Hybrid parallel reduction algorithms for the multi-level CMFD acceleration in the neutron transport code PANDAS-MOC

f

The coarse mesh finite difference (CMFD) technique is considered efficiently in accelerating the convergence of the iterative solutions in the computational intensive 3D whole-core pin-resolved neutron transport simulations. However, its parallel performance in the hybrid MPI/OpenMP parallelism is inadequate, especially when running with larger number of threads. In the original Whole-code OpenMP threading hybrid model (WCP) model of the PANDAS-MOC neutron transport code, the hybrid MPI/OpenMP reduction has been determined as the principal issue that restraining the parallel speedup of the multi-level coarse mesh finite difference solver. In this paper, two advanced reduction algorithms are proposed: Count-Update-Wait reduction and Flag-Save-Update reduction, and their parallel performances are examined by the C5G7 3D core. Regarding the parallel speedup, the Flag-Save-Update reduction has attained better results than the conventional hybrid reduction and Count-Update-Wait reduction.

1 Introduction

3D whole-core pin-resolved modeling is the state-of-the-art of computational simulation of the neutron transport in the nuclear reactors. Nevertheless, the computational intensiveness makes solving such problems quite challenging, especially for time-dependent transient analysis, where multiple steady-sate eigenvalue and transient fixed-source problems need to be resolved. One popular low-order acceleration scheme for accelerating the convergence of transport solutions is the coarse mesh finite difference (CMFD) method, which was first proposed for nodal diffusion calculation in 1983 (Smith, 1983). It formulates the pinwise core matrices based on the 3D spatial and energy meshes that can be solved simultaneously, and therefore, considerably increases the converge rate of the transport equation.

PANDAS-MOC (Purdue Advanced Neutronics Design and Analysis System with Methods of Characteristics) is a neutron transport code being developed at Purdue University (Tao and Xu, 2022b), and the purpose of which is to provide 3D high-fidelity modeling and simulation of the neutronics analysis in reactor cores. In this code, the 2D/1D method is utilized to estimate the essential parameters to the safety assessment, such as criticality, reactivity, and 3D pin-resolved power distributions, etc. Specifically, the radial solution is determined by the Method of Characteristics (MOC), the axial solution is resolved by the Nodal Expansion Method (NEM), and they are coupled by the transverse leakage. Furthermore, the transport solver is accelerated by the multi-level (ML) CMFD, which is composed by the mutually accelerated multi-group (MG) and one-group (1G) CMFD schemes. However, in the serial computing, the ML-CMFD solver has consumed about 30% of the computation time of the steady state (initial state) calculation in the C5G7 3D test (Tao and Xu, 2022b). Therefore, further acceleration tools shall be considered to improve its efficiency while maintaining the accuracy for the rapid flux changes.

With the considerable increase in the computational power, parallel computing has been widely considered in the high-fidelity neutronics analysis codes, such as DeCART (Joo et al., 2004), MPACT (Larsen et al., 2019), nTRACER (Choi et al., 2018), OpenMOC (Boyd et al., 2016), STREAM (Choi et al., 2021), ARCHER (Zhu et al., 2022) etc., in order to improve the performance of solving the neutron transport equations in the nuclear reactors. Similarly, several parallel models of the PANDAS-MOC have been developed based on the nature of distributed and shared memory architectures, including the Pure MPI parallel model (PMPI), Segment OpenMP threading hybrid model (SGP), and Whole-code OpenMP threading hybrid model (WCP). The detailed design descriptions and parallel performance are presented in Ref (Tao and Xu, 2022a). It is demonstrated that the WCP model costs less memory to finish the calculation, but still needs further improvement in the ML-CMFD solver and the MOC sweep solver in order to attain comparable, even exceptional, performance to the PMPI code in order to show the benefits of the hybrid memory architectures. The improvement of the MOC sweep solver is discussed in Ref. (Tao and Xu, 2022c), and this article will concentrate on the optimization of the ML-CMFD solver.

Additionally, while executing large amounts of processors in hybrid MPI/OpenMP cases, the parallel performance of CMFD could be quite inadequate (Tao and Xu, 2020), which is also true in the WCP model of PANDAS-MOC. In Ref (Tao and Xu, 2022a), it is found that one major challenge of the hybrid parallel of ML-CMFD is the reduction operation, which is the principal problem we are trying to resolve in this work. In this paper, we will firstly discuss the conventional hybrid OpenMP/MPI reduction pattern, which is also utilized in the WCP code in the first place. Then two innovative reduction algorithms will be proposed: Count-Update-Wait reduction and Flag-Save-Update reduction. Next, the parallel performance for the ML-CMFD solver implementing those three reduction methods are measured and contrasted with each other, which is expected to demonstrate the breakthrough of the newly designed reduction methods. Last, the performance of the optimized WCP mode will be briefly discussed to show the overall improvement from the novel hybrid reduction algorithm and MOC parallelization schemes.

2 Methodology

2.1 PANDAS-MOC methodology

This section will briefly introduce the methodology of the PANDAS-MOC, highlighting the concepts that are most relevant for this work. The detailed derivations can be found in Ref. (Tao and Xu, 2022b). The transient method starts with the 3D time-dependent neutron transport equation Eq. 1 and the precursor equations Eq. 2:

$\frac{1}{v_g\left(r\right)}\frac{\partial {\phi }_g\left(r,\mathrm{\Omega },t\right)}{\partial t}=-\mathrm{\Omega }\cdot \nabla {\phi }_g\left(r,\mathrm{\Omega },t\right)-{\mathrm{\Sigma }}_{tg}\left(r,t\right){\phi }_g\left(r,\mathrm{\Omega },t\right)+S_{sg}\left(r,\mathrm{\Omega },t\right)+\frac{{\chi }_g\left(r\right)}{4\pi }{S}_F\left(r,t\right)+\frac{1}{4\pi }\sum _k{\chi }_{\mathit{dgk}}\left({\lambda }_k{C}_k\left(r,t\right)-{\beta }_k{S}_F\left(r,t\right)\right)(1)$

$\frac{\partial C_k\left(r,t\right)}{\partial t}={\beta }_k\left(r\right)S_F\left(r,t\right)-{\lambda }_k\left(r\right)C_k\left(r,t\right),k=\mathrm{1,2},\dots ,6(2)$

The terms χ_g, S_sg and S_F are the average fission neutron spectrum, scattered neutron source, and prompt fission neutron source, and they are defined as Eq. 3, Eq. 4, and Eq. 5 respectively. The definitions of the rest variables are summarized in Table 1.

${\chi }_g={\chi }_{pg}+\sum _k{\beta }_k\left({\chi }_{\mathit{dgk}}-{\chi }_{pg}\right)(3)$

$S_{sg}\left(r,\mathrm{\Omega },t\right)=\sum _{g^{\prime }}{\int }_{4\pi }{\mathrm{\Sigma }}_{g^{\prime }g}\left(r,{\mathrm{\Omega }}^{\prime }\cdot \mathrm{\Omega },t\right){\phi }_{g^{\prime }}\left(r,{\mathrm{\Omega }}^{\prime },t\right)d{\mathrm{\Omega }}^{\prime }(4)$

$S_F\left(r,t\right)=\frac{1}{k_{\mathit{eff}}^s}\sum _{g^{\prime }}\nu {\mathrm{\Sigma }}_{f{g}^{\prime }}\left(r,t\right){\int }_{4\pi }{\phi }_{g^{\prime }}\left(r,\mathrm{\Omega },t\right)d\mathrm{\Omega }(5)$

TABLE 1

TABLE 1. Definitions of terms in the time dependent transport equation.

To numerically solve the transport equation, several approximations are considered:

1. Angular flux: Exponential transformation

2. Time derivative term: Implicit scheme of temporal integration method

3. Fission source: Exponential transformation and linear change in each time step

4. Densities of delayed neutron precursors: integrating Eq.2 over time step

Accordingly, Eq. 1 can be transformed to the Transient Fix Source Equation, and the Cartesian form of which is:

$\begin{array}{c}\hfill \left(\eta \frac{\partial }{\partial x}+ϵ\frac{\partial }{\partial y}+\mu \frac{\partial }{\partial z}\right){\phi }_g^n\left(r,\mathrm{\Omega }\right)+{\mathrm{\Sigma }}_{tg}^n\left(r\right){\phi }_g^n\left(r,\mathrm{\Omega }\right)=S_{sg}^n\left(r,\mathrm{\Omega }\right)+\frac{1}{4\pi }\left[{\chi }_g\left(r\right)S_F^n\left(r\right)+S_{\mathit{ntg}}^n\left(r\right)+S_{\mathit{trg}}^{n-1}\left(r\right)\right]\end{array}(6)$

where

$\begin{array}{c}r=\left(x,y,z\right),\mathrm{\Omega }=\left(\mu ,\alpha \right),\eta =\sin \theta \cos \alpha ,ϵ=\sin \theta \sin \alpha \\ S_{\mathit{trg}}^{n-1}\left(r\right)=S_{\mathit{dcg}}^{n-1}\left(r\right)+S_{\mathit{dtg}}^{n-1}\left(r\right),S_{\mathit{dcg}}^{n-1}\left(r\right)=\sum _k{\chi }_{\mathit{dkg}}{\lambda }_k{\widehat{C}}_k^{n-1}\left(r\right)\\ S_{\mathit{dtg}}^{n-1}\left(r\right)=\frac{{\varphi }_g^{n-1}\left(r\right)}{E_g^n\left(r\right)\mathrm{\Delta }{t}_n{v}_g\left(r\right)},S_{\mathit{ntg}}^n\left(r\right)={\widehat{\chi }}_g{S}_F^n\left(r\right)-{\mathrm{\Sigma }}_{dg}^n{\varphi }_g^n\\ E_g^n\left(r\right)=e^{-{\alpha }_g^n\left(r\right)\mathrm{\Delta }{t}_n},{\alpha }_g^n=\left(\log P_n^{\mathit{tot}}-\log P_{n-1}^{\mathit{tot}}\right)/{\mathrm{\Delta }}_{n-1},{\mathrm{\Sigma }}_{dg}^n=\frac{{\alpha }_g^n}{v_g}+\frac{1}{\mathrm{\Delta }{t}_n{v}_g}\end{array}$

Instead of directly resolve the computational-intensive 3D problem, it is converted to a radial 2D problem and an axial 1D problem, which is conventionally referred to as the 2D/1D method. The 2D equation is obtained by integrating Eq. 6 axially over the axial plane $({\int }_{z_b}^{z_t}dz)$ and solved by the MOC method, and the 1D equation is obtained by radially integrating over a box (∫ ∫_Adxdy) and solved by the NEM method. Then the 2D radial solution and 1D axial solution are coupled by the transverse leakage. Besides, the ML-CMFD approach is implemented to accelerate the convergence for solutions to the Transient Fix Source Equation. Since this paper concentrates on the performance improvement on the ML-CMFD solver, the details of MOC and NEM are omitted for brevity and the details could be found in Ref (Xu and Downar, 2012) (Tao and Xu, 2022b) (Tao and Xu, 2022c).

2.2 Multi-level CMFD method

The transport equation is generally very hard to be solved for large reactor cores. But the finite difference equation for neutron diffusion equation can be solved very efficiently for nuclear reactor (Hao et al., 2018) (Tao and Xu, 2020). In the PANDAS-MOC implementation, the CMFD is implemented by overlaying a 2D Cartesian mesh over the FSR meshes. The coarse mesh layout used for solving a 17 × 17 PWR assembly problem is illustrated in Figure 1B, where each colored cell denotes a different region. While performing MOC sweeping, each CMFD region could be further discretized to multiple flat source regions, as shown in Figure 1C. The bridges connecting two mesh layouts are the variable homogenization and current coupling coefficients.

FIGURE 1

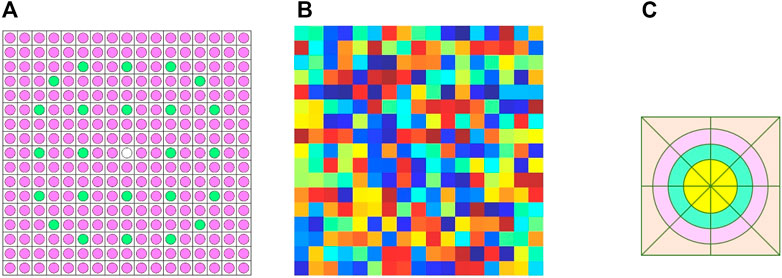
FIGURE 1. CMFD and FSR mesh layout for a 17 × 17 PWR assembly. (A) PWR assembly (B) CMFD mesh layout (C) FSR layout in one CMFD mesh.

The MG-CMFD formulations are obtained from integrating the transient transport equation over a 4π and over the node n of interest. The equation for steady state is listed in Eq. 7 and for transient analysis is written in Eq.9. In addition, the 1G-CMFD equations are determined via collapsing the energy dimension from the MG-CMFD formula, and Eq.8 and Eq.10 are the steady state and transient equation respectively.

$\frac{1}{V^c}\sum _s{A}_s^c\left({\widetilde{\stackrel{̃}{D}}}_{g,s}^c{\bar{\varphi }}_g^n-{\widetilde{\stackrel{̃}{D}}}_{g,c}^s{\bar{\varphi }}_g^{n,s}\right)+{\mathrm{\Sigma }}_{rg}^n{\varphi }_g^n-\sum _{g^{\prime }\ne g}{\mathrm{\Sigma }}_{g{g}^{\prime }}^n{\varphi }_{g^{\prime }}^n={\lambda }^{n-1}{\chi }_g{S}_F^{n-1}(7)$

$\frac{1}{V^c}\sum _s{A}_s^c\left({\widetilde{\stackrel{̃}{D}}}_{A,s}^c{\bar{\varphi }}_A^n-{\widetilde{\stackrel{̃}{D}}}_{A,c}^s{\bar{\varphi }}_A^{n,s}\right)+\left({\mathrm{\Sigma }}_{rA}^n-{\lambda }_s\nu {\mathrm{\Sigma }}_{fA}^n\right){\varphi }_A^n=\left({\lambda }^{n-1}-{\lambda }_s\right)S_F^{n-1}(8)$

$\frac{1}{V^c}\sum _s{A}_s^c\left({\widetilde{\stackrel{̃}{D}}}_{g,s}^c{\bar{\varphi }}_g^n-{\widetilde{\stackrel{̃}{D}}}_{g,c}^s{\bar{\varphi }}_g^{n,s}\right)+{\tilde{\mathrm{\Sigma }}}_{rg}^n{\varphi }_g^n-\sum _{g^{\prime }\ne g}{\mathrm{\Sigma }}_{g{g}^{\prime }}^n{\varphi }_{g^{\prime }}^n=\left({\chi }_g+{\widehat{\chi }}_g\right)S_F^n+S_{\mathit{dcg}}^n+S_{\mathit{dtg}}^n(9)$

$\frac{1}{V^c}\sum _s{A}_s^c\left({\widetilde{\stackrel{̃}{D}}}_{A,s}^c{\bar{\varphi }}_A^n-{\widetilde{\stackrel{̃}{D}}}_{A,c}^s{\bar{\varphi }}_A^{n,s}\right)+\left\{{\tilde{\mathrm{\Sigma }}}_{rA}^n-\left[1+\sum _k{\lambda }_k^n{\mathrm{\Omega }}_k^n-\beta \right]\lambda \nu {\mathrm{\Sigma }}_{fA}^n\right\}{\varphi }_A^n=S_{\mathit{dcA}}^n+S_{\mathit{dtA}}^n(10)$

In the ML-CMFD technique, the multi-group solution and one-group solution are employed to mutually speed up the convergence. Once the multi-group node average flux and the surface current are ready, the one-group parameters can then be updated accordingly. And this new 1G-CMFD linear system can render next-generation of one-group flux distribution which will be used to update the multi-group flux parameters to benefit the eigenvalue convergence. The flowchart of its implementation in the PANDAS-MOC is illustrated in Figure 2. Moreover, the ML-CMFD scheme used for the steady state case and the transient case are approximately the same, except that there is no update of the eigenvalue for the transient evaluation. Therefore, the steady state module terminates when the change of the eigenvalue and the norm of the difference of the MOC flux between two consecutive iterations have both satisfied the convergence criteria, while the transient iteration stops when the norm of the MOC flux difference is satisfied. More details can be found in Ref (Tao and Xu, 2022b).

FIGURE 2

FIGURE 2. SS/TS Multi-level CMFD (dashed step is only valid for SS).

Meanwhile, the CMFD Eqs 7–10 are large sparse asymmetric linear systems, and can be rearranged to classic matrix notation, Ax = b, where A is a block-diagonal sparse matrix corresponding to the coefficients and cross-section parameters whose dimension is about hundreds of millions with respect to the large reactor size, and b represents the source term. To further accelerate the convergence of the solution to this sparse linear system, the preconditioned generalized minimal residual method (GMRES) is employed because it can sufficiently take advantage of the sparsity of the matrix and is easy to implement (Saad, 2003). In addition, Givens rotation is applied in the GMRES solver, since it can preserve better orthogonality and is more efficient than other processes for the QR factorization of the Hessenberg matrix.

2.3 Hybrid parallelism of ML-CMFD

Generally speaking, there are two ways to convert the serial program to multithreading form for large problems: MPI-only and hybrid MPI/OpenMP. In many cases, the hybrid programs execute faster than the pure MPI program because they have lower communication overhead (Quinn, 2003). Suppose the program is executed on a cluster of a multiprocessors and each has b CPUs. The program using MPI must create ab processors to use every CPU, thus all ab processors are involved in the communication. On the contrary, the program using hybrid MPI/OpenMP only need to create a processors, and each processor then spawns b threads to divide the workload in the parallel sections, which also has employed every CPU. Nevertheless, only that a processors are active during the communication procedure, which will give the hybrid program lower communication overhead than the MPI program. In this paper, all work are performed based on the previous developed whole-code OpenMP threading hybrid model (WCP) of the PANDAS-MOC, which partitioned the entire workload by the MPI and OpenMP simultaneously in order to get rid of the repetitious creation and suspension of the OpenMP parallel regions. The detailed information on the WCP model could be found in Ref (Tao and Xu, 2022a).

As indicated by the CMFD Eqs 7–10, the principal target of the ML-CMFD is to find the solution x to the linear system Ax = b by the GMRES iterative scheme. Therefore, the major work included in this part is the matrix and vector operations, such as the vector-vector dot product, matrix-vector multiplication, and matrix-matrix multiplication. Take vector-vector dot product as an example, the general way to compute dot-product using hybrid MPI/OpenMP scheme is listed in Algorithm 1, where nx, ny, nz are the spatial dimensions and ng is the neutron energy group dimension. In order to find the dot-product result, three steps are involved: 1) each OpenMP thread compute the partial result on their own, 2) a local result will be collected for each MPI processor from its launched OpenMP threads by the omp reduction clause, 3) the global result is computed and broadcasted by the MPI_Allreduce() routine. This reduction conception is also implemented in the WCP in the first place, and its performance will be discussed in the following Section 4 in details.

Algorithm 1.

2.4 Performance metrics

The measurement of parallel performance is the speedup, which is defined as the ratio of the sequential runtime (T_s) which is approximated using the runtime with 1 processor (T₁) in pure MPI model, and the parallel runtime while utilizing p processors (T_p) to solve the same problem. Also, efficiency (ϵ) is a metric of the utilization of the resources of the parallel system, the value of which is typically between 0 and 1.

$S_p=\frac{T_s}{T_p}\approx \frac{T_1}{T_p},{ϵ}_p=\frac{S_p}{p}(11)$

3 Test problem

The parallel performance of designed codes in this work are determined by a steady state problem, in which all control rods are removed from the C5G7 3D core from the OECD/NEA deterministic time-Dependent neutron transport benchmark, which is proposed to verify the ability and performance of the neutronics codes without neutron cross-sections spatial homogenization above the fuel pin level (Boyarinov et al., 2016) (Hou et al., 2017). It is a miniature light water reactor with 8 uranium oxide (UO₂) assemblies, 8 mixed oxide (MOX) assemblies, and surrounding water moderator/reflector. Besides, the C5G7 3D model is a quarter-core and fuel assemblies are arranged in the top-left corner. For the sake of symmetry, reflected condition is used for the north and west boundaries, and vacuum condition is considered for the rest six surfaces. Figure 3A is the planar and axial configuration of the C5G7 core. The size of the 3D core is 64.26 cm × 64.26 cm × 171.36 cm, and the axial thickness is equally divided into 32 layers.

FIGURE 3

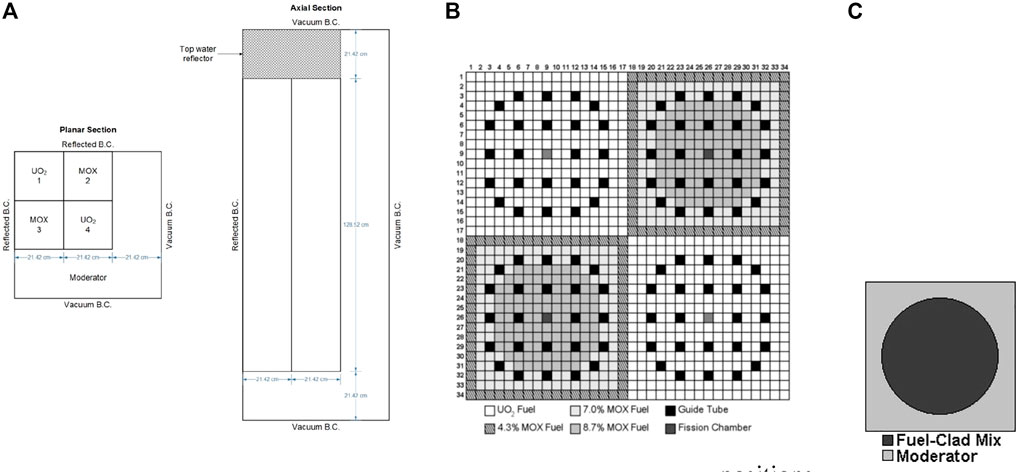
FIGURE 3. Geometry and composition of C5G7-TD benchmark. (A) Planar and axial view of 1/4 core map (B) Fuel pin compositions and number scheme (C) Pin cell.

Moreover, the UO₂ assemblies and MOX assemblies have the same geometry configurations. The assembly size is 21.42 cm × 21.42 cm. There are 289 pin cells in each assembly arranged as a 17 × 17 square (Figure 3B), including 264 fuel pins, 24 guide tubes, and 1 instrument tube for a fission chamber in the center of the assembly. The UO₂ assemblies contains only UO₂ fuel, while the MOX assemblies includes MOX fuels with 3 levels of enrichment: 4.3%, 7.0%, and 8.7%. Besides, each pin is simplified as 2 zones in this benchmark. Zone 1 is the homogenized fuel pin from the fuel, gap, cladding materials, and zone 2 is the outside moderator (Figure 3C). The pin (zone 1) radius is 0.54 cm, and the pin pitch is 1.26 cm.

While running the 3D benchmark problem, the essential parameters are defined as following. For the MOC sweeping, all cases were performed with Tabuchi-Yamamoto quadrature set with 64 azimuthal angles, 3 polar angles, the ray-spacing was 0.03 cm. The fuel pin-cells are discretized into 8 azimuthal flat source regions and 3 radial rings (Figure 1C), and the moderator cells were divided into 1 by 1 or 6 by 6 coarse meshes, which depends on their locations in the core. Meanwhile, for the numerical iterative functions, the convergence criteria of the GMRES method in the ML-CMFD solver was set as 10⁻¹⁰, and the convergence criteria for the eigenvalue was 10⁻⁶ and for the flux was 10⁻⁵. No preconditioners were employed to show the improvement from the algorithm update.

This study is conducted in the “Current” cluster at Purdue University, the mode of which is Intel(R) Xeon(R) Gold 6152 CPU @ 2.10GHz, and it has 2 NUMA nodes, 22 cores for each node, and 1 thread per core. The parallel performance is measured using Intel(R) MPI Library 2018 Update 3, and the compiler is mpigcc (gcc version 4.8.5).

4 Parallelism of reduction

According to the numerical experiments in Ref. (Tao and Xu, 2022a), the predominant factors that hurt the hybrid parallel performance of the ML-CMFD solver are the repetitious construct and destruct of the OpenMP parallel region and the reduction procedure. The former has been tackled in the WCP design, which has moderately improved the speedup of the ML-CMFD solver. This section will first discuss the difficulties of the conventional method of the hybrid MPI/OpenMP reduction, and then propose two novel reduction designs to further advance the efficiency of the parallelism in the ML-CMFD solver.

4.1 Hybrid default reduction

The majority work in the multi-level CMFD solver are the matrix-vector, matrix-matrix, and vector-vector product, which means that summing the partial results given by each thread is playing a vital role to the computation accuracy and efficiency. In general, such reduction process in the hybrid MPI/OpenMP program is finished by the omp reduction clause from OpenMP library in the first place and then by the MPI_Allreduce() routine from MPI library (Figure 4A), which is referred as ”hybrid default reduction” in the context hereafter. The shortcoming of this reduction manner is that the omp reduction only conducts the data synchronization when all spawned threads have finished their tasks due to the implicit barrier, which may slow down the calculation. Figure 4B is an example of the hybrid default reduction. If thread 0 need t_p,0 time to finish its task, yet thread 2 only need t_p,2 time, then thread 2 will be staying idle and wait for t_w,2 time before the OpenMP reduction can be executed. Of course, this will happen again on the MPI processors before the MPI_Allreduction() operation can be performed. In addition, if “nowait” is specified to override such implicit barriers simultaneously with the omp reduction clause, it will cause race condition and unpredicted behaviors. To overcome the impacts caused by the implicit barrier after the OpenMP reduction and reduce the thread idle time, here we designed two different reduction algorithms.

FIGURE 4

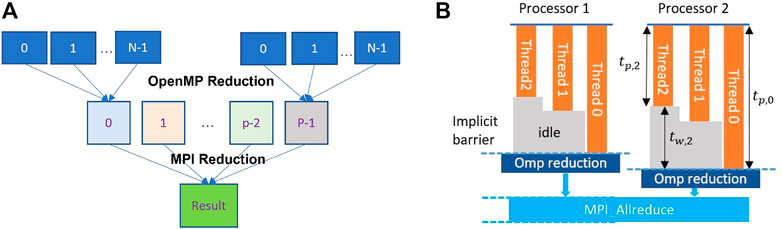
FIGURE 4. Example of hybrid default reduction. (A) Hybrid MPI + OpenMP reduction (B) Reduction time.

4.2 Count-update-wait reduction

Instead of waiting for all OpenMP threads having their partial results ready, this method immediately gathers the partial result once a thread has finished its calculation and uses a global counter to count the number of collected data. Till all threads have provided their partial results, in the zeroth OpenMP thread, the MPI_Allreduction() routine is utilized to compute the global result and reset the counter and variables. For example, to compute the hybrid reduction sum, the defined function is listed in Algorithm 2 and illustrated in Figure 5, in which the counting and summation processes are performed atomically to take advantage of the hardware provided atomic increment operation. Furthermore, the Count-Update-Wait reduction functions for finding the global maximum value, global minimum value, or any combinations of those operations were written in the similar fashion, except that the counting and local result updating operations are protected by the omp critical directive if necessary.

FIGURE 5

FIGURE 5. Illustration of count-update-wait reduction.

In the implementation, the omp reduction clause is removed from the OpenMP #pragma statement and the nowait clause is applied to override the implicit OpenMP barrier. In that regard, the Count-Update-Wait algorithm has one barrier less than the default reduction method. However, the trade-offs are the incurred synchronization overhead every time a thread enters and exits the atomic or critical section and the inherent cost of serialization.

Algorithm 2.

4.3 Flag-save-update reduction algorithm

In the previous Count-Update-Wait Reduction algorithm, the atomic and critical clauses, which are utilized to guarantee the race-free conditions, introduce synchronization overhead and serialization cost and hence decrease the computation efficiency. Since the purposes of the atomic and critical clauses are restricting a specific memory location or a structured block to be accessed by a single thread at a time, which otherwise is considered as a race condition, they can be eliminated from the code if the partial results are saved in different memory locations before the final reduction.

In the Flag-Save-Update Reduction, the MPI reduction is still performed by the MPI_Allreduction() routine, and the improvement is carried out on the OpenMP reduction procedure.

Firstly, the OpenMP threads are deliberately configured as a tree structure. In such sense, this procedure allows us to collect the data in log₂(N_threads) stages, rather than N_threads−1 stages, which can be a huge saving in reduction. The maximum number of children to each thread is determined as:

$N_{\text{children}}=⌞{\log }_2{N}_{\mathit{threads}}⌟(12)$

Next, two global arrays are allocated to store the partial results and the status flag of each OpenMP thread, darray and notready, and their sizes are defined as N_threads*D, where D is the spacing distance that isolates the element from each OpenMP thread and prevents the potential false sharing and race condition problems. Once the thread partial result is evaluated, it will be stored to the corresponding location in the darray and the flag in the notready will be updated, as showing in Figure 6. Since all locations are separated from each other, reading and modifying their values will not incur any race condition issues for the appropriate D value. We are going to use D = 128 in this work to measure the performance hereafter, which is chosen from sample experimentation.

FIGURE 6

FIGURE 6. Arrays structure.

Furthermore, in this method, a global status flag and a thread-private status flag are designed to control the calculation flow in order to make sure that the collected data are fresh and to avoid issues like missing data or recurrently reading the same data.

The Flag-Save-Update reduction algorithm is designed according to the executed number of OpenMP threads and MPI processors and listed in Algorithm 3. Figure 7 is an illustration of the thread scheme when the total OpenMP thread is 12, in which arrows with different colors indicate different computation stages. To perform the OpenMP reduction, threads having a different number of children threads are defined behaving differently:

1. If a thread has no children, then flip its thread-private flag, save its result to darray, and update status in the notready array

2. If a thread has children, for example, when d₁, d₃, d₅, and d₉ are ready, their results are collected and then store to d₁ location in darray, and update status at the corresponding locations in the notready as well.

3. All partial results should be collected to d₀ after log₂(N_threads) stages of reduction.

FIGURE 7

FIGURE 7. Parent-child layout of OpenMP threads (total threads = 12).

Furthermore, MPI_Allreduce() is called at thread 0 to perform the mpi reduction if it is necessary, and the global flag is flipped to allow all threads to access and read the final result.

With respect to its implementation in the PANDAS-MOC code, the reduction clause is removed from the OpenMP pragmas, and the ”nowait” clause is specified to override the implicit barrier after the OpenMP regions. Therefore, it contains neither implicit nor explicit barriers in the work flow, comparing to the hybrid default reduction and the Count-Update-Wait reduction.

Algorithm 3.

4.4 Performance

In order to compare the hybrid parallel performance, the total executed number of threads were fixed as 36. Given that the C5G7 3D core has 32 layers in the axial direction, the number of MPI processors applied in the axial direction are the common factors of 32 and 36 to achieve better load balance. All combinations of number of MPI processors and OpenMP threads and the x−y−z distribution of MPI processors are tabulated in Table 2. Besides, all tests were executed 5 times to minimize the measurement error and their average run-time were used for the further data analysis.

TABLE 2

TABLE 2. Combinations of tested number of MPI and OpenMP threads.

The measured speedup and efficiency for the ML-CMFD solver using the hybrid default reduction, Count-Update-Wait reduction, and Flag-Save-Update reduction are computed based on the run-time for the ML-CMFD solver from the pure MPI model (PMPI) with single MPI processor (2196.113 s) (Tao and Xu, 2022a), and they are presented in Figure 8, which presents big improvement from the default reduction to the Flag-Save-Update reduction, especially when testing with large number of OpenMP threads.

FIGURE 8

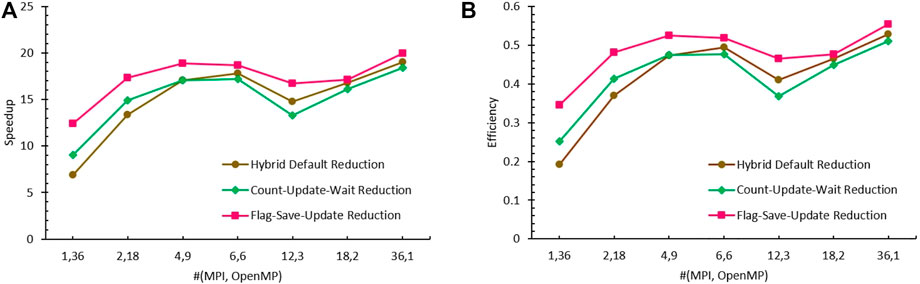
FIGURE 8. Comparison of ML-CMFD solver performance using different reduction algorithms. (A) Speedup (B) Efficiency.

All hybrid reductions have their largest speedup at (36, 1). Although theoretically results are expected similar to each other when running with a single thread, the actual measured speedup shows that Flag-Save-Update reduction $>$ hybrid default reduction $>$ Count-Update-Wait reduction, and they all present sublinear speedup. In this test, the inherent overhead of OpenMP is unavoidable, such as the process of generating multi-threading and walking through the included OpenMP directives even though there was only a single thread spawned by each MPI processor. Among three hybrid methods, the Flag-Save-Update reduction rendered the largest speedup because the synchronization points have been deliberately eliminated as many as possible from the algorithm. Besides, even though the Count-Update-Wait reduction had one implicit barrier less than the hybrid default reduction, it still had slightly larger natural overhead due to the existence of the atomic or critical structure. In the hybrid default reduction, the implicit barrier introduced by the “reduction” clause forces all threads to wait until all threads in the same team have arrived to this place and then gathers their partial results. In the Count-Update-Wait reduction, its counterpart is the atomic/critical structure, which collects the partial results from the threads immediately when they are arrived (Algorithm 2). When running with single thread, the implicit barrier in the hybrid default reduction could hardly slow down the calculation, whereas the serialization cost incurred by the atomic/critical structure not negligible. The measured difference between them indicates that the serialization cost incurred by the atomic or critical is more expensive than the implicit barrier in this circumstance.

The observed trend of speedup from Count-Update-Wait reduction and from hybrid default reduction came cross at (4,9). When the number of executed OpenMP threads is smaller than 9, the speedup accomplished by the Count-Update-Wait reduction is about 96%–97% of the hybrid default reduction. This is because the workload assigned to each OpenMP thread is not significantly biased, the waiting to completion time are trivial in both algorithms. Yet, the overhead brought by the atomic and critical serializations for collecting the OpenMP partial results and updating the counters will introduce extra cost and slow down the calculation. However, as more OpenMP threads contributed, the benefit of owning fewer synchronization barriers has been demonstrated as the Count-Update-Wait reduction reached larger speedup. After compensating the inherent cost of serialization because of omp atomic and critical blocks, its speedup at (1, 36) is about 30.9% higher than the hybrid default reduction.

On the other hand, the Flag-Save-Update reduction has achieved larger speedup than the other two algorithms for all tests due to lacking of synchronization points, even when there is only a single OpenMP contributing to the calculation [i.e., (36,1)]. Moreover, this advantage was more obvious when larger number of OpenMP threads were executed. In Figure 8, the speedup ratio of the Flag-Save-Update reduction to the hybrid default reduction has augmented from 1.05 to 1.80 from right to left as more OpenMP contributed and fewer MPI devoted. Concerning the Flag-Save-Update reduction, the obtained speedup of most tests falls within the range of (17, 19). However, The speedup could also be weakened by the communications and data synchronizations among MPI processors if there were domain decomposition in the x-y plane, for instance the drop in (12,3). Despite that, the Flag-Save-Update reduction can compensate part of this overhead, since its ratio of speedup at (12,3) and at (4,9) was larger than the other two reduction methods. Furthermore, overall tests, (1, 36) has attained the smallest speedup. Other than the OpenMP thread load balance among and inherent overhead from the algorithm per se, the parallel performance of this group could possibly be restricted by the hardware properties, such as memory bandwidth, cache size and cache hit rate. For example, the size of darray, the type of elements contained in which is double, is about N_threads × D × 8/1024 kb = 36 × 128 × 8/1024 kb = 36 kb, however the size of the Ld1 and Ldi cache of the ”Current” cluster are 32 kb.

5 WCP optimizations

As explained in the Ref (Tao and Xu, 2022a), the parallel performance achieved from the original WCP model is better than the SGP model which is the conventional fashion of hybrid MPI/OpenMP parallelization, yet not comparable to the PMPI model. The advancement of the hybrid reduction in ML-CMFD solver and parallelism of MOC sweeping are desired to optimize the WCP code and make it at least comparable to the PMPI code. In this article, we have proposed several innovative algorithms to conduct the hybrid reduction, and the most promising one is the Flag-Save-Update reduction. Its collected performance is better than the hybrid default reduction, regardless that it is still slower than the MPI_Allreduction() standalone in the PMPI mode while using the identical total number of threads (Figures 8, 9A). On the other hand, the improvement on the parallelism of MOC sweeping is thoroughly discussed in Ref (Tao and Xu, 2022c) and here is a brief description.

FIGURE 9

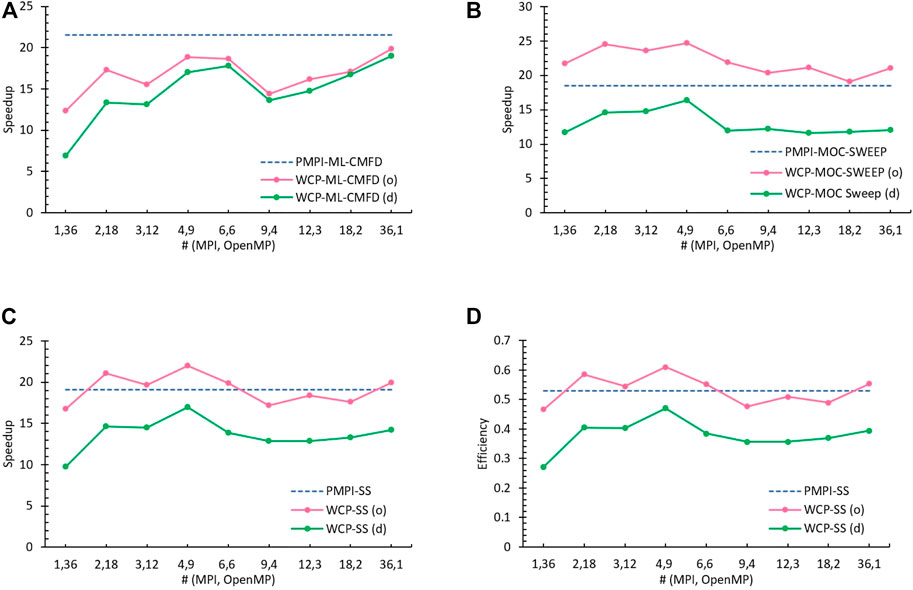
FIGURE 9. Performance Comparison with total threads as 36 (o: optimized algorithm, d: default method). (A) Speedup: ML-CMFD (d: hybrid default reduction, o: Flag-Save-Update reduction) (B) Speedup: MOC sweep (d: long-track schedule (default), o: No-Atomic schedule) (C) Speedup: Steady State (D) Efficiency: Steady State.

While using the OpenMP directives to partition the characteristic rays sweeping, it is found that the speedup of the MOC sweep are limited by the unbalanced workload among threads and the serialization overhead caused by the omp atomic clause for assuring the correctness of MOC angular flux and current update (Tao and Xu, 2022a). Two schedules are designed to resolve these two obstacles: Equal Segment (SEG) schedule and No-Atomic schedule. The SEG resolves the unbalanced issue, in which the average number of segments are determined in the first step according to the total number of segments and number of executed threads, and then long-tracks are partitioned based on this average number so that the number of segments (i.e., actual computational workload) are distributed among OpenMP threads as equalized as possible. Based on SEG, the No-Atomic schedule further removes all omp atomic structures to improve the computational efficiency by pre-defining the sweeping sequence of long-track batches across all threads to create a race-free job. The implementation details could be found in Ref. (Tao and Xu, 2022c). After repeating the same tests on each schedule, it is confirmed that the No-Atomic schedule is capable to achieve much better performance than the other schedules, and even outperforms the PMPI sweeping with the identical total number of threads.

The comparison of the parallel performance obtained from the PMPI (dashed blue line), the original WCP using default methods [green line, labeled as (d)], and the optimized WCP with Flag-Save-Update reduction and No-Atomic schedule [pink line, labeled as (o)] are illustrated in Figure 9. Although the speedup of the ML-CMFD solver using the Flag-Save-Update reduction is still slower than the PMPI using MPI_Allreduction() (Figure 9A), the enhancement accomplished from the optimized No-Atomic MOC sweep is large enough to compensate such weakness (Figure 9B). Therefore, pertaining to the overall steady state calculation, the optimized WCP code has managed to obtain much better speedup than the original WCP code, and comparable to or even greater than the PMPI code as explained in Figures 9C,D.

6 Summary remarks

The CMFD technique is commonly used in the neutron transport simulations to accelerate the convergence of the iterative solutions. However, the performance of its implementation in the hybrid MPI/OpenMP parallelism is inadequate, especially when running with larger number of threads. In the original WCP model of the PANDAS-MOC code, the hybrid MPI/OpenMP reduction has been determined as the principal issue that restraining the parallel speedup of the ML-CMFD solver. Conventionally, the hybrid reduction operation is finished by exploiting the omp reduction clause and MPI_Allreduction() routine, which was referred to as “hybrid default reduction” in the previous context. Other than that, two original hybrid reduction algorithms were presented in this paper: Count-Update-Wait reduction and Flag-Save-Update reduction. The first algorithm had fewer barriers than the hybrid default reduction yet introduced extra synchronization points, such as atomic or critical sections, to count and assure that all partial results were collected from the launched OpenMP threads. Besides, the second algorithm was accomplished by using the global arrays and status flags, and establishing the tree configuration of all threads, where includes no implicit and explicit barriers. The hybrid parallel performance for three algorithms were examined using the C5G7 3D core and the total number of threads were set as 36. The Flag-Save-Update reduction yielded the best speedup at all tested cases, and its superiority was more obvious as more OpenMP threads were contributed. For instance, when using (1, 36), the obtained speedup of Flag-Save-Update reduction algorithm is about 1.8 times of the speedup achieved by the hybrid default reduction. In spite of the fact that it is less efficient than the MPI_Allreduction() routine in PMPI model, this disadvantage can be offset by the great advance from the optimized MOC sweep scheme, and together they are able to reach larger speedup than the PMPI model when using identical total number of threads.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

All authors contributed to the conception and methodology of the study. ST performed the coding and data analysis under YX supervision, and wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boyarinov, V., Fomichenko, P., Hou, J., Ivanov, K., Aures, A., Zwermann, W., et al. (2016). Deterministic time-dependent neutron transport benchmark without spatial homogenization (c5g7-td). Paris, France: Nuclear Energy Agency Organisation for Economic Co-operation and Development NEA-OECD.

Google Scholar

Boyd, W., Siegel, A., He, S., Forget, B., and Smith, K. (2016). Parallel performance results for the openmoc neutron transport code on multicore platforms. Int. J. High Perform. Comput. Appl. 30, 360–375. doi:10.1177/1094342016630388

CrossRef Full Text | Google Scholar

Choi, N., Kang, J., and Joo, H. G. (2018). “Preliminary performance assessment of gpu acceleration module in ntracer,” in Transactions of the Korean nuclear society autumn meeting (yeosu, korea).

Google Scholar

Choi, S., Kim, W., Choe, J., Lee, W., Kim, H., Ebiwonjumi, B., et al. (2021). Development of high-fidelity neutron transport code stream. Comput. Phys. Commun. 264, 107915. doi:10.1016/j.cpc.2021.107915

CrossRef Full Text | Google Scholar

Hao, C., Xu, Y., and Downar, J. T. (2018). Multi-level coarse mesh finite difference acceleration with local two-node nodal expansion method. Ann. Nucl. Energy 116, 105–113. doi:10.1016/j.anucene.2018.02.002

CrossRef Full Text | Google Scholar

Hou, J. J., Ivanov, K. N., Boyarinov, V. F., and Fomichenko, P. A. (2017). Oecd/nea benchmark for time-dependent neutron transport calculations without spatial homogenization. Nucl. Eng. Des. 317, 177–189. doi:10.1016/j.nucengdes.2017.02.008

CrossRef Full Text | Google Scholar

Joo, H. G., Cho, J. Y., Kim, K. S., Lee, C. C., and Zee, S. Q. (2004). “Methods and performance of a three-dimensional whole-core transport code decart,” in Physor 2004 (Chicago, IL: American Nuclear Society).

Google Scholar

Larsen, E., Collins, B., Kochunas, B., and Stimpson, S. (2019). “MPACT theory manual (version 4.1),” in Tech. Rep. CASL-U-2019-1874-001. Oak Ridge, TN, United States: (University of Michigan, Oak Ridge National Laboratory).

Google Scholar

Quinn, M. (2003). Parallel programming in C with MPI and OpenMP. Boston: McGraw-Hill.

Google Scholar

Saad, Y. (2003). Iterative methods for sparse linear systems. 2nd Edition. Philadelphia, PA: Society for Industrial and Applied Mathematics.

Google Scholar

Smith, K. S. (1983). “Nodal method storage reduction by nonlinear iteration”in ANS annual meeting, Detroit, MI, United States, June 12–June 17, 1983, (Transactions of the American Nuclear Society), 44, 265–266.

Google Scholar

Tao, S., and Xu, Y. (2020). “Hybrid parallel computing for solving 3d multi-group neutron diffusion equation via multi-level cmfd acceleration,” in Transactions of the American nuclear society (virtual conference).

Google Scholar

Tao, S., and Xu, Y. (2022a). Hybrid parallel strategies for the neutron transport code pandas-moc. Front. Nucl. Eng. 1. doi:10.3389/fnuen.2022.1002951

CrossRef Full Text | Google Scholar

Tao, S., and Xu, Y. (2022b). Neutron transport analysis of c5g7-td benchmark with pandas-moc. Ann. Nucl. Energy 169, 108966. doi:10.1016/j.anucene.2022.108966

CrossRef Full Text | Google Scholar

Tao, S., and Xu, Y. (2022c). Parallel schedules for moc sweep in the neutron transport code pandas-moc. Front. Nucl. Eng. 1. doi:10.3389/fnuen.2022.1002862

CrossRef Full Text | Google Scholar

Xu, Y., and Downar, T. (2012). “Convergence analysis of a cmfd method based on generalized equivalence theory,” in Physor 2012: Conference on advances in reactor physics - linking research, industry, and education Knoxville: American Nuclear Society. Apr 15-20 (TN (United States)).

Google Scholar

Zhu, K., Kong, B., Hou, J., Zhang, H., Guo, J., and Li, F. (2022). Archer - a new three-dimensional method of characteristics neutron transport code for pebble-bed htr with coarse mesh finite difference acceleration. Ann. Nucl. Energy 177, 109303. doi:10.1016/j.anucene.2022.109303

CrossRef Full Text | Google Scholar