- 1 State Key Laboratory of Cognitive Neuroscience and Learning, Beijing Normal University, Beijing, China
- 2 Phyllis Green and Randolph Cõwen Institute for Pediatric Neuroscience, New York University Langone Medical Center, New York, NY, USA
In the past decade, resting-state functional MRI (R-fMRI) measures of brain activity have attracted considerable attention. Based on changes in the blood oxygen level-dependent signal, R-fMRI offers a novel way to assess the brain’s spontaneous or intrinsic (i.e., task-free) activity with both high spatial and temporal resolutions. The properties of both the intra- and inter-regional connectivity of resting-state brain activity have been well documented, promoting our understanding of the brain as a complex network. Specifically, the topological organization of brain networks has been recently studied with graph theory. In this review, we will summarize the recent advances in graph-based brain network analyses of R-fMRI signals, both in typical and atypical populations. Application of these approaches to R-fMRI data has demonstrated non-trivial topological properties of functional networks in the human brain. Among these is the knowledge that the brain’s intrinsic activity is organized as a small-world, highly efficient network, with significant modularity and highly connected hub regions. These network properties have also been found to change throughout normal development, aging, and in various pathological conditions. The literature reviewed here suggests that graph-based network analyses are capable of uncovering system-level changes associated with different processes in the resting brain, which could provide novel insights into the understanding of the underlying physiological mechanisms of brain function. We also highlight several potential research topics in the future.
Introduction
As a novel, non-invasive way to measure spontaneous neural activity in the human brain, resting-state functional magnetic resonance imaging (R-fMRI) has attracted considerable attention (Biswal et al., 1995 ; Fox and Raichle, 2007 ). R-fMRI measures the endogenous or spontaneous brain activity as low-frequency fluctuations in blood oxygen level-dependent (BOLD) signals. This low-frequency fluctuation phenomenon is vital for a better understanding of human brain function because extremely disproportionate energy consumption appears within the regions showing high resting metabolisms (Raichle et al., 2001 ; Raichle, 2006 ). Beginning with a seminal demonstration of highly coherent low-frequency fluctuations within the brain motor system (Biswal et al., 1995 ), R-fMRI has been extensively used to investigate normal brain function (Greicius et al., 2003 ; Beckmann et al., 2005 ; Fox et al., 2005 ; Margulies et al., 2007 ; Di Martino et al., 2008 ; Roy et al., 2009 ; Smith et al., 2009 ; Yan et al., 2009b ), trait variability and behavioral characteristics (Hampson et al., 2006 ; Fox et al., 2007 ; Hesselmann et al., 2008 ; Kelly et al., 2008 ; Di Martino et al., 2009 ; Yan et al., 2009a ), as well as various clinical populations (for reviews, see Greicius, 2008 ; Broyd et al., 2009 ; Zhang and Raichle, 2010 ). To date, many R-fMRI methods have been developed to explore the nature of resting-state brain.
Currently, there are two main types of R-fMRI methods used to characterize spontaneous brain activity. One measures specific regional characteristics of R-fMRI signals within a brain region (e.g., voxels or parcellation units), such as regional homogeneity (Zang et al., 2004 ), network homogeneity (Uddin et al., 2008 ), amplitude of low-frequency fluctuations (ALFF) (Zang et al., 2007 ), fractional ALFF (Zou et al., 2008 ) and fractal complexity (Wink et al., 2006 ). In contrast, the other measures the relationship between different brain units (i.e., highly coherent spontaneous fluctuations or functional connectivity), such as seed-based functional connectivity analysis (Biswal et al., 1995 ), clustering (Cordes et al., 2002 ) and independent component analysis (ICA) (van de Ven et al., 2004 ). Connectivity-based methods have been widely used to detect functionally connected brain networks, including motor (Biswal et al., 1995 ), auditory (Cordes et al., 2001 ), visual (Lowe et al., 1998 ), language (Hampson et al., 2002 ), default-mode (Greicius et al., 2003 ), and attention systems (Fox et al., 2006 ). These brain networks have demonstrated high consistency and reproducibility across subjects and sessions (Damoiseaux et al., 2006 ; Chen et al., 2008a ; Meindl et al., 2009 ; Zuo et al., 2010a ), high test–retest reliability (Shehzad et al., 2009 ; Zuo et al., 2010a ), high reproducibility across different analytic approaches (Long et al., 2008 ; Franco et al., 2009 ) and a striking correspondence to task activation maps (Smith et al., 2009 ). More recently, using novel graph theory-based approaches, these identified biologically plausible brain networks were found to topologically organize in a non-trivial manner (e.g., small-world architecture and modular structure) that support efficient information processing of the brain.
Graph theory-based approaches model the brain as a complex network represented graphically by a collection of nodes and edges. In the virtual graph, nodes indicate anatomical elements (e.g., brain regions), and edges represent the relationships between nodes (e.g., connectivity). After the network modeling procedure, various graph theoretical metrics can be used to investigate the organizational mechanism underlying the relevant networks. In contrast to those widely used R-fMRI analytic methods (e.g., ALFF, seed-based functional connectivity and ICA), the graph-based network analyses allow us not only to visualize the overall connectivity pattern among all the elements of the brain (e.g., brain regions) but also to quantitatively characterize the global organization. In addition, this approach also gives insight into the topological reconfiguration of the brain in response to external task modulation (Eguiluz et al., 2005 ; Pachou et al., 2008 ; Bassett et al., 2009 ; Micheloyannis et al., 2009 ; Wang et al., 2010 ) or pathological attacks (for reviews, see Bassett and Bullmore, 2009 and He et al., 2009a ). Moreover, it provides a vital framework to elucidate the relationship between brain structure and function (Honey et al., 2010 ). Both structural and functional brain networks have been demonstrated to organize intrinsically as highly modular small-world architectures capable of efficiently transferring information at a low wiring cost as well as formatting highly connected hub regions (Salvador et al., 2005 ; Achard et al., 2007 ; He et al., 2007 , 2009b ; Chen et al., 2008b ; Hagmann et al., 2008 ; Gong et al., 2009a ). Furthermore, the utility of graph-based techniques has been proven by an increasing number of studies to probe potential mechanisms involved in normal development (Fair et al., 2007 , 2008 , 2009 ; Supekar et al., 2009 ), aging (Achard and Bullmore, 2007 ; Gong et al., 2009b ; Meunier et al., 2009a ; Micheloyannis et al., 2009 ; Wang et al., 2010 ), and various brain disorders (Stam et al., 2007 ; He et al., 2008 , 2009c ; Liu et al., 2008 ; Supekar et al., 2009 ; Wang et al., 2009b ; Buckner et al., 2009 ). Given the lack of relevant reviews that focus exclusively on graph-based brain network research using R-fMRI, the purpose of the present review is to increase multi-discipline appreciation and cooperation on this burgeoning field. In addition, this work provides the opportunity to revolutionize our view of brain organization and function by re-examining the progress made in this field.
In this review, we will summarize the recent progress made in the study of functional brain networks constructed by intrinsic brain activity measured by R-fMRI. The paper is organized to three main sections. First, some basic concepts regarding brain connectivity and graph theoretical approaches are introduced, along with a review of recent graph-based work on revealing the normal topological architecture and underlying organization of functional brain networks. Then, we survey various R-fMRI applications of graph-based approaches to uncover changes in the network properties of brain development, aging and disorders. Finally, we highlight some technical challenges and future directions in this rapidly emerging research area.
Basic Conceptions
Brain Connectivity Networks
A network is a collection of nodes and edges, where nodes indicate basic elements within the system of interest and edges indicate the associations among those elements. An accurate method for defining the most essential elements of a network (i.e., nodes and edges) is vital for network construction. Specifically, for brain networks, they can be described at different spatial levels, such as microscale, mesoscale, and macroscale or large-scale (Sporns et al., 2005 ). Given technical limitations and computational demand, most current studies focus on the macroscale or large-scale brain networks. In this review, we will also concentrate on the macroscale brain networks.
In a macroscale brain network, nodes can be defined as EEG electrodes, MEG channels, or regions of interest (ROI) derived from anatomical atlases in MRI. After the definition of nodes, the edges among nodes can be defined by the functional or structural associations among different neuronal elements of the brain. To date, functional associations are measured by either the temporal correlation between spatially remote neurophysiological events, often referred to as the functional connectivity, or the influence that one neural system exerts over another, also termed effective connectivity (Friston et al., 1993 ). Structural associations can be measured by examining either direct diffusion-based anatomical connectivity or indirect morphology-based statistical interdependencies across populations (Bullmore and Sporns, 2009 ; He and Evans, 2010 ). Once these two basic elements of a network, nodes and edges, are extracted from the dataset, the constructed brain connectivity network can be further characterized using graph theoretical approaches. Figure 1 illustrates the schematic representation of network constructions using R-fMRI.
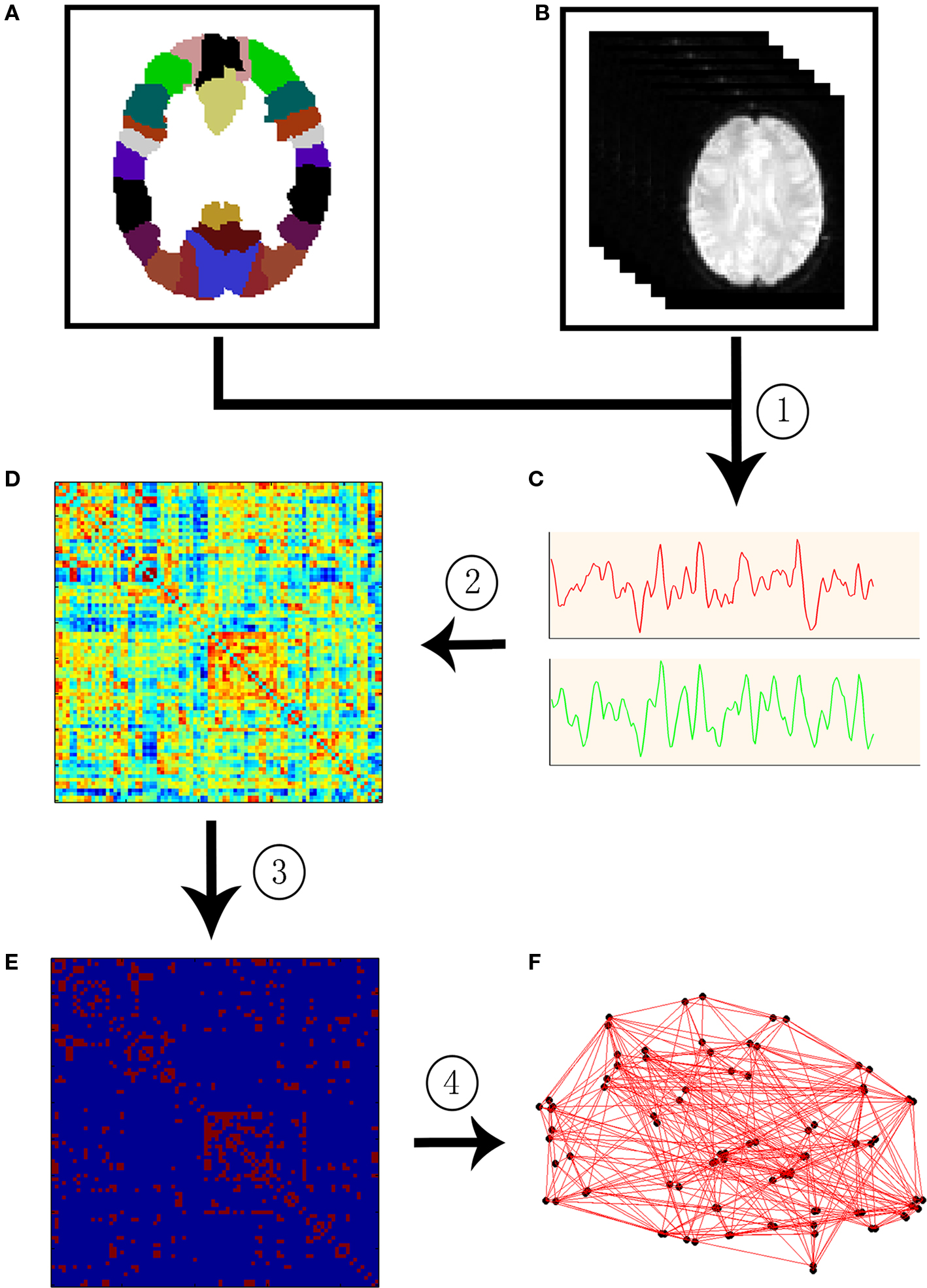
Figure 1. A flowchart for the construction of functional brain network in the human brain by R-fMRI. (1) Extraction of the time course (C) from R-fMRI data (B) within each anatomical unit (i.e., network node). (B) Anatomical units are obtained according to a prior brain atlas (A) or voxels; (2) Calculation of a functional connectivity (i.e., network edge) correlation matrix (D) between any pairs of nodes; (3) Thresholding the correlation matrix into a binary connectivity matrix (i.e., association matrix, E); (4) Visualization of the association matrix as a graph (F).
Graph Theoretical Approaches
Graph theory is the natural framework for the exact mathematical representation of complex networks. Formally, a complex network can be represented as a graph by G(N, K), with N denoting the number of nodes and K the number of edges in graph G. Graphs can be classified as directed or undirected based on whether the edges have sense of direction information. Likewise, graphs can also be divided into unweighted (binary) graphs if every edge in the graph has an equal weight of 1 or weighted graphs if its edges are assigned with different strengths. In this review, we will only focus on undirected and unweighted graphs. The descriptions for other types of graphs can be found in previous literature (Boccaletti et al., 2006 ; Bang-Jensen and Gutin, 2008 ).
For an undirected and unweighted graph G(N, K), the connectivity pattern can be completely described by an N × N symmetric square matrix named adjacency matrix A whose entry aij (i,j = 1,…,N) is 1 if there exists an edge between node i and j or 0 if one does not. Now we will list some important metrics that are frequently used in the field of neuroscience.
Degree and degree distribution
In a graph G(N, K), the degree of node i is the number of edges linked to it and is calculated as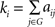 
, where aij is the ith row and jth column element of adjacency matrix 
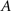. Degree is a simple measurement for the connectivity of a node with the rest of the nodes in a network. The mean of degrees over all the nodes in G, referred to as the average degree, measures the extent to which the graph is connected. The degree distribution P(k) is defined as the probability that a node chosen uniformly at random has degree k or, equivalently, as the fraction of nodes in the graph having degree k. In terms of the form of degree distribution, networks can be classified into different categories (e.g., power law or scale-free networks where nodal degrees are extremely heterogeneous) that possess distinct resilience to the removal of nodes. For example, networks of exponentially truncated power law degree were demonstrated to be equally resilient to random failures (random removal of nodes) but more resilient to targeted attacks (selective removal of nodes, such as those with the highest degrees) compared with the scale-free network in spontaneous human brain functional networks (Achard et al., 2006
).
Small-world
The small-world (Watts and Strogatz, 1998
) is an important model to characterize the organization principles that govern a remarkable variety of social, economic, and biological complex networks. A small-world network can be described by high local clustering, characterized by a high clustering coefficient, Cp, and low minimum path length between any pair of nodes, characterized by a low characteristic path length, Lp (Watts and Strogatz, 1998
). The Cp of a network is defined as the average of the clustering coefficients over all nodes in the network where the clustering coefficient Ci of a node i is calculated as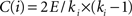 
, with E denoting the number of existing connections among the node i’s neighbors and ki representing the degree of node i. Cp quantifies the extent of local interconnectivity or cliquishness of a network. The Lp is defined as the average of the shortest path lengths (minimum number of edges needed to link one node to another) between any pair of nodes in the network. Lp measures the distance (i.e., number of edges) between any pair of nodes in a network or the extent of overall communication efficiency of a network. A shorter distance means higher routing efficiency because information is exchanged via fewer steps. Notably, this original definition of Lp is problematic in networks with multiple components where there exist nodal pairs that have no connecting path. The shortest path lengths for such disconnected node pairs are infinite. To avoid this problem, Lp can be measured by using a “harmonic mean” distance between any pairs of network nodes as proposed by Newman (2003)
, that is, the reciprocal of the average of the reciprocals. Notably, Lp calculated by “harmonic mean” distance is numerically the inverse of global efficiency (see below for the definition of global efficiency). Mathematically, a real network would be considered as small-world if it meets the following two conditions: γ = Cp/Cp−rand > 1 and λ = Lp/Lp−rand ≈ 1, where Cp−rand and Lp−rand are the mean clustering coefficient and characteristic path length of the matched random networks (random networks have low Cp and short Lp), respectively. These two conditions can also be summarized into a simple quantitative measurement, small-worldness, σ = γ/λ > 1 (Humphries et al., 2005). Small-world is an attractive model for the description of complex brain networks because it not only supports both specialized/modularized and integrated/distributed information processing but also maximizes the efficiency of information transfer at a relatively low wiring cost (Sporns et al., 2004
; Bassett and Bullmore, 2006
). Using these measurements, small-world topology has been recently demonstrated in many complex brain networks across multiple species in both healthy and diseased states (for reviews, see Stam and Reijneveld, 2007
; Bassett and Bullmore, 2009
; Bullmore and Sporns, 2009
; He et al., 2009a
).
Network efficiency
Efficiency is a more biologically relevant metric to describe brain networks from the perspective of information flow, which can deal with the disconnected graphs, nonsparse graphs or both (Latora and Marchiori, 2001
; Bassett and Bullmore, 2006
). For a graph G(N,K), the global efficiency is defined as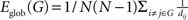 
, where dij is the shortest path length between node i and node j in G. The local efficiency of G is measured as 
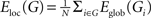, where Eglob(Gi) is the global efficiency of 
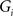, the sub-graph composed of the neighbors of node i. Global efficiency and local efficiency measure the ability of a network to transmit information at the global and local level, respectively (Latora and Marchiori, 2001
, 2003
). An important metric that concisely couples with network efficiency is network cost, which measures how expensive it is to build a network. For an unweighted and undirected network, network cost can be defined as the ratio of the existing number of edges to the number of all possible edges in the network. Using these measurements, networks with high efficiency, both local and global, and low cost are said to be economic small-world networks (Achard et al., 2007
; Wang et al., 2009b
).
Nodal centrality
Nodal centrality quantifies how important a node is within a network. Several different metrics exist for measuring nodal centrality, such as degree centrality, nodal efficiency (Achard and Bullmore, 2007
), closeness centrality (Freeman, 1979
), and betweenness centrality (Freeman, 1977
). For a node i in a network G(N,K), the degree is defined as the number of edges linked directly to it. The nodal efficiency of node i is computed as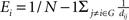 
. Nodal efficiency measures the ability of a node to propagate information with the other nodes in a network. The closeness centrality of node i is computed as 
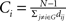, and it reflects the average distance from a node to all the other nodes in a network. The betweenness centrality captures the influence that one node has over the flow of information between all other nodes in the network and can be calculated as 
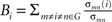, where 
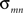is the total number of shortest paths from node m to node n and 
is the number of shortest paths from node m to node n that pass through node i. A node with high centrality is considered a hub in the network (Sporns et al., 2007
; He et al., 2008
; Buckner et al., 2009
).
Modularity
Modularity reflects the degree to which a network is organized into a modular or community structure. Modules refer to a set of nodes with denser links among them but sparser links with the rest of the network (Newman, 2006 ). Detection and characterization of modular structure in the brain system can help us to identify groups of anatomically and/or functionally associated components that perform specific biological functions. Several optimization algorithms are currently available, each with different advantages (Clauset et al., 2004). Based on the identified modular structure, hubs can be further subdivided in terms of their roles in maintaining intra- or inter-module connectivity. Provincial hubs are connected mainly to nodes in their own modules, whereas connector hubs are connected to nodes in other modules (Guimera et al., 2005 ; Chen et al., 2008; He et al., 2009b ).
Hierarchy
Hierarchical structure is a fundamental characteristic of many social and biological networks (Ravasz et al., 2002 ; Ravasz and Barabasi, 2003 ; Sales-Pardo et al., 2007 ). In a hierarchical network, highly connected nodes (hubs) are connected predominantly to nodes that are not otherwise connected to each other. That is, the larger the degree, the lower the clustering coefficient. Such a hierarchical organization favors top-down relationships between nodes and minimizes wiring costs, but it is vulnerable to attacks on hubs (Ravasz and Barabasi, 2003 ; Sakata et al., 2005 ). Mathematically, this phenomenon can be quantified by the β value, an exponent of the power law relationship between clustering coefficient, Ci, and degree, ki, of the nodes in the network: C ≈ k−β. A large positive value of β signifies a typical hierarchical structure. Such a hierarchy has been found to exist in both structural (Bassett et al., 2008 ) and functional (Supekar et al., 2009 ) human brain networks.
For more details regarding the construction of brain networks, frequently used graph-based metrics in brain networks, and the final interpretations of results, see (Bullmore and Sporns, 2009 ; He et al., 2009a ; Rubinov and Sporns, 2009 ).
Resting-State Functional Brain Networks
Spontaneous neural activity can be recorded by multiple imaging techniques, such as EEG, MEG, and R-fMRI, each with different advantages. Several studies have successfully used EEG or MEG to construct intrinsic brain connectivity networks and further investigated state-dependent alterations in network topological properties (Stam and Reijneveld, 2007 ; Bassett and Bullmore, 2009 ). More recently, R-fMRI-based network analysis has gained popularity because of its high spatial and temporal resolution. This review will primarily focus on graph-based brain network studies using R-fMRI. Table 1 presents the relevant literature reviewed here.
Table 1. Ggraph-based brain functional network studies by R-fMRI.
Normal Population
Region-based resting-state brain networks
Salvador et al. (2005) were the first to utilize R-fMRI to investigate the whole brain functional network. Based on a prior Automated Anatomical Labeling (AAL) atlas, a 90-node group-level network generated from 12 healthy volunteers was constructed. Graph theoretical methods revealed that the brain functional network showed a small-world topology characterized by high local clustering and short path lengths linking different brain regions. Further hierarchical clustering and multidimensional scaling analyses demonstrated that the network included several major functional clusters corresponding to four neocortical lobes (frontal, temporal, parietal-(pre)motor, and occipital), the medial temporal lobe and subcortical nuclei. In a following study that also utilized the AAL atlas, Achard et al. (2006) investigated frequency-dependent spontaneous brain networks in five healthy volunteers. They found that the small-world topology was most salient in the low-frequency (0.03–0.06 Hz) brain network. Furthermore, several heteromodal association cortex regions were found to act as hubs in the brain network. The authors also found that the network obeys an exponentially truncated power law degree distribution, which appears to confer a distinctive tolerance against random failures and target attacks compared with scale-free or power law distribution. Recently, Wang et al. (2009a) investigated the topological organization of functional brain networks constructed from two different brain atlases [AAL atlas (90 parcellation units) and Automatic Nonlinear Imaging Matching and Anatomical Labeling (ANIMAL) atlas (70 parcellation units)]. They found that the spontaneous functional brain networks exhibited robust small-world topology and a common form of exponentially truncated power law degree distribution regardless of parcellation strategies. This suggests a stable intrinsic architecture in the resting human brain. More importantly, they observed significant parcellation-related differences in multiple network topological parameters (e.g., small-worldness and network efficiency) between the two sets of networks. For example, the global efficiency of networks based on the AAL atlas was higher than those based on the ANIMAL atlas. Given that most current studies construct the brain networks using prior brain templates, this work has important implications for the consideration of parcellation-related effects in future brain network studies.
Using R-fMRI, He et al. (2009b) demonstrated modular structures of intrinsic functional brain networks (Figure 2 ). A group-level brain connectivity network was obtained and fed into a simulated annealing algorithm to detect the modular structure. The results showed that the resting-state brain network was modularly configured and optimally organized into five modules: somatosensory/motor and auditory, vision, attention, default-mode, and limbic/paralimbic and sub-cortical systems. Interestingly, when the modularity detection algorithm was iteratively applied to those identified modules, several more segregated sub-modules were observed, suggesting a hierarchical modularity. Furthermore, they demonstrated significant differences in the network structure between modules and the whole brain network, suggesting module-specific organization patterns. In a more detailed exploration, specific sets of connector nodes and bridge edges that were involved in different modules were shown to be important for maintaining the connectivity and stability of the functional brain networks. Another similar study from Meunier et al. (2009b) also demonstrated the hierarchical modularity in resting-state functional networks of the human brain. In this case, a larger brain network, consisting of 1808 regional nodes, was constructed for each of the 18 right-handed healthy volunteers and was fed into a multi-level method for detecting the hierarchical modularity. The results indicated a significant hierarchical modularity of the resting-state brain functional network, with the five largest modules observed at the highest level of the hierarchy: medial occipital, lateral occipital, central, parieto-frontal, and fronto-temporal systems. Intriguingly, the occipital modules showed less sub-modular organization in comparison with other modules, implying that distinctive organizational principles exist in function-specific sub-systems, which is consistent with previous findings (He et al., 2009b ). Additionally, the nodal roles analysis indicated that connector nodes and inter-modular connections were largely concentrated in posterior modules that contain regions of association cortex. In addition to the studies mentioned above, Ferrarini et al. (2009) also validated small-world properties and hierarchical modularity by focusing on revising a clustering algorithm to detect the modularity of resting-state functional networks of the human brain.
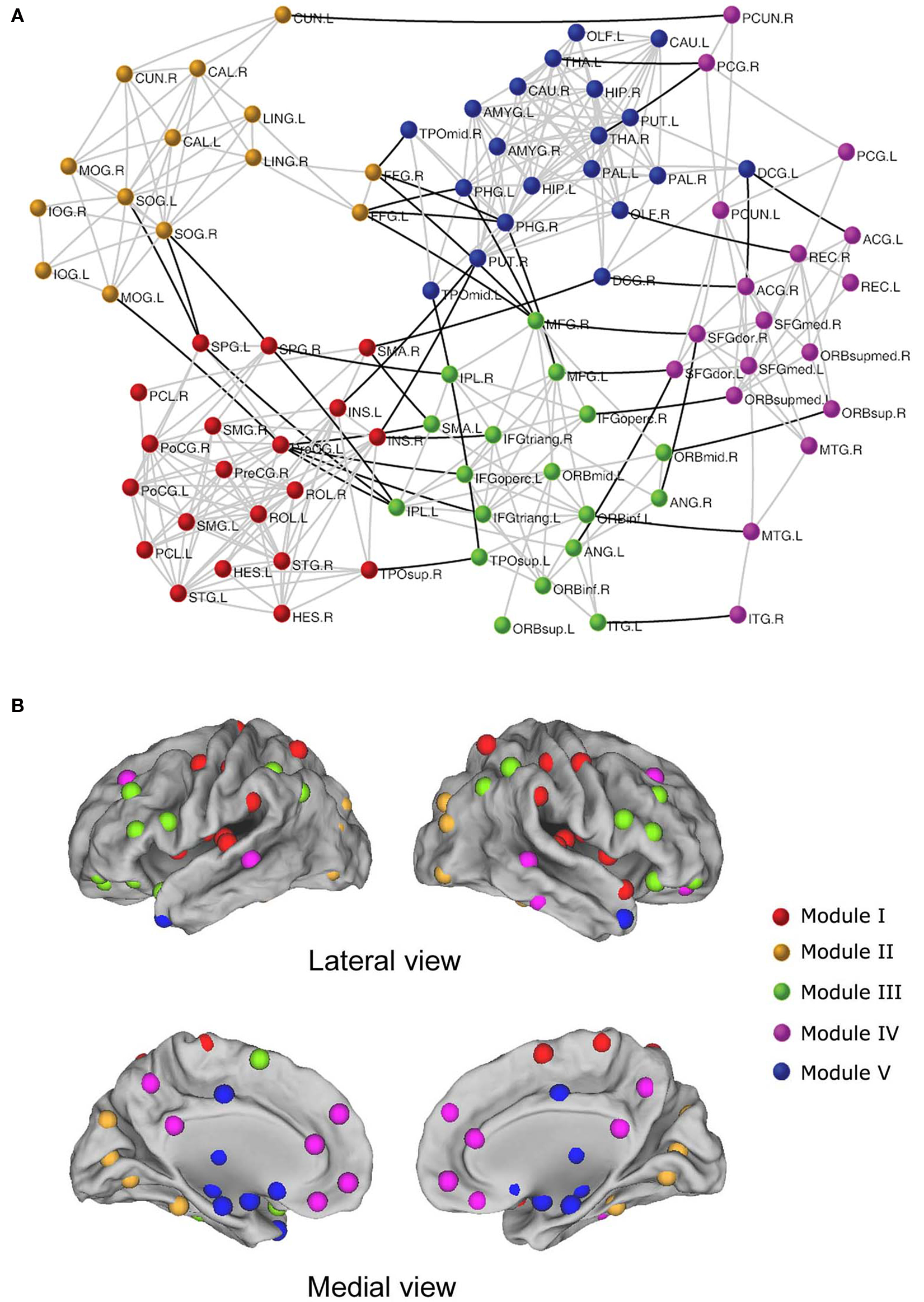
Figure 2. The modular architecture of resting-state functional brain network (He et al., 2009b ). (A) Five modules were identified in a functional network of the human brain, represented by five different colors. The geometric distance between brain regions on the drawing space approximates the shortest path length between them. The network is visualized with Pajek (http://vlado.fmf.uni-lj.si/pub/networks/pajek/ ). The intra-module and inter-module connections are shown in gray and dark lines, respectively. For the abbreviations of the regions, see He et al. (2009b) . (B) Surface representation of modular architecture of a functional brain network. All 90 brain regions are marked by using different colored spheres (different colors represent distinct network modules) and further mapped onto the cortical surfaces in the lateral and medial views, respectively. Notably, the regions are located according to their centroid stereotaxic coordinates. For visualization purposes, the subcortical regions are projected to the medial cortical surface according to their y and z centroid stereotaxic coordinates.
Beyond the region-level explorations of the intrinsic topology mentioned above, brain network analyses have been done at the voxel-level. Although some intriguing results were demonstrated in intrinsic large-scale (region-level) functional brain networks, these findings may be biased by the fact that all of the analyses were restricted to predefined anatomical structures. Specifically, at the region-level, inter-regional connectivity was routinely evaluated in terms of representative time courses obtained by averaging the signals within predefined parcellation structures. However, despite the simplicity, the averaging process may simultaneously lead to a possible blurring out of some local specific information, particularly for those functionally heterogeneous parcellation units. The high spatial resolution (e.g., 4 mm) provided by R-fMRI allows investigation of the topological properties of brain networks at a finer-grained voxel-level, which is beneficial to our understanding of brain organization at a more refined level (e.g., 20,000 nodes). The next section will be devoted to reviewing some work in this area.
Voxel-based resting-state brain networks
Eguiluz et al. (2005) conducted the first study of human brain functional networks constructed at the voxel-level and found general scale-free small-world architecture under multiple task conditions. Focusing on the same features, van den Heuvel et al. (2008a) first examined the resting-state functional network of the human brain at voxel-level. After constructing individual brain networks for 28 participants, the graph theoretical analysis confirmed the small-world organization in spontaneous brain network consistent with previous region-level network analyses. This finding suggests that small-world topology is a robust organizational principle governing the global pattern of coherent fluctuations in spontaneous neural activity across multiple spatial scales (i.e., region-level and voxel-level). However, in contrast to the exponentially truncated power law degree distribution observed frequently in region-level brain networks, the voxel-level brain network exhibited a scale-free or power law form. This discrepancy implies that intrinsic functional networks of the human brain may organize differently at different spatial scales, at least in some features, therefore pointing out the need to elucidate how the organization of brain networks depends on the scale in which they are constructed.
Instead of global small-world architecture, several groups have focused on the identification of intrinsic modular/community structure in resting-state brain networks at voxel-level. Using a normalized cut graph clustering algorithm, van den Heuvel et al. (2008b) found seven resting-state networks, such as default-mode network, parietal-frontal network and motor and visual network, resembling those sub-networks or components revealed by ICA studies on R-fMRI datasets. This consistency of modularity structure or sub-systems in intrinsic functional brain networks across analytical methods was also validated by more recent voxel-level network studies (Laurienti et al., 2009 ; Valencia et al., 2009 ). Valencia et al. (2009) constructed voxel-level functional brain networks for seven healthy subjects and then investigated the modular architecture of these networks using a random-walk-based method. It is not surprising that all individuals exhibited significant modular structure with moderate stability. Refreshingly, the authors compared the spatial distribution of retrieved modules with a prior anatomical AAL atlas and found that some modules aligned well with certain brain systems. For example, 75% of the primary visual area, V1, was gathered into one module. More importantly, some modules included functionally related but spatially distant regions. These results imply that the modular organization has an underlying basis of neural functions, rather than being a consequence of vascular processes or local physiological activities. Another notable finding from this work is the exponentially truncated power law model of degree distribution for intrinsic brain networks, which contrasts with the observation of power law form by van den Heuvel et al. (2008b) . This discrepancy may be attributed to the different network construction methods (i.e., network nodes were abstracted from gray matter voxels by van den Heuvel et al. vs. whole brain by Valencia et al.) given the findings of tissue specific organization that networks constructed from white matter and cerebral spinal fluid voxels did not exhibited typical power law degree distribution (van den Heuvel et al., 2008b ). Almost simultaneously, Laurienti et al. (2009) combined R-fMRI and graph theory to explore the modular structure of resting-state brain networks derived from six normal young adults. Modular architecture was again uncovered in spite of the use of a different module detection algorithm of QCut. It is noteworthy that the default-mode network was separated into three primary modules: the module of the medial frontal cortex, the module of sections from the parietal lobe and parahippocampal gyrus and the module of portions from the cuneus gyrus, parietal cortex and middle frontal gyrus. This was consistent with the finding of functional brain networks (He et al., 2009b ). The split of the default-mode network into multiple sub-networks is also observed in previous ICA studies (Zuo et al., 2010a ) and could imply functional segregation or heterogeneity within the default-mode network (Buckner et al., 2008 ; Harrison et al., 2008 ; Kiviniemi et al., 2009 ; Uddin et al., 2009 ). Given the high sensitivity of the default-mode network to numerous mental disorders (Broyd et al., 2009 ), studies that focus on the pattern within and between these sub-modules may lead to new insights into the pathophysiology of these disorders.
Rather than work with whole brain network studies, Dosenbach et al. (2007) concentrated exclusively on a putative task-control network. Thirty-nine ROIs associated with task-control were selected as the network nodes, and a group-level network from 74 young adults was formed. Analogous to the whole brain network, the sub-network of task-control system also exhibited small-world features. Further visualization of the network connectivity pattern revealed eight disconnected components, including the fronto-parietal component and cingulo-opercular component, which were clearly associated with task control. More importantly, the authors found that the wiring patterns of the fronto-parietal and cingulo-opercular components to other parts of the brain were obviously different. The fronto-parietal component preferentially connected with cerebellar regions, whereas the cingulo-opercular component tended to connect firstly with putative downstream sensory regions in the occipital cortex. Inspired by this phenomenon, the authors proposed a ‘‘dual-network’’ hypothesis to model task control, in which the fronto-parietal network supports adaptive control function and the cingulo-opercular network handles stable set-maintenance function.
Development/Aging
The mature human brain has been optimally organized into a collection of specialized functional networks that flexibly interact in rapid response to various cognitive demands. Studying the formation of the architecture in a maturing brain from a global level may provide more insights into the organizing principle that guides the maturation process. In this topic, Fair and colleagues carried out a series of experiments to explore the mechanisms of development using R-fMRI and modern network techniques. They first studied a task control related network (Fair et al., 2007 ), containing 39 nodes (i.e., task control regions). Three group-level networks covering different ages were generated: 49 children (7–9 years; mean 8.6), 43 adolescents (10–15 years; mean 11.9), and 47 adults (20–31 years; mean 24.1). Visualization analysis showed a clear dynamic reorganization of brain network structure over the course of development. For example, the interconnected fronto-parietal and cingulo- opercular components in children gradually became two disconnected networks in adults. Using similar methods, the authors also demonstrated a more densely connected network structure in the adult default-mode network when compared with children, implying an increased functional integration during development (Fair et al., 2008 ). Moving beyond a single functional network, the authors expanded their interests to a wide system that included four functional networks: cingulo-opercular, fronto-parietal, default-mode and cerebellar. Based on large R-fMRI datasets (210 subjects: 66 aged 7–9; 53 aged 10–15; 91 aged 19–31), they studied the dynamic developmental trajectory of functional brain network organization using a sliding boxcar grouping method (Fair et al., 2009 ). The most important finding was the observation of concurrent segregation and integration in brain networks during development, which was revealed by both qualitative and quantitative analyses. This dichotomy of development was further found to be related to a general decrease in short-range connections and an increase in long-range connections. Another interesting result in this study was the comparable small-world topology observed across the entire range of ages examined, from 8 to 25 years old, as indicated by very little changes in path lengths and clustering coefficients. This suggests a largely conserved architecture over age. All the aforementioned studies focused on some specific brain functional systems, such as the default network or control network, leaving development effects on whole brain network organization unclear. Filling this gap, Supekar et al. (2009) assessed development-related alterations in brain functional networks in great detail using R-fMRI and graph theoretical techniques. After the construction of brain networks for each of 23 children (7–9 years) and 22 IQ-matched young-adult subjects (19–22 years), obvious differences were found in both global and local properties of functional brain networks between children and young adults. For example, children showed a globally lower level of hierarchical organization in the whole network and locally higher efficiency in sub-cortical division. Of particular importance, combining with DTI-based fiber tracking, the authors found a pattern of simultaneous emergence of decreased functional segregation and increased functional integration with development, characterized by lower short-range and higher long-range functional connectivity in young adults when compared with children. Taken together, these results show that development is strongly related to a weakening of short-range functional segregation and a strengthening of long-range functional integration, which suggests a general developmental principle for intrinsic functional brain architecture.
In addition to development-related changes, some groups have also investigated the effects of normal aging on the functional organization of large-scale brain networks during rest (Achard et al., 2007 ; Meunier et al., 2009a ). Using graph theoretical approaches, Achard et al. (2007) tested the hypothesis that resting-state functional brain networks have economical small-world properties and that their performance would be disrupted by normal aging. R-fMRI data were collected from 11 old and 15 young healthy volunteers, and individual brain networks were constructed using the methods from Achard et al. (2006) . The results confirmed the economic small-world configuration hypothesis of intrinsic functional brain networks in both young and old people. However, normal aging significantly reduced the global and local efficiency of parallel information processing. Furthermore, regional efficiency analysis found that the detrimental effects of aging were mainly localized to frontal and temporal cortical and sub-cortical regions. Notably, in this study the authors also successfully detected alterations in the overall performance of economical small-world properties in intrinsic functional brain networks associated with the pharmacological blockade of dopamine neurotransmission. This finding highlights the potential value of graph theoretical tools for characterizing the mechanisms involved in different pathophysiological processes, such as the role of dopamine transmission system. In another study of normal aging, Meunier et al. (2009a) studied aging-related changes in the module or community structure of resting-state brain functional networks from two groups: 17 younger participants (18–33 years, mean age = 24.3 years) and 13 older participants (62–76 years, mean age = 67.3 years). The module structure analyses showed that both age groups exhibited significant, non-random, and robust modularity. However, both module size and composition differed between the age groups. For instance, five modules were detected in young brain functional networks, whereas six were seen in the older group. Interestingly, the authors found a trend for modules to segregate into multiple components in the brain networks of older people compared with younger people. For example, the dorsal fronto-cingulo-parietal module in the young brain network was segregated into two smaller and more local modules in the old brain network, a dorsal prefronto-striato-thalamic module and a medial posterior module. Thereby, tracing the profile of modular architecture throughout both development and aging will be an important topic.
Overall, the use of R-fMRI and graph theoretical approaches has demonstrated that normal development and aging are associated with alterations of brain organization, particularly in the modular architecture. The reconfiguration of network structure may allow for more flexibility to meet the demands during different states of life, such as high plasticity and fast learning at young ages. Future longitudinal studies could help address this question.
Applications in Clinical Population
To date, the combination of R-fMRI and graph theory-based network approaches has proven to be a powerful tool to investigate the abnormalities in the organization of intrinsic brain networks under different pathological conditions (Bassett and Bullmore, 2009 ; Bullmore and Sporns, 2009 ; He et al., 2009a ).
Alzheimer’s disease
Supekar et al. (2008) were the first to study Alzheimer’s disease (AD)-related changes in the coordination of large-scale brain functional networks using R-fMRI. After constructing functional brain networks for each of 21 AD patients and 18 age-matched controls, they found that AD patients showed deterioration of the small-world network properties, characterized by a significantly lower normalized clustering coefficient, implying disrupted local network connectivity. Furthermore, the differences in the normalized clustering coefficient can distinguish the AD participants from the controls with a sensitivity of 72% and a specificity of 78%, suggesting that these network measures could serve as an imaging-based biomarker in AD diagnosis. These findings suggested that AD is associated with disrupted functional integrity in the intrinsic spontaneous neuronal activity of the brain functional system. In a relevant large- and multiple-datasets study, Buckner et al. (2009) performed another AD-related study using graph theoretical approaches and R-fMRI to address the spatial distribution and stability of hub regions in intrinsic functional brain networks of human. They also assessed whether the identified hubs had a preferential vulnerability to AD pathology. One hundred twenty-seven healthy young adults participated in MRI sessions, and 39 older adults (29 controls and 10 AD patients) participated in PET sessions. The results showed that hub regions were dominated mainly by heteromodal areas of the association cortex, such as the posterior cingulate and medial/lateral prefrontal cortices, consistent with previous studies (Achard et al., 2006 ). Of more importance, the pattern of hubs was highly consistent between datasets and activity states (passive fixation vs. semantic classification task), suggesting that this is a stable property of cortical network architecture. Finally, the authors demonstrated a striking overlap and strong correlation (r = 0.68) between the pattern of cortical hubs derived from young subjects and the Aβ deposition map in AD patients. The results imply a dual role for hubs in brain networks. On one hand, they act as critical stations for information processing, and on the other hand, they are preferential candidates of pathology.
Schizophrenia
Using R-fMRI, Liu et al. (2008) utilized graph-based network analysis to characterize networks in schizophrenia patients. Individual brain networks were built for 31 schizophrenia patients and 31 age- and gender-matched healthy subjects. Subsequent graph theoretical analysis revealed that schizophrenia patients showed abnormalities in multiple network attributes, including lower absolute clustering coefficients, normalized clustering coefficient, small-worldness and network efficiency, as well as longer absolute path length. In addition, multiple nodal characteristics were altered in several specific regions predominately located in prefrontal, parietal and temporal lobes in schizophrenia patients. Collectively, these abnormalities suggest a dysfunctional organization of the intrinsic functional brain network in schizophrenia. It is worth noting that multiple network metrics, such as the absolute clustering coefficient and local network efficiency, were found to have a significant negative correlation with the duration of illness and the dose of medication, suggesting a potential use of the graph theoretical tool in monitoring the progression and therapy evaluation of schizophrenia.
Attention-deficit hyperactivity disorder
Wang et al. (2009b) were the first to apply graph theoretical approaches to explore the spontaneous brain networks in patients with attention-deficit hyperactivity disorder (ADHD). Based upon R-fMRI datasets from 29 ADHD and 27 control boys, the authors found that the functional brain networks in both groups exhibited economic small-world behaviors. However, the ADHD group exhibited significant increases in local efficiency but statistically unchanged global efficiency in comparison with the control subjects, suggesting a shift toward regular networks in ADHD children. In addition, the authors also tested regional nodal efficiency and found decreased nodal efficiency in the medial prefrontal, temporal, and occipital cortex regions and increased nodal efficiency in the inferior frontal cortex and sub-cortical regions. These differences imply a loss of the optimal organization pattern in ADHD children.
Epilepsy
The first study of mesial temporal lobe epilepsy (mTLE) to use graph theoretical approaches was performed by Liao et al. (2010) . They constructed endogenous brain connectivity networks for 18 mTLE patients and 27 healthy controls using R-fMRI signals. A direct between-group comparison in functional connectivity revealed significantly increased connectivity within the medial temporal lobes but decreased connectivity within the frontal and parietal lobes and between frontal and parietal lobes in mTLE patients relative to controls. Subsequent graph theoretical analyses demonstrated that regions showing a significantly decreased number of connections were mainly from components of default-mode networks in mTLE patients. In addition, normalized path length was also found to be significantly lower in mTLE patients. These alterations in functional connectivity and topological properties may be used to define tentative disease markers for mTLE after the validation of repeatability.
Others
In addition to the application of this approach to neuropsychopathic diseases, graph theoretical approaches have also been used to explore the changes in intrinsic functional brain networks during recovery from traumatic brain injury (Nakamura et al., 2009 ) and in drug addicts (Liu et al., 2009 ). Nakamura et al. (2009) studied the changes of intrinsic coordinated brain connectivity networks in six subjects in recovery from severe traumatic brain injury. They found that high-value functional connections decreased with recovery but the overall number of connections maintained relatively stable. Further analyses revealed multiple altered topological indices during the recovery timeline, such as a significant reduction of global and local efficiency in brain networks at 6 months post injury compared with those at 3 months post injury. These results suggest that graph-based network techniques could be useful in evaluating the adaptation of intrinsic brain networks to neural disruption during recovery. Liu et al. (2009) concentrated on a specific population of chronic heroin users and evaluated the impairments of their brain functions from a functional integration perspective. The results demonstrated a typical small-world configuration in the brain networks constructed from 12 chronic heroin users; however, the extent of small-worldness (i.e., σ) was much smaller than that of non-drug users. Furthermore, some regions in the prefrontal cortex, ventral striatum, and limbic/paralimbic area were found to have dysfunctional connectivity, which may be responsible for the decreased self-control, impaired inhibitory function and deficits in stress regulation observed in chronic heroin users.
Taken together, these results demonstrate the utility of the combination of R-fMRI and graph theoretical techniques in capturing the abnormal alterations in topological organization of spontaneous brain networks caused by different brain disorders. Further studies are needed to ascertain whether this kind of topology-based approach could be used as a novel way to identify biomarkers for the diagnosis and monitoring of these diseases.
Technical Challenge and Future Perspectives
In this review, we summarized the recent advances in the application of modern graph theory-based network analysis techniques to study the intrinsic or spontaneous human brain functional networks derived from R-fMRI. Several consistent characteristics are demonstrated in the normal population, such as small-world topology, modular structure, and core regions, some of which are sensitive to normal development, aging and neuropsychiatric disease. These findings provide novel insights into the functional architecture of the human brain and its adaptive reconfiguration in brain maturing, aging and against pathological attacks. However, we should acknowledge that the studies of complex brain networks formed by spontaneous activity, even in normal subjects, are still in the early stages. There are still a number of unanswered questions in this research field.
First, given that the human brain is a complex network at multiple spatial and time scales, how to appropriately represent the brain as a network that can precisely reflect the natural state of the brain is a considerable task. For instance, what are the nodes and edges in a brain network? Which time scale is best suited for the brain network? As Butts (2009) stated, the inappropriate representation of nodes and edges in a network and failure to consider the dynamics of the system of interest will lead to misleading conclusions and generally poor results. Recent evidence has demonstrated the meaningful influence of node choice on the properties of resulting networks (Hayasaka and Laurienti, 2009 ; Wang et al., 2009a ; Zalesky et al., 2010 ). For example, Hayasaka and Laurienti constructed functional brain networks at multiple resolutions (90∼160,000 nodes) using the same R-fMRI dataset from 10 normal subjects and found more prominent small-worldness and robustness against network fragmentation in networks at the voxel-level compared with the region-level. In parallel with the definition of nodes, how to determine the functional connectivity-based edges in functional brain networks is another important issue. Multiple choices are currently available for estimating the functional connectivity between brain areas, such as partial correlation, Pearson correlation and mutual information that depict the functional associations from different angles. Our recent work (not published) demonstrates significant connectivity-related differences in the architecture of resting brain networks, implying that different organization patterns can be generated using different functional connectivity measures. Therefore, a combined analysis of multiple connectivity metrics could be more fruitful for brain network studies. In addition to intuitively conceivable nodes and edges, the human brain is a dynamic system over multiple time scales with ongoing and adaptive functional activities (Honey et al., 2009 ). Therefore, capturing the dynamic network behaviors at different time scales is an important topic in future.
Second, although graph theoretical brain network analysis based on R-fMRI attracts a great deal of attention, the reliability and reproducibility of network measurements, both across subjects and over time, needs to be addressed. R-fMRI has shown reliability in local low-frequency fluctuations (Zuo et al., 2010b ), ROI-based functional connectivity (Shehzad et al., 2009 ) and ICA components (Zuo et al., 2010a ). However, the reliability of topological structures has not yet been validated in R-fMRI brain networks. Nonetheless, a recent magnetoencephalography study has shown that graph metrics exhibited sufficient reliability both in resting-state and during performance of the n-back working memory task, though greater reliability was seen in the performance of the n-back task compared with resting-state (Deuker et al., 2009 ). We speculate that graph-based metrics in R-fMRI may also have acceptable reliability and reproducibility, but this hypothesis needs to be tested directly by multi-center and longitudinal datasets.
Third, how do resting-state functional brain networks relate to individual traits and genetic factors? The answer to these questions may provide new insights into brain function. Smit et al. (2008) demonstrated that individual differences in the topological properties of resting-state functional brain networks constructed using EEG signals are heritable. van den Heuvel et al. (2009b) found that the overall organization of spontaneous functional brain networks had a strong association with intelligence quotient (IQ) as characterized by a negative correlation between the normalized characteristic path length and IQ, consistent with the findings from a recent structural brain network study (Li et al., 2009 ). Accordingly, it is of great interest to further investigate the relationship between network organization and individual characteristics, such as genotype and education level.
Fourth, only a few articles concentrate on the topological architecture of neuronal networks during the performance of tasks. Eguiluz et al. demonstrated scale-free small-world topology in human brain networks across different task conditions. Bassett et al. (2006) indicated that behavioral state in a finger-tapping task did not strongly influence the global topology of the human brain network derived from MEG signals during rest but was associated with emergence of some long-range connections. Their subsequent work (Bassett et al., 2009 ) further demonstrated that the superior task performance of work memory was positively correlated with the cost-efficiency (the difference between the global efficiency and cost of a network) of the β-band brain networks. More recently, Wang et al. (2010) investigated the age-related changes of functional brain networks during memory encoding and recognition, and they found longer path length in older adults due to the loss of long-range connections. Consequently, studying the brain networks under both resting and task conditions as well as the transition between these states may offer new insights into the rapid adaptive reconfiguration of neuronal assemblies that underlie the change between cognitive states.
Finally, the relationship between brain structure and function, both how brain function emerges from its structural substrate and inversely how experience-related functional plasticity reshapes brain structure, is an important future topic. The current review mainly focused on recent studies of R-fMRI based brain networks. It has been demonstrated that brain networks can also be constructed by using other imaging modalities (e.g., structural MRI, diffusion MRI, and EEG/MEG). For instance, researchers have been capable of constructing structural brain networks by measuring inter-regional correlations of cortical thickness or gray matter volume across populations (He et al., 2007 , 2008 , 2009c ; Bassett et al., 2008 ), and found that the resultant networks had small-world properties. Several diffusion MRI studies have utilized deterministic or probabilistic white-matter tractography approaches to build structural brain networks, and also showed small-world topology and high connected hubs in the medial parietal and frontal regions. Of note, the brain networks derived from different imaging modalities have been found to show many common topological properties such as the small-world attributes and network hubs but specific features for each modality such as network modules (Hagmann et al., 2008 ; Chen et al., 2009; He et al., 2009b ). Moreover, several studies have directly compared DTI-based structural connectivity and R-fMRI based functional connectivity, and largely convergent results were found that the strength of resting-state functional connectivity correlated positively with structural connectivity strength (for a review, see Damoiseaux and Greicius, 2009 ). This implies that functionally linked resting brain networks likely reflect underlying structural connectivity (Greicius et al., 2009 ; van den Heuvel et al., 2009a ; Teipel et al., 2010 ). In particular, by focusing on the whole brain connectivity pattern, previous studies have demonstrated overall, though imperfect, agreement between functional and structural connectivity at different spatial levels (Skudlarski et al., 2008 ; Honey et al., 2009 ). In spite of these efforts, the exact nature of the bi-directional interaction between brain structure and function, especially in the global topological organization remains unclear. Concentrating on this point, Park et al. (2008) demonstrated significantly distinct topological features between structural and functional brain networks. For example, structural brain networks showed higher efficiency than the functional brain networks. Collectively, by combining multiple imaging modalities (e.g., fMRI, sMRI, and DTI), direct comparisons of the network properties using large-sample neuroimaging data would be vital to address these issues. Specifically, we need to point out that the public release of the “1000 Functional Connectomes Project” dataset (1200+ resting-state R-fMRI and structural MRI datasets independently collected at 35 sites, http://www.nitrc.org/projects/fcon_1000/ ) (Biswal et al., 2010 ) will be extremely important for the exploration and refinement of topological organization and relevant approaches to structural and functional networks in the human brain.
Conclusion
Through the combination of R-fMRI and graph theory-based network analysis techniques, intrinsic functional networks of the human brain have been generated and demonstrate converging and highly conserved topological organization over different scales and types of measurement, such as small-world and modular structures. More importantly, some of these features exhibit specific changes associated with normal development, aging and various pathological attacks, which indicates the potential value of these approaches in capturing and monitoring the brain organization under different mental states. With the advances in brain imaging techniques (e.g., higher spatiotemporal resolution) and the maturity and perfection of multiple analytical approaches on complex system in parallel, we can expect important progress in our understanding of how the brain works and how it interacts with other systems of the body.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The work was supported by the National Natural Science Foundation of China (Grant No. 30870667), Beijing Natural Science Foundation (Grant No. 7102090) and the Scientific Research Foundation for the Returned Overseas Chinese Scholars (State Education Ministry). We thank American Journal Experts (http://www.journalexperts.com/ ) for English editing and proofreading.
References
Achard, S., and Bullmore, E. T. (2007). Efficiency and cost of economical brain functional networks. PLoS Comput. Biol. 3, e17. doi:10.1371/journal.pcbi.0030017.
Achard, S., Salvador, R., Whitcher, B., Suckling, J., and Bullmore, E. T. (2006). A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 26, 63–72.
Bang-Jensen, J., and Gutin, G. Z. (2008). Digraphs: Theory, Algorithms and Applications. Berlin: Springer-Verlag Press.
Bassett, D. S., and Bullmore, E. T. (2006). Small-world brain networks. Neuroscientist. 12, 512–523.
Bassett, D. S., and Bullmore, E. T. (2009). Human brain networks in health and disease. Curr. Opin. Neurol. 22, 340–347.
Bassett, D. S., Bullmore, E. T., Meyer-Lindenberg, A., Apud, J. A., Weinberger, D. R., and Coppola, R. (2009). Cognitive fitness of cost-efficient brain functional networks. Proc. Natl. Acad. Sci. U.S.A. 106, 11747–11752.
Bassett, D. S., Bullmore, E. T., Verchinski, B. A., Mattay, V. S., Weinberger, D. R., and Meyer-Lindenberg, A. (2008). Hierarchical organization of human cortical networks in health and schizophrenia. J. Neurosci. 28, 9239–9248.
Bassett, D. S., Meyer-Lindenberg, A., Achard, S., Duke, T., and Bullmore, E. T. (2006). Adaptive reconfiguration of fractal small-world human brain functional networks. Proc. Natl. Acad. Sci. U.S.A. 103, 19518–19523.
Beckmann, C. F., DeLuca, M., Devlin, J. T., and Smith, S. M. (2005). Investigations into resting-state connectivity using independent component analysis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 1001–1013.
Biswal, B. B., Mennes, M., Zuo, X. N., Gohel, S., Kelly, C., Smith, S. M., Beckmann, C. F., Adelstein, J. S., Buckner, R. L., Colcombe, S., Dogonowski, A. M., Ernst, M., Fair, D., Hampson, M., Hoptman, M. J., Hyde, J. S., Kiviniemi, V. J., Kotter, R., Li, S. J., Lin, C. P., Lowe, M. J., Mackay, C., Madden, D. J., Madsen, K. H., Margulies, D. S., Mayberg, H. S., McMahon, K., Monk, C. S., Mostofsky, S. H., Nagel, B. J., Pekar, J. J., Peltier, S. J., Petersen, S. E., Riedl, V., Rombouts, S. A., Rypma, B., Schlaggar, B. L., Schmidt, S., Seidler, R. D., Siegle, G. J., Sorg, C., Teng, G. J., Veijola, J., Villringer, A., Walter, M., Wang, L., Weng, X. C., Whitfield-Gabrieli, S., Williamson, P., Windischberger, C., Zang, Y. F., Zhang, H. Y., Castellanos, F. X., and Milham, M. P. (2010). Toward discovery science of human brain function. Proc Natl Acad Sci U.S.A. 107, 4734–4739.
Biswal, B., Yetkin, F. Z., Haughton, V. M., and Hyde, J. S. (1995). Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson. Med. 34, 537–541.
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and Hwang, D. U. (2006). Complex networks: Structure and dynamics. Phys. Rep. 424, 175–308.
Broyd, S. J., Demanuele, C., Debener, S., Helps, S. K., James, C. J., and Sonuga-Barke, E. J. (2009). Default-mode brain dysfunction in mental disorders: a systematic review. Neurosci. Biobehav. Rev. 33, 279–296.
Buckner, R. L., Andrews-Hanna, J. R., and Schacter, D. L. (2008). The brain’s default network: anatomy, function, and relevance to disease. Ann. N. Y. Acad. Sci. 1124, 1–38.
Buckner, R. L., Sepulcre, J., Talukdar, T., Krienen, F. M., Liu, H., Hedden, T., Andrews-Hanna, J. R., Sperling, R. A., and Johnson, K. A. (2009). Cortical hubs revealed by intrinsic functional connectivity: mapping, assessment of stability, and relation to Alzheimer’s disease. J. Neurosci. 29, 1860–1873.
Bullmore, E., and Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198.
Chen, S., Ross, T. J., Zhan, W., Myers, C. S., Chuang, K. S., Heishman, S. J., Stein, E. A., and Yang, Y. (2008a). Group independent component analysis reveals consistent resting-state networks across multiple sessions. Brain Res. 1239, 141–151.
Chen, Z. J., He, Y., Rosa-Neto, P., Germann, J., and Evans, A. C. (2008b). Revealing modular architecture of human brain structural networks by using cortical thickness from MRI. Cereb. Cortex 18, 2374–2381.
Cordes, D., Haughton, V., Carew, J. D., Arfanakis, K., and Maravilla, K. (2002). Hierarchical clustering to measure connectivity in fMRI resting-state data. Magn. Reson. Imaging 20, 305–317.
Cordes, D., Haughton, V. M., Arfanakis, K., Carew, J. D., Turski, P. A., Moritz, C. H., Quigley, M. A., and Meyerand, M. E. (2001). Frequencies contributing to functional connectivity in the cerebral cortex in “resting-state” data. AJNR Am. J. Neuroradiol. 22, 1326–1333.
Damoiseaux, J. S., and Greicius, M. D. (2009). Greater than the sum of its parts: a review of studies combining structural connectivity and resting-state functional connectivity. Brain Struct. Funct. 213, 525–533.
Damoiseaux, J. S., Rombouts, S. A., Barkhof, F., Scheltens, P., Stam, C. J., Smith, S. M., and Beckmann, C. F. (2006). Consistent resting-state networks across healthy subjects. Proc. Natl. Acad. Sci. U.S.A. 103, 13848–13853.
de Haan, W., Pijnenburg, Y. A., Strijers, R. L., van der Made, Y., van der Flier, W. M., Scheltens, P., and Stam, C. J. (2009). Functional neural network analysis in frontotemporal dementia and Alzheimer’s disease using EEG and graph theory. BMC Neurosci. 10, 101.
Deuker, L., Bullmore, E. T., Smith, M., Christensen, S., Nathan, P. J., Rockstroh, B., and Bassett, D. S. (2009). Reproducibility of graph metrics of human brain functional networks. Neuroimage 47, 1460–1468.
Di Martino, A., Scheres, A., Margulies, D. S., Kelly, A. M., Uddin, L. Q., Shehzad, Z., Biswal, B., Walters, J. R., Castellanos, F. X., and Milham, M. P. (2008). Functional connectivity of human striatum: a resting state FMRI study. Cereb. Cortex 18, 2735–2747.
Di Martino, A., Shehzad, Z., Kelly, C., Roy, A. K., Gee, D. G., Uddin, L. Q., Gotimer, K., Klein, D. F., Castellanos, F. X., and Milham, M. P. (2009). Relationship between cingulo-insular functional connectivity and autistic traits in neurotypical adults. Am. J. Psychiatry 166, 891–899.
Dosenbach, N. U., Fair, D. A., Miezin, F. M., Cohen, A. L., Wenger, K. K., Dosenbach, R. A., Fox, M. D., Snyder, A. Z., Vincent, J. L., Raichle, M. E., Schlaggar, B. L., and Petersen, S. E. (2007). Distinct brain networks for adaptive and stable task control in humans. Proc. Natl. Acad. Sci. U.S.A. 104, 11073–11078.
Eguiluz, V. M., Chialvo, D. R., Cecchi, G. A., Baliki, M., and Apkarian, A. V. (2005). Scale-free brain functional networks. Phys. Rev. Lett. 94, 018102.
Fair, D. A., Cohen, A. L., Dosenbach, N. U., Church, J. A., Miezin, F. M., Barch, D. M., Raichle, M. E., Petersen, S. E., and Schlaggar, B. L. (2008). The maturing architecture of the brain’s default network. Proc. Natl. Acad. Sci. U.S.A. 105, 4028–4032.
Fair, D. A., Cohen, A. L., Power, J. D., Dosenbach, N. U., Church, J. A., Miezin, F. M., Schlaggar, B. L., and Petersen, S. E. (2009). Functional brain networks develop from a “local to distributed” organization. PLoS Comput. Biol. 5, e1000381. doi:10.1371/journal.pcbi.1000381.
Fair, D. A., Dosenbach, N. U., Church, J. A., Cohen, A. L., Brahmbhatt, S., Miezin, F. M., Barch, D. M., Raichle, M. E., Petersen, S. E., and Schlaggar, B. L. (2007). Development of distinct control networks through segregation and integration. Proc. Natl. Acad. Sci. U.S.A. 104, 13507–13512.
Ferrarini, L., Veer, I. M., Baerends, E., van Tol, M. J., Renken, R. J., van der Wee, N. J., Veltman, D. J., Aleman, A., Zitman, F. G., Penninx, B. W., van Buchem, M. A., Reiber, J. H., Rombouts, S. A., and Milles, J. (2009). Hierarchical functional modularity in the resting-state human brain. Hum. Brain Mapp. 30, 2220–2231.
Fox, M. D., Corbetta, M., Snyder, A. Z., Vincent, J. L., and Raichle, M. E. (2006). Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proc. Natl. Acad. Sci. U.S.A. 103, 10046–10051.
Fox, M. D., and Raichle, M. E. (2007). Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat. Rev. Neurosci. 8, 700–711.
Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen, D. C., and Raichle, M. E. (2005). The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci. U.S.A. 102, 9673–9678.
Fox, M. D., Snyder, A. Z., Vincent, J. L., and Raichle, M. E. (2007). Intrinsic fluctuations within cortical systems account for intertrial variability in human behavior. Neuron 56, 171–184.
Franco, A. R., Pritchard, A., Calhoun, V. D., and Mayer, A. R. (2009). Interrater and intermethod reliability of default mode network selection. Hum. Brain Mapp. 30, 2293–2303.
Freeman, L. C. (1979). Centrality in social networks conceptual clarification. Soc. Networks 1, 215–239.
Friston, K. J., Frith, C. D., Liddle, P. F., and Frackowiak, R. S. (1993). Functional connectivity: the principal- component analysis of large (PET) data sets. J. Cereb. Blood Flow Metab. 13, 5–14.
Gong, G., He, Y., Concha, L., Lebel, C., Gross, D. W., Evans, A. C., and Beaulieu, C. (2009a). Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography. Cereb. Cortex 19, 524–536.
Gong, G., Rosa-Neto, P., Carbonell, F., Chen, Z. J., He, Y., and Evans, A. C. (2009b). Age- and gender-related differences in the cortical anatomical network. J. Neurosci. 29, 15684–15693.
Greicius, M. (2008). Resting-state functional connectivity in neuropsychiatric disorders. Curr. Opin. Neurol. 21, 424–430.
Greicius, M. D., Krasnow, B., Reiss, A. L., and Menon, V. (2003). Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc. Natl. Acad. Sci. U.S.A. 100, 253–258.
Greicius, M. D., Supekar, K., Menon, V., and Dougherty, R. F. (2009). Resting-state functional connectivity reflects structural connectivity in the default mode network. Cereb. Cortex 19, 72–78.
Guimera, R., Mossa, S., Turtschi, A., and Amaral, L. A. (2005). The worldwide air transportation network: anomalous centrality, community structure, and cities’ global roles. Proc. Natl. Acad. Sci. U.S.A. 102, 7794–7799.
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J., Wedeen, V. J., and Sporns, O. (2008). Mapping the structural core of human cerebral cortex. PLoS Biol. 6, e159. doi:10.1371/journal.pbio.0060159.
Hampson, M., Driesen, N. R., Skudlarski, P., Gore, J. C., and Constable, R. T. (2006). Brain connectivity related to working memory performance. J. Neurosci. 26, 13338–13343.
Hampson, M., Peterson, B. S., Skudlarski, P., Gatenby, J. C., and Gore, J. C. (2002). Detection of functional connectivity using temporal correlations in MR images. Hum. Brain Mapp. 15, 247–262.
Harrison, B. J., Pujol, J., Lopez-Sola, M., Hernandez-Ribas, R., Deus, J., Ortiz, H., Soriano-Mas, C., Yucel, M., Pantelis, C., and Cardoner, N. (2008). Consistency and functional specialization in the default mode brain network. Proc. Natl. Acad. Sci. U.S.A. 105, 9781–9786.
Hayasaka, S., and Laurienti, P. J. (2009). Comparison of characteristics between region-and voxel-based network analyses in resting-state fMRI data. Neuroimage 2, 499–508.
He, Y., and Evans, A. (2010). Graph theoretical modeling of brain connectivity. Curr. Opin. Neurol., in press.
He, Y., Chen, Z., and Evans, A. (2008). Structural insights into aberrant topological patterns of large-scale cortical networks in Alzheimer’s disease. J. Neurosci. 28, 4756–4766.
He, Y., Chen, Z. J., and Evans, A. C. (2007). Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb. Cortex 17, 2407–2419.
He, Y., Chen, Z., Gong, G., and Evans, A. (2009a). Neuronal networks in Alzheimer’s disease. Neuroscientist. 15, 333–350.
He, Y., Wang, J., Wang, L., Chen, Z. J., Yan, C., Yang, H., Tang, H., Zhu, C., Gong, Q., Zang, Y., and Evans, A. C. (2009b). Uncovering intrinsic modular organization of spontaneous brain activity in humans. PLoS ONE 4, e5226. doi:10.1371/journal.pone.0005226.
He, Y., Dagher, A., Chen, Z., Charil, A., Zijdenbos, A., Worsley, K., and Evans, A. (2009c). Impaired small-world efficiency in structural cortical networks in multiple sclerosis associated with white matter lesion load. Brain 132, 3366–3379.
Hesselmann, G., Kell, C. A., Eger, E., and Kleinschmidt, A. (2008). Spontaneous local variations in ongoing neural activity bias perceptual decisions. Proc. Natl. Acad. Sci. U.S.A. 105, 10984–10989.
Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P., Meuli, R., and Hagmann, P. (2009). Predicting human resting-state functional connectivity from structural connectivity. Proc. Natl. Acad. Sci. U.S.A. 106, 2035–2040.
Honey, C. J., Thivierge, J. P., and Sporns, O. (2010). Can structure predict function in the human brain? NeuroImage [Epub ahead of print].
Kelly, A. M., Uddin, L. Q., Biswal, B. B., Castellanos, F. X., and Milham, M. P. (2008). Competition between functional brain networks mediates behavioral variability. Neuroimage 39, 527–537.
Kiviniemi, V., Starck, T., Remes, J., Long, X., Nikkinen, J., Haapea, M., Veijola, J., Moilanen, I., Isohanni, M., Zang, Y. F., et al. (2009). Functional segmentation of the brain cortex using high model order group PICA. Hum. Brain Mapp. 30, 3865–3886.
Latora, V., and Marchiori, M. (2001). Efficient behavior of small-world networks. Phys. Rev. Lett. 87, 198701.
Latora, V., and Marchiori, M. (2003). Economic small-world behavior in weighted networks. Eur. Phys. J. B Condens Matter Complex Syst V 32, 249–263.
Laurienti, P., Hugenschmidt, C. E., and Hayasaka, S. (2009). “Modularity maps reveal community structure in the resting human brain,” in Nature Precedings. http://hdl.handle.net/10101/npre.2009.3069.1
Li, Y., Liu, Y., Li, J., Qin, W., Li, K., Yu, C., and Jiang, T. (2009). Brain anatomical network and intelligence. PLoS Comput. Biol. 5, e1000395. doi:10.1371/journal.pcbi.1000395.
Liao, W., Zhang, Z., Pan, Z., Mantini, D., Ding, J., Duan, X., Luo, C., Lu, G., and Chen, H. (2010). Altered functional connectivity and small-world in mesial temporal lobe epilepsy. PLoS ONE 5, e8525. doi:10.1371/journal.pone.0008525.
Liu, J., Liang, J., Qin, W., Tian, J., Yuan, K., Bai, L., Zhang, Y., Wang, W., Wang, Y., Li, Q., et al. (2009). Dysfunctional connectivity patterns in chronic heroin users: an fMRI study. Neurosci. Lett. 460, 72–77.
Liu, Y., Liang, M., Zhou, Y., He, Y., Hao, Y., Song, M., Yu, C., Liu, H., Liu, Z., and Jiang, T. (2008). Disrupted small-world networks in schizophrenia. Brain 131, 945–961.
Long, X. Y., Zuo, X. N., Kiviniemi, V., Yang, Y., Zou, Q. H., Zhu, C. Z., Jiang, T. Z., Yang, H., Gong, Q. Y., Wang, L., et al. (2008). Default mode network as revealed with multiple methods for resting-state functional MRI analysis. J. Neurosci. Methods 171, 349–355.
Lowe, M. J., Mock, B. J., and Sorenson, J. A. (1998). Functional connectivity in single and multislice echoplanar imaging using resting-state fluctuations. Neuroimage 7, 119–132.
Margulies, D. S., Kelly, A. M. C., Uddin, L. Q., Biswal, B. B., Castellanos, F. X., and Milham, M. P. (2007). Mapping the functional connectivity of anterior cingulate cortex. Neuroimage 37, 579–588.
Meindl, T., Teipel, S., Elmouden, R., Mueller, S., Koch, W., Dietrich, O., Coates, U., Reiser, M., and Glaser, C. (2009). Test–retest reproducibility of the default-mode network in healthy individuals. Hum. Brain Mapp. 31, 237–246.
Meunier, D., Achard, S., Morcom, A., and Bullmore, E. T. (2009a). Age-related changes in modular organization of human brain functional networks. Neuroimage 44, 715–723.
Meunier, D., Lambiotte, R., Fornito, A., Ersche, K. D., and Bullmore, E. T. (2009b). Hierarchical modularity in human brain functional networks. Front. Neuroinformatics 3, 37.
Micheloyannis, S., Vourkas, M., Tsirka, V., Karakonstantaki, E., Kanatsouli, K., and Stam, C. J. (2009). The influence of ageing on complex brain networks: a graph theoretical analysis. Hum. Brain Mapp. 30, 200–208.
Nakamura, T., Hillary, F. G., and Biswal, B. B. (2009). Resting network plasticity following brain injury. PLoS ONE 4, e8220. doi:10.1371/journal.pone.0008220.
Newman, M. E. (2006). Modularity and community structure in networks. Proc. Natl. Acad. Sci. U.S.A. 103, 8577–8582.
Pachou, E., Vourkas, M., Simos, P., Smit, D., Stam, C. J., Tsirka, V., and Micheloyannis, S. (2008). Working memory in schizophrenia: an EEG study using power spectrum and coherence analysis to estimate cortical activation and network behavior. Brain Topogr. 21, 128–137.
Park, C.-H., Kim, S. Y., Kim, Y.-H., and Kim, K. (2008). Comparison of the small-world topology between anatomical and functional connectivity in the human brain. Phys. A. Stat. Mech. Appl. 387, 5958–5962.
Raichle, M. E., MacLeod, A. M., Snyder, A. Z., Powers, W. J., Gusnard, D. A., and Shulman, G. L. (2001). A default mode of brain function. Proc. Natl. Acad. Sci. U.S.A. 98, 676–682.
Ravasz, E., and Barabasi, A. L. (2003). Hierarchical organization in complex networks. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 67, 026112.
Ravasz, E., Somera, A. L., Mongru, D. A., Oltvai, Z. N., and Barabasi, A. L. (2002). Hierarchical organization of modularity in metabolic networks. Science 297, 1551–1555.
Roy, A. K., Shehzad, Z., Margulies, D. S., Kelly, A. M., Uddin, L. Q., Gotimer, K., Biswal, B. B., Castellanos, F. X., and Milham, M. P. (2009). Functional connectivity of the human amygdala using resting state fMRI. Neuroimage 45, 614–626.
Rubinov, M., and Sporns, O. (2009). Complex network measures of brain connectivity: uses and interpretations. Neuroimage [Epub ahead of print].
Sakata, S., Komatsu, Y., and Yamamori, T. (2005). Local design principles of mammalian cortical networks. Neurosci. Res. 51, 309–315.
Sales-Pardo, M., Guimera, R., Moreira, A. A., and Amaral, L. A. (2007). Extracting the hierarchical organization of complex systems. Proc. Natl. Acad. Sci. U.S.A. 104, 15224–15229.
Salvador, R., Suckling, J., Coleman, M. R., Pickard, J. D., Menon, D., and Bullmore, E. (2005). Neurophysiological architecture of functional magnetic resonance images of human brain. Cereb. Cortex 15, 1332–1342.
Shehzad, Z., Kelly, A. M., Reiss, P. T., Gee, D. G., Gotimer, K., Uddin, L. Q., Lee, S. H., Margulies, D. S., Roy, A. K., Biswal, B. B., et al. (2009). The resting brain: unconstrained yet reliable. Cereb. Cortex 19, 2209–2229.
Skudlarski, P., Jagannathan, K., Calhoun, V. D., Hampson, M., Skudlarska, B. A., and Pearlson, G. (2008). Measuring brain connectivity: diffusion tensor imaging validates resting state temporal correlations. Neuroimage 43, 554–561.
Smit, D. J., Stam, C. J., Posthuma, D., Boomsma, D. I., and de Geus, E. J. (2008). Heritability of “small-world” networks in the brain: a graph theoretical analysis of resting-state EEG functional connectivity. Hum. Brain Mapp. 29, 1368–1378.
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M., Mackay, C. E., Filippini, N., Watkins, K. E., Toro, R., Laird, A. R., et al. (2009). Correspondence of the brain’s functional architecture during activation and rest. Proc. Natl. Acad. Sci. U.S.A. 106, 13040–13045.
Sporns, O., Chialvo, D. R., Kaiser, M., and Hilgetag, C. C. (2004). Organization, development and function of complex brain networks. Trends Cogn. Sci. (Regul. Ed.) 8, 418–425.
Sporns, O., Honey, C. J., and Kotter, R. (2007). Identification and classification of hubs in brain networks. PLoS ONE 2, e1049. doi:10.1371/journal.pone.0001049.
Sporns, O., Tononi, G., and Kotter, R. (2005). The human connectome: a structural description of the human brain. PLoS Comput. Biol. 1, e42. doi:10.1371/journal.pcbi.0010042.
Stam, C. J., Jones, B. F., Nolte, G., Breakspear, M., and Scheltens, P. (2007). Small-world networks and functional connectivity in Alzheimer’s disease. Cereb. Cortex 17, 92–99.
Stam, C. J., and Reijneveld, J. C. (2007). Graph theoretical analysis of complex networks in the brain. Nonlinear Biomed. Phys. 1, 3. doi:10.1186/1753-4631-1-3
Supekar, K., Menon, V., Rubin, D., Musen, M., and Greicius, M. D. (2008). Network analysis of intrinsic functional brain connectivity in Alzheimer’s disease. PLoS Comput. Biol. 4, e1000100. doi:10.1371/journal.pcbi.1000100.
Supekar, K., Musen, M., and Menon, V. (2009). Development of large-scale functional brain networks in children. PLoS Biol. 7, e1000157. doi:10.1371/journal.pbio.1000157.
Teipel, S. J., Bokde, A. L., Meindl, T., Amaro, E. Jr., Soldner, J., Reiser, M. F., Herpertz, S. C., Moller, H. J., and Hampel, H. (2010). White matter microstructure underlying default mode network connectivity in the human brain. Neuroimage 49, 2021–2032.
Uddin, L. Q., Kelly, A. M., Biswal, B. B., Margulies, D. S., Shehzad, Z., Shaw, D., Ghaffari, M., Rotrosen, J., Adler, L. A., Castellanos, F. X., and Milham, M. P. (2008). Network homogeneity reveals decreased integrity of default-mode network in ADHD. J. Neurosci. Methods 169, 249–254.
Uddin, L. Q., Kelly, A. M., Biswal, B. B., Xavier Castellanos, F., and Milham, M. P. (2009). Functional connectivity of default mode network components: correlation, anticorrelation, and causality. Hum. Brain Mapp. 30, 625–637.
Valencia, M., Pastor, M. A., Fernandez-Seara, M. A., Artieda, J., Martinerie, J., and Chavez, M. (2009). Complex modular structure of large-scale brain networks. Chaos 19, 023119.
van den Heuvel, M. P., Stam, C. J., Boersma, M., and Hulshoff Pol, H. E. (2008a). Small-world and scale-free organization of voxel-based resting-state functional connectivity in the human brain. Neuroimage 43, 528–539.
van den Heuvel, M., Mandl, R., and Hulshoff Pol, H. (2008b). Normalized cut group clustering of resting-state FMRI data. PLoS ONE 3, e2001. doi:10.1371/journal.pone.0002001.
van den Heuvel, M. P., Mandl, R. C., Kahn, R. S., and Hulshoff Pol, H. E. (2009a). Functionally linked resting-state networks reflect the underlying structural connectivity architecture of the human brain. Hum. Brain Mapp. 30, 3127–3141.
van den Heuvel, M. P., Stam, C. J., Kahn, R. S., and Hulshoff Pol, H. E. (2009b). Efficiency of functional brain networks and intellectual performance. J. Neurosci. 29, 7619–7624.
van de Ven, V. G., Formisano, E., Prvulovic, D., Roeder, C. H., and Linden, D. E. (2004). Functional connectivity as revealed by spatial independent component analysis of fMRI measurements during rest. Hum. Brain Mapp. 22, 165–178.
Wang, J., Wang, L., Zang, Y., Yang, H., Tang, H., Gong, Q., Chen, Z., Zhu, C., and He, Y. (2009a). Parcellation-dependent small-world brain functional networks: a resting-state fMRI study. Hum. Brain Mapp. 30, 1511–1523.
Wang, L., Zhu, C., He, Y., Zang, Y., Cao, Q., Zhang, H., Zhong, Q., and Wang, Y. (2009b). Altered small-world brain functional networks in children with attention-deficit/hyperactivity disorder. Hum. Brain Mapp. 30, 638–649.
Wang, L., Li, Y., Metzak, P., He, Y., and Woodward, T. S. (2010). Age-related changes in topological patterns of large-scale brain functional networks during memory encoding and recognition. Neuroimage 50, 862–872.
Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442.
Wink, A. M., Bernard, F., Salvador, R., Bullmore, E. T., and Suckling, J. (2006). Age and cholinergic effects on hemodynamics and functional coherence of human hippocampus. Neurobiol. Aging 27, 1395–1404.
Yan, C., Liu, D., He, Y., Zou, Q., Zhu, C., Zuo, X., Long, X., and Zang, Y. (2009a). Spontaneous brain activity in the default mode network is sensitive to different resting-state conditions with limited cognitive load. PLoS ONE 4, e5743. doi:10.1371/journal.pone.0005743.
Yan, H., Zuo, X. N., Wang, D., Wang, J., Zhu, C., Milham, M. P., Zhang, D., and Zang, Y. (2009b). Hemispheric asymmetry in cognitive division of anterior cingulate cortex: a resting-state functional connectivity study. Neuroimage 47, 1579–1589.
Zalesky, A., Fornito, A., Harding, I. H., Cocchi, L., Yucel, M., Pantelis, C., and Bullmore, E. T. (2010). Whole-brain anatomical networks: does the choice of nodes matter? Neuroimage 50, 970–983.
Zang, Y., Jiang, T., Lu, Y., He, Y., and Tian, L. (2004). Regional homogeneity approach to fMRI data analysis. Neuroimage 22, 394–400.
Zang, Y., Yong, H., Chao-Zhe, Z., Qing-Jiu, C., Man-Qiu, S., Meng, L., Li-Xia, T., Tian-Zi, J., and Yu-Feng, W. (2007). Altered baseline brain activity in children with ADHD revealed by resting-state functional MRI. Brain Dev. 29, 83–91.
Zou, Q. H., Zhu, C. Z., Yang, Y., Zuo, X. N., Long, X. Y., Cao, Q. J., Wang, Y. F., and Zang, Y. F. (2008). An improved approach to detection of amplitude of low-frequency fluctuation (ALFF) for resting-state fMRI: fractional ALFF. J. Neurosci. Methods 172, 137–141.
Zuo, X. N., Kelly, C., Adelstein, J. S., Klein, D. F., Castellanos, F. X., and Milham, M. P. (2010a). Reliable intrinsic connectivity networks: Test–retest evaluation using ICA and dual regression approach. Neuroimage 49, 2163–2177.
Keywords: resting-state, functional connectivity, human connectome, small-world, functional MRI, graph theory, brain, network
Citation: Wang J, Zuo X and He Y (2010) Graph-based network analysis of resting-state functional MRI. Front. Syst. Neurosci. 4:16. doi: 10.3389/fnsys.2010.00016
Received: 04 February 2010;
Paper pending published: 27 February 2010;
Accepted: 11 May 2010;
Published online: 07 June 2010
Edited by:
Lucina Q. Uddin, Stanford University, USAReviewed by:
Sophie Achard, University of Cambridge, UKEdward T. Bullmore, University of Cambridge, UK
Alex Fornito, University of Melbourne, Australia
Copyright: © 2010 Wang, Zuo and He. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Yong He, State Key Laboratory of Cognitive Neuroscience and Learning, Beijing Normal University, Beijing, China. e-mail: yong.he@bnu.edu.cn