Developmental neuroscience of time and number: implications for autism and other neurodevelopmental disabilities

Estimations of time and number share many similarities in both non-humans and man. The primary focus of this review is on the development of time and number sense across infancy and childhood, and neuropsychological findings as they relate to time and number discrimination in infants and adults. Discussion of these findings is couched within a mode-control model of timing and counting which assumes time and number share a common magnitude representation system. A basic sense of time and number likely serves as the foundation for advanced numerical and temporal competence, and aspects of higher cognition—this will be discussed as it relates to typical childhood, and certain developmental disorders, including autism spectrum disorder. Directions for future research in the developmental neuroscience of time and number (NEUTIN) will also be highlighted.

Introduction

The interval timing and numerical abilities identified in nonhuman animals, human infants, and children may represent biological and developmental precursors of adults' highly developed computational abilities (Buhusi and Cordes, 2011; Lustig, 2011; Williams, 2011). For instance, at the perceptual level, non-humans and infants appear capable of making magnitude estimates of duration, numerosity and area (i.e., that a given stimulus is presented for “more” time than another, or contains “more” elements—this basic ability is the focus of our review). The ability to imagine events in the future (which must by implication, require some form of internal time sense) has been postulated to be related to our ability to “anticipate future mental processes and motivational and emotional states” (Pezzulo and Rigoli, 2011:1), and adults at least appear able to comprehend metaphysical and higher concepts of time and space (e.g., imagining the size of the galaxy, or how long it has been around). It seems parsimonious to suppose that the basic ability to represent time, space and numerosity is a basic developmental “building block” for math ability, and abstract mental representations and concepts of metaphysical time and space (see Casasanto and Boroditsky, 2008).

The processing of sensory information according to its spatial, temporal, and numerical properties is a requirement of the central nervous system. Navon (1978) “considered the issue of how we apprehend stimuli that vary along several dimensions. We may often overlook some aspects, and sometimes be unable to ignore others” (1978:3). He suggested that time occupies the dominant dimension, followed by space. In non-humans and humans, there are a variety of interaction effects between our estimates of time, space, and number, and these have been taken as support for mode-control models of (sensory) time and number perception (e.g., Meck and Church, 1983), and those that suppose our ability to make sense of time, space, and numerosity develops from a single magnitude processing system (A Theory of Magnitude, ATOM; Walsh, 2003). In fact, in humans at least, they are most likely component processes in a cognitive system: a “raw substrate” magnitude estimate of time and number is likely processed by some ordinal magnitude comparator (which is recruited to make “how much” or “more than and less than” judgments) that apparently deals with many different dimensions (time, space, numerosity, loudness and luminance, and even emotional expression; e.g., see Smith and Sera, 1992; Holmes and Lourenco, 2009). Although ATOM assumes that “time and quantity estimation operate on similar and partly shared accumulation principles” of the type described in the mode-control model, these two forms of account (Meck and Church, 1983; Walsh, 2003) may be theoretically dissociated at the developmental level—for instance, the mode-control model assumes numerosity is the product of an internal (primitive) count, which is “built in,” and according to ATOM, numerosity is acquired by learning associations between magnitudes of different dimensions, as “specializations for time, space and quantity develop from a single magnitude system operating from birth” (2003:484). ATOM does not describe the nature of a shared accumulation system as the mode-control model does. ATOM grounds the ontogeny of multi-dimension magnitude estimation abilities on the basis of the need for action, and the translation from sensory to motor, and this is germane to infant development (i.e., Piaget's sensorimotor stage from 0 to 2 years). It is reasoned in ATOM that the infant is born with a “one-bit” magnitude system, and number sense is mapped onto the magnitude system, which is argued to have a spatial basis (given its emphasis for action).

The primary focus of our review is how we develop the ability to integrate (or “stitch together”) representations of duration and numerosity magnitudes, operating at the level of processing incoming sensory input, couched within the influential “mode-control” approach (Meck and Church, 1983). This assumes the substrate for time and number judgments can be represented by an “accumulated” magnitude, and there is quantitative equivalence between an estimate of number and a unit of time (Meck et al., 1985)—space (area) will also be discussed but to a lesser extent (but see Gallistel, 1989). Accordingly, we refer to “time” (time sense) as the ability to estimate duration magnitude in the seconds to minutes range, and “number” (number sense) as the ability to estimate non-symbolic numerosity (i.e., number of dots in an array).

There are three main areas of coverage in this review:

1. We discuss animal findings relating to the neuroscience of time and number sense (NEUTIN), and comparable human studies of time, space, and number magnitude estimation in infants and adults. We also highlight cross-dimensional interaction effects (e.g., between time, space, and number) in non-humans and humans.
2. We review the “mini-evolution” of the development of time and number sense in infancy and childhood. We also comment on the correspondence between number sense and more advanced numerical abilities (symbolic representations of number, counting, math ability), and how children are considered to develop higher-order concepts of time, speed, distance and space.
3. Children with developmental disabilities, particularly those with difficulties as they relate to time and number abilities (developmental dyscalculia, autism, attention-deficit hyperactivity disorder, Down and Williams syndrome) will also be discussed. Studying the atypical development of NEUTIN has the potential to developmentally tease apart the aforementioned accounts, but also to improve understanding of these disorders and their therapeutic and educational remediation. With the exception of Williams and Down syndrome (which have a genetic basis), the disorders included in this review are characterized on the basis of observable behavioral (rather than biomedical) features, and as such, it is useful to know the extent of sensitivity and adaption to time, numerosity and space in these populations—as these types of impairments might contribute to clinical symptoms (and have a “knock-on” effect in development; see also Williams, 2011).

Basic Approach to Temporal and Numerical Integration

The psychological process of actively representing time and number magnitude estimations (see Meck et al., 1985), and the form this integration may take, is expected to be among the premier topics to unite systems, cellular, computational, and cognitive neuroscience for the foreseeable future (Meck, 2003). Temporal processing has been a topic of interest since the dawn of modern experimental psychology—perhaps as a function of its ties to philosophy and physics involving the investigation of absolute vs. relative time perception (Myers, 1971; Wackermann, 2008; Buhusi and Meck, 2009a,b; Lustig, 2011) as well as the impressive ability of humans and other animals to learn and adapt to the temporal and numerical qualities of environmental events (Skinner, 1938; Gibbon, 1977; Gibbon et al., 1997). The mode-control model (for time and number) is related to “scalar expectancy theory” (SET; for time only, Gibbon et al., 1984). These types of accounts were stimulated by studies of rodents (and pigeons) operating on fixed-interval schedules (an event occurs at a fixed period in time). With training, rats and pigeons demonstrate “expectancy” (or anticipation) of an event around the time it is scheduled (Church and Gibbon, 1982; Roberts and Boisvert, 1998), and the accuracy of their temporal expectancies (duration judgment) can be neuropsychologically manipulated (e.g., by pharmacological agents, task load, sensory qualities; e.g., see Meck, 1983, 1996). Their behavioral expectancies conform to the scalar property (discussed in the next section). Animals also appear to perform “superstitious behaviors” (Skinner, 1948) or sequences of actions to “count” (or parse) the passage of time (Killeen and Fetterman, 1988). Rats, pigeons, and monkeys can also discriminate the number of entities in a set when non-numerical dimensions (such as surface area, density, perimeter, duration, and rate) are strictly controlled for, and their performance reflects the use of similar analog representations of number to those of adult humans (e.g., Fetterman and MacEwen, 1989; Brannon and Terrace, 1998, 2000; Emmerton, 1998). These animals can also be trained to press a lever a specific number of times (fixed-ratio schedules), and appear sensitive to the rate of reinforcement (rate is defined as number divided by time)—there is also evidence that certain animals can perform simple arithmetic reasoning (addition, subtraction; see Gallistel and Gelman, 2000 for a fuller discussion).

Mode-Control Model of Meck and Church (1983)

The mode-control model of counting and timing (see Figure 1; Meck and Church, 1983) was developed to account for such findings, and provides a unified theory of numerosity and timing by positing the existence of a functioning isomorphism (formal correspondence) between number and duration. It assumes a similar functional network operates to process either time or number (see; Meck et al., 1985; Church and Broadbent, 1990; Meck, 1997; Carey, 1998, 2001; Gelman and Cordes, 2001; Nieder et al., 2002; Nieder and Miller, 2003, 2004a,b; Pessoa and Desimone, 2003). In this account, “pulses” are accumulated (or integrated) to provide a given estimate of magnitude, and this is then compared to some stored (or remembered) criterion tally (of a given duration or number). Rats show similarities in their discrimination of continuous (time) or segmented (number) signals such that 1-s segmented signal is equivalent to 200 ms of continuous signal (this has been referred to as a “quantal unit”; Meck et al., 1985). This type of organization (in particular, the required comparison between current and stored magnitude estimates) may also facilitate arithmetic processing of basic time and number magnitudes (see Gallistel and Gelman, 2000), as an alternative to cross-dimensional statistical learning process that are proposed in ATOM (Walsh, 2003).

FIGURE 1

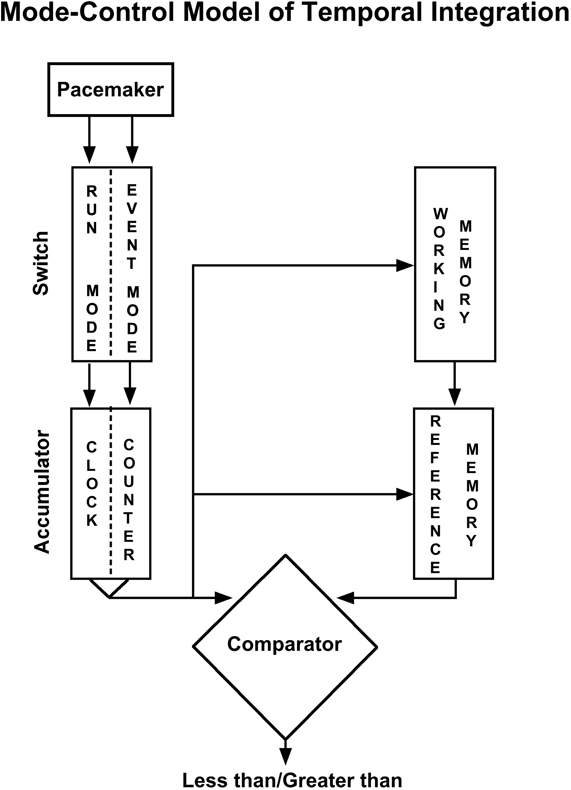
Figure 1. The information-processing “mode-control” model of timing and counting. A pacemaker emits pulses which are gated into an accumulator; it is a counter if operating in the event mode, and a clock if operating in the run mode (see text for details). The current accumulator value can be held in working memory and compared to a previous accumulator value stored in reference memory. A decision process determines the appropriate response [adapted from Meck and Church (1983)].

The way the integration mechanism is applied in the model is that at the onset of a relevant stimulus pulses are directed into an accumulator by a “mode switch” that allows pulses to flow (into the accumulator) in one of three different modes (run and stop modes for time, and an event mode for number) depending on the nature of the stimulus (see, Church and Meck, 1984; Meck et al., 1985; Broadbent et al., 1993; Meck, 1997). There is no mode nor accumulation process detailing the comparable process for space (although this is not to say the model might not be able to be adapted to do so). “An animal may be said to be timing if the duration of an event serves as a discriminative stimulus; an animal may be said to be counting if the number of events serves as a discriminative stimulus” (Meck and Church, 1983: 320).

A word of caution should be given here to the term “counting.” As it relates to the mode-control model, “counting” refers to non-symbolic numerosity accumulation. In the human literature, “counting” typically refers to related symbolic number representations (and related cognitive processes; e.g., Wynn, 1990). We shall highlight the development of symbolic counting abilities in children later.

Event Mode

The magnitude estimation of number occurs in the event mode, when the mode-control model is assumed to be a model of (non-symbolic) counting. In this mode, discrete numerosities are represented by the linear magnitude of a “batch” of pulses from a pacemaker accumulated upon stimulus onset. (Borrowing the analogy of Gallistel and Gelman, 2000; akin to adding a discrete cupful of liquid to a container all at once; n.b. in the experiments by Meck and Church, 1983, 1985, number was signaled by a series of pulses).

Run Mode

The magnitude estimation of time occurs in run mode. In the model time is represented as the linear magnitude of pacemaker pulses that are accumulated over the course of stimulus duration. (Akin to pouring liquid in from a continuous free-flowing source).

Temporal Integration

Represents the numerosity of events or objects collected in the accumulator (a total tally) and thus constitutes this model's proposed numeron, just as this same temporal integration process represents duration when pulses are gated through the switch in the run mode. (Akin to the scale on the container measuring how much liquid it contains; see Gallistel and Gelman, 2000).

A further point to note, is that according to mode-control models, if timing pulses are counted when a “neural network” is running (i.e., the ON signal is true) then percentage of time the “neural network” is in use can be calculated by comparing the total count with the elapsed time. This calculation is simple even though the “neural network” may start and stop many times during the monitoring. In order to do this, the counter must have a switch input, as well as its normal count input. You connect the neural network's ON signal to the switch and a source of clock pulses to the normal count input, making the measurements within the counter.

Four Phylogenic Similarities in Time and Number Sense that the Mode-Control Model can Account for

The mode-control model is successful as it can accommodate four fundamental phylogenic (and ontogenetic) similarities common to both time and number sense (e.g., Meck et al., 1985; Fetterman, 1993; Roberts, 1995, 2002; Roberts et al., 1995, 2000; Roberts and Boisvert, 1998), which we shall outline. Another strength of this model (see also, Gibbon, 1977; Gibbon et al., 1984) is that the shape of obtained time and number psychophysical discrimination functions correspond to functioning of the various aspects of the model (Figure 1; see Allman and Meck, 2012 for a fuller discussion), and these types of indices are informative with respect to the typical and atypical development of NEUTIN. For example, on a bisection task (where two “anchor” exemplars are trained, and intermediates are classified) non-humans and humans reveal a subjective mid-point between the geometric and arithmetic mean of the “anchor” (smallest and largest) stimuli (durations, numerosities, line length; see, Church and Deluty, 1977; Meck, 1983; Allan and Gibbon, 1991; Wearden, 1991; Wearden and Ferrara, 1995, 1996; McCormack et al., 1999; Melgire et al., 2005; Droit-Volet et al., 2008; Penney et al., 2008; Kopec and Brody, 2010).

1. Both time and number transfer to novel stimuli, and operate simultaneously in a similar manner. Rats trained to press one lever in response to a “short,” 2-s, 2-pulse tone sequence and another lever in response to a “long” 8-s, 8-pulse tone sequence reveal they have represented both time and number properties of these compound stimuli (second/pulse). For instance, rats' will continue to use the “short” response when presented with a novel 4-s, 2-pulse sequence and use the “long” response for a novel 4-s, 8-pulse tone sequence. Similarly, they will respond “short” in response to a new 2-s, 4-pulse sequence and “long” to a new 8-s, 4-pulse sequence. In other words, there appears a correspondence and “meaning” to their nature (Meck and Church, 1983).
2. Magnitude estimations of time and number are transferable to an equivalent extent, such that the contents of an accumulator in the “event” (count) mode can be compared to a stored value in “run” (time) mode. Timing and counting in rats also transfers to a similar extent between different stimulus modalities (i.e., auditory to cutaneous) suggesting that amodal estimates of time and number can be extracted from many types of events (Meck and Church, 1983).
3. Certain pharmacological agents; particularly those that modulate dopaminergic, glutamatergic and cholinergic systems, can influence time and number estimations in equivalent ways. The produced magnitude estimate is modulated in a dose-dependent manner by administration of indirect dopamine agonists such as amphetamine and cocaine, which produces an overestimation of both duration and number. Dopamine antagonists (e.g., haloperidol) have the opposite effect, effectively producing an underestimation of time and number (e.g., Meck, 1983, 1996; Meck and Church, 1987; Meck and Williams, 1997; Matell et al., 2004, 2006; Lustig and Meck, 2005; Cheng et al., 2006, 2008).
4. Time and number have identical discriminability and appear bound to the scalar property. For instance, rats reveal equivalent sensitivity to a proportional 4:1 ratio of counts and times (Meck and Church, 1983). This reflects the use of analog mental representations that obey the psychophysical tenets of Weber's law, found in other forms of perception (Moyer and Landauer, 1967; Buckley and Gilman, 1974). “The ‘scalar property’ refers to the fact that the variance (or ‘noisiness’) of a cardinal memory magnitude representation is proportional to the objective magnitude (bigger = noisier). When mental magnitudes have scalar variability, the discriminability of values obeys Weber’s law, because the degree of overlap between representations remains constant when the ratio of the means is held constant. Thus the amount by which two scalar quantities must differ in order to meet a constant criterion of discriminability is proportional to their magnitude” (Weber's law; Whalen et al., 1999:130). Thus “the overlap between two [magnitude] distributions with scalar variability is determined by the ratio of their means” (Cordes et al., 2001:698). The mode-control model accommodates the scalar property at the level of memory distribution (rather than through variance in the pulse accumulation process).

Non-Symbolic “Sense” of Number and Time

The mode control model is specifically designed to explain time and number magnitude estimates in animals (see Meck and Church, 1983; Meck et al., 1985), but may provide a useful frame of reference for understanding the development of non-symbolic counting and timing processes in non-verbal infants, young children, and adults (e.g., Gallistel and Gelman, 1992; Wynn, 1992, 1995, 1996, 1998; Broadbent et al., 1993; Roberts and Mitchell, 1994; Roberts, 1995; Meck, 1997; Breukelaar and Dalrymple-Alford, 1998; Wynn and Chiang, 1998; Dehaene et al., 1999; Xu and Spelke, 2000; Spelke, 2000; Wynn et al., 2002; Brannon and Roitman, 2003; Xu, 2003; Cordes et al., 2007).

In Infancy

Evidence of a primitive time and number sense in early development includes reports that very young infants (and in some cases, newborns) can discriminate small numbers of syllables and tones (Bijeljac-Babic et al., 1993; van Marle and Wynn, 2006), simple dots (Starkey and Cooper, 1980; Antell and Keating, 1983), moving objects and collections of objects (van Loosbroek and Smitsman, 1990; Wynn et al., 2002), can enumerate heterogeneous arrays of objects as well homogeneous arrays (e.g., Strauss and Curtis, 1981; Feigenson, 2005), and can discriminate between numerosity with the same precision in all modalities (Feigenson, 2007). Infants have also been shown to represent small numerical quantities across modalities (Jordan and Brannon, 2006), and discriminate between large numerosities (Lipton and Spelke, 2003). It even appears that “nuisance” task-irrelevant sensory information may improve infants' numerical precision (Jordan et al., 2008). Infants also show interchangeability between numerosities of different dimensions such as between two-or three drumbeats and two-or three objects, even when duration is controlled for (Starkey et al., 1983; Kobayashi et al., 2004; Feron et al., 2006; Izard et al., 2009). Collectively these studies suggest that an innate form of abstraction exists between different types of the same numerical magnitude in early life.

As it relates to time sense, infants possess sensitivity to temporal rhythm (Trehub and Thorpe, 1989) and are able to synchronize and adapt their sucking behavior (and other forms of motor activity) with the tempo of an external stimulus (Bobin-Bègue et al., 2006). There is also evidence to suggest that infants attend to the temporal features of stimuli in their environment (Clifton, 1974; Jusczyk et al., 1983). For example, by 2 months of age, infants are sensitive to the duration of sounds that differ by less than 1-s (Jusczyk et al., 1983), and similar results have been obtained for speech sounds (Eimas and Miller, 1980).

Lourenco and Longo (2010) revealed that 9-month-old infants can (bi-directionally) transfer learned associations (a mapping between stimulus color and relative magnitude) between greater/lesser durations, size and numerosity. This points to a (at least partly) shared general magnitude representation system, and is consistent with both the mode-control model (although it was not adapted for space) and ATOM. These findings reveal, “representations of magnitude information are (at least partially) abstracted from the specific dimensions” (Lourenco and Longo, 2010:873). They lean away from the mode-control model as findings suggest, “the relation between number and time is only one type of association in a more general system of magnitude representation” (Lourenco and Longo, 2010:79).

Perhaps the most striking support for the mode-control approach is evidence from young infants that magnitude estimates of time and number show scalar variability. Recall that in the mode-control model, ratio dependency (a larger ratio difference is easier to discriminate) is explained due to (a decrease in) the noisiness of stored time and number magnitude estimations (i.e., their spread is reduced, so they overlap less). ATOM acknowledges that the scalar property is a quality of multisensory perception. Intriguingly, the scalar property is also a quality of early social interactions for the infant (e.g., Stern and Gibbon, 1978; Jaffe et al., 2001). Like our other senses, it appears time and number sense is based on ratio (rather than absolute) differences (in magnitude). Furthermore, this appears to be honed during the first year of life (e.g., there are quantitative developmental changes between 6- and 10-months of age in both time and number sense). These findings endorse a common system of magnitude representation between time and number (in the context of the mode-control model; Church and Meck, 1983; Gallistel and Gelman, 2000).

For instance, Xu and Spelke (2000) as well as Xu et al. (2005) report that 6-month-old infants can discriminate visual numerical arrays that differ by a 1:2 ratio (e.g., 8 vs. 16 dots) even when contour length (density, surface area, etc) is controlled for, but these infants do not discriminate visual arrays that differ by a 2:3 ratio (e.g., 16 vs. 24 dots). Although this pattern of results has also been obtained when numerosity is signaled by sequences of tones (which must be integrated across time, Lipton and Spelke, 2003), and actions (Wood and Spelke, 2005) a recent study in 6-month olds has revealed numerical sensitivity to ratios including 2:3, 1:3, 1:4, but only if tested under certain arrangements (Libertus and Brannon, 2010). Moreover, individual differences in preference for a numerically changing display are stable, and the sensitivity to detect (ratio) numerical change at 6-months of age is predictive of numerical change detection scores at 9-months of age (Libertus and Brannon, 2010). Cordes and Brannon (2009) examined the ability of 7-month-old infants to compare small and large number sets under a variety of ratio conditions (e.g., 1:2 and 1:4), and report that small and large number sets could both be discriminated given a fourfold, but not a twofold change in number. In contrast, Wood and Spelke (2005) report that 1:2 ratio dependence in 6-month olds holds for larger numbers of actions (greater than 4), but not for small numbers of actions (less than 4). We shall extend our discussion of small vs. large numbers in a later section.

There are a handful of studies that have behaviorally assessed duration discrimination thresholds in infants between 4- and 10-months of age (Brannon et al., 2004a, 2008; van Marle and Wynn, 2006; Provasi et al., 2011). For example, van Marle and Wynn (2006) revealed 6-month-old infants can discriminate between durations of 2- and 4-s, but not between 3-s and 4.5-s. That is to say, typical 10-month-old infants can discriminate between durations (time) that differ according to a 1:2 ratio, as 6-month olds can, in addition to a 2:3 ratio, which 6-month-old infants cannot (as is the case for number, see Brannon et al., 2007).

Support for the idea that other dimensions (i.e., space) are also represented as noisy magnitudes, and perhaps a shared representational currency is provided by Brannon et al. (2006). These authors report that 6-month infants reveal the same ratio-dependency when discriminating size/area (i.e., 1:2, but not 2:3) as for time and number. To-date, it is unknown whether precision for area similarly increases with age (e.g., by 10 months). In addition, Möhring et al. (2012) revealed the same 1:2–2:3 ratio improvements between infants 6- and 10-months of age when discriminating different speeds (time/distance).

Given that psychophysical functions superimpose (with scalar variability), it appears young infants possess similar subjective sensitivity for different dimensions (i.e., time, number, area, line-length, speed), which supports the idea that all quantities (continuous or not) are represented by analog magnitudes with scalar variability, and the ability to represent magnitudes improves according to a developmental trajectory set into motion in early life.

In Childhood

Sensitivity for time and number sense, perhaps not surprisingly, continues to improve during childhood (we shall go on to discuss findings as they relate to time and number in children separately). For instance, Halberda and Feigenson (2008) revealed a marked improvement in the performance of 3-and 6-old year-old children during number discrimination from a 3:4 ratio to 5:6 with increasing age (adults were as high as 10:11), and between the ages of 5–7 years, children become able to discriminate number with increasing precision (e.g., see, Huntley-Fenner and Cannon, 2000; Huntley-Fenner, 2001). Four-year-old children can accurately select the visual array of dots that corresponds numerically to a sequence of sounds while younger children cannot (Mix et al., 1996). Siegler and Booth (2004) report age-related changes between 6 and 8 years of age in children's representation of the “mental number line” (described in more detail later). Specifically, younger children reveal logarithmic spacing and older children linear spacing between numbers. Logarithmic spacing (noise independent of magnitude) is inconsistent with the scalar property (noise proportional to magnitude), and aforementioned non-human and infant findings demonstrating simple arithmetic reasoning (see Gibbon and Church, 1981; Brannon et al., 2001).

Droit-Volet et al. (2003) employed a bisection task with 5-and 8-year-old children (and adults), which required selective attention to either time or number when they were both simultaneously presented (ignore one dimension). They report that for younger children, number interferes with time, but time does not interfere with number (an effect attenuated in older children; but present in adults, Dormal et al., 2006). Droit-Volet and colleagues subsequently examined time, number and line-length, with number and line-length presented sequentially (through time) and non-sequentially (Droit-Volet et al., 2008). During non-sequential presentation, the obtained psychophysical functions for number and line-length were comparable in both 5- and 8-year olds, but there was a relatively larger subjective mid-point, and index of reduced sensitivity, for timing functions from all children. Moreover, when number and line-length were presented sequentially, these dimensional differences disappeared. They interpreted their results in the context of the mode-control model and the pulse accumulation process for time, which is suited to sequential magnitude estimation. They contend that this type of processing demands attentional and working memory abilities (and are themselves components of these models; Figure 1) and this system is “tapped into” during sequential presentation of other dimensions (e.g., line-length, however the model is not presently designed to accommodate such dimensions).

Development of Temporal Competence in Childhood

Correspondences between age-related changes in sensitivity to different dimensions suggests that between the ages of 5- and 8-years old, sensitivity for time lags behind sensitivity for number (Droit-Volet et al., 2003); time appears to be a dimension that younger children may find less salient and less likely to attend to (Gautier and Droit-Volet, 2002). In fact, it is historically considered in developmental psychology (Piaget, 1946; Fraisse, 1967; Ornstein, 1969) that children are not equipped with temporal abilities; instead these derive from superior abilities in the processing of other dimensions (e.g., speed, number; although studies highlighted in this review have since rebutted this).

For instance, the timing functions obtained with 3-, 5- and 8-year-old children reveal (the scalar property, and) temporal judgments become more precise across development, which may be related to attentional and working memory function (see, Droit-Volet and Wearden, 2001; McCormack et al., 2004; Rattat and Droit-Volet, 2005; Wearden, 2005; Droit-Volet and Meck, 2007; Droit-Volet et al., 2007).

Theoretical and computer modeling (in the context of scalar expectancy theory; Gibbon et al., 1984) of temporal magnitude data from children, tends to support the notion that various components of the mode-control model, particularly “reference memory” and attention, undergo age-related changes (see Droit-Volet and Wearden, 2001; Droit-Volet et al., 2001; Droit-Volet, 2002, 2003a,b). As such, the development of psychological variables closely associated with “timing ability” (e.g., attention, memory), may also play a role in the development of timing performance across childhood and old age (e.g., Lustig and Meck, 2001, 2011; Lustig et al., 2005). Modeling of the timing functions from children (interpreted within the context of scalar expectancy theory) has also suggested that younger children make more random responses than older children (i.e., between 3- and 8-years old; Droit-Volet and Wearden, 2001).

Recently, Zélanti and Droit-Volet (2011) revealed discriminations between relatively small temporal magnitudes are easier than larger ones, and there are age-related improvements (between 5- and 9-years of age), with temporal sensitivity improving earlier for the short than for the long durations. Age-related improvements for “shorter” durations were predictive of the development of the span of short-term memory, whereas improved competence for “longer” durations was related to the development of attention and executive functions. However only age, and no cognitive abilities, were found to predict individual differences in time discrimination between the shortest and longest durations.

It has also been reported the psychophysical timing functions of children aged 3-, 5- and to a lesser extent 8- year olds, become flatter (less sensitive) when interval timing is either interrupted or tested after a (e.g., 24-h) retention delay. Rattat and Droit-Volet (2005) also reveal an interruption task tends to lengthen the subjective magnitude estimation, particularly in 5-year olds, which they attributed to stored representations of trained temporal magnitudes in memory. Furthermore, temporal estimations in children are inflated if the stimulus is bigger or brighter (Levin, 1977, 1979, 1982). This represents known properties of the psychophysiological modulation of time perception in adults (Gibbon et al., 1997; Buhusi and Meck, 2005). Children also tend to overestimate time on perception tasks, and under-reproduce a given duration, and their duration judgments are less stable (see Block et al., 1999).

It has been proposed that children under the age of 8 years, do not tend to spontaneously count while timing (Wilkening et al., 1987), and Clément and Droit-Volet (2006) report that temporal magnitude estimations of 5-year olds display the scalar property in both counting and non-counting conditions, but by 8-years and adulthood, counting during timing results in a violation the scalar property (see also, Hinton and Rao, 2004). This finding can be explained according to the mode-control approach. “Counting is a multistep process, with the number of steps proportional to the numerosity counted. If there is some probability of error (either skipping an item or counting it twice) at every step, then the more steps there are, the greater the expected accumulation of miscounts. The variability in counts from this source should, however…grow in proportion to the square root of the numerosity…discriminations should get relatively better as numerosities increase. That is, the discrimination of 30 from 20 should be more accurate than the discrimination of 3 from 2, contrary to Weber's law” (Cordes et al., 2001:699).

Lustig and Meck (2011) demonstrated that 8-year-old children (and younger and older adults), showed “typical” sensory modality asymmetry for durations signaled by either “sights” or “sounds.” Usually it is found that a magnitude estimation for time can be influenced by the modality, such that a given stimulus duration (i.e., 5-s) is perceived as a longer if it is signaled by a sound rather than a light (Wearden et al., 1998; Penney et al., 2000). It is assumed by the mode-control model that the clock runs faster for auditory stimuli as they capture and hold attention relatively automatically—thus they are more efficient at holding the switch closed, allowing larger pulse accumulations (see Figure 1)—whereas attending to visual stimuli requires controlled attention (Meck, 1984). In addition, a memory distribution (of a given duration) may be composed of “mixed-modality” memories, such that there might be a bias by skew of over-represented modality (see Chen and Yeh, 2009; Gu and Meck, 2011). Lustig and Meck (2011) report children tend to overestimate auditory stimuli compared to adults (they are comparable for visual stimuli). “Auditory stimuli are disadvantaged relative to visual stimuli in children's long-term memory and age-related declines in attention” (Lustig and Meck, 2011:2). In a separate study, Droit-Volet et al. (2004) report that 5-year olds have greater variability in their judgments of visual stimuli than auditory ones, indicating improved developmental temporal sensitivity for “sounds” rather than “sights.”

It has also been reported that although 3-year-old children can “time” an event, they have difficulty timing the duration between events (Droit, 1994). Young children are also found to base their ability to estimate duration through action (Droit, 1995) or an external “ticking” clock (Droit, 1994), but this is reduced by around age five, and they seem aware of temporal rules governing their behavior (Droit et al., 1990; Pouthas et al., 1990). It has also been reported that 3-year olds produce more accurate temporal magnitude estimates when they are asked to press harder than press longer, and press for longer and harder when asked to press harder. Droit-Volet and Rattat (1999) reveal five-and-a-half-year olds are able to transfer a target duration across different actions, but 3 year-olds cannot, suggesting children do not dissociate time from action, or develop abstract concepts of time, until around 5 years of age. This is consistent with ATOM which emphasizes a single magnitude system arose from the need for action. According to Droit-Volet (1998) “children's feeling that something is resisting them through their action may be the first step toward the understanding of duration” (1998:247).

The Development of Numerical Ability and Symbolic Number Across Infancy and Childhood

As has been discussed, there is much evidence to support the idea that a primitive time and number sense (at least) is ontogenetically “built in,” but there is much debate as to the form this may play in numerical development. In fact, preverbal counting may be a precursor to verbal counting abilities, as the basic number sense may provide the basis for the verbal system and arithmetic computation (Gallistel and Gelman, 1992). There are some comparative findings with non-humans to suggest that animals can learn to map symbolic Arabic digits (1–9) to objects and appropriately make use of this knowledge through symbolic labeling (e.g., see, Matsuzawa, 1985; Washburn and Rumbaugh, 1991; Brannon and Terrace, 1998, 2000; Pepperberg, 2006). “A more controversial question is whether there is ontogenetic continuity in numerical cognition” (Brannon, 2002:224). We shall now highlight children's development of counting and symbolic number representation.

The mode-control approach has been influential in the debate surrounding the foundations of numerical thinking and verbal counting ability during human development (e.g., Gallistel, 1990; Starkey et al., 1990; Wynn, 1990; Gallistel and Gelman, 1992; Dehaene et al., 1999; Grondin et al., 1999; Whalen et al., 1999; Brannon et al., 2001). Instead of using the representational convention whereby (symbolic) numbers are used to represent linear magnitudes, the mode-control model supposes the nervous system uses numerosity magnitudes to represent symbolic number. Accordingly, numerate individuals are presumed to have learned to map magnitudes of basic number sense to number words and numerals (i.e., from non-symbolic to symbolic; see Gallistel and Gelman, 2000). ATOM supposes, “when we later learn about [symbolic] number, the scaling mechanisms used for [all continuous] dimensions with action-relevant magnitude information will be co-opted in development for the scaling of [symbolic discrete] number” (Bueti and Walsh, 2009:1836).

In Infancy

Although the aforementioned findings support the notion that the ability to represent and compare numerosity appears early in development, other studies suggest that infants attend to continuous spatial dimensions such as surface area and contour length rather than number per se (Clearfield and Mix, 1999; Feigenson et al., 2002), challenging the notion that numerical representation is present in infancy (see, Mix et al., 2002; Newcombe, 2002). An alternative view is numerical competence in infancy is the product of an automated system for tracking and reasoning about small numbers of (non-numerical) “object files” or object-tracking mechanisms (e.g., Kahneman et al., 1992; Trick and Pylyshyn, 1994). By this form of account, object-file representations (rather than analog magnitudes) form the foundation of the verbal counting system (see, Carey, 1998, 2001; Spelke, 2000; Le Corre and Carey, 2007, 2008).

In support of this view, Feigenson et al. (2002) report that 10- and 12-month-old infants use object-file (size) rather than numerical ratio to track sequentially hidden objects, as they can compare representations of objects, and make ordinal “more” or “less” judgments—but only when the magnitudes were relatively small and within the limits (of about four items) of the “object-file” system (i.e., 1 vs. 2, or 2 vs. 3; but not 4 vs. 6). However Brannon (2002) has revealed that the ability to make ordinal number judgments develops between 9- and 11-months of age, even for numerosities that exceed the bounds of the object-file system (see also Dehaene and Changeux, 1993). Discrepancies between small and large numerosities may also reflect different conditions that direct young infants attention to number (Xu, 2003; Feigenson et al., 2004; Wood and Spelke, 2005).

The “magic number four” has been taken as evidence that infants ability to numerate small numbers is related to “subitizing” (Trick and Pylyshyn, 1994), and that symbolic (verbal) representations of number provide the basis for developing a (non-symbolic) understanding of numerosity (rather than the other way around, as supposed by the mode-control model). Of course, this type of account is at odds with aforementioned findings that infants can discriminate between large numerosities (with a large ratio difference), and can successfully reason about the “magical disappearance” of a large number (specifically, a collection) of objects (Chiang and Wynn, 2000).

Essentially, the dichotomy between small and larger numbers speaks to the issue of whether they are represented by the same or different cognitive system (see Buhusi and Cordes, 2011; Hyde, 2011), and was first addressed by Jevons (1871): are numerosities less than the “magic number four” processed as individual entities (subitizing, effectively filling in pockets of space), while larger numbers are represented through the approximate number system? (ANS; Feigenson et al., 2004). Alternatively, all magnitudes (small and large; as proposed by the mode-control model) may be represented by a single system, such as ANS (Gallistel and Gelman, 2000; Cordes et al., 2001; Cordes and Brannon, 2009), with the accumulated magnitude representing a cardinal value. However it has been cautioned that “accurate theories of numerical cognition must take seriously the notion that, under many conditions, small numbers are represented as arrays of numerically distinct individuals, not as sets with approximate cardinal values” (Hyde and Spelke, 2012:13). Of course, if numerosities below the “magic number” are integers rather than real-valued magnitudes, they should violate scalar variability.

McCrink and Wynn (2004) examined infants' numerical computation explicitly using large numbers, and found that 9-month olds appear to conduct arithmetic operations (addition and subtraction) over estimates of numerical magnitude, further supporting the idea that number sense supports numerical manipulations and operations.

In Childhood

A puzzling inconsistency is that infants are often purported to possess numerical abilities that young children do not seem capable of when tested in explicit choice paradigms (Huttenlocher et al., 1994; Mix et al., 1996, 2002; Newcombe, 2002). For example, Huttenlocher et al. (1994) showed that children younger than 3 years of age could not predict the numerical outcome of a nonverbal addition and subtraction task. Four-year-old children could accurately select the visual array of dots that corresponded numerically to a sequence of sounds while younger children performed at chance. These accounts of numerical development suggest that children gradually develop the ability to form and manipulate abstract representations of number.

Cantlon et al. (2010) report that 3-year-old children appear to represent analog numerical magnitudes when enumerating sets of objects, even those within the “magic number four” subitizing range, and numerical judgments were influenced by area. These authors observed ratio-dependence (scalar variance) for numbers both within and beyond the “magic number four” subitizing range. Young children in this study also appeared to preferentially attend to number over area.

Piaget (1952) reports abstract knowledge of arithmetic requires considerable learning (i.e., is not “built-in”) and does not emerge until a child is between 4 and 7 years of age, but studies have since revealed young children (between one-and-a-half-year to four years of age) master number conversion (e.g., see Gelman and Gallistel, 1978; Starkey, 1992), and preschool children possess an abstract representation of number and simple addition (Brannon and Van de Walle, 2001; Barth et al., 2005).

Spelke (2000) attributes the acquisition of mathematical skills to object knowledge (permanence through space and time) and numerosity, and it has been asserted that children must “possess a magnitude-based estimation system for representing numerosities that also supports procedures for numerical computation” (McCrink and Wynn, 2004:776). Despite the infamous (debunked) “clever Hans” demonstrations—the horse that apparently had mastered symbolic calculation—it has been revealed in children at least, that basic number sense (and numerosity estimation) is related to math ability and the development of mathematical intelligence (e.g., Carey, 1998, 2001; Gallistel and Gelman, 2000; Gelman and Gallistel, 2004).

Booth and Siegler (2006, 2008) report an association between 5-year-old children's school math achievement and linear (as opposed to logarithmic) sequencing of symbolic (Arabic) numbers along a spatial schematic number line—this suggests the spatial arrangement of numerical representations affects math abilities (Siegler and Ramani, 2009). The ability to quickly make ordinal comparisons between symbolic numbers also appears to be related to arithmetic calculation in older children (6–10-year olds; e.g., De Smedt et al., 2009).

Recently, Libertus et al. (2011a) reported that the acuity (sensitivity) of preschoolers' number sense was predictive of school math ability, even prior to the onset of formal mathematics instruction, and controlling for age and verbal skills. There are other studies that report stable individual differences in school-based math ability (verbal counting, ordinal comparison, arithmetic) in young children early into their formal education (Jordan et al., 2006, 2007, 2008, 2009). Collectively, these studies provide evidence that a primitive number sense lays the foundation for more advanced numerical abilities.

By 3 years of age, children appear to have mastery of some parts of the one to ten count sequence (Wynn, 1992), and between the ages of three-and-a-half and four and-a-half children are skilled with the decade count order (10, 20, 30, etc; Fuson, 1992). Also, behavioral response times reveal marked age-related changes and improves between the ages of 2 and 7 years (Huntley-Fenner and Cannon, 2000; Huntley-Fenner, 2001). By the age of 5 years, not all children have developed the ability to link symbolic symbols with non-symbolic quantities (Lipton and Spelke, 2005).

A related line of research examines how counting typically becomes related to determining numerosity (cardinal word principle)—this may be related to one-to-one correspondence between items and number tags (Gelman and Gallistel, 1978; Mix et al., 2011). In other words, children need to learn how count, but also why we count (and that the last count represents a magnitude estimate). The fact that small numerosities (<4) can be determined without counting (“subitizing”) may be at the root of developing this knowledge. The representation of the words “one,” “two, “three, “four” is progressive, but for other number words the child needs to understand the equivalence between the order of the words in the counting list and the successive numbers that are related by the function “+1” (see Carey, 2004). In much the same way, two, 2, and •• are equivalent in their “two-ness.”

Wynn (1990) revealed that children aged between 2- and 3-years old generalize counting such that they can count sounds, actions and objects. This is informative as the number of objects might be determined by counting them in any order, but actions and sounds must be counted in a certain order (i.e., when they occur). If asked “how many” after counting, children younger than 3-years of age are unable to produce an estimation of magnitude that corresponds to the last number counted, whereas children older than 3-years can. Moreover, if required to “give-a-number” (i.e., perform an action a certain number of times), children over 3-years of age will count as they perform the task, whereas younger children do not (they tend to give only one or two; see also Zur and Gelman, 2004).

It has been postulated that acquiring symbolic language enables children to become able to make conceptual inferences (e.g., see Spelke, 2011), by allowing them to selectively attend to relevant information (e.g., Sandhofer and Smith, 1999). This has led some researchers to propose that the numerical concepts demonstrated by infants are not obviously related to the later numerical concepts exhibited by preschool children as they begin to count verbally (Mix, 1999; Mix et al., 2002; Newcombe, 2002; Rousselle et al., 2004). In a study of how children judge the numerical equivalence of arrays of objects, Mix (1999) found that children gradually develop the ability to identify numerical equivalence. Children between 3- and 4-years of age could recognize numerical equivalence among homogeneous arrays in which elements were similar to one another, but could not reliably recognize numerical equivalence among heterogeneous arrays, which was only found in 5-year olds. The ability to identify numerical equivalence for heterogeneous arrays was correlated with children's verbal counting ability, independent of age. Mix (1999) argues that number words allow children to acquire abstract number concepts, even within the context of a nonverbal matching task (see also Mix et al., 1996)—children become better able to ignore superficial object features as they master the verbal counting system because number words embody abstract numerical categories. In other words, children gradually develop the ability to represent number as they acquire linguistic and symbolic knowledge. Previous studies of numerical cognition that required verbal identification of the number of objects in an array have obtained similar results (Von Gast, 1957; Siegel, 1974).

Since Piaget's (1952) studies using the number conservation task, it is well known that children before the age of 6 or 7 years will judge the number of counters in two parallel rows to be equal if the counters are arranged opposite to each other (i.e., in one-to-one correspondence), but a longer (or shorter) row (e.g., created by spreading out/pushing together the counters) is consistently judged to have more (or less counters, respectively; see also Mix et al., 2011). In ATOM, Walsh (2003:486) points out “is perhaps maladaptive for an infant brain not to use a common metric [for different magnitudes] as it is difficult for an older child to unbind these three elements [time, space, and quantity],” and is highly dependent upon the ability to learn associations between them.

Magnitude Estimation in Adulthood

As it relates to number (and time) sense, it is found in both non-humans and adults, that the speed and accuracy of estimates of magnitude can be influenced by distance and size effects (see Rumbaugh et al., 1987; Washburn, 1994; Brannon and Terrace, 2000; Brannon and Roitman, 2003). Of course, this relates to ratio-dependence (the scalar property); the ability to discriminate two numbers improves as the numerical distance between them increases, and sensitivity worsens as numerical size increases. These effects are obtained for both non-symbolic and symbolic number. Typically it is observed that temporal estimation in adults conforms to the scalar property, to both short and large durations (for a review see, Meck, 2003; Buhusi and Meck, 2005).

In a seminal paper, Moyer and Landauer (1967) report that during a task of symbolic Arabic number discrimination, “decision time was an approximately linear inverse function of the numerical distance between the two stimulus digits” (as for other dimensions) and when describing the data, “a reasonable fit is of the same general class as those usually found to describe … differences between physical quantities such as pitch and line-length” (Moyer and Landauer, 1967:1520).

When required to press a response key a certain number of times, there is scalar variability of adults pressing for small and large numbers, both within and beyond the subitizing range, however this effect is abolished when participants are asked to verbally count their presses out loud (Cordes et al., 2001). Whalen et al. (1999) report proportionality (scalar variability) between the number of taps generated following a specific request (i.e., 7–25).

As it pertains to the “two process” theories of number development, Revkin et al. (2008) report disproportionately higher sensitivity for numbers in the subitizing range (1–4) than for larger numbers in adults (see also, Trick and Pylyshyn, 1994). The authors reconcile the violation of Weber's law by suggesting “that in the small-number range, variables other than the ratio between stimuli (possibly variables relating to spatial arrangement or to other perceptual factors) boost number discriminability” and this “seems hard to separate from the original subitizing hypothesis” (Revkin et al., 2008:613). In adults, Dormal and Pesenti (2007) found that space influences number judgments, but number does not influence spatial judgments, and Roitman et al. (2007) report “short/few” and “long/many” classifications transfer between time and number, with improved sensitivity for number. Temporal judgments can also be biased by spatial-numerical associations of response code (SNARC-type) effects (Dehaene, 1997). Human findings have revealed: greater Arabic digits (Oliveri et al., 2008); larger stimuli (Xuan et al., 2007); visualized forwards motion (Vicario et al., 2007); visuomotor shifts to the right (Frassinetti et al., 2009) and greater distances (DeLong, 1981; Sarrazin et al., 2004) are associated with longer estimated durations (see also, Nicholls et al., 2011b). Secondary tasks tend to disrupt temporal magnitude estimates, but only mental arithmetic is impaired by a temporal task (Brown, 1997). It has also been recently reported that adults' ability to estimate time is somewhat predictive of their mathematical intelligence (Kramer et al., 2011).

Numerical magnitudes (i.e., 1–10) appear spatially organized from left to right, and this phenomenon is referred to as the mental number line (see de Hevia et al., 2008), and is believed to correspond to the orienting of visual attention. It has been considered that the mere presentation of symbolic digits can impose a spatial attentional bias (i.e., left for a small number), and this shift modulates time judgments (Oliveri et al., 2008). It has been recently reported that it is the process of comparing size differences between numerical cues, rather than the size of the number itself, which appears to bias time estimation (Vicario, 2011). The subjective mid-point during number bisection has also been found to vary as a function of spatial attention to the mental number line, i.e., presenting stimuli in near and far space (Longo and Lourenco, 2010), turning one's head to the left or right also modulates (smaller or larger, respectively) random number generation (Loetscher et al., 2008), and the left and hand rights respond faster (during an odd/even number discrimination) to smaller and larger numbers (respectively, Dehaene et al., 1993). Space and number effects are also found when there is no lateralized (left/right) response (Casarotti et al., 2007) or if events are presented in an orthogonal arrangement (Nicholls et al., 2008; see also Nicholls et al., 2011a). It is not beyond the scope of possibility that (SNARC-type) spatial mappings might be related to a cultural bias (i.e., in the Western world) to read across (and scale) from left to right, and the correspondence to left-lateralized language systems.

It has been suggested that spontaneous cross-modal interaction effects might not be as profuse in adulthood as during infancy and childhood (see Walsh, 2003; Izard et al., 2009)—it might make developmental sense to be equipped with a general magnitude estimator to facilitate comparing functionally equivalent co-varying quantities (e.g., to learn relations between size, weight and length). Any such effects are also taken as support for a general magnitude system, one in which unidirectional asymmetries exist between different dimensions. However, it is important to note that stimulus magnitude effects (intensity, size, number, emotional valence) are precisely known to bias interval time perception, and pulse accumulation, and so caution should be taken before attributing them to a more generalized process. This is particularly important from a developmental perspective, when the attempt is essentially to establish “which comes first?” (see also, Ansari, 2008).

Differences in Developmental Disabilities

Various findings examining the relative development of time and number sense in pediatric developmental disorder populations have emerged. These may shed light on some of the questions surrounding the typical development of NEUTIN. For instance, Spaepen et al. (2011) report that deaf individuals (who live in a remote Nicaraguan culture) who lack a language for number (i.e., no sign language) employ gestures to represent number, but have markedly reduced accuracy in “how many” and “give a number” type tasks for large numerosities (i.e., over three).

Developmental Dyscalculia

Problems with mathematics may readily present in educational environments with academic demands, and thus (at-risk) school-aged children may be identified as having mathematics disorder or developmental dyscalculia. This is one of the most well defined disabilities as it may thus relate to number sense. This is a disorder of numerical competence and arithmetical skill, such as retrieval of antithetic facts and dependence on finger counting when attempting number problems, in children of normal intelligence with no neurological injuries (see Temple, 1992).

Children who experience difficulties with mathematics reveal differences on number-comparison tasks with both symbolic and non-symbolic stimuli. This may suggest problems linking symbolic and approximate, to non-symbolic numerical representations. For example, Rousselle and Noël (2007) tested number magnitude estimates in children with mathematic learning disabilities. They report impairments in Arabic number comparison, number writing and trans-coding of tokens into Arabic numerals (symbolic number), but intact abilities for addition and subtraction (non-symbolic number). Furthermore, those with mathematical disability revealed a propensity to represent number magnitude over physical size (on a Stroop task), and they report a larger numerical distance effect. Ashkenazi et al. (2009) report a larger numerical distance and size effects for double-digit numbers, and interpret their findings to difficulties with subitizing and counting in this population (see Henik et al., 2011).

Ashkenazi and Henik (2010) administered a physical line and symbolic number bisection task to adults with developmental dyscalculia, and revealed affected individuals show a greater (than typical) tendency to underestimate the subjective mid-point (and reveal an absence of a typical bias for line bisection). They discuss their findings within the context of differences in the development of the mental number line, and an over-reliance on logarithmic (rather than linear) spacing (see also Geary et al., 2007).

Collectively, these findings were taken as evidence that children with mathematics disabilities do have a basic number sense (numerosity) but may experience problems relating numerical magnitudes to symbols (see also Landerl et al., 2004; Butterworth, 2010).

Williams and Down Syndrome

It has been revealed that young children (around 3 years old) with Williams syndrome (WS) are able to enumerate small numbers in dot arrays, but only when they differ by the 1:2 but not 2:3 ratio-requirement (Van Herwegen et al., 2008). O'Hearn et al. (2011) examined individuals with WS on a visual counting task, and asked them “how many?” (cardinality principle) with a rapidly presented array of dots. Those with WS revealed comparatively normal performance in the counting task, but were only able to (rapidly) accurately enumerate a (comparatively) smaller magnitude, even when arrays were presented for a longer period. These findings were taken as evidence for a limited subitizing system in WS (i.e., a “magic number three”). Ansari et al. (2005) reported the ability of children with WS to understand cardinality was predicted by their verbal language scores. That is, affected children may use language (rather than visuo-spatial skills, as is typical) to develop the cardinality principle (for a review, see O'Hearn and Luna, 2009). It has also been reported that individuals with WS may experience specific difficulties with the “mental number line” (number-space interaction effects) as they are less accurate on tasks such as “is five closer to nine or six?” (O'Hearn and Landau, 2007; see also, Krajcsi et al., 2009).

In an attempt to examine whether numerosity relies upon approximate estimates of magnitude (visuo-spatial) and symbolic number upon verbally mediated language processes, Paterson et al. (2006) made direct comparisons between WS (characteristically aspects of language are spared, but spatial abilities are impaired) and Down syndrome (DS; spatial spared, aspects of language impaired). On a task displaying small numbers of objects, they report infants with DS are impaired in their ability to discriminate small numerosities, but infants with WS are not. On a non-symbolic numerical distance task (using dot arrays) with affected older children and adults, they report those with WS do not reveal an expected distance effect, but those with DS do, suggestive of impaired analog numerical magnitude representation in WS (but not DS). They also report WS impairments on a variety of other tasks, particularly those that require mental manipulation of numbers, such as putting them in order (rote counting was generally in tact). This pattern was interpreted as a problem linking non-symbolic and symbolic forms of number in WS.

Children with Down syndrome display difficulties on counting and cardinal number tests (i.e., reporting “how many”; Gelman and Cohen, 1988), and may be less likely to notice violations of counting principles (Porter, 1999). For example, Nye et al. (2001) required children with DS to verbally count items in a set, and select a certain number of items (i.e., cardinality). Children with DS produced shorter count sequences and could count smaller sets. Camos (2009) required children with DS to enumerate large numerosities (dot arrays) that they were able to do with a 1:2 ratio, but not a 2:3 ratio (comparison participants showed age-related ratio improvements).

ADHD and Autism Spectrum Disorder

It has been reported (Zentall et al., 1994) that children with attention deficit hyperactivity disorder (ADHD) reveal lower (and slower) problem solving for math concepts on timed arithmetic tests, and the authors attributed these findings to difficulties with spatio-temporal organization. Kaufmann and Neurk, 2008 (see also 2006) tested 9- to 12-year-old children with ADHD on a variety of number tasks, including; placing an Arabic digit on an analogue scale, number discrimination at a range of distances, counting, non-symbolic (dot) enumeration (so-called “core” number abilities) and simple and complex mental and written calculation; and report particular difficulties with the first two in children with ADHD, particularly when numerical distance is small (the remainder were not affected). There is a variety of evidence to suggest individuals with ADHD also experience pathophysiological differences in temporal processing (see Barkley et al., 1997; Gooch et al., 2011; Allman and Meck, 2012). For instance, Valko et al. (2010) report impairments on reproduced temporal magnitude estimates (in the supra-seconds range) and temporal discrimination (in the sub-seconds range), and age-related changes between children and adults with ADHD.

The question of whether there is disordered processing of the temporal quality of information in autism spectrum disorder, and the extent to which this may impact the autistic behavioral phenotype, is beginning to be studied (Allman, 2011; Falter and Noreika, 2011), but has much anecdotal and clinical support. Although in their infancy, there are at least some empirical grounds (see also Szelag et al., 2004; Martin et al., 2009; Allman et al., 2011; Kwakye et al., 2011; but see Wallace and Happé, 2008; Jones et al., 2009a) and published commentaries supporting the temporal deficit hypothesis of autism (Boucher, 2001; Wimpory, 2002; Allman and DeLeon, 2009; Allman, 2011).

For example, Allman et al. (2011) report the timing functions across a wide age range (7–17 years) of affected individuals, and reveal (using a bisection task) potentially characteristic differences in the location of the subjective mid-point—which is found to be somewhat predictive of diagnostic communication and working memory impairment for shorter durations. They also reveal poorer temporal sensitivity for longer durations. These authors make modeling comparisons with previous reports from typically developing children (Droit-Volet and Wearden, 2001) and report that those with autism spectrum disorder appear to have more variable temporal memories, to an extent comparable with typically developing 5 year olds; and were likely to truncate (shorten) the “anchor” durations, to an extent that was comparable with typically developing 3 year olds. This lends support to the claim that time sense may be developmentally delayed in affected individuals, and may even contribute to diagnostic symptoms.

Assuming this is indeed the case in autism spectrum disorder, it might be conjectured that there may be relative differences and/or insensitivities in the “run” and “event” modes in the magnitude accumulation system (in a mode-control model). Presumably, given the shared mechanism but different mode of representation between basic time and number estimation, a fault operating in one mode (i.e., run) might produce a compensatory over-reliance upon using the other mode (i.e., event). Of course, we might also expect both time and number sense to be impaired if there are central problems in the function of the integration system, or if magnitude estimation is a more “generalized” process (i.e., ATOM).

If an atypically developing child finds it difficult to make sense of events according to their temporal properties, an adaptive strategy might be to use their numerical (or other stimulus) properties instead. As it pertains to oddities with number, it is common for children with autism spectrum disorder to have preoccupations for symbolic numbers; assigning numbers as labels for objects, events and animate beings; knowing how many parts there are to objects or events, and their order or calendrical quality. To-date it is unknown whether there is preserved number sense (i.e., ANS) and typical magnitude interaction effects (i.e., “mental number line”) in this disorder, and like Williams syndrome, perhaps these individuals “over” rely upon rote formal instruction, and symbolic numerical processing (although individuals may also have language problems, unlike in WS). Although not characteristic of the disorder per se, for a review of mathematical ability in autism spectrum disorders see Chiang and Lin (2007) and Jones et al. (2009b).

Intriguingly with respect to posited deficits in temporal processing in autism spectrum disorder, and an compensation on symbolic number (or other dimensions), it is not uncommon for affected individuals to have unusual interests in timetables, calendars, and routines, which might serve as useful “external” temporal supports (e.g., Lalli et al., 1994). There is evidence that children and teenagers with autism spectrum disorder reveal impairments in higher-order temporal cognition (Boucher et al., 2007), including the ability to 1) think about past or future changes of think about a current situation; 2) understand that entities change over time but are still the same thing; 3) comprehend that successive events are part of a unitary process, which is not attributable to non-temporal cognitive factors such as inabilities with inferencing or generativity, motivation or attention. Parents of children with autism spectrum disorder (like parents of children with attention-deficit hyperactivity disorder) tend to describe them as having a “poor” sense of time (Barkley et al., 1997; Allman et al., 2011). At face value, these studies endorse a developmental association between a basic time sense and higher concepts and adaptability to time.

It is curious to wonder whether differences with time (and number) are somehow related to the outstanding skills of savants, which fall into five categories; mathematics (human calculator), calendar calculating and music (external representations of time), art and mechanical or spatial skills; particularly as these relate to different analog modes of stimulus representation (i.e., number, time, and length; see Droit-Volet et al., 2008; also González-Garrido et al., 2002; Thioux et al., 2006).

Neuroscience of Time and Number Ability (NEUTIN)

Although researchers have identified particular brain areas that function as neural integrators, and thus would likely serve good candidates for the supposed pulse accumulation process (of the type described by the mode-control model), a full explanation of how neurons integrate time and number is still lacking (Matell et al., 2003, 2011; Matell and Meck, 2004; Meck, 2006a,b; Meck et al., 2008; Coull et al., 2011). As it relates to making magnitude estimates, the basal ganglia, prefrontal cortex and inferior and posterior parietal cortex are usually recruited on tasks examining number and time magnitude estimation (Breukelaar and Dalrymple-Alford, 1999; Casini and Ivry, 1999; Rao et al., 2001; Macar et al., 2002; Hinton et al., 2004; Buhusi and Meck, 2005; Pouthas et al., 2005; Jahanshahi et al., 2006) and these findings tend to support comparative findings from animals (Schubotz et al., 2000; Schubotz and von Cramon, 2001). Although, as we have highlighted, there is much support for the idea that magnitudes of different dimensions (at least partly) share a common basis, they can be dissociated in adults with left-and right lateralized parietal lesions, who reveal selective impairments with number and time. For instance Cappelletti et al. (2011) report a patient with left lesion displayed otherwise intact temporal processing that was influenced by irrelevant numbers, which themselves could not be adequately processed; and a patient with a right lesion revealed impaired time estimation that could be modulated by preserved numerical processing (neither patient showed numerical processing could be influenced by time). The same patient with the right parietal lesion had previously been reported to show impaired temporal processing (a tendency to underestimate duration), but intact spatial and numerical processing and number-time interaction effects (i.e., small numbers perceived as shorter, long numbers perceived as longer; Cappelletti et al., 2009).

Evidence from electrophysiological recordings in animals reveals neurons (single cells) with periodical firing patterns, those tuned to specific magnitudes, and neurons with monotonically increasing firing as a function of increases in magnitude, for both time and number (e.g., see Nieder et al., 2002; Matell et al., 2003; Nieder, 2004; Nieder and Miller, 2004b; Dehaene and Brannon, 2010). For instance, Nieder et al. (2002) revealed individual neurons in monkey prefrontal cortex appear to code for specific cardinal numerosities, and revealed size and distance effects (at least partly accounted for by the mode-control model). It is also revealed that neurons in the intraparietal sulcus (IPS) are active before those in prefrontal cortex, suggesting number might be represented in the parietal cortex and sent to PFC for further processing (e.g., number related responses). In monkeys trained to perform a temporal comparison task, neurons in intraparietal regions were tuned to the temporal durations of the comparison stimuli (Leon and Shadlen, 2003).

ATOM (Walsh, 2003; Bueti and Walsh, 2009) supposes the parietal cortex is the “seat” of the generalized magnitude system, as this region is often recruited during spatial (Sereno et al., 2001; Pinel et al., 2004), numerical (Dehaene et al., 1999; Piazza et al., 2007) and temporal (Maquet et al., 1996; Leon and Shadlen, 2003) processing. This shared neural basis (parietal cortex) of the representation of number (numerical value) and size (size of digits; see Dehaene et al., 2003; Fias et al., 2003; Pinel et al., 2004; Kadosh et al., 2005) is undoubtedly reflected in behavioral similarities between magnitude estimation judgments between time and number, and other quantities (i.e., line length). It is often found that number (with its symbolic connotations to language) and number tasks that require calculation (held to use verbal coding), involve left or bilateral parietal cortex, while time and space activates the right parietal cortex. In other words, “dimensions may have become lateralized from one another due to their output—number requires verbal representations, and time and space are more important for coordinating action” (Walsh, 2003:485). Cohen and Dehaene (1996) have suggested both (left and right) inferior parietal cortices are necessary for analogue magnitude representation.

As it relates to time sense, the striatal beat frequency (SBF) model (Matell and Meck, 2004) is a neurobiological instantiation of the pulse accumulator model of scalar expectancy theory (Gibbon et al., 1984; see Meck et al., 2008; Coull et al., 2011). Oscillatory neural inputs from the activity of large areas of cortex constitute the time code, and patterns of oscillatory activity are detected by striatal medium spiny neurons (input cells of the basal ganglia). The memory stage of the model (of the type described by the mode-control model) is attributed to the adjustment of cortico-striatal weights (which become “tuned”), and is assumed to depend upon the same neural representation of a specific stimulus as working memory (see Lustig and Meck, 2005; Lustig et al., 2005). From a computational perspective, it has recently been proposed that “chains of integrators constructed from mechanisms exhibiting a range of intrinsic time constraints (ranging from slow protein synthesis to rapidly ramping neural firing rates) may…perform interval timing” (Simen et al., 2011:1). In this account, magnitude estimates of time (in the seconds-to-minutes range) are mediated by chains of leaky accumulators.

In Infancy

Recall that time and number discrimination in infancy shows ratio-dependent improvements between 6- and 10-months of age (e.g., Brannon et al., 2007; Cordes and Brannon, 2009; Cantlon et al., 2010). The same pattern of results has also been found in electrophysiological recordings from infant brains. For instance, Libertus et al. (2009) demonstrated 7-month-old infants are able to detect novel numerosities (following habituation to a standard number). The magnitude of the “spike” of the deviant-triggered (“odd-ball”) amplitude produced in the brain to the unexpected change in numerosity (or duration, to be discussed) constitutes an event-related potential (ERP). These authors report that the ERP varied in accordance to changes in number—specifically, the greater the relative difference between numerosities (1:3 ratio vs. 1:2 ratio) rather than their absolute difference, the bigger the ERP. Additionally, Hyde and Spelke (2011) recorded ERP's from 6- to 7.5-month-old infants and also obtained evidence that representation of large numerosities in infants are approximate and ratio-dependent. Specifically, large numbers evoked a (mid-latency parietal) ERP that was dependent upon stimulus numerosity, whereas small numbers evoked an (occipital-temporal) ERP that was dependent upon the cardinal value of stimuli (i.e., not ratio-dependent). This finding was interpreted as support for the idea that there might be different cognitive systems for small and large numerosities.

In a recent study, Libertus et al. (2011b) observed that following steady-state repetition of the same numerosity, a proportional change in numerosity produced a proportion change in electrophysiological entrainment (Weber's law). Moreover, neural entrainment predicted infants' number discrimination measured behaviorally 2 months later. Hyde et al. (2010) showed the latency of the ERP after a change in shape (space) occurred much later (i.e., after 5–8 s) compared to when number was changed (i.e., after 2–5 s) in 6-month-old infants. Further, they report a right lateralized response to number changes (see also Izard et al., 2008). This is in contrast to other reports that have found bilateral activity (Cantlon et al., 2006). As it may relate to the development of a “two-part” number system and the “magic number four,” Hyde and Spelke (2011) report that 6-month olds display patterns of electrical brain activity which follows the scalar property (i.e., the ERP scaled with the ratio between numbers), but only for the processing of larger, but not smaller numbers (i.e., those in the subitizing range).

In relation to time sense, Brannon et al. (2008) employed a timing-interval oddball paradigm coupled with electrophysiological recording in 10-month-old infants, and examined the amplitude to an time-interval triggered (“odd-ball”) spike to deviations in duration, comparing infants' performance with a group of adults. The peak magnitude of the ERP has been shown to vary as a function of the standard to deviant ratio in both infants and adults (1:2, 2:3: 1:3, and 1:4; Brannon et al., 2008). Moreover, when ratio was held constant and absolute values were made to vary, the ERP did not vary. That is, the “hallmark” scalar property is also obtained in the firing patterns of neurons coding for time (see also, Brannon et al., 2004b). Infants also revealed a slight right lateralization in the ERP for time magnitude estimation.

In Childhood

Electrophysiological studies in children suggest that number processing in the inferior parietal cortex begins as a right-lateralized process and the left hemisphere gradually takes over, while right-lateralized activity does not show such age-related changes (e.g., Ansari and Dhital, 2006). More recently, Heine et al. (2011) studied elementary school children (around 7 years of age) on a non-symbolic number discrimination task using a range of numerical magnitudes, both within and beyond the subitizing range. They report late parietal ERP's that were proportionally affected by the relative distance between the magnitudes, and which were more right- than left-lateralized, including those in the subitizing range. Temple and Posner (1998) have shown that the brain activity associated with symbolic number discrimination shows little change between the age of 5-years and adulthood. They report that while the reaction times for numerical comparisons of Arabic numerals and dot arrays dropped threefold between 5 years and adulthood, the numerical distance ERP effects and the loci of activity remained constant between children and adults. The consistency in patterns of brain activity is impressive given that dramatic changes in numerical language and skill occur between 5 and 20 years of age.

It has been revealed through functional neuroimaging (fMRI) that young children can discriminate between numerical values across different notation systems, both symbolic and non-symbolic, and recruit the same parts of the brain as adults when doing so (occipitio-temporal and parietal cortex), plus a few regions more (inferior frontal; e.g., Cantlon et al., 2009). For instance, Cantlon et al. (2006) tested non-symbolic and area discrimination in 4-year olds, and revealed similar IPS activation to number as in adults.

This approach also reveals age-related fronto-parietal shifts in number processing, of basic and advanced numerical tasks (Ansari and Dhital, 2006; Ansari, 2008; Holloway and Ansari, 2010). The decreasing involvement of prefrontal cortex is assumed to reflect a developmental disengagement of domain-general processes related to executive control and working memory (Ansari et al., 2005; Rivera et al., 2005). These findings can be taken as support for the idea that a core neural system integrates notation-independent numerical representations, and that mental arithmetic may have functional specialization on the left inferior parietal cortex.

Kaufmann et al. (2006, 2008) have reported neural overlap between non-symbolic numerical and spatial processing in children around 8 years old (using hand and finger stimuli). In contrast to adults, children reveal increased activity in bilateral supramarginal gyrus, post-and-precentral gyrus, and anterior-lateral portions of the IPS. Cantlon et al. (2011) attempted to measure activity to symbols (numbers and letters, and a variety of other comparison stimuli), and compared to adults, children reveal comparable left-lateralized mid-fusiform/inferior temporal gyrus activity for both letters and numbers.

As pertains to developmental disabilities, individuals with developmental dyscalculia also present with presumed neuropsychological damage to the IPS, thus providing additional support for this neurological locus in numerical processing and abstract number. It has been thought this disorder may characterize a deficit with the “mental number line” (Bachot et al., 2005) or in the linking between non-symbolic magnitude and symbolic notation (Rubinsten and Henik, 2005; Rousselle and Noël, 2007). Kaufmann et al. (2009) reveal that during non-symbolic number processing, children with dyscalculia reveal stronger activations in the left inferior parietal cortex and reduced deactivations in the right inferior parietal cortex, perhaps suggestive of an impaired number sense and compensatory neural activity. However, Mussolin et al. (2009) required affected children aged 9–11 years old to identify the larger numeral in a pair (with a variety of numerical distances; i.e., 2 vs. 4; 2 vs. 8) and report that affected children show absence of typical numerical distance effect modulations of the IPS (as typical children do). They also observed other differences between typical and dyscalculic children: typically there is stronger right intraparietal sulcus (IPS; and right middle frontal gyrus) activation for small than large numerical distances, while children with dyscalculia show left supramarginal gyrus and middle frontal gyrus activation; affected children also revealed postcentral gyrus activation for number in contrast to color comparison.

It has been revealed that older children (10–15 years) with ADHD show decreased activation on a time discrimination task contrasted by a temporal order task in right dorsolateral and inferior frontal cortex, and right anterior cingulate into SMA (Smith et al., 2008). There is unpublished fMRI data to suggest that children with autism spectrum disorder reveal differences in activity in cortico-cerebellar and cortico-striatal circuits when timing relatively short (2-s) and longer (8-s) durations: children with autism may recruit a “longer” timing system for shorter durations (Allman et al., in preparation).

In Adults

Electrophysiological recordings in adults have revealed the magnitude of an ERP is proportional to the ratio of the difference between temporal and numerical magnitudes (scalar property). As it relates to time estimation, there has been much speculation as to whether brain rhythms may serve as the “tick” of a clock (Treisman, 1984). This includes alpha and theta rhythms, and event-related de-synchronizations. Perhaps the most oft cited is the slow negative wave called the contingent negative variation (CNV; for a discussion, see Pouthas, 2003). However it has recently been suggested that rather than being directly implicated in the accumulation process, the CNV likely represents time-based decision and response processes (van Rijn et al., 2011).

Szucs and Soltesz (2007) were able to dissociate ERP's associated with both facilitation and interference on the (number-size) numerical Stroop paradigm (i.e., judge number magnitude with physically smaller and bigger Arabic digits). “In a nutshell, in the numerical task we found an ERP facilitation effect related to perceptual processing” (Szucs and Soltesz, 2007:3196). They also report that number had a slower processing speed than size, and an ERP numerical distance effect which was stronger over right (than left) parietal regions. The timing of the ERP was also associated with distance effects, and occurred at the same time as the Stroop facilitation effect, “suggesting the facilitation effect appeared when numerical information was just being evaluated or was already available…Most probably, the faster processed irrelevant size information could prime and accelerate the processing of the slower processed numerical information in the common magnitude representation” system (Szucs and Soltesz, 2007:3197).

As it relates to numerical processing, Libertus et al. (2007) employed non-symbolic (dots) and symbolic (Arabic digits; 1–10) numbers and required adults to judge whether the presented number was less/more than five. For symbolic numbers, they report distance-related ERP modulation across parietal and temporal-occipital regions, and greater right-lateralized posterior positive ERP's for symbolic digits closer to the comparison (5; than those further apart, e.g., 9), however this was not found small non-symbolic number distances; and ERP's increased as numerosity increased (size effect). With a greater range of values (8–30) they did obtain similar ERP distance effects as symbolic digits (indicative of input-notation independence).

As it relates to the question of the “magic number four,” there is evidence that small and large number processing can be dissociated in adults at the electrophysiological level with respect to both pattern and time: small cardinal numbers (within the ‘subitizing’ range) invoke an early visuo-spatial attentional component, and the ERP is largest for three objects, then two, then one; while larger numbers modulate a mid-latency component in the right intraparietal region that is sensitive to ratios. In the same study, Hyde and Spelke (2012) also report lateralization effects, and identified several distinct loci, for small and large non-symbolic numbers. The authors surmised a single system represents all numerosities, but is constrained by cognitive processes related to the limits of an early attentional selection processes; small numbers (e.g., four objects) might be selected (by attentional processing) as a group, but larger numbers likely require (more demanding) parallel processing.

In a procedure combining electrophysiological and fMRI, it has been shown that patterns of cortical activity are attributable to the input of symbolic notation (verbal or Arabic). For instance, bilateral extrastriate cortices and a left-lateralized precentral region are more activated during verbal (than Arabic) numbers, while activity in right fusiform gyrus (the “expert” area), bilateral inferior parietal and frontal regions is greater for Arabic (than verbal) notation. Bilateral activation along the interparietal sulcus and precuneus that corresponds to numerical distance was also noted (Pinel et al., 2001). This is consistent with a basic notation-independent system of magnitude (see also, Piazza et al., 2007). Piazza et al. (2004) report the percent signal change of IPS response to deviant numerosities increased with the disparity between the habituated and deviant numerosities. The general conclusion of this study was that the IPS responds to changes in the numerical quantity of a stimulus even when explicit comparison of stimuli is not required and regardless of whether the stimuli involve Arabic numerals or dot arrays (but see, Shuman and Kanwisher, 2004).

Using fMRI, Pinel et al. (2004) examined adults' magnitude estimation for size, luminance and number; and revealed at both the behavioral and neural level, number interfered with size, but not with luminance. It has also been suggested that number-space interactions (i.e., “mental number line”) might be mediated by shared parietal circuits for external attention to space and internal representations of number (Hubbard et al., 2005). For instance, it has been reported that there is left-lateralized parietal activation when participants' attention is directed to time, right-lateralized parietal activation when attending to space, and bilateral activation when processing both dimensions simultaneously (Coull and Nobre, 1998), and patients with spatial neglect (i.e., damage to right parietal cortex produces failure to attend or response to left space) reveal a variety of timing deficits (e.g., see Danckert et al., 2007; Hoeckner et al., 2008; Calabria et al., 2011). For example, Vuilleumier et al. (2004) report patients with neglect are slower to classify numbers (Arabic) if they are smaller (than larger) than a target number, which they attributed to difficulties spatially representing numbers in the left side of the mental number line.

In adults, symbolic number processing (and complex math ability) is usually characterized by bilateral, and in some instances, left-lateralized IPS activity (for details, see Dehaene et al., 2003; Santens et al., 2010). For instance, Piazza et al. (2002) report the IPS is active when participants estimate numerosity across non-symbolic numerical stimuli such as sets of visual objects or auditory events, and Kadosh et al. (2005) report notation-independent activity in IPS between symbolic (digits, number words) and non-symbolic number (dots; see also, Naccache and Dehaene, 2001; Eger et al., 2003). Further, right-lateralized IPS activation is greater when participants compare the values of Arabic numerals (or numerosity, ANS) than when they compare stimuli of other such semantic categories as animals, body parts, or abstract symbols along continuous dimensions like ferocity, relative position, and orientation (Le Clec'h et al., 2000). Bilateral IPS is selectively activated when participants perform approximate arithmetic calculations on symbolic numerical stimuli such as Arabic numerals and number words (Pesenti et al., 2000; Simon et al., 2004; for reviews see, Dehaene, 2003; Dehaene et al., 2004). This activation is not related to factual knowledge of arithmetic outcomes because greater IPS activation is also found when participants roughly estimate the answers to arithmetic problems. The activation can be dissociated from the patterns of IPS activation associated with the calculation of precise arithmetic outcomes (Dehaene et al., 1999). For example, when participants are presented with the problem “4 + 5,” the IPS is activated when they choose the closest answer from the options “8 or 3” but the IPS is not activated when they identify the answer precisely from the choices “7 or 9.” IPS activation is found when participants are asked to compute the outcomes of various addition and subtraction computations but not when they are simply asked to read number words (e.g., Chochon et al., 1999). The bilateral posterior superior parietal lobe is believed to correspond to spatial attention along the “mental number line,” while the left angular gyrus supports verbally learned facts (e.g., 2 + 2 = 4).

Pinel and Dehaene (2010) investigated whether individual differences in functional asymmetry (left-lateralization) in areas involved in sentence listening and reading are mirrored in the asymmetry of areas involved in mental arithmetic, and found this to be the case. They report arithmetic processing recruits frontal, parietal and subcortical regions. “Specifically, the profile of asymmetry in the posterior superior temporal sulcus during sentence processing co-varied with the asymmetry of calculation-induced activation in the IPS” (Pinel and Dehaene, 2010:48).

As it relates to time estimation, similar patterns of activation are observed during supra-second perception or production timing tasks and all timing tasks (i.e., even those involving “thinking” about time) typically activate motor regions such as the basal ganglia, supplemental motor area (SMA) and pre-SMA (for a review, see Macar et al., 2002; Kotz and Schwartze, 2011; van Rijn et al., 2011). It is widely held that relatively small (less than a second) and longer duration magnitudes (in the seconds to minutes range) may be represented by different timing systems (e.g., see Buhusi and Meck, 2005; Jahanshahi et al., 2006; Buhusi and Cordes, 2011). Sub-second timing may be more cerebellar-dependent due to this region's role in motor coordination, and timing in the supra-seconds range may depend more upon the basal ganglia and prefrontal regions, as this type of temporal processing recruits more attentional (switch and accumulator) and working memory processes (see Figure 1; see also Hinton and Meck, 1997), however they are not mutually exclusive as cerebellar activation is also found in adult fMRI studies using supra-second durations (and basal ganglia for millisecond durations). Similarly, different molecular and neurophysiological systems underlie interval and circadian (i.e., 24-h) timing (see Agostino et al., 2011). Given the wealth of such findings (as it relates to humans and adults), a complete account of neurophysiological findings of timing and time perception in adults is beyond the scope of this review (e.g., but see, Harrington and Haaland, 1999; Matell and Meck, 2000; Meck and Benson, 2002; Meck, 2003, 2005; Nenadic et al., 2003; Hinton and Meck, 2004; Meck and Malapani, 2004; Pastor et al., 2004; Buhusi and Meck, 2005; Coull et al., 2011; Allman and Meck, 2012). However, a common feature of many adult neuroimaging studies is the explicit attempt to dissect the contribution of different timing components (e.g., clock, memory, and decision stages) as it relates to a neurobiological instantiation of scalar expectancy theory (Gibbon et al., 1984).

For example using fMRI, Harrington et al. (2010); see also, Harrington et al. (2004) examined patterns of neural activity during the perceptual (encoding), memory and decision stages of a duration (and pitch) ordinality task. Encoding of time selectively activated the striatum; the striatum was equally active for time (as for pitch) during the maintenance stage, and striatal activation was greatest for time during the decision stage. As acknowledged by the authors, these findings are consistent with the SBF model of interval timing (Matell and Meck, 2004). fMRI studies have revealed the preSMA and basal ganglia likely serve a function in the “accumulation processes” as there is increased activation in these regions to longer durations (e.g., see Coull et al., 2004; Pouthas et al., 2005); memory processes are likely served by lateral premotor and right inferior frontal corticies (see Rao et al., 2001; Pouthas et al., 2005) and decision processes by the anterior cingulate (see also Rao et al., 2001).

In their study, Coull et al. (2004) made use of dynamically changing visual stimulus attributes (e.g., color and duration), requiring selective attention (on the part of the participants) to either dimension. Increasing attentional allocation to time selectively increased activity in a cortico-striatal network that included the pre-supplementary motor area, the right frontal operculum, and the right putamen.

Harrington et al. (2011) scanned adults while studying the “sounds are judged longer than lights” effect. Subjective perceptions of time slowing or quickening were associated with different patterns of superior temporal, posterior insula, and middle occipital activity, which reveal stronger effective connectivity when time was dilated. The within-trial evolution of interval timing has also been examined (Rao et al., 2001), and it was found that activation in the basal ganglia (right putamen and caudate) occurred early and continued into the trial and was uniquely associated with encoding time intervals, whereas cerebellar activation unfolded later, suggesting an involvement of processes other than explicit timing. Early activation in right inferior parietal cortex (and bilateral premotor) was associated with encoding, implicating these systems in attention and temporary maintenance of intervals. Later activation in the right dorsolateral prefrontal cortex emerged during comparison of time intervals.

Summary and Conclusions

Evidence from infants, children and adults, and non-human animals, suggests numerical and temporal processes are remarkably accurate, and conform to qualities of sensory perception (i.e., scalar property), across a variety of different methods: behavioral looking patterns of infants, social timing, behavioral responses in children as young as 3-years old, and in the electrophysiological potentials of neurons.

The studies cited in this review tend to support the notion that typical infants possess a “built in” time and number sense (e.g., Brannon and Roitman, 2003). Performance on time and number tasks is modulated by ratio-dependence in children and adults, and this is found with non-symbolic and symbolic stimuli (e.g., Arabic numerals and words). Typically developing 6-month-old infants reveal sensitivity to numerosity in temporal sequences and spatial arrays, and sensitivity to time with respect to deviant durations, area, speed and distance, but only when constrained by the 1:2 ratio requirement, although this quite quickly develops (over a few months) to encompass “more difficult” 2:3 ratio sensitivities. This review has attempted to reconcile such findings within a “mode-control” model perspective (Meck and Church, 1983; Church and Meck, 1984). In this model, temporal and numerical quantity is measured by the accumulation of pulses (in the run/stop and event modes, respectively).

As studies examining the relative extent of conformities between magnitude estimation for different dimensions continue, so too does support for the idea that there is a general principle (of the type described by the mode-control model) operating on a multitude of dimensions (of the type described by ATOM) upon which we rely to make sense of events in our world (time, area, number, size, distance, speed). However there is (as yet) no model that is able to provide a complete account of multi-dimensional magnitude estimation (accumulation) processes. Both types of account predict cross-dimension interaction effects (between time and number; across different quantities). Of course, given the co-linearity between time and numerosity in the mode-control model, and in ATOM (Walsh, 2003), it becomes difficult to dissociate between these two types of accounts given the aforementioned developmental similarities between magnitude estimates of time and number.

Infants are able to perform numerical addition and subtraction, and more advanced temporal and numerical abilities also require similar forms of arithmetic operations of magnitudes, such as calculating speed (space divided by time) or rate of return (number divided by time), and number sense appears to be associated with math ability. The fact that infants resources are being directed toward improving sensitivity to different quantities at such a critical period in brain development, speaks to the importance of this as a “foundational” ability for other cognitive and behavioral functions. Of course during infancy, a wide variety of abilities are starting to take shape (e.g., walking, inhibiting actions) and it comes as no surprise that the time from birth to 2 years and middle to late childhood is particularly important for the development of NEUTIN. It will be useful for future research to identify the precise developmental sequences of sensitivities to different quantities, and how they relate to other forms of cognitive development (e.g., attention, memory), and to adapt the mode-control to accommodate findings for different dimensions (see also, Lustig, 2011).

Given the literature, it seems likely that a (right-lateralized) non-symbolic number system provides the foundation for the (left-lateralized) symbolic number system over the course of development (see Cantlon et al., 2009). Across childhood, it appears the discrimination of analogue magnitudes improves with age, which is perhaps inextricably linked with the development of attentional capacities or the ability to maintain information in working memory. There is debate about whether smaller magnitude estimates (i.e., numerosities) are processed differently than larger ones. The question of how the brain develops a sense of number and time raises serious computational issues for cognitive neuroscience. As adults, we have the ability to make decisions based on abstract mental representations of magnitudes of time (e.g., “do I have enough time to get to the shop”) and complex number abstractions (e.g., calculating change left over from a purchase at the shop), and of course our attention is distributed in time and space, and our subjective experience of time is modulated by attention (see Coull et al., 2004).

It will be important for future research to identify the neural correlates of time and number representation in children, and corresponding changes in brain function that underlie normative developments in these domains (i.e., brain maturation and the relationship to timing and counting). This is relevant to children with developmental disabilities, particularly those with apparent difficulty with time and number (e.g., math disability, autism spectrum disorder, Williams syndrome), as it offers a “bench-to-bedside” approach with therapeutic potential. For example, there is evidence that external temporal supports (e.g., picture schedules, timers) are extremely effective in the training and treatment of individuals with autism, and other neurological populations who experience problems with cognitive adaptation (for details, see Allman and Meck, 2012).

A developmental perspective to time and number can also help unravel interactions among seemingly disparate levels of organization, such as the molecular biology of gene expression and the development of cognitive abilities. For example, assuming a basic deficit in time sense in those with autism spectrum disorder, it should follow that aspects of the behavioral phenotype are related to subtle and early neuropathology that ultimately affects multiple neural systems involved in number and time representation, directly and through compensatory experience-dependent reorganization. This is still yet to be determined, but this idea is congruous with current theories of autism spectrum disorder that emphasize differences in “neural signatures” (Kaiser et al., 2010), or the adaptive functioning of long-range (multiple neural systems) in neurocognitive function (Allman, 2011; Barttfield et al., 2011). Potentially at least, this type of neural-systems approach to the development of NEUTIN may provide a neural signature or “endophenotype” that corresponds to impairments in autism spectrum disorder (and potentially, to co-morbid disorders). The goal for the quest for the “endophenotype” is to identify pathophysiological mechanisms that “cause” the disorder (Kaiser et al., 2010).

On a final note, it is parsimonious (from an ontogenic developmental perspective) to surmise that our “built in” quantity sense and “integration” mechanism is likely at the root of our cognitive ability to think about metaphysical aspects of time and space, such as pondering how big or old the milky way is, and what the word “vast” means to our subjective estimations of magnitude.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported in part by a Pathway to Independence award to Melissa J. Allman from the Eunice Kennedy Shriver National Institute of Child Health and Human Development (K99 HD058698). The authors are grateful to the reviewers for their comments.

References

Agostino, P. V., Golombek, D. A., and Meck, W. H. (2011). Unwinding the molecular basis of interval and circadian timing. Front. Integr. Neurosci. 5:64. doi: 10.3389/fnint.2011.00064

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Allan, L. G., and Gibbon, J. (1991). Human bisection at the geometric mean. Learn. Motiv. 22, 39–58.

Allman, M. J. (2011). Deficits in temporal processing associated with autistic disorder. Front. Integr. Neurosci. 5:2. doi: 10.3389/fnint.2011.00002

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Allman, M. J., and DeLeon, I. G. (2009). “No time like the present: time perception in autism,” in Causes and Risks for Autism, eds A. C. Giordano and V. A. Lombardi (New York, NY: Nova Science Publishers), 65–76.

Allman, M. J., DeLeon, I. G., and Wearden, J. H. (2011). A psychophysical assessment of timing in individuals with autism. Am. J. Intellect. Dev. Disabil. 116, 165–178.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Allman, M. J., and Meck, W. H. (2012). Pathophysiological distortions in time perception and timed performance. Brain 135, 656–677.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ansari, D. (2008). Effects of development and enculturation on number representation in the brain. Nat. Rev. Neurosci. 9, 278–291.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ansari, D., and Dhital, B. (2006). Age-related changes in the activation of the intraparietal sulcus during nonsymbolic magnitude processing: an event-related functional magnetic resonance imaging study. J. Cogn. Neurosci. 18, 1820–1828.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ansari, D., Garcia, N., Lucas, E., Hamon, K., and Dhital, B. (2005). Neural correlates of symbolic number processing in children and adults. Neuroreport 16, 1769–1773.

Pubmed Abstract | Pubmed Full Text

Ansari, D., Donlan, C., Thomas, M. S. C., Ewing, S. A., Peen, T., and Karmiloff-Smith, A. (2003). What makes counting count? Verbal and visuo-spatial contributions to typical and atypical number development. J. Exp. Child Psychol. 85, 50–62.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Antell, S. E., and Keating, D. P. (1983). Perception of numerical invariance in neonates. Child Dev. 54, 695–701.

Pubmed Abstract | Pubmed Full Text

Ashkenazi, S., and Henik, A. (2010). Attentional networks in developmental dyscalculia. Behav. Brain Funct. 6, 2.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ashkenazi, S., Mark-Zigdon, N., and Henik, A. (2009). Numerical distance effect in developmental dyscalculia. Cogn. Dev. 24, 387–400.

Bachot, J., Gevers, W., Fias, W., and Roeyers, H. (2005). Number sense in children with visuospatial disabilities: orientation of the mental number line. Psychol. Sci. 47, 172–183.

Barkley, R. A., Koplowitz, S., Anderson, T., and McMurray, M. B. (1997). Sense of time in children with ADHD: effects of duration, distraction and stimulant medication. J. Int. Neuropsychol. Soc. 3, 359–369.

Pubmed Abstract | Pubmed Full Text

Barth, H., La Mont, K., Lipton, J., and Spelke, E. S. (2005). Abstract number and arithmetic in young children. Proc. Natl. Acad. Sci. U.S.A. 39, 14117–14121.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barttfield, P., Wicker, B., Cukier, S., Navarta, S., Lew, S., and Sigman, M. (2011). A big-world network in ASD: dynamical connectivity analysis reflects a deficit in long-range connections and an excess of short-range connections. Neuropsychologia 49, 254–263.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Block, R. A., Zakay, D., and Hancock, P. A. (1999). Developmental changes in human duration judgments: a meta-analytic review. Dev. Rev. 19, 183–211.

Bijeljac-Babic, R., Bertoncini, J., and Mehler, J. (1993). How to 4-day old infants categorize multisyllabic utterances? Dev. Psychol. 29, 711–721.

Bobin-Bègue, A., Provasi, J., Marks, A., and Pouthas, V. (2006). Influence of auditory tempo on the endogenous rhythm of non-nutritive sucking. Eur. Rev. Appl. Psychol. 56, 239–245.

Booth, J. L., and Siegler, R. S. (2006). Developmental and individual differences in pure numerical estimation. Dev. Psychol. 42, 189–201.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Booth, J. L., and Siegler, R. S. (2008). Numerical magnitude representations influence arithmetic learning. Child Dev. 79, 1016–1031.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Boucher, J. (2001). “Lost in a sea of time: Time-parsing and autism,” in Time and Memory, eds C. Hoerl and T. McCormack (Oxford, UK: Oxford University Press), 111–135.

Boucher, J., Pons, F., Lind, S., and Williams, D. (2007). Temporal cognition in children with autistic spectrum disorder: tests of diachronic thinking. J. Autism Dev. Disord. 37, 1413–29.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brannon, E. M. (2002). The development of ordinal numerical knowledge in infancy. Cognition 83, 223–240.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brannon, E. M., Abbott, S., and Lutz, D. J. (2004a). Number bias for the discrimination of large visual sets in infancy. Cognition 93, B59–B68.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brannon, E. M., Roussel, L. W., Meck, W. H., and Woldorff, M. (2004b). Timing in the baby brain. Cogn. Brain Res. 21, 227–233.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brannon, E. M., Libertus, M. E., Meck, W. H., and Woldorff, M. G. (2008). Electrophysiological measures of time processing in infant and adult brains: Weber's law holds. J. Cogn. Neurosci. 20, 193–203.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brannon, E. M., Lutz, D., and Cordes, S. (2006). The development of area discrimination and its implications for number representation in infancy. Dev Sci. 9, F59–64.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brannon, E. M., and Roitman, J. D. (2003). “Nonverbal representations of time and number in animals and human infants,” in Functional and Neural Mechanisms of Interval Timing, ed W. H. Meck (Boca Raton, FL: CRC Press), 143–182.

Brannon, E. M., Suanda, S., and Libertus, K. (2007). Temporal discrimination increases in precision over development and parallels the development of numerosity discrimination. Dev. Sci. 10, 770–777.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brannon, E. M., and Terrace, H. S. (1998). Ordering of the numerosities 1 to 9 by monkeys. Science 282, 746–749.

Pubmed Abstract | Pubmed Full Text

Brannon, E. M., and Terrace, H. S. (2000). Representation of the numerosities 1–9 by rhesus macaques (Macaca mulatta). J. Exp. Psychol. Anim. Behav. Process. 26, 31–49.

Pubmed Abstract | Pubmed Full Text

Brannon, E. M., and Van de Walle, G. A. (2001). The development of ordinal numerical competence in young children. Cogn. Psychol. 43, 53–81.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brannon, E. M., Wusthoff, C. J., Gallistel, C. R., and Gibbon, J. (2001). The subjective scaling of number representation. Psychol. Sci. 12, 238–243.

Pubmed Abstract | Pubmed Full Text

Breukelaar, J. W. C., and Dalrymple-Alford, J. C. (1998). Timing ability and numerical competence in rats. J. Exp. Psychol. Anim. Behav. Process. 24, 84–97.

Pubmed Abstract | Pubmed Full Text

Breukelaar, J. W. C., and Dalrymple-Alford, J. C. (1999). Effects of lesions to the cerebellar vermis and hemispheres on timing and counting in rats. Behav. Neurosci. 113, 78–90.

Pubmed Abstract | Pubmed Full Text

Broadbent, H. A., Rakitin, B. C., Church, R. M., and Meck, W. H. (1993). “Quantitative relationships between timing and counting,” in The Development of Numerical Competence: Animal and Human Models, eds S. Boysen and E. J. Capaldi (Hillsdale, NJ: Erlbaum), 171–187.

Brown, S. W. (1997). Attentional resources in timing: interference effects in concurrent temporal and non-temporal working memory tasks. Percept. Psychophys. 5, 1118–1140.

Pubmed Abstract | Pubmed Full Text

Buckley, P. B., and Gilman, C. B. (1974). Comparison of digits and dot patterns. J. Exp. Psychol. 103, 1131–1136.

Pubmed Abstract | Pubmed Full Text

Bueti, D., and Walsh, V. (2009). The parietal cortex and the representation of time, space, number and other magnitudes. Philos. Trans. R. Soc. Lond. B Bio. Sci. 364, 1831–1840.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buhusi, C. V., and Cordes, S. (2011). Time and number: the privileged status of small values in the brain. Front. Integr. Neurosci. 5:67. doi: 10.3389/fnint.2011.00067

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buhusi, C. V., and Meck, W. H. (2005). What makes us tick? Functional and neural mechanisms of interval timing. Nat. Rev. Neurosci. 6, 755–765.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buhusi, C. V., and Meck, W. H. (2009a). Relative time sharing: new findings and an extension of the resource allocation model of temporal processing. Phil. Trans. R. Soc. Lond. B Biol. Sci. 364, 1875–1885.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buhusi, C. V., and Meck, W. H. (2009b). Relativity theory and time perception: single or multiple clocks? PLoS One 4:e6268. doi:10.1371/journal.pone.0006268

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Butterworth, B. (2010). Foundational numerical capacities and the origins of dyscalculia. Trends Cogn. Sci. 14, 534–541.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Calabria, M., Jacquin-Courtois, S., Miozzo, A., Rossetti, Y., Padovani, A., Cotelli, M., and Miniussi, C. (2011). Time perception in spatial neglect: a distorted representation. Neuropsychology 25, 193–200.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Camos, V. (2009). Numerosity discrimination in children with Down syndrome. Dev. Neuropsychol. 34, 435–447.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cantlon, J. F., Brannon, E. M., Carter, E. J., and Pelphrey, K. A. (2006). Functional imaging of numerical processing in adults and four-year-old children. PLoS Biol. 4:0844–0854. doi: 10.1371/journal.pbio.0040125

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cantlon, J. F., Libertus, M. E., Pinel, P., Dehaene, S., Brannon, E. M., and Pelphrey, K. A. (2009). The neural development of an abstract concept of number. J. Cogn. Neurosci. 21, 2217–2229.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cantlon, J. F., Pinel, P., Dehaene, S., and Pelphrey, K. A. (2011). Cortical representations of symbols, objects, and faces are pruned back during early childhood. Cereb. Cortex 21, 191–199.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cantlon, J. F., Safford, K. E., and Brannon, E. M. (2010). Spontaneous analog number representations in 3-year-old children. Dev. Sci. 13, 289–297.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cappelletti, M., Freeman, E. D., and Cipolotti, L. (2009). Dissociations and interactions between time, numerosity and space processing. Neuropsychologia 47, 2732–2748.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cappelletti, M., Freeman, E. D., and Cipolotti, L. (2011). Numbers and time doubly dissociate. Neuropsychologia 49, 3078–3092.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Carey, S. (1998). Knowledge of number: its evolution and ontogenesis. Science 242, 641–642.

Pubmed Abstract | Pubmed Full Text

Carey, S. (2001). “On the very possibility of discontinuties in conceptual development,” in Language, Brain, and Cognitive Development: Essays in Honor of Jacques Mehler, ed E. Dupoux (Cambridge, MA: MIT Press), 303–324.

Carey, S. (2004). Bootstrapping and the origin of concepts. Daedalus 133, 59–68.

Casini, L., and Ivry, R. B. (1999). Effects of divided attention on temporal processing in patients with lesions of the cerebellum or frontal lobe. Neuropsychology 13, 10–21.

Pubmed Abstract | Pubmed Full Text

Casasanto, D., and Boroditsky, L. (2008). Time in the mind: using space to think about time. Cognition 106, 579–593.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Casarotti, M., Michielin, M., Zorzi, M., and Umiltà, C. (2007). Temporal order judgment reveals how number magnitude affects visuospatial attention. Cognition 102, 101–117.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chen, K.-M., and Yeh, S.-L. (2009). Asymmetric cross-modal effects in time perception. Acta Psychol. 130, 225–234.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cheng, R. K., MacDonald, C. J., and Meck, W. H. (2006). Differential effects of cocaine and ketamine on time estimation: implications for neurobiological models of interval timing. Pharmacol. Biochem. Behav. 85, 114–122.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cheng, R. K., MacDonald, C. J., Williams, C. L., and Meck, W. H. (2008). Prenatal choline supplementation alters the timing, emotion, and memory performance (TEMP) of adult male and female rats as indexed by differential reinforcement of low-rate schedule behavior. Learn. Mem. 15, 153–162.

Pubmed Abstract | Pubmed Full Text

Chiang, H. M., and Lin, Y. H. (2007). Mathematical ability of students with Asperger syndrome and high-functioning autism: a review of the literature. Autism 11, 547–556.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chiang, W. C., and Wynn, K. (2000). Infants' tracking of objects and collections. Cognition 77, 169–195.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chochon, F., Cohen, L., van de Moortele, P. F., and Dehaene, S. (1999). Differential contributions of the left and right inferior parietal lobules to number processing. J. Cogn. Neurosci. 11, 617–630.

Pubmed Abstract | Pubmed Full Text

Church, R. M., and Broadbent, H. A. (1990). Alternative representations of time, number and rate. Cognition 37, 55–81.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Church, R. M., and Deluty, M. Z. (1977). Bisection of temporal intervals. J. Exp. Psychol. Anim. Behav. Process. 3, 216–228.

Pubmed Abstract | Pubmed Full Text

Church, R. M., and Gibbon, J. (1982). Temporal generalization. J. Exp. Psychol. Anim. Behav. Process. 8, 165–186.

Pubmed Abstract | Pubmed Full Text

Church, R. M., and Meck, W. H. (1984). “The numerical attribute of stimuli,” in Animal Cognition, eds H. L. Roitblat, T. G. Bever, and H. S. Terrace (Hillsdale, NJ: Erlbaum), 445–464.

Clearfield, M. W., and Mix, K. S. (1999). Number versus contour length in infants' discrimination of small visual sets. Psychol. Sci. 10, 408–411.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Clément, A., and Droit-Volet, S. (2006). Counting in a time discrimination task in children and adults. Behav. Process. 71, 164–171.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Clifton, R. K. (1974). Heart rate conditioning in the newborn infant. J. Exp. Child Psychol. 18, 9–21.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cohen, L., and Dehaene, S. (1996). Cerebral networks for number processing: evidence from a case of posterior callosal lesion. Neurocase 155–174.

Cordes, S., and Brannon, E. M. (2009). Crossing the divide: infants discriminate small from large numerosities. Dev. Psychol. 45, 1583–1594.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cordes, S., Gelman, R., Gallistel, C. R., and Whalen, J. (2001). Variability signatures distinguish verbal from nonverbal counting for both large and small numbers. Psychon. Bull. Rev. 8, 698–707.

Pubmed Abstract | Pubmed Full Text

Cordes, S., Williams, C. L., and Meck, W. H. (2007). Common representations of abstract quantities. Curr. Dir. Psychol. Sci. 16, 156–161.

Coull, J. T., Cheng, R. K., and Meck, W. H. (2011). Neuroanatomical and neurochemical substrates of timing. Neuropsychopharmacology 36, 3–25.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Coull, J. T., and Nobre, A. C. (1998). Where and when to pay attention: the neural systems for directing attention to spatial locations and to time intervals as revealed by both PET and fMRI. J. Neurosci. 18, 7426–7435.

Coull, J. T., Vidal, F., Nazarian, B., and Macar, F. (2004). Functional anatomy of the attentional modulation of time estimation. Science 303, 1506–1508.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Danckert, J., Ferber, S., Pun, C., Broderick, C., Striemer, C., Rock, S., and Stewart, D. (2007). Neglected time: impaired temporal perception of multisecond intervals in unilateral neglect. J. Cogn. Neurosci. 19, 1706–1720.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dehaene, S. (1997). The1 Number Sense: How the Mind Creates Mathematics. New York, NY: Oxford University Press.

Dehaene, S. (2003). The neural basis of the Weber-Fechner law: a logarithmic mental number line. Trends Cogn. Sci. 7, 145–147.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dehaene, S., Bossini, S., and Giraux, P. (1993). The mental representation of parity and number magnitude. J. Exp. Psychol. Gen. 122, 371–396.

Dehaene, S., and Brannon, E. M. (2010). Space, time, and number: a Kantian research program. Trends Cogn. Sci. 14, 517–519.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dehaene, S., and Changeux, J. (1993). Development of elementary numerical abilities: a neuronal model. J. Cogn. Neurosci. 5, 390–407.

Dehaene, S., Molko, N., Cohen, L., and Wilson, A. J. (2004). Arithmetic and the brain. Curr. Opin. Neurobiol. 14, 218–224.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dehaene, S., Piazza, M., Pinel, P., and Cohen, L. (2003). Three parietal circuits for number processing. Cogn. Neuropsychol. 20, 487–506.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dehaene, S., Spelke, E., Pinel, P., Stanescu, R., and Tsivkin, S. (1999). Sources of mathematical thinking: behavioral and brain-imaging evidence. Science 284, 970–974.

Pubmed Abstract | Pubmed Full Text

DeLong, A. J. (1981). Phenomenological space-time: toward an experiential relativity. Science 213, 681–683.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

de Hevia, M. D., Girelli, L., Bricolo, E., and Vallar, G. (2008). The representational space of numerical magnitude: illusions of length. Q. J. Exp. Psychol. 61, 1496–1514.

Pubmed Abstract | Pubmed Full Text

De Smedt, B., Verschaffel, L., and Ghesqiere, P. (2009). The predictive value of numerical magnitude comparison for individual differences in mathematics achievement. J. Exp. Child Psychol. 103, 469–479.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dormal, V., and Pesenti, M. (2007). Numerosity-length interference: a Stroop Experiment. Exp. Psychol. 54, 289–297.

Pubmed Abstract | Pubmed Full Text

Dormal, V., Seron, X., and Pesenti, M. (2006). Numerosity-duration interference: a Stroop experiment. Acta Psychol. (Amst) 121, 109–124.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit, S. (1994). Temporal regulation of behavior with an external clock in 3-year-old children: differences between waiting and response duration tasks. J. Exp. Child Psychol. 58, 332–345.

Droit, S. (1995). Learning by doing in 3- and 4-year-old children: adapting to time. Eur. Bull. Cogn. Psychol. 14, 283–299.

Droit, S., Pouthas, V., and Jacquet, A. Y. (1990). Temporal learning in 4 12- and 6-year-old children: role of instructions and prior knowledge. J. Exp. Child Psychol. 50, 305–321.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit-Volet, S. (1998). Time estimation in young children: an initial force rule governing time production. J. Exp. Child Psychol. 68, 236–249.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit-Volet, S. (2002). Scalar timing in temporal generalization in children with short and long durations. Q. J. Exp. Psychol. A 55, 1193–1209.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit-Volet, S. (2003a). “Temporal experience and timing in children,” in Functional and Neural Mechanisms of Interval Timing, ed W. H. Meck (Boca Raton, FL: CRC Press LLC), 183–208.

Droit-Volet, S. (2003b). Alerting attention and time perception in children. J. Exp. Child Psychol. 85, 372–384.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit-Volet, S., Cle&#x02018;ıment, A., and Fayol, M. (2003). Time and number discrimination in a bisection task with a sequence of stimuli: a developmental approach. J. Exp. Child Psychol. 84, 63–76.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit-Volet, S., Cle&#x02018;ıment, A., and Fayol, M. (2008). Time, number and length: similarities and differences in discrimination in adults and children. Q. J. Exp. Psychol. 61, 1827–1846.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit-Volet, S., Clément, A., and Wearden, J. H. (2001). Temporal generalization in 3- to 8-year-old children. J. Exp. Child Psychol. 80, 271–288.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit-Volet, S., and Meck, W. H. (2007). How emotions colour our perception of time. Trends Cogn. Sci. 11, 504–513.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit-Volet, S., Meck, W. H., and Penney, T. B. (2007). Sensory modality and time perception in children and adults. Behav. Processes 74, 244–250.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit-Volet, S., and Rattat, A-C. (1999). Are time and action dissociated in young children's time estimation? Cogn. Dev. 14, 573–595.

Droit-Volet, S., Tourret, S., and Wearden, J. (2004). Perception of the duration of auditory and visual stimuli in children and adults. Q. J. Exp. Psychol. A 57, 797–818.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Droit-Volet, S., and Wearden, J. H. (2001). Temporal bisection in children. J. Exp. Child Psychol. 80, 142–159.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eger, E., Sterzer, P., Russ, M. O., Giraud, A. L., and Kleinschmidt, A. (2003). A supramodal number representation in human intraparietal cortex. Neuron 37, 719–725.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eimas, P. D., and Miller, J. L. (1980). Contextual effects in infant speech perception. Science 209, 1140–1141.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Emmerton, J. (1998). Numerosity differences and effects of stimulus density on pigeons' discrimination performance. Anim. Learn. Behav. 26, 243–256.

Falter, C. M., and Noreika, V. (2011). Interval timing deficits and abnormal cognitive development. Front. Integr. Neurosci. 5:26. doi: 10.3389/fnint.2011.00026

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Feigenson, L. (2005). A double-dissociation in infants' representations of object arrays. Cognition 95, B37–48.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Feigenson, L. (2007). The equality of quantity. Trends Cogn. Sci. 11, 185–187.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Feigenson, L., Carey, S., and Hauser, M. D. (2002). Infant's spontaneous judgements of ordinality. Psychol. Sci. 13, 150–156.

Pubmed Abstract | Pubmed Full Text

Feigenson, L., Carey, S., and Spelke, E. (2002). Infants' discrimination of number vs. continuous extent. Cogn. Psychol. 44, 33–66.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Feigenson, L., Dehaene, S., and Spelke, E. (2004). Core systems of number. Trends Cogn. Sci. 8, 307–314.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Feron, J., Gentaz, E., and Streri, A. (2006). Evidence of amodal representation of small numbers across visuo-tactile modalities in 5-month-old infants. Cogn. Dev. 21, 81–92.

Fetterman, J. G. (1993). Numerosity discrimination: both time and number matter. J. Exp. Psychol. Anim. Behav. Process. 19, 149–164.

Pubmed Abstract | Pubmed Full Text

Fetterman, J. G., and MacEwen, D. (1989). Short-term memory for responses: the “choose-small” effect. J. Exp. Anal. Behav. 52, 311–324.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fias, W., Lammertyn, J., Reynvoet, B., Dupont, P., and Orban, G. A. (2003). Parietal representation of symbolic and nonsymbolic magnitude. J. Cogn. Neurosci. 15, 47–56.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fraisse, P. (1967). Psychology of Time. Paris: PUF.

Frassinetti, F., Magnani, B., and Oliveri, M. (2009). Prismatic lenses shift time perception. Psychol. Sci. 20, 949–954.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fuson, K. (1992). “Relationships between counting and cardinality from age 2 to age 8,” in Pathways to Number: Children's Developing Numerical Abilities, eds J. Bideaud, C. Meljac, and J. P. Fischer (Hillsdale, NJ: Lawrence Erlbaum Associates), 349–361.

Gallistel, C. R. (1989). Animal cognition: the representation of space, time and number. Ann. Rev. Psychol. 40, 155–189.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gallistel, C. R. (1990). The Organization of Learning. Cambridge, MA: MIT Press.

Gallistel, C. R., and Gelman, R. (1992). Preverbal and verbal counting and computation. Cognition 44, 43–74.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gallistel, C. R., and Gelman, R. (2000). Non-verbal numerical cognition: from reals to integers. Trends Cogn. Sci. 4, 59–65.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gautier, T., and Droit-Volet, S. (2001). Attention and time estimation in 5- and 8-year-old children: a dual-task procedure. Behav. Processes. 28, 57–66.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Geary, D. C., Hoard, M. K., Byrd-Craven, J., Nugent, L., and Numtee, C. (2007). Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Dev. 78, 1343–1359.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gelman, R., and Cohen, M. (1988). “Qualitative differences in the way Down syndrome and normal children solve a novel counting problem,” in The Psychobiology of Down's Syndrome, ed L. Nadel (Cambridge, MA: MIT Press), 51–99.

Gelman, R., and Cordes, S. (2001). “Counting in animals and humans,” in Language, Brain, and Cognitive Development: Essays in Honor of Jacques Mehler, ed E. Dupoux (Cambridge, MA: MIT Press), 279–301.

Gelman, R., and Gallistel, C. R. (1978). The Child's Understanding of Number. Cambridge, MA: Harvard University Press.

Gelman, R., and Gallistel, C. R. (2004). Language and the origin of numerical concepts. Science 306, 441–443.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gibbon, J. (1977). Scalar expectancy theory and Weber's Law in animal timing. Psychol. Rev. 84, 279–325.

Gibbon, J., and Church, R. M. (1981). Time left: linear versus logarithmic subjective time. J. Exp. Psychol. Anim. Behav. Process. 7, 87–107.

Pubmed Abstract | Pubmed Full Text

Gibbon, J., Church, R. M., and Meck, W. H. (1984). Scalar timing in memory. Ann. N.Y. Acad. Sci. 423, 52–77.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gibbon, J., Malapani, C., Dale, C. L., and Gallistel, C. (1997). Toward a neurobiology of temporal cognition: advances and challenges. Curr. Opin. Neurobiol. 7, 170–184.

Pubmed Abstract | Pubmed Full Text

Grondin, S., Meilleur-Wells, G., and Lachance, R. (1999). When to start explicit counting in a time-intervals discrimination task: a critical point in the timing process of humans. J. Exp. Psychol. Hum. Percept. Perform. 25, 993–1004.

González-Garrido, A. A., Ruiz-Sandoval, J. L., Gomez-Velazquez, F. R., de Alba, J. L., and Villasenor-Cabrera, T. (2002). Hypercalculia in savant syndrome: central executive failure. Arch. Med. Res. 33, 586–589.

Pubmed Abstract | Pubmed Full Text

Gooch, D., Snowling, M., and Hulme, C. (2011). Time perception, phonological skills and executive function in children with dyslexia and/or ADHD symptoms. J. Child Psychol. Psychiatry 52, 195–203.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gu, B. M., and Meck, W. H. (2011). New perspectives on Vierordt's law: memory-mixing in ordinal temporal comparison tasks. Lect. Notes Comp. Sci. 6789 LNAI, 67–78.

Halberda, J., and Feigenson, L. (2008). Developmental change in the acuity of the “Number Sense”: the approximate number system in 3-, 4-, 5-, and 6- year olds and adults. Dev. Psychol. 44, 1457–1465.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harrington, D. L., Boyd, L. A., Mayer, A. R., Sheltraw, D. M., Lee, R. R., Huang, M., and Rao, S. M. (2004). Neural representation of interval encoding and decision making. Cogn. Brain Res. 21, 193–205.

Pubmed Abstract | Pubmed Full Text

Harrington, D. L., Castillo, G. N., Fong, C. H., and Reed, J. D. (2011). Neural underpinnings of distortions in the experience of time across senses. Front. Integr. Neurosci. 5:32. doi: 10.3389/fnint.2011.00032

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harrington, D. L., and Haaland, K. Y. (1999). Neural underpinnings of temporal processing: a review of focal lesion, pharmacological, and functional imaging research. Rev. Neurosci. 10, 91–116.

Pubmed Abstract | Pubmed Full Text

Harrington, D. L., Zimbelman, J. L., Hinton, S. C., and Rao, S. M. (2010). Neural modulation of temporal encoding, maintenance, and decision processes. Cereb Cortex. 20, 1274–1285.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Henik, A., Rubinsten, O., and Ashkenazi, S. (2011). The “where” and “what” in developmental dyscalculia. Clin. Neuropsychol. 25, 989–1008.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Heine, A., Tamm, S., Wissmann, J., and Jacobs, A. M. (2011). Electrophysiological correlates of non-symbolic numerical magnitude processing in children: joining the dots. Neuropsychologia 49, 3238–3246.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hinton, S. C., Harrington, D. L., Binder, J. R., Durgerian, S., and Rao, S. M. (2004). Neural systems supporting timing and chronometric counting: an FMRI study. Cogn. Brain Res. 21, 183–192.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hinton, S. C., and Meck, W. H. (1997). The ‘internal clocks’ of circadian and interval timing. Endeavour 21, 82–87.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hinton, S. C., and Meck, W. H. (2004). Frontal-striatal circuitry activated by human peak-interval timing in the supra-seconds range. Cogn. Brain Res. 21, 171–182.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hinton, S. C., and Rao, S. M. (2004). “One-thousand one \dots one-thousand two \dots ”: chronometric counting violates the scalar property in interval timing. Psychon. Bull. Rev. 11, 24–30.

Pubmed Abstract | Pubmed Full Text

Hoeckner, S. H., Moeller, K., Zauner, H., Wood, G., Haider, C., Gassner, A., and Nuerk, H. C. (2008). Impairments of the mental number line for two-digit numbers in neglect. Cortex 44, 429–438.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Holloway, I. D., and Ansari, D. (2010). Developmental specialization in the right intraparietal sulcus for the abstract representation of numerical magnitude. J. Cogn. Neurosci. 22, 2627–2637.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Holmes, K. J., and Lourenco, S. F. (2009). “Spatial organization of magnitude in the representation of number and emotion,” in Proceedings of the 31th Annual Conference of the Cognitive Science Society, eds N. A. Taatgen and H. van Rijn (Austin, TX: Cognitive Science Society), 2402–2407.

Hubbard, E. M., Piazza, M., Pinel, P., and Dehaene, S. (2005). Interactions between number and space in parietal cortex. Nat. Rev. Neurosci. 6, 435–448.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Huntley-Fenner, G. (2001). Children's understanding of number is similar to adults' and rats': numerical estimation by 5–7-year-olds. Cognition 78, B27–40.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Huntley-Fenner, G., and Cannon, E. (2000). Preschoolers' magnitude comparisons are mediated by a preverbal analog mechanism. Psychol. Sci. 11, 147–152.

Pubmed Abstract | Pubmed Full Text

Huttenlocher, J., Jordan, N. C., and Levine, S. C. (1994). A mental model for early arithmetic. J. Exp. Psychol. Gen. 123, 284–296.

Pubmed Abstract | Pubmed Full Text

Hyde, D. C. (2011). Two systems of non-symbolic numerical cognition. Front. Hum. Neurosci. 5:150. doi: 10.3389/fnhum.2011.00150

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hyde, D. S., Boas, D. A., Blair, C., and Carey, S. (2010). Near-infrared spectroscopy shows right parietal specialization for number in pre-verbal infants. Neuroimage 53, 647–652.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hyde, D. C., and Spelke, E. S. (2011). Neural signatures of number processing in human infants: evidence for two core systems underlying numerical cognition. Dev. Sci. 360–371.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hyde, D. C., and Spelke, E. S. (2012). Spatiotemporal dynamics of processing nonsymbolic number: an event-related potential source localization study. Hum. Brain Mapp. (in press).

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izard, V., Dehaene-Lambertz, G., and Dehaene, S. (2008). Distinct cerebral pathways for object identity and number in human infants. PLoS Biol. 6:e11. doi: 10.1371/journal.pbio.0060011

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izard, V., Sann, C., Spelke, E. S., and Streri, A. (2009). Newborn infants perceive abstract numbers. Proc. Natl. Acad. Sci. U.S.A. 106, 10382–10385.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jaffe, J., Beebe, B., Feldstein, S., Crown, C., and Jasnow, M. (2001). Rhythms of dialogue in infancy. Monogr. Soc. Res. Child Dev. 66 (2 Serial No. 265).

Pubmed Abstract | Pubmed Full Text

Jahanshahi, M., Jones, C. R., Dirnberger, G., and Frith, C. D. (2006). The substantia nigra pars compacta and temporal processing. J. Neurosci. 22, 12266–12273.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jevons, W. S. (1871). The power of numerical discrimination. Nature 363–372.

Jones, C. R., Happé, F., Baird, G., Simonoff, E., Marsden, A. J., Tregay, J., Phillips, R. J., Goswami, U., Thomson, J. M., and Thompson, J. M. (2009a). Auditory discrimination and auditory sensory behaviors in autism spectrum disorders. Neuropsychologia 47, 2850–2858.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jones, C. R., Happé, F., Golden, H., Marsden, A. J., Tregay, J., Simonoff, E., Pickles, A., Baird, G., and Charman, T. (2009b). Reading and arithmetic in adolescents with autism spectrum disorders: peak and dips in attainment. Neuropsychology 23, 718–728.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jordan, K. E., and Brannon, E. M. (2006). The multisensory representation of number in infancy. Proc. Natl. Acad. Sci. U.S.A. 103, 3486–3489.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jordan, N. C., Kaplan, D., Olah, L. N., and Locuniak, M. N. (2006). Number sense growth in kindergarten: a longitudinal investigation of children at risk for mathematics difficulties. Child Dev. 77, 153–175.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jordan, N. C., Kaplan, D., Locuniak, M. N., and Ramineni, C. (2007). Predicting first-grade math achievement from developmental number sense trajectories. Learn. Disabil. Res. Pract. 22, 36–46.

Jordan, K. E., Suanda, S. H., and Brannon, E. M. (2008). Intersensory redundancy accelerates preverbal numerical competence. Cognition 108, 210–212.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jordan, N. C., Kaplan, D., Ramineni, C., and Locuniak, M. N. (2009). Early math matters: kindergarten number competence and later mathematics outcomes. Dev. Psychol. 45, 850–867.

Pubmed Abstract | Pubmed Full Text

Jusczyk, P. W., Pisoni, D. B., Reed, M. A., Fernald, A., and Myers, M. (1983). Infants' discrimination of the duration of a rapid spectrum change in nonspeech signals. Science 222, 175–177.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kadosh, R. C., Kadosh, K. C., Linden, D. E. J., Gevers, W., Berger, A., and Henik, A. (2005). The brain locus of interaction between number and size: a combined functional magnetic resonance imaging and event-related potential study. J. Cogn. Neurosci. 19, 957–970.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kahneman, D., Treisman, A., and Gibbs, B. J. (1992). The reviewing of object files: object-specific integration of information. Cogn. Psychol. 24, 175–219.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kaiser, M. D., Hudac, C. M., Shultz, S., Lee, S. M., Cheung, C., Berken, A. M., Deen, B., Pitskel, N. B., Sugrue, D. R., Voos, A. C., Saulnier, C. A., Ventola, P., Wolf, J. M., Klin, A., Vander Wyk, B. C., and Pelphrey, K. A. (2010). Neural signatures of autism. Proc. Natl. Acad. Sci. U.S.A. 107, 21223–21228.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kaufmann, L., Koppelstaetter, F., Siedentopf, C., Haala, I., Haberlandt, E., Zimmerhackl, L-B., Felber, S., and Ischebeck, A. (2006). Neural correlates of a number–size interference task in children. Neuroreport 17, 587–591.

Pubmed Abstract | Pubmed Full Text

Kaufmann, L., and Nuerk, H. C. (2006). Interference effects in a numerical Stroop paradigm in 9- to 12-year-old children with ADHD-C. Child Neuropsychol. 12, 223–243.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kaufmann, L., and Neurk, H. C. (2008). Basic number processing deficits in ADHD: a broad examination of elementary and complex number processing skills in 9- to 12-year-old children with ADHD-C. Dev. Sci. 11, 692–699.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kaufmann, L., Vogel, S. E., Starke, M., Kremser, C., Schocke, M., and Wood, G. (2009). Developmental dyscalculia: compensatory mechanisms in left intraparietal regions in response to nonsymbolic magnitudes. Behav. Brain Funct. 5, 35.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kaufmann, L., Vogel, S. E., Wood, G., Kremser, C., Schocke, M., Zimmerhacki, L. B., and Koten, J. W. (2008). A developmental fMRI study of nonsymbolic numerical and spatial processing. Cortex 44, 376–385.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Killeen, P. R., and Fetterman, J. G. (1988). A behavioral theory of timing. Psychol. Rev. 95, 274–295.

Pubmed Abstract | Pubmed Full Text

Kobayashi, T., Hiraki, K., Mugitani, R., and Hasegawa, T. (2004). Baby arithmetic: one object plus one tone. Cognition 91, B23–B34.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kopec, C. D., and Brody, C. D. (2010). Human pereformance on the temporal bisection task. Brain Cogn. 74, 262–272.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kotz, S. A. E., and Schwartze, M. (2011). Differential input of the supplementary motor area to a dedicated temporal processing network: functional and clinical implications. Front. Integr. Neurosci. 5:86. doi: 10.3389/fnint.2011.00086

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Krajcsi, A., Lukacs, A., Igacs, J., Racsmany, M., and Pleh, C. (2009). Numerical abilities in Williams syndrome: dissociating the analogue magnitude system and verbal retrieval. J. Clin. Exp. Neuropsychol. 31, 439–446.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kramer, P., Bressan, P., and Grassi, M. (2011). Time estimation predicts mathematical intelligence. PLoS One 6:e28621. doi: 10.1371/journal.pone.0028621

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kwakye, L. D., Foss-Feig, J. H., Cascio, C. J., Stone, W. L., and Wallace, M. T. (2011). Altered auditory and multisensory temporal processing in autism spectrum disorders. Front. Integr. Neurosci. 4:129. doi: 10.3389/fnint.2010.00129

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lalli, J. S., Casey, S., Goh, H., and Merlino, J. (1994). Treatment of escape-maintained aberrant behavior with escape extinction and predictable routines. J. Appl. Behav. Anal. 27, 705–714.

Pubmed Abstract | Pubmed Full Text

Landerl, K., Bevan, A., and Butterworth, B. (2004). Developmental dyscalculia and basic numerical capacities: a case study of 8–9-year-old students. Cognition 93, 99–125.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Le Clec'h, H. G., Dehaene, S., Cohen, L., Mehler, J., Dupoux, E., Poline, J. B., Lehéricy, S., van de Moortele, P. F., and Le Bihan, D. (2000). Distinct cortical areas for names of numbers and body parts independent of language and input modality. Neuroimage 12, 381–391.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Le Corre, M., and Carey, S. (2007). One, two, three, four, nothing more: an investigation of the conceptual sources of the verbal counting principles. Cognition 105, 395–438.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Le Corre, M., and Carey, S. (2008). Why the verbal counting principles are constructed out of representations of small sets of individuals: a reply to Gallistel. Cognition 107, 650–662.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Leon, M. I., and Shadlen, M. N. (2003). Representation of time by neurons in the posterior parietal cortex of the macaque. Neuron 38, 317–327.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Levin, I. (1977). The development of time concepts in young children: reasoning about duration. Child Dev. 48, 435–444.

Levin, I. (1979). Interference of time related and unrelated cues with duration comparisons of young children: analysis of Piaget's formulation of the relation of time and speed. Child Dev. 50, 469–477.

Pubmed Abstract | Pubmed Full Text

Levin, I. (1982). “The nature and development of time concepts in children. The effects of interfering cues,” in The Developmental Psychology of Time, ed W. J. Friedman (New York, NY: Academic Press), 47–85.

Libertus, M. E., and Brannon, E. M. (2010). Stable individual differences in number discrimination in infancy. Dev. Sci. 13, 900–906.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Libertus, M. E., Feigenson, L., and Halberda, J. (2011a). Preschool acuity of the approximate number system correlates with school math ability. Dev. Sci. 14, 1292–1300.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Libertus, M. E., Brannon, E. M., and Woldorff, M. G. (2011b). Parallels in stimulus-driven oscillatory brain responses to numerosity changes in adults and seven-month-old infants. Dev. Neuropsychol. 36, 651–667.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Libertus, M. E., Pruitt, L. B., Woldorff, M. G., and Brannon, E. M. (2009). Induced alpha-band oscillations reflect ratio-dependent number discrimination in the infant brain. J. Cogn. Neurosci. 21, 2398–2406.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Libertus, M. E., Woldorff, M. G., and Brannon, E. M. (2007). Electrophysiological evidence for notation independence in numerical processing. Behav. Brain Funct. 3, 1.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lipton, J. S., and Spelke, E. S. (2003). Origins of number sense. Large-number discrimination in human infants. Psychol. Sci. 14, 396–401.

Pubmed Abstract | Pubmed Full Text

Lipton, J. S., and Spelke, E. S. (2005). Preschool children's mapping of number words to nonsymbolic numerosities. Child Dev. 76, 978–988.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Loetscher, T., Schwarz, U., Schubiger, M., and Brugger, P. (2008). Head turns bias the brain's internal random generator. Curr. Biol. 18, R60–R62.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Longo, M. R., and Lourenco, S. F. (2010). Bisecting the mental number line in near and far space. Brain Cogn. 72, 362–367.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lourenco, S. F., and Longo, M. R. (2010). General magnitude representation in human infants. Psychol. Sci. 21, 873–881.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lustig, C. (2011). The neuroscience of time and number: untying the Gordian knot. Front. Integr. Neurosci. 5:47. doi: 10.3389/fnint.2011.00047

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lustig, C., Matell, M. S., and Meck, W. H. (2005). Not “just” a coincidence: frontal-striatal synchronization in working memory and interval timing. Memory 13, 441–448.

Pubmed Abstract | Pubmed Full Text

Lustig, C., and Meck, W. H. (2001). Paying attention to time as one gets older. Psychol. Sci. 12, 478–484.

Pubmed Abstract | Pubmed Full Text

Lustig, C., and Meck, W. H. (2005). Chronic treatment with haloperidol induces working memory deficits in feedback effects of interval timing. Brain Cogn. 58, 9–16.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lustig, C., and Meck, W. H. (2011). Modality differences in timing and temporal memory throughout the lifespan. Brain Cogn. 77, 298–303.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Macar, F., Lejeune, H., Bonnet, M., Ferrara, A., Pouthas, V., Vidal, F., and Maquet, P. (2002). Activation of the supplementary motor area and of attentional networks during temporal processing. Exp. Brain Res. 142, 475–485.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Martin, J. S., Poirier, M., and Bowler, D. M. (2009). Brief report: impaired temporal reproduction performance in adults with autism spectrum disorder. J. Austim Dev. Disord. 40, 640–646.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Matell, M. S., Bateson, M., and Meck, W. H. (2006). Single-trials analyses demonstrate that increases in clock speed contribute to the methamphetamine-induced horizontal shifts in peak-inetrval timing functions. Psychopharmacology 188, 201–212.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Matell, M. S., King, G. R., and Meck, W. H. (2004). Differential adjustment of interval timing by the chronic administation of intermittent or continuous cocaine. Behav. Neurosci. 118, 150–156.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Matell, M. S., and Meck, W. H. (2000). Neuropsychological mechanisms of interval timing behavior. Bioessays 22, 94–103.

Pubmed Abstract | Pubmed Full Text

Matell, M. S., and Meck, W. H. (2004). Cortico-striatal circuits and interval timing: coincidence-detection of oscillatory processes. Cogn. Brain Res. 21, 139–170.

Pubmed Abstract | Pubmed Full Text

Matell, M. S., Meck, W. H., and Nicolelis, M. A. L. (2003). Interval timing and the encoding of signal duration by ensembles of cortical and striatal neurons. Behav. Neurosci. 117, 760–773.

Pubmed Abstract | Pubmed Full Text

Matell, M. S., Shea-Brown, E., Gooch, C., Wilson, A. G., and Rinzel, J. (2011). A heterogeneous population code for elapsed time in rat medial agranular cortex. Behav. Neurosci. 125, 54–73.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Matsuzawa, T. (1985). Use of numbers by a chimpanzee. Nature 315, 57–59.

Pubmed Abstract | Pubmed Full Text

Maquet, P., Lejeune, H., Pouthas, V., Bonnet, M., Casini, L., Macar, F., Timsit-Berthier, M., Vidal, F., Ferrara, A., Degueldre, C., Quaglia, L., Delfiore, G., Luxen, A., Woods, R., Mazziotta, J. C., and Comar, D. (1996). Brain activation induced by estimation of duration: a PET study. Neuroimage 3, 119–126.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McCormack, T., Brown, G. D. A., Maylor, E. A., Darby, R. J., and Green, D. (1999). Developmental changes in time estimation: comparing childhood and old age. Dev. Psychol. 35, 1143–1155.

Pubmed Abstract | Pubmed Full Text

McCormack, T., Brown, G. D., Smith, M. C., and Brock, J. (2004). A timing-specific memory disortion effects in young children. J. Exp. Child Psychol. 87, 33–56.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McCrink, K., and Wynn, K. (2004). Large-number addition and subtraction by 9-month-old infants. Psychol. Sci. 15, 776–781.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Meck, W. H. (1983). Selective adjustment of the speed of internal clock and memory processes. J. Exp. Psychol. Anim. Behav. Process. 9, 171–201.

Pubmed Abstract | Pubmed Full Text

Meck, W. H. (1984). Attentional bias between modalities: effect on the internal clock, memory, and decision stages used in animal time discrimination. Ann. N.Y. Acad. Sci. 423, 528–541.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Meck, W. H. (1996). Neuropharmacology of timing and time perception. Cogn. Brain Res. 3, 227–242.

Pubmed Abstract | Pubmed Full Text

Meck, W. H. (1997). “Application of a mode-control model of temporal integration to counting and timing behaviour,” in Time and Behaviour: Psychological and Neurobiological Analyses, eds. C. M. Bradshaw and E. Szabadi (New York, NY: Elsevier), 133–184.

Meck, W. H. (2003). Functional and Neural Mechanisms of Interval Timing. Boca Raton, FL: CRC Press LLC.

Meck, W. H. (2005). Neuropsychology of timing and time perception. Brain Cogn. 58, 1–8.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Meck, W. H. (2006a). Frontal cortex lesions eliminate the clock speed effect of dopaminergic drugs on interval timing. Brain Res. 1108, 157–167.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Meck, W. H. (2006b). Neuroanatomical localization of an internal clock: a functional link between mesolimbic, nigrostriatal, and mesocortical dopaminergic systems. Brain Res. 1109, 93–107.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Meck, W. H., and Benson, A. M. (2002). Dissecting the brain's internal clock: how frontal-stratial circuitry keeps time and shifts attention. Brain Cogn. 48, 195–211.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Meck, W. H., and Church, R. M. (1983). A mode-control model of counting and timing processes. J. Exp. Psychol. Anim. Behav. Process. 9, 320–334.

Pubmed Abstract | Pubmed Full Text

Meck, W. H., and Church, R. M. (1987). Cholinergic modulation of the content of temporal memory. Behav. Neurosci. 101, 457–464.

Pubmed Abstract | Pubmed Full Text

Meck, W. H., Church, R. M., and Gibbon, J. (1985). Temporal integration in duration and number discrimination. J. Exp. Psychol. Anim. Behav. Process. 11, 591–597.

Pubmed Abstract | Pubmed Full Text

Meck, W. H., and Malapani, C. (2004). Neuroimaging of interval timing. Cogn. Brain Res. 21, 133–137.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Meck, W. H., Penney, T. B., and Pouthas, V. (2008). Cortico-striatal representation of time in animals and humans. Curr. Opin. Neurobiol. 18, 145–152.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Meck, W. H., and Williams, C. L. (1997). Characterization of the facilitative effects of perinatal choline supplementation on timing and temporal memory. Neuroreport 8, 2831–2835.

Pubmed Abstract | Pubmed Full Text

Melgire, M., Ragot, R., Samson, S., Penney, T. B., Meck, W. H., and Pouthas, V. (2005). Auditory/visual duration bisection in patients with left or right medial-temporal lobe resection. Brain Cogn. 58, 119–124.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mix, K. S. (1999). Preschoolers' recognition of numerical equivalence: sequential sets. J. Exp. Child Psychol. 74, 309–332.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mix, K. S., Huttenlocher, J., and Levine, S. C. (1996). Do preschool children recognize auditory-visual numerical correspondences? Child Dev. 67, 1592–1608.

Pubmed Abstract | Pubmed Full Text

Mix, K. S., Huttenlocher, J., and Levine, S. C. (2002). Multiple cues for quantification in infancy: is number one of them? Psychol. Bull. 128, 278–294.

Pubmed Abstract | Pubmed Full Text

Mix, K. S., Moore, J. A., and Holcomb, E. (2011). One-to-one correspondence promotes numerical equivalence concepts. J. Cogn. Dev. 12, 463–480.

Möhring, W., Libertus, M. E., and Bertin, E. (2012). Speed discrimination in 6- and 10-month-old infants follows Weber's law. J. Exp. Child Psychol. 111, 405–418.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Moyer, R. S., and Landauer, T. K. (1967). Time required for judgments of numerical inequality. Nature 215, 1519–1520.

Pubmed Abstract | Pubmed Full Text

Mussolin, C., De Volder, A., Grandin, C., Schlogel, X., Nassogne, M-C., and Noel, M-P. (2009). Neural correlates of symbolic number comparison in developmental dyscalculia. J. Cogn. Neurosci. 22, 860–874.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Myers, G. E. (1971). Williams James on time perception. Philos. Sci. 38, 353–360.

Naccache, L., and Dehaene, S. (2001). The priming method: imaging unconscious repetition priming reveals an abstract representation of number in the parietal lobes. Cereb. Cortex 11, 966–974.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Navon, D. (1978). On a conceptual hierarchy of time, space, and other dimensions. Cognition 6, 223–228.

Nenadic, I., Gaser, C., Volz, H. P., Rammsayer, T., Hager, F., and Sauer, H. (2003). Processing of temporal information and the basal ganglia: new evidence from fMRI. Exp. Brain Res. 148, 238–246.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Newcombe, N. S. (2002). The nativist-empiricist controversy in the context of recent research on spatial and quantitative development. Psychol. Sci. 13, 395–401.

Pubmed Abstract | Pubmed Full Text

Nicholls, M. E., Forte, J. D., Loetscher, T., Orr, C. A., Yates, M. J., and Bradshaw, J. L. (2011a). Near, yet so far: the effect of pictorial cues on spatial attention. Brain Cogn. 76, 349–352.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nicholls, M. E., Lew, M., Loetscher, T., and Yates, M. J. (2011b). The importance of response type to the relationship between temporal order and numerical magnitude. Atten. Percept. Psychophys. 73, 1604–1613.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nicholls, M. E. R., Loftus, A., and Gevers, W. (2008). Look, no hands: a perceptual task shows that number magnitude induces shifts of attention. Psychon. Bull. Rev. 15, 413–418.

Pubmed Abstract | Pubmed Full Text

Nieder, A. (2004). The number domain- can we count on parietal cortex? Neuron 44, 407–409.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nieder, A., Freedman, D. J., and Miller, E. K. (2002). Representation of the quantity of visual items in the primate prefrontal cortex. Science 297, 1708–1711.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nieder, A., and Miller, E. K. (2003). Coding of cognitive magnitude: compressed scaling of numerical information in the primate prefrontal cortex. Neuron 37, 149–157.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nieder, A., and Miller, E. K. (2004a). Analog numerical representations in Rhesus monkeys: evidence for parallel processing. J. Cogn. Neurosci. 16, 889–901.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nieder, A., and Miller, E. K. (2004b). A parieto-frontal network for visual numerical information in the monkey. Proc. Natl. Acad. Sci. U.S.A. 101, 7457–7462.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nye, J., Fluck, M., and Buckley, S. (2001). Counting and cardinal understanding in children with Down syndrome and typically developing children. Down Syndr. Res. Pract. 7, 68–78.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O'Hearn, K., Hoffman, J. E., and Landau, B. (2011). Small subitizing range in people with Williams syndrome. Vis. Cogn. 19, 289–312.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O'Hearn, K., and Luna, B. (2009). Mathematical skills in Williams syndrome: Insight into the importance of underlying representations. Dev. Disabil. Res. Rev. 15, 11–20.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O'Hearn, K., and Landau, B. (2007). Mathematical skill in individuals with Williams syndrome: evidence from a standardized mathematics battery. Brain Cogn. 64, 238–246.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Oliveri, M., Vicario, C. M., Salerno, S., Koch, G., Turriziani, P., Mangano, R., Chillemi, G., and Caltagirone, C. (2008). Perceiving numbers alters time perception. Neurosci. Lett. 438, 308–311.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ornstein, R. (1969). On the Experience of Time. Harmondsworth, UK: Penguin.

Pastor, M. A., Day, B. L., Macaluso, E., Friston, K. J., and Frackowiak, R. S. (2004). The functional neuroanatomy of temporal discrimination. J. Neurosci. 24, 2585–2591.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Paterson, S. J., Girelli, L., Butterworth, B., and Karmiloff-Smith, A. (2006). Are numerical impairments syndrome specific? Evidence from Williams syndrome and Down's syndrome. J. Child Psychol. Psychiatry 47, 190–204.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Penney, T. B., Gibbon, J., and Meck, W. H. (2000). Differential effects of auditory and visual signals on clock speed and temporal memory. J. Exp. Psychol. Hum. Percept. Perform. 26, 1770–1787.

Pubmed Abstract | Pubmed Full Text

Penney, T. B., Gibbon, J., and Meck, W. H. (2008). Categorical scaling of duration bisection in pigeons (Columba livia), mice (Mus musculus), and humans (homo sapiens). Psychol. Sci.19, 1103–1109.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pepperberg, I. M. (2006). Ordinality and inferential abilities of a Grey Parrot (Psittacus erithacus). J. Comp. Psychol. 120, 205–216.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pesenti, M., Thioux, M., Seron, X., and De Volder, A. (2000). Neuroanatomical substrates of Arabic number processing, numerical comparison, and simple addition: a PET study. J. Cogn. Neurosci. 12, 461–479.

Pubmed Abstract | Pubmed Full Text

Pessoa, L., and Desimone, R. (2003). From humble neural beginnings comes knowledge of numbers. Neuron 37, 4–6.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pezzulo, G., and Rigoli, F. (2011). The value of foresight: how prospection affects decision-making, Front. Neurosci. 5:79. doi: 10.3389/fnins.2011.00079

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Piaget, J. (1946). The Development of the Notion of Time in Children. Paris: PUF.

Piaget, J. (1952). The Child's Conception of Number. New York, NY: Norton.

Piazza, M., Izard, V., Pinel, P., Le Bihan, D., and Dehaene, S. (2004). Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron 44, 547–555.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Piazza, M., Mechelli, A., Butterworth, B., and Price, C. J. (2002). Are subitizing and counting implemented as separate or functionally overlapping processes? Neuroimage 15, 435–446.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Piazza, M., Pinel, P., Le Bihan, D., and Dehaene, S. (2007). A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron 53, 293–305.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pinel, P., and Dehaene, S. (2010). Beyond hemispheric dominance: brain regions underlying the joint lateralization of language and arithmetic to the left hemisphere. J. Cogn. Neurosci. 22, 48–66.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pinel, P., Dehaene, S., Rivière, D., and LeBihan, D. (2001). Modulation of parietal activation by semantic distance in a number comparison task. Neuroimage 14, 1013–1026.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pinel, P., Piazza, M., Le Bihan, D., and Dehaene, S. (2004). Distributed and overlapping cerebral representations of number, size, and luminance during comparative judgments. Neuron 41, 983–993.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Porter, J. (1999). Learning to count: a difficult task? Down Syndr. Res. Pract. 6, 85–94.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pouthas, V. (2003). “Electrophysiological evidence for specific processing of temporal information in humans,” in Functional and Neural Mechanisms of Interval Timing, ed W. H. Meck (Boca Raton, FL: CRC Press LLC), 439–456.

Pouthas, V., Droit, S., Jacquet, A. Y., and Wearden, J. (1990). Temporal differentiation of response duration in children of different ages: developmental changes in relations between verbal and nonverbal behavior. J. Exp. Anal. Behav. 53, 21–31.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pouthas, V., George, N., Poline, J. B., Pfeuty, M., Vandemoorteele, P. F., Hugueville, L., Ferrandez, A. M., Lehéricy, S., Lebihan, D., and Renault, B. (2005). Neural network involved in time perception: an fMRI study comparing long and short interval estimation. Hum. Brain Mapp. 25, 433–441.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Provasi, J., Rattat, A. C., and Droit-Volet, S. (2011). Temporal bisection in 4-month olds. J. Exp. Psychol. Anim. Behav. Process. 37, 108–113.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rao, S. M., Mayer, A. R., and Harrington, D. L. (2001). The evolution of brain activation during temporal processing. Nat. Neurosci. 4, 317–323.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rattat, A. C., and Droit-Volet, S. (2005). The long-term retention of time: a developmental study. Q. J. Exp. Psychol. B 58, 163–176.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Revkin, S. K., Piazza, M., Izard, V., Cohen, L., and Dehaene, S. (2008). Does subitizing reflect numerical estimation? Psychol. Sci. 19, 607–614.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rivera, S. M., Reiss, A. L., Eckert, M. A., and Menon, V. (2005). Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cereb. Cortex 15, 1779–1790.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Roberts, W. A. (1995). Simultaneous numerical and temporal processing in the pigeon. Curr. Dir. Psychol. Sci. 4, 47–51.

Roberts, W. A. (2002). Are animals stuck in time? Psychol. Bull. 128, 473–489.

Pubmed Abstract | Pubmed Full Text

Roberts, W. A., and Boisvert, M. J. (1998). Using the peak procedure to measure timing and counting processes in pigeons. J. Exp. Psychol. Anim. Behav. Process. 24, 416–430.

Roberts, W. A., Coughlin, R., and Roberts, S. (2000). Pigeons flexibly time or count on cue. Psychol. Sci. 11, 218–222.

Pubmed Abstract | Pubmed Full Text

Roberts, W. A., Macuda, T., and Brodbeck, D. R. (1995). Memory for number of light flashes in the pigeon. Anim. Learn. Behav. 23, 182–188.

Roberts, W. A., and Mitchell, S. (1994). Can a pigeon simultaneously process temporal and numerical information? J. Exp. Psychol. Anim. Behav. Process. 20, 66–78.

Roitman, J. D., Brannon, E. M., Andrews, J. R., and Platt, M. L. (2007). Nonverbal representation of time and number in adults. Acta Psychol. 124, 296–318.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rousselle, L., and Noël, M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: a comparison of symbolic vs. non-symbolic number magnitude processing. Cognition 102, 361–395.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rousselle, L., Palmers, E., and Noel, M. P. (2004). Magnitude comparison in preschoolers: what counts? Influence of perceptual variables. J. Exp. Child Psychol. 87, 57–84.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rubinsten, O., and Henik, A. (2005). Automatic activation of internal magnitudes: a study of developmental dyscalculia. Neuropsychology 5, 641–648.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rumbaugh, D. M., Savage-Rumbaugh, S., and Hegel, M. T. (1987). Summation in the chimpanzee (Pan troglodytes). J. Exp. Psychol. Anim. Behav. Process. 13, 107–115.

Pubmed Abstract | Pubmed Full Text

Sandhofer, C. M., and Smith, L. B. (1999). Learning color words involves learning a system of mappings. Dev. Psychol. 35, 668–679.

Pubmed Abstract | Pubmed Full Text

Santens, S., Roggeman, C., Fias, W., and Verguts, T. (2010). Number processing pathways in human parietal cortex. Cereb. Cortex 20, 77–88.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sarrazin, J. C., Giraudo, M. D., Pailhous, J., and Bootsma, R. J. (2004). Dynamics of balancing space and time in memory: tau and kappa effects revisited. J. Exp. Psychol. Hum. Percept. Perform. 30, 411–430.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schubotz, R. I., Friederici, A. D., and von Cramon, D. Y. (2000). Time perception and motor timing: a common cortical and subcortical basis revealed by fMRI. Neuroimage 11, 1–12.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schubotz, R. I., and von Cramon, D. Y. (2001). Interval and ordinal properties of sequences are associated with distinct premotor areas. Cereb. Cortex 11, 210–222.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sereno, M. I., Pitzalis, S., and Martinez, A. (2001). Mapping of contralateral space in retinotopic coordinates by a parietal cortical area in humans. Science 294, 1350–1354.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shuman, M., and Kanwisher, N. (2004). Numerical magnitude in the human parietal lobe; tests of representational generality and domain specificity. Neuron 44, 557–569.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Siegel, L. S. (1974). Heterogeneity and spatial factors as determinants of numeration ability. Child Dev. 45, 532–534.

Siegler, R. S., and Booth, J. L. (2004). Development of numerical estimation in young children. Child Dev. 75, 428–444.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Siegler, R. S., and Ramani, G. B. (2009). Playing linear number board games-but not circular ones-improves low-income preschoolers' numerical understanding. J. Educ. Psychol. 101, 545–560.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Simen, P., Balci, F., deSouza, J., Cohen, J. D., and Holmes, P. (2011). Interval timing by long-range temporal integration. Front. Integr. Neurosci. 5:28. doi: 10.3389/fnint.2011.00028

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Simon, O., Kherif, F., Flandin, G., Poline, J. B., Riviere, D., Mangin, J. F., LeBihan, D., and Dehane, S. (2004). Automatized clustering and functional geometry of human parietofrontal networks for language, space and number. Neuroimage 23, 1192–1202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Skinner, B. F. (1938). The Behavior of Organisms. New York, NY: Appleton-Century.

Skinner, B. F. (1948). “Superstition” in the pigeon. J. Exp. Psychol. 38, 168–172.

Pubmed Abstract | Pubmed Full Text

Smith, L. B., and Sera, M. D. (1992). A developmental analysis of the polar structure of dimensions. Cogn. Psychol. 24, 99–142.

Pubmed Abstract | Pubmed Full Text

Smith, A. B., Taylor, E., Brammer, M., Halari, R., and Rubia, K. (2008). Reduced activation in right lateral prefrontal cortex and anterior cingulated gyrus in medication-naïve adolescents with attention deficit hyperactivity disorder during time discrimination. J. Child Psychol. Psychiatry 49, 977–985.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Spaepen, E., Coppola, M., Spelke, E. S., Carey, S. E., and Goldin-Meadow, S. (2011). Number without a language model. Proc. Natl. Acad. Sci. U.S.A. 108, 3163–3168.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Spelke, E. (2000). Core knowledge. Am. Psychol. 55, 1233–1243.

Pubmed Abstract | Pubmed Full Text

Spelke, E. (2011). Quinian bootstrapping or Fodorian combination? Core and constructed knowledge of number. Behav. Brain Sci. 34, 149–150.

Starkey, P. (1992). The early development of numerical reasoning. Cognition 43, 93–126.

Pubmed Abstract | Pubmed Full Text

Starkey, P., and Cooper, R. G. Jr. (1980). Perception of numbers by human infants. Science 210, 1033–1035.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Starkey, P., Spelke, E. S., and Gelman, R. (1983). Detection of intermodal numerical correspondences by human infants. Science 222, 179–181.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Starkey, P., Spelke, E. S., and Gelman, R. (1990). Numerical abstraction by human infants. Cognition 36, 97–127.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Strauss, M. S., and Curtis, L. E. (1981). Infant perception of numerosity. Child Dev. 52, 1146–1152.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stern, D., and Gibbon, J. (1978). “Temporal expectancies of social behaviors in mother-infant play,” in Origins of the Infant's Social Responsiveness, ed. E. Thoman (New York, NY: Wiley), 409–429.

Szelag, E., Kowalska, J., Galkowski, T., and Poppel, E. (2004). Temporal processing deficits in high-functioning children with autism. Br. J. Psychol. 95, 269–282.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Szucs, D., and Soltesz, F. (2007). Event-related potentials dissociate facilitation and interference effects in the numerical Stroop paradigm. Neuropsychology 45, 3190–3202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Temple, C. M. (1992). “Developmental dyscalculia,” in Handbook of Neuropsychology: Vol. 7, Child Neuropsychology, eds S. J. Segalowitz and I. Rapin (New York, NY: Elsevier), 211–222.

Temple, E., and Posner, M. I. (1998). Brain mechanisms of quantity are similar in 5-year-old children and adults. Proc. Natl. Acad. Sci. U.S.A. 95, 7836–7841.

Pubmed Abstract | Pubmed Full Text

Thioux, M., Stark, D. E., Klaiman, C., and Schulz, R. T. (2006). The day of the week when you were born in 700 ms: calendar computation in an Autistic savant. J. Exp. Psychol. Hum. Percept. Perform. 32, 1155–1168.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Trehub, S. E., and Thorpe, L. A. (1989). Infants' perception of rhythm: categorization of auditory sequences by temporal structure. Can. J. Psychol. 43, 217–229.

Pubmed Abstract | Pubmed Full Text

Treisman, M. (1984). Temporal rhythms and cerebral rhythms. Ann. N.Y. Acad. Sci. 423, 542–565.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Trick, L. M., and Pylyshyn, Z. W. (1994). Why are small and large numbers enumerated differently? A limited-capacity preattentive stage in vision. Psychol. Rev. 101, 80–102.

Pubmed Abstract | Pubmed Full Text

Valko, L., Schneider, G., Doehnert, M., Müller, U., Brandeis, D., Steinhausen, H-C., and Drechsler, R. (2010). Time processing in children and adults with ADHD. J. Neural. Transm. 117, 1213–1228.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Van Herwegen, J., Ansari, D., Xu, F., and Karmiloff-Smith, A. (2008). Small and large number processing in infants and toddlers with Williams syndrome. Dev. Sci. 11, 637–643.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Loosbroek, E., and Smitsman, A. D. (1990). Visual perception of numerosity in infancy. Dev. Psychol. 26, 916–922.

van Marle, K., and Wynn, K. (2006). Six-month old infants use analog magnitudes to represent duration. Dev. Sci. 9, F41–49.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Rijn, H., Kononowicz, T. W., Meck, W. H., Ng, K. K., and Penney, T. B. (2011). Contingent negative variation and its relation to time estimation: a theoretical evaluation. Front. Integr. Neurosci. 5:91. doi: 10.3389/fnint.2011.00091

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vicario, C. M. (2011). Perceiving numbers affects the subjective temporal midpoint. Perception 40, 23–29.

Pubmed Abstract | Pubmed Full Text

Vicario, C. M., Caltagirone, C., and Oliveri, M. (2007). Optokinetic stimulation affects temporal estimation in healthy humans, Brain Cogn. 64, 68–73.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Von Gast, H. (1957). Der Umgang mit Zahlen und Zahlge- bilden in der frühen Kindheit. Zeitschrift für Psychologie 161, 1–90.

Pubmed Abstract | Pubmed Full Text

Vuilleumier, P., Ortigue, S., and Brugger, P. (2004). The number space and neglect. Cortex 40, 399–410.

Pubmed Abstract | Pubmed Full Text

Wackermann, J. (2008). Measure of time: a meeting point of psychophyscis and fundamental physics. Mind Matter 6, 9–50.

Wallace, G. L., and Happé, F. (2008). Time perception in autism spectrum disorders. Res. Autism Spectr. Disord. 2, 447–455.

Walsh, V. (2003). A theory of magnitude: common cortical metrics of time, space and quantity. Trends Cogn. Sci. 7, 483–488.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Washburn, D. A. (1994). Stroop-like effects for monkeys and humans: processing speed or strength of association? Psychol. Sci. 5, 375–379.

Pubmed Abstract | Pubmed Full Text

Washburn, D. A., and Rumbaugh, D. M. (1991). Ordinal judgments of numerical symbols by macaques (Macaca Mulatto). Psychol. Sci. 2, 190–193.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wearden, J. H. (1991). Do humans possess an internal clock with scalar timing properties? Learn. Motiv. 22, 59–83.

Wearden, J. H. (2005). “The wrong tree: time perception and time experience in the elderly,” in Measuring the Mind: Speed, Age and Control, eds. J. Duncan, L. Philips, and P. McLeod (Oxford: Oxford University Press), 137–158.

Wearden, J. H., Edwards, H., Fakhri, M., and Percival, A. (1998). Why “sounds are judged longer than lights”: application of a model of the internal clock in humans. Q. J. Exp. Psychol. 51B, 97–120.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wearden, J. H., and Ferrara, A. (1995). Stimulus spacing effects in temporal bisection by humans. Q. J. Exp. Psychol. 48B, 289–310.

Pubmed Abstract | Pubmed Full Text

Wearden, J. H., and Ferrara, A. (1996). Stimulus range effects in temporal bisection by humans. Q. J. Exp. Psychol. 49B, 24–44.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Whalen, J., Gallistel, C. R., and Gelman, R. (1999). Non-verbal counting in humans: the psychophysics of number representation. Psychol. Sci. 10, 130–137.

Wilkening, F., Levin, I., and Druyan, S. (1987). Children's counting strategies for time quantification and integration. Dev. Psychol. 23, 822–883.

Williams, C. L. (2011). Sex differences in counting and timing. Front. Integr. Neurosci. 5:88. doi: 10.3389/fnint.2011.00088

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wimpory, D. (2002). Social timing, clock genes and autism: a new hypothesis. J. Intellect. Disabil. Res. 46, 352–358.

Pubmed Abstract | Pubmed Full Text

Wood, J. N., and Spelke, E. (2005). Infants' enumeration of actions: numerical discrimination and its signature limits. Dev. Sci. 8, 173–181.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wynn, K. (1990). Children's understanding of counting. Cognition 36, 155–193.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wynn, K. (1992). Addition and subtraction by human infants. Nature 358, 749–750.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wynn, K. (1995). Infants possess a system of numerical knowledge. Curr. Dir. Psychol. Sci. 4, 172–177.

Wynn, K. (1996). Infants' individuation and enumeration of actions. Psychol. Sci. 7, 164–169.

Wynn, K. (1998). Psychological foundations of number: numerical competence in human infants. Trends Cogn. Sci. 2, 296–303.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wynn, K., Bloom, P., and Chiang, W-C. (2002). Enumeration of collective entities by 5-month-old infants. Cognition 83, B55–B62.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wynn, K., and Chiang, W-C. (1998). Limits to infants' knowledge of objects: the case of magical appearance. Psychol. Sci. 9, 448–455.

Xu, F. (2003). Numerosity discrimination in infants: evidence for two systems of representations. Cognition 89, B15–B25.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Xu, F., and Spelke, E. (2000). Large number discrimination in 6-month-old infants. Cognition 74, B1–B11.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Xu, F., Spelke, E. S., and Goddard, S. (2005). Number sense in human infants. Dev. Sci. 8, 88–101.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Xuan, B., Zhang, D., He, S., and Chen, X. C. (2007). Larger stimuli are judged to last longer. J. Vis. 7, 1–5.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zélanti, P. S., and Droit-Volet, S. (2011). Cognitive abilities explaining age-related changes in time perception of short and long durations. J. Exp. Child Psychol. 109, 143–157.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zentall, S. S., Smith, Y. N., Lee, Y. B., and Wieczorek, C. (1994). Mathematical outcomes of attention-deficit hyperactivity disorder. J. Learn. Disabil. 27, 510–519.

Pubmed Abstract | Pubmed Full Text

Zur, O., and Gelman, R. (2004). Young children can add and subtract by predicting and checking. Early Child. Res. Q. 19, 121–137.