
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
METHODS article
Front. Neurosci. , 12 July 2022
Sec. Brain Imaging Methods
Volume 16 - 2022 | https://doi.org/10.3389/fnins.2022.963082
This article is part of the Research Topic Current Advances in Multimodal Human Brain Imaging and Analysis Across the Lifespan: From Mapping to State Prediction View all 6 articles
 Haoteng Tang1
Haoteng Tang1 Lei Guo1
Lei Guo1 Xiyao Fu1
Xiyao Fu1 Benjamin Qu2
Benjamin Qu2 Olusola Ajilore3
Olusola Ajilore3 Yalin Wang4
Yalin Wang4 Paul M. Thompson5
Paul M. Thompson5 Heng Huang1
Heng Huang1 Alex D. Leow3
Alex D. Leow3 Liang Zhan1*
Liang Zhan1*Brain networks have attracted increasing attention due to the potential to better characterize brain dynamics and abnormalities in neurological and psychiatric conditions. Recent years have witnessed enormous successes in deep learning. Many AI algorithms, especially graph learning methods, have been proposed to analyze brain networks. An important issue for existing graph learning methods is that those models are not typically easy to interpret. In this study, we proposed an interpretable graph learning model for brain network regression analysis. We applied this new framework on the subjects from Human Connectome Project (HCP) for predicting multiple Adult Self-Report (ASR) scores. We also use one of the ASR scores as the example to demonstrate how to identify sex differences in the regression process using our model. In comparison with other state-of-the-art methods, our results clearly demonstrate the superiority of our new model in effectiveness, fairness, and transparency.
Understanding brain structural and functional changes and its relationship to other phenotypes (e.g., behavior and demographical variables or clinical outcomes) are of prime importance in the neuroscience field. One of the key research directions is to use neuroimaging data for predictive or regression analyses and identify phenotype-related imaging biomarkers. Many previous studies (Rusinek et al., 2003; Sabuncu et al., 2015; Seo et al., 2015; Duffy et al., 2018; Kim et al., 2019) focus on predicting phenotypes using imaging features from voxels or region-of-interests (ROIs). However, increasing evidences show that most of the phenotypes are the outcomes of the interactions among many brain regions (Lehrer, 2009; Van Den Heuvel et al., 2012; Sporns, 2013; Mattar and Bassett, 2019), therefore, using brain network for this prediction task attracts more and more attentions. Brain network (Sporns et al., 2004; Power et al., 2010; Sporns, 2011) represents a 3D brain graph model, comprising the nodes and the edges connecting to the nodes. The nodes are brain ROIs and the edges can be defined using diffusion-MRI derived fiber tracking or functional-MRI-derived correlation. Brain network has the potential to gain system-level insights into the brain dynamics related to those phenotypes.
Many studies have been conducted to relate brain networks to behavioral, clinical measures or demographical variables and identify the most predictive network features (Eichele et al., 2008; Uddin et al., 2013; Brown et al., 2017; Beaty et al., 2018; Tang et al., 2019, 2022; Li C. et al., 2020). However, most of these studies (Chennu et al., 2017; Li et al., 2017; Warren et al., 2017; Du et al., 2019; D́ıaz-Arteche and Rakesh, 2020; Kuo et al., 2020) focus on exploring correlations between the pre-defined network features (e.g., clustering coefficient, small-worldness, characteristic path length, etc.) and the measures to be predicted (such as cognitive impairment, biological variables, behavior profile, psychopathological scores, etc.). This may be sub-optimal since those derived brain network features contain less information than the original networks and may ignore important brain network attributes. Although using the entire brain network for the task can solve this issue, it will introduce another challenge in how to handle the high dimensional network data during the task. Obviously, the traditional linear regression method may not be a good choice and more advanced methods (Székely et al., 2007; Székely and Rizzo, 2009; Simpson et al., 2011, 2012; Varoquaux and Craddock, 2013; Craddock et al., 2015; Dai et al., 2017; Wang et al., 2017; Zhang et al., 2019b; Xia et al., 2020; Lehmann et al., 2021; Tomlinson et al., 2021) have been proposed for this purpose. Additionally, recently years have witnessed a great success in the deep learning tools which have been widely used to discover the biological characteristics of brain network-phenotype associations (Hu et al., 2016; Ju et al., 2017; Mirakhorli et al., 2020).
To analyze the complex network data (e.g., brain networks), deep graph learning techniques (Kipf and Welling, 2016; Hamilton et al., 2017; Veličković et al., 2017; Gao et al., 2018; Zhang and Huang, 2019; Zhang et al., 2019a) have gained significant attention. A typical category of deep graph learning techniques are the graph neural networks (GNNs), which are proposed based on the message passing mechanism. In general, GNNs can be summarized as (1) message aggregation across nodes and (2) message transformation (e.g., non-linear transformation) as updated node features. A graph convolution operation in GNNs enables each graph node to aggregate information from its neighbor nodes. Generally, one graph convolution layer can enable the graph node to aggregate local information from one-hop neighbors (i.e., directly connected nodes), while stacked graph convolution layers may enable the graph node to aggregate higher-level information from multi-hops neighbors (Dehmamy et al., 2019), where richer semantic information can be found. However, when stacking too many graph convolution layers, not only the effective information will be captured but also much noise will be introduced, which will break the network representation (Li et al., 2018; Chen et al., 2020). Therefore, an important issue for current graph learning methods is how to effectively capture the higher-level brain network features. Another issue for current graph learning techniques is that the models are not easy to interpret. Although many existing graph learning methods may well achieve good predictive performances for certain tasks (e.g., classification of diseases or prediction of clinical scores), they might be difficult to provide meaningful biological explanations or heuristic insights into the results (Wee et al., 2019; Xuan et al., 2019; Li Y. et al., 2020; Wang et al., 2021). This should be attributed to the black-box nature of the neural networks. Although it is easy to know what the neural network predicts (i.e., the output of the black-box model), it is difficult to understand how the neural networks make the decision (i.e., heuristic intermediate results inside the black box). To address these, a few recent studies (Cui et al., 2021; Li et al., 2021) have been conducted to explore interpretable discoveries from deep graph models on brain networks. However, Cui et al. (2021) focuses on explaining the message passing mechanism across the brain ROIs while ignoring the high-level network patterns within the brain networks. Li et al. (2021) tries to explain how the model generates high-level network patterns based on the graph communities. However, they only preserve the center node and discard all other nodes in the communities during the designed pooling operation.
In this work, we propose a new explainable graph representation learning framework and illustrate our method on a task predicting behavioral measures from multi-model brain connectomes in young healthy adults. We hypothesize that the intrinsic higher-level graph patterns can be preserved from the graph communities in brain networks in a hierarchical manner. Based on this assumption, we design a graph community pooling module to summarize the higher-order graph patterns. This hierarchical patterns from brain networks can be used to guide the information flow during the AI model training and increase the transparency and interpretability of the model. We demonstrate this new framework by predicting several behavioral measures using the entire brain network for each gender and investigate whether there is any significant sex difference in the results. The main contributions are summarized as follows:
• We propose a new interpretable hierarchical graph representation learning framework for brain network regression analysis.
• Comparing to state-of-the-arts methods, the regression results on Human Connectome Project (HCP) dataset demonstrate the superiority of our proposed framework.
• In order to explore the interpretability of our framework, we adopt graph saliency maps to highlight brain regions selected by the model and provide biological explanations.
The brain network data used in this study was obtained from Zhang et al. (2020), which we summarize below. The original data was from the Human Connectome Project (HCP) 1200 Subjects Data Release (Van Essen et al., 2013). 246 region-of-interests (ROIs) from the Brainnetome atlas (Fan et al., 2016) was adopted to define the resting-state functional network and diffusion-MRI-derived structural network. Functional network was computed using CONN toolbox (Whitfield-Gabrieli and Nieto-Castanon, 2012) and structural network was processed using FSL bedpostx (Behrens et al., 2003) and probtrackx (Behrens et al., 2007). The reconstructing pipelines for these two brain networks (Ajilore et al., 2013; Zhan et al., 2015) have been described in our previous publications. In order to evaluate our framework, we selected 10 Achenbach Adult Self-Report (ASR) (Achenbach and Rescorla, 2003) measures from each subject as our prediction objectives. These 10 measures include: Anxious/Depressed Score (ANXD), Withdrawn Score (WITD), Somatic Complaints Score (SOMA), Thought Problems Score (THOT), Attention Problems Score (ATTN), Aggressive Behavior Score (AGGR), Rule Breaking Behavior Score (RULE), Intrusive Score (INTR), Internalizing Score (INTN), and Externalizing Score (EXTN). After quality control assessment of head motion and global signal changes for both scan types (diffusion MRI and resting-state fMRI) and removal of those with missing data, we included 738 young healthy subjects (mean age = 28.62±3.67, 337 males) in our study.
In sum, each subject has a 246 × 246 structural network from diffusion MRI, a 246 × 246 functional network from resting-state fMRI, and 10 ASR scores. Table 1 summarizes the ASR statistics for each gender and details of the HCP dataset can be found in footnote 1.1
In this section, we first provide some preliminaries for graph learning. Then, we will explain our new framework, in which we will delve into the proposed graph pooling layer which down-scales the brain network and generates the coarse representation of brain network based on the network communities. Finally, we will briefly describe the training procedure to show that our proposed framework can be trained in an end-to-end manner.
We denote any attributed graph (i.e., brain network) with N nodes as G = (A, X). is the graph adjacency matrix saving the node connections in the graph which can be defined as:
Particularly, in the functional brain networks, the edge weights measures the relationships between the BOLD signals of different brain regions (e.g., Aij is the Pearson Correlation of BOLD signals between brain node i and j) (Bathelt et al., 2013; Fischer et al., 2014). By contrast, in the diffusion MRI-derived structural networks, the edge weights describe the connectivity of white matter tracts between brain regions. is the node feature matrix, where the dimension of the feature is d. We also denote as the latent feature matrix embedded by the graph convolution layers, where c is the dimension of the node latent features. is the i-th row of matrix Z representing the latent feature of the i-th node. Given a set of labeled data where is the regression value to the corresponding graph , the graph regression task is learning a mapping, .
Graph Neural Network (GNN) is an effective message-passing architecture to embed the graph nodes as well as their local structures. In general, GNN layer can be formulated as:
where θ is the trainable parameters.
F(·) is the forward function of GNN layer to combine and transform the messages across the graph nodes. Different expressions of F(·) are proposed in the previous work such as Graph Convolution Network (GCN) (Kipf and Welling, 2016) and Graph Attention Network (GAT) (Veličković et al., 2017). In this work, we adopt GCN to generate the node latent features. Following Kipf and Welling (2016), the layer of the graph neural network (i.e., Equation 2) can be instantiated as:
where à = A+I, is the degree matrix, σ(·) is a non-linear activation function (e.g., ReLU).
The goal of this new brain network representation learning framework is to capture community structures of brain networks in a hierarchical manner, and to generate a representation of the whole brain network based on the preserved community information. Moreover, the proposed framework should be able to utilize derived brain network representations to achieve graph-level learning tasks (e.g., graph regression). The proposed brain network representation learning framework, as shown in Figure 1, consists of three components which are (1) nodes and local structures embedding modules, (2) community-based brain network pooling modules and (3) a task-specific prediction module. In the nodes and local structures embedding module, graph convolution layers are deployed to embed the brain network nodes and the corresponding local structures into the latent feature space. In stead of using single graph convolution layer (i.e., 1 GCN layer), we here deploy stacked graph convolution layers (i.e., stacked GCN layers, Dehmamy et al., 2019) which can promote each graph node to aggregate higher order information from a broader receptive field (i.e., to capture the information beyond one-hop neighborhoods to several-hops neighborhoods).
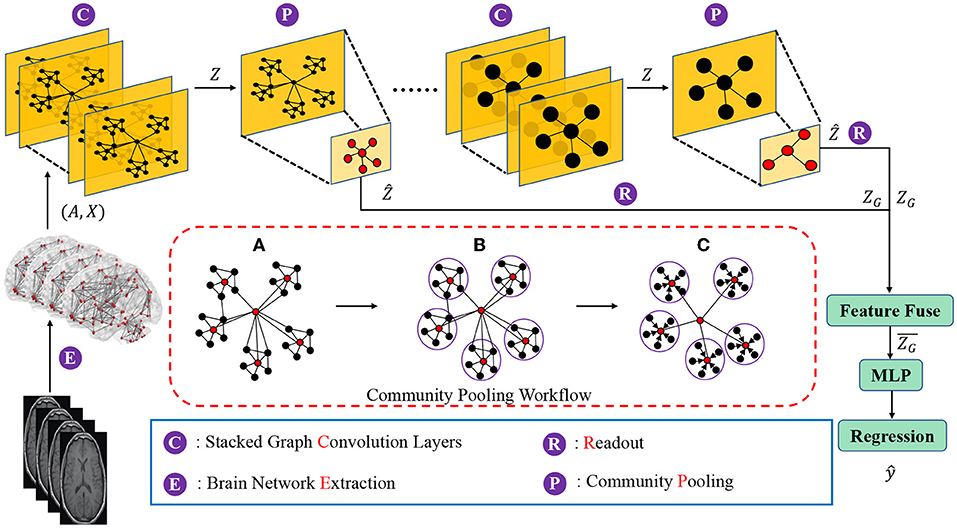
Figure 1. Diagram of the proposed hierarchical brain network learning framework, including stacked graph convolution layers, community pooling modules, and an Multilayer perceptron (MLP) block for the regression task. The workflow details of the proposed community pooling module are presented in the red box, including: (A) Compute the center node probability () and select the nodes with top-M scores as center nodes. (B) Assign each node into the closest community. (C) Aggregate features of community member nodes to the corresponding center node and down scale the graph based on the captured communities.
Given a brain network (i.e., G = (A, X)), the nodes and local structures embedding module can embed the network node features with its local structures in to the latent space as node latent features . The next question is that how to use these node latent features to generate the high-level graph representations? The graph convolution layers focus on the node-level representation learning and only propagate information across edges of the graph in a “flat” way (Ying et al., 2018; Tang et al., 2021). Some previous studies (Lin et al., 2013; Li et al., 2015; Vinyals et al., 2015; Zhang et al., 2018) adopted global pooling which sums, averages or concatenates all the node features as the graph-level representation and use it for graph-level tasks (e.g., graph classification, graph similarity learning). However, these methods may ignore the hierarchical structures during the global pooling process, which leads to the models ineffective in graph-level tasks. To address this issue, our proposed brain network pooling module down scales the network from N nodes to M(< N) nodes based on the network community which is an important graph hierarchical structures. Specifically, the proposed brain network pooling can down scale the network latent features to . Details of the proposed brain network pooling module are discussed in the next subsection.
After the network pooling, a readout operation is adopted to summary the whole graph representation at the current scale of the graph. Assume that we obtain the network latent feature matrix from the network pooling module, the readout operation generates the whole graph representation by a linear layer with an activation function:
where is the trainable parameters within the linear layer and σ(·) is an activation function (i.e., ReLu).
In the task-specific prediction module, we first fuse (e.g., concatenate, sum, average, etc.) all the graph representation ZG obtained in different scales of graphs as the hierarchical graph representation for the further graph-level prediction (i.e., graph regression in this work). Then, an Multilayers Perception (MLP) is deployed to utilize the hierarchical graph representation for the graph regression task.
As mentioned before, the brain network pooling module down scales the node latent features to the based on the network community structures. To achieve this, two basic steps are involved in the brain network pooling module including network community partition and community representation. We will discuss these two steps in sequence.
To partition the network nodes and generate the network community, the pooling module will first identify the community center nodes and then assign other nodes to the nearest community. Inspired by the density-based partition methods (Ester et al., 1996; Heuvel van den and Sporns, 2013) that community center nodes are always densely encircled by a group of nodes with a high probability, we compute the feature distance (i.e., Euclidean distance of feature vector) as a metric to approximate the probability that measures the possibility for a node to be a center node. Specifically, a node with a smaller feature distances to all other nodes is more likely to be a community center. Based on node feature vectors, we construct the probability vector, to measure the possibility that each node to be a community center node where is formulated as:
where S (i.e., Si, j = ||Zi−Zj||L1) is the feature distance matrix. Finally, we select M nodes with Top-M -values as M community center nodes.
When we identify M community center nodes, we assign other graph nodes to the nearest the community. We denote Ω = {Ω1, Ω2, …, ΩM} as the set of all M communities. Then the representation of i-th community (i.e., Ẑi) can be computed by:
where Zci is the latent feature of the center node of i-th community. vj are the community member nodes in the corresponding community.
As aforementioned, we fuse all graph representations ZG obtained from different graph scales as the final hierarchical graph representation . Then, an MLP takes as input to generate the regression prediction value ŷ. We optimize the Mean squared error (MSE) loss (i.e., ℓMSE) to minimize the difference between the ground-truth y and the prediction ŷ. Meanwhile, to make the feature of community members closer to the corresponding community center node, we minimize:
The total loss function can be formulated as follows:
where the η1 and η2 are the loss weights. We train the proposed brain network learning framework by minimizing this regression loss and the whole training procedure is therefore in an end-to-end manner.
We will apply the proposed framework to predict ASR scores. The prediction performance will be evaluated using Mean Absolute Error (MAE). Since the community pooling module in our framework will select a group of nodes or brain regions, we can identify which brain regions (or brain network nodes) are directly linked to the prediction objects (i.e., ASR score in our study) from the last pooling module. Please be noted that this “link” doesn't mean the direct correlation since the relationship captured by our framework is non-linear by nature. We name these nodes as effecting nodes. And the last community pooling layer in our framework will generate a group of “effecting” nodes. Due to the individual difference, the effecting nodes for each subject are not exact the same. Then we count how many times each node is selected as the effecting node during the testing and normalize this number by the total number of testing subject in each group. The resulted number will be treated as the frequency of this node to be the effecting node. As a result, we can get the nodal frequency distribution for each group (male or female). Then the normalized mutual information (NMI) is used to quantify the group difference between male and female and we adopt permutation approach to evaluate the significance of the group difference.
For each prediction task, we randomly split the entire dataset into five disjoint sets for 5-fold cross-validations. All the prediction accuracy are calculated as the mean ± standard deviation values obtained from these 5 folders. We utilize the diffusion MRI-derived brain structural networks as the adjacency matrix input of our framework. We treat each row in the resting-state functional network as the feature for each node, so the initial nodal feature dimension is 246. We also consider using Principal Component Analysis (PCA) to reduce the nodal feature dimension. During the training stage, we optimize the parameters in the framework using the Adam optimizer (Kingma and Ba, 2015) with a batch size of 256. The initial learning rate is set to 0.001 and decayed by . We also regularize the framework training with an L2 weight decay of 1e−5. Following the previous studies (Shchur et al., 2018; Lee et al., 2019), we adopt an early stopping criterion if the validation loss did not improve for 20 epochs in an epoch termination condition with a maximum of 500 epochs. We implement all experiments based on PyTorch (Paszke et al., 2019) and the torch-geometric graph learning library (Fey and Lenssen, 2019). All the experiments are deployed on 1 NVIDIA TITAN RTX GPUs.
In this section, we put all subjects (male and female) into one group and apply our method to predict ASR scores. We compare the prediction performance of our framework with 7 baseline methods to show the superiority of our framework. Two dimension reduction methods [i.e., PCA and Spectral Clustering (Ng et al., 2002) with linear regression] and five graph neural network (GNN) based models [i.e., Stacked GCN with Global-POOL, SAG-POOL (Lee et al., 2019), DIFFPOOL (Ying et al., 2018), HGP-SL (Zhang et al., 2019c) and StructPOOL (Yuan and Ji, 2020)] with different pooling layers are set as our compared baselines. The GNN based models can co-embed the brain structural networks (i.e., as adjacency matrices) and brain functional networks (i.e., as node feature matrices) into the latent space, however, two dimension reduction methods can only analyze one type of brain networks. To make a fair comparison, we only utilize brain structural networks to present the regression performance here in Table 2. Particularly, we conduct two dimension reduction methods on the brain structural networks to reduce the network dimension. Then, the linear regression is adopted on the dimension reduced networks for the regression task. Meanwhile, for the 5 GNN-based baseline models as well as ours, we initialize the node feature matrix by using all-ones vector (i.e., ) and only utilize the brain structural networks as the adjacency matrices. For the 5 hierarchical graph pooling models (i.e., SAG-POOL, DIFFPOOL, HGP-SL, StructPOOL and ours), we deployed 3 hierarchical graph pooling modules. Table 2 shows that our proposed framework achieves the best performance with a lowest regression Mean Absolute Error (MAE) comparing to all other methods. Meanwhile, the GNN-based methods are generally superior to the dimension reduction ones. This may result from that GNN-based methods can better extract the network local and global topological structures which are important to represent the brain networks. Moreover, the group of hierarchical graph pooling models perform better than the global pooling method, which may be explained by that our hierarchical pooling method can not only extract the graph local structures as the low-level features but also preserve these low-level features into the high level space in an hierarchical manner, while the global pooling method can only extract the graph low-level features and combine these features in a naive way (e.g., by concatenating, averaging, etc.).
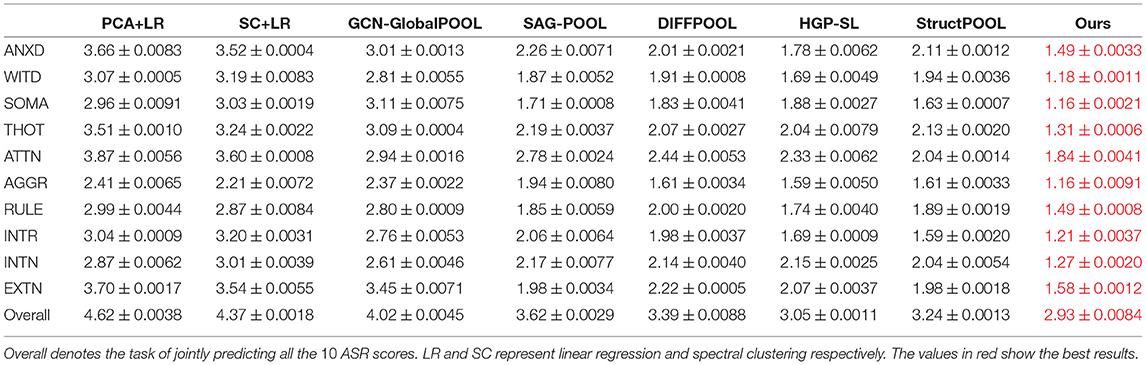
Table 2. Regression Mean Absolute Error (MAE) with corresponding standard deviations under five-fold cross-validation on 10 ASR scores.
We search the loss weights of η1 and η2 in range of [0.1, 0.5, 1] and [0.01, 0.05, 0.1], respectively, (see Figure 2) for the Overall ASR regression. The best loss weights are determined as η1 = 0.5 and η2 = 0.01. Figure 2 indicates that the performance of our framework is relatively consistent under different loss weights. We use the same loss weights setting for each single ASR prediction, although the optimal loss weights may slightly different for different prediction.
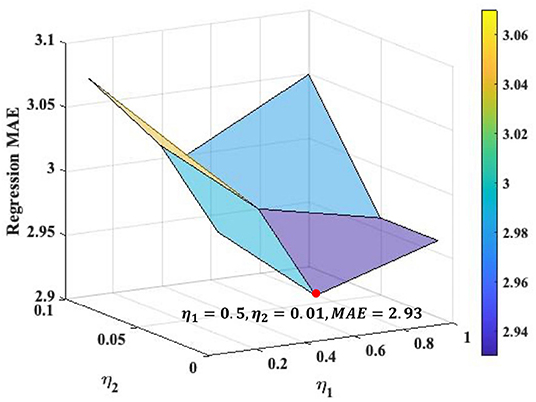
Figure 2. Loss weights analysis for the Overall ASR regression task. The optimal values of η1 and η2 are 0.5 and 0.01, respectively, where the MAE of overall regression achieves as 2.93.
In this section, we evaluate how the number of Community Pooling modules affect the prediction performance on 10 ASR scores. We deployed different number of pooling modules (i.e., from 1 to 5) and set the pooling ratio in each pooling module as 0.5 (i.e., only 50% nodes will be preserved after each pooling module). The MAE of ASR scores obtained by the proposed framework with different number of pooling modules are shown in the Figure 3A. Figure 3A shows that the regression performance obtained by our proposed framework are consistent among different ASR scores. In general, with the increasing number of pooling modules, the MAE values first decline and then incline with the minimum MAE value is achieved when 3 pooling modules are deployed. The possible explanation is as follows: when the number of pooling modules is insufficient (e.g., 1 or 2), the high-level features related to the prediction object haven't been extracted enough; while when too many pooling modules (e.g., 4 or 5) are deployed, the extracted features may be too “coarse”, where the key discriminative information have been mosaicked.
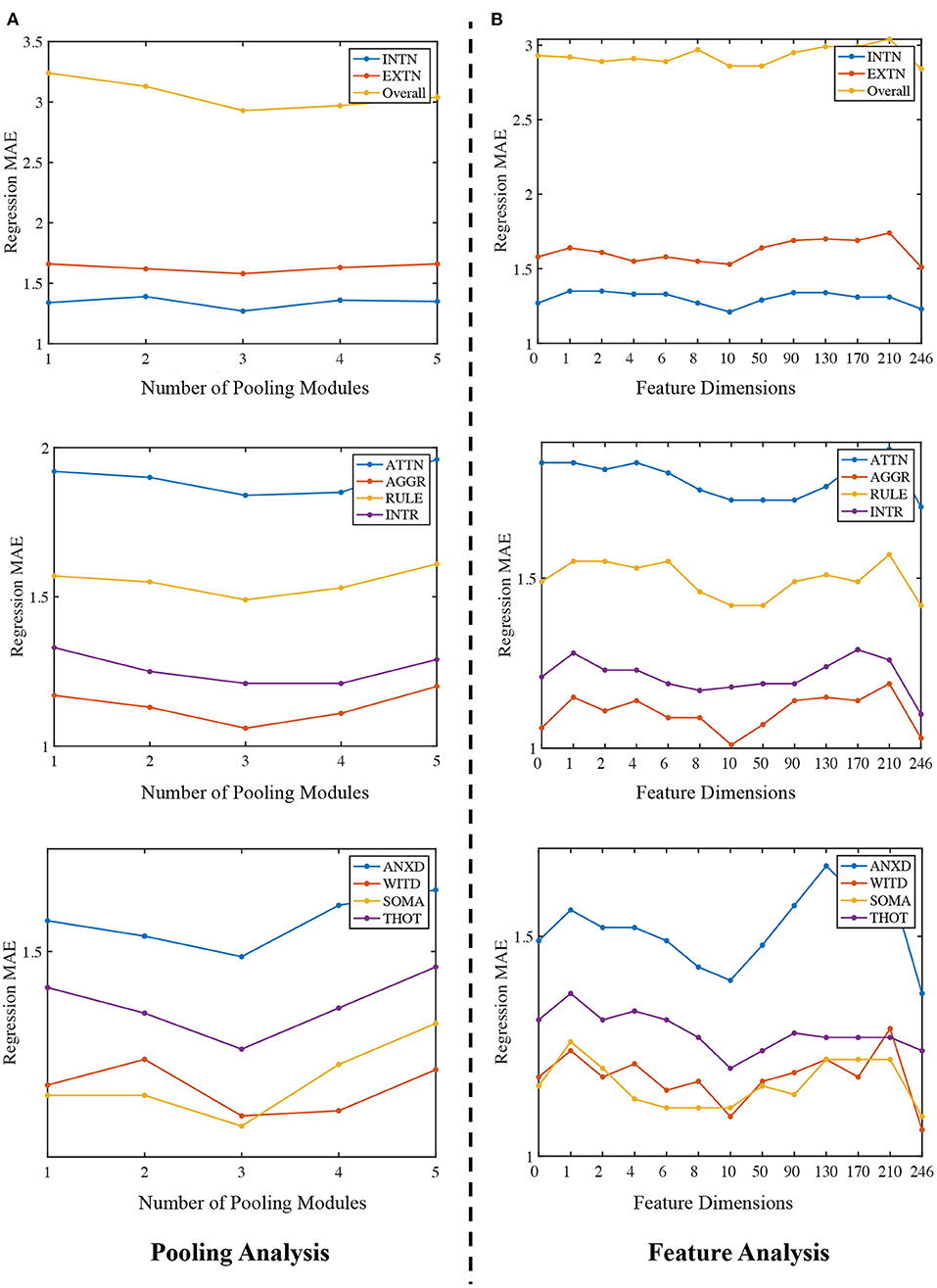
Figure 3. Ablation study. (A) Regression MAE under different number of pooling modules. The x-axis is 1 to 5, representing the number of community pooling modules and y-axis is the corresponding MAE. (B) Regression MAE obtained by the proposed framework when using different number of node features. The x-axis ranges from 0 to 246, representing different number of nodal features and y-axis is the corresponding MAE.
Firstly, the number of the pooling modules is fixed as 3 for all experiments in this section. Then, we predict the ASR scores without using any nodal features and treat the feature dimension as zero. This is implemented by setting the node feature matrix as ). After that, we use PCA algorithm to extract different number of features (from 1 to 240) and use them as the nodal features for the predictions. Lastly, we directly apply the functional network as the nodal feature matrix for the same tasks and in this situation, feature dimension is 246. Therefore, we can compare how the number of nodal features affect the prediction performance, and our results are summarized in the Figure 3B.
There are two main findings in Figure 3B. Firstly, the proposed framework can generally achieve better prediction performance by using the functional network as the node feature matrix. Secondly, we expected that using the principle components of the functional networks as the nodal features could further improve the regression or prediction performance. Among the feature dimension range from 1 to 240, the best result (i.e., the lowest MAE) is achieved at 10, in other words, using the top 10 PCs to form the feature matrix can achieve the best performance when compared with other dimension options. Moreover, although the performance obtained with 10 PCs is close to that obtained by using full functional networks (dimension = 246), using full functional network as the feature matrix (dimension = 246) generally has a better prediction performance than using PCs as the feature input, which indicate there the topological structures in the full functional networks may not be well preserved in the PCA processing. There may have some better choices for the nodal features or dimension reduction techniques, which will be considered in our future research.
In this section, we will demonstrate how to apply this new framework to identify sex differences. Here, sex is referred as the biological sex, as available data does not permit us to disentangle the influence of social culturally defined gender influences from biological sex effect.
We firstly apply our framework to predict each of the ASR scores for each sex. Table 3 summarizes the estimation errors (mean ± standard deviation) for each gender (column 1 and 2 for male and female respectively). Column 3 in Table 3 shows the student t-test P-values for evaluating whether there is any significant difference in the estimation errors between sexes. None of these are significant, in other words, these results demonstrates the fairness of our framework in terms of the variable “sex”.
Next, we adopt the permutation approach to evaluate whether there are significant sex differences in the “effecting” node distributions for each ASR score (Please refer to Section 4.1 for technique details). We randomly shuffle the subjects between male and female groups and conduct 100 permutations. All permutation tests are conducted using the computation resource in the Pittsburgh Supercomputing Center (PSC) (Towns et al., 2014; Nystrom et al., 2015). Our permutation results show that there are significant sex differences (p < 0.01) in the effecting node distributions for 7 ASR variables except ANXD, SOMA and INTN, which is consistent with the conclusions from Table 1. Here we choose ATTN as an example to show the sex differences in the effecting nodal distribution. Attention problem score (ATTN) (Achenbach and Rescorla, 2003) indicates the tendency to be easily distracted and unable to concentrate more than momentarily. Figure 4 shows the effecting node distributions for male and female, and the hot color indicates the stronger involvements of that ROI in this psychiatric process (or ATTN) and the cool color indicate the opposite. Our results show there are multiple brain regions (including Left Paracentral lobule, Right Posterior cingulate and Left dorsomedial prefrontal cortex, Right Precuneus, and Left Premotor, highlighted using black circle in Figure 4) showing significantly different involvements in this psychiatric process between sexes.
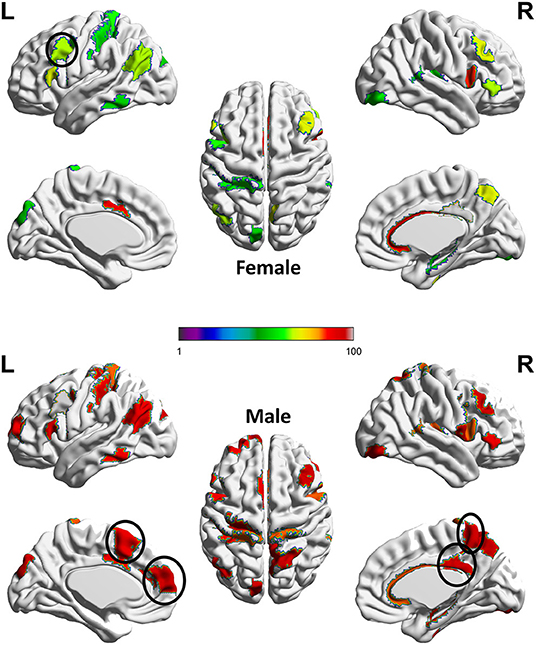
Figure 4. Sex difference identified for ATTN. The color indicates the region involved in the ATTN process and the hotter color indicate the stronger involvement and the cooler color indicate the inverse. Permutation tests have been adopted to confirm the significance of this sex difference (p < 0.01).The main sex differences are in several regions, which are highlighted using a black circle. These regions include Left Paracentral lobule, Right Posterior cingulate and Left dorso-medial prefrontal cortex, Right Precuneus, and Left Premotor.
Previous studies reported that paracentral lobule is activated in covert shifts of attention (Grosbras et al., 2005) and auditory attention shifting (Huang et al., 2012). Moreover, Dickstein et al. (2006) reported that right paracentral lobule had a greater probability of activation in patients with Attention-deficit/hyperactivity disorder (ADHD) than in controls while our results show that part of sex differences for healthy controls is in the left paracentral lobule, which deserves further investigations in the future. The posterior cingulate cortex (PCC) is a central node of the default mode network (DMN) and many evidence suggests that the PCC plays a direct role in attentionally demanding tasks (Gusnard and Raichle, 2001; Vogt and Laureys, 2005; Hampson et al., 2006; Hahn et al., 2007; Leech et al., 2011; Leech and Sharp, 2014). The dorsomedial prefrontal cortex (dmPFC) receives afferent input from sensory and parietal regions of the cortex, which presumably enable the dmPFC to respond to situations that require immediate attention and respond with appropriate actions (Narayanan and Laubach, 2006; Venkatraman et al., 2009; Park et al., 2016). Additionally, Precuneus has been reported to highly involve in attention shift (Cavanna and Trimble, 2006) while Premotor is involved in Reorienting attention (Rizzolatti et al., 1987) and attention-deficit/hyperactivity disorder (Mostofsky et al., 2002). All these clearly indicate that our new AI framework can discover potential biologically-meaningful results for regression studies.
In this study, we proposed a novel interpretable graph learning framework for brain network regression analysis. We demonstrated that our new framework has better prediction performances than state-of-the-arts graph learning methods in predicting young health subjects' psychiatric scores. Additionally, we chose one of the psychiatric scores to demonstrate how this new framework can be used to study sex differences. Future work will focus on how to modify our framework for the signed graph data.
Publicly available datasets were analyzed in this study. This data can be found here: https://www.humanconnectome.org/study/hcp-young-adult/document/1200-subjects-data-release.
HT took charge of conception and design, method implementation, statistical analysis, and interpretation, as well as manuscript writing and revising. LZ took charge of project design, data preprocessing, analysis and interpretation, manuscript writing/revising. LG, XF, BQ, OA, YW, PT, HH, and AL took charge of experiment design, results discussion, and manuscript proofreading. All authors contributed to the article and approved the submitted version.
This study was partially supported by the National Institutes of Health (R01AG071243, R01MH125928, and U01AG068057) and National Science Foundation (IIS 2045848 and IIS 1837956).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank MGH-USC Consortium (Principal Investigators: Bruce R. Rosen, Arthur W. Toga, and Van Wedeen; U01MH093765), which was funded by the NIH Blueprint Initiative for Neuroscience Research grant; the National Institutes of Health grant P41EB015896; and the Instrumentation Grants S10RR023043, 1S10RR023401, 1S10RR019307, which provides the Human Connectome Project data for our work. We thank the Extreme Science and Engineering Discovery Environment (XSEDE), which was supported by National Science Foundation (NSF) grant number ACI-1548562 and NSF award number ACI-1445606, which provide the computation resources based on Pittsburgh Supercomputing Center (PSC) for part of our work.
Achenbach, T. M., and Rescorla, L. (2003). Manual for the Aseba Adult Forms & Profiles. Burlington, VT: University of Vermont, Research Center for Children, Youth.
Ajilore, O., Zhan, L., GadElkarim, J., Zhang, A., Feusner, J., Yang, S., et al. (2013). Constructing the resting state structural connectome. Front. Neuroinform. 7:30. doi: 10.3389/fninf.2013.00030
Bathelt, J., O'Reilly, H., Clayden, J. D., Cross, J. H., and de Haan, M. (2013). Functional brain network organisation of children between 2 and 5 years derived from reconstructed activity of cortical sources of high-density eeg recordings. Neuroimage 82, 595–604. doi: 10.1016/j.neuroimage.2013.06.003
Beaty, R. E., Kenett, Y. N., Christensen, A. P., Rosenberg, M. D., Benedek, M., Chen, Q., et al. (2018). Robust prediction of individual creative ability from brain functional connectivity. Proc. Natl. Acad. Sci. U.S.A. 115, 1087–1092. doi: 10.1073/pnas.1713532115
Behrens, T. E., Berg, H. J., Jbabdi, S., Rushworth, M. F., and Woolrich, M. W. (2007). Probabilistic diffusion tractography with multiple fibre orientations: what can we gain? Neuroimage 34, 144–155. doi: 10.1016/j.neuroimage.2006.09.018
Behrens, T. E., Woolrich, M. W., Jenkinson, M., Johansen-Berg, H., Nunes, R. G., Clare, S., et al. (2003). Characterization and propagation of uncertainty in diffusion-weighted mr imaging. Magnet. Reson. Med. 50, 1077–1088. doi: 10.1002/mrm.10609
Brown, C. J., Moriarty, K. P., Miller, S. P., Booth, B. G., Zwicker, J. G., Grunau, R. E., et al. (2017). “Prediction of brain network age and factors of delayed maturation in very preterm infants,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Quebec City, QC: Springer), 84–91. doi: 10.1007/978-3-319-66182-7_10
Cavanna, A. E., and Trimble, M. R. (2006). The precuneus: a review of its functional anatomy and behavioural correlates. Brain 129, 564–583. doi: 10.1093/brain/awl004
Chen, D., Lin, Y., Li, W., Li, P., Zhou, J., and Sun, X. (2020). “Measuring and relieving the over-smoothing problem for graph neural networks from the topological view,” in Proceedings of the AAAI Conference on Artificial Intelligence (New York, NY: ACM), 3438–3445. doi: 10.1609/aaai.v34i04.5747
Chennu, S., Annen, J., Wannez, S., Thibaut, A., Chatelle, C., Cassol, H., et al. (2017). Brain networks predict metabolism, diagnosis and prognosis at the bedside in disorders of consciousness. Brain 140, 2120–2132. doi: 10.1093/brain/awx163
Craddock, R. C., Tungaraza, R. L., and Milham, M. P. (2015). Connectomics and new approaches for analyzing human brain functional connectivity. Gigascience 4, s13742-s13015. doi: 10.1186/s13742-015-0045-x
Cui, H., Dai, W., Zhu, Y., Li, X., He, L., and Yang, C. (2021). Brainnnexplainer: an interpretable graph neural network framework for brain network based disease analysis. arXiv[Preprint]. arXiv:2107.05097. doi: 10.48550/arXiv.2107.05097
Dai, T., Guo, Y., and Alzheimer's Disease Neuroimaging Initiative (2017). Predicting individual brain functional connectivity using a Bayesian hierarchical model. Neuroimage 147, 772–787. doi: 10.1016/j.neuroimage.2016.11.048
Dehmamy, N., Barabási, A.-L., and Yu, R. (2019). “Understanding the representation power of graph neural networks in learning graph topology,” in Advances in Neural Information Processing Systems, eds H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Vancouver, BC), 15413–15423.
Díaz-Arteche, C., and Rakesh, D. (2020). Using neuroimaging to predict brain age: insights into typical and atypical development and risk for psychopathology. J. Neurophysiol. 124, 400–403. doi: 10.1152/jn.00267.2020
Dickstein, S. G., Bannon, K., Xavier Castellanos, F., and Milham, M. P. (2006). The neural correlates of attention deficit hyperactivity disorder: an ale meta-analysis. J. Child Psychol. Psychiatry 47, 1051–1062. doi: 10.1111/j.1469-7610.2006.01671.x
Du, J., Wang, Y., Zhi, N., Geng, J., Cao, W., Yu, L., et al. (2019). Structural brain network measures are superior to vascular burden scores in predicting early cognitive impairment in post stroke patients with small vessel disease. Neuroimage Clin. 22, 101712. doi: 10.1016/j.nicl.2019.101712
Duffy, B. A., Zhang, W., Tang, H., Zhao, L., Law, M., Toga, A. W., et al. (2018). Retrospective correction of motion artifact affected structural MRI images using deep learning of simulated motion. Neuroimage 230, 117756. doi: 10.1016/j.neuroimage.2021.117756
Eichele, T., Debener, S., Calhoun, V. D., Specht, K., Engel, A. K., Hugdahl, K., et al. (2008). Prediction of human errors by maladaptive changes in event-related brain networks. Proc. Natl. Acad. Sci. U.S.A. 105, 6173–6178. doi: 10.1073/pnas.0708965105
Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996). “A density-based algorithm for discovering clusters in large spatial databases with noise,” in KDD'96: Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (Portland, OR), 226–231.
Fan, L., Li, H., Zhuo, J., Zhang, Y., Wang, J., Chen, L., et al. (2016). The human brainnetome atlas: a new brain atlas based on connectional architecture. Cereb. Cortex 26, 3508–3526. doi: 10.1093/cercor/bhw157
Fey, M., and Lenssen, J. E. (2019). Fast graph representation learning with pytorch geometric. arXiv[Preprint]. arXiv:1903.02428. doi: 10.48550/arXiv.1903.02428
Fischer, F. U., Wolf, D., Scheurich, A., and Fellgiebel, A. (2014). Association of structural global brain network properties with intelligence in normal aging. PLoS ONE 9, e86258. doi: 10.1371/journal.pone.0086258
Gao, H., Wang, Z., and Ji, S. (2018). “Large-scale learnable graph convolutional networks,” in Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (London), 1416–1424. doi: 10.1145/3219819.3219947
Grosbras, M.-H., Laird, A. R., and Paus, T. (2005). Cortical regions involved in eye movements, shifts of attention, and gaze perception. Hum. Brain Mapp. 25, 140–154. doi: 10.1002/hbm.20145
Gusnard, D. A., and Raichle, M. E. (2001). Searching for a baseline: functional imaging and the resting human brain. Nat. Rev. Neurosci. 2, 685–694. doi: 10.1038/35094500
Hahn, B., Ross, T. J., and Stein, E. A. (2007). Cingulate activation increases dynamically with response speed under stimulus unpredictability. Cereb. Cortex 17, 1664–1671. doi: 10.1093/cercor/bhl075
Hamilton, W. L., Ying, R., and Leskovec, J. (2017). “Inductive representation learning on large graphs,” in Proceedings of the 31st International Conference on Neural Information Processing Systems, eds I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett (Long Beach, CA), 1025–1035.
Hampson, M., Driesen, N. R., Skudlarski, P., Gore, J. C., and Constable, R. T. (2006). Brain connectivity related to working memory performance. J. Neurosci. 26, 13338–13343. doi: 10.1523/JNEUROSCI.3408-06.2006
Heuvel van den, M. P., and Sporns, O. (2013). Network hubs in the human brain. Trends Cogn. Sci. 17, 683–696. doi: 10.1016/j.tics.2013.09.012
Hu, C., Ju, R., Shen, Y., Zhou, P., and Li, Q. (2016). “Clinical decision support for Alzheimer's disease based on deep learning and brain network,” in 2016 IEEE International Conference on Communications (ICC) (Kuala Lumpur: IEEE), 1–6. doi: 10.1109/ICC.2016.7510831
Huang, S., Belliveau, J. W., Tengshe, C., and Ahveninen, J. (2012). Brain networks of novelty-driven involuntary and cued voluntary auditory attention shifting. PLoS ONE 7, e44062. doi: 10.1371/journal.pone.0044062
Ju, R., Hu, C., Zhou, P., and Li, Q. (2017). Early diagnosis of Alzheimer's disease based on resting-state brain networks and deep learning. IEEE/ACM Trans. Comput. Biol. Bioinform. 16, 244–257. doi: 10.1109/TCBB.2017.2776910
Kim, H., Irimia, A., Hobel, S. M., Pogosyan, M., Tang, H., Petrosyan, P., et al. (2019). The loni qc system: a semi-automated, web-based and freely-available environment for the comprehensive quality control of neuroimaging data. Front. Neuroinform. 13, 60. doi: 10.3389/fninf.2019.00060
Kingma, D. P., and Ba, J. (2015). “Adam: a method for stochastic optimization,” in International Conference on Learning Representations (San Diego, CA).
Kipf, T. N., and Welling, M. (2016). Semi-supervised classification with graph convolutional networks. arXiv[Preprint]. arXiv:1609.02907. doi: 10.48550/arXiv.1609.02907
Kuo, C.-Y., Lee, P.-L., Hung, S.-C., Liu, L.-K., Lee, W.-J., Chung, C.-P., et al. (2020). Large-scale structural covariance networks predict age in middle-to-late adulthood: a novel brain aging biomarker. Cereb. Cortex 30, 5844–5862. doi: 10.1093/cercor/bhaa161
Lee, J., Lee, I., and Kang, J. (2019). “Self-attention graph pooling,” in International Conference on Machine Learning (Long Beach, CA: PMLR), 3734–3743.
Leech, R., Kamourieh, S., Beckmann, C. F., and Sharp, D. J. (2011). Fractionating the default mode network: distinct contributions of the ventral and dorsal posterior cingulate cortex to cognitive control. J. Neurosci. 31, 3217–3224. doi: 10.1523/JNEUROSCI.5626-10.2011
Leech, R., and Sharp, D. J. (2014). The role of the posterior cingulate cortex in cognition and disease. Brain 137, 12–32. doi: 10.1093/brain/awt162
Lehmann, B., Henson, R., Geerligs, L., Can, C., and White, S. (2021). Characterising group-level brain connectivity: a framework using Bayesian exponential random graph models. Neuroimage 225, 117480. doi: 10.1016/j.neuroimage.2020.117480
Li, C., Tang, H., Deng, C., Zhan, L., and Liu, W. (2020). “Vulnerability vs. reliability: disentangled adversarial examples for cross-modal learning,” in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (San Diego, CA), 421–429. doi: 10.1145/3394486.3403084
Li, Q., Han, Z., and Wu, X.-M. (2018). “Deeper insights into graph convolutional networks for semi-supervised learning,” in Thirty-Second AAAI Conference on Artificial Intelligence (New Orleans, LA: AAAI). doi: 10.1609/aaai.v32i1.11604
Li, X., Li, Y., and Li, X. (2017). “Predicting clinical outcomes of Alzheimer's disease from complex brain networks,” in International Conference on Advanced Data Mining and Applications (Singapore: Springer), 519–525. doi: 10.1007/978-3-319-69179-4_36
Li, X., Zhou, Y., Dvornek, N., Zhang, M., Gao, S., Zhuang, J., et al. (2021). Braingnn: Interpretable brain graph neural network for fmri analysis. Med. Image Anal. 74, 102233. doi: 10.1016/j.media.2021.102233
Li, Y., Qian, B., Zhang, X., and Liu, H. (2020). Graph neural network-based diagnosis prediction. Big Data 8, 379–390. doi: 10.1089/big.2020.0070
Li, Y., Tarlow, D., Brockschmidt, M., and Zemel, R. (2015). Gated graph sequence neural networks. arXiv[Preprint]. arXiv:1511.05493. doi: 10.48550/arXiv.1511.05493
Lin, M., Chen, Q., and Yan, S. (2013). Network in network. arXiv[Preprint]. arXiv:1312.4400. doi: 10.48550/arXiv.1312.4400
Mattar, M. G., and Bassett, D. S. (2019). “Brain network architecture: implications for human learning,” in Network Science in Cognitive Psychology, ed M. S. Vitevitch (Routledge), 30–44. doi: 10.4324/9780367853259-3
Mirakhorli, J., Amindavar, H., and Mirakhorli, M. (2020). A new method to predict anomaly in brain network based on graph deep learning. Rev. Neurosci. 31, 681–689. doi: 10.1515/revneuro-2019-0108
Mostofsky, S. H., Cooper, K. L., Kates, W. R., Denckla, M. B., and Kaufmann, W. E. (2002). Smaller prefrontal and premotor volumes in boys with attention-deficit/hyperactivity disorder. Biol. Psychiatry 52, 785–794. doi: 10.1016/S0006-3223(02)01412-9
Narayanan, N. S., and Laubach, M. (2006). Top-down control of motor cortex ensembles by dorsomedial prefrontal cortex. Neuron 52, 921–931. doi: 10.1016/j.neuron.2006.10.021
Ng, A. Y., Jordan, M. I., and Weiss, Y. (2002). “On spectral clustering: analysis and an algorithm,” in Advances in Neural Information Processing Systems, eds T. Dietterich, S. Becker, and Z. Ghahramani (Vancouver, BC), 849–856.
Nystrom, N. A., Levine, M. J., Roskies, R. Z., and Scott, J. R. (2015). “Bridges: a uniquely flexible HPC resource for new communities and data analytics,” in Proceedings of the 2015 XSEDE Conference: Scientific Advancements Enabled by Enhanced Cyberinfrastructure (St. Louis, MO), 1–8. doi: 10.1145/2792745.2792775
Park, J., Wood, J., Bondi, C., Del Arco, A., and Moghaddam, B. (2016). Anxiety evokes hypofrontality and disrupts rule-relevant encoding by dorsomedial prefrontal cortex neurons. J. Neurosci. 36, 3322–3335. doi: 10.1523/JNEUROSCI.4250-15.2016
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). “Pytorch: an imperative style, high-performance deep learning library,” in Advances in Neural Information Processing Systems Vol. 32, eds H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, R. Garnett (Vancouver, BC), 8026–8037.
Power, J. D., Fair, D. A., Schlaggar, B. L., and Petersen, S. E. (2010). The development of human functional brain networks. Neuron 67, 735–748. doi: 10.1016/j.neuron.2010.08.017
Rizzolatti, G., Riggio, L., Dascola, I., and Umiltá, C. (1987). Reorienting attention across the horizontal and vertical meridians: evidence in favor of a premotor theory of attention. Neuropsychologia 25, 31–40. doi: 10.1016/0028-3932(87)90041-8
Rusinek, H., De Santi, S., Frid, D., Tsui, W.-H., Tarshish, C. Y., Convit, A., et al. (2003). Regional brain atrophy rate predicts future cognitive decline: 6-year longitudinal mr imaging study of normal aging. Radiology 229, 691–696. doi: 10.1148/radiol.2293021299
Sabuncu, M. R., Konukoglu, E., Initiative, A. D. N., et al. (2015). Clinical prediction from structural brain mri scans: a large-scale empirical study. Neuroinformatics 13, 31–46. doi: 10.1007/s12021-014-9238-1
Seo, S., Mohr, J., Beck, A., Wüstenberg, T., Heinz, A., and Obermayer, K. (2015). Predicting the future relapse of alcohol-dependent patients from structural and functional brain images. Addict. Biol. 20, 1042–1055. doi: 10.1111/adb.12302
Shchur, O., Mumme, M., Bojchevski, A., and Günnemann, S. (2018). Pitfalls of graph neural network evaluation. arXiv[Preprint]. arXiv:1811.05868. doi: 10.48550/arXiv.1811.05868
Simpson, S. L., Hayasaka, S., and Laurienti, P. J. (2011). Exponential random graph modeling for complex brain networks. PLoS ONE 6, e20039. doi: 10.1371/journal.pone.0020039
Simpson, S. L., Moussa, M. N., and Laurienti, P. J. (2012). An exponential random graph modeling approach to creating group-based representative whole-brain connectivity networks. Neuroimage 60, 1117–1126. doi: 10.1016/j.neuroimage.2012.01.071
Sporns, O.. (2011). The human connectome: a complex network. Ann. N. Y. Acad. Sci. 1224, 109–125. doi: 10.1111/j.1749-6632.2010.05888.x
Sporns, O.. (2013). The human connectome: origins and challenges. Neuroimage 80, 53–61. doi: 10.1016/j.neuroimage.2013.03.023
Sporns, O., Chialvo, D. R., Kaiser, M., and Hilgetag, C. C. (2004). Organization, development and function of complex brain networks. Trends Cogn. Sci. 8, 418–425. doi: 10.1016/j.tics.2004.07.008
Székely, G. J., and Rizzo, M. L. (2009). Brownian distance covariance. Ann. Appl. Stat. 3, 1236–1265. doi: 10.1214/09-AOAS312
Székely, G. J., Rizzo, M. L., and Bakirov, N. K. (2007). Measuring and testing dependence by correlation of distances. Ann. Stat. 35, 2769–2794. doi: 10.1214/009053607000000505
Tang, H., Guo, L., Dennis, E., Thompson, P. M., Huang, H., Ajilore, O., et al. (2019). “Classifying stages of mild cognitive impairment via augmented graph embedding,” in Multimodal Brain Image Analysis and Mathematical Foundations of Computational Anatomy (Shenzhen: Springer), 30–38. doi: 10.1007/978-3-030-33226-6_4
Tang, H., Guo, L., Fu, X., Qu, B., Thompson, P. M., Huang, H., et al. (2022). “Hierarchical brain embedding using explainable graph learning,” in 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI) (Kolkata: IEEE), 1–5. doi: 10.1109/ISBI52829.2022.9761543
Tang, H., Ma, G., He, L., Huang, H., and Zhan, L. (2021). Commpool: an interpretable graph pooling framework for hierarchical graph representation learning. Neural Netw. 143, 669–677. doi: 10.1016/j.neunet.2021.07.028
Tomlinson, C. E., Laurienti, P. J., Lyday, R. G., and Simpson, S. L. (2021). A regression framework for brain network distance metrics. Netw. Neurosci. 6, 49–68. doi: 10.1101/2021.02.26.432910
Towns, J., Cockerill, T., Dahan, M., Foster, I., Gaither, K., Grimshaw, A., et al. (2014). Xsede: accelerating scientific discovery. Comput. Sci. Eng. 16, 62–74. doi: 10.1109/MCSE.2014.80
Uddin, L. Q., Supekar, K., Lynch, C. J., Khouzam, A., Phillips, J., Feinstein, C., et al. (2013). Salience network-based classification and prediction of symptom severity in children with autism. JAMA Psychiatry 70, 869–879. doi: 10.1001/jamapsychiatry.2013.104
Van Den Heuvel, M. P., Kahn, R. S., Go ni, J., and Sporns, O. (2012). High-cost, high-capacity backbone for global brain communication. Proc. Natl. Acad. Sci. U.S.A. 109, 11372–11377. doi: 10.1073/pnas.1203593109
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E., Yacoub, E., Ugurbil, K., et al. (2013). The wu-minn human connectome project: an overview. Neuroimage 80, 62–79. doi: 10.1016/j.neuroimage.2013.05.041
Varoquaux, G., and Craddock, R. C. (2013). Learning and comparing functional connectomes across subjects. Neuroimage 80, 405–415. doi: 10.1016/j.neuroimage.2013.04.007
Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., and Bengio, Y. (2017). Graph attention networks. arXiv[Preprint]. arXiv:1710.10903. doi: 10.48550/arXiv.1710.10903
Venkatraman, V., Rosati, A. G., Taren, A. A., and Huettel, S. A. (2009). Resolving response, decision, and strategic control: evidence for a functional topography in dorsomedial prefrontal cortex. J. Neurosci. 29, 13158–13164. doi: 10.1523/JNEUROSCI.2708-09.2009
Vinyals, O., Bengio, S., and Kudlur, M. (2015). Order matters: sequence to sequence for sets. arXiv[Preprint]. arXiv:1511.06391. doi: 10.48550/arXiv.1511.06391
Vogt, B. A., and Laureys, S. (2005). Posterior cingulate, precuneal and retrosplenial cortices: cytology and components of the neural network correlates of consciousness. Prog. Brain Res. 150, 205–217. doi: 10.1016/S0079-6123(05)50015-3
Wang, J., Ma, A., Chang, Y., Gong, J., Jiang, Y., Qi, R., et al. (2021). scGNN is a novel graph neural network framework for single-cell RNA-Seq analyses. Nat. Commun. 12, 1–11. doi: 10.1038/s41467-021-22197-x
Wang, L., Durante, D., Jung, R. E., and Dunson, D. B. (2017). Bayesian network-response regression. Bioinformatics 33, 1859–1866. doi: 10.1093/bioinformatics/btx050
Warren, D. E., Denburg, N. L., Power, J. D., Bruss, J., Waldron, E. J., Sun, H., et al. (2017). Brain network theory can predict whether neuropsychological outcomes will differ from clinical expectations. Arch. Clin. Neuropsychol. 32, 40–52. doi: 10.1093/arclin/acw091
Wee, C.-Y., Liu, C., Lee, A., Poh, J. S., Ji, H., Qiu, A., et al. (2019). Cortical graph neural network for ad and mci diagnosis and transfer learning across populations. Neuroimage Clin. 23, 101929. doi: 10.1016/j.nicl.2019.101929
Whitfield-Gabrieli, S., and Nieto-Castanon, A. (2012). Conn: a functional connectivity toolbox for correlated and anticorrelated brain networks. Brain Connect. 2, 125–141. doi: 10.1089/brain.2012.0073
Xia, C. H., Ma, Z., Cui, Z., Bzdok, D., Thirion, B., Bassett, D. S., et al. (2020). Multi-Scale Network Regression for Brain-Phenotype Associations. Technical report, Wiley Online Library. doi: 10.1002/hbm.24982
Xuan, P., Pan, S., Zhang, T., Liu, Y., and Sun, H. (2019). Graph convolutional network and convolutional neural network based method for predicting lncrna-disease associations. Cells 8, 1012. doi: 10.3390/cells8091012
Ying, Z., You, J., Morris, C., Ren, X., Hamilton, W., and Leskovec, J. (2018). “Hierarchical graph representation learning with differentiable pooling,” in Advances in Neural Information Processing Systems, eds S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Montreal, QC), 4805–4815.
Yuan, H., and Ji, S. (2020). “Structpool: structured graph pooling via conditional random fields,” in Proceedings of the 8th International Conference on Learning Representations (Addis Ababa).
Zhan, L., Zhou, J., Wang, Y., Jin, Y., Jahanshad, N., Prasad, G., et al. (2015). Comparison of nine tractography algorithms for detecting abnormal structural brain networks in Alzheimer's disease. Front. Aging Neurosci. 7, 48. doi: 10.3389/fnagi.2015.00048
Zhang, M., Cui, Z., Neumann, M., and Chen, Y. (2018). “An end-to-end deep learning architecture for graph classification,” in Thirty-Second AAAI Conference on Artificial Intelligence (New Orleans, LA: AAAI). doi: 10.1609/aaai.v32i1.11782
Zhang, W., Zhan, L., Thompson, P., and Wang, Y. (2020). “Deep representation learning for multimodal brain networks,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Lima: Springer), 613–624. doi: 10.1007/978-3-030-59728-3_60
Zhang, Y., and Huang, H. (2019). “New graph-blind convolutional network for brain connectome data analysis,” in International Conference on Information Processing in Medical Imaging (Hong Kong: Springer), 669–681. doi: 10.1007/978-3-030-20351-1_52
Zhang, Y., Zhan, L., Cai, W., Thompson, P., and Huang, H. (2019a). “Integrating heterogeneous brain networks for predicting brain disease conditions,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Shenzhen: Springer), 214–222. doi: 10.1007/978-3-030-32251-9_24
Zhang, Z., Allen, G. I., Zhu, H., and Dunson, D. (2019b). Tensor network factorizations: Relationships between brain structural connectomes and traits. Neuroimage 197, 330–343. doi: 10.1016/j.neuroimage.2019.04.027
Keywords: multimodal brain networks, human connectome project, graph learning, interpretable AI, adult self-report score
Citation: Tang H, Guo L, Fu X, Qu B, Ajilore O, Wang Y, Thompson PM, Huang H, Leow AD and Zhan L (2022) A Hierarchical Graph Learning Model for Brain Network Regression Analysis. Front. Neurosci. 16:963082. doi: 10.3389/fnins.2022.963082
Received: 07 June 2022; Accepted: 22 June 2022;
Published: 12 July 2022.
Edited by:
Xi Jiang, University of Electronic Science and Technology of China, ChinaReviewed by:
Li Wang, University of North Carolina at Chapel Hill, United StatesCopyright © 2022 Tang, Guo, Fu, Qu, Ajilore, Wang, Thompson, Huang, Leow and Zhan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liang Zhan, bGlhbmcuemhhbkBwaXR0LmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.