Identification of Epileptic EEG Signals Through TSK Transfer Learning Fuzzy System

We propose a new model to identify epilepsy EEG signals. Some existing intelligent recognition technologies require that the training set and test set have the same distribution when recognizing EEG signals, some only consider reducing the marginal distribution distance of the data while ignoring the intra-class information of data, and some lack of interpretability. To address these deficiencies, we construct a TSK transfer learning fuzzy system (TSK-TL) based on the easy-to-interpret TSK fuzzy system the transfer learning method. The proposed model is interpretable. By using the information contained in the source domain and target domains more effectively, the requirements for data distribution are further relaxed. It realizes the identification of epilepsy EEG signals in data drift scene. The experimental results show that compared with the existing algorithms, TSK-TL has better performance in EEG recognition of epilepsy.

Introduction

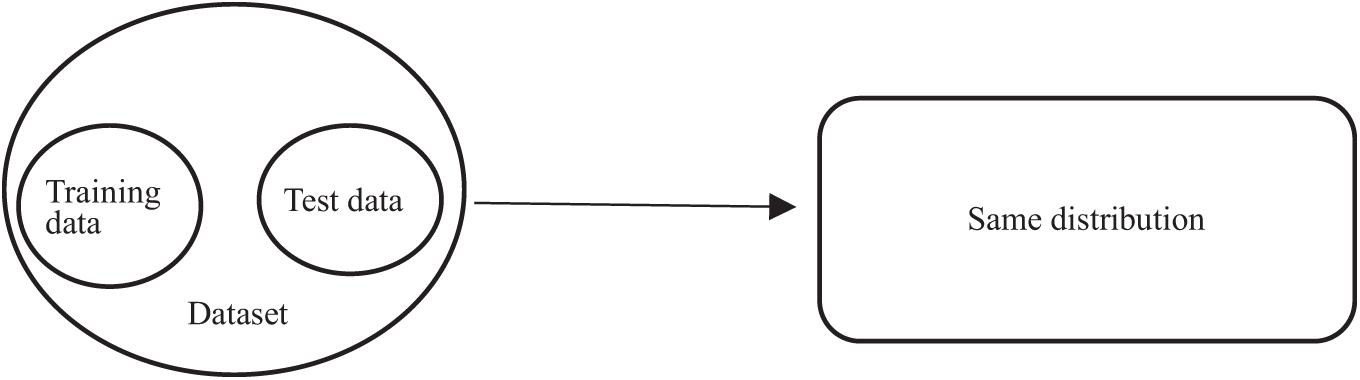
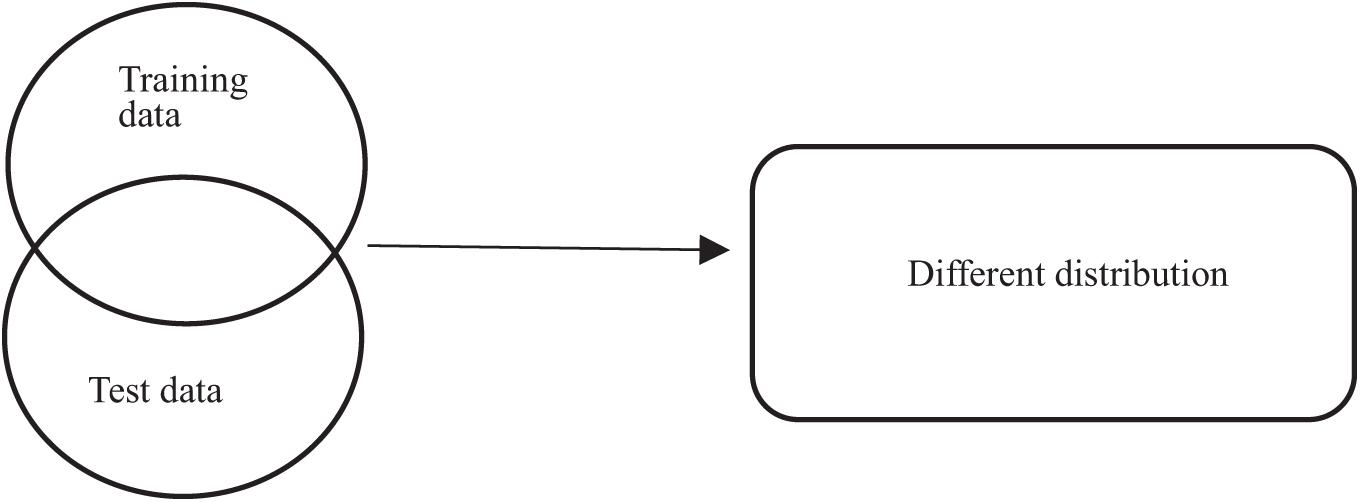
Epilepsy is a disease caused by the sudden discharge of cerebral neurons. EEG technology (Suk et al., 2018) can monitor the changes of brain electrical signals, so we often use EEG intelligent recognition technology to detect epilepsy (Litt et al., 2001; Iasemidis et al., 2003; Dorai and Ponnambalam, 2010). Nowadays, many machines learn algorithms (Wang et al., 2015; Zhang et al., 2021) have been used to recognize epileptic signals, such as Decision Tree (Wang et al., 2015), nearest neighbor (KNN) (Iscan et al., 2011), Naive Bayes Algorithm (NB; Iscan et al., 2011), support vector machines (SVM; Yang et al., 2014), and fuzzy system (Aarabi et al., 2009; Rabbi and Fazel-Rezai, 2012; Deng et al., 2014a, b, 2018; Jiang et al., 2015). It has been proved that these algorithms can detect epilepsy faster and more accurately than doctors. However, as shown in Figure 1, only when the training set and test set obey the similar distribution can they show good classification performance. However, in most cases, as shown in Figure 2, the distribution characteristics of EEG data are not exactly the same. In order to make full use of their similar information, some researchers have proposed to use transfer learning algorithm, such as LMPROJ (Yang et al., 2014) and STL (Wang et al., 2018), applying the old knowledge we have gained to new fields. Different from traditional machine learning, which acquires knowledge from data and applies it to new problems, transfer learning focuses on transferring the learned knowledge to new problems. Although the problem of different data distribution has been solved to a certain extent, these transfer learning algorithms only consider reducing the marginal distribution probability or conditional distribution probability (Deng et al., 2018) of data, without comprehensive balance, and these algorithms lack of interpretability.

FIGURE 1

Figure 1. Data distribution scenarios required by traditional methods.

FIGURE 2

Figure 2. Actual data distribution scenario.

To solve these problems, we propose a new method of EEG recognition based on transfer learning and a fuzzy system. The traditional method has a single model structure, so it cannot achieve good results in the face of complex scenes. Different from the traditional method, we pay attention to how to make full use of the previously marked data while ensuring the accuracy of the model on the new task. We not only minimize the marginal distribution or conditional distribution probability, but also combine them to minimize the joint probability distribution (Deng et al., 2018), and reach the best balance between marginal distribution and conditional distribution. In terms of ensuring interpretability, we use the TSK fuzzy system. Its IF-THEN rules can help us understand the rules of model operation more clearly. It has been widely used in data flow modeling, mining tasks, metacognitive learning, and multi-task learning. In order to realize this system, a TSK fuzzy system construction method based on transfer learning (TSK-TL) was developed. The experimental results show that compared with the existing algorithms, TSK-TL has better performance in EEG recognition of epilepsy.

Our contributions are mainly reflected on: (1) The introduction of transfer learning technology (Wang and Mahadevan, 2011; Quanz et al., 2012; Xiao and Guo, 2012), the proposed model in ensuring the accuracy of recognition At the same time, it has higher interpretability; (2) It has stronger robustness and can handle more complex data scenes; (3) It realizes the more accurate identification of epileptic EEG signals in data drift scenarios.

The rest of the manuscript is organized as follows. In the section “Backgrounds,”we briefly introduced the EEG data set, the classical TSK model and the related contents of transfer learning. In section “Identification of Epileptic EEG Signals Through TSK Transfer Learning fuzzysystem,”we first introduced the framework based on transfer learning, and then proposed the objective function of the TSK-TL. In section “Experimental Process and Result Analysis,” we introduce the details of our experiment to test the performance of TSK-TL. The conclusion is given in the last section.

Backgrounds

This section introduces the data sets and their processing methods used in the research, the classical TSK fuzzy system and the related content of transfer learning.

Epilepsy EEG Signal Dataset

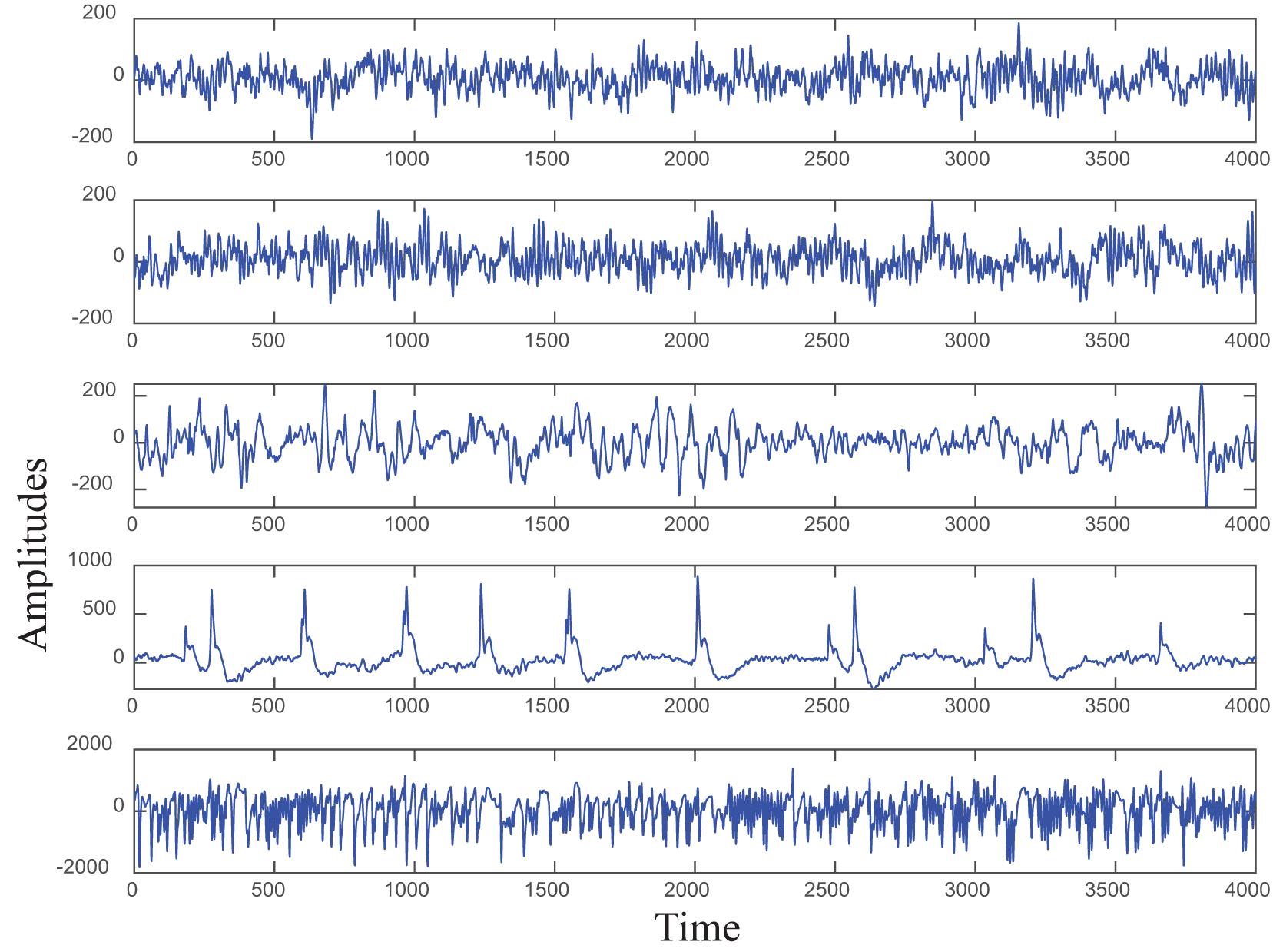
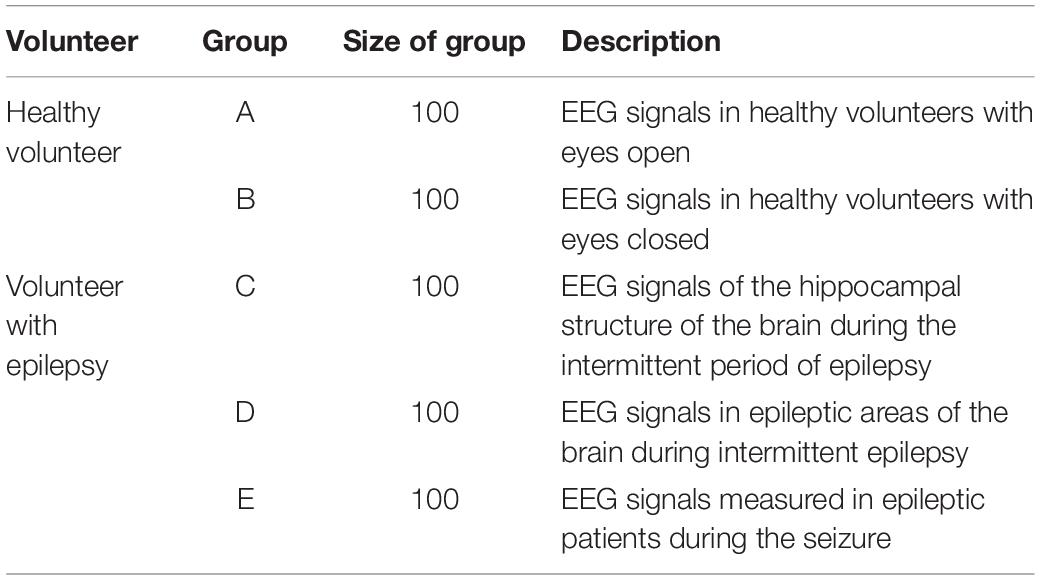
The original epileptic EEG data set used in this study is divided into five groups, i.e., Group A to Group E, each group contains 100 single-channel signal segments, and the sampling rate of all samples is adjusted to 173.6 Hz. Among them, the data from healthy people are divided into groups A and B. The difference is that the eyes of group A are opened and group B is closed. The data of groups C, D, and E are obtained from volunteers with epilepsy in different states (Li, 2021). Figure 3 shows the five groups of original epilepsy EEG signals. Table 1 presents these five groups in detail.

FIGURE 3

Figure 3. Original epilepsy EEG signals.

TABLE 1

Table 1. Description of the dataset.

The distribution law of EEG signals changes with time. Its amplitude is very small, and it is easy to be affected by other human biological currents such as ECG, EOG, and EMG. At the same time, it has strong randomness, and the noise in the signal is very complicated. Therefore, the experimental results obtained by using the original EEG signal directly are not ideal. According to previous work (Jiang et al., 2017; Tsujikawal et al., 2018), WPD, STFT, and KPCA are three typical feature extraction methods to process epileptic EEG signals (Blanco et al., 1997; Zhang et al., 2000; Srinivasan et al., 2005; Vivaldi and Bassi, 2006; Tzallas et al., 2009; Tang and Durand, 2012; Teng et al., 2017). Figure 4 shows the sample of group A processed by the three feature extraction methods.

FIGURE 4

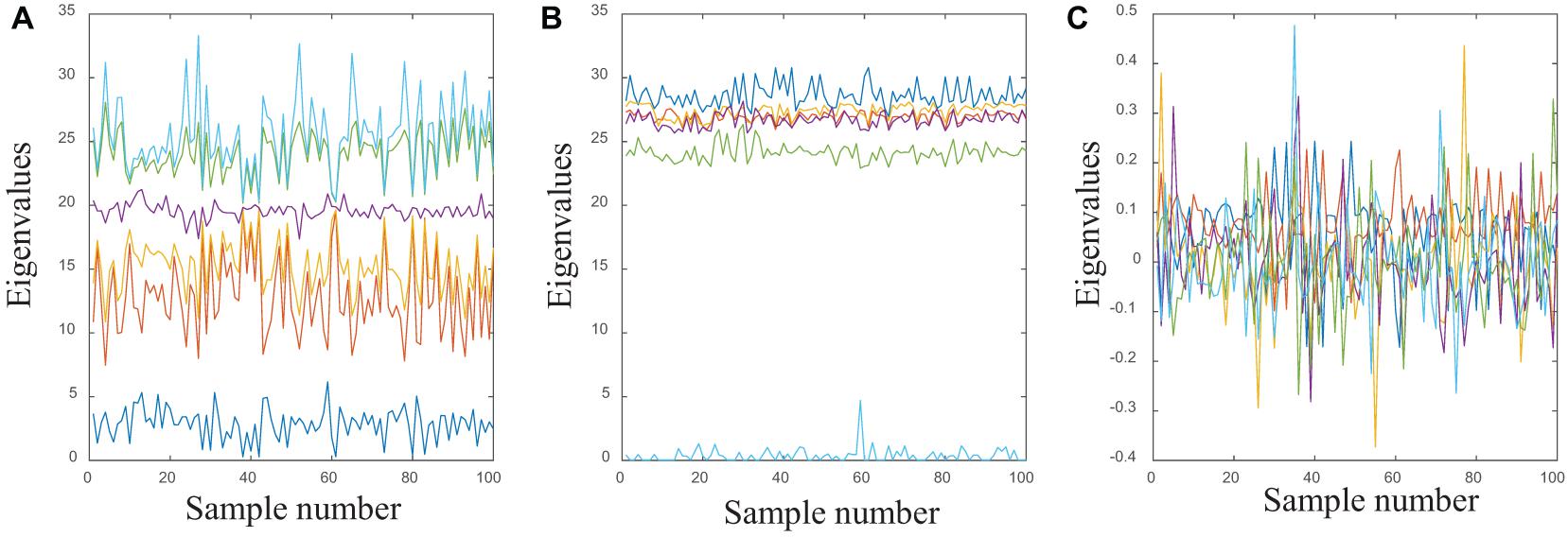
Figure 4. (A) The samples of group A processed through WPD; (B) the samples of group A processed through STFT; (C) the samples of group A processed through KPCA.

Classical TSK Fuzzy System

Because of its unique interpretability, fuzzy systems has been widely used in modeling and intelligent control. In addition, the output of TSK fuzzy system is more concise. The training process can be transformed into a linear regression problem or a quadratic programming problem, which makes the training process more efficient (Deng et al., 2012; Jiang et al., 2017).

The inference rules of TSK fuzzy system are usually defined as:

$$R^k:\text{IF}{x}_1\text{is}{A}_1^k\mathrm{\wedge }{x}_2\text{is}{A}_2^k\mathrm{\wedge }\mathrm{\cdots }\mathrm{\wedge }{x}_d\mathrm{is}{A}_d^k,(1)$$

$$\text{Then}{f}^k\left(\text{x}\right)=p_0^k+p_1^k{x}_1+\mathrm{\cdots }+p_d^k{x}_d,k=1,\mathrm{\cdots },K$$

K is the number of fuzzy rules. Each rule is premised on the input vector x = [x₁, x₂, x_d]^T and maps the fuzzy set in the input space A^k ⊂ R^d to the change single case represented by f^k(x). $A_i^k$ is the fuzzy subset of the ith dimension of the input vector x under the kth rule. ∧ is a fuzzy conjunction operator. According to previous work (Jiang et al., 2017) the result of the TSK fuzzy model can be expressed as

$$y^0=\sum _{k=1}^K\frac{{\mu }^k\left(\mathbf{x}\right)f^k\left(\mathbf{x}\right)}{{\sum }_{k^{\prime }=1}^K{\mu }^{k^{\prime }}\left(\mathbf{x}\right)}=\sum _{k=1}^K{\tilde{\mu }}^k\left(\mathbf{x}\right)f^k\left(\mathbf{x}\right)(\mathrm{2.a})$$

where

$${\mu }^k\left(\mathbf{x}\right)=\prod _{i=1}^d{\mu }_{A_i^k}(x_i)(\mathrm{2.b})$$

and

$${\tilde{\mathrm{\mu }}}^k\left(\mathbf{x}\right)={\mu }^k(\mathbf{x})/\sum _{k^{\prime }=1}^K{\mu }^{k^{\prime }}\left(\mathbf{x}\right)(\mathrm{2.c})$$

we use the Gaussian membership function, i.e.,

$${\mu }_{A_i^k}\left(x_i\right)=\text{exp}\left(\frac{-{(x_i-c_i^k)}^2}{2{\delta }_i^k}\right)(\mathrm{2.d})$$

as the fuzzy membership function. In the paper, we use the FCM algorithm to obtain $c_i^k$ and ${\delta }_i^k$. They can be estimated by the following expressions

$$c_i^k=\sum _{j=1}^N{u}_{jk}{x}_{ji}/\sum _{j=1}^N{u}_{jk}(2.e)$$

$${\delta }_i^k=h\cdot \sum _{j=1}^N{u}_{jk}{(x_{ji}-c_i^k)}^2/\sum _{j=1}^N{u}_{jk}(\mathrm{2.f})$$

u_jk is the fuzzy membership corresponding to the jth sample in the kth cluster. And h is the artificially adjustable scale parameter. After determining these antecedent parameters, let

$${\mathbf{\text{x}}}_e={(1,{\mathbf{\text{x}}}^T)}^T(\mathrm{3.a})$$

$${\widetilde{\mathbf{\text{x}}}}^k={\tilde{\mathrm{\mu }}}^k\left(\mathbf{x}\right){\mathbf{\text{x}}}_e(\mathrm{3.b})$$

$${\mathbf{\text{x}}}_g={({\left({\widetilde{\mathbf{\text{x}}}}^1\right)}^T,{\left({\widetilde{\mathbf{\text{x}}}}^2\right)}^T,\mathrm{\dots },{\left({\widetilde{\mathbf{\text{x}}}}^K\right)}^T)}^T(\mathrm{3.c})$$

$${\mathbf{\text{p}}}^k={(p_0^k,p_1^k,\mathrm{\dots },p_d^k)}^T(\mathrm{3.d})$$

$${\mathbf{\text{p}}}_g={({\left({\mathbf{\text{p}}}^1\right)}^T,{\left({\mathbf{\text{p}}}^2\right)}^T,\mathrm{\dots },{\left({\mathbf{\text{p}}}^K\right)}^T)}^T(3.e)$$

According to the above transformation, Eq. 2a be converted to the following linear regression problem (Jiang et al., 2017).

$$y^o={\mathbf{\text{p}}}_g^T{\mathbf{\text{x}}}_g(\mathrm{3.f})$$

A well-performing algorithm is proposed (Jiang et al., 2017) to train the classic TSK-FS. The objective function of this algorithm is

$$\underset{{\mathbf{p}}_g}{min}{J}_{TSK-FS}({\mathbf{\text{P}}}_g)=\frac{1}{2}{\mathbf{\text{P}}}_g^{\mathbf{T}}{\mathbf{\text{P}}}_g+\frac{{}_{{\lambda }_1}}{2}{||{\mathbf{\text{P}}}_g^{\text{T}}\mathbf{\text{X}}-\mathbf{\text{Y}}||}^2(4)$$

where $\frac{1}{2}{\mathbf{\text{P}}}_g^{\mathbf{T}}{\mathbf{\text{P}}}_g$ is the regularization term, which can effectively promote the generalization ability of the TSK-FS; P_g is a consequent parameter; X is the matrix obtained by (5c); ₁ is a regularization parameter. It can adjust the balance between model complexity and error tolerance; [Y = y₀, y₁, …, y_n] is the label matrix.

In order to obtain the optimal P_g, the derivative of J_TSK−FS(P_g) with respect to P_g can be set to 0, and then the optimal solution of P_g can be obtained as follows:

$${\mathbf{\text{P}}}_g={(\mathbf{\text{I}}+{\lambda }_1\cdot {\mathbf{\text{XX}}}^{\mathbf{T}})}^{-1}\cdot \left({\lambda }_1\cdot \mathbf{\text{XY}}\right)(5)$$

Through the optimal prior and posterior parameters, we can establish a classic TSK fuzzy system.

Preparatory Knowledge of Transfer Learning

There are three methods for transfer learning: data distribution adaptation, feature selection, and subspace learning (Shi et al., 2013; Zheng, 2021). The basic concept of data distribution adaptation is to make the probability distribution of the data of the source domain (𝒟_s) and the target domain (𝒟_t) the same or similar through some transformations. Feature selection method considers that the source domain and the target domain contain some common features, and their data distribution is similar. Then, the common features are extracted through the machine learning method, and the model can be built based on these features. The subspace learning method usually assumes that the data of the source domain and target domain will have similar distributions in the transformed subspace, and then learn through statistical feature transformation or manifold transformation.

The joint distribution adaptation (Wang et al., 2018) adopted in the paper belongs to the data distribution adaptive methods. Specifically, the core of joint distribution adaptation is to simultaneously minimize the marginal probability distribution and the conditional probability distribution of the two domains. The distance in machine learning has various forms. Here we use the MMD (Long et al., 2012) as a distance measurement. It can be calculated as follows:

$$MM{D}_H^2(D_s,D_t)={||\frac{1}{n}\sum _{i=1}^n\mathrm{\varnothing }\left({\mathbf{\text{x}}}_i\right)-\frac{1}{m}\sum _{j=n+1}^{n+m}\mathrm{\varnothing }\left({\mathbf{\text{x}}}_j\right)||}^2(6)$$

where ∅ is a feature mapping, n is the number of samples in the source domain and m indicates the number of samples in the target domain.

Identification of Epileptic EEG Signals Through TSK Transfer Learning Fuzzysystem

In this section, we will introduce in detail the transfer learning techniques we use. Combined with the analysis and research on the rules and parameter learning strategies of the classical TSK fuzzy system, a TSK-TL method for detecting epileptic signals is proposed.

Framework Based on Transfer Learning

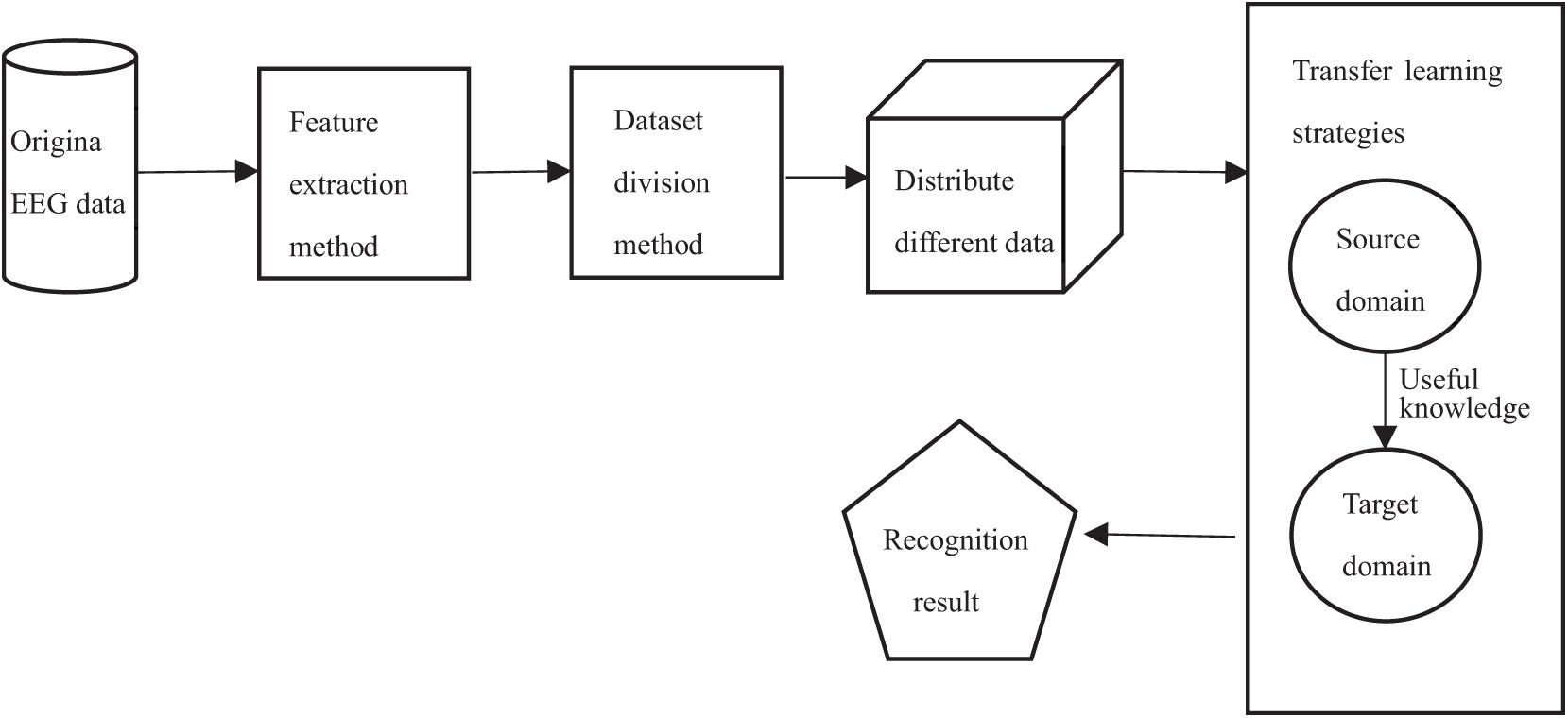
The transfer learning strategy used in this study is divided into two parts: joint distribution adaptation (Zheng, 2021) and historical knowledge learning mechanism. As shown in Figure 5, the framework of epilepsy EEG signals recognition based on transfer learning theory is given. In order to make full use of the information of source domain and target domain, our work mainly includes three steps: (1) minimizing the marginal probability distribution, (2) minimizing the conditional probability distribution, and (3) further learning with historical knowledge.

FIGURE 5

Figure 5. Framework of EEG signal recognition based on transfer learning.

(1) Minimize the marginal probability distribution

The marginal distributions of the source domain and target domain are represented by P_s and P_t, respectively. The paper builds a new model based on TSK-FS, P_g can be taken as a projected vector, x_g is a projected vector. And in order to make MMD a proper regularization for the classifier, we adopt the projected MMD (Long et al., 2013). Then the marginal probability distribution can be obtained by

$$D(P_s,P_t)={||\frac{1}{n}\sum _{\mathrm{i}=1}^n{\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{x}}}_{si}-\frac{1}{m}\sum _{\mathrm{j}=1}^m{\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{x}}}_{tj}||}^2(7)$$

where x_si is the ith sample of the source domain, x_tj is the jth sample of the target domain, n and m indicate the number of samples in the source domain and target domain, respectively.

(2) Minimize the conditional probability distribution

Reducing the distance of conditional distribution is actually to achieve intra-class migration, but we don’t know the label of the target domain. In the paper, we use some traditional classification algorithms (such as SVM) to obtain the pseudo-label of the target domain. At the same time, we assume that the calculated pseudo-class centroid may be located not far from the real class centroid (Long et al., 2012). Therefore, we can calculate the distance of conditional probability distribution by using both true label and pseudo label. The conditional probability distribution of source domain and target domain are represented by Q_s and Q_t, and then the conditional distribution can be calculated as follows:

$$D^{\left(c\right)}(Q_s,Q_t)={||\frac{1}{n^{(c)}}\sum _{{\mathbf{X}}_i\in {𝒟}_s^{(c)}}{\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{x}}}_i-\frac{1}{m^{(c)}}\sum _{{\mathbf{X}}_j\in {𝒟}_t^{(c)}}{\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{x}}}_j||}^2(8)$$

where c ∈ {0, 1, …, C} is the category tag. ${𝒟}_s^{(c)}$ is a set of the data belonging to class c in the source domain and $n^{(c)}=\left|{𝒟}_s^{(c)}\right|$. Correspondingly, ${𝒟}_t^{(c)}$ is a set of the data belonging to class c in the target domain and $m^{(c)}=\left|{𝒟}_t^{(c)}\right|$.

By integrating Equations 9 and 10, the joint probability distribution distance can be calculated as follows:

$$D(J_s,J_t)=D(P_s,P_t)+\sum _{c=1}^C{D}^{\left(c\right)}(Q_s,Q_t)(9)$$

(3) Combine the historical knowledge to further learn

The parameter P_g0 obtained through classic TSK-FS is used to further guide the learning, and then the complete tranfer learning item is

$$D({𝒟}_s,{𝒟}_t)=D(J_s,J_t)+{\lambda }_{3}D({\mathbf{\text{P}}}_{g_0},{\mathbf{\text{P}}}_g)(10)$$

where

$$D({\mathbf{\text{P}}}_{g_0},{\mathbf{\text{P}}}_g)={||{\mathbf{\text{P}}}_{g_0}-{\mathbf{\text{P}}}_g||}^2(11)$$

The Objective Function of TSK-TL

We design the objective function of TSK-TL as

$$\underset{{\mathbf{P}}_g}{min}{J}_{TSK-TL}\left({\mathbf{\text{P}}}_g\right)=g+{\lambda }_{2}D(J_s,J_t)+{\lambda }_{3}D({\mathbf{\text{P}}}_{g_0},{\mathbf{\text{P}}}_g)(\mathrm{12.a})$$

where

$$g=\frac{1}{2}{\mathbf{\text{P}}}_g^{\mathbf{T}}{\mathbf{\text{P}}}_g+\frac{{\lambda }_1}{2}{||{\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{X}}}_s-\mathbf{\text{Y}}||}^2(\mathrm{12.b})$$

$$D(J_s,J_t)=D(P_s,P_t)+\sum _{c=1}^{C}D(Q_s,Q_t)$$

$$={||\frac{1}{n}\sum _{\mathrm{i}=1}^n{\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{x}}}_{si}-\frac{1}{m}\sum _{\mathrm{j}=1}^m{\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{x}}}_{tj}||}^2$$

$$+{||\frac{1}{n^{(c)}}\sum _{{\mathbf{X}}_i\in D_s^{(c)}}{\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{x}}}_i-\frac{1}{m^{(c)}}\sum _{{\mathbf{X}}_j\in D_t^{(c)}}{\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{x}}}_j||}^2(\mathrm{12.c})$$

$$D({\mathbf{\text{P}}}_{g_0},{\mathbf{\text{P}}}_g)={||{\mathbf{\text{P}}}_{g_0}-{\mathbf{\text{P}}}_g||}^2(\mathrm{12.d})$$

where P_g is the expected projection of TSK-TL, P_g0 is the consequent parameter of the classical TSK model. X_s is a data matrix from the source domain. Y = [y₀, y₁, …, y_n] is the label matrix, if the ith sample belongs to healthy volunteers, then y_i is 1, otherwise y_i is -1. And _{1, 2, 3} are the regularization parameters.

Then we further explain the above formula as follows:

(1) Equation 12b is the training model of the classic TSK fuzzy system, so the TSK-TL we proposed inherits all its advantages.

(2) When experimenting with the classical TSK fuzzy system, the result is poor because of the distribution difference of data. By Equation 12c, the joint probability distribution distance is minimized to optimize the experimental results.

(3) In Equation 12d, P_g is further optimized by measuring the distance between P_g0 and P_g. If ₃ is infinite and the term is optimal, then P_g0 and P_g are equal.

(4) The regularization parameters ₁ 0, ₂ 0, and ₃ 0 are used to control the balance between different terms. We use the grid search method to determine their values.

Solution of TSK-TL

In Equation 12c, the first term can be converted as follows:

$$\begin{array}{rcl}& & {\left|\right|\frac{1}{n}\sum _{\mathrm{i}=1}^n{\mathbf{P}}_g^{\mathrm{T}}{\mathbf{x}}_{si}-\frac{1}{m}\sum _{\mathrm{j}=1}^m{\mathbf{P}}_g^{\mathrm{T}}{\mathbf{x}}_{tj}\left|\right|}^2\\ & & =\left|\right|\frac{1}{n}{\mathbf{P}}_g^{\mathrm{T}}{[{\mathbf{x}}_{s1}{\mathbf{x}}_{s2}\cdots {\mathbf{x}}_{sn}]}_{1^{\ast }n}{\left[\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right]}_{n^{\ast }1}\\ & & {-\frac{1}{m}{\mathbf{P}}_g^{\mathrm{T}}{[{\mathbf{x}}_{t1}{\mathbf{x}}_{t2}\cdots {\mathbf{x}}_{tn}]}_{1^{\ast }m}{\left[\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right]}_{m^{\ast }1}\left|\right|}^2\\ & & =\mathrm{t}\mathrm{r}(\frac{1}{n^2}{\mathbf{P}}_g^{\mathrm{T}}{\mathbf{X}}_s\mathbf{1}{\left({\mathbf{P}}_g^{\mathrm{T}}{\mathbf{X}}_s\mathbf{1}\right)}^{\mathrm{T}}+\frac{1}{m^2}{\mathbf{P}}_g^{\mathrm{T}}{\mathbf{X}}_t\mathbf{1}{\left({\mathbf{P}}_g^{\mathrm{T}}{\mathbf{X}}_t\mathbf{1}\right)}^{\mathrm{T}}\\ & & -\frac{1}{nm}{\mathbf{P}}_g^{\mathrm{T}}{\mathbf{X}}_s\mathbf{1}{\left({\mathbf{P}}_g^{\mathrm{T}}{\mathbf{X}}_s\mathbf{1}\right)}^{\mathrm{T}}-\frac{1}{nm}{\mathbf{P}}_g^{\mathrm{T}}{\mathbf{X}}_t\mathbf{1}{\left({\mathbf{P}}_g^{\mathrm{T}}{\mathbf{X}}_t\mathbf{1}\right)}^{\mathrm{T}})\\ & & +\mathrm{t}\mathrm{r}[{\mathbf{P}}_g^{\mathrm{T}}(\frac{1}{n^2}\mathbf{1}{\mathbf{1}}^{\mathrm{T}}{\mathbf{X}}_s^{\mathrm{T}}{\mathbf{X}}_s+\frac{1}{m^2}\mathbf{1}{\mathbf{1}}^{\mathrm{T}}{\mathbf{X}}_t^{\mathrm{T}}{\mathbf{X}}_t\\ & & -\frac{1}{nm}\mathbf{1}{\mathbf{1}}^{\mathrm{T}}{\mathbf{X}}_s^{\mathrm{T}}{\mathbf{X}}_t\mathbf{-}\frac{1}{nm}\mathbf{1}{\mathbf{1}}^{\mathrm{T}}{\mathbf{X}}_t^{\mathrm{T}}{\mathbf{X}}_s){\mathbf{P}}_g]\\ & & =\mathrm{t}\mathrm{r}\left({\mathbf{P}}_g^{\mathrm{T}}\mathbf{X}{\mathbf{M}}_0{\mathbf{X}}^{\mathrm{T}}{\mathbf{P}}_g\right)\end{array}$$

Similarly, the second term can be converted as:

$$\text{tr}\left({\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{XM}}}_{\text{c}}{\mathbf{\text{X}}}^{\text{T}}{\mathbf{\text{P}}}_g\right)$$

where X is a matrix composed of the source domain and target domain data. M_c is MMD matrix computed as:

$${({\mathbf{\text{M}}}_{\text{c}})}_{\text{ij}}=\{\begin{array}{c}\hfill \frac{1}{n^{(c)}{n}^{(c)}},{\mathbf{\text{x}}}_i,{\mathbf{\text{x}}}_j\in {𝒟}_s^{(c)}\hfill \\ \hfill \frac{1}{m^{(c)}{m}^{(c)}},{\mathbf{\text{x}}}_i,{\mathbf{\text{x}}}_j\in {𝒟}_t^{(c)}\hfill \\ \\ \hfill \frac{-1}{n^{(c)}{m}^{(c)}},\{\begin{array}{c}\hfill {\mathbf{\text{x}}}_i\in {𝒟}_s^{(c)},{\mathbf{\text{x}}}_j\in {𝒟}_t^{(c)}\hfill \\ \hfill {\mathbf{\text{x}}}_j\in {𝒟}_s^{(c)},{\mathbf{\text{x}}}_i\in {𝒟}_t^{(c)}\hfill \end{array}\hfill \\ \hfill \mathrm{\hspace{0.33em}0},\text{otherwise}\hfill \end{array}(13)$$

So

$$D(J_s,J_t)=\mathrm{tr}\left({\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{XMX}}}^{\text{T}}{\mathbf{\text{P}}}_g\right)\mathbf{\text{M}}=\sum _{\mathrm{c}=0}^{\text{C}}{\mathbf{\text{M}}}_{\text{c}}$$

Then,

$$\begin{array}{c}\underset{{\mathbf{P}}_g}{min}{J}_{TSK-TL}\left({\mathbf{\text{P}}}_g\right)=\frac{1}{2}{\mathbf{\text{P}}}_g^{\mathbf{T}}{\mathbf{\text{P}}}_g+\frac{{\lambda }_1}{2}{||{\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{X}}}_s-\mathbf{\text{Y}}||}^2\hfill \\ +{\lambda }_2\text{tr}\left({\mathbf{\text{P}}}_g^{\text{T}}{\mathbf{\text{XMX}}}^{\text{T}}{\mathbf{\text{P}}}_g\right)+{\lambda }_3{||{\mathbf{\text{P}}}_{g_0}-{\mathbf{\text{P}}}_g||}^2\hfill \end{array}$$

By setting the derivative of J_TSK–TL with respect to P_g to zero, i.e., $\frac{\partial J_{TSK-TL}}{{\mathbf{P}}_g}=0$, we can get the optimal solution of P_g as follows:

$${\mathbf{\text{P}}}_g={({}_2(\mathbf{\text{XM}}+{\mathbf{\text{XM}}}^{\text{T}}){\mathbf{\text{X}}}^{\text{T}}+{\lambda }_1{\mathbf{\text{X}}}_s{\mathbf{\text{X}}}_s^{\text{T}}+{\lambda }_3\mathbf{\text{I}})}^{-1}({\lambda }_1{\mathbf{\text{X}}}_s{\mathbf{\text{Y}}}^{\text{T}}+{\lambda }_3{\mathbf{\text{P}}}_{g_0})(14)$$

By (7), (15), and (16), we can obtain the optimal posterior parameter P_g. Then based on P_g, the final decision function can be obtained as follows

$$f\left({\mathbf{\text{x}}}_{gi}\right)=\mathrm{sign}({\mathbf{\text{P}}}_g{\mathbf{\text{x}}}_{gi})(15)$$

The details of the proposed TSK-TL algorithm are as follows:

Algorithm of TSK-TL.

Initialization: Set the number of fuzzy rules K, the regularization parameters λ1, λ2, and λ3.

Stage 1: Construction of datasets for linear regression

Step 1: Through classical FCM or other partition techniques to divide the input space of training data to determine the premise of TSK-FS.

Step 2: Construct the new training dataset and test dataset through (3a)–(3c).

Stage 2: Computation of historical knowledge parameter Pg0

Step 3: Obtain the Pg0 by (5).

Stage 3: Obtain the parameter Pg of TSK-TL

Step 4: Compute the MMD matrix by (13).

Step 5: Compute the consequent parameter Pg of TSK-TL through (14).

Step 6: Generate the TSK-TL by (15).

Experimental Process and Results Analysis

In this section, the proposed TSK-TL method is evaluated by classifying EEG signals of epilepsy patients and healthy people. In addition, a comparative study of five traditional machine learning algorithms and two transfer learning algorithms is carried out. Details of the experiments are as follows.

Experimental Setup

In this paper, we use three classical feature extraction methods, namely WPD, STFT, and KPCA, to obtain EEG datasets from three different views and perform experiments on them, respectively. In each experiment, we set up 10 experimental datasets, and every dataset is composed of part of the data from two or three different groups in this view. The details of these datasets are shown in Table 2. The structure of this dataset ensures that there is no or only a part of the data comimg from the same group. In short, there is no or only a part of the data in the source domain and the test domain has the same distribution.

TABLE 2

Table 2. Structure of experimental datasets.

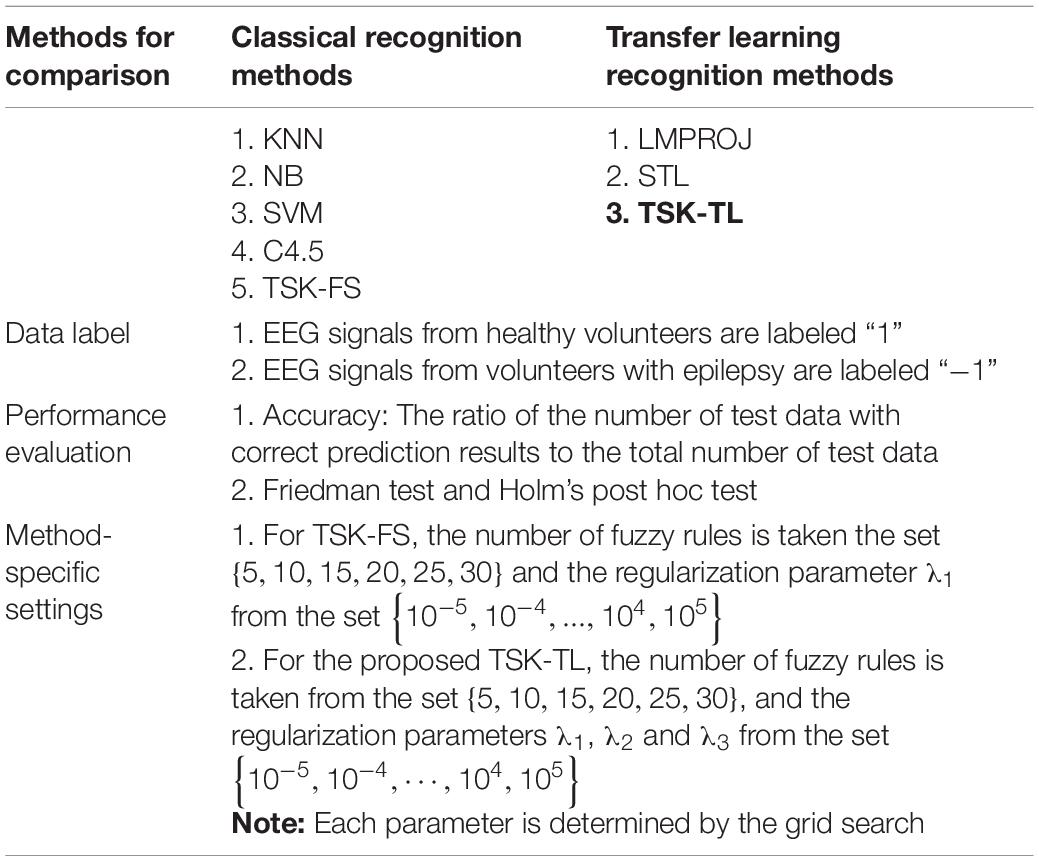
During the experiment, the experiment of each experimental dataset is repeated 10 times. And take the average result of 10 times to evaluate the performance. The optimal hyperparameters of each experimental model are determined by the grid search. All the algorithms are implemented using MATLAB on a computer with Intel i5-4590 3.3 GHz CPU, 12 GB of RAM. The details of the experimental setup are shown in Table 3.

TABLE 3

Table 3. Experimental setup.

Recognition Performance

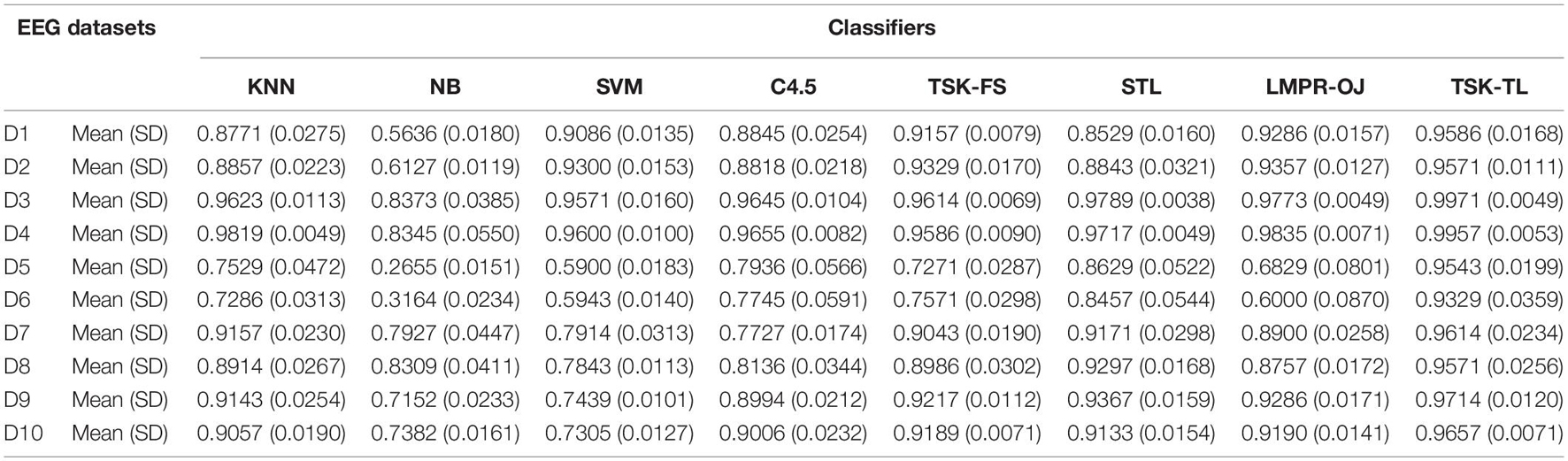
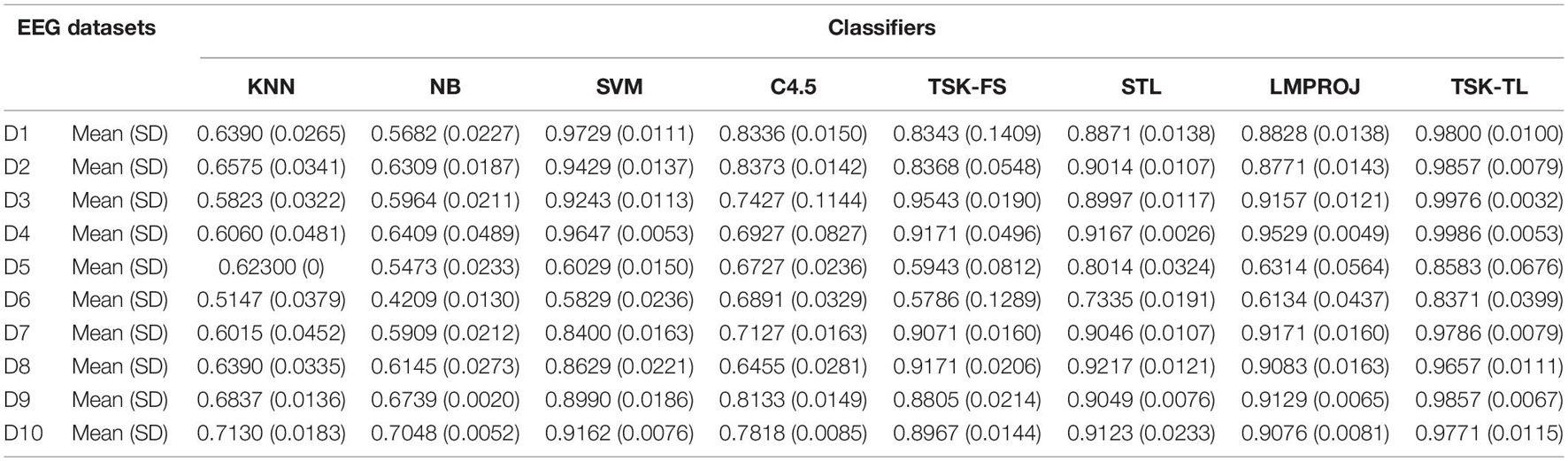
In our experiment, five traditional machine learning algorithms and two transfer learning algorithms, i.e., LMPROJ and STL are used for comparative experiments. The results are shown in Tables 4–6. By observing these results, three conclusions can be drawn as follows.

(1) The proposed TSK-TL method not only reduces the difference of data distribution, but also optimizes the formation of new knowledge parameters through the prior knowledge parameters obtained from the classical TSK-FS model. The results show that our method can improve the accuracy of EEG signal recognition.

(2) Compared with the two transfer learning classifiers LMPROJ and STL, TSK-TL is superior to LMPROJ in recognition of epileptic EEG signals, and its performance is better than or at least comparable to the STL method. STL method uses affinity within the class to transfer knowledge within the class, and then to learn. The LMPROJ method only reduces the marginal distribution of data based on the SVM algorithm.

(3) The TSK-TL method we proposed has a good recognition effect in the three views, and the average recognition accuracy in the WPD view is the highest, which points out the direction for us to select an appropriate feature extraction method in practical applications. At the same time, it can be observed that when processing the D5 and D6 data sets, the recognition accuracy is greatly improved compared with other methods, which further verifies that our proposed method has a better effect in the face of data with large differences in data distribution.

TABLE 4

Table 4. Experimental results of eight classifiers in the WPD view.

TABLE 5

Table 5. Experimental results of eight classifiers in the STFT view.

TABLE 6

Table 6. Experimental results of eight classifiers in the KPCA view.

Statistical Analysis

We evaluated the experimental results from a statistical point of view through the Friedman test (Demšar, 2006; Garcia and Herrera, 2008) and the Holm’s post hoc test (Demšar, 2006; Garcia and Herrera, 2008). Friedman test is used to calculate the average ranking of the compared methods and to determine whether the observed difference are statistically significant. We set the significance level of the test to 0.05. If the p-value is less than 0.05, the null hypothesis H0 is rejected and we can confirm that there are significant difference. The Holm’s post hoc test is then performed to evaluate the statistical differences between the control (i.e., the method that achieves the best Friedman rank) and other methods. The results of the Friedman test are shown in Table 7, and the results of the Holm’s post hoc test are shown in Table 8.

TABLE 7

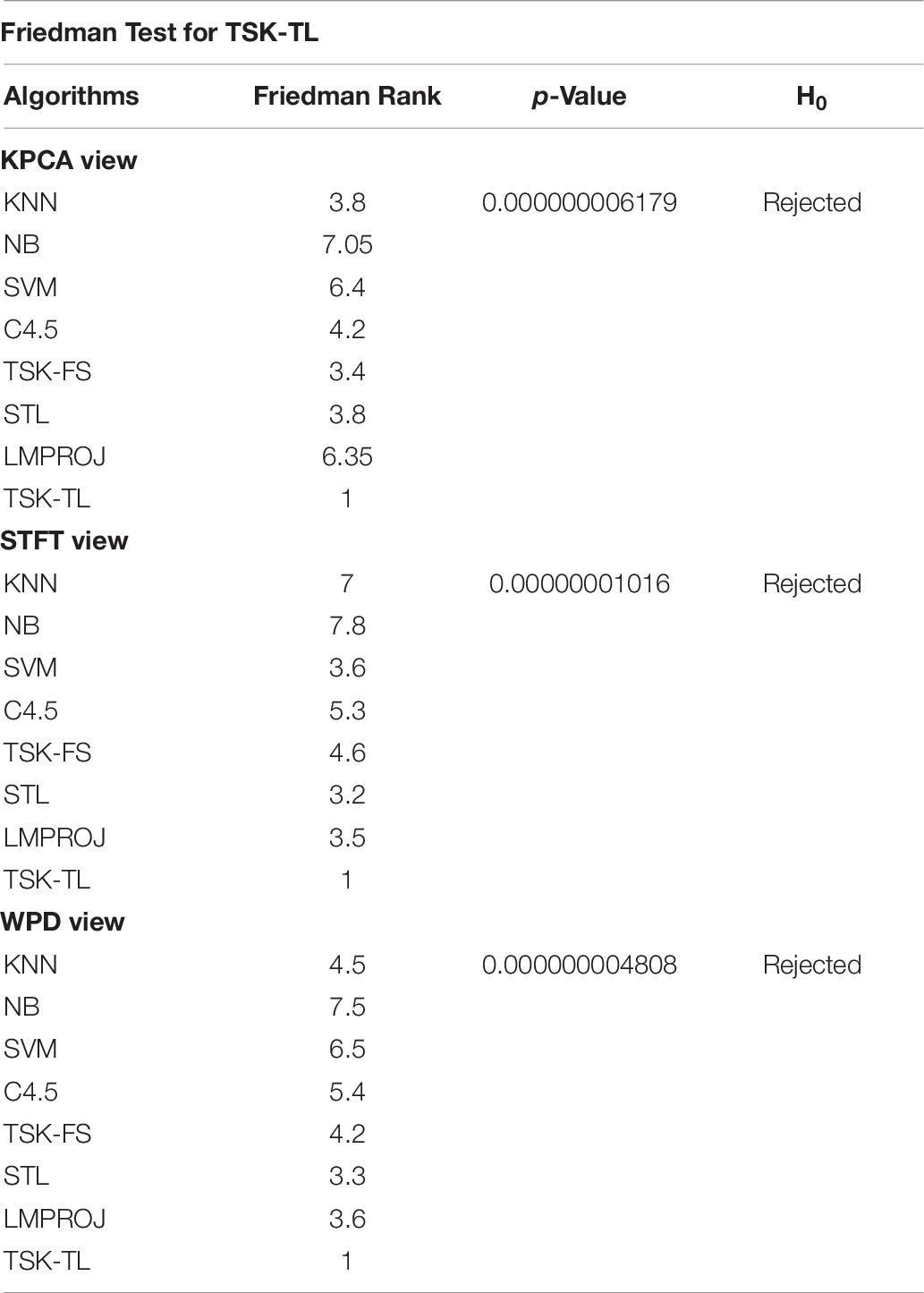
Table 7. Comparison of average performance of TSK-Tl and other seven methods using Friedman test (A = 0.05).

TABLE 8

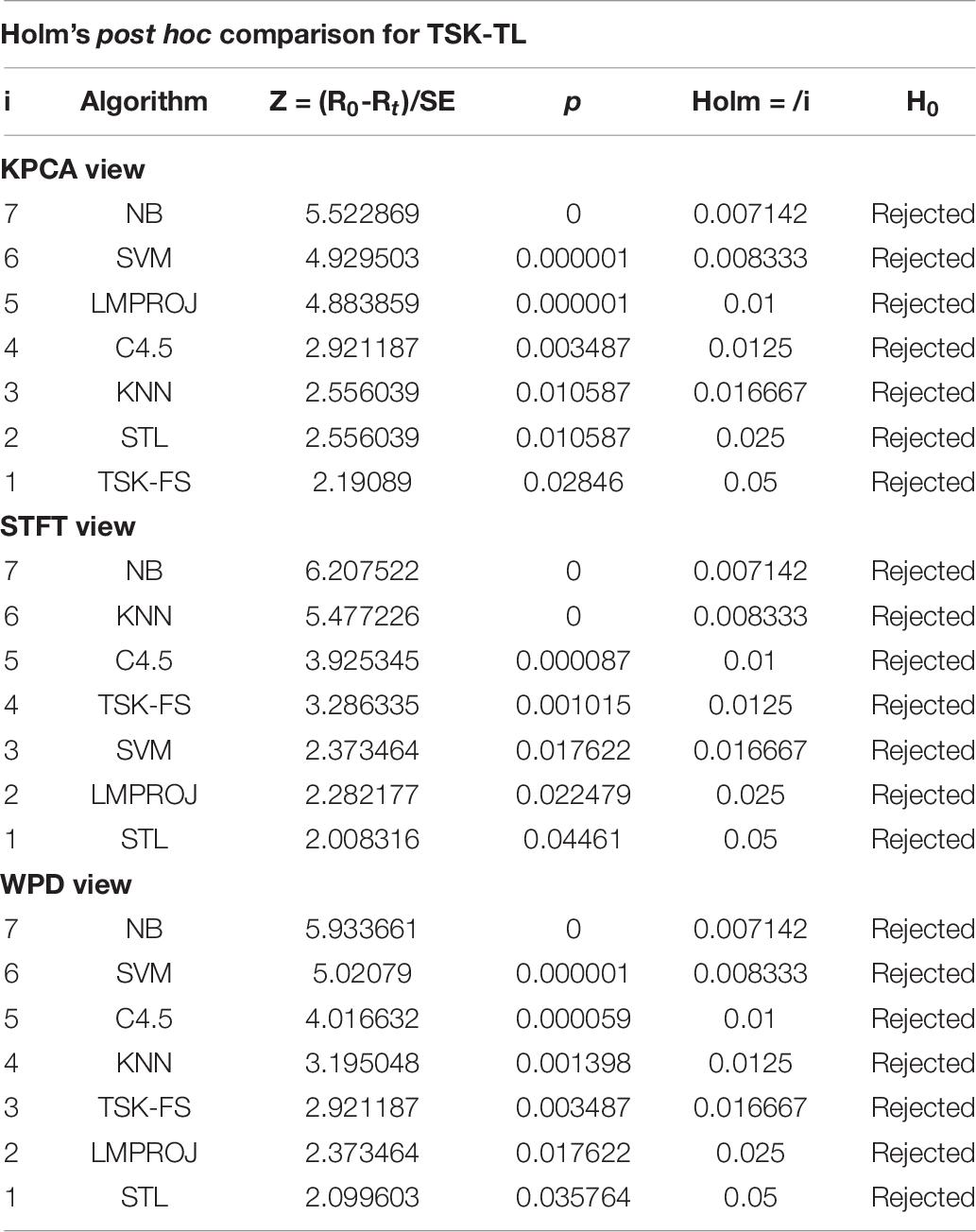
Table 8. Holm’s post hoc comparison of the results of Friedman procedure of TSK-TL and other seven methods

As shown in Table 7, the Friedman test results reveal that the TSK-TL method performs better than the other seven classification methods in classification accuracy. And the results of Holm’s post hoc in Table 8 also show that compared with other methods, TSK-TL—TL has better performance. This once again proves that our proposed TSK-TL has achieved better results in the detection of epileptic EEG signals.

Model Analysis

In this section, TSK-TL is analyzed through the model trained from the D2 dataset in the KPCA view. Table 9 gives an example of the model, these model parameters prove that TSK-TL inherits the interpretability of the classical TSK fuzzy system. In this example, we set up five fuzzy rules. Figure 6 shows the corresponding MF of each fuzzy set, where each MF has a fuzzy rule description, such as “the energy of a band of EEG signal is Low” (A little low, Medium, A little high or High). Because medical experts in different fields have different interpretations of fuzzy rules, the language description given is only a possible example.

TABLE 9

Table 9. TSK-TL Model with five rules trained on the dataset D2 for the KPCA view.

FIGURE 6

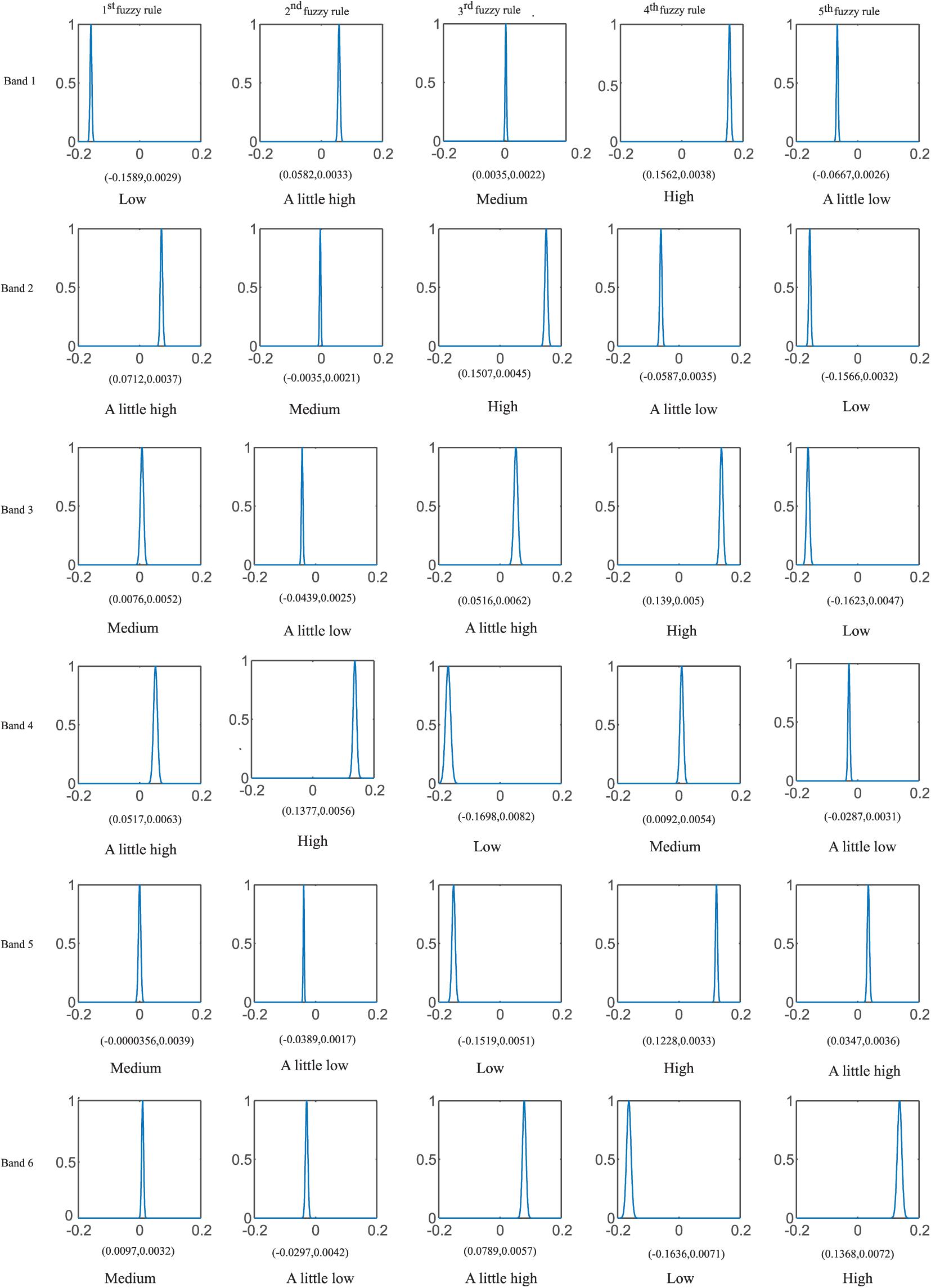
Figure 6. The membership function of each fuzzy rule and the linguistic interpretation of each fuzzy subset of the TSK fuzzy system are obtained from the KPCA view.

According to the central value from low to high, these five MFs can be expressed as “Low,” “A little low,” “Medium,” “A little high,” and “High”. Finally, through the language expression of the IF-part of the fuzzy rule and the linear function corresponding to the THEN-part of the fuzzy rule, five fuzzy rules of the KPCA view are given:

The first fuzzy rule:

If the energy of EEG signal from band 1 to band 6 is Low, A little high, Medium, A little high, Medium, and Medium, respectively,

THEN the decision value under this rule is obtained by the following formula:

$$\begin{array}{c}{f}^1\left(\mathbf{x}\right)=[-2.7245-0.5118x_1+0.9243x_2-0.295x_3\hfill \\ -0.0378x_4-0.58x_5-1.1201x_6]\hfill \end{array}$$

The second fuzzy rule:

If the energy of EEG signal from band 1 to band 6 is A little high, Medium, A little Low, High, A little Low and A little Low, respectively,

THEN the decision value under this rule is obtained by the following formula:

$$\begin{array}{c}{f}^2\left(\mathbf{x}\right)=[10.9842-8.5028x_1-0.9881x_2+4.7443x_3\hfill \\ -1.8692x_4+3.2596x_5-3.0533x_6]\hfill \end{array}$$

The third fuzzy rule:

If the energy of EEG signal from band 1 to band 6 is Medium, High, A little high, Low, Low and A little high, respectively,

THEN the decision value under this rule is obtained by the following formula:

$$\begin{array}{c}{f}^3\left(\mathbf{x}\right)=[2.045+3.995x_1-4.3315x_2-1.4117x_3\hfill \\ -0.9264x_4-0.0619x_5+0.4859x_6]\hfill \end{array}$$

The fourth fuzzy rule:

If the energy of EEG signal from band 1 to band 6 is High, A little low, High, Medium, High and Low, respectively,

THEN the decision value under this rule is obtained by the following formula:

$$\begin{array}{c}{f}^4\left(\mathbf{x}\right)=[-3.8877-2.2364x_1-0.7276x_2\hfill \\ -1.1165x_3+0.1062x_4-1.3669x_{5}0.9594x_6]\hfill \end{array}$$

The fifth fuzzy rule:

If the energy of EEG signal from band 1 to band 6 is A little Low, Low, Low, A little low, A little high, and High, respectively,

THEN the decision value under this rule is obtained by the following formula:

$$\begin{array}{c}{f}^5\left(\mathbf{x}\right)=[2.0489+4.0366x_1-4.2784x_2-1.4602x_3\hfill \\ -1.0065x_4+0.0086x_5+0.9774x_6]\hfill \end{array}$$

According to the final output value, i.e., y = -1 or y = 1, it can be judged whether the patient has epilepsy.

Conclusion

The study combines the classic TSK fuzzy system with transfer learning technology and proposes a TSK fuzzy system (TSK-TL) that is interpretable and can better adapt to scenarios of data distribution differences. It expands the application scenarios of the model and realizes the recognition of epileptic EEG signals with large data distribution differences in reality.

Although we have proved the effectiveness of TSK-TL, it can be further optimized. For example, there are several predefined parameters in the TSK-TL algorithm. When optimizing them, the optimization process of these parameters takes a lot of time. In the future, we will study the problem and develop more effective algorithms.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/benfulcher/hctsaTutorial_BonnEEG.

Author Contributions

ZZ developed the theoretical framework and model in this work and drafted the manuscript. XD gave support for medical knowledge. ZZ, XD, JY, and AC implemented the algorithm and performed experiments and result analysis. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grants U20A20228, 61772241, and 61873321, in part by the Science and Technology Demonstration Project of Social Development of Jiangsu Province under Grant BE2019631, and in part by the 2018 Six Talent Peaks Project of Jiangsu Province under Grant XYDXX-127.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aarabi, A., Fazel-Rezai, R., and Aghakhani, Y. (2009). A fuzzy rule-based system for epileptic seizure detection in intracranial EEG. Clin. Neurophysiol. 120, 1648–1657. doi: 10.1016/j.clinph.2009.07.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Blanco, S., Kochen, S., Rosso, O. A., and Salgado, P. (1997). Applying time-frequency analysis to seizure EEG activity. IEEE Engin. Med. Biol. Magaz. 16, 64–71. doi: 10.1109/51.566156

CrossRef Full Text | Google Scholar

Demšar, J. (2006). Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 7, 1–30.

Google Scholar

Deng, Z., Choi, K. S., Jiang, Y., and Wang, S. (2014b). Generalized hidden-mapping ridge regression, knowledge-leveraged inductive transfer learning for neural networks, fuzzy systems and kernel methods. IEEE Trans. Cybernet. 44, 2585–2599. doi: 10.1109/tcyb.2014.2311014

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, Z., Jiang, Y., Chung, F. L., Choi, K. S., and Wang, S. (2014a). Transfer prototype-based fuzzy clustering. IEEE Trans. Fuzzy Syst. 24, 1210–1232. doi: 10.1109/tfuzz.2015.2505330

CrossRef Full Text | Google Scholar

Deng, Z., Jiang, Y., Chung, F. L., Ishibuchi, H., and Wang, S. (2012). Knowledge-leverage-based fuzzy system and its modeling. IEEE Trans. Fuzzy Syst. 21, 597–609. doi: 10.1109/tfuzz.2012.2212444

CrossRef Full Text | Google Scholar

Deng, Z., Peng, X., Xie, L., Choi, K. S., and Wang, S. (2018). Transductive joint-knowledge-transfer tsk-fs for recognition of epileptic eeg signals. IEEE Trans. Neural Syst. Rehabil. Engin. 26, 1481–1494.

Google Scholar

Dorai, A., and Ponnambalam, K. (2010). Automated epileptic seizure onset detection. International Conference on Autonomous & Intelligent Systems. New York, NY: IEEE.

Google Scholar

Garcia, S., and Herrera, F. (2008). An extension on” Statistical Comparisons of Classifiers over Multiple Data Sets” for all pairwise comparisons. J. Mach. Learn. Res. 9, 2677–2694.

Google Scholar

Iasemidis, L. D., Shiau, D. S., Chaovalitwongse, W., Sackellares, J. C., Pardalos, P. M., Principe, J. C., et al. (2003). Adaptive epileptic seizure prediction system. IEEE Trans. Biomed. Engin. 50, 616–627.

Google Scholar

Iscan, Z., Dokur, Z., and Demiralp, T. (2011). Classification of electroencephalogram signals with combined time and frequency features. Expert Syst. Appl. 38, 10499–10505. doi: 10.1016/j.eswa.2011.02.110

CrossRef Full Text | Google Scholar

Jiang, Y., Deng, Z., Chung, F. L., and Wang, S. (2015). Multi-task TSK fuzzy system modeling using inter-task correlation information. Inform. Sci. 298, 512–533. doi: 10.1016/j.ins.2014.12.007

CrossRef Full Text | Google Scholar

Jiang, Y., Deng, Z., Chung, F. L., Wang, G., Qian, P., Choi, K. S., et al. (2017). Recognition of epileptic eeg signals using a novel multiview tsk fuzzy system. IEEE Trans. Fuzzy Syst. 25, 3–20. doi: 10.1109/tfuzz.2016.2637405

CrossRef Full Text | Google Scholar

Li, L. (2021). DSP for condition monitoring equipment in real-time. ASP Trans. Neural Inform. Comput. 1, 22–25.

Google Scholar

Litt, B., Esteller, R., Echauz, J., D’Alessandro, M., Shor, R., Henry, T., et al. (2001). Epileptic seizures may begin hours in advance of clinical onset: a report of five patients. Neuron 30, 51–64. doi: 10.1016/s0896-6273(01)00262-8

CrossRef Full Text | Google Scholar

Long, M., Wang, J., Ding, G., Cheng, W., Zhang, X., and Wang, W. (2012). Dual transfer learning. In Proceedings of the 2012 SIAM International Conference on Data Mining. Thailand: Society for Industrial and Applied Mathematics, 540–551.

Google Scholar

Long, M., Wang, J., Ding, G., Sun, J., and Yu, P. S. (2013). Transfer feature learning with joint distribution adaptation. In Proceedings of the IEEE international conference on computer vision. New York, NY: IEEE, 2200–2207.

Google Scholar

Quanz, B., Huan, J., and Mishra, M. (2012). Knowledge transfer with low-quality data: A feature extraction issue. IEEE Trans. Knowl. Data Engin. 24, 1789–1802. doi: 10.1109/tkde.2012.75

CrossRef Full Text | Google Scholar

Rabbi, A. F., and Fazel-Rezai, R. (2012). A fuzzy logic system for seizure onset detection in intracranial EEG. Comput. Intell. Neurosci. 12, 7051401–70514012.

Google Scholar

Shi, X., Liu, Q., Fan, W., and Philip, S. Y. (2013). Transfer across completely different feature spaces via spectral embedding. IEEE Trans. Knowl. Data Engin. 25, 906–918. doi: 10.1109/tkde.2011.252

CrossRef Full Text | Google Scholar

Srinivasan, V., Eswaran, C., and Sriraam, A. N. (2005). Artificial neural network based epileptic detection using time-domain and frequency-domain features. J. Med. Syst. 29, 647–660. doi: 10.1007/s10916-005-6133-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Suk, K. H., Daesub, Y., Soon, S. H., and Hee, P. C. (2018). Predicting the eeg level of a driver based on driving information. IEEE Trans. Intell. Transport. Syst. 20, 1215–1225. doi: 10.1109/tits.2018.2848300

CrossRef Full Text | Google Scholar

Tang, Y., and Durand, D. (2012). A tunable support vector machine assembly classifier for epileptic seizure detection. Expert Syst. Appl. 39, 3925–3938. doi: 10.1016/j.eswa.2011.08.088

PubMed Abstract | CrossRef Full Text | Google Scholar

Teng, T., Bi, L., and Liu, Y. (2017). Eeg-based detection of driver emergency braking intention for brain-controlled vehicles. IEEE Trans. Intell. Transport. Syst. 19, 1766–1773. doi: 10.1109/tits.2017.2740427

CrossRef Full Text | Google Scholar

Tsujikawal, M., Onishil, Y., Kiuchil, Y., Ogatsul, T., and Hashimoto, S. (2018). Drowsiness Estimation from Low-Frame-Rate Facial Videos using Eyelid Variability Features. 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). New York, NY: IEEE.

Google Scholar

Tzallas, A. T., Tsipouras, M. G., and Fotiadis, D. I. (2009). Epileptic seizure detection in eegs using time–frequency analysis. IEEE Trans. Inf. Technol. Biomed. 13, 703–710. doi: 10.1109/titb.2009.2017939

PubMed Abstract | CrossRef Full Text | Google Scholar

Vivaldi, E. A., and Bassi, A. (2006). Frequency domain analysis of sleep EEG for visualization and automated state detection. In 2006 International Conference of the IEEE Engineering in Medicine and Biology Society. New York: IEEE, 3740–3743.

Google Scholar

Wang, C., and Mahadevan, S. (2011). Heterogeneous domain adaptation using manifold alignment. In Twenty-second international joint conference on artificial intelligence. Barcelona: IJCAI.

Google Scholar

Wang, G., Deng, Z., and Choi, K. S. (2015). Detection of Epileptic Seizures in EEG Signals with Rule-Based Interpretation by Random Forest Approach. International Conference on Intelligent Computing. Cham: Springer.

Google Scholar

Wang, J., Feng, W., Chen, Y., Yu, H., Huang, M., and Yu, P. S. (2018). Visual domain adaptation with manifold embedded distribution alignment. In Proceedings of the 26th ACM international conference on Multimedia. New York, NY: Association for Computing Machinery, 402–410.

Google Scholar

Xiao, M., and Guo, Y. (2012). Semi-supervised kernel matching for domain adaptation. In Twenty-Sixth AAAI Conference on Artificial Intelligence. Palo Alto, CA: AAAI Press.

Google Scholar

Yang, C., Deng, Z., Choi, K. S., Jiang, Y., and Wang, S. (2014). Transductive domain adaptive learning for epileptic electroencephalogram recognition. Artific. Intell. Med. 62, 165–177. doi: 10.1016/j.artmed.2014.10.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Fan, C., Zhang, L., and Kong, M. (2021). K Algorithm for microstrip peocessor design. ASP Trans. Neural Inform. Comput. 1, 15–21.

Google Scholar

Zhang, Z., Kawabata, H., and Liu, Z. Q. (2000). EEG analysis using fast wavelet transform. In Smc 2000 conference proceedings. 2000 ieee international conference on systems, man and cybernetics.’cybernetics evolving to systems, humans, organizations, and their complex interactions’(cat. no. 0, Vol. 4. New York: IEEE, 2959–2964.

Google Scholar

Zheng, M. (2021). PCNN for power distribution network. ASP Trans. Neural Inform. Comput. 1, 9–14.

Google Scholar