Inter- and Intra-subject Template-Based Multivariate Synchronization Index Using an Adaptive Threshold for SSVEP-Based BCIs

The steady-state visually evoked potential (SSVEP) has been widely used in brain-computer interfaces (BCIs). Many studies have proved that the Multivariate synchronization index (MSI) is an efficient method for recognizing the frequency components in SSVEP-based BCIs. Despite its success, the recognition accuracy has not been satisfactory because the simplified pre-constructed sine-cosine waves lack abundant features from the real electroencephalogram (EEG) data. Recent advances in addressing this issue have achieved a significant improvement in recognition accuracy by using individual calibration data. In this study, a new extension based on inter- and intra-subject template signals is introduced to improve the performance of the standard MSI method. Through template transfer, inter-subject similarity and variability are employed to enhance the robustness of SSVEP recognition. Additionally, most existed methods for SSVEP recognition utilize a fixed time window (TW) to perform frequency domain analysis, which limits the information transfer rate (ITR) of BCIs. For addressing this problem, a novel adaptive threshold strategy is integrated into the extension of MSI, which uses a dynamic window to extract the temporal features of SSVEPs and recognizes the stimulus frequency based on a pre-set threshold. The pre-set threshold contributes to obtaining an appropriate and shorter signal length for frequency recognition and filtering ignored-invalid trials. The proposed method is evaluated on a 12-class SSVEP dataset recorded from 10 subjects, and the result shows that this achieves higher recognition accuracy and information transfer rate when compared with the CCA, MSI, Multi-set CCA, and Individual Template-based CCA. This paper demonstrates that the proposed method is a promising approach for developing high-speed BCIs.

1. Introduction

The Brain-Computer Interfaces (BCIs) provide humans with a direct communication and control channel between human brains and external devices by utilizing brain signals produced along the cerebral cortex within the brain to directly control external devices without the aid of muscular movements (Dornhege et al., 2007; Faller et al., 2010). People with disabilities, such as limb loss, spinal cord injury, and amyotrophic lateral sclerosis, can draw support from BCIs to assist with the activities involved in daily life. Further research is being conducted on developing the EEG-Based Brain-Computer Interfaces due to its non-invasive nature, high temporal resolution, ease of acquisition, and beneficial cost-effectiveness (Nicolas-Alonso and Gomez-Gil, 2012; Al-Hudhud, 2016).

In recent years, several specific brain activity patterns, including Slow Cortical Potentials (SCPs), P300 evoked potentials, Steady-State Visually Evoked Potentials (SSVEPs), Event-Related Desynchronization (ERD), and Synchronization (ERS), have been investigated extensively, as these have served as the source of stimulation signals for BCI control (Zhang et al., 2014b). Among these, the SSVEP paradigm has become a promising option in BCI applications due to its high signal-to-noise ratio (SNR), high information transfer rate (ITR), reliability, and design flexibility (Bin et al., 2009; Zhu et al., 2010; Bakardjian et al., 2011). The SSVEP-BCIs rely on oscillatory responses occurring in the occipital and the occipito-parietal cortex that are elicited from a stimulus flickering at a specific frequency (Vu et al., 2016; Georgiadis et al., 2018). While people focus attention on a visual stimulation at a fixed frequency, such as flashing lights or flickering icons on a computer screen, the SSVEP signals can be observed at the same fundamental frequency as the stimulation and also at higher harmonics of the driving stimulus (Muller-Putz and Pfurtscheller, 2007; Bakardjian et al., 2010; Zhang Z. et al., 2018). Hence, the SSVEP signals are the inherent response of the brain, and the SSVEP-based BCI systems required minimal to no training (Bin et al., 2009).

In the past few decades, many studies have revealed that the SSVEP pattern is effective for BCI control, and various SSVEP-based brain-computer interface (BCI) systems have been proposed by numerous laboratories and research groups (Poryzala and Materka, 2014). It has been verified that four driving rates in an evoked potential interface system are distinguishable (Skidmore and Hill, 1991). In the study, the stimulation frequency was set at 35.050, 23.367, 17.525, and 14.020 Hz, and it was found that the responses corresponding to the stimulation frequencies were generated during the analysis. The SSVEP-based BCI system with high transfer rates was also used to help operators input phone numbers (Cheng et al., 2002) in which four buttons flickering at different frequencies represented the four directions. The operators could move the cursor in different directions to the target position by gazing at these buttons. Finally, eight of the 13 subjects completed the task where subjects were asked to select the correct number on the telephone keypad to input phone numbers with the help of the SSVEP-based BCI system. In another work, a new dual-frequency-SSVEP for BCI systems was developed that could increase the number of selections through different combinations of four frequencies, i.e., 16.4, 17.5, 19.1, and 20.2 Hz (Shyu et al., 2010). The result indicated that this dual-frequency approach was effective for an SSVEP BCI system.

Previous studies for SSVEP recognition focused on the amplitude and spatial distribution of SSVEP responses (Zhang et al., 2013a; Norcia et al., 2015). However, these traditional methods using single-channel EEG data [e.g., Power spectral density analysis (PSDA)] are sensitive to noise and require a long period of recognition time to improve the accuracy of the results. Moreover, these SSVEP recognition techniques cannot detect and identify harmonic stimulation frequencies (Zhang et al., 2011, 2015). Therefore, many advanced multichannel approaches have been developed to enhance the recognition performance of SSVEPs. For frequency recognition, the Canonical Correlation Analysis (CCA) algorithm was first introduced to find the correlation between the multichannel EEG data and reference signals consisting of sin-cosine waves at each of the target frequencies (Lin et al., 2006). Recent work has already validated that the CCA method could achieve better recognition performance than the traditional power spectral density analysis (Zhang et al., 2014c). Until now, there have been many methods proposed to improve recognition accuracy further by optimizing the pre-constructed sine-cosine reference signals, such as Multiway Canonical Correlation Analysis (MCCA) (Zhang et al., 2011), L1-regularized Multiway Canonical Correlation (L1-MCCA) (Zhang et al., 2013b), and Multi-set Canonical Correlation Analysis (Multi-set CCA) (Zhang et al., 2014c)—all proposed as multiway extensions of standard CCA. Although the sine-cosine reference signals usually perform well for specific frequency components recognition, the simplified single or multiple frequency signals are incapable of exactly representing the complex neural responses, which are collaboratively created by several neural populations in the visual cortex rather than a single signal source. Recently, researchers constructed a laminar microcircuits model consisting of two visual areas (V1 and V2) to imitate the dynamics of neuronal population response in the visual cortex, which revealed the modulation mechanism of the SSVEP, confirming the hypothesis (Zhou et al., 2013; Yang et al., 2019). Beside this, the new spatial filtering method, known as Minimum Energy Combination (MEC), found a linear combination of multichannel signals, which reduces the number of channels, to minimize the noise energy (Friman et al., 2007; Nan et al., 2011). Nakanishi et al. used multiple spatial filters to remove the EEG background artifacts, enhance discriminability and SNR of the signals (Nakanishi et al., 2017). Zhang et al. introduced the Correlated Component Analysis (CORCA) to find linear combinations of electrodes across subjects and maximize correlation between them (Zhang et al., 2018a,b). Recently, the Multivariate Synchronization Index (MSI) (Zhang et al., 2014b) has attracted attention as a novel feature extraction method, which calculates the synchronization index between the multichannel EEG data and the pre-constructed reference signals, showing better recognition performance than both CCA and MEC.

Although previous studies have demonstrated that the MSI method is an efficient method for frequency component recognition, the temporal features of the EEG signals have not been explored yet. The analysis of Global Field Power highlighted time periods results in the most robust performance (Jrad and Congedo, 2012), showing the importance of time domain analysis for recognizing the specific frequency in SSVEPs. Recent research has also confirmed that considering temporal information of EEG signals can improve the performance of the algorithm, such as the temporal local structure of the signals (Wang and Zheng, 2008), the time-delayed copy (Lemm et al., 2005), and certain temporal features (Jrad and Congedo, 2012). To address this issue, Zhang et al. proposed a temporally local MSI (TMSI) method, which explicitly considers the time-local information of the EEG signal, further improving the accuracy of the recognition algorithm for SSVEP-Based BCIs (Zhang et al., 2016). The time delay embedding method has also been employed to extend MSI (known as EMSI), further enhancing the performance of SSVEP, which combined the first-order time-delayed version of EEG data during the calculation of the synchronous index (Zhang et al., 2017). Zhang combined adaptive TWL selection strategy with the MSI method, which is superior to fixed TWL in SSVEP recognition (Zhang et al., 2014a).

In the present study, the reference signals of sine-cosine waves are replaced with inter-subject and intra-subject template signals. The intra-subject template signals, also termed as the individual template signals, are obtained by averaging multichannel EEG data of the individual training dataset and provided more abundant subject-specific and inter-trial information for correlation analysis. It has been shown that the CCA based on the individual template signals significantly outperforms the standard CCA (Bin et al., 2011; Nan et al., 2011). Additionally, the inter-subject template signals are obtained by averaging the partial trials selected from other subjects. Recent studies have demonstrated inter-subject similarity in neural responses occurs because subjects are instructed to perform a specific task over time (Saha and Baumert, 2019). Yuan et al. presented transfer template-based canonical correlation analysis (tt-CCA) to enhance the detection of SSVEPs by exploiting inter-subject information (Yuan et al., 2015). Several studies attempted to apply session-to-session and inter-subject transfer to simplify the training procedure (Nakanishi et al., 2016; Waytowich et al., 2016). This paper proposes an efficient way for transfer learning to improve SSVEP-based BCIs performance. After this, an expanding time window over time is used to extract temporal features of SSVEP, and the stimulus frequency is recognized based on the pre-set threshold. Dynamic window recognition algorithms are often integrated into other algorithms to adaptively control the recognition time while maintaining a high accuracy, which significantly improves the information transfer rate (ITR), and adaptability of systems to different individuals (Zhang et al., 2014a; Cao et al., 2015; Yang et al., 2018). In the method presented in this paper, the pre-set threshold obtained from the training dataset of individual subjects makes the algorithm shutdown at the appropriate data length and filters the potentially invalid trial resulted from attention lapses (Russell et al., 2016) or the reaction times of subjects considered to be too long. It has been reported that attention lapses may lead to an increase of reaction times and the number of incorrect responses because irrelevant information cannot be effectively suppressed, shifting attention to irrelevant visual stimuli (Ko et al., 2017; Wang et al., 2018). The novel extension of multivariate synchronization index method is verified with an SSVEP dataset involving 10 healthy subjects and compared to the CCA, standard MSI, Multi-set CCA, and Individual Template-based CCA. The results in this paper show that the proposed method significantly enhances the individual recognition performance of SSVEP frequency, resulting in an improvement in overall accuracy and the information transfer rate.

2. Methods

2.1. The Standard Multivariate Synchronization Index

The MSI method aims to estimate the synchronization between the multichannel EEG data and the reference signals for frequency detection. Let $X\in {ℝ}^{N_1\times M}$ denote the multivariate EEG signals and $Y\in {ℝ}^{N_2\times M}$ denote the reference signal, which is constructed as follows:

$\begin{array}{ll}Y=\left(\begin{array}{c}sin(2\pi f_{i}t)\\ cos(2\pi f_{i}t)\\ ⋮\\ sin(2\pi N_h{f}_{i}t)\\ cos(2\pi N_h{f}_{i}t)\end{array}\right),t=\frac{1}{Fs},\frac{2}{Fs},\dots ,\frac{M}{Fs}& (1)\end{array}$

where N_h denotes the number of harmonics, Fs is the sampling rate. N₁ and N₂ are the number of channels, respectively, and M is the number of samples. X and Y are normalized to have zero mean and unit variance without loss of generality. The covariance matrix of concatenation of X and Y can subsequently be calculated as

$\begin{array}{ll}C=\left(\begin{array}{cc}{C}_{11}& C_{12}\\ C_{21}& C_{22}\end{array}\right)& (2)\end{array}$

where

$\begin{array}{ll}{C}_{11}=\frac{1}{M}X{X}^T& (3)\end{array}$

$\begin{array}{ll}{C}_{22}=\frac{1}{M}Y{Y}^T& (4)\end{array}$

$\begin{array}{ll}{C}_{12}=\frac{1}{M}X{Y}^T=C_{21}^T& (5)\end{array}$

Because both the autocorrelation and cross-correlation of matrix C, which is calculated from the concatenation of X and Y, could influence the synchronization computing, a linear transformation is employed:

$\begin{array}{ll}U=\left(\begin{array}{cc}{C}_{11}^{-\frac{1}{2}}& 0\\ 0& C_{22}^{-\frac{1}{2}}\end{array}\right)& (6)\end{array}$

Then, the transformed correlation matrix can be described as follows:

$\begin{array}{ll}R=UC{U}^T& (7)\end{array}$

Assume λ₁, λ₂, …, λ_P are the eigenvalues of matrix R. Then, the normalized eigenvalues are represented by

$\begin{array}{ll}{\lambda }_i^{\prime }=\frac{{\lambda }_i}{{\displaystyle {\sum }_{i=1}^P}{\lambda }_i}=\frac{{\lambda }_i}{tr(R)}& (8)\end{array}$

where P = N₁ + N₂. Finally, the synchronization index between two multivariate signals can be calculated using the following formula:

$\begin{array}{ll}S=1+\frac{{\displaystyle {\sum }_{i=1}^P}{\lambda }_i^{\prime }log({\lambda }_i^{\prime })}{log(P)}& (9)\end{array}$

Based on the formula (9), the synchronization index of each frequency f_i(i = 1, …, K) used in SSVEP-based BCI can be calculated. The target frequency f_t can now be computed by the formula.

$\begin{array}{ll}{f}_t={\displaystyle \underset{f_i}{max}}{S}_i,i=1,\dots ,K& (10)\end{array}$

2.2. Inter- and Intra-subject Template-Based Multivariate Synchronization Index (IIST-MSI)

We propose a variant version of multivariate synchronization index based on transferred inter- and intra-subject template signals. Considering ${\chi }_{i,h}\in {ℝ}^{N_c\times N_t}$, which is the h-th trial from the individual training set corresponding to the stimulus frequency f_i, an individual template signal $Y_i\in {ℝ}^{N_c\times N_t}$ is obtained by averaging training trials as

$\begin{array}{ll}{Y}_i=\frac{1}{N_n}{\displaystyle \sum _{h=1}^{N_n}}{\chi }_{i,h}& (11)\end{array}$

where N_c, N_t, and N_n are the numbers of channels, samples, and trials, respectively. For structuring the transferred inter-subject templates, the core issue is how to pick up credible trials. We propose a threshold policy for supervised adaptation of trials. Assume ${\chi }_{p,i,h}\in {ℝ}^{N_c\times N_t}$ is the h-th trial recorded from the subject p corresponding to the stimulus frequency f_i. The confidence of this trial is defined as

$\begin{array}{ll}{C}_{p,i,h}=\frac{S_{p,i,h}}{\frac{1}{K}{\displaystyle {\sum }_{k=1}^K}{S}_{p,k,h}}& (12)\end{array}$

where K is the number of stimulus frequencies, S_p,i,h is the multivariate synchronization index between EEG signals and the sine-cosine reference signals at the labeled stimulus frequency f_i, and S_p,k,h is the multivariate synchronization index between EEG signals and the sine-cosine reference signals at the stimulus frequency f_k. Only high-confidence trials are selected for transfer learning, and the threshold function for confidence is formulated as

$\begin{array}{ll}f(C_{p,i,h})=\{\begin{array}{cc}1,& C_{p,i,h}>1+\ln (\frac{N_t}{F_s}),\\ -\text{1,}& otherwise\text{.}\end{array}& (13)\end{array}$

where Fs is the sampling rate. Suppose A_p,i is a set composed of high-confidence trials belonging to subject p, and the initial set is the empty set (A_p,i = ∅). The trial selection procedure establishes an iterator to loop over all trials corresponding to the stimulus frequency f_i and pick up high-confidence trials:

$\begin{array}{ll}{A}_{p,i}\leftarrow \{\begin{array}{cc}{A}_{p,i}\cup \left\{{\chi }_{p,i,h}\right\},\hfill & f(C_{p,i,h})>0\hfill \\ A_{p\text{,}i}\text{,}\hfill & otherwise\text{.}\hfill \end{array}& (14)\end{array}$

If P is the set of ideal subjects used for templates, the inter-subject template is obtained by averaging high-confidence trials across subjects:

$\begin{array}{ll}{Y}_i^{*}=\frac{1}{|P|}{\displaystyle \sum _{p\in P}}\frac{1}{|A_{p,i}|}{\displaystyle \sum _{{\chi }_{p,i,h}\in A_{p,i}}}{\chi }_{p,i,h}& (15)\end{array}$

Then, the sine-cosine reference signals of the standard MSI can be replaced by the inter- and intra-subject template signals. The multivariate synchronization index $S_i^{*}$ and S_i between the inter- and intra-subject template signals and the test trial can be calculated with the formula (2–9), respectively. Finally, a sum-of-squares γ_i based the multivariate synchronization index represents the final detection score for the stimulus frequency f_i:

$\begin{array}{ll}{\gamma }_i={(S_i)}^2+{(S_i^{*})}^2& (16)\end{array}$

The target frequency f_t can be recognized by the formula:

$\begin{array}{ll}{f}_t={\displaystyle \underset{f_i}{max}}{\gamma }_i,i=1,\dots ,K& (17)\end{array}$

2.3. Dynamic Window-Based Adaptive Threshold (AT) Strategy

In order to exploit the temporal features of EEG signal, a dynamic window approach is incorporated into the IIST-MSI method. In a trial where the EEG data is continuously received, the inter- and intra-subject template-based multivariate synchronization index of a small initial time window (ITW) corresponding to each stimulus frequency can be first computed. The probability ratio r_{1, i} of the stimulus frequency f_i can be then defined as

$\begin{array}{ll}{r}_{1,i}=\frac{\sqrt{{\gamma }_{1,i}}}{\frac{1}{K}{\displaystyle {\sum }_{k=1}^K}\sqrt{{\gamma }_{1,k}}}& (18)\end{array}$

where K is the number of stimulus frequencies. The probability ratio reflects the confidence of each stimulus frequency. When the probability ratio of each stimulus frequency is less than the pre-set threshold, it indicates that the current data length is not enough to make a reasonable decision, so the algorithm requires more data. A time window increment (TWI) is appended to the last data segment, and the algorithm recalculates the probability ratio of this new data segment corresponding to each stimulus frequency. A joint probability of the new data segment and the last data segment can then be computed. After m subsequences, the joint probability J_i of the stimulus frequency f_i is calculated as:

$\begin{array}{ll}{J}_i\leftarrow J_i\times r_{m,i}& (19)\end{array}$

where the initial value is set as J_i ← r_{1, i}. The threshold T_c serves as the cut-off condition for this method. To paraphrase, if max{J₁, …, J_K} < T_c, the iterative process is continued. When all EEG signals are depleted, and max{J₁, …, J_K} still is less than T_c, the trial is regarded as an invalid trial. Once the method reaches the threshold T_c, the target stimulus frequency f_t can be computed as follows:

$\begin{array}{ll}{f}_t={\displaystyle \underset{f_i}{max}}{J}_i,i=1,\dots ,K& (20)\end{array}$

where K is the number of stimulus frequencies used in SSVEP-based BCI. Figure 1 illustrates the frequency recognition method.

FIGURE 1

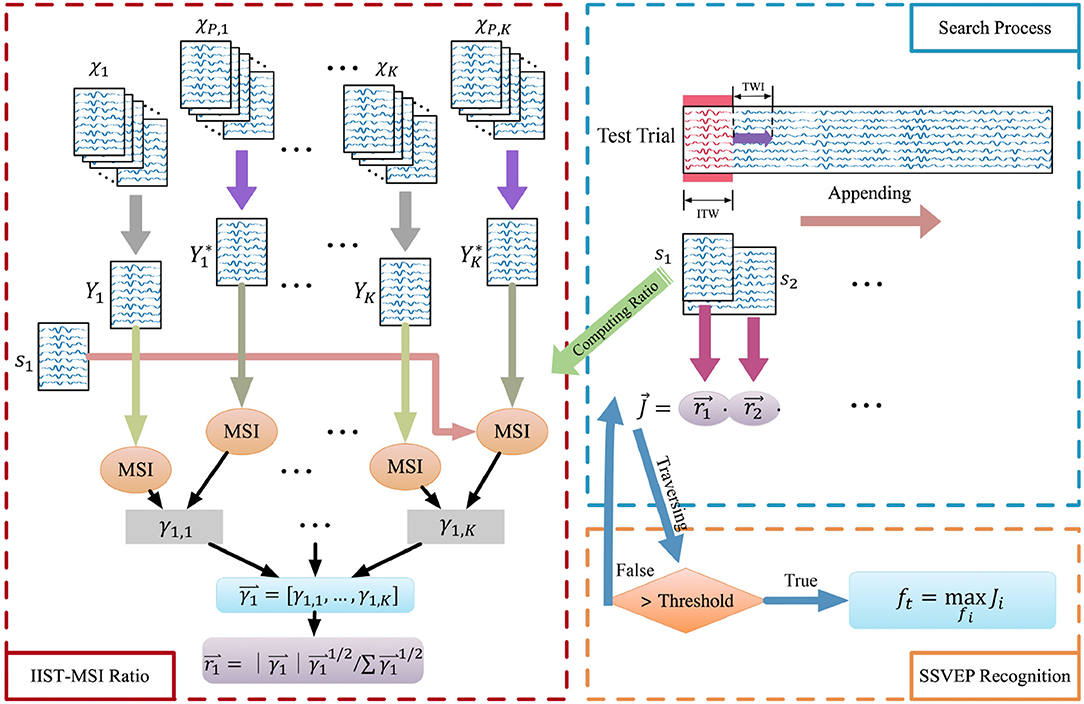
Figure 1. The flowchart of the IIST-MSI-AT method for SSVEP frequency recognition. χ₁, χ₂, …, χ_K, and χ_{P, 1}, χ_{P, 2}, …, χ_{P, K} denote the individual training dataset and that of other selected subjects corresponding to the stimulus frequency f₁, f₂, …, f_K, respectively. $Y_1^{*},Y_2^{*},\dots ,Y_K^{*}$, and Y₁, Y₂, …, Y_K are the inter- and intra-subject templates. Then the synchronization index and the probability ratio of each frequency can be calculated. The probability ratio of each frequency is multiplied, and the result is compared with the threshold. When the threshold is exceeded, the SSVEP frequency can be recognized by the formula (20).

2.4. Contrast Method

For validating effectiveness for frequency recognition in SSVEPs, the classification performance of the proposed method is compared with various algorithms, including Canonical Correlation Analysis (CCA), the standard Multivariate Synchronization Index (MSI), Multi-set CCA, and Individual Template-based CCA.

2.4.1. Canonical Correlation Analysis

Canonical Correlation Analysis (CCA) is a multivariable statistical technique used to reveal the underlying correlation between two multidimensional variables (Hardoon et al., 2004). Given two sets of random variables $X\in {ℝ}^{N_1\times M}$, $Y\in {ℝ}^{N_2\times M}$. Their linear combinations can be define as $\tilde{x}=w^{\text{T}}X$ and $\tilde{y}=v^{\text{T}}X$, respectively. The CCA method is aimed at finding a pair of vectors $w\in {ℝ}^{N_1\times 1}$ and $v\in {ℝ}^{N_2\times 1}$, such that the correlation between $\tilde{x}$ and $\tilde{y}$ is maximized. In other words, the following optimization problem is solved:

$\begin{array}{ll}\rho ={\displaystyle \underset{w,v}{max}}\frac{E\left[\tilde{x}\tilde{y}\right]}{\sqrt{E\left[{\tilde{x}}^2\right]E\left[{\tilde{y}}^2\right]}}=\frac{w^{\text{T}}X{Y}^{\text{T}}v}{w^{\text{T}}X{X}^{\text{T}}w{v}^{\text{T}}Y{Y}^{\text{T}}v}& (21)\end{array}$

The maximum canonical correlation between the canonical variates $\tilde{x}$ and $\tilde{y}$ is the maximum of ρ. Assume X represents a multichannel EEG data, and Y is the reference signal constructed according to the formula (1). The maximum canonical correlation of each frequency f_i(i = 1, …, K) can thus be calculated. Then, the target frequency f_t can be recognized by the formula.

$\begin{array}{ll}{f}_t={\displaystyle \underset{f_i}{max}}{\rho }_i,i=1,\dots ,K& (22)\end{array}$

2.4.2. Multi-Set Canonical Correlation Analysis

Multi-set canonical correlation analysis (Multi-set CCA) is developed as an extension of CCA to analyze linear relationships between multiple sets of features. In order to improve the classification accuracy of SSVEPs, The Multi-set CCA method is implemented to optimize the reference signal, and the pre-constructed sine-cosine waves, by learning from the joint spatial filtering of training sets of EEG signals (Zhang et al., 2014c).

Assume the h-th training trial of EEG signals corresponding to the stimulus frequency f_i is ${\chi }_{i,h}\in {ℝ}^{N_c\times N_s}$, and the spatial filters used to extract common features of training sets are w₁, …, w_n. To maximize the sum of the pairwise correlation between multiple sets of training data, the optimization problem of Multi-set CCA is presented as follows:

$\begin{array}{ll}\begin{array}{c}{\tilde{w}}_{i,1},\dots ,{\tilde{w}}_{i,n}=\underset{w_1,\dots ,w_n}{argmax}{\displaystyle \sum _{h_1\ne h_2}^n}{w}_{h_1}^T{\chi }_{i,h_1}{\chi }_{i,h_2}^T{w}_{h_2}\\ \text{subject to}\frac{1}{n}{\displaystyle \sum _{h_1=1}^n}{w}_{h_1}^T{\chi }_{i,h_1}{\chi }_{i,h_1}^T{w}_{h_1}=1\end{array}& (23)\end{array}$

The objective function can then be transformed into the following generalized eigenvalue problem with the Lagrange multipliers:

$\begin{array}{ll}(R_i-S_i)w=\rho S_{i}w& (24)\end{array}$

where

$R_i=\left[\begin{array}{ccc}{\chi }_{i,1}{\chi }_{i,1}^T& \dots & {\chi }_{i,1}{\chi }_{i,n}^T\\ ⋮& \ddots & ⋮\\ {\chi }_{i,n}{\chi }_{i,1}^T& \dots & {\chi }_{i,n}{\chi }_{i,n}^T\end{array}\right],$

$S_i=\left[\begin{array}{ccc}{\chi }_{i,1}{\chi }_{i,1}^T& \dots & 0\\ ⋮& \ddots & ⋮\\ 0& \dots & {\chi }_{i,n}{\chi }_{i,n}^T\end{array}\right],$

$w=\left[\begin{array}{c}{w}_1\\ ⋮\\ w_n\end{array}\right]$

After obtaining the multiple linear transforms w₁, …, w_n and utilizing the joint spatial filtering ${\tilde{z}}_{i,h}={\tilde{w}}_{i,h}^T{\chi }_{i,h}$, the optimized reference signal is constructed as

$\begin{array}{ll}{Z}_n={\left[{\tilde{z}}_{i,1}^T,{\tilde{z}}_{i,2}^T,\dots ,{\tilde{z}}_{i,n}^T\right]}^T& (25)\end{array}$

Next, the maximum canonical correlation between the test data and the optimized reference signal can be calculated using CCA, and the target stimulus frequency f_t can be recognized with the formula (22).

2.4.3. Individual Template Based CCA

To explore temporal features of EEG signals, the Individual Template-based CCA (IT-CCA) approach was proposed for SSVEP detection (Bin et al., 2011). For each stimulus frequency f_i, the individual template signal $Y_i\in {ℝ}^{N_c\times N_t}$ is obtained by averaging training trials using the formula (11). The CCA process can then be used to calculate the maximum canonical correlation between the test data and the individual template signal, and the target stimulus frequency f_t can be recognized with the formula (22).

2.5. Experiment and Data

To validate our proposed method, a 12-class joint frequency-phase modulated SSVEP dataset from Nakanishi et al. (2015) is used, which contains ten healthy subjects (nine males and one female, the average age being 28 years old), each having 15 trials corresponding to all 12 stimulus frequencies. In their experiment, the 12-target stimuli were presented on an LCD screen with a 60 Hz refresh rate. These stimuli were placed in a 4 × 3 matrix regarded as a virtual keypad, as shown in Figure 2A, and tagged with different frequencies ranging from 9.25 to 14.75 Hz and phases ranging from 0 to 1.5π, as shown in Figure 2B.

FIGURE 2

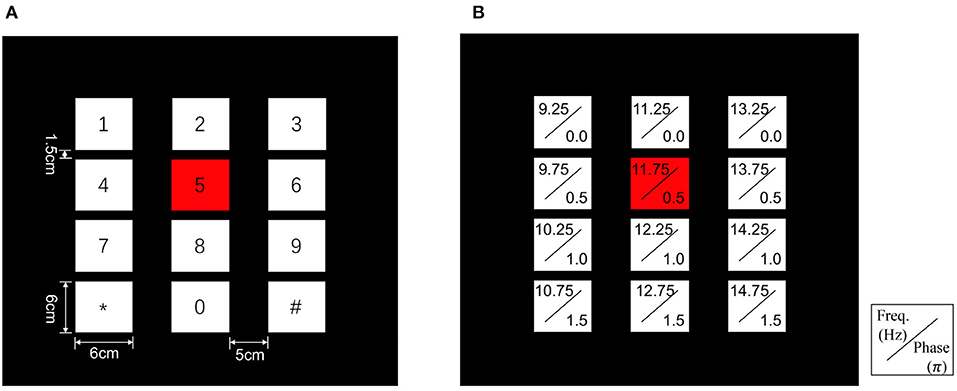
Figure 2. Stimulus design of the 12-target BCI system. (A) The user interface of the virtual keypad. (B) Frequency and phase values for each target.

When conducting this experiment, the subjects were seated on a comfortable chair within a dim room, with their eyes 60 cm away from the LCD screen. The visual stimuli were presented by the stimulus program in random order. At the beginning of a trial, a red square emerged at the position of the target stimulus for 1 s, which indicated that the subjects should shift their gaze to the target. Afterward, all stimuli started to flicker simultaneously and the subjects were required to stare at the visual stimuli for 4 s. At the same time, EEG signals were recorded with eight electrodes placed over the occipital area with reference to the CMS electrode close to Cz. In this experiment, each subject completed 15 trials corresponding to all 12 targets.

Considering that visual stimulation emerged at the 15th millisecond, the data epochs were extracted from 0.15 to 4.15 s. Each epoch was band-pass filtered from 6 to 80 Hz with an infinite impulse response (IIR) filter and was then used as the input for recognition algorithms.

To determine ideal subjects used for templates, we selected subjects in descending order of the MSI accuracy. For adaptive threshold strategy, the initial time window ITW and the time window increment TWI were set to 0.5 s. The threshold T_c took values from a range (d ≤ 1s: ranging from 1 to 2 with an interval of 0.05; 1s < d ≤ 2s: ranging from 1 to 4 with an interval of 0.1; 2s < d ≤ 3s: ranging from 3 to 8 with an interval of 0.2; and 3s < d ≤ 4s: ranging from 3 to 16 with an interval of 0.4). The number of harmonics pre-defined for reference signals was 3 uniquely. During the process of performing parameter optimization, the combination of parameters would be discarded once the proportion of invalid trials was more than 20%. In the end, an optimum set of parameters was obtained by tuning the parameters to reach maximum recognition accuracy on the training dataset, and the optimal parameters were then applied to frequency recognition of the test dataset.

2.6. Evaluation Methods

The classification accuracy is estimated using three-fold cross-validation to evaluate the proposed method. The sample dataset is divided into the training set for choosing the optimal parameter (i.e., the threshold T_c) and test set for estimating the performance of the model for frequency recognition. The accuracy is defined as the percentage of valid trials classified correctly. Thus, the classification accuracy is calculated as follows:

$\begin{array}{ll}acc=\frac{1}{3}{\displaystyle \sum _{i=1}^3}\frac{P_i}{N_i}\times 100\%& (26)\end{array}$

where P_i is the number of valid trials correctly classified and N_i is the number of valid trials from the i-th fold.

In addition to the classification accuracy, the information transfer rate (ITR) is adopted to evaluate the communication capacity of the BCI system (Wolpaw et al., 2002):

$\begin{array}{ll}B=logN+PlogP+(1-P)log\frac{1-P}{N-1}& (27)\end{array}$

$\begin{array}{ll}ITR=B\times 60/T& (28)\end{array}$

where P denotes the classification accuracy, N is the number of possible selections, and T is the average time required to select a command. Here, the ITR is calculated using different values of T (Target gazing time: 0.5 to 4.0 s with an interval of 0.5 s; Gaze shifting time: 1 s).

3. Results

Since the number of subjects used for transfer |P| plays an important role in the IIST-MSI method, we explore the effects of varying |P| on the recognition performance firstly. As a special case, the individual template-based MSI (IT-MSI) is the same as the IIST-MSI with |P| = 0. Figure 3 shows the averaged accuracy and ITR obtained by the IIST-MSI with the |P| varying from 0 to 6 and TWs from 0.5 to 4 s. When TW is <1 s, the method only using the individual template performs better than that using the combined inter- and intra-subject templates. When TW is more than 2 s, the result is the contrary. For |P| = 4, the IIST-MSI achieved the best recognition performance. In the following analysis, the performance of the IIST-MSI with fixed |P| = 4 is compared with that of other methods.

FIGURE 3

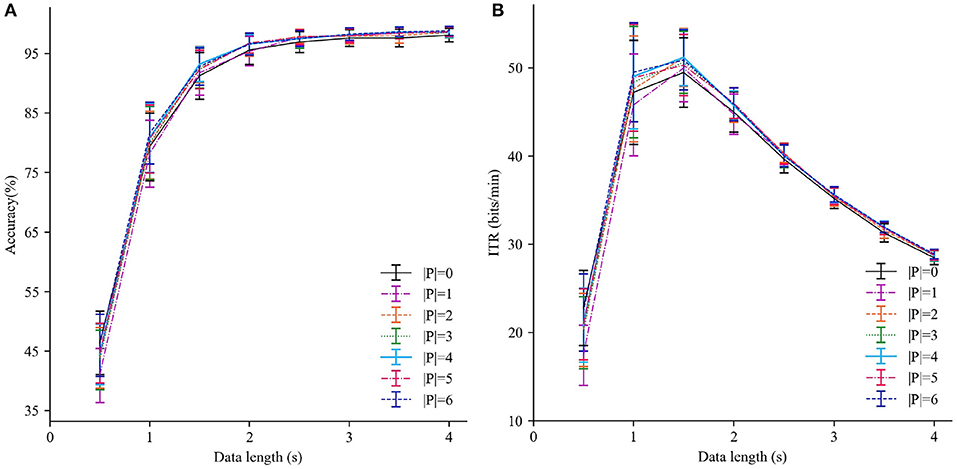
Figure 3. Performance comparison of IIST-MSI with various |P|. (A) The averaged accuracy and (B) ITR across all subjects with different data lengths from 0.5 to 4 s. Error bars show standard errors.

Figure 4 depicts the averaged SSVEP recognition accuracy of ten subjects derived by CCA, MSI, Multi-set CCA, IT-CCA, IT-MSI and IIST-MSI with different data epochs lengths, ranging from 0.5 to 4 s, which shows that the recognition accuracy of subject 2 and 7 is significantly improved by the IIST-MSI. The one-way repeated-measure ANOVA results show that there is a statistically significant difference in the accuracy between these methods under the data length ranging from 0.5 to 3 s [d = 0.5 s: F_{(5, 45)} = 29.402, p < 0.001; d = 1s: F_{(5, 45)} = 52.036, p < 0.001; d = 1.5s: F_{(5, 45)} = 11.894, p < 0.001; d = 2s: F_{(5, 45)} = 5.269, p < 0.01; d = 2.5s: F_{(5, 45)} = 3.395, p < 0.05; d = 3s: F_{(5, 45)} = 2.592, p < 0.05; d = 3.5s: F_{(5, 45)} = 1.819, 0.1 < p; and d = 4s: F_{(5, 45)} = 1.396, 0.1 < p]. For a more intuitive comparison of these methods, Figures 5A,B depict the averaged accuracy and the ITR across all subjects with different data lengths from 0.5 to 4 s. In terms of the mean classification accuracies of all ten subjects, from 1 to 4 s, the IIST-MSI method achieves a higher accuracy than the other methods.

FIGURE 4

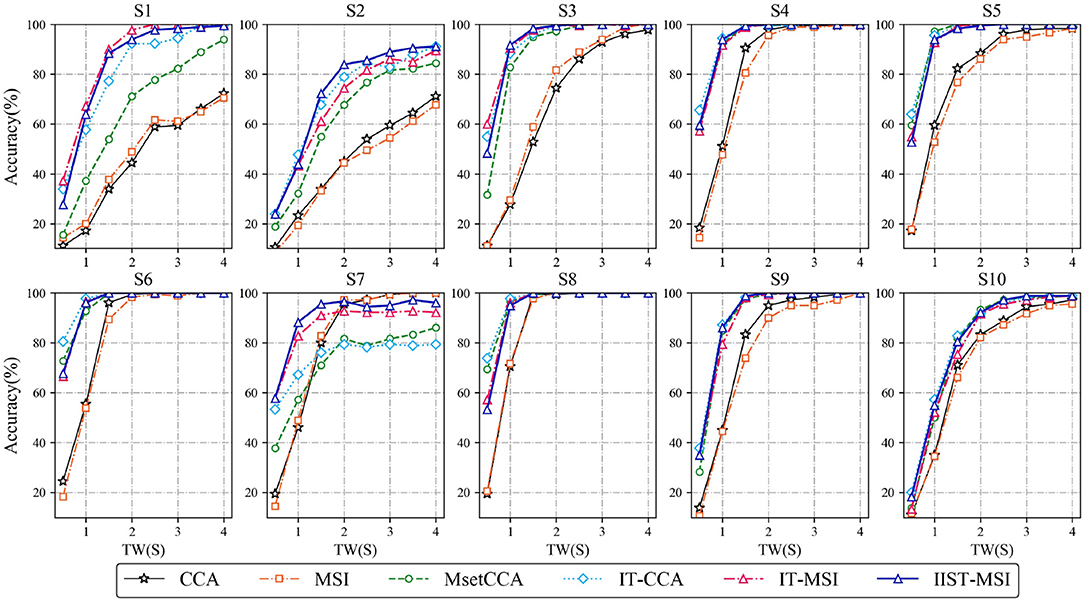
Figure 4. Averaged SSVEP recognition accuracies of 10 subjects derived by CCA, MSI, Multi-set CCA, IT-CCA, IT-MSI, and IIST-MSI, with different length of data epochs from 0.5 to 4 s.

FIGURE 5

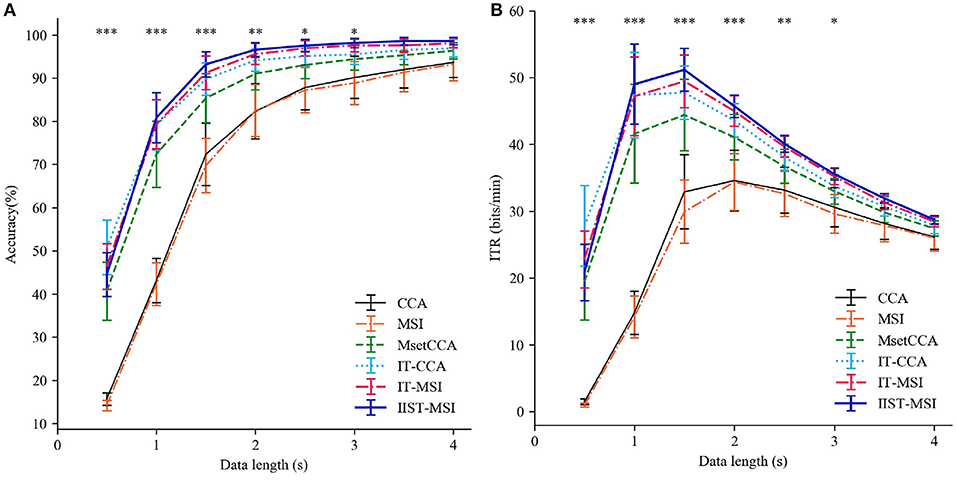
Figure 5. Performance comparison between IIST-MSI and other methods. (A) The averaged accuracy and (B) ITR across all subjects with different data lengths from 0.5 to 4 s. Error bars show standard errors. The asterisk indicates the statistically significant differences (*p < 0.05; **p < 0.01; ***p < 0.001).

To investigate the superiority of adaptive threshold strategy, the IIST-MSI using adaptive threshold (IIST-MSI-AT) is compared with the basic IIST-MSI. Figure 6 depicts the mean detection accuracy and ITR for the basic and the combined version of IIST-MSI method. The paired-sample t-test shows there are no statistical differences in the accuracy between them, but there are significant differences in the ITR from 1.5 to 4 s. The experimental result coincides with the expectation that the dynamic window algorithm can adaptively determine the shorter time window, while maintaining high accuracy. Hence the IIST-MSI-AT method significantly outperformed the other methods in terms of ITR. The highest ITR obtained by the IIST-MSI-AT method is 53.08 ± 3.65 bits/min.

FIGURE 6

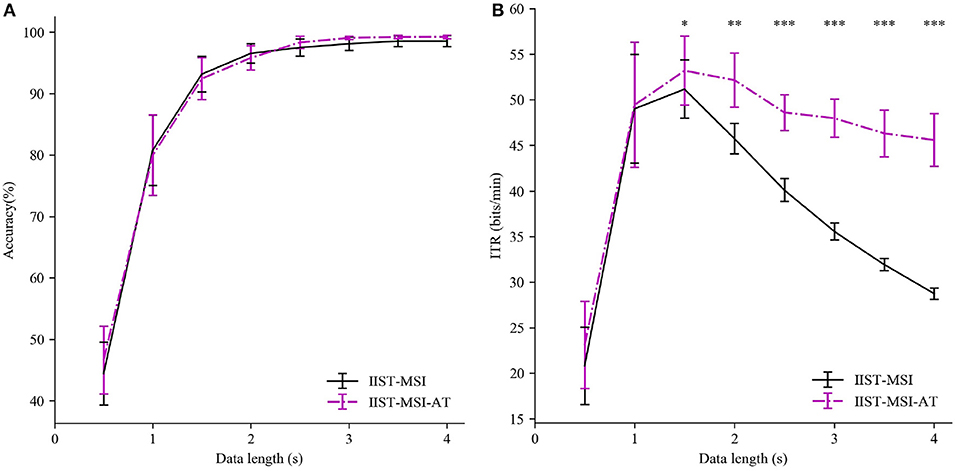
Figure 6. Performance comparison between IIST-MSI and IIST-MSI-AT. (A) The averaged accuracy and (B) ITR across all subjects with different data lengths from 0.5 to 4 s. Error bars show standard errors. The asterisk indicates the statistically significant differences (paired t-tests, *p < 0.05; **p < 0.01; ***p < 0.001).

Table 1 presents the recognition accuracy and ITR obtained by CCA, MSI, Multi-set CCA, IT-CCA, and IIST-MSI-AT for each subject with a 4 s data length. Here, the accuracy of CCA, MSI, Multi-set CCA, and IT-CCA are the average values computed over 180 trials for each subject. The accuracy of IIST-MSI-AT is described as the average accuracy of the test set in a three-fold cross-validation as formulated in the equation (26). For the epoch length of 4 s, the IIST-MSI-AT method gets the highest accuracy (99.23 ± 0.29%),which achieves an increase of 5.62% compared to CCA (93.61 ± 3.48%), 6.06% compared to MSI (93.17 ± 3.82%), 2.90% compared to Multi-set CCA (96.33 ± 1.84%), and 2.34% compared to IT-CCA (96.89 ± 2.02%). These results demonstrate that the proposed method is a promising way to develop more high-performance SSVEP-based brain-computer interface systems.

TABLE 1

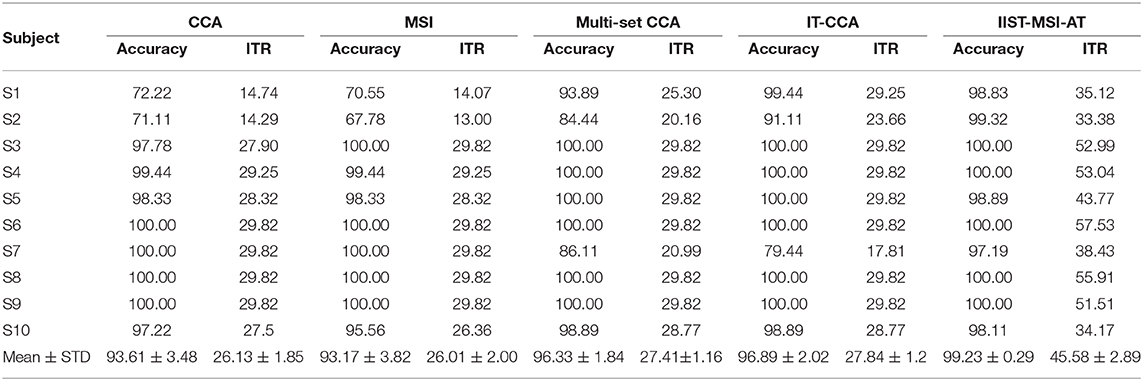
Table 1. Classification accuracy (%) and ITR (bits/min) of CCA, MSI, Multi-set CCA, IT-CCA, and IIST-MSI-AT for each subject with 4s data length.

4. Discussion

The most recent state-of-the-art methods for SSVEP recognition use the individual calibration data as the template of correlation analysis and significantly improve the detection performance (Nakanishi et al., 2015). The individual templates can accumulate the frequency components while maintaining the phase information and, conversely, reduce the effect of the background EEG artifacts. Furthermore, it contributes to improving the individual adaptability of methods, as the individual templates can learn spontaneous EEG signals from calibration data. However, the training data collection process may be time-consuming. The visual fatigue and attention lapses make the training data not perfect enough for every subject. For addressing this problem, inter-subject transfer learning is exploited to provide inter-subject similarity and variability for enhancing target recognition in SSVEP-based BCIs. For each subject, the frequency components of SSVEPs induced by a specific target frequency are similar, but the visual latencies in the visual system are various. According to the superposition principle, the averaged inter-subject transferred templates can contain the same frequency and little phase differences (Yuan et al., 2015). Based on this, this study replaces the commonly used sine-cosine reference signals with the inter- and intra-subject templates for improving adaptability and robustness of the MSI method. Indeed, the experimental results show that the detection accuracy of a few individuals is obviously improved.

On the other hand, this paper employs a dynamic time window to explore the temporal features of SSVEP signals neglected by the standard MSI method and a pre-set threshold to determine when to stop the algorithm, which can balance the recognition accuracy and data length. Hence, the proposed method can significantly improve the information transmission rate, which is critical to the development of high-speed BCIs. Considering the limited reliability of short data, the threshold not only acts as the stopping condition but assists in filtering these invalid trials to avoid wrong commands. Accordingly, the method will improve the effectiveness of the dry-electrode based BCI system with a low signal-to-noise ratio by filtering invalid trials, which can avoid mistakes and ensure the stability of BCI.

5. Conclusion

In this paper, we introduce a novel method based on the inter- and intra-subject template and adaptive threshold strategy to enhance the detection of SSVEPs for high-speed BCIs. The experimental results on ten subjects indicate that our approach obtains higher recognition accuracy and ITR than the CCA, MSI, Multi-set CCA, and Individual Template-based CCA. The results remind us that the inter-subject template transfer and the threshold search based on other methods could further improve the performance of BCIs, which will be investigated in our future work.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/mnakanishi/12JFPM_SSVEP.

Author Contributions

HW contributed conception and realization of algorithm. SC organized the database. WZ performed the statistical analysis. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the Grants from the National Key R &D Program of China (2018YFC1314700), the National Natural Science Foundation of China (91748122, 81671307), and the Priority of Shanghai Key Discipline of Medicine (2017ZZ02020).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Al-Hudhud, G. (2016). Smart brain interaction systems for office access and control in smart city context. Smart Cities Technol. 101, 101–119. doi: 10.5772/65902

CrossRef Full Text | Google Scholar

Bakardjian, H., Tanaka, T., and Cichocki, A. (2010). Optimization of ssvep brain responses with application to eight-command brain-computer interface. Neurosci. Lett. 469, 34–38. doi: 10.1016/j.neulet.2009.11.039

PubMed Abstract | CrossRef Full Text | Google Scholar

Bakardjian, H., Tanaka, T., and Cichocki, A. (2011). Emotional faces boost up steady-state visual responsesforbrain-computer interface. Neuroreport 22, 121–125. doi: 10.1097/WNR.0b013e32834308b0

PubMed Abstract | CrossRef Full Text | Google Scholar

Bin, G., Gao, X., Wang, Y., Li, Y., Hong, B., and Gao, S. (2011). A high-speed BCI based on code modulation VEP. J. Neural Eng. 8:025015. doi: 10.1088/1741-2560/8/2/025015

PubMed Abstract | CrossRef Full Text | Google Scholar

Bin, G., Gao, X., Yan, Z., Hong, B., and Gao, S. (2009). An online multi-channel SSVEP-based brain-computer interface using a canonical correlation analysis method. J. Neural Eng. 6:046002. doi: 10.1088/1741-2560/6/4/046002

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, L., Ju, Z., Li, J., Jian, R., and Jiang, C. (2015). Sequence detection analysis based on canonical correlation for steady-state visual evoked potential brain computer interfaces. J. Neurosci. Methods 253, 10–17. doi: 10.1016/j.jneumeth.2015.05.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, M., Gao, X., Gao, S., and Xu, D. (2002). Design and implementation of a brain-computer interface with high transfer rates. IEEE Trans. Biomed. Eng. 49, 1181–1186. doi: 10.1109/TBME.2002.803536

PubMed Abstract | CrossRef Full Text | Google Scholar

Dornhege, G., Millan, J. d. R., Hinterberger, T., McFarland, D. J., and Müller, K.-R. (2007). Toward Brain-Computer Interfacing. MIT Press. doi: 10.7551/mitpress/7493.001.0001

CrossRef Full Text | Google Scholar

Faller, J., Müller-Putz, G., Schmalstieg, D., and Pfurtscheller, G. (2010). An application framework for controlling an avatar in a desktop-based virtual environment via a software SSVEP brain-computer interface. Presence 19, 25–34. doi: 10.1162/pres.19.1.25

CrossRef Full Text | Google Scholar

Friman, O., Volosyak, I., and Graser, A. (2007). Multiple channel detection of steady-state visual evoked potentials for brain-computer interfaces. IEEE Trans. Biomed. Eng. 54, 742–750. doi: 10.1109/TBME.2006.889160

PubMed Abstract | CrossRef Full Text | Google Scholar

Georgiadis, K., Laskaris, N., Nikolopoulos, S., and Kompatsiaris, I. (2018). Discriminative codewaves: a symbolic dynamics approach to SSVEP recognition for asynchronous BCI. J. Neural Eng. 15:026008. doi: 10.1088/1741-2552/aa904c

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardoon, D. R., Szedmak, S., and Shawe-Taylor, J. (2004). Canonical correlation analysis: an overview with application to learning methods. Neural Comput. 16, 2639–2664. doi: 10.1162/0899766042321814

PubMed Abstract | CrossRef Full Text | Google Scholar

Jrad, N., and Congedo, M. (2012). Identification of spatial and temporal features of EEG. Neurocomputing 90, 66–71. doi: 10.1016/j.neucom.2012.02.032

CrossRef Full Text | Google Scholar

Ko, L.-W., Komarov, O., Hairston, W. D., Jung, T.-P., and Lin, C.-T. (2017). Sustained attention in real classroom settings: an EEG study. Front. Hum. Neurosci. 11:388. doi: 10.3389/fnhum.2017.00388

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemm, S., Blankertz, B., Curio, G., and Muller, K.-R. (2005). Spatio-spectral filters for improving the classification of single trial EEG. IEEE Trans. Biomed. Eng. 52, 1541–1548. doi: 10.1109/TBME.2005.851521

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, Z., Zhang, C., Wu, W., and Gao, X. (2006). Frequency recognition based on canonical correlation analysis for SSVEP-based BCIs. IEEE Trans. Biomed. Eng. 53, 2610–2614. doi: 10.1109/TBME.2006.886577

PubMed Abstract | CrossRef Full Text | Google Scholar

Muller-Putz, G. R., and Pfurtscheller, G. (2007). Control of an electrical prosthesis with an SSVEP-based BCI. IEEE Trans. Biomed. Eng. 55, 361–364. doi: 10.1109/TBME.2007.897815

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakanishi, M., Wang, Y., Chen, X., Wang, Y.-T., Gao, X., and Jung, T.-P. (2017). Enhancing detection of SSVEPs for a high-speed brain speller using task-related component analysis. IEEE Trans. Biomed. Eng. 65, 104–112. doi: 10.1109/TBME.2017.2694818

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakanishi, M., Wang, Y., and Jung, T.-P. (2016). “Session-to-session transfer in detecting steady-state visual evoked potentials with individual training data,” in International Conference on Augmented Cognition (Toronto, ON: Springer), 253–260. doi: 10.1007/978-3-319-39955-3_24

CrossRef Full Text | Google Scholar

Nakanishi, M., Wang, Y., Wang, Y.-T., and Jung, T.-P. (2015). A comparison study of canonical correlation analysis based methods for detecting steady-state visual evoked potentials. PLoS ONE 10:e0140703. doi: 10.1371/journal.pone.0140703

PubMed Abstract | CrossRef Full Text | Google Scholar

Nan, W., Wong, C. M., Wang, B., Wan, F., Mak, P. U., Mak, P. I., et al. (2011). “A comparison of minimum energy combination and canonical correlation analysis for SSVEP detection,” in 2011 5th International IEEE/EMBS Conference on Neural Engineering (Cancun), 469–472. doi: 10.1109/NER.2011.5910588

CrossRef Full Text | Google Scholar

Nicolas-Alonso, L. F., and Gomez-Gil, J. (2012). Brain computer interfaces, a review. Sensors 12, 1211–1279. doi: 10.3390/s120201211

PubMed Abstract | CrossRef Full Text | Google Scholar

Norcia, A. M., Appelbaum, L. G., Ales, J. M., Cottereau, B. R., and Rossion, B. (2015). The steady-state visual evoked potential in vision research: a review. J. Vis. 15:4. doi: 10.1167/15.6.4

PubMed Abstract | CrossRef Full Text | Google Scholar

Poryzala, P., and Materka, A. (2014). Cluster analysis of CCA coefficients for robust detection of the asynchronous SSVEPs in brain-computer interfaces. Biomed. Signal Process. Control 10, 201–208. doi: 10.1016/j.bspc.2013.11.003

CrossRef Full Text | Google Scholar

Russell, B. A., Russo, J. C., Warfield, I. P., and Casebeer, W. D. (2016). “Monitoring attention with embedded frequency markers for simulation environments,” in International Conference on Augmented Cognition (Toronto, ON: Springer), 394–403. doi: 10.1007/978-3-319-39955-3_37

CrossRef Full Text | Google Scholar

Saha, S., and Baumert, M. (2019). Intra-and inter-subject variability in EEG-based sensorimotor brain computer interface: a review. Front. Comput. Neurosci. 13:87. doi: 10.3389/fncom.2019.00087

PubMed Abstract | CrossRef Full Text | Google Scholar

Shyu, K.-K., Lee, P.-L., Liu, Y.-J., and Sie, J.-J. (2010). Dual-frequency steady-state visual evoked potential for brain computer interface. Neurosci. Lett. 483, 28–31. doi: 10.1016/j.neulet.2010.07.043

PubMed Abstract | CrossRef Full Text | Google Scholar

Skidmore, T., and Hill, H. (1991). “The evoked potential human-computer interface,” in Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vol. 13 (Orlando, FL), 407–408.

Google Scholar

Vu, H., Koo, B., and Choi, S. (2016). “Frequency detection for SSVEP-based BCI using deep canonical correlation analysis,” in 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC) (Budapest), 001983–001987.

Google Scholar

Wang, H., and Zheng, W. (2008). Local temporal common spatial patterns for robust single-trial EEG classification. IEEE Trans. Neural Syst. Rehabil. Eng. 16, 131–139. doi: 10.1109/TNSRE.2007.914468

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y.-K., Jung, T.-P., and Lin, C.-T. (2018). Theta and alpha oscillations in attentional interaction during distracted driving. Front. Behav. Neurosci. 12:3. doi: 10.3389/fnbeh.2018.00003

PubMed Abstract | CrossRef Full Text | Google Scholar

Waytowich, N. R., Faller, J., Garcia, J. O., Vettel, J. M., and Sajda, P. (2016). “Unsupervised adaptive transfer learning for steady-state visual evoked potential brain-computer interfaces,” in 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC) (Budapest), 004135–004140. doi: 10.1109/SMC.2016.7844880

CrossRef Full Text | Google Scholar

Wolpaw, J. R., Birbaumer, N., McFarland, D. J., Pfurtscheller, G., and Vaughan, T. M. (2002). Brain-computer interfaces for communication and control. Clin. Neurophysiol. 113, 767–791. doi: 10.1016/S1388-2457(02)00057-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, C., Han, X., Wang, Y., Saab, R., Gao, S., and Gao, X. (2018). A dynamic window recognition algorithm for SSVEP-based brain-computer interfaces using a spatio-temporal equalizer. Int. J. Neural Syst. 28:1850028. doi: 10.1142/S0129065718500284

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z., Guo, D., Zhang, Y., Wu, S., and Yao, D. (2019). Visual evoked response modulation occurs in a complementary manner under dynamic circuit framework. IEEE Trans. Neural Syst. Rehabil. Eng. 27, 2005–2014. doi: 10.1109/TNSRE.2019.2940712

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, P., Chen, X., Wang, Y., Gao, X., and Gao, S. (2015). Enhancing performances of SSVEP-based brain-computer interfaces via exploiting inter-subject information. J. Neural Eng. 12:046006. doi: 10.1088/1741-2560/12/4/046006

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Guo, D., Li, F., Yin, E., Zhang, Y., Li, P., et al. (2018a). Correlated component analysis for enhancing the performance of SSVEP-based brain-computer interface. IEEE Trans. Neural Syst. Rehabil. Eng. 26, 948–956. doi: 10.1109/TNSRE.2018.2826541

CrossRef Full Text | Google Scholar

Zhang, Y., Guo, D., Xu, P., Zhang, Y., and Yao, D. (2016). Robust frequency recognition for SSVEP-based BCI with temporally local multivariate synchronization index. Cogn. Neurodyn. 10, 505–511. doi: 10.1007/s11571-016-9398-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Guo, D., Yao, D., and Xu, P. (2017). The extension of multivariate synchronization index method for SSVEP-based BCI. Neurocomputing 269, 226–231. doi: 10.1016/j.neucom.2017.03.082

CrossRef Full Text | Google Scholar

Zhang, Y., Ma, H., Jin, J., and Wang, X. (2014a). “Adaptive strategy for time window length in SSVEP-based brain-computer interface,” in 2014 international Conference on Mechatronics and Control (ICMC) (Jinzhou), 140–143. doi: 10.1109/ICMC.2014.7231535

CrossRef Full Text | Google Scholar

Zhang, Y., Xu, P., Cheng, K., and Yao, D. (2014b). Multivariate synchronization index for frequency recognition of SSVEP-based brain-computer interface. J. Neurosci. Methods 221, 32–40. doi: 10.1016/j.jneumeth.2013.07.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Xu, P., Huang, Y., Cheng, K., and Yao, D. (2013a). SSVEP response is related to functional brain network topology entrained by the flickering stimulus. PLoS ONE 8:e72654. doi: 10.1371/journal.pone.0072654

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Yin, E., Li, F., Zhang, Y., Tanaka, T., Zhao, Q., et al. (2018b). Two-stage frequency recognition method based on correlated component analysis for SSVEP-based BCI. IEEE Trans. Neural Syst. Rehabil. Eng. 26, 1314–1323. doi: 10.1109/TNSRE.2018.2848222

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Zhou, G., Jin, J., Wang, M., Wang, X., and Cichocki, A. (2013b). L1-regularized multiway canonical correlation analysis for SSVEP-based BCI. IEEE Trans. Neural Syst. Rehabil. Eng. 21, 887–896. doi: 10.1109/TNSRE.2013.2279680

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Zhou, G., Jin, J., Wang, X., and Cichocki, A. (2014c). Frequency recognition in SSVEP-based BCI using multiset canonical correlation analysis. Int. J. Neural Syst. 24:1450013. doi: 10.1142/S0129065714500130

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Zhou, G., Jin, J., Wang, X., and Cichocki, A. (2015). SSVEP recognition using common feature analysis in brain-computer interface. J. Neurosci. Methods 244, 8–15. doi: 10.1016/j.jneumeth.2014.03.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Zhou, G., Zhao, Q., Onishi, A., Jin, J., Wang, X., and Cichocki, A. (2011). “Multiway canonical correlation analysis for frequency components recognition in SSVEP-based BCIs,” in International Conference on Neural Information Processing (Shanghai: Springer), 287–295. doi: 10.1007/978-3-642-24955-6_35

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Wang, C., Ang, K. K., Wai, A. A. P., and Nanyang, C. G. (2018). “Spectrum and phase adaptive CCA for SSVEP-based brain computer interface,” in 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 311–314. doi: 10.1109/EMBC.2018.8512267

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, D., Rangan, A. V., McLaughlin, D. W., and Cai, D. (2013). Spatiotemporal dynamics of neuronal population response in the primary visual cortex. Proc. Natl. Acad. Sci. U.S.A. 110, 9517–9522. doi: 10.1073/pnas.1308167110

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, D., Bieger, J., Molina, G. G., and Aarts, R. M. (2010). A survey of stimulation methods used in SSVEP-based BCIs. Comput. Intell. Neurosci. 2010:702357. doi: 10.1155/2010/702357

PubMed Abstract | CrossRef Full Text | Google Scholar