Closed-loop stimulation of a delayed neural fields model of parkinsonian STN-GPe network: a theoretical and computational study

Several disorders are related to pathological brain oscillations. In the case of Parkinson's disease, sustained low-frequency oscillations (especially in the β-band, 13–30 Hz) correlate with motor symptoms. It is still under debate whether these oscillations are the cause of parkinsonian motor symptoms. The development of techniques enabling selective disruption of these β-oscillations could contribute to the understanding of the underlying mechanisms, and could be exploited for treatments. A particularly appealing technique is Deep Brain Stimulation (DBS). With clinical electrical DBS, electrical currents are delivered at high frequency to a region made of potentially heterogeneous neurons (the subthalamic nucleus (STN) in the case of Parkinson's disease). Even more appealing is DBS with optogenetics, which is until now a preclinical method using both gene transfer and deep brain light delivery and enabling neuromodulation at the scale of one given neural network. In this work, we rely on delayed neural fields models of STN and the external Globus Pallidus (GPe) to develop, theoretically validate and test in silico a closed-loop stimulation strategy to disrupt these sustained oscillations with optogenetics. First, we rely on tools from control theory to provide theoretical conditions under which sustained oscillations can be attenuated by a closed-loop stimulation proportional to the measured activity of STN. Second, based on this theoretical framework, we show numerically that the proposed closed-loop stimulation efficiently attenuates sustained oscillations, even in the case when the photosensitization effectively affects only 50% of STN neurons. We also show through simulations that oscillations disruption can be achieved when the same light source is used for the whole STN population. We finally test the robustness of the proposed strategy to possible acquisition and processing delays, as well as parameters uncertainty.

1. Introduction

Pathological conditions in Parkinson's disease, Huntington's disease or epileptic seizures are often associated with abnormal oscillations in specific brain areas (Bragin et al., 2010; Devergnas and Wichmann, 2014). In particular, parkinsonian motor symptoms result from a dopamine depletion in the striatum and strong neural synchronization, bursting and sustained oscillations in low frequencies can be observed (Bergman et al., 1994; Brown et al., 2001; Jenkinson and Brown, 2011). This oscillatory activity is especially detectable in global signals such as local field potentials (LFPs) (Stein and Bar-Gad, 2013). The precise relation between these sustained oscillations and motor symptoms is still a matter of debate. Nonetheless, there is clear evidence that low-frequencies activity in the LFP of the subthalamic nucleus (STN) is correlated to parkinsonian motor deficit. More precisely, bradykinesia and rigidity are related to strong and sustained activity in β-frequencies (13–30 Hz) (Kühn et al., 2006; Hammond et al., 2007; Little et al., 2012), while low γ-frequencies (31–45 Hz) correlate with tremor severity (Beudel et al., 2015). Sustained β-activity is not reported in healthy conditions (Bar-Gad et al., 2003; Heimer et al., 2006; Schwab et al., 2013). Among the possible hypotheses for the mechanisms underlying this pathological synchronization onset, a possible pacemaker role of the network formed by the excitatory STN and the inhibitory external globus pallidus (GPe) has been proposed based on in vitro experiments (Plenz and Kital, 1999). With striatal origins and cortical STN patterning, this role of the STN-GPe as a pacemaker is one of the main hypotheses for this pathological oscillations onset (Bevan et al., 2002; Lang and Zadikoff, 2005). Experiments conducted on non-human primate models of Parkinson's disease confirm the importance of reciprocal STN-GPe connections on oscillatory activity onset (Nambu and Tachibana, 2014). Although not formally proven in vivo, this pacemaker effect of the STN-GPe network is supported by mathematical models, fitted to neurophysiological data, which effectively reproduce sustained oscillations in parkinsonian conditions (Terman et al., 2002; Holgado et al., 2010; Merrison et al., 2013; Pasillas-Lépine, 2013). In order to test this hypothesis, there is a critical need for developing theoretical strategies of neuromodulation that could be implemented experimentally in order to control sustained oscillations in the STN.

Deep Brain Stimulation (DBS, Benabid et al., 1991) is a neuromodulation method that consists in chronically implanting electrodes in specific targeted brain areas and in applying electrical currents to alleviate neurological symptoms (Lozano and Lipsman, 2013). In the case of Parkinson's disease, three different targets (thalamus, globus pallidus pars internalis and subthalamic nucleus) have been identified to reduce motor symptoms such as tremor or/and rigidity, akinesia, the STN being the most prescribed. Although the electrical DBS's mechanisms of action are still a matter of debate, it has been suggested that DBS of the STN may affect β-synchrony in the targeted neural population (Eusebio et al., 2011). In most existing DBS treatments, the electrical signal is delivered in an open-loop manner, meaning regardless of the patient's state or brain activity. As reviewed in Carron et al. (2013), several attempts have recently been made to optimize DBS by taking into account some measurements of the patient brain activity. These include adaptive and on-demand stimulation (Marceglia et al., 2007; Graupe et al., 2010; Rosin et al., 2011; Santaniello et al., 2011; Little et al., 2013), delayed and multi-site stimulation (Omel chenko et al., 2008; Batista et al., 2010; Pfister and Tass, 2010; Lysyansky et al., 2011; Tass et al., 2012), optimal control strategies (Feng et al., 2007), and closed-loop firing rate regulation (Wagenaar et al., 2005; Luo et al., 2009; Franci et al., 2011; Pasillas-Lépine et al., 2013). Another strategy, not included in that review, is Schiff (2010), which advocates for the use of Kalman filtering to enhance DBS strategies. The review Carron et al. (2013) underlines a clear gap between model-based closed-loop DBS strategies, whose efficiency is most of the time assessed in silico, and the DBS signals actually tested in vivo.

Optogenetics is a promising tool to unravel pathological oscillations onset mechanisms and to explore closed-loop strategies to optimize DBS treatment. Using a viral vector, genes coding for neuronal membrane ionic channels, sensitive to precise wavelengths, are selectively transferred to precisely targeted neurons, which become photosensitive. Thus, simple pulses of intense light, e.g., through implanted optical fibers, can induce the response of the photosensitized neurons (Boyden et al., 2005; Pastrana, 2010). By contrast with electrostimulation, optical neuromodulation does not induce any stimulation artifacts on electrical recordings. It also allows sharpest targeting of specific neuronal subpopulations. In addition, the development of bi-color optogenetics stimulation and bi-switchable opsins such as Halo-ChR2 (Han and Boyden, 2007), now allows for simultaneous excitation and inhibition of the neural population in a controlled way, whereas electrical DBS may perform both excitation and inhibition on different compartments of the same neurons or on different neurons depending on their orientations relative to the electrical field (Ranck, 1975; McIntyre et al., 2004). Thus, combined with electrode measurements, optogenetics may offer unprecedented possibilities to achieve closed-loop stimulation of neural structures, in particular for counteracting pathological oscillations in animal models (Chaillet et al., 2014). First experimental attempts include those described by Paz et al. (2012), where closed-loop optical stimulation was used on rats in order to interrupt seizures after cortical injury.

A particular way to avoid the generation of sustained oscillations in a parkinsonian STN-GPe network is to artificially reduce the gain of the STN-GPe loop. This strategy has been developed in Pasillas-Lépine et al. (2013)¹ using tools from linear control theory. That theoretical paper demonstrates that, by delivering a photostimulation whose frequency is proportional to the measured unitary activity, sustained oscillations are impeded in the parkinsonian basal ganglia model proposed in Holgado et al. (2010). It further proposes a filtering strategy to cope with inherent acquisition and processing delays. In view of its simplicity and ease of technological implantation, this closed-loop DBS strategy is very appealing. Nonetheless, this encouraging result still suffers from important limitations. The main one stands in the employed model, which summarizes the activity of each neural population by a single averaged variable and thus fails at taking into account spatial heterogeneity within STN and GPe. The first aim of this theoretical paper is to propose a model of the parkinsonian STN-GPe network, able to take into account both temporal and spatial evolutions of the activity.

Another limitation of the study conducted in Pasillas-Lépine et al. (2013) is that it relies on a linearized model, and thus neglects the inherent nonlinear effects arising from the neurons f-I curves and the saturation of the stimulation signal. The works Faye and Faugeras (2010); Veltz and Faugeras (2011) provide a relevant mathematical framework to study the proposed spatiotemporal model analytically, despite the combined effects of delays and nonlinearities. The second objective of this paper is to propose a closed-loop stimulation strategy enabling disruption of sustained oscillations in this spatiotemporal model of the STN-GPe network, and to prove its efficiency both mathematically and numerically. This stimulation signal is designed to be realistically implementable in order to test the role of sustained oscillations in parkinsonian symptoms in future experiments.

The third objective of this paper is to validate both the model and the associated closed-loop stimulation signal based on in silico experiments that take into account specific experimental constraints that would occur in an in vivo testing. These constraints include parameter uncertainties, imperfect photosensitization or insufficient illumination of STN neurons, use of a single light source for the whole STN population, and unavoidable acquisition and processing delays.

2. Materials and Methods

2.1. Neural Fields Model of the STN-GPe Network

In parkinsonian conditions, pathological oscillations are commonly observed in the dorsolateral region of the STN (Zaidel et al., 2010). We focus on this specific area and on the GPe neurons that either project or receive projections from that region. From now on, we will simply refer to these regions as STN and GPe for simplicity. A finer study of the pathological oscillations onset in the parkinsonian STN-GPe network requires to include the evolution of their activity in both time and space. To this aim, we model the STN and GPe populations as delayed neural fields (Coombes, 2005; Bressloff, 2012). Indicating the STN and GPe populations with indexes 1 and 2 respectively, the STN-GPe network is thus modeled as coupled delayed neural fields:

$\begin{array}{cc}\begin{array}{l}{\tau }_1\frac{\partial z_1}{\partial t}(r,t)=-z_1(r,t)\\ +S_1\left({\displaystyle \sum _{j=1}^2{\displaystyle {\int }_{\Omega }{w}_{1j}}}(r,r^{\prime })z_j(r^{\prime },t-d_j(r,r^{\prime }))d{r}^{\prime }+I_1^{\text{ext}}(r,t)\right)\end{array}& (1\text{a})\end{array}$

$\begin{array}{cc}\begin{array}{l}{\tau }_2\frac{\partial z_2}{\partial t}(r,t)=-z_2(r,t)\\ +S_2\left({\displaystyle \sum _{j=1}^2{\displaystyle {\int }_{\Omega }{w}_{2j}}}(r,r^{\prime })z_j(r^{\prime },t-d_j(r,r^{\prime }))d{r}^{\prime }+I_2^{\text{ext}}(r,t)\right).\end{array}& (1\text{b})\end{array}$

z₁(r, t) and z₂(r, t) represent the neuronal activity of the neurons at position r and at time t for STN and GPe respectively. Ω denotes a compact set of ℝ^p, p ∈ {1,2,3}, representing the physical support of the network neuronal populations. τ₁ and τ₂ are the time constant STN and GPe activities. w_ij(r, r') describes the synaptic strength between location r' in population j and location r in population i. d₁(r, r') and d₂(r, r') represent the axonal time delays between a pre-synaptic neuron at position r' and a post-synaptic neuron at position r. S₁ and S₂ are the activation functions of STN and GPe respectively. I₁^ext(r, t) and I₂^ext(r, t) account for the external inputs of STN and GPe. In this work, we consider that the STN neurons expresses the gene that codes for photoactivatable proteins and receive sufficient illumination from the stimulation device. In other words, the STN activity can be modulated with light stimulation. I₁^ext(r, t) thus decomposes into a stimulation signal u(r, t) that we can regulate and the inputs I₁(r, t) from other cerebral structures, especially cortical inputs. The GPe is not directly affected by the stimulation and hence sums up to inputs I₂(r, t) from other brain areas, specifically from the striatum. The overall setup is depicted by Figure 1.

FIGURE 1

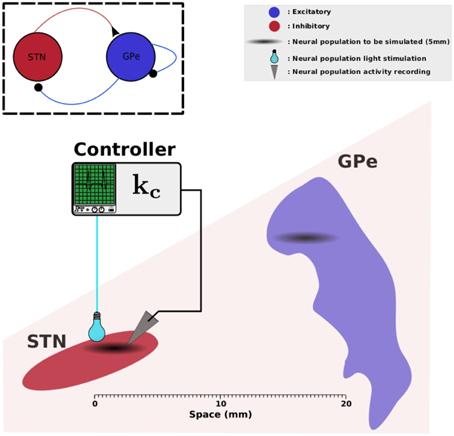
Figure 1. STN-GPe network. This figure illustrates the physical arrangement of STN and GPe. We assume that the zones involved in pathological oscillations in STN and GPe measure 2.5 mm each (Zaidel et al., 2010); they are indicated in black clouds. The light-green box illustrates a controller that reads data from STN and applies a photostimulation to the same neural population. Elements of this figure have been found in Wikipedia and they are licensed according to CC (http://creativecommons.org/licenses/by-sa/3.0).

2.2. Closed-loop Stimulation Signal

As will be seen in Section 3, the STN-GPe model (Equation 1) may exhibit sustained oscillations even when the exogenous inputs I₁^ext and I₂^ext are constant in time. These oscillations result from the combined effects of transmission delays and too strong synaptic weights between STN and GPe. As originally proposed in Holgado et al. (2010), these increased synaptic gains in pathological conditions may result from dopamine depletion. In order to attenuate these pathological oscillations, we rely on a proportional stimulation law, in the spirit of Pasillas-Lépine et al. (2013). Proportional control constitutes the basics of control theory; it consists in applying an input which is proportional to the difference between the measured state and a targeted reference:

$\begin{array}{cc}u(r,t)=-k_c\left(z_1(r,t)-z_{ref}(r)\right),& (2)\end{array}$

where k_c is a positive control gain that can be adjusted at will, and z_ref(r) represents a prescribed rate for the STN population. The stimulation signal is thus assumed to act as an external rate on the STN. It may act as an either inhibitory or excitatory input, depending on the sign of u(r, t). This is in agreement with the recent development of bi-color optogenetics stimulation and bi-switchable opsins such as Halo-ChR2 (Han and Boyden, 2007), which enables both excitation and inhibition of the same neuronal population.

The rationale behind this proportional closed-loop stimulation is rather intuitive: when the measured STN activity z₁(r, t) overpasses the prescribed rate z_ref(r), the stimulation tends to decrease the STN activity, translating in a negative sign of the stimulation signal u(r, t). On the contrary, when the measured STN activity is too low compared to the target rate, the stimulation excites the STN (u(r, t) comes with a positive sign). In both cases, the amplitude of the delivered stimulation signal is proportional to the difference between the STN measured activity and the prescribed one. Note that the implementation of this closed-loop stimulation signal requires the real-time measurement of the STN activity. No measurements on the GPe or other brain areas are needed.

Plugging the closed-loop stimulation signal (Equation 2) into the spatiotemporal model (Equation 1) leads to the following dynamics:

$\begin{array}{cc}\begin{array}{l}{\tau }_1\frac{\partial z_1}{\partial t}=-z_1+S_1({\displaystyle \sum _{j=1}^2{\displaystyle {\int }_{\Omega }{w}_{ij}}}(r,r^{\prime })z_j(r^{\prime },t-d_j(r,r^{\prime }))d{r}^{\prime }\\ +I_1(r,t)-k_c\alpha (r)\left(z_1(r,t)-z_{ref}(r)\right))\end{array}& (3\text{a})\end{array}$

$\begin{array}{cc}\begin{array}{l}{\tau }_2\frac{\partial z_2}{\partial t}=-z_2+S_2({\displaystyle \sum _{j=1}^2{\displaystyle {\int }_{\Omega }{w}_{ij}}}(r,r^{\prime })z_j(r^{\prime },t-d_j(r,r^{\prime }))d{r}^{\prime }\\ +I_2(r,t)).\end{array}& (3\text{b})\end{array}$

α(r) ≥ 0 is a position-dependent gain accounting for the strength of the stimulation influence at position r. It typically decreases as a function of the distance to the stimulation device, due to light absorption in brain tissues (Deng et al., 2014). Its value may also be affected by the quality of photosensitization of the targeted neurons. In the case when photosensitization is not effective or light stimulation is not received, it holds that α(r) = 0.

2.3. Tools to Assess Performance and Robustness

In order to numerically investigate the effects of the proposed closed-loop DBS method described above, we propose five in silico experimental protocols.

• Protocol A tests the ability of the proposed spatiotemporal model to generate sustained oscillations in the β band. This test is conducted both on a nominal set of parameters deduced from data available in the literature (see Section 2.4) and on variations around these nominal values.

• Protocol B assesses the efficiency of the proposed closed-loop stimulation signal to disrupt these sustained oscillations.

• Protocol C studies the performance of the closed-loop stimulation signals in case of poor STN photosensitization.

• Protocol D tests the implementability of the closed-loop stimulation policy when a single light source is available for the whole STN population.

• Protocol E investigates how acquisition and processing delays may affect the performance of the closed-loop stimulation signal.

2.4. Parameters Selection

For simplicity and clarity of exposition, we consider only 1-dimensional spatial distributions: Ω is picked as the interval [0, 15]mm, as the STN and GPe are both contained in zone of length 15mm in adult human brain. The STN activity lies in the subregion Ω₁ = [0, 2.5]mm, while the GPe stands in the subregion Ω₂ = [12.5, 15] mm. All these values are in accordance with adult human brain physiology (Mai et al., 1997).

An advanced identification of parkinsonian activity of STN and GPe rate dynamics has been performed in Holgado et al. (2010) based on experimental data available in the literature. We partly rely on that work to identify some parameters of the model. More precisely, in that reference, the time constants τ₁ and τ₂ were taken as the membrane time constants of the neurons involved and can be taken as 6 ms and 14 ms according to e.g., Paz et al. (2005) and Kita and Kitai (1991) respectively. The activation functions S₁ and S₂ were fitted to experimental data available in Kita and Kitai (1991) and Deister et al. (2009) among others. They were taken as sigmoidal functions:

$S_i(x)=\frac{m_i{b}_i}{b_i+(m_i-b_i)e^{-4x/m_i}},$

where m₁ = 300 spk/s, b₁ = 17 spk/s, m₂ = 400 spk/s and b₂ = 75 spk/s. It can easily be checked that the maximum slopes of these functions are ℓ₁ = ℓ₂ = 1.

The remaining parameters cannot be readily taken from Holgado et al. (2010) as they are space-dependent, while Holgado et al. (2010) relied on an averaged model. The axonal delays d_i(r, r') are derived based on the physical distance between r and r' and the velocity c_i of spike propagation along the axons under concern:

$d_j(r,r^{\prime })=\frac{|r-r^{\prime }|}{c_j}.$

We picked c₁ = 2.5 m/s and c₂ = 1.4 m/s, in accordance with Kita et al. (1983). The inputs I₁(r, t) and I₂(r, t) encompass activities from other brain areas, mainly from cortex for STN and from striatum for GPe. Although they were assumed constant in time in our theoretical analysis (see Section 3.1), we have taken them as white noises with variance 0.05 centered at 27 spk/s for cortex and 2 spk/s for striatum (the values have been taken from Holgado et al., 2010). Also in line with Holgado et al. (2010), these input rates were multiplied by uniform synaptic weights of 12.5 (cortical input to STN) and 110 (striatal input to GPe). The addition of a noise to these constant inputs makes the cortical and striatal influences more physiologically plausible and in turn allows to test the robustness of the proposed closed-loop stimulation strategy. The striatal influence on GPe being mostly inhibitory (Kita, 2007), I₂(r, t) was taken with a minus sign.

The kernel w₁₁ accounting for synaptic coupling within STN was taken as zero since there is no evidence of self-excitatory STN connections (Marani et al., 2008). The other kernels, modeling synaptic weights between the populations (w₁₂ and w₂₁) or within the GPe (w₂₂), were taken as Gaussian functions as represented by Figure 2 (left panel). Synaptic strengths w₁₂ and w₂₁ follow the principle of short-range excitation/inhibition. This implies that if a neuron of STN project to a neuron of GPe, the former excites the neighbor neurons in GPe as well. More precisely, w₁₂ and w₂₁ were taken as²

$\begin{array}{l}{w}_{12}(r,r^{\prime })=-g_{12}(|r-r^{\prime }-{\mu }_2|),\forall r\in {\Omega }_1,r^{\prime }\in {\Omega }_2\\ w_{21}(r,r^{\prime })=g_{21}(|r-r^{\prime }-{\mu }_1|),\forall r\in {\Omega }_2,r^{\prime }\in {\Omega }_1\\ w_{22}(r,r^{\prime })=-|r-r^{\prime }|g_{22}(|r-r^{\prime }|),\forall r,r^{\prime }\in {\Omega }_2,\end{array}$

where μ₁ = 1.25mm and μ₂ = 13.25mm indicate the centers of STN and GPe respectively, and the Gaussian functions g_ij are defined as

$g_{ij}(x):=K_{ij}\exp \left(-\frac{x^2}{2{\sigma }_{ij}}\right).$

FIGURE 2

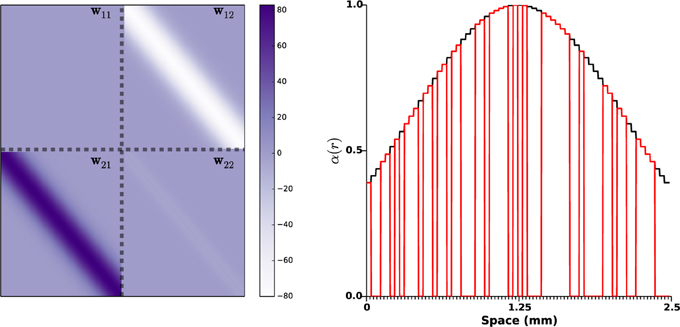
Figure 2. Synaptic weights distributions and photosensitization distribution. On the left side panel, the distributions w_ij of the synaptic strengths are represented. The gray dashed lines indicate the space between STN and GPe (10 mm in an adult human brain, Mai et al., 1997). Right panel shows a realization of function α(r), the black curve indicates a STN photosensitization of 100%, the red line corresponds to a random photosensitization of 50%.

The variance σ₁₂ and σ₂₁ were taken identical (0.03 mm²) based on the numerical and computational studies (Terman et al., 2002; Park et al., 2011), which indicate that STN and GPe neurons are connected to a small portion of GPe and STN neurons respectively. The variance σ₂₂ within GPe is taken smaller (σ₂₂ = 0.015) as GPe lateral projections are more local (François et al., 1984). The amplitudes K_ij of the synaptic weights distribution were picked in order for the mean activity to fit the simulations presented in Holgado et al. (2010): K₁₂ = 30, K₂₁ = 38, and K₂₂ = 2.55. Note that the amplitude of w₂₂ is much lower than the other two, as the number of lateral connections within GPe is small (Sadek et al., 2005). w₁₂ and w₂₂ were taken negative as the projections from GPe neurons are mostly GABAergic (Sato et al., 2000a); on the other hand w₂₁ was picked positive, as STN projections are mostly glutamatergic (Sato et al., 2000b). Note that, although this has little influence on the simulations result, w₂₂ is not a pure Gaussian function: it is zero when r = r'. This was done in order to provide little synaptic coupling with GPe neurons in the immediate vicinity as little correlations have been observed between neighboring neurons in the GPe (Bar-Gad et al., 2003). This parameters choice lead to a L₂-norm of lateral GPe connections ℓ₂||w₂₂|| = 1 × 0.95 < 1, thus fulfilling the requirement (Equation 4) of our theoretical result. This rather small value can be interpreted as the absence of endogenous oscillations within GPe (see Section 3.1 for details). In line with e.g., Plenz and Kital (1999); Nambu and Tachibana (2014), the observed pathological oscillations do not find their roots within GPe, but result from interactions between neuronal populations.

Finally, the function α(r) accounting for the impact of light stimulation was taken as a Gaussian function (zero outside Ω₁) of amplitude 1, centered at the middle of the STN population (1.25mm), and variance 1.25 mm²: see right panel of Figure 2. This choice corresponds to a photo-sensitization of all STN neurons and takes into account light absorption in the medium (as the central STN neurons are more impacted by stimulation than neurons in the periphery).

The parameters used in each in silico protocols are summarized in Table 1.

TABLE 1

Table 1. Model parameters in each protocol.

2.5. Simulation Details

In order to simulate the delayed neural fields described by Equation (3), we normalized the spatial domain to Ω_sim = [0, 1]. All synaptic strengths and delays are computed according to this normalized interval. We discretized Ω_sim using m spatial nodes representing unitary subregions of the populations: m/6 for the STN, m/6 for the GPe and the rest for silent neurons modeling the physical distance between STN and GPe. The temporal integration of the system has been done by the Forward Euler method. All the simulation parameters are gathered in Table 2.

TABLE 2

Table 2. Simulation parameters.

We run all the simulations on a Dell Desktop Machine equipped with an Intel i5 processor and 8 GB memory. The average running time of a simulation was 0.7 s. All the simulations are written in Python (Numpy, Scipy, Matplotlib). The source code is freely distributed under the GPL License and can be found on-line at Github³.

3. Results

3.1. Provable Disruption of Pathological Oscillations

Our main theoretical result states that the delayed neural fields (Equation 3) can always be stabilized by the proportional closed-loop stimulation (Equation 2), provided that the GPe does not exhibit endogenous sustained oscillations. More precisely, we have the following result, whose proof is provided in Appendix.

---

Consider any admissible target pattern z_ref(r). Let the activation functions S₁ and S₂ be bounded, increasing, and with maximum slope ℓ₁ and ℓ₂ respectively. Assume that the lateral synaptic weights in the GPe satisfy

$\begin{array}{cc}\sqrt{{\displaystyle {\int }_{\Omega }{\displaystyle {\int }_{\Omega }{w}_{22}{(r,r^{\prime })}^{2}d{r}^{\prime }dr}}}<\frac{1}{{\ell }_2},& (4)\end{array}$

and that the photosensitization is efficient over all STN, meaning that α(r) > 0 for all r ∈ Ω. Assume further that the inputs I₁(r, t) and I₂(r, t) from other brain areas are constant in time. Then, for any feedback gain k_c sufficiently large, the neural fields under closed-loop stimulation (Equation 2) is stable and, from almost all admissible initial conditions⁴, the STN and GPe activities exponentially converge to constant patterns.

---

Condition (Equation 4) requires a sufficiently small L₂-norm for the lateral synaptic weights w₂₂ of the GPe. It has a physical interpretation: it imposes that the internal dynamics of the GPe should not exhibit instability (see e.g., Faye and Faugeras, 2010). Thus, proportional closed-loop stimulation can compensate for oscillations generated either within the STN (large w₁₁) or due to too strong interactions between the STN and GPe (large w₁₂ or w₂₁), but might be insufficient to tackle endogenous oscillations within the GPe (large w₂₂).

3.2. Protocol A: Sensitivity Analysis

We start by assessing the capability of the proposed model (Equation 3) to robustly produce sustained oscillations with the parameters choice described in Section 2.4. Tight parameters identification is usually incompatible with experimental constraints: the robustness of the model is therefore a crucial necessity. To this aim, we systematically modified the amplitude of the synaptic weights distribution (K₁₂, K₂₁, and K₂₂) and the axonal transmission velocities (c₁ and c₂) in ranges of plus or minus 35% their nominal values. Ten values in this range were tested for each parameter, thus corresponding to a total of 10⁵ simulations. No stimulation was applied in this protocol (k_c = 0). For each simulation, we estimated the main harmonic of the STN and GPe activity, as the maximum peak of the Fourier transform of the signals after transients. The result is summarized by a histogram that illustrates the different oscillations frequencies that can be generated by the model: see Figure 3.

FIGURE 3

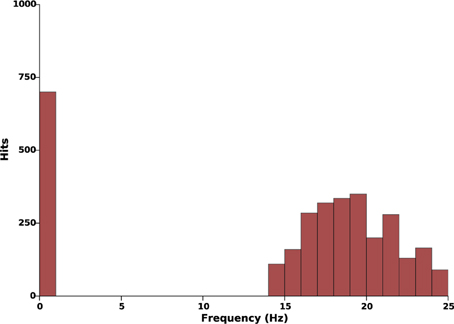
Figure 3. Effects of parameters uncertainty on the frequency of sustained oscillations. This histogram illustrates the occurrences of different oscillations frequencies when the parameters K₁₂, K₂₁, K₂₂, c₁, and c₂ evolve in a range of ±35% their nominal values (see Tables 1, 2). In all 10⁵ simulations, when oscillations take place, they lie within the β-band.

This histogram suggests reasonable robustness to parameter uncertainty as, in all simulations, the main oscillations harmonic either lied within 13–25 Hz or was zero. In other words, in these parameters ranges, oscillations either take place in the β-band or do not take place at all.

In order to assess more tightly the role of each parameters in the sustained oscillations onset, we estimated their frequency by varying only two parameters in a wider range, while leaving all other parameters to their nominal values. It appeared that the amplitude K₂₂ of lateral GPe synaptic weights may result in sustained oscillations or constant activity, but has little effect on the oscillations frequencies (curves not reported). On the contrary, the synaptic weights between STN and GPe (K₁₂ and K₂₂) and the axonal velocities (c₁ and c₂) do play a crucial role in the frequency of sustained oscillations. Figure 4 shows the frequencies as a function of K₁₂ and K₂₁ (left panel) and as a function of c₁ and c₂ (right panel).

FIGURE 4

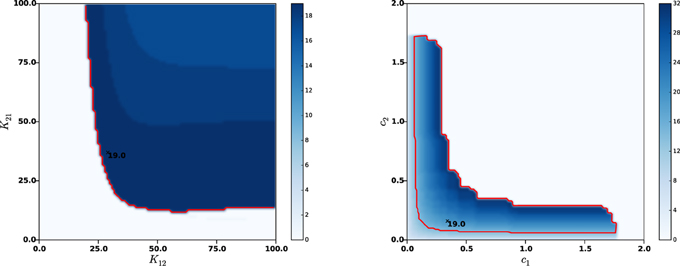
Figure 4. Effects of synaptic strengths and axonal velocities on the frequency of oscillations. Left panel: main harmonic frequency of STN and GPe oscillations as a function of the synaptic distributions amplitudes K₁₂ and K₂₁ between STN and GPe (left panel) and as a function of the axonal propagation delays c₁ and c₂ (right panel). The red contour indicates β-band frequencies. The nominal values of the parameters are indicated with a black cross, together with the corresponding oscillations frequency.

It can be observed that each of the considered parameters can be significantly modified without compromising the β nature of sustained oscillations. Nonetheless, too low synaptic weights or two high axonal velocities (meaning lower transmission delays between STN and GPe) may compromise the very oscillations onset. This is in agreement with the analyses conducted on an averaged rate model in Holgado et al. (2010) and Pasillas-Lépine (2013), which clearly showed that sustained oscillations results from the combined effects of two factors: too strong synaptic coupling between STN and GPe resulting from dopamine depletion and axonal propagation delays. This is also in agreement with the basics of control theory, which predicts that instability is favored by high coupling and delays.

3.3. Protocol B: Sustained Oscillations Disruption

As seen in the above section, the nominal parameters lead to sustained β-oscillations (approximately 19 Hz) in both STN and GPe. In order to counteract these pathological oscillations, we apply the proposed closed-loop stimulation (Equation 2) from time t = 0.5 s. The results are presented in Figure 5, which clearly shows oscillations disruption. Once stimulation is ON, the remaining oscillations mostly result from the cortical and the striatal stochastic inputs (I₁(r, t) and I₂(r, t)).

FIGURE 5

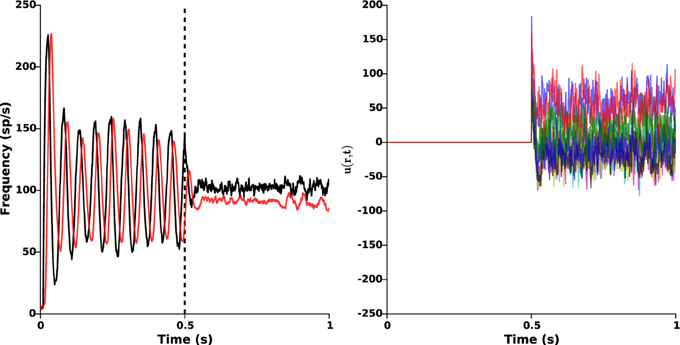
Figure 5. Oscillations disruption. The left panel illustrates the disruption of pathological β-oscillations by applying the closed-loop stimulation signal with gain k_c = 2 and target reference z_ref(r) = 0 from time t = 0.5 s. Red and black curves indicate the time evolution of the GPe and STN mean activities, respectively. Right panel shows the evolution of the control signal u(r, t) = −k_c(z₁(r, t) − z_ref(r)).

3.4. Protocol C: Poor STN Photosensitization

Depending on the efficacy of transgenesis linked to the viral vector itself, its envelope, its promoter, and to the targeted neurons, it may happen that photosensitization does not affect all STN neurons. It is important to check whether the closed-loop stimulation signal still succeeds in disrupting pathological oscillations. To that end, we randomly put to zero 50% of the values of α(r), corresponding to a photosensitization of only half of the STN population (see Figure 2, right panel), while keeping the same value of the feedback gain (k_c = 2). The results are presented in Figure 6. They indicate that the proposed closed-loop stimulation signal is robust to poor photosensitization, as the oscillations are still reduced although less efficiently than when all STN cells are successfully photosensitized.

FIGURE 6

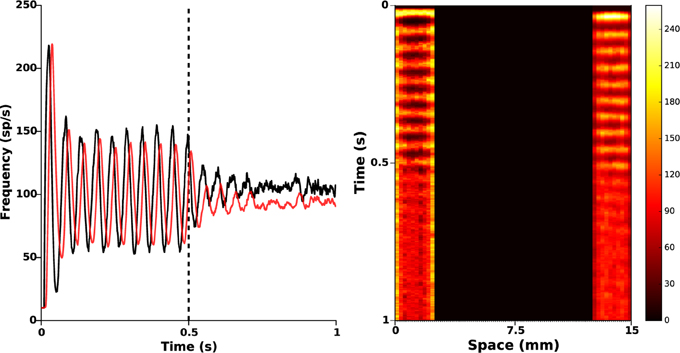
Figure 6. Poor STN photosensitization. 50% of the function α(r) was randomly silenced. Closed-loop stimulation is applied from time t = 0.5 s with gain k_c = 2 and target reference z_ref(r) = 0. Left: red and black curves illustrate time evolution of the mean activities of GPe and STN, respectively. It is apparent that the attenuation is not as successful as in Figure 5, but oscillations are still attenuated. Right: spatiotemporal evolution of the activity in STN (left) and GPe (right).

In order to further investigate the link between the level of photosensitization of STN neurons and the efficacy of the proposed closed-loop stimulation strategy, we plot the maximum amplitude of observed β-oscillations as a function of the α(r) degeneracy (meaning the percentage of STN cells that do not respond to light stimulation). The results are presented in Figure 7, for various values of the percentage of STN neurons that do not respond to light stimulation (0, 25, 50, 75, and 100%) and of the stimulation gain k_c (2, 6, and 12).

FIGURE 7

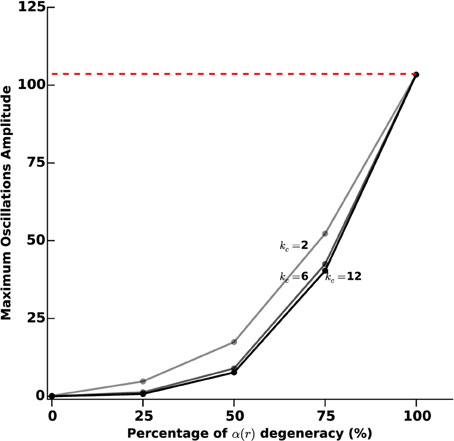
Figure 7. Sustained oscillations amplitude vs. photosensitization degeneracy. We measure the efficiency of the proposed closed-loop stimulation through the amplitude of the remaining oscillations. We consider an increasing degeneracy of α(r), corresponding to an increasing number of STN neurons that do not respond to photostimulation. The three curves correspond to different values of the feedback gain k_c (2, 6, and 12). The darkest curve corresponds to the highest value and the lighter one to the lowest value. The red dashed line indicates the oscillations maximum amplitude when no stimulation is applied.

Not surprisingly, the efficacy of the stimulation diminishes as α(r) degeneracy increases. While a degeneracy of 50% has an impact on oscillations disruption for k_c = 2 (amplitudes of approximatively 30 sp/s), it can efficiently be tackled by using a larger k_c (k_c = 6 leads to low-amplitude remaining oscillations).

3.5. Protocol D: Single Light Source

The size of the STN impedes the use of several light sources. Although holographic techniques could be envisioned (see Section 4 for a discussion about this), it is crucial to test the validity of the proposed closed-loop stimulation signal when only one light source is available for the whole STN population. To this end, we applied the following closed-loop stimulation signal:

$\begin{array}{cc}u(r,t)=u(t)=-k_c{\displaystyle {\int }_{{\Omega }_1}\left(z_1(r,t)-z_{ref}(r)\right)}dr.& (5)\end{array}$

This closed-loop stimulation signal can be seen as a spatial average of the original one proposed in Equation (2) over the whole STN population. Like Equation (2), this averaged stimulation signal relies on measurement of STN activity only. Nonetheless, it owns the advantage of being no longer dependent on position: it is taken proportional to the mean STN activity, and is the same for all STN neurons (modulo the function α(r)). In this case, a larger feedback gain is required to efficiently disrupt oscillations (k_c = 6.5). The results are presented in Figure 8, and show that proper β-oscillations disruption is achieved. We did not succeed in showing this analytically yet. Surprisingly enough, the required amplitude of stimulation is smaller when a single light source is used (compare the right panels of Figures 5, 8).

FIGURE 8

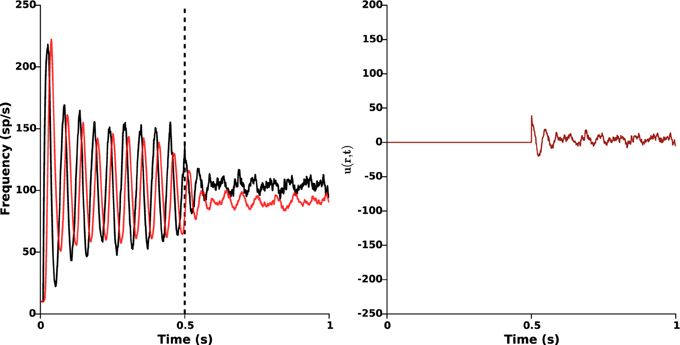
Figure 8. Single light source. The same stimulation signal (Equation 5) is provided to all STN neurons (modulo the function α(r)), with feedback gain k_c = 6.5 and target reference z_ref(r) = 0. Stimulation is ON at time t = 0.5 s. Left: time evolution of the mean activities of GPe (red) and STN (black). Right: time evolution of the closed-loop stimulation signal (Equation 5) (no longer position-dependent). This figure validates the possibility to apply proportional closed-loop stimulation by using a single light source.

3.6. Protocol E: Effect of Acquisition and Processing Delays

The experimental implementation of the proposed closed-loop stimulation signal in an animal model of Parkinson’s disease would require a real-time estimation of the activity in the STN based on the measurements provided by the recording electrodes. This signal acquisition and its processing require some time, which is likely to induce a significant delay in the applied stimulation signal. In order to test the robustness of the proposed strategy to acquisition and processing delays, we consider the following closed-loop stimulation signal:

$\begin{array}{cc}u(r,t)=-k_c(z_1(r,t-T)-z_{ref}(r)),& (6)\end{array}$

where T indicates the time needed to acquire and process the STN activity. The results are presented in Figure 9 for a feedback gain k_c = 2.

FIGURE 9

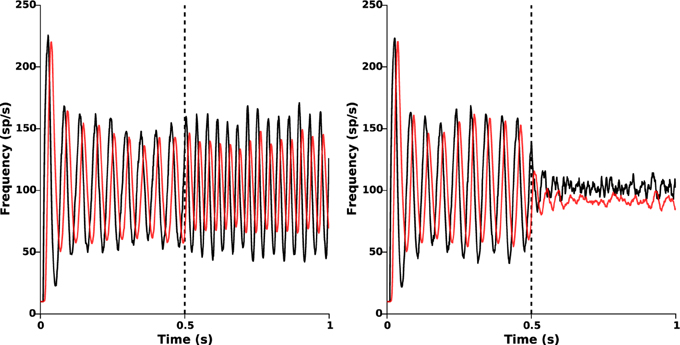
Figure 9. Effect of acquisition and processing delays. Time evolution of the mean activities of STN (black) and GPe (red) when the delayed closed-loop stimulation (Equation 6) is applied at time t = 0.5 s. Left: oscillations disruption is lost for too large delays (T = 10 ms). Right: β-oscillations disruption is still efficiently achieved for an acquisition and processing delay T = 5 ms.

When T is too large (T ≥ 10 ms), β-oscillations are no longer disrupted (Figure 9, left panel) and can even be amplified by the stimulation, as already observed in Pasillas-Lépine et al. (2013) in an averaged rate model. Nevertheless, if T is reasonably small, oscillations disruption remains satisfactorily achieved (Figure 9, right panel, T = 5 ms). This indicates that strong attention should be paid on the code optimization for data processing in view of experimental implementation. Filtering strategies, such as the one presented in Pasillas-Lépine et al. (2013) and a careful choice of the target reference z_ref(r) could probably increase robustness to acquisition and processing delays (not implemented here).

In order to assess more finely the impact of acquisition and processing delays T and their link with the feedback gain k_c, we tested 10 different delays (1, 3, 5, 7, 8, 9, 10, 13, 15, and 20 ms). For each delay, we measured the oscillations amplitude after transients for different values of k_c (2, 6, and 12), as we did for protocol D. The results are reported in Figure 10.

FIGURE 10

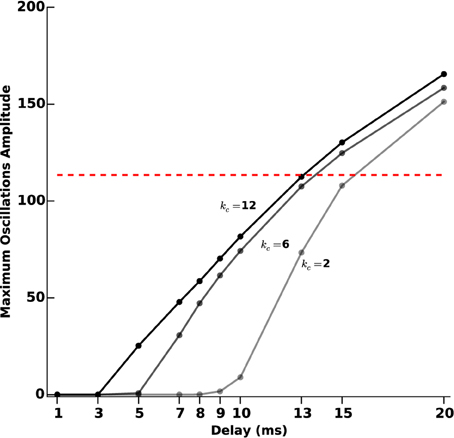
Figure 10. Oscillations amplitude vs. acquisition and processing delays. We measure the efficiency of the closed-loop stimulation (Equation 6), which includes processing and acquisition delays T, through the amplitude of the remaining oscillations after transients. We consider increasing values of T (1, 3, 5, 7, 8, 9, 10, 13, 15, and 20 ms). The three curves correspond to different values of the feedback gain k_c (2, 6, and 12). The darkest line corresponds to the highest value and the lighter to the lowest value. The red dashed line indicates the oscillations maximum amplitude when no stimulation is applied.

For small gains (k_c = 2), the model is quite robust to acquisition and processing delays: only delays above 9 ms significantly degrade the performance of the stimulation. This robustness to delays decreases as the feedback gain increases. Depending on the delay value, it may happen that stimulation is even counter-productive, in the sense that sustained oscillations get enhanced rather than disrupted.

4. Discussion

In this theoretical work, we have proposed a model of the STN-GPe network able to take into account both temporal and spatial evolutions of electrophysiological activity, and a closed-loop stimulation strategy to suppress sustained oscillations related to Parkinson's disease and test their causality in future experiments with animal models.

Our model is based on delayed neural fields to account for spatiotemporal dynamics. The need to consider spatial heterogeneity in STN and GPe arises from the facts that: (i) the efficiency of DBS requires a fine positioning of the stimulation electrodes (a millimetric scale precision is required, Anheim et al., 2008; Luján et al., 2009), thus indicating a strong position-dependency of the populations sensitivity; (ii) connectivity organization between neurons among a population or between populations cannot be taken into account in averaged models, although some studies underline its crucial role in oscillations onset (Schwab et al., 2013); (iii) the complex functioning of the structures involved, assimilated in Montgomery (2007) to a hierarchical interconnection of multiple nested, loosely coupled oscillators, requires spatially distributed models; (iv) the use of multi-plot electrodes with the most recent technologies permits a spatial resolution below 50 μ m, which cannot be exploited in averaged models; and (v) human recordings indicate a possible role of spatial correlation of STN synchronization in the parkinsonian motor symptoms (Cagnan et al., 2015).

We chose to model this spatiotemporal dynamics of the STN-GPe network by neural fields (Coombes, 2005; Bressloff, 2012). Neural fields were originally introduced by Amari (1977) to model cortical layers. They have been extensively used in the study of many different cortical phenomena such as propagating waves (Cremers and Herz, 2002; Bressloff and Webber, 2012; Meijer and Coombes, 2014), synaptic depression (Bressloff and Kilpatrick, 2011), and neural oscillations (Hutt et al., 2008). As proposed in Holgado et al. (2010) and confirmed in this work, transmission delays between STN and GPe are likely to play a key role in pathological oscillations onset and are thus included in the model. Neural fields affected by axonal propagation and synaptic delays have been studied in Faye and Faugeras (2010); Veltz and Faugeras (2011), which provide the mathematical framework this study relies on. They have been used in (Modolo et al., 2010) for closed-loop stimulation, using a term-cancellation that requires precise knowledge of the dynamics involved, including synaptic weights distributions.

The proposed spatiotemporal STN-GPe model reproduces sustained β-oscillations in a robust way, meaning even for relatively large uncertainty on parameters. We have proposed a closed-loop stimulation policy that provably disrupts sustained oscillations in this spatiotemporal model of the STN-GPe network. Inspired by Pasillas-Lépine et al. (2013), this closed-loop stimulation signal is taken proportional to the STN activity. Assuming that STN neurons have successfully undergone photosensitization, we have formally shown that, provided that no endogenous oscillations take place within the GPe, stabilization of the whole network can always be achieved by this closed-loop stimulation if the feedback gain is taken sufficiently large. This result shows that any oscillations generated within the STN or resulting from a pacemaker effect between STN and GPe populations can be tackled in this model. It is worth stressing that the assumptions of this theoretical result do not rely on the precise knowledge of the parameters and functions involved in the model. No precise information on the activation functions are required: an estimate of their maximum slopes is enough. Similarly, the synaptic weight distributions do not need to be known precisely: all we need to know is whether the intensity of the lateral GPe connections is strong or weak. Also, no knowledge is required on the time constants or on the delays. Finally, no precise tuning of the feedback gain is required: it is enough to pick it sufficiently large. These features make our closed-loop stimulation signal intrinsically robust to parameter uncertainties and promising from an experimental testing perspective. The requirement that lateral synaptic gains of the GPe be low enough is in agreement with the experimental findings of Bar-Gad et al. (2003), where functional correlations between GPe neurons have been reported as either weak or non-existent.

The spatial nature of the model allows to conduct more precise in silico experiments exploiting the geometry of STN and GPe and the synaptic distributions of neurons within and between these structures. Our numerical experiments revealed that the model is robust to poor STN photosensitization and that, in case of low photosensitization, a larger feedback gain can be used in order to successfully preserve oscillations disruption.

From an experimental testing in animal models of Parkinson's disease perspective, we stress that the use of optogenetics neuromodulation is crucial since it enables simultaneous neuro-excitation, neuro-inhibition and neural recordings, with biotechnological tools already validated experimentally (Han and Boyden, 2007). Moreover, these numerical findings point toward a necessary trade-off between robustness to poor photosensitization, which is favored by the use of large feedback gains, and robustness to acquisition and processing delays, which is better with small feedback gains. Simulations revealed that the proposed strategy is little robust to acquisition and processing delays if a large feedback gain is used. This issue needs to be carefully taken into account when performing experimentations in animal models of Parkinson's disease. Careful attention should be paid to the optimization of the acquisition algorithms in order to reduce the round-trip-time as much as possible. Future work should be conducted to make the proposed closed-loop stimulation more robust to these delays. This may take the form of a low-pass filter, as in Pasillas-Lépine et al. (2013), or of more advanced strategies inspired from control theory (including predictive features).

For experimental translation, the ability to deliver a space-dependent light for photostimulation is also crucial. Light stimulation is usually delivered through an optical fiber connected to a laser or directly by a light-emitting diode, so that all neurons expressing opsins and receiving photons are simultaneously photo-stimulated, receiving a number of photons depending simply on the output of the fiber, the distance to the fiber and the physical properties of the biological tissue interacting with photons. Patterned illumination constitutes a promising way to illuminate precisely shaped regions of interest, with neighboring neurons receiving potentially different patterns of illumination in intensity and in time (Bovetti and Fellin, 2015). Patterned illumination can be performed by phase modulation of light: liquid crystal spatial light modulators (LC-SLMs) can modulate two-photon light according to arbitrary shapes, thus allowing simultaneous illumination of multiple neurons with different phase maps over time in order to probe neuronal networks with complex spatial and temporal patterns of neuronal activation. For instance, optogenetic neuromodulation with millisecond temporal precision and cellular regulation has been performed in retinal ganglion cells expressing channel-rhodopsins (Reutsky-Gefen et al., 2013). Although we have shown through simulations that proportional stimulation remains efficient even when a single light source is used for the entire controlled population, holographic optogenetics thus constitutes a promising technique to provide precise time and space resolution of the closed-loop stimulation signal.

Future work should deepen the dynamics induced by light stimulation in optogenetics experiments. The model used in this work assumes that the impact of photostimulation is similar to that of a fictitious afferent neural population whose rate and excitatory/inhibitory features can be regulated in real time. In particular, the combined effects of intensity and frequency of light stimulation are not captured by the present model. Tighter modeling could be developed in the future based on existing works such as Nikolic et al. (2009).

Synaptic plasticity and homeostasis are not taken into account in the employed model. Recent studies evoke the role of synaptic plasticity in the long-term effects of DBS (Tass et al., 2012; van Hartevelt et al., 2014). Neural fields models including learning mechanisms have been studied in Galtier et al. (2012); Detorakis and Rougier (2014); Fix (2014) and we believe that the results presented here could constitute a relevant framework to deepen the analysis by including plasticity or homeostasis mechanisms.

Furthermore, the analysis conducted here focuses on the STN-GPe interaction. The theoretical result presented here can be readily adapted to more than two neuronal populations by modifying the synaptic coupling distributions. Consequently, our framework is well fitted to assess the possible role of other brain structures in the pathological oscillations onset.

Finally, as stressed in the introduction, the precise mechanisms of parkinsonian oscillations in deep brain structures is still a matter of debate (Bevan et al., 2002; Lang and Zadikoff, 2005). This paper focuses on one possible mechanism, namely the STN-GPe network acting as a pacemaker. This hypothesis is supported by in vitro experiments reported in Plenz and Kital (1999) using mature organotypic cortex-striatum-STN-GPe cultures. To the best of our knowledge, no in vivo experiments has yet confirmed or infirmed this hypothesis, although Nambu and Tachibana (2014) underlines the role played by STN-GPe reciprocal connections. We believe that the theoretical insights provided by the model presented here and its associated closed-loop stimulation constitute interesting bases for further experimental investigations in animal models of Parkinson's disease in order to confront this hypothesis with other possible mechanisms, including cortical patterning of STN (Magill et al., 2001) and striatal origins of oscillations (McCarthy et al., 2011).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was partially supported by a public grant overseen by the French ANR as part of the Investissements d'Avenir program, through the iCODE institute, research project funded by the IDEX Paris-Saclay, ANR-11-IDEX-0003-02, and by the ANR JCJC project SynchNeuro.

Footnotes

1. ^Journal extended version submitted to Biological Cybernetics under the title “A firing-rate regulation strategy for closed-loop deep brain stimulation.”

2. ^All these functions are taken as zero outside their domain.

3. ^https://github.com/gdetor/neuralfieldDBSmodel.

4. ^We call admissible any initial condition that lies within the ranges of S₁ and S₂.

References

Amari, S.-I. (1977). Dynamics of pattern formation in lateral-inhibition type neural fields. Biol. Cybern. 27, 77–87. doi: 10.1007/BF00337259

PubMed Abstract | CrossRef Full Text | Google Scholar

Anheim, M., Batir, A., Fraix, V., Silem, M., Chabardès, S., Seigneuret, E., et al. (2008). Improvement in Parkinson's disease by subthalamic nucleus stimulation based on electrode placement: effects of reimplantation. Arch. Neurol. 65, 2–616. doi: 10.1001/archneur.65.5.612

PubMed Abstract | CrossRef Full Text | Google Scholar

Bar-Gad, I., Heimer, G., Ritov, Y., and Bergman, H. (2003). Functional correlations between neighboring neurons in the primate globus pallidus are weak or nonexistent. J. Neurosci. 23, 4012–4016.

PubMed Abstract | Google Scholar

Batista, C. A. S., Lopes, S. R., Viana, R. L., and Batista, A. M. (2010). Delayed feedback control of bursting synchronization in a scale-free neuronal network. Neural Netw. 23, 114–124. doi: 10.1016/j.neunet.2009.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Benabid, A. L., Pollak, P., Hoffmann, D., Gervason, C., Hommel, M., Perret, J. E., et al. (1991). Long-term suppression of tremor by chronic stimulation of the ventral intermediate thalamic nucleus. Lancet 337, 403–406. doi: 10.1016/0140-6736(91)91175-T

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergman, H., Wichmann, T., Karmon, B., and DeLong, M. R. (1994). “Parkinsonian tremor is associated with low frequency neuronal oscillations in selective loops of the basal ganglia,” in The Basal Ganglia IV (Boston, MA: Springer US), 317–325. doi: 10.1007/978-1-4613-0485-2_33

CrossRef Full Text | Google Scholar

Beudel, M., Little, S., Pogosyan, A., Ashkan, K., Foltynie, T., Limousin, P., et al. (2015). Tremor reduction by deep brain stimulation is associated with gamma power suppression in Parkinson's disease. Neuromodulation 18, 349–354. doi: 10.1111/ner.12297

PubMed Abstract | CrossRef Full Text | Google Scholar

Bevan, M. D., Magill, P. J., Terman, D., Bolam, J. P., and Wilson, C. J. (2002). Move to the rhythm: oscillations in the subthalamic nucleus–external globus pallidus network. Trends Neurosci. 25, 525–531. doi: 10.1016/S0166-2236(02)02235-X

PubMed Abstract | CrossRef Full Text

Bovetti, S., and Fellin, T. (2015). Optical dissection of brain circuits with patterned illumination through the phase modulation of light. J. Neurosci. Methods 15, 66–77. doi: 10.1016/j.jneumeth.2014.12.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Boyden, E. S., Zhang, F., Bamberg, E., Nagel, G., and Deisseroth, K. (2005). Millisecond-timescale, genetically targeted optical control of neural activity. Nat. Neurosci. 8, 1263–1268. doi: 10.1038/nn1525

PubMed Abstract | CrossRef Full Text | Google Scholar

Bragin, A., Engel, J. Jr., and Staba, R. J. (2010). High-frequency oscillations in epileptic brain. Curr. Opin. Neurol. 23:151. doi: 10.1097/WCO.0b013e3283373ac8

PubMed Abstract | CrossRef Full Text | Google Scholar

Bressloff, P. C. (2012). Spatiotemporal dynamics of continuum neural fields. J. Phys. A 45:033001. doi: 10.1088/1751-8113/45/3/033001

CrossRef Full Text | Google Scholar

Bressloff, P. C., and Kilpatrick, Z. P. (2011). Two-dimensional bumps in piecewise smooth neural fields with synaptic depression. SIAM J. Appl. Math. 71, 379–408. doi: 10.1137/100799423

CrossRef Full Text | Google Scholar

Bressloff, P. C., and Webber, M. A. (2012). Front propagation in stochastic neural fields. SIAM J. Appl. Dyn. Syst. 11, 708–740. doi: 10.1137/110851031

CrossRef Full Text | Google Scholar

Brown, P., Oliviero, A., Mazzone, P., Insola, A., Tonali, P., and Di Lazzaro, V. (2001). Dopamine dependency of oscillations between subthalamic nucleus and pallidum in Parkinson's disease. J. Neurosci. 21, 1033–1038.

PubMed Abstract | Google Scholar

Cagnan, H., Duff, E. P., and Brown, P. (2015). The relative phases of basal ganglia activities dynamically shape effective connectivity in Parkinson's disease. Brain 138, 1667–1678. doi: 10.1093/brain/awv093

PubMed Abstract | CrossRef Full Text | Google Scholar

Carron, R., Chaillet, A., Filipchuk, A., Pasillas-Lépine, W., and Hammond, C. (2013). Closing the loop of deep brain stimulation. Front. Syst. Neurosci. 7:112. doi: 10.3389/fnsys.2013.00112

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaillet, A., Da Silva, D., Detorakis, G., Pouzat, C., and Senova, S. (2014). Optogenetics to unravel the mechanisms of parkinsonian symptoms and optimize deep brain stimulation. ERCIM News Spec. Issue Cyberphys. Syst. 97, 1–2.

Google Scholar

Coombes, S. (2005). Waves, bumps, and patterns in neural field theories. Biol. Cybern. 93, 91–108. doi: 10.1007/s00422-005-0574-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Cremers, D., and Herz, A. V. (2002). Traveling waves of excitation in neural field models: equivalence of rate descriptions and integrate-and-fire dynamics. Neural Comput. 14, 1651–1667. doi: 10.1162/08997660260028656

PubMed Abstract | CrossRef Full Text | Google Scholar

Deister, C. A., Chan, C. S., Surmeier, D. J., and Wilson, C. J. (2009). Calcium-activated sk channels influence voltage-gated ion channels to determine the precision of firing in globus pallidus neurons. J. Neurosci. 29, 8452–8461. doi: 10.1523/JNEUROSCI.0576-09.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, W., Goldys, E. M., Farnham, M. M., and Pilowsky, P. M. (2014). Optogenetics, the intersection between physics and neuroscience: light stimulation of neurons in physiological conditions. Am. J. Physiol. Regul. Integr. Comp. Physiol. 307, R1292–R1302. doi: 10.1152/ajpregu.00072.2014

PubMed Abstract | CrossRef Full Text | Google Scholar

Detorakis, G. I., and Rougier, N. P. (2014). Structure of receptive fields in a computational model of area 3b of primary sensory cortex. Front. Comput. Neurosci. 8:76. doi: 10.3389/fncom.2014.00076

PubMed Abstract | CrossRef Full Text | Google Scholar

Devergnas, A., and Wichmann, T. (2014). “Local field potential and movement disorders,” in Encyclopedia of Computational Neuroscience, eds D. Jaeger and R. Jung (New York, NY: Springer), 1–13. doi: 10.1007/978-1-4614-7320-6_551-1

CrossRef Full Text | Google Scholar

Eusebio, A., Thevathasan, W., Doyle, G. L., Pogosyan, A., Bye, E., Foltynie, T., et al. (2011). Deep brain stimulation can suppress pathological synchronisation in parkinsonian patients. J. Neurol. Neurosurg. Psychiatry 82, 569–573. doi: 10.1136/jnnp.2010.217489

PubMed Abstract | CrossRef Full Text | Google Scholar

Faye, G., and Faugeras, O. (2010). Some theoretical and numerical results for delayed neural field equations. Physica D 239, 561–578. doi: 10.1016/j.physd.2010.01.010

CrossRef Full Text | Google Scholar

Feng, X., Greenwald, B., Rabitz, H., Shea-Brown, E., and Kosut, R. (2007). Toward closed-loop optimization of deep brain stimulation for Parkinson's disease: concepts and lessons from a computational model. J. Neural Eng. 4, L14. doi: 10.1088/1741-2560/4/2/L03

PubMed Abstract | CrossRef Full Text | Google Scholar

Fix, J. (2014). “Dynamic formation of self-organizing maps,” in Advances in Self-Organizing Maps and Learning Vector Quantization, eds T. Villmann, F.-M. Schleif, M. Kaden, and M. Lange (Springer International Publishing), 25–34. doi: 10.1007/978-3-319-07695-9_2

CrossRef Full Text | Google Scholar

Franci, A., Chaillet, A., and Pasillas-Lépine, W. (2011). Existence and robustness of phase-locking in coupled Kuramoto oscillators under mean-field feedback. Automatica SI Biol. Syst. 47, 1193–1202. doi: 10.1016/j.automatica.2011.03.003

CrossRef Full Text | Google Scholar

François, C., Percheron, G., Yelnik, J., and Heyner, S. (1984). A golgi analysis of the primate globus pallidus. i. inconstant processes of large neurons, other neuronal types, and afferent axons. J. Comp. Neurol. 227, 182–199. doi: 10.1002/cne.902270205

PubMed Abstract | CrossRef Full Text | Google Scholar

Galtier, M. N., Faugeras, O. D., and Bressloff, P. C. (2012). Hebbian learning of recurrent connections: a geometrical perspective. Neural Comput. 24, 2346–2383. doi: 10.1162/NECO/a/00322

PubMed Abstract | CrossRef Full Text | Google Scholar

Graupe, D., Basu, I., Tuninetti, D., Vannemreddy, P., and Slavin, K. (2010). Adaptively controlling deep brain stimulation in essential tremor patient via surface electromyography. Neurol. Res. 32, 899–904. doi: 10.1179/016164110X12767786356354

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammond, C., Bergman, H., and Brown, P. (2007). Pathological synchronization in Parkinson's disease: networks, models and treatments. Trends Neurosci. 30, 357–364. doi: 10.1016/j.tins.2007.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, X., and Boyden, E. S. (2007). Multiple-color optical activation, silencing, and desynchronization of neural activity, with single-spike temporal resolution. PLoS ONE 2:e299. doi: 10.1371/journal.pone.0000299

PubMed Abstract | CrossRef Full Text | Google Scholar

Heimer, G., Rivlin, M., Israel, Z., and Bergman, H. (2006). Synchronizing activity of basal ganglia and pathophysiology of Parkinson's disease. J. Neural Tran. Suppl. 70, 17–20. doi: 10.1007/978-3-211-45295-0/4

PubMed Abstract | CrossRef Full Text | Google Scholar

Holgado, A. N., Terry, J., and Bogacz, R. (2010). Conditions for the generation of beta oscillations in the subthalamic nucleus-globus pallidus network. J. Neurosci. 30:12340. doi: 10.1523/JNEUROSCI.0817-10.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutt, A., Sutherland, C., and Longtin, A. (2008). Driving neural oscillations with correlated spatial input and topographic feedback. Phys. Rev. E 78:021911. doi: 10.1103/PhysRevE.78.021911

PubMed Abstract | CrossRef Full Text | Google Scholar

Jenkinson, N., and Brown, P. (2011). New insights into the relationship between dopamine, beta oscillations and motor function. Trends Neurosci. 34, 611–618. doi: 10.1016/j.tins.2011.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Kita, H. (2007). “Globus pallidus external segment,” in Gaba and the Basal Ganglia From Molecules to Systems, Progress in Brain Research, Vol. 160, eds M. James, E. D. A. Tepper, and J. P. Bolam (Elsevier), 111–133.

Google Scholar

Kita, H., Chang, H., and Kitai, S. (1983). Pallidal inputs to subthalamus: intracellular analysis. Brain Res. 264, 255–265. doi: 10.1016/0006-8993(83)90823-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Kita, H., and Kitai, S. (1991). Intracellular study of rat globus pallidus neurons: membrane properties and responses to neostriatal, subthalamic and nigral stimulation. Brain Res. 564, 296–305. doi: 10.1016/0006-8993(91)91466-E

PubMed Abstract | CrossRef Full Text | Google Scholar

Kühn, A. A., Kupsch, A., Schneider, G.-H., and Brown, P. (2006). Reduction in subthalamic 835 hz oscillatory activity correlates with clinical improvement in parkinson's disease. Eur. J. Neurosci. 23, 1956–1960. doi: 10.1111/j.1460-9568.2006.04717.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lang, A. E., and Zadikoff, C. (2005). Parkinsonian tremor. Neurol. Dis. Ther. 70:195. doi: 10.1201/b14115-16

CrossRef Full Text | Google Scholar

Little, S., Pogosyan, A., Kuhn, A. A., and Brown, P. (2012). beta band stability over time correlates with Parkinsonian rigidity and bradykinesia. Exp. Neurol. 236, 383–388. doi: 10.1016/j.expneurol.2012.04.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Little, S., Pogosyan, A., Neal, S., Zavala, B., Zrinzo, L., Hariz, M., et al. (2013). Adaptive deep brain stimulation in advanced Parkinson disease. Ann. Neurol. 73, 449–457. doi: 10.1002/ana.23951

PubMed Abstract | CrossRef Full Text | Google Scholar

Lozano, A. M., and Lipsman, N. (2013). Probing and regulating dysfunctional circuits using deep brain stimulation. Neuron 77, 406–424. doi: 10.1016/j.neuron.2013.01.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Luján, J. L., Noecker, A. M., Butson, C. R., Cooper, S. E., Walter, B. L., Vitek, J. L., et al. (2009). Automated 3-dimensional brain atlas fitting to microelectrode recordings from deep brain stimulation surgeries. Stereotact. Funct. Neurosurg. 87, 229. doi: 10.1159/000225976

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, M., Wu, Y., and Peng, J. (2009). Washout filter aided mean field feedback desynchronization in an ensemble of globally coupled neural oscillators. Biol. Cybern. 101, 241–246. doi: 10.1007/s00422-009-0334-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Lysyansky, B., Popovych, O. V., and Tass, P. A. (2011). Desynchronizing anti-resonance effect of m:n ON–OFF coordinated reset stimulation. J. Neural Eng. 8:036019. doi: 10.1088/1741-2560/8/3/036019

PubMed Abstract | CrossRef Full Text | Google Scholar

Magill, P., Bolam, J. P., and Bevan, M. (2001). Dopamine regulates the impact of the cerebral cortex on the subthalamic nucleus–globus pallidus network. Neuroscience 106, 313–330. doi: 10.1016/S0306-4522(01)00281-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Mai, J. K., Assheuer, J., and Paxinos, G. (1997). Atlas of the Human Brain. San Diego, CA: Academic Press.

Google Scholar

Marani, E., Heida, T., Lakke, E. A., and Usunoff, K. G. (2008). The Subthalamic Nucleus: Part I: Development, Cytology, Topography and Connections, Vol. 198. Berlin; Heidelberg: Springer Science & Business Media.

Google Scholar

Marceglia, S., Rossi, L., Foffani, G., Bianchi, A. M., Cerutti, S., and Priori, A. (2007). Basal ganglia local field potentials: applications in the development of new deep brain stimulation devices for movement disorders. Expert Rev. Med. Devices 4, 605–614. doi: 10.1586/17434440.4.5.605

PubMed Abstract | CrossRef Full Text | Google Scholar

McCarthy, M., Moore-Kochlacs, C., Gu, X., Boyden, E. S., Han, X., and Kopell, N. (2011). Striatal origin of the pathologic beta oscillations in Parkinson's disease. Proc. Natl. Acad. Sci. U.S.A. 108, 11620. doi: 10.1073/pnas.1107748108

PubMed Abstract | CrossRef Full Text | Google Scholar

McIntyre, C. C., Grill, W. M., Sherman, D. L., and Thakor, N. V. (2004). Cellular effects of deep brain stimulation: model-based analysis of activation and inhibition. J. Neurophysiol. 91, 1457–1469. doi: 10.1152/jn.00989.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Meijer, H. G., and Coombes, S. (2014). Travelling waves in a neural field model with refractoriness. J. Math. Biol. 68, 1249–1268. doi: 10.1007/s00285-013-0670-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Merrison, R. J., Yousif, N., Njap, F., Hofmann, U. G., Burylko, O., and Borisyuk, R. (2013). An interactive channel model of the basal ganglia: bifurcation analysis under healthy and parkinsonian conditions. J. Math. Neurosci. 3:14. doi: 10.1186/2190-8567-3-14

PubMed Abstract | CrossRef Full Text | Google Scholar

Modolo, J., Bhattacharya, B., Edwards, R., Campagnaud, J., Legros, A., and Beuter, A. (2010). Using a virtual cortical module implementing a neural field model to modulate brain rhythms in Parkinson's disease. Front. Neurosci. 4:45. doi: 10.3389/fnins.2010.00045

PubMed Abstract | CrossRef Full Text | Google Scholar

Montgomery, E. B. Jr. (2007). Basal ganglia physiology and pathophysiology: a reappraisal. Parkinsonism Relat. Disord. 13, 455–465. doi: 10.1016/j.parkreldis.2007.07.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Nambu, A., and Tachibana, Y. (2014). Mechanism of parkinsonian neuronal oscillations in the primate basal ganglia: some considerations based on our recent work. Front. Syst. Neurosci. 8:74. doi: 10.3389/fnsys.2014.00074

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolic, K., Grossman, N., Grubb, M. S., Burrone, J., Toumazou, C., and Degenaar, P. (2009). Photocycles of Channelrhodopsin2. Photochem. Photobiol. 85, 400–411. doi: 10.1111/j.1751-1097.2008.00460.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Omel chenko, O., Hauptmann, C., Maistrenko, Y., and Tass, P. A. (2008). Collective dynamics of globally coupled phase oscillators under multisite delayed feedback stimulation. Physica D 237, 365–384. doi: 10.1016/j.physd.2007.09.019

CrossRef Full Text | Google Scholar

Park, C., Worth, R. M., and Rubchinsky, L. L. (2011). Neural dynamics in parkinsonian brain: the boundary between synchronized and nonsynchronized dynamics. Phys. Rev. E 83:042901. doi: 10.1103/PhysRevE.83.042901

PubMed Abstract | CrossRef Full Text | Google Scholar

Pasillas-Lépine, W. (2013). Delay-induced oscillations in Wilson and Cowan’s model: an analysis of the subthalamo-pallidal feedback loop in healthy and parkinsonian subjects. Biol. Cybern. 107, 289–308. doi: 10.1007/s00422-013-0549-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Pasillas-Lépine, W., Haidar, I., Chaillet, A., and Panteley, E. (2013). “Closed-loop deep brain stimulation based on firing-rate regulation,” in Proceedings 6th IEEE EMBS Conference on Neural Engineering (San Diego, CA: IEEE). 166–169. doi: 10.1109/NER.2013.6695898

CrossRef Full Text

Pastrana, E. (2010). Optogenetics: controlling cell function with light. Nat. Methods 8, 24–25. doi: 10.1038/nmeth.f.323

CrossRef Full Text | Google Scholar

Paz, J. T., Davidson, T. J., Frechette, E. S., Delord, B., Parada, I., Peng, K., et al. (2012). Closed-loop optogenetic control of thalamus as a tool for interrupting seizures after cortical injury. Nat. Neurosci. 16, 64–70. doi: 10.1038/nn.3269

PubMed Abstract | CrossRef Full Text | Google Scholar

Paz, J. T., Deniau, J.-M., and Charpier, S. (2005). Rhythmic bursting in the cortico-subthalamo-pallidal network during spontaneous genetically determined spike and wave discharges. J. Neurosci. 25, 2092–2101. doi: 10.1523/JNEUROSCI.4689-04.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Pfister, J.-P., and Tass, P. A. (2010). STDP in oscillatory recurrent networks: theoretical conditions for desynchronization and applications to deep brain stimulation. Front. Comput. Neurosci. 4:22. doi: 10.3389/fncom.2010.00022

PubMed Abstract | CrossRef Full Text | Google Scholar

Plenz, D., and Kital, S. T. (1999). A basal ganglia pacemaker formed by the subthalamic nucleus and external globus pallidus. Nature 400, 677–682. doi: 10.1038/23281

PubMed Abstract | CrossRef Full Text | Google Scholar

Ranck, J. B. (1975). Which elements are excited in electrical stimulation of mammalian central nervous system: a review. Brain Res. 98, 417–440. doi: 10.1016/0006-8993(75)90364-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Reutsky-Gefen, I., Golan, L., Farah, N., Schejter, A., Tsur, L., Brosh, I., et al. (2013). Holographic optogenetic stimulation of patterned neuronal activity for vision restoration. Nat. Commun. 4, 1509. doi: 10.1038/ncomms2500

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosin, B., Slovik, M., Mitelman, R., Rivlin-Etzion, M., Haber, S. N., Israel, Z., et al. (2011). Closed-Loop deep brain stimulation is superior in ameliorating parkinsonism. Neuron 72, 370–384. doi: 10.1016/j.neuron.2011.08.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadek, A.-R., Magill, P. J., and Bolam, J. P. (2005). “Local connectivity between neurons of the rat globus pallidus,” in The asal Ganglia VIII, eds J. P. Bolam, C. A. Ingham, P. J. Magill (Springer), 611–619. doi: 10.1007/0-387-28066-9_59

CrossRef Full Text | Google Scholar

Santaniello, S., Fiengo, G., Glielmo, L., and Grill, W. M. (2011). Closed-loop control of deep brain stimulation: a simulation study. IEEE Trans. Neural Syst. Rehabil. Eng. 19, 15–24. doi: 10.1109/TNSRE.2010.2081377

PubMed Abstract | CrossRef Full Text | Google Scholar

Sato, F., Lavallée, P., Lévesque, M., and Parent, A. (2000a). Single-axon tracing study of neurons of the external segment of the globus pallidus in primate. J. Comp. Neurol. 417, 17–31. doi: 10.1002/(SICI)1096-9861(20000131)417:1<17::AID-CNE2>3.0.CO;2-I

PubMed Abstract | CrossRef Full Text | Google Scholar

Sato, F., Parent, M., Levesque, M., and Parent, A. (2000b). Axonal branching pattern of neurons of the subthalamic nucleus in primates. J. Comp. Neurol. 424, 142–152.. doi: 10.1002/1096-9861(20000814)424:1<142::AID-CNE10>3.0.CO;2-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Schiff, S. J. (2010). Towards model-based control of parkinson's disease. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 368, 2269–2308. doi: 10.1098/rsta.2010.0050

CrossRef Full Text | Google Scholar

Schwab, B. C., Heida, T., Zhao, Y., Marani, E., van Gils, S. A., and Van Wezel, R. J. (2013). Synchrony in Parkinson's disease: importance of intrinsic properties of the external globus pallidus. Front. Syst. Neurosci. 7:60. doi: 10.3389/fnsys.2013.00060

PubMed Abstract | CrossRef Full Text | Google Scholar

Stein, E., and Bar-Gad, I. (2013). Beta oscillations in the cortico-basal ganglia loop during parkinsonism. Exp. Neurol. 245, 52–59. doi: 10.1016/j.expneurol.2012.07.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Tass, P. A., Qin, L., Hauptmann, C., Dovero, S., Bezard, E., Boraud, T., et al. (2012). Coordinated reset has sustained aftereffects in Parkinsonian monkeys. Ann. Neurol. 72, 816–820. doi: 10.1002/ana.23663

PubMed Abstract | CrossRef Full Text | Google Scholar

Terman, D., Rubin, J., Yew, A., and Wilson, C. (2002). Activity patterns in a model for the subthalamopallidal network of the basal ganglia. J. Neurosci. 22, 2963–2976.

PubMed Abstract | Google Scholar

van Hartevelt, T. J., Cabral, J., Deco, G., Møller, A., Green, A. L., Aziz, T. Z., et al. (2014). Neural plasticity in human brain connectivity: the effects of long term deep brain stimulation of the subthalamic nucleus in Parkinsons disease. PLoS ONE 9:e86496. doi: 10.1371/journal.pone.0086496

PubMed Abstract | CrossRef Full Text | Google Scholar

Veltz, R., and Faugeras, O. (2011). Stability of the stationary solutions of neural field equations with propagation delays. J. Math. Neurosci. 1:1. doi: 10.1186/2190-8567-1-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagenaar, D. A., Madhavan, R., Pine, J., and Potter, S. M. (2005). Controlling bursting in cortical cultures with closed-loop multi-electrode stimulation. J. Neurosci. 25, 680–688. doi: 10.1523/JNEUROSCI.4209-04.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Zaidel, A., Spivak, A., Grieb, B., Bergman, H., and Israel, Z. (2010). Subthalamic span of β oscillations predicts deep brain stimulation efficacy for patients with Parkinsons disease. Brain 133, 2007–2021. doi: 10.1093/brain/awq144

PubMed Abstract | CrossRef Full Text | Google Scholar

Appendix

Proof of the Theoretical Result

A thorough analysis of delayed neural fields has been conducted in Faye and Faugeras (2010); Veltz and Faugeras (2011). In particular, given any continuous initial conditions defined on [−d_max; 0], where d_max is such that d₁(r, r'), d₂(r, r') ≤ d_max for all r, r' ∈ Ω, the solutions z₁ and z₂ are known to exist at all times in the whole domain Ω and to be continuous with respect to time (Faye and Faugeras, 2010, Theorem 3.2.1).

Given any constant inputs I₁(r) and I₂(r), any equilibrium pattern (z₁*, z₂*) of the neural fields model (3) is given by the following two implicit equations

$\begin{array}{cc}\begin{array}{l}{z}_1^{\ast }(r)=S_1({\displaystyle \sum _{j=1}^2{\displaystyle {\int }_{\Omega }{w}_{1j}(r,r^{\prime })z_j^{\ast }(r^{\prime })d{r}^{\prime }}}\\ +I_1(r)-k_c\alpha (r)(z_1^{\ast }(r)-z_{ref}(r)))\end{array}& (\text{A}1\text{a})\end{array}$

$\begin{array}{cc}{z}_2^{\ast }(r)=S_2\left({\displaystyle \sum _{j=1}^2{\displaystyle {\int }_{\Omega }{w}_{2j}(r,r^{\prime })z_j^{\ast }(r^{\prime })d{r}^{\prime }+I_2(r)}}\right).& (\text{A}1\text{b})\end{array}$

We start by operating a change of variables in order to rewrite the neural fields (Equation 3) in terms of the difference between the firing rate the resulting equilibrium pattern (z₁*, z₂*), the existence of which is assumed in the statement. To this end, we let x₁(r, t): = z₁(r, t) − z₁*(r) and x₂(r, t): = z₂(r, t) − z₂*(r). Combining Equation (A1) with Equation (3), the stability of the equilibrium pattern (x₁*, x₂*) for Equation (3) is equivalent to the stability of the origin for the neural field

$\begin{array}{cc}\begin{array}{l}{\tau }_1{\dot{x}}_1=-x_1+{{S}}_1({\displaystyle {\int }_{\Omega }{w}_{11}(r,r^{\prime })x_1(r^{\prime },t-d_1(r,r^{\prime }))d{r}^{\prime }}\\ +{\displaystyle {\int }_{\Omega }{w}_{12}(r,r^{\prime })x_2(r^{\prime },t-d_2(r,r^{\prime }))d{r}^{\prime }-k_c{\alpha }_1(r)x_1})\end{array}& (\text{A}2\text{a})\end{array}$

$\begin{array}{cc}\begin{array}{l}{\tau }_2{\dot{x}}_2=-x_2+{{S}}_2({\displaystyle {\int }_{\Omega }{w}_{21}(r,r^{\prime })x_1(r^{\prime },t-d_1(r,r^{\prime }))d{r}^{\prime }}\\ +{\displaystyle {\int }_{\Omega }{w}_{22}(r,r^{\prime })x_2(r^{\prime },t-d_2(r,r^{\prime }))d{r}^{\prime }}),\end{array}& (\text{A}2\text{b})\end{array}$

where we omitted the argument (r, t) of some functions for the sake of notation conciseness and, for each i ∈ {1, 2},

$\begin{array}{cc}\begin{array}{l}{{S}}_i(x):=S_i(x+{\displaystyle \sum _{j=1}^2{\displaystyle {\int }_{\Omega }{w}_{ij}(r,r^{\prime })z_j^{\ast }(r)}})\\ -S_i({\displaystyle \sum _{j=1}^2{\displaystyle {\int }_{\Omega }{w}_{ij}(r,r^{\prime })z_j^{\ast }(r)}}),\forall x\in ℝ.\end{array}& (\text{A}3)\end{array}$

Note that 𝒮_i(0) = 0, which confirms the fact that (Equation A2) has an equilibrium at the origin. In order to proceed to the stability analysis of Equation (A2), we rely on the following technical lemma, which provides a useful upper bound on the time derivative of the Lyapunov-Krasovskii functional proposed in Faye and Faugeras (2010) along the solutions of the system under concern. For the sake of generality, we state it in the case of n interconnected neuronal populations. Its proof is omitted but results from rather standard computations.

Lemma 1. Let 𝒮₁, 𝒮₂ : ℝ → ℝ be any bounded continuous increasing functions satisfying |𝒮_i(x)| ≤ ℓ_i|x| for all x ∈ ℝ, where ℓ₁ and ℓ₂ denote nonnegative constants. Let α₁, α₂: Ω → ℝ_>0 be such that inf_r∈Ω αi(r) > 0. Consider the function

$\begin{array}{l}{𝒱}(t)=\frac{1}{2}{\displaystyle \sum _{i=1}^2{\displaystyle {\int }_{\Omega }{\tau }_i{x}_i{(r,t)}^{2}dr}}\\ +{\displaystyle {\int }_{\Omega }{\displaystyle \sum _{i=1}^n{\beta }_i}(r){\displaystyle {\int }_{\Omega }^{}{\displaystyle {\int }_{-d_i(r,r^{\prime })}^0{x}_i}}{(r^{\prime },t-\theta )}^{2}d\theta d{r}^{\prime }dr,}\end{array}$

where β₁, β₂ : Ω → ℝ_>0. Then, given any k₁ ≥ 0, there exists γ₁(k₁) satisfying γ₁(k₁) > 0 for all k₁ > 0 and lim_k1→+∞γ₁(k₁) = +∞ such that, given any functions λ_ij : Ω→ℝ_>0, the derivative of 𝒱 along the solutions of the delayed neural field

$\begin{array}{cc}\begin{array}{l}{\tau }_1{\dot{x}}_1(r,t)=-a_1{x}_1(r,t)+{{S}}_1({\displaystyle \sum _{j=1}^2{\displaystyle {\int }_{\Omega }{w}_{1j}(r,r^{\prime })x_j(r^{\prime },t}}\\ -d_j(r,r^{\prime }))d{r}^{\prime }-k_1{\alpha }_1(r)x_1(r,t))\end{array}& (\text{A}4\text{a})\end{array}$

$\begin{array}{cc}\begin{array}{l}{\tau }_2{\dot{x}}_2(r,t)=-a_2{x}_2(r,t)+{{S}}_2\\ \left({\displaystyle \sum _{j=1}^2{\displaystyle {\int }_{\Omega }{w}_{2j}(r,r^{\prime })x_j(r^{\prime },t-d_j(r,r^{\prime }))d{r}^{\prime }}}\right)\end{array}& (\text{A}4\text{b})\end{array}$

satisfies, for any admissible initial conditions,

$\begin{array}{l}\stackrel{.}{{𝒱}}(t)\le -{\displaystyle \sum _{i=1}^n{\displaystyle {\int }_{\Omega }(a_i+{\gamma }_i(k_i)-{\displaystyle {\int }_{\Omega }^{}{\beta }_i}(r^{\prime })d{r}^{\prime }}}\\ -\frac{1}{2}{\displaystyle \sum _{j=1}^n\frac{{\overline{w}}_{ij}(r)}{{\lambda }_{ij}(r)}})x_i{(r,t)}^{2}dr\\ -{\displaystyle \sum _{i=1}^n{\displaystyle {\int }_{\Omega }({\beta }_i(r)-\frac{1}{2}{\displaystyle \sum _{j=1}^n{\lambda }_{ij}}(r))}}\\ {\displaystyle {\int }_{\Omega }{x}_i{(r^{\prime },t-d_i(r,r^{\prime }))}^{2}d{r}^{\prime }dr,\forall t\ge 0,}\end{array}$

where w_ij : Ω → ℝ_≥0 denote any positive functions satisfying

$\begin{array}{cc}{\overline{w}}_{ij}(r)\ge {\ell }_i^2{\displaystyle {\int }_{\Omega }{w}_{ij}{(r,r^{\prime })}^{2}d{r}^{\prime },}\forall r\in \Omega .& (\text{A}5)\end{array}$

Note that the influence of the delayed and non-delayed terms in the estimate of $\stackrel{.}{{𝒱}}$ can be weighted, to some extent, by the functions λ_ij which can be arbitrarily tuned.

Remark 1. We stress that, in the statement of Lemma 1, the functions w_ij can be taken as close as the functions r ↦ ℓ_i² ∫_Ω w_ij(r, r')²dr' as we want. More precisely, given any function ε : Ω → ℝ_>0, there exists a positive function w_ij satisfying (Equation A5) and $\left|{\overline{w}}_{ij}(r)-{\ell }_i^2{\displaystyle {\int }_{\Omega }^{}{w}_{ij}}{(r,r^{\prime })}^{2}d{r}^{\prime }\right|\le \epsilon (r)$ for all r ∈ Ω. For instance, the choice ${\overline{w}}_{ij}(r)=\max \left\{\epsilon (r);{\ell }_i^2{\displaystyle {\int }_{\Omega }^{}{w}_{ij}}{(r,r^{\prime })}^{2}d{r}^{\prime }\right\}$ fits these requirements.

Observe that the neural fields (Equation A2) can be written as Equation (A1) by letting α₁(r) = α(r) and a₁ = a₂ = 1. Moreover, note that Equation (A3) and the fact that the functions S_i are ℓ_i-Lipschitz ensure that |𝒮_i(x)| ≤ ℓ_i|x| for all x ∈ ℝ. Invoking Lemma 1 it follows that, given any k_c > 0, there exists γ(k_c) > 0 satisfying lim_kc→+∞ γ(k_c) = +∞ such that, given any functions β_i, λ_ij:Ω → ℝ_>0, i, j ∈ {1,2}, the derivative of the function

$\begin{array}{l}{𝒱}(t)=\frac{1}{2}{\displaystyle \sum _{i=1}^2{\displaystyle {\int }_{\Omega }{\tau }_i{x}_i{(r,t)}^{2}dr}}\\ +{\displaystyle {\int }_{\Omega }{\displaystyle \sum _{i=1}^2{\beta }_i}(r)}{\displaystyle {\int }_{\Omega }{\displaystyle {\int }_{-d_i(r,r^{\prime })}^0{x}_i}{(r^{\prime },t-\theta )}^{2}d\theta d{r}^{\prime }dr,}\end{array}$

along the solutions of Equation (A2) satisfies, for all admissible initial conditions,

$\begin{array}{l}\stackrel{.}{{𝒱}}(t)\le -{\displaystyle {\int }_{\Omega }(1+\gamma (k_c)-\frac{{\overline{w}}_{11}(r)}{2{\lambda }_{11}(r)}-\frac{{\overline{w}}_{12}(r)}{2{\lambda }_{12}(r)}}\\ -{\displaystyle {\int }_{\Omega }{\beta }_1(r^{\prime })d{r}^{\prime }})x_1{(r,t)}^{2}dr\\ -{\displaystyle {\int }_{\Omega }(1-\frac{{\overline{w}}_{21}(r)}{2{\lambda }_{21}(r)}-\frac{{\overline{w}}_{22}(r)}{2{\lambda }_{22}(r)}-{\displaystyle {\int }_{\Omega }{\beta }_2(r^{\prime })d{r}^{\prime }})x_2{(r,t)}^{2}dr}\\ -{\displaystyle \sum _{i=1}^2{\displaystyle {\int }_{\Omega }{\displaystyle {\int }_{\Omega }({\beta }_i(r)-\frac{1}{2}{\displaystyle \sum _{j=1}^2{\lambda }_{ji}}(r))x_i(r^{\prime },t}}}\\ -d_j(r,r^{\prime }){)}^{2}d{r}^{\prime }dr,\end{array}$

where the functions w_ij were defined in Equation (A5). The right-hand side of this inequality is a negative definite function in terms of the non-delayed terms provided that, for all r ∈ Ω,

$\begin{array}{cc}1+\gamma (k_c)>\frac{{\overline{w}}_{11}(r)}{2{\lambda }_{11}(r)}+\frac{{\overline{w}}_{12}(r)}{2{\lambda }_{12}(r)}+{\displaystyle {\int }_{\Omega }{\beta }_1(r^{\prime })d{r}^{\prime }}& (\text{A}6\text{a})\end{array}$

$\begin{array}{cc}1>\frac{{\overline{w}}_{21}(r)}{2{\lambda }_{21}(r)}+\frac{{\overline{w}}_{22}(r)}{2{\lambda }_{22}(r)}+{\displaystyle {\int }_{\Omega }{\beta }_2(r^{\prime })d{r}^{\prime }}& (\text{A}6\text{b})\end{array}$

$\begin{array}{cc}2{\beta }_1(r)\ge {\lambda }_{11}(r)+{\lambda }_{21}(r)& (\text{A}6\text{c})\end{array}$

$\begin{array}{cc}2{\beta }_2(r)\ge {\lambda }_{12}(r)+{\lambda }_{22}(r).& (\text{A}6\text{d})\end{array}$

Recalling that W₂₂ = ∫_Ω w₂₂(r')dr', it can be checked that the following choices satisfy (Equations A6b–d):

$\begin{array}{l}{\lambda }_{11}(r)=2{\overline{w}}_{11}(r)\\ {\lambda }_{12}(r)=\frac{1-{\overline{W}}_{22}}{2\left(2-{\overline{W}}_{22}\right)}{\overline{w}}_{22}(r)\\ {\lambda }_{21}(r)=\frac{2(3-{\overline{W}}_{22})}{(1-{\overline{W}}_{22})(2-{\overline{W}}_{22})}{\overline{w}}_{21}(r)\\ {\lambda }_{22}(r)=\frac{3-{\overline{W}}_{22}}{2\left(2-{\overline{W}}_{22}\right)}{\overline{w}}_{22}(r)\\ {\beta }_1(r)={\overline{w}}_{11}(r)+\frac{3-{\overline{W}}_{22}}{(1-{\overline{W}}_{22})(2-{\overline{W}}_{22})}{\overline{w}}_{21}(r)\\ {\beta }_2(r)=\frac{{\overline{w}}_{22}(r)}{2}.\end{array}$

In view of Equation (4), Remark 1 ensures that w₂₂ can be picked in such a way that W₂₂ = ∫_Ω w₂₂(r')dr' < 1. Consequently, the functions λ_ij and β_i are all positive as required. With these choices, the condition (Equation A6a) boils down to

$\begin{array}{l}\gamma (k_c)>\frac{(2-{\overline{W}}_{22}){\overline{w}}_{12}(r)}{(1-{\overline{W}}_{22}){\overline{w}}_{22}(r)}+{\displaystyle {\int }_{\Omega }{\overline{w}}_{11}(r^{\prime })d{r}^{\prime }}\\ +\frac{3-{\overline{W}}_{22}}{(1-{\overline{W}}_{22})(2-{\overline{W}}_{22})}{\displaystyle {\int }_{\Omega }{\overline{w}}_{21}(r^{\prime })d{r}^{\prime }.}\end{array}$

In view of Remark 1 and Equation (A5), a sufficient condition for this to hold is

$\begin{array}{l}\gamma (k_c)>\text{}\text{}\frac{(2-{\overline{W}}_{22}){\displaystyle {\int }_{\Omega }^{}{\ell }_1^2}{w}_{12}{(r,r^{\prime })}^{2}d{r}^{\prime }}{(1-{\overline{W}}_{22}){\overline{w}}_{22}(r)}\text{}+\text{}{\displaystyle {\int }_{\Omega }{\displaystyle {\int }_{\Omega }{\ell }_1^2{w}_{11}{(r,r^{\prime })}^{2}d{r}^{\prime }dr}}\\ +\frac{3-{\overline{W}}_{22}}{(1-{\overline{W}}_{22})(2-{\overline{W}}_{22})}{\displaystyle {\int }_{\Omega }{\displaystyle {\int }_{\Omega }{\ell }_2^2{w}_{21}{(r,r^{\prime })}^{2}d{r}^{\prime }d{r}^{\prime },}}\end{array}$

Recalling that γ(k_c) can be picked as large as we want provided that k_c is taken sufficiently large, this condition can always be fulfilled. We thus obtain that, for all admissible initial conditions,

$\dot{V}(t)\le -ϵ{\displaystyle {\int }_{\Omega }\left(x_1{(r,t)}^2+x_2{(r,t)}^2\right)dr,}\forall t\ge 0.$

A straightforward adaptation of (Faye and Faugeras, 2010, Theorem 4.2.2) then ensures the existence of positive constants η₁, η₂ such that

$\Vert x_1(·,t){\Vert }^2+\Vert x_2(·,t){\Vert }^2\le {\eta }_1\left(\Vert {\varphi }_1{\Vert }^2+\Vert {\varphi }_2{\Vert }^2\right)e^{-{\eta }_{2}t},\forall t\ge 0,$

for all admissible initial conditions ϕ_i, i ∈ {1,2}, meaning continuous functions from [−d_max;0] to ℝ with bounded L₂-norm over Ω and satisfying S_i < ϕ_i(r) < S_i for all r ∈ Ω. The conclusion follows.