
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Neurosci. , 23 March 2011
Sec. Decision Neuroscience
volume 5 - 2011 | https://doi.org/10.3389/fnins.2011.00041
This article is part of the Research Topic Neurobiology of Choice View all 12 articles
Choosing which hand to use for an action is one of the most frequent decisions people make in everyday behavior. We developed a simple reaching task in which we vary the lateral position of a target and the participant is free to reach to it with either the right or left hand. While people exhibit a strong preference to use the hand ipsilateral to the target, there is a region of uncertainty within which hand choice varies across trials. We manipulated the reinforcement rates for the two hands, either by increasing the likelihood that a reach with the non-dominant hand would successfully intersect the target or decreasing the likelihood that a reach with the dominant hand would be successful. While participants had minimal awareness of these manipulations, we observed an increase in the use of the non-dominant hand for targets presented in the region of uncertainty. We modeled the shift in hand use using a Q-learning model of reinforcement learning. The results provided a good fit of the data and indicate that the effects of increasing and decreasing the rate of positive reinforcement are additive. These experiments emphasize the role of decision processes for effector selection, and may point to a novel approach for physical rehabilitation based on intrinsic reinforcement.
Reaching to grasp an object is one of our most common actions. In the process of planning a reaching movement, people have two principle decisions (Horowitz and Newsome, 1999): Where to reach (target selection) and which limb to reach with (effector specification). Target selection decisions are often dictated by a desired goal. If we want to take a break from our writing, we may decide to reach for the cup of coffee. The decision processes underlying effector selection are less clear. While people prefer to use their dominant hand, we also show impressive flexibility in hand choice in our everyday behavior (Johansson et al., 2006). For example, we sometimes use the left hand to pick up the cup and other times use the right hand. Similar flexibility is observed in a variety of behaviors such as pointing out directions to a lost traveler or pressing the elevator call button.
A substantial literature has focused exclusively on the problem of target selection, or more generally, decisions that require the person to make a choice between different objects. This literature has explored the relative importance of cost and reward in decision making (Rudebeck et al., 2006), the neural representation of the value of competing perceptual targets (Sugrue et al., 2004; Cisek and Kalaska, 2005; Churchland et al., 2008), and the effector-specific nature of these representations (Tosoni et al., 2008; Gershman et al., 2009). Goal-related activity in posterior parietal cortex (PPC) has been modeled as an accumulation process, resulting in the selection of one action over another (Batista and Anderson, 2001; Huk and Shadlen, 2005; Churchland et al., 2008; Seo et al., 2009). Similar patterns of activation have been observed in frontal motor areas. Interestingly, activity in dorsal premotor cortex may reflect the presence of multiple response options, pointing to the parallel preparation of candidate movements, with the final selection of a single action dependent on a threshold process (Cisek, 2006).
These studies have generally been restricted to experimental tasks in which a single effector is used (e.g., point to the chosen object) or effector selection is used to indicate the chosen object (e.g., use the left hand to chose object on the left). Work in humans (Medendorp et al., 2005; Beurze et al., 2007) and non-human primates (Hoshi and Tanji, 2000) has demonstrated that target and body-part information are integrated in premotor cortex and the PPC. However, an external cue is typically used in these studies to specify the target and effector. Few studies have been conducted in which the participant must self-select which effector to use to reach for a single target. One exception here has been the work of Schieber and colleagues. When monkeys are free to use either hand to retrieve a food reward, their choice is strongly biased by hand preference (Lee and Schieber, 2006). However, this bias can be modulated by other factors such as the location of the stimulus, with the animals exhibiting a preference to reach to eccentric targets with the ipsilateral hand (Schieber, 2000; Gabbard and Helbig, 2004; Gardiner et al., 2006), and head position (Dancause and Schieber, 2010). Interestingly, hand/target choices were more closely linked with prior success for particular head/hand/location pairs rather than with movement speed, indicating that hand choice may be related to reinforcement history.
In the present pair of experiments, we examine the role of reinforcement on effector selection during reaching. Reinforcement is likely related to hand preference: We are more likely to be successful in producing a skilled action when using our dominant limb. Of course this is a bit of a chicken-and-egg question. Do we become more skilled with one hand because of an intrinsic preference for one hand over the other? Or do we choose the preferred hand because it is, intrinsically more coordinated? Ontologically, the answer is probably a bit of both, with handedness constituting a self-reinforcing process. Nonetheless, over a shorter time scale, people exhibit flexibility in hand choice and their choices here may reflect recent reinforcement history. You can imagine that if you spilled your coffee when last using the left hand to pick up the cup, you would become more likely to use the right hand the next time. However, if you are holding something with the right hand, you might still choose to use your left hand to pick up the coffee cup.
In this way, hand choice can be viewed as a decision process, with relative costs and rewards being assigned to competing action alternatives. Given that the likelihood of reward involves the effort of a particular action and the accuracy or proficiency of that action, we hypothesized that the competitive process underlying effector choice would be influenced by limb-dependent task success. To investigate the effect of reinforcement on hand choice, we varied limb-dependent task success in a target interception task. We first established a psychometric function describing hand choice as a function of target location in a task in which participants were free to use either their right or left hand. We then introduced an experimental manipulation in which we modified the reinforcement rate. Exploiting the fact that right-handed participants show an overall right-hand bias, we either increased the rate of positive reinforcement for the left hand, decreased the rate of positive reinforcement for the right hand, or simultaneously applied both manipulations. We compare the effectiveness of these manipulations in producing a shift in hand choice. Given this reinforcement-learning framework, we applied a Q-learning model to characterize the change in behavior over time.
Fifty-six participants (27 females; age range 18–24) participated in Experiment 1 and received course credit for their participation. Twenty-seven (16 females; age range 19–30) participated in Experiment 2 and were paid for their participation. All participants were right-handed. Data from six participants (three for each experiment) were excluded. Five participants were excluded because they almost always used one hand (right only = 4; left only = 1). One participant from Experiment 2 did not return for the second session. The protocol was approved by the UC Berkeley Institutional Review Board and all participants provided informed written consent at the start of the test session.
The experiment was performed in a virtual environment that interfaced with a 3-D robotic manipulandum (PHANToM 1.5 System, SensAble Technologies). A mirrored projection system was used to display the visual stimuli (Figure 1). The participants’ task was to reach through a target that appeared at one of seven locations along a semicircular array. The participant held a robotic manipulandum in each hand and moved this device to reach through the target location. Movements were confined to the horizontal plane.
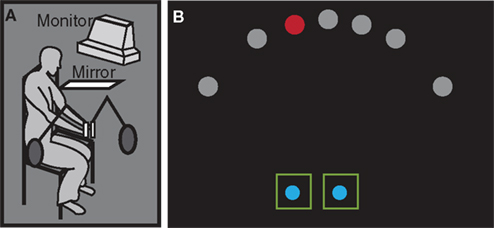
Figure 1. (A) A computer monitor projected stimuli onto a mirror, creating the impression that the stimuli were in the same plane as the participant’s hands. The robotic device restricted movement to this plane. (B) Stimuli appeared in one of seven locations in Experiment 1 (shown here) and one of nine locations in Experiment 2. While the visible size of the targets remained constant, a staircase algorithm adjusted the radius of a virtual target region that was used to achieve a specified reward rate.
Two green squares (2 cm × 2 cm) centered 4.5 cm apart indicated the starting location for the hands. At the beginning of each trial, participants were instructed to move two spherical cursors, corresponding to the positions of the two hands, into these start squares. After the start positions were maintained for 200 ms, the blue cursors disappeared and a red target appeared at one of seven locations along a semicircular array approximately 9 cm from the start positions. The exact radius of the array was scaled to each individual’s arm length. The participants were instructed to reach with one hand until they saw the target explode, indicating a hit, or heard a tone (242 ms), indicating a miss. Vision of their hands was occluded by the mirror and the hand cursor was not displayed during the reaching movement. Thus, participants could not make online corrections to their movements.
The participants were trained to move at a comfortable speed. Auditory feedback was also used to indicate if the movement time fell outside a criterion window of approximately 300–700 ms. The precise time window depended on the arm-length scaled target distance. One sound was played if the movement time was too short (duration: 232 ms) and another sound was played if the movement time was too long (duration: 1200 ms). A high pitched beep was played if subjects stopped reaching before they hit the target (duration: 135 ms). These reaches were coded as errors and accounted for less than 3% of the trials.
Participants completed 12 experimental blocks of 100 trials each (1200 trials total). Within a block of 100 trials, the target appeared at the ±55° locations on eight trials, the ±30° and ±17.4° locations on 16 trials, and at the center location on 20 trials. This distribution was chosen to increase the sampling rate at locations in which participants were expected to use both hands (ambiguous locations). The eccentric, 55° locations, were included to decrease the likelihood that participants would adopt a strategy of using one hand to reach to all of the targets. The sequence of target locations was randomized.
Across the 12 blocks, we manipulated the target reward rate. The first four blocks served as the baseline phase. During these blocks, the target reward rate was set to 68% for each hand (see below for description of how we controlled the reward rate). Blocks 5–8 constituted the manipulation phase. During these blocks, the target reward rate was adjusted differently for four participant groups: BOOST (n = 12): The left hand reward rate was increased to 86% while the right hand reward rate remained at 68%; TAX (n = 14): Right hand reward rate was reduced to 50% while the left hand reward rate was maintained at 68%; BOTH (n = 13): The reward rates for the left and right hands were adjusted to 86 and 50%, respectively; NOMANIP: (n = 14): The target reward rates for both hands remained at 68%. The final four blocks served as the post-manipulation phase. Here the reward rate for all four groups was set to 68% for both hands.
The desired target reward rate was experimentally controlled using a variable ratio staircase procedure (Garcia-Perez, 1998) in which the size of the virtual target was adjusted. The target displayed to the subjects was a consistent visual size (radius 4 mm). However, we also defined a virtual target region; the hand had to pass within this region for the trial to result in a successful reach (i.e., a hit). The staircase procedure was used to adjust the size of the virtual target region. The size was decreased after a hit and increased after a miss. Following a miss, the radius of the virtual target region was always increased by 1.5 mm. Following a hit, the radius was reduced, with the amount of the reduction a function of the target reward rate. Reductions of 0.3, 0.6, and 1.5 mm were used for target reward rates of 86, 68, and 50%, respectively. Note that the radius of the virtual target was limb specific since the target reward rate for the two hands could differ during the manipulation phase.
To increase subject motivation, a point counter at the center of the screen kept a running tally on the number of hits. Between each block, the score for that block, as well as the total current score, were displayed.
Before the start of the experimental blocks, participants performed one practice block of 100 trials. During the practice blocks, participants had online feedback of their hand position during the reaches (i.e., the spherical cursors remained visible). The virtual target and visible target were identical in this block and reinforcement was based on whether or not the participant’s hand passed through the target. We also provided 10 practice trials with online feedback at the start of each of the 12 experimental blocks. These practice trials were included so that the participants remained calibrated throughout the experiment.
Awareness. We included a debriefing survey to assess participants’ awareness of the experimental manipulation. Participants were asked if they had noticed any change over the course of the experiment. Specifically they were asked if the task got easier, harder, or stayed the same for the right and left hand. Additionally they were asked if they used one hand more than the other, and if this changed over the course of the experiment.
The apparatus and stimulus displays were slightly modified in Experiment 2. First, we updated the virtual environment to include angled mirrors, providing for better 3-D vision. Movements were again confined to the horizontal plane. Second, the density of targets near the midline was increased such that a target could also appear at ±8.6°, increasing the number of target locations from seven to nine. The eccentric target was moved in to ±45° from ±55°. In a 100-trial test block, targets appeared at the eccentric ±45° locations on six trials, at the three intermediary locations (±30°, ±17.4°, ±8.6°) on 12 trials each, and at the midline location on 16 trials. Third, approximate reach lengths were 11 cm compared to 9 cm in Experiment 1 (again scaled to arm length). Slightly longer reaches were possible given the new apparatus configuration. Fourth, a variable delay (50–250 ms) was introduced between the time the participants positioned their hands in the start squares and the onset of the target. Fifth, the point counter was not visible during the experimental blocks; summary feedback was only presented between blocks.
The design of Experiment 2 involved two primary changes in the experimental design. First, to obtain a better understanding of the differences in the effects of increasing and decreasing positive reinforcement on hand choice, a within-subject design was adopted with testing limited to the BOOST and TAX conditions. Second, we modified the target reward rates so they were identical for the BOOST and TAX conditions in the manipulation phase. For the BOOST condition, the target reward rate was 70% for each hand in the baseline and post-manipulation phases. During the manipulation phase, the reward rate for the left hand was set to 84% and the right hand remained at 70%. For the TAX condition, the target reward rate was 84% for both hands during the baseline and post-manipulation blocks. During the manipulation phase, the reward rate dropped to 70% for the right hand and remained at 84% for the left hand. Thus, the manipulation phase always involved a change in the reward rate of 14% for one hand, and resulted in target rates of 70 and 84% for the right and left hands, respectively. We again used a staircase procedure to produce the desired reward rates. The base step size was increased to 3 mm in Experiment 2, given the increase in reach distance and pilot work that indicated this would provide better experimental control of the reward rates.
The BOOST and TAX conditions were tested in separate sessions, separated by 1 day. Within each session, the participants completed 12 experimental blocks with 100 trials each (1200 trials total), divided into four baseline blocks, four manipulation blocks, and four post-manipulations blocks. Half of the participants started with BOOST and the other half started with TAX.
As in Experiment 1, participants completed a practice block of 100 trials at the start of the test session.
Awareness. We again included a debriefing survey to assess participants’ awareness of the experimental manipulation. This survey was only given at the end of the second session. Participants were informed that they had been randomly assigned to one of two groups: Group A in which the reward rate for each hand was consistent throughout the experiment or Group B in which the reward rate changed in a way that corresponded to their particular condition. They were asked to indicate their perceived group assignment.
To measure hand preference, we calculated the total percent right hand use across all targets for each block. This value was also calculated for each target to obtain a psychometric function of hand choice as a function of target location. By fitting a logistic regression to this curve, we estimated the point of subjective equality (PSE), the theoretical point where the participant was equally likely to use his/her right or left hand. This procedure was performed separately for the three phases. To obtain estimates of the PSE values when performance was relatively stable, we limited the data set to the final two blocks of each phase (baseline: Blocks 3–4; manipulation: Blocks 7–8; post-manipulation: Blocks 11–12). These values were entered into an ANOVA to determine the effectiveness of the experimental manipulations of reward rate.
We quantified sequential effects by calculating the probability of using the right hand at the center target on trial t given that the previous trial t − 1 was either a right hand hit, a right hand miss, a left hand hit, or a left hand miss. Given the small amount of data for each pair of locations, the data were collapsed over the experimental phases and conditions. We also combined the data over all previous t − 1 locations in an ANOVA designed to assess the probability of choosing the right hand on the current trial as a function of the hand (right or left) and outcome (hit or miss) from the previous trial.
Reaction time was defined as the interval between the onset of the target and the time at which the chosen hand left the start box. Our primary focus with these data was to compare the reaction time to targets at the center location to those at the more peripheral locations (±30°, ±17.4° in Experiment 1 and ±30°, ±17.4°, ±8.6° in Experiment 2). We did not include the data from the most eccentric locations in the RT analysis since these locations were used much less frequently. We excluded the data from the first block since we observed that participants’ generally showed a considerable reduction in RT over the first 100 trials as they became familiar with the task. In order to have the same amount of data in each phase, we also excluded the first block for the manipulation and post-manipulation phases.
A reinforcement learning model based on a temporal difference (TD) algorithm was fit to the data (Gershman et. al., 2009; Watkins and Dayan, 1992; Kaelbling et al., 1996; Sutton and Barto, 1998; ). The model assigns a value to each state–action pair where the state (s) is the target location and the action (a) is a right or left hand reach. The action values are learned and updated each trial t using the following update rule:
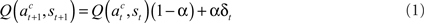
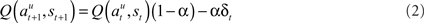
where st represents the target location at the current trial t, and for the action, a, the superscript c or u refers to chosen and unchosen hand, respectively. The learning rate α is a free parameter. δ is the prediction error defined by the following equation:

The probability by which a particular action is chosen on trial t is a function of the current action–state value Q and is given by a “softmax” (logistic) rule:

On each trial, the probability of a particular action given by the softmax function was compared to a threshold of PT = 0.5 such that:

The Q values were initialized using the average percent right hand use (PER) over the baseline phase (first four blocks). The Q values were set to PER − 0.5, bounding them between −0.5 and 0.5.
The model was fit to the data from the manipulation and post-manipulation phases (Blocks 5–12). We compared three models: Alpha_4: For this model, we allowed alpha to have a different value for each condition (Experiment 1: αBOOST, αTAX, αBOTH, αNOMANIP; Experiment 2: αBOOST-Day1, αTAX-Day1, αBOOST-Day2, αTAX-Day2); Alpha_1: Alpha was constrained to take on a single value for each experiment; No_Learn: A reinforcement-free model in which alpha was fixed at zero. The No_Learn model serves as a null model. Here, hand choice is restricted to the biases exhibited during the baseline phase and does not depend on changes in reinforcement history. In contrast, hand choice can vary with reinforcement history in the Alpha_1 and Alpha_4 models. For the former, hand choice will vary with reward rate in the same manor in all four types of manipulations. For the latter, the learning rates may vary as a function of the type of manipulation. In particular, we included the Alpha_4 model to ask whether learning rate differed for changes related to increasing the rate positive reinforcement, decreasing the rate of reinforcement, or, in Experiment 1, both manipulations.
To obtain the best fitting values for the free parameter alpha in these Alpha_1 and Alpha_4 models, we minimized the negative log likelihood (−LL). For each value of alpha, the average percent hand use for each block, calculated from the data, was compared to the model prediction. The alpha values ranged from 0.01 to 0.49 and was incremented in steps of 0.01.
We used a bootstrapping (Fisher, 1993) procedure to determine the best fit learning rate (alpha) for each of the models Alpha_1 and Alpha_4. We generated 1000 group averaged data sets by randomly resampling with replacement from the original participant pool and fit the models to each data set. To evaluate the model fits, we used the likelihood ratio test statistic (LR):
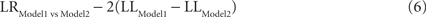
We also calculated the Pearson correlation coefficient (R2). To compare Alpha_4 and Alpha_1 to No_learn models, we calculated a pseudo-R2 statistic defined as (R − Q)/R where R is the −LL for the No_learn model and Q is the −LL for the Alpha_4 and Alpha_1 (Gershman et al., 2009).
We explored models with more parameters. These included models in which different learning rates were set for the right and left hands, different learning rates were set for the chosen and unchosen hand, and models in which a temperature parameter that dictated how exclusively choices were restricted to the highest valued action was allowed to vary. These models did not significantly improve the obtained fits and introduced considerable variability in the parameter selection. While a more complex model may capture nuances in the data, we focus on a simplistic model that can capture the way in which recent reinforcement history affects hand choice.
The observed reward rates were close to the desired target reward rates (Figure 2A). Participants were rewarded slightly more often during the baseline and post-manipulation blocks than expected (69.3% compared to target rate of 68%). During the manipulation phase, the reward rate increased to 83.1 ± 0.3% for the left hand in the BOOST condition and fell to 49.9 ± 0.1% for the right hand in the TAX condition. Thus, while the experiment was designed to produce an 18% shift for both the BOOST and TAX conditions, the actual changes were approximately 14 and 19%. For the BOTH condition, the observed reward rates during the manipulation phase were 83.3 ± 0.3% and 50.7 ± 0.2% for the left and right hands, respectively.
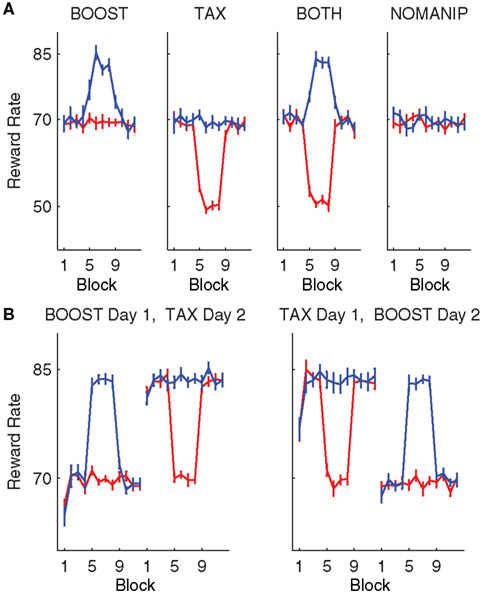
Figure 2. Observed rewards rates for the right hand (red) and left hand (blue). Target reward rate was fixed for Blocks 1–4 (baseline), adjusted in Blocks 5–8 (manipulation), and then returned to the initial rates in Blocks 9–12 (post-manipulation). (A) Experiment 1 reward rates for the four experimental conditions (BOOST: increase reward rate for left hand, TAX: decrease reward rate of right hand, BOTH: both tax and boost manipulations, NOMANIP: no manipulation). (B) Experiment 2 reward rates for the two experimental conditions and two subjects groups.
The psychometric function for hand choice was very steep (Figure 3A). Participants almost always used the right hand to reach for the three target locations in the right visual field, even during the manipulation phase when the reward rates favored left hand use. The left hand was selected for the majority of left visual field targets, but there were some trials in which the right hand was selected. More variability was evident at the center location, both within and across subjects. During the baseline phase, the right hand was used on 82.3 ± 1.9% (across all 53 participants) of the trials to reach to the center location. Right hand use decreased during manipulation phase for the BOOST, TAX, and BOTH conditions (Figure 3B). This shift was not evident in the control, NOMANIP condition.
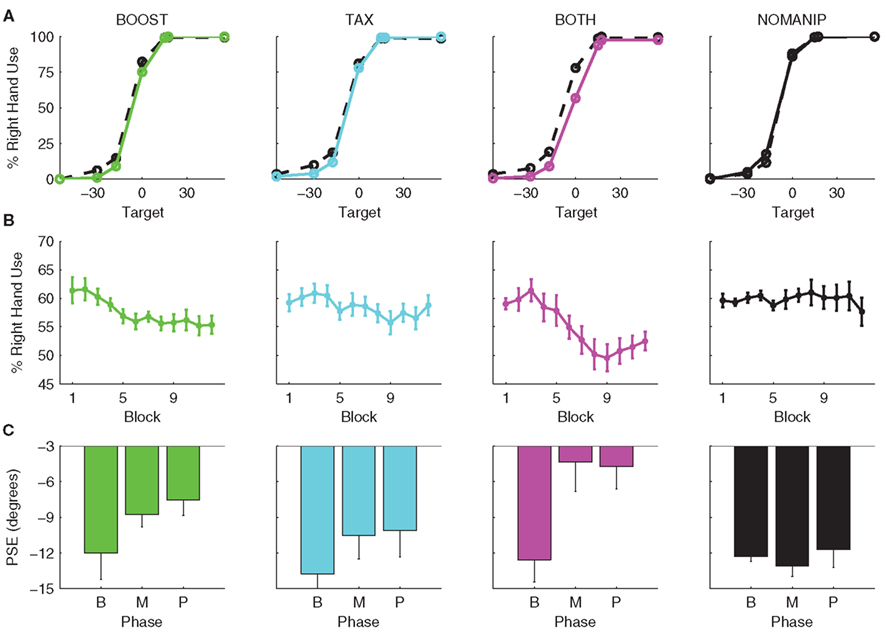
Figure 3. Hand choice results for Experiment 1 in the BOOST (green), TAX (cyan), BOTH (magenta), NOMANIP (black) conditions. (A) Mean probability of right hand use as a function of target location. Solid lines are for data from the last two blocks of the manipulation phase (Blocks 7–8) and dotted lines are for data from the last two blocks of the baseline phase (Blocks 3–4). (B) Percent right hand use across all targets as a function of block number. (C) PSE values, calculated from the data for the last two blocks of each phase (B, baseline; M, manipulation; P, post-manipulation).
To quantify these effects, PSE values were estimated for each phase. As can be seen in Figure 3C, the PSE values were all negative during the baseline phase, consistent with the right hand bias evident in the psychometric functions. During the manipulation phase, these values became less negative, indicative of greater left hand use. The main effect of phase was significant [F(2,98) = 13.89, p < 0.0001], and this factor interacted with condition [F(6,294) = 2.80, p = 0.02]. When compared to the NOMANIP condition, the decrease in right hand use was reliable for all three conditions: BOOST [t(23) = 2.30, p = 0.01], TAX [t(25) = 2.24, p = 0.02], and BOTH [t(24) = 3.50, p < 0.001]. Furthermore, changing the reward rate simultaneously for both hands had a larger effect on right hand use than either increasing the reward rate for the left hand [BOOST vs BOTH: t(23) = 1.90, p = 0.04] or decreasing the reward rate for the right hand [TAX vs BOTH: t(25) = 1.98, p = 0.03]. There was no difference between the shift in hand use between the BOOST and TAX conditions [t(24) = 0.03, p = 0.49].
This decrease in right hand use was maintained during the post-manipulation phase, and correspondingly, the PSEs during the post-manipulation phase were less negative than the PSEs during the baseline phase. In a series of pair-wise comparisons between the baseline PSE and the post-manipulation PSE, reliable effects were observed for the BOOST [t(11) = 2.90, p < 0.01] and BOTH [t(12) = 3.60, p = 0.02] conditions. The effect for the TAX condition was marginally significant [t(13) = 1.75, p = 0.052]. Again, there was no change in right hand use for the NOMANIP condition [t(12) = 0.32, p = 0.38].
Given that hand choice was influenced, albeit in a subtle manner, by the change in reinforcement rate, we performed a sequential analysis, asking if the cause of these shifts might be evident in the local reinforcement history. We note at the outset that this analysis is problematic because the shift in hand choice was most pronounced at the central location and targets only appeared at this location on 20% of the trials. As such, the trial-by-trial pairs involving non-central targets on trial t involve reaches where hand choice was dominated by target location.
Nonetheless, we focus here on a qualitative analysis of reaches to the more ambiguous, center location, asking if hand choice on these trials is influenced by the location of the target, hand choice, and outcome on trial t − 1. If hand choice was impervious to local history, then these functions would be flat. As can be seen in Figure 4A, sequential effects are evident in hand choices made to central targets. First, there is a bias for participants to use the same hand as was selected on the previous trial. This is most evident when the target on trial t − 1 was also at the center location, but is also evident at the other locations (e.g., right hand at center location is greater after a right visual field target compared to a left visual field target). Second, there is a “contrast” effect in the sequential data. The more eccentric a target was on trial t − 1, the more likely the participant was to switch hands when the target on trial t appeared at the center location. This effect was present for both hands.
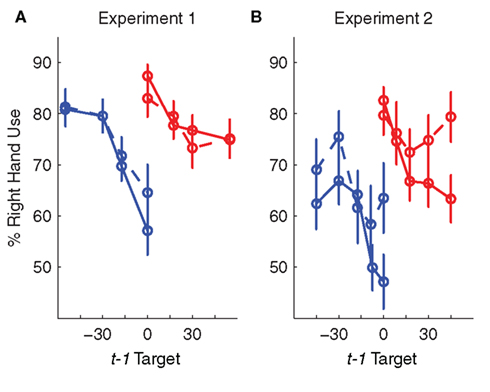
Figure 4. Sequential analysis of hand choice for Experiment 1 (A) and Experiment 2 (B). The functions depict the probability of right hand use for targets at the center location (0°) as a function of the previous trial (n − 1), divided by the location of the last target, the hand used on the last trial, and the outcome on that trial. Right miss (red dashed), right hit (red solid), left miss (blue dashed), left hit (blue solid).
The functions in Figure 4A indicate a modest effect of reinforcement on hand choice. Participants were more likely to use their right hand to reach to the center target if the left hand had missed a target on the previous trial (77.0 ± 2.7%) compared to when the left hand has successfully reached a target on the previous trial (73.9 ± 2.7%). Conversely, the participants were more likely to use their right hand if that hand had successfully intercepted a target on the previous trial (79.1 ± 2.5%) compared to a right-hand miss (77.7 ± 3.2%). In an ANOVA collapsing across t − 1 target location, there was no main effect of the hand used on the previous trial [F(1,49) = 1.50, p = 0.23] nor on the outcome (hit or miss) of the previous trial [F(1,49) = 0.93, p = 0.34]. However, these two factors did interact [F(1,49) = 5.12, p = 0.03], consistent with the hypothesis that hand choice was more likely to switch after a miss.
Figure 5 plots the RT data as a function of target position. We combined the data for targets at −30° and −17.4° using only left hand reaches and the data for the +30° and +17.4° targets using only right hand reaches. For the central target, the data are divided into right and left hand reaches. Note the number of observations is not equal for the two hands given the hand choice biases. Two trends are evident in the figure. First, right hand reaches were initiated faster than left hand reaches [F(1,49) = 30.29, p < 0.001, main effect of hand]. Second, RTs to the center location were slower than RTs to more peripheral locations [F(1,49) = 68.12, p < 0.001, main effect of target]. The hand by location interaction was also reliable [F(1,49) = 15.73, p < 0.001] due to the fact that the peripheral advantage was more pronounced for right hand reaches.
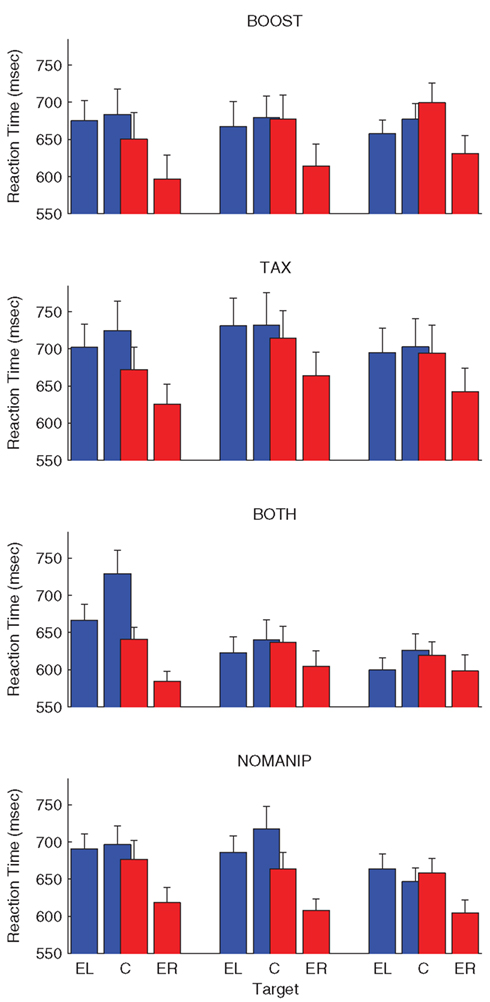
Figure 5. Left (blue) and right (red) hand reaction time data for Experiment 1. For each condition, the data are plotted separately for the three phases (baseline: left cluster; manipulation: center cluster; post-manipulation: right cluster). Within each cluster, the data were combined for eccentric targets at ±30° and ±17.4° for the left and right hands (EL and ER). Data for the central target (C) is depicted separately for right and left hand reaches.
No participants spontaneously reported being aware of the experimental manipulation. Two participants in BOOST, two in TAX, eight in BOTH, and three in the NOMANIP condition commented that they used their left hand more over the course of the experiment. In general, these participants reported being concerned about the accuracy of their left hand initially, but became more confident over time. They tended to attribute the increase in left hand use to intrinsic factors. One subject remarked that they might have used their left hand more than they would have expected because they spend a lot of time playing video games, while another subject reported that over the course of the experiment they “put a little more faith” in their left hand.
When directly asked whether the task became easier, harder, or stayed the same for the right and left hands, participants in the TAX and BOOST conditions were nearly equally likely to say that the difficulty remained the same across the experimental session as they were to state that the difficulty changed in accordance with their particular experimental manipulation. For example, 42% of the participants in the BOOST condition reported that the task got easier for the left hand, compared to 25% who reported it got harder. However, for the TAX condition, 46% also reported that the task got easier for the right hand! Participants were more sensitive to the experimental manipulations in the BOTH condition. Here 57% reported that the task became harder for the right hand (compared to 14% who reported it got easier) and 64% reported that the task became easier for the left hand (compared to 0% who reported it got harder). While the participants in the NOMANIP group distributed their responses across the three choices with near-identical frequencies for the right hand, they were more likely to report that left hand reaches became easier (39%) compared to harder (15%). Thus, this control condition suggests that participants experienced a general practice effect when using their non-dominant limb.
The results of Experiment 1 indicate that hand choice was sensitive to reinforcement. Regardless of whether we reduced the reinforcement rate for the right hand, increased the rate for the left hand, or introduced both manipulations, participants exhibited a spontaneous increase in the use of their left hand. The shift was generally restricted to regions in which hand choice exhibited some ambiguity in the baseline phase, and was of comparable values for the TAX and BOOST conditions. The increase in left hand use for these conditions occurred despite the participants’ lack of awareness of the experimental manipulation.
Our interpretation of this finding is that the change in reward rates led to a change in the value state associated with left and right hand choices, thus influencing the outcome of a competitive process underlying hand choice. The RT data are in accord with this hypothesis: Participants were slower to initiate responses when the target appeared at the ambiguous, central location.
Although we did not observe a differential effect of increasing and decreasing the rate of positive reinforcement in Experiment 1, the data showed a trend for a larger effect of BOOST in the post-manipulation phase, the condition in which the left hand reward rate was increased. However, Experiment 1 might not provide a fair contrast of BOOST and TAX since the absolute reinforcement rates, as well as change in reinforcement rates, differ for the two conditions during the manipulation phase. Moreover, despite our efforts to use a constant size shift (18%), the observed changes in reward rates differed for the two conditions. To better compare the effects of increasing and decreasing the rate of positive reinforcement, we used a more powerful within-subject design in Experiment 2. In addition, we equated the reward rates in the BOOST and TAX conditions during the manipulation phase and added target locations at ±8.6°, close to the central location, to more densely sample the ambiguous area.
In Experiment 2, the average reward rates during the last three blocks of baseline and last three blocks of post-manipulation were 69.5 ± 0.1% and 69.6 ± 0.1% for the right and left hands, respectively in the BOOST condition. For the TAX condition, the observed reward rates were 83.7 ± 0.2% for each hand over these two phases. These values are very close to the desired values of 70 and 84% (Figure 2B). During the manipulation phase, the reward rates for the two groups were near-identical [BOOST: 69.8 ± 0.1% (right), 83.5 ± 0.2% (left); TAX: 69.7 ± 0.3% (right), 83.6 ± 0.2% (left)].
As in Experiment 1, the psychometric functions were very steep, with participants overwhelmingly preferring to use the ipsilateral hand when reaching to peripheral targets (Figure 6A). A right-hand bias was again observed at the center location (71.5 ± 2.6%), although there were a significant number of left hand reaches to this location during the baseline phase. The inclusion of target locations just off-center (±8.6°) increased the occurrence of off-center ambiguity, with the right-hand being used to cross the midline on 20.2 ± 1.8% of the trials during the baseline phase. Interestingly, the inclusion of these locations may have reduced participants’ willingness to use the right hand to reach to the −17.4° target (left of midline): The percentage of right hand reaches to this location during the baseline phase was only 5.8 ± 1.3%, compared to 16.1 ± 1.7% in Experiment 1. We did not analyze this effect given the various methodological differences between the two experiments.
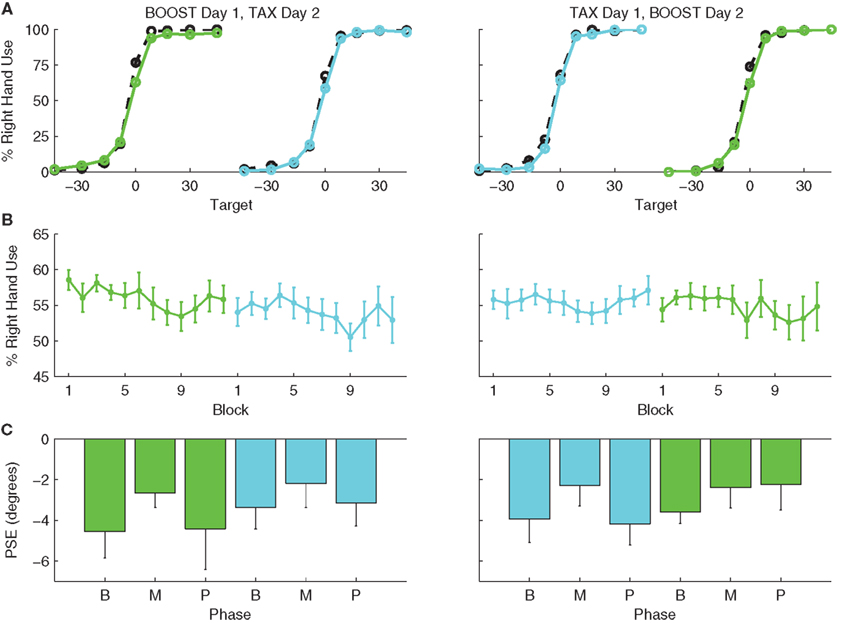
Figure 6. Hand choice results for Experiment 2 for participants who were tested on BOOST in day 1 (left side) or TAX on day 1 (right side). BOOST is shown in green and TAX in cyan. (A) Mean probability of right hand use as a function of target location. Solid lines are for data from the last two blocks of the manipulation phase (Blocks 7–8) and dotted lines are for data from the last two blocks of the baseline phase (Blocks 3–4). (B) Percent right hand use across all targets as a function of block number. (C) PSE values, calculated from the data for the last two blocks of each phase (B, baseline; M, manipulation; P, post manipulation).
Figures 6B,C depict the shift in right hand use and corresponding changes in PSEs over the course of the experiment. In the ANOVA of the PSE data (within-subject factors: phase and condition, between-subject factor: order of conditions), we observed a marginally reliable main effect of phase [F(2,44) = 2.57, p = 0.09]. The main effects of condition [F(1,22) = 0.03, p = 0.87] and test order were not reliable [F(1,22) = 0.15, p = 0.70], nor did any of the two-way or three-way interactions approach significance. In pair-wise comparisons of the scores between baseline and manipulation phases, we observed a marginal shift in the PSEs during the manipulation phase for BOOST [t(22) = 1.52, p = 0.07] and a reliable shift for TAX [t(22) = 2.92, p < 0.01]. Unlike Experiment 1, this shift was not maintained in the post-manipulation phase for either condition, relative to baseline [BOOST: t(22) = −0.59, p = 0.28; TAX: t(22) = −0.002, p = 0.50].
Figure 4B shows the sequential analysis for Experiment 2, again restricted to trials in which the target on trial t appeared at the center location. As in Experiment 1, participants exhibited a bias to reach with the hand used on the last trial (on top of an overall bias to use the right hand). Moreover, hand switches were more likely to occur when the center location was preceded by a target at a more eccentric location, an effect that was especially pronounced after hits.
Unlike Experiment 1, we did not observe a win-stay/lose-shift strategy. There was a main effect of the hand used on the previous trial [F(1,23) = 6.85, p < 0.01] and an effect of the outcome of the last trial [F(1,23) = 13.14, p = 0.001]. However, these factors did not interact [F(1,23) = 0.01, p = 0.92]. Rather, there was an unexpected outcome-related sequential effect in Experiment 2: Independent of whether the last reach was with the right or left hand, participants were more likely to use their right hand after a miss compared to a hit. The probability of using the right hand at the center target after a left miss was 65.7 ± 4.7% compared to 59.7 ± 4.5% after a left hand hit. Surprisingly, the probability of using the right hand at the center target after a right hand hit was 76.1 ± 3.6% compared to 70.5 ± 3.6% after a right hand miss. One interpretation of this effect is that participants became more reliant on their dominant hand after an error, independent of which hand has produced the error.
The reaction time data were very similar to those observed in Experiment 1 (Figure 7). Participants were faster to initiate reaches with the right hand [F(1,22) = 16.20, p = 0.001] and showed an RT cost when the target appeared at the center location compared to the more peripheral locations [F(1,22) = 14.46, p = 0.001]. Unlike Experiment 1, the hand by target interaction was not reliable [F(1,22) = 0.42, p = 0.52].
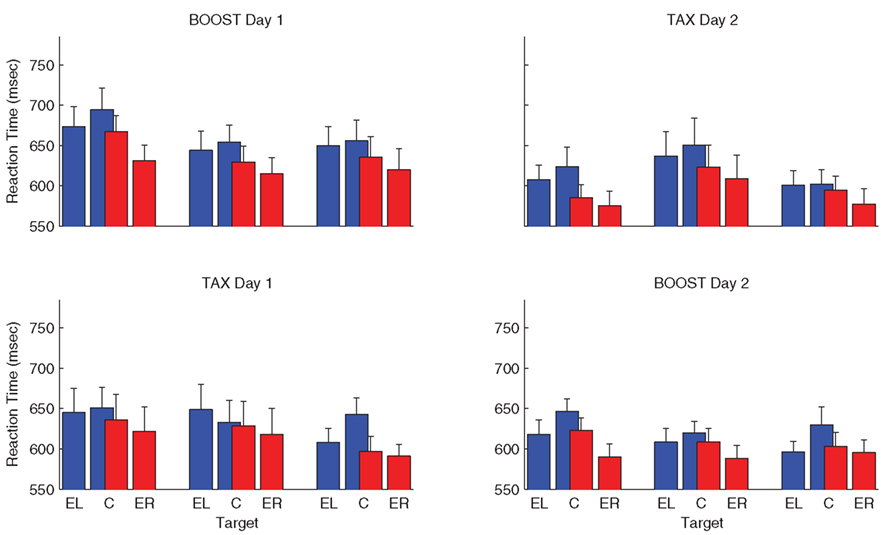
Figure 7. Left (blue) and right (red) hand reaction time data for Experiment 2. The data are plotted for the three phases (baseline: left cluster; manipulation: center cluster; post-manipulation: right cluster). Within each cluster, the data were combined for eccentric targets at ±30°, ±17.4°, and ±8.6° for the left and right hands (EL and ER). Data for the central target (C) is depicted separately for right and left hand reaches.
As in Experiment 1, participants did not spontaneously report becoming aware of the experimental manipulations during either session of the experiment. Due to a filing error, the survey data were not retained for nine participants. For the other 18, 11 judged that they had been in a group in which the reward rate remained unchanged over the course of the experiment, with the percentage similar for the BOOST and TAX conditions.
In Experiment 2 we equated the TAX and BOOST manipulations by employing different reward rates during the baseline phase. In both conditions, we observed an increase in left hand use when the reinforcement rates were altered for one of the two hands, although these effects were only marginally reliable in the overall ANOVA. We had hoped to observe more ambiguous target locations in Experiment 2 by including a denser sampling of midline targets (targets at ±8.6°). However, the inclusion of this target may have reduced the (small) ambiguity observed at more eccentric locations, and as such, effectively reduced the range of ambiguity compared to Experiment 1. The smaller sample of ambiguous targets could account for the smaller shift in hand choice observed in Experiment 2, as well as the lack of persistence of the hand choice shift during the post-manipulation phase (see Discussion).
As in Experiment 1, we failed to observe any obvious differential effect of increasing or decreasing the rate of positive reinforcement. We examine this issue in more detail in the following section in which we apply a reinforcement learning model.
We fit the hand choice data to a Q-learning model. We used the data from the baseline phase to establish initial Q values at each location. These data capture the biases of the participants to respond to eccentric targets with the ipsilateral hand and to prefer the dominant over the non-dominant hand (for most participants) for central locations. We then fit the data for the manipulation and post-manipulation phases. By comparing three models, we addressed two questions. First, is a better fit obtained when the model reflects recent reinforcement history? To address this question, we compared models that included a learning rate parameter, alpha, to a model in which hand choice preferences remained invariant over the course of the experiment (null model). Note that if reinforcement history modifies hand choice, we may observe an improved fit with the alpha model even in the condition in which we did not alter the success rate (NOMANIP in Experiment 1). Second, we compared two classes of models, one in which a single alpha value was set for all of the experimental conditions compared to one in which alpha was free to vary across experimental conditions. In this way, we could ask if hand choice was differentially affected by increasing or decreasing the rate of positive reinforcement, as well as whether choice behavior changed at a different rate when the success rate for both hands was simultaneously adjusted.
The model fits and free parameter estimates are presented in Table 1. For both experiments, the Alpha_1 models provide a much better fit than the null model. A likelihood-ratio test as approximated by Chi-square test of the log likelihood ratios showed that the fit was much better for the Alpha_1 model compared to the null model in both experiments [Experiment 1: χ2(1) = 1191, p < 0.0001; Experiment 2: χ2(1) = 1358, p < 0.0001]. Indeed, the percentage of variance accounted for (R2) was low for the set of null models, but rose to 94 and 97% for the Alpha_1 models in Experiments 1 and 2, respectively. Thus, while the effect of reinforcement was relatively modest in the group-averaged data of hand choice, recent reinforcement history had a significant impact on hand choice preferences. The R2 values are also very high for each condition in the Alpha_4 models.
It should be noted that the improved fit for Alpha_4 as compared to the corresponding null model holds even for the NOMANIP condition in Experiment 1, where we did not vary reinforcement rate. Thus, the effect of reinforcement history on hand choice does not require that the system be perturbed with a change in reinforcement rate: The current data suggest that hand choice preferences are constantly being updated as a function of success rates, at least when reaching to ambiguous locations. This observation is consistent with the fact that the participants exhibited minimal awareness of the experimental manipulation of reinforcement rates, yet altered their hand choice preferences.
The goodness-of-fit was similar for the Alpha_1 and Alpha_4 models. A Chi-square test of the likelihood ratios did not show a reliable difference between the two alpha models in Experiment 1 [χ2(3) = 2, p = 1]. While the Alpha_4 model did provide a significant improvement over the Alpha_1 model in Experiment 2 [χ2(3) = 24, p < 0.0001]. This effect is relatively modest, and likely reflects the fact that the alpha values were different for the two subject groups, and not for the two reinforcement manipulations. Thus, the modeling results confirm that participants were equally sensitive to reinforcement changes that either increased the success rate of the left hand or decreased the success rate for the right hand. While our manipulation confounds the form of reinforcement and hand, the results suggest that increasing or decreasing the rate of positive reinforcement operate through a common mechanism.
In terms of the estimates of learning rate, the alpha values for the four conditions in Experiment 1 were not reliably different from one another as estimated by a bootstrapping procedure (p > 0.055, significance criterion p < 0.0125 to correct for multiple comparisons) and were quite similar to the alpha value obtained for the Alpha_1 model. Of note here is that the estimate of the alpha rate for the BOTH condition is similar to the estimates for the TAX and BOOST conditions. Thus, it appears that simultaneously increasing and decreasing reinforcement rates has an additive effect on behavior.
The alpha estimates are more problematic for Experiment 2. Here we observed a much larger estimate of alpha for the participants who were tested in the BOOST condition on day 1 compared to those who were first tested in the TAX condition. While this might suggest greater sensitivity to positive reinforcement (or a manipulation targeted at the non-dominant hand), two features of the data suggest that this difference may be idiosyncratic to these particular groups of individuals. First, these differences were also evident in the estimates obtained from the day 2 data. Second, the actual reinforcement rates are identical for the BOOST conditions in Experiments 1 and 2 (shift from 70/70 reinforcement rates during baseline to 85/70 during the manipulation phase). Nonetheless, the estimates of alpha were much larger in Experiment 2 for the BOOST data on day 1.
In summary, a reinforcement learning model provided an excellent fit to the data in both experiments. Participants altered their hand choice preferences for each location (Q values) as a function of their recent success or failure in reaching to targets at that location. Moreover, the modeling results indicate that participants were equally sensitive to manipulations that increased or decreased the rate of positive reinforcement. Not only were the estimates of alpha similar across conditions in Experiment 1 and within conditions in Experiment 2, but a model with a single learning rate performed essentially as well as one with separate learning rates for each condition.
The pair of experiments reported here demonstrate that hand choice in an unconstrained reaching task can be influenced by limb-dependent task success. Both decreasing the rate of positive reinforcement for the dominant hand and/or increasing the rate of positive reinforcement for the non-dominant hand increased the likelihood that participants would use their non-dominant to reach to ambiguous target locations. We were able to account for these transient changes in performance within a reinforcement learning framework using a Q-learning model.
Previous work on the behavioral and neural correlates of decision making during reaching has focused on target selection (Sugrue et al., 2004; Cisek and Kalaska, 2005; Churchland et al., 2008). The current studies suggest that hand choice may also be viewed as a competitive process. Participants exhibited between-trial variability in hand choice at locations near the midline. Moreover, RTs at these ambiguous locations(s) were slower than RTs to targets at neighboring locations, an effect we interpret as a signature of a competitive process. This RT cost is not observed when the responses are limited to a single hand (Oliveira et al., 2010). Interestingly, participants were faster when using their right hand in the current studies, whereas they showed a surprising left hand advantage in Oliveira et al. (2010). This difference may reflect the accuracy requirements used here. RTs were approximately 200 ms slower in the current experiments, likely due to the fact that accuracy constraints had to be incorporated in trajectory planning processes given that online corrections were precluded (Sainburg and Kalakanis, 2000).
By viewing hand choice as a competitive process, it is reasonable to think that this simple decision might be affected by recent reinforcement history. An increase in the rate of positive reinforcement for the non-dominant limb or decrease in the rate for the dominant limb led to an increase in the use of the non-dominant limb. The small size of the shift likely arises from at least two factors. First, hand choice was strongly constrained by target position – the participants showed a large bias to use their ipsilateral hand to reach to eccentric targets, an effect that may be especially pronounced when head position and fixation are centered near the midline (Dancause and Schieber, 2010). Thus, the effects of reinforcement are intermixed with other constraints determining hand choice. Second, the change in reinforcement rates was relatively subtle, an increase or decrease of around 20%, changes that are much smaller than those used in many studies of reinforcement learning (Daw et al., 2006; Seymour et al., 2007). We opted to use these values so that we could examine the effects of reinforcement in the absence of awareness. Indeed, none of the participants in the TAX and BOOST conditions of either experiment reported being aware of the experimental manipulation. Those who had a sense of increasing their left hand use tended to attribute the change in their behavior to intrinsic factors.
The implicit nature of the changes observed here may have important implications for physical rehabilitation after neurological injury. Patients with hemiparesis frequently exhibit compensatory strategies, using the arm on their unaffected side to accomplish tasks previously performed with the affected limb. This shift may persist even after the individual exhibits considerable recovery with the affected limb, creating a significant loss of functional recovery. This effect has come to be referred to as learned non-use (Taub, 1980) and has been attributed to behavioral factors such as attention, motivation, and sense of effort (Sterr et al., 2002). That is, the patient’s internal assessment, at least during the first months after the stroke, may be that use of the affected limb is not only much more effortful, but also less likely to be behaviorally successful. This experience is reinforcing, increasing the likelihood that the individual will continue to use the unaffected limb at the expense of the affected limb.
Clinical trials have been designed to counteract the effects of learned non-use. One approach is to force the individual to use the affected limb through constraint induced movement therapy (Taub et al., 1993; Wolf et al., 2006) and/or with virtual reality environments that augment feedback (Merians et al., 2002; Piron et al., 2010). However, the benefits of such interventions are modest and the mechanisms underlying such benefits remain unknown (Wolf, 2007). The limited success of guided therapeutic interventions such as constraint-induced therapy may, in part, be related to their reliance on extrinsic manipulations of behavior. The person is physically restrained from using the affected limb. Such procedures, while producing improvements within the therapeutic setting, may not generalize well when the contextual cue is absent. Our implicit, reinforcement manipulation is designed to alter behavior through intrinsic processes. Altering the person’s internal sense of success may prove to be an important component of inducing long-term changes in behavior.
We did not find a reliable difference in the efficacy of increasing and decreasing the rate of positive reinforcement for inducing changes in hand choice preference. The modeling results also suggest that the learning rate is comparable for conditions in which the rate of positive reinforcement is increased compared to conditions in which the rate of positive reinforcement is decreased. This suggests that a common underlying mechanism may be sensitive to these two types of reinforcement. It is important to note that, although we describe our experimental manipulations in terms of varying the rates of positive reinforcement, we did not test models in which we allowed different alpha values for updating the Q-values following hits vs misses.
The neural mechanisms involved in limb selection, and how this process is influenced by reinforcement, remain to be explored. Using a similar task to that employed here, Oliveira et al. (2010) observed that stimulation of PPC of the left hemisphere increased left hand use, an effect especially pronounced around the PSE. This effect suggests that activity in PPC contributes to effector selection. Other studies point to a role for premotor cortex in such decisions (Beurze et al., 2007, 2009). Here we show that shifts in hand use can also be induced by short-term changes in reinforcement rates. The dopaminergic system has been implicated as facilitating learning for both positive and negative reinforcement. Dopamine bursts are associated with positive reinforcement, and through associative mechanisms, with prediction errors to a stimulus that foreshadows an unanticipated reward (Schultz et al., 1997; O’Doherty et al., 2003; O’Doherty, 2004). Although the evidence is less compelling, a drop in the firing rate of dopaminegeric neurons can be observed when an expected reward is withheld (Schultz et al., 1997; O’Doherty et al., 2003; O’Doherty, 2004). Similarly, high amounts of dopamine facilitate learning from positive reinforcement, while low amounts of dopamine facilitate learning from negative reinforcement (Frank et al., 2004). The modulatory effect of dopamine is especially pronounced under conditions of uncertainty (Cooper and Knutson, 2008; Koch et al., 2008), something that should be prominent in our experimental task given the relatively high error rates. Future studies can directly address the role of dopamine in modulating hand choice preferences, designed to ask if the effects on effector selection are similar to those observed in tasks examining goal selection.
The Q-learning model was successful in capturing the gradual shifts in hand choice preferences as a function of reinforcement. However, the model fails to account for some of the trial-by-trial effects observed in the data (see Figure 4). First, when the target appeared at the same location on two successive trials, participants exhibited a pronounced bias to repeat the reach with the same hand. In its current form, location biases are established by choices exhibited in the baseline phase. Similarly, the model cannot account for the fact that the likelihood of a hand switch was greater when the distance between successive targets increased. The updating of the Q-values following reinforcement was restricted to the pair of values associated with actions to the target location for that trial. Additional parameters would be required to impose additional biases related to repetition or “contrast” effects.
Reinforcement learning should decrease the likelihood that a given action will be chosen following an error (and conversely, increase the likelihood of that action following a hit). Of course this does not mean that behavior will exhibit win-stay/lose-shift tendencies. The reinforcement-related changes may be insufficient to alter preferences to use one hand or the other at a given location. A win-stay/lost-shift tendency was observed in Experiment 1. However, we observed an unexpected sequential effect in Experiment 2: Participants were more likely to use the right hand after an error, regardless of whether that error was produced with the left or right hand. We hypothesize that the decrease in positive feedback may have biased the participants to resort to their dominant hand, reflecting a greater comfort level in using this hand to make accurate movements. It remains unclear why we observed different sequential effects in the two experiments.
A second difference between the two experiments was observed in the post-manipulation phase. On average, participants in Experiment 1 continued to use their non-dominant limb more often than during the baseline phase, whereas those in Experiment 2 returned to baseline choice preferences. Given that the patterns within an experiment were quite consistent across experimental conditions, we expect the difference is related to the methodological changes introduced in Experiment 2. For example, we increased the step size of the staircase procedure and added a new target location to increase the number of trials involving reaches to ambiguous locations. The former change, adopted to help ensure that the average reward rate over an entire block of trials was more consistent across participants, may have increased the rate of learning. The latter may have increased the sensitivity of the experiment to learning effects, now evident during both the manipulation and post-manipulation phases. Models of hemiparesis suggest that efforts to increase the use of an affected limb should accelerate once some minimum threshold of use is achieved (Han et al., 2008). Reinforcement manipulations may facilitate this process, especially if the observed rate of reinforcement exceeds the expected rate. In terms of rehabilitation, it will be desirable to design experimental manipulations that produce stronger and lasting changes in hand choice preferences than those observed with our current procedures.
Goal-oriented behavior requires the operation of decision processes at multiple levels. Fluid behavior involves that we successfully operate in a variable environment that presents a stream of choices. Moreover, the manner in which we interact with the environment is variable and context-dependent. We have focused here on a neglected, but fundamental decision process for motor control, the choice between executing an action with the right or left hand. In many situations, this choice is highly constrained, reflecting factors such as the position of the object with respect to the body or a lifetime preference for the dominant limb. Yet for many actions, especially those that do not involve tools, people exhibit considerable flexibility, switching readily between the two limbs. The experiments presented here demonstrate that principles derived from studies of goal-selection, can shed insight into the processes underlying limb selection.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors would like to thank Robert Lamorena and Andy Noblet for their assistance with data collection. This study was supported by the National Institutes of Health (P01 NS040813) and the National Science Foundation (IIS 0703787).
Batista, A., and Anderson, R. (2001). The parietal reach region codes the next planned movement in a sequential reach task. J. Neurophysiol. 85, 539–544.
Beurze, S. M., de Lange, F. P., Toni, I., and Medendorp, W. P. (2007). Integration of target and effector information in the human brain during reach planning. J. Neurophysiol. 97, 188–199.
Beurze, S. M., de Lange, F. P., Toni, I., and Medendorp, W. P. (2009). Spatial and effector processing in the human parietofrontal network for reaches and saccades. J. Physiol. 101, 3053–3062.
Churchland, A. K., Roozbeh, K., and Shadlen, M. N. (2008). Decision-making with multiple alternatives. Nat. Neurosci. 11, 693–702.
Cisek, P. (2006). Integrated neural processes for defining potential actions and deciding between them: a computational model. J. Neurosci. 26, 9761–9770.
Cisek, P., and Kalaska, J. F. (2005). Neural correlates of reaching decisions in dorsal premotor cortex: specification of multiple direction choices and final selection of action. Neuron 45, 801–886.
Cooper, J. C., and Knutson, B. (2008). Valence and salience contribute to nucleus accumbens activation. Neuroimage 39, 538–547.
Dancause, N., and Schieber, M. (2010). The impact of head direction on lateralized choices of target and hand. Exp. Brain Res. 201, 821–835.
Daw, N., O’Doherty, J. P., Dayan, P, Seymour, B., and Dolan, R. J. (2006). Cortical substrates for exploratory decisions in humans. Nature 441, 876–879.
Frank, M. J., Seeberger, L. C., and O’Reilly, R. C. (2004). By carrot or by stick: cognitive reinforcement learning in Parkinsonism. Science 306, 1940–1943.
Gabbard, C., and Helbig, C. (2004). What drives children’s limb selection for reaching in hemispace? Exp. Brain Res. 156, 325–332.
Garcia-Perez, M. A. (1998). Forced-choice staircases with fixed step sizes: asymptotic and small-sample properties. Vision Res. 38, 1861–1881.
Gardiner, J., Franco, V., and Schieber, M. H. (2006). Interaction between lateralized choices of hand and target. Exp. Brain Res. 170, 149–159.
Gershman, S. J., Pesaran, B., and Daw, N. (2009). Human reinforcement learning subdivides structured. Action spaces by learning effector-specific values. J. Neurosci. 29, 13524–13531.
Han, C. E., Arbib, M. A., and Schweighofer, N. (2008). Stroke rehabilitation reaches a threshold. PLoS Comput. Biol. 4, e1000133. doi: 10.1371/journal.pcbi.1000133
Horowitz, G. D., and Newsome, W. T. (1999). Separate signals for target selection and movement specification in the superior colliculus. Science 284, 1158–1161.
Hoshi, E., and Tanji, J. (2000). Integration of target and body-part information in the premotor cortex when planning action. Nature 408, 466–470.
Huk, A. C., and Shadlen, M. N. (2005). Neural activity in macaque parietal cortex reflects temporal integration of visual motion signals during perceptual decision making. J. Neurosci. 25, 10420–10436.
Johansson, R. S., Theorin, A., Westling, G., Andersson, M., Ohki, Y., and Nyberg, L. (2006). How a lateralized brain supports symmetrical bimanual tasks. PLoS Biol. 4, 1025–1034. doi: 10.1371/journal.pbio.0040158
Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996). Reinforcement learning: a survey. J. Artif. Intell. Res. 4, 237–285.
Koch, K., Schachtzabel, C., and Wagner, G. (2008). The neural correlates of reward-related trial-and-error learning: an fMRI study with a probabilistic learning task. Learn. Mem. 85, 728–778.
Lee, D., and Schieber, M. (2006). Serial correlation in lateralized choices of hand and target. Exp. Brain Res. 174, 499–509.
Medendorp, P., Goltz, H., Crawford, J. D., and Villis, T. (2005). Integration of target and effector information in human posterior parietal cortex for the planning of action. J. Neurophysiol. 93, 954–962.
Merians, A. S., Jack, D., Boian, R., Tremaine, M., Burdea, G. C., Adamovich, S. V., Recce, M., and Poizner, H. (2002). Virtual reality–augmented rehabilitation for patients following stroke. Phys. Ther. 82, 898–915.
O’Doherty, J. (2004). Reward representations and reward-related learning in the human brain: insights from human neuroimaging. Curr. Opin. Neurobiol. 14, 769–776.
O’Doherty, J., Critchley, H., Deichmann, R., and Dolan, R. J. (2003). Dissociating valence of outcome from behavioral control in human orbital and ventral prefrontal cortices. J. Neurosci. 23, 7931–7939.
Oliveira, F. T. P., Diedrichsen, J., Verstynen, T., Duque, J,, and Ivry, R. (2010). Transcranial magnetic stimulation of posterior parietal cortex affects decisions of hand choice. Proc. Natl. Acad. Sci. U.S.A. 107, 1–6.
Piron, L., Turolla, A., Agostini, M., Zucconi, C. S., Ventura, L., Tonin, P., and Dam, M. (2010). Motor learning principles for rehabilitation: a pilot randomized controlled study in poststroke patients. Neurorehabil. Neural. Repair 24, 501–508.
Rudebeck, P. H., Walton, M. E., Smyth, A. N., Bannerman, D. M., and Rushworth, M. F. S. (2006). Separate neural pathways process different decision costs. Nat. Neurosci. 9, 1161–1168.
Sainburg, R. L., and Kalakanis, D. (2000). Differences in control of limb dynamics during dominant and non-dominant arm reaching. J. Neurophysiol. 83, 2661–2675.
Schieber, M. H. (2000). Inactivation of the ventral premotor cortex biases the laterality of motoric choices. Exp. Brain Res. 130, 497–507.
Schultz, W., Dayan, P., and Montague, P. R. (1997). A neural substrate of prediction and reward. Science 275, 1593–1599.
Seo, H., Barraclough, D. J., and Lee, D. (2009). Lateral intraparietal cortex and reinforcement learning during a mixed-strategy game. J. Neurosci. 29, 7278–7289.
Seymour, B., Daw, N., Dayan, P., Singer, T., and Dolan, R. (2007). Differential encoding of losses and gains in the human striatum. J. Neurosci. 27, 4826–2831.
Sterr, A., Freivogel, S., and Schmalohr, D. (2002). Neurobehavioral aspects of recovery: assessment of the learned nonuse phenomenon in hemiparetic adolescents. Arch. Phys. Med. Rehabil. 83, 1726–1731.
Sugrue, L. P., Corrado, G. S., and Newsome, W. T. (2004). Matching behavior and the representation of value in the parietal cortex. Science 304, 1782–1787.
Taub, E. (1980). “Somatosensory deafferentation research with monkeys: implications for rehabilitation medicine,” in Behavioral Psychology in Rehabilitation Medicine: Clinical Applications, ed. L. P. Ince (New York, NY: Williams & Wilkins), 371–401.
Taub, E., Miller, N. E., Novack, T. A., Cook, E. W. III, Fleming, W. C., Nepomuceno, C. S., Connell, J. S., and Crago, J. E. (1993). Technique to improve chronic motor deficit after stroke. Arch. Phys. Med. Rehabil. 74, 347–354.
Tosoni, A., Galati, G., Romani, G. L., and Corbetta, M. (2008). Sensory-motor mechanisms in human parietal cortex underlie arbitrary visual decisions. Nat. Neurosci. 11, 8646–8653.
Wolf, S. L. (2007). Revisiting constraint-induced movement therapy: are we too smitten with the mitten? Is all nonuse “learned”? and other quandaries. Phys. Ther. 87, 1212–1223.
Wolf, S. L., Winstein, C. J., Miller, J. P., Taub, E., Uswatte, G., Morris, D., Giuliani, C., Light, K. E., Nichols-Larsen, D., and EXCITE Investigators. (2006). Effect of constraint-induced movement therapy on upper extremity function 3 to 9 months after stroke: the EXCITE randomized clinical trial. JAMA 296, 2095–2104.
Keywords: motor control, decision making, action selection, reinforcement learning, reaching
Citation: Stoloff RH, Taylor JA, Xu J, Ridderikhoff A and Ivry RB (2011) Effect of reinforcement history on hand choice in an unconstrained reaching task. Front. Neurosci. 5:41. doi: 10.3389/fnins.2011.00041
Received: 15 January 2011;
Accepted: 14 March 2011;
Published online: 23 March 2011.
Edited by:
Julia Trommershaeuser, New York University, USAReviewed by:
Stefan Pollmann, Otto-von-Guericke University, GermanyCopyright: © 2011 Stoloff, Taylor, Xu, Ridderikhoff and Ivry. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Richard B. Ivry, University of California Berkeley, 3210 Tolman Hall, Berkeley, CA 94720-1650, USA. e-mail:aXZyeUBiZXJrZWxleS5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.