Local Label Point Correction for Edge Detection of Overlapping Cervical Cells

Accurate labeling is essential for supervised deep learning methods. However, it is almost impossible to accurately and manually annotate thousands of images, which results in many labeling errors for most datasets. We proposes a local label point correction (LLPC) method to improve annotation quality for edge detection and image segmentation tasks. Our algorithm contains three steps: gradient-guided point correction, point interpolation, and local point smoothing. We correct the labels of object contours by moving the annotated points to the pixel gradient peaks. This can improve the edge localization accuracy, but it also causes unsmooth contours due to the interference of image noise. Therefore, we design a point smoothing method based on local linear fitting to smooth the corrected edge. To verify the effectiveness of our LLPC, we construct a largest overlapping cervical cell edge detection dataset (CCEDD) with higher precision label corrected by our label correction method. Our LLPC only needs to set three parameters, but yields 30–40% average precision improvement on multiple networks. The qualitative and quantitative experimental results show that our LLPC can improve the quality of manual labels and the accuracy of overlapping cell edge detection. We hope that our study will give a strong boost to the development of the label correction for edge detection and image segmentation. We will release the dataset and code at: https://github.com/nachifur/LLPC.

1. Introduction

Medical image datasets are generally annotated by professional physicians (Demner-Fushman et al., 2016; Almazroa et al., 2017; Johnson et al., 2019; Zhang et al., 2019; Lin et al., 2021; Ma et al., 2021; Wei et al., 2021). To construct an annotated dataset for edge detection or image segmentation tasks, annotators often need to annotate points and connect them into an object outline. In the manual labeling process, it is difficult to control label accuracy due to human error. Northcutt et al. (2021) found that label errors are numerous and universal: the average error rate in 10 datasets is 3.4%. These wrong labels seriously affect the accuracy of model evaluation and destabilize benchmarks, which will ultimately spill over model selection and deployment. For example, the deployed model in learning-based computer-aided diagnosis (Saha et al., 2019; Song et al., 2019, 2020; Wan et al., 2019; Zhang et al., 2020) is selected from many candidate models based on evaluation accuracy, which means that inaccurate annotations may ultimately affect accurate diagnosis. To mitigate labeling errors, an image is often annotated by multiple annotators (Arbelaez et al., 2010; Almazroa et al., 2017; Zhang et al., 2019), which generates multiple labels for one image. However, even if the annotation standard is unified, differences between different annotators are inevitable. Another way is to correct the labels manually (Ma et al., 2021). In fact, multi-person annotation and manual label correction are time-consuming and labor-intensive. Therefore, it is of great value to develop label correction methods based on manual annotation for supervised deep learning methods.

Most label correction works are focused on weak supervision (Zheng et al., 2021), semi-supervision (Li et al., 2020), crowdsourced labeling (Bhadra and Hein, 2015; Nicholson et al., 2016), classification (Nicholson et al., 2015; Kremer et al., 2018; Guo et al., 2019; Liu et al., 2020; Wang et al., 2021; Li et al., 2022), and natural language processing (Zhu et al., 2019). However, label correction in these tasks is completely different from correcting object contours. To automatically correct edge labels, we propose a local label point correction method for edge detection and image segmentation. Our method contains three steps: gradient-guided point correction, point interpolation, and local point smoothing. We correct the annotation of the object contours by moving label points to the pixel gradient peaks and smoothing the edges formed by these points. To verify the effectiveness of our label correction method, we construct a cervical cell edge detection dataset. Experiments with multiple state-of-the-art deep learning models on the CCEDD show that our LLPC can greatly improve the quality of manual annotation and the accuracy of overlapping cell edge detection, as shown in Figure 1. Our unique contributions are summarized as follows:

• We are the first to propose a label correction method based on annotation points for edge detection and image segmentation. By correcting the position of these label points, our label correction method can generate higher-quality label, which contributes 30–40% AP improvement on multiple baseline models.

• We construct a largest publicly cervical cell edge detection dataset based on our LLPC. Our dataset is ten times larger than the previous datasets, which greatly facilitates the development of overlapping cell edge detection.

• We present the first publicly available label correction benchmark for improving contour annotation. Our study serves as a potential catalyst to promote label correction research and further paves the way to construct accurately annotated datasets for edge detection and image segmentation.

FIGURE 1

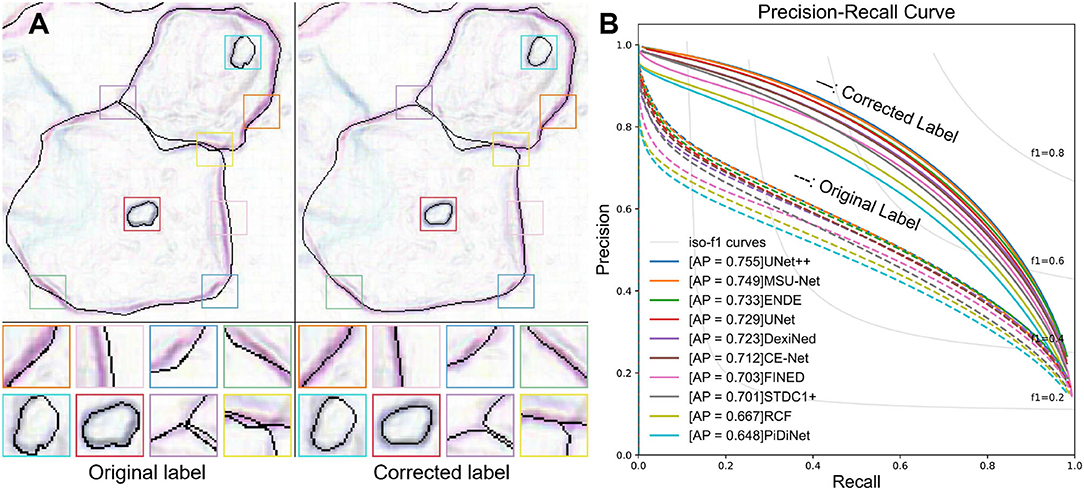
Figure 1. (A) Visual comparison of the original label and our corrected label. Our LLPC can improve the edge positioning accuracy and generate more accurate edge labels. (B) Precision-Recall curves of edge detection methods on our CCEDD dataset. The average precision (AP) is significantly improved over multiple baseline models by using our corrected labels.

2. Related Work

2.1. Label Correction

Deep learning is developing rapidly with the help of big computing (Jouppi et al., 2017) and big data (Deng et al., 2009; Sun et al., 2017; Zhou et al., 2017). Some works (Radford et al., 2019; Brown et al., 2020; Raffel et al., 2020) focus on feeding larger models with more data for better performance and generalization, while others design task-specific model structures and loss functions (Hu et al., 2019; Huang et al., 2021; Zhao et al., 2022) to improve performance on a fixed dataset. Recently, data itself has received a lot of attention. Ng et al. (2021) led the data revolution of deep learning and successfully organized the first “Data-Centric AI” competition. The competition aims to improve data quality and develop data optimization pipelines, such as label correction, data synthesis, and data augmentation (Motamedi et al., 2021). Competitors mine data potential instead of optimizing model structure to improve performance. Northcutt et al. (2021) found that if the error rate of test labels only increases by 6%, ResNet18 outperforms ResNet-50 on ImageNet (Deng et al., 2009). To improve data quality and accurately evaluate models, there is an urgent need to develop label correction algorithms. In weak supervision and semi-supervision (Li et al., 2020; Zheng et al., 2021), pseudo label correction is usually implemented due to the lack of supervision from real labels. Zheng et al. (2021) correct the noisy labels by using a meta network for image recognition and text classification. For supervised learning, bad data can be discarded by data preprocessing, but bad labels seem inevitable in large-scale datasets. In crowdsourcing (Bhadra and Hein, 2015; Nicholson et al., 2016), an image is annotated by multiple people to improve the accuracy of classification task (Nicholson et al., 2015; Kremer et al., 2018; Guo et al., 2019). Guo et al. (2019) trained a model by using a small amount of data and design a label completion method to generate labels (negative or positive) for the mostly unlabeled data. However, label correction in these tasks is significantly different from correcting object contours. In this paper, to eliminate edge location errors and inter-annotator differences in manual annotation, we propose an label correction method based on annotation points for edge detection and image segmentation. Besides, we compare our LLPC with conditional random fields (CRF) (Sutton et al., 2012), which is popular as post-processing for other segmentation methods (Chen et al., 2017; Sun et al., 2020; Fan et al., 2021a; Lu et al., 2021; Ma et al., 2022; Zhang et al., 2022). Dense CRF (Krähenbühl and Koltun, 2011) improves the labeling accuracy by optimizing energy function based on coarse segmentation images, while our LLPC is a label correction method based on annotation points, which are two different technical routes of label correction for image segmentation. More discussion in Section 5.3.

2.2. Cervical Cell Dataset

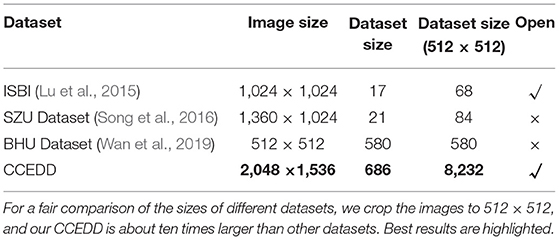
Currently, cervical cell datasets include ISBI 2015 challenge dataset (Lu et al., 2015), Shenzhen University dataset (Song et al., 2016), and Beihang University dataset (Wan et al., 2019). Supervised deep learning based methods require large amounts of data with accurate annotations. However, the only public ISBI dataset (Lu et al., 2015) has a small amount of data and simple image types, which are difficult to train deep neural networks. In this paper, we construct a largest high-accuracy cervical cell edge detection dataset based on our label correction method. Our CCEDD contains overlapping cervical cell masses in a variety of complex backgrounds and high-precision corrected labels, which are sufficient in quantity and richness to train various deep learning models.

3. Label Correction

Our LLPC contains three steps: gradient-guided point correction (GPC), point interpolation (PI) and local point smoothing (LPS). I(x, y) is a cervical cell image and g(x, y) is the gradient image of I(x, y) after Gaussian smoothing. $x_s^i$ is an original label point of I(x, y). First, we correct the points $x_s^i$ to the nearest gradient peak on g(x, y), as shown in Figure 2A, i.e., $\left\{x_s^i\right\}\to \left\{x_c^i\right\}$. i ∈ {1, 2, …, n_s}. Second, we insert more points in large gaps, as shown in Figure 2B, i.e., $\left\{x_c^i\right\}\to \left\{x_I^j\right\}$. j ∈ {1, 2, …, n_I}. n_s and n_I are the number of points before and after interpolation, respectively. Third, we divide the point set $\left\{x_I^j\right\}$ into n_c groups. Each group of points is expressed as Φ_k. We fit a curve C_k on Φ_k. k ∈ {1, 2, …, n_c}. All curves {C_k} are merged into a closed curve C_c, as shown in Figure 2C. Finally, we sample C_c to obtain discrete edges C_d, as shown in Figure 2D. In fact, the closed discrete edges generated by multiple curves fusion are not smooth at the stitching nodes. Therefore, we propose a local point smoothing method without curves splicing and sampling in Section 3.3.

FIGURE 2

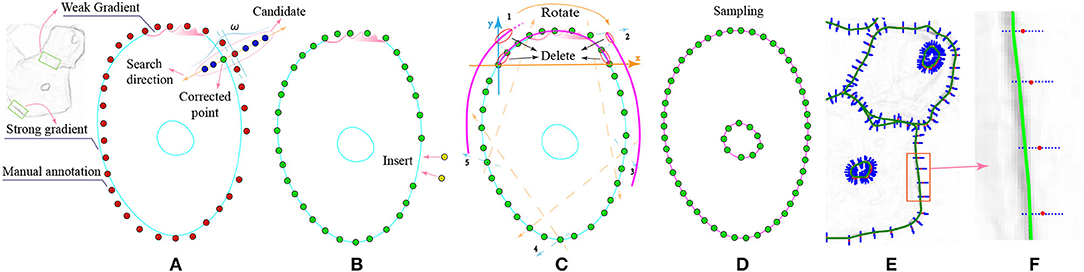
Figure 2. The workflow of our LLPC algorithm. (A) Gradient-guided point correction (the red points → the green points); (B) Insert points at large intervals; (C) Piecewise curve fitting (the purple curve); (D) Curve sampling; (E) The gradient image with the corrected edge label (the green edges); (F) Magnification of the gradient image. The whole label correction process is to generate the corrected edge (green edges) from original label points (red points) in (F).

3.1. Gradient-Guided Point Correction

Although the annotations of cervical cell images are provided by professional cytologists, due to human error, the label points usually deviate from the pixel gradient peaks. To solve this problem, we design a gradient-guided point correction (GPC) method based on gradient guidance. We correct the label points only in the strong gradient region to eliminate human error, while preserving the original label points in the weak gradient region to retain the correct high-level semantics in human annotations. Our point correction consists of three steps as follows:

1. Determine whether the position of each label point is in strong gradient regions.

2. Select a set of candidate points for a label point.

3. Move the label point to the position of the point with the largest gradient value among these candidate points.

The processing object of our LLPC is a set of label points ($\left\{x_s^i\right\}$) corresponding to a closed contour. For an original label point $x_s^i$, we select candidate points along the normal direction of label edge, as shown in Figure 2A. These points constitute a candidate point set ${\Omega }_{x_s^i}$, and $x_{max}^i$ is the point with the largest gradient in ${\Omega }_{x_s^i}$. We move $x_s^i$ to the position of $x_{max}^i$ to obtain the corrected label point $x_c^i$.

$\begin{array}{ll}{x}_c^i=\{\begin{array}{cc}{x}_{max}^i& if\Delta >0\\ x_s^i& otherwise\end{array}& (1)\end{array}$

where

$\begin{array}{ll}\Delta =\left|max({\omega }_j·g(x_{s_j}^i))-min({\omega }_j·g(x_{s_j}^i))\right|-{\lambda }_t·max({\omega }_j).& (2)\end{array}$

$x_{s_j}^i$ is a candidate point in ${\Omega }_{x_s^i}$. We judge whether a point $x_s^i$ is in strong gradient regions through Δ. If Δ > 0, the point will be corrected; otherwise, it will not be moved. In this way, when the radius (r) of ${\Omega }_{x_s^i}$ is larger, our method can correct larger annotation errors. However, this will increase the correction error of label points due to image noise and interference from adjacent edges. To balance the contradiction, the gradient value of the candidate point $g(x_{s_j}^i)$ is weighted by ω_j, which allows setting a larger radius to correct larger annotation errors. We compute the weight as

$\begin{array}{ll}{\omega }_j=K({\Vert x_{s_j}^i-x_s^i\Vert }_2,h_1),& (3)\end{array}$

where

$\begin{array}{ll}K(x,h)=\kappa (x/h)/h.& (4)\end{array}$

K(x, h) is a weighted kernel function with bandwidth h. κ(x) is a Gaussian function with zero mean and one variance. After point correction, $\left\{x_s^i\right\}\to \left\{x_c^i\right\}$.

3.2. Piecewise Curve Fitting

The edge generated directly from the point set $\left\{x_c^i\right\}$ is not smooth due to the errors in point correction process (see Section 5.4). To eliminate the errors, we fit multiple curve segments and stitch them together. In the annotation process of manually drawing cell contours, the annotators perform dense point annotations near large curvatures, and sparse annotations near small curvatures to accurately and quickly outline cell contours. Since the existence of large intervals is not conducive to curve fitting, we perform linear point interpolation (PI) on these intervals before curve fitting.

3.2.1. Point Interpolation

The sparse label point pairs can be represented as,

$\begin{array}{ll}\left\{(x_c^i,x_c^{i+1})|{\Vert x_c^i-x_c^{i+1}\Vert }_2>2·gap\right\},& (5)\end{array}$

where i = 0, 1…n_s − 1. Then, we insert points between the sparse points pairs to satisfy

$\begin{array}{ll}{\Vert x_I^j-x_I^{j+1}\Vert }_2<gap,& (6)\end{array}$

as shown in Figure 2B. j = 0, 1…n_I − 1. n_s and n_I are the number of points before and after interpolation, respectively. gap is the maximum interval between adjacent point pair. After interpolation, $\left\{x_c^i\right\}\to \left\{x_I^j\right\}$.

3.2.2. Curve Fitting

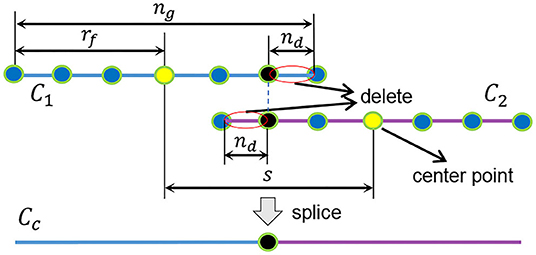
We divide $\left\{x_I^j\right\}$ into n_c groups. Each group is expressed as ${\Phi }_k=\left\{x_I^{1+k·s},x_I^{2+k·s},\dots ,x_I^{n_g+k·s}\right\}$. k = 0, 1…n_c − 1. n_c = ⌈n_I/s⌉. As shown in Figure 3, s = 2(r_f − n_d) is the interval between the center points of each group; r_f = ⌊(n_g − 1)/2⌋ is the group radius; n_g is the number of points in the group. To reduce the fitting error at both ends of the curve, there is overlap between adjacent curves. The overlapping length is 2n_d. To fit a curve on Φ_k, we create a new coordinate system, as shown in Figure 2C. The x-axis passes through the $x_I^{1+k·s}$ point and the $x_I^{n_g+k·s}$ point. The point set in the new coordinate system is ${\Phi }_k^r$. We obtain a curve C_k by local linear fitting (McCrary, 2008) on ${\Phi }_k^r$. This is equivalent to solving the following problem at the target point x_t = (x, y) on the curve C_k.

$\begin{array}{ll}{\displaystyle \underset{{\beta }_0(x),{\beta }_1(x)}{min}}{\displaystyle \sum _{j=1+k·s}^{n_g+k·s}}{\omega }_j(x)(y_j-{\beta }_0(x)-{\beta }_1(x)·x_j)& (7)\end{array}$

β₀(x) and β₁(x) are the curve parameter at the point x_t. (x_j, y_j) denotes the coordinates of point $x_I^j$ in ${\Phi }_k^r$. The weight function is

$\begin{array}{ll}{\omega }_j(x)=K({\Vert x-x_j\Vert }_2,h_2)/{\displaystyle \sum _{m=1+k·s}^{n_g+k·s}}K({\Vert x-x_m\Vert }_2,h_2).& (8)\end{array}$

If the distance between the point $x_I^j$ and the target point x_t is larger, the weight ω_j(x) will be smaller. The matrix representation of the above parameter solution is

$\begin{array}{ll}\beta ={(X^T\omega X)}^{-1}{X}^T\omega Y,& (9)\end{array}$

where $X=\left[\begin{array}{cc}1& x_{1+k·s}\\ 1& x_{2+k·s}\\ ⋮& ⋮\\ 1& x_{n_g+k·s}\end{array}\right]$, $Y=\left[\begin{array}{c}{y}_{1+k·s}\\ y_{2+k·s}\\ ⋮\\ y_{n_g+k·s}\end{array}\right]$, $\beta =\left[\begin{array}{c}{\beta }_0(x)\\ {\beta }_1(x)\end{array}\right]$,

$\omega =\left[\begin{array}{cccc}{\omega }_{1+k·s}(x)& & & \\ & {\omega }_{2+k·s}(x)& & \\ & & \ddots & \\ & & & {\omega }_{n_g+k·s}(x)\end{array}\right].$

The matrix ω is zero except for the diagonal. Each ${\Phi }_k^r$ corresponds to a curve C_k. We stitch n_c curves into a closed curve C_c, as shown in Figures 2C, 3. Then, we sample on the interval $\left[x_I^{1+k·s+n_d},x_I^{n_g+k·s-n_d}\right]$ as shown in Figure 2D. We convert the coordinates of these sampling points to the original image coordinate system. Finally, we can obtain a discrete edge C_d, as shown in Figures 2E,F.

FIGURE 3

Figure 3. Merge multiple curves (C₁ and C₂) into one curve(C_c).

3.3. Local Point Smoothing

In Section 3.2, we stitch multi-segment curves to obtain a closed cell curve, and then sample the curve to generate a discrete edge. In fact, there is no smoothness at the splice nodes. To generate a smooth closed discrete edge, we design a local point smoothing (LPS) method without curves splicing and sampling. As shown in Figure 4A, we insert more points in large intervals (gap = 1). As shown in Figure 4B, we only correct the center point of ${\Phi }_k^r$ by fitting a curve (C_k). By shifting the local coordinate system by one step (s = 1), each point in $\left\{x_I^j\right\}$ will be corrected by fitting a curve. These correction points constitute a discrete edge C_d. Because no curves are spliced, the generated edge is smooth at each point. The pipeline of our LLPC is shown in Algorithm 1.

FIGURE 4

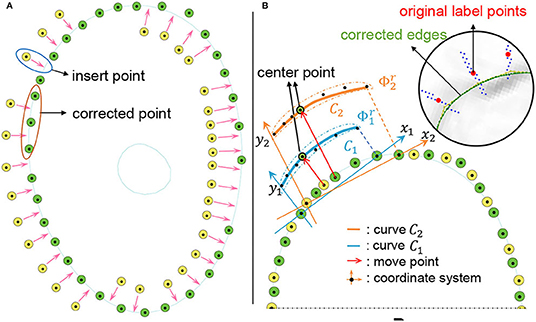
Figure 4. Local point smoothing to generate smooth closed discrete edges. (A) Insert points; (B) Move the coordinate system and correct each point by curve fitting. All corrected points constitute a discrete edge.

ALGORITHM 1

Algorithm 1: LLPC Label Correction Algorithm.

3.4. Parameter Setting

In Section 3.1, we set the parameters r = 15, λ_t = 4 and h₁ = r/2. In Section 3.2, we set n_g = 14. r_f = ⌊(n_g − 1)/2⌋. h₂ = r_f/2. When gap = 1 and s = 1, the Section 3.3 is a special case of the Section 3.2. See Section 5.4 for more discussion of parameter selection.

4. Experimental Design

4.1. Data Aquisition and Processing

We compare our CCEDD with other cervical cytology datasets in Table 1. Our dataset was collected from Liaoning Cancer Hospital & Institute between 2016 and 2017. We capture digital images with a Nikon ELIPSE Ci slide scanner, SmartV350D lens and a 3-megapixel digital camera. For patients with negative and positive cervical cancer, the optical magnification is 100× and 400×, respectively. All of the cases are anonymized. All processes of our research (image acquisition and processing, etc.) follow ethical principles. Our CCEDD dataset includes 686 cervical images with a size of 2,048×1,536 pixels (Table 2). Six expert cytologists outline the closed contours of the cytoplasm and nucleus in cervical cytological images by an annotation software (labelme; Wada, 2016).

TABLE 1

Table 1. Comparison with other cervical cytology datasets.

TABLE 2

Table 2. The detailed description of CCEDD.

We randomly shuffle our dataset and split it into training, validation and test sets. To ensure test reliability, we set this ratio to 6:1:3. To be able to train various complex neural networks on a GPU, we crop a large-size image into small-size images. If an image is cut as shown in Figure 5A, it will result in incomplete edge at the cut boundary. To maximize data utilization efficiency, we move the cutting grid, as shown in Figures 5B–D. After label correction, we cut an image with a size of 2,048×1,536 into 49 image patches with a size of 512×384 pixels.

FIGURE 5

Figure 5. Image cutting method. (A) 4×4 cutting grid; (B) move the grid right; (C) move the grid down; (D) move the grid right and down.

4.2. Baseline Model and Evaluation Metrics

4.2.1. Baseline Model

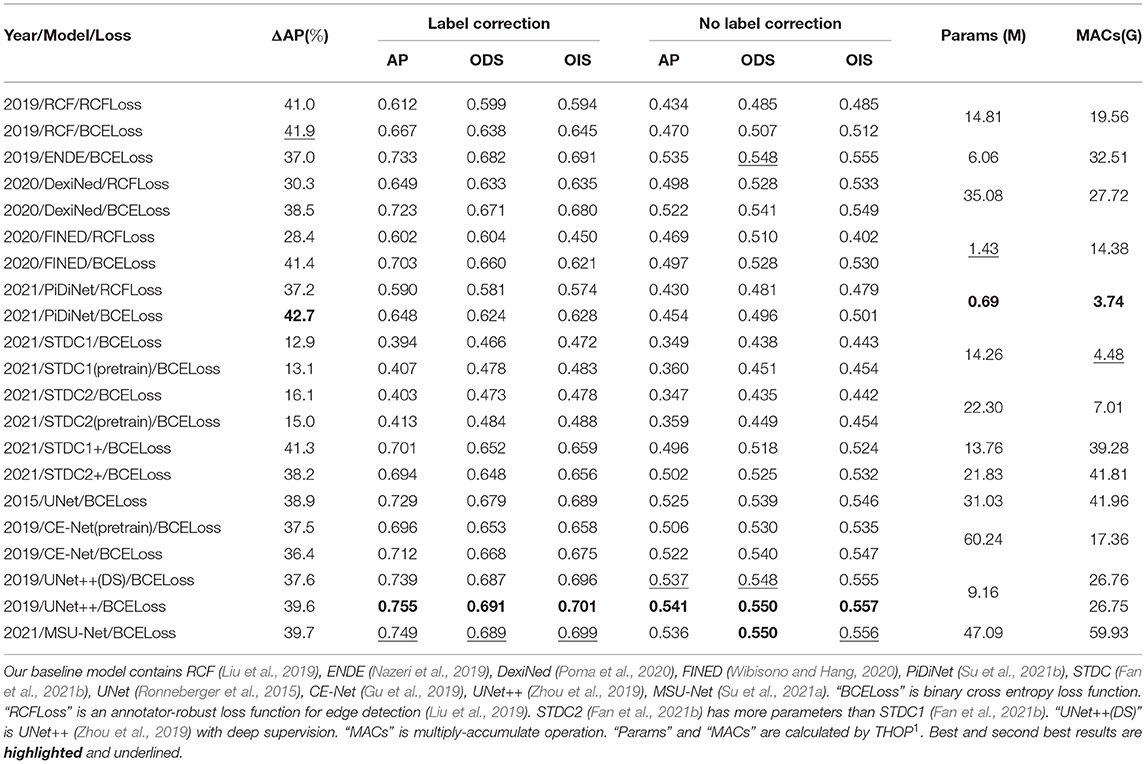
Our baseline detectors are 10 state-of-the-art models. We evaluate multiple edge detectors, such as RCF (Liu et al., 2019), ENDE (Nazeri et al., 2019), DexiNed (Poma et al., 2020), FINED (Wibisono and Hang, 2020), and PiDiNet (Su et al., 2021b). Furthermore, we explore more network structures for edge detection by introducing segmentation networks, which usually only requires simple modifications of the last layer of networks. These segmentation networks include STDC (Fan et al., 2021b), UNet (Ronneberger et al., 2015), UNet++ (Zhou et al., 2019), CENet (Gu et al., 2019), MSU-Net (Su et al., 2021a). To aggregate more shallow features for edge detection, we modify multiple layers of STDC, i.e., STDC+. More details of these network structure can be found in our code implementation.

4.2.2. Evaluation Metrics

We quantitatively evaluate the edge detection accuracy by calculating three standard measures (ODS, OIS, and AP) (Arbelaez et al., 2010). The average precision (AP) is the area under the precision-recall curve (Figure 1B). F1-score$=\frac{2·precision·recall}{precision+recall}$ is the harmonic average of precision and recall. ODS is the best F1-score for a fixed scale, while OIS is the F1-score for the best scale in each image.

4.3. Experimental Setup

4.3.1. Training Strategy

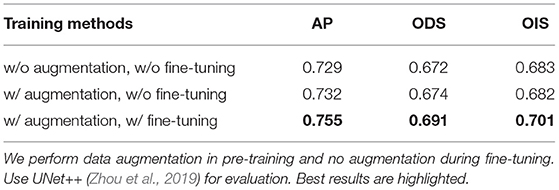
Data augmentation can improve model generalization and performance (Bloice et al., 2019). In training, we perform rotation and shearing operations, which require padding zero pixels around an image. In testing, there is no zero pixel padding. This lead to different distributions of training and testing sets and degrade the model performance. Therefore, we perform data augmentation in pre-training and no augmentation during fine-tuning.

Due to the different structures and parameters of baseline networks, a fixed number of training iterations may lead to overfitting or underfitting. For accurate evaluation, we adaptively adjust the iteration number by evaluating the average accuracy (AP) on the validation set. The period of model evaluation is set 1 epoch for pre-training and 0.1 epoch for fine-tuning. After the i-th model evaluation, we can obtain Model_i and AP_i (i = 1, 2, ⋯ , 50). If AP_i < min(AP_i−j), the training ends and we obtain the optimal model Model_j|max(APj). j = 1, 2, 3 in pre-training and j = 1, 2, ⋯ , 10 in fine-tuning. The maximum iteration number is 50 epochs for pre-training and fine-tuning. Besides, we also dynamically adjust the learning rate to improve performance. The learning rate l decays from 1⁻⁴ to 1⁻⁵. If AP_i < AP_i−1, l_i = l_i−1/2.

4.3.2. Implementation Details

We use the Adam optimizer (Kingma and Ba, 2015) to optimize all baseline networks on PyTorch (β₁ = 0, β₂ = 0.9). We use random normal initialization to initialize these networks. To be able to train various complex neural networks on a GPU, we resize the image to 256×192. The batch size is set 4. We perform color adjustment, affine transformation and elastic deformation for data augmentation (Bloice et al., 2019). All experiments are implemented on a workstation equipped with a Intel Xeon Silver 4110 CPUs and a NVIDIA RTX 3090 GPU.

5. Experimental Results and Discussion

5.1. Edge Detection of Overlapping Cervical Cells

We show the visual comparison results on our CCEDD in Figure 6. The quantitative comparison is shown in Table 4 and Figure 1B. These results have important guiding implications for accurate edge detection of overlapping cervical cells. We analyze several factors affecting the performance of overlapping edge detection.

• Loss function design. RCFLoss (Liu et al., 2019) produces coarser edges, as shown in Figure 7. This may be robust for natural images, but poor localization accuracy for accurate cervical cell edge detection.

• Network structure design. Long-distance skip connections can fuse shallow and deep features for constructing multi-scale features. Our experiments show that the U-shaped structure is effective for overlapping edge detection [e.g., UNet (Ronneberger et al., 2015), UNet++ (Zhou et al., 2019) and MSU-Net (Su et al., 2021a)].

• Pre-training. Due to the huge distribution difference between natural and medical images, pre-training may degrade performance (e.g., CE-Net; Gu et al., 2019) or have limited improvement (e.g., STDC; Fan et al., 2021b).

FIGURE 6

Figure 6. Visual comparison results on CCEDD dataset. (A) Slightly overlapping cells. (B,C) Highly overlapping cells. (D,E) Overlapping cell masses. (F,G) Blurred overlapping cells. (H,I) Overlapping cells in complex environments.

FIGURE 7

Figure 7. Visual comparison of different loss functions. (A) Input; (E) Ground truth; (B,F) PiDiNet (Su et al., 2021b); (C,G) RCF (Liu et al., 2019); (D,H) DexiNed (Poma et al., 2020); (B–D) BCELoss; (F–H) RCFLoss (Liu et al., 2019). “BCELoss” is binary cross entropy loss function. Compared with BCELoss, RCFLoss (Liu et al., 2019) can produce coarser edges.

5.2. Effectiveness of Label Correction

In our LLPC, the position of label points is locally corrected to the pixel gradient peak. As shown in Figures 1A, 8B, Our LLPC can generate more accurate edge labels. Besides, we can easily generate corrected masks from corrected points in the labelme software (Wada, 2016). Compared with the original mask in Figure 8C, our corrected mask has higher edge localization accuracy and smoother edges, as shown in Figure 8D.

FIGURE 8

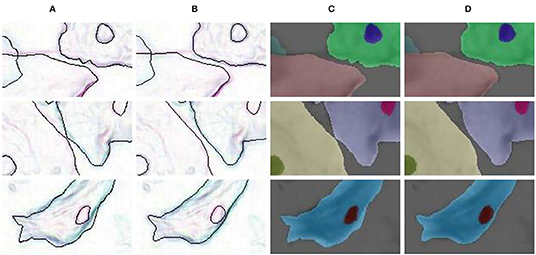
Figure 8. Label correction for edge detection and semantic segmentation. (A) Original edge; (B) Corrected edge; (C) Original mask; (D) Corrected mask.

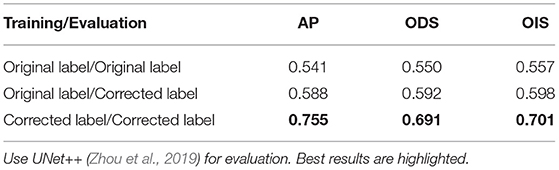
We train multiple networks using original label and corrected label. The quantitative comparison results is shown in Table 3 and Figure 1B. Compared with the original label, using the corrected label to train multiple networks can significantly improve AP (30–40%), which verifies the effectiveness of our label correction method. Table 4 shows that the performance improvement comes from two aspects. First, our corrected label can improve the evaluation accuracy in testing (0.541 → 0.588). Second, using our corrected label to train network can improve the accuracy of overlapping edge detection in training (0.588 → 0.755), as shown in Figure 9.

TABLE 3

Table 3. Edge detection results on our CCEDD dataset.

TABLE 4

Table 4. Performance improvement analysis of label correction.

FIGURE 9

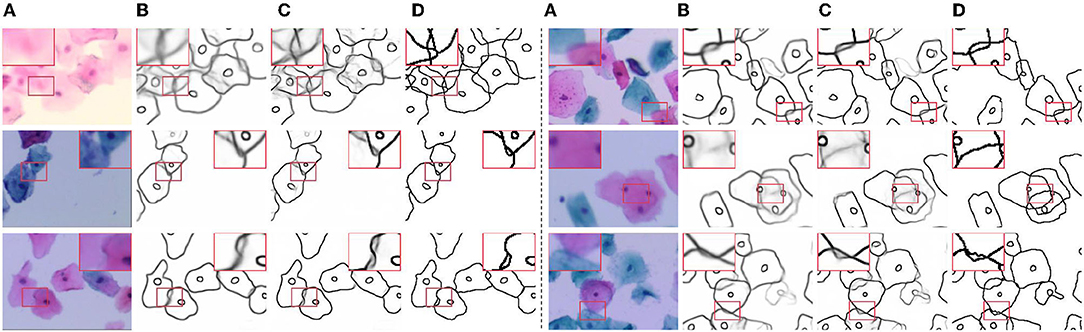
Figure 9. Visual comparison results of training with different labels. (A) Input image; (B) UNet++ (Zhou et al., 2019)/BCELoss + Original label; (C) UNet++ (Zhou et al., 2019)/BCELoss + Corrected label; (D) Corrected labels. Compared with the original label, the corrected label can improve the accuracy of overlapping edge detection.

5.3. Comparison With Other Label Correction Methods

In Figures 10, 11, we compare our LLPC with active contours (Chan and Vese, 2001) and dense CRF (Krähenbühl and Koltun, 2011). We observed that active contours (Chan and Vese, 2001) is refinement failure of nucleus contours in Figure 10F, and dense CRF (Krähenbühl and Koltun, 2011) fails due to complex overlapping cell contours in Figure 11C. Since active contours (Chan and Vese, 2001) and dense CRF (Krähenbühl and Koltun, 2011) are global iterative optimization methods based on segmented images, which are uncontrollable for label correction of object contours and ultimately lead to these failed results. Our LLPC is the local label point correction without iterative optimization. Therefore, the correction error of our LLPC is controllable and the error in one place does not spread to other places, which is crucial for robust label correction. Besides, dense CRF (Krähenbühl and Koltun, 2011) is nonplussed over overlapping instance segmentation refinement, while our LLPC corrects label based on annotation point and can handle overlapping label correction, as shown in Figure 11E.

FIGURE 10

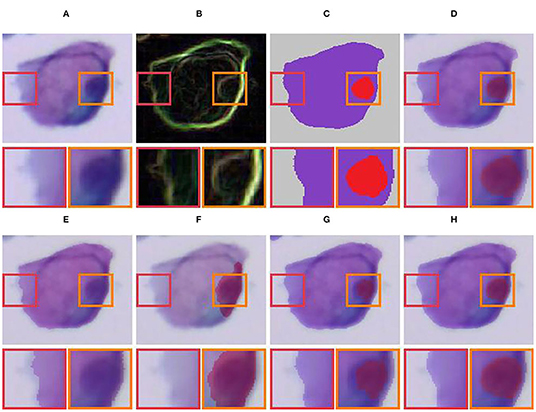
Figure 10. Qualitative comparison of single-cell label correction. (A) Input; (B) Gradient image; (C) Original mask; (D) Input + original mask; (E) Active contours (Chan and Vese, 2001) for cytoplasm; (F) Active contours (Chan and Vese, 2001) for nucleus; (G) Dense CRF (Krähenbühl and Koltun, 2011); (H) Our LLPC.

FIGURE 11

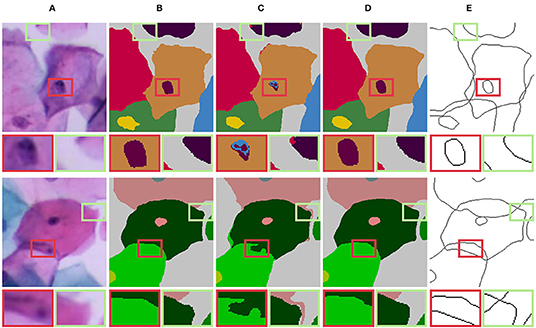
Figure 11. Qualitative comparison of label correction for overlapping cell masses. (A) Input; (B) Original mask; (C) Dense CRF (Krähenbühl and Koltun, 2011); (D) Our LLPC (mask); (E) Our LLPC (edge).

5.4. Ablation Experiment

5.4.1. Ablation of Label Correction Method

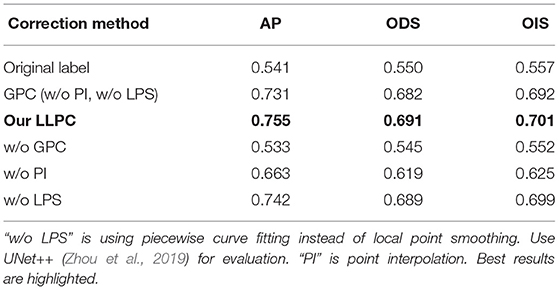
Our LLPC contains three steps: gradient-guided point correction (GPC), point interpolation (PI), and local point smoothing (LPS). Although our GPC can correct label points to pixel gradient peaks, there is still some error in the correction process. LPS can smooth the edges corrected by GPC, as shown in Figure 12A. Table 5 shows that GPC is the most important part of our LLPC (0.541 → 0.731), while PI and LPS can further improve the annotation quality by smoothing edges (0.731 → 0.755). Only smoothing the original labels (“w/o GPC”) is ineffective (0.541 → 0.533). Because this may lead to larger annotation errors. Compared to piecewise curve fitting in Section 3.2, LPS can generate smoother edges, as shown in Figure 12B. These qualitative and quantitative results verify that the three components of our LLPC are essential.

FIGURE 12

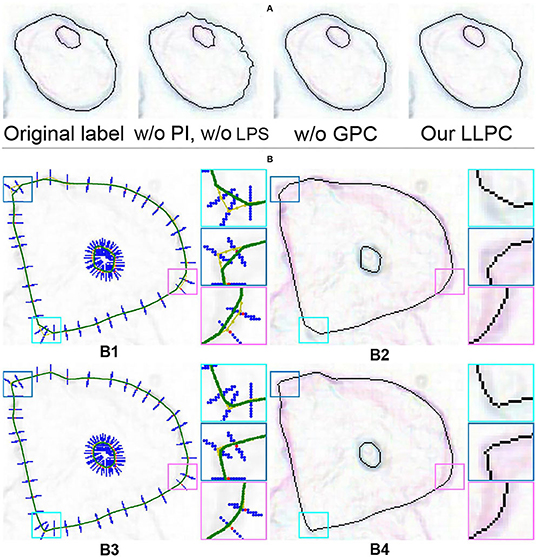
Figure 12. (A) Ablation of gradient-guided point correction. “GPC” is gradient-guided point correction. (B) Visual comparison of different label correction methods. (B1) The green curves generated by piecewise curve fitting (w/o LPS); (B2) The discrete edge sampled from the curves in (B1); (B3) The curves smoothed by LPS; (B4) The discrete edges without curve sampling.

TABLE 5

Table 5. Ablation of our LLPC. “GPC” is gradient-guided point correction.

5.4.2. Selection of Hyper-Parameters

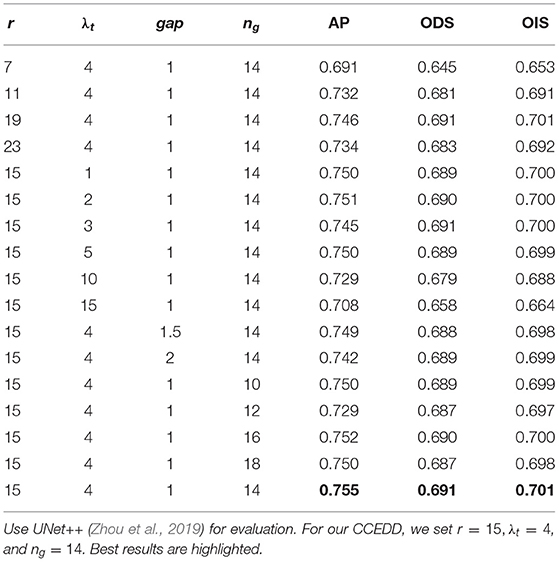
To set the optimal parameters, we conduct parameters ablation experiments in Table 6. gap can control the point density in PI. For local curve fitting, gap = 1 is optimal. Therefore, for an unknown dataset, our LLPC only needs to set three parameters, i.e., r, λ_t and n_g. A qualitative comparison of these parameters with different settings is shown in Figure 13. r controls the maximum error correction range in human annotations. If r is too small, large label errors cannot be corrected. If r is too large, the error of point correction is larger. r limits the correction range in space, while λ_t is the threshold for a limitation of gradient values variation during the correction process. If λ_t is large, label points are corrected only when the gradient value changes sharply in the search direction. n_g controls the scale of the local smoothing. For our CCEDD, r = 15, λ_t = 4, and n_g = 14.

TABLE 6

Table 6. Parameters ablation of our label correction method.

FIGURE 13

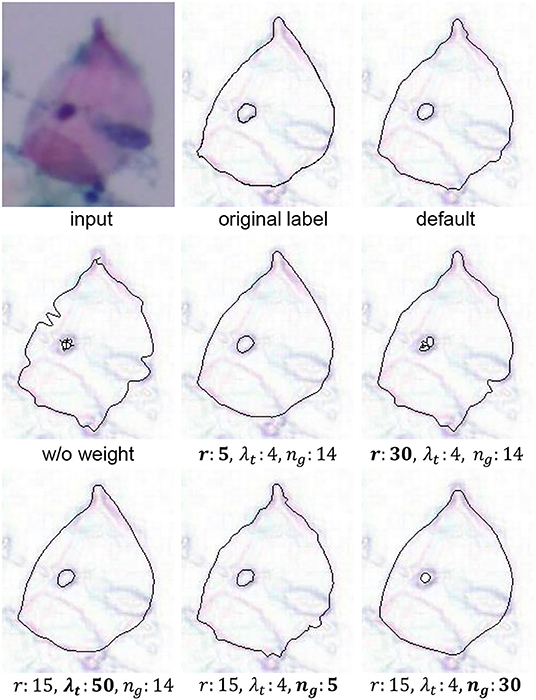
Figure 13. Visual comparison results for different parameters settings in our LLPC. “Default” is r = 15, λ_t = 4, and n_g = 14. “w/o weight” is ω_j = 1 in Equation (3).

5.4.3. Ablation of Training Strategy

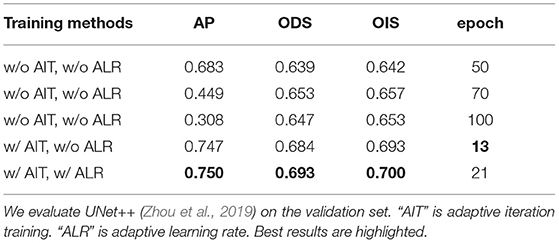
Our training strategy can eliminate the influence of different distributions of the training and test sets due to data augmentation, and improve the AP by 3.6% in Table 7. To fairly evaluate multiple networks with different structures and parameters, we employ adaptive iteration and learning rate adjustment to avoid overfitting and underfitting. Table 8 and Figure 14A verify the effectiveness of our adaptive training strategy.

TABLE 7

Table 7. Ablation of two-stage training strategy.

TABLE 8

Table 8. Ablation of adaptive training strategy.

FIGURE 14

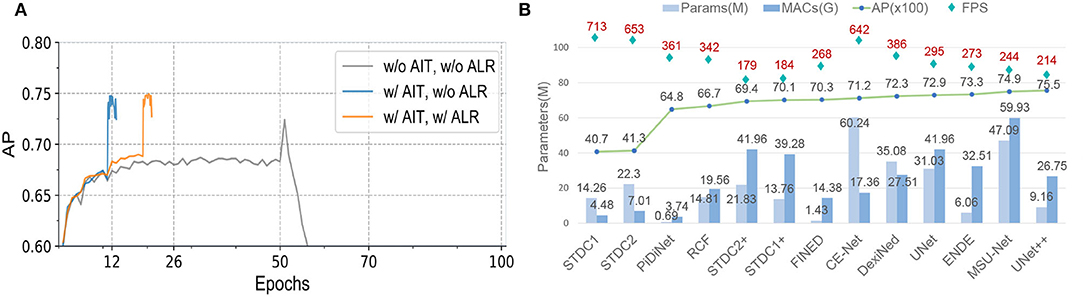
Figure 14. (A) Training schedules. “AIT” is adaptive iteration training. “ALR” is adaptive learning rate. We evaluate UNet++ (Zhou et al., 2019) on the validation set. (B) Comparison of network parameters, running efficiency and edge detection performance. “MACs” is multiply-accumulate operation. “FPS” is the average speed by evaluating 10,413 images with a resolution of 256×192.

5.5. Computational Complexity

5.5.1. Label Correction

Our LLPC takes 270 s to generate 100 corrected edge images with a size of 2,048×1,536 pixels on CPU. Because our label correction algorithm is offline and does not affect the inference time of a neural network, we have not further optimized it. If the algorithm runs on GPU, the speed can be further improved, which can save more time for label correction of large-scale datasets.

5.5.2. Model Evaluation

We rewrite the evaluation code (Arbelaez et al., 2010) on GPU for fast evaluation. The average FPS using the UNet++ (Zhou et al., 2019) is 173 for 10,143 test images with a size of 256×192 pixels. In training, we need to calculate the AP of the validation set to adaptively control the learning rate and the number of iterations (see Section 4.3). Fast evaluation greatly accelerates our training process.

5.5.3. Neural Network Inference

We test the inference speed of UNet++ (Zhou et al., 2019). For 207 images with a resolution of 1,024×768, the average FPS is 9. For 207 images with a resolution of 512×512, the average FPS is 26. For 10,413 images with a resolution of 256×192, the average FPS is 295. Figure 14B shows the running efficiency comparison of multiple benchmark models. According to the report of Wan et al. (2019), the methods of Wan et al. (2019), Lu et al. (2015), and Lu et al. (2016), took 17.67, 35.69m and 213.62 s for an image a resolution of 512×512, respectively. Compared with these method, the UNet++ (Zhou et al., 2019) is significantly faster. Many cervical cell segmentation approaches (Phoulady et al., 2017; Tareef et al., 2017, 2018; Wan et al., 2019; Zhang et al., 2020) consist of three stages, including nucleus candidate detection, cell localizations, and cytoplasm segmentation. Fast edge detection of overlapping cervical cell means that the detected edges can be used as a priori input of these segmentation networks to improve performance at a small cost.

6. Discussion

6.1. Label Correction for Natural Images

Our label correction method can correct a closed contour by correcting the position of label points, which does not require additional prior assumptions (e.g., contour shape, object size). We annotated several images in the PASCAL VOC dataset (Everingham et al., 2010) with labelme (Wada, 2016) and corrected the label (r = 7, λ_t = 4, and n_g = 9). As shown in Figure 15, our label correction method can generate more accurate object contours, which demonstrates the feasibility of our label correction method for natural images.

FIGURE 15

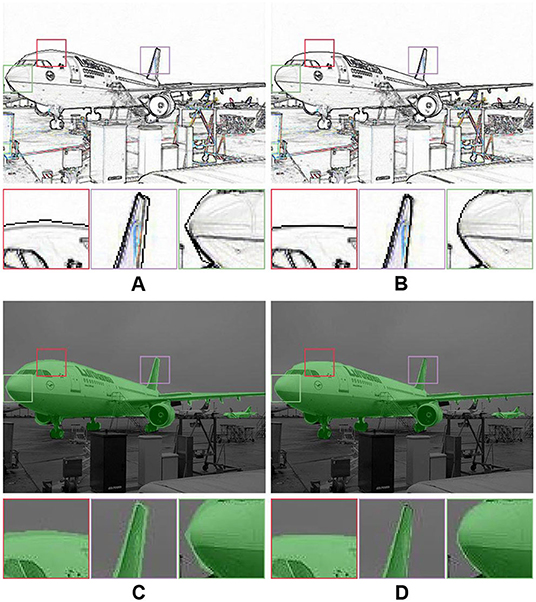
Figure 15. Label correction for natural images. (A) Original edge; (B) Corrected edge; (C) Original mask; (D) Corrected mask.

6.2. Overlapping Edge Detection

Overlapping edge detection of cervical cell is a challenging task due to the presence of strong and weak gradient edges. For edges with strong gradients, it only requires low-level detail features. For edges with weak gradients in overlapping region, it may require high-level semantics to reason contours and connect edges based on the context in strong gradient regions. While Unet++ (Zhou et al., 2019) achieves the best results on our CCEDD, there is no difference in the detection of these two different types of edges. Designing new network structures and loss functions for overlapping edge detection may be a way to further address this challenge.

7. Conclusions

We propose a local label point correction method for edge detection and image segmentation, which is the first benchmark for label correction based on annotation points. Our LLPC can improve the edge localization accuracy and mitigate labeling error from different annotators in manual annotation. Only three parameters need to be set in our LLPC, but using the label corrected by our LLPC to train multiple networks can yield 30–40% AP improvement. Besides, we construct a largest overlapping cervical cell edge detection dataset based on our LLPC, which will greatly facilitate the development of overlapping cell edge detection. In future work, we plan to develop a label point correction method with local adaptive parameter adjustment.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://github.com/nachifur/LLPC.

Author Contributions

JL: conceptualization, methodology, software, validation, writing—original draft, and visualization. HF: investigation, resources, writing—review and editing, supervision, project administration, and funding acquisition. QW: writing—review and editing. WL: investigation. YT: writing—review and editing and supervision. DW: investigation, resources, and data curation. MZ and LC: investigation and resources. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (61873259, 62073205, and 61821005), the Key Research and Development Program of Liaoning (2018225037), and the Youth Innovation Promotion Association of Chinese Academy of Sciences (2019203).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnote

1. ^https://github.com/Lyken17/pytorch-OpCounter

References

Almazroa, A., Alodhayb, S., Osman, E., Ramadan, E., Hummadi, M., Dlaim, M., et al. (2017). Agreement among ophthalmologists in marking the optic disc and optic cup in fundus images. Int. Ophthalmol. 37, 701–717. doi: 10.1007/s10792-016-0329-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Arbelaez, P., Maire, M., Fowlkes, C., and Malik, J. (2010). Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 33, 898–916. doi: 10.1109/TPAMI.2010.161

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhadra, S., and Hein, M. (2015). Correction of noisy labels via mutual consistency check. Neurocomputing 160, 34–52. doi: 10.1016/j.neucom.2014.10.083

CrossRef Full Text | Google Scholar

Bloice, M. D., Roth, P. M., and Holzinger, A. (2019). Biomedical image augmentation using augmentor. Bioinformatics 35, 4522–4524. doi: 10.1093/bioinformatics/btz259

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., et al. (2020). “Language models are few-shot learners,” in Advances in Neural Information Processing Systems eds H. Larochelle, M. Ranzato, R. Hadsell, M. Balcan, and H. Lin. Available online at: https://proceedings.neurips.cc/paper/2020/hash/1457c0d6bfcb4967418bfb8ac142f64a-Abstract.html

Google Scholar

Chan, T. F., and Vese, L. A. (2001). Active contours without edges. IEEE Trans. Image Process. 10, 266–277. doi: 10.1109/83.902291

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L.-C., Papandreou, G., Kokkinos, I., Murphy, K., and Yuille, A. L. (2017). Deeplab: semantic image segmentation with deep convolutional nets, Atrous convolution, and fully connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 40, 834–848. doi: 10.1109/TPAMI.2017.2699184

PubMed Abstract | CrossRef Full Text | Google Scholar

Demner-Fushman, D., Kohli, M. D., Rosenman, M. B., Shooshan, S. E., Rodriguez, L., Antani, S., et al. (2016). Preparing a collection of radiology examinations for distribution and retrieval. J. Am. Med. Inform. Assoc. 23, 304–310. doi: 10.1093/jamia/ocv080

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, J., Dong, W., Socher, R., Li, L., and Kai Li, Li Fei-Fei (2009). “Imagenet: a large-scale hierarchical image database,” in 2009 IEEE Conference on Computer Vision and Pattern Recognition (Miami, FL: IEEE Computer Society), 248–255. doi: 10.1109/CVPR.2009.5206848

CrossRef Full Text | Google Scholar

Everingham, M., Van Gool, L., Williams, C. K. I., Winn, J., and Zisserman, A. (2010). The pascal visual object classes (VOC) challenge. Int. J. Comput. Vis. 88, 303–338. doi: 10.1007/s11263-009-0275-4

CrossRef Full Text | Google Scholar

Fan, D.-P., Li, T., Lin, Z., Ji, G.-P., Zhang, D., Cheng, M.-M., et al. (2021a). Re-thinking co-salient object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2021.3060412. doi: 10.1109/TPAMI.2021.3060412

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, M., Lai, S., Huang, J., Wei, X., Chai, Z., Luo, J., et al. (2021b). “Rethinking bisenet for real-time semantic segmentation,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (Computer Vision Foundation/IEEE), 9716–9725. doi: 10.1109/CVPR46437.2021.00959

CrossRef Full Text | Google Scholar

Gu, Z., Cheng, J., Fu, H., Zhou, K., Hao, H., Zhao, Y., et al. (2019). CE-NET: context encoder network for 2d medical image segmentation. IEEE Trans. Med. Imag. 38, 2281–2292. doi: 10.1109/TMI.2019.2903562

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, K., Cao, R., Kui, X., Ma, J., Kang, J., and Chi, T. (2019). LCC: towards efficient label completion and correction for supervised medical image learning in smart diagnosis. J. Netw. Comput. Appl. 133, 51–59. doi: 10.1016/j.jnca.2019.02.009

CrossRef Full Text | Google Scholar

Hu, X., Fu, C.-W., Zhu, L., Qin, J., and Heng, P.-A. (2019). Direction-aware spatial context features for shadow detection and removal. IEEE Trans. Pattern Anal. Mach. Intell. 42, 2795–2808. doi: 10.1109/TPAMI.2019.2919616

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Z., Wei, Y., Wang, X., Liu, W., Huang, T. S., and Shi, H. (2021). AlignSeg: feature-aligned segmentation networks. IEEE Trans. Pattern Anal. Mach. Intell. 44, 550–557. doi: 10.1109/TPAMI.2021.3062772

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, A. E., Pollard, T. J., Greenbaum, N. R., Lungren, M. P., Deng, C.-y., Peng, Y., et al. (2019). MIMIC-CXR-JPG, a large publicly available database of labeled chest radiographs. arXiv preprint arXiv:1901.07042. doi: 10.1038/s41597-019-0322-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Jouppi, N. P., Young, C., Patil, N., Patterson, D., Agrawal, G., Bajwa, R., et al. (2017). “In-datacenter performance analysis of a tensor processing unit,” in Proceedings of the 44th Annual International Symposium on Computer Architecture (Toronto, ON: ACM), 1–12. doi: 10.1145/3140659.3080246

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. (2015). “Adam (2014), a method for stochastic optimization,” in Proceedings of the 3rd International Conference on Learning Representations, Vol. 1412 (San Diego, CA). Available online at: http://arxiv.org/abs/1412.6980

Google Scholar

Krähenbühl, P., and Koltun, V. (2011). Efficient inference in fully connected CRFs with Gaussian edge potentials. Proceedings of the 24th International Conference on Neural Information Processing Systems (Red Hook, NY: Curran Associates Inc). 24, 109–117. doi: 10.5555/2986459.2986472

CrossRef Full Text | Google Scholar

Kremer, J., Sha, F., and Igel, C. (2018). “Robust active label correction,” in International Conference on Artificial Intelligence and Statistics eds A. J. Storkey, F. Pérez-Cruz (PMLR), 84, 308–316.

PubMed Abstract | Google Scholar

Li, J., Socher, R., and Hoi, S. C. (2020). “Dividemix: learning with noisy labels as semi-supervised learning,” in Proceedings of the 8th International Conference on Learning Representations. Available online at: https://openreview.net/forum?id=HJgExaVtwr

Google Scholar

Li, S.-Y., Shi, Y., Huang, S.-J., and Chen, S. (2022). Improving deep label noise learning with dual active label correction. Mach. Learn. 111, 1103–1124. doi: 10.1007/s10994-021-06081-9

CrossRef Full Text | Google Scholar

Lin, Z., Wei, D., Petkova, M. D., Wu, Y., Ahmed, Z., Zou, S., et al. (2021). “NUCMM dataset: 3d neuronal nuclei instance segmentation at sub-cubic millimeter scale,” in International Conference on Medical Image Computing and Computer-Assisted Intervention eds M. Bruijne, P. C. Cattin, S. Cotin, N. Padoy, S. Speidel, Y. Zheng, et al.(Springer) 12901, 164–174. doi: 10.1007/978-3-030-87193-2_16

CrossRef Full Text | Google Scholar

Liu, S., Niles-Weed, J., Razavian, N., and Fernandez-Granda, C. (2020). “Early-learning regularization prevents memorization of noisy labels,” in Advances in Neural Information Processing Systems, Vol. 33. Available online at: https://proceedings.neurips.cc/paper/2020/hash/ea89621bee7c88b2c5be6681c8ef4906-Abstract.html

Google Scholar

Liu, Y., Cheng, M., Hu, X., Bian, J., Zhang, L., Bai, X., et al. (2019). Richer convolutional features for edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 41, 1939–1946. doi: 10.1109/TPAMI.2018.2878849

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, X., Wang, W., Shen, J., Crandall, D., and Van Gool, L. (2021). Segmenting objects from relational visual data. IEEE Trans. Pattern Anal. Mach. Intell. 2021:3115815. doi: 10.1109/TPAMI.2021.3115815

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Z., Carneiro, G., and Bradley, A. P. (2015). An improved joint optimization of multiple level set functions for the segmentation of overlapping cervical cells. IEEE Trans. Image Process. 24, 1261–1272. doi: 10.1109/TIP.2015.2389619

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Z., Carneiro, G., Bradley, A. P., Ushizima, D., Nosrati, M. S., Bianchi, A. G., et al. (2016). Evaluation of three algorithms for the segmentation of overlapping cervical cells. IEEE J. Biomed. Health Informatics 21, 441–450. doi: 10.1109/JBHI.2016.2519686

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, J., Zhang, Y., Gu, S., Zhu, C., Ge, C., Zhang, Y., et al. (2021). AbdomenCT-1K: is abdominal organ segmentation a solved problem. IEEE Trans. Pattern Anal. Mach. Intell. 2021:3100536. doi: 10.1109/TPAMI.2021.3100536

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, T., Wang, Q., Zhang, H., and Zuo, W. (2022). Delving deeper into pixel prior for box-supervised semantic segmentation. IEEE Trans. Image Process. 31, 1406–1417. doi: 10.1109/TIP.2022.3141878

PubMed Abstract | CrossRef Full Text | Google Scholar

McCrary, J. (2008). Manipulation of the running variable in the regression discontinuity design: a density test. J. Econ. 142, 698–714. doi: 10.1016/j.jeconom.2007.05.005

CrossRef Full Text | Google Scholar

Motamedi, M., Sakharnykh, N., and Kaldewey, T. (2021). A data-centric approach for training deep neural networks with less data. arXiv preprint arXiv:2110.03613.

Google Scholar

Nazeri, K., Ng, E., Joseph, T., Qureshi, F., and Ebrahimi, M. (2019). “Edgeconnect: structure guided image inpainting using edge prediction,” in Proceedings of the IEEE/CVF International Conference on Computer Vision Workshop (IEEE), 3265–3274. doi: 10.1109/ICCVW.2019.00408

CrossRef Full Text | Google Scholar

Ng, A., Laird, D., and He, L. (2021). Data-Centric AI Competition. Available online at: https://https-deeplearning-ai.github.io/data-centric-comp/ (accessed August, 2021).

Nicholson, B., Sheng, V. S., and Zhang, J. (2016). Label noise correction and application in crowdsourcing. Expert Syst. Appl. 66, 149–162. doi: 10.1016/j.eswa.2016.09.003

CrossRef Full Text | Google Scholar

Nicholson, B., Zhang, J., Sheng, V. S., and Wang, Z. (2015). “Label noise correction methods,” in IEEE International Conference on Data Science and Advanced Analytics, 1–9. doi: 10.1109/DSAA.2015.7344791

CrossRef Full Text | Google Scholar

Northcutt, C. G., Athalye, A., and Mueller, J. (2021). Pervasive label errors in test sets destabilize machine learning benchmarks. arXiv preprint arXiv:2103.14749.

Google Scholar

Phoulady, H. A., Goldgof, D., Hall, L. O., and Mouton, P. R. (2017). A framework for nucleus and overlapping cytoplasm segmentation in cervical cytology extended depth of field and volume images. Comput. Med. Imaging Graph. 59, 38–49. doi: 10.1016/j.compmedimag.2017.06.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Poma, X. S., Riba, E., and Sappa, A. (2020). “Dense extreme inception network: towards a robust CNN model for edge detection,” in Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (Snowmass Village, CO: IEEE), 1923–1932.

Google Scholar

Radford, A., Wu, J., Child, R., Luan, D., Amodei, D., Sutskever, I., et al. (2019). Language models are unsupervised multitask learners. OpenAI blog. 1, 8–9.

Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., et al. (2020). Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res. 21, 1–67. Available online at: http://jmlr.org/papers/v21/20-074.html

Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. (2015). “U-net: convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention, eds N. Navab, J. Hornegger, W. M. Wells III, A. F. Frangi (Springer) 234–241. doi: 10.1007/978-3-319-24574-4_28

CrossRef Full Text | Google Scholar

Saha, R., Bajger, M., and Lee, G. (2019). “SRM superpixel merging framework for precise segmentation of cervical nucleus,” in Digital Image Computing: Techniques and Applications (IEEE), 1–8. doi: 10.1109/DICTA47822.2019.8945887

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, Y., Qin, J., Lei, B., He, S., and Choi, K.-S. (2019). “Joint shape matching for overlapping cytoplasm segmentation in cervical smear images,” in IEEE 16th International Symposium on Biomedical Imaging (IEEE), 191–194. doi: 10.1109/ISBI.2019.8759259

CrossRef Full Text | Google Scholar

Song, Y., Tan, E.-L., Jiang, X., Cheng, J.-Z., Ni, D., Chen, S., et al. (2016). Accurate cervical cell segmentation from overlapping clumps in PAP smear images. IEEE Trans. Med. Imaging 36, 288–300. doi: 10.1109/TMI.2016.2606380

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, Y., Zhu, L., Lei, B., Sheng, B., Dou, Q., Qin, J., et al. (2020). Constrained multi-shape evolution for overlapping cytoplasm segmentation. arXiv preprint arXiv:2004.03892.

Google Scholar

Su, R., Zhang, D., Liu, J., and Cheng, C. (2021a). MSU-NET: multi-scale U-Net for 2d medical image segmentation. Front. Genet. 12:140. doi: 10.3389/fgene.2021.639930

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, Z., Liu, W., Yu, Z., Hu, D., Liao, Q., Tian, Q., et al. (2021b). “Pixel difference networks for efficient edge detection,” in Proceedings of the IEEE/CVF International Conference on Computer Vision (Montreal, QC: IEEE), 5117–5127. doi: 10.1109/ICCV48922.2021.00507

CrossRef Full Text | Google Scholar

Sun, C., Shrivastava, A., Singh, S., and Gupta, A. (2017). “Revisiting unreasonable effectiveness of data in deep learning era,” in Proceedings of the IEEE International Conference on Computer Vision (Venice: IEEE Computer Society), 843–852. doi: 10.1109/ICCV.2017.97

CrossRef Full Text | Google Scholar

Sun, G., Wang, W., Dai, J., and Van Gool, L. (2020). “Mining cross-image semantics for weakly supervised semantic segmentation,” in European Conference on Computer Vision eds A. Vedaldi, Horst . Bischof, T. Brox, J. Frahm (Glasgow: Springer), 347–365. doi: 10.1007/978-3-030-58536-5_21

PubMed Abstract | CrossRef Full Text | Google Scholar

Sutton, C.McCallum, A., et al. (2012). An introduction to conditional random fields. Found. Trends Mach. Learn. 4, 267–373. doi: 10.1561/2200000013

CrossRef Full Text | Google Scholar

Tareef, A., Song, Y., Cai, W., Huang, H., Chang, H., Wang, Y., et al. (2017). Automatic segmentation of overlapping cervical smear cells based on local distinctive features and guided shape deformation. Neurocomputing 221, 94–107. doi: 10.1016/j.neucom.2016.09.070

CrossRef Full Text | Google Scholar

Tareef, A., Song, Y., Huang, H., Feng, D., Chen, M., Wang, Y., et al. (2018). Multi-pass fast watershed for accurate segmentation of overlapping cervical cells. IEEE Trans. Med. Imaging 37, 2044–2059. doi: 10.1109/TMI.2018.2815013

PubMed Abstract | CrossRef Full Text | Google Scholar

Wada, K. (2016). Labelme: Image Polygonal Annotation with Python. doi: 10.5281/zenodo.5711226

CrossRef Full Text

Wan, T., Xu, S., Sang, C., Jin, Y., and Qin, Z. (2019). Accurate segmentation of overlapping cells in cervical cytology with deep convolutional neural networks. Neurocomputing 365, 157–170. doi: 10.1016/j.neucom.2019.06.086

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Hua, Y., Kodirov, E., Clifton, D. A., and Robertson, N. M. (2021). “ProSelflC: Progressive self label correction for training robust deep neural networks,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (Computer Vision Foundation/IEEE), 752–761. doi: 10.1109/CVPR46437.2021.00081

CrossRef Full Text | Google Scholar

Wei, D., Lee, K., Li, H., Lu, R., Bae, J. A., Liu, Z., et al. (2021). “AxonEM dataset: 3d axon instance segmentation of brain cortical regions,” in International Conference on Medical Image Computing and Computer-Assisted Intervention eds M. Bruijne, P. C. Cattin, S. Cotin, N. Padoy, S. Speidel, Y. Zheng, et al. (Strasbourg: Springer), 175–185. doi: 10.1007/978-3-030-87193-2_17

CrossRef Full Text | Google Scholar

Wibisono, J. K., and Hang, H.-M. (2020). Fined: Fast inference network for edge detection. arXiv preprint arXiv:2012.08392. doi: 10.1109/ICME51207.2021.9428230

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, C., Liu, D., Wang, L., Li, Y., Chen, X., Luo, R., et al. (2019). “DCCL: a benchmark for cervical cytology analysis,” in International Workshop on Machine Learning in Medical Imaging eds H. Suk, M. Liu, P. Yan, C. Lian (Shenzhen: Springer), 63–72. doi: 10.1007/978-3-030-32692-0_8

CrossRef Full Text | Google Scholar

Zhang, H., Zhu, H., and Ling, X. (2020). Polar coordinate sampling-based segmentation of overlapping cervical cells using attention u-net and random walk. Neurocomputing 383, 212–223. doi: 10.1016/j.neucom.2019.12.036

CrossRef Full Text | Google Scholar

Zhang, Z., Peng, Q., Fu, S., Wang, W., Cheung, Y.-M., Zhao, Y., et al. (2022). A componentwise approach to weakly supervised semantic segmentation using dual-feedback network. IEEE Trans. Neural Netw. Learn. Syst. 1–14. doi: 10.1109/TNNLS.2022.3144194

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, J., Yan, S., and Feng, J. (2022). Towards age-invariant face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 44, 474–487. doi: 10.1109/TPAMI.2020.3011426

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, G., Awadallah, A. H., and Dumais, S. (2021). “Meta label correction for noisy label learning,” in Proceedings of the 35th AAAI Conference on Artificial Intelligence (AAAI Press). 11053–11061.

Google Scholar

Zhou, B., Lapedriza, A., Khosla, A., Oliva, A., and Torralba, A. (2017). Places: a 10 million image database for scene recognition. IEEE Trans. Pattern Anal. Mach. Intell. 40, 1452–1464. doi: 10.1109/TPAMI.2017.2723009

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Z., Siddiquee, M. M. R., Tajbakhsh, N., and Liang, J. (2019). UNet++: Redesigning skip connections to exploit multiscale features in image segmentation. IEEE Trans. Med. Imaging 39, 1856–1867. doi: 10.1109/TMI.2019.2959609

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, X., Liu, G., Su, B., and Nees, J. P. (2019). “Dynamic label correction for distant supervision relation extraction via semantic similarity,” in CCF International Conference on Natural Language Processing and Chinese Computing eds J. Tang, M. Kan, D. Zhao, S. Li, H. Zan (Dunhuang: Springer), 16–27. doi: 10.1007/978-3-030-32236-6_2

CrossRef Full Text | Google Scholar