Fireworks explosion boosted Harris Hawks optimization for numerical optimization: Case of classifying the severity of COVID-19

Harris Hawks optimization (HHO) is a swarm optimization approach capable of handling a broad range of optimization problems. HHO, on the other hand, is commonly plagued by inadequate exploitation and a sluggish rate of convergence for certain numerical optimization. This study combines the fireworks algorithm's explosion search mechanism into HHO and proposes a framework for fireworks explosion-based HHo to address this issue (FWHHO). More specifically, the proposed FWHHO structure is comprised of two search phases: harris hawk search and fireworks explosion search. A search for fireworks explosion is done to identify locations where superior hawk solutions may be developed. On the CEC2014 benchmark functions, the FWHHO approach outperforms the most advanced algorithms currently available. Moreover, the new FWHHO framework is compared to four existing HHO and fireworks algorithms, and the experimental results suggest that FWHHO significantly outperforms existing HHO and fireworks algorithms. Finally, the proposed FWHHO is employed to evolve a kernel extreme learning machine for diagnosing COVID-19 utilizing biochemical indices. The statistical results suggest that the proposed FWHHO can discriminate and classify the severity of COVID-19, implying that it may be a computer-aided approach capable of providing adequate early warning for COVID-19 therapy and diagnosis.

1. Introduction

Numerical optimization is currently a hot topic for research in both science and technology. It is becoming increasingly difficult to deal with these issues with discontinuous, non-convex, and non-differentiable properties (Cui et al., 2017). In many cases, traditional gradient-based methods are ineffective because of their stringent use conditions and local convergence. As a result of these and other natural phenomena, many meta-heuristic algorithms (MHAs) have been developed in the last few decades by researchers around the world. Genetic algorithm (GA) (Mathew, 2012), differential evolution (DE) (Price, 2013), particle swarm optimization (PSO) (Poli et al., 2007), ant colony optimization (Paniri et al., 2020), and harris hawks optimization (HHO) (Heidari et al., 2019) are some of the most popular MHAs. For numerical optimization problems, these algorithms have proven to be extremely effective.

HHO (Heidari et al., 2019) is a meta-heuristic algorithm with population theory that mimics harris hawks' intelligent hunting behavior. HHO is proposed to assault the rabbit in four distinct ways: soft besiege, hard besiege, soft besiege with progressive rapid dives, and hard besiege with progressive rapid dives. Compared to other optimizers, HHO has a small number of parameters and a high capacity for exploration. Due to its simplicity, ease of implementation, and performance, HHO has garnered considerable attention and has been applied to a variety of real-world optimization problems, such as job-shop scheduling (Li C. et al., 2021), internet of vehicles application (Dehkordi et al., 2021), engineering optimization (Kamboj et al., 2020), and estimation of photovoltaic parameters (Chen et al., 2020b; Jiao et al., 2020). Although HHO has demonstrated competitive performance on a variety of problems when compared to other algorithms, such as PSO and GA, it still has some shortcomings in terms of exploitation (Alabool et al., 2021). However, an efficient search strategy should strike a good balance between global exploration and local exploitation, favoring exploration at first and turning to exploitation as the iteration counts increase. Thus, the development of a new search strategies to improve HHO's exploration–exploitation balance is crucial for increasing its performance on difficult numerical optimization tasks.

The fireworks algorithm (FWA) was developed by Tan and Zhu (2010) as a novel MHA technique. The fireworks explosion search is FWA's most productive operator, as it generates new individuals in the vicinity of several promising individuals that have been evenly distributed. The old will be replaced by new, more fitting individuals. FWA simulates a global search by bursting fireworks. The method possesses (1) an explosive search pattern and (2) a framework for the interaction of many (sub)populations. Since its conception, the FWA has drawn considerable research and has been widely applied to real-world optimization, most notably as a minimalist global optimizer (Li and Tan, 2018), multimodal function optimization (Li and Tan, 2017), and flowshop scheduling (He et al., 2019).

In this article, we propose a framework for fireworks explosion-based Harris Hawks optimization (FWHHO), which incorporates fireworks explosion search into the HHO algorithm. To be more specific, the FWHHO framework recommends two stages of search: one for hawks and another for fireworks explosions. After completing the four hawks' search phases soft besiege, hard besiege, soft besiege with progressive rapid dives, and hard besiege with progressive rapid dives, exploitation of prospective places is accomplished by the use of a fireworks explosion search. From populations, some individuals with a widespread are picked, and new individuals are generated in their vicinity. Experiments on CEC2014 benchmark functions reveal that using fireworks explosion search to optimize HHO algorithms can greatly enhance their performance. The FWHHO algorithm outperforms state-of-the-art meta-heuristic algorithms on the CEC2014 benchmark functions. Furthermore, the proposed FWHHO framework is applied to four existing HHO algorithms and fireworks algorithms, and the experimental results demonstrate that FWHHO shows the obvious property over existing HHO algorithms and fireworks algorithms. Finally, the proposed FWHHO is used to evolve a kernel extreme learning machine for the purpose of diagnosing COVID-19 using biochemical indexes. The main contributions of this study are as follows:

• The fireworks explosion-based Harris Hawks optimization is proposed in this article (FWHHO), and fireworks explosion operators are integrated into the original HHO.

• The FWHHO's performance is validated using CEC2014 benchmarks, and its capabilities clearly outperforms the original HHO.

• The FWHHO method considerably outperforms state-of-the-art techniques, existing HHO algorithms, and a variety of fireworks algorithms.

• The FWHHO can evolve a kernel extreme learning machine for the purpose of diagnosing COVID-19 using biochemical indexes successfully.

The following sections describe the structure of this article. Section 2 summarizes HHO algorithm research. Section 3 contains a detailed discussion of the FWHHO algorithms. Section 4 gives the details of the experimental designs. The results of the experiments are analyzed and discussed in Section 5. Section 6 includes the conclusion and future work.

2. Literature survey

Numerous improved HHO algorithms have been developed in recent years to improve performance. These algorithms can be classified into two categories: modification of HHO with new search equations and hybrid with other metaheuristic algorithms.

(1) Modification of HHO with new search operators: The search operators in HHO are used to direct the search and develop new solutions. Numerous new search operators have been developed to enhance the search capacity of the HHO. Song et al. (2021) proposed a new GCHHO with Gaussian mutation, and a dimension-decision strategy that was used in the cuckoo. The results show that GCHHO is very good at getting better results. A hybrid QRHHO algorithm was created by Fan et al. (2020). Fan et al. combined the exploration of HHO with the use of a quasi-reflection-based learning mechanism (QRBL). Gupta et al. (2020) suggested an opposition-based learning-based HHO (m-HHO), in which OBL improves the search efficiency of HHO and alleviates the problems of a standstill at suboptimal solutions and premature convergence. Zheng-Ming et al. (2019) developed a more efficient HHO algorithm based on the tent map. The results indicate that the tent map has the potential to enhance the HHO algorithm's capabilities. Qu et al. (2020) utilized information sharing for HHO and information from the cooperative foraging area and collaborators' location areas, so establishing that information exchange is shared. Ridha et al. (2020) introduced a boosted HHO (BHHO) algorithm with random exploratory steps and a strong mutation scheme, in which methods not only accelerate the convergence rate of the BHHO algorithm but also aid it in scanning additional parts of the search basins. Devarapalli and Bhattacharyya (2019) proposed a modified HHO algorithm with a squared decay rate (MHHOS) as a damping controller for power system oscillations. Yousri et al. (2020) designed a modified HHO with the biological features of the rabbit (MHHO) for optimal photovoltaic array reconfiguration.

(2) Hybridization with other algorithms: Hybridizing HHO with other algorithms enables the advantages of two algorithms to be combined and their shortcomings overcome. This is another method for enhancing HHO's performance. Kamboj et al. (2020) suggested a hybrid algorithm called hHHO-SCA using a sine cosine algorithm, in which the SCA is employed to keep the exploration and exploitation phases balanced. Dhawale and Kamboj (2020) proposed a hybridized HHO with enhanced gray wolf optimization (IGWO) to boost population diversity and convergence. Zhong et al. (2020) hybridized HHO with the first-order reliability (FORM), and the HHO-FORM method was developed to extract the global optimal solutions for problems with high dimensions. Yıldız et al. (2019) proposed the hybridization HHO with Nelder-Mead called H-HHONM, in which the process parameters in milling operations are successfully optimized. A hybrid algorithm, termed hybrid HHO with simulated annealing algorithm (HHOSA), was introduced by Kurtuluş et al. (2020) to accelerate the convergence speed. SA is added into the hawks' phase to increase the convergence pace of the process. Fu et al. (2020a) proposed the hybridization HHO with a mutation sine cosine algorithm (MSCA) to diagnose the faults in rolling bearings. Aiming at accelerating HHO's exploitation, Fu et al. (2020b) proposed the hybridization HHO with mutation-based GWO (MHHOGWO), in which mutation-based GWO can improve the property of HHO. Bao et al. (2019) presented a hybrid HHO (HHO-DE) with a differential evolution algorithm (DE), where the DE is used to augment the required global and local search capabilities. Abd Elaziz et al. (2020) proposed a hybrid HHO (HHOSSA) with the salp swarm method (SSA) for picture segmentation issues to boost population diversity and improve the convergence rate. An enhanced hybrid version of fireworks method and HHO together with dynamic competition idea has been proposed in Li W. et al. (2021).

Although a large number of research work has paid attention to the HHO, some room for improvement still exists, especially when the algorithm is used to solve some new application scenarios. On the one hand, just like the no free lunch (Wolpert and Macready, 1997) that no one universal algorithm can solve all existing optimization problems, which demonstrates that no one can build an all-time-best-performing algorithm capable of solving all optimization problems. This means that while some algorithms excel at solving a subset of problems, they cannot guarantee the success of all optimization tasks involving diverse or complex scenes. Addressing this mindset, new optimization approaches or modified versions of existing techniques should be provided in the future to tackle subgroups of challenges in many disciplines. In addition, HHO is frequently plagued by inadequate exploitation and delayed convergence (Alabool et al., 2021), and the possibility of local optimal stagnation also exists for some multimodal or complex numerical optimization tasks. In this article, we propose a framework for fireworks explosion-based Harris Hawks optimization (FWHHO), which incorporates fireworks explosion search into the HHO algorithm for improving its performance on complex optimization problems. To the best of our knowledge, fireworks explosion is introduced into HHO for the first time in all the literature.

3. Proposed FWHHO algorithm

3.1. Basic HHO

Heidari et al. (2019) created the Harris Hawks optimization (HHO), a swarm-based optimization technique. HHO's primary objective is to imitate hawk's team coordination and prey escape in nature to develop answers to the single-objective problem. The HHO model consisted of three major stages: the exploration phase, the transition from exploring to exploiting, and the exploitation phase. These three stages are explained in the next few sections.

3.1.1. Execution exploration

In this part, hawks detect prey in exploring by Equation 1; first, a population X_i (i = 1, 2, 3, 4…N) is randomly generated, where N is the number of hawks. When q ≥ 0.5 (a random value in [0, 1]), X_i(t + 1) = X_rand(t) − r₁|X_rand(t) − 2r₂X(t)|; X_i(t + 1) = (X_prey(t) − X_m(t) − Y), when q < 0.5. These two ways describe how hawks identify prey using a random perch and the true individual's position, respectively.

$\begin{array}{ll}{X}_i(t+1)=\{\begin{array}{ll}{X}_{\text{rand }}(t)-r_1\left|X_{\text{rand }}(t)-2r_{2}X(t)\right|,\hfill & q\ge 0.5\hfill \\ \left(X_{\text{prey }}(t)-X_{\text{m}}(t)-Y\right),\hfill & q<0.5\hfill \end{array}& (1)\end{array}$

Where X_i(t + 1) is the i^th new position of hawks in the (t + 1)^th iteration. X_rand(t) is the i^th position of hawks in the t^th iteration, r₁, r₂, r₃, and r₄ are all random values in [0, 1]. X_prey(t) is the current prey position in the t^th iteration. X_m(t) is calculated by Y = r₃(Lb + r₄(Ub − Lb)) and reflects the difference between variables' upper and lower limits.

3.1.2. Execution from exploration to exploitation

The escaping energy (E) controls the behavior of hawks from exploration to exploitation. The E is calculated by E = 2E₀(1 − (t/T)), where E₀ is the initial energy of the prey that randomly changes in (–1, 1). If |E| ≥ 1, the exploration phase will still execute; if |E| < 1, the exploitation phase is activated.

3.1.3. Execution exploitation

This phase seeks to simulate the surprise pounce (seven kills) behavior of the hawk on the examined target. Four chasing tactics are offered to do this, namely (1) soft besiege, (2) hard besiege, (3) soft besiege with progressive rapid dives, and (4) hard besiege with progressive rapid dives.

Soft besiege If |E| ≥ 0.5 and r ≥ 0.5, soft besiege is activated. This behavior is modeled as X_i(t + 1) = ΔX(t) − E|JX_prey(t) − X(t)|, where ΔX(t) is calculated as ΔX(t) = X_prey(t) − ∣X(t), ΔX(t) is the difference between the rabbit's position vector and its current location in the t^th iteration. U = 2(1 − r₅) strategy for evading prey that varied randomly in each repetition. r₅ is a random value in [0, 1].

Hard besiege Hard besiege is activated when |E| < 0.5 and r ≥ 0.5. This signifies that the victim is unable to flee successfully due to exhaustion. The new positions of hawks can be obtained by X(t + 1) = X_prey(t) − E|ΔX(t)|.

Soft besiege with progressive rapid dives Soft besiege with progressive rapid dives is activated when |E| ≥ 0.5 and r < 0.5. Hawks must then choose the optimal dive angle toward the prey in this situation by evaluating the new moves using Y = X_prey(t) − E|JX_prey(t) − X(t)|. If the comparison result does not result in determining the best dive toward the prey, team rapid dives based on the levy flight LF are performed to improve the exploitation capacity as modeled by Z = Y + S× LF(D), where D is the number of dimensions, S represents random vector by size 1 × D, and LF is calculated as follows:

$\begin{array}{ll}\mathrm{LF}(X)=\frac{u\times \sigma }{|v{|}^{\frac{1}{\beta }}},\sigma ={\left(\frac{\text{Γ}(1+\beta )\times \sin \left(\frac{\pi \beta }{2}\right)}{\text{Γ}\left(\frac{1+\beta }{2}\right)\times \beta \times 2^{\left(\frac{\beta -1}{2}\right)}}\right)}^{\frac{1}{\beta }}& (2)\end{array}$

Where u and v represent random values in [0, 1]. B is a constant with 1.5. Therefore, in this way, the new positions X(t + 1) of hawks can be calculated as X(t + 1) = Y if F(Y) < F(X(t)); X(t + 1) = Z if F(Z) < F(X(t)), where F is a fitness function for an optimization problem.

Hard besiege with progressive rapid dives In this strategy, prey had no energy to escape |E| < 0.5, and hawks constructed hard besiege r < 0.5. The new positions X(t + 1) of hawks can be calculated as X(t + 1) = Y if F(Y′) < F(X(t)), X(t + 1) = Z if F(Z′) < F(X(t)), where Y′ = X_prey(t) − E|JX_prey(t) − X_m(t)|, and Z′ = Y′ + S × LF(D). The distinction between this strategy and the previous one (soft besiege with progressive rapid dives) is that the hawks are striving to reduce the average distance between their location and their prey.

3.2. FWHHO framework

HHO is an excellent prospector but a poor exploitation candidate, although it has several local search mechanisms. However, an efficient search process demands a high level of exploration to discover prospective solutions inside the board search space, as well as a high level of exploitation to further increase the attributes of those solutions. Tan and Zhu (2010) recently presented a fireworks algorithm (FWA). The primary FWA operator is fireworks explosion search, which results in the creation of new persons in the vicinity of a few potential individuals. This operator can efficiently use data to find better solutions (Zhang et al., 2014). A novel hybrid FWHHO framework will be proposed in this research, which incorporates the fireworks explosion search. The FWHHO framework generates an initial population of N and then progresses through four search phases: (1) exploration, (2) transition from exploration to exploitation, (3) exploitation, and (4) fireworks explosion search. The first three phases are formed by HHO, whereas the fourth phase is formed by FWA.

3.2.1. Fireworks algorithm

Following three levels of hawk search, a small number of individuals are chosen to do the fireworks explosion search. The best candidate is chosen first, followed by those who are closest to the top candidate. The following formula is used to calculate the distance between two food individuals as $R(X_i)=\sum _{j\in K}d(X_i,X_j)=\sum _{j\in K}||X_i-X_j||$, where X_i and X_j(j ≠ i) are the different individuals, and K is the number of individuals. The chance of an individual being selected for a search for fireworks explosions is calculated by p(X_i) = R(X_i)/∑_j∈KR(X_j). When a spark explodes, several sparks emerge around it, generating new people. The operator also has two parameters to be determined. The number of sparks S_i is calculated as follows:

$\begin{array}{ll}{S}_i=\widehat{S}·\frac{Y_{\max }-f\left(X_i\right)+\epsilon }{{\displaystyle {\sum }_{i=1}^{ke}\left(Y_{\max }-f\left(X_i\right)\right)}}& (3)\end{array}$

Where the i^th individual generates the S_i sparks, the number of sparks is Ŝ, and the total number of people chosen for the explosion search is ke. Y_max is the best individual. f(X_i) is the i^th individual. The amount of sparks is restricted by an upper constraint S_max and a lower bound S_min in order to avoid overpowering impacts of pyrotechnics in desirable locations. If S_i < S_min, S_i = S_min, then S_i > S_max, S_i = S_max.

The second parameter is the amplitude of the generated sparks $A_i^g$. The magnitude of the explosion is dynamically adjusted. If g = 1, $A_i^g=A_i^1$, then $f(V_{\text{best}}^{\text{g}})\ge f(X_i^{\text{g}})$, $A_i^g=C_r{A}_i^{g-1}$, $A_i^g=C_a{A}_i^{g-1}$ when $f(V_{\text{best}}^{\text{g}})<f(X_i^{\text{g}})$, where $A_i^g$ denotes the amplitude of the i^th individual's explosion, while the diameter of the search zone is denoted by the first generation's amplitude. $V_{\text{best}}^g$ is the best spark created, while g denotes the generation count. If the objective function value of the best spark is greater than the value of the individual, the amplitude multiplies with a coefficient C_a > 1; otherwise, it multiplies with a coefficient C_a < 1.

In this case, the amplitude is too small to make more progress and should be increased; if a better solution is not found, it means that the amplitude is too long and should be cut down. The dynamic amplitude can be used to make more space around possible solutions.

3.2.2. Proposed FWHHO

The FWHHO is intended to overcome the inherent flaws of the original HHO through inefficient exploitation and slow convergence. The fireworks algorithm's explosive search mechanism is included in HHO in this research, along with a framework for fireworks explosion-based Harris Hawks optimization (FWHHO). More precisely, the suggested FWHHO structure is divided into two search stages: Harris Hawks and fireworks explosion. A search for fireworks explosions is conducted to identify suitable places for developing improved hawk solutions. To the best of our knowledge, this is the first time that the HHO is integrated with operators of fireworks explosions. In the proposed FWHHO, three sections are available for discussion. The first step is to carry out the initialization of the search population in the database. The second step is to complete the execution of the algorithm operators in the original HHO, and the third step is to complete the execution of the newly introduced operators generated from the fireworks explosion that was introduced earlier. Algorithm 1 presents the pseudocode for the FWHHO algorithm utilizing the basic HHO.

ALGORITHM 1

Algorithm 1. FWHHO.

4. Experimental designs

In this study, some experiments are executed to verify the proposed FWHHO, which is composed of a comparison between FWHHO and state-of-the-art algorithms, a comparison of FWHHO on existing HHO algorithms, a comparison between FWHHO and fireworks algorithms, and an application of FWHHO on machine learning evolution. For comparison between FWHHO and state-of-the-art algorithms, existing HHO algorithms, fireworks algorithms, and the CEC2014 benchmark functions (Liang et al., 2013) are used which has 30 functions including F1–F3 (unimodal functions), F4–F16 (simple multimodal functions), F17–F22 (hybrid functions), and F23–F30 (composition functions). The CEC2014 benchmark has the most typical and comprehensive test function and can effectively test the performance of the algorithm. The maximum number of function evaluations is 5*10⁴. To record the statistical data, each algorithm is run 30 times independently on each function. For the application of FWHHO on machine learning evolution, the key parameters and optimal subfeatures of the support vector machine on medical diagnosis. Take note that all tests are run on Windows Server 2018 R2 with MATLAB2020b on a Xeon CPU i5-2660 V3 (2.60 GHz) and 16 GB RAM.

5. Experimental and analytical results

5.1. Comparison between FWHHO and state-of-the-art algorithms

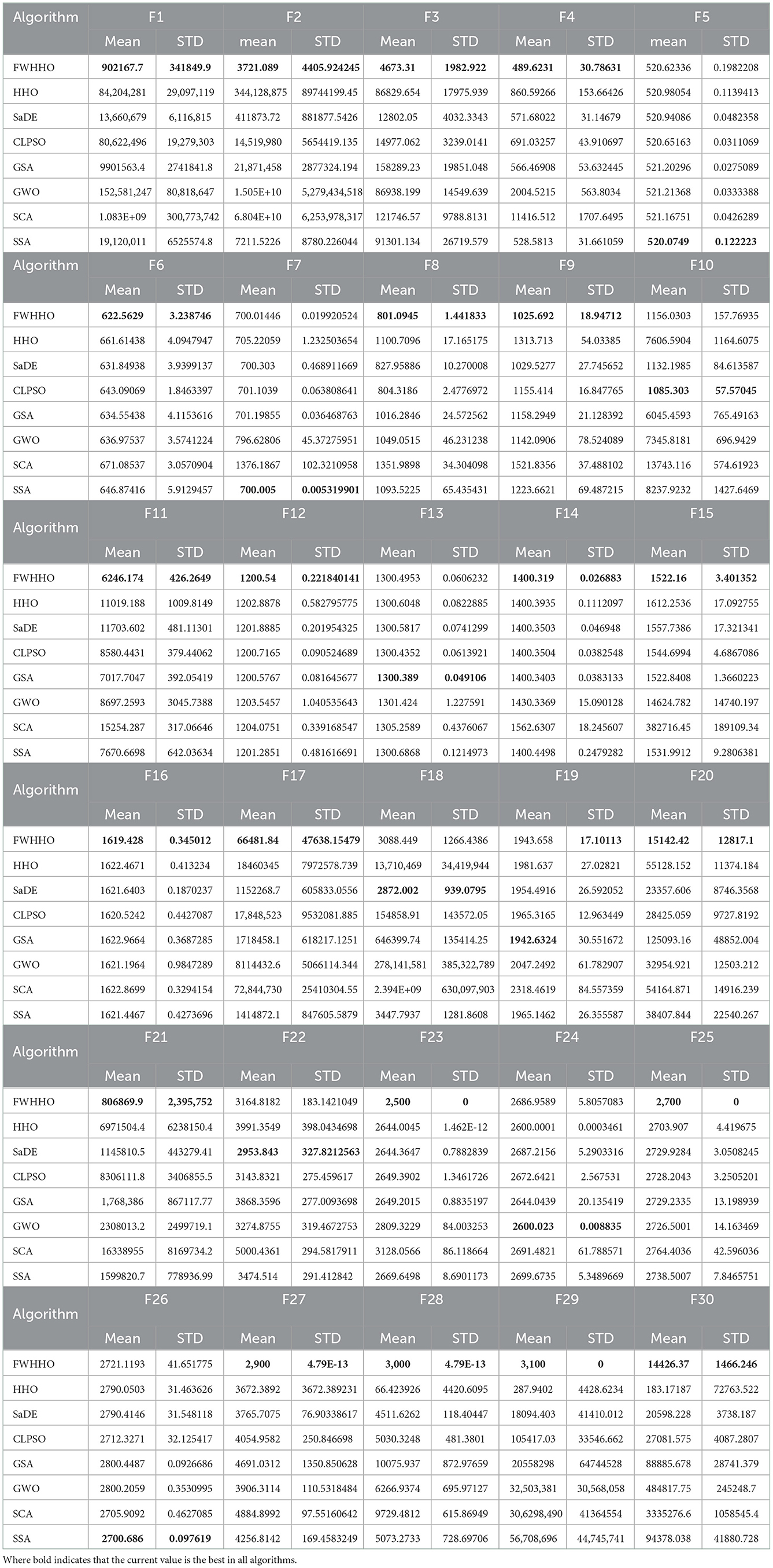
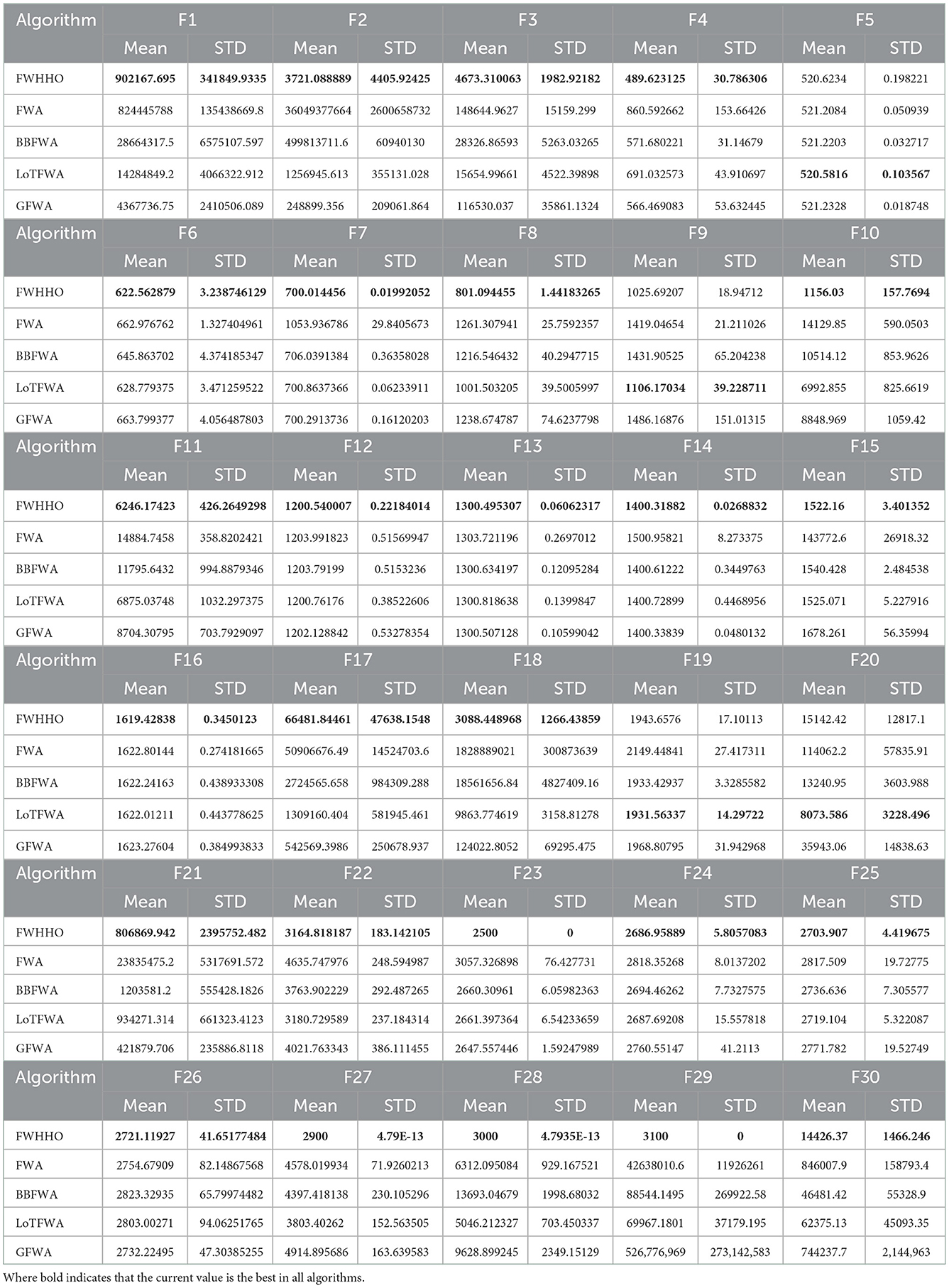
In this section, the proposed FWHHO is compared to several state-of-the-art algorithms on CEC 2014 benchmarks and each algorithm is carried out 30 times independently. These state-of-the-art algorithms are composed of original HHO (Heidari et al., 2019), self-adaptive differential evolution (SaDE) (Qin et al., 2008), comprehensive learning particle swarm optimization (CLPSO) (Liang et al., 2006), gravitational search algorithm (GSA) (Rashedi et al., 2009), gray wolf optimizer (GWO) (Mirjalili et al., 2014), sine cosine algorithm (SCA) (Mirjalili, 2016), and salp swarm algorithm (SSA) (Mirjalili et al., 2017). These algorithms' parameters have been set in accordance with the original article. As shown in Table 1, the mean and standard deviation (STD) values demonstrate the accuracy of the experimental findings.

TABLE 1

Table 1. Comparison of FWHHO and state-of-the-art algorithms.

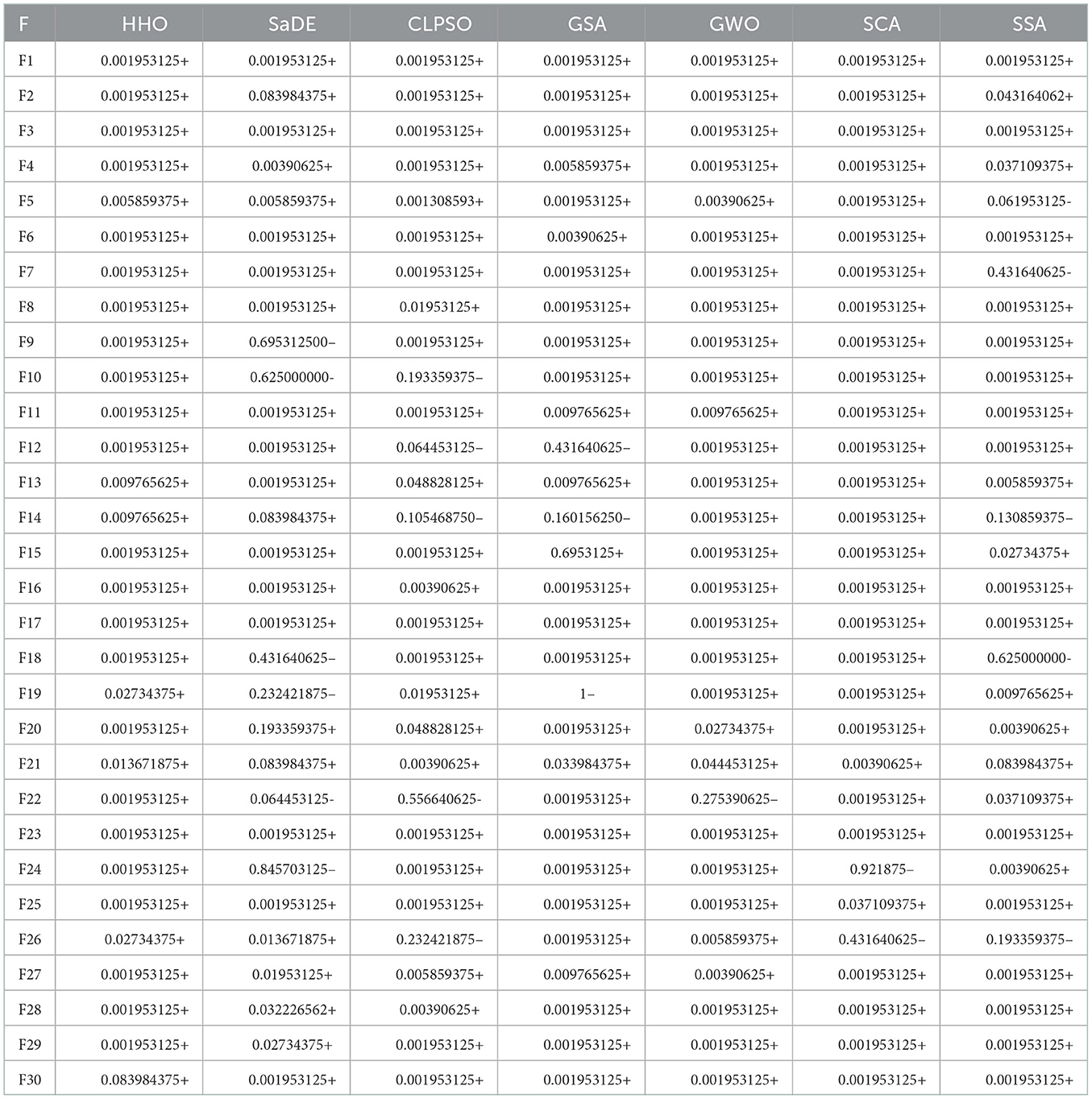
Even if it may not perform well in all circumstances, it can be seen that the proposed FWHHO has the best average value performance among most benchmarks. To establish how significant the gains were, the Wilcoxon sign rank test was also utilized. P < 0.05 show that FWHHO works better than the other optimizer. In this case, the gains are not statistically significant. Table 2 contains the calculated p-values. P > 0.05 are highlighted in Table 2, indicating that the difference is not statistically significant. The calculated p-values of FWHHO and other state-of-the-art algorithms on CEC2014 benchmarks are shown in Table 2. As shown in Table 2, most of the p < 0.05, demonstrating that FWHHO outperformed the original HHO and other state-of-the-art algorithms.

TABLE 2

Table 2. The calculated p-values for FWHHO vs. state-of-the-art algorithms.

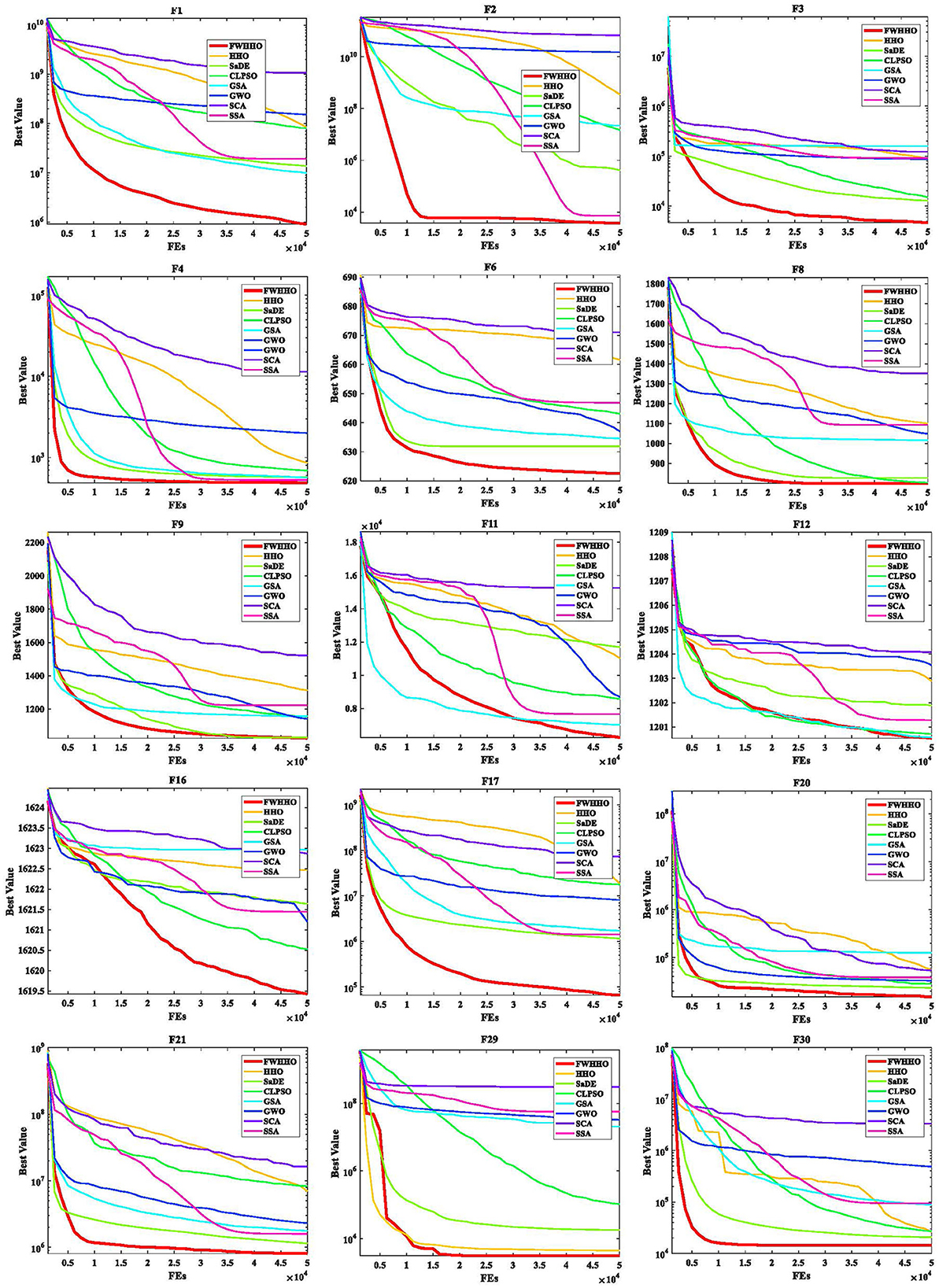
Additionally, Figure 1 illustrates the convergence curves of various algorithms for a selection of benchmarks. It can be observed that the presented FWHHO has a fast search ability of convergence on most benchmarks such as F2, F3, F4, F8 F20, and F30, to ensure that it achieves the best theoretical value in a short time and the apparent superiority to all other competitors in these benchmarks. Convergence can occur quickly during the early stages of algorithm execution, particularly for F4, F29, and F30. Although the convergence ability of F11, F12, and F16 are relatively weak in the early stages of algorithm execution, as the number of iterations rises, it can achieve quick convergence in the later stages. In a nutshell, it can be stated that the original HHO's properties can be significantly enhanced.

FIGURE 1

Figure 1. Convergence curves of FWHHO and state-of-the-art algorithms.

5.2. Comparison between FWHHO and existing HHO algorithms

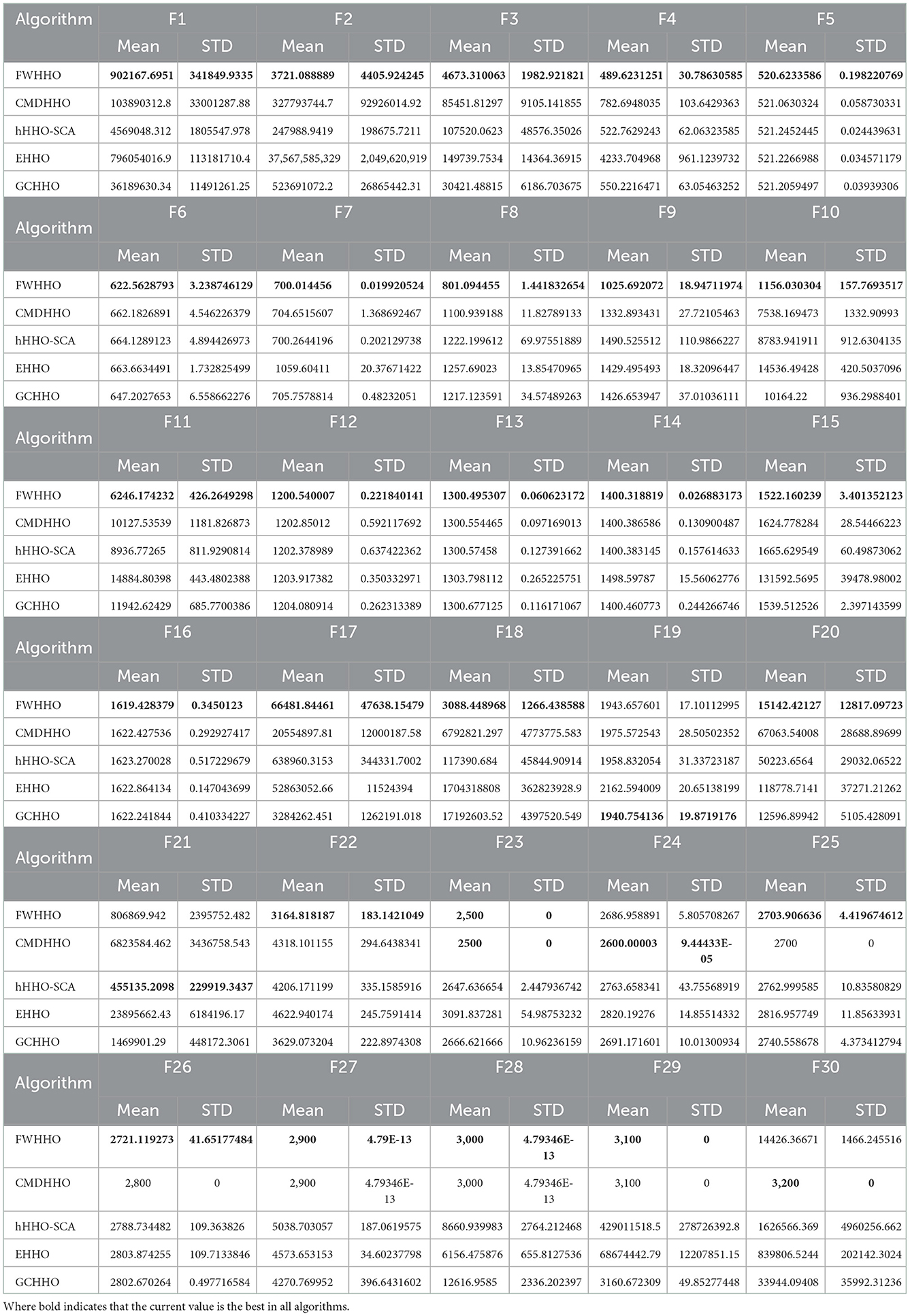
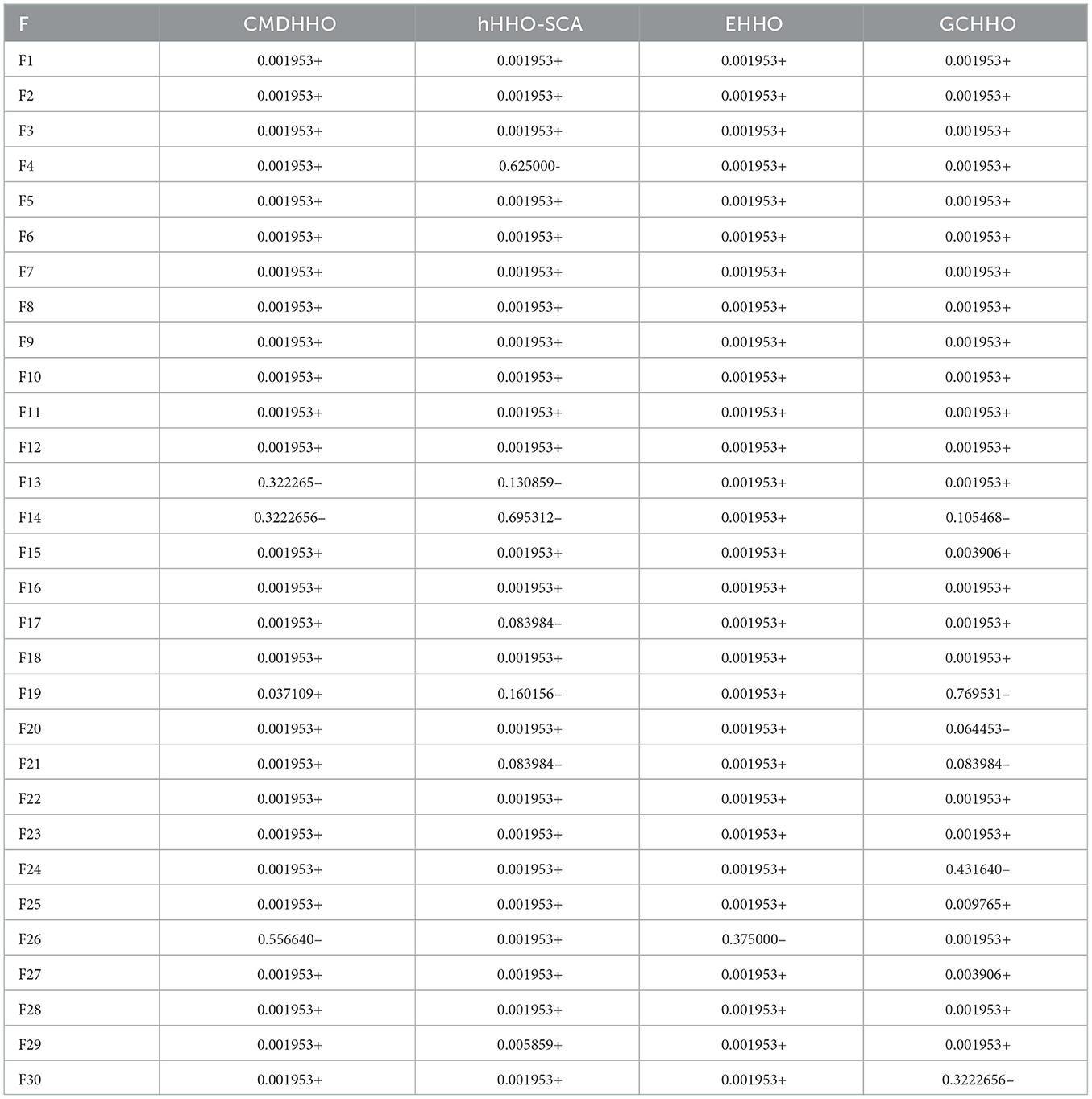
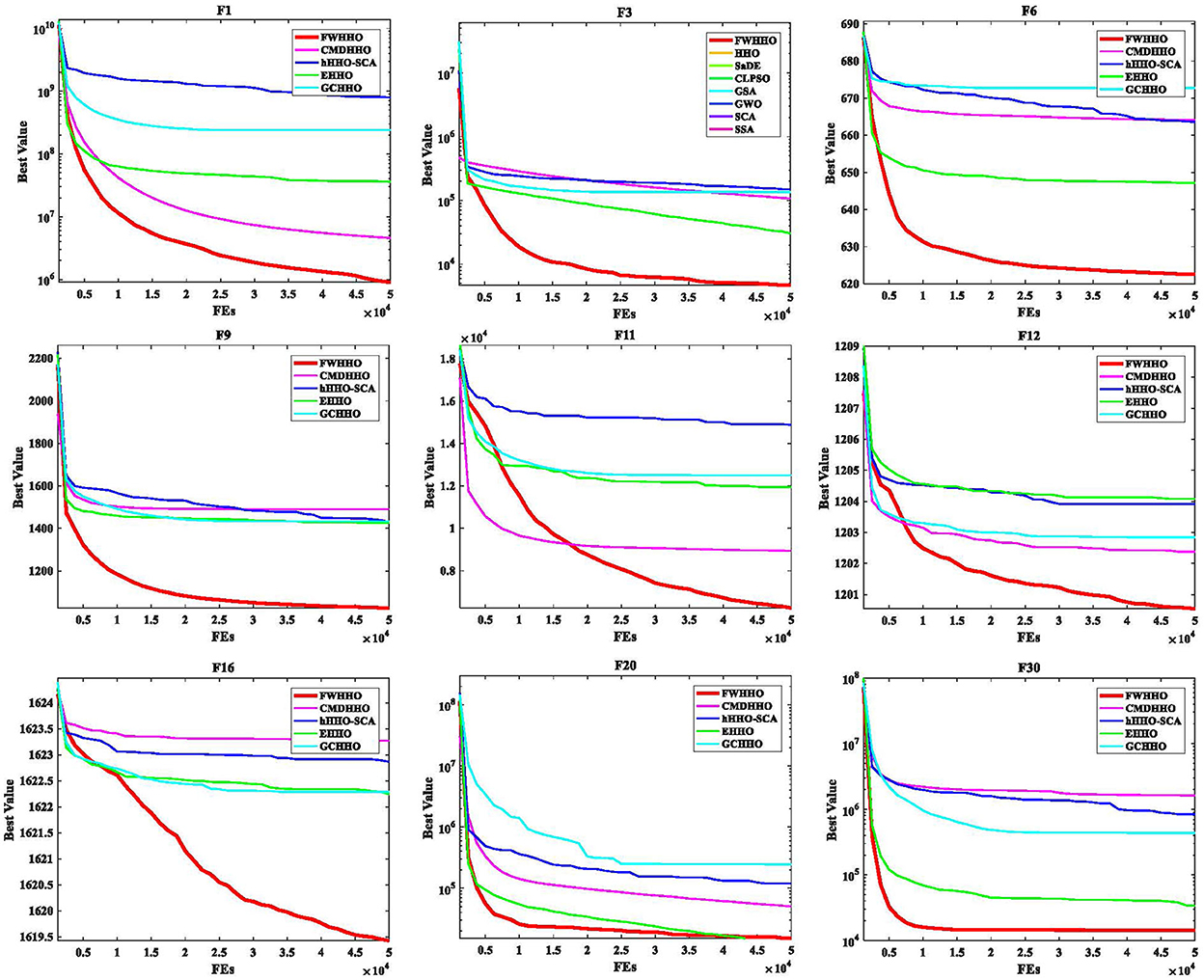
On the CEC2014 benchmarks, this section compares the proposed FWHHO and existing HHO algorithms. The existing HHO algorithms are composed of CMDHHO (enriched HHO with chaos strategy, multi-population mechanism, and DE strategy) (Chen et al., 2020a), hHHO-SCA (hybrid harris hawks-sine cosine algorithm) (Kamboj et al., 2020), EHHO (enriched Harris Hawks optimization with chaotic drifts) (Chen et al., 2020b), and GCHHO (HHO with Gaussian mutation and cuckoo search strategy) (Song et al., 2021). All of these algorithms' parameters have been set in accordance with the original article. Table 3 compares the performance of FWHHO and existing HHO algorithms on the CEC2014 benchmark with 50 dimensions. As can be shown, FWHHO obviously surpasses these current HHO algorithms in terms of not only mean error values but also standard deviations for the majority of functions, while FWHHO may perform badly in contrast to other existing FWA algorithms for F19, F21, F24, and F30. On F19, the GCHHO produces the best mean error values, while the hHHO-SCA produces the best mean error values. On F24 and F30, the CMDHHO obtains the best mean error values.

TABLE 3

Table 3. Comparison of FWHHO and existing HHO algorithms.

Table 4 presents the p-values for the FWHHO and other existing HHO algorithms on the CEC2014 benchmark with 50 dimensions. As can be seen, the majority of cases are smaller than 0.05, indicating that FWHHO outperforms CMDHHO, hHHO-SCA, EHHO, and GCHHO. A preliminary result is that the FWHHO approach is superior to other existing HHO methods in terms of numerical optimization potential. In addition, the convergence curves of FWHHO and other existing HHO methods for several selected benchmarks are exhibited in Figure 3. The proposed FWHHO shows the best fast convergence speed among all these existing HHO methods on these functions. The estimated optimal solution can be reached fast during the early stages of FWHHO execution; in contrast, other algorithms did not complete convergence until the end of the iteration number.

TABLE 4

Table 4. The calculated p-values for FWHHO vs. existing HHO algorithms.

5.3. Comparison between FWHHO and fireworks algorithms

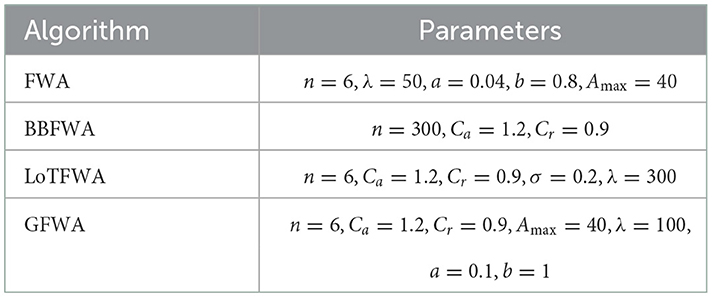
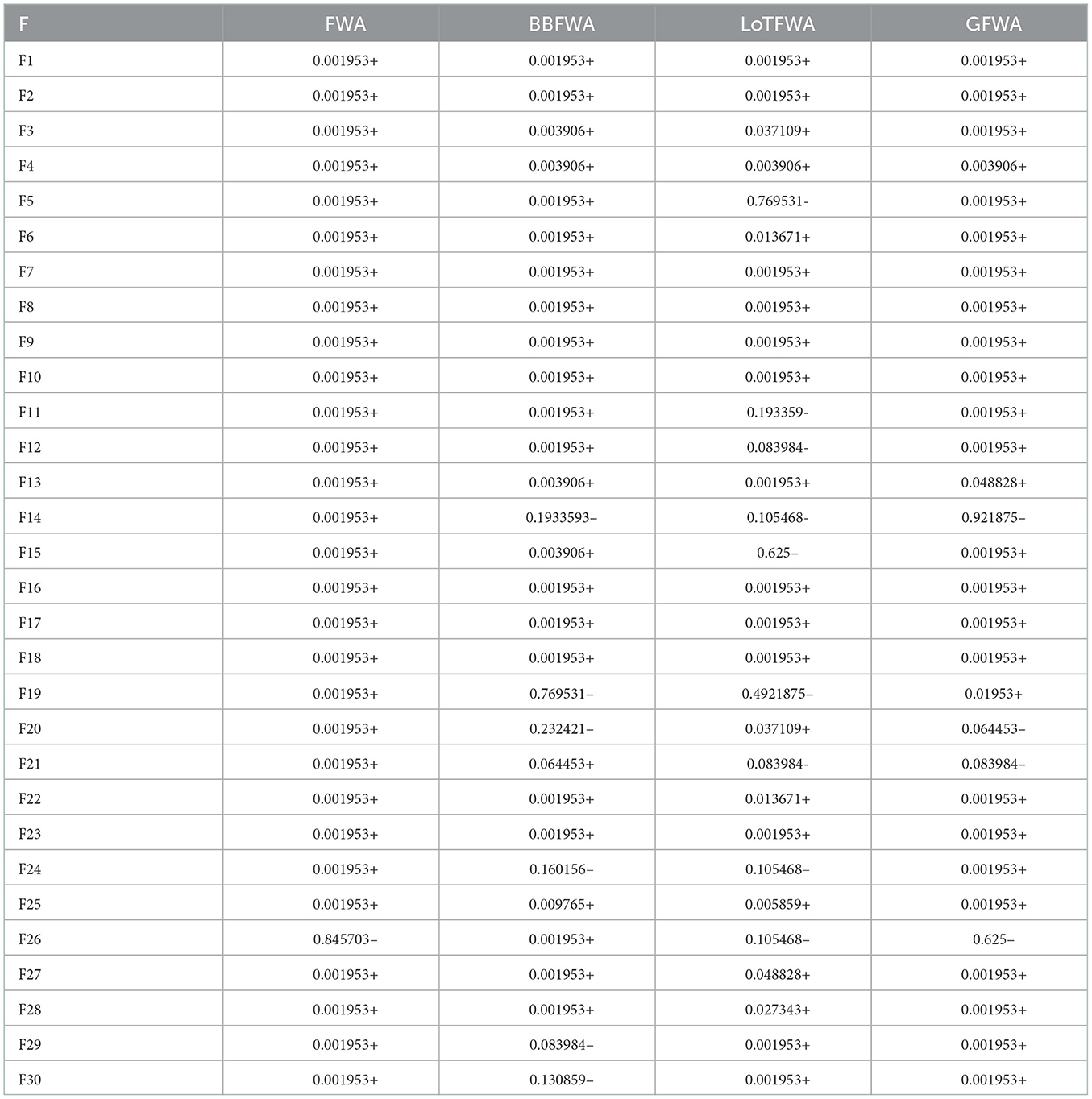
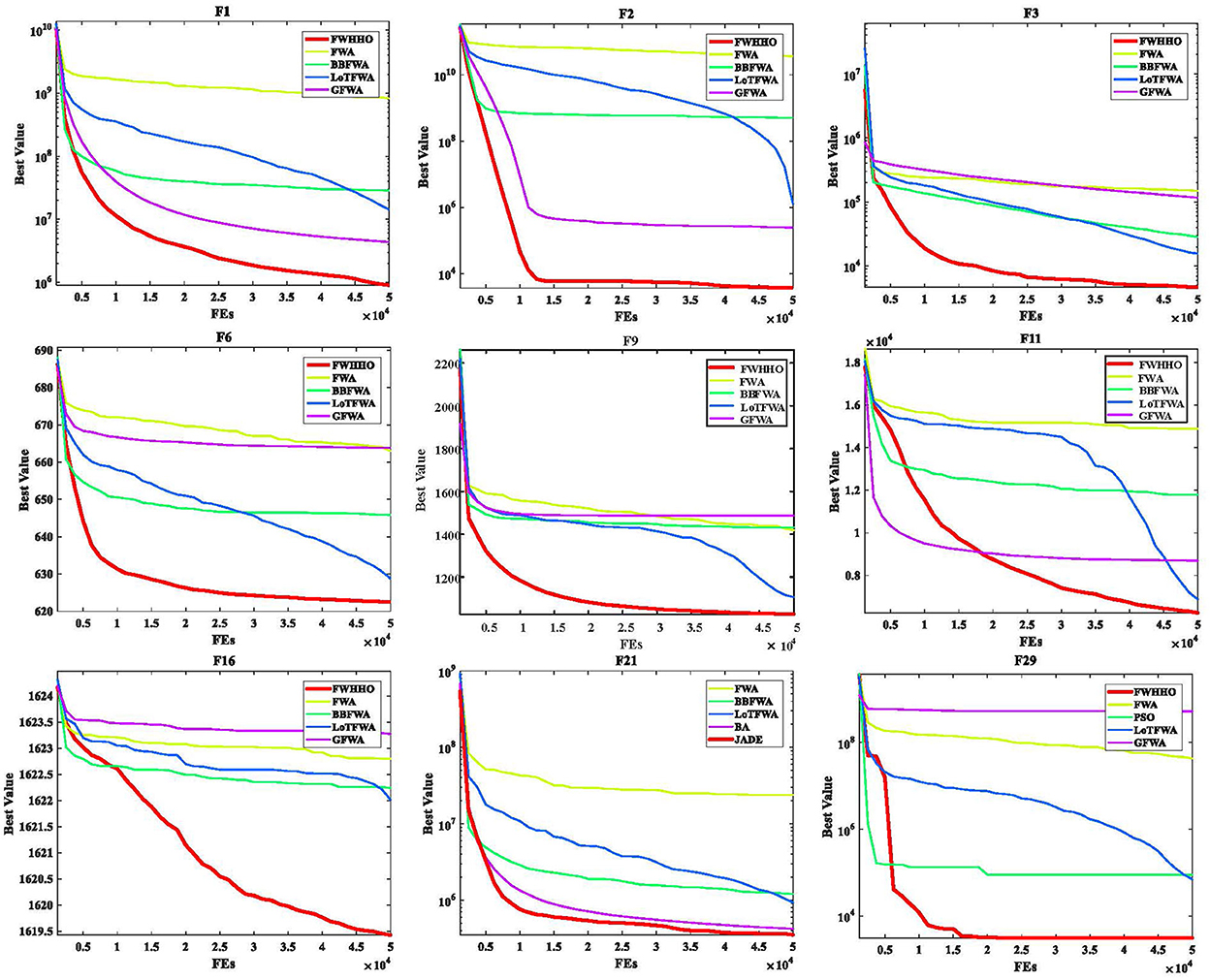
The new FWHHO algorithm is compared to many current fireworks algorithms on CEC2014 benchmarks in this section. The extant fireworks algorithms include the original FWA, the BBFWA (bare bones FWA) (Li and Tan, 2018), the LoTFWA (loser-out tournament-based FWA) (Li and Tan, 2017), and the GFWA (Guide FWA) (Li et al., 2016). Table 5 illustrates how these algorithms' parameters are set. The results of the statistical comparison between FWHHO and existing FWA algorithms on the CEC2014 benchmark with 50 dimensions are shown in Table 6. As can be seen, the FWHHO approach delivers the most thorough results in terms of mean error values and standard deviations for the majority of functions, although it may perform badly in contrast to other current FWA algorithms for F5, F9, F19, and F20. It is worth noticing that the mean values and standard deviations for F5, F6, F12, and F16 for all methods are rather similar. LoTFWA outperforms FWHHO, BBFWA, and GFWA on the F5, F9, F19, and F20 functions and the proposed FWHHO on all other functions.

TABLE 5

Table 5. Parameters for fireworks algorithms.

TABLE 6

Table 6. Comparison of FWHHO and fireworks algorithms.

Table 7 presents the p-values for the FWHHO and other existing FWA algorithms on the CEC2014 benchmark with 50 dimensions. As can be seen, the majority of cases are smaller than 0.05, indicating that FWHHO considerably outperforms GFWA, BBFWA, LoTFWA, and FWA. A preliminary conclusion can be drawn that the algorithm proposed FWHHO in this study has the perfect potential ability for numerical optimization than other existing FWA methods. In addition, the convergence curves of FWHHO and other existing FWA methods for several selected benchmarks are exhibited in Figure 2. It can be observed that the suggested FWHHO has the fastest convergence speed of all the known FWA techniques on these functions. The approximate optimum solution may be promptly found in the early stage of FWHHO execution for F2, F21, and F29, but other algorithms did not complete the convergence until the end of the iteration number to acquire the approximate optimal solution. Overall, the technique suggested in this research has been first validated for several numerical optimization problems.

TABLE 7

Table 7. The calculated p-values for FWHHO vs. fireworks algorithms.

FIGURE 2

Figure 2. Convergence curves of FWHHO and existing HHO algorithms.

FIGURE 3

Figure 3. Convergence curves of FWHHO and existing FWA algorithms.

5.4. Application of FWHHO on machine learning evolution

The property of FWHHO with fireworks explosion has been verified based on the aforementioned experimental results. In this section, the FWHHO is used to evolve a kernel extreme learning machine (KELM) for the purpose of diagnosing COVID-19 using biochemical indexes. The classification performance of KELM depends entirely on two of the key parameters and the optimal feature subset (Shi et al., 2021). The FWHHO is used to optimize the parameters and subfeatures of KELM concurrently with biochemical indexes for diagnosing COVID-19. The data used in this experiment are the data we used and published earlier (Shi et al., 2021). A total of 51 patients with COVID-19 were included in the analysis retroactively between 21 January and 20 March 2020. Each patient with COVID-19 was evaluated for gender, age, biochemical index, and blood electrolyte values. Biochemical indices and blood electrolytes were determined using an automated biochemical analyzer at the clinical biochemistry laboratory at the Affiliated Yueqing Hospital of Wenzhou Medical University (BS-190; Mindray, Shenzhen, China). This data set consists of 25 biochemical index features. Moreover, several other state-of-the-art algorithms, such as ECPA, CPA, GWO, MFO, and PSO, are utilized to optimize the parameters and subfeatures of KELM; the original KELM, SVM, and KNN are used as comparisons, and 10-fold cross-validation is used in this work. Each algorithm is run independently 10 times diagnose COVID-19 utilizing biochemical indexes.

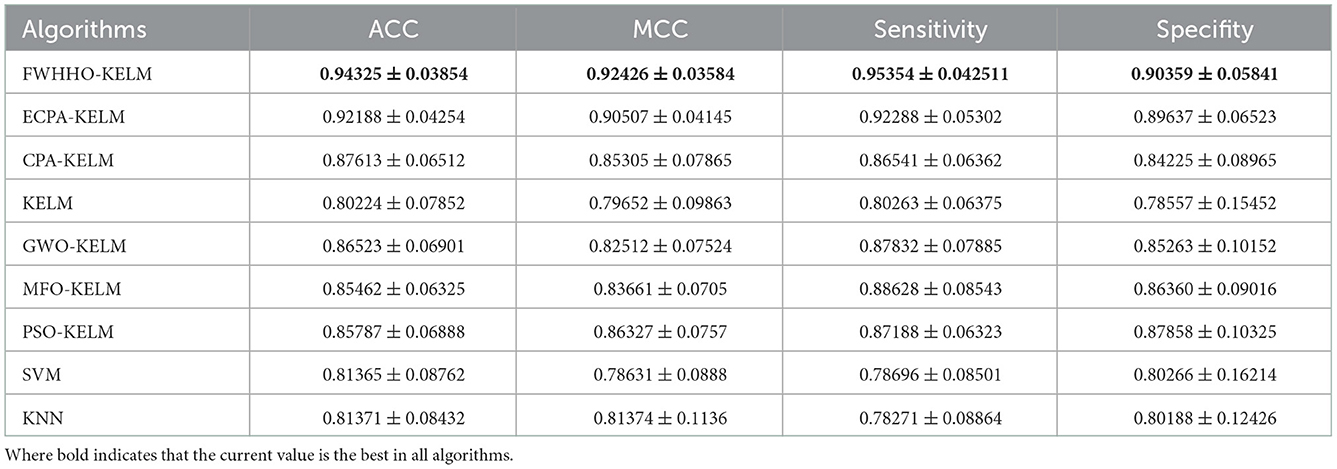
Comparison of the statistical results of the proposed FWHHO-KELM algorithm with existing competitive algorithms, such as ECPA-KEML, CPA-KELM, CPA-KELM, GWO-KELM, MFO-KELM, PSO-KELM, SVM, and KNN, is presented in Table 8. In comparison to existing algorithms, the suggested FWHHO-KELM has the best ACC (0.94320), MCC (0.92420), sensitivity (0.95354), specificity (0.90359), and sensitivity (0.95354). The best standard deviation is also obtained by the proposed FWHHO-KELM with 0.03854, 0.03584, 0.042511, and 0.05841. The results of the algorithm proposed in this article on this data set are higher than the results of the previous ECPA-KELM algorithm: 2.3%, 2.1%, 3.3%, and 0.8% in terms of four metrics. The original KELM and SVM algorithms perform poorly in the absence of swarm optimization algorithm evolution; however, the GWO-KELM, MFO-KELM, and PSO-KELM algorithms outperform the original KELM, SVM, and KNN algorithms. This experiment reveals that FWHHO-KELM can acquire the best property across all of these competing models automatically, owing mostly to the improved FWHHO, which can automatically select the optimal KELM parameters and subset of features for diagnosing COVID-19 using biochemical indices.

TABLE 8

Table 8. The statistical study comparing outcomes in terms of the four criteria.

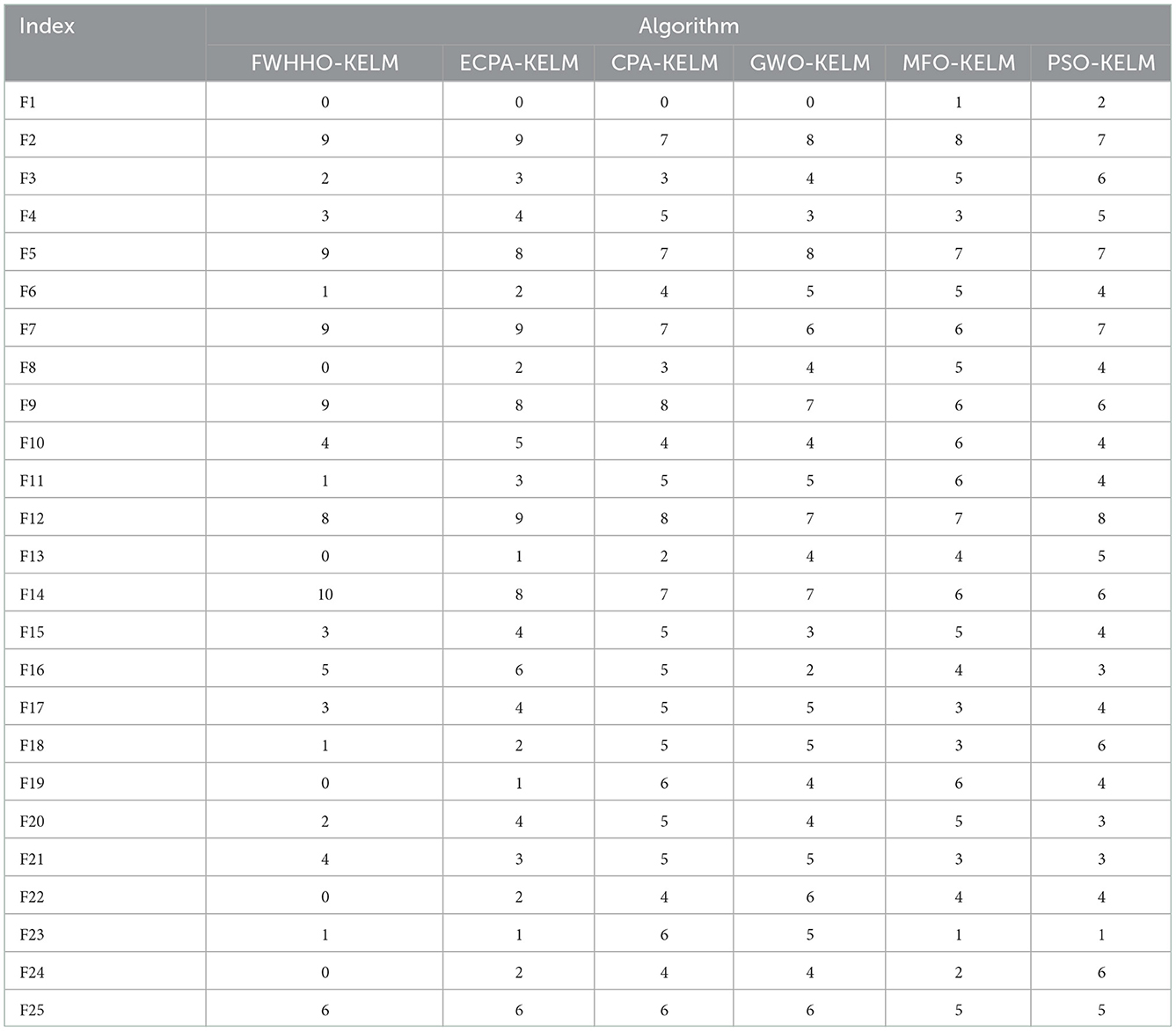
In addition, the proposed FWHHO is utilized to optimize settings and choose optimal subfeatures for KELM concurrently to diagnose COVID-19 using biochemical indicators. In addition, the numbers of the selected features in each 10-fold cycle by these algorithms are shown in Table 9. As shown in Table 9, the FWHHO-KELM proposal clearly beats others, and in terms of statistics, the FWHHO-KELM picked the characteristics AGE, ALT, ALB, A/G, AST, and LDH with values of 9, 9, 9, 8, and 10, respectively, whereas the other features were chosen far less frequently. As a result of their frequent appearance, such qualities may aid in the early diagnosis of COVID-19 and the discrimination of other low-frequency features. Due to the underlying details in these frequency aspects, these AGE, ALT, ALB, A/G, AST, and LDH traits should be given additional care in clinical practice. In short, the proposed FWHHO can successfully crack numerical optimization problems.

TABLE 9

Table 9. The numbers of selected feature.

6. Conclusion and future work

The purpose of this research is to develop a novel HHO frame based on the fireworks explosions to enhance the performance of the original HHO for challenging numerical optimization tasks. The FWHHO framework suggests performing searches in two phases: first for hawks, then for fireworks explosions. Following the conclusion of the four stages of the hawks' search, a fireworks explosion search is performed to explore promising locations and potential food supplies. It then looks for adjacent fireworks explosions after selecting persons based on their proximity to one another. In addition, the dynamic amplitude is used to calculate the step size for searching for fireworks bursts. At first, the amplitude is considerable, allowing for exploration of prospective areas; as iteration progresses, the amplitude decreases, allowing for full exploitation of the space surrounding a potential solution. To be more precise, it selects several individuals based on their proximity to one another and then does a search for fireworks explosions in their vicinity. In addition, the dynamic amplitude is used to determine the step size of the search for fireworks explosions. At first, the amplitude is considerable, allowing for exploration of prospective locations; as iterations progress, the amplitude decreases, allowing for complete exploitation of the space surrounding a potential solution. Furthermore, FWHHO is compared with state-of-the-art algorithms, existing HHO algorithms, and existing fireworks algorithms, and the statistical findings demonstrate that FWHHO is superior in terms of solution quality and search efficiency.

There might be limitations to this research. The projected FWHHO may still have room for development. The proposed method, although effective, does need a significant amount of extra computing time and resources to implement. To this end, we will likely investigate ways to parallelize the implementation of the method in the near future. Complex engineering optimization issues, such as optimal control in industry and energy management, are prime candidates for the FWHHO algorithm.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

MW: designing experiments, programming, and executing experiments. LC: revision, editing, software, visualization, and investigation. AH: algorithm design and experimental data statistics. HC: financial support, manuscript polishing, and provision of experimental equipment. All authors contributed to the article and approved the submitted version.

Funding

This study was supported by the Youth Program of Jiangsu Natural Science Foundation (BK20210204).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abd Elaziz, M., Heidari, A. A., Fujita, H., and Moayedi, H. (2020). A competitive chain-based Harris Hawks optimizer for global optimization and multi-level image thresholding problems. Appl. Soft. Comput. 95, 106347. doi: 10.1016/j.asoc.2020.106347

CrossRef Full Text | Google Scholar

Alabool, H. M., Alarabiat, D., Abualigah, L., and Heidari, A. A. (2021). Harris Hawks optimization: a comprehensive review of recent variants and applications. Neural Comput. Appl. 33, 8939–8980. doi: 10.1007/s00521-021-05720-5

CrossRef Full Text | Google Scholar

Bao, X., Jia, H., and Lang, C. (2019). A novel hybrid Harris Hawks optimization for color image multilevel thresholding segmentation. IEEE Access 7, 76529–76546. doi: 10.1109/ACCESS.2019.2921545

CrossRef Full Text | Google Scholar

Chen, H., Heidari, A. A., Chen, H., Wang, M., Pan, Z., and Gandomi, A. H. (2020a). Multi-population differential evolution-assisted Harris Hawks optimization: framework and case studies. Future Generat. Comput. Syst. 111, 175–198. doi: 10.1016/j.future.2020.04.008

CrossRef Full Text | Google Scholar

Chen, H., Jiao, S., Wang, M., Heidari, A. A., and Zhao, X. (2020b). Parameters identification of photovoltaic cells and modules using diversification-enriched Harris Hawks optimization with chaotic drifts. J. Clean Prod. 244, 118778. doi: 10.1016/j.jclepro.2019.118778

CrossRef Full Text | Google Scholar

Cui, L., Li, G., Wang, X., Lin, Q., Chen, J., Lu, N., et al. (2017). A ranking-based adaptive artificial bee colony algorithm for global numerical optimization. Inf. Sci. 417, 169–185. doi: 10.1016/j.ins.2017.07.011

CrossRef Full Text | Google Scholar

Dehkordi, A. A., Sadiq, A. S., Mirjalili, S., and Ghafoor, K. Z. (2021). Nonlinear-based chaotic Harris Hawks optimizer: Algorithm and internet of vehicles application. Appl. Soft Comput. 2021, 107574. doi: 10.1016/j.asoc.2021.107574

CrossRef Full Text | Google Scholar

Devarapalli, R., and Bhattacharyya, B. (2019). “Application of modified Harris Hawks optimization in power system oscillations damping controller design,” in 2019 8th International Conference on Power Systems (ICPS) (Jaipu: IEEE), 1–6.

Google Scholar

Dhawale, D., and Kamboj, V. K. (2020). “Hhho-igwo: a new hybrid Harris Hawks optimizer for solving global optimization problems,” in 2020 International Conference on Computation, Automation and Knowledge Management (ICCAKM) (Dubai: IEEE), 52–57.

Google Scholar

Fan, Q., Chen, Z., and Xia, Z. (2020). A novel quasi-reflected Harris Hawks optimization algorithm for global optimization problems. Soft Comput. 24, 14825–14843. doi: 10.1007/s00500-020-04834-7

CrossRef Full Text | Google Scholar

Fu, W., Shao, K., Tan, J., and Wang, K. (2020a). Fault diagnosis for rolling bearings based on composite multiscale fine-sorted dispersion entropy and svm with hybrid mutation sca-hho algorithm optimization. IEEE Access 8, 13086–13104. doi: 10.1109/ACCESS.2020.2966582

CrossRef Full Text | Google Scholar

Fu, W., Wang, K., Tan, J., and Zhang, K. (2020b). A composite framework coupling multiple feature selection, compound prediction models and novel hybrid swarm optimizer-based synchronization optimization strategy for multi-step ahead short-term wind speed forecasting. Energy Conversi. Manag. 205, 112461. doi: 10.1016/j.enconman.2019.112461

CrossRef Full Text | Google Scholar

Gupta, S., Deep, K., Heidari, A. A., Moayedi, H., and Wang, M. (2020). Opposition-based learning Harris Hawks optimization with advanced transition rules: principles and analysis. Expert. Syst. Appl. 158, 113510. doi: 10.1016/j.eswa.2020.113510

CrossRef Full Text | Google Scholar

He, L., Li, W., Zhang, Y., and Cao, Y. (2019). A discrete multi-objective fireworks algorithm for flowshop scheduling with sequence-dependent setup times. Swarm Evolution. Comput. 51, 100575. doi: 10.1016/j.swevo.2019.100575

CrossRef Full Text | Google Scholar

Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., and Chen, H. (2019). Harris Hawks optimization: algorithm and applications. Future Generat. Comput. Syst. 97, 849–872. doi: 10.1016/j.future.2019.02.028

CrossRef Full Text | Google Scholar

Jiao, S., Chong, G., Huang, C., Hu, H., Wang, M., Heidari, A. A., et al. (2020). Orthogonally adapted Harris Hawks optimization for parameter estimation of photovoltaic models. Energy 203, 117804. doi: 10.1016/j.energy.2020.117804

CrossRef Full Text | Google Scholar

Kamboj, V. K., Nandi, A., Bhadoria, A., and Sehgal, S. (2020). An intensify Harris Hawks optimizer for numerical and engineering optimization problems. Appl. Soft. Comput. 89, 106018. doi: 10.1016/j.asoc.2019.106018

CrossRef Full Text | Google Scholar

Kurtuluş, E., Yıldız, A. R., Sait, S. M., and Bureerat, S. (2020). A novel hybrid harris hawks-simulated annealing algorithm and rbf-based metamodel for design optimization of highway guardrails. Mater. Test. 62, 251–260. doi: 10.3139/120.111478

CrossRef Full Text | Google Scholar

Li, C., Li, J., Chen, H., and Heidari, A. A. (2021). Memetic Harris Hawks optimization: developments and perspectives on project scheduling and qos-aware web service composition. Expert. Syst. Appl. 171, 114529. doi: 10.1016/j.eswa.2020.114529

CrossRef Full Text | Google Scholar

Li, J., and Tan, Y. (2017). Loser-out tournament-based fireworks algorithm for multimodal function optimization. IEEE Trans. Evolut. Comput. 22, 679–691. doi: 10.1109/TEVC.2017.2787042

CrossRef Full Text | Google Scholar

Li, J., and Tan, Y. (2018). The bare bones fireworks algorithm: a minimalist global optimizer. Appl. Soft. Comput. 62, 454–462. doi: 10.1016/j.asoc.2017.10.046

CrossRef Full Text | Google Scholar

Li, J., Zheng, S., and Tan, Y. (2016). The effect of information utilization: Introducing a novel guiding spark in the fireworks algorithm. IEEE Trans. Evolution. Comput. 21, 153–166. doi: 10.1109/TEVC.2016.2589821

CrossRef Full Text | Google Scholar

Li, W., Shi, R., Zou, H., and Dong, J. (2021). “Fireworks harris hawk algorithm based on dynamic competition mechanism for numerical optimization,” in International Conference on Swarm Intelligence (Cham: Springer), 441–450.

Google Scholar

Liang, J. J., Qin, A. K., Suganthan, P. N., and Baskar, S. (2006). Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evolution. Comput. 10, 281–295. doi: 10.1109/TEVC.2005.857610

CrossRef Full Text | Google Scholar

Liang, J. J., Qu, B. Y., and Suganthan, P. N. (2013). Problem definitions and evaluation criteria for the cec 2014 special session and competition on single objective real-parameter numerical optimization. Computational Intelligence Laboratory, Zhengzhou University, Zhengzhou China and Technical Report, Nanyang Technological University, Singapore.

Google Scholar

Mathew, T. V. (2012). Genetic Algorithm. Report submitted at IIT Bombay.

Google Scholar

Mirjalili, S. (2016). Sca: a sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 96, 120–133. doi: 10.1016/j.knosys.2015.12.022

CrossRef Full Text | Google Scholar

Mirjalili, S., Gandomi, A. H., Mirjalili, S. Z., Saremi, S., Faris, H., and Mirjalili, S. M. (2017). Salp swarm algorithm: a bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 114, 163–191. doi: 10.1016/j.advengsoft.2017.07.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi: 10.1016/j.advengsoft.2013.12.007

CrossRef Full Text | Google Scholar

Paniri, M., Dowlatshahi, M. B., and Nezamabadi-pour, H. (2020). Mlaco: a multi-label feature selection algorithm based on ant colony optimization. Knowl. Based Syst. 192, 105285. doi: 10.1016/j.knosys.2019.105285

CrossRef Full Text | Google Scholar

Poli, R., Kennedy, J., and Blackwell, T. (2007). Particle swarm optimization. Swarm Intell. 1, 33–57. doi: 10.1007/s11721-007-0002-0

CrossRef Full Text | Google Scholar

Price, K. V. (2013). “Differential evolution,” in Handbook of Optimization (Berlin; Heidelberg: Springer), 187–214.

Google Scholar

Qin, A. K., Huang, V. L., and Suganthan, P. N. (2008). Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evolution. Comput. 13, 398–417. doi: 10.1109/TEVC.2008.927706

PubMed Abstract | CrossRef Full Text | Google Scholar

Qu, C., He, W., Peng, X., and Peng, X. (2020). Harris Hawks optimization with information exchange. Appl. Math. Model 84, 52–75. doi: 10.1016/j.apm.2020.03.024

CrossRef Full Text | Google Scholar

Rashedi, E., Nezamabadi-Pour, H., and Saryazdi, S. (2009). Gsa: a gravitational search algorithm. Inf. Sci. 179, 2232–2248. doi: 10.1016/j.ins.2009.03.004

CrossRef Full Text | Google Scholar

Ridha, H. M., Heidari, A. A., Wang, M., and Chen, H. (2020). Boosted mutation-based Harris Hawks optimizer for parameters identification of single-diode solar cell models. Energy Convers. Manag. 209, 112660. doi: 10.1016/j.enconman.2020.112660

CrossRef Full Text | Google Scholar

Shi, B., Ye, H., Zheng, L., Lyu, J., Chen, C., Heidari, A. A., et al. (2021). Evolutionary warning system for COVID-19 severity: colony predation algorithm enhanced extreme learning machine. Comput. Biol. Med. 136, 104698. doi: 10.1016/j.compbiomed.2021.104698

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, S., Wang, P., Heidari, A. A., Wang, M., Zhao, X., Chen, H., et al. (2021). Dimension decided Harris Hawks optimization with gaussian mutation: balance analysis and diversity patterns. Knowl. Based Syst. 215, 106425. doi: 10.1016/j.knosys.2020.106425

CrossRef Full Text | Google Scholar

Tan, Y., and Zhu, Y. (2010). “Fireworks algorithm for optimization,” in International Conference in Swarm Intelligence (Berlin; Heidelberg: Springer), 355–364.

Google Scholar

Wolpert, D. H., and Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Trans. Evolution. Comput. 1, 67–82. doi: 10.1109/4235.585893

CrossRef Full Text | Google Scholar

Yıldız, A. R., Yıldız, B. S., Sait, S. M., Bureerat, S., and Pholdee, N. (2019). A new hybrid harris hawks-nelder-mead optimization algorithm for solving design and manufacturing problems. Mater. Test. 61, 735–743. doi: 10.3139/120.111378

CrossRef Full Text | Google Scholar

Yousri, D., Allam, D., and Eteiba, M. B. (2020). Optimal photovoltaic array reconfiguration for alleviating the partial shading influence based on a modified Harris Hawks optimizer. Energy Convers. Manag. 206, 112470. doi: 10.1016/j.enconman.2020.112470

CrossRef Full Text | Google Scholar

Zhang, B., Zhang, M.-X., and Zheng, Y.-J. (2014). “A hybrid biogeography-based optimization and fireworks algorithm,” in 2014 IEEE Congress on Evolutionary Computation (CEC) (Beijing: IEEE), 3200–3206.

Google Scholar

Zheng-Ming, G., Juan, Z., Yu-Rong, H., and Chen, H.-F. (2019). “The improved harris hawk optimization algorithm with the tent map,” in 2019 3rd International Conference on Electronic Information Technology and Computer Engineering (EITCE) (Xiamen: IEEE), 336–339.

Google Scholar

Zhong, C., Wang, M., Dang, C., Ke, W., and Guo, S. (2020). First-order reliability method based on Harris Hawks optimization for high-dimensional reliability analysis. Struct. Multidisc. Optim. 62, 1951–1968. doi: 10.1007/s00158-020-02587-3

CrossRef Full Text | Google Scholar