A commentary has been posted on this article:
One vs. two non-symbolic numerical systems? Looking to the ATOM theory for clues to the mystery
- Laboratory for Developmental Studies, Department of Psychology, Harvard University, Cambridge, MA, USA
Studies of human adults, infants, and non-human animals demonstrate that non-symbolic numerical cognition is supported by at least two distinct cognitive systems: a “parallel individuation system” that encodes the numerical identity of individual items and an “approximate number system” that encodes the approximate numerical magnitude, or numerosity, of a set. The exact nature and role of these systems, however, have been debated for over a 100-years. Some argue that the non-symbolic representation of small numbers (<4) is carried out solely by the parallel individuation system and the non-symbolic representation of large numbers (>4) is carried out solely by the approximate number system. Others argue that all numbers are represented by the approximate number system. This debate has been fueled largely by some studies showing dissociations between small and large number processing and other studies showing similar processing of small and large numbers. Recent work has addressed this debate by showing that the two systems are present and distinct from early infancy, persist despite the acquisition of a symbolic number system, activate distinct cortical networks, and engage differentially based attentional constraints. Based on the recent discoveries, I provide a hypothesis that may explain the puzzling findings and makes testable predictions as to when each system will be engaged. In particular, when items are presented under conditions that allow selection of individuals, they will be represented as distinct mental items through parallel individuation and not as a numerical magnitude. In contrast, when items are presented outside attentional limits (e.g., too many, too close together, under high attentional load), they will be represented as a single mental numerical magnitude and not as distinct mental items. These predictions provide a basis on which researchers can further investigate the role of each system in the development of uniquely human numerical thought.
Introduction
The brain has at least two systems for representing number non-symbolically; however, these systems represent number in qualitatively different ways (see Feigenson et al., 2004 or Piazza, 2010 for reviews). The approximate number system encodes an imprecise estimate of the numerical magnitude, or numerosity1, of a set of objects (see Gallistel, 1990; Butterworth, 1999; Nieder and Dehaene, 2009; Dehaene, 2011 for reviews). The mental representations formed by this system can be used to compare and combine numerical magnitudes. Importantly, this system uses one mental symbol to summarize the set. In contrast, the parallel individuation system forms a distinct mental symbol for each item (see Carey, 2009 or Scholl, 2002 for reviews). This system privileges spatiotemporal information to initiate a mental index, or object file, for each item. Although inherently non-numerical in nature, these representations afford numerical content by retaining information about numerical identity – mentally stored items can be compared on a one-to-one basis with visible objects in the scene to detect numerical matches or mismatches.
These systems are further characterized by their contrasting limits (see Feigenson et al., 2004 for a review). The imprecision of the approximate number system systematically increases as numerosity increases. As a result, the ability to estimate numerosity has no particular upper bound, but discrimination of any two numerical quantities follows Weber’s Law, as it is a function of the ratio between the two quantities to be compared. In contrast, the ability to simultaneously represent and track objects through parallel individuation is limited to only a few items (usually about 3–4)2. Representations through parallel individuation afford more fine-grained numerical discriminations than those of the approximate number system if numbers are within the range of this system, but comparisons fail when the limits of this system are surpassed. The signature limits of ratio and capacity have allowed researchers to find evidence of the two numerical systems across age-groups and species, suggesting these systems are innate, arise very early in human infancy, and are shared with a wide variety of non-human animals.
One difficulty in understanding the nature and function of these systems has been in specifying the conditions under which each system is engaged. This difficulty has been historically compounded in experiments that contrast the processing of small (<∼4) and large numbers (>4; e.g., Jevons, 1871; Kaufman et al., 1949; Trick and Pylyshyn, 1994). Jevons (1871) was the first to demonstrate empirically a dissociation between small and large number processing by asking subjects to count the number of beans tossed into a shallow pan. He showed that enumeration of 1–4 items was perfectly accurate, while errors increased as the number of items to be enumerated increased beyond 4. The phenomenon of precise, accurate, and seemingly instantaneous enumeration of a small number of items, in contrast to the slower, more inaccurate process for larger number of items, was later termed “subitizing” to distinguish it from counting (Kaufman et al., 1949).
The most striking dissociations seen between small and large numbers, however, come from human infants without symbolic counting abilities (e.g., Xu, 2003; Lipton and Spelke, 2004; Feigenson and Carey, 2005; Wood and Spelke, 2005). For example, after watching an experimenter sequentially place 1 food item in one bucket and 2 food items in a different bucket, human infants reliably search in the bucket with 2 food items (e.g., Feigenson et al., 2002; Feigenson and Carey, 2003, 2005). In similar comparisons of 1 vs. 3 and 2 vs. 3, they search in the bucket with numerically and physically more food items. However, in cases where more than 3 items are placed in any given bucket (e.g., 2 vs. 4; 1 vs. 4), infants are not able to reliably choose the bucket with more food items. These highly replicable failures, seen in a variety of paradigms with infants (e.g., Feigenson and Carey, 2003, 2005; Xu, 2003; Lipton and Spelke, 2004), combined with the processing dissociations in human adults (e.g., Jevons, 1871; Kaufman et al., 1949; Trick and Pylyshyn, 1994), have led some to propose that parallel individuation is engaged exclusively when processing sets with a small number of objects (1–3 or 4) and the approximate number system is engaged exclusively when processing sets with larger numbers of objects (>4; see Simon et al., 1995; Uller et al., 1999; Feigenson et al., 2002, 2004; Xu, 2003; Lipton and Spelke, 2004; Ansari et al., 2007; Van Herwegen et al., 2008). Under this view, what will be called here the “two systems view,” the parallel individuation system is specialized to represent small numbers and the approximate number system is specialized to represent large numbers; numerical range determines when each system will be engaged.
Other evidence, however, suggests that the approximate number system operates over both large and small numbers (e.g., Moyer and Landauer, 1967, 1973; Meck and Church, 1983; Brannon and Terrace, 1998; Cordes et al., 2001; Cantlon and Brannon, 2006). For example, Cordes et al. (2001) showed that when adult subjects were asked to tap a table a given number of times while under articulatory suppression, their tapping of both small and large numerosities showed the systematic variability characteristic of the approximate number system. Similarly, Brannon and colleagues have shown that the ability to order small and large numerosities is a function of the ratio between the numbers to be ordered in non-human primates and adults under articulatory suppression, suggesting the approximate number system is operating over the entire range of numbers used (e.g., Brannon and Terrace, 1998; Cantlon and Brannon, 2006). In addition, most formal mathematical models of non-symbolic number representation in the brain assume all numbers are represented by the approximate number system (e.g., Meck and Church, 1983; Church and Broadbent, 1990; Dehaene and Changeux, 1993; Zorzi and Butterworth, 1999; Verguts and Fias, 2004; Nieder and Merten, 2007). This type of evidence has led some to adopt, what will be called here the “one system view” of numerical cognition. Importantly, proponents of the “one system view” do not deny the existence of the parallel individuation system, but contest that the approximate number system operates over the entire range of numbers, large and small. From this view, it is unclear exactly what conditions elicit differential representations from parallel individuation and approximate number. One proposal is that both types of representations are formed over sets simultaneously and under some conditions representations of parallel individuation override those of approximate numerosity when acting on the world (e.g., Cordes and Brannon, 2009; Burr et al., 2010, 2011). Another proposal is that object file representations are formed over small numbers initially and then these representations are converted to approximate numerosity representations (e.g., Cordes and Brannon, 2009).
In sum, most researchers agree that humans and many non-human animals possess both the ability to represent a set as an approximate numerical value or as distinct object files. Furthermore, there is accord that the ability to represent individual items in parallel is limited to only several items at a given moment. Until recently, however, the field has disagreed as to the conditions that activate each system and, in particular, whether these systems are specialized for small and large numbers. Recent work in psychophysics and, in particular, cognitive neuroscience, with non-human animals, human infants, and human adults has provided empirical evidence for the distinctness of these systems in the brain and a better understanding of the experimental conditions that elicit representations from each system3. Furthermore, this recent work suggests a hybrid view of the “two systems” and “one system” views by delineating the conditions under which each system is engaged and the cognitive constraints that underlie this delineation.
Recent Insights
Distinct Representations
Recent work has directly contrasted small and large number processing using common measures and methods. This work has shown that under many conditions small numbers are represented differently than large numbers. For example, a recent event-related potential (ERP) study showed that human adults spontaneously encode number while passively viewing dot arrays; however, small and large numbers are encoded differently (Hyde and Spelke, 2009). Small numbers (1–3 items) evoke an early posterior parietal response (N1) that scales with the number of individuals in the set irrespective of the number in the array that preceded it. In contrast, large numbers evoke a later, mid-latency component over posterior parietal scalp (P2p) that scales with the ratio of numerical change between successive sets (Hyde and Spelke, 2009). These signatures mirror the behavioral signature limits of the two systems (Feigenson et al., 2004) to suggest that the approximate number system and the parallel individuation system are being differentially engaged over large and small numbers under these conditions. Similarly, in an ERP number comparison task, Libertus et al. (2007) also observed distinct early signatures for small numbers (Libertus et al., 2007).
Psychophysics has further confirmed the qualitative distinction between small and large number processing (Revkin et al., 2008; Piazza et al., 2011). For example, Revkin et al. (2008) showed that estimates of large and small numbers differ in reaction time, accuracy, and the distribution of the answers. Furthermore, individual variability in the small number range does not correlate with individual variability in the large number range and individual differences in subitizing capacity do not correlate with individual differences in large non-symbolic number comparison precision (Revkin et al., 2008; Piazza et al., 2011). Together these results suggest small number subitizing relies on a distinct cognitive mechanism from estimation of larger numbers and that, under these conditions, small numbers are not being represented as approximate numerical magnitudes.
It is reasonable to posit that the distinct signatures for small compared to large numbers arise from the extensive practice human adults have at enumerating, visualizing, and remembering small numbers of items, 1–3, compared to larger numbers of items like 8 or 32. As mentioned above, previous work showing differences in small and large number processing in non-human animals and pre-verbal human infants suggests that this may not be the case. Recent work has strengthened the case for an innate difference between small and large number processing, as opposed to an experiential difference. For example, Cordes and Brannon (2009) used a habituation method to show that young infants fail to dishabituate to changes in number that cross the small/large number divide and it is only when the ratio is increased to a 1:4 ratio (e.g., 2 vs. 8) that infants succeed at discriminating a large and a small number. Furthermore, Hyde and Spelke (2011a), using the same ERP measure and similar passive viewing methods as in adults, showed distinct brain signatures for small and large numbers in human infants that parallel those observed in adults (Hyde and Spelke, 2009, 2011a; but see Izard et al., 2008). These results in infants without any numerical education, symbolic number practice, and/or spoken language present a strong case for innate differences between small and large number processing that are not dependent on formal numerical experience or language.
Directly comparing small and large numbers has also resulted in qualitative and quantitative dissociations in animals evolutionarily far removed from humans (Agrillo et al., 2007; Rugani et al., 2008, 2010; Piffer et al., 2011). For example, Agrillo et al. (2007) showed that fish are able to discriminate between two social groups of peers at a closer ratio (e.g., 2 vs. 3 or 3 vs. 4) when groups are made up of smaller numbers of fish, compared to the ratio at which they can discriminate between two social groups that contain larger numbers of fish (Agrillo et al., 2007). Furthermore, like human infants, fish fail to discriminate between numbers that cross the small/large divide (3 vs. 5) until the ratio difference is increased (Piffer et al., 2011). Similarly, young chickens have been shown to discriminate between two small numbers, but fail to discriminate between a large and a small number, or two large numbers unless the ratio between them is increased substantially (Rugani et al., 2008, 2010). These results, in species far removed from humans, further support the idea of innate representational differences between small and large number processing.
Together this evidence suggests that the “one system view” does not always hold. That is, approximate number representations are not always formed over sets of small numbers of objects under experimental conditions where they are clearly formed over large numbers.
Distinct Neural Mechanisms
Recent neurophysiological and neuroimaging work also suggests that the distinct neural and behavioral signatures of the two systems arise from anatomically distinct brain regions. For example, Hyde and Spelke (2011b) used the low resolution electromagnetic tomography (LORETA) source localization algorithm to estimate the neural origin of ERP signatures of small and large number processing. Early, distinctly small number ERPs signatures (modulation by cardinal value) appeared to arise from extrastriate visual regions including superior and lateral portions of visual cortex and later small number processing appeared to arise from right temporal–parietal junction (RTPJ) and left parietal regions, whereas distinctly large number processing (modulation by numerical ratio of change between successive images) appeared to arise primarily from right intraparietal regions.
In a similar vein, Ansari and colleagues used functional magnetic resonance imaging (fMRI) to measure the brain response as subjects performed a number comparison task. They found that small number comparisons elicited an increase activity in the RTPJ, whereas large number comparisons elicited a decrease in activity in the RTPJ and an increase in activity in the parietal occipital sulcus (Ansari et al., 2007). Similar RTPJ activity has independently been observed in anther study contrasting enumeration of small and large numbers (Vetter et al., 2011). Both groups attribute the small number RTPJ activity to stimulus driven attention, that is not present or not present to the same extent in large number processing.
Finally, a complementary line of functional neuroimaging work suggests encoding of individual objects may occur within the IPS as well (Culham et al., 1998, 2001; Xu and Chun, 2006; Xu, 2009). More specifically, recent work suggests that inferior IPS activity scales with the number of objects in scene up to about three to four and then plateaus while the superior IPS responds to differences in object identity, but not number. These results suggest that portions of the inferior IPS support the initial selection and individuation of a limited number of objects from a scene (up to about four), in contrast to the lateral occipital complex and the superior IPS, which seem to support object identification (Xu and Chun, 2006; Xu, 2009).
In sum, recent neuroimaging results further contest the “one system view” that approximate number representations are formed over small numbers, as small number processing under many conditions elicits qualitatively distinct patterns of brain activity in anatomically distinct regions compared to activity elicited for large numerosities.
Differential Engagement of Attention
The functional neuroimaging and electrophysiological evidence provided above points to the possibility that small and large numbers differentially recruit attention. Specifically, ERP markers of attentional processing (e.g., N1 component) are modulated in qualitatively different ways for small and large numbers; early ERPs increase as number increases for small but not large numbers (e.g., Hyde and Spelke, 2009, 2011a,b). Furthermore, small and large number processing recruit at least some distinct brain regions (Ansari et al., 2007; Vetter et al., 2011; Hyde and Spelke, 2011b). The particular brain regions recruited distinctly for small numbers (or modulated by small, but not large numbers), such as a portion of the inferior IPS and RTPJ (see Corbetta and Shulman, 2002 for a review), have been linked to attentional effects whereas the regions uniquely identified for large numbers (or that respond more to large than small numbers) and some of the regions that respond to both large and small numbers have not necessarily been linked to attentional effects. The most recent and exciting work contrasting small and large numbers has experimentally tested what the above reported results imply, attention and/or working memory operate differentially over small and large numbers.
One line of this work looks at the role of attention and working memory in enumeration of small and large numbers (subitizing small numbers vs. counting or estimation of larger numbers). For example, one recent study showed that subitizing (rapid, quick, and near perfect enumeration of small numbers) is inhibited during a dual task with high attentional load but estimation is not (Burr et al., 2010; but see Vetter et al., 2008 for contradictory results). Another study showed that individual differences in subitizing correlated with individual differences in working memory, but not individual differences in estimation abilities (Piazza et al., 2011). Furthermore, holding several items in working memory while jointly attempting to subitize reduced the capacity limit of the subitizing range. Importantly, the same working memory dual task does not impair estimation abilities (Piazza et al., 2011). Impairments to subitizing are also observed using an attentional blink paradigm (Egeth et al., 2008; Olivers and Watson, 2008; Xu and Liu, 2008). Interestingly, increasing viewing eccentricity also decreases enumeration accuracy for small numbers but not large numbers (Palomares et al., 2011).
Another exciting line of work investigating the role of attention in numerical processing has looked at neural adaptation to number. This research has typically shown that the brain adapts to the numerosity of large but not small numbers (Burr and Ross, 2008). One recent study, however, looked at the ability of the brain to adapt to numerosity under attentional load. Adaptation to numerosity was observed for small and large numbers when subjects were under high attentional load but was only seen for large numerosities when subjects are not under an attentional load (Burr et al., 2011). Another recent study measured the electrophysiological brain response to passive viewing of small and large numbers under conditions within and beyond the limits of attention (Hyde and Wood, 2011). When subjects viewed small numbers presented beyond the resolution limits (smaller individual items, crowded, and in the periphery) or under high attentional load (performing an attention demanding rapid serial visual presentation task) the brain signatures of the approximate number system and not parallel individuation were observed for small numbers. In contrast, when items were viewed within the resolution of attention (larger, further spaced items) or under no additional attentional load (same visual stimuli with no dual task), the brain signatures of parallel individuation, but not the approximate number system, were observed for small numbers.
These results, like those presented above, contest the “one system view” by showing that when stimuli are presented within the limits of attention, approximate number representations are not formed over small numbers. However, these results also contest the “two systems view” to suggest that the two systems are not specialized for small or large numbers per se, but rather are engaged differentially depending on the nature of the visual stimuli presented and the attentional or working memory constraints in place (Burr et al., 2010, 2011; Hyde and Wood, 2011; Piazza et al., 2011).
A Unifying Theory of the Two Numerical Systems
Recent studies bring together findings of both similarities and differences between small and large number processing to suggest: (1) The two systems are qualitatively and anatomically distinct. (2) The two systems are not specialized for small and large numbers. (3) The two systems are crucially affected by limits to early visual, attentional, and working memory. These novel results unify the “one system view” and the “two systems view” to provide an account of the conditions under which each system is engaged over a set of items.
General constraints on visual processing, attention, and working memory determine if a given set of items is represented as individual object files or as an approximate numerical magnitude (Burr et al., 2010, 2011; Hyde and Wood, 2011; Piazza et al., 2011). Small numbers are often represented distinctly from large numbers because they fall within the limits of the brain to individuate and track simultaneously (see Feigenson et al., 2004). In fact, when items are presented within the limits of the brain to form object files, parallel individuation may be the default. Importantly, under these conditions, small numbers do not appear to be represented as approximate numerical magnitudes. That is, none of the evidence accrued to this point suggests that small numbers are spontaneously represented both through the parallel individuation system and through the approximate number system. Dichotomous and qualitatively different representations explain striking developmental failures in infants and some non-human animals to distinguish numbers that cross the small/large divide, as well as the differential behavioral and brain signatures of small and large number processing observed in infants and adults (Feigenson and Carey, 2003, 2005; Xu, 2003; Cordes and Brannon, 2009; Hyde and Spelke, 2009, 2011a,b).
Large numerosities, in contrast, always fall beyond the limits of the brain to encode, remember, and simultaneously track distinct individual items. Therefore, the default, at least for simultaneously presented large quantities, appears to be representation as a numerical magnitude. Furthermore, if small number sets are presented beyond the limits of the brain to encode as individual object files (e.g., too close together) or if sufficient attentional/working memory resources are not available (e.g., because resources are tied up in another task), it appears that small numbers are also represented as approximate numerical magnitudes like large numbers. This can explain the cases where processing of small quantities shows the signatures of approximate number representation (Cordes et al., 2001; Burr et al., 2011; Hyde and Wood, 2011). For example, articulatory suppression, attentional blink, or dual task paradigms, which demand substantial attentional resources, often lead small number processing to show variability consistent with the approximate number representation (e.g., Cordes et al., 2001).
This proposal can also potentially explain studies showing infant success at discriminating numbers across the small/large boundary (evidence for common representation of small and large numbers; e.g., Cordes and Brannon, 2009). The experimental manipulation through which successful discrimination across the small/large boundary is achieved (increasing the ratio between the small and large number from 2 vs. 4 to 2 vs. 8) also correlates with a substantial decrease in the spacing of individual objects (as a by-product of the non-numerical controls employed). It is plausible, given the evidence provided above, that the decrease in spacing of objects in the 2 vs. 8 condition, not the increase in ratio in and of itself, exceeded the limits of the infant visual attention system to encode the items as object files, resulting in representation of the set as an approximate numerical magnitude. If this were correct, decreasing the spacing of objects in the 2 vs. 4 condition beyond the attentional limits to form object files, would also produce success (without increasing the ratio).
Figure 1 presents a graphical representation of how the current proposal might work. When presented with a set of items, numerical representation through parallel individuation occurs if attention selects individual items and subsequently forms a mental symbol, or object file, for each individual item in the set. Each object file is then stored in working memory and the specific properties of each item can then be bound to the mental representation of each specific individual (e.g., size, color, type, category, meaning, etc.). If attention is not able to select individuals because the limits are surpassed (e.g., too many, they are too close together, engaged in another attention demanding task, etc.), the set is summarized by a single mental symbol and properties of the set, or ensemble statistics, will be calculated, approximate numerosity being one property of the set.
FIGURE 1
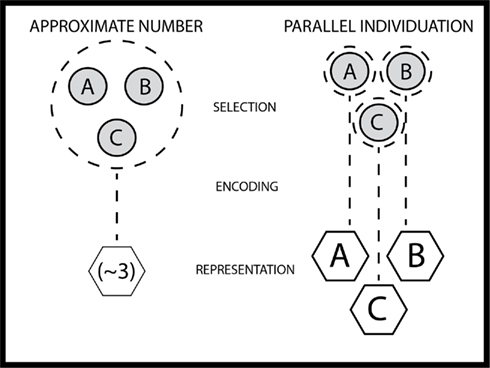
Figure 1. Schematic depiction of number representation through the approximate number system and the parallel individuation system.
Limitations and Future Directions
One open question is if number can be simultaneously represented through parallel individuation and the approximate number system over a single set or subset of objects4. None of the evidence accrued to this point suggests that the same items are being simultaneously represented as individual object files and as an approximate numerical magnitudes. On the contrary, the evidence to date suggests that early attentional selection and subsequent cognitive encoding determine whether a given set of objects will be spontaneously represented as set of individual object files or as a set with an approximate numerical magnitude (e.g., Burr et al., 2011; Hyde and Wood, 2011). However, such a dichotomous process, if it exists, is certainly only a bias of spontaneous mental representation of number. It is certainly the case that a set of objects can be reanalyzed and encoded differently. This undoubtedly occurs in real world situations where our initial analysis of the visual scene has to be quickly revised or refocused for our current action.
Most of the work cited presents items simultaneously and often quickly. Less explored is the representation of number during sequential processing. Although sequential presentation has been used developmentally (e.g., Feigenson and Carey, 2003, 2005) and has produced some interesting similarities and differences to simultaneous processing, it has not been adequately explored and directly contrasted with simultaneous presentation to study numerical cognition. Sequential presentation is important for future work to determine if the same numerical signatures of the two systems hold and if attentional and working memory constraints similarly operate.
It is also unclear if the current proposal generalizes to other sensory domains such as audition and somatosensation. Systematic studies comparing numerical cognition across sensory modalities would be helpful in elucidating potential sensory-specific contributions to the mental representation of numerosity. A promising recent line of work appears to show that limits on parallel individuation/object file representation are not restricted to perceptual processes, as they extend to the planning of actions as well (Gallivan et al., 2011). However, at this point, it is still unclear if the general principles established for visual numerical representation apply equally or differentially to other sensory modalities. For example, Wood and Spelke (2005) showed similar development from 6 to 9 months in precision of representing number of actions (number of times a puppet jumped) as have been shown with visual stimuli (e.g., Xu, 2003). More specifically, 6-month-old infants can tell the difference between 4 and 8 jumps, but not between 4 vs. 6 or 2 vs. 4 jumps. On the other hand, vanMarle and Wynn (2009) found that infants could discriminate 2 from 4 tones, but not 2 from 3 tones. They interpreted this behavioral pattern to suggest infants were using the approximate number system in the auditory domain and that the limits of this system are similar in the auditory and visual domains (because infants of this age fail at 2 vs. 3 ratios but not at 1:2 ratios with large numbers in the visual domain). While it is certainly the case that infants could have been engaging the approximate number system here and this is consistent with the proposal above, it is unclear why they succeed at 2 vs. 4 in the auditory domain, but fail in the visual domain (e.g., Xu, 2003; Cordes and Brannon, 2009). A better understanding of the attentional limits in simultaneously representing individuals in other sensory domains may provide some insight into this puzzle.
Here we display work showing a variety of constraints on attentional resources change the way the brain represents objects numerically. Beyond the scope of this paper, however, there is a vast literature showing that attention can be divided into different sub-types, namely bottom-up and top-down attention, and different types of attention are constrained by different factors (see Corbetta and Shulman, 2002 for a review). For example, top-down attentional processing is constrained by increasing perceptual or working memory load, while bottom-up attentional processing is constrained by stimulus degradation (e.g., Lavie and de Fockert, 2003; Lavie, 2005; Awh et al., 2006). It may also be the case that perceptual or cognitive factors that facilitate grouping items vs. treating them individuals interact with attention to bias the way in which numerosity is represented. For example, Gestalt principles such as proximity, similarity, or closure (for a review see Todorovic, 2007) or cognitive factors such as whether items are seen as an “object” (e.g., Egly et al., 1994) may differentially bias how attention is allocated, thereby influencing whether items will be represented as a group with an approximate numerical magnitude instead of individual items. Future work on numerical cognition should carefully consider the role and/or interaction of top-down and bottom-up attentional processing, as well as the particular environmental constraints present, in the representation of numerosity through the two systems.
Future work should also investigate potential distinctions and interactions between attention and working memory in non-symbolic number representation. Early ERP signatures suggest attention is distributed differentially when a set of items is encoded as individual object files compared to when it is encoded as an approximate numerical magnitude (Hyde and Spelke, 2009, 2011a,b; Hyde and Wood, 2011). Other work on remembering and tracking objects shows sensitivity in later processing to remembering and tracking objects (e.g., Luck and Vogel, 1997; Drew and Vogel, 2008). One question for future work would be how these early attentional effects interface with working memory representations of non-symbolic number downstream. More generally, numerical cognition may provide an avenue to further investigate attention and working memory, their respective limits, and the interplay.
Finally, certain insights gained from this proposal, namely early attentional constraints determine the nature of number representation, must be considered when investigating the role of each system in the development of uniquely human numerical and mathematical abilities. The field has shown a surge of excitement from recent work linking the precision of approximate number representations with numerical and mathematical achievement in school (Halberda et al., 2008; Gilmore et al., 2010; Piazza et al., 2010; Bugden and Ansari, 2011); Furthermore, at least one leading proposal as to how children acquire natural number concepts implicates parallel individuation as a crutch in this process (Le Corre and Carey, 2007; Carey, 2009). Future work should carefully examine individual differences in parallel individuation, approximate number representation, as well as the influence of individual differences in attention and working memory, to form a better understanding of the role each of these cognitive abilities plays in forming uniquely human numerical and mathematical concepts.
Conclusion
The emerging picture from recent work is that the two established systems of non-symbolic number representation do not operate in isolation from other cognitive and perceptual limits, nor do they appear to operate in parallel of each other. Rather, numerical information is encoded differentially from a set of objects based on what is presented and what else the brain is doing.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I would like to thank Elizabeth Spelke for her suggestions on an early version of this manuscript and Justin Wood for his input into this line of thought more generally.
Footnotes
- ^As a reviewer aptly pointed out, a distinction should be made between “number” as a mathematical entity and “numerosity” as a cardinal value of a set of items. When referring to primitive numerical representations, specifically those of the approximate number system, I am referencing the notion of a cardinal value of a set of items, or numerosity, rather than “number” as a mathematical entity. In the paper I also use the term “non-symbolic number representation” to refer to “numerosity.”
- ^It should be noted that the current proposal could be applied to a fixed slot/item-limited model (e.g., Luck and Vogel, 1997; Cowan, 2001; Zhang and Luck, 2008) or resource/information-limited model of working memory (e.g., Alvarez and Cavanagh, 2004; Wilken and Ma, 2004). This debate is intentionally avoided here because it seems to be unresolved in the literature more generally.
- ^The current literature review focuses on work conducted within the last 5 years.
- ^This question is different from the question of whether number can be estimated for multiple sets in parallel, which evidence suggests is the case (Halberda et al., 2006).
References
Agrillo, C., Dadda, M., and Bisazza, A. (2007). Quantity discrimination in female mosquitofish. Anim. Cogn. 10, 63–70.
Alvarez, G. A., and Cavanagh, P. (2004). The capacity of visual short-term memory is set both by visual information load and by number of objects, Psychol. Sci. 15, 106–111.
Ansari, D., Lyons, I. M., van Eimeren, L., and Xu, F. (2007). Linking visual attention and number processing in the brain: the role of the right temporal–parietal junction in the small and large non-symbolic number comparison, J. Cogn. Neurosci. 19, 1845–1853.
Awh, E., Vogel, E. K., and Oh, S.-H. (2006). Interactions between attention and working memory, Neuroscience 139, 201–208.
Brannon, E. M., and Terrace, H. S. (1998). Ordering of the numerosities 1–9 by monkeys, Science 282, 746–749.
Bugden, S., and Ansari, D. (2011). Individual differences in children’s mathematical competence are related to the intentional but not automatic processing of Arabic numerals, Cognition 118, 35–47.
Burr, D. C., Anobile, G., and Turi, M. (2011). Adaptation affects both high and low (subitized) numbers under conditions of high attentional load, Seeing Perceiving 24, 141–150.
Burr, D. C., Turi, M., and Anobile, G. (2010). Subitizing but not estimation of numerosity requires attentional resources, J. Vis. 6, 20.
Cantlon, J. F., and Brannon, E. M. (2006). Shared system for ordering small and large numbers in monkeys and humans, Psychol. Sci. 17, 401–406.
Church, R. M., and Broadbent, H. A. (1990). Alternative representations of time, number, and rate, Cognition 37, 55–81.
Corbetta, M., and Shulman, G. L. (2002). Control of goal-directed and stimulus-driven attention in the brain, Nat. Rev. Neurosci. 3, 215–229.
Cordes, S., and Brannon, E. M. (2009). Crossing the divide: infants discriminate small from large numerosities, Dev. Psychol. 45, 1583–1594.
Cordes, S., Gelman, R., and Gallistel, C. R. (2001). Variability signatures distinguish verbal from nonverbal counting in both large and small numbers, Psychon. Bull. Rev. 8, 698–707.
Cowan, N. (2001). The magical number 4 in short-term memory: a reconsideration of mental storage capacity, Behav. Brain Sci. 24, 87–185.
Culham, J. C., Brandt, S. A., Cavanagh, P., Kanwisher, N. G., Dale, A. M., and Tootell, R. B. H. (1998). Cortical fMRI activation produced by attentive tracking of moving targets, J. Neurophysiol. 88, 2657–2670.
Culham, J. C., Cavanagh, P., and Kanwisher, N. G. (2001). Attention response functions: characterizing brain areas using fMRI activation during parametric variations of attentional load, Neuron 32, 737–745.
Dehaene, S. (2011). The Number Sense: How the Mind Creates Mathematics, Revised and Updated Edition. New York: Oxford University Press.
Dehaene, S., and Changeux, J. P. (1993). Development of elementary numerical abilities: a neuronal model, J. Cogn. Neurosci. 5, 390–407.
Drew, T., and Vogel, E. K. (2008). Neural measures of individual differences in selecting and tracking multiple moving objects, J. Neurosci. 28, 4183–4191.
Egeth, H. E., Leonard, C. J., and Palomares, M. (2008). The role of attention in subitizing: is the magical number 1? Vis. Cogn. 16, 463–473.
Egly, R., Driver, J., and Rafal, R. D. (1994). Shifting visual attention between objects and locations: evidence from normal and parietal lesion subjects, J. Exp. Psychol. Gen. 123, 161–177.
Feigenson, L., and Carey, S. (2003). Tracking individuals via object files: evidence from infants’ manual search, Dev. Sci. 6, 568–584.
Feigenson, L., and Carey, S. (2005). On the limits of infants’ quantification of small object arrays, Cognition 97, 295–313.
Feigenson, L., Carey, S., and Hauser, M. D. (2002). The representations underlying infants’ choice of more: object files versus analog magnitudes, Psychol. Sci. 13, 150–156.
Feigenson, L., Dehaene, S., and Spelke, E. S. (2004). Core systems of number, Trends Cogn. Sci. (Regul. Ed.) 8, 307–314.
Gallivan, J. P., Chapman, C. S., Wood, D. K., Milne, J. L., Ansari, D., Culham, J. C., and Goodale, M. A. (2011). One to four, but nothing more: Non-conscious parallel object individuation in action, Psychol. Sci. 22, 803–811.
Gilmore, C. K., McCarthy, S. E., and Spelke, E. S. (2010). Non-symbolic arithmetic abilities and achievement in the first year of formal schooling in mathematics, Cognition 115, 394–406.
Halberda, J., Mazzocco, M., and Feigenson, L. (2008). Individual differences in nonverbal estimation ability predict maths achievement, Nature 455, 665–669.
Halberda, J., Sires, S. F., and Feigenson, L. (2006). Multiple spatially-overlapping sets can be enumerated in parallel, Psychol. Sci. 17, 572–576.
Hyde, D. C., and Spelke, E. S. (2009). All numbers are not equal: an electrophysiological investigation of large and small number representations, J. Cogn. Neurosci. 21, 1039–1053.
Hyde, D. C., and Spelke, E. S. (2011a). Neural signatures of number processing in infants: evidence for two core systems underlying numerical cognition, Dev. Sci. 14, 360–371.
Hyde, D. C., and Spelke, E. S. (2011b). Spatiotemporal dynamics of processing nonsymbolic number: an event-related potential source localization study, Hum. Brain Mapp. doi: 10.1002/hbm.21352. [Epub ahead of print].
Hyde, D. C., and Wood, J. N. (2011). Spatial attention determines the nature of non-verbal numerical cognition, J. Cogn. Neurosci. 23, 2336–2351.
Izard, V., Dehaene-Lambertz, G., and Dehaene, S. (2008). Distinct cerebral pathways for object identity and number in 3-month-old infants, PLoS Biol. 6, e11. doi:10.1371/journal.pbio.0060011
Kaufman, E. L., Lord, M. W., Reese, T. W., and Volkmann, J. (1949). The discrimination of visual number, Am. J. Psychol. 62, 498–525.
Lavie, N. (2005). Distracted and confused?: selective attention under load, Trends Cogn. Sci. (Regul. Ed.) 9, 75–82.
Lavie, N., and de Fockert, J. W. (2003). Contrasting effects of sensory limits and capacity limits in visual selective attention, Percept. Psychophys. 65, 202–212.
Le Corre, M., and Carey, S. (2007). One, two, three, four, nothing more: an investigation of the conceptual sources of the verbal counting principles, Cognition 105, 395–438.
Libertus, M. E., Woldorff, M. G., and Brannon, E. M. (2007). Electrophysiological evidence for notation intendance in numerical processing, Behav. Brain Funct. 3, 1.
Lipton, J. S., and Spelke, E. S. (2004). Discrimination of large and small numerosities by human infants, Infancy 5, 271–290.
Luck, S. J., and Vogel, E. K. (1997). The capacity of visual working memory for features and conjunctions, Nature 390, 279–281.
Meck, W. H., and Church, R. M. (1983). A mode control model of counting and timing processes, J. Exp. Psychol. Anim. Behav Process. 9, 320–334.
Moyer, R. S., and Landauer, T. K. (1967). Time required for judgments of numerical inequality, Nature 215, 1519–1520.
Moyer, R. S., and Landauer, T. K. (1973). Determinants of reaction time for digit inequality judgments, Bull. Psychon. Soc. 1, 167–168.
Nieder, A., and Dehaene, S. (2009). Representation of number in the brain, Ann. Rev. Neurosci. 32, 185–208.
Nieder, A., and Merten, K. (2007). A labeled-line code for small and large numerosities in the monkey prefrontal cortex, J. Neurosci. 27, 5986–5993.
Palomares, M., Smith, P. R., Pitts, C. H., and Carter, B. M. (2011). The effect of viewing eccentricity on enumeration, PLoS ONE 6, e20779. doi:10.1371/journal.pone.0020779
Piazza, M. (2010). Neurocognitive start-up tools for symbolic number representations, Trends Cogn. Sci. (Regul. Ed.) 14, 542–551.
Piazza, M., Facoetti, A., Trussardi, A. N., Bertletti, I., Conte, S., Lucangeli, D., Dehaene, S., and Zorzi, M. (2010). Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia, Cognition 116, 33–41.
Piazza, M., Fumarola, A., Chinello, A., and Melcher, D. (2011). Subitizing reflects visuo-spatial object individuation capacity, Cognition 121, 147–153.
Piffer, L., Agrillo, C., and Hyde, D. C. (2011). Small and large number discrimination in guppies, Anim. Cogn. doi: 10.1007/s10071-011-0447-9. [Epub ahead of print].
Revkin, S. K., Piazza, M., Izard, V., Cohen, L., and Dehaene, S. (2008). Does subitizing reflect numerical estimation? Psychol. Sci. 19, 607–614.
Rugani, R., Regolin, L., and Vallortigara, G. (2008). Discrimination of small numerosities in young chicks, J. Exp. Psychol. Anim. Behav. Process. 34, 388–399.
Rugani, R., Regolin, L., and Vallortigara, G. (2010). Imprinted numbers: Newborn chicks’ sensitivity to number vs. continuous extent of objects they have been reared with, Dev. Sci. 13, 790–797.
Simon, T. J., Hespos, S. J., and Rochat, P. (1995). Do infants understand simple arithmetic? A replication of Wynn (1992). Cogn. Dev. 10, 253–269.
Trick, L. M., and Pylyshyn, Z. W. (1994). Why are small and large numbers enumerated differently? A limited capacity preattentive stage in vision, Psychol. Rev. 101, 80–102.
Uller, C., Carey, S., Huntley-Fenner, G., and Klatt, L. (1999). What representations might underlie infant numerical knowledge? Cogn. Dev. 14, 1–36.
Van Herwegen, J., Ansari, D., Elsabbagh, M., Xu, F., and Karmiloff-Smith, A. (2008). Small mall and large number processing in infants and toddlers with Williams syndrome, Dev. Sci. 11, 637–643.
vanMarle, K., and Wynn, K. (2009). Infants’ auditory enumeration: evidence for analog magnitudes in the small number range, Cognition 111, 302–316.
Verguts, T., and Fias, W. (2004). Representation of number in animals and humans: a neural model, J. Cogn. Neurosci. 16, 1493–1504.
Vetter, P., Butterworth, B., and Bahrami, B. (2008). Modulating attentional load affects numerosity estimation: evidence against a pre-attentive subitizing mechanism, PLoS ONE 3, e3269. doi:10.1371/journal.pone.0003269
Vetter, P., Butterworth, B., and Bahrami, B. (2011). A candidate for the attentional bottleneck: set-size specific modulation of right TPJ during attentive enumeration, J. Cogn. Neurosci. 23, 728–736.
Wilken, P., and Ma, W. J. (2004). A detection theory account of change detection, J. Vis. 4, 1120–1135.
Wood, J. N., and Spelke, E. S. (2005). Infants’ enumeration of actions: Numerical discrimination and its signature limits, Dev. Sci. 8, 173–181.
Xu, F. (2003). Numerosity discrimination in infants: evidence for two systems of representations, Cognition 89, B15–B25.
Xu, X., and Liu, C. (2008). Can subitizing survive the attentional blink? An ERP study, Neurosci. Lett. 440, 140–144.
Xu, Y. (2009). Distinctive neural mechanisms supporting visual object individuation and identification, J. Cogn. Neurosci. 21, 511–518.
Xu, Y., and Chun, M. M. (2006). Dissociable neural mechanisms supporting visual short-term memory for objects, Nature 440, 91–95.
Keywords: number, cognition, representation, ERP, fMRI, attention, memory
Citation: Hyde DC (2011) Two systems of non-symbolic numerical cognition. Front. Hum. Neurosci. 5:150. doi: 10.3389/fnhum.2011.00150
Received: 02 September 2011;
Paper pending published: 27 October 2011;
Accepted: 09 November 2011;
Published online: 29 November 2011.
Edited by:
Daniel Ansari, The University of Western Ontario, CanadaReviewed by:
Ian Mark Lyons, University of Chicago, USAAngela Heine, Freie Universität Berlin, Germany
Copyright: © 2011 Hyde. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Daniel C. Hyde, Laboratory for Developmental Studies, Department of Psychology, Harvard University, 1118 WJH, 33 Kirkland Street, Cambridge, MA 02138, USA. e-mail: dchyde@fas.harvard.edu