- 1 Department of Psychiatry, Yale University School of Medicine, New Haven, CT, USA
- 2 Department of Neurobiology, Yale University School of Medicine, New Haven, CT, USA
- 3 Interdepartmental Neuroscience Program, Yale University School of Medicine, New Haven, CT, USA
Error detection is critical to the shaping of goal-oriented behavior. Recent studies in non-human primates delineated a circuit involving the lateral habenula (LH) and ventral tegmental area (VTA) in error detection. Neurons in the LH increased activity, preceding decreased activity in the VTA, to a missing reward, indicating a feedforward signal from the LH to VTA. In the current study we used connectivity analyses to reveal this pathway in humans. In 59 adults performing a stop signal task during functional magnetic resonance imaging, we identified brain regions showing greater psychophysiological interaction with the habenula during stop error as compared to stop success trials. These regions included a cluster in the VTA/substantia nigra (SN), internal segment of globus pallidus, bilateral amygdala, and insula. Furthermore, using Granger causality and mediation analyses, we showed that the habenula Granger caused the VTA/SN, establishing the direction of this interaction, and that the habenula mediated the functional connectivity between the amygdala and VTA/SN during error processing. To our knowledge, these findings are the first to demonstrate a feedforward influence of the habenula on the VTA/SN during error detection in humans.
Introduction
Goal-oriented behavior requires outcome monitoring. Many studies in non-human primates described the role of the saliency/reward pathway, involving the ventral tegmental area (VTA) and substantia nigra (SN), in outcome and error processing (Montague et al., 1996; Schultz et al., 1997; Holroyd and Coles, 2002; Schultz, 2002; Fiorillo et al., 2003; Bayer and Glimcher, 2005). Neurons in the VTA/SN increase activity to an unexpected reward and decrease activity to a missing reward. These roles of VTA/SN in error-related cognitive processes have recently been substantiated in humans (D’Ardenne et al., 2008; Carter et al., 2009; Duzel et al., 2009).
Anatomical and electrophysiological studies converged to suggest a function of the epithalamus/habenula in regulating outcome-related signals in the VTA/SN (Matsuda and Fujimura, 1992; Scheibel, 1997; Ji and Shepard, 2007; Matsumoto and Hikosaka, 2007, 2009; Hikosaka et al., 2008; Morissette and Boye, 2008). For instance, neurons in the habenula and midbrain were each excited and inhibited by no-reward-predicting targets; and electrical stimulation of lateral habenula (LH) decreased activity in the dopaminergic neurons (Matsumoto and Hikosaka, 2007).
In an earlier functional magnetic resonance imaging (fMRI) study of humans performing a target prediction task, hemodynamic responses were observed in the anterior cingulate cortex, inferior anterior insula, and habenula during negative feedback (Ullsperger and von Cramon, 2003). The authors suggested a role of the habenula in error monitoring and as a critical modulatory relay between the limbic forebrain structures and the midbrain. In another study, co-activation of the habenula and midbrain was observed during negative but not positive feedback (Shepard et al., 2006). A recent study with more detailed anatomical mapping confirmed the habenula as the locus responding to negative rewards (Salas et al., 2010). However, it remains unclear whether the habenula signals to the VTA/SN in outcome monitoring, as has been demonstrated in non-human primates. The current study aimed to fill this gap of knowledge.
In previous studies, we observed activation of subcortical structures including the habenula during error trials in a stop signal task (Li et al., 2008b). Here we substantiated the functional connectivity of the habenula and VTA/SN, using psychophysiological interaction (PPI), Granger causality analysis (GCA), and mediation analysis. PPI is a voxel-wise method widely used to examine whether correlation in activity between two brain areas is modulated by psychological contexts (Friston et al., 1997; Gitelman et al., 2003; Stephan et al., 2003; O’Reilly et al., 2008; Hare et al., 2009). We used PPI to establish greater connectivity between the habenula and VTA/SN during stop error (SE) as compared to stop success (SS) trials. However, PPI does not specify the direction of influence between brain regions. In contrast, GCA has been used to model directional interaction between blood oxygenation level dependent (BOLD) time series (Goebel et al., 2003; Roebroeck et al., 2005; Abler et al., 2006; Stilla et al., 2007; Deshpande et al., 2008; Duann et al., 2009; Sato et al., 2009; Ide and Li, 2011). We thus used GCA to ascertain the direction of connectivity between the habenula and VTA/SN. Furthermore, with mediation analysis we established that the habenula projected directly to the VTA/SN.
Materials and Methods
Subjects and Behavioral Task
Fifty-nine healthy adult subjects (30 men, 22–45 years of age) participated in the study according to a protocol approved by Yale University Human Investigation Committee.
We employed a simple reaction time task in this stop signal paradigm (Logan et al., 1984; Li et al., 2006, 2008a, 2009). There were two trial types: “go” and “stop,” randomly intermixed. A small dot appeared on the screen to engage attention at the beginning of a go trial. After a randomized time interval (fore-period) between 1 and 5 s, the dot turned into a circle (the “go” signal), prompting the subjects to quickly press a button. The circle vanished at a button press or after 1 s had elapsed, whichever came first, and the trial terminated. A premature button press prior to the appearance of the circle also terminated the trial. Approximately three quarters of all trials were go trials. The remaining one quarter were stop trials. In a stop trial, an additional “X,” the “stop” signal, appeared after and replaced the go signal. The subjects were told to withhold button press when they saw the stop signal. Likewise, a trial terminated at button press or when 1 s had elapsed since the appearance of the stop signal. The stop signal delay (SSD) – the time interval between the go and stop signal – started at 200 ms and varied from one stop trial to the next according to a staircase procedure: if the subject succeeded in withholding the response, the SSD increased by 64 ms; conversely, if they failed, SSD decreased by 64 ms (Levitt, 1971). There was an inter-trial-interval of 2 s. Subjects were instructed to respond to the go signal quickly while keeping in mind that a stop signal could come up in a small number of trials. All participants had a practice session outside the scanner and completed four 10-min runs of the task in the scanner. Depending on the actual stimulus timing (trials varied in fore-period duration) and speed of response, the total number of trials varied slightly across subjects in an experiment. With the staircase procedure we anticipated that the subjects would succeed in withholding their response in approximately half of the stop trials.
As a control experiment, we also imaged 30 subjects during a 10-min resting state session, in which subjects were instructed to stay awake and relaxed, with their eyes closed (Duann et al., 2009).
Imaging Protocol
Conventional T1-weighted spin echo sagittal anatomical images were acquired for slice localization using a 3-T scanner (Siemens Trio). Anatomical images of the functional slice locations were next obtained with spin echo imaging in the axial plane parallel to the AC–PC line with TR = 300 ms, TE = 2.5 ms, bandwidth = 300 Hz/pixel, flip angle = 60°, field of view = 220 mm × 220 mm, matrix = 256 × 256, 32 slices with slice thickness = 4 mm and no gap. Functional, BOLD signals were then acquired with a single-shot gradient echo echoplanar imaging (EPI) sequence. Thirty-two axial slices parallel to the AC–PC line covering the whole brain were acquired with TR = 2,000 ms, TE = 25 ms, bandwidth = 2,004 Hz/pixel, flip angle = 85°, field of view = 220 mm × 220 mm, matrix = 64 × 64, 32 slices with slice thickness = 4 mm and no gap. Three hundred images were acquired in each session.
Spatial Pre-Processing of Brain Images
Data were analyzed with Statistical Parametric Mapping 8 (Wellcome Department of Imaging Neuroscience, University College London, UK). Images from the first five TRs at the beginning of each trial were discarded to enable the signal to achieve steady-state equilibrium between RF pulsing and relaxation. Images of each individual subject were first corrected for slice timing, realigned (motion-corrected) and unwarped (Andersson et al., 2001; Hutton et al., 2002). A mean functional image volume was constructed for each subject for each run from the realigned image volumes. These mean images were co-registered with the high resolution structural image and then segmented for normalization to an Montreal Neurological Institute (MNI) EPI template with affine registration followed by non-linear transformation (Ashburner and Friston, 1999, 2005). The normalization parameters determined for the mean functional volume were then applied to the corresponding functional image volumes for each subject. Finally, images were smoothed with a Gaussian kernel of 6 mm at full width at half maximum.
General Linear Modeling
We followed our previous studies in the statistical modeling of imaging data (Li et al., 2006, 2008a). Briefly, four trial types were distinguished: go success (G), go error (F), SS, and SE trials. A statistical analytical design was constructed for each individual subject, using the general linear model (GLM) with the onsets of go signal in each of these trial types convolved with a canonical hemodynamic response function (HRF) and with the temporal derivative of the canonical HRF entered as regressors in the model (Friston et al., 1995). We entered reaction time (RT) and SSD as parametric modulators for go and stop trials, respectively, in the GLM. Realignment parameters in all six dimensions were also entered in the model. The data were high-pass filtered (128 s cutoff) to remove low-frequency signal drifts, and serial autocorrelation caused by aliased cardiovascular and respiratory signals was corrected by a first-degree autoregressive or AR (1) model (Friston et al., 2000; Della-Maggiore et al., 2002). Across subjects, there were: 281.6 ± 19.6 G trials, 11.2 ± 12.0 F trials, 47.2 ± 4.7 SS trials, and 40.8 ± 7.2 SE trials. We did not include F trials in the current analyses, because they comprised less than 3% of all trials.
In the first-level analysis, we constructed for each individual subject a contrast SE > SS in order to identify regional brain activations associated with error detection (Li et al., 2008b). Our previous work showed that the contrasts SS > G and SE > G activated brain regions that overlapped those of SE > SS, including the anterior cingulate cortex (both SS > G and SE > G) as well as the thalamus and midbrain (SE > G; Li et al., 2008b). Thus, to demonstrate the specificity of the contrast SE > SS in PPI, we examined SE > G and SS > G for comparison (see below). The contrast images (con) of the first-level analysis were used for random-effect analysis (Penny et al., 2004) to obtain group T maps using a one-sample t test. Brain regions were identified using an atlas (Duvernoy, 2003; Mai et al., 2008).
Psychophysiological Interaction
We used PPI to describe how functional connectivity between brain regions was altered as a result of psychological context (Friston et al., 1997). We hypothesized that the habenula showed greater PPI with the VTA and SN during SE compared to SS trials. With the contrast SE > SS, we identified a mask of the habenula comprising two symmetric spheres each of 6 mm in radius and centered at MNI coordinates [−1, −25, 1] and [1, −25, 1]. This mask was well within the area identified as habenula in Ullsperger and von Cramon, 2003 (Talairach and approximate MNI coordinates: [−5/6, −25, 8] and [−6/6, −25, 5]). On the basis of the GLM, we extracted the time series of the first eigenvariate of the BOLD signal of the habenula for each individual subject. The eigenvariate value, inside a region of interest (ROI), corresponds to the average BOLD signal weighted by the voxel significance, and it is more robust to outliers (Gitelman et al., 2003). This time series constituted the physiological variable. The time series were de-convolved to remove the effects of HRF, multiplied by the psychological variable (SE > SS, i.e., “1” for SE and “−1” for SS conditions), and re-convolved with the canonical HRF to obtain the interaction term or PPI variable (Gitelman et al., 2003). The three variables were entered as regressors in a whole-brain GLM. PPI analysis was performed for each individual subject, and the resulting positive contrast images (i.e., “1” for the PPI regressors) were used in random-effect group analysis (Penny et al., 2004). Group results were reported for p < 0.001, uncorrected. To check whether PPI results were specific to the contrast SE > SS, we also used SE > G and SS > G as psychological variables of PPI for comparison.
To ascertain the specificity of brain regions of PPI with the habenula during error processing, we performed another PPI analysis with a “control” seed region, involving the error activated thalamic cluster (MNI coordinates [14, −12, 5] and [−14, −20, 10], 5,600 mm3), exclusively masked by a larger area encompassing the habenula (two spheres of 10 mm in radius and centered at [−1, −25, 1] and [1, −25, 1]). This mask was to ensure the exclusion of the habenula from the control seed region.
For the regression slope analysis, multivariate GCA, and mediation analysis, we referred to the habenula and the regions identified with PPI as the ROIs or only the latter brain regions as ROIs.
Multivariate Granger Causality Analysis
The analysis of PPI identified areal interaction but did not specify the direction of influence. In order to confirm our hypothesis that the habenula signals the VTA in error detection and not the other way around, we used a multivariate GCA (Stilla et al., 2007; Deshpande et al., 2009) to examine the direction of the influence between the ROIs of PPI and the habenula.
Multivariate GCA was implemented as in our previous work (Duann et al., 2009; Ide and Li, 2011). We considered two models; the first one included the habenula and all four regions identified from PPI as ROIs, and the second model included the habenula and three PPI regions (all except the globus pallidus; see below). Multivariate GCA was performed for individual subjects. For each subject and each ROI, a summary time series was computed by averaging across voxels inside the ROI for each time point. These average time series were concatenated across four sessions, after de-trending and normalization (Ding et al., 2000). Afterward, the pre-processed time series were entered into multivariate autoregressive (MAR) modeling (Harrison et al., 2003). We used the Akaike Information Criterion (AIC), which imposes a complexity penalty on the number of parameters and avoids over-fitting of the data (Akaike, 1974). The application of MAR modeling required that each ROI time series was covariance stationary, which we examined with the Augmented Dickey Fuller (ADF) test (Hamilton, 1994). The ADF test verified that there was no unit root in the modeled time series. The residuals of MAR modeling were used to compute the Granger causality measures (F values) of each possible connection between ROIs. Since MAR modeling often involves highly interdependent residuals (Deshpande et al., 2009), we used permutation resampling (Hesterberg et al., 2005; Seth, 2010) to obtain an empirical null distribution of no causality, as suggested in Roebroeck et al. (2005), in order to estimate the Fcritical, and assess the statistical significance of Granger causality measures. With resampling, we produced surrogate data by randomly generating time series with the same mean, variance, autocorrelation function, and spectrum as the original data (Theiler et al., 1992), as implemented in previous EEG (Kaminski et al., 2001; Kus et al., 2004), and fMRI studies (Deshpande et al., 2009). We used binomial test to assess statistical significance in group analysis (Duann et al., 2009; Uddin et al., 2009); for each connection, we counted the number of subjects that had F > Fcritical (i.e., significant connection) and estimated its significance using a binomial distribution with parameters n = 59 trials and p = q = 0.5 (same probability to observe a connection or not). Multiple comparisons were corrected for false discovery rate (FDR; Genovese et al., 2002).
We applied the same multivariate GCA procedures to resting state data of the 30 subjects, following our previous work (Duann et al., 2009), as an additional control for false positive connectivities. The absence of functional connectivity in the resting data would suggest that the task-related connectivity is not an artifact of HRF variability across the brain (see next section for more details).
GCA: methodological considerations
Although some investigators argued the importance of causality based on temporal precedence and the utility of GCA in connectivity analyses (e.g., Roebroeck et al., 2009), others discussed the limitations of GCA (e.g., Friston, 2009). As detailed in a recent review of GCA in neuroimaging (Bressler and Seth, 2010), the utility of Granger causality measures depends on successfully estimating autoregressive (AR) models of stochastic processes. Successful applications of GCA to fMRI data (Roebroeck et al., 2005; Stilla et al., 2007; Bressler et al., 2008; Deshpande et al., 2009; Duann et al., 2009; Kayser et al., 2009; Ide and Li, 2011) appeared to have some elements in common. First, it is crucial that the modeled time series are wide-sense stationary (WSS; i.e., they have constant mean and variance). Otherwise, non-stationary time courses are known to produce spurious regression results (Granger and Newbold, 2001). Second, it is also important to have a number of observations (time points) adequate to estimate the AR model coefficients. In the current GCA modeling, by concatenating BOLD time series across four sessions for each individual (a total of 1,180 time points) after de-trending and normalization, we obtained time series (averaged inside each ROI) that were sufficiently long and covariance stationary, the latter verified by the ADF test. Third, we applied spatial but not temporal filtering to the original BOLD signals because temporal (e.g., bandpass) filtering is known to introduce severe confounds in GCA of neuroimaging time series (Florin et al., 2010; Seth, 2010). These procedures were also successfully applied in our previous studies (Duann et al., 2009; Ide and Li, 2011).
An additional consideration is the effects of HRF variability and down-sampling of BOLD signals on autoregressive modeling. A popular approach is to use the “difference of influence” (DOI) between two regions (Roebroeck et al., 2005; Stilla et al., 2007) to ameliorate these effects. However, this approach is no longer valid for multivariate GCA. In such cases, a useful practice is to analyze Granger causality during different experimental conditions (e.g., by studying both task and resting conditions; Duann et al., 2009; Kayser et al., 2009), since the effects of HRF variability and signal down-sampling are not expected to vary across conditions.
A few studies in the literature presented less successful results from GCA. In a study of simultaneous electroencephalographic recordings and fMRI in rats, David et al. (2008) showed spurious connectivities derived from GCA due to HRF variability. However, one should note that the HRF variability was outside normal physiological range. Furthermore, in a recent investigation using simulated BOLD signals by convolving a standard HRF with local field potentials recorded from macaque cortex, Deshpande et al. (2010) showed that, even considering real and normal range of HRF variability (Handwerker et al., 2004) and a signal-to-noise ratio of 1 unit and a TR = 2 s, GCA reliably detected neuronal delays around 700 ms (Deshpande et al., 2010). Witt and Meyerand (2009) reported poor performance of GCA but it is not clear whether these experiments were biased because of simulated fMRI time series generated using Dynamic Causal Modeling (Friston, 2009) or whether these simulated time series were covariance stationary.
Taken together, although GCA presents some technical challenges, we believe that, when it is carefully applied and done without over-interpretation of the results, GCA is a useful exploratory tool to delineate effective connectivity of the complex human brain.
Mediation Analysis
We performed mediation analyses to further characterize functional connectivity between the ROIs (MacKinnon et al., 2007), using the toolbox M3, developed by Tor Wager and Martin A. Lindquist1. Mediation analyses are widely used in social and economic research to examine whether a relationship between two variables is mediated by an intervening variable (Maccorquodale and Meehl, 1948; Baron and Kenny, 1986). It was successfully applied to fMRI of emotion regulation (Wager et al., 2008; Lebrecht and Badre, 2008) and more recently to analyses of functional connectivity (Hare et al., 2010). In a mediation analysis, the relation between the independent variable X and dependent variable Y, i.e., X → Y, is tested to see if it is significantly mediated by a variable M. The mediation test is performed by employing three regression equations (MacKinnon et al., 2007):
Y = i1 + cX + e1
Y = i2 + c′X + bM + e2
M = i3 + aX + e3
where a represents X → M, b represents M → Y (controlling for X), c′ represents X → Y (controlling for M), and c represents X → Y. In the literature, a, b, c, and c′ were referred as path coefficients or simply paths (MacKinnon et al., 2007; Wager et al., 2008), and we followed this notation. Variable M is said to be a mediator of connection X → Y, if (c − c′) is significantly different from 0, which is mathematically equivalent to the product of the paths a × b (MacKinnon et al., 2007). If the product a × b and the paths a and b are significant, one concludes that X → Y is mediated by M. In addition, if path c′ is not significant, it indicates that there is no direct connection from X to Y and that X → Y is completely mediated by M. Note that path b is the relation between Y and M, controlling for X, and it should not be confused with the correlation coefficient between Y and M.
Mediation analyses: methodological considerations
As with other methods based on structural equation models, one assumed that all relevant variables are included in the analysis; i.e., one could not rule out the existence of mediating factors not tested in the model (Lebrecht and Badre, 2008). In addition, mediation analysis is only valid upon correct specification of the causal orders (MacKinnon et al., 2007). We believe that these limitations were addressed to a significant extent in the current study: whole-brain PPI identified all relevant ROIs functionally connected to the habenula during errors; and multivariate GCA provided important information regarding causal orders. Finally, as pointed out by Wager et al. (2008), an additional limitation of using mediation analysis in fMRI is that models are made on the basis of naturally occurring variance over subjects, and thus conclusions are made with the assumption that inter-subject variability does not affect the coupling between dependent variables. This restriction also applies to the study. One could control the variability by simply removing the regression outliers (Chatterjee and Hadi, 1986) or, alternatively, develop multilevel mediation models that consider the mediation path coefficients as random effects (MacKinnon et al., 2007).
Results
Brain Regions of PPI with the Habenula
With general linear modeling we examined and confirmed error-related regional brain activations during the stop signal task (Li et al., 2008b). Compared to SS, SE trials evoked greater activations in the medial frontal cortex including the dorsal anterior cingulate cortex (dACC) and pre-supplementary motor area (preSMA), as well as the anterior inferior insulas, thalamus, habenula, and structures in the midbrain, at p < 0.05, corrected for family-wise error (FWE) of multiple comparisons (Figure 1; Table 1).
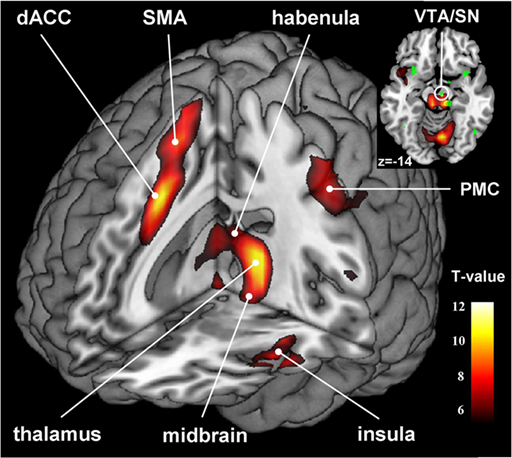
Figure 1. Error-related activations during a stop signal task: stop error > stop success; p < 0. 05, corrected for FWE. dACC, dorsal anterior cingulate cortex; SMA, supplementary motor area; PMC, primary motor cortex. The inset on the top depicts the error-related activations in relation to regions functionally connected to habenula (in green, results from psychophysiological interaction, Figure 2).
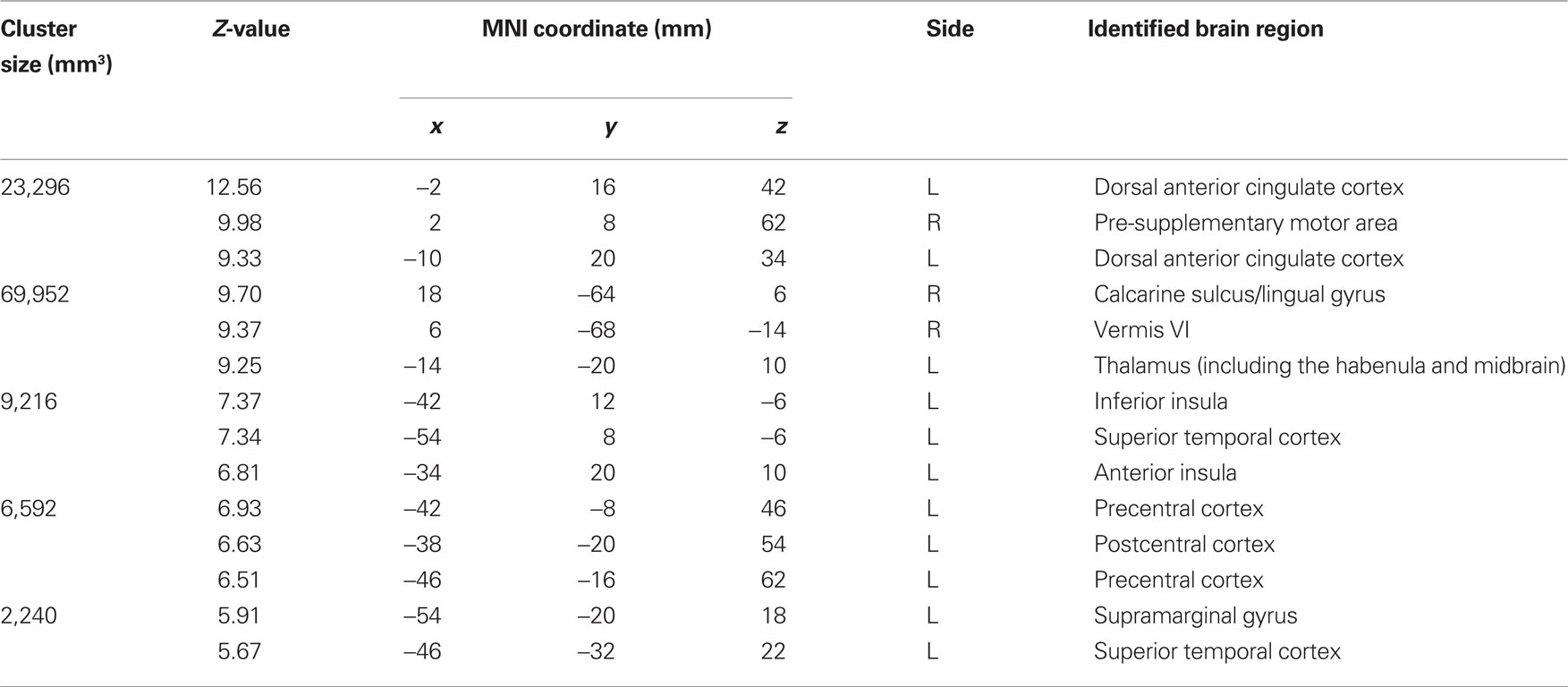
Table 1. Brain regions showing greater activation during stop error (SE), compared to stop success (SS), trials in the stop signal task (p < 0.05, corrected for FWE).
In PPI, we identified brain regions that were functionally connected with the habenula. Compared to SS trials, SE trials evoked greater PPI with the habenula in the VTA/SN, bilateral anterior inferior insula, amygdala, and the internal segment of the globus pallidus (GPi), at p < 0.001, uncorrected (Figure 2; Table 2). To test our hypothesis targeting the VTA/SN, we also performed a ROI analysis, using small volume correction for a spherical mask centered at [2, −16, −10] and 6 mm in radius (Carter et al., 2009). The results identified a peak of activation at [6, −16, −14], p < 0.005, corrected for FWE. In addition, on the basis of the literature (Seeley et al., 2007; Hikosaka et al., 2008; Haber and Knutson, 2010), the insula, amygdala, and GPi were also significant at p < 0.05, corrected for FWE, after small volume correction using anatomical masks from the Automated Anatomical Labeling atlas (Tzourio-Mazoyer et al., 2002). Conversely, no brain regions showed greater connectivity with the habenula during SS compared to SE trials (p < 0.01, uncorrected).
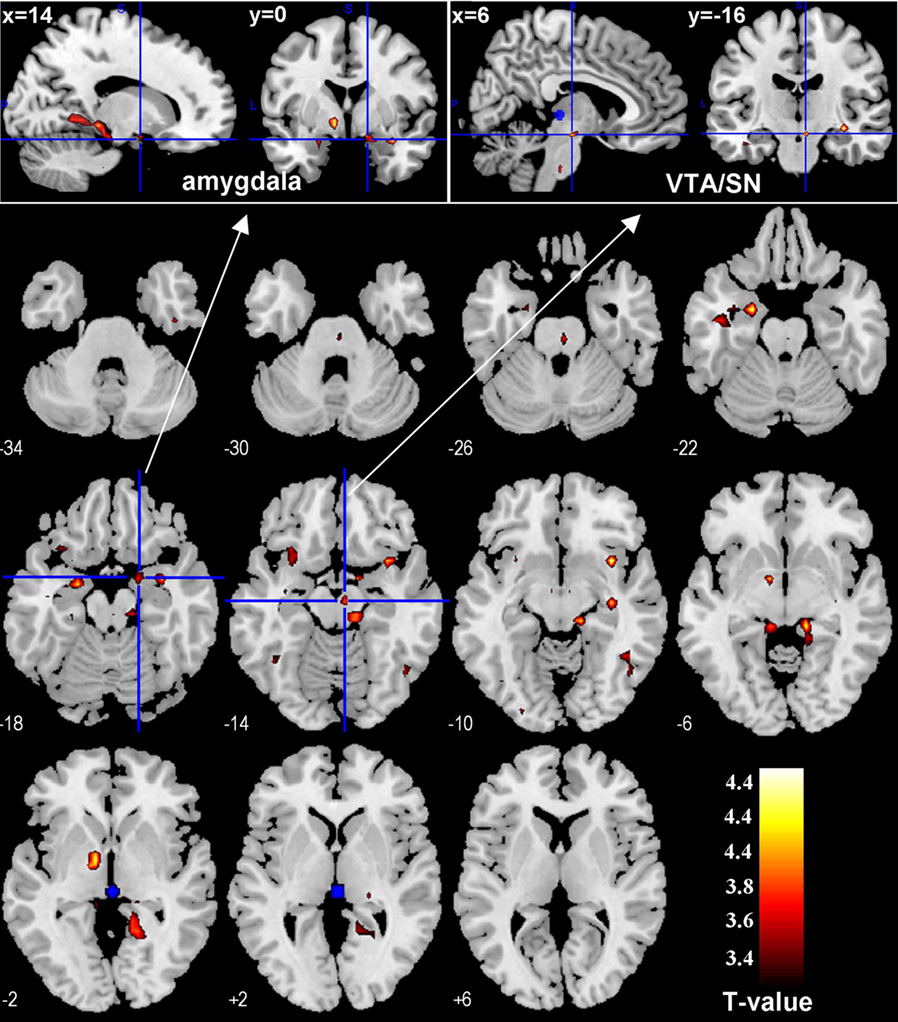
Figure 2. Regions showing psychophysiological interaction (in hot color) with the habenula (blue) during stop error as compared to stop success in the stop signal task. T maps were thresholded at p < 0.001, uncorrected. The insets on the top highlight locations of the right amygdala (left) and the ventral tegmental area/substantia nigra (VTA/SN, right) on sagittal and coronal sections. Interestingly, this VTA/SN cluster has little overlay with error-related activations in the midbrain area (see inset in Figure 1), i.e., these identified dopaminergic midbrain clusters were mostly not activated during stop error > stop success.
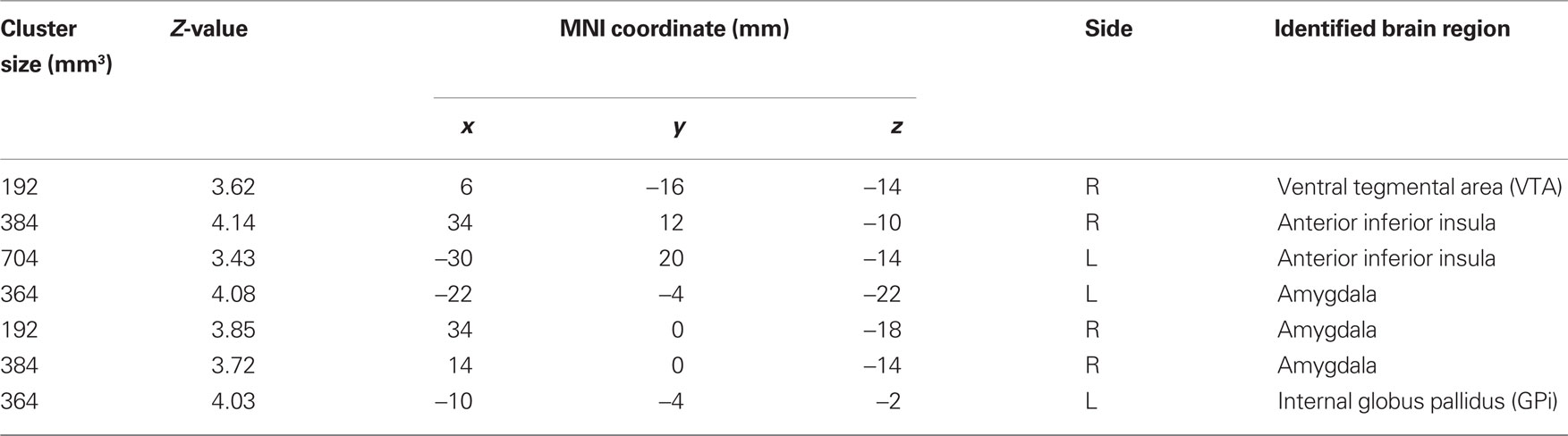
Table 2. Brain regions with psychophysiological interaction with the habenula during stop error > stop success (p < 0.001, uncorrected).
In comparison, PPI with SE > G and SS > G as psychological variables each revealed activations in the bilateral insula (SE > G) and precuneus (G > SE), and the right insula (SS > G) as well as posterior cingulate cortex and the precuneus (G > SS), p < 0.001, uncorrected (Figures 3 and 4). No foci were observed in the area of the VTA/SN or the amygdala (p < 0.01, uncorrected).
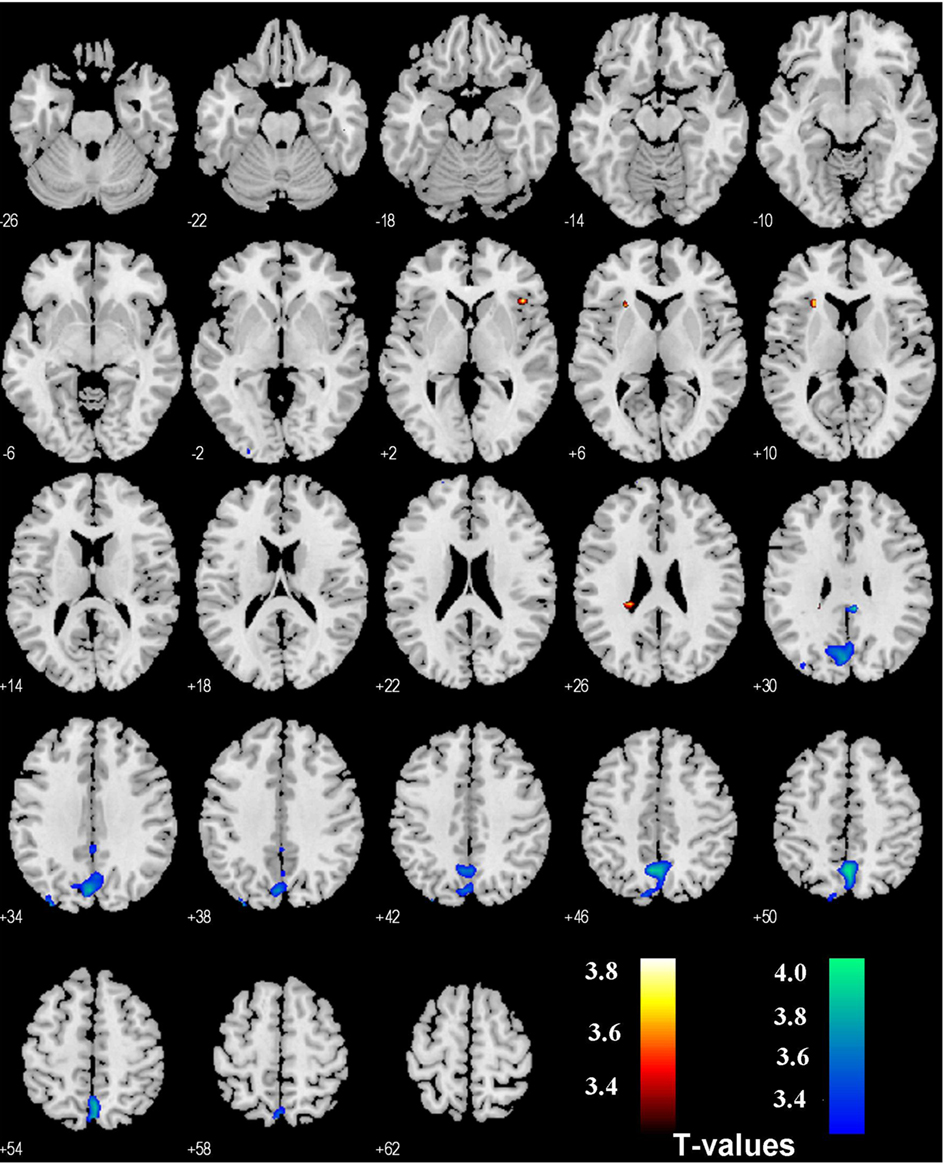
Figure 3. Regions showing psychophysiological interaction with the habenula during stop error (SE) as compared to go success (G, in hot color), and during G > SE (in cold color) in the stop signal task. T maps were thresholded at p < 0.001, uncorrected.
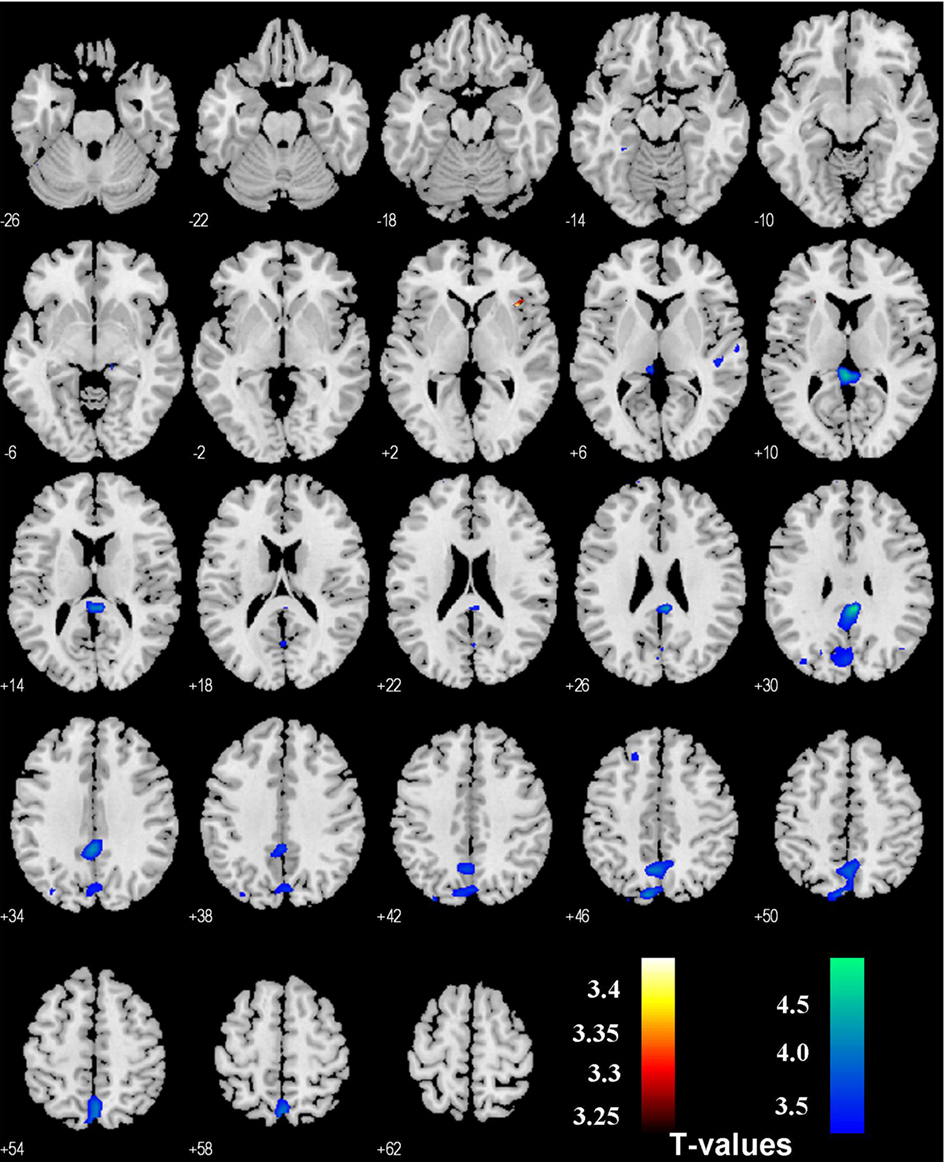
Figure 4. Regions showing psychophysiological interaction with the habenula during stop success (SS) as compared to go success (G, in hot color), and during G > SS (in cold color) in the stop signal task. T maps were thresholded at p < 0.001, uncorrected.
Because voxel smoothing in image pre-processing diminished spatial specificity of the results, we examined brain regions of PPI with the thalamic cluster “minus the habenula” as a control. The results showed that, at the same statistical threshold, regions showing PPI with the thalamus included the occipital cortices, fusiform gyrus, temporal cortex, insula, supplementary motor area, and prefrontal cortex (Figure 5; Table 3). No activation was observed in the VTA/SN region (p < 0.01, uncorrected). Thus, the PPI of the VTA/SN, bilateral amygdala, and the GPi appeared to be specific to the habenula.
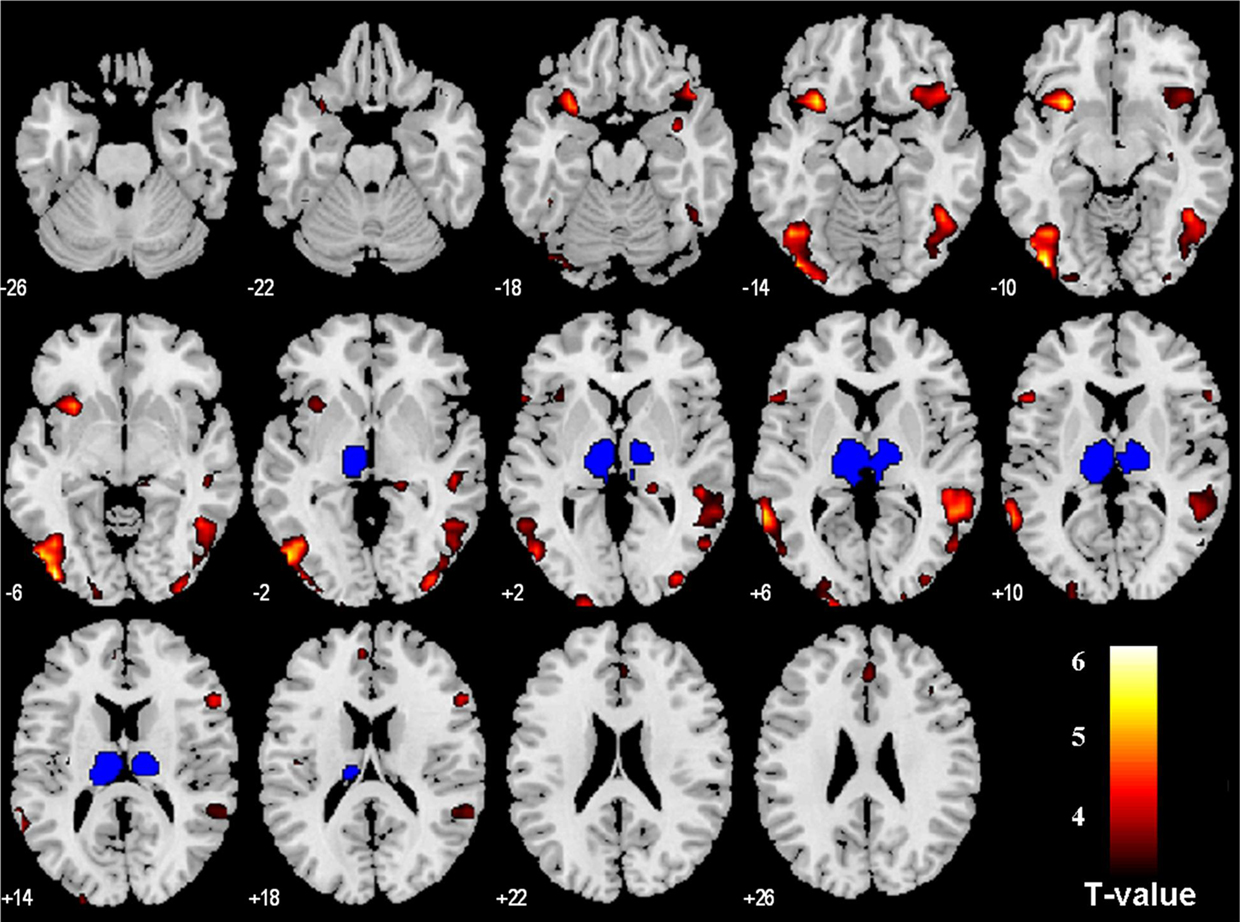
Figure 5. Regions (in hot color) of psychophysiological interaction (PPI) with the thalamus cluster “minus the habenula” (blue), during stop error as compared to stop success; p < 0. 001, uncorrected. These brain regions are summarized in Table 3. Note that, except for the left insula, the brain regions of PPI with the thalamus cluster did not overlap those of PPI with the habenula (Figure 2).
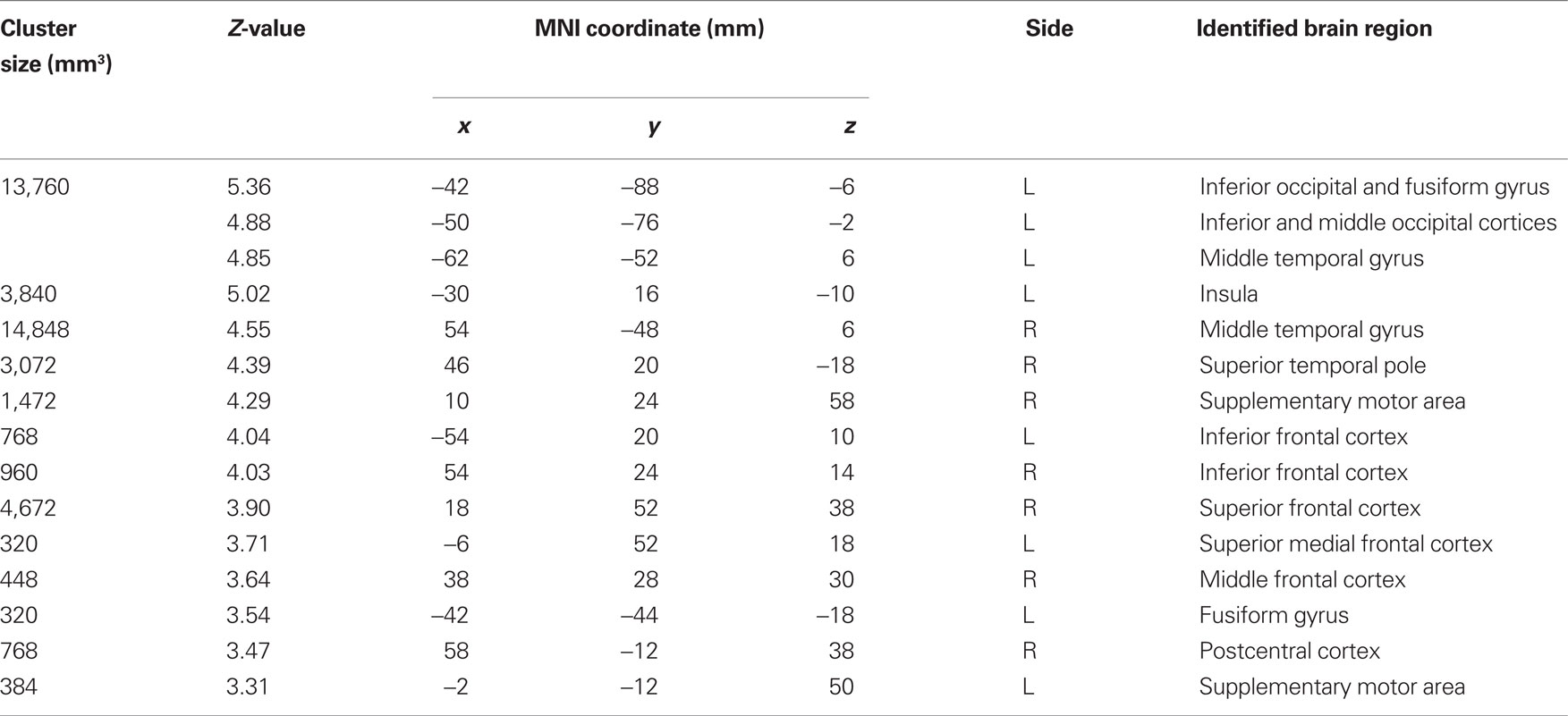
Table 3. Brain regions with psychophysiological interaction with the thalamus cluster “minus habenula” during stop error > stop success (p < 0.001, uncorrected).
Granger Causality Analysis
With multivariate GCA, we determined the direction of influence between the habenula and ROIs of PPI (Figure 6). In one model we included the habenula, VTA/SN, GPi, bilateral amygdala, and insula. To minimize model complexity and facilitate interpretation of the results, we combined bilateral amygdala as a single ROI. Similarly, we combined bilateral insula as a single region. For each individual subject we tested all possible connections between regions at p < 0.05, corrected for FDR, against an empirical statistical null distribution (see Materials and Methods). In a binomial test (p < 0.05) for the group, the results showed significant projections from the habenula to the VTA/SN, insula, and amygdala, but not to the GPi (Figure 6A). Thus, in a second model, we excluded the GPi, and again obtained significant projections from the habenula to the VTA/SN but not from the VTA/SN to the habenula (Figure 6B). Thirty-eight of the 59 participants also showed a significant projection from the amygdala to the VTA, compared to 44 with projection from the habenula to the VTA/SN.
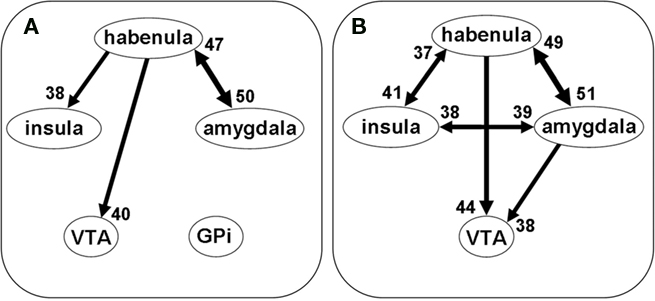
Figure 6. Granger causality analysis (GCA) indicated the directions of influence between the BOLD time series of regions of interest. (A) Shows the results of five ROIs: habenula, insula, amygdala, ventral tegmental area/substantia nigra (VTA/SN), and internal globus pallidus (GPi). The GPi did not show Granger causality with any other brain regions. Thus, we removed the GPi in a second model (B) of multivariate GCA. The results at (B) show that the habenula, insula, and amygdala are bidirectionally connected, while the habenula and amygdala unilaterally project to the VTA/SN. GCA was performed and evaluated for each connection of each individual subject, at p < 0.05, corrected for FDR. Group results were obtained using a binomial test for each connection (p < 0.05). The numbers next to the arrows indicate the number of subjects out of 59 who have that connection.
In contrast to these task-related connectivity patterns, no significant Granger causality was observed (binomial test, p > 0.50, in both models) for any of the connections in the resting state time series, providing evidence that these task-related connections were not spurious, such as resulting from HRF variability across the brain.
Mediation Analysis
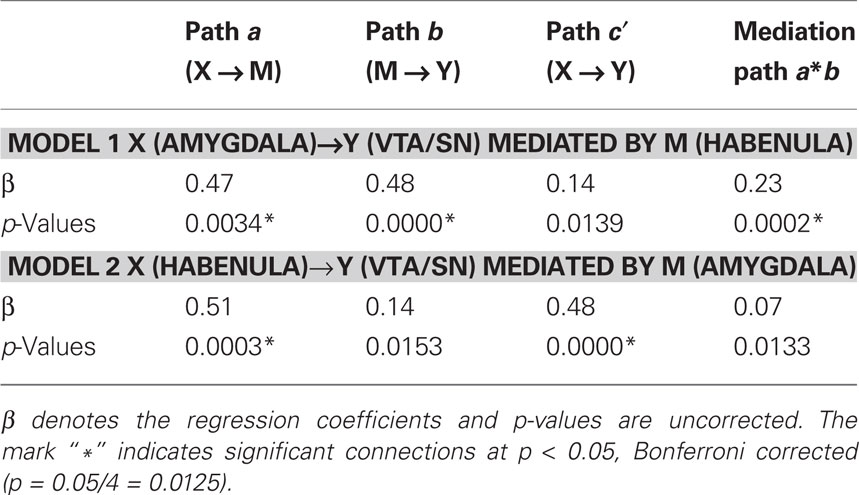
We performed mediation analyses to further characterize the functional connectivity between the habenula, amygdala, and VTA/SN during error processing. In particular, we tested the hypothesis that the projection amygdala → VTA/SN was mediated by the habenula. We derived for each individual subject the effect-size of SE > SS of the three ROIs for a single-level mediation analysis (MacKinnon et al., 2007); i.e., one single value (the effect-size of SE > SS; Brett et al., 20022). We tested two models. In the first model, the effect-sizes of the amygdala and VTA/SN, habenula were set as X, Y, and mediator variable M, respectively. In the second model, we tested if the projection from habenula (X) to VTA/SN (Y) was mediated by amygdala (M).
Figure 7 and Table 4 summarized the results. The results of the first model confirmed the hypothesis of the habenula mediating the connection from amygdala to VTA/SN during error processing. The results of the second model confirmed the lack of a projection from the amygdala to the VTA/SN.
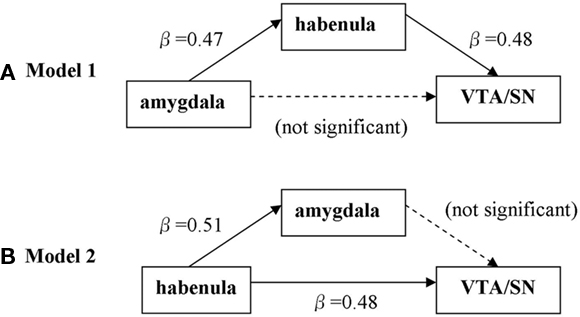
Figure 7. Single-level mediation analysis of the error-related effect-size (SE > SS) across subjects. (A) Model to test whether habenula mediates the correlation between amygdala and VTA/SN. (B) Model to test whether amygdala mediates the correlation between habenula and VTA/SN.
Discussion
The VTA/SN, bilateral amygdala, insula, and GPi showed greater PPI with the habenula during SE as compared to SS trials. In contrast, except for the left insula, none of these areas showed a PPI with the thalamic cluster. Thus, with the exception of the left insula, these brain regions altered activation to SE as compared to SS trials in specific association with the habenula in the stop signal task. Furthermore, the connectivity between the habenula and VTA/SN was contrast-specific as PPI of SS > G or SE > G did not reveal this connection.
As described in the above, PPI analyses did not provide information about the direction of influence between brain regions. Thus, we performed GCA, which confirmed a feedforward connection from the habenula to VTA/SN but not vice versa. The amygdala also showed a significant projection to the VTA/SN in addition to a bidirectional connection with the habenula, broadly consistent with evidence of anatomical projections from the amygdala to the VTA (Kaufling et al., 2009) and the role of amygdala in reward and saliency processing (Baxter and Murray, 2002; Etkin et al., 2006; Murray, 2007; Haber and Knutson, 2010; Linke et al., 2010; see also Delgado et al., 2008 for a review). On the other hand, Granger causality did not describe event-related relationship between time series. Thus, we used mediation analyses to further characterize the functional connectivities between the habenula, amygdala, and VTA/SN during error processing. The results supported the hypothesis that the error-related connectivity between the amygdala and VTA/SN was largely mediated by the habenula and that the error-related connectivity between the habenula and VTA/SN was not mediated by the amygdala. Taken together, the results of these complementary analyses support a robust error-related signal from the habenula to VTA/SN during the stop signal task.
Unlike single-unit recordings, which could determine the “sign” of influence of neuronal activities in one brain region on those in another, the BOLD signals in fMRI represented an indirect measure of neural activity (Logothetis, 2008). Thus, although the current findings demonstrated a feedforward connectivity between the habenula and the VTA/SN, they did not indicate whether the influence is excitatory or inhibitory. Indeed, Ji and Shepard (2007) and Hikosaka et al. (2008) showed that neurons in the LH might exert inhibitory effects on neurons in the VTA/SN by exciting local GABAergic neurons. Furthermore, dopaminergic neurons in the VTA/SN may respond to stimuli with both positive and negative motivational value (Matsumoto and Hikosaka, 2009). These issues may lead one to consider whether the functional connectivity between the habenula and the midbrain had more to do with saliency than the motivational valence of errors. On the other hand, both SE and SS trials are more salient than G trials. Our supplementary results showing a largely lack of activation in the VTA/SN during PPI with SE > G and SS > G suggested that the feedforward influence of the habenula on VTA/SN was contingent upon a contrast between negative and positive motivational value.
In rodent studies, Jhou et al. (2009) reported the mesopontine rostromedial tegmental (RMTg) nucleus mediating the projections of the LH to VTA/SN. In the PPI analyses, we did not observe any significant clusters in the brain stem that might correspond in location to the RMTg nucleus. In contrast, we observed activation in a cluster around the pretectal area (Figure 2, z = −14), consistent with an earlier work showing projection from the superior colliculus and pretectal area to SN during the detection of salient visual events (Comoli et al., 2003). Although the GPi was functionally connected to the habenula during PPI, neither GCA or regression slope analysis could further confirm its role in this circuit. The latter result thus needs to be reconciled with findings from single-unit recordings of monkeys showing habenula-projecting neurons in the GPi (Hong and Hikosaka, 2008).
Methodological Considerations
Some methodological issues need to be considered. First, the volume of the VTA is approximately 60 mm3 (Paxinos and Huang, 1995); and the volume of the SN, pars compacta, is approximately 190 mm3, estimated based on atlas plates (Mai et al., 2008). Thus, the total volume of the VTN/SN in the current data set corresponded approximately to 250 mm3 or 4 voxels (1 voxel = 4 mm × 4 mm × 4 mm). A cluster of this size is difficult to localize precisely in fMRI. Thus, we compared and noted that the coordinates of the VTA/SN (MNI: [6, −16, −14]; and Talairach: [5, −17, −8]), converted from MNI coordinates using the BioImage Suite coordinate converter (Lacadie et al., 2008) were very close to those reported in previous fMRI studies: VTA in MNI coordinate [4, −16, −10] (Carter et al., 2009); VTA/SN in MNI coordinates [8, −20, −18] (Bunzeck and Duzel, 2006); VTA/SN in Talairach coordinates [6, −18, −12] (Schott et al., 2007); and SN in Talairach coordinate [6, −21, −12] (Wittmann et al., 2005).
The same localization issue applies to the habenula, a small structure with a size of approximately 3 mm × 3 mm × 6 mm (Salas et al., 2010). We sought to obtain the functional time course reflecting the habenula activity, by computing the average BOLD signal of a mask with a volume of approximately 1,344 mm3 or ∼29 voxels. Note that this mask included voxels in the white matter and CSF and raised the question whether the functional connectivities were specific to the habenula. We wish to address this issue from two perspectives. First, as described in the Section Materials and Methods, aliased cardiovascular and respiratory signals were removed with high pass filtering and AR (1) in analyses (Friston et al., 2000; Della-Maggiore et al., 2002). Second, the PPI of the habenula mask showed results that were anatomically specific while the control mask (which also contained white matter and CSF) did not. We feel that signal artifacts of the CSF or white matter are unlikely to account for the current results. In addition, we computed PPI for a “control” region that excluded this habenula mask for comparison.
Second, GCA per se does not involve modulation of the connectivity by experimental conditions, as does PPI analysis. Thus, GCA alone does not guarantee “causality” between regional brain activations in response to specific events in the cognitive task. That is, it was possible that the causalities observed between the habenula, amygdala, and the VTA/SN was due to signals unrelated to error processing. For this reason, we used mediation analyses to examine the correlation of activity between these brain regions. In particular, compared to the habenula, the amygdala showed a less significant projection (Granger causality) to the VTA/SN, raising the possibility that the habenula may mediate the projection from the amygdala to VTA/SN during error processing. The results of mediation analyses substantiated this hypothesis. Error-related activity of the habenula was significantly correlated with the VTA/SN even with the amygdala as an intervening variable; in contrast, amygdala correlated with the VTA/SN largely through its connection with the habenula.
Finally, a contrast of SE > SS involved differences in motor responses in addition to error processing (Table 1). Although to our knowledge the habenula has never been implicated in motor control, the current results need to be considered in the context of this limitation.
Conclusion
The complementary results of psychophysiological, regression slope, Granger causality, and mediation analyses delineated a feedforward connection from the habenula to the VTA/SN in humans. These new findings extend recent work in rodents and non-human primates on the role of this subcortical circuit in error detection.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This study was supported by NIH grants R01DA023248 (Chiang-Shan R. Li), K02DA026990 (Chiang-Shan R. Li), R21AA018004 (Chiang-Shan R. Li), and a Clinical Translational Science Award (NIH-UL1RR024139, Robert Sherwin). The NIH had no further role in study design; in the collection, analysis, and interpretation of data; in the writing of the report; or in the decision to submit the paper for publication. We thank Drs. Wager and Lindquist for making the toolbox of mediation analysis freely available on the web. We also thank Drs. Sheng Zhang, Sien Hu, Olivia Hendrick, and Sarah Bednarski for their many helpful discussions.
Footnotes
References
Abler, B., Roebroeck, A., Goebel, R., Hose, A., Schonfeldt-Lecuona, C., Hole, G., and Walter, H. (2006). Investigating directed influences between activated brain areas in a motor-response task using fMRI. Magn. Reson. Imaging 24, 181–185.
Akaike, H. (1974). A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19, 716–723.
Andersson, J. L., Hutton, C., Ashburner, J., Turner, R., and Friston, K. (2001). Modeling geometric deformations in EPI time series. Neuroimage 13, 903–919.
Ashburner, J., and Friston, K. J. (1999). Nonlinear spatial normalization using basis functions. Hum. Brain Mapp. 7, 254–266.
Baron, R. M., and Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J. Pers. Soc. Psychol. 51, 1173–1182.
Bayer, H. M., and Glimcher, P. W. (2005). Midbrain dopamine neurons encode a quantitative reward prediction error signal. Neuron 47, 129–141.
Bressler, S. L., and Seth, A. K. (2010). Wiener–Granger causality: a well established methodology. Neuroimage doi: 10.1016/j.neuroimage.2010.02.059. [Epub ahead of print].
Bressler, S. L., Tang, W., Sylvester, C. M., Shulman, G. L., and Corbetta, M. (2008). Top-down control of human visual cortex by frontal and parietal cortex in anticipatory visual spatial attention. J. Neurosci. 28, 10056–10061.
Brett, M., Anton, J. L., Valabregue, R., and Poline, J. B. (2002). “Region of interest analysis using an SPM toolbox (abstract),” in Paper Presented at the 8th International Conference on Functional Mapping of the Human Brain, Sendai, Japan.
Bunzeck, N., and Duzel, E. (2006). Absolute coding of stimulus novelty in the human substantia nigra/VTA. Neuron 51, 369–379.
Carter, R. M., Macinnes, J. J., Huettel, S. A., and Adcock, R. A. (2009). Activation in the VTA and nucleus accumbens increases in anticipation of both gains and losses. Front. Behav. Neurosci. 3:21. doi: 10.3389/neuro.08.021.2009
Chatterjee, S., and Hadi, A. S. (1986). Influential observations, high leverage points, and outliers in linear regression. Stat. Sci. 1, 379–416.
Comoli, E., Coizet, V., Boyes, J., Bolam, J. P., Canteras, N. S., Quirk, R. H., Overton, P. G., and Redgrave, P. (2003). A direct projection from superior colliculus to substantia nigra for detecting salient visual events. Nat. Neurosci. 6, 974–980.
D’Ardenne, K., McClure, S. M., Nystrom, L. E., and Cohen, J. D. (2008). BOLD responses reflecting dopaminergic signals in the human ventral tegmental area. Science 319, 1264–1267.
David, O., Guillemain, I., Saillet, S., Reyt, S., Deransart, C., Segebarth, C., and Depaulis, A. (2008). Identifying neural drivers with functional MRI: an electrophysiological validation. PLoS Biol. 6, 2683–2697. doi: 10.1371/journal.pbio.0060315
Delgado, M. R., Li, J., Schiller, D., and Phelps, E. A. (2008). The role of the striatum in aversive learning and aversive prediction errors. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 363, 3787–3800.
Della-Maggiore, V., Chau, W., Peres-Neto, P. R., and McIntosh, A. R. (2002). An empirical comparison of SPM preprocessing parameters to the analysis of fMRI data. Neuroimage 17, 19–28.
Deshpande, G., Hu, X., Stilla, R., and Sathian, K. (2008). Effective connectivity during haptic perception: a study using Granger causality analysis of functional magnetic resonance imaging data. Neuroimage 40, 1807–1814.
Deshpande, G., LaConte, S., James, G. A., Peltier, S., and Hu, X. (2009). Multivariate Granger causality analysis of fMRI data. Hum. Brain Mapp. 30, 1361–1373.
Deshpande, G., Sathian, K., and Hu, X. (2010). Effect of hemodynamic variability on Granger causality analysis of fMRI. Neuroimage 52, 884–896.
Ding, M., Bressler, S. L., Yang, W., and Liang, H. (2000). Short-window spectral analysis of cortical event-related potentials by adaptive multivariate autoregressive modeling: data preprocessing, model validation, and variability assessment. Biol. Cybern. 83, 35–45.
Duann, J. R., Ide, J. S., Luo, X., and Li, C. S. (2009). Functional connectivity delineates distinct roles of the inferior frontal cortex and presupplementary motor area in stop signal inhibition. J. Neurosci. 29, 10171–10179.
Duzel, E., Bunzeck, N., Guitart-Masip, M., Wittmann, B., Schott, B. H., and Tobler, P. N. (2009). Functional imaging of the human dopaminergic midbrain. Trends Neurosci. 32, 321–328.
Etkin, A., Egner, T., Peraza, D. M., Kandel, E. R., and Hirsch, J. (2006). Resolving emotional conflict: a role for the rostral anterior cingulate cortex in modulating activity in the amygdala. Neuron 51, 871–882.
Fiorillo, C. D., Tobler, P. N., and Schultz, W. (2003). Discrete coding of reward probability and uncertainty by dopamine neurons. Science 299, 1898–1902.
Florin, E., Gross, J., Pfeifer, J., Fink, G. R., and Timmermann, L. (2010). The effect of filtering on Granger causality based multivariate causality measures. Neuroimage 50, 577–588.
Friston, K. (2009). Causal modelling and brain connectivity in functional magnetic resonance imaging. PLoS Biol. 7, e1000033. doi: 10.1371/journal.pbio.1000033
Friston, K. J., Buechel, C., Fink, G. R., Morris, J., Rolls, E., and Dolan, R. J. (1997). Psychophysiological and modulatory interactions in neuroimaging. Neuroimage 6, 218–229.
Friston, K. J., Holmes, A. P., Worsley, K. J., Poline, J. P., Frith, C. D., and Frackowiak, R. S. J. (1995). Statistical parametric maps in functional imaging: a general linear approach. Hum. Brain Mapp. 2, 189–210.
Friston, K. J., Josephs, O., Zarahn, E., Holmes, A. P., Rouquette, S., and Poline, J. (2000). To smooth or not to smooth? Bias and efficiency in fMRI time-series analysis. Neuroimage 12, 196–208.
Genovese, C. R., Lazar, N. A., and Nichols, T. (2002). Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage 15, 870–878.
Gitelman, D. R., Penny, W. D., Ashburner, J., and Friston, K. J. (2003). Modeling regional and psychophysiologic interactions in fMRI: the importance of hemodynamic deconvolution. Neuroimage 19, 200–207.
Goebel, R., Roebroeck, A., Kim, D. S., and Formisano, E. (2003). Investigating directed cortical interactions in time-resolved fMRI data using vector autoregressive modeling and Granger causality mapping. Magn. Reson. Imaging 21, 1251–1261.
Granger, C. W. J., and Newbold, P. (2001). “Spurious regressions in econometrics,” in Essays in Econometrics: Collected Papers of Clive W. J. Granger, eds E. Ghysels, N. R. Swanson, and M. W. Watson (Cambridge, MA: Harvard University Press), 109–118.
Haber, S. N., and Knutson, B. (2010). The reward circuit: linking primate anatomy and human imaging. Neuropsychopharmacology 35, 4–26.
Handwerker, D. A., Ollinger, J. M., and D’Esposito, M. (2004). Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. Neuroimage 21, 1639–1651.
Hare, T. A., Camerer, C. F., Knoepfle, D. T., and Rangel, A. (2010). Value computations in ventral medial prefrontal cortex during charitable decision making incorporate input from regions involved in social cognition. J. Neurosci. 30, 583–590.
Hare, T. A., Camerer, C. F., and Rangel, A. (2009). Self-control in decision-making involves modulation of the vmPFC valuation system. Science 324, 646–648.
Harrison, L., Penny, W. D., and Friston, K. (2003). Multivariate autoregressive modeling of fMRI time series. Neuroimage 19, 1477–1491.
Hesterberg, T., Moore, D. S., Monaghan, S., Clipson, A., and Epstein, R. (2005). “Bootstrap methods and permutation tests,” in Introduction to the Practice of Statistics, 5th Edn., eds D. S. Moore and G. P. McCabe (New York: WH Freeman & Co.), 14.11–14.70.
Hikosaka, O., Sesack, S. R., Lecourtier, L., and Shepard, P. D. (2008). Habenula: crossroad between the basal ganglia and the limbic system. J. Neurosci. 28, 11825–11829.
Holroyd, C., and Coles, M. G. H. (2002). The neural basis of human error processing: reinforcement learning, dopamine, and the error-related negativity. Psychol. Rev. 109, 679–709.
Hong, S., and Hikosaka, O. (2008). The globus pallidus sends reward-related signals to the lateral habenula. Neuron 60, 720–729.
Hutton, C., Bork, A., Josephs, O., Deichmann, R., Ashburner, J., and Turner, R. (2002). Image distortion correction in fMRI: a quantitative evaluation. Neuroimage 16, 217–240.
Ide, J. S., and Li, C. R. (2011). A cerebellar thalamic cortical circuit for error-related cognitive control. Neuroimage 54, 455–464.
Jhou, T. C., Geisler, S., Marinelli, M., Degarmo, B. A., and Zahm, D. S. (2009). The mesopontine rostromedial tegmental nucleus: a structure targeted by the lateral habenula that projects to the ventral tegmental area of Tsai and substantia nigra compacta. J. Comp. Neurol. 513, 566–596.
Ji, H., and Shepard, P. D. (2007). Lateral habenula stimulation inhibits rat midbrain dopamine neurons through a GABA(A) receptor-mediated mechanism. J. Neurosci. 27, 6923–6930.
Kaminski, M., Ding, M., Truccolo, W. A., and Bressler, S. L. (2001). Evaluating causal relations in neural systems: granger causality, directed transfer function and statistical assessment of significance. Biol. Cybern. 85, 145–157.
Kaufling, J., Veinante, P., Pawlowski, S. A., Freund-Mercier, M. J., and Barrot, M. (2009). Afferents to the GABAergic tail of the ventral tegmental area in the rat. J. Comp. Neurol. 513, 597–621.
Kayser, A. S., Sun, F. T., and D’Esposito, M. (2009). A comparison of Granger causality and coherency in fMRI-based analysis of the motor system. Hum. Brain Mapp. 30, 3475–3494.
Kus, R., Kaminski, M., and Blinowska, K. J. (2004). Determination of EEG activity propagation: pair-wise versus multichannel estimate. IEEE Trans. Biomed. Eng. 51, 1501–1510.
Lacadie, C. M., Fulbright, R. K., Rajeevan, N., Constable, R. T., and Papademetris, X. (2008). More accurate Talairach coordinates for neuroimaging using non-linear registration. Neuroimage 42, 717–725.
Lebrecht, S., and Badre, D. (2008). Emotional regulation, or: how I learned to stop worrying and love the nucleus accumbens. Neuron 59, 841–843.
Levitt, H. (1971). Transformed up-down methods in psychoacoustics. J. Acoust. Soc. Am. 49(Suppl. 2), 467–477.
Li, C. S., Chao, H. H., and Lee, T. W. (2009). Neural correlates of speeded as compared with delayed responses in a stop signal task: an indirect analog of risk taking and association with an anxiety trait. Cereb. Cortex 19, 839–848.
Li, C. S., Huang, C., Constable, R. T., and Sinha, R. (2006). Imaging response inhibition in a stop-signal task: neural correlates independent of signal monitoring and post-response processing. J. Neurosci. 26, 186–192.
Li, C. S., Yan, P., Sinha, R., and Lee, T. W. (2008a). Subcortical processes of motor response inhibition during a stop signal task. Neuroimage 41, 1352–1363.
Li, C. S., Yan, P., Chao, H. H., Sinha, R., Paliwal, P., Constable, R. T., Zhang, S., and Lee, T. W. (2008b). Error-specific medial cortical and subcortical activity during the stop signal task: a functional magnetic resonance imaging study. Neuroscience 155, 1142–1151.
Linke, J., Kirsch, P., King, A. V., Gass, A., Hennerici, M. G., Bongers, A., and Wessa, M. (2010). Motivational orientation modulates the neural response to reward. Neuroimage 49, 2618–2625.
Logan, G. D., Cowan, W. B., and Davis, K. A. (1984). On the ability to inhibit simple and choice reaction time responses: a model and a method. J. Exp. Psychol. Hum. Percept. Perform. 10, 276–291.
Maccorquodale, K., and Meehl, P. E. (1948). On a distinction between hypothetical constructs and intervening variables. Psychol. Rev. 55, 95–107.
MacKinnon, D. P., Fairchild, A. J., and Fritz, M. S. (2007). Mediation analysis. Annu. Rev. Psychol. 58, 593–614.
Mai, J. K., Paxinos, G., and Voss, T. (2008). Atlas of the Human Brain, 3rd Edn. New York: Academic Press.
Matsuda, Y., and Fujimura, K. (1992). Action of habenular efferents on ventral tegmental area neurons studied in vitro. Brain Res. Bull. 28, 743–749.
Matsumoto, M., and Hikosaka, O. (2007). Lateral habenula as a source of negative reward signals in dopamine neurons. Nature 447, 1111–1115.
Matsumoto, M., and Hikosaka, O. (2009). Representation of negative motivational value in the primate lateral habenula. Nat. Neurosci. 12, 77–84.
Montague, P. R., Dayan, P., and Sejnowski, T. J. (1996). A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J. Neurosci. 16, 1936–1947.
Morissette, M. C., and Boye, S. M. (2008). Electrolytic lesions of the habenula attenuate brain stimulation reward. Behav. Brain Res. 187, 17–26.
O’Reilly, J. X., Mesulam, M. M., and Nobre, A. C. (2008). The cerebellum predicts the timing of perceptual events. J. Neurosci. 28, 2252–2260.
Penny, W. D., Holmes, A. P., and Friston, K. J. (2004). “Random-effects analysis,” in Human Brain Function, 2nd Edn., eds R. S. J. Frackowiak, C. Frith, R. Dolan, K. J. Friston, C. J. Price, S. Zeki, J. Ashburner, and W. D. Penny (New York: Academic Press), 843–850.
Roebroeck, A., Formisano, E., and Goebel, R. (2005). Mapping directed influence over the brain using Granger causality and fMRI. Neuroimage 25, 230–242.
Roebroeck, A., Formisano, E., and Goebel, R. (2009). The identification of interacting networks in the brain using fMRI: model selection, causality and deconvolution. Neuroimage. doi: 10.1016/j.neuroimage.2009.09.036. [Epub ahead of print].
Salas, R., Baldwin, P., De Biasi, M., and Montague, P. R. (2010). BOLD responses to negative reward prediction errors in human habenula. Front. Hum. Neurosci. 4:36. doi: 10.3389/fnhum.2010.00036
Sato, J. R., Takahashi, D. Y., Arcuri, S. M., Sameshima, K., Morettin, P. A., and Baccala, L. A. (2009). Frequency domain connectivity identification: an application of partial directed coherence in fMRI. Hum. Brain Mapp. 30, 452–461.
Scheibel, A. B. (1997). The thalamus and neuropsychiatric illness. J. Neuropsychiatry Clin. Neurosci. 9, 342–353.
Schott, B. H., Niehaus, L., Wittmann, B. C., Schutze, H., Seidenbecher, C. I., Heinze, H. J., and Duzel, E. (2007). Ageing and early-stage Parkinson’s disease affect separable neural mechanisms of mesolimbic reward processing. Brain 130, 2412–2424.
Schultz, W., Dayan, P., and Montague, P. R. (1997). A neural substrate of prediction and reward. Science 275, 1593–1599.
Seeley, W. W., Menon, V., Schatzberg, A. F., Keller, J., Glover, G. H., Kenna, H., Reiss, A. L., and Greicius, M. D. (2007). Dissociable intrinsic connectivity networks for salience processing and executive control. J. Neurosci. 27, 2349–2356.
Seth, A. K. (2010). A MATLAB toolbox for Granger causal connectivity analysis. J. Neurosci. Methods 186, 262–273.
Shepard, P. D., Holcomb, H. H., and Gold, J. M. (2006). Schizophrenia in translation: the presence of absence: habenular regulation of dopamine neurons and the encoding of negative outcomes. Schizophr. Bull. 32, 417–421.
Stephan, K. E., Marshall, J. C., Friston, K. J., Rowe, J. B., Ritzl, A., Zilles, K., and Fink, G. R. (2003). Lateralized cognitive processes and lateralized task control in the human brain. Science 301, 384–386.
Stilla, R., Deshpande, G., LaConte, S., Hu, X., and Sathian, K. (2007). Posteromedial parietal cortical activity and inputs predict tactile spatial acuity. J. Neurosci. 27, 11091–11102.
Theiler, J., Eubank, S., Longtin, A., Galdrikian, B., and Doyne, F. J. (1992). Testing for nonlinearity in time series: the method of surrogate data. Physica D 58, 77–94.
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F., Etard, O., Delcroix, N., Mazoyer, B., and Joliot, M. (2002). Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273–289.
Uddin, L. Q., Kelly, A. M., Biswal, B. B., Xavier Castellanos, F., and Milham, M. P. (2009). Functional connectivity of default mode network components: correlation, anticorrelation, and causality. Hum. Brain Mapp. 30, 625–637.
Ullsperger, M., and von Cramon, D. Y. (2003). Error monitoring using external feedback: specific roles of the habenular complex, the reward system, and the cingulate motor area revealed by functional magnetic resonance imaging. J. Neurosci. 23, 4308–4314.
Wager, T. D., Davidson, M. L., Hughes, B. L., Lindquist, M. A., and Ochsner, K. N. (2008). Prefrontal-subcortical pathways mediating successful emotion regulation. Neuron 59, 1037–1050.
Witt, S. T., and Meyerand, M. E. (2009). The effects of computational method, data modeling, and TR on effective connectivity results. Brain Imaging Behav. 3, 220–231.
Keywords: epithalamus, VTA, negative feedback, reward, stop signal task, PPI
Citation: Ide JS and Li C-S R (2011) Error-related functional connectivity of the habenula in humans. Front. Hum. Neurosci. 5:25. doi: 10.3389/fnhum.2011.00025
Received: 29 October 2010;
Accepted: 01 March 2011;
Published online: 16 March 2011.
Edited by:
Hauke R. Heekeren, Max Planck Institute for Human Development, GermanyReviewed by:
Markus Ullsperger, Max Planck Institute for Neurological Research, GermanyMarios Philiastides, Max Planck Institute for Human Development, Germany
Copyright: © 2011 Ide and Li. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Chiang-Shan R. Li, Connecticut Mental Health Center, S112, Department of Psychiatry, Yale University School of Medicine, 34 Park Street, New Haven, CT 06519, USA. e-mail: chiang-shan.li@yale.edu