- 1 Department of Neurology, Berlin NeuroImaging Center, Charité – Universitaetsmedizin Berlin, Berlin, Germany
- 2 Department of Psychology, Humboldt-Universitaet zu Berlin, Berlin, Germany
- 3 Berlin School of Mind and Brain, Humboldt-Universitaet zu Berlin, Berlin, Germany
- 4 Department of Electrical and Computer Engineering, AU Magnetic Resonance Imaging Research Center, Auburn University, Auburn, AL, USA
- 5 Department of Psychology, Auburn University, Auburn, AL, USA
- 6 Department of Molecular Neuroscience, Krasnow Institute for Advanced Study, George Mason University, Fairfax, VA, USA
- 7 Center of Excellence Cognitive Sciences, Department of Linguistics, University of Potsdam, Potsdam, Germany
Fluid intelligence is the ability to think flexibly and to understand abstract relations. People with high fluid intelligence (hi-fluIQ) perform better in analogical reasoning tasks than people with average fluid intelligence (ave-fluIQ). Although previous neuroimaging studies reported involvement of parietal and frontal brain regions in geometric analogical reasoning (which is a prototypical task for fluid intelligence), however, neuroimaging findings on geometric analogical reasoning in hi-fluIQ are sparse. Furthermore, evidence on the relation between brain activation and intelligence while solving cognitive tasks is contradictory. The present study was designed to elucidate the cerebral correlates of geometric analogical reasoning in a sample of hi-fluIQ and ave-fluIQ high school students. We employed a geometric analogical reasoning task with graded levels of task difficulty and confirmed the involvement of the parieto-frontal network in solving this task. In addition to characterizing the brain regions involved in geometric analogical reasoning in hi-fluIQ and ave-fluIQ, we found that blood oxygenation level dependency (BOLD) signal changes were greater for hi-fluIQ than for ave-fluIQ in parietal brain regions. However, ave-fluIQ showed greater BOLD signal changes in the anterior cingulate cortex and medial frontal gyrus than hi-fluIQ. Thus, we showed that a similar network of brain regions is involved in geometric analogical reasoning in both groups. Interestingly, the relation between brain activation and intelligence is not mono-directional, but rather, it is specific for each brain region. The negative brain activation–intelligence relationship in frontal brain regions in hi-fluIQ goes along with a better behavioral performance and reflects a lower demand for executive monitoring compared to ave-fluIQ individuals. In conclusion, our data indicate that flexibly modulating the extent of regional cerebral activity is characteristic for fluid intelligence.
Introduction
Mathematics comprises various areas such as arithmetic, algebra, analysis, set theory, geometry, and probability, just to name a few. Although the content and demands of these areas differ, they all require the understanding of relations and the ability to mentally manipulate symbols or structure relations. These abilities are also referred to as fluid intelligence (Cattell, 1963, 1987; Horn and Cattell, 1966). Interindividual differences in math performance are associated with interindividual differences in fluid intelligence (Spinath et al., 2010). Recently, there have been increasingly more attempts to characterize the neural foundations of mathematical cognition. Until now, there has been a promising number of studies investigating the cerebral correlates of number representation, number competences (Dehaene et al., 2003; Feigenson et al., 2004; Nieder and Dehaene, 2009), and arithmetic (Rickard et al., 2000; Zago et al., 2001; Ischebeck et al., 2006; Grabner et al., 2009; Landgraf et al., 2010; Santens et al., 2010). However, those studies have examined fundamental areas of mathematics and have not gone beyond arithmetic or basic algebra. Only recently have experimental approaches within the tight limitations of functional neuroimaging setups examined higher-order mathematics, such as differentiation or integration (e.g., Krueger et al., 2008). Still, to understand the mechanisms underlying higher-order mathematical cognition, further research approaches are needed.
Thus, we pursued a novel approach: Instead of focusing on an area- or domain-specific ability, interindividual differences in fluid intelligence as a cognitive foundation of higher-order mathematics were investigated. Little is known about functional cerebral correlates related to interindividual differences in fluid intelligence and cognitive performance. Therefore, we studied high school students differing in levels of fluid intelligence by using a geometric analogical reasoning task with graded levels of task difficulty, which prototypically demands fluid intelligence.
Fluid Intelligence
Fluid intelligence is a prerequisite for solving novel problems and for coping with unfamiliar situations, situations that thereby allow an individual to acquire new knowledge and obtain new insights. The Raven’s advanced progressive matrices (RAPM; Raven et al., 1980) are a common measure of fluid intelligence. In this test, participants have to select the missing parts of visuo-spatial patterns (i.e., matrices) from given alternatives. This task involves flexibility in thinking, pattern matching abilities, and relational reasoning (Bethell-Fox et al., 1984; Carpenter et al., 1990).
Individuals differ in their fluid intelligence level. In general, people with high fluid intelligence (hi-fluIQ) outperform people with average or low fluid intelligence on cognitive tasks (Horn and Cattell, 1966; Kane and Engle, 2002; Ackerman et al., 2005). This finding is corroborated by associations between fluid intelligence and shorter reaction times, as well as increased task performance for a number of memory tasks as reported by Vernon (1983) and Grabner et al. (2004) as well as for elementary cognitive tasks (i.e., the Hick, Sternberg, and Posner paradigms; Neubauer et al., 1997).
Cerebral correlates of fluid intelligence
Interindividual differences in fluid intelligence correlate with behavioral performance differences as well as with differences in structural or functional characteristics of the brain. The possibility of integrating functional neuroimaging with psychometric and behavioral data continues to grow in the cognitive sciences. Recently, there has been extensive neuroscience research on human intelligence and interindividual differences in intelligence (e.g., Jung and Haier, 2007; Neubauer and Fink, 2009a; Deary et al., 2010; Geake and Hansen, 2010). Here, we will shortly present some findings of cerebral correlates of fluid intelligence, intelligence differences, and analogical reasoning, which are most relevant for our study. Newman and Just (2005) and Jung and Haier (2007) have argued that intelligent behavior cannot be broken down and localized in one single and specialized brain region, but rather that it originates from a large-scale network of several interacting parieto-frontal brain areas. The dynamics of that network and the interplay of various brain regions upon a cognitive demand determine fluid intelligence. After reviewing neuroimaging studies on functional and structural correlates of intelligence, Jung and Haier (2007) derived their parieto-frontal integration theory of intelligence (P-FIT): According to this model, an extensive and distinct network of frontal and parietal brain areas is involved in reasoning. The supramarginal and angular gyri, superior parietal cortex, dorsolateral prefrontal cortex (PFC), as well as superior, middle, and inferior frontal gyri constitute the parieto-frontal network. The interaction of these components is crucial for intelligent behavior.
Likewise, Gray et al. (2003) found activity in the left and right lateral PFC, left dorsal anterior cingulate cortex (ACC), and left and right parietal and temporal cortex to be positively correlated with fluid intelligence. As involvement of frontal brain regions has been reported for tasks that demand intelligence (e.g., Duncan et al., 2000; Duncan, 2003), we hypothesize that individuals with hi-fluIQ recruit a more extensive network of prefrontal brain regions when solving a task that demands fluid intelligence as compared to individuals with average fluid intelligence (ave-fluIQ). However, improvement in behavioral performance due to training was reported to be related to decrease of parietal and frontal brain activation (Ischebeck et al., 2006, 2007). Thus, performance differences due to differences in fluid intelligence might also be related to the recruitment of a less extensive parieto-frontal network.
Relationship between brain activation and fluid intelligence
In addition to attempts at identifying correlates of fluid intelligence in frontal and parietal brain regions, other studies have examined the important question of how fluid intelligence and the extent of task-induced brain activation are related. However, findings on this issue have been ambiguous: There have been some studies reporting a positive correlation between brain activation and intelligence (Larson et al., 1995; Lee et al., 2006; Grabner et al., 2007). This means that when solving a cognitive task, brain activation is increased in more intelligent participants as compared to averagely intelligent participants. Yet, other studies have reported a negative correlation between brain activation and intelligence (e.g., Haier et al., 1988; Jausovec, 2000; Neubauer et al., 2004). This means that when solving a cognitive task, brain activation is lower in the more intelligent participants as compared to averagely intelligent participants. Haier et al. (1988) probably were the first to name this latter phenomenon neural efficiency. They reported a negative correlation between RAPM performance and task-related cortical metabolic rates measured by positron emission tomography (PET). Haier et al. (1988) argue that intelligence is a function of neural efficiency and according to the neural efficiency hypothesis (NEH), increased behavioral performance in intelligent individuals goes along with decreased (i.e., more efficient) brain metabolism or cortical activity when performing a cognitive task. In a comprehensive review of findings on the NEH, Neubauer and Fink (2009b) thoroughly compiled evidence that moderating variables such as task type, task difficulty, sex, extent of training, and brain region account for the contradictory evidence on the brain activation–intelligence relationship. Furthermore, differences in methods or definitions of intelligence may also be reasons for the contradictory findings. The NEH suggests that individuals with hi-fluIQ deploy their cerebral resources more adaptively, depending on task demand and practice level (Neubauer and Fink, 2009b). Thus, the interplay of resource availability, adaptability of the cerebral networks, interregional communication within cerebral networks, and structural anatomical features should have an impact on intelligent behavior (Newman and Just, 2005; Just and Varma, 2007). Yet, the precise nature of the brain activation–intelligence relationship is not completely understood and currently under debate.
Consequently, the following patterns of cerebral characteristics of hi-fluIQ may exist: There may be a positive or negative brain activation–intelligence relationship, or there may be intelligence-related differences with respect to which brain regions are recruited when performing a cognitive task that demands fluid intelligence. To find out about the cerebral characteristics of hi-fluIQ, we employed an analogical reasoning task that demands fluid intelligence and applied it to a sample of individuals with hi-fluIQ.
Analogical Reasoning
The cognitive ability to draw inferences from given facts and circumstances is called reasoning. Analogical reasoning is the ability to find relations between structures and to explain new concepts in terms of familiar ones (French, 2002). Analogical reasoning is important for every day life in a multitude of situations. It is essential for accessing new knowledge and making insights. Analogical reasoning ability is closely linked to fluid intelligence as individuals with hi-fluIQ usually perform well on analogical reasoning tasks (Hofstadter, 1997, 2001; Prabhakaran et al., 1997; Holyoak and Morrison, 2005).
In the example analogy A:A′ = B:B′ (A is to A′ as B is to B′), the relations between the two structure pairs are similar or equivalent: that is, they are analogical. The relation between structure A and structure A′ is called the base or source relation. The relation between structure B and structure B′ is called the target relation. Analogical reasoning generally requires performing the following sub-processes: (i) building representations of the structures in question, (ii) identifying the source relation of the first two structures by selecting relevant characteristics and inhibiting irrelevant ones, (iii) mapping the source and the target relation by transferring the source relation onto the target structures, and (iv) evaluating the analogy (Mulholland et al., 1980; Gentner, 1983; Holyoak and Kroger, 1995; Kokinov and French, 2003). Interindividual differences in geometric analogical reasoning performance are most likely related to interindividual differences in accuracy and/or speed in performing one or more of these sub-processes.
Geometric analogical reasoning is one form of analogical reasoning. Comparing characteristics of geometric patterns requires flexibility in thinking and in mentally manipulating structures and relations. Solving geometric analogical reasoning tasks does not necessarily rely on verbal responses and relies only to a limited degree on domain-specific knowledge. These geometric analogical reasoning tasks can therefore be assumed to measure analogical reasoning more purely than verbal analogies do (Hosenfeld et al., 1997). Hence, geometric analogies are a prototypical fluid intelligence task and therefore provide an adequate experimental approach for studying interindividual differences in fluid intelligence.
As fluid intelligence is fundamental to mathematical performance and understanding mathematics in class, it is thus of high significance in research on mathematical cognition.
Cerebral correlates of analogical reasoning
There have been some functional neuroimaging studies reporting the recruitment of frontal and parietal brain regions during geometric analogical reasoning. In a block-design PET study, Wharton et al. (2000) presented geometric shapes to participants who had to decide whether their relations were analogical. Wharton et al. found that the left medial and inferior frontal cortices and the left inferior parietal cortex were involved in analogy detection. When applying the same task to participants who received repetitive transcranial magnetic stimulation (rTMS) over the left PFC, reaction time increased significantly (Boroojerdi et al., 2001). The authors of that study concluded that the left PFC is relevant for geometric analogy detection. In a precursor task to the one reported here, our group identified a bilateral parieto-frontal network that is involved in geometric analogical reasoning and is modulated by task difficulty and training (Wartenburger et al., 2009). As Prabhakaran et al. (1997) reported, solving fluid reasoning problems (RAPM) recruits bilateral frontal and parietal brain regions, including the precuneus and the medial occipital gyrus.
Studies on relational reasoning using verbal material have frequently identified prefrontal brain regions and the ACC as involved in those tasks (Luo et al., 2003; Bunge et al., 2005; Wendelken et al., 2008; Ferrer et al., 2009). Bunge et al. (2005) reported that the PFC mediates verbal analogical reasoning in general, whereas the frontopolar cortex is involved in relation integration. Moreover, Wendelken et al. (2008) found that the rostrolateral PFC is involved in relation comparison.
Effective Connectivity
In addition to characterizing the brain regions which are involved in geometric analogical reasoning and their modulation by fluid intelligence and/or task difficulty, investigating the effective connectivity within the parieto-frontal network contributes to understanding of interregional cerebral communication during geometric analogical reasoning and its modulation by fluid intelligence. The patterns of effective connectivity which involve frontal brain regions allow the testing of assumptions about executive monitoring during task-solving. The patterns of effective connectivity which involve parietal brain regions allow the testing of assumptions about task-related spatial processing and attentional processes. Prescott et al. (2010) reported enhanced intra-hemispheric parieto-frontal connectivity, as well as enhanced inter-hemispheric frontal connectivity in mathematically gifted adolescents during a 3-D mental rotation task. Consequently, we expect stronger interregional connectivity within the parieto-frontal network for individuals with hi-fluIQ as compared to individuals with ave-fluIQ.
Aim of the Study
The aim of this study was to elucidate the cerebral correlates of hi-fluIQ using geometric analogical reasoning as a paradigm that measures this ability very purely without demanding additional context knowledge, as for example, verbal tasks do. Hence, we recruited a sample of two matched groups of healthy young participants who did not differ in psychometric or demographic characteristics except for their fluid intelligence as measured with the RAPM. To our knowledge, this is the first study on the influence of interindividual differences in fluid intelligence using a non-verbal geometric analogical reasoning task. As Neubauer and Fink (2009b) suggested, intelligence level and task difficulty both modulate brain activation. Thus, we applied a graded variation of task difficulty. In general, we hypothesized that parietal and frontal brain regions would be involved in geometric analogical reasoning in individuals with high respectively ave-fluIQ. Furthermore, we expected interindividual differences in the brain activation–intelligence relationship, in the modulation of brain activity by task difficulty and stronger effective connectivity within the parieto-frontal network in individuals with hi-fluIQ.
Materials and Methods
Sample
In order to be able to characterize cerebral correlates of hi-fluIQ, we drew a sample consisting of two sub-groups: an experimental group with distinctly hi-fluIQ level and a control group with ave-fluIQ level. Approximately 4 months before the first experimental session, we conducted a screening test session of 120 11th grade students from three college-preparatory high schools in Berlin, Germany. The RAPM (Raven et al., 1980) was used as a proxy to assess fluid intelligence, and the results were used to select participants and assign them to one of the two intelligence groups. Students with an IQ score>115 had above-average intelligence and thus met inclusion criteria for the hi-fluIQ group. Students with an IQ score ≥85 and ≤115 had an IQ score within 1 SD of the population average of 100. They thus met inclusion criteria for the ave-fluIQ group and served as a control group. Students with an IQ score < 85 were excluded from the sample.
Furthermore, students could take part in this study only if (a) they and their parents consented to taking part in the functional magnetic resonance imaging (fMRI) study; (b) they met MRI safety criteria; (c) they took part in the compulsory training session 4 weeks prior to the experimental session; (d) they were right-handed as determined by the Edinburgh Handedness Inventory (Oldfield, 1971); and (e) they were free of past and present signs of psychiatric and neurological disorders as assessed with the SKID-I screening interview (Strukturiertes Klinisches Interview fuer DSM-IV; Wittchen et al., 1997).
This resulted in a final sample of 41 participants. There were technical difficulties with data acquisition in one ave-fluIQ participant, leaving a total of 40 participants with data for the final analyses. Twenty-two participants constituted the hi-fluIQ group (IQ range 119–145, mean IQ 130, SD 8). Nineteen participants constituted the ave-fluIQ group (IQ range 91–110, mean IQ 104, SD 7). The two groups differed statistically in intelligence (T(38) = 11.2, p <0.01). In addition, groups were matched for other demographic factors. The groups did not differ in age (hi-fluIQ: mean age 17; 3 years (SD 0.5 months), ave-fluIQ: mean age 17;3 years (SD 0.5 months), T(38) = 0.2, p ≫ 0.05). The groups did not differ in years of education. All participants attended 11th grade. One participant from each group had previously repeated one school year and one participant from each group had previously skipped one school year. Visual acuity was normal or corrected to normal in all participants. Written informed consent was provided prior to the investigation by all participants and their parents (when underage). All participants were reimbursed for their participation. The study was approved by the local ethics committee of the Charité – Universitaetsmedizin Berlin. The study was in compliance with the Declaration of Helsinki and was conducted following the guidelines of good scientific practice and the APA Standards for Educational and Psychological Testing.
Task
The geometric analogical reasoning task makes use of geometric patterns as previously described in related studies (Preusse et al., 2010; van der Meer et al., 2010). In every trial, two pairs of patterns (source pair A:A′ and target pair B:B′) were presented side by side. The left part of each pair was one of the geometric patterns in its original version (A resp. B). The right partner of the pair was the mirror image of the first (A′ resp. B′) mirrored either on one of the orthogonal axes, one of the two diagonal axes, or not manipulated at all (identity condition). According to behavioral pretests, these five conditions constituted a graded variation of task difficulty with identity condition being the easiest, followed by vertical mirroring, horizontal mirroring, mirroring on the diagonal tilted left, and mirroring on the diagonal tilted right being the most difficult manipulation to detect. Patterns were constructed such that any mirrorings were unambiguous. The geometric analogical reasoning task consisted of 150 items in total. In half the trials, the mirroring relation between the source pair and the target pair was analogous (A:A′ = B:B′; analogy trials). The remaining 75 trials consisted of pairs with unlike mirroring relations (A:A′ 1 B:B′; distractor trials; see Figure 1).
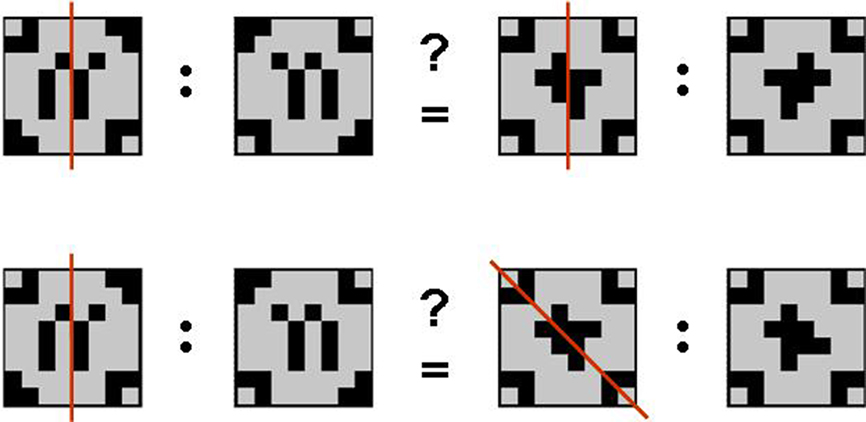
Figure 1. Geometric analogies. Examples of an analogy item (mirroring on the vertical axis in both pattern pairs; top) and a distractor item (mirroring on the vertical axis in the source pair and mirroring on the diagonal axis tilted to the left in the target pair; bottom). Note that the mirroring axes (red) were not displayed in the experiment.
Hence, there were 15 target trials for each level of task difficulty. Target and distractor trials for all levels of difficulty were displayed in a pseudo-randomized order. Each trial started with a fixation cross that stayed on the screen for a pseudo-randomized duration of either 1, 2, or 3 s and was then followed by the actual item (pattern pairs). For each item, participants were to decide whether – with respect to the mirroring relation – the two pattern pairs were analogical (= target) or not (= distractor) by pressing the answer button for “yes” (left hand index finger) or “no” (left hand middle finger). Immediately after the button press a checkerboard-like mask appeared for 2 s, marking the end of the trial. In case the participant did not respond, presentation of the pattern pairs stopped automatically after 12 s. Trials answered incorrectly and unanswered trials were classified as errors. Participants received extensive training on the task 4 weeks prior to the experimental session. The experimental session finished with an anatomical scan of the brain.
Data Acquisition and Analysis
The Presentation software package (version 9.101) was used for stimulus delivery, experimental control, and collecting behavioral data.
Functional magnetic resonance imaging data were acquired on a 1.5 T scanner (Siemens Sonata, Erlangen, Germany) with a standard head coil and an echoplanar single-shot pulse sequence (30 slices covering the whole brain, 4 mm × 4 mm × 4 mm resolution, TE = 40 ms, TR = 2 s, flip angle = 90°, FoV = 256 mm, no interslice gap, interleaved acquisition of AC–PC oriented images).
Anatomical high resolution T1-weighted scans (MDEFT sequence, 176 slices, sagittal orientation, voxel size 1 mm × 1 mm × 1 mm, TE = 3.56 ms, TR = 12.24 ms, flip angle = 23°, FoV = 256 mm, fat saturation, phase coding: A ≫ P; Deichmann, 2005) were acquired after all cognitive tasks were completed.
A vacuum head cushion was used to immobilize the participants’ heads and necks in order to reduce movement. Earplugs were provided to attenuate background noise, and headphones were used to communicate with participants.
Analyses of behavioral and psychometric data were computed with the statistical software SPSS 16.0 for Windows (Rel. 16.0.2 2008, SPSS Inc., Chicago, IL, USA).
Imaging data were analyzed using FSL 4.1 (FMRIB’s Software Library2; Smith et al., 2004; Woolrich et al., 2009). Single-subject analyses were carried out using FEAT (FMRI Expert Analysis Tool) Version 5.98, part of FSL. The following pre-statistical processing was applied: motion correction using MCFLIRT (Jenkinson et al., 2002); slice-timing correction using Fourier-space time series phase-shifting; non-brain removal using BET (Smith, 2002); spatial smoothing using a Gaussian kernel of FWHM 5 mm; grand-mean intensity normalization of the entire 4-D dataset by a single multiplicative factor; high-pass temporal filtering (Gaussian-weighted least-squares straight line fitting, with sigma = 20 s). Registration to high resolution structural and standard space images was carried out using FLIRT (Jenkinson and Smith, 2001; Jenkinson et al., 2002). Single-subject time series statistical analysis was carried out using FILM with local autocorrelation correction (Woolrich et al., 2001). The five levels of task difficulty were modeled as explanatory variables and convolved with a standard gamma hemodynamic response function (HRF). All statistical fMRI analyses included correct target trials (i.e., analogies) only. Error trials and distractor trials were modeled as regressors of no interest because the cognitive processes underlying an error or a no-analogy decision remain elusive in our experimental design.
Both interindividual differences in fluid intelligence level and graded levels of task difficulty are directly associated with differences in reaction times. However, intertrial variance in the fMRI-signal due to differences in reaction times within and between participants and levels of task difficulty constitute a confound. In order to avoid this confounding effect, we fixed the time window for the analysis to the last 2 s of each trial (i.e., the last 2 s before the button press). It can be assumed that processes most relevant to the recognition of an analogy (i.e., retrieving relations from source and target and mapping them) occur in the time window immediately before a participant arrives at a decision (Zarahn et al., 1997; Wartenburger et al., 2009; Mayer et al., 2010; Preusse et al., 2010). We set the time window of interest to 2 s because this corresponds to the fastest reaction times in the easiest condition. However, we also ran the analysis of the full trial durations for reasons of completeness. There were only marginal differences between the results for the two approaches. Reporting of results will here be restricted to the last-2-s approach.
Higher-level group analysis was carried out using FMRIB’s local analysis of mixed effects (FLAME) stage 1 (Beckmann et al., 2003; Woolrich et al., 2004; Woolrich, 2008). Z (Gaussianized T/F) statistical images were initially uncorrected and later thresholded using clusters determined by Z = 2.9 and a corrected cluster significance threshold of p = 0.05. For the main effect of task difficulty, the threshold was elevated to Z = 3.3 to avoid emergence of only one huge cluster stretching from the occipital lobe via the parietal lobe into the frontal lobe, and thus to allow differentiation of separate brain regions of interest (ROIs) and multiple peak voxels.
Statistical analyses were performed to assess the main effects of task difficulty and fluid intelligence and their interaction. First, a whole brain parametric contrast of the main effect of task difficulty was computed. This allowed for the identification of brain regions that were involved in geometric analogical reasoning and were modulated by task difficulty across the two groups. The higher task demand of the two diagonal conditions led to higher error rates than in the other three conditions (especially in the ave-fluIQ, see Results below), which left fewer correct trials for the analysis. To assure a sufficient number of trials for the fMRI analysis, we combined the two diagonal mirroring conditions into one regressor. Therefore, the parametric contrast of task difficulty is made up of four grade increments (both diagonals > horizontal > vertical > identity). To assess the main effect of fluid intelligence, we computed a contrast comparing all correct target trials between the two groups. This allowed us to identify brain regions that were differentially involved in geometric analogical reasoning in the two groups. Additionally, to visualize the results, we extracted parameter estimates from those brain regions modulated by task difficulty and intelligence. Last, we computed the interaction of task difficulty and fluid intelligence. Data were visualized using AFNI3 (Cox, 1996; Cox and Hyde, 1997). Anatomical labels were given on the basis of AFNIs Talairach Daemon using the Talairach–Tournoux Atlas (Talairach and Tournoux, 1988).
As little is known about intelligence-related differences in effective connectivity in the parieto-frontal network, a multivariate Granger causality mapping complements the fMRI activation results and helps to better characterize cognitive processing in geometric analogical reasoning and fluid intelligence. Granger causality mapping attributes a directed causal influence from one brain region onto another brain region, if the temporal characteristics of the first region at present helps predict the temporal characteristics of the second region at a future time instant (Granger, 1969; Krueger et al., 2010). To investigate the effective connectivity between brain ROIs during geometric analogical reasoning in the two groups, we applied the basic principles of multivariate Granger causality mapping (Deshpande et al., 2009), with some modification to include the dynamics as described in the next paragraph. We extracted the raw time series data from eight ROIs as determined by the results of the blood oxygenation level dependency (BOLD) fMRI activation analysis (left and right inferior parietal lobe, left precuneus, right superior parietal lobe, left middle temporal gyrus, left and right middle frontal gyrus, and left inferior frontal gyrus) and normalized the time series from each participant by subtracting the mean and dividing by its SD. These normalized time series were input into the model described below.
A dynamic multivariate autoregressive model (dMVAR) was defined such that its coefficients are a function of time and simultaneous directional influences between multiple ROIs could be captured. Dynamic correlation-purged Granger causality (CPGC; Deshpande et al., 2010a,b; Lacey et al., 2011) was obtained for the complete time series and for every subject using a first order dMVAR model. As shown before, CPGC is capable of inferring causal interactions without being contaminated by instantaneous correlation between time series arising due to the external input (Deshpande et al., 2010b). Further, since the coefficients of dMVAR are a function of time (Lacey et al., 2011), unlike previous implementations (Deshpande et al., 2009), it is possible to tease out only those causalities which covary with the external input. Accordingly, the boxcar function corresponding to the experimental paradigm was smoothed by a standard HRF and entered into the design matrix. Using a general linear model (GLM), the beta values indicating the strength of covariance between CPGC paths and the experimental paradigm were determined on a group level using separate GLMs for hi-fluIQ and ave-fluIQ. The betas from the subject level analysis were entered into an unpaired t-test in order to determine the paths which were significantly different between the groups. This approach formulates connectivity investigation within the methodological framework of “activity detection,” which makes it easier to interpret the relationship between activity and connectivity (Lacey et al., 2011). Intrinsic causality which is not entrained to the stimulus, though interesting, is not relevant to the specific brain mechanism being investigated using the geometric analogical reasoning task. Also, since hemodynamic variability does not change with time, the results obtained from this model are not influenced by the variability of the hemodynamic response across regions and participants.
Results
Behavioral Results
An overview of mean reaction times and reaction accuracy presented by levels of task difficulty and for the fluid intelligence groups is provided in Figure 2.
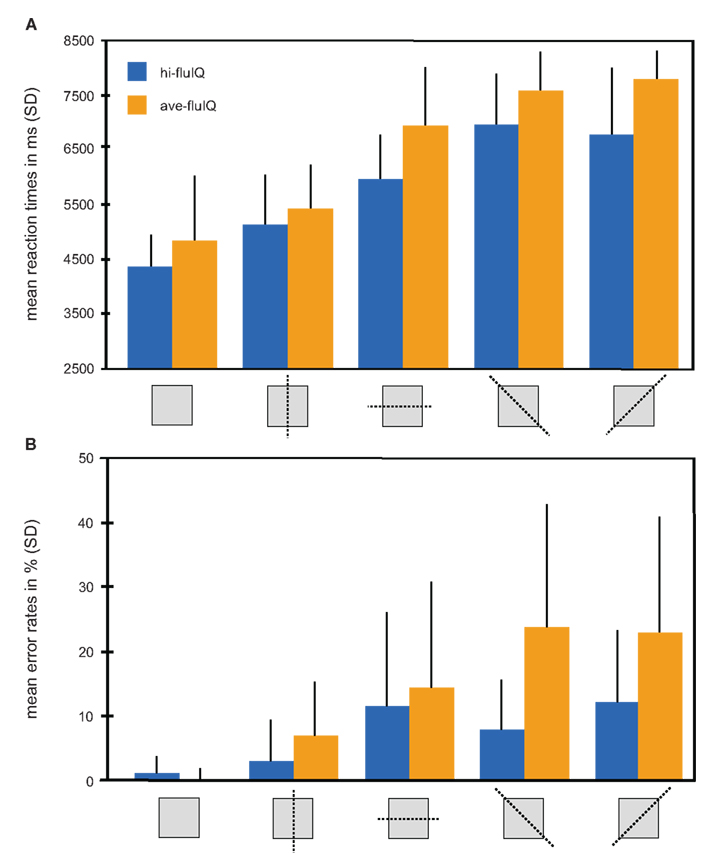
Figure 2. Behavioral results color coded for the two groups. (A) Mean reaction times in millisecond (with SD) for the five levels of task difficulty (mirroring relation indicated by pictograms) and for both groups. (B) Mean reaction accuracy given as percent errors (with SD) for the five levels of task difficulty (mirroring relation indicated by pictograms) and for both groups.
We conducted a two-way repeated measures analysis of variance (ANOVA) with the factors task difficulty (five levels, within-subjects factor) and fluid intelligence (two levels, between-subjects factor), and with mean reaction times as the dependent variable. This ANOVA revealed a main effect of task difficulty (F(4, 38) = 110.2, p < 0.001). Mean reaction times generally increased with increasing task difficulty. The main effect of fluid intelligence failed to reach statistical significance (F(1, 38) = 3.5, p = 0.07). Mean reaction times were slightly shorter for hi-fluIQ than for ave-fluIQ. There was no interaction between task difficulty and fluid intelligence. Median reaction times were slightly lower than mean reaction times for both groups and for all levels of task difficulty. However, the overall picture of results remained the same for median reaction times: There was a main effect of task difficulty but no main effect of fluid intelligence and no interaction of the two factors on reaction times.
All participants showed above-chance reaction accuracy for all levels of difficulty. We conducted a two-way repeated measures ANOVA with the factors task difficulty (five levels, within-subjects factor) and fluid intelligence (two levels, between-subjects factor) with reaction accuracy as the dependent variable. This ANOVA revealed a main effect of task difficulty (F(4, 38) = 24.7, p < 0.001). Mean reaction accuracy generally decreased with increasing task difficulty. Furthermore, this ANOVA revealed a main effect of fluid intelligence (F(1, 38) = 10.7, p < 0.01). Mean reaction accuracy was higher for hi-fluIQ than for ave-fluIQ. Also, there was an interaction between task difficulty and fluid intelligence (F(4, 152) = 4.9, p < 0.01). The decrease in reaction accuracy with increasing task difficulty was stronger for ave-fluIQ than for hi-fluIQ.
Please note, in post-task interviews the two groups did not differ in terms of which strategy they reported to employ for task-solving. However, when explaining the task-solving process, hi-fluIQ accompanied their explanations with more movement gestures related to the process of mirroring than ave-fluIQ did (see Sassenberg et al., 2011).
FMRI Results
Main effects
To elucidate which brain areas were generally involved in geometric analogical reasoning and modulated by task difficulty, we analyzed the main effect of task difficulty. It revealed greater BOLD signal changes in the left and right inferior parietal lobe stretching to the superior parietal lobe, to the precuneus, and to the angular gyrus. Moreover, the left middle and inferior frontal gyrus, the right superior and middle frontal gyrus, and an area in the left occipito-temporal junction showed greater BOLD signal changes for this contrast (see Figure 3; Table 1). Activity of these brain areas was modulated by task difficulty with greater BOLD signal changes for more difficult trials.
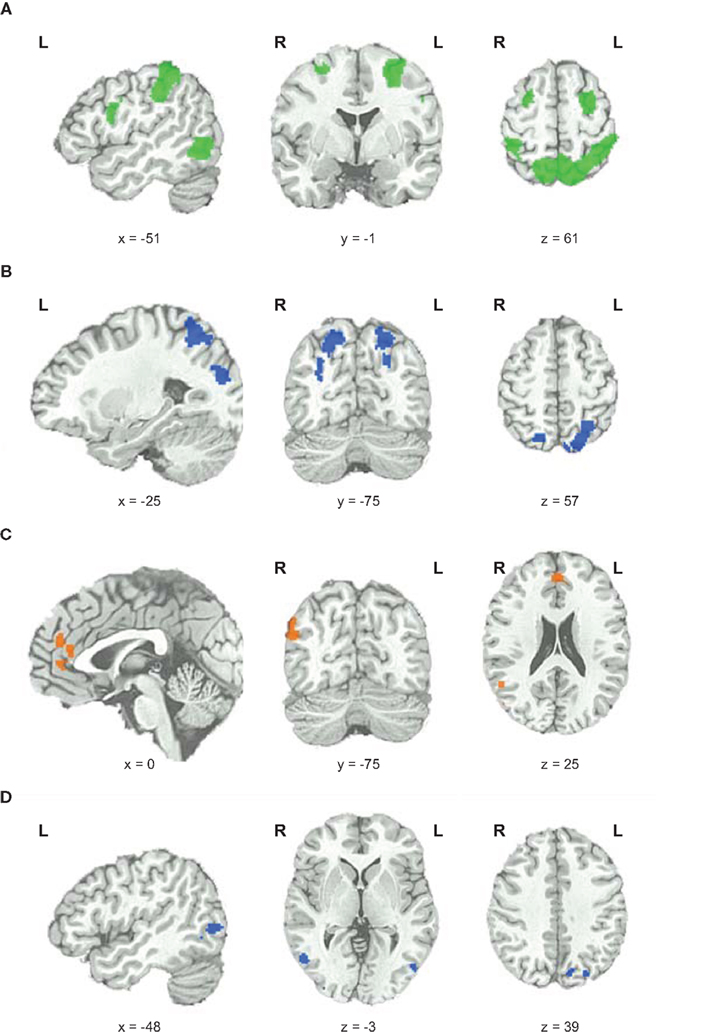
Figure 3. Functional magnetic resonance imaging results. (A) Main effect of task difficulty, increases in BOLD signal changes with increasing task difficulty color coded in green. (B) Main effect of fluid intelligence for hi-fluIQ > ave-fluIQ color coded in blue. (C) Main effect of fluid intelligence for ave-fluIQ > hi-fluIQ color coded in orange. (D) Interaction of task difficulty and fluid intelligence color coded in blue.
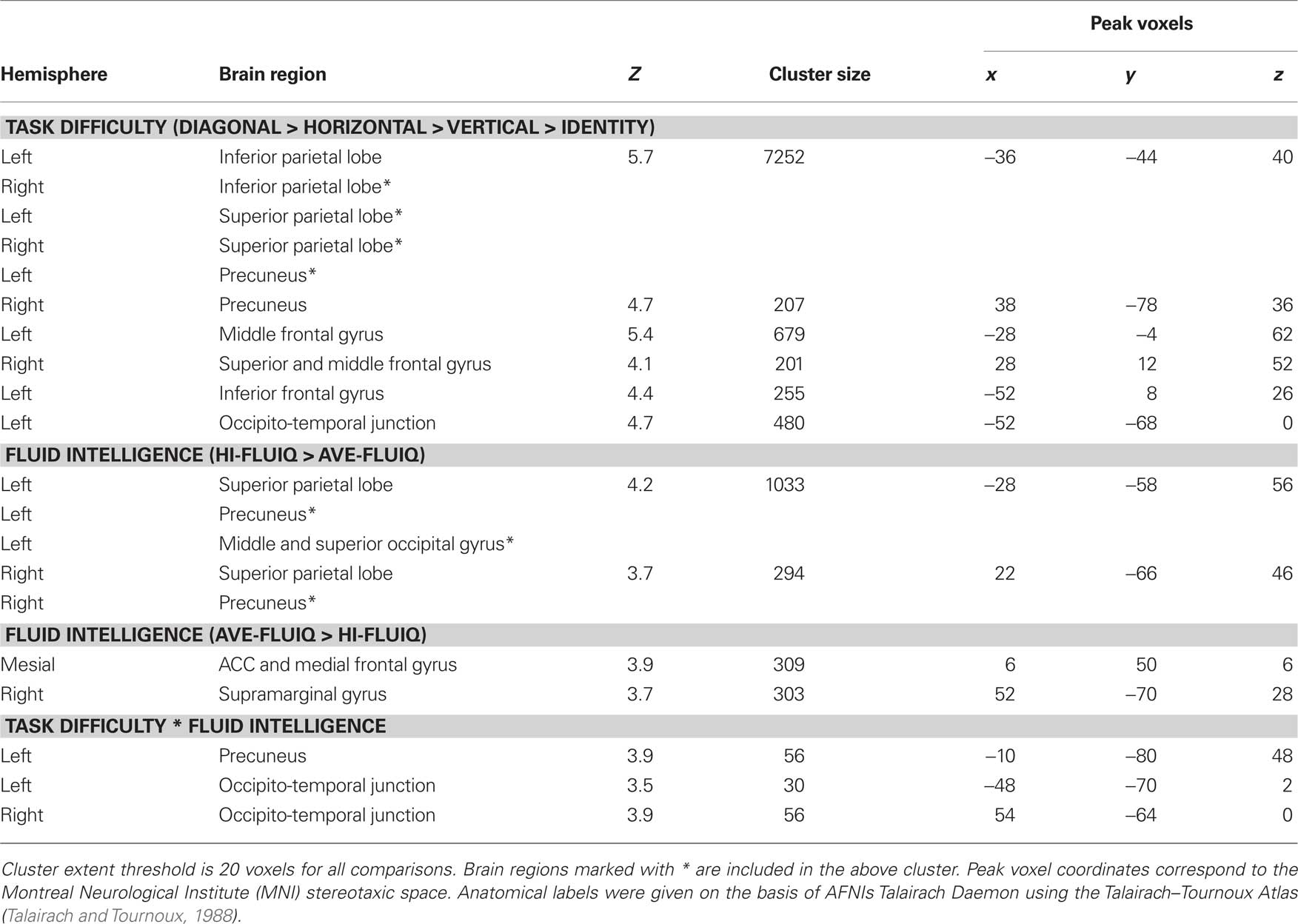
Table 1. Significant activation clusters for parametric effect of task difficulty, fluid intelligence, and the interaction of task difficulty and fluid intelligence.
When comparing the two groups (main effect of fluid intelligence), hi-fluIQ showed greater BOLD signal changes than ave-fluIQ in the left and right superior parietal lobe and precuneus, and in an area in the left middle and superior occipital gyrus. Ave-fluIQ showed greater BOLD signal changes than hi-fluIQ in the ACC and medial frontal gyrus, as well as in an area in the right supramarginal gyrus (see Figure 3; Table 1).
Interaction effects
The interaction of the two main effects (task difficulty × fluid intelligence) revealed greater BOLD signal changes in the left precuneus and bilaterally in the occipito-temporal junction (see Figure 3; Table 1). Inspection of the data indicated that for these brain regions, there was greater modulation by task difficulty in hi-fluIQ than in ave-fluIQ.
Effective Connectivity
We used the dMVAR model (Lacey et al., 2011) to investigate the effective connectivity during geometric analogical reasoning in the two groups. Again, we found differential group effects within the parieto-frontal network. The effective connectivity patterns differed between the fluid intelligence groups: For hi-fluIQ, the network included significant (p < 0.05) paths of effective connectivity between the following ROIs: within the frontal cortex, from the left inferior frontal gyrus to left and right parietal brain regions, and also from the left precuneus to the left middle temporal gyrus. In contrast, for ave-fluIQ the network included significant (p < 0.05) paths of effective connectivity from the right middle frontal gyrus to left and right parietal brain regions, and also within the parietal regions.
Discussion
In this study, we characterized the behavioral and cerebral correlates related to interindividual differences in fluid intelligence in a geometric analogical reasoning task. This task had graded levels of difficulty and is a prototypical task for demanding the application of fluid intelligence. Recruitment of the parieto-frontal brain network was modulated by both task difficulty and fluid intelligence.
As the behavioral results showed, hi-fluIQ participants achieve better task performance in terms of accuracy compared to ave-fluIQ. As indicated by the interaction of task difficulty and fluid intelligence, groups differ in the more difficult task conditions in particular. This is in line with findings from the literature on the relation of fluid intelligence and behavioral task performance (Horn and Cattell, 1966; Kane and Engle, 2002; Ackerman et al., 2005; van der Meer et al., 2010). There was no main effect of fluid intelligence for reaction times. That is, although the hi-fluIQ were slightly faster in all conditions, the groups did not differ statistically. This may be due to the extensive training on the task participants received prior to the experimental session. In short, hi-fluIQ reached a higher accuracy performance level at the same velocity. As expected, there was a modulatory effect of task difficulty on both reaction times and accuracy. Reaction times increased with increasing task demand and accuracy rates decreased with increasing task demands.
Parieto-Frontal Network Modulation by Task Difficulty
We demonstrated main effects of task difficulty and fluid intelligence for the neuroimaging results. Parietal and frontal as well as occipito-temporal brain areas are involved in solving the geometric analogical reasoning task and are modulated by task difficulty. This is in line with findings from studies on visuo-spatial and analogical reasoning (Wharton et al., 2000; Wartenburger et al., 2009; Preusse et al., 2010) and with the postulates of the P-FIT theory (Jung and Haier, 2007). Employing a similar task in a forerunner study (Wartenburger et al., 2009), we showed that a fronto-parietal network is engaged when solving geometric analogies. Wharton et al. (2000) reported a left hemispheric fronto-parietal network (left middle frontal gyrus and the left inferior parietal cortex) to be involved in the processing of simple geometric analogies and identity decisions. Interestingly, in a 1-year follow up with the hi-fluIQ we demonstrated that the task-related BOLD response stays stable over this time period (Preusse et al., 2010), which further corroborates the present findings.
In the present study, we operationalized task difficulty with a graded variation of task demand using identical stimuli and instructional demands for all levels of difficulty. This approach distinguishes our study from others that varied task difficulty by either contrasting distinct tasks that varied demand on reasoning ability (Lee et al., 2006), or by varying the visual complexity of the stimuli (Prabhakaran et al., 1997). Our findings are in line with reports from Kalbfleisch et al. (2007) who found that the BOLD signal in the left middle frontal gyrus was correlated with variance in the difficulty of a fluid reasoning task. Also, D’Esposito et al. (1998) reported that tasks requiring spatial working memory activate the middle frontal gyrus.
According to Ungerleider (Ungerleider and Haxby, 1994; Ungerleider et al., 1998), the so-called ventral and dorsal stream are involved in processing visuo-spatial information. The ventral stream involves occipito-temporal brain regions and is associated with object recognition and form representation. The dorsal stream runs from the striate cortex to the superior parietal cortex and is involved in processing object location, spatial relations of objects, and motion information. We found that brain regions from both streams were involved in geometric analogical reasoning. Brain regions from the ventral stream were probably involved in detecting individual pattern features that may be relevant for recognizing the spatial relation of the two patterns of a pair. Brain regions from the dorsal stream probably aided in identifying the specific mirroring relation within a pattern pair and to compare source and target pair. Hence, as our data suggest, geometric analogical reasoning requires the interplay of both processing streams and there is increased visuo-spatial processing demand for both streams with increasing task difficulty. Geometric analogical reasoning requires complex information processing and information integration. Further research is needed to elucidate cerebral correlates of underlying cognitive sub-processes in greater detail.
Parieto-Frontal Network Modulation by Fluid Intelligence
In general, a similar network of brain regions is involved in geometric analogical reasoning in both groups. Interestingly, we were able to show that modulation of activation of the parietal network components is related to fluid intelligence.
According to the literature, parietal brain regions are associated with task-related processing (Gevins and Smith, 2000; Lee et al., 2006; Rypma et al., 2006; Neubauer and Fink, 2009b). Stronger recruitment of parietal task-related brain regions in hi-fluIQ is correlated to better behavioral performance in the geometric analogical reasoning task. This is in line with Jung and Haier (2007) who argued that the dynamics of the parieto-frontal network and the interplay of brain regions upon a cognitive demand determine fluid intelligence.
As expected, the geometric analogical reasoning task is more demanding for ave-fluIQ than for hi-fluIQ. This is reflected in higher error rates. Interestingly, there is increased brain activity in the ACC and medial frontal gyrus in ave-fluIQ compared to hi-fluIQ. According to the literature, the ACC is attributed an important role in executive monitoring and also in cognitive functions that are central to intelligent behavior, such as problem solving and adaptive responses to changing conditions (Allman et al., 2001). The ACC seems to be especially involved when cognitive effort is needed to carry out a task, when integrating conflicting information, or when a task is unfamiliar. Duncan et al. (2000) found the lateral frontal cortex to be bilaterally involved and the ACC to be particularly involved while adult participants solved novel spatial reasoning tasks that were highly demanding of fluid intelligence. Moreover, Duncan and Owen (2000) reported frontal lobe activations (specifically, mid-dorsolateral, mid-ventrolateral, and ACC) to be associated with a multitude of cognitive demands, such as, for example, executive control or problem solving. From the similarity of activation for different cognitive demands, Duncan and Owen concluded that this common frontal network is generally involved in cognitive problem solving. As on the one hand ave-fluIQ show stronger involvement of medial frontal brain regions, and on the other hand there is no differential recruitment of lateral frontal brain regions when solving the geometric analogical reasoning task, we conclude that ave-fluIQ need to exert more cognitive control and stronger executive monitoring than hi-fluIQ.
Our findings are in line with further findings from the literature. Grabner et al. (2004) reported lower event-related desynchronization of brain activity in the EEG upper alpha frequency band (i.e., a negative correlate of cortical activation) of left frontal brain regions in a working memory task for participants with hi-fluIQ. Rypma et al. (2006) found less cortical activity in PFC and greater cortical activity in parietal regions for faster-performing individuals compared to slower-performing individuals in a digit-symbol substitution test. Yet, there are also findings of a positive correlation between fluid intelligence and ACC activation. Gray et al. (2003) reported a positive association between fluid intelligence and activity in the left dorsal ACC in a working memory task. However, that task involved a larger amount of trial interference than the geometric analogical reasoning task did. Hence, these opposing findings may be due to differences in the specific cognitive demands of the tasks. Our data suggest that hi-fluIQ can more easily make up for the demands of the geometric analogical reasoning task because focused executive control and information integration processes from frontal brain regions are less relevant for task-solving than in their ave-fluIQ peers. The greater parietal activation observed in hi-fluIQ may reflect group differences in processing spatial information.
As the two groups differ both in their behavioral performance and in the cerebral correlates underlying geometric analogical reasoning, it can be assumed that there are differences in the cognitive information processing. The interaction of task difficulty and fluid intelligence revealed greater BOLD signal changes bilaterally in the occipito-temporal junction for hi-fluIQ and for increasing task difficulty. The differential recruitment of higher-order visual brain regions may reflect a differential approach to the imagination of motion and spatial orientation while solving the task. As could be learned from post-task interviews, the two groups did not differ in their verbally reported intentional task-solving strategy. However, they differed in the usage of movement gestures and gesture frequency on the process of mirroring when explaining the task-solving process (Sassenberg et al., 2011). Considering this along with the aforementioned brain activation patterns in the occipito-temporal region, this may hint to group differences in how vividly the mirroring is imagined during the task-solving.
Relationship between brain activation and fluid intelligence
Neural efficiency hypothesis assumes that increased behavioral performance level in more intelligent individuals goes along with decreased (i.e., more efficient) cortical activity when performing a cognitive task (Haier et al., 1988; Neubauer and Fink, 2009b). Generally, we found frontal and parietal brain regions to be involved in geometric analogical reasoning in both groups. Yet, the modulation of the extent of brain activation is different depending on fluid intelligence level and brain region. We found brain regions that show greater BOLD signal changes for hi-fluIQ as well as brain regions that show greater BOLD signal changes for ave-fluIQ. Hence, we cannot globally characterize the direction of the brain activation–intelligence relationship to be exclusively positive or exclusively negative, but rather it is region specific. In their review on intelligence and neural efficiency Neubauer and Fink (2009b) conclude that neural efficiency is not a feature of the whole brain, but they assume that it is limited to frontal brain regions. Our data are in line with the assumption of a localized negative brain activation–intelligence relationship for frontal brain regions. Yet, as we also demonstrated a positive brain activation–intelligence relationship for parietal brain regions, we conclude that the flexibility of modulating the extent of cerebral activity region- and task-specifically is characteristic for fluid intelligence.
Interindividual differences in recruitment of parietal and frontal brain regions cannot be interpreted as causative for interindividual differences in fluid intelligence. Rather, it is generally assumed that the brain activation–intelligence relationship acts bi-directionally. That is, there is a mutual interaction between fluid intelligence and structural or functional characteristics of the brain (Jung and Haier, 2007): Differences in fluid intelligence are correlated to differences in brain activation patterns (including differences in the functional interplay among brain regions), and conversely, differences in brain characteristics are correlated to differences in behavioral performance in cognitive tasks. In the present study we demonstrated that flexible modulation of the parieto-frontal network is correlated to hi-fluIQ.
Effective connectivity
Dynamic multivariate Granger causality mapping was used to identify the paths of interregional communication in the parieto-frontal network during geometric analogical reasoning. For hi-fluIQ we found significant paths of effective connectivity within frontal brain regions and from the left inferior frontal gyrus to left and right parietal brain regions. For ave-fluIQ we found significant paths of effective connectivity within parietal brain regions and from the right middle frontal gyrus to left and right parietal brain regions. Communication within frontal brain regions is assumed to reflect executive processes, while communication within parietal brain regions is assumed to reflect visuo-spatial and task-related processing. Parieto-frontal connectivity is assumed to reflect the link between visuo-spatial operations and executive processes in order to ultimately arrive at a decision.
Studies on effective connectivity in reasoning are still sparse and findings are inconsistent (e.g., Rypma et al., 2006; Krueger et al., 2010; Prescott et al., 2010). This may be because of differences in the employed tasks, the frequent use of performance measures rather than intelligence measures, or differences in methodology. Our findings differ from Krueger et al. (2010) who report stronger inter-hemispheric connectivity between the left and right parietal lobe in high performers in a mental multiplication task. Individuals performing low in this task based their calculations more strongly on a right intra-hemispheric circuit between frontal and parietal brain regions. Since that study did not investigate the dynamics, it is possible that the causalities reported there were both intrinsic and stimulus-entrained. However, our study investigated only stimulus-entrained causality as it is of most relevance to the brain systems being investigated using the task. Owing to these methodological differences, one should only carefully compare the results of our study with Krueger et al. (2010). Using a simple speeded-processing task Rypma et al. (2006) found that faster performers were characterized by a less pronounced parieto-frontal communication and slower performers showed more directed influences from frontal to parietal brain regions. However, as Rypma et al. (2006) regarded task performance rather than fluid intelligence, this might account for the differences in comparison to our results. Thus, in order to learn more about the modulation of interregional connectivity by fluid intelligence, further research is of paramount interest.
With respect to inter-hemispheric frontal connectivity, our results are consistent with the findings of Prescott et al. (2010). They reported stronger inter-hemispheric frontal connectivity in mathematically gifted adolescents during a 3-D mental rotation task and attribute this to the significance of executive processes to high intelligence. However, as intra-hemispheric parieto-frontal connectivity was not specifically enhanced in hi-fluIQ in our study (as opposed to inter-hemispheric parieto-frontal connectivity), our data do not support assumptions of hemispheric lateralization of effective connectivity in geometric analogical reasoning in hi-fluIQ.
The significant paths of effective connectivity within the frontal brain regions for the hi-fluIQ were coupled with lower BOLD signal changes in these regions and better behavioral performance. In order to reconcile these findings, we need to understand the complex interplay between brain activation and effective connectivity: To obtain higher effective connectivity between two regions from the dMVAR model, the delay between the two must wax and wane according to the external input. This is quite possible without the BOLD signal itself being strongly positively correlated with the paradigm. Hence, though high activation and strong effective connectivity can co-exist, the presence of the former is not required for the latter. Therefore, stronger effective connectivity within the frontal brain regions for the hi-fluIQ with simultaneously lower BOLD signal changes in these regions may indicate that efficient communication between these regions was possible without using too many resources.
Directions for Future Research
Note that the results of the present study display characteristics of hi-fluIQ. Yet, they do not allow conclusions about underlying causations of high cognitive ability. Further research on the relationship between cerebral characteristics, fluid intelligence, and behavioral performance is needed.
The results presented here need to be considered along with some limitations. As mentioned above, fluid intelligence is (among others) correlated to performance in cognitive tasks and also to scholastic achievements. Yet, in everyday life fluid intelligence is rarely ever demanded exclusively. Rather, everyday cognitive or scholastic demands usually pair fluid intelligence with other cognitive abilities (e.g., memory demands or world knowledge, the latter is also referred to as crystallized intelligence). As the geometric analogical reasoning task we employed demands fluid intelligence very purely, it remains relatively abstract from everyday cognitive demands. Thus, on the basis of our findings and the current knowledge about interindividual differences in fluid intelligence and reasoning, further research on influencing factors of cognitive task performance and scholastic achievements is desirable.
Blood oxygenation level dependency signal changes due to training or motivation were controlled for and thus not regarded in the present study. However, it is desirable to conduct research on the influence of further trait or state factors on interindividual differences in cerebral correlates of geometric analogical reasoning.
In our study design we compared a group of individuals with distinctly hi-fluIQ to a group of individuals with ave-fluIQ and determined cerebral correlates of geometric analogical reasoning for those two groups. Perspective future research could provide further insight by correlating individual intelligence scores to behavioral performance measures, measures of cerebral activation, or interregional connectivity patterns. In order to carry out such a study, one would need a different sample composition with some more participants rating between 110 and 120 on fluid intelligence scales such that the basic population is evenly represented in a continuum of fluid intelligence rather than examining two distinct groups as in the present study, which restricts statements to characteristics of hi-fluIQ. As we did not recruit a sample group with below-average intelligence, the pattern of results cannot be transferred to the whole spectrum of fluid intelligence.
Furthermore, it is important to note that fluid intelligence level is not stable but it can change over the life-span. It reaches its highest level at late adolescence and starts declining from about the mid-twenties on (Cattell, 1943). As the human brain is plastic, this study would most probably come to different results if we repeated it when the participants have reached their middle age. Thus, it is of paramount interest to investigate the cerebral and behavioral correlates of fluid intelligence and geometric analogical reasoning in longitudinal developmental studies.
Conclusion
In summary, we conclude that hi-fluIQ are able to solve the geometric analogical reasoning task with greater accuracy than ave-fluIQ, and at the same speed. On the cerebral level, hi-fluIQ display stronger task-related recruitment of parietal brain regions on the one hand and a negative brain activation–intelligence relationship in frontal brain regions on the other hand. Cattell defined fluid intelligence as the ability to solve problems adaptively and to cope with novel situations or circumstances independently of acquired knowledge. One key characteristic of fluid intelligence is the ability to perceive and manipulate relations (Cattell, 1963; Horn and Cattell, 1966). This means, people with a hi-fluIQ level possess a high level of flexibility concerning order and the relation of structures. In Cattell’s theory of fluid intelligence, this flexibility is meant only for the cognitive domain – although he postulated that there is a physiological basis for fluid intelligence. According to the results presented here, we might, however, expand the scope of this theory and transfer the flexibility approach to the cerebral level: hi-fluIQ are able to adapt the allocation of cerebral resources more flexibly to task requirements when solving a geometric analogical reasoning task, which is known to demand fluid intelligence. The modulation of parietal brain activation with task demand, along with neural efficiency in frontal brain regions, displays adaptivity of the brain toward external cognitive demands. Adapting more flexibly to such demands – on both the behavioral and the cerebral level – together with more efficient interregional frontal communication seems to be a significant feature of hi-fluIQ. This ultimately allows hi-fluIQ to outperform ave-fluIQ.
In the present study, we characterized the parieto-frontal network as differentially involved in geometric analogical reasoning in hi-fluIQ and ave-fluIQ. By using a qualified task and a well characterized sample, we were able to expand results from the literature to a sample with hi-fluIQ. We showed that the relationship between brain activation and fluid intelligence is not mono-directional, but rather, frontal and parietal brain regions are differentially modulated by fluid intelligence when participants carry out the geometric analogical reasoning task. That flexibility of region-specific modulation of cerebral activation with task demand appears to be significant for hi-fluIQ.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by grants from the German Bundesministerium fuer Bildung und Forschung (Neuroscience, Instruction, and Learning program (grant number 01GJ0802); and Berlin NeuroImaging Center). Isabell Wartenburger is supported by the Stifterverband fuer die Deutsche Wissenschaft (Claussen–Simon–Stiftung). The authors thank Manja Foth, Boris Bornemann, and Jan Ries for their help with study design and recruitment and Jan-Ole Christian and Manja Homberg for their help with data acquisition. In addition, the authors thank the two anonymous reviewers for their time and for their helpful comments on an earlier version of this manuscript.
Footnotes
References
Ackerman, P. L., Beier, M. E., and Boyle, M. O. (2005). Working memory and intelligence: the same or different constructs? Psychol. Bull. 131, 30–60.
Allman, J. M., Hakeem, A., Erwin, J. M., Nimchinsky, E., and Hof, P. (2001). The anterior cingulate cortex. Ann. N. Y. Acad. Sci. 935, 107–117.
Beckmann, C. F., Jenkinson, M., and Smith, S. M. (2003). General multilevel linear modeling for group analysis in FMRI. Neuroimage 20, 1052–1063.
Bethell-Fox, C. E., Lohmann, D. F., and Snow, R. E. (1984). Adaptive reasoning: componential and eye movement analysis of geometric analogy performance. Intelligence 8, 205–238.
Boroojerdi, B., Phipps, M., Kopylev, L., Wharton, C. M., Cohen, L. G., and Grafman, J. (2001). Enhancing analogic reasoning with rTMS over the left prefrontal cortex. Neurology 56, 526–528.
Bunge, S. A., Wendelken, C., Badre, D., and Wagner, A. D. (2005). Analogical reasoning and prefrontal cortex: evidence for separable retrieval and integration mechanisms. Cereb. Cortex 15, 239–249.
Carpenter, P. A., Just, M. A., and Shell, P. (1990). What one intelligence test measures: a theoretical account of the processing in the Raven progressive matrices test. Psychol. Rev. 97, 404–431.
Cattell, R. B. (1963). Theory of fluid and crystallized intelligence: a critical experiment. J. Educ. Psychol. 54, 1–22.
Cattell, R. B. (1987). Intelligence: Its Structure, Growth, and Action. Amsterdam: Elsevier Science Publishers BV.
Cox, R. W. (1996). AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput. Biomed. Res. 29, 162–173.
Cox, R. W., and Hyde, J. S. (1997). Software tools for analysis and visualization of FMRI Data. NMR Biomed. 10, 171–178.
Deary, I. J., Penke, L., and Johnson, W. (2010). The neuroscience of human intelligence differences. Nat. Rev. Neurosci. 11, 201–211.
Dehaene, S., Piazza, M., Pinel, P., and Cohen, L. (2003). Three parietal circuits for number processing. Cogn. Neuropsychol. 20, 487–506.
Deichmann, R. (2005). Fast high-resolution T1 mapping of the human brain. Magn. Reson. Med. 54, 20–27.
Deshpande, G., Hu, X., Lacey, S., Stilla, R., and Sathian, K. (2010a). Object familiarity modulates effective connectivity during haptic shape perception. Neuroimage 49, 1991–2000.
Deshpande, G., LaConte, S., James, G. A., Peltier, S., and Hu, X. (2009). Multivariate Granger causality analysis of fMRI data. Hum. Brain Mapp. 30, 1361–1373.
Deshpande, G., Sathian, K., and Hu, X. (2010b). Assessing and compensating for zero-lag correlation effects in time-lagged Granger causality analysis of fMRI. IEEE Trans. Biomed. Eng. 57, 1446–1456.
D’Esposito, M., Aguirre, G. K., Zarahn, E., Ballard, D., Shin, R. K., and Lease, J. (1998). Functional MRI studies of spatial and nonspatial working memory. Cogn. Brain Res. 7, 1–13.
Duncan, J. (2003). Intelligence tests predict brain response to demanding task events. Nat. Neurosci. 6, 207–208.
Duncan, J., and Owen, A. M. (2000). Common regions of the human frontal lobe recruited by diverse cognitive demands. Trends Neurosci. 23, 475–483.
Duncan, J., Seitz, R. J., Kolodny, J., Bor, D., Herzog, H., Ahmed, A., Newell, F. N., and Emslie, H. (2000). A neural basis for general intelligence. Science 289, 457–460.
Feigenson, L., Dehaene, S., and Spelke, E. (2004). Core systems of number. Trends Cogn. Sci. 8, 307–314.
Ferrer, E., O’Hare, E. D., and Bunge, S. A. (2009). Fluid reasoning and the developing brain. Front. Neurosci. 3:1. doi: 10.3389/neuro.01.003.2009
Geake, J. G., and Hansen, P. C. (2010). Functional neural correlates of fluid and crystallized analogizing, Neuroimage 49, 3489–3497.
Gevins, A., and Smith, M. E. (2000). Neurophysiological measures of working memory and individual differences in cognitive ability and cognitive style. Cereb. Cortex 10, 829–839.
Grabner, R. H., Ansari, D., Koschutnig, K., Reishofer, G., Ebner, F., and Neuper, C. (2009). To retrieve or to calculate? Left angular gyrus mediates the retrieval of arithmetic facts during problem solving. Neuropsychologia 47, 604–608.
Grabner, R. H., Ansari, D., Reishofer, G., Stern, E., Ebner, F., and Neuper, C. (2007). Individual differences in mathematical competence predict parietal brain activation during mental calculation. Neuroimage 38, 346–356.
Grabner, R. H., Fink, A., Stipacek, A., Neuper, C., and Neubauer, A. C. (2004). Intelligence and working memory systems: evidence of neural efficiency in alpha band ERD. Cogn. Brain Res. 20, 212–225.
Granger, C. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37, 424–438.
Gray, J. R., Chabris, C. F., and Braver, T. S. (2003). Neural mechanisms of general fluid intelligence. Nat. Neurosci. 6, 316–322.
Haier, R. J., Siegel, B. V., Nuechterlein, K. H., and Hazlett, E. (1988).Cortical glucose metabolic rate correlates of abstract reasoning and attention studied with positron emission tomography. Intelligence 12, 199–217.
Hofstadter, D. (2001). “Analogy as the core of cognition,” in The Analogical Mind: Perspectives From Cognitive Science, eds D. Gentner, K. J. Holyoak, and B. N. Kokinov (Cambridge, MA: MIT Press), 504–537.
Hofstadter, D. R. (1997). Fluid Concepts and Creative Analogies: Computer Models of the Fundamental Mechanisms of Thought. London: Penguin Press.
Holyoak, K. J., and Kroger, J. K. (1995). Forms of reasoning: insight into prefrontal functions? Ann. N. Y. Acad. Sci. 769, 253–264.
Holyoak, K. J., and Morrison, R. (2005). The Cambridge Handbook of Thinking and Reasoning. Cambridge: University Press.
Horn, J. L., and Cattell, R. B. (1966). Refinement and test of the theory of fluid and crystallized general intelligences. J. Educ. Psychol. 57, 253–270.
Hosenfeld, B., Boom, D. C., and Resing, W. C. M. (1997). Constructing geometric analogies for the longitudinal testing of elementary school children. J. Educ. Meas. 34, 367–372.
Ischebeck, A., Zamarian, L., Egger, K., Schocke, M., and Delazer, M. (2007). Imaging early practice effects in arithmetic. Neuroimage 36, 993–1003.
Ischebeck, A., Zamarian, L., Siedentopf, C., Koppelstaetter, F., Benke, T., Felber, S., and Delazer, M. (2006). How specifically do we learn? Imaging the learning of multiplication and subtraction. Neuroimage 30, 1365–1375.
Jausovec, N. (2000). Differences in cognitive processes between gifted, intelligent, creative, and average individuals while solving complex problems: an EEG study. Intelligence 28, 213–237.
Jenkinson, M., Bannister, P., Brady, M., and Smith, S. (2002). Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 17, 825–841.
Jenkinson, M., and Smith, S. (2001). A global optimisation method for robust affine registration of brain images. Med. Image Anal. 5, 143–156.
Jung, R. E., and Haier, R. J. (2007). The parieto-frontal integration theory (P-FIT) of intelligence: converging neuroimaging evidence. Behav. Brain Sci. 30, 135–154.
Just, M. A., and Varma, S. (2007). The organization of thinking: what functional brain imaging reveals about the neuroarchitecture of complex cognition. Cogn. Affect. Behav. Neurosci. 7, 153–191.
Kalbfleisch, M. L., van Meter, J. W., and Zeffiro, T. A. (2007). The influences of task difficulty and response correctness on neural systems supporting fluid reasoning. Cogn. Neurodyn. 1, 71–84.
Kane, M. J., and Engle, R. W. (2002). The role of prefrontal cortex in working-memory capacity, executive attention, and general fluid intelligence: an individual-differences perspective. Psychon. Bull. Rev. 9, 637–671.
Kokinov, B., and French, R. M. (2003). “Computational models of analogy-making,” in Encyclopedia of Cognitive Science, Vol. 1, ed. L. Nadel (London: Nature Publishing Group), 113–118.
Krueger, F., Landgraf, S., van der Meer, E., Deshpande, G., and Hu, X. (2010). Effective connectivity of the multiplication network: a functional MRI and multivariate Granger causality mapping study. Hum. Brain Mapp. [Epub ahead of print]
Krueger, F., Spampinato, M. V., Pardini, M., Pajevic, S., Wood, J. N., Weiss, G. H., Landgraf, S., and Grafman, J. (2008). Integral calculus problem solving: an fMRI investigation. Neuroreport 19, 1095–1099.
Lacey, S., Hagtvedt, H., Patrick, V. M., Anderson, A., Stilla, R., Deshpande, G., Hu, X., Sato, J. R., Reddy, S., and Sathian, K. (2011). Art for reward’s sake: visual art recruits the ventral striatum. Neuroimage 55, 420–433.
Landgraf, S., van der Meer, E., and Krueger, F. (2010). Cognitive resource allocation for neural activity underlying mathematical cognition: a multi-method study. ZDM 42, 579–590.
Larson, G. E., Haier, R. J., LaCasse, L., and Hazen, K. (1995). Evaluation of a “mental effort” hypothesis for correlations between cortical metabolism and intelligence. Intelligence 21, 267–278.
Lee, K. H., Choi, Y. Y., Gray, J. R., Cho, S. H., Chae, J.-H., Lee, S., and Kim, K. (2006). Neural correlates of superior intelligence: stronger recruitment of posterior parietal cortex. Neuroimage 29, 578–586.
Luo, Q., Perry, C., Peng, D., Jin, Z., Xu, D., Ding, G., and Xu, S. (2003). The neural substrate of analogical reasoning: an fMRI study. Cogn. Brain Res. 17, 527–534.
Mayer, J. S., Roebroeck, A., Maurer, K., and Linden, D. E. (2010). Specialization in the default mode: task-induced brain deactivations dissociate between visual working memory and attention. Hum. Brain Mapp. 31, 126–139.
Mulholland, T. M., Pellegrino, J. W., and Glaser, R. (1980). Components of geometric analogy solution. Cogn. Psychol. 12, 252–284.
Neubauer, A. C., and Fink, A. (2009a). Intelligence and neural efficiency: measures of brain activation versus measures of functional connectivity in the brain. Intelligence 37, 223–229.
Neubauer, A. C., and Fink, A. (2009b). Intelligence and neural efficiency. Neurosci. Biobehav. Rev. 33, 1004–1023.
Neubauer, A. C., Grabner, R. H., Freudenthaler, H. H., Beckmann, J. F., and Guthke, J. (2004). Intelligence and individual differences in becoming neurally efficient. Acta Psychol. 116, 55–74.
Neubauer, A. C., Riemann, R., Mayer, R., and Angleitner, A. (1997). Intelligence and reaction times in the Hick, Sternberg and Posner paradigms. Pers. Individ. Dif. 22, 885–894.
Newman, S. D., and Just, M. A. (2005). “The neural bases of intelligence: a perspective based on functional neuroimaging,” in Cognition and Intelligence: Identifying the Mechanisms of the Mind, eds J. Sternberg and J. Pretz (New York: Cambridge University Press), 88–103.
Nieder, A., and Dehaene, S. (2009). Representation of number in the brain. Annu. Rev. Neurosci. 32, 185–208.
Oldfield, R. C. (1971). The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9, 97–113.
Prabhakaran, V., Smith, J. A., Desmond, J. E., Glover, G. H., and Gabrieli, J. D. (1997). Neural substrates of fluid reasoning: an fMRI study of neocortical activation during performance of the Raven’ progressive matrices test. Cogn. Psychol. 33, 43–63.
Prescott, J., Gavrilescu, M., Cunnington, R., O’Boyle, M. W., and Egan, G. F. (2010). Enhanced brain connectivity in math-gifted adolescents: an fMRI study using mental rotation. Cogn. Neurosci. 1, 277–288.
Preusse, F., van der Meer, E., Ullwer, D., Brucks, M., Krueger, F., and Wartenburger, I. (2010). Long-term characteristics of analogical processing in high-school students with high fluid intelligence: an fMRI study. ZDM 42, 635–647.
Raven, J., Court, J., and Raven, J. J. (1980). RAVEN-Matrizen-Test. Advanced Progressive Matrices. Weinheim: Beltz Test Gesellschaft.
Rickard, T. C., Romero, S. G., Basso, G., Wharton, C., Flitman, S., and Grafman, J. (2000). The calculating brain: an fMRI study. Neuropsychologia 38, 325–335.
Rypma, B., Berger, J. S., Prabhakaran, V., Bly, B. M., Kimberg, D. Y., Biswal, B. B., and D’Esposito, M. (2006). Neural correlates of cognitive efficiency. Neuroimage 33, 969–979.
Santens, S., Roggeman, C., Fias, W., and Verguts, T. (2010). Number processing pathways in human parietal cortex. Cereb. Cortex 20, 77–88.
Sassenberg, U., Foth, M., Wartenburger, I., and van der Meer, E. (2011). Show your hands – are you really clever? Reasoning, gesture production, and intelligence. Linguistics 49, 105–134.
Smith, S. M., Jenkinson, M., Woolrich, M. W., Beckmann, C. F., Behrens, T. E. J., Johansen-Berg, H., Bannister, P. R., Luca, M. D., Drobnjak, I., Flitney, D. E., Niazy, R. K., Saunders, J., Vickers, J., Zhang, Y., Stefano, N. D., Brady, J. M., and Matthews, P. M. (2004). Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 23(Suppl. 1), S208–S219.
Spinath, B., Freudenthaler, H. H., and Neubauer, A. C. (2010). Domain-specific school achievement in boys and girls as predicted by intelligence, personality and motivation. Pers. Individ. Dif. 48, 481–486.
Talairach, J., and Tournoux, P. (1988). Co-planar Stereotaxic Atlas of the Human Brain. 3-Dimensional Proportional System: An Approach to Cerebral Imaging. New York: Thieme Medical Publishers.
Ungerleider, L. G., Courtney, S. M., and Haxby, J. V. (1998). A neural system for human visual working memory. Proc. Natl. Acad. Sci. U.S.A. 95, 883–890.
Ungerleider, L. G., and Haxby, J. V. (1994). “What” and “where” in the human brain. Curr. Opin. Neurobiol. 4, 157–165.
van der Meer, E., Beyer, R., Horn, J., Foth, M., Bornemann, B., Ries, J., Kramer, J., Warmuth, E., Heekeren, H. R., and Wartenburger, I. (2010). Resource allocation and fluid intelligence: insights from pupillometry. Psychophysiology 47, 158–169.
Vernon, P. A. (1983). Speed of information processing and general intelligence. Intelligence 7, 53–70.
Wartenburger, I., Heekeren, H. R., Preusse, F., Kramer, J., and van der Meer, E. (2009). Cerebral correlates of analogical processing and their modulation by training. Neuroimage 48, 291–302.
Wendelken, C., Nakhabenko, D., Donohue, S. E., Carter, C. S., and Bunge, S. A. (2008). “Brain is to thought as stomach is to ??”: investigating the role of rostrolateral prefrontal cortex in relational reasoning. J. Cogn. Neurosci. 20, 682–693.
Wharton, C. M., Grafman, J., Flitman, S. S., Hansen, E. K., Brauner, J., Marks, A., and Honda, M. (2000). Toward neuroanatomical models of analogy: a positron emission tomography study of analogical mapping. Cogn. Psychol. 40, 173–197.
Wittchen, H.-U., Zaudig, M., and Fydrich, T. (1997). Strukturiertes Klinisches Interview für DSM-IV. Goettingen: Hogrefe.
Woolrich, M. W., Behrens, T. E. J., Beckmann, C. F., Jenkinson, M., and Smith, S. M. (2004). Multilevel linear modelling for FMRI group analysis using Bayesian inference. Neuroimage 21, 1732–1747.
Woolrich, M. W., Jbabdi, S., Patenaude, B., Chappell, M., Makni, S., Behrens, T., Beckmann, C., Jenkinson, M., and Smith, S. M. (2009). Bayesian analysis of neuroimaging data in FSL. Neuroimage 45(Suppl. 1), S173–S186.
Woolrich, M. W., Ripley, B. D., Brady, M., and Smith, S. M. (2001). Temporal autocorrelation in univariate linear modeling of FMRI data. Neuroimage 14, 1370–1386.
Zago, L., Pesenti, M., Mellet, E., Crivello, F., Mazoyer, B., and Tzourio-Mazoyer, N. (2001). Neural correlates of simple and complex mental calculation. Neuroimage 13, 314–327.
Keywords: high fluid intelligence, geometric analogical reasoning, task difficulty, functional magnetic resonance imaging, parieto-frontal network
Citation: Preusse F, van der Meer E, Deshpande G, Krueger F and Wartenburger I (2011) Fluid intelligence allows flexible recruitment of the parieto-frontal network in analogical reasoning. Front. Hum. Neurosci. 5:22. doi: 10.3389/fnhum.2011.00022
Received: 29 September 2010;
Accepted: 17 February 2011;
Published online: 01 March 2011.
Edited by:
Neal J. Cohen, University of Illinois, USACopyright: © 2011 Preusse, van der Meer, Deshpande, Krueger and Wartenburger. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Franziska Preusse, Department of Neurology, Berlin NeuroImaging Center, Charité – Universitaetsmedizin Berlin CCM, AG Wartenburger, Charitéplatz 1, 10117 Berlin, Germany. e-mail:ZnJhbnppc2thLnByZXVzc2VAY2hhcml0ZS5kZQ==


 Gopikrishna Deshpande4,5
Gopikrishna Deshpande4,5