Abrar Faiyaz
Marvin M. Doyley
Giovanni Schifitto
Md Nasir Uddin- 1Department of Electrical and Computer Engineering, University of Rochester, Rochester, NY, United States
- 2Department of Imaging Sciences, University of Rochester, Rochester, NY, United States
- 3Department of Biomedical Engineering, University of Rochester, Rochester, NY, United States
- 4Department of Neurology, University of Rochester, Rochester, NY, United States
Artificial intelligence (AI) has made significant advances in the field of diffusion magnetic resonance imaging (dMRI) and other neuroimaging modalities. These techniques have been applied to various areas such as image reconstruction, denoising, detecting and removing artifacts, segmentation, tissue microstructure modeling, brain connectivity analysis, and diagnosis support. State-of-the-art AI algorithms have the potential to leverage optimization techniques in dMRI to advance sensitivity and inference through biophysical models. While the use of AI in brain microstructures has the potential to revolutionize the way we study the brain and understand brain disorders, we need to be aware of the pitfalls and emerging best practices that can further advance this field. Additionally, since dMRI scans rely on sampling of the q-space geometry, it leaves room for creativity in data engineering in such a way that it maximizes the prior inference. Utilization of the inherent geometry has been shown to improve general inference quality and might be more reliable in identifying pathological differences. We acknowledge and classify AI-based approaches for dMRI using these unifying characteristics. This article also highlighted and reviewed general practices and pitfalls involving tissue microstructure estimation through data-driven techniques and provided directions for building on them.
1. Introduction
The microstructural estimation of biological tissue through histological analysis is reliable. However, it has limitations, including its invasive nature (1). In contrast, diffusion MRI (dMRI) is a non-invasive technique for encoding information about tissue structure at the microscopic scale in the human brain (2–4). It is based on the restricted diffusion of water molecules in the local microstructural environment. Diffusion tensor imaging (DTI), a widely used dMRI approach, has been shown to be sensitive to pathological changes in the brain (5). However, water diffusion in DTI has been assumed to be a Gaussian process, and microscopic inspection of the neuronal environment invalidated this assumption (6, 7). Thus, DTI is not specific to microstructural properties such as cell size, axon diameter, orientation dispersion, and neurite density (8).
Consequently, multi-compartment modeling in dMRI has emerged as a powerful non-Gaussian tool for studying neuropathogenesis and holds potential for both research and clinical applications, including providing insight into the biological mechanisms of disease and improving diagnosis and treatment monitoring (9). Models such as free water imaging (FWI) and Neurite Orientation Dispersion and Density Imaging (NODDI) helped early multicompartmental modeling become more widely adopted in the field (10, 11). However, most of the advanced multi-compartment dMRI models suffer estimation errors due to highly non-linear signal representations, underlying simplifying assumptions, and sometimes motion artifacts due to longer acquisition times for multiple b-values and diffusion gradient directions (8, 12).
Artificial intelligence (AI) commonly involves creating systems capable of tasks requiring human senses and intelligence, such as speech, image, and natural language synthesis. Deep/machine learning (DL/ML) subsets of AI train deep artificial neural networks to make predictions or decisions from data in a common gradient update framework. AI algorithms have evolved with DL/ML techniques due to skyrocketing computing power and resources (13, 14). Recently, AI-based approaches have been proposed to address issues such as denoising and artifact reduction (15–18), fiber tractography (19–21), resolution enhancement (22–25), and quantification of microstructural properties (20–22, 26–31). These techniques have been particularly useful for working with clinical and challenging datasets and have led to advances in dMRI parameter mapping and image quality assessment and improvement. With that said, it is important to understand that there are potential pitfalls of using such data-driven techniques, e.g., tomographic hallucination, training bias, etc. (32–34); thus, the application of such an approach in clinical dMRI needs to follow the best practices; otherwise, it can lead to inaccurate or unreliable results, proving itself to be a double-edged sword. Best practices for AI in clinical dMRI include proper protocol design and optimization, accurate image acquisition and noise-redacted reconstruction for standardized ground truth, and careful interpretation of the data (13). Further, efforts are currently being made to quantitatively understand how much clinically relevant information can be retrieved through DL/ML architectures, which is another important aspect of clinical dMRI besides general image/parameter reconstruction (35).
This study briefly generalized common features related to some of the leading biophysical models that have practically established sensitivity to the designed parameters for the models and mainly reviewed the concurrent AI alternatives to these models with their general architecture/results to probe the best practices. This article also discussed the challenges of existing AI approaches and future perspectives in tissue microstructure estimation. We identified the gross development of these algorithms in the targeted microarchitecture modeling. This includes highlighting efforts/innovations in data engineering, feature design, common practices in these techniques, or differences that set the methods apart for better/worse results.
2. Biophysical models of dMRI
2.1. The domain of dMRI sensitivity in biophysical models
In dMRI techniques, diffusion-weighted (DW) images are acquired with multiple b-values at a different number of gradient directions (2, 36–38). Then, microstructure information in each voxel of the image can be extracted via either signal representations (e.g., DTI, diffusion kurtosis imaging DKI, fiber orientation distribution function fODF) or biophysical models (e.g., NODDI, spherical mean technique SMT, white matter tissue integrity WMTI) (5, 39–41).
Signal representations explain the DW signal behavior and provide effective summary statistics at a given voxel that do not rely on assumptions about the underlying tissue properties, which is clinically demanding but estimated parameters lack specificity. On the other hand, biophysical models are mathematical models aiming to explain the physical properties of biological systems. The parameters of the biophysical models in dMRI are intentionally designed to be adjustable, mimicking the biological constructs to fit the measured DW signals. These constructs may include biophysically meaningful parameters such as tissue volume fractions and other properties that are specific to the system being studied (40). For example, white matter models vastly differ from gray matter models, leading to differentiated assumptions and geometrical functions (42, 43). A detailed explanation of the steps involved in constructing a biophysical model for dMRI can be found in Jelescu et al. (9).
The advent of computational power, complex mathematics, and geometrical formulations has led to a good number of biophysical models of brain tissue to date, including the standard model, SMT, AxCaliber (44), diffusion basis spectrum imaging (DBSI) (45), NODDI (11), WMTI (46), simple harmonic oscillator-based reconstruction and estimation (SHORE) (47) and soma and neurite density imaging (SANDI) (48). Biophysical models with their DL/ML alternatives/improvements found in the past decade are considered within the scope of this study and are displayed in Table 1 Block-A and Supplementary Table S1.
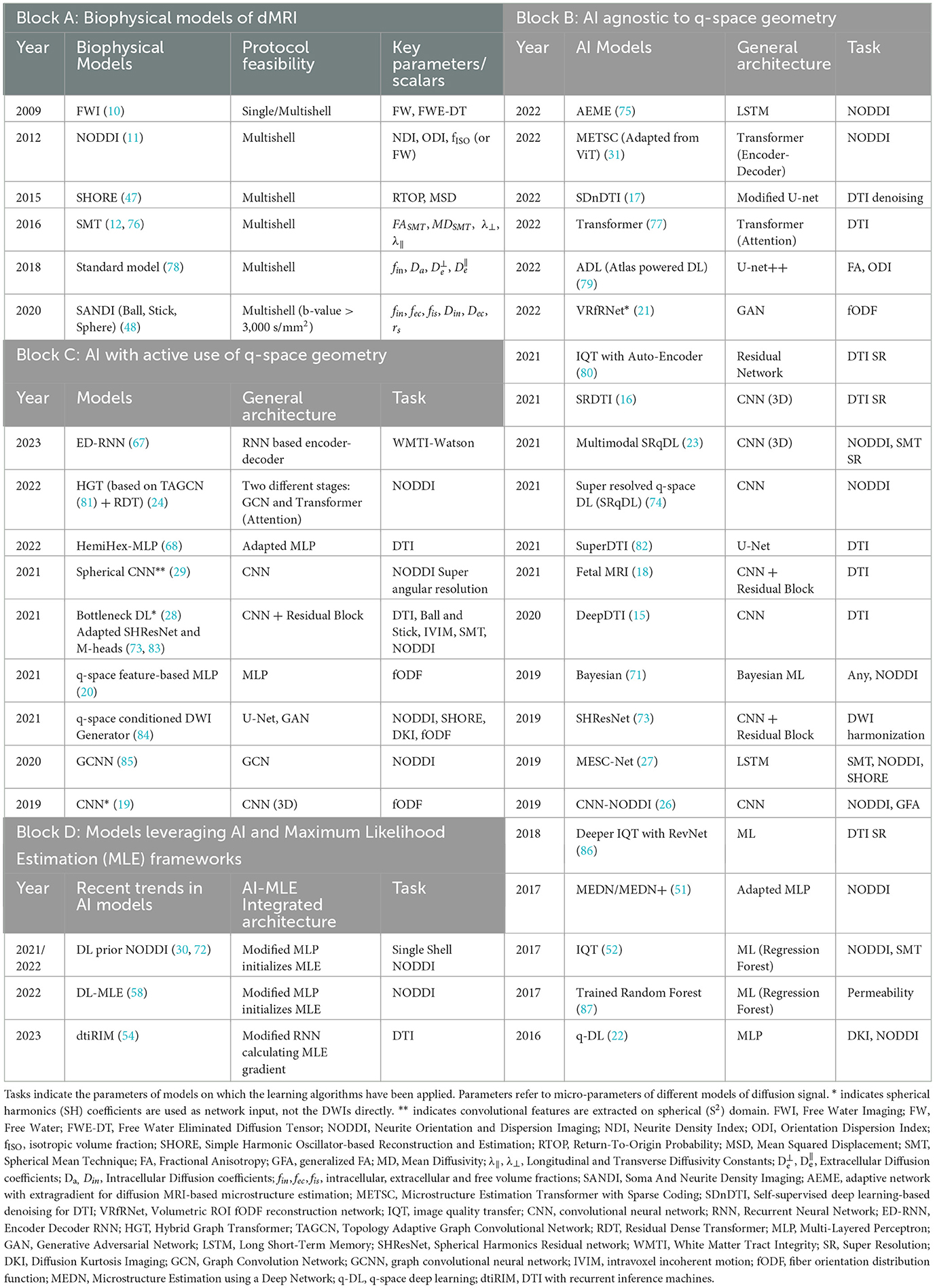
Table 1. Summary of biophysical models with their key parameters and studies conducted on diffusion MRI using AI in human brain.
2.2. Parametrizations, estimation, and validation
Overparameterization in biophysical models is necessary but results in a loss of uniqueness of the DW signals and estimated tissue microparameters, leading to higher ill-posedness in solving inverse problems (9, 40, 49, 50). A general schematic framework is illustrated in Figure 1A for parametrizing and solving inverse problems devised with a biophysical model. Like most other problems in practice, figuring out these parameters is often ill-posed by nature, which means that for a voxel, there can be multiple sets of plausible parameters that are able to explain the DWI signals. These ill-posed cases can be addressed with further contrast or geometrical priors available from the data. The ML/DL techniques can also be used to generate additional priors to solve such problems.
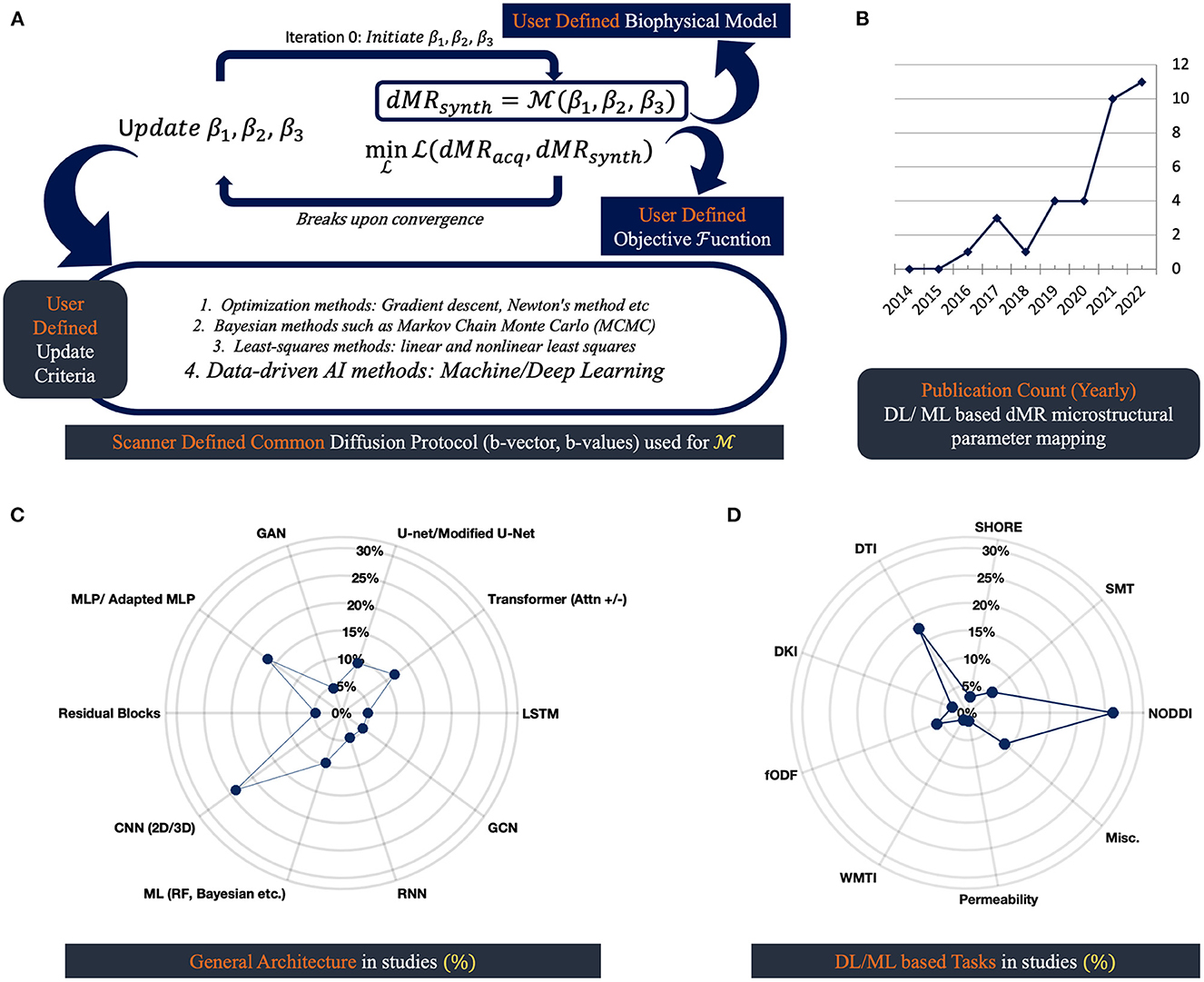
Figure 1. dMRI based microstructural reconstruction in human brain: schematics and progress through AI: (A) general schematics of microstructural reconstruction using biophysical model; (B) displays the number of AI approaches proposed over the last decade; (C) shows type of architectures these approaches use; (D) shows the biophysical models these AI approaches are applied to.
Once we have robust priors that distinguish the relevant features, optimization techniques need to be chosen empirically based on performance, and this is subject to validation. A fitting strategy refers to the methods and techniques used to train a model, such as gradient descent or genetic algorithms. The choice of optimization and fitting strategies can have a significant impact on the performance of a model and the ability to find a globally optimal solution (25). The following approaches—numerical analysis, Monte Carlo, animal models, phantoms, tissue fixation experiments, etc.—are commonly used to validate these models (50). The validation modes can often lead to good training data sources in DL/ML practice (30, 51).
3. AI in dMRI microstructure estimation
AI algorithms have been applied widely throughout the dMRI field, including signal reconstruction, denoising, detection and removal of artifacts, segmentation, co-registration, spatial and angular super-resolution of the dMRI signal, and tissue microstructure modeling (18, 21, 24, 30, 52–54). Table 1 identifies such approaches (Block B-D) and lists relevant biophysical models on which DL/ML approaches have been used (Block A). Details are provided in Supplementary Tables S1–S4.
3.1. Maximum likelihood frameworks for AI
Figure 1A depicts the three basic components of extracting microstructure from scanner-derived dMRI data. Voxel-wise processing of DW data requires us to have a mathematical representation or biophysical model, an optimization algorithm, and an objective function that fundamentally designs the goal of the optimizer. Before the advent of DL tools, gradient descent, Newton's method, and the Levenberg-Marquardt algorithm were popular for solving inverse problems (55). These algorithms have been used with objective functions that closely mimic the noise distribution of the data. Gaussian or Rician noise is a common find in MRI, so the optimizers are tasked with generally maximizing the log-likelihood given measured DW data for such noise distributions. Also, in some cases, the problems are reformatted in a sparse dictionary framework (56). Common practice involves adding regularization terms with objective functions in cases where problems are heavily ill-posed. To stabilize the ill-posedness of the problems, Lasso (L1), Ridge (L2), Tikhonov, etc., regularizing frameworks are used (34, 56, 57). Limitations of the maximum likelihood estimation (MLE) frameworks often involved the solution stopping at local minima, which heavily depended on the set of parameters used for initializing the biophysical model (11, 58). That's why grid-searching approaches are common to get a good starting point for the algorithms. Also, these approaches are computationally heavy (49, 59). However, a sparse dictionary representation of such a model is shown to reduce computational redundancy at the cost of accuracy (56).
Imaging reconstruction practices involving optimizers are now heavily shifting toward DL/ML. A major advantage of these approaches is generalization, but this major advantage doesn't come bias-free (60), and promising workarounds help to overcome these limitations. Data engineering is a promising approach that minimizes training-data bias by increasing data priors either by leveraging problem geometry or employing different available modalities that work as a prior. This can be easily termed “prior regularization” since it pushes the solution out of local minima. The objective values have been shown to improve and reduce bias when the starting points of the MLE are determined through an adapted multiple-layer perceptron (MLP) (30, 58).
The usage of DL/ML architectures is on the rise (Figure 1B). Different proposed approaches to data-driven strategies lack standardization in nomenclature and make it hard to track the underlying generic architecture in use. Figures 1C, D summarizes the general architectures in practice that are included in this study in a quantifiable manner. It is crucial to monitor the underlying architectures, as they come with specific limitations and pose distinctive biases. For example, it is common for convolutional neural network (CNN), U-net, and generative adversarial networks (GAN) architectures to hallucinate complex structures that might be clinically misleading (13, 33, 34, 61, 62). And for general MLP, overparameterization with noise generalizes the outcome as the mean of the training data (60).
We focused on providing the reader with a transparent view of the generic form of the algorithms in use through Table 1, with further details available in Supplementary Tables S1–S4, hoping this would create a meaningful approach to understanding data-driven AI strategies to solve the problem of microstructure estimation. The novelty of these approaches is evidently in data engineering, hyperparameter tuning, and leveraging synthetic or data-inherent priors that closely relate to the estimated parameters.
3.2. Unified AI (DL/ML) strategies for biophysical models: application and advancements
Based on how the DL/ML algorithms are applied to estimate tissue microparameters from dMRI data (single- or multishell DW data), including NODDI parameters such as NDI, ODI, and fISO defined in Table 1 Block-A, we have divided them into three categories found in Table 1 (Blocks B, C, and D) and in Supplementary Tables S2–S4.
AI agnostic to dMR q-space: The first category of AI algorithms focuses on direct DWI signal mapping and is generally agnostic to q-space geometry or how the sampling scheme is oriented for the signal. Some of these algorithms are analogous to the Natural Language Processing (NLP) algorithms that are often used in speech data processing. Examples include recurrent neural networks (RNN), short-term long memory (LSTM), GAN, attention mechanisms, etc. (63–66). The memory/forget block in some of these architectures allows for the development of signal orientation priors that are not directly sensitive to the geometry of the sampling scheme (27). These artificially generated priors might be misleading when substantial noise is present (34), as it has been noted in the literature that with lower SNR, AI algorithms are more susceptible to training data bias (60).
AI with active use of q-space: The second category of algorithms is much more diverse in its use of the geometry of the q-space. An inherent property of some of the architectures in this group helps to preserve this preceding geometry information. For example, graph and spherical convolutional (GCN/SCN) approaches are used to extract features that are relevant to the geometry of the acquisition schemes (24, 29). As the geometry of the q-space is incorporated, the mapping algorithms in the first category have been shown to be used in parallel to further enhance their performance (67). Q-space dMRI regression is yet another unexplored area that has shown promising results when used with an optimized protocol and a subsampling scheme (35, 68). Further, embeddings specifically designed over q-space analogous to zonal features have been shown to map fODF using adapted MLPs (20). Thus, we believe q-space is a natural characteristic of the diffusion protocol with enough potential to exploit.
AI and MLE integrated frameworks: The third category of algorithms embraces the recent trend of enhancing the Maximum Likelihood framework's performances through Deep Learners. Gradient update computation and initialization are challenging areas for which MLE algorithms often become stuck in the local minima (58). The advent of DL/ML has contributed to the generalization of the gradient update framework for processing variant forms of data. Previously, signals and systems being analyzed with a forward model contributed to system-specific gradient computation either analytically or numerically, which often posed computational and tedious derivation challenges, specifically with complex biophysical models such as NODDI and SMT, and this complexity increased with new parameters introduced to the system. With that said, system-specific derivatives with a good choice of optimization framework in MLE can be more powerful to rid bias and ensure specificity, which is important clinically. As spatial networks such as CNN, U-net, and GAN-based models often contribute to hallucination and systemic bias, this is often a risky bet in clinical implementation, and this recent shift in DL-based instructions for improving MLE can help overcome such issues effectively (30, 54, 58).
3.3. Challenges and possible solutions for implementing AI in dMRI microstructure estimation
Despite the promising results, reliable applications of AI in dMRI microstructure estimation are still challenging. Everyday challenges to data-driven techniques are often related to over- or underfitting, non-convergence, noise, hyperparameter tuning, etc. These are frequently encountered in every form of ML/DL algorithm. Therefore, we focused on challenges that are unique to clinical dMRI and biophysical models of learning. They are listed below with possible resolutions:
• Over/underfitting: If validation loss was significantly higher or lower than training loss, they were an indicator of over/underfitting; the validation loss trend was expected to be slightly higher than in training (30).
To resolve the issue, one can check for inconsistencies in the training and validation data. If the data check out, relevant hyperparameters of the optimization algorithm (e.g., learning rate, momentum, etc.) need to be tested.
• DWI noise: With higher b-values, we often have DW images with lower SNR. And with lower SNR, the DLs are shown to be training data biased (60).
Possible solutions include principal component analysis (PCA), DL-based denoising (15, 17, 69, 70), or using high-resolution priors (30). PCA accounts for noise by projecting data onto dimensions with the highest variances (60), whereas DL-based approaches mostly focus on spatial learning to improve SNR. However, this may not always be suitable in a clinical context due to the risk of hallucinations. High SNR priors have been shown to reliably help in DL-based estimation (30).
• Non-uniqueness: Often, biophysical models have multiple solutions that are all consistent with the data.
The non-uniqueness problem in AI architectures must be dealt with by incorporating necessary boundary conditions and additional priors (71). Regularization also addresses this issue by removing fitting noise. Neural networks often use dropout layers or apply L1/L2 regularization in their proposed objective functions to resolve this problem.
• Clinical training data scarcity: The amount of data available to fit a model is often limited clinically, which limits inference confidence.
Possible solutions include in-vivo simulations and data augmentation (71). In dMRI, the number of clinical subjects required can be substantially reduced by reducing spatial priors in the architecture. We recommend incorporating q-space priors for better clinical relevance over spatial networks (30). Generalizing the model on q-space for dMRI also increases the training samples and helps satisfy the learning goals effectively.
• High dimensionality: When the number of parameters in a model is high, it can be difficult to determine the correct solution with too many plausible combinations of parameters.
The Bayesian solution has been shown to address such problems (71). It's also possible to find embeddings that are common to high-dimensional parameters (28). The so-called “embeddings” are mappings of lower-dimensional data to higher dimensions through the deep layers. In this context, AI-MLE architectures are another way to resolve this problem (54, 72). AI-MLE architectures can leverage Rician noise-based likelihood functions and optimize quickly and reliably.
• Incorporating model limitations: Some models have limitations on the range of parameter values that they can accurately represent, making it difficult to fit them.
Conditions can be imposed on such limitations, followed by normalization (27, 51).
• Multi-site data: Some data may have non-stationary properties, meaning that the statistical properties of the data may change over time. This is commonly found in clinical dMRI as a multi-scanner harmonization problem.
DL harmonization is seen as a potential solution (73). Data harmonization is a technique that aims to statistically standardize data from different sources so that they can be used together. Moreover, AI-MLE variants such as dtiRIM (54), which work by estimating learning gradient, have shown to be generalizable in simulation with different diffusion protocols in clinical and research settings.
• Uncertainty quantification: DL/ML are advanced statistical tools that should practice uncertainty quantification, a practice that is scarcely observed in the field (74). After all, only by recognizing the extent of one's ignorance can one truly grasp the depth of his/her understanding, which is true for both natural and artificial intelligence.
4. Future perspectives on AI in dMRI microstructure estimation
The future role of AI is highly dependent on the clinical reliability and feasibility of proposed algorithms in practice. Feasibility challenges include the number of required subjects needed for training the AI models, incompleteness and ill-posedness in the training domain, dMRI protocol complexity and scan time, and multi-scanner dataset handling. Reliability challenges include a lack of explicit instructions on extrapolation, uncertainty quantification of the proposed models, biophysical models, and inverse solvers with higher specificity, which are ideally desired but often pose limiting assumptions, etc. Since active use of q-space geometry ensures inherent priors for inference and MLE warrants likelihood with a known noise distribution framework, adapting these practices with AI is highly likely to ensure the feasibility and reliability challenges mentioned above. On the other hand, the use of spatial networks in dMRI would be more prone to deviate from clinical relevance, as it is known to be biased on spatial relevance for inference. Clinical validation has become necessary to further probe into these architectures.
5. Conclusion
This article has described an overview of the AI methods used for microstructure estimation/enhancement through dMRI data. The growth of AI is a captivating development, beginning with neural networks and advancing into sophisticated DL structures, allowing us to investigate brain microstructures in millimeter-scale clinical-dMRI data. While concerns regarding bias in training data exist, certain architectures have demonstrated solutions that align with diffusion biophysical models. Despite this progress, there are obstacles to overcome, particularly in clinical validation, liability for widespread adoption, and ethical and legal concerns.
Author contributions
AF: study concept and design and writing the original draft of the manuscript. MD: revision of the manuscript for intellectual content. GS: revision of the manuscript for intellectual content and funding acquisition. MU: study concept and design, critical revision of the manuscript, and supervision. All authors read and approved the final version of the manuscript.
Funding
This study was supported by the National Institutes of Health (NIH) grants R01-AG054328 and R01-MH118020.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fneur.2023.1168833/full#supplementary-material
Abbreviations
AI, Artificial Intelligence; CNN, convolutional neural network; DL, Deep Learning; dMRI, Diffusion Magnetic Resonance Imaging; DW, Diffusion Weighted; DTI, Diffusion Tensor Imaging; Diffusion Kurtosis Imaging; DBSI, Diffusion Basis Spectrum Imaging; fODF, fiber orientation distribution function; FWI, free water imaging; GAN, Generative Adversarial Networks; GCN, Graph Convolution Network; LSTM, Long Short-Term Memory; ML, Machine Learning; MLP, Multi-Layer Perceptron; MLE, Maximum Likelihood Estimation; NODDI, Neurite Orientation Dispersion and Density Imaging; NLP, Natural Language Processing; NDI, Neurite Density Index; ODI, Orientation Dispersion Index; PCA, Principal Component Analysis; RNN, Recurrent Neural Network; SCN, Spherical Convolution Network; SNR, Signal to Noise Ratio; SMT, Spherical Mean Technique; SHORE, Simple Harmonic Oscillator-Based Reconstruction and Estimation; SANDI, Soma And Neurite Density Imaging; WMTI, White Matter Tissue Integrity.
References
1. Gurcan MN, Boucheron LE, Can A, Madabhushi A, Rajpoot NM, Yener B. Histopathological image analysis: a review. IEEE Rev Biomed Eng. (2009) 2:147–71. doi: 10.1109/RBME.2009.2034865
2. Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. (1994) 66:259–67. doi: 10.1016/S0006-3495(94)80775-1
3. Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B. (1996) 111:209–19. doi: 10.1006/jmrb.1996.0086
4. Johansen-Berg H, Behrens T. Diffusion MRI: From Quantitative Measurement to In vivo Neuroanatomy: Second Edition. Elsevier (2013). Available online at: https://ora.ox.ac.uk/objects/uuid:15e45ac3-dab3-4f0f-a980-e4e56e1682ad (accessed February 4, 2023).
5. Figley CR, Uddin MN, Wong K, Kornelsen J, Puig J, Figley TD. Potential pitfalls of using fractional anisotropy, axial diffusivity, and radial diffusivity as biomarkers of cerebral white matter microstructure. Front Neurosci. (2022) 15:1855. doi: 10.3389/fnins.2021.799576
6. Lee HH, Yaros K, Veraart J, Pathan JL, Liang FX, Kim SG, et al. Along-axon diameter variation and axonal orientation dispersion revealed with 3D electron microscopy: implications for quantifying brain white matter microstructure with histology and diffusion MRI. Brain Struct Funct. (2019) 224:1469–88. doi: 10.1007/s00429-019-01844-6
7. Kleinnijenhuis M, Johnson E, Mollink J, Jbabdi S, Miller KL. A Semi-Automated Approach to Dense Segmentation of 3D White Matter Electron Microscopy. bioRxiv (2020). Available online at: https://www.biorxiv.org/content/10.1101/2020.03.19.979393v1 (accessed January 12, 2023).
8. Novikov DS, Fieremans E, Jespersen SN, Kiselev VG. Quantifying brain microstructure with diffusion MRI: theory and parameter estimation. NMR Biomed. (2019) 32:e3998. doi: 10.1002/nbm.3998
9. Jelescu IO, Palombo M, Bagnato F, Schilling KG. Challenges for biophysical modeling of microstructure. J Neurosci Methods. (2020) 344:108861. doi: 10.1016/j.jneumeth.2020.108861
10. Pasternak O, Sochen N, Gur Y, Intrator N, Assaf Y. Free water elimination and mapping from diffusion MRI. Magn Reson Med. (2009) 62:717–30. doi: 10.1002/mrm.22055
11. Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage. (2012) 61:1000–16. doi: 10.1016/j.neuroimage.2012.03.072
12. Kaden E, Kelm ND, Carson RP, Does MD, Alexander DC. Multi-compartment microscopic diffusion imaging. NeuroImage. (2016) 139:346–59. doi: 10.1016/j.neuroimage.2016.06.002
13. Davatzikos C. Machine learning in neuroimaging: progress and challenges. NeuroImage. (2019) 197:652–6. doi: 10.1016/j.neuroimage.2018.10.003
14. Nielsen AN, Barch DM, Petersen SE, Schlaggar BL, Greene DJ. Machine learning with neuroimaging: evaluating its applications in psychiatry. Biol Psychiatry Cogn Neurosci Neuroimaging. (2020) 5:791–8. doi: 10.1016/j.bpsc.2019.11.007
15. Tian Q, Bilgic B, Fan Q, Liao C, Ngamsombat C, Hu Y, et al. DeepDTI: high-fidelity six-direction diffusion tensor imaging using deep learning. NeuroImage. (2020) 219:117017. doi: 10.1016/j.neuroimage.2020.117017
16. Tian Q, Li Z, Fan Q, Ngamsombat C, Hu Y, Liao C, et al. SRDTI: Deep Learning-Based Super-Resolution for Diffusion Tensor MRI. arXiv (2021). Available online at: http://arxiv.org/abs/2102.09069 (accessed January 2, 2023).
17. Tian Q, Li Z, Fan Q, Polimeni JR, Bilgic B, Salat DH, et al. SDnDTI: Self-supervised deep learning-based denoising for diffusion tensor MRI. NeuroImage. (2022) 253:119033. doi: 10.1016/j.neuroimage.2022.119033
18. Karimi D, Jaimes C, Machado-Rivas F, Vasung L, Khan S, Warfield SK, et al. Deep learning-based parameter estimation in fetal diffusion-weighted MRI. NeuroImage. (2021) 243:118482. doi: 10.1016/j.neuroimage.2021.118482
19. Lin Z, Gong T, Wang K, Li Z, He H, Tong Q, et al. Fast learning of fiber orientation distribution function for MR tractography using convolutional neural network. Med Phys. (2019) 46:3101–16. doi: 10.1002/mp.13555
20. Karimi D, Vasung L, Jaimes C, Machado-Rivas F, Khan S, Warfield SK, et al. A machine learning-based method for estimating the number and orientations of major fascicles in diffusion-weighted magnetic resonance imaging. Med Image Anal. (2021) 72:102129. doi: 10.1016/j.media.2021.102129
21. Jha RR, Pathak SK, Nath V, Schneider W, Kumar BVR, Bhavsar A, et al. VRfRNet: volumetric ROI fODF reconstruction network for estimation of multi-tissue constrained spherical deconvolution with only single shell dMRI. Magn Reson Imaging. (2022) 90:1–16. doi: 10.1016/j.mri.2022.03.004
22. Golkov V, Dosovitskiy A, Sperl JI, Menzel MI, Czisch M, Sämann P, et al. q-space deep learning: twelve-fold shorter and model-free diffusion MRI scans. IEEE Trans Med Imaging. (2016) 35:1344–51. doi: 10.1109/TMI.2016.2551324
23. Qin Y, Li Y, Zhuo Z, Liu Z, Liu Y, Ye C. Multimodal super-resolved q-space deep learning. Med Image Anal. (2021) 71:102085. doi: 10.1016/j.media.2021.102085
24. Chen G, Jiang H, Liu J, Ma J, Cui H, Xia Y, et al. Hybrid Graph Transformer for Tissue Microstructure Estimation with Undersampled Diffusion MRI Data. In: Medical Image Computing and Computer Assisted Intervention – MICCAI 2022. Cham: Springer Nature Switzerland (2022). p. 113–22. (Lecture Notes in Computer Science).
25. HashemizadehKolowri S, Chen RR, Adluru G, DiBella EVR. Jointly estimating parametric maps of multiple diffusion models from undersampled q-space data: a comparison of three deep learning approaches. Magn Reson Med. (2022) 87:2957–71. doi: 10.1002/mrm.29162
26. Gibbons EK, Hodgson KK, Chaudhari AS, Richards LG, Majersik JJ, Adluru G, et al. Simultaneous NODDI and GFA parameter map generation from subsampled q-space imaging using deep learning. Magn Reson Med. (2019) 81:2399–411. doi: 10.1002/mrm.27568
27. Ye C, Li X, Chen J. A deep network for tissue microstructure estimation using modified LSTM units. Med Image Anal. (2019) 55:49–64. doi: 10.1016/j.media.2019.04.006
28. Nath V, Ramadass K, Schilling KG, Hansen CB, Fick R, Pathak SK, et al. DW-MRI microstructure model of models captured via single-shell bottleneck deep learning. In: Computational Diffusion MRI. Cham: Springer International Publishing. (2021). p. 147–57 (Mathematics and Visualization).
29. Sedlar S, Alimi A, Papadopoulo T, Deriche R, Deslauriers-Gauthier S. A spherical convolutional neural network for white matter structure imaging via dMRI. In: MICCAI 2021 - 24th International Conference on Medical Image Computing and Computer Assisted Intervention. Strasbourg/Virtual, France, Part III; volume 12903. (2021). p. 529–39. Available online at: https://hal.archives-ouvertes.fr/hal-03307031 (accessed November 23, 2022).
30. Faiyaz A, Doyley M, Schifitto G, Zhong J, Uddin MN. Single-shell NODDI using dictionary-learner-estimated isotropic volume fraction. NMR Biomed. (2022) 35:e4628. doi: 10.1002/nbm.4628
31. Zheng T, Sun C, Zheng W, Shi W, Li H, Sun Y, et al. A Microstructure Estimation Transformer Inspired by Sparse Representation for Diffusion MRI. arXiv (2022). Available online at: http://arxiv.org/abs/2205.06450 (accessed January 2, 2023).
32. Jollans L, Boyle R, Artiges E, Banaschewski T, Desrivières S, Grigis A, et al. Quantifying performance of machine learning methods for neuroimaging data. NeuroImage. (2019) 199:351–65. doi: 10.1016/j.neuroimage.2019.05.082
33. Antun V, Renna F, Poon C, Adcock B, Hansen AC. On instabilities of deep learning in image reconstruction and the potential costs of AI. Proc Natl Acad Sci USA. (2020) 117:30088–95. doi: 10.1073/pnas.1907377117
34. Bhadra S, Kelkar VA, Brooks FJ, Anastasio MA. On hallucinations in tomographic image reconstruction. IEEE Trans Med Imaging. (2021) 40:3249–60. doi: 10.1109/TMI.2021.3077857
35. MICCAI Challenge (QuaD22) (2022). Available online at: https://www.lpi.tel.uva.es/quad22/ (accessed February 4, 2023).
36. Callaghan PT, Eccles CD, Xia Y. NMR microscopy of dynamic displacements: k-space and q-space imaging. J Phys. (1988) 21:820. doi: 10.1088/0022-3735/21/8/017
37. Torrey HC. Bloch equations with diffusion terms. Phys Rev. (1956) 104:563–5. doi: 10.1103/PhysRev.104.563
38. Finkelstein A, Cao X, Liao C, Schifitto G, Zhong J. Diffusion encoding methods in mri: perspectives and challenges. Investig Magn Reson Imaging. (2022) 26:208–19. doi: 10.13104/imri.2022.26.4.208
39. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. (2005) 53:1432–40. doi: 10.1002/mrm.20508
40. Jelescu IO, Budde MD. Design and validation of diffusion MRI models of white matter. Front Phys. (2017) 5:61. doi: 10.3389/fphy.2017.00061
41. Novikov DS, Kiselev VG, Jespersen SN. On modeling. Magn Reson Med. (2018) 79:3172–93. doi: 10.1002/mrm.27101
42. Jelescu IO, de Skowronski A, Geffroy F, Palombo M, Novikov DS. Neurite Exchange Imaging (NEXI): a minimal model of diffusion in gray matter with inter-compartment water exchange. NeuroImage. (2022) 256:119277. doi: 10.1016/j.neuroimage.2022.119277
43. Drobnjak I, Zhang H, Ianuş A, Kaden E, Alexander DC. PGSE, OGSE, and sensitivity to axon diameter in diffusion MRI: insight from a simulation study. Magn Reson Med. (2016) 75:688–700. doi: 10.1002/mrm.25631
44. Assaf Y, Blumenfeld-Katzir T, Yovel Y, Basser PJ. AxCaliber: a method for measuring axon diameter distribution from diffusion MRI. Magn Reson Med. (2008) 59:1347–54. doi: 10.1002/mrm.21577
45. Wang Y, Wang Q, Haldar JP, Yeh FC, Xie M, Sun P, et al. Quantification of increased cellularity during inflammatory demyelination. Brain J Neurol. (2011) 134:3590–601. doi: 10.1093/brain/awr307
46. Fieremans E, Benitez A, Jensen JH, Falangola MF, Tabesh A, Deardorff RL, et al. Novel white matter tract integrity metrics sensitive to Alzheimer disease progression. AJNR Am J Neuroradiol. (2013) 34:2105–12. doi: 10.3174/ajnr.A3553
47. Ning L, Westin CF, Rathi Y. Estimating diffusion propagator and its moments using directional radial basis functions. IEEE Trans Med Imaging. (2015) 34:2058–78. doi: 10.1109/TMI.2015.2418674
48. Palombo M, Ianus A, Guerreri M, Nunes D, Alexander DC, Shemesh N, et al. SANDI: a compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI. NeuroImage. (2020) 215:116835. doi: 10.1016/j.neuroimage.2020.116835
49. Kamiya K, Hori M, Aoki S. NODDI in clinical research. J Neurosci Methods. (2020) 346:108908. doi: 10.1016/j.jneumeth.2020.108908
50. Afzali M, Pieciak T, Newman S, Garyfallidis E, Özarslan E, Cheng H, et al. The sensitivity of diffusion MRI to microstructural properties and experimental factors. J Neurosci Methods. (2021) 347:108951. doi: 10.1016/j.jneumeth.2020.108951
51. Ye C. Tissue microstructure estimation using a deep network inspired by a dictionary-based framework. Med Image Anal. (2017) 42:288–99. doi: 10.1016/j.media.2017.09.001
52. Alexander DC, Zikic D, Ghosh A, Tanno R, Wottschel V, Zhang J, et al. Image quality transfer and applications in diffusion MRI. NeuroImage. (2017) 152:283–98. doi: 10.1016/j.neuroimage.2017.02.089
53. Anctil-Robitaille B, Théberge A, Jodoin PM, Descoteaux M, Desrosiers C, Lombaert H. Manifold-aware Synthesis of High-resolution Diffusion from Structural Imaging. arXiv (2021). Available online at: http://arxiv.org/abs/2108.04135 (accessed January 22, 2023).
54. Sabidussi ER, Klein S, Jeurissen B, Poot DHJ. dtiRIM: a generalisable deep learning method for diffusion tensor imaging. NeuroImage. (2023) 269:119900. doi: 10.1016/j.neuroimage.2023.119900
55. Kumaraswamy B. 6 - Neural networks for data classification. In: Binu D, Rajakumar BR, editors. Artificial Intelligence in Data Mining. Academic Press (2021). p. 109–31. Available online at: https://www.sciencedirect.com/science/article/pii/B9780128206010000112 (accessed February 5, 2023).
56. Daducci A, Canales-Rodríguez EJ, Zhang H, Dyrby TB, Alexander DC, Thiran JP. Accelerated microstructure imaging via convex optimization (AMICO) from diffusion MRI data. NeuroImage. (2015) 105:32–44. doi: 10.1016/j.neuroimage.2014.10.026
57. Liu X, Xu W, Ye X. The ill-posed problem and regularization in parallel magnetic resonance imaging. In: 2009 3rd International Conference on Bioinformatics and Biomedical Engineering. (2009). p. 1–4.
58. Ting G, Grussu F, Wheeler-Kingshott CG, Alexander D, Zhang H. Deep-learning-informed parameter estimation improves reliability of spinal cord diffusion MRI. In: Proc Intl Soc Mag Reson Med. 30. UK (2022). Available online at: https://cds.ismrm.org/protected/22MPresentations/abstracts/0394.html (accessed January 12, 2023).
59. Tariq M, Schneider T, Alexander DC, Gandini Wheeler-Kingshott CA, Zhang H. Bingham–NODDI: mapping anisotropic orientation dispersion of neurites using diffusion MRI. NeuroImage. (2016) 133:207–23. doi: 10.1016/j.neuroimage.2016.01.046
60. Gyori NG, Palombo M, Clark CA, Zhang H, Alexander DC. Training data distribution significantly impacts the estimation of tissue microstructure with machine learning. Magn Reson Med. (2022) 87:932–47. doi: 10.1002/mrm.29014
61. Thesing L, Antun V, Hansen AC. What Do AI Algorithms Actually Learn? - On False Structures in Deep Learning. arXiv (2019). Available online at: http://arxiv.org/abs/1906.01478 (accessed cited January 26, 2023).
62. Kelkar VA, Bhadra S, Anastasio MA. Compressible latent-space invertible networks for generative model-constrained image reconstruction. IEEE Trans Comput Imaging. (2021) 7:209–23. doi: 10.1109/TCI.2021.3049648
63. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, et al. Attention is all you need. In: Advances in Neural Information Processing Systems. Curran Associates, Inc. (2017). Available online at: https://proceedings.neurips.cc/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html (accessed February 9, 2023).
64. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial nets. In: Advances in Neural Information Processing Systems. Curran Associates, Inc. (2014). Available online at: https://papers.nips.cc/paper/2014/hash/5ca3e9b122f61f8f06494c97b1afccf3-Abstract.html (accessed February 9, 2023).
65. Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput. (1997) 9:1735–80. doi: 10.1162/neco.1997.9.8.1735
66. Rumelhart DE, McClelland JL. Learning internal representations by error propagation. In: Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations. MIT Press (1987). p. 318–62. Available online at: https://ieeexplore.ieee.org/document/6302929 (accessed February 9, 2023).
67. Diao Y, Jelescu I. Parameter estimation for WMTI-Watson model of white matter using encoder–decoder recurrent neural network. Magn Reson Med. (2023) 89:1193–206. doi: 10.1002/mrm.29495
68. Faiyaz A, Uddin MN, Schifitto G. Angular Upsampling in Diffusion MRI Using Contextual HemiHex Sub-Sampling in q-Space.arXiv (2022). Available online at: http://arxiv.org/abs/2211.00240 (accessed January 19, 2023).
69. A diffusion-matched principal component analysis (DM-PCA) based two-channel denoising procedure for high-resolution diffusion-weighted MRI. PLoS ONE. (2018) 13:e0195952. doi: 10.1371/journal.pone.0195952
70. MP-PCA denoising for diffusion MRS data: promises and pitfalls. NeuroImage. (2022) 263:119634. doi: 10.1016/j.neuroimage.2022.119634
71. Reisert M, Kellner E, Dhital B, Hennig J, Kiselev VG. Disentangling micro from mesostructure by diffusion MRI: a Bayesian approach. NeuroImage. (2017) 147:964–75. doi: 10.1016/j.neuroimage.2016.09.058
72. Faiyaz A, Doyley M, Schifitto G, Zhong J, Uddin MN. Single-Shell NODDI Using Dictionary Learner Estimated Isotropic Volume Fraction. arXiv (2021). Available online at: http://arxiv.org/abs/2102.02772 (accessed January 25, 2023).
73. Koppers S, Bloy L, Berman JI, Tax CMW, Edgar JC, Merhof D. Spherical harmonic residual network for diffusion signal harmonization. In: Computational Diffusion MRI: International MICCAI Workshop. Springer International Publishing (2019). p. 173–82. doi: 10.1007/978-3-030-05831-9_14
74. Qin Y, Liu Z, Liu C, Li Y, Zeng X, Ye C. Super-Resolved q-Space deep learning with uncertainty quantification. Med Image Anal. (2021) 67:101885. doi: 10.1016/j.media.2020.101885
75. Zheng T, Zheng W, Sun Y, Zhang Y, Ye C, Wu D. An Adaptive Network with Extragradient for Diffusion MRI-Based Microstructure Estimation. In: Medical Image Computing and Computer Assisted Intervention – MICCAI 2022. Cham: Springer Nature Switzerland. (2022). p. 153–62. (Lecture Notes in Computer Science).
76. Kaden E, Kruggel F, Alexander DC. Quantitative mapping of the per-axon diffusion coefficients in brain white matter. Magn Reson Med. (2016) 75:1752–63. doi: 10.1002/mrm.25734
77. Karimi D, Gholipour A. Diffusion tensor estimation with transformer neural networks. Artif Intell Med. (2022) 130:102330. doi: 10.1016/j.artmed.2022.102330
78. Novikov DS, Veraart J, Jelescu IO, Fieremans E. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. NeuroImage. (2018) 174:518–38. doi: 10.1016/j.neuroimage.2018.03.006
79. Karimi D, Gholipour A. Atlas-powered deep learning (ADL) – application to diffusion weighted MRI. arXiv (2022). Available online at: http://arxiv.org/abs/2205.03210 (accessed January 2, 2023).
80. Ma W, Peng L. Image quality transfer with auto-encoding applied to dMRI super-resolution. In: 2021 4th International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE). (2021). p. 828–31.
81. Du J, Zhang S, Wu G, Moura JMF, Kar S. Topology adaptive graph convolutional networks. arXiv. (2018) Available online at: http://arxiv.org/abs/1710.10370 (accessed January 25, 2023).
82. Li H, Liang Z, Zhang C, Liu R, Li J, Zhang W, et al. SuperDTI: ultrafast DTI and fiber tractography with deep learning. Magn Reson Med. (2021) 86:3334–47. doi: 10.1002/mrm.28937
83. Lee S, Purushwalkam S, Cogswell M, Crandall D, Batra D. Why M Heads are Better than One: Training a Diverse Ensemble of Deep Networks. arXiv (2015). Available online at: http://arxiv.org/abs/1511.06314 (accessed January 25, 2023).
84. Ren M, Kim H, Dey N, Gerig G. Q-space conditioned translation networks for directional synthesis of diffusion weighted images from multi-modal structural MRI. In: Medical Image Computing and Computer Assisted Intervention – MICCAI 2021. Cham: Springer International Publishing (2021). p. 530–40. (Lecture Notes in Computer Science).
85. Chen G, Hong Y, Zhang Y, Kim J, Huynh KM, Ma J, et al. Estimating tissue microstructure with undersampled diffusion data via graph convolutional neural networks. In: Medical Image Computing and Computer Assisted Intervention – MICCAI 2020. Cham: Springer International Publishing (2020). p. 280–90. (Lecture Notes in Computer Science).
86. Blumberg SB, Tanno R, Kokkinos I, Alexander DC. Deeper image quality transfer: training low-memory neural networks for 3D images. In: Medical Image Computing and Computer Assisted Intervention – MICCAI 2018. Cham: Springer International Publishing (2018). p. 118–25. (Lecture Notes in Computer Science).
Keywords: artificial intelligence, machine learning, deep learning, diffusion MRI (dMRI), neuroimaging, brain, microstructure, biophysical model
Citation: Faiyaz A, Doyley MM, Schifitto G and Uddin MN (2023) Artificial intelligence for diffusion MRI-based tissue microstructure estimation in the human brain: an overview. Front. Neurol. 14:1168833. doi: 10.3389/fneur.2023.1168833
Received: 18 February 2023; Accepted: 27 March 2023;
Published: 21 April 2023.
Edited by:
Jean Chen, University of Toronto, CanadaReviewed by:
Rabia Saleem, University of Leicester, United KingdomCopyright © 2023 Faiyaz, Doyley, Schifitto and Uddin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Md Nasir Uddin, bmFzaXJfdWRkaW4mI3gwMDA0MDt1cm1jLnJvY2hlc3Rlci5lZHU=