Predicting Vasovagal Responses: A Model-Based and Machine Learning Approach

Vasovagal syncope (VVS) or neurogenically induced fainting has resulted in falls, fractures, and death. Methods to deal with VVS are to use implanted pacemakers or beta blockers. These are often ineffective because the underlying changes in the cardiovascular system that lead to the syncope are incompletely understood and diagnosis of frequent occurrences of VVS is still based on history and a tilt test, in which subjects are passively tilted from a supine position to 20° from the spatial vertical (to a 70° position) on the tilt table and maintained in that orientation for 10–15 min. Recently, is has been shown that vasovagal responses (VVRs), which are characterized by transient drops in blood pressure (BP), heart rate (HR), and increased amplitude of low frequency oscillations in BP can be induced by sinusoidal galvanic vestibular stimulation (sGVS) and were similar to the low frequency oscillations that presaged VVS in humans. This transient drop in BP and HR of 25 mmHg and 25 beats per minute (bpm), respectively, were considered to be a VVR. Similar thresholds have been used to identify VVR's in human studies as well. However, this arbitrary threshold of identifying a VVR does not give a clear understanding of the identifying features of a VVR nor what triggers a VVR. In this study, we utilized our model of VVR generation together with a machine learning approach to learn a separating hyperplane between normal and VVR patterns. This methodology is proposed as a technique for more broadly identifying the features that trigger a VVR. If a similar feature identification could be associated with VVRs in humans, it potentially could be utilized to identify onset of a VVS, i.e, fainting, in real time.

Introduction

A neurogenically induced vasodilation and corresponding inappropriate bradycardia can lead to hypotension and transient loss of body tone and consciousness, that is, fainting. This condition has been termed neurogenic or vasovagal syncope (VVS) (1–4). Many nerves connect to the heart and blood vessels, which help control the beat frequency of the heart and the dilation and contraction of the blood vessels that control blood pressure (BP). Usually, these control signals are coordinated so that a decrease in BP is compensated by an increase in heart rate (HR) so that proper blood flow to the brain is maintained through sympathetic outflow (5). If the nerve signals are not coordinated, it could create a condition where the blood vessels dilate while the heart rate slows causing blood to pool in the legs and not enough reaches the brain, resulting in syncope (5). Although VVS is not considered harmful because lying down causes a resumption of blood flow to the brain, it can result in falls, fractures, and in some cases death (1, 2). Thus, a correct diagnosis of frequent occurrences of VVS is critical for the management of this disease. Yet, diagnosis of VVS is usually based on history and a tilt test, in which subjects are passively tilted from a supine position to 20° from the spatial vertical (to a 70° position) on a tilt table and maintained in that orientation for 10–15 min. This maneuver usually brings on the symptoms of fainting and returning subjects to a reclining position makes them go away. Treatment of recurrent VVS using implanted pacemakers or beta blockers is often ineffective (6–10), because the underlying changes in the cardiovascular system that lead to the syncope are still incompletely understood (11, 12), although there has been an acknowledgment that the relative timing of BP and HR plays an important role in VVS generation (3, 4). The role of the vestibular system in generating the timing has only recently been explored and has suggested ways of habituating VVS as a treatment option (13).

The interest in better managing VVS has seen a concerted attempt to relate VVS to drops in blood pressure (BP) and heart rate (HR), which have been termed vasovagal responses (VVR's). There have been suggestions that BP oscillations during tilt testing are a predictive marker for VVS (14). In support of this idea, multiresolution analysis with wavelets demonstrated that there was increased power in low frequency modulations of BP that presage an episode of VVS in a human fainter (15). Recently, VVRs have been generated in anesthetized rats by repetitively activating the Vestibulo-Sympathetic Reflex (VSR), using sinusoidal galvanic vestibular stimulation (sGVS) or with 70° head-up tilts and ±70° oscillation in pitch (16–18). Although in anesthetized rats there is no concept of fainting, the VVRs are surprisingly similar to those in humans and we postulated that they would be a good animal model for VVRs in humans and their corresponding VVS responses (16).

In the studies on the rat, vasovagal oscillations were induced by sinusoidal galvanic vestibular stimulation (sGVS) with low frequency oscillations (16–18) in each of six rats. These low frequency modulations in BP and HR were referred to as vasovagal oscillations (18). In some instances, sGVS induced a substantial fall in BP and HR, that is, the transient VVR, which recovered over several minutes. We identified this transient component as a VVR, if there was a drop in BP and HR of 25 mmHg and 25 beats per minute (bpm), respectively. Similar thresholds have been used to identify VVR's in human studies as well (14, 15). These data have shown that VVRs may be an outcome of an aberrant type of vestibular stimulation of the vestibulosympathetic reflex and not a disease (17). The data also show that the rat may be a useful animal model for understanding how human VVRs may be generated and studied. However, this arbitrary threshold of identifying a VVR from BP drops does not give a clear understanding of the identifying features of a VVR nor what triggers a vasovagal response. The purpose of this study is to utilize our model of VVR generation (19) together with a machine learning approach to identify a separating hyperplane (20) between a normal and VVR, based on simultaneous BP and HR changes. This technique would more broadly identify the features that trigger VVRs. If a similar feature identification could be associated with VVRs in humans, it potentially could be utilized to identify VVS onset of fainting in real time.

Methods

Experimental Methods

Adult, male Long-Evan rats (Harlan Laboratories, MA) weighing 300–400 g were used in these studies. All experiments were approved by the Institutional Care and Use Committee of the Mount Sinai School of Medicine. In this study, the data were taken from previous studies (16, 17, 21). We give a brief summary of the surgical and sGVS procedures.

Surgical Procedures

The implantation of a blood pressure measurement device and a head fixation mount were accomplished during the same aseptic surgical session. Throughout the surgery, rats were kept on a heating-pad controlled by the feedback of a rectal temperature probe. The surgery and testing were conducted under isoflurane anesthesia (4% induction, 2% maintenance).

Implantation of Bolts to Allow Painless Fixation of the Head During Experiments

Bolts were secured with dental acrylic cement, and two nuts were encased semisoft acrylic. A telemetric blood pressure sensor (DSI, St Paul, MN) was implanted in the abdominal aorta. These animals were utilized in a series of experiments performed over the next 2 months [see (16) for details].

Sinusoidal Galvanic Vestibular Stimulation for Inducing VVR

During testing, the heads of the rats were immobilized using the head mounts attached to a cylindrical holder for the animal's body. Sinusoidal currents generated by a computer-controlled stimulator (22) were delivered via two Ag/AgCl needle electrodes inserted into the skin over the mastoids, behind the external auditory meati. sGVS was given binaurally with currents of 1–4 mA and frequencies of 0.008 to 0.5 Hz. Current and frequencies were randomized, and 15–30 min were allowed to elapse between stimuli to reduce possible effects of habituation.

Tilt Protocol to Initiate VVR

The rats were statically tilted 70° and held in this position until they developed a vasovagal response. If a vasovagal response developed or if there was no response after several minutes, they were then brought back to the prone position.

Data Collection and Analysis

BP in response to sGVS was recorded continuously using customized A/D conversion hardware (Grass Technologies, West Warwick, RI) and Polyview software (Grass technologies) and stored at a rate of 1 KHz. BP data from the telemetric sensors were collected via a wand receiver (DSI, St Paul, MN) at 1 KHz with 12 bit resolution (Data Translation, Inc.) using our data collection program. The data were converted for analysis into what we have referred to as Virtual Memory File (VMF) format. The data format is comprised of channels that represent stimuli and responses and can be representations of analog data, that are acquired via an A/D converter or event channels that associate an event with a time of occurrence. The VMF application software that we developed contains modules, which operate on the data and perform a wide range of transformations, such as a correlation analysis, power spectral analysis, timing of events, etc. The program also has visualization capabilities so that data can be displayed as time functions. The transformed data can also be displayed in the frequency domain or as one variable against another [See (23) for a more thorough description].

BP was utilized to obtain heart rate (HR) off-line. HR was identified from the peaks in BP. Stored pulses were converted to instantaneous frequency (beats·s⁻¹) and stored in a separate channel for further analysis. Mean square sinusoidal fits to the data were used to estimate variations of BP and HR to the sinusoidal oscillations.

Results

Data Underpinnings of Modeling Vasovagal Responses

There were two characteristics of typical data that characterized a VVR during sGVS and tilts in anesthetized rats that were used to model the response (Figure 1). At a 2 s time scale, there were triangular type oscillations corresponding to the rapid transition (systole) and the slower transitions (diastole) (Figure 1A, inset). At a 1,000 s time scale, there was a coordinated drop in the in BP oscillations (Figure 1A) as well as in HR (Figure 1B) during sGVS (Figure 1C). Similar kinds of drops in BP (Figure 1C) and HR (Figure 1E) occurred during head up tilts of 70° (Figure 1F). The responses of BP and HR are similar to that observed during head up tilts when testing for fainting (15) and strategies for stopping VVS by leg-crossing and muscle tensing (24). The model therefore encompassed the systolic-diastolic oscillations and a central control structure to predict the drops in BP and HR over the longer time scale (19). The modeling approach in this paper considers what features of the model can be used to better identify the drops in BP and HR using the data and machine learning.

FIGURE 1

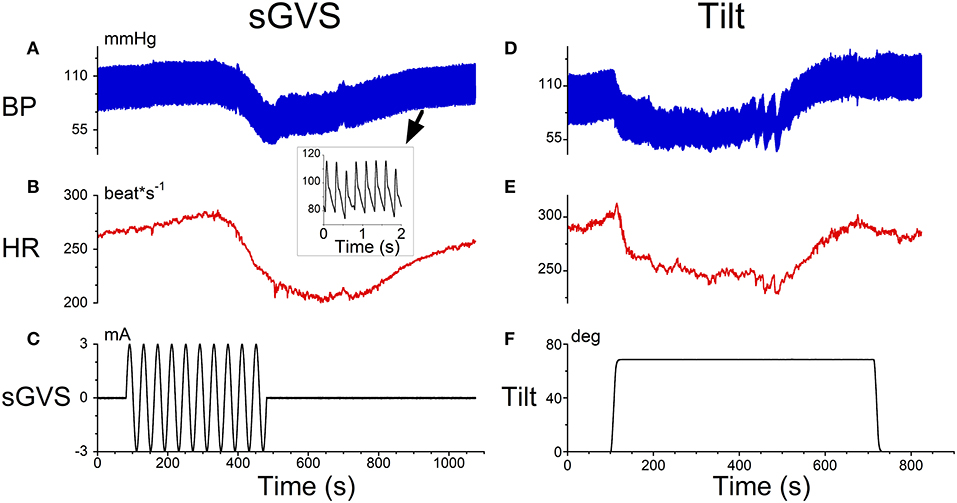
Figure 1. Typical data that initiated a VVR in an anesthetized rat obtained from sGVS (A–C) and head up tilts of 70°. The inset in (A) shows a 2 s time scale. There were triangular type oscillations corresponding to the rapid transition (systole) and the slower transitions (diastole). (A) At a 1,000 s time scale, there was a coordinated drop in the in BP oscillations (A) as well as in HR (B) during sGVS (C). Similar drops in BP (D) and HR (E) occurred during head up tilts of 70° (F).

Modeling Approach

The basis of the model (Figure 2) that generates the triangular systolic-diastolic oscillations is a relaxation oscillator (19, 25). There is a signal Desired Blood Pressure (BP_d), which acts as input that maintains the relaxation oscillations and is dependent on metabolic needs of the muscles and cells (26). This model not only simulates the basic diastolic and systolic behavior of BP as monitored by an intra-aortic sensor, but also predicts their variations in response to vestibular stimuli. The model also showed that alterations in BP_d changed the oscillation amplitude and its frequency, which compared favorably with data on systolic BP, pulse pressure, and Baroreflex Sensitivity (BRS) (19). It also predicts that as the BP drops, the period of the systolic-diastolic oscillations increases, and therefore HR drops (19). It is this relationship that is explored in this paper to elucidate the features that best describe a VVR and by extrapolation to predict a VVS.

FIGURE 2

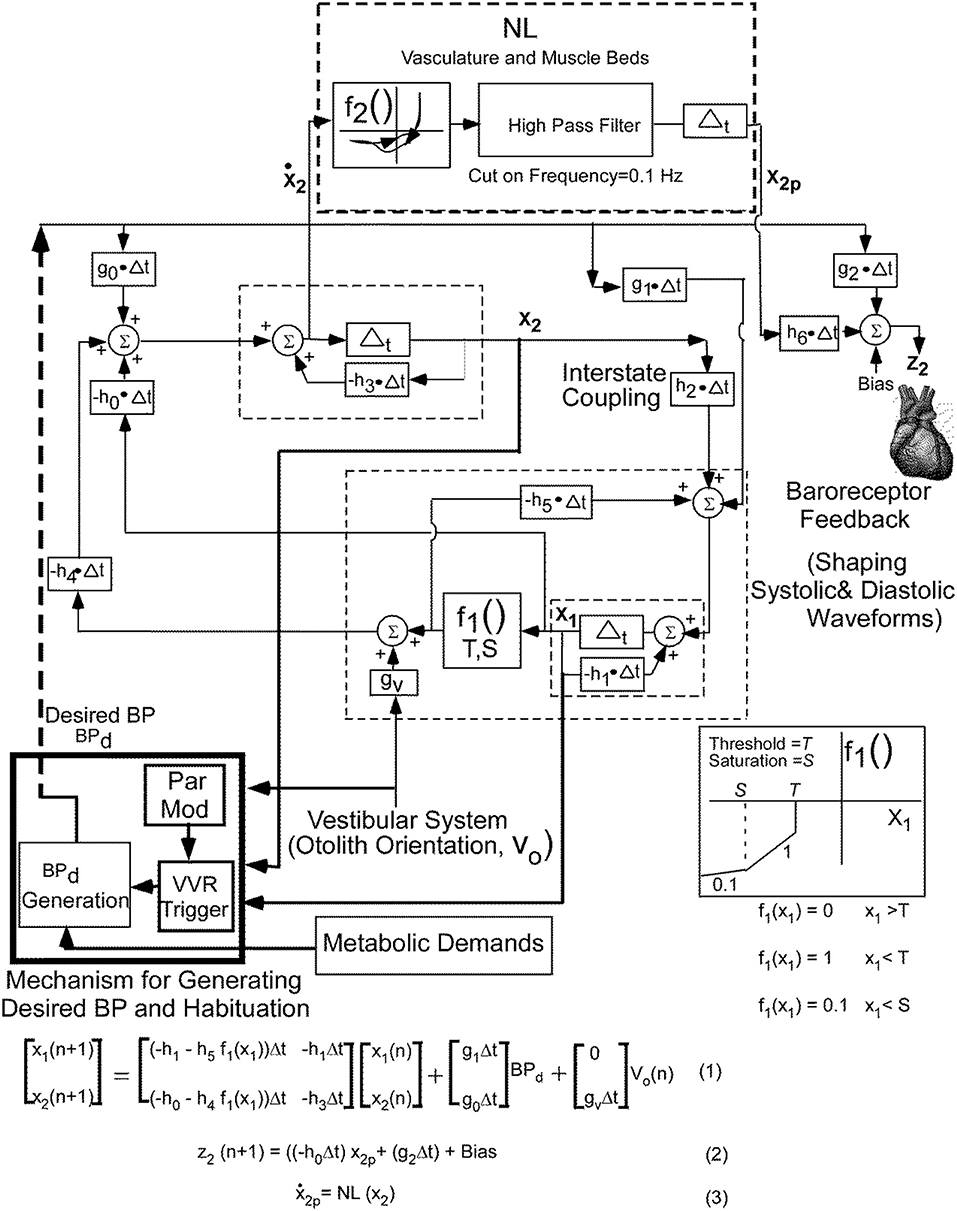
Figure 2. Non-linear relaxation oscillator model that generates the systoles and diastoles seen in the blood pressure signal together with the central mechanisms that control the BP and HR variations and adaptations. See text for details. This figure has been modified and extended from (19).

Briefly, the relaxation oscillator model, which is of second order, has two states, x₁ and x₂, which are generated by delays Δ_t with feedback elements that are discrete representations of leaky integrators (dashed rectangles) in continuous system models (27). The non-linear element (f₁, Figure 1), was modeled as piecewise linear with threshold, T, and saturation, S. This nonlinear feedback is responsible for making the system oscillate, mimics the non-linear feedback present in the baroreflex (28, 29) and is a minimal structure for inducing relaxation oscillations (25). The realization of these integrators by central circuits is not known, but may be accomplished through functional commissural connections between neurons in the rostral ventrolateral medulla (RVLM) and those in the nucleus tractus solitarius NTS) (30, 31). The vestibular system affects the oscillator in two ways: First, by adding an input in the feedback loop from the otolith orientation signal V₀ through g_v. Second it affects the parameter modification of the VVR trigger, which causes a drop in Bp_d, initiating a VVR (Figure 2).

In order to fit the data better on both systole-diastole transition and its derivative, a non-linear function (NL, f₂) of the derivative of the integrator state (x₂) was implemented as an enhancement of the model developed in Raphan et al. (19) (Figure 2). The output of this non-linearity was processed by a high pass filter with a cut-in frequency of 0.1 Hz and then processed by an integrator, whose output has been labeled x_2p. We postulate that this output combined with BP_d through parameters h₆ and g₂, which is offset by a bias (Bias) generates the signal z₂ that controls BP and presumably the Volumetric Flow rate by constricting and dilating the muscle beds (32, 33). The purpose of the high pass filter was to prevent drifts at the output of the integrator due to any level component (DC) generated by the non-linearity, f₂. The oscillator maintained the systolic to diastolic transitions and the non-linearity shaped and constrained the BP and its derivative, which fit the data. The equations below the model (Figure 2) were implemented in Matlab and used to simulate model predictions.

Model Predictions of Data and Defining the Features for Identifying a VVR

The simulations presented here are only those that have a direct bearing on the VVR. A more complete analysis of the model performance and the testing of the model against a wide range of data is given in (19). When activated by a constant BP_d, the output of the model, z₂, oscillated at a fixed frequency and the systolic and diastolic phases compared favorably with those from an anesthetized rat when there was no external vestibular stimulus (Figure 3, BP_d = 50). When BP_d was dropped at t = 5 s from 50 to 40 (Figure 3), due to the peak to peak amplitude of each simulated systole was reduced (Figure 3), and BP had the same properties as the experimental data (18, 19). Thus, the model had the flexibility to simulate experimental data not only in the normal state, but also during a VVR. Altering parameters, such as the threshold, or other parameters did not produce a VVR with these characteristics (19). Thus, a key prediction of the model is that it is a drop in BP_d that triggers a VVR.

FIGURE 3

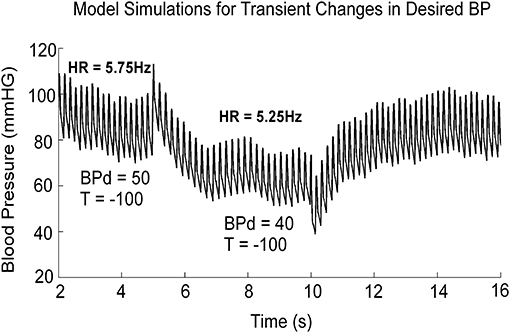
Figure 3. Model simulation showing the effects of dropping BP_d from 50 to 40 mmHG. The threshold, T, in the feedback loop, responsible for the transition from diastole to systole was held constant at −100. BP_d is the only parameter that effectively mimics a VVR when it is dropped from its stable value. This figure was adapted from (19).

From the above findings, we hypothesize that in non-susceptible animals, or in animals that are habituated, the internal signal, BP_d, is prevented from dropping (13). We have also postulated that the BP_d signal originated in specific circuits that reconstruct this signal from states of the relaxation oscillator. We have further postulated that there is a specific trigger circuit that monitors the states and output variables of the relaxation oscillator in the brainstem as well as vestibular inputs to the baroreflex feedback, correlates these signals and determines whether to initiate a VVR. In order to determine the signals that activate this mechanism, we propose a new method for identifying VVRs, which utilizes a metric that combines features associated with both BP and HR.

These features were derived as follows: we incorporated stochastic variations in threshold of the baroreflex feedback, T. When this was done, the model predicted what has commonly been referred to as baroreflex sensitivity (BRS) (Figure 4), which has been defined as the slope of the regression when R-R interval is plotted as a function of previous systolic pressure (34, 35). When the threshold, T, was varied randomly, the model output achieved varying systolic levels and intersystolic intervals (Figure 4A). This was the approximate behavior of the systolic levels and intersystolic intervals in the alert rat (Figure 4B). When the intersystolic interval was plotted as a function of Systolic Pressure (BRS), the model predicted a positive correlation for the BRS for vestibular input V₀ =0 in the model (Figure 4C, Shaded dotted line, slope = 0.31). This compared favorably with the data obtained in the alert rat (Figure 4D) as well as habituated anesthetized rats (13). It also predicted the BRS of anesthetized rats (Figure 4C, slope = 0). For a constant input V₀ = 10, the slope was increased to 0.6, which was the range of the baroreceptor in humans (34). The slopes could be altered by changes in sinusoidal vestibular input. (Figure 4C, slope −0.78), showing the wide range of baroreflex sensitivities that could be obtained from the model.

FIGURE 4

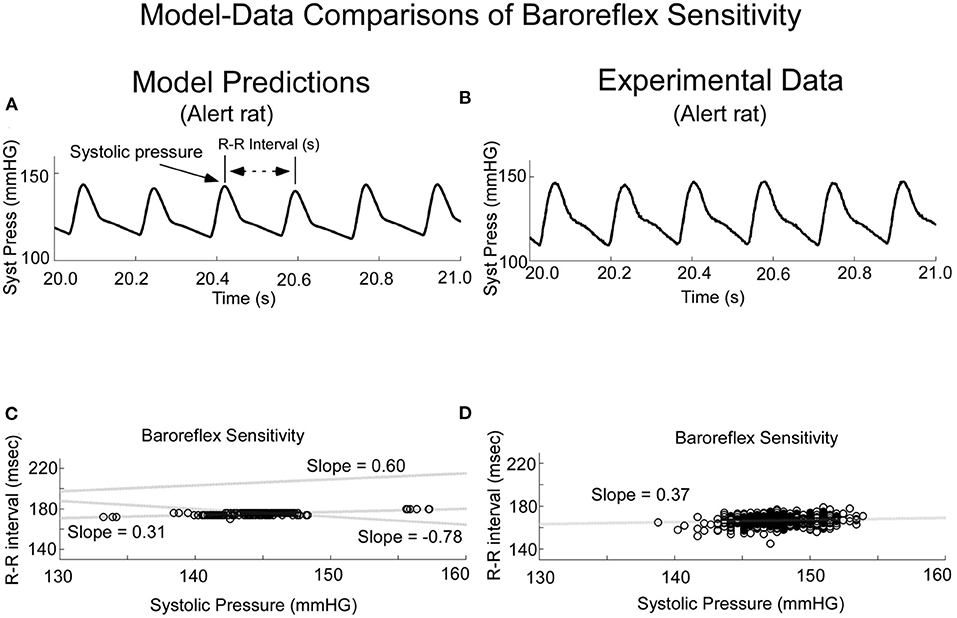
Figure 4. Comparison of Model Predictions (A,C) and Experimental Data (B,D) of Baroreceptor Sensitivity (BRS). The model predicted the experimental data (A,B) and had the flexibility to predict the Baroreflex Sensitivity (C,D). This figure was taken from (19).

It has been noted that both BP and HR drops characterize a VVR (18, 36, 37). We have identified a signal BP_d that when it drops, both BP and the inverse of intersystolic interval drop. It is therefore of interest that baroreflex sensitivity is a parameter that is determined from a ratio of intersystolic interval and systolic BP. Thus, the BRS parameter has information about instantaneous HR and BP, rather than BP alone and could be the important trigger signal for VVR initiation. In this study, we therefore examined the temporal variations in BRS to determine the normal variation in anesthetized and alert states and the threshold that needs to be reached to generate a VVR.

We then considered an instantaneous Baroreflex Sensitivity function (ΔBRS) to determine whether this feature is a better prognosticator of VVRs and determine how the states of the model are related to ΔBRS. The computation of ΔBRS was implemented as a moving average window of instantaneous ratios of changes in intersystolic interval (related to HR) to changes in systolic BP. When a VVR occurred, the peak drop in systolic BP, BPmaxdrop, was plotted vs. the maximum of ΔBRS (ΔBRS_max). This plot had a considerable overlap in classifying a VVR according to a criterion based on maximal drops in BP alone (Figure 5). If the threshold for BPmaxdrop is chosen at 25 mmHG, then there are many VVRs that are missed (Figure 4, orange circles below 25 mmHG). If the threshold for classifying a VVR is 18 mmHG, many non-VVRs are classified as VVRs (Figure 5, blue circles). This shows that choosing a threshold for BPMaxdrop alone for identifying a VVR is an insufficient metric. A “Machine Learning” algorithm was used to find the discriminant function between what we termed normal vs. VVR (Figure 5 Separating Linear function of orange from blue circles). First a small “test set” of what had been identified as VVRs using large values of BPmaxdrop was clasiified (Figure 5, purple star). The remaining data points were classified using the learned discriminant function based on the test set. There was improved identification and separation of a VVR from a non-VVR (Figure 5). This shows that a linear combination of BP_Maxdrop and ΔBRS was a more appropriate metric.

FIGURE 5

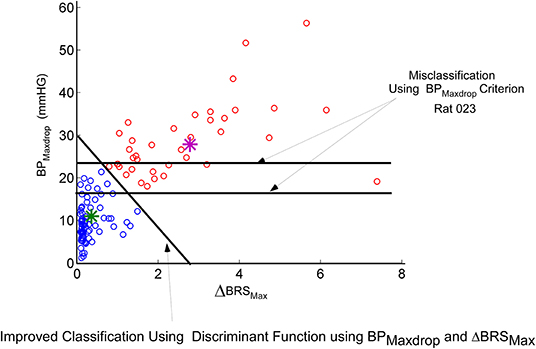
Figure 5. Machine learning approach to finding a linear discriminant function that seperates a known VVR from normal. The blue circles are not VVRs while the others are VVRs. The features that are being plotted are the maximum drop in BP (BP_Maxdrop) vs. maximum change in the new metric ΔBRS (See Text). Using a threshold on BP_Maxdrop alone (horizontal lines) misclassifies a significant greater VVRs than does the learned linear discriminant function, which utilizes a combination of BP_Maxdrop and ΔBRS.

Because ΔBRS is an important part of classifying a VVR, we then considered whether the time series ΔBRS (Figure 6B) or its derivative (Figure 6D) could be used (Figure 6A) to predict the triggering of a VVR. The polynomial fit to ΔBRS (Figure 6C) is an intermediate step in finding the derivative and suggests that the derivative of ΔBRS reaches a threshold, Tvvr (Figure 6D), before there is a drop in systolic level of BP (Figure 6, Dotted Vertical Line). This threshold metric, Tvvr, which is derived from the temporal characteristics of the derivative of ΔBRS, is consistent with the idea that ΔBRS is an important part of the discriminant function that separates a VVR from a non-VVR. Therefore, this newly defined ΔBRS function and its derivative are better predictors of a VVR and could be a metric that combines both BP and HR as determinants of an impending VVR and associated VVS in humans if a large data set were utilized.

FIGURE 6

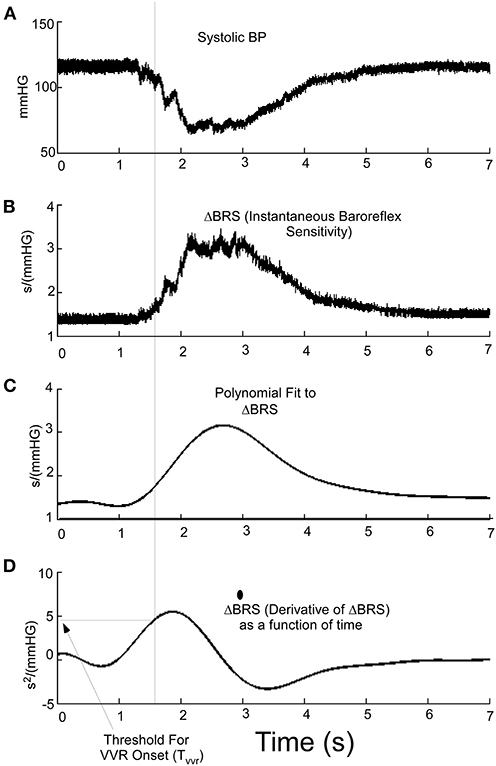
Figure 6. (A) Systolic BP as a function of time during a VVR. (B) Using the instantaneous baroreflex sensitivity, ΔBRS, allows for the polynomial fitting (C) and determining the derivative where a threshold (T_vvr) (D) aligns and is a predictor of the drop in systolic pressure at the beginning of a VVR.

Discussion

This study has shown that this newly defined function, ΔBRS, and its derivative are predictive of a VVR and potentially could be important in predicting VVS in humans. This is consistent with the finding that a better discriminant for identifying a VVR is when BP_max is combined with ΔBRS_Max. This new metric takes into account a critical feature of VVRs in humans and rats as the simultaneous occurrence of both bradycardia and hypotension at the onset of the VVR (38). It is supported by the idea that it is the loss of baroreflex function that triggers a VVS (17, 36, 39). Consistent with this, there is also an immediate loss of the baroreflex-generated Muscle Sympathetic Nerve Activity (MSNA) at the onset of syncope (40–42). The pathophysiological mechanism and significance of the baroreflex disengagement in producing bradycardia and hypotension have been conjectured to be the basis for VVS (3, 4), but no specific mechanism has been identified that could produce these changes. As such, despite being relatively common (1, 12, 43), the origin and neural basis of VVRs, which are related to VVS are not known (2, 36, 38) and there are no physical signs of neurogenically mediated VVR. Therefore, identifying the features that could be correlated with triggering the a VVR that underlies VVS, could be important in predicting their onset and managing the condition.

The pressure and flow dynamics are not easily modeled from a biophysical perspective. We have therefore taken a system theoretic approach to this problem to model the neural control of the cardiovascular oscillations as an internal model that entrains the natural cardiovascular oscillations (19). This approach encompasses not only the physical volumetric flow rate and pressure dynamics, but also how the BP and HR system is controlled by sensory-motor neural mechanisms that constrain the shape of the systolic-diastolic oscillatory waves (19). It had been suggested that the systolic-diastolic oscillations in BP had characteristics of a relaxation oscillator (44, 45). Recently, we demonstrated how relaxation oscillations could be embedded in a control system that could regulate its performance. In this model, the shape of the systolic/diastolic waveform is not determined strictly by the heart, but by a neural network, which mimics the oscillation features of the heart, referred to as the internal model. The feedback mechanisms implement closed loop control and drive actuators through non-linear mechanisms that can rapidly control the constriction of the arteries and vascular beds (33), regulating volumetric blood flow rate and BP (19). This kind of control is referred to as Model Reference Adaptive Control (MRAC) (46–48). The output of the internal model is compared to a feedback signal from baro-receptors that code BP, generating an error signal whose control parameters are updated based on this error signal. The control parameters then converge to ideal values that cause the actual BP and HR to ~match the response of the reference model. We have simulated the reference model behavior as a function of alteration of specific parameters and tested the predictions against data. This kind of control is different from eye movement control or leg control. These systems are stationary and need to be activated to have them move. The blood pressure and heart rate control requires the maintenance of oscillations by an already oscillating system. Therefore, it is reasonable that the control strategies would be different.

The model was implemented as a state determined second order relaxation oscillator, whose oscillation characteristics are governed essentially by a threshold and saturation mechanism in the feedback loop and a driving signal that maintains the oscillations. The threshold non-linearity, which has been observed in the baroreflex feedback (28, 29, 49), puts the system into systolic or diastolic mode. The model was adapted from work done on modeling oculomotor oscillations during nystagmus (25) and repetitive motion of the legs during locomotion (50, 51) where there are also oscillating fast and slow components of the stepping. An important enhancement to the model above over that presented previously (19), is a component, which we have labeled Mechanism for Generating BP_d and habituation. We propose that this component generates BP_d to maintain the relaxation oscillations. We also postulate that it correlates the signals arising from the states of the relaxation oscillator that is responsible for activating the VVR trigger, which inhibits BP_d Generation and initiates a VVR. Finally, it is responsible for activating the Par Mod component during habituation that adapts the parameters of BP_d Generation, which raises the threshold for triggering a VVR as habituation is ongoing (13).

There is some evidence that mechanism for generating BP_d and the parameter modification for maintaining BP oscillations or initiating a VVR is performed in the uvula. Optogenetic inhibition of Purkinje cell activity in the uvula modulates BP when anesthetized rats are tilted (52). There are also afferent (53) and efferent (54) connections to autonomic nuclei in the rabbit. These findings together with the fact that neural activity in the caudal medial, lateral and descending VN (55–58) are critical for VSR (59, 60) may contain a mediator that modulates BP (61–63) is consistent with the model structure that is being proposed.

In conclusion, much of the efforts in identifying the onset of a VVR has been focused on BP (14, 15, 18). The VVRs in rats were associated with increased power in the low frequency band (0.025–0.05 Hz) with synchronous oscillations in BP and HR, which have been termed vasovagal Oscillations; higher frequencies of sGVS rarely induced a VVR (18). The approach in this study was to base our criteria for predicting a VVR on a model that (1) predicted the approximate triangular shape of systolic/diastolic oscillations. (2) identified parameters, which could modify the oscillations. (3) Encompassed a theory for how amplitudes and frequencies of these systolic/diastolic oscillations could be controlled by vestibular input (4). Better Identified the features that could be used to separate a VVR from the normal systolic/diastolic oscillations using a machine learning technique.

The method developed was based on small data set, yet proved valuable in finding a separation between the systolic-diastolic beats during VVR and normal beats. Finding discriminant functions using a “Big Data” set for each animal should give us a better understanding of how BP and HR are processed to generate a VVR and how it is reflected in our newly defined ΔBRS function and its derivative. If a similar feature identification could be associated with VVRs in humans, it potentially could be utilized to identify onset of fainting in real time.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The animal study was reviewed and approved by IACUC, Icahn School of Medicine at Mount Sinai Hospital.

Author Contributions

TR contributed to the overall conceptual framework of this study. TR was responsible for developing the model, defining and testing the parameters that were used to identify VVRs and showing the plausibility of such an approach. TR also was responsible for the organization and writing of the manuscript. SY contributed by performing the experiments on the rats as well as contributing of the writing of the manuscript.

Funding

The authors gratefully acknowledge the support of the Jewish Communal fund donated by Mrs. Pheobe Cohen to support the research of TR. The work was also supported by grant NIH/NIDC DC 012573 (TR). SY was supported by NIH/NIDCD DC018390.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank G. P. Martinelli for implanting the Blood pressure monitors. We would like to acknowledge the funding obtained by BC (deceased) that support the experimental work.

References

1. Gendelman HE, Linzer M, Gabelman M, Smoller S, Scheuer J. Syncope in a general hospital patient population. Usefulness of the radionuclide brain scan, electroencephalogram, and 24-hour Holter monitor. N Y State J Med. (1983) 83:1161–5.

PubMed Abstract | Google Scholar

2. Moya A, Sutton R, Ammirati F, Blanc JJ, Brignole M, Dahm JB, et al. Guidelines for the diagnosis and management of syncope (version 2009). Task Force for the Diagnosis and Management of Syncope; European Society of Cardiology (ESC); European Heart Rhythm Association (EHRA); Heart Failure Association (HFA); Heart Rhythm Society (HRS). Eur Heart J. (2009) 30:2631–71. doi: 10.1093/eurheartj/ehp298

CrossRef Full Text

3. Saal DP, Thijs RD, van Zwet EW, Bootsma M, Brignole M, Benditt DG, et al. Temporal relationship of a systole to onset of transient loss of conciousness in tilt Induced reflex syncope. JACC: Clinical Electrophysiol. (2017) 3:1592–8. doi: 10.1016/j.jacep.2017.07.006

CrossRef Full Text | Google Scholar

4. van Dijk JG, van Rossum IA, Thijs RD. Timing of circulatory and neurological events in syncope. Front Cardiovasc Med. (2020) 7:36. doi: 10.3389/fcvm.2020.00036

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Wallin BG, Sundlof G. Sympathetic outflow to muscles during vasovagal syncope. J Auton Nerv Syst. (1982) 6: 287–91.

PubMed Abstract | Google Scholar

6. Calkins H. Pharmacological approaches to therapy for vasovagal syncope. Am J Cardiol. (1999) 84:20Q–5Q.

Google Scholar

7. Sheldon R. Role of pacing in the treatment of vasovagal syncope. Am J. Cardiol. (1999) 84:26Q−32Q.

PubMed Abstract | Google Scholar

8. Sheldon R, Connolly S. Second Vasovagal Pacemaker Study (VPS II): rationale, design, results, and implications for practice and future clinical trials. Card Electrophysiol Rev. (2003) 7:411–5. doi: 10.1023/B:CEPR.0000023157.37745.76

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sheldon R, Rose S, Connolly S. Prevention of syncope trial (POST): a randomized clinical trial of beta blockers in the prevention of vasovagal syncope; rationale and study design. Europace. (2003) 5:71–5. doi: 10.1053/eupc.2002.0284

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Kapoor JR. Predicting the effectiveness of beta-blocker therapy in vasovagal syncope. J Am Coll Cardiol. (2008) 51:2372. doi: 10.1016/j.jacc.2008.02.070

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Sutton R, Bloomfeld DM. Indications, methodology, and classification of results of tilt-table testing. Am J. Cardiol. (1999) 84:10Q–9Q.

PubMed Abstract | Google Scholar

12. Grubb BP. Neurocardigenic syncope. N Engl J Med. (2005) 352:1004–10. doi: 10.1056/NEJMcp042601

CrossRef Full Text | Google Scholar

13. Cohen B, Martinelli GP, Xiang Y, Raphan T, Yakushin SB. Vestibular activation habituates the vasovagal response in the rat. Front Neurol. (2017) 8:83. doi: 10.3389/fneur.2017.00083

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Hausenloy DJ, Arhi C, Chandra N, Franzen-McManus A-C, Meyer A, Sutton R. Blood pressure oscillations during tilt testing as a predictive marker of vasovagal syncope. Eurospace. (2009) 11:1696–701. doi: 10.1093/eurospcae/eup338

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Nowak JA, Ocon A, Taneja I, Medow MS, Steward JM. Multiresolution wavelet analysis of time dependent physiological response in syncopal youths. Am J Physiol Heart Circ Physiol. (2009) 296:H171–9. doi: 10.1152/ajpheart.00963.2008

CrossRef Full Text | Google Scholar

16. Cohen B, Martinelli GP, Ogorodnikov D, Xiang Y, Raphan T, Holstein GR, et al. Sinusoidal galvanic vestibular stimulation (sGVS) induces a vasovagal response in the rat. Exp Brain Res. (2011) 210:45–55. doi: 10.1007/s00221-011-2604-4

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Cohen B, Martinelli GP, Raphan T, Schaffner A, Xiang Y, Holstein GR, et al. The vaso-vagal response (VVR) of the rat: its relation to the vestibulo-sympathetic reflex (VSR) and to Mayer waves. FASEB. (2013) 27:2564–72. doi: 10.1096/fj.12-226381

CrossRef Full Text | Google Scholar

18. Yakushin SB, Martinelli GP, Raphan T, Xiang Y, Holstein GR, Cohen B. Vasovagal oscillations and vasovagal responses produces by the vestibulo-sympathetic reflex in the rat. Front Neurol. (2014) 5:1–11. doi: 10.3389/fneur.2014.00037.ecollections 2014

CrossRef Full Text | Google Scholar

19. Raphan T, Cohen B, Xiang Y, Yakushin SB. A model of blood pressure, heart rate, and vaso-vagal responses produced by vestibulo-sympathetic activation. Front Neurosci. (2016) 10:1–16. doi: 10.3389/fnins.2016.00096

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Bishop CM. Pattern Recognition and Machine Learning. New York, NY: Springer Science +Business Media (2006). p. 738.

Google Scholar

21. Yakushin SB, Martinelli GP, Raphan T, Cohen B. The response of the vestibulosympathetic reflex to linear acceleration in the rat. J Neurophysiol. (2016) 116: 2752–64. doi: 10.1152/jn.00217.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Kaufmann H, Biaggioni I, Voustianiouk A, Diedrich A, Costa F, Clarke R, et al. Vestibular control of sympathetic activity. An otolith-sympathetic reflex in humans. Exp Brain Res. (2002) 143:463–9. doi: 10.1007/s00221-002-1002-3

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Rudowsky I, Kulyba O, Kunin M, Ogarodnikov D, Raphan T. A relational database application in support of integrated neuroscience research. J Integr Neurosci. (2004) 3:363–78. doi: 10.1142/S0219635204000609

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Krediet CTP, van Dijk N, Linzer M, van Lieshout JJ, Wouter W. Management of vasovagal Syncope controlling or aborting faints by leg crossing and muscle tensing. Circulation. (2002) 106:1684–9. doi: 10.1161/01.CIR.0000030939.12646.8F

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Raphan T. A parameter adaptive approach to oculomotor system modeling. In: Engineering. New York, NY: CUNY (1976). p. 204.

26. Berne RM, Levy MN. Cardiovascular Physiology. Philadelphia, PA: Mosby (2001).

Google Scholar

27. Zadeh LA, Desoer CA. Linear System Theory: The State Space Approach. Series in Systems Science. New York, NY: McGraw Hill (1963). p. 628.

Google Scholar

28. Chen HI, Kuo-Chu C. Assessment of threshold and saturation pressure in the baroreflex function curve: a new mathematical analysis. Jpn J Physiol. (1991) 41:861–77.

PubMed Abstract | Google Scholar

29. Chen S, Shi X. Re-parameterization of the logistic model in assessing changes in baroreceptor reflex. Neurosci Med. (2011) 2: 110–6. doi: 10.4236/nm.2011.22016

CrossRef Full Text | Google Scholar

30. Blessing WW. The Lower Brainstem and Bodily Homeostasis. Oxford: Oxford University Press (1997).

31. Granata AR. Modulatory inputs on sympathetic neurons in the rostral ventrlateral medulla in the rat. Cell Mol Neurobiol. (2003) 23:665–80. doi: 10.1023/a:1025040600812

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Barcroft H, Edholm OG, Mcmichael J, Sharpey-Schafer EP. Posthaemorrhagic fainting: study by cardiac output and forearm flow. Lancet. (1944):489–90.

Google Scholar

33. Barcroft H, Edholm OG. On the vasodilation in human skeletal muscle during post-haemorrhagic fainting. J Physiol. (1945) 104.2:161–75.

Google Scholar

34. Davos CH, Davies LC, Piepoli M. The effect of baroreceptor activity on cardiovascular regulation. Hellenic J Cardiol. (2002) 43:145–55.

Google Scholar

35. La Rovere M, Pinna G, Raczak G. Baroreflex sensitivity: measurement and clinical implications. Ann Noninv Electrocardiol. (2008) 13:191–207. doi: 10.1111/j.1542-474X.2008.00219.x

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Julu POO, Cooper VL, Hansen S, Hainsworth R. Cardiovascular regulation in the period preceding vasovagal syncope in concious humans. J Physiol. (2003) 549:299–311. doi: 10.1113/jphysiol.2002.036715

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Kaufmann H, Hainsworth R. Why do we faint? Muscle Nerve. (2001) 24:981–3. doi: 10.1002/mus.1102

CrossRef Full Text | Google Scholar

38. Lewis T. Vasovagal syncope and the carotid sinus mechanism. Br Med J. (1932) 3723: 873–6.

PubMed Abstract | Google Scholar

39. Thomson HL, Wright K, Frenneaux M. Baroreflex sensitivity in patients with vasovagal syncope. Circulation. (1997) 95:395–400.

PubMed Abstract | Google Scholar

40. Morillo CA, Eckberg DL, Ellenbogen KA, Beightol LA, Hoag JB, Tahvanainen KU, et al. Vagal and sympathetic mechanisms in patients with orthostatic vasovagal syncope. Circulation. (1997) 96:2509–13.

PubMed Abstract | Google Scholar

41. Morillo CA, Villar JC. Neurocardiology. Neurogenic syncope. Baillieres Clin Neurol. (1997) 6:357–80.

Google Scholar

42. Mosqueda-Garcia R, Furlan R, Fernandez-Violante R, Desai T, Snell M, Jarai Z, et al. Sympathetic and baroreceptor reflex function in neurally mediated syncope evoked by tilt. J Clin Invest. (1997) 99: 2736–44.

PubMed Abstract | Google Scholar

43. Soteriades ES. Incidence and prognosis of syncope. N Engl J Med. (2002) 347:875–85. doi: 10.1056/NEJMoa012407

CrossRef Full Text | Google Scholar

44. van Der Pol B. On relaxation-oscillations. The London, Edinburgh and Dublin. Phil Mag Sci. (1926) 2:978–92. doi: 10.1080/1478644260856127

CrossRef Full Text

45. Noble PJ, Noble D, A historical perspective on the development of models of rhythm in the heart. In: Tripathi ON, Ravens U, Sanguinetti MC, editors. Heart Rate and Rhythm. New York, NY: Springer Verlag (2011). p. 155–74.

46. Horrocks T. Investigations into model reference adaptive control systems. Proc IEEE. (1964) 3:1894–906.

Google Scholar

47. Landau ID. Adaptive Control: The Model Reference Approach. New York NY: Marcel Dekker (1979).

Google Scholar

48. White AJ. Analysis and design of model-reference adaptive control systems. Proc IEEE. (1966) 113:175–84.

Google Scholar

49. Chen LY, Benditt DG. Perhaps past performance does predict future results after all: a key to evaluating treatment interventions in vasovagal syncope. J Cardiovasc Electrophysiol. (2010) 21:1381–3. doi: 10.1111/j.1540-8167.2010.01881.x

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Osaki Y, Kunin M, Cohen B, Raphan T. Three-dimensional kinematics and dynamics of the foot during walking: a model of central control mechanisms. Exp Brain Res. (2007) 176:476–96. doi: 10.1007/s00221-006-0633-1

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Osaki Y, Kunin M, Cohen B, Raphan T. Relative contribution of walking velocity and stepping frequency to the neural control of locomotion. Exp Brain Res. (2008) 185: 121–35. doi: 10.1007/s00221-007-1139-1

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Tsubota T, Ohashi Y, Tamura K, Miyashita Y. Optogenetic inhibition of Purkinje cell activity reveals cerebellar control of blood pressure during postural alterations in anesthetized rats. Neuroscience. (2012) 210: 137–44. doi: 10.1016/j.neuroscience.2012.03.014

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Bradley DJ, Ghelarducci B, La Noce A, Paton JFR, Spyer KM, Withington-Wray DJ. An electrophysiological and anatomical study of afferents reaching the cerebellar uvula in the rabbit. Exp Physiol. (1990) 75:163–77.

PubMed Abstract | Google Scholar

54. Paton JFR, La Noce A, Sykes RM, Sebastiani L, Bagnoli P, Ghelarducci B, et al. Efferent connections of lobule IX of the posterior cerebellar cortex in the rabbit—some functional considerations. J Auton Nerv Syst. (1991) 36:209–24.

PubMed Abstract | Google Scholar

55. Yates BJ, Grelot L, Kerman IA, Balaban CD, Jakus J, Miller AD. Organization of vestibular inputs to nucleus tractus solitarius and adjacent structures in cat brain stem. Am J Physiol. (1994) 267(4 Pt. 2): R974–83.

PubMed Abstract | Google Scholar

56. Doba N, Reis DJ. Changes in regional blood flow and cardiodynamics evoked by electrical stimulation of the fastigial nucleus in the cat and their similarity to orthstatic reflexes. J Phusiol (Lond.). (1972) 227: 729–47.

PubMed Abstract | Google Scholar

57. Pan PS, Zhang YS, Chen YZ. Role of the nucleus vestibularis medialis in vestibulo-sympathetic response in rats. Acta Physiol Sin, Chinese. (1991) 43:184–8.

PubMed Abstract | Google Scholar

58. Uchino Y, Kudo N, Tsuda K, Iwamura Y. Vestibular inhibition of sympathetic nerve activities. Brain Res. (1970) 22:195–206.

PubMed Abstract | Google Scholar

59. Yates BJ. Vestibular influences on the sympathetic nervous system. Brain Res. (1992) 17:51–9.

PubMed Abstract | Google Scholar

60. Yates BJ, Goto T, Kerman I, Bolton PS. Responses of caudal medullary raphe neurons to natural vestibular stimulation. J Neurophysiol. (1993) 70:938–46.

PubMed Abstract | Google Scholar

61. Bozdagi O, Wang XB, Martinelli GP, Prell G, Friedrich VL Jr, Huntley GW, et al. Imidazoleacetic acid-ribotide induces depression of synaptic responses in hippocampus through activation of imidazoline receptors. J Neurophysiol. (2011) 105:1266–75. doi: 10.1152/jn.00263.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Martinelli GP, Friedrich VL Jr, Prell GD, Holstein GR. Vestibular neurons in the rat contain imidazoleacetic acid-ribotide, a putative neurotransmitter involved in blood pressure regulation. J Comp Neurol. (2007) 501:568–81. doi: 10.1002/cne.21271

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Prell GD, Martinelli GP, Holstein GR, Matulic-Adamic J, Watanabe KA, Chan SLF, et al. Imidazoleacetic acid-ribotide: an endogenous ligand that stimulates imidazol(in)e receptors. Proc Natl Acad Sci. (2004) 101:13677–82. doi: 10.1073/pnas.0404846101

PubMed Abstract | CrossRef Full Text | Google Scholar