- Département de Physiologie and Groupe de Recherche sur le Système Nerveux Central, Université de Montréal, Montréal, QC, Canada
Previous studies have shown that neural activity in primate dorsal premotor cortex (PMd) can simultaneously represent multiple potential movement plans, and that activity related to these movement options is modulated by their relative subjective desirability. These findings support the hypothesis that decisions about actions are made through a competition within the same circuits that guide the actions themselves. This hypothesis further predicts that the very same cells that guide initial decisions will continue to update their activities if an animal changes its mind. For example, if a previously selected movement option suddenly becomes unavailable, the correction will be performed by the same cells that selected the initial movement, as opposed to some different group of cells responsible for online guidance. We tested this prediction by recording neural activity in the PMd of a monkey performing an instructed-delay reach selection task. In the task, two targets were simultaneously presented and their border styles indicated whether each would be worth 1, 2, or 3 juice drops. In a random subset of trials (FREE), the monkey was allowed a choice while in the remaining trials (FORCED) one of the targets disappeared at the time of the GO signal. In FORCED-LOW trials the monkey was forced to move to the less valuable target and started moving either toward the new target (Direct) or toward the target that vanished and then curved to reach the remaining one (Curved). Prior to the GO signal, PMd activity clearly reflected the monkey's subjective preference, predicting his choices in FREE trials even with equally valued options. In FORCED-LOW trials, PMd activity reflected the switch of the monkey's plan as early as 100 ms after the GO signal, well before movement onset (MO). This confirms that the activity is not related to feedback from the movement itself, and suggests that PMd continues to participate in action selection even when the animal changes its mind on-line. These findings were reproduced by a computational model suggesting that switches between action plans can be explained by the same competition process responsible for initial decisions.
Introduction
Natural behavior requires animals to make many kinds of decisions. For example, an animal is often faced with selecting between different movements that accomplish the same behavioral goal, such as different directions to run to escape a predator. At a higher level of selection, the same animal may decide between different types of activity, such as running away versus turning around to fight. Still other kinds of decisions may involve purely abstract choices, which are not (at least immediately) associated with any specific action. In human behavior, such decisions may be extremely abstract, such as choosing what kind of career to pursue in life. Because the brain was built through continuous evolutionary refinement, we expect that the neural mechanisms of decisions at different levels of abstraction share many aspects of their architecture, and that consideration of simple spatial decisions between movement options may yield insights into decision-making in general (Cisek and Kalaska, 2010).
Recent work has suggested that, at least in the case of selecting between actions, decision-making is intimately integrated with sensorimotor control (Basso and Wurtz, 1998; Platt and Glimcher, 1999; Romo et al., 2004; Cisek and Kalaska, 2005; Gold and Shadlen, 2007). This has led to the proposal that while an animal is deciding between actions, neural activity in the sensorimotor system represents several movements simultaneously and the decision is made by selecting between these parallel representations (Kim and Shadlen, 1999; Cisek, 2007; Cisek and Kalaska, 2010). For example, Cisek and Kalaska (2005) found that while a monkey is deciding between two different potential reaching movements, neural activity in dorsal premotor cortex (PMd) represents both options simultaneously and reflects the selection of one over the other when the monkey makes his choice. This is consistent with earlier proposals suggesting parallel movement preparation (Fagg and Arbib, 1998; Tipper et al., 1998; Erlhagen and Schoner, 2002), and with the hypothesis that action selection is accomplished through a biased competition within a sensorimotor map of potential actions (Cisek, 2006).
This “affordance competition” hypothesis (Cisek, 2007) stands in contrast to the classical serial model, in which decisions are made in higher cognitive centers and the resulting choice passed down to the sensorimotor system for execution. Instead, it suggests that decisions are determined when a competition between actions is resolved within the sensorimotor system—e.g., for reaching, within the fronto-parietal cortex and associated corticostriatal loops. This means that although the biases that influence the decision may come from many sources, including the activity of higher cognitive regions, it is in the sensorimotor system that the final decision is taken. For selecting between actions, this makes good sense from an ecological perspective: the systems most sensitive to the spatial and dynamic attributes of the candidate actions are best qualified to make the final selection that takes all of these factors into account. For example, when choosing between actions, the spatial layout of the immediate environment directly specifies the options and is of critical importance for evaluating what is the best choice in terms of payoffs and costs. Indeed, all else being equal, humans select the action that is least demanding from a biomechanical perspective (Cos et al., 2011), suggesting that the same “forward models” (Shadmehr et al., 2010) useful for predicting the consequences of motor commands may also play a role in selecting the actions themselves by biasing activity in sensorimotor cortices.
Decision-making within a sensorimotor map is particularly useful for spatial choices, such as selecting among different ways to escape a predator through an environment filled with obstacles. If two escape routes are close together, then you should not waste time deciding but instead run between them and choose in flight. In contrast, if you are up against a wall then a clear “winner-take-all” decision is critical, even if it takes a little more time to resolve. Finally, even during ongoing escape, you must continuously evaluate and update the options presented by the environment in case what appeared as an escape route turns out to be a dead end and/or if a new and better option presents itself. If that new option is already partially represented in sensorimotor maps of potential actions, then switching to it will be very fast.
In an analogy to the above scenario, here we consider selection between reaching movements to different spatially specified targets. The affordance competition hypothesis predicts that if we present a monkey with multiple reaching options associated with different rewards, neural activity in PMd will be modulated by the relative value of those rewards. However, if a single option is present, then its value will not influence PMd activity because there is no competition. A recent study in our lab (Pastor-Bernier and Cisek, 2011) confirmed both of these predictions, showing relative value modulation when two targets were presented but no value modulation with one target. Furthermore, it was found that the competition between options was strongest when they were furthest apart—just as predicted in the prey escape example described above. All of these results are consistent with the idea that the competition unfolds within a sensorimotor map that respects the pragmatic issues of selecting actions in space, and all of them could be simulated with a simple model of biased competition among populations of tuned cells (Cisek, 2006).
In summary, previous studies have shown that the process of deciding between actions involves the very same brain regions that are implicated in sensorimotor guidance of actions, consistent with the affordance competition hypothesis (Cisek, 2007). However, the hypothesis also makes a complementary prediction: that the same cells involved in selecting the initial action will continue to be involved in adjusting and even switching between actions during overt behavior. In other words, if the environment changes and old opportunities are lost or new ones become available, the same integrated selection and sensorimotor guidance system should reflect the switch of the plan. Here, we investigate this issue by examining neural activity in PMd after a monkey has chosen one of two actions, but the selected option becomes unavailable. We examined the same cells whose delay period activity showed relative value modulation in our previous work (Pastor-Bernier and Cisek, 2011) but extended our analysis to the activity after the GO signal, with particular interest in trials in which the option with highest payoff becomes unavailable. Some of these results have been previously presented in abstract form (Pastor-Bernier et al., 2011).
Materials and Methods
Instrumentation and Technical Procedures
A male monkey (Macaca mulatta) performed a planar center-out reaching task illustrated in Figure 1A. The task involved moving a cursor from a central circle (2 cm radius) to one of six possible targets (2.4 cm radius) spaced at 60° intervals around a 12.6 cm radius circle. The monkey performed movements using a cordless stylus whose position was recorded (125 Hz) by a digitizing tablet (CalComp). Target stimuli and continuous cursor feedback were projected onto a mirror suspended between the monkey's gaze and the tablet, creating the illusion that they are in the plane of the tablet. Oculomotor behavior was unconstrained, as eye movements do not strongly influence arm-related PMd activity (Cisek and Kalaska, 2002), but was monitored with an infrared oculometer (ASL). Neural activity was recorded with 3–4 independently moveable microelectrodes (NAN microdrive) and data acquisition was performed with AlphaLab (Alpha-Omega). On-line spike discrimination was used to estimate cell preferred directions for choosing target locations. All analog waveforms were stored on disk for offline sorting using principal components (Plexon). All task events, trajectory data and spike times were stored in a database (Microsoft SQL Server 2005) accessed through custom scripts for data analysis (Matlab). After completing training, the animal was implanted under general anesthesia with a titanium head post and a recording chamber placed using MRI images (Brainsight primate). The chamber was centered on the arm area of PMd, between the precentral dimple and the junction of the arcuate sulcus and spur (Figure 1B). All procedures followed university and national guidelines for animal care.
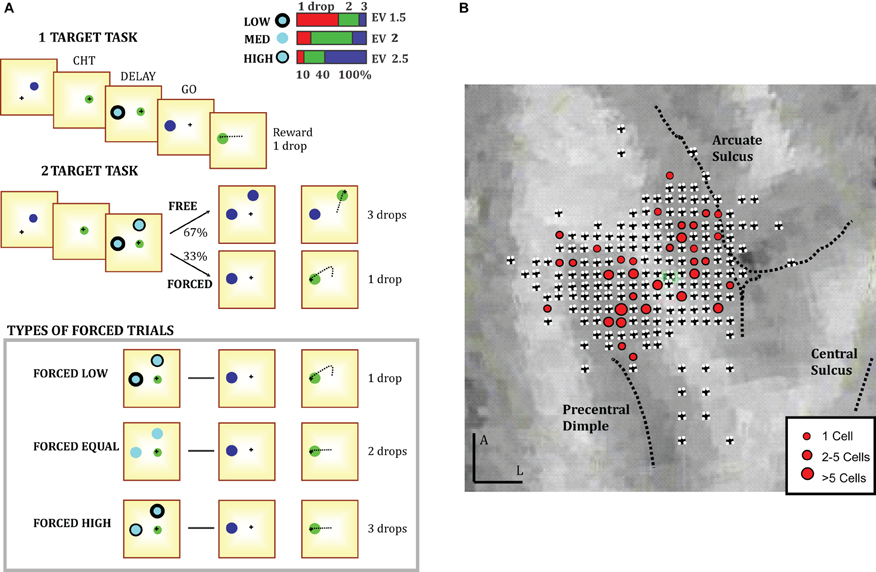
Figure 1. (A) Behavioral tasks. The tasks involve moving a cursor from a central circle to one of six possible target locations. At the beginning of each trial the monkey placed the cursor in the center and two targets appeared. Each target was associated with different rewards indicated by different border styles (legend shows the probability of receiving 1 (red), 2 (green), or 3 (blue) drops of juice for each border style). The monkey had to keep the cursor in the center until the targets changed color (GO signal). Then, it moved to one of the targets and held the cursor there to get a reward. In one variant of the task, the monkey was presented with only one target (1T). In a second variant two targets were presented, and the monkey was either free to move to either of them after the GO signal (FREE trials), or one disappeared after GO leaving the monkey with only the remaining option (FORCED trials). (B) The recording locations in PMd. Black crosses indicate recording sites. The locations for cells modulated by relative value (RV cells) are shown with red circles (N = 52).
Behavioral task
The monkey began each trial by placing the cursor in the central circle for a 350–650 ms Center-Hold-Time (CHT). Next, one or two cyan targets appeared, with border styles indicating the amount of juice that the monkey was likely to receive for reaching to that target (See Figure 1A, inset). The reward was determined probabilistically to encourage the monkey to explore available options (Herrnstein, 1961). A “low-value” target (L, thick border) had a 60% chance of yielding 1 drop, 30% chance of yielding 2, and 10% chance of yielding 3 (Expected value, EV = 1.5). A “medium-value” target (M, no border) was worth 2 (60%), 1 (20%), or 3 drops (20%) (EV = 2). A “high-value” target (H, thin border) was worth 3 (60%), 2, (30%), or 1 drop (10%) (EV = 2.5). The non-monotonic relationship between border thickness and value was used to dissociate motivational factors from physical properties of stimuli. In particular, the most visually salient cue with a thick border style is deliberately chosen to have a small payoff (“low value”) to dissociate saliency from value effects. The monkey held the cursor in the center for an instructed delay period (DELAY, 700–1300 ms) until a GO signal was indicated by a change in target color and the disappearance of the central circle. After the GO signal, the monkey had to initiate the movement within a 550 ms reaction time (RT) (which had to be at least 100 ms, to discourage anticipation). To receive a reward, the monkey had to move to a target within a maximum 550 ms movement time (MT) and hold the cursor there for 500 ms (Target-Hold-Time, THT). When cells were isolated, we first ran a block of 90 trials in which only one target was presented (1T), to identify the DELAY-period preferred target (PT) of each cell. Next, we ran a block of 180 two-target trials (2T), including ones where the PT target was present and low, medium, or high-valued, while the other target (OT) appeared at 60°, 120°, or 180° away and was low, medium, or high-valued. Each block also included 30 trials in which the targets were 120° apart but neither was in the direction of the PT. In this paper we focus only on trials in which the targets are 120° apart (90 trials per 2T block) and at least one of the presented targets was the cell's PT. In 67% of 2T trials (FREE), the monkey was free to move to either target after the GO signal. In 33% of 2T trials (FORCED), one of the targets disappeared at GO and the monkey had to move to the remaining one. FREE and FORCED trials were randomly interleaved to encourage the animal to keep both options partially prepared. FORCED trials were classified according to the value of the target that disappears after the GO signal. In FORCED LOW trials the target with the higher expected value disappears (inset in Figure 1A bottom), while the opposite is true in FORCED HIGH trials. In a FORCED EQUAL trial both the target that disappears and the target that remains have the same value.
Kinematic Analysis
Movement trajectories were re-sampled at a constant rate (200 Hz) and filtered using a two-way butterworth filter [0 phase lag, 4th order, norm. cutoff 0.05 (∼20 Hz)] using Matlab functions butter and filtfilt (Mathworks). The initial direction vector (IDV) was calculated as the X and Y coordinate cartesian arctangent (atan2) between the position at movement onset (MO) and the position 100 ms later. Trials were sorted by short RT (<180 ms), medium RT (between 180 ms and 240 ms) or long RT (>240 ms). The mean trajectory profiles and mean IDVs were calculated for each RT group independently. To determine whether the IDV was pointing to a given target in space, we calculated the mean IDV in the 1T condition for each target individually. Then, 2T trials were classified as “direct” to the selected target if their IDV fell within ±60 degrees of that target's mean IDV in the 1T condition. Trials whose IDV pointed away from the ultimately acquired target were classified as “curved.”
Cell Tuning and Relative Value Discrimination
We investigated only cells that had both spatial tuning and relative value discrimination (see Pastor-Bernier and Cisek, 2011) during DELAY. We calculated directional tuning preferences for the cells during each behavioral epoch (DELAY, MT, and THT) and assessed significance with a non-parametric bootstrap test (1000 shuffles, p < 0.05; Cisek et al., 2003). To assess whether a cell discriminated relative value during DELAY, we examined whether the cell showed statistically significant differences in firing rate between a “HIGH” value condition (value in PT was larger than OT) and a “LOW” value condition (value in OT larger than PT) for the last 300 ms prior to the GO signal (One-Way ANOVA, p < 0.05). This was done to verify whether the same cells that are involved in the initial decision continue to reflect plan switches after the GO signal. Cells satisfying both requirements were used for post-GO analyses. Discrimination latencies were obtained using a sliding ANOVA method adapted from Peng et al., 2008 (window: 50 ms, step: 5 ms, p < 0.05) to perform a statistical temporal analysis between the HIGH and LOW value conditions. We obtained latencies for relative value discrimination with respect to the GO signal by aligning the neural activity on GO and parsing each trial backwards for 700 ms (shortest variable DELAY duration). This chosen interval ensured that all trials had a similar time range for firing rate comparisons. The latency of relative-value discrimination was obtained as the last 80 ms sliding time-window for which a statistical difference could be observed. The cells that satisfied both the One-Way ANOVA and sliding-ANOVA requirements were called relative value discriminating cells (RV cells, N: 52). This population is identical to the data-set described previously (Pastor-Bernier and Cisek, 2011) in which relative-value effects were assessed for particular value combinations (PTvsOT: 3vs1, 2vs1, 3vs2) using paired ANOVA and Tukey–Kramer tests.
Plan-Switch Analysis
FORCED LOW trials were of particular interest for plan-switching analysis because they represent conflict situations in which the more desirable option must be replaced by the less desirable option. In these “plan-switch” cases, DELAY activity prior to GO (pre-GO plan) was compared with activity after GO (post-GO plan). We further distinguished cases where the target that disappears is located in the cell's PT or in the OT, giving rise to two different kinds of FORCED LOW trials. In FORCED LOW PT2OT trials the pre-GO DELAY activity reflects an initial plan to PT and the post-GO activity a final plan to OT. In FORCED LOW OT2PT trials the pre-GO DELAY activity reflects a movement plan to OT and the post-GO activity a final plan to PT. To obtain plan-switch latencies FORCED LOW trials were compared with trials belonging to the FREE condition in which the animal naturally chose the high valued option (FORCED-FREE comparison). To obtain the switch latency from an initial plan to PT to a final plan to OT (SwitchPT2OT) the activity of FORCED LOW PT2OT trials was compared with FREE trials in which PT was the plan selected (FREE HIGH PT). This type of switch is illustrated in Figure 3A. The plan-switch latency was obtained by parsing the neural activity for both types of trials from GO to movement offset using a sliding ANOVA method (window: 50 ms, step: 5 ms, p < 0.05) and calculated as the first moment in time in which they were significantly different for at least 80 ms after the GO signal. For the plan-switch latency to be valid we also required that there be no significant difference between the FORCED LOW PT2OT and the FREE HIGH PT types of trial for at least 300 ms before the GO signal (One-Way ANOVA, p < 0.05 ms). To calculate the switch latency from an initial OT plan to a final PT plan (SwitchOT2PT) the activity of FORCED LOW OT2PT trials was compared to FREE HIGH OT trials in which OT was selected. Figure 3B illustrates an example of this type of switch. We define as “convergence” the situation in which the pre-GO DELAY activity for two types of trials represents different movement plans, while the post-GO activity represents the same plan. The time of convergence to a plan in the PT direction (CONV) is found by comparing FORCED LOW OT2PT trials with FREE HIGH PT trials (Figure 3C). Convergence to an OT plan cannot be determined from the activity of cells because activity to OT is generally low. To obtain CONV latency a similar sliding ANOVA method was used, although the time of convergence was defined as the first moment after the GO signal in which the difference between the two types of trial was not significant (p > 0.05) for at least 80 ms. We also required the pre-GO DELAY activity between FORCED LOW OT2PT and FREE HIGH PT to be different for at least 300 ms (One-Way ANOVA, p < 0.05). In a variant of the plan-switch latency study we used FORCED HIGH trials instead of FREE HIGH trials for the calculation of plan-switch latencies (FORCED-FORCED comparison). This allowed us to address whether differences in visual input after the GO signal (the number of remaining targets) could have an effect on the plan-switching process.
The population's mean switch latencies (ms) were calculated using the sliding-ANOVA method mentioned above. The confidence intervals (CI) at 95% probability (p < 0.05) were obtained as ±Z × √E, where Z represents the critical area for the distribution of mean switch latencies across trials. Z can be approximated to ±1.96 assuming by the central limit theorem (Polya, 1920) that the mean distribution tends to normality with large sample sizes. The variable E represents the error variance of the mean and was calculated using the expression correcting for overlapping intervals described in Müller (1993) (Equation 3.7) and cited elsewhere (Dacorogna et al., 2001; Hansen and Lunde, 2006).
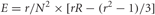
where r = min(m,N), R = max(m,N) and where m is the overlap between intervals and N is the number of samples per time interval.
In our case we have a 50 ms window sliding by 5 ms bins. Therefore, m = 45 and N = 10. Because m > N, then r = N, and R = m, and the previous expression takes the form:
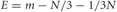
Solving numerically with m = 45 and N = 10, we obtain E = 41.7 and therefore,
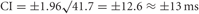
With no overlap m = 0, r = 0, R = 1, N = 1, and the error of overlap E = 0.
Computational Modeling
The model (Cisek, 2006) is aimed at explaining and predicting systems-level phenomena such as response patterns over large population of neurons. It is implemented with a set of equations describing the activity of several populations of neurons that correspond to specific cortical regions. Each population is organized as a layer of neurons that are tuned to spatial directions of potential actions. Each neuron in a layer behaves according to an expression that defines how its activity changes over time as a function of four terms: passive decay, excitation toward saturation, inhibition, and noise. This expression can also be called “mean-rate leaky integrator” (Grossberg, 1973) and takes the following form:
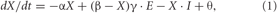
where X is the mean firing rate of a given neuron, dX/dt is the change in rate over time, E is the excitatory input, I is the inhibitory input, α is a decay rate, β is the maximum activity of a neuron, γ is the excitatory gain, and θ is the Gaussian noise. The connections between each layer are hardwired and organized to respect basic neuroanatomical connection patterns. Further details concerning connectivity patterns and model behavior have been described previously elsewhere (Cisek, 2006). For purposes of the present task the model's “prefrontal” activity was scaled by a signal related to the absolute value of each target (low = 0.3, medium = 0.7, high = 1.0). To simulate plan switches, we removed one of the two presented targets (high valued target in FORCED LOW trials) at the beginning of the GO epoch. All parameter settings were identical to Cisek (2006), except that we used a gradual GO signal that allows the activity in PMd to gradually spill into the M1 layer. The gradual GO signal is defined as a multiplicative factor that scales the input from PMd to M1 and is zero before the GO instruction. After the GO instruction, it grows as 2.5·t where t is the time since the GO instruction.
Note that the model in its present form is not intended to simulate the movement itself. Activity in the model M1 population simply indicates the initial direction of movement, computed as the preferred direction of the first M1 cell that crosses a threshold of activity equal to 1.75.
Behavioral Results
In 1T trials the monkey's success rate was 98%, in 2T FREE it was 99%, and in 2T FORCED it was 96% (in all cases N > 60,000). In 2T FREE trials the monkey selected the more valuable target 90% of the time, indicating that he understood the meaning of the stimulus cues. We found that movement times (MT) were shorter to higher-valued targets in 1T trials (400 ms to high-value and 416 ms to low-value targets). Although the difference was small, it was significant (Kolmogorov–Smirnov test (KS), p < 0.01). RTs in 1T trials did not depend on target value (KS-test p > 0.05 for all comparisons).
We observed an interaction effect between RT and trajectory kinematics in 2T trials. Trajectories belonging to short RT trials were generally more curved than trajectories belonging to medium or long RT trials (Figure 2A). This effect was accentuated by the value of the unselected target with respect to the value of the selected target in the FORCED condition. Trajectories in the FORCED LOW condition (Figure 2A, rightmost panel) were generally more curved than the ones in the FORCED HIGH or FREE HIGH conditions (Figure 2A, left and middle panels). These curved movements have an initial launching direction toward the target that vanishes and are corrected later to the remaining target. To quantify this we obtained the mean trajectory IDV across all conditions (Figure 2B). We observed that a great deal of the curvature in FORCED LOW trials was due to movements launching to the target that becomes unavailable after GO (High value). This effect was particularly strong for short RT trials and moderate for intermediate RT trials. Long RT trials were essentially straight toward the remaining target (Figure 2B, rightmost panel). We didn't see this effect when the monkey was forced to move to the high value target or when the monkey was free to choose among the two targets, because in either situation the preferred and available target were the same. We further investigated the interaction between RT, relative value, and initial launching direction by comparing raw RT distributions. The mean RTs in FREE HIGH (266 ms, light-brown dashed histogram), FORCED HIGH (271 ms, dark-brown dashed histogram), and FORCED LOW (279 ms, black dashed histogram), were very similar (Figure 2D) with only small differences between the mean RTs in FREE HIGH and FORCED LOW distributions (KS-test, p < 0.01). This could be due to the contribution of a higher proportion of correct trials in FREE HIGH than in FORCED LOW trials (3% difference). Most importantly we observed that the mean RT in FORCED LOW trials with “direct” trajectories (red histogram, 291 ms) was significantly longer (21 ms difference, KS-test, p < 0.01) than the mean RT in FORCED LOW trials with “curved” trajectories (blue histogram, 270 ms). In comparison, FORCED LOW “curved” trials and FORCED HIGH trials did not show RT differences (KS-test, p > 0.05) (Figure 2D).
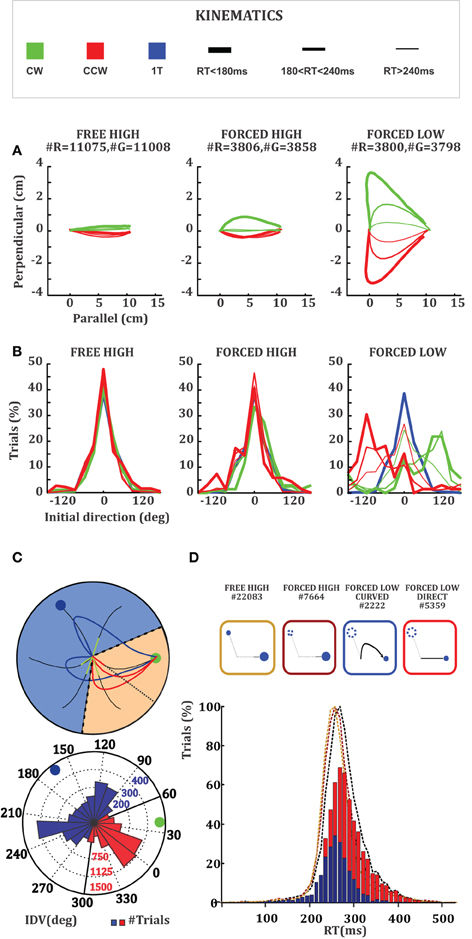
Figure 2. (A) Average trajectories for 2T trials with the unselected target located 120° clockwise (red) or counterclockwise (green) to the selected target (always on the right). The three panels from left to right represent FREE, FORCED HIGH, and FORCED LOW trials. The line thickness represents trials classified by their RT. Thick lines correspond to long RT (>240 ms), medium sized lines to intermediate RT (between 180 and 240 ms) and thin lines short RT (<180 ms) (See Method sections for details). (B) Distribution of initial launching directions, with selected target at 0°. The color and line thickness code is the same as in Figure 2A. Blue histograms represent 1T trials to the selected target. (C) Method used to classify trials as direct (red) or curved (blue). The top panel shows individual FORCED LOW trials when the remaining target is to the right and the vanished target is to the upper left. Small arrows indicate the IDVs and the red region indicates the 120° angle around the average, within which trials were considered to be “direct.” The bottom panel shows a rose plot of the distribution of individual IDVs. (D) The RT distributions of FORCED LOW (black dash) trials, including FORCED LOW “direct” (red solid) and “curved” (blue solid) trials along with the RT distributions of FREE HIGH (light brown dash) and FORCED HIGH (dark brown dash).
Neural Results
PMd Activity Predicts Switching of Motor Plans Ahead of Movement Onset
Activity was recorded from 327 cells from the arm area of PMd (Figure 1B) of which 226 (69%) had significant directional tuning during at least one epoch (DELAY, MT, THT) and were considered task-related. Here, we focus on cells with DELAY-period tuning (181/226, 80%), 52 of which (29%) were modulated by relative value combinations during DELAY (One-Way ANOVA, p < 0.05) and were considered further for the plan-switch analyses (relative value, RV cells). In the first variant of this analysis we compared neural activity in FORCED LOW versus FREE HIGH conditions (FORCED-FREE). Figures 3A–C shows three individual cells illustrating the different types of plan-switch analyses. In a SwitchPT2OT (Figure 3A) we compare trials that had a pre-GO plan to PT and a post-GO plan to OT (FORCED LOW PT2OT, green trace) with trials that had both a pre-GO and post-GO plan to PT (FREE HIGH PT, red trace). In a SwitchOT2PT (Figure 3B) we compare trials with a pre-GO plan to OT and a post-GO plan to PT (FORCED LOW OT2PT, blue trace) with trials that had both a pre-GO and post-GO plan to OT (FREE HIGH OT, pink trace). In a convergence (CONV) the pre-GO plan is different for two types of trials (FORCED LOW OT2PT and FREE HIGH PT) but is the same (movement plant to PT) after the GO signal (Figure 3C). Figures 3D–G show additional examples that had statistically significant plan switches at the individual cell level. Thirty-seven of the 52 (71%) RV cells showed statistically significant modulation (sliding ANOVA p < 0.05) in at least one plan-switch analysis in the FORCED-FREE latency comparison and are referred to as Switch cells. Switches of activity of the other cells did not reach statistical significance, often because those cells were recorded during only a few trials of each type.
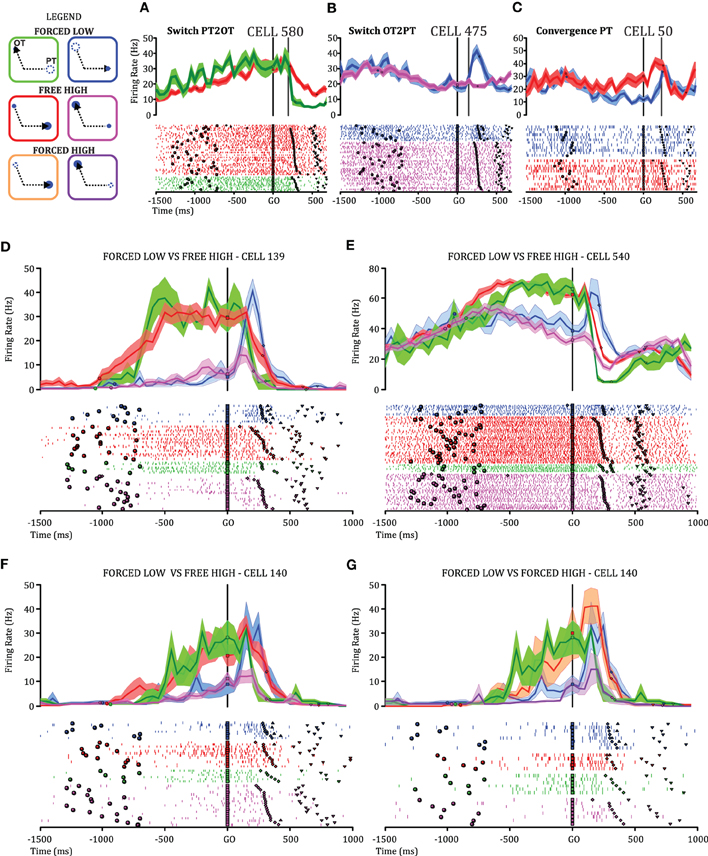
Figure 3. Top-left: The different types of trials are represented in color boxes. Target position is indicated by a blue circle in PT or in OT. The target value is indicated by circle size. In a “FORCED LOW” condition the most valuable option disappears after the GO signal (dashed circles) giving rise to two possibilities: whether the target with the larger value (big circle) was the cell's PT (green box) or the other target (blue box). In both cases the monkey is forced to move to the remaining option (small circle). We compare these trials with “FREE HIGH” trials, in which the monkey is free to choose the target located either in PT or OT (red or pink) and selects the option with higher value (FORCED-FREE comparison). We also separately compare FORCED LOW trials with “FORCED HIGH” trials in which the target that disappeared after the GO signal was the less valuable one (orange and violet) (FORCED-FORCED comparison). In all panels bold black arrowheads indicate the selected option. (A–G) Examples of the activity of individual cells illustrating the switching of movement plans observed between the pre-GO and the post-GO period. Cell activity is depicted as firing-rate histograms, with mean ± s.t.e., and rasters in which black marks indicate cue onset, go signal, movement onset and offset, with trials sorted by RT. A switch from PT to OT (SwitchPT2OT) is seen by comparing trials that have a pre-GO plan to PT and a post-GO plan to OT (green) with trials that have both a pre-GO and post-GO plan to PT (red). The time of the switch is indicated by a gray vertical bar (only in Figures 1A–C for simplicity). The alignment of activity on the GO signal for rasters and firing rate histograms is indicated by a black vertical bar in all panels. A switch from OT to PT (SwitchOT2PT) is seen by comparing trials that have a pre-GO plan to OT and a post-GO plan to PT (blue) with trials that have both a pre-GO and post-GO plan to OT (pink). The time of convergence to a plan in the PT direction (CONV) is found by comparing trials with a pre-GO and post-GO plan to PT (red) with trials with a pre-GO plan to OT but a post-GO plan to PT (blue). Convergence to an OT plan cannot be determined from the activity of cells because activity to OT is generally low.
To address the role of visual input (the number of targets remaining after GO) on the plan-switching process, we also compared FORCED LOW versus FORCED HIGH conditions (FORCED-FORCED comparison). Figures 3F–G illustrates a single cell example in which plan switches were obtained both for the FORCED-FREE comparison (Figure 3F) and for the FORCED-FORCED comparison (Figure 3G). Twenty-eight out of 52 (54%) RV cells showed statistically significant modulation to plan switches in the FORCED-FORCED comparison. Table 1 summarizes the cell counts for the different types of switch in both comparisons.
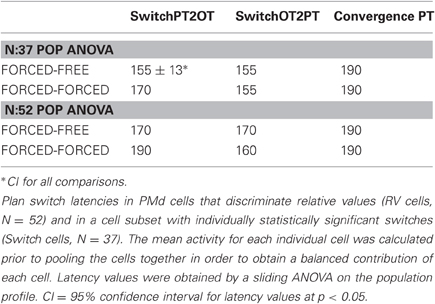
To test whether the plan-switch pattern observed at the individual cell level also held at the population level, we obtained the population profile for plan-switching in Switch Cells and all RV cells separately and for both FORCED-FREE (Figures 4A–B) and FORCED-FORCED (Figures 4C–D) comparisons. We observed that the latency of SwitchPT2OT and SwitchOT2PT for Switch Cells was 155 ± 13 ms (95% CI) after the GO signal and, therefore, well before MO (300 ± 50 ms) in both FORCED-FREE and FORCED-FORCED comparisons (Figures 4E–F). Convergence to a plan occurred later, 190 ms ± 13 ms after the GO signal, but still well-ahead of MO. These results held for both the Switch cell or RVcell populations, although we observed that switch latencies in the larger RV cell population were later than in the Switch cell population by about 15–20 ms (this difference did not reach statistical significance, ANOVA p > 0.05), and was presumably due to the presence, in the RV population, of cells with very few trials resulting in a larger standard error. Table 2 summarizes the latency results for each cell population and comparison.
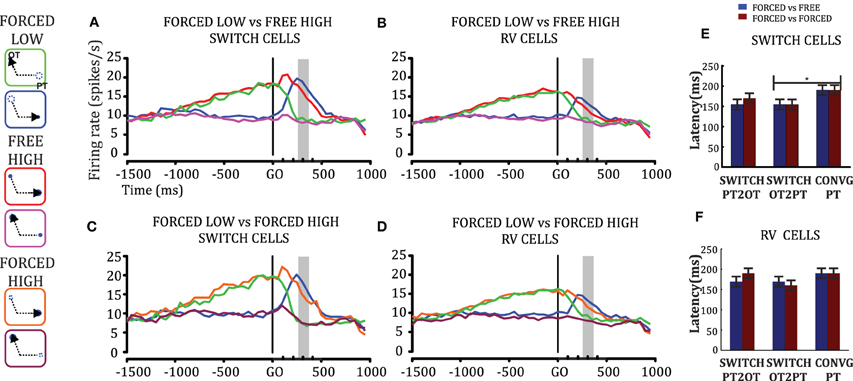
Figure 4. Population activity. Cells with statistically significant plan switches (Switch Cells, N = 37) and all cells discriminating relative values (RV Cells, N = 52) were examined separately for switch latencies in the FORCED vs. FREE (A–B) and FORCED vs. FORCED comparisons (C–D). The gray bar indicates the time range of movement onset. The legend has the same color code as in Figures 3E–F. Comparison of the latencies of SwitchPT2OT, SwitchOT2PT, and CONV in these two groups of cells in FORCED-FREE (blue bars) and FORCED-FORCED comparisons (brown bars). The horizontal line above the histograms represent comparisons that were statistically significant (ANOVA, p < 0.05).
PMd Contribution to Kinematics Prior to Movement Onset (Initial Direction) is Observed in Situations where there is no Relative Value Bias
We examined the cell responses in the plan-switch paradigm taking into account the initial direction of the reach movements in each trial. By doing so we classified trajectories as initially aiming to the selected target (“direct,” to PT or OT) or initially aiming to the unselected target (“curved”). We compared both direct and curved movements in the conditions that were more likely to provoke curvatures due to plan-switches, namely the FORCED LOW and FORCED EQUAL conditions. Figures 5A–C shows population histograms for Switch cells and RV cells, comparing FORCED LOW direct and curved trials. We observed that curvature is not predicted by DELAY activity in the FORCED LOW condition. We did not observe statistically significant differences either between activity in the FORCED LOW PT2OT direct trials and FORCED LOW PT2OT curved trials, or between FORCED LOW OT2PT direct and FORCED LOW PT2OT curved (ANOVA, p > 0.05 in both cases). However, DELAY activity in the FORCED EQUAL conditions does predict whether a trial will be curved or straight. During the 600 ms prior to the GO signal, we observed statistically significant differences (ANOVA, p < 0.05) between FORCED EQUAL direct and FORCED EQUAL curved trials, for both Switch cell and RV cell populations (Figures 5D–F). It is noteworthy to mention that these differences take place only during DELAY prior to the monkey's knowledge of which target will disappear (GO), and reflect pre-GO selection biases. That is, among the FORCED EQUAL trials there are some in which the pre-GO activity happens to be strongly biased toward one target, and when that target disappears, the bias is likely to cause a curved movement (green and blue traces).
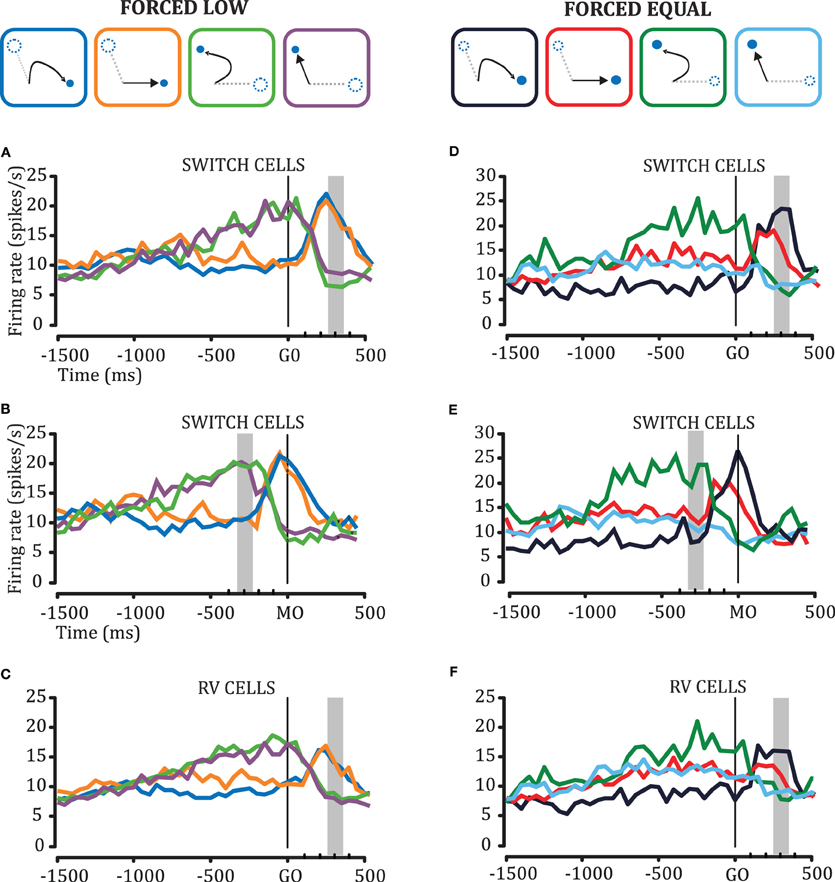
Figure 5. Cell responses in the plan switch paradigm taking into account the initial direction of the reach movements in each trial. (A–C) Comparison of direct and curved movements in the FORCED LOW condition for Switch Cells(A–B) and RV Cells(C). Trajectories are classified as curved to PT (blue box), curved to OT (green box), direct to PT (orange), or direct to OT (violet). (D–F) Comparison of straight and curved movements in the FORCED EQUAL condition for Switch Cells(D–E) and RV Cells(F). Trajectories are classified as curved to PT (dark blue box), curved to OT (dark green box), direct to PT (magenta) or direct to OT (cyan). In panels A, C, D, and F the data is aligned on GO and the gray bar represents the time range of movement onset. Panels B and E replot the data in A and D, respectively, with alignment on movement onset (MO), and the grey bar indicates the time range of the GO signal.
Note that, as shown in Figures 5B,E, when we align activity on the MO we can see that the switch of the plan (computed at the population level) occurs approximately 150 ms before MO. This is interesting because in the curved trials the monkey still launches to the now non-existent target.
A Biased Competition Model can Reproduce the Dynamics of the Plan-Switch
Cisek (2006) described a “biased competition” model of action selection, in which populations of cells along the dorsal stream implement a distributed representation of potential actions that compete against each other through lateral inhibition (Figure 6A, see Methods). The model simulates relative value effects reported previously when reward-related biasing signals are introduced into PFC (Pastor-Bernier and Cisek, 2011). Here, we used the same model to simulate plan switches by removing one of the two presented targets at the beginning of the GO epoch and by letting the activity in PMd gradually spill into the M1 layer (see Methods). Figure 6D shows the activity of a simulated neuron illustrating plan switches from OT2PT, PT2OT, and convergence to PT. Note that the timing of the PT2OT and OT2PT plan switches occur simultaneously and prior to MO. This is also the case for convergence to PT. These results are compatible with the experimental data and suggest that PMd contains all the information concerning the final action plan before MO. Figure 6B shows RT distributions from FORCED LOW simulations for trials in which the model launched toward the target that vanished (blue) or the remaining target (red). We observe that RTs are shorter for trials initiated toward the vanishing target, in agreement with behavioral data (Figure 2D). Figure 6C shows the distribution of initial launching directions. Note that the blue distribution (which comprises the majority of early RT trials) is aimed toward the target that vanished, predicting that if the model were equipped with online feedback during the movement itself, it would produce curved trajectories as in the behavioral data. Figure 6E shows the model's Parietal, PFC (rostral and caudal), PMd (rostral to caudal), and M1 population patterns of activity during a FORCED LOW trial where we observe a plan switch that is completed before MO. In contrast, in the trial shown in Figure 6F, the model launches the movement before the plan switch is complete. We observe that the timing of plan switches in all PMd layers is before MO, in agreement with our experimental results.
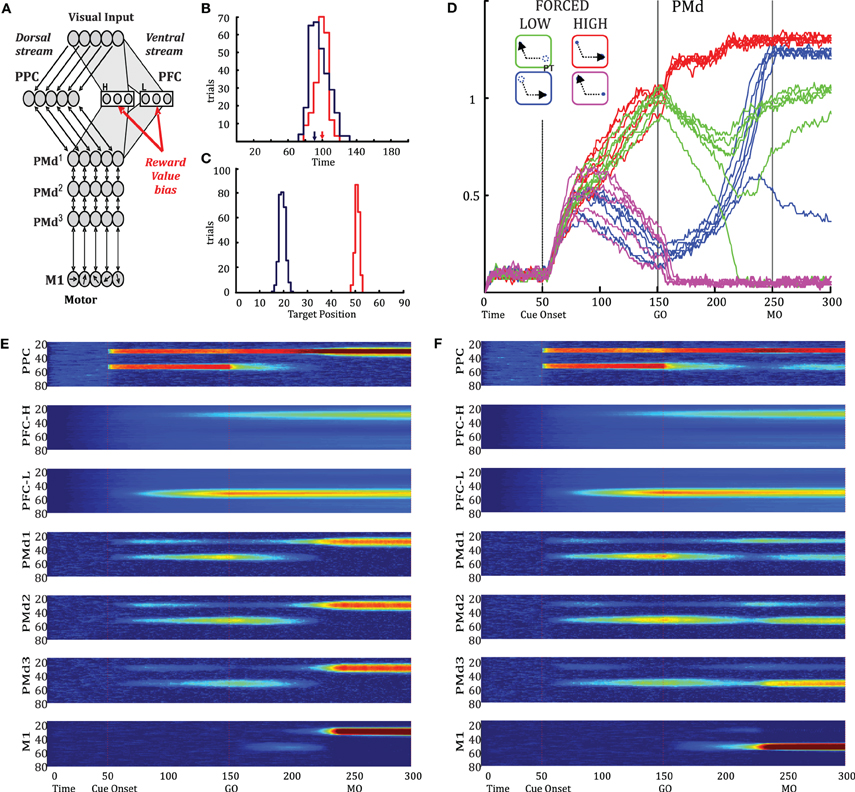
Figure 6. (A) Model of action selection, in which populations of cells along the dorsal stream implement a distributed representation of potential actions that compete against each other through lateral inhibition. Each population is modeled as a set of tuned neurons with “on-center-off-surround” recurrent connectivity. The model includes posterior parietal cortex (PPC), prefrontal cortex (PFC), three regions of PMd (rostral to caudal), and primary motor cortex (M1). Biasing signals related to absolute reward value (High, H or Low, L) enter as independent inputs to particular PFC layers (PFC-H, PFC-L). (B) RT distributions for trials in which the model launched to the target that vanished (blue) or to the remaining target (red). (C) Initial launching directions toward the vanishing target (blue, at position 20) or remaining target (red, at position 50). (D) A simulated neuron showing activity during four compared conditions: FORCED LOW OT2PT (blue), FORCED HIGH OT (purple), FORCED LOW PT2OT (green), and FORCED HIGH PT (red). Individual lines represent individual simulated trials. (E) Patterns of activity in the model's Parietal, PFC, PMd (rostral to caudal) and M1 populations, during a FORCED LOW trial in which the target at position 50 was more valuable but vanished at the time of the GO signal, and the plan switch was completed prior to MO. (F) Patterns of activity in another FORCED LOW trial, but in which the movement was launched before the plan switch was complete, initiating to the target at position 50.
Discussion
Recent studies have shown that while a monkey is deciding between two potential reaching movements, neural activity in the dorsal PMd can specify both movements simultaneously (Cisek and Kalaska, 2002, 2005; Klaes et al., 2011), and the neural representations of these movements are modulated by their relative subjective desirability (Pastor-Bernier and Cisek, 2011). These findings suggest that decisions between reaching actions are made within the same brain regions involved in the execution of the actions themselves, in agreement with research on reaching (Cisek, 2007; Pesaran et al., 2008; Cisek and Kalaska, 2010) and oculomotor control (for reviews, see Glimcher, 2003; Gold and Shadlen, 2007). In fact, decisions about eye movements appear to involve even the superior colliculus, a brainstem structure that is just two synapses away from the motor neurons that move the eye (Basso and Wurtz, 1998; Carello and Krauzlis, 2004; Horwitz et al., 2004; Ignashchenkova et al., 2004; Thevarajah et al., 2009).
However, the finding that decision variables (such as relative value) influence neural activity in sensorimotor regions does not necessarily imply that these same cells continue to be involved in the on-line guidance of movement. It is plausible that once a decision is made and an action is launched toward a given target, the decision-related cells fall silent while a separate circuit becomes responsible for guiding movement toward the selected target. The results presented here suggest that this is not the case. We found that the very same PMd cells previously shown to reflect relative value during a delay period continue to update their activity to reflect when the monkey changes its plan during situations in which a previously selected action becomes unavailable. This argues against the distinction between regions responsible for choosing an action and those responsible for its guidance through on-line feedback, and in favor of the hypothesis that decisions emerge through a competition within the same circuit that guides movement execution (Cisek, 2007).
A number of earlier studies provide converging evidence consistent with this integrated view. For example, it has been shown that humans and monkeys can quickly and smoothly update their movement plans when the location of the reach target suddenly and unpredictably changes (Georgopoulos et al., 1981, 1983; Prablanc and Martin, 1992; Desmurget et al., 1999; Day and Lyon, 2000; Archambault et al., 2009, 2011; Gritsenko et al., 2011), even when they are not consciously aware of the change. During these “target jump” experiments, neural activity in fronto-parietal cortex smoothly transitions between the original and final motor plan (Archambault et al., 2009, 2011), without any “refractory period” for aborting the previous plan before preparing a new one. Among the regions tested, the earliest changes in neural activity were found in PMd, in which 50% of cells reflected the new plan about 140 ms after a target jump, followed by M1 at 180 ms and dorsal area 5 at 200 ms (Archambault et al., 2011). This is comparable to the latency of responses to target jumps in earlier studies by Georgopoulos et al. (1983), who observed latencies of about 130–150 ms in the rostral part of M1.
Interestingly, the neural latencies to target jumps are comparable to the latencies of plan switches observed in PMd in our study—about 155 ms for both increases (SwitchOT2PT) and decreases of activity (SwitchPT2OT). They are also comparable to the latencies reported by Wise and Mauritz (1985) in a study in which the stimulus that instructed the plan switches was presented during the delay period, well before the GO signal. In that study, it was found that PMd cells reflected the switch with a median latency of 140–150 ms. In other words, the latency with which neural activity in PMd reflects a plan change is approximately 140–150 ms after the sensory stimulus which instructs that plan change. This holds true regardless of whether that stimulus is the change of a target from one location to another during the delay period (Wise and Mauritz, 1985), the displacement of a target during RT or movement (Georgopoulos et al., 1983; Archambault et al., 2009, 2011), or the offset of a PT that leaves only a less-desirable one available (present study). Furthermore, we found that the latency at which cells became suppressed when their PT disappeared (SwitchPT2OT) was not statistically different than the latency with which their discharge increased when their PT, which was initially less desirable, suddenly became the only remaining option (SwitchOT2PT). The similarity of these neural latencies across different experimental conditions demonstrates that in all cases, neural activity in PMd remains sensitive to new information pertinent to available actions and their values. This suggests a view whereby sensory information continuously flows into the motor system (Coles et al., 1985; Cisek, 2007), as opposed to a view of separate computational stages involved in canceling one motor program and computing a new one.
The neural processes of canceling a planned movement have been studied in the frontal eye fields (Hanes et al., 1998), superior colliculus (Pare and Hanes, 2003) and for arm-reaching studies in the supplementary motor area (SMA), pre-SMA (Scangos and Stuphorn, 2010) and PMd (Mirabella et al., 2011) using the countermanding task (Logan et al., 1984). In this task, subjects are asked to make a saccade or reach to a target, but to inhibit the movement if an infrequent STOP-signal is presented after a variable delay following the GO signal. As the delay increases, it becomes increasingly difficult to successfully inhibit the movement, making it possible to estimate a given subject's “stop-signal reaction time” (SSRT). Although many cortical areas such as motor cortex (M1) and supplemental cortical areas (pre-SMA and SMA) harbor neurons with DELAY activity related to movement planning (Okano and Tanji, 1987) it is unlikely that these areas are involved in processes causally related to movement cancellation because their responses to a stop signal take place after the SSRT (Scangos and Stuphorn, 2010). In contrast, Mirabella et al. (2011) found that during successful STOP trials, neurons in PMd show activity changes prior to the SSRT, making it possible that this region is involved in inhibiting the movement. This is consistent with the findings reported here that the suppression of PMd activity tuned to the target which vanished (SwitchPT2OT) occurs well before MO.
Our behavioral results are compatible with the proposal that at the end of the DELAY period, the movement to the higher-valued target is more strongly prepared than the movement to the lower-valued target. When the higher target disappears in a FORCED LOW trial, then one of two things can happen. If the RT is short, then the movement initiates toward the location of the unavailable target and the monkey must later turn around (curved trials, Figure 2D blue). If the RT is long, then the monkey completes his plan switch and initiates directly to the remaining target (direct trials, Figure 2D red). Nevertheless, what is surprising is that in both cases, neural activity in PMd already clearly reflects the change of plan more than 150 ms before the MO. This can be seen in Figures 5A,B. For example, the green traces illustrate trials in which the monkey initiated the movement toward the PT of recorded cells, which was the more valuable of the targets present during the DELAY. However, that target vanished and so the monkey curved its movement trajectory and arrived at the remaining target. Although the neural activity becomes suppressed within 200 ms of the GO signal, reflecting the change of plan away from the PT, the initial movement some 100 ms later is still launched in the direction of the original plan. This happens most often during trials with short RTs (Figures 2B,D) suggesting that the motor system has a certain “inertia” that cannot be easily overcome. That is, movement initiation and muscle contraction could be starting to take place shortly after the GO signal despite the possibility that the more desirable choice will become unavailable. In this sense, the short-RT curved movements would be a natural consequence of the monkey's impulsivity and a strategy of reaching quickly and correcting the trajectory when necessary. In FORCED LOW trials, we found no significant difference in PMd activity between curved versus direct trials (Figures 5A–C), suggesting that other regions (presumably M1) may be more strongly responsible for determining whether the movement launches toward the initially selected or not. In FORCED EQUAL trials, we did observe differences in PMd activity when comparing curved versus direct movements (Figures 5D–F), but we believe this is simply due to selection bias: Curved movements (dark blue and green traces) are more likely to occur when the monkey happens to be strongly biased during DELAY toward the target that vanished, while direct movements could result equally from trials in which DELAY activity is biased to the PT, the OT, or neither, and the average DELAY activity of these three groups of trials will lie somewhere in the middle (red and cyan traces).
Cisek (2006) described a model of biased competition between action plans, which was originally designed to capture neural data on the simultaneous specification of multiple movements (Cisek and Kalaska, 2005) and behavioral data on the distributions of initial directions in short-RT pointing tasks (Favilla, 1997; Ghez et al., 1997). That same model, without any changes in parameters, was able to simulate more recent data on the modulation of PMd activity by relative subjective desirability (Pastor-Bernier and Cisek, 2011). In the model, potential actions are encoded as hills of activity in populations of directionally tuned neurons with short-range mutual excitation between similarly tuned cells and long-range lateral inhibition among cells with different tuning. The distance dependence of these lateral interactions is responsible for producing both the distance-dependent distributions of initial reach directions (Favilla, 1997; Ghez et al., 1997) and the distance-dependent influence of the value of one target on the PMd activity related to another (Pastor-Bernier and Cisek, 2011). That same model, only slightly modified with a gradual GO signal, is also able to reproduce our current results on plan switches (Figure 6D) and the distributions and timing of initial launching directions (Figures 6B,C). Note, however, that the model makes no attempt whatsoever to explain activity after MO—it includes no dynamics for producing or guiding movement, and its M1 activity should only be interpreted as capturing the initial pattern around the time of MO. Nevertheless, despite the absence of any movement production mechanisms in the present form of the model, it is consistent with models in which the movement trajectory is generated through continuous feedback via proprioceptive and visual signals (Bullock and Grossberg, 1988; Bullock et al., 1998; McIntyre and Bizzi, 1993; Burnod et al., 1999; Shadmehr and Wise, 2005) and through internal forward models (Bullock et al., 1993; Miall and Wolpert, 1996; Shadmehr et al., 2010). The model is compatible with general theories proposing that movements unfold as a dynamical system that is guided by the continuously updated pattern of activity within a distributed sensorimotor map. These patterns of activity can be shaped by a variety of processes, including attention (Tipper et al., 1998; Baldauf and Deubel, 2010), decision-variables (Cisek, 2007), and continuous spatial information from the dorsal visual stream (Goodale and Milner, 1992; Milner and Goodale, 1995; Desmurget et al., 1999; Day and Lyon, 2000).
That a relatively simple “biased competition” model can explain this fairly large set of data is particularly interesting given that the same mechanism is often used to explain the neural mechanisms of spatial attention (Desimone and Duncan, 1995; Boynton, 2005). This supports the conjecture (Allport, 1987; Rizzolatti et al., 1987; Neumann, 1990; Duncan, 2006; Cisek, 2007) that both attention and decision-making are related aspects of a general process of selection necessary to arbitrate between the many demands and opportunities for action that animals are continuously faced with in their natural environment. In this view, sensory information is continuously winnowed along the dorsal stream as it is converted into information specifying potential actions and ultimately guiding their execution. In all cases, this winnowing process involves a biased competition, but the specific dynamics of the process may be somewhat different in different brain regions.
For example, Louie et al. (2011) showed that activity in LIP was best described as
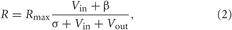
where R is the firing rate, Rmax is the maximum firing rate, Vin is the value of targets in the receptive field, Vout is the total value of targets outside the receptive field, and β and σ are the baseline activity and semi-saturation terms, respectively, (see Reynolds and Heeger, 2009). Note that, as shown by Grossberg (1973), the normalization computation described by Equation (2) can be produced by the steady-state solution of Equation (1) if the excitation term E is equal to Vin and the inhibition term I is equal to Vout (see Cohen and Grossberg, 1983, for a proof of Lyapunov stability for a general class of such networks). In other words, divisive normalization may result from the competitive interactions within neural populations.
Louie et al. (2011) found that to explain their LIP data, the parameter σ had to be large, implying incomplete normalization such that LIP cells exhibited value-related modulation even with a single target. In contrast, our results suggest that PMd exhibits complete or nearly complete divisive normalization, because in the 1T task we found no value-related modulation whatsoever (Pastor-Bernier and Cisek, 2011), as if the σ parameter is zero. This raises the intriguing question of whether partial divisive normalization is the trend in parietal cortex, which is still far from overt execution, while activity is more fully normalized in regions closer to motor output, such as PMd. This would make good sense if PMd is most closely related to the process of final arbitration between potential actions, but a deeper understanding of these differences between LIP and PMd requires further investigation.
To summarize, we found evidence that PMd neurons, which appear to be involved in the competition determining the initial selection of action, continue to take part in action selection after MO, reflecting a change of plan when a selected target becomes unavailable. This finding is compatible with previous studies of plan changes during the delay period (Wise and Mauritz, 1985) and during target jump paradigms (Georgopoulos et al., 1983; Archambault et al., 2009, 2011), as well as with the suggestion that PMd activity may be causally involved in the voluntary inhibition of movement (Mirabella et al., 2011). Taken together, these results provide support for the general hypothesis that the brain mechanisms for selecting between actions involve the same circuits that guide the execution of the actions during overt behavior.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Marie-Claude Labonté for technical support and Pascal Poisson-Fortier for valuable comments regarding the manuscript and analyses. This work was supported by research grants from the Canadian Institutes of Health Research and the EJLB Foundation, a GRSNC doctoral fellowship to Alexandre Pastor-Bernier, and an infrastructure grant from the Fonds de la recherche en Santé du Québec.
References
Allport, D. A. (1987). “Selection for action: some behavioral and neurophysiological considerations of attention and action,” in Perspectives on Perception and Action, eds Heuer, H., Sanders, A. F. (Hillsdale, NJ: Lawrence Erlbaum Associates), 395–419.
Archambault, P. S., Caminiti, R., and Battaglia-Mayer, A. (2009). Cortical mechanisms for online control of hand movement trajectory: the role of the posterior parietal cortex. Cereb. Cortex 19, 2848–2864.
Archambault, P. S., Ferrari-Toniolo, S., and Battaglia-Mayer, A. (2011). Online control of hand trajectory and evolution of motor intention in the parietofrontal system. J. Neurosci. 31, 742–752.
Baldauf, D., and Deubel, H. (2010). Attentional landscapes in reaching and grasping. Vision Res. 50, 999–1013.
Basso, M. A., and Wurtz, R. H. (1998). Modulation of neuronal activity in superior colliculus by changes in target probability. J. Neurosci. 18, 7519–7534.
Bracewell, R. M., Mazzoni, P., Barash, S., and Andersen, R. A. (1996). Motor intention activity in the macaque's lateral intraparietal area. II. Changes of motor plan. J. Neurophysiol. 76, 1457–1464.
Bullock, D., Cisek, P., and Grossberg, S. (1998). Cortical networks for control of voluntary arm movements under variable force conditions. Cereb. Cortex 8, 48–62.
Bullock, D., and Grossberg, S. (1988). Neural dynamics of planned arm movements: emergent invariants and speed-accuracy properties during trajectory formation. Psychol. Rev. 95, 49–90.
Bullock, D., Grossberg, S., and Guenther, F. H. (1993). A self-organizing neural model of motor equivalent reaching and tool use by a multijoint arm. J. Cogn. Neurosci. 5, 408–435.
Burnod, Y., Baraduc, P., Battaglia-Mayer, A., Guigon, E., Koechlin, E., Ferraina, S., Lacquaniti, F., and Caminiti R. (1999). Parieto-frontal coding of reaching: an integrated framework. Exp. Brain Res. 129, 325–346.
Carello, C. D., and Krauzlis, R. J. (2004). Manipulating intent: evidence for a causal role of the superior colliculus in target selection. Neuron 43, 575–583.
Cisek, P. (2006). Integrated neural processes for defining potential actions and deciding between them: a computational model. J. Neurosci. 26, 9761–9770.
Cisek, P. (2007). Cortical mechanisms of action selection: the affordance competition hypothesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 362, 1585–1599.
Cisek, P., Crammond, D. J., and Kalaska, J. F. (2003). Neural activity in primary motor and dorsal premotor cortex in reaching tasks with the contralateral versus ipsilateral arm. J. Neurophysiol. 89, 922–942.
Cisek, P., and Kalaska, J. F. (2002). Simultaneous encoding of multiple potential reach directions in dorsal premotor cortex. J. Neurophysiol. 87, 1149–1154.
Cisek, P., and Kalaska, J. F. (2005). Neural correlates of reaching decisions in dorsal premotor cortex: specification of multiple direction choices and final selection of action. Neuron 45, 801–814.
Cisek, P., and Kalaska, J. F. (2010). Neural mechanisms for interacting with a world full of action choices. Annu. Rev. Neurosci. 33, 269–298.
Cohen, M. A., and Grossberg, S. (1983). Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Man Cybern. SMC−13, 815–826.
Coles, M. G., Gratton, G., Bashore, T. R., Eriksen, C. W., and Donchin, E. (1985). A psychophysiological investigation of the continuous flow model of human information processing. J. Exp. Psychol. Hum. Percept. Perform. 11, 529–553.
Cos, I., Belanger, N., and Cisek, P. (2011). The influence of predicted arm biomechanics on decision making. J. Neurophysiol. 105, 3022–3033.
Dacorogna, M., Gençay, R., Müller, U., and Pictet, O. (2001). Effective return, risk aversion and drawdowns. Physica A Stat. Mech. Appl. 289, 229–248.
Day, B. L., and Lyon, I. N. (2000). Voluntary modification of automatic arm movements evoked by motion of a visual target. Exp. Brain Res. 130, 159–168.
Desimone, R., and Duncan, J. (1995). Neural mechanisms of selective visual attention. Annu. Rev. Neurosci. 18, 193–222.
Desmurget, M., Epstein, C. M., Turner, R. S., Prablanc, C., Alexander, G. E., and Grafton, S. T. (1999). Role of the posterior parietal cortex in updating reaching movements to a visual target. Nat. Neurosci. 2, 563–567.
Duncan, J. (2006). EPS mid-career award 2004: brain mechanisms of attention. Q. J Exp. Psychol. (Colchester.) 59, 2–27.
Erlhagen, W., and Schoner, G. (2002). Dynamic field theory of movement preparation. Psychol. Rev. 109, 545–572.
Fagg, A. H., and Arbib, M. A. (1998). Modeling parietal-premotor interactions in primate control of grasping. Neural Netw. 11, 1277–1303.
Favilla, M. (1997). Reaching movements: concurrency of continuous and discrete programming. Neuroreport 8, 3973–3977.
Georgopoulos, A. P., Kalaska, J. F., Caminiti, R., and Massey, J. T. (1983). Interruption of motor cortical discharge subserving aimed arm movements. Exp. Brain Res. 49, 327–340.
Georgopoulos, A. P., Kalaska, J. F., and Massey, J. T. (1981). Spatial trajectories and reaction times of aimed movements: effects of practice, uncertainty, and change in target location. J. Neurophysiol. 46, 725–743.
Ghez, C., Favilla, M., Ghilardi, M. F., Gordon, J., Bermejo, R., and Pullman, S. (1997). Discrete and continuous planning of hand movements and isometric force trajectories. Exp. Brain Res. 115, 217–233.
Glimcher, P. W. (2003). The neurobiology of visual-saccadic decision making. Annu. Rev. Neurosci. 26, 133–179.
Gold, J. I., and Shadlen, M. N. (2007). The neural basis of decision making. Annu. Rev. Neurosci. 30, 535–574.
Goodale, M. A., and Milner, A. D. (1992). Separate visual pathways for perception and action. Trends Neurosci. 15, 20–25.
Gritsenko, V., Kalaska, J. F., and Cisek, P. (2011). Descending corticospinal control of intersegmental dynamics. J. Neurosci. 31, 11968–11979.
Grossberg, S. (1973). Contour enhancement, short term memory, and constancies in reverberating neural networks. Stud. Appl. Math. 52, 213–257.
Hanes, D. P., Patterson, W. F. 2nd, and Schall, J. D. (1998). Role of frontal eye fields in countermanding saccades: visual, movement, and fixation activity. J. Neurophysiol. 79, 817–834.
Hansen, P. R., and Lunde, A. (2006). Realized variance and market microstructure noise. Bus. Econ. Stat. 24, 127–161.
Herrnstein, R. J. (1961). Relative and absolute strength of response as a function of frequency of reinforcement. J. Exp. Anal. Behav. 4, 267–272.
Horwitz, G. D., Batista, A. P., and Newsome, W. T. (2004). Representation of an abstract perceptual decision in macaque superior colliculus. J. Neurophysiol. 91, 2281–2296.
Ignashchenkova, A., Dicke, P. W., Haarmeier, T., and Thier, P. (2004). Neuron-specific contribution of the superior colliculus to overt and covert shifts of attention. Nat. Neurosci. 7, 56–64.
Kim, J. N., and Shadlen, M. N. (1999). Neural correlates of a decision in the dorsolateral prefrontal cortex of the macaque. Nat. Neurosci. 2, 176–185.
Klaes, C., Westendorff, S., Chakrabarti, S., and Gail, A. (2011). Choosing goals, not rules: deciding among rule-based action plans. Neuron 70, 536–548.
Logan, G. D., Cowan, W. B., and Davis, K. A. (1984). On the ability to inhibit simple and choice reaction time responses: a model and a method. J. Exp. Psychol. Hum. Percept. Perform. 10, 276–291.
Louie, K., Grattan, L. E., and Glimcher, P. W. (2011). Reward value-based gain control: divisive normalization in parietal cortex. J. Neurosci. 31, 10627–10639.
McIntyre, J., and Bizzi, E. (1993). Servo hypotheses for the biological control of movement. J. Mot. Behav. 25, 193–202.
Miall, R. C., and Wolpert, D. M. (1996). Forward models for physiological motor control. Neural Netw. 9, 1265–1279.
Milner, A. D., and Goodale, M. A. (1995). The Visual Brain in Action. Oxford: Oxford University Press.
Mirabella, G., Pani, P., and Ferraina, S. (2011). Neural correlates of cognitive control of reaching movements in the dorsal premotor cortex of rhesus monkeys. J. Neurophysiol. 106, 1454–1466.
Müller, U. (1993). Statistics of Variables Observed Over Overlapping Intervals Internal Document UAM. 1993−06−18. Olsen and Associates. Available at http://citeseer.ist.psu.edu/muller93statistics.html
Neumann, O. (1990). “Visual attention and action,” in Relationships Between Perception and Action: Current Approaches, eds Neumann, O., Prinz, W. (Berlin: Springer-Verlag), 227–267.
Okano, K., and Tanji, J. (1987). Neuronal activities in the primate motor fields of the agranular frontal cortex preceding visually triggered and self-paced movement. Exp. Brain Res. 66, 155–166.
Pare, M., and Hanes, D. P. (2003). Controlled movement processing: superior colliculus activity associated with countermanded saccades. J. Neurosci. 23, 6480–6489.
Pastor-Bernier, A., and Cisek, P. (2011). Neural correlates of biased competition in premotor cortex. J. Neurosci. 31, 7083–7088.
Pastor-Bernier, A., Tremblay, E., and Cisek, P. (2011). “Dorsal premotor cortex is involved in switching motor plans,” Program No. 405.05. 2011, Neuroscience Meeting Planner. (Washington, DC: Society for Neuroscience). [Online].
Pesaran, B., Nelson, M. J., and Andersen, R. A. (2008). Free choice activates a decision circuit between frontal and parietal cortex. Nature 453, 406–409.
Peng, X., Sereno, M. E., Silva, A. K., Lehky, S. R., and Sereno, A. B. (2008). Shape selectivity in primate frontal eye field. J. Neurophysiol. 100, 796–814.
Platt, M. L., and Glimcher, P. W. (1999). Neural correlates of decision variables in parietal cortex. Nature 400, 233–238.
Polya, G. (1920). Über den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung und das Momentenproblem. Math. Z. 8, 171–181.
Prablanc, C., and Martin, O. (1992). Automatic control during hand reaching at undetected two-dimensional target displacements. J. Neurophysiol. 67, 455–469.
Reynolds, J. H., and Heeger, D. J. (2009). The normalization model of attention. Neuron 61, 168–185.
Rizzolatti, G., Riggio, L., Dascola, I., and Umilta, C. (1987). Reorienting attention across the horizontal and vertical meridians: evidence in favor of a premotor theory of attention. Neuropsychologia 25, 31–40.
Romo, R., Hernandez, A., and Zainos, A. (2004). Neuronal correlates of a perceptual decision in ventral premotor cortex. Neuron 41, 165–173.
Scangos, K. W., and Stuphorn, V. (2010). Medial frontal cortex motivates but does not control movement initiation in the countermanding task. J. Neurosci. 30, 1968–1982.
Shadmehr, R., Smith, M. A., and Krakauer, J. W. (2010). Error correction, sensory prediction, and adaptation in motor control. Annu. Rev. Neurosci. 33, 89–108.
Shadmehr, R., and Wise, S. P. (2005). The Computational Neurobiology of Reaching and Pointing: A Foundation for Motor Learning. Cambridge, MA: MIT Press.
Thevarajah, D., Mikulic, A., and Dorris, M. C. (2009). Role of the superior colliculus in choosing mixed-strategy saccades. J. Neurosci. 29, 1998–2008.
Tipper, S. P., Howard, L. A., and Houghton, G. (1998). Action-based mechanisms of attention. Philos. Trans. R. Soc. Lond. BBiol. Sci. 353, 1385–1393.
Keywords: decision-making, movement preparation, reach, motor planning, free choice, monkey, computational model, biased competition
Citation: Pastor-Bernier A, Tremblay E and Cisek P (2012) Dorsal premotor cortex is involved in switching motor plans. Front. Neuroeng. 5:5. doi: 10.3389/fneng.2012.00005
Received: 24 January 2012; Paper pending published: 23 February 2012;
Accepted: 11 March 2012; Published online: 04 April 2012.
Edited by:
Giovanni Mirabella, La Sapienza University, ItalyReviewed by:
Hun-Kuk Park, Kyung Hee University, Korea (South)Vassiliy Tsytsarev, University of Maryland School of Medicine, USA
Giovanni Mirabella, La Sapienza University, Italy
Copyright: © 2012 Pastor-Bernier, Tremblay and Cisek. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Paul Cisek, Département de Physiologie, Université de Montréal, C.P. 6218 Succursale Centre-ville, Montréal, QC H3C 3J7, Canada. e-mail:cGF1bC5jaXNla0B1bW9udHJlYWwuY2E=