
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Comput. Neurosci., 16 May 2023
Volume 17 - 2023 | https://doi.org/10.3389/fncom.2023.1189853
The self-organization of the brain matrix of serotonergic axons (fibers) remains an unsolved problem in neuroscience. The regional densities of this matrix have major implications for neuroplasticity, tissue regeneration, and the understanding of mental disorders, but the trajectories of its fibers are strongly stochastic and require novel conceptual and analytical approaches. In a major extension to our previous studies, we used a supercomputing simulation to model around one thousand serotonergic fibers as paths of superdiffusive fractional Brownian motion (FBM), a continuous-time stochastic process. The fibers produced long walks in a complex, three-dimensional shape based on the mouse brain and reflected at the outer (pial) and inner (ventricular) boundaries. The resultant regional densities were compared to the actual fiber densities in the corresponding neuroanatomically-defined regions. The relative densities showed strong qualitative similarities in the forebrain and midbrain, demonstrating the predictive potential of stochastic modeling in this system. The current simulation does not respect tissue heterogeneities but can be further improved with novel models of multifractional FBM. The study demonstrates that serotonergic fiber densities can be strongly influenced by the geometry of the brain, with implications for brain development, plasticity, and evolution.
The self-organization of the brain serotonergic matrix remains an unsolved problem in neuroscience. This matrix, or a meshwork of axons (fibers), is present in virtually all brain regions, likely across the entire vertebrate clade (Wolters et al., 1985; Challet et al., 1991, 1996; Stuesse et al., 1991; Metzger et al., 2002; López and González, 2014; Janušonis, 2018; Awasthi et al., 2021; Bhat and Ganesh, 2023). It appears to be fundamentally associated with neuroplasticity (Lesch and Waider, 2012; Teissier et al., 2017; Daws et al., 2022), raising new questions (Vargas et al., 2023), and is remarkable in its ability to robustly regenerate in the adult mammalian brain (Jin et al., 2016; Cooke et al., 2022). In mammals, serotonergic axons originate exclusively in the brainstem raphe nuclei; the total number of serotonin (5-hydroxytryptamine, 5-HT)-synthesizing neurons has been estimated at 20,000–26,000 in mice and rats and at around 450,000 in humans (Jacobs and Azmitia, 1992; Okaty et al., 2019). Comprehensive analyses have shown that this population of neurons is extremely diverse in its transcriptomes (Okaty et al., 2019, 2020; Ren et al., 2019).
Recent studies have led to an intriguing picture of this system. On the one hand, state-of-the-art methods, such as single-cell RNA-seq and viral-genetic tract-tracing, have revealed its deep, deterministic-like organization. In particular, specific transcriptome profiles (including neurotransmitter complements and excitability signatures) have been mapped to nested neuron clusters, each with its anatomically-defined set of projections (Ren et al., 2018, 2019; Okaty et al., 2019, 2020). On the other hand, serotonergic axons have been shown to be strongly stochastic in their trajectories. These trajectories can be viewed as unique paths (realizations) of rigorously-defined spatial stochastic processes (Janušonis and Detering, 2019; Janušonis et al., 2019, 2020; Vojta et al., 2020). Both approaches are innovative in that they seek to reveal how precisely-specified events at the single-neuron level result in the self-organization of the entire serotonergic system, in space and time. Their conceptual underpinnings can be traced back several decades (Katz et al., 1984; Waterhouse et al., 1986).
The emerging duality of the serotonergic system, with well-defined deterministic and stochastic components, may reflect the fundamental principles of the self-assembly of neural tissue. The constructive interplay between dynamic determinism and stochasticity has been suggested by studies that have used various experimental platforms. An individual serotonergic neuron may express a specific gene network, distinctly different from other “adjacent” networks, but it may still be able to perform switch-like transitions among them, in the presence of environmental “noise” (Okaty et al., 2019; Ren et al., 2019). Dorsal raphe serotonergic neurons vary in their firing rates, but this variability may be captured by a single normal distribution, across different anatomical locations (Mlinar et al., 2016). Several classes of serotonergic axons have been defined based on their morphology (Kosofsky and Molliver, 1987), but recent studies have demonstrated that axonal morphology may undergo significant changes in a regionally- and developmentally-dependent manner (Gagnon and Parent, 2014; Maddaloni et al., 2017; Nazzi et al., 2019; Okaty et al., 2019; Andersson et al., 2020). In primary cell cultures, adjacent axon segments of serotonergic neurons can strongly vary in their caliber, varicosity size, and other features (Hingorani et al., 2022). This variability is likely to be partially stochastic, as a consequence of the strongly stochastic properties of neural tissue at the microscopic level (Jang et al., 2010; Nicholson and Hrabetova, 2017; Hrabetova et al., 2018; Hingorani et al., 2022). Furthermore, different neuron clusters may show preference for different targets; however, individual serotonergic axons within the same cluster may differ in their collateralization and target specificity (Gagnon and Parent, 2014; Ren et al., 2019). Also, serotonergic neurons that send their axons to the same anatomical region may not be physically clustered (Okaty et al., 2019). In experimental brain injury models, regenerating serotonergic fibers do not follow their previous trajectories and create new tortuous paths (Jin et al., 2016).
This study sought to investigate the potential of the purely stochastic component of the serotonergic fibers, with regard to the self-organization of their regional densities. Individual serotonergic fibers were modeled as paths of fractional Brownian motion (FBM), a continuous-time stochastic process (Mandelbrot and Van Ness, 1968; Biagini et al., 2010). FBM generalizes normal Brownian motion (BM) in that it allows positive and negative correlations among displacement increments (in BM, used to describe free diffusion of particles, non-overlapping displacements are assumed to be statistically independent). FBM process is parametrized with the Hurst index (0 < H < 1), which leads to three distinctly different regimes: subdiffusion (H < 0.5), BM (H = 0.5), and superdiffusion (H > 0.5). We have previously shown that serotonergic fiber trajectories can be modeled with superdiffusive FBM (H≈0.8) (Janušonis et al., 2020).
In a previous study, we have analyzed the distributions of FBM-driven fibers in a selected set of two-dimensional (2D) shapes based on coronal sections of the adult mouse brain (Janušonis et al., 2020). However, the long-range dependence among spatial displacements implies that the trajectory of a fiber at a given coronal level depends on its history in the three-dimensional (3D) space (e.g., at more rostral or caudal coronal sections). In this study, we performed a supercomputing simulation of a large number of fibers in a complex 3D-shape that was constructed from a serially sectioned mouse brain. The simulation was based on reflected (boundary-limited) FBM (rFBM), the theoretical properties of which have been investigated by our group (Wada and Vojta, 2018; Guggenberger et al., 2019; Vojta et al., 2020). It is a major extension of the previous study in that the simulation captured the entire 3D-geometry of the brain, virtually eliminating the dependence of the results on the sectioning plane.
In the adult mouse brain, this geometry contains some elaborate elements (e.g., the folded hippocampus) and is enriched with many dense, fully developed axon tracts. These tracts (e.g., the anterior commissure, the corpus callosum, and the fasciculus retroflexus) are nearly impermeable to serotonergic axons and act as obstacles in simulations (Janušonis et al., 2020). To reduce this complexity, a late-embryonic mouse brain (at embryonic day [E] 17.5) was used to construct the 3D-shape. This selection is further justified by the evidence that serotonergic neurons mature early; by this age, their axons are already present in the telencephalon and reach the cortical plate in mice and rats (Wallace and Lauder, 1983; Brüning et al., 1997; Janušonis et al., 2004). The geometries (e.g., curvatures, distances) of the embryonic and adult brain are not identical, but they share the same fundamental topology and major features. Strictly speaking, neither the embryonic brain nor the adult brain is the “correct” static shape in this context: a developmentally accurate approach would require simulating fiber trajectories as the shape itself increases in size and morphs. However, without accurate experimental information about the relative dynamics of both processes such simulations are unlikely to produce robust results. State-of-the-art imaging techniques have provided new insights into the growth dynamics of single serotonergic axons (Jin et al., 2016; Hingorani et al., 2022), but live-imaging of serotonergic fibers in the intact developing brain needs further technological advances.
The verification of simulation results requires accurate information about actual serotonergic fiber densities. These densities have been a major focus of investigation since the discovery of 5-HT-producing neurons in the brain (Hokfelt, 2016). Their regionally-specific estimates, independent of the neuroanatomical origin of the fibers, initially relied on the detection of 5-HT or the serotonin transporter (SERT) (Steinbusch, 1981; Lidov and Molliver, 1982; Foote and Morrison, 1984; Mize and Horner, 1989; Lavoie and Parent, 1990, 1991; Voigt and de Lima, 1991a; Sur et al., 1996; Bjarkam et al., 2003, 2005; Way et al., 2007; Vertes et al., 2010; Parent et al., 2011; Linley et al., 2013; Belmer et al., 2017). These markers are specific to serotonergic neurons and strongly overlap (Belmer et al., 2019), with some caveats (Lebrand et al., 1996, 2006; Maddaloni et al., 2017). However, they are directly associated with local 5-HT accumulation and release, and therefore may not visualize fibers or their segments with low 5-HT levels (e.g., if they have a fine caliber and contain no varicosities). The 5-HT signal can show striking variability along the path of a single fiber in cell-culture preparations (Hingorani et al., 2022). In addition, the relative abundance of SERT may depend on the local diffusivity of extracellular 5-HT, which in turn depends on the local properties of the extracellular space (Syková and Nicholson, 2008; Hrabetova et al., 2018; Okaty et al., 2019). Furthermore, serotonergic neurons can release other neurotransmitters, such as glutamate, and their terminals can segregate by the preferred neurotransmitter (Okaty et al., 2019).
In the past several decades, studies have mapped the projections of specific raphe nuclei, often using sensitive visualization procedures (e.g., efficient neural tract tracers combined with immunoperoxidase detection) (Vertes, 1991; Morin and Meyer-Bernstein, 1999; Vertes et al., 1999). These connectomics-driven approaches are independent of 5-HT accumulation, but the obtained densities reflect only the contribution of the selected nucleus. In addition, they strongly depend on the uptake efficiency of the tracer (i.e., some serotonergic neurons and their axons are likely to remain unlabeled).
More recently, transgenic mouse models have allowed extremely accurate visualization of all serotonergic axons, irrespective of their anatomical origin or 5-HT content. For example, a fluorescent reporter (e.g., EGFP) can be expressed under the promoter of a serotonergic neuron-specific gene (e.g., Tph2) and further enhanced with immunohistochemistry. Since reporter proteins can be transported to distal axon segments, they can reveal the dynamics and susceptibility of serotonergic fibers with unprecedented precision (Maddaloni et al., 2017, 2018). However, these studies have focused on targeted brain regions, due to the complexity of single-fiber analyses.
These research trends have resulted in a paradoxical lack of modern, comprehensive atlases of serotonergic fiber densities. Such atlases should (1) cover the entire brain and (2) detect all physically present serotonergic fibers—with high specificity and sensitivity, irrespective of their signaling state (e.g., 5-HT content). The recent publication of a detailed topographical map of the serotonergic fiber densities in the entire adult mouse brain has now partially filled this knowledge gap (Awasthi et al., 2021). This map, based on the expression of EGFP under the SERT gene promoter, currently does not include the adult female mouse brain or developmental stages.
In summary, this study brings together several recent developments: the models of serotonergic fibers as rFBM-paths, the advances in the theory of rFBM, and the new comprehensive map of serotonergic fiber densities. By using a supercomputing simulation, we attempted to predict regional fiber densities based purely on the geometry of the brain and compared them to the neuroanatomical data.
A timed-pregnant mouse (Charles River Laboratories) was deeply anesthetized at E17.5 with a mixture of ketamine (200 mg/kg) and xylazine (20 mg/kg), and the embryos were dissected into cold 0.1 M phosphate-buffered saline (PBS, pH 7.2). They were immediately decapitated, and their brains were dissected with fine forceps under a stereoscope. Two embryonic brains were rinsed in PBS and immersion-fixed in 4% paraformaldehyde overnight at 4°C. They were cryoprotected in 30% sucrose for 2 days at 4°C and embedded in 20% gelatin (type A) in a Peel-A-Way mold, with an insect pin pushed through the mold in the rostro-caudal orientation just dorsal to the brain. After 1 h at 4°C, the gelatin block was removed, trimmed, and incubated for 3 h in formalin with 20% sucrose at room temperature. It was sectioned coronally from the olfactory bulbs to the caudal midbrain at 40 μm thickness on a freezing microtome into 96-well trays with PBS. The lower brainstem and the cerebellum were not included. In order to avoid distance distortions in the rostro-caudal axis, empty wells were used to mark damaged or missing sections. Every other section was mounted onto gelatin/chromium-subbed glass slides, allowed to air-dry, and imaged uncoverslipped on a Zeiss Axio Imager Z1 in bright field with a 1 × objective (NA = 0.025) (Figure 1A). All animal procedures have been approved by the UCSB Institutional Animal Care and Use Committee.
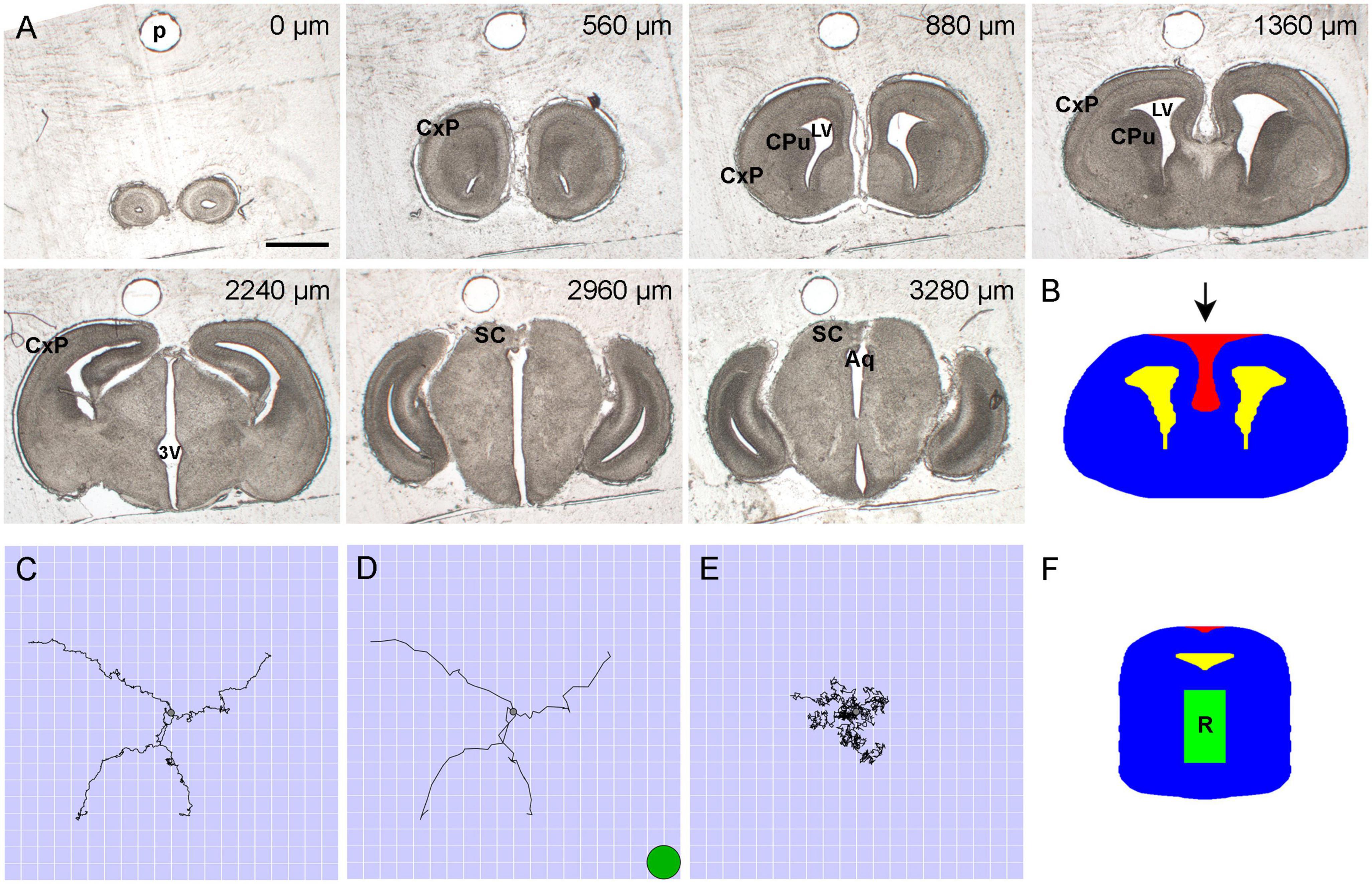
Figure 1. (A) Representative bright-field images of unstained and uncoverslipped coronal brain sections (E17.5) used in the set. The rostrocaudal distances are shown at the top of the panels. In the simulation, tissue heterogeneities were disregarded. Aq, cerebral aqueduct; CxP, cortical plate; CPu, caudate-putamen; LV, lateral ventricle; SC, superior colliculus; 3V, third ventricle. Scale bar = 1 mm. (B) Each of the constitutive shapes in a section was fully described by its leftmost and rightmost points at each dorsoventral level. The 2D-shape represents the section at the rostrocaudal distance of 1,360 μm. The allowed region is shown in blue; the forbidden regions are shown in yellow and red (the lateral ventricles and the dorsomedially oriented concavity, respectively). (C) Four sample FBM (H = 0.8) trajectories with mean zero and σ = 0.4 spatial units, from 0 to 20 time-units with the walk-step of 0.05 time-units. The side of one cell is one spatial unit (corresponding to 6.6 μm in the physical brain). All trajectories start at the center (gray circle) of the region containing 20 × 20 grid cells. The small step is used to show the fine details of the process. (D) The same trajectories shown with the walk-step of one time-unit (as actually used in the simulation). The green circle shows the relative size of a typical neuronal soma in the adult brain (with the diameter of around 13 μm). (E) Four sample trajectories of normal Brownian motion (H = 0.5) with mean zero and σ = 0.4 spatial units, from 0 to 20 time-units with the walk-step of 0.05 time-units. The trajectories are shown for comparison (normal Brownian motion was not used in the simulation; it produces trajectories with uncorrelated increments). (F) All fibers started in the rostral raphe region (R), approximated by a cuboid under the aqueduct.
The section series of both brains were examined, and one series was selected for further processing. The sections were aligned in the rostro-caudal axis in Reconstruct (SynapseWeb), as shown in our previous publication (Flood et al., 2012). The pin-hole in the gelatin was used as a fiducial marker (Figure 1A). The aligned images were imported into Photoshop 23 (Adobe, Inc., San Jose, CA, United States), and brain contours were outlined by an expert neuroanatomist using the magnetic or polygonal lasso tools. The contours were converted into binary images (white shapes on a black background). If a section contained more than one shape (e.g., the outer outline and ventricular spaces), they were saved as separate images, in the same aligned geometric space. In order to reduce the complexity of the geometry, the folding of the hippocampus was not respected (i.e., the hippocampus was represented by a medial pallial region with no internal structure).
The binary images were imported into Wolfram Mathematica 13 (Wolfram Research, Inc.) and processed as previously described (Janušonis et al., 2020). Briefly, each closed contour was converted into an ordered set of points, smoothed, bilaterally symmetrized, and transformed into a different format represented by an N × 3 matrix (where N is the number of the rows). The rows represented the consecutive y-coordinates (with no gaps), from the most dorsal level to the most ventral level of the contour. Each row contained three values: a y-coordinate and the leftmost and rightmost x-coordinates of the contour at this y-coordinate (both x- and y-coordinates were integers). Since this format cannot capture concavities oriented in the dorsoventral direction, they were coded as separate contours representing “forbidden” regions (in addition to the ventricular spaces) (Figure 1B). In this two-dimensional (2D)-integer grid, the side of each square cell represented the physical distance of 6.6 μm in the physical brain.
Next, a three-dimensional brain model was built from the section stack. First, missing or damaged sections were recreated by linear interpolation between neighboring sections to maintain even (80 μm) rostro-caudal steps between any two consecutive sections. This process was guided by the known anatomy, and the resulting interpolated sections were checked manually for anatomical correctness. Second, in order to produce a three-dimensional simulation grid, each section was further subdivided into a set of twelve virtual sections of around 6.6 μm in thickness using linear interpolation. The resulting simulation grid cells (voxels) were thus cubes whose linear size corresponded to 6.6 μm in the physical brain.
The fiber densities were produced by 960 simulated fibers. Each fiber was represented by the path of a discrete three-dimensional FBM (Qian, 2003). Specifically, the trajectory of the random walker moved according to the recursion relation rn + 1=rn + ξn, where rn is the (three-dimensional) walker position, and the steps (increments) ξn are a three-component discrete fractional Gaussian noise (Figures 1C, D). The statistically-independent x, y, and z components of ξn were Gaussian random numbers with mean zero and variance σ2, and each component had long-range correlations between steps [in contrast to normal Brownian motion (Figure 1E)]. The corresponding noise covariance function between steps m and m+n was given by , where H is the Hurst index, δij is the Kronecker delta, and i, j = x, y, z denotes the three space dimensions. The Fourier-filtering method (Makse et al., 1996) was employed to generate these long-range correlated, stationary random numbers on the computer (Wada and Vojta, 2018; Vojta et al., 2020). This efficient method allowed us to create particularly long trajectories. The main simulations were performed for H = 0.8, but we also tested other H-values. The root mean-square step size was set to σ = 0.4 grid units, corresponding to 2.6 μm in the physical brain (smaller than the diameter of a single neuron). All paths started in the rostral raphe region, given by a cuboid with the approximate physical dimensions 680 × 1,200 × 400 μm3 in the mediolateral, dorsoventral, and rostrocaudal directions, respectively (Figure 1F). Each trajectory consisted of 225≈33.6 million walk-steps (each 1 time-unit). The length of the trajectories was sufficient for the relative densities to reach a steady state.
If the extending fiber encountered a boundary (i.e., an outer or inner contour), it was reflected. Our previous extensive analyses have shown that the choice of the reflection condition has virtually no effect on the simulation results, with the exception of a very narrow region (a few steps wide) at the boundary (Vojta et al., 2020). Therefore, the following simulation used the simple condition under which a step that would move the leading fiber end into the forbidden region was simply not carried out. Deciding whether a given point is inside or outside of a complex three-dimensional shape is a complicated problem in computational geometry. Our approach to modeling the geometry in terms of virtual sections and boundary contours within each section (as described above) allowed us to implement an efficient local inside-outside test. The most rostral and caudal sections of the model brain geometry were treated as reflecting boundaries in the rostro-caudal direction.
After the simulation, the resultant densities were evaluated in non-overlapping cubes (composed of 2 × 2 × 2 grid cells, to suppress noise and achieve more robust estimates). The local density (ds) was determined by counting the total number of random-walk segments inside each cell. These local densities were normalized to the total sum of one in the entire 3D-brain volume, to remove any dependence of the results on the arbitrarily chosen trajectory length. To facilitate comparisons between the simulated fiber densities and published densities (typically, in immunostained sections), the raw simulation densities were transformed to “optical densities” using a Beer-Lambert law-like transformation do=1−−exp(−kds) (Janušonis et al., 2020), with an empirically optimized k-value (k = 108.3). This transformation constrained density values to a finite interval (from zero to one). They were used for all further analyses and figures. The graphical density maps were produced in Mathematica 13, using the “rainbow” and “heat” color schemes.
All supercomputing simulations were written in Fortran 2018 and carried out on the Pegasus cluster at the Missouri University of Science and Technology, using parallel processing on several hundred CPU cores.
The simulated fiber densities were evaluated using a comprehensive map of the serotonergic fiber densities in the adult male mouse brain (on the C57BL/6J background) (Awasthi et al., 2021) and an atlas of the developing mouse brain (Paxinos et al., 2020).
The fiber densities obtained in the simulation are shown in Figure 2. For accurate quantitative comparisons, the density values along selected cuts (1D-segments) are included (Figure 3).
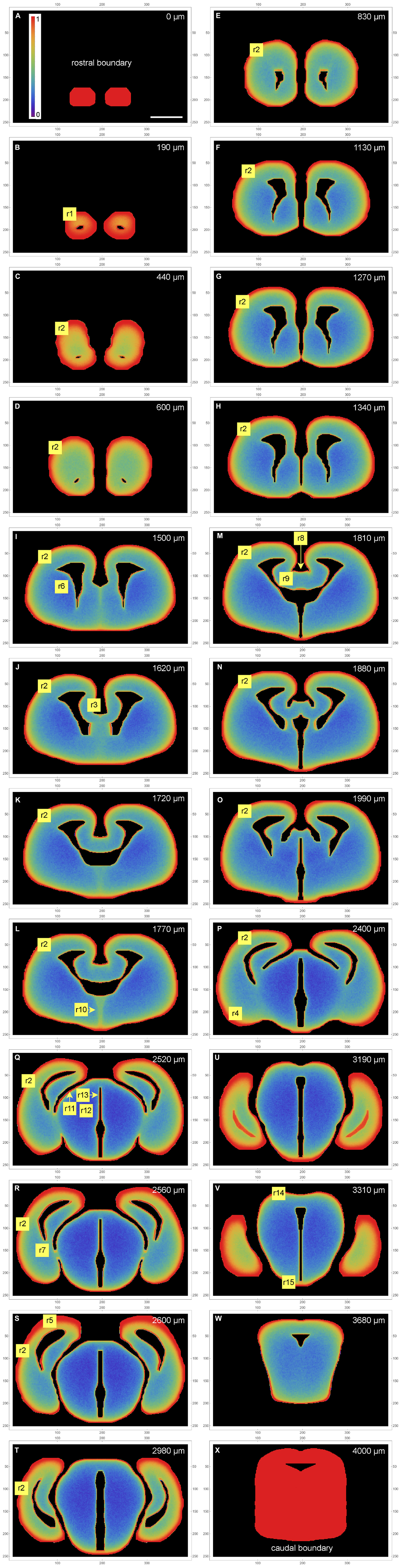
Figure 2. A color-map atlas of the simulated fiber densities in coronal sections (A–X) from the rostral brain pole (A) to the most caudal section in the set (X). Low densities are blue, medium densities are green, and high densities are red. Key rostrocaudal levels and transitions are shown (note that the rostrocaudal distances between panels vary; they are shown at the top of the panels). The selected regions (r1-r15) are discussed in the results section. The frame numbers indicate square cells after the 2 × 2 pooling. Scale bar = 1 mm.
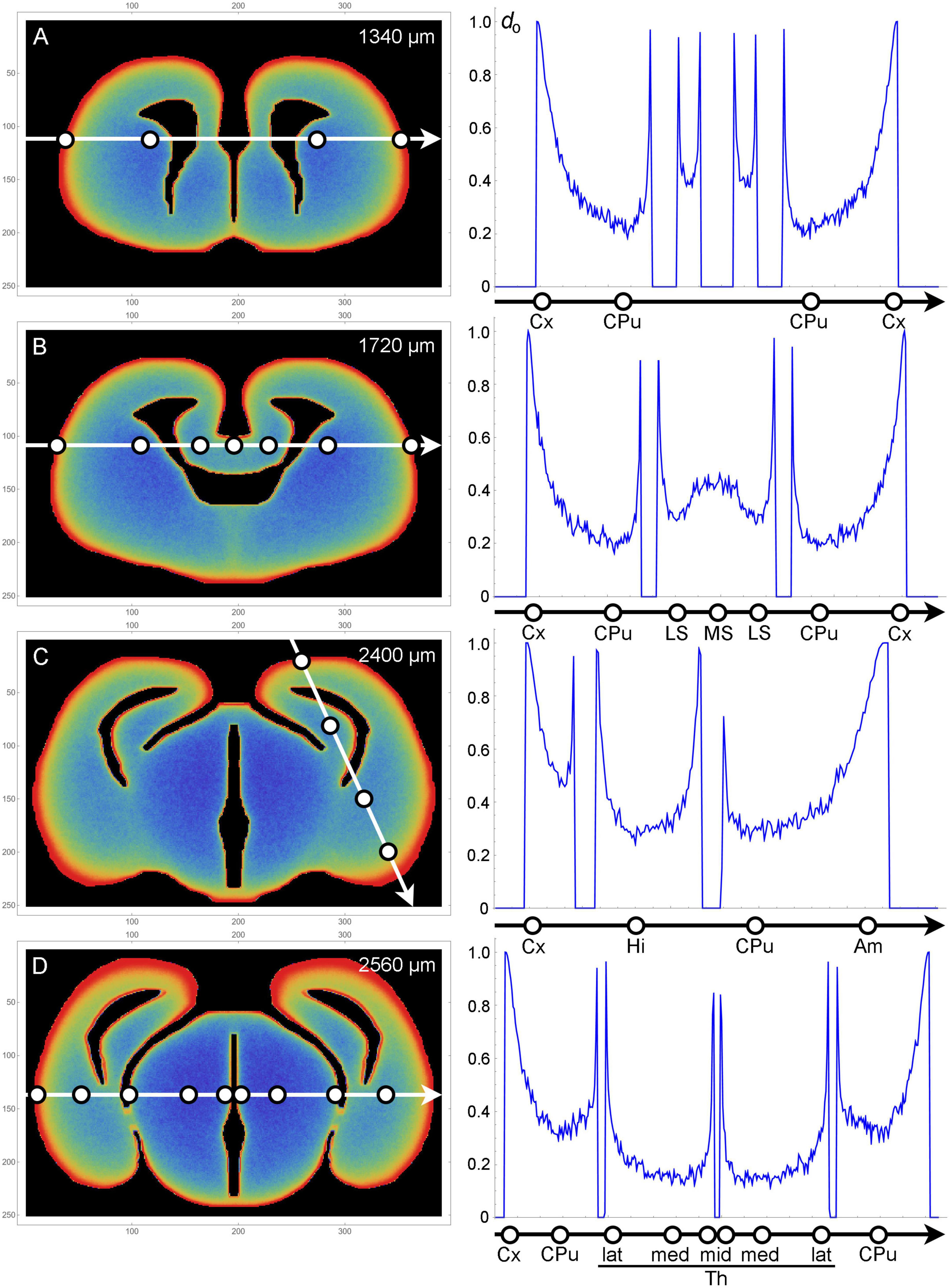
Figure 3. Plots of fiber densities (right) along selected one-dimensional cuts across sections (left) at four coronal levels (A–D). Regions important for comparisons with the actual serotonergic fiber densities are marked with circles. Am, amygdala region; CPu, caudate-putamen; Cx, cortex; Hi, hippocampal (medial pallial) region; LS, lateral septum; MS, medial septum; Th, thalamus (lat, lateral; med, medial; mid, midline); do, optical density (0–1). The frame numbers indicate square cells after the 2 × 2 pooling.
The extremely high accumulation of fibers in the most rostral section (Figure 2A) reflects its position as a coronal boundary of the 3D-shape (i.e., fibers cannot advance rostrally beyond it). The actual olfactory bulb extends a little further, but this section can also be considered to be the most superficial layer of the rostral pole.
Generally, the simulated fibers produced the highest fiber densities close to the tissue borders (the pia as the outer border and the ependyma of the ventricular system as the inner border). However, the memory (autocorrelation) of the fibers and the complex shape they interacted with led to other density variations that could not be predicted purely from the local geometry. We next discuss the key findings and compare them to the experimentally established densities of serotonergic fibers in the adult mouse brain, based on the comprehensive map of Awasthi et al. (2021). In this map, regional densities (d) are semi-quantitatively evaluated on the scale of 0 (extremely low) to 6 (extremely high).
In the olfactory bulb, the dense accumulation of the simulated fibers at the outer border (Figure 2B [r1]) corresponds to the glomerular layer, the layer with the highest serotonergic fiber density in this structure (d = 5). In the telencephalon proper, the neural tissue at the outer and inner borders corresponds to the adult cortical layer I and periventricular regions, respectively. In most regions, the high-density band at the outer border (r2) was considerably thicker than the bands at the inner borders (Figures 2C-T). This pattern was in register with the high densities (d = 5) of serotonergic fibers in layer I of virtually all, functionally different adult cortical regions (in which no other layer exceeds the layer I density). These regions cover the entire rostro-caudal and medio-lateral extents and include the prefrontal cortex, the motor cortex, the somatosensory cortex, the auditory cortex, and the piriform cortex, with the minor exception of the retrosplenial cortex (RSC; d = 3). However, the RSC [areas A29c and A30 of the cingulate cortex (Vogt and Paxinos, 2014)] has an extensive, prominently flattened cortical region (A29c), where the two hemispheres press against each other at the midline. The exact boundaries of A29c are not readily identifiable in the embryonic mouse brain (Paxinos et al., 2020), but in the simulation similar flat cingulate regions showed narrower high-density bands (Figure 2J [r3]). The basolateral amygdala (BLA) has an exceptionally high density of serotonergic fibers (d = 5–6), with the adjacent regions showing a similar pattern [the basomedial amygdala (BMA) and the piriform cortex: d = 3–5; the endopiriform nucleus: d = 5–6]. The simulated fibers produced a particularly thick high-density band in the corresponding region (Figure 2P [r4], Figure 3C). However, the simulated fibers did not show the tendency to decrease in density in cortical regions in the rostro-caudal direction, as reported by Awasthi et al. (2021), and produced another thick high-density band in a region corresponding to the future visual cortex (Figure 2S [r5]). This discrepancy may reflect limitations of the model, but it can also be due to other causes: in the adult brain the visual cortex extends more caudally (to the cerebellum); serotonergic neurons that reach the most caudal cortical regions incur an energetic cost in supporting extremely long axons (with no such limitation in simulations); and the detection of distal axonal segments can be affected by the long-distance transport of EGFP, the protein used for fiber visualization.
The simulated fibers produced a low density in the region corresponding to the caudate-putamen (Figure 2I [r6], Figures 3A, B), despite its proximity to the medially-bulging edge of the lateral ventricles. The fiber density increased in the more caudal caudate-putamen regions (Figure 2R [r7], Figures 3A-C), generally consistent with the low-to-moderate (d = 2–4) densities of serotonergic fibers in this region, with the same gradient.
The complex geometry of the septal region led to a subtly higher density of simulated fibers in the medial septum than in the lateral septum (Figure 2M [r8, r9], Figure 3B). With the exception of the rostral part of the lateral septum, the brain shows a similar gradient of serotonergic fiber densities (the medial septum: d = 3–5; the lateral septum: d = 1–3).
Just rostral to the transition to the third ventricle, simulated fibers produced a distinct median band with an elevated fiber density (Figure 2L [r10]). This region corresponds to the region of the preoptic hypothalamus, which has a high density of serotonergic fibers (e.g., d = 5 in the median preoptic nucleus and parts of the medial preoptic area). The higher density was induced by the location of this region in the 3D-space. Specifically, it represents a coronal boundary to medially located fibers that move caudally: they cannot enter the third ventricle at the adjacent caudal levels and are “reflected,” with an accumulation. This same geometry may be a contributing factor in the actual brain.
In the diencephalon and mesencephalon, the highest serotonergic fiber densities tend to be located near the outer tissue border or around the ventricular spaces [see Figure 5 of Awasthi et al. (2021)]. This general pattern is strongly consistent with the density distributions produced by the simulated fibers (Figures 2O–W). In the actual brain, it can be interrupted by major axon fascicles (e.g., the cerebral peduncle) that cannot be easily penetrated by individual serotonergic fibers (Janušonis et al., 2020; Awasthi et al., 2021). The thalamic lateral posterior (LP), lateral dorsal (LD), and lateral geniculate (LG) nuclei, all contributing to the dorsal outer border of the thalamus, have high serotonergic fiber densities (d = 4–5, d = 4–5, d = 6, respectively). The simulated fibers also produced high densities in this region (Figure 2Q [r11], Figure 3D). Notably, in the adult mouse brain the LG has the highest outer curvature. In contrast, the deeper thalamic nuclei, such as the ventral posteromedial and posterolateral nuclei (VPM and VPL), the ventromedial nucleus (VM), the posterior nucleus (PO), and the deep part of the medial geniculate nucleus (MG), have serotonergic fiber densities that are among the lowest in the entire brain (d = 2 in the MG and d < 1 in the rest of the set). The simulated fibers also produced especially low densities in this region (Figure 2Q [r12], Figure 3D). The thalamic midline nuclei, located close to the third ventricle, again have high serotonergic fiber densities (d = 6), consistent with the accumulation of the simulated fibers at inner borders (Figure 2Q [r13], Figure 3D).
The mesencephalon followed a similar general pattern. The simulated fibers produced the highest densities in the regions of the superior colliculus (SC) (Figure 2V [r14]) and the broadly defined ventral tegmental region (Figure 2V [r15]), both of which have high serotonergic fiber densities (Awasthi et al., 2021). Despite this consistency, caution should be exercised at this coronal level because it is close to the origin of the serotonergic fibers (emerging from the raphe nuclei under the cerebral aqueduct) and it also contains several major axon fascicles deep in the tissue. Also, the caudal mesencephalon represents an unnatural boundary of the simulated central nervous system (Figure 2X), which in reality is given by the caudal end of the spinal cord.
A selected subset of the sections is shown in pseudo-monochrome, to support direct comparisons with densities visualized with immunohistochemical procedures (Figure 4).
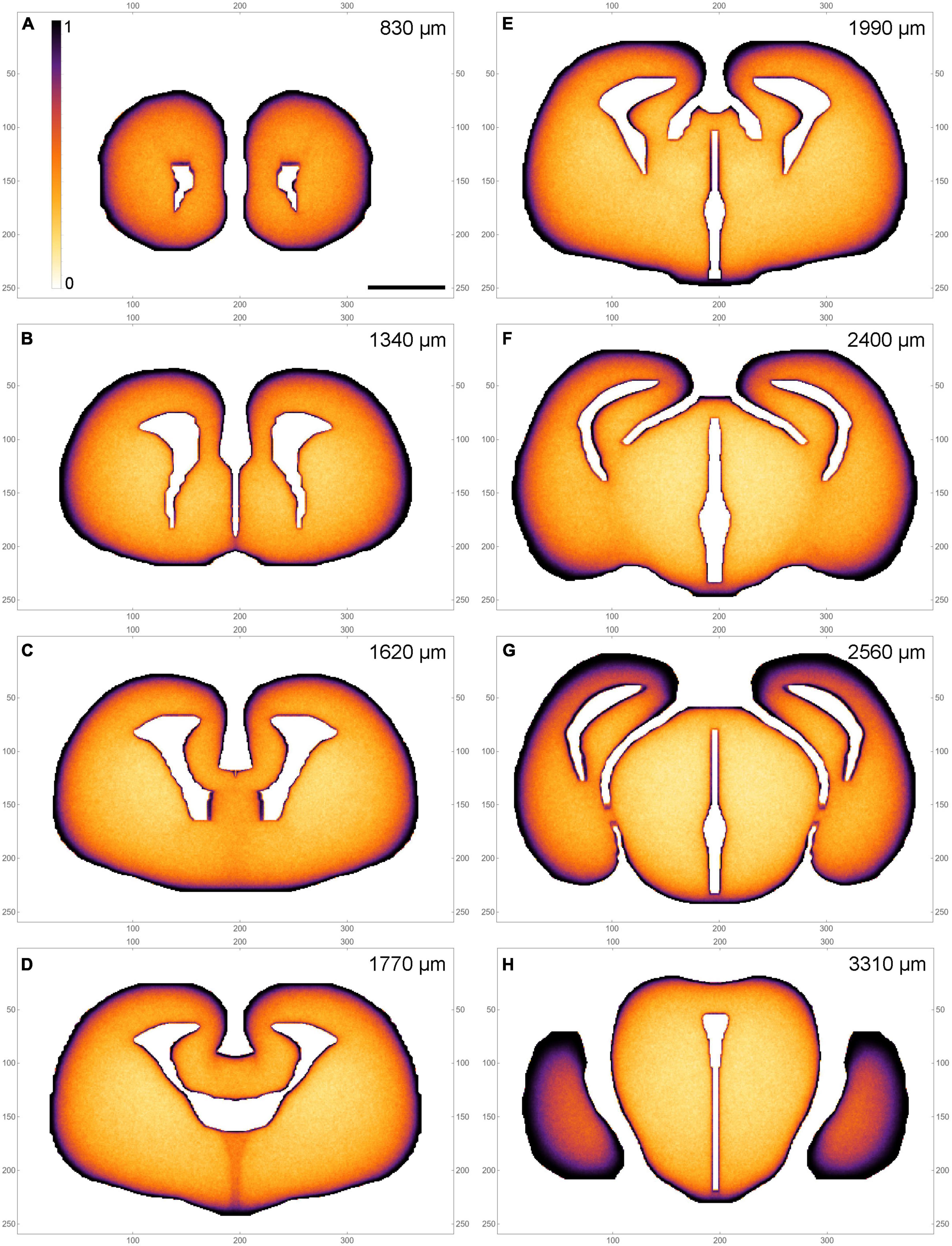
Figure 4. A pseudo-monochrome map atlas of the simulated fiber densities at selected coronal levels (A–H) (a subset of the set in Figure 2). The colors simulate immunohistochemical visualization with 3,3’-diaminobenzidine (DAB); low densities are light, high densities are dark. The rostrocaudal distances are shown at the top of the panels. The frame numbers indicate square cells after the 2 × 2 pooling. Scale bar = 1 mm.
The supercomputing simulation produced a predictive map of serotonergic fiber densities, based on the model of fibers as rFBM paths. In addition to its contribution to neuroscience, this work is the first simulation of rFBM in any complex 3D-shape, with potential applications in other fields (Vojta et al., 2020).
The obtained densities depended only on the fundamental properties of rFBM as a stochastic process and the geometry of the 3D-shape (including the ventricular spaces). Despite this conceptual simplicity, the simulated densities approximated the relative intensities of serotonergic fiber densities in many brain regions. Exact quantitative comparisons are currently infeasible because regional serotonergic densities are traditionally reported only descriptively or as observer scores limited to a small set of discrete values [e.g., 0−6 in Awasthi et al. (2021)]. This approach is partially motivated by the need to combine the overall signal intensity with the morphology of individual fibers; for example, the same overall signal intensity can be produced by a high density of fine-caliber fibers or by a lower density of larger-caliber axons. As a consequence, the semi-quantitative scores are assigned by expert viewers but can still be influenced by subjective biases. In contrast, assessments of relative densities, especially in adjacent or similar brain regions, are likely to be highly accurate. Therefore, we followed the same approach in our comparisons, which were nearly independent of the shape of the monotonic function used to transform raw simulated fiber densities to the corresponding (immunohistochemistry-like) signal intensities.
As expected from our previous simulations in 2D-shapes, high fiber densities were produced near the borders of the 3D-shape (Janušonis et al., 2020). Elevated serotonergic fiber densities have been reported in many of the corresponding brain regions, despite major differences in their functional roles (Awasthi et al., 2021). These regions include the most superficial layer (layer I) of virtually all cortical areas, the thalamic nuclei at the lateral and medial (ventricular) borders, the superior colliculus, the hypothalamus, the ventral region of the tegmentum, and other major neuroanatomical structures (Figures 2-4). The local border curvature and the geometry of adjacent regions further contributed to the intensities and gradients of fiber densities. In particular, this effect produced a high-density region in the area corresponding to the amygdala complex. This region extended deep into the tissue (Figure 3C), consistent with the actual serotonergic fiber densities in the brain (Awasthi et al., 2021). Generally, high serotonergic fiber densities in these regions have been reported in other mapping studies (Vertes, 1991; Morin and Meyer-Bernstein, 1999; Vertes et al., 1999, 2010; Linley et al., 2013), with some variability due to the technical limitations discussed in the Introduction (e.g., the targeting of specific raphe nuclei).
The border effect has been reported in different species, but it usually has been interpreted in a brain region-centric way, without generalizing the pattern. Interesting examples are provided by the telencephalon of the New Zealand white rabbit (Bjarkam et al., 2003, 2005) and the tadpole telencephalon of the Indian burrowing frog (Bhat and Ganesh, 2023). A study of serotonergic densities in the hamster brain has noted that, “in the thalamus, there is a general theme of denser 5-HT-IR [serotonergic] innervation surrounding a sparsely innervated core” (Morin and Meyer-Bernstein, 1999). We are aware of only one descriptive study that has attempted to quantitatively evaluate the decrease of a fiber density as a function of the distance from the edge; this analysis has been performed in the cat superior colliculus (Mize and Horner, 1989). Relatively few studies have investigated serotonergic fibers in the ependymal layer (which surrounds ventricular spaces), but this region is known to have high fiber densities (Dinopoulos and Dori, 1995), consistent with the simulation results. Actual serotonergic fiber densities can decrease more gradually away from a border; however, this property can be mirrored in simulated densities by changing the convexity of the transforming function (effectively, by deciding at which density value intensities saturate and become virtually indistinguishable).
The hippocampal complex was modeled as a featureless, unfolded medial pallial region (Butler and Hodos, 2005; Striedter and Northcutt, 2020). This representation was deliberately inaccurate, to avoid the 3D-reconstruction of a complex, layered structure (with the correctly placed entrance and exit zones for fibers). Unsurprisingly, the low simulated density in this area (Figure 3C) deviated strongly from the generally high density of serotonergic fibers in the hippocampus (Awasthi et al., 2021). However, if the folding had been simulated, a high fiber density would have been observed in the superficial layer of this cortical structure (the archicortex). In the hippocampus proper, this superficial layer corresponds to the stratum lacunosum moleculare, which has the highest serotonergic fiber density among all layers (Vertes et al., 1999; Nazzi et al., 2019; Awasthi et al., 2021). Likewise, the molecular layer of the mouse dentate gyrus has been reported to have the highest serotonergic fiber density among all layers (Awasthi et al., 2021). A slightly different pattern has been reported in another study that has focused only on the fibers originating in the median raphe nucleus of the rat (Vertes et al., 1999). This discrepancy may be due to an incomplete labeling of fibers with the tracer.
The mediolateral fiber-density profile in the septum (Figure 3B) was remarkably consistent with the reported serotonergic densities in this region (Awasthi et al., 2021), with a high peak in the medial septum, a deep trough in the medial part of the lateral septum, and another peak in the lateral part of the lateral septum, at the edge of the lateral ventricle [see Figure 11 of Vertes et al. (1999)]. This close match may be coincidental, but it may also reflect the potential of the proposed approach. The observed profile cannot be deduced from a single coronal section and it may also have a developmental component, since in the adult brain this region is dorsally limited by the thick band of the corpus callosum (which was not modeled in the used 3D-shape).
The current model cannot capture local variations in serotonergic fiber densities that are not accounted for by the geometry of the borders. For example, the cortical layers below layer I often do not follow a descending gradient and can produce local density peaks deeper in the tissue, such as in layers IV or V (Linley et al., 2013; Awasthi et al., 2021). Likewise, individual nuclei in the amygdala complex can be located close to one another but differ strongly in their serotonergic fiber densities (Awasthi et al., 2021). This local variability may be due to local biological factors that control the growth and branching of fibers. These discrepancies do not signal fundamental limitations of the proposed model which assumed that the interior of the 3D-shape was a uniform medium, with no spatial heterogeneities. In reality, such heterogeneities are always present in natural neural tissue and can be easily observed even in unstained preparations (Figure 1). They may include regional variations in neuron packing densities (Erö et al., 2018; Keller et al., 2018), extracellular space (Hrabetova et al., 2018), viscoelasticity (Cherstvy et al., 2019; Antonovaite et al., 2021), and other variables. It is currently unclear which of these factors can affect the resultant densities of simulated fibers; for example, our limited analysis of rFBM-fibers in 2D-shapes with densely packed cells (small obstacles) produced results similar to those in corresponding shapes with no cells (Janušonis et al., 2020). The incorporation of spatial heterogeneities requires advances in the theory of FBM, where a non-constant H poses challenges in mathematical specifications of the process. We are currently developing new theoretical models that can overcome these difficulties (Wang et al., 2023). It is worth noting that the densities of glial cells show surprisingly little regional variability, and even little variability across mammalian species (Herculano-Houzel, 2014; Dos Santos et al., 2020). Quantitative estimates of some parameters of the brain extracellular space (e.g., tortuosity) also suggest strong uniformity across brain regions (Nicholson, 2005; Syková and Nicholson, 2008).
In order to keep the simulation manageable, it was performed in a static shape based on a late-embryonic brain. The actual biology is more complex in that serotonergic fibers gradually “fill” the brain as the brain itself rapidly expands, in embryonic and postnatal development (Slaten et al., 2010; Flood et al., 2012). This growth includes changes in local tissue properties, due to cell migration, myelination, and other processes (Iwashita et al., 2014; Guo et al., 2019). In mouse postnatal development, fiber densities can steadily increase in some brain regions (e.g., in the caudate-putamen and basolateral amygdala), but they can show transient peaks in others (e.g., in the medial prefrontal cortex and hippocampus) (Maddaloni et al., 2017). The present simulation cannot replicate these more complex patterns. Simulating fibers in evolving 3D-shapes might capture them, but this transition poses challenges in mathematical specifications (e.g., a dynamic border may drag adjacent fibers or move independently of them) and requires further upscaling of computing resources. Despite the current limitations, the general validity of the static brain model is supported by the observation that serotonergic fibers accumulate at the surface of the future cerebral cortex as soon as they reach it (i.e., in the marginal zone, the future cortical layer I) (Wallace and Lauder, 1983; Voigt and de Lima, 1991b; Brüning et al., 1997; Janušonis et al., 2004). It should also be noted that the model did not include the medial forebrain bundle, a major pathway that the rostrally-projecting serotonergic fibers follow before dispersing (Wallace and Lauder, 1983). In simulations, fibers can be forced to deterministically move away from the raphe nuclei, as a compact bundle, before they acquire stochastic properties. However, it would not have a major effect on their final, equilibrium densities outside the bundle.
The primary aim of the simulation was not to fully replicate the regional densities of serotonergic fibers but rather to examine to what extent these densities can be explained by the intrinsic stochastic properties of the fibers, as they interact with the basic geometry of the brain. We note that different axon types may lie at different points along the stochastic-deterministic continuum. For example, the trajectories of the retinogeniculate and corticospinal axons can be considered strongly deterministic. In contrast, serotonergic fibers appear to be strongly stochastic; in the adult brain they typically produce highly tortuous trajectories (sometimes with complete loops), can meet at any angles (Janušonis et al., 2019), and do not fasciculate. The stochasticity of axon growth has been acknowledged by a small number of other studies (Katz et al., 1984; Maskery and Shinbrot, 2005; Betz et al., 2006; Yurchenko et al., 2019), but thus far these approaches have not led to major applications in neuroscience. The fundamental problem of the self-organization of serotonergic fiber densities may motivate this line of research, which can be enriched with other theoretical insights, such Brownian ratchet theory and Wiener sausage-like constructs.
At the qualitative level, the rFBM-model of serotonergic fibers can make intriguing predictions. For example, the accumulation of fibers at a border is likely to be higher if the border has a high local curvature. We have demonstrated this phenomenon in 2D-shapes (Janušonis et al., 2020; Vojta et al., 2020). Since the size of neurons and axons is physically constrained, it implies that larger brains might have relatively lower serotonergic fiber densities at the surface—unless the curvature is restored with gyrification. It also implies that the shape of the brain, whether molded by evolution (Striedter and Northcutt, 2020), artificial selection, or artificial cranial deformation (Meiklejohn et al., 1992) might affect the distribution of serotonergic fibers, with potential implications for regional neuroplasticity.
Irrespective of the exact specification of the used stochastic process, this study highlights the possibility that serotonergic fiber densities are never truly local. In order to reach a specific target, fibers have to traverse other regions, introducing spatial correlations. Also, the absence of physical tissue or the emergence of obstacles in adjacent planes prevents fibers from advancing in this direction and may give the impression of an external guiding force when viewed in only one plane.
The strong stochasticity of serotonergic fibers does not exclude other factors that may guide their interaction with the environment and with one another. These factors include brain-derived neurotrophic factor (BDNF) (Mamounas et al., 1995; Popova and Naumenko, 2019), the growth factor S100β (Sodhi and Sanders-Bush, 2004), GAP-43 (Donovan et al., 2002), the microtubule-associated STOP proteins (Fournet et al., 2010), protocadherins (Katori et al., 2009, 2017; Chen et al., 2017), and neurexins (Cheung et al., 2023). In addition, 5-HT itself may affect the growth of serotonergic fibers (Whitaker-Azmitia, 2001; Migliarini et al., 2013), but these effects are neuroanatomically subtle (Lesch et al., 2012; Montalbano et al., 2015; Mosienko et al., 2015). They can also be masked by the availability of placenta-derived 5-HT in fetal brain development (Bonnin and Levitt, 2011). Interestingly, serotonergic fibers themselves may guide postnatal neuroblast migration (García-González et al., 2017).
Alterations in regional serotonergic fiber densities have been associated with a number of mental disorders and conditions, such as autism spectrum disorder (Azmitia et al., 2011), epilepsy (Maia et al., 2019), major depressive disorder (Numasawa et al., 2017), social isolation (Keesom et al., 2018), and the abuse of 3,4-methylenedioxy-methamphetamine (MDMA, Ecstasy) (Adori et al., 2011). In the healthy brain, 5-HT signaling plays major roles in the sleep-wake cycle (Brown et al., 2012) and reward circuits (Liu et al., 2020). It suggests that predictive models of the self-organization and dynamics of serotonergic fibers may advance not only basic neuroscience but also find applications in the biomedical field.
The dataset generated in this study is available in the following online repositories: Dryad (https://doi.org/doi:10.25349/D9802S) and Scholars’ Mine (https://scholarsmine.mst.edu/phys_facwork/2305/).
This animal study was reviewed and approved by the UCSB IACUC.
SJ proposed that the self-organization of serotonergic densities can be modeled with FBM-paths, produced the embryonic brain section series (with JH), wrote the Mathematica scripts to convert raw section images into the simulation-compatible format, and wrote the first draft of the manuscript. TV performed all supercomputing simulations. RM contributed to the theoretical development of the used approaches. SJ, RM, and TV are the Principal Investigators of their respective research programs. All authors contributed to the article and approved the submitted version.
This research was supported by an NSF-BMBF (USA-Germany) CRCNS grant (NSF #2112862 and BMBF #STAXS).
We thank Dr. Kasie Mays (UCSB) for the advice on published serotonergic density maps and Parsa Madinei (UCSB) for the assistance with histology.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Adori, C., Ando, R. D., Szekeres, M., Gutknecht, L., Kovacs, G. G., Hunyady, L., et al. (2011). Recovery and aging of serotonergic fibers after single and intermittent MDMA treatment in Dark Agouti rat. J. Comp. Neurol. 519, 2353–2378. doi: 10.1002/cne.22631
Andersson, M., Kjer, H. M., Rafael-Patino, J., Pacureanu, A., Pakkenberg, B., Thiran, J. P., et al. (2020). Axon morphology is modulated by the local environment and impacts the noninvasive investigation of its structure-function relationship. Proc. Natl. Acad. Sci. U.S.A. 117, 33649–33659. doi: 10.1073/pnas.2012533117
Antonovaite, N., Hulshof, L. A., Hol, E. M., Wadman, W. J., and Iannuzzi, D. (2021). Viscoelastic mapping of mouse brain tissue: relation to structure and age. J. Mech. Behav. Biomed. Mater. 113:104159. doi: 10.1016/j.jmbbm.2020.104159
Awasthi, J. R., Tamada, K., Overton, E. T. N., and Takumi, T. (2021). Comprehensive topographical map of the serotonergic fibers in the male mouse brain. J. Comp. Neurol. 529, 1391–1429. doi: 10.1002/cne.25027
Azmitia, E. C., Singh, J. S., and Whitaker-Azmitia, P. M. (2011). Increased serotonin axons (immunoreactive to 5-HT transporter) in postmortem brains from young autism donors. Neuropharmacology 60, 1347–1354. doi: 10.1016/j.neuropharm.2011.02.002
Belmer, A., Beecher, K., Jacques, A., Patkar, O. L., Sicherre, F., and Bartlett, S. E. (2019). Axonal non-segregation of the vesicular glutamate transporter VGLUT3 within serotonergic projections in the mouse forebrain. Front. Cell Neurosci. 13:193. doi: 10.3389/fncel.2019.00193
Belmer, A., Klenowski, P. M., Patkar, O. L., and Bartlett, S. E. (2017). Mapping the connectivity of serotonin transporter immunoreactive axons to excitatory and inhibitory neurochemical synapses in the mouse limbic brain. Brain Struct. Funct. 222, 1297–1314. doi: 10.1007/s00429-016-1278-x
Betz, T., Lim, D., and Käs, J. A. (2006). Neuronal growth: a bistable stochastic process. Phys. Rev. Lett. 96:098103. doi: 10.1103/PhysRevLett.96.098103
Bhat, S. K., and Ganesh, C. B. (2023). Organization of serotonergic system in Sphaerotheca breviceps (Dicroglossidae) tadpole brain. Cell Tissue Res. 391, 67–86. doi: 10.1007/s00441-022-03709-7
Biagini, F., Hu, Y., Oksendal, B., and Zhang, T. (2010). Stochastic Calculus For Fractional Brownian Motion and Applications. London: Springer.
Bjarkam, C. R., Sørensen, J. C., and Geneser, F. A. (2003). Distribution and morphology of serotonin-immunoreactive axons in the hippocampal region of the New Zealand white rabbit. I. Area dentata and hippocampus. Hippocampus 13, 21–37. doi: 10.1002/hipo.10042
Bjarkam, C. R., Sørensen, J. C., and Geneser, F. A. (2005). Distribution and morphology of serotonin-immunoreactive axons in the retrohippocampal areas of the New Zealand white rabbit. Anat Embryol. 210, 199–207. doi: 10.1007/s00429-005-0004-x
Bonnin, A., and Levitt, P. (2011). Fetal, maternal, and placental sources of serotonin and new implications for developmental programming of the brain. Neuroscience 197, 1–7. doi: 10.1016/j.neuroscience.2011.10.005
Brown, R. E., Basheer, R., McKenna, J. T., Strecker, R. E., and McCarley, R. W. (2012). Control of sleep and wakefulness. Physiol. Rev. 92, 1087–1187. doi: 10.1152/physrev.00032.2011
Brüning, G., Liangos, O., and Baumgarten, H. G. (1997). Prenatal development of the serotonin transporter in mouse brain. Cell Tissue Res. 289, 211–221. doi: 10.1007/s004410050868
Butler, A. B., and Hodos, W. (2005). Comparative Vertebrate Neuroanatomy, 2nd Edn. Hoboken, NJ: Wiley-Interscience.
Challet, E., Miceli, D., Pierre, J., Repérant, J., Masicotte, G., Herbin, M., et al. (1996). Distribution of serotonin-immunoreactivity in the brain of the pigeon (Columba livia). Anat. Embryol. 193, 209–227. doi: 10.1007/bf00198325
Challet, E., Pierre, J., Repérant, J., Ward, R., and Miceli, D. (1991). The serotoninergic system of the brain of the viper, Vipera aspis. An immunohistochemical study. J. Chem. Neuroanat. 4, 233–238. doi: 10.1016/0891-0618(91)90015-5
Chen, W. V., Nwakeze, C. L., Denny, C. A., O’Keeffe, S., Rieger, M. A., Mountoufaris, G., et al. (2017). Pcdhαc2 is required for axonal tiling and assembly of serotonergic circuitries in mice. Science 356, 406–411. doi: 10.1126/science.aal3231
Cherstvy, A. G., Thapa, S., Wagner, C. E., and Metzler, R. (2019). Non-Gaussian, non-ergodic, and non-Fickian diffusion of tracers in mucin hydrogels. Soft. Matter 15, 2526–2551. doi: 10.1039/c8sm02096e
Cheung, A., Konno, K., Imamura, Y., Matsui, A., Abe, M., Sakimura, K., et al. (2023). Neurexins in serotonergic neurons regulate neuronal survival, serotonin transmission, and complex mouse behaviors. Elife 12:e85058. doi: 10.7554/eLife.85058
Cooke, P., Janowitz, H., and Dougherty, S. E. (2022). Neuronal redevelopment and the regeneration of neuromodulatory axons in the adult mammalian central nervous system. Front. Cell Neurosci. 16:872501. doi: 10.3389/fncel.2022.872501
Daws, R. E., Timmermann, C., Giribaldi, B., Sexton, J. D., Wall, M. B., Erritzoe, D., et al. (2022). Increased global integration in the brain after psilocybin therapy for depression. Nat. Med. 28, 844–851. doi: 10.1038/s41591-022-01744-z
Dinopoulos, A., and Dori, I. (1995). The development of the serotonergic fiber network of the lateral ventricles of the rat brain: a light and electron microscopic immunocytochemical analysis. Exp. Neurol. 133, 73–84. doi: 10.1006/exnr.1995.1009
Donovan, S. L., Mamounas, L. A., Andrews, A. M., Blue, M. E., and McCasland, J. S. (2002). GAP-43 is critical for normal development of the serotonergic innervation in forebrain. J. Neurosci. 22, 3543–3552. doi: 10.1523/jneurosci.22-09-03543.2002
Dos Santos, S. E., Medeiros, M., Porfirio, J., Tavares, W., Pessôa, L., Grinberg, L., et al. (2020). Similar microglial cell densities across brain structures and mammalian species: implications for brain tissue function. J. Neurosci. 40, 4622–4643. doi: 10.1523/jneurosci.2339-19.2020
Erö, C., Gewaltig, M. O., Keller, D., and Markram, H. (2018). A cell atlas for the mouse brain. Front. Neuroinform. 12:84. doi: 10.3389/fninf.2018.00084
Flood, Z. C., Engel, D. L., Simon, C. C., Negherbon, K. R., Murphy, L. J., Tamavimok, W., et al. (2012). Brain growth trajectories in mouse strains with central and peripheral serotonin differences: relevance to autism models. Neuroscience 210, 286–295. doi: 10.1016/j.neuroscience.2012.03.010
Foote, S. L., and Morrison, J. H. (1984). Postnatal development of laminar innervation patterns by monoaminergic fibers in monkey (Macaca fascicularis) primary visual cortex. J. Neurosci. 4, 2667–2680. doi: 10.1523/JNEUROSCI.04-11-02667.1984
Fournet, V., Jany, M., Fabre, V., Chali, F., Orsal, D., Schweitzer, A., et al. (2010). The deletion of the microtubule-associated STOP protein affects the serotonergic mouse brain network. J. Neurochem. 115, 1579–1594. doi: 10.1111/j.1471-4159.2010.07064.x
Gagnon, D., and Parent, M. (2014). Distribution of VGLUT3 in highly collateralized axons from the rat dorsal raphe nucleus as revealed by single-neuron reconstructions. PLoS One 9:e87709. doi: 10.1371/journal.pone.0087709
García-González, D., Khodosevich, K., Watanabe, Y., Rollenhagen, A., Lübke, J. H. R., and Monyer, H. (2017). Serotonergic projections govern postnatal neuroblast migration. Neuron 94, 534–549.e9. doi: 10.1016/j.neuron.2017.04.013
Guggenberger, T., Pagnini, G., Vojta, T., and Metzler, R. (2019). Fractional Brownian motion in a finite interval: correlations effect depletion or accretion zones of particles near boundaries. N. J. Phys. 21:022002. doi: 10.1016/j.icarus.2017.03.021
Guo, J., Bertalan, G., Meierhofer, D., Klein, C., Schreyer, S., Steiner, B., et al. (2019). Brain maturation is associated with increasing tissue stiffness and decreasing tissue fluidity. Acta Biomater. 99, 433–442. doi: 10.1016/j.actbio.2019.08.036
Herculano-Houzel, S. (2014). The glia/neuron ratio: how it varies uniformly across brain structures and species and what that means for brain physiology and evolution. Glia 62, 1377–1391. doi: 10.1002/glia.22683
Hingorani, M., Viviani, A. M. L., Sanfilippo, J. E., and Janušonis, S. (2022). High-resolution spatiotemporal analysis of single serotonergic axons in an in vitro system. Front. Neurosci. 16:994735. doi: 10.3389/fnins.2022.994735
Hokfelt, T. (2016). Early attempts to visualize cortical monoamine nerve terminals. Brain Res. 1645, 8–11. doi: 10.1016/j.brainres.2016.01.024
Hrabetova, S., Cognet, L., Rusakov, D. A., and Nagerl, U. V. (2018). Unveiling the extracellular space of the brain: from super-resolved microstructure to in vivo function. J. Neurosci. 38, 9355–9363. doi: 10.1523/jneurosci.1664-18.2018
Iwashita, M., Kataoka, N., Toida, K., and Kosodo, Y. (2014). Systematic profiling of spatiotemporal tissue and cellular stiffness in the developing brain. Development 141, 3793–3798. doi: 10.1242/dev.109637
Jacobs, B. L., and Azmitia, E. C. (1992). Structure and function of the brain serotonin system. Physiol. Rev. 72, 165–229. doi: 10.1152/physrev.1992.72.1.165
Jang, K. J., Kim, M. S., Feltrin, D., Jeon, N. L., Suh, K. Y., and Pertz, O. (2010). Two distinct filopodia populations at the growth cone allow to sense nanotopographical extracellular matrix cues to guide neurite outgrowth. PLoS One 5:e15966. doi: 10.1371/journal.pone.0015966
Janušonis, S. (2018). Some galeomorph sharks express a mammalian microglia-specific protein in radial ependymoglia of the telencephalon. Brain Behav. Evol. 91, 17–30. doi: 10.1159/000484196
Janušonis, S., and Detering, N. (2019). A stochastic approach to serotonergic fibers in mental disorders. Biochimie 161, 15–22. doi: 10.1016/j.biochi.2018.07.014
Janušonis, S., Detering, N., Metzler, R., and Vojta, T. (2020). Serotonergic axons as fractional Brownian motion paths: insights into the self-organization of regional densities. Front. Comput. Neurosci. 14:56. doi: 10.3389/fncom.2020.00056
Janušonis, S., Gluncic, V., and Rakic, P. (2004). Early serotonergic projections to Cajal-Retzius cells: relevance for cortical development. J. Neurosci. 24, 1652–1659. doi: 10.1523/jneurosci.4651-03.2004
Janušonis, S., Mays, K. C., and Hingorani, M. T. (2019). Serotonergic axons as 3D-walks. ACS Chem. Neurosci. 10, 3064–3067. doi: 10.1021/acschemneuro.8b00667
Jin, Y., Dougherty, S. E., Wood, K., Sun, L., Cudmore, R. H., Abdalla, A., et al. (2016). Regrowth of serotonin axons in the adult mouse brain following injury. Neuron 91, 748–762. doi: 10.1016/j.neuron.2016.07.024
Katori, S., Hamada, S., Noguchi, Y., Fukuda, E., Yamamoto, T., Yamamoto, H., et al. (2009). Protocadherin-α family is required for serotonergic projections to appropriately innervate target brain areas. J. Neurosci. 29, 9137–9147. doi: 10.1523/jneurosci.5478-08.2009
Katori, S., Noguchi-Katori, Y., Okayama, A., Kawamura, Y., Luo, W., Sakimura, K., et al. (2017). Protocadherin-αC2 is required for diffuse projections of serotonergic axons. Sci. Rep. 7:15908. doi: 10.1038/s41598-017-16120-y
Katz, M. J., George, E. B., and Gilbert, L. J. (1984). Axonal elongation as a stochastic walk. Cell Motil. 4, 351–370. doi: 10.1002/cm.970040505
Keesom, S. M., Morningstar, M. D., Sandlain, R., Wise, B. M., and Hurley, L. M. (2018). Social isolation reduces serotonergic fiber density in the inferior colliculus of female, but not male, mice. Brain Res. 1694, 94–103. doi: 10.1016/j.brainres.2018.05.010
Keller, D., Erö, C., and Markram, H. (2018). Cell densities in the mouse brain: a systematic review. Front. Neuroanat. 12:83. doi: 10.3389/fnana.2018.00083
Kosofsky, B. E., and Molliver, M. E. (1987). The serotoninergic innervation of cerebral cortex: different classes of axon terminals arise from dorsal and median raphe nuclei. Synapse 1, 153–168. doi: 10.1002/syn.890010204
Lavoie, B., and Parent, A. (1990). Immunohistochemical study of the serotoninergic innervation of the basal ganglia in the squirrel monkey. J. Comp. Neurol. 299, 1–16. doi: 10.1002/cne.902990102
Lavoie, B., and Parent, A. (1991). Serotoninergic innervation of the thalamus in the primate: an immunohistochemical study. J. Comp. Neurol. 312, 1–18. doi: 10.1002/cne.903120102
Lebrand, C., Cases, O., Adelbrecht, C., Doye, A., Alvarez, C., El Mestikawy, S., et al. (1996). Transient uptake and storage of serotonin in developing thalamic neurons. Neuron 17, 823–835. doi: 10.1016/s0896-6273(00)80215-9
Lebrand, C., Gaspar, P., Nicolas, D., and Hornung, J. P. (2006). Transitory uptake of serotonin in the developing sensory pathways of the common marmoset. J. Comp. Neurol. 499, 677–689. doi: 10.1002/cne.21137
Lesch, K. P., and Waider, J. (2012). Serotonin in the modulation of neural plasticity and networks: implications for neurodevelopmental disorders. Neuron 76, 175–191. doi: 10.1016/j.neuron.2012.09.013
Lesch, K. P., Araragi, N., Waider, J., van den Hove, D., and Gutknecht, L. (2012). Targeting brain serotonin synthesis: insights into neurodevelopmental disorders with long-term outcomes related to negative emotionality, aggression and antisocial behaviour. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 367, 2426–2443.
Lidov, H. G., and Molliver, M. E. (1982). An immunohistochemical study of serotonin neuron development in the rat: ascending pathways and terminal fields. Brain Res. Bull. 8, 389–430. doi: 10.1016/0361-9230(82)90077-6
Linley, S. B., Hoover, W. B., and Vertes, R. P. (2013). Pattern of distribution of serotonergic fibers to the orbitomedial and insular cortex in the rat. J. Chem. Neuroanat. 48-49, 29–45. doi: 10.1016/j.jchemneu.2012.12.006
Liu, Z., Lin, R., and Luo, M. (2020). Reward contributions to serotonergic functions. Annu. Rev. Neurosci. 43, 141–162. doi: 10.1146/annurev-neuro-093019-112252
López, J. M., and González, A. (2014). Organization of the serotonergic system in the central nervous system of two basal actinopterygian fishes: the Cladistians Polypterus senegalus and Erpetoichthys calabaricus. Brain Behav. Evol. 83, 54–76. doi: 10.1159/000358266
Maddaloni, G., Bertero, A., Pratelli, M., Barsotti, N., Boonstra, A., Giorgi, A., et al. (2017). Development of serotonergic fibers in the post-natal mouse brain. Front. Cell Neurosci. 11:202. doi: 10.3389/fncel.2017.00202
Maddaloni, G., Migliarini, S., Napolitano, F., Giorgi, A., Nazzi, S., Biasci, D., et al. (2018). Serotonin depletion causes valproate-responsive manic-like condition and increased hippocampal neuroplasticity that are reversed by stress. Sci. Rep. 8:11847. doi: 10.1038/s41598-018-30291-2
Maia, G. H., Soares, J. I., Almeida, S. G., Leite, J. M., Baptista, H. X., Lukoyanova, A. N., et al. (2019). Altered serotonin innervation in the rat epileptic brain. Brain Res. Bull. 152, 95–106. doi: 10.1016/j.brainresbull.2019.07.009
Makse, H. A., Havlin, S., Schwartz, M., and Stanley, H. E. (1996). Method for generating long-range correlations for large systems. Phys. Rev. E. 53, 5445–5449.
Mamounas, L. A., Blue, M. E., Siuciak, J. A., and Altar, C. A. (1995). Brain-derived neurotrophic factor promotes the survival and sprouting of serotonergic axons in rat brain. J. Neurosci. 15, 7929–7939.
Mandelbrot, B. B., and Van Ness, J. W. (1968). Fractional Brownian motions, fractional noises and applications. SIAM Rev. 10, 422–437.
Maskery, S., and Shinbrot, T. (2005). Deterministic and stochastic elements of axonal guidance. Annu. Rev. Biomed. Eng. 7, 187–221. doi: 10.1146/annurev.bioeng.7.060804.100446
Meiklejohn, C., Agelarakis, A., Akkermans, P. A., Smith, P. E. L., and Solecki, R. (1992). Artificial cranial deformation in the proto-neolithic and neolithic Near East and its possible origin: evidence from four sites. Paleorient 18, 83–97.
Metzger, M., Toledo, C., and Braun, K. (2002). Serotonergic innervation of the telencephalon in the domestic chick. Brain Res. Bull. 57, 547–551. doi: 10.1016/s0361-9230(01)00688-8
Migliarini, S., Pacini, G., Pelosi, B., Lunardi, G., and Pasqualetti, M. (2013). Lack of brain serotonin affects postnatal development and serotonergic neuronal circuitry formation. Mol. Psychiatry 18, 1106–1118. doi: 10.1038/mp.2012.128
Mize, R. R., and Horner, L. H. (1989). Origin, distribution, and morphology of serotonergic afferents to the cat superior colliculus: a light and electron microscope immunocytochemistry study. Exp. Brain Res. 75, 83–98. doi: 10.1007/bf00248533
Mlinar, B., Montalbano, A., Piszczek, L., Gross, C., and Corradetti, R. (2016). Firing properties of genetically identified dorsal raphe serotonergic neurons in brain slices. Front. Cell Neurosci. 10:195. doi: 10.3389/fncel.2016.00195
Montalbano, A., Waider, J., Barbieri, M., Baytas, O., Lesch, K. P., Corradetti, R., et al. (2015). Cellular resilience: 5-HT neurons in Tph2(-/-) mice retain normal firing behavior despite the lack of brain 5-HT. Eur. Neuropsychopharmacol. 25, 2022–2035. doi: 10.1016/j.euroneuro.2015.08.021
Morin, L. P., and Meyer-Bernstein, E. L. (1999). The ascending serotonergic system in the hamster: comparison with projections of the dorsal and median raphe nuclei. Neuroscience 91, 81–105. doi: 10.1016/s0306-4522(98)00585-5
Mosienko, V., Beis, D., Pasqualetti, M., Waider, J., Matthes, S., Qadri, F., et al. (2015). Life without brain serotonin: reevaluation of serotonin function with mice deficient in brain serotonin synthesis. Behav. Brain Res. 277, 78–88. doi: 10.1016/j.bbr.2014.06.005
Nazzi, S., Maddaloni, G., Pratelli, M., and Pasqualetti, M. (2019). Fluoxetine induces morphological rearrangements of serotonergic fibers in the hippocampus. ACS Chem. Neurosci. 10, 3218–3224. doi: 10.1021/acschemneuro.8b00655
Nicholson, C. (2005). Factors governing diffusing molecular signals in brain extracellular space. J. Neural Transm. 112, 29–44. doi: 10.1007/s00702-004-0204-1
Nicholson, C., and Hrabetova, S. (2017). Brain extracellular space: the final frontier of neuroscience. Biophys. J. 113, 2133–2142. doi: 10.1016/j.bpj.2017.06.052
Numasawa, Y., Hattori, T., Ishiai, S., Kobayashi, Z., Kamata, T., Kotera, M., et al. (2017). Depressive disorder may be associated with raphe nuclei lesions in patients with brainstem infarction. J. Affect. Disord. 213, 191–198. doi: 10.1016/j.jad.2017.02.005
Okaty, B. W., Commons, K. G., and Dymecki, S. M. (2019). Embracing diversity in the 5-HT neuronal system. Nat. Rev. Neurosci. 20, 397–424. doi: 10.1038/s41583-019-0151-3
Okaty, B. W., Sturrock, N., Escobedo Lozoya, Y., Chang, Y., Senft, R. A., Lyon, K. A., et al. (2020). A single-cell transcriptomic and anatomic atlas of mouse dorsal raphe Pet1 neurons. Elife 9:e55523. doi: 10.7554/eLife.55523
Parent, M., Wallman, M. J., Gagnon, D., and Parent, A. (2011). Serotonin innervation of basal ganglia in monkeys and humans. J. Chem. Neuroanat. 41, 256–265. doi: 10.1016/j.jchemneu.2011.04.005
Paxinos, G., Watson, C., Kassem, M. S., and Halliday, G. (2020). Atlas of the developing mouse brain. Cambridge, MA: Elsevier.
Popova, N. K., and Naumenko, V. S. (2019). Neuronal and behavioral plasticity: the role of serotonin and BDNF systems tandem. Expert Opin. Ther. Targets 23, 227–239. doi: 10.1080/14728222.2019.1572747
Qian, H. (2003). “Fractional Brownian motion and fractional Gaussian noise,” in Processes With Long-Range Correlations: Theory and Applications, eds G. Rangarajan and M. Ding (Berlin: Springer), 22–33.
Ren, J., Friedmann, D., Xiong, J., Liu, C. D., Ferguson, B. R., Weerakkody, T., et al. (2018). Anatomically defined and functionally distinct dorsal raphe serotonin sub-systems. Cell 175, 472.e–487.e. doi: 10.1016/j.cell.2018.07.043
Ren, J., Isakova, A., Friedmann, D., Zeng, J., Grutzner, S. M., Pun, A., et al. (2019). Single-cell transcriptomes and whole-brain projections of serotonin neurons in the mouse dorsal and median raphe nuclei. Elife 8:e49424. doi: 10.7554/eLife.49424
Slaten, E. R., Hernandez, M. C., Albay, R. III, Lavian, R., and Janušonis, S. (2010). Transient expression of serotonin 5-HT4 receptors in the mouse developing thalamocortical projections. Dev. Neurobiol. 70, 165–181. doi: 10.1002/dneu.20775
Sodhi, M. S., and Sanders-Bush, E. (2004). Serotonin and brain development. Int. Rev. Neurobiol. 59, 111–174. doi: 10.1016/s0074-7742(04)59006-2
Steinbusch, H. W. (1981). Distribution of serotonin-immunoreactivity in the central nervous system of the rat-cell bodies and terminals. Neuroscience 6, 557–618. doi: 10.1016/0306-4522(81)90146-9
Striedter, G. F., and Northcutt, R. G. (2020). Brains Through Time. New York, NY: Oxford University Press.
Stuesse, S. L., Cruce, W. L., and Northcutt, R. G. (1991). Localization of serotonin, tyrosine hydroxylase, and leu-enkephalin immunoreactive cells in the brainstem of the horn shark, Heterodontus francisci. J. Comp. Neurol. 308, 277–292. doi: 10.1002/cne.903080211
Sur, C., Betz, H., and Schloss, P. (1996). Immunocytochemical detection of the serotonin transporter in rat brain. Neuroscience 73, 217–231.
Syková, E., and Nicholson, C. (2008). Diffusion in brain extracellular space. Physiol. Rev. 88, 1277–1340. doi: 10.1152/physrev.00027.2007
Teissier, A., Soiza-Reilly, M., and Gaspar, P. (2017). Refining the role of 5-HT in postnatal development of brain circuits. Front. Cell Neurosci. 11:139.
Vargas, M. V., Dunlap, L. E., Dong, C., Carter, S. J., Tombari, R. J., Jami, S. A., et al. (2023). Psychedelics promote neuroplasticity through the activation of intracellular 5-HT2A receptors. Science 379, 700–706. doi: 10.1126/science.adf0435
Vertes, R. P. (1991). A PHA-L analysis of ascending projections of the dorsal raphe nucleus in the rat. J. Comp. Neurol. 313, 643–668. doi: 10.1002/cne.903130409
Vertes, R. P., Fortin, W. J., and Crane, A. M. (1999). Projections of the median raphe nucleus in the rat. J. Comp. Neurol. 407, 555–582.
Vertes, R. P., Linley, S. B., and Hoover, W. B. (2010). Pattern of distribution of serotonergic fibers to the thalamus of the rat. Brain Struct. Funct. 215, 1–28. doi: 10.1007/s00429-010-0249-x
Vogt, B. A., and Paxinos, G. (2014). Cytoarchitecture of mouse and rat cingulate cortex with human homologies. Brain Struct. Funct. 219, 185–192. doi: 10.1007/s00429-012-0493-3
Voigt, T., and de Lima, A. D. (1991a). Serotoninergic innervation of the ferret cerebral cortex. I. Adult pattern. J. Comp. Neurol. 314, 403–414. doi: 10.1002/cne.903140214
Voigt, T., and de Lima, A. D. (1991b). Serotoninergic innervation of the ferret cerebral cortex. II. Postnatal development. J. Comp. Neurol. 314, 415–428. doi: 10.1002/cne.903140215
Vojta, T., Halladay, S., Skinner, S., Janušonis, S., Guggenberger, T., and Metzler, R. (2020). Reflected fractional Brownian motion in one and higher dimensions. Phys. Rev. E. 102:032108. doi: 10.1103/PhysRevE.102.032108
Wada, A. H. O., and Vojta, T. (2018). Fractional Brownian motion with a reflecting wall. Phys. Rev. E. 97:020102. doi: 10.1103/PhysRevE.97.020102
Wallace, J. A., and Lauder, J. M. (1983). Development of the serotonergic system in the rat embryo: an immunocytochemical study. Brain Res. Bull. 10, 459–479. doi: 10.1016/0361-9230(83)90144-2
Wang, W., Balcerek, M., Burnecki, K., Chechkin, A. V., Janušonis, S., Slezak, J., et al. (2023). Memory-multi-fractional Brownian motion with continuous correlations. arXiv [Preprint] doi: 10.48550/arXiv.2303.01551
Waterhouse, B. D., Mihailoff, G. A., Baack, J. C., and Woodward, D. J. (1986). Topographical distribution of dorsal and median raphe neurons projecting to motor, sensorimotor, and visual cortical areas in the rat. J. Comp. Neurol. 249, 460–476, 478–481. doi: 10.1002/cne.902490403
Way, B. M., Lacan, G., Fairbanks, L. A., and Melega, W. P. (2007). Architectonic distribution of the serotonin transporter within the orbitofrontal cortex of the vervet monkey. Neuroscience 148, 937–948. doi: 10.1016/j.neuroscience.2007.06.038
Whitaker-Azmitia, P. M. (2001). Serotonin and brain development: role in human developmental diseases. Brain Res. Bull. 56, 479–485.
Wolters, J. G., ten Donkelaar, H. J., Steinbusch, H. W., and Verhofstad, A. A. (1985). Distribution of serotonin in the brain stem and spinal cord of the lizard Varanus exanthematicus: an immunohistochemical study. Neuroscience 14, 169–193. doi: 10.1016/0306-4522(85)90172-1
Keywords: 5-hydroxytryptamine, serotonin, axons, density, stochastic process, anomalous diffusion, fractional Brownian motion, geometry
Citation: Janušonis S, Haiman JH, Metzler R and Vojta T (2023) Predicting the distribution of serotonergic axons: a supercomputing simulation of reflected fractional Brownian motion in a 3D-mouse brain model. Front. Comput. Neurosci. 17:1189853. doi: 10.3389/fncom.2023.1189853
Received: 20 March 2023; Accepted: 24 April 2023;
Published: 16 May 2023.
Edited by:
Yu-Guo Yu, Fudan University, ChinaReviewed by:
Massimo Pasqualetti, University of Pisa, ItalyCopyright © 2023 Janušonis, Haiman, Metzler and Vojta. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Skirmantas Janušonis, amFudXNvbmlzQHVjc2IuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.