- Brain Science Institute, Korea Institute of Science and Technology, Seoul, Republic of Korea
Although it may appear infeasible and impractical, building artificial intelligence (AI) using a bottom-up approach based on the understanding of neuroscience is straightforward. The lack of a generalized governing principle for biological neural networks (BNNs) forces us to address this problem by converting piecemeal information on the diverse features of neurons, synapses, and neural circuits into AI. In this review, we described recent attempts to build a biologically plausible neural network by following neuroscientifically similar strategies of neural network optimization or by implanting the outcome of the optimization, such as the properties of single computational units and the characteristics of the network architecture. In addition, we proposed a formalism of the relationship between the set of objectives that neural networks attempt to achieve, and neural network classes categorized by how closely their architectural features resemble those of BNN. This formalism is expected to define the potential roles of top-down and bottom-up approaches for building a biologically plausible neural network and offer a map helping the navigation of the gap between neuroscience and AI engineering.
1. Introduction
Turing's idea of building a thinking machine by replacing an organism with artifacts, part by part (Turing, 1948), has inspired scientists and engineers because it was the first clear statement of a bottom-up approach toward building artificial intelligence (AI). In general, the term “bottom-up” refers to the directionality of an approach that begins with specifics or minutiae to arrive at a comprehensive solution. Thus, the bottom-up approach to developing a brain-like intelligence system begins with spatiotemporal local properties and their organized combinations. Local properties are presented in neurons or synapses, namely, single computational units and their combinations directly depict the connectivity and architecture of a neural circuit. Because these details and their effects are covered by the discipline of neuroscience, developing AI from the ground up using an understanding of neuroscience is straightforward. However, even the latest neuroscience field lacks comprehensive knowledge of neural circuits, their functions, and the mapping between them, indicating that the operating principle of neural networks is absent in practice (Goodfellow et al., 2016; Jonas and Kording, 2017). Thus, experimental attempts to translate up-to-date piecemeal information on various characteristics of neurons, synapses, and neural circuits into AI are the only viable options under these circumstances. Given that replacing a component of an artificial neural network (ANN) with the counterpart of a biological neural network (BNN) generally does not outperform the original ANN and is often not very influential, a bottom-up approach appears to be infeasible and impractical although it does not imply inherent impossibility, as Turing contested (Turing, 1948).
Nonetheless, we believe exploring the gap between neuroscience and AI engineering using a bottom-up approach should be encouraged. Although no unified principle governing multiscale neural network features has been found, there are several useful models describing phenomena at different scales. Good examples include the Hebbian learning principle and its modifications, encompassing various forms of long-term synaptic plasticity (Dayan and Abbott, 2001). Considering the history of AI development, it is unsurprising that an ANN incorporates specific principles from neuroscience and computational neuroscience. The birth of successful modern approaches, such as deep neural networks and their learning algorithms, is partly attributable to this type of strategy (Goodfellow et al., 2016). Furthermore, given the massive amount of resources required to operate such systems (Schuman et al., 2022), further information behind the efficient computation by the BNN should be uncovered and implanted into the ANN. To accelerate exploration using a bottom-up approach, cooperation between neuroscientists and AI engineers can be promoted through mutual benefits. One of the goals of neuroscience is to reveal the neural network mechanisms underlying a particular mental state or behavior that the neural network principle can encapsulate. This process requires confirmation by observations made in a controlled setting or laboratory experiments; however, because of their complexity, the brain and neural circuits are often inaccessible in a properly controlled manner. Furthermore, confirming a unified operating mechanism is challenging because of the low practicality of long-term and large-scale manipulation of the brain and neural system. AI engineering can serve as a valuable analogical model spanning several spatiotemporal scales, from a cellular level to behavioral consequences. Hence, an ANN based on the BNN features provides a proof-of-concept for a particular neural network principle, demonstrating how a neural circuit produces a specific behavior. On the other hand, the neural network principle contributes to a better understanding of how ANNs work. Considering that currently successful ANNs require improved explainability and interpretability (Gunning et al., 2019; Vilone and Longo, 2021; Nussberger et al., 2022), bottom-up approaches equipped with neural network principles can help AI designers better understand the outcomes of their ANN models. Thus, this review preferentially introduces studies that focused on the conceptual similarity between the components of a given ANN and its corresponding BNN, regardless of the model's performance on the tasks designed for ANNs.
On the other hand, because other types of approaches toward well-functioning intelligence systems have been successful, such as the recent advancement of large-scale language models (Devlin et al., 2019; Brown et al., 2020) and text-to-image models (Ramesh et al., 2022; Rombach et al., 2022), approaches under purely engineering goals seem to dispense with the need for a bottom-up approach. However, such approaches merely offer an explanation of how the brain is capable of many cognitive functions with BNN, contrary to the mutual benefit expected from the bottom-up approach. Top-down approaches like “brain-inspired” AI (Chen et al., 2019; Robertazzi et al., 2022; Zeng et al., 2022) partly enhance our understanding of the brain, especially the cognitive process of a certain task, and improve performances simultaneously, whereas their goals do not reach the circuit-level mechanism of BNN. At the other extreme, attempts to emulate BNN have been made to copy a mesoscopic neural circuit and demonstrate that copied BNN indeed show the same activity measured from experiments (Markram et al., 2015). They are useful for replacing invasive experiments in the future and for simulating virtually controlled experiments. However, these detailed models are not directly applicable to AI systems because of their low cost-effectiveness and relatively simple output pattern, despite large-scale computation with a large number of parameters to be optimized. Therefore, this review focuses on studies that consider the mutual benefits between scientific and engineering goals at the proper level of BNN abstraction.
Considering the rudiments of deep neural networks, the first step was to construct a neural network and select a training algorithm after determining the task and training dataset. Unlike ANN, nature handles the search for a BNN architecture and builds a training strategy. Thus, we begin the review with ANN's architecture search and training algorithm, which was inspired by the natural process of network structure optimization and its updates. As the optimization process continues, the properties of the single computational units and the architecture of the neural circuit are updated, which can be viewed as the outcome of successful optimization. This implies that understanding BNN properties and their impact on computation can be advantageous because such properties of BNN studied have already been refined by nature. Hence, the following sections of this review focus on the montage of useful BNN properties and the efforts related to the direct utilization of BNN properties in ANN design (summarized in Figure 1).
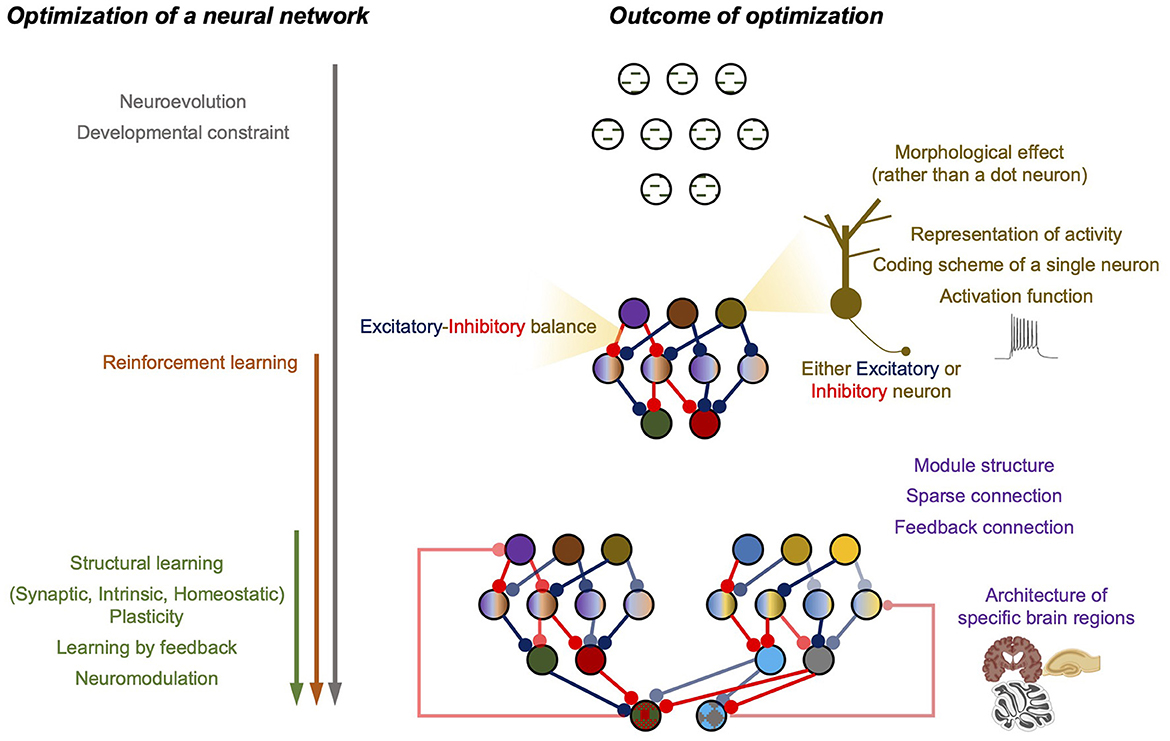
Figure 1. Summary figure of the review. (Left) The optimization processes of a neural network. Arrows represent the involvement of each process with time. (Right) The outcome of the optimization.
To develop a systematic manner as opposed to a random search of proper links between neuroscience and AI engineering, we defined the set of objectives that neural networks try to achieve as “the problem space” and categorized neural network models based on how closely their architectural features resemble those of BNN. Such formalization may offer an approximate map, including the limitations of ANN and what we should aim for when constructing a biologically plausible neural network. Using this map, we proposed the potential roles of neuroscience and AI engineering and their cooperative workflow pipeline. We believe that this pipeline will encourage reciprocal advantages by demonstrating how top-down and bottom-up approaches from neuroscience can offer useful information for AI engineering and, conversely, how AI engineering advances our understanding of the brain and its function.
2. Optimization strategy: multiscale credit assignment
All biologically intelligent agents interact with their environments and attempt to survive and reproduce. A combination of hereditary mutations and epigenetic adaptations builds up a biological agent's fitness, and the agents are eventually evaluated for survival (or death) and reproduction (or nonproliferation). One of the essential organs in an individual agent is the brain, which is optimized using the same process (Tosches, 2017). Although the entire optimization process can be understood in parts by dividing it into different temporal scales, each part still encounters the common conundrum of how much each spatiotemporal local parameter should be updated to improve fitness. Thus, this issue can be described as a multiscale credit assignment problem (Valiant, 2013). Assuming that the properties of the computational units, network architecture, and overall performance of the network are the outcomes of BNN optimization, it is worthwhile to imitate this strategy to achieve superior biologically plausible neural networks. In this review, we simply hypothesized that a longer time-scale optimization relates to the architectural search process through evolution and development, whereas a shorter-scale optimization corresponds to the learning process in a neural circuit or brain.
2.1. Architecture search: evolution and development
The process of evolution includes the development and learning of a neural circuit; therefore, it is a credit assignment process with the longest temporal scale. Genes that must be evaluated for fitness are prepared by mutations, and the neural circuit variants built from these genes are eventually tested by natural selection (Tosches, 2017; Hasson et al., 2020). The artificial counterpart of the mutation-selection process, namely, the evolutionary algorithm (EA), has been applied in numerous domains for decades, and “neuroevolution” refers to the application of EA to neural networks (Yao and Liu, 1998; Stanley et al., 2019; Galván and Mooney, 2021). Although the neuroevolution scheme simplified or omitted numerous aspects of the biological evolution process, it successfully captured the essentials and performed well in rediscovering the BNN properties (Risi and Stanley, 2014) and optimizing the ANN architecture (Liang et al., 2018; Zoph et al., 2018). In addition to structural connectivity, network architecture comprises the functional features of a network, such as the activation function of each neuron and its hyperparameters or initial synaptic weights. For example, the hyperparameters of different neuronal activation functions can be optimized using the EA (Cui et al., 2019). In deep learning, EA and reinforcement learning have been widely employed for the automated network model selection, termed neural architecture search (NAS; Elsken et al., 2019; Liu Y. et al., 2021).
In a BNN, developmental processes add diversity or constraints to neural networks through their stochastic nature or spatial arrangement, respectively (Smith, 1999; Tosches, 2017; Luo, 2021), in addition to a genetic code-driven architecture search. During development, neurons are ready to grow and connect to others, controlled by internally produced proteins (genetic codes) and external cues. Biological studies have revealed sequentially proceeding developmental processes: neuralation, proliferation, cell migration, differentiation, synaptogenesis, synapse pruning, and myelination (Tierney and Nelson, 2009). The first three steps indicate the orchestrated positioning of neuronal nodes in space, and the consecutive processes drive the formation of proper connections. Although genetic codes can drive the overall coordination of neuronal nodes in a three-dimensional space, chemical cues, such as morphogens, are constantly exposed to stochastic fluctuations (van Ooyen, 2011; Goodhill, 2018; Razetti et al., 2018; Llorca et al., 2019; Staii, 2022). Additionally, considering that synaptogenesis induces the randomly generated overproduction of synapses and connectivity is polished by pruning and myelination processes (van Ooyen, 2011; Goodhill, 2018; Razetti et al., 2018), the potential intervention of probabilistic diversification to differentiate connectivity is highly likely. Such stochasticity depends on the environment to which the brain is exposed. Thus, the common skeleton of the BNN architecture across individuals is an essential structure of a neural network to perform naturalistic tasks stably, and the variability in each individual agent is a sign of adaptation to different environments. This implies that by introducing such variability, we may be able to expand the range of searches in the parametric space of a neural network compared with relying only on genetic codes and mutations.
Although the evolution and development of BNN have potential advantages during ANN construction, direct and thorough imitation of these processes does not necessarily guarantee better ANN performance. First, when nature searches for answers through evolution and development, it utilizes an extremely efficient parallel search by preparing variable groups of individuals and combinations between groups (Foster and Baker, 2004; Traulsen and Nowak, 2006). To emulate such a process on a conventional computer, each individual needs to be stored in memory and evolved through a series of calculations, greatly increasing the computational burden. Thus, some processes should be simplified, and we need to capture the essential parts like the neuroevolution approach although an ensemble neural network strategy that shares the concept of group selection has been applied to construct and optimize ANN (Krogh and Vedelsby, 1994; Zhou et al., 2002; Liu and Yao, 2008; Zhang S. et al., 2020). The second aspect is platform dependency; as mentioned above, the optimization processes occurring in the brain depend on the spatial arrangement of computing units and chemicals as well as genetic codes, which implies that the distance between neurons can limit wiring (van Ooyen, 2011; Goodhill, 2018). Because the spatial arrangement of neurons and wiring costs do not matter in the simulation of an ANN, the direct translation of evolution and developmental processes for the BNN is not an effective option. Thus, only when we construct an ANN on a platform where the wiring cost can be defined, the emulation of the BNN formation through the direct imitation of evolution and development may offer a better architecture search algorithm. Third, evolution and development are primarily driven by the environment. In contrast to the well-specified task and dataset in ANN, the environment to which the BNN has to adapt is vast and carries an intensive amount of information, which blurs the boundary of essential information for training specific neural circuits. A notable recent study circumvented these problems and demonstrated that simplified developmental and evolutionary processes can select a biologically plausible neural circuit (Hiratani and Latham, 2022). This study utilized a rather simple feedforward neural network to approximate olfactory information in an environment, which was considered a teacher network to train a student network that corresponds to a biological olfactory circuit consisting of expansion-contraction coding architecture; eventually, such a simple approach successfully met with the scaling laws in BNN. This study showed a model case of how a mutually beneficial investigation can be designed to enhance the understanding of both BNN and ANN.
2.2. Learning algorithm
Once the fundamental architecture is determined by genetic codes and developmental processes, as described above, the BNN begins to be rapidly trained by interacting with the environment. Both structural and functional changes are involved in the biological implementation of this training process, which we call learning. Structural changes include neurogenesis, neuronal death, synaptogenesis, and pruning, while functional changes indicate the plasticity of neurons and synapses in the brain. Considering that local chemical and physiological mechanisms mediate these changes, achieving global adaptation through learning is a problem that the BNN must resolve, which we refer to as the populational credit assignment problem of computing units (Friedrich et al., 2011; Zou et al., 2023). Additionally, when instruction information for a proper change is provided by a circuit mechanism, such as a feedback connection, it is accompanied by an unavoidable delay that eventually causes a temporal credit assignment problem (Friedrich et al., 2011; Zou et al., 2023).
2.2.1. Local attributes: structural changes
Structural changes in the brain occur throughout the lifespan of an animal. However, considering that neurogenesis is a rare event and is observed in confined brain regions in adults, if any (Sorrells et al., 2018, 2021; Abdissa et al., 2020; Moreno-Jiménez et al., 2021), and significant neuronal death is expected to take place in old age or a pathological brain (Mattson and Magnus, 2006), simply assuming that the number of nodes of a neural network is determined by development is in the range of biological plausibility. In brain regions where we can expect significantly observable neurogenesis, such as the dentate gyrus in the hippocampus, a notable study reported that newly added neuronal nodes could contribute to neural network performance by working as a neural regularizer to avoid overfitting (Tran et al., 2022). In contrast to the addition of neuronal nodes, neuronal death may be superficially interpreted as the negative regulation of neural networks as observed in the aging or degenerative pathology of the brain (Mattson and Magnus, 2006). However, considering that some cognitive features can improve with age (Murman, 2015; Veríssimo et al., 2022), well-regulated neuronal death may not directly indicate the total dysfunction of a neural network. Two potential biological mechanisms account for this paradoxical positive regulation by removing neuronal nodes. First, as observed in biological studies (Kuhn et al., 2001; Merlo et al., 2019) and implied by computational studies (Barrett et al., 2016; Tan et al., 2020; Terziyan and Kaikova, 2022), a biological system often prepares compensatory mechanisms against sudden changes that can function as a temporary or partial advantage in neural computation. Another possibility is the intrinsic advantage achieved by removing neuronal nodes. In ANN, similar negative structural regulations have already been utilized as a form of “drop-out” or “sparsification” by intentionally removing neuronal nodes (Goodfellow et al., 2016; Tan et al., 2020; Hoefler et al., 2022). Because cognitive advantage with gradually increased neuronal death and its circuit mechanisms are largely unexplored, ANNs that include neuronal deaths and show partially or temporarily improved performances can offer new insights for both neuroscience and AI engineering.
Unlike the structural changes caused by neuronal addition or removal, new synapse formation and synaptic elimination by pruning, which are the addition and removal of edges in a neural network, occur more generally in the brain. The axon of a presynaptic neuron and the dendrite of a postsynaptic neuron should be within a proper distance before making a new synapse, and then a new synapse can be formed by the Hebbian type activity-dependent synaptogenesis (Südhof, 2018). However, the local mechanism of edge addition is insufficient for the optimization of an entire network and can result in excessive connectivity redundancy between activity-correlated neurons unless there is a regulatory mechanism. To participate in the optimization of a neural network, neurons must utilize information other than local synaptic activity. Negative regulatory mechanisms, such as synaptic elimination, are required to properly adjust the number of edges, which is widely utilized as an algorithm for the sparsification of a neural network to reduce the model (Luo, 2020; Hoefler et al., 2022). Adaptive synaptogenesis (Miller, 1998; Thomas et al., 2015), reinforcement signals from reward and punishment (Dos Santos et al., 2017), or other types of neuromodulation (Garcia et al., 2014; Speranza et al., 2017) may achieve such orchestration between positive and negative regulation. The counterparts of edge number regulation by synapse formation and elimination in ANN are the additive update of a synaptic weight from zero-weight connection and making a synaptic weight to zero, respectively, implying that the structural changes in synapses can be interpreted as the on-off switch type of functional changes. Interestingly, beyond the dichotomy of synapses or no synapses, a contact point between two neurons is ready to be switched on by the Hebbian-type learning rule in the form of a silent synapse (Kerchner and Nicoll, 2008; Hanse et al., 2013), which is also found in filopodia lacking AMPA receptors and containing NMDA receptors in the adult neocortex (Vardalaki et al., 2022). Considering that the brain should adapt to an increase in the amount of information to be stored, such a substrate for readiness is a valuable mechanism (Fusi et al., 2005; Vardalaki et al., 2022). Additionally, because a stable consolidation of acquired information into already stored information is accompanied by the rearrangement of the synaptic weights and connectivity, on- and off-type regulation should be appropriately utilized (Jedlicka et al., 2022). For ANN simulation on the current computer form, zero-weight synapse costs roughly the same as any other weight value in the allowed range; however, in BNN, physical wiring and its maintenance require additional resources. Hence, when constructing an ANN on a platform where the cost can be reduced by eliminating connections, a NAS strategy must be considered based on various types of structural changes in the BNN.
Similar to our categorization, a recent review (Maile et al., 2022) also regarded these structural changes after the developmental period as “structural learning,” which implies that NAS across a multi-temporal scale needs to continue for the whole life. In summary, structural changes in a neural network achieved by controlling the number of neurons or synapses are the key concepts that optimize a neural network architecture during its lifespan, and their implementation in an ANN can contribute to the construction of a better-performing neural network with reduced resource requirements under specific platforms.
2.2.2. Local attributes: functional changes
Although functional changes in a neural network are less explicit than physically expressed structural changes, they occur much more often in the brain and are essential for the fineness of adaptation. Various types of plasticity occurring at synapses or neurons are key components of the functional changes in a neural network.
Considering that a neuron transmits information as a spiking electrical signal, the so-called action potential, any change that alters the probability of generating action potentials under the same input indicates a change in neuronal excitability, which is called intrinsic plasticity. Thus, the intrinsic plasticity of a neuron can be interpreted as a transition from a certain state of neuronal excitability to a different state (Titley et al., 2017; Debanne et al., 2019). In a BNN, the concept of intrinsic plasticity is suitable for implementing memory mechanisms. Input-dependent stable changes in neuronal excitability can be directly paired with the hypothesis of the cellular level memory engram (Titley et al., 2017; Alejandre-García et al., 2022). Additionally, because the parameters of synaptic plasticity are significantly affected by the average activities of both pre- and post-synaptic neurons, as indicated by the Bienenstock-Cooper-Munro (BCM) model (Bienenstock et al., 1982; Dayan and Abbott, 2001), intrinsic plasticity can also be interpreted as a means of metaplasticity (Sehgal et al., 2013). Thus, implementing intrinsic plasticity in an ANN can improve the representability of the given information. In an ANN, the concept of neuronal excitability is expressed as a bias before the activation function determines the neuron's output. In many ANN cases, bias is considered a common constant within a layer or even set to zero. We can expect significantly better performances by introducing intrinsic plasticity into ANN or spiking neurons (Zhang and Li, 2019; Zhang et al., 2019). A similarity between the simplified intrinsic plasticity introduced in ANN and batch normalization has also been reported (Shaw et al., 2020).
The concept of synaptic plasticity involves changes in the efficacy of synaptic transmission across multiple temporal scales. Because a neuron propagates information through spikes, the main mechanism of synaptic plasticity is expected to depend on spike timing rather than amplitude by considering a uniform voltage level of action potential firing. Although the extent to which the synaptic weight should be adjusted depending on the timing differences between the presynaptic spike and postsynaptic spike varies with neuronal types, synaptic properties, or the existence of neuromodulation, synaptic plasticity occurring timing difference can be categorized as spike-timing-dependent-plasticity (STDP; qiang Bi and ming Poo, 1998). Under an ultra-sparse firing regime, STDP may be the sole mechanism to implement synaptic plasticity, which features Hebbian plasticity, in which neurons that fire together wire together (Song et al., 2000; Caporale and Dan, 2008). However, because information encoding is not always at the level of a single action potential firing, the description of synaptic plasticity at the level of each spike cannot explain the computational implications of the consequences of such plasticity. Thus, it is necessary to build a description of synaptic plasticity that depends on momentary information transmitted through the synapse. Rate-dependent encoding occurs at a longer timescale or under a denser spiking regime (Gerstner et al., 1997). Classical computational neuroscience has already depicted such plasticity by formalizing and improving Hebbian plasticity using additional terms (Dayan and Abbott, 2001). In fact, Hebbian plasticity and its variants could well describe synaptic plasticities in BNN, and by introducing the concept of sliding threshold, metaplasticity could be incorporated into formalism (Abraham, 2008; Laborieux et al., 2021). However, because these phenomenological models focus on simple but accurate descriptions of various synaptic plasticities in BNN, they require ad hoc terms or modifications if more diverse dynamics in synaptic plasticity and metaplasticity are observed. In contrast, mechanistic models can be more useful for generalizing various types of synaptic plasticity by introducing the dynamics of biological synaptic components. For example, considering that short-term plasticity can be utilized to stably represent information for a certain short period in a buffer-like neural network, analogous cognitive mechanisms such as working memory can be modeled (Masse et al., 2019), which may open up more promising future applications to the artificial memory system by introducing more detailed synaptic components. Indeed, a mechanistic model for short-term plasticities, such as the Tsodyks-Markram model (Tsodyks and Markram, 1997), could be utilized to explain working memory modulation (Rodriguez et al., 2022) and may help to build a better neuromorphic device (Zhang et al., 2017; Li et al., 2023) or a better artificial working memory system (Averbeck, 2022; Kozachkov et al., 2022; Rodriguez et al., 2022). The mechanical description of long-term synaptic plasticity is often composed of several processes responsible for multiple-timescale mechanisms, as indicated in the cascade model of binary switches constructed using positive feedback loops with multiple time constants (Kawato et al., 2011; Helfer and Shultz, 2018; Smolen et al., 2020). Although the readout of biological synaptic plasticity is the same as the weight adjustment in ANN, such mechanistic models may largely help construct a new type of metaplasticity algorithm in ANN. Considering the recent spotlight on metaplasticity as one of the solutions to catastrophic forgetting (Jedlicka et al., 2022), it has become more important to understand how synapses in BNN can form their metastable states and how synaptic plasticity can exploit the transition between these states to enhance the representation of information (Fusi et al., 2005; Benna and Fusi, 2016; Abraham et al., 2019).
2.2.3. Global optimization
An orchestrated strategy is required for these local processes of plasticity to result in the learning of a certain function. Learning is the adaptation of a neural network to approximate a function that maps from the input from the environment to the target output, which is a global optimization process (Zhang H. et al., 2020). The optimization target and the algorithm for efficiently reaching the target by combining local processes should be elucidated to define this optimization. Although how the brain can optimize neural networks and what kind of target it tries to minimize or maximize are generally unknown, there are several phenomena observed in BNN that can be the hint or the starting point toward building biologically plausible optimization algorithms. For example, homeostatic control of neuronal activity has been observed in various neural networks across multiple spatiotemporal scales from locally occurring Hebbian plasticity to global synaptic scaling or homeostatic intrinsic plasticity (Turrigiano et al., 1998; Turrigiano and Nelson, 2004; Naudé et al., 2013; Toyoizumi et al., 2014). The impact of locally occurring homeostatic plasticity (Naudé et al., 2013) and how global homeostatic plasticity regulates neural network dynamics (Zierenberg et al., 2018) has been simulated in biological recurrent networks. However, it has not been tested in ANN to improve the performance, and no attempt has been made to find a similar concept in the current ANN optimization algorithm. Recent experimental confirmation also supports the idea that a neural network utilizes a plasticity rule that maximizes information (Toyoizumi et al., 2005) or minimizes free energy (Isomura and Friston, 2018; Gottwald and Braun, 2020; Isomura et al., 2022). Additionally, considering that the wiring between neurons requires metabolic resources in the BNN, as mentioned in the NAS and structural learning sections, we can also define the cost function that includes the constraints introduced by limited physical resources (Chen et al., 2006; Tomasi et al., 2013; Rubinov et al., 2015; Goulas et al., 2019). Although the target functions for a neural network to optimize are explicit in these examples, how the optimization results in learning a cognitive task remain elusive. However, they have inspired the ANN method to approach the learning of relationships among data to approximate the probability distribution of inputs or latent variables, which is an example of an unsupervised learning paradigm (Goodfellow et al., 2016; Pitkow and Angelaki, 2017). On the other hand, supervised learning can be defined more easily by quantifying the difference between the function to learn and the current state of a neural network, which is generally called the loss function in an ANN (Goodfellow et al., 2016). The strategy for minimizing the loss function and assigning the adjustment of each weight is characterized by a backpropagation algorithm (Rumelhart et al., 1986). While no explicit evidence has been found that the brain uses error backpropagation for learning, a hypothetical learning algorithm class, “neural gradient representation by activity differences (NGRAD),” has been suggested, which states that the information of activity difference is reflected as synaptic change, driving the learning or behavioral change of the network (Lillicrap et al., 2020). Considering that the backpropagation algorithm in ANN and error-dependent learning are not directly comparable because of the difference in encoding (scalar value vs. spikes) and the questionable existence of mandatory symmetric backward connections in BNN, organized feedback of error or target information is necessary for the implementation of NGRAD in a biologically plausible neural network (Guerguiev et al., 2017; Sacramento et al., 2018; Whittington and Bogacz, 2019; Lillicrap et al., 2020; Fernández et al., 2021). In a large neural network with physical constraints, relying only on the global feedback information provided through the environment is inefficient because of the long delay (Nijhawan, 2008; Foerde and Shohamy, 2011; Cameron et al., 2014). For example, when an animal tries to visually follow a fast-moving prey, moving the eyeballs at the proper speed and forming a proper percept without mental preparation by predicting sensory consequences is difficult (Greve, 2015; Palmer et al., 2015; Sederberg et al., 2018). Therefore, a neural system is known to utilize predictive coding, and the prediction error may be an appropriate teaching signal for optimizing each component in a hierarchical neural network (Rao and Ballard, 1999; Millidge et al., 2022; Pezzulo et al., 2022). A recent study theoretically suggested and experimentally validated that even a single neuron can predict future activity and use a predictive learning rule to minimize surprises; this is derived from a contrastive Hebbian learning rule (Luczak et al., 2022). Thus, this study has important implications for the bottom-up principle of local learning rules to form a learning algorithm for intelligent agents. The neuromodulatory system can participate in slower feedback or more implicit teaching signals (Johansen et al., 2014; Liu Y. H. et al., 2021; Mei et al., 2022). In fact, the three-factor rule constructed by simply adding a factor, such as neuromodulation, to pairwise synaptic plasticity can include diverse information about reward or learning hyperparameters (Gil et al., 1997; Nadim and Bucher, 2014; Łukasz Kuśmierz et al., 2017; Brzosko et al., 2019). Given the experimentally examined role of neurotransmitters in the neuromodulatory system and the local physiological dynamics affected by such neurotransmitters, the brain's mechanism of dealing with vast amounts of information from the natural environment can be explained by a combination of diverse modulatory inputs and the distinctive distribution of receptor subtypes (Noudoost and Moore, 2011; Rogers, 2011; Fischer and Ullsperger, 2017; Doya et al., 2021; Cools and Arnsten, 2022). Investigating global optimization algorithm and understanding it across multiple scales is important not only for neuroscience pursuing the answer of mechanisms of neural processes in the brain but also for constructing a better biologically plausible neural network capable of “general intelligence.”
3. Outcome of optimization: single computational unit properties
As Cajal's (1888) confirmation of the neuron doctrine implied, McCulloch and Pitts's (1943) theory of artificial neurons shaped the idea that a neuron is the single unit of computation, and a synapse is the single communication channel between two neurons. Although neurons and synapses have been intensively studied, several fundamental questions remain to be answered, including those regarding the computational roles of neuronal and synaptic properties. In ANN, a representative precedent, such as introducing a rectified linear unit (ReLU; Fukushima, 1975; Nair and Hinton, 2010), helped dramatically advance the field. Because single computational units in BNN are largely unexplored owing to their diversity and nonlinear properties, carefully searching computationally influential properties may enable us to build better neural networks.
3.1. Representation of the activity and coding scheme of a single neuron
The governing dynamics of the electrical properties of a neuron have been well-described and integrated into Hodgkin and Huxley's (1952) monumental work. This set of nonlinear differential equations can regenerate the dynamic excitability and action potential firing. A simpler description of the dynamics using the leaky integrate-and-fire model (Hill, 1936) can be utilized to reduce the complexity and extend the applicability to various types of firing patterns. In addition, direct reverse engineering of the spike parameters was successfully implemented (Izhikevich, 2003). In these neuronal models of the BNN, two distinctive aspects were noticeable, when compared with the ANN. One is that a set of continuous-time differential equations describes neuronal activities, and the other is that there is no explicit activation function except in the integrate-and-fire model and its variants. Although the information encoded in the spiking dynamics along continuous time in the BNN is not yet fully understood, several strategies that the BNN may utilize have been investigated. The well-known dichotomy of such strategies is the rate vs. temporal code (Gerstner et al., 1997; Guo et al., 2021). The rate code encodes target information using the firing rate, corresponding to a neuron's positive scalar value encoding in ANN. Temporal coding refers to an encoding strategy that utilizes the timing of spikes, and the specific coding scheme can vary depending on the time a neuron uses to represent information. For example, a period of silence is a candidate for inter-spike interval coding or time-to-first-spike coding (Dayan and Abbott, 2001; Park et al., 2020; Guo et al., 2021), or the absolute timing of multiple sparse spikes can be used to convey information under a proper decoding scheme (Comşa et al., 2021). The other aspect of the coding strategy, which extends the capacity for encoding, is to deploy a population of neurons to represent the information (Averbeck et al., 2006; Panzeri et al., 2015; Pan et al., 2019). Because the spiking patterns in a population of neurons can be statistically interpreted by considering each spike in each neuron as a sample of a specific random variable, an abundant representation form can be implemented. Different types of information can be conveyed through multiplexing by alternating coding schemes or mixing up heterogeneous neurons in a population (Harvey et al., 2013; Akam and Kullmann, 2014; Lankarany et al., 2019; Jun et al., 2022). For example, a sensor that waits for sparsely occurring inputs of various intensities can encode the input by timely bursting spikes upon an input arrival (Guo et al., 2021). Such a strategy is advantageous for richer dynamics and encoding capacity as well as lower power consumption by considering silence (off period) as another piece of information (Cao et al., 2015; Pfeiffer and Pfeil, 2018). Therefore, spiking neural networks (SNN) has become an essential type of ANN and are widely utilized in neuromorphic engineering (Kornijcuk et al., 2019; Kabilan and Muthukumaran, 2021; Parker et al., 2022). Because various models can describe a neuron's spike activity and each spike can represent distinctive information depending on the coding scheme, we can expect a much larger diversity of neuronal activation processes compared to ANN. Exploring various coding schemes with diverse temporal and populational spike patterns (Comşa et al., 2021; Guo et al., 2021) and heterogeneous distribution of diverse types of neurons (Stöckl et al., 2022) is necessary to represent complex information better and build more biologically plausible neural networks. Diverse types of neurons and their computational impacts have been tested and have demonstrated better performance in typical ANN by varying the type of activation function (Lee et al., 2018). Although groundbreaking improvements are rarely achieved by changing the activation functions in the deep learning field (Goodfellow et al., 2016), combinations of representations of activities in a neuron (spike), consequential spike-based synaptic plasticity (spike-timing-dependent-plasticity and spike-driven synaptic plasticity), various coding schemes (temporal, rate, population, and phase), and heterogeneous neuronal types have not yet been fully examined.
3.2. Dale's principle and input balance
Although the strongest interpretation of Dale's principle, which indicates one neurotransmitter type for one neuron, has become outdated and proven incorrect through accumulated experimental results (Osborne, 1979), it still offers an important framework for analyzing neural networks: the distinction between excitatory and inhibitory neurons (Eccles et al., 1976; Cornford et al., 2021). If we compare the synaptic efficacy in the BNN with that in the ANN, a direct correspondence can be found in the weights of the connection from one neuron to another. In contrast, the weight value in the ANN can vary between positive and negative values, and an input(presynaptic) neuron can include outward connections with both positive and negative weights unlike BNN neurons. Introducing the implications of Dale's principle to an ANN involves fixing a given neuronal identity to either an excitatory or inhibitory neuron, with the weights of its outward connections having the same signs. This is quite a strong constraint, but careful modification did not harm the network performance (Cornford et al., 2021) and provided more diverse computation (Tripp and Eliasmith, 2016) although there was no dramatic improvement in performance. Practical computational implications of the segregation of excitation and inhibition have not yet been established; however, by mathematical treatment of such a neural network, optimal dynamics of the neural network (Catsigeras, 2013) and efficient learning (Haber and Schneidman, 2022) have been carefully suggested as benefits. In BNN, it has long been suggested that a stable but sensitive representation of information can be achieved by balancing excitatory and inhibitory inputs, the so-called E-I balance (Denève and Machens, 2016; Hennequin et al., 2017). The implications of the E-I balance can be roughly explained by comparing it with other extremities. In an excitatory-dominant regime, excessive firing interferes with the expressibility of information by a neuron, whereas in an inhibitory-dominant regime, the frequency of firing drops, and the neuron cannot express the information that lies within a certain time scale. However, tightly balanced inputs can modulate a neuron to fire during a period of tiny temporal discrepancies between excitation and inhibition. Consequently, with an optimal number of firings, a neuron can efficiently represent multiple timescale inputs. The E-I balance has been restated and utilized to explain the performance and efficiency of biological neural circuit models (Denève et al., 2017; Zhou and Yu, 2018; Bhatia et al., 2019; Sadeh and Clopath, 2021) and the malfunctions of an imbalance regime (Sohal and Rubenstein, 2019). In ANN applications (Song et al., 2016; Ingrosso and Abbott, 2019; Tian et al., 2020), balanced inputs are utilized to optimize neural networks for better performance, with the advantages shown in BNN models. Because the concept of E-I balance covers a wide range of extents of balance (Hennequin et al., 2017), defining an alternative type of balanced network (Khajeh et al., 2022) is also possible. Considering that balancing is not just an artificial constraint but also the outcome of optimization (Trapp et al., 2018), applying excitatory-inhibitory segregation and its balance seem to be another prominent way to build better biologically plausible neural networks.
3.3. Morphological effect: dendritic computation
The types of neurons in a BNN are extremely diverse; one criterion is their heterogeneous morphology (Kepecs and Fishell, 2014; Cembrowski and Spruston, 2019). Unlike in a point neuron model, spatially separated input, processor, and output units are implemented as dendrites, somas, and axons, respectively, in a BNN. Thus, the morphological effect refers to the emerging directionality of information flow and the information contents affected by each unit. Notably, the input part (dendrite) is spatially distributed over a larger space than the output pathway (axon) that is often found as a minimally branched fiber consisting of somewhat homogeneous segments with small cross-sectional areas (Chklovskii, 2004). Hence, axonal fibers are expected to be primarily employed to faithfully convey the generated electrical signal (action potential) to distal postsynaptic neurons (Scott, 1975). In contrast, dendrites have many branches with thicker shafts capable of accommodating complex cellular organelles, except the nucleus. The complex branching pattern and spacious cytosol indicate that intracellular processes also occur in dendrites and may be spatially heterogeneous (Shemer et al., 2008; Dittmer et al., 2019). Because synapses are distributed across such heterogeneous substrates, information processed through synapses can be highly heterogeneous even when exposed to uniform presynaptic activity. Specifically, given that the change in shaft thickness varies with the branching or distance from the soma (Harris and Spacek, 2016), differentiating the electrical processing of each input from another is expected to depend on the location of the input (Guerguiev et al., 2017; Sezener et al., 2022; Pagkalos et al., 2023). A simple but remarkable aspect of such a structure and implication is the sequential processing of inputs from the distal location toward the soma, as the directionality of the information flow in a passive cable indicates. As a single action potential from a presynaptic neuron can be interpreted as a Boolean activation input, a recent study attempted to simplify the dendritic processing of many inputs as a layered neural network by adding active dendritic computation to the directionality (Beniaguev et al., 2021). This study highlighted the role of NMDA receptors capable of tuning the plasticity in each excitatory synapse and generating dendritic calcium spikes, which can be interpreted as the integration and firing of local inputs converging to a dendritic segment. Thus, each dendritic segment that generates spikes can be assumed to be a computing layer of converging Boolean inputs through a dendritic arbor, simplifying the complex information processing of a neuron and corresponding to the ANN. In neuroscience, there have been many observations of the active computation of dendrites via spike generation (Cook and Johnston, 1997; Poirazi and Mel, 2001; London and Häusser, 2005; Johnston and Narayanan, 2008). These examples also imply that various types of inputs are spatially and functionally segregated on distinctive branches or dendritic segments (Wybo et al., 2019; Francioni and Harnett, 2022); therefore, a neuron can work as a functional unit capable of more diverse performance than a point neuron. Because of the additional nonlinearity compared to a model point neuron, better expressibility can be expected (Wu et al., 2018), and electrical compartmentalization and active dendritic properties can be applied to ANNs (Chavlis and Poirazi, 2021; Iyer et al., 2022; Sezener et al., 2022). The segregated electrical properties also indicate that homeostatic control can occur separately in distinct dendritic branches (Tripodi et al., 2008; Bird et al., 2021; Shen et al., 2021). Such an adjustment of weights in each dendritic branch toward a certain homeostatic level is similar to the normalization step in ANN (Shen et al., 2021), which also improves learning in sparsely connected neural networks, such as BNN (Bird et al., 2021). The typical structure of a cortical pyramidal neuron consists of two distinctive directions of dendritic outgrowth from the soma: basal and apical dendrites (DeFelipe and Farias, 1992). These differ from each other not only in the direction of growth but also in the branching pattern. Additionally, owing to the vertical alignment of the dendrites of a cortical pyramidal neuron across the cortical laminar layer structure, basal and apical dendrites are exposed to inputs at different layers (Park et al., 2019; Pagkalos et al., 2023). Different branching patterns indicate distinctive information processing in the dendrites, as shown in the aforementioned study. Different input contents combined with different processing methods imply that diverse computations can occur at the microcircuit level, comprising several neurons. One remarkable application of this property is the assumption that a neuron processes both feedforward and feedback inputs, simultaneously. By postulating that error-conveying feedback and feedforward inputs containing external information are separately processed in distinct dendritic branches, the problem of credit assignment can also be explained (Guerguiev et al., 2017; Sacramento et al., 2018), as discussed in Section 2.2.3. Considering that in the biophysical model of a neuron, spontaneous orchestration of the dendritic properties of a neuron to learn a nonlinear function has been identified (Bicknell and Häusser, 2021), the computational implication of dendritic computation is no longer an assumption from the observation of morphology but becomes an essential governing principle of a single neuronal information processing.
4. Outcome of optimization: network architecture
Because single biological computing units exhibit numerous unexplored properties, large-scale combinations of these properties may enable neural networks to reveal complexities that can significantly affect neural network functions (Hermundstad et al., 2011; Braganza and Beck, 2018; Navlakha et al., 2018). The complexity that underlies the BNN emerges from other characteristics, such as high heterogeneity (Liu, 2020), overall sparse connectivity (Eavani et al., 2015; Cayco-Gajic et al., 2017), and hierarchical modularization (Meunier et al., 2010; Hilgetag and Goulas, 2020; D'Souza et al., 2022).
4.1. General distinctive characteristics of the network structure in BNN
The construction and maintenance of hard wiring from one neuron to another involve metabolic and volumetric costs (Chen et al., 2006; Tomasi et al., 2013; Rubinov et al., 2015; Goulas et al., 2019); thus, in a BNN, it is difficult to imagine dense connections, as in an ANN, where we often encounter fully connected layers. The sparse connectivity in the BNN inspired the construction of a lightweight deep learning architecture (Wang C. H. et al., 2022). Model compression by the sparsification of connectivity has led to a large reduction in power consumption, while minimizing performance reduction (Han et al., 2015; Barlaud and Guyard, 2021; Hoefler et al., 2022) and improving performance (Luo, 2020). Identifying the sweet spot between optimized sparsity and performance is the next challenge (Hoefler et al., 2022), and as explored in Section 2, EA may be a suitable choice (Mocanu et al., 2018). As the outcome of a properly chosen sparsification algorithm, the connectivity map of an optimal sparse network also directly improves neural network interpretability because the putative essential connections to process the task are presumably spared, while the unnecessary connections are pruned (Hoefler et al., 2022).
Combining high heterogeneity with sparse connectivity results in modular structures (Mukherjee and Hill, 2011; Miscouridou et al., 2018), and the highly modular structure of the BNN shows the same set of advantages as sparse connectivity. The modular structure can be interpreted as an aggregation of computational units employed for the same function. These units (neurons) are usually located near each other and activated at the same developmental stage, which implies that the general wiring principle in BNN, involving activity- and distance-dependent wiring, may shape the modular structure (van Ooyen, 2011). Contrary to the constructive algorithm by the developmental process, learning-based decomposition into modules is also possible (Kirsch et al., 2018; Pan and Rajan, 2020), enhancing the interpretability and convenience of troubleshooting. In addition, connecting modules that perform distinct functions enables the task-specific design of a comprehensive neural network (Amer and Maul, 2019; Michaels et al., 2020; Duan et al., 2022). Because each module can be considered a building block of a neural network, the evolutionary strategy may perform best in identifying the entire architecture optimized for a certain task (Clune et al., 2013; Lin et al., 2021). Such a strategy eventually maximizes the functional performance of each building block and implies scalability without interfering with the performance of other modules (Ellefsen et al., 2015), while maintaining a minimal number of additional connections. This example is directly related to the answer regarding how the brain can acquire and store multiple memories by not harming old ones and not interfering with new learning with a finite number of hardware units. Such a problem can be characterized by catastrophic forgetting and interference during continual learning, and many candidate mechanisms that the brain may utilize to solve these problems have been suggested (Hadsell et al., 2020; Jedlicka et al., 2022). The modular structures combined with the sparse representation are a more intuitive solution than others because it assigns each piece of information to a separate hardware, implying faster and more precise access to the memory unit. Although the number of neurons and synapses is still not enough to afford all the information which an intelligent agent learns during their lifespan, the modular structure may play a key role in efficient continual learning by harnessing other mechanisms regarding common information.
4.2. Connectivity in a specific brain region
Considering that the largest scale of the module structure is the functional modularization of the brain into each brain region, the most straightforward way for AI to acquire a certain function is to copy the connectivity of the specific brain region that regulates that particular function. Although the current brain-wide or regional wiring map is far from completion, several brain areas are known to have relatively organized connectivity and regulate well-defined functions.
One of these brain regions is the cerebellum. Because of its relatively simple and organized structure, the cerebellum was the first target for computational modeling as attempted by Marr (1969), Albus (1971). Major streams of the cerebellar information processing can be divided into a feedforward network through granule cells and Purkinje cells, and a feedback connection from inferior olive where a part of the cerebellar outputs projects. Because the feedforward stream conveys the information from the cortex and the olivary feedback sends the error between sensory feedback and sensory prediction, the Purkinje cell where these streams converge has been assumed to adapt to minimize the error signal (Raymond and Medina, 2018). This conjecture based on the structure was directly applied to a cerebellar model articulation controller (CMAC; Albus, 1975), which is based on the fact that the cerebellum is involved in smooth motor control. CMAC is still utilized with modifications (Tsa et al., 2018; Le et al., 2020). Because the cerebellum is not a sole motor controller, the whole motor control process should be analyzed by including the initial command generator and motor plant. Considering that the cerebellum receives inputs from the cerebral cortex through pontine nuclei and propagate outputs to the cortex through deep cerebellar nuclei to thalamic projection, the loop between the cortex and the cerebellum can be interpreted as the continuous corrector of the ongoing motor control. The importance of such a brain-wide loop structure in which a cerebellum is involved has been recently raised and integrated into ANN models (Iwadate et al., 2014; Tanaka et al., 2020; Boven et al., 2023). Furthermore, in recent decades, our understanding of the cerebellum and its functions has deepened considerably, including the non-motor output from the cerebellum (Kang et al., 2021; Hwang et al., 2023) and multi-dimensional structural organization (Apps et al., 2018; Beckinghausen and Sillitoe, 2019). Although, currently, we barely understand the detailed network architecture underlying such diverse functions and gross anatomy, further research will lead us to implement the control of broad behavioral modality through the cerebellum.
The hippocampus is also a brain area that deserves a brief introduction here. The hippocampus has well-defined functional roles in episodic memory and spatial cognition, and the overall information flow across the sub-regions is also known (Bird and Burgess, 2008; Kovács, 2020; Li et al., 2020). The improved artificial memory system has drawn more attention regarding the memory mechanisms and implementation of the memory circuit (Berger et al., 2012; van de Ven et al., 2020). Traditionally, the auto-associative connectivity in CA3 was characterized and inspired the Hopfield-type memory network (Hopfield, 1982; Ishizuka et al., 1990; Bennett et al., 1994). In addition, considering that the well-known connections from CA3 to CA1 roughly form a hetero-associative network, the stored information can migrate along the feedforward organization within the hippocampus (Graham et al., 2010; Miyata et al., 2013). However, because such associative memory structures are known to have limited capacity (McEliece et al., 1988; Kuo and Zhang, 1994; Bosch and Kurfess, 1998), additional structure or functional extension is necessary to reach the biological memory capacity level which can store dense information during a whole lifespan. Considering that the hippocampus receives inputs from the cortex through the dentate gyrus and projects back to the cortex through CA1 output, the interaction between the hippocampus and the cortex has been suggested to have the role of the memory buffer and consolidation (Rothschild et al., 2017). In addition to the modular structure with sparse representation as mentioned in a previous section, working mechanisms of this interplay have been suggested, such as generative replay and metaplasticity (Hadsell et al., 2020; van de Ven et al., 2020; Jedlicka et al., 2022), by resolving how to efficiently reorganize the representation of the information with time across the network. Considering that these mechanisms are inferred by the observations of both functional data and the architecture, the applications of these mechanisms to ANN (Hadsell et al., 2020; van de Ven et al., 2020; Wang L. et al., 2022) propose more intense collaboration between neuroscience and AI engineering toward a neural network design containing both bioplausibility and better performance.
Besides the cerebellum and hippocampus, other unexplored brain areas can be used to build biologically plausible neural networks. Since the recent advances in neuroscience have revealed not only the map of structural and functional connections within a region and across regions but also the relationship between the structure and function, careful imitation of other brain areas with proper simplification and interfacing will be demanding.
5. Discussion
5.1. The goal and limitation of a bottom-up approach
Putting aside the hardware issue and the question of intrinsic infeasibility, whether copying a BNN by artifacts can generate the intelligence possessed by a human or animal directly requires the goal and limitation of a bottom-up approach. While we have partially reviewed recent advances in bottom-up approaches to construct neural networks, it should be noted that replacing only a certain part of the ANN with one from the BNN usually does not improve the performance measured by the criteria for ANN. In other words, if we introduce a new concept from a BNN, the entire framework must be changed. For example, to utilize spike-timing-dependent plasticity, a change from an ANN to an SNN is necessary, and consequently, the task design needs to be modified. For certain tasks, such as predicting the digit annotation from the images drawn from the MNIST dataset (LeCun et al., 2010) after supervised learning, the ANN can achieve the best precision, while the SNN may not be able to outperform it. However, when implemented in hardware, SNNs have a considerably greater advantage in terms of power consumption, as observed in modern neuromorphic hardware (Cao et al., 2015; Pfeiffer and Pfeil, 2018; Cui et al., 2019; Kornijcuk et al., 2019; Kabilan and Muthukumaran, 2021; Parker et al., 2022). In addition, as mentioned in Section 3.1, SNNs may have the advantage of dealing with intermittently activated inputs (Pfeiffer and Pfeil, 2018). Thus, this example prompts us to build an alternative interpretation that the advantages of a certain neural network can vary with the type of problem that the neural network must solve.
To generalize these observations, first, we defined “the problem space,” which is the set of problems that neural networks try to solve. “A problem” (P) is defined by the task itself (T), including the dataset and goal, and by the performance measure of the task (R), including the efficiency measure like power consumption or the number of required computations or platforms to perform the task. By mapping P, these attributes represent a point in the problem space ℙ. For a certain problem, if we set the naturalistic task and try to achieve the evaluation measure in the range of humans or animals, the problem is a point in the “natural problem space” in Figure 2. By simply assuming that there is a subset of ℙ that consists of points mapped from the biological range of T, R (Tbio, Rbio), the set of natural problems (natural problem space) can be defined as ℙ as follows:
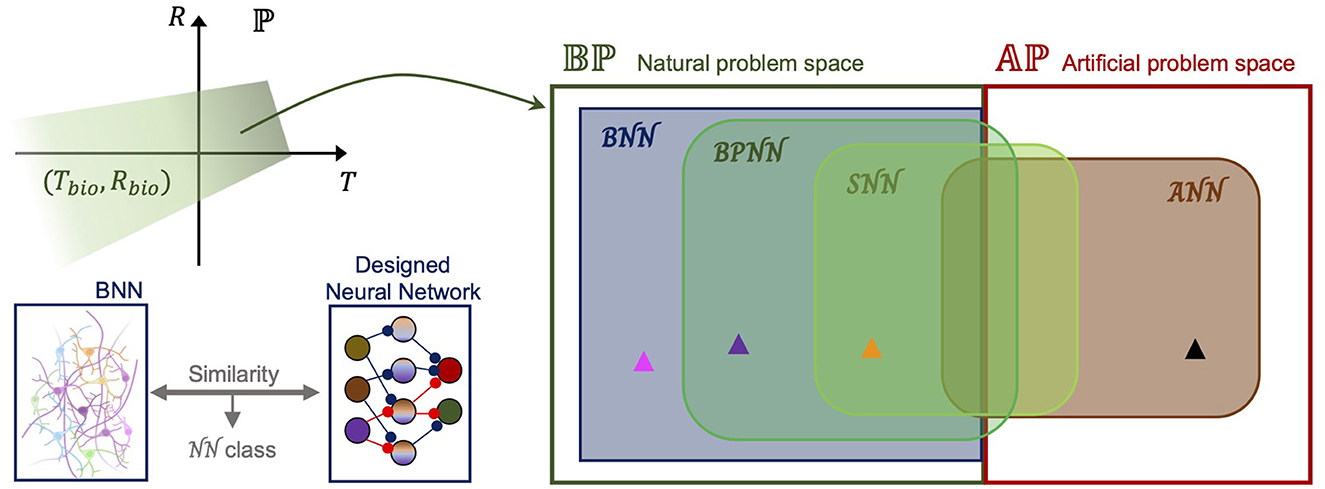
Figure 2. Problem spaces and cover sets by neural network designs. (Left top) In the entire problem space (ℙ), natural problems can be defined as the green region where both the task (T which includes the dataset and the goal) and the performance measure (R which includes the efficiency measure, the number of required computations, and platforms to perform the task) are within the biological range. (Left bottom) Neural network class can be defined by comparing a designed neural network with a biological neural network. The similarity decides its class. (Right) Binary division of the problem space into the natural problem space (Bℙ) and artificial problem space (Aℙ) as aforementioned. Neural network classes are: , artificial neural network; , biological neural network; , biologically plausible neural network; , spiking neural network. The black arrowhead represents the problems for ANN supremacy. Magenta: BNN supremacy; Purple: BPNN supremacy; Yellow: SNN supremacy, compared with ANN.
and all the non-natural problems belong to the “artificial problem space” (Aℙ). For example, tracking fast-moving prey without intensive pretraining is a natural problem, but identifying a fingerprint from a vast database is an artificial problem. In fact, determining a problem type can be taken care of by neuroscience, specifically, by a top-down approach, because it ultimately determines whether this task is one of what can be done with the brain, in Turing's (1948) terms.
These problems in Bℙ or Aℙ can be solved using neural networks; however, the coverage differs depending on the class of a neural network. ANNs have shown powerful performance, at least for problems in Aℙ, and have also been employed to solve natural problems by reducing power consumption and minimizing training. Thus, as shown in the Venn diagram in Figure 2, the class covers some natural problems and a larger part of the artificial problem space. On the other hand, the neural network class has been utilized to solve more natural problems than artificial problems. For instance, by hardware implementation, an SNN can greatly reduce the required resources with similar precision to an ANN in image classification, but an ANN can show better optimization for performance on a typical computer after training with a large dataset. Therefore, as shown in Figure 1, the and intersect in both problem spaces, and the intersection in the natural problem space is a subset of the . By contrast, the class is a subset of the natural problem space that covers most of the Bℙ region. Because we defined natural problems as those that the brain can solve, it is reasonable to assume that a BNN as a unit of the brain can be employed to process most natural problems not covered by other classes of neural networks. We would like to call the relative complement in the “BNN supremacy regime,” which is the actively used phrase in quantum computing (Arute et al., 2019). Thus, when building a biologically plausible neural network, the task, its performance measure, and the neural network architecture need to be changed to prove a better performance of a designed neural network than an ANN. Given the assumption that the class of biologically plausible neural networks, , is defined by the similarity to BNN architecture, our practical short-term goal is not only to construct a BNN-like architecture but also to demonstrate the “BPNN supremacy” by finding a proper problem in Bℙ. There have been attempts at formalization with similar motivations on SNN (Maass, 1996; Kwisthout and Donselaar, 2020) or ANN (Balcazar et al., 1997), and solving the shortest path problem is a problem in the relative complement of in that has been discovered (Aimone et al., 2021). Eventually, formalization and a mathematical approach are necessary to better define the problem spaces and investigate the spectrum in a set.
5.2. The role of neuroscience in the bottom-up approach to explore the BNN supremacy regime
How can we discover points in the problem spaces, specifically within the BNN or BPNN supremacy regime? Does a proper design of a BNN or BPNN always exist for certain problems? We do not have a concrete formalization scheme or rough map of problem spaces to answer these questions fundamentally using mathematical proofs. Furthermore, we do not have any information regarding the proper design of neural networks. Thus, we suggest the pipeline shown in Figure 3, which starts with neuroscientific discoveries and shows how to define a problem specifically in the natural problem space. Accumulated data related to neuroscience can help define the task goal and the corresponding dataset to train neural networks through a top-down approach that specifically pursues the neural network mechanism by starting from observations at the level of the cognitive behavior of an intelligent agent. Thus, a top-down approach may be able to define a point in the problem space and distinguish between points in the Bℙ and Aℙ. Simultaneously, a bottom-up approach may enable the design of a neural network by combining many essential properties of the targeted BNN with the generalized principles of a neural network. However, because the definition of the problem in Bℙ may be too complicated to completely formulate, and it is difficult to judge whether the designed neural network can solve the problem before emulation, the defined problem and the hypothesized neural network design should be embedded in an already built scheme such as ANN or SNN to utilize feasible engineering techniques. Such hybridization is necessary for estimating the solvability of the problem without a full emulation. We speculate that persistent exploration by following the suggested pipeline will fill the information in the diagram shown in Figure 2, which can eventually enable a formal investigation to derive the set boundary. We believe that this type of slow but straightforward bottom-up approach and collaboration with a top-down approach and interfacing with current ANN will help us to light up the way to build a thinking machine like the human on the concrete foundation of neural circuit principles. Moreover, this pipeline could promote improved communication between neuroscience and AI engineering.
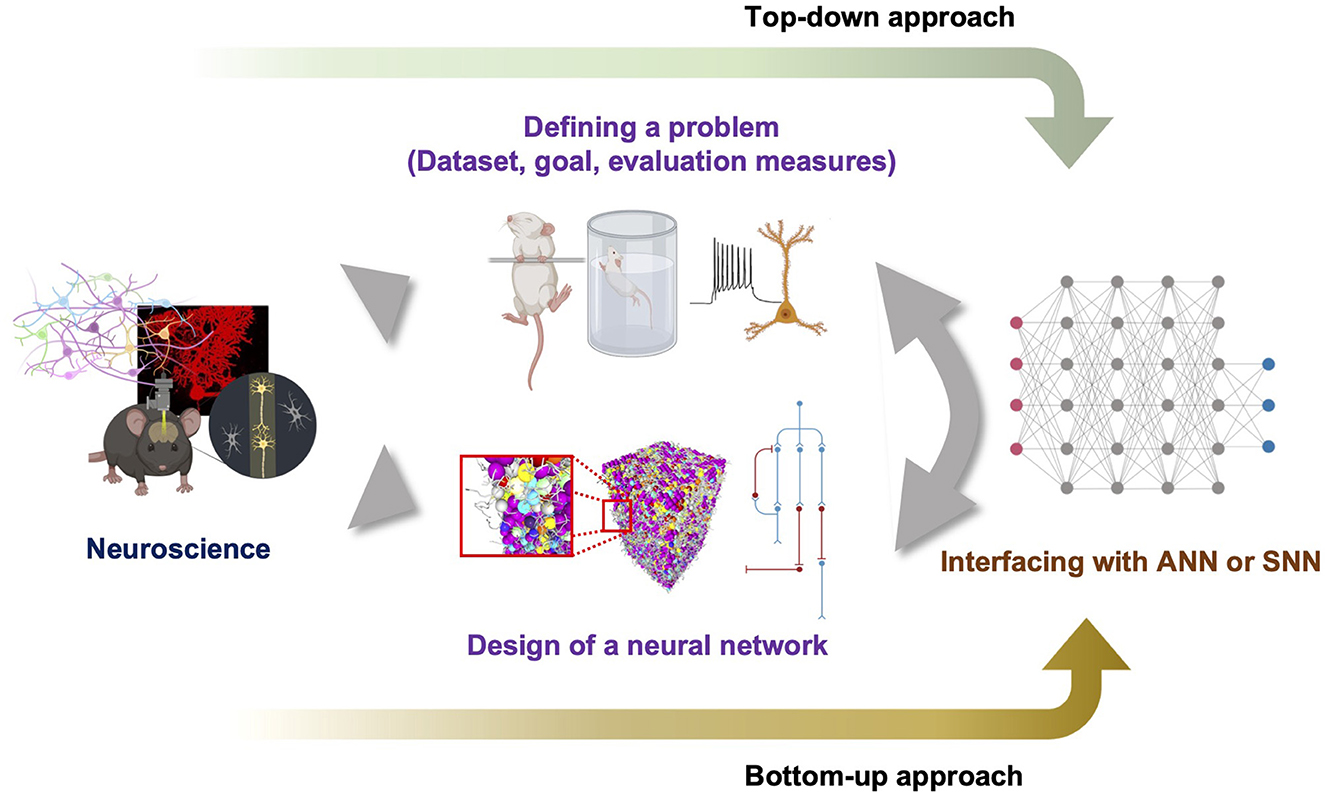
Figure 3. Suggested pipeline to explore problem spaces and proper design of neural networks. The top-down approach defines the problem to solve based on the findings of neuroscience and the bottom-up approach designs a neural network. To determine whether the problem can be solved by a designed neural network without slow search, both need to be hybridized with feasible neural networks such as ANN or SNN.
Author contributions
IJ and TK searched and analyzed the references. IJ wrote the draft. TK arranged the original idea and revised the draft. All authors contributed to the article and approved the submitted version.
Funding
This research was supported by the Original Technology Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (no. 2021M3F3A2A01037811) and by the KIST Institutional Program (project no., 2E32211).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdissa, D., Hamba, N., and Gerbi, A. (2020). Review article on adult neurogenesis in humans. Transl. Res. Anat. 20:100074. doi: 10.1016/j.tria.2020.100074
Abraham, W. C. (2008). Metaplasticity: tuning synapses and networks for plasticity. Nat. Rev. Neurosci. 9, 387–387. doi: 10.1038/nrn2356
Abraham, W. C., Jones, O. D., and Glanzman, D. L. (2019). Is plasticity of synapses the mechanism of long-term memory storage? NPJ Sci. Learn. 4:9. doi: 10.1038/s41539-019-0048-y
Aimone, J. B., Ho, Y., Parekh, O., Phillips, C. A., Pinar, A., Severa, W., et al. (2021). “Provable advantages for graph algorithms in spiking neural networks,” in Proceedings of the 33rd ACM Symposium on Parallelism in Algorithms and Architectures, SPAA '21 (New York, NY: Association for Computing Machinery), 35–47. doi: 10.1145/3409964.3461813
Akam, T., and Kullmann, D. M. (2014). Oscillatory multiplexing of population codes for selective communication in the mammalian brain. Nat. Rev. Neurosci. 15, 111–122. doi: 10.1038/nrn3668
Albus, J. S. (1971). A theory of cerebellar function. Math. Biosci. 10, 25–61. doi: 10.1016/0025-5564(71)90051-4
Albus, J. S. (1975). A new approach to manipulator control: the cerebellar model articulation controller (CMAC). J. Dyn. Syst. Measure. Control 97, 220–227. doi: 10.1115/1.3426922
Alejandre-García, T., Kim, S., Pérez-Ortega, J., and Yuste, R. (2022). Intrinsic excitability mechanisms of neuronal ensemble formation. eLife 11:e77470. doi: 10.7554/eLife.77470
Amer, M., and Maul, T. (2019). A review of modularization techniques in artificial neural networks. Artif. Intell. Rev. 52, 527–561. doi: 10.1007/s10462-019-09706-7
Apps, R., Hawkes, R., Aoki, S., Bengtsson, F., Brown, A. M., Chen, G., et al. (2018). Cerebellar modules and their role as operational cerebellar processing units. Cerebellum 17, 654–682. doi: 10.1007/s12311-018-0952-3
Arute, F., Arya, K., Babbush, R., Bacon, D., Bardin, J. C., Barends, R., et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510. doi: 10.1038/s41586-019-1666-5
Averbeck, B. B. (2022). Pruning recurrent neural networks replicates adolescent changes in working memory and reinforcement learning. Proc. Natl. Acad. Sci. U.S.A. 119:e2121331119. doi: 10.1073/pnas.2121331119
Averbeck, B. B., Latham, P. E., and Pouget, A. (2006). Neural correlations, population coding and computation. Nat. Rev. Neurosci. 7, 358–366. doi: 10.1038/nrn1888
Balcazar, J., Gavalda, R., and Siegelmann, H. (1997). Computational power of neural networks: a characterization in terms of kolmogorov complexity. IEEE Trans. Inform. Theory 43, 1175–1183. doi: 10.1109/18.605580
Barlaud, M., and Guyard, F. (2021). “Learning sparse deep neural networks using efficient structured projections on convex constraints for green AI,” in 2020 25th International Conference on Pattern Recognition (ICPR) (Milan), 1566–1573. doi: 10.1109/ICPR48806.2021.9412162
Barrett, D. G., Denève, S., and Machens, C. K. (2016). Optimal compensation for neuron loss. eLife 5:e12454. doi: 10.7554/eLife.12454
Beckinghausen, J., and Sillitoe, R. V. (2019). Insights into cerebellar development and connectivity. Neurosci. Lett. 688, 2–13. doi: 10.1016/j.neulet.2018.05.013
Beniaguev, D., Segev, I., and London, M. (2021). Single cortical neurons as deep artificial neural networks. Neuron 109, 2727–2739.e3. doi: 10.1016/j.neuron.2021.07.002
Benna, M. K., and Fusi, S. (2016). Computational principles of synaptic memory consolidation. Nat. Neurosci. 19, 1697–1706. doi: 10.1038/nn.4401
Bennett, M. R., Gibson, W. G., and Robinson, J. (1994). Dynamics of the ca3 pyramidial neuron autoassociative memory network in the hippocampus. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 343, 167–187. doi: 10.1098/rstb.1994.0019
Berger, T. W., Song, D., Chan, R. H. M., Marmarelis, V. Z., LaCoss, J., Wills, J., et al. (2012). A hippocampal cognitive prosthesis: multi-input, multi-output nonlinear modeling and VLSI implementation. IEEE Trans. Neural Syst. Rehabil. Eng. 20, 198–211. doi: 10.1109/TNSRE.2012.2189133
Bhatia, A., Moza, S., and Bhalla, U. S. (2019). Precise excitation-inhibition balance controls gain and timing in the hippocampus. eLife 8:e43415. doi: 10.7554/eLife.43415
Bicknell, B. A., and Häusser, M. (2021). A synaptic learning rule for exploiting nonlinear dendritic computation. Neuron 109, 4001–4017.e10. doi: 10.1016/j.neuron.2021.09.044
Bienenstock, E., Cooper, L., and Munro, P. (1982). Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. J. Neurosci. 2, 32–48. doi: 10.1523/JNEUROSCI.02-01-00032.1982
Bird, A. D., Jedlicka, P., and Cuntz, H. (2021). Dendritic normalisation improves learning in sparsely connected artificial neural networks. PLoS Comput. Biol. 17:e1009202. doi: 10.1371/journal.pcbi.1009202
Bird, C. M., and Burgess, N. (2008). The hippocampus and memory: insights from spatial processing. Nat. Rev. Neurosci. 9, 182–194. doi: 10.1038/nrn2335
Bosch, H., and Kurfess, F. J. (1998). Information storage capacity of incompletely connected associative memories. Neural Netw. 11, 869–876. doi: 10.1016/S0893-6080(98)00035-5
Boven, E., Pemberton, J., Chadderton, P., Apps, R., and Costa, R. P. (2023). Cerebro-cerebellar networks facilitate learning through feedback decoupling. Nat. Commun. 14, 1–18. doi: 10.1038/s41467-022-35658-8
Braganza, O., and Beck, H. (2018). The circuit motif as a conceptual tool for multilevel neuroscience. Trends Neurosci. 41, 128–136. doi: 10.1016/j.tins.2018.01.002
Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., et al (2020). “Language models are few-shot learners,” in Advances in Neural Information Processing Systems, Vol. 33, eds H. Larochelle, M. Ranzato, R. Hadsell, M. Balcan, and H. Lin (Vancouver, CA; Red Hook, NY: Curran Associates, Inc.), 1877–1901.
Brzosko, Z., Mierau, S. B., and Paulsen, O. (2019). Neuromodulation of spike-timing-dependent plasticity: past, present, and future. Neuron 103, 563–581. doi: 10.1016/j.neuron.2019.05.041
Cajal, R. Y. (1888). Revista trimestral de histología normal y patológica. Barcelona: Casa Provincial de la Caridad, 1
Cameron, B., de la Malla, C., and López-Moliner, J. (2014). The role of differential delays in integrating transient visual and proprioceptive information. Front. Psychol. 5:50. doi: 10.3389/fpsyg.2014.00050
Cao, Y., Chen, Y., and Khosla, D. (2015). Spiking deep convolutional neural networks for energy-efficient object recognition. Int. J. Comput. Vis. 113, 54–66. doi: 10.1007/s11263-014-0788-3
Caporale, N., and Dan, Y. (2008). Spike timing-dependent plasticity: a Hebbian learning rule. Annu. Rev. Neurosci. 31, 25–46. doi: 10.1146/annurev.neuro.31.060407.125639
Catsigeras, E. (2013). Dale's principle is necessary for an optimal neuronal network's dynamics. Appl. Math. 4, 15–29. doi: 10.4236/am.2013.410A2002
Cayco-Gajic, N. A., Clopath, C., and Silver, R. A. (2017). Sparse synaptic connectivity is required for decorrelation and pattern separation in feedforward networks. Nat. Commun. 8:1116. doi: 10.1038/s41467-017-01109-y
Cembrowski, M. S., and Spruston, N. (2019). Heterogeneity within classical cell types is the rule: lessons from hippocampal pyramidal neurons. Nat. Rev. Neurosci. 20, 193–204. doi: 10.1038/s41583-019-0125-5
Chavlis, S., and Poirazi, P. (2021). Drawing inspiration from biological dendrites to empower artificial neural networks. Curr. Opin. Neurobiol. 70, 1–10. doi: 10.1016/j.conb.2021.04.007
Chen, B. L., Hall, D. H., and Chklovskii, D. B. (2006). Wiring optimization can relate neuronal structure and function. Proc. Natl. Acad. Sci. U.S.A. 103, 4723–4728. doi: 10.1073/pnas.0506806103
Chen, S., Zhang, S., Shang, J., Chen, B., and Zheng, N. (2019). Brain-inspired cognitive model with attention for self-driving cars. IEEE Trans. Cogn. Dev. Syst. 11, 13–25. doi: 10.1109/TCDS.2017.2717451
Chklovskii, D. B. (2004). Synaptic connectivity and neuronal morphology: two sides of the same coin. Neuron 43, 609–617. doi: 10.1016/S0896-6273(04)00498-2
Clune, J., Mouret, J.-B., and Lipson, H. (2013). The evolutionary origins of modularity. Proc. R. Soc. B: Biol. Sci. 280:20122863. doi: 10.1098/rspb.2012.2863
Comša, I.-M., Potempa, K., Versari, L., Fischbacher, T., Gesmundo, A., and Alakuijala, J. (2021). “Temporal coding in spiking neural networks with alpha synaptic function: learning with backpropagation,” in ICASSP 2020 - 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 8529–8533, doi: 10.1109/ICASSP40776.2020.9053856
Cook, E. P., and Johnston, D. (1997). Active dendrites reduce location-dependent variability of synaptic input trains. J. Neurophysiol. 78, 2116–2128. doi: 10.1152/jn.1997.78.4.2116
Cools, R., and Arnsten, A. F. T. (2022). Neuromodulation of prefrontal cortex cognitive function in primates: the powerful roles of monoamines and acetylcholine. Neuropsychopharmacology 47, 309–328. doi: 10.1038/s41386-021-01100-8
Cornford, J., Kalajdzievski, D., Leite, M., Lamarquette, A., Kullmann, D. M., and Richards, B. (2021). “Learning to live with dale's principle: ANNs with separate excitatory and inhibitory units,” in 9th International Conference on Learning Representations (Austria). doi: 10.1101/2020.11.02.364968
Cui, P., Shabash, B., and Wiese, K. C. (2019). “EvoDNN - an evolutionary deep neural network with heterogeneous activation functions,” in 2019 IEEE Congress on Evolutionary Computation (CEC) (Wellington), 2362–2369. doi: 10.1109/CEC.2019.8789964
Dayan, P., and Abbott, L. (2001). Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Cambridge, MA: Massachusetts Institute of Technology Press.
Debanne, D., Inglebert, Y., and Russier, M. (2019). Plasticity of intrinsic neuronal excitability. Curr. Opin. Neurobiol. 54, 73–82. doi: 10.1016/j.conb.2018.09.001
DeFelipe, J., and Fariñas, I. (1992). The pyramidal neuron of the cerebral cortex: morphological and chemical characteristics of the synaptic inputs. Prog. Neurobiol. 39, 563–607. doi: 10.1016/0301-0082(92)90015-7
Denève, S., Alemi, A., and Bourdoukan, R. (2017). The brain as an efficient and robust adaptive learner. Neuron 94, 969–977. doi: 10.1016/j.neuron.2017.05.016
Denève, S., and Machens, C. K. (2016). Efficient codes and balanced networks. Nat. Neurosci. 19, 375–382. doi: 10.1038/nn.4243
Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. (2019). “BERT: pre-training of deep bidirectional transformers for language understanding,” in Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, eds J. Burstein, C. Doran, and T. Solorio (Association for Computational Linguistics), 4171–4186. doi: 10.18653/v1/n19-1423
Dittmer, P. J., Dell'Acqua, M. L., and Sather, W. A. (2019). Synaptic crosstalk conferred by a zone of differentially regulated ca < sup>2+ < /sup> signaling in the dendritic shaft adjoining a potentiated spine. Proc. Natl. Acad. Sci. U.S.A. 116, 13611–13620. doi: 10.1073/pnas.1902461116
Dos Santos, M., Salery, M., Forget, B., Garcia Perez, M. A., Betuing, S., Boudier, T., et al. (2017). Rapid synaptogenesis in the nucleus accumbens is induced by a single cocaine administration and stabilized by mitogen-activated protein kinase interacting kinase-1 activity. Biol. Psychiatry 82, 806–818. doi: 10.1016/j.biopsych.2017.03.014
Doya, K., Miyazaki, K. W., and Miyazaki, K. (2021). Serotonergic modulation of cognitive computations. Curr. Opin. Behav. Sci. 38, 116–123. doi: 10.1016/j.cobeha.2021.02.003
D'Souza, R. D., Wang, Q., Ji, W., Meier, A. M., Kennedy, H., Knoblauch, K., et al. (2022). Hierarchical and nonhierarchical features of the mouse visual cortical network. Nat. Commun. 13, 1–14. doi: 10.1038/s41467-022-28035-y
Duan, S., Yu, S., and Príncipe, J. C. (2022). Modularizing deep learning via pairwise learning with kernels. IEEE Trans. Neural Netw. Learn. Syst. 33, 1441–1451. doi: 10.1109/TNNLS.2020.3042346
Eavani, H., Satterthwaite, T. D., Filipovych, R., Gur, R. E., Gur, R. C., and Davatzikos, C. (2015). Identifying sparse connectivity patterns in the brain using resting-state fMRI. NeuroImage 105, 286–299. doi: 10.1016/j.neuroimage.2014.09.058
Eccles, J. C., Jones, R. V., and Paton, W. D. M. (1976). From electrical to chemical transmission in the central nervous system: the closing address of the sir henry dale centennial symposium Cambridge, 19 September 1975. Notes Rec. R. Soc. Lond. 30, 219–230. doi: 10.1098/rsnr.1976.0015
Ellefsen, K. O., Mouret, J.-B., and Clune, J. (2015). Neural modularity helps organisms evolve to learn new skills without forgetting old skills. PLoS Comput. Biol. 11:e1004128. doi: 10.1371/journal.pcbi.1004128
Elsken, T., Metzen, J. H., and Hutter, F. (2019). Neural architecture search: a survey. J. Mach. Learn. Res. 20, 1997–2017. doi: 10.1007/978-3-030-05318-5_3
Fernández, J. G., Hortal, E., and Mehrkanoon, S. (2021). “Towards biologically plausible learning in neural networks,” in 2021 IEEE Symposium Series on Computational Intelligence (SSCI) (Orlando, FL), 1–8. doi: 10.1109/SSCI50451.2021.9659539
Fischer, A. G., and Ullsperger, M. (2017). An update on the role of serotonin and its interplay with dopamine for reward. Front. Hum. Neurosci. 11:484. doi: 10.3389/fnhum.2017.00484
Foerde, K., and Shohamy, D. (2011). Feedback timing modulates brain systems for learning in humans. J. Neurosci. 31, 13157–13167. doi: 10.1523/JNEUROSCI.2701-11.2011
Foster, S. A., and Baker, J. A. (2004). Evolution in parallel: new insights from a classic system. Trends Ecol. Evol. 19, 456–459. doi: 10.1016/j.tree.2004.07.004
Francioni, V., and Harnett, M. T. (2022). Rethinking single neuron electrical compartmentalization: dendritic contributions to network computation in vivo. Neuroscience, 489, 185–199. doi: 10.1016/j.neuroscience.2021.05.038
Friedrich, J., Urbanczik, R., and Senn, W. (2011). Spatio-temporal credit assignment in neuronal population learning. PLoS Comput. Biol. 7:e1002092. doi: 10.1371/journal.pcbi.1002092
Fukushima, K. (1975). Cognitron: a self-organizing multilayered neural network. Biol. Cybern. 20, 121–136. doi: 10.1007/BF00342633
Fusi, S., Drew, P. J., and Abbott, L. (2005). Cascade models of synaptically stored memories. Neuron 45, 599–611. doi: 10.1016/j.neuron.2005.02.001
Galván, E., and Mooney, P. (2021). Neuroevolution in deep neural networks: current trends and future challenges. IEEE Trans. Artif. Intell. 2, 476–493. doi: 10.1109/TAI.2021.3067574
Garcia, I., Quast, K., Huang, L., Herman, A., Selever, J., Deussing, J., et al. (2014). Local CRH signaling promotes synaptogenesis and circuit integration of adult-born neurons. Dev. Cell 30, 645–659. doi: 10.1016/j.devcel.2014.07.001
Gerstner, W., Kreiter, A. K., Markram, H., and Herz, A. V. M. (1997). Neural codes: firing rates and beyond. Proc. Natl. Acad. Sci. U.S.A. 94, 12740–12741. doi: 10.1073/pnas.94.24.12740
Gil, Z., Connors, B. W., and Amitai, Y. (1997). Differential regulation of neocortical synapses by neuromodulators and activity. Neuron 19, 679–686. doi: 10.1016/S0896-6273(00)80380-3
Goodhill, G. J. (2018). Theoretical models of neural development. iScience 8, 183–199. doi: 10.1016/j.isci.2018.09.017
Gottwald S, and Braun, D. A.. (2020). The two kinds of free energy and the Bayesian revolution. PLoS Comput. Biol. 16:e1008420. doi: 10.1371/journal.pcbi.1008420
Goulas, A., Betzel, R. F., and Hilgetag, C. C. (2019). Spatiotemporal ontogeny of brain wiring. Sci. Adv. 5:eaav9694. doi: 10.1126/sciadv.aav9694
Graham, B. P., Cutsuridis, V., and Hunter, R. (2010). Associative Memory Models of Hippocampal Areas CA1 and CA3. New York, NY: Springer New York, 459–494. doi: 10.1007/978-1-4419-0996-1_16
Greve, P. F. (2015). The role of prediction in mental processing: a process approach. New Ideas Psychol. 39, 45–52. doi: 10.1016/j.newideapsych.2015.07.007
Guerguiev, J., Lillicrap, T. P., and Richards, B. A. (2017). Towards deep learning with segregated dendrites. eLife 6:e22901. doi: 10.7554/eLife.22901
Gunning, D., Stefik, M., Choi, J., Miller, T., Stumpf, S., and Yang, G.-Z. (2019). XAI-explainable artificial intelligence. Sci. Robot. 4:eaay7120. doi: 10.1126/scirobotics.aay7120
Guo, W., Fouda, M. E., Eltawil, A. M., and Salama, K. N. (2021). Neural coding in spiking neural networks: a comparative study for robust neuromorphic systems. Front. Neurosci. 15:638474. doi: 10.3389/fnins.2021.638474
Haber, A., and Schneidman, E. (2022). “The computational and learning benefits of daleian neural networks,” in Advances in Neural Information Processing Systems 35: NeurIPS 2022, New Orleans, Louisiana, USA, eds S. Koyejo and S. Mohamed and A. Agarwal and D. Belgrave and K. Cho and A. Oh (Red Hook, NY: Curran Associates Inc.), 5194–5206. Available online at: https://proceedings.neurips.cc/paper_files/paper/2022/file/21cb5931c39d7bd21b34b3b8f14a125c-Paper-Conference.pdf
Hadsell, R., Rao, D., Rusu, A. A., and Pascanu, R. (2020). Embracing change: continual learning in deep neural networks. Trends Cogn. Sci. 24, 1028–1040. doi: 10.1016/j.tics.2020.09.004
Han, S., Pool, J., Tran, J., and Dally, W. (2015). “Learning both weights and connections for efficient neural network,” in Proceedings of the 28th International Conference on Neural Information Processing Systems (Montreal, QC), 1135–1143.
Hanse, E., Seth, H., and Riebe, I. (2013). Ampa-silent synapses in brain development and pathology. Nat. Rev. Neurosci. 14, 839–850. doi: 10.1038/nrn3642
Harris, K. M., and Spacek, J. (2016). “Dendrite structure,” in Dendrites, eds G. Stuart, N. Spruston, and M. Häusser (Oxford: Oxford University Press). doi: 10.1093/acprof:oso/9780198745273.003.0001
Harvey, M. A., Saal, H. P., Dammann, J. F. III, and Bensmaia, S. J. (2013). Multiplexing stimulus information through rate and temporal codes in primate somatosensory cortex. PLoS Biol. 11:e1001558. doi: 10.1371/journal.pbio.1001558
Hasson, U., Nastase, S. A., and Goldstein, A. (2020). Direct fit to nature: an evolutionary perspective on biological and artificial neural networks. Neuron 105, 416–434. doi: 10.1016/j.neuron.2019.12.002
Helfer, P., and Shultz, T. R. (2018). Coupled feedback loops maintain synaptic long-term potentiation: a computational model of PKMZETA synthesis and AMPA receptor trafficking. PLoS Comput. Biol. 14:e1006147. doi: 10.1371/journal.pcbi.1006147
Hennequin, G., Agnes, E. J., and Vogels, T. P. (2017). Inhibitory plasticity: balance, control, and codependence. Annu. Rev. Neurosci. 40, 557–579. doi: 10.1146/annurev-neuro-072116-031005
Hermundstad, A. M., Brown, K. S., Bassett, D. S., and Carlson, J. M. (2011). Learning, memory, and the role of neural network architecture. PLoS Comput. Biol. 7:e1002063. doi: 10.1371/journal.pcbi.1002063
Hilgetag, C. C., and Goulas, A. (2020). “Hierarchy” in the organization of brain networks. Philos. Trans. R. Soc. B 375:20190319. doi: 10.1098/rstb.2019.0319
Hill, A. V. (1936). Excitation and accommodation in nerve. Proc. R. Soc. Lond. Ser. B Biol. Sci. 119, 305–355. doi: 10.1098/rspb.1936.0012
Hiratani, N., and Latham, P. E. (2022). Developmental and evolutionary constraints on olfactory circuit selection. Proc. Natl. Acad. Sci. U.S.A. 119:e2100600119. doi: 10.1073/pnas.2100600119
Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544. doi: 10.1113/jphysiol.1952.sp004764
Hoefler, T., Alistarh, D., Ben-Nun, T., Dryden, N., and Peste, A. (2022). Sparsity in deep learning: pruning and growth for efficient inference and training in neural networks. J. Mach. Learn. Res. 22, 1–124.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U.S.A. 79, 2554–2558. doi: 10.1073/pnas.79.8.2554
Hwang, K.-D., Baek, J., Ryu, H.-H., Lee, J., Shim, H. G., Kim, S. Y., et al. (2023). Cerebellar nuclei neurons projecting to the lateral parabrachial nucleus modulate classical fear conditioning. Cell Rep. 42:112291. doi: 10.1016/j.celrep.2023.112291
Ingrosso, A., and Abbott, L. (2019). Training dynamically balanced excitatory-inhibitory networks. PLoS ONE 14:e0220547. doi: 10.1371/journal.pone.0220547
Ishizuka, N., Weber, J., and Amaral, D. G. (1990). Organization of intrahippocampal projections originating from CA3 pyramidal cells in the rat. J. Compar. Neurol. 295, 580–623. doi: 10.1002/cne.902950407
Isomura, T., and Friston, K. (2018). In vitro neural networks minimise variational free energy. Sci. Rep. 8:16926. doi: 10.1038/s41598-018-35221-w
Isomura, T., Shimazaki, H., and Friston, K. J. (2022). Canonical neural networks perform active inference. Commun. Biol. 5:55. doi: 10.1038/s42003-021-02994-2
Iwadate, K., Suzuki, I., Watanabe, M., Yamamoto, M., and Furukawa, M. (2014). “An artificial neural network based on the architecture of the cerebellum for behavior learning,” in Soft Computing in Artificial Intelligence (Berlin: Springer), 143–151. doi: 10.1007/978-3-319-05515-2_13
Iyer, A., Grewal, K., Velu, A., Souza, L. O., Forest, J., and Ahmad, S. (2022). Avoiding catastrophe: active dendrites enable multi-task learning in dynamic environments. Front. Neurorobot. 16:846219. doi: 10.3389/fnbot.2022.846219
Izhikevich, E. (2003). Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569–1572. doi: 10.1109/TNN.2003.820440
Jedlicka, P., Tomko, M., Robins, A., and Abraham, W. C. (2022). Contributions by metaplasticity to solving the catastrophic forgetting problem. Trends Neurosci. 45, 656–666. doi: 10.1016/j.tins.2022.06.002
Johansen, J. P., Diaz-Mataix, L., Hamanaka, H., Ozawa, T., Ycu, E., Koivumaa, J., et al. (2014). Hebbian and neuromodulatory mechanisms interact to trigger associative memory formation. Proc. Natl. Acad. Sci. U.S.A. 111, E5584–E5592. doi: 10.1073/pnas.1421304111
Johnston, D., and Narayanan, R. (2008). Active dendrites: colorful wings of the mysterious butterflies. Trends Neurosci. 31, 309–316. doi: 10.1016/j.tins.2008.03.004
Jonas, E., and Kording, K. P. (2017). Could a neuroscientist understand a microprocessor? PLoS Comput. Biol. 13:e1005268. doi: 10.1371/journal.pcbi.1005268
Jun, N. Y., Ruff, D. A., Kramer, L. E., Bowes, B., Tokdar, S. T., Cohen, M. R., et al. (2022). Coordinated multiplexing of information about separate objects in visual cortex. eLife 11:e76452. doi: 10.7554/eLife.76452
Kabilan, R., and Muthukumaran, N. (2021). “A neuromorphic model for image recognition using SNN,” in 2021 6th International Conference on Inventive Computation Technologies (ICICT) (Coimbatore), 720–725. doi: 10.1109/ICICT50816.2021.9358663
Kang, S., Jun, S., Baek, S., Park, H., Yamamoto, Y., and Tanaka-Yamamoto, K. (2021). Recent advances in the understanding of specific efferent pathways emerging from the cerebellum. Front. Neuroanat. 15:759948. doi: 10.3389/fnana.2021.759948
Kawato, M., Kuroda, S., and Schweighofer, N. (2011). Cerebellar supervised learning revisited: biophysical modeling and degrees-of-freedom control. Curr. Opin. Neurobiol. 21, 791–800. doi: 10.1016/j.conb.2011.05.014
Kepecs, A., and Fishell, G. (2014). Interneuron cell types are fit to function. Nature 505, 318–326. doi: 10.1038/nature12983
Kerchner, G. A., and Nicoll, R. A. (2008). Silent synapses and the emergence of a postsynaptic mechanism for LTP. Nat. Rev. Neurosci. 9, 813–825. doi: 10.1038/nrn2501
Khajeh, R., Fumarola, F., and Abbott, L. (2022). Sparse balance: excitatory-inhibitory networks with small bias currents and broadly distributed synaptic weights. PLoS Comput. Biol. 18:e1008836. doi: 10.1371/journal.pcbi.1008836
Kirsch, L., Kunze, J., and Barber, D. (2018). “Modular networks: learning to decompose neural computation,” in Advances in Neural Information Processing Systems 31: NeurIPS 2018, Montréal, QC, eds S. Bengio, H. M. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Red Hook, NY: Curran Associates Inc.), 2414–2423.
Kornijcuk, V., Park, J., Kim, G., Kim, D., Kim, I., Kim, J., et al. (2019). Reconfigurable spike routing architectures for on-chip local learning in neuromorphic systems. Adv. Mater. Technol. 4:1800345. doi: 10.1002/admt.201800345
Kovács, K. A. (2020). Episodic memories: how do the hippocampus and the entorhinal ring attractors cooperate to create them? Front. Syst. Neurosci. 14:559168. doi: 10.3389/fnsys.2020.559186
Kozachkov, L., Tauber, J., Lundqvist, M., Brincat, S. L., Slotine, J.-J., and Miller, E. K. (2022). Robust and brain-like working memory through short-term synaptic plasticity. PLoS Comput. Biol. 18:e1010776. doi: 10.1371/journal.pcbi.1010776
Krogh, A., and Vedelsby, J. (1994). “Neural network ensembles, cross validation, and active learning,” in Advances in Neural Information Processing Systems, Vol. 7, eds G. Tesauro, D. Touretzky, and T. Leen (Cambridge, MA: MIT Press).
Kuhn, H. G., Palmer, T. D., and Fuchs, E. (2001). Adult neurogenesis: a compensatory mechanism for neuronal damage. Eur. Arch. Psychiatry Clin. Neurosci. 251, 152–158. doi: 10.1007/s004060170035
Kuo, I.-C., and Zhang, Z. (1994). “Capacity of associative memory,” in Proceedings of 1994 IEEE International Symposium on Information Theory (Trondheim), 222. doi: 10.1109/ISIT.1994.394746
Kwisthout, J., and Donselaar, N. (2020). “On the computational power and complexity of spiking neural networks,” in Proceedings of the Neuro-Inspired Computational Elements Workshop, NICE '20 (New York, NY: Association for Computing Machinery). doi: 10.1145/3381755.3381760
Laborieux, A., Ernoult, M., Hirtzlin, T., and Querlioz, D. (2021). Synaptic metaplasticity in binarized neural networks. Nat. Commun. 12:2549. doi: 10.1038/s41467-021-22768-y
Lankarany, M., Al-Basha, D., Ratt, S., and Prescott, S. A. (2019). Differentially synchronized spiking enables multiplexed neural coding. Proc. Natl. Acad. Sci. U.S.A. 116, 10097–10102. doi: 10.1073/pnas.1812171116
Le, T.-L., Huynh, T.-T., Hong, S.-K., and Lin, C.-M. (2020). Hybrid neural network cerebellar model articulation controller design for non-linear dynamic time-varying plants. Front. Neurosci. 14:695. doi: 10.3389/fnins.2020.00695
LeCun, Y., Cortes, C., and Burges, C. (2010). MNIST Handwritten Digit Database. ATT Labs [Online]. Available online at: http://yann.lecun.com/exdb/mnist
Lee, A., Lam, B., Li, W., Lee, H., Chen, W., Chang, M., et al. (2018). Conditional activation for diverse neurons in heterogeneous networks. CoRR, abs/1803.05006. arXiv [preprint] arXiv:1803.05006.
Li, C., Zhang, X., Chen, P., Zhou, K., Yu, J., Wu, G., et al. (2023). Short-term synaptic plasticity in emerging devices for neuromorphic computing. iScience 26:106315. doi: 10.1016/j.isci.2023.106315
Li, T., Arleo, A., and Sheynikhovich, D. (2020). Modeling place cells and grid cells in multi-compartment environments: entorhinal-hippocampal loop as a multisensory integration circuit. Neural Netw. 121, 37–51. doi: 10.1016/j.neunet.2019.09.002
Liang, J., Meyerson, E., and Miikkulainen, R. (2018). “Evolutionary architecture search for deep multitask networks,” in Proceedings of the Genetic and Evolutionary Computation Conference, GECCO '18 (New York, NY: Association for Computing Machinery), 466–473. doi: 10.1145/3205455.3205489
Lillicrap, T. P., Santoro, A., Marris, L., Akerman, C. J., and Hinton, G. (2020). Backpropagation and the brain. Nat. Rev. Neurosci. 21, 335–346. doi: 10.1038/s41583-020-0277-3
Lin, Y., Li, G., Zhang, X., Zhang, W., Chen, B., Tang, R., et al. (2021). “ModularNAS: towards modularized and reusable neural architecture search,” in Proceedings of Machine Learning and Systems, Vol. 3, eds A. Smola, A. Dimakis, and I. Stoica (Virtual), 413–433.
Liu, Y., Sun, Y., Xue, B., Zhang, M., Yen, G. G., and Tan, K. C. (2021). A survey on evolutionary neural architecture search. IEEE Trans. Neural Netw. Learn. Syst. 34, 550–570. doi: 10.1109/TNNLS.2021.3100554
Liu, Y., and Yao, X. (2008). Nature inspired neural network ensemble learning. J. Intell. Syst. 17(Suppl.), 5–26. doi: 10.1515/JISYS.2008.17.S1.5
Liu, Y. H., Smith, S., Mihalas, S., Shea-Brown, E., and Sümbül, U. (2021). Cell-type-specific neuromodulation guides synaptic credit assignment in a spiking neural network. Proc. Natl. Acad. Sci. U.S.A. 118:e2111821118. doi: 10.1073/pnas.2111821118
Llorca, A., Ciceri, G., Beattie, R., Wong, F. K., Diana, G., Serafeimidou-Pouliou, E., et al. (2019). A stochastic framework of neurogenesis underlies the assembly of neocortical cytoarchitecture. eLife 8:e51381. doi: 10.7554/eLife.51381
London, M., and Häusser, M. (2005). Dendritic computation. Annu. Rev. Neurosci. 28, 503–532. doi: 10.1146/annurev.neuro.28.061604.135703
Luczak, A., McNaughton, B. L., and Kubo, Y. (2022). Neurons learn by predicting future activity. Nat. Mach. Intell. 4, 62–72. doi: 10.1038/s42256-021-00430-y
Łukasz Kuśmierz Isomura, T., and Toyoizumi, T. (2017). Learning with three factors: modulating Hebbian plasticity with errors. Curr. Opin. Neurobiol. 46, 170–177. doi: 10.1016/j.conb.2017.08.020
Luo, L. (2021). Architectures of neuronal circuits. Science 373:eabg7285. doi: 10.1126/science.abg7285
Luo, W. (2020). Improving neural network with uniform sparse connectivity. IEEE Access 8, 215705–215715. doi: 10.1109/ACCESS.2020.3040943
Maass, W. (1996). Lower bounds for the computational power of networks of spiking neurons. Neural Comput. 8, 1–40. doi: 10.1162/neco.1996.8.1.1
Maile, K., Hervé, L., and Wilson, D. G. (2022). Structural learning in artificial neural networks: a neural operator perspective. Trans. Mach. Learn. Res. Available online at: https://openreview.net/forum?id=gzhEGhcsnN
Markram, H., Muller, E., Ramaswamy, S., Reimann, M., Abdellah, M., Sanchez, C., et al. (2015). Reconstruction and simulation of neocortical microcircuitry. Cell 163, 456–492. doi: 10.1016/j.cell.2015.09.029
Marr, D. (1969). A theory of cerebellar cortex. J. Physiol. 202, 437–470. doi: 10.1113/jphysiol.1969.sp008820
Masse, N. Y., Yang, G. R., Song, H. F., Wang, X.-J., and Freedman, D. J. (2019). Circuit mechanisms for the maintenance and manipulation of information in working memory. Nat. Neurosci. 22, 1159–1167. doi: 10.1038/s41593-019-0414-3
Mattson, M. P., and Magnus, T. (2006). Ageing and neuronal vulnerability. Nat. Rev. Neurosci. 7, 278–294. doi: 10.1038/nrn1886
McCulloch, W. S., and Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5, 115–133. doi: 10.1007/BF02478259
McEliece, R. J., Posner, E. C., Rodemich, E. R., and Venkatesh, S. S. (1988). The Capacity of the Hopfield Associative Memory. Washington, DC: IEEE Computer Society Press, 100–121.
Mei, J., Muller, E., and Ramaswamy, S. (2022). Informing deep neural networks by multiscale principles of neuromodulatory systems. Trends Neurosci. 45, 237–250. doi: 10.1016/j.tins.2021.12.008
Merlo, S., Spampinato, S. F., and Sortino, M. A. (2019). Early compensatory responses against neuronal injury: a new therapeutic window of opportunity for Alzheimer's disease? CNS Neurosci. Therap. 25, 5–13. doi: 10.1111/cns.13050
Meunier, D., Lambiotte, R., and Bullmore, E. T. (2010). Modular and hierarchically modular organization of brain networks. Front. Neurosci. 4:200. doi: 10.3389/fnins.2010.00200
Michaels, J. A., Schaffelhofer, S., Agudelo-Toro, A., and Scherberger, H. (2020). A goal-driven modular neural network predicts parietofrontal neural dynamics during grasping. Proc. Natl. Acad. Sci. U.S.A. 117, 32124–32135. doi: 10.1073/pnas.2005087117
Miller, K. D. (1998). Equivalence of a sprouting-and-retraction model and correlation-based plasticity models of neural development. Neural Comput. 10, 529–547. doi: 10.1162/089976698300017647
Millidge, B., Seth, A., and Buckley, C. L. (2022). Predictive coding: a theoretical and experimental review. arXiv [preprint] arXiv:2107.12979.
Miscouridou, X., Caron, F., and Teh, Y. W. (2018). “Modelling sparsity, heterogeneity, reciprocity and community structure in temporal interaction data,” in Proceedings of the 32nd International Conference on Neural Information Processing Systems, NIPS'18 (Red Hook, NY: Curran Associates Inc.), 2349–2358.
Miyata, R., Ota, K., and Aonishi, T. (2013). Optimal design for hetero-associative memory: hippocampal ca1 phase response curve and spike-timing-dependent plasticity. PLoS ONE 8:e77395. doi: 10.1371/journal.pone.0077395
Mocanu, D. C., Mocanu, E., Stone, P., Nguyen, P. H., Gibescu, M., and Liotta, A. (2018). Scalable training of artificial neural networks with adaptive sparse connectivity inspired by network science. Nat. Commun. 9, 1–12. doi: 10.1038/s41467-018-04316-3
Moreno-Jiménez, E. P., Terreros-Roncal, J., Flor-García, M., Rábano, A., and Llorens-Martín, M. (2021). Evidences for adult hippocampal neurogenesis in humans. J. Neurosci. 41, 2541–2553. doi: 10.1523/JNEUROSCI.0675-20.2020
Mukherjee, S., and Hill, S. M. (2011). Network clustering: probing biological heterogeneity by sparse graphical models. Bioinformatics 27, 994–1000. doi: 10.1093/bioinformatics/btr070
Murman, D. L. (2015). The impact of age on cognition. Semin. Hear. 36, 111–121. doi: 10.1055/s-0035-1555115
Nadim, F., and Bucher, D. (2014). Neuromodulation of neurons and synapses. Curr. Opin. Neurobiol. 29, 48–56. doi: 10.1016/j.conb.2014.05.003
Nair, V., and Hinton, G. E. (2010). “Rectified linear units improve restricted Boltzmann machines,” in Proceedings of the 27th International Conference on International Conference on Machine Learning, ICML'10 (Madison, WI: Omnipress), 807–814.
Naudé, J., Cessac, B., Berry, H., and Delord, B. (2013). Effects of cellular homeostatic intrinsic plasticity on dynamical and computational properties of biological recurrent neural networks. J. Neurosci. 33, 15032–15043. doi: 10.1523/JNEUROSCI.0870-13.2013
Navlakha, S., Bar-Joseph, Z., and Barth, A. L. (2018). Network design and the brain. Trends Cogn. Sci. 22, 64–78. doi: 10.1016/j.tics.2017.09.012
Nijhawan, R. (2008). Visual prediction: psychophysics and neurophysiology of compensation for time delays. Behav. Brain Sci. 31, 179–198. doi: 10.1017/S0140525X08003804
Noudoost, B., and Moore, T. (2011). The role of neuromodulators in selective attention. Trends Cogn. Sci. 15, 585–591. doi: 10.1016/j.tics.2011.10.006
Nussberger, A.-M., Luo, L., Celis, L. E., and Crockett, M. J. (2022). Public attitudes value interpretability but prioritize accuracy in artificial intelligence. Nat. Commun. 13:5821. doi: 10.1038/s41467-022-33417-3
Osborne, N. N. (1979). Is dale's principle valid? Trends Neurosci. 2, 73–75. doi: 10.1016/0166-2236(79)90031-6
Pagkalos, M., Chavlis, S., and Poirazi, P. (2023). Introducing the dendrify framework for incorporating dendrites to spiking neural networks. Nat. Commun. 14:131. doi: 10.1038/s41467-022-35747-8
Palmer, S. E., Marre, O., Berry, M. J., and Bialek, W. (2015). Predictive information in a sensory population. Proc. Natl. Acad. Sci. U.S.A. 112, 6908–6913. doi: 10.1073/pnas.1506855112
Pan, R., and Rajan, H. (2020). “On decomposing a deep neural network into modules,” in Proceedings of the 28th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, ESEC/FSE 2020 (New York, NY: Association for Computing Machinery), 889–900. doi: 10.1145/3368089.3409668
Pan, Z., Wu, J., Chua, Y., Zhang, M., and Li, H. (2019). “Neural population coding for effective temporal classification,” in International Joint Conference on Neural Networks (Budapest), 1–8. doi: 10.1109/IJCNN.2019.8851858
Panzeri, S., Macke, J. H., Gross, J., and Kayser, C. (2015). Neural population coding: combining insights from microscopic and mass signals. Trends Cogn. Sci. 19, 162–172. doi: 10.1016/j.tics.2015.01.002
Park, J., Papoutsi, A., Ash, R. T., Marin, M. A., Poirazi, P., and Smirnakis, S. M. (2019). Contribution of apical and basal dendrites to orientation encoding in mouse v1 l2/3 pyramidal neurons. Nat. Commun. 10:5372. doi: 10.1038/s41467-019-13029-0
Park, S., Kim, S., Na, B., and Yoon, S. (2020). “T2FSNN: deep spiking neural networks with time-to-first-spike coding,” in 2020 57th ACM/IEEE Design Automation Conference (DAC) (Virtual), 1–6. doi: 10.1109/DAC18072.2020.9218689
Parker, L., Chance, F., and Cardwell, S. (2022). “Benchmarking a bio-inspired SNN on a neuromorphic system,” in Neuro-Inspired Computational Elements Conference, NICE 2022 (New York, NY: Association for Computing Machinery), 63–66. doi: 10.1145/3517343.3517365
Pezzulo, G., Parr, T., and Friston, K. (2022). The evolution of brain architectures for predictive coding and active inference. Philos. Trans. R. Soc. B Biol. Sci. 377:20200531. doi: 10.1098/rstb.2020.0531
Pfeiffer, M., and Pfeil, T. (2018). Deep learning with spiking neurons: opportunities and challenges. Front. Neurosci. 12:774. doi: 10.3389/fnins.2018.00774
Pitkow, X., and Angelaki, D. E. (2017). Inference in the brain: statistics flowing in redundant population codes. Neuron 94, 943–953. doi: 10.1016/j.neuron.2017.05.028
Poirazi, P., and Mel, B. W. (2001). Impact of active dendrites and structural plasticity on the memory capacity of neural tissue. Neuron 29, 779–796. doi: 10.1016/S0896-6273(01)00252-5
Qiang Bi, G., and Ming Poo, M. (1998). Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998
Ramesh, A., Dhariwal, P., Nichol, A., Chu, C., and Chen, M. (2022). Hierarchical text-conditional image generation with clip latents. arXiv [preprint] arXiv:2204.06125.
Rao, R. P. N., and Ballard, D. H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 2, 79–87. doi: 10.1038/4580
Raymond, J. L., and Medina, J. F. (2018). Computational principles of supervised learning in the cerebellum. Annu. Rev. Neurosci. 41, 233–253. doi: 10.1146/annurev-neuro-080317-061948
Razetti, A., Medioni, C., Malandain, G., Besse, F., and Descombes, X. (2018). A stochastic framework to model axon interactions within growing neuronal populations. PLoS Comput. Biol. 14:e1006627. doi: 10.1371/journal.pcbi.1006627
Risi, S., and Stanley, K. O. (2014). “Guided self-organization in indirectly encoded and evolving topographic maps,” in Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, GECCO '14 (New York, NY: Association for Computing Machinery), 713–720. doi: 10.1145/2576768.2598369
Robertazzi, F., Vissani, M., Schillaci, G., and Falotico, E. (2022). Brain-inspired meta-reinforcement learning cognitive control in conflictual inhibition decision-making task for artificial agents. Neural Netw. 154, 283–302. doi: 10.1016/j.neunet.2022.06.020
Rodriguez, H. G., Guo, Q., and Moraitis, T. (2022). “Short-term plasticity neurons learning to learn and forget,” in International Conference on Machine Learning, Vol. 162, eds K. Chaudhuri, S. Jegelka, L. Song, C. Szepesvári, G. Niu, and S. Sabato (MLR Press), 18704–18722. Available online at: https://proceedings.mlr.press/v162/rodriguez22b.html
Rogers, R. D. (2011). The roles of dopamine and serotonin in decision making: evidence from pharmacological experiments in humans. Neuropsychopharmacology 36, 114–132. doi: 10.1038/npp.2010.165
Rombach, R., Blattmann, A., Lorenz, D., Esser, P., and Ommer, B. (2022). “High-resolution image synthesis with latent diffusion models,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (New Orleans, LA: IEEE), 10674–10685. doi: 10.1109/CVPR52688.2022.01042
Rothschild, G., Eban, E., and Frank, L. M. (2017). A cortical-hippocampal-cortical loop of information processing during memory consolidation. Nat. Neurosci. 20, 251–259. doi: 10.1038/nn.4457
Rubinov, M., Ypma, R. J. F., Watson, C., and Bullmore, E. T. (2015). Wiring cost and topological participation of the mouse brain connectome. Proc. Natl. Acad. Sci. U.S.A. 112, 10032–10037. doi: 10.1073/pnas.1420315112
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning representations by back-propagating errors. Nature 323, 533–536. doi: 10.1038/323533a0
Sacramento, J., Ponte Costa, R., Bengio, Y., and Senn, W. (2018). “Dendritic cortical microcircuits approximate the backpropagation algorithm,” in Advances in Neural Information Processing Systems 31: NeurIPS 2018, Montréal, Canada, eds S. Bengio, H. M. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Red Hook, NY: Curran Associates Inc.), 31, 8735–8746.
Sadeh, S., and Clopath, C. (2021). Excitatory-inhibitory balance modulates the formation and dynamics of neuronal assemblies in cortical networks. Sci. Adv. 7:eabg8411. doi: 10.1126/sciadv.abg8411
Schuman, C. D., Kulkarni, S. R., Parsa, M., Mitchell, J. P., Date, P., and Kay, B. (2022). Opportunities for neuromorphic computing algorithms and applications. Nat. Comput. Sci. 2, 10–19. doi: 10.1038/s43588-021-00184-y
Scott, A. C. (1975). The electrophysics of a nerve fiber. Rev. Mod. Phys. 47, 487–533. doi: 10.1103/RevModPhys.47.487
Sederberg, A. J., MacLean, J. N., and Palmer, S. E. (2018). Learning to make external sensory stimulus predictions using internal correlations in populations of neurons. Proc. Natl. Acad. Sci. U.S.A. 115, 1105–1110. doi: 10.1073/pnas.1710779115
Sehgal, M., Song, C., Ehlers, V. L., and Moyer, J. R. (2013). Learning to learn-intrinsic plasticity as a metaplasticity mechanism for memory formation. Neurobiol. Learn. Mem. 105, 186–199. doi: 10.1016/j.nlm.2013.07.008
Sezener, E., Grabska-Barwińska, A., Kostadinov, D., Beau, M., Krishnagopal, S., Budden, D., et al. (2022). A rapid and efficient learning rule for biological neural circuits. bioRxiv. doi: 10.1101/2021.03.10.434756
Shaw, N. P., Jackson, T., and Orchard, J. (2020). Biological batch normalisation: how intrinsic plasticity improves learning in deep neural networks. PLoS ONE 15:e0238454. doi: 10.1371/journal.pone.0238454
Shemer, I., Brinne, B., Tegnér, J., and Grillner, S. (2008). Electrotonic signals along intracellular membranes may interconnect dendritic spines and nucleus. PLoS Comput. Biol. 4:e1000036. doi: 10.1371/journal.pcbi.1000036
Shen, Y., Wang, J., and Navlakha, S. (2021). A correspondence between normalization strategies in artificial and biological neural networks. Neural Comput. 33, 3179–3203. doi: 10.1162/neco_a_01439
Smith, J. M. (1999). Shaping Life: Genes, Embryos, and Evolution. Darwinism Today Series. New Haven: Yale University Press.
Smolen, P., Baxter, D. A., and Byrne, J. H. (2020). Comparing theories for the maintenance of late LTP and long-term memory: computational analysis of the roles of kinase feedback pathways and synaptic reactivation. Front. Comput. Neurosci. 14:569349. doi: 10.3389/fncom.2020.569349
Sohal, V. S., and Rubenstein, J. L. R. (2019). Excitation-inhibition balance as a framework for investigating mechanisms in neuropsychiatric disorders. Mol. Psychiatry 24, 1248–1257. doi: 10.1038/s41380-019-0426-0
Song, H. F., Yang, G. R., and Wang, X.-J. (2016). Training excitatory-inhibitory recurrent neural networks for cognitive tasks: a simple and flexible framework. PLoS Comput. Biol. 12:e1004792. doi: 10.1371/journal.pcbi.1004792
Song, S., Miller, K. D., and Abbott, L. F. (2000). Competitive hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926. doi: 10.1038/78829
Sorrells, S. F., Paredes, M. F., Cebrian-Silla, A., Sandoval, K., Qi, D., Kelley, K. W., et al. (2018). Human hippocampal neurogenesis drops sharply in children to undetectable levels in adults. Nature 555, 377–381. doi: 10.1038/nature25975
Sorrells, S. F., Paredes, M. F., Zhang, Z., Kang, G., Pastor-Alonso, O., Biagiotti, S., et al. (2021). Positive controls in adults and children support that very few, if any, new neurons are born in the adult human hippocampus. J. Neurosci. 41, 2554–2565. doi: 10.1523/JNEUROSCI.0676-20.2020
Speranza, L., Labus, J., Volpicelli, F., Guseva, D., Lacivita, E., Leopoldo, M., et al. (2017). Serotonin 5-ht7 receptor increases the density of dendritic spines and facilitates synaptogenesis in forebrain neurons. J. Neurochem. 141, 647–661. doi: 10.1111/jnc.13962
Stanley, K. O., Clune, J., Lehman, J., and Miikkulainen, R. (2019). Designing neural networks through neuroevolution. Nat. Mach. Intell. 1, 24–35. doi: 10.1038/s42256-018-0006-z
Stöckl, C., Lang, D., and Maass, W. (2022). Structure induces computational function in networks with diverse types of spiking neurons. bioRxiv. doi: 10.1101/2021.05.18.444689
Südhof, T. C. (2018). Towards an understanding of synapse formation. Neuron 100, 276–293. doi: 10.1016/j.neuron.2018.09.040
Tan, S. Z. K., Du, R., Perucho, J. A. U., Chopra, S. S., Vardhanabhuti, V., and Lim, L. W. (2020). Dropout in neural networks simulates the paradoxical effects of deep brain stimulation on memory. Front. Aging Neurosci. 12:273. doi: 10.3389/fnagi.2020.00273
Tanaka, H., Ishikawa, T., Lee, J., and Kakei, S. (2020). The cerebro-cerebellum as a locus of forward model: a review. Front. Syst. Neurosci. 14:19. doi: 10.3389/fnsys.2020.00019
Terziyan, V., and Kaikova, O. (2022). Neural networks with disabilities: an introduction to complementary artificial intelligence. Neural Comput. 34, 255–290. doi: 10.1162/neco_a_01449
Thomas, B. T., Blalock, D. W., and Levy, W. B. (2015). Adaptive synaptogenesis constructs neural codes that benefit discrimination. PLoS Comput. Biol. 11:e1004299. doi: 10.1371/journal.pcbi.1004299
Tian, G., Li, S., Huang, T., and Wu, S. (2020). Excitation-inhibition balanced neural networks for fast signal detection. Front. Comput. Neurosci. 14:79. doi: 10.3389/fncom.2020.00079
Tierney, A. L., and Nelson, C. A. I. (2009). Brain development and the role of experience in the early years. Zero Three 30, 9–13.
Titley, H. K., Brunel, N., and Hansel, C. (2017). Toward a neurocentric view of learning. Neuron 95, 19–32. doi: 10.1016/j.neuron.2017.05.021
Tomasi, D., Wang, G.-J., and Volkow, N. D. (2013). Energetic cost of brain functional connectivity. Proc. Natl. Acad. Sci. U.S.A. 110, 13642–13647. doi: 10.1073/pnas.1303346110
Tosches, M. A. (2017). Developmental and genetic mechanisms of neural circuit evolution. Dev. Biol. 431, 16–25. doi: 10.1016/j.ydbio.2017.06.016
Toyoizumi, T., Kaneko, M., Stryker, M., and Miller, K. (2014). Modeling the dynamic interaction of hebbian and homeostatic plasticity. Neuron 84, 497–510. doi: 10.1016/j.neuron.2014.09.036
Toyoizumi, T., Pfister, J.-P., Aihara, K., and Gerstner, W. (2005). “Generalized Bienenstock-Cooper-Munro rule for spiking neurons that maximizes information transmission,” in Proceedings of the National Academy of Sciences, Vol. 102. p. 5239–5244. doi: 10.1073/pnas.0500495102
Tran, L. M., Santoro, A., Liu, L., Josselyn, S. A., Richards, B. A., and Frankland, P. W. (2022). Adult neurogenesis acts as a neural regularizer. Proc. Natl. Acad. Sci. U.S.A. 119:e2206704119. doi: 10.1073/pnas.2206704119
Trapp, P., Echeveste, R., and Gros, C. (2018). E-i balance emerges naturally from continuous Hebbian learning in autonomous neural networks. Sci. Rep. 8:8939. doi: 10.1038/s41598-018-27099-5
Traulsen, A., and Nowak, M. A. (2006). Evolution of cooperation by multilevel selection. Proc. Natl. Acad. Sci. U.S.A. 103, 10952–10955. doi: 10.1073/pnas.0602530103
Tripodi, M., Evers, J. F., Mauss, A., Bate, M., and Landgraf, M. (2008). Structural homeostasis: Compensatory adjustments of dendritic arbor geometry in response to variations of synaptic input. PLoS Biol. 6:e60260. doi: 10.1371/journal.pbio.0060260
Tripp, B., and Eliasmith, C. (2016). Function approximation in inhibitory networks. Neural Netw. 77, 95–106. doi: 10.1016/j.neunet.2016.01.010
Tsa, Y., Chu, H.-C., Fang, S.-H., Lee, J., and Lin, C.-M. (2018). Adaptive noise cancellation using deep cerebellar model articulation controller. IEEE Access 6, 37395–37402. doi: 10.1109/ACCESS.2018.2827699
Tsodyks, M., and Markram, H. (1997). The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc. Natl. Acad. Sci. U.S.A. 94, 719–723. doi: 10.1073/pnas.94.2.719
Turrigiano, G. G., Leslie, K. R., Desai, N. S., Rutherford, L. C., and Nelson, S. B. (1998). Activity-dependent scaling of quantal amplitude in neocortical neurons. Nature 391, 892–896. doi: 10.1038/36103
Turrigiano, G. G., and Nelson, S. B. (2004). Homeostatic plasticity in the developing nervous system. Nat. Rev. Neurosci. 5, 97–107. doi: 10.1038/nrn1327
Valiant, L. (2013). Probably Approximately Correct: Nature's Algorithms for Learning and Prospering in a Complex World. New York City, NY: Basic Books, Inc.
van de Ven, G. M., Siegelmann, H. T., and Tolias, A. S. (2020). Brain-inspired replay for continual learning with artificial neural networks. Nat. Commun. 11:4069. doi: 10.1038/s41467-020-17866-2
van Ooyen, A. (2011). Using theoretical models to analyse neural development. Nat. Rev. Neurosci. 12, 311–326. doi: 10.1038/nrn3031
Vardalaki, D., Chung, K., and Harnett, M. T. (2022). Filopodia are a structural substrate for silent synapses in adult neocortex. Nature 612, 323–327. doi: 10.1038/s41586-022-05483-6
Veríssimo, J., Verhaeghen, P., Goldman, N., Weinstein, M., and Ullman, M. T. (2022). Evidence that ageing yields improvements as well as declines across attention and executive functions. Nat. Hum. Behav. 6, 97–110. doi: 10.1038/s41562-021-01169-7
Vilone, G., and Longo, L. (2021). Notions of explainability and evaluation approaches for explainable artificial intelligence. Inform. Fus. 76, 89–106. doi: 10.1016/j.inffus.2021.05.009
Wang, C.-H., Huang, K.-Y., Yao, Y., Chen, J.-C., Shuai, H.-H., and Cheng, W.-H. (2022). Lightweight deep learning: an overview. IEEE Consum. Electron. Mag. 1–12. doi: 10.1109/MCE.2022.3181759
Wang, L., Lei, B., Li, Q., Su, H., Zhu, J., and Zhong, Y. (2022). Triple-memory networks: a brain-inspired method for continual learning. IEEE Trans. Neural Netw. Learn. Syst. 33, 1925–1934. doi: 10.1109/TNNLS.2021.3111019
Whittington, J. C., and Bogacz, R. (2019). Theories of error back-propagation in the brain. Trends Cogn. Sci. 23, 235–250. doi: 10.1016/j.tics.2018.12.005
Wu, X., Liu, X., Li, W., and Wu, Q. (2018). “Improved expressivity through dendritic neural networks,” in Advances in Neural Information Processing Systems 31: NeurIPS 2018, Montréal, Canada, eds S. Bengio, H. M. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Red Hook, NY: Curran Associates Inc.), 31, 8068–8079.
Wybo, W. A., Torben-Nielsen, B., Nevian, T., and Gewaltig, M.-O. (2019). Electrical compartmentalization in neurons. Cell Rep. 26, 1759–1773.e7. doi: 10.1016/j.celrep.2019.01.074
Yao, X., and Liu, Y. (1998). Towards designing artificial neural networks by evolution. Appl. Math. Comput. 91, 83–90. doi: 10.1016/S0096-3003(97)10005-4
Zeng, Y., Zhao, D., Zhao, F., Shen, G., Dong, Y., Lu, E., et al. (2022). Braincog: a spiking neural network based brain-inspired cognitive intelligence engine for brain-inspired AI and brain simulation. arXiv [preprint] arXiv:2207.08533. doi: 10.2139/ssrn.4278957
Zhang, H., Sun, J., and Xu, Z. (2020). Learning to be global optimizer. arXiv [preprint] arXiv:2003.04521.
Zhang, S., Liu, M., and Yan, J. (2020). “The diversified ensemble neural network,” in Advances in Neural Information Processing Systems, Vol. 33, eds H. Larochelle, M. Ranzato, R. Hadsell, M. Balcan, and H. Lin (Curran Associates, Inc.), 16001–16011.
Zhang, S., Zhang, A., Ma, Y., and Zhu, W. (2019). Intrinsic plasticity based inference acceleration for spiking multi-layer perceptron. IEEE Access 7, 73685–73693. doi: 10.1109/ACCESS.2019.2914424
Zhang, W., and Li, P. (2019). Information-theoretic intrinsic plasticity for online unsupervised learning in spiking neural networks. Front. Neurosci. 13:31. doi: 10.3389/fnins.2019.00031
Zhang, X., Liu, S., Zhao, X., Wu, F., Wu, Q., Wang, W., et al. (2017). Emulating short-term and long-term plasticity of bio-synapse based on CU/A-SI/PT memristor. IEEE Electr. Device Lett. 38, 1208–1211. doi: 10.1109/LED.2017.2722463
Zhou, S., and Yu, Y. (2018). Synaptic E-I balance underlies efficient neural coding. Front. Neurosci. 12:46. doi: 10.3389/fnins.2018.00046
Zhou, Z.-H., Wu, J., and Tang, W. (2002). Ensembling neural networks: many could be better than all. Artif. Intell. 137, 239–263. doi: 10.1016/S0004-3702(02)00190-X
Zierenberg, J., Wilting, J., and Priesemann, V. (2018). Homeostatic plasticity and external input shape neural network dynamics. Phys. Rev. X 8:031018. doi: 10.1103/PhysRevX.8.031018
Zoph, B., Vasudevan, V., Shlens, J., and Le, Q. V. (2018). “Learning transferable architectures for scalable image recognition,” in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (Salt Lake City, UT), 8697–8710. doi: 10.1109/CVPR.2018.00907
Keywords: bottom-up approach, biologically plausible neural network, optimization of neural network, biological neural network supremacy, neural network architecture, balanced network, dendritic computation, Dale's principle
Citation: Jeon I and Kim T (2023) Distinctive properties of biological neural networks and recent advances in bottom-up approaches toward a better biologically plausible neural network. Front. Comput. Neurosci. 17:1092185. doi: 10.3389/fncom.2023.1092185
Received: 07 November 2022; Accepted: 12 June 2023;
Published: 28 June 2023.
Edited by:
Jiyoung Kang, Pukyong National University, Republic of KoreaReviewed by:
Chang-Eop Kim, Gachon University, Republic of KoreaSeok Jun Hong, Sungkyunkwan University, Republic of Korea
Copyright © 2023 Jeon and Kim. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Taegon Kim, dGFlZ29uLmtpbUBraXN0LnJlLmty
 Ikhwan Jeon
Ikhwan Jeon Taegon Kim
Taegon Kim