Dynamics of a model for the degradation mechanism of aggregated α-synuclein in Parkinson's disease

Accumulation of the misfolded synaptic protein α-synuclein (αSyn^*) is a hallmark of neurodegenerative disease in Parkinson's disease (PD). Recent studies suggest that the autophagy lysosome pathway (ALP) including both the Beclin1-associated and mTOR-signaling pathways is involved in the αSyn^* clearance mechanism. In this study, a mathematical model is proposed for the degradation of αSyn^* by ALP with the crosstalk element of mTOR. Using codimension-1 bifurcation analysis, the tri-stability of αSyn^* is surveyed under three different stress signals and, in addition, consideration is given to the regulatory mechanisms for the Beclin1- and mTOR-dependent rates on αSyn^* degradation using the codimension-1 and−2 bifurcation diagrams. It was found that, especially under internal and external oxidative stresses (S₁), the bistable switch of the aggregation of αSyn^* can be transformed from an irreversible to a reversible condition through the ALP degradation pathways. Furthermore, the robustness of the tri-stable state for the stress S₁ to the parameters related to mTOR-mediated ALP was probed. It was confirmed that mTOR-mediated ALP is important for maintaining the essential dynamic features of the tri-stable state. This study may provide a promising avenue for conducting further experiments and simulations of the degradation mechanism of dynamic modeling in PD.

Introduction

Parkinson's disease (PD) is the second most frequent neurodegenerative disease, after Alzheimer's disease, with an incidence rate among humans as high as 2% after 65 years of age (Goedert et al., 2013; Bridi and Hirth, 2018). From a neuropathological point of view, the hallmark of PD is the loss of dopaminergic neurons in the substantia nigra pars compacta (SNc). It is most likely caused by the presence of neuronal cytoplasmic inclusions called Lewy bodies (LBs) due to abnormal accumulation of α-synuclein (αSyn) (Maries et al., 2003; Ruiperez et al., 2010; Gallegos et al., 2015; Choi et al., 2020).

Increased levels of αSyn have been demonstrated to cause the loss of mitochondria electron transport chain complex I activity resulting in increased reactive oxygen species (ROS) (Cali et al., 2011; Schapira and Jenner, 2011; Blesa et al., 2015; Scialo et al., 2017). Subsequently, excessive levels of ROS result in the upregulation of misfolded αSyn (αSyn^*) and damage to dopaminergic neurons in PD (Kolodkin et al., 2020; Thorne and Tumbarello, 2022). Cloutier and Wellstead (2012) have proposed a double positive feedback loop for the mutual promotion between ROS and αSyn^* within a PD model. The model contains multiple complex interactions involving molecular pathways and cellular processes, and hence the model has been further simplified to highlight the central feedback motif of αSyn^* and ROS with stress signals (Cloutier et al., 2012).

Autophagy is a “self-eating” process arising through the digestion of cellular components (Komatsu et al., 2007; Harris and Rubinsztein, 2011; Zhao et al., 2015; Fussi et al., 2018; Sotthibundhu et al., 2018). The upregulation of the autophagy lysosome pathway (ALP) promoting the degradation of αSyn^* is a very important degradation mechanism for maintaining homeostasis in the pathology of PD (Spencer et al., 2009; Vilchez et al., 2014; Erustes et al., 2018; Malik et al., 2019; Bekker et al., 2021). However, the aforementioned models of the central feedback structure of ROS and αSyn^* do not allow for the vital clearance mechanisms of ALP to degrade αSyn^*.

The mammalian target of rapamycin (mTOR) is a central regulator and modulates multiple aspects of ALP; hence, it is a novel therapeutic target for PD (Bove et al., 2011; Jiang et al., 2013; Xu et al., 2014; Zhu et al., 2019). The activation of mTOR is known to inactivate Beclin1-induced autophagy and promote Caspases-induced apoptosis under stress (Li et al., 2011; Siddiqui et al., 2015; Tavassoly et al., 2015; Cooper, 2018; Lu et al., 2020). Recent research suggests a complex network of mTOR signaling pathways implicated in the control of ALP which determines cell life and death (Sarkar et al., 2009; Jung et al., 2010; Kondratskyi et al., 2013; Shen et al., 2013). In consequence, the crosstalk element mTOR which regulates ALP to degrade the aggregation of αSyn^* may become one of the most crucial targets for the treatment of PD (Ebrahimi-Fakhari et al., 2014; Lan et al., 2017).

The aggregation of αSyn^* will trigger an appropriate endoplasmic reticulum (ER) stress response to decide cell survival or death (Kim et al., 2008; Cybulsky, 2017; Gomez-Suaga et al., 2018; Ren et al., 2021). Under tolerable stress conditions, autophagy plays a clearance role in removing aggregated αSyn^* for maintaining neuro homeostasis (Booth et al., 2014; Liu et al., 2018). However, under conditions of too long or too excessive stress levels, autophagy will switch to apoptosis as a “self-killing” pathway for better adaptation to the living environment (Heath-Engel et al., 2008; Djavaheri-Mergny et al., 2010; Wu et al., 2014; Chung et al., 2018). Kapuy et al. (2014) have presented a mathematical model that contains an interplay between major autophagy and apoptosis proteins mediated by mTOR. In that study, Beclin1, as the main protein regulator of autophagy, is activated by the endoplasmic reticulum stress sensor (ERS), and Caspases, as a primary inducer of apoptosis, is also activated by ERS.

In the present study, we seek to establish a mathematical model of mTOR-mediated ALP as the major protein clearance for the degradation of aggregated αSyn^*. Two key points will be addressed: (1) the aggregation of αSyn^* promoted by ROS triggers the activation of ERS and then ALP and Caspases-dependent apoptosis and (2) mTOR crosstalk controls ALP with respect to the degradation of the aggregated αSyn^*. Abundant non-linear dynamic analysis in the model expounds the tendency of protein concentrations to play an important role in clarifying whether the disease emerges or not.

Furthermore, recent studies show that in neurodegenerative disease, it is quite possible that a critical state, as evidenced by the existence of a tipping point, exists between healthy and disease states (Liu R. et al., 2019; McClellan and King, 2021). In this study, we seek to clarify the existence of healthy, critical, and disease states in the pathology of PD, based on the presence of low, intermediate, and high steady-state levels of αSyn^*, respectively, as depicted in Figure 1A. Therefore, in the context of the tri-stability of αSyn^*, it is considered noteworthy to study critical states to gain a better understanding of the pathogenesis of PD.

FIGURE 1

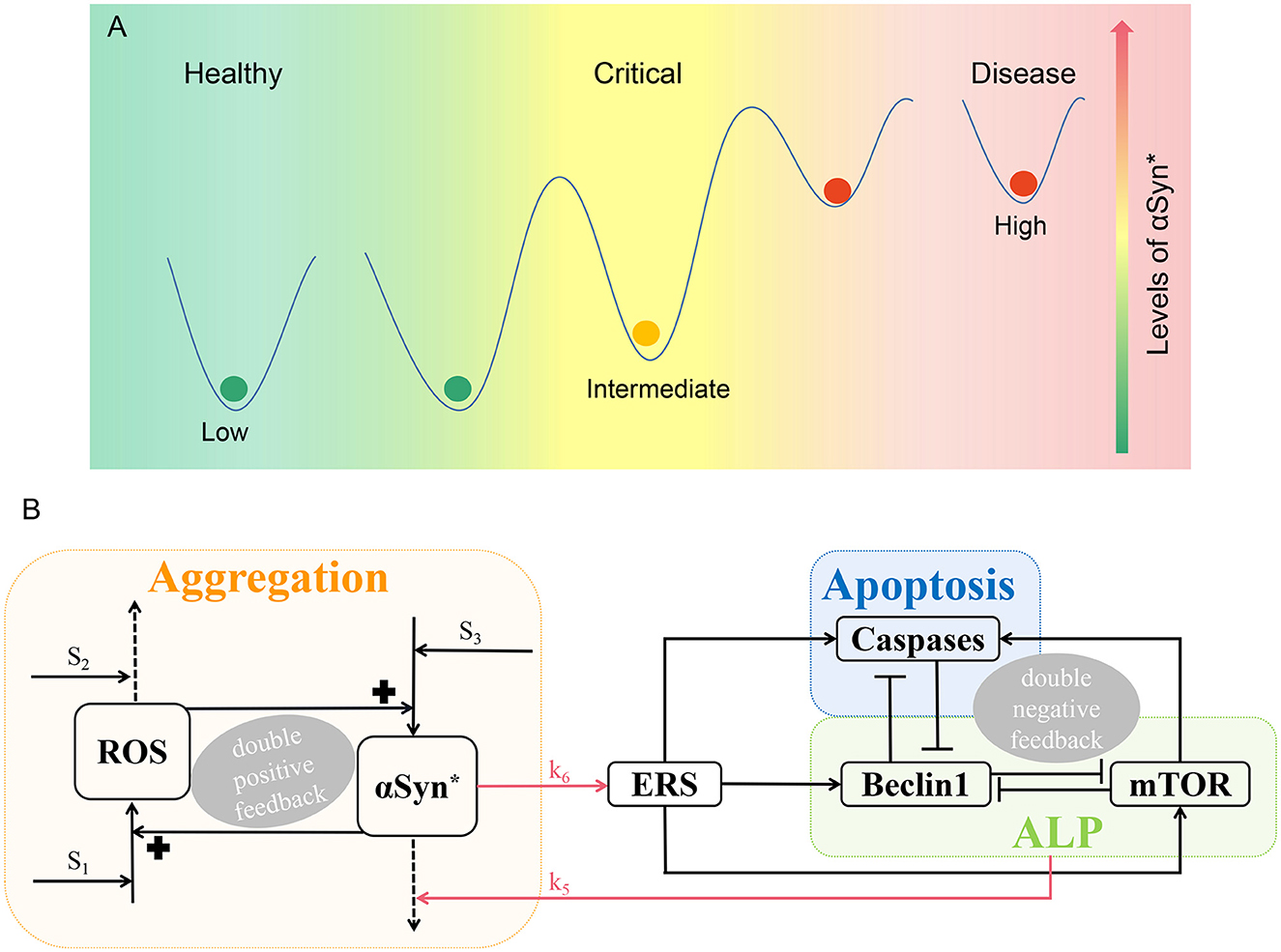
Figure 1. Schematic illustration of PD. (A) According to the levels of αSyn*, there are three different states, i.e., the low, intermediate, and high steady states parallel to the healthy, critical, and disease states, respectively. (B) A three-module model network characterizing aggregation, ALP, and apoptosis. The promotion, degradation, and inhibition are denoted by solid lines with arrowheads, dotted lines with arrowheads, and blocked end lines, respectively.

To investigate the characteristic of αSyn^* with tri-stability, the focus is given to the key molecules Beclin1 and mTOR in ALP which degrade αSyn^* under three different stresses, i.e., internal and external oxidative stresses (S₁), age-related anti-oxidative mechanisms (S₂), and the influence of genetic damage (S₃) through codimension-1 bifurcation diagrams. Moreover, bifurcation analysis is used to survey the tri-stability under the three stresses controlled by the ALP-dependent degradation rates. In addition, all possible steady-state regions are explored by codimension-2 bifurcation analyses as well as the effect of the steady-state levels of αSyn^* under different initial conditions. We find that ALP related to Beclin1 and mTOR correlates to the bistable state which switches from the irreversible to the reversible state for the stress signal S₁, which may have significant implications for the pathogenesis of PD. Finally, we investigate the robustness of the tri-stable state with respect to the mTOR-associated regulatory mechanisms. Overall, our findings provide new insights into the complex tri-stability dynamics as being a key regulatory mechanism where ALP mediated by mTOR degrades αSyn^* in PD.

Methods

Model of ALP regulated by mTOR for degradation of αSyn^*

The mathematical network model is divided into three functional modules with Aggregation (orange), ALP (green), and Apoptosis (blue) illustrated in Figure 1B.

Aggregation is represented by a positive feedback loop between αSyn^* and ROS under three stresses S₁, S₂, and S₃. Internal or external oxidative stress (such as nutrient starvation, mitochondria dysfunction, and the loss of dopamine) S₁ promotes ROS, while stress S₂ with mechanisms of age-related anti-oxidative (such as reduced energy metabolism and anti-oxidative capability) degrade ROS. Stress S₃ which is characterized by having damaged protein mechanisms for over-expression that promotes the formation of αSyn^* (Cloutier et al., 2012).

Endoplasmic reticulum stress activated by αSyn^* (upper red arrow) promotes the activation of Beclin1-dependent autophagy via ALP, Caspases-dependent apoptosis, and mTOR (Kapuy et al., 2014). αSyn^* is aggregated through ALP (lower red arrow) including both mTOR signaling and Beclin1-associated pathways with protein clearance mechanisms. Three double-negative feedback loops are formed by mutual inhibitions between Beclin1 and Caspases, between Beclin1 and mTOR, and among Beclin1, Caspases, and mTOR when the activated mTOR promotes Caspases.

Dynamic equations

The model is formulated as a coupled system of non-linear ordinary differential equations (ODEs) (1)–(6), which includes six components: the concentrations of [ROS], [αSyn^*], [ERS], [mTOR], [Beclin1], and [Caspases].

The double-positive feedback loops between [ROS] and [αSyn^*] are described in Equations (1) and (2). The first term in Equation (1) represents [ROS] generated by the background synthesis, stimuli S₁, and [αSyn^*]. The second term represents [ROS] degraded by stimuli S₂. The dynamics of aggregated αSyn^* in Equation (2) includes [ROS] which promotes the generation of αSyn^* within the first term, and the basal and Beclin-1-dependent removal within the second term. There are two terms in Equation (3), the first term corresponds to [ROS]-dependent and basal activation of [ERS], while the second term corresponds to the basal inactivation of [ERS]. As described by Equation (4), the dynamics of [mTOR] involve the basal and [ERS]-dependent activation, as well as the basal and [Beclin1]-dependent inactivation. The double-negative feedback motif between [Beclin1] and [Caspases] is described in Equations (5) and (6). For the dynamics of [Beclin1] in Equation (4), the first term represents the basal and ERS-dependent activation of [Beclin1], and the second term represents the basal and [Caspases]-dependent inactivation of [Beclin1]. Equation (5) accounts for the dynamics of [Caspases] with two terms, i.e., the basal and [ERS]-dependent activation and the basal and [Beclin1]-dependent inactivation.

Parameters in the model are mostly determined based on the literature (Cloutier et al., 2012; Kapuy et al., 2014) concerning both the simulation results and the experimental data. The initial values for all these variables are set at zero biologically (Cloutier et al., 2012; Kapuy et al., 2014), and the significance of each parameter with its default value is shown in Table 1. The numerical simulations and the bifurcation diagrams of the ODEs are solved by XPPAUT (Ermentrout, 2003).

$\begin{array}{l}\frac{d[ROS]}{dt}=k_1\left[1+S_1+d_{\alpha Syn}\left(\frac{{\left(\frac{[\alpha Sy{n}^{*}]}{k_{\alpha Syn}}\right)}^4}{1+{\left(\frac{[\alpha Sy{n}^{*}]}{k_{\alpha Syn}}\right)}^4}\right)\right]\\ -k_2\cdot [ROS]\cdot S_2& (1)\end{array}$

$\begin{array}{l}\frac{d[\alpha Sy{n}^{*}]}{dt}=k_3\cdot [ROS]\cdot S_3-k_4\cdot \left[\alpha Sy{n}^{*}\right]\cdot k_5\cdot ([Beclin1]\\ \cdot [mTOR])& (2)\end{array}$

$\begin{array}{l}\frac{d[ERS]}{dt}=k_6\cdot \left[\alpha Sy{n}^{*}\right]\cdot k_7\cdot (ERST-[ERS])\\ -k_8\cdot [ERS]& (3)\end{array}$

$\begin{array}{l}\frac{d[mTOR]}{dt}=(k_9+k_{10}\cdot [ERS])\cdot (mTORT-[mTOR])\\ -(k_{11}+k_{12}\cdot [Beclin1])\cdot [mTOR]& (4)\end{array}$

$\begin{array}{l}\frac{d[Beclin1]}{dt}=\frac{(k_{13}+k_{14}\cdot [ERS])\cdot (Beclin1T-[Beclin1])}{(Jbe+Beclin1T-[Beclin1])}\\ -\frac{(k_{15}+k_{16}\cdot [Caspases]+k_{17}\cdot [mTOR])\cdot [Beclin1]}{(Jbe+[Beclin1])}& (5)\end{array}$

$\begin{array}{l}\frac{d[Caspases]}{dt}=\\ \frac{(k_{18}+k_{19}\cdot [ERS]+k_{20}\cdot [mTOR])\cdot (CaspasesT-[Caspases])}{Jca+CaspasesT-[Caspases]}\\ -\frac{(k_{21}+k_{22}\cdot [Beclin1])\cdot [Caspases]}{(Jca+[Caspases])}& (6)\end{array}$

TABLE 1

Table 1. Description of parameters used in models (1)–(6).

Results

Bifurcations analysis under the three stresses

First, we have attempted to understand how every one of the stresses S_i (i = 1, 2, 3) changes the activation of [αSyn^*], [Caspases], and [Beclin1] in the positive-feedback loop between αSyn^* and ROS.

From a dynamic point of view, bifurcation diagrams of the [αSyn^*] concentration as well as the [Caspases] and [Beclin1] concentrations for the stresses S_i (i = 1, 2, 3) were prepared as shown in Figures 2A–C, respectively. There exist multiple stable (red solid lines) and unstable (black dotted lines) bifurcating branches arising from multiple fold points F_i(i = 1, 2, …, 6), whose locations enable us to decide on the occurrence of tri-stability, bistability, or monostability for the three stresses. In addition, there exist Hopf bifurcation points (HB) on the bifurcation curves for the stresses S₁ and S₃ in Figures 2A, C, respectively. However, only a very small stable limit cycle (green) appears and then disappears via saddle homoclinic (HC) bifurcation (see insets in Figures 2A, C).

FIGURE 2

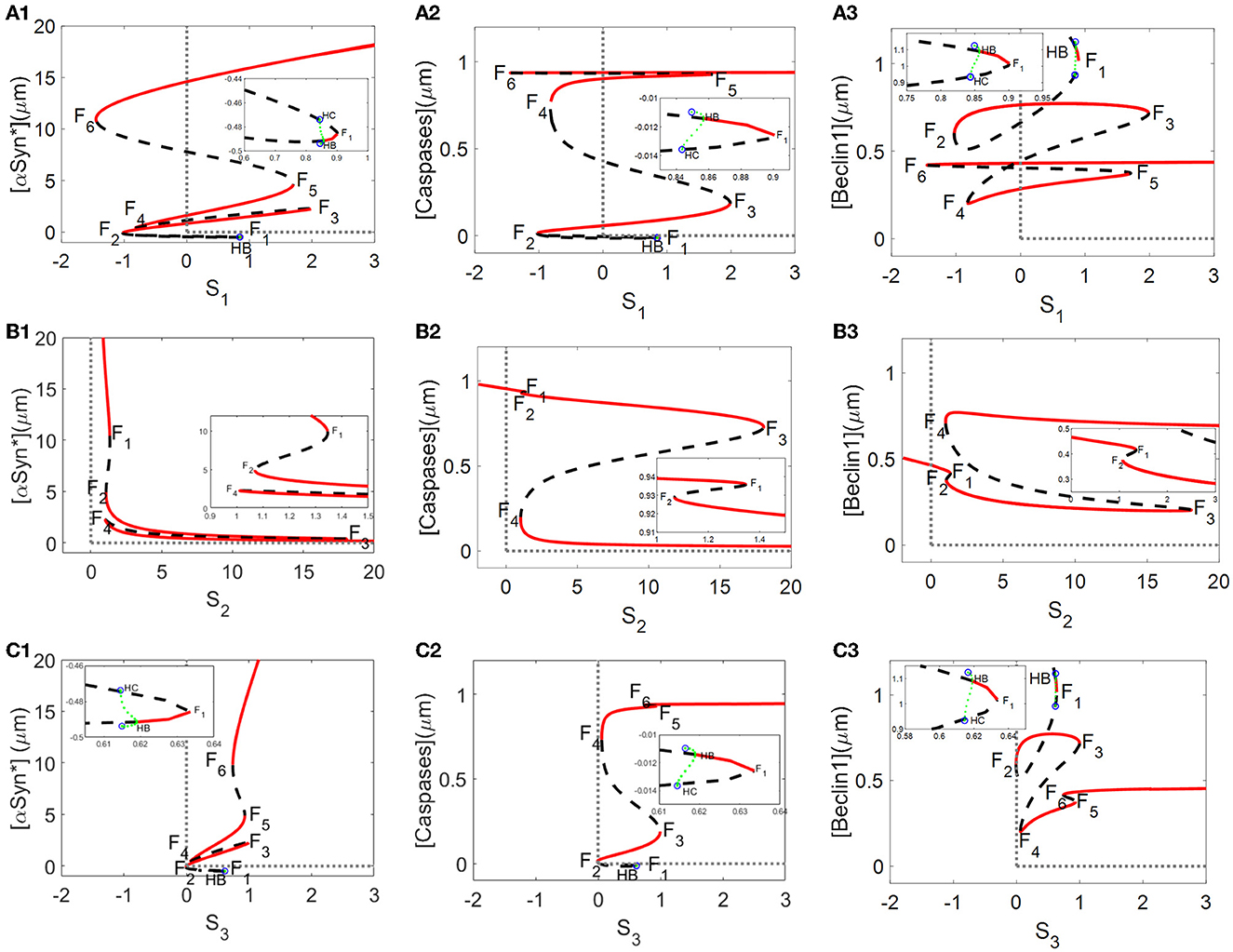
Figure 2. Bifurcation diagrams of [αSyn*], [Caspases], and [Beclin1] for the stresses S₁, S₂, and S₃ [the first lines in (A–C), respectively], where stable and unstable steady states are represented by red solid and black dotted lines, respectively, and F₁–F₆ are fold bifurcation points.

Here, a relatively large range of values [0, 20] for the stresses S_I (i = 1, 2, 3) was set on the ordinate to better display the three coexisting stable steady states. As shown in Figures 2A–C, the tri-stability state dominates the range [1, 1.8] for S₁, being more substantial than the ranges [1.07, 1.34] for S₂ and [1, 1.3] for S₃. It should be pointed out that the results of the three different stable states are from a dynamic standpoint. In fact, the intermediate and high states for [Caspases] almost have the same levels, coinciding with the “0–1” state for [Caspases] in terms of biological significance.

Given that the non-negative stresses in the model are of biological significance, the non-negative half-axis of the (S_i, y)-plane surrounded by the gray dotted lines is given some focus of attention. All switches between any two stable states are reversible for the stresses S₂ and S₃ (see Figures 2B, C) but irreversible for the stress S₁ due to the fold bifurcation points F₂ and F₄ located in the negative part of the x-axis (see Figure 2A). The reversibility of the stresses S₂ and S₃ guaranteeing arbitrary switching between any two stable states lowers the high [αSyn^*] concentrations with increasing stress S₂ (see Figure 2B1) or decreasing stress S₃ (see Figure 2C1). Nevertheless, the irreversibility of stress S₁ fails to activate the switch between any two stable states so that the high [αSyn^*] concentration always remains high (see Figure 2A1).

Tri-stability initiated from different values of the [αSyn^*] concentration

From Figures 2A–C, it can be deduced that the tri-stability state occupies the ranges of [1, 1.8] for stress S₁, [1.07, 1.34] for S₂, and [1, 1.3] for S₃, respectively. Furthermore, attempts to capture possible states for the initial values of [αSyn^*] eventually arrive at any of the three steady states for the stresses S_i (i = 1, 2, 3) in Figure 3. Within the tri-stable ranges of the three stresses on the vertical axis, all the initiated values of the [αSyn^*] concentrations (in dark blue, light blue, and yellow) are depicted on the abscissa in Figures 3A1–C1, respectively. To reflect the consequences of different initial values of [αSyn^*] more intuitively, the time courses for the [αSyn^*], [Caspases], and [Beclin1] concentrations in the second, third, and fourth columns are presented in Figure 3, respectively, when setting the stress S_i (i = 1, 2, 3) at some specific values, i.e., S₁ = 1, S₂ = 1.2, and S₃ = 0.9. In accordance with the results for the bifurcation diagrams in Figures 2A–C, the [αSyn^*] and [Caspases] concentrations finally reach the lower, middle, and upper stable branches, while the [Beclin1] concentration reaches exactly the upper, lower, and middle stable branches.

FIGURE 3

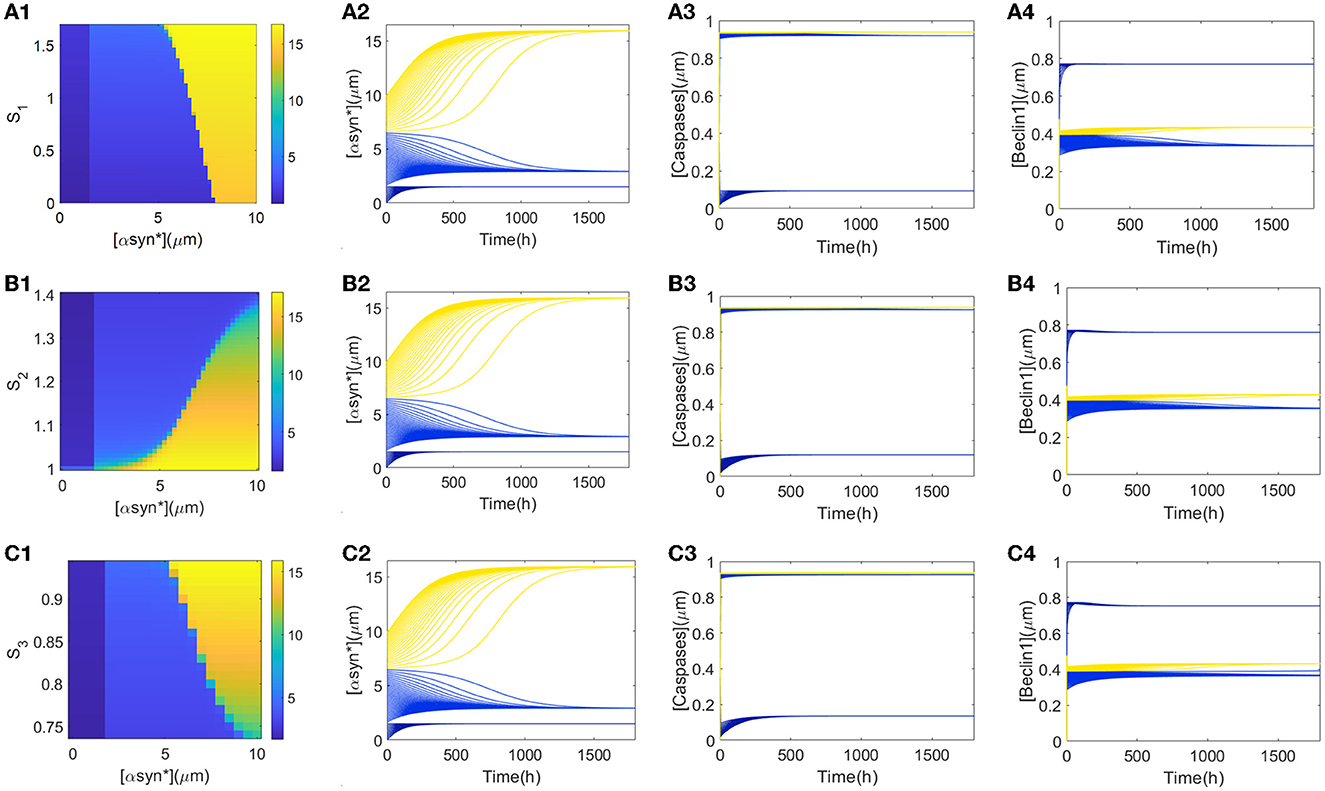
Figure 3. (A1, B1, C1) show the three αSyn* levels as a function of the initial values of [αSyn*] (x-axis) and S_i (i = 1, 2, 3) (y-axis). Time series of [αSyn*], [Caspases], and [Beclin1] reach their own three steady-states with the input signal S₁ = 1 (A2–A4), S₂ = 1.2 (B2–B4), and S₃ = 0.9 (C2–C4), respectively.

Furthermore, explanations regarding the biological significance of the tendencies for the time series of [αSyn^*], [Caspases], and [Beclin1] concentrations in Figure 3 are now considered. First, small initial values of [αSyn^*] tend to evoke low [αSyn^*] concentrations accompanied by high [Beclin1] and low [Caspases] concentrations (dark blue lines in time-series diagrams in Figure 3), which correspond to the health state with a low [αSyn^*] concentration. From a biological standpoint, Beclin1-induced autophagy takes advantage of the whole process to degrade most of the [αSyn^*] concentration. Then, medium initial values of [αSyn^*] lead to a relatively intermediate [αSyn^*] concentration accompanied by a low [Beclin1] but the intermediate [Caspases] concentrations (light blue lines in time-series diagrams in Figure 3) correspond to critical state with a relatively low [αSyn^*] concentration. The fact that the [Beclin1] concentration is much lower than the [Caspases] concentration indicates that apoptosis dominates the [αSyn^*] concentration at this health state. Finally, large initial values of [αSyn^*] bring about high [αSyn^*] concentrations, as well as high [Caspases] concentrations, but the intermediate [Beclin1] concentrations (yellow lines in the time-series diagrams in Figure 3) correspond to a disease state due to the high [αSyn^*] concentrations.

Tri-stability under the three stresses controlled by the ALP-dependent degradation rate k₅

Abnormal accumulation of αSyn^* is also degraded by ALP via both the mTOR-signaling and Beclin1-associated pathways (Shen et al., 2013). In the present model, the ALP-dependent αSyn^* degradation rate constant, k₅, bridges the two modules via the degradation mechanism of ALP. Here, different values of the parameter k₅ were selected to reveal how the bifurcation curves of αSyn^* change with the stress signals S₁, S₂, and S₃ (see Figure 4).

FIGURE 4

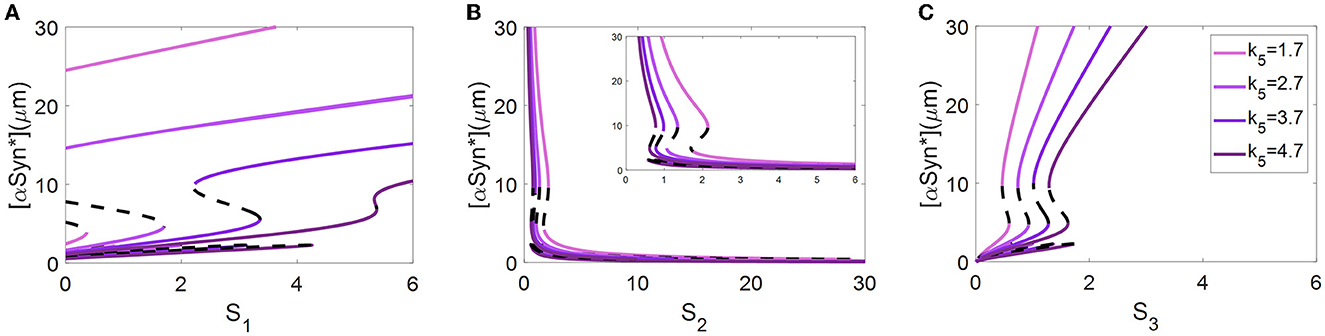
Figure 4. At three different values of k₅, bifurcation diagrams of [αSyn*] for the stress signals S₁ (A), S₂ (B), and S₃ (C), respectively.

The values of k₅, varying from small to large, resulting in shifting of the bifurcation curves for S₁ and S₃ from left to right (see Figures 4A, C) but for S₂ moves in the opposite direction (see Figure 4B). In particular, the increase in the parameter k₅ results in a change from irreversibility to the reversibility of the bistable switch between the middle and the upper stable states for S₁ in Figure 4A, which further benefits the transition from the upper to the middle stable state. Moreover, the increase in the parameter k₅ significantly lowers the upper stable states to reduce the [αSyn^*] levels for S₁ in Figure 4A. For example, an increase in k₅ from 2.7 to 3.7 reduces the [αSyn^*] concentration from 19.27 to 13.27, i.e., a reduction of nearly 31.14%. All of these variations fully support the contention that the aggregation of αSyn^* has the possibility to be modulated by the parameter k₅ via the ALP degradation pathways. This result may offer a plausible explanation of how the switchover states between irreversibility and reversibility are controlled by ALP which is medicated by mTOR.

Regions of tri-stable steady states in codimension-2 bifurcation diagrams

The parameter k₅ impacts on the bifurcation curves as well as the switches between the stable steady states. This fact encourages us to identify more globally all the steady-state regions controlled by k₅ through codimension-2 bifurcation diagrams in the (S_i, k₅) -planes (i = 1, 2, 3 ).

In codimension-2 bifurcation diagrams on the (S₁, k₅)-plane in Figure 5A, four fold bifurcation curves f₁–f₄ (blue) and an Hopf bifurcation curve h (black) near f₃ are obtained by the saddle-node bifurcation points F₄, F₁, F₅, and F₃ and the Hopf bifurcation point HB in Figure 2A, respectively. Furthermore, the fold curve f₁ collides with f₂ at the cusp bifurcation points CP1 and f₃ collides with f₄ at CP2. The fold curves f₁, f₂, and f₄ divide the (S₁, k₅)-plane into tri-stable (T, green), bistable (B, pink), and monostable (M, yellow) regions. Here, the stability seems to be unchanged when passing through the fold curve f₃ from left to right. In fact, the number of stable equilibria is added by one via fold bifurcation on the fold curve f₃ but reduced by one via the Hopf bifurcation on the Hopf curve h.

FIGURE 5

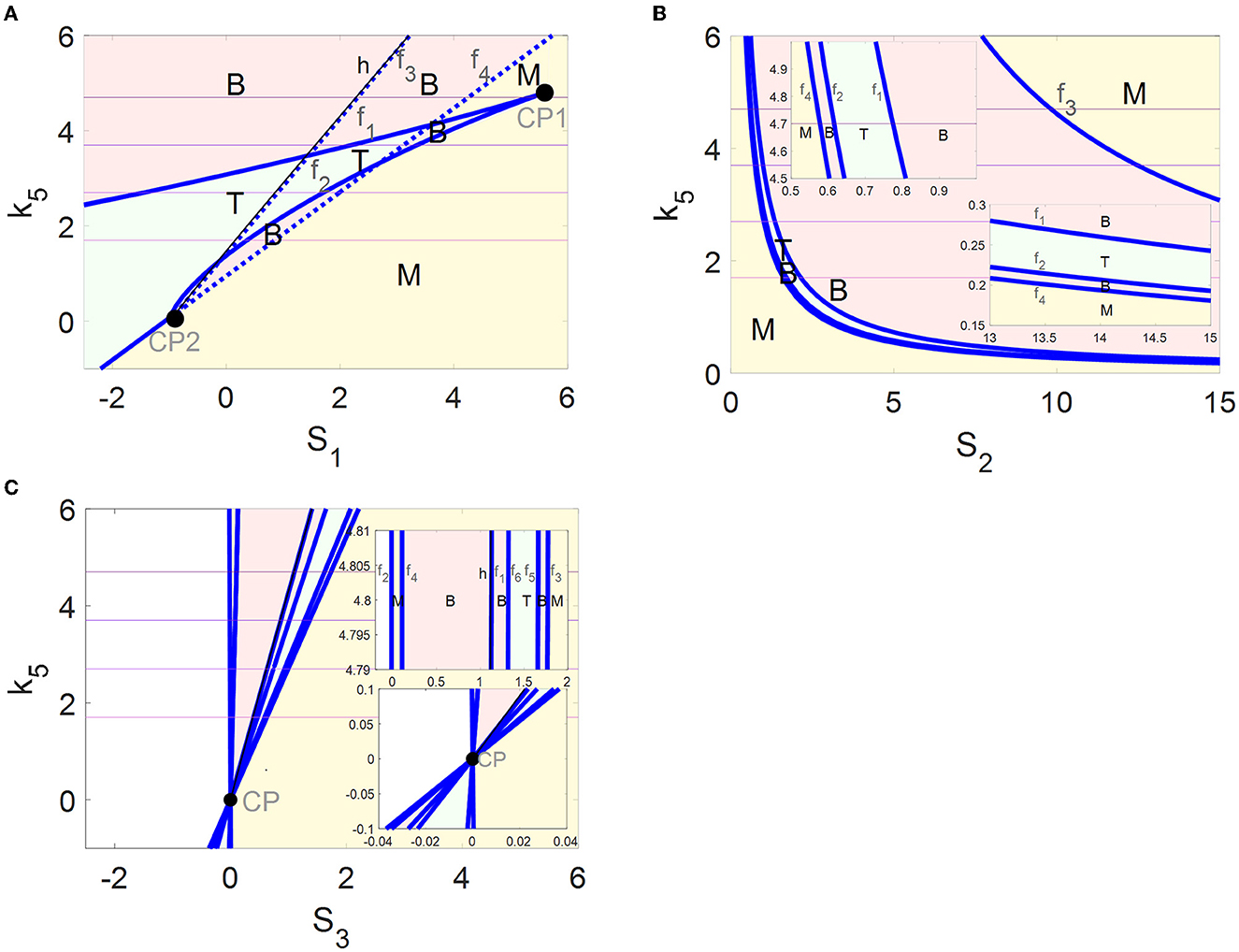
Figure 5. Codimension-2 bifurcation diagrams of αSyn* with respect to S₁ (A), S₂ (B), and S₃ (C), where blue and black curves depict the saddle-node bifurcation points and Hopf bifurcation points, respectively, and T, B, and M denote the tri-stable (green), bistable (pink), and monostable (yellow) states, respectively.

The four fold curves f₁–f₄ in Figure 5B originated from the saddle-node bifurcation points F₁–F₄ (Figure 2B1), where the (S₂, k₅)-plane is divided into regions M, B, T, B, and M from bottom left to top right. In addition, some enlarged views of the upper left and the lower right of the (S₂, k₅)-plane are inserted in Figure 5B.

The saddle-node bifurcation points F₁–F₆ and the Hopf bifurcation point HB in Figure 2C1 form fold bifurcation curves f₁-and the Hopf bifurcation curve h in Figure 5C, respectively. It may be pointed out that all the fold curves intersect at one cusp bifurcation point CP. The (S₃, k₅)-plane is divided by f₂–f₆ into regions M, B, T, B, and M from left to right. Here, the stability is still unchanged when passing through the fold curve f₁ and the Hopf curve h.

The multi-stability in the regions of M, B, and T with the coexistence of steady states are exhibited more comprehensively by the codimension-2 diagrams in Figure 5. In addition, the dynamics of the tri-stable state in region T should be highlighted, where the healthy state may transform the critical state to avoid transiting to the disease state directly and rapidly. Moreover, the regions of the tri-stability for T that exist in the (S₁, k₅)-plane are much larger than those in the (S₂, k₅)- and the (S₃, k₅)-planes. Furthermore, the irreversible switch transits to the reversible one in the tri-stable region T in the (S₁, k₅)-plane with increasing k₅. Thus, more attention is focused on the tri-stable state for the stress S₁ by the ALP degradation pathways regulated by k₅.

Fluctuation of the [αSyn^*] steady-state levels under different initiated conditions

The choice of initial values is also an important factor in the accumulation of αSyn^* as it may lead to the different stable states for tri-stability. From a global perspective, a further survey on the tendency of different initial conditions to affect the steady-state levels of [αSyn^*] for the three stresses S_i (i = 1, 2, 3) and the parameter k₅ was undertaken. Here, the three initial values of [αSyn^*] were still set at 0, 2, and 10 (see rows 1–3 in Figure 6). In Figure 6, the same results in the 3D and 2D contour maps are presented. The former is to illustrate the variation of the [αSyn^*] concentration more completely and the latter is to help better understand the response more intuitively. Surfaces of different stable steady states with color bars were constructed for the stresses S_i (x-axis) and the parameter k₅ (y-axis), and the contour maps are projected onto the planes of (S_i, k₅) (i = 1, 2, 3) in Figures 6A–C, respectively.

FIGURE 6

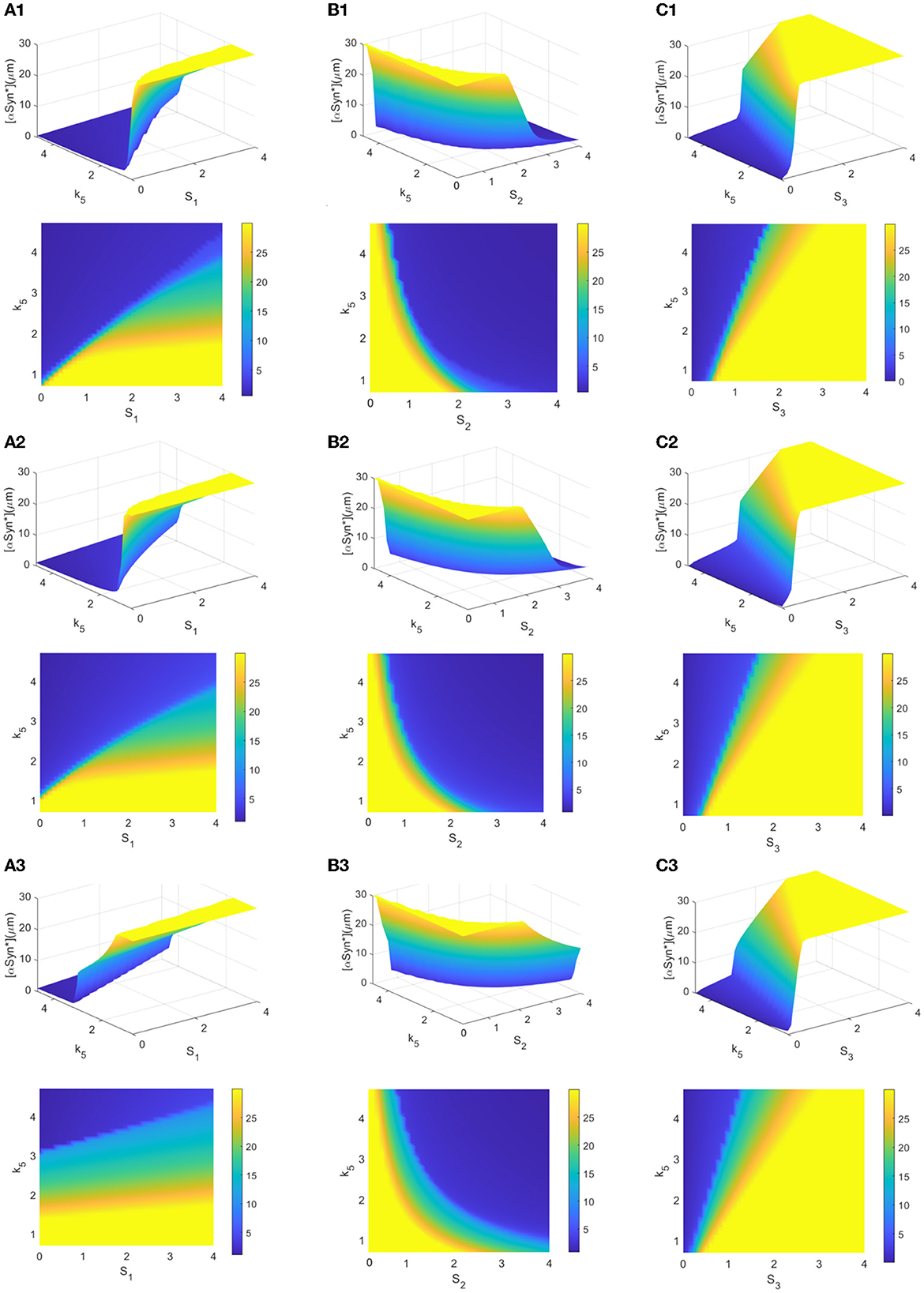
Figure 6. (A–C) 3D plots and their contour maps for the [αSyn*] levels at three steady states (blue, green, and yellow) as a function of the stresses S_i and k₅ at the initial values 0, 2, and 10 of αSyn* (rows), respectively.

The increasing initial value of [αSyn^*] from 0 to 2 to 10 elevates the steady-state levels and so inevitably shrinks the regions of the lower stable steady states (blue). Particularly, the extent of shrinking in the (S₁, k₅)-plane in Figure 6A is much sharper than those in the (S₂, k₅)- and (S₃, k₅)-planes in Figures 6B, C. However, the larger k₅ expands the regions of the lower stable steady-state levels for the three stresses S_i (i = 1, 2, 3) more to possibly reduce the [αSyn^*] levels in Figure 6. Especially so for the larger k₅ and the smaller stresses S₁ and S₃ while the larger stress S₂ expands more the regions of the lower stable steady states. In summary, the parameter k₅ contributes to the regulation of the [αSyn^*] concentration, especially in the case of stress S₁ for the prevention and treatment of PD.

Robustness of tri-stable state to the parameters of mTOR-related regulations

An investigation of the robustness of the tri-stable regions in the (S₁, k₅)-plane to variations in other key parameters was attempted. Here, we consider three important parameters associated with mTOR, i.e., the αSyn^*-dependent rate constant of ERS activation k₆ as well as the basal rates of mTOR activation and inactivation, k₉ and k₁₁. The raw values of the parameters k₆ (see Figure 7A), k₉ (see Figure 7B), and k₁₁ (see Figure 7C) were increased or decreased in the codimension-2 bifurcation diagrams in the (S₁, k₅)-plane in Figure 5A.

FIGURE 7

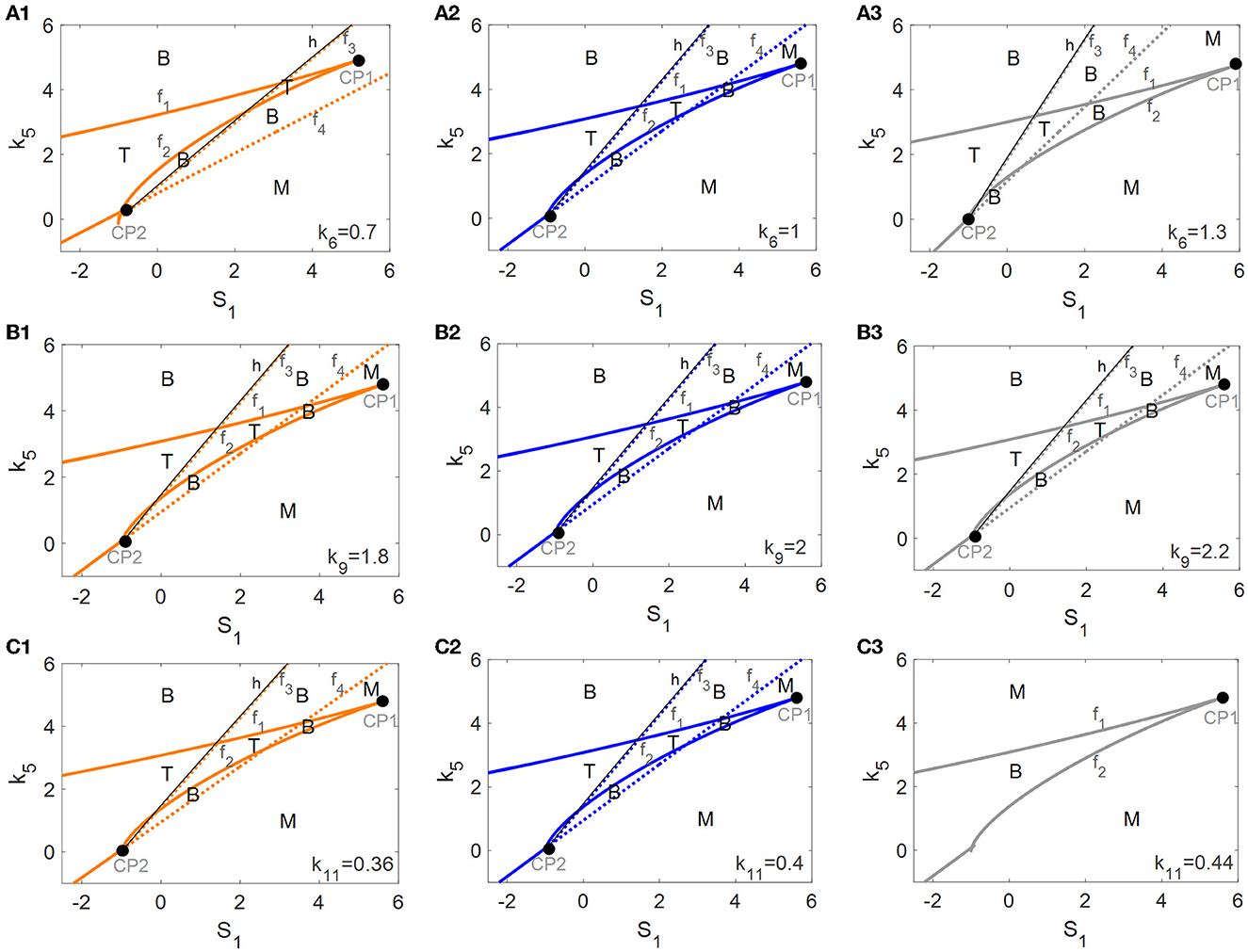
Figure 7. Codimension-2 bifurcation diagrams of S₁ and k₅ for the parameters k₆ (A), k₉ (B), and k₁₁ (C), where the left, middle, and right columns represent the smaller, the raw, and the larger values for k_i (i = 6, 9, 11).

With the increase of k₆ from left to right in Figure 7A, the fold bifurcation curves f₁ and f₂ changes little while the fold bifurcation curves f₃ and f₄ shifted to the left. Thus, the tri-stable region T between f₁ and f₂ shrinks while the bistable region B between f₁ and f₂ expands a little. However, k₉ hardly changed any of the bifurcation curves as well as any of the steady-state regions as illustrated in Figure 7B, implying that the dynamic behavior is robust to perturbation of the parameter k₉. Unexpectedly, with the increase of k₁₁, there are only twofold curves f₁ and f₂ dividing the (S₁, k₅)-plane into monostable and bistable regions, so the tri-stable state is transformed to the bistable state which in turn reverts to the monostable state as shown in Figure 7C.

In summary, the dynamic behavior of the tri-stable state in the (S₁, k₅)-plane changed the most under perturbation of parameter k₁₁. This result implies that the mTOR-mediated ALP is crucial to maintaining the essential dynamic feature of the tri-stable state for this biological system.

Discussion

It is widely considered that the aggregation of αSyn^* is closely related to the pathogenesis of PD; however, the underlying mechanism is still not fully understood. Indeed, it should be pointed out that the progression of many complex diseases may be divided into three states, i.e., normal state, pre-disease (or tipping point), and disease states (Liu et al., 2017; Liu R. et al., 2019; Liu X. et al., 2019). Especially in neurodegenerative disease (Liu X. et al., 2019; McClellan and King, 2021; Qi et al., 2021), it is quite possible that a critical state may serve as an early-warning signal prior to the rapid switch between healthy and disease states. Therefore, identifying the critical state is crucial and represents a challenge to prevent qualitative deterioration in PD. In this study, we have proposed a mathematical model whereby ALP regulated by mTOR is considered the major protein clearance pathway for degrading the aggregated αSyn^*; moreover, we have also surveyed the tri-stability dynamics for the three states of PD.

A large amount of aggregated αSyn^* which may trigger the spontaneous development of PD may be influenced by multifaceted factors associated with S₁, S₂, and S₃ at the same time, such as exposure to an environmental toxin (external oxidative stress from toxins to increase S₁), advanced age (reduction in the age-related anti-oxidative mechanism of S₂), and a genetic defect (αSyn overexpression or increase in S₃) (Cloutier and Wellstead, 2012). In this research, the key molecules Beclin1 and mTOR in ALP to degrade αSyn^* under three different stresses have been highlighted and studied.

The dynamics of tri-stability for the different stress signals S_i (i = 1, 2, 3) are captured by codimension-1 bifurcation analysis, in which the lower, middle, and upper stable steady states correspond to the healthy, critical, and disease states in the progression of PD, respectively. Although a small step toward the identification of the intermedium state in PD is taken, the challenges in describing and characterizing faithfully the biological system are expected to be improved in further biodynamic modeling of PD.

It has been established that the bistable switches are irreversible for stress S₁ but reversible for stresses S₂ and S₃. The irreversibility of stress S₁ may ensure that a high concentration of [αSyn^*] is maintained. From a biological perspective, mitochondria dysfunction plays a crucial role in PD etiopathogenesis, given that it is an important source of S₁ and leads to significantly higher ROS in cells to indirectly accelerate the formation of αSyn^* (Cali et al., 2011; Scialo et al., 2017). Moreover, it has been found that the ALP-dependent rate constant of αSyn^* degradation, k₅, changes the bistable switch from irreversible to reversible for S₁ and increasing k₅ greatly alters the higher stable states of the αSyn^* levels for S₁. It has been confirmed that the ALP degradation pathways offer the possibility to control the aggregation of αSyn^* to protect dopaminergic neuron cells from death. More globally, in uncovering all the steady-state regions in the codimension-2 bifurcation diagrams, it was discovered that the regions of tri-stability in the (S₁, k₅)-plane are much larger than those in the (S₂, k₅) and (S₃, k₅)-planes.

Furthermore, it was revealed that mTOR-mediated ALP plays an important role in regulating the degradation of αSyn^* based on the robustness of the tri-stable regions in the (S₁, k₅)-plane with respect to the three important parameters associated with mTOR. Unexpectedly, the tri-stable dynamic behavior vanished under the disturbance of the k₁₁ parameter, implying that mTOR-mediated ALP is important to maintaining the essential dynamic features of tri-stability for biological systems. In addition, it is well-known that the function of mTOR signaling is of great importance in restoring neuron death induced by toxins, such as the huge accumulation of αSyn^* in PD (Ebrahimi-Fakhari et al., 2014; Lan et al., 2017).

In conclusion, the clearance mechanism of ALP plays an important role in tri-stability in our model where mTOR-mediated ALP degrades αSyn^*. The model links experimental and theoretical biology to realize a more comprehensive understanding of the precise regulatory mechanisms of the degradation of αSyn^* by ALP and mediated by mTOR. In future, the essential properties of tri-stability may be applied to experiments and studies of PD, and relevant molecular aspects should be considered for biomathematical modeling and dynamic analysis of PD.

The intermediate state as a barrier prevents the system from switching from the lower to the upper steady state directly. Thus, the critical state (the intermediate state) in tri-stability is an alert warning for avoiding more aggregation of αSyn^* and causing PD, thus treatment for the critical state in neuron cells will be vital for modeling PD dynamic networks. Our study may provide a promising avenue for further experiments and simulations of the degradation mechanisms for dynamic modeling in PD. This research may ultimately lead to novel therapeutic approaches for the treatment of PD.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BY was responsible for manuscript development, model concept, and writing the manuscript. ZY supervised the study design and manuscript development. LH collaborated on manuscript development and concept. All authors have read and approved the final manuscript.

Funding

This study is supported by the National Natural Science Foundation of China under Grant Nos. 11872084, 11932003, and 11902221.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bekker, M., Abrahams, S., Loos, B., and Bardien, S. (2021). Can the interplay between autophagy and apoptosis be targeted as a novel therapy for Parkinson's disease? Neurobiol. Aging. 100, 91–105. doi: 10.1016/j.neurobiolaging.2020.12.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Blesa, J., Trigo-Damas, I., Quiroga-Varela, A., and Jackson-Lewis, V. R. (2015). Oxidative stress and Parkinson's disease. Front. Neuroanat. 9, 91. doi: 10.3389/fnana.2015.00091

PubMed Abstract | CrossRef Full Text | Google Scholar

Booth, L. A., Tavallai, S., Hamed, H. A., Cruickshanks, N., and Dent, P. (2014). The role of cell signalling in the crosstalk between autophagy and apoptosis. Cell Signal. 26, 549–555. doi: 10.1016/j.cellsig.2013.11.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Bove, J., Martinez-Vicente, M., and Vila, M. (2011). Fighting neurodegeneration with rapamycin: mechanistic insights. Nat. Rev. Neurosci. 12, 437–452. doi: 10.1038/nrn3068

PubMed Abstract | CrossRef Full Text | Google Scholar

Bridi, J. C., and Hirth, F. (2018). Mechanisms of alpha-synuclein induced synaptopathy in Parkinson's disease. Front. Neurosci. 12, 80. doi: 10.3389/fnins.2018.00080

PubMed Abstract | CrossRef Full Text | Google Scholar

Cali, T., Ottolini, D., and Brini, M. (2011). Mitochondria, calcium, and endoplasmic reticulum stress in Parkinson's disease. Biofactors 37, 228–240. doi: 10.1002/biof.159

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, I., Zhang, Y., Seegobin, S. P., Pruvost, M., Wang, Q., and Purtell, K., et al. (2020). Microglia clear neuron-released alpha-synuclein via selective autophagy and prevent neurodegeneration. Nat. Commun. 11, 1386. doi: 10.1038/s41467-020-15119-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung, Y., Lee, J., Jung, S., Lee, Y., Cho, J. W., and Oh, Y. J. (2018). Dysregulated autophagy contributes to caspase-dependent neuronal apoptosis. Cell Death Dis. 9, 1189. doi: 10.1038/s41419-018-1229-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Cloutier, M., Middleton, R., and Wellstead, P. (2012). Feedback motif for the pathogenesis of Parkinson's disease. IET Syst. Biol. 6, 86–93. doi: 10.1049/iet-syb.2011.0076

PubMed Abstract | CrossRef Full Text | Google Scholar

Cloutier, M., and Wellstead, P. (2012). Dynamic modelling of protein and oxidative metabolisms simulates the pathogenesis of Parkinson's disease. IET Syst. Biol. 6, 65–72. doi: 10.1049/iet-syb.2011.0075

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooper, K. F. (2018). Till death do us part: the marriage of autophagy and apoptosis. Oxid. Med. Cell. Longevity 2018, 4701275. doi: 10.1155/2018/4701275

PubMed Abstract | CrossRef Full Text | Google Scholar

Cybulsky, A. V. (2017). Endoplasmic reticulum stress, the unfolded protein response and autophagy in kidney diseases. Nat. Rev. Nephrol. 13, 681–696. doi: 10.1038/nrneph.2017.129

PubMed Abstract | CrossRef Full Text | Google Scholar

Djavaheri-Mergny, M., Maiuri, M. C., and Kroemer, G. (2010). Cross talk between apoptosis and autophagy by caspase-mediated cleavage of Beclin1. Oncogene 29, 1717–1719. doi: 10.1038/onc.2009.519

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebrahimi-Fakhari, D., Wahlster, L., Hoffmann, G. F., and Kolker, S. (2014). Emerging role of autophagy in pediatric neurodegenerative and neurometabolic diseases. Pediatr. Res. 75, 217–226. doi: 10.1038/pr.2013.185

PubMed Abstract | CrossRef Full Text | Google Scholar

Ermentrout, B. (2003). Simulating, analyzing, and animating dynamical systems: a guide to XPPAUT for researchers and students. SIAM 56, B53 doi: 10.1115/1.1579454

CrossRef Full Text | Google Scholar

Erustes, A. G., Stefani, F. Y., Terashima, J. Y., Stilhano, R. S., Monteforte, P. T., and Pereira, G. J. D., et al. (2018). Overexpression of alpha-synuclein in an astrocyte cell line promotes autophagy inhibition and apoptosis. J. Neurosci. Res. 96, 160–171. doi: 10.1002/jnr.24092

PubMed Abstract | CrossRef Full Text | Google Scholar

Fussi, N., Hollerhage, M., Chakroun, T., Nykanen, N. P., Rosler, T. W., and Koeglsperger, T., et al. (2018). Exosomal secretion of alpha-synuclein as protective mechanism after upstream blockage of macroautophagy. Cell Death Dis. 9, 757. doi: 10.1038/s41419-018-0816-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Gallegos, S., Pacheco, C., Peters, C., Opazo, C. M., and Aguayo, L. G. (2015). Features of alpha-synuclein that could explain the progression and irreversibility of Parkinson's disease. Front. Neurosci. 9, 59. doi: 10.3389/fnins.2015.00059

PubMed Abstract | CrossRef Full Text | Google Scholar

Goedert, M., Spillantini, M. G., Del Tredici, K., and Braak, H. (2013). 100 years of Lewy pathology. Nat. Rev. Neurol. 9, 13–24. doi: 10.1038/nrneurol.2012.242

PubMed Abstract | CrossRef Full Text | Google Scholar

Gomez-Suaga, P., Bravo-San Pedro, J. M., Gonzalez-Polo, R. A., Fuentes, J. M., and Niso-Santano, M. (2018). ER-mitochondria signaling in Parkinson's disease. Cell Death Dis. 9, 337. doi: 10.1038/s41419-017-0079-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, H., and Rubinsztein, D. C. (2011). Control of autophagy as a therapy for neurodegenerative disease. Nat. Rev. Neurol. 8, 108–117. doi: 10.1038/nrneurol.2011.200

PubMed Abstract | CrossRef Full Text | Google Scholar

Heath-Engel, H. M., Chang, N. C., and Shore, G. C. (2008). The endoplasmic reticulum in apoptosis and autophagy: role of the BCL-2 protein family. Oncogene 27, 6419–6433. doi: 10.1038/onc.2008.309

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, T. F., Zhang, Y. J., Zhou, H. Y., Wang, H. M., Tian, L. P., and Liu, J., et al. (2013). Curcumin ameliorates the neurodegenerative pathology in A53T alpha-synuclein cell model of Parkinson's disease through the downregulation of mTOR/p70S6K signaling and the recovery of macroautophagy. J. Neuroimmune Pharm. 8, 356–369. doi: 10.1007/s11481-012-9431-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Jung, C. H., Ro, S. H., Cao, J., Otto, N. M., and Kim, D. H. (2010). mTOR regulation of autophagy. FEBS Lett. 584, 1287–1295. doi: 10.1016/j.febslet.2010.01.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Kapuy, O., Vinod, P. K., and Banhegyi, G. (2014). mTOR inhibition increases cell viability via autophagy induction during endoplasmic reticulum stress: an experimental and modeling study. FEBS Open Biol. 4, 704–713. doi: 10.1016/j.fob.2014.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, I., Xu, W., and Reed, J. C. (2008). Cell death and endoplasmic reticulum stress: disease relevance and therapeutic opportunities. Nat. Rev. Drug Discov. 7, 1013–1030. doi: 10.1038/nrd2755

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolodkin, A. N., Sharma, R. P., Colangelo, A. M., Ignatenko, A., Martorana, F., Jennen, D., et al. (2020). ROS networks: designs, aging, Parkinson's disease and precision therapies. NPJ Syst. Biol. Appl. 6, 34. doi: 10.1038/s41540-020-00150-w

PubMed Abstract | CrossRef Full Text

Komatsu, M., Ueno, T., Waguri, S., Uchiyama, Y., Kominami, E., and Tanaka, K. (2007). Constitutive autophagy: vital role in clearance of unfavorable proteins in neurons. Cell Death Differ. 14, 887–894. doi: 10.1038/sj.cdd.4402120

PubMed Abstract | CrossRef Full Text | Google Scholar

Kondratskyi, A., Yassine, M., Kondratska, K., Skryma, R., Slomianny, C., and Prevarskaya, N. (2013). Calcium-permeable ion channels in control of autophagy and cancer. Front. Physiol. 4, 272. doi: 10.3389/fphys.2013.00272

PubMed Abstract | CrossRef Full Text | Google Scholar

Lan, A. P., Chen, J., Zhao, Y., Chai, Z., and Hu, Y. (2017). mTOR signaling in Parkinson's disease. Neuromol. Med. 19, 1–10. doi: 10.1007/s12017-016-8417-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Wang, P., Yu, J., and Zhang, L. (2011). Cleaving Beclin1 to suppress autophagy in chemotherapy-induced apoptosis. Autophagy 7, 1239–1241. doi: 10.4161/auto.7.10.16490

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, C., Yan, D. Y., Tan, X., Ma, Z., Wang, C., and Deng, Y. (2018). Effect of the cross-talk between autophagy and endoplasmic reticulum stress on Mn-induced alpha-synuclein oligomerization. Environ. Toxicol. 33, 315–324. doi: 10.1002/tox.22518

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, R., Zhong, J., Yu, X., Li, Y., and Chen, P. (2019). Identifying critical state of complex diseases by single-sample-based hidden Markov model. Front. Genet. 10, 285. doi: 10.3389/fgene.2019.00285

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X., Chang, X., Leng, S., Tang, H., Aihara, K., and Chen, L. (2019). Detection for disease tipping points by landscape dynamic network biomarkers. Natl. Sci. Rev. 6, 775–785. doi: 10.1093/nsr/nwy162

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X., Chang, X., Liu, R., Yu, X., Chen, L., and Aihara, K. (2017). Quantifying critical states of complex diseases using single-sample dynamic network biomarkers. PLoS Comput. Biol. 13, e1005633. doi: 10.1371/journal.pcbi.1005633

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Z. Y., Cheng, M. H., Yu, C. Y., Lin, Y. S., Yeh, T. M., and Chen, C. L. (2020). Dengue non-structural protein 1 maintains autophagy through retarding caspase-mediated cleavage of Beclin-1. Int. J. Mol. Sci. 21, 24. doi: 10.3390/ijms21249702

PubMed Abstract | CrossRef Full Text | Google Scholar

Malik, B. R., Maddison, D. C., Smith, G. A., and Peters, O. M. (2019). Autophagic and endo-lysosomal dysfunction in neurodegenerative disease. Mol. Brain 12, 100. doi: 10.1186/s13041-019-0504-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Maries, E., Dass, B., Collier, T. J., Kordower, J. H., and Steece-Collier, K. (2003). The role of alpha-synuclein in Parkinson's disease: insights from animal models. Nat. Rev. Neurosci. 4, 727–738. doi: 10.1038/nrn1199

PubMed Abstract | CrossRef Full Text | Google Scholar

McClellan, J. M., and King, M. C. (2021). A tipping point in neuropsychiatric genetics. Neuron 109, 1411–1413. doi: 10.1016/j.neuron.2021.04.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, H., Li, Z. C., Wang, S. M., Wu, L., Xu, F., Liu, Z. L., et al. (2021). Tristability in mitochondrial permeability transition pore opening. Chaos 31, 123108. doi: 10.1063/5.0065400

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, H., Zhai, W., Lu, X., and Wang, G. (2021). The cross-links of endoplasmic reticulum stress, autophagy, and neurodegeneration in Parkinson's disease. Front. Aging Neurosci. 13, 691881. doi: 10.3389/fnagi.2021.691881

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruiperez, V., Darios, F., and Davletov, B. (2010). Alpha-synuclein, lipids and Parkinson's disease. Prog. Lipid Res. 49, 420–428. doi: 10.1016/j.plipres.2010.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarkar, S., Ravikumar, B., Floto, R. A., and Rubinsztein, D. C. (2009). Rapamycin and mTOR-independent autophagy inducers ameliorate toxicity of polyglutamine-expanded huntingtin and related proteinopathies. Cell Death Differ. 16, 46–56. doi: 10.1038/cdd.2008.110

PubMed Abstract | CrossRef Full Text | Google Scholar

Schapira, A. H., and Jenner, P. (2011). Etiology and pathogenesis of Parkinson's disease. Mov. Disord. 26, 1049–1055. doi: 10.1002/mds.23732

PubMed Abstract | CrossRef Full Text | Google Scholar

Scialo, F., Fernandez-Ayala, D. J., and Sanz, A. (2017). Role of mitochondrial reverse electron transport in ROS signaling: potential roles in health and disease. Front. Physiol. 8, 428. doi: 10.3389/fphys.2017.00428

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, Y. F., Tang, Y., Zhang, X. J., Huang, K. X., and Le, W. D. (2013). Adaptive changes in autophagy after UPS impairment in Parkinson's disease. Acta Pharmacol. Sin. 34, 667–673. doi: 10.1038/aps.2012.203

PubMed Abstract | CrossRef Full Text | Google Scholar

Siddiqui, W. A., Ahad, A., and Ahsan, H. (2015). The mystery of BCL2 family: BCL-2 proteins and apoptosis: an update. Arch. Toxicol. 89, 289–317. doi: 10.1007/s00204-014-1448-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Sotthibundhu, A., Promjuntuek, W., Liu, M., Shen, S., and Noisa, P. (2018). Roles of autophagy in controlling stem cell identity: a perspective of self-renewal and differentiation. Cell Tissue Res. 374, 205–216. doi: 10.1007/s00441-018-2829-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Spencer, B., Potkar, R., Trejo, M., Rockenstein, E., Patrick, C., and Gindi, R. (2009). Beclin1 gene transfer activates autophagy and ameliorates the neurodegenerative pathology in alpha-synuclein models of Parkinson's and Lewy body diseases. J. Neurosci. 29, 13578–13588. doi: 10.1523/JNEUROSCI.4390-09.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Tavassoly, I., Parmar, J., Shajahan-Haq, A. N., Clarke, R., Baumann, W. T., and Tyson, J. J. (2015). Dynamic modeling of the interaction between autophagy and apoptosis in mammalian cells. CPT Pharmacomet. Syst. Pharmacol. 4, 263–272. doi: 10.1002/psp4.29

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, N. J., and Tumbarello, D. A. (2022). The relationship of alpha-synuclein to mitochondrial dynamics and quality control. Front. Mol. Neurosci. 15, 947191. doi: 10.3389/fnmol.2022.947191

PubMed Abstract | CrossRef Full Text | Google Scholar

Vilchez, D., Saez, I., and Dillin, A. (2014). The role of protein clearance mechanisms in organismal ageing and age-related diseases. Nat. Commun. 5, 5659. doi: 10.1038/ncomms6659

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, H., Che, X., Zheng, Q., Wu, A., Pan, K., and Shao, A., et al. (2014). Caspases: a molecular switch node in the crosstalk between autophagy and apoptosis. Int. J. Biol. Sci. 10, 1072–1083. doi: 10.7150/ijbs.9719

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Y., Liu, C., Chen, S., Ye, Y., Guo, M., and Ren, Q. (2014). Activation of AMPK and inactivation of Akt result in suppression of mTOR-mediated S6K1 and 4E-BP1 pathways leading to neuronal cell death in vitro models of Parkinson's disease. Cell Signal. 26, 1680–1689. doi: 10.1016/j.cellsig.2014.04.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, G. X., Pan, H., Ouyang, D. Y., and He, X. H. (2015). The critical molecular interconnections in regulating apoptosis and autophagy. Ann. Med. 47, 305–315. doi: 10.3109/07853890.2015.1040831

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Z., Yang, C., Iyaswamy, A., Krishnamoorthi, S., Sreenivasmurthy, S. G., and Liu, J. (2019). Balancing mTOR signaling and autophagy in the treatment of Parkinson's disease. Int. J. Mol. Sci. 20, 728. doi: 10.3390/ijms20030728

PubMed Abstract | CrossRef Full Text | Google Scholar