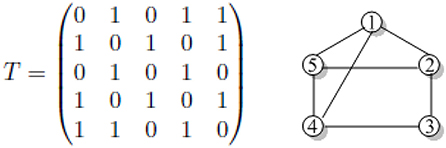Computing the partition dimension of certain families of Toeplitz graph

Let G = (V(G), E(G)) be a graph with no loops, numerous edges, and only one component, which is made up of the vertex set V(G) and the edge set E(G). The distance d(u, v) between two vertices u, v that belong to the vertex set of H is the shortest path between them. A k-ordered partition of vertices is defined as β = {β₁, β₂, …, β_k}. If all distances d(v, β_k) are finite for all vertices v ∈ V, then the k-tuple (d(v, β₁), d(v, β₂), …, d(v, β_k)) represents vertex v in terms of β, and is represented by r(v|β). If every vertex has a different presentation, the k-partition β is a resolving partition. The partition dimension of G, indicated by pd(G), is the minimal k for which there is a resolving k-partition of V(G). The partition dimension of Toeplitz graphs formed by two and three generators is constant, as shown in the following paper. The resolving set allows obtaining a unique representation for computer structures. In particular, they are used in pharmaceutical research for discovering patterns common to a variety of drugs. The above definitions are based on the hypothesis of chemical graph theory and it is a customary depiction of chemical compounds in form of graph structures, where the node and edge represent the atom and bond types, respectively.

1. Introduction

Mathematics plays a key role in social science such as computer science, physics, and chemistry. If L = {l₁, l₂, …, l_k} is a graph's ordered set of vertices and v ∈ G, then the k-tuple r(v|L) = (r(v, l₁), r(v, l₂), …, r(v, l_k)). The notation r is the representation of v with regard to L, and the symbol L is said to be a resolving set if the different vertices of G have different representations regard to L. H's metric dimension, indicated by dim(H), is the minimal number of vertices in the resolving set. The task of computing a graph's locating set is a Non-deterministic Polynomial time problem or NP-hard (Lewis et al., 1983). These ideas have been mentioned in the literature (Chvatal, 1983; Slater, 1988; Khuller et al., 1996; Chartrand et al., 2000a, 2003; Buczkowski et al., 2003; Caceres et al., 2007).

Another form of dimension is partition dimension, which is similar to the metric dimension (Chartrand et al., 2000b) as follows: The k-ordered partition is designed as β = {β₁, …, β_k} and r(v|β) = {d(v, β₁), d(v, β₂), …, d(v, β_k)} are named as k-tuple representations. If each v in V(G) has a unique representation with regard to β, then the resolving partition of the vertex set is termed β, and the least value of the resolving partition set of V(G) is called the partition dimension of G and is indicated as pd(G) (Chartrand et al., 2000b). The metric dimension problem's computational complexity and NP-hardness were studied in Lewis et al. (1983). Because computing the pd is a more advanced variant of computing the metric dimension, it is likewise an NP-complete task. For simple graphs, there is a well-known inequality between dim, and pd (Chartrand et al., 2000b).

$\begin{array}{ll}pd(G)\le dim(G)+1.& (1)\end{array}$

A n × n matrix A = a_xy is a Toeplitz matrix if a_xy = a_x+1,y+1 for each x, y = 1, 2, ..., n − 1. A loopless and having no multi-edges graph termed as T_n is Toeplitz graph if the matrix is the symmetric Toeplitz matrix. The Topelitz graph T_n〈t₁, t₂, t₃, …, t_p〉, where 0 < t₁ < t₂ < …t_p < n with V(H) = {1, 2, 3, …, n} has E(H) = {(x, y), 1 ≤ x ≤ y ≤ n}, iff y − 1 = t_q for some q, 1 ≤ q ≤ p (Liu et al., 2019). Let n = 5, k = 2, t₁ = 1, t₂ = 3, and t₃ = 4. Figure 1 highlight the adjacency matrix T and its corresponding Toeplitz graphs T₅〈1, 3, 4〉.

FIGURE 1

Figure 1. The corresponding Toeplitz graph and the adjacency matrix T T₅〈1, 3, 4〉.

Toeplitz matrices play a major role in physical data-processing and in determining the discrete form of an integral and differential equations are considered as applications. Furthermore, matrices also contributed in process of stationary, the theories of polynomials of orthogonals and moment problem (Heinig and Rost, 1984) for more details reader can see (Ku and Kuo, 1992; Hua et al., 2010).

The researchers in Harary and Melter (1976) founded the concept of resolvability in graphs. Chartrand et al. (2000b) first time introduced the concept of pd. Javaid and Shokat (2008) discussed the pd of wheel graphs. Yero and Velázquez (2010) computed the pd of the cartesian product of graphs. Fehr et al. (2006) disproved a conjecture regarding the pd of products of graphs. The upper bound for the pd of the parallel composition of any graph was studied by Mohan et al. (2019). They also came up with an exact solution for the parallel composition of pathways of various lengths. Some updated references are (Ahmad et al., 2021; Ali et al., 2021; Azeem et al., 2021, 2022; Shanmukha et al., 2022a,b,c; Usha et al., 2022).

Resolvability of the graph has application in many fields of science such as in chemistry for representing chemical compounds (Browsable, 1998), Djokovic-Winkler relation (Caceres et al., 2007), strategies for the mastermind game (Chvatal, 1983), pattern recognition and image processing, hierarchical data structures (Melter and Tomescu, 1984), and robots navigation in networks (Khuller et al., 1994). For a better understanding of this topic, some very detailed articles are (Chartrand et al., 2000b; Saenpholphat and Zhang, 2002; Javaid et al., 2012; Velazquez et al., 2012; Velázquez et al., 2014; Yero et al., 2014; Siddiqui and Imran, 2015; Alatawi et al., 2022; Alshehri et al., 2022; Khabyah et al., 2022; Koam et al., 2022,a,b; Nadeem et al., 2022).

The theorems that follow are quite useful for calculating the pd of graphs.

Theorem 1 (Chartrand et al., 2000b). “Let G be a connected graph of order n ≥ 2. Then pd(G) = 2 if and only if G = P_n”.

Theorem 2 Chartrand et al. (2000b) “Let ϕ be a resolving partition of ε(⋎) and ϵ₁, ϵ₂ ∈ ε(⋎). If d(ϵ₁, w) = d(ϵ₂, w) for all vertices w ∈ ε(⋎)\(ϵ₁, ϵ₂), then ϵ₁, ϵ₂ belong to different classes of ϕ.”

This study's findings the pd of Toeplitz graph with two generators 1 and t in Section 2 and Toeplitz graph partition dimension with three generators 1, 2, and t in Section 3.

2. Partition dimension of T_n〈1, t〉

The coming section is containing the discussion on the pd of the Toeplitz graph T_n〈1, t〉, for t ≥ 2 the pd of the graph is three.

Theorem 2.1. A Toeplitz graph with n ≥ 4 is T_n〈1, 2〉. After that, pd(T_n〈1, 2〉) = 3.

Proof. Let the Toeplitz graph with n ≥ 4 is T_n〈1, 2〉 Then we will show that the Toeplitz graph with generators 1 and 2 consist a resolving partition set, β = {β₁, β₂, β₃} with three elements, where β₁ = {v₁}, β₂ = {_{vk}k≡0(mod 2)}, β₃ = {_{vk}k≡1(mod 2)}. Let β = {β₁, β₂, β₃} resolve the vertices of graph G with V(G) = β₁ ∪ β₂ ∪ β₃.

When k = 1, 2, …, n. In terms of resolving partition set β, we have the following representations of v_k.

$r(v_k|\beta )=\left(\lfloor \frac{k}{2}\rfloor ,\frac{{(-1)}^{k+1}+1}{2},\{\begin{array}{ll}1\hfill & k=1\hfill \\ \frac{{(-1)}^k+1}{2}\hfill & k\ge 2\hfill \end{array}\right)$

Because all of the representations of different vertices are distinct

$\begin{array}{ll}pd(T_n\text{〈}1,2\text{〉})\le 3.\hfill & (2)\end{array}$

Conversely: Now, we will show that pd(T_n〈1, 2〉) ≥ 3. Suppose on contrary that pd(T_n〈1, 2〉) = 2. We know that pd(G) = 2, iff G is a path graph by Theorem 1, it is not possible for T_n〈1, 2〉. Thus,

$\begin{array}{ll}pd(T_n\text{〈}1,2\text{〉})\ge 3.& (3)\end{array}$

Hence, from Inequalities (2) and (3), we have

$\begin{array}{l}pd(T_n\text{〈}1,2\text{〉})=3.\end{array}$

Theorem 2.2. Let a Toeplitz graph T_n〈1, 3〉 with n ≥ 5. Then pd(T_n〈1, 3〉) = 3.

Proof. Let a Toeplitz graph T_n〈1, 3〉 with n ≥ 5. We will show that the Toeplitz graph with generators 〈1, 3〉 consist of a resolving partition set, β = {β₁, β₂, β₃} with three elements, where β₁ = {v₁}, β₂ = {v₂, …, v_t}, β₃ = {v_t+1, …, v_n}. There are two cases for β:

Case 1: If 1 ≤ k ≤ 3, then we can write the representation of v_k with respect to β as

$r(v_k|\beta )=(k-1,q,1)$

where $q=\lfloor \frac{1}{k}\rfloor ,$ this shows that all the representations are different so β resolves the vertex set of graph T_n〈1, 3〉.

Case 2: If 4 ≤ k ≤ n, then we can write the representation of v_k with respect to β a

$\begin{array}{l}r(v_k|\beta )=(q+j,q,0)\end{array}$

where $q=\lceil \frac{k-3}{3}\rceil$ and k − 1 ≡ j(mod 3), this shows that all the representations are different, thus,

$\begin{array}{ll}pd(T_n\text{〈}1,3\text{〉})\le 3.& (4)\end{array}$

Conversely: We will prove that pd(T_n〈1, 3〉) ≥ 3. On contrary suppose that pd(T_n〈1, 3〉) = 2. Theorem 1 demonstrates that pd(G) = 2, iff G is a path graph, then it is not possible for T_n〈1, 3〉. Thus,

$\begin{array}{ll}pd(T_n\text{〈}1,3\text{〉})\ge 3.& (5)\end{array}$

Hence, from Inequalities (4) and (5), we have

$\begin{array}{l}pd(T_n\text{〈}1,3\text{〉})=3.\end{array}$

Theorem 2.3. Let a Toeplitz graph with notation T_n〈1, t〉 with even generator t ≥ 4, n ≥ t+2. Then pd(T_n〈1, t〉) = 3.

Proof. Let a Toeplitz graph with notation T_n〈1, t〉 with even generator t ≥ 4, n ≥ t+2. The Toeplitz graph with generators 〈1, t〉 consisting of a resolving partition set will be demonstrated. β = {β₁, β₂, β₃}, where β₁ = {v₁}, ${\beta }_2=\left\{v_{\frac{t+2}{2}}\right\},$ β₃ = {∀v_k|v_k ∉ β₁, β₂}. There are three cases with respect to v_k, which are the following;

Case 1: When $k\equiv 2,3,\dots ,\frac{t}{2}(modt).$ We have the following representation of v_k with regard to resolving partition set β;

$\begin{array}{l}r(v_k|\beta )=\left(k-\rho t+\rho -1,\frac{(2\rho +1)t+2(\rho -k+1)}{2},0\right)\end{array}$

where $\rho =\lfloor \frac{k}{t}\rfloor .$

Case 2: When $k\equiv \frac{t+2}{2}(modt).$ We have the following representation of v_k with respect to resolving partition set β;

$\begin{array}{l}r(v_k|\beta )=\left(k-\rho t+\rho -1,\frac{2(\rho +k-1)-(2\rho +1)t}{2},z\right)\end{array}$

where $\rho =\lfloor \frac{k}{t}\rfloor ,$ z = 1 when $k=\frac{t+2}{2}$ and otherwise z = 0.

Case 3: When $k\equiv 0,1,\frac{t+4}{2},\frac{t+6}{2},\dots ,t-1(modt).$ We have the following representation of v_k with respect to resolving partition set β;

$\begin{array}{l}r(v_k|\beta )=\left(\rho t-k+\rho +1,\frac{2(\rho +k-2)-(2\rho -1)t}{2},z\right)\end{array}$

where $\rho =\lfloor \frac{2k+t}{2t}\rfloor ,$ z = 1 when k = 1 and otherwise z = 0.

It is clear that no two vertices have the same representation, implying that there are not any two vertices with the same representation.

$\begin{array}{ll}pd(T_n\text{〈}1,t\text{〉})\le 3.& (6)\end{array}$

On contrary, we shall now demonstrate that pd(T_n〈1, t〉) ≥ 3. Suppose on the contrary that pd(T_n〈1, t〉) = 2. We know that by Theorem 1, it is not possible for even t of graph T_n〈1, t〉. Thus,

$\begin{array}{ll}pd(T_n\text{〈}1,t\text{〉})\ge 3.& (7)\end{array}$

Hence, from Inequalities (6) and (7), we have

$\begin{array}{l}pd(T_n\text{〈}1,t\text{〉})=3.\end{array}$

Theorem 2.4. Let a Toeplitz graph T_n〈1, t〉 with odd t ≥ 5, n ≥ t+2. Then pd(T_n〈1, t〉) = 3.

Proof. Let a Toeplitz graph T_n〈1, t〉 with odd t ≥ 5, n ≥ t+2. We will show that the Toeplitz graph with generators 1 and t, consists of a resolving partition set, β = {β₁, β₂, β₃} with three elements, where β₁ = {v₁, v₂, v_t+1}, ${\beta }_2=\left\{v_{\frac{t+1}{2}},v_{\frac{t+3}{2}}\right\},$ β₃ = {∀v_k|v_k ∉ {β₁, β₂}}.

There are two cases for β₁

$\begin{array}{l}r(v_k|{\beta }_1)\\ =\{\begin{array}{ll}k-2+q_1(1-t),\hfill & k\equiv 2,\dots ,\frac{t+1}{2}+1(modt)\hfill \\ t+1-k+(t+1)\left(q_2-s\right)+s,\hfill & k\equiv 0,1,\frac{t+1}{2}+2,\mathrm{...},t-1(modt)\hfill \end{array}\end{array}$

where $q_1=\lfloor \frac{k}{t}\rfloor ,$ $q_2=\lfloor \frac{k}{t+2}\rfloor$, and $s=\lfloor \frac{1}{k}\rfloor .$

There are two cases for β₂

$\begin{array}{l}r(v_k|{\beta }_2)\\ =\{\begin{array}{ll}t+1-k+(t+1)q_1-s,\hfill & k\equiv 2,3,\dots ,\frac{t+1}{2}(modt)\hfill \\ k-1-\left(\frac{t+1}{2}\right)+q_2(1-t)+st,\hfill & k\equiv 0,1,\frac{t+1}{2}+1,\dots ,t-1(modt)\hfill \end{array}\end{array}$

where $q_1=\lfloor \frac{k}{t}\rfloor$ and $s=\frac{t+1}{2}.$ where $q_2=\lfloor \frac{k}{t+2}\rfloor$ and $s=\lfloor \frac{1}{k}\rfloor .$

For β₃, we have the following values

$\begin{array}{ll}r(v_k|{\beta }_2)\hfill & =\{\begin{array}{ll}2\hfill & fork=1\hfill \\ 1\hfill & fork=\frac{t+1}{2},\frac{t+3}{2},t+1\hfill \\ 0\hfill & otherwise\hfill \end{array}\hfill \end{array}$

From all these cases of β₁, β₂, and β₃

$\begin{array}{l}r(v_k|\beta )=\left(r(v_k|{\beta }_1),r(v_k|{\beta }_2),r(v_k|{\beta }_3)\right)\end{array}$

We conclude that all representations are unique, and no two vertices have identical representations.

$\begin{array}{ll}pd(T_n\text{〈}1,t\text{〉})\le 3& (8)\end{array}$

In contrary, we shall now demonstrate that pd(T_n〈1, t〉) ≥ 3. Suppose on the contrary that pd(T_n〈1, t〉) = 2. We know that by Theorem 1, it is not possible for odd t of graph T_n〈1, t〉. So

$\begin{array}{ll}pd(T_n\text{〈}1,t\text{〉})\ge 3& (9)\end{array}$

Hence, from Inequalities (8) and (9), we can say that

$\begin{array}{l}pd(T_n\text{〈}1,t\text{〉})=3\end{array}$

3. Partition dimension of T_n〈1, 2, t〉

In this section, we are going to discuss the partition dimension of T_n〈1, 2, t〉. If t = 3, 4, 5, and t = 2i, i ≥ 3, n ≥ t + 2 then partition dimension is 4.

Theorem 3.1. Let T_n〈1, 2, t〉 be a Toeplitz graph. Then pd(T_n〈1, 2, t〉) = 4.

Proof. We split our theorem into three cases.

Case A: When t = 3, 4, 5.

Let T_n〈1, 2, t〉 be a Toeplitz graph with t = 3, 4, 5, n ≥ t+2, then we will show that vertices of the Toeplitz graph with three generators consist of a resolving partition set, β = {β₁, β₂, β₃, β₄} where β₁ = {v₁}, β₂ = {v₂}, β₃ = {v₃, …, v_t}, and β₄ = {v_t+1, …, v_n}. Then there are the three cases that follow:

Case 1: If k ≡ 1(mod t), then we can write the unique position of v_k regarding β as;

$\begin{array}{l}r(v_k|\beta )=\left(q-k+1,q-k+2-\lfloor \frac{3}{t}\rfloor s,q-k+2-s,w\right)\end{array}$

where $q=(t+1)\lfloor \frac{k}{t}\rfloor ,$ $s=\frac{k-1}{k}$, and $w=\lfloor \frac{t}{k+t-1}\rfloor .$ This shows that all the representations are different so β resolves the vertices of T_n〈1, 2, t〉

Case 2: If k ≡ 2, 3(mod t), we can write the representations of v_k regarding β as;

$\begin{array}{l}r(v_k|\beta )=\left(q+1,k-2+(1-t)q,q+\lfloor \frac{2}{k}\rfloor ,s\right)\end{array}$

where $q=\lfloor \frac{k-1}{t}\rfloor$ and $s=\lfloor \frac{t}{k+t-3}\rfloor .$ This indicates that all the representations are different so β resolves the vertices of T_n〈1, 2, t〉.

Case 3: If k ≡ 4, 5(mod t), we can write the representations of v_k with respect to β as

$\begin{array}{l}r(v_k|\beta )=\left(q+2,\lfloor \frac{k}{t}\rfloor +\lfloor \frac{t}{5}\rfloor ,q,\lfloor \frac{t}{k}\rfloor \right)\end{array}$

where $q=\lfloor \frac{k-1}{t}\rfloor .$ This shows that all the representations are different so β resolve the vertices. From all three cases, we conclude that

$\begin{array}{ll}pd(T_n\text{〈}1,2,t\text{〉})\le 4& (10)\end{array}$

Case B: When t = 6, 8.

Let β = {β₁, β₂, β₃, β₄} be a resolving partition set. Where β₁ = {v₁}, β₂ = {v₂, v_t}, β₃ = {v₃, …, v_t−2}, and β₄ = {v_t−1, v_t+1, …, v_n}. We have different cases on v_k, which are following;

There are two cases for β₁;

$\begin{array}{l}r(v_k|{\beta }_1)\\ =\{\begin{array}{ll}\lfloor \frac{k}{2}\rfloor -\left(\frac{t-2}{2}\right)\lfloor \frac{k}{t}\rfloor -z_1,\hfill & k\equiv 1,2,3,4,5(modt)\hfill \\ \left(\frac{t-2}{2}+6-k\right)+\left(t+1\right)\lfloor \frac{k-1}{t}\rfloor +z,\hfill & k\equiv 0,6,7,\dots ,t-1(modt)\hfill \end{array}\end{array}$

where z₁ = 1 when k = even, z = 1 when k ≡ 0(mod 8) and otherwise both are 0.

There are three cases for β₂;

$\begin{array}{l}r(v_k|{\beta }_2)\\ =\{\begin{array}{ll}\lfloor \frac{k}{2}\rfloor -1-\left(\frac{t-2}{2}\right)\lfloor \frac{k}{t}\rfloor +z_1,\hfill & k\equiv 2,3,4(modt)\hfill \\ \left(\frac{t-4}{2}+6-k\right)-\lfloor \frac{k}{2}\rfloor +\left(\frac{t+2}{2}\right)\lfloor \frac{k}{t}\rfloor +z,\hfill & k\equiv 5,\dots ,t-1(modt)\hfill \\ \lfloor \frac{k-1}{t}\rfloor ,\hfill & k\equiv 0,1(modt)\hfill \end{array}\end{array}$

where z = 0 when 5 ≤ k ≤ t−1 and otherwise z = 2, and z₁ has defined in β₁.

There are three cases for β₃;

$r(v_k|{\beta }_3)=\{\begin{array}{ll}\lfloor \frac{k+1}{2}\rfloor -\left(\frac{t-2}{2}\right)\lfloor \frac{k}{t}\rfloor ,\hfill & k\equiv 1,2(modt)\hfill \\ \lfloor \frac{k}{t}\rfloor ,\hfill & k\equiv 3,\dots ,t-2(modt)\hfill \\ \lfloor \frac{k+1}{t}\rfloor ,\hfill & k\equiv 0,t-1(modt)\hfill \end{array}$

There is the only case for β₄;

$\begin{array}{ll}r(v_k|{\beta }_4)\hfill & =\{\begin{array}{ll}1\hfill & k=1,\dots t-4\hfill \\ 0\hfill & otherwise\hfill \end{array}\hfill \end{array}$

It is clear that no two vertices have the same representation, implying that there are no two vertices with the same representation.

$\begin{array}{ll}pd(T_n\text{〈}1,2,t\text{〉})\le 4.& (11)\end{array}$

Case C: When t = 2i, i ≥ 5.

Let β = {β₁, β₂, β₃, β₄} be a resolving partition set. Where β₁ = {v₂}, β₂ = {v₆}, β₃ = {v_a}, and β₄ = {∀v_k|v_k ∉ β₁, β₂, β₃}. where $a=2\lceil \frac{t+6}{4}\rceil .$

The following is a representation of all vertices v_k with regard to the resolving partition set β.

There are two cases for β₁;

$\begin{array}{l}r(v_k|{\beta }_1)\\ =\{\begin{array}{ll}\lfloor \frac{k-1}{2}\rfloor -\left(\frac{t-2}{2}\right)\lfloor \frac{k}{2}\rfloor ,\hfill & k\equiv 3,4,\dots ,t-3(modt)\hfill \\ 3-\lfloor |\frac{k-t+2}{2}|\rfloor +\left(\frac{t+2}{2}\right)\lfloor \frac{k}{t+3}\rfloor +\lfloor \frac{1}{k}\rfloor ,\hfill & k\equiv 0,1,2,t-2,t-1(modt)\hfill \end{array}\end{array}$

There are four cases for β₂;

$\begin{array}{ll}r(v_k|{\beta }_2)\hfill & =\{\begin{array}{ll}\lfloor \frac{3}{k}\rfloor -\left(\frac{t-2}{2}\right)\lfloor \frac{k}{t+1}\rfloor +\lfloor \frac{k-\frac{t}{2}}{2}\rfloor ,\hfill & k\equiv 0,1(modt)t=10,12\hfill \\ \lfloor \frac{3}{k}\rfloor +\lfloor \frac{5\left(k-1\right)}{t}\rfloor -4\lfloor \frac{k}{t+1}\rfloor ,\hfill & k\equiv 0,1(modt),t\ge 14\hfill \\ 2-\lfloor \frac{k-2}{2}\rfloor +\left(\frac{t+2}{2}\right)\lfloor \frac{k}{t}\rfloor ,\hfill & k\equiv 2,3,\dots ,6(modt)\hfill \\ \lfloor \frac{k-5}{2}\rfloor -\left(\frac{t-2}{2}\right)\lfloor \frac{k}{t}\rfloor ,\hfill & k\equiv 7,8,\dots ,t-1(modt)\hfill \end{array}\hfill \end{array}$

There are four cases for β₃;

$\begin{array}{ll}r(v_k|{\beta }_3)\hfill & =\{\begin{array}{ll}\lceil \frac{t}{4}\rceil ,\hfill & k=1,2\hfill \\ \lceil \frac{t+2}{4}\rceil -k+3,\hfill & k=3,4\hfill \\ \lfloor \frac{k-2a}{2}\rfloor -\left(\frac{t-2}{2}\right)\lfloor \frac{k-5}{t}\rfloor +z_1,\hfill & k\equiv 0,\dots ,4,2a,2a+1,\dots ,\hfill \\ \hfill & t-1(modt),k\ge 2a\hfill \\ \frac{t-6}{2}-\lfloor \frac{k-5}{2}\rfloor +\left(\frac{t+2}{2}\right)\lfloor \frac{k}{t}\rfloor -z_2,\hfill & k\equiv 5,\dots ,t-3(modt)\hfill \end{array}\hfill \end{array}$

where z₁ = 0 when k = even, otherwise 1 and z₂ = 1 when k = odd, otherwise 0.

There is the only case for β₄;

$r(v_k|{\beta }_4)=\{\begin{array}{ll}1,\hfill & k=2,6,a\hfill \\ 0,\hfill & otherwise\hfill \end{array}$

It is clear that no two vertices have the same representation, implying that there does not exist two vertices with the same representation.

$\begin{array}{ll}pd(T_n\text{〈}1,2,t\text{〉})\le 4.& (12)\end{array}$

Converse A, B, and C:

We will show that pd(T_n〈1, 2, t〉) ≥ 4. On contrary, suppose that pd(T_n〈1, 2, t〉) = 3.

Different cases on behalf of our assumption that pd(T_n〈1, 2, t〉) is 3. If ${\beta }^n=\left\{{\beta }_1,{\beta }_2,{\beta }_3\right\},$ where βⁿ consists of sets of different resolving partition set that are following:

Case 1: β₁ = {v₁, v₂}, β₂ = {v₃, v₄}, ${\beta }_3={\left\{v_i\right\}}_{i=5}^{i=n},$ then we have the following different vertices with same representation; $r(v_3|{\beta }^n)=r(v_4|{\beta }^n)=(1,0,1).$

Case 2: β₁ = {v₁, v₃}, β₂ = {v₂, v₄}, ${\beta }_3={\left\{v_i\right\}}_{i=5}^{i=n},$ then we have the following different vertices with same representation; $r(v_2|{\beta }^n)=r(v_4|{\beta }^n)=(1,0,1).$

Case 3: β₁ = {v₁, v₂, v₃}, β₂ = {v₄}, ${\beta }_3={\left\{v_i\right\}}_{i=5}^{i=n},$ then we have the following different vertices with same representation; $r(v_2|{\beta }^n)=r(v_3|{\beta }^n)=(0,1,1).$

Case 4: β₁ = {v₁, v₂}, β₂ = {v₃}, ${\beta }_3={\left\{v_i\right\}}_{i=4}^{i=n},$then we have the following different vertices with same representation; $r(v_1|{\beta }^n)=r(v_2|{\beta }^n)=(0,1,1).$

Case 5: β₁ = {v₁}, β₂ = {v₂, v₃}, ${\beta }_3={\left\{v_i\right\}}_{i=4}^{i=n},$ then we have the following different vertices with same representation; $r(v_{t+2}|{\beta }^n)=r(v_{t+3}|{\beta }^n)=(2,1,0).$

Case 6: β₁ = {v₁, v₂, v₄}, β₂ = {v₃}, ${\beta }_3={\left\{v_i\right\}}_{i=5}^{i=n},$ then we have the following different vertices with same representation; $r(v_2|{\beta }^n)=r(v_4|{\beta }^n)=(0,1,1).$

Case 7: β₁ = {v₁, v₃, v₄}, β₂ = {v₂}, ${\beta }_3={\left\{v_i\right\}}_{i=5}^{i=n},$ then we have the following different vertices with same representation; $r(v_{t+3}|{\beta }^n)=r(v_{t+3}|{\beta }^n)=(1,2,0).$

Case 8: β₁ = {v₁}, β₂ = {v₂, v₄}, ${\beta }_3={\left\{v_3,v_i\right\}}_{i=5}^{i=n},$ then we have the following different vertices with same representation; $r(v_3|{\beta }^n)=r(v_6|{\beta }^n)=(1,1,0).$

Case 9: β₁ = {v₁}, β₂ = {v₂, v₃, v₄}, ${\beta }_3={\left\{v_i\right\}}_{i=5}^{i=n},$ then we have the following different vertices with same representation; $r(v_2|{\beta }^n)=r(v_3|{\beta }^n)=(1,0,1).$

Case 10: β₁ = {v₁}, β₂ = {v₂, v₃, v₅}, ${\beta }_3={\left\{v_3,v_i\right\}}_{i=5}^{i=n},$ then we have the following different vertices with same representation; $r(v_{t+3}|{\beta }^n)=r(v_{2t+1}|{\beta }^n)=\left(2,\lfloor \frac{t+1}{3}\rfloor ,0\right).$

Case 11: β₁ = {v₁, v₅}, β₂ = {v₂, v₄}, ${\beta }_3={\left\{v_3,v_i\right\}}_{i=6}^{i=n},$ then we have the following different vertices with same representation; $r(v_1|{\beta }^n)=r(v_5|{\beta }^n)=(0,1,1).$

Case 12: β₁ = {v₁, v₄}, β₂ = {v₃, v₅}, ${\beta }_3={\left\{v_2,v_i\right\}}_{i=6}^{i=n},$ then we have the following different vertices with same representation; $r(v_1|{\beta }^n)=r(v_4|{\beta }^n)=(0,1,1).$

Case 13: β₁ = {v₁, v₄}, β₂ = {v₂, v₅}, ${\beta }_3={\left\{v_3,v_i\right\}}_{i=6}^{i=n},$ then we have the following different vertices with same representation; $r(v_2|{\beta }^n)=r(v_4|{\beta }^n)=(1,0,1).$

Case 14: β₁ ≡ 1(mod 3), β₂ ≡ 2(mod 3), β₃ ≡ 0(mod 3), then we have the following different vertices with same representation; $r(v_1|{\beta }^n)=r(v_4|{\beta }^n)=r(v_7|{\beta }^n)=(0,1,1).$

According to the above cases, we can easily conclude that our supposition is wrong, and we can not resolve the vertices of T_n〈1, 2, t〉 into three resolving partition sets. Thus,

$\begin{array}{ll}pd(T_n\text{〈}1,2,t\text{〉})\ge 4& (13)\end{array}$

Hence, from Inequalities (1-3) and (13), we can say that

$\begin{array}{l}pd(T_n\text{〈}1,2,t\text{〉})=4\end{array}$

4. Conclusion and open problems

In this study, we looked at different families of Toeplitz graphs and established that the partition dimension of each family is the constant, if the Toeplitz graph consists of two generators, then pd(T_n〈1, t〉)=3, where t ≥ 2 and if Toeplitz graph consists of three generators, pd(T_n(〈1, 2, t〉)) = 4, where t = 3, 5 and t = 2i and i ≥ 2.

In this paper, inequality (1) also satisfied the metric dimension results (Liu et al., 2019) with our results for partition dimension (Figure 2).

Open Problem 1. The partition dimension of the Toeplitz graph with two generators k ≥ 2, s ≥ 3 and gcd(k, s) = 1, is constant, bounded or unbounded?

Open Problem 2. The partition dimension of the Toeplitz graph with three generators k ≥ 2, s ≥ 3, t ≥ 4 and gcd(k, s, t) = 1, is constant, bounded or unbounded?

Open Problem 3. If the generators of the Toeplitz graph are increasing then the partition dimension either increasing or decreasing ?

FIGURE 2

Figure 2. Toeplitz graph T₈〈1, 2, 3〉 with partition dimension 4.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

RL conceived of the presented idea. AK developed the theory and performed the computations. AA and MA verified the analytical methods. GI and MN investigated and supervised the findings of this work. All authors discussed the results and contributed to the final manuscript.

Funding

This study was supported by the National Science Foundation of China (11961021 and 11561019), Guangxi Natural Science Foundation (2020GXNSFAA159084), and Hechi University Research Fund for Advanced Talents (2019GCC005).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmad, A., Ali, N. A., Koam, Siddiqui, M. H. F., Azeem, M., et al. (2021). Resolvability of the starphene structure and applications in electronics. Ain Shams Eng. J. 13, 101587. doi: 10.1016/j.asej.2021.09.014

CrossRef Full Text | Google Scholar

Alatawi, M. S., Ahmad, A., Koam, A. N. A., Husain, S., and Azeem, M. (2022). Computing vertex resolvability of benzenoid tripod structure. AIMS Math. 7, 6971–6983. doi: 10.3934/math.2022387

CrossRef Full Text | Google Scholar

Ali, N. A., Koam, Ahmad, A., Asim, M. A., and Azeem, M. (2022b). Computation of vertex and edge resolvability of benzenoid tripod structure. J. King Saud Univer. Sci. 34, 102208. doi: 10.1016/j.jksus.2022.102208

CrossRef Full Text | Google Scholar

Ali, N. A., Koam, Ahmad, A., and Azeem, M. (2021). Metric and fault-tolerant metric dimension of hollow coronoid. IEEE Access 9, 81527–81534. doi: 10.1109/ACCESS.2021.3085584

CrossRef Full Text | Google Scholar

Alshehri, H., Ahmad, A., Alqahtani, Y., and Azeem, M. (2022). Vertex metric-based dimension of generalized perimantanes diamondoid structure. IEEE Access 10, 43320–43326. doi: 10.1109/ACCESS.2022.3169277

CrossRef Full Text | Google Scholar

Azeem, M., Imran, M., and Nadeem, M. F. (2021). Sharp bounds on partition dimension of hexagonal Möbius ladder. J. King Saud Univer. Sci. 34, 101779. doi: 10.1016/j.jksus.2021.101779

CrossRef Full Text | Google Scholar

Azeem, M., Jamil, M. K., Javed, A., and Ahmad, A. (2022). Verification of some topological indices of Y-junction based nanostructures by M-polynomials. J. Math. 2022, 8238651. doi: 10.1155/2022/8238651

CrossRef Full Text | Google Scholar

Browsable, M. A. J. (1998). “Structure-activity datasets R. Carb-Dorca, ” in Advances in Molecular Similarity, ed P. Mezey (London: JAI Press Connecticut), 153–170.

Google Scholar

Buczkowski, P. S., Chartrand, G., Poisson, C., and Zhang, P. (2003). On k-dimensional graphs and their bases. Periodica Math. Hung. 46, 9–15. doi: 10.1023/A:1025745406160

CrossRef Full Text | Google Scholar

Caceres, J., Hernando, C., Mora, M., Pelayo, I. M., Puertas, M. L., Seara, C., et al. (2007). On the metric dimension of Cartesian product of graphs. SIAM J. Disc. Math. 2, 423–441. doi: 10.1137/050641867

CrossRef Full Text | Google Scholar

Chartrand, G., and Zhang, P. (2003). The theory and applications of resolvability in graphs. Congress. Numer. 160, 47–68.

Google Scholar

Chartrand, G., Eroh, L., Johnson, M. A., and Oellermann, O. R. (2000a). Resolvability in graphs and the metric dimension of a graph. Discrete Appl. Math. 105, 99–113. doi: 10.1016/S0166-218X(00)00198-0

CrossRef Full Text | Google Scholar

Chartrand, G., Salehi, E., and Zhang, P. (2000b). The partition dimension of a graph. Aequat. Math. 59, 45–54. doi: 10.1007/PL00000127

CrossRef Full Text | Google Scholar

Chvatal, V. (1983). Mastermind. Combinatorica 3, 325–329. doi: 10.1007/BF02579188

CrossRef Full Text | Google Scholar

Fehr, M., Gosselin, S., and Oellermann, O. R. (2006). The partition dimension of Cayley digraphs. Aequat. Math. 71, 1–18. doi: 10.1007/s00010-005-2800-z

CrossRef Full Text | Google Scholar

Harary, F., and Melter, R. A. (1976). On the metric dimension of a graph. Ars Combinat. 2, 191–195.

Google Scholar

Heinig, G., and Rost, K. (1984). Algebric Methods for Toeplitz-Like Matrices Operators. Boston, MA: Birkhäuser.

Google Scholar

Hua, Y., Wen-Quan, W., and Zhong, L. (2010). “Application of Toeplitz matrix in image restoration,” in 2010 IEEE Fifth International Conference on Bio-Inspired Computing (Changsha: IEEE).

Google Scholar

Javaid, I., Raja, N. K., Salman, M., and Azhar, M. N. (2012). The partition dimension of circulant graphs. World Appl. Sci. J. 18, 1705–1717. doi: 10.5829/idosi.wasj.2012.18.12.1590

CrossRef Full Text | Google Scholar

Javaid, I., and Shokat, S. (2008). On the partition dimension of some wheel graphs. J. Prime Res. Math. 4, 154–164.

Google Scholar

Khabyah, A. A., Jamil, M. K., Koam, A. N. A., Javed, A., and Azeem, M. (2022). Partition dimension of COVID antiviral drug structures. Math. Biosci. Eng. 19, 10078–10095. doi: 10.3934/mbe.2022471

PubMed Abstract | CrossRef Full Text | Google Scholar

Khuller, S., Raghavachari, B., and Rosenfeld, A. (1994). Localization in Graphs. Technical Report. UMIACS-TR-94-R-92, College Park, MD: University of Maryland.

Google Scholar

Khuller, S., Raghavachari, B., and Rosenfeld., S. (1996). Landmarks in graphs. Discrete Appl. Math. 70, 217–229. doi: 10.1016/0166-218X(95)00106-2

CrossRef Full Text | Google Scholar

Koam, A. N. A., Ahmad, A., Azeem, M., Khalil, A., and Nadeem, M. F. (2022a). On adjacency metric dimension of some families of graph. J. Funct. Spaces. 2022, 6906316. doi: 10.1155/2022/6906316

PubMed Abstract | CrossRef Full Text | Google Scholar

Koam, A. N. A., Ahmad, A., Azeem, M., and Nadeem, M. F. (2022). Bounds on the partition dimension of one pentagonal carbon nanocone structure. Arabian J. Chem. 15, 103923. doi: 10.1016/j.arabjc.2022.103923

CrossRef Full Text | Google Scholar

Ku, T. K., and Kuo, C. J. (1992). Design and analysis of Toeplitz preconditioners. IEEE Trans. Signal Process. 40, 129–141. doi: 10.1109/78.157188

CrossRef Full Text | Google Scholar

Lewis, H. R., Garey, M. R., and Johnson, D. S. (1983). Computers and Intractability. A guide to the theory of NP-completeness. W.H. Freeman and Company, San Franciscoc 1979. J. Symbolic Logic. 48, 498–500. doi: 10.2307/2273574

CrossRef Full Text | Google Scholar

Liu, J. B., Nadeem, M. F., Siddiqui, H. M. A., and Nazir, W. (2019). Computing metric dimension of certain families of Toeplitz graphs. IEEE Access 4, 1–8. doi: 10.1109/ACCESS.2019.2938579

CrossRef Full Text | Google Scholar

Melter, R. A., and Tomescu, I. (1984). Metric bases in digital geometry. Comput. Vis. Graphics Image Process. 25, 113–121. doi: 10.1016/0734-189X(84)90051-3

CrossRef Full Text | Google Scholar

Mohan, C. M., Santhakumar, S., Arockiaraj, M., and Liu, J. B. (2019). Partition dimension of certain classes of series parallel graphs. Theor. Comput. Sci. 778, 47–60. doi: 10.1016/j.tcs.2019.01.026

CrossRef Full Text | Google Scholar

Nadeem, M. F., Qu, S., Ahmad, A., and Azeem, M. (2022). Metric dimension of some generalized families of Toeplitz graphs. Math. Problems Eng. 2022, 9155291. doi: 10.1155/2022/9155291

CrossRef Full Text | Google Scholar

Saenpholphat, V., and Zhang, P. (2002). “Connected partition dimensions of graphs,” in Discussiones Mathematicae 305 Graph Theory, Vol. 22 (Zielona Góra: University of Zielona Góra), 305–323.

Google Scholar

Shanmukha, M. C., Kumar, K. N. A., Basavarajappa, N. S., and Usha, A. (2022b). Neighborhood topological indices of metal organic networks. Jnanabha 52, 174–181.

Google Scholar

Shanmukha, M. C., Usha, A., Praveen, B. M., and Douhadji, A. (2022a). Degree based molecular descriptors and QSPR analysis of breast cancer drugs. J. Math. 2022, 1–13. doi: 10.1155/2022/5880011

CrossRef Full Text | Google Scholar

Shanmukha, M. C., Usha, A., Siddiqui, M. K., Asefa Fufa, S., and Tuah, A. (2022c). Degree-based molecular descriptors of guar gum and its chemical derivatives. J. Chem. 2022, 7371538. doi: 10.1155/2022/7371538

CrossRef Full Text | Google Scholar

Siddiqui, H. M. A., and Imran, M. (2015). Computation of metric dimension and partition dimension of nanotubes. J. Comput. Theor. Nanosci. 12, 199–203. doi: 10.1166/jctn.2015.3717

CrossRef Full Text | Google Scholar

Slater, P. J. (1988). Dominating and reference sets in graphs. J. Math. Phys. Sci. 22, 445–455.

Google Scholar

Usha, A., Shanmukha, M. C., Praveen, B. M., Krishnan, S. Y., and Shilpa, K. C. (2022). Variation of adriatic and wiener indices for different cycle lengths and paths. Discrete Math. Algorithms Appl. doi: 10.1142/S1793830922501257

CrossRef Full Text | Google Scholar

Velazquez, J. A. R., Yero, I. G., and Kuziak, D. (2012). The partition dimension of corona product graphs. arXiv:1010.5144. doi: 10.48550/arXiv.1010.5144

CrossRef Full Text | Google Scholar

Velázquez, P. A. R., Yero, I. G., and Lemańska, M. (2014). On the partition dimension of trees. Discrete Appl. Math. 166, 204–209. doi: 10.1016/j.dam.2013.09.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Yero, I. G., Jakovac, M., Kuziak, D., and Taranenko, A. (2014). The partition dimension of strong product graphs and cartesian product graphs. Discrete Math. 331, 43–52. doi: 10.1016/j.disc.2014.04.026

CrossRef Full Text | Google Scholar

Yero, I. G., and Velázquez, J. A. R. (2010). A note on the partition dimension of cartesian product graphs. Appl. Math. Comput. 217, 3571–3574. doi: 10.1016/j.amc.2010.08.038

CrossRef Full Text | Google Scholar