
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Comput. Neurosci., 16 November 2022
Volume 16 - 2022 | https://doi.org/10.3389/fncom.2022.1062678
This article is part of the Research TopicBrain-inspired Cognition and Understanding for Next-generation AI: Computational Models, Architectures and Learning AlgorithmsView all 15 articles
Backpropagation has been regarded as the most favorable algorithm for training artificial neural networks. However, it has been criticized for its biological implausibility because its learning mechanism contradicts the human brain. Although backpropagation has achieved super-human performance in various machine learning applications, it often shows limited performance in specific tasks. We collectively referred to such tasks as machine-challenging tasks (MCTs) and aimed to investigate methods to enhance machine learning for MCTs. Specifically, we start with a natural question: Can a learning mechanism that mimics the human brain lead to the improvement of MCT performances? We hypothesized that a learning mechanism replicating the human brain is effective for tasks where machine intelligence is difficult. Multiple experiments corresponding to specific types of MCTs where machine intelligence has room to improve performance were performed using predictive coding, a more biologically plausible learning algorithm than backpropagation. This study regarded incremental learning, long-tailed, and few-shot recognition as representative MCTs. With extensive experiments, we examined the effectiveness of predictive coding that robustly outperformed backpropagation-trained networks for the MCTs. We demonstrated that predictive coding-based incremental learning alleviates the effect of catastrophic forgetting. Next, predictive coding-based learning mitigates the classification bias in long-tailed recognition. Finally, we verified that the network trained with predictive coding could correctly predict corresponding targets with few samples. We analyzed the experimental result by drawing analogies between the properties of predictive coding networks and those of the human brain and discussing the potential of predictive coding networks in general machine learning.
The human brain has an intricate and heterogeneous structure that consists of a high recurrent and nonlinear neural network (Felleman and Van Essen, 1991; Friston, 2008; Bertolero et al., 2015). It is commonly understood that the learning system of the human brain operates on the synaptic plasticity mechanism (Hebb, 2005), wherein the modulation in synaptic weights varies according to the intrinsic or extrinsic stimuli (Power and Schlaggar, 2017). Specifically, neural plasticity regulates the process of synaptic transmission as a fundamental property of neurons (Citri and Malenka, 2008; Mateos-Aparicio and Rodŕıguez-Moreno, 2019). Based on this property, the neuronal responses to sensory stimuli enable the robust recognition (Ohayon et al., 2012; Denève et al., 2017; Geirhos et al., 2017; Wardle et al., 2020) and noise-resistance learning (Suzuki et al., 2015; Perez-Nieves et al., 2021) in human perception.
Based on the human brain architecture, artificial neural networks (ANNs) were suggested to simulate the pattern of the human decision-making process for recognition tasks. Rumelhart et al. (1986) introduced the backpropagation algorithm that adjusts the network parameters to achieve reliable performance. Backpropagation iteratively updates the network parameters relying on the error signal generated at the end of the network between the produced output and the desired output. In the last decade, with the benefits of backpropagation (Rumelhart et al., 1986), ANNs have exceeded human-level performance on classification, segmentation, and detection (He et al., 2016; Dosovitskiy et al., 2020). However, learning ANNs with backpropagation have been criticized for their biological implausibility, wherein its behavior conflicts with the activity of real neurons in the human brain (Akrout et al., 2019; Illing et al., 2021). First, the human brain operates according to neural plasticity, which indicates the capability for modifying neural circuit connectivity or degree of interaction (Neves et al., 2008). Second, global error-guided learning requires the forward weight matrices to propagate the error signal flow to the lower layer, that is weight transport problem (Grossberg, 1987). Multiple learning algorithms have been proposed to alleviate the previously mentioned issues based on strong constraints of backpropagation and reinforce its biological plausibility (Liao et al., 2016; Lillicrap et al., 2016; Whittington and Bogacz, 2017; Woo et al., 2021; Dellaferrera and Kreiman, 2022). This study explored the predictive coding network (Whittington and Bogacz, 2017) among the various biologically plausible learning and its characteristics.
A predictive coding network (Whittington and Bogacz, 2017) was introduced to resolve the biological limitations of backpropagation depending on the hierarchically organized visual cortex of the human brain (Rao and Ballard, 1999; Friston, 2008). With respect to biological plausibility, a predictive coding network concentrates on local and Hebbian plasticity by minimizing the prediction errors between expected and actual inputs (Rao and Ballard, 1999; Millidge et al., 2020). The learning mechanism of the predictive coding network is different from that of backpropagation, which updates the network parameters using only one error derived from the last layer (Rumelhart et al., 1986). Predictive coding is regarded as a local learning algorithm because its learning is performed with local error nodes and global error nodes. A learning network with predictive coding approximates the learning dynamics of backpropagation (Whittington and Bogacz, 2017) and can also be expanded to arbitrary computational graphs (Millidge et al., 2020). Multiple works (Han et al., 2018; Wen et al., 2018; Choksi et al., 2021) inspired by the property of prediction itself have been proposed, and some studies (Choksi et al., 2021; Salvatori et al., 2021) demonstrated that the potential of the predictive manner related to human perception.
However, despite the remarkable accomplishment of ANN architectures and their learning algorithms, there remains a performance gap between machine and human intelligence in some applications. We collectively refer to these tasks as machine-challenging tasks (MCTs); MCTs are difficult for machine intelligence while easy for human intelligence. This study considers the representative MCTs as incremental learning, long-tailed recognition, and few-shot learning (Hassabis et al., 2017). A more detailed definition and explanation of MCTs will be presented in Section 2.2. Humans progressively and ceaselessly acquire new knowledge and preserve it by virtue of the hippocampus (Preston and Eichenbaum, 2013). The primary function of the hippocampus is that it enables long-term memory of the spatial and sequential order from the human experience (Bird and Burgess, 2008; Davachi and DuBrow, 2015). This property makes the human intelligence exhibits robust and performs better than machine intelligence (Goodfellow et al., 2014; Zhou and Firestone, 2019; Liu et al., 2021). Meanwhile, ANNs trained with backpropagation tend to forget what it learned when it learns new information, that is catastrophic forgetting (McCloskey and Cohen, 1989; French, 1999; Goodfellow et al., 2013). As another example, machine intelligence shows unsatisfactory performance under limited or imperfect training data recognition (De Man et al., 2019; Liu et al., 2019a). When training ANNs for classification tasks in a long-tail scenario, the classifier can be easily biased toward the majority classes that contain the most data and show poor performance in minority classes (Johnson and Khoshgoftaar, 2019). These phenomena result from the fundamental differences in visual processing between the brain and ANNs (Xu and Vaziri-Pashkam, 2021). Inspired by Hassabis et al. (2017), we hypothesized that the closer the learning algorithm is to the human brain, the more effective it is for the MCTs.
Similar to our assumption on the MCTs, the learning algorithms inspired by the brain are consistently studied to reduce the performance gap between machine intelligence and human intelligence based on human's various attributes. In terms of human learning mechanisms, a spiking neural network (SNN) is considered a promising solution to replicate the neural processing process of the brain. On the other hand, recent studies reported that the neural network trained biologically plausible manner embodies specific memory functions in the human memory system. Therefore, based on previous studies, we speculated that predictive coding has other latent properties. This study aimed to discover hidden properties and extend the scope of predictive coding to MCTs. Contrary to the conventional solutions for the MCTs, our study focused on the predictive coding algorithm itself employed for the optimization of the network parameters. In incremental learning, it is confirmed that predictive coding better reveals the plasticity-stability property and enables faster adaptation to new tasks than backpropagation. In long-tailed recognition, it reduces the classification bias problem of minority classes.
This paper is organized as follows: In Section 2, the predictive coding network is briefly reviewed. In Section 3, the experiments on incremental learning based on a predictive coding network are presented. In Section 4, the experiments on limited data recognition based on a predictive coding network, such as long-tailed recognition and few-shot learning, are described. In Section 5, we discuss why predictive coding network improves the performance of MCTs. In Section 6, related work to help understand our paper is presented. In Section 7, we conclude the paper with limitations and a summary.
Our contributions can be summarized as follows:
• The study characterized the MCTs, which are easy for human intelligence and difficult for machine intelligence, in machine learning fields and proposed a hypothesis that the brain-inspired learning algorithm improves the performance of MCTs.
• Predictive coding, a biologically plausible learning algorithm, was adopted for MCTs, such as incremental learning and limited data recognition. In addition, extensive experiments were performed by reimplementing the learning with backpropagation with predictive coding.
• The effect of learning algorithms close to brain learning on MCTs in terms of neuroscience was presented. Mainly, the experimental results were analyzed with respect to the plasticity-stability dilemma and interplay between the hippocampus and prefrontal cortex.
The backpropagation algorithm (Rumelhart et al., 1986), which simulates the properties of the human brain, has achieved excellent progress in various machine learning tasks. The algorithm calculates the global error by comparing the predicted outputs and the actual targets at the network's end to achieve an objective. Then, it propagates the error signal to the front of the network to update parameters. Although backpropagation is the most popular learning algorithm for ANNs, it is often regarded as a biologically implausible algorithm from a neuroscience perspective. The main reason is that backpropagation does not operate following the local synaptic plasticity (Takesian and Hensch, 2013; Mateos-Aparicio and Rodŕıguez-Moreno, 2019) as a fundamental property of the nervous system. Synaptic plasticity refers to the ability to reorganize structures or connections by intrinsic or extrinsic stimuli. Another reason is that the backpropagation requires a copy of the weight matrices to transfer backward error signal (Grossberg, 1987). However, retaining synaptic weights on each neuron is impractical in the human brain. So, Lillicrap et al. (2016) replaced the backward weight matrices with fixed random weights to avoid those problems. Liao et al. (2016) reported that the signs of backward weight matrices were important, and when the signs between the forward and backward matrices were concordant, the same or better performance could be achieved. Furthermore, various learning algorithms have been proposed to reinforce biological plausibility while maintaining the classification performance (Lee et al., 2015; Whittington and Bogacz, 2017; Ahmad et al., 2020; Lindsey and Litwin-Kumar, 2020; Pogodin and Latham, 2020). Among them, predictive coding, based on the predictive process of the brain, was suggested to achieve better biologically plausible properties than the backpropagation algorithm and achieved comparable performance to the backpropagation on arbitrary computational graphs (Whittington and Bogacz, 2017).
ANNs have achieved comparable or superior performances to humans by backpropagation in visual recognition (Russakovsky et al., 2015; Geirhos et al., 2017). However, ANNs have unsatisfactory performance in certain tasks regarded as simple and easy for human intelligence (Goodfellow et al., 2013; Snell et al., 2017; Cao et al., 2019). As detailed in Section 1, these types of tasks as MCTs (e.g., incremental learning, long-tailed recognition, and few-shot recognition).
Humans ceaselessly take new information from multiple sensory organs and reorganize it in the brain (Felleman and Van Essen, 1991; Denève et al., 2017). These processes proceed in a lifelong manner because knowledge construction is affected by previous experiences. In addition, humans can refine or transfer knowledge acquired from different types of previous tasks built in an incremental manner (Preston and Eichenbaum, 2013; Davachi and DuBrow, 2015). In contrast to human intelligence, ANNs have catastrophic forgetting in which the collected information is lost after training of subsequent tasks (Goodfellow et al., 2013). Moreover, the human visual system shows robust performances even in limited data recognition, such as long-tailed and few-shot visual recognition. Real-world data commonly follow long-tailed distribution wherein the majority classes occupy the significant part of the dataset and have an open-ended distribution (Liu et al., 2019b). The primary purpose of long-tailed recognition is to correctly classify the minority class samples to the corresponding targets, reducing the classification bias effect (Cao et al., 2019). Further, the classification of tail class samples can be regarded as a few-shot recognition problem as the degree of imbalance increases (Samuel et al., 2021).
The discrepancy in learning performances between humans and ANNs is closely related to the characteristics of the human brain. First, the human brain operates under two properties: plasticity and stability (Takesian and Hensch, 2013). Plasticity refers to the brain's change in connectivity and circuitry that enables humans to acquire knowledge, keep memories, and adapt to the external environment (Power and Schlaggar, 2017). Meanwhile, stability refers to the ability of long-term memory where stable memory is relevant to stable neuron connectivity (Susman et al., 2019). A balance between plasticity and stability is achieved with excitatory and inhibitory circuit activity in the visual cortex (Takesian and Hensch, 2013). Second, the brain engages the hippocampus and neocortex, as explained by the complementary learning system theory that characterizes learning in the brain (Preston and Eichenbaum, 2013). The hippocampus focuses on acquiring new knowledge, and knowledge is transferred and generalized to the neocortex via the memory consolidation process. Such mechanisms do not exist in backpropagation. However, they can be indirectly performed in learning predictive coding through the free-energy minimization process of predictive coding. As such, we assume that humans can achieve superior performance in MCTs.
Most architectures in ANNs follow an L-layer structure wherein each layer consists of a set of neurons (Rumelhart et al., 1986). The training with the backpropagation algorithm can be explained to minimize a global error generated at the last layer of a network. In the backpropagation algorithm, an activation value of each layer is defined as follows:
where i is the indices of layers, and θi is the parameters of i-th layer. The goal of backpropagation algorithm is to minimize a loss function between the ground-truth target y and the prediction value ŷ. The final layer output is derived from the forward pass as follows:
In the backward pass, the optimization of parameters is performed by the derivative of the loss function. The gradient of each layer is computed in reverse order as follows:
and
where δi and dθi are the error signal and the gradient from i-th layer, respectively.
Meanwhile, in the predictive coding algorithm, an error node is defined in every layer, and the goal of learning is to minimize the collective energy function (Friston, 2003; Bogacz, 2017; Buckley et al., 2017), which is the sum of prediction errors as illustrated in Figure 1. A predictive coding network assumes the network as a directed acyclic computational graph to deliver an error from the last layer to the first layer. and are defined as a set of error nodes and a set of activation nodes at every layer.
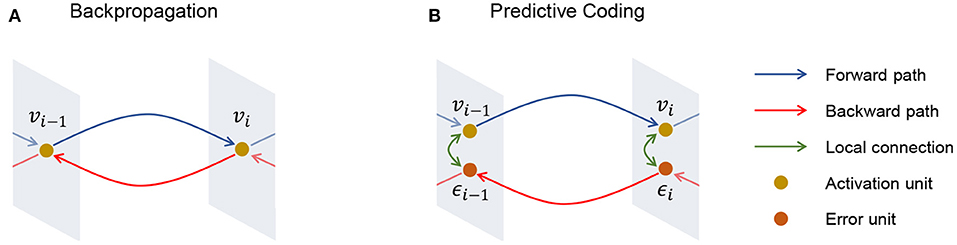
Figure 1. Illustration of (A) backpropagation and (B) predictive coding. Different from backpropagation, predictive coding has an error unit ϵi for each activation unit vi and this enables predictive coding to perform local learning.
By analogy to the cortical hierarchy in the human brain, predictive coding can be formulated as a variational inference algorithm (Friston, 2005; Buckley et al., 2017). Millidge et al. (2020) extended predictive coding to an arbitrary computational graph considering its hierarchical and generative structure. Given a computational graph , the feedforward prediction is defined as and variational posterior is derived as , where indicates the set of parent nodes and denotes the set of child nodes for the given node x. Each activation node has the prediction for i-th layer. Based on this, Millidge et al. (2020) defined a objective function of predictive coding as the variational free energy as follows (Friston, 2005; Buckley et al., 2017):
where a prediction error of each layer ei. The i-th error node ei can be calculated as follows:
where vi−1 is the activation node value of the previous layer.
In the backward phase of predictive coding, network parameters θ containing activation nodes {vi} and error nodes {ei} are updated via gradient descent of each layer as follows:
The learning is performed by minimizing the variational free energy until converges as follows:
where η is the weight learning rate. Parameters are updated as follows:
The equation 10 indicates the local learning rule of the predictive coding where the parameters of i-th layer are only updated based on the ei and vi−1.
Based on previous studies (Hassabis et al., 2017; Perez-Nieves et al., 2021), our fundamental assumption is that the more biologically plausible the learning algorithm, closely replicating the learning mechanism of the brain, the more effective it will be for MCTs. Previous studies focused on confirming that the predictive coding network itself inherits the physiological characteristics of the brain. Motivated by the previous study, the current research assumed that predictive coding networks have a latent ability to consolidate the sequentially acquired knowledge in the human memory system. Therefore, we propose a predictive coding framework for incremental learning and verify the efficacy of MCTs. The task of incremental learning can be mainly categorized into two categories (Masana et al., 2020): class-incremental learning and task-incremental learning. The current study focused on the former. In class-incremental learning, the knowledge from previously seen classes is no longer available when a network learns the knowledge of unseen classes, and the learned network aims to achieve favorable classification accuracy for all tasks without forgetting. Multiple tasks were sequentially learned based on the pre-defined order to validate our assumption, and each task with its validation set finishing the training of the given task was evaluated. The algorithms are detailed in Algorithm 1.
A 3-layer predictive coding network with ReLU non-linearity, where the number of the hidden nodes was 800 for the simple dataset such as MNIST (LeCun et al., 1998) and FMNIST (Xiao et al., 2017), was employed. Similar to the study by Serra et al. (2018), a simplified Alexnet architecture (Krizhevsky et al., 2012) consisting of three convolutional layers was used for the complex dataset such as CIFAR-10 (Krizhevsky et al., 2009). The three convolutional layers comprised 64, 128, and 256 channels.
We refined the data to formulate sequential incremental tasks. The data were divided into multiple portions following the representative incremental learning approaches (Lee et al., 2017; Sokar et al., 2021), and constructed four datasets: disjoint-MNIST, disjoint-FMNIST, split-MNIST, and split-CIFAR-10. Disjoint-MNIST and disjoint-FMNIST were organized by separating MNIST and FMNIST into two tasks. In addition, a more complex dataset, called split-MNIST and split-CIFAR-10, was also established, where all classes were separated into five tasks, and each task contained two categories. The details of the tasks on the multiple datasets are described in Tables 1 and 2. Finally, we evaluated incremental learning performance. We trained a network with sequential order and measured that the acquired knowledge was maintained after each task's training, same as Serra et al. (2018).
A learning rate of 0.05 was used, and the learning rate was divided by 1/3 to perform incremental learning, if there was no advancement in the validation loss for five consecutive epochs. In predictive coding, the weight learning rate was set as 0.1 while keeping the other hyperparameters. The minimum learning rate was set as 1e−4 and batch size as 64. All experiments were conducted using data split according to five different seeds. We provide the code to reproduce the results in the manuscript at https://github.com/jangho2001us/PredictiveCoding_IncrementalLearning.
Incremental learning was performed on disjoint-MNIST and disjoint-FMNIST using the predictive coding framework to validate our hypothesis. To implement the incremental learning task in a predictive coding manner, we integrated the code of Serra et al. (2018) and Rosenbaum (2021) by replacing the network learning from the backpropagation with the predictive coding networks. The performance of each task was evaluated after completing the learning of each task in Tables 3 and 4. The performance in all tasks learned was evaluated using the best model of the last task. In this case, the best model refers to the model with the highest performance in the given task. Moreover, the other backpropagation-based incremental approaches containing SGD (Goodfellow et al., 2013), SGD-F (Goodfellow et al., 2013), EWC (Kirkpatrick et al., 2017), IMM (Lee et al., 2017), LFL (Jung et al., 2016), and LWF (Li and Hoiem, 2017) were evaluated to observe whether the predictive coding framework itself is effectual for preventing catastrophic forgetting. For all datasets, the average performance of the network trained with SGD based on the predictive coding manner outperformed the performance of the network trained with SGD based on backpropagation. Furthermore, learning with predictive coding exceeds strong competitor EWC (Kirkpatrick et al., 2017) on disjoint-MNIST and split-MNIST.
To make the challenging experimental settings, we combined two classes into one task and created five tasks using MNIST and CIFAR-10, similar to the study by Sokar et al. (2021). Incremental learning performance of backpropagation and predictive coding on split-MNIST and split-CIFAR-10 is shown in Tables 5 and 6. The performance of incremental learning based on predictive coding was also compared with that of conventional approaches (Goodfellow et al., 2013; Jung et al., 2016; Kirkpatrick et al., 2017; Lee et al., 2017; Li and Hoiem, 2017). To observe its ability to retain previously obtained knowledge, we visualized the average accuracy of trained tasks in Figure 2. Figure 2 and Table 5 are the experimental results from the same protocol (split-MNIST). After finishing every epoch, we evaluated the performance of all the tasks and drew Figure 2. While Table 5 shows the results of the average evaluation five times using the best model derived from each task. It was confirmed that catastrophic forgetting occurred in both learning algorithms, but the degree of forgetting was certainly more severe in the experimental results of backpropagation. Learning with predictive coding showed stable performance even when the learning task changed, in contrast to the pattern of backpropagation. In the backpropagation experiment, when the network acquired the knowledge of task 3, the knowledge of task 2 was forgotten. Further, when the network learned knowledge of task 5, it was confirmed that the discriminative information of tasks 1 and 2 was removed from the memories. These experimental results confirm that a biologically plausible learning algorithm reduces catastrophic forgetting in incremental learning and enhances the performance of incremental learning as one of MCTs.
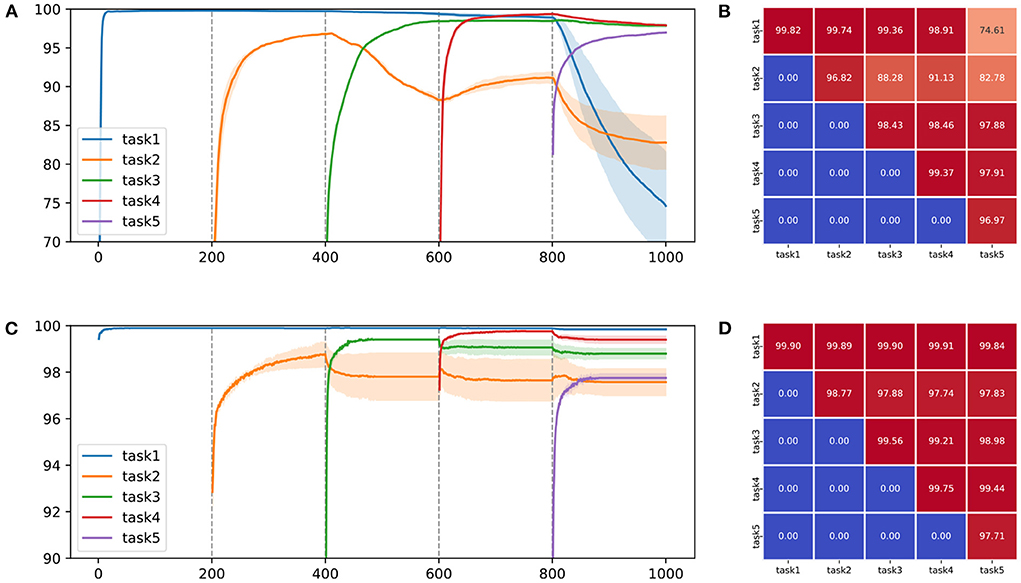
Figure 2. Qualitative and quantitative performance comparison on two learning schemes for (A,B) backpropagation and (C,D) predictive coding on split-MNIST. In (A,C), the solid line indicates the average accuracy for each task and the transparent region represents the standard deviation on five random seeds. The vertical dashed line refers to the point at which the task to be learned changes. In (B,D), each value indicates the performance each task measured by the final model.
We carried out additional experiments to demonstrate the advantages of learning with the brain-inspired algorithm. We implemented the predictive coding version of EWC (Kirkpatrick et al., 2017), IMM-MEAN (Lee et al., 2017), and IMM-MODE (Lee et al., 2017) algorithms and evaluated their performance on disjoint-MNIST. In the EWC algorithm, learning with predictive coding improves the average performance from 95.64% to 97.52%. In addition, learning with predictive coding enhances the average performance 0.21% and 5.42% in IMM-MEAN and IMM-MODE, respectively.
The potential of predictive coding networks for limited data recognition was then investigated. Specifically, the efficacy of predictive coding networks in long-tailed recognition and few-shot recognition type of MCTs was analyzed. First, real-world datasets are often highly imbalanced following long-tail distribution in which data category accounts for a significant portion of the overall data (Johnson and Khoshgoftaar, 2019; Liu et al., 2019b). Owing to the skewed class distribution of the dataset, the network trained with a class-imbalanced dataset may show a classification bias problem in which the samples of tail classes are predicted as head classes (Cao et al., 2019). In addition, managing few-shot samples in an open-world setting is crucial because it is similar to the situation in which the human recognition system can be encountered. Second, to achieve more human-like recognition performance, effectively managing few-shot examples in an open-world setting is crucial. Two experimental scenarios are significant because it is realistic situations that human recognition can encounter.
The cortical neuron in the human brain can learn with only a few repetitions owing to the local synaptic plasticity (Yger et al., 2015), and it is widely known that such plasticity contributes to the interactions between limited data (Wu et al., 2022). It has been demonstrated that the changes in synaptic connections assist in learning new information and long-term memory formation (Yang et al., 2009). Given the characteristics of synaptic plasticity, experiments with a predictive coding framework were performed on the class-imbalanced data, and the biologically plausible learning algorithm that helped limited data recognition was identified.
The same architecture used in the previous section consisting of three-layer MLP was used in long-tailed recognition. The number of hidden neurons was set as 800 with ReLU non-linearity and dropout. We used MNIST (LeCun et al., 1998) for our experiment and synthesized the long-tailed data with an imbalance ratio γ. The imbalance ratio was defined as the proportion of the samples of the highest number of classes to the lowest number of classes as . Although it differed depending on the imbalance ratio, in general, Nmax and Nmin usually followed the relationship, Nmax≫Nmin. Exponential distribution and the number of samples Nl in l-th class was defined as . The four types of imbalanced data distribution were then synthesized as previously described (Kim et al., 2020). To train a network, we set a batch size of 128 and optimized a model until 100 epochs. When backpropagation was used for learning, the learning rate was increased from 0.0001 to 0.5 by growing five times, and the best performance results among them were determined. When predictive coding was used for the optimization, a learning rate of 0.002 with a weight decay of 2e−4 was used. Additionally, the weight learning rate η was set as 0.1 and the number of iterations as 20 as hyperparameters for predictive coding networks. All the experiments with predictive coding were performed under the fixed prediction assumption. We provide the code to reproduce the results in the manuscript at https://github.com/jangho2001us/PredictiveCoding_LongTailedRecognition.
In few-shot recognition, the same experimental settings with those of Snell et al. (2017), which comprised four convolutional blocks with Batch normalization, ReLU, and MaxPool were used. Experiments on few-shot recognition were conducted with Omniglot (Lake et al., 2011) dataset containing 1623 categories of handwritten characters. The performance of few-shot recognition is commonly measured by N-way k-shot classification, where N implies the number of given classes and k indicates the number of samples in each category. The current study extended the experimental protocol of the original paper to 30-way k-shot experiment settings because those evaluation protocols are more difficult because the number of classes for the candidate group increases. The learning rate was set to 1e−3 and then reduced by 1/10 every 20 epoch to train a network. For learning networks with a predictive coding framework, the same learning rate, weight decay, weight learning rate, and iterations were used. For more information, please refer to the original paper (Snell et al., 2017). We provide the code to reproduce the results in the manuscript at https://github.com/jangho2001us/PredictiveCoding_FewShotRecognition.
In Table 7, we compared the long-tailed recognition performance with Cross-Entropy (CE) loss, Mixup approach (Zhang et al., 2017), Focal loss (Lin et al., 2017), Class-Balanced Focal (CB Focal) loss (Cui et al., 2019), Label-Distribution-Aware-Margin (LDAM) loss (Cao et al., 2019), and Balanced Meta-Softmax (BALMS) loss (Ren et al., 2020). Further details on multiple learning objectives are provided in the Supplementary material. The experimental results showed the benefit of learning with predictive coding networks. First, the long-tailed recognition performance was higher by 4.45% in learning the network with a predictive coding framework than that in learning with CE loss under severe class imbalance of data distribution. Similar results in the following experiments were observed when the network was trained with other learning objectives such as Focal (Lin et al., 2017) and BALMS (Ren et al., 2020). In this experiment, the performance improvement is evaluated using the predictive coding framework rather than comparing performance between different learning objectives. The results shown in Table 7 indicate that the learning algorithm close to the human brain brings a positive effect on MCTs, confirming our assumption.
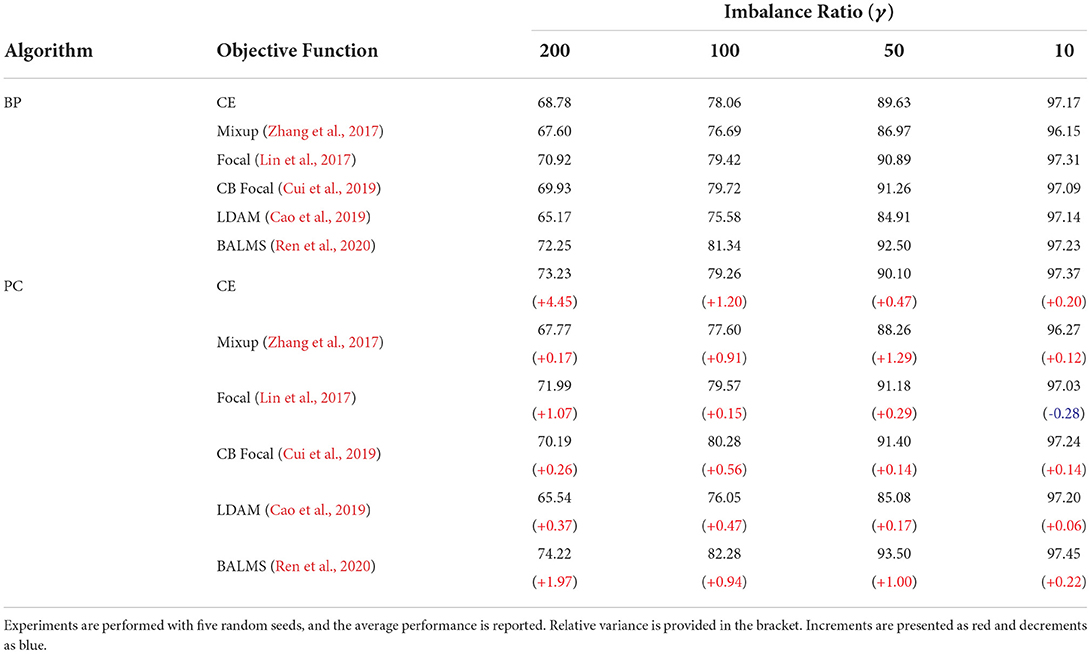
Table 7. Comparison of classification performance (%) on MNIST under four different imbalance distributions.
The few-shot recognition performance trained with backpropagation and predictive coding framework is shown in Table 8, Learning with predictive coding enabled robust recognition under the various few-shot experimental protocols. Additionally, predictive coding networks showed their potential ability under challenging inference settings such as 20-way 1-shot and 30-way 1-shot rather than 20-way 5-shots and 30-way 5-shots. The experimental results confirmed our assumptions and supported that the brain-like learning algorithm was effective for MCTs.
The plasticity-stability dilemma is a well-known problem widely studied in biology (Mateos-Aparicio and Rodŕıguez-Moreno, 2019). This phenomenon is related to the power of consolidation of new information without forgetting previously acquired information (Mermillod et al., 2013). Further, it is an essential issue in incremental learning with ANNs (Lin et al., 2022). The human brain is well-controlled to learn new information and to prevent the learned information from being overridden by the new information (Takesian and Hensch, 2013). However, ANNs naturally induce catastrophic forgetting and expose the trade-off between plasticity and stability (Kirkpatrick et al., 2017).
To confirm that predictive coding achieves a better plasticity-stability trade-off than backpropagation, we experimented with split-MNIST by controlling the stability of two learning mechanisms. Adjusting the learning rate is not directly related to stability, but it was used because it was considered as a factor that could adjust stability in our experiments. In Figure 3, we report the experimental results and compare the learning schemes by adjusting the learning rate of backpropagation and the weight learning rate of predictive coding. In backpropagation experiments, the learning is reduced from 0.01 to 0.0001 to decrease forgetting of acquired knowledge. When the learning rate was 0.0001, the network forgot less information to perform task 2. However, it still showed limited performance in tasks 1 and 2. Thus, maintaining stability by reducing the learning rate may not be acceptable because it deteriorates the overall performance. Meanwhile, performance was consistently high for each task in predictive coding experiments. These results implied predictive coding had better plasticity properties than backpropagation while maintaining stability.
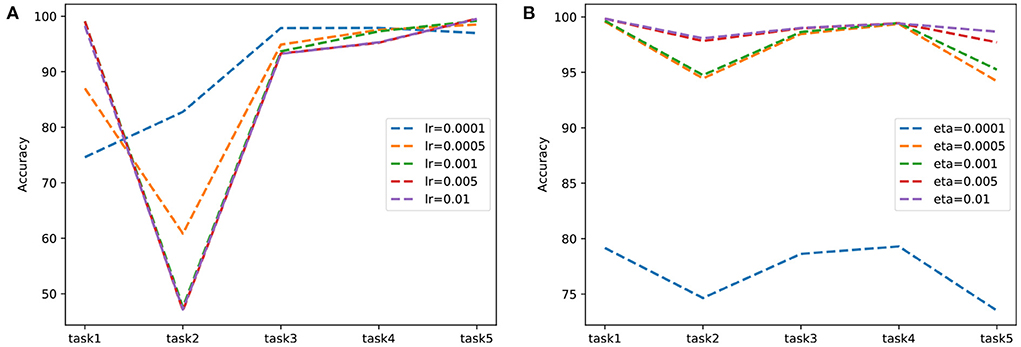
Figure 3. Comparison of learning with (A) backpropagation and (B) predictive coding on split-MNIST in two learning schemes. To adjust network stability, the learning rate of backpropagation and the weight learning rate of predictive coding are varied.
The hippocampus plays an essential role in episodic memory at the top of the cortical processing hierarchy (Felleman and Van Essen, 1991). In incremental learning, the ability to regulate learned information and retrieve context-appropriate memories is essential. We can understand the effectiveness of predictive coding in incremental learning as the interaction between the hippocampus and the prefrontal cortex in the human brain (Eichenbaum, 2017; Barron et al., 2020). It is well known that the hippocampus can quickly encode new information, stabilize memory traces, and organize memory networks (Preston and Eichenbaum, 2013). In addition, this mechanism has been physiologically proven through functional magnetic resonance imaging studies (Hindy et al., 2019).
We have shown that the learning process of predictive coding networks is analogous to the interaction between the hippocampus and the prefrontal cortex in the human brain (Eichenbaum, 2017). As described in Algorithm 1, the learning process based on predictive coding networks can be divided into two phases: forward and backward pass. In the forward phase, the predictive coding network computes its predictions for every layer. In the backward phase, the predictive coding network minimizes the free-energy summation as a learning objective. The two-phase learning of predictive coding networks corresponds to acquiring and consolidating information in the hippocampus and prefrontal cortex. The predictive coding framework promotes the two processes and enables accurate inference when data containing information corresponding to the previously learned task are received.
The reason why we selected predictive coding as a brain-inspired algorithm is as follows. As described in Section 2, predictive coding is potentially more biologically plausible because local learning rules perform parameter updates. This property is distinct from the update of backpropagation executed from the global error signal. It will be ideal if the parameter update is performed asynchronously in a different layer, such as the neural plasticity of the human brain. However, the parameter update of predictive coding occurs under the fixed prediction assumption (Millidge et al., 2020). The fixed prediction assumption implies that the parameters are updated based on the fixed predictions of the forward phase. Whittington and Bogacz (2017) demonstrated that a predictive coding network with a fixed prediction assumption performs the same parameter updates as backpropagation. Another limitation of predictive coding is the degree of convergence of variational free energy used as a learning objective. The convergence of the backward phase is achieved by setting a specific number of iterations (Rosenbaum, 2021). Depending on the number of backward iterations, learning with predictive coding may converge or diverge. Although these two issues introduced earlier remain open questions, we conducted our experiments using predictive coding because we thought its advantages outweighed its disadvantages.
This study empirically demonstrated the potential effectiveness of predictive coding in MCTs. However, despite this, the predictive coding algorithm still has some limitations. First, predictive coding requires a longer training time than backpropagation because it executes backward iteration until the error nodes and activation nodes converge. Although we expanded our experiments for large networks such as VGGNet and ResNet (He et al., 2016; Krizhevsky et al., 2017), we could not perform the experiments on MCTs because of the excessive training time. Second, to conduct learning with predictive coding, the network should be an architecture composed of sequential layers. For example, if shortcut connections exist, it is challenging to implement them into a predictive coding layer. In this case, we set the block unit, which is the boundary of the shortcut, as the predictive coding layer. If predictive coding combines learning speed and scalability, there will be infinite opportunities for development as a learning algorithm that can replace backpropagation.
In summary, we extensively analyze the benefits of learning ANNs with predictive coding frameworks for MCTs. MCTs can be described as tasks that are easy for human intelligence while difficult for machine intelligence. Based on our hypothesis, we empirically demonstrate that brain-inspired predictive coding has advantages in incremental learning on MNIST and CIFAR, long-tailed recognition on MNIST, and few-shot recognition on Omniglot. In neuroscience, especially the intrinsic properties of the human brain, we discuss why training ANNs with a predictive coding framework improves the performance of MCTs. The study concludes that predictive coding learning is similar to the plasticity-stability property of the human brain and mainly mimics the interaction between the hippocampus and prefrontal cortex. Finally, it is an interesting avenue for future work to reduce the training time under the fixed prediction assumption and relax the constraint of predictive coding while maintaining the performance.
The original contributions presented in the study are publicly available. The data can be found here: http://yann.lecun.com/exdb/mnist and https://www.cs.toronto.edu/~kriz/cifar.html.
JL contributed to the design of the study and performed the experiments. JL, JJ, BL, and J-HL developed the algorithm and performed the result analysis, and wrote the revised manuscript. SY conceived and supervised the project, checked ideas and terminology, performed result analysis, editing, and revision of the manuscript.
This work was supported by Electronics and Telecommunications Research Institute (ETRI) grant funded by the Korean government [22ZS1100, Core Technology Research for Self-Improving Integrated Artificial Intelligence System], and the BK21 FOUR program of the Education and Research Program for Future ICT Pioneers, Seoul National University in 2022.
The authors would like to thank Hyemi Jang and Bonggyun Kang for their contribution in the early stages of this study.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fncom.2022.1062678/full#supplementary-material
Ahmad, N., van Gerven, M. A., and Ambrogioni, L. (2020). “Gait-prop: a biologically plausible learning rule derived from backpropagation of error,” in Advances in Neural Information Processing Systems 33, 10913–10923.
Akrout, M., Wilson, C., Humphreys, P., Lillicrap, T., and Tweed, D. B. (2019). “Deep learning without weight transport,” in Advances in Neural Information Processing Systems 32, NeurIPS 2019, Vancouver.
Barron, H. C., Auksztulewicz, R., and Friston, K. (2020). Prediction and memory: a predictive coding account. Prog. Neurobiol. 192, 101821. doi: 10.1016/j.pneurobio.2020.101821
Bertolero, M. A., Yeo, B. T., and D92Esposito, M. (2015). The modular and integrative functional architecture of the human brain. Proc. Natl. Acad. Sci. U.S.A. 112, E6798–E6807. doi: 10.1073/pnas.1510619112
Bird, C. M., and Burgess, N. (2008). The hippocampus and memory: insights from spatial processing. Nat. Rev. Neurosci. 9, 182–194. doi: 10.1038/nrn2335
Bogacz, R. (2017). A tutorial on the free-energy framework for modelling perception and learning. J. Math. Psychol. 76, 198–211. doi: 10.1016/j.jmp.2015.11.003
Buckley, C. L., Kim, C. S., McGregor, S., and Seth, A. K. (2017). The free energy principle for action and perception: a mathematical review. J. Math. Psychol. 81, 55–79. doi: 10.1016/j.jmp.2017.09.004
Cao, K., Wei, C., Gaidon, A., Arechiga, N., and Ma, T. (2019). “Learning imbalanced datasets with label-distribution-aware margin loss,” in Advances in Neural Information Processing Systems 32, NeurIPS 2019, Vancouver.
Choksi, B., Mozafari, M., Biggs O'May, C., Ador, B., Alamia, A., and VanRullen, R. (2021). Predify: “Augmenting deep neural networks with brain-inspired predictive coding dynamics,” in Advances in Neural Information Processing Systems 34, NeurIPS 2021.
Citri, A., and Malenka, R. C. (2008). Synaptic plasticity: multiple forms, functions, and mechanisms. Neuropsychopharmacology 33, 18–41. doi: 10.1038/sj.npp.1301559
Colom, R., Karama, S., Jung, R. E., and Haier, R. J. (2022). Human intelligence and brain networks. Dialogues Clin. Neurosci. 12, 489–501. doi: 10.31887/DCNS.2010.12.4/rcolom
Cui, Y., Jia, M., Lin, T.-Y., Song, Y., and Belongie, S. (2019). “Class-balanced loss based on effective number of samples,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, 9268–9277. doi: 10.1109/CVPR.2019.00949
Davachi, L., and DuBrow, S. (2015). How the hippocampus preserves order: the role of prediction and context. Trends Cogn. Sci. 19, 92–99. doi: 10.1016/j.tics.2014.12.004
De Man, R., Gang, G. J., Li, X., and Wang, G. (2019). Comparison of deep learning and human observer performance for detection and characterization of simulated lesions. J. Med. Imaging 6, 025503. doi: 10.1117/1.JMI.6.2.025503
Dellaferrera, G., and Kreiman, G. (2022). “Error-driven input modulation: solving the credit assignment problem without a backward pass,” in Proceedings of the 39th International Conference on Machine Learning, Baltimore, MA, 4937–4955.
Denéve, S., Alemi, A., and Bourdoukan, R. (2017). The brain as an efficient and robust adaptive learner. Neuron 94, 969–977. doi: 10.1016/j.neuron.2017.05.016
Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., et al. (2020). An image is worth 16x16 words: transformers for image recognition at scale. arXiv preprint arXiv:2010.11929. doi: 10.48550/arXiv.2010.11929
Eichenbaum, H. (2017). Prefrontal-hippocampal interactions in episodic memory. Nat. Rev. Neurosci. 18, 547–558. doi: 10.1038/nrn.2017.74
Felleman, D. J., and Van Essen, D. C. (1991). Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47. doi: 10.1093/cercor/1.1.1
French, R. M. (1999). Catastrophic forgetting in connectionist networks. Trends Cogn. Sci. 3, 128–135. doi: 10.1016/S1364-6613(99)01294-2
Friston, K. (2003). Learning and inference in the brain. Neural Netw. 16, 1325–1352. doi: 10.1016/j.neunet.2003.06.005
Friston, K. (2005). A theory of cortical responses. Philos. Trans. R. Soc. B Biol. Sci. 360, 815–836. doi: 10.1098/rstb.2005.1622
Friston, K. (2008). Hierarchical models in the brain. PLoS Comput. Biol. 4, e1000211. doi: 10.1371/journal.pcbi.1000211
Geirhos, R., Janssen, D. H., Schütt, H. H., Rauber, J., Bethge, M., and Wichmann, F. A. (2017). Comparing deep neural networks against humans: object recognition when the signal gets weaker. arXiv preprint arXiv:1706.06969. doi: 10.48550/arXiv.1706.06969
Goodfellow, I. J., Mirza, M., Xiao, D., Courville, A., and Bengio, Y. (2013). An empirical investigation of catastrophic forgetting in gradient-based neural networks. arXiv preprint arXiv:1312.6211.
Goodfellow, I. J., Shlens, J., and Szegedy, C. (2014). Explaining and harnessing adversarial examples. arXiv preprint arXiv:1412.6572. doi: 10.48550/arXiv.1412.6572
Grossberg, S. (1987). Competitive learning: from interactive activation to adaptive resonance. Cogn. Sci. 11, 23–63. doi: 10.1111/j.1551-6708.1987.tb00862.x
Han, K., Wen, H., Zhang, Y., Fu, D., Culurciello, E., and Liu, Z. (2018). “Deep predictive coding network with local recurrent processing for object recognition,” in Advances in Neural Information Processing Systems 31, NeurIPS 2018, Montreal.
Hassabis, D., Kumaran, D., Summerfield, C., and Botvinick, M. (2017). Neuroscience-inspired artificial intelligence. Neuron 95, 245–258. doi: 10.1016/j.neuron.2017.06.011
He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, GA, 770–778. doi: 10.1109/CVPR.2016.90
Hindy, N. C., Avery, E. W., and Turk-Browne, N. B. (2019). Hippocampal-neocortical interactions sharpen over time for predictive actions. Nat. Commun. 10, 1–13. doi: 10.1038/s41467-019-12016-9
Illing, B., Ventura, J., Bellec, G., and Gerstner, W. (2021). “Local plasticity rules can learn deep representations using self-supervised contrastive predictions,” in Advances in Neural Information Processing Systems 34.
Johnson, J. M., and Khoshgoftaar, T. M. (2019). Survey on deep learning with class imbalance. J. Big Data 6, 1–54. doi: 10.1186/s40537-019-0192-5
Jung, H., Ju, J., Jung, M., and Kim, J. (2016). Less-forgetting learning in deep neural networks. arXiv preprint arXiv:1607.00122. doi: 10.48550/arXiv.1607.00122
Kim, J., Hur, Y., Park, S., Yang, E., Hwang, S. J., and Shin, J. (2020). “Distribution aligning refinery of pseudo-label for imbalanced semi-supervised learning,” in Advances in Neural Information Processing Systems 33, 14567–14579.
Kirkpatrick, J., Pascanu, R., Rabinowitz, N., Veness, J., Desjardins, G., Rusu, A. A., et al. (2017). Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. U.S.A. 114, 3521–3526. doi: 10.1073/pnas.1611835114
Krizhevsky, A., and Hinton, G. (2009). Learning Multiple Layers of Features From Tiny Images. Technical Report, University of Toronto, Toronto, ON, Canada.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “ImageNet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems 25, NeurIPS 2012, Lake Tahoe.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2017). ImageNet classification with deep convolutional neural networks. Commun. ACM 60, 84–90. doi: 10.1145/3065386
Lake, B., Salakhutdinov, R., Gross, J., and Tenenbaum, J. (2011). “One shot learning of simple visual concepts,” in Proceedings of the Annual Meeting of the Cognitive Science Society.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324. doi: 10.1109/5.726791
Lee, D.-H., Zhang, S., Fischer, A., and Bengio, Y. (2015). “Difference target propagation,” in Joint European Conference on Machine Learning and Knowledge Discovery in Databases (Proto: Springer), 498–515. doi: 10.1007/978-3-319-23528-8_31
Lee, S.-W., Kim, J.-H., Jun, J., Ha, J.-W., and Zhang, B.-T. (2017). “Overcoming catastrophic forgetting by incremental moment matching,” in Advances in Neural Information Processing Systems 30, NeurIPS 2017, Long Beach, CA.
Li, Z., and Hoiem, D. (2017). Learning without forgetting. IEEE Trans. Pattern Anal. Mach. Intell. 40, 2935–2947. doi: 10.1109/TPAMI.2017.2773081
Liao, Q., Leibo, J., and Poggio, T. (2016). “How important is weight symmetry in backpropagation?” in Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, doi: 10.1609/aaai.v30i1.10279
Lillicrap, T. P., Cownden, D., Tweed, D. B., and Akerman, C. J. (2016). Random synaptic feedback weights support error backpropagation for deep learning. Nat. Commun. 7, 1–10. doi: 10.1038/ncomms13276
Lin, G., Chu, H., and Lai, H. (2022). “Towards better plasticity-stability trade-off in incremental learning: a simple linear connector,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, AK, 89–98. doi: 10.1109/CVPR52688.2022.00019
Lin, T.-Y., Goyal, P., Girshick, R., He, K., and Dollár, P. (2017). “Focal loss for dense object detection,” in Proceedings of the IEEE International Conference on Computer Vision, Venice, 2980–2988. doi: 10.1109/ICCV.2017.324
Lindsey, J., and Litwin-Kumar, A. (2020). “Learning to learn with feedback and local plasticity,” in Advances in Neural Information Processing Systems 33, 21213–21223.
Liu, K., Li, X., Zhou, Y., Guan, J., Lai, Y., Zhang, G., et al. (2021). Denoised internal models: a brain-inspired autoencoder against adversarial attacks. arXiv preprint arXiv:2111.10844. doi: 10.1007/s11633-022-1375-7
Liu, X., Faes, L., Kale, A. U., Wagner, S. K., Fu, D. J., Bruynseels, A., et al. (2019a). A comparison of deep learning performance against health-care professionals in detecting diseases from medical imaging: a systematic review and meta-analysis. Lancet Digit. Health 1, e271–e297. doi: 10.1016/S2589-7500(19)30123-2
Liu, Z., Miao, Z., Zhan, X., Wang, J., Gong, B., and Yu, S. X. (2019b). “Large-scale long-tailed recognition in an open world,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, 2537–2546. doi: 10.1109/CVPR.2019.00264
Masana, M., Liu, X., Twardowski, B., Menta, M., Bagdanov, A. D., and van de Weijer, J. (2020). Class-incremental learning: survey and performance evaluation on image classification. arXiv preprint arXiv:2010.15277. doi: 10.48550/arXiv.2010.15277
Mateos-Aparicio, P., and Rodriguez-Moreno, A. (2019). The impact of studying brain plasticity. Front. Cell. Neurosci. 13, 66. doi: 10.3389/fncel.2019.00066
McCloskey, M., and Cohen, N. J. (1989). “Catastrophic interference in connectionist networks: the sequential learning problem,” in Psychology of Learning and Motivation, Vol. 24 (Elsevier), 109–165. doi: 10.1016/S0079-7421(08)60536-8
Mermillod, M., Bugaiska, A., and Bonin, P. (2013). The stability-plasticity dilemma: investigating the continuum from catastrophic forgetting to age-limited learning effects. Front. Psychol. 4, 504. doi: 10.3389/fpsyg.2013.00504
Millidge, B., Tschantz, A., and Buckley, C. L. (2020). Predictive coding approximates backprop along arbitrary computation graphs. arXiv preprint arXiv:2006.04182. doi: 10.48550/arXiv.2006.04182
Neves, G., Cooke, S. F., and Bliss, T. V. (2008). Synaptic plasticity, memory and the hippocampus: a neural network approach to causality. Nat. Rev. Neurosci. 9, 65–75. doi: 10.1038/nrn2303
Ohayon, S., Freiwald, W. A., and Tsao, D. Y. (2012). What makes a cell face selective? The importance of contrast. Neuron 74, 567–581. doi: 10.1016/j.neuron.2012.03.024
Perez-Nieves, N., Leung, V. C., Dragotti, P. L., and Goodman, D. F. (2021). Neural heterogeneity promotes robust learning. Nat. Commun. 12, 1–9. doi: 10.1038/s41467-021-26022-3
Pogodin, R., and Latham, P. (2020). “Kernelized information bottleneck leads to biologically plausible 3-factor Hebbian learning in deep networks,” in Advances in Neural Information Processing Systems 33, 7296–7307.
Power, J. D., and Schlaggar, B. L. (2017). Neural plasticity across the lifespan. Wiley Interdiscipl. Rev. Dev. Biol. 6, e216. doi: 10.1002/wdev.216
Preston, A. R., and Eichenbaum, H. (2013). Interplay of hippocampus and prefrontal cortex in memory. Curr. Biol. 23, R764–R773. doi: 10.1016/j.cub.2013.05.041
Rao, R. P., and Ballard, D. H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 2, 79–87. doi: 10.1038/4580
Ren, J., Yu, C., Ma, X., Zhao, H., Yi, S., et al. (2020). “Balanced meta-softmax for long-tailed visual recognition,” in Advances in Neural Information Processing Systems 33, 4175–4186.
Rosenbaum, R. (2021). On the relationship between predictive coding and backpropagation. arXiv preprint arXiv:2106.13082. doi: 10.1371/journal.pone.0266102
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning representations by back-propagating errors. Nature 323, 533–536. doi: 10.1038/323533a0
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., et al. (2015). Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 115, 211–252. doi: 10.1007/s11263-015-0816-y
Salvatori, T., Song, Y., Hong, Y., Sha, L., Frieder, S., Xu, Z., et al. (2021). “Associative memories via predictive coding,” in Advances in Neural Information Processing Systems 34, NeurIPS 2021.
Samuel, D., Atzmon, Y., and Chechik, G. (2021). “From generalized zero-shot learning to long-tail with class descriptors,” in Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, 286–295. doi: 10.1109/WACV48630.2021.00033
Serra, J., Suris, D., Miron, M., and Karatzoglou, A. (2018). “Overcoming catastrophic forgetting with hard attention to the task,” in International Conference on Machine Learning (PMLR), Stockholm, 4548–4557.
Snell, J., Swersky, K., and Zemel, R. (2017). “Prototypical networks for few-shot learning,” in Advances in Neural Information Processing Systems 30, NeurIPS 2017, Long Beach, CA.
Sokar, G., Mocanu, D. C., and Pechenizkiy, M. (2021). Addressing the stability-plasticity dilemma via knowledge-aware continual learning. arXiv preprint arXiv:2110.05329. doi: 10.48550/arXiv.2110.05329
Susman, L., Brenner, N., and Barak, O. (2019). Stable memory with unstable synapses. Nat. Commun. 10, 1–9. doi: 10.1038/s41467-019-12306-2
Suzuki, Y., Ikeda, H., Miyamoto, T., Miyakawa, H., Seki, Y., Aonishi, T., et al. (2015). Noise-robust recognition of wide-field motion direction and the underlying neural mechanisms in Drosophila melanogaster. Sci. Rep. 5, 1–12. doi: 10.1038/srep10253
Takesian, A. E., and Hensch, T. K. (2013). Balancing plasticity/stability across brain development. Prog. Brain Res. 207, 3–34. doi: 10.1016/B978-0-444-63327-9.00001-1
Wardle, S. G., Taubert, J., Teichmann, L., and Baker, C. I. (2020). Rapid and dynamic processing of face pareidolia in the human brain. Nat. Commun. 11, 1–14. doi: 10.1038/s41467-020-18325-8
Wen, H., Han, K., Shi, J., Zhang, Y., Culurciello, E., and Liu, Z. (2018). “Deep predictive coding network for object recognition,” in International Conference on Machine Learning (PMLR), 5266–5275.
Whittington, J. C., and Bogacz, R. (2017). An approximation of the error backpropagation algorithm in a predictive coding network with local hebbian synaptic plasticity. Neural Comput. 29, 1229–1262. doi: 10.1162/NECO_a_00949
Woo, S., Park, J., Hong, J., and Jeon, D. (2021). “Activation sharing with asymmetric paths solves weight transport problem without bidirectional connection,” in Advances in Neural Information Processing Systems 34, NeurIPS 2021.
Wu, Y., Zhao, R., Zhu, J., Chen, F., Xu, M., Li, G., et al. (2022). Brain-inspired global-local learning incorporated with neuromorphic computing. Nat. Commun. 13, 1–14. doi: 10.1038/s41467-021-27653-2
Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms. arXiv preprint arXiv:1708.07747. doi: 10.48550/arXiv.1708.07747
Xu, Y., and Vaziri-Pashkam, M. (2021). Limits to visual representational correspondence between convolutional neural networks and the human brain. Nat. Commun. 12, 1–16. doi: 10.1038/s41467-021-22244-7
Yang, G., Pan, F., and Gan, W.-B. (2009). Stably maintained dendritic spines are associated with lifelong memories. Nature 462, 920–924. doi: 10.1038/nature08577
Yang, S., Gao, T., Wang, J., Deng, B., Azghadi, M. R., Lei, T., et al. (2022a). SAM: a unified self-adaptive multicompartmental spiking neuron model for learning with working memory. Front. Neurosci. 16, 850945. doi: 10.3389/fnins.2022.850945
Yang, S., Linares-Barranco, B., and Chen, B. (2022b). Heterogeneous ensemble-based spike-driven few-shot online learning. Front. Neurosci. 16, 850932. doi: 10.3389/fnins.2022.850932
Yang, S., Tan, J., and Chen, B. (2022c). Robust spike-based continual meta-learning improved by restricted minimum error entropy criterion. Entropy 24, 455. doi: 10.3390/e24040455
Yger, P., Stimberg, M., and Brette, R. (2015). Fast learning with weak synaptic plasticity. J. Neurosci. 35, 13351–13362. doi: 10.1523/JNEUROSCI.0607-15.2015
Zhang, H., Cisse, M., Dauphin, Y. N., and Lopez-Paz, D. (2017). mixup: beyond empirical risk minimization. arXiv preprint arXiv:1710.09412. doi: 10.48550/arXiv.1710.09412
Keywords: brain-inspired learning, biologically plausible learning, deep learning, backpropagation, predictive coding
Citation: Lee J, Jo J, Lee B, Lee J-H and Yoon S (2022) Brain-inspired Predictive Coding Improves the Performance of Machine Challenging Tasks. Front. Comput. Neurosci. 16:1062678. doi: 10.3389/fncom.2022.1062678
Received: 06 October 2022; Accepted: 28 October 2022;
Published: 16 November 2022.
Edited by:
Yuqi Han, Tsinghua University, ChinaReviewed by:
Yuxuan Zhao, Institute of Automation (CAS), ChinaCopyright © 2022 Lee, Jo, Lee, Lee and Yoon. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sungroh Yoon, c3J5b29uQHNudS5hYy5rcg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.