- 1School of Computer Science and Technology, Xidian University, Xi'an, China
- 2National Engineering Laboratory for Video Technology, Department of Computer Science and Technology, Peking University, Beijing, China
- 3Centre for Systems Neuroscience, Department of Neuroscience, Psychology and Behaviour, University of Leicester, Leicester, United Kingdom
The majority of neurons in the neuronal system of the brain have a complex morphological structure, which diversifies the dynamics of neurons. In the granular layer of the cerebellum, there exists a unique cell type, the unipolar brush cell (UBC), that serves as an important relay cell for transferring information from outside mossy fibers to downstream granule cells. The distinguishing feature of the UBC is that it has a simple morphology, with only one short dendritic brush connected to its soma. Based on experimental evidence showing that UBCs exhibit a variety of dynamic behaviors, here we develop two simple models, one with a few detailed ion channels for simulation and the other one as a two-variable dynamical system for theoretical analysis, to characterize the intrinsic dynamics of UBCs. The reasonable values of the key channel parameters of the models can be determined by analysis of the stability of the resting membrane potential and the rebound firing properties of UBCs. Considered together with a large variety of synaptic dynamics installed on UBCs, we show that the simple-structured UBCs, as relay cells, can extend the range of dynamics and information from input mossy fibers to granule cells with low-frequency resonance and transfer stereotyped inputs to diverse amplitudes and phases of the output for downstream granule cells. These results suggest that neuronal computation, embedded within intrinsic ion channels and the diverse synaptic properties of single neurons without sophisticated morphology, can shape a large variety of dynamic behaviors to enhance the computational ability of local neuronal circuits.
1. Introduction
The vast majority of neurons in the neuronal systems of the brain have a complex morphology with a tree-like structure of the dendritic field. Each spine on the dendrite represents a synaptic contact that receives its input from a presynaptic neuron. The integration of these tremendous synapses is computationally complicated with dendritic non-linearity (Poirazi et al., 2003). However, there are other neurons with a relatively simple dendritic structure, but still conducting complex computation, as the important factors for single neuronal dynamics consist of a series of interactions between intrinsic and synaptic dynamics (Abbott and Regehr, 2004; Harvey et al., 2009; Torres et al., 2019).
The cerebellum, as one of the most stereotyped brain areas, has been traditionally suggested to play an essential role in motor control (Zeeuw et al., 1997). In recent years, a large body of studies has shown that the cerebellum is also involved in the processing of higher cognition (Ito, 2008; Strick et al., 2009; Tsai et al., 2012; Wagner et al., 2017; Bostan and Strick, 2018; Raymond and Medina, 2018). From a classical viewpoint, the cerebellum combines all sensory information about the body and outside environment to compute a series of motor sequences for controlling body movements and correcting the body position in space. For the granular layer of the cerebellum, all of these computations are started from mossy fibers (MFs) as outside inputs and ended with granule cells (GCs) as outputs.
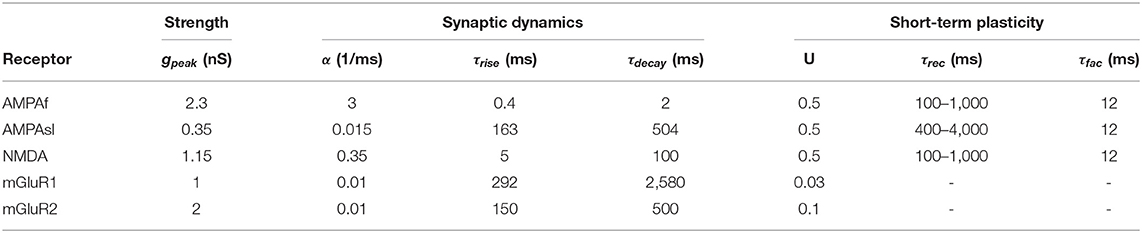
In the granular layer, there is a high density of compact GCs. On average, each GC only receives four presynaptic inputs. However, one of the unique features of the connection between MF inputs and well-studied GCs is the presence of an additional type of neuron, termed a unipolar brush cell (UBC) (Mugnaini et al., 1997), that constitutes an independent relay line for external MF signals. Therefore, UBCs have been suggested as internal MFs playing the important role of determining how the information from external MFs is transferred and encoded by the cerebellar cortex (Mugnaini et al., 1994, 2011; Jaarsma et al., 1995; Kinney et al., 1997; Diño et al., 1999; Nunzi et al., 2002; Ann et al., 2014; Stijn and Zeeuw, 2014; Carolina and Trussell, 2015; Zampini et al., 2016). Information flows into the granular layer through external MFs and is then relayed by UBCs as a version of internal MFs, such that GCs receive external MFs and transcoded UBCs. Besides, there are cascaded connections between UBCs formed as internal transcode lines from external MFs to GCs, as illustrated in Figure 1A, where the evidence from experimental and computational studies shows that UBCs make a significant contribution to transfer and relay of external MF activity for downstream GCs and Purkinje cells (Ann et al., 2014; Carolina and Trussell, 2015; Zampini et al., 2016).
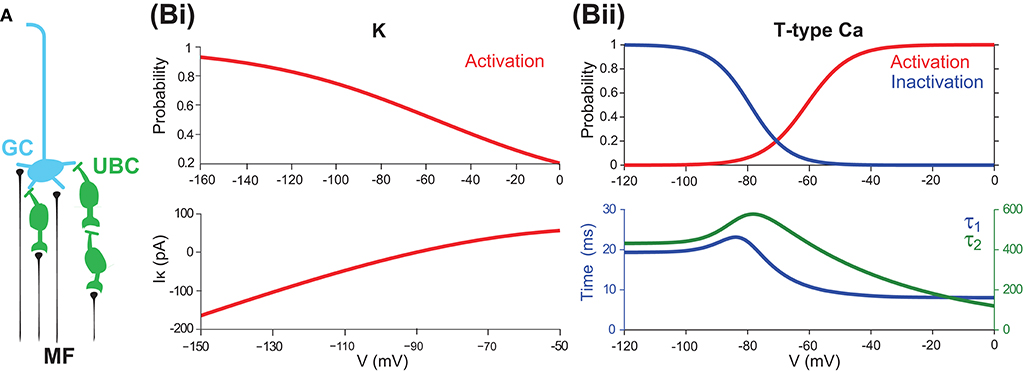
Figure 1. UBCs as relay cells between MFs and GCs (A) A typical GC receives four presynaptic inputs from MFs and/or UBCs. (B) Channel properties of mGluR2-dependent rectifier K and T-type Ca currents. (Bi) mGluR2-dependent rectifier K (IK) steady-state activation curve (top) and its current as a function of membrane potential (bottom). (Bii) T-type Ca steady-state activation and inactivation curves (top) and voltage sensitive time constants τ1 and τ2. Note that τ2 is much larger than τ1.
The unique feature of UBCs is that they are glutamatergic interneurons receiving a single excitatory synapse from MF and several inhibitory buttons from Golgi cells on their short dendritic brush (Mugnaini et al., 2011). Experimental studies have demonstrated that the unusually large MF-UBC synapse may entrap glutamate in the synaptic cleft that can prolong the excitatory postsynaptic currents mediated by various receptors in UBCs following MF stimulation (Rossi et al., 1995; Kinney et al., 1997; Morin et al., 2001). Together with inhibition from Golgi cells, there is a large variety of dynamic properties of the UBCs from pure excitation to pure inhibition, and a mix of both (Carolina and Trussell, 2015; Zampini et al., 2016).
The variation of biophysical components in UBCs enables them to exhibit a rich range of dynamics. On the one hand, the strong feedforward excitation encoded by UBCs can amplify the external MF signal as an ON signal for downstream GCs. On the other hand, the inhibition mediated by UBCs plays the role of an OFF signal to rectify the inputs (Carolina and Trussell, 2015; Zampini et al., 2016). Together with other mixed excitation and inhibition from UBCs, the input-output relationship of the granular layer can be modulated in a highly dynamical way (Ann et al., 2014). Various synaptic properties of UBCs make them send fast and slow types of excitation and inhibition down to the GCs (Stijn and Zeeuw, 2014; Zampini et al., 2016). At the same time, the intrinsic properties of UBCs are also determinant factors for their computational properties and shape their synaptic responses and firing patterns (Subramaniyam et al., 2014).
Despite the granular layer being relatively well-understood, the dynamics and functional properties of UBCs remain unclear due to the complex combinations of ion channels and synaptic receptors. In this study, we investigate the relationship between the activity displayed by UBCs and underlying voltage-dependent ion channels and various types of synaptic receptors with a modeling approach. We use a full model of a UBC with a number of ion channels and a reduced minimal model with essential T-type calcium and rectifier potassium channels to study the intrinsic properties of UBC and clarify the role of these two channels in shaping the dynamics of UBC response while maintaining the stability of the UBC resting membrane potential. Rebound firing after inhibition offset and low-frequency resonance are also exhibited by both versions of the model. Finally, the UBC firing patterns determined by intrinsic properties are also regulated by different types of synaptic receptors, such that UBCs can show a large variation of temporal dynamics, as observed in experiments.
2. Methods
2.1. Full UBC Model
Here, the full UBC model is a model with all essential ion channels to generate experimental observations, although a more detailed model was derived previously (Subramaniyam et al., 2014). The UBC was modeled as an integration-and-fire neuron but with additional T-type calcium (Ca) (IT), L-type Ca (IL), and mGluR2-dependent rectifier potassium K (IK) current, as well as h-type (Ih) current. The membrane potential V is changed with time according to the following equation when V < Vthr,
where C = 20 pF is the cell capacitance, gl = 1 nS and El = −67 mV represent the conductance and resting potential of the leak current, and Iinput is the input current. When the threshold Vthr = −50 mV is reached at the spiking time t = tspk, V is set to Vpeak = 40 mV for a duration of the spike of τdur = 1 ms. Then, after the spike at t = tspk + τdur, the repolarizing potential is set to Vreset = −67 mV, and the after hyperpolarization conductance (gAHP) is activated with EK = −90 mV. gAHP is a dynamical conductance changed as follows:
where τAHP = 2 ms, and the δ function is used to add an increment ḡAHP = 1 nS where a spike occurs. The refractory period is set as τref = 2 ms.
Looking more closely at these channels, there are two channels that are particularly interesting. The first is the rectifier K channel, which plays an important role in maintaining the stability of the resting membrane potential, controlling excitability, and shaping the initial depolarization (Chung et al., 2010). For UBCs, there is a specific type of K channel, the mGluR2-dependent rectifier type, which can be modeled based on experimental data (Zampini et al., 2016) as
where gK is the conductance, which is a free parameter, and EK = −90 mV is the reversal potential. m∞, K represents the activation state. Figure 1Bi shows the typical behavior, activation curve, and voltage-current curve of this channel followed by the model. Half-point activation is reached at -55 mV for the rectifier K channel. Note that this current has a fast and instantaneous activation time constant, such that the output current at the given membrane potential can be computed directly by this steady state, as an input-output, or voltage-current, mapping as in Figure 1Bi (bottom).
The other channel of interest is the fast-inactivating T-type Ca current, which produces low-threshold spikes, triggering the high-frequency bursts, and generating powerful Ca transients in the brush and soma (Diana et al., 2007; Birnstiel et al., 2009). The T-type Ca current can be modeled as
where gT is the conductance, which is a free parameter, ECa = 120 mV is the reversal potential, m∞, T represents the activation state, and h is the inactivation described below.
The T-type Ca current inactivates rapidly during maintained depolarization yet recovers slowly from inactivation. To reconcile these observations, a two-step kinetic scheme is used for the inactivation gate. All the time constants in this scheme are voltage-dependent. To account for these effects, we consider a model that has two closed states (C1 and C2) and one open (O) state (Wang et al., 1991),
Considerable low transition rates into and out of the deep closed state C2 provide the mechanism for the slower state of inactivation. h, d, and s are defined as the fractions of inactivation gates in the states O, C1, and C2, respectively. Since h+d+s = 1, the equations for h and s are
In this model, there are four rate coefficient kinetics: K1, K2, τ1, and τ2, or equivalently,
Assuming K1 = K2, h∞ = 1/(1 + K + K2). One can solve three rate coefficients by using the following experimental estimation (Diana et al., 2007),
With this model, one can analyze the steady state of membrane potential for the T-type Ca as shown in Figure 1Bii with steady-state activation and inactivation curves fitted with a Boltzmann function. The threshold for T-type Ca (measured as the point of 10% activation) is −76 mV, and half-activation is reached at −61 mV. Half-point inactivation is reached at −79 mV. These values are consistent with those experimental values (Edward, 2003; Diana et al., 2007). Furthermore, the overlap of activation and inactivation curves suggests that the full steady-state inactivation is not achieved between −71 and −50 mV, thus giving the UBC a tonic inward current and Ca influx at subthreshold potentials, similar to what has been reported in thalamocortical relay cells (Vincenzo et al., 2005).
In addition, we also consider two other typical ion channels. One is the L-type current IL modeled according to experimental data as (Diana et al., 2007)
with gL = 0.5 nS and ECa = 120 mV. The other is the h-type current Ih modeled according to experimental data as (Diana et al., 2007)
where gh = 1.5 nS and Eh = −40 mV.
2.2. Minimal UBC Model for Stability Analysis
Given the full model of UBC as above, note that the intrinsic currents IT and IK play a dominant role in maintaining the resting potential Vrest and generating responses for subthreshold input. To study the functional role of the T-type Ca channel and rectifier K channel in shaping the intrinsic dynamics of UBC membrane potential, we can simplify the full model as follows. First, one can ignore all other intrinsic currents except Il, IT, and IK. Then, for the IT current, considering the relationship between the two time constants such that τ2 ≫ τ1, as shown in Figure 1Bii (bottom), we can further simplify the IT component to ignore the slow time constant such that In this way, one can obtain a reduced minimal UBC model as a two-variable dynamical system,
To consider the stability of the steady state of membrane potential at Vrest, we explored a wide range of two parameters, gT and gK, while keeping the other parameters fixed. For this two-variable dynamical system, denote
The stability of Vrest is then obtained by calculating eigenvalues of the Jacobian matrix evaluated at V = Vrest:
The signs of the real part of eigenvalues determine the stability: a positive (negative) sign means V = Vrest is unstable (stable). The bifurcation points are where the sign changes.
2.3. UBC Synaptic Dynamics
Experimental studies have found that synaptic receptors expressed in UBCs are heterogeneous, with significant variation (Stijn and Zeeuw, 2014; Carolina and Trussell, 2015; Zampini et al., 2016), so that UBCs can express excitatory AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid), NMDA (N-methyl-D-aspartate), and mGluR1 (metabotropic glutamate receptor type 1) and inhibitory mGluR2 (metabotropic glutamate receptor type 2) receptors. There is also a slow spillover excitatory AMPA current (Zampini et al., 2016). Therefore, we modeled postsynaptic currents in a UBC with fast AMPA (AMPAf), slow spillover AMPA (AMPAsl), NMDA, and mGluR1, as well as mGluR2 dynamics:
The gating variable r(t) for all types of synapses was modeled as:
where the value of α was chosen so as to make the peak value of r as U induced by the first spike. In all synapses except mGluR1 and mGluR2, Ru was induced for short-term plasticity, which was modeled as previously (Markram et al., 1998; Izhikevich, 2003):
where R(u) is the short-term depression (facilitation) variable with the time constant τrec (τfac) and subjected to the pulsed decrease uR [increase U(1−u)] due to the n-th spike. The cumulative synaptic efficacy at any time is the product Ru that is incorporated into single synaptic dynamics. In summary, all synaptic parameters are listed in Table 1. All the simulations were done in MATLAB.
3. Results
3.1. Stability of the Resting Membrane Potential in UBCs
UBCs are relay cells between external MF inputs and GCs (Ann et al., 2014; Zampini et al., 2016), as illustrated in Figure 1A. Besides, the axons of UBCs themselves form a version of internal MFs to connect with other UBCs and GCs and establish an intrinsic relay network that can synchronize, amplify, and relay MFs inputs to downstream GCs (Birnstiel et al., 2009; Zampini et al., 2016). Moreover, the intrinsic properties of UBCs are important determinant factors for the computational performance of this relay network (Diana et al., 2007). To study these properties, we set up a full UBC model with all essential ion channels to generate experimental observations. The model is based on an integration-and-fire neuron but with additional T-type Ca (IT), L-type Ca (IL), mGluR2-dependent rectifier K (IK), and h-type (Ih) ion channel currents (see section Methods). In contrast to a detailed UBC model with all known ion channels and morphology (Subramaniyam et al., 2014), it should be noted that the full model here is simply to include the necessary, but a subset of all, component channels to explain UBC dynamics.
Within the full model above, the intrinsic properties of IT and IK play a dominant role in maintaining the resting membrane potential, modulating subthreshold responses as well as spiking activity. To study the functional role of those two channels, we simplified the full model to a reduced minimal UBC model that becomes a simple two-variable dynamical system with a Jacobian matrix to evaluate eigenvalues for stability analysis (see section Methods).
The stability of the resting membrane potential is used to study the steady state of the resting membrane potential Vrest. As we consider those the two most important channels, we computed Jacobian matrices at a wide range of key parameters; in this case, the conductances of gT and gK. The sign of the real part of eigenvalues determines the stability: a positive (negative) sign means V = Vrest is unstable (stable). The bifurcation points are where the sign changes. Theoretical results with eigenvalues λ are shown in Figure 2 in the parameter space of gT and gK.
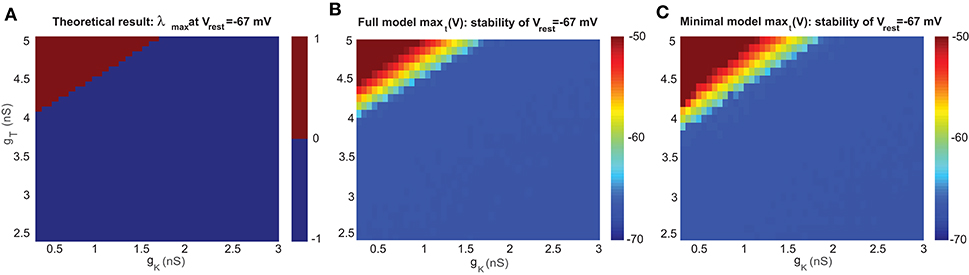
Figure 2. Stability analysis of the resting membrane potential of a UBC. (A) Bifurcation diagram based on theoretical analysis of eigenvalue λ at Vrest=-67 mV. The upper part of the bifurcation diagram (red) indicates that the UBC is unstable with positive eigenvalue, and the lower part (blue) is stable with a negative one. (B) Bifurcation diagram simulated by the full model at Vrest=-67 mV. (C) Similar to (B) but for the minimal model.
For the steady state of membrane potential, it is the leakage potential El in the model that is equivalent to the resting potential Vrest measured in experiments. Experimental observation found that there is no spontaneous firing when the single UBC is recorded by blocking all receptors, which that means Vrest is stable. Figure 2A shows the theoretical bifurcation diagram of the Jacobian matrix evaluated at Vrest = −67 mV, the value measured by experiments (Diana et al., 2007).
To analyze the stability property in detail, we compared the Jacobian matrix of the theoretical analysis with the simulated membrane potentials in the full and minimal models at El = −67 mV. With the same set of values for parameters gT and gK, both versions of the UBC model were simulated for a period of t=1 s, and then the maximum value of stimulated membrane potential maxt (V) over this period t was obtained for each pair of gT and gK. The results of maxt (V) are presented as the corresponding bifurcation diagrams in Figure 2B for the full model and Figure 2C for the minimal model. max(V) = −50 mV is the threshold for firing a spike in the model, so the membrane potential below this value is in the stable state. The comparison shows that the results of the two models are consistent with the theoretical result in the sense that the values of gT and gK are within a similar range for the stable resting potential, while the minimal model shifts the boundary line of stability by a small amount due to ignoring several ion channels in the model. These stability diagrams can give an estimate of the possible parameter values of gT and gK for future simulations below.
3.2. Rebound Firing in a UBC
Experimental observations show that some types of UBCs have a particular feature of rebound firing after the offset of inhibitory stimulus, which plays a functional role in information timing and encoding (Zampini et al., 2016). Similar to other types of neurons showing rebound firing in the cortex, the low threshold voltage-gated T-type Ca channel is thought to contribute to rebound firing because it can activate and inactivate with relatively little depolarization as shown in Figure 1Bii. It has been suggested that several mechanisms could produce hyperpolarization rebound, which could signal specific patterns of animal behavior (Diana et al., 2007).
A typical property of the T-type current in neurons is to generate rebound firing when an inhibitory current is injected. Figures 3A,B shows a few typical examples of UBC voltage traces simulated with both models at different settings of gT and gK. Similar to the stability diagram, the firing patterns of the UBC are shaped by ion channels. Higher gT values set the UBC to an unstable state, and lower values are for the stable state. However, for those values close to the bifurcation boundary, there is a regime of rebound firing after the offset of inhibitory current stimulation.
Figure 3. Stability diagram of a UBC with rebound firing at Vrest = −67 mV. (A) Examples of UBC response in the full model with different combinations of gT and gK for unstable state (top), rebound firing (middle), and stable state (bottom) after the offset of a constant inhibitory current. (B) Similar to (A) but with the minimal model. (C) Stability diagram of the UBC in the full model at Vrest =-67 mV showing three regions of unstable state (maxt (V) >-50 mV), rebound firing (maxt (V) ∈ [-60−50] mV), and stable state (maxt (V) <-60 mV) in the parameter space of gT and gK. (D) Similar to (C) but with the minimal model.
We measured the maximal value of membrane potentials after stimulation offset and obtained the rebound firing diagram simulated with UBC models by varying gT and gK, as shown in Figures 3C,D. The theoretical results suggest that the values of gT and gK in a UBC should be close to the bifurcation boundary in the stability diagram to generate rebound firing, where V ∈ [−60 −50] mV is marked as the rebound firing regime. Within the stable regime of Figure 2, the UBC presents rebound firing activity, as shown in experiments. A typical membrane voltage trace of the full model for rebound firing is shown in Figure 3A (middle) by using the parameter values measured in experiments for the conductance gT = 3.5 nS and gK = 0.3 nS. With these values, the UBC does not present spontaneous firing but shows rebound firing with an inhibitory current. We then fix the two parameters at these values for the rest of the paper. These results suggest that the intrinsic T-type Ca channel can profoundly shape the response to MF input and mediate rebound firing in a UBC.
3.3. UBC Subthreshold Resonance
Generation of action potentials in neurons depends on how relatively weaker inputs influence the dynamics of subthreshold voltage without firing activity. One typical behavior for subthreshold neuronal dynamics is showing membrane potential resonance, i.e., there there is a maximal subthreshold response at a non-zero frequency (Ostojic et al., 2015). To investigate the subthreshold resonance of a UBC, we injected a sinusoidal zap current with increasing frequency. If there were a significant resonance response at a certain frequency, the membrane potential would be amplified. To obtain the resonance frequency, Fast Fourier Transform (FFT) was used for the voltage response of the UBC to get a spectrum of response amplitude. The frequency at which the maximal amplitude is observed is called the resonance frequency, which is set by a combination of passive and active intrinsic membrane properties of neurons (Hutcheon and Yarom, 2000).
Figure 4 shows the subthreshold dynamics of UBC models with linearly (Figures 4A,C) and non-linearly (Figures 4D–F) increasing frequency. There are significant resonance responses for both types of inputs, and the amplitude of membrane potential first increases and then decreases, so that there is a low-frequency (~6 Hz) subthreshold potential resonance in both models, as seen with FFT. Such a subthreshold resonance in UBCs is similar to that in thalamic neurons, which also involves T-type Ca current (Wang et al., 1991). The resonance frequencies of the two UBC models are similar, presumably due to the fact that the T-type Ca current plays an important role in resonance generation. The nature of resonance is intrinsic and independent of whether the input pattern is linear or non-linear. These results reveal that the subthreshold resonance is related to intrinsic properties but independent of the exact types of external inputs.
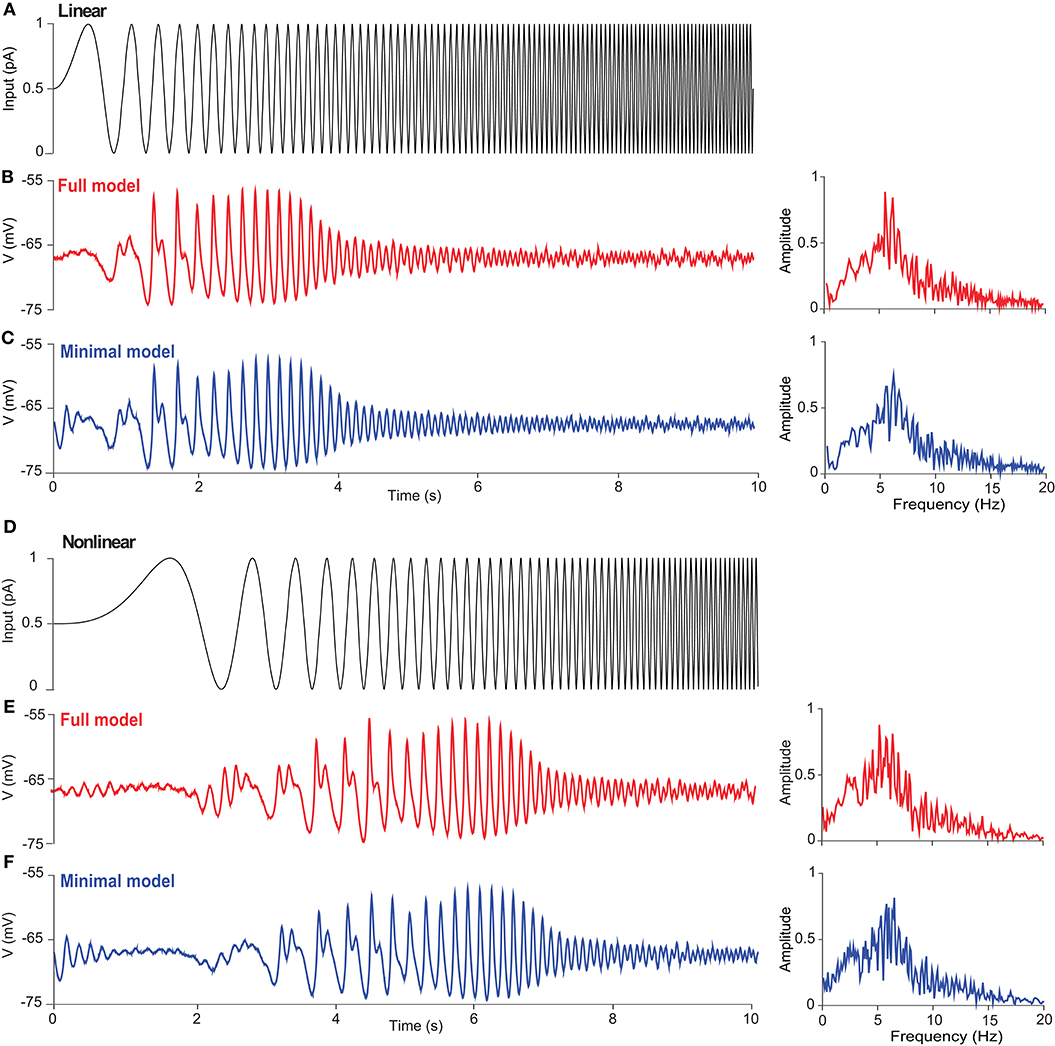
Figure 4. Subthreshold resonance of a UBC in response to sinusoidal inputs with linearly and non-linearly increasing frequency. (A) Zap current input from 0 to 10 Hz linearly as Iinput = Iampsin(2f(t)t) with f(t) = fmaxt/T at Iamp = 1 pA, fmax = 10 Hz, and T = 10 s. (B) UBC voltage response triggered by the stimulus given in (A) in the full model. (Right) Fourier transform of UBC response showing the resonance of UBC dynamics with a peak frequency around 6 Hz. (C) Similar to (B) but simulated with the minimal model. (D) Zap current input from 0 to 10 Hz non-linearly as at Iamp = 1 pA. (E,F) Similar to (B,C) showing UBC response and resonance.
3.4. UBC Response to Current Input
In the classical protocol of in vivo recording, when the animal was rotating its head, it was found that the responses of different types of neurons in the vestibular cerebellum presented phase shifts in different degrees (Barmack and Vadim, 2008), where the firing activity of a UBC could be modulated by the input current. When the response is fitted with a sinusoidal function, the phase shifts between UBC response and input current are distributed uniformly, and it has been shown that this uniform distribution contributes to the relaying of input MF information (Zampini et al., 2016).
We set out to investigate the firing-rate modulation of UBCs using both models with oscillating input currents with a fixed amplitude (10 pA) but at different frequencies; the three typical inputs are shown in Figure 5A (top). Compared to the full model (Figure 5A, middle), the minimal model generates fewer spikes under the same current input (Figure 5A, bottom), presumably due to the absence of L-type and h-type ion channels, which could induce firing via a pacemaking mechanism. After fitting the average UBC firing activity over several input cycles, one can obtain the amplitude and phase shift of modulation with respect to the input. Interestingly, the phase shift of the modulation exhibits a similar behavior for both models (Figure 5B), while the amplitude of the modulation in the full model is larger than that of the minimal model (Figure 5C). This difference is a direct consequence of the higher firing activity in the full model induced by L-type and h-type channels. These results suggest that the phase shifts of the input modulation observed in UBC experiments are not induced by intrinsic ion channel properties, which only contribute to the amplitude of firing rate.
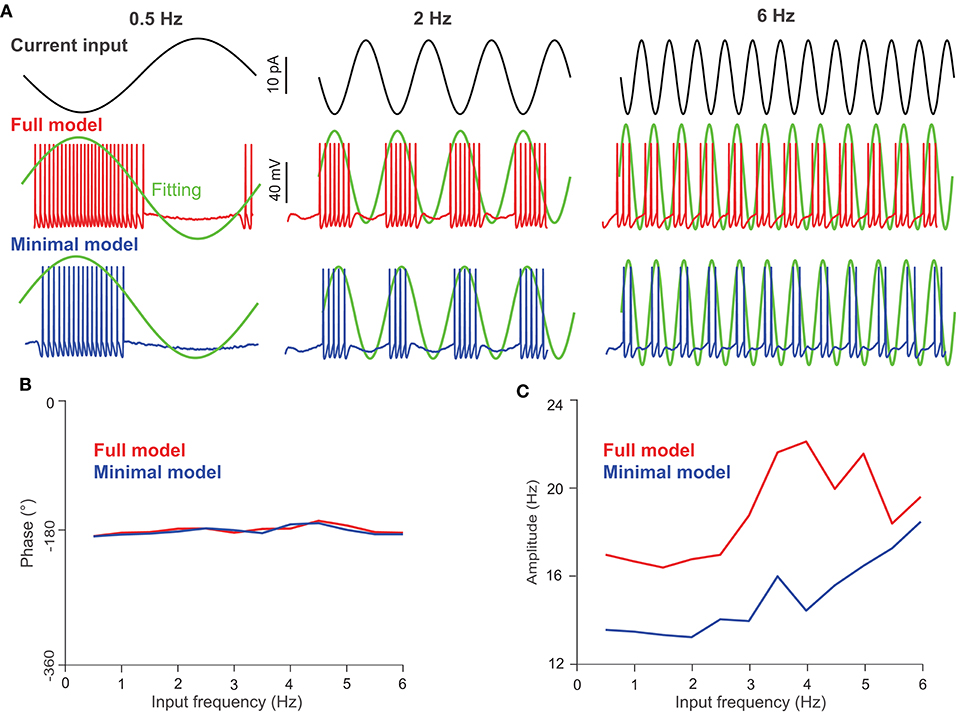
Figure 5. UBC response to oscillating current inputs. (A) Response of UBC models to sinusoidal current inputs with 0.5, 2, and 6 Hz frequencies and 10 pA amplitude. (Top) Current inputs of three frequencies. UBC voltage traces obtained from the full (middle) and minimal (bottom) models with fitting curves (green) to compute the phase in degree and amplitude in Hz of UBC responses. The fitting curve was obtained by fitting the instantaneous firing rate of UBC responses. (B) The phase shift of UBC response relative to the input phase in the full (red) and minimal (blue) model as a function of modulation frequency. (C) Similar to (B) but for UBC response amplitude.
3.5. UBC Response to Synaptic Input
So far, we have studied the intrinsic properties of UBCs through different ion channels and the dynamics of UBCs in response to current input. In real scenarios, the firing activity of a single MF encodes the velocity of head rotation in animals (Arenz et al., 2008). Since a single UBC only receives one MF, a mono-connection from MF to UBC makes it easy to study how the firing activity of the UBC is changed by presynaptic inputs.
Recent experiments show that a UBC can embed a large variety of synaptic receptors such that there is a rich diversity of dynamics in its firing activity (Carolina and Trussell, 2015; Zampini et al., 2016). UBC brushes are endowed with different types of synaptic receptors, including the AMPA, NMDA, mGluR1, and mGluR2 receptors (Billups et al., 2002; Zampini et al., 2016). The presynaptic element of these synapses shows the typical mossy fiber terminal but forms an exceptionally extended synaptic contact that can entrap glutamate for several hundred milliseconds, thus enabling unusually long excitatory responses (Ann et al., 2014; Stijn and Zeeuw, 2014; Zampini et al., 2016).
To understand how a UBC may transcode its synaptic inputs, we examined the synaptic response of a UBC by using different types of receptors. Based on the experimental data of UBCs recorded (Zampini et al., 2016), five types of synapses can be modeled: fast AMPA (AMPAf), slow spillover AMPA (AMPAsl), excitatory NMDA and mGluR1, and inhibitory mGluR2 (see section Methods).
To simulate the UBC response to the synaptic current of each type of receptor, Poisson stimulations of a single mossy fiber at different frequencies were used, and the UBC voltage was fixed at -57 mV under simulated voltage clamp. We used the minimal UBC model, which has a lower firing activity compared to that of the full model. In this way, one can clearly examine the difference between different receptors to avoid saturation at high firing rate under strong stimulation. Figure 6A shows the simulated excitatory/inhibitory postsynaptic currents of the five individual receptors in the UBC over 4 s using Possion stimuli with the frequency of 1, 20, and 50 Hz, respectively. It can be observed that only the mGluR2 current is positive (inhibitory), while the currents of the other four receptors are negative (excitatory). The output current of the fast AMPA receptor shows a typical behavior of rapid increase and decay. The responses of slow AMPA and mGluR2 are relatively larger and longer than those of the other receptors, so these two play a major role in shaping the response of a UBC to low-frequency stimulation. When Poisson stimulation is changed to higher frequencies, the response currents of these receptors vary significantly. If the stimulation frequency is greater than 20 Hz, the response currents of mGluR1 and mGluR2 increase and saturate over time, and the current after stabilization is much larger than that in the other receptors. Taken together, these synaptic dynamics can individually or together express on different individual UBCs to generate a large variety of temporal dynamics for information relay (Carolina and Trussell, 2015; Zampini et al., 2016).
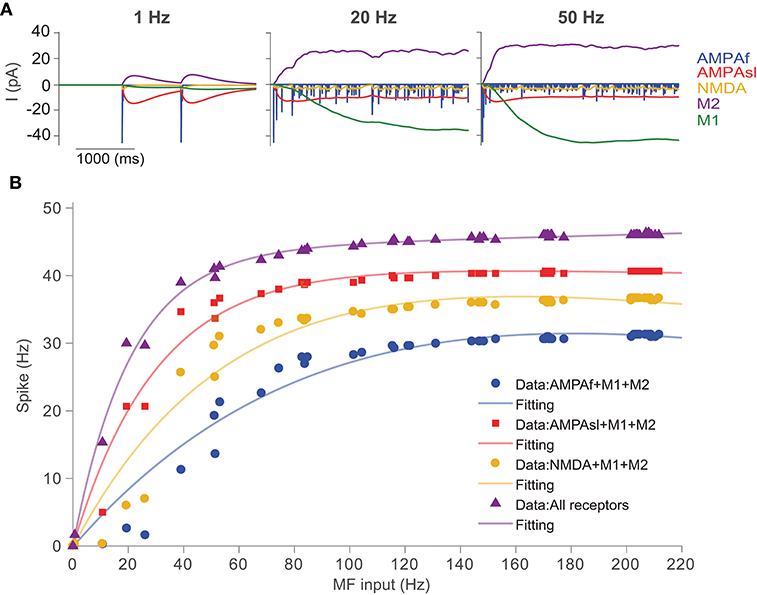
Figure 6. UBC response to synaptic inputs with different types of receptors. (A) Receptor dynamics of fast AMPA (AMPAf), slow AMPA (AMPAsl), NMDA, mGluR1 (M1), and mGluR2 (M2) triggered by mossy fiber Poisson spike trains at frequencies of 1, 20, and 50 Hz. (B) Spiking output of UBCs with different combinations of synaptic receptors in response to Poisson stimulation of MF inputs.
We then study the input-output relationship of UBC response, which is determined predominantly by the properties of the synapses and their short-term plasticities. The cerebellum can control high-precise motor patterns with millisecond resolution by using a wide range of action potential firing rates. Figure 6B shows the results for the UBC firing rate response with different combinations of synaptic receptors. We measured the spiking response obtained from simulated membrane voltage traces of the UBC model during a single mossy fiber Poisson stimulus with a wide range of frequencies (1-220 Hz) and calculated the UBC output firing frequency, which can be fitted with a double exponential function.
In order to investigate the effects of different receptors on UBC response output, we changed the receptor type of the MF-UBC synapse in the model by combining mGluR1 and mGluR2 with the other three receptors respectively. In this way, the slow dynamics of mGluR1 and mGluR2 can be balanced to amplify the other three receptors, AMPAf, AMPAsl, and NMDA. The results show that the output firing rate is changed when the types of synaptic receptors are altered. A non-linear relationship between output firing frequency and input MF stimulation frequency can be observed. The output discharge frequency increases at the low-frequency stimuli. For higher frequencies, the output discharge frequency increases gradually and then saturates. These results suggest that, for the low frequencies, the slow spillover mechanism of AMPA receptors predominates in coding the frequency of synaptic firing rate. However, all receptors can cooperate to regulate synaptic firing at all frequencies of inputs.
Next, we examined the firing rate modulation of continuous MF input by different receptors using the full model. For simplicity, we only consider the AMPAf, AMPAsl, and NMDA receptors, as they are shown to generate enough phase shifts for UBCs (Zampini et al., 2016). The UBC voltage traces for different receptors to the same sinusoidal MF input with a modulated firing rate at the frequency of 1 Hz are shown in Figure 7A, where firing rates are significantly different between receptors. Again, the average firing rate of a UBC over several stimulation cycles was fitted by a sinusoidal function to compute the modulation phase (Figure 7B) and amplitude (Figure 7C) in UBC responses. These three types of receptors, AMPAf, AMPAsl, and NMDA, can induce different phase shifts relative to the MF input due to their dynamics occurring at different time scales. These results show that the phase shifts of UBC response relative to the MF input are induced by different types of receptors. Together with the variation of synaptic connection weights, UBCs can relay the MF input over a full spectrum of any direction in the phase space (Zampini et al., 2016).
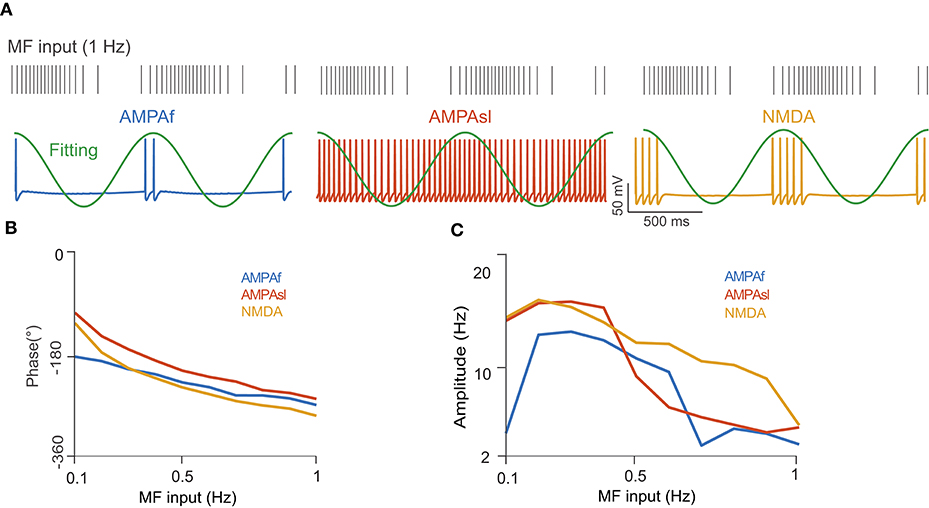
Figure 7. UBC response to MF input with a modulated firing rate. (A) (Top) MF spike train input sampled from a modulated sinusoidal firing rate A sin(2πft) + A with 1 Hz frequency and amplitude A = 20 Hz. Vertical ticks indicate spike times. (Bottom) UBC voltage traces simulated with different receptors of AMPAf, AMPAsl, and NMDA, respectively. Fitting curves (green) are sinusoidal functions to compute UBC response modulation in terms of phase shift and amplitude. (B) The phase shift of UBC response relative to MF sinusoidal input with three types of receptors as a function of MF input frequencies. (C) Similar to (B) but for UBC response amplitude.
4. Discussion
To understand how information is processed in a brain region, it is crucial to study the intrinsic properties of the neurons within the circuitry. Here, we developed two models for a UBC in the granular layer of the cerebellum based on the experimental data obtained in the literature. We clarified the functional role of the T-type Ca and K channels in shaping the dynamics of UBCs by stability analysis of the resting membrane potential, rebound firing after inhibitory current injection, and subthreshold response resonance. Furthermore, we demonstrated that the rich types of synaptic receptors expressed on UBCs can modulate their strength of firing activity, as well as the amplitude and phase shift of the firing rate relative to presynaptic MF input.
The only known source of excitation for UBCs is their single giant dendritic brush, which can receive the external MFs. The outside input passes into MFs, which can be spontaneously active at high frequency in vivo (Arenz et al., 2008) and are thus likely to drive the complex pattern of activity of UBCs observed in experiments. However, UBCs do not discharge spontaneously at rest. We showed, by using mathematical analysis of a reduced minimal model, that the T-type Ca and mGluR2-dependent rectifier K channels play a particularly important role in maintaining the stable state of the resting membrane potential. By comparing simulations with both full and minimal models with theoretical results, we found that the resting potential of a UBC at Vrest = −67 mV yields reasonable values for the conductance parameters gT and gK, which are consistent with experimental measurements (Diana et al., 2007). These types of analysis and mechanisms may be useful for studying other types of neurons that have no spontaneous activity, for instance, the retinal ganglion cells in the retina of the salamander (Liu and Gollisch, 2015). However, the existence of spontaneous activity, even in the retina, depends on a number of biophysical properties of neurons (Sernagor and Grzywacz, 1999; Margolis and Detwiler, 2007).
UBCs can display rebound burst-firing upon hyperpolarization from their resting membrane potential. Rebound firing has been suggested to play an important role in cerebellar function (Aizenman et al., 1998; Aizenman and Linden, 1999; Kistler and Zeeuw, 2003; Pugh and Raman, 2006) under different in vitro and in vivo experimental conditions (Karina et al., 2008). In the current study, the experimental and modeling results indicate that UBCs can generate rebound firing with inhibitory current injection, similar to what has been documented in experimental studies (Zampini et al., 2016). In addition, the parameter values of the conductance of the mGluR2-dependent K channel as 0.3 nS and the T-type Ca channel as 3.5 nS are within a reasonable range of experimental conditions. Therefore, the rebound firing of UBCs is most likely mediated by T-type calcium channels, which is consistent with previous findings (Aizenman and Linden, 1999; Molineux et al., 2006).
One of the non-linear features in neuronal computation is that neurons can generate resonance, i.e., enhanced response at a particular preferential frequency (Hutcheon and Yarom, 2000). In the cerebellum, GCs show theta-frequency resonance around 6-8 Hz, which was suggested to be due to the existence of a slow repolarizing K current (D'Angelo et al., 2001). Here, we found that injecting the UBC model with sinusoidal currents of different frequencies can generate resonant responses as well and that subthreshold resonance occurs at a low frequency (~6 Hz). Considering that GCs typically fire at a low frequency (~5–6 Hz), UBCs, as a relay between MFs and GCs, may utilize their subthreshold resonance to maximize the information carried by subthreshold membrane potentials for downstream granule cells (Ann et al., 2014; Zampini et al., 2016).
As well as its intrinsic properties, the UBC has a short dendrite as a presynaptic terminal receiving afferent synaptic input from external MFs. The unique feature of the MF-UBC synapse is that there exists a very extensive synaptic apposition with multiple release sites (Billups et al., 2002) as well as a large variety of synapse receptors, as modeled in the current study. Specifically, UBCs can be classified as ON and OFF types according to their expression of synaptic receptors (Carolina and Trussell, 2015; Zampini et al., 2016). The ON type of UBC shows excitatory responses to glutamate inputs resulting from high expression of AMPARs and mGluR1, whereas the OFF type of UBC shows inhibitory responses to glutamate inputs due to mGluR2 activation. Therefore, receptor heterogeneity can induce a large diversity of dynamics in ring activity, as shown in this work. We found that the slow spillover AMPA receptors, besides typical AMPA and NMDA, play an important role in shaping dynamics, similar to experimental observations (Zampini et al., 2016). Altogether, different synaptic receptors in UBCs seems to play different roles in neuronal computation (Ann et al., 2014; Stijn and Zeeuw, 2014; Carolina and Trussell, 2015; Zampini et al., 2016). The most important part of these computations is to generate different relays, or shifts in terms of phase of MF input, which provide a temporal basis for GCs and Purkinje cells (Ann et al., 2014; Zampini et al., 2016), eventually enabling the fulfillment of the complex computation done by the cerebellum (Raymond and Medina, 2018).
In the current work, due to its simple dendritic structure, we employed a specific type of neuron in the cerebellum, the UBC, to explain how the intrinsic and synaptic properties of a neuron shape diverse behaviors of single neuronal dynamics. The important computational properties for single neurons consist of both intrinsic and synaptic dynamics (Abbott and Regehr, 2004; Harvey et al., 2009). Intrinsic properties play a dominant role in subthreshold response and spiking activity, whereas the synaptic dynamics rely on spikes passing between neurons. Therefore, intrinsic properties can be combined with synaptic dynamics at different time scales to shape diverse neural dynamics (Latorre et al., 2016; Torres et al., 2019). Such interactions become more prominent at the network level (Buonomano and Maass, 2009; Liu and Buonomano, 2009; Liu, 2011). A detailed model with multiple compartments and morphological structure is particularly useful for validating experiments (Subramaniyam et al., 2014). However, to study the network dynamics, modeling of single neurons mostly relies on computationally efficient models similar to the ones used in this work to strike a balance between detail and abstraction (Herz et al., 2006). Eventually, the dynamics of single neurons together with a population of neurons within the same neuronal circuit and across different brain areas form rich dynamical behaviors and computations (Buonomano and Maass, 2009; Yang et al., 2019).
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
LA, ZY, and JL: conceptualization and project administration. LA, YT, DW, and SJ: formal analysis. LA, QP, QW, and JL: funding acquisition. LA, YT, and DW: investigation. LA, YT, ZY, and JL: methodology and writing—original draft. YT, DW, and JL: software. LA, QW, and JL: supervision. YT and ZY: validation. YT, ZY, SJ, and JL: visualization.
Funding
This work was supported by the Key Program of NSFC-Tongyong Union Foundation, China (Grant No. U1636209), National Natural Science Foundation of China (Grant Nos. 61572385, and 61902292), Key Research and Development Programs of Shanxi, China (Grant Nos. 2019ZDLGY13-07 and 2019ZDLGY13-04), Zhejiang Lab, China (Grant Nos. 2019KC0AB03 and 2019KC0AD02), and Royal Society Newton Advanced Fellowship, UK (Grant No. NAF-R1-191082).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abbott, L. F., and Regehr, W. G. (2004). Synaptic computation. Nature 431, 796–803. doi: 10.1038/nature03010
Aizenman, C. D., and Linden, D. J. (1999). Regulation of the rebound depolarization and spontaneous firing patterns of deep nuclear neurons in slices of rat cerebellum. J. Neurophysiol. 82:1697. doi: 10.1152/jn.1999.82.4.1697
Aizenman, C. D., Manis, P. B., and Linden, D. J. (1998). Polarity of long-term synaptic gain change is related to postsynaptic spike firing at a cerebellar inhibitory synapse. Neuron 21, 827–835. doi: 10.1016/S0896-6273(00)80598-X
Ann, K., Greg, W., Patrick, K., Karina, A., Abbott, L. F., and Sawtell, N. B. (2014). A temporal basis for predicting the sensory consequences of motor commands in an electric fish. Nat. Neurosci. 17, 416–22. doi: 10.1038/nn.3650
Arenz, A., Silver, R. A., Schaefer, A. T., and Margrie, T. W. (2008). The contribution of single synapses to sensory representation in vivo. Science 321, 977–980. doi: 10.1126/science.1158391
Barmack, N. H., and Vadim, Y. (2008). Functions of interneurons in mouse cerebellum. J. Neurosci. 28, 1140–1152. doi: 10.1523/JNEUROSCI.3942-07.2008
Billups, D., Liu, Y. B., Birnstiel, S., and Slater, N. T. (2002). NMDA receptor-mediated currents in rat cerebellar granule and unipolar brush cells. J. Neurophysiol. 87, 1948–1959. doi: 10.1152/jn.00599.2001
Birnstiel, S., Slater, N. T., Mccrimmon, D. R., Mugnaini, E., and Hartell, N. A. (2009). Voltage-dependent calcium signaling in rat cerebellar unipolar brush cells. Neuroscience 162, 702–712. doi: 10.1016/j.neuroscience.2009.01.051
Bostan, A. C., and Strick, P. L. (2018). The basal ganglia and the cerebellum: nodes in an integrated network. Nat. Rev. Neurosci. 19:338. doi: 10.1038/s41583-018-0002-7
Buonomano, D. V., and Maass, W. (2009). State-dependent computations: spatiotemporal processing in cortical networks. Nat. Rev. Neurosci. 10, 113–125. doi: 10.1038/nrn2558
Carolina, B. M., and Trussell, L. O. (2015). On and off unipolar brush cells transform multisensory inputs to the auditory system. Neuron 85, 1029–1042. doi: 10.1016/j.neuron.2015.02.009
Chung, S. H., Kim, C. T., Jeong, Y. G., and Lee, N. S. (2010). Tbr2-immunopsitive unipolar brush cells are associated with ectopic zebrin II-immunoreactive purkinje cell clusters in the cerebellum of scrambler mice. Anat. Cell Biol. 43:72. doi: 10.5115/acb.2010.43.1.72
D'Angelo, E., Nieus, T., Maffei, A., Armano, S., Rossi, P., Taglietti, V., et al. (2001). Theta-frequency bursting and resonance in cerebellar granule cells: experimental evidence and modeling of a slow k+-dependent mechanism. J. Neurosci. 21, 759–770. doi: 10.1523/JNEUROSCI.21-03-00759.2001
Diana, M. A., Yo, O., Gilliane, M., Thibault, C., Mireille, C., and Stephane, D. (2007). T-type and L-type ca2+ conductances define and encode the bimodal firing pattern of vestibulocerebellar unipolar brush cells. J. Neurosci. 27, 3823–38. doi: 10.1523/JNEUROSCI.4719-06.2007
Diño, M. R., Willard, F. H., and Mugnaini, E. (1999). Distribution of unipolar brush cells and other calretinin immunoreactive components in the mammalian cerebellar cortex. J. Neurocytol. 28, 99–123. doi: 10.1023/A:1007072105919
Edward, P. R. (2003). Molecular physiology of low-voltage-activated T-type calcium channels. Physiol. Rev. 83, 117–161. doi: 10.1152/physrev.00018.2002
Harvey, C. D., Collman, F., Dombeck, D. A., and Tank, D. W. (2009). Intracellular dynamics of hippocampal place cells during virtual navigation. Nature 461, 941–946. doi: 10.1038/nature08499
Herz, A. V., Gollisch, T., Machens, C. K., and Jaeger, D. (2006). Modeling single-neuron dynamics and computations: a balance of detail and abstraction. Science 314, 80–5. doi: 10.1126/science.1127240
Hutcheon, B., and Yarom, Y. (2000). Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci. 23, 216–222. doi: 10.1016/S0166-2236(00)01547-2
Ito, M. (2008). Control of mental activities by internal models in the cerebellum. Nat. Rev. Neurosci. 9, 304–313. doi: 10.1038/nrn2332
Izhikevich, E. M. (2003). Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569–72. doi: 10.1109/TNN.2003.820440
Jaarsma, D., Wenthold, R. J., and Mugnaini, E. (1995). Glutamate receptor subunits at mossy fiber-unipolar brush cell synapses: light and electron microscopic immunocytochemical study in cerebellar cortex of rat and cat. J. Comp. Neurol. 357, 145–160. doi: 10.1002/cne.903570113
Karina, A., Walter, J. T., Adam, K., Graham, E. D., and Kamran, K. (2008). Questioning the role of rebound firing in the cerebellum. Nat. Neurosci. 11:1256. doi: 10.1038/nn.2195
Kinney, G. A., Overstreet, L. S., and Slater, N. T. (1997). Prolonged physiological entrapment of glutamate in the synaptic cleft of cerebellar unipolar brush cells. J. Neurophysiol. 78, 1320–33. doi: 10.1152/jn.1997.78.3.1320
Kistler, W. M., and Zeeuw, C. I. D. (2003). Time windows and reverberating loops: a reverse-engineering approach to cerebellar function. Cerebellum 2, 44–54. doi: 10.1080/14734220309426
Latorre, R., Torres, J. J., and Varona, P. (2016). Interplay between subthreshold oscillations and depressing synapses in single neurons. PLoS ONE 11:e0145830. doi: 10.1371/journal.pone.0145830
Liu, J. K. (2011). Learning rule of homeostatic synaptic scaling: presynaptic dependent or not. Neural Comput. 23, 3145–3161. doi: 10.1162/NECO_a_00210
Liu, J. K., and Buonomano, D. V. (2009). Embedding multiple trajectories in simulated recurrent neural networks in a self-organizing manner. J. Neurosci. 29, 13172–13181. doi: 10.1523/JNEUROSCI.2358-09.2009
Liu, J. K., and Gollisch, T. (2015). Spike-triggered covariance analysis reveals phenomenological diversity of contrast adaptation in the retina. PLoS Comput. Biol. 11:e1004425. doi: 10.1371/journal.pcbi.1004425
Margolis, D. J., and Detwiler, P. B. (2007). Different mechanisms generate maintained activity in on and off retinal ganglion cells. J. Neurosci. 27, 5994–6005. doi: 10.1523/JNEUROSCI.0130-07.2007
Markram, H., Wang, Y., and Tsodyks, M. (1998). Differential signaling via the same axon of neocortical pyramidal neurons. Proc. Natl. Acad. Sci. U.S.A. 95, 5323–5328. doi: 10.1073/pnas.95.9.5323
Molineux, M. L., McRory, J. E., McKay, B. E., Hamid, J., Mehaffey, W. H., Rehak, R., et al. (2006). Specific T-type calcium channel isoforms are associated with distinct burst phenotypes in deep cerebellar nuclear neurons. Proc. Natl. Acad. Sci. U.S.A. 103, 5555–5560. doi: 10.1073/pnas.0601261103
Morin, F., Dino, M. R., and Mugnaini, E. (2001). Postnatal differentiation of unipolar brush cells and mossy fiber-unipolar brush cell synapses in rat cerebellum. Neuroscience 104, 1127–1139. doi: 10.1016/S0306-4522(01)00144-0
Mugnaini, E., Dino, M. R., and Jaarsma, D. (1997). The unipolar brush cells of the mammalian cerebellum and cochlear nucleus: cytology and microcircuitry. Prog. Brain Res. 114, 131–150. doi: 10.1016/S0079-6123(08)63362-2
Mugnaini, E., Floris, A., and Mary, W. G. (1994). Extraordinary synapses of the unipolar brush cell: an electron microscopic study in the rat cerebellum. Synapse 16, 284–311. doi: 10.1002/syn.890160406
Mugnaini, E., Sekerkova, G., and Martina, M. (2011). The unipolar brush cell: a remarkable neuron finally receiving deserved attention. Brain Res. Rev. 66, 220–245. doi: 10.1016/j.brainresrev.2010.10.001
Nunzi, M. G., Ryuichi, S., and Enrico, M. (2002). Differential expression of calretinin and metabotropic glutamate receptor mglur1alpha defines subsets of unipolar brush cells in mouse cerebellum. J. Comp. Neurol. 451, 189–199. doi: 10.1002/cne.10344
Ostojic, S., Szapiro, G., Schwartz, E., Barbour, B., Brunel, N., and Hakim, V. (2015). Neuronal morphology generates high-frequency firing resonance. J. Neurosci. 35:7056. doi: 10.1523/JNEUROSCI.3924-14.2015
Poirazi, P., Brannon, T., and Mel Bartlet, W. (2003). Arithmetic of subthreshold synaptic summation in a model CA1 pyramidal cell. Neuron 37, 977–987. doi: 10.1016/S0896-6273(03)00148-X
Pugh, J. R., and Raman, I. M. (2006). Potentiation of mossy fiber EPSCs in the cerebellar nuclei by NMDA receptor activation followed by postinhibitory rebound current. Neuron 51, 113–123. doi: 10.1016/j.neuron.2006.05.021
Raymond, J. L., and Medina, J. F. (2018). Computational principles of supervised learning in the cerebellum. Annu. Rev. Neurosci. 41:233. doi: 10.1146/annurev-neuro-080317-061948
Rossi, D. J., Alford, S., Mugnaini, E., and Slater, N. T. (1995). Properties of transmission at a giant glutamatergic synapse in cerebellum: the mossy fiber-unipolar brush cell synapse. J. Neurophysiol. 74, 24–42. doi: 10.1152/jn.1995.74.1.24
Sernagor, E., and Grzywacz, N. M. (1999). Spontaneous activity in developing turtle retinal ganglion cells: pharmacological studies. J. Neurosci. 19, 3874–3887. doi: 10.1523/JNEUROSCI.19-10-03874.1999
Stijn, V. D., and Zeeuw, C. I. D. (2014). Variable timing of synaptic transmission in cerebellar unipolar brush cells. Proc. Natl. Acad. Sci. U.S.A. 111, 5403–5408. doi: 10.1073/pnas.1314219111
Strick, P. L., Dum, R. P., and Fiez, J. A. (2009). Cerebellum and nonmotor function. Annu. Rev. Neurosci. 32, 413–434. doi: 10.1146/annurev.neuro.31.060407.125606
Subramaniyam, S., Solinas, S., Perin, P., Locatelli, F., Masetto, S., and D'Angelo, E. (2014). Computational modeling predicts the ionic mechanism of late-onset responses in unipolar brush cells. Front. Cell. Neurosci. 8:237. doi: 10.3389/fncel.2014.00237
Torres, J. J., Baroni, F., Latorre, R., and Varona, P. (2019). Temporal discrimination from the interaction between dynamic synapses and intrinsic subthreshold oscillations. bioRxiv 727735. doi: 10.1101/727735
Tsai, P. T., Court, H., Yunxiang, C., Emily, G. C., Sadowski, A. R., Leech, J. M., et al. (2012). Autistic-like behaviour and cerebellar dysfunction in Purkinje cell Tsc1 mutant mice. Nature 488, 647–51. doi: 10.1038/nature11310
Vincenzo, C., Toth, T. I., Cope, D. W., Kate, B., and Hughes, S. W. (2005). The ‘window' T-type calcium current in brain dynamics of different behavioural states. J. Physiol. 562, 121–129. doi: 10.1113/jphysiol.2004.076273
Wagner, M. J., Kim, T. H., Savall, J., Schnitzer, M. J., and Luo, L. (2017). Cerebellar granule cells encode the expectation of reward. Nature 544, 96–100. doi: 10.1038/nature21726
Wang, X. J., Rinzel, J., and Rogawski, M. A. (1991). A model of the T-type calcium current and the low-threshold spike in thalamic neurons. J. Neurophysiol. 66, 839–850. doi: 10.1152/jn.1991.66.3.839
Yang, M., Zhou, Z., Zhang, J., Jia, S., Li, T., Guan, J., et al. (2019). MATRIEX imaging: multiarea two-photon real-time in vivo explorer. Light Science Appl. 8:109. doi: 10.1038/s41377-019-0219-x
Zampini, V., Jian, K. L., Diana, M. A., Maldonado, P. P., Brunel, N., and Dieudonne, S. (2016). Mechanisms and functional roles of glutamatergic synapse diversity in a cerebellar circuit. Elife 5:e15872. doi: 10.7554/eLife.15872
Keywords: neural dynamic modeling, stability analysis, rebound firing, synaptic dynamics, dynamical system
Citation: An L, Tang Y, Wang D, Jia S, Pei Q, Wang Q, Yu Z and Liu JK (2020) Intrinsic and Synaptic Properties Shaping Diverse Behaviors of Neural Dynamics. Front. Comput. Neurosci. 14:26. doi: 10.3389/fncom.2020.00026
Received: 06 December 2019; Accepted: 18 March 2020;
Published: 21 April 2020.
Edited by:
Germán Mato, Bariloche Atomic Centre (CNEA), ArgentinaReviewed by:
Pablo Varona, Autonomous University of Madrid, SpainErvin Wolf, University of Debrecen, Hungary
Copyright © 2020 An, Tang, Wang, Jia, Pei, Wang, Yu and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lingling An, YW4ubGluZ2xpbmdAZ21haWwuY29t; Zhaofei Yu, eXV6ZjEyQHBrdS5lZHUuY24=
 Lingling An
Lingling An Yuanhong Tang
Yuanhong Tang Doudou Wang1
Doudou Wang1 Shanshan Jia
Shanshan Jia Zhaofei Yu
Zhaofei Yu Jian K. Liu
Jian K. Liu