
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Comput. Neurosci. , 30 July 2014
Volume 8 - 2014 | https://doi.org/10.3389/fncom.2014.00080
This article is part of the Research Topic Hierarchical Object Representations in the Visual Cortex and Computer Vision View all 20 articles
The remarkable abilities of the primate visual system have inspired the construction of computational models of some visual neurons. We propose a trainable hierarchical object recognition model, which we call S-COSFIRE (S stands for Shape and COSFIRE stands for Combination Of Shifted FIlter REsponses) and use it to localize and recognize objects of interests embedded in complex scenes. It is inspired by the visual processing in the ventral stream (V1/V2 → V4 → TEO). Recognition and localization of objects embedded in complex scenes is important for many computer vision applications. Most existing methods require prior segmentation of the objects from the background which on its turn requires recognition. An S-COSFIRE filter is automatically configured to be selective for an arrangement of contour-based features that belong to a prototype shape specified by an example. The configuration comprises selecting relevant vertex detectors and determining certain blur and shift parameters. The response is computed as the weighted geometric mean of the blurred and shifted responses of the selected vertex detectors. S-COSFIRE filters share similar properties with some neurons in inferotemporal cortex, which provided inspiration for this work. We demonstrate the effectiveness of S-COSFIRE filters in two applications: letter and keyword spotting in handwritten manuscripts and object spotting in complex scenes for the computer vision system of a domestic robot. S-COSFIRE filters are effective to recognize and localize (deformable) objects in images of complex scenes without requiring prior segmentation. They are versatile trainable shape detectors, conceptually simple and easy to implement. The presented hierarchical shape representation contributes to a better understanding of the brain and to more robust computer vision algorithms.
Shape is perceptually the most important visual characteristic of an object. Although there is no formal definition—as with most perceptual related concepts—it is understood that the two-dimensional shape of an object is characterized by the relative spatial positions of a collection of contour-based features.
Let us consider, for instance, the square in Figure 1A, which we refer to as a reference or prototype object. From the point of view of visual perception the incomplete object in Figure 1B is very similar to the prototype even though it is composed of only 25% of the contour pixels of the reference object. On the contrary, the closed polygon in Figure 1C, which has the bottom half equivalent to that of the prototype is perceptually less similar to it. Furthermore, there is little perceptual similarity between the prototype and its scrambled contour parts shown in Figure 1D.
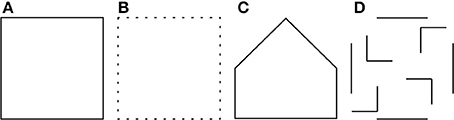
Figure 1. (A) A prototype shape. (B) A test pattern that has only 25% similarity (computed by template matching) to the prototype is perceptually more similar to the prototype than the polygon in (C) and the set of contour parts in (D), both of which have 50% similarity (computed by template matching) to the prototype.
As a matter of fact, there is neurophysiological evidence that objects, such as faces, are recognized by detecting certain features that are spatially arranged in a certain way (Kobatake and Tanaka, 1994). By means of single-cell recordings in adult monkeys it was, for instance, found that a neuron in inferotemporal cortex gives similar responses for the two images shown in Figures 2A,B. The icon presented in Figure 2B is a simplified version of the monkey's face shown in Figure 2A. It only consists of a circle that surrounds a horizontally-aligned pair of spots on top of a horizontal bar. Removing one of these features, Figures 2C,D, causes the concerned cell to give very small response.

Figure 2. (A–D) A set of stimuli used in an electrophysiological study Kobatake and Tanaka (1994) to test the selectivity of a neuron in inferotemporal cortex. (Bottom) The activity of the concerned neuron for the corresponding stimuli. The neuron gives high response only when the stimulus contains a detailed or simplified representation of the face boundary that surrounds a pair of eyes on top of a mouth. If any of these features is missing, the neuron gives negligible response.
Another neurophysiological study (Brincat and Connor, 2004) reveals that some neurons in inferotemporal cortex integrate information about the curvatures, orientations, and positions of multiple (typically 2–4) simple contour elements, such as angles or curved contour segments. In that study the authors argue that their findings are in line with other studies that support parts-based shape representation theories (Marr and Nishihara, 1978; Riesenhuber and Poggio, 1999; Mel and Fiser, 2000; Edelman and Intrator, 2003), and suggest that non-linear integration in the inferotemporal cortex might help to extend sparseness of shape representation along the ventral stream.
Tsotsos (1990) showed that hierarchical architectures are more appropriate for object detection in contrast to unbounded visual search which is known to be NP-complete. This has led to the proposal of a number of hierarchical models (Mel and Fiser, 2000; Scalzo and Piater, 2005; DiCarlo and Cox, 2007; Rodríguez-Sánchez and Tsotsos, 2012). Existing approaches that consider the spatial relationship of features include the so-called standard model (Serre et al., 2007), some probabilistic techniques, such as the generative constellation model (Fergus et al., 2003; Fei-Fei et al., 2007) and a hierarchical model of object categories (Fidler and Leonardis, 2007; Fidler et al., 2008). These approaches rely on summation of the responses of elementary feature detectors and may find the images in Figures 1C,D quite similar to the prototype in Figure 1A. For instance, such a technique may consider a circle with a horizontal line within it as a face even though the representations of the eyes are missing, Figures 2C,D.
We introduce a hierarchical object detection technique which is motivated by the shape selectivity of some neurons in inferotemporal cortex. The principal idea is to construct a shape-selective filter that combines the responses of some simpler filters that detect some partial features of the concerned shape in specific positions that are characteristic of that shape. We call this approach to the construction of filters Combination Of Shifted Filter REsponses (COSFIRE). We successfully applied this approach to the construction of line and edge detectors (Azzopardi and Petkov, 2012; Azzopardi et al., 2014) and simple contour-related features, such as vascular bifurcations (Azzopardi and Petkov, 2013b). In Azzopardi and Petkov (2013b) we demonstrated how the collective responses of multiple COSFIRE filters to segmented patterns, such as handwritten digits, can be used to form a shape descriptor with high discrimination ability. That descriptor, however, does not take into account the relative spatial arrangement of the concerned features. Similar to other shape descriptors (Belongie et al., 2002; Grigorescu and Petkov, 2003; Ghosh and Petkov, 2005; Latecki et al., 2005; Lauer et al., 2007; Ling and Jacobs, 2007; Goh, 2008; Almazan et al., 2012) that approach works well with segmented objects, but it is not effective for the detection of objects embedded in complex scenes. In order to distinguish the two types of filter, we refer to the composite shape-selective filter that we propose in this paper as S-COSFIRE and to the filter proposed in Azzopardi and Petkov (2013b) as V-COSFIRE (S and V stand for shape and vertex, respectively).
There are three aspects in which the S-COSFIRE filters that we propose differ from other hierarchical models that also consider the spatial geometric arrangement of parts. First, our model is implemented in a filter that gives a scalar response (between 0 and 1) for each position in the image. The higher the value the more similar the shape around the concerned location is to the prototype shape. An S-COSFIRE filter can be thought of a model of a shape-selective neuron in inferotemporal cortex of the type studied in Kobatake and Tanaka (1994); Brincat and Connor (2004), which fires only when a specific arrangement of contour-based features is present in its receptive field. It addresses object recognition and localization as a joint problem, which is in line with how Marr (1982) defined the sense of seeing: “… to know what is where by looking.” In contrast, the other methods referred to above use multiple prototypes and consider several responses from different feature detectors to form a mixture of probability distributions or a vector of responses. For these methods, the geometrical spatial arrangement of the concerned prototype defining parts is achieved by training a supervised classifier and subsequently the similarity between a test pattern and a prototype is computed by a distance metric. Moreover, they suffer from insufficient robustness to localization because they treat this matter at a region level (sliding window) rather than at a pixel level.
Second, since the omission of an object part can radically change shape perception, we regard every feature (and its relative position) that forms part of a prototype shape as essential. This aspect is implemented as an AND-type operation of an S-COSFIRE filter. It is in contrast to other models that rely on summation, and therefore achieve a response even when any of the prototype-defining features is missing. These models may thus match objects that are perceptually different.
Third, while the S-COSFIRE approach that we present achieves invariance to rotation, scaling, and reflection by simply manipulating some model parameters, the other techniques can only achieve invariance to such geometric transformations by extending the training set with example objects that are rotated, scaled and/or reflected versions of a prototype.
The rest of the paper is organized as follows: in section 2 we present the proposed hierarchical S-COSFIRE model. In section 3, we demonstrate its effectiveness in two applications: keyword spotting in handwritten manuscripts and vision for a home tidying pickup robot. Section 4 contains a discussion on the properties of the S-COSFIRE filters and finally we draw conclusions in section 5.
The following example illustrates the main idea of the proposed method. We consider the triangle, shown in Figure 3A, as a shape of interest and we call it prototype. We use this prototype to automatically configure an S-COSFIRE filter that will respond to shapes that are identical with or similar to this prototype.
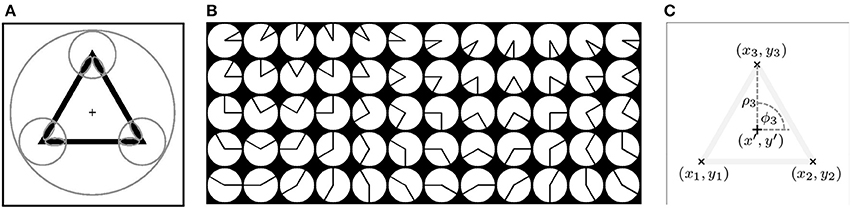
Figure 3. (A) The triangle is the prototype shape of interest and the “+” marker indicates the center of the user-specified large circle. The small circles indicate the supports of three vertex detectors that are identified as relevant for the concerned prototype shape. The small ellipses represent the supports of line detectors that are selective for the contour parts of the corresponding vertices. (B) A data set of 60 synthetic vertices, f1, …, f60 (left-to-right, top-to-bottom). A V-COSFIRE filter Vfk is selective for a vertex fk. (C) Configuration of an S-COSFIRE filter. The “×” markers indicate the locations, (x1, y1), (x2, y2), (x3, y3), where the corresponding three V-COSFIRE filters, Vf13, Vf17, Vf21, achieve the maximum responses. These locations correspond to the three vertices of the prototype shape, which is rendered here with low contrast. The Cartesian coordinates of each point (xi, yi) are converted into the polar coordinates (ρi, ϕi) with respect to the given point of interest (x′, y′), indicated by the “+” marker.
A shape-selective S-COSFIRE filter takes input from simpler filters; here filters that are selective for vertices. We use vertex-selective COSFIRE filters of the type proposed in Azzopardi and Petkov (2013b) to detect the vertices of the prototype shape. Such a filter, which we refer to it as V-COSFIRE, combines the responses of line detectors, the areas of support of which are indicated by the small ellipses in Figure 3A.
The response of an S-COSFIRE filter is computed by combining the responses of the concerned V-COSFIRE filters in the centers of the corresponding circles by weighted geometric mean. The preferred orientations and the preferred apertures of these filters together with the locations at which we take their responses are determined by analysing the responses of a set of V-COSFIRE filters to the prototype shape. Consequently, the S-COSFIRE filter will be selective for the given spatial arrangement of vertices of specific orientations and apertures. Taking the responses of V-COSFIRE filters at different locations around a point can be implemented by shifting the responses appropriately before using them for the pixel-wise evaluation of a multivariate function which gives the S-COSFIRE filter output.
We denote by rVfi(x, y) the response of a V-COSFIRE filter Vfi that is selective for a vertex fi. We threshold these responses at a given fraction t1 (0 ≤ t1 ≤ 1) of the maximum response across all image coordinates (x, y) and denote these thresholded responses by |rVfi(x, y)|t1. We use the publicly available Matlab implementation1 of V-COSFIRE filters. Such a filter uses as input the responses of given channels of a bank2 of Gabor filters. For further technical details about the properties of V-COSFIRE filters we refer to Azzopardi and Petkov (2013b).
We use a bank of V-COSFIRE filters that are selective for vertices of different orientations (in intervals of π/6 radians) and different apertures (in intervals of π/6 radians), Figure 3B. For the considered prototype the strongest responses are obtained by three V-COSFIRE filters that are selective for vertices of the types f13, f17, and f21, shown in Figure 3B. The corresponding locations, (x1, y1), (x2, y2), (x3, y3), at which they obtain the maximum responses are indicated in Figure 3C.
An S-COSFIRE filter uses as input the responses of selected V-COSFIRE filters Vfji, i = 1 … n, each selective for some vertex fji, around a certain position (ρi, ϕi) with respect to the center of the S-COSFIRE filter. A 3-tuple (Vfji, ρi, ϕi) that consists of a V-COSFIRE filter specification Vfji and two scalar values (ρi, ϕi) characterizes the properties of a vertex that is present in the given prototype shape: Vfji represents a V-COSFIRE filter that is selective for a vertex fji and (ρi, ϕi) are the polar coordinates of the location at which its response is taken with respect to the center of the S-COSFIRE filter. In the following we explain how we obtain the parameter values of such vertices around a given point of interest.
For each location in the input image of the prototype shape we take the maximum value of all responses achieved by the bank of V-COSFIRE filters mentioned above. The positions that have values greater than those of their corresponding 8-neighbors are chosen as the points that have local maximum responses. For each such point (xi, yi) we determine the polar coordinates (ρi, ϕi) with respect to the center of the S-COSFIRE filter, Figure 3C. Then we determine the V-COSFIRE filters, the responses of which are greater than a fraction t2 = 0.75 of the maximum response rVfi(x, y) for all i ∈ {1, … nf} where nf is the number of V-COSFIRE filters used across all locations in the input image. Thus, multiple V-COSFIRE filters can be significantly activated for the same location (ρi, ϕi). The selected points characterize the dominant vertices in the given prototype shape of interest.
We denote by SS = {(Vfji, ρi, ϕi) | i = 1 … nf} the set of parameter value combinations, which describes the properties and locations of a number of vertices. The subscript S stands for the prototype shape of interest. Every tuple in set SS specifies the parameters of some vertex in prototype S. For the prototype shape of interest in Figure 3A, the selection method described above results in three vertices with parameter values specified by the tuples in the following set: SS = {(Vfj1 = 21, ρ1 = 50, ϕ1 = π/2), (Vfj2 = 13, ρ2 = 50, ϕ2 = 7π/6), (Vfj3 = 17, ρ3 = 50, ϕ3 = 5π/3)}.
The above configuration results in an S-COSFIRE filter that is selective for a preferred spatial arrangement of three vertices forming an equilateral triangle. Next, we use the responses of the V-COSFIRE filters that are selective for the corresponding vertices to compute the output of the S-COSFIRE filter as follows.
First, we blur the responses of the V-COSFIRE filters in order to allow for some tolerance in the position of the respective vertices. This increases the generalization ability of the S-COSFIRE filter under construction. We define the blurring operation as the computation of maximum value of the weighted thresholded responses of a V-COSFIRE filter. For weighting we use a Gaussian function Gσ(x, y), the standard deviation σ of which is a linear function of the distance ρ from the center of the S-COSFIRE filter: σ = σ0 + αρ where σ0 and α are constants. The choice of this linear function is inspired by the visual system of the brain for which we provide more detail in section 4. For α > 0, which we use, the tolerance to the position of the respective vertices increases with an increasing distance ρ from the support center of the concerned S-COSFIRE filter.
Second, we shift the blurred responses of each V-COSFIRE filter by a distance ρi in the direction opposite to ϕi. With this shifting the concerned V-COSFIRE filter responses, which are located at different positions (ρi, ϕi) meet at the support center of the S-COSFIRE filter. The output of the S-COSFIRE filter can then be evaluated as a pixel-wise multivariate function of the shifted and blurred responses of V-COSFIRE filter responses. In polar coordinates, the shift vector is specified by (ρi, ϕi + π), and in Cartesian coordinates, it is (Δxi, Δyi) where Δxi = −ρi cos ϕi, and Δyi = −ρi sin ϕi. We denote by sVfji, ρi, ϕi(x, y), the blurred and shifted thresholded response of a V-COSFIRE filter that is specified by the i-th tuple (Vfji, ρi, ϕi) in the set SS:
Figure 4 illustrates the blurring and shifting operations for this S-COSFIRE filter, applied to the image shown in Figure 3A.
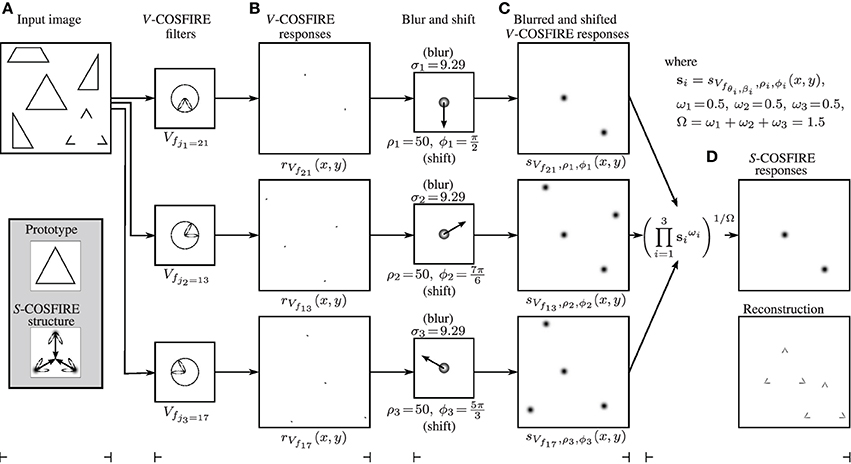
Figure 4. (A) Input image (of size 512 × 512 pixels). The enframed inlay images show (top) the enlarged prototype shape of interest, which is identical to the equilateral triangle in the input image and (bottom) the structure of the S-COSFIRE filter that is configured by this prototype. The ellipses illustrate the wavelengths and orientations of the Gabor filters that are used by the V-COSFIRE filters, and the dark blobs are intensity maps for blurring (Gaussian) functions. The blurred responses are then shifted by the corresponding vectors. (B) The V-COSFIRE filters that are automatically identified from the prototype shape and the corresponding response images to the input image. (C) We then blur (here we use σ0 = 0.1 and α = 0.0853 to compute σi) the thresholded (here at t1 = 0) response |rVfi(x, y)|t1 of each concerned V-COSFIRE filter and subsequently shift the resulting blurred response images by corresponding polar-coordinate vectors (ρi, ϕi + π). (D) We use weighted geometric mean (here σ′ = 91.44) of all the blurred and shifted V-COSFIRE filters to compute (top) the output of the S-COSFIRE filter and show (bottom) the reconstruction of the detected features. The reconstruction is achieved by superimposing the Gabor filter responses that give input to the S-COSFIRE filter. The two local maxima in the output of the S-COSFIRE filter correspond to the triangle and to the perceived one in the input image. For better clarity we use inverted gray-level rendering to show the images in the right of the columns (B–D).
We define the response rSS (x, y) of an S-COSFIRE filter as the weighted geometric mean of the blurred and shifted thresholded responses of the selected V-COSFIRE filters sVfji, ρi, ϕi (x, y):
where |.|t3 stands for thresholding the response at a fraction t3 of its maximum across all image coordinates (x, y). For 1/σ′ = 0, the computation of the S-COSFIRE filter is equivalent to the standard geometric mean, where the s-quantities have the same contribution. Otherwise, for 1/σ′>0, the input contribution of s-quantities decreases with an increasing value of the corresponding parameter ρ. In our experiments we use a value of the standard deviation σ′ that is computed as a function of the maximum value of the given set of ρ values: σ′ = (− ρmax2/2 ln 0.5)1/2, where ρmax = maxi∈{1…|SS|}{ρi}. We make this choice in order to achieve a maximum value ω = 1 of the weights in the center (for ρ = 0), and a minimum value ω = 0.5 in the periphery (for ρ = ρmax).
Figure 4D shows the output of an S-COSFIRE filter which is defined as the weighted geometric mean of three blurred and shifted response images obtained by the three concerned V-COSFIRE filters. Note that this filter responds in the middle of a spatial arrangement of three vertices that is identical with or similar to that of the prototype shape S, which was used for the configuration of the S-COSFIRE filter. In this example, the S-COSFIRE filter reacts strongly in a given point that is surrounded by three vertices each having an aperture of π/3 radians: one northward-pointing, another one south-west-pointing and a south-east-pointing vertex to the north, south-west, and south-east of that point, respectively. Besides the complete triangle that was used for configuration, the concerned filter also detects the Kanizsa-type illusory triangle. This is in line with neurophysiological and psychophysical evidence, in that the visual system is capable of detecting a shape with illusory contours, based on its visible salient parts. A thorough review of this phenomenon is provided in Roelfsema (2006).
The proposed S-COSFIRE filters are tolerant to rotations, scales and reflections. Similar to a V-COSFIRE filter, such a tolerance is achieved by manipulating the values of some parameters rather than by configuring separate filters by rotated, scaled, and reflected versions of the prototype shape of interest.
Using the set SS that defines the concerned S-COSFIRE filter, we form a new set ℜψ(SS) that defines a new filter, which is selective for a version of the prototype shape S that is rotated by an angle ψ:
For each tuple (Vfji, ρi, ϕi) in the original filter SS that describes a certain vertex of the prototype shape, we provide a counterpart tuple (ℜψ(Vfji), ρi, ϕi + ψ) in the new set ℜψ(SS). The set ℜψ(Vfji) defines3 a V-COSFIRE filter that is selective for vertex fji that is also rotated by an angle ψ. The orientation of the concerned vertex and its polar angle position ϕi with respect to the support center of the S-COSFIRE filter are off-set by an angle ψ relative to the values of the corresponding parameters of the original vertex.
A rotation-invariant response is achieved by taking the maximum value of the responses of filters that are obtained with different values of the parameter ψ:
where Ψ is a set of nψ equidistant orientations defined as .
Tolerance to scaling is achieved in a similar way. Using the set SS that defines the concerned S-COSFIRE filter, we form a new set Tυ(SS) that defines a new filter, which is selective for a version of the prototype shape S that is scaled in size by a factor υ:
For each tuple (Vfji, ρi, ϕi) in the original S-COSFIRE filter SS that describes a certain vertex of the prototype shape, we provide a counterpart tuple (Tυ(Vfji), υρi, ϕi) in the new set Tυ(SS). The set Tυ(Vfji) defines1 a V-COSFIRE filter that responds to a version of the vertex fji scaled by the factor υ. The size of the concerned vertex and its distance to the center of the filter are scaled by the factor υ relative to the original values of the corresponding parameters.
A scale-invariant response is achieved by taking the maximum value of the responses of filters that are obtained with different values of the parameter υ:
where ϒ is a set of υ values equidistant on a logarithmic scale defined as .
As to reflection invariance we first form a new set ŚS from the set SS as follows:
The set defines1 a new V-COSFIRE filter that is selective for the corresponding vertex fji reflected about the y–axis. Similarly, the new S-COSFIRE filter ŚS is selective for a reflected version of the prototype shape S also about the y−axis. A reflection-invariant response is achieved by taking the maximum value of the responses of the filters SS and ŚS:
An S-COSFIRE filter achieves tolerance to all the above geometric transformations by taking the maximum value of the rotation- and scale-tolerant responses of the filters SS and ŚS that are obtained with different values of the parameters ψ and υ:
In the following we demonstrate the effectiveness of the proposed S-COSFIRE filters by applying them in two practical applications: the spotting of keywords in handwritten manuscripts and the spotting of objects in complex scenes for the computer vision system of a domestic robot.
The automatic recognition of keywords in handwritten manuscripts is an application that has been extensively investigated for several decades (Plamondon and Srihari, 2000; Frinken et al., 2012). Despite this effort the problem has not been solved yet.
As a demonstration, in Figure 5 we show how to detect the keyword “Germany” in two handwritten manuscripts. We use the keyword prototype “Germany” that is shown enframed in Figure 5A to configure an S-COSFIRE filter that receives input from 13 V-COSFIRE filters, Figure 5E. Figures 5C,D show the responses of the concerned S-COSFIRE filter (t1 = 0.1, t2 = 0.75, t3 = 0.1, σ0 = 0.67, and α = 0.1.) to the two manuscript images4 in Figures 5A,B. It spots all the six instances of the keyword “Germany” and does not produce any false positives.

Figure 5. An example of spotting the keyword “Germany” in (A,B) two handwritten manuscripts taken from the IAM offline database (Marti and Bunke, 2002). The indicated keyword “Germany” in (A) is used as a prototype to configure an S-COSFIRE filter. (E) The circles indicate the support areas of 13 V-COSFIRE filters that are used to provide input to the concerned S-COSFIRE filter with the “+” marker indicating its support center. (C,D) Normalized responses of this filter to the images in (A,B) rendered by shading of the spotted words. All six instances are detected. The strongest response is achieved for the word that was used for the configuration of the S-COSFIRE filter.
The S-COSFIRE filters that are selective for specific words may correspond to neurons or networks of neurons in a certain area in the posterior lateral-occipital cortex. This area receives input from V4 and is selective for combinations of vertices. It has been shown to play a role in the recognition of words and has been named Visual Word Form Area (Szwed et al., 2011).
Daily service robots that perform routine tasks are becoming popular as household appliances. Such tedious tasks include, but are not limited to, vacuum cleaning, setting up and cleaning up a dinner table, tidying up toys, and organizing closets. The design of domestic robots is a growing research area (Bandera et al., 2012; Jiang et al., 2012).
We demonstrate how the S-COSFIRE filters that we propose can be used by a personal robot to visually recognize objects of interest in indoor environments. As an illustration we consider a task for a tidying pickup robot to detect shoes in different rooms of a home that match the prototype shoe shown in Figure 6A.
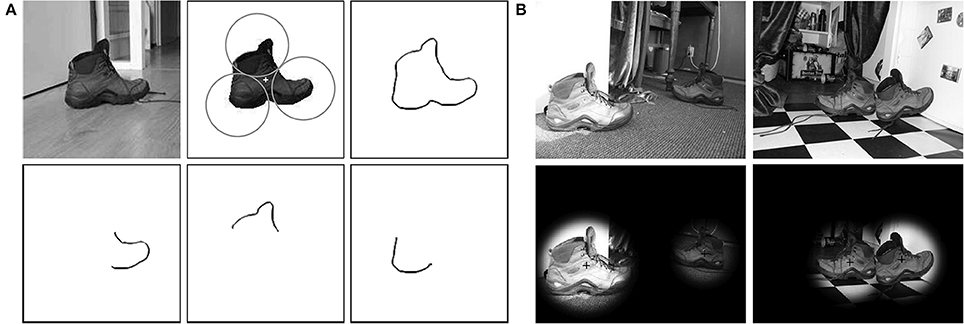
Figure 6. Detection of shoes in complex scenes. (A) A protoype shoe used for the configuration of an S-COSFIRE filter. The circles represent the non-overlapping supports of three V-COSFIRE filters, and the “+” marker indicates the center of support of the concerned S-COSFIRE filter. (Top right) The superimposed (inverted) thresholded responses (t1 = 0.3) of a bank of Gabor energy filters with one wavelength (λ = 4) and 16 orientations in intervals of π/8. (Bottom) Reconstructions of the local patterns for which the three resulting V-COSFIRE filters are selective. (B) Detection results to two input images (of size 256 × 342 pixels) from the RUG-Shoes data set with filenames (a) Shoes03_1.jpg, (c) Shoes17_2.jpg, (e) Shoes58_2.jpg, and (g) Shoes38_1.jpg.
We use a segmented prototype image of the shoe to configure an S-COSFIRE filter. The concerned S-COSFIRE filter receives input from three V-COSFIRE filters that are selective for different parts of the shoe. These parts are automatically chosen by the system from a circular local neighborhood of a point of interest that is indicated by a “+” marker. In practice, the concerned point of interest and the radius of the corresponding local neighborhood are manually specified by the user. The radii of the three circles are automatically computed in such a way that the circles touch each other. For the configuration of the concerned V-COSFIRE filters we use a bank of Gabor energy filters5 with one wavelength (λ = 4) and 16 equidistant orientations , and we threshold the responses with t1 = 0.3. Within each of the three circles, we consider a number of concentric circles, the radii of which increment in intervals of 4 pixels starting from 0. For the concerned three V-COSFIRE filters as well as the S-COSFIRE filter we use the same values of parameters α (α = 0.67) and σ0 (σ0 = 0.1) in order to allow the same tolerance in the position of the involved edges and curvatures.
We created a data set that we call RUG-Shoes of 60 color images (of size 256 × 342 pixels) by taking pictures in different rooms of the same house. Of these images, 39 contain a pair of shoes of interest, another nine contain a single shoe and the remaining 12 do not contain any shoes. The distance above ground of the digital camera was varied between 50 cm and 1 m. All pictures of shoes were taken from the side view of the corresponding shoes. The shoes were, however, arranged in different orientations and their distances from the camera varied by at most 25% as compared to the distance which we used to take the image of the prototype shoe. We made the RUG-Shoes data set publicly available6.
We use the configured S-COSFIRE filter to detect shoes in the data set of 60 images. We first convert every color image to grayscale and subsequently apply the concerned S-COSFIRE filter in reflection-, scale- and partially rotation-invariant mode. The Gabor energy filters that we use to provide inputs to the V-COSFIRE filters are applied with isotropic suppression (Grigorescu et al., 2004) in order to reduce responses to texture. We threshold the responses of the concerned S-COSFIRE filter with t3 = 0.1 and for each image we consider only the highest two responses. We obtain a perfect detection and recognition performance for all the 60 images in the RUG-Shoes data set. This means that we detect all the shoes in the given images with no false positives. Figure 6B illustrates the detection of some shoes in two of the images.
The trainable S-COSFIRE filters that we propose are part of a hierarchical object recognition approach that shares similarity with the ventral stream of visual cortex. In the first layer we detect lines and edges by Gabor filters, which are inspired by the function of orientation-selective cells in primary visual cortex (Daugman, 1985). Their responses are projected to a second layer and used by V-COSFIRE filters that detect vertices and curved contour segments. In our previous work (Azzopardi and Petkov, 2013b), we showed that such filters give responses that are qualitatively similar to a class of cells in area V4 in visual cortex. Finally, in a third layer we have S-COSFIRE filters that combine the responses of certain V-COSFIRE filters. Such a filter is selective for a given spatial configuration of vertices and curved contour segments that defines a simple to moderately complex shape. S-COSFIRE filters share similar properties with shape-selective neurons in inferotemporal cortex, which provided inspiration for this work.
This hierarchical object recognition approach is, however, not restricted to three layers. The addition of further layers may be more appropriate for prototype objects of higher deformation complexity. For instance, let us consider a prototype shape of a simplistic human-body figure that is composed of a head, a pair of eyes, a nose, a mouth, two arms, two hands, a torso, two legs, and two feet. We may configure an S-COSFIRE filter to be selective for the entire body with its center being at the center of mass of the body. Such a filter receives input from V-COSFIRE filters that are selective for distinct body parts. With this type of configuration the tolerance in the position of the body parts is computed with the same function that depends on the distance from the center of the S-COSFIRE filter. However, we know that certain body parts may require more tolerance or may be more correlated than others. For instance, the positions of the eyes, the nose and the mouth depend more on the position of the head than on the position of the legs. By taking this aspect in consideration it would be better to construct a hierarchical filter in the following way: configure an S-COSFIRE filter to be selective for the spatial arrangement of the head components (eyes, nose, and mouth), an S-COSFIRE filter for a hand and an arm, another one for a foot and a leg and a fourth one for the torso. Then, the responses of these four S-COSFIRE filters may be used as inputs to another, more complex S-COSFIRE filter.
The configuration of an S-COSFIRE filter determines which responses of which V-COSFIRE filters need to be multiplied in order to obtain the output of the filter. The number of V-COSFIRE filters used is a model parameter that is specified by the user. This value depends on the shape complexity of the concerned prototype (as represented by the number of vertex features). The selectivity of an S-COSFIRE filter increases with an increasing number of V-COSFIRE filters. The sizes of the V-COSFIRE supports and their position are automatically determined in such a way that they do not overlap each other. In future work, we will incorporate a learning mechanism in the configuration stage. It will use multiple prototype examples of the object of interest (instead of only one prototype that we use here) and negative examples (e.g., other objects and scenes). It will learn the optimal number of V-COSFIRE filters as well as the size and position of their support in order to maximize selectivity and generalization abilities.
An S-COSFIRE filter achieves a response when all parts of a shape of interest are present in a specific spatial arrangement around a given point in an image. The rigidity of this geometrical configuration may vary according to the application at hand. The standard deviation of a blurring (Gaussian) function that we use to allow for some tolerance depend on the distance from the center of the concerned S-COSFIRE filter: it grows linearly with a rate that is defined by the parameter α. Small values of α are more appropriate for the selectivity of rigid objects. Generalization ability increases with an increasing value of α. This mechanism is inspired by neurophysiological evidence that the average diameter of receptive fields of some neurons in visual cortex increases with the eccentricity (Gattass et al., 1988).
The specific type of function that we use to combine the responses of costituent (V-COSFIRE) filters for the considered applications is a weighted geometric mean. This output function, which is also used to compute a V-COSFIRE filter response, proved to give better results than various forms of addition. Furthermore, there is psychophysical evidence that human visual processing of shape is likely performed by a non-linear neural operation that multiplies afferent responses (Gheorghiu and Kingdom, 2009). In future work, we plan to experiment with functions other than (weighted) geometric mean.
The application of the home tidying robot in section 3.2 demonstrates the benefits of the rotation, scale and reflection invariances that we use. With one S-COSFIRE filter that is configured by a single prototype, the filter is able to achieve responses to different views of the object used for training. While this ability implies more operations, the computational cost does not grow linearly with the number of considered views. This is attributable to the fact that the responses of the bank of Gabor filters at the bottom layer can be shared among the involved V-COSFIRE filters, irrespective of the view. We refer the reader to Azzopardi and Petkov (2013a,b) for the technical details. The majority of the new operations required due to the invariances are shifting computations, which have very low computational cost. In practice, the shoe-selective filter used in section 3.2 takes 3.5 s to process an image (256 × 342 pixels) with no invariances, and less than 5 s with rotation-, scale-, and reflection-invariance.
The proposed S-COSFIRE filters are particularly useful due to their versatility and selectivity, in that an S-COSFIRE filter can be configured to be selective for any given deformable object and used to detect other objects embedded in complex scenes that are perceptually similar to it. This effectiveness is attributable to taking into account the mutual spatial positions of the responses of certain V-COSFIRE filters that are selective for simpler object parts.
The S-COSFIRE filters that we propose are highly effective to detect and recognize deformable objects that are embedded in complex scenes without prior segmentation. This effectiveness is due to the deployment of both the presence of certain object-characteristic features and their mutual spatial arrangement. They are versatile shape detectors as they can be trained to be selective for any given visual pattern of interest.
An S-COSFIRE filter is conceptually simple and easy to implement: the filter output is computed as the weighted geometric mean of blurred and shifted responses of simpler V-COSFIRE filters.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1. ^The Matlab implementation of a V-COSFIRE filter can be downloaded from http://matlabserver.cs.rug.nl/
2. ^Here we use a bank of Gabor filters with five wavelengths λ = {4, 4, 8, 8, 16} and six equidistant orientations
3. ^We refer to Azzopardi and Petkov (2013b) for the technical details about the invariance that is achieved by a V-COSFIRE filter.
4. ^The images in Figures 5A,B are extracted from the files named b01-049.png and b01-044.png, respectively, in the IAM offline database.
5. ^The response of a Gabor energy filter is computed as the L2-norm of the responses of a symmetric and anti-symmetric Gabor filters.
6. ^The RUG-Shoes data set can be downloaded from http://matlabserver.cs.rug.nl/
Almazan, J., Fornes, A., and Valveny, E. (2012). A non-rigid appearance model for shape description and recognition. Pattern Recogn. 45, 3105–3113. doi: 10.1016/j.patcog.2012.01.010
Azzopardi, G., and Petkov, N. (2012). A CORF computational model of a simple cell that relies on LGN input outperforms the Gabor function model. Biol. Cybernet. 106, 177–189. doi: 10.1007/s00422-012-0486-6
Azzopardi, G., and Petkov, N. (2013a). Automatic detection of vascular bifurcations in segmented retinal images using trainable COSFIRE filters. Pattern Recogn. Lett. 34, 922–933. doi: 10.1016/j.patrec.2012.11.002
Azzopardi, G., and Petkov, N. (2013b). Trainable COSFIRE Filters for Keypoint Detection and Pattern Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 35, 490–503. doi: 10.1109/TPAMI.2012.106
Azzopardi, G., Rodriguez Sanchez, A., Piater, J., and Petkov, N. (2014). A push-pull CORF model of a simple cell with antiphase inhibition improves SNR and contour detection. PLoS ONE 9:e98424. doi: 10.1371/journal.pone.0098424
Bandera, J. P., Rodriguez, J. A., Molina-Tanco, L., and Bandera, A. (2012). A survey of vision-based architectures for robot learning by imitation. Int. J. Human. Robot. 9:1250006. doi: 10.1142/S0219843612500065
Belongie, S., Malik, J., and Puzicha, J. (2002). Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 24, 509–522. doi: 10.1109/34.993558
Brincat, S. L., and Connor, C. E. (2004). Underlying principles of visual shape selectivity in posterior inferotemporal cortex. Nat. Neurosci. 7, 880–886. doi: 10.1038/nn1278
Daugman, J. G. (1985). Uncertainty relation for resolution in space, spatial-frequency, and orientation optimized by two-dimensional visual cortical filters. J. Optic. Soc. Am. Optic. Image Sci. Vis. 2, 1160–1169. doi: 10.1364/JOSAA.2.001160
DiCarlo, J., and Cox, D. (2007). Untangling invariant object recognition. Trends Cogn. Sci. 11, 333–341. doi: 10.1016/j.tics.2007.06.010
Edelman, S., and Intrator, N. (2003). Towards structural systematicity in distributed, statically bound visual representations. Cogn. Sci. 27, 73–109. doi: 10.1207/s15516709cog2701_3
Fei-Fei, L., Fergus, R., and Perona, P. (2007). Learning generative visual models from few training examples: an incremental Bayesian approach tested on 101 object categories. Comput. Vis. Image Understand. 106, 59–70. doi: 10.1016/j.cviu.2005.09.012. 2nd International Workshop on Generative-Model Based Vision, Washington, DC, 2005.
Fergus, R., Perona, P., and Zisserman, A. (2003). “Object class recognition by unsupervised scale-invariant learning,” in Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Vol. 2, Technical Committee on Pattern Analysis and Machine Intelligence (TCPAMI) (Madison, WI), 264–271.
Fidler, S., Boben, M., and Leonardis, A. (2008). “Similarity-based cross-layered hierarchical representation for object categorization,” in 2008 IEEE Conference on Computer Vision and Pattern Recognition, Vol. 1–12 (Anchorage, AK), 525–532. doi: 10.1109/CVPR.2008.4587409
Fidler, S., and Leonardis, A. (2007). “Towards scalable representations of object categories: learning a hierarchy of parts,” in 2007 IEEE Conference on Computer Vision and Pattern Recognition, Vol. 1–8 (Minneapolis, MN), 2295–2302. doi: 10.1109/CVPR.2007.383269
Frinken, V., Fischer, A., Manmatha, R., and Bunke, H. (2012). A novel word spotting method based on recurrent neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 34, 211–224. doi: 10.1109/TPAMI.2011.113
Gattass, R., Sousa, A. P., and Gross, C. G. (1988). Visuotopic organization and extent of v3 and v4 of the macaque. J. Neurosci. 8, 1831–1845.
Gheorghiu, E., and Kingdom, F. A. A. (2009). Multiplication in curvature processing. J. Vis. 9, 1–17. doi: 10.1167/9.2.23
Ghosh, A., and Petkov, N. (2005). Robustness of shape descriptors to incomplete contour representations. IEEE Trans. Pattern Anal. Mach. Intell. 27, 1793–1804. doi: 10.1109/TPAMI.2005.225
Goh, W. B. (2008). Strategies for shape matching using skeletons. Comput. Vis. Image Understand. 110, 326–345. doi: 10.1016/j.cviu.2007.09.013
Grigorescu, C., and Petkov, N. (2003). Distance sets for shape filters and shape recognition. IEEE Trans. Image Process. 12, 1274–1286. doi: 10.1109/TIP.2003.816010
Grigorescu, C., Petkov, N., and Westenberg, M. A. (2004). Contour and boundary detection improved by surround suppression of texture edges. Image Vis. Comput. 22, 609–622. doi: 10.1016/j.imavis.2003.12.004
Jiang, Y., Lim, M., Zheng, C., and Saxena, A. (2012). Learning to place new objects in a scene. Int. J. Robot. Res. 31, 1021–1043. doi: 10.1177/0278364912438781
Kobatake, E., and Tanaka, K. (1994). Neuronal selectivities to complex object features in the ventral visual pathway of the macaque cerebral-cortex. J. Neurophysiol. 71, 856–867.
Latecki, L., Lakaemper, R., and Wolter, D. (2005). Optimal partial shape similarity. Image Vis. Comput. 23, 227–236. doi: 10.1016/j.imavis.2004.06.015. 11th International Conference on Discrete Geometry for Computer Imagery, Italian Inst Philosoph Studies, Naples, Italy, Nov 19-21, 2003.
Lauer, F., Suen, C. Y., and Bloch, G. (2007). A trainable feature extractor for handwritten digit recognition. Pattern Recogn. 40, 1816–1824. doi: 10.1016/j.patcog.2006.10.011
Ling, H., and Jacobs, D. W. (2007). Shape classification using the inner-distance. IEEE Trans. Pattern Anal. Mach. Intell. 29, 286–299. doi: 10.1109/TPAMI.2007.41
Marr, D. (1982). Vision: A Computational Investigation Into The Human Respresentation and Processing of Visual Information. New York, NY: Freeman.
Marr, D., and Nishihara, H. K. (1978). Representation and recognition of spatial-organization of 3-dimensional shapes. Proc. R. Soc. London B Biol. Sci. 200, 269–294. doi: 10.1098/rspb.1978.0020
Marti, U.-V., and Bunke, H. (2002). The IAM-database: an english sentence database for offline handwriting recognition. Int. J. Doc. Anal. Recogn. 5, 39–46. doi: 10.1007/s100320200071
Mel, B. W., and Fiser, J. (2000). Minimizing binding errors using learned conjunctive features (vol 12, pg 247, 1999). Neural Comput. 12, 731–762. doi: 10.1162/089976600300015574
Plamondon, R., and Srihari, S. (2000). On-line and off-line handwriting recognition: a comprehensive survey. IEEE Trans. Pattern Anal. Mach. Intell. 22, 63–84. doi: 10.1109/34.824821
Riesenhuber, M., and Poggio, T. (1999). Hierarchical models of object recognition in cortex. Nat. Neurosci. 2, 1019–1025. doi: 10.1038/14819
Rodríguez-Sánchez, A. J., and Tsotsos, J. K. (2012). The roles of endstopped and curvature tuned computations in a hierarchical representation of 2d shape. PLoS ONE 7:e42058. doi: 10.1371/journal.pone.0042058
Roelfsema, P. R. (2006). Cortical algorithms for perceptual grouping. Annu. Rev. Neurosci. 29, 203–227. doi: 10.1146/annurev.neuro.29.051605.112939
Scalzo, F., and Piater, J. (2005). “Statistical learning of visual feature hierarchies,” in IEEE Computer Society Conference on Computer Vision and Pattern Recognition - Workshops, 2005. CVPR Workshops (San Diego, CA), 44.
Serre, T., Wolf, L., Bileschi, S., Riesenhuber, M., and Poggio, T. (2007). Robust object recognition with cortex-like mechanisms. IEEE Trans. Pattern Anal. Mach. Intell. 29, 411–426. doi: 10.1109/TPAMI.2007.56
Szwed, M., Dehaene, S., Kleinschmidt, A., Eger, E., Valabregue, R., Amadon, A., et al. (2011). Specialization for written words over objects in the visual cortex. Neuroimage 56, 330–344. doi: 10.1016/j.neuroimage.2011.01.073
Keywords: hierarchical representation, object recognition, shape, ventral stream, vision and scene understanding, robotics, handwriting analysis
Citation: Azzopardi G and Petkov N (2014) Ventral-stream-like shape representation: from pixel intensity values to trainable object-selective COSFIRE models. Front. Comput. Neurosci. 8:80. doi: 10.3389/fncom.2014.00080
Received: 14 April 2014; Accepted: 09 July 2014;
Published online: 30 July 2014.
Edited by:
Antonio J. Rodriguez-Sanchez, University of Innsbruck, AustriaReviewed by:
Bart Ter Haar Romeny, Eindhoven University of Technology, NetherlandsCopyright © 2014 Azzopardi and Petkov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: George Azzopardi, Intelligent Systems, Johann Bernoulli Institute for Mathematics and Computer Science, University of Groningen, P.O. Box 800, 9700 AV Groningen, Netherlands e-mail:Zy5henpvcGFyZGlAcnVnLm5s
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.