Sustained activity in hierarchical modular neural networks: self-organized criticality and oscillations

Cerebral cortical brain networks possess a number of conspicuous features of structure and dynamics. First, these networks have an intricate, non-random organization. In particular, they are structured in a hierarchical modular fashion, from large-scale regions of the whole brain, via cortical areas and area subcompartments organized as structural and functional maps to cortical columns, and finally circuits made up of individual neurons. Second, the networks display self-organized sustained activity, which is persistent in the absence of external stimuli. At the systems level, such activity is characterized by complex rhythmical oscillations over a broadband background, while at the cellular level, neuronal discharges have been observed to display avalanches, indicating that cortical networks are at the state of self-organized criticality (SOC). We explored the relationship between hierarchical neural network organization and sustained dynamics using large-scale network modeling. Previously, it was shown that sparse random networks with balanced excitation and inhibition can sustain neural activity without external stimulation. We found that a hierarchical modular architecture can generate sustained activity better than random networks. Moreover, the system can simultaneously support rhythmical oscillations and SOC, which are not present in the respective random networks. The mechanism underlying the sustained activity is that each dense module cannot sustain activity on its own, but displays SOC in the presence of weak perturbations. Therefore, the hierarchical modular networks provide the coupling among subsystems with SOC. These results imply that the hierarchical modular architecture of cortical networks plays an important role in shaping the ongoing spontaneous activity of the brain, potentially allowing the system to take advantage of both the sensitivity of critical states and the predictability and timing of oscillations for efficient information processing.

1 Introduction

The impact of network topology on the dynamical behavior of network systems is a topic of central importance for the understanding of complex systems, and has attracted much attention in the complex network field (Strogatz, 2001); Albert and Barabási, 2002; Boccaletti et al., 2006; Arenas et al., 2008). Understanding the large-scale organization of the structure and dynamics in the brain from the viewpoint of complex networks has become a new frontier in neuroscience (Sporns et al., 2004; Bassett and Bullmore, 2006; Reijneveld et al., 2007; Bullmore and Sporns, 2009).

Neural networks in the brain have a highly intricate structural organization. One prominent feature of this organization is modularity. It is known from the anatomy of the brain that cortical architecture is organized in a hierarchical and modular way, from cellular micro-circuits in cortical columns at the lowest level, via cortical areas at the intermediate level, to sets of highly connected brain regions at the global systems level (Mountcastle, 1997; Hilgetag et al., 2000; Hilgetag and Kaiser, 2004). This means that neurons within a column, an area or a set of areas are more densely linked with each other than with neurons in the rest of the network (Hilgetag et al., 2000; Hilgetag and Kaiser, 2004; Sporns et al., 2004; Kaiser et al., 2007), resulting in the multi-scale organization of a hierarchical modular network (HMN).

Brain dynamics are also organized in an intricate way. First, the brain can sustain irregular activity in the absence of external stimuli. Such irregular sustained activity (ISA) represents internal self-organized states of the nervous systems, and has attracted great attention (Vreeswijk and Sompolinsky, 1996, 1998; Brunel, 2000; Roxin et al., 2004; Galán, 2008). The phenomenon is important in the study of various neural functions, such as signal propagation (Vogels and Abbott, 2005) and neural coding (Lewis et al., 2009). It was shown that networks of sparsely connected spiking neurons can produce highly irregular chaotic activity without external stimuli, due to the balance between excitation and inhibition (Vreeswijk and Sompolinsky, 1996; Vogels and Abbott, 2005). However, little is known about the impact of complex network topology, especially the HMN architecture, on the organization of sustained activity and particular ISA.

The sustained resting state activity of the brain is far from simply noisy. To the contrary, rhythmic oscillations with characteristic frequencies, such as α, β, γ waves are abundant (Buzsáki, 2006). The relationship between cognitive functions and brain rhythms as well as synchronization of the rhythms has been a central topic in neuroscience over the last decade (Engel et al., 2001; Fries, 2005). How oscillations emerge in the brain and how they are related to the network architecture, however, is still largely an open question.

In addition to sustained complex oscillations and waves, avalanches of neuronal firing activity have been demonstrated in neural networks. It was shown that avalanche activity in neural systems reaches self-organized critical states. Self-organized criticality (SOC) is a concept proposed in physics that mimics the avalanche of sandpiles, and is a widespread property of complex systems, such as piling of granular media, earthquakes, and forest fires, etc., (Bak et al., 1987, 1988; Bak, 1996; Jensen, 1998). In such systems, as one unit exceeds a threshold, it promotes other units by interaction and may cause them to cross the threshold as well. Activity emerges as a cascade propagating through the system. The concept asserts that a system self-organized into a critical state is characterized by scale invariance, which is usually identified as a power-law distribution of variables, such as the size of the avalanche, duration of the event or the waiting time between events (Bedard et al., 2006). At such a critical state, signals and perturbations can efficiently propagate over broad spatio-temporal scales. In neural systems, SOC has been observed experimentally (Beggs and Plenz, 2003, 2004) and studied in models (Eurich et al., 2002; de Arcangelis et al., 2006; Levina et al., 2007). Critical behavior in neural models has been shown to bring about optimal computational capabilities, optimal transmission, storage of information, and sensitivity to sensory stimuli (Kinouchi and Copelli, 2006; Levina et al., 2007).

Studying the interplay between the modular architecture and dynamical activity of neural networks may deliver important insights for the understanding of structure–function relationships in neural systems. Previous investigations have shown several interesting results. The study of synchronization dynamics in the cerebral cortical network demonstrated that the clusters of the functional networks coincide with the anatomical communities (Zhou et al., 2006, 2007; Honey et al., 2007; Müller-Linow et al., 2008). In a model of spreading neural activity, persistent, and scalable network activation could be produced in HMNs, but not in same-size random networks, implying that the hierarchical cluster architecture is a potential basis for the stable and diverse functional patterns in cortical networks (Kaiser et al., 2007; Kaiser and Hilgetag, 2010). It was also shown that HMNs satisfy constraints of stability under dynamical changes (Robinson et al., 2009).

To summarize, sustained activity occurs and coexists with rhythmic oscillations and SOC in the brain, which has a HMN structure. However, it has not yet been studied whether these prominent structural and dynamical properties are inherently related. This question, however, is crucial for understanding the functional roles of spontaneous brain activity. Classical theories of cognitive neuroscience viewed the brain as a passive, stimulus-driven device. In this view, the spontaneous on going activity of the brain was regarded as noise. Over the last decades, the paradigm has shifted to consider the brain as an active network that can generate meaningful activity by itself, which has significant impact on the selective responses to stimuli (Engel et al., 2001; Fries, 2005; Knight, 2007).

Here we investigate the impact of HMN architecture on sustained neural activity in a neural network model with balanced excitation and inhibition, with the principal aim to reveal relationships between the structural and dynamic features. In previous studies of random networks, it was shown that both large size and small density of neural networks are needed for sustained activity in the balanced network (Vreeswijk and Sompolinsky, 1996, 1998). The brain network as a whole has a very sparse connectivity, while cerebral cortical columns consisting of a small number of neurons in a local region are often densely connected internally, due to their modular organization. The questions we are going to address are: how does the balance mechanism for sustaining the irregular activity of a large sparse network support the sustained activity in small modules and in HMNs? What is the difference between the sustained activity in HMNs and that in homogeneous random networks? What is the role of hierarchical modular structure in the emergence of slow waves and SOC?

Our computational simulations show that HMNs can sustain irregular activity in larger parameter regions for the strength of excitatory and inhibitory synapses than homogeneous networks of the same size and connection density. In the regime of ISA, the dynamics of modules displays intermittent activity rather than the continuous activity observed in homogeneous networks. The intermittent activity of modules induces the emergence of low-frequency oscillations in HMNs. The size and the interval of the activity of modules are distributed according to power laws, which is consistent with the experimental observation of SOC in neural systems. We show that small, dense modules cannot support sustained activity without external input, but display SOC in the presence of weak inputs. Therefore, HMNs can be regarded as coupled SOC subsystems where the avalanches from some modules can provide weak input to the other modules. Since systems with SOC are very sensitive to weak perturbation, quite sparse connections between the modules can maintain the sustained activity.

Our work provides a generic and simple cortex-like neural network model which exhibits several important dynamical properties consistent with experimental findings. These findings may be of significance in studying the structure–dynamics–function relationship in the brain. First, the findings provide some principal understanding of the mechanism underlying the structure–dynamics relationship in the brain. Hierarchical modular brain architecture plays an essential role in simultaneously supporting diverse and non-trivial dynamical features. Second, the coexistence of SOC and oscillations may allow the cortical network to simultaneously take advantage of these two dynamical properties in information processing. For example, SOC would allow the system to have a broad responding region in the presence of external stimuli, while oscillations could provide timing, predictability, and integration necessary in various cognitive functions. The present work may stimulate further large-scale network simulations in studying the structural and dynamical mechanism underlying the emergence of ongoing activity and its interaction with external stimuli.

2 Model

2.1 Balanced Model of Sustained Activity

Our investigation started from a random neural network model which exhibits sustained activity (Vogels and Abbott, 2005). The network consists of a large number N of leaky integrate-and-fire neurons, sparsely, and randomly connected with a connection probability P₀ = 0.01. The ratio of excitatory to inhibitory neurons in the network is taken as 4:1. Whenever the membrane potential of a neuron crosses a spiking threshold of −50 mV, an action potential is generated and the membrane potential is reset to the resting potential V_rest, where it remains clamped for a 5-ms refractory period. We use a conductance-based model of neurons (Vogels and Abbott, 2005). The dynamics of the membrane potential is described as

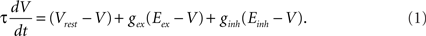
The value of the time constant is τ = 20 ms, the resting membrane potential is V_rest = −60 mV. Reversal potentials of synapses for excitatory and inhibitory neurons are E_ex = 0 mV and E_inh = −80 mV, respectively. The synaptic conductances g_ex and g_inh are expressed in units of the resting membrane conductance, which is set to 1/(100 MΩ).

When a neuron fires, the appropriate synaptic variables of its postsynaptic targets are increased, g_ex → g_ex + Δg_ex for an excitatory presynaptic neuron and g_inh → g_inh + Δg_inh for an inhibitory presynaptic neuron. Otherwise, these parameters obey the following equations:

and

where synaptic time constants are τ_ex = 5 ms and τ_inh = 10 ms.

2.2 The Hierarchical Modular Network Model

We obtain HMNs by rewiring the random network described in Section 2.1 in a top-down way. The network is divided randomly into two groups of the same size, and a modular architecture is obtained by rewiring connections between the two groups. In particular, with a probability R, each of the inter-modular connections (i → j) is rewired back into the module from which the connection projects, that is, deleting the link from i to j and connecting i to k which is randomly selected in the same module of node i. The rewiring probabilities for excitatory and inhibitory synapses are denoted by R_ex and R_inh, respectively. In this way we obtain a 1-level (flat) modular network. This method is applied recursively to generate HMNs with (l + 1)-levels, in which each module in the l-level network is split into two submodules, and the connections between them are rewired with the probabilities R_ex and R_inh. This rewiring method can transfer a large sparse network into a network composed of local units which are small and dense. See Figure 1 for an example of a 4-level HMN with 16 units, each having N/16 = 625 neurons. For studying the dynamics of network modules at different levels, we also cut inter-module connections of HMNs to isolate the densely connected smallest modules, and assemble these units by recovering the inter-module connections in a bottom-up manner.

FIGURE 1

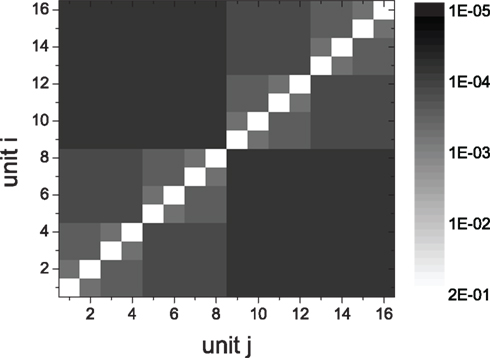
Figure 1. Connection density matrix of a 4-level HMN. Network size is N = 10,000. The connection density of the initial random networks is 0.01. The rewiring probabilities of excitatory links and inhibitory links are R_ex = 0.99 and R_inh = 1, respectively. The matrix is averaged over 100 network realizations.

Considering the fact that inhibitory couplings are formed by local connections and excitatory couplings by local or long-distance connections (Albus and Wahle, 1994; Bosking et al., 1997; Battaglia et al., 2007), we take R_inh = 1, and R_ex as a value in (0, 1). In HMNs, the connection density in a module is defined in the same way as in a random network, as the ratio of the number of connections to the total number of possible connections. The connection density between two modules is the ratio of the actual number of inter-module links to the number of possible links between them. The matrix of connection density between the modular units in a 4-level HMN is shown in Figure 1. With the parameter R_ex = 0.99, the connection density in elementary modules can be about 15 times larger than that of the whole network. Since we assume that the rewiring probability R_ex is the same across different levels of hierarchy, the density shown in Figure 1 can be expressed by an easily derived formula. For each unit the local connection density is

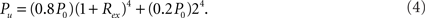
The connection density between a pair of modules of the i-level is

For example, for the two 1-level modules (i = 1), the initial connection density between them is P₀. After all the inhibitory connections from 20% of inhibitory neurons are rewired into the modules (R_inh = 1), the density becomes 0.8P₀. Further rewiring the excitatory connections with rate R_ex results in the density P₁ =(0.8P₀)(1 − R_ex) as given in Eq. (6) for i = 1.

The model can be easily generalized by splitting a module into m submodules of equal size at each level. In this case, the connection density between the modules of the ith level is

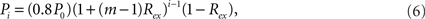
where i = 1,…,l, if a network is rewiring into a l-level HMN. The connection density within each unit of the network, that is, the l-level module, is

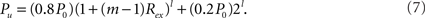
In the present work, we consider a large and sparse initial random network with size N = 10,000 and connection probability P₀ = 0.01. For HMNs, we report results for m = 2. The results remain qualitatively the same when other values of m are considered.

3 Results

3.1 The Balanced Region in HMNs

In random networks, balance between excitation and inhibition exists in a region of the parameter space of the strength of the excitatory and inhibitory synapses (Δg_inh, Δg_ex), which allows the neural network to sustain irregular activity without external input. The HMN structure can enlarge the balanced parameter region. We performed a parameter search by varying the strength of excitatory (Δg_ex) and inhibitory (Δg_inh) synapses, limited to the upper boundary Δg_ex = 1, Δg_inh = 10 following Vogels and Abbott (2005). Network activations were simulated by providing each node with background noise activation for 200 ms, and then removing the noise to check whether the networks could sustain the activity on their own. The duration of network activity was determined by numerical simulations lasting up to 1000 ms after the removal of noise.

The results of the average duration over many realizations of simulations are illustrated in Figure 2. The results for the random network are shown in Figure 2A for comparison. In the red regions the networks sustain their activity throughout the simulations. The sustained activity in the upper-left region regular sustained (RS) corresponds to RS activity. Here excitation is dominant and all the neurons of a network fire spikes synchronously. In the blue region excitatory transient (ET), the excitatory couplings tend to synchronize neurons in the networks if there is external excitation. However, the signals generated by neuronal firing arrive synchronously at postsynaptic neurons during their refractory period. Therefore, after the ET activity, all neurons turn silent if the external stimulation is removed. On the other hand, in the blue region inhibitory transient (IT), the inhibitory couplings dominate the network, and the activity is too weak to sustain. When stimulation is removed, all neurons turn to silent after the IT process. The other red region IS represents ISA (Vogels and Abbott, 2005). This overall picture remains similar for the HMNs with various rewiring probabilities R_ex, as seen in Figures 2B–D. Compared to the random networks, in the 4-level HMNs obtained with the rewiring probability of excitatory links R_ex = 0.8, the parameter regions of both irregular and RS activity are enlarged (Figure 2B). The regions are further enlarged with R_ex = 0.9 (Figure 2C). When the rewiring probability R_ex = 0.99, the region of ISA shifts toward the top and is decreased. When R_ex is very close to 1.0, the modules become effectively disconnected, and the communication between the modules is too weak to maintain ISA at the level of the whole network.

FIGURE 2

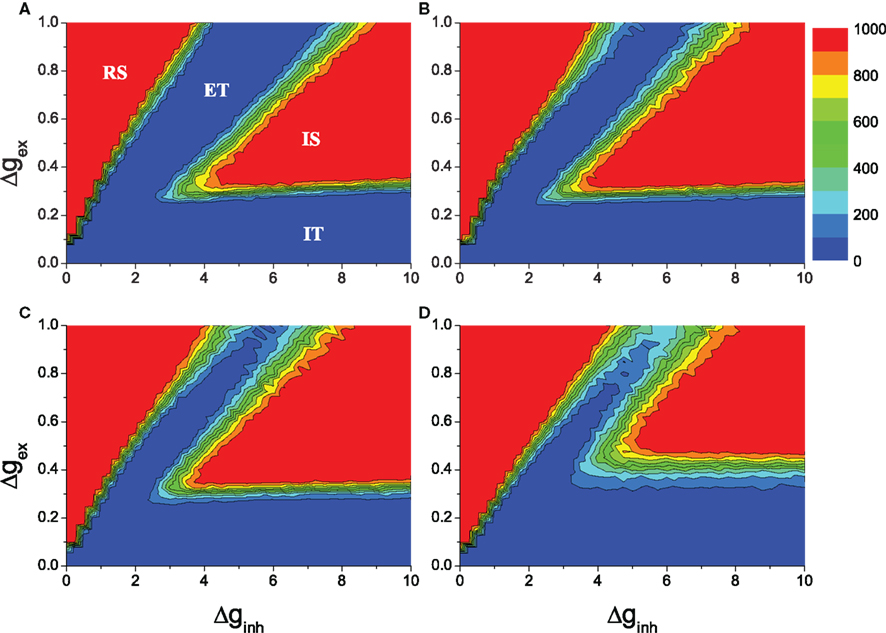
Figure 2. Average duration of network activity in the parameter space (Δginh, Δgex). The network has regular sustained activity (RS) in region RS, irregular sustained activity (IS) in region IS and cannot sustain activity in regions ET and IT. The network size is N = 10,000, the overall connection density is P₀ = 0.01. (A): random networks. (B–D): 4-level HMNs with the rewiring probability R_ex = 0.8, R_ex = 0.9, and R_ex = 0.99, respectively. The results are averaged over 100 network realizations.

In contrast to the previous result suggesting that irregular activity can sustain only in large and sparse networks (Vreeswijk and Sompolinsky, 1996; Vogels and Abbott, 2005), surprisingly, it appears that sustained activity also exists in networks with dense and small modules. Given the HMN organization, the network model simultaneously possesses both the higher connection probabilities found among neighboring neurons and the lower connectivity between neurons separated by modules. Thus our model shows that sustained activity can exist in a broad parameter region in more realistic cortex-like neural networks.

We note that in order to sustain irregular activity, the inhibitory strength is several times larger than the excitatory strength due to a smaller proportion of inhibitory neurons in the system. This is physiologically realistic, since inhibitory synapses are often closer to the cell body of postsynaptic neurons, corresponding to greater physiological impact (Somogyi et al., 1998; Buzsáki, 2006).

The similarity of the sustained region for the homogeneous random network and HMNs implies that the balance of excitation and inhibition plays a crucial role in sustaining irregular activity. However, we here show that the detailed mechanisms are quite different. For random networks, it is known that the network can sustain irregular activity in the balanced region, because in such sparse large networks, the average current into a neuron is around zero; however, it fluctuates strongly and can exceed the firing threshold occasionally to maintain the activity (Vreeswijk and Sompolinsky, 1996; Vogels and Abbott, 2005). Therefore, dense and small networks cannot sustain activity without external signals. However, we show that such isolated dense modules, when perturbed, can produce firing avalanches that display the characteristic of SOC due to the balance of excitation and inhibition. Such SOC modules are sensitive to very weak inputs. When connected into a hierarchical modular structure, they can maintain sustained activity due to the mutual triggering of the avalanches. A more detailed analysis of this new mechanism is present in Sections 3.4 and 3.5 (Figures 6–8). In the following, we describe different firing patterns in the sustained activity of the HMNs due to such firing avalanches. In most of the following analysis, if not specified, the synapse strengths are fixed to Δg_inh = 8.0, and Δg_ex = 0.5, a point in the middle of the sustained region IS.

3.2 Variation of Firing Patterns

The patterns of the irregular dynamics in HMNs are distinctly different from random networks when the modularity increases at large R_ex. We compared the activity of one module in a 4-level HMN obtained at R_ex = 0.99 and the activity of the corresponding ensemble of neurons in the random network before rewiring. Both the HMN and random network sustain irregular activity as a whole. The population activity of the ensemble of neurons in a random network is shown in Figure 3A and that of the corresponding module in a HMN in Figure 3B. The HMN displays an intermittent activity with bursts of relatively strong activity separated by distinct silent periods, while the activity in the random network generally proceeds at a lower level, but without discernible silent intervals. The corresponding spike raster of these neurons in Figures 3C,D shows that in the module of the HMN, the neurons fire with stronger coherence due to dense connections.

FIGURE 3

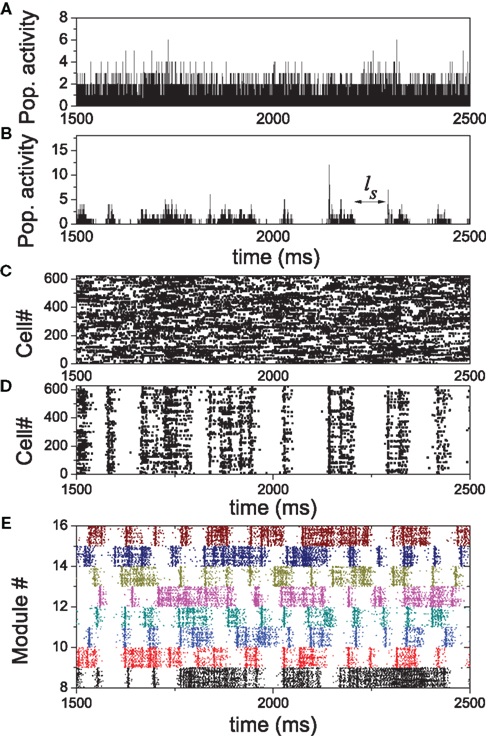
Figure 3. Comparison of the activity patterns in a random network and HMN. (A,B) population activity of an ensemble of neurons in a random network and of the same ensemble neurons which form a module in the HMN rewired from the random network, respectively. (C,D) the corresponding spike rasters of the ensembles. (E) The spike rasters of eight modules in the HMN.

The intermittent firing patterns provide new insight into the mechanism underlying the sustained activity in HMNs: the dense modules can support temporally coherent activity which will terminate eventually if the modules are isolated. However, a silent module can be activated again due to the input from some other modules which are still active. This behavior is manifested by the spike rasters of several modules in Figure 3E. The avalanches of some of the modules are relatively synchronized within a time window, the correlation: however, does not last for a very long time. Since the modules cannot be so strongly synchronized as to move the whole network into silence simultaneously, such intermittent activity will continue, leading to sustained activity in the whole network. This behavior suggests that the network dynamics has the ability to become coordinated but is also very flexible to desynchronize.

3.3 Critical Behavior in HMNs

The intermittent activity of a module is a response of the module to weak input signals from other modules. The intermittent activity exhibits the characteristics of an avalanche. It has been shown that criticality of avalanches is useful for information propagation and processing in neural networks (Beggs and Plenz, 2003). Therefore, we investigated whether the activity of the networks has properties of criticality. We analyzed the distribution of the size of each activity of a module and the length l_s of the silent interval between two active periods (Figure 2B). Activity size is measured as the number of spikes fired in an active period.

Figures 4A,B compare the distribution of l_s in a module of HMNs with a corresponding subnetwork of the random network. The data are cumulated from 60,000 time steps. The distribution of the silent period in the random network follows a straight line with a slope of −0.24 ± 0.01 when plotted in log-linear form, showing that the silent period in random networks follows an exponential distribution (Figure 4A). Very rarely one can observe a silent period larger than 2 ms in the ensemble. By contrast, the distribution of the module in the HMN displays a straight line in the log–log plot (Figure 4B). Therefore, in the HMN, the silent period is distributed according to a power law, with an exponent −2.54 ± 0.05. In these networks, one can observe silent intervals as long as tens of milliseconds to one hundred millisecond. The distribution of the size of activity is shown in Figures 4C,D. For random networks, it follows an exponential function with the exponent −0.16 ± 0.01. For the HMN, the size of the activity displays a power-law distribution with the exponent −2.08 ± 0.08, followed by an exponential cut-off, most clearly seen by the cumulative distribution in the inset. Such a cut-off is mainly due to finite-size effects of the dense module. Indeed, when we enlarge the network size, the power-law distribution of the avalanche size is extended to larger magnitudes (Figure 5). However, systematic simulation of even larger networks is beyond our computational capacity.

FIGURE 4

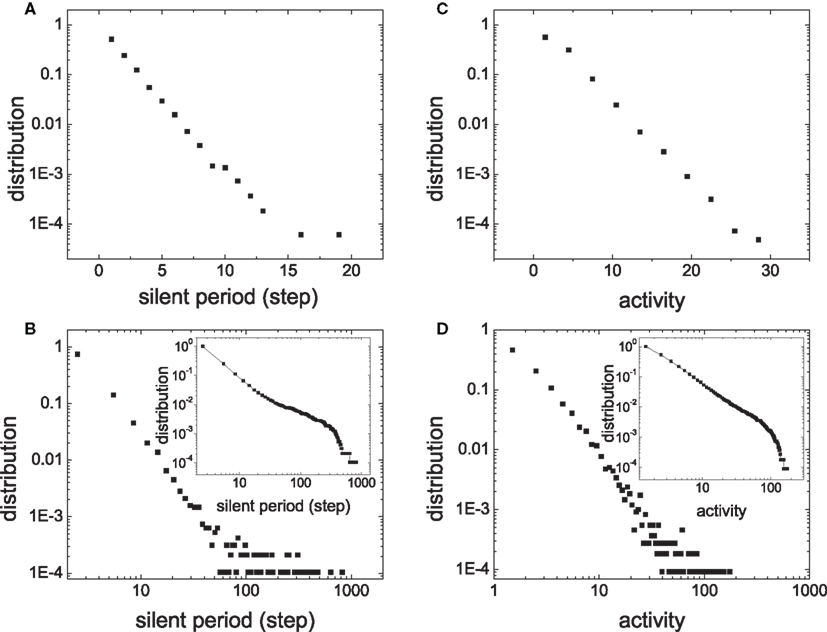
Figure 4. Distribution of the silent period ls and the activity size in an ensemble of N/16 neurons in random network (A) and (C) and in a module of 4-level HMN (B) and (D). The whole networks have the same size N = 10,000 and the rewiring probability for generating HMN is R_ex = 0.99. The insets in (B) and (D) shows the cumulative distribution, that is, the number of intervals larger than a given value, which manifests an exponential cut-off in the distribution.

FIGURE 5

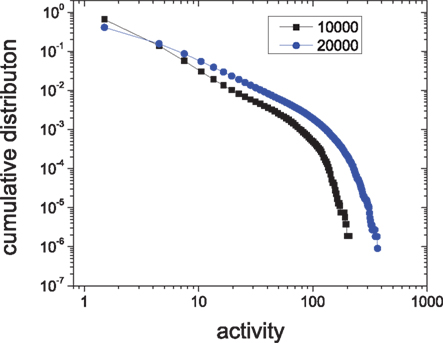
Figure 5. The cumulative distribution of the activity size of modules in 4-level HMNs with N = 10,000, P₀ = 0. 01 (squares) and N = 20,000, P₀ = 0.006 (circles). Δg_ex = 0.5, Δg_inh = 8.0.

A power-law distribution of avalanche size is the fingerprint of SOC. These results show that HMNs are close to critical states, while the random networks are not. The observation of critical states is consistent with experimental data which showed a power-law distribution (also with cut-off) of the neuronal avalanche size (Beggs and Plenz, 2003) or the intervals between large energy fluctuations (Worrell et al., 2002). Here, both the intervals between avalanches and the avalanche sizes of the modules exhibit power-law distributions in the balanced HMNs with sustained irregular activity.

3.4 Mechanism of the Sustained Activity

The SOC feature in the avalanches of the modules suggests a new mechanism of sustained activity of neuronal networks, as follows. In HMNs, all elementary modules are small and dense and cannot sustained their activity independently. However, the modules can exhibit SOC in the presence of weak perturbations. The sparse connections between modules could provide such weak perturbation. Thus, the whole network with sustained activity can be regarded as a system of coupled SOC subsystems.

To verify this new mechanism, we need to show that isolated modules can also display SOC when they are weakly perturbed and that the hierarchical coupling of such modules will gradually lead to sustained activity. In Figure 6A we show the sustained probability of an isolated module versus the connection density (random connections, 4:1 ratio of excitatory to inhibitory neurons). When the connection density of the module is equal to the value in above 4-level HMN, indicated by the arrow in Figure 6, the sustaining probability is effectively zero and the module cannot sustained its activity. Then we investigate the response of the isolated module to weak input. In the simulations, we provide one spike into a randomly selected node from the module at each time step. With such a small input, the module can intermittently produce large avalanches and one obtains a power-law distribution of the activity size, as shown in Figure 6B. The distribution also has an exponential cut-off due to finite size, as seen more clearly by the cumulative distribution in the inset. Thus, the isolated modules can reach the self-organized critical state in the presence of weak external perturbations, very similar to that in the self-sustained HMNs without external signal. One needs to emphasize that a balance of excitation and inhibition is important for the approximate critical state in the module. For the same inhibition strength Δg_in = 8.0, if the excitatory strength is small, Δg_ex < 0.3, the module is clearly in the subcritical regime with only small avalanches, or even cannot generate any response for the weak input. By contrast, for a much larger excitatory strength Δg_ex > 1.0 above the region IS, the module is evidently in the supercritical regime, with high probability for generating large avalanches covering the whole module, or simply displays self-sustained periodic activity. The examples of subcritical (Δg_ex = 0.28) and supercritical (Δg_ex = 1.30) regimes are shown in the inset of Figure 6B for comparison with the approximate critical state at Δg_ex = 0.50. The approximate critical states occur in a broad parameter regions without fine-tuning of system parameters, which is the feature of SOC.

FIGURE 6

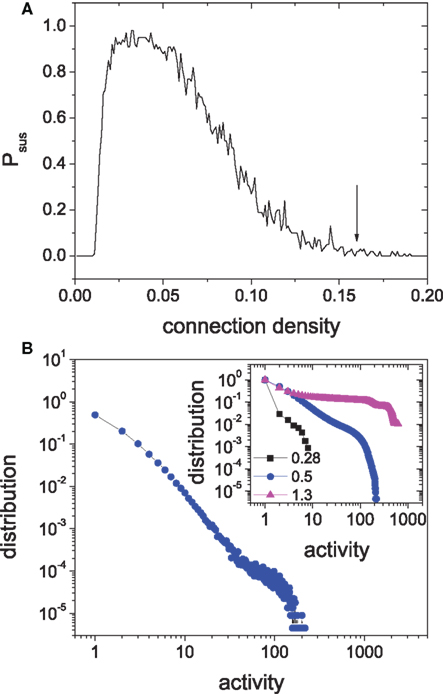
Figure 6. (A) The relation between the sustaining probability of random networks and the connection density. Δg_ex = 0.5, Δg_inh = 8.8, N = 625. (B) The distribution of avalanche size of the isolated module driven by external input. Inset: the cumulative distributions of clearly subcritical state (Δg_ex = 0.28) and supercritical state (Δg_ex = 1.3) are compared to the approximate critical state (Δg_ex = 0.5).

Next we show that the interaction among modules can strongly affect the sustained activity of modules, although the inter-module coupling is very sparse compared to the intra-module coupling. To show the effect of inter-module interactions, we build HMNs in a bottom-up way. We take the isolated modules of a 4-level HMN as basic units for building hierarchical networks with various levels. We assemble the units according to the connection density matrix (Figure 1) from lower to higher levels. Figure 7 shows the sustaining probability of networks built by assembling units in this bottom-up way. When the units are coupled, the sustaining probability increases. In the 4-level HMN the sustaining probability is equal to 1.

FIGURE 7

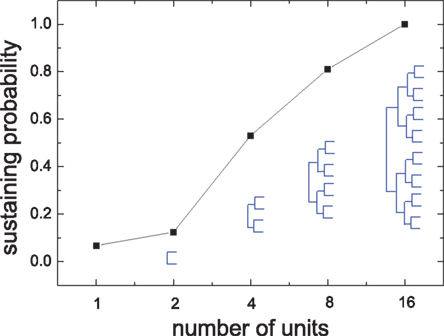
Figure 7. Sustaining probability in networks which are built by assembling the isolated modules of the 4-level HMN according to the connection density matrix shown in Figure 1. The labels on the x-axis represent the number of modules used in recovering HMNs in the bottom-up way. The resulting HMNs are indicated by the hierarchical trees. Δg_ex = 0.5, Δg_inh = 8.0.

These results verify our speculation of the new mechanism of sustained activity in HMNs as coupled SOC subsystems. The sparse coupling between the modules transmits a small portion of the avalanches to act as the weak input into the other temporally silent modules, maintaining them at approximate critical state and inducing avalanches of various sizes. With increases in the number of hierarchical levels and total number of modules in the system, such mutual triggering leads to self-sustained activity.

3.5 Transition from Sustained Activity to Silence at High Rewiring Probability

Systems close to a critical state are sensitive to weak perturbation over a broad range of magnitudes (Kinouchi and Copelli, 2006; Levina et al., 2007). Therefore, we expect that sustained activity in HMNs can be achieved for a range of parameters of sparse coupling between the modules. Figure 2 shows the variation of the parameter region of sustained activity for several values of the rewiring probability R_ex. Here we study the probability P_sus of sustaining the activity in the HMNs with respect to R_ex for given values of synaptic strength (Δg_ex = 0.5, Δg_inh = 8.0). As shown in Figure 8, the sustaining probability only starts to decrease when the rewiring probability is larger than 0.99. After that, we obtain a finite probability that the whole network becomes silent after the removal of the external noise signal. When R_ex > 0.999, the probability that the whole network possesses sustained activity becomes eventually zero, but some of the modules can support sustained activity while the others are silent, since the modules are effectively disconnected. It is notable that the transition of the sustaining probability occurs at a large value of the rewiring probability, confirming that HMNs only need a very small amount of inter-module connections to sustain the activity of the whole network due to the sensitivity of SOC to weak perturbations.

FIGURE 8

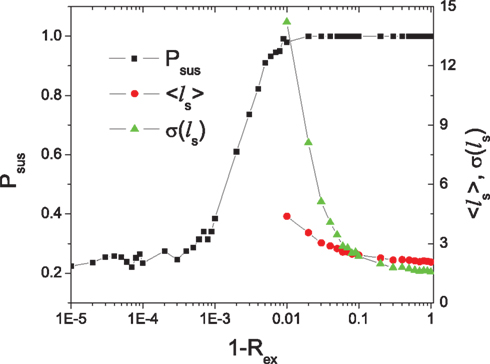
Figure 8. The sustaining probability of a 4-level HMN as a function of rewiring probability R_ex. The average 〈l_s〉 and SD σ〈l_s〉 of the silent period l_s in a module is also shown as functions of R_ex. N = 10,000, Δg_ex = 0.5, Δg_inh = 8.0.

We can characterize the difference in the activity of random and HMNs in a more quantitative way by the statistics of the silent period l_s (in the unit of simulation time steps of 0.1 ms) during which no neuron in the considered ensemble fires a spike. The average value 〈l_s〉 and the SD σ〈l_s〉 are shown in Figure 8 as a function of the rewiring probability R_ex. Both of them increase rapidly when R_ex > 0.9. Large value of σ〈l_s〉 in a broad range of R_ex close to the transition point of the sustained activity implies robust critical behavior in the system.

3.6 Emergence of a Low-Frequency Component in Network Activity

Another significant effect of the intermittent dynamics in HMN is the emergence of low-frequency oscillatory activity. Here we perform an analysis by calculating the power spectrum density (PSD) of the average potential of networks with N = 10,000 and overall connectivity P₀ = 0.01. Figure 9A shows that in random networks the power decays as the frequency increases. When we rewire the network into a HMN with R_ex = 0.99 and R_inh = 1.0, a peak appears at low frequencies around 15 Hz.

FIGURE 9

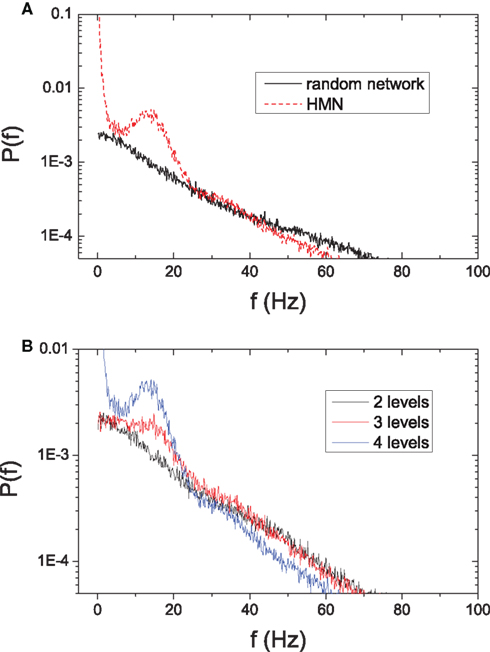
Figure 9. (A) Comparison of the power spectrum density of average potentials in random networks and HMNs with N = 10,000 and P₀ = 0. 01. Solid line: random network. Dashed line: 4-level hierarchical modular network with R_ex = 0.99. (B) Power spectrum density of average potential of hierarchical modular networks with different depth of hierarchy. The parameters are N = 10,000, P₀ = 0.01, and R_ex = 0.99. Black: 2-level HMN; red: 3-level HMN; blue: 4-level HMN.

The low-frequency oscillations are closely related to the intermittent dynamics of modules. When the random network is rewired into a 3-level HMN with the same rewiring probability, the isolated modules are not as densely connected and the temporal activity within them is not very strong. When connected into 3-level HMNs, the intermittent activity is not as pronounced as in a 4-level network. As a result, the low-frequency peak of PSD of the 3-level HMN is lower than that of a 4-level HMN (Figure 9B). When the random network is rewired into a 2-level HMN, its isolated modules can almost always support sustained activity. However, the modules do not display pronounced intermittent activity and a peak is no longer clearly observed at low frequency in the PSD of the 2-level HMN (Figure 9B).

To further illustrate the features of the oscillations, in Figure 10A we show the time series of the average membrane potentials of a few modules in the HMN. A significant randomness exists in the oscillations, corresponding to the broadband background. As discussed in Figure 3, the relation between the activities of the modules is quite complex. It is seen that clear synchronization of the oscillations can occur among some modules for some periods of time. We can manifest such synchronization–desynchronization process by correlation of a pair of modules using a moving window of 500 ms. The correlation is defined as

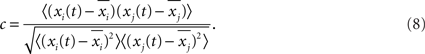
Figure 10B shows an example of c between two modules. The short time correlation has a large fluctuation, and clear correlation may be persistent for hundreds of millisecond. We also compute the correlation between modules over long time window. The correlation can reveal the hierarchical modular structure, as shown in Figure 10C. Averaging the correlation for the modules within the same level shows a clear increase with the hierarchical level (Figure 10D). The largest correlation is between two modules which are neighbors at level 4, for example, modules 1 and 2 illustrated in Figure 10C. Conversely, the smallest correlation is between modules which are only very sparsely connected at level 1, e.g., modules 1 and 9. Thus, the correlation between modules in the model can reveal the network structure over long time periods, but exhibits significant fluctuations in short intervals. These properties are consistent with previous observations on models of functional networks of the brain (Honey et al., 2007).

FIGURE 10

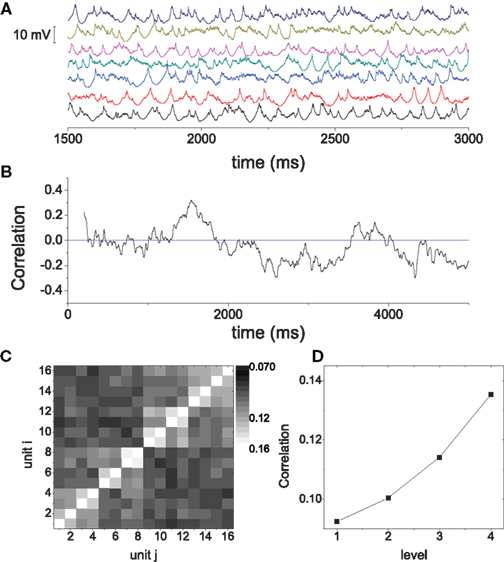
Figure 10. (A) The average membrane potential of several modules in the HMN networks. (B) The correlation between the average potential of two modules, computed with a moving window of 500 ms. (C) The correlation matrix C(i,j). The entries are the correlation between the module i and the module j which are computed in a long window of 6000 ms and averaged over 100 realizations. (D) The average correlation between modules from the same level, as a function of the level.

Both the sustained activity and slow oscillations originate from the interaction of SOC within different modules. The activity in a module is characterized by many small events separated with small intervals, both following power-law distributions. Through sparse connections between the modules, such small but frequently occurring events slightly change the membrane potential of the neurons in other silent modules, slowly drive the system and induce power-law activity in these modules. Such induced activity can further activate the other silent modules. Therefore, the whole network can support sustained irregular activity due to mutual triggering of SOC with very sparse connections among the modules. The slow oscillations are related to the finite-size effects of the SOC within the dense, small modules. As shown by the cumulative distributions in the insets of Figures 4B,D, the largest activities have a cut-off and therefore possess typical scales. Indeed, if we pay particular attention to the statistics of these large events by applying different thresholds, we can see that the intervals between two large events exhibit a distribution peaked around 60 ms. Furthermore, the mean activity of the whole network is mainly contributed by such large events. The combination of these effects leads to the slow oscillations with a frequency of about 15 Hz < 1/60 ms.

So far, we have mainly presented the findings of critical states and slow oscillations for one particular parameters set Δg_ex = 0.5, Δg_inh = 8.0. These behaviors, however, are quite robust to the variation of the parameters in the irregular sustained region when the network modularity is strong enough at large R_ex. This is demonstrated in Figure 11 where the power-law distributions of the silent period and the size of activity and the peaked distribution of PSD are shown for several points as indicated in the parameter space. We can see that the magnitudes of the avalanches, the power and frequency of the oscillations depend on the system parameters.

FIGURE 11

Figure 11. Self-organized criticality and slow oscillations are common in the HMNs in the regime of sustained irregular activity. For various points indicated by the white symbols in the parameter space (A), the peaks in the spectra of the mean potential of the whole network (B), the power-law distributions of the silent period (C) and activity of the modules (D) are robust. The insets in (C) and (D) are the corresponding cumulative distributions.

Here we would like to further discuss the cut-off of the power-law distribution. The cut-off of the avalanche magnitude results from several factors. Firstly, in our model, modules have small size, so the avalanche size is limited. Secondly, inhibitory couplings in the model prevent avalanches from reaching the module size. Both of these two factors can be adjusted by network parameters while maintaining power-law distributions, but affect the cut-off of the avalanche size. In Figure 11 we see that the magnitude of avalanches increases with the excitatory coupling strength. In larger networks the power-law distribution is extended, as shown in Figure 5. Furthermore, SOC is often reflected by an approximate power-law distribution in a broad parameter space, but is not necessarily tied to the exact critical point. Deviation from such an exact critical point will also typically result in an exponential cut-off. In our modular networks, the state is close to the critical states, and the network dynamics in the broad region of ISA are similar. However, due to highly demanding computation in modeling the HMNs, it is difficult to identify the exact critical point using systematic finite-size analysis.

3.7 Realistic Network

We proceed to testing these results on realistic biological data for the cortical network of the cat (Scannell et al., 1999; Zhou et al., 2006). The cat cortical network consists of 53 areas which are linked by 830 fiber connections of different densities. It forms a weighted complex network and exhibits a hierarchically modular structure. The connection matrix {a_ij} is shown in Figure 12. The cortex network has modules that broadly agree with four functional cortical subdivisions, that is, visual cortex (V), auditory (A), somato-motor (SM), and fronto-limbic (FL) (Hilgetag et al., 2000; Hilgetag and Kaiser, 2004).

FIGURE 12

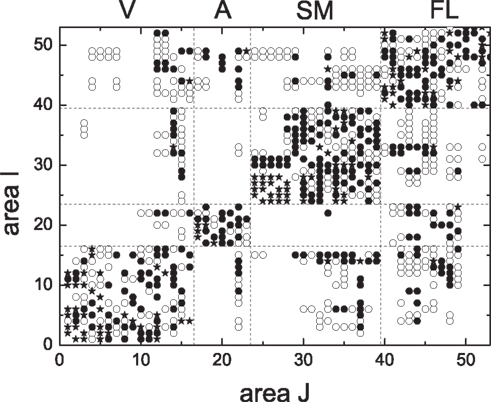
Figure 12. The connection matrix {a_ij} of the cortical network of the cat brain. The symbols represent different densities of the fiber connections: 1 (•, sparse), 2(○, intermediate), and 3(⋆, dense). a_ij represents the connection density from area i to area j.

In the present work, a pair of interacting areas is represented by a 4-level HMN as in Figure 1, so that each area of the cat network is represented by one of the two modules (3-level HMN) in the 4-level HMN, and the connection density between the two areas is given by that between the two 3-level modules. The 3-level HMN in each cortical area has 4000 neurons with the overall connection probability P₀ = 0.02. The rewiring probability is R_ex = 0.999 and R_inh = 1.0. Here a larger R_ex is considered since we have 53 areas so that smaller inter-module connections are necessary to maintain the intermittent activity in the system. With these parameters, connection probability between area i and area j is a_ijP_c with P_c = 8.0 × 10⁻⁶, where P_c is the connection density between the two modules of the 4-level network.

The distributions of the silent period and the size of activity are shown in Figure 13. Both the silent period and the size of activity are distributed according to a power law. The scale exponent of the distribution of the silent period is −2.58 ± 0.08. The scale exponent of the distribution of the size of activity is −3.04 ± 0.09. They are similar to the values obtained in our previous simpler model. The distribution of the PSD in Figure 14 shows a peak around a low frequency. These results show that both criticality and low-frequency oscillations are quite robust when HMNs are embedded in more complex realistic cortical networks, implying that the combination of the hierarchical modular architecture and the balance of excitation with inhibition may generally play an important role in the activity of the brain.

FIGURE 13

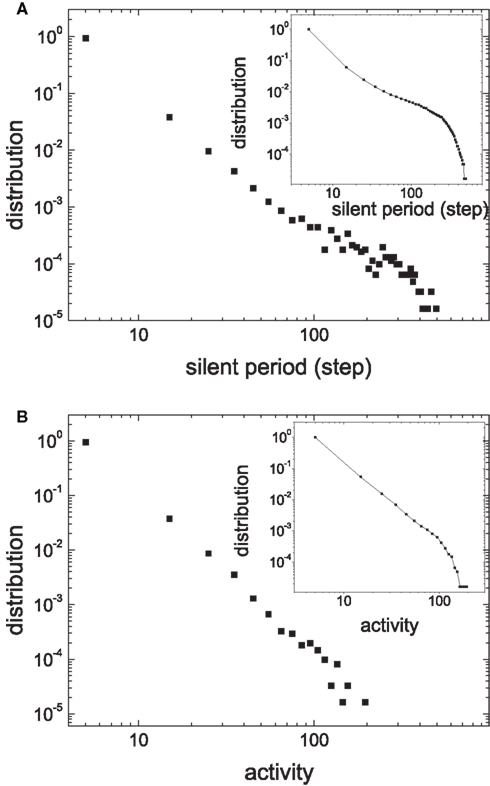
Figure 13. Distribution of the silent period (A) and the size of activity (B) of one area of the cat cortical network model. The insets are the corresponding cumulative distributions.

FIGURE 14

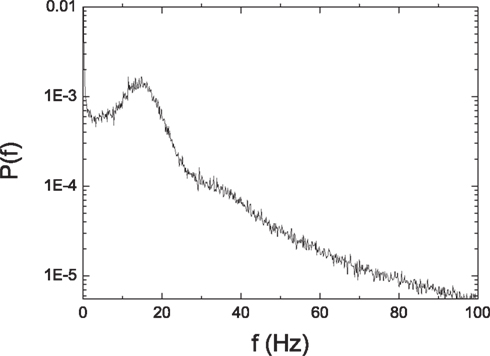
Figure 14. Power spectrum density of the average membrane potential of the cat cortical network model.

The analysis of modular organization in human cortical connectivity data from magnetic resonance imaging (MRI) or diffusion spectrum imaging (DSI) has shown that brain networks have many levels of hierarchy. The number of modules and the sizes of the modules vary at different levels (Bassett et al., 2010), and the number of hierarchy increases from 2 in MRI data (parcellation into 104 regions) to 3 in DSI data (1000 regions). It is likely that more refined levels can be detected in smaller scales if connectivity data with higher resolution could become available in the future. Recent simulation of a simple spreading model in HMNs shows that the persistence of scalable activation is optimal for certain combination of depth of the hierarchy l, the number of modular division m (Kaiser and Hilgetag, 2010). In our biologically meaningful HMN model with balanced excitation and inhibition, a more systematic analysis of the dependence of the activity on the network parameters, such as the depth of the hierarchy l, the number of modular division m, the overall average density P₀ and the modularity related to the rewiring probabilities R_ex and R_inh can shed light on the organization of HMNs in the whole brain in terms of these organization parameters. This will be a topic for future explorations.

4 Discussion

Among the most basic and prominent features of the neural networks of the brain are the mixture of excitatory and inhibitory neurons and the network organization into a hierarchical modular graph. Here we studied effects of the hierarchical modular organization on the dynamics of the sustained activity of neural networks with balanced excitation and inhibition. We found that the combination of these two structural features can simultaneously support sustained irregular activity, critical states of neural avalanches and slow oscillations in the mean activity of the neural networks.

The hierarchical modular structure enables the brain networks to have both ISA and dense local subnetworks, which cannot support sustained activity in isolation. The mechanism unveiled in this work is that very weak interactions between modules ensure the sustained activity of the HMNs, which extends the balanced parameter region between excitatory and inhibitory synapses. For given strengths of excitatory and inhibitory synapses, the modules in silent periods cannot be activated by the input from the other active modules as the synaptic connections between modules become too sparse, and the whole network looses the ability to support sustained activity. In a region close to the transition point, the modules display an intermittent dynamics, while the whole network sustains irregular activity.

Within the modules, the intermittent activity exhibits several other non-trivial properties. We can observe relatively large synchronized firing of the neurons which is not present in the subnetworks of the corresponding random networks. Such synchronization was also observed experimentally in the spontaneous activity in slices of mouse visual cortex (Mao et al., 2001; Cossart et al., 2003; Ikegaya et al., 2004; Grinstein and Linsker, 2005). A model investigation into the role of network structure in the generation of synchrony suggested that networks with hubs are able to exhibit synchrony peaks (Grinstein and Linsker, 2005). Here we show that modular network structure provides another potential mechanism of generating synchronization. Very recently, the existence of hub neurons has been demonstrated experimentally (Bonifazi et al., 2009). It will be interesting for future work to investigate the activity patterns of HMNs with hubs (Müller-Linow et al., 2008).

Our more detailed statistical analysis of the activity within the modules of balanced HMNs shows that the dynamic behavior possesses characteristics of SOC. Both the silent period and the size of the activity are distributed according to a power-law, which is consistent with several experimental findings on neuronal avalanches (Worrell et al., 2002; Beggs and Plenz, 2003). The exponents of the distribution depend on various network parameters, which will be analyzed in more detail in the future. In experiments, it was also shown that the exponents are related to various components in the configuration of neural systems (Worrell et al., 2002). For example, in Beggs and Plenz (2003) it was shown that the exponent depends on the spatial and temporal resolution of the data. Our model is different from the usual neural network models for the simulation of critical behavior. In those models, a separation of timescales is assumed and external random input is needed for driving a system to avalanche (Eurich et al., 2002; de Arcangelis et al., 2006; Levina et al., 2007). In our model, a slow and random perturbation of a module results from the weak interaction with the avalanche activity of other modules. Self-organized critical states within the dense modules can be obtained by mutual triggering among the modules. These findings show that the modular structure of brain networks naturally provides the substrates for the system to simultaneously support global sustained activity and local critical states, so that the advantages of both of them could be employed for information processing (Beggs and Plenz, 2003; Vogels and Abbott, 2005; Lewis et al., 2009).

Interestingly, the coexistence of local critical states and global sustained activity can lead to slow waves in the mean activity of HMNs. While much research has been devoted to study oscillations in complex brain activity and their relevance to functions of the brain (Engel et al., 2001; Fries, 2005; Buzsáki, 2006), the generating mechanisms for oscillations are still largely an open question. On the one hand, in terms of non-linear dynamics, feedback projections with inhibition and delays are supposed to play an important role. On the other hand, it has been stated that slow waves are related to slow neuronal oscillations composed of silent phases (down-state) and burst phases (up-state; Buzsáki, 2006). There has been much work on modeling the dynamics based on burst firing of individual neurons (Belykh et al., 2005; Hill and Tononi, 2005). Here we demonstrated that the hierarchical modular architecture of the brain could play an important role in generating oscillations from the mutual triggering of critical states. Although the individual model nodes do not possess up- or down-states, the modular structure induces a burst-like behavior of the modules and the slow oscillations of the whole network. Since the large-scale neural network in the brain has more levels of hierarchical modular architecture and strongly heterogeneous organization in the modules, it is likely that such a structural organization underlies the emergence of complex oscillations covering a broad range of scales when interacting with feedbacks by inhibition and delays. More detailed exploration of the underlying mechanism should provide new insights into the structure–function relationships which are mediated by the sustained, critical, and oscillatory dynamical activity of the brain.

There are other important questions that need to be addressed in the future. For example, what are the reasons for neural systems to organize into a HMN architecture? No doubt, there are numerous constraints on the network organization to meet requirements of efficient information processing during diverse functions. Our analysis demonstrates possible functional advantages of the hierarchical modular organization for supporting simultaneously various dynamical properties which may be beneficial for information processing. The modular architecture also provides the neural systems with an increased parameter space for sustained activity (Kaiser et al., 2007; Kaiser and Hilgetag, 2010) as well as balanced functional segregation and integration (Sporns et al., 2000; Zhao et al., 2010). Of additional relevance could be constraints from wiring and metabolic costs. It was shown that small-world connectivity provides a wiring-efficient solution while enabling synchronization of neural systems (Buzsáki et al., 2004). It will be interesting to see whether the hierarchical modular organization could provide an even more efficient solution.

In summary, we discovered a new mechanism of dynamical organization in cortex-like hierarchical modular neural networks. Dense and small modules display avalanches with characteristic features of SOC in the presence of weak inputs, and HMNs integrate these modules as a system of coupled SOC subsystems. Very weak interactions between modules guarantee the sustained activity of the HMNs due to high sensitivity of critical states to weak perturbations. The balance between excitation and inhibition is crucial for maintaining SOC in the modules. Further studies will focus on investigating how the self-sustaining HMNs interact with external signals and how the advantages of the sensitivity of SOC and the predictability of oscillations can be employed in information processing. These investigations of the dynamical mechanisms could make significant contributions to understanding the general impact of spontaneous brain activity on brain dynamics and function.

5 Conclusion

We studied the effect of hierarchical modular structure on the dynamics of sustained activity of neural networks with both excitatory and inhibitory neurons. The hierarchical modular organization can support ISA and extend the balanced parameter region between excitatory and inhibitory synapses. More importantly, the dynamics of the HMNs is different from homogeneous networks. The isolated dense small modules cannot sustain activity without external stimulus, however, they can generate avalanches of various sizes in the presence of weak inputs. The power-law distribution of the avalanches shows that they display SOC. When modules are coupled, sparse inter-module connections enable the network to sustain its activity without external signal through mutual triggering of avalanches of the modules. This is due to high sensitivity of SOC to weak perturbations. As a result, the dynamics of modules in self-sustained HMNs also displays the characteristic of SOC. The HMNs also exhibit slow oscillations because of the intermittent dynamics of modules. The power and frequency of the oscillations can be adjusted by network parameters. These results were also obtained in the model using cat cortio-corticall network connectivity. Our results provide a new mechanism of sustaining activity and generating oscillations in cortex-like neural networks that capture the most prominent structural features: the hierarchical modular organization and the coexistence of excitatory and inhibitory neurons.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The work described in this paper was supported by Hong Kong Baptist University, the Research Grants Council of Hong Kong (HKBU 202710) and a grant from the Germany/Hong Kong Joint Research Scheme sponsored by the Research Grants Council of Hong Kong and the German Academic Exchange Service (Reference No. G-HK 006/08).

References

Albert, R., and Barabási, A. (2002). Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97.

CrossRef Full Text

Albus, K., and Wahle, P. (1994). The topography of tangential inhibitory connections in the postnatally developing and mature striate cortex of the cat. Eur. J. Neurosci. 6, 779–792.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Arenas, A., Díaz-Guilera, A., Kurths, J., Moreno, Y., and Zhou, C. (2008). Synchronization in complex networks. Phys. Rep. 469, 93–153.

CrossRef Full Text

Bak, P. (1996). How Nature Works: The Science of Self-Organized Criticality (Copernicus), 1st Edn. New York, NY: Springer-Verlag.

Bak, P., Tang, C., and Wiesenfeld, K. (1987). Self-organized criticality: an explanation of the 1/f noise. Phys. Rev. Lett. 59, 381–384.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bak, P., Tang, C., and Wiesenfeld, K. (1988). Self-organized criticality. Phys. Rev. A 38, 364–374.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bassett, D., and Bullmore, E. (2006). Small-world brain networks. Neuroscientist 12, 512.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bassett, D. S., Greenfield, D. L., Meyer-Lindenberg, A., Weinberger, D. R., Moore, S. W., and Bullmore, E. T. (2010). Efficient physical embedding of topologically complex information processing networks in brains and computer circuits. PLoS Comput. Biol. 6, e1000748. doi: 10.1371/journal.pcbi.1000748

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Battaglia, D., Brunel, N., and Hansel, D. (2007). Temporal decorrelation of collective oscillations in neural networks with local inhibition and long-range excitation. Phys. Rev. Lett. 99, 238106.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bedard, C., Kroeger, H., and Destexhe, A. (2006). Does the 1/f frequency scaling of brain signals reflect self-organized critical states? Phys. Rev. Lett. 97, 118102.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Beggs, J., and Plenz, D. (2003). Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167.

Pubmed Abstract | Pubmed Full Text

Beggs, J., and Plenz, D. (2004). Neuronal avalanches are diverse and precise activity patterns that are stable for many hours in cortical slice cultures. J. Neurosci. 24, 5216.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Belykh, I., de Lange, E., and Hasler, M. (2005). Synchronization of bursting neurons: what matters in the network topology. Phys. Rev. Lett. 94, 188101.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and Hwang, D.-U. (2006). Complex networks: structure and dynamics. Phys. Rep. 424, 175–308.

CrossRef Full Text

Bonifazi, P., Goldin, M., Picardo, M., Jorquera, I., Cattani, A., Bianconi, G., Represa, A., Ben-Ari, Y., and Cossart, R. (2009). GABAergic hub neurons orchestrate synchrony in developing hippocampal networks. Science 326, 1419.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bosking, W., Zhang, Y., Schofield, B., and Fitzpatrick, D. (1997). Orientation selectivity and the arrangement of horizontal connections in tree shrew striate cortex. J. Neurosci. 17, 2112.

Pubmed Abstract | Pubmed Full Text

Brunel, N. (2000). Dynamics of networks of randomly connected excitatory and inhibitory spiking neurons. J. Physiol. Paris 94, 445–463.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bullmore, E., and Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buzsáki, G. (2006). Rhythms of the Brain. New York, NY: Oxford University Press.

Buzsáki, G., Geisler, C., Henze, D., and Wang, X. (2004). Interneuron diversity series: circuit complexity and axon wiring economy of cortical interneurons. Trends Neurosci. 27, 186–193.

CrossRef Full Text

Cossart, R., Aronov, D., and Yuste, R. (2003). Attractor dynamics of network UP states in the neocortex. Nature 423, 283–288.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

de Arcangelis, L., Perrone-Capano, C., and Herrmann, H. (2006). Self-organized criticality model for brain plasticity. Phys. Rev. Lett. 96, 28107.

CrossRef Full Text

Engel, A., Fries, P., and Singer, W. (2001). Dynamic predictions: oscillations and synchrony in top–down processing. Nat. Rev. Neurosci. 2, 704–716.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eurich, C., Herrmann, J., and Ernst, U. (2002). Finite-size effects of avalanche dynamics. Phys. Rev. E 66, 66137.

CrossRef Full Text

Fries, P. (2005). A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn. Sci. (Regul. Ed.) 9, 474–480.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Galán, R. (2008). On how network architecture determines the dominant patterns of spontaneous neural activity. PLoS ONE 3, e2148. doi: 10.1371/journal.pone.0002148

CrossRef Full Text

Grinstein, G., and Linsker, R. (2005). Synchronous neural activity in scale-free network models versus random network models. Proc. Natl. Acad. Sci. U.S.A. 102, 9948.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hilgetag, C., Burns, G., O’Neill, M., Scannell, J., and Young, M. (2000). Anatomical connectivity defines the organization of clusters of cortical areas in the macaque monkey and the cat. Philos. Trans. R. Soc. Lond. B Biol. Sci 355, 91.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hilgetag, C., and Kaiser, M. (2004). Clustered organization of cortical connectivity. Neuroinformatics 2, 353–360.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hill, S., and Tononi, G. (2005). Modeling sleep and wakefulness in the thalamocortical system. J. Neurophysiol. 93, 1671–1698.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Honey, C., Kötter, R., Breakspear, M., and Sporns, O. (2007). Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc. Natl. Acad. Sci. U.S.A. 104, 10240.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ikegaya, Y., Aaron, G., Cossart, R., Aronov, D., Lampl, I., Ferster, D., and Yuste, R. (2004). Synfire chains and cortical songs: temporal modules of cortical activity. Science 304, 559.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jensen, H. J. (1998). Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems. Cambridge, MA: Cambridge University Press.

Kaiser, M., Görner, M., and Hilgetag, C. (2007). Criticality of spreading dynamics in hierarchical cluster networks without inhibition. New J. Phys. 9, 110.

CrossRef Full Text

Kaiser, M., and Hilgetag, C. (2010). Optimal hierarchical modular topologies for producing limited sustained activation of neural networks. Front. Neuroinform. 4:8. doi: 10.3389/fninf.2010.00008

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kinouchi, O., and Copelli, M. (2006). Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2, 348–351.

CrossRef Full Text

Knight, R. (2007). Neural networks debunk phrenology. Science 316, 1578.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Levina, A., Herrmann, J. M., and Geisel, T. (2007). Dynamical synapses causing self-organized criticality in neural networks. Nat. Phys. 3, 857–860.

CrossRef Full Text

Lewis, C., Baldassarre, A., Committeri, G., Romani, G., and Corbetta, M. (2009). Learning sculpts the spontaneous activity of the resting human brain. Proc. Natl. Acad. Sci. U.S.A. 106, 17558.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mao, B., Hamzei-Sichani, F., Aronov, D., Froemke, R., and Yuste, R. (2001). Dynamics of spontaneous activity in neocortical slices. Neuron 32, 883–898.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mountcastle, V. (1997). The columnar organization of the neocortex. Brain 120, 701.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Müller-Linow, M., Hilgetag, C. C., and Hütt, M. T. (2008). Organization of excitable dynamics in hierarchical biological networks. PLoS Comput. Biol. 4, e1000190. doi: 10.1371/journal.pcbi.1000190

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Reijneveld, J., Ponten, S., Berendse, H., and Stam, C. (2007). The application of graph theoretical analysis to complex networks in the brain. Clin. Neurophysiol. 118, 2317–2331.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Robinson, P. A., Henderson, J. A., Matar, E., Riley, P., and Gray, R. T. (2009). Dynamical reconnection and stability constraints on cortical network architecture. Phys. Rev. Lett. 103, 108104.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Roxin, A., Riecke, H., and Solla, S. (2004). Self-sustained activity in a small-world network of excitable neurons. Phys. Rev. Lett. 92, 198101.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Scannell, J., Burns, G., Hilgetag, C., O’Neil, M., and Young, M. (1999). The connectional organization of the cortico-thalamic system of the cat. Cereb. Cortex 9, 277.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Somogyi, P., Tamas, G., Lujan, R., and Buhl, E. (1998). Salient features of synaptic organisation in the cerebral cortex1. Brain Res. Rev. 26, 113–135.

CrossRef Full Text

Sporns, O., Chialvo, D., Kaiser, M., and Hilgetag, C. (2004). Organization, development and function of complex brain networks. Trends Cogn. Sci. (Regul. Ed.) 8, 418–425.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sporns, O., Tononi, G., and Edelman, G. (2000). Theoretical neuroanatomy: relating anatomical and functional connectivity in graphs and cortical connection matrices. Cereb. Cortex 10, 127.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Strogatz, S. (2001). Exploring complex networks. Nature 410, 268–276.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vogels, T. P., and Abbott, L. F. (2005). Signal propagation and logic gating in networks of integrate-and-fire neurons. J. Neurosci. 25, 10786–10795.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vreeswijk, C., and Sompolinsky, H. (1996). Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274, 1724.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vreeswijk, C., and Sompolinsky, H. (1998). Chaotic balanced state in a model of cortical circuits. Neural. Comput. 10, 1321–1371.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Worrell, G., Cranstoun, S., Echauz, J., and Litt, B. (2002). Evidence for self-organized criticality in human epileptic hippocampus. Neuroreport 13, 2017.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zhao, M., Zhou, C., Chen, Y., Hu, B., and Wang, B. (2010). Complexity versus modularity and heterogeneity in oscillatory networks: combining segregation and integration in neural systems. Phys. Rev. E 82, 046225.

CrossRef Full Text

Zhou, C., Zemanová, L., Zamora, G., Hilgetag, C., and Kurths, J. (2006). Hierarchical organization unveiled by functional connectivity in complex brain networks. Phys. Rev. Lett. 97, 238103.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zhou, C., Zemanová, L., Zamora-Lopez, G., Hilgetag, C., and Kurths, J. (2007). Structure–function relationship in complex brain networks expressed by hierarchical synchronization. New J. Phys. 9, 178.

CrossRef Full Text