- Biomedical Engineering, Oregon Health and Science University, Portland, OR, USA
Adaptive sensory processing influences the central nervous system’s interpretation of incoming sensory information. One of the functions of this adaptive sensory processing is to allow the nervous system to ignore predictable sensory information so that it may focus on important novel information needed to improve performance of specific tasks. The mechanism of spike-timing-dependent plasticity (STDP) has proven to be intriguing in this context because of its dual role in long-term memory and ongoing adaptation to maintain optimal tuning of neural responses. Some of the clearest links between STDP and adaptive sensory processing have come from in vitro, in vivo, and modeling studies of the electrosensory systems of weakly electric fish. Plasticity in these systems is anti-Hebbian, so that presynaptic inputs that repeatedly precede, and possibly could contribute to, a postsynaptic neuron’s firing are weakened. The learning dynamics of anti-Hebbian STDP learning rules are stable if the timing relations obey strict constraints. The stability of these learning rules leads to clear predictions of how functional consequences can arise from the detailed structure of the plasticity. Here we review the connection between theoretical predictions and functional consequences of anti-Hebbian STDP, focusing on adaptive processing in the electrosensory system of weakly electric fish. After introducing electrosensory adaptive processing and the dynamics of anti-Hebbian STDP learning rules, we address issues of predictive sensory cancelation and novelty detection, descending control of plasticity, synaptic scaling, and optimal sensory tuning. We conclude with examples in other systems where these principles may apply.
Expectations and predictions are essential for efficient processing sensory information (Barlow, 1990). If expected sensory patterns are subtracted from sensory signals, then novel sensory patterns, important to the survival of an organism, are accentuated. Any novel stimulus that is persistently associated with other neural signals will eventually become predictable. Hence, sensory processing systems must continually adapt to changing sensory environmental conditions to take full advantage of such predictive coding strategies.
Because biological processes interact across different time scales in adaptive sensory systems, mathematical modeling is helpful to untangle multiple causes from their effects. This review discusses attempts that have been made to model adaptive sensory filters based on spike-timing-dependent plasticity (STDP). The model systems are found in electrosensory systems, but the principles discussed here are applicable to many sensory systems.
The two types of electrosensory systems that we will discuss in terms of modeling are the passive and active electrosensory system of weakly electric fish. We will focus on the initial processing structure in the electrosensory lateral line lobe (ELL) of mormyrid electric fish, where passive and active electrosensory information is conveyed and processed by separate sensory pathways. The basic functional structure of these two electrosensory pathways is the convergence of primary electrosensory input with a variety of sensory and motor signals that could serve to predict changes in the electrosensory input (Figure 1). Spike-timing-dependent synaptic plasticity at the synapse carrying predictive signals sculpts a negative image of predictable sensory input patterns from a background of sensorimotor activity. The summation of these negative images with the sensory input results in a cancelation of predictable features.
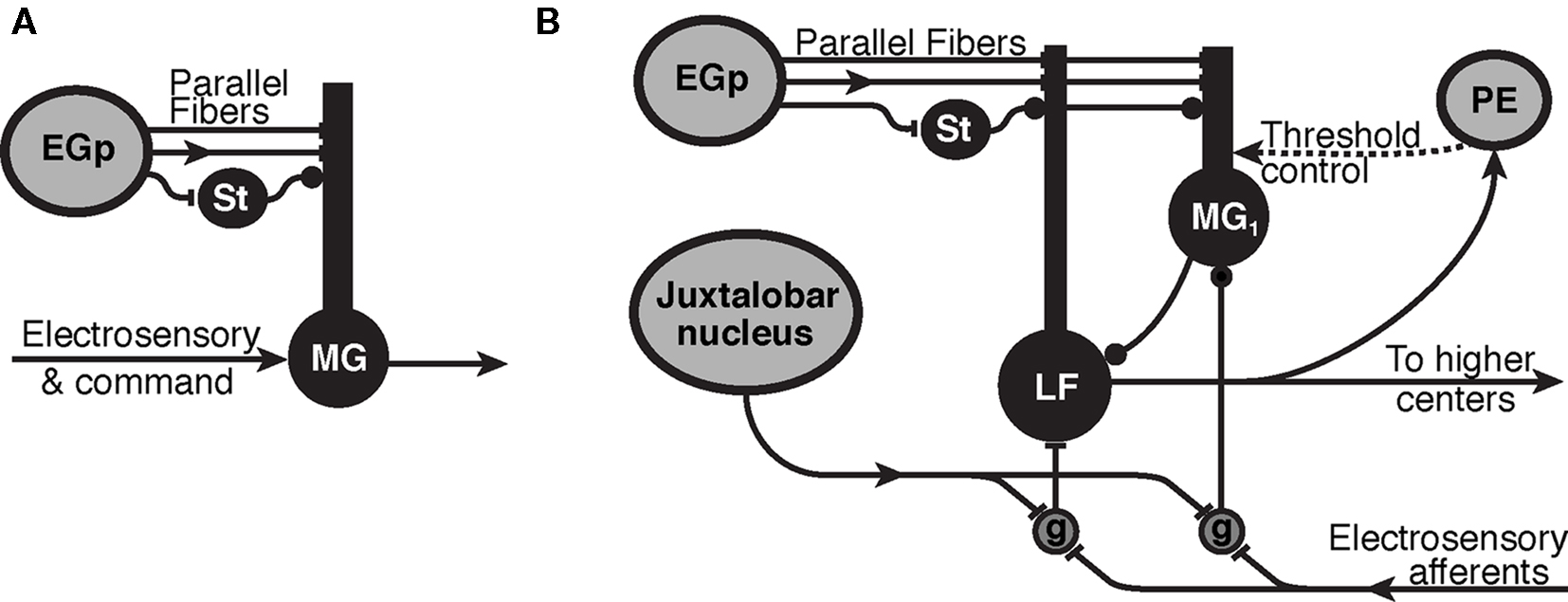
Figure 1. Synaptic organization of cerebellum-like structures in mormyrid fish. (A) Simplified circuit of electrosensory lateral line lobe (ELL) used for modeling of the passive electrosensory system. Parallel fibers originate in the eminentia granularis posterior (EGp) and synapse onto the apical dendrites of medium ganglion (MG) cell with excitatory synapses (bar terminals) and inhibitory stellate cells (St) synapse in the same layer with inhibitory synapses (disk terminals). The parallel fibers carry a sequence of delayed inputs that convey the timing of the EOD command. The Purkinje-like MG cell cancels expected electrosensory signals with an STDP mechanism at the synapse from parallel fibers and stellate cells. Arrows represent the flow of information and mixed inputs. (B) ELL circuitry for the active electrosensory system. Mormyromast electroreceptors transform the field intensity at the skin into a spike latency code that is transformed into a spike burst duration code by deep granular cells (g) controlled by centrally generated corollary discharge input from the juxtalobar nucleus. The electrosensory signal is then transferred to the adaptive stage of electrosensory processing (type-1 medium ganglion (MG1) and large fusiform (LF) cells), and the expected sensory responses are subtracted. Recurrent connections, modulated by higher centers (preeminential nucleus, PE), are hypothesized to control the threshold of back-propagating broad (dendritic) spikes in MG1 cells.
1 Mormyrid Electrosensory System
Mormyrid electric fish have an electric organ in their tail that generates a weak electric field. A motor command causes the electric organ to discharge in pulses (Bennett, 1970; Hopkins, 1995), like the flexing of a muscle. By detecting distortions caused by external objects in the fish’s own electric field, mormyrids can navigate through their environment without vision (Assad et al., 1999; Von der Emde, 1999). This active electrolocation system is similar to echolocation in bats. The electric organ discharge (EOD) is also used for communication with conspecifics (Hopkins, 1988).
Mormyrids have three types of electroreceptors that serve three different functions (Bodznick and Montgomery, 2005; Kawasaki, 2005): active electrolocation, communication, and passive detection of external sources of electric fields, such as moving organisms. Behaviorally relevant stimuli associated with prey result in extremely small changes in the fish’s self-generated field detected by receptors for active electrolocation and relatively weak fields caused by the prey’s movement detected by receptors for passive electrolocation.
In both the active and passive pathways, the challenge for the electrosensory system is to detect small behaviorally relevant signals in the midst of much larger signals resulting from the fish’s own behavior. In the active system, moving the tail changes the position of the electric organ relative to the electroreceptors on the body surface and produces large changes in the electric field the receptors are exposed to. In the passive system, the fish’s EOD swamps the receptors that need to detect weak, externally generated fields. In order to detect weak changes in signals, the fish integrates self-generated proprioceptive and timing information about where and when the EODs, information that could be used to process re-afferent signals. We will focus on the passive system first and the mechanism of canceling the EOD using timing information.
2 Expectation Cancelation in Passive Electrosensory Systems
The command to generate an EOD is sent to the electric organ, and results in a following sensory re-afferent signal (von Holst and Mittelstaedt, l950) from electroreceptors responding to the EOD signal that central neurons in the ELL. Simultaneously, information about the timing of the motor command is relayed to the ELL through another neural pathway as a corollary discharge signal.
The ELL is a laminar, cerebellum-like structure where electrosensory afferents enter from the deep layer. There is a layer of large cells in the ELL, called the ganglion layer, where the cells show strong adaptation to changing sensory images (Bell, 1982). We focus on one class of principal cells in this layer, the medium ganglion (MG) cells, because they receive the most parallel fiber synapses Meek and Grant (1994). MG cells have basal dendrites that receive the electrosensory afferent input and apical dendrites that reach into the molecular layer to receive a variety of synaptic inputs from parallel fibers (PF). The PF originate externally to the ELL, as granule cells that respond to the corollary discharge in the eminentia granularis posterior (EGp) nucleus, PF also drive inhibitory interneurons (stellate cells) that synapse onto MG cells (Figure 1A).
Recordings from the EGp nucleus containing granule cells suggest that the granule cells do not respond to the corollary discharge simultaneously, but their responses appear to be distributed sequentially during the time following the command signal (Bell et al., 1992; Sawtell, 2010).Following each EOD motor command, different granule cells fire at different latencies so that PF carry a distribution of spikes timed at different delays following each EOD. Because corollary discharge information on electric discharge timing arrives at MG cells through PF, a likely candidate for an adaptive mechanism would be the synapse between the PF and the apical dendrites of MG cells.
Medium ganglion cells respond to a depolarizing input with two types of spikes: a small narrow spike and a large, broad spike that is generated at a higher threshold than the narrow spike and mediates synaptic plasticity. Experimental evidence suggests that the small spike is axonal and the broad spike propagates into the dendrites (Grant et al., 1998). The dendritic spike would inform the parallel fiber synapses of strong depolarization caused by afferent sensory input to the basilar dendrites and mediates plasticity at the synapses from the PF to the MG cells.
Within each network shown in Figure 1, the main process is that principal cells are excited by a large set of inputs that carry contextual information. In addition, the principal MG cells are inhibited via inhibitory interneurons that respond to the same large set of inputs. The convergence of contextual information onto a Purkinje-like neuron suggests that associative plasticity at the synapses onto MG cells may provide the system a means of sorting the incoming information for sensory processing. In addition, the plasticity should be dependent on the timing of broad (dendritic) spikes in MG cells.
To test for spike-timing-dependent changes at the parallel fiber synapse onto MG cells, Bell et al. (1997d) used a slice preparation of the ELL to stimulate the PF and measure the resulting parallel fiber-evoked excitatory postsynaptic potential (EPSP). In these experiments, changes in the size of the EPSPs were taken as a proxy for changes in the strength of excitatory parallel fiber synapses. The MG cell was depolarized to generate a broad spike at various delays from the parallel fiber stimulus. After repeatedly pairing a stimulation with a broad spike at a certain delay, the strength of the synapse was remeasured. Some delays increased the synaptic strength, while others decreased it. When all the changes were plotted as a function of the delays, it was found that the synapse was depressed if the broad spikes immediately followed the stimulation; otherwise the synaptic strength was enhanced. Furthermore, the depression was in a window of about the same duration, and coincident with, the EPSP evoked by PF.
The activity dependent changes do not appear to be limited to parallel fiber EPSPs. Some experiments showed spike-timing-dependent changes in parallel fiber-evoked, postsynaptic potentials, which were mostly inhibitory (IPSP; Bell et al., 1997c). The synapses where these changes take place are most likely from stellate cells in the molecular layer onto the MG cells. The precise characterization of the STDP learning rules led to theoretical investigations (Roberts, 2000b; Roberts and Bell, 2000, 2001) of the effects of STDP at both excitatory and inhibitory synapses to determine how the form of the STDP learning rule affects the function of adaptive sensory processing.
2.1 Formal Model of the Mormyrid Passive Electrosensory System
Several possible approaches present themselves to formalize the neuronal architecture of the ELL, such as conductance-based compartmental models that lead to complex dynamics described by a large set of differential equations. If the questions to be answered by modeling are about the precise spike dynamics of the principal cells in response to the inputs, a conductance-based model would be essential and will be demonstrated in Section 3.3.
However, we are presently interested in the adaptation of responses through many stimulation cycles, so that the details of individual spikes do not affect these dynamics. This leads to a modification, or a “coarse graining,” of our model so that only those changes during time intervals greater than individual spikes will be represented. In this approach, only the spike times would be calculated, not the exact form of individual spikes. The different equations that result from this level of modeling emphasize changes in spike rates of the system, though the timing of individual spikes may be preserved. Although the equations are different in these approaches, there should be overlap in their results at certain time scales, if they are both to represent the actual dynamics of the system.
We now describe the analytical methods that have been used for investigating the adaptive responses of MG cell (Roberts, 2000b; Roberts and Bell, 2000, 2001). The MG cells have been modeled by a spike response model (Gerstner and van Hemmen, 1992) with no relative refractory period and two thresholds: a lower threshold for narrow spikes and a higher threshold for broad spikes which mediate plasticity.
There are two time scales in the model. The fast scale is limited to the duration of each EOD cycle on the scale of tens of milliseconds. The slow scale represents the adaptation of synaptic strengths due to synaptic plasticity lasting many EOD cycles and is on the scale of several minutes. These time scales are separated in the model into two components, fast and slow. The x-component is the time in milliseconds following the EOD, and the t-component represents the number of EOD cycles. These coordinates are typically used for representing electrophysiological data such as spike rasters showing changes in a spike response pattern during repeated presentation of a stimulus. In the present application, the x-component is discretized so that xn = n(Δx), with n an integer. The discretization in xn is related to the times that the various delayed versions of the corollary discharge arrives at MG cells in the ELL. It is assumed that each presynaptic neuron n fires only once per cycle (i.e., at time xn). Thus, the dynamical variables in the model are dependent on two temporal variables. For instance, the average membrane potential, denoted by V(xn, t), is a function of both xn and t. The probability of a broad spike at time xn in EOD cycle t is a sigmoidal function of the average membrane potential. With threshold θ, and noise parameter μ, the spike probability is given by the expression, f(xn,t) = (1 + exp[−μ(V(xn, t) − θ)])−1. The instantaneous spike frequency is obtained by multiplying the spike probability by the maximum spike frequency.
The membrane potential, in the absence of noise, is the sum of all external inputs. The sensory image representing the re-afferent EOD signal is denoted by Vel(xn). This function is only dependent on xn because it is held constant in t as the system adapts. The functional form of Vel(xn) represents the stereotyped response of sensory afferents to the EOD.
Excitatory synapses from PF are represented by the sum of a temporal series of weighted EPSP waveforms, E(xn). The weighting factors, w(xm, t), change in t as the system adapts due to a learning rule that depends on the relative timing of pre- and postsynaptic spikes (Gerstner et al., 1996; Abbott and Song, 1999; Kempter et al., 1999; Xie and Seung, 2000). The x-component in the argument of w(xm, t) labels the beginning of the EPSP. The contribution of PF to the MG cell’s membrane potential at time xn in EOD cycle t is
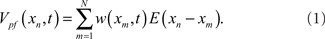
The fast time scale is discretized to the time of each synaptic input and N is the number of synaptic inputs so that the period of the EOD cycle is N(Δx).
Likewise, inhibitory synapses from stellate cells are included in the model by subtracting a set of weighted IPSP waveforms, 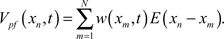 The IPSP waveform, I(xn), was derived from data collected in Dr. Bell’s lab where postsynaptic potentials were recorded with and without the presence of bicuculline, a blocker of inhibitory synaptic currents (Grant et al., 1998). The difference yields the inhibitory contribution. The total membrane potential is the sum of the electrosensory input, the parallel fiber input, and the stellate input, V(xn, t) = Vel(xn) + Vpf(xn, t) + Vst(xn, t).
The IPSP waveform, I(xn), was derived from data collected in Dr. Bell’s lab where postsynaptic potentials were recorded with and without the presence of bicuculline, a blocker of inhibitory synaptic currents (Grant et al., 1998). The difference yields the inhibitory contribution. The total membrane potential is the sum of the electrosensory input, the parallel fiber input, and the stellate input, V(xn, t) = Vel(xn) + Vpf(xn, t) + Vst(xn, t).
The spike-timing-dependent learning rules are implemented by changing the synaptic weights with a function that is dependent on the timing of a postsynaptic broad spike, xb (Roberts and Bell, 2000). The learning rules have two components: a non-associative part and an associative part (Bell et al., 1997d). The change in each excitatory synaptic weight per cycle is
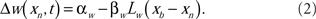
The parameters αw and βw denote the non-associative and associative learning rates. The learning function, Lw(xb − xn), is positive definite and has an area of unity. Similarly, the change in each inhibitory synaptic weight is,
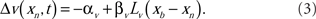
In the following calculations, the learning functions are set equal to their respective postsynaptic potential waveforms, Lw(xn) = E(xn) and Lv(xn) = I(xn).
The ensemble average weight change per EOD cycle calculated using the broad spike probability function, f(xp, t),
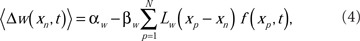
for excitatory synapses and similarly for the inhibitory synapses, but with the sign of the learning rates reversed. The system-level rate of adaptation is calculated by using the averaged changes in weights. The resultant equations were used to derive analytic results in the continuum approximation (Roberts, 1999; Roberts and Bell, 2000), and for numerical simulations (Figure 2). Both approaches have shown that the synaptic learning rule causes the system to adapt to cancel predictable inputs.

Figure 2. Results of MG cell adaptation simulation. Membrane potential (solid line), dendritic spike threshold (dashed line), and synaptic weights (separate dots) for a model MG cell. (A) The idealized waveform represents the corollary discharge with the parallel fiber synaptic strengths, given a random initial weight distribution (arbitrary units where maximum weight = 1.0 and maximum potential V = 100). The horizontal location of the weights represents the delay following the EOD motor command where input begins, and the height represents the synaptic strength. (B) After adaptation, the spike-timing-dependent learning rule adjusted the synaptic weights. The synaptic weights for parallel fibers onto the model MG cell are depressed, resulting in a cancelation of the corollary discharge-evoked EPSP.
2.2 Questions Answered by the Formal Model
When the learning rules in Eqs (2) and (3) are used in the model, the spike output of the MG cell approaches a fixed point at which the spike probability IS constant in x. The fixed point is at the constant broad spike probability

Although the spike probability is constant in t at the fixed point, the weights will be constant only if the learning rates of the excitatory synapses are equivalent to the learning rates of the inhibitory synapses. Otherwise, the weights will drift in such a way that the change in the excitatory input exactly balances the change in the inhibitory input. The drift rate is
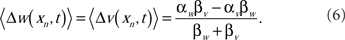
The result of this drift is that, in the generic case where the learning rates are not equal, the weights will saturate at their lowest or highest levels. This result is independent of whether the inhibitory inputs are correlated with the EOD cycle. When the inhibitory spikes from stellate cells were uncorrelated with respect to the EOD, then MG cell output reached an equilibrium level, but the inhibitory inputs did not help to cancel the re-afferent sensory image. In fact, if the learning rates of the inhibitory synapses were not set exactly to that of the excitatory synapse, then the synapses drifted to saturate at a level where sensory image cancelation was poor.
However, if the inhibitory spikes were correlated with respect to the EOD, then the system adapted better than without inhibitory inputs. Furthermore, the synaptic weight drift caused by a mismatch between the learning rates of the inhibitory and excitatory synapses would cause the system to save resources by reducing the synaptic input to the minimum that is necessary to cancel the re-afferent sensory image. These analyses suggest that the combination of stable STDP learning dynamics in both excitatory and inhibitory synapses can provide a mechanism for synaptic scaling (Turrigiano, 1999) that minimizes the global synaptic current into a neuron.
To test the stability of the image cancelation under perturbations of the learning rule for excitatory synapses, we analyzed the stability of the fixed point (Williams et al., 2003; Roberts et al., 2006). The negative image is stable only if the timing window for associative depression of excitatory synapses is close to the EPSP. In addition, stability could result if we relax the assumption that the learning function is positive definite to include associative potentiation. Some evidence of such associative potentiation has been observed in vivo (Bell et al., 1993) but the evidence has not been shown to be statistically significant in vitro (Bell et al., 1997d). All other forms of the STDP learning rule would destroy the function of adaptive mechanism by generating oscillations in the weights within each EOD cycle resulting in oscillating activity that would overwhelm any external stimuli.
In other analyses of the relationship between neural computation and the functional form of the learning rule, Toyoizumi et al. (2005) showed that a match between the learning function and the EPSP would maximize the mutual information. This principle of maximum information for non-predictable stimuli was found in ELL by Sawtell and Williams (2008) who demonstrated that the information about the position of an object was independent of the tail position after processing by ELL, but not in the primary afferents. In a different context, Pfister et al. (2006) showed that if the postsynaptic neuron is constrained to fire at a constant rate, then the time constant of the learning function has to be matched to the postsynaptic potential for precise timing.
2.3 Characterization of Synaptic Weight Distributions
Rate-dependent learning models involve, by definition, averaging over many spike events (either in time, or across a statistical ensemble). Consequently random fluctuations between events are naturally averaged out. In such models, synaptic dynamics are naturally described by deterministic differential equations.
The discovery that synaptic changes are mediated by processes sensitive to the relative timing between individual pre- and postsynaptic events voided traditional models based on spike rates. The random variation in the broad spike timing relative to the PSP (c.f. the broad spike probability from Section 2.1) and the experimentally observed variability in synaptic change even at constant timing, suggest that in contrast to rate-dependent models, the dynamics in our system are more appropriately described by stochastic dynamics.
In our models, the random fluctuations in the weight changes Δw and Δv arise from fluctuations in the postsynaptic broad spike time xb in Eqs (2) and (3). These fluctuations enter the model through the broad spike probability function f(xb)1. In other researchers’ models, fluctuations enter learning models from other sources. For example, van Rossum et al. (2000) model the Hebbian learning rule observed by Bi and Mu-Ming Poo (1998) in hippocampal neurons by a learning rule that has exponential dependence on the relative timing between presynaptic and postsynaptic events, and has additive noise whose variance is proportional to the synaptic weight.
Regardless of the source of the fluctuations, the time evolution of synaptic weights under STDP is conveniently treated by stochastic dynamics. A large class of learning rules, including our models of STDP in the mormyrid ELL and the model that van Rossum et al. (2000) apply to hippocampal neuron, follow a Markov process described by a suitable master equation. Several other authors have modeled STDP by such Markov processes. Authors usually replace the master equation (see below) that describes these processes with a pseudo-approximation – the Fokker–Planck equation (FPE) – obtained by truncating to second order an expansion in powers of the synaptic jumps. As cited above, van Rosum et al. use FPE to model the equilibrium distribution of synaptic weights in the STDP learning rule discovered by Bi and Poo. Their analytic equilibrium distribution agrees well with Monte Carlo simulations, and provides qualitative agreement with experimental quantal amplitude distributions observed in a pyramidal. Cateau and Fukai (2003) use a numerically integrated FPE to determine the equilibrium distribution of synaptic strengths under learning rules similar to those observed in rat hippocampus CA1 neurons. Kepecs et al. (2002) use the FPE to analytically calculate equilibrium distributions arising from learning rules with STDP, and to confirm that Monte Carlo simulations have reached equilibrium. Masuda and Aihara (2004) use the FPE to analyze synaptic competition and the formation of functional clusters. Their theoretical equilibrium distributions match Monte Carlo simulations well. Finally, Burkitt et al. (2004) use the FPE to predict equilibrium synaptic distributions, and compare their analytic results with histograms from Monte Carlo simulations of the learning rules they study. Hence, there is wide agreement that the dynamics of STDP are appropriately treated by stochastic dynamics, in many cases well-described by a Markov process2. We note however that average ensemble behavior, which can be illuminated by deterministic dynamics, is certainly of interest. For example, Saudargiene et al. (2004) developed a biophysical model of asymmetric STDP learning from a differential Hebbian learning rule in a deterministic framework.
In this description, the synaptic weights w(xn, t) (respectively v(xn, t)) are random variables with density function Pw(w(xn), t) (respectively Pv(v(xn), t)). The dynamics of these densities, together with inputs to the circuitry and the response functions of the cells, determine the functional properties of the network. In particular, the stable negative image equilibria of the network correspond to fixed points of the average weight changes; that is, 〈Δw(xn)〉 = 0 in Eq. (4) (and similarly 〈Δv(xn)〉 = 0). (Equation (5) expresses the equilibrium in terms of the broad spike probability.) A consequence of the random fluctuations in the learning rule is that the negative image will be imprecise. The equilibrium density Pw(w(xn), t → ∞) for the weights will have, in general, non-zero variance. Hence individual weight values at equilibrium will differ from the average value <w(xn))> corresponding to the negative image given by Roberts and Bell (2000). This variability, captured by the covariance of w, leads to imprecision in the cancelation of the re-afferent signal.
This is a familiar situation in engineering adaptive filter theory and statistical estimation by stochastic approximation algorithms (a.k.a. on-line learning in the machine learning; Haykin, 2002). In the language of adaptive filter theory, one of the ELL’s tasks is to estimate parameters (the synaptic weights from the PF onto the MG cells) so that the network filters out the re-afferent signal. However, the weight-adjustment procedure is noisy, and hence we get noisy estimates of the optimal weights3.
2.3.1 Mathematical Formulation of the Synaptic Distribution
The Master Equation for learning under the Markov process in Eq. (2) reads
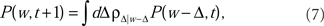
where P(w, t) is the probability density for the weight w at trial t, and ρ(Δ | w) is the probability density of taking a step of size Δ in one EOD cycle, starting from point w (see for example Gardiner, 1985). The step probability ρ(Δ | w) is governed by the learning rule Eq. (2). The full development was fleshed out by us in Williams et al. (2004) with the resulting master equation
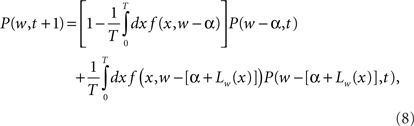
where α is the non-associative learning rate, Lw(x) is the learning function that represents the spike timing dependence, and T is the period of the EOD cycle.
Master equations such as this are, for the most part, intractable. A common approach in computational neuroscience is to substitute a more tractable non-linear FPE for the full master equation as discussed above (van Rossum et al., 2000; Kepecs et al., 2002; Cateau and Fukai, 2003; Burkitt et al., 2004; Masuda and Aihara, 2004). This has met with success, but we advise more care than wholesale adoption of the FPE. The conditions under which the discrete random walk can be properly described by a non-linear FPE are quite narrow as discussed by van Kampen (1992). The required conditions are nearly universally overlooked by practitioners in computational neuroscience.
In our work, we have adopted the random walk in Eq. (8) directly, and approximate a solution by replacing the broad spike firing probability f(x) is with its linear approximation. This approximation is equivalent to assuming that the tails of the equilibrium synaptic weight density P(w, t → ∞) do not penetrate significantly into the non-linear parts of sigmoidal-shaped density f. We verified that for the physiologically relevant parameter range this assumption is valid.
Our analysis (Williams et al., 2004) includes expressions for the first four moments of the equilibrium synaptic weight density for a model consisting of a single synapse. For the more interesting case of multiple synapses, we give a recurrence relation for the equilibrium moments, and solve the recurrence for the equilibrium mean and covariance function
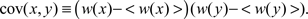
As discussed in Section 2.3 above, the equilibrium covariance affects the precision of the negative image; its contribution to the variance of the true negative image around the optimum is
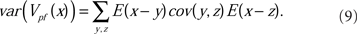
Theoretical prediction of the weight variance for physiologically relevant model parameters, and Monte Carlo simulations confirming the analytic predictions were developed fully in Williams et al. (2004). The results confirm that the error of the negative image estimation is within the tolerance of the sensory image cancelation function for a large number of PF found in cerebellum-like structures.
3 Modification of STDP Dynamics in Active Electrolocation
3.1 Active Electrolocation System in Mormyrids
The active electrosensory system is an elaboration of the passive electrosensory system discussed in the previous section, and has additional sources of corollary discharge inputs that refine sensory processing. In addition to the corollary discharge in PF, the active system has deep layer inputs that appear to be necessary for reading out latency coded information about the strength of the electric field. In the passive system, the corollary discharge conveyed by PFs exhibit anti-Hebbian plasticity to eliminate electrosensory responses caused by the EOD. The significance of this plasticity is less clear in the active system, which is designed to specifically process re-afferent signals. One possibility is that plasticity implements a simple gain control so that plastic electric organ corollary discharge inputs serve to control the level of response to maintain best sensitivity. Another possibility is a similar function as in the passive system, to eliminate the effects of predictable signals from the sensory image. However, sensory cancelation algorithm must be more subtle in the active system because it must preserve details in the image related to distortions of the electric field. To clarify the differences in function between the passive and active systems, we introduce further physiological details that appear in the active system.
Specialized mormyromast electroreceptors sense the self-generated field and its distortions. Afferent fibers from this type of electroreceptors responds to the fish’s own EOD with a small number of spikes that encode the strength of the electric field in the latency of the first spike following the EOD. These responses are conveyed to the cortex of the ELL where the fibers terminate in the mormyromast zone (Bell, 1990).
With each EOD, the ELL cortex is affected not only by inputs from the periphery but also by electric organ corollary discharge signals that originate centrally. These corollary discharge signals are time-locked with the EOD motor command, which elicits the EOD (Zipser and Bennet, 1976). The corollary discharge signals arise from various central structures, one of which is the juxtalobar nucleus (JLN), which provides a short, fixed latency timing signal to the deeper layers of the ELL (Figure 1B). A second such structure is the EGp, which gives rise to the PF of ELL (Figure 1). EGp receives corollary discharge signals at various delays to about 80 ms (Bell et al., 1992).
A clear example of the mechanisms of central control of sensory processing is present in the deeper layers of the region of ELL dedicated to activation electrolocation, where a centrally originating corollary discharge signal from the JLN provides the timing signal (Mohr et al., 2003a) for the decoding of afferent latency as a measure of stimulus intensity. Mormyromast afferents respond to the EOD with a single spike (or short burst). The strength of electrosensory stimuli is encoded as the latency to the leading spike (Bell, 1990; Sawtell and Williams, 2008). The JLN fibers converge onto granular cells that also receive primary afferent inputs. The granular cells act as a coincidence detector that measure the time difference between corollary discharge and the arrival of the mormyromast afferent spike (Meek and Grant, 1994).
Electrosensory processing in the mormyrid is highly specialized for discriminating precise timing of mormyromast afferent signals. Behavioral studies reveal that the fish can discriminate afferent timing changes of less than 100 μs (Hall et al., 1995). In addition, timing is remarkably well-preserved in the pathway from the EOD motor command to the corollary discharge signal in the ELL. Although this signal traverses five synaptic junctions, the signal maintains a variability of less than 50 μs (Bell and Emde, 1995).
As we focus on adaptive processing in the active system, we are first confronted by a serious discrepancy; the output of MG cells should be constant throughout the EOD cycle as in passive system, but MG cells respond with a burst to each EOD command. There are two reasons why this would be functionally expected. First, the active system is designed to detect small changes in the re-afferent signal, not eliminate it like the passive system, so some modulation of the MG cell response should be expected. Secondly, MG cells are interneurons that inhibit efferent cells (Figure 1B), so their activity does not represent the final output of the ELL. However, the dynamical stability of the learning rule contradicts the observation of the MG cell spike bursts in the active system. This contradiction suggested that another mechanism is at play to control how the dynamics of STDP regulate electrosensory processing.
3.2 Dendritic Spike Threshold Control to Regulate Synaptic Plasticity
In the passive circuit of the ELL, the principal cells respond to the combined external electrical signals with a constant output spike rate that is modulated by novel sensory patterns. However, if the principal cells in the active circuit responded with a constant output spike rate, then no information about distortions of the fish’s own field could be used to identify external objects. To avoid cancelation of critical information, the learning dynamics are altered by controlling the threshold of back-propagating spikes in the principal cells (Mohr et al., 2003b; Sawtell et al., 2007). This mechanism allows for the neurons of the ELL to respond with a burst of spikes to every command in spite of the dynamics of the STDP learning rule. In addition, this mechanism of controlling the learning dynamics allows control of adaptation in the initial sensory processing stage by higher centers.
Recent studies by Sawtell et al. (2007) suggest that centrally generated signals actively control the threshold of dendritic spikes following the EOD motor command and, thus, control synaptic plasticity and adaptive sensory processing in the ELL. We wish to resolve the apparently paradoxical empirical observation that MG cells are inhibited in the part of the cell where dendritic spikes are initiated, while they are excited in another part of the cell where axon spikes are initiated.
We have constructed a morphologically accurate model of a MG cell that we have used to test the hypotheses that inhibitory synaptic inputs to the apical dendrites that are time-locked to the corollary discharge increase the threshold of dendritic spikes while excitatory inputs simultaneously excite axon spikes. Our simulation demonstrates that inhibitory synaptic current in the dendrites shunt depolarizing currents and modulate the propagation of dendritic spikes during an EPSP that increases the rate of axon spikes.
Our analytic model of the region of ELL that is used for active electrolocation showed that an increase of the dendritic spike threshold relative to the axon spike threshold during the EOD is necessary to reproduce the qualitative features of the MG cell response to the mormyromast burst (Roberts, 2000a; Roberts and Bell, 2003). This prediction was confirmed by Mohr et al. (2003b) in experimental observations of a pause in dendritic spike activity during the command response (Figure 3B).

Figure 3. Effects of an increased dendritic spike threshold. Membrane potential (solid line), dendritic spike threshold (dashed line), and synaptic weights (separate dots) for a model MG cells. (A) The modified model in which the dendritic spike threshold increases during the time course of the juxtalobar nucleus evoked EPSP, allowing this waveform to persist in the presence of parallel fiber synaptic plasticity (arbitrary units where maximum weight = 1.0 and maximum potential V = 100). (B) Intracellular recordings by Mohr et al. (2003a) showing several sweeps triggered to the EOD motor command with many broad (dendritic) spikes. There is a pause in broad spikes during the corollary discharge response, even though the average membrane potential (black) increases.
Subsequent experiments showed that the threshold for generating a dendritic spike threshold increases during the corollary discharge response of MG cells (Mohr et al., 2003a). This increase is sufficient to explain the response of MG cells to the corollary discharge. In our simulation, we inserted the predicted increase in the dendritic spike threshold during the corollary discharge into our numerical model neurons (Figure 3A). The simulation showed that the corollary discharge-driven EPSP is still present. This modification of the dendritic spike threshold causes the system to be globally stable under the STDP learning rule (Roberts et al., 2006), consistent with the experimentally demonstrated corollary discharge-driven EPSP.
3.3 MG Cell Model: Morphology and Currents
To evaluate how descending inputs could modify the dendritic spike threshold, and thereby control STDP we developed a conductance-based model of an MG cell. An MG cell of mormyrid ELL, that was classified as an MG2, broad spiking cell, was traced (Engelmann et al., 2008) and converted to the format of the NEURON simulation package (Hines and Carnevale, 1997). The original tracing by adding axonal compartments to generate axonal, narrow spikes, and a passive hillock to reduce the size of the narrow spikes as measured at the some, to match the known electrophysiology (Bell et al., 1997b,d).
Each of the 276 compartments of the model neuron obeyed the membrane current balance equation of the Hodgkin–Huxley formalism (Hodgkin and Huxley, l952). The membrane potential, V, was computed by numerically integrating the equation for each compartment:
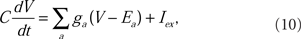
where C is the membrane capacitance, ga is the ionic conductance of an a-type ion channel, and Ea is the reversal potential of an a-type ion channel. The sum is over all types of ion conductances in the model, and Iex represents an externally applied current.
The voltage-sensitive membrane conductances were calculated using activation (xa) and inactivation (ya) variables:
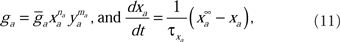
where 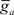 is the maximum ionic conductance, and na is the power of the activation variable. The asymptote
is the maximum ionic conductance, and na is the power of the activation variable. The asymptote 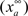 and decay
and decay 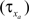 constants are functionally related to the first-order rate constants
constants are functionally related to the first-order rate constants 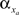 and
and 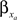 by
by 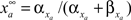 and
and 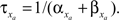 The inactivation variables obey a similar first-order equation. The rate constants are themselves dependent on the membrane potential, V, through empirically derived relations for each channel type.
The inactivation variables obey a similar first-order equation. The rate constants are themselves dependent on the membrane potential, V, through empirically derived relations for each channel type.
Although it is likely that a reduced model with fewer compartments (Rall, 1964) would exhibit similar behavior, we wish to show that a morphologically accurate MG cell could regulate the broad (dendritic) spike threshold without silencing the narrow (axonal) spikes. In addition, the detailed model allows us to identify the precise location of the dendritic spike initiation zone and supports the hypothesis that inputs to the deep molecular layer regulate dendritic spikes in vivo.
3.4 MG Cell Dendritic Spike Simulation
In vitro experiments showed that dendritic spikes are dependent on sodium ion channels (Bell et al., 1997b). The simplest choice of conductance types to generate spikes is a fast, inactivating sodium current, INa−f, and a delayed rectifier potassium current, IK−V. In addition, a leak current, Il, was added to each compartment of the model neuron with a reversal potential of El = −70 mV.
To yield a model with a broad spike threshold that was higher than the axonal spike threshold required a INa−f density that was sparser in the dendrites than in the axon. A broadening of the dendritic spikes required a reduced ratio of IK−V density to INa−f density. In a previous MG model, we used active currents that were based on the classical Hodgkin–Huxley kinetics of the squid axon. We found it difficult to replicate the physiological broadness of dendritic spikes, though the depolarization of the dendritic tree would sum to yield a broad spike in the soma. Since we knew that recordings in the dendritic branches were also broad (Mohr et al., 2003a,b), we sought to improve the dendritic spike representation in the present model. Since MG cells are Purkinje neurons, we used the kinetics of INa−f and IK−V from Purkinje cells (DeSchutter and Bower, 1994). In our new simulations, the resulting broad spikes were robustly as broad as the physiologically observed broad spikes in dendrites of MG cells.
To simulate dendritic and axonal spikes, we applied parameter settings in the MG model neuron from Table 1. The soma and dendrites were initialized with passive properties: 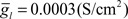 and El = −70 mV. INa−f and IK−V conductances were added to the axon to generate independent axon spikes. The result of a 50 ms, 0.5 nA pulse is shown in Figure 4, where the red trace is the voltage at the distal end of the axon, the blue trace is the voltage at the distal end of one of the dendrites, and the black trace is the voltage in the soma. The resultant dendritic spike propagates from the soma outward.
and El = −70 mV. INa−f and IK−V conductances were added to the axon to generate independent axon spikes. The result of a 50 ms, 0.5 nA pulse is shown in Figure 4, where the red trace is the voltage at the distal end of the axon, the blue trace is the voltage at the distal end of one of the dendrites, and the black trace is the voltage in the soma. The resultant dendritic spike propagates from the soma outward.
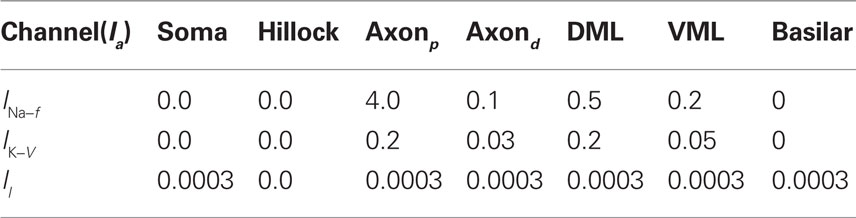
Table 1. Maximum current densities, 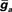 (S/cm2), for active membrane currents of MG cell by morphological region. The proximal compartments of the axon (axonp) are the spike initiation zone and have a higher INa−f density than the distal axon compartments (axond). The dendritic spikes of the apical dendrites are initiated in compartments in the ventral molecular layer (VML), and propagate into apical dendritic compartments in the dorsal molecular layer (DML). The basilar dendrites are passive in this model.
(S/cm2), for active membrane currents of MG cell by morphological region. The proximal compartments of the axon (axonp) are the spike initiation zone and have a higher INa−f density than the distal axon compartments (axond). The dendritic spikes of the apical dendrites are initiated in compartments in the ventral molecular layer (VML), and propagate into apical dendritic compartments in the dorsal molecular layer (DML). The basilar dendrites are passive in this model.

Figure 4. Conductance-based compartmental model of a MG cell. (A) Morphology of MG cell model. Synaptic inputs were applied to both the dorsal molecular layer (DML) dendrites and the ventral molecular layer (VML) regions of the apical dendrites, but the broad spike regulating synaptic current was applied only to the VML. The basal dendrites received electrosensory inputs representing inputs from deep layers of the ELL. (B) Simulated small and broad spikes from three different compartments, soma (black trace), axon (red), and tip of a dendrite (blue). Current pulse at soma, 0.05 nA for 50 ms.
This simulation suggests that the properties of the two spike types arise from the morphology and membrane conductance densities in different segments of the model neuron. We next investigate how inhibitory synaptic inputs increase the threshold of dendritic spikes. The difference between the axon and broad dendritic spike thresholds will be controlled by the density of INa−f and IK−V currents in the soma. The dependence of the axon-to-dendritic spike threshold ratio on the conductance properties of the soma suggests that membrane currents, which we have not yet tested, alter that ratio. A gap in narrow spikes followed the initiation of each broad spike because of inactivation of INa−f in the axonal compartments, as noted in recent physiological observations (Sawtell et al., 2007).
3.5 Threshold Control of Broad Spikes by Inhibitory Synaptic Currents
We simulated the effects of background parallel fiber activity and stellate cell activity by assigning AMPA and GABAA synaptic currents with random latencies on each of the apical dendritic segments. The maximum GABAA currents were adjusted to recover the original spike thresholds and responses to current injections so that the background inputs were balanced between excitation and inhibition.
These inputs were divided into ventral (VML) and dorsal (DML) molecular layer regions. The maximum GABAA current was increased until the broad spike, generated by a 0.5-pA current step, was blocked. The VML inhibitory inputs were over twice as effective as the DML inputs at blocking the broad spike. The maximum inhibitory synaptic currents for broad spike blockage are 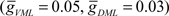 and
and 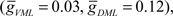 where
where  was used as the balanced background GABAA current.
was used as the balanced background GABAA current.
Electric organ discharge corollary discharge inputs from the JLN excite MG cells via the basilar dendrites. These timing inputs were modeled by injecting bursts of 1 ms current pulses (0.05 nA) into each segment of the basilar dendrites to simulate electrical synapses. The burst durations at each dendritic segment were randomized uniformly from one to six spikes per burst, with 5 ms inter-spike interval. The initial spike latency was also randomized from 10 to 30 ms. During each simulation run, the latencies of inputs and burst durations at each segment was randomized. This initial randomization simulated synaptic and spike propagation failures in the inputs, and yielded a Monte Carlo simulation of the response of MG cells to the EOD command.
To compare Monte Carlo samples of responses given randomized synaptic latencies, we simulated command-evoked parallel fiber inputs by adding an α-function distribution of latencies of excitatory AMPA synapses to the simulation ( PF-onset = α(τ = 20 ms)). The results of five trials is shown in the Figure 5A as overlays of membrane voltages. The latencies of the broad spikes are near the crest of the parallel fiber inputs distribution as would be expected if there were no broad spike gap.
PF-onset = α(τ = 20 ms)). The results of five trials is shown in the Figure 5A as overlays of membrane voltages. The latencies of the broad spikes are near the crest of the parallel fiber inputs distribution as would be expected if there were no broad spike gap.
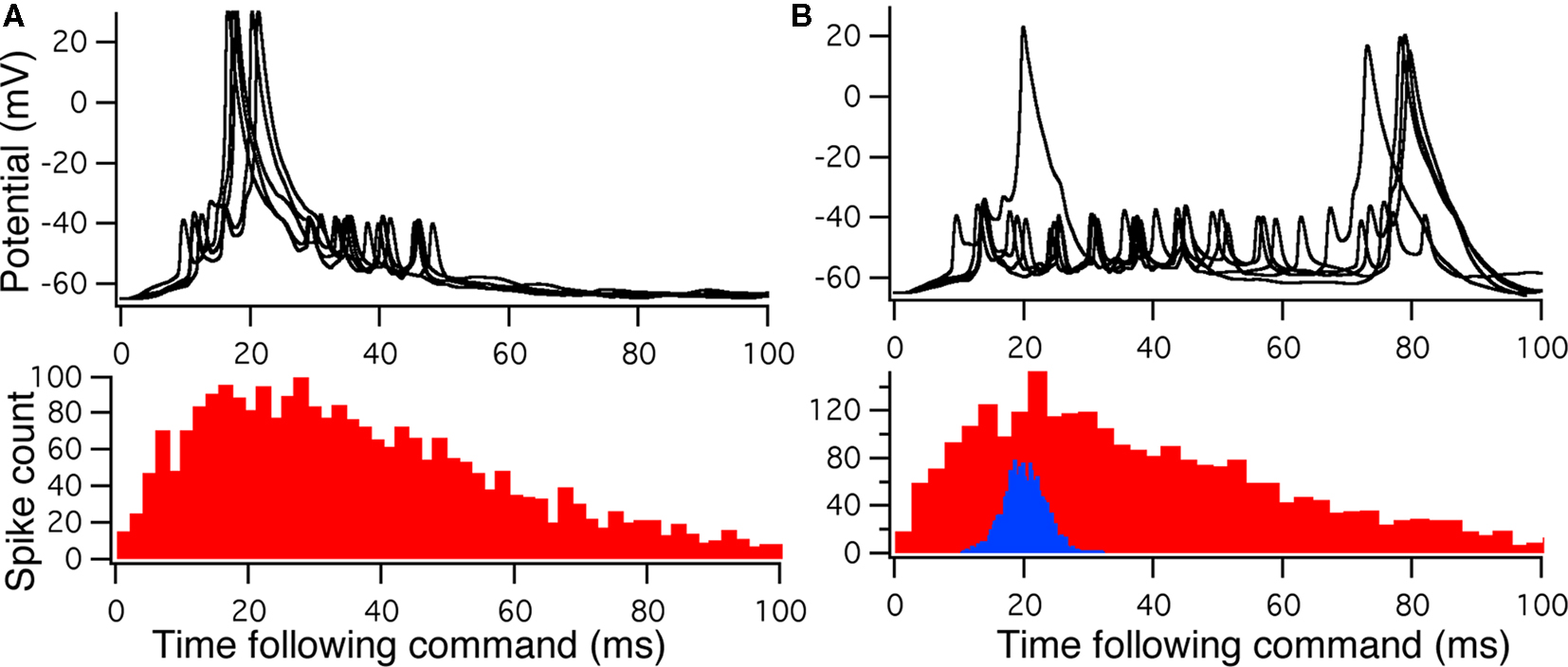
Figure 5. Monte Carlo samples of responses to the electric organ discharge command. (A) Only background inhibition in VML dendritic sections yields broad spikes centered near the beginning of the command-evoked burst of spikes (top panel). The distribution of command-driven (non-background) parallel fiber latencies is shown in the histogram (bottom panel). (B) Inhibitory GABA synaptic inputs are injected in the VML dendritic segments with a latencies normally distributed (blue histogram in bottom panel). The broad spikes are nearly eliminated during the burst, but the narrow spikes are not strongly affected by the inhibition.
Command-driven GABA synaptic inputs were added to the model to determine whether the broad spike activity could be controlled independently of the narrow spikes. In Figure 5B, a narrow, normal distribution of GABA input latencies were applied in the VML dendritic sections (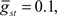 PF-onset = Normal (20 ms ± 10)). The GABA inputs resulted in delays of most of the broad spikes until late in the cycle.
PF-onset = Normal (20 ms ± 10)). The GABA inputs resulted in delays of most of the broad spikes until late in the cycle.
The main finding here is that we could suppress dendritic spikes in the model without silencing the narrow spikes, even though the distance between the spike generation zones is merely across the soma. The mechanism is a shunting of the Na currents in the VML-dendrites (see Figure 5A) so that the dendritic (broad) spike cannot propagate into the dendrites. Detailed inspection of the dendritic spike initiation reveals that the initiation zone is less than 50 μm from the soma, in a single dendritic branch, and then the depolarization spreads to other branches as it propagates up the dendritic tree.
4 Functional Consequences of Anti-Hebbian STDP in Other Systems
The principle of predictable image cancelation is found in other electrosensory systems, both passive and active (Bell et al., 1997a), such as the octavolateral nucleus of sharks and rays (Montgomery and Bodznick, 1994; Bodznick et al., 1999) and the gymnotid ELL (Bastian, 1995). In sharks and rays, the electroreceptors are affected by a current flow between the gills and the rest of the fish’s body. This current flow is modulated by gill movement. Gill movement, therefore, affects the electrosensory system. The effects of movements on the electrosensory signal appear to be filtered out by neurons in a primary sensory structure similar to ELL. Principal neurons of ascending efferent neurons, do not modulate their spike output in response to gill movements. Thus, although the primary afferents are modulated by the gill movements, other inputs to the structure (Conley and Bodznick, 1994; Bodznick et al., 1999) are used to eliminate this predictable modulation of the electrosensory pattern caused by gill movements.
The final requirement for this system to operate as an adaptive filter is for the gain control of inputs that carry information about gill movements to be sensitive to changes in the electrosensory signals. If the synaptic learning rule is anti-Hebbian, then the synapses should reduce in strength during persistent correlated firing. Also, in order to decorrelate the parallel fiber inputs relative to the sensory inputs, a mechanism must be present for increasing the synaptic strength. Such bi-directional plasticity has been observed (Bodznick et al., 1999) by directly stimulating the inputs if followed by a reduction in the responses to electrosensory signal that have paired with the stimulation.
Nelson and Paulin (1995) developed a formal model of the elasmobranch electrosensory system to support this conceptual model. Given biologically realistic afferent currents, the model was used to test whether the synaptically driven adaptive processes would be sufficient to flatten the response of the electrosensory neurons during the respiratory cycle. The functional results is that the effects of gill movements on the electrosensory signal is eliminated so that the fish becomes more sensitive to external sources of electrical signals. Numerical simulations determined that the cancelation of predictable afferent patterns was possible only if the synaptic learning rule were anti-Hebbian.
Similar studies have been carried out in gymnotid fish (Bastian, 1995). These weakly electric fish have an active electrosensory system that has been shown to adjust the gain of the responses of principal cells in ELL to movements of the tail. Proprioceptive information is used to cancel the predicted changes in the electrosensory response caused by the fish’s own movements. Anti-Hebbian plasticity has been observed in the gymnotid ELL, but it is not clear whether underlying mechanism of sensory adaptation is an STDP learning rule similar to the one found in mormyrid fish.
Another feature of the gymnotid ELL is that descending feedback is an active part of electrosensory processing (Bastian and Bratton, 1990; Bratton and Bastian, 1990), and that dendritic spikes may be controlled by these descending inputs. The functional similarities with the mormyrid ELL are striking in spite of anatomical differences (Bell et al., 1997a), and suggest that the mechanism of descending control of STDP plasticity may be a general principle in sensory processing.
The dorsal cochlear nucleus (DCN) is one of the two initial sites of auditory processing in the mammalian brainstem and is another cerebellum-like structure similar to the above electrosensory systems. Along with receiving primary auditory inputs, the DCN receives additional ascending and descending auditory and non-auditory inputs. This convergence of information may be important for utilizing synaptic plasticity to alter auditory responses to predictable stimuli. The function of the DCN from the standpoint of its similarity to the cerebellum and cerebellar-like structures suggests that anti-Hebbian synaptic plasticity functions to cancel out the neural activity derived from self-generated movements (Roberts and Portfors, 2008) as in ELL. A similar form of STDP has been shown in the DCN of mouse (Tzounopoulos et al., 2004) suggesting that similar adaptive mechanisms may exist in both structures.
The stability of the learning dynamics associated with the anti-Hebbian learning rule discussed here provides a compelling basis for interpreting the functional consequences of STDP in sensory processing. Some of the principles presented here, such as control of STDP by regulating dendritic spike thresholds, are likely to be general principles found other parts of the nervous system besides early sensory processing.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We wish to thank Jacob Engelmann for providing the medium ganglion tracing. This work was supported in part by the National Science Foundation under Grant No. CRCNS IIS-0827722 and IIS-0812687.
Footnotes
- ^Our deterministic learning rule is an idealization of the original data shown by Bell et al. (1997d). Those data show that for given fixed time difference the presynaptic event and the broad spike, there is significant variability (noise) about the mean synaptic change. Hence, even at the level of individual learning events, there is randomness in the mormyrid ELL system.
- ^We are not here advocating the use of the FPE to treat these systems since the non-linear Fokker–Planck equation can generate misleading results. We have constructed and applied rigorous perturbation methods in place of the FPE and will make those available in future work. The point here is that stochastic dynamics is an appropriate tool to describe the evolution of synaptic weights under learning rules described by STDP, particularly as in our case where the fluctuations around the weight equilibrium have consequences for the sensory functioning of the circuitry.
- ^The fluctuations about the optimal weights arise here because of noise in the learning rule. This is distinct from the usual variance in statistical estimates owing to sample size restrictions.
References
Abbott, L. F., and Song, S. (1999). “Temporally asymmetric Hebbian learning, spike timing and neuronal response variability,” in Advances in Neural Information Processing Systems 11, eds M. Kearns, S. A. Solla, and D. Cohn (Cambridge: MIT Press), 69–75.
Assad, C., Rasnow, B., and Stoddard, P. (1999). Electric organ discharges and electric images during electrolocation. J. Exp. Biol. 202, 1185.
Barlow, H. (1990). Conditions for versatile learning, Helmholtz’s unconscious inference, and the task of perception. Vision Res. 30, 1561–1571.
Bastian, J. (1995). Pyramidal-cell plasticity in weakly electric fish: a mechanism for attenuating responses to reafferent electrosensory inputs. J. Comp. Physiol. A 176, 63–73.
Bastian, J., and Bratton, B. (1990). Descending control of electroreception. I. Properties of nucleus praeeminentialis neurons projecting indirectly to the electrosensory lateral line lobe. J. Neurosci. 10, 1226.
Bell, C. C. (1982). Properties of a modifiable efference copy in an electric fish. J. Neurophysiol. 47, 1043–1056.
Bell, C. C. (1990). Mormyromast electroreceptor organs and their afferent fibers in mormyrid fish. II. Intra-axonal recordings show initial stages of central processing. J. Neurophysiol. 63, 303–318.
Bell, C. C., Bodznick, D., Montgomery, J., and Bastian, J. (1997a). The generation and subtraction of sensory expectations within cerebellum-like structures. Brain Behav. Evol. 50(Suppl. 1), 17–31.
Bell, C. C., Caputi, A., and Grant, K. (1997b). Physiology and plasticity of morphologically identified cells in the mormyrid electrosensory lobe. J. Neurosci. 17, 6409–6423.
Bell, C. C., Han, V., Sugawara, Y., and Grant, K. (1997c). Direction of change in synaptic efficacy following pairing depends on the temporal relation of presynaptic input and postsynaptic spike during pairing. Soc. Neurosci. Abstr. 23, 1840.
Bell, C. C., Han, V., Sugawara, Y., and Grant, K. (1997d). Synaptic plasticity in a cerebellum-like structure depends on temporal order. Nature 387, 278–281.
Bell, C. C., Caputi, A., Grant, K., and Serrier, J. (1993). Storage of a sensory pattern by anti-Hebbian synaptic plasticity in an electric fish. Proc. Natl. Acad. Sci. U.S.A. 90, 4650–4654.
Bell, C. C., and Emde, G. v. (1995). Electric organ corollary discharge pathways in mormyrid fish. II. The medial juxtalobar nucleus. J. Comp. Physiol. A 177, 463–479.
Bell, C. C., Grant, K., and Serrier, J. (1992). Sensory processing and corollary discharge effects in the mormyromast regions of the mormyrid electrosensory lobe: I. Field potentials and cellular activity in associated structures. J. Neurophysiol. 68, 843–858.
Bi, Q., and Poo, M.-M. (1998). Precise spike timing determines the direction and extent of synaptic modifications in cultured hippocampal neurons. J. Neurosci. 18, 10464–10472.
Bodznick, D., and Montgomery, J. C. (2005). “The physiology of low-frequency electrosensory systems,” in Electroreception. Vol. 21 of Springer Handbook of Auditory Research, eds R. R. Fay, A. N. Popper, T. H. Bullock, C. D. Hopkins, A. N. Popper, and R. R. Fay (New York: Springer), 132–153.
Bodznick, D., Montgomery, J. C., and Carey, M. (1999). Adaptive mechanisms in the elasmobranch hindbrain. J. Exp. Biol. 202, 1357–1364.
Bratton, B., and Bastian, J. (1990). Descending control of electroreception. II. Properties of nucleus praeeminentialis neurons projecting directly to the electrosensory lateral line lobe. J. Neurosci. 10, 1241.
Burkitt, A., Meffin, H., and Grayden, D. (2004). Spike-timing-dependent plasticity: the relationship to rate-based learning for models with weight dynamics determined by a stable fixed point. Neural Comput. 16, 885–940.
Cateau, H., and Fukai, T. (2003). A stochastic method to predict the consequence of arbitrary forms of spike-timing-dependent plasticity. Neural Comput. 15, 597–620.
Conley, R. A., and Bodznick, D. (1994). The cerebellar dorsal granular ridge in an elasmobranch has proprioceptive and electroreceptive representations and projects homotopically to the medullary electrosensory nucleus. J. Comp. Physiol. A 174, 707–721.
DeSchutter, E., and Bower, J. M. (1994). Simulated responses of cerebellar Purkinje cells are independent of the dendritic location of granule cell synaptic inputs. Proc. Natl. Acad. Sci. U.S.A. 91, 4736–4740.
Engelmann, J., van den Burg, E., Bacelo, J., de Ruijters, M., Kuwana, S., Sugawara, Y., and Grant, K. (2008). Dendritic backpropagation and synaptic plasticity in the mormyrid electrosensory lobe. J. Physiol. (Paris) 102, 233–245.
Gerstner, W., Kempter, R., van Hemmen, J. L., and Wagner, H. (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76–78.
Gerstner, W., and van Hemmen, J. L. (1992). Associative memory in a network of ‘spiking’ neurons. Network 3, 139–164.
Grant, K., Sugawara, Y., Gomes, L., Han, V., and Bell, C. C. (1998). The mormyrid electrosensory lobe in vitro: physiology and pharmacology of cells and circuits. J. Neurosci. 18, 6009–6025.
Hall, C., Bell, C. C., and Zelick, R. (1995). Behavioral evidence of a latency code for stimulus intensity in mormyrid electric fish. J. Comp. Physiol. A 177, 29–39.
Hines, M., and Carnevale, T. (1997). The neuron simulation environment. Neural Comput. 9, 1179–1209.
Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (Lond.) 108, 37–77.
Hopkins, C. (1995). Convergent designs for electrogenesis and electroreception. Curr. Opin. Neurobiol. 5, 769–777.
Kawasaki, M. (2005). “Physiology of tuberous electrosensory systems,” in Electroreception. Vol. 21 of Springer Handbook of Auditory Research, eds R. R. Fay, A. N. Popper, T. H. Bullock, C. D. Hopkins, A. N. Popper, R. R. Fay (New York: Springer), 154–194.
Kempter, R., Gerstner, W., and van Hemmen, J. L. (1999). Hebbian learning and spiking neurons. Phys. Rev. E 59, 4498–4514.
Kepecs, A., van Rossum, M., Song, S., and Tegner, J. (2002). Spike-timing-dependent plasticity: common themes and divergent vistas. Biol. Cybern. 87, 446–458.
Masuda, N., and Aihara, K. (2004). Self-organizing dual coding based on spike-time-dependent plasticity. Neural Comput. 16, 627–663.
Meek, J., and Grant, K. (1994). The role of motor command feedback in electrosensory processing. Eur. J. Morphol. 32, 225–234.
Mohr, C., Roberts, P. D., and Bell, C. C. (2003a). Cells of the mormyrid electrosensory lobe: II. Responses to input from central sources. J. Neurophysiol. 90, 1211–1223.
Mohr, C., Roberts, P. D., and Bell, C. C. (2003b). Cells of the mormyrid electrosensory lobe: I. Responses to the electric organ corollary discharge and to electrosensory stimuli. J. Neurophysiol. 90, 1193–1210.
Montgomery, J. C., and Bodznick, D. (1994). An adaptive filter that cancels self-induced noise in the electrosensory and lateral line mechanosensory systems of fish. Neurosci. Lett. 174, 145–148.
Nelson, M. E., and Paulin, M. G. (1995). Neural simulations of adaptive reafference suppression in the elasmobranch electrosensory system. J. Comp. Physiol. A 177, 723–736.
Pfister, J., Toyoizumi, T., Barber, D., and Gerstner, W. (2006). Optimal spike-timing-dependent plasticity for precise action potential firing in supervised learning. Neural Comput. 18, 1318–1348.
Rall, W. (1964). “Theoretical significance of dendritic trees for neuronal input–output relations,” in Neural Theory and Modeling, ed. R. Reiss (Stanford: Stanford University Press), 73–97.
Roberts, P. D. (1999). Computational consequences of temporally asymmetric learning rules: I. Differential Hebbian learning. J. Comput. Neurosci. 7, 235–246.
Roberts, P. D. (2000a). Electrosensory response mechanisms in mormyrid electric fish. Neurocomputing 32–33, 243–248.
Roberts, P. D. (2000b). Modeling inhibitory plasticity in the electrosensory system of mormyrid electric fish. J. Neurophysiol. 84, 2035–2047.
Roberts, P. D., and Bell, C. C. (2000). Computational consequences of temporally asymmetric learning rules: II. Sensory image cancellation. J. Comput. Neurosci. 9, 67–83.
Roberts, P. D., and Bell, C. C. (2001). Mutual inhibition increases adaptation rate in an electrosensory system. Neurocomputing 38–40, 845–850.
Roberts, P. D., and Bell, C. C. (2003). Active control of spike-timing dependent synaptic plasticity in an electrosensory system. J. Physiol. (Paris) 96, 445–449.
Roberts, P. D., Lafferriere, G., Sawtell, N., Williams, A., and Bell, C. C. (2006). Dynamic regulation of spike-timing dependent plasticity in electrosensory processing. Neurocomputing 69, 1195–1198.
Roberts, P., and Portfors, C. (2008). Design principles of sensory processing in cerebellum-like structures. Biol. Cybern. 98, 491–507.
Saudargiene, A., Porr, B., and Wörgötter, F. (2004). How the shape of pre- and postsynaptic signals can influence STDP: a biophysical model. Neural Comput. 16, 595–625.
Sawtell, N. (2010). Multimodal integration in granule cells as a basis for associative plasticity and sensory prediction in a cerebellum-like circuit. Neuron 66, 573–584.
Sawtell, N., and Williams, A. (2008). Transformations of electrosensory encoding associated with an adaptive filter. J. Neurosci. 28, 1598.
Sawtell, N. B., Williams, A., and Bell, C. C. (2007). Central control of dendritic spikes shapes the responses of Purkinje-like cells through spike timing-dependent synaptic plasticity. J. Neurosci. 27, 1552–1565.
Toyoizumi, T., Pfister, J. P., Aihara, K., and Gerstner, W. (2005). Generalized Bienenstock–Cooper–Munro rule for spiking neurons that maximizes information transmission. Proc. Natl. Acad. Sci. U.S.A. 102, 5239–5244.
Turrigiano, G. G. (1999). Homeostatic plasticity in neuronal networks: the more things change, the more they stay the same. Trends Neurosci. 22, 221–227.
Tzounopoulos, T., Kim, Y., Oertel, D., and Trussell, L. O. (2004). Cell-specific, spike timing-dependent plasticities in the dorsal cochlear nucleus. Nat. Neurosci. 7, 719–725.
van Rossum, M. C. W., Bi, G. Q., and Turrigiano, G. G. (2000). Stable Hebbian learning from spike timing-dependent plasticity. J. Neurosci. 20, 8812–8821.
Von der Emde, G. (1999). Active electrolocation of objects in weakly electric fish. J. Exp. Biol. 202, 1205.
Williams, A., Leen, T. K., and Roberts, P. D. (2004). Random walks for spike-timing dependent plasticity. Phys. Rev. E 70, 021916.
Williams, A., Roberts, P. D., and Leen, T. K. (2003). Stability of negative-image equilibria in spike-timing-dependent plasticity. Phys. Rev. E 68, 021923.
Xie, X.-H., and Seung, H. S. (2000). “Spike-based learning rules and stabilization of persistent neural activity,” in Advances in Neural Information Processing Systems 12, eds S. A. Solla, T. K. Leen, and K.-R. Muller (Cambridge: MIT Press), 164–170.
Keywords: Keyword: electrosensory, mormyrid, learning dynamics, stability, descending control, stochastic
Citation: Roberts PD and Leen TK (2010) Anti-Hebbian spike-timing-dependent plasticity and adaptive sensory processing. Front. Comput. Neurosci. 4:156. doi: 10.3389/fncom.2010.00156
Received: 21 February 2010;
Accepted: 15 December 2010;
Published online: 31 December 2010.
Edited by:
Wulfram Gerstner, Ecole Polytechnique Fédérale de Lausanne, SwitzerlandReviewed by:
Bruce A. Carlson, Washington University in St. Louis, USAJean-Pascal Pfister, Cambridge University, UK
Copyright: © 2010 Roberts and Leen. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Patrick D. Roberts, Biomedical Engineering, Oregon Health and Science University, Portland, OR 97239, USA. e-mail:cm9iZXJ0cGFAb2hzdS5lZHU=

