The abrupt development of adult-like grid cell firing in the medial entorhinal cortex

Understanding the development of the neural circuits subserving specific cognitive functions such as navigation remains a central problem in neuroscience. Here, we characterize the development of grid cells in the medial entorhinal cortex, which, by nature of their regularly spaced firing fields, are thought to provide a distance metric to the hippocampal neural representation of space. Grid cells emerge at the time of weaning in the rat, at around 3 weeks of age. We investigated whether grid cells in young rats are functionally equivalent to those observed in the adult as soon as they appear, or if instead they follow a gradual developmental trajectory. We find that, from the very youngest ages at which reproducible grid firing is observed (postnatal day 19): grid cells display adult-like firing fields that tessellate to form a coherent map of the local environment; that this map is universal, maintaining its internal structure across different environments; and that grid cells in young rats, as in adults, also encode a representation of direction and speed. To further investigate the developmental processes leading up to the appearance of grid cells, we present data from individual medial entorhinal cortex cells recorded across more than 1 day, spanning the period before and after the grid firing pattern emerged. We find that increasing spatial stability of firing was correlated with increasing gridness.

Grid cells in the medial entorhinal cortex (mEC) are active when the animal's position coincides with the vertices of a triangular grid covering the whole of the local environment (Hafting et al., 2005). The regularly spaced and repeating nature of grid cell firing, along with the findings that the mEC also contains neural representations of direction, speed and local boundaries (Sargolini et al., 2006; Solstad et al., 2008), suggests that it is a critical brain structure for navigation, combining path integration with local cue information in order to calculate an animal's position.

Since the discovery of grid cells in 2005, a sustained effort has been made toward modeling the neural circuits that produce grid firing in adult rats. Two major categories of theories have become prominent: those positing that grid cells are wired to form a continuous attractor representation of space (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Burak and Fiete, 2009; Navratilova et al., 2011; Sreenivasan and Fiete, 2011), and those which suggest that the regularly repeating patterns of firing of grid cells emerge from the summation of distinct oscillators beating at differing frequencies (Burgess et al., 2007; Giocomo et al., 2007; Blair et al., 2008; Burgess, 2008; Zilli and Hasselmo, 2010). Despite this progress, less emphasis has been placed on understanding how either of these network architectures might be set up during the organism's ontogenetic development (see McNaughton et al., 2006; Welinder et al., 2008; Widloski and Fiete, 2010, for exceptions), leaving open the question of how the grid cell circuit is wired during brain development.

In recent work, we and others have characterized the developmental timeline of the emergence of spatially responsive cells in the hippocampal formation of pre-weanling rats (Langston et al., 2010; Scott et al., 2010; Wills et al., 2010). These studies indicate that head-direction cells are the earliest developing spatial response, appearing fully mature at postnatal day 16 (P16). Rudimentary place cell firing is also present at this age, but continues to improve gradually as the animals age (until at least P45; Scott et al., 2010). Grid cells emerged later, with adult-like grid cell firing present around 3–4 weeks of age. Although the different spatial responses follow distinct developmental trajectories, all the basic components of the hippocampal navigation system are in place by 3 weeks of age, coinciding with the time when weanlings first start to leave their nest (Gerrish and Alberts, 1996).

However, beyond noting the first appearance of grid cell firing and the spatial stability of grid fields, the Wills et al. (2010) and Langston et al. (2010) studies did not offer a detailed investigation of the development of grid cell firing in immature rats. For instance, it is still an open question whether all the aspects that define the adult grid cell system are present from the first appearance of grid firing or if, similarly to place cells, grid cells follow a gradual developmental trajectory. The focus of this study, therefore, is to provide a fuller characterization of grid cell development. With minor exceptions, we find that, as soon as grid cells are present, the grid cell network possesses all of the characteristic properties observed in the adult. We also present data from a small number of mEC cells that were recorded across 2 days, both before and after stable grid firing emerged. We found that different cells display different patterns of development, and that increasing spatial stability of firing may be an important factor in grid cell development.

Methods

Implantation of Extracellular Recording Electrodes in Medial Entorhinal Cortex

The data used for analyses in this paper have previously been presented in Wills et al. (2010): detailed methods relating to extra-cellular recording of mEC cells in awake and behaving pre-weanling rats were described in that study. For methods relating to adult control data, see Barry et al. (2007). In summary, 28 male Lister Hooded rat pups, aged P14–P23 at the time of surgery, were chronically implanted with microdrives loaded with 4 tetrodes (HM-L coated 90% platinum-10% iridium 17 μm diameter wire). Microelectrodes were aimed at the mEC using co-ordinates 3.8 mm lateral to the midline and 0.2–0.3 mm anterior to the transverse sinus, with electrodes angled 9° tip anterior. After surgery rats were placed in a heated chamber until they had fully recovered from the gas anesthetic (1% isofluorane; 30 min recovery time), and were then returned to the dam and littermates. After completion of the experiments, rats were perfused transcardially with saline followed by 4% paraformaldehyde. Brains were sliced parasagitally into 30 μm thick sections and Nissl stained to aid visualization of the electrode track.

Single-Unit Recording in Behaving Rats

Rats were allowed a 1 day postoperative recovery, after which microelectrodes were advanced ventrally by 60–250 μm/day. When mEC cells were found, recording sessions began. Single unit data was acquired using the Axona DACQ system (Axona, UK). Two LEDs spaced 7 cm apart and placed in a fixed orientation with respect to the animal's head were used to track the position and directional heading of the animal. Isolation of single units from multi-unit data was performed manually on the basis of peak-to-trough amplitude. Cells were selected for further analysis if they had: (a) spike width >200 μs, (b) an overall mean rate less than 10 Hz, and (c) fired at least 100 spikes during the trial.

Behavioral Testing

Single-unit recording trials took place in a square-walled (62 cm sides, 50 cm high) light-gray wooden box, placed on a black platform, while the rat searched for drops of soya-based infant formula milk randomly scattered on the floor of the environment. The floor was not washed between trials. Trials were 15 min long. Distal visual cues were available in the form of the fixed apparatus of the laboratory. Rats were kept in a separate holding box (30 × 30 cm, 30 cm high walls) between recording trials (inter-trial intervals were 15 min). Cells were used for analysis if they were recorded in a trial where total path length exceeded 45 m, and the recording session involved at least two trials (to assess for reproducibility of firing).

Firing Rate Maps

Firing rate maps were constructed by sorting position data into 2 × 2 cm bins. The binned position and spike data were then smoothed using the adaptive smoothing rule described in (Skaggs and McNaughton, 1998), where the smoothing radius for each bin was expanded until the amount of dwell time (in seconds) multiplied by square root of the number of spikes within the radius was greater than 200. Firing rates in each bin were then calculated by dividing the total number of action potentials during occupancy of the bin by the total duration of occupancy. The ten colors of the firing-rate maps were auto-scaled to represent 10% of the peak rate—red (top 10%) to dark blue (bottom 10%). Unvisited bins are shown in white.

Auto-Correlograms and Gridness Score

Following Hafting et al. (2005), the spatial autocorrelogram of the firing rate map was calculated as:

$r\left({\tau }_x,{\tau }_y\right)=\frac{n{\displaystyle \sum {\lambda }_1\left(x,y\right){\lambda }_2\left(x-{\tau }_x,y-{\tau }_y\right)}-{\displaystyle \sum {\lambda }_1\left(x,y\right){\displaystyle \sum {\lambda }_2\left(x-{\tau }_x,y-{\tau }_y\right)}}}{\sqrt{n{\displaystyle \sum {\lambda }_1{\left(x,y\right)}^2}-{\left({\displaystyle \sum {\lambda }_1}\left(x,y\right)\right)}^2\times \sqrt{n{{\displaystyle \sum {\lambda }_2\left(x-{\tau }_x,y-{\tau }_y\right)}}^2-{\left({\displaystyle \sum {\lambda }_2\left(x-{\tau }_x,y-{\tau }_y\right)}\right)}^2}}}$

where r(τ_x,τ_y) is the autocorrelation between bins with spatial offset of τ_x and τ_y. λ₁ (x, y) and λ₂(x, y) are equivalent for an autocorrelation and indicate the mean firing rate in bin (x, y) and n is the number of bins over which the estimate was made. The six central peaks of the autocorrelogram were defined as the six local maxima, with r > 0.3, closest to (but excluding) the central peak. Gridness was calculated by defining a mask on the spatial autocorrelogram centered on the central peak, but excluding the peak itself (r > 0.5), bounded by a circle defined by the mean distance from the center of the six closest peaks, multiplied by 1.25. Gridness was then expressed as the lowest correlation obtained for rotations of 60° and 120°, versus the unrotated mask, minus the highest correlation obtained at 30°, 90°, or 150°. Grid cell wavelength was calculated as the mean distance from the central peak to the six surrounding peaks in the spatial autocorrelogram (expressed in cm). Grid field size (radius) was calculated as the square root of the area of the central peak of the autocorrelogram (r > 0.5) divided by π.

Classification of mEC Cells as Grid Cells

Grid cells were identified by comparing gridness scores of mEC cells to a threshold value calculated as the 95 percentile value of the gridness scores of a shuffled data null population (for more details see Wills et al., 2010). For any single trial, randomized data was generated by shifting the whole spike train with respect to the position data by a random amount (>20 s). This process was repeated a sufficient number of times for there to be 20,000 shuffled rate maps for each age. The gridness thresholds obtained in this study were 0.36 for young rats, and 0.29 for adults. In order to reduce the influence of false positive grid classifications (expected as 5% of a total 727 cells = 36 cells in this study), data was only included in further analyses if at least one cell in the recording session was classified as a grid cell on more than one trial. Cells shown in Figure 5 were selected by the following criteria: (1) electrodes were not moved between Day N and Day N + 1; (2) clusters were identifiable between Day N and Day N + 1; (3) the waveform of the cell in question had not substantially changed; (4) the cell met the grid cell criterion (see above) on at least one trial on Day N + 1; (5) the cell's mean gridness increased between Day N and Day N + 1.

Cross-Correlograms and Grid Field Phase Offset

Cross-correlograms between two rate maps were calculated as for autocorrelograms, with the exception that λ₁(x, y) and λ₂(x, y) indicate the mean firing rate in bin (x, y) in the two different rate maps. The phase offset of the grid fields was defined as the vector between the center of the cross-correlogram and the closest local maxima of the cross-correlogram (r > 0.3). Gridness was calculated from cross-correlograms (Figure 1A) or population vector cross-correlograms (Figure 2D) by offsetting the cross-correlogram such that the local maxima closest to the center is placed at the center of the cross-correlogram, and then calculating gridness as described above.

FIGURE 1

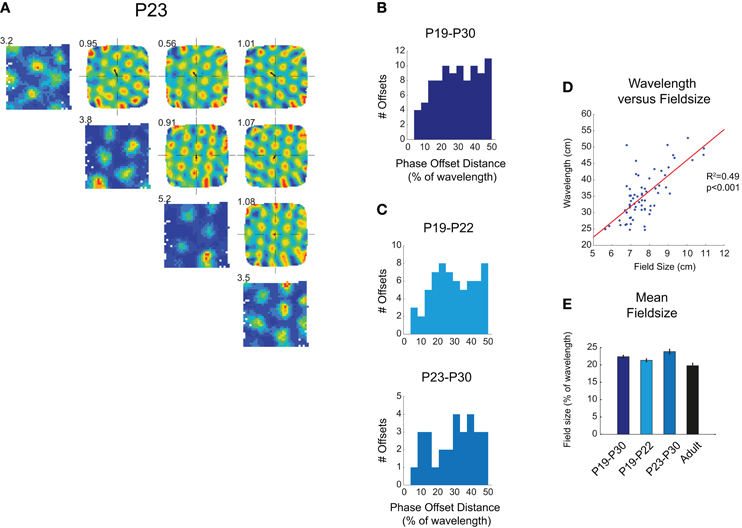
Figure 1. (A–C) Simultaneously recorded grid fields in immature rats share the same wavelength and orientation, and tessellate to cover the whole environment surface. (A) Diagonal row shows firing rate maps for four grid cells simultaneously recorded at P23. Peak firing rate is shown at top left of map. Top-right quadrant of (A) shows spatial cross-correlograms which compare firing rate maps. These show clear hexagonal symmetry, demonstrating a repeating grid structure that is shared between different cells. The distance between the center of the cross-correlogram and the closest peak (small black arrow) represents the phase offset between different firing fields. Numbers on the top-left of cross correlograms show the gridness score calculated from the cross-correlogram. (B) Phase offsets for all simultaneously recorded grid cells from P19 to P30. Offsets are evenly distributed between 0% and 50% of grid wavelength (C) Phase offsets are equally distributed in both younger (light blue) and older (blue-gray) developing rats. (D) Scatter plot showing the wavelength for each grid cell (ages P19–P30) versus the field size. Red line shows significant linear regression between wavelength and field size, R² and p-values for regression are shown to left of plot. (E) Mean field size as a percentage of wavelength, ±SEM. Field size in pups is slightly larger than that in adults, but there is no trend for field size to decrease during the period P19–P30.

FIGURE 2

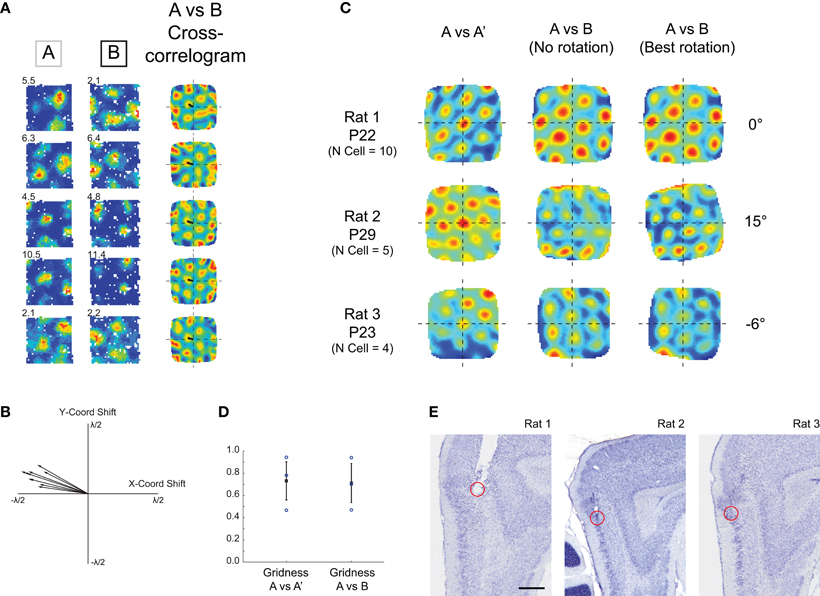
Figure 2. Grid cells simultaneously recorded in young rats maintain their relative spatial structure in different environments. (A) Example cells recorded at P22 in two different environments. Left-hand column: rate map for cell in Env A, middle column: rate map for cell in Env B, right-hand column: cross-correlogram for Env A rate map vs. Env B rate map. Note that all cross-correlograms show the same hexagonal symmetry and the same phase offset (small black arrow), indicating that all cells have shifted their firing fields coherently between Env A and Env B. (B) Phase offset vectors for all grid cells recorded in experiment shown in (A) are clustered together. (C) Population vector cross-correlograms for three simultaneously recorded grid cell ensembles. Left-column: population vector cross-correlogram for two different trials in Env A. Hexagonal structure shows repeatable grid firing in two consecutive trials in the same environment. Middle column: population vector cross-correlogram for Env A versus Env B. Two ensembles (P29 and P23) show some degradation in the hexagonal symmetry. Right column: cross-correlogram after rotation of Env B rate maps. Hexagonal symmetry is restored in the P29 and P23 ensembles, demonstrating a coherent rotation of grid cell firing fields between Env A and Env B. (D) Gridness scores calculated from population vector cross-correlograms, for within-environment and across-environment comparisons. (E) Estimated recording locations for the three ensembles of simultaneously recorded cells. Ensembles from Rats 2 and 3 were most likely recorded from mEC LII, the ensemble from Rat 1 was most likely recorded from just below the mEC/Parasubiculum border zone. Scale bar = 0.5 mm.

Different Environment Probe, Phase Offset Variability, and Population Vector Cross-Correlograms

Young rats were exposed to a different environment which was in the same room as the standard testing environment, but completely enclosed within black curtains, such that there were no common visual cues. The second environment was a 62 × 62 cm square, with interior walls coated in brown masking tape. The floor was translucent Perspex overlaid on a black surface, which was washed before every trial. In all data shown, rats had been exposed at least three times to this environment. To test whether phase offsets were significantly clustered, we calculated the variability of a group of phase offsets, defined as the mean length of the vectors connecting the phase offset coordinates with the center-point of the group (mean x and y coordinate). To take account of the sixfold symmetry of the autocorrelogram, all phase offsets were first mapped onto the range 0–60°, by taking the remainder modulo 60 of the offset vector angle. The offset variabilities of the three ensembles in the environment A versus environment B condition (A–B) were compared to the offset variabilities for environment A versus a repeat trial of the same environment (A–A′). The A–B ensemble variabilities were then further compared to the variability between all cells (i.e., from across ensembles) in the A–B condition. Population vector cross-correlograms were calculated following Fyhn et al. (2007). Briefly, rate maps from simultaneously recorded cells were stacked into a three-dimensional matrix with the two spatial dimensions on the x and y axes and cell identity on the z axis. Each vector in the z-dimension of the matrix, therefore, described the set of firing rates from all simultaneously recorded cells in one trial, in one particular spatial 2 × 2 cm bin. The cross-correlation between two different trials was defined as the mean of all dot products between vectors from spatially corresponding bins in different trials (dot products were first normalized to vector length to yield a number between 0 and 1). Then, to compute a spatial cross-correlogram, one matrix was shifted in 2 cm steps in the x and y dimensions, to cover all possible offsets between the two matrices in x and y, and the mean population vector cross-correlation at each offset was re-calculated. Cross-correlations at each offset were only used in the cross-correlogram if the number of overlapping bins at each offset was >50. To test for rotations of grid firing, one matrix was rotated in 3° increments and the cross-correlogram recalculated. The rotation yielding the maximum gridness score is shown in Figure 2C (rightmost column).

Identification of Conjunctive Cells

For all grid cells, directional data was sorted into 1° bins and smoothed with 14.5° boxcar window. Firing rate polar plots were computed by dividing the number of spikes that the cell fired when the animal was pointing its head in a specific direction by the time spent facing that direction. The Rayleigh vector was defined as the length of the mean resultant vector derived from the binned, smoothed directional rate map. Grid cells were classified as conjunctive cells if the length of the Rayleigh vector exceeded the threshold of the 95th percentile value of the Rayleigh vector lengths of a shuffled data null population (obtained similarly to gridness classification, see above). The resulting threshold values were 0.18 for young rats and 0.15 for adults. The stability of directional tuning was assessed by (1) correlating rate values of spatially corresponding bins from two consecutive trials, and (2) testing whether the inter-trial differences between preferred firing directions (defined as the circular means of the firing rate maps), significantly differed from 0°.

Speed Modulaltion of Firing Rate and Intrinsic Frequency

Position and spike data from trials in which grid cells were recorded were filtered by running speed into eight bins, using the following boundary values (in cm/s): 2.5, 3.5, 4.5, 5.5, 7, 8.5, 10, 12.5, 15, 20. Data in which running speed was less than 2.5 cm/s or greater than 20 cm/s were discarded. Each bin represented a 10 ± 1% percentile range of the entire speed data set. The mean rate for each speed bin was defined as the number of spikes divided by the dwell time in each speed bin. Linear regression was used to test for a significant relationship between speed and mean rate. Adult data was analyzed using both the same speed bins as above (Figure 4G) and a set of percentile-matched bins to account for greater running speed in adult rats (Figure 4F). The boundary values for these were (cm/s): 5, 7.54, 10.03, 12.44, 15.75, 18.87, 21.83, 26.37, 30.69, 39.12. To estimate the intrinsic frequency of the cell, data was filtered into slow (2.5–8 cm/s) or fast (8–20 cm/s) speed bins. The spike train autocorrelogram for each segment of data (with duration ≥ 0.5 s after filtering) was calculated, segments were then combined (weighted by the duration of the segment of data) and mean normalized. The power spectrum for the combined autocorrelogram was then obtained using the fast Fourier transform, smoothed (Gaussian kernel with standard deviation 0.375 Hz), and the intrinsic frequency was defined as the peak value in the 4–10 Hz band. The theta modulation of a cell was defined as the ratio between the mean power ±0.5 Hz from the intrinsic frequency peak, and the mean power of the remaining power spectrum between 2 and 125 Hz. Only cells with theta modulation >5 were used for analysis of intrinsic frequency modulation with speed.

Results

The data used for analyses in this paper have previously been presented in Wills et al. (2010). 727 mEC cells were recorded in rats aged between postnatal day 16 and 30 (P16–P30). Of these, 65 cells were classified as grid cells, which were recorded between the ages of P19 and P30 (see Methods for details).

Grid Cell Firing Fields are Adult-Like from Their First Appearance in Development

In the adult rat, most grid cells in the same local patch of mEC share the same wavelength and orientation, but are offset in spatial phase (Hafting et al., 2005). The population of grid cells in a local patch of mEC, therefore, forms a coherent neural representation of space, in which the firing fields of a relatively small number of cells tessellate the whole surface of the environment. We have previously shown that in young rats, similarly to what observed in adults, the wavelength and orientation of simultaneously recorded grid cells are clustered together (Figure 1A; see also Wills et al., 2010 supporting figure 16). Here we also asked whether grid fields exhaustively tessellate the whole environment: if so, phase offset vectors should be evenly distributed between 0 (overlapping fields) and 50% of ensemble wavelength (maximum offset). This was found to be the case for all simultaneously recorded grid cell ensembles (P19–P30; Figure 1B; χ² goodness-of-fit of uniform distribution: χ²₍₁₁₎ = 14.3, p = 0.21), and also for those ensembles recorded at the earliest stages of grid development (P19–P22; Figure 1C; χ²₍₁₁₎ = 12.6, p = 0.32). From this data we can infer that local groups of grid cells, as soon as they appear, form a coherent map covering the entire environment.

In adults, the size of individual grid firing fields is closely related to the spacing between fields (Hafting et al., 2005). We found that this was true also in young rats: there was a close correlation between the field size and the wavelength of the grid (Figure 1D; linear regression between wavelength and field size: R²=0.49, p < 0.001). This was also true when just those grid cells from the youngest animals (P19–P22) were considered (R²= 0.37, p < 0.001). Are grid fields more diffuse in rat pups compared to adults? Field size as a proportion of wavelength was found to be slightly, but significantly larger than that in adults (Figure 1E; t-test P19–P30 versus adult: t = 3.00, df = 282, p = 0.003), though there was no trend for field size to decrease between the ages of P19 and P30 (Figure 1E). The grid circuit in rat pups, therefore, has the same internal structure as that in the adult, although grid firing fields appear to be slightly more diffuse in young rats.

The Grid Cell Map of Space Maintains its Internal Structure in Different Environments

If adult rats are exposed to different testing environments grid cell fields will rotate and shift their spatial phase. Simultaneously recorded local groups of cells will shift and rotate in unison, such that the internal structure of the grid cell map is maintained (Fyhn et al., 2007). We asked whether local groups of grids cells have the same fixed phase structure early in development. If the internal structure of the grid network is not fixed, cells could adopt different phase offsets when introduced into a different environment. Figure 2A shows firing fields for five simultaneously recorded cells from a 22-day-old animal introduced into two different testing environments (Env A and Env B). The spatial cross-correlograms for the Env A rate map versus the Env B rate map show that all cells share the same phase offset. Figure 2B similarly shows that phase offset vectors for all cells recorded from this animal are closely clustered together. To quantify whether phase offset vectors were significantly clustered for all simultaneously recorded cells, we tested whether the variability between phase offsets within ensembles increased when animals were placed in Env B (A-B condition, see Methods), and found no such effect (2-sample t-test: t = −0.70, df = 4, p = 0.52). Furthermore, the offset variability across ensembles (in the A–B condition) was significantly greater than that within ensembles (1-sample t-test: t = −5.23, df = 2, p = 0.034). To further quantify whether local groups of grid cells maintain their fixed phase structure in different environments, we compared activity of the entire grid cell ensemble using population vector-based cross-correlograms (Fyhn et al., 2007; see Methods). Figure 2C (left-hand column) shows the population cross-correlogram comparing two different trials in Env A. The symmetrical hexagonal structure, with a strong peak in the center of the correlogram demonstrates stable, fixed grid cell activity upon exposure to the same environment during two temporally contiguous trials. When the Env A ensemble firing is compared to that of Env B (Figure 2C middle column), the cross-correlogram for Rat 1 shows an equally strong hexagonal symmetry, although offset in spatial phase, indicating a coherent shift in grid firing. Rat 2 and Rat 3 ensembles show some degradation of hexagonal symmetry when compared directly (Figure 2C middle column), but this degradation is rescued when Env B firing rate maps are rotated (all maps being rotated by the same angle), demonstrating that grid ensemble firing has coherently rotated and shifted between Env A and Env B. Figure 2C right-hand column shows the population cross-correlogram for the rotation that resulted in the highest gridness score for each rat. After rotation, there was no significant difference between the gridness scores calculated from the population cross-correlogram for the A–A′ condition and the A–B condition (Figure 2D, t-test: t = 0.11, df = 4, p = 0.91). At the earliest stages of grid cell development, therefore, local groups of grid cells maintain a stable phase offset structure upon exposure to distinct environments.

Conjunctive Representation of Distance and Direction in the Earliest Grid Cells

The entorhinal cortex encodes a combined representation of distance, direction and speed, which allows the computation of position based on heading direction and distance travelled (Sargolini et al., 2006). Previous work has shown that head direction cells recorded from both the mEC and the Presubiculum have adult-like properties very early on during postnatal development (P16; Langston et al., 2010; Wills et al., 2010). In adult rats, representations of direction and distance are encoded in single cells, the so called “conjunctive cells,” found throughout the parahippocampal cortices (Sargolini et al., 2006). It is not known when conjunctive cells emerge during development. We analyzed our grid cell data set to look for directional tuning, quantified by the length of the mean resultant vector (“Rayleigh vector”) of the directional firing rate map. Figure 3A shows three examples of conjunctive cells recorded from three different rats aged between P20 and P23. The preferred direction of the cells' firing is stable over two consecutive trials in the same environment. This was assessed by computing the correlation between the two firing rate maps (Figure 3B; t-test young versus adult correlation: t = 0.29, df = 22, p = 0.77), and by calculating the inter-trial differences in the preferred firing directions: these were closely clustered around 0° (all young rats mean difference = 3°, 95% confidence interval ±8°; P19–P22 group mean difference = 1°, 95% confidence interval ±8.5°). Figure 3C shows the distribution of directionality versus gridness for all mEC cells that were classified as grid cells. All grid cells with a mean vector length greater than the 95th percentile of a null distribution from spatially shuffled data (red dashed line) were classified as conjunctive cells. Do conjunctive cells emerge abruptly and at the same time as grid cells, or is there an extended period during which they gradually emerge? When the data was split into two groups, P19–P22 and P23–P30, there were no significant differences in the proportions of grid cells with directional correlates across these age groups, and compared to adults (Figures 3D,E; χ²= 0.44, df = 2, p = 0.80). The combined representation of distance and direction in single mEC cells is, therefore, present from the earliest ages at which grid cells emerge.

FIGURE 3

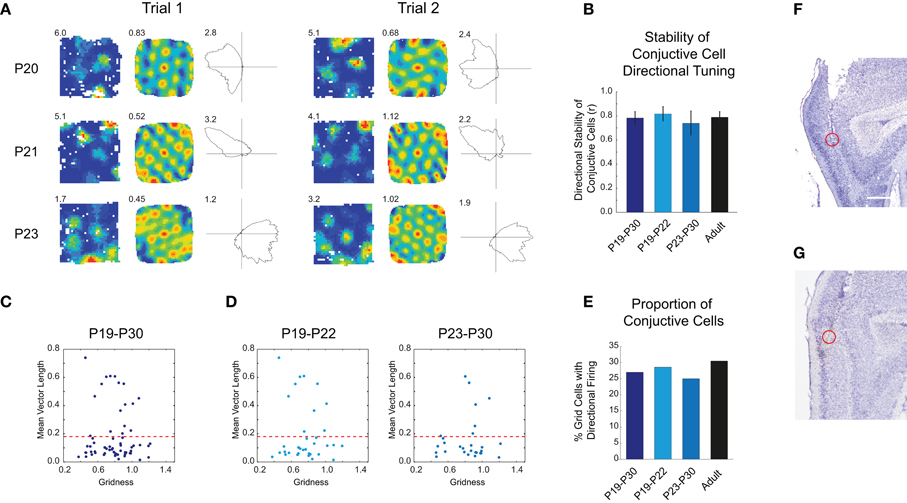
Figure 3. Conjunctive grid-head direction cells exist at the earliest stages of grid cell development. (A) Three example of conjunctive cells recorded from three different rats at P20, P21, and P23, for two consecutive trials. For each trial, the left-hand column shows the firing rate map with peak firing rate, the middle column the auto-correlogram with the gridness score, and the right-hand column the directional firing rate map, with the peak directional firing rate. The directional firing correlate is stable between consecutive trials. (B) The mean stability of the directional correlate of conjunctive cells is at adult levels from the earliest emergence of conjunctive cell firing. Bar chart shows mean inter-trial stability of the directional component of conjunctive cell firing for different age groups, ±SEM. (C) Scatter plot showing gridness versus the mean vector length of the directional rate map. The red dashed line shows the threshold for classifying cells as directional, based on the 95th percentile of a shuffled data null distribution. (D) Distributions of gridness and mean vector lengths are similar for both young (P19–P22) and older developing rats (P23–P30) rats. (E) The proportions of grid cells classified as conjunctive do not significantly change during development. (F,G) Representative recording location for conjunctive cells, which were most likely recorded from mEC LIII. Scale bar = 0.5 mm.

Grid Cells in Immature Rats Show Rate Modulation by Running Speed

Is grid cell firing in young rats also affected by the running speed of the animal? To test how many grid cells showed modulation of firing rate by running speed in young rats, we calculated the overall mean firing rates at different running speeds for each cell. No attempt was made to separate within-field from out-of-field firing. After finding the mean firing rate for each of the seven speed bins (see Methods for details), we tested whether there was a significant linear correlation between firing rate and running speed. In 70% of grid cells recorded from young rats (44/63), we found a significant rate-speed relationship. Four examples are shown in Figures 4A–C. In each case, when rate maps are constructed from data filtered for fast running speeds, grid field firing rates are higher than when rate maps are constructed from data filtered for low running speeds (Figure 4B). The increase in mean rate (combined in- and out- of field firing rate) with speed for these cells can be seen in Figure 4C. Note that both the slope and the intercept of the relationship between rate and speed differ between cells, but the large majority increase rate with speed: the distributions of slope and intercept values for all cells are shown in Figure 4D. Between the ages of P19–P22 and P23–P30, there is a trend for both slope and intercept to decrease, though these trends reach significance only for intercepts (Figure 4E, t-test slopes: t = 1.42, df = 42, p = 0.16; intercepts: t = 2.23, df = 42, p = 0.03).

FIGURE 4

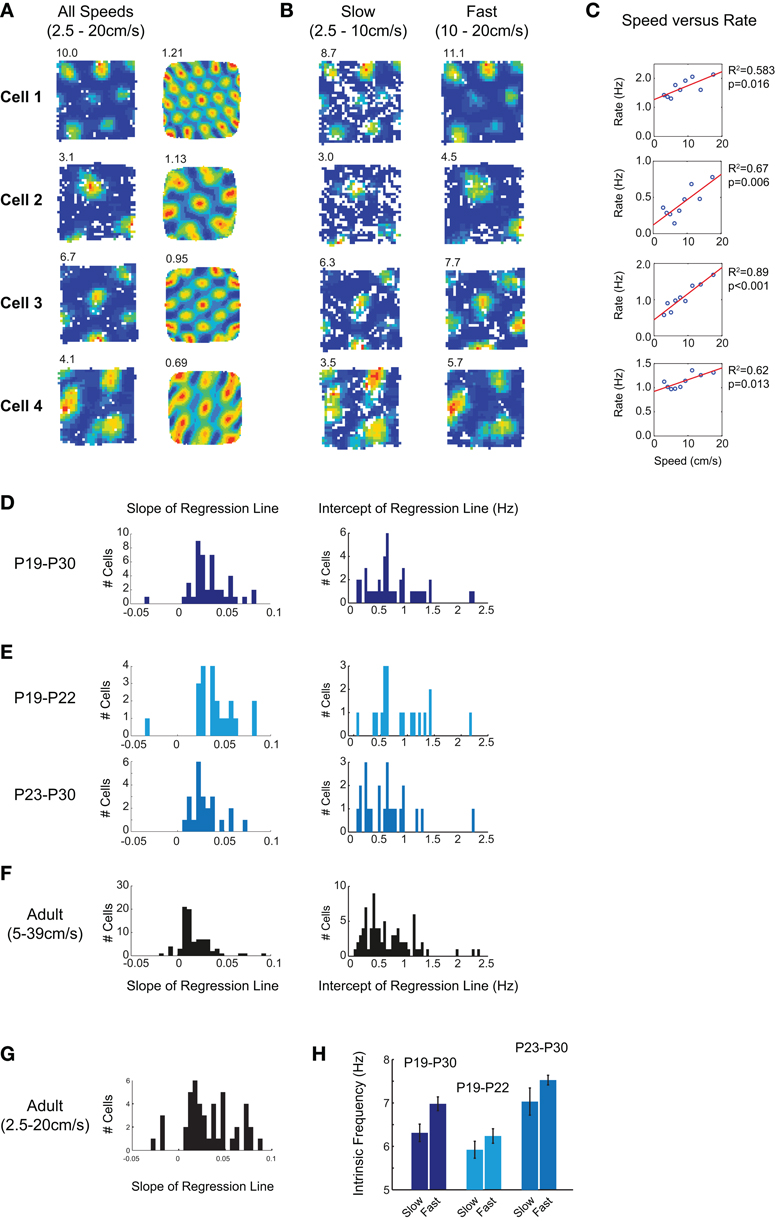
Figure 4. Grid cell firing rate in young rats is modulated by running speed. (A) Firing rate maps and autocorrelograms for four grid cells. Peak firing rate is top left of rate map, gridness score is top left of autocorrelogram. Firing rate maps are constructed from data in which the running speed was 2.5–20 cm/s. (B) Firing rate maps for the same four cells, with data filtered by either slow (2.5–10 cm/s; left column) or fast (10–20 cm/s; right column) running speeds. The grid firing field is preserved at both fast and slow speeds, but firing rates increase with running speed. (C) Scatter plots of mean firing rate versus running speed for the same four grid cells. The mean rates shown include both in- and out- of field firing. The red lines show linear regression fits to the speed versus firing rate data: R² and p values for these fits are shown to the right of the plots. (D) Distribution of regression line slopes and intercepts for all grid cells with a significant linear fit between speed and firing rate. Most cells increase firing rate with running speed, and all intercept values are positive. (E) Distribution of regression line slopes for younger (P19–P22; top) and older (P23–P30; bottom) developing rats. Grid cells are speed modulated when they first emerge during development, though the slope and the intercept of the regression line tends to decrease with age. (F,G) Speed modulation of grid cell firing in adults. (F) When regression lines are fitted over a range of speeds scaled to reflect the faster running of adults, regression slopes are significantly lower than those seen in young rats. (G) When the same absolute speed range as for young rats is used, fewer grid cells show a significant speed modulation, but those which do show similar slope values to those seen in young rats. (H) Intrinsic frequency of grid cell firing increases with running speed. Bars show mean intrinsic frequency of theta-modulated grid cells, ±SEM. “Slow” bars show data where speed lies between 2.5 and 8 cm/s, “Fast” bars from 8 and 20 cm/s. Dark blue shows all young rats, light blue P19–P22, and gray P23–P30.

How similar is the speed modulation of immature rat grid cells to that seen in adults? When adult cells are tested using a set of speed bins scaled to match faster running speeds in adults (5–39 cm/s, see Methods), 42% of adult cells (85/208) had a significant linear relationship between firing rate and running speed. Figure 4E shows the distributions of slope and intercept values for these 85 cells. Although there was no difference between immature and adult intercepts (t = 0.39, df = 127, p = 0.69), adult slope values are significantly lower than those in immature rats (Adult mean = 0.0162, Immature mean = 0.0284; t = 4.90, df = 127, p < 0.001). Does this difference truly reflect a greater degree of speed modulation in young rat firing rates, or does it instead reflect the different speed ranges covered by adults and immature rats? To check this, we re-ran the analysis on the adult data, this time using the same absolute values of speed bin as for immature rats (2.5–20 cm/s). Using these speeds, fewer cells showed significant modulation (50/208), but those that were modulated had slope values similar to those seen in young rats (Adult mean slope = 0.0263; adult versus immature t-test: t = 0.23, df = 92, p = 0.81). Over the range of speeds covered by immature rats, therefore, the percentage of adult cells modulated by speed is considerably lower, but the degree of speed modulation of firing rate in those cells appears to be similar.

Oscillatory interference models of grid cell firing predict that the frequency of intrinsic oscillation should increase with running speed (Burgess et al., 2007). Does the modulation of rate by speed reflect an increase in the intrinsic frequency of grid cells with faster running speed? We calculated an estimate of intrinsic frequency from the spike train autocorrelogram of grid cells (see Methods), for both slow (2.5–8 cm/s) and fast (8–20 cm/s) runs. Intrinsic frequency increases with running speed in young rats (Figure 4H, t-test slow versus fast: t = 2.71, df = 44, p = 0.009). This pattern holds true also for the younger and older groups of rats (Figure 4H, middle and right). At the earliest ages at which grid cells appear, therefore, the grid cell network also contains an adult-like representation of the speed of the animal.

The Emergence of Grid Firing in Individual mEC Cells

From the data presented so far it appears that the grid cells recorded from immature rats are adult-like as soon as they appear. The abrupt emergence of adult-like grid cell firing at around P19 poses an experimental conundrum: how is one to study the development of grid cells if, upon their first emergence, they appear to be mature in most respects? In other words, in the absence of a reliable physiological identifier (as in the case of CA1 pyramidal cells), how are we to know what is the activity of nascent grid cells, if they are fully developed as soon as they can be detected? To begin to answer this question, we looked at whether we could track the same cell across different days. Electrodes were moved after most recording sessions, and this, combined with the natural growth of the brain, meant that stably tracked cells were rarely found. However, we have identified six grid cells from our dataset which we can track across 2 days on the basis of their extracellular waveform characteristics. Crucially we recorded these cells on the day before they exhibited a recognizable grid firing pattern. In all six cells, the mean gridness score increased between the first day (“Day N”) and second day (“Day N + 1”) of recording. Figures 5A,B show these six cells, recorded on two consecutive trials on the first (A), and the second day of recording (B). The ages at which grid firing first emerged in these cells ranged from P20 to P24. Cells 1 and 2 show multiple, discrete firing fields on Day N (P19), though these are not arranged hexagonally, and show a degree of instability between trials. On Day N + 1, their firing fields become more stable, and hexagonally arranged. Cells 3–5, by contrast, show more diffuse firing patterns on Day N, which “sharpens up,” on Day N + 1, increasing their in- to out- of field firing ratio. However, some hexagonal symmetry can also be observed on Day N, despite the diffuse firing. Cell 6 seems to be different again: sharply peaked firing fields with hexagonal symmetry are already present on the first day. However, time is needed for the south-western field to detach itself from the wall, such that a precise equilateral triangle, consistent with grid cell firing, is formed.

FIGURE 5

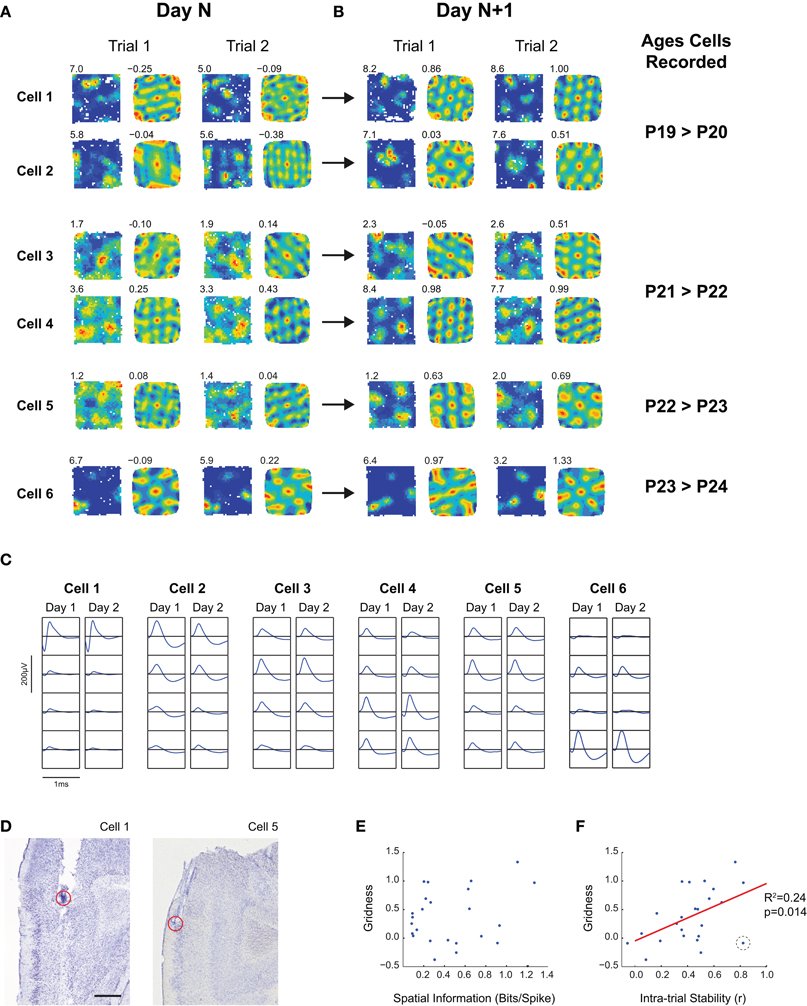
Figure 5. The development of grid firing in individual mEC cells. (A,B) Firing rate maps and autocorrelograms for six mEC cells which were tracked for more than 1 day, and which developed stable grid cell firing patterns on the second day of recording. Text top left of firing rate maps shows peak firing, top-left of autocorrelogram shows gridness score for the trial. (A) shows two consecutive trials on the first day for which the cell was recorded (“Day N”), (B) shows two consecutive trials for the second day of recording (“Day N + 1”). The ages, in postnatal days, corresponding to Day N and Day N + 1 are shown to the right of (B). (C) Extracellular waveforms for the six mEC cells shown in (A,B). Each column shows the waveforms on the four wires of the tetrode on which the cell was recorded. For each cell, the left column shows the waveform for the last recording trial of Day N, the right column shows the recording trial of Day N + 1 with the highest gridness score. The vertical and horizontal scale bars (200 μV and 1 ms, respectively) apply to all waveform plots. (D) Estimated recording locations for cells shown in (A) for which recording locations are not shown elsewhere in the paper. For the recording location of Cell 2, see Figure 3G; for Cell 3–4, see Figure 2E, “Rat 1”; and for Cell 6 see Figure 3F. Scale bar = 0.5 mm. (E,F) Scatter plots of Spatial Information (E) and Intra-trial stability (F) against Gridness. Each point represents a trial on Day N or Day N + 1 [i.e., all trials shown in (A)]. There is a significant relationship between Gridness and Intra-trial Stability (R² and p value for linear regression shown to right of plot), but not for Gridness and Spatial Information. The data point in (F) highlighted by a black dashed circle, which has a high stability but low gridness, corresponds to Cell 6, Trial 1 on P23 (see text for details).

Is it possible to make any generalizations about the mechanisms of grid cell development based on these 6 examples? We looked at the development of two fundamental properties of spatial firing: spatial specificity (measured by spatial information) and spatial stability (measured as the correlation between firing in the first and second halves of each trial), and tested for correlations between these two measures and gridness on a trial-by-trial basis (Figures 5E,F). We found a significant relationship between stability and gridness (linear regression; R²= 0.24, p = 0.014), but no significant relationship between spatial information and gridness (R²= 0.06, p = 0.21). Figure 5F shows one outlier with high stability but low gridness (circled in black), and removing this point strengthens the relationship between stability and gridness (R²= 0.40, p = 0.001). This data point corresponds to Cell 6 Trial 1 on Day N: in this case, the environment wall may have stabilized the firing field, despite grid firing had not yet fully developed. The increases in gridness and stability likely reflected developmental processes rather than increased familiarity with the environment: there was no significant relationship between either of these measures and the total number of exposures to the environment (Gridness: linear regression, R²< 0.001, p = 0.98; Stability: linear regression, R²= 0.03, p = 0.39). On the basis of this limited dataset, therefore, we can conclude that there may be different patterns of maturation for different grid cells, but that increasing spatial stability of firing may be an important factor in grid cell development.

This data can also tell us about the time course of grid cell development in individual cells. In several cells, a rudimentary hexagonal symmetry is present on the day preceding mature grid firing, suggesting that, at the single cell level, the transition from rudimentary to fully mature grid cell firing takes place over the time course of approximately 24 h.

Discussion

In this study, we have attempted to provide a full characterization of the emergence of grid cell firing during rat post-natal development. We have shown that grid cells first emerge around 3 weeks of age, and that the development of their functional properties occurs rapidly. Indeed, as soon as grid cells can be detected, they possess almost all of the properties that characterize adult grid cell firing. Grid fields in immature rats evenly cover the whole explored environment, exhaustively mapping it (c.f. Hafting et al., 2005 for adult grid cells). These neural maps appear to be universal even in young rats: different grid cells maintain their phase offsets in different environments, even though absolute firing field positions shift and rotate (c.f. Fyhn et al., 2007), similarly to the rigid relationships seen in simultaneously recorded head direction cells (Taube et al., 1990). Conjunctive representations of place and direction co-exist in grid cells in immature rats, and these grid cells are also modulated by the running speed of the animal (c.f. Sargolini et al., 2006). The emergence of stable, adult-like grid firing fields appears to be relatively abrupt, occurring around the beginning of the fourth week of life in the rat (see also Wills et al., 2010). Individual grid cells may mature over the course of approximately 1 day, though we cannot rule out that the time needed for the maturation of the whole mEC grid cell network is longer than this. Although early grid cells share most of the properties of their adult counterparts, it should be noted that some properties of the grid cell network at P19–P30 differ from those of adults. For example, the proportion of grid cells with a significant speed modulation is higher in pups, and the overall proportion of grid cells in the mEC is slightly lower in pups than in adults (see Wills et al., 2010).

One other previous study has characterized the timeline of grid cell development in the hippocampal formation (Langston et al., 2010). In agreement with Wills et al. (2010), grid cells were also found to be the slowest to develop with respect to head direction and place cells, with no adult-like grids seen until P19 at the earliest. Langston et al also reported an abrupt change to adult-like values for the proportion of grid cells, the levels of mean gridness and the grid spatial stability (though this occurred somewhat later than observed in our data, at around P28). However, consistent with what we report here and in Wills et al. (2010), Langston et al. show clear examples of adult like grid cells at P19 and P23. Furthermore, the abrupt appearance, at P22, of sub-threshold membrane synchrony in mEC stellate cells reported by Langston et al. (2010) is suggestive of a sudden maturational step occurring in mEC circuits around this age.

We have also presented data tracking the patterns of development in individual nascent grid cells. Grid cells represent a sub-set of all spatially modulated responses reported in the adult mEC (Fyhn et al., 2004; Sargolini et al., 2006), and there is no extra-cellular physiological signature unique to grid cells. Tracking the development of individual cells is, therefore, the only way to investigate the developmental stages leading up to the expression of grid cell firing using our current technology. In the data presented, cells showed diverse patterns of development, suggesting more than one mechanism for grid cell development. Despite the differences between cells, one common theme was that grid cell firing correlated with increased spatial stability. Although grid firing clearly could not occur in the complete absence of stability, it is noteworthy that stability is correlated with the development of gridness, whereas the spatial information conveyed by the cells' firing is not, and furthermore, that spatial stability does occur in the absence of grid firing. Increasing spatial stability in mEC could be due to increasing quality of the sensory information available to the mEC, for example through developmental of the visual or vestibular systems (Lannou et al., 1979; Fagiolini et al., 1994), or an increase in the spatial stability of the place signaling feeding into the mEC. Further technological developments will be required in order to track the development of larger numbers of cells through optogenetic and/or in vivo imaging means (Dombeck et al., 2010; Osakada et al., 2011).

Can the developmental programme of grid cells inform us about mechanisms of grid cell firing in adults? More specifically, is the pattern of grid cell development shown here consistent with the two major classes of theories seeking to explain grid cell firing (the attractor network and oscillatory interference models)? The early emergence of a universal fixed phase relationship between grid cells is consistent with the early development of recurrent connections between cells of similar phases, as required by continuous attractor models (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Burak and Fiete, 2009), whilst not being predicted by oscillatory interference models. The development of subthreshold membrane synchrony across stellate cells at P22 (Langston et al., 2010) also suggests that recurrent connectivity is set up in the mEC around this age, though whether such recurrent connections are direct or indirect remains an open question (Dhillon and Jones, 2000; Quilichini et al., 2010). Tracking the anatomical development of intra-mEC connectivity, ideally in combination with the functional correlates of the cells (Ko et al., 2011), would be necessary to fully understand the role of recurrent connectivity in grid cell development. The presence of head direction- and speed-modulation of grid firing at the earliest stages of development is also consistent with attractor network models, according to which these cells' function is to shift the network activity “bump” depending on the animals' velocity (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Burak and Fiete, 2009; Navratilova et al., 2011).

In this and other studies (Wills et al., 2010) we have also tested whether the temporal dynamics of grid cells during early development are consistent with the oscillatory interference class of models. We have previously shown that grid cell firing is temporally modulated at a frequency slightly higher than the theta-band LFP at all stages of development (Wills et al., 2010; as predicted in Burgess et al., 2007; Giocomo et al., 2007). In the present study, we have also shown that the intrinsic frequency of grid cells in young rats increases with running speed at all ages, consistent with a central concept of oscillatory inference models, that a velocity-modulated oscillator is used to integrate displacement over time (Burgess et al., 2007; Hasselmo et al., 2007; Blair et al., 2008; Burgess, 2008). Also consistent with oscillatory inference models is the finding that theta-band sub-threshold oscillations in mEC stellate cells, proposed to be one of the two oscillatory components (Burgess et al., 2007; Giocomo et al., 2007), emerge shortly before grid cells, at P18 (Burton et al., 2008). One outstanding question for both types of model is the nature of the velocity signal which grid cells use to track distance. This question is particularly pertinent to weanling rats, in which body size, and associated motor and proprioceptive systems, are scaled down by a factor of approximately 3, but grid field spacing is only 20–25% less than the smallest grids seen in adults (Hafting et al., 2005; Wills et al., 2010).

Do our results support any of the theories proposed for the mechanisms of grid cell development? McNaughton et al. (2006) suggested that patterns of recurrent connectivity in the mEC could be created by waves of spontaneous cortical activity in the first 2 weeks of life. The resulting network would be topographically arranged (with cells anatomically proximal sharing similar spatial phases, in contrast to what is seen in mEC grid cells), and would act as a teaching network for mEC grid cells. The later emergence of grid cell firing at 3 weeks of age (Langston et al., 2010; Wills et al., 2010) argues against this model (for further objections, see Welinder et al., 2008), though it remains possible that the correct internal mEC connectivity pre-exists the emergence of stable grid cell firing, and that the critical developmental step is the stabilization of grid fields through the maturation of afferent projections conveying speed, visual or other sensory information. Welinder et al. (2008; see also Widloski and Fiete, 2010) proposed that patterns of recurrent activity needed for an attractor network could be achieved through a self-organizing process, in which velocity signals signifying speed and direction, and local position cues from place cells, set up mEC network connectivity using a combination of symmetric and asymmetric spike-timing dependent plasticity rules. An experience-dependent learning process is consistent with the emergence of grid cells after a period of exploratory behavior (Langston et al., 2010; Wills et al., 2010), but further work is needed to fully test this hypothesis. Finally, it has been pointed out that the 60° symmetry of grid cells could be achieved through a self-organizing integration of one-dimensional band-like firing patterns (Mhatre et al., 2010; see also Burgess et al., 2007), though whether such one-dimensional bands are observed in immature mEC firing will require further investigation (see also Krupic et al., 2011).

Can studying the development of spatially responsive cells in the hippocampal formation help to explain the ontogeny of spatial learning and exploratory behavior? Various lines of evidence suggest that the ability to construct and use a cognitive map of the environment (Tolman, 1948; O'Keefe and Nadel, 1978) emerges around 3 weeks of age. Young rats will learn to find a hidden platform in a water maze using only distal cues (“place learning”) at P20–P21 (Schenk, 1985; Rudy et al., 1987; Brown and Whishaw, 2000; Akers et al., 2007). Learning the position of a platform marked by a proximal visual cue precedes place learning by 1 or 2 days (Rudy et al., 1987; Akers et al., 2007; although see Brown and Whishaw, 2000), suggesting that the physical demands of the task are not the limiting step delaying the emergence of place learning. Likewise, rats will learn a delayed alternation T-maze task at P21, but not at P15 (Green and Stanton, 1989), and spontaneous alternation in the T-maze appears around P25 (Kirkby, 1967). Young rats also show an abrupt increase in the tendency to explore the environment away from the “huddle” of their littermates on P20, and furthermore, have the ability to “home” directly back to their littermates after exploration, suggesting that path integration is already in place at this age (Loewen et al., 2005). Interestingly, there is evidence that spatial competence emerges abruptly in individual animals (Kirkby, 1967; Nadel, 1990), mirroring the abrupt emergence of adult like grid cells described here.

Convergent evidence, therefore, points to the appearance of place learning and exploration at around P20, coinciding with the sudden development of grid cell firing in our data. By contrast, the gradual developmental trajectory of CA1 place cells is not marked by any corresponding step change at this age. This suggests that the functional maturation of the mEC at this age is a critical factor for the expression of spatial behavior. However, it should also be noted that, despite the first evidence for spatial learning appearing at around 3 weeks, levels of performance on several spatial tasks do not reach adult levels until much later (Schenk, 1985; Rossier and Schenk, 2003) consistent with the protracted development of hippocampal CA1 spatial responses (Scott et al., 2010). It is, therefore, plausible that the full complement of spatial cognitive ability requires both mEC and hippocampus proper networks to be fully mature. Furthermore, if spatial stability is key for grid cell development, then it may be that an increasingly stable spatial signal originating in CA1 represents the critical developmental ingredient needed in order to set up spatially stable grid cell firing (Burgess et al., 2007; Hasselmo, 2008). More experimental effort will be needed to address these questions.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to acknowledge the following funding: The Royal Society (Fellowship to Thomas J. Wills), Research Councils UK (Fellowship to Francesca Cacucci), EU FP7 (“SPACEBRAIN” grant), an ERC fellowship (“DEVSPACE”; to Francesca Cacucci), the BBSRC. Caswell Barry and Thomas J. Wills were additionally supported by the Wellcome Trust. We also thank John O'Keefe and Neil Burgess for helpful discussions regarding the manuscript.

References

Akers, K. G., Candelaria, F. T., and Hamilton, D. A. (2007). Preweanling rats solve the Morris water task via directional navigation. Behav. Neurosci. 121, 1426–1430.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barry, C., Hayman, R., Burgess, N., and Jeffery, K. J. (2007). Experience-dependent rescaling of entorhinal grids. Nat. Neurosci. 10, 682–684.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Blair, H. T., Gupta, K., and Zhang, K. (2008). Conversion of a phase- to a rate-coded position signal by a three-stage model of theta cells, grid cells, and place cells. Hippocampus 18, 1239–1255.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brown, R. W., and Whishaw, I. Q. (2000). Similarities in the development of place and cue navigation by rats in a swimming pool. Dev. Psychobiol. 37, 238–245.

Pubmed Abstract | Pubmed Full Text

Burak, Y., and Fiete, I. R. (2009). Accurate path integration in continuous attractor network models of grid cells. PLoS Comput. Biol. 5:e1000291. doi: 10.1371/journal.pcbi.1000291

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burgess, N. (2008). Grid cells and theta as oscillatory interference: theory and predictions. Hippocampus 18, 1157–1174.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burgess, N., Barry, C., and O'Keefe, J. (2007). An oscillatory interference model of grid cell firing. Hippocampus 17, 801–812.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burton, B. G., Economo, M. N., Lee, G. J., and White, J. A. (2008). Development of theta rhythmicity in entorhinal stellate cells of the juvenile rat. J. Neurophysiol. 100, 3144–3157.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dhillon, A., and Jones, R. S. (2000). Laminar differences in recurrent excitatory transmission in the rat entorhinal cortex in vitro. Neuroscience 99, 413–422.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dombeck, D. A., Harvey, C. D., Tian, L., Looger, L. L., and Tank, D. W. (2010). Functional imaging of hippocampal place cells at cellular resolution during virtual navigation. Nat. Neurosci. 13, 1433–1440.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fagiolini, M., Pizzorusso, T., Berardi, N., Domenici, L., and Maffei, L. (1994). Functional postnatal development of the rat primary visual cortex and the role of visual experience: dark rearing and monocular deprivation. Vision Res. 34, 709–720.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fuhs, M. C., and Touretzky, D. S. (2006). A spin glass model of path integration in rat medial entorhinal cortex. J. Neurosci. 26, 4266–4276.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fyhn, M., Hafting, T., Treves, A., Moser, M. B., and Moser, E. I. (2007). Hippocampal remapping and grid realignment in entorhinal cortex. Nature 446, 190–194.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fyhn, M., Molden, S., Witter, M. P., Moser, E. I., and Moser, M. B. (2004). Spatial representation in the entorhinal cortex. Science 305, 1245–1246.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerrish, C. J., and Alberts, J. R. (1996). Environmental temperature modulates onset of independent feeding: warmer is sooner. Dev. Psychobiol. 29, 483–495.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Giocomo, L. M., Zilli, E. A., Fransen, E., and Hasselmo, M. E. (2007). Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science 315, 1719–1722.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Green, R. J., and Stanton, M. E. (1989). Differential ontogeny of working memory and reference memory in the rat. Behav. Neurosci. 103, 98–105.

Pubmed Abstract | Pubmed Full Text

Hafting, T., Fyhn, M., Molden, S., Moser, M. B., and Moser, E. I. (2005). Microstructure of a spatial map in the entorhinal cortex. Nature 436, 801–806.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hasselmo, M. E. (2008). Grid cell mechanisms and function: contributions of entorhinal persistent spiking and phase resetting. Hippocampus 18, 1213–1229.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hasselmo, M. E., Giocomo, L. M., and Zilli, E. A. (2007). Grid cell firing may arise from interference of theta frequency membrane potential oscillations in single neurons. Hippocampus 17, 1252–1271.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kirkby, R. J. (1967). A maturation factor in spontaneous alteration. Nature 215, 784.

Pubmed Abstract | Pubmed Full Text

Ko, H., Hofer, S. B., Pichler, B., Buchanan, K. A., Sjostrom, P. J., and Mrsic-Flogel, T. D. (2011). Functional specificity of local synaptic connections in neocortical networks. Nature 473, 87–91.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Krupic, J., Burgess, N., and O'Keefe, J. (2011). Periodic bands are the building blocks of locational firing in the Parahippocampal Formation. Soc. Neurosci. Abstr. 729.13.

Langston, R. F., Ainge, J. A., Couey, J. J., Canto, C. B., Bjerknes, T. L., Witter, M. P., Moser, E. I., and Moser, M. B. (2010). Development of the spatial representation system in the rat. Science 328, 1576–1580.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lannou, J., Precht, W., and Cazin, L. (1979). The postnatal development of functional properties of central vestibular neurons in the rat. Brain Res. 175, 219–232.

Pubmed Abstract | Pubmed Full Text

Loewen, I., Wallace, D. G., and Whishaw, I. Q. (2005). The development of spatial capacity in piloting and dead reckoning by infant rats: use of the huddle as a home base for spatial navigation. Dev. Psychobiol. 46, 350–361.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McNaughton, B. L., Battaglia, F. P., Jensen, O., Moser, E. I., and Moser, M. B. (2006). Path integration and the neural basis of the ‘cognitive map’. Nat. Rev. Neurosci. 7, 663–678.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mhatre, H., Gorchetchnikov, A., and Grossberg, S. (2010). Grid cell hexagonal patterns formed by fast self-organized learning within entorhinal cortex. Hippocampus 22, 320–334.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nadel, L. (1990). Varieties of spatial cognition. Psychobiological considerations. Ann. N.Y. Acad. Sci. 608, 613–626.

Pubmed Abstract | Pubmed Full Text

Navratilova, Z., Giocomo, L. M., Fellous, J. M., Hasselmo, M. E., and McNaughton, B. L. (2011). Phase precession and variable spatial scaling in a periodic attractor map model of medial entorhinal grid cells with realistic after-spike dynamics. Hippocampus 22, 772–789.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O'Keefe, J., and Nadel, L. (1978). The Hippocampus as a Cognitive Map. Oxford, UK: Oxford University Press.

Osakada, F., Mori, T., Cetin, A. H., Marshel, J. H., Virgen, B., and Callaway, E. M. (2011). New rabies virus variants for monitoring and manipulating activity and gene expression in defined neural circuits. Neuron 71, 617–631.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Quilichini, P., Sirota, A., and Buzsaki, G. (2010). Intrinsic circuit organization and theta-gamma oscillation dynamics in the entorhinal cortex of the rat. J. Neurosci. 30, 11128–11142.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rossier, J., and Schenk, F. (2003). Olfactory and/or visual cues for spatial navigation through ontogeny: olfactory cues enable the use of visual cues. Behav. Neurosci. 117, 412–425.

Pubmed Abstract | Pubmed Full Text

Rudy, J. W., Stadler-Morris, S., and Albert, P. (1987). Ontogeny of spatial navigation behaviors in the rat: dissociation of “proximal”- and “distal”-cue-based behaviors. Behav. Neurosci. 101, 62–73.

Pubmed Abstract | Pubmed Full Text

Sargolini, F., Fyhn, M., Hafting, T., McNaughton, B. L., Witter, M. P., Moser, M. B., and Moser, E. I. (2006). Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312, 758–762.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schenk, F. (1985). Development of place navigation in rats from weaning to puberty. Behav. Neural Biol. 43, 69–85.

Pubmed Abstract | Pubmed Full Text

Scott, R. C., Richard, G. R., Holmes, G. L., and Lenck-Santini, P. P. (2010). Maturational dynamics of hippocampal place cells in immature rats. Hippocampus 21, 346–353.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Skaggs, W. E., and McNaughton, B. L. (1998). Spatial firing properties of hippocampal CA1 populations in an environment containing two visually identical regions. J. Neurosci. 18, 8455–8466.

Pubmed Abstract | Pubmed Full Text

Solstad, T., Boccara, C. N., Kropff, E., Moser, M. B., and Moser, E. I. (2008). Representation of geometric borders in the entorhinal cortex. Science 322, 1865–1868.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sreenivasan, S., and Fiete, I. (2011). Grid cells generate an analog error-correcting code for singularly precise neural computation. Nat. Neurosci. 14, 1330–1337.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Taube, J. S., Muller, R. U., and Ranck, J. B. Jr. (1990). Head-direction cells recorded from the postsubiculum in freely moving rats. II. Effects of environmental manipulations. J. Neurosci. 10, 436–447.

Pubmed Abstract | Pubmed Full Text

Tolman, E. C. (1948). Cognitive maps in rats and men. Psychol. Rev. 55, 189–208.

Pubmed Abstract | Pubmed Full Text

Welinder, P. E., Burak, Y., and Fiete, I. R. (2008). Grid cells: the position code, neural network models of activity, and the problem of learning. Hippocampus 18, 1283–1300.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Widloski, J., and Fiete, I. (2010). Spike time-dependent synaptic plasticity can organize a recurrent network to generate grid cell responses. Soc. Neurosci. Abstr. 100.4.

Wills, T. J., Cacucci, F., Burgess, N., and O'Keefe, J. (2010). Development of the hippocampal cognitive map in preweanling rats. Science 328, 1573–1576.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zilli, E. A., and Hasselmo, M. E. (2010). Coupled noisy spiking neurons as velocity-controlled oscillators in a model of grid cell spatial firing. J. Neurosci. 30, 13850–13860.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text