Intrinsic electrophysiological properties of entorhinal cortex stellate cells and their contribution to grid cell firing fields

The medial entorhinal cortex (MEC) is an increasingly important focus for investigation of mechanisms for spatial representation. Grid cells found in layer II of the MEC are likely to be stellate cells, which form a major projection to the dentate gyrus. Entorhinal stellate cells are distinguished by distinct intrinsic electrophysiological properties, but how these properties contribute to representation of space is not yet clear. Here, we review the ionic conductances, synaptic, and excitable properties of stellate cells, and examine their implications for models of grid firing fields. We discuss why existing data are inconsistent with models of grid fields that require stellate cells to generate periodic oscillations. An alternative possibility is that the intrinsic electrophysiological properties of stellate cells are tuned specifically to control integration of synaptic input. We highlight recent evidence that the dorsal-ventral organization of synaptic integration by stellate cells, through differences in currents mediated by HCN and leak potassium channels, influences the corresponding organization of grid fields. Because accurate cellular data will be important for distinguishing mechanisms for generation of grid fields, we introduce new data comparing properties measured with whole-cell and perforated patch-clamp recordings. We find that clustered patterns of action potential firing and the action potential after-hyperpolarization (AHP) are particularly sensitive to recording condition. Nevertheless, with both methods, these properties, resting membrane properties and resonance follow a dorsal-ventral organization. Further investigation of the molecular basis for synaptic integration by stellate cells will be important for understanding mechanisms for generation of grid fields.

Introduction

Stellate cells in layer II of the medial entorhinal cortex (MEC) are a crucial component of the neural circuit for representation of space. These neurons receive synaptic input from diverse cortical areas and send axonal projections to the dentate gyrus of the hippocampus (Steward and Scoville, 1976; Schwartz and Coleman, 1981; Ruth et al., 1982; Ruth and Collier, 1988; Insausti et al., 1997; Dolorfo and Amaral, 1998; Burwell, 2000; van Groen et al., 2003; Witter, 2007). They are defined by a stellate dendritic architecture and distinctive electrophysiological properties (Ramón y Cajal, 1995; Alonso and Llinás, 1989; Alonso and Klink, 1993; Jones, 1994; Klink and Alonso, 1997a; Heinemann et al., 2000; Erchova et al., 2004; Burton et al., 2008; Garden et al., 2008). Stellate cells received considerable attention initially because of their possible role in theta-frequency (4–12 Hz) oscillations that are associated with exploratory spatial behaviors (Mitchell and Ranck, 1980; Alonso and García-Austt, 1987; Dickson et al., 1995; Buzsáki, 1996; White et al., 1998; Hasselmo et al., 2002).

The discovery that cells in layer II of the MEC have grid-like spatial firing fields has given further motivation to investigation of the functional properties of stellate cells (Fyhn et al., 2004; Hafting et al., 2005). Several observations suggest that grid cells in layer II of the MEC are stellate cells. Stellate cells are the main excitatory neuron type in the layer where grid cells are most frequently found (Alonso and Klink, 1993; Hafting et al., 2005; Sargolini et al., 2006), and they were recently shown to encode spatial information during navigation on linear tracks (Burgalossi et al., 2011). The topographical organization of the spatial resolution of grid firing fields along the dorsal-ventral axis of the MEC (Hafting et al., 2005; Sargolini et al., 2006; Barry et al., 2007; Brun et al., 2008; Fyhn et al., 2008) is mirrored by differences between stellate cells in their intrinsic theta-frequency activity and resonance (Giocomo et al., 2007; Boehlen et al., 2010; Dodson et al., 2011; Yoshida et al., 2011), and in their integration of synaptic responses (Garden et al., 2008). The intrinsic electrophysiological properties of stellate cells may, therefore, offer vital clues and experimental targets for the investigation of cellular mechanisms involved in the neuronal representation of space (Giocomo et al., 2011b; O'Donnell and Nolan, 2011).

With this goal in mind we review the known intrinsic electrophysiological properties of stellate cells in layer II of the MEC and introduce new data obtained using perforated patch-clamp methods. We begin by considering the identity and nature of the ion channels that stellate cells express. We then examine how these channels influence membrane properties of stellate cells typically measured with recordings from brain slices. We compare the voltage dependence of key membrane properties of stellate cells (Figures 1A,B) with that of their ion channels (Figure 1C). We show that new data obtained with the perforated patch-clamp method can reconcile differences between results obtained with whole-cell and sharp electrode recordings (Figures 2–9). Finally, we consider evidence for how the intrinsic properties of stellate cells influence neuronal computations important for the representation of space in behaving animals. We argue that models that require stellate cells to generate periodic oscillations are not consistent with existing data. We suggest that establishing how stellate cells integrate their synaptic input (Garden et al., 2008) will be crucial for understanding the cellular basis for grid cell firing fields.

FIGURE 1

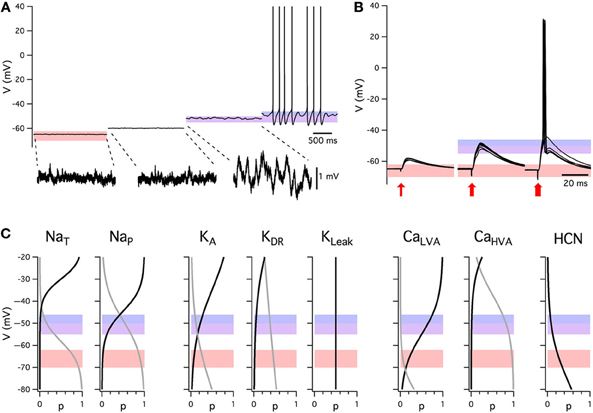
Figure 1. Summary of intrinsic electrophysiological properties of stellate cells from layer II of the medial entorhinal cortex. (A) Example of membrane potential activity at rest and during injection of constant current. Shading indicates the range of typical resting membrane potentials (orange), peri-threshold theta-frequency activity (purple), and threshold for initiation of action potential firing (blue). Subthreshold activity is shown on an expanded voltage-scale below. (B) Examples of excitatory post-synaptic potentials evoked by stimuli of increasing amplitude (left to right). Each block shows five consecutive responses to stimuli of identical intensity. Data in A and B are obtained with whole-cell patch-clamp recordings from the same stellate cell in the presence of picrotoxin (50 μM) and CGP55845 (1μM) to block inhibitory synaptic transmission. (C) Voltage dependence of stellate cell conductances. Boltzmann fits for activation (black) and inactivation (gray). From left: Na_T: activation (V_1/2 = −29.9 mV, k = 3.9 mV) and inactivation (V_1/2 = −58.2 mV, k = −5 mV) [Magistretti and Alonso (1999a)]; Na_P: activation (V_1/2 = −44.4 mV, k = 5.2 mV), inactivation (V_1/2 = −48.8 mV, k = −10 mV) [Magistretti and Alonso (1999a)]; K_A: activation (V_1/2 = −34.7 mV, k = 12 mV), inactivation (V_1/2 = −80.3 mV, k = −12 mV) where V_1/2 parameters were calculated in [Eder and Heinemann (1996)] and the slopes were estimated from Figure 2A [Eder and Heinemann (1996)]; K_DR: activation (V_1/2 = −34.8 mV, k = 11 mV), inactivation (V_1/2 = −74.3 mV, k = −15 mV) where V_1/2 given in [Eder and Heinemann (1996)] and the slopes were estimated from Figure 2B [Eder and Heinemann (1996)]; K_Leak; Ca_LVA activation (V_1/2 = −45 mV, k = 8 mV), estimated from threshold and peak amplitude data in [Bruehl and Wadman (1999)], inactivation (V_1/2 = −89 mV, k = −6.9 mV) [Bruehl and Wadman (1999)]; Ca_HVA activation (V_1/2 = −11.1 mV, k = 8.4 mV) [Castelli and Magistretti (2006)], inactivation (V_1/2 = −37 mV, k = −8.7 mV) [Bruehl and Wadman (1999)]. HCN activation (V_1/2 = −83.1 mV, k = −8.1 mV) [Nolan et al. (2007)].

FIGURE 2

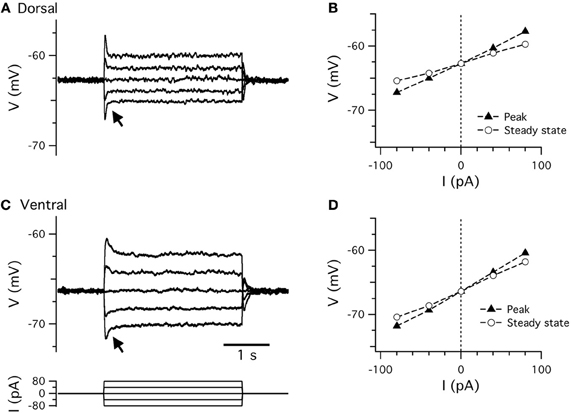
Figure 2. Resting membrane properties. (A,C) Examples of perforated patch-clamp recordings of membrane potential responses to current steps (C, lower) recorded from dorsal (A) and ventral (C) stellate cells. Arrows indicate the membrane potential “sag.” (B,D) Peak (closed triangles) and steady-state (open circles) membrane potential responses plotted as a function of current step amplitude for data from dorsal (B) and ventral (D) stellate cells in (A,C).

Results and Discussion

Ion Channels Determining the Intrinsic Excitability of Stellate Cells

Sodium channels

Three types of sodium conductance have been identified in stellate cells (Figure 1C). Depolarization to membrane potentials above approximately –50 mV activates a transient sodium current (Na_T) with rapid kinetics (White et al., 1993; Magistretti and Alonso, 1999b, 2007; Magistretti et al., 1999b). This current consists of a component that is sensitive to the classic Na⁺ channel blocker tetrodotoxin (TTX) and a component that is relatively insensitive (White et al., 1993). The kinetics and voltage dependence of these two components are indistinguishable, but the TTX-resistant component of Na_T is more sensitive to block by Cd²⁺, La³⁺, and Zn²⁺ (White et al., 1993). The sensitivity to Zn²⁺ may be of functional relevance as Zn²⁺ is found at high levels in the neuropil of the MEC (Haug, 1976; Holm and Geneser, 1989; Slomianka, 1992). The TTX-insensitive component of Na_T is smaller than the TTX-sensitive component (White et al., 1993).

In addition to Na_T, stellate cells express a prominent voltage-gated, persistent sodium current (Na_P) (Alonso and Llinás, 1989; Jones, 1994; Magistretti and Alonso, 1999a,b, 2002, 2007; Magistretti et al., 1999a,b, 2003). The threshold for activation of Na_P is approximately 10–15 mV lower than Na_T (Magistretti et al., 1999b) and in contrast to Na_T it inactivates relatively slowly with a half-maximal inactivation voltage of approximately −60 mV (Magistretti and Alonso, 1999a,b) (Figure 1C). These properties suggest that in stellate cells Na_P is active at membrane potentials below the threshold for action potential firing (Figures 1A,B).

A series of elegant studies have investigated the properties of Na_P using single channel recordings (Magistretti and Alonso, 1999a, 2002, 2007; Magistretti et al., 1999a,b, 2003). This approach has the advantages that it is not subject to voltage errors associated with whole-cell recordings, provides information about channel location and gives useful insights into channel gating mechanisms. Single channels with properties of Na_P and Na_T are found on the dendrites as well as the cell bodies of stellate cells (Magistretti et al., 1999a). Na_P is mediated by relatively high conductance single channels (∼20 pS) compared to Na_T (∼16 pS) (Magistretti et al., 1999b). The voltage-dependence of activation of the macroscopic Na_P current appears to depend on the strong voltage dependence of single channel opening times during bursts of channel activity (Magistretti and Alonso, 2002). Increases in closure duration between such bursts may underlie the slow inactivation of the current (Magistretti and Alonso, 2002). Further detailed analysis suggests that ion channels mediating Na_P exist in one of two preferred gating modes (Magistretti et al., 2003) and have at least six different sub-states between fully open and closed (Magistretti and Alonso, 2007). Given the likely importance of stochastic gating of Na_P for computation by stellate cells (White et al., 1998; Dorval and White, 2005), it will be important in the future to generate complete kinetic schemes of Na_P gating that fully account for these observations.

Potassium channels

Stellate cells express at least four major types of potassium current: leak, delayed rectifier, A-type, and calcium-activated (Figure 1C). They are distinguished by their kinetics, voltage dependence, and pharmacology. An M-type current has also been investigated (Yoshida and Alonso, 2007; Heys et al., 2010), but is yet to be isolated with voltage-clamp experiments.

A substantial potassium leak conductance found in stellate cells is relatively independent of membrane potential and is at least in part blocked by Ba²⁺, low pH, and quinidine (Deng et al., 2007; Garden et al., 2008), suggesting that it is mediated by two-pore domain (K_2P) potassium channels. Consistent with this idea, immunohistochemical data demonstrate that the two-pore-domain channels TASK-1 (Kcnk3), TASK-3 (Kcnk9), TWIK-1 (Kcnk1), TREK-1 (Kcnk2), and TREK-2 (Kcnk10) are all present in layer II of MEC (Deng et al., 2009). At present it is not completely clear which of these channels are open at rest, but pharmacological data point to a role for TASK channels (Deng et al., 2007). Two-pore domain channels are likely to be important targets for modulation of stellate cells (Deng et al., 2007, 2009).

A delayed rectifier potassium current (K_DR) activates in stellate cells on depolarization to potentials above approximately −45 mV (Eder et al., 1991; Eder and Heinemann, 1996) (Figure 1C). K_DR shows considerable rundown (∼80% within 60 min) in the whole-cell recording configuration, with small shifts in steady-state activation and much larger shifts in steady-state inactivation, suggesting that it is under metabolic control. Rundown can be avoided with the use of perforated patch-clamp techniques (Eder et al., 1991). This current has a greater density in stellate cells than pyramidal cells (Eder and Heinemann, 1994). Its molecular basis is unclear.

An A-type current (K_A) recorded from stellate cells is distinguished from K_DR by its strong inactivation (Eder et al., 1991; Eder and Heinemann, 1996) (Figure 1C). Consequently, activation of K_A first requires removal of inactivation by hyperpolarization of the membrane to potentials below −60 mV. Depolarization to voltages positive to −50 mV then activates K_A. The density of K_A is lower in stellate cells than in neighboring pyramidal cells (Eder and Heinemann, 1994). Its molecular basis is again not clear.

Other voltage-gated potassium channels are much less prominent in stellate cells. M-current blockade has small effects on stellate cell properties (Yoshida and Alonso, 2007; Heys et al., 2010). Nevertheless, there is reasonably high expression of mRNA for Kv7 subunits in layer II in Allen Brain Atlas data (Garden et al., 2008), although this could be due to expression in non-stellate cells, where M current blockade has a greater effect (Yoshida and Alonso, 2007). There is evidence that stellate cells express inward-rectifying potassium channels. This comes from a small, Ba²⁺-sensitive rectification in the instantaneous current-voltage relationship at voltages negative to −80 mV (Dickson et al., 2000b). However, this current has not been studied further and these findings could also be consistent with properties of some K_2P channels.

Stellate cells also express calcium-activated potassium channels (K_Ca) (Khawaja et al., 2007). These channels are activated indirectly following depolarization as a result of Ca²⁺ influx through voltage-gated Ca²⁺ channels. The K_Ca current recorded from stellate cells has a large relatively fast component and a smaller slow component (Khawaja et al., 2007). Neither component is sensitive to apamin, which blocks small conductance K_Ca channels, but the slow component can be modulated by the cAMP pathway, as forskolin reduces the amplitude of K_Ca currents (Khawaja et al., 2007). The molecular basis for these currents is unclear. MEC layer II neurons express RNA for apamin-sensitive K_Ca2.2 (SK2) and K_Ca2.3 (SK3) subunits and the apamin-insensitive K_Ca2.1 (SK1) subunit of small-conductance channels (Stocker and Pedarzani, 2000; D'Hoedt et al., 2004). It is either possible that the apamin-sensitive subunits are expressed by non-stellate cells, or that they are expressed by stellate cells, but have functions that have not yet been investigated in stellate cells, for example to control local synaptic depolarizations (Ngo-Anh et al., 2005).

Calcium channels

Two calcium currents have been described in MEC stellate cells (Figure 1C). A high-voltage-activated calcium current (Ca_HVA) is mediated by channels that open on depolarization to potentials positive to approximately −50 mV (Bruehl and Wadman, 1999; Visan et al., 2002; Castelli and Magistretti, 2006), whereas a low-voltage activated current (Ca_LVA) is mediated by channels that open with depolarization above approximately −60 mV (Bruehl and Wadman, 1999; Visan et al., 2002). The two channel populations are further distinguished by the membrane potentials at which they inactivate. Both currents slowly inactivate on depolarization, but Ca_HVA inactivates at more depolarized potentials compared with Ca_LVA (Bruehl and Wadman, 1999; Visan et al., 2002). This difference is important as it means that depolarization from potentials in the region of −50 mV will activate Ca_HVA, but not Ca_LVA. In contrast, depolarization from more hyperpolarized voltages will activate both currents. Ca_HVA currents appear to have similar properties in stellate and pyramidal cells (Bruehl and Wadman, 1999; Castelli and Magistretti, 2006), suggesting that they are not responsible for the distinct electrophysiological properties of stellate cells (Castelli and Magistretti, 2006). There is some evidence that the density of Ca_HVA currents is larger in pyramidal cells (Bruehl and Wadman, 1999), but this may be specific to older animals and could be confounded by inclusion of layer III cells in the analysis (Castelli and Magistretti, 2006).

Several calcium channel types appear to contribute to the Ca_HVA current. These include L-type channels (∼50%), N-type (∼23–30%), P/Q-type (∼22–24%) and a component that is insensitive to pharmacological block of these channel types (11–13%) (Castelli and Magistretti, 2006). This residual current is reduced by 57–62% by the Ca_v2.3 channel blocker SNX-482 (Castelli and Magistretti, 2006). Ca_LVA has properties consistent with T-type channels, but again the molecular identity of the current remains to be established.

HCN channels

Hyperpolarization activated cation currents (I_h) have been extensively studied in stellate cells. Unlike most other voltage-gated currents, I_h activates when the membrane is hyperpolarized and de-activates on depolarization (Robinson and Siegelbaum, 2003). Its presence in stellate cells was initially established from the observation of a sag-like response during injection of negative current steps (Alonso and Llinás, 1989; Jones, 1994). Subsequent voltage-clamp experiments have investigated the kinetics, voltage dependence, and pharmacology of I_h in stellate cells (Richter et al., 1997, 2000; Dickson et al., 2000b; Nolan et al., 2007; Giocomo and Hasselmo, 2008). Interestingly, the density of I_h increases with age from newborn to adult (Richter et al., 1997), with a peak approximately three weeks after birth (Burton et al., 2008), suggesting its importance for function of the mature MEC circuit.

Typically, I_h in stellate cells activates at voltages negative to −50 mV (Dickson et al., 2000b; Richter et al., 2000; Nolan et al., 2007), shows half-maximal activation at −80 mV (Dickson et al., 2000b; Nolan et al., 2007) and has a reversal potential of approximately −20 mV (Dickson et al., 2000b). It is blocked by ZD7288 (Richter et al., 1997; Dickson et al., 2000b; Nolan et al., 2007) and Cs⁺ (Alonso and Llinás, 1989; Klink and Alonso, 1993; Dickson et al., 2000b; Richter et al., 2000). I_h in stellate cells, but not MEC pyramidal cells, can be activated by the cAMP analog 8-Bromo-c-AMP (Richter et al., 2000). The kinetics of I_h are relatively slow compared to transient potassium and sodium currents. The time course of activation of I_h is best fit with a sum of two exponentials (Dickson et al., 2000b; Nolan et al., 2007). When measured at room temperature to better isolate currents, the fast component has a time constant of approximately ∼80 ms on hyperpolarization to −90 mV, whereas the slow component has a time constant of approximately ∼400 ms (Dickson et al., 2000b; Nolan et al., 2007). The relative amplitude of the fast component increases with hyperpolarization (Dickson et al., 2000b; Nolan et al., 2007). Deactivation is also relatively slow, with kinetics that speed-up on depolarization (Dickson et al., 2000b; Nolan et al., 2007). While these kinetics are accelerated at physiological temperatures (Nolan et al., 2007), it is important to recognize that they are nevertheless much slower than the voltage-gated channels underlying the action potential. These kinetics are important for certain models of grid cell firing fields discussed further below.

The molecular basis for I_h has been investigated in more detail than that of other ion channels expressed by stellate cells. Four genes (HCN1–4) encode channels with properties of I_h (Robinson and Siegelbaum, 2003). A direct role for HCN1 is evident from experiments using mice in which the HCN1 gene is deleted. This deletion reduces the amplitude of I_h in stellate cells by approximately two-thirds and abolishes the fast activation of the current (Nolan et al., 2007). The residual I_h has slower kinetics and a more negative voltage-dependence than the wild-type current (Nolan et al., 2007). This suggests that the two components of the wild-type current are unlikely to be a simple arithmetic sum of independent currents mediated by HCN1 and other HCN subunits. Rather, a substantial fraction of the wild-type current is likely to be mediated by heteromers containing HCN1 and one or more additional subunits. The kinetics of the wild-type current most closely resemble those of heteromers of HCN1 and HCN2 (Santoro et al., 2000; Chen et al., 2001; Ulens and Tytgat, 2001). Nevertheless, more direct experiments will be required to clearly establish the molecular identity of the additional HCN subunits expressed by stellate cells.

Consistent with these electrophysiological data, gene expression data from the Allen Brain Atlas indicates that mRNA levels of HCN1 and HCN2 are particularly high in layer II of the MEC. Antibody labeling also suggests strong HCN1 expression in superficial layers of the MEC (Notomi and Shigemoto, 2004; Nolan et al., 2007), whilst HCN2 and HCN3 show moderate expression (Notomi and Shigemoto, 2004). However, antibody labeling could reflect HCN1 channels expressed in the dendrites of pyramidal cells with somata in layers III and V (Shah et al., 2004; Rosenkranz, 2006). The use of HCN1 channel knockout mice to establish links between cellular properties of neurons and spatial behavior (Nolan et al., 2004; Giocomo et al., 2011a) is discussed below.

Other ion channels

A non-specific cation current, I_NCM, has also been identified as a potentially important contributor to stellate cell function. It is activated during muscarinic receptor-dependent depolarization and is sensitive to Ca²⁺ influx through voltage-gated channels (Klink and Alonso, 1997a; Shalinsky et al., 2002; Magistretti et al., 2004). It possesses a transient tail and sustained plateau component (Magistretti et al., 2004), the former of which may be of functional relevance to action potential firing patterns (Yoshida and Alonso, 2007). Interestingly, this current is analogous to that mediated by TRP channels (Shalinsky et al., 2002) and there is evidence that TRP channels mediate I_NCM in layer V neurons (Zhang et al., 2011). Immunohistochemical analysis shows that the TRPC5 and TRPC1 channels are present in layer II of MEC (Bohlen und Halbach et al., 2005).

Intrinsic Excitable Properties of Stellate Cells

Since initial pioneering investigations (Alonso and Llinás, 1989), it has been clear that intrinsic voltage-gated ion channels play an important role in determining the membrane potential trajectory of stellate cells prior to initiation of action potential firing. Ion channels that activate at membrane potentials below the threshold for action potential firing may contribute to the generation of intrinsic activity that is independent of synaptic input (Figures 1A,C), and will also shape integration of synaptic responses as the membrane potential moves toward the action potential threshold (Figures 1B,C). Ion channels that open at more depolarized voltages influence action potential initiation and repolarization (Figures 1A–C). We will consider below key integrative properties of stellate cells at sub-threshold and supra-threshold membrane potentials.

Because there are differences between data obtained from stellate cells with the two techniques most frequently used for investigating their membrane properties—sharp electrode and whole-cell patch-clamp recording (Erchova et al., 2004; Nolan et al., 2007; Boehlen et al., 2010)—we will also introduce new data obtained with the perforated patch-clamp recording method (Figures 2–9). With this technique a high resistance seal is formed between a patch-clamp electrode and the recorded cell. Electrical access to the inside of the cell is then obtained through small pores in the membrane formed by an antibiotic included in the pipette solution (Horn and Marty, 1988; Mathias et al., 1991). Perforated patch-clamp recordings overcome a potential limitation of whole-cell recording by avoiding dialysis of the cell and possible rundown or washout of membrane currents (Horn and Marty, 1988). At the same time, because a tight seal is maintained between the recording electrode and the cell membrane, errors associated with sharp electrode recordings are also avoided (Spruston and Johnston, 1992).

Resting properties

In the absence of significant synaptic input stellate cells do not fire action potentials and have a stable resting membrane potential. At physiological temperatures in brain slices from mature (>30 day) rodents the resting membrane potential of a stellate cell is typically in the range of −60 mV to −70 mV (Alonso and Llinás, 1989; Alonso and Klink, 1993; Jones, 1994; Erchova et al., 2004; Nolan et al., 2007; Garden et al., 2008; Boehlen et al., 2010). In anesthetized rats the resting potential is approximately −70 mV (Quilichini et al., 2010). Input resistance is typically between 20 and 80 MΩ and the membrane time constant is in the range 5–15 ms (Alonso and Llinás, 1989; Alonso and Klink, 1993; Jones, 1994; Erchova et al., 2004; Nolan et al., 2007; Garden et al., 2008; Boehlen et al., 2010). These properties appear similar in rats and mice [cf. (Nolan et al., 2007; Garden et al., 2008; Boehlen et al., 2010)], change during development (Burton et al., 2008) and are substantially different when measured at room temperature (Dickson et al., 2000b). A large part of the within-study variation in input resistance and time constant can be explained by differences in neuronal location along the dorsal-ventral axis of the MEC (Garden et al., 2008; Boehlen et al., 2010)(see below).

A further source of variation between studies is the recording method used to investigate stellate cell properties. After accounting for a neuron's position, it appears that sharp electrode recordings produce membrane potentials that are typically more negative, input resistance that is lower and membrane time constants that are shorter compared with data from whole-cell recordings (Boehlen et al., 2010). We find that the direction of the difference between perforated patch-clamp and whole-cell measures of resting potential and input resistance (Table 1) is opposite to that between sharp electrode and whole-cell measures (Boehlen et al., 2010). Therefore, as for hippocampal neurons (Spruston and Johnston, 1992), sharp electrode recordings may under-estimate input resistance and the membrane time constant of stellate cells. Nevertheless, whole-cell recordings also appear to modify the resting membrane potential and input resistance of stellate cells, suggesting the importance of validating key results with perforated patch-clamp methods.

TABLE 1

Table 1. Sub-threshold membrane properties.

The ionic basis for the stellate cell resting potential involves a balance between a depolarizing drive from I_h and a hyperpolarizing drive from leak potassium channels. I_h depolarizes the resting membrane potential by approximately 10 mV (Dickson et al., 2000b; Haas et al., 2007; Nolan et al., 2007) and appears to contribute approximately 50% of the resting membrane conductance, with a large component requiring HCN1 channels (Nolan et al., 2007). Leak potassium channels that are open at rest in stellate cells have properties consistent with the Ba²⁺- and acid-sensitive TASK sub-type of K_2P channel and may account for the majority of the remaining resting membrane conductance (Deng et al., 2007; Garden et al., 2008). It is possible that the resting membrane potential is also influenced by a depolarizing leak Na⁺ conductance (Garden et al., 2008).

Control of the resting potential by leak potassium currents is important for actions of neuromodulators on stellate cells. Serotonin and GABA modulate K_2P channels through 5-HT_1A and GABA_B receptors, respectively. GABA_B receptors are highly expressed in stellate cells (Mizukami et al., 2002). Baclofen, a GABA_B receptor agonist, hyperpolarizes stellate cells and reduces their input resistance by activating TREK-2 channels (Deng et al., 2009). This modulation may be critical in spatial learning (Deng et al., 2009). Serotonin modulation occurs through activation of the quinidine-sensitive channel TWIK-1, which depends on 5-HT_1A receptor activation (Deng et al., 2007). HCN channels may also be targets for modulation (Heys et al., 2010).

Membrane potential sag

Small perturbations of the membrane potential of a stellate cell are opposed after a short delay, leading to a characteristic “sag” response (Alonso and Llinás, 1989; Alonso and Klink, 1993; Klink and Alonso, 1993, 1997b; Jones, 1994; van der Linden and Lopes da Silva, 1998; Dickson et al., 2000b; Nolan et al., 2007). The sag response is prominent in previous whole-cell and sharp electrode recordings, and using perforated patch-clamp recordings (Figure 2 and Table 1). The sag response is due to a change in the depolarizing inward current provided by I_h (Dickson et al., 2000b; Nolan et al., 2007). During responses to negative current steps the membrane potential hyperpolarizes and I_h slowly activates, thus causing a return depolarization. Conversely, when the membrane potential depolarizes I_h slowly deactivates, causing the membrane potential to then hyperpolarize. I_h block by Cs⁺ or ZD7288 abolishes the sag (Klink and Alonso, 1993; Jones, 1994; Dickson et al., 2000b; Haas et al., 2007; Nolan et al., 2007), while deletion of HCN1 reduces the amplitude and slows the kinetics of the sag (Giocomo and Hasselmo, 2009; Nolan et al., 2007).

Theta-frequency resonance

A complementary approach to investigating the integrative properties of stellate cells is through their response to sinusoidally modulated current inputs. Membrane potential responses are largest to inputs that vary at frequencies in the theta range (4–12 Hz) (Haas and White, 2002; Erchova et al., 2004; Schreiber et al., 2004) (Figure 3). This theta-frequency resonance distinguishes stellate cells from other nearby neurons (Erchova et al., 2004). At lower frequencies the membrane potential response also has a small phase advance relative to the injected current, whereas at higher frequencies the membrane potential lags behind the injected current (Erchova et al., 2004; Nolan et al., 2007; Heys et al., 2010) (Figure 3).

FIGURE 3

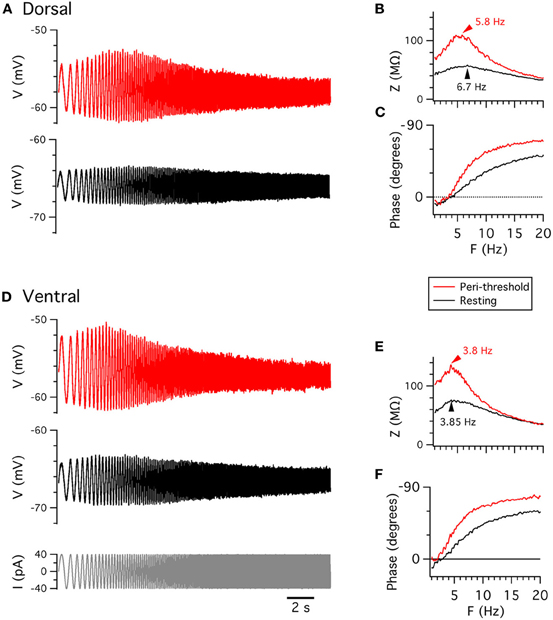
Figure 3. Membrane potential resonance. (A,D) Examples of perforated patch-clamp recordings of membrane potential responses from resting potential (black) and from depolarized membrane potential (red) to ZAP current waveforms (D, lower), from dorsal (A) and ventral (D) stellate cells. (B,E) Membrane impedance plotted as a function of frequency. (C,F) Membrane phase plotted as a function of frequency. B,C and E,F are calculated from data in A and D, respectively.

Resonant properties also appear to be sensitive to recording method. Two properties are often used to describe resonance: the frequency of the resonance peak (F) and the relative amplitude of the peak (Q) (Hutcheon et al., 1996). Previous studies indicate that F is greater for sharp-electrode compared (Erchova et al., 2004; Boehlen et al., 2010) with whole-cell recordings (Nolan et al., 2007; Boehlen et al., 2010; Heys et al., 2010). We find that F is similar, at either resting membrane potentials or peri-threshold potentials (approximately −50 to −55 mV), when measured with whole-cell or perforated patch-clamp methods (Table 2). Q also does not differ significantly between the two methods (Table 2), although with perforated patch-clamp recordings Q is significantly smaller at peri-threshold compared to resting membrane potentials (Table 3). Our finding here that with whole-cell recordings Q is similar when measured at resting potential (−65 mV) and peri-threshold potentials (−50 to −55 mV), while previous results indicate that Q is reduced on depolarization from −70 to −60 mV (Nolan et al., 2007), may be explained by resonance at peri-threshold potentials resulting from a different mechanism to that observed at resting potentials. Together, these data suggest that sharp electrode recordings may over-estimate the F at both resting and peri-threshold potentials, while whole-cell methods appear to provide estimates of resonant properties that are comparable to perforated patch-clamp data.

TABLE 2

Table 2. Resonant properties.

TABLE 3

Table 3. Action potential properties.

At resting membrane potentials the attenuation of low frequency signals that is essential for resonance in stellate cells requires HCN1 channels (Nolan et al., 2007). Deletion of HCN1 or pharmacological block of I_h abolishes resonance by increasing the amplitude of responses to current inputs with frequencies less than 4 Hz (Haas et al., 2007; Nolan et al., 2007). The phase advance is also abolished (Nolan et al., 2007). Thus, resonance at resting membrane potentials can be explained by I_h opposing slow changes in the membrane potential (Hutcheon and Yarom, 2000; Nolan et al., 2007; Dudman and Nolan, 2009; Dodson et al., 2011). Roles for other ion channels in resonance are less clear. In other cell types persistent sodium currents and M-type potassium currents can contribute to resonance at more depolarized voltages (Hu et al., 2007). In stellate cells the M-current blocker XE991 reduces the frequency and amplitude of the resonance peak at more depolarized voltages, but not at resting membrane potentials, although the frequency shift is on average less than 1 Hz and the reduction in amplitude appears quite small (Heys et al., 2010).

Theta-frequency resonance is also observed when stellate cells are probed with non-periodic frozen-noise inputs (Schreiber et al., 2004). However, the relationship between resonance and stellate cell responses to more physiological inputs is not fully understood. For excitatory glutamatergic synaptic input, stimulation at theta frequency produces little or no temporal summation of the response, whereas stimulation at gamma frequencies (40–80 Hz) causes strong temporal summation (Garden et al., 2008). This frequency dependence may reflect the fact that glutamatergic synaptic currents are very short compared with the membrane time constant (Garden et al., 2008) and so fast synaptic inputs will have very different temporal structure to the continuous sinusoidal inputs that are typically used to investigate resonant properties.

Peri-threshold theta-frequency membrane potential activity

When the membrane potential of a stellate cell is depolarized from rest to close to the threshold for action potential firing it becomes unstable, appearing to oscillate with frequency in the theta range (4–12 Hz) (Figure 1A) (Alonso and Llinás, 1989; Alonso and Klink, 1993; Dickson et al., 2000b; Erchova et al., 2004; Nolan et al., 2007; Dodson et al., 2011; Yoshida et al., 2011). This is of considerable interest first because it suggests a cellular correlate of the network theta rhythm recorded from the MEC and other hippocampal regions in vivo (Stewart et al., 1992; Dickson et al., 2000a; Mizuseki et al., 2009), and second because it has been argued that theta-frequency oscillations may be a substrate for encoding of spatial information by grid cells (Burgess et al., 2007; Giocomo et al., 2007).

Peri-threshold theta-frequency activity is consistently recorded from stellate cells with both sharp electrode and whole-cell techniques. However, the frequency of membrane potential activity during whole-cell recordings (Giocomo et al., 2007; Nolan et al., 2007; Giocomo and Hasselmo, 2009; Boehlen et al., 2010; Dodson et al., 2011) appears to be lower than during sharp electrode recordings (Alonso and Llinás, 1989; Klink and Alonso, 1993; White et al., 1998; Erchova et al., 2004; Boehlen et al., 2010). We find with perforated patch-clamp recordings that all stellate cells generate significant theta-frequency activity at membrane potentials close to spike threshold (Figure 4). In spectrograms the activity is characterized by brief epochs of power at theta frequencies (Figures 4B,G). Use of long windows for spectrograms as in some previous studies (Yoshida et al., 2011) may cause transient activity to appear sustained, whereas with shorter windows spectral peaks are revealed as non-stationary (cf Figures 4B–C, G–H). When activity is analyzed with Lomb periodograms of adjacent segments of activity (see Dodson et al., 2011 for details), the instability is manifest as variability in the frequency of the most significant activity peak and as multiple peaks in each segment (Figures 4D,I). This variability is clear from representative data (Figures 4E,J). Variability in the frequency of activity is also apparent during periods between action potential clusters (Figure 4K). Considering only the most significant peak in each of five epochs of duration 3 s, the mean frequency is 3.6 ± 0.5 Hz, while the range of significant frequencies across all five epochs is 3.2 ± 0.55 Hz. These results are similar to data from previous whole-cell recordings (Dodson et al., 2011).

FIGURE 4

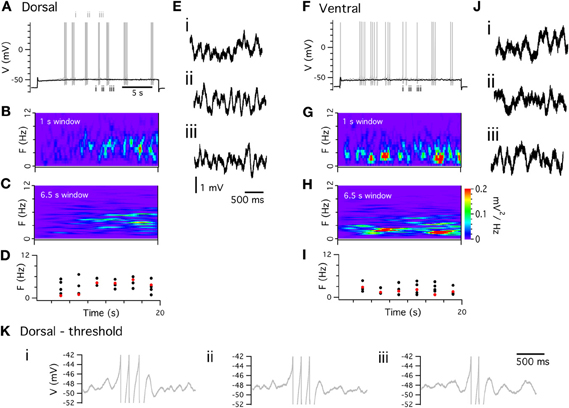
Figure 4. Peri-threshold theta-frequency activity. (A,F) Examples of perforated patch-clamp recordings of peri-threshold (black) and threshold (gray) membrane potential responses to current steps. (B,G) Spectograms from peri-threshold responses in A,F, calculated with 1 s windows. (C,H) Spectrograms from the same traces calculated using 6.5 s windows. (D,I) Frequency of most significant component (red) and all other significant frequencies (black) of peri-threshold membrane potential activity in A,F. Frequencies are obtained from Lomb periodograms of contiguous 3 s segments of data. (E,J) Examples of consecutive 2 s segments of data from peri-threshold activity in A,F (K) Examples of 1.5 s segments of membrane potential activity triggered by final spikes of three consecutive clusters of action potentials in A. Note the different frequency of the theta activity following each spike cluster.

The mechanism responsible for peri-threshold theta-frequency activity has been subject to debate. One class of ionic mechanism proposes that theta-frequency activity is generated by a periodic oscillator. This follows from the consideration that addition of an amplifying conductance, such as Na_P, to a resonator can lead to the generation of oscillations (Hutcheon and Yarom, 2000). Consistent with this idea, models of stellate cells that include Na_P and I_h can produce periodic membrane potential oscillations at peri-threshold potentials (Dickson et al., 2000b; Fransén et al., 2004). An important test of this oscillator model is whether the theta activity is periodic. In this case power spectra of the activity will have a single spectral peak that will have a stable frequency in consecutive analysis windows (Hajimiri and Lee, 1998; Dodson et al., 2011). The theta-frequency activity, recorded with perforated patch-clamp methods (Figure 4), and in previous whole-cell recordings (Nolan et al., 2007; Dodson et al., 2011), does not match this prediction (Figures 4B–D, G–I). Instead, the theta activity during sub-threshold sweeps and between spikes during suprathreshold sweeps (Figure 4K) has a frequency that changes apparently unpredictably. These observations are evidence against some models of grid cell firing fields that we discuss below. While these properties could perhaps be explained by variation in the period of an oscillator (Zilli et al., 2009), the variation would be so high that this would amount to an oscillatory system with dynamics that are essentially swamped by stochastic fluctuations.

A second class of ionic mechanism that can account for peri-threshold theta-frequency activity is based on evidence that stochastic gating of membrane ion channels can cause the membrane potential to fluctuate at theta frequencies (White et al., 1998). Direct support for this mechanism comes from experiments in which theta-frequency activity is abolished by pharmacologically blocking Na_P. When a dynamic clamp is then used to reintroduce a purely deterministic version of Na_P theta-frequency fluctuations remain absent (Dorval and White, 2005). In contrast, reintroduction of stochastic Na_P channels restores theta-frequency activity (Dorval and White, 2005). Consistent with this mechanism, detailed models of stellate cells, in which all ion channels gate stochastically, reproduce spectral properties of theta-frequency activity (Dudman and Nolan, 2009; Dodson et al., 2011). Nevertheless, because these models represent stellate cells as a single compartment, whereas the electrical properties of stellate cells are primarily determined by their dendrites (Garden et al., 2008), it will be important to establish whether theta-frequency activity is also accounted for by models that include stochastic gating of dendritic ion channels (Cannon et al., 2010).

Considering these data together, it is unlikely that theta-frequency membrane potential fluctuations reflect the output of a periodic oscillatory process. Instead, they appear most consistent with filtering of membrane potential noise resulting from stochastic ion channel gating. In this scenario, resonance due to voltage-gated ion channels likely plays an important role in shaping the frequency of the noise-driven membrane potential activity (White et al., 1998; Haas et al., 2007). It remains to be determined whether this intrinsic theta-frequency activity originates in the cell body or dendrites of stellate cells. For example, membrane potential changes at the cell body may reflect much larger stochastic events originating in the dendrites (Cannon et al., 2010).

The action potential and its after-polarization

Stellate cells generate action potentials when their membrane potential is depolarized above approximately −50 mV (Alonso and Klink, 1993; Jones, 1994). When action potentials are initiated during injection of constant positive current they are followed immediately by an after-polarization with several components (Figure 5). First, there is a shallow and rapid AHP, which is followed by a brief after-depolarization (ADP). Finally, at typical physiological spiking rates (<∼20 Hz) (Sargolini et al., 2006), there is a slower AHP which maintains the membrane potential below its peri-threshold value (Alonso and Klink, 1993). These properties are seen with whole-cell and sharp electrode recordings, but their relative prominence may differ (Boehlen et al., 2010). We find that with perforated patch-clamp recordings these characteristic features of the action potential and its AHP are also maintained (Figure 5). We note that when action potentials are triggered by brief synaptic input, the waveform of the after-polarization differs (Figure 1B), but while this difference may be important for physiological activation of stellate cells it has so far received very little attention.

FIGURE 5

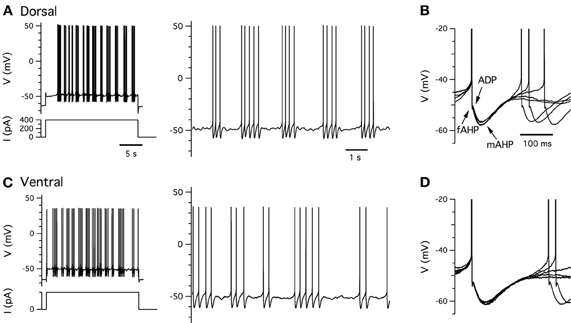
Figure 5. Clustered firing patterns. (A,C) Examples of perforated patch-clamp recordings of supra-threshold membrane potential responses (upper left) to positive current steps (lower left) from dorsal (A) and ventral (C) stellate cells. Action potentials on an expanded time base are shown to the right. (B,D) Examples of five consecutive action potential afterhyperpolarizations captured from traces in (A,C). Arrows indicate components of the after polarization.

Initiation of the action potential is blocked by TTX (Alonso and Llinás, 1989), but not by riluzole (Dorval and White, 2005), indicating that it requires Na_T, but not Na_P. As for many other neuron types, the duration of the action potential is increased by blocking voltage-gated potassium channels (Klink and Alonso, 1993). This is consistent with K_DR channels mediating rapid repolarization. Ca²⁺-dependent activation of K_Ca is important for the later stages of repolarization and for the AHP (Klink and Alonso, 1993; Khawaja et al., 2007). The recovery of the membrane potential to rest following the peak of the AHP is accelerated by activation of I_h mediated by HCN1 channels (Nolan et al., 2007). Further experimental investigation of the action potential AHP is likely to be important, particularly as the AHP and ADP are difficult to fully account for in current biophysical models of stellate cells (Fransén et al., 2004; Dudman and Nolan, 2009) and may play important roles in generation of grid cell firing fields (Navratilova et al., 2012).

Clustering of action potentials

Compared with other neuron types, stellate cells generate distinctive clustered patterns of action potentials during maintained supra-threshold depolarization (Alonso and Klink, 1993; Klink and Alonso, 1993; Nolan et al., 2007; Engel et al., 2008; Fernandez and White, 2008) (Figures 1A, 5). During whole-cell recordings, spikes within a cluster have similar inter-spike intervals that are independent of the overall firing frequency and that are often in the high theta range (about 8–12 Hz) (Nolan et al., 2007; Fernandez and White, 2008). Clustered patterns of spikes are most robust when the overall spike frequency is less than 5 Hz, with the inter-cluster interval sometimes being a second or longer (Nolan et al., 2007). At higher overall spike frequencies clustered patterns of spikes are no longer detectable. Spike trains show very little frequency adaptation at firing rates below the typical physiological maximum (∼20 Hz) (Alonso and Klink, 1993; Sargolini et al., 2006). Importantly, while clustered patterns of action potential firing have peaks in their power spectra in the theta-frequency range, the underlying mechanism is distinct from that of sub-threshold theta-frequency resonance (Nolan et al., 2007; Fernandez and White, 2008).

When recorded with perforated-patch methods clustered firing is exceptionally robust (Figures 5A,C). The probability that a spike is within a cluster is substantially greater when recorded with perforated patch compared to whole-cell methods (Table 3). The frequency of spikes within clusters is also higher for perforated patch recordings, whereas the number of spikes per cluster is similar to measurements with whole-cell recordings (Nolan et al., 2007). These data suggest that during whole-cell recordings there may be washout of a conductance that is not necessary for clustered firing patterns, but that increases their probability of occurrence.

We took advantage of the relatively large differences between whole-cell and perforated patch-clamp methods in the duration of the AHP and the probability that a spike is part of a cluster to estimate the time course of changes that takes place during intracellular dialysis associated with whole-cell recording from stellate cells (Figure 6). We found that even within 2 min of break in to the whole-cell configuration—the shortest interval within which we could reliably estimate the threshold current to trigger spike firing—the probability that spikes are part of a cluster differed significantly from that measured with perforated patch-clamp recording (Figure 6). This property and the AHP half-duration continued to change during the first 30 min following break-in (Figure 6). These data suggest that signaling pathways sensitive to washout during whole-cell recording regulate the firing properties of stellate cells.

FIGURE 6

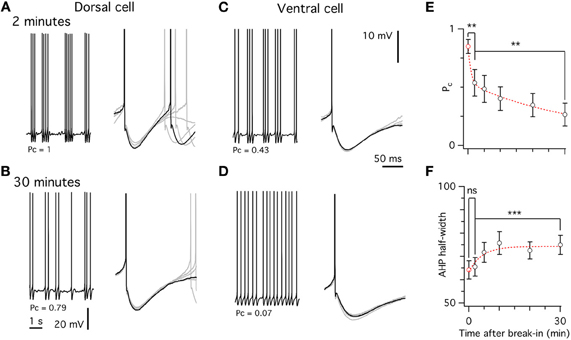
Figure 6. Washout of spiking properties during whole-cell recording. (A,C) Spiking pattern (left) and after-hyperpolarization (right) in a dorsal (A) and ventral (C) stellate cell approximately 2 min after break in. (B,D) Spiking pattern and after-hyperpolarization from the same cells as in A,C, 30 min after break-in. (E) Decrease of the probability of spikes occurring in a cluster (Pc) over time after break-in. (F) Increase in the after-hyperpolarization width at half-height over time. In E,F the red data point at time zero is from the perforated patch data. ANCOVA was used for comparisons between data obtained using different recording methods and Student's paired t-test to test differences within cells at different time points.

Ion channels that determine the amplitude and duration of the AHP appear to be critical for determining the pattern of spiking activity generated by stellate cells (Fransén et al., 2004; Nolan et al., 2007; Fernandez and White, 2008; Dudman and Nolan, 2009). Deletion of HCN1 or block of I_h greatly reduces spike clustering (Nolan et al., 2007). This can be explained by a model in which action potentials are triggered by stochastic fluctuations in membrane potential (Dudman and Nolan, 2009). In this model HCN channels engaged during the AHP provide a depolarizing drive that transiently increases the probability that membrane potential noise will trigger an action potential (Dudman and Nolan, 2009). Alternatively, termination of spike clusters could be achieved through incremental elevation of intracellular Ca²⁺ following each action potential (Fransén et al., 2004). However, with this mechanism it is difficult to explain the probabilistic properties of clustered spike firing that are accounted for by stochastic models (Dudman and Nolan, 2009). A model based on inductor-dependent resonance can also reproduce statistics of clustered spiking trains (Engel et al., 2008). However, this model appears inconsistent with experiments showing that the dominant frequency of spike train power spectral densities can be manipulated independently from that of peri-threshold membrane potential activity (Fernandez and White, 2008).

Synaptic Integration

A typical stellate cell has 6–10 primary dendrites that are densely populated with dendritic spines (Klink and Alonso, 1997b; Buckmaster et al., 2004; Garden et al., 2008). These spines are likely to be the main sites of excitatory synaptic input to stellate cells, but while the experiments considered so far evaluate stellate cell output in response to current injected through an experimental electrode, much less are known about how stellate cells respond to synaptic inputs. Stimulation of layer I evokes excitatory postsynaptic potentials (EPSPs) in stellate cells that can trigger action potentials (Figure 1B) (Alonso et al., 1990; Garden et al., 2008). The origin of these inputs is not clear, but might include axons from neurons in the neocortex (Dolorfo and Amaral, 1998; Burwell, 2000). Synaptic potentials can also be evoked in stellate cells by stimulation in the parasubiculum or deeper layers of the MEC (Jones, 1994). Recent experiments using localized photo-uncaging of glutamate to activate inputs from neurons at anatomically defined locations have begun to establish principles for the organization of local microcircuits containing stellate cells (Kumar et al., 2007; Beed et al., 2010). These experiments suggest that stellate cells receive local excitatory input from neurons in layer II of the MEC as well as from deeper layers. However, dual intracellular recordings from over 100 pairs of layer II principle cells did not find evidence for excitatory connections between stellate cells, suggesting that if recurrent excitation is present within layer II it is very sparse (Dhillon and Jones, 2000). The neurotransmitter receptors that mediate synaptic responses of stellate cells appear to have properties similar to other central neurons. EPSPs have fast components mediated by AMPA (non-NMDA) receptors and slower NMDA receptor components (Alonso et al., 1990; Jones, 1994). Fast synaptic inhibition is mediated by GABA_A receptors (Jones, 1994), while slower synaptic inhibition is through GABA_B receptors (Jones, 1994; Deng et al., 2009). Inputs from different locations can differentially activate plasticity mechanisms in stellate cells (Ma et al., 2008), but it is unclear whether they also engage distinct integrative mechanisms.

How do non-synaptic ion channels modify the responses of stellate cells to synaptic input? As the main ion channels open at rest (Figure 1C), leak potassium channels and HCN channels are important determinants of integration of sub-threshold synaptic responses (Garden et al., 2008). Both channel types determine the time window for detection of coincident inputs and summation of inputs activated at gamma frequencies (Garden et al., 2008). If either channel is blocked the coincidence detection time window becomes wider and summation of gamma frequency inputs increases. In contrast, the interval between synaptic responses evoked at theta frequency is too long for interactions between successive responses to be influenced by these integrative mechanisms (Garden et al., 2008). Unlike for some other neuron types (Stuart and Sakmann, 1994; Schiller et al., 2000), it is not yet clear whether synaptic input to dendrites of stellate cells can initiate local spikes. The role of Na_P is also unclear, although experiments in other neuron types suggest it may be important for amplification of EPSPs (Stuart and Sakmann, 1995).

Dorsal-Ventral Organization of Membrane Properties

Grid cells are organized topographically according to the spatial resolution of their firing fields, such that more dorsal cells have smaller firing fields that are spaced closer together compared with more ventral cells (Hafting et al., 2005; Sargolini et al., 2006; Barry et al., 2007; Brun et al., 2008; Fyhn et al., 2008). Several of the integrative properties of stellate cells that we describe above follow a similar dorsal-ventral organization. This correlation is of potential importance as it may reflect cellular computations important for generation of grid fields (Giocomo et al., 2011b; O'Donnell and Nolan, 2011). However, to test whether such correlations play a causal role in establishing grid cell firing fields, it is essential to first understand their underlying mechanisms. We describe below evidence for dorsal-ventral organization of ion channel properties, resting membrane properties, frequency selectivity, action potential clustering, and synaptic integration. We will suggest how these observations can be explained by increasing density of currents mediated by HCN and leak potassium channels in stellate cells located at dorsal compared to more ventral locations (Garden et al., 2008).

Ion channel function

There is evidence for a dorsal-ventral gradient in the density of a leak potassium conductance (Garden et al., 2008) and in either the density (Garden et al., 2008) or kinetics of I_h (Giocomo and Hasselmo, 2008). In one study, when pharmacologically isolated I_h was measured by two independent methods—from tail currents and from currents sensitive to the blocker ZD7288—the amplitude of I_h appeared to be smaller for neurons located at progressively more ventral locations (Garden et al., 2008). Differences in morphology between cells at different locations were insufficient to explain the differences in the measured currents (Garden et al., 2008). These data are consistent with in situ hybridization data in the Allen Brain Atlas, which suggests that mRNA levels of HCN1 and HCN2 follow a dorsal-ventral gradient in expression in layer II of the MEC. In this study there was very little variability in the time constant of I_h (Garden et al., 2008). In contrast to these data, a different study suggests that time constants, but not the amplitude of I_h, vary across the dorsal-ventral extent of the MEC (Giocomo and Hasselmo, 2008). Because these differences lead to very different functional predictions for the roles of I_h in stellate cells, it will be important for future work to clarify their cause, for example young (Giocomo and Hasselmo, 2008) vs. mature animals (Garden et al., 2008), or rats (Giocomo and Hasselmo, 2008) vs. mice (Garden et al., 2008).

Resting membrane properties

Stellate cells at dorsal locations have lower input resistance and faster membrane time constants than those at ventral locations (Garden et al., 2008; Boehlen et al., 2010). Consistent with these data, in perforated patch-clamp experiments we also find a significant dorsal-ventral organization of the input-resistance and membrane time constant, but not the resting membrane potential (Figures 7A–C). This organization can be accounted for by differences in the density of both leak potassium channels and HCN channels that mediate I_h (Garden et al., 2008). Thus, in dorsal neurons a greater density of leak potassium and HCN conductances lowers the input resistance and membrane time constant compared with more ventral neurons.

FIGURE 7

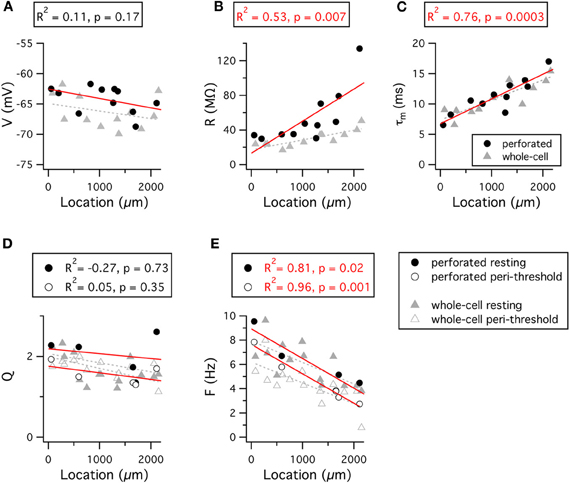
Figure 7. Dorsal-ventral organization of resting and resonant membrane properties. (A–E) Resting membrane potential (A), input resistance (B), membrane time constant (C), resonance amplitude (D) and resonant frequency (E) are plotted as a function of the location of the recorded stellate cell. Red lines indicate fits to the perforated patch-clamp data. Grey dashed lines indicate fits to the whole-cell data. Adjusted R² value and significance of the fit for the perforated patch-clamp data are stated above each plot. The R² and significance values for fits of the whole-cell data are as follows: V, R² = 0.04, p = 0.24; R, R² = 0.59, p = 0.0009; τ_m, R² = 0.64, p = 0.0003; Q_rest, R² = 0.22, p = 0.052; Q_peri, R² = 0.006, p = 0.32; F_rest, R² = 0.46, p = 0.005; F_peri, R² = 0.5, p = 0.003. Location refers to distance from the dorsal border of the MEC.

Frequency selectivity

Stellate cells exhibit a gradient in their frequency selectivity, with dorsal cells having a resting resonance peak at higher frequencies than cells from more ventral locations (Giocomo et al., 2007; Boehlen et al., 2010). Results from perforated patch-clamp experiments are consistent with these data (Figures 7D–E). Differences in the density of currents through HCN channels could account for this organization of resonance frequencies, as greater I_h amplitude in dorsal cells will more effectively oppose slow changes in membrane potential, thus causing greater attenuation of low frequency inputs (Nolan et al., 2007; Heys et al., 2010). While not found in mature neurons (Garden et al., 2008), differences in the kinetics of I_h could in principle also account for the dorsal-ventral organization of membrane resonance (Giocomo and Hasselmo, 2008), but this would not explain the dorsal-ventral organization of input resistance (Garden et al., 2008).

Just as for the resonant response to injected current, the properties of peri-threshold theta-frequency activity also follow a dorsal-ventral gradient (Giocomo et al., 2007; Giocomo and Hasselmo, 2008, 2009; Dodson et al., 2011; Yoshida et al., 2011). With perforated patch-clamp recordings the frequency of the most significant peak in a 15 s window varies steeply as a function of location (Figures 8A–C). These data are consistent with previous observations from whole-cell and sharp electrode recordings (Giocomo et al., 2007; Giocomo and Hasselmo, 2008, 2009; Dodson et al., 2011; Yoshida et al., 2011). The dependence of the significant frequencies on the length of the analysis time window (Figures 8A–B) and their variability between consecutive time windows (Figure 8C) is consistent with the idea that theta-frequency activity reflects filtering of a noise source (Dodson et al., 2011).

FIGURE 8

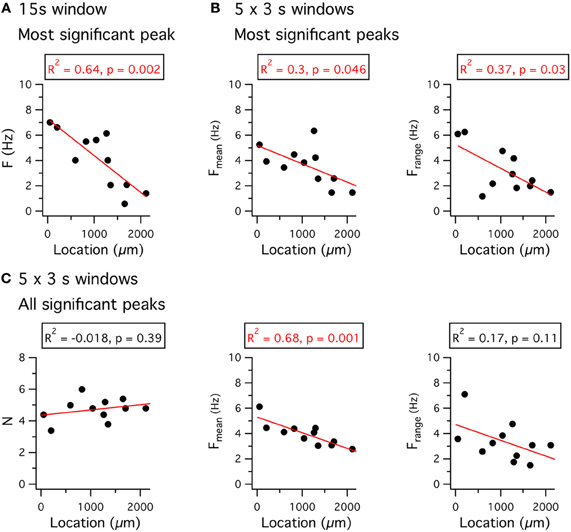
Figure 8. Dorsal-ventral organization of theta-frequency activity. (A) The frequency of the most significant peak in a Lomb periodogram of 15 s of peri-threshold membrane potential activity is plotted as a function of the location of the recorded neuron. (B) The mean frequency (left) and the range of frequencies (right) of the most significant peak of Lomb periodograms, obtained from five consecutive 3 s duration segments of peri-threshold activity, is plotted as a function of the location of the recorded neuron. (C) The number of significant peaks (left), the mean frequency (middle) of all significant peaks, and the range of frequencies of all significant peaks (right), obtained from five consecutive 3 s duration segments of peri-threshold activity, plotted as a function of the location of the recorded neuron. Data analyzed were from 5 s to 20 s after the onset of the largest amplitude current step that did not trigger action potential firing. Adjusted R² value and significance of the fit for the perforated patch-clamp data are stated above each plot. Location refers to distance from the dorsal border of the MEC.

The ionic basis for the dorsal-ventral organization of theta-frequency activity appears to involve differences in I_h. Knockout of the HCN1 subunit flattens the frequency gradient of the fluctuations (Giocomo and Hasselmo, 2009), although following pharmacological block of I_h a gradient nevertheless remains (Dodson et al., 2011). If the theta-frequency activity was periodic then these differences could be explained by models in which ion channels gate deterministically and the kinetics of I_h vary with location (Yoshida et al., 2011). However, as we discuss above, models of this kind do not appear to account for the stochastic nature of theta-frequency activity. In contrast, both the variability and the frequency of the largest amplitude activity are accounted for by models in which all ion channels gate stochastically and in which the density of HCN and leak potassium channels follows a dorsal-ventral organization (Dodson et al., 2011). It is, therefore, possible that the dorsal-ventral organization of intrinsic theta-frequency activity is a secondary consequence of control of the resting integrative properties of stellate cells by these ion channels.

Clustering of action potentials

Stellate cells also demonstrate a dorsal-ventral gradient in their pattern of action potential firing (Figures 9A–C). This organization of stellate cell firing patterns has not previously been described. With perforated patch-clamp recordings we find that, although spike clustering remains high in stellate neurons along the full dorsal-ventral extent of the MEC (Figure 9A), the frequency with which spikes occur within clusters follows a gradient (Figure 9B). In contrast, in our whole-cell recordings clustering appears to be reduced in more ventral cells, leading to the emergence of a gradient in the probability that an action potential is part of a clustered firing pattern (Figure 9A). The number of spikes per cluster is independent of location and recording method.

FIGURE 9

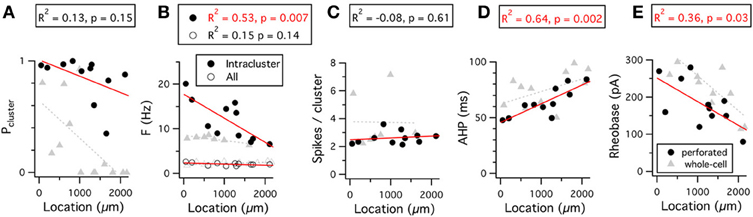
Figure 9. Dorsal-ventral organization of firing properties. (A–E) Probability that a spike is part of a cluster (A), frequency of spikes throughout the 15 s duration analysis window (open circles) or within a cluster (closed circles) (B), number of spikes per cluster (C), duration of the action potential after-hyperpolarization (D), and rheobase (E), are plotted as a function of the location of the recorded neuron. Data analyzed were from 5 s to 20 s after the onset of the current steps that triggered action potential firing at frequencies in the range 1–3 Hz. Adjusted R² value and significance of the fit for the perforated patch-clamp data are stated above each plot. The R² and significance values for fits of the whole-cell data are as follows: P_cluster, R² = 0.35, p = 0.02; F_intracluster, R² = 0.56, p = 0.03; F_all, R² = 0.19, p = 0.08; Spikes/cluster, R² = 0.38, p = 0.08; AHP, R² = 0.19, p = 0.08; Rheobase, R² = 0.61, p = 0.0009. Location refers to distance from the dorsal border of the MEC.

This organization of the pattern of spike firing by stellate cells can be explained by differences in the density of current through HCN channels (Garden et al., 2008) and their influence on the action potential AHP (Nolan et al., 2007; Dudman and Nolan, 2009). Because activation of HCN channels accelerates repolarization following the peak of the action potential AHP (Nolan et al., 2007; Dudman and Nolan, 2009), the greater density of HCN channels in dorsal cells will reduce the duration of the AHP and, therefore, increase the intra-cluster spike frequency. Consistent with this explanation, the AHP duration is shortest in more dorsal cells and increases for cells at progressively more ventral locations (Figure 9D) (Boehlen et al., 2010). The dependence of the probability of clustered firing on location found with whole-cell recordings is consistent with a strong correlation between these parameters in whole-cell recording conditions (Nolan et al., 2007; Fernandez and White, 2008). The absence of this gradient from perforated-patch recordings suggests wash-out during whole-cell recordings of a factor that promotes clustered patterns of activity in ventral cells. One possible explanation is that wash-out during whole-cell recordings causes a shift in the voltage dependence of HCN channels that reduces their influence on the AHP.

The threshold-current required to initiate action potential firing also follows a dorsal-ventral organization (Garden et al., 2008; Boehlen et al., 2010). This organization is maintained in perforated patch-clamp and whole-cell recordings (Figure 9E). The organization of the threshold-current is at least in part explained by the lower input resistance of dorsal compared to more ventral neurons, resulting from their higher density of leak potassium and HCN channels (Garden et al., 2008).

Synaptic integration

The waveforms of evoked and spontaneous excitatory synaptic potentials recorded from stellate cells follow a dorsal-ventral organization that is also explained by the density of currents through HCN and leak potassium channels. For neurons located more dorsally, EPSPs are shorter than for neurons located more ventrally (Garden et al., 2008). One consequence is that gamma frequency inputs to stellate cells at ventral locations sum more effectively relative to cells at more dorsal locations (Garden et al., 2008). Another is that dorsal cells have narrower time windows for detection of coincident synaptic activity than ventral cells and may, therefore, be better at temporal discrimination (Garden et al., 2008). Importantly, either leak potassium channels or HCN channels alone can support the gradient in integrative properties, although block of either channel increases the duration of EPSPs (Garden et al., 2008). Simulations suggest that gradients in the amplitude of the currents that organize synaptic integration are sufficient to also account for the dorsal-ventral organization of peri-threshold theta-frequency activity (Dodson et al., 2011).

From Ion Channels to Grid Firing Fields

The electrophysiological investigations of stellate cells described above provide a foundation to begin addressing questions about cellular mechanisms for spatial computations carried out within the MEC. For example, what is the relationship between computational properties evaluated with in vitro experiments and generation of grid firing fields? What are the roles in generation of grid firing fields of particular ion channels expressed by stellate cells? Does modulation of the intrinsic electrophysiological properties of stellate cells play roles in firing during spatial behaviors? Answering these and related questions will require integration of cellular data with predictive models for computation carried out during spatial behaviors, and testing of these models using recordings from behaving animals and specific manipulation of cellular properties of stellate cells.

Constraining models based on intrinsic electrophysiological properties

Two general classes of abstract model have been proposed to account for generation of grid firing fields (Burgess and O'Keefe, 2011; Giocomo et al., 2011b). In one, grid fields are produced by interference between oscillations with frequency sensitive to an animal's velocity (Burgess et al., 2007; Giocomo et al., 2007; Blair et al., 2008; Burgess, 2008; Hasselmo, 2008). In the second, grid fields result from bumps in an attractor network that are shifted by velocity inputs (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Burak and Fiete, 2009; Navratilova et al., 2012). We consider below how known intrinsic electrophysiological properties of stellate cells constrain the ways in which each class of abstract model can be implemented, and how knowledge of ion channel function in stellate cells can be used to distinguish between different models.

Models that compute location through oscillatory interference rely on periodic oscillators that are sensitive to velocity. Initial versions of these models proposed that theta-frequency activity of stellate cells reflected one or more oscillations of this kind (Burgess et al., 2007; Giocomo et al., 2007). However, several cellular properties argue against this mechanism. First, while theta-frequency activity can be interpreted as the output of a periodic oscillator (Dickson et al., 2000a; Fransén et al., 2004), the data discussed above suggests it is more likely to reflect filtered stochastic noise (White et al., 1998; Nolan et al., 2007; Dodson et al., 2011). This is a substantial problem as filtered noise signals are not periodic and computation by oscillatory interference mechanisms is extremely sensitive to noise (Burak and Fiete, 2009). Second, models that require independent oscillators in different dendrites appear to be impossible to implement given known cable properties of dendrites (Remme et al., 2010). Third, theta-frequency activity is abolished by synaptic conductances that mimic activity that might occur in vivo (Fernandez and White, 2008).

Alternative implementations of oscillatory interference models assume that neurons that act as velocity-sensitive oscillators are located upstream of grid cells (Blair et al., 2008; Burgess, 2008; Hasselmo, 2008). Recent evidence suggests that firing of “theta cells” in the anterior thalamus, hippocampus and medial septum may perform this function (Welday et al., 2011). In these cells theta-frequency bursts of action potentials are modulated by both movement speed and movement direction. For further evaluation of this theory it will be important to determine if these cells synapse with stellate cells and how the intrinsic properties of stellate cells influence responses to these inputs. For example, dorsal-ventral gradients in theta-frequency resonance or synaptic integration might contribute to decoding of inputs from velocity sensitive oscillators.

In models of grid cell firing that rely on network attractor states the influence of stellate cell integrative properties has received less direct attention. While these models are typically implemented using abstract neurons, in all cases tuning of neuronal gain is necessary for the network to produce attractor states (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Burak and Fiete, 2009; Navratilova et al., 2012). Therefore models of this kind can also be used to make predictions for how intrinsic properties of stellate cells might influence grid firing fields. A recent attractor model predicts possible roles for the AHP and ADP, along with synaptic NMDA conductances, in grid cell firing, periodicity, and phase precession (Navratilova et al., 2012). This model assumes dorsal-ventral tuning of NMDA kinetics, but observations of dorsal-ventral organization of synaptic integration (Garden et al., 2008) would likely also predict experimentally observed dorsal-ventral spacing of grid firing fields using models of this kind (Navratilova et al., 2012). Dorsal-ventral gradients in the AHP waveform are also consistent with this model (Figure 9) (Boehlen et al., 2010).

Ion channel manipulation in behaving animals

One of the most promising approaches for understanding the contribution of the intrinsic electrical properties of hippocampal and entorhinal neurons to spatial behavior is using animals in which key ion channels are genetically deleted. So far most attention has been directed toward the HCN1 ion channel (Nolan et al., 2004; Giocomo et al., 2011a; Hussaini et al., 2011). When the HCN1 channel is deleted from forebrain neurons spatial memory is enhanced (Nolan et al., 2004). Removal of HCN1 also increases the amplitude of the theta rhythm recorded in the hippocampus (Nolan et al., 2004). Consistent with these results and the effects of HCN1 deletion on the intrinsic properties of stellate cells (Nolan et al., 2007), grid-like firing fields of neurons in layer II of the MEC and place fields of hippocampal CA1 neurons are maintained in mice with deletion of HCN1 from forebrain neurons (Giocomo et al., 2011a; Hussaini et al., 2011). Together, these observations provide strong evidence against models for neuronal representation of space that require functions attributed to HCN1, including models based on interference between intrinsic oscillations. These results also argue against the view that HCN channels in the entorhinal cortex are pacemakers of theta-frequency activity.

Recent experiments that record from grid cells in mice with deletion of HCN1 from forebrain neurons are of further interest because they suggest that HCN1 plays important regulatory roles in the encoding of space (Giocomo et al., 2011a; Hussaini et al., 2011). Most intriguingly, grid cells and place cells observed following deletion of HCN1 appear to be larger and are more stable than in control animals (Giocomo et al., 2011a; Hussaini et al., 2011). The spacing between grid fields is also increased, while the dorsal-ventral organization of grid fields is maintained, so that on average firing fields at all locations are larger and further apart in HCN1 knockout compared to control mice (Giocomo et al., 2011a). While a potential caveat in interpretation of these observations is that deletion of HCN1 is throughout the forebrain, including neurons upstream of grid cells, they nevertheless raise important new questions. For example, why does deletion of HCN1 make grid fields larger and wider? One possibility is that this reflects the increased time-window for synaptic integration or summation of synaptic responses in stellate cells (Garden et al., 2008). Another is that it reflects place field expansion in CA1 (Hussaini et al., 2011), possibly in turn resulting from increased synaptic plasticity of CA1 pyramidal cells (Nolan et al., 2004). What mechanisms maintain the dorsal-ventral organization of grid field properties in the absence of HCN1? A possibility is that control of synaptic integration by the dorsal-ventral organization of leak potassium channels is sufficient to coordinate these properties of grid fields (Garden et al., 2008). What aspects of HCN1 channel function are critical to the behavioral roles of the channel? On the one hand, these behavioral roles may reflect control of sub-threshold resonant or oscillatory dynamics of stellate cells through voltage-dependent gating of HCN1 (Nolan et al., 2007; Giocomo and Hasselmo, 2009). On the other hand, the pattern of spike output from stellate cells may be independent of sub-threshold resonant properties (Fernandez and White, 2008), and instead the key function of HCN1 may be simply through its contribution to the resting membrane potential and conductance (Nolan et al., 2007). Further experimental investigation will be required to address these and other questions about the relationship between HCN1 channels, leak potassium channels and grid firing fields.

A further possible caveat in interpretation of behavioral results from knockout mice is that adaptation may mask roles of the deleted protein. For example, while data from knockout mice indicates that HCN1 is not required for generation of grid firing fields, this does not rule out the possibility that in wild-type animals HCN1 plays a central role that can nevertheless be compensated for when the channel is deleted. Comparison of intrinsic electrophysiological properties of stellate cells from control and HCN1 deletion mice during block of I_h does not reveal evidence of adaptation (Nolan et al., 2007). However, in pyramidal neurons from the somatosensory cortex there is strong evidence for up-regulation of a tonic GABA_A receptor conductance following deletion of HCN1 (Chen et al., 2010). This up-regulation is not found in hippocampal neurons (Nolan et al., 2004; Chen et al., 2010), and is not consistent with data from stellate neurons (Nolan et al., 2007), suggesting it may be specific to neocortical neurons. Nevertheless, these results highlight the need for additional approaches to corroborate results from knockout mice. New pharmacological tools that discriminate between HCN subunits may be of use [e.g., (Del Lungo et al., 2011; McClure et al., 2011)], although interpretation of in vivo effects of existing HCN channel blockers is difficult because of their off-target effects (Chevaleyre and Castillo, 2002). Viruses that knockdown HCN1 in mature mice may in the future also have important experimental roles (White et al., 2011).

Stellate cells across species

Comparison of stellate cell properties between species may give additional insights into their roles in generation of grid firing fields. Grid fields have so far been directly observed in neurons from layer II of the MEC of rats, mice and bats (Hafting et al., 2005; Fyhn et al., 2008; Yartsev et al., 2011). There is also strong evidence that neurons in the human entorhinal cortex have grid firing fields (Doeller et al., 2010). Given that the anatomical organization of entorhinal and hippocampal circuits is similar in each species it is likely that cellular mechanisms critical for representation of space will also be conserved across species. Consistent with this notion, basic electrophysiological properties of stellate cells in rats and mice, including their prominent sag response, theta-frequency peri-threshold activity and clustered spike firing, are also found in primates (Buckmaster et al., 2004). However, primate stellate cells have more primary dendrites, more dendritic branches and a greater total dendritic length (Buckmaster et al., 2004). They also have a less pronounced sag, and slower and less robust sub-threshold theta-frequency activity (Buckmaster et al., 2004). Stellate cells in humans (Mikkonen et al., 2000) are larger than in rats (Klink and Alonso, 1997b). While there are differences between studies in properties of stellate cells from mouse and rat, it seems likely that they could reflect technical differences such as experimental preparation and age of the animals. Nevertheless, more systematic study of this issue and comparison with species differences in spatial encoding may lead to useful insights.

Conclusion

Stellate cells in layer II of the MEC are a striking example of neurons in which single-cell computations are controlled by voltage-gated ion channels that open prior to initiation of action potentials. We have highlighted in this review that Na_P, HCN, and K_2P ion channels in particular influence properties such as resonance and temporal summation of synaptic inputs, suggesting they will be important for computation in behaving animals. We suggest that the influence of these ion channels on integration of synaptic input may be central to the computation carried out by stellate cells. We believe this will be a particularly important area for future investigation. In contrast, one of the most studied aspects of stellate cell activity, the theta-frequency activity, may be a secondary consequence of tuning ion channels to control integration of synaptic inputs.

To establish how stellate cell ion channels influence computations that underlie spatial representation, it will be important in the future to manipulate channels such as Na_P, HCN, and K_2P specifically in stellate cells while recording membrane potential or spiking activity in behaving animals. This will help demonstrate which of the intrinsic electrophysiological properties are critical for behavior. An important step toward this goal is the demonstration that forebrain HCN1 channels are not required for generation or dorsal-ventral organization of grid firing fields, but instead may be critical modulators of grid field size, spacing, and stability (Giocomo et al., 2011a). Correspondence between these results and previous cellular data suggests the importance of tuning of synaptic integration for grid cell computation (Garden et al., 2008). It also highlights the significance of ion channels in addition to HCN1, for example the K_2P ion channels, in the topographic organization of stellate cell integrative properties (Garden et al., 2008). These studies point toward the exciting prospect of a cellular and molecular level understanding of the neural representation of space.

Materials and Methods

Slice Preparation and Maintenance

Sagittal brain slices with thickness of 400 μm were prepared from 30 to 53 day old mice using previously described procedures (Garden et al., 2008; Dodson et al., 2011). Slices were maintained in physiological artificial cerebrospinal fluid of the following composition (mM): NaCl 124, NaH₂PO₄ 1.2, KCl 2.5, NaHCO₃ 25, Glucose 20, CaCl₂ 2, MgCl₂ 1. Patch electrodes were filled with an intracellular solution of the following composition (mM): K Gluconate 130; KCl 10, HEPES 10, MgCl₂ 2, EGTA 0.1, Na₂ATP 2, Na₂GTP 0.3, NaPhosphoCreatine 10. Excitatory glutamate receptor-mediated and inhibitory GABA receptor-mediated synaptic transmission was blocked with NBQX (5 μM), D-APV (50 μM), picrotoxin (50 μM) and CGP55845 (1 μM).

Data Collection

All recordings were made at 34–37°C. Recording electrodes had a tip resistance of 3–7 MΩ. All membrane seals had resistance of >2 GΩ as calculated by the current response to 10 mV pulses in voltage-clamp. A liquid junction potential of 8.1 mV (bath relative to pipette) was not corrected for. Stellate cells were identified in the superficial part of layer II by their large soma, the presence of multiple similar sized primary dendrites and their characteristic electrophysiological properties including the presence of prominent sag potentials and bi-phasic spike after-hyperpolarization (AHP).

For the perforated patch recordings the electrodes were front-filled with standard intracellular solution and then back-filled with an intracellular solution containing the antibiotic amphotericin B (final concentration 0.075–0.15 mg/ml) dissolved in DMSO (final concentration 3–6 μl/ml). For these recordings, after rapidly establishing a cell-attached configuration, rather than rupturing the membrane to achieve a whole-cell configuration, we waited for the antibiotic to permeabilize the membrane. We confirmed that spontaneous break-in did not occur by including a fluorescent label (Alexa 488) in the intracellular solution. Using this technique, access resistances of 24–85 MΩ were achieved after a delay lasting from 20 min to an hour after seal formation. Whole-cell patch recordings had access resistances <30 MΩ. All access resistances were fully compensated for using the bridge-balance technique. All signals were recorded in current clamp using a Multiclamp 700B amplifier (Molecular Devices), low pass filtered at 10 kHz (two pole Bessel filter), converted with an ADC (National Instruments ITC-18) and sampled at 20 kHz.

Data Analysis

Data analysis was performed as previously described (Nolan et al., 2007; Garden et al., 2008; Dodson et al., 2011) using Axograph and custom written MATLAB routines. Statistical calculations were done using R (www.r-project.org). All results are reported as mean ± standard error.

Time frequency analysis

To examine the persistence of spectral components across time we used Lomb analysis to identify significant frequencies in contiguous 3 s segments perithreshold recordings as previously described (Dodson et al., 2011). Spectrograms (in Figure 4) had windows of 1 s or 6.5 s, with 32768 or 131072 points and had 90% or 95% overlap. The first second of each 20 s trace was ignored to eliminate high frequency transients associated with current injection steps.

Spike clustering

We used a previously described algorithm (Nolan et al., 2007) to calculate the spike clustering coefficient, Pc, the proportion of spikes occurring in a cluster. Briefly, a group of spikes was considered a cluster if no inter-spike interval in the group exceeded 250 ms and if the inter-cluster interval was at least 300 ms.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by the Biotechnology and Biological Sciences Research Council (Matthew F. Nolan), the Engineering and Physical Sciences Research Council (Hugh Pastoll and Helen Ramsden) and the Commonwealth Scholarships Commission (Hugh Pastoll).

References

Alonso, A., de Curtis, M., and Llinás, R. (1990). Postsynaptic Hebbian and non-Hebbian long-term potentiation of synaptic efficacy in the entorhinal cortex in slices and in the isolated adult guinea pig brain. Proc. Natl. Acad. Sci. U.S.A. 87, 9280–9284.

Pubmed Abstract | Pubmed Full Text

Alonso, A., and García-Austt, E. (1987). Neuronal sources of theta rhythm in the entorhinal cortex of the rat. II. Phase relations between unit discharges and theta field potentials. Exp. Brain Res. 67, 502–509.

Pubmed Abstract | Pubmed Full Text

Alonso, A., and Klink, R. (1993). Differential electroresponsiveness of stellate and pyramidal-like cells of medial entorhinal cortex layer II. J. Neurophysiol. 70, 128.

Pubmed Abstract | Pubmed Full Text

Alonso, A., and Llinás, R. R. (1989). Subthreshold Na+-dependent theta-like rhythmicity in stellate cells of entorhinal cortex layer II. Nature 342, 175–177.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barry, C., Hayman, R., Burgess, N., and Jeffery, K. J. (2007). Experience-dependent rescaling of entorhinal grids. Nat. Neurosci. 10, 682–684.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Beed, P., Bendels, M. H. K., Wiegand, H. F., Leibold, C., Johenning, F. W., and Schmitz, D. (2010). Analysis of excitatory microcircuitry in the medial entorhinal cortex reveals cell-type-specific differences. Neuron 68, 1059–1066.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Blair, H. T., Gupta, K., and Zhang, K. (2008). Conversion of a phase- to a rate-coded position signal by a three-stage model of theta cells, grid cells, and place cells. Hippocampus 18, 1239–1255.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Boehlen, A., Heinemann, U., and Erchova, I. (2010). The range of intrinsic frequencies represented by medial entorhinal cortex stellate cells extends with age. J. Neurosci. 30, 4585–4589.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bohlen und Halbach, O., Hinz, U., Unsicker, K., and Egorov, A. V. (2005). Distribution of TRPC1 and TRPC5 in medial temporal lobe structures of mice. Cell Tissue Res. 322, 201–206.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bruehl, C., and Wadman, W. J. (1999). Calcium currents in acutely isolated stellate and pyramidal neurons of rat entorhinal cortex. Brain Res. 816, 554–562.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brun, V. H., Solstad, T., Kjelstrup, K. B., Fyhn, M., Witter, M. P., Moser, E. I., and Moser, M-B. (2008). Progressive increase in grid scale from dorsal to ventral medial entorhinal cortex. Hippocampus 18, 1200–1212.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buckmaster, P. S., Alonso, A., Canfield, D. R., and Amaral, D. G. (2004). Dendritic morphology, local circuitry, and intrinsic electrophysiology of principal neurons in the entorhinal cortex of macaque monkeys. J. Comp. Neurol. 470, 317–329.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burak, Y., and Fiete, I. R. (2009). Accurate path integration in continuous attractor network models of grid cells. PLoS Comput. Biol. 5:e1000291. doi: 10.1371/journal.pcbi.1000291

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burgalossi, A., Herfst, L., von Heimendahl, M., Förste, H., Haskic, K., Schmidt, M., and Brecht, M. (2011). Microcircuits of functionally identified neurons in the rat medial entorhinal cortex. Neuron 70, 773–786.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burgess, N. (2008). Grid cells and theta as oscillatory interference: theory and predictions. Hippocampus 18, 1157–1174.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burgess, N., Barry, C., and O'Keefe, J. (2007). An oscillatory interference model of grid cell firing. Hippocampus 17, 801–812.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burgess, N., and O'Keefe, J. (2011). Models of place and grid cell firing and theta rhythmicity. Curr. Opin. Neurobiol. 21, 734–744.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burton, B. G., Economo, M. N., Lee, G. J., and White, J. A. (2008). Development of theta rhythmicity in entorhinal stellate cells of the juvenile rat. J. Neurophysiol. 100, 3144–3157.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burwell, R. D. (2000). The parahippocampal region: corticocortical connectivity. Ann. N.Y. Acad. Sci. 911, 25–42.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buzsáki, G. (1996). The hippocampo-neocortical dialogue. Cereb. Cortex 6, 81–92.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cannon, R. C., O'Donnell, C., and Nolan, M. F. (2010). Stochastic ion channel gating in dendritic neurons: morphology dependence and probabilistic synaptic activation of dendritic spikes. PLoS Comput. Biol. 6:e1000886. doi: 10.1371/journal.pcbi.1000886

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Castelli, L., and Magistretti, J. (2006). High-voltage-activated Ca²⁺ currents show similar patterns of expression in stellate and pyramidal cells from rat entorhinal cortex layer II. Brain Res. 1090, 76–88.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chen, S., Wang, J., and Siegelbaum, S. A. (2001). Properties of hyperpolarization-activated pacemaker current defined by coassembly of HCN1 and HCN2 subunits and basal modulation by cyclic nucleotide. J. Gen. physiol. 117, 491–504.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chen, X., Shu, S., Schwartz, L. C., Sun, C., Kapur, J., and Bayliss, D. A. (2010). Homeostatic regulation of synaptic excitability: tonic GABA(A) receptor currents replace I(h) in cortical pyramidal neurons of HCN1 knock-out mice. J. Neurosci. 30, 2611–2622.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chevaleyre, V., and Castillo, P. E. (2002). Assessing the role of Ih channels in synaptic transmission and mossy fiber LTP. Proc. Natl. Acad. Sci. U.S.A. 99, 9538–9543.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

D'Hoedt, D., Hirzel, K., Pedarzani, P., and Stocker, M. (2004). Domain analysis of the calcium-activated potassium channel SK1 from rat brain. Functional expression and toxin sensitivity. J. Biol. Chem. 279, 12088–12092.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Del Lungo, M., Melchiorre, M., Guandalini, L., Sartiani, L., Mugelli, A., Koncz, I., Szel, T., Varro, A., Romanelli, M. N., and Cerbai, E. (2011). Novel blockers of hyperpolarization-activated current with isoform selectivity in recombinant cells and native tissue. Br. J. Pharmacol. doi: 10.1111/j.1476-5381.2011.01782.x. [Epub ahead of print].

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Deng, P-Y., Poudel, S. K. S., Rojanathammanee, L., Porter, J. E., and Lei, S. (2007). Serotonin inhibits neuronal excitability by activating two-pore domain k+ channels in the entorhinal cortex. Mol. Pharmacol. 72, 208–218.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Deng, P.-Y., Xiao, Z., Yang, C., Rojanathammanee, L., Grisanti, L., Watt, J., Geiger, J. D., Liu, R., Porter, J. E., and Lei, S. (2009). GABA(B) receptor activation inhibits neuronal excitability and spatial learning in the entorhinal cortex by activating TREK-2 K+ channels. Neuron 63, 230–243.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dhillon, A., and Jones, R. S. (2000). Laminar differences in recurrent excitatory transmission in the rat entorhinal cortex in vitro. Neuroscience 99, 413–422.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dickson, C. T., Kirk, I. J., Oddie, S. D., and Bland, B. H. (1995). Classification of theta-related cells in the entorhinal cortex: cell discharges are controlled by the ascending brainstem synchronizing pathway in parallel with hippocampal theta-related cells. Hippocampus 5, 306–319.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dickson, C. T., Magistretti, J., Shalinsky, M., Hamam, B., and Alonso, A. (2000a). Oscillatory activity in entorhinal neurons and circuits. Mechanisms and function. Ann. N.Y. Acad. Sci. 911, 127–150.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dickson, C. T., Magistretti, J., Shalinsky, M. H., Fransén, E., Hasselmo, M. E., and Alonso, A. (2000b). Properties and role of I(h) in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. J. Neurophysiol. 83, 2562–2579.

Pubmed Abstract | Pubmed Full Text

Dodson, P. D., Pastoll, H., and Nolan, M. F. (2011). Dorsal-ventral organization of theta-like activity intrinsic to entorhinal stellate neurons is mediated by differences in stochastic current fluctuations. J. Physiol. 589, 2993–3008.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Doeller, C. F., Barry, C., and Burgess, N. (2010). Evidence for grid cells in a human memory network. Nature 463, 657–661.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dolorfo, C. L., and Amaral, D. G. (1998). Entorhinal cortex of the rat: organization of intrinsic connections. J. Comp. Neurol. 398, 49–82.

Pubmed Abstract | Pubmed Full Text

Dorval, A. D., and White, J. A. (2005). Channel noise is essential for perithreshold oscillations in entorhinal stellate neurons. J. Neurosci. 25, 10025–10028.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dudman, J. T., and Nolan, M. F. (2009). Stochastically gating ion channels enable patterned spike firing through activity-dependent modulation of spike probability. PLoS Comput. Biol. 5:e1000290. doi: 10.1371/journal.pcbi.1000290

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eder, C., Ficker, E., Gündel, J., and Heinemann, U. (1991). Outward currents in rat entorhinal cortex stellate cells studied with conventional and perforated patch recordings. Eur. J. Neurosci. 3, 1271–1280.

Pubmed Abstract | Pubmed Full Text

Eder, C., and Heinemann, U. (1994). Current density analysis of outward currents in acutely isolated rat entorhinal cortex cells. Neurosci. Lett. 174, 58–60.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eder, C., and Heinemann, U. (1996). Potassium currents in acutely isolated neurons from superficial and deep layers of the juvenile rat entorhinal cortex. Pflügers Arch. 432, 637–643.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Engel, T. A., Schimansky-Geier, L., Herz, A. V. M., Schreiber, S., and Erchova, I. (2008). Subthreshold membrane-potential resonances shape spike-train patterns in the entorhinal cortex. J. Neurophysiol. 100, 1576–1589.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Erchova, I., Kreck, G., Heinemann, U., and Herz, A. V. M. (2004). Dynamics of rat entorhinal cortex layer II and III cells: characteristics of membrane potential resonance at rest predict oscillation properties near threshold. J. Physiol. 560, 89–110.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fernandez, F. R., and White, J. A. (2008). Artificial synaptic conductances reduce subthreshold oscillations and periodic firing in stellate cells of the entorhinal cortex. J. Neurosci. 28, 3790.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fransén, E., Alonso, A. A., Dickson, C. T., Magistretti, J., and Hasselmo, M. E. (2004). Ionic mechanisms in the generation of subthreshold oscillations and action potential clustering in entorhinal layer II stellate neurons. Hippocampus 14, 368–384.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fuhs, M. C., and Touretzky, D. S. (2006). A spin glass model of path integration in rat medial entorhinal cortex. J. Neurosci. 26, 4266–4276.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fyhn, M., Hafting, T., Witter, M. P., Moser, E. I., and Moser, M.-B. (2008). Grid cells in mice. Hippocampus 18, 1230–1238.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fyhn, M., Molden, S., Witter, M. P., Moser, E. I., and Moser, M. B. (2004). Spatial representation in the entorhinal cortex. Science 305, 1258–1264.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Garden, D. L. F., Dodson, P. D., O'Donnell, C., White, M. D., and Nolan, M. F. (2008). Tuning of synaptic integration in the medial entorhinal cortex to the organization of grid cell firing fields. Neuron 60, 875–889.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Giocomo, L. M., and Hasselmo, M. E. (2008). Time constants of h current in layer ii stellate cells differ along the dorsal to ventral axis of medial entorhinal cortex. J. Neurosci. 28, 9414–9425.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Giocomo, L. M., and Hasselmo, M. E. (2009). Knock-out of HCN1 subunit flattens dorsal-ventral frequency gradient of medial entorhinal neurons in adult mice. J. Neurosci. 29, 7625–7630.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Giocomo, L. M., Hussaini, S. A., Zheng, F., Kandel, E. R., Moser, M. B., and Moser, E. I. (2011a). Grid cells use HCN1 channels for spatial scaling. Cell 147, 1159–1170.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Giocomo, L. M., Moser, M. B., and Moser, E. I. (2011b). Computational models of grid cells. Neuron 71, 589–603.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Giocomo, L. M., Zilli, E. A., Fransén, E., and Hasselmo, M. E. (2007). Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science 315, 1719–1722.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Haas, J. S., Dorval, A. D., and White, J. A. (2007). Contributions of Ih to feature selectivity in layer II stellate cells of the entorhinal cortex. J. Comput. Neurosci. 22, 161–171.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Haas, J. S., and White, J. A. (2002). Frequency selectivity of layer II stellate cells in the medial entorhinal cortex. J. Neurophysiol. 88, 2422–2429.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hafting, T., Fyhn, M., Molden, S., Moser, M.-B., and Moser, E. I. (2005). Microstructure of a spatial map in the entorhinal cortex. Nature 436, 801–806.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hajimiri, A., and Lee, T. H. (1998). A general theory of phase noise in electrical oscillators. Solid-State Circuits, IEEE J. 33, 179–194.

Hasselmo, M. E. (2008). Grid cell mechanisms and function: contributions of entorhinal persistent spiking and phase resetting. Hippocampus 18, 1213–1229.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hasselmo, M. E., Hay, J., Ilyn, M., and Gorchetchnikov, A. (2002). Neuromodulation, theta rhythm and rat spatial navigation. Neural Netw. 15, 689–707.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Haug, F. M. (1976). Sulphide silver pattern and cytoarchitectonics of parahippocampal areas in the rat. Special reference to the subdivision of area entorhinalis (area 28) and its demarcation from the pyriform cortex. Adv. Anat. Embryol. Cell Biol. 52, 3–73.

Pubmed Abstract | Pubmed Full Text

Heinemann, U., Schmitz, D., Eder, C., and Gloveli, T. (2000). Properties of entorhinal cortex projection cells to the hippocampal formation. Ann. N.Y. Acad. Sci. 911, 112–126.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Heys, J. G., Giocomo, L. M., and Hasselmo, M. E. (2010). Cholinergic modulation of the resonance properties of stellate cells in layer II of medial entorhinal cortex. J. Neurophysiol. 104, 258–270.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Holm, I. E., and Geneser, F. A. (1989). Histochemical demonstration of zinc in the hippocampal region of the domestic pig: I. Entorhinal area, parasubiculum, and presubiculum. J. Comp. Neurol. 287, 145–163.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Horn, R., and Marty, A. (1988). Muscarinic activation of ionic currents measured by a new whole-cell recording method. J. Gen. Physiol. 92, 145–159.

Pubmed Abstract | Pubmed Full Text

Hu, H., Vervaeke, K., and Storm, J. F. (2007). M-channels (Kv7/KCNQ channels) that regulate synaptic integration, excitability, and spike pattern of CA1 pyramidal cells are located in the perisomatic region. J. Neurosci. 27, 1853–1867.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hussaini, S. A., Kempadoo, K. A., Thuault, S. J., Siegelbaum, S. A., and Kandel, E. R. (2011). Increased size and stability of CA1 and CA3 Place Fields in HCN1 knockout mice. Neuron 72, 643–653.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hutcheon, B., Miura, R. M., and Puil, E. (1996). Subthreshold membrane resonance in neocortical neurons. J. Neurophysiol. 76, 683–697.

Pubmed Abstract | Pubmed Full Text

Hutcheon, B., and Yarom, Y. (2000). Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci. 23, 216–222.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Insausti, R., Herrero, M. T., and Witter, M. P. (1997). Entorhinal cortex of the rat: cytoarchitectonic subdivisions and the origin and distribution of cortical efferents. Hippocampus 7, 146–183.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jones, R. S. (1994). Synaptic and intrinsic properties of neurons of origin of the perforant path in layer II of the rat entorhinal cortex in vitro. Hippocampus 4, 335–353.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Khawaja, F. A., Alonso, A. A., and Bourque, C. W. (2007). Ca(2+)-dependent K(+) currents and spike-frequency adaptation in medial entorhinal cortex layer II stellate cells. Hippocampus 17, 1143–1148.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Klink, R., and Alonso, A. (1993). Ionic mechanisms for the subthreshold oscillations and differential electroresponsiveness of medial entorhinal cortex layer II neurons. J. Neurophysiol. 70, 144–157.

Pubmed Abstract | Pubmed Full Text

Klink, R., and Alonso, A. (1997a). Ionic mechanisms of muscarinic depolarization in entorhinal cortex layer II neurons. J. Neurophysiol. 77, 1829–1843.

Pubmed Abstract | Pubmed Full Text

Klink, R., and Alonso, A. (1997b). Morphological characteristics of layer II projection neurons in the rat medial entorhinal cortex. Hippocampus 7, 571–583.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kumar, S. S., Jin, X., Buckmaster, P. S., and Huguenard, J. R. (2007). Recurrent circuits in layer II of medial entorhinal cortex in a model of temporal lobe epilepsy. J. Neurosci. 27, 1239–1246.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ma, L., Alonso, A., and Dickson, C. T. (2008). Differential induction of long-term potentiation in the horizontal versus columnar superficial connections to layer II cells of the entorhinal cortex. Neural plast. 2008, 814815.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Magistretti, J., and Alonso, A. (1999a). Biophysical properties and slow voltage-dependent inactivation of a sustained sodium current in entorhinal cortex layer-II principal neurons. J. Gen. physiol. 114, 491.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Magistretti, J., and Alonso, A. (1999b). Slow voltage-dependent inactivation of a sustained sodium current in stellate cells of rat entorhinal cortex layer II. Ann. N.Y. Acad. Sci. 868, 84–87.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Magistretti, J., and Alonso, A. (2002). Fine gating properties of channels responsible for persistent sodium current generation in entorhinal cortex neurons. J. Gen. Physiol. 120, 855–873.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Magistretti, J., and Alonso, A. (2007). Multiple conductance substates in pharmacologically untreated Na⁺ channels generating persistent openings in rat entorhinal cortex neurons. J. Membr. Biol. 214, 165–180.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Magistretti, J., Ma, L., Shalinsky, M. H., Lin, W., Klink, R., and Alonso, A. (2004). Spike patterning by Ca²⁺-dependent regulation of a muscarinic cation current in entorhinal cortex layer II neurons. J. Neurophysiol. 92, 1644–1657.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Magistretti, J., Ragsdale, D. S., and Alonso, A. (1999a). Direct demonstration of persistent Na⁺ channel activity in dendritic processes of mammalian cortical neurones. J. Physiol. 521(Pt 3), 629–636.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Magistretti, J., Ragsdale, D. S., and Alonso, A. (1999b). High conductance sustained single-channel activity responsible for the low-threshold persistent Na(+) current in entorhinal cortex neurons. J. Neurosci. 19, 7334–7341.

Pubmed Abstract | Pubmed Full Text

Magistretti, J., Ragsdale, D. S., and Alonso, A. (2003). Kinetic diversity of single-channel burst openings underlying persistent Na(+) current in entorhinal cortex neurons. Biophys. J. 85, 3019–3034.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mathias, R. T., Riquelme, G., and Rae, J. L. (1991). Cell to cell communication and pH in the frog lens. J. Gen. Physiol. 98, 1085–1103.

Pubmed Abstract | Pubmed Full Text

McClure, K. J., Maher, M., Wu, N., Chaplan, S. R., Eckert, W. A. III, Lee, D. H., Wickenden, A. D., Hermann, M., Allison, B., Hawryluk, N., Breitenbucher, J. G., and Grice, C. A. (2011). Discovery of a novel series of selective HCN1 blockers. Bioorg. Med. Chem. Lett. 21, 5197–5201.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McNaughton, B. L., Battaglia, F. P., Jensen, O., Moser, E. I., and Moser, M.-B. ((2006)). Path integration and the neural basis of the “cognitive map”. Nat. Rev. Neurosci. 7, 663–678.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mikkonen, M., Pitkänen, A., Soininen, H., Alafuzoff, I., and Miettinen, R. (2000). Morphology of spiny neurons in the human entorhinal cortex: intracellular filling with lucifer yellow. Neuroscience 96, 515–522.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mitchell, S. J., and Ranck, J. B. (1980). Generation of theta rhythm in medial entorhinal cortex of freely moving rats. Brain Res. 189, 49–66.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mizukami, K., Ishikawa, M., Hidaka, S., Iwakiri, M., Sasaki, M., and Iritani, S. (2002). Immunohistochemical localization of GABAB receptor in the entorhinal cortex and inferior temporal cortex of schizophrenic brain. Prog. Neuropsychopharmacol. Biol. Psychiatry 26, 393–396.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mizuseki, K., Sirota, A., Pastalkova, E., and Buzsáki, G. (2009). Theta oscillations provide temporal windows for local circuit computation in the entorhinal-hippocampal loop. Neuron 64, 267–280.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Navratilova, Z., Giocomo, L. M., Fellous, J-M., Hasselmo, M. E., and McNaughton, B. L. (2012). Phase precession and variable spatial scaling in a periodic attractor map model of medial entorhinal grid cells with realistic after-spike dynamics. Hippocampus. 22, 772–789.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ngo-Anh, T., Bloodgood, B., Lin, M., Sabatini, B., Maylie, J., and Adelman, J. (2005). SK channels and NMDA receptors form a Ca²⁺-mediated feedback loop in dendritic spines. Nat. Neurosci. 8, 642–649.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nolan, M. F., Dudman, J. T., Dodson, P. D., and Santoro, B. (2007). HCN1 channels control resting and active integrative properties of stellate cells from layer II of the entorhinal cortex. J. Neurosci. 27, 12440.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nolan, M. F., Malleret, G., Dudman, J. T., Buhl, D. L., Santoro, B., Gibbs, E., Vronskaya, S., Buzsáki, G., Siegelbaum, S. A., Kandel, E. R., and Morozov, A. (2004). A behavioral role for dendritic integration: HCN1 channels constrain spatial memory and plasticity at inputs to distal dendrites of CA1 pyramidal neurons. Cell 119, 719–732.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Notomi, T., and Shigemoto, R. ((2004)). Immunohistochemical localization of Ih channel subunits, HCN1–4, in the rat brain. J. Comp. Neurol. 471, 241–276.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O'Donnell, C., and Nolan, M. F. (2011). Tuning of synaptic responses: an organizing principle for optimization of neural circuits. Trends Neurosci. 34, 51–60.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Quilichini, P., Sirota, A., and Buzsáki, G. (2010). Intrinsic circuit organization and theta-gamma oscillation dynamics in the entorhinal cortex of the rat. J. Neurosci. 30, 11128–11142.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ramón y Cajal, S. (1995). Histology of the Nervous System, vol. II. (Trans. N. Swanson and L. W. Swanson). New York, NY: Oxford University Press.

Remme, M. W. H., Lengyel, M., and Gutkin, B. S. (2010). Democracy-independence trade-off in oscillating dendrites and its implications for grid cells. Neuron 66, 429–437.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Richter, H., Heinemann, U., and Eder, C. (2000). Hyperpolarization-activated cation currents in stellate and pyramidal neurons of rat entorhinal cortex. Neurosci. Lett. 281, 33–36.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Richter, H., Klee, R., Heinemann, U., and Eder, C. (1997). Developmental changes of inward rectifier currents in neurons of the rat entorhinal cortex. Neurosci. Lett. 228, 139–141.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Robinson, R. B., and Siegelbaum, S. A. (2003). Hyperpolarization-activated cation currents: from molecules to physiological function. Annu. Rev. Physiol. 65, 453–480.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rosenkranz, J. A. (2006). Dopaminergic regulation of neuronal excitability through modulation of Ih in layer V entorhinal cortex. J. Neurosci. 26, 3229–3244.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ruth, R. E., and Collier, T. J. (1988). Topographical relationship between the entorhinal cortex and the septotemporal axis of the dentate gyrus in rats: II. Cells projecting from lateral entorhinal subdivision. J. Comp. Neurol. 270, 506–516.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ruth, R. E., Collier, T. J., and Routtenberg, A. (1982). Topography between the entorhinal cortex and the dentate septotemporal axis in rats: I. Medial and intermediate entorhinal projecting cells. J. Comp. Neurol. 209, 69–78.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Santoro, B., Chen, S., Luthi, A., Pavlidis, P., Shumyatsky, G. P., Tibbs, G. R., and Siegelbaum, S. A. (2000). Molecular and functional heterogeneity of hyperpolarization-activated pacemaker channels in the mouse CNS. J. Neurosci. 20, 5264–5275.

Pubmed Abstract | Pubmed Full Text

Sargolini, F., Fyhn, M., Hafting, T., McNaughton, B. L., Witter, M. P., Moser, M-B., and Moser, E. I. (2006). Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312, 758–762.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schiller, J., Major, G., Koester, H. J., and Schiller, Y. (2000). NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature 404, 285–289.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schreiber, S., Erchova, I., Heinemann, U., and Herz, A. V. M. (2004). Subthreshold resonance explains the frequency-dependent integration of periodic as well as random stimuli in the entorhinal cortex. J. Neurophysiol. 92, 408–415.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schwartz, S. P., and Coleman, P. D. (1981). Neurons of origin of the perforant path. Exp. Neurol. 74, 305–312.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shah, M. M., Anderson, A. E., Leung, V., Lin, X., and Johnston, D. (2004). Seizure-induced plasticity of h channels in entorhinal cortical layer III pyramidal neurons. Neuron 44, 495–508.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shalinsky, M. H., Magistretti, J., Ma, L., and Alonso, A. A. (2002). Muscarinic activation of a cation current and associated current noise in entorhinal-cortex layer-II neurons. J. Neurophysiol. 88, 1197–1211.

Pubmed Abstract | Pubmed Full Text

Slomianka, L. (1992). Neurons of origin of zinc-containing pathways and the distribution of zinc-containing boutons in the hippocampal region of the rat. Neuroscience 48, 325–352.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Spruston, N., and Johnston, D. (1992). Perforated patch-clamp analysis of the passive membrane properties of three classes of hippocampal neurons. J. Neurophysiol. 67, 508–529.

Pubmed Abstract | Pubmed Full Text

Steward, O., and Scoville, S. A. (1976). Cells of origin of entorhinal cortical afferents to the hippocampus and fascia dentata of the rat. J. Comp. Neurol. 169, 347–370.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stewart, M., Quirk, G. J., Barry, M., and Fox, S. E. (1992). Firing relations of medial entorhinal neurons to the hippocampal theta rhythm in urethane anesthetized and walking rats. Exp. Brain Res. 90, 21–28.

Pubmed Abstract | Pubmed Full Text

Stocker, M., and Pedarzani, P. (2000). Differential distribution of three Ca(2+)-activated K(+) channel subunits, SK1, SK2, and SK3, in the adult rat central nervous system. Mol. Cell. Neurosci. 15, 476–493.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stuart, G., and Sakmann, B. (1995). Amplification of EPSPs by axosomatic sodium channels in neocortical pyramidal neurons. Neuron 15, 1065–1076.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stuart, G. J., and Sakmann, B. (1994). Active propagation of somatic action potentials into neocortical pyramidal cell dendrites. Nature 367, 69–72.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ulens, C., and Tytgat, J. (2001). Functional heteromerization of HCN1 and HCN2 pacemaker channels. J. Biol. Chem. 276, 6069–6072.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van der Linden, S., and Lopes da Silva, F. H. (1998). Comparison of the electrophysiology and morphology of layers III and II neurons of the rat medial entorhinal cortex in vitro. Eur. J. Neurosci. 10, 1479–1489.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Groen, T., Miettinen, P., and Kadish, I. (2003). The entorhinal cortex of the mouse: organization of the projection to the hippocampal formation. Hippocampus 13, 133–149.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Visan, V., Heinemann, U., Volynets, A., and Müller, W. (2002). Calcium currents in rat entorhinal cortex layer II stellate and layer III pyramidal neurons in acute brain slice. Neurosci. Lett. 327, 153–156.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Welday, A. C., Shlifer, I. G., Bloom, M. L., Zhang, K., and Blair, H. T. (2011). Cosine directional tuning of theta cell burst frequencies: evidence for spatial coding by oscillatory interference. J. Neurosci. 31, 16157–16176.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

White, J. A., Alonso, A., and Kay, A. R. (1993). A heart-like Na+ current in the medial entorhinal cortex. Neuron 11, 1037–1047.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

White, J. A., Klink, R., Alonso, A., and Kay, A. R. (1998). Noise from voltage-gated ion channels may influence neuronal dynamics in the entorhinal cortex. J. Neurophysiol. 80, 262–269.

Pubmed Abstract | Pubmed Full Text

White, M. D., Milne, R. V., and Nolan, M. F. (2011). A molecular toolbox for rapid generation of viral vectors to Up- or Down-Regulate neuronal gene expression in vivo. Front. Mol. Neurosci. 4:8. doi: 10.3389/fnmol.2011.00008

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Witter, M. P. (2007). The perforant path: projections from the entorhinal cortex to the dentate gyrus. Prog. Brain Res. 163, 43–61.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yartsev, M. M., Witter, M. P., and Ulanovsky, N. (2011). Grid cells without theta oscillations in the entorhinal cortex of bats. Nature 479, 103–107.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yoshida, M., and Alonso, A. (2007). Cell-type specific modulation of intrinsic firing properties and subthreshold membrane oscillations by the M(Kv7)-current in neurons of the entorhinal cortex. J. Neurophysiol. 98, 2779–2794.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yoshida, M., Giocomo, L. M., Boardman, I., and Hasselmo, M. E. (2011). Frequency of subthreshold oscillations at different membrane potential voltages in neurons at different anatomical positions on the dorsoventral axis in the rat medial entorhinal cortex. J. Neurosci. 31, 12683–12694.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zhang, Z., Reboreda, A., Alonso, A., Barker, P. A., and Séguéla, P. (2011). TRPC channels underlie cholinergic plateau potentials and persistent activity in entorhinal cortex. Hippocampus 21, 386–397.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zilli, E. A., Yoshida, M., Tahvildari, B., Giocomo, L. M., and Hasselmo, M. E. (2009). Evaluation of the oscillatory interference model of grid cell firing through analysis and measured period variance of some biological oscillators. PLoS Comput. Biol. 5:e1000573. doi: 10.1371/journal.pcbi.1000573

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text