Mathematical model of mechanobiology of acute and repeated synaptic injury and systemic biomarker kinetics

Background: Blast induced Traumatic Brain Injury (bTBI) has become a signature casualty of military operations. Recently, military medics observed neurocognitive deficits in servicemen exposed to repeated low level blast (LLB) waves during military heavy weapons training. In spite of significant clinical and preclinical TBI research, current understanding of injury mechanisms and short- and long-term outcomes is limited. Mathematical models of bTBI biomechanics and mechanobiology of sensitive neuro-structures such as synapses may help in better understanding of injury mechanisms and in the development of improved diagnostics and neuroprotective strategies.

Methods and results: In this work, we formulated a model of a single synaptic structure integrating the dynamics of the synaptic cell adhesion molecules (CAMs) with the deformation mechanics of the synaptic cleft. The model can resolve time scales ranging from milliseconds during the hyperacute phase of mechanical loading to minutes-hours acute/chronic phase of injury progression/repair. The model was used to simulate the synaptic injury responses caused by repeated blast loads.

Conclusion: Our simulations demonstrated the importance of the number of exposures compared to the duration of recovery period between repeated loads on the synaptic injury responses. The paper recognizes current limitations of the model and identifies potential improvements.

GRAPHICAL ABSTRACT

Graphical Abstract.

1. Introduction

Repeated concussions, relatively common in contact sports, have been recognized as serious medical events that can cause sustained cognitive and psychiatric changes, as well as neurodegeneration (McKee et al., 2009; Prins et al., 2013; Greco et al., 2019; Zetterberg et al., 2019; Kashyap et al., 2022). Recently, it has become evident that non-injurious sub-concussive repeated head impacts, such as frequent heading in soccer, may result in acute and chronic neurological effects (Ashton et al., 2020; Kakavas et al., 2021; McCunn et al., 2021; Sandmo et al., 2022). Blast induced traumatic brain injury (bTBI) has been referred to as a hallmark neurological signature in servicemen exposed to blast waves generated by improvised explosive devices (IED) during recent military operations (Cernak, 2017; DePalma and Hoffman, 2018

Elder et al., 2019; Siedhoff et al., 2022). During training, military personnel may be repeatedly exposed to LLB while using breaching explosives to gain entry and firing of the heavy weapon systems such as artillery, mortars, and shoulder mounted recoilless rifles. Just as in the civilian sports, military medics observed neurocognitive deficits in servicemen exposed to repeated low level blast (LLB) waves during military heavy weapons training (Carr et al., 2015; Engel et al., 2019; Modica et al., 2021). The neurological and neurocognitive changes experienced by those who have sustained repeated LLB blast exposures may have different cellular and anatomical underpinnings compared to those with clinically-diagnosed concussion.

Following recommendations from the U.S. Congress, the U.S. Department of Defense (DoD) is taking steps to understand and mitigate any potentially harmful effects from the occupational blast exposure. The goal of that program is to register the blast pressure profiles, referred to as a “dose”, using wearable sensors on individual serviceman during weapon training and to collect the medical data, “response” at various times post-exposure. However, to date there are no clear methods to correlate the dose and response parameters that could be used for definite medical diagnostics.

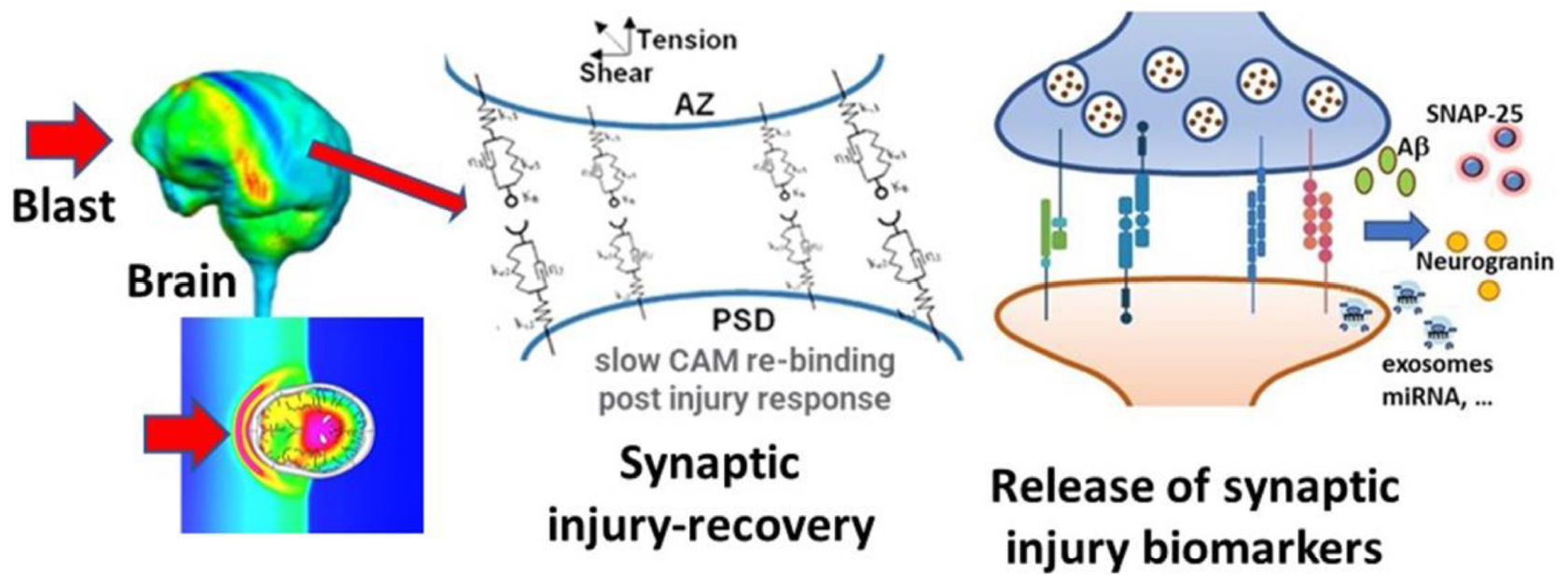
Mathematical models of brain injury biomechanics (Gupta and Przekwas, 2013; Garimella and Kraft, 2017; Garimella et al., 2018), coupled to mechanobiology of injury sensitive neuroaxonal structures (Przekwas et al., 2016) and neuro signaling pathways could help in better understanding and quantitation of the dose-response challenge. Reported mathematical models of brain-scale blast-induced biomechanics can predict local brain tissue stress-strain profiles (Gupta et al., 2017). However, in spite of large volume of work on mathematical modeling of synaptic, axonal and neuronal neurotransmission, metabolism and signaling pathways very little has been reported on modeling synaptic mechanobiology (Przekwas et al., 2016; Hall et al., 2021; Keating and Cullen, 2021; Hoffe and Holahan, 2022; Procès et al., 2022). In the present paper we introduce an initial formulation of a computational model of a mechanobiological “response” of a neuronal synapse to acute and repeated sub-concussive blast loads. We focused on the mechanobiology of a synaptic cleft for its very sensitive structural morphology and its extreme metabolic and neurophysiological activity. Our goal is to develop a prototype mathematical model of the acute and repeated mechanical injury of the synaptic cleft, linked to the sub-acute/chronic synaptic biochemical responses and release of biomarkers that could be detected in body fluids. This model will be introduced as a part of the computational framework, CoBi-Neuro, linking the dose represented by blast induced brain scale biomechanics and the micro-mechanics of injury sensitive neuro-structures and the response simulated by mechanobiology of these structures, release of injury biomarkers, and their bio-distribution in human body fluids, Figure 1.

FIGURE 1

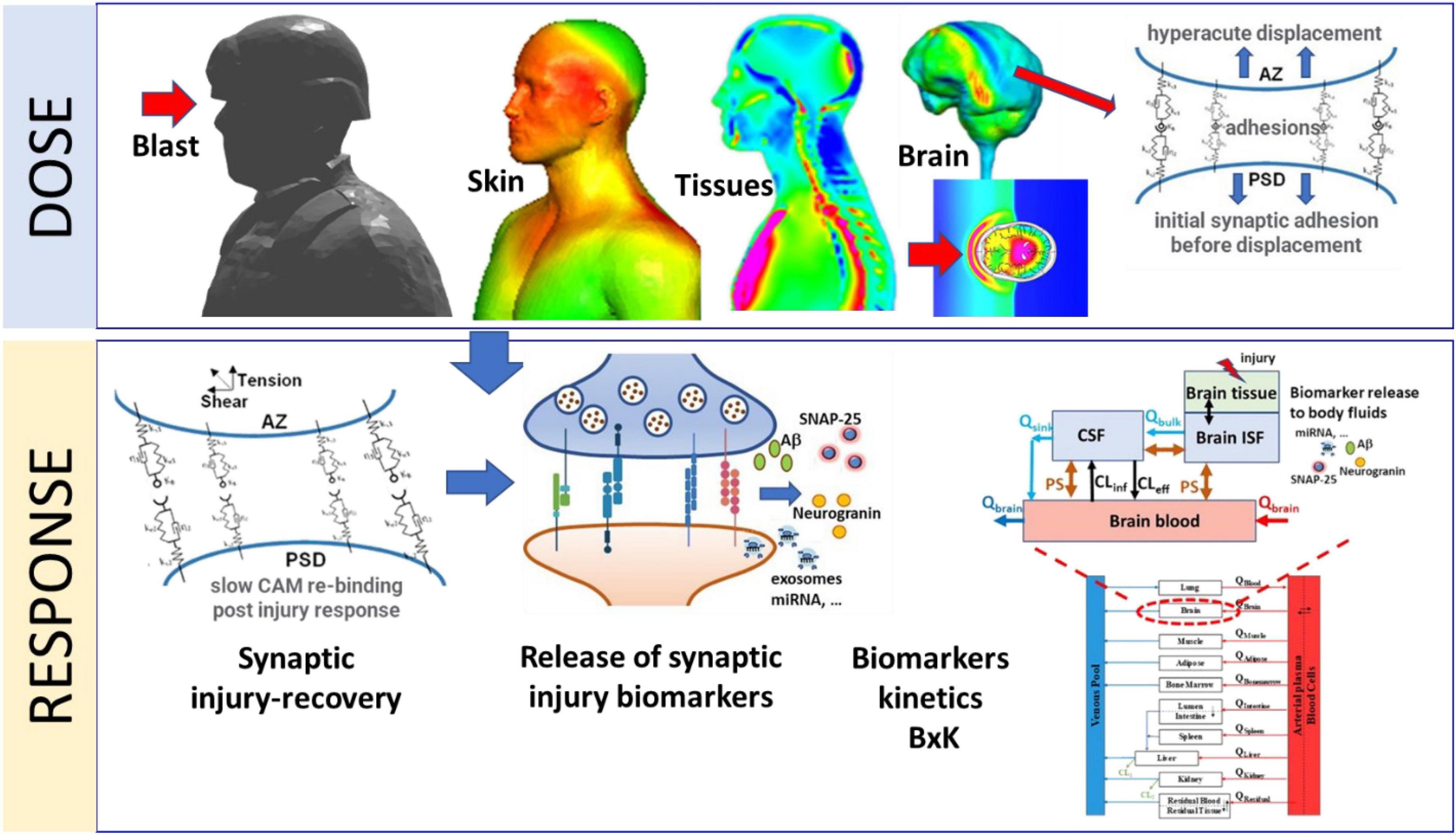
Figure 1. Schematic representation of major components of the Dose-Response modeling framework for blast induced synaptic brain injury and biomarkers kinetics. The Dose module computes blast induced brain macro-biomechanics and the hyper-acute micro-mechanics of synaptic adhesion molecules. The Response module simulates kinetics of synaptic cell adhesion molecules, synaptic damage/repair, release of synaptic biomarkers into CNS fluids and their whole-body kinetics (BxK).

Due to the anatomical and neurological complexity of the human brain and wide range of spatial and temporal scales such computational model inherently involves various approximations and assumptions (Gupta et al., 2017). Development and validation of such a model requires experimental data for the dose and the response model components. Reliable experimental data of blast wave loads on the human physical surrogate body/head can be collected and used to validate the dose model. Moreover, the blast dose on the US servicemen involved in weapon training can be computed using the wearable pressure sensor and weapon blast signature data (Przekwas et al., 2021). Acquisition of direct and objective data for the development and validation of the human neuro-response model is not feasible. Experimental data from animal models and in-vitro devices such as brain-on-chip, could provide some of the mechanobiological data but the translation to humans is debatable. However, medical imaging and body fluid biomarkers data can provide an indirect data for the development and validation of the neuro-response model. In this work we use brain injury biomarkers collected from the body fluids at various time points post-blast exposure (Gupta et al., 2017) to develop a prototype neuro-response model. Figure 1 schematically identifies major components of the CoBi-Neuro repeated brain injury dose-response framework.

2. Materials and methods

2.1. Mechanobiology of synaptic injury: Model description

We first present a novel mathematical framework to study temporally multiscale synaptic damage mechanisms. In this work, we use the term synapse as a short-hand for the chemical synapses in the brain. Synapses are comprised of three main components. First, a pre-synaptic membrane which contains a high concentration of mitochondria and neurotransmitter vesicles. Second, synaptic cleft is the gap between two nerve cells across which neurotransmitters diffuse after release from vesicles. Third, a post-synaptic membrane that contains receptor sites to which neurotransmitters bind leading to permeability change that produces the post-synaptic potential.

Motivated by models of immunological synapse assembly (Qi et al., 2001), we postulate that the configuration of the synapse is governed by the mechanical inter-membrane separation distance that drives the system to the minimum free energy functional. We assume that the pre- and post-synaptic membranes form two parallel rigid planes, where the synaptic cleft size is moderated via cell adhesion molecules (CAMs) complexes. CAMs populate the surface of the pre- and post-synapse, bind to their counterparts on the opposite membrane, and form a spring-damper-type network that structurally supports the synapse structure (Przekwas et al., 2016). In fact, CAM complex (re)formation, modulated by binding and dissociation of individual CAMs, plays a pivotal role in the response of synapse to a forced membrane separation (e.g., in blast-induced deformations). The ability of the CAMs to form complexes following a separation depends on their distance and the force acting on their inter-molecular bond. In addition to CAM-CAM interactions, connection of a CAM to the pre- or post-synaptic membrane may also play a role in synaptic damage and recovery. For instance, a fast separation of the synaptic membranes may lead to detachment of some CAMs from their cytoplasmic anchor, effectively inhibiting their rebinding.

More than twenty different families of synaptic CAMs have been identified with diverse adhesive behaviors, calcium sensitivities, and functions (Bukalo and Dityatev, 2012). However, only three representative families of CAM complexes are considered in this work to reduce the model and parameter complexities: (1) Neurexin:Neuroligin, (2) Synaptic CAMs (SynCAMs), and (3) N-Cadherins (NCADs). Neurexins (pre-synaptic) and neuroligins (post-synaptic) are CAMs that trans-synaptically interact to provide connectivity between membranes and ensure proper synaptic functions. In addition to providing mechanical support, neurexins (NX) and neuroligins (NL) play crucial roles in neurotransmission and differentiation of synapses, as well as maintaining NMDA and AMPA receptor function (Heine et al., 2008). Pathologically, NX-NL complexes (XL) are involved in amyloid β (Aβ) synaptotoxicity in Alzheimer’s disease (Brito-Moreira et al., 2017). SynCAM1-4 are immunoglobin proteins that constitute a family of CAMs central in synaptogenesis (Fowler et al., 2017). In addition, although SynCAM1-4 can form homophilic bonds, they preferentially assemble into heterophilic complexes (Fogel et al., 2007). Lastly, NCADs are a subgroup of the super-family of Ca²⁺-dependent CAMs that homophilically bind together to form the NCAD:NCAD complex and contribute to formation stability of the synapses (Arikkath and Reichardt, 2008). The cytoplasmic end of cadherins form a strong catch bond with catenins where force strengthens the bound state (Buckley et al., 2014).

2.2. Mechanobiology of synaptic injury: Model formulation

In this section, we present the mathematical model of the dynamics of synaptic injury and recovery and binding/unbinding of CAMs constrained in pre- and post-synaptic membranes. The model is described by a set of ordinary differential equations (ODEs). In all the formulations we assume that thermal noise is negligible compared to other terms. In addition, we assume a uniform distribution of synaptic CAMs on the membrane surfaces and neglect their diffusion.

Our model has been adapted from an immunological synapse model (Qi et al., 2001) which accounts for intra-membrane diffusion of both receptors and complexes. Such model becomes multidimensional (at least 2D axisymmetric). It was feasible to calibrate that model, lasting several minutes, using in vitro imaging data. We decided to simplify the immune synapse model for two reasons: (1) in the neuronal synapse there is a myriad of other transmembrane proteins that would complicate the diffusion model, and (2) at present there is lack of data for calibration of the diffusive transport of adhesion molecules and their complexes. We have also neglected interstitial fluid flow in the synaptic cleft during sudden mechanical extension and slow recoil.

Neurexin-Neuroligin Reactions: The kinetics of NX, NL, and their complex XL are expressed using the reaction equations

$\frac{d{C}_{NX}}{dt}=-k_{on,XL}\cdot C_{NX}\cdot C_{NL}+k_{off,XL}\left(f_{XL}\right)\cdot C_{XL}$

$-k_{rup}^{NX}{C}_{NX}+k_{syn}^{NX},(1)$

$\frac{d{C}_{NL}}{dt}=-k_{on,XL}\cdot C_{NX}\cdot C_{NL}+k_{off,XL}\left(f_{XL}\right)\cdot C_{XL}$

$-k_{rup}^{NL}{C}_{NL}+k_{syn}^{NL},\text{and}(2)$

$\frac{d{C}_{XL}}{dt}=+k_{on,XL}\cdot C_{NX}\cdot C_{NL}-k_{off,XL}\left(f_{XL}\right)$

$\cdot C_{XL}-\underset{downregulation}{\underbrace{\left(1-P_{XL}\right)k_{break,XL}{C}_{XL}}},(3)$

where C_NX, C_NL, and C_XL are surface concentrations of NX, NL, and XL, respectively. The unbinding rate k_off,XL varies with force acting on the intermolecular bond (Bell, 1978)

$k_{off,XL}=k_{off,XL}^0\cdot e^{\frac{f_{XL}}{f_{0,XL}}},(4)$

where $k_{off,XL}^0$ is the baseline unbinding rate, f_XL is the total force generated in XLs during synapse separation. Total force is normalized by a reference force f_0,XLwhich we define as

$f_{0,XL}=N_{XL}\frac{K_{B}T}{x_{XL}}(5)$

where N_XLthe total number bound XLs, K_B and T are Boltzmann’s constant and temperature, respectively, and x_XL is the distance between potential energies of the intact and broken states (Ahmadzadeh et al., 2015). The binding rate is assumed to follow a Gaussian distribution centered around optimal cleft distance (z₀)

$k_{on,XL}=k_{on,XL}^0\cdot e^{-\frac{{\left(z-z_0\right)}^2}{2{\mathrm{\sigma }}^2}},(6)$

with baseline $k_{on,XL}^0$ and distribution width σ. Furthermore, a portion of XL complexes may detach from their cytoplasmic connections during the insult. There are two potential parametrizations for this CAM-membrane detachment: pulling rate dependent and rupture force dependent. In this work, we use the pulling rate as the determining factor for the CAM detachment from membrane assuming that the detachment only occurs during the insult (separation of the cleft). We must note that rate dependent surface detachment are widely studied in adhesive viscoelastic material research (Violano et al., 2021). This detachment is represented by the “down-regulation” term in Eq. (3), where P_XLis defined as

$P_{XL}=e^{-\frac{s\left(t\right)}{v_{break,XL}}}.(7)$

In this formulation, pulling rate, s(t), is normalized by a factor v_break,XL. We assume that this down-regulation only affects the CAM complexes since the individual unbound CAMs can move with their base membrane during the insult. During a slow pulling process, the down-regulation term will vanish (P_XL ≈ 1), while during a fast pulling, this term becomes dominant (P_XL ≈ 0). Moreover, we assume that the NX and NL are produced ($k_{syn}^{NX}$ and $k_{syn}^{NL})$ and degraded ($k_{rup}^{NX}$ and $k_{rup}^{NL}$) at a constant rate. Therefore, the damage induced by the fast pulling can be remedied via natural turnover of NX and NL over time. However, we will refer to this damage as irreversible with regards to the timescale of our analysis here. We must note that the stoichiometry of NL is 2:2 (Comoletti et al., 2008), however, their dimer concentrations are considered in this work.

SynCAM Compartment (the complex is SynC12): SynCAM1 preferentially binds SynCAM2 to form a complex (Fogel et al., 2010), hence we use SynC12 for their complex. However, for simplicity we assume that SynCAM1 and SynCAM2 have the same properties and concentrations. Therefore, the kinetics of SynCAM and associated complex SynC12 can be written as

$\frac{d{C}_{SynC}}{dt}=-k_{on,SynC}\cdot C_{SynC}^2+k_{off,SynC}\left(f_{SynC12}\right)\cdot C_{SynC12}$

$\mathrm{\hspace{1em}}-k_{rup}^{SynC}{C}_{SynC}+k_{syn}^{SynC},(8)$

$\frac{d{C}_{SynC12}}{dt}\mathrm{}=+k_{on,SynC}\cdot C_{SynC}^2-k_{off,SynC}\left(f_{SynC12}\right)\cdot C_{SynC12}$

$\mathrm{\hspace{1em}}-\left(1-P_{SynC12}\right)k_{break,SynC12}{C}_{SynC12}.(9)$

Similar to Neurexin-Neuroligin compartment, C_SynC and C_SynC12 are surface concentrations of SynCAM and SynC12, respectively. Moreover, the corresponding unbinding rate, binding rate, and down-regulation factor are defined as

$k_{off,SynC}=k_{off,SynC}^0\cdot e^{\frac{f_{SynC}}{f_{0,SynC12}}},(10)$

$\mathrm{}{k}_{on,SynC}=k_{on,SynC}^0\cdot e^{-\frac{{\left(z-z_0\right)}^2}{2{\mathrm{\sigma }}^2}},and(11)$

$P_{SynC12}=e^{-\frac{s\left(t\right)}{v_{break,SynC}}},(12)$

where f_SynC is the total force in SynC12 CAMs, $k_{off,SynC}^0$ and $k_{on,SynC}^0$ are respectively the baseline unbinding and binding rates, and v_break,SynC is a pulling-rate normalization factor. Furthermore, a reference force is defined as

$f_{0,SynC12}=N_{SynC12}\frac{K_{B}T}{x_{SynC12}}(13)$

where N_SynC12 and x_SynC12 are similar to their counterparts in Eq. (5).

NCAD Compartment: NCADs homophilically bind together to form the NCAD:NCAD complex. The cytoplasmic end of cadherins form a strong catch bond with catenins where force strengthens the bound state (Buckley et al., 2014). Thus, we ignore the detachment (down-regulation) term for NCAD and NCAD:NCAD kinetics

$\frac{d{C}_{NCAD}}{dt}\mathrm{}=-k_{on,NCAD}\cdot C_{NCAD}^2+k_{off,NCAD}\left(f_{NCAD:NCAD}\right)\cdot$

$C_{NCAD:NCAD}-k_{rup}^{NCAD}{C}_{NCAD}+k_{syn}^{NCAD},(14)$

$\frac{d{C}_{NCAD:NCAD}}{dt}=+k_{on,NCAD}\cdot C_{NCAD}^2$

$\mathrm{\hspace{1em}}\mathit{\hspace{1em}}-k_{off,NCAD}\left(f_{NCAD:NCAD}\right)\cdot C_{NCAD:NCAD}.(15)$

The concentration of unbound NCADs on the pre- and post-synaptic membranes are assumed to be equal and represented by C_NCAD. Similar to the other CAMs, the binding and unbinding rates are

$k_{off,NCAD}=k_{off,NCAD}^0\cdot e^{\frac{f_{NCAD:NCAD}}{f_{0,NCAD}}},$

$k_{on,NCAD}=k_{on,NCAD}^0\cdot e^{-\frac{{\left(z-z_0\right)}^2}{2{\mathrm{\sigma }}^2}}(16)$

where f_NCAD:NCAD is the total force in NCAD:NCAD complexes, $k_{off,NCAD}^0$ and $k_{on,NCAD}^0$ are respectively the baseline unbinding and binding rates.

Mechanics of Synaptic Adhesion: Following (Qi et al., 2001), the free energy functional corresponding to CAM complex deformations can be written as penalties associated with bond deformation

$F=\sum _i\frac{{\lambda }_i}{2}{C}_i\left(t\right){\left(z\left(t\right)-z_{0,i}\right)}^2,i\in \{XL,SynC12,NCAD:NCAD\}(17)$

where λ_i is the curvature of binding energy well for ith complex, and z(t) and z_0,i are the synaptic cleft and optimal complex heights (all equal to z₀ here), respectively. Assuming a constant λ_i, total force as a function of CAM complex deformation and concentration is

$f=\sum _i{f}_i,=\sum _i{\mathrm{\lambda }}_i{C}_i\left(t\right)(z\left(t\right)-z_{0,i}).(18)$

Finally, the time evolution of synaptic cleft distance z(t) is described by a time-dependent equation, as a functional derivative of the free energy, input displacement and s(t),

$\frac{dz}{dt}=-M\frac{\mathrm{\delta }F}{\mathrm{\delta }z}+s\left(t\right),(19)$

where M is a phenomenological constant for membrane response to free energy. The synaptic response to an insult is modeled as a two-step process: (1) a fast injury marked by a forced separation of pre- and post-synaptic membranes induced by tension and shear [s(t) = 0], and (2) synaptic release [s(t) = 0] characterized a relatively slow recovery of the synapse where the synaptic CAMS form bounds and pull the membranes together. The configuration of the synaptic cleft and associated CAM complexes are shown in Figure 2A. The full implementation of ODEs are provided in Supplementary material A.

FIGURE 2

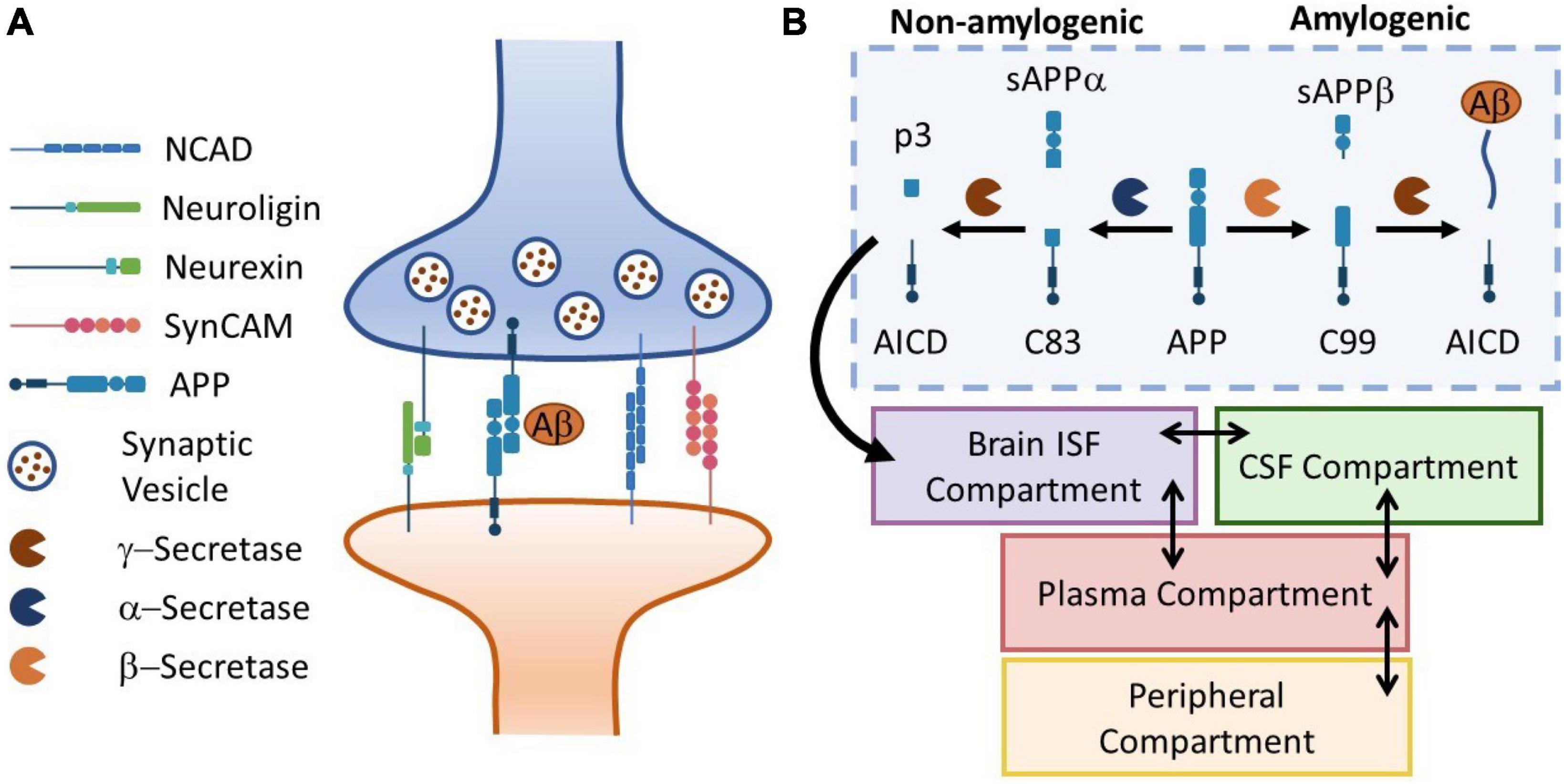
Figure 2. Panel (A) the schematic representation of a neuronal synapse with four representative families of CAMs. Aß release and kinetics is used to drive the biomarker kinetics model. Panel (B) the APP cleavage pathways in brain ISF diverge in to amylogenic and non-amylogenic braches, depending on the activity of sBACE (ß-secretase) and ADAM10 (α-secretase), respectively. Here, a simple four-compartment model is used to simulate transport of Aß peptides in the body. Temporal kinetics of synaptic injury biomarkers can be monitored in body fluids (plasma, CSF, saliva, …).

2.3. Biomarker kinetics model description

In this section, we demonstrate the utility of our model in simulating the release and distribution of injury biomarkers in human body fluids. Several families of synaptic CAMs share common effectors with neurodegenerative diseases such as Alzheimer’s disease (AD). For instance, Presenilin-1 (PS1), the catalytic subunit of γ-secretase (a main component of Amyloid ß production), regulates the processing of neurexins (Saura et al., 2011). Moreover, animal studies have shown elevated amyloid precursor protein (APP) levels (Edwards et al., 2017) following exposure to repeated mild TBI. Interestingly, increasing evidence suggest that APP itself is a CAM (Sosa et al., 2017). Motivated by such observations, we incorporate our mechanobiology model in a biomarker kinetics framework. In this work, we use Aß₄₂ production as an illustrative example. To describe the release and distribution of Aß₄₂ in the body, we use a 4-compartment model adapted from Madrasi et al. (2021), where Aß₄₂ is produced in brain interstitial fluid (ISF) and peripheral compartments. Moreover, we neglect the oligomerization process in the brain ISF. Figure 2B shows the schematic of APP processing pathways, Aß₄₂ generation, release, transport and bio-distribution in the body (section “2.3. Biomarker kinetics model description”).

To link the mechanobiology model to the biomarker release model, we define a phenomenological function quantifying the long-term synaptic dysfunction based on the perturbation of CAM complex concentrations from their homeostatic baseline

$SD(t)=w_1\frac{C_{XL}\left(t\right)-C_{XL}^0}{C_{XL}^0}+w_2\frac{C_{SynC12}\left(t\right)-C_{SynC12}^0}{C_{SynC12}^0}$

$\mathrm{\hspace{1em}}\mathit{\hspace{1em}}+w_3\frac{C_{NCAD:NCAD}\left(t\right)-C_{NCAD:NCAD}^0}{C_{NCAD:NCAD}^0},(20)$

where w₁, w₂, and w₃ are the weights associated with each CAM complex and $C_i^0$ are the initial (equilibrium) concentrations. We assume that the synaptic dysfunction linearly elevates the APP synthesis rate in the brain ISF, i.e.,

$K_{BISF,synth}=K_{BISF,synth}^0+K_{SD}SD\left(t\right),(21)$

where $K_{BISF,synth}^0$ is the baseline rate and K_SD is a constant. The full description of ODEs and parameters for Aß₄₂ release and production are provided in Supplementary material B.

2.4. Parameter selection and global sensitivity analysis

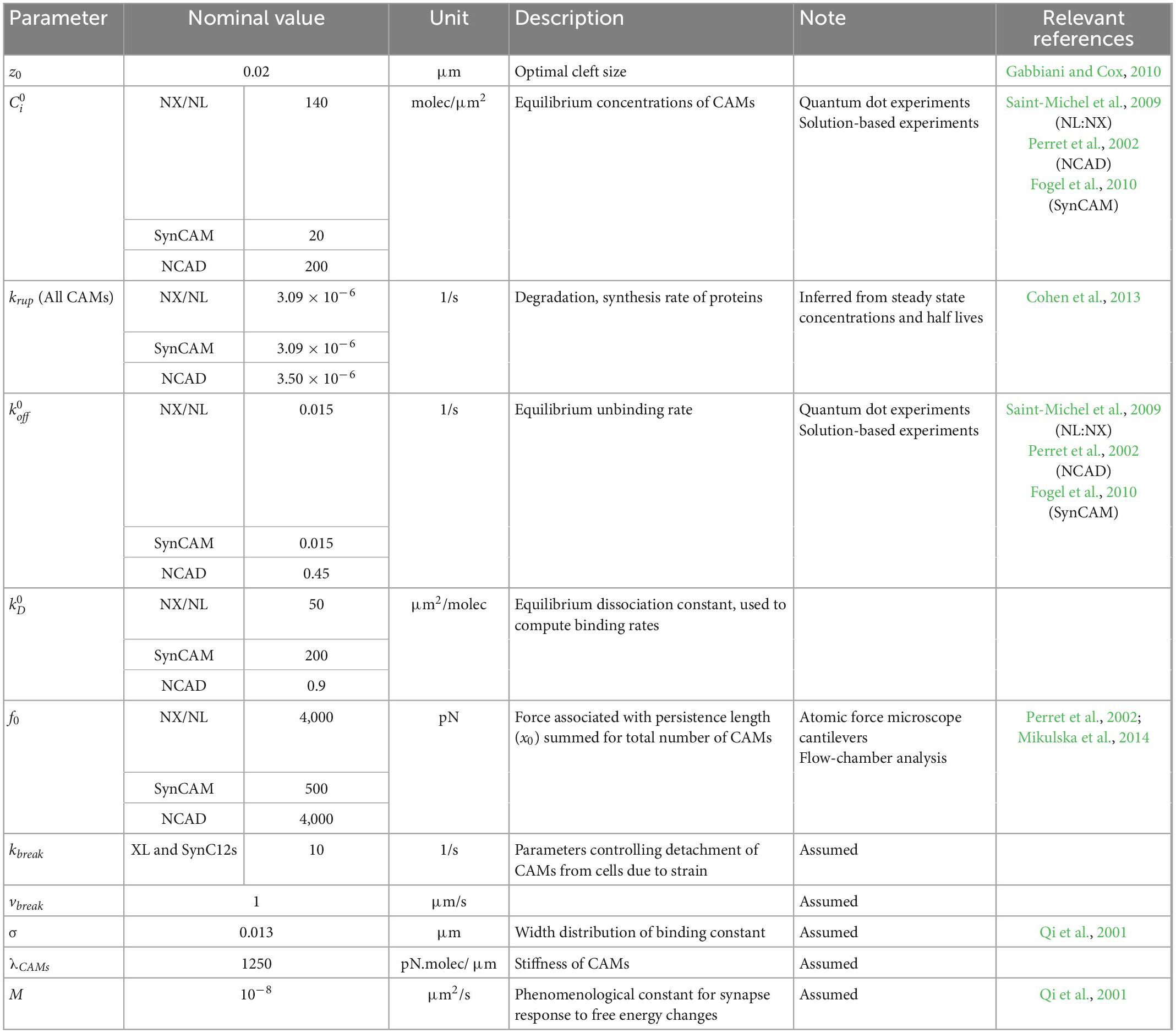
The parameters of the mechanobiology model are adopted or inferred from the available data literature. Table 1 summarizes the parameters, their nominal value, their description, the reference used for parameters, and the experiment used in the reference.

TABLE 1

Table 1. List of parameters in the mechanobiology model.

We use a Sobol sensitivity analysis technique to measure the contribution of each parameter and its interactions with other parameters to the output variance. Excluding z₀ and equilibrium concentrations ($C_i^0)$from the sensitivity analysis, a total of 18 parameters were used in the sensitivity analysis. To incorporate the inherent large uncertainty in the biological model parameters, each parameter is varied from 0.01 to 100 times the nominal value with a log-uniform distribution. The area-under-curve (AUC) of synaptic dysfunction following an acute insult, with w₁ = w₂ = w₃ = 1 is used for this analysis. To implement the Sobol method, a Saltelli’s (Saltelli et al., 2010) sampling scheme was used with a total of 38,912 model evaluations. The sample generation and calculation of total Sobol index was performed via open-source Python’s SALib (Herman and Usher, 2017).

3. Results

3.1. Acute response to LLB exposure and global sensitivity analysis

An acute exposure to LLB is simulated via a forced separation of pre- and post-synaptic membranes with a pulling rate of 0.01 μm/ms, cleft size 0.02 μm and duration of 0.5 ms, i.e., equivalent to a strain rate of 500 1/s ($s=\frac{0.01\mathrm{\mu }\mathrm{m}/\mathrm{ms}}{0.02\mathrm{\mu }\text{m}}$ 500 1/s), which of the same order of magnitude as computed in finite element models of blast-induced brain injury (Panzer et al., 2012). Once the injury duration is over, the synapse is released and allowed to slowly recover via rebinding of CAMs.

Figure 3 shows the synaptic response to an acute injury, characterized by a fast separation of membranes followed by a slow recovery. Synaptic cleft recovers its original size after a few minutes. In addition, the model shows a sharp increase in the total force generated in CAMs followed by a slow decrease, similar to a viscoelastic response. In the physiological conditions the adhesion molecules linking the pre- and post-synaptic terminals will be under an initial tension force. Our model, derived from the immune synapse model, assumes that the force is relative to the initial state.

FIGURE 3

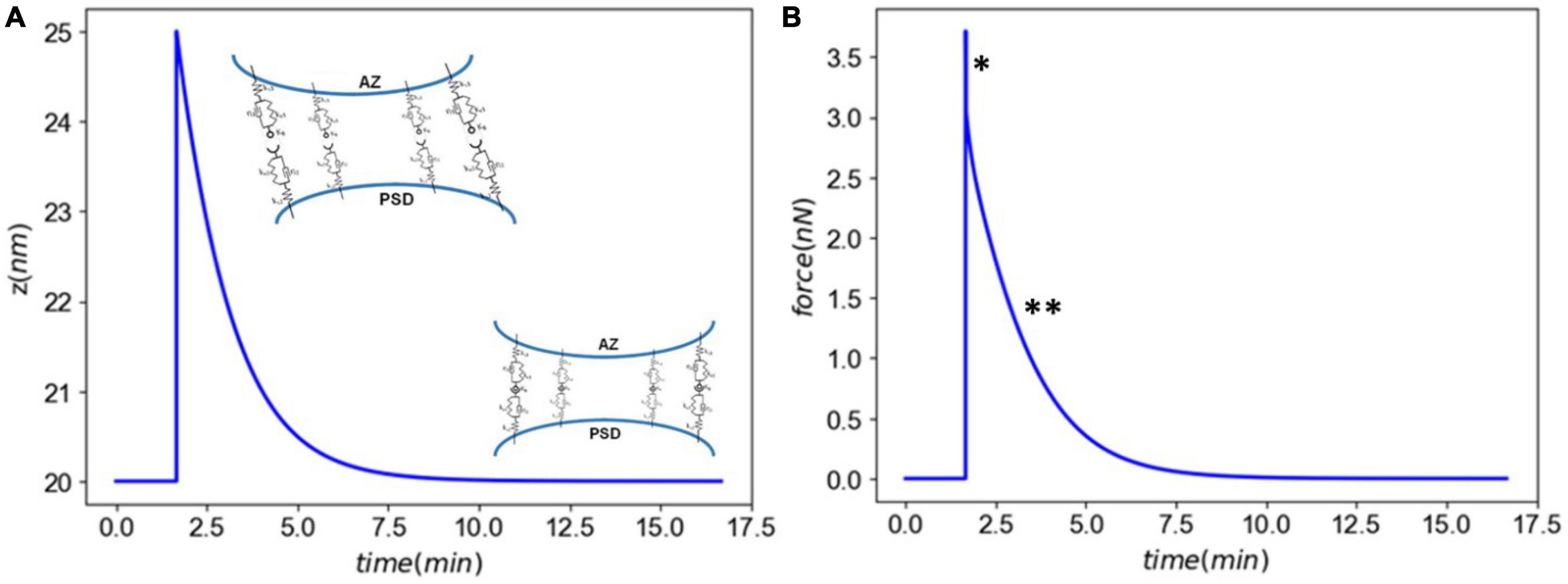
Figure 3. Panel (A) the synaptic cleft distance marked by a fast injury (∼ms) and slow recovery (∼minutes). Panel (B) the total force generated in CAMs marked by a a viscoelastic-type response. The astrics (*) and (^**) delineate different modes of force generated by CAMs.

Figure 4 shows the CAM responses to the insult. The XL complexes almost return back to their normal levels minutes after injury (Figure 4A). However, a closer examination shows that the insult causes a slight, yet sustained, loss of CAM complexes. This loss is more pronounced in SynCAM12 complexes. In both XL and SynC12 cases, the loss will be remedied by the replenishment of lost proteins via the natural synthesis and degradation process over days-months after the insult (Supplementary material C). As discussed in the “2. Materials and methods” section, the NCADs create a strong catch bond with catenins at their cytoplasmic end. Therefore, they will not detach from the membranes and are able to fully rebind within minutes after the injury.

FIGURE 4

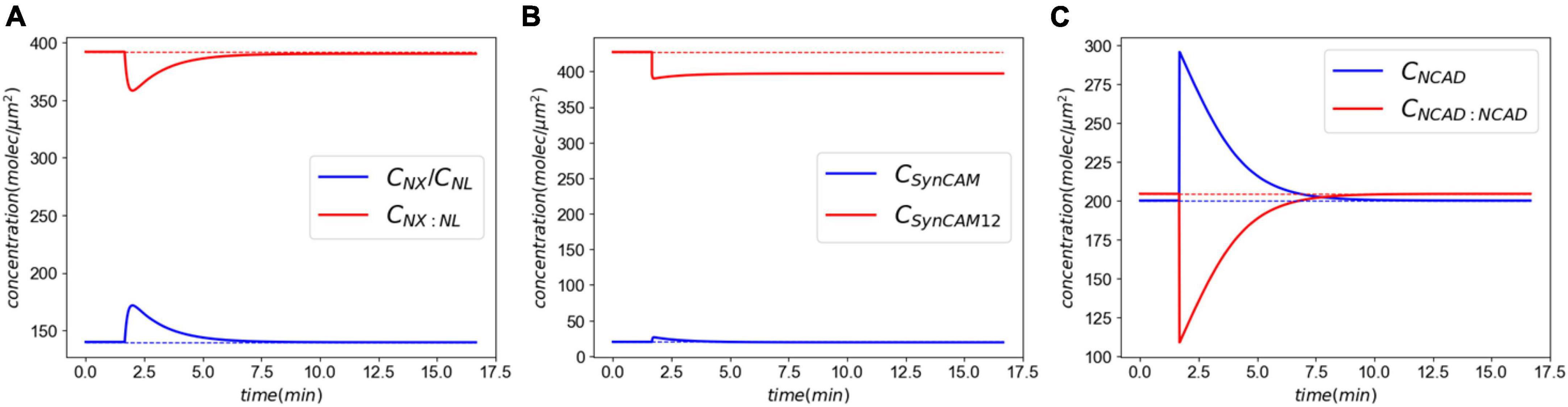
Figure 4. Molecular response to an acute insult. Panel (A) shows the XL and its constitutive CAMs response. The initial concentrations are almost fully recovered minutes after the insult. Panel (B) shows the SynCAM response. A clear loss of SynCAM12 complexes are predicted as a result of the injury. This loss will be remedied days-months via natural degradation and synthesis of SynCAMs. Conversely, the loss of NCADs minutes after the insult panel (C) due to lack of the pulling rate dependent down-regulation.

Importantly, the mechanobiology model of synaptic damage and recovery captures responses multiple timescales: (1) the <1 ms of injury, (2) minutes of partial recovery mediated by rebinding of dissociated proteins, and (3) days-months of full recovery facilitated by the natural synthesis of CAMs.

To further evaluate the model behavior, we varied the synaptic membrane pulling rate (s) across three orders of magnitude leading to strain rates 50–500–5,000 1/s while keeping the insult duration constant. Figure 5 shows the results of this parametric study. A strain rate of 50 1/s leads to a relatively small 0.5 nm cleft separation. However, even with a small separation, our model predicts a degree of CAM loss as seen on panels Figures 5C–E. As the strain rate is increased 10- and 100-fold, the synaptic cleft separation elevates to 5 and 50 nm, respectively. This separation leads to a significant drop in the concentrations of CAM complexes and delays their recovery (via rebinding) time. The long-term loss of SynCAM12 complexes is 4.4, 7.0, and 7.1% for smallest, medium, and largest strain rates, respectively, suggesting that our model and parameters produce a saturated CAM loss response as a function of strain rates. Interestingly, the total force complexes display a multipeak behavior when strain rate is increased to 5,000 1/s (Figure 5B). The first peak, consistent with smaller strain rates, pertains to the fast CAM complex stretch during the insult. During the recovery phase of the synapse, the CAMs rebind and pull the membranes together, where we have assumed a Gaussian function for this cleft distance-dependent rebinding with a 13 nm spread (Eq. 6). The lower-level strain rates (50 and 500 1/s) do not move the synaptic cleft outside of the Gaussian spread, whereas the strain rate of 5,000 1/s causes the rebinding to reduce to almost zero. At zero rebinding, the only driver for recovery is the energy stored in the remaining CAM complexes. However, once the synapse recovers the rebinding accelerates following the Gaussian curve while the CAM complexes are still stretched. This leads to a secondary peak in the force shown on Figure 5B. We must note that a 50 nm cleft separation will likely lead to an irrecoverable damage to synapses which is out of the scope of the current model. Nevertheless, this parametric study demonstrates an extreme model behavior which may be seen in mild-strong strain rates (500–5,000 1/s).

FIGURE 5

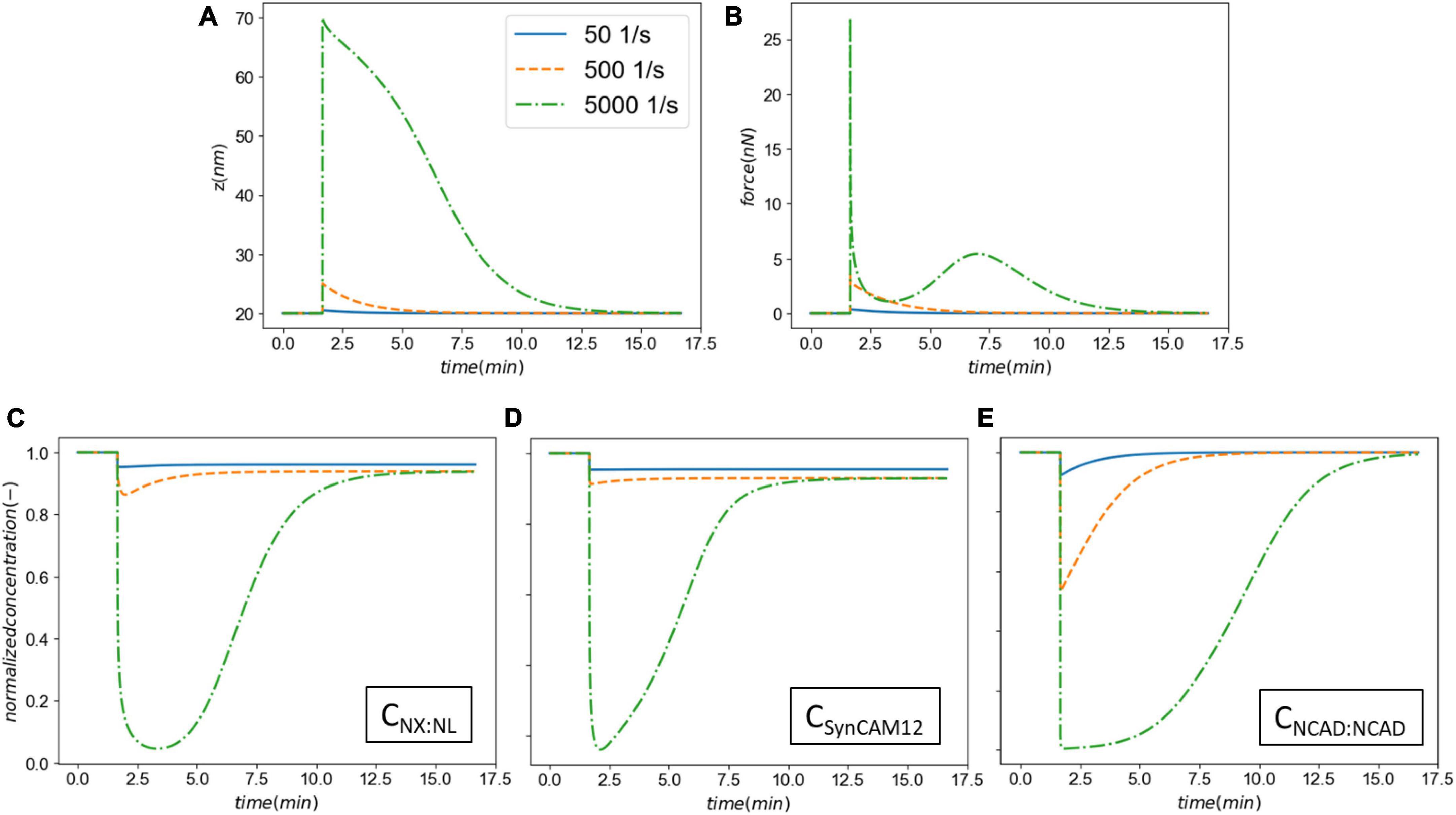
Figure 5. The effect the strain rate on the synaptic cell adhesion molecules (CAM) mechanics and concentrations. Panel (A) shows the cleft size before, during and after the insult. Panel (B) shows the total force applied on the intermolecular bonds. Panels (C–E) show the normalized CAM complex concentrations for NX:NL, SynCAM12, and NCAD:NCAD, respectively.

Figure 6 shows the resulting parameter sensitivities ranked based on the total-order Sobol index. The most sensitive parameters are M and σ. Parameter M corresponds to the overall response of synapse and to a large degree controls the synaptic recovery time course. Similarly, parameter σ is the spread if the Gaussian used for the binding rates, shared across all CAMs. These parameters are followed by the parameters controlling the unbinding of SynCAM and XL complexes. Due to lack of insult-induced long-term (∼days to months) loss of NCADs, its associated parameters rank lower compared to their XL and SynCAM counterparts. The least sensitive parameters based on this analysis are parameters defining the natural turnover of CAMs.

FIGURE 6

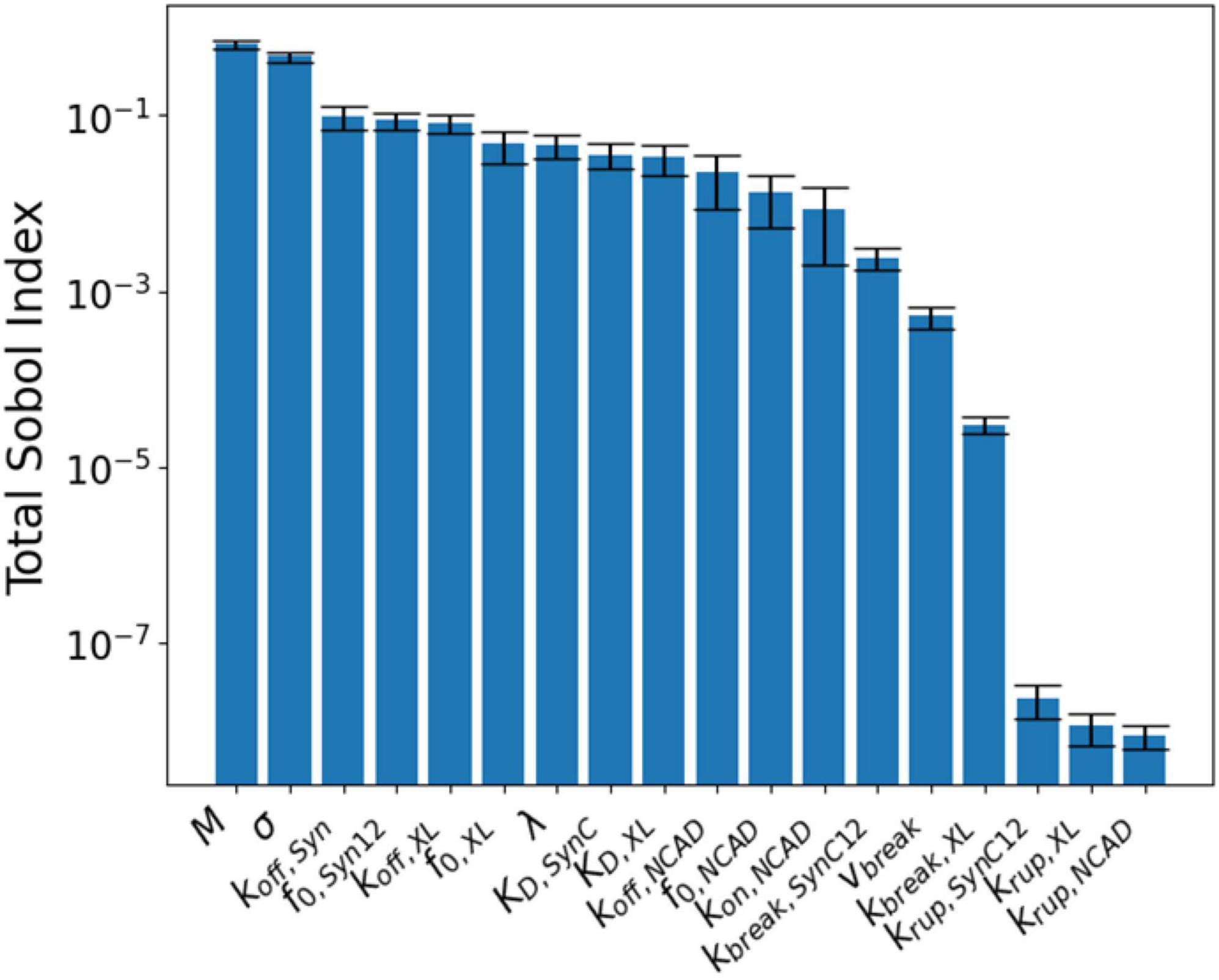
Figure 6. Global sensitivity analysis results ranked according to their total-order Sobol index (S_T).

3.2. Synaptic damage due to exposure to repeated LLBs

In this section, we extend the acute response model to simulate exposure to repeated LLBs. We consider six identical insults (pulling rate of 0.01 μm/ms and duration of 0.5 ms) in two exposure scenarios, Case 1: insults every 10 min, and Case 2: insults every 30 min. Figure 7 shows the results of exposure to repeated blasts. The loss of XL and SynCAM complexes has markedly increased due to repeated injuries with a 2.6 and 35% loss in XLs and SynCAMs, respectively, 10 min after the last insult for both cases. These losses remain almost constant in the timescale of hours after the insults. Similar to the acute response, slow recovery of detached CAMs is due to their long half-lives and slow synthesis rates (Cohen et al., 2013). In contrast, the loss of NCADs is 0.25% after 10 min which drops to 0.08% after 20 min. The NCAD response is largely modulated by rebinding of homophilic CAMs.

FIGURE 7

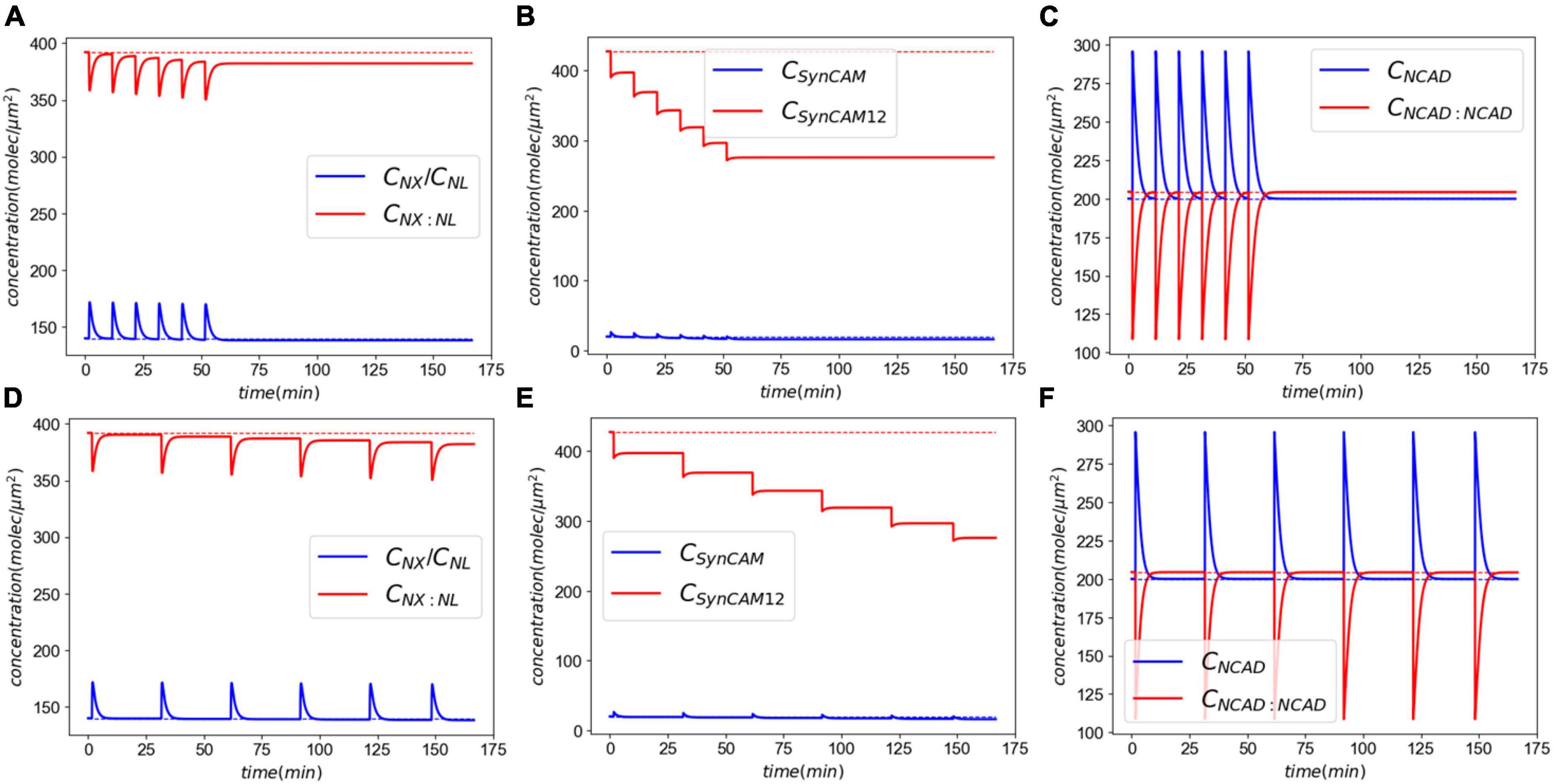
Figure 7. Molecular response to exposure to repeated LLBs. Panels (A–C) show the response to six insults every 10 min. Panels (D–F) show the response to six insults every 30 min.

3.3. Biomarker release and distribution following exposure to LLBs

Next, we show illustrative results of the biomarker release kinetics following repeated blast exposure. Our APP processing model simulates generation of both the amylogenic (sAPPβ, Aβ40, Aβ42) and non-amylogenic (sAPPα, p3) peptides that may be detected in body fluids. Here we only report results for generation of APP and Aß₄₂ peptides and their kinetics in plasma for which human data have been recently reported (Boutté et al., 2021, 2022). We set w₁ = 1, w₂ = 0.1, and w₃ = 0 in the synaptic dysfunction model [Eq. (20)]. In addition, we assumed that $K_{SD}=10=K_{BISF,synth}^0$. The rest of the parameters for this model were taken from Madrasi et al. (2021). The biomarker release and kinetics are simulated for 21 days following the exposure to single or repetitive blasts. Three scenarios were simulated in this section: (1) single mild insult (pulling rate of 0.01 μm/ms and duration of 0.5 ms), (2) six repeated mild insults, and (3) six repeated moderate insults (pulling rate of 0.04 μm/ms and duration of 1.0 ms). Figure 8A shows the synaptic dysfunction for the three cases. The spikes in this figure correspond to dynamics of short-term response of CAMs (shown in Figure 7) that are followed by a slower decline in synaptic dysfunction over following days. Figure 8B shows the concentration of APP in the brain ISF which increase 40, 370, and 800% for simulated exposures. Biomarker Aß₄₂ follows the dynamics of APP with a noticeable delay, reaching a maximum around 1–1.4 days following the exposure (Figure 8C). The demarcation line at 2.5 above the physiological level has been to demonstrate the potential “window” for biomarker collection, with approximately 2 days post-mild blast exposure and 5 days for moderate exposure. The model will have to be calibrated, but the reported human data show similar time windows for plasma Aβ (Boutté et al., 2021). Lastly, our model predicts that a single mild insult cannot induce enough damage for a detectable brain injury.

FIGURE 8

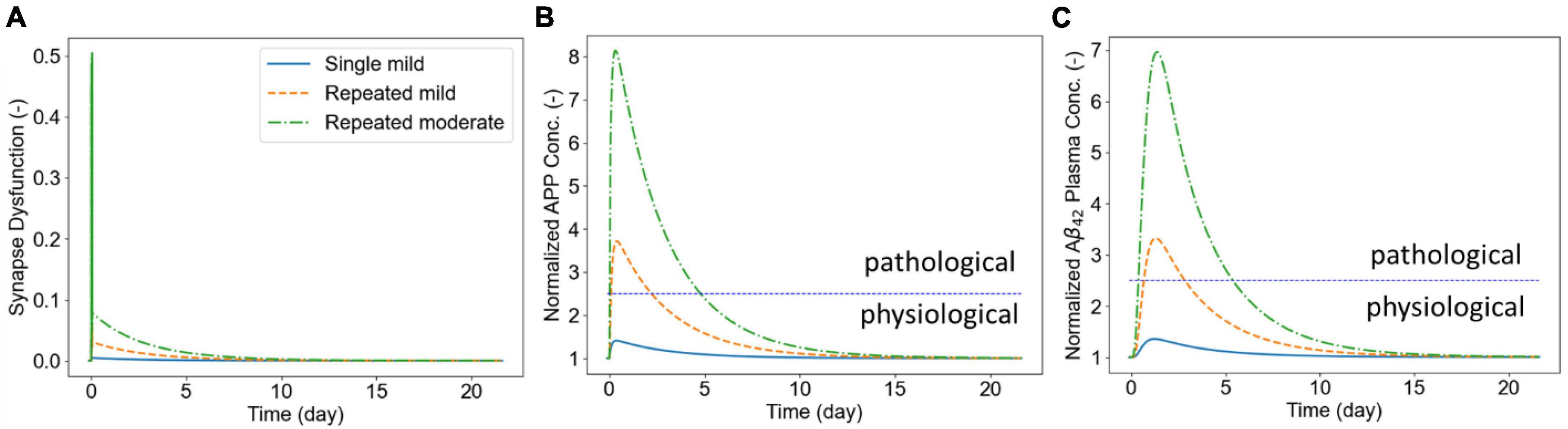
Figure 8. Panel (A) shows the synaptic dysfunction. Panel (B) shows the elevation in APP following the exposure to LLBs. Panel (C) shows the plasma concentrations of Aß₄₂ following exposure to repeated insults.

4. Discussion

Billions of neurons in the human brain connected to one another by trillions of synapses are continuously subjected to mechanical forces communicated via adhesion molecules, cell membranes, extracellular and intracellular matrix. This endogenous physiological neuro-mechanobiology affects CNS cellular neurotransmission, metabolism and plasticity. However, external mechanical forces may cause synaptic structural damage and initiate a cascade of mechanical and biochemical deleterious and recovery responses. Mathematical models of synaptic mechanobiology supported by laboratory in vitro and in vivo experiments may help in better understanding of brain injury, diagnostics and protection. Mathematical modeling of CNS synaptic mechanobiology is challenging due to the immense number of brain synapses and heterogeneity of their morphologies as well as extreme range of spatial and temporal scales involved in brain injury responses (Procès et al., 2022). Structural mechanics of CAMs can be simulated at various scales using molecular and coarse-grained dynamics models, spring-mass-damper models or finite element type models. However, the spatial and time-step limitations make them impractical for longer duration (seconds to hours) simulation periods.

In this work, we formulated a dynamic model of a single synaptic structure using a network of ligand-receptor binding kinetics of synaptic CAMs and quasi-equilibrium energy-displacement model. The model can resolve time scales ranging from milliseconds during the hyperacute phase of mechanical loading to minutes-hours acute/chronic phase of injury progression/repair. Such synaptic mechanobiology model can be coupled with other models such as biomarker kinetics (BxK), neurotransmission, neuroimmune responses, and synaptic plasticity. Here we demonstrated a link between the synaptic mechanobiology model and a minimal model of synaptic processing of amyloid precursor protein and generation and kinetics of related amyloid biomarkers that can be detected in CSF and plasma.

First, we established our model’s capability in simulating the synaptic response to an acute injury characterized by a single separation of synapse over a 0.5 ms, almost equivalent to the positive phase duration of low-level blast waves. As a response to acute injury, our model predicted a viscoelastic-type behavior in which the synaptic cleft and force slowly restore their baseline values 8 min after the insult (Figure 3). During the synaptic cleft separation, initially a sharp spike is seen in the total forces generated in CAMs [marked by (*) in Figure 3B]. The sudden rise in force is due to the stretch of bound CAMs and their associated stiffnesses which resist the cleft separation. Conversely, the large generated force sharply increases the CAM complex unbinding rates which leads to their rapid dissociation, reduction in their concentrations, and eventually a decrease in force. The spike is then followed by a less steep reduction in force [marked by (^**) in Figure 3B] which is the result of competition between unbinding due to remaining intermolecular force and distance-dependent rebinding of detached CAMs. The CAM forces vanish when the synapse cleft recovers its initial dimensions. However, since a significant loss is observed in SynC12 concentrations, a full recovery of synapse is not yet achieved (Figure 4B). In this work, SynC12 have a relatively higher dissociation constant and detachment parameter (k_break), and thus, a greater portion of bound SynC12 are irreversibly detached from the membranes. The recovery of SynC12 requires natural turnover of unbound SynCAM1/2. Conversely, we assumed that NCAD do not detach from their cytoplasmic ends. Therefore, there is enough unbound NCAD on both sides of synapse to recover their baseline values within minutes after the acute insult.

To understand the effect of model parameters on the simulation results, a global sensitivity analysis was performed (Figure 6). The analysis results indicated that M (a constant modulating the synapse response to free energy changes) and σ (width distribution of binding constants) are the most sensitive parameters. We must note that M is a parameter for the synapse structure, and σ is shared between different CAM families. Among CAM specific parameters, SynCAM parameters are generally more sensitive and NCAD parameters are less sensitive. This is expected since the model output is considered long-term synaptic dysfunction, while NCAD complexes recover their initial concentrations minutes after the insult.

Next, we extended our model to simulate the synaptic response to multiple LLBs within a timeframe comparable to military weapon training scenarios. Exposure to repeated LLBs noticeably increases the long-term effects of damage. This is particularly evident in Figure 7 where after each insult, the XL and SynC12 concentrations progressively fall. Decreasing the frequency of exposures from every 10 min to every 30 min, however, did not have a significant effect on the long-term effects. Therefore, our model predicts that in a weapon training setting where shots are fired minutes apart, the number of exposures rather than their firing interval could be the determining factor in long-term effects of synaptic injury. We must note that while cumulative effects of exposure to repeated blasts on brain tissue integrity have been established (Trotter et al., 2015), the relationship between blast exposure frequency and brain pathology is currently unclear (Heyburn et al., 2021). Long-term recovery of CAMs and their complexes are largely modulated by the natural turnover of SynCAMs, NX, and NL. Cohen et al. (Cohen et al., 2013) reported half-lives of 2.56 and 2.63 days for SYNCAM1/2 and NX/NL, respectively. Accordingly, the loss of these CAMs is eventually recovered via their natural turn-over process after ∼3 months and ∼9 months for XL/NL and SynCAMs, respectively. We must note that this recovery time is predicted in absence of intrinsic homeostatic compensatory mechanisms which might expedite the CAM recoveries.

Finally, we illustrated the utility of our model in quantifying biomarker release and kinetics after exposure to repeated blasts (Figure 8). In this work, we only accounted for the amylogenic pathway shown in Figure 2. However, the non-amylogenic pathway could be useful for diagnostic, prophylactic, or therapeutic investigations of APP-affecting enzymes such as ADAM10 (Appel et al., 2021). Our results highlighted that the dynamics of biomarker (Aß₄₂) following LLBs are demonstrably slower than the synaptic responses. This is particularly depicted in brain interstitial APP and plasma Aß₄₂ peaking at around 1 and 2 days after the exposure, respectively. Moreover, our model predicts that the plasma biomarkers remain elevated for months after the initial exposure. Our findings of increased Aß₄₂ in plasma 3–5 days post-blast exposure compare relatively well to recently reported human plasma Aß₄₂ and Aß₄₀ levels 1-, 2- and 3-days post-weapon blast exposure in military sniper training (Thangavelu et al., 2020; Boutté et al., 2021). We are collecting related human blast dose biomarker response data for more quantitative model validation. Several experimental studies have shown that the elevated of soluble Aß₄₂ in TBI might induce oligomerization and aggregation leading to accelerated neurocognitive disease progression (e.g., Alzheimer’s disease) (Roberts et al., 1994; Washington et al., 2014). Taken together, these results underscore the importance computational models that delineate neuro-response and their link to clinical biomarker markers in LLB exposure.

In this work we have only considered mechanobiology of a single synapse in response to single and repeated blast injury. In the human CNS there are several other cellular and molecular adhesion structures susceptible to external loads including the axons, astrocytes, blood-brain barrier as well as extracellular matrix and intracellular cytoskeletal networks. The present “minimal” model of synaptic mechanobiology can be improved by accounting not only for tension loads but also shear loads. The model should be parametrized to account for variable morphology and composition of CAMs in excitatory and inhibitory synapses. Moreover, the present model is largely focused on the mechanics and kinetics CAM-CAM interactions. The mechanics of CAM connections to their respective synaptic membranes, however, is less understood. For instance, neuroligins and neurexins both have relatively short intracellular domains that potentially bind to several PDZ-domain scaffolding proteins (Meyer et al., 2004). This lack of mechanistic understanding of the proteins inside the cell motivated us to use a phenomenological pulling rate dependent down-regulation term for the detachment of SynCAMs and NX and NL from their synaptic membrane. This term is particularly crucial in understanding the recovery phase and biomarker kinetics. Further improvements could couple the present synapse model with reduced order mechanical models of the connected pre-synaptic axon segment and post-synaptic dendritic spine models e.g., spring-damper-mass models accounting for the elastic and damping effects of the extracellular matrix. The present mechanobiology model could be also adapted for modeling CAM effects between the axon and myelin junctions next to nodes of Ranvier and the adhesion dynamics between intraconal microtubule network and the microtubule-associated Tau proteins.

The present model needs to be calibrated and validated on experimental data collected from in vitro imaging of neuro-axonal structures and generation of injury related biomarkers. At present, we have linked the synaptic mechanobiology model with simple model of amyloid beta (Aß₄₂) responses. More advanced models of generations of soluble synaptic biomarkers exist that could be incorporated in the present framework and validated on experimental data. Furthermore, several experimental and clinical studies have highlighted the neuro-immune responses such as neuroinflammation and microglial priming in repeated TBI (Kokiko-Cochran and Godbout, 2018). Accordingly, minimal or extended models of cytokine-mediate microglial activation from resting to pro- and anti-inflammatory phenotypes could be integrated in the presented framework to investigate neuroinflammation (Donat et al., 2017; Amato and Arnold, 2021).

5. Conclusion

Synaptic injury mechanisms are largely unknown and have only recently begun to attract interest of neuroscientists partially because of experimental challenges at such small length and timescales. Whether the synaptic injury is a primary result of the mechanical loads or a secondary effect of axonal injury remains to be determined. Most likely both mechanisms occur at the same time at different locations in the brain and induce mutual secondary effects (Jamjoom et al., 2021). This paper presented a novel reduced order model of synaptic mechanobiology caused by an acute and repeated blast brain injury. The model integrates the adhesion dynamics of the synaptic CAMs with the deformation mechanics of the synaptic cleft. Depending on the blast load level it predicts the reversible CAM adhesion recovery after lower level and slower rate loads and irreversible disconnect of some CAMs caused by bigger and faster rate loads. The model has been used to simulate the synaptic injury responses caused by repeated blast loads. It demonstrated the relevance of the duration of recovery period between repeated loads on the synaptic injury responses. In this work, we have linked the synaptic mechanobiology model with a minimal model of biomarker (Aβ₄₂) kinetics. The model can be extended to simulate not only tension but also shear loads on both excitatory and inhibitory synapses, account for ECM effects and link to a synaptic neurotransmission model. Most importantly, the model needs to be further calibrated and validated on in vitro experimental data.

Data availability statement

The original contributions presented in this study are included in this article/Supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

HG and AP formulated the model. RG formulated modeling requirements for repeated blast TBI, CFDRC team (HG, HTG, ZC, and AP in equal contribution) implemented the model and conducted simulations and reviewed the results and the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work, performed by CFDRC, has been supported by the US DoD Defense Health Agency (DHA) SBIR Phase IIE project titled “Tools for Warfighter Repeated Blast Exposure Monitoring in Military Heavy Weapon Training”, Award No. W81XWH-21-C-0020.

Acknowledgments

The authors gratefully acknowledge the reviewers for their valuable time and insightful comments during the review process. It helped to improve the quality of the manuscript.

Conflict of interest

HG, HTG, ZC, and AP were employed by CFD Research Corporation.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author disclaimer

The views expressed in this manuscript are those of the authors and may not necessarily be endorsed by the U.S. Army or U.S. Department of Defense.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fncel.2023.1007062/full#supplementary-material

References

Ahmadzadeh, H., Smith, D., and Shenoy, V. (2015). Mechanical effects of dynamic binding between tau proteins on microtubules during axonal injury. Biophys. J. 109, 2328–2337. doi: 10.1016/j.bpj.2015.09.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Amato, S., and Arnold, A. (2021). Modeling microglia activation and inflammation-based neuroprotectant strategies during ischemic stroke. Bull. Math. Biol. 83, 1–27.

Google Scholar

Appel, D., Hummel, R., Weidemeier, M., Endres, K., Gölz, C., and Schäfer, M. (2021). Pharmacologic inhibition of ADAM10 attenuates brain tissue loss, axonal injury and pro-inflammatory gene expression following traumatic brain injury in mice. Front. Cell Dev. Biol. 9:661462. doi: 10.1007/s11538-021-00905-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Arikkath, J., and Reichardt, L. (2008). Cadherins and catenins at synapses: Roles in synaptogenesis and synaptic plasticity. Trends Neurosci. 31:487. doi: 10.3389/fcell.2021.661462

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashton, J., Coyles, G., Malone, J., and Roberts, J. (2020). Immediate effects of an acute bout of repeated soccer heading on cognitive performance. Sci. Med. Footb. 5, 181–187. doi: 10.1016/j.tins.2008.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, G. (1978). Models for the specific adhesion of cells to cells. Science 200, 618–627. doi: 10.1080/24733938.2020.1846769

PubMed Abstract | CrossRef Full Text | Google Scholar

Boutté, A., Thangavelu, B., and Anagli, J. (2022). Opinion: The Potential role of amyloid beta peptides as biomarkers of subconcussion and concussion. Front. Neurol. 13:1370. doi: 10.1126/science.347575

PubMed Abstract | CrossRef Full Text | Google Scholar

Boutté, A., Thangavelu, B., Nemes, J., Lavalle, C., Egnoto, M., Carr, W., et al. (2021). Neurotrauma biomarker levels and adverse symptoms among military and law enforcement personnel exposed to occupational overpressure without diagnosed traumatic brain injury. JAMA Netw. Open 4, e216445–e216445. doi: 10.3389/fneur.2022.941151

PubMed Abstract | CrossRef Full Text | Google Scholar

Brito-Moreira, J., Lourenco, M. V., Oliveira, M., Ribeiro, F., Ledo, J., Diniz, L., et al. (2017). Interaction of amyloid-β (Aβ) oligomers with neurexin 2α and neuroligin 1 mediates synapse damage and memory loss in mice. J. Biol. Chem. 292, 7327–7337. doi: 10.1001/jamanetworkopen.2021.6445

PubMed Abstract | CrossRef Full Text | Google Scholar

Buckley, C., Tan, J., Anderson, K., Hanein, D., Volkmann, N., Weis, W., et al. (2014). The minimal cadherin-catenin complex binds to actin filaments under force. Science 346:1254211. doi: 10.1074/jbc.M116.761189

PubMed Abstract | CrossRef Full Text | Google Scholar

Bukalo, O., and Dityatev, A. (2012). Synaptic cell adhesion molecules. Adv. Exp. Med. Biol. 970, 97–128. doi: 10.1126/science.1254211

PubMed Abstract | CrossRef Full Text | Google Scholar

Carr, W., Polejaeva, E., Grome, A., Crandall, B., La Valle, C., Eonta, S., et al. (2015). Relation of repeated low-level blast exposure with symptomology similar to concussion. J. Head Trauma Rehabil. 30, 47–55. doi: 10.1007/978-3-7091-0932-8_5

CrossRef Full Text | Google Scholar

Cernak, I. (2017). Understanding blast-induced neurotrauma: How far have we come? Concussion 2:CNC42. doi: 10.1097/HTR.0000000000000064

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, L., Zuchman, R., Sorokina, O., Müller, A., Dieterich, D., Armstrong, J., et al. (2013). Metabolic turnover of synaptic proteins: Kinetics, interdependencies and implications for synaptic maintenance. PLoS One 8:e63191. doi: 10.2217/cnc-2017-0006

PubMed Abstract | CrossRef Full Text | Google Scholar

Comoletti, D., Grishaev, A., Whitten, A., Taylor, P., and Trewhella, J. (2008). Characterization of the solution structure of a neuroligin/beta-neurexin complex. Chem. Biol. Interact. 175, 150–155. doi: 10.1371/journal.pone.0063191

PubMed Abstract | CrossRef Full Text | Google Scholar

DePalma, R., and Hoffman, S. (2018). Combat blast related traumatic brain injury (TBI): Decade of recognition; promise of progress. Behav. Brain Res. 340, 102–105. doi: 10.1016/j.cbi.2008.04.040

PubMed Abstract | CrossRef Full Text | Google Scholar

Donat, C., Scott, G., Gentleman, S., and Sastre, M. (2017). Microglial activation in traumatic brain injury. Front. Aging Neurosci. 9:208. doi: 10.1016/j.bbr.2016.08.036

PubMed Abstract | CrossRef Full Text | Google Scholar

Edwards, G., Moreno-Gonzalez, I., and Soto, C. (2017). Amyloid-beta and tau pathology following repetitive mild traumatic brain injury. Biochem. Biophys. Res. Commun. 483, 1137–1142. doi: 10.3389/fnagi.2017.00208

PubMed Abstract | CrossRef Full Text | Google Scholar

Elder, G., Ehrlich, M., and Gandy, S. (2019). Relationship of traumatic brain injury to chronic mental health problems and dementia in military veterans. Neurosci. Lett. 707:134294. doi: 10.1016/j.bbrc.2016.07.123

PubMed Abstract | CrossRef Full Text | Google Scholar

Engel, C., Hoch, E., and Simmons, M. (2019). The neurological effects of repeated exposure to military occupational blast: Implications for prevention and health: Proceedings, findings, and expert recommendations from the seventh department of defense state-of-the-science meeting. Santa Monica, CA: RAND Corporation. doi: 10.1016/j.neulet.2019.134294

PubMed Abstract | CrossRef Full Text | Google Scholar

Fogel, A., Akins, M., Krupp, A., Stagi, M., Stein, V., and Biederer, T. (2007). SynCAMs organize synapses through heterophilic adhesion. J. Neurosci. 27, 12516–12530. doi: 10.7249/CF380.1

CrossRef Full Text | Google Scholar

Fogel, A., Li, Y., Giza, J., Wang, Q., Lam, T., Modis, Y., et al. (2010). N-glycosylation at the SynCAM (Synaptic cell adhesion molecule) immunoglobulin interface modulates synaptic adhesion. J. Biol. Chem. 285, 34864–34874. doi: 10.1523/JNEUROSCI.2739-07.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Fowler, D., Peters, J., Williams, C., and Washbourne, P. (2017). Redundant postsynaptic functions of SynCAMs 1–3 during synapse formation. Front. Mol. Neurosci. 10:24. doi: 10.1074/jbc.M110.120865

PubMed Abstract | CrossRef Full Text | Google Scholar

Gabbiani, F., and Cox, S. J. (2010). Mathematics for neuroscientists. Amsterdam: Academic Press.

Google Scholar

Garimella, H., and Kraft, R. (2017). Modeling the mechanics of axonal fiber tracts using the embedded finite element method. Int. J. Numer. Method Biomed. Eng. 33:e2823. doi: 10.1016/B978-0-12-374882-9.00012-5

CrossRef Full Text | Google Scholar

Garimella, H., Kraft, R., and Przekwas, A. (2018). Do blast induced skull flexures result in axonal deformation? PLoS One 13:e0190881. doi: 10.1002/cnm.2823

PubMed Abstract | CrossRef Full Text | Google Scholar

Greco, T., Ferguson, L., Giza, C., and Prins, M. (2019). Mechanisms underlying vulnerabilities after repeat mild traumatic brain injuries. Exp. Neurol. 317, 206–213. doi: 10.1371/journal.pone.0190881

PubMed Abstract | CrossRef Full Text | Google Scholar

Gupta, R., and Przekwas, A. (2013). Mathematical models of blast-induced TBI: Current status, challenges, and prospects. Front. Neurol. 4:59. doi: 10.1016/j.expneurol.2019.01.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Gupta, R., Tan, X., Somayaji, M., and Przekwas, A. (2017). Multiscale modelling of blast-induced TBI mechanobiology - from body to neuron to molecule. Def. Life Sci. J. 2, 3–13. doi: 10.3389/fneur.2013.00059

PubMed Abstract | CrossRef Full Text | Google Scholar

Hall, C., Moeendarbary, E., and Sheridan, G. (2021). Mechanobiology of the brain in ageing and Alzheimer’s disease. Eur. J. Neurosci. 53, 3851–3878. doi: 10.14429/dlsj.2.10369

CrossRef Full Text | Google Scholar

Heine, M., Thoumine, O., Mondin, M., Tessier, B., Giannone, G., and Choquet, D. (2008). Activity-independent and subunit-specific recruitment of functional AMPA receptors at neurexin/neuroligin contacts. Proc. Natl. Acad. Sci. U.S.A. 105, 20947–20952. doi: 10.1111/ejn.14766

PubMed Abstract | CrossRef Full Text | Google Scholar

Herman, J., and Usher, W. (2017). SALib: An open-source python library for sensitivity analysis. J. Open Source Softw. 2:97. doi: 10.1073/pnas.0804007106

PubMed Abstract | CrossRef Full Text | Google Scholar

Heyburn, L., Abutarboush, R., Goodrich, S., Urioste, R., Batuure, A., Wheel, J., et al. (2021). Repeated low-level blast acutely alters brain cytokines, neurovascular proteins, mechanotransduction, and neurodegenerative markers in a rat model. Front. Cell. Neurosci. 15:636707. doi: 10.21105/joss.00097

CrossRef Full Text | Google Scholar

Hoffe, B., and Holahan, M. (2022). Hyperacute excitotoxic mechanisms and synaptic dysfunction involved in traumatic brain injury. Front. Mol. Neurosci. 15:61. doi: 10.3389/fncel.2021.636707

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamjoom, A., Rhodes, J., Andrews, P., and Grant, S. (2021). The synapse in traumatic brain injury. Brain 144:18. doi: 10.3389/fnmol.2022.831825

PubMed Abstract | CrossRef Full Text | Google Scholar

Kakavas, G., Malliaropoulos, N., Blach, W., Bikos, G., Migliorini, F., and Maffulli, N. (2021). Ball heading and subclinical concussion in soccer as a risk factor for anterior cruciate ligament injury. J. Orthop. Surg. Res. 16, 1–4. doi: 10.1093/brain/awaa321

PubMed Abstract | CrossRef Full Text | Google Scholar

Kashyap, P., Shenk, T., Svaldi, D., Lycke, R., Lee, T., Gregory, G., et al. (2022). Normalized Brain tissue–level evaluation of volumetric changes of youth athletes participating in collision sports. Neurotrauma Rep. 3:57. doi: 10.1186/s13018-021-02711-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Keating, C., and Cullen, D. (2021). Mechanosensation in traumatic brain injury. Neurobiol. Dis. 148:105210. doi: 10.1089/neur.2021.0060

PubMed Abstract | CrossRef Full Text | Google Scholar

Kokiko-Cochran, O., and Godbout, J. (2018). The Inflammatory continuum of traumatic brain injury and Alzheimer’s disease. Front. Immunol. 9:672. doi: 10.1016/j.nbd.2020.105210

PubMed Abstract | CrossRef Full Text | Google Scholar

Madrasi, K., Das, R., Mohmmadabdul, H., Lin, L., Hyman, B., Lauffenburger, D., et al. (2021). Systematic in silico analysis of clinically tested drugs for reducing amyloid-beta plaque accumulation in Alzheimer’s disease. Alzheimers Dement. 17, 1487–1498. doi: 10.3389/fimmu.2018.00672

PubMed Abstract | CrossRef Full Text | Google Scholar

McCunn, R., Beaudouin, F., Stewart, K., Meyer, T., and MacLean, J. (2021). Heading in football: Incidence, biomechanical characteristics and the association with acute cognitive function—a three-part systematic review. Sport Med. 51, 2147–2163. doi: 10.1002/alz.12312

PubMed Abstract | CrossRef Full Text | Google Scholar

McKee, A., Cantu, R., Nowinski, C., Hedley-Whyte, E., Gavett, B., Budson, A., et al. (2009). Chronic traumatic encephalopathy in athletes: Progressive tauopathy after repetitive head injury. J. Neuropathol. Exp. Neurol. 68, 709–735. doi: 10.1007/s40279-021-01492-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, G., Varoqueaux, F., Neeb, A., Oschlies, M., and Brose, N. (2004). The complexity of PDZ domain-mediated interactions at glutamatergic synapses: A case study on neuroligin. Neuropharmacology 47, 724–733. doi: 10.1097/NEN.0b013e3181a9d503

PubMed Abstract | CrossRef Full Text | Google Scholar

Mikulska, K., Strzelecki, J., and Nowak, W. (2014). Nanomechanics of β-rich proteins related to neuronal disorders studied by AFM, all-atom and coarse-grained MD methods. J. Mol. Model. 20, 1–10. doi: 10.1016/j.neuropharm.2004.06.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Modica, L., Egnoto, M., Statz, J., Carr, W., and Ahlers, S. (2021). Development of a blast exposure estimator from a department of defense-wide survey study on military service members. J. Neurotrauma 38, 1662–1669. doi: 10.1007/s00894-014-2144-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Panzer, M., Myers, B., Capehart, B., and Bass, C. (2012). Development of a finite element model for blast brain injury and the effects of CSF cavitation. Ann. Biomed. Eng. 40, 1530–1544. doi: 10.1089/neu.2020.7405

PubMed Abstract | CrossRef Full Text | Google Scholar

Perret, E., Benoliel, A., Nassoy, P., Pierres, A., Delmas, V., Thiery, J., et al. (2002). Fast dissociation kinetics between individual E-cadherin fragments revealed by flow chamber analysis. EMBO J. 21, 2537–2546. doi: 10.1007/s10439-012-0519-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Prins, M., Alexander, D., Giza, C., and Hovda, D. (2013). Repeated mild traumatic brain injury: Mechanisms of cerebral vulnerability. J. Neurotrauma 30, 30–38. doi: 10.1093/emboj/21.11.2537

PubMed Abstract | CrossRef Full Text | Google Scholar

Procès, A., Luciano, M., Kalukula, Y., Ris, L., and Gabriele, S. (2022). Multiscale mechanobiology in brain physiology and diseases. Front. Cell Dev. Biol. 10:823857. doi: 10.1089/neu.2012.2399

PubMed Abstract | CrossRef Full Text | Google Scholar

Przekwas, A., Garimella, H., Chen, Z., Zehnbauer, T., Gupta, R., Skotak, M., et al. (2021). Fast-running tools for personalized monitoring of blast exposure in military training and operations. Mil Med. 186(Suppl. 1), 529–536. doi: 10.3389/fcell.2022.823857

PubMed Abstract | CrossRef Full Text | Google Scholar

Przekwas, A., Somayaji, M., and Gupta, R. (2016). Synaptic mechanisms of blast-induced brain injury. Front. Neurol. 7:2. doi: 10.1093/milmed/usaa341

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, S., Groves, J., and Chakraborty, A. (2001). Synaptic pattern formation during cellular recognition. Proc. Natl. Acad. Sci. U.S.A. 98, 6548–6553. doi: 10.3389/fneur.2016.00002

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, G., Gentleman, S., Lynch, A., Murray, L., Landon, M., and Graham, D. (1994). Beta amyloid protein deposition in the brain after severe head injury: Implications for the pathogenesis of Alzheimer’s disease. J. Neurol. Neurosurg. Psychiatry 57, 419–425. doi: 10.1073/pnas.111536798

PubMed Abstract | CrossRef Full Text | Google Scholar

Saint-Michel, E., Giannone, G., Choquet, D., and Thoumine, O. (2009). Neurexin/neuroligin interaction kinetics characterized by counting single cell-surface attached quantum dots. Biophys. J. 97:480. doi: 10.1136/jnnp.57.4.419

PubMed Abstract | CrossRef Full Text | Google Scholar

Saltelli, A., Annoni, P., Azzini, I., Campolongo, F., Ratto, M., and Tarantola, S. (2010). Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 181, 259–270. doi: 10.1016/j.bpj.2009.04.044

PubMed Abstract | CrossRef Full Text | Google Scholar

Sandmo, S., Matyasova, K., Filipcik, P., Cente, M., Koerte, I., Pasternak, O., et al. (2022). Changes in circulating microRNAs following head impacts in soccer. Brain Inj. 36, 560–571. doi: 10.1016/j.cpc.2009.09.018

CrossRef Full Text | Google Scholar

Saura, C., Servián-Morilla, E., and Scholl, F. (2011). Presenilin/γ-secretase regulates neurexin processing at synapses. PLoS One 6:e19430. doi: 10.1080/02699052.2022.2034042

PubMed Abstract | CrossRef Full Text | Google Scholar

Siedhoff, H., Chen, S., Song, H., Cui, J., Cernak, I., Cifu, D., et al. (2022). Perspectives on primary blast injury of the brain: Translational insights into non-inertial low-intensity blast injury. Front. Neurol. 12:818169. doi: 10.1371/journal.pone.0019430

PubMed Abstract | CrossRef Full Text | Google Scholar

Sosa, L., Cáceres, A., Dupraz, S., Oksdath, M., Quiroga, S., and Lorenzo, A. (2017). The physiological role of the amyloid precursor protein as an adhesion molecule in the developing nervous system. J. Neurochem. 143, 11–29. doi: 10.3389/fneur.2021.818169

PubMed Abstract | CrossRef Full Text | Google Scholar

Thangavelu, B., LaValle, C., Egnoto, M., Nemes, J., Boutté, A., and Kamimori, G. (2020). Overpressure exposure from.50-caliber rifle training is associated with increased amyloid beta peptides in serum. Front. Neurol. 11:620. doi: 10.1111/jnc.14122

PubMed Abstract | CrossRef Full Text | Google Scholar

Trotter, B., Robinson, M., Milberg, W., McGlinchey, R., and Salat, D. (2015). Military blast exposure, ageing and white matter integrity. Brain 138:2278. doi: 10.3389/fneur.2020.00620

PubMed Abstract | CrossRef Full Text | Google Scholar

Violano, G., Chateauminois, A., and Afferrante, L. (2021). Rate-dependent adhesion of viscoelastic contacts, Part I: Contact area and contact line velocity within model randomly rough surfaces. Mech. Mater. 160:103926. doi: 10.1093/brain/awv139

PubMed Abstract | CrossRef Full Text | Google Scholar

Washington, P., Morffy, N., Parsadanian, M., Zapple, D., and Burns, M. (2014). Experimental traumatic brain injury induces rapid aggregation and oligomerization of amyloid-beta in an Alzheimer’s disease mouse model. J. Neurotrauma 31, 125–134. doi: 10.1016/j.mechmat.2021.103926

CrossRef Full Text | Google Scholar

Zetterberg, H., Winblad, B., Bernick, C., Yaffe, K., Majdan, M., Johansson, G., et al. (2019). Head trauma in sports - clinical characteristics, epidemiology and biomarkers. J. Intern. Med. 285, 624–634. doi: 10.1089/neu.2013.3017

PubMed Abstract | CrossRef Full Text | Google Scholar