Buffering by Transporters Can Spare Geometric Hindrance in Controlling Glutamate Escape

The surface of astrocyte processes that often surround excitatory synapses is packed with high-affinity glutamate transporters, largely preventing extrasynaptic glutamate escape. The shape and prevalence of perisynaptic astroglia vary among brain regions, in some cases providing a complete isolation of synaptic connections from the surrounding tissue. The perception has been that the geometry of perisynaptic environment is therefore essential to preventing extrasynaptic glutamate escape. To understand to what degree this notion holds, we modelled brain neuropil as a space filled with a scatter of randomly sized, overlapping spheres representing randomly shaped cellular elements and intercellular lumen. Simulating release and diffusion of glutamate molecules inside the interstitial gaps in this medium showed that high-affinity transporters would efficiently constrain extrasynaptic spread of glutamate even when diffusion passages are relatively open. We thus estimate that, in the hippocampal or cerebellar neuropil, the bulk of glutamate released by a synaptic vesicle is rapidly bound by transporters (or high-affinity target receptors) mainly in close proximity of the synaptic cleft, whether or not certain physiological or pathological events change local tissue geometry.

Introduction

Glutamatergic circuitry of the brain has long been associated with a “wired,” one-to-one type of transmission that carries excitatory signals between individual nerve cells. This type of connectivity has provided a basis upon which the computation logic of neural-network learning algorithms was established and benefited from. To ensure that glutamate released into the synaptic cleft does not escape activating its receptors beyond the target cell, excitatory synapses are often surrounded by perisynaptic astrocyte processes (PAPs), part of the sponge-like morphology of brain astroglia. PAPs vary extensively in shape and size, and their membrane surface is densely packed with high-affinity glutamate transporters, among other signalling molecules (reviewed in Heller and Rusakov, 2015; Bazargani and Attwell, 2016; Murphy-Royal et al., 2017; Rose et al., 2017; Verkhratsky and Nedergaard, 2018). At some specialised synaptic connections, PAPs form a comprehensive isolating shield around one or several synaptic contacts (Barbour, 1993; Grosche et al., 1999; Rollenhagen et al., 2007; Borst and Soria van Hoeve, 2012). However, common (small) cortical synapses normally have only a varied fraction of their immediate neuropil environment (20–80%) occupied by PAPs (Spacek and Harris, 1998; Ventura and Harris, 1999; Witcher et al., 2007; Lushnikova et al., 2009; Patrushev et al., 2013; Bernardinelli et al., 2014; Medvedev et al., 2014; Pannasch et al., 2014; Gavrilov et al., 2018; Henneberger et al., 2020). It has often been argued that the synapse has to be comprehensively surrounded by the transporter-enriched PAPs, to prevent synaptically released glutamate from spilling over to the neighbouring tissue. Whilst the latter would indeed stop glutamate from escaping, whether the commonly observed partial PAP coverage is as effective in this respect has remained uncertain, prompting intense theoretical and experimental exploration of extrasynaptic glutamate escape (Diamond, 2001; Rusakov, 2001; Scimemi et al., 2004; Szapiro and Barbour, 2007; Zheng et al., 2008; Scimemi et al., 2009; Henneberger et al., 2020).

This issue has been somewhat blurred by the “aqueous” connotation arising from the commonly used term “glutamate spillover.” In reality, glutamate molecules do not flow or spill over as do liquids. They undergo rapid Brownian diffusion, bouncing off multiple nanoscale obstacles (such as water molecules) millions of times, moving into random directions, in nanoscale steps. Thus, any diffusing glutamate molecule has a chance to encounter a PAP surface populated with high-affinity glutamate transporters. The other issue affecting our perception of extrasynaptic glutamate actions is our understanding of the extracellular space architecture. The classical electron micrographs of fixed brain tissue tend to depict the interstitial space as a system of thin gaps between adjacent cell membranes. It has emerged, however, that in live brain the extracellular space occupies ∼20% of neuropil tissue volume, with interstitial gaps sometimes as wide as 200 nm (Thorne and Nicholson, 2006; Tonnesen et al., 2018; Paviolo et al., 2020). These data suggest that there could be much less geometric hindrance to diffusion in the brain neuropil than commonly perceived. Our aim was therefore to understand better, in comparative terms, the roles of geometric hindrance and of glutamate transporter binding in regulating extrasynaptic escape of glutamate, as predicted by physics. To this end, we explored detailed Monte Carlo simulations of particle diffusion and (transporter) binding in complex, quasi-randomly shaped geometries representing the extracellular space.

Methods

Monte Carlo Simulations of Particle Diffusion

Monte Carlo algorithms for particle diffusion were designed and run with MATLAB: they were previously described in detail, and tested and constrained using various experimental settings (Savtchenko et al., 2013, 2021; Sylantyev et al., 2013). The simulation arena was a 3 μm wide cube, with 2,000 particles “released” instantaneously at the centre. Particles positioned at time t at point r_i(x,y,z) were moved, over time step Δt, to point r_{i + 1}(x + 2δ_xΔ_1D,y + 2δ_yΔ_1D,z + 2δ_zΔ_1D) where Δ_1D stands for the mean square displacement in the Einstein’s diffusion equation for 1D Brownian motion ${\mathrm{\Delta }}_{1\mathrm{D}}^2=2D\mathrm{\Delta }t$, D = 0.65 μm²/ms is the glutamate diffusion coefficient in the interstitial space (Zheng et al., 2017), and δ_{x| y| z} denotes a “delta-correlated” (independently seeded, uncorrelated) uniform random number from the (–1, 1) range. The latter ensures that Brownian particles are equally likely to move into either direction whereas scale factor 2 for δ gives the average elementary displacement in x-y-z either –Δ_1D or +Δ_1D. This algorithm provided the duty-cycle translational particle movements in a contiguous 3D space, over all directions with varied 3D steps, rather than over the rectangular 3D-lattice vertices used by us and many others previously. The randomness of the displacement vector helped avoid occasional numerical deadlocks for particles trapped near the space dead-ends formed by aggregated overlapped spheres. The time step Δt (usually < 0.1 μs) was set to be small enough to prevent particles from “tunnelling” through the smallest obstacles, and the actual value of D was verified at regular intervals.

The interaction with obstacles was simulated either as an elastic collision, or as a permanent bond (the catchment layer of ± 3 nm of the sphere surface, comparable with the maximal elementary displacement Δ_1D), with the probability as indicated. Because the characteristic diffusion time from the centre to the arena boundary (<1 ms) was much shorter than the time constant of glutamate unbinding from glial glutamate transporter (GLT1 type), particle binding to the spheres on the millisecond scale was set as permanent.

Simulating Sphere-Filled Space Representing Brain Neuropil

There were at least two reasons to believe that randomly sized overlapping spheres would be a more realistic representation of neuropil compared to regular lattices of regular shapes, a tissue model used extensively by us and others previously. Firstly, multiple intersecting spheres give randomly shaped and randomly sized cellular elements and extracellular channels, as opposed to uniform or regular structures. Secondly, this approach provides a mixture of concave and convex shapes, including “diffusion dead-ends” which are considered an important trait of brain neuropil (Hrabe et al., 2004). Both features therefore reflect reality better than do regular lattices.

Filling the space with overlapping spheres followed the routines described in detail previously (Savtchenko et al., 2021). In brief, the key parameter controlling this procedure was the volume fraction β occupied by the spheres: β = 1-α where α commonly stands for medium porosity, such as the volume fraction of the extracellular space in brain tissue. The β-value was calculated by (a) scattering 10⁵ test points uniformly randomly throughout the arena, and (b) calculating the proportion of the point falling outside the spheres. We verified that increasing the number of such test points to 10⁶ altered β by < 1%, pointing to asymptotic accuracy.

To fill the space with overlapping spheres that have a distributed size, we generated random co-ordinates of sphere centroids across the arena, and the random radius value for each sphere, in accord with the designated diameter distribution, which in our case was uniformly random between 20 and 100 nm. The initial number of spheres was estimated based on their average volume and the average size (to give the required β-value), and we left the co-ordinate origin unoccupied by any sphere. The space-filling cycle was repeated, with adjusted sphere numbers, until β approached the required value with ∼5% accuracy.

Our initial tests revealed that introducing transporter binding effectively restricted free particle movement across the simulated arena within ∼1 ms. We therefore limited simulated time to 1 ms.

Computing Environment

Monte Carlo simulations were run on a dedicated 8-node BEOWULF-style diskless PC cluster running under the Gentoo LINUX operating system (kernel 4.12.12), which was an upgraded, ad hoc built version of the cluster described earlier (Zheng et al., 2008). Individual nodes comprised an HP ProLiant DL120 G6 Server containing a quad-core Intel Xeon X3430 processor and 8 GB of DDR3 RAM. Nodes were connected through a NetGear Gigabit Ethernet switch to a master computer that distributes programs and collects the results on its hard disk. Parallelisation and optimisation of the algorithms and program codes were implemented by AMC Bridge LLC (Waltham, MA).

Results

Surface Binding Is Efficient in Curtailing Particle Diffusion Even in Highly Porous Environment

In a porous medium, the diffusion transfer rate scales, at least to a first approximation, with medium porosity α (Tartakovsky and Dentz, 2019), which in the brain represents tissue volume fraction of the extracellular space (Sykova and Nicholson, 2008). Thus, narrowing interstitial passages in the neuropil will slow down escape of glutamate released at the synapse. To understand how this would affect the scatter of glutamate molecules away from the release site, we simulated brain neuropil as a space filled by randomly sized, overlapping spheres representing cellular structures: this procedure formed a porous, randomly shaped medium, with volume fraction β occupied by spheres, or porosity α = 1-β (see section “Methods”) (Savtchenko et al., 2021).

For the sake of comparison, we first tracked the fate of 2,000 diffusing particles representing glutamate molecules released in the middle of a 3 μm cube arena, with space porosity of either α = 0.7 or α = 0.2, the latter representing an adult mammalian brain (Thorne and Nicholson, 2006; Tonnesen et al., 2018). The diffusion coefficient for glutamate was set at D = 0.65 μm²/ms, as measured through diffusion retardation in the interstitial brain space using time-resolved fluorescence anisotropy imaging (Suhling et al., 2015; Zheng et al., 2017). Because the characteristic free-diffusion time over the arena was < 1 ms, our simulations ran for 1 ms. The outcome showed that narrowing diffusion passages by 3.5 times slowed down particle escape, so that the molecular scatter became 1.5–2 times narrower (Figures 1A,B).

FIGURE 1

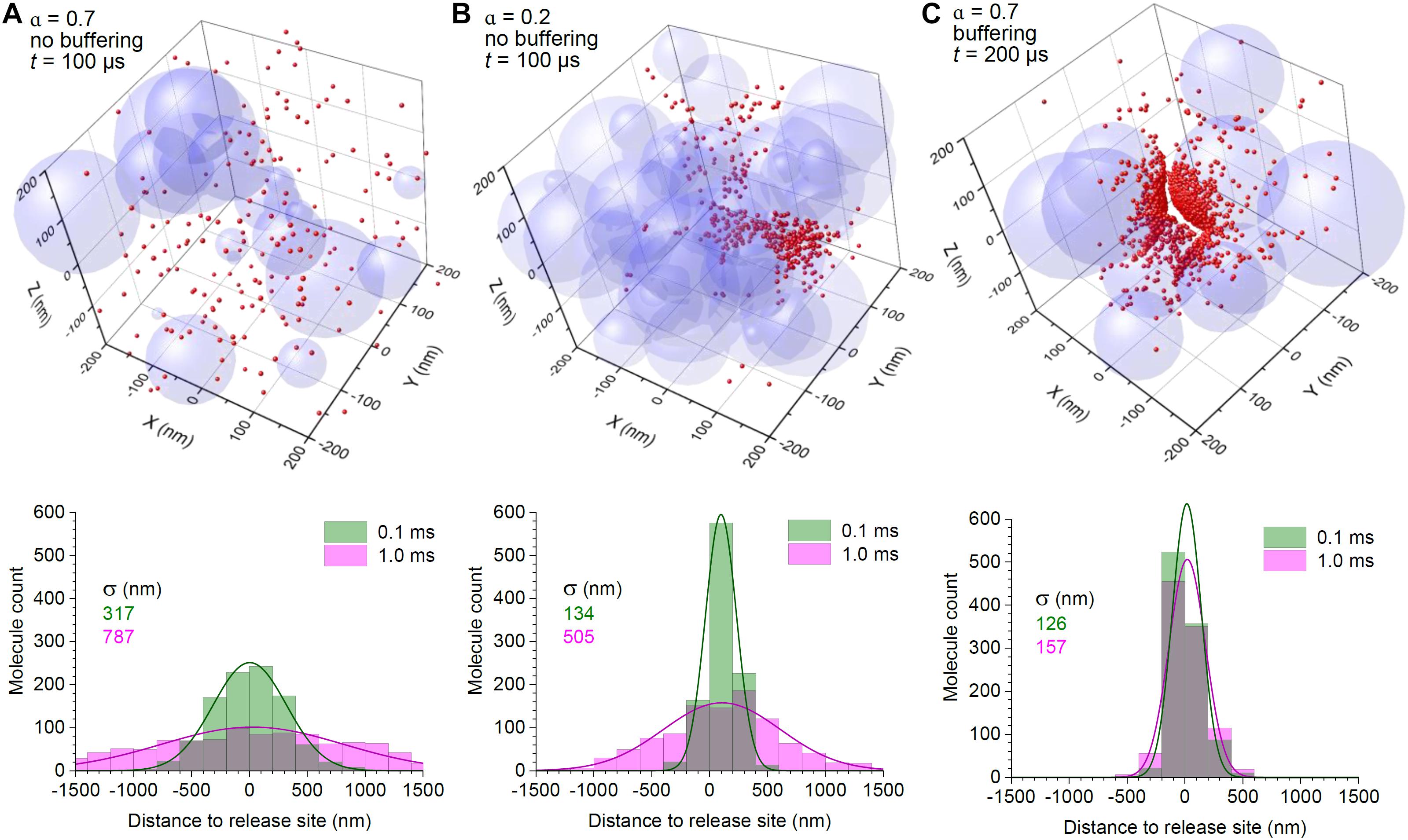
Figure 1. Surface binding to high-affinity transporters provides efficient control of extrasynaptic glutamate escape even in high-porosity tissue. (A) 3D graph: A snapshot of the simulated molecular scatter (400 nm wide fragment of the 3 μm wide simulation arena), 0.1 ms after release of 2,000 particles in the centre, with a scatter of overlapping spheres representing 3D obstacles to diffusion; α = 0.7, medium porosity (volume fraction of the free space). Histogram: spatial distribution of diffusing particles across the simulation arena, at two time points post-release, as indicated; solid lines, best-fit Gaussian distribution; σ, distribution dispersion (standard deviation). (B) Simulations as in (A), but with medium porosity α = 0.2; note that the particle scatter is skewed because of the asymmetric geometry of diffusion obstacles (sphere aggregates); other notations as in (A). (C) Simulations as in (A), but with the particle-surface binding enabled; particle catchment occurs at a distance of ± 3 nm of the surface, to reflect the elementary diffusion displacement Δ_1D (see section “Methods”); other notations as in (A).

Next, instead of narrowing the extracellular space, we equipped surfaces of the spheres with the ability to hold diffusing molecules that “bumped” into them. This arrangement reflects the scenario when astroglial surfaces that are densely populated with GLT1 transporters (up to 10⁵ μm^–2; Lehre and Danbolt, 1998; Lehre and Rusakov, 2002) represent all cell membranes in the nearby neuropil. Again, the time constant characterising glutamate unbinding or the glutamate uptake rate for the main glial glutamate transporter GLT1 is much longer than the diffusion time of < 1 ms (Bergles et al., 2002; Savtchenko et al., 2018). Thus, a permanent bond was fully representative of glutamate-transporter interaction on this time scale. Simulations showed that in these conditions the molecules remained within the vicinity of the release site, with little progression of the spread, even though 80% of the medium was available for free diffusion (Figure 1C).

Glutamate Escape in Realistic Neuropil

The results above illustrate that, in principle, binding to glutamate transporters could provide an efficient barrier to diffusion even when the diffusion passages are widely open. However, it was important to relate these observations to a set of parameters characteristic of the real brain neuropil. Whilst α = 0.2 is thought to faithfully represent brain tissue porosity across regions (Nicholson and Phillips, 1981; Sykova and Nicholson, 2008; Tonnesen et al., 2018), astroglial coverage of synapse varies significantly. Stereological estimates based on quantitative electron microscopy suggest that in the neuropil of the rodent cerebellum (molecular layer) and hippocampus (area CA1), astroglial surfaces represent a ∼30 and 13% fraction, respectively, of all cell membrane surfaces (Lehre and Danbolt, 1998; Lehre and Rusakov, 2002; Savtchenko et al., 2018), whereas in the supraoptic nucleus cortex this fraction could exceed 50% (Pilgrim et al., 1982).

Based on these measurements, we first simulated glutamate release and diffusion in a modelled neuropil with α = 0.2 as in Figure 1B, but with the probability for individual molecules to be bound by the surface of either 0.3 or 0.13, thus representing the occurrence of transporter-enriched astroglial membranes in the cerebellar molecular layer or hippocampal area CA1, respectively. This approach assumes that the occurrence of astroglial and non-astroglial membranes near excitatory synapses does not follow any regular pattern but is arbitrary, which appears in line with the quantitative analyses of synaptic environment (Lehre and Rusakov, 2002; Patrushev et al., 2013; Medvedev et al., 2014). The other important assumption here is that the numbers of glutamate transporters expressed in perisynaptic astroglial membranes are much higher than the numbers of released glutamate molecules, a relationship consistent with single-vesicle release (Lehre and Danbolt, 1998; Savtchenko et al., 2013). We have also introduced a 320 nm wide, 20 nm thick synaptic cleft (free of transporters) based on the typical dimensions of such clefts at CA3-CA1 synapses (Harris and Stevens, 1989; Harris et al., 1992), centred at the arena co-ordinate origin, coinciding with the glutamate release site.

The results suggest that the bulk of glutamate escaping from cerebellar molecular layer synapses is bound to transporters within ∼100 nm from the cleft, so that virtually all molecules become immobile very rapidly after ∼0.1 ms (Figure 2A). In these simulations, the distribution histograms represent all, both free and transporter-bound, molecules, so that the spatiotemporal dynamics of freely diffusing glutamate is reflected in how this distribution changes in time (see section “Discussion”). In the hippocampus, where astroglial presence is three times lower, the glutamate profile does change from 0.1 to 1 ms post-release, allowing for a more widespread “tail” of diffusing molecules, even though the majority of them still remain bound in close proximity to the cleft (Figure 2B).

FIGURE 2

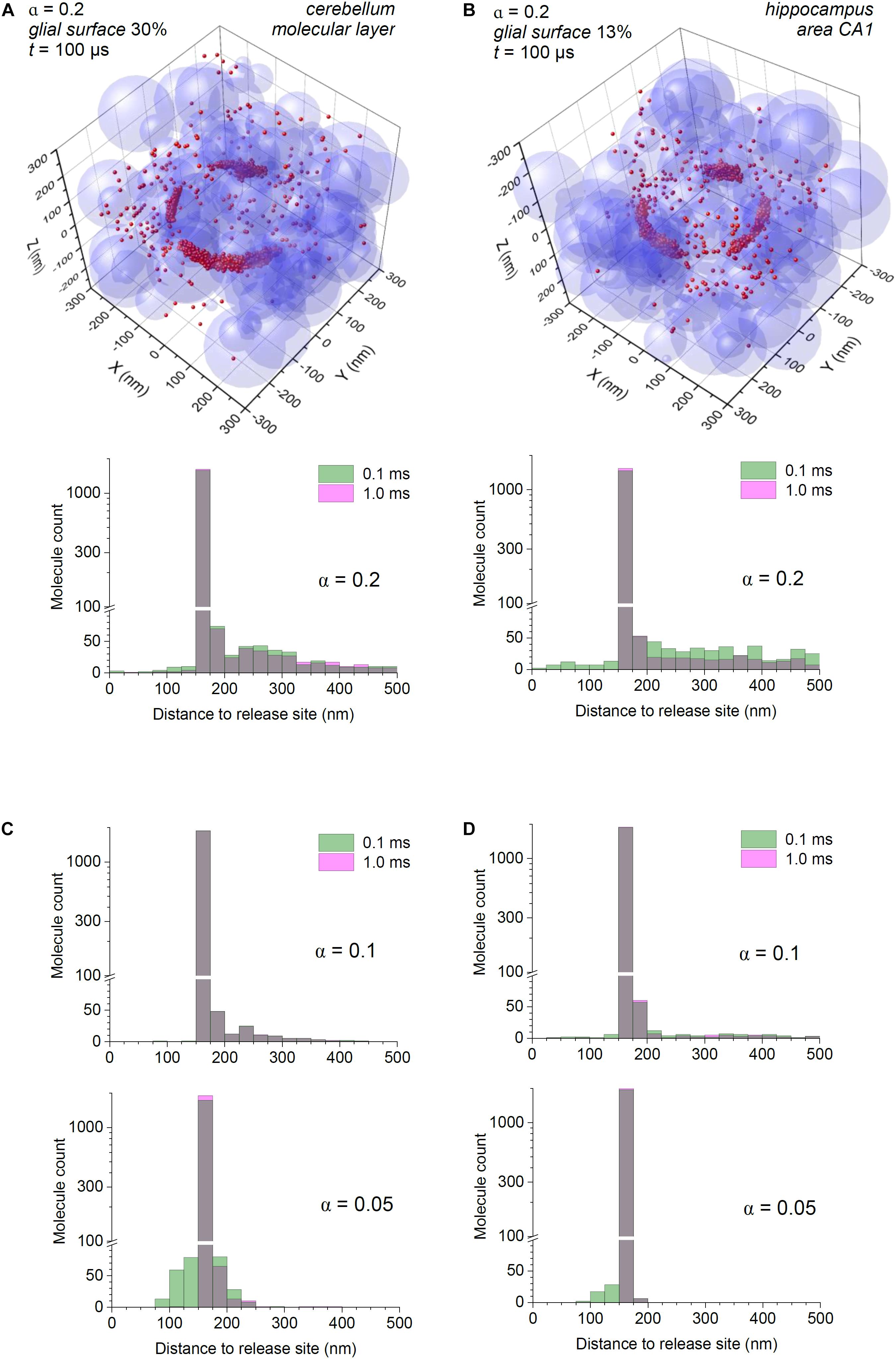
Figure 2. Astroglial high-affinity transporters control the scatter of escaping glutamate molecules in the modelled cerebellar and hippocampal neuropil. (A) Simulations as in Figure 1B, with the synaptic cleft (diameter 320 nm, height 20 nm) placed in the co-ordinate origin (also glutamate release site); particle-surface binding enabled, for each particle with probability of 0.3 (to mimic 30% chance of encountering cell membranes representing astroglia); medium porosity α = 0.2. Histogram: spatial distribution of glutamate molecules (free and transporter-bound combined) across the simulation arena, at two time points post-release, as indicated; note two scales (one log-scale) of the ordinate. (B) Simulations as in (A), with the particle-surface binding enabled, for each particle with probability of 0.13 (to mimic 13% of neuropil cell membranes representing astroglia); other notations as in (A). (C) Simulation outcome (molecule distribution histograms) for the model shown (A), but with tissue porosity values α = 0.1 and α = 0.05, as indicated); other notations as in (A). (D) Simulation outcome (molecule distribution histograms) for the model shown (B), but with tissue porosity values α = 0.1 and α = 0.05, as indicated); other notations as in (B).

The Effect of Extracellular Space Shrinkage or Expansion

It has long been known that during intense excitatory activity, or in some pathological conditions such as epilepsy or ischemia, the extracellular space of the brain can shrink (Lux et al., 1986; Vorisek and Sykova, 1997; Vargova et al., 2001; Witcher et al., 2010). We have therefore asked whether such changes could significantly affect extrasynaptic escape of glutamate, by repeating our simulations for reduced porosity values. As expected, decreasing tissue porosity α from 0.2 to 0.1 and further to 0.05 led to a lower number of molecules escaping away from the cleft. However, the main feature of glutamate escape, its intense binding in cleft proximity, remained (Figures 2C,D).

Finally, we asked what could happen when the extracellular space is significantly expanded, which is thought to be the case during postnatal development (Lehmenkuhler et al., 1993), but also in the human cerebellum (Cragg, 1979). Simulations adopting α = 0.5 still indicated perisynaptic binding as a prevalent feature even though glutamate molecules have a significantly wider spread, and a longer free-diffusion span than in cases with lower α (Figure 3).

FIGURE 3

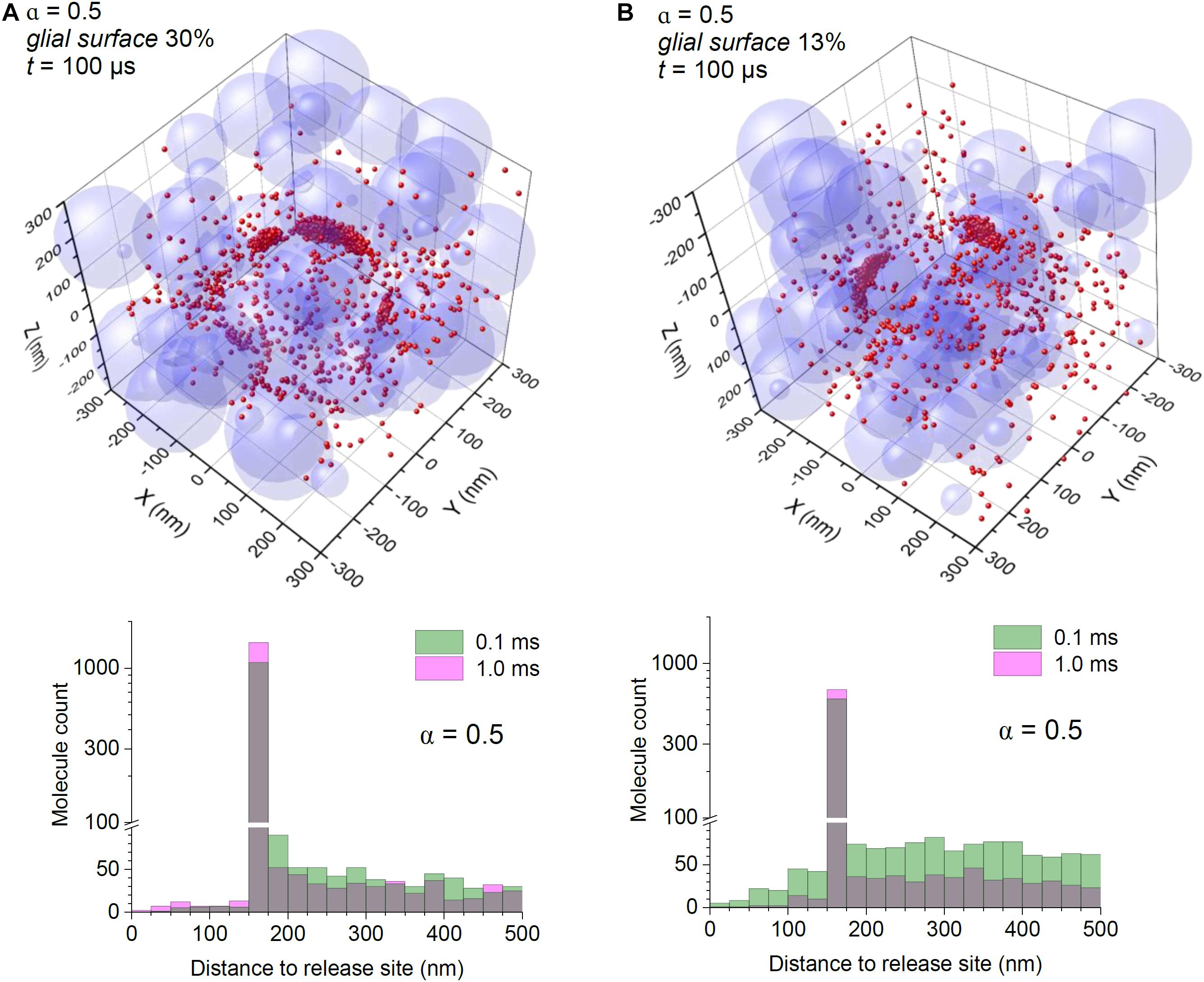
Figure 3. Astroglial high-affinity transporters control the scatter of escaping glutamate molecules under conditions of expanded extracellular space. (A) Simulations as in Figure 2, with the particle-surface binding enabled, for each particle with probability of 0.3 (to mimic 30% chance of encountering cell membranes representing astroglia); tissue porosity α = 0.5; other notations as in Figure 2A. (B) Simulations as in (A), but with the particle-surface binding enabled, for each particle with probability of 0.13 (to mimic 13% of neuropil cell membranes representing astroglia); other notations as in (A).

Discussion

Scope and Limitations

It this study we asked which aspects of the perisynaptic environment are prevalent in controlling glutamate escape from excitatory synapses. Our primary purpose was therefore to understand whether geometric hindrance by tissue elements, and high-affinity binding by glutamate transporters, play comparable roles, in this context. The goal was neither to firmly establish the “true” glutamate escape profile for a particular synaptic type nor to expand such claims to various synaptic types featuring varied morphologies. The modelling relied on several basic assumptions, such as (a) single-vesicle glutamate release hence non-saturation of local glutamate transporters, (b) random distribution of glial and non-glial cellular surfaces in the neuropil, with the ratio established purely by the probability of encountering one or the other surface, and (c) negligible binding inside the synaptic cleft (numbers of glutamate receptors much smaller than that of released glutamate molecules). Clearly, these assumptions impose certain interpretability limitations: repetitive synaptic discharges or highly asymmetric occurrence of perisynaptic astroglia may produce a somewhat different dynamic picture of glutamate escape.

Empirical Relevance

Our estimates are generally consistent with the previous theoretical assessments that used alternative modelling approaches (Scimemi et al., 2004; Zheng et al., 2008; Scimemi et al., 2009; Zheng and Rusakov, 2015; Armbruster et al., 2020) predicting a very rapid fall of free glutamate concentration the cleft. However, the distributions of mainly bound molecules obtained here could be particularly relevant to the experimental measurements of extrasynaptic glutamate escape using optical glutamate sensors (Hires et al., 2008; Jensen et al., 2019; Armbruster et al., 2020; Henneberger et al., 2020). Because such sensors feature the glutamate binding rate on the same scale as do glutamate transporters, one could simply assume that in our simulations a proportion of the binding sites represents glutamate sensors. In this case, the local sensor/transporter concentration ratio would reflect the ratio of glutamate molecules bound to the two respective targets. In other words, assuming no significant difference between the spatial arrangement of either transporters and sensors (e.g., as in the case of astroglia-expressing iGluSnFR), the distribution profiles obtained here for bound glutamate molecules should be equally relevant to sensor-bound molecules.

One may argue that the experimental fluorescence profiles of glutamate-bound iGluSnFR around synapses are much smoother, and with no “voids” indicating the synaptic cleft, compared with the profiles shown here (Jensen et al., 2019). However, this is most likely because fluorescence signal is blurred over the point-spread function of an optical system (∼0.4 μm in the xy plane and ∼1 μm in the z direction), and because imaged synapses will have their cleft randomly oriented with respect to the focal plane. Exploring 3D simulation results by mimicking optical projections to match a particular imaging setting should bring theoretical findings closer to a faithful representation of experimental readout.

In this context, one novelty element of the present simulations is tissue modelling that uses randomly sized, randomly positioned intersecting spheres. As explained in the section “Methods,” we believe that this approach should provide a fairer representation of brain neuropil than would regular lattices of regular shapes that we and others employed previously. Also, we presented examples of individual trials rather than averaged outcome because “average synapse geometry” is a non-existing entity in which important “outlier” features of perisynaptic architecture could be unduly smoothed out. We therefore considered it intuitively more revealing, in this particular case, to illustrate individual Monte Carlo realisations.

Extracellular Space in Pathology

Our basic results suggest that glutamate transporters can efficiently restrict glutamate diffusion even when the diffusion escape passages are relatively open. As mentioned, dynamic changes of the extracellular space volume, such as its transient or long-term shrinkage, have long been associated with pathological brain conditions such as in epilepsy or stroke (Lux et al., 1986; Vorisek and Sykova, 1997; Sykova, 2001; Vargova et al., 2001; Witcher et al., 2010). At the same time, physiological studies of neurodegenerative diseases, stroke, or addiction have found reduced expression of glial glutamate transporters in brain tissue (Maragakis and Rothstein, 2004; Fontana, 2015; Kruyer et al., 2019), which normally undergo rapid recycling on astroglial surfaces (Michaluk et al., 2021). The present results suggests that, over a wide range of tissue porosities, high-affinity transporters remain the principal factor in curtailing glutamate escape. Thus, the availability of high-affinity glutamate transporters appears a prevalent mechanism to control extrasynaptic actions of glutamate in pathological conditions affecting brain tissue architectonics.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

LS designed and carried out computer simulations. KZ designed and provided cluster computing facilities. DR narrated the study, designed specific tests, and wrote the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Wellcome Trust Principal Fellowship (212251_Z_18_Z), ERC Advanced Grant (323113), and European Commission NEUROTWIN grant (857562), to DR.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Parallelisation and optimisation of the algorithms and program codes were implemented by AMC Bridge LLC (Waltham, MA).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fncel.2021.707813/full#supplementary-material

References

Armbruster, M., Dulla, C. G., and Diamond, J. S. (2020). Effects of fluorescent glutamate indicators on neurotransmitter diffusion and uptake. Elife 9:e54441.

Google Scholar

Barbour, B. (1993). Synaptic currents evoked in purkinje-cells by stimulating individual granule cells. Neuron 11, 759–769. doi: 10.1016/0896-6273(93)90085-6

CrossRef Full Text | Google Scholar

Bazargani, N., and Attwell, D. (2016). Astrocyte calcium signaling: the third wave. Nat. Neurosci. 19, 182–189. doi: 10.1038/nn.4201

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergles, D. E., Tzingounis, A. V., and Jahr, C. E. (2002). Comparison of coupled and uncoupled currents during glutamate uptake by GLT-1 transporters. J. Neurosci. 22, 10153–10162. doi: 10.1523/jneurosci.22-23-10153.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernardinelli, Y., Muller, D., and Nikonenko, I. (2014). Astrocyte-synapse structural plasticity. Neural Plast. 2014:232105.

Google Scholar

Borst, J. G., and Soria van Hoeve, J. (2012). The calyx of held synapse: from model synapse to auditory relay. Annu. Rev. Physiol. 74, 199–224. doi: 10.1146/annurev-physiol-020911-153236

PubMed Abstract | CrossRef Full Text | Google Scholar

Cragg, B. (1979). Overcoming the failure of electron-microscopy to preserve the brains extracellular-space. Trends Neurosci. 2, 159–161. doi: 10.1016/0166-2236(79)90062-6

CrossRef Full Text | Google Scholar

Diamond, J. S. (2001). Neuronal glutamate transporters limit activation of NMDA receptors by neurotransmitter spillover on CA1 pyramidal cells. J. Neurosci. 21, 8328–8338. doi: 10.1523/jneurosci.21-21-08328.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Fontana, A. C. (2015). Current approaches to enhance glutamate transporter function and expression. J. Neurochem. 134, 982–1007. doi: 10.1111/jnc.13200

PubMed Abstract | CrossRef Full Text | Google Scholar

Gavrilov, N., Golyagina, I., Brazhe, A., Scimemi, A., Turlapov, V., and Semyanov, A. (2018). Astrocytic coverage of dendritic spines, dendritic shafts, and axonal boutons in hippocampal neuropil. Front. Cell Neurosci. 12:248.

Google Scholar

Grosche, J., Matyash, V., Moller, T., Verkhratsky, A., Reichenbach, A., and Kettenmann, H. (1999). Microdomains for neuron-glia interaction: parallel fiber signaling to Bergmann glial cells. Nat. Neurosci. 2, 139–143. doi: 10.1038/5692

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, K. M., Jensen, F. E., and Tsao, B. (1992). Three-dimensional structure of dendritic spines and synapses in rat hippocampus (CA1) at postnatal day 15 and adult ages: implications for the maturation of synaptic physiology and long-term potentiation. J. Neurosci. 12, 2685–2705. doi: 10.1523/jneurosci.12-07-02685.1992

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, K. M., and Stevens, J. K. (1989). Dendritic spines of CA 1 pyramidal cells in the rat hippocampus: serial electron microscopy with reference to their biophysical characteristics. J. Neurosci. 9, 2982–2997. doi: 10.1523/jneurosci.09-08-02982.1989

PubMed Abstract | CrossRef Full Text | Google Scholar

Heller, J. P., and Rusakov, D. A. (2015). Morphological plasticity of astroglia: Understanding synaptic microenvironment. Glia 63, 2133–2151. doi: 10.1002/glia.22821

PubMed Abstract | CrossRef Full Text | Google Scholar

Henneberger, C., Bard, L., Panatier, A., Reynolds, J. P., Kopach, O., Medvedev, N. I., et al. (2020). LTP induction boosts glutamate spillover by driving withdrawal of perisynaptic astroglia. Neuron 108:e911.

Google Scholar

Hires, S. A., Zhu, Y., and Tsien, R. Y. (2008). Optical measurement of synaptic glutamate spillover and reuptake by linker optimized glutamate-sensitive fluorescent reporters. Proc. Natl. Acad. Sci. U.S.A. 105, 4411–4416. doi: 10.1073/pnas.0712008105

PubMed Abstract | CrossRef Full Text | Google Scholar

Hrabe, J., Hrabetova, S., and Segeth, K. (2004). A model of effective diffusion and tortuosity in the extracellular space of the brain. Biophys. J. 87, 1606–1617. doi: 10.1529/biophysj.103.039495

PubMed Abstract | CrossRef Full Text | Google Scholar

Jensen, T. P., Zheng, K. Y., Cole, N., Marvin, J. S., Looger, L. L., and Rusakov, D. A. (2019). Multiplex imaging relates quantal glutamate release to presynaptic Ca2+ homeostasis at multiple synapses in situ. Nat. Commun. 10:1414.

Google Scholar

Kruyer, A., Scofield, M. D., Wood, D., Reissner, K. J., and Kalivas, P. W. (2019). Heroin cue-evoked astrocytic structural plasticity at nucleus accumbens synapses inhibits heroin seeking. Biol. Psychiatry 86, 811–819. doi: 10.1016/j.biopsych.2019.06.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmenkuhler, A., Sykova, E., Svoboda, J., Zilles, K., and Nicholson, C. (1993). Extracellular-space parameters in the rat neocortex and subcortical white-matter during postnatal-development determined by diffusion analysis. Neuroscience 55, 339–351. doi: 10.1016/0306-4522(93)90503-8

CrossRef Full Text | Google Scholar

Lehre, K. P., and Danbolt, N. C. (1998). The number of glutamate transporter subtype molecules at glutamatergic synapses: chemical and stereological quantification in young adult rat brain. J. Neurosci. 18, 8751–8757. doi: 10.1523/jneurosci.18-21-08751.1998

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehre, K. P., and Rusakov, D. A. (2002). Asymmetry of glia near central synapses favors presynaptically directed glutamate escape. Biophys. J. 83, 125–134. doi: 10.1016/s0006-3495(02)75154-0

CrossRef Full Text | Google Scholar

Lushnikova, I., Skibo, G., Muller, D., and Nikonenko, I. (2009). Synaptic potentiation induces increased glial coverage of excitatory synapses in CA1 hippocampus. Hippocampus 19, 753–762. doi: 10.1002/hipo.20551

PubMed Abstract | CrossRef Full Text | Google Scholar

Lux, H. D., Heinemann, U., and Dietzel, I. (1986). Ionic changes and alterations in the size of the extracellular space during epileptic activity. Adv. Neurol. 44, 619–639.

Google Scholar

Maragakis, N. J., and Rothstein, J. D. (2004). Glutamate transporters: animal models to neurologic disease. Neurobiol. Dis. 15, 461–473. doi: 10.1016/j.nbd.2003.12.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Medvedev, N., Popov, V., Henneberger, C., Kraev, I., Rusakov, D. A., and Stewart, M. G. (2014). Glia selectively approach synapses on thin dendritic spines. Philos. Trans. R. Soc. Lond. B Biol. Sci. 369:20140047. doi: 10.1098/rstb.2014.0047

PubMed Abstract | CrossRef Full Text | Google Scholar

Michaluk, P., Heller, J. P., and Rusakov, D. A. (2021). Rapid recycling of glutamate transporters on the astroglial surface. Elife 10:64714.

Google Scholar

Murphy-Royal, C., Dupuis, J., Groc, L., and Oliet, S. H. R. (2017). Astroglial glutamate transporters in the brain: Regulating neurotransmitter homeostasis and synaptic transmission. J. Neurosci. Res. 95, 2140–2151. doi: 10.1002/jnr.24029

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicholson, C., and Phillips, J. M. (1981). Ion diffusion modified by tortuosity and volume fraction in the extracellular micro-environment of the rat cerebellum. J. Physiol. Lond. 321, 225–257. doi: 10.1113/jphysiol.1981.sp013981

PubMed Abstract | CrossRef Full Text | Google Scholar

Pannasch, U., Freche, D., Dallerac, G., Ghezali, G., Escartin, C., Ezan, P., et al. (2014). Connexin 30 sets synaptic strength by controlling astroglial synapse invasion. Nat. Neurosci 17, 549–558. doi: 10.1038/nn.3662

PubMed Abstract | CrossRef Full Text | Google Scholar

Patrushev, I., Gavrilov, N., Turlapov, V., and Semyanov, A. (2013). Subcellular location of astrocytic calcium stores favors extrasynaptic neuron-astrocyte communication. Cell Calcium 54, 343–349. doi: 10.1016/j.ceca.2013.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Paviolo, C., Soria, F. N., Ferreira, J. S., Lee, A., Groc, L., Bezard, E., et al. (2020). Nanoscale exploration of the extracellular space in the live brain by combining single carbon nanotube tracking and super-resolution imaging analysis. Methods 174, 91–99. doi: 10.1016/j.ymeth.2019.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Pilgrim, C., Reisert, I., and Grab, D. (1982). Volume densities and specific surfaces of neuronal and glial tissue elements in the rat supraoptic nucleus. J. Comp. Neurol. 211, 427–431. doi: 10.1002/cne.902110409

PubMed Abstract | CrossRef Full Text | Google Scholar

Rollenhagen, A., Satzler, K., Rodriguez, E. P., Jonas, P., Frotscher, M., and Lubke, J. H. (2007). Structural determinants of transmission at large hippocampal mossy fiber synapses. J. Neurosci. 27, 10434–10444. doi: 10.1523/jneurosci.1946-07.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Rose, C. R., Felix, L., Zeug, A., Dietrich, D., Reiner, A., and Henneberger, C. (2017). Astroglial glutamate signaling and uptake in the hippocampus. Front. Mol. Neurosci. 10:451.

Google Scholar

Rusakov, D. A. (2001). The role of perisynaptic glial sheaths in glutamate spillover and extracellular Ca2+ depletion. Biophys. J. 81, 1947–1959. doi: 10.1016/s0006-3495(01)75846-8

CrossRef Full Text | Google Scholar

Savtchenko, L. P., Bard, L., Jensen, T. P., Reynolds, J. P., Kraev, I., Medvedev, N., et al. (2018). Disentangling astroglial physiology with a realistic cell model in silico. Nat. Commun. 9:3554.

Google Scholar

Savtchenko, L. P., Sylantyev, S., and Rusakov, D. A. (2013). Central synapses release a resource-efficient amount of glutamate. Nat. Neurosci. 16, 10–U163.

Google Scholar

Savtchenko, L. P., Zheng, K., and Rusakov, D. A. (2021). Conductance of porous media depends on external electric fields. Biophys. J. 120, 1431–1442. doi: 10.1016/j.bpj.2021.02.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Scimemi, A., Fine, A., Kullmann, D. M., and Rusakov, D. A. (2004). NR2B-containing receptors mediate cross talk among hippocampal synapses. J. Neurosci. 24, 4767–4777. doi: 10.1523/jneurosci.0364-04.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Scimemi, A., Tian, H., and Diamond, J. S. (2009). Neuronal transporters regulate glutamate clearance. NMDA receptor activation, and synaptic plasticity in the hippocampus. J. Neurosci. 29, 14581–14595. doi: 10.1523/jneurosci.4845-09.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Spacek, J., and Harris, K. M. (1998). Three-dimensional organization of cell adhesion junctions at synapses and dendritic spines in area CA1 of the rat hippocampus. J. Comp. Neurol. 393, 58–68. doi: 10.1002/(sici)1096-9861(19980330)393:1<58::aid-cne6>3.0.co;2-p

CrossRef Full Text | Google Scholar

Suhling, K., Hirvonen, L. M., Levitt, J. A., Chung, P.-H., Tregidgo, C., Le Marois, A., et al. (2015). Fluorescence lifetime imaging (FLIM): basic concepts and some recent developments. Med. Photon. 27, 3–40. doi: 10.1016/j.medpho.2014.12.001

CrossRef Full Text | Google Scholar

Sykova, E. (2001). Glial diffusion barriers during aging and pathological states. Prog. Brain Res. 132, 339–363. doi: 10.1016/s0079-6123(01)32087-3

CrossRef Full Text | Google Scholar

Sykova, E., and Nicholson, C. (2008). Diffusion in brain extracellular space. Physiol. Rev. 88, 1277–1340. doi: 10.1152/physrev.00027.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Sylantyev, S., Savtchenko, L. P., Ermolyuk, Y., Michaluk, P., and Rusakov, D. A. (2013). Spike-driven glutamate electrodiffusion triggers synaptic potentiation via a homer-dependent mGluR-NMDAR link. Neuron 77, 528–541. doi: 10.1016/j.neuron.2012.11.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Szapiro, G., and Barbour, B. (2007). Multiple climbing fibers signal to molecular layer interneurons exclusively via glutamate spillover. Nat. Neurosci. 10, 735–742. doi: 10.1038/nn1907

PubMed Abstract | CrossRef Full Text | Google Scholar

Tartakovsky, D. M., and Dentz, M. (2019). Diffusion in Porous Media: Phenomena and Mechanisms. Transport Porous Media 130, 105–127. doi: 10.1007/s11242-019-01262-6

CrossRef Full Text | Google Scholar

Thorne, R. G., and Nicholson, C. (2006). In vivo diffusion analysis with quantum dots and dextrans predicts the width of brain extracellular space. Proc. Natl. Acad. Sci. U.S.A. 103, 5567–5572. doi: 10.1073/pnas.0509425103

PubMed Abstract | CrossRef Full Text | Google Scholar

Tonnesen, J., Inavalli, V. V. G. K., and Nagerl, U. V. (2018). Super-resolution imaging of the extracellular space in living brain tissue. Cell 172, 1108–1121. doi: 10.1016/j.cell.2018.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Vargova, L., Jendelova, P., Chvatal, A., and Sykova, E. (2001). Glutamate, NMDA, and AMPA induced changes in extracellular space volume and tortuosity in the rat spinal cord. J. Cereb. Blood Flow Metab. 21, 1077–1089. doi: 10.1097/00004647-200109000-00005

PubMed Abstract | CrossRef Full Text | Google Scholar

Ventura, R., and Harris, K. M. (1999). Three-dimensional relationships between hippocampal synapses and astrocytes. J. Neurosci. 19, 6897–6906. doi: 10.1523/jneurosci.19-16-06897.1999

PubMed Abstract | CrossRef Full Text | Google Scholar

Verkhratsky, A., and Nedergaard, M. (2018). Physiology of astroglia. Physiol. Rev. 98, 239–389. doi: 10.1152/physrev.00042.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

Vorisek, I., and Sykova, E. (1997). Ischemia-induced changes in the extracellular space diffusion parameters, K+, and pH in the developing rat cortex and corpus callosum. J. Cereb. Blood Flow Metab. 17, 191–203. doi: 10.1097/00004647-199702000-00009

PubMed Abstract | CrossRef Full Text | Google Scholar

Witcher, M. R., Kirov, S. A., and Harris, K. M. (2007). Plasticity of perisynaptic astroglia during synaptogenesis in the mature rat hippocampus. Glia 55, 13–23. doi: 10.1002/glia.20415

PubMed Abstract | CrossRef Full Text | Google Scholar

Witcher, M. R., Park, Y. D., Lee, M. R., Sharma, S., Harris, K. M., and Kirov, S. A. (2010). Three-dimensional relationships between perisynaptic astroglia and human hippocampal synapses. Glia 58, 572–587.

Google Scholar

Zheng, K., and Rusakov, D. A. (2015). Efficient integration of synaptic events by NMDA receptors in three-dimensional neuropil. Biophys. J. 108, 2457–2464. doi: 10.1016/j.bpj.2015.04.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, K., Scimemi, A., and Rusakov, D. A. (2008). Receptor actions of synaptically released glutamate: the role of transporters on the scale from nanometers to microns. Biophys. J. 95, 4584–4596. doi: 10.1529/biophysj.108.129874

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, K. Y., Jensen, T. P., Savtchenko, L. P., Levitt, J. A., Suhling, K., and Rusakov, D. A. (2017). Nanoscale diffusion in the synaptic cleft and beyond measured with time-resolved fluorescence anisotropy imaging. Sci. Rep. 7:42022.

Google Scholar