- 1Division of Neurobiology, Department of Biology II, Ludwig-Maximilians-Universitaet Muenchen, Martinsried, Germany
- 2Department of Behavioural Neurobiology, Max Planck Institute for Ornithology, Seewiesen, Germany
- 3Princeton Neuroscience Institute, Princeton University, Princeton, NJ, United States
- 4Howard Hughes Medical Institute, Princeton University, Princeton, NJ, United States
Axons functionally link the somato-dendritic compartment to synaptic terminals. Structurally and functionally diverse, they accomplish a central role in determining the delays and reliability with which neuronal ensembles communicate. By combining their active and passive biophysical properties, they ensure a plethora of physiological computations. In this review, we revisit the biophysics of generation and propagation of electrical signals in the axon and their dynamics. We further place the computational abilities of axons in the context of intracellular and intercellular coupling. We discuss how, by means of sophisticated biophysical mechanisms, axons expand the repertoire of axonal computation, and thereby, of neural computation.
1. Introduction
Neurons are compartmentalized into input compartments formed by dendrites and somas, and an output compartment, the axon. However, in the current era, there is a widespread tendency to consider that the biophysics of single neurons do not matter to understand neuronal dynamics and behavior. Neurons are often treated as point processes with disregard of the complex biophysical machinery that they have evolved. Moreover, neuronal computations are assumed to be mostly performed by dendrites or at synapses (Südhof and Malenka, 2008; Stuart et al., 2016), and axons are reduced to simple, static, and reliable devices. However, a wealth of literature supports that this is not the case: axons form complex structures that ensure a variety of sophisticated functions and they are highly dynamic. Here, we aim to review evidence that axons perform complex computations which depend on a myriad of biophysical details and ensure the generation and propagation of neuronal outputs. We will not discuss biophysics of synaptic release, reviewed elsewhere (Südhof and Malenka, 2008).
More than six decades after seminal discoveries in experimentally accessible invertebrate axons (Hodgkin and Huxley, 1952), axonal research has unraveled previously-unsuspected, rich and dynamical electrical signaling in axons, which consists of a hybrid of analog and digital signaling. Contrary to the giant invertebrate axons studied in the early days (Hodgkin and Huxley, 1952; Furshpan and Potter, 1959), most invertebrate and vertebrate axons are thin and present complex extended arborizations (e.g., Figure 1), making it difficult to record from them. However, successful electrophysiological recordings from axons and terminals have been performed (Hu and Jonas, 2014; Kawaguchi and Sakaba, 2015) and electron and optical microscopy have made it possible to deepen our understanding of fine axonal structures (Rash et al., 2016; D'Este et al., 2017). Moreover, the combination of new structural imaging techniques with electrophysiology has made it possible to study how structural changes at the sub-micrometer scale impact function (Chéreau et al., 2017).
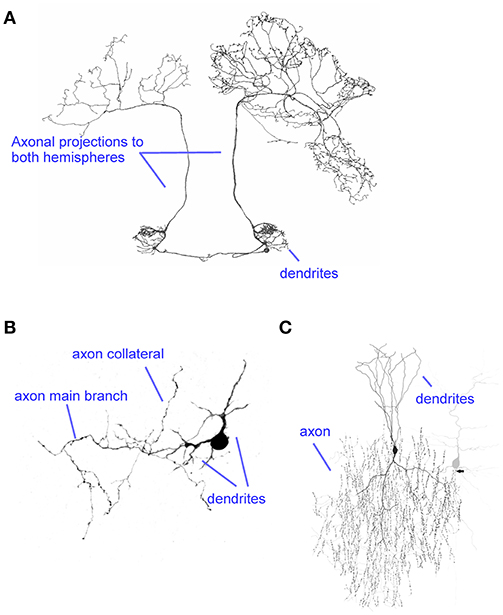
Figure 1. Diversity of axons. (A) The axon of the BAC cell in the honeybee projects onto the left and right hemispheres, targeting a large number of regions. Modified from Zwaka et al. (2016) (CC-BY). (B) A cerebellar rat stellate cell axon illustrates a small local axon. Modified from Alcami and Marty (2013). (C) The extensive arborization of a cortical chandelier cell targets the axon initial segment of many postsynaptic cells (example shown in gray). Modified from Wang et al. (2016) (CC-BY).
We will first illustrate general signaling principles in axons, before delving into the generation and propagation of action potentials (APs) and their dynamical regulation. We will comment on the computational abilities enabled by different mechanisms throughout the article. Finally, we will position axons in the context of their interactions with other compartments and with each other, by virtue of axo-axonal coupling (Katz and Schmitt, 1940; Furshpan and Potter, 1959) and finally, indirectly via glial cells.
2. Review of Axonal Computations
2.1. General Principles: Signaling in Axons
2.1.1. Of Axons and Brains
The propagation of electrical signals along axons controls the reliability and the timing with which neural networks communicate. The spatial extent of axonal trees introduces delays between the generation of an AP in a neuron and its arrival to the presynaptic site, where information is relayed to a postsynaptic cell. Thereby, the axonal propagation delay influences the temporal relationship of presynaptic and postsynaptic activity (Izhikevich et al., 2004).
The delays in AP propagation encode information (Seidl et al., 2010) and contribute to re-configuring neural circuits through plastic mechanisms such as spike timing dependent plasticity (Bi and Poo, 1998; Izhikevich et al., 2004). Each synapse is characterized by its own “critical window,” given by the delay between presynaptic and postsynaptic activity, to induce synaptic plasticity. The speed at which signals travel along axons can vary over four orders of magnitude, from tens of centimeters per second in thin unmyelinated axons to 100 m/s in giant myelinated fibers (Xu and Terakawa, 1999; Schmidt-Hieber et al., 2008); highlighting the ability of biophysical specializations of different axons to conduct APs at different speeds. In computational terms these specializations allow signals to travel at different speeds in neural circuits, diversifying and expanding the timescales at which neural computations take place. Moreover, they modulate the speed of information processing in neural circuits.
Axons have evolved different intricate geometries (Figure 1), revealing specific structure-function specializations. Constraints to axonal morphology include (1) spatial constraints: axons occupy large volumes of nervous systems, yet they require internal components necessary to their function such as mitochondria, which constrain their minimal functional size; (2) energetic requirements may have evolutionary exerted a selection pressure on axonal properties (Perge et al., 2009; Harris and Attwell, 2012); (3) efficiency of electrical information processing in relation to structure-function specializations. The last point on electrical information processing will be the main focus of the current review.
One first needs to define what a computation is in the context of neuronal information processing. We can state that the role of a neuron is to generate and transmit electrical signals. Ultimately, subthreshold signals and spikes propagate in axons, conveying a combined functional output message to the synaptic terminals (reviewed in Zbili and Debanne, 2019). These output signals need to first be generated by integrating input information received by soma and dendrites. Any modification of the input/output relation is to be considered a computation (Silver, 2010) since it contributes to the transformations that ultimately generate the functional message carried by axons. It is important to note that these modifications are inherently non-linear as they deviate from computations by a linear and static cable.
2.1.2. Propagation of Electrical Signals in the Axon
Propagation of electrical signals in the axon results from a combination of specialized active and passive mechanisms. Active properties are shaped by neuronal voltage-gated ion channels recruited as a function of the dynamics of the membrane potential whereas passive properties are determined by the axonal membrane at rest and by axonal geometry.
As increasingly appreciated, APs are not just an on/off switch, and electrical signaling in the axon should be regarded as a hybridization of analog and digital signaling (Shu et al., 2006) (Figure 2). Furthermore, APs are strongly regulated by the background analog activity provided by subthreshold postsynaptic events. For example, the inactivation of potassium Kv1 channels in the axon initial segment broadens the axonal AP waveform and increases unitary excitatory postsynaptic potentials (EPSP) amplitude in layer V pyramidal neurons (Kole et al., 2007). Interestingly, Nav channels have also been implicated in analog-digital signaling. The recovery from inactivation of axonal Nav channels can increase AP amplitude, enhancing synaptic transmission (Rama et al., 2015). Note that some neurons do not encode information with APs but only with graded signals (graded potential neurons; Borst and Haag, 1996).
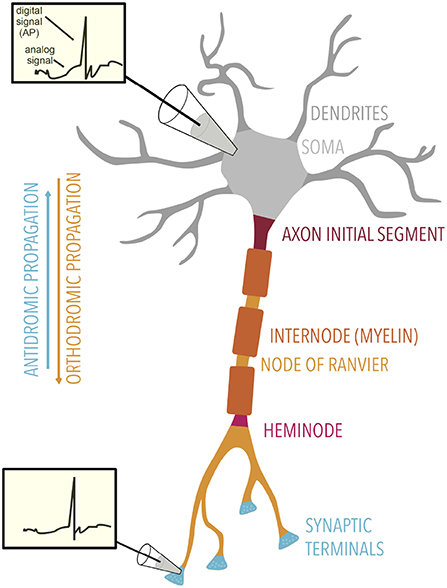
Figure 2. Overview of axonal electrical signaling. Axonal signaling is formed by a mixture of analog and digital signaling. Insets: membrane potential traces show both the analog and digital components, the former being attenuated with distance. Electrical signals can propagate orthodromically or antidromically. Specialized regions of the axon are labeled.
2.1.3. Non-electrical Changes
Signaling in axons and neurons is usually regarded as purely electrical. However, electrical signals are accompanied by other biophysical changes in the neuronal membrane, some of which may further contribute to signaling. The AP is accompanied by changes in many biophysical properties such as temperature, mechanical membrane properties, and optical birefringence (Abbott et al., 1965; Cohen et al., 1970; Howarth, 1975; Howarth et al., 1975; Tasaki and Iwasa, 1982b; Tasaki and Byrne, 1992). For example the changes in the optical properties of the axon during propagation have been at the basis of the label free interferometric imaging of APs in in-vitro systems (Akkin et al., 2007; Oh et al., 2012; Batabyal et al., 2017).
Mechanical displacements associated with the AP have been measured in many experimental contexts (Hill et al., 1977; Iwasa and Tasaki, 1980; Tasaki and Iwasa, 1982a,b). These mechanical displacements can be regarded as propagating surface modes that are elicited via the large electrostatic force produced by the AP. In this regard, the AP is an electro-mechanical pulse (El Hady and Machta, 2015). Interestingly, converging evidence suggests that mechanics play a role in electrical signaling (Tyler, 2012). Moreover, there is mounting evidence that some voltage sensitive channels such as sodium and potassium channels are mechanically modulated locally and that many neurons express mechanically-activated channels (Schmidt and MacKinnon, 2008; Schmidt et al., 2012; Ranade et al., 2015). Interestingly, mechanically sensitive ion channels are present in the internodes of myelinated axons (Brohawn et al., 2019). Future research is needed to establish the functional relevance of non-electrical changes that accompany action potentials, including in particular the relevance of mechanical displacements.
2.2. Biophysics of Action Potential Generation
2.2.1. A Brief Historical Perspective on the Action Potential
At the resting, non-excited state, mostly potassium channels are open and the resting potential is, as a consequence, close to the reversal potential for potassium, maintained around −70 mV. In 1939, Hodgkin and Huxley published the first trace of an AP recorded from the squid axon using an intracellular electrode where one can see a very clear overshoot. Following this in 1949, the proposal that sodium ions are the main mediator of AP generation was put forward by Hodgkin and Katz (1949). They studied the effect of systematically varying the concentration of sodium ions and measured its impact on the amplitude of the AP recorded. Subsequently, Keynes managed to show that nerve excitation leads to an increase in the transmembrane flow of sodium ions by tracing the movement of the radioactive isotope Na24 in repeatedly stimulated squid axons (Keynes, 1951). These seminal findings confirmed that sodium ions are the main contributors to AP generation.
2.2.2. Variations of Action Potentials
APs are characterized by a width, a height and an overshoot magnitude (i.e., referring to the AP height beyond 0 mV). Despite sharing a general biophysical mechanism for initiation, the shape of APs varies in different types of neurons. For example, there are cells that exhibit very narrow APs of a few hundreds of microseconds in width, reflecting a fast spiking behavior, such as some GABAergic interneurons, Purkinje neurons which are GABAergic projection neurons, glutamatergic neurons of the subthalamic nucleus, and Medial nucleus of the trapezoid body (MNTB) cells in the superior olivary complex. CA1 pyramidal neurons in the hippocampus have, in contrast, a relatively wide AP and dopaminergic neurons have an even wider AP of up to 4 ms (reviewed in Bean, 2007).
Apart from the shape of the single spike, neurons can exhibit a diversity of firing patterns. For example, they can be bursting or non-bursting on one hand and they can be adapting or non-adapting on the other hand. Adaptation during a train of APs refers to the process by which AP properties, typically rate and amplitude, decrease within the spike train. There are many biophysical mechanisms by which spike frequency adaptation can happen. The most prominent mechanisms are an increase in outward current flowing through calcium-activated potassium channels and an increasing outward current produced by the electrogenic sodium-potassium pump (Powers et al., 1999). Moreover, there is also a substantial sodium channel inactivation induced by a long lasting depolarization (Sawczuk et al., 1997).
The diversity of AP shapes along with the firing patterns are a result of the different combinations of ion channels that the neuron expresses (reviewed in Marder and Goaillard, 2006). The expression of ion channels impacts the computational abilities of neurons (e.g., narrow action potentials and short after-hyperpolarizations allow cells to generate high firing rates). Narrow action potentials allow neurons to follow high frequency inputs with higher fidelity than cells with wide action potentials and long refractory periods. Remarkably, in addition to constraining bandwidth of information processing, different AP widths may convey different information content (Borst and Sakmann, 1999).
2.2.3. The Axon Initial Segment
Before delving into the mechanistic details of AP generation, it is crucial to appreciate the complex anatomy of the Axon Initial Segment (AIS), the site of AP initiation (Figure 3A). The AIS is the main computational unit in axons, allowing them to integrate input signals and generate outputs (APs). Its distance from the soma can vary from 20–60 μm (Somogyu and Hamori, 1976; Sloper and Powell, 1979; Duflocq et al., 2011) to 120 μm (dopaminergic cells; Moubarak et al., 2019). The specific length of the AIS is variable across neurons as it has to adapt it to its own excitability properties. The excitability of the AIS is modulated by varying compositions of sodium and potassium channels clustered at the AIS.
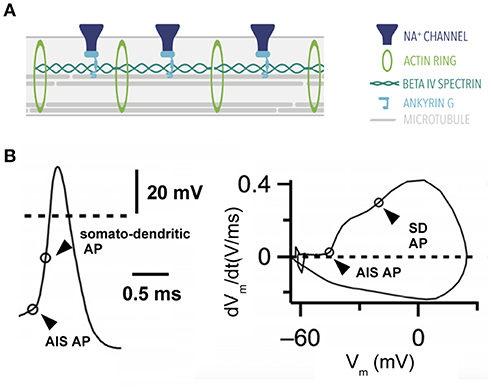
Figure 3. Action potential generation. (A) Ultrastructure of the axon initial segment. A highly-structured spatial organization characterizes proteins at the AIS. (B) Action potential of a stellate cell from the cochlear nucleus with two components: a fast rising phase of the action potential contributed by the AIS and a second phase contributed by the somatodendritic (SD) compartment. Right, phase plane plot of this cell. Modified from Yang et al. (2016) (CC-BY).
The AIS contains a highly-specialized protein machinery that gives it a distinct character (reviewed in Leterrier, 2016). One such protein is Ankyrin G, a scaffolding protein that is also present at the nodes of Ranvier (Kordeli et al., 1995). Ankyrin G anchors voltage-gated channels such as voltage-gated sodium (Nav) and potassium channels (Kv) to the membrane along with other adhesion molecules (Davis et al., 1996). Beta IV spectrin is another protein expressed in the axon initial segment. Beta IV spectrin's main function is to cluster sodium channels at the axon initial segment while simultaneously binding to the actin cytoskeleton (reviewed in Rasband, 2010; Figure 3A).
The AIS in mammalian neurons has been established as the site of the AP initiation following a series of seminal studies that began in the mid 1950s (Araki and Otani, 1955; Coombs et al., 1957; Fatt, 1957). The location of AP initiation has been further confirmed by combining precise electrophysiological measurements and imaging technologies. These allow to precisely identify the locus of AP initiation which was established to be in the distal part of the AIS, 20–40 μm from the soma (Palmer and Stuart, 2006; Kole et al., 2007; Meeks and Mennerick, 2007; Atherton et al., 2008; Foust et al., 2010; Palmer et al., 2010). The AIS is considered to be the site of AP initiation also because of several key properties. It contains a high sodium channel density. Furthermore, AIS sodium channels show a voltage dependence shifted to lower voltages, favoring their activation at less depolarized voltages than at the soma (Hu et al., 2009). Finally, the relatively large electrotonic distance of the AIS from the soma renders distal sodium influx more efficient in evoking a local membrane depolarization, compared to an AIS that would start at the soma. Note that electrophysiological recordings from invertebrates have shown that the initiation of the AP can happen at multiple locations acting in an independent manner (Calabrese and Kennedy, 1974; Meyrand et al., 1992; Maratou and Theophilidis, 2000), as will be discussed below. Along with its specialized protein machinery and acting as the site of AP initiation, the AIS also acts as a diffusion barrier between the somatodendritic and axonal compartments, filtering transport materials passing from soma to axon (Song et al., 2009; Brachet et al., 2010). Note however that the AIS length and its distance from the soma can be regulated in an activity-dependent manner (Grubb and Burrone, 2010; Kuba et al., 2014) and that in some neurons, AP initiation has been reported to occur at the first node of Ranvier (Clark et al., 2005; Lehnert et al., 2014), as will be developed later.
2.2.4. The Sodium Ionic Dynamics and Action Potential Initiation
The extent to which the density of sodium channels is higher in the AIS and the contribution of this high density of sodium channels to AP initiation is a matter of active investigation. There is a consensus that sodium channel density is higher in the AIS but the order of magnitude is still unclear. Immunostaining of sodium channels consistently indicates that there is a higher channel density in the AIS of various neuron types (Wollner and Catterall, 1986; Boiko et al., 2003; Meeks and Mennerick, 2007). Lorincz and Nusser (2010) counted around 200 Nav 1.6 sodium channels per square micrometer in the AIS of hippocampal pyramidal cells using electron microscopy. Given that the conductance of a single sodium channel is around 15 pS (Colbert and Johnston, 1996), one would expect a conductance density of about 3,000 pS per square micrometer. On the contrary, electrophysiological measurements from membrane patches pinpoint that sodium channel density is about 3–4 channels per square micrometer in the AIS, which is the same as the somatic density (Colbert and Johnston, 1996; Colbert and Pan, 2002). A similar conclusion was reached on the basis of recordings from blebs that form when cortical axons are cut in in vitro preparations. This might be due to the inability to draw AIS Na+ channels into the patch-clamp recording pipette due to their tight coupling to the actin cytoskeleton (Kole et al., 2008). In this article, the authors record a much larger sodium current after disruption of the actin cytoskeleton (Kole et al., 2008).
Kinetics of sodium currents underlying AP generation have been extensively studied. Hodgkin and Huxley have proposed that the activity of sodium channels can be fitted by m3 activation kinetics. Baranauskas and Martina (2006) found that sodium currents in three types of central neurons (prefrontal cortical cells, dentate gyrus granule cells and CA1 pyramidal cells) activate faster than predicted by Hodgkin-Huxley type kinetics following m2 activation kinetics. Moreover, it was found that the half activation voltage of voltage-gated sodium channels in layer 5 pyramidal neurons is 7–14 mV lower in the distal AIS compared to the soma and decreases further with increasing distance from the soma (Colbert and Pan, 2002; Hu et al., 2009). Nav1.6 channels, which are predominantly expressed in the axon initial segment and have a lower half activation voltage (Rush et al., 2005), are proposed to be primarily responsible for the initial slope of the AP. Furthermore, sodium channels at the AIS are more capable of producing a persistent sodium current (Stuart and Sakmann, 1995; Astman et al., 2006). The persistent sodium current has a significant influence on the AP threshold (Kole et al., 2008). Moreover, it is implicated in the generation of the AP afterdepolarization and it therefore contributes directly to the generation of high frequency AP bursts (Azouz et al., 1996).
Using sodium imaging to follow sodium influx in axon, soma and basal dendrites (Fleidervish et al., 2010), the authors suggest that the ratios of Nav channel densities in these regions are approximately 3:1:0.3. Interestingly in another study by Lazarov et al. (2018), APs were initiated in the AIS, even when axonal Nav channel density was reduced to about 10% in a beta IV spectrin mutant mouse. This experimental finding indicates to a great extent that AP initiation in the AIS does not require such a high local channel density. However in that study, the precision of AP timing was substantially compromised when axonal channel density was reduced. Likewise, the temporal accuracy of AP generation from MNTB cells decreases in a beta IV spectrin mutant mouse (Kopp-Scheinpflug and Tempel, 2015).
The aforementioned section highlights the complexity of sodium ion dynamics and begs for novel imaging modalities that allow tying ultra-fast dynamics with the axonal ultrastructures in order to get insights into the intricate biophysical mechanisms underlying the very first microseconds of AP initiation. The kinetics of sodium channel activation contribute to the speed at which neurons can generate action potentials. Thereby, they constitute a crucial factor in setting the computational speed of neural circuits. The existence of a diversity of sodium kinetics in different cell types likely allows neurons to be recruited at different speeds in different circuits.
2.2.5. The Action Potential Rapidness
A simple but very informative way to study the properties of APs is to plot the time derivative of the voltage (dV/dt) versus the voltage. This is called “phase-plane plot.” The spike threshold can be easily visualized in such a representation, where it corresponds to the voltage at which dV/dt rises abruptly. Coombs et al. (1957) noticed that the main spike is preceded by a smaller earlier component (referred to as a “kink”). This component is interpreted as reflecting initiation of the spike in the initial segment of the axon. One can record such a component in somatic spikes in many central neurons, including neocortical pyramidal neurons which we will focus our discussion on here. As mentioned above, one of the most striking features of the AP recorded from cortical neurons has been the existence of a “kink” at the initiation of the AP. One can define the rapidness of AP onset in this cell as the slope of the phase-plane plot at dV/dt = 10 mV /ms. The AP rapidness can also be referred to as rate of voltage change. In Naundorf et al. (2006), the AP rapidness was measured from the cat visual cortical cells. AP rapidness varied between around 20–60 ms−1. It is important to mention that sharp, step-like onsets of APs have been recorded in vivo in many preparations (cat visual cortex: Azouz and Gray, 1999, and cat somatosensory cortex: in Yamamoto et al., 1990).
Several hypothesis have been proposed to explain the origin of the AP kink: (1) the backpropagation to the soma of a smoother AP generated at the AIS; (2) an abrupt opening of sodium channels due to the biophysics of neuronal compartmentalization; (3) a decreased membrane time constant due to the loading of the dendritic compartment; and (4) the cooperativity of sodium channels at the AIS.
The “lateral current hypothesis” states that the “kink” at spike onset reflects lateral current coming from the axon which becomes sharper through backpropagation from the initiation site to the soma while initiation is smooth at the initiation site (McCormick et al., 2007; Yu et al., 2008). In Yu et al. (2008), authors perform simultaneous recordings from axon blebs and soma, finding a smoother AP onset in the axon, additionally reproducing these results in a model. It is important to note that this study supporting the lateral current hypothesis was done in bleb recordings which are injured axons that may have undergone severe cytoskeletal reorganization (Spira et al., 2003) affecting sodium channels dynamics. This reorganization might alter the true dynamics of AP initiation.
Although the kink indeed might reflect the lateral current coming from the axon (Milescu et al., 2010), this hypothesis fails to account for the ability of neurons to follow 200–300 Hz frequency inputs. In order to account for this discrepancy, Brette (2013) proposed that the compartmentalization and the distance between the soma and the AIS leads to spike initiation sharpness. In his proposal, Brette suggests that the rapidness arises from the geometrical discontinuity between the soma and the AIS, rather than from the backpropagation of axonal APs. When sodium channels are placed in a thin axon, they open abruptly rather than gradually as a function of somatic voltage, as an all-or-none phenomenon.
Another proposal that takes into account the geometry of neurons is Eyal et al. (2014), in which the authors propose that increasing the dendritic membrane surface area (the dendritic impedance load) both enhances the AP onset in the axon and also shifts the cutoff frequency of the modulated membrane potential to higher frequencies. This “dendritic size effect” is the consequence of the decrease in the effective time constants of the neuron with increasing dendritic impedance load. The authors have shown this in a computational model of reconstructed layer 2/3 pyramidal neurons of humans and rats. The firing pattern at the axon is strongly shaped by the size of the dendritic tree. Authors predict that neurons with larger dendritic trees have a faster AP onset.
A last proposal to interpret AP onset rapidness is that sodium channels, which are assumed to be opening independently within the Hodgkin-Huxley framework, are gated cooperatively. The cooperativity model proposed that the half-activation voltage of the channels becomes dependent on the probability of the opening of the neighboring channels. These cooperative effects might happen mechanistically on very fast timescales either through a purely electrical, mechanical, or electro-mechanical coupling. Though there is no direct experimental test of the cooperativity of neuronal sodium channels at the AIS, it can theoretically account for the observed discrepancy between the sodium channel density and the very rapid rise of the AP at the site of initiation in the initial segment (Naundorf et al., 2006). It is important to note that cooperative gating has been previously observed in calcium, potassium, and HCN channels (Marx et al., 2001; Dekker and Yellen, 2006; Kim et al., 2014).
Apart from its mechanistic underpinnings, the fast rise of APs has attracted both experimental and theoretical approaches to study its functional implications on the biophysics of neuronal populations. Before detailing those functional implications, it is important here to go through a useful theoretical abstraction: a typical cortical neuron, embedded in a cortical network in vivo, receives about 10,000 synaptic inputs. Assuming that each of these synaptic inputs is active with a rate on the order of 1–10 Hz, incoming signals arrive at a rate of 10 kHz. As a result, the membrane voltage exhibits strong, temporally irregular fluctuations. To understand the computational capabilities of e.g., cortical circuits, it is essential to characterize single neuron computation under such realistic operating conditions. To control the activity of entire neuronal circuits while preserving their natural firing characteristics, it would be advantageous to introduce artificial input components mimicking intrinsically generated synaptic input under precise experimental control. In order to study the dynamical properties of cortical neurons, experimenters have mimicked synaptic bombardment in vitro by injecting stochastic inputs modeled as an Ornstein-Uhlenbeck process in which sinusoidal inputs are embedded (Destexhe et al., 2001; Tchumatchenko et al., 2010; Neef et al., 2013). This experimental setting has allowed the measurement of the dynamic gain of neurons, which means how much neurons attenuate their input in the frequency domain and how fast they are able to follow a rapidly-fluctuating input. This has led to the establishment of the ability of cortical neurons to follow high frequency inputs up to 200–300 Hz (Higgs et al., 2006; Higgs and Spain, 2009; Tchumatchenko et al., 2011). Moreover, there has been a series of theoretical studies exploring the dependence of encoding capacity on the active properties of the AP initiation (Fourcaud-Trocmé et al., 2003; Wei and Wolf, 2011; Huang et al., 2012).
2.2.6. AP Trajectories Beyond the Rapidness of Initiation
Although we have mostly concentrated on the initial spike rapidness, note that the phase plot can display a variety of trajectories after the onset of the AP (Figure 3). These trajectories are determined by additional ion channels in conjunction with sodium channels. Potassium channels are typically responsible for the repolarizing phase of the AP. The relative temporal profiles of activation of sodium and potassium channels and their subunit composition determine the width of the AP (Lien and Jonas, 2003). Furthermore, the spatial location of ion channels also contributes to the shape of AP trajectories (Yang et al., 2016; Figure 3B). Interestingly, Kole et al. (2007) showed that APs become thinner during axonal propagation due to the specific expression of Kv1 channels in the axons of layer 5 pyramidal neurons. It has also been shown that the AP shape affects calcium currents and transmitter release [calix of Held: (Borst and Sakmann, 1999); dentate gyrus granule cells: (Geiger and Jonas, 2000); layer 5 pyramidal neurons: (Shu et al., 2006; Kole et al., 2007); CA3 pyramidal neurons (Bialowas et al., 2015; Rama et al., 2015); cerebellar interneurons: (Rowan et al., 2016); cerebellar Purkinje cells: (Kawaguchi and Sakaba, 2015)]. Therefore, the AP shape beyond the initial spike rapidness provides an extra dimension for information encoding on a variety of timescales.
2.2.7. The Action Potential at Nodes of Ranvier
Although the AP is generated at the AIS, the nodes of Ranvier contain a machinery to regenerate the AP. It is important to note that there are striking similarities between axon initial segment and nodes of Ranvier. A great deal of the protein machinery in the axon initial segment is also present in the nodes of Ranvier where the regeneration of the AP is performed. Ankyrin G, the major scaffolding protein in the AIS and the ring-like arrangement of actin and beta IV spectrin are also found in the nodes of Ranvier (D'Este et al., 2017). Nodes of Ranvier are distributed spatially along the axon to guarantee the faithful propagation of the AP. In addition, the first node of Ranvier was found to be crucial for high bandwidth bursting activity in neocortical layer 5 pyramidal neurons (Kole, 2011). In that study, the author shows that nodal persistent sodium currents at the first node of Ranvier hyperpolarize AP threshold and amplify the afterdepolarization. The study opens up the space for a computational role of the first node of Ranvier beyond the regeneration of the propagating AP. The first node faithfully follows spike frequencies with a approximately 100 μs delay (Khaliq and Raman, 2006; Palmer and Stuart, 2006; Foust et al., 2010; Palmer et al., 2010). This had led to the speculation that the nodes of Ranvier, and in particular the first node, may have an active computational role in modulating the AP initiation itself.
It is worth noting that nodes of Ranvier also express NaV 1.6, the same sodium channel subtype that is expressed in the AIS. It is even more striking that the sodium channels at the nodes also undergo the developmental changes from NaV 1.2 to NaV 1.6 during postnatal development, following a similar developmental trajectory as those found in the AIS (Rios et al., 2003). NaV is highly clustered at the nodes of Ranvier in the order of 1,200 channels per micrometers square (Rosenbluth, 1976), while internodes contain 20–25 channels per micrometers square (Ritchie and Rogart, 1977). This very high density ensures high-fidelity regeneration of the AP. Given the close proximity of the first node to the cell body and high density of NaV channels, it has been postulated that, in addition to securing propagation, it could potentially generate the AP (Colbert and Pan, 2002; Clark et al., 2005; Lehnert et al., 2014). Although this might be happening, the overwhelming evidence favors that the AP initiation is happening at the AIS.
2.2.8. Ectopic Spiking
AP initiation at the AIS and its subsequent orthodromic propagation have been extensively investigated. However, a number of studies demonstrates that distally generated spikes or “ectopic” APs co-exist in invertebrate and vertebrate neurons (Mulloney and Selverston, 1972; Maranto and Calabrese, 1984; Meyrand et al., 1992; Sheffield et al., 2010; Dugladze et al., 2012; Lehnert et al., 2014). Marked differences in somatic AP recordings are observed when APs are generated at the AIS or in a distal part of the axon. In particular, APs have more negative thresholds when APs are generated in distal parts of the axon. This is likely due to the fact that they do not show the strong coupling of soma to AIS which is responsible for the inactivation of sodium channels at the AIS and for a more depolarized AP generation threshold. Interestingly, given the different potential at which ectopic spikes are generated, the conductances activated during AP generation may differ between distal and proximal APs (Meyrand et al., 1992).
In invertebrates, numerous examples of ectopic spikes and of their functional relevance have been described (Mulloney and Selverston, 1972; Maranto and Calabrese, 1984; Meyrand et al., 1992). Ectopic spikes in neurons that target the hearts of the leech have been proposed to control the heart firing frequency (Maranto and Calabrese, 1984). In the somatogastric ganglion of the crab, ectopic spikes are typically observed in the lateral gastric motor neuron only when the muscles remain attached to the preparation, ectopic spikes being induced by motor contraction (Meyrand et al., 1992). Remarkably, ectopic spikes in Meyrand et al. (1992) fail to depolarize terminals onto interneurons located close to the soma, whereas they efficiently excite a distal postsynaptic target, the muscle. Thus, orthodromically-propagating spikes generated close to the soma and antidromically-propagating spikes generated distally co-exist and they can reach synapses that target different postsynaptic neurons.
Ectopic spikes have also been observed in vertebrates. In principal cells from CA3 area in the hippocampus during rhythmic activity in the gamma range (Dugladze et al., 2012), axons fire APs at five times the firing frequency detected at the soma. This is due to the activity of a specific interneuron, the axo-axonic cell, that inhibits the initial segment, thereby avoiding the backpropagation of axonal spikes to the soma. Another noteworthy case of co-ocurrence of AIS and ectopic spikes has been reported in Lehnert et al. (2014) in auditory medial superior olive (MSO) neurons. A realistic model of MSO neurons which takes into account their axonal structure and ion channel composition generates APs at both the AIS and the first node of Ranvier. Additionally, under certain pathological conditions, e.g., in epilepsy, hyperexcitable axons have been reported to generate ectopic spikes in the hippocampus (Stasheff et al., 1993). To conclude, we would like to emphasize that ectopic spikes occur in some neurons because of their multiple action potential generation sites, that is, specialized regions that act as action—potential generating computational units.
We would like to make at this point a clarification: although “action potential” and “spike” are two terms used to refer to the sodium AP generated at the axon initial segment, the term spike seems preferentially used in the literature to refer to spikes that can differ in their location (dendritic or ectopic spikes) and in their underlying ionic mechanism (e.g., calcium spike, see below).
2.2.9. Beyond the Sodium Spike
The spike initiated through sodium influx is not the only spike that can propagate in the axon. In some axons, there are spikes that are generated through the influx of calcium. In the giant axon of the jellyfish Aglantha digitale (order Hydromedusae), both sodium and calcium spikes propagate in the axon (Mackie and Meech, 1985). Sodium-dependent spikes are responsible for fast swimming and calcium spikes mediate slow swimming.
In vertebrates, calcium spikes are typically restricted to the dendritic compartment where there is a calcium spike generation mechanism. The biophysical mechanisms contributing to the dendritic spikes initiation in the distal apical trunk and proximal tuft of hippocampal CA1 pyramidal neurons (Gasparini et al., 2004) are dendritic sodium and potassium channels that set AP shape and propagation properties, the highly synchronized inputs, their spatial clustering and the activation of NMDA receptors. In the olfactory bulb mitral cells and in hippocampal and cortical pyramidal cells, dendritic spikes can trigger one or more axonal APs (Stuart et al., 1997; Golding and Spruston, 1998; Larkum et al., 1999, 2001; Chen et al., 2002; Ariav et al., 2003). In addition, backpropagating axonal APs can themselves promote dendritic spikes, a reciprocal interaction that can lead to a burst of axonal APs (Pinsky and Rinzel, 1994; Mainen and Sejnowski, 1996; Larkum et al., 1999, 2001; Doiron et al., 2002).
2.3. Biophysics of Action Potential Propagation
2.3.1. An Equivalent Electrical Circuit for Axons
The passive properties of axons can be modeled by an equivalent electrical circuit (Figure 4A). The axonal membrane can be reduced to two circuit elements: the lipid bilayer, modeled by a capacitor and ion channels, by a resistor. The resistance to axial current flow can be modeled by an additional resistance.
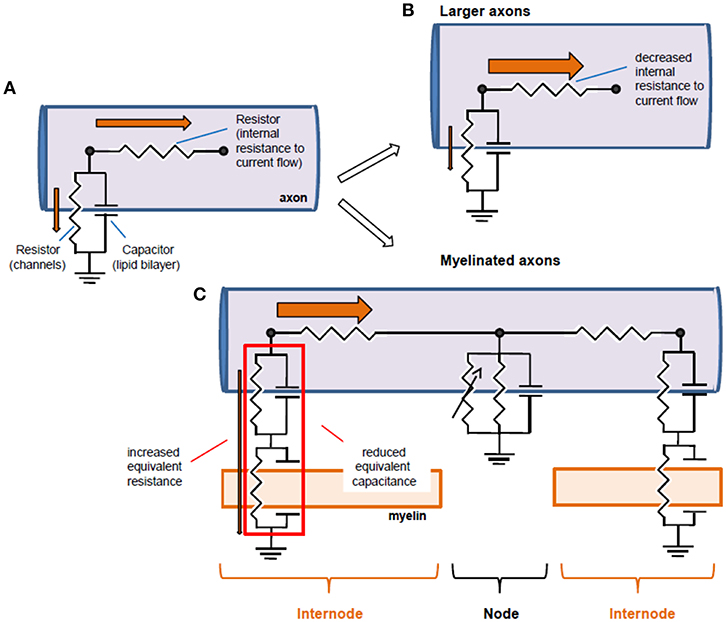
Figure 4. Equivalent circuits of axons and structural biophysical specializations that improve conduction. (A) An axon can be reduced to an equivalent electrical circuit involving an axial resistor (parallel to the membrane) conveyed by the intracellular medium of the axon (axoplasm), and a parallel “RC circuit” formed by the membrane resistance and the membrane capacitance. (B) Conduction can be improved by increasing axon diameter, thereby decreasing longitudinal resistance to current flow. This allows for a larger current flow in the axon relative to the membrane resistor, and thereby a larger space constant and faster conduction. (C) An alternative circuit modification occurs with myelination: additional capacitances conveyed by myelin in series with axonal capacitance reduce the effective capacitance and additional resistance increase the effective resistance, increasing propagation speed and space constant, respectively. Note that the battery associated to the membrane has been omitted for simplification purposes. Orange arrows represent the current flow, and their thickness is indicative of the relative current flow in the axoplasm and in the radial direction out of the axon.
How fast signals propagate is critically controlled by the capacitance. Electrical currents need to first charge the membrane capacitance, that opposes the flow of electric current, before electrically-charged membranes can undergo voltage changes. Capacitances are proportional to the membrane capacity (capacitance per surface area) and to the membrane surface area. The capacity of neuronal membranes is in the order of 1 μF per cm2 (Gentet et al., 2000). Capacitance measurements from small axons are in the range of tens of picoFahrads (pF) (Mejia-Gervacio et al., 2007). Capacitances of larger neurons (i.e., strongly-ramifying interneurons and projection neurons) are therefore expected to be in the range of hundreds of pF to nF. Remarkably, dynamic changes in membrane capacitance are suggested by activity-dependent changes in the size of axons (e.g., Chéreau et al., 2017). However, little is known about dynamical changes in capacitance due to temperature, lipid composition, and whether these may significantly impact the propagation of electrical signals along the axon.
The membrane resistance plays a major role in controlling how far signals spread in space along the axon before membrane potential changes become imperceptible. This is typically measured by the space constant, defined as the distance over which the membrane potential decays to 37% of its initial value. The more open channels are available at the membrane, the more the axial current is attenuated in space along the axon due to current leakage through membrane channels. Remarkably, the membrane resistance can change (reviewed in Debanne et al., 2019), providing a potential source of variation in the conduction of electrical signals along axons.
The axonal axial resistance to current flow results from the combination of the resistivity of the axoplasm (that is, the cytoplasm of the axon), given in Ohms*cm, and the diameter of the cylinder. Axial resistivity values are in the range of approximately 100 Ω.cm (Carpenter et al., 1975; Cole, 1975). Computational models of the calyx of Held suggest that the latency and amplitude of signals propagating between release sites is highly sensitive to changes in axial resistivity, and that these changes may have a large impact on synaptic release (Spirou et al., 2008). However, changes in resistivity have not been reported so far experimentally. The axon diameter can vary in three orders of magnitude, from hundred nanometers to hundreds of micrometers in diameter. Giant fibers found in invertebrates are an example of specialized large-diameter structures that propagate electrical signals with high speed over long distances (in Hodgkin and Huxley, 1952; Xu and Terakawa, 1999; Figure 4B). The larger the diameter of the axon, the faster the electrical signal propagates. Taking into account cable theoretic considerations, the propagation speed increases with the square root of the diameter. Remarkably, the axon diameter, as well as the diameter of synaptic boutons, are not static properties of axons. In fact, axon diameter has been shown to be regulated in hippocampal principal cells in an activity-dependent manner. Plasticity protocols induced changes in axonal diameter which were accompanied by significant changes in AP conduction velocity along CA3 pyramidal cell axons (Chéreau et al., 2017; Figure 5A).
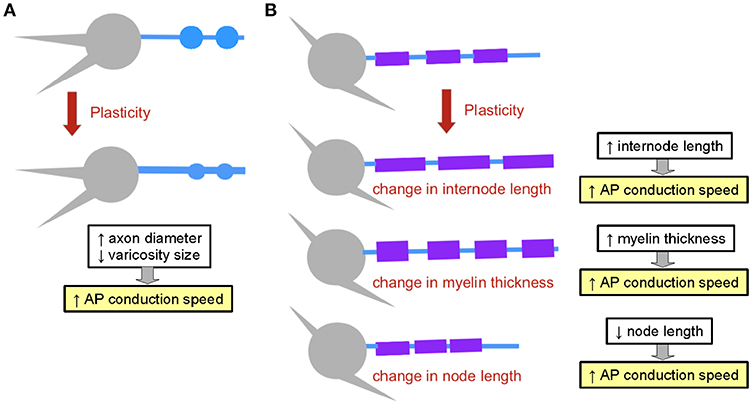
Figure 5. Structural plasticity mechanisms affecting the propagation of electrical signals. (A) Axon structural plasticity. Axons can change their diameter and bouton size. (B) Myelin structural plasticity can involve changes in internode length, in myelin thickness or in node length. The impact of each mechanism on AP propagation speed is outlined.
2.3.2. Propagation of Subthreshold Signals
Subthreshold signals propagate passively in axons, reaching synaptic terminals, where they influence spike-evoked synaptic release (Alle and Geiger, 2006). Subthreshold membrane fluctuations consist of synaptic events, typically in the range of 100 s of μVs to mVs, which in cortical neurons approximate highly stochastic background dynamics in vivo (Rudolph and Destexhe, 2003). Their propagation, referred to as analog, in comparison to the digital nature of the AP, modulates the efficiency of APs to induce neurotransmitter release in synaptic terminals (Shu et al., 2006). Given that subthreshold signals are not regenerated along the axon, analog signaling is more prominent in proximal portions of the axon. The presence of combined analog and digital signals in axons has been termed hybrid analog-digital signaling (reviewed in Zbili and Debanne, 2019).
Of particular interest is that the propagation of slow analog subthreshold signals does not only reach chemical synapses. Subthreshold signals also reach axonal electrical synapses, at which the signal is expected to be conveyed with high efficiency to the postsynaptic site due to the continuous and low-pass filtering properties of electrical transmission (reviewed in Alcami and Pereda, 2019).
The co-existence of subthreshold signals and suprathreshold signals (APs) illustrate two co-existing signaling modalities and computations in axons (reviewed in Zbili and Debanne, 2019).
2.3.3. Reliability of Propagation and Action Potential Failures
Before we consider how signals propagate along axons, let us discuss the reliability of propagation. In small axons, modeling shows that APs can propagate with a large variability in their kinetics and amplitude due to channel noise (Neishabouri and Faisal, 2014). Furthermore, APs do not always efficiently propagate. In fact, failures in AP propagation are observed in many neuron types at high firing frequencies (Krnjevic and Miledi, 1959; Grossman et al., 1979; Monsivais et al., 2005).
Although geometry can generate failures (e.g., at branch points, see next section), failures typically involve active mechanisms during repetitive activation of axons as observed in a number of vertebrate and invertebrate preparations (Krnjevic and Miledi, 1959; Mar and Drapeau, 1996; Monsivais et al., 2005). Repetitive activity typically leads to extracellular potassium accumulation and subsequently to the depolarization of the axon, inducing failures of conduction by inactivating sodium channels (Grossman et al., 1979). In other cases however, repetitive activation induces AP propagation failures via hyperpolarization of the membrane (Mar and Drapeau, 1996). Additionally, computational modeling suggests that axonal gap junctions, by leaking current to coupled axons, may induce propagation failures in thin axons (Hull et al., 2015).
Note that propagation failures likely affect only a fraction of APs at physiological firing rates, and that most APs succeed in propagating. Remarkably, auditory axons are able to transmit action potentials at very high firing rates up to 1 kHz without failures (Kim et al., 2013).
Interestingly, changes in AP failure can also occur in response to membrane fluctuations, e.g., in response to synaptic inputs. Indeed, specific potassium channels of the type IA underlie a hyperpolarization-mediated conduction block in hippocampal pyramidal cells (Debanne et al., 1997). Remarkably, the activation and de-inactivation kinetics of IA allow for a history-dependent conduction block of APs.
Propagation failures, that occur under specific conditions or under high frequency firing, induce a mismatch between action potentials at the AIS and at more distal portions of the axon where synapses are located. Interestingly, this mismatch may impact the ability of neurons to drive synapses at high frequencies, even when AIS spiking could be driven at such high frequencies. Thereby, propagation failures represent under specific conditions, a limitation to the reliable propagation of action potentials.
2.3.4. More Than Linear Cables: Impact of Axonal Branching and Inhomogeneities
Axons are typically formed by complex trees and spatial heterogeneities. These include branching points, varicosities (local enlargements of the axon containing the release machinery of chemical presynaptic sites) and large structures specialized in the interaction with other cells. Examples of such structures are the “basket” formed by a specific type of interneuron, basket cells, around principal cells in many brain regions; the glomerular collateral of the climbing fiber in the cerebellum; the “pinceau” structure surrounding cerebellar Purkinje cells (Palay and Chan-Palay, 2012) or the calyx of Held in the auditory system.
Changes in axon diameter at varicosities or branching points are characterized by an impedance mismatch, that is, a need of a larger current to flow in one of the two directions to electrically load axonal branches, provoking changes in AP propagation speed (Goldstein and Rall, 1974; Manor et al., 1991). Due to this impedance mismatch, when APs need to load a larger impedance as they propagate from one mother branch into two daughter branches, their propagation will be delayed relative to the speed that they would have had if no branching was present.
In the most extreme case, the electrical signal fails to load one or two of the branches, resulting in AP propagation failure. Propagation failures have been shown to occur in branches of a number of neurons (Yau, 1976; Grossman et al., 1979; Gu et al., 1991). An interesting example is provided by the medial pressure sensory neuron in the leech, where the failure of APs to propagate can differentially affect postsynaptic cells contacted by distinct presynaptic branches (Gu et al., 1991).
Finally, branching points can also provoke a surprising effect: APs can be slowed down in the ms range, up to a level that allows the mother branch to overcome the refractory period for AP generation. As a consequence, the AP can “reflect” (that is, travel backwards), increasing synaptic release at synapses present in the branch where the AP reflects (Baccus, 1998; Baccus et al., 2000).
The impact of axonal morphologies on AP propagation is likely to be relevant in the complex axonal ramification patterns of many neurons, including vertebrate interneurons (Ofer et al., 2019). The usage of voltage sensitive-dyes that track membrane voltage with sub-millisecond precision (Palmer and Stuart, 2006) should allow following large portions of axons both in vitro and in vivo, and characterize the propagation of APs along complex axonal structures.
At this point, we would like to comment on the relevance of the physiological phenomena constrained by the morphology of axons discussed above to non-linear processing by neurons, and therefore on their computational abilities. They introduce non-linear transformations in specific axonal compartments. Thereby, they allow for a differential encoding in different regions of the axonal tree, modulating the functional impact of APs onto different post-synaptic targets. In other words, there is not one axon, but multiple compartments in one axon. The details of AP propagation in these compartments have been explored by computational modeling, creating a detailed knowledge of how electrical activity flows in single cells (Peterson et al., 2011; Xylouris et al., 2011; Agudelo-Toro and Neef, 2013)
2.3.5. Biophysical Properties of Myelinated Fibers
Many vertebrate and some invertebrate fibers are myelinated, a specialization endowed by the glial ensheathment of axons that appeared several times during evolution (Castelfranco and Hartline, 2015). Myelin, formed by compact lipidic layers produced by the membranes of glial cells (oligodendrocytes in the central nervous system and Schwann cells in the peripheral nervous system), strongly impacts the propagation of electrical signals.
In his seminal study, Lillie (1925) wrapped an iron wire placed in an acidic solution with an insulating glass cylinder. This increased the speed of propagation of electrical signals along the wire, which he postulated to occur in myelinated fibers. His prediction was confirmed decades later in axons by recording electrical signals at nodes, leading to the concept of the “saltatory” nature of transmission of electrical signals in myelinated fibers (Huxley and Stämpfli, 1949). Saltatory comes from the latin verb “saltare” (to jump), an analogy describing the very fast propagation of electrical signals between nodes of Ranvier.
Myelin modifies the electrical circuit that models the passive properties of axons described above by adding compact membrane layers in series with the axonal membrane. As a consequence, myelin increases the effective radial resistance and decreases the effective capacitance of the axon (Figure 4C). These two effects are due to the different properties of series resistors and series capacitors added to the circuit: series resistors sum their resistances whereas the inverse of capacitances from capacitors in series sums. The increase in effective membrane resistance (Bakiri et al., 2011) and the decrease in effective membrane capacitance by myelin have two major consequences. On the one hand, the increase in the effective axonal resistance by myelin increases the length constant. On the other hand, as a consequence of the decrease in the effective axonal capacitance, the time required to effectively load axons decreases, dramatically accelerating the propagation of electrical signals. This speeding of electrical propagation by a reduced effective capacitance underlies saltatory conduction between nodes of Ranvier (Huxley and Stämpfli, 1949; Castelfranco and Hartline, 2015). Therefore, adding myelin to an axon allows it to overcome the passive constraints that limit its computational abilities, including the speed of propagation and the distance of effective propagation of electrical signals. It additionally impacts the reliability and the jitter at which APs propagate, as will be discussed below.
2.3.6. Geometry of Axons and Myelin
Theoretical studies have shown that specific myelination parameters maximize the space constant and the conduction velocity of electrical signals in axons. In particular, the ratio of the axonal diameter d to the fiber diameter D (the summed diameter of axon and myelin sheath), defined as the “g-ratio,” controls the conduction of electrical signals. Rushton (1951) developed a biophysical formalism to model current flow in a myelinated axon. He deduced the relation between the ratio l/D (internode length l over D) and the g-ratio. He further demonstrated that the ratio l/D is maximal when g = 0.6, a value also found analytically to maximize the space constant. In an independent approach, Deutsch (1969) mathematically derived the geometry of axonal and myelin properties that maximize, this time, conduction velocity. He deduced that the propagation velocity is inversely proportional to the RC time constant given by the internal resistance of the axon R and the capacitance of the membrane C. Maximizing conduction speed requires minimizing the time constant of the circuit. This resulted in the same geometrical properties as those derived by Rushton: a g-ratio of 0.6. Additional modeling studies including a more complete description of myelinated fibers converged to similar conclusions (Goldman and Albus, 1968). Therefore, due to the biophysical constraints posed by the thickness of myelin and axonal size, both conduction speed and efficient spatial propagation of electrical signals are maximized by specific axonal and myelin geometries. It is noteworthy that the geometry of axons and myelin does not only control AP propagation speed (Rushton, 1951; Deutsch, 1969) but also AP temporal jitter (Kim et al., 2013).
It seems difficult to imagine that neurons have fine-tuned their dendritic computations in a cell-type specific manner (Stuart et al., 2016), but that axons would, on the contrary, be invariant and homogeneously optimizing speed by their geometry. Additionally, we know that nervous systems adapt and fine tune a plethora of properties to accomplish specific functions (Marder and Taylor, 2011). Axons indeed adjust different parameters which impact the speed of propagation of electrical signals (Seidl et al., 2010; Ford et al., 2015; Arancibia-Carcamo et al., 2017) to obtain different speeds of computation.
An illustrative example of how the geometry of axons and myelin is tuned to adjust AP propagation speed, deviating from a g-ratio of 0.6, is provided by the axon properties which encode spatial location in the avian brain (Seidl et al., 2010). The longer contralateral fibers have larger-diameter axons and longer internodal distances, compensating in this manner for an otherwise larger conduction delay relative to the shorter fibers on the ipsilateral side. In this manner, axons ensure a coincident arrival of contralateral and ipsilateral signals to the synaptic terminals. As a consequence, post-synaptic cells can act as coincidence detectors, a key computational feature that allows neural circuits to locate sounds. Another interesting example is provided by fibers specialized in carrying information for low-frequency sounds, which show larger diameters than those carrying high-frequency sounds, but also shorter internodes. In doing so, these fibers deviate from the classical dependence of both variables established by Rushton. This specialization is proposed to ensure a proper function of the circuit (Ford et al., 2015). Moreover, internode length and node diameter show graded properties as they approach the terminal in the auditory granular bushy cell axon, implementing an efficient invasion of the axon terminal by APs (Ford et al., 2015).
We have seen that a large number of structural myelination parameters act in concert to control the speed of AP propagation (Goldman and Albus, 1968). It is noteworthy to mention that myelin has introduced new degrees of freedom in the regulation of AP speed: speed depends on distance between nodes of Ranvier, on node length, node composition, and thickness of myelin (Rushton, 1951; Wu et al., 2012; Ford et al., 2015; Arancibia-Carcamo et al., 2017). These parameters can be modulated independently or in combination, thereby increasing the number of available mechanisms by which nervous systems tune the axonal propagation of electrical signals. Furthermore, dynamical changes in axons and myelin (Sampaio-Baptista et al., 2013; McKenzie et al., 2014; Fields, 2015; Sinclair et al., 2017) suggest that nervous systems dynamically adjust the properties of their fibers to achieve the specific behaviors that they control. Adding myelin has allowed axonal conduction speed to be regulated by additional mechanisms other than their diameter. Indeed new adjustable parameters appeared evolutionary with myelination (e.g., myelin thickness, node length, etc.) to dynamically fine tune the computational speed of neural circuits.
2.3.7. Active Contributions to Variations of Action Potentials Along the Axon
Each active AP regeneration site along the axon can potentially generate AP variants due to their specific state and composition of ion channels and membrane potential. In particular, myelinated fibers are characterized by the presence of non-myelinated sections, which concentrate the machinery to generate APs. These include nodes, the heminode (last unmyelinated portion before the terminal) and synaptic terminals. Remarkably, AP shape can be modified along the axon by the active channels present in these locations.
An example of local variations in AP shape through active mechanisms is found at presynaptic mossy fiber terminals (present in the axon of dentate gyrus granule cells), where local potassium channels modulate spike shape (Alle et al., 2011). Another example is provided by the exclusion of sodium channels from the terminals in the calix of Held, while being concentrated at the heminode. Such compartmental specialization has been suggested to produce APs with a shorter width in the calix (Leão et al., 2005). At the Purkinje cell nodes of Ranvier, the activation of calcium-dependent potassium channels repolarizes membranes, de-inactivating sodium channels which can then generate fast frequency spikes, and in this manner prevent AP failure at high frequencies (Gründemann and Clark, 2015). Additionally, changes in membrane voltage in the axon induced by active mechanisms can impact the efficiency of AP propagation. For example, in the leech touch cells, adaptation in response to repetitive AP firing consists of a hyperpolarization, resulting in the blockade of AP propagation (Van Essen, 1973).
We previously described how actively-generated signals can differently be passed on by two bifurcating branches, illustrating how passive properties can filter actively-generated signals (Gu et al., 1991). Remarkably, active properties of axonal branches can prevent failures by potentiating signals in specific branches in cultured hippocampal neurons (Cho et al., 2017). Failures that would occur as a consequence of the passive filtering of electrical signals can be prevented in a branch-specific manner by the presence of the sodium channel subunit NavβII, which potentiates AP propagation. Thus, the combination of passive and active properties fine tunes the computational properties of axonal branches.
2.3.8. The Geometries of Axons and Myelin Are Plastic
Geometrical properties of both axons and myelin have been shown to be highly plastic. Indeed, the diameter of axons can change as a function of neuronal activity (Chéreau et al., 2017; Sinclair et al., 2017). Furthermore, the understanding of the mechanisms of myelination has revealed that properties of nodes and internodes are subject to plasticity (Young et al., 2013; reviewed in Kaller et al., 2017). Interestingly, major macroscopic changes in myelination occur in response to training paradigms in mice, allowing the acquisition of motor skills (Sampaio-Baptista et al., 2013; McKenzie et al., 2014; Xiao et al., 2016), and models of injury induce strong remodeling of myelination patterns in the auditory brainstem (Sinclair et al., 2017). Changes in myelination can involve several mechanisms: changes in internode length (Etxeberria et al., 2016), in myelin thickness (Sinclair et al., 2017) and in node length (suggested in Arancibia-Carcamo et al., 2017; Figure 5B). Remarkably, plasticity of myelination allows circuits to adjust their speed of computation, adding computational flexibility to neural networks.
2.3.9. Nanostructures With Unknown Function
The evolutionary appearance of myelin has led to new specialized microstructures or microdomains (namely nodes, paranodes, juxtaparanodes, heminodes). Electron microscopy and recently superresolution imaging have revealed additional structures whose contribution to axonal computation remains mysterious. These structures can be observed at the nanometer scale in a highly regular spatial organization (D'Este et al., 2017), rising the question of the function of these periodic structures. For example, d'Este et al. show that the voltage-dependent potassium channel subunit Kv1.2 channels, found at the juxtaparanodes, correlates in space with the underlying actin cytoskeleton. An additional structure is the Schmidt-Lanterman incisure, a spiral cytoplasmic expansion from the outer tongue of myelin to the inner tongue. Incisures express gap junctions and their contribution to the electrical properties of myelin remain mysterious (Kamasawa et al., 2005). Likewise, exquisite arrangements of structures apposing glial and neuronal membranes and also with other glial membranes in the form of “rosettes” formed by ion channels at the paranode are still poorly understood (Rash et al., 2016).
These findings open up the following question: how do these nanostructures impact function? One would expect that further perturbing and studying those nanoscale structures in the future will further our understanding of how they contribute to axonal computations.
2.4. Axons Are Not Alone: Intracellular and Intercellular Coupling
2.4.1. Crosstalk of Axons With Other Compartments
Although we have done a treatment of the axon as an isolated cable as has classically been performed in the early days (Lillie, 1925; Huxley and Stämpfli, 1949; Hodgkin and Huxley, 1952), the axonal cable is coupled to the somatic and dendritic compartment at one end and, additionally, directly or indirectly to electrically-coupled cells, which also functionally act like an electrical compartment (Furshpan and Potter, 1959; Alcami and Marty, 2013; Eyal et al., 2014). Electrical coupling between the axon and the soma, and indirectly to dendrites and electrically-coupled cells, influences AP generation in the axon (Bekkers and Häusser, 2007; Eyal et al., 2014; Amsalem et al., 2016; Alcami, 2018; Goldwyn et al., 2019). Loading of these non-axonal compartments was shown to impact AP threshold and speed (Bekkers and Häusser, 2007; Eyal et al., 2014; Amsalem et al., 2016). Their contribution to the effective membrane time constant is substantial. The somato-dendritic compartment has been shown to, by this mechanism, modify both the threshold and the initial rise of the AP (Eyal et al., 2014).
It is further interesting to consider the axon in the context of synaptic integration, that is, the computation of information received at synapses. Similar to the somato-dendritic and junctional compartments, which act as current sinks, influencing the effective kinetics and strength of excitatory inputs recorded at the soma, before they reach the AIS (Nörenberg et al., 2010; Alcami, 2018), the axonal membrane also behaves as a current sink, leaking current generated at synapses in the somatic and dendritic compartments. This phenomenon has been shown to, through a passive mechanism, accelerate the time-course of somatically-recorded excitatory synaptic events (Mejia-Gervacio et al., 2007). It has additionally been suggested to also accelerate the time-course of spikelets generated by electrically-coupled cells (Alcami and Marty, 2013). Mejia-Gervacio and collaborators (Mejia-Gervacio et al., 2007) show that the capacitive loading of axons introduces in cerebellar molecular layer interneurons a computational time constant of about 3 ms, which is one order of magnitude slower than the faster time constant to load the somatodendritic compartment. This relatively slowly-charging process of the axonal membrane accelerates the decay of excitatory postsynaptic potentials, reducing the time window for AP generation. Therefore, electrical signals that arrive to the axon are not only passively influenced by other compartments, but they also influence passive computation by the non-axonal compartments, as part of a system formed by coupled compartments.
Let us now turn our attention onto the signals propagating in axons as cells receive synaptic events in their somas and dendrites, which is a consequence of the current flow in the axon evoked by synaptic events received in dendrites and somas. These signals propagate at long distances before their complete attenuation (contributing to the analog signaling in the axon that was previously introduced). The space constant at the hippocampal unmyelinated granule cell axon is in the range of hundreds of micrometers (Alle and Geiger, 2006) and the subthreshold propagation of voltage depolarizations has been shown to increase AP evoked release (Shu et al., 2006). Interestingly, subthreshold signals do not only travel orthodromically toward the terminals, but signals generated in the axon, e.g., by synaptic receptors present on the presynaptic membrane, also travel antidromically to the soma (Trigo et al., 2010). As a consequence, these axonal events depolarize the soma and influence AP generation (de San Martin et al., 2015). In summary, intracellular and intercellular coupling render the computations of all compartments inter-dependent: axons don't carry out their computations independently from other compartments of the same cell or from other cells, and non-axonal compartments don't carry their computations independently of axons.
2.4.2. Direct Coupling Between Axons
Direct coupling between axons was suggested in early work, bringing up the concept that networks of axons may directly interact with each other (Katz and Schmitt, 1940). These interactions can be explained by two forms of electrical transmission (Figure 6A): ephaptic transmission due to the generation of an electric field by an axon, affecting the excitability of a neighboring axon (Katz and Schmitt, 1940; Blot and Barbour, 2014; Han et al., 2018), and transmission mediated by gap junction-mediated electrical synapses (Furshpan and Potter, 1959; Watanabe and Grundfest, 1961; Bennett et al., 1963; Robertson et al., 1963; Schmitz et al., 2001). As a matter of fact, electrical synapses were first discovered in axons in a variety of preparations (Furshpan and Potter, 1959; Watanabe and Grundfest, 1961; Bennett et al., 1963; Robertson et al., 1963).
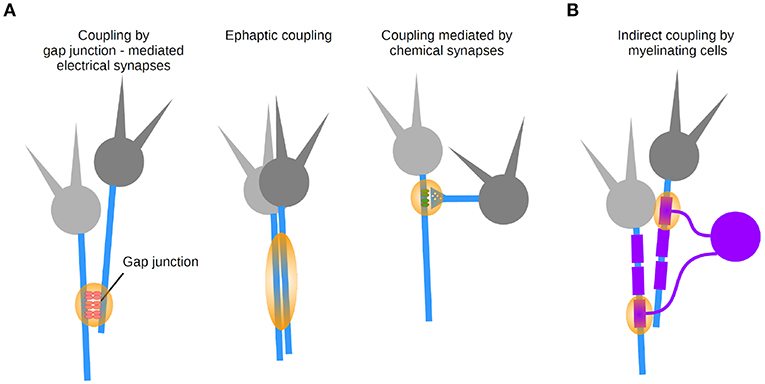
Figure 6. Coupling modalities between axons. (A) Three types of synapse-mediated coupling: through axo-axonal gap junctions (left), ephaptic coupling (middle), and chemical axonic synapses (right). (B) Indirect coupling via myelinating cells.
Axonal electrical synapses are expected to strongly affect electrical signals by adding a conductance pathway directly in the axon. Remarkably, axonal gap junctions allow inputs to arrive at the axon directly, blurring the pure “output” role of axons: an AP in a presynaptic axon induces a spikelet (a low-pass filtered version of the presynaptic AP) in the postsynaptic axon. Spikelets excite distal parts of the axon where the gap junctions are located. When the spikelet depolarizes the membrane potential sufficiently, they are able to evoke APs (Chorev and Brecht, 2012). Interestingly, in vivo recordings from hippocampal principal cells in CA regions from rodents revealed two types of APs: one type was preceded by a “shoulder” which was identical to the rising phase of the spikelet, and the other was a full-blown AP lacking the shoulder (Epsztein et al., 2010). Spikelets correlate with AP firing from nearby cells, confirming that they are generated by electrically-coupled cells, and not by spontaneous AP firing of distal axons (Chorev and Brecht, 2012). Altogether, these studies suggest that hippocampal pyramidal cell axons are excited through electrical synapses under physiological conditions in behaving animals, as it had been previously shown in slices (Schmitz et al., 2001).
Axonal gap junctions have additionally been proposed to underlie fast synchronization of neuronal ensembles in both physiological and pathophysiological conditions (Schmitz et al., 2001; Roopun et al., 2010). Interestingly, axo-axonal gap junctions can have a strong impact on spike coordination and coding efficiency (Wang et al., 2017). They may additionally induce AP propagation failures in thin axons as shown in a model of a brainstem networks in frog tadpoles (Hull et al., 2015). In this model, gap junction-mediated failures can be prevented by increasing gap junction resistance or membrane excitability.
Last but not least, direct axo-axonal coupling can be mediated by chemical synapses onto axons (Figure 6A) which are typically performed by a specific type of interneuron targeting the AIS of principal cells (chandelier cells in the neocortex; Somogyi et al., 1985). GABAergic terminals made onto neocortical and hippocampal pyramidal cells axons exert inhibitory control over AP initiation (Dugladze et al., 2012). Owing to axo-axonal coupling, populations of axons can be regarded as a computational unit.
2.4.3. Axons Interact Indirectly via Glial Cells
Finally, let us consider the contribution of glial cells to axonal function as an indirect coupling pathway between axons (Figure 6B). The biophysical properties of myelin are achieved by glial cells that produce myelin. Since several axons are typically contacted by a myelinating oligodendrocyte, this introduces de facto an indirect coupling pathway between axons. A number of transmission mechanisms has been described between axons and myelin (reviewed in Micu et al., 2017), whose dynamic properties depend on signaling from neurons (Hines et al., 2015). A better understanding of axo-axonal coupling mediated by glial cells will in the long run help us understand the computations of populations of axons regulated by glial cells in health and disease.
3. Overview of Axonal Computations
Let us at this point recall the definition of computation stated beforehand. We defined computations as modifications in the input/output transformations performed by axons. In this section, we will summarize the diverse axonal computations afforded by the various physiological processes discussed throughout the article beside the well established canonical computation of action potential generation at the AIS.
1. Axons compute with both analog and digital signals. This can also be termed “hybrid computation” since both signals co-exist and are tightly intermingled.
2. Axons can vary the shape of APs in terms of width and rise time by combining ion channels with specific kinetics and by distributing them in specific spatial configurations along the axon. These variations modulate their postsynaptic impact.
3. Owing to specializations in morphology, active properties of axons or electrical coupling between axons, (i) APs can fail to propagate, (ii) their efficient propagation can be ensured, or (iii) they may reflect to the mother branch. This implies that an AP in the AIS may correspond at the terminal to more than one AP (reflection case), or less than one AP (failure case).
4. By fine-tuning axonal morphology, active and passive mechanisms, axons can introduce anisotropies in AP propagation speed along the axon.
5. Axons modulate synaptic integration by fine-tuning AIS function and by leaking currents in the axonal tree.
6. By generating AIS spikes and ectopic spikes, and propagating them orthodromically and antidromically respectively, axons can carry parallel computations.
7. By virtue of their plasticity, axons and myelin readjust AP propagation speed.
8. Axons can add and relocate computational “hotspots” that generate non-linear transformations at specialized locations: AIS, nodes, ectopic spike generation sites, heminode, branching points, daughter branches, terminals.
9. Axons can compute information at the level of populations of axons owing to the various modalities of inter-axonal coupling.
10. Axon can, in addition to their output role, act as input structures by receiving information at electrical synapses, chemical axo-axonic synapses, and axonal receptors.
4. Conclusion
Here, we have reviewed the biophysical nature of computations performed by the axon. We have shown that the axon is not just a cable on which electrical pulses propagate but rather a computational device that modulates signaling and adds to the complexity of information processing in the brain. It should be appreciated that these computations are sophisticated enough to contribute to network level phenomena up to behavior in vivo. Relating axonal computation to behavioral phenomenology is still a nascent area which will complement studies that have focused almost exclusively on somas, dendrites or a coarse grained view of neurons. The study of axonal computation is hurdled by technical challenges, but there is already an emerging interest in developing technologies that will allow to electrophysiologically and structurally study axonal processes. Further complication arises when one realizes that axons do not act alone but in concert, exhibiting collective modes of computation conveyed by inter-axonal signaling. We propose that axonal biophysics are of vital importance for understanding not only how single neurons process information but also how neural networks coordinate their activity.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
PA was funded by the Munich Center for Neurosciences. AE was funded by the Howard Hughes Medical Institute.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to Emily Jane Dennis for the drawing of the neuron in Figure 2 and the AIS in Figure 3. We are grateful to Conny Kopp-Scheinflug and Henrique von Gersdorff for their feedback on previous versions of this manuscript. We are thankful to the reviewers for their insightful comments.
References
Abbott, B., Howarth, J., and Ritchie, J. (1965). The initial heat production associated with the nerve impulse in crustacean and mammalian non-myelinated nerve fibres. J. Physiol. 178, 368–383. doi: 10.1113/jphysiol.1965.sp007633
Agudelo-Toro, A., and Neef, A. (2013). Computationally efficient simulation of electrical activity at cell membranes interacting with self-generated and externally imposed electric fields. J. Neural Eng. 10:026019. doi: 10.1088/1741-2560/10/2/026019
Akkin, T., Joo, C., and De Boer, J. F. (2007). Depth-resolved measurement of transient structural changes during action potential propagation. Biophys. J. 93, 1347–1353. doi: 10.1529/biophysj.106.091298
Alcami, P. (2018). Electrical synapses enhance and accelerate interneuron recruitment in response to coincident and sequential excitation. Front. Cell. Neurosci. 12:156. doi: 10.3389/fncel.2018.00156
Alcami, P., and Marty, A. (2013). Estimating functional connectivity in an electrically coupled interneuron network. Proc. Natl. Acad. Sci. U.S.A. 110, E4798–E4807. doi: 10.1073/pnas.1310983110
Alcami, P., and Pereda, A. E. (2019). Beyond plasticity: the dynamic impact of electrical synapses on neural circuits. Nat. Rev. Neurosci. 20, 253-?271. doi: 10.1038/s41583-019-0133-5
Alle, H., and Geiger, J. R. (2006). Combined analog and action potential coding in hippocampal mossy fibers. Science 311, 1290–1293. doi: 10.1126/science.1119055
Alle, H., Kubota, H., and Geiger, J. R. (2011). Sparse but highly efficient Kv3 outpace BKCa channels in action potential repolarization at hippocampal mossy fiber boutons. J. Neurosci. 31, 8001–8012. doi: 10.1523/JNEUROSCI.0972-11.2011
Amsalem, O., Van Geit, W., Muller, E., Markram, H., and Segev, I. (2016). From neuron biophysics to orientation selectivity in electrically coupled networks of neocortical l2/3 large basket cells. Cereb. Cortex 26, 3655–3668. doi: 10.1093/cercor/bhw166
Araki, T., and Otani, T. (1955). Response of single motoneurons to direct stimulation in toad's spinal cord. J. Neurophysiol. 18, 472–485. doi: 10.1152/jn.1955.18.5.472
Arancibia-Carcamo, I. L., Ford, M. C., Cossell, L., Ishida, K., Tohyama, K., and Attwell, D. (2017). Node of ranvier length as a potential regulator of myelinated axon conduction speed. Elife 6:e23329. doi: 10.7554/eLife.23329
Ariav, G., Polsky, A., and Schiller, J. (2003). Submillisecond precision of the input-output transformation function mediated by fast sodium dendritic spikes in basal dendrites of CA1 pyramidal neurons. J. Neurosci. 23, 7750–7758. doi: 10.1523/JNEUROSCI.23-21-07750.2003
Astman, N., Gutnick, M. J., and Fleidervish, I. A. (2006). Persistent sodium current in layer 5 neocortical neurons is primarily generated in the proximal axon. J. Neurosci. 26, 3465–3473. doi: 10.1523/JNEUROSCI.4907-05.2006
Atherton, J. F., Wokosin, D. L., Ramanathan, S., and Bevan, M. D. (2008). Autonomous initiation and propagation of action potentials in neurons of the subthalamic nucleus. J. Physiol. 586, 5679–5700. doi: 10.1113/jphysiol.2008.155861
Azouz, R., and Gray, C. M. (1999). Cellular mechanisms contributing to response variability of cortical neurons in vivo. J. Neurosci. 19, 2209–2223. doi: 10.1523/JNEUROSCI.19-06-02209.1999
Azouz, R., Jensen, M. S., and Yaari, Y. (1996). Ionic basis of spike after-depolarization and burst generation in adult rat hippocampal CA1 pyramidal cells. J. Physiol. 492(Pt 1), 211–223. doi: 10.1113/jphysiol.1996.sp021302
Baccus, S. A. (1998). Synaptic facilitation by reflected action potentials: enhancement of transmission when nerve impulses reverse direction at axon branch points. Proc. Natl. Acad. Sci. U.S.A. 95, 8345–8350. doi: 10.1073/pnas.95.14.8345
Baccus, S. A., Burrell, B. D., Sahley, C. L., and Muller, K. J. (2000). Action potential reflection and failure at axon branch points cause stepwise changes in EPSPs in a neuron essential for learning. J. Neurophysiol. 83, 1693–1700. doi: 10.1152/jn.2000.83.3.1693
Bakiri, Y., Káradóttir, R., Cossell, L., and Attwell, D. (2011). Morphological and electrical properties of oligodendrocytes in the white matter of the corpus callosum and cerebellum. J. Physiol. 589, 559–573. doi: 10.1113/jphysiol.2010.201376
Baranauskas, G., and Martina, M. (2006). Sodium currents activate without a hodgkin and huxley-type delay in central mammalian neurons. J. Neurosci. 26, 671–684. doi: 10.1523/JNEUROSCI.2283-05.2006
Batabyal, S., Satpathy, S., Bui, L., Kim, Y.-T., Mohanty, S., Bachoo, R., et al. (2017). Label-free optical detection of action potential in mammalian neurons. Biomed. Opt. Exp. 8, 3700–3713. doi: 10.1364/BOE.8.003700
Bean, B. P. (2007). The action potential in mammalian central neurons. Nat. Rev. Neurosci. 8:451. doi: 10.1038/nrn2148
Bekkers, J. M., and Häusser, M. (2007). Targeted dendrotomy reveals active and passive contributions of the dendritic tree to synaptic integration and neuronal output. Proc. Natl. Acad. Sci. U.S.A. 104, 11447–11452. doi: 10.1073/pnas.0701586104
Bennett, M. V., Aljure, E., Nakajima, Y., and Pappas, G. D. (1963). Electrotonic junctions between teleost spinal neurons: electrophysiology and ultrastructure. Science 141, 262–264. doi: 10.1126/science.141.3577.262
Bi, G.-Q., and Poo, M.-M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998
Bialowas, A., Rama, S., Zbili, M., Marra, V., Fronzaroli-Molinieres, L., Ankri, N., et al. (2015). Analog modulation of spike-evoked transmission in CA 3 circuits is determined by axonal Kv1.1 channels in a time-dependent manner. Eur. J. Neurosci. 41, 293–304. doi: 10.1111/ejn.12787
Blot, A., and Barbour, B. (2014). Ultra-rapid axon-axon ephaptic inhibition of cerebellar purkinje cells by the pinceau. Nat. Neurosci. 17, 289–295. doi: 10.1038/nn.3624
Boiko, T., Van Wart, A., Caldwell, J. H., Levinson, S. R., Trimmer, J. S., and Matthews, G. (2003). Functional specialization of the axon initial segment by isoform-specific sodium channel targeting. J. Neurosci. 23, 2306–2313. doi: 10.1523/JNEUROSCI.23-06-02306.2003
Borst, A., and Haag, J. (1996). The intrinsic electrophysiological characteristics of fly lobula plate tangential cells: I. passive membrane properties. J. Comput. Neurosci. 3, 313–336. doi: 10.1007/BF00161091
Borst, J. G. G., and Sakmann, B. (1999). Effect of changes in action potential shape on calcium currents and transmitter release in a calyx–type synapse of the rat auditory brainstem. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 354, 347–355. doi: 10.1098/rstb.1999.0386
Brachet, A., Leterrier, C., Irondelle, M., Fache, M.-P., Racine, V., Sibarita, J.-B., et al. (2010). Ankyrin G restricts ion channel diffusion at the axonal initial segment before the establishment of the diffusion barrier. J. Cell Biol. 191, 383–395. doi: 10.1083/jcb.201003042
Brette, R. (2013). Sharpness of spike initiation in neurons explained by compartmentalization. PLoS Comput. Biol. 9:e1003338. doi: 10.1371/journal.pcbi.1003338
Brohawn, S. G., Wang, W., Schwarz, J. R., Handler, A., Campbell, E. B., and MacKinnon, R. (2019). The mechanosensitive ion channel traak is localized to the mammalian node of ranvier. bioRxiv. doi: 10.1101/713990
Calabrese, R. L., and Kennedy, D. (1974). Multiple sites of spike initiation in a single dendritic system. Brain Res. 82, 316–321. doi: 10.1016/0006-8993(74)90612-X
Carpenter, D. O., Hovey, M. M., and Bak, A. F. (1975). Resistivity of axoplasm. II. internal resistivity of giant axons of squid and myxicola. J. Gen. Physiol. 66, 139–148. doi: 10.1085/jgp.66.2.139
Castelfranco, A. M., and Hartline, D. K. (2015). The evolution of vertebrate and invertebrate myelin: a theoretical computational study. J. Comput. Neurosci. 38, 521–538. doi: 10.1007/s10827-015-0552-x
Chen, W. R., Shen, G. Y., Shepherd, G. M., Hines, M. L., and Midtgaard, J. (2002). Multiple modes of action potential initiation and propagation in mitral cell primary dendrite. J. Neurophysiol. 88, 2755–2764. doi: 10.1152/jn.00057.2002
Chéreau, R., Saraceno, G. E., Angibaud, J., Cattaert, D., and Nägerl, U. V. (2017). Superresolution imaging reveals activity-dependent plasticity of axon morphology linked to changes in action potential conduction velocity. Proc. Natl. Acad. Sci. U.S.A. 114, 1401–1406. doi: 10.1073/pnas.1607541114
Cho, I. H., Panzera, L. C., Chin, M., and Hoppa, M. B. (2017). Sodium channel β2 subunits prevent action potential propagation failures at axonal branch points. J. Neurosci. 37, 9519–9533. doi: 10.1523/JNEUROSCI.0891-17.2017
Chorev, E., and Brecht, M. (2012). In vivo dual intra-and extracellular recordings suggest bidirectional coupling between CA1 pyramidal neurons. J. Neurophysiol. 108, 1584–1593. doi: 10.1152/jn.01115.2011
Clark, B. A., Monsivais, P., Branco, T., London, M., and Häusser, M. (2005). The site of action potential initiation in cerebellar purkinje neurons. Nat. Neurosci. 8, 137–139. doi: 10.1038/nn1390
Cohen, L., Hille, B., and Keynes, R. (1970). Changes in axon birefringence during the action potential. J. Physiol. 211, 495–515. doi: 10.1113/jphysiol.1970.sp009289
Colbert, C. M., and Johnston, D. (1996). Axonal action-potential initiation and Na+ channel densities in the soma and axon initial segment of subicular pyramidal neurons. J. Neurosci. 16, 6676–6686. doi: 10.1523/JNEUROSCI.16-21-06676.1996
Colbert, C. M., and Pan, E. (2002). Ion channel properties underlying axonal action potential initiation in pyramidal neurons. Nat. Neurosci. 5, 533–538. doi: 10.1038/nn0602-857
Cole, K. (1975). Resistivity of axoplasm. I. resistivity of extruded squid axoplasm. J. Gen. Physiol. 66, 133–138. doi: 10.1085/jgp.66.2.133
Coombs, J., Curtis, D., and Eccles, J. (1957). The generation of impulses in motoneurones. J. Physiol. 139, 232–249. doi: 10.1113/jphysiol.1957.sp005888
Davis, J. Q., Lambert, S., and Bennett, V. (1996). Molecular composition of the node of ranvier: identification of ankyrin-binding cell adhesion molecules neurofascin (mucin+/third FNIII domain-) and nrCAM at nodal axon segments. J. Cell Biol. 135, 1355–1367. doi: 10.1083/jcb.135.5.1355
de San Martin, J. Z., Jalil, A., and Trigo, F. F. (2015). Impact of single-site axonal gabaergic synaptic events on cerebellar interneuron activity. J. Gen. Physiol. 146, 477–493. doi: 10.1085/jgp.201511506
Debanne, D., Guerineau, N. C., Gähwiler, B. H., and Thompson, S. M. (1997). Action-potential propagation gated by an axonal I(A)-like K+ conductance in hippocampus. Nature 389, 286–289. doi: 10.1038/38502
Debanne, D., Inglebert, Y., and Russier, M. (2019). Plasticity of intrinsic neuronal excitability. Curr. Opin. Neurobiol. 54, 73–82. doi: 10.1016/j.conb.2018.09.001
Dekker, J. P., and Yellen, G. (2006). Cooperative gating between single hcn pacemaker channels. J. Gen. Physiol. 128, 561–567. doi: 10.1085/jgp.200609599
D'Este, E., Kamin, D., Balzarotti, F., and Hell, S. W. (2017). Ultrastructural anatomy of nodes of ranvier in the peripheral nervous system as revealed by sted microscopy. Proc. Natl. Acad. Sci. U.S.A. 114, E191–E199. doi: 10.1073/pnas.1619553114
Destexhe, A., Rudolph, M., Fellous, J.-M., and Sejnowski, T. J. (2001). Fluctuating synaptic conductances recreate in vivo-like activity in neocortical neurons. Neuroscience 107, 13–24. doi: 10.1016/S0306-4522(01)00344-X
Deutsch, S. (1969). The maximization of nerve conduction velocity. IEEE Trans. Syst. Sci. Cybern. 5, 86–91. doi: 10.1109/TSSC.1969.300249
Doiron, B., Laing, C., Longtin, A., and Maler, L. (2002). Ghostbursting: a novel neuronal burst mechanism. J. Comput. Neurosci. 12, 5–25. doi: 10.1023/A:1014921628797
Duflocq, A., Chareyre, F., Giovannini, M., Couraud, F., and Davenne, M. (2011). Characterization of the axon initial segment (AIS) of motor neurons and identification of a para-ais and a juxtapara-ais, organized by protein 4.1B. BMC Biol. 9:66. doi: 10.1186/1741-7007-9-66
Dugladze, T., Schmitz, D., Whittington, M. A., Vida, I., and Gloveli, T. (2012). Segregation of axonal and somatic activity during fast network oscillations. Science 336, 1458–1461. doi: 10.1126/science.1222017
El Hady, A., and Machta, B. B. (2015). Mechanical surface waves accompany action potential propagation. Nat. Commun. 6:6697. doi: 10.1038/ncomms7697
Epsztein, J., Lee, A. K., Chorev, E., and Brecht, M. (2010). Impact of spikelets on hippocampal CA1 pyramidal cell activity during spatial exploration. Science 327, 474–477. doi: 10.1126/science.1182773
Etxeberria, A., Hokanson, K. C., Dao, D. Q., Mayoral, S. R., Mei, F., Redmond, S. A., et al. (2016). Dynamic modulation of myelination in response to visual stimuli alters optic nerve conduction velocity. J. Neurosci. 36, 6937–6948. doi: 10.1523/JNEUROSCI.0908-16.2016
Eyal, G., Mansvelder, H. D., de Kock, C. P., and Segev, I. (2014). Dendrites impact the encoding capabilities of the axon. J. Neurosci. 34, 8063–8071. doi: 10.1523/JNEUROSCI.5431-13.2014
Fatt, P. (1957). Electric potentials occurring around a neurone during its antidromic activation. J. Neurophysiol. 20, 27–60. doi: 10.1152/jn.1957.20.1.27
Fields, R. D. (2015). A new mechanism of nervous system plasticity: activity-dependent myelination. Nat. Rev. Neurosci. 16, 756–767. doi: 10.1038/nrn4023
Fleidervish, I. A., Lasser-Ross, N., Gutnick, M. J., and Ross, W. N. (2010). Na+ imaging reveals little difference in action potential–evoked Na+ influx between axon and soma. Nat. Neurosci. 13, 852–860. doi: 10.1038/nn.2574
Ford, M. C., Alexandrova, O., Cossell, L., Stange-Marten, A., Sinclair, J., Kopp-Scheinpflug, C., et al. (2015). Tuning of ranvier node and internode properties in myelinated axons to adjust action potential timing. Nat. Commun. 6:8073. doi: 10.1038/ncomms9073
Fourcaud-Trocmé, N., Hansel, D., Van Vreeswijk, C., and Brunel, N. (2003). How spike generation mechanisms determine the neuronal response to fluctuating inputs. J. Neurosci. 23, 11628–11640. doi: 10.1523/JNEUROSCI.23-37-11628.2003
Foust, A., Popovic, M., Zecevic, D., and McCormick, D. A. (2010). Action potentials initiate in the axon initial segment and propagate through axon collaterals reliably in cerebellar purkinje neurons. J. Neurosci. 30, 6891–6902. doi: 10.1523/JNEUROSCI.0552-10.2010
Furshpan, E. J., and Potter, D. D. (1959). Transmission at the giant motor synapses of the crayfish. J. Physiol. 145, 289–325. doi: 10.1113/jphysiol.1959.sp006143
Gasparini, S., Migliore, M., and Magee, J. C. (2004). On the initiation and propagation of dendritic spikes in CA1 pyramidal neurons. J. Neurosci. 24, 11046–11056. doi: 10.1523/JNEUROSCI.2520-04.2004
Geiger, J. R., and Jonas, P. (2000). Dynamic control of presynaptic Ca2+ inflow by fast-inactivating K+ channels in hippocampal mossy fiber boutons. Neuron 28, 927–939. doi: 10.1016/S0896-6273(00)00164-1
Gentet, L. J., Stuart, G. J., and Clements, J. D. (2000). Direct measurement of specific membrane capacitance in neurons. Biophys. J. 79, 314–320. doi: 10.1016/S0006-3495(00)76293-X
Golding, N. L., and Spruston, N. (1998). Dendritic sodium spikes are variable triggers of axonal action potentials in hippocampal Ca1 pyramidal neurons. Neuron 21, 1189–1200. doi: 10.1016/S0896-6273(00)80635-2
Goldman, L., and Albus, J. S. (1968). Computation of impulse conduction in myelinated fibers; theoretical basis of the velocity-diameter relation. Biophys. J. 8, 596–607. doi: 10.1016/S0006-3495(68)86510-5
Goldstein, S. S., and Rall, W. (1974). Changes of action potential shape and velocity for changing core conductor geometry. Biophys. J. 14, 731–757. doi: 10.1016/S0006-3495(74)85947-3
Goldwyn, J. H., Remme, M. W., and Rinzel, J. (2019). Soma-axon coupling configurations that enhance neuronal coincidence detection. PLoS Comput. Biol. 15:e1006476. doi: 10.1371/journal.pcbi.1006476
Grossman, Y., Parnas, I., and Spira, M. E. (1979). Differential conduction block in branches of a bifurcating axon. J. Physiol. 295, 283–305. doi: 10.1113/jphysiol.1979.sp012969
Grubb, M. S., and Burrone, J. (2010). Activity-dependent relocation of the axon initial segment fine-tunes neuronal excitability. Nature 465, 1070–1074. doi: 10.1038/nature09160
Gründemann, J., and Clark, B. A. (2015). Calcium-activated potassium channels at nodes of ranvier secure axonal spike propagation. Cell Rep. 12, 1715–1722. doi: 10.1016/j.celrep.2015.08.022
Gu, X. N., Muller, K. J., and Young, S. R. (1991). Synaptic integration at a sensory-motor reflex in the leech. J. Physiol. 441, 733–754. doi: 10.1113/jphysiol.1991.sp018776
Han, K.-S., Guo, C., Chen, C. H., Witter, L., Osorno, T., and Regehr, W. G. (2018). Ephaptic coupling promotes synchronous firing of cerebellar purkinje cells. Neuron 100, 564–578.e3. doi: 10.1016/j.neuron.2018.09.018
Harris, J. J., and Attwell, D. (2012). The energetics of CNS white matter. J. Neurosci. 32, 356–371. doi: 10.1523/JNEUROSCI.3430-11.2012
Higgs, M. H., Slee, S. J., and Spain, W. J. (2006). Diversity of gain modulation by noise in neocortical neurons: regulation by the slow afterhyperpolarization conductance. J. Neurosci. 26, 8787–8799. doi: 10.1523/JNEUROSCI.1792-06.2006
Higgs, M. H., and Spain, W. J. (2009). Conditional bursting enhances resonant firing in neocortical layer 2–3 pyramidal neurons. J. Neurosci. 29, 1285–1299. doi: 10.1523/JNEUROSCI.3728-08.2009
Hill, B. C., Schubert, E. D., Nokes, M. A., and Michelson, R. P. (1977). Laser interferometer measurement of changes in crayfish axon diameter concurrent with action potential. Science 196, 426–428. doi: 10.1126/science.850785
Hines, J. H., Ravanelli, A. M., Schwindt, R., Scott, E. K., and Appel, B. (2015). Neuronal activity biases axon selection for myelination in vivo. Nat. Neurosci. 18, 683–689. doi: 10.1038/nn.3992
Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544. doi: 10.1113/jphysiol.1952.sp004764
Hodgkin, A. L., and Katz, B. (1949). The effect of sodium ions on the electrical activity of the giant axon of the squid. J. Physiol. 108, 37–77. doi: 10.1113/jphysiol.1949.sp004310
Howarth, J. (1975). Heat production in non-myelinated nerves. Philos. Trans. R. Soc. Lond. B Biol. Sci. 270, 425–432. doi: 10.1098/rstb.1975.0020
Howarth, J., Keynes, R., Ritchie, J., and Von Muralt, A. (1975). The heat production associated with the passage of a single impulse in pike olfactory nerve fibres. J. Physiol. 249, 349–368. doi: 10.1113/jphysiol.1975.sp011019
Hu, H., and Jonas, P. (2014). A supercritical density of Na(+) channels ensures fast signaling in gabaergic interneuron axons. Nat. Neurosci. 17, 686—693. doi: 10.1038/nn.3678
Hu, W., Tian, C., Li, T., Yang, M., Hou, H., and Shu, Y. (2009). Distinct contributions of Na(v)1.6 and Na(v)1.2 in action potential initiation and backpropagation. Nat. Neurosci. 12, 996–1002. doi: 10.1038/nn.2359
Huang, M., Volgushev, M., and Wolf, F. (2012). A small fraction of strongly cooperative sodium channels boosts neuronal encoding of high frequencies. PLoS ONE 7:e37629. doi: 10.1371/journal.pone.0037629
Hull, M. J., Soffe, S. R., Willshaw, D. J., and Roberts, A. (2015). Modelling the effects of electrical coupling between unmyelinated axons of brainstem neurons controlling rhythmic activity. PLoS Comput. Biol. 11:e1004240. doi: 10.1371/journal.pcbi.1004240
Huxley, A. F., and Stämpfli, R. (1949). Evidence for saltatory conduction in peripheral myelinated nerve fibres. J. Physiol. 108, 315–339. doi: 10.1113/jphysiol.1949.sp004335
Iwasa, K., and Tasaki, I. (1980). Mechanical changes in squid giant axons associated with production of action potentials. Biochem. Biophys. Res. Commun. 95, 1328–1331. doi: 10.1016/0006-291X(80)91619-8
Izhikevich, E. M., Gally, J. A., and Edelman, G. M. (2004). Spike-timing dynamics of neuronal groups. Cereb. Cortex 14, 933–944. doi: 10.1093/cercor/bhh053
Kaller, M. S., Lazari, A., Blanco-Duque, C., Sampaio-Baptista, C., and Johansen-Berg, H. (2017). Myelin plasticity and behaviour—connecting the dots. Curr. Opin. Neurobiol. 47, 86–92. doi: 10.1016/j.conb.2017.09.014
Kamasawa, N., Sik, A., Morita, M., Yasumura, T., Davidson, K., Nagy, J., et al. (2005). Connexin-47 and connexin-32 in gap junctions of oligodendrocyte somata, myelin sheaths, paranodal loops and schmidt-lanterman incisures: implications for ionic homeostasis and potassium siphoning. Neuroscience 136, 65–86. doi: 10.1016/j.neuroscience.2005.08.027
Katz, B., and Schmitt, O. H. (1940). Electric interaction between two adjacent nerve fibres. J. Physiol. 97, 471–488. doi: 10.1113/jphysiol.1940.sp003823
Kawaguchi, S.-Y., and Sakaba, T. (2015). Control of inhibitory synaptic outputs by low excitability of axon terminals revealed by direct recording. Neuron 85, 1273—1288. doi: 10.1016/j.neuron.2015.02.013
Keynes, R. (1951). The ionic movements during nervous activity. J. Physiol. 114, 119–150. doi: 10.1113/jphysiol.1951.sp004608
Khaliq, Z. M., and Raman, I. M. (2006). Relative contributions of axonal and somatic Na channels to action potential initiation in cerebellar purkinje neurons. J. Neurosci. 26, 1935–1944. doi: 10.1523/JNEUROSCI.4664-05.2006
Kim, G. E., Kronengold, J., Barcia, G., Quraishi, I. H., Martin, H. C., Blair, E., et al. (2014). Human slack potassium channel mutations increase positive cooperativity between individual channels. Cell Rep. 9, 1661–1672. doi: 10.1016/j.celrep.2014.11.015
Kim, J. H., Renden, R., and Von Gersdorff, H. (2013). Dysmyelination of auditory afferent axons increases the jitter of action potential timing during high-frequency firing. J. Neurosci. 33, 9402–9407. doi: 10.1523/JNEUROSCI.3389-12.2013
Kole, M. H., Letzkus, J. J., and Stuart, G. J. (2007). Axon initial segment Kv1 channels control axonal action potential waveform and synaptic efficacy. Neuron 55, 633–647. doi: 10.1016/j.neuron.2007.07.031
Kole, M. H. P. (2011). First node of ranvier facilitates high-frequency burst encoding. Neuron 71, 671–682. doi: 10.1016/j.neuron.2011.06.024
Kole, M. H. P., Ilschner, S. U., Kampa, B. M., Williams, S. R., Ruben, P. C., and Stuart, G. J. (2008). Action potential generation requires a high sodium channel density in the axon initial segment. Nat. Neurosci. 11, 178–186. doi: 10.1038/nn2040
Kopp-Scheinpflug, C., and Tempel, B. L. (2015). Decreased temporal precision of neuronal signaling as a candidate mechanism of auditory processing disorder. Hear. Res. 330, 213–220. doi: 10.1016/j.heares.2015.06.014
Kordeli, E., Lambert, S., and Bennett, V. (1995). Ankyrin a new ankyrin gene with neural-specific isoforms localized at the axonal initial segment and node of ranvier. J. Biol. Chem. 270, 2352–2359. doi: 10.1074/jbc.270.5.2352
Krnjevic, K., and Miledi, R. (1959). Presynaptic failure of neuromuscular propagation in rats. J. Physiol. 149, 1–22. doi: 10.1113/jphysiol.1959.sp006321
Kuba, H., Adachi, R., and Ohmori, H. (2014). Activity-dependent and activity-independent development of the axon initial segment. J. Neurosci. 34, 3443–3453. doi: 10.1523/JNEUROSCI.4357-13.2014
Larkum, M. E., Zhu, J. J., and Sakmann, B. (1999). A new cellular mechanism for coupling inputs arriving at different cortical layers. Nature 398, 338–341. doi: 10.1038/18686
Larkum, M. E., Zhu, J. J., and Sakmann, B. (2001). Dendritic mechanisms underlying the coupling of the dendritic with the axonal action potential initiation zone of adult rat layer 5 pyramidal neurons. J. Physiol. 533(Pt 2), 447–466. doi: 10.1111/j.1469-7793.2001.0447a.x
Lazarov, E., Dannemeyer, M., Feulner, B., Enderlein, J., Gutnick, M. J., Wolf, F., et al. (2018). An axon initial segment is required for temporal precision in action potential encoding by neuronal populations. Sci. Adv. 4:eaau8621. doi: 10.1126/sciadv.aau8621
Leão, R. M., Kushmerick, C., Pinaud, R., Renden, R., Li, G.-L., Taschenberger, H., et al. (2005). Presynaptic Na+ channels: locus, development, and recovery from inactivation at a high-fidelity synapse. J. Neurosci. 25, 3724–3738. doi: 10.1523/JNEUROSCI.3983-04.2005
Lehnert, S., Ford, M. C., Alexandrova, O., Hellmundt, F., Felmy, F., Grothe, B., et al. (2014). Action potential generation in an anatomically constrained model of medial superior olive axons. J. Neurosci. 34, 5370–5384. doi: 10.1523/JNEUROSCI.4038-13.2014
Leterrier, C. (2016). “The axon initial segment, 50 years later: a nexus for neuronal organization and function,” in Current Topics in Membranes, Vol. 77, ed V. Bennett (Elsevier), 185–233. Available online at: https://www.elsevier.com/books/dynamic-plasma-membranes-portals-between-cells-and-physiology/bennett/978-0-12-805404-8
Lien, C.-C., and Jonas, P. (2003). Kv3 potassium conductance is necessary and kinetically optimized for high-frequency action potential generation in hippocampal interneurons. J. Neurosci. 23, 2058–2068. doi: 10.1523/JNEUROSCI.23-06-02058.2003
Lillie, R. S. (1925). Factors affecting transmission and recovery in the passive iron nerve model. J. Gen. Physiol. 7, 473–507. doi: 10.1085/jgp.7.4.473
Lorincz, A., and Nusser, Z. (2010). Molecular identity of dendritic voltage-gated sodium channels. Science 328, 906–909. doi: 10.1126/science.1187958
Mackie, G. O., and Meech, R. W. (1985). Separate sodium and calcium spikes in the same axon. Nature 313, 791–793. doi: 10.1038/313791a0
Mainen, Z. F., and Sejnowski, T. J. (1996). Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382, 363–366. doi: 10.1038/382363a0
Manor, Y., Koch, C., and Segev, I. (1991). Effect of geometrical irregularities on propagation delay in axonal trees. Biophys. J. 60, 1424–1437. doi: 10.1016/S0006-3495(91)82179-8
Mar, A., and Drapeau, P. (1996). Modulation of conduction block in leech mechanosensory neurons. J. Neurosci. 16, 4335–4343. doi: 10.1523/JNEUROSCI.16-14-04335.1996
Maranto, A. R., and Calabrese, R. L. (1984). Neural control of the hearts in the leech, Hirudo medicinalis. J. Comp. Physiol. A 154, 381–391. doi: 10.1007/BF00605237
Maratou, E., and Theophilidis, G. (2000). An axon pacemaker: diversity in the mechanism of generation and conduction of action potentials in snail neurons. Neuroscience 96, 1–2. doi: 10.1016/S0306-4522(99)00529-1
Marder, E., and Goaillard, J.-M. (2006). Variability, compensation and homeostasis in neuron and network function. Nat. Rev. Neurosci. 7, 563–574. doi: 10.1038/nrn1949
Marder, E., and Taylor, A. L. (2011). Multiple models to capture the variability in biological neurons and networks. Nat. Neurosci. 14, 133–138. doi: 10.1038/nn.2735
Marx, S. O., Gaburjakova, J., Gaburjakova, M., Henrikson, C., Ondrias, K., and Marks, A. R. (2001). Coupled gating between cardiac calcium release channels (ryanodine receptors). Circ. Res. 88, 1151–1158. doi: 10.1161/hh1101.091268
McCormick, D. A., Shu, Y., and Yu, Y. (2007). Hodgkin and huxley model —still standing? Nature 445, E1–E2. doi: 10.1038/nature05523
McKenzie, I. A., Ohayon, D., Li, H., Paes de Faria, J., Emery, B., Tohyama, K., et al. (2014). Motor skill learning requires active central myelination. Science 346, 318–322. doi: 10.1126/science.1254960
Meeks, J. P., and Mennerick, S. (2007). Action potential initiation and propagation in Ca3 pyramidal axons. J. Neurophysiol. 97, 3460–3472. doi: 10.1152/jn.01288.2006
Mejia-Gervacio, S., Collin, T., Pouzat, C., Tan, Y. P., Llano, I., and Marty, A. (2007). Axonal speeding: shaping synaptic potentials in small neurons by the axonal membrane compartment. Neuron 53, 843–855. doi: 10.1016/j.neuron.2007.02.023
Meyrand, P., Weimann, J., and Marder, E. (1992). Multiple axonal spike initiation zones in a motor neuron: serotonin activation. J. Neurosci. 12, 2803–2812. doi: 10.1523/JNEUROSCI.12-07-02803.1992
Micu, I., Plemel, J. R., Caprariello, A. V., Nave, K.-A., and Stys, P. K. (2017). Axo-myelinic neurotransmission: a novel mode of cell signalling in the central nervous system. Nat. Rev. Neurosci. 19, 49–58. doi: 10.1038/nrn.2017.128
Milescu, L. S., Yamanishi, T., Ptak, K., and Smith, J. C. (2010). Kinetic properties and functional dynamics of sodium channels during repetitive spiking in a slow pacemaker neuron. J. Neurosci. 30, 12113–12127. doi: 10.1523/JNEUROSCI.0445-10.2010
Monsivais, P., Clark, B. A., Roth, A., and Häusser, M. (2005). Determinants of action potential propagation in cerebellar purkinje cell axons. J. Neurosci. 25, 464–472. doi: 10.1523/JNEUROSCI.3871-04.2005
Moubarak, E., Engel, D., Dufour, M. A., Tapia, M., Tell, F., and Goaillard, J.-M. (2019). Robustness to axon initial segment variation is explained by somatodendritic excitability in rat substantia nigra dopaminergic neurons. J. Neurosci. 39, 5044–5063. doi: 10.1523/JNEUROSCI.2781-18.2019
Mulloney, B., and Selverston, A. (1972). Antidromic action potentials fail to demonstrate known interactions between neurons. Science 177, 69–72. doi: 10.1126/science.177.4043.69
Naundorf, B., Wolf, F., and Volgushev, M. (2006). Unique features of action potential initiation in cortical neurons. Nature 440, 1060–1063. doi: 10.1038/nature04610
Neef, A., Hady, A. E., Nagpal, J., Bröking, K., Afshar, G., Schlüter, O. M., et al. (2013). Continuous dynamic photostimulation-inducing in-vivo-like fluctuating conductances with channelrhodopsins. arXiv preprint arXiv:1305.7125.
Neishabouri, A., and Faisal, A. A. (2014). Axonal noise as a source of synaptic variability. PLoS Comput. Biol. 10:e1003615. doi: 10.1371/journal.pcbi.1003615
Nörenberg, A., Hu, H., Vida, I., Bartos, M., and Jonas, P. (2010). Distinct nonuniform cable properties optimize rapid and efficient activation of fast-spiking gabaergic interneurons. Proc. Natl. Acad. Sci. U.S.A. 107, 894–899. doi: 10.1073/pnas.0910716107
Ofer, N., Shefi, O., and Yaari, G. (2019). Axonal tree morphology and signal propagation dynamics improve interneuron classification. bioRxiv. doi: 10.1101/414615
Oh, S., Fang-Yen, C., Choi, W., Yaqoob, Z., Fu, D., Park, Y., et al. (2012). Label-free imaging of membrane potential using membrane electromotility. Biophys. J. 103, 11–18. doi: 10.1016/j.bpj.2012.05.020
Palay, S. L., and Chan-Palay, V. (2012). Cerebellar Cortex: Cytology and Organization. Berlin; Heidelberg: Springer-Verlag.
Palmer, L. M., Clark, B. A., Gründemann, J., Roth, A., Stuart, G. J., and Häusser, M. (2010). Rapid report: initiation of simple and complex spikes in cerebellar purkinje cells. J. Physiol. 588, 1709–1717. doi: 10.1113/jphysiol.2010.188300
Palmer, L. M., and Stuart, G. J. (2006). Site of action potential initiation in layer 5 pyramidal neurons. J. Neurosci. 26, 1854–1863. doi: 10.1523/JNEUROSCI.4812-05.2006
Perge, J. A., Koch, K., Miller, R., Sterling, P., and Balasubramanian, V. (2009). How the optic nerve allocates space, energy capacity, and information. J. Neurosci. 29, 7917–7928. doi: 10.1523/JNEUROSCI.5200-08.2009
Peterson, E., Izad, O., and Tyler, D. J. (2011). Predicting myelinated axon activation using spatial characteristics of the extracellular field. J. Neural Eng. 8:046030. doi: 10.1088/1741-2560/8/4/046030
Pinsky, P. F., and Rinzel, J. (1994). Intrinsic and network rhythmogenesis in a reduced traub model for Ca3 neurons. J. Comput. Neurosci. 1, 39–60. doi: 10.1007/BF00962717
Powers, R. K., Sawczuk, A., Musick, J. R., and Binder, M. D. (1999). Multiple mechanisms of spike-frequency adaptation in motoneurones. J. Physiol. 93, 101–114. doi: 10.1016/S0928-4257(99)80141-7
Rama, S., Zbili, M., Bialowas, A., Fronzaroli-Molinieres, L., Ankri, N., Carlier, E., et al. (2015). Presynaptic hyperpolarization induces a fast analogue modulation of spike-evoked transmission mediated by axonal sodium channels. Nat. Commun. 6:10163. doi: 10.1038/ncomms10163
Ranade, S. S., Syeda, R., and Patapoutian, A. (2015). Mechanically activated ion channels. Neuron 87, 1162–1179. doi: 10.1016/j.neuron.2015.08.032
Rasband, M. N. (2010). The axon initial segment and the maintenance of neuronal polarity. Nat. Rev. Neurosci. 11, 552–562. doi: 10.1038/nrn2852
Rash, J. E., Vanderpool, K. G., Yasumura, T., Hickman, J., Beatty, J. T., and Nagy, J. I. (2016). Kv1 channels identified in rodent myelinated axons, linked to Cx29 in innermost myelin: support for electrically active myelin in mammalian saltatory conduction. J. Neurophysiol. 115, 1836–1859. doi: 10.1152/jn.01077.2015
Rios, J. C., Rubin, M., Martin, M. S., Downey, R. T., Einheber, S., Rosenbluth, J., et al. (2003). Paranodal interactions regulate expression of sodium channel subtypes and provide a diffusion barrier for the node of ranvier. J. Neurosci. 23, 7001–7011. doi: 10.1523/JNEUROSCI.23-18-07001.2003
Ritchie, J. M., and Rogart, R. B. (1977). Density of sodium channels in mammalian myelinated nerve fibers and nature of the axonal membrane under the myelin sheath. Proc. Natl. Acad. Sci. U.S.A. 74, 211–215. doi: 10.1073/pnas.74.1.211
Robertson, J. D., Bodenheimer, T. S., and Stage, D. E. (1963). The ultrastructure of mauthner cell synapses and nodes in goldish brains. J. Cell Biol. 19, 159–199. doi: 10.1083/jcb.19.1.159
Roopun, A. K., Simonotto, J. D., Pierce, M. L., Jenkins, A., Nicholson, C., Schofield, I. S., et al. (2010). A nonsynaptic mechanism underlying interictal discharges in human epileptic neocortex. Proc. Natl. Acad. Sci. U.S.A. 107, 338–343. doi: 10.1073/pnas.0912652107
Rosenbluth, J. (1976). Intramembranous particle distribution at the node of ranvier and adjacent axolemma in myelinated axons of the frog brain. J. Neurocytol. 5, 731–745. doi: 10.1007/BF01181584
Rowan, M. J., DelCanto, G., Jianqing, J. Y., Kamasawa, N., and Christie, J. M. (2016). Synapse-level determination of action potential duration by K+ channel clustering in axons. Neuron 91, 370–383. doi: 10.1016/j.neuron.2016.05.035
Rudolph, M., and Destexhe, A. (2003). Characterization of subthreshold voltage fluctuations in neuronal membranes. Neural Computation 15, 2577–2618. doi: 10.1162/089976603322385081
Rush, A. M., Dib-Hajj, S. D., and Waxman, S. G. (2005). Electrophysiological properties of two axonal sodium channels, Nav1.2 and Nav1.6, expressed in mouse spinal sensory neurones. J. Physiol. 564(Pt 3), 803–815. doi: 10.1113/jphysiol.2005.083089
Rushton, W. A. H. (1951). A theory of the effects of fibre size in medullated nerve. J. Physiol. 115, 101–122. doi: 10.1113/jphysiol.1951.sp004655
Sampaio-Baptista, C., Khrapitchev, A. A., Foxley, S., Schlagheck, T., Scholz, J., Jbabdi, S., et al. (2013). Motor skill learning induces changes in white matter microstructure and myelination. J. Neurosci. 33, 19499–19503. doi: 10.1523/JNEUROSCI.3048-13.2013
Sawczuk, A., Powers, R. K., and Binder, M. D. (1997). Contribution of outward currents to spike-frequency adaptation in hypoglossal motoneurons of the rat. J. Neurophysiol. 78, 2246–2253. doi: 10.1152/jn.1997.78.5.2246
Schmidt, D., del Mármol, J., and MacKinnon, R. (2012). Mechanistic basis for low threshold mechanosensitivity in voltage-dependent K+ channels. Proc. Natl. Acad. Sci. U.S.A. 109, 10352–10357. doi: 10.1073/pnas.1204700109
Schmidt, D., and MacKinnon, R. (2008). Voltage-dependent k+ channel gating and voltage sensor toxin sensitivity depend on the mechanical state of the lipid membrane. Proc. Natl. Acad. Sci. U.S.A. 105, 19276–19281. doi: 10.1073/pnas.0810187105
Schmidt-Hieber, C., Jonas, P., and Bischofberger, J. (2008). Action potential initiation and propagation in hippocampal mossy fibre axons. J. Physiol. 586, 1849–1857. doi: 10.1113/jphysiol.2007.150151
Schmitz, D., Schuchmann, S., Fisahn, A., Draguhn, A., Buhl, E. H., Petrasch-Parwez, E., et al. (2001). Axo-axonal coupling: a novel mechanism for ultrafast neuronal communication. Neuron 31, 831–840. doi: 10.1016/S0896-6273(01)00410-X
Seidl, A. H., Rubel, E. W., and Harris, D. M. (2010). Mechanisms for adjusting interaural time differences to achieve binaural coincidence detection. J. Neurosci. 30, 70–80. doi: 10.1523/JNEUROSCI.3464-09.2010
Sheffield, M. E. J., Best, T. K., Mensh, B. D., Kath, W. L., and Spruston, N. (2010). Slow integration leads to persistent action potential firing in distal axons of coupled interneurons. Nat. Neurosci. 14, 200–207. doi: 10.1038/nn.2728
Shu, Y., Hasenstaub, A., Duque, A., Yu, Y., and McCormick, D. A. (2006). Modulation13 of intracortical synaptic potentials by presynaptic somatic membrane potential. Nature 441, 761–765. doi: 10.1038/nature04720
Sinclair, J. L., Fischl, M. J., Alexandrova, O., Heβ, M., Grothe, B., Leibold, C., et al. (2017). Sound-evoked activity influences myelination of brainstem axons in the trapezoid body. J. Neurosci. 37, 8239–8255. doi: 10.1523/JNEUROSCI.3728-16.2017
Sloper, J., and Powell, T. P. S. (1979). A study of the axon initial segment and proximal axon of neurons in the primate motor and somatic sensory cortices. Philos. Trans. R. Soc. Lond. B Biol. Sci. 285, 173–197. doi: 10.1098/rstb.1979.0004
Somogyi, P., Freund, T. F., Hodgson, A. J., Somogyi, J., Beroukas, D., and Chubb, I. W. (1985). Identified axo-axonic cells are immunoreactive for gaba in the hippocampus visual cortex of the cat. Brain Res. 332, 143–149. doi: 10.1016/0006-8993(85)90397-X
Somogyu, P., and Hamori, J. (1976). A quantitative electron microscopic study of the purkinje cell axon initial segment. Neuroscience 1, 361–365. doi: 10.1016/0306-4522(76)90127-5
Song, A.-h., Wang, D., Chen, G., Li, Y., Luo, J., Duan, S., et al. (2009). A selective filter for cytoplasmic transport at the axon initial segment. Cell 136, 1148–1160. doi: 10.1016/j.cell.2009.01.016
Spira, M. E., Oren, R., Dormann, A., and Gitler, D. (2003). Critical calpain-dependent ultrastructural alterations underlie the transformation of an axonal segment into a growth cone after axotomy of cultured aplysia neurons. J. Compar. Neurol. 457, 293–312. doi: 10.1002/cne.10569
Spirou, G., Chirila, F., von Gersdorff, H., and Manis, P. (2008). Heterogeneous Ca2+ influx along the adult calyx of held: a structural and computational study. Neuroscience 154, 171–185. doi: 10.1016/j.neuroscience.2008.04.002
Stasheff, S. F., Hines, M., and Wilson, W. A. (1993). Axon terminal hyperexcitability associated with epileptogenesis in vitro. I. origin of ectopic spikes. J. Neurophysiol. 70, 961–975. doi: 10.1152/jn.1993.70.3.961
Stuart, G., and Sakmann, B. (1995). Amplification of EPSPs by axosomatic sodium channels in neocortical pyramidal neurons. Neuron 15, 1065–1076. doi: 10.1016/0896-6273(95)90095-0
Stuart, G., Spruston, N., and Häusser, M. (2016). Dendrites. Oxford University Press. Available online at: http://www.dendrites.org/dendrites-book
Stuart, G., Spruston, N., Sakmann, B., and Häusser, M. (1997). Action potential initiation and backpropagation in neurons of the mammalian CNS. Trends Neurosci. 20, 125–131. doi: 10.1016/S0166-2236(96)10075-8
Südhof, T. C., and Malenka, R. C. (2008). Understanding synapses: past, present, and future. Neuron 60, 469–476. doi: 10.1016/j.neuron.2008.10.011
Tasaki, I., and Byrne, P. M. (1992). Heat production associated with a propagated impulse in bullfrog myelinated nerve fibers. Jpn. J. Physiol. 42, 805–813. doi: 10.2170/jjphysiol.42.805
Tasaki, I., and Iwasa, K. (1982a). Further studies of rapid mechanical changes in squid giant axon associated with action potential production. Jpn. J. Physiol. 32, 505–518. doi: 10.2170/jjphysiol.32.505
Tasaki, I., and Iwasa, K. (1982b). Rapid pressure changes and surface displacements in the squid giant axon associated with production of action potentials. Jpn. J. Physiol. 32, 69–81. doi: 10.2170/jjphysiol.32.69
Tchumatchenko, T., Malyshev, A., Geisel, T., Volgushev, M., and Wolf, F. (2010). Correlations and synchrony in threshold neuron models. Phys. Rev. Lett. 104:058102. doi: 10.1103/PhysRevLett.104.058102
Tchumatchenko, T., Malyshev, A., Wolf, F., and Volgushev, M. (2011). Ultrafast population encoding by cortical neurons. J. Neurosci. 31, 12171–12179. doi: 10.1523/JNEUROSCI.2182-11.2011
Trigo, F. F., Bouhours, B., Rostaing, P., Papageorgiou, G., Corrie, J. E., Triller, A., et al. (2010). Presynaptic miniature gabaergic currents in developing interneurons. Neuron 66, 235–247. doi: 10.1016/j.neuron.2010.03.030
Tyler, W. J. (2012). The mechanobiology of brain function. Nat. Rev. Neurosci. 13, 867–878. doi: 10.1038/nrn3383
Van Essen, D. C. (1973). The contribution of membrane hyperpolarization to adaptation and conduction block in sensory neurones of the leech. J. Physiol. 230, 509–534. doi: 10.1113/jphysiol.1973.sp010201
Wang, S., Borst, A., Zaslavsky, N., Tishby, N., and Segev, I. (2017). Efficient encoding of motion is mediated by gap junctions in the fly visual system. PLoS Comput. Biol. 13, 1–22. doi: 10.1371/journal.pcbi.1005846
Wang, Y., Zhang, P., and Wyskiel, D. R. (2016). Chandelier cells in functional and dysfunctional neural circuits. Front. Neural Circ. 10:33. doi: 10.3389/fncir.2016.00033
Watanabe, A., and Grundfest, H. (1961). Impulse propagation at the septal and commissural junctions of crayfish lateral giant axons. J. Gen. Physiol. 45, 267–308. doi: 10.1085/jgp.45.2.267
Wei, W., and Wolf, F. (2011). Spike onset dynamics and response speed in neuronal populations. Phys. Rev. Lett. 106:088102. doi: 10.1103/PhysRevLett.106.088102
Wollner, D. A., and Catterall, W. A. (1986). Localization of sodium channels in axon hillocks and initial segments of retinal ganglion cells. Proc. Natl. Acad. Sci. U.S.A. 83, 8424–8428. doi: 10.1073/pnas.83.21.8424
Wu, L. M. N., Williams, A., Delaney, A., Sherman, D. L., and Brophy, P. J. (2012). Increasing internodal distance in myelinated nerves accelerates nerve conduction to a flat maximum. Curr. Biol. 22, 1957–1961. doi: 10.1016/j.cub.2012.08.025
Xiao, L., Ohayon, D., McKenzie, I. A., Sinclair-Wilson, A., Wright, J. L., Fudge, A. D., et al. (2016). Rapid production of new oligodendrocytes is required in the earliest stages of motor-skill learning. Nat. Neurosci. 19, 1210–1217. doi: 10.1038/nn.4351
Xu, K., and Terakawa, S. (1999). Fenestration nodes and the wide submyelinic space form the basis for the unusually fast impulse conduction of shrimp myelinated axons. J. Exp. Biol. 202, 1979–1989.
Xylouris, K., Queisser, G., and Wittum, G. (2011). A three-dimensional mathematical model of active signal processing in axons. Comput. Visual. Sci. 13:409. doi: 10.1007/s00791-011-0155-7
Yamamoto, T., Samejima, A., and Oka, H. (1990). The mode of synaptic activation of pyramidal neurons in the cat primary somatosensory cortex: an intracellular HRP study. Exp. Brain Res. 80, 12–22. doi: 10.1007/BF00228842
Yang, Y., Ramamurthy, B., Neef, A., and Xu-Friedman, M. A. (2016). Low somatic sodium conductance enhances action potential precision in time-coding auditory neurons. J. Neurosci. 36, 11999–12009. doi: 10.1523/JNEUROSCI.1475-16.2016
Yau, K. W. (1976). Receptive fields, geometry and conduction block of sensory neurones in the central nervous system of the leech. J. Physiol. 263, 513–538. doi: 10.1113/jphysiol.1976.sp011643
Young, K. M., Psachoulia, K., Tripathi, R. B., Dunn, S.-J., Cossell, L., Attwell, D., et al. (2013). Oligodendrocyte dynamics in the healthy adult CNS: evidence for myelin remodeling. Neuron 77, 873–885. doi: 10.1016/j.neuron.2013.01.006
Yu, Y., Shu, Y., and McCormick, D. A. (2008). Cortical action potential backpropagation explains spike threshold variability and rapid-onset kinetics. J. Neurosci. 28, 7260–7272. doi: 10.1523/JNEUROSCI.1613-08.2008
Zbili, M., and Debanne, D. (2019). Past and future of analog-digital modulation of synaptic transmission. Front. Cell. Neurosci. 13:160. doi: 10.3389/fncel.2019.00160
Keywords: analog-digital signaling, action potential generation, propagation, resistance, capacitance, myelin, axo-axonal coupling
Citation: Alcami P and El Hady A (2019) Axonal Computations. Front. Cell. Neurosci. 13:413. doi: 10.3389/fncel.2019.00413
Received: 03 May 2019; Accepted: 27 August 2019;
Published: 18 September 2019.
Edited by:
Dominique Debanne, INSERM U1072 Neurobiologie des canaux Ioniques et de la Synapse, FranceReviewed by:
Mickael Zbili, INSERM U1028 Centre de Recherche en Neurosciences de Lyon, FranceAlon Korngreen, Bar-Ilan University, Israel
Copyright © 2019 Alcami and El Hady. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pepe Alcami, YWxjYW1pQGJpby5sbXUuZGU=; Ahmed El Hady, YWhhZHlAcHJpbmNldG9uLmVkdQ==
 Pepe Alcami
Pepe Alcami Ahmed El Hady
Ahmed El Hady