Modeling the Cerebellar Microcircuit: New Strategies for a Long-Standing Issue

The cerebellar microcircuit has been the work bench for theoretical and computational modeling since the beginning of neuroscientific research. The regular neural architecture of the cerebellum inspired different solutions to the long-standing issue of how its circuitry could control motor learning and coordination. Originally, the cerebellar network was modeled using a statistical-topological approach that was later extended by considering the geometrical organization of local microcircuits. However, with the advancement in anatomical and physiological investigations, new discoveries have revealed an unexpected richness of connections, neuronal dynamics and plasticity, calling for a change in modeling strategies, so as to include the multitude of elementary aspects of the network into an integrated and easily updatable computational framework. Recently, biophysically accurate “realistic” models using a bottom-up strategy accounted for both detailed connectivity and neuronal non-linear membrane dynamics. In this perspective review, we will consider the state of the art and discuss how these initial efforts could be further improved. Moreover, we will consider how embodied neurorobotic models including spiking cerebellar networks could help explaining the role and interplay of distributed forms of plasticity. We envisage that realistic modeling, combined with closed-loop simulations, will help to capture the essence of cerebellar computations and could eventually be applied to neurological diseases and neurorobotic control systems.

Introduction

The “Realistic” Modeling Approach

In contrast to the classical top-down modeling strategies guided by researcher’s intuitions about the structure-function relationship of brain circuits, much attention has recently been given to bottom-up strategies. In the construction of bottom-up models, the system is first reconstructed through a reverse engineering process integrating available biological features. Then, the models are carefully validated against a complex dataset not used to construct them, and finally their performance is analyzed as they were the real system. The biological precision of these models can be rather high so that they merit the name of realistic models. The advantage of realistic models is two-fold. First, there is limited selection of biological details that might be relevant to function (this issue will be important in the simplification process considered below). Secondly, with these models it is possible to monitor the impact of microscopic variables on the whole system. A drawback is that some details may be missing, although they can be introduced at a later stage providing proofs on their relevance to circuit functioning (model upgrading). Another potential drawback of realistic models is that they may lose insight into the function being modeled. However, this insight can be recovered at a later stage, since realistic models can incorporate sufficient details to generate microcircuit spatio-temporal dynamics and explain them on the basis of elementary neuronal and connectivity mechanisms (Brette et al., 2007).

Realistic modeling responds to the general intuition that complexity in biological systems should be exploited rather that rejected (Pellionisz and Szentágothai, 1974; Jaeger et al., 1997; De Schutter, 1999; Fernandez et al., 2007; Bower, 2015). For example, the essential computational aspects of a complex adaptive system may reside in its dynamics rather than just in the structure-function relationship (Arbib et al., 1997, 2008), and require therefore closed-loop testing and the extraction of rules from models running in a virtual environment (see below). Moreover, the multilevel organization of the brain often prevents from finding a simple relationship between elementary properties (e.g., neuronal firing) and higher functions (e.g., motor control or cognition). Network connectivity on different scales exploits local neuronal computations and eventually generates the algorithms subtending brain operations. An important new aspect of the realistic modeling approach is that it is now much more affordable than in the past, when it was less used due to the lack of sufficient biophysical data on one hand and of computational power and infrastructures on the other. Now that these all are becoming available, the realistic modeling approach represents a new exciting opportunity for understanding the inner nature of brain functioning. In a sense, realistic modeling is emerging as one of the most powerful tools in the hands of neuroscientists (Davison, 2012; Gerstner et al., 2012; Markram, 2013). The cerebellum has actually been the work bench for the development of ideas and tools fuelling realistic modeling over almost 40 years (for review see Bhalla et al., 1992; Baldi et al., 1998; Cornelis et al., 2012a; D’Angelo et al., 2013a; Bower, 2015; Sudhakar et al., 2015).

Cerebellar Microcircuit Modeling: Foundations

In the second half of the 20th century David Marr, in a classical triad, developed theoretical models for the neocortex, the hippocampus and the cerebellum, setting landmarks for the development of theoretical and computational neuroscience (for review see, Ito, 2006; Honda et al., 2013). Since then, the models have advanced alternatively in either one or the other of these brain areas.

The striking anatomical organization of the cerebellar circuit has been the basis for initial models. In 1967, the future Nobel Laureate J.C. Eccles envisaged that the cerebellum could operate as a neuronal “timing” machine (Eccles, 1967). This prediction was soon followed by the theoretical models of Marr and Albus, who proposed the Motor Learning Theory (Marr, 1969; Albus, 1971) emphasizing the cerebellum as a “learning machine” (for a critical vision on this issue, see Llinás, 2011). These latter models integrated a statistical description of circuit connectivity with intuitions about the function the circuit has in behavior (Marr, 1969; Albus, 1971). These models have actually been only partially implemented and simulated as such (Tyrrell and Willshaw, 1992; see below) or transformed into mathematically tractable versions like the adaptive filter model (AFM; Dean and Porrill, 2010, 2011; Porrill et al., 2013).

While Marr himself framed his own efforts to understand brain function by contrasting “bottom up” and “top down” approaches (he believed his approach was “bottom up”), in initial models the level of realism was limited (at that time, little was known on the ionic channels and receptors of the neuronal membrane, by the way). Since then, several models of the cerebellum and cerebellar subcircuits have been developed incorporating realistic details to a different extent (Maex and De Schutter, 1998; Medina et al., 2000; Solinas et al., 2010). In the most recent models, neurons and synapses incorporate Hodgkin-Huxley-style mechanisms and neurotransmission dynamics (Yamada et al., 1989; Tsodyks et al., 1998; D’Angelo et al., 2013a). As far as microcircuit connectivity is concerned, this has been reconstructed by applying combinatorial rules similar to those that have inspired the original Marr’s model. Recently, an effort has allowed the reconstruction and simulation of the neocortical microcolumn (Markram et al., 2015) showing construction rules that may also be used for different brain areas. The approach used for the neocortical microcircuit is based on precise determination of cell densities, on cell morphologies and on a set of rules for synaptic connectivity based on proximity of the neuronal processes (density-morphology-proximity or DMP rule). One question is now whether the construction rules used for the neocortex can also be applied to the cerebellar network. Moreover, since ontogenetic factors play a critical role in network formation, taking a snapshot of the actual state of the mature cerebellar network may not be enough to implement its connectivity and investigate its function. Again, while developmental models have been devised for the cerebral cortex (Zubler et al., 2013; Roberts et al., 2014), their application to the cerebellum remains to be investigated. Therefore, advancement on the neocortical front may now inspire further development in cerebellar modeling.

The most recent realistic computational models of the cerebellum have been built using an extensive amount of information taken from the anatomical and physiological literature and incorporate neuronal and synaptic models capable of responding to arbitrary input patterns and of generating multiple response properties (Maex and De Schutter, 1998; Medina et al., 2000; Santamaria et al., 2002, 2007; Santamaria and Bower, 2005; Solinas et al., 2010; Kennedy et al., 2014). Each neuron model is carefully reconstructed through repeated validation steps at different levels: at present, accurate models of the GrCs, GoCs, UBCs, PCs, DCN neurons and IOs neurons are available (De Schutter and Bower, 1994a,b; D’Angelo et al., 2001; D’Angelo et al., 2016; Nieus et al., 2006, 2014; Solinas et al., 2007a, b; Vervaeke et al., 2010; Luthman et al., 2011; Steuber et al., 2011; De Gruijl et al., 2012; Subramaniyam et al., 2014; Masoli et al., 2015). Clearly, realistic models have the intrinsic capacity to resolve the still poorly understood issue of brain dynamics, an issue critical to understand how the cerebellum operates (for e.g., see Llinás, 2014).

That understanding cerebellar neuron dynamics can bring beyond a pure structure-function relationships was early recognized but the issue is not resolved yet. There are several correlated aspects that, in cascade from macroscopic to microscopic, need to be considered in detail (see below). Eventually, cerebellar functioning may exploit internal dynamics to regulate spike-timing and to store relevant network configurations through distributed plasticity (Ito, 2006; D’Angelo and De Zeeuw, 2009; Gao et al., 2012). The testing of integrated hypotheses of this kind is exactly what a realistic computational model, once properly reconstructed and validated, should be able to promote.

A further crucial consideration is that the cerebellum has a similar microcircuit structure in all its parts, whose functions differentiate over a broad range of sensori-motor and cognitive control functions depending on the specific anatomical connections (Schmahmann and Sherman, 1998; Schmahmann, 2004; Ito, 2006; Schmahmann and Caplan, 2006; D’Angelo and Casali, 2013; Koziol et al., 2014). It appears therefore that the intuition about the network role in learning and behavior of the original models of Marr-Albus-Ito can be implemented now by integrating realistic models into a closed-loop robotic environment. This allows the interaction of the microcircuit with ongoing actions and movements and the subsequent learning and extraction of rules from the analysis of neuronal and synaptic properties under closed-loop testing (Caligiore et al., 2013, 2016). In this article, we are reviewing an extended set of critical data that could impact on realistic modeling and are proposing a framework for cerebellar model development and testing. Since not all the aspects of cerebellar modeling have evolved at similar rate, more emphasis has been given to those that will help more in exemplifying prototypical cases.

Realistic Modeling Techniques: The Cerebellum as Workbench

Realistic modeling allows reconstruction of neuronal functions through the application of principles derived from membrane biophysics. The membrane and cytoplasmic mechanisms can be integrated in order to explain membrane potential generation and intracellular regulation processes (Koch, 1998; De Schutter, 2000; D’Angelo et al., 2013a). Once validated, neuronal models can be used for reconstructing entire neuronal microcircuits. The basis of realistic neuronal modeling is the membrane equation, in which the first time derivative of potential is related to the conductances generated by ionic channels. These, in turn, are voltage- and time-dependent and are usually represented either through variants of the Hodgkin-Huxley formalism, through Markov chain reaction models, or using stochastic models (Hodgkin and Huxley, 1952; Connor and Stevens, 1971; Hepburn et al., 2012). All these mechanisms can be arranged into a system of ordinary differential equations, which are solved by numerical methods. The model can contain all the ion channel species that are thought to be relevant to explain the function of a given neuron, which can eventually generate all the known firing patterns observed in real cells. In general, this formalism is sufficient to explain the properties of a membrane patch or of a neuron with very simple geometry, so that one such model may collapse all properties into a single equivalent electrical compartment. In most cases, however, the properties of neurons cannot be explained so easily, and multiple compartments (representing soma, dendrites and axon) have to be included thus generating multicompartment models. This strategy requires an extension of the theory based on Rall’s equation for muticompartmental neuronal structures (Rall et al., 1992; Segev and Rall, 1998). Eventually, the ionic channels will be distributed over numerous different compartments communicating one with each other through the cytoplasmic resistance. Up to this point, the models can usually be satisfactorily constrained by biological data on neuronal morphology, ionic channel properties and compartmental distribution. However, the main issue that remains is to appropriately calibrate the maximum ionic conductances of the different ionic channels. To this aim, recent techniques have made use of genetic algorithms that can determine the best data set of multiple conductances through a mutation/selection process (Druckmann et al., 2007, 2008).

As well as membrane excitation, synaptic transmission mechanisms can also be modeled at a comparable level of detail. Differential equations can be used to describe the presynaptic vesicle cycle and the subsequent processes of neurotransmitter diffusion and postsynaptic receptor activation (Tsodyks et al., 1998). This last step consists of neurotransmitter binding to receptors, followed by the opening ion channels or modulation of intracellular cascades, and it is often accounted by stochastic receptor models. The synapses can also be endowed with mechanisms generating various forms of short- and long-term plasticity (Migliore et al., 1995). Appropriate synaptic modeling provides the basis for assembling neuronal circuits.

In all these cases, the cerebellum has provided a work bench that has remarkably contributed to write the history of realistic modeling. Examples are the development of integrated simulation platforms (Bhalla et al., 1992; Bower and Beeman, 2007), the definition of model optimization and evaluation strategies (Baldi et al., 1998; Vanier and Bower, 1999; Cornelis et al., 2012a,b; Bower, 2015), the generation of complex neuron models as exemplified by the Purkinje cells (De Schutter and Bower, 1994a,b; Bower, 2015; Masoli et al., 2015) and the GrCs (D’Angelo et al., 2001; Nieus et al., 2006; Diwakar et al., 2009) and the generation of complex microcircuit models (Maex and De Schutter, 1998; Medina and Mauk, 2000; Solinas et al., 2010). Now, the cerebellar neurons, synapses and network pose new challenges for realistic modeling depending on recent discoveries on neuron and circuit biology and on the possibility of including large-scale realistic circuit models into closed loop robotic simulations.

Critical Structural Properties of the Cerebellar Network

In the Marr-Albus models, the core hypothesis was that the GCL performs sparse coding of mf information, so that the specific patterns of activity presented to PCs can be optimally learned at the pf-PC synapse under cf control. In these models the cerebellar cortex processes incoming information serially (Altman and Bayer, 1997; Sotelo, 2004) and its output impinges on the DCN, while the IO plays an instructing or teaching role by activating PCs through the cfs. These models reflect the anatomical concept of the cerebellar cortical microzone, which, once connected to the DCN and IO, forms the cerebellar microcomplex (Ito, 1984) representing the functional unit of the cerebellum. Recently, this fundamental modular organization has been extended by including recurrent loops between DCN and GCL and also between the DCN and IO. Moreover, the cerebellum turns out to be divided into longitudinal stripes that intersect the transverse lamella of the folia and can be subdivided into various anatomo-functional regions connected to specific brain structures forming nested and multiple feed-forward and feed-back loops with the spinal cord, brain stem and cerebral cortex. Thus, the cerebellar connectivity, both on the micro-scale, meso-scale and macro-scale, is far from being as simple as originally assumed but it rather appears to generate a complex multidimensional hyperspace. A main challenge for future modeling efforts is thus to consider these different scales of complexity and recurrent connectivity.

Microscale Organization

The cerebellar inputs are elaborated in the GCL before being further processed in the ML and distributed to PCs, from which signals are sent to DCN. While signals flow along the GrC → PC → DCN neuronal chain, they are thought to undergo an initial “expansion recoding” in the GCL followed by a “perceptron-like” sampling in PCs before converging onto the DCN (the validity of these assumptions is further considered below). Local computations in the cerebellar cortex are regulated by two extended inhibitory interneuron networks, one in the GCL and one in the ML. Since the DCN is also activated by mf collaterals, the cerebellar cortex de facto operates as a modulator of DCN activity. Finally, the IO → PC → DCN neuronal chain forms another pathway probably implied in controlling network learning and timing capabilities. Recently, relevance has been given to recurrent DCN → GrC and DCN → IO connections, which can directly send output information back to the input. Of great importance for network conceptualization and modeling are not just the convergence/divergence ratios and cell densities reported in Table 1 but also the specific geometries of connectivity reported in Figures 1, 2 (neuron and microcircuit dynamics are considered in the next chapter). It turns out that, differently from the neocortex that has neurons almost isotropically organized inside microcolumns, the cerebellar cortex shows precisely oriented neuronal structures and connections.

TABLE 1

Table 1. Statistics of connectivity.

FIGURE 1

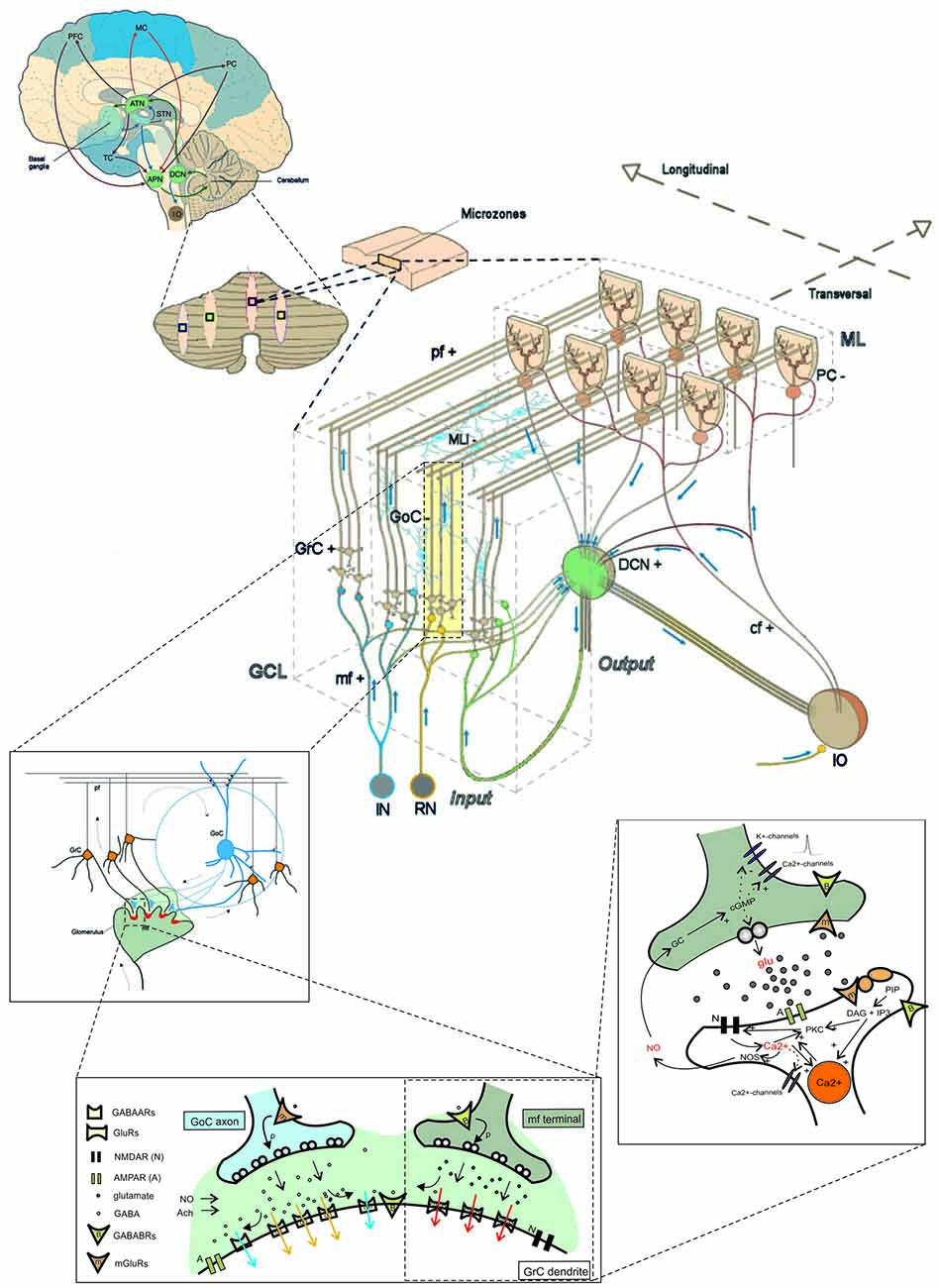
Figure 1. The multi-level organization of the cerebellum. This schematic representation shows how the core cerebellar microcircuit is wired inside the whole brain and how it can be further dissected into levels of increasing cellular and molecular complexity. The drawing at the center shows the cerebellar cortex subdivided into three layers (GCL, granular cell layer; PCL, Purkinje cell layer; ML, Molecular layer), which contain different types of excitatory and inhibitory neurons (cf, climbing fiber; DCN, deep cerebellar nuclei; GoC, Golgi cell; GrC, granule cell; IO, inferior olive; APN, anterior pontine nucleus; RN, reticular nucleus; MLI, molecular layer interneuron; mf, mossy fiber; pf, parallel fiber; PC, Purkinje cell; the signs indicate the excitatory or inhibitory nature of the cell or fiber). A cortical microzone is connected to IO and DCN to form a cerebellar microcomplex. The expansion to the top, which shows a flattened representation of the cerebellar cortex, indicates how a cerebellar microcomplex can extend to include several microzones located in separated cerebellar regions. A further expansion to the top shows the main circuit loops formed by the cerebellum with the cerebral cortex (PFC, prefrontal cortex; MC, motor cortex; PC, parietal cortex; TC, temporal cortex) through the DCN and the anterior thalamic nuclei (ATN) on the efferent pathway and through the anterior pontine nuclei (APN) on the afferent pathway. The connection with basal ganglia (BG) and subthalamic nucleus (STN) is also indicated. The insets to the bottom show, expand in cascade the wiring in the granular layer to show glomerular connectivity, glomerular neurotransmission and synaptic transduction mechanisms. The receptors involved (labeled in the inset) and the intracellular cascades include several identified molecular elements (glu, glutamate; PKC, protein kinase C; DAG, diacyl-glycerol; IP3, inositol-triphosphate; PIP, phosphatidyl-inositol-phosphate; NO, nitric oxide synthase; NOS, nitric oxide synthase; NO, nitric oxide; Ca²⁺, calcium ions; GC, guanyl cyclase; cGMP, cyclic GMP; Modified from D’Angelo and Peres, 2011; Mapelli et al., 2014).

FIGURE 2

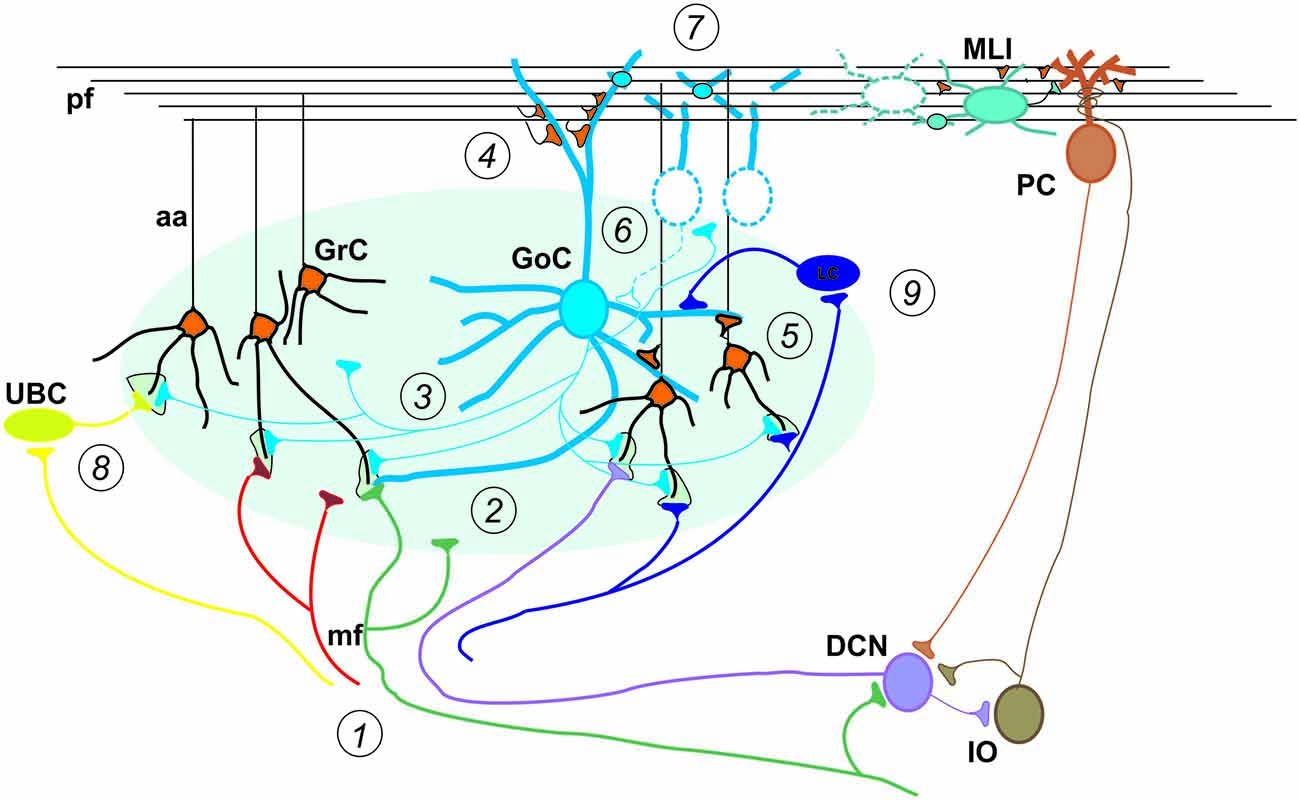
Figure 2. Special properties of GCL connectivity. The figure shows schematically the most important properties of GCL connectivity that have emerged from a complex set of physiological and structural experiments. (1) Divergence of mossy fibers onto different cell types. Formation of multiple glomeruli per mossy fiber. Multiple inputs onto the same GrC but different inputs on each granule cell dendrite. (2) Glomerular integration: a cerebellar glomerulus contains a mossy fiber terminal as well as GoC axonal terminals and dendrites. (3) Feed-forward inhibitory loops pass through the MF→GoC→GrC circuit. (4) Feed-back inhibitory loops pass through the MF→GC→GoC→GrC circuit. (5) GrCs activate GoCs both on basal dendrites and apical dendrites (4). (6) GoC→GoC reciprocal inhibition through reciprocal synapses. (7) GoC→GoC communication through gap-junctions. (8) UBC pathway: MF→UBC→ GrC. (9) Lugaro Cell pathway: MF→LC→ GoC. (aa, Ascending axon; other labels and symbols as in Figure 1). Modified from Mapelli et al. (2014).

The Double mf and cf Input

The main input to the cerebellum comes through the mfs. The mfs originate from neurons located in the brain-stem nuclei (including the cuneate nucleus, vestibular nucleus, reticular nucleus, red nucleus and APN) and spinal cord (dorsal columns). Moreover, relevant to external connectivity, GrCs have recently been shown to receive a blend of modalities from brain-stem and cortical afferences (Huang et al., 2013; Ishikawa et al., 2015). In the GCL, mfs, GrC dendrites, GoC dendrites and axons interact into specialized structures called glomeruli. The mfs emit collaterals forming synapses in the DCN. The other important input originates from a brain-stem nucleus, the IO, giving rise to the cfs contacting PCs and DCNs.

The Geometry of Microcircuit Connectivity

The mfs, after entering the GCL, branch longitudinally (i.e., orthogonally to the main axis of the folia) generating numerous “rosettes” (i.e., clusters of glomeruli). The basal GoC dendrites spread around the soma, while the apical dendrites ascend into the ML and the GoC axons remains confined into the GCL also spreading longitudinally (Wu et al., 1999; Sultan, 2001; Sultan and Heck, 2003). There are just 3–5 short GrC dendrites that are connected to as many different glomeruli, whereas the GrC axons pass vertically the PCL and the ML until they divide into pfs running transversally (i.e., along the main axis of the folia). The flattened dendritic trees of PCs form an ordered palisade perpendicular to the folia (Person and Raman, 2012a) and are crossed by pfs connecting arrays of PCs aligned along the pf bundle. The SCs are located in the upper part of the ML and the BCs in the lower of the ML (Briatore et al., 2010; Alcami and Marty, 2013) with the dendritic trees perpendicular to the folium and axons spreading to some distance both along and across the pf bundle. In turn, the cfs branch longitudinally and contact the dendrites of clusters of PCs. Therefore, perhaps the most striking aspect in the cerebellar microcircuit is that, while mfs, cfs, GoC axons and PC dendrites are oriented longitudinally, they are orthogonal to the pfs that cross the PC dendritic trees.

The Inhibitory Interneuron Networks

The cerebellum is characterized by two extended inhibitory interneuron networks. The GCL layer inhibitory network is made of feedforward and feedback loops driven by mfs: (i) the mfs excite GrC and GoC dendrites and these latter inhibit GrCs in a feedforward loop, and (ii) the mfs excite GrCs and then pfs excite GoCs and these latter inhibit GrCs in a feedback loop (Simões de Souza and De Schutter, 2011; Mapelli et al., 2014). The GoCs are interconnected through gap-junctions and reciprocal inhibitory synapses. The ML inhibitory network is formed by a series of MLIs (SCs and BCs) activated by pfs and inhibiting PCs in feed-forward (Santamaria et al., 2002, 2007). The MLIs are interconnected through gap-junctions and reciprocal inhibitory synapses (Astori et al., 2009; Alcami and Marty, 2013).

Mesoscale Organization

Beyond the combinatorial and geometrical architecture described above, which is valid for the whole cerebellar cortex, there are higher orders of organization.

Cortical Microzones and Cerebellar Modules

Tracing studies have revealed longitudinal zones that elongate in the rostro-caudal direction and run perpendicular to the long axis of the lobules. The longitudinal zones include the olivocerebellar afferents (cfs) and the corticonuclear (PC) efferents. The somatotopic distribution of cfs are directed to one or two longitudinal zones, while mfs have a more extended transverse branching and terminate in multiple longitudinal zones. Some longitudinal zones can be split into smaller units called microzones. The microzones receiving the same cf inputs from the multizonal microcomplexes and are important for the parallel processing and integration of information coming from mf inputs. Thus, while the neocortex is characterized by microcolums and columns, the cerebellum can be divided into anatomo-functional modules deriving from the assembly of microzones (Cerminara, 2010). Recently, by combining in vitro recordings with optogenetics, it has been possible to identify stereotyped patterns of functional synaptic organization between GrCs and PCs, GoCs and MLIs. All these connections displayed position-specific patterns of GrC synaptic inputs that did not strictly match with anatomical boundaries and could connect distant cortical modules, indicating that specific microcircuit connectivity rules have also to be taken into account (Valera et al., 2016).

Longitudinal Organization: The Zebrin Stripes

The so-called zones are long cerebellar stripes ranging from the anterior to posterior poles of the cerebellum and can be identified histochemically and functionally (Andersson and Oscarsson, 1978; Apps and Garwicz, 2005; Apps and Hawkes, 2009; Voogd, 2011). Each stripe is defined by the PC type depending on the expression of Aldolase-C (Zebrin II) as well as of other enzymes (e.g., NOS and PKC isoforms) and ionic channels (e.g., TRIP). PCs expressing Zebrin II (Z+) show a slower spontaneous firing (40 Hz) compared to PCs not expressing Zebrin II (Z−; 90–100 Hz; Zhou et al., 2014). Moreover, Z+ and Z− PCs differ as for their ability to generate plasticity at the pf-PC synapse (Wadiche and Jahr, 2005; Wang et al., 2011). It has recently been shown that GoC somata and dendrites are restricted to the same PC Zebrin II stripe (Sillitoe et al., 2008). The restriction of GoCs in specific stripes may influence network activity, since GoCs are connected through gap junctions (Vervaeke et al., 2010) and could have a role in controlling GCL oscillations (Simões de Souza and De Schutter, 2011). The PCs output on specific DCNs is then retransmitted to the IO trough the nucleo-olivary pathway and this pathway has been seen to influence the responses of the IO to their target PCs (Voogd, 2011).

Macroscale Organization

Major Anatomical Subdivisions

The cerebellum, on each side of the midline, is divided into three regions running along the rostral to caudal axis: the vermis, the paravermis and the hemisphere. Each of these regions is folded into lobules and each lobule is subdivided into folia. Remarkably, the afferent and efferent connections of the cerebellar cortex, as well as the corresponding DCNs, are strictly related to this anatomical arrangement, as recently confirmed by viral tracing in experimental animals (Huang et al., 2013; Watson et al., 2014) and MRI data in humans (Balsters et al., 2010; Diedrichsen et al., 2011; Sokolov et al., 2012; Palesi et al., 2015). Projections from the cerebral cortex are conveyed to the anterior pontine nuclei and then relayed mostly to the posterior-lateral parts of the cerebellum through the medium cerebellar peduncle. Projections from the pons and spinal cord are relayed mostly to the vermis and anterior cerebellum through the inferior and superior cerebellar peduncle. These same cerebellar regions project to the spinal cord, brainstem and cerebral cortex through different subdivisions of the DCNs (e.g., see Eccles, 1967; Ito, 1984).

Extracerebellar Connectivity and Recurrent Loops

Beyond anatomical details, what is relevant here is that the cerebellum is involved in major connections with brainstem, spinal cord and cerebral cortex as well as with basal ganglia (BG) and hippocampus. These connections generate multiple loops, in which the cerebellum is wired as a pivotal node (Caligiore et al., 2013, 2016; D’Angelo and Casali, 2013).

– The most renowned recurrent loop passes through the IO. The small DCN GABAergic neurons inhibit the IO cells regulating their coupling and oscillations (Najac and Raman, 2015).

– The DCNs are involved in the cerebellar circuitry with a one way connection between the glycinergic DCN, projecting to the GCL, inhibiting GABAergic GoCs and the glutamatergic DCN that excite the GRCs and GOCs (Ankri et al., 2015; Houck and Person, 2015; Gao et al., 2016). A similar connectivity characterizes the medial vestibular nucleus in the vestibulo-cerebellum.

– There are several loops formed with the cerebellum by the brainstem, passing through different cerebellar nuclei (except the dentate) and involving the red nucleus and the reticular nucleus.

– The major loops connecting the cerebellum to the forebrain, start from the dentate nucleus and pass through the anterior ventrolateral thalamus mostly to reach the cerebral cortex, then return through the anterior pontine nuclei and the medial cerebellum peduncle.

– Afferent sensory fibers are relayed to the cerebellum through nuclei located in the spinal cord (e.g., in the Deiter’s columns), brain stem (e.g., the cuneate nucleus), and superior and inferior colliculi.

Functionally, it is important to note that all these loops are normally closed, in that fibers leave and then return to the cerebellum through a different pathway. The most remarkable loops are formed with the cerebral cortex and with the peripheral motor system, so that the cerebellum is actually embedded in loops controlling movement planning and the sensory consequences of movement execution. These loops are the substrates of what are usually referred to as the cerebellar “feed-forward” and “feed-back” controllers (see below).

Critical Dynamic Properties of the Cerebellar Microcircuit

The neurons and synapses of cerebellum are amongst the most intensely studied in the whole brain and biophysically detailed models of several cerebellar neurons and synapses are available (Figures 3, 4; Table 2). These models are based on realistic multicompartmental morphologies and incorporate a detailed description of membrane mechanisms including various ionic channels, synaptic receptors, ionic pumps, intracellular calcium dynamics and some cytoplasmic processes. These models, together with detailed connectivity rules, are fundamental to reconstruct realistic microcircuit dynamics.

FIGURE 3

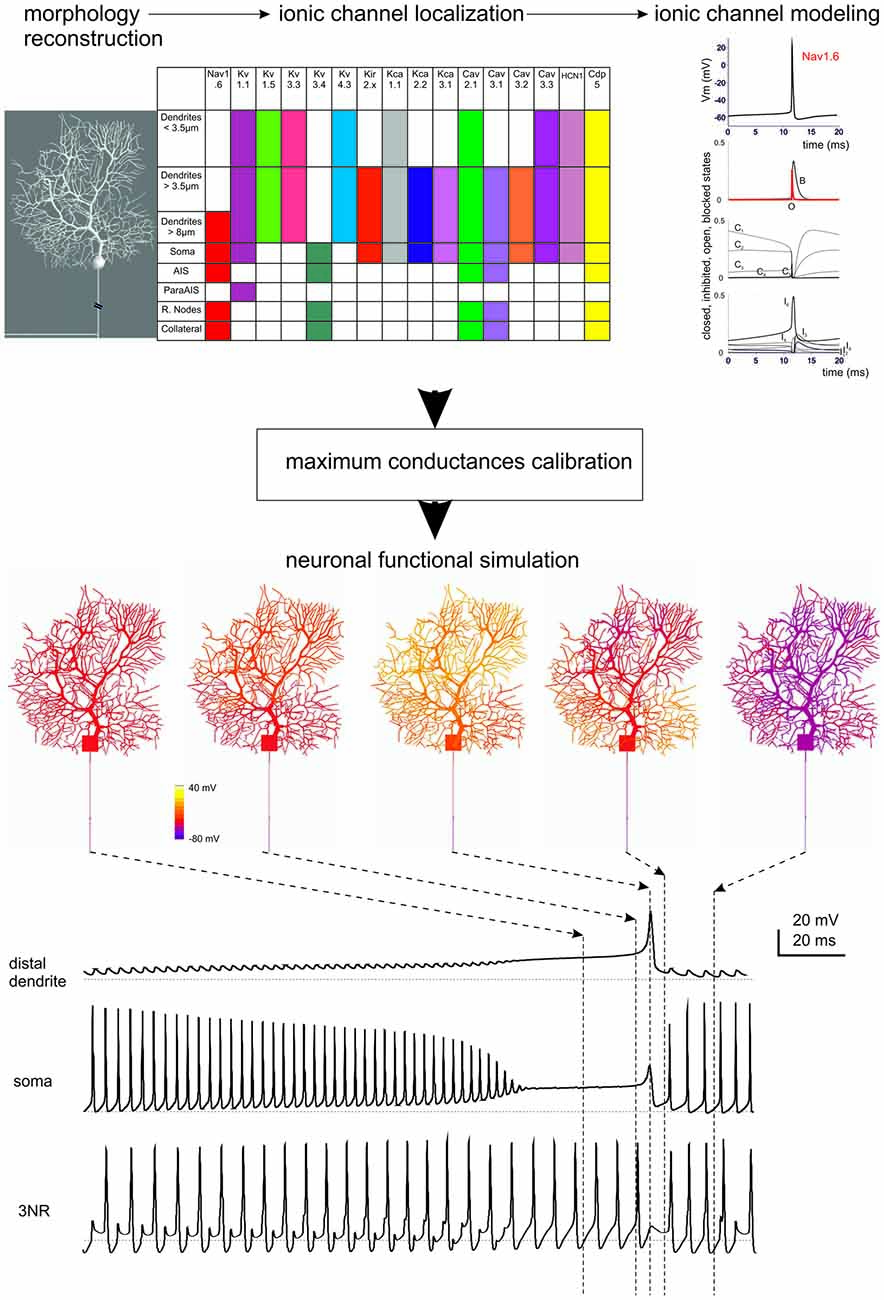
Figure 3. Ionic channel types, distribution and gating properties in a PC model. The investigation of cerebellar neurons physiology and biophysics has classically followed the same procedures used for other central neurons. Most experiments have been carried out in mice and rats in acute brain slice preparations with the aim of determining their intrinsic electroresponsiveness. Voltage-clamp analysis of membrane currents has mostly been dedicated to synaptic events, since space-clamp problems have in most cases hindered an accurate determination of current kinetics (except for GrCs, which are electrotonically compact). In some neurons, relevant information has been gained through single-unit and even patch-clamp recordings in vivo. Modeling reconstruction has, in most cases, exploited the knowledge of ionic currents identified kinetically and pharmacologically and the corresponding gating models have been derived from ion-channel libraries. The maximum ionic channel conductances have been iteratively adjusted by fitting complex sets of experimental data derived from current-clamp recordings. (Top) The diagram shows a 3D representation of PC morphology. This has been divided into eight distinct sections illustrated in the table on the right and endowed with ionic mechanisms according to immunohistochemical data. The ionic mechanisms include the sodium channel (Nav1.6), LVA and HVA calcium channels (Cav2.1, Cav3.1, Cav3.2, Cav3.3), potassium channels (Kv3.4, Kv1.1, Kv4.3, Kv1.5, Kv3.3), potassium calcium dependent channels (KCa1.1, KCa3.1, KCa2.2), inward rectified potassium channel (Kir2.x), cationic channel (HCN1) and a Ca buffering system composed by Calbindin and Parvalbumin (CDP5). The graph represents the state variables of the Nav1.6 channel during an action potential. C, I, O, B, indicate closed, inactivated, open and blocked states. Vertical dashed lines indicate the approximate action potential threshold (−50 mV). (Bottom) The drawings show PC membrane potential at different times (arrows) during complex bursting (membrane potential is color-coded) in distal dendrites, soma and third node of Ranvier (3NR). At the end of the spike burst, the PC model depolarizes starting from distal dendrites before the depolarization invades the whole dendritic tree. A large Ca spike is the most relevant depolarizing event in terminal dendrites, while fast Na spikes are most evident in AIS. In the 3RN, there is no firing pause during the dendritic Ca spike. (Modified from Masoli et al., 2015).

FIGURE 4

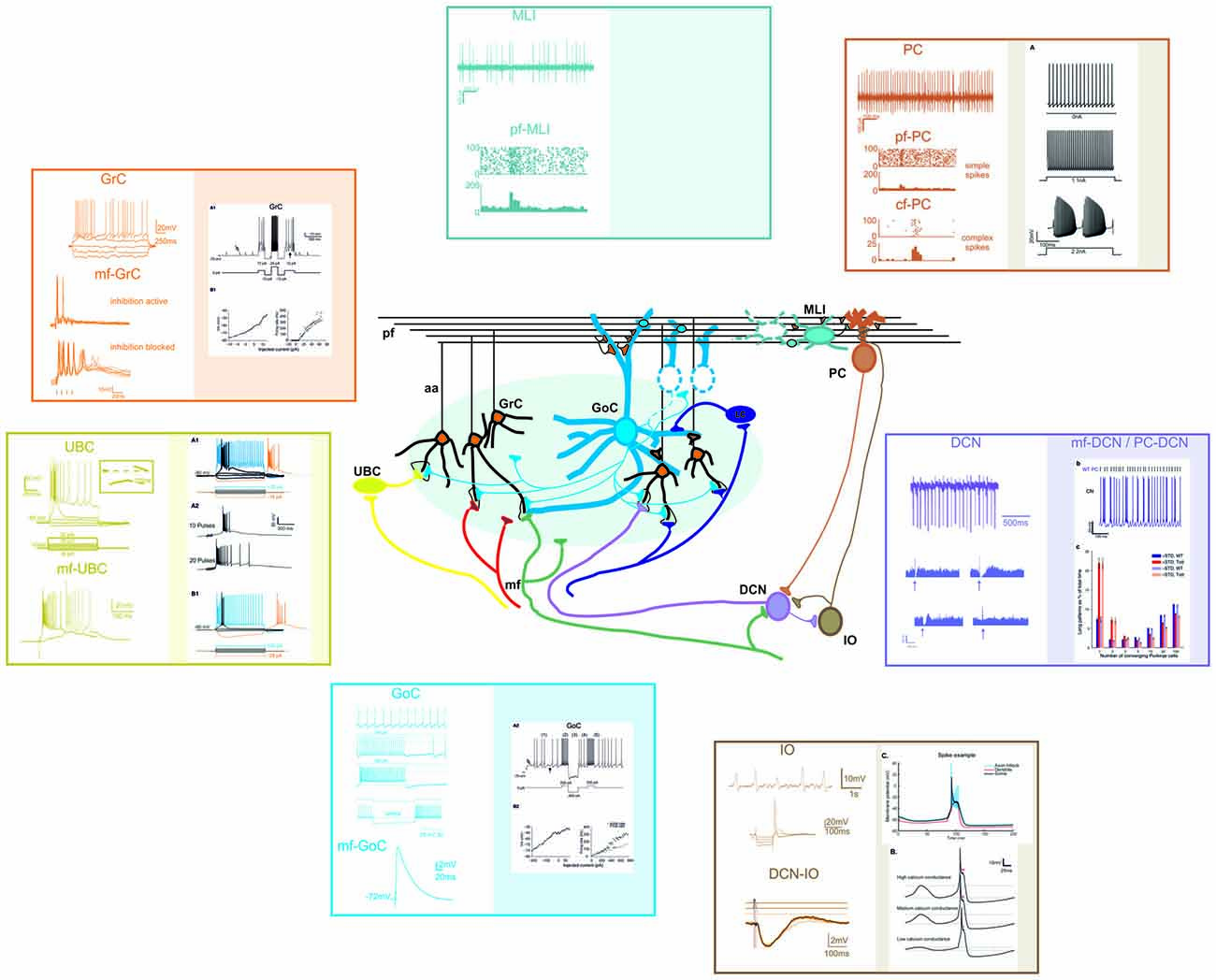
Figure 4. Different electrophysiological properties of cerebellar neurons and their biophysical modeling. At present, accurate realistic models have been constructed for most cerebellar neurons, except for MLIs and Lugaro cells. In the different panels, the figure shows schematically the most important properties of cerebellar neurons (left) and their biophysical reconstruction (right). For GCL and IO neurons, example tracings are taken from intracellular current-clamp recordings. For PC, MLI and DCN neurons, example tracings are reported along with raster plots and PSTH of activity. The traces are modified from: (GrC) Experiments: Nieus et al. (2014). Model: Solinas et al. (2010). (UBC) Experiments: Locatelli et al. (2013). Model: Subramaniyam et al. (2014). (GoC) Experiments: Bureau et al. (2000); Forti et al. (2006); D’Angelo et al. (2013b). Model: Solinas et al. (2010). (PC) Experiments: Ramakrishnan et al. (2016). Model: Masoli et al. (2015). (MLI) Experiments: Ramakrishnan et al. (2016). (DCN) Experiments: Rowland and Jaeger (2005); Uusisaari et al. (2007). Model: Luthman et al. (2011). (IO) Experiments: Lampl and Yarom (1997); Lefler et al. (2014). Model: De Gruijl et al. (2012).

TABLE 2

Table 2. Neuronal electroresponsive properties.

Neuronal Intrinsic Excitability

Neurons of the cerebellum show complex nonlinear properties that are likely to play a key role in controlling network functions. Firstly, several neurons are autorhythmic, with frequencies varying between a few up to around 100 Hz. The spikes have different shapes and properties and can configure various patterns in response to current injection or synaptic activation. Secondly, for some neurons, evidence for resonance in the theta-frequency band has emerged. Thirdly, neurons express non-linear firing properties suitable for processing burst generation and burst-pause responses. Finally, several neurons have inward rectification controlling resting membrane potential and rebound excitation. These properties emerge from the specific ionic channel complement and involve differentially the soma, dendrites and axons. For most of these neurons, there are advanced Hodgkin-Huxley style models, which have helped understanding how the specific electroresponsive properties are generated and as noted above, have set landmarks for realistic modeling strategy (for an extended review see D’Angelo et al., 2016).

The Purkinje cell is probably the most apparent example of this (for a recent review, see Bower, 2015). Early in the 60’s, Rodolfo Llinas claimed that Purkinje cell dendrites were electrically active (Llinás et al., 1968). Following a lively scientific debate, the demonstration came from a double proof provided by the advent of intracellular PC recordings (Llinás and Sugimori, 1980) followed by the first model of active dendrites (Pellionisz and Szentágothai, 1973, 1974). Then, following precise morpho-electrical reconstruction of a guinea-pig PC (Rapp et al., 1994), the first PC model based on realistic construction principles was presented (De Schutter and Bower, 1994a,b) and then widely used for network simulations for over 20 years (Santamaria et al., 2002; Steuber et al., 2007; Bower, 2010; Maex and Steuber, 2013). Recently, based on the same morphology, a new PC model has been developed using an updated set of ionic channels and accounting for the axonal generation mechanism of simple spikes (Masoli et al., 2015). A compressed version has also been presented (Marasco et al., 2013).

The granule cell has been first approximated to a McCulloc-Pitt neuron by a realistic model based on a limited set of ionic currents (Gabbiani et al., 1994). Then GrCs were shown to generate non-linear input-output relationships and were fully modeled based on a more complex set of ionic currents and validated against a rich repertoire of electroresponsive properties including near-threshold oscillations and resonance (D’Angelo et al., 2001). Interestingly, this last model still represents a unique example of full Hodgkin-Huxley style reconstruction based on ionic currents recorded directly from the same neuron, therefore implying minimal assumptions even for the calibration of maximum ionic conductances. The model has subsequently been updated to incorporate detailed synaptic inputs (Nieus et al., 2006, 2014) and to include the dendrites and axon demonstrating the mechanisms of action potential initiation and spike back-propagation (Diwakar et al., 2009). The model has then been used for network simulations (Solinas et al., 2010).

The DCN cells have been modeled, although not for all the neuronal subtypes. A model of the glutamatergic DCN neurons, based on realistic morphological reconstruction with active channels (Steuber et al., 2011), was used to analyze synaptic integration and DCN rebound firing after inhibition. More advanced versions have been used to study the dependence of neuronal encoding on short-term synaptic plasticity (Luthman et al., 2011) and the impact of Kv1 channels in spontaneous spike generation (Ovsepian et al., 2013). These models have been used to predict the impact of the cerebellar output on extracerebellar circuits (Kros et al., 2015).

The IO neurons were modeled to investigate the interaction of different ionic currents in mono compartmental models (Manor et al., 1997; Torben-Nielsen et al., 2012) showing modifications to sub threshold oscillations (STO) when two neurons where connected through gap junctions. A bi-compartment model (Schweighofer et al., 1999) was able to reproduce the typical STO and the particular spikes generated by the interaction of sodium and calcium currents in the soma/dendritic compartments. A three compartment model was then built to account for the interaction between the dendrites, soma and the AIS in generating the STO and spike output of the IO neurons (De Gruijl et al., 2012). Different versions of IO neuron models have been used to simulate the properties of the IO network (Manor et al., 1997; Torben-Nielsen et al., 2012).

Interneurons

The Golgi cells were modeled reproducing the basis of their intrinsic electroreponsiveness, showing complex non linear behaviors such as pacemaking, resonance and phase reset and uncovering the role of gap junctions in oscillatory synchronization (Solinas et al., 2007a,b; Dugué et al., 2009; Vervaeke et al., 2010). The model of UBCs reproduced the nonlinear behaviors of this neuron including bursts, rebounds and the late-onset burst response. This latter property contributes to generate transmission delays in the circuit (Subramaniyam et al., 2014). Concerning MLIs (Llano and Gerschenfeld, 1993; Alcami and Marty, 2013) no detailed conductance-based models are available yet and simplified IF models of these neurons were connected with the PCs to investigate the ML subcircuit (Santamaria et al., 2007; Lennon et al., 2014).

Synaptic Transmission and Plasticity

A wealth of experimental investigations has addressed the functional properties of cerebellar synapses and will not be considered in detail here (for review see e.g., Mapelli et al., 2014; for the granular layer, Barmack and Yakhnitsa, 2008; for ML). Almost all cerebellar synapses present different forms of short-term plasticity (short-term facilitation: STF; short-term depression: STD) and long-term plasticity (LTP, LTD; De Zeeuw et al., 2011; Gao et al., 2012). In general, short-term plasticity is suitable to regulate transmission during bursts. STD prevails at the mf-GrC synapse, STF prevails at the pf-PC synapse, and STD occurs at the PC-DCN synapses (Häusser and Clark, 1997; Mitchell and Silver, 2000a,b; Nielsen et al., 2004; Sargent et al., 2005; Nieus et al., 2006; DiGregorio et al., 2007; Szapiro and Barbour, 2007; Kanichay and Silver, 2008; Duguid et al., 2012; Powell et al., 2015; Wilms and Häusser, 2015; van Welie et al., 2016). While neurotransmitter dynamics involving vesicular release as well as postsynaptic receptor desensitization proved critical for controlling neurotransmission dynamics, an intriguing observation has been that spillover in the cerebellar glomerulus and in the ML might have a more important role than expected (e.g., see Mitchell and Silver, 2000a,b; Szapiro and Barbour, 2007).

Likewise, there are more than 15 forms of long-term synaptic plasticity in the cerebellar network, appearing both as LTP or LTD with multiple and different mechanisms of induction and expression (for review, see Ito, 2002; Gao et al., 2012; D’Angelo, 2014). Plasticity has been reported not just in acute brain slices but also in vivo (Jörntell and Ekerot, 2002; Roggeri et al., 2008; Diwakar et al., 2011; Johansson et al., 2014; Ramakrishnan et al., 2016), revealing that patterned sensory inputs can determine a complex set of changes encompassing multiple synaptic relays. Importantly several of the cerebellar synapses may show forms of spike-timing-dependent plasticity (STDP), linking intracerebellar oscillations to the ability of generating plasticity (D’Angelo et al., 2015; Garrido et al., 2016; Luque et al., 2016). Understanding the importance of these forms of plasticity may greatly benefit from integrated network modeling. At present, models incorporating dynamics presynaptic vesicle cycling (Tsodyks et al., 1998) have been developed for the mf-GrC, mf-GoC, GoC-GrC and GrC-GoC synapses (Nieus et al., 2006, 2014).

Microcircuit Dynamics: Timing and Learning

The cerebellar microcircuit has been shown to develop dynamic behaviors, although their investigation is still limited. The EEG cannot normally be recorded from the cerebellum, although some MEG data have been reported showing increased power in the theta-band during motor processing (Gross et al., 2001, 2002). Recordings in the experimental animal in vivo have focused on PC discharge patterns. PCs have been shown to activate in spots forming transient clusters (Velarde et al., 2004), to exploit burst-pause coding (Herzfeld et al., 2015) and to encode the prediction of ongoing motor states (Balsters et al., 2010). A recent report has shown that locomotion was associated with widespread increased activity in GrCs and interneurons, consistent with an increase in mossy fiber drive, and that dendrites of different PC showed increased co-activation, reflecting increased synchrony of climbing fiber activity. At the same time, responses to external stimuli in all three cell types were strongly suppressed showing that climbing and mossy fiber representations can shift together within a fraction of a second between responses to movement-associated or external stimuli (Ozden et al., 2012). However, the spatio-temporal reconfiguration of signals expected to occur in the GCL remains to be fully addressed in vivo and it is not fully clear how signals coming from different sources are redistributed through the different internal channels of the cerebellum.

Relevant to cerebellar circuit dynamics are its oscillating and resonant properties. On one hand, the GCL can be entrained into coherent oscillations by external inputs, possibly exploiting the resonance properties of its neurons (Pellerin and Lamarre, 1997; Hartmann and Bower, 1998; D’Angelo et al., 2001; Courtemanche et al., 2002, 2013; Solinas et al., 2007a; D’Angelo and De Zeeuw, 2009; Gandolfi et al., 2013; Garrido et al., 2016). On the other hand, spontaneous oscillations occur in the IO, that might have the role of coordinating cerebellar activity generating patterns that could be used for timing motor, sensory and cognitive tasks (Lampl and Yarom, 1997; Jacobson et al., 2008; Llinás, 2014). In 2011, these two observations have been merged with a large set of experimental data to propose a 3-level hypothesis, in which: (1) the spatio-temporal reconfiguration of incoming signals in the GCL is followed by; (2) their synthesis in the ML and DCN; while (3) the DCN/PC/IO loop controls a modular synchronization of cerebellar sub-fields based on circuit recurrent dynamics and selective frequency-dependent signal transmission (D’Angelo, 2011). The issue of oscillations is particularly relevant not just for microcircuit computation but also for microcircuit learning through STDP rules (see also “Model Simplification and Implementation in Closed-loop Robotic Testing” Section below). Once again, timing to learning appear as complementary aspects of the same mechanisms rather than alternative mechanisms of function, as it was suggested by the original models (Marr, 1969; Eccles, 1973).

Signal Transmission in Local Microcircuits

Despite its extensive investigation, several fundamental issues about signal transmission in local microcircuits are still incompletely understood.

There has been a long debate, which is not fully resolved yet, on the modality of PC activation by GCL inputs. While punctuate peripheral stimulation in vivo generates activity spots on the cerebellar surface (Bower and Woolston, 1983; Rokni et al., 2007), local pf stimulation elicits stripes of activity along the pf bundles (Ebner and Pasalar, 2008; Ebner, 2013). A recent work using localized Glu uncaging in acute cerebellar slices suggests that the organization of connections between the GCL and PCs may actually be even more complex than originally thought (Valera et al., 2016). From a functional viewpoint, following GCL stimulation, high-frequency modulated bursts are reliably transmitted vertically from the GCl to PCs, while only low-frequencies are transmitted transversally along the pfs (Mapelli et al., 2010). This observation suggested that a frequency-dependent selection of transmission lines, together with a specific micro-connectivity, may allow the formation of functional modules of active spots emerging vertically at the intersection of multiple pf bundles running along the folia with cfs fibers branching orthogonally to them (D’Angelo, 2011). At these intersection points, PCs may be able to decode the phase of IO oscillations and regulate pf gain (Ohtsuki et al., 2009).

A correlated issue concerns signal spread in the ML and PC inhibition. The pure feed-forward inhibition of PCs has inspired initial functional models taking the move from the observation that SCs and BCs inhibit PC activity with specific spatial organization and timing along and across the pf bundle (Eccles, 1967; Ito, 1984). This structural-functional relationship has recently been revisited highlighting the differential effect of inhibition on PC excitation mediated by aa and parallel fiber synapse (Mann-Metzer and Yarom, 1999, 2000, 2002; Santamaria et al., 2002, 2007; Mittmann et al., 2005; Santamaria and Bower, 2005; Mittmann and Häusser, 2007; Rieubland et al., 2014). Several dynamic phenomena have been reported to intervene in determining how the ML actually operates. SCs are pacemaking and are electrically coupled thus forming an oscillating interneuron network (Mann-Metzer and Yarom, 1999, 2000, 2002; Alcami and Marty, 2013). The analysis of these electrical and chemical SC microcircuits has recently revealed that transitivity of chemical connectivity is directed vertically in the sagittal plane, and electrical synapses appear strictly confined to the sagittal plane (Rieubland et al., 2014). The effect of ML inhibition is not confined to regulate PC activity, but it can also regulate generation of LTD and LTP at pf-PC synapses (Mittmann et al., 2005; Mittmann and Häusser, 2007). On the side of ML coding, SC inhibition deeply affects the burst-pause pattern of PC output (Steuber et al., 2007; Herzfeld et al., 2015). Moreover, a form of interconnectivity between PCs has been proposed to generate traveling waves of activity in the ML (Watt et al., 2009).

Finally, the dynamics of the IO-PC-DCN subcircuit remain still incompletely understood. The well-known contention about the role of cfs, that has been proposed either to control cerebellar learning or timing (Ito, 2000; Jacobson et al., 2008; Llinás, 2009, 2011, 2014), is not yet over. What is becoming clear is that this subcircuit has all the ingredients to subserve both functions. The IO operates as a pattern generator exploiting gap-junctions and local synaptic inhibition coming from the DCN in order to organize internal activity patterns that are then conveyed to PCs (Jacobson et al., 2008; Chen et al., 2010; Libster et al., 2010; Lefler et al., 2013; Libster and Yarom, 2013). This cf pattern, in turn, could be used to select mossy fiber patterns in specific groups of PCs. It can be argued that the coincidence of these cf and mf patterns could be instrumental to generate various forms of plasticity at PC and DCN synapses (see D’Angelo, 2014) raising again the duality of the timing-plasticity issue in the cerebellar circuit.

Realistic Models of the Cerebellar Microcircuit

Realistic models of the cerebellar network have to take into account a series of experimental observations, some used for construction, others for validation. In general, morphological measurements are the most relevant for constructing the network structure, electrophysiological data are needed to implement neurons and synaptic models, microcircuit-scale functional measurements (imaging and electrophysiology) are fundamental for validation.

The Most Compelling Example: The Model of the GCL Subcircuit

Construction

The wealth of anatomical data reported above (Figures 1, 2) and of cellular data (Figures 3, 4) provides the basis for reconstructing the cerebellar microcircuit (Figure 5). The state of the art for the cerebellar GCL is currently set by the 2010 model (Solinas et al., 2010), which was intended to generate a core computational element of the GCL microcircuit (about 10,000 neurons). This model was built by carefully reproducing the cerebellar GCL network anatomical properties and then validating the response against a large set of available physiological data. A peculiarity of the cerebellar network is that of being highly defined in terms of number of elements, convergence/divergence ratios and even in the number of synapses impinging on individual neurons. Moreover, the geometric orientation of processes is not isotropic but rather geometrically oriented, so that this network is quasi-crystalline in nature. This has allowed the application of a “direct approach”, in which:

– The appropriate number of neuronal elements has been randomly dislocated in a 3D space (density).

– The connectivity rules have been implemented to respect the convergence/divergence ratios.

– The connections have been limited to specific network sub-spaces with well defined innervation territories. This, together with the estimates of cell densities and of the number of synapses, allowed to implement an equivalent 3D connectivity even if the axonal plexus was not represented explicitly.

– The neurons, though very accurate, had an equivalent rather than a realistic morphology, either monocompartmental (GrCs) or multicompartmental (GoCs).

FIGURE 5

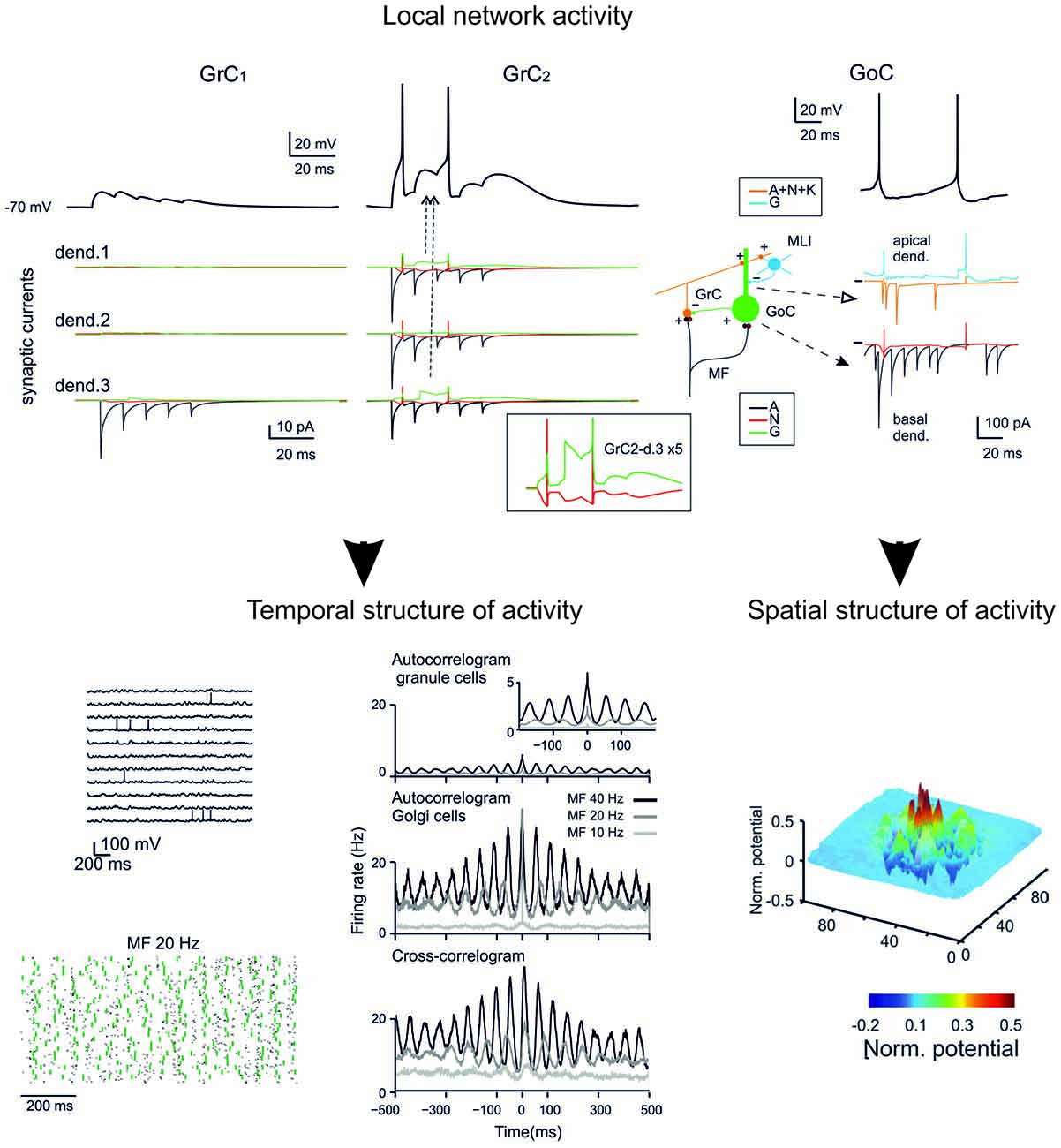
Figure 5. GCL modeling. The reconstruction of the microcircuit model of the GCL involves a precise representation of neurons, synapses and network connectivity. Interestingly, the model accounted for all the spatio-temporal dynamics of the GCL known at the moment. The model can therefore provide relevant information about the inner structure of neuronal activity during specific patterns of activity and reveal the relationship between individual synaptic and neuronal elements and the ensemble network response. (Top) synaptic currents in the dendrites of two different GrCs and receptor-specific components (AMPA, A; NMDA, N; GABA, G). (Bottom) Spatio-temporal dynamics of the network under noisy inputs reveal coherent low-frequency oscillations in the GC populations (left). Spatial response of GCs to a collimated mf bursts reveal a center-surround structure (right). (Modified from Solinas et al., 2010).

Given that the data were sufficient to determine microcircuit connectivity, it was not necessary to implement DMP rules (see below). Moreover, since the neurons were very accurate in reproducing the neuronal electrophysiological properties (Table 2), there was no need to implement realistic morphologies. Therefore, this network represents a “special case” of a more general network reconstruction procedure, as explained below.

Validation

Network validation has been performed against a relevant experimental dataset:

– First of all, it was considered whether the model neurons, which were calibrated beforehand on acute slice data (D’Angelo et al., 2001; Nieus et al., 2006; Solinas et al., 2007a,b), showed properties observed using patch-clamp recordings in vivo (Rancz et al., 2007; Arenz et al., 2008; Duguid et al., 2012, 2015; Chadderton et al., 2014). This actually happened, suggesting that a simulation of the role played by specific ionic channels during network processing is actually possible.

– Secondly, it was assessed how the model network reacted to random inputs distributed across the mfs. The model correctly generated coherent GrC oscillations in the theta band (Pellerin and Lamarre, 1997; Hartmann and Bower, 1998) provided that an appropriate balance between the MF and PF input to GoC was maintained.

– Thirdly, it was considered whether the high-pass filtering properties of the GCL emerged. Again this happened, with a correct cut-off around 50 Hz. Importantly, this property depended on NMDA receptors but much less so on GABA-A receptors, as observed experimentally (Mapelli et al., 2010).

– Finally, the network response to collimated mf bursts was tested. According to previous observations using MEA recordings, the typical center-surround organization of GCL responses emerged (Mapelli and D’Angelo, 2007).

Therefore, the GCL network model successfully reproduced the whole set of functional properties known at that time, suggesting that it could be used for predicting emerging network behaviors. Nonetheless, several issues remained unresolved, mostly concerning the GoC inhibitory network, and the range of network properties has in the meantime been extended by new findings.

– The relative weight of the feed-forward and feed-back inhibitory loop generated by GoCs was a free parameter, whose impact was explored explicitly. A strong feed-back loop favored coherent GCL network oscillations, as predicted by a previous modeling layout (Maex and De Schutter, 1998), while a strong fed-forward loop was needed to implement the time-windowing effect (D’Angelo and De Zeeuw, 2009). It still remains unclear how the two loops balanced. It is possible that the oscillating mode dominates over large network areas and that selective mf inputs to GoCs project restricted regions into the time-window mode, a hypothesis that needs to be tested (Duguid et al., 2015).

– The inhibitory input to GoCs was supposed to derive from MLIs, but now this hypothesis is less creditable, since recent data support the existence of inhibitory GoC-GoC connections (Hull and Regehr, 2012).

– The excitatory input to GoCs is more complex than previously thought, GrCs form contacts onto GoC dendrites (Cesana et al., 2013), and GoCs are connected through gap-junctions (Dugué et al., 2009; Vervaeke et al., 2010).

– The modality of GoC-GrC connectivity in the glomerulus is not clear yet. While each GrC receives a single inhibitory contact from GoCs, it is not clear if all the GrCs in each individual glomerulus receive inhibition from the same GoC axon or rather if they receive connections from different GoCs.

– Finally, the small-scale of the 2010 network precluded the analysis of extended spatio-temporal effects, for example of those concerning interaction of different active clusters and the spatial distribution of responses along the pf axis.

– The microscopic structure of GCL network activation can now be compared with the multispot two-photon microscopy data, which provide a new level of microcircuit validation (Gandolfi et al., 2014).

Eventually, improvements of specific structural properties and of membrane and intracellular mechanisms could also be considered. For example, the dendrites of GoCs are likely to be active and this has to be accounted for in future models (Rudolph et al., 2015). Multicompartment GrC models perform better than monocompartment ones in controlling spike properties and delays (Diwakar et al., 2009) and so they should be developed and adopted for all neurons in the network model. Specific issues concern the cerebellar glomerulus: at present, this structure has a fictive morphology but it could be designed to incorporate a closed diffusion space allowing the generation of glomerular homeostatic mechanisms balancing excitatory and inhibitory neurotransmitter release during repetitive synaptic activity (Mapelli et al., 2014; Nieus et al., 2014). Another specific issue concerns the mechanisms of postsynaptic calcium regulation, signal transduction and plasticity in GrCs and GoCs dendrites, for reason that will become evident below.

The model of the GCL is fundamental since it generates the input to the subsequent stages of the cerebellar cortex. Although, in a local perspective, a microcircuit made of GrCs and GoCs is enough to generate meaningful outputs for ML and PCs, the incorporation of the GCL in an extended macrocircuit requires a set of extensions. These concern additional control subcircuits that include the UBC subcircuit, that predicted to play an important role in generating delay lines inside the GCL (Kennedy et al., 2014), and the LC subcircuit, that provides a control loop regulating GoC activity (Dieudonné and Dumoulin, 2000; Barmack and Yakhnitsa, 2008).

Perspectives for Modeling Other Cerebellar Network Subcircuits and The Whole Cerebellar Network

The GCL network provides the most advanced computational model of the cerebellum at the moment. The impact of GCL modeling becomes even more relevant once the GCL output is used to activate the ML. At this level, mapping of GCL activity onto PCs and MLIs occurs serially, as there is no evidence of direct feed-back from the ML to the GCL (though it occurs through DCN and extracerebellar loops, see also below). A reference model for the ML has been proposed over 10 years ago to explain PC activation (Santamaria et al., 2007), but the main connectivity aspects of BCs and SCs with PCs need now to updated with recent data that revealed potentially important physiological and molecular details. For example, ephaptic synapses need to be added on the PC axonal initial segment (Blot and Barbour, 2014) and short-term plasticity needs to be implemented at all the ML synapses (Liu et al., 2008; Lennon et al., 2015). Likewise, while models for the fundamental properties of IO and DCN neurons are available, they also need to be updated. For example, IO neuron axonal burst generation (Mathy et al., 2009) still needs to be resolved. All these properties are likely to have a relevant impact on cerebellar computation dynamics. The same connectivity inside the IO-DCN-PC subcircuit has never been modeled in full although relevant progress has been done (De Schutter and Steuber, 2009; Steuber and Jaeger, 2013). In principle, the IO-DCN-PC subcircuit should be modeled independently and tested and then wired with the cerebellar cortical model.

A first series of effects is expected from the integration of the different subcircuits (granular, molecular and IO-DCN-PC) into a whole-cerebellum network model. This assembly, by including a set of recurrent loops, breaks down the serial processing scheme adopted when modeling the cerebellar subcircuits separately. In this way, the intrinsic dynamics of the IO-DCN-PC subsystem will be integrated with the activity patterns carried by the mfs and processed in the GCL and ML. Eventually, this whole-cerebellum network model will help facing the basic question of how PC and DCN firing is regulated by the cerebellar cortical circuit activity.

A second series of effects is expected from the integration of the whole-cerebellum network model into extracerebellar loops. This step is essential to analyze how the cerebellar network operates. For example, properties like resonance or STDP are relevant only in the context of rhythmic patterns of activity in closed-loop circuits formed by the cerebellum with the DCN (Kistler and De Zeeuw, 2003), the cerebral cortex, brain stem and spinal-cord. The needing of connecting the cerebellum model with external brain structures brings about a series of additional modeling questions.

Relevant Properties of the mf Input

Several anatomical and functional observations become relevant when considering the internal and external connectivity of the cerebellum. The mfs connecting to a certain GrC are probably not all of the same nature but rather they come from different sources. For example, there are GrCs receiving combinations of cortical and spinal afferences and some show a multimodal response to sensory stimulation (Huang et al., 2013; Ishikawa et al., 2015). Thus, each GrC may work as a coincidence detector of different signal sources. However, in some areas GrCs may operate as threshold detectors for the intensity of signal sources deriving from a specific modality or somatic subregions (Bengtsson and Jörntell, 2009). Implementing these connections requires to know how mfs from different sources combine in individual GrC and requires therefore a specific redistribution of glomeruli inside the GCL (Billings et al., 2014). Ideally, the combination of different fibers in GrCs allows direct coincidence detection of signals from different areas carrying “congruent” information that needs to be associated before further processing in the cerebellum. Some mfs also come from the DCN imposing further constraints on the internal distribution of connections. The GrCs receiving the internal feed-back from DCN may be able to associate the coincidence between DCN and extracerebellar inputs. These observations suggest that understanding the cerebellar GCL should consider the distribution of glomeruli deriving from mfs originating from various sources.

Relevant Properties of Zonal and Regional Organization

Perhaps the aspect most relevant to cerebellar modeling on the mesoscale is the organization of subcircuits, in which the cfs and the mfs contacting a certain group of PCs and DCN neurons are connected to the same area of origin to form fully connected cerebellar modules. Furthermore, the cerebellar modules can be organized according to the longitudinal stripes, in which some neuronal and synaptic mechanisms are differentiated depending on the type (Z+ or Z−) of the stripe (Wadiche and Jahr, 2005; Wang et al., 2011; Zhou et al., 2014). In turn, a model on the macroscale has to be composed of multiple modules, each one connected to specific extracerebellar regions. These aspects will have to be considered once the cerebellum model will be wired with extracerebellar areas (see below).

New Modeling Strategies for New Challenging Questions

Realistic cerebellar modeling has to face two main challenges. First, it has to able to incorporate realistic morphologies and to improve details on the molecular and cellular microscale. Secondly, it has to be expanded toward the mesoscale and macroscale. In order to do so, a general and flexible implementation strategy is needed, and in this process cerebellar modeling has once again been acting to promoting the development of general model strategies (Bhalla et al., 1992; Bower and Beeman, 2007).

The cerebellar network is probably the most ordered structure of the brain, and this has allowed a precise modeling reconstruction of its internal connectivity based on extended datasets derived from mice and rats (Maex and De Schutter, 1998; Medina and Mauk, 2000; Medina et al., 2000; Solinas et al., 2010). A further advancement would benefit of an approach based on structured multiscale simulators (Hines and Carnevale, 2001; Bower and Beeman, 2003; Gleeson et al., 2007; Ramaswamy et al., 2015). This would allow to extend cerebellum modeling performed in mice and rats to other species (e.g., humans) and to paracerebellar structures, including the dorsal cochlear nucleus in all vertebrates and the paracerebellar organs in electric fishes (Oertel and Young, 2004; Requarth and Sawtell, 2011; Kennedy et al., 2014). This approach would facilitate the incorporation of new cell types (like the UBCs or the LCs), provided that their detailed single neuron models are available. This approach can host morphological and functional variants of the different neurons, thus moving from canonical neuronal models to neuron model families expressing all the richness of electrophysiological properties that characterize biological networks.

The cerebellum is fundamentally a plastic structure and its function is hard to understand if plasticity is not considered. The cerebellum drives adaptation through plasticity. Moreover, the cerebellum attains the adult network organization through a blend of plastic processes guided by the interaction of genetic programs with epigenetic cues. Thus the interaction of the cerebellar network with the rest of the brain and with ongoing behavior is key not just to determine how the cerebellum operates but also how the cerebellum forms its internal structure and connections. Plasticity during development and in adulthood are probably the most fascinating aspects of the cerebellum and pose challenging questions for modeling.

In adulthood, the cerebellar synapses express various forms of plasticity with learning rules showing different pattern sensitivity, induction and expression mechanisms (D’Angelo, 2014). The corresponding learning rules are embedded into these mechanisms and although it would be desirable that these are eventually represented using dynamics synaptic models (Migliore et al., 1995, 1997, 2015; Tsodyks et al., 1998; Migliore and Lansky, 1999; Rothman and Silver, 2014) at present no such models are available. Nonetheless, theoretical rules based on Hebbian coincidence detectors and STDP have been developed in some cases (Garrido et al., 2016; see below). Eventually a realistic model incorporating learning rules resolved at the molecular level should be able to give insight on the adaptable properties of the network.

As far as ontogenetic network self-organization is concerned, a reference model has been developed for the cerebral cortex accounting for synapse formation through an interaction/pruning process guided by Hebbian rules (Zubler et al., 2013). The dendrite extension/pruning process would by itself solve problems like the crystalline convergence/divergence ratio of the mf-GrC relay and of the cf-PC connectivity. In a way, it can be envisaged that the selection rules of DMP algorithm will eventually be implemented using growing plastic rules. Moreover, once connection pathways are prescribed, the self-organizing system should be able to generate the appropriate distribution of the mf-glomeruli into the cerebellar GCL and to prime the ontogenetic development of the whole network, aligning transmission channels and optimizing circuit performance by setting the appropriate associations of fiber types.

Thus the problem is not just to determine and model the plasticity rules, but also to apply them to the network, as this would require the cerebellum model to be inserted in a whole-brain system interacting with the environment.

Model Simplification and Implementation in Closed-Loop Robotic Testing

The ultimate challenge appears then to run the whole-cerebellum network model in a simulated brain operating in closed-loop. While a radical approach is out of reach at the moment (it would require, in addition to fully developed cerebellum models, also realistic models of large brain sections outside the cerebellum), a first attempt has been done by reducing the complexity of cerebellar models and using simplified versions to run closed-loop robotic simulations (Casellato et al., 2012, 2014, 2015; Garrido et al., 2013; Luque et al., 2014, 2016).

Complexity Reduction

The way complexity reduction is achieved is critical, since it has to be performed in a way that preserves the fundamental biological properties relevant to the process under investigation. Two recent approaches have been proposed. Realistic PC models currently involve about 1500 electrical compartments and up to 15 active ionic conductances (De Schutter and Bower, 1994a,b). This complexity has been remarkably reduced by applying Strahler’s analysis to reduce up to 200-fold the run time but yet maintaining an appropriate response to synaptic inputs (Marasco et al., 2012, 2013). Likewise, the granular layer network has been simplified using analytical tools by increasing the simulation speed at least 270 times but yet reproducing salient features of neural network dynamics such as local microcircuit synchronization, traveling waves, center-surround, and time-windowing (Cattani et al., 2016). In all these cases, a well defined relationship is maintained between the simplified models and their more complex realistic counterparts. These attempts open the way to a guided simplification procedure, at least for some cerebellar neurons and subnetworks. When the whole cerebellar network has to be represented in a macro-scale model, simplifications that are computationally efficient may be preferable in a first instance. Clearly, in this case a top-down approach is adopted and the relationship of the simplified model with the real system is a matter of speculation. This approach has been used to generate cerebellar spiking networks (SNN) allowing to reproduce a single basic cerebellar module running with high efficiency in a robotic controller yet maintaining some fundamental features of neurons and connections (Casellato et al., 2012, 2014, 2015; Garrido et al., 2013; Luque et al., 2014, 2016). For example, in these models, neurons were represented by integrate-and-fire single-compartment elements, the local inhibitory interneuron networks were not included and the GCL was not fully implemented resorting to the concept of a non-recurrent states in a liquid-state machine (Yamazaki and Tanaka, 2007). Nonetheless, the model incorporated multiple forms of bidirectional plasticity at the PC and DCN synapses. This compromise had to be accepted in order to generate a spiking cerebellum model running in real-time inside a closed-loop robotic control system and to perform system level analysis of complex tasks like active manipulation.

Spiking Neural Networks of the Cerebellum

Despite the simplicity of the cerebellar SNN (Figure 6), the robots that incorporated it revealed remarkable emerging properties (Casellato et al., 2012, 2014, 2015). The SNN robots correctly performed multiple associative learning and correction tasks, which ranged from eye-blink conditioning to vestibulo-ocular reflex (VOR) and force-field correction. Importantly, the robots were not designed for any specific one of these tasks but could cope equally well with all of them demonstrating generalized learning and computational capabilities. The robots could also generalize their previous stored patterns to analogous cases with a learning rate approaching that observed in real life. This system could easily fit human EBCC data predicting dual-rate learning in the network. Again, the outcome of the closed-loop simulation have been validated against real experiments carried out in humans (Monaco et al., 2014; D’Angelo et al., 2015) and the challenge is now to see whether it is predictive with respect to human pathologies.

FIGURE 6

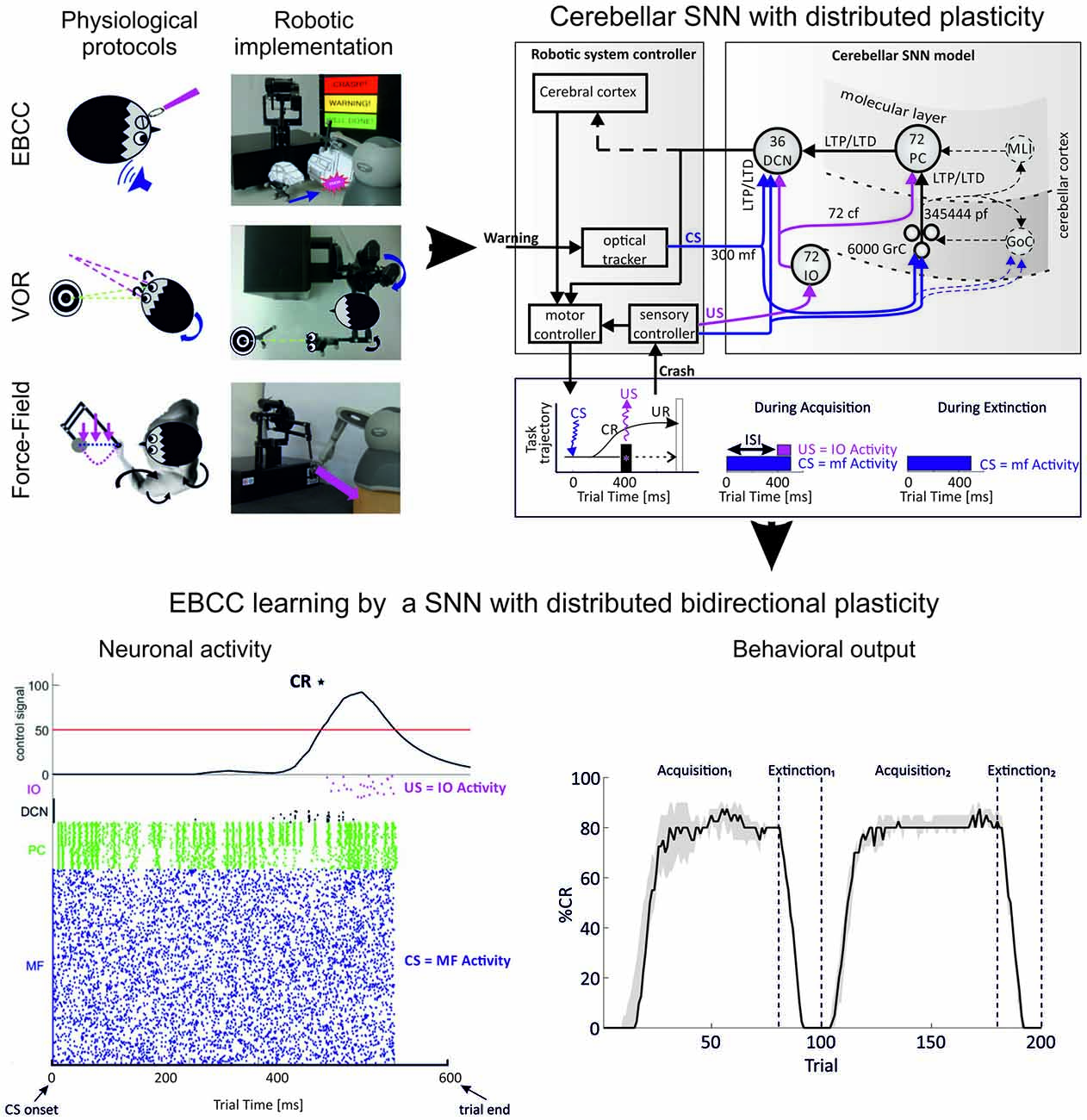
Figure 6. Simulating an associative learning task using a cerebellar spiking neural network (SNN). The cerebellum circuit was simplified and embedded into a robotic control system, in which it provided the substrate to integrate spatio-temporal information in different associative learning tasks. Real robot paradigms (top left panel): eye blink classical conditioning (EBCC)-like, vestibulo-ocular reflex (VOR) and upper limb reaching perturbed by force fields. The EBCC-like Pavlovian task is reproduced into the robotic platform as a collision-avoidance task. The conditioned stimulus (CS) onset is based on the distance between the moving robot end-effector and the fixed obstacle placed along the trajectory, detected by the optical tracker. The unconditioned stimulus (US) is the collision event. The DCNs trigger the conditioned response (anticipated stop). The VOR is reproduced into the robotic platform by using the second joint of the robotic arm as the head (imposed rotation) and the third joint (determining the orientation of the second link) as the eye. The misalignment between the gaze direction and the environmental target to be looked at is computed through geometric equations from the optical tracker recording. The DCNs modulate the eye compensatory motion. The perturbed reaching is reproduced into the robotic platform by applying a viscous force field on the moving robotic arm by means of the other robotic device attached at its end-effector. The DCNs modulate the anticipatory corrective torque. (Modified from Casellato et al., 2014). EBCC-like control system embedding spiking cerebellar network (top right panel). US is fed into the cf pathway; CS into the mf pathway. CS and US co-terminate (as in the “delay” EBCC). The SNN learns to produce conditioned responses (CRs), i.e., a stop of the robotic arm (collision avoidance) anticipating the US onset. The figure highlights the major forms of plasticity embedded in the cerebellar network and driving the learning, namely synaptic long-term potentiation (LTP) and synaptic long-term depression (LTD), both at cortical and nuclear levels (distributed plasticity). The protocol is made up of acquisition and extinction phases; in the acquisition trials CS-US pairs are presented at a constant Inter-Stimuli Interval (ISI); in the extinction trials CS alone is presented. Each trial lasts 600 ms. The number of cell in the circuit is indicated. All labels as in previous figures. (Modified from D’Angelo et al., 2015). Network activity and output behavior during EBCC training (bottom panel). After learning, the response of PCs to inputs decreases, and this increases the discharge in DCN neurons (raster plot and integral of neuronal activity, left). Since the DCN spike pattern changes occur before the US arrival, the DCN discharge accurately predicts the US and therefore facilitates the release of an anticipatory behavioral response. Number of CRs (%) along trials (80 acquisition trials and 20 extinction trials for two sessions in a row; CR% is computed as percentage number of CR occurrence within blocks of 10 trials each). The black curve (right plot) represents the behavior generated by the cerebellar SNN equipped with only one plasticity site at the cortical layer (median on 15 tests with interquartile intervals). Despite uncertainty and variability introduced by the direct interaction with a real environment, the SNN progressively learns to generate CRs anticipating the US, to rapidly extinguish them and to consolidate the learnt association to be exploited in the re-test session. (Modified from Casellato et al., 2015; D’Angelo et al., 2015; Antonietti et al., 2016).

An important aspect of these models is to incorporate learning rules that allow to test the impact of learning on cerebellar computation. While a precise correspondence with long-term synaptic plasticity is not at the level of molecular mechanisms (we are dealing with simplified models by the way), these learning rules can effectively capture the learning dynamics of the system. Importantly, faster learning rates at PC than DCN synapses allow fast acquisition and subsequent transfer of memory in a consolidated state (Luque et al., 2014) and STDP rules allow learning to accurately match the network temporal dynamics (Luque et al., 2016). These models allowed to evaluate the impact of known forms of bidirectional LTP/LTD at pf-PC, PC-DCN and mf-DCN synapses and to predict a critical role for plasticity at IO-DCN synapses. The implementation of GCL plasticity poses a formidable problem as it is hard to determine its supervision process. A recent proposal suggests that the issue could be solved by exploiting multi-step learning with an initial pattern storage in the inhibitory interneuron network formed by Golgi cells (Garrido et al., 2016).

Advanced Robotic Simulations of Manipulation Tasks

When manipulating a tool, the cerebellar network acquires a dynamic and kinematic model of the tool. In this way, the manipulated tool becomes de facto as an extension of the arm allowing to perform accurate movements of the arm-object system as a whole. This unique capability is to a large extent based on the cerebellum sensory-motor integration properties. In order to establish a functional link between specific properties of neurons, network organization, plasticity rules and behavior, the cerebellar model needs to be integrated with a body (a simulated or real robotic sensory-motor system). Sensory signals need to be translated into biologically plausible codes to be delivered to the cerebellar network, and also cerebellar outputs need to be translated into representations suitable to be transferred to actuators (Luque et al., 2012). The experimental set-up is defined so as to monitor how accurately the system performs pre-defined movements when manipulating objects that significantly affect the arm/object kinematics and dynamics (Figure 7).

FIGURE 7

Figure 7. Biologically plausible cerebellar control loops. (Top left) The target trajectory followed by the robotic arm model is defined along three degrees of freedom in joint coordinates and Cartesian coordinates. (Top right) In the feedback cerebellar (recurrent) control loop, the adaptive cerebellar controller infers a model from the error signal related to a sensorimotor input to produce effective corrective position and velocity terms. In this way, instead of propagating data from input to output as the forward architecture does, the recurrent architecture also propagates data from later processing stages to earlier ones. In the feedforward cerebellar control loop, the adaptive cerebellar module is embedded in the forward control loop and delivers add-on corrective torque values to compensate deviations in the base dynamics of the robotic arm model. The idealized correspondence with anatomical parts and processing functions is also indicated. (Bottom) Weight evolution in the cerebellar model manipulating different payloads operating with multiple plasticity mechanisms. Simulations were performed using plasticity at PF-PC, MF-DCN, and PC-DCN synapses and a custom-configured IO-DCN connection for manipulating 2 kg external payloads during 500 trials. The initial cerebellar system gain was properly set to operate with no payload. Evolution of the average error (MAE, black curve on the left) of the three robot joints during the learning process for 2 kg payload. The red curves on the left indicate the evolution of synaptic weight at the different synapses. Note that weights change rapidly at the beginning but then the cerebellar system works almost in open loop and no remarkable corrective action are applied by the cerebellar adapting system. PC and DCN neuron activity during a single trial show oscillations dictating the precise timing of force delivery to the joints in different trials. (Modified from Luque et al., 2011a, 2014).

At this level, the cerebellar network is assumed to integrate sensory-motor signals by delivering corrective terms during movement execution (here a top-down approach is applied). In the framework of a biologically relevant task such as accurate object manipulation, different issues need to be addressed and defined by adopting specific working hypothesis and simplifications. For example: (i) PCs and DCN can be arranged in microcomplexes dealing with different degrees of freedom; (ii) error-related signal coming from the IO are delivered to PCs and drive learning at pf-PC synapses; (iii) neurons and connection can be simplified still maintaining the fundamental cerebellar network structure and functionality. There are different modeling approaches that have been simulated and tested (Luque et al., 2011a,b):

(1)  Integrating the cerebellum in a feed-forward scheme delivering corrective terms to the spinal cord. In this case the cerebellum receives sensory inputs and produces motor corrective terms (the cerebellum implements an “inverse model”). Thus in this case the input and output representation spaces are different and the sensori-motor transformation needs to be performed also in the cerebellar network.

(2)  Integrating the cerebellum in a feed-back (recurrent) scheme delivering corrective terms to the cerebellar cortex. In this case the cerebellum receives sensory-motor inputs and produces sensory corrective terms (the cerebellum implements a “forward model”; Kawato et al., 1988; Miyamoto et al., 1988; Gomi and Kawato, 1993; Yamazaki et al., 2015; Hausknecht et al., 2016).

Eventually, closed-loop robotic simulations allow to investigate the original issue of how the cerebellar microcircuit controls behavior in a novel manner. Here neurons and SNN are running in the robot. The challenge is clearly now to substitute the current simplified models of neurons and microcircuits with more realistic ones, so that from their activity during a specific behavioral task, the scientists should be able to infer the underlying coding strategies at the microscopic level.

Current Perspectives for Realistic Cerebellar Modeling

On one hand, realistic cerebellar modeling is now advanced enough to generate predictions that may guide the subsequent search for critical physiological phenomena amongst the many that could be otherwise investigated. On the other hand, several new challenges await to be faced in terms of model construction and validation in order to explore physiological phenomena that have emerged from experiments. Realistic modeling is therefore becoming more and more an interactive tool for cerebellar research.

Predictions of Realistic Cerebellar Modeling and their Experimental Testing

Cerebellar modeling is providing new opportunities for predicting biological phenomena that can be subsequently searched for experimentally. This procedure is relevant for several reasons. First, as discussed above, the computational models implicitly generate hypotheses providing the way for their subsequent validation or rejection. Secondly, the computational models can help focusing researcher’s interest toward specific questions. There are several examples that apply to different levels of cerebellar physiology.

In 2001, an advanced GrC model, based on the ionic conductance complement of the same neuron, predicted that a slow K current was needed to explain certain aspects of GrC firing and intrinsic GrC theta-band resonance. This current has been then looked for experimentally and its subsequent identification allowed to successfully complete the model and explain bursting and resonance in mechanistic terms (D’Angelo et al., 2001). In 2006, a mossy fiber-granule cell neurotransmission model, based on specific quantal release and receptor properties (Nieus et al., 2006), predicted that plasticity of intrinsic excitability could control rate coding while plasticity of release probability could control spike timing, as indeed verified experimentally. In 2007, a Golgi cell model actually predicted that Golgi cells were resonant in the theta-band a property that was then demonstrated experimentally (Solinas et al., 2007a,b). In 2007, a PC model predicted the coding properties of PCs in relation to LTD (Steuber et al., 2007). In 2009–2010 two models of the Golgi cell network predicted the impact of gap-junctions in regulating local GrC discharge and Golgi cell synchronization (Dugué et al., 2009; Vervaeke et al., 2010). In 2013, a theoretical article predicted that bidirectional plasticity had to exist at the mossy fiber—Golgi cell synapse (Garrido et al., 2013). This plasticity has subsequently been demonstrated (Locatelli et al., 2015). In 2014, a model including both excitatory and inhibitory neurotransmission predicted that phasic inhibitory mechanisms can dynamically regulate output spike patterns, as well as calcium influx and NMDA currents, at the mossy fiber-granule cell relay of cerebellum (Nieus et al., 2014). Again this prediction was accurately matched by the experiments. In 2015, a computational model predicted that the number of GrC dendrites that maximizes information transfer is actually coincident with that measured anatomically (Billings et al., 2014).

Yet other predictions are awaiting for experimental verification. In 2014, a closed-loop simulation predicted that cerebellar learning would accelerate toward biological levels if a form of mid-term plasticity would exist between the IO and DCN neurons (Luque et al., 2014). In 2016, another work predicted that STDP has the intrinsic capacity of binding learning to temporal network dynamics (Luque et al., 2016). Finally, very recently a mechanism of STDP learning involving the inhibitory interneuron network has been proposed (Garrido et al., 2016), that could be applicable to the GCL and explain how learning takes place in this cerebellar subnetwork. Thus, a new perspective for the near future is to extend the feed-back between computational models and experiments generating de facto a new powerful tool for cerebellar network investigation.

New Challenges for Cerebellar Physiology and their Realistic Modeling

Amongst the new challenges that may benefit from enhanced and extended realistic models of the cerebellum, some have been highlighted in the present review and are summarized here.

There is a wealth of molecular and cellular phenomena, whose biological significance has been inferred experimentally, that could be incorporated into a realistic cerebellar model in order to investigate their implications for function. These include: the role of specific ionic channel properties in regulating neuronal excitation (amongst known examples see Jaeger et al., 1997; Bower and Beeman, 1998; Kubota and Bower, 2001; Ovsepian et al., 2013); the role of synaptic receptor properties in neuronal excitation and plasticity, like the voltage-dependence of NMDA receptor subtypes (Schwartz et al., 2012); the role of diffusible messengers like nitric oxide in coordinating long-term synaptic plasticity (Garthwaite, 2016); the role of intracellular biochemical cascades in the induction and expression of long-term synaptic plasticity (Tsukada et al., 1995; Schweighofer and Ferriol, 2000; Billings et al., 2014).

There are several properties of local microcircuits that are being discovered and that could be further understood by realistic cerebellar modeling. We have already mentioned the critical issue on how the cerebellum processes incoming information involving numerous molecular and cellular mechanisms that are only partially known. An issue that needs to be revisited, as it appears critical to understand the whole cerebellar functioning, is how the PC are activated by GrC through their aa (Gundappa-Sulur et al., 1999; Huang et al., 2006). Moreover, recent discoveries have opened new issues: ephaptic synapses have recently been revealed between basket cells (BCs) and PCs (Blot and Barbour, 2014), the connectivity of MLI involves complex spatial rules (Bower, 2010; Rieubland et al., 2014), the inhibitory network in the cerebellar granular layer involves gap junctions and reciprocal inhibitory synapses (Dugué et al., 2009; Szoboszlay et al., 2016; van Welie et al., 2016), the inferior olivary neurons are connected through gap junctions (Rothman et al., 2009; Rancz and Häusser, 2010; Lefler et al., 2014).

There are aspects of intracerebellar organization and connectivity that remain to be incorporated into large-scale realistic models, including the granular layer-molecular layer projections (Valera et al., 2016), the PC-DCN convergence (Person and Raman, 2012b), the DCN-granular layer projections (Houck and Person, 2015), the PC-DCN-IO loops (Libster and Yarom, 2013). Beyond this, these are needed for guided cerebellar model simplification and incorporation into large-scale networks running into robotic controllers and simulated environments (Garrido et al., 2013; Casellato et al., 2015; Yamazaki et al., 2015).

On the pathophysiological side (Chen et al., 2010; Libster et al., 2010; Ovsepian et al., 2013; Kros et al., 2015), there is a wealth of hypothesis that have or would benefit of realistic modeling. Ataxia has long been attributed to cerebellar dysfunction. Recently, several ionic channel and neuronal alterations have been linked to ataxia (Libster et al., 2010) and to the disruption of dynamics in the olivo-cerebellar circuit (Chen et al., 2010). There are specific properties of the cerebellar output that are critical for controlling extracerebellar networks and their pathological states, like in cebro-cortical spike-and-wave discharge (e.g., see Ovsepian et al., 2013; Kros et al., 2015). This kind of observations may provide critical test-benches for realistic model validation and prediction.

Finally, in perspective, the connectivity of the cerebellar network in long-range loops appears to be critical to understand microcircuit functions. Following the fundamental recognition of its involvement in sensory-motor coordination and learning, the cerebellum is now also believed to take part in the processing of cognition and emotion (Schmahmann, 2004) by exploiting the connectivity of the cerebellar modules with specific brain structures through different cerebro-cerebellar loops. It has been proposed that a similar circuit structure in all cerebellar areas may carry out various operations using a common computational scheme (D’Angelo and Casali, 2013). Since there is an intimate interplay between timing and learning at the cellular level that is reminiscent of the “timing and learning machine” capabilities long attributed to the cerebellum, it is conceivable that realistic models developed for sensori-motor control might also apply to cognitive-emotional control once integrated into the appropriate loops.

A Manifesto for Collaborative Cerebellar Modeling

This review has summarized some relevant aspects characterizing the cerebellar circuit showing how these have been conceptualized and modeled. Still, there are several issues that deserve attention, ranging from molecular to neuronal, microcircuit, macrocircuit and integrative aspects, and even more it is clear that all these aspects are tightly bound. There is no solution through a single experiment or model, so that understanding the structure-function-dynamics relationship of the cerebellum requires a continuous bottom-up top-down dialog (Akemann et al., 2009).

Realistic modeling is now opening new perspectives. The main challenge is to join precise network wiring with accurate representations of neuronal and synaptic properties in order to be able to simulate local network dynamics. The introduction of synaptic and non-synaptic plasticity in its various forms and locations could then allow to understand how input patterns can reconfigure the network during ontogenetic development and in the mature state. Finally, full exploitation of cerebellar network capabilities would require simulations operated in closed-loop in robotic systems. It is envisaged that such systems will be able in the future to emulate physiological and pathological states, providing the basis for protocols of network-guided robotic neurorehabilitation.

Large-scale simulations running efficiently on supercomputers are now possible, and software development systems have been designed and tested (Bhalla et al., 1992; Hines and Carnevale, 1997; Bower and Beeman, 2007; Gleeson et al., 2007, 2010; Davison et al., 2009; Hines et al., 2009; Cornelis et al., 2012a). While this may be sufficient for elaborating complex codes in an iterative reconstruction/validation process, simulating network adaptation during learning would require several repetitions over prolonged time periods. In this scenario, a large-scale cerebellar network embedding synaptic learning rules should be running inside a whole sensory-motor control system generating a massive computational load and leading to unaffordable simulation times. To this aim, efficient codes have been developed (Eppler et al., 2008; Bednar, 2009; Zaytsev and Morrison, 2014). The problem that remains will be that of providing efficient model simplifications still maintaining the salient computational properties of the network (e.g., see the chapter above Casellato et al., 2012, 2014, 2015; Garrido et al., 2013; Luque et al., 2014). Eventually, neuromorphic hardware platforms will have to be considered for the cerebellum as well as for the cerebral cortex (Pfeil et al., 2013; Galluppi et al., 2015; Lagorce et al., 2015). It can be envisaged that realistic modeling of the cerebellum, with the reconstruction of neurons and large-scale networks based on extended data-sets and running on supercomputing infrastructures, will require a world-wide collaborative effort as it has been proposed for other brain structures like the neocortex and hippocampus (Markram, 2006; Cornelis et al., 2012a; Crook et al., 2012; Kandel et al., 2013; Bower, 2015; Ramaswamy et al., 2015).

Author Contributions

ED’A coordinated and wrote the article helped by all the other authors.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge the REALNET (FP7-ICT270434) and CEREBNET (FP7-ITN238686) consortium for the fruitful interactions that fueled cerebellar research in the last years and posed the grounds for the present article. The article was supported by Human Brain Project (HBP-604102) to ED’A and ER and by HBP-RegioneLombardia to AP.

Abbreviations

aa, ascending axon; APN, anterior pontine nucleus; ATN, anterior thalamic nuclei; BC, basket cell; BG, basal ganglia; cf, climbing fiber; Ca²⁺, calcium ions; cGMP, cyclic GMP; DCN, deep cerebellar nuclei; DAG, diacyl-glycerol; GoC, Golgi cell; glu, glutamate; GC, guanyl cyclase; GCL, granular cell layer; GrC, granule cell; IO, inferior olive; IP3, inositol-triphosphate; LC, Lugaro cell; ML, molecular layer; MLI, molecular layer interneuron; mf, mossy fiber; MC, motor cortex; NO, nitric oxide; NOS, nitric oxide synthase; PKC, protein kinase C; pf, parallel fiber; PC, Purkinje cell; PC, parietal cortex; PIP, phosphatidyl-inositol-phosphate; PFC, prefrontal cortex; PCL, Purkinje cell layer; RN, reticular nucleus; SC, stellate cell; TC, temporal cortex; STN, subthalamic nucleus; UBC, unipolar brush cell.

References

Akemann, W., Middleton, S. J., and Knöpfel, T. (2009). Optical imaging as a link between cellular neurophysiology and circuit modeling. Front. Cell. Neurosci. 3:5. doi: 10.3389/neuro.03.005.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Albus, J. S. (1971). A theory of cerebellar function. Math. Biosci. 10, 25–61. doi: 10.1016/0025-5564(71)90051-4

CrossRef Full Text | Google Scholar

Alcami, P., and Marty, A. (2013). Estimating functional connectivity in an electrically coupled interneuron network. Proc. Natl. Acad. Sci. U S A 110, E4798–E4807. doi: 10.1073/pnas.1310983110

PubMed Abstract | CrossRef Full Text | Google Scholar

Altman, J., and Bayer, S. A. (1997). Development of the Cerebellar System in Relation to its Evolution, Structure and Function. Boca Raton, FL: CRC Press.

Google Scholar

Andersson, G., and Oscarsson, O. (1978). Climbing fiber microzones in cerebellar vermis and their projection to different groups of cells in the lateral vestibular nucleus. Exp. Brain Res. 32, 565–579. doi: 10.1007/bf00239553

PubMed Abstract | CrossRef Full Text | Google Scholar

Ankri, L., Husson, Z., Pietrajtis, K., Proville, R., Léna, C., Yarom, Y., et al. (2015). A novel inhibitory nucleo-cortical circuit controls cerebellar Golgi cell activity. Elife 4:e06262. doi: 10.7554/eLife.06262

PubMed Abstract | CrossRef Full Text | Google Scholar

Antonietti, A., Casellato, C., Garrido, J. A., Luque, N. R., Naveros, F., Ros, E., et al. (2016). Spiking neural network with distributed plasticity reproduces cerebellar learning in eye blink conditioning paradigms. IEEE Trans. Biomed. Eng. 63, 210–219. doi: 10.1109/TBME.2015.2485301

PubMed Abstract | CrossRef Full Text | Google Scholar

Apps, R., and Garwicz, M. (2005). Anatomical and physiological foundations of cerebellar information processing. Nat. Rev. Neurosci. 6, 297–311. doi: 10.1038/nrn1646

PubMed Abstract | CrossRef Full Text | Google Scholar

Apps, R., and Hawkes, R. (2009). Cerebellar cortical organization: a one-map hypothesis. Nat. Rev. Neurosci. 10, 670–681. doi: 10.1038/nrn2698

PubMed Abstract | CrossRef Full Text | Google Scholar

Arbib, M. A., Erdi, P., and Szentagothai, J. (1997). Neural Organization: Structure, Function and Dynamics. Cambridge, MA: MIT Press.

Google Scholar

Arbib, M. A., Metta, G., and van der Smagt, P. (2008). “Neurorobotics: from vision to action,” in Springer Handbook of Robotics, eds B. Siciliano and O. Khatib (New York, NY: Springer-Verlag), 1453–1480.

Google Scholar

Arenz, A., Silver, R. A., Schaefer, A. T., and Margrie, T. W. (2008). The contribution of single synapses to sensory representation in vivo. Science 321, 977–980. doi: 10.1126/science.1158391

PubMed Abstract | CrossRef Full Text | Google Scholar

Astori, S., Luján, R., and Köhr, G. (2009). GABA release from cerebellar stellate cells is developmentally regulated by presynaptic GABA(B) receptors in a target-cell-specific manner. Eur. J. Neurosci. 30, 551–559. doi: 10.1111/j.1460-9568.2009.06856.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Baldi, P., Vanier, M. C., and Bower, J. M. (1998). On the use of Bayesian methods for evaluating compartmental neural models. J. Comput. Neurosci. 5, 285–314. doi: 10.1023/A:1008887028637

PubMed Abstract | CrossRef Full Text | Google Scholar

Balsters, J. H., Cussans, E., Diedrichsen, J., Phillips, K. A., Preuss, T. M., Rilling, J. K., et al. (2010). Evolution of the cerebellar cortex: the selective expansion of prefrontal-projecting cerebellar lobules. Neuroimage 49, 2045–2052. doi: 10.1016/j.neuroimage.2009.10.045

PubMed Abstract | CrossRef Full Text | Google Scholar

Barmack, N. H., and Yakhnitsa, V. (2008). Functions of interneurons in mouse cerebellum. J. Neurosci. 28, 1140–1152. doi: 10.1523/JNEUROSCI.3942-07.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Baumel, Y., Jacobson, G. A., and Cohen, D. (2009). Implications of functional anatomy on information processing in the deep cerebellar nuclei. Front. Cell. Neurosci. 3:14. doi: 10.3389/neuro.03.014.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Bednar, J. A. (2009). Topographica: building and analyzing map-level simulations from python, C/C++, MATLAB, NEST, or NEURON components. Front. Neuroinform. 3:8. doi: 10.3389/neuro.11.008.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Bengtsson, F., and Jörntell, H. (2009). Sensory transmission in cerebellar granule cells relies on similarly coded mossy fiber inputs. Proc. Natl. Acad. Sci. U S A 106, 2389–2394. doi: 10.1073/pnas.0808428106

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhalla, U. S., Bilitch, D. H., and Bower, J. M. (1992). Rallpacks: a set of benchmarks for neuronal simulators. Trends Neurosci. 15, 453–458. doi: 10.1016/0166-2236(92)90009-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Billings, G., Piasini, E., Lorincz, A., Nusser, Z., and Silver, R. A. (2014). Network structure within the cerebellar input layer enables lossless sparse encoding. Neuron 83, 960–974. doi: 10.1016/j.neuron.2014.07.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Blot, A., and Barbour, B. (2014). Ultra-rapid axon-axon ephaptic inhibition of cerebellar Purkinje cells by the pinceau. Nat. Neurosci. 17, 289–295. doi: 10.1038/nn.3624

PubMed Abstract | CrossRef Full Text | Google Scholar

Bower, J. M. (2010). Model-founded explorations of the roles of molecular layer inhibition in regulating purkinje cell responses in cerebellar cortex: more trouble for the beam hypothesis. Front. Cell. Neurosci. 4:27. doi: 10.3389/fncel.2010.00027

PubMed Abstract | CrossRef Full Text | Google Scholar

Bower, J. M. (2015). The 40-year history of modeling active dendrites in cerebellar Purkinje cells: emergence of the first single cell “community model”. Front. Comput. Neurosci. 9:129. doi: 10.3389/fncom.2015.00129

PubMed Abstract | CrossRef Full Text | Google Scholar

Bower, J. M., and Beeman, D. (1998). “Ion channels in bursting neurons,” in The Book of GENESIS, eds J. M. Bower and D. Beeman (New York, NY: Springer New York), 97–130.

Bower, J. M., and Beeman, D. (2003). The Book of GENESIS: Exploring Realistic Neural Models with the General Neural Simulation System. New York, NY: Springer-Verlag New York, Inc.

Google Scholar

Bower, J. M., and Beeman, D. (2007). Constructing realistic neural simulations with GENESIS. Methods Mol. Biol. 401, 103–125. doi: 10.1007/978-1-59745-520-6_7

PubMed Abstract | CrossRef Full Text | Google Scholar

Bower, J. M., and Woolston, D. C. (1983). Congruence of spatial organization of tactile projections to granule cell and Purkinje cell layers of cerebellar hemispheres of the albino rat: vertical organization of cerebellar cortex. J. Neurophysiol. 49, 745–766.

PubMed Abstract | Google Scholar

Brette, R., Rudolph, M., Carnevale, T., Hines, M., Beeman, D., Bower, J. M., et al. (2007). Simulation of networks of spiking neurons: a review of tools and strategies. J. Comput. Neurosci. 23, 349–398. doi: 10.1007/s10827-007-0038-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Briatore, F., Patrizi, A., Viltono, L., Sassoè-Pognetto, M., and Wulff, P. (2010). Quantitative organization of GABAergic synapses in the molecular layer of the mouse cerebellar cortex. PLoS One 5:e12119. doi: 10.1371/journal.pone.0012119

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, K. M., Sugihara, I., Shinoda, Y., and Ascoli, G. A. (2012). Digital morphometry of rat cerebellar climbing fibers revals distinct branch and bouton types. J. Neurosci. 32, 14670–14684. doi: 10.1523/JNEUROSCI.2018-12.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

Bureau, I., Dieudonne, S., Coussen, F., and Mulle, C. (2000). Kainate receptor-mediated synaptic currents in cerebellar Golgi cells are not shaped by diffusion of glutamate. Proc. Natl. Acad. Sci. U S A 97, 6838–6843. doi: 10.1073/pnas.97.12.6838

PubMed Abstract | CrossRef Full Text | Google Scholar

Caligiore, D., Pezzulo, G., Baldassarre, G., Bostan, A. C., Strick, P. L., Doya, K., et al. (2016). Consensus paper: towards a systems-level view of cerebellar function: the interplay between cerebellum, basal ganglia and cortex. Cerebellum doi: 10.1007/s12311-016-0763-3 [Epub ahead of print].

PubMed Abstract | CrossRef Full Text | Google Scholar

Caligiore, D., Pezzulo, G., Miall, R. C., and Baldassarre, G. (2013). The contribution of brain sub-cortical loops in the expression and acquisition of action understanding abilities. Neurosci. Biobehav. Rev. 37, 2504–2515. doi: 10.1016/j.neubiorev.2013.07.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Casellato, C., Antonietti, A., Garrido, J. A., Carrillo, R. R., Luque, N. R., Ros, E., et al. (2014). Adaptive robotic control driven by a versatile spiking cerebellar network. PLoS One 9:e112265. doi: 10.1371/journal.pone.0112265

PubMed Abstract | CrossRef Full Text | Google Scholar

Casellato, C., Antonietti, A., Garrido, J. A., Ferrigno, G., D’Angelo, E., and Pedrocchi, A. (2015). Distributed cerebellar plasticity implements generalized multiple-scale memory components in real-robot sensorimotor tasks. Front. Comput. Neurosci. 9:24. doi: 10.3389/fncom.2015.00024

PubMed Abstract | CrossRef Full Text | Google Scholar

Casellato, C., Pedrocchi, A., Garrido, J. A., Luque, N. R., Ferrigno, G., D’Angelo, E., et al. (2012). “An integrated motor control loop of a human-like robotic arm: feedforward, feedback and cerebellum-based learning,” in 2012 4th IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics Rome, 562–567.

Google Scholar

Cattani, A., Solinas, S., and Canuto, C. (2016). A hybrid model for the computanionally-efficient simulation of the cerebellar granular layer. Front. Comput. Neurosci. 10:30 doi: 10.3389/fncom.2016.00030

CrossRef Full Text

Cerminara, N. L. (2010). Cerebellar modules: individual or composite entities? J. Neurosci. 30, 16065–16067. doi: 10.1523/JNEUROSCI.4823-10.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Cesana, E., Pietrajtis, K., Bidoret, C., Isope, P., D’Angelo, E., Dieudonné, S., et al. (2013). Granule cell ascending axon excitatory synapses onto Golgi cells implement a potent feedback circuit in the cerebellar granular layer. J. Neurosci. 33, 12430–12446. doi: 10.1523/JNEUROSCI.4897-11.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Chadderton, P., Schaefer, A. T., Williams, S. R., and Margrie, T. W. (2014). Sensory-evoked synaptic integration in cerebellar and cerebral cortical neurons. Nat. Rev. Neurosci. 15, 71–83. doi: 10.1038/nrn3648

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Kovalchuk, Y., Adelsberger, H., Henning, H. A., Sausbier, M., Wietzorrek, G., et al. (2010). Disruption of the olivo-cerebellar circuit by Purkinje neuron-specific ablation of BK channels. Proc. Natl. Acad. Sci. U S A 107, 12323–12328. doi: 10.1073/pnas.1001745107

PubMed Abstract | CrossRef Full Text | Google Scholar

Connor, J. A., and Stevens, C. F. (1971). Prediction of repetitive firing behaviour from voltage clamp data on an isolated neurone soma. J. Physiol. 213, 31–53. doi: 10.1113/jphysiol.1971.sp009366

PubMed Abstract | CrossRef Full Text | Google Scholar

Cornelis, H., Coop, A. D., and Bower, J. M. (2012a). A federated design for a neurobiological simulation engine: the CBI federated software architecture. PLoS One 7:e28956. doi: 10.1371/journal.pone.0028956

PubMed Abstract | CrossRef Full Text | Google Scholar

Cornelis, H., Rodriguez, A. L., Coop, A. D., and Bower, J. M. (2012b). Python as a federation tool for GENESIS 3.0. PLoS One 7:e29018. doi: 10.1371/journal.pone.0029018

PubMed Abstract | CrossRef Full Text | Google Scholar

Courtemanche, R., Pellerin, J.-P., and Lamarre, Y. (2002). Local field potential oscillations in primate cerebellar cortex: modulation during active and passive expectancy. J. Neurophysiol. 88, 771–782. doi: 10.1152/jn.00718.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Courtemanche, R., Robinson, J. C., and Aponte, D. I. (2013). Linking oscillations in cerebellar circuits. Front. Neural Circuits 7:125. doi: 10.3389/fncir.2013.00125

PubMed Abstract | CrossRef Full Text | Google Scholar

Crook, S. M., Bednar, J. A., Berger, S., Cannon, R., Davison, A. P., Djurfeldt, M., et al. (2012). Creating, documenting and sharing network models. Network 23, 131–149. doi: 10.3109/0954898X.2012.722743

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Angelo, E. (2011). Neural circuits of the cerebellum: hypothesis for function. J. Integr. Neurosci. 10, 317–352. doi: 10.1142/s0219635211002762

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Angelo, E. (2014). The organization of plasticity in the cerebellar cortex: from synapses to control. Prog. Brain Res. 210, 31–58. doi: 10.1016/B978-0-444-63356-9.00002-9

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Angelo, E., and Casali, S. (2013). Seeking a unified framework for cerebellar function and dysfunction: from circuit operations to cognition. Front. Neural Circuits 6:116. doi: 10.3389/fncir.2012.00116

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Angelo, E., and De Zeeuw, C. I. (2009). Timing and plasticity in the cerebellum: focus on the granular layer. Trends Neurosci. 32, 30–40. doi: 10.1016/j.tins.2008.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Angelo, E., Mapelli, L., Casellato, C., Garrido, J. A., Luque, N., Monaco, J., et al. (2015). Distributed circuit plasticity: new clues for the cerebellar mechanisms of learning. Cerebellum 15, 139–151. doi: 10.1007/s12311-015-0711-7

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Angelo, E., Masoli, S., Rizza, M., and Casali, S. (2016). “Single-neuron and network computation in realistic models of the cerebellar cortex,” in The Neuronal Codes of the Cerebellum, ed. D. H. Heck. (San Diego, CA: Academic Press), 239–260.

Google Scholar

D’Angelo, E., Nieus, T., Maffei, A., Armano, S., Rossi, P., Taglietti, V., et al. (2001). Theta-frequency bursting and resonance in cerebellar granule cells: experimental evidence and modeling of a slow k+-dependent mechanism. J. Neurosci. 21, 759–770.

PubMed Abstract | Google Scholar

D’Angelo, E., and Peres, A. (2011). Fisiologia. ed. Ediermes.

D’Angelo, E., Solinas, S., Garrido, J., Casellato, C., Pedrocchi, A., Mapelli, J., et al. (2013a). Realistic modeling of neurons and networks: towards brain simulation. Funct. Neurol. 28, 153–166. doi: 10.11138/FNeur/2013.28.3.153

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Angelo, E., Solinas, S., Mapelli, J., Gandolfi, D., Mapelli, L., and Prestori, F. (2013b). The cerebellar Golgi cell and spatiotemporal organization of granular layer activity. Front. Neural Circuits 7:93. doi: 10.3389/fncir.2013.00093

PubMed Abstract | CrossRef Full Text | Google Scholar

Davison, A. P. (2012). Collaborative Modelling: the future of computational neuroscience? Network 23, 157–166. doi: 10.3109/0954898X.2012.718482

PubMed Abstract | CrossRef Full Text | Google Scholar

Davison, A. P., Brüderle, D., Eppler, J., Kremkow, J., Muller, E., Pecevski, D., et al. (2009). PyNN: a common interface for neuronal network simulators. Front. Neuroinform. 2:11. doi: 10.3389/neuro.11.011.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Dean, P., and Porrill, J. (2010). The cerebellum as an adaptive filter: a general model? Funct. Neurol. 25, 173–180.

PubMed Abstract | Google Scholar

Dean, P., and Porrill, J. (2011). Evaluating the adaptive-filter model of the cerebellum. J. Physiol. 589, 3459–3470. doi: 10.1113/jphysiol.2010.201574

PubMed Abstract | CrossRef Full Text | Google Scholar

De Gruijl, J. R., Bazzigaluppi, P., de Jeu, M. T. G., and De Zeeuw, C. I. (2012). Climbing fiber burst size and olivary sub-threshold oscillations in a network setting. PLoS Comput. Biol. 8:e1002814. doi: 10.1371/journal.pcbi.1002814

PubMed Abstract | CrossRef Full Text | Google Scholar

De Schutter, E. (1999). Using realistic models to study synaptic integration in cerebellar Purkinje cells. Rev. Neurosci. 10, 233–245. doi: 10.1515/revneuro.1999.10.3-4.233

PubMed Abstract | CrossRef Full Text | Google Scholar

De Schutter, E. (2000). “Computational neuroscience: realistic modeling for experimentalists,” in Methods and New Frontiers in Neuroscience, eds E. D. Schutter and R. C. Cannon (Boca Raton, FL: CRC Press), 347–348.

Google Scholar

De Schutter, E., and Bower, J. M. (1994a). An active membrane model of the cerebellar Purkinje cell. I. Simulation of current clamps in slice. J. Neurophysiol. 71, 375–400.

PubMed Abstract | Google Scholar

De Schutter, E., and Bower, J. M. (1994b). Simulated responses of cerebellar Purkinje cells are independent of the dendritic location of granule cell synaptic inputs. Proc. Natl. Acad. Sci. U S A 91, 4736–4740. doi: 10.1073/pnas.91.11.4736

PubMed Abstract | CrossRef Full Text | Google Scholar

De Schutter, E., and Steuber, V. (2009). Patterns and pauses in Purkinje cell simple spike trains: experiments, modeling and theory. Neuroscience 162, 816–826. doi: 10.1016/j.neuroscience.2009.02.040

PubMed Abstract | CrossRef Full Text | Google Scholar

De Zeeuw, C. I., Hoebeek, F. E., Bosman, L. W. J., Schonewille, M., Witter, L., and Koekkoek, S. K. (2011). Spatiotemporal firing patterns in the cerebellum. Nat. Rev. Neurosci. 12, 327–344. doi: 10.1038/nrn3011

PubMed Abstract | CrossRef Full Text | Google Scholar

Diedrichsen, J., Maderwald, S., Küper, M., Thürling, M., Rabe, K., Gizewski, E. R., et al. (2011). Imaging the deep cerebellar nuclei: a probabilistic atlas and normalization procedure. Neuroimage 54, 1786–1794. doi: 10.1016/j.neuroimage.2010.10.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Dieudonné, S., and Dumoulin, A. (2000). Serotonin-driven long-range inhibitory connections in the cerebellar cortex. J. Neurosci. 20, 1837–1848.

PubMed Abstract | Google Scholar

DiGregorio, D. A., Rothman, J. S., Nielsen, T. A., and Silver, R. A. (2007). Desensitization properties of AMPA receptors at the cerebellar mossy fiber granule cell synapse. J. Neurosci. 27, 8344–8357. doi: 10.1523/JNEUROSCI.2399-07.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Diwakar, S., Lombardo, P., Solinas, S., Naldi, G., and D’Angelo, E. (2011). Local field potential modeling predicts dense activation in cerebellar granule cells clusters under LTP and LTD control. PLoS One 6:e21928. doi: 10.1371/journal.pone.0021928

PubMed Abstract | CrossRef Full Text | Google Scholar

Diwakar, S., Magistretti, J., Goldfarb, M., Naldi, G., and D’Angelo, E. (2009). Axonal Na+ channels ensure fast spike activation and back-propagation in cerebellar granule cells. J. Neurophysiol. 101, 519–532. doi: 10.1152/jn.90382.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Druckmann, S., Banitt, Y., Gidon, A., Schürmann, F., Markram, H., and Segev, I. (2007). A novel multiple objective optimization framework for constraining conductance-based neuron models by experimental data. Front. Neurosci. 1, 7–18. doi: 10.3389/neuro.01.1.1.001.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Druckmann, S., Berger, T. K., Hill, S., Schürmann, F., Markram, H., and Segev, I. (2008). Evaluating automated parameter constraining procedures of neuron models by experimental and surrogate data. Biol. Cybern. 99, 371–379. doi: 10.1007/s00422-008-0269-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Dugué, G. P., Brunel, N., Hakim, V., Schwartz, E., Chat, M., Lévesque, M., et al. (2009). Electrical coupling mediates tunable low-frequency oscillations and resonance in the cerebellar golgi cell network. Neuron 61, 126–139. doi: 10.1016/j.neuron.2008.11.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Duguid, I., Branco, T., Chadderton, P., Arlt, C., Powell, K., and Häusser, M. (2015). Control of cerebellar granule cell output by sensory-evoked Golgi cell inhibition. Proc. Natl. Acad. Sci. U S A 112, 13099–13104. doi: 10.1073/pnas.1510249112

PubMed Abstract | CrossRef Full Text | Google Scholar

Duguid, I., Branco, T., London, M., Chadderton, P., and Hausser, M. (2012). Tonic inhibition enhances fidelity of sensory information transmission in the cerebellar cortex. J. Neurosci. 32, 11132–11143. doi: 10.1523/JNEUROSCI.0460-12.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebner, T. J. (2013). “Cerebellum and internal models,” in Handbook of the Cerebellum and Cerebellar Disorders, eds M. Manto, J. D. Schmahmann, F. Rossi, D. L. Gruol, and N. Koibuchi (Dordrecht: Springer, Netherlands), 1279–1295.

Google Scholar

Ebner, T. J., and Pasalar, S. (2008). Cerebellum predicts the future motor state. Cerebellum 7, 583–588. doi: 10.1007/s12311-008-0059-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Eccles, J. C. (1967). Circuits in the cerebellar control of movement. Proc. Natl. Acad. Sci. U S A 58, 336–343. doi: 10.1073/pnas.58.1.336

PubMed Abstract | CrossRef Full Text | Google Scholar

Eccles, J. C. (1973). The cerebellum as a computer: patterns in space and time. J. Physiol. 229, 1–32. doi: 10.1113/jphysiol.1973.sp010123

PubMed Abstract | CrossRef Full Text | Google Scholar

Eppler, J. M., Helias, M., Muller, E., Diesmann, M., and Gewaltig, M.-O. (2008). PyNEST: a convenient interface to the NEST simulator. Front. Neuroinform. 2:12. doi: 10.3389/neuro.11.012.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernandez, F. R., Engbers, J. D. T., and Turner, R. W. (2007). Firing dynamics of cerebellar purkinje cells. J. Neurophysiol. 98, 278–294. doi: 10.1152/jn.00306.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Forti, L., Cesana, E., Mapelli, J., and D’Angelo, E. (2006). Ionic mechanisms of autorhythmic firing in rat cerebellar Golgi cells. J. Physiol. 574, 711–729. doi: 10.1113/jphysiol.2006.110858

PubMed Abstract | CrossRef Full Text | Google Scholar

Gabbiani, F., Midtgaard, J., and Knöpfel, T. (1994). Synaptic integration in a model of cerebellar granule cells. J. Neurophysiol. 72, 999–1009.

PubMed Abstract | Google Scholar

Galluppi, F., Lagorce, X., Stromatias, E., Pfeiffer, M., Plana, L. A., Furber, S. B., et al. (2015). A framework for plasticity implementation on the SpiNNaker neural architecture. Front. Neurosci. 8:429. doi: 10.3389/fnins.2014.00429

PubMed Abstract | CrossRef Full Text | Google Scholar

Gandolfi, D., Lombardo, P., Mapelli, J., Solinas, S., and D’Angelo, E. (2013). θ-frequency resonance at the cerebellum input stage improves spike timing on the millisecond time-scale. Front. Neural Circuits 7:64. doi: 10.3389/fncir.2013.00064

PubMed Abstract | CrossRef Full Text | Google Scholar

Gandolfi, D., Pozzi, P., Tognolina, M., Chirico, G., Mapelli, J., and D’Angelo, E. (2014). The spatiotemporal organization of cerebellar network activity resolved by two-photon imaging of multiple single neurons. Front. Cell. Neurosci. 8:92. doi: 10.3389/fncel.2014.00092

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Z., Proietti-Onori, M., Lin, Z., Ten Brinke, M. M., Boele, H.-J., Potters, J.-W., et al. (2016). Excitatory cerebellar nucleocortical circuit provides internal amplification during associative conditioning. Neuron 89, 645–657. doi: 10.1016/j.neuron.2016.01.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Z., van Beugen, B. J., and De Zeeuw, C. I. (2012). Distributed synergistic plasticity and cerebellar learning. Nat. Rev. Neurosci. 13, 619–635. doi: 10.1038/nrn3312

PubMed Abstract | CrossRef Full Text | Google Scholar

Garrido, J. A., Luque, N. R., D’Angelo, E., and Ros, E. (2013). Distributed cerebellar plasticity implements adaptable gain control in a manipulation task: a closed-loop robotic simulation. Front. Neural Circuits 7:159. doi: 10.3389/fncir.2013.00159

PubMed Abstract | CrossRef Full Text | Google Scholar

Garrido, J. A., Luque, N. R., Tolu, S., and D’Angelo, E. (2016). Oscillation-driven spike-timing dependent plasticity allows multiple overlapping pattern recognition in inhibitory interneuron networks. Int. J. Neural Syst. 26:1650020. doi: 10.1142/s0129065716500209

PubMed Abstract | CrossRef Full Text | Google Scholar

Garthwaite, J. (2016). From synaptically localized to volume transmission by nitric oxide. J. Physiol. 594, 9–18. doi: 10.1113/JP270297

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerstner, W., Sprekeler, H., and Deco, G. (2012). Theory and simulation in neuroscience. Science 338, 60–65. doi: 10.1126/science.1227356

PubMed Abstract | CrossRef Full Text | Google Scholar

Gleeson, P., Crook, S., Cannon, R. C., Hines, M. L., Billings, G. O., Farinella, M., et al. (2010). NeuroML: a language for describing data driven models of neurons and networks with a high degree of biological detail. PLoS Comput. Biol. 6:e1000815. doi: 10.1371/journal.pcbi.1000815

PubMed Abstract | CrossRef Full Text | Google Scholar

Gleeson, P., Steuber, V., and Silver, R. A. (2007). neuroConstruct: a tool for modeling networks of neurons in 3D space. Neuron 54, 219–235. doi: 10.1016/j.neuron.2007.03.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Gomi, H., and Kawato, M. (1993). Neural network control for a closed-loop system using feedback-error-learning. Neural Netw. 6, 933–946. doi: 10.1016/s0893-6080(09)80004-x

CrossRef Full Text | Google Scholar

Gross, J., Kujala, J., Hamalainen, M., Timmermann, L., Schnitzler, A., and Salmelin, R. (2001). Dynamic imaging of coherent sources: studying neural interactions in the human brain. Proc. Natl. Acad. Sci. U S A 98, 694–699. doi: 10.1073/pnas.98.2.694

PubMed Abstract | CrossRef Full Text | Google Scholar

Gross, J., Timmermann, L., Kujala, J., Dirks, M., Schmitz, F., Salmelin, R., et al. (2002). The neural basis of intermittent motor control in humans. Proc. Natl. Acad. Sci. U S A 99, 2299–2302. doi: 10.1073/pnas.032682099

PubMed Abstract | CrossRef Full Text | Google Scholar

Gundappa-Sulur, G., De Schutter, E., and Bower, J. M. (1999). Ascending granule cell axon: an important component of cerebellar cortical circuitry. J. Comp. Neurol. 408, 580–596. doi: 10.10.1002/(SICI)1096-9861(19990614)408:4<580::AID-CNE11>3.0.CO;2-O

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartmann, M. J., and Bower, J. M. (1998). Oscillatory activity in the cerebellar hemispheres of unrestrained rats. J. Neurophysiol. 80, 1598–1604.

PubMed Abstract | Google Scholar

Hausknecht, M., Li, W.-K., Mauk, M., and Stone, P. (2016). Machine learning capabilities of a simulated cerebellum. IEEE Trans. Neural Netw. Learn. Syst. 99, 1–13. doi: 10.1109/tnnls.2015.2512838 [Epub ahead of print].

PubMed Abstract | CrossRef Full Text | Google Scholar

Häusser, M., and Clark, B. A. (1997). Tonic synaptic inhibition modulates neuronal output pattern and spatiotemporal synaptic integration. Neuron 19, 665–678. doi: 10.1016/s0896-6273(00)80379-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hepburn, I., Chen, W., Wils, S., and De Schutter, E. (2012). STEPS: efficient simulation of stochastic reaction-diffusion models in realistic morphologies. BMC Syst. Biol. 6:36. doi: 10.1186/1752-0509-6-36

PubMed Abstract | CrossRef Full Text | Google Scholar

Herzfeld, D. J., Kojima, Y., Soetedjo, R., and Shadmehr, R. (2015). Encoding of action by the Purkinje cells of the cerebellum. Nature 526, 439–442. doi: 10.1038/nature15693

PubMed Abstract | CrossRef Full Text | Google Scholar

Hines, M. L., and Carnevale, N. T. (1997). The NEURON simulation environment. Neural Comput. 9, 1179–1209. doi: 10.1162/neco.1997.9.6.1179

PubMed Abstract | CrossRef Full Text | Google Scholar

Hines, M. L., and Carnevale, N. T. (2001). NEURON: a tool for neuroscientists. Neuroscientist 7, 123–135. doi: 10.1177/107385840100700207

PubMed Abstract | CrossRef Full Text | Google Scholar

Hines, M. L., Davison, A. P., and Muller, E. (2009). NEURON and python. Front. Neuroinform. 3:1. doi: 10.3389/neuro.11.001.2009

CrossRef Full Text | Google Scholar

Hodgkin, A., and Huxley, A. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544. doi: 10.1113/jphysiol.1952.sp004764

PubMed Abstract | CrossRef Full Text | Google Scholar

Honda, M., Urakubo, H., Koumura, T., and Kuroda, S. (2013). A common framework of signal processing in the induction of cerebellar LTD and cortical STDP. Neural Netw. 43, 114–124. doi: 10.1016/j.neunet.2013.01.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Houck, B. D., and Person, A. L. (2015). Cerebellar premotor output neurons collateralize to innervate the cerebellar cortex. J. Comp. Neurol. 523, 2254–2271. doi: 10.1002/cne.23787

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, C. C., Sugino, K., Shima, Y., Guo, C., Bai, S., Mensh, B. D., et al. (2013). Convergence of pontine and proprioceptive streams onto multimodal cerebellar granule cells. Elife 2013:e00400. doi: 10.7554/eLife.00400

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, C., Wang, L., and Huang, R. H. (2006). Cerebellar granule cell: ascending axon and parallel fiber. Eur. J. Neurosci. 23, 1731–1737. doi: 10.1111/j.1460-9568.2006.04690.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hull, C., and Regehr, W. G. (2012). Identification of an inhibitory circuit that regulates cerebellar golgi cell activity. Neuron 73, 149–158. doi: 10.1016/j.neuron.2011.10.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishikawa, T., Shimuta, M., and Häusser, M. (2015). Multimodal sensory integration in single cerebellar granule cells in vivo. Elife 4:e12916. doi: 10.7554/eLife.12916

PubMed Abstract | CrossRef Full Text | Google Scholar

Ito, M. (1984). The Cerebellum and Neural Control. New York, NY: Raven Press.

Ito, M. (2000). Mechanisms of motor learning in the cerebellum. Brain Res. 886, 237–245. doi: 10.1016/s0006-8993(00)03142-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ito, M. (2002). The molecular organization of cerebellar long-term depression. Nat. Rev. Neurosci. 3, 896–902. doi: 10.1038/nrn962

PubMed Abstract | CrossRef Full Text | Google Scholar

Ito, M. (2006). Cerebellar circuitry as a neuronal machine. Prog. Neurobiol. 78, 272–303. doi: 10.1016/j.pneurobio.2006.02.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Jacobson, G. A., Rokni, D., and Yarom, Y. (2008). A model of the olivo-cerebellar system as a temporal pattern generator. Trends Neurosci. 31, 617–625. doi: 10.1016/j.tins.2008.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaeger, D., De Schutter, E., and Bower, J. M. (1997). The role of synaptic and voltage-gated currents in the control of Purkinje cell spiking: a modeling study. J. Neurosci. 17, 91–106.

PubMed Abstract | Google Scholar

Johansson, F., Jirenhed, D.-A., Rasmussen, A., Zucca, R., and Hesslow, G. (2014). Memory trace and timing mechanism localized to cerebellar Purkinje cells. Proc. Natl. Acad. Sci. U S A 111, 14930–14934. doi: 10.1073/pnas.1415371111

PubMed Abstract | CrossRef Full Text | Google Scholar

Jörntell, H., and Ekerot, C. F. (2002). Reciprocal bidirectional plasticity of parallel fiber receptive fields in cerebellar Purkinje cells and their afferent interneurons. Neuron 34, 797–806. doi: 10.1016/s0896-6273(02)00713-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Kandel, E. R., Markram, H., Matthews, P. M., Yuste, R., and Koch, C. (2013). Neuroscience thinks big (and collaboratively). Nat. Rev. Neurosci. 14, 659–664. doi: 10.1038/nrn3578

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanichay, R. T., and Silver, R. A. (2008). Synaptic and cellular properties of the feedforward inhibitory circuit within the input layer of the cerebellar cortex. J. Neurosci. 28, 8955–8967. doi: 10.1523/JNEUROSCI.5469-07.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Kawato, M., Uno, Y., Isobe, M., and Suzuki, R. (1988). Hierarchical neural network model for voluntary movement with application to robotics. IEEE Control Syst. Mag. 8, 8–15. doi: 10.1109/37.1867

CrossRef Full Text | Google Scholar

Kennedy, A., Wayne, G., Kaifosh, P., Alviña, K., Abbott, L. F., and Sawtell, N. B. (2014). A temporal basis for predicting the sensory consequences of motor commands in an electric fish. Nat. Neurosci. 17, 416–422. doi: 10.1038/nn.3650

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, J., Lee, S., Tsuda, S., Zhang, X., Asrican, B., Gloss, B., et al. (2014). Optogenetic mapping of cerebellar inhibitory circuitry reveals spatially biased coordination of interneurons via electrical synapses. Cell Rep. 7, 1601–1613. doi: 10.1016/j.celrep.2014.04.047

PubMed Abstract | CrossRef Full Text | Google Scholar

Kistler, W. M., and De Zeeuw, C. I. (2003). Time windows and reverberating loops: a reverse-engineering approach to cerebellar function. Cerebellum 2, 44–54. doi: 10.1080/14734220309426

PubMed Abstract | CrossRef Full Text | Google Scholar

Koch, C. (1998). Biophysics of Computation: Information Processing in Single Neurons. New York, NY: Oxford Unit.

Google Scholar

Korbo, L., and Andersen, B. B. (1995). The distributions of Purkinje cell perikaryon and nuclear volume in human and rat cerebellum with the nucleator method. Neuroscience 69, 151–158. doi: 10.1016/0306-4522(95)00223-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Korbo, L., Andersen, B. B., Ladefoged, O., and Møller, A. (1993). Total numbers of various cell types in rat cerebellar cortex estimated using an unbiased stereological method. Brain Res. 609, 262–268. doi: 10.1016/0006-8993(93)90881-m

PubMed Abstract | CrossRef Full Text | Google Scholar

Koziol, L. F., Budding, D., Andreasen, N., D’Arrigo, S., Bulgheroni, S., Imamizu, H., et al. (2014). Consensus paper: the cerebellum’s role in movement and cognition. Cerebellum 13, 151–177. doi: 10.1007/s12311-013-0511-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kros, L., Eelkman Rooda, O. H. J., Spanke, J. K., Alva, P., van Dongen, M. N., Karapatis, A., et al. (2015). Cerebellar output controls generalized spike-and-wave discharge occurrence. Ann. Neurol. 77, 1027–1049. doi: 10.1002/ana.24399

PubMed Abstract | CrossRef Full Text | Google Scholar

Kubota, Y., and Bower, J. M. (2001). Transient versus asymptotic dynamics of CaM kinase II: possible roles of phosphatase. J. Comput. Neurosci. 11, 263–279. doi: 10.1023/A:1013727331979

PubMed Abstract | CrossRef Full Text | Google Scholar

Lagorce, X., Stromatias, E., Galluppi, F., Plana, L. A., Liu, S. C., Furber, S. B., et al. (2015). Breaking the millisecond barrier on spiNNaker: implementing asynchronous event-based plastic models with microsecond resolution. Front. Neurosci. 9:206. doi: 10.3389/fnins.2015.00206

PubMed Abstract | CrossRef Full Text | Google Scholar

Lampl, I., and Yarom, Y. (1997). Subthreshold oscillations and resonant behavior: two manifestations of the same mechanism. Neuroscience 78, 325–341. doi: 10.1016/s0306-4522(96)00588-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lefler, Y., Torben-Nielsen, B., and Yarom, Y. (2013). Oscillatory activity, phase differences and phase resetting in the inferior olivary nucleus. Front. Syst. Neurosci. 7:22. doi: 10.3389/fnsys.2013.00022

PubMed Abstract | CrossRef Full Text | Google Scholar

Lefler, Y., Yarom, Y., and Uusisaari, M. (2014). Cerebellar inhibitory input to the inferior olive decreases electrical coupling and blocks subthreshold oscillations. Neuron 81, 1389–1400. doi: 10.1016/j.neuron.2014.02.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Lennon, W., Hecht-Nielsen, R., and Yamazaki, T. (2014). A spiking network model of cerebellar Purkinje cells and molecular layer interneurons exhibiting irregular firing. Front. Comput. Neurosci. 8:157. doi: 10.3389/fncom.2014.00157

PubMed Abstract | CrossRef Full Text | Google Scholar

Lennon, W., Yamazaki, T., and Hecht-Nielsen, R. (2015). A model of in vitro plasticity at the parallel fiber–molecular layer interneuron synapses. Front. Comput. Neurosci. 9:150. doi: 10.3389/fncom.2015.00150

PubMed Abstract | CrossRef Full Text | Google Scholar

Libster, A. M., Lefler, Y., Yaron-Jakoubovitch, A., and Yarom, Y. (2010). Ataxia and the olivo-cerebellar module. Funct. Neurol. 25, 129–133.

PubMed Abstract | Google Scholar

Libster, A. M., and Yarom, Y. (2013). In and out of the loop: external and internal modulation of the olivo-cerebellar loop. Front. Neural Circuits 7:73. doi: 10.3389/fncir.2013.00073

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, S. J., Lachamp, P., Liu, Y., Savtchouk, I., and Sun, L. (2008). Long-term synaptic plasticity in cerebellar stellate cells. Cerebellum 7, 559–562. doi: 10.1007/s12311-008-0057-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Llano, I., and Gerschenfeld, H. M. (1993). Inhibitory synaptic currents in stellate cells of rat cerebellar slices. J. Physiol. 468, 177–200. doi: 10.1113/jphysiol.1993.sp019766

PubMed Abstract | CrossRef Full Text | Google Scholar

Llinás, R. R. (2009). Inferior olive oscillation as the temporal basis for motricity and oscillatory reset as the basis for motor error correction. Neuroscience 162, 797–804. doi: 10.1016/j.neuroscience.2009.04.045

PubMed Abstract | CrossRef Full Text | Google Scholar

Llinás, R. R. (2011). Cerebellar motor learning versus cerebellar motor timing: the climbing fibre story. J. Physiol. 589, 3423–3432. doi: 10.1113/jphysiol.2011.207464

PubMed Abstract | CrossRef Full Text | Google Scholar

Llinás, R. R. (2014). The olivo-cerebellar system: a key to understanding the functional significance of intrinsic oscillatory brain properties. Front. Neural Circuits 7:96. doi: 10.3389/fncir.2013.00096

PubMed Abstract | CrossRef Full Text | Google Scholar

Llinás, R., Nicholson, C., Freeman, J. A., and Hillman, D. E. (1968). Dendritic spikes and their inhibition in alligator Purkinje cells. Science 160, 1132–1135. doi: 10.1126/science.160.3832.1132

PubMed Abstract | CrossRef Full Text | Google Scholar

Llinás, R., and Sugimori, M. (1980). Electrophysiological properties of in vitro Purkinje cell dendrites in mammalian cerebellar slices. J. Physiol. 305, 197–213. doi: 10.1113/jphysiol.1980.sp013358

PubMed Abstract | CrossRef Full Text | Google Scholar

Locatelli, F., Bottà, L., Prestori, F., Masetto, S., and D’Angelo, E. (2013). Late-onset bursts evoked by mossy fiber bundle stimulation in unipolar brush cells: evidence for the involvement of H- and TRP-currents. J. Physiol. 591, 899–918. doi: 10.1113/jphysiol.2012.242180

PubMed Abstract | CrossRef Full Text | Google Scholar

Locatelli, F., Soda, T., Mapelli, L., Prestori, F., and D’Angelo, E. (2015). “Evidence for long-term synaptic plasticity at the mossy fiber–Golgi cell synapse of cerebellum,” in 66th SIF National Congress: Programme and Abstracts (Genoa).

Luque, N. R., Garrido, J. A., Carrillo, R. R., Coenen, O. J. D., and Ros, E. (2011a). Cerebellar input configuration toward object model abstraction in manipulation tasks. IEEE Trans. Neural Netw. 22, 1321–1328. doi: 10.1109/TNN.2011.2156809

PubMed Abstract | CrossRef Full Text | Google Scholar

Luque, N. R., Garrido, J. A., Carrillo, R. R., Tolu, S., and Ros, E. (2011b). Adaptive cerebellar spiking model embedded in the control loop: context switching and robustness against noise. Int. J. Neural Syst. 21, 385–401. doi: 10.1142/s0129065711002900

PubMed Abstract | CrossRef Full Text | Google Scholar

Luque, N. R., Garrido, J. A., Carrillo, R. R., D’Angelo, E., and Ros, E. (2014). Fast convergence of learning requires plasticity between inferior olive and deep cerebellar nuclei in a manipulation task: a closed-loop robotic simulation. Front. Comput. Neurosci. 8:97. doi: 10.3389/fncom.2014.00097

PubMed Abstract | CrossRef Full Text | Google Scholar

Luque, N. R., Garrido, J. A., Naveros, F., Carrillo, R. R., D’Angelo, E., and Ros, E. (2016). Distributed cerebellar motor learning: a spike-timing-dependent plasticity model. Front. Comput. Neurosci. 10:17. doi: 10.3389/fncom.2016.00017

PubMed Abstract | CrossRef Full Text | Google Scholar

Luque, N. R., Garrido, J. A., Ralli, J., Laredo, J. J., and Ros, E. (2012). From sensors to spikes: evolving receptive fields to enhance sensorimotor information in a robot-arm. Int. J. Neural Syst. 22:1250013. doi: 10.1142/S012906571250013X

PubMed Abstract | CrossRef Full Text | Google Scholar

Luthman, J., Hoebeek, F. E., Maex, R., Davey, N., Adams, R., De Zeeuw, C. I., et al. (2011). STD-dependent and independent encoding of input irregularity as spike rate in a computational model of a cerebellar nucleus neuron. Cerebellum 10, 667–682. doi: 10.1007/s12311-011-0295-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Maex, R., and De Schutter, E. (1998). Synchronization of golgi and granule cell firing in a detailed network model of the cerebellar granule cell layer. J. Neurophysiol. 80, 2521–2537.

PubMed Abstract | Google Scholar

Maex, R., and Steuber, V. (2013). An integrator circuit in cerebellar cortex. Eur. J. Neurosci. 38, 2917–2932. doi: 10.1111/ejn.12272

PubMed Abstract | CrossRef Full Text | Google Scholar

Mann-Metzer, P., and Yarom, Y. (1999). Electrotonic coupling interacts with intrinsic properties to generate synchronized activity in cerebellar networks of inhibitory interneurons. J. Neurosci. 19, 3298–3306.

PubMed Abstract | Google Scholar

Mann-Metzer, P., and Yarom, Y. (2000). Electrotonic coupling synchronizes interneuron activity in the cerebellar cortex. Prog. Brain Res. 124, 115–122. doi: 10.1016/s0079-6123(00)24012-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Mann-Metzer, P., and Yarom, Y. (2002). Pre- and postsynaptic inhibition mediated by GABA(B) receptors in cerebellar inhibitory interneurons. J. Neurophysiol. 87, 183–190. doi: 10.1152/jn.00344.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Manor, Y., Rinzel, J., Yarom, Y., and Segev, I. (1997). Low-amplitude oscillations in the inferior olive: a model based on electrical coupling of neurons with heterogeneous channel densities. J. Neurophysiol. 77, 2736–2752.

PubMed Abstract | Google Scholar

Mapelli, J., and D’Angelo, E. (2007). The spatial organization of long-term synaptic plasticity at the input stage of cerebellum. J. Neurosci. 27, 1285–1296. doi: 10.1523/jneurosci.4873-06.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Mapelli, J., Gandolfi, D., and D’Angelo, E. (2010). Combinatorial responses controlled by synaptic inhibition in the cerebellum granular layer. J. Neurophysiol. 103, 250–261. doi: 10.1152/jn.00642.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Mapelli, L., Solinas, S., and D’Angelo, E. (2014). Integration and regulation of glomerular inhibition in the cerebellar granular layer circuit. Front. Cell. Neurosci. 8:55. doi: 10.3389/fncel.2014.00055

PubMed Abstract | CrossRef Full Text | Google Scholar

Marasco, A., Limongiello, A., and Migliore, M. (2012). Fast and accurate low-dimensional reduction of biophysically detailed neuron models. Sci. Rep. 2:928. doi: 10.1038/srep00928

CrossRef Full Text | Google Scholar

Marasco, A., Limongiello, A., and Migliore, M. (2013). Using strahler’s analysis to reduce up to 200-fold the run time of realistic neuron models. Sci. Rep. 3:2934. doi: 10.1038/srep02934

PubMed Abstract | CrossRef Full Text | Google Scholar

Markram, H. (2006). The blue brain project. Nat. Rev. Neurosci. 7, 153–160. doi: 10.1038/nrn1848

PubMed Abstract | CrossRef Full Text | Google Scholar

Markram, H. (2013). Seven challenges for neuroscience. Funct. Neurol. 28, 145–151. doi: 10.11138/FNeur/2013.28.3.144

PubMed Abstract | CrossRef Full Text | Google Scholar

Markram, H., Muller, E., Ramaswamy, S., Reimann, M. W., Abdellah, M., Sanchez, C. A., et al. (2015). Reconstruction and simulation of neocortical microcircuitry. Cell 163, 456–492. doi: 10.1016/j.cell.2015.09.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Marr, B. Y. D. (1969). A theory of cerebellar cortex. J. Physiol. 202, 437–470. doi: 10.1113/jphysiol.1969.sp008820

PubMed Abstract | CrossRef Full Text | Google Scholar

Masoli, S., Solinas, S., and D’Angelo, E. (2015). Action potential processing in a detailed Purkinje cell model reveals a critical role for axonal compartmentalization. Front. Cell. Neurosci. 9:47. doi: 10.3389/fncel.2015.00047

PubMed Abstract | CrossRef Full Text | Google Scholar

Mathy, A., Ho, S. S. N., Davie, J. T., Duguid, I. C., Clark, B. A., and Häusser, M. (2009). Encoding of oscillations by axonal bursts in inferior olive neurons. Neuron 62, 388–399. doi: 10.1016/j.neuron.2009.03.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Medina, J. F., Garcia, K. S., Nores, W. L., Taylor, N. M., and Mauk, M. D. (2000). Timing mechanisms in the cerebellum: testing predictions of a large-scale computer simulation. J. Neurosci. 20, 5516–5525.

PubMed Abstract | Google Scholar

Medina, J. F., and Mauk, M. D. (2000). Computer simulation of cerebellar information processing. Nat. Neurosci. 3, 1205–1211. doi: 10.1038/81486

PubMed Abstract | CrossRef Full Text | Google Scholar

Migliore, M., Alicata, F., and Ayala, G. F. (1995). A model for long-term potentiation and depression. J. Comput. Neurosci. 2, 335–343. doi: 10.1007/BF00961444

PubMed Abstract | CrossRef Full Text | Google Scholar

Migliore, M., Alicata, F., and Ayala, G. F. (1997). Possible roles of retrograde messengers on LTP, LTD and associative memory. Biosystems 40, 127–132. doi: 10.1016/0303-2647(96)01638-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Migliore, M., De Simone, G., and Migliore, R. (2015). Effect of the initial synaptic state on the probability to induce long-term potentiation and depression. Biophys. J. 108, 1038–1046. doi: 10.1016/j.bpj.2014.12.048

PubMed Abstract | CrossRef Full Text | Google Scholar

Migliore, M., and Lansky, P. (1999). Long-term potentiation and depression induced by a stochastic conditioning of a model synapse. Biophys. J. 77, 1234–1243. doi: 10.1016/s0006-3495(99)76975-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, S. J., and Silver, R. A. (2000a). GABA spillover from single inhibitory axons suppresses low-frequency excitatory transmission at the cerebellar glomerulus. J. Neurosci. 20, 8651–8658.

PubMed Abstract | Google Scholar

Mitchell, S. J., and Silver, R. A. (2000b). Glutamate spillover suppresses inhibition by activating presynaptic mGluRs. Nature 404, 498–502. doi: 10.1038/35006649

PubMed Abstract | CrossRef Full Text | Google Scholar

Mittmann, W., and Häusser, M. (2007). Linking synaptic plasticity and spike output at excitatory and inhibitory synapses onto cerebellar Purkinje cells. J. Neurosci. 27, 5559–5570. doi: 10.1523/jneurosci.5117-06.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Mittmann, W., Koch, U., and Häusser, M. (2005). Feed-forward inhibition shapes the spike output of cerebellar Purkinje cells. J. Physiol. 563, 369–378. doi: 10.1113/jphysiol.2004.075028

PubMed Abstract | CrossRef Full Text | Google Scholar

Miyamoto, H., Kawato, M., Setoyama, T., and Suzuki, R. (1988). Feedback-error-learning neural network for trajectory control of a robotic manipulator. Neural Netw. 1, 251–265. doi: 10.1016/0893-6080(88)90030-5

CrossRef Full Text | Google Scholar

Monaco, J., Casellato, C., Koch, G., and D’Angelo, E. (2014). Cerebellar theta burst stimulation dissociates memory components in eyeblink classical conditioning. Eur. J. Neurosci. 40, 3363–3370. doi: 10.1111/ejn.12700

PubMed Abstract | CrossRef Full Text | Google Scholar

Najac, M., and Raman, I. M. (2015). Integration of Purkinje cell inhibition by cerebellar nucleo-olivary neurons. J. Neurosci. 35, 544–549. doi: 10.1523/JNEUROSCI.3583-14.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Nielsen, T. A., DiGregorio, D. A., and Silver, R. A. (2004). Modulation of glutamate mobility reveals the mechanism underlying slow-rising AMPAR EPSCs and the diffusion coefficient in the synaptic cleft. Neuron 42, 757–771. doi: 10.1016/j.neuron.2004.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Nieus, T. R., Mapelli, L., and D’Angelo, E. (2014). Regulation of output spike patterns by phasic inhibition in cerebellar granule cells. Front. Cell. Neurosci. 8:246. doi: 10.3389/fncel.2014.00246

PubMed Abstract | CrossRef Full Text | Google Scholar

Nieus, T., Sola, E., Mapelli, J., Saftenku, E., Rossi, P., and D’Angelo, E. (2006). LTP regulates burst initiation and frequency at mossy fiber-granule cell synapses of rat cerebellum: experimental observations and theoretical predictions. J. Neurophysiol. 95, 686–699. doi: 10.1152/jn.00696.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Oertel, D., and Young, E. D. (2004). What’s a cerebellar circuit doing in the auditory system? Trends Neurosci. 27, 104–110. doi: 10.1016/j.tins.2003.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohtsuki, G., Piochon, C., and Hansel, C. (2009). Climbing fiber signaling and cerebellar gain control. Front. Cell. Neurosci. 3:4. doi: 10.3389/neuro.03.004.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Ovsepian, S. V., Steuber, V., Le Berre, M., O’Hara, L., O’Leary, V. B., and Dolly, J. O. (2013). A defined heteromeric KV1 channel stabilizes the intrinsic pacemaking and regulates the output of deep cerebellar nuclear neurons to thalamic targets. J. Physiol. 591, 1771–1791. doi: 10.1113/jphysiol.2012.249706

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozden, I., Dombeck, D. A., Hoogland, T. M., Tank, D. W., and Wang, S. S.-H. (2012). Widespread state-dependent shifts in cerebellar activity in locomoting mice. PLoS One 7:e42650. doi: 10.1371/journal.pone.0042650

PubMed Abstract | CrossRef Full Text | Google Scholar

Palesi, F., Tournier, J. D., Calamante, F., Muhlert, N., Castellazzi, G., Chard, D., et al. (2015). Contralateral cerebello-thalamo-cortical pathways with prominent involvement of associative areas in humans in vivo. Brain Struct. Funct. 220, 3369–3384. doi: 10.1007/s00429-014-0861-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Pellerin, J. P., and Lamarre, Y. (1997). Local field potential oscillations in primate cerebellar cortex during voluntary movement. J. Neurophysiol. 78, 3502–3507.

PubMed Abstract | Google Scholar

Pellionisz, A., and Szentágothai, J. (1973). Dynamic single unit simulation of a realistic cerebellar network model. Brain Res. 49, 83–99. doi: 10.1016/0006-8993(73)90403-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Pellionisz, A., and Szentágothai, J. (1974). Dynamic single unit simulation of a realistic cerebellar network model. II. Purkinje cell activity within the basic circuit and modified by inhibitory systems. Brain Res. 68, 19–40. doi: 10.1016/0006-8993(74)90531-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Person, A. L., and Raman, I. M. (2012a). Synchrony and neural coding in cerebellar circuits. Front. Neural Circuits 6:97. doi: 10.3389/fncir.2012.00097

PubMed Abstract | CrossRef Full Text | Google Scholar

Person, A., and Raman, I. (2012b). Purkinje neuron synchrony elicits time-locked spiking in the cerebellar nuclei. Nature 481, 502–505. doi: 10.1038/nature10732

PubMed Abstract | CrossRef Full Text | Google Scholar

Pfeil, T., Grübl, A., Jeltsch, S., Müller, E., Müller, P., Petrovici, M. A., et al. (2013). Six networks on a universal neuromorphic computing substrate. Front. Neurosci. 7:11. doi: 10.3389/fnins.2013.00011

PubMed Abstract | CrossRef Full Text | Google Scholar

Porrill, J., Dean, P., and Anderson, S. R. (2013). Adaptive filters and internal models: multilevel description of cerebellar function. Neural Netw. 47, 134–149. doi: 10.1016/j.neunet.2012.12.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Powell, K., Mathy, A., Duguid, I., and Häusser, M. (2015). Synaptic representation of locomotion in single cerebellar granule cells. Elife 4:e07290. doi: 10.7554/eLife.07290

PubMed Abstract | CrossRef Full Text | Google Scholar

Rall, W., Burke, R. E., Holmes, W. R., Jack, J. J., Redman, S. J., and Segev, I. (1992). Matching dendritic neuron models to experimental data. Physiol. Rev. 72, S159–S186.

PubMed Abstract | Google Scholar

Ramakrishnan, K. B., Voges, K., De Propris, L., De Zeeuw, C. I., and D’Angelo, E. (2016). Tactile stimulation evokes long-lasting potentiation of purkinje cell discharge in vivo. Front. Cell. Neurosci. 10:36. doi: 10.3389/fncel.2016.00036

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramaswamy, S., Courcol, J.-D., Abdellah, M., Adaszewski, S. R., Antille, N., Arsever, S., et al. (2015). The neocortical microcircuit collaboration portal: a resource for rat somatosensory cortex. Front. Neural Circuits 9:44. doi: 10.3389/fncir.2015.00044

PubMed Abstract | CrossRef Full Text | Google Scholar

Rancz, E. A., and Häusser, M. (2010). Dendritic spikes mediate negative synaptic gain control in cerebellar Purkinje cells. Proc. Natl. Acad. Sci. U S A 107, 22284–22289. doi: 10.1073/pnas.1008605107

PubMed Abstract | CrossRef Full Text | Google Scholar

Rancz, E. A., Ishikawa, T., Duguid, I., Chadderton, P., Mahon, S., and Häusser, M. (2007). High-fidelity transmission of sensory information by single cerebellar mossy fibre boutons. Nature 450, 1245–1248. doi: 10.1038/nature05995

PubMed Abstract | CrossRef Full Text | Google Scholar

Rapp, M., Segev, I., and Yarom, Y. (1994). Physiology, morphology and detailed passive models of guinea-pig cerebellar Purkinje cells. J. Physiol. 474, 101–118. doi: 10.1113/jphysiol.1994.sp020006

PubMed Abstract | CrossRef Full Text | Google Scholar

Requarth, T., and Sawtell, N. B. (2011). Neural mechanisms for filtering self-generated sensory signals in cerebellum-like circuits. Curr. Opin. Neurobiol. 21, 602–608. doi: 10.1016/j.conb.2011.05.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Rieubland, S., Roth, A., and Häusser, M. (2014). Structured connectivity in cerebellar inhibitory networks. Neuron 81, 913–929. doi: 10.1016/j.neuron.2013.12.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, A., Conte, D., Hull, M., Merrison-Hort, R., al Azad, A. K., Buhl, E., et al. (2014). Can simple rules control development of a pioneer vertebrate neuronal network generating behavior? J. Neurosci. 34, 608–621. doi: 10.1523/JNEUROSCI.3248-13.2014

PubMed Abstract | CrossRef Full Text | Google Scholar

Roggeri, L., Rivieccio, B., Rossi, P., and D’Angelo, E. (2008). Tactile stimulation evokes long-term synaptic plasticity in the granular layer of cerebellum. J. Neurosci. 28, 6354–6359. doi: 10.1523/JNEUROSCI.5709-07.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Rokni, D., Llinas, R., and Yarom, Y. (2007). Stars and stripes in the cerebellar cortex: a voltage sensitive dye study. Front. Syst. Neurosci. 1:1. doi: 10.3389/neuro.06.001.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Rothman, J. S., Cathala, L., Steuber, V., and Silver, R. A. (2009). Synaptic depression enables neuronal gain control. Nature 457, 1015–1018. doi: 10.1038/nature07604

PubMed Abstract | CrossRef Full Text | Google Scholar

Rothman, J. S., and Silver, R. A. (2014). Data-driven modeling of synaptic transmission and integration. Prog. Mol. Biol. Transl. Sci. 123, 305–350. doi: 10.1016/B978-0-12-397897-4.00004-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Rowland, N. C., and Jaeger, D. (2005). Coding of tactile response properties in the rat deep cerebellar nuclei. J. Neurophysiol. 94, 1236–1251. doi: 10.1152/jn.00285.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Rudolph, S., Hull, C., and Regehr, W. G. (2015). Active dendrites and differential distribution of calcium channels enable functional compartmentalization of Golgi cells. J. Neurosci. 35, 15492–15504. doi: 10.1523/JNEUROSCI.3132-15.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Santamaria, F., and Bower, J. M. (2005). Background synaptic activity modulates the response of a modeled purkinje cell to paired afferent input. J. Neurophysiol. 93, 237–250. doi: 10.1152/jn.00458.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Santamaria, F., Jaeger, D., De Schutter, E., and Bower, J. M. (2002). Modulatory effects of parallel fiber and molecular layer interneuron synaptic activity on Purkinje cell responses to ascending segment input: a modeling study. J. Comput. Neurosci. 13, 217–235. doi: 10.1023/A:1020266315730

PubMed Abstract | CrossRef Full Text | Google Scholar

Santamaria, F., Tripp, P. G., and Bower, J. M. (2007). Feedforward inhibition controls the spread of granule cell-induced Purkinje cell activity in the cerebellar cortex. J. Neurophysiol. 97, 248–263. doi: 10.1152/jn.01098.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Sargent, P. B., Saviane, C., Nielsen, T. A., DiGregorio, D. A., and Silver, R. A. (2005). Rapid vesicular release, quantal variability and spillover contribute to the precision and reliability of transmission at a glomerular synapse. J. Neurosci. 25, 8173–8187. doi: 10.1523/jneurosci.2051-05.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Schild, R. F. (1970). On the inferior olive of the albino rat. J. Comp. Neurol. 140, 255–260. doi: 10.1002/cne.901400302

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmahmann, J. D. (2004). Disorders of the cerebellum: ataxia, dysmetria of thought and the cerebellar cognitive affective syndrome. J. Neuropsychiatry Clin. Neurosci. 16, 367–378. doi: 10.1176/jnp.16.3.367

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmahmann, J. D., and Caplan, D. (2006). Cognition, emotion and the cerebellum. Brain 129, 290–292. doi: 10.1093/brain/awh729

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmahmann, J. D., and Sherman, J. C. (1998). The cerebellar cognitive affective syndrome. Brain 121, 561–579. doi: 10.1093/brain/121.4.561

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwartz, E. J., Rothman, J. S., Dugué, G. P., Diana, M., Rousseau, C., Silver, R. A., et al. (2012). NMDA receptors with incomplete Mg2+ block enable low-frequency transmission through the cerebellar cortex. J. Neurosci. 32, 6878–6893. doi: 10.1523/JNEUROSCI.5736-11.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

Schweighofer, N., Doya, K., and Kawato, M. (1999). Electrophysiological properties of inferior olive neurons: a compartmental model. J. Neurophysiol. 82, 804–817.

PubMed Abstract | Google Scholar

Schweighofer, N., and Ferriol, G. (2000). Diffusion of nitric oxide can facilitate cerebellar learning: a simulation study. Proc. Natl. Acad. Sci. U S A 97, 10661–10665. doi: 10.1073/pnas.97.19.10661

PubMed Abstract | CrossRef Full Text | Google Scholar

Segev, I., and Rall, W. (1998). Excitable dendrites and spines: earlier theoretical insights elucidate recent direct observations. Trends Neurosci. 21, 453–460. doi: 10.1016/s0166-2236(98)01327-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Sillitoe, R. V., Chung, S.-H., Fritschy, J.-M., Hoy, M., and Hawkes, R. (2008). Golgi cell dendrites are restricted by Purkinje cell stripe boundaries in the adult mouse cerebellar cortex. J. Neurosci. 28, 2820–2826. doi: 10.1523/JNEUROSCI.4145-07.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Simões de Souza, F. M., and De Schutter, E. (2011). Robustness effect of gap junctions between Golgi cells on cerebellar cortex oscillations. Neural Syst. Circuits 1:7. doi: 10.1186/2042-1001-1-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Sokolov, A. A., Erb, M., Gharabaghi, A., Grodd, W., Tatagiba, M. S., and Pavlova, M. A. (2012). Biological motion processing: the left cerebellum communicates with the right superior temporal sulcus. Neuroimage 59, 2824–2830. doi: 10.1016/j.neuroimage.2011.08.039

PubMed Abstract | CrossRef Full Text | Google Scholar

Solinas, S., Forti, L., Cesana, E., Mapelli, J., De Schutter, E., and D’Angelo, E. (2007a). Computational reconstruction of pacemaking and intrinsic electroresponsiveness in cerebellar Golgi cells. Front. Cell. Neurosci. 1:2. doi: 10.3389/neuro.03.002.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Solinas, S., Forti, L., Cesana, E., Mapelli, J., De Schutter, E., D’Angelo, E., et al. (2007b). Fast-reset of pacemaking and theta-frequency resonance patterns in cerebellar golgi cells: simulations of their impact in vivo. Front. Cell. Neurosci. 1:4. doi: 10.3389/neuro.03.004.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Solinas, S., Nieus, T., and D’Angelo, E. (2010). A realistic large-scale model of the cerebellum granular layer predicts circuit spatio-temporal filtering properties. Front. Cell. Neurosci. 4:12. doi: 10.3389/fncel.2010.00012

PubMed Abstract | CrossRef Full Text | Google Scholar

Sotelo, C. (2004). Cellular and genetic regulation of the development of the cerebellar system. Prog. Neurobiol. 72, 295–339. doi: 10.1016/j.pneurobio.2004.03.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Steuber, V., and Jaeger, D. (2013). Modeling the generation of output by the cerebellar nuclei. Neural Netw. 47, 112–119. doi: 10.1016/j.neunet.2012.11.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Steuber, V., Mittmann, W., Hoebeek, F. E., Silver, R. A., De Zeeuw, C. I., Häusser, M., et al. (2007). Cerebellar LTD and pattern recognition by Purkinje cells. Neuron 54, 121–136. doi: 10.1016/j.neuron.2007.03.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Steuber, V., Schultheiss, N. W., Silver, R. A., De Schutter, E., and Jaeger, D. (2011). Determinants of synaptic integration and heterogeneity in rebound firing explored with data-driven models of deep cerebellar nucleus cells. J. Comput. Neurosci. 30, 633–658. doi: 10.1007/s10827-010-0282-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Subramaniyam, S., Solinas, S., Perin, P., Locatelli, F., Masetto, S., and D’Angelo, E. (2014). Computational modeling predicts the ionic mechanism of late-onset responses in unipolar brush cells. Front. Cell. Neurosci. 8:237. doi: 10.3389/fncel.2014.00237

PubMed Abstract | CrossRef Full Text | Google Scholar

Sudhakar, S. K., Torben-Nielsen, B., and De Schutter, E. (2015). Cerebellar nuclear neurons use time and rate coding to transmit purkinje neuron pauses. PLoS Comput. Biol. 11:e1004641. doi: 10.1371/journal.pcbi.1004641

PubMed Abstract | CrossRef Full Text | Google Scholar

Sultan, F. (2001). Distribution of mossy ber rosettes in the cerebellum of cats and mice: evidence for a parasagittal organization on the single ber level. Eur. J. Neurosci. 13, 2123–2130. doi: 10.1046/j.0953-816x.2001.01593.x

CrossRef Full Text | Google Scholar

Sultan, F., and Heck, D. (2003). Detection of sequences in the cerebellar cortex: numerical estimate of the possible number of tidal-wave inducing sequences represented. J. Physiol. Paris 97, 591–600. doi: 10.1016/j.jphysparis.2004.01.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Szapiro, G., and Barbour, B. (2007). Multiple climbing fibers signal to molecular layer interneurons exclusively via glutamate spillover. Nat. Neurosci. 10, 735–742. doi: 10.1038/nn1907

PubMed Abstract | CrossRef Full Text | Google Scholar

Szoboszlay, M., Lõrincz, A., Lanore, F., Vervaeke, K., Silver, R. A., and Nusser, Z. (2016). Functional properties of dendritic gap junctions in cerebellar golgi cells. Neuron 90, 1043–1056. doi: 10.1016/j.neuron.2016.03.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Torben-Nielsen, B., Segev, I., and Yarom, Y. (2012). The generation of phase differences and frequency changes in a network model of Inferior Olive subthreshold oscillations. PLoS Comput. Biol. 8:e1002580. doi: 10.1371/journal.pcbi.1002580

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsodyks, M., Pawelzik, K., and Markram, H. (1998). Neural networks with dynamic synapses. Neural Comput. 10, 821–835. doi: 10.1162/089976698300017502

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsukada, M., Yamazaki, Y., and Koizumi, A. (1995). Changes in nitric oxide synthase activities in the cerebellum during development and aging of C57BL/6 mice. Tohoku J. Exp. Med. 176, 69–74. doi: 10.1620/tjem.176.69

PubMed Abstract | CrossRef Full Text | Google Scholar

Tyrrell, T., and Willshaw, D. (1992). Cerebellar cortex: its simulation and the relevance of Marr’s theory. Philos. Trans. R. Soc. Lond. B Biol. Sci. 336, 239–257. doi: 10.1098/rstb.1992.0059

PubMed Abstract | CrossRef Full Text | Google Scholar

Uusisaari, M., and Knöpfel, T. (2011). Functional classification of neurons in the mouse lateral cerebellar nuclei. Cerebellum 10, 637–646. doi: 10.1007/s12311-010-0240-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Uusisaari, M., Obata, K., and Knöpfel, T. (2007). Morphological and electrophysiological properties of GABAergic and non-GABAergic cells in the deep cerebellar nuclei. J. Neurophysiol. 97, 901–911. doi: 10.1152/jn.00974.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Valera, A. M., Binda, F., Pawlowski, S. A., Dupont, J.-L., Casella, J.-F., Rothstein, J. D., et al. (2016). Stereotyped spatial patterns of functional synaptic connectivity in the cerebellar cortex. Elife 5:e09862. doi: 10.7554/eLife.09862

PubMed Abstract | CrossRef Full Text | Google Scholar

Vanier, M. C., and Bower, J. M. (1999). A comparative survey of automated parameter-search methods for compartmental neural models. J. Comput. Neurosci. 7, 149–171. doi: 10.1023/A:1008972005316

PubMed Abstract | CrossRef Full Text | Google Scholar

van Welie, I., Roth, A., Ho, S. S. N., Komai, S., and Häusser, M. (2016). Conditional spike transmission mediated by electrical coupling ensures millisecond precision-correlated activity among interneurons in vivo. Neuron 90, 810–823. doi: 10.1016/j.neuron.2016.04.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Velarde, M. G., Nekorkin, V. I., Makarov, V. A., Makarenko, V. I., and Llinàs, R. R. (2004). Clustering behavior in a three-layer system mimicking olivo-cerebellar dynamics. Neural Netw. 17, 191–203. doi: 10.1016/j.neunet.2003.07.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Vervaeke, K., LÖrincz, A., Gleeson, P., Farinella, M., Nusser, Z., and Silver, R. A. (2010). Rapid desynchronization of an electrically coupled interneuron network with sparse excitatory synaptic input. Neuron 67, 435–451. doi: 10.1016/j.neuron.2010.06.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Voogd, J. (2011). Cerebellar zones: a personal history. Cerebellum 10, 334–350. doi: 10.1007/s12311-010-0221-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Wadiche, J. I., and Jahr, C. E. (2005). Patterned expression of Purkinje cell glutamate transporters controls synaptic plasticity. Nat. Neurosci. 8, 1329–1334. doi: 10.1038/nn1539

PubMed Abstract | CrossRef Full Text | Google Scholar

Wadleigh, A., and Valenzuela, C. F. (2012). Ethanol increases GABAergic transmission and excitability in cerebellar molecular layer interneurons from GAD67-GFP knock-in mice. Alcohol Alcohol. 47, 1–8. doi: 10.1093/alcalc/agr147

PubMed Abstract | CrossRef Full Text | Google Scholar

Walter, J. T., Dizon, M.-J., and Khodakhah, K. (2009). The functional equivalence of ascending and parallel fiber inputs in cerebellar computation. J. Neurosci. 29, 8462–8473. doi: 10.1523/JNEUROSCI.5718-08.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Chen, G., Gao, W., and Ebner, T. J. (2011). Parasagittally aligned, mGluR1-dependent patches are evoked at long latencies by parallel fiber stimulation in the mouse cerebellar cortex in vivo. J. Neurophysiol. 105, 1732–1746. doi: 10.1152/jn.00717.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, T. C., Becker, N., Apps, R., and Jones, M. W. (2014). Back to front: cerebellar connections and interactions with the prefrontal cortex. Front. Syst. Neurosci. 8:4. doi: 10.3389/fnsys.2014.00004

PubMed Abstract | CrossRef Full Text | Google Scholar

Watt, A. J., Cuntz, H., Mori, M., Nusser, Z., Sjöström, P. J., and Häusser, M. (2009). Traveling waves in developing cerebellar cortex mediated by asymmetrical Purkinje cell connectivity. Nat. Neurosci. 12, 463–473. doi: 10.1038/nn.2285

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilms, C. D., and Häusser, M. (2015). Reading out a spatiotemporal population code by imaging neighbouring parallel fibre axons in vivo. Nat. Commun. 6:6464. doi: 10.1038/ncomms7464

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, H. S., Sugihara, I., and Shinoda, Y. (1999). Projection patterns of single mossy fibers originating form the lateral reticular nucleus in the rat cerebellar cortex and nuclei. J. Comp. Neurol. 411, 97–118. doi: 10.1002/(SICI)1096-9861(19990816)411:1<97::aid-cne8>3.0.CO;2-O

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamada, W. M., Koch, C., and Adams, P. R. (1989). “Multiple channels and calcium dynamics” in Methods Neuronal Model, eds C. Koch and I. Segev (Cambridge, MA: MIT Press), 97–133.

Google Scholar

Yamazaki, T., Nagao, S., Lennon, W., and Tanaka, S. (2015). Modeling memory consolidation during posttraining periods in cerebellovestibular learning. Proc. Natl. Acad. Sci. U S A 112, 3541–3546. doi: 10.1073/pnas.1413798112

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamazaki, T., and Tanaka, S. (2007). The cerebellum as a liquid state machine. Neural Netw. 20, 290–297. doi: 10.1016/j.neunet.2007.04.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Zaytsev, Y. V., and Morrison, A. (2014). CyNEST: a maintainable Cython-based interface for the NEST simulator. Front. Neuroinform. 8:23. doi: 10.3389/fninf.2014.00023

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, H., Lin, Z., Voges, K., Ju, C., Gao, Z., Bosman, L. W., et al. (2014). Cerebellar modules operate at different frequencies. Elife 3:e02536. doi: 10.7554/eLife.02536

PubMed Abstract | CrossRef Full Text | Google Scholar

Zubler, F., Hauri, A., Pfister, S., Bauer, R., Anderson, J. C., Whatley, A. M., et al. (2013). Simulating cortical development as a self constructing process: a novel multi-scale approach combining molecular and physical aspects. PLoS Comput. Biol. 9:e1003173. doi: 10.1371/journal.pcbi.1003173

PubMed Abstract | CrossRef Full Text | Google Scholar