Calmodulin as a major calcium buffer shaping vesicular release and short-term synaptic plasticity: facilitation through buffer dislocation

Action potential-dependent release of synaptic vesicles and short-term synaptic plasticity are dynamically regulated by the endogenous Ca²⁺ buffers that shape [Ca²⁺] profiles within a presynaptic bouton. Calmodulin is one of the most abundant presynaptic proteins and it binds Ca²⁺ faster than any other characterized endogenous neuronal Ca²⁺ buffer. Direct effects of calmodulin on fast presynaptic Ca²⁺ dynamics and vesicular release however have not been studied in detail. Using experimentally constrained three-dimensional diffusion modeling of Ca²⁺ influx–exocytosis coupling at small excitatory synapses we show that, at physiologically relevant concentrations, Ca²⁺ buffering by calmodulin plays a dominant role in inhibiting vesicular release and in modulating short-term synaptic plasticity. We also propose a novel and potentially powerful mechanism for short-term facilitation based on Ca²⁺-dependent dynamic dislocation of calmodulin molecules from the plasma membrane within the active zone.

Introduction

Calmodulin (CaM) is a major neuronal protein that acts as a key mediator of multiple Ca²⁺-dependent intracellular signaling cascades in the brain. CaM regulates synaptic transmission and synaptic plasticity via Ca²⁺-dependent binding to its target proteins in both the pre- and the post-synaptic compartments. These include protein kinases, adenylyl cyclases, calcineurin, Munc13s, and voltage-gated Ca²⁺ channels (VGCCs) (Xia and Storm, 2005; Pang et al., 2010; Sun et al., 2010; Lipstein et al., 2013; Ben-Johny and Yue, 2014). It has been recently demonstrated that CaM binds Ca²⁺ ions with much faster kinetics than other major neuronal Ca²⁺ buffers such as calbindin-D28k (CB), parvalbumin, and calretinin (Faas et al., 2011). However, in comparison to the other buffers direct effects of CaM-dependent Ca²⁺ buffering on action potential (AP)-evoked presynaptic Ca²⁺ dynamics and vesicular release have not been systematically studied.

In this work we performed realistic, experimentally constrained model simulations of AP-evoked presynaptic Ca²⁺ dynamics and synaptic vesicle fusion in small excitatory synapses. We compared the relative contributions of Ca²⁺ buffering by CB and CaM to modulation of vesicular release probability and short-term synaptic plasticity. Our simulations demonstrate that, at physiologically relevant concentrations, fast Ca²⁺ binding to the N-lobe of CaM has a dominant effect in inhibiting AP-evoked vesicular release. We also show that the predicted effect of CaM Ca²⁺ buffering on short-term synaptic plasticity strongly depends on the location and mobility of CaM molecules.

Finally, we propose a novel mechanism for a dynamic regulation of presynaptic strength based on Ca²⁺-dependent interaction of CaM with membrane-associated proteins that contain the isoleucine–glutamine (IQ) binding motif (e.g., neuromodulin and VGCCs) (Alexander et al., 1988; Xia and Storm, 2005; Ben-Johny and Yue, 2014). Our simulations demonstrate that Ca²⁺-induced dislocation of CaM molecules from the plasma membrane could lead to a significant reduction of Ca²⁺ buffering capacity within the active zone (AZ). This in turn, leads to an increase of vesicular release probability during repeated APs. Thus, AP-evoked dislocation of CaM may provide a powerful mechanism for short-term facilitation of synaptic transmission.

Materials and Methods

Modeling of Presynaptic Ca²⁺ Dynamics

Three-dimensional modeling of dynamic AP-evoked presynaptic Ca²⁺ influx, buffering, and diffusion, on a millisecond timescale, was performed in the Virtual Cell (VCell) simulation environment (http://vcell.org) using the fully implicit finite volume regular grid solver and a 10 nm mesh. In contrast to the simplified steady-state and/or non-stationary single compartment models that are normally used to approximate presynaptic Ca²⁺ dynamics on tens to hundreds of milliseconds timescale (Neher, 1998; Sabatini and Regehr, 1998; Scott and Rusakov, 2006; Ermolyuk et al., 2012), no assumptions regarding Ca²⁺ buffer binding and/or diffusional equilibration were made in the VCell model used here. VCell simulations using a 10 nm mesh produced solutions for presynaptic Ca²⁺ dynamics at vesicular release sensors similar to those obtained in our previous work with a 5 nm mesh (Ermolyuk et al., 2013). The use of the larger mesh substantially increased the computation speed and allowed us to simulate Ca²⁺ dynamics in the whole presynaptic bouton on the longer time scale.

The presynaptic bouton was considered as a truncated sphere (Figure 1A) of radius R_bout = 0.3 μm (described by the equation [x² + y² + z² ≤ 0.09] · [z ≤ 0.25], all distances are in μm). The AZ containing VGCCs was modeled as a circle of radius R_AZ = 0.16 μm situated in the center of the truncated plane z = 0.25 μm. VGCCs were evenly distributed within a rectangular cluster (40 by 80 nm) which was placed in the center of the AZ. The cluster contained 7 P/Q-type, 8 N-type, and 1 R-type VGCCs (Ermolyuk et al., 2013).

FIGURE 1

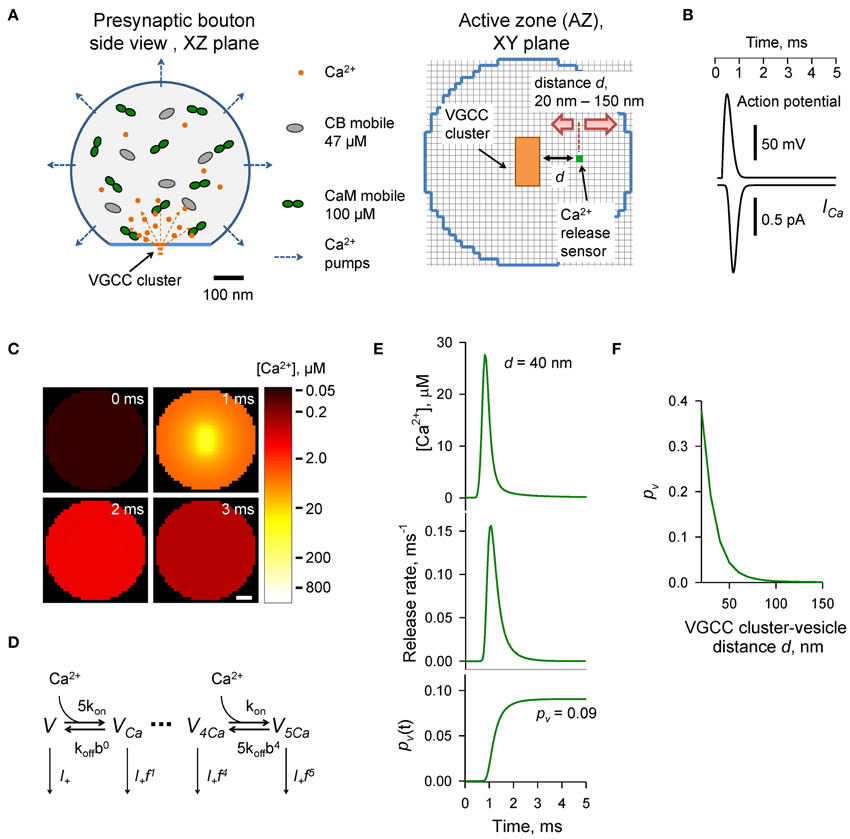
Figure 1. Modeling of AP-evoked synaptic vesicle exocytosis in a small presynaptic bouton. (A) Presynaptic bouton geometry. Left, side view of a bouton modeled as a truncated sphere of R_bout = 0.3 μm. Right, the AZ plane containing the VGCC cluster modeled as a 40 × 80 nm rectangle (orange); red arrows depict the range of tested coupling distances d (20–150 nm) between the VGCC cluster and the vesicular Ca²⁺ release sensor (green dot). Grid 10 nm. (B) AP waveform (top trace) and corresponding average Ca²⁺ current I_Ca (bottom trace) through 7 P/Q-type, 8 N-type, and 1 R-type VGCCs. (C) Snapshots of spatial AP-evoked [Ca²⁺] within a 10 nm thick plane immediately above the AZ, scale bar 50 nm. Logarithmic color coding bar is shown on the right. (D) Allosteric model of Ca²⁺ activation of vesicle fusion (Lou et al., 2005) (E) Results of simulations for a representative VGCC—Ca²⁺ sensor coupling distance d = 40 nm: [Ca²⁺] time course (top trace), corresponding vesicular release rate time course (middle trace), and time dependency of cumulative vesicular release probability p_v(t) (bottom trace). Final AP-evoked vesicular release probability p_v is shown in the insert. This was determined as the horizontal asymptote of a cumulative probability after the AP (in practice we defined it as a value of p_v(t) at 5 ms) (F) Dependency of p_v on distance d.

The model assumed Ca²⁺ binding to the three endogenous buffers present in the presynaptic bouton: CaM, CB, and ATP. Ca²⁺ interaction with free CaM was simulated using a two-step cooperative binding model to the N- and the C-lobes of CaM molecule (Faas et al., 2011):

$N_T{N}_T+C{a}^{2+}\underset{k_{off}^{(T),N}}{\overset{2·k_{on}^{(T),N}}{\rightleftarrows }}Ca{N}_T{N}_R+C{a}^{2+}\underset{2·k_{off}^{(R),N}}{\overset{k_{on}^{(R),N}}{\rightleftarrows }}Ca{N}_{R}Ca{N}_R,$

$C_T{C}_T+C{a}^{2+}\underset{k_{off}^{(T),C}}{\overset{2·k_{on}^{(T),C}}{\rightleftarrows }}Ca{C}_T{C}_R+C{a}^{2+}\underset{2·k_{off}^{(R),C}}{\overset{k_{on}^{(R),C}}{\rightleftarrows }}Ca{C}_{R}Ca{C}_R,$

k^(T),N_on = 770 μM⁻¹ s⁻¹, k^(T),N_off = 1.6 × 10⁵ s⁻¹, k^(R),N_on = 3.2 × 10⁴ μM⁻¹ s⁻¹, k^(R),N_off = 2.2 × 10⁴ s⁻¹, k^(T),C_on = 84 μM⁻¹ s⁻¹, k^(T),C_off = 2.6 × 10³ s⁻¹, k^(R),C_on = 25 μM⁻¹ s⁻¹, k^(R),C_off = 6.5 s⁻¹. The total average CaM concentration was [CaM]_tot = 100 μM (Faas et al., 2011). Depending on the type of simulation (as indicated in the text) CaM was considered either as a mobile buffer with diffusion coefficient D_CaM = 20 μm² s⁻¹, or as an immobile buffer which was either evenly distributed throughout the bouton volume or bound to the plasma membrane (within a 10 nm single layer adjacent to the bouton membrane in VCell simulations). In the case of CaM associated with neuromodulin we assumed that k^(R),C_off was increased 50-fold (Gaertner et al., 2004; Hoffman et al., 2014) (k^(R),C_off = 325 s⁻¹).

Each CB molecule contained four independent Ca²⁺ binding sites (two fast and two slow) (Nagerl et al., 2000):

$\begin{array}{l}C{B}_{fast}+C{a}^{2+}\underset{k_{off}^{CB\_fast}}{\overset{k_{on}^{CB\_fast}}{\rightleftarrows }}CaC{B}_{fast},\\ C{B}_{slow}+C{a}^{2+}\underset{k_{off}^{CB\_slow}}{\overset{k_{on}^{CB\_slow}}{\rightleftarrows }}CaC{B}_{slow},\end{array}$

k^CB_fast_on = 87 μM⁻¹ s⁻¹, k^CB_fast_off = 35.8 s⁻¹, k^CB_slow_on = 11 μM⁻¹ s⁻¹, k^CB_slow_off = 2.6 s⁻¹. The diffusion coefficient for both Ca²⁺-free and Ca²⁺-bound CB molecules was D_CB = 20 μm² s⁻¹ and the total CB concentration was [CB]_tot = 47.5 μM (Muller et al., 2005).

Ca²⁺ binding to ATP was modeled as a second order reaction:

$ATP+C{a}^{2+}\underset{k_{off}^{ATP}}{\overset{k_{on}^{ATP}}{\rightleftarrows }}CaATP,$

k^ATP_on = 500 μM⁻¹ s⁻¹, k^ATP_off = 1.0 × 10⁵ s⁻¹. The diffusion coefficient of free and Ca²⁺ bound ATP was D_ATP = 220 μm² s⁻¹ (Meinrenken et al., 2002). The total ATP concentration was [ATP]_tot = 0.9 mM, corresponding to 58 μM [ATP]_free at resting physiological conditions (assuming 1 mM intracellular [Mg²⁺]) (Faas et al., 2011).

Ca²⁺ extrusion by the bouton surface pumps (excluding the AZ) was approximated by a first-order reaction: j_extr = −k_extr · ([Ca²⁺]−[Ca²⁺]_rest) (Matveev et al., 2006; Ermolyuk et al., 2013), with k_extr = 125 μm s⁻¹ and [Ca²⁺]_rest = 50 nM.

AP-evoked Ca²⁺ currents through P/Q-, N-, and R-type VGCCs were modeled in the NEURON simulation environment (Hines and Carnevale, 1997) using a six-state channel gating kinetic model of P/Q-, N-, and R-type VGCCs in hippocampal mossy fiber boutons (Li et al., 2007) as described in detail previously (Ermolyuk et al., 2013). The mean AP-evoked Ca²⁺ current at the VGCC cluster was approximated by averaging 500 independent NEURON simulations of AP-evoked Ca²⁺ currents for each channel sub-type, followed by fitting the sum of average Ca²⁺ currents corresponding to 7 P/Q-type, 8 N-type, and 1 R-type VGCCs with the function I_Ca(t) = $\frac{A}{t}$ exp [−B · [ln(t/t₀)]²], where A = 9.2246 × 10⁻⁴ pA s, B = 15.78, t₀ = 8.036 × 10⁻⁴ s (Figure 1B). We did not consider any possible effects of AP waveform changes during repeated AP stimulations and assumed that the magnitude of Ca²⁺ influx was the same at each AP. Access to the VCell simulations is available upon request.

Modeling of Ca²⁺-triggered Synaptic Vesicle Fusion

Vesicular release rates were calculated using a previously published six-state allosteric model of Ca²⁺ activation of vesicle fusion in the calyx of Held (Lou et al., 2005) (Figure 1D). The model parameters were: k_on = 1 × 10⁸ M⁻¹ s⁻¹, k_off = 4 × 10³ s⁻¹, b = 0.5, f = 31.3, and I₊ = 2 × 10⁻⁴ s⁻¹. The model was solved using a variable-order stiff multistep method based on the numerical differentiation formulas (function ode15s in MATLAB, MathWorks USA) for AP-evoked Ca²⁺ concentration profiles obtained in VCell simulations at each of the 10 × 10 × 10 nm voxels located immediately above the AZ plane (Figure 1C). MATLAB computer code is enclosed (Supplementary MATLAB code).

The time-dependent vesicular release probability at each voxel in the AZ was calculated as p_v(t) = 1 − ∑_i V_i(t), where ∑_i V_i(t) is the sum of occupancies of all six model states V_i (Figure 1D). The release rate was then calculated as R_rel = dp_v(t)/dt. In this work we were specifically interested in dissecting the relative effects of CaM and CB on vesicular release and short-term facilitation. Therefore, we did not take into account any changes in the number of release-ready vesicles that occur during paired-pulse stimulation due to vesicle depletion and replenishment. We thus considered that at the onsets of both the first and second APs the vesicular release sensor was in Ca²⁺ unbound state V_{t = 0ms} = V_{t = 20ms} = (1,0,0,0,0,0). To account for sensitivity of AP-evoked release observed in small excitatory hippocampal and neocortical synapses to the slow endogenous buffer EGTA (e.g., Rozov et al., 2001; Ermolyuk et al., 2013), voxels located closer than 20 nm to the VGCC clusters were excluded from the analysis.

Results

Experimentally Constrained Model of AP-evoked Synaptic Vesicle Exocytosis in Small Central Synapses

To compare the effects of CB and CaM Ca²⁺ buffering on AP-evoked vesicular release and short-term synaptic plasticity we used a realistic experimentally constrained three-dimensional model of AP-evoked VGCC-mediated Ca²⁺ influx, Ca²⁺ buffering and diffusion, and Ca²⁺-dependent activation of vesicular release sensors. The modeling framework consisted of two steps: simulation of buffered Ca²⁺ diffusion in the presynaptic bouton using VCell environment, and calculation of vesicular release rates and fusion probabilities p_v using an allosteric model of the Ca²⁺ activation of vesicle fusion developed in the calyx of Held (Lou et al., 2005) (Materials and Methods).

The presynaptic bouton was considered as a truncated sphere (R_bout = 0.3 μm) with the AZ located at the truncated plane (Figure 1A). Immunogold electron microscopy has shown that P/Q-type VGCCs in small excitatory CA3 hippocampal synapses are mainly situated in small oval-shaped clusters with typical dimensions of 50–100 nm, and that the number of such clusters linearly scales with the size of the AZ (Holderith et al., 2012). To simplify our model we assumed that the AZ had only a single VGCC cluster of rectangular shape: 40 × 80 nm (Figure 1A). Indeed, several studies have argued that for a given release-ready vesicle docked at the AZ its AP-evoked release probability p_v is mainly determined by the closest VGCC cluster (Meinrenken et al., 2002; Ermolyuk et al., 2013; Nakamura et al., 2015).

AP-evoked release in small central excitatory synapses is triggered by mixed populations of P/Q-, N-, and R-type VGCCs (Wu and Saggau, 1994; Reid et al., 1998; Li et al., 2007; Holderith et al., 2012; Sheng et al., 2012). Based on experimental data for the relative numbers of P/Q-, N-, and R-type VGCCs in small hippocampal boutons (Ermolyuk et al., 2013) and for the average channel density within VGCC clusters (Holderith et al., 2012) we considered that the VGCC cluster contains 7 P/Q-type, 8 N-type, and 1 R-type VGCCs. In this simplified model we did not take into account the stochastic behavior of individual VGCCs during an AP and assumed that all channels are evenly distributed within the VGCC cluster. Thus, total AP-evoked Ca²⁺ influx at the VGCC cluster was approximated as the sum of average Ca²⁺ currents corresponding to 7 P/Q-type, 8 N-type, and 1 R-type VGCCs (Figure 1B and Materials and Methods).

We considered that in addition to ATP the presynaptic bouton contains two major presynaptic Ca²⁺ buffers found in central excitatory synapses: CB [physiological [CB]_tot ~ 47.5 μM, total concentration of Ca²⁺ binding sites 190 μM; (Berggard et al., 2002; Jackson and Redman, 2003; Muller et al., 2005; Scott and Rusakov, 2006)] and CaM (physiological [CaM]_tot ~ 100 μM, total concentration of Ca²⁺ binding sites 400 μM; Faas et al., 2011). In the first set of simulations we assumed that CaM molecules are mobile and have the same coefficient of diffusion in Ca²⁺-free and Ca²⁺-bound states equal to that of CB (D_CaM = D_CB = 20 μm² s⁻¹).

To calculate the AP-evoked synaptic vesicle release probability p_v as a function of distance between the VGCC cluster and the vesicular release sensor (coupling distance d, Figure 1A) we extracted from the three-dimensional VCell model Ca²⁺ dynamics at the AZ (Figure 1C) and then calculated p_v at different d using the allosteric model of Ca²⁺-triggered synaptic vesicle fusion (Figure 1D). Consistent with experimental data (Murthy et al., 2001; Ariel and Ryan, 2010; Ermolyuk et al., 2012) the model predicted that physiologically relevant p_v-values (0.05–0.15 range) should correspond to an average coupling distance d within a 30–50 nm range (Figures 1E,F).

Dominant Effect of CaM Ca²⁺ Buffering on AP-evoked Vesicular Release

To compare the relative contributions of CB and CaM to buffering of AP-evoked [Ca²⁺] transients at the AZ (and, as a consequence, to inhibition of vesicular release) we performed simulations using different combinations of CB and CaM either absent or present at physiological concentrations (Figures 2A,B). The model predicted that each buffer on its own efficiently inhibited AP-evoked AZ [Ca²⁺] transients and p_v. At a typical coupling distance d = 40 nm CB caused ~ 50% reduction of p_v (from 0.58 to 0.31) relative to control simulations without CB and CaM. CaM had even stronger inhibitory effect: ~80% reduction of p_v at d = 40 nm (from 0.58 to 0.12). Consistent with the steep power relationship between vesicular release rate and [Ca²⁺] at the release sensors (Mintz et al., 1995; Lou et al., 2005) Ca²⁺ buffering by CB and CaM caused a non-additive supralinear reduction of p_v. Notably, addition of CB on top of CaM caused only a minor further decrease of p_v (e.g., from 80 to 85% at d = 40 nm).

FIGURE 2

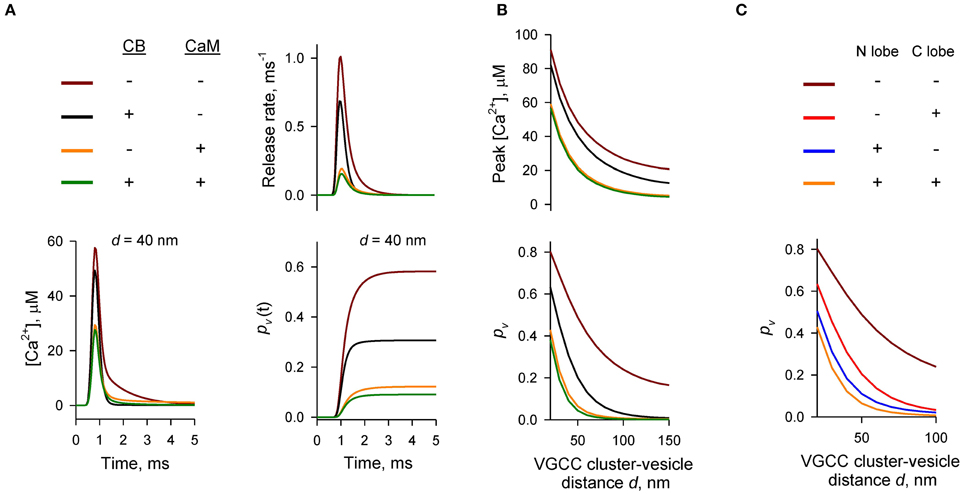
Figure 2. Dominant effect of CaM on inhibition of AP-evoked vesicular release probability p_v. (A,B) Simulation results for different presynaptic Ca²⁺ buffer mixtures, color codes are shown on the top left in (A). (A) Time courses for [Ca²⁺] (bottom left), vesicular release rate (top right), and cumulative vesicular release probability p_v(t) (bottom right) for a representative VGCC—Ca²⁺ sensor coupling distance d = 40 nm. (B) Dependencies of peak [Ca²⁺] at release sensor (top) and p_v (bottom) on distance d. (C) Relative contributions of the N- and C-lobes of CaM to inhibition of p_v at different distances d. CB was absent in this set of simulations.

We next compared the relative contributions of the fast Ca²⁺ binding to the CaM N-lobe (limiting rate constant k^(T),N_on = 770 μM⁻¹ s⁻¹) and the slower Ca²⁺ binding to the CaM C-lobe (limiting rate constant k^(T),C_on = 84 μM⁻¹ s⁻¹) to inhibition of p_v. Consistent with its ~ ten-fold higher Ca²⁺ binding rate the N-lobe had a dominant effect in reducing AP-evoked [Ca²⁺] transients at the AZ and p_v (Figure 2C). The C-lobe on its own produced an inhibitory effect similar to that of CB.

Thus, our simulations show that fast synchronous AP-evoked vesicular release at synapses that contain both CB and CaM is mainly inhibited by fast Ca²⁺ binding to the N-lobe of CaM and that the CaM C-lobe and CB play only secondary roles.

Effect of Mobile CaM on Paired-pulse Facilitation

At certain types of central synapses CB has been shown to contribute to short-term facilitation of AP-evoked vesicular release through Ca²⁺ buffer saturation (e.g., Blatow et al., 2003; Jackson and Redman, 2003). Given the predicted dominant effect of CaM on AP-evoked release we asked how Ca²⁺ buffering by CaM affects short-term synaptic plasticity in presynaptic boutons that contain both CB and CaM. Facilitation through buffer saturation strongly depends on the mobility of the endogenous Ca²⁺ buffers (e.g., Matveev et al., 2004). CaM binds to multiple soluble and membrane-bound proteins (Xia and Storm, 2005; Villarroel et al., 2014). However, the precise distribution of presynaptic CaM molecules between the mobile and immobile states is not known. Therefore, we explored several limiting cases with respect to the diffusional properties and spatial distribution of presynaptic CaM.

We first considered the case of mobile CaM (Figure 3, see also Figures 1, 2). We modeled Ca²⁺ dynamics and vesicular release during 50 Hz paired-pulse AP stimulation (inter-spike interval Δt_AP = 20 ms) and calculated the dependencies of paired-pulse ratios (PPRs) on the coupling distance d both for peak [Ca²⁺] (PPR [Ca²⁺]_peak = [Ca²⁺]^AP2_peak/[Ca²⁺]^AP1_peak) and for the vesicular release probability (PPR_pv = p^AP2_v/p^AP1_v) (Figures 3A–C). It should be noted that because we were specifically interested in the effects of CaM and CB on shaping the vesicular release, when calculating PPR_pv we did not consider any changes in the number of release-ready vesicles that may occur as a result of vesicle depletion and replenishment during repetitive stimulation (Materials and Methods).

FIGURE 3

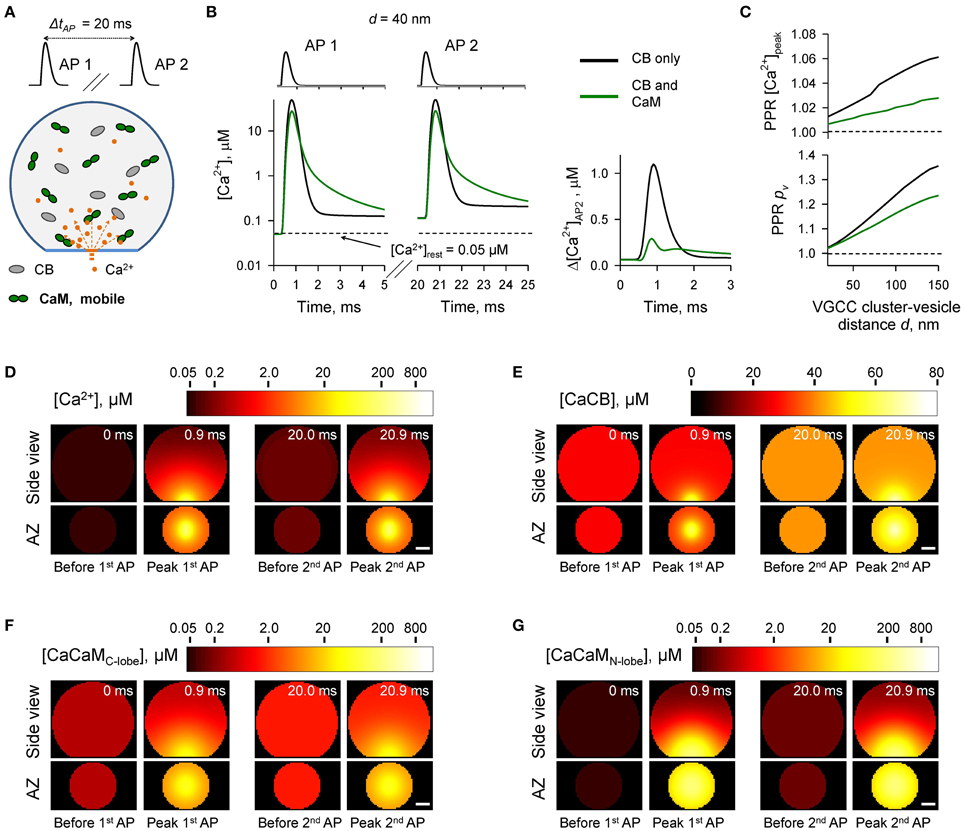
Figure 3. Effect of mobile CaM on short-term synaptic plasticity. (A) Schematic representation of the paired-pulse simulation experiment (Δt_AP = 20 ms) with mobile CaM, see text for details. (B) Comparison of [Ca²⁺] time courses at the vesicular release Ca²⁺ sensor for a representative coupling distance d = 40 nm during paired-pulse stimulation (AP 1 and AP 2) with and without mobile CaM in the presynaptic bouton. Left, [Ca²⁺] transients; right, net increase of [Ca²⁺] at the second AP (Δ[Ca²⁺]_AP2 = [Ca²⁺]_AP2 − [Ca²⁺]_AP1). (C) Dependencies of PPR[Ca²⁺]_peak = [Ca²⁺]^AP2_peak/[Ca²⁺]^AP1_peak and PPR_pv = p_v^AP2/p_v^AP1 on the coupling distance d. p_v^AP1 and p_v^AP2 were determined as the horizontal asymptotes of p_v^AP1(t) and p_v^AP2(t) after the first and the second APs respectively. (D–G) Snapshots of spatial distribution of Ca²⁺ (D, [Ca²⁺]), Ca²⁺ bound to CB (E, [CaCB] = [CaCB_fast] + [CaCB_slow]), and Ca²⁺ bound to the C-lobe (F, [CaCaM_C-lobe] = [CaC_TC_R] + 2 · [CaC_RCaC_R]) and the N-lobe (G, [CaCaM_N-lobe] = [CaN_TN_R] + 2 · [CaN_RCaN_R]) of CaM during paired-pulse stimulation. Side view, XZ plane through the center of the bouton (as in A); AZ, 10 nm thick plane immediately above the AZ. Scale bar 100 nm.

In comparison to the control simulations where only CB was present, inclusion of mobile CaM led to a noticeable decrease of both PPR [Ca²⁺]_peak and PPR_pv (Figure 3C). CB has a relatively high affinity to Ca²⁺ (K^eff_{D CB} = 0.31 μM, Supplementary Figure 1) and binds Ca²⁺ ions that enter the bouton during the first AP both within the transient Ca²⁺-nano/microdomain (local [Ca²⁺] up to 10–100 μM within 20–150 nm from the VGCC cluster) and in the rest of the bouton volume (global [Ca²⁺] ~ 1.0–1.5 μM) (Figures 3D,E). Thus, at the onset of the second AP the concentration of free CB binding sites was noticeably reduced in comparison to the first AP (by ~ 10%, from 163.0 to 148.5 μM, Supplementary Figure 2). In contrast both the C- and the N-lobes of CaM have low Ca²⁺ affinities (K^eff_{D C−lobe} = 2.84 μM and K^eff_{D N−lobe} = 12.0 μM, Supplementary Figure 1) and bind Ca²⁺ ions mainly within the Ca²⁺-nano/microdomain (Figures 3F,G). Therefore, because of the diffusional equilibration at the onset of the second AP over 99% of CaM Ca²⁺ binding sites at the AZ remained in the unbound state (Supplementary Figure 2). Thus, the presence of mobile CaM, which directly competes with CB for Ca²⁺ in the AZ, occludes the short-term facilitation caused by saturation of CB.

Effect of Immobile CaM on Paired-pulse Facilitation

In the next set of simulations (Figure 4) we considered another limiting case and assumed that all CaM molecules were immobile (e.g., bound to immobile target proteins) and were evenly distributed throughout the bouton volume. The presence of immobile CaM still led to a reduction of paired-pulse facilitation mediated by buffer saturation, although on a smaller scale than in the case of mobile CaM (Figures 4A–C). This was due to the contribution of partial saturation of the immobile CaM C-lobe within the Ca²⁺-nano/microdomain (Figure 4F, snapshot “Before 2^nd AP”). Ca²⁺ unbinding from the fully occupied C-lobe occurs on a longer timescale (Ca²⁺ dwell time ~ 150 ms, k^(R),C_off = 6.5 s⁻¹) than the 20 ms inter-spike interval. Therefore, at a typical coupling distance d = 40 nm only 80% of Ca²⁺ binding sites on the C-lobe were free at the onset of the second AP (Supplementary Figure 3). In contrast Ca²⁺ unbinding from the N-lobe occurs on a much faster timescale (Ca²⁺ dwell time ~ 0.05 ms, k^(R),N_off = 2.2 × 10⁴ s⁻¹). Therefore, concentrations of the available N-lobe Ca²⁺ binding sites were similar at the onsets of the first and the second APs, which led to occlusion of the paired-pulse facilitation caused by saturation of CB and the C-lobe of CaM. In this set of simulations we used Ca²⁺ binding kinetics determined for free CaM (Faas et al., 2011). However, CaM Ca²⁺ binding properties are affected by binding of CaM to its target proteins. These can either increase (e.g., CaM kinase II) or decrease (e.g., neuromodulin) Ca²⁺ affinity of CaM (Gaertner et al., 2004; Xia and Storm, 2005). Therefore, the effects of the immobile CaM on vesicular release probability p_v and short-term plasticity are expected to be also influenced by the distribution of bound CaM among different target proteins.

FIGURE 4

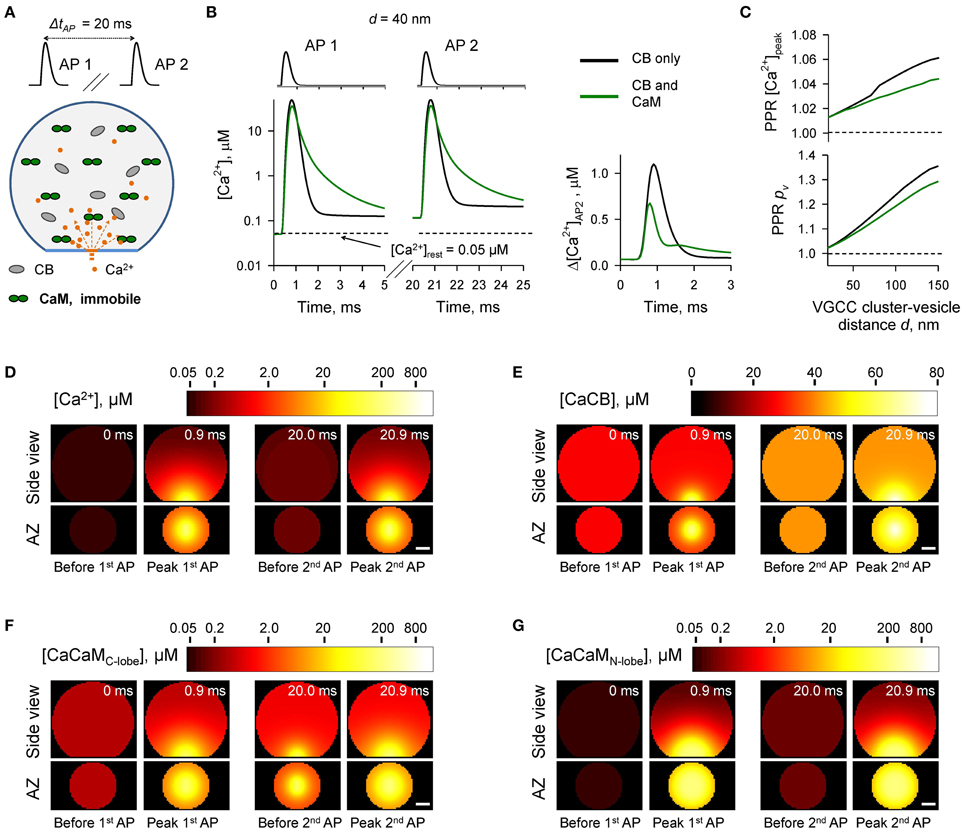
Figure 4. Effect of immobile CaM on short-term synaptic plasticity. (A) Schematic representation of the paired-pulse simulation experiment (Δt_AP = 20 ms) with immobile CaM, see text for details. (B) Comparison of [Ca²⁺] time courses at the vesicular release Ca²⁺ sensor for a representative coupling distance d = 40 nm during paired-pulse stimulation (AP 1 and AP 2) with and without immobile CaM in the presynaptic bouton. Left, [Ca²⁺] transients; right, net increase of [Ca²⁺] at the second AP. (C) Dependencies of PPR[Ca²⁺]_peak and PPR_pv on the coupling distance d. (D–G) Snapshots of spatial distribution of Ca²⁺ (D), Ca²⁺ bound to CB (E), and Ca²⁺ bound to the C-lobe (F) and the N-lobe (G) of CaM during paired-pulse stimulation. Side view, XZ plane through the center of the bouton (as in A); AZ, 10 nm thick plane immediately above the AZ. Scale bar 100 nm.

The Case of Membrane-bound CaM

Many CaM binding partners are located on the presynaptic plasma membrane. In particular, neuromodulin is an abundant presynaptic protein which is found in the brain at similar levels to CaM (Alexander et al., 1988; Xia and Storm, 2005; Kumar et al., 2013). Neuromodulin is a member of the IQ motif family of CaM-binding proteins which also includes neurogranin and PEP-19 (Putkey et al., 2003; Xia and Storm, 2005). CaM binds to the IQ motif via the C-lobe at low [Ca²⁺], and dissociates when Ca²⁺ levels increase (Alexander et al., 1988; Xia and Storm, 2005; Kumar et al., 2013). It was proposed that at resting [Ca²⁺]_rest most of presynaptic CaM is bound to the membrane anchored neuromodulin (Xia and Storm, 2005). Indeed, our model predicts that at [Ca²⁺]_rest = 50 nM, over 99.8% of CaM C-lobes should be in the Ca²⁺-free apo-state which has high affinity of binding to neuromodulin.

We first considered a limiting case where all CaM molecules were irreversibly bound to neuromodulin molecules located in the bouton plasma membrane. In the VCell simulations we assumed that all CaM molecules were located within a single 10 nm layer adjacent to the plasma membrane (Figure 5). This led to ~ a ten-fold increase of [CaM]_tot near the plasma membrane (1023 μM) in comparison to the case with evenly distributed CaM (100 μM). The detailed Ca²⁺ binding kinetics to CaM associated with neuromodulin remains unknown. However, binding of CaM to the post-synaptically expressed neurogranin (which contains a similar CaM-binding IQ motif) has been shown to decrease Ca²⁺ affinity of the CaM C-lobe because of ~ a fifty-fold acceleration of Ca²⁺ dissociation rate k^(R),C_off (Gaertner et al., 2004; Hoffman et al., 2014). Therefore, in this set of simulations we also increased k^(R),C_off 50-fold (from 6.5 to 325 s⁻¹).

FIGURE 5

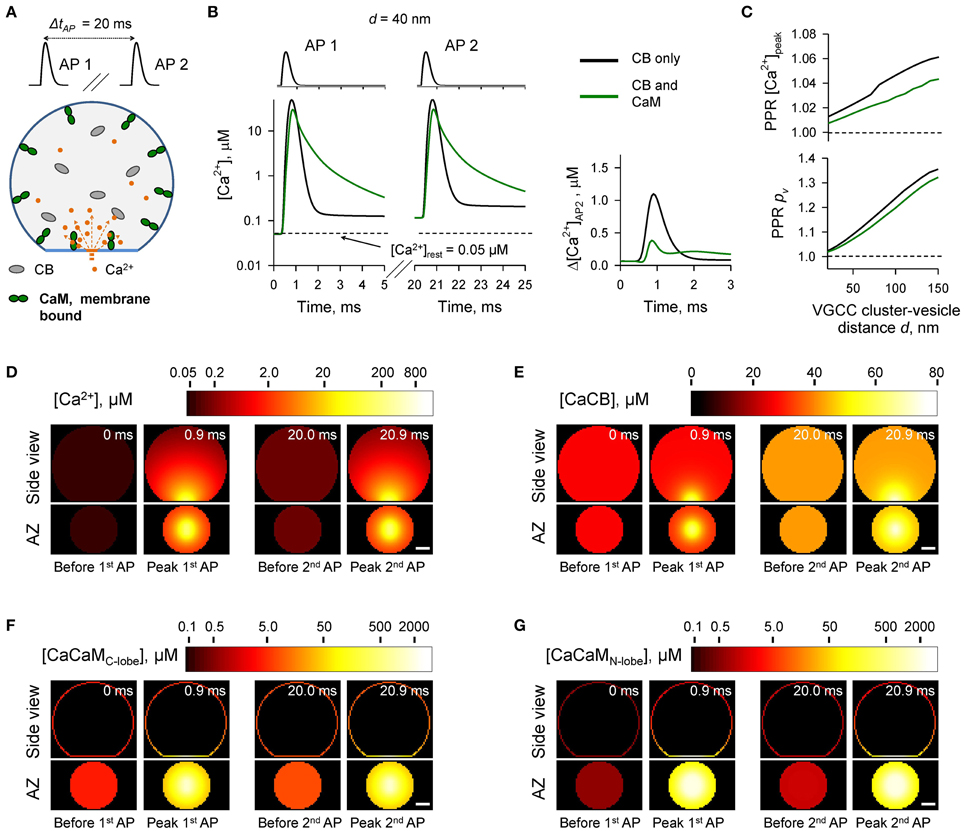
Figure 5. Effect of membrane-bound CaM on short-term synaptic plasticity. (A) Schematic representation of the paired-pulse simulation experiment (Δt_AP = 20 ms) with membrane-bound CaM, see text for details. (B) Comparison of [Ca²⁺] time courses at the vesicular release Ca²⁺ sensor for a representative coupling distance d = 40 nm during paired-pulse stimulation (AP 1 and AP 2) with and without membrane-bound CaM in the presynaptic bouton. Left, [Ca²⁺] transients; right, net increase of [Ca²⁺] at the second AP. (C) Dependencies of PPR[Ca²⁺]_peak and PPR_pv on the coupling distance d. (D–G) Snapshots of spatial distribution of Ca²⁺ (D), Ca²⁺ bound to CB (E), and Ca²⁺ bound to the C-lobe (F) and the N-lobe (G) of CaM during paired-pulse stimulation. Side view, XZ plane through the center of the bouton (as in A); AZ, 10 nm thick plane immediately above the AZ. Scale bar 100 nm.

The simulations revealed that in the case of irreversible binding of CaM to membrane associated neuromodulin, the presence of CaM still partially occludes the short-term facilitation caused by saturation of CB (Figure 5 and Supplementary Figure 4) to the degree similar to that observed in the case of evenly distributed immobile CaM (Figure 4 and Supplementary Figure 3).

Short-term Facilitation through Ca²⁺-induced Dislocation of CaM from the Plasma Membrane

We next considered a more realistic case of dynamic Ca²⁺-dependent interaction between CaM and neuromodulin. Ca²⁺ binding by the C-lobe of CaM reduces its affinity to neuromodulin several fold which leads to dissociation of CaM—neuromodulin complex (Alexander et al., 1988; Kumar et al., 2013; Hoffman et al., 2014). This prompts the hypothesis that Ca²⁺-induced dislocation of CaM molecules from the membrane bound neuromodulin may decrease the Ca²⁺ buffering capacity at the AZ during repetitive AP stimulation, which, in turn, should lead to a use-dependent increase in the vesicular release probability p_v.

To test the feasibility of this hypothesis we modeled how Ca²⁺-dependent dislocation of CaM molecules from the plasma membrane to the cytosol affects presynaptic Ca²⁺ dynamics and vesicular release during paired-pulse stimulation (Figure 6). As in Section The Case of Membrane-bound CaM we considered that at the beginning of each simulation ([Ca²⁺]_rest = 50 nM) all CaM molecules were bound to the plasma membrane via the interaction with neuromodulin. We assumed that upon binding of two Ca²⁺ ions by the C-lobe (independently of the Ca²⁺ occupancy of the N-lobe), a CaM molecule can irreversibly dissociate from the plasma membrane and freely diffuse in the cytosol (with D_CaM = 20 μm² s⁻¹) (Figure 6A). The dissociation rate of the Ca²⁺ bound C-lobe from neuromodulin (k^CaM_off) is unknown, but based on thermodynamics principles it is likely to be comparable to the effective Ca²⁺ dissociation rate. Therefore, we assumed that upon Ca²⁺ binding by the C-lobe there is a 50% chance of CaM dissociation from neuromodulin (i.e., k^CaM_off = 2 · k^(R),C_off = 650 s⁻¹).

FIGURE 6

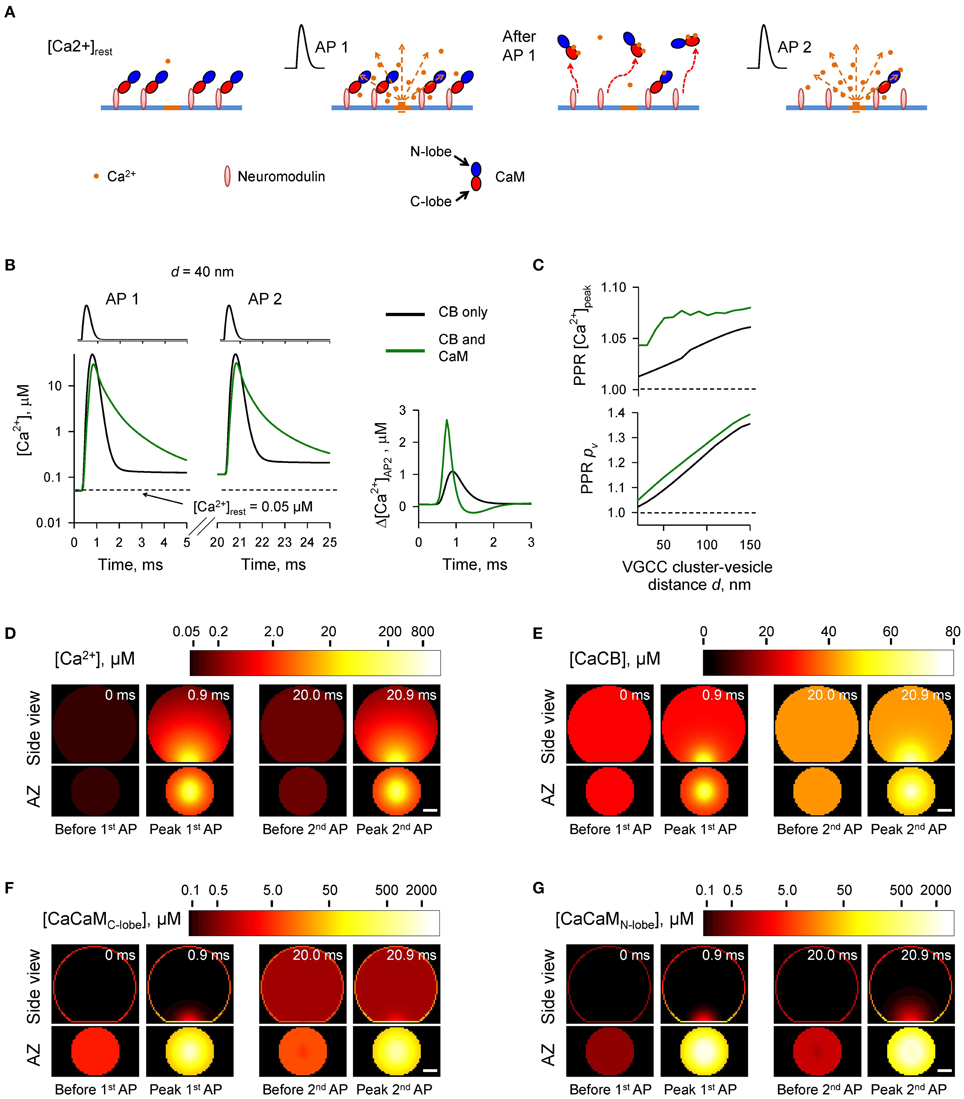
Figure 6. Ca²⁺-dependent CaM dislocation from the AZ as a mechanism of short-term facilitation. (A) Schematics depicting the model of Ca²⁺-dependent CaM dislocation from the membrane during paired-pulse simulation experiment. We assumed that at resting [Ca²⁺]_rest all CaM molecules were in the Ca²⁺-free apo state and bound via the C-lobes to the membrane-associated neuromodulin molecules. Binding of two Ca²⁺ ions by the C-lobe during the first AP leads to its dissociation from neuromodulin and to reduction of Ca²⁺ buffering at the AZ during the second AP. (B) Comparison of [Ca²⁺] time courses at the vesicular release Ca²⁺ sensor for a representative coupling distance d = 40 nm during paired-pulse stimulation (AP 1 and AP 2) with and without CaM in the presynaptic bouton. Left, [Ca²⁺] transients; right, net increase of [Ca²⁺] at the second AP. (C) Dependencies of PPR[Ca²⁺]_peak and PPR_pv on the coupling distance d. (D–G) Snapshots of spatial distribution of Ca²⁺ (D), Ca²⁺ bound to CB (E), and Ca²⁺ bound to the C-lobe (F) and the N-lobe (G) of CaM during paired-pulse stimulation. Side view, XZ plane through the center of the bouton (as in A); AZ, 10 nm thick plane immediately above the AZ. Scale bar 100 nm.

Simulations revealed a reduction of [CaM]_tot in the AZ caused by Ca²⁺ influx during the first AP (Figures 6F,G and Supplementary Figure 5). In comparison to the simulations where paired-pulse facilitation was mediated only by the buffer saturation mechanism (Figures 3–5) CaM dislocation led to a noticeably stronger increase in peak [Ca²⁺] and p_v at the second AP (Figures 6B,C). Indeed, in the case of buffer dislocation the decrease of Ca²⁺ buffering at the second AP was not only due to saturation of the relatively slow CB and CaM C-lobe Ca²⁺ binding sites, but also due to a direct reduction in fast Ca²⁺ binding to the N-lobe of CaM, which dominates regulation of fast AP-evoked Ca²⁺-nano/microdomain dynamics and p_v (Figure 2).

Finally we considered the effect of CaM membrane dislocation on AP-evoked release during physiological firing patterns typical for CA1 hippocampal pyramidal cells. These are characterized by short high-frequency bursts of APs that are interleaved by single APs (O'Keefe and Dostrovsky, 1971; Dobrunz and Stevens, 1999). We modeled AP-evoked presynaptic Ca²⁺ dynamics and vesicular release during a 50 Hz burst of six APs which was followed by a single AP 300 ms after the burst (Figure 7A). The results of our simulations show that cumulative dislocation of CaM from the AZ plasma membrane during the AP burst leads to a prominent and lasting longer facilitation of vesicular release, as evidently from the comparison with the control simulations where all CaM molecules were irreversibly bound to the plasma membrane (Figure 7).

FIGURE 7

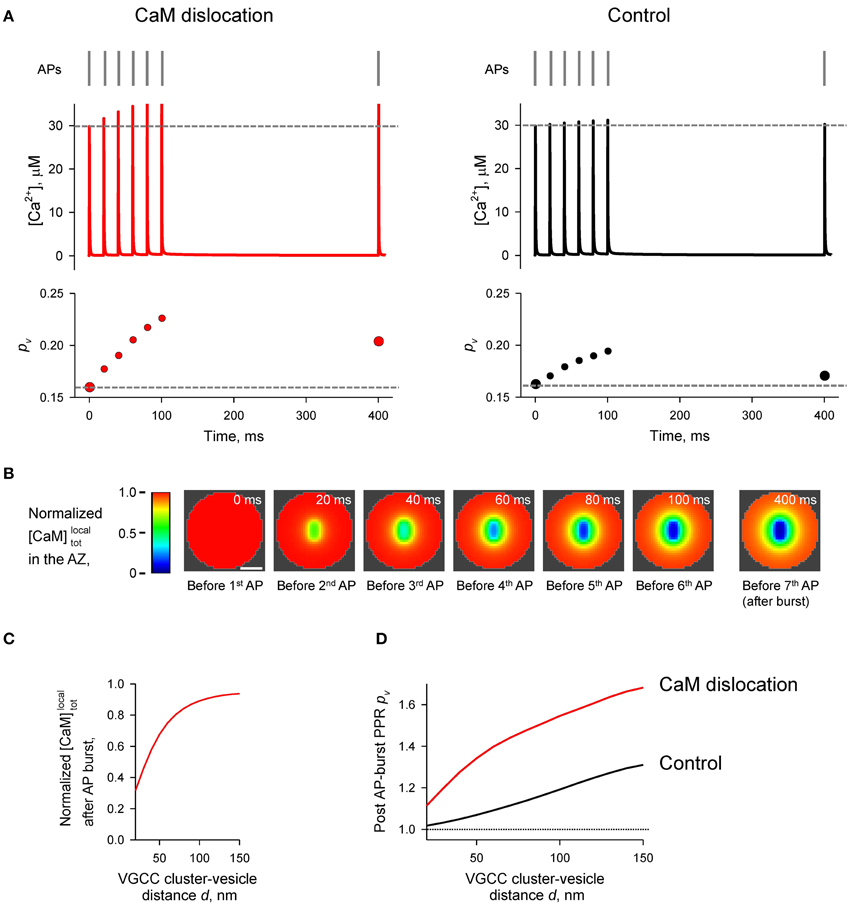
Figure 7. Effect of CaM dislocation on short-term facilitation during physiological patterns of AP firing. (A) Comparison of Ca²⁺ dynamics and vesicular release probability p_v at a representative coupling distance d = 40 nm for the case of Ca²⁺-dependent CaM dislocation (left) and for the control case of irreversible membrane bound CaM (right). Top, physiological AP stimulus pattern; middle, [Ca²⁺] time courses; bottom, p_v plots. (B) Snapshots of spatial distribution of normalized local total [CaM]^local_tot (which accounts for all CaM molecules in a given voxel, irrespective of their Ca²⁺ binding state) in the AZ, illustrating progressive dislocation of CaM from the AZ during the burst of APs [the same stimulation pattern as in (A)]. Scale bar 100 nm. (C) Dependency of normalized [CaM]^local_tot after the burst of APs on the coupling distance d. Normalized [CaM]^local_tot in (B) and (C) were calculated by dividing the spatially dependent [CaM]^local_tot by the initial total [CaM]_tot = 1023 μM. (D) Dependences of post-AP burst PPR_pv on the coupling distance d calculated for the single AP at t = 400 ms and for the first AP in the burst.

Discussion

This modeling study investigates the effects of Ca²⁺ buffering by CaM on AP-evoked synaptic vesicle release and short-term synaptic plasticity. The multiple roles of CaM in modulating synaptic transmission, which it exerts via interactions with its target proteins, have been extensively characterized (Xia and Storm, 2005; Pang et al., 2010; Sun et al., 2010; Lipstein et al., 2013; Ben-Johny and Yue, 2014). Hitherto however, the direct effects of Ca²⁺ buffering by CaM on AP-evoked presynaptic Ca²⁺ dynamics and vesicular release have not been systematically investigated.

We used a realistic three-dimensional computational model of AP-evoked presynaptic [Ca²⁺] dynamics and Ca²⁺-triggered vesicular fusion in small excitatory synapses (Ermolyuk et al., 2013). We systematically compared the effects of physiologically relevant concentrations of CaM and CB (the two major Ca²⁺ buffers found in central excitatory synapses) on vesicular release probability and short-term synaptic plasticity. To constrain the model parameters we used recently published detailed kinetics of Ca²⁺ binding to CaM (Faas et al., 2011), which reveal that the N-lobe of CaM binds Ca²⁺ much faster than any other characterized presynaptic Ca²⁺ buffer, whilst the CaM C-lobe binds Ca²⁺ with a rate comparable to that of CB. Consistently with this, our modeling shows that fast Ca²⁺ binding by the N-lobe of CaM plays a dominant role in shaping [Ca²⁺] within the transient AP-evoked Ca²⁺-nano/microdomains and as a consequence in inhibition of vesicular release probability p_v. In contrast, slower Ca²⁺ binding by the CaM C-lobe and by CB plays only a secondary role.

Our simulations also demonstrate that, depending on its mobility and location, CaM may exert opposite effects on short-term facilitation of synaptic responses. First, the fast Ca²⁺ binding/unbinding by the CaM N-lobe generally occludes paired-pulse facilitation of vesicular release caused by partial saturation of CB and the CaM C-lobe (which release Ca²⁺ on a slow time scale). Such an occlusion mechanism, and possible differences in concentration, location and mobility of CaM may explain why Ca²⁺ saturation of CB contributes to short-term facilitation only in certain types of synapses (e.g., Blatow et al., 2003; Muller et al., 2005; Bornschein et al., 2013).

Second, we propose a novel mechanism of short-term facilitation through Ca²⁺-induced dislocation of CaM from the plasma membrane. It is thought that at resting conditions most of the presynaptic CaM is bound to the membrane-associated protein neuromodulin (Alexander et al., 1988; Xia and Storm, 2005). The binding occurs at low [Ca²⁺] via interaction between the apoCaM C-lobe and the IQ-motif of neuromodulin. Upon Ca²⁺ binding by the C-lobe when [Ca²⁺] increases this interaction becomes weaker and CaM dissociates from neuromodulin (Xia and Storm, 2005; Kumar et al., 2013). Thus, we hypothesize that transient increase of [Ca²⁺] within Ca²⁺-nano/microdomains may lead to a dislocation of CaM molecules from the plasma membrane at the AZ into the cytosol.

Indeed, our simulations show that even a single AP would lead to a reduction in [CaM]_tot in the AZ. Such a stimulation-dependent reduction of Ca²⁺ buffering capacity within the AZ results in a noticeable increase in the paired-pulse ratio when compared to the control simulation with irreversible membrane-bound CaM. The effect of Ca²⁺-dependent CaM dislocation was even more prominent during the physiological burst-like AP firing of pyramidal cells.

When modeling the effect of Ca²⁺-dependent CaM dislocation we assumed that the effective concentration of CaM at the membrane was ~1000 μM (to maintain the experimentally estimated [CaM]_tot in the entire bouton at 100 μM). This corresponds to ~25 CaM molecules located at an average sized AZ with an area S_AZ = 0.04 μm² (Schikorski and Stevens, 1997; Holderith et al., 2012). In reality it is likely that the density of CaM molecules bound at the AZ is even higher than that because at [Ca²⁺]_rest apoCaM molecules are also bound to the presynaptic VGCCs via a similar IQ-motif interaction (Ben-Johny and Yue, 2014).

In this work we used a simplified model that did not take into account the mobility of VGCCs in the presynaptic membrane (Schneider et al., 2015) and also assumed irreversible dissociation of CaM from neuromodulin when both binding sites on the CaM C-lobe were occupied by Ca²⁺ ions. Yet, the detailed kinetics of CaM and neuromodulin interaction in the presence and in the absence of Ca²⁺ remains largely unknown. Thus, further experimental and modeling work is required to obtain more realistic models of the complex kinetics of Ca²⁺-dependent interaction of CaM with its binding partners at the AZ. Furthermore, activity-dependent phosphorylation of neuromodulin and other IQ-motif containing proteins prevents their interaction with CaM (Xia and Storm, 2005; Kumar et al., 2013). This should lead to long-lasting changes in the distribution of CaM molecules between the membrane-bound and mobile states, thus regulating Ca²⁺ buffering capacity at the AZ and p_v on a longer timescale. Our theoretical modeling study thus argues that Ca²⁺-dependent CaM dislocation from the plasma membrane could provide a powerful mechanism for dynamic modulation of vesicular release during physiological patterns of activity, and calls for direct experimental testing of this hypothesis.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This study was supported by the Welcome Trust. The Virtual Cell simulation environment is supported by NIH Grant Number P41 GM103313 from the National Institute for General Medical Sciences. We are grateful to J. Jepson, S. Krishnakumar, D. M. Kullmann, I. Pavlov, and S. Schorge for critical reading of the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fncel.2015.00239

References

Alexander, K. A., Wakim, B. T., Doyle, G. S., Walsh, K. A., and Storm, D. R. (1988). Identification and characterization of the calmodulin-binding domain of neuromodulin, a neurospecific calmodulin-binding protein. J. Biol. Chem. 263, 7544–7549.

PubMed Abstract | Google Scholar

Ariel, P., and Ryan, T. A. (2010). Optical mapping of release properties in synapses. Front. Neural Circuits 4:18. doi: 10.3389/fncir.2010.00018

PubMed Abstract | CrossRef Full Text | Google Scholar

Ben-Johny, M., and Yue, D. T. (2014). Calmodulin regulation (calmodulation) of voltage-gated calcium channels. J. Gen. Physiol. 143, 679–692. doi: 10.1085/jgp.201311153

PubMed Abstract | CrossRef Full Text | Google Scholar

Berggard, T., Miron, S., Onnerfjord, P., Thulin, E., Akerfeldt, K. S., Enghild, J. J., et al. (2002). Calbindin D28k exhibits properties characteristic of a Ca2+ sensor. J. Biol. Chem. 277, 16662–16672. doi: 10.1074/jbc.M200415200

PubMed Abstract | CrossRef Full Text | Google Scholar

Blatow, M., Caputi, A., Burnashev, N., Monyer, H., and Rozov, A. (2003). Ca2+ buffer saturation underlies paired pulse facilitation in calbindin-D28k-containing terminals. Neuron 38, 79–88. doi: 10.1016/S0896-6273(03)00196-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Bornschein, G., Arendt, O., Hallermann, S., Brachtendorf, S., Eilers, J., and Schmidt, H. (2013). Paired-pulse facilitation at recurrent Purkinje neuron synapses is independent of calbindin and parvalbumin during high-frequency activation. J. Physiol. 591, 3355–3370. doi: 10.1113/jphysiol.2013.254128

PubMed Abstract | CrossRef Full Text | Google Scholar

Dobrunz, L. E., and Stevens, C. F. (1999). Response of hippocampal synapses to natural stimulation patterns. Neuron 22, 157–166. doi: 10.1016/S0896-6273(00)80687-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Ermolyuk, Y. S., Alder, F. G., Surges, R., Pavlov, I. Y., Timofeeva, Y., Kullmann, D. M., et al. (2013). Differential triggering of spontaneous glutamate release by P/Q-, N- and R-type Ca(2+) channels. Nat. Neurosci. 16, 1754–1763. doi: 10.1038/nn.3563

PubMed Abstract | CrossRef Full Text | Google Scholar

Ermolyuk, Y. S., Alder, F. G., Henneberger, C., Rusakov, D. A., Kullmann, D. M., and Volynski, K. E. (2012). Independent regulation of basal neurotransmitter release efficacy by variable Ca2+ influx and bouton size at small central synapses. PLoS Biol. 10:e1001396. doi: 10.1371/journal.pbio.1001396

PubMed Abstract | CrossRef Full Text | Google Scholar

Faas, G. C., Raghavachari, S., Lisman, J. E., and Mody, I. (2011). Calmodulin as a direct detector of Ca2+ signals. Nat. Neurosci. 14, 301–304. doi: 10.1038/nn.2746

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaertner, T. R., Putkey, J. A., and Waxham, M. N. (2004). RC3/Neurogranin and Ca2+/calmodulin-dependent protein kinase II produce opposing effects on the affinity of calmodulin for calcium. J. Biol. Chem. 279, 39374–39382. doi: 10.1074/jbc.M405352200

PubMed Abstract | CrossRef Full Text | Google Scholar

Hines, M. L., and Carnevale, N. T. (1997). The NEURON simulation environment. Neural Comput. 9, 1179–1209. doi: 10.1162/neco.1997.9.6.1179

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoffman, L., Chandrasekar, A., Wang, X., Putkey, J. A., and Waxham, M. N. (2014). Neurogranin alters the structure and calcium binding properties of calmodulin. J. Biol. Chem. 289, 14644–14655. doi: 10.1074/jbc.M114.560656

PubMed Abstract | CrossRef Full Text | Google Scholar

Holderith, N., Lorincz, A., Katona, G., Rozsa, B., Kulik, A., Watanabe, M., et al. (2012). Release probability of hippocampal glutamatergic terminals scales with the size of the active zone. Nat. Neurosci. 15, 988–997. doi: 10.1038/nn.3137

PubMed Abstract | CrossRef Full Text | Google Scholar

Jackson, M. B., and Redman, S. J. (2003). Calcium dynamics, buffering, and buffer saturation in the boutons of dentate granule-cell axons in the hilus. J. Neurosci. 23, 1612–1621.

PubMed Abstract | Google Scholar

Kumar, V., Chichili, V. P., Zhong, L., Tang, X., Velazquez-Campoy, A., Sheu, F. S., et al. (2013). Structural basis for the interaction of unstructured neuron specific substrates neuromodulin and neurogranin with Calmodulin. Sci. Rep. 3:1392. doi: 10.1038/srep01392

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, L., Bischofberger, J., and Jonas, P. (2007). Differential gating and recruitment of P/Q-, N-, and R-type Ca2+ channels in hippocampal mossy fiber boutons. J. Neurosci. 27, 13420–13429. doi: 10.1523/JNEUROSCI.1709-07.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Lipstein, N., Sakaba, T., Cooper, B. H., Lin, K. H., Strenzke, N., Ashery, U., et al. (2013). Dynamic control of synaptic vesicle replenishment and short-term plasticity by Ca(2+)-calmodulin-Munc13-1 signaling. Neuron 79, 82–96. doi: 10.1016/j.neuron.2013.05.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Lou, X., Scheuss, V., and Schneggenburger, R. (2005). Allosteric modulation of the presynaptic Ca2+ sensor for vesicle fusion. Nature 435, 497–501. doi: 10.1038/nature03568

PubMed Abstract | CrossRef Full Text | Google Scholar

Matveev, V., Bertram, R., and Sherman, A. (2006). Residual bound Ca2+ can account for the effects of Ca2+ buffers on synaptic facilitation. J. Neurophysiol. 96, 3389–3397. doi: 10.1152/jn.00101.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Matveev, V., Zucker, R. S., and Sherman, A. (2004). Facilitation through buffer saturation: constraints on endogenous buffering properties. Biophys. J. 86, 2691–2709. doi: 10.1016/S0006-3495(04)74324-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Meinrenken, C. J., Borst, J. G., and Sakmann, B. (2002). Calcium secretion coupling at calyx of held governed by nonuniform channel-vesicle topography. J. Neurosci. 22, 1648–1667.

PubMed Abstract | Google Scholar

Mintz, I. M., Sabatini, B. L., and Regehr, W. G. (1995). Calcium control of transmitter release at a cerebellar synapse. Neuron 15, 675–688. doi: 10.1016/0896-6273(95)90155-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Muller, A., Kukley, M., Stausberg, P., Beck, H., Muller, W., and Dietrich, D. (2005). Endogenous Ca2+ buffer concentration and Ca2+ microdomains in hippocampal neurons. J. Neurosci. 25, 558–565. doi: 10.1523/JNEUROSCI.3799-04.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Murthy, V. N., Schikorski, T., Stevens, C. F., and Zhu, Y. (2001). Inactivity produces increases in neurotransmitter release and synapse size. Neuron 32, 673–682. doi: 10.1016/S0896-6273(01)00500-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagerl, U. V., Novo, D., Mody, I., and Vergara, J. L. (2000). Binding kinetics of calbindin-D(28k) determined by flash photolysis of caged Ca(2+). Biophys. J. 79, 3009–3018. doi: 10.1016/S0006-3495(00)76537-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, Y., Harada, H., Kamasawa, N., Matsui, K., Rothman, J. S., Shigemoto, R., et al. (2015). Nanoscale distribution of presynaptic Ca(2+) channels and its impact on vesicular release during development. Neuron 85, 145–158. doi: 10.1016/j.neuron.2014.11.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Neher, E. (1998). Usefulness and limitations of linear approximations to the understanding of Ca2+ signals. Cell Calcium 24, 345–357. doi: 10.1016/S0143-4160(98)90058-6

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Keefe, J., and Dostrovsky, J. (1971). The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 34, 171–175. doi: 10.1016/0006-8993(71)90358-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Pang, Z. P., Cao, P., Xu, W., and Sudhof, T. C. (2010). Calmodulin controls synaptic strength via presynaptic activation of calmodulin kinase II. J. Neurosci. 30, 4132–4142. doi: 10.1523/JNEUROSCI.3129-09.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Putkey, J. A., Kleerekoper, Q., Gaertner, T. R., and Waxham, M. N. (2003). A new role for IQ motif proteins in regulating calmodulin function. J. Biol. Chem. 278, 49667–49670. doi: 10.1074/jbc.C300372200

PubMed Abstract | CrossRef Full Text | Google Scholar

Reid, C. A., Bekkers, J. M., and Clements, J. D. (1998). N- and P/Q-type Ca2+ channels mediate transmitter release with a similar cooperativity at rat hippocampal autapses. J. Neurosci. 18, 2849–2855.

PubMed Abstract | Google Scholar

Rozov, A., Burnashev, N., Sakmann, B., and Neher, E. (2001). Transmitter release modulation by intracellular Ca2+ buffers in facilitating and depressing nerve terminals of pyramidal cells in layer 2/3 of the rat neocortex indicates a target cell-specific difference in presynaptic calcium dynamics. J. Physiol. 531, 807–826. doi: 10.1111/j.1469-7793.2001.0807h.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Sabatini, B. L., and Regehr, W. G. (1998). Optical measurement of presynaptic calcium currents. Biophys. J. 74, 1549–1563. doi: 10.1016/S0006-3495(98)77867-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Schikorski, T., and Stevens, C. F. (1997). Quantitative ultrastructural analysis of hippocampal excitatory synapses. J. Neurosci. 17, 5858–5867.

PubMed Abstract | Google Scholar

Schneider, R., Hosy, E., Kohl, J., Klueva, J., Choquet, D., Thomas, U., et al. (2015). Mobility of calcium channels in the presynaptic membrane. Neuron 86, 672–679. doi: 10.1016/j.neuron.2015.03.050

PubMed Abstract | CrossRef Full Text | Google Scholar

Scott, R., and Rusakov, D. A. (2006). Main determinants of presynaptic Ca2+ dynamics at individual mossy fiber-CA3 pyramidal cell synapses. J. Neurosci. 26, 7071–7081. doi: 10.1523/JNEUROSCI.0946-06.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheng, J., He, L., Zheng, H., Xue, L., Luo, F., Shin, W., et al. (2012). Calcium-channel number critically influences synaptic strength and plasticity at the active zone. Nat. Neurosci. 15, 998–1006. doi: 10.1038/nn.3129

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, T., Wu, X. S., Xu, J., McNeil, B. D., Pang, Z. P., Yang, W., et al. (2010). The role of calcium/calmodulin-activated calcineurin in rapid and slow endocytosis at central synapses. J. Neurosci. 30, 11838–11847. doi: 10.1523/JNEUROSCI.1481-10.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Villarroel, A., Taglialatela, M., Bernardo-Seisdedos, G., Alaimo, A., Agirre, J., Alberdi, A., et al. (2014). The ever changing moods of calmodulin: how structural plasticity entails transductional adaptability. J. Mol. Biol. 426, 2717–2735. doi: 10.1016/j.jmb.2014.05.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, L. G., and Saggau, P. (1994). Pharmacological identification of two types of presynaptic voltage-dependent calcium channels at CA3-CA1 synapses of the hippocampus. J. Neurosci. 14, 5613–5622.

PubMed Abstract | Google Scholar

Xia, Z., and Storm, D. R. (2005). The role of calmodulin as a signal integrator for synaptic plasticity. Nat. Rev. Neurosci. 6, 267–276. doi: 10.1038/nrn1647

PubMed Abstract | CrossRef Full Text | Google Scholar