- 1Shenzhen Academy of Robotics, Shenzhen, Guangdong Province, China
- 2Faculty of Applied Science, Macao Polytechnic University, Macau, Macao SAR, China
- 3Harbin Institute of Technology, Harbin, Heilongjiang Province, China
- 4Information Engineering College, Zhijiang College of Zhejiang University of Technology, Shaoxing, China
Introduction: As an interactive method gaining popularity, brain-computer interfaces (BCIs) aim to facilitate communication between the brain and external devices. Among the various research topics in BCIs, the classification of motor imagery using electroencephalography (EEG) signals has the potential to greatly improve the quality of life for people with disabilities.
Methods: This technology assists them in controlling computers or other devices like prosthetic limbs, wheelchairs, and drones. However, the current performance of EEG signal decoding is not sufficient for real-world applications based on Motor Imagery EEG (MI-EEG). To address this issue, this study proposes an attention-based bidirectional feature pyramid temporal convolutional network model for the classification task of MI-EEG. The model incorporates a multi-head self-attention mechanism to weigh significant features in the MI-EEG signals. It also utilizes a temporal convolution network (TCN) to separate high-level temporal features. The signals are enhanced using the sliding-window technique, and channel and time-domain information of the MI-EEG signals is extracted through convolution.
Results: Additionally, a bidirectional feature pyramid structure is employed to implement attention mechanisms across different scales and multiple frequency bands of the MI-EEG signals. The performance of our model is evaluated on the BCI Competition IV-2a dataset and the BCI Competition IV-2b dataset, and the results showed that our model outperformed the state-of-the-art baseline model, with an accuracy of 87.5 and 86.3% for the subject-dependent, respectively.
Discussion: In conclusion, the BFATCNet model offers a novel approach for EEG-based motor imagery classification in BCIs, effectively capturing relevant features through attention mechanisms and temporal convolutional networks. Its superior performance on the BCI Competition IV-2a and IV-2b datasets highlights its potential for real-world applications. However, its performance on other datasets may vary, necessitating further research on data augmentation techniques and integration with multiple modalities to enhance interpretability and generalization. Additionally, reducing computational complexity for real-time applications is an important area for future work.
1 Introduction
The brain-computer interface (BCI) is an emerging interactive communication method that enables the neural control of prostheses and external devices, as well as post-stroke motor rehabilitation by decoding signals generated from brain activity. This state-of-the-art technology has the potential to revolutionize various aspects of life and significantly enhance the overall quality of life. BCIs have a wide range of applications, ranging from medical assistance to human enhancement (Ahmed et al., 2022; Altaheri et al., 2023). Typically, electroencephalogram (EEG) signals reflect the electrical activity of the brain and are recorded non-invasively by placing an array of electrodes on the scalp. Obtaining real values (time and channel) Two-dimensional EEG signal matrix enables direct communication between people and external devices (Graimann et al., 2010).
Motor imagery (MI) is an activity of thinking about how to move a certain part of the body without moving the body. EEG-based MI activity has been widely used in vehicle control, drone control, environmental control, smart home, security, and other non-medical fields (Altaheri et al., 2023). However, the decoding of MI-EEG signals remains a challenging task. In this task, other physiological signals, such as facial muscle activity, eye blinking, and electromagnetic interference in the environment, contaminate the recorded MI-EEG signals and result in a low signal-to-noise ratio (Lotte et al., 2018). Individual differences in MI-EEG patterns are influenced by variations in brain structure and function across participants. Additionally, the EEG system exhibits a level of correlation between signal channels, further complicating the signals processing procedure (Altaheri et al., 2022).
In traditional methods for classifying and recognizing EEG signals, there is often a reliance on domain-specific knowledge. This has led to an increased focus on developing effective feature extraction and classification techniques, primarily due to the low signal-to-noise ratio inherent in EEG signals (Huang et al., 2019). Various feature extraction methods have been commonly utilized, including independent component analysis (Barbati et al., 2004; Delorme and Makeig, 2004; Porcaro et al., 2015; Ruan et al., 2018), wavelet transform (Xu et al., 2018), common spatial pattern (Gaur et al., 2021), and empirical mode decomposition (Tang et al., 2020). After preprocessing the EEG signals, essential features are extracted from the processed signals and fed into a classifier to determine the class of input instances (Vaid et al., 2015). Traditional feature extraction methods often involve hand-designed feature extractors such as Filter Bank Shared Space Pattern (FBCSP) (Ang et al., 2008) or Riemannian Covariance (Hersche et al., 2018) features. Ang et al. (2012) used the Filter Bank Common Spatial Pattern (FBCSP) algorithm to optimize the subject-specific frequency band of Common Spatial Pattern (CSP) on MI-EEG and then employed the Mutual Information-based Best Individual Feature (MIBIF) algorithm and Mutual Information-based Rough Set Reduction (MIRSR) algorithm to extract discriminative CSP features from the signals. Finally, we use the CSP algorithm for classification and obtain good performance. It is important to note that all of these steps are computationally time-consuming.
Although traditional methods have improved the signal-to-noise ratio of EEG signals through preprocessing methods, EEG signals collected from different timestamps and subjects usually exhibit different patterns due to the inter- and intra-subject variability of the EEG signals, leading to a poor generalization of traditional methods to datasets with unknown subjects. In contrast, Deep Learning (DL) has significant advantages because it can learn complex and meaningful features directly from raw EEG signals without time-consuming preprocessing or manual feature extraction, focuses on and learns important signals from raw EEG signals, and improves the generalization of the model. DL has demonstrated remarkable success in diverse domains, such as image, video, audio, and text analysis (Hossain et al., 2018; Ahmed et al., 2019; Altaheri et al., 2019; Qamhan et al., 2021). Consequently, researchers have increasingly turned to deep learning algorithms in recent years to address EEG classification tasks, capitalizing on the significant advancements achieved by deep learning in other fields.
In recent years, there has been a surge in the use of deep learning techniques for MI-EEG classification tasks. Researchers have introduced various deep learning network models, including Convolutional Neural Networks (CNNs) (Zhang et al., 2020), Recurrent Neural Networks (RNNs) (Luo et al., 2018; Kumar et al., 2021), Deep Belief Networks (DBNs) (Xu et al., 2020), and Autoencoder (AE) structures (Hassanpour et al., 2019). Among these models, CNNs have been widely adopted, and a variety of CNN network designs have been proposed. These designs aim to learn complex and meaningful features directly from raw EEG signals, thereby improving the signal-to-noise ratio, and eliminating the need for time-consuming preprocessing or manual feature extraction. Examples of these designs include residual-based CNN (Liu and Yang, 2021), multiscale CNN (Li et al., 2020), multilayer CNN (Amin et al., 2019), and attention-based CNN (Altuwaijri et al., 2022). Bai et al. (2018) proposed a novel variant of CNNs known as temporal convolutional network for time-series modeling and classification tasks. TCN has exhibited superior performance compared to other CNNs and recurrent networks like Long Short-Term Memory (LSTM) and Gated Recurrent Units (GRU) in sequence-related tasks. The advantages of TCN are that the size of the receptive field can be expanded exponentially, the number of parameters increases linearly, and they are not affected by gradient disappearance or explosion problems. Ingolfsson et al. (2020) proposed an EEGTCN model that combines TCN and EEGNet (Lawhern et al., 2018) to maintain high classification accuracy while reducing memory footprint and computational complexity. In addition, Altaheri et al. (2022) proposed a model called ATCNet, which combines TCN, EEGNet architecture (Lawhern et al., 2018), and a multi-attention mechanism. It extracts advanced time features through TCN and EEGNet architecture, highlights the most valuable features in MI-EEG signals through the multi-attention mechanism and surpasses the performance of EEGTCN. Superior performance is achieved in subject-centered and non-subject-centered modes, respectively.
The attention mechanism is an artificial neural network structure inspired by the selective attention process of the human brain, which enables the network to focus on pertinent information. Integrating the attention mechanism into deep learning models allows for automatic learning of key features from input signals, which in combination with CNN networks can alleviate some of the limitations in MI-EEG classification, such as low signal-to-noise ratios and inter- and intra-subject variability. One of the earliest attention-based neural network models is the attention layer within the encoder-decoder framework proposed for language modeling (Hassanpour et al., 2019). The challenge lies in efficiently learning attention weights. To address this, Luong et al. (2015) introduced multiplicative attention, which further improved efficiency. The multi-head attention network, proposed by researchers at Google, further optimized attention computation (Vaswani et al., 2017). Initially, these foundational attention models were applied in the field of natural language processing (NLP) and achieved success. Subsequently, they were extended to the domain of computer vision. Attention mechanisms proposed for the visual domain include squeeze-and-excitation blocks (Hu et al., 2018) and convolutional block attention modules (CBAMs) (Woo et al., 2018). These mechanisms facilitate the network in learning the correlations between different time steps and channels, thereby enhancing its ability to capture relevant visual information. Zhang et al. (2020) proposed a Graph-based Convolutional Recurrent Attention Model (G-CRAM). The model buildings a graph structure to represent the positioning information of EEG and employs a convolutional recurrent attention mechanism to learn spatial and temporal EEG features, with a focus on the most discriminative temporal periods, which overcomes the challenges of complexity, dynamics, and low signal-to-noise ratio of the EEG signals, and obtains superior performance in the MI-EEG classification task. Altuwaijri et al. (2022) proposed a novel model called Multi-Branch EEGNet with squeeze-and-excitation blocks (MBEEGSE) for decoding EEG-based motor imagery. The model aims to overcome the challenges of inter-subject and intra-subject variability of EEG signal and low signal-to-noise ratio to extract high-level features of EEG signal. The model employs a multi-branch convolutional neural network architecture with attention blocks to capture channel interdependencies and adaptively modify channel-wise feature responses. Superior performance is obtained in MI-EEG classification tasks.
In the future, MI-EEG classification tasks could benefit from research on artificial general intelligence methods to achieve high levels of intelligence, high precision, high robustness, and low power consumption. In this regard, Yang et al. put forward a series of innovative methods. First, Yang et al. (2022) propose a novel spike-based framework with minimum error entropy, called MeMEE, The framework combines entropy theory and recurrent spiking neural network (SNN) architecture and establishes a gradient-based online meta-learning scheme to improve the accuracy and robustness of SNN in various tasks. Second, Yang and Chen (2023) propose a novel and flexible learning framework termed high-order spike-based information bottleneck (HOSIB) leveraging the surrogate gradient technique for peak-based machine intelligence. The framework utilizes the surrogate gradient technique second-order information bottleneck (SOIB) and third-order information bottleneck (TOIB) to explore the underlying architecture and peak-based intrinsic information in SNN models. By discarding redundant information, the HOSIB framework improves the generalization and robustness of SNN models. Experiments show that the framework has superior generalization ability, robustness, and power efficiency. In addition, Yang et al. (2023) proposes an efficient learning mechanism for spiking dendrites, addressing the challenge of designing efficient learning mechanisms with dendrites. The method utilizes a multi-scale learning rule with dendritic predictive characteristics and employs a two-phase learning mechanism based on burst-related plateau potential dynamics of spiking dendrites. The experimental results have demonstrated that the proposed algorithm improves learning accuracy and reduces synaptic operations. This reduction in synaptic operations and spike numbers in the output layer leads to a reduction of power consumption on neuromorphic hardware. The combination of the three-factor dendritic prediction principle and two-phase plateau potential activities enhances learning capability and sparsity within a single neuron, while also improving robustness and learning convergence speed.
This study presents a novel bidirectional feature pyramid network attention-based temporal convolutional network, BFATCNet, for decoding MI-EEG brain signals. To enhance the input signals, data augmentation techniques such as data blending, Gaussian noise addition, and signal scaling are employed. The proposed BFATCNet model follows a four-stage process for processing MI-EEG signals. First, the MI-EEG signal undergoes the encoding stage using a combination of CNN, CBAM, and Bidirectional Feature Pyramid Network (Bi-FPN) to generate a series of high-level temporal representations. This stage aims to capture the correlations between different channels and time steps, resulting in time series signals for various frequency bands. Second, an attention layer is utilized to highlight the most salient information within the time series of different frequency bands. This attention mechanism assists the model in focusing on significant features and enhancing the discriminative power of the network. Third, a temporal convolutional layer is employed to extract high-level temporal features from the attention-highlighted information. This layer leverages temporal relationships in the signals to capture important patterns and dynamics. Finally, a fully connected layer analyzes the extracted high-level temporal features for classification purposes. This study makes several significant contributions:
1. The proposed BFATCNet model integrates the mechanisms of TCN, CBAM, Bi-FPN, attention, and convolution-based sliding window to achieve state-of-the-art performance in the BCI Contest IV-2a dataset.
2. The incorporation of CBAM facilitates the model's ability to capture correlations between different channels and time steps in the signals. Moreover, the multi-head attention mechanism enhances the model's focus on important MI information within the MI-EEG signals, allowing for effective learning and utilization of essential patterns and relationships.
3. The utilization of the Bi-FPN structure addresses the limitation of previous models that only focus on a single frequency band of EEG. By considering the information from the time series of different frequency bands, the model can improve its performance by leveraging the diverse and complementary information available across various frequency bands. This demonstrates the effectiveness of the Bi-FPN structure in enhancing the model's understanding of the MI-EEG signals.
2 Design of the BFATCNet model
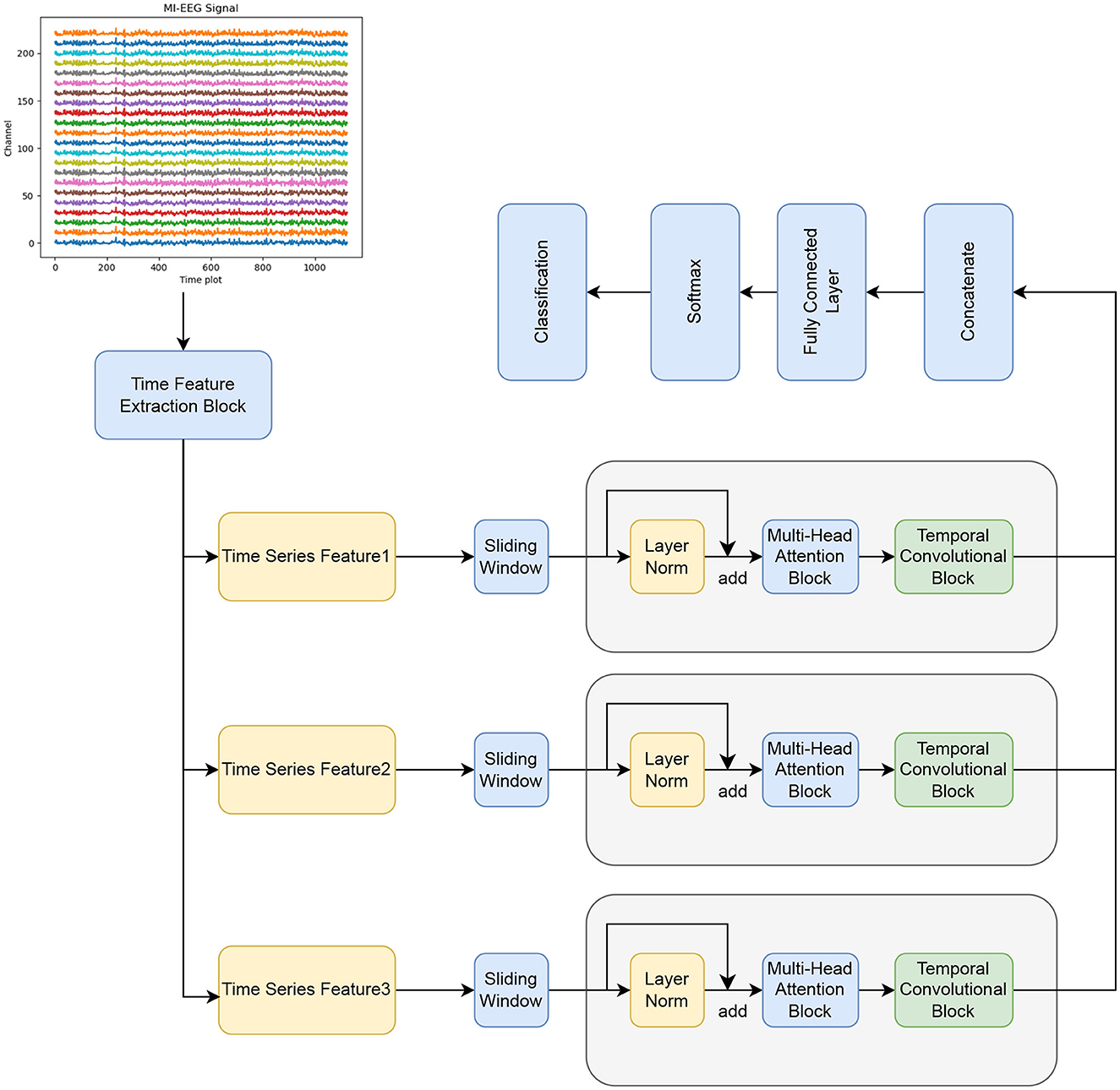
The proposed BFATCNet model consists of four main blocks: temporal feature block, attention (AT) block, and temporal convolution (TC) block with full connectivity, as shown in Figure 1. The temporal feature block encodes the original MI-EEG signals using temporal convolution layers, which include temporal convolution, channel depth convolution, and spatial convolution. It also incorporates the channel attention mechanism CBAM and the Bi-FPN structure. The block learns the correlation between channels and different time steps, extracts low-level temporal feature representations for different frequency bands and time steps, and resolves the effects of inter- and intra-subject variability and low signal-to-noise ratios of EEG signals on the classification performance of the model. Next, the AT block utilizes the Multiple Self-Attention (MSA) mechanisms to emphasize the components of the time series that have the highest correlation between different features, enhancing the generalization of the model to unknown subject datasets. Finally, the TC block applies TCN to extract high-level temporal features in the time series. The temporal features from different frequency bands are then concatenated and fed into the fully connected block for classification and identification.
The output of the time series generated by the temporal feature block can be divided into multiple windows. Each window is separately processed by the AT/TC block. The outputs of all windows are then concatenated and passed through the softmax classifier. This approach enhances data efficiency and improves accuracy. More information about the BFATCNet block is provided in the subsequent subsections.
2.1 Temporal feature block
The temporal feature block is based on the EEGNet architecture originally proposed by Lawhern et al. (2018), but with modifications. Unlike the original design that uses separable convolution, the temporal feature block utilizes 2D convolution, which has shown enhanced performance. Additionally, this block incorporates the CBAM attention mechanism to capture correlations between channels and different time steps. Moreover, the Bi-FPN architecture is employed to obtain representations of the time series in various frequency bands. The temporal feature block is used to extract high-dimensional features of different bands in EEG signals, and the CBAM attention mechanism is used to capture the correlation between channels and different time steps, which improves the generalization of the model.
The temporal feature block consists of four convolution (conv) layers and the CBAM attention mechanism, as shown in Figure 2. Firstly, a temporal convolution is applied using F1 filters with a size of (1, Fs/4), where Fs/4 represents the length of the filter along the time axis. In the BCI-2a dataset, which has a sampling rate of 250 Hz, Fs/4 becomes 62.5. To conform to standard lengths, the closest value, 64, is selected. This choice ensures the extraction of temporal information associated with frequencies above 4 Hz. The output of this layer corresponds to the F1 temporal feature maps. This design facilitates the extraction of temporal information related to higher frequencies within the time series signals, enabling the capture of subtle changes and dynamic features present in the signals.
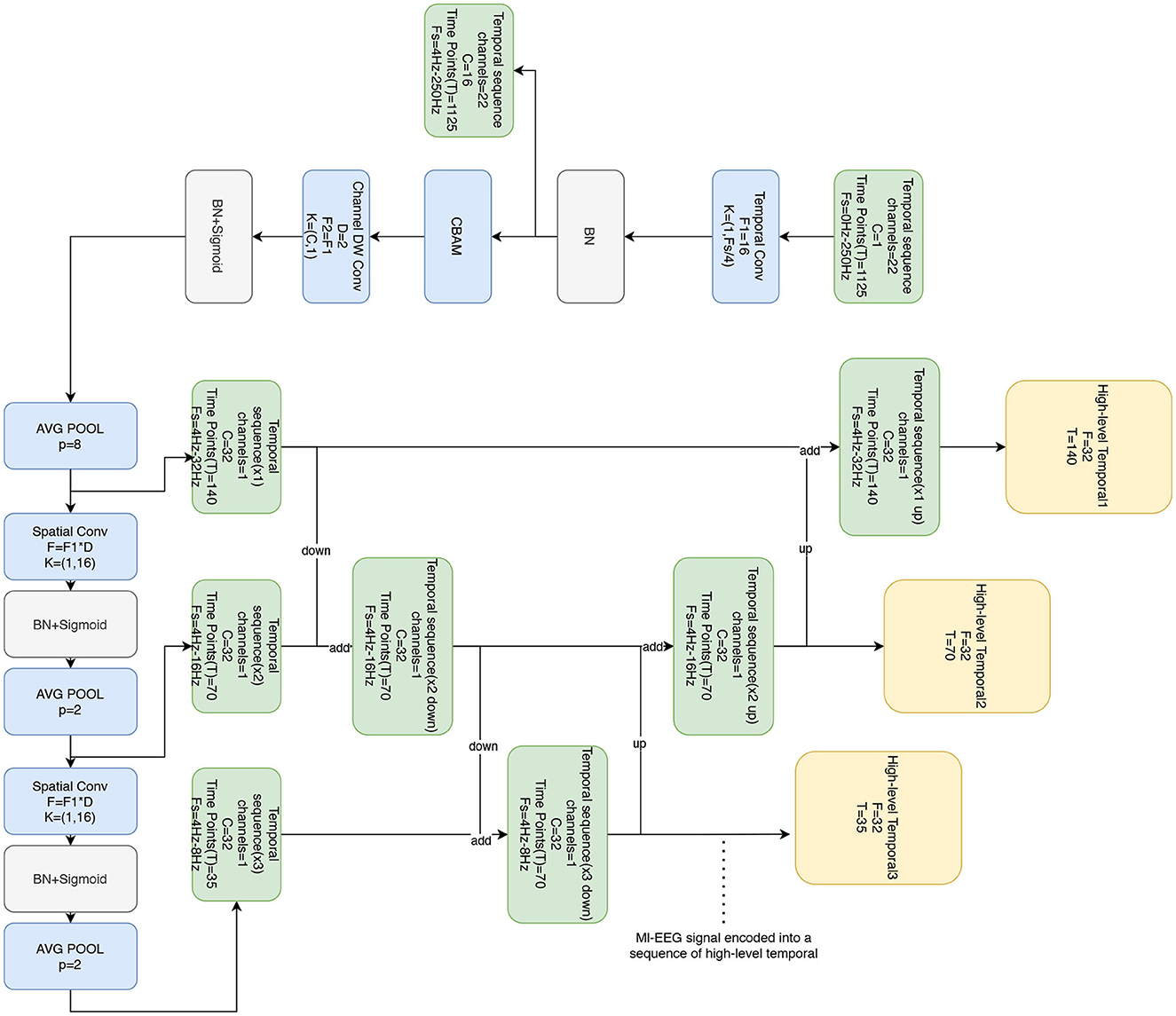
Figure 2. Temporal feature block consists of four convolutional layers and CBAM attention mechanism, which receives the original MI-EEG signals and outputs the temporal signals in different frequency bands.
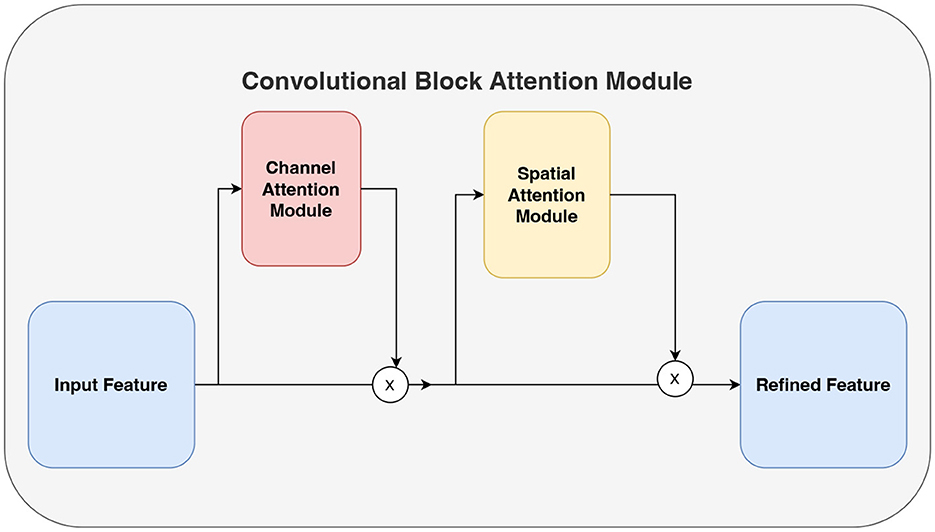
Convolutional block attention module (CBAM) (Woo et al., 2018) comprises both channel attention and spatial attention mechanisms as shown in Figure 3. The channel attention mechanism focuses on extracting significant information from the input signals along the channel dimension. It consists of three main components: the Adaptive Average Pooling Layer (AdaptiveAvgPool2d), the Adaptive Maximum Pooling Layer (AdaptiveMaxPool2d), and the Shared Multi-Layer Perceptron (SharedMLP). Initially, the input signals undergo pooling operations using the adaptive average pooling layer and adaptive maximum pooling layer, resulting in the average pooled output and maximum pooled output, respectively. Subsequently, the shared multi-layer perceptron applies a convolution operation to these outputs, allowing the extraction of feature representations within the channel dimensions. Finally, the convolution output is activated by a sigmoid function, producing the channel attention weights. These weights are then used to emphasize important channel information by appropriately weighting the different channels of the input signals.
On the other hand, the spatial attention mechanism aims to extract significant information from the input signals along the spatial dimension. It consists of a convolutional layer (Conv2d) that is subsequently followed by a sigmoid activation function. The input to this convolutional layer is the data that has been processed by the channel attention mechanism, resulting in a two-channel input. After the convolution operation, the output is activated by the sigmoid function, producing spatial attention weights. These weights are used to highlight important spatial information by assigning different weights to different spatial locations of the input signals accordingly. The integration of the channel attention mechanism and the spatial attention mechanism enables the model to learn correlations between channels and different time steps, thereby enhancing its understanding of the signals.
The second layer utilizes deep convolution with F2 filters of size (C, 1), where C denotes the number of EEG channels. This deep convolution allows each filter to extract spatial features, particularly features related to the EEG channels, from a single temporal feature map. As a result, the output of this layer consists of F2×D feature maps, where D represents the number of filters associated with each temporal feature map in the previous layer. Based on practical experience and signal characteristics, the value for D is determined as 2.
After the deep convolution layer, an average pooling layer with a size of (1, 8) is utilized to achieve an eight-fold abstraction of the temporal signals. This pooling operation reduces the signal's sampling rate to approximately 32 Hz. The rationale behind this design choice is to improve the extraction of spatial features and abstract the signal. By enabling more effective feature extraction and dimensionality reduction of the signals, this approach enhances the overall performance of the model.
The third and fourth layers involve spatial convolutions using F2×D filters with a size of (1, 16) to perform spatial convolutions. The filter length along the time axis is 16, and these convolutions are applied to decode the 4–32 Hz motor imagery (MI) activity and 4–16 Hz activities, respectively. To decrease the sampling rate and adjust the length of the resulting time series, an average pooling layer with a size of (1, 2) is used. Additionally, batch normalization is implemented to expedite network training. The nonlinear activation function applied in these layers is the sigmoid activation function.
The Bi-FPN is critical in improving the model's performance by effectively integrating feature map information from different layers. In this case, the time series outputs from convolutional layers 2, 3, and 4 are fed into the Bi-FPN. As a result, integrated outputs for layers 2, 3, and 4 are obtained, encompassing the 4–32, 4–16, and 4–8 Hz time series across three distinct frequency bands.
The temporal feature block outputs three-time series in three different frequency bands consisting of time vectors Tc of 140, 70, and 35 respectively. We empirically set d to 32. The length of the time series zj is determined by , where T refers to the time point of the original EEG signal, and P is the cumulative multiplication of the kernel of the pooling layer that has passed through.
2.2 Sliding window
To capture the dynamic properties and timing patterns of the signals more effectively, a sliding window approach is employed instead of directly inputting the entire zj into subsequent layers (Schirrmeister et al., 2017). By utilizing a sliding window of length Tw, the time series zj is systematically divided into multiple windows denoted as , where w represents the window index ranging from 1 to n, the total number of windows. Subsequently, each window is individually processed by the subsequent Attention block and Temporal Convolutional block. According to Equation (1), a specific value for the window length Tw can be calculated in the following way:
Suppose the temporal feature block utilizes three pooling layers with respective sizes of P1 = 8, P2 = 2, and P3 = 2. In that case, it generates three time series z1i, z2i, and z3i comprising three vectors of size T1 = 140, T2 = 70, and T3 = 35, respectively. Each of these time series represents 32 (= 8 × 2 × 2), 16 (= 8 × 2), and 8-time points, respectively, from the original MI-EEG signal x. Therefore, one step of sliding in z1i, z2i, and z3i corresponds to 32, 16, and 8 steps of sliding in the original signal x.
2.3 Attention (AT) block
The attention mechanism, introduced by Vaswani et al. (2017), is a neural network structure that emulates the selective information-focusing behavior observed in the human brain. By integrating the attention mechanism into deep learning models, it becomes possible to automatically extract essential information from the input signals. Improving the generalization of the model. An important feature of the multi-head attention mechanism is the internal variability, which allows the model to learn different attention weights among different heads, thus further improving the generalization performance. Following the division of the time series into multiple segments through the sliding window approach, N segments of , where i represents the ith head and j denotes the jth vector of ei, are created, corresponding to the number of heads N in the multi-head attention mechanism. Each instance of the time series, denoted as , is then multiplied by Wq, Wk, and Wv to derive the respective query vector qj, key vector kj, and value vector vj as shown in Equations 2–4:
The attention value is computed based on the query vector , key vector , and value vector . To calculate the normalized correlation score between the ath coding vector and the bth coding vector , as shown in Equation 5
where dk is the dimension of . Then, the attention-weighted output is defined as Equation 6
where T is the number of rows of the vi matrix set to coincide with the time length of the time series output from the temporal series block empirically. Finally, zis are spliced as Z = [z1, z2, ..., z8] to obtain the time series after highlighting the important information.
2.4 Temporal convolutional (TC) block
TCN architecture is composed of multiple residual blocks. Each residual block comprises two dilated causal convolution layers (Ingolfsson et al., 2020), followed by batch normalization and Exponential Linear Unit (ELU) activation, as depicted in Figure 4. The adoption of dilated causal convolution exponentially extends the receptive field, ensuring that no information propagates from future time steps to past time steps. Therefore, the output of time tis completely dependent on the input of time tor before, so that the relationship in the long series can be better learned, ensuring that the model is invariant to the translation of the time series, that is, robust to the translation of the signal in time. The residual block employed in the TCN performs element-level summation, denoted as F(x)+x, on the input and output feature maps. This summation aids in learning constant functions and prevents the vanishing or exploding of gradients in the model. With residual blocks, the model can be sensitive to translation while learning local changes and global trends in the time series data. When the signal shifts in time, residual blocks can help the model adapt better to this change, thus improving translation invariance. Within the residual blocks, a constant mapping strategy is employed, resulting in an exponential increase in the receptive field size (RFS) of the TCN with the number of stacked residual blocks L. This increase is attributed to the exponential expansion D observed in each subsequent block. The RFS is computed as in Equation 7 and is determined by two key parameters: the number of remaining blocks L and the convolutional kernel size KT.
A typical configuration of the TC block in BFATCNet consists of L = 2 residual blocks and 32 filters of size KT = 4 for all convolutional layers, so RFS is 19. With this setting, the TCN can process up to 19 elements in a sequence.
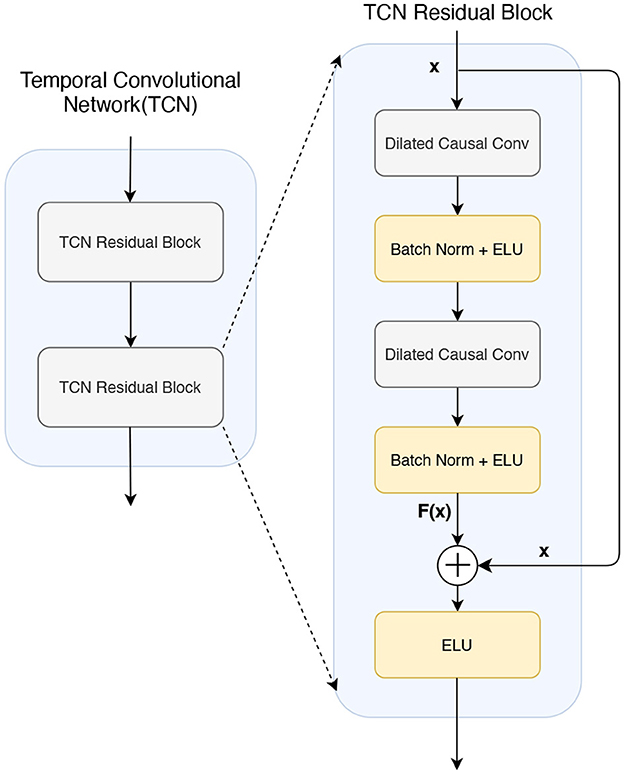
Figure 4. The architecture of a temporal convolutional network (TCN) consists of two residual blocks.
2.5 Fully connected block
In the final stage of the proposed model, three groups of time series with distinct frequency bands undergo sliding window, AT block, and TCN processing. Following the derivation of advanced time features, Adaptive Average Pooling is implemented on the three groups of advanced time features to compress them into predetermined features. The flattened advanced time features are then concatenated and subsequently passed through a three-layer fully connected layer. To expedite network training, batching is employed in combination with the fully connected layers. Additionally, Dropout is utilized to mitigate overfitting. Finally, the resulting outputs are fed into a softmax function for probability computation. The hyperparameters of the model are determined empirically and further tuned using Optuna (Akiba et al., 2019). The specific values of these hyperparameters are as follows: for the AT block, two attention heads are used with a head size of 32. For the TC block, two residual blocks are utilized with a kernel size of 4 and a total of 32 filters. The dropout rate for both AT blocks and TC blocks is set to 0.12.
3 Experimental results and discussion
3.1 Datasets and data enhancement
The BCI Contest IV-2a (BCI-2a) dataset (Brunner et al., 2008) is a widely recognized publicly available dataset for Motor Imagery Electroencephalography (MI-EEG) analysis. This dataset serves as a benchmark for MI-EEG decoding research. The BCI-2a dataset includes EEG data recorded from nine subjects, with 22 channels sampled at a rate of 250 Hz. During the data collection process, participants were given instructions to perform four different motor imagery tasks: left-hand movement, right-hand movement, foot movement, and tongue movement. Two sessions were conducted for each subject on separate days, resulting in a total of 288 trials per session. In each trial, participants performed motor imagery from the interval of 2s to 6s. It's important to note that only one session in the dataset contains class labels for all trials, whereas the other session was used as the target domain.
The BCI Contest IV-2b (BCI-2b) dataset (Leeb et al., 2008) is a widely recognized publicly available dataset for Motor Imagery Electroencephalography (MI-EEG) analysis. This dataset serves as a benchmark for MI-EEG decoding research. In the BCI-2b dataset, EEG data from three channels (C3, Cz, and C4) were captured at a sampling rate of 250 Hz from nine subjects. During the experiments, after the cue appeared, all subjects were instructed to imagine left or right-hand movements for four seconds. Each subject was provided with five sessions, with each session consisting of 120 trials. The first three sessions in the dataset were well-labeled, while the last two sessions were not. In the conducted experiments, the first three sessions were treated as source domains, and the remaining two sessions were considered as target domains. Additionally, since the first three sessions were collected at different times, they naturally represent three distinct source domains.
The proposed model is evaluated using subject-dependent (subject-specific). The model is trained and tested based on the data of individual subjects. Data augmentation was applied to the BCI-2a dataset and BCI-2b dataset to enhance the model's generalization capabilities and improve noise robustness. The augmentation involved mixing the signals from two different samples with the same label, adding Gaussian noise n, and scaling the signal using the formula where w ∈ (0, 1), noise level ∈ (0, 0.3), and scale ∈ (0.8, 1.2), as shown in Equations (8, 9, 10).
To assess the impact of the data enhancement process on model performance, we evaluated the performance of two models: accuracy and kappa, on the BCI-2a dataset and the BCI-2b dataset. We compared the performance of the model using data enhancement with that of the model without data enhancement. The results show that on the BCI-2a dataset, the overall accuracy of the model using data augmentation increased by 13.3% and kappa increased by 0.17. On the BCI-2b dataset, the overall accuracy of the model using data augmentation increased by 4.5% and kappa increased by 0.08. The results show that data augmentation improves the performance of the model on different datasets with a certain effect, especially the performance improvement on the BCI-2a dataset is more significant.
3.2 Performance metrics
In this study, the model performance was assessed using the following methods Accuracy (Acc), Equation 11 and κ score, Equation 12.
where TPi is the true positives, Hi is the number of samples in class i, and n denotes the number of classes;
where Pa is the actual percent agreement, and Pe is the expected percent agreement probability (Cohen, 1960).
3.3 Training procedure
The models in this study were trained and evaluated using the PyTorch framework. A consistent configuration was followed for the training process. The model parameters were initialized with weights drawn from a normal distribution with a mean of 0 and a standard deviation of 0.01. The AdamW optimizer was used for training the models, with a learning rate of 1.795 × 10−3 and a weight decay rate of 5.015 × 10−8. A batch size of 128 was utilized, and the training was conducted for more than 40 epochs. The categorical cross-entropy loss function was used as the objective function during training. To mitigate overfitting, a dropout rate of 0.12 was applied. These hyper-parameters were determined through a series of experiments, coupled with Optuna tuning, to ensure optimal generalization of the model. The proposed BFATCNet model achieved an impressive overall accuracy of 87.5% and a κ score of 0.83, surpassing the state-of-the-art performance in this domain.
3.4 Ablation study
Table 1 presents the impact of removing one or more blocks from the BFATCNet model on MI classification performance, using the BCI-2a dataset. The blocks were removed before training and validation procedures. The results demonstrate that the Bi-FPN blocks contribute significantly to the overall accuracy of the model, improving it by 8%, while the CBAM block improves the accuracy by 2.4%. The combination of Bi-FPN and CBAM blocks leads to an overall accuracy improvement of 8.7%. Table 2 presents the impact of removing one or more blocks from the BFATCNet model on MI classification performance, using the BCI-2b dataset. The blocks were removed before training and validation procedures. The results demonstrate that the Bi-FPN blocks contribute significantly to the overall accuracy of the model, improving it by 10%, while the CBAM block improves the accuracy by 2.8%. The combination of Bi-FPN and CBAM blocks leads to an overall accuracy improvement of 11.5%. These findings underscore the pivotal role of the Bi-FPN block in the BFATCNet model, primarily through the acquisition of multiple time series featuring distinct frequency bands. Additionally, the incorporation of the CBAM block also contributes to improving performance. Notably, the combination of Bi-FPN and CBAM blocks results in a synergistic effect that amplifies the benefits of each block, leading to a greater improvement in the overall accuracy of the model.
3.5 Comparison with recent studies
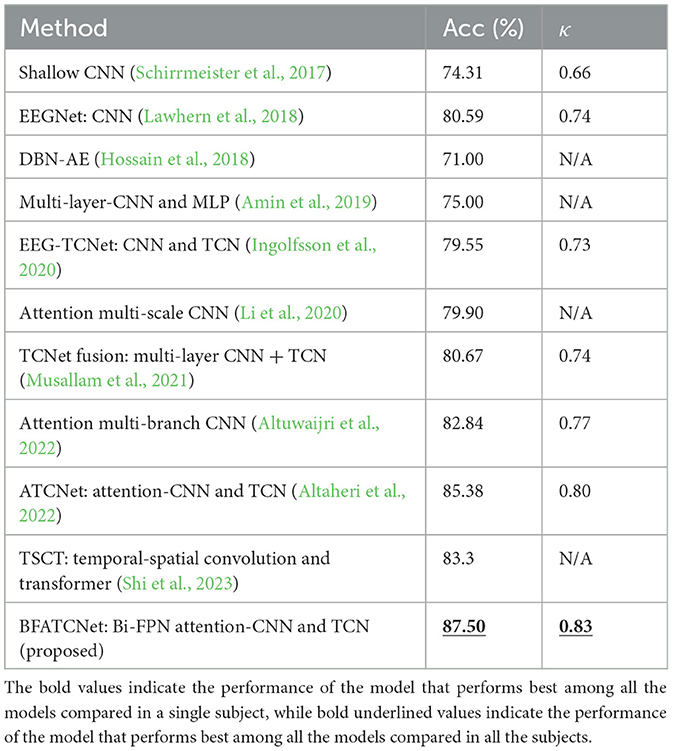
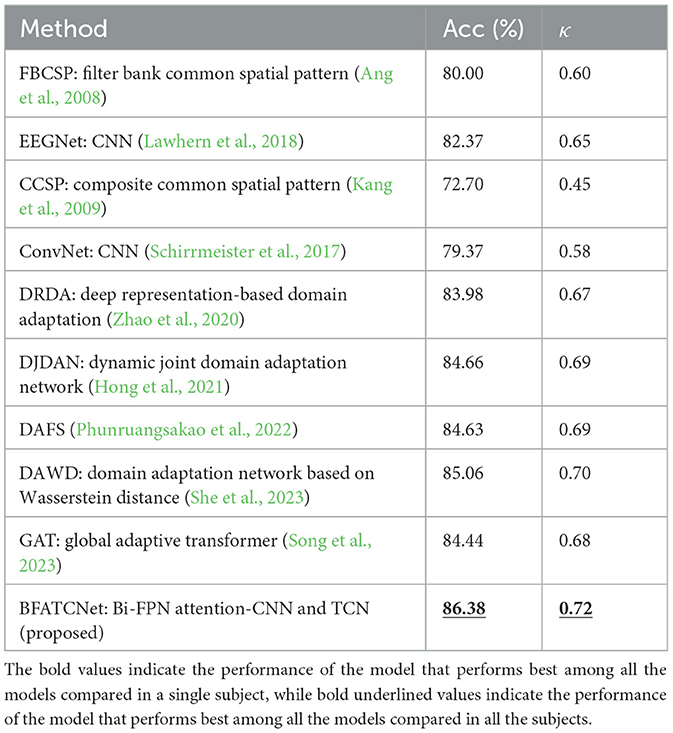
Table 3 presents a comprehensive summary of the accuracy and kappa scores achieved by the BFATCNet model and its comparison model on the BCI-2a dataset for different subjects. The results demonstrate that the BFATCNet model, the ATCNet model, and the TSCT model exhibit the capability to learn distinct attention weights based on the EEG signals from different subjects, utilizing the multi-head attention mechanism to enhance generalization performance. They have shown superior performance compared to other models in terms of average accuracy and standard deviation of accuracy. The BFATCNet model, in particular, leverages the features of different frequency bands in the EEG signals, resulting in further improved model performance. It outperforms the other models with an average accuracy of 87.5% and a kappa score of 0.83. Table 4 presents a comprehensive summary of the average accuracy and kappa scores achieved by the BFATCNet model and its comparison model on the BCI-2b dataset for different subjects. A comparison is made with other similar models: DRDA, DAFS, DAWD, GAT, and DJDAN. The results clearly show that the GAT model uses an attention-based domain adaptation approach for capturing globally correlated features between the source and target domains to address inter- and intra-subject variability of EEG signals and to enhance the generalization performance. The BFATCNet model learns different attention weights based on EEG signals from different subjects through the multi-attention mechanism algorithm, which enhances the generalization performance. It outperforms the other models with an average accuracy of 86.3% and a kappa score of 0.72.
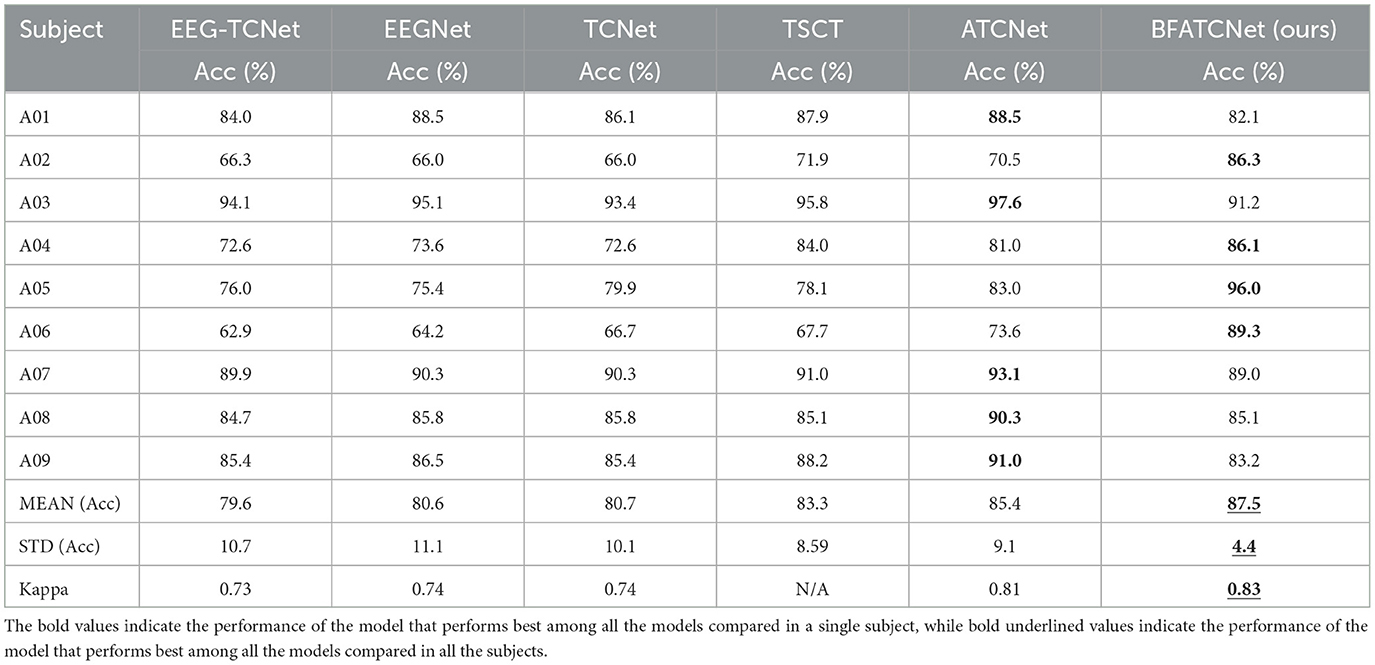
Table 3. Comparison of the performance between the proposed model and other replicated models for topic-specific classification using the BCI-2a dataset.
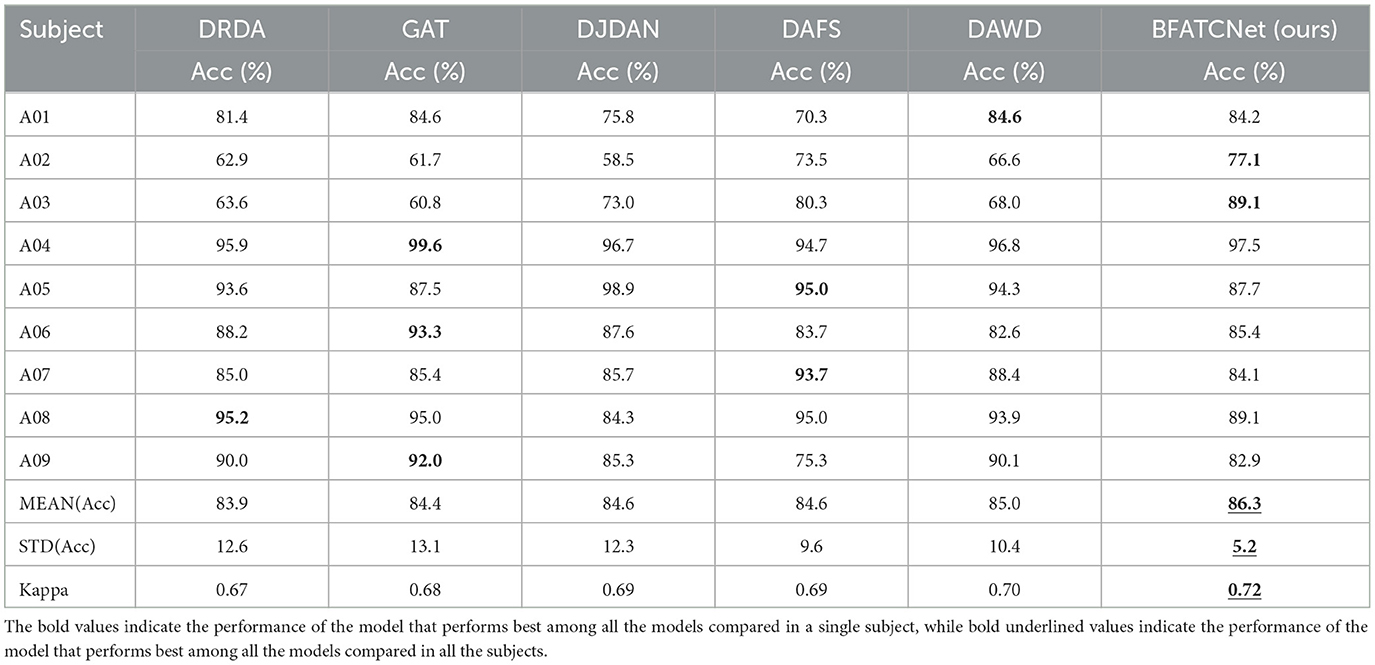
Table 4. Comparison of the performance between the proposed model and other replicated models for topic-specific classification using the BCI-2b dataset.
It is worth noting that the standard deviation of BFATCNet's performance is only 4.4% across subjects in the BCI-2a dataset and 5.2% across subjects in the BCI-2b dataset, which suggests that it has a high degree of stability in its classification effect across individuals. In addition, the performance consistency of the BFATCNet model among different users is also improved. In addition, the BFATCNet model shows higher performance consistency among different users.
According to the results in Tables 5, 6, the BFATCNet model outperformed the other models in decoding all MI categories in a subject-specific motor imagery (MI) categorization study. In particular, the BFATCNet model showed higher overall accuracy and kappa scores in a per-subject MI-EEG classification task compared to recent studies using raw EEG signals. These findings suggest that the BFATCNet model learns different attention weights for different subjects' EEG signals through a multi-head attention mechanism that adapts to the individual differences of different subjects, which enables the BFATCNet model to better decode the MI task for a specific subject, showing higher performance and accuracy compared to other models.
4 Conclusion
The present study proposes a novel attention-based bidirectional Feature Pyramid Network temporal convolution network (BFATCNet) for EEG-based motor imagery classification. BFATCNet comprises four key blocks: a temporal feature block, an attention (AT) block, a temporal convolution (TC) block, and a fully connected block. The temporal feature block encodes the raw MI-EEG signals using a temporal convolutional layer, a channel attention mechanism CBAM, and a Bi-FPN structure. The low-level temporal feature representations of different frequency bands and time steps are extracted to learn the correlation between cross-channel signals and different time steps and to address the impact of inter- and intra-subject variability and low signal-to-noise ratio of EEG signals on the classification performance of the model. Second, the AT block uses the Multihead Self-Attention mechanism to learn different attention weights based on the EEG signals from different subjects to emphasize the components of the time series with the highest correlation between different features and improve the generalization performance. Finally, the TC block utilizes TCN to extract high-level temporal features in the time series. The temporal features of different frequency bands are then concatenated and fed to the fully connected block for classification and identification.
Furthermore, this study implements the combination of Bi-FPN and CBAM modules. The ablation analysis reveals that both Bi-FPN and CBAM blocks contribute significantly to the performance of the BFATCNet model. In the BCI-2a dataset, CBAM improved the overall accuracy by 2.4%, BiFPN improved the overall accuracy by 8%, and the combination of BiFPN and CBAM improved the overall accuracy by 8.7%. In the BCI-2b dataset, CBAM improved the overall accuracy by 2.8%, BiFPN improved the overall accuracy by 10%, and the combination of BiFPN and CBAM improved the overall accuracy by 11.5%.
The proposed BFATCNet model surpasses state-of-the-art techniques for MI-EEG classification using the BCI-2a dataset and BCI-2b dataset, achieving accuracy of 87.5 and 86.3% for the subject-dependent, respectively. The model demonstrates an exceptional ability to extract MI features from raw EEG signals, without the need for data preprocessing operations such as artifact removal, major component extraction, and signal filtering. The augmentation of the BCI-2a dataset and BCI-2b dataset through data blending, signal scaling, and the addition of Gaussian noise contributes to improving the model's generalization ability and increasing its noise immunity. BFATCNet exhibits an overall improvement in EEG decoding for all MI categories and all subjects in the BCI-2a dataset and BCI-2b dataset, indicating its potential to learn universal EEG representations across categories and subjects.
However, our approach does have certain limitations. The model's performance evaluation is primarily based on the BCI-2a dataset and BCI-2b dataset, which may result in decreased performance when applied to other datasets. Although data augmentation has been applied to the BCI-2a dataset and BCI-2b dataset, the effectiveness of data augmentation may vary for different datasets or real-world data. Additionally, the complexity and computational requirements of the model may impose restrictions on its usage in real-time applications or embedded systems.
In future work, the proposed model can be further improved by researching and validating the effectiveness and applicability of data augmentation methods in different scenarios. Additionally, cross-modal deep learning models can be explored to integrate brainwave signals with other modalities such as functional magnetic resonance imaging (fMRI, eye-tracking data, text) to obtain a more comprehensive understanding of brain functionality. By combining multiple modalities, the interpretability and generalization of the model can be enhanced for brainwave signals. Alternatively, research can be conducted on reducing the computational complexity of the model to achieve higher performance and efficiency in real-time brain-computer interface applications.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Ethics statement
The studies involving humans were approved by Ethics Review Board of Shenzhen Academy of Robotics. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required from the participants or the participants' legal guardians/next of kin in accordance with the national legislation and institutional requirements.
Author contributions
XX: Conceptualization, Data curation, Software, Validation, Visualization, Writing – original draft. LC: Investigation, Writing – original draft, Writing – review & editing. SQ: Conceptualization, Data curation, Funding acquisition, Methodology, Project administration, Supervision, Writing – review & editing, Writing – original draft. FZ: Funding acquisition, Project administration, Writing – review & editing. XF: Methodology, Supervision, Writing – review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the National Key Research and Development Program of China under Grant 2020YFB1313400, and by the Basic Research Program of Shenzhen (JCYJ20180504170303184 and JCYJ20190806172007629).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmed, I., Din, S., Jeon, G., and Piccialli, F. (2019). Exploring deep learning models for overhead view multiple object detection. IEEE Internet Things J. 7, 5737–5744. doi: 10.1109/JIOT.2019.2951365
Ahmed, I., Jeon, G., and Piccialli, F. (2022). From artificial intelligence to explainable artificial intelligence in industry 4.0 a survey on what, how, and where. IEEE Trans. Ind. Inform. 18, 5031–5042. doi: 10.1109/TII.2022.3146552
Akiba, T., Sano, S., Yanase, T., Ohta, T., and Koyama, M. (2019). “Optuna: a next-generation hyperparameter optimization framework, in Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (New York, NY: ACM), 2623–2631. doi: 10.1145/3292500.3330701
Altaheri, H., Alsulaiman, M., and Muhammad, G. (2019). Date fruit classification for robotic harvesting in a natural environment using deep learning. IEEE Access 7, 117115–117133. doi: 10.1109/ACCESS.2019.2936536
Altaheri, H., Muhammad, G., and Alsulaiman, M. (2022). Physics-informed attention temporal convolutional network for EEG-based motor imagery classification. IEEE Trans. Ind. Inform. 19, 2249–2258. doi: 10.1109/TII.2022.3197419
Altaheri, H., Muhammad, G., Alsulaiman, M., Amin, S. U., Altuwaijri, G. A., Abdul, W., et al. (2023). Deep learning techniques for classification of electroencephalogram (EEG) motor imagery (MI) signals: a review. Neural Comput. Appl. 35, 14681–14722. doi: 10.1007/s00521-021-06352-5
Altuwaijri, G. A., Muhammad, G., Altaheri, H., and Alsulaiman, M. (2022). A multi-branch convolutional neural network with squeeze-and-excitation attention blocks for EEG-based motor imagery signals classification. Diagnostics 12:995. doi: 10.3390/diagnostics12040995
Amin, S. U., Alsulaiman, M., Muhammad, G., Mekhtiche, M. A., and Hossain, M. S. (2019). Deep learning for EEG motor imagery classification based on multi-layer cnns feature fusion. Future Gener. Comput. Syst. 101, 542–554. doi: 10.1016/j.future.2019.06.027
Ang, K. K., Chin, Z. Y., Zhang, H., and Guan, C. (2008). “Filter bank common spatial pattern (FBCSP) in brain-computer interface,” in 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence) (Piscataway, NJ: IEEE), 2390–2397.
Ang, K. K., Chin, Z. Y., Wang, C., Guan, C., and Zhang, H. (2012). Filter bank common spatial pattern algorithm on BCI competition iv datasets 2a and 2b. Front. Neurosci. 6:39. doi: 10.3389/fnins.2012.00039
Bai, S., Kolter, J. Z., and Koltun, V. (2018). An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv. [Preprint]. doi: 10.48550/arXiv.1803.01271
Barbati, G., Porcaro, C., Zappasodi, F., Rossini, P. M., and Tecchio, F. (2004). Optimization of an independent component analysis approach for artifact identification and removal in magnetoencephalographic signals. Clin. Neurophysiol. 115, 1220–1232. doi: 10.1016/j.clinph.2003.12.015
Brunner, C., Leeb, R., Müller-Putz, G., Schlögl, A., and Pfurtscheller, G. (2008). “BCI competition 2008-graz data set a,” in Institute for Knowledge Discovery (Laboratory of Brain-Computer Interfaces) (Vol. 16. Graz: Graz University of Technology), 1–6.
Cohen, J. (1960). A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 20, 37–46. doi: 10.1177/001316446002000104
Delorme, A., and Makeig, S. (2004). Eeglab: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 134, 9–21. doi: 10.1016/j.jneumeth.2003.10.009
Gaur, P., Gupta, H., Chowdhury, A., McCreadie, K., Pachori, R. B., Wang, H., et al. (2021). A sliding window common spatial pattern for enhancing motor imagery classification in EEG-BCI. IEEE Trans. Instrum. Meas. 70, 1–9. doi: 10.1109/TIM.2021.3051996
Graimann, B., Allison, B., and Pfurtscheller, G., (eds) (2010). “Brain-computer interfaces: a gentle introduction,” in Brain-computer Interfaces: Revolutionizing Human-computer Interaction (Berlin: Springer), 1–27. doi: 10.1007/978-3-642-02091-9
Hassanpour, A., Moradikia, M., Adeli, H., Khayami, S. R., and Shamsinejadbabaki, P. (2019). A novel end-to-end deep learning scheme for classifying multi-class motor imagery electroencephalography signals. Expert Syst. 36:e12494. doi: 10.1111/exsy.12494
Hersche, M., Rellstab, T., Schiavone, P. D., Cavigelli, L., Benini, L., Rahimi, A., et al. (2018). “Fast and accurate multiclass inference for MI-BCIS using large multiscale temporal and spectral features,” in 2018 26th European Signal Processing Conference (EUSIPCO) (Rome: IEEE), 1690–1694. doi: 10.23919/EUSIPCO.2018.8553378
Hong, X., Zheng, Q., Liu, L., Chen, P., Ma, K., Gao, Z., et al. (2021). Dynamic joint domain adaptation network for motor imagery classification. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 29, 556–565. doi: 10.1109/TNSRE.2021.3059166
Hossain, M. S., Al-Hammadi, M., and Muhammad, G. (2018). Automatic fruit classification using deep learning for industrial applications. IEEE Trans. Ind. Inform. 15, 1027–1034. doi: 10.1109/TII.2018.2875149
Hu, J., Shen, L., and Sun, G. (2018). “Squeeze-and-excitation networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Salt Lake City, UT: IEEE), 7132–7141. doi: 10.1109/CVPR.2018.00745
Huang, Q., Zhang, Z., Yu, T., He, S., and Li, Y. (2019). An EEG-/EOG-based hybrid brain-computer interface: application on controlling an integrated wheelchair robotic arm system. Front. Neurosci. 13:1243. doi: 10.3389/fnins.2019.01243
Ingolfsson, T. M., Hersche, M., Wang, X., Kobayashi, N., Cavigelli, L., Benini, L., et al. (2020). “EEG-TCNeT: an accurate temporal convolutional network for embedded motor-imagery brain-machine interfaces,” in 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC) (Toronto, ON: IEEE), 2958–2965. doi: 10.1109/SMC42975.2020.9283028
Kang, H., Nam, Y., and Choi, S. (2009). Composite common spatial pattern for subject-to-subject transfer. IEEE Signal Process. Lett. 16, 683–686. doi: 10.1109/LSP.2009.2022557
Kumar, S., Sharma, R., and Sharma, A. (2021). Optical+: a frequency-based deep learning scheme for recognizing brain wave signals. Peerj Comput. Sci. 7:e375. doi: 10.7717/peerj-cs.375
Lawhern, V. J., Solon, A. J., Waytowich, N. R., Gordon, S. M., Hung, C. P., Lance, B. J., et al. (2018). EEGNET: a compact convolutional neural network for EEG-based brain-computer interfaces. J. Neural Eng. 15:056013. doi: 10.1088/1741-2552/aace8c
Leeb, R., Brunner, C., Müller-Putz, G., Schlögl, A., and Pfurtscheller, G. (2008). BCI Competition 2008-Graz Data Set b, Volume 16. Graz: Graz University of Technology, 1–6.
Li, D., Xu, J., Wang, J., Fang, X., and Ji, Y. (2020). A multi-scale fusion convolutional neural network based on attention mechanism for the visualization analysis of EEG signals decoding. IEEE Trans. Neural Syst. Rehabil. Eng. 28, 2615–2626. doi: 10.1109/TNSRE.2020.3037326
Liu, T., and Yang, D. (2021). A densely connected multi-branch 3D convolutional neural network for motor imagery EEG decoding. Brain Sci. 11, 197. doi: 10.3390/brainsci11020197
Lotte, F., Jeunet, C. Mladenović, J., N'Kaoua, B., and Pillette, L. (2018). A BCI Challenge for the Signal Processing Community: Considering the User in the Loop. London: IET.
Luo, T.-j., Zhou, C.-l., and Chao, F. (2018). Exploring spatial-frequency-sequential relationships for motor imagery classification with recurrent neural network. BMC Bioinform. 19, 1–18. doi: 10.1186/s12859-018-2365-1
Luong, M.-T., Pham, H., and Manning, C. D. (2015). Effective approaches to attention-based neural machine translation. arXiv. [Preprint]. doi: 10.48550/arXiv.1508.04025
Musallam, Y. K. AlFassam, N. I., Muhammad, G., Amin, S. U., Alsulaiman, M., Abdul, W., et al. (2021). Electroencephalography-based motor imagery classification using temporal convolutional network fusion. Biomed. Signal Process. Control 69:102826. doi: 10.1016/j.bspc.2021.102826
Phunruangsakao, C., Achanccaray, D., and Hayashibe, M. (2022). Deep adversarial domain adaptation with few-shot learning for motor-imagery brain-computer interface. IEEE Access 10, 57255–57265. doi: 10.1109/ACCESS.2022.3178100
Porcaro, C., Medaglia, M. T., and Krott, A. (2015). Removing speech artifacts from electroencephalographic recordings during overt picture naming. Neuroimage 105, 171–180. doi: 10.1016/j.neuroimage.2014.10.049
Qamhan, M. A., Altaheri, H., Meftah, A. H., Muhammad, G., and Alotaibi, Y. A. (2021). Digital audio forensics: microphone and environment classification using deep learning. IEEE Access 9, 62719–62733. doi: 10.1109/ACCESS.2021.3073786
Ruan, J., Wu, X., Zhou, B., Guo, X., and Lv, Z. (2018). An automatic channel selection approach for ica-based motor imagery brain computer interface. J. Med. Syst. 42, 1–13. doi: 10.1007/s10916-018-1106-3
Schirrmeister, R. T., Springenberg, J. T., Fiederer, L. D. J., Glasstetter, M., Eggensperger, K., Tangermann, M., et al. (2017). Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 38, 5391–5420. doi: 10.1002/hbm.23730
She, Q., Chen, T., Fang, F., Zhang, J., Gao, Y., Zhang, Y., et al. (2023). Improved domain adaptation network based on Wasserstein distance for motor imagery EEG classification. IEEE Trans Neural Syst. Rehabil. Eng. 31, 1137–1148. doi: 10.1109/TNSRE.2023.3241846
Shi, X., Li, B., Wang, W., Qin, Y., Wang, H., Wang, X., et al. (2023). Classification algorithm for electroencephalogram-based motor imagery using hybrid neural network with spatio-temporal convolution and multi-head attention mechanism. Neuroscience 527, 64–73. doi: 10.1016/j.neuroscience.2023.07.020
Song, Y., Zheng, Q., Wang, Q., Gao, X., and Heng, P.-A. (2023). Global adaptive transformer for cross-subject enhanced EEG classification. IEEE Trans. Neural Sys. Rehabil. Eng. 31, 2767–2777. doi: 10.1109/TNSRE.2023.3285309
Tang, X., Li, W., Li, X., Ma, W., and Dang, X. (2020). Motor imagery EEG recognition based on conditional optimization empirical mode decomposition and multi-scale convolutional neural network. Expert Syst. Appl. 149:113285. doi: 10.1016/j.eswa.2020.113285
Vaid, S., Singh, P., and Kaur, C. (2015). “EEG signal analysis for BCI interface: a review,” in 2015 Fifth International Conference on Advanced Computing and Communication Technologies (Haryana: IEEE), 143–147. doi: 10.1109/ACCT.2015.72
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. Adv. Neural Inf. Process. Syst. 30, 1–15. doi: 10.48550/arXiv.1706.03762
Woo, S., Park, J., Lee, J.-Y., and Kweon, I. S. (2018). “CBAM: convolutional block attention module,” in Proceedings of the European Conference on Computer Vision (ECCV) (Ithaca, NY; Berlin: arXiv; Springer), 3–19. doi: 10.1007/978-3-030-01234-2_1
Xu, B., Zhang, L., Song, A., Wu, C., Li, W., Zhang, D., et al. (2018). Wavelet transform time-frequency image and convolutional network-based motor imagery EEG classification. IEEE Access 7, 6084–6093. doi: 10.1109/ACCESS.2018.2889093
Xu, J., Zheng, H., Wang, J., Li, D., and Fang, X. (2020). Recognition of EEG signal motor imagery intention based on deep multi-view feature learning. Sensors 20:3496. doi: 10.3390/s20123496
Yang, S., and Chen, B. (2023). Effective surrogate gradient learning with high-order information bottleneck for spike-based machine intelligence. IEEE Trans. Neural Netw. Learn. Syst. 1–15. doi: 10.1109/TNNLS.2023.3329525. [Epub ahead of print].
Yang, S., Pang, Y., Wang, H., Lei, T., Pan, J., Wang, J., et al. (2023). Spike-driven multi-scale learning with hybrid mechanisms of spiking dendrites. Neurocomputing 542:126240. doi: 10.1016/j.neucom.2023.126240
Yang, S., Tan, J., and Chen, B. (2022). Robust spike-based continual meta-learning improved by restricted minimum error entropy criterion. Entropy 24:455. doi: 10.3390/e24040455
Zhang, D., Chen, K., Jian, D., and Yao, L. (2020). Motor imagery classification via temporal attention cues of graph embedded EEG signals. IEEE J. Biomed. Health Inf. 24, 2570–2579. doi: 10.1109/JBHI.2020.2967128
Keywords: deep learning, temporal convolutional networks, multihead attention, electroencephalogram, motion imagery
Citation: Xie X, Chen L, Qin S, Zha F and Fan X (2024) Bidirectional feature pyramid attention-based temporal convolutional network model for motor imagery electroencephalogram classification. Front. Neurorobot. 18:1343249. doi: 10.3389/fnbot.2024.1343249
Received: 23 November 2023; Accepted: 15 January 2024;
Published: 30 January 2024.
Edited by:
Ming-Feng Ge, China University of Geosciences Wuhan, ChinaReviewed by:
Shuangming Yang, Tianjin University, ChinaQi Li, Changchun University of Science and Technology, China
Copyright © 2024 Xie, Chen, Qin, Zha and Fan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shujia Qin, cWluc2h1amlhQHN6YXJvYm90cy5jb20=; Fusheng Zha, emhhZnVzaGVuZ0BoaXQuZWR1LmNu
 Xinghe Xie
Xinghe Xie Liyan Chen1
Liyan Chen1 Shujia Qin
Shujia Qin Fusheng Zha
Fusheng Zha