Learning geometric Jensen-Shannon divergence for tiny object detection in remote sensing images

Tiny objects in remote sensing images only have a few pixels, and the detection difficulty is much higher than that of regular objects. General object detectors lack effective extraction of tiny object features, and are sensitive to the Intersection-over-Union (IoU) calculation and the threshold setting in the prediction stage. Therefore, it is particularly important to design a tiny-object-specific detector that can avoid the above problems. This article proposes the network JSDNet by learning the geometric Jensen-Shannon (JS) divergence representation between Gaussian distributions. First, the Swin Transformer model is integrated into the feature extraction stage as the backbone to improve the feature extraction capability of JSDNet for tiny objects. Second, the anchor box and ground-truth are modeled as two two-dimensional (2D) Gaussian distributions, so that the tiny object is represented as a statistical distribution model. Then, in view of the sensitivity problem faced by the IoU calculation for tiny objects, the JSDM module is designed as a regression sub-network, and the geometric JS divergence between two Gaussian distributions is derived from the perspective of information geometry to guide the regression prediction of anchor boxes. Experiments on the AI-TOD and DOTA datasets show that JSDNet can achieve superior detection performance for tiny objects compared to state-of-the-art general object detectors.

1. Introduction

With the rapid development of satellite technology, remote sensing images collected by optical payloads often have a large width and high resolution, so the remote sensing images often contain a large number of tiny objects, which makes remote sensing object detection challenging in applications such as maritime search and rescue, flight scheduling, and ground surveillance. Despite the significant success of deep learning and convolutional neural networks (CNNs), many object detectors can perform various visual detection tasks with high quality (Liu et al., 2016, 2020; Ren et al., 2017; Bochkovskiy et al., 2020), such as salient object detection and crowd density detection. Since the object size and distribution of these scenes are very different with remote sensing images, it is particularly important to design a tiny object detection method suitable for remote sensing scenes.

The latest research in tiny object detection has mainly focused on multi-scale feature learning (Zhang X. et al., 2022), context-based detection (Zhang K. et al., 2022), network structure-based optimization (Lu et al., 2023), data augmentation strategies (Kim and Hwang, 2022) and so on. The above methods are all implemented by the CNN architecture, which drives the data training by enhancing the tiny object feature representation. In addition to the representation of tiny object features, the computation of the IoU for network training is also affected by object scale changes (Li et al., 2021). The IoU between the ground-truth and anchor box directly reflects the positive and negative categories of the current anchor box, but the IoU is sensitive to objects of different pixel sizes, and a small position offset leads to a large change in the IoU value. As shown in Figure 1, the results of the IoU calculation for objects with different pixel sizes are different. For example, when the offset pixel is 2, the IoU value of the object of 8 × 8 pixels is calculated as 0.39, and the IoU value of the object of 96 × 96 pixels is calculated as 0.92. Thus, the results are different. Then, when the IoU threshold is used to determine the positive and negative sample labels of the current anchor box, there is inaccurate classification of the respective labels. Therefore, the IoU calculation method is not suitable for the anchor-box label assignment mechanism of tiny objects. In addition, when there is no overlap or mutual inclusion between the anchor boxes and the ground-truth, the value of IoU remains unchanged and cannot reflect the positional regression relationship between the current anchor box and the ground-truth. This is often the case with tiny objects in remote sensing image.

FIGURE 1

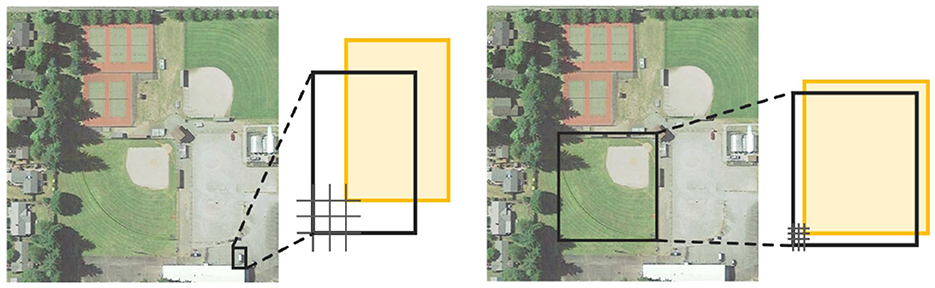
Figure 1. The area difference of the IoU calculation with objects of different pixel sizes. It shows that the IoU calculation method is sensitive to tiny remote-sensing objects.

Based on the application potential of the Swin Transformer model (Liu et al., 2021) in the remote sensing field, this article proposes a new object metric representation learning method (JSDNet), which uses the geometric JS divergence to measure the distribution distance of anchor boxes and the ground-truth. The closed form of geometric JS divergence was previously used to train Bayesian neural networks in reference (Deasy et al., 2020; Thiagarajan and Ghosh, 2022), which brings new inspiration to train deep networks. In this article, feature extraction based on Swin Transformer is firstly performed to find deeper feature representations and richer semantic information. Second, an object regression module (JSDM) is designed to model the object bounding box as a 2D Gaussian distribution, and we use the proposed geometric JS divergence with a closed-form to measure the similarity between the anchor boxes and ground-truth, avoiding the traditional IoU calculation which results in pixel offset sensitivity for tiny objects. The experiments on AI-TOD (Xu et al., 2022) and DOTA (Xia et al., 2018) datasets demonstrate the advanced performance of the proposed method.

We summarize the main contributions as follows:

1. Swin Transformer is integrated into the CNN architecture, and a remote sensing tiny object detector called JSDNet is proposed. The semantic features of the object are extracted by Swin Transformer, and the CNN network is used for the classification and regression processes.

2. The geometric JS divergence with a closed-form is used as the distance measure between Gaussian distributions, which guides the regression loss branch of the object detection network, avoids the sensitivity of the IoU calculation method to tiny objects, and improves the detection performance of remote sensing tiny objects.

3. The regression loss is described from the perspective of information geometry, which provides a new thinking for the algorithm improvement in the tiny object detection field.

2. Related works

2.1. Tiny object detection

Currently, research on tiny object detection mainly focuses on anchor-based optimization, network structure-based optimization, multi-scale feature learning, context-based information, and label classification strategy.

2.1.1. Anchor-based optimization

Anchors are multiple bounding boxes with different sizes and aspect ratios that are generated centered on each pixel of the image. Yang et al. (2018) propose a dynamic mechanism named MetaAnchor, which can select appropriate anchor for dynamic generation. Zhang et al. (2017) propose a scale compensation anchor matching mechanism to improve the recall rate for tiny objects. Duan et al. (2019) propose using center points to improve the discrimination and screening ability of anchor. Tian et al. (2019) solved the problem of hyperparametric calculation caused by too many anchors. Yang et al. (2019) use point sets to represent the bounding box of tiny objects. Due to the large and dense number of tiny objects in the image, the effectiveness of current tiny object detection algorithms based on anchor still needs to be improved.

2.1.2. Network structure-based optimization

Optimizing backbone and neck can generally enhance feature extraction for objects and improve the performance of tiny object detection (Bochkovskiy et al., 2020). Qiao et al. (2021) designed a recursive feature pyramid as a backbone network. Kong et al. (2020) designed new detection heads that can directly learn the possibility of tiny objects. Cai and Vasconcelos (2018) proposed a multi-stage network structure to improve the value of IoU layer by layer, solving the problem of over fitting in training.

2.1.3. Multi-scale feature learning

Shallow networks contain coordinate information of tiny objects, and using multi-scale feature learning can better fuse and enhance the features of tiny objects. Liu et al. (2016) proposed a single shot multi box detector (SSD) algorithm for hierarchical detection of feature maps of different scales. Lu et al. (2019) designed grid points for spatial feature information fusion. Han et al. (2022) proposed a multi-scale residual block, which obtains multi-scale context information by using dilated convolution in cascaded residual blocks. Literature (Deng et al., 2022; Zeng et al., 2022) improves the feature pyramid network, which can effectively solve the problem that feature coupling at different scales affects the performance of tiny object detection.

2.1.4. Context-based information

Effectively utilizing the background environment information around tiny objects can effectively improve the performance of tiny object detection. Feng et al. (2021) introduced the global context aware enhancement module, which activates the characteristics of the entire object by capturing the global visual context. Li et al. (2019), Leng et al. (2021), Cui et al. (2022) improved the performance of tiny object detection by constructing high-resolution and strong semantic feature maps.

2.1.5. Label classification strategy

Assigning high-quality anchor boxes to tiny objects is challenging, and many recent work has been carried out (Ge et al., 2021). Kim and Lee (2020) proposed probabilistic anchor assignment, which assumes that the joint loss distribution of positive and negative samples follows a Gaussian distribution. Xu et al. (2022) proposed a ranking-based allocation strategy, significantly improving the impact of label allocation on tiny object detection.

2.2. 2D Gaussian modeling for remote sensing object

IoU guided regression losses in object detection may lead to deviations in numerical calculations due to the following two issues: The loss form is not differentiable, and the loss calculated by IoU is inconsistent with the assessment. In order to solve the above challenges in remote sensing images, Yang et al. (2021a,b, 2023) proposed to represent an oriented object as a two-dimensional Gaussian distribution of rotation, which brought new inspiration for object detection. Modeling a remote sensing object as a 2D Gaussian distribution N(m, Σ) at any angle:

$\begin{array}{ll}\{\begin{array}{l}m=(x,y{)}^T\\ {\Sigma }^{1/2}=R\Lambda R^T\end{array}& (1)\end{array}$

where, R represents a 2D rotation matrix and Λ represents a diagonal matrix of eigenvalues. Specifically, the anchor box and the ground-truth of the object are modeled as two 2D rotational Gaussian distributions, and then the distance between the two Gaussian distributions is measured to guide the regression network in training. The design of regression loss function can effectively adapt to the situation of orienting and dense object distribution in remote sensing image. Yang et al. (2021a) used Wasserstein distance for spatial distance measurement, while Yang et al. (2021b) used Kullback-Leibler divergence. These metrics are not closed forms in information geometry field.

3. Proposed method

3.1. Overall framework

The proposed tiny-object-detection framework JSDNet is shown in Figure 2, using RetinaNet (Lin et al., 2020) as the baseline algorithm. The framework comprises three main parts: the window attention backbone, the feature fusion network and the detection sub-network. First, Swin Transformer is used as the backbone for feature extraction. Owing to the large width and high pixel characteristics of remote sensing images, the original backbone of RetinaNet cannot effectively extract fine small object features from remote sensing images. Therefore, it is theoretically valid to use window-based self-attention operations. Swin Transformer processes the image into patches, proposes the concept of a moving window, and only calculates self-attention inside the window, which can effectively reduce the length of the sequence and reduce the computational complexity. JSDNet uses Swin Transformer as the backbone, which can handle the problem of different scale features hierarchically and then optimize the detection of remote sensing tiny objects by multi-scale feature maps. Second, JSDNet inputs the obtained multi-scale feature map into the feature pyramid network for feature fusion. The fusion process adopts a top-down transfer method to transfer the high-level feature semantics to the underlying structure. This is the same as the original feature fusion structure of RetinaNet.

FIGURE 2

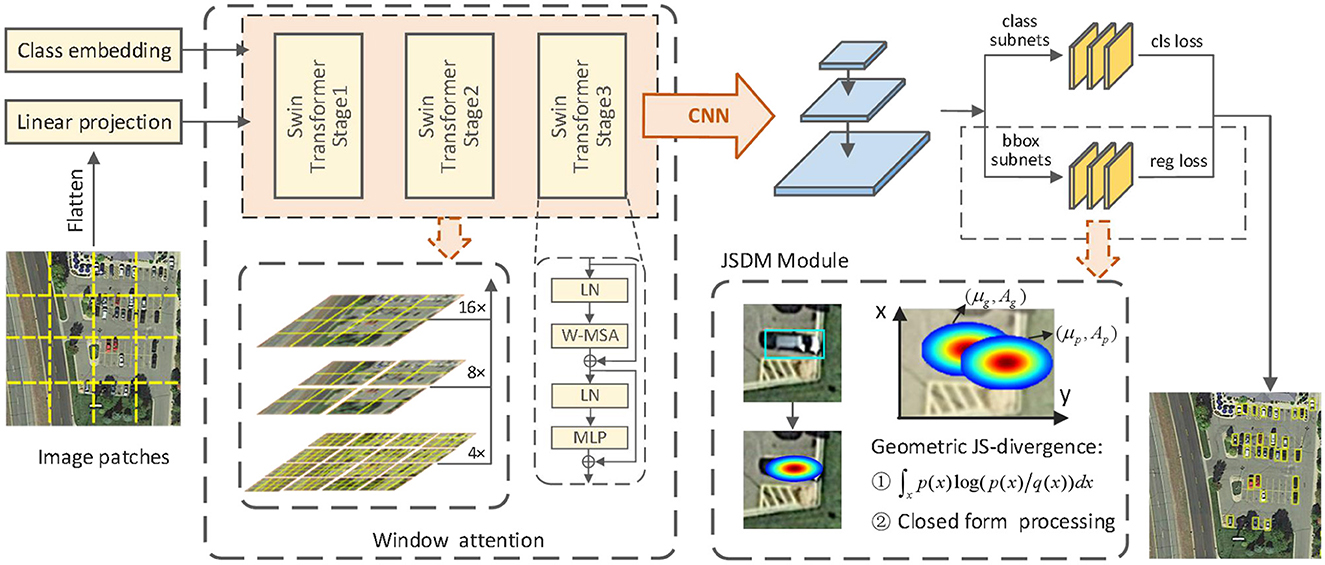
Figure 2. The proposed JSDNet framework. It consists of the Swin Transformer backbone, feature fusion module, and classification and regression sub-networks. The regression sub-network JSDM uses the geometric JS divergence for closed-form processing.

Then, JSDNet feeds the fused features into the detection sub-network, which performs label classification and bounding-box regression tasks. In the bounding-box regression task, the JSDM models the object as a 2D Gaussian distribution from information geometry perspective and uses the abstract mean to calculate the geometric JS divergence, so that the JS divergence can be approximated as a similarity measurement of two Gaussian distributions that can produce closed-form expressions.

3.2. Gaussian distribution modeling for bounding box

Yang et al. (2021a,b, 2023) proposed that the oriented object is represented as a rotating 2D Gaussian distribution, which brings new inspiration for object detection. However, a tiny object has a small number of pixels in the image, and the IoU calculation method is easily affected by the threshold setting. Modeling the tiny object as a 2D Gaussian distribution can avoid this problem and can also distinguish the object information from the redundant background. Specifically, the anchor box and ground-truth are represented by four parameters (x₀, y₀, w, h) of a centroid notation, where (x₀, y₀) represents the coordinates of the rectangle center point, w and h are the length and width of the rectangle, respectively. At this time, it is described as an inscribed ellipse as follows:

$\begin{array}{ll}\frac{4{(x-x_0)}^2}{w^2}+\frac{4{(y-y_0)}^2}{h^2}=1& (2)\end{array}$

where $\frac{w}{2}$ and $\frac{h}{2}$ are semi-major axes of the ellipse, which are equivalent to half the length and width of the rectangle, respectively.

According to probability statistics, the probability density function of the 2D Gaussian distribution is as follows:

$\begin{array}{ll}f(\text{x | }\mu ,\sum )=\frac{\exp (-\frac{1}{2}{(x-\mu )}^{\text{T}}{\displaystyle \sum }^{-1}(x-\mu ))}{2\pi |{\displaystyle \sum {|}^{\frac{1}{2}}}}& (3)\end{array}$

where x denotes the coordinate variable (x, y), μ denotes the mean vector, and ∑ denotes the covariance matrix. When the inscribed ellipse in (1) is set as a standard 2D Gaussian distribution, there is a conversion relationship between the elliptic and the Gaussian distribution in (3):

$\begin{array}{ll}\mu =\left[\begin{array}{c}{x}_0\\ y_0\end{array}\right],{\displaystyle \sum =}\left[\begin{array}{cc}\frac{w^2}{4}& 0\\ 0& \frac{h^2}{4}\end{array}\right]& (4)\end{array}$

At this time, both the ground-truth and anchor box can be modeled as a 2D Gaussian distribution according to the above-mentioned corresponding relationship.

3.3. Closed-form metrics for geometric JS divergence

Let (χ, F) be the measurable space of the image plane, χ be the sample space, and F be the σ−algebra of the measurable events. Denote the distribution variable established in last section as a positive measure μ, the predicted frame of the object as P(μ₁, Σ₁), and the true frame of the object as G(μ₂, Σ₂). At this time, the most basic distribution distance KL Divergence can be defined as follows:

$\begin{array}{ll}KL(P:G):=KL*(G:P)=\int plog(p/g)d\mu & (5)\end{array}$

where p and g represent the Radon-Nikodym derivatives of the Gaussian distribution P and G for the positive measure μ, respectively, and “*” represents the inverse distance. It is clear that the KL divergence is an asymmetric distance. One method to achieve symmetric KL divergence is to convert to standard JS divergence, as follows:

$\begin{array}{ll}JS(P:G):=\frac{1}{2}(KL(P:\frac{P+G}{2})+KL(G:\frac{P+G}{2}))& (6)\end{array}$

Yang et al. (2021b) discussed the use of JS divergence for distance measurement. However, the direct application of the above JS divergence to the distance metric leads to a problem where we ignore that the JS divergence between two Gaussian distributions is not available in closed form. Thus, we can hardly obtain a strict distance metric result and thus cannot accurately guide the regression process of the anchor box. Therefore, the JS divergence calculation for remote sensing tiny objects needs to use the closed-form formula, and the closed form can be obtained according to the given exponential family.

Definition 1 (Abstract mean function, AM). The abstract mean function AM(., .) is a continuous binary function, and on the domain of definition S ⊂ ℝ₊, it satisfies the bounded range as follows:

$\begin{array}{ll}inf\left\{x,y\right\}\le AM(x,y)\le sup\left\{x,y\right\},\forall x,y\in S& (7)\end{array}$

According to Frank (2019), based on AM, we construct a weighted expression AM_α(p, g) for probability distributions with densities p and g, where α ∈ [0, 1].

Definition 2 (Geometric statistical mixture, GSM). For the abstract mean function AM_α(p, g), with probability densities p and g, the mixture of distributions P and G with respect to the geometric mean M can be defined as:

$\begin{array}{l}{\left(PG\right)}_{\alpha }^M(\mu ):=\frac{A{M}_{\alpha }(P(\mu ),G(\mu ))}{N_{\alpha }^M\left(P:G\right)}\\ =\exp \left((1\text{}-\text{}\alpha )P\text{}+\text{}\alpha G\text{}-\text{}\log N_{\alpha }^M\left(P\text{}:\text{}G\right)\right)& (8)\end{array}$

where $N_{\alpha }^M(:)$ is the normalization sub-function. Now, for the distributions P and G, a statistical mixture function weighted by the geometric is obtained.

Definition 3 (Mean JS-divergence, AM-JS-divergence). Extending the concept of a geometric statistical mixture to the JS-divergence of two exponential family distributions, we obtain a generalized weighted form of geometric JS-divergence, and it is geometrically symmetric. The definition of mean JS divergence is as follows:

$\begin{array}{ll}{(JS)}^M:=(1-\alpha )KL(P:{(PG)}_{\alpha }^M)+\alpha KL(G:{(PG)}_{\alpha }^M)& (9)\end{array}$

In particular, when α = 0 or α = 1, no significant mean JS divergence is obtained. The weights α imply a geometrical statistical mixture, so when α ∈ ∀(0, 1), (JS)^M can be used as the generalized JS divergence of the two exponential family distributions P and G.

Proposition Assuming that the prediction box and ground-truth in the image conform to the 2D Gaussian distribution in the exponential family distribution and are denoted as P(μ₁, Σ₁) and G(μ₂, Σ₂), respectively, the geometric mean JS divergence between them can be expressed as follows:

$\begin{array}{l}{\left(JS\right)}^{G_{\alpha }}(p({\mu }_1,{\Sigma }_1):p({\mu }_2,{\Sigma }_2))\\ =\frac{1}{2}(tr\left({\Sigma }_{\alpha }^{-1}((1\text{}-\text{}\alpha ){\Sigma }_1\text{}+\text{}\alpha {\Sigma }_2)\right)+\log \frac{\left|{\Sigma }_{\alpha }\right|}{{\left|{\Sigma }_1\right|}^{1-\alpha }{\left|{\Sigma }_2\right|}^{\alpha }}-\text{}2+\\ (1\text{}-\text{}\alpha )({\mu }_{\alpha }\text{}-\text{}{\mu }_1{)}^{\text{T}}{\Sigma }_{\alpha }^{-1}({\mu }_{\alpha }\text{}-\text{}{\mu }_1)\text{}+\text{}\alpha ({\mu }_{\alpha }\text{}-\text{}{\mu }_2{)}^{\text{T}}{\Sigma }_{\alpha }^{-1}({\mu }_{\alpha }\text{}-\text{}{\mu }_2))& (10)\end{array}$

where (μ_α, Σ_α) is the center of gravity of the matrix harmonics:

$\begin{array}{l}{\mu }_{\alpha }=({\mu }_1{\mu }_2{)}_{\alpha }^{\mu }={\Sigma }_{\alpha }\left((1-\alpha ){\Sigma }_1^{-1}{\mu }_1+\alpha {\Sigma }_2^{-1}{\mu }_2\right),\\ {\Sigma }_{\alpha }=({\Sigma }_1{\Sigma }_2{)}_{\alpha }^{\Sigma }={\left((1-\alpha ){\Sigma }_1^{-1}+\alpha {\Sigma }_2^{-1}\right)}^{-1}& (11)\end{array}$

According to proposition, JSDNet can learn the JS divergence representation between the prediction box and ground-truth, and then as the regression process of the anchor box (x₀, y₀, w, h). Specifically, the anchor-box regression process is realized by calculating the offset, which is the same as the fine-tuning mechanism of the parameter change of RetinaNet.

Figure 3 shows the two-dimensional spatial regression calculation process of the JSDM module. First, the bounding box of a tiny object is modeled to obtain a 2D ellipse. Then, the geometric mean JS divergence is used as distance measure between two 2D Gaussian distributions. Finally, update the four parameters of the prediction box to make the regression network converge.

FIGURE 3

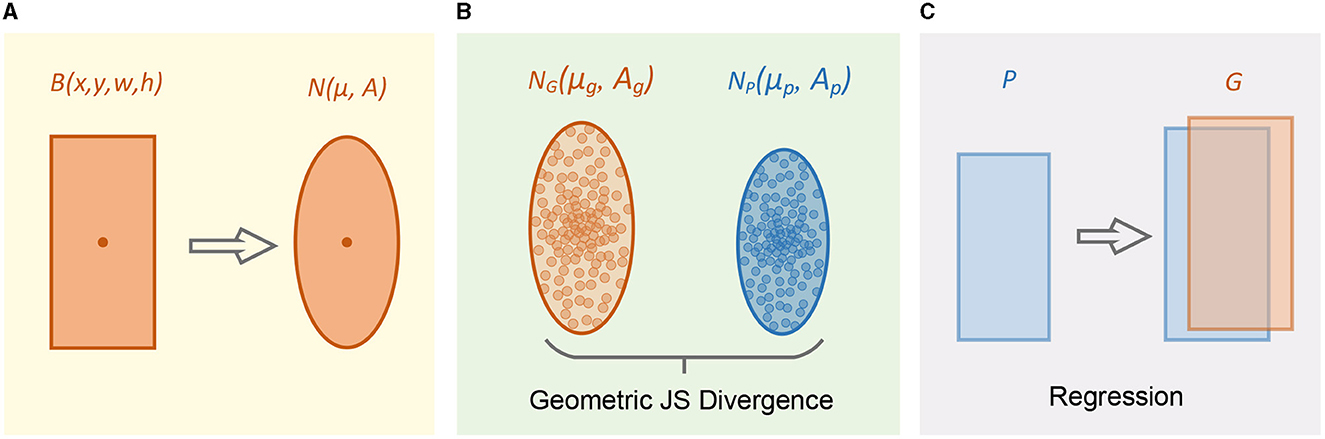
Figure 3. 2D space approximation process of geometric mean JS divergence module. (A) Modeling a Gaussian distribution for bounding box. (B) Calculate geometric JS divergence in 2D space. (C) Adjust predicted box to approximate two distributions.

3.4. JSDNet training

This section defines the classification and regression loss function for JSDNet. First, a nonlinear relationship between the distance function and the geometric mean JS divergence is established. Specifically, square the geometric mean JS divergence in the proposition and convert it into a fractional form, as follows:

$\begin{array}{ll}{(JS)}^{G_{\alpha }}(N_P,N_G)=\frac{1}{\tau +f\left[{(JS)}^{G_{\alpha }}(N_P:N_G)\right]},\tau \ge 1& (12)\end{array}$

where, τ is the offset hyperparameter, f(.) is the square operation of the distance function, and belongs to a nonlinear expression. Tiny objects in remote sensing usually occupy a small proportion of pixels, so horizontal bounding boxes are chosen to locate tiny objects. Assuming that the predicted bounding box of tiny objects follows a Gaussian distribution N_P and the ground-truth follows a Gaussian distribution N_G, each horizontal bounding box uses a four parameter definition method (x₀, y₀, w, h) to represent the center point coordinates and side length of the rectangle. Therefore, the calculation relationship between the relative translation (δ_x, δ_y) and the size scaling (δ_w, δ_h) is as follows, which can guide the horizontal bounding box of tiny objects to update coordinates.

$\begin{array}{l}{\delta }_x=(G_x-x_a)/w_a,{\delta }_y=(G_y-y_a)/h_a\\ {\delta }_w=\log (G_w/w_a),{\delta }_h=\log (G_h/h_a)& (13)\end{array}$

where, (x_a, y_a, w_a, h_a) represents an anchor box for the regression process. The differential calculation of the anchor box regression process may result in a very small value for (13). This typically results in regression losses that are much smaller than classification losses. Therefore, normalizing the mean and variance of (δ_x, δ_y, δ_w, δ_h), and incorporating the geometric mean form JS divergence in the previous section into the standard regression loss function, as shown in Equation (14), can avoid the limitations of traditional IoU loss.

$\begin{array}{ll}{\mathcal{L}}_{reg}=1-{(JS)}^{G_{\alpha }}(N_P:N_G)& (14)\end{array}$

4. Experiments

Our experiments are conducted on the AI-TOD and DOTA1.0 datasets and compared with advanced general object detectors to verify the effectiveness of the proposed method for remote sensing tiny object detection.

4.1. Experimental settings

(1) Dataset: AI-TOD dataset is a remote sensing tiny object dataset with 28,036 images of 800 × 800 pixels, including eight categories and 700,621 tiny objects. These instances are different from objects in other datasets, as the instances have a small number of pixels. Therefore, the dataset is suitable for training and testing the tiny object detector proposed in this article. We abbreviate the AI-TOD object classes as airplane (APL), bridge (BR), storage-tank (ST), ship (SH), swimming-pool (SP), vehicle (VE), person (PE), and wind-mill (WM). The DOTA1.0 dataset is a public large-scale remote sensing image object detection dataset, with 2,806 satellite or aerial images of about 4,000 × 4,000 pixels, including 15 object categories and 188,282 instances. We only use data augmentation on the DOTA1.0 dataset to avoid network training overfitting.

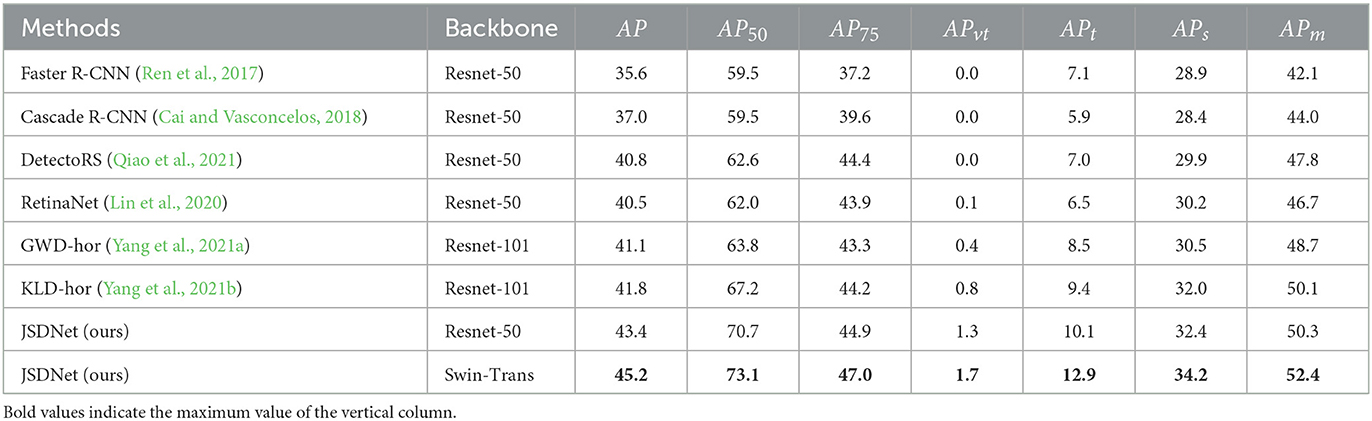
(2) Evaluation Metrics: We use average precision (AP) and mean average precision (mAP) to compare the performance of different detectors. Also, we refer to the evaluation indicators definition in AI-TOD dataset, including AP calculation under different IoU thresholds, and the evaluation of different scales of pixels (AP_vt, AP_t, AP_s and AP_m represent 2-8 pixels, 8-16 pixels, 16-32 pixels, and 32-64 pixels, respectively), along with the accuracy calculations for each category.

(3) Details: All experiments are performed on a workstation with an NVIDIA RTX 3090 GPU (24G). We use Swin Transformer as the pretrained model for network fine-tuning. During model training, the SGD optimizer is used for gradient descent and updates, the initial learning rate is set to 0.001, and the weight coefficient α are compared with multiple sets of values. The strides for training AI-TOD and DOTA datasets are 320K and 360K, respectively; the weight momentum and decay are set to 0.9 and 0.0001, respectively; and the batch size for training each model is set to 4.

4.2. Ablation studies

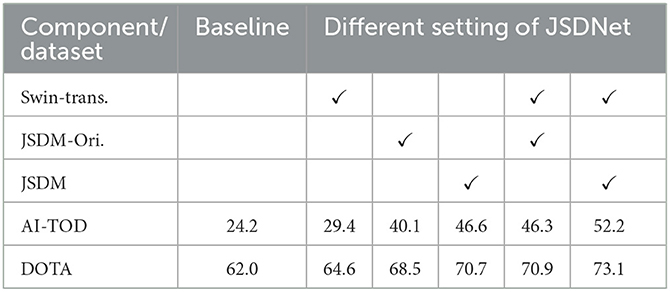
To verify the effectiveness of the proposed method composition structure, we conduct ablation analysis on two datasets. Table 1 shows the results of using AP₅₀ ablation to analyze the effect of each component in JSDNet, including the effect of the Transformer structure integrated into the CNN network, the effect of directly using the original JS divergence formula, and the improved effect of using the geometric JS divergence. The comparison shows that the model based on the Transformer backbone can slightly improve the object feature extraction ability. Compared with the baseline algorithm, the AI-TOD and DOTA datasets increase the AP value by 5.2% and 2.6% respectively. Compared with the original JS divergence formula, the improved geometric JS divergence with closed-form formula can better improve the performance of object detectors, and the AP value is increased by 5.9% and 2.2% respectively. We believe that the JSDM module can greatly improve the detection results. This module provides a more accurate anchor box regression calculation method, which alleviates two shortcomings of IoU threshold calculation (i.e., imbalance in the number of positive and negative samples for tiny objects and imbalance in scale samples). Compared to using the original JS divergence formula, geometric JS divergence belongs to a more accurate closed form, which can reduce the systematic error of numerical calculation, and thus obtain better detection results for tiny objects.

TABLE 1

Table 1. Ablation study on AI-TOD and DOTA datasets.

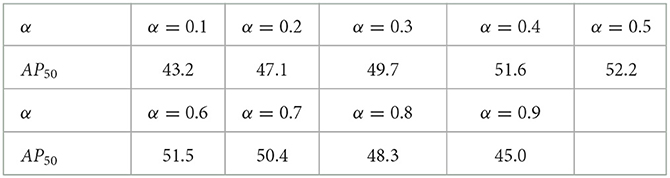
Table 2 explores the impact of the weight coefficients of geometric JS divergence on detection performance on the AI-TOD dataset. As can be seen, when α = 0.5, the detector was able to achieve the optimal detection effect, with the AP₅₀ value reaching 52.2%. The smaller or larger the value of α, the more unbalanced the coupling between the covariance matrices of the two Gaussian distributions. This will lead to deviations in the regression constraints, and weakening the detection effect. The experiment shows that the improved geometric JS divergence can obtain closed form calculation results. When the covariance matrices of two Gaussian distributions are balanced coupled together, better detection results can be obtained, and these results are approximately symmetric.

TABLE 2

Table 2. Effect study of different α values on AI-TOD dataset.

4.3. Comparison and discussion

This section evaluates JSDNet and various algorithms on AI-TOD and DOTA datasets.

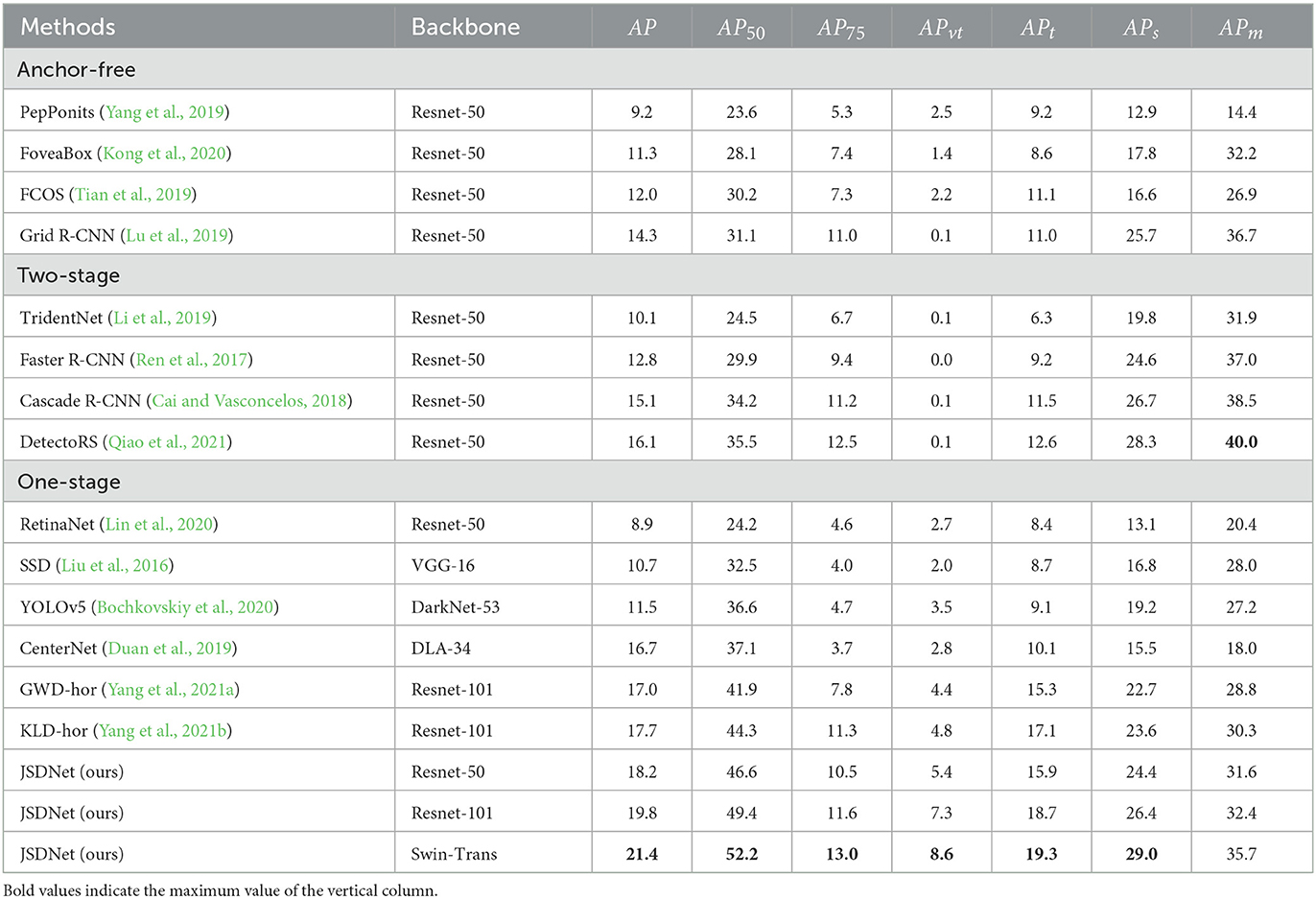
(1) AI-TOD dataset: We have conducted experiments on some baseline object detectors, including methods with and without anchor box. Table 3 is a comparison of the quantitative results of the algorithm, listing the AP value calculation results for different thresholds and scales. It can be seen that the proposed algorithm significantly improves the detection performance of tiny objects in remote sensing. JSDNet achieved 52.2% on the AP₅₀ and 13.0% on the AP₇₅, leading other methods, including the GWD and KLD methods under horizontal bounding box detection. CenterNet and YOLOv5 have achieved good results in traditional detectors, but it is clear that these methods are weak for tiny object detection. Experiment results demonstrate the effectiveness of using the analytic form of geometric JS divergence in the measurement of object detection distribution, and achieve the most advanced performance. The AP_vt and AP_t represent the evaluation of tiny object detection, with JSDNet reaching 8.6% and 19.3%, respectively, which is better than other methods, indicating that JSDNet can effectively learn the geometric JS divergence representation of remote sensing tiny objects, thereby avoiding the traditional IoU calculation.

TABLE 3

Table 3. Comparison of quantitative results of different indicators on AI-TOD.

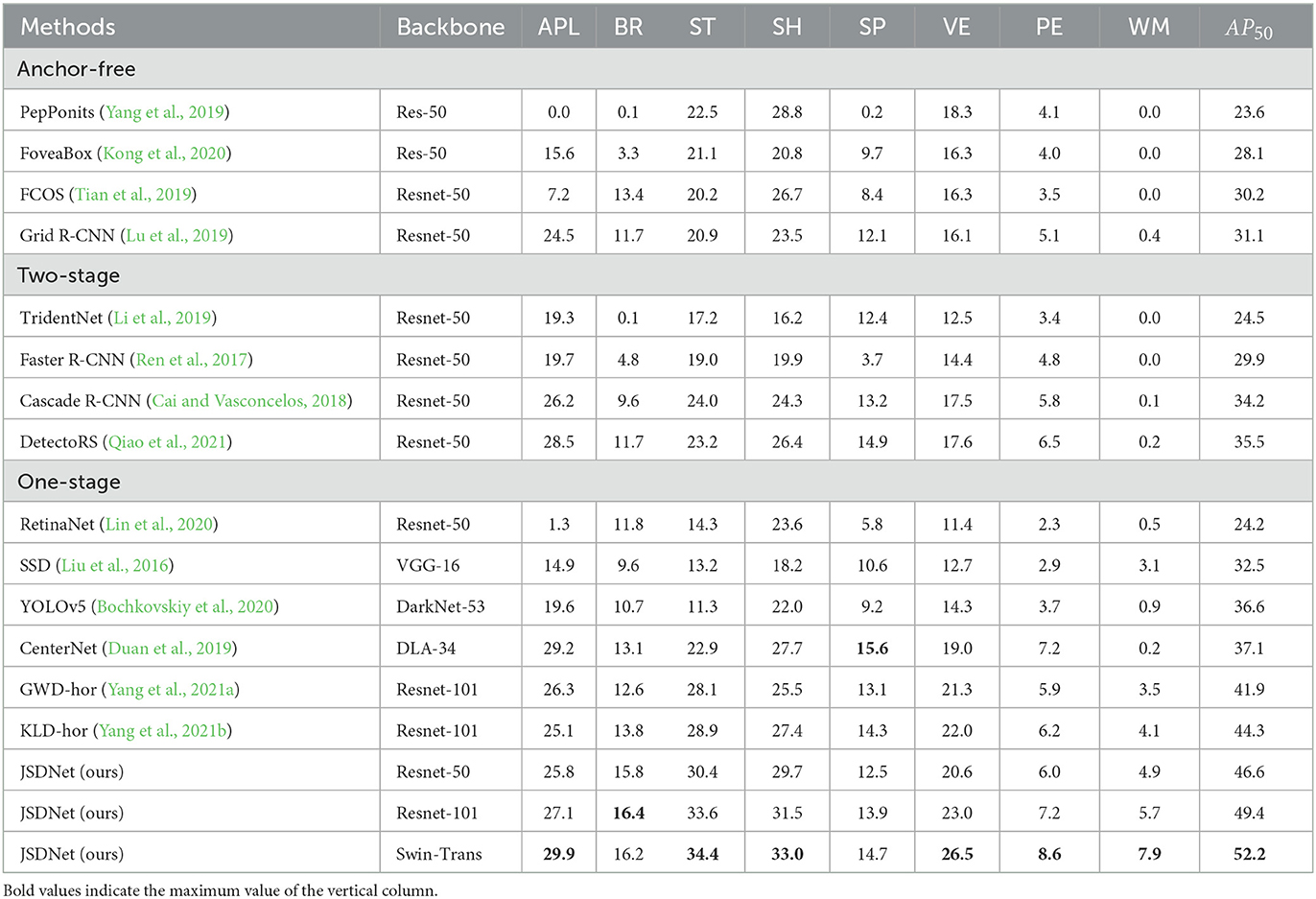
Table 4 shows the detection results for eight object categories in the AI-TOD dataset. The proposed method is leading in terms of effectiveness in six categories, only second to the optimal results in the other two categories. The horizontal bounding box detection results using Wasserstein distance and KL divergence for distance measurement are listed in the table. Although they have also achieved good results, they are not closed formulas in information geometry, resulting in errors in the similarity measurements. Therefore, using the geometric JS divergence method achieves better detection performance. In addition, in some challenging object categories, such as SP, PE, WM, etc., JSDNet has advantages in detection effectiveness. The distribution of samples in these categories is uneven, and the background around the object is complex. Therefore, all methods have obtained lower AP values. Figure 4 shows some qualitative reasoning results for JSDNet. It is worth noting that JSDNet can accurately detect densely distributed tiny objects, such as vehicles, ships, storage tanks, and so on. Although JSDNet uses a horizontal bounding box, from the visual effect, the horizontal box is more suitable for positioning tiny objects in remote sensing image, and using a rotation box has little significance.

TABLE 4

Table 4. Comparison of quantitative results of different categories on AI-TOD.

FIGURE 4

Figure 4. Qualitative inference results of JSDNet on AI-TOD. (A) Airplane. (B) Bridge. (C) storage tank. (D) Ship. (E) Swimming pool. (F) Vehicle. (G) Person. (H) Wind mill.

(2) DOTA dataset: Table 5 lists the detection results of JSDNet and some baseline algorithms on the DOTA dataset. When using Resnet-50 as the backbone network, the detection results of this method are still good, with AP₅₀ achieving 70.7%. In terms of AP_vt and AP_t indicators, some general detectors performed weakly. We believe that this is due to the impact of IoU calculation and threshold setting for tiny objects, while the GWD, KLD and JSDNet with horizontal bounding box have improved this issue somewhat. When using Swin Transformer as the backbone network, JSDNet can extract features of tiny objects more sufficient, improving the detection results. The AP₅₀ achieved 73.1%. Figure 5 is visual result of JSDNet on the DOTA test set. JSDNet can accurately regress the spatial location information of tiny objects. The figure shows the detection effect of bridges and airplanes, which belong to smaller objects in the dataset and can still be accurately located.

TABLE 5

Table 5. Comparison of quantitative results on DOTA.

FIGURE 5

Figure 5. Qualitative inference results of JSDNet on DOTA. (A) Bridge. (B) Plane.

5. Conclusion

The sensitivity of tiny object detection in remote sensing images to the IoU threshold and the IoU calculation process makes a robust tiny object detector particularly important. A small position offset leads to a large change in the IoU value. Therefore, this article has adopted the closed-form of geometric JS divergence representation of tiny objects as the similarity measure for bounding-box distribution. In this article, the Swin Transformer model is adaptively integrated into the tiny object detection network to efficiently extract tiny features. The JSDM module is based on the Gaussian distribution modeling of the ground-truth and anchor box, and then the geometric JS divergence with the closed-form formula is applied to measure the distribution distance. The ablation and comparison experiments have been carried out on AI-TOD and DOTA datasets, and the results show that the proposed JSDNet can effectively improve the performance of remote sensing tiny object detection and can fully learn the geometric JS divergence representation of tiny objects.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SN: Conceptualization, Resources, Writing—review & editing. CL: Methodology, Writing—review & editing. HW: Software, Writing—original draft. YLi: Validation, Writing—review & editing. YLia: Formal analysis, Investigation, Writing—review & editing. NL: Writing—review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China under Grant Nos. 61805283, 61805284, and 61906213.

Acknowledgments

The authors would like to thank all reviewers and editors for their comments on this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bochkovskiy, A., Wang, C.-Y., and Liao, H.-Y. M. (2020). YOLOv4: Optimal speed and accuracy of object detection. arXiv [preprint]. doi: 10.48550/arXiv.2004.10934

CrossRef Full Text | Google Scholar

Cai, Z., and Vasconcelos, N. (2018). “Cascade r-cnn: delving into high quality object1 detection,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Piscataway: IEEE), 6154–6162.

Google Scholar

Cui, L., Lv, P., Jiang, X., Gao, Z., Zhou, B., Zhang, L., et al. (2022). Context-aware block net for small object detection. IEEE Trans. Cybern. 52, 2300–2313. doi: 10.1109/TCYB.2020.3004636

PubMed Abstract | CrossRef Full Text | Google Scholar

Deasy, J., Simidjievski, N., and Liò, P. (2020). “Constraining variational inference with geometric jensen-shannon divergence,” in Proceedings of Advances in Neural Information Processing Systems (Massachusetts: Cambridge).

Google Scholar

Deng, C., Wang, M., Liu, L., Liu, L., and Jiang, Y. (2022). Extended feature pyramid network for small object detection. IEEE Trans. Multimedia 24, 1968–1979. doi: 10.1109/TMM.2021.3074273

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, K., Bai, S., and Xie, L. (2019). “Centernet: keypoint triplets for object detection,” in Proceedings of IEEE International Conference on Computer Vision (Piscataway: IEEE), 6568–6577.

Google Scholar

Feng, X., Han, J., Yao, X., and Cheng, G. (2021). Tcanet: triple context-aware network for weakly supervised object detection in remote sensing images. IEEE Trans. Geosci. Remote Sens. 59, 6946–6955. doi: 10.1109/TGRS.2020.3030990

CrossRef Full Text | Google Scholar

Frank, N. (2019). On the jensen–shannon symmetrization of distances relying on abstract means. Entropy 21, 1–23. doi: 10.3390/e21050485

CrossRef Full Text | Google Scholar

Ge, Z., Liu, S., Li, Z., Yoshie, O., and Sun, J. (2021). “Ota: optimal transport assignment for object detection,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Piscataway: IEEE), 303–312.

Google Scholar

Han, W., Kuerban, A., Yang, Y., Huang, Z., Liu, B., and Gao, J. (2022). Multi-vision network for accurate and real-time small object detection in optical remote sensing images. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi: 10.1109/LGRS.2020.3044422

CrossRef Full Text | Google Scholar

Kim, J., and Hwang, Y. (2022). Gan-based synthetic data augmentation for infrared small target detection. IEEE Trans. Geosci. Remote Sens. 60, 1–12. doi: 10.1109/TGRS.2022.3179891

CrossRef Full Text | Google Scholar

Kim, K., and Lee, H. (2020). “Probabilistic anchor assignment with iou prediction for object detection,” in Proceedings of the European Conference on Computer Vision (Piscataway: IEEE), 355–371.

Google Scholar

Kong, T., Sun, F., Liu, H., Jiang, Y., Li, L., and Shi, J. (2020). Foveabox: beyound anchor-based object detection. IEEE Trans. Image Process. 29, 7389–7398. doi: 10.1109/TIP.2020.3002345

CrossRef Full Text | Google Scholar

Leng, J., Ren, Y., Jiang, W., Sun, X., and Wang, Y. (2021). Realize your surroundings: exploiting context information for small object detection. Neurocomputing 433:287–299. doi: 10.1016/j.neucom.2020.12.093

CrossRef Full Text | Google Scholar

Li, Y., Chen, Y., Wang, N., and Zhang, Z. (2019). “Scale-aware trident networks for object detection,” in Proceedings of IEEE International Conference on Computer Vision (Piscataway: IEEE), 6054–6063.

Google Scholar

Li, Y., Huang, Q., and Pei, X. (2021). Cross-layer attention network for small object detection in remote sensing imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 14, 2148–2161. doi: 10.1109/JSTARS.2020.3046482

CrossRef Full Text | Google Scholar

Lin, T., Goyal, P., Girshick, R., He, K., and Dollar, P. (2020). Focal loss for dense object detection. IEEE Trans. Pattern Anal. Mach. Intell. 42, 317–328. doi: 10.1109/TPAMI.2018.2858826

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, L., Ouyang, W., Wang, X., Feiguth, P., Chen, J., Liu, X., et al. (2020). Deep learning for generic object detection: a survey. Int. J. Comput. Vision 128, 261–318. doi: 10.1007/s11263-019-01247-4

CrossRef Full Text | Google Scholar

Liu, W., Anguelov, D., and Erhan, D. (2016). “SSD: single shot multibox detector,” in Proceedings of the European Conference on Computer Vision (Berlin: Springer), 21–37.

Google Scholar

Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., et al. (2021). “Swin transformer: hierarchical vision transformer using shifted windows,” in Proceedings of the IEEE Conference on Computer Vision, 10012–10022.

Google Scholar

Lu, W., Lan, C., and Niu, C. (2023). A cnn-transformer hybrid model based on cswin transformer for uav image object detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 16, 1211–1231. doi: 10.1109/JSTARS.2023.3234161

CrossRef Full Text | Google Scholar

Lu, X., Li, B., Yue, Y., Li, Q., and Yan, J. (2019). “Grid r-cnn,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Piscataway: IEEE), 7363–7372.

Google Scholar

Qiao, S., Chen, L.-C., and Yuille, A. (2021). “Detectors: detecting objects with recursive feature pyramid and switchable atrous convolution,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Piscataway: IEEE), 10213–10224.

PubMed Abstract | Google Scholar

Ren, S., He, K., Girshick, R., and Sun, J. (2017). Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 39, 1137–1149. doi: 10.1109/TPAMI.2016.2577031

PubMed Abstract | CrossRef Full Text | Google Scholar

Thiagarajan, P., and Ghosh, S. (2022). Jensen-shannon divergence based novel loss functions for bayesian neural networks. arXiv [preprint]. doi: 10.48550/arXiv.2209.1136

CrossRef Full Text | Google Scholar

Tian, Z., Shen, C., and Chen, H. (2019). “Fcos: Fully convolutional one-stage object detection,” in Proceedings of the IEEE Conference on Computer Vision (Piscataway: IEEE), 9627–9636.

Google Scholar

Xia, G.-S., Bai, X., Ding, J., Zhu, Z., Belongie, S., Luo, J., et al. (2018). “Dota: a large-scale dataset for object detection in aerial images,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Piscataway: IEEE), 3974–3983.

Google Scholar

Xu, C., Wang, J., Yang, W., Yu, H., Yu, L., and Xia, G. (2022). Detecting tiny objects in aerial images: a normalized wasserstein distance and a new benchmark. ISPRS J. Photogr. Remote Sens. 190, 79–93. doi: 10.1016/j.isprsjprs.2022.06.002

CrossRef Full Text | Google Scholar

Yang, T., Zhang, X., and Li, Z. (2018). “Metaanchor: learning to detect objects with customized anchors,” in Proceedings of the Advances in Neural Information Processing Systems (Massachusetts: Cambridge), 318–328.

Google Scholar

Yang, X., Yan, J., Ming, Q., Wang, W., Zhang, X., and Tian, Q. (2021a). “Rethinking rotated object detection with gaussian wasserstein distance loss,” in Proceedings of the 24th International Conference on Machine Learning (New York, NY: ACM), 11830–11841.

Google Scholar

Yang, X., Yang, X., Yang, J., Ming, Q., Wang, W., Tian, Q., et al. (2021b). “Learning high-precision bounding box for rotated object detection via kullback-leibler divergence,” in Proceedings of the Advances in Neural Information Processing Systems (Massachusetts: Cambridge), 18381–18394.

Google Scholar

Yang, X., Zhang, G., Yang, X., Zhou, Y., Wang, W., Tang, J., et al. (2023). Detecting rotated objects as gaussian distributions and its 3-d generalization. IEEE Trans. Pattern Anal. Mach. Intell. 45, 4335–4354. doi: 10.1109/TPAMI.2022.3197152

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z., Liu, S., Hu, H., Wang, L., and Lin, S. (2019). “Reppoints: point set representation for object detection,” in Proceedings of the International Conference on Computer Vision (Piscataway: IEEE), 9657–9666.

Google Scholar

Zeng, N., Wu, P., Wang, Z., Li, H., Liu, W., and Liu, X. (2022). A small-sized object detection oriented multi-scale feature fusion approach with application to defect detection. IEEE Trans. Instrum. Meas. 71, 1–14. doi: 10.1109/TIM.2022.3153997

CrossRef Full Text | Google Scholar

Zhang, K., Wu, Y., Wang, J., and Wang, Q. (2022). A hierarchical context embedding network for object detection in remote sensing images. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi: 10.1109/LGRS.2022.3161938

CrossRef Full Text | Google Scholar

Zhang, S., Zhu, X., and Lei, Z. (2017). “S3fd: single shot scale-invariant face detector,” in Proceedings of the International Conference on Computer Vision (Piscataway: IEEE), 192–201.

Google Scholar

Zhang, X., Feng, Y., and Zhang, S. (2022). Finding nonrigid tiny person with densely cropped and local attention object detector networks in low-altitude aerial images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 15, 4371–4385. doi: 10.1109/JSTARS.2022.3175498

CrossRef Full Text | Google Scholar