
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Neurorobot. , 22 December 2022
Volume 16 - 2022 | https://doi.org/10.3389/fnbot.2022.1105177
This article is part of the Research Topic Learning and control in robotic systems aided with neural dynamics View all 6 articles
In a complicated forest environment, it is usual to install many ground-fixed devices, and patrol personnel periodically collects data from the device to detect forest pests and valuable wild animals. Unlike human patrols, UAV (Unmanned Aerial Vehicles) may collect data from ground-based devices. The existing UAV path planning method for fixed-point devices is usually acceptable for simple UAV flight scenes. However, it is unsuitable for forest patrol. Meanwhile, when collecting data, the UAV should consider the timeliness of the collected data. The paper proposes two-point path planning and multi-point path planning methods to maximize the amount of fresh information collected from ground-fixed devices in a complicated forest environment. Firstly, we adopt chaotic initialization and co-evolutionary algorithmto solve the two-point path planning issue considering all significant UAV performance and environmental factors. Then, a UAV path planning method based on simulated annealing is proposed for the multi-point path planning issue. In the experiment, the paper uses benchmark functions to choose an appropriate parameter configuration for the proposed approach. On simulated simple and complicated maps, we evaluate the effectiveness of the proposed method compared to the existing pathplanning strategies. The results reveal that the proposed ways can effectively produce a UAV patrol path with higher information freshness in fewer iterations and at a lower computing cost, suggesting the practical value of the proposed approach.
Many ground-based fixed-point Internet of Things devices (also called IoT equipment) must be deployed during forest pest and disease prevention and rare species monitoring in order to collect ecological factors, various types of images, and other crucial data. Due to the fact that these devices are typically used in forests, which have high crown densities, complex environments, and no internet access, manual methods are typically used to regularly patrol fixed-point equipment in the forest and collect perception data. Manual data collection during patrols is time-consuming, ineffective, and increases patrol costs. Perceived data is frequently not obtained in a timely manner, leading to data quality issues like data loss. This is especially true when fixed-point equipment is deployed in challenging mountain environments. These have a significant impact on the precision of disaster and other warnings, as well as forest protection.
The UAV (unmanned aerial vehicle) has a wide load platform, high cruising efficiency on fixed routes, and other features. The data collected by the ground fixed-point equipment in the fixed-point cruise mode can be obtained in complex mountain environments by the multi-source sensor equipment mounted on the UAV, and the data can then be stored in the data center for further processing and analysis when the UAV returns. UAV patrol has gradually taken the place of manual patrol in maintaining some national forest parks and keeping an eye on the area close to cities.
Path planning allows for the prompt collection of data from fixed-point equipment deployed in the challenging mountain environment, solving the issue of manual data collection. Under a variety of constraints, including the performance of the UAV, its maximum flight length, potential environmental threats, flight altitude, maximum turning angle, and maximum climb/dive angle, traditional UAV path planning can be seen as a feasible flight path from the starting point to the target point. Numerous researchers, including (Yingkun, 2018; Hu et al., 2020; Kiani et al., 2022), have investigated UAV cruise problems and track path planning techniques and proposed a range of models and methods for urban security, agricultural patrol, and other scenarios. These techniques, however, typically only work for the starting and stopping points of a fixed-point track problem. The requirements of the forest point patrol data collection are not met because the scenario where the navigation needs to cover multiple points is not taken into account. The accuracy and timeliness of the data used in wildlife monitoring, forest disaster warning, and other specialized fields are also based on how quickly the patrol collects data. As a result, when the UAV is on patrol, the timeliness of data collection should also be prioritized.
Therefore, this paper focuses on the optimal trajectory planning problem of UAV fixed-point data collection in complex forest environments, with the goal of effectively obtaining a feasible trajectory planning path that satisfies fundamental requirements like flight performance and equal-height obstacle avoidance through the co-evolution method with domain adaptation. The perception data from all types of ground fixed point equipment has a significant time sensitivity when it comes to data collection during the forest patrol process. To assess how timely UAV data collection is, the age of information (AoI) index was created. As a result of AoI’s critical importance in patrol planning, AoI was included in the goals of UAV patrol planning. The paper’s specific contributions consist of:
(1) A path planning method for UAV fixed-point collection of forest floor monitoring data with comprehensive navigation performance, AoI, and other factors in complicated forest environments is provided. This method is targeted at time-sensitive forest monitoring tasks such as wildlife patrol, forest fire prevention, and pest monitoring.
(2) The plan took into account a wide range of variables, including the UAV data collection mode, the patrol or monitoring information timeliness, the UAV navigation posture, the obstacle avoidance in complex environments, and others. It methodically abstracted the objectives and constraints (terrain, threat, etc.) of UAV path planning in various intricate scenarios.
(3) An algorithm for co-evolving UAV patrol paths through complex forests is put forth. The algorithm continuously improves the dominant strategy applicable to the current scene from multiple evolutionary strategies through enhanced learning, then solves the UAV patrol flight path in an efficient and adaptive manner based on the characteristics of the patrol environment and AoI requirements.
Unmanned aerial vehicles path planning is a crucial component of UAV system design and serves as the foundation for UAV edge calculations, networking data transmission, and UAV flight control (Pehlivanoglu and Pehlivanoǧlu, 2021). At the moment, there are two main areas of UAV path planning research. The first step is to use domain problem modeling to attempt an accurate description of the domain characteristics and essential components of UAV solutions. The second is to design a UAV path planning algorithm that is efficient and satisfies the domain modeling characteristics.
Environment modeling and UAV modeling are two common examples of domain problem modeling. Environmental modeling is primarily used in UAV application scenarios, such as those involving city, mountain, and weapon threat models. Maximum flight height, maximum deflection angle, maximum pitch angle, maximum energy power, and longest flight path are among the flight characteristics that are primarily taken into account in UAV modeling.
Many researchers have adopted AoI as a crucial metric to assess the timeliness of data collection in UAV modeling in recent years because the perception data collected by UAV should be delivered to the data collector as soon as possible (Abbas et al., 2022). In 2012, (Kaul et al., 2012) first put forth the conception of AoI and described it as the interval from the time of packet generation to the present. Following that, many academics studied UAV path planning based on AoI and tailored to the needs of the field (Abd-Elmagid et al., 2019). Jointly optimized UAV flight trajectory using deep reinforcement learning framework, aiming for the least weighted sum of AoI (Jia et al., 2019) aiming to minimize the average AoI of sensors, optimizing UAVs’ flight trajectory and data collection mode through dynamic programming algorithms (Liu et al., 2018) took the maximum AoI optimal trajectory, averaged AoI optimal trajectory as targets, and used a dynamic programming algorithm and genetic algorithm to design the path planning of UAV in two-dimensional space (Tong et al., 2019) continued their research based on (Liu et al., 2018), using the nearest neighbor propagation algorithm to form sensor networks by clustering, reducing the influence of sensor size on algorithm efficiency through the specific collection points of each sensor network. Then designing the ideal trajectory using the dynamic programming algorithm (Liu et al., 2021) investigated the data collection technique used by unmanned aerial vehicles in wireless sensor networks based on AoI.
According to all of the aforementioned studies, AoI-based UAV path planning modeling has emerged as the most effective way to address the issue of the timing of domain perception data collection. The aforementioned studies, however, mainly concentrate on two-dimensional or approximate plane scenes. Complex forest scene patrol scenes cannot be directly applied to the relatively simple constraints taken into account in scene abstraction and the formation of target routes. Building a domain problem model for effective data collection from multi-point equipment at various altitudes based on AoI and complex conditions such as geographic factors, UAV performance, and UAV collision remains a necessary challenge for complex forest scene patrol.
In the aspect of UAV path planning algorithm design, heuristic algorithm or bionics algorithm has become the leading technical route. For example, Neural Networks (NNs) (Yan et al., 2020; Jin et al., 2022b; Shi et al., 2022; Xie et al., 2022), Dijkstra Algorithm (Maini and Sujit, 2016), Ant Colony Algorithm (ACO) (He et al., 2013), Artificial Potential Field Method (APF) (Chen et al., 2016a), Particle Swarm Optimization (PSO) (Zhang et al., 2013), Artificial Bee Colony (ABC) (Goel and Singh, 2013), Simulated Annealing Algorithm (SA) (Turker et al., 2015), and Genetic Algorithm (GA) (Xiao-Ting et al., 2013; Wang and Chen, 2014). Some scholars improved the above methods to build a more efficient UAV path-solving algorithm. Pehlivanoglu (2012) designed a multi-frequency vibration genetic algorithm (MVGA) that supports the Voronoi diagram to solve the problem of UAV path planning (Yang and Yoo, 2018) designed a UAV flight path planning method based on information such as no-fly zone, geographical positioning conditions, and sensor deployment by using a multi-objective biologically-inspired algorithm (Nikolos and Tsourvelouds, 2009) combined the traditional genetic algorithm and the improved proliferation genetic algorithm to design a path planner for the autonomous navigation of UAVs (Chen et al., 2016b) improved the path planning method through improved Particle Swarm Optimization (PSO) algorithm and Genetic Algorithm (GA) (Liu et al., 2016) solved the PSO algorithm’s efficiency problem in solving path planning from multiple perspectives, such as particle search space limitation and sensitivity.
The aforementioned research demonstrates that the key to increasing the effectiveness of UAV path planning is optimizing a single evolutionary strategy, coordinating multiple evolutionary strategies, and adapting to solve problems. However, in a complex forest environment, the UAV patrol path must deal with the accuracy of fixed point equipment’s data collection and ensure that UAV performance consumption and obstacle avoidance in a three-dimensional complex forest scene. The overall optimization algorithm structure, collaborative method of calculation strategy, algorithm execution efficiency, and domain problem ability must still be combined to create a UAV path planning algorithm with high problem execution efficiency, robustness, and scene generalization ability.
The actual patrol path of UAVs in a complex forest environment can be planned in two steps to gather data on ground equipment dispersed in various locations (Figure 1). In the first stage, a smooth multi-track flight path was built between the data collection points of two fixed points on the ground by combining flight obstacle avoidance, flight energy consumption, and other factors. The optimal path between every two points is successively obtained in the second stage, and the patrol path—capable of patrolling all the ground equipment at the points—is constructed on the basis of the smooth path between the points constructed in the first stage. The first stage, which will be abstracted in Section “3.1.1 Scenario of UAV two-point path planning,” can be represented as a flight path planning scenario of the flight path between two fixed-point devices. The second stage, which will be abstracted in Section “3.1.2 Scenario of UAV multi-point path planning,” can be represented as a global path planning scenario of flight paths between all fixed point equipment.
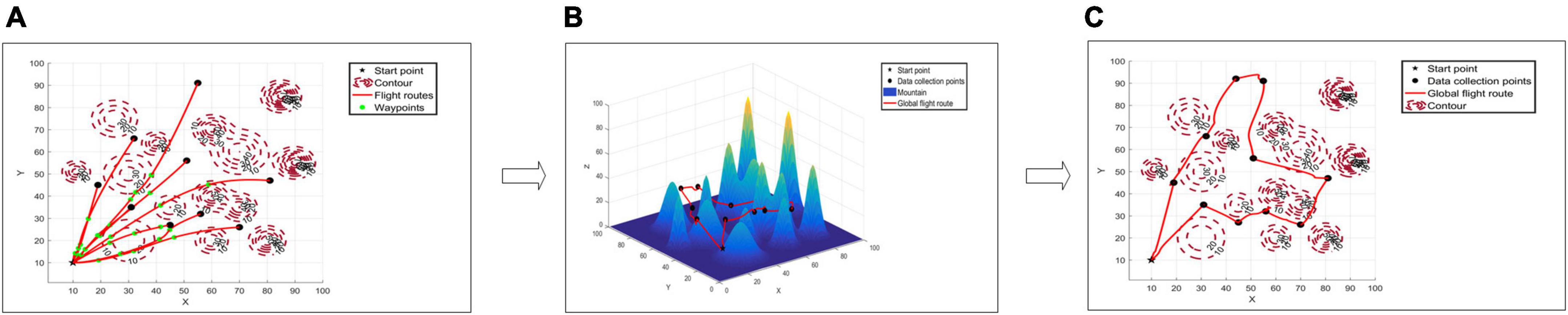
Figure 1. Unmanned aerial vehicles (UAV) forest fixed-points patrol diagram. Panel (A) is the top view of two-point path planning, panel (B) is the route map of multi-point path planning, and panel (C) is the top view of route map of multi-point path planning.
To ensure that the UAV can successfully avoid flight obstacles while adhering to energy consumption restrictions, take into account the complex landforms, numerous obstacles, and other features present in the forest scene that the UAV is inspecting. Thus, in order to create the three-dimensional path planning scene for the UAV, flight paths must be constructed for every pair of two points in the multi-point path planning in Section “3.1.2 Scenario of UAV multi-point path planning.”
In the two-point path planning, when there are obstacles such as high mountains in the process of flying from point vk to point vk + 1, the flight path of the UAV is no longer a simple straight line, but connects point vk to point vk+ 1 and avoids multiple obstacles. The three-dimensional spatial curve path (vk, d1, d2, …, dp, vk + 1) is composed of p intermediate points (Yang et al., 2015) (d1, d2, …, dp) (Figure 2).
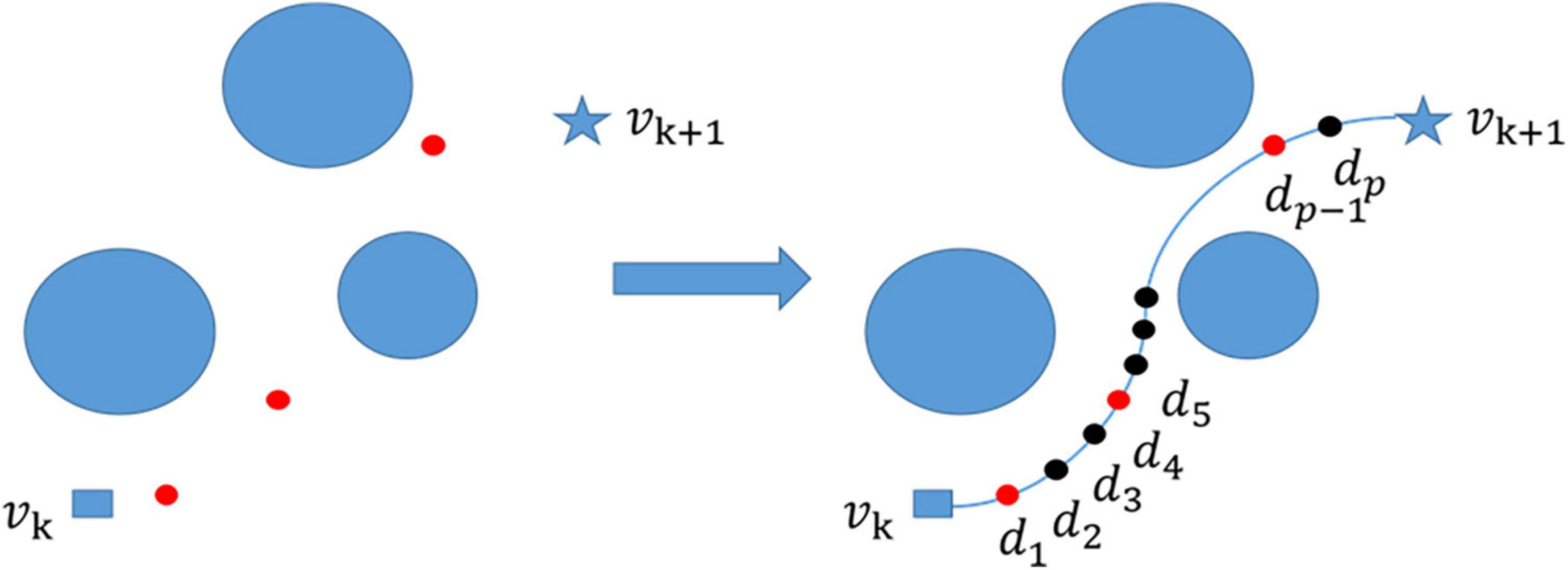
Figure 2. Path smoothing, generate a number of waypoints (red points) between the start point and end point, then generate a large number of intermediate points (black points) based on path smoothing, and finally connect them into a smooth curve.
According to the two-point path planning scenario representation method, the time required for the UAV to move from point vk and point vk+ 1 is shown in formula (1). η(k),(k+ 1) represents the time spent going from vk to vk+ 1 on the two-point path.
Among this v represents the speed of the drone, and when s is 1, l1 represents the Euclidean distance from vk to d1, ls represents the Euclidean distance from ds−1 to ds,when s is p+1, lp+ 1 represents the Euclidean distance from dp to vk+ 1.
In the UAV multi-point path planning scenario, the UAV will fly over the ground sequentially to gather data on wildlife, forest and grass disaster warning, and other time-sensitive data collected at the fixed points (Liu et al., 2018). Each location is traversed by the UAV, which collects all the data and sends it back to the data center. In order to obtain and excavate crucial data in the forest and grass field, such as forest and grass early warning and priceless animal habitat, the data center will conduct additional analysis and processing of the data collected by the UAV.
The set V = {v1,…,vN} is used to represent the location of fixed equipment to be flown over during UAV patrol, and the data center point of the UAV return position is indicated by v0. For any point vk ∈ {v0} ∪V,vk = (xk, yk, zk), among them, xk, yk, zk represent the spatial location of the k-th data collection point, respectively, in multi-point path planning scenarios, this parameter must be met:
xmin,xmax,ymin,ymax,zmin,zmax represent the boundaries of the environment, respectively. The solution of multi-point path planning can be regarded as taking v0 as the starting point and the endpoint, a primary loop containing each point in V, the node sequence with no repetition in the loop except v0, and each point in V appears, such as v0→v1 → v2 →—vN→v0,vk ∈ V represents the k -th data collection point, and the form of the actual multi-point planning path in the UAV patrol scenario is shown in Figure 3.
Since the data collected by UAV during patrol is time-sensitive, it is necessary to introduce the age of information and construct the representation method of the age of information. When the data is collected from the fixed-point device vk and is collected when the UAV is hovering above vk at tk, the age Γk(t) of the collected data information in vk can be represented as Γk(t) = (t−tk) +, where tk represents the moment when the UAV reaches the k-th sensor node, (x) + max (Hu et al., 2020). ζk represents the time taken for vk to upload the data to the drone. In multi-point path planning scenarios, it is generally assumed that the upload time of fixed point equipment, the flight time of UAV, the sampling time of each fixed point equipment and communication overhead can be ignored (Tong et al., 2019). The k-th node data information age is the sum of the upload data time on the path and the flight time of the UAV, as shown in formula (3).
Among these, η(n),(n + 1) represents the time when the drone flies back to the data center from the last data collection point. According to formula (3), on the multi-point path planning, the average AoI (Tong et al., 2019) of the UAV flying over all ground fixed-point locations can be shown in formula (4).
Two-point path planning and multi-point path planning make up the UAV forest patrol’s path planning, according to Section “3.1 Scene modeling.” The two scenarios mentioned above are combined to create the respective objective functions.
The objective function of multi-point path planning was built from the perspective of path length cost and mountain obstacle threat cost, taking into account the complex characteristics of the forest flight environment and the three-dimensional curve characteristics of the two-point patrol trajectory.
Formula (1) states that the shorter the actual route length of the UAV’s two-point curve is, the less time is required, and the simpler it is to gather the perception data in a timely manner during obstacle avoidance flight. Formula (5) shows the cost of building the two-point path planning length.
Among this L represents the sum of distances between all adjacent intermediate track points from the two data collection points. p represents the number of intermediate points (xs,ys,zs) is the coordinate of the s-th intermediate node in the path, with s equal to 0, the starting coordinate vk, and s equal to p+1, the ending coordinate vk+ 1.
The primary obstacle avoidance targets for UAV forest patrol in complex forest environments are mountain peaks. Mountain obstacle threat costs are added to ensure that UAV can reasonably avoid mountain peaks, as shown in formula (6). Formula (6) states that the adaptability of this path can be decreased if the middle track point of two-point planning intersects with the surface of a mountain peak or is inside a mountain peak, leading to this path being viewed as an infeasible path in the planning process.
To quantify the freshness of the data collected from UAV missions, many scholars have used AoI as an objective function for UAV trajectory optimization (Meng et al., 2021; Wu et al., 2021). In the process of forest patrol, to timely collect more valuable ground fixed point equipment perception data, the goal of UAV multi-point path planning is to minimize the average AoI of UAV data collection, that is, the minimum .
The energy consumption, flight attitude, and other performance constraints as well as the environmental constraints of various UAVs must be taken into account when planning UAV tracks.
The energy consumption model of UAV patrol is created based on the current mainstream fixed-wing and rotary-wing UAV products to guarantee that the energy consumed by UAV during flight must be less than its maximum energy.
Energy consumption model of rotary wing UAV. When the UAV flies at the speed v, the generated propulsion power consumption can be expressed as (Zeng et al., 2019):
In formula (7), is leaf profile power, is induced power, and is parasitic power. Among them, P0 and Pi is constant, respectively for the UAV hovering state blade profile power and induced power, Utip said rotor blade tip speed, ν0 means hovering rotor average induction speed, d0 and s, respectively for UAV fuselage resistance ratio and rotor strength, related to the type of UAV, ρ and A, respectively said air density and rotor disk area.
Energy consumption model of fixed-wing UAV. The energy consumption model of fixed-wing UAV depends on the flight speed and acceleration of the UAV (Hua et al., 2018), which can be expressed as
Among these ν and α are the flight speed and acceleration of the UAV, respectively, c1 and c2 are the parameters related to its weight, wing area, and air density, g = 9.8m/s2 is the gravity acceleration, and m is the mass of the UAV and its load. When the fixed-wing UAV flies smoothly at speed v, its energy consumption model can be reduced to the following form
The propulsion energy of a UAV during flight can be expressed as:
The c1 and c2 are constant and are related to UAV weight, wing area, air density, etc. The δ is the length of time in the unit time slot.
The maximum horizontal rotation angle, the maximum climbing angle, and the minimum and maximum flight altitude of the UAV flight will all have an impact on the flight energy consumption in the three-dimensional path flight.
First, the UAV’s turning angle should not be too large due to its own performance constraints. Second, while turning, the UAV will slightly veer from the intended flight path; at this point, the flight path curvature should be taken into account to maintain a safe distance between the flight path and the terrain. In other words, it should not exceed the maximum turning Angle.
The ability of the UAV to maneuver, flight altitude, and weather conditions are the main factors limiting the climbing angle of the UAV in 3D space flight path planning. Therefore, during flight, the UAV’s climbing Angle should not exceed its maximum climbing Angle.
The minimum altitude of each track point in the UAV track search must not be less than a specified terrain altitude, and the flight altitude must not be higher than the maximum flight altitude.
The main danger to UAVs using ground sensors in challenging mountain environments is the danger posed by the mountains. UAVs should therefore avoid running into mountains while in the air.
To ensure that the planned path of two points can be used as the smooth trajectory of actual UAV flight, it is also necessary to construct a smooth flight path for the track points between two adjacent points in multiple points. Based on this, cubic B-spline curve (Chai et al., 2022) was introduced in this paper to smooth the flight path of UAVs and build a feasible flight path. The red points represent the algorithm-generated waypoints and the black points represent the points generated by the cubic B-spline curve (Figure 2).
Chaos is a spontaneously generated instability in deterministic systems, commonly found in nonlinear systems. Due to the ergodic nature of chaos, cango through all states in a certain range without repetition. Using chaotic variables for optimization is superior to blind and disorderly random searches. In this paper, chaos theory is introduced to population initialization. The main idea of chaotic search is to generate chaotic sequences in some iterative way, and generally most logistic equations are used to generate chaotic sequences, as shown in Equation (11):
The logistic mapping is in a fully chaotic state at the bifurcation parameter 3.57< μ ≤ 4, and the trajectory of the equations in this interval shows chaotic characteristics. In this paper, we take μ = 3.98.
No single algorithm is the most efficient for solving all optimization problems, according to the “No-free-lunch” theorem, and many researchers are working to increase the generalization ability of the approaches by hybridizing the characteristics of the problems that have been solved (Shi and Zhang, 2020; Jin et al., 2022a; Liu et al., 2022).
Coevolution algorithms have the ability to actively learn the properties of the solution space in accordance with the properties of the issue, adaptively select the dominant strategy suitable for the algorithm’s convergence from a variety of evolutionary strategies, significantly increase the algorithm’s generalization ability to the problem, and produce superior results while addressing active complex optimization problems.
In a complex forest environment, UAV two-point path planning is the key to avoiding obstacles and collecting fixed-point data efficiently. This paper uses GA and SA strategies to design the parallel evolutionary algorithm (GASA). Under parameter control, the GA is an adaptive global search strategy, and the SA can reflect good local search capabilities. During the co-evolutionary process, the two evolutionary techniques complement each other and can improve the algorithm’s convergence speed and improve path planning efficiency.
Set the relevant parameters and map boundaries of the GASA coevolution algorithm, which include population size popNum, chromosome length chromLength, crossover probability p_crs, mutation probability p_mut, iteration number iterMax, initial temperature T, termination temperature Tf, annealing rate k, Markov chain length L, and probability selection step r.
The set of waypoint coordinates between two data collection points is considered as an individual, the chromosome length of the individual is chromLength, and the path between data collection point v_k and data collection point vk+1 is denoted as (vi,d1,d2,…,dp,vi + 1). First take the random number vectors a_1, b_1, c_1 initial values between 0 ∼ 1.
Then a new vector is generated according to the form of the logistic mapping.
Where i = 1,2,…,popNum
The resulting chaotic variables are mapped into the three-dimensional space to obtain the set of three-dimensional coordinates of the i-th individual of the initial population. The i-th individual in the population popi = (Xi,Yi,Zi).
Superior genes can be kept in the population by using selection, crossover, and mutation operations to create new populations and keeping elite particles out of crossover and mutation operations.
Randomly select an individual for annealing operation to generate a new population of the received particles. After the evolution is finished, the annealing temperature of the SA strategy is updated in time.
Optimize populations by eliminating some particles according to constraints.
After the evolution of the GA strategy or SA strategy, the parent population and the child population are fused and ranked according to the fitness value. The individuals with the population are retained to form a new population. Suppose the number of individuals from the parent population is more than the number of individuals from the offspring population. In that case, the corresponding algorithm is the dominant strategy and the probability of selection of this algorithm should be increased according to formula (21), and vice versa, the probability of selection of the algorithm should be decreased according to formula (22).
The pseudo-code for solving the shortest path between two points (vi,vj) using the GASA coevolution algorithm is shown in Table 1.
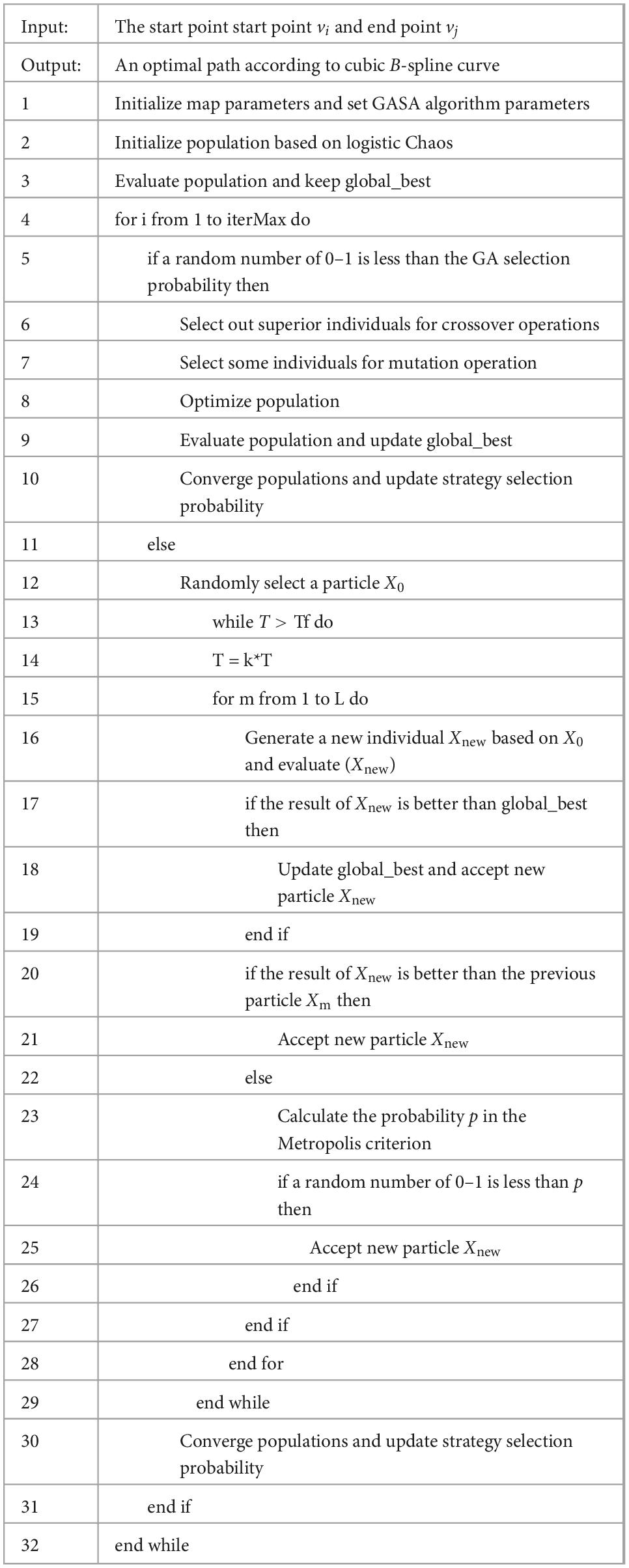
Table 1. GASA coevolution algorithm pseudo-code to solve the optimal path between two points(vi,vj).
A full alignment of the data collection points makes up one particle of the simulated annealing algorithm, and the process calculates the total fitness value of the entire path, accepting and updating the global optimum if it is better than the global one, accepting if it is better than the previous one, and accepting probabilistically if it is worse than the previous one.
The locations of the data collection points to be flown by the UAV in this study are known, and the UAV starts from a fixed starting point v_0 and flies over each fixed point device only once, and finally returns to the starting point v_0 with the minimum average AoI of all nodes.
It is known from formula (1) that the timeliness of the data and the flight path are proportional to one another when the UAV flies at a particular speed. This study applies the GASA coevolution algorithm to discover the shortest path between two points in order to achieve the time-optimal path of the UAV from the current collection point to the next target point. This work employs the simulated annealing process to determine the best solution for the issue of minimizing the average information age of all nodes; the algorithm pseudo-code is displayed in Table 2. Figure 4 depicts the SA algorithm swap operation.
Four distinct sorts of experiments are set in this chapter to test the usefulness of the suggested method. The first experiment is a fundamental experiment for selecting the proper probability choice step parameter r, the second experiment is an experiment to verify the algorithm on the Benchmark function, and the third experiment is an experiment to compare two-point path planning simulations based on simulation maps. The fourth experiment is a multi-point comparative simulation experiment involving multiple data gathering points in two different circumstances.
On a Windows 10 computer with an Intel Core i7-6700HQ processor, 8 GB of memory, and the Matlab2016a platform, all experiments in this paper were simulated.
Theoretically, selecting a greater r will cause the algorithm to be over-sensitive to changes in the probability of strategy selection, resulting in over-fitting. When r is too little, the sensitivity to a problem is insufficient to achieve the benefit of adaptive learning. To further determine the optimum probability selection step parameter r, this work analyzes the statistics of the adaptation of the matching results provided by GASA when r = 0.1, 0.2, 0.3, 0.4, 0.5, and presents the results of 3-dimensional experiments as an example. The values in Table 3 are the mean, median, and standard deviation of the Ackley function and Griewank function in 10 independent experiments.
According to the experimental results, the various statistics are better when r = 0.2. In the subsequent experiments, r = 0.2.
In order to prove the effectiveness of chaotic initialization, this paper tests the convergence rate and optimal function value of GA algorithm, Logistic chaotic initialization-based GA algorithm, SA algorithm, GA algorithm, GASA coevolution algorithm, and Logistic chaotic initialization based GASA coevolution algorithm on Ackley function. The experimental parameters are shown in Table 4. The experimental results (Figure 5) show that GA algorithm converges in the 47th generation, and the optimal Ackley function value is 2.196. The GA algorithm improved based on logistic chaos initialization converges in the 23rd generation, and the optimal Ackley function value is 2.194, which can accelerate the convergence speed of GA algorithm. Although the two final results are similar, the convergence speed of the improved GA algorithm is increased by 100%. Logistic chaos initialization can accelerate the convergence of GA algorithm. Compared with the other three algorithms, the GASA coevolution algorithm based on logistic chaos initialization has better convergence speed and accuracy and optimization ability.
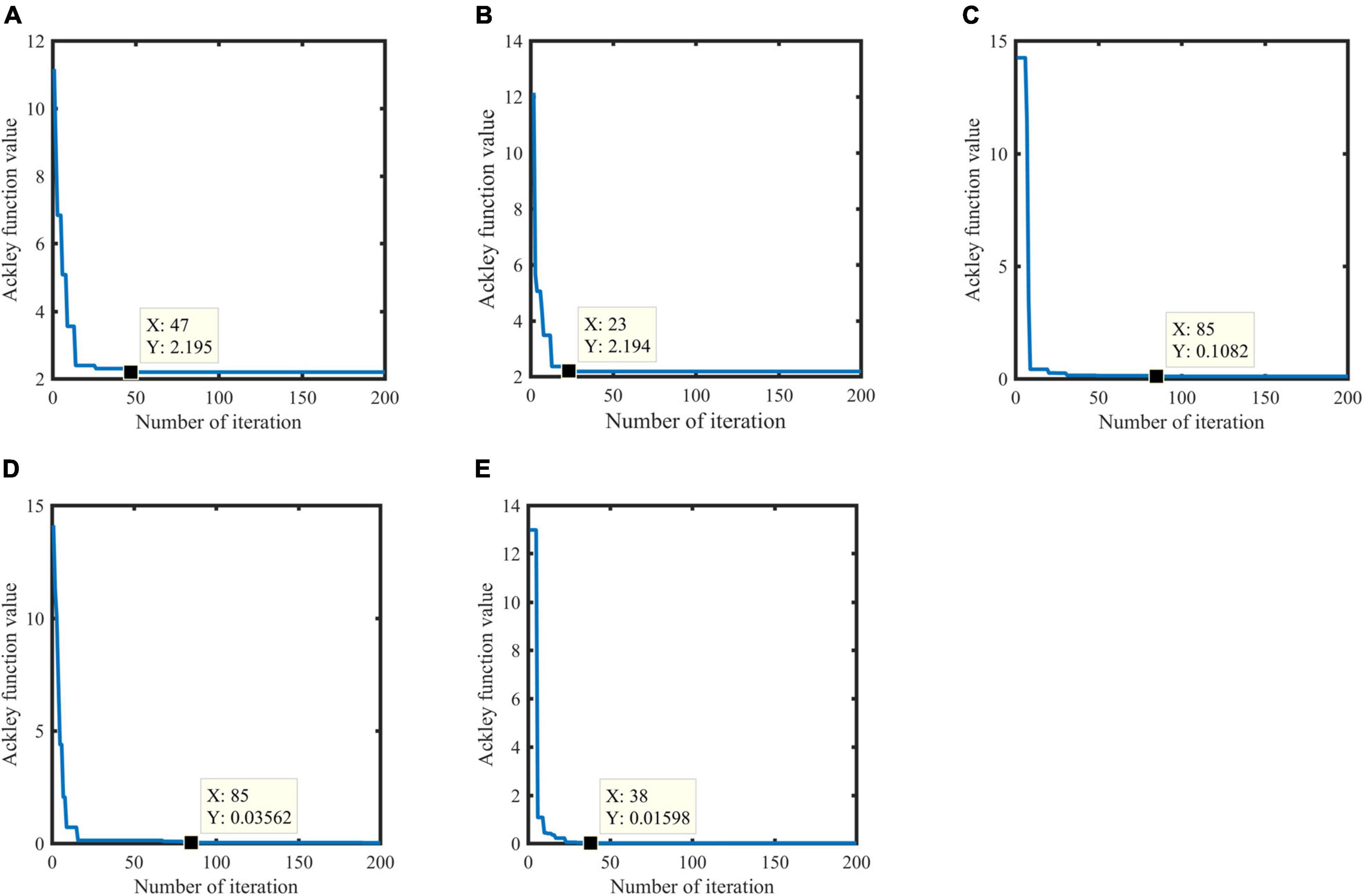
Figure 5. Results based on the Ackley function. Genetic Algorithm (GA) algorithm (A), GA algorithm based on logistic chaos initialization (B), Simulated Annealing Algorithm (SA) algorithm (C), GASA coevolution algorithm (D), an GASA coevolution algorithm based on logistic chaos initialization (E).
This paper constructs a simulation map for the simulation experiment to test the validity of the GASA coevolution algorithm in the path planning problem between two points. To test the effect of population size and the number of iterations on the GASA coevolution algorithm, we fine-tuned the selection range of parameters and did several sets of comparison experiments, and the results of the experiments showed that the effect of the parameters was small, and we later chose the most suitable parameters to compare with other algorithms. It contrasts the PSO algorithm, GA algorithm, ACO algorithm, and ABC algorithm in terms of convergence speed, path cost, and three-dimensional track diagram. Table 5 displays the precise experimental parameters.
The convergence speed and objective function values of all algorithms are shown in Table 6. GASA coevolution algorithm converges in the 5th generation. The optimal path length is 70.34, and the linear distance between the two points of the starting point and the end point is 68.91, which is close to that of the GASA coevolution algorithm. The path cost of the GASA coevolution algorithm is much lower than the GA and ACO algorithms. Although the final objective function value of PSO algorithm is not much different from that of the GASA coevolution algorithm, the PSO algorithm does not converge until the 60th generation, and the convergence speed is slower than that of the GASA coevolution algorithm. The optimal path length obtained by the ABC algorithm is 71.91, but it does not converge until the 70th generation, and the convergence speed is slower. It can be seen from the above that GASA coevolution algorithm has the optimal planning result, which can effectively restrain the precocity of traditional genetic algorithm and accelerate the rate of algorithm convergence.
From the experimental simulation results (Figure 6), it can be seen that the GASA coevolution algorithm proposed in this paper can plan the flight path of UAVs and improve the optimization accuracy of the original algorithm. Compared with the GA algorithm, GASA coevolution algorithm can better jump out of the local optimal in the middle and later optimization stage, restrain algorithm precocity and accelerate algorithm convergence speed. Moreover, compared with the GA algorithm, PSO algorithm, ACO algorithm and ABC algorithm, GASA coevolution algorithm has higher optimization accuracy and faster convergence speed. It can better plan an optimal flight path for UAVs.
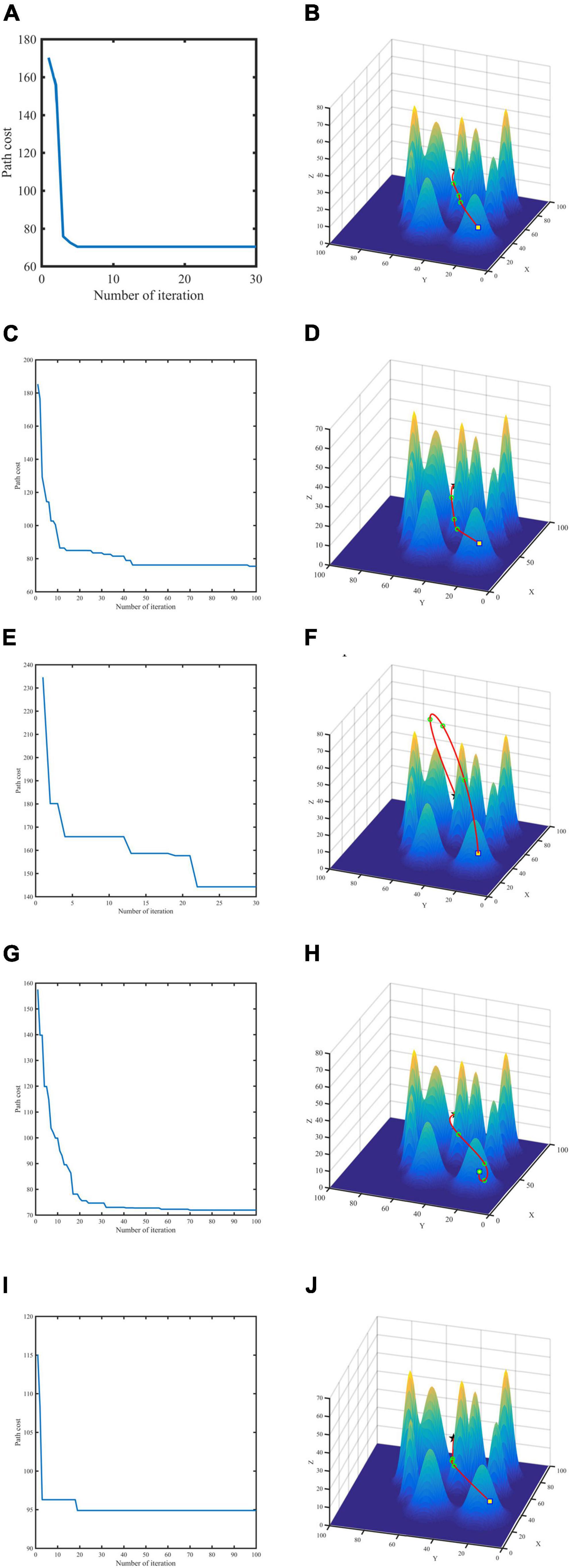
Figure 6. Convergence curve and flight path for two-point planning. GASA (A,B), Particle Swarm Optimization (PSO) (C,D), Genetic Algorithm (GA) (E,F), Ant Colony Algorithm (ACO) (G,H), Artificial Bee Colony (ABC) (I,J).
To verify the effectiveness of the proposed algorithm in multi-point path planning, this paper constructs two different terraforms, simple scenario, and complex scenario (Figures 7, 8), sets different numbers of data collection points, and compares the average AoI of data collection points. The starting point of the route is (10,10,20). We employ the PSO algorithm for comparison to test the validity of SA for multiple-point planning. In addition, for the inner two-point path planning algorithm, we compare the PSO and ABC algorithms from Section “5.4 Two-point path planning experiment” with the GASA collaborative algorithm. The experimental results indicate that the SA algorithm is a highly stable method. When conducting path planning experiments in simple and complicated maps, the average AoI of SA algorithm is better than that of the PSO algorithm, according to Table 7.
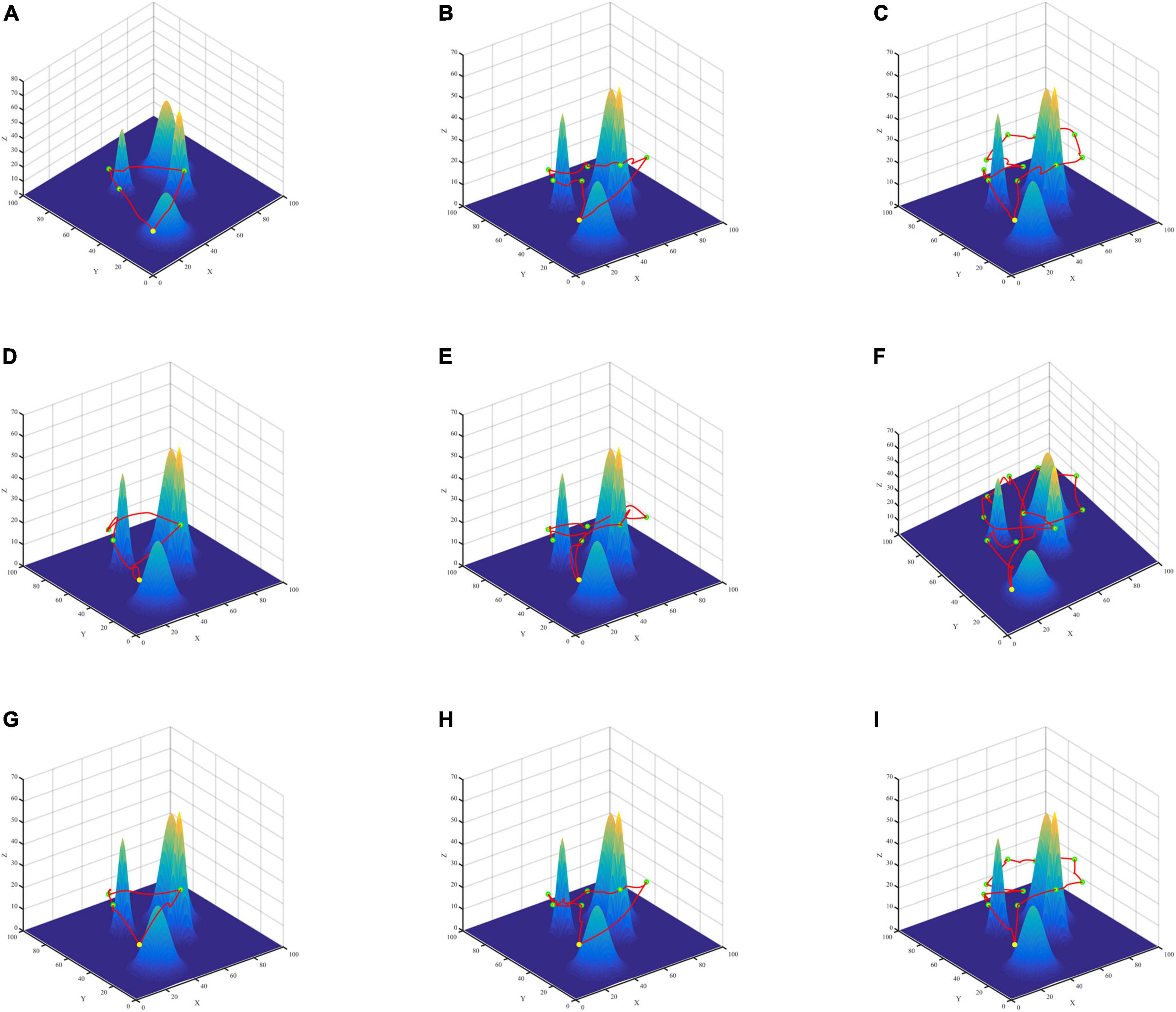
Figure 7. Three algorithms for multi-point path planning trajectory maps in simple maps. GASA (A–C), Particle Swarm Optimization (PSO) (D–F), Artificial Bee Colony (ABC) (G–I).
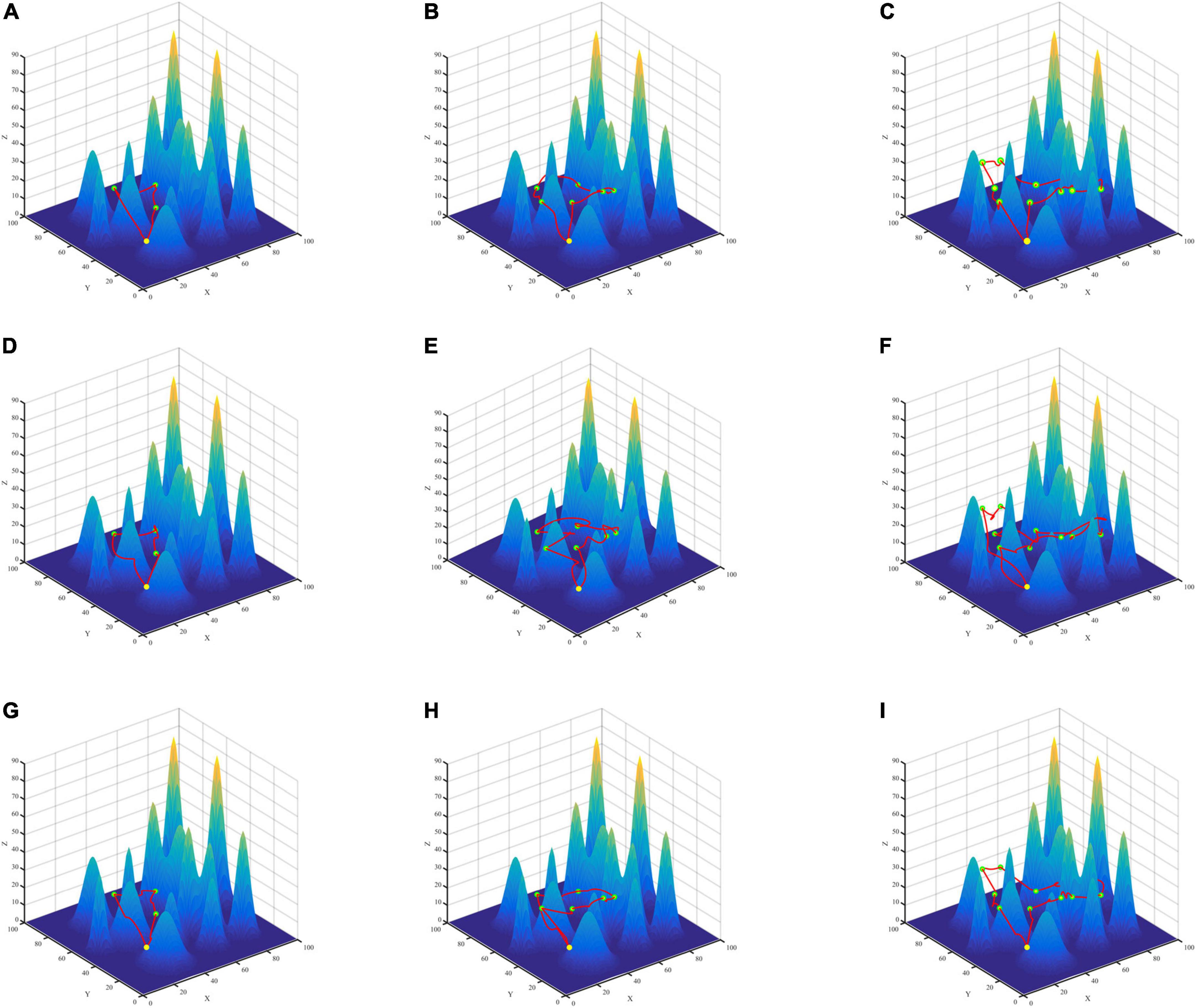
Figure 8. Three algorithms for multi-point path planning trajectory maps in complex maps. GASA (A–C), Particle Swarm Optimization (PSO) (D–F), Artificial Bee Colony (ABC) (G–I).
According to the results (Table 7), compared with PSO algorithm and ABC algorithm, the GASA algorithm proposed in this paper can reduce the average AoI of the collected data and improve the freshness of the data. Compared with the PSO algorithm, the average AoI of data in the simple map is reduced by 16.31, 20.67, and 23.33% at 3, 6, and 10 data collection points, respectively. In the complex map, the average data AoI decreased by 11.45, 19.47, and 24.87% at 3, 6, and 10 data collection points, respectively. Compared with the ABC algorithm, the average AoI of data in the simple map is reduced by 5.14, 3.87, and 1.49% at 3, 6, and 10 data collection points, respectively. In the complex map, the mean AoI of data decreased by 1.7, 0.05, and 0.02% at 3, 6, and 10 data collection points, respectively.
In this paper, the UAV path planning method in complex environment is designed for forest pest monitoring, wildlife protection and resource monitoring process, where the UAV needs to efficiently collect data from fixed-point monitoring devices. With the information freshness as the main optimization objective, the two-point and multi-point path planning process is integrated to design the UAV path planning method facing the complex mountain environment. In the multi-point path planning, the UAV patrol path between multiple fixed-point devices is obtained by simulated annealing method with the goal of information freshness. In the two-point path planning, the UAV 3D smooth patrol path between two fixed-point devices is obtained by integrating information freshness, flight attitude, and complex environment elements through the coevolution algorithm. In the experiment, the reasonable configuration of parameters of the proposed method is determined using the benchmark function, and then, the effectiveness of the two-point path planning method and the multi-point path planning method is verified using simulated complex mountain environments with different configurations of the number of fixed points. Then, the effectiveness of the two-point path planning method and the multi-point path planning method is verified using simulated complex mountain environments with different configurations of the number of fixed points. When the outer algorithm uses the SA algorithm and the inner two-point path planning GASA coevolution algorithm is compared with the existing method PSO, the proposed two-point optimization method reduces 11.4, 19.4, 24.8% in terms of AoI in the complex environment, and when the inner algorithm When the inner layer algorithms are the same, the proposed multi-point optimization method SA is more stable in the complex environment, and the AoI is reduced by 2.3, 3.7, and 4.5%.
The method proposed in this paper is an exploration of the UAV with fixed time path planning method for complex mountainous environments. In the subsequent research, the applicability and practical application value of the algorithm can be improved in terms of scene migration and method improvement. In the scenario migration, the multi-objective optimization method applicable to other UAV patrol scenarios can be constructed by combining the UAV patrol needs of simple urban suburban environments and introducing airtime, etc. as the objective function. In the convenience of method improvement, it can be combined with the actual wildlife monitoring needs and domain expert knowledge to construct the illuminating information optimization objective function of the optimization method, meanwhile, some new optimization methods can be combined with the existing methods to construct the co-evolutionary algorithm to verify the applicability of different evolutionary strategies in the forest patrol problem.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
XC and CM: conceptualization, writing—review and editing, and funding acquisition. XC, YW, and SY: methodology. YW and HL: coding. XC and YW: writing—original draft preparation. XC, YW, and CM: significance contributions to the manuscript. All authors read and agreed to the published version of the manuscript.
This research was funded by the Fundamental Research Funds for the Central Universities (BLX202140), Beijing Forestry University “Double First-Class” Construction Project (450-GK112203008), and Beijing Forestry University National Training Program of Innovation and Entrepreneurship for Undergraduates.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbas, Q., Zeb, S., Hassan, S. A., Mumtaz, R., and Zaidi, S. A. R. (2022). “Joint optimization of Age of information and energy efficiency in IoT networks,” in Proceedings of the 2020 IEEE 91st vehicular technology conference (VTC2020-Spring), (Antwerp: IEEE), 1–5.
Abd-Elmagid, M. A., Ferdowsi, A., Dhillon, H. S., and Saad, W. (2019). “Deep reinforcement learning for minimizing age-of-information in UAV-assisted networks,” in Proceedings of the 2019 IEEE global communications conference, (Waikoloa, HI: GLOBECOM), 1–6.
Chai, X., Zheng, Z., Xiao, J., Yan, L., Qu, B., Wen, P., et al. (2022). Multi-strategy fusion differential evolution algorithm for UAV path planning in complex environment. Aerosp. Sci. Technol. 121:107287. doi: 10.1016/j.ast.2021.107287
Chen, Y., Luo, G., Mei, Y., Yu, J., and Su, X. (2016a). UAV path planning using artificial potential field method updated by optimal control theory. Int. J. Syst. Sci. 47, 1407–1420. doi: 10.1080/00207721.2014.929191
Chen, Y., Yu, J., Mei, Y., Wang, Y., and Su, X. (2016b). Modified central force optimization (MCFO) algorithm for 3D UAV path planning. Neurocomputing 171, 878–888. doi: 10.1016/j.neucom.2015.07.044
Goel, P., and Singh, D. (2013). An improved ABC algorithm for optimal path planning. Int. J. Sci. Res. 2:4.
He, Y., Zeng, Q., Liu, J., Xu, G., and Deng, X. (2013). “Path planning for indoor UAV based on Ant Colony Optimization,” in Proceedings of the 2013 25th chinese control and decision conference (CCDC), (Guiyang: IEEE), 2919–2923. doi: 10.1109/CCDC.2013.6561444
Hu, X., Pang, B., Dai, F., and Low, K. H. (2020). Risk assessment model for UAV cost-effective path planning in urban environments. IEEE Access 8, 150162–150173. doi: 10.1109/ACCESS.2020.3016118
Hua, M., Wang, Y., Zhang, Z., Li, C., Huang, Y., and Yang, L. (2018). Power-efficient communication in UAV-aided wireless sensor networks. IEEE Commun. Lett. 22, 1264–1267. doi: 10.1109/lcomm.2018.2822700
Jia, Z., Qin, X., Wang, Z., and Liu, B. (2019). “Age-based path planning and data acquisition in UAV-assisted iot networks,” in Proceedings of the 2019 IEEE international conference on communications workshops (ICC Workshops, (Shanghai: IEEE). doi: 10.1109/ICCW.2019.8756751
Jin, L., Liang, S., Luo, X., and Zhou, M. (2022a). Distributed and time-delayed k-winner-take-all network for competitive coordination of multiple robots. IEEE Trans. Cybern. 2022, 1–12. doi: 10.1109/TCYB.2022.3159367
Jin, L., Wei, L., and Li, S. (2022b). Gradient-based differential neural-solution to time-dependent nonlinear optimization. IEEE Trans. Autom. Contr. 2022, 1–1. doi: 10.1109/tac.2022.3144135
Kaul, S., Yates, R., and Gruteser, M. (2012). “Real-time status: How often should one update?,” in 2012 Proceedings IEEE INFOCOM, (Piscataway, NJ: IEEE), 2731–2735.
Kiani, F., Seyyedabbasi, A., Nematzadeh, S., Candan, F., Çevik, T., Anka, F. A., et al. (2022). Adaptive metaheuristic-based methods for autonomous robot path planning: Sustainable agricultural applications. Appl. Sci. 12:943. doi: 10.3390/app12030943
Liu, J., Tong, P., Wang, X., Bai, B., and Dai, H. (2021). UAV-aided data collection for information freshness in wireless sensor networks. IEEE Trans. Wirel. Commun. 20, 2368–2382. doi: 10.1109/TWC.2020.3041750
Liu, J., Wang, X., Bai, B., and Dai, H. (2018). “Age-optimal trajectory planning for UAV-assisted data collection,” in IEEE INFOCOM 2018 - IEEE conference on computer communications workshops, (Honolulu, HI: INFOCOM WKSHPS), 553–558. doi: 10.3390/s18051519
Liu, M., Zhang, X., Shang, M., and Jin, L. (2022). Gradient-based differential kWTA network with application to competitive coordination of multiple robots. IEEE/CAA J. Autom. Sinica 9, 1452–1463. doi: 10.1109/jas.2022.105731
Liu, Y., Zhang, X., Guan, X., and Delahaye, D. (2016). Adaptive sensitivity decision based path planning algorithm for unmanned aerial vehicle with improved particle swarm optimization. Aerosp. Sci. Technol. 58, 92–102. doi: 10.1016/J.AST.2016.08.017
Maini, P., and Sujit, P. B. (2016). “Path planning for a UAV with kinematic constraints in the presence of polygonal obstacles,” in Proceedings of the 2016 international conference on unmanned aircraft systems (ICUAS), (Arlington, VA: IEEE), 62–67.
Meng, K., Li, D., He, X., and Liu, M. (2021). Space pruning based time minimization in delay constrained multi-task UAV-based sensing. IEEE Trans. Veh. Technol. 70, 2836–2849. doi: 10.1109/tvt.2021.3061243
Nikolos, I., and Tsourvelouds, N. C. (2009). “Path planning for cooperating unmanned vehicles over 3-D terrain,” in Informatics in control, automation and robotics. Lecture notes in electrical engineering, Vol. 24, eds J. Filipe, J. A. Cetto, and J. Ferrier (Berlin: Springer). doi: 10.1007/978-3-540-85640-5_12
Pehlivanoglu, Y. V. (2012). A new vibrational genetic algorithm enhanced with a voronoi diagram for path planning of autonomous UAV. Aerosp. Sci. Technol. 16, 47–55. doi: 10.1016/J.AST.2011.02.006
Pehlivanoglu, Y. V., and Pehlivanoǧlu, P. (2021). An enhanced genetic algorithm for path planning of autonomous UAV in target coverage problems. Appl. Soft Comput. 112:107796. doi: 10.1016/J.ASOC.2021.107796
Shi, Y., and Zhang, Y. (2020). New discrete-time models of zeroing neural network solving systems of time-variant linear and nonlinear inequalities. IEEE Trans. Syst. Man Cybern. Syst. 50, 565–576. doi: 10.1109/tsmc.2017.2751259
Shi, Y., Jin, L., Li, S., Li, J., Qiang, J., and Gerontitis, D. K. (2022). Novel discrete-time recurrent neural networks handling discrete-form time-variant multi-augmented sylvester matrix problems and manipulator application. IEEE Trans. Neural. Netw. Learn. Syst. 33, 587–599. doi: 10.1109/TNNLS.2020.3028136
Tong, P., Liu, J., Wang, X., and Bai, B. (2019). “UAV-Enabled age-optimal data collection in wireless sensor networks,” in Proceedings of the 2019 IEEE international conference on communications workshops (ICC Workshops), (Shanghai: IEEE). doi: 10.1109/ICCW.2019.8756665
Turker, T., Sahingoz, O. K., and Yilmaz, G. (2015). “2D path planning for UAVs in radar threatening environment using simulated annealing algorithm,” in Proceedings of the 2015 international conference on unmanned aircraft systems (ICUAS), (Denver, CO: IEEE), 56–61.
Wang, Y., and Chen, W. (2014). “Path planning and obstacle avoidance of unmanned aerial vehicle based on improved genetic algorithms,” in 2014 33rd chinese control conference (CCC), (Nanjing: IEEE), 8612–8616.
Wu, F., Zhang, H., Wu, J., Han, Z., Poor, H. V., and Song, L. (2021). UAV-to-device underlay communications: Age of information minimization by multi-agent deep reinforcement learning. IEEE Trans. Commun. 69, 4461–4475. doi: 10.1109/tcomm.2021.3065135
Xiao-Ting, J., Hai-Bin, X., Li, Z., and Sheng-De, J. (2013). “Flight path planning based on an improved genetic algorithm,” in Proceedings of the 2013 third international conference on intelligent system design and engineering applications (ISDEA), (Piscataway, NJ: IEEE), 775–778.
Xie, Z., Jin, L., Luo, X., Hu, B., and Li, S. (2022). An Acceleration-level data-driven repetitive motion planning scheme for kinematic control of robots with unknown structure. IEEE Trans. Syst. Man Cybern. Syst. 52, 5679–5691. doi: 10.1109/tsmc.2021.3129794
Yan, C., Xiang, X., and Wang, C. (2020). Towards real-time path planning through deep reinforcement learning for a UAV in dynamic environments. J. Intell. Robot. Syst. 98, 297–309. doi: 10.1007/s10846-019-01073-3
Yang, P., Tang, K., Lozano, J. A., and Cao, X. (2015). IEEE Trans. Robot. 31, 1130–1146. doi: 10.1109/TRO.2015.2459812
Yang, Q., and Yoo, S.-J. (2018). Optimal UAV path planning: Sensing data acquisition over iot sensor networks using multi-objective bio-inspired algorithms. IEEE Access 6, 13671–13684. doi: 10.1109/ACCESS.2018.2812896
Yingkun, Z. (2018). “Flight path planning of agriculture UAV based on improved artificial potential field method,” in Proceedings of the 2018 Chinese control and decision conference (CCDC), (Shenyang: IEEE), 1526–1530. doi: 10.3389/fpls.2022.998962
Zeng, Y., Xu, J., and Zhang, R. (2019). Energy minimization for wireless communication with rotary-wing UAV. IEEE Trans. Wireless Commun. 18, 2329–2345. doi: 10.1109/twc.2019.2902559
Keywords: UAV, fixed-point path planning, multi-point path planning, two-point path planning, co-evolutionary algorithm
Citation: Cui X, Wang Y, Yang S, Liu H and Mou C (2022) UAV path planning method for data collection of fixed-point equipment in complex forest environment. Front. Neurorobot. 16:1105177. doi: 10.3389/fnbot.2022.1105177
Received: 22 November 2022; Accepted: 08 December 2022;
Published: 22 December 2022.
Edited by:
Long Jin, Lanzhou University, ChinaReviewed by:
Xuyang Teng, Hangzhou Dianzi University, ChinaCopyright © 2022 Cui, Wang, Yang, Liu and Mou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chao Mou, ✉ Y2hhb19tQGJqZnUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.