- Merchant Marine College, Shanghai Maritime University, Shanghai, China
This paper presents an online recorded data-based composite neural finite-time control scheme for underactuated marine surface vessels (MSVs) subject to uncertain dynamics and time-varying external disturbances. The underactuation problem of the MSVs was solved by introducing the line-of-sight (LOS) method. The uncertain dynamics of MSVs are approximated by the composite neural networks (NNs). A modified prediction error signal is designed by virtue of online recorded data. The weight updating law of NN is driven by both tracking error and prediction error, introducing additional correction information to the weights of NN, thus improving the learning ability of the NN. Furthermore, disturbance observers can be devised to estimate the compound disturbances consisting of the approximation errors of NNs and external disturbances. Moreover, the smooth function is inserted into the design of the control scheme, and the finite-time composite neural trajectory tracking control of MSVs is achieved. The stability of the MSVs trajectory tracking closed-loop control system is guaranteed rigorously by the Lyapunov approach, and the tracking error will converge to the set of residuals around zero within a finite time. The simulation tests on an MSV verify the effectiveness of the proposed control scheme.
1. Introduction
Due to the rapid exploitation of marine resources, marine surface vehicles (MSVs) have been extensively deployed in various fields, such as scientific research applications, commercial cargo transport, missions related to maritime search and maritime emergency rescue (Dai et al., 2015; He and Geng, 2021). The trajectory tracking of MSVs plays a significant and important role in accomplishing different missions at sea (Xiao and Yin, 2018; Zhu et al., 2021b). However, in the complex maritime environment, MSVs will inevitably be affected by unknown external disturbances and uncertain dynamics, which bring great challenges to accurate trajectory tracking control.
In recent years, scholars have proposed fruitful approaches to mitigate the effects of unknown external disturbances and uncertain dynamics, such as neural network (NN) control (Rout et al., 2020; Zhu et al., 2021a), fuzzy control (Wang et al., 2018, 2020), observer-based nonlinear control (Gao and Guo, 2019; Van, 2019; Guo and Zhang, 2020), and the finite-time control (Ning et al., 2020; Wang and Deng, 2020; Zhu et al., 2020). The NNs and fuzzy logic systems are introduced to approximate the uncertain terms of the MSVs, including unmodeled dynamics and unknown dynamics in Wang et al. (2018, 2020), Rout et al. (2020), and Zhu et al. (2021a). In Gao and Guo (2019), Van (2019), and Guo and Zhang (2020), the nonlinear disturbance observers (NDOs) have been devised to estimate the compound uncertainties consisting of model parameter perturbations and unknown disturbances. Combining parameter adaptive technique and backstepping vector design scheme, the unmodeled dynamics of MSVs were addressed in Do (2016) and Ghommam and Saad (2018).
However, most of the literature mentioned above only focuses on the control problem of fully actuated MSVs. In fact, for most MSVs, there are three degrees of freedom, but only two control inputs are available for control, which means that they are underactuated. The methods to solve the problem of underactuation control mainly focus on additional control methods (Do, 2010; Seok Park, 2014; Park and Yoo, 2016), output redefinition control (Shojaei and Arefi, 2015; Zhu et al., 2021c), line-of-sight (LOS) (Shojaei, 2015; Gao et al., 2017; Elhaki and Shojaei, 2021), etc.
The problems of uncertain dynamics and time-varying disturbances deserve further attention, although the above-mentioned literature has yielded fruitful results. The purpose of approximating system uncertainty information with NN has been completed in Xu (2017) and Xu and Sun (2018). To obtain better tracking control performance, uncertain dynamic terms need to be approximated as accurately as possible. By constructing a serial-parallel estimation model, the model prediction error can be obtained in Peng et al. (2016), and it is integrated into the design of the weight update rate of the NN, which effectively improves the transient performance of the system. To reduce the high-frequency oscillations and improve the transient performance of the system, adaptive control modification (Yucelen and Haddad, 2013) and auxiliary filters (Na et al., 2015, 2017; Huang et al., 2018) were introduced to design the adaptive law and NN weight update law, respectively. The error feedback information is embedded into the reference model in Gibson et al. (2013) to reduce the oscillation caused by large gain. The updating law of NNs weights was designed by fusing model prediction errors and the system tracking errors in Xu et al. (2014).
In the above literature, the tracking error of a closed-loop control system can only reach uniformly boundedness. However, tracking errors of MSVs frequently require achieving finite time convergence. Recently, finite-time (FT) control methods have been intensively investigated and adopted for various control systems because of their advantages of fast convergence and strong robustness (Yang et al., 2021, 2022a). For the FT convergence problem, scholars have proposed a large number of advanced FT control techniques, In addition to the sliding-mode-based FT control method, uniformity and the addition of a power integrator (API) are also effective methods to achieve FT stability. Scholars have proposed a large number of effective techniques to achieve FT control, including sliding-mode based FT control methods, homogeneity, and the addition of power integrators (Wang et al., 2017, 2018). The FT trajectory tracking control (Wang et al., 2016) and formation Control (Zhang et al., 2020; Yang et al., 2022b) of the MSVs are well implemented. It can be clearly seen that the control performance of the MSV system is obviously improved under FT control. However, the FT control of MSVs is still a largely open problem suffering from unknown external disturbances and uncertain dynamics.
In this article, we develop an online recorded data-based FT composite neural control scheme for underactuated MSVs suffering from uncertain dynamics and unknown external disturbances. Moreover, the contributions of this article can be listed as follows.
• In this article, an FT composite neural control scheme based on online recorded data is proposed for underactuated MSVs suffering from uncertain dynamics and unknown external disturbances for the first time, and high precision tracking is guaranteed. Compared with the control scheme based on NN, the proposed control scheme can achieve both higher tracking accuracy, faster tracking speed, and a more precise approximation of uncertain dynamics.
• Unlike existing composite learning control schemes, which either converge exponentially (Xu and Shou, 2018; Xu et al., 2019) or in finite time (Pan et al., 2022) but exhibit potential singularity problems, we introduce a smoothing function into the design of the composite learning control scheme such that the tracking errors can achieve FT converge to the neighborhood of zero without singularity.
The remainder of this article is organized as follows. Section 2 introduces the mathematical model of MSV, the problem formulation, some preliminaries, and the principle of NN. Section 3 describes the details of the control scheme design process. The simulation results and comparison are shown in Section 4. Section 5 concludes this paper. Notations: indicates the error value between • and its estimate , which satisfies that .
2. Problem formulation
2.1. Mathematical model of MSV
The mathematical model of underactuated MSVs moving in the horizontal plane is given by
where (x, y) represents the position and φ denotes the orientation of MSVs in the earth-fixed frame. Here, [u, v, r]T represents surge velocity, sway velocity, and angular rate of MSVs in the body-fixed frame, respectively. The m11, m22, and m33 are nominal values of the inertia mass. The d11, d22, and d33 are hydrodynamic damping parameters. The τeu, τev, and τer denote unknown external disturbances. represents uncertain dynamics including uncertain parts of the model parameters of the MSVs. τu and τr are the control input signal in the surge and yaw directions.
Assumption 1. The unknown external disturbances τej, (j = u, q, r) satisfies that and , where and are unknown positive constants.
Assumption 2. The desired trajectory signal xd, yd and their first two time derivatives are available.
The position error in the body-fixed frame is given
Differentiating (Equations 2a,b) with respect to time yields
Then, we can describe the position error ze and angle error θe as
Together with Equations (2a,b), we can obtain
A user-design positive constant z0 is embedded in the design of virtual control law to avoid possible singularity. The main objective of this article is to conceive an online recorded data-based FT composite neural control scheme for underactuated MSVs satisfying Assumptions 1–2 suffering from uncertain dynamics and environmental disturbances tracking the desired trajectory satisfies that tracking errors ze and θe can converge to a small residual set within a finite time.
2.2. Some preliminaries
Lemma 1 (Qi et al., 2020). Consider the nonlinear system , g(0) = 0, ε ∈ Rn, if Lyapunov function V(ε) satisfies that
where a and b are positive constants and 0 < J < 1. The system is finite-time stable and there exists a setting time function T
Lemma 2 (Zhang and Zhang, 2014). For arbitrarily positive constant f and 0 < δ < 1, the following inequality always holds.
Lemma 3 (Wang and Lin, 2015). For arbitrarily positive constant ϖ and positive constant ϱ, the following inequality always holds.
2.3. Introduction to the principle of radial basis function NN
In general, for any continuous function L(X) that can be parameterized through the Radial Basis Function NNs with approximation errors ξ, and can be described as
where Φ(X) is the basis function vector. ch and bh denote the center and the width of the basis function, respectively. N represents the number of the node. ξ is the approximation error that satisfies |ξ| ≤ ξm and ξm is an unknown positive constant. Ŵ is the estimate of the W. In practice, the uncertain nonlinear function can usually be expressed as .
3. Details of control law design and stability analysis
Together with Equations (4a) and (5a)-(5b), differentiating ze with respect to time yields
where ζ1 and ζ2 are expressed as
The virtual control law αu is designed as
where kz1, kz2, and ιz are positive user-designed constants.
In the surge direction, the velocity error can be expressed as ue = u − αu. From Equation (13), the Equation (11) can be further rewritten as
In the light of Equations (1d) and (13), the equation for the derivative of ue is given by
The uncertain dynamic of MSVs can be estimated using NN such that . Here, let du = ξu + τeu. The ξu is the approximation error of NN and the time derivative of ξu is bound.
In the light of Assumption 1, we have
where Υu0 and Υu are positive constants.
The following error equation is further expressed as
Then, the following control law is constructed
where ku1, ku2, and ιu are positive constants.
Therefore, the Equation (17) can be expressed as
The prediction error is designed as
where pu and Au are constructed as
where τd is an integral interval.
From Equations (21) to (23) can be expressed as
where .
The composite neural update law can be designed as
where γu, kwu, ϑu1, and ϑu2 are positive parameters.
The NDO for the surge direction is designed as
where σu is the auxiliary variable.
Using Equations (1d) and (25a)-(25b), taking the time derivative of , we can get
Combining Equation (4b) and (5a)-(5b), taking the time derivative of θe
The virtual control law αr can be designed as
where kθ1, kθ2, and ιθ are positive constants.
In the yaw direction, the velocity error can be expressed as re = r−αr. From Equation (28), the Equation (27) can be further rewritten as
In the light of Equations (1f) and (28), the equation for the derivative of re is given by
The uncertain dynamic of MSVs can be estimated using NN such that . Here, let dr = ξr + τer. The ξr is the approximation error of NN and the time derivative of ξr is bound.
In the light of Assumption 1, we have
where Υr0 and Υr are positive constants.
The following error equation is further expressed as
Then, the following control law is constructed
where kr1 and kr2 are positive constants.
Therefore, the Equation (32) can be expressed as
The prediction error is designed as
where pr and Ar are constructed as
From Equations (36–38) can be expressed as
where .
The composite learning update law can be designed as
where γr, kwr, and ϑr are positive parameters.
The NDO for the yaw direction is designed as
where σr is the auxiliary variable.
Using Equations (1f) and (40a)-(40b), taking the time derivative of , we can get
Remark 1. In the view of Equations (24) and (39), the online recorded data-based prediction errors and tracking errors are fused to construct the composite NN weight updating. More information is introduced to construct the weight updating to approximate uncertain dynamics. Hence, the trajectory tracking speed and accuracy of MSVs are improved.
Remark 2. Different from Xu and Shou (2018) and Xu et al. (2019), prediction errors are constructed through online data recording and a smooth function, which realizes the FT converge under the composite neural control scheme based on online recorded data.
Remark 3. kwu and kwr in Equations (24) and (39) are designed to enhance the learning competence of the NN. The magnitude of the values of kwu and kwr determines whether the values of Ŵu and Ŵr mainly depend on the tracking error or the prediction error.
Remark 4. Combined with the approximation results of uncertain dynamics of MSVs, the NDOs were designed to estimate the lumped disturbances consisting of approximation residuals of NNs and unknown external disturbances. In this article, the developed control scheme guarantees both higher tracking accuracy and a more precise approximation of uncertain dynamics.
The compounded unknown information lumped by the uncertain dynamics of MSVs and unknown external disturbances is represented as Du and Dr.
Remark 5. It is worth noting that one cannot definitively tell whether and can approximate the m22vr − d11u + fu and (m11 − m22)uv − d33r + fr, respectively. Because the NNs and NDOs are sharing each other's information, which means both are sharing “estimation work”. If the estimation and can closely follow the compounded unknown information Du and Dr, respectively, then the purpose of composite neural using NNs and NDOs is realized effectively.
Theorem 1: Applying the virtual control laws equation (13), (28), the NN updating laws equation (24), (39), NDOs equation (25a)-(25b), (40a)-(40b) to the MSVs trajectory tracking system (1a)-(1c) and (2a)-(2c) with uncertain dynamics and unknown external disturbances under Assumptions 1–2. Tracking errors can achieve FT converge to the neighborhood of zero. All the signals in MSVs trajectory tracking closed-loop system are uniformly ultimately bounded.
Proof: The Lyapunov function can be selected as
Taking the time derivative of Equation (43), we have
Along with Equations (14) and (29), Lemma 3, and Young's inequality, we have
In the light of Equations (19) and (34) and Lemma 3, we have
In view of Equations (24) and (39), we can get
From Equations (26) and (41), we can get
The Equation (44) can be rearranged as
where , g = u, r. From Equations (16) and (31), has the supreme expressed as .
According to Young's inequality, we can get
Similarly, we can obtain
The Equation (53) can be further rearranged as
According to Young's inequality, Equations (16) and (31), we can get
Then, the Equation (56) can be further rearranged as
According to Young's inequality and the Lemma 3, we have the following fact
where μu and μr are positive constants, ||Φu|| ≤ ϖu and ||Φr|| ≤ ϖr.
Therefore, the Equation (61) is further scaled as
Therefore, we have
where a = min{(2kz2 − 1), (2kθ2 − 1), (2ku2 − 1), (2kr2 − 1), , h = min{2kz1, 2kθ1, 2ku1, 2kr2, ϑu, ϑr, 1} and .
From Equation (67), we can obtain
According to Equation (68), if we have
From Lemma 1, V converges around within a setting time
The theorem has been proved.
4. Simulation results and comparison
To validate the superiority of the proposed control scheme in this article, simulation investigations together with comprehensive comparisons of an MSV are addressed in Do and Pan (2004), whereby the main parameters are as follows: m11 d11
Next, the performance advantages of the proposed control scheme (FT-ORDCL) are presented through a comprehensive comparison with other neural network-based finite-time control schemes (FT-NN). The simulations are carried out under the proposed trajectory tracking control scheme in the following two cases.
Case 1: Uncertain dynamics of MSV are assumed as . The unknown external disturbances are assumed as [104 sin(0.3t − π/4) + 104 cos(0.2t + π/4) + 2 × 104N, 103 sin(0.2t − π/4) + 103 cos(0.3t − π/4) + 3 × 103N · m, 105 sin(0.2t + π/6) + 105 cos(0.5t − π/4) − 3 × 105N · m]T.
The desired trajectory signal is given as xd = 200 sin(0.02t),yd = 200 cos(0.02t). User-defined parameters for FT-ORDCL and FT-NN control schemes are as follows: [x(0), y(0), φ(0), u(0), v(0), r(0)] = [20, 190, −0.02π, 0, 0, 0]. z0 = 10, kz1 = 0.02, kz2 = 0.55, ιz = 0.2, kθ1 = 0.001, ιθ = 0.3, kθ2 = 0.8, ku1 = 5, ιu = 0.2, , kr1 = 3, ιr = 0.3, , γu = 100, γr = 10, kwu = kwr = 50, ϑu1 = ϑr1 = 0.0001, ϑu2 = ϑr2 = 0.001, τd = 0.05.
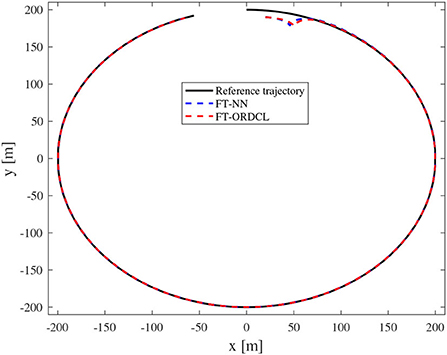
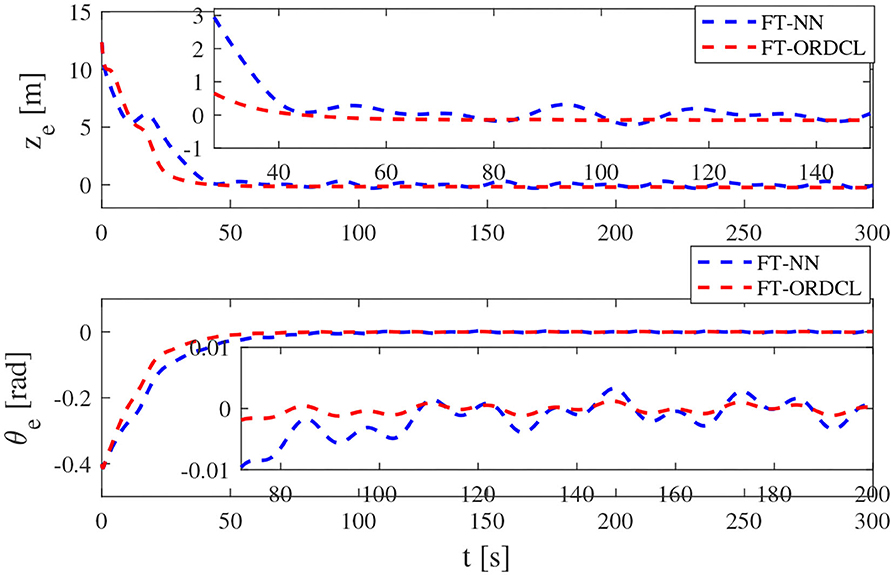
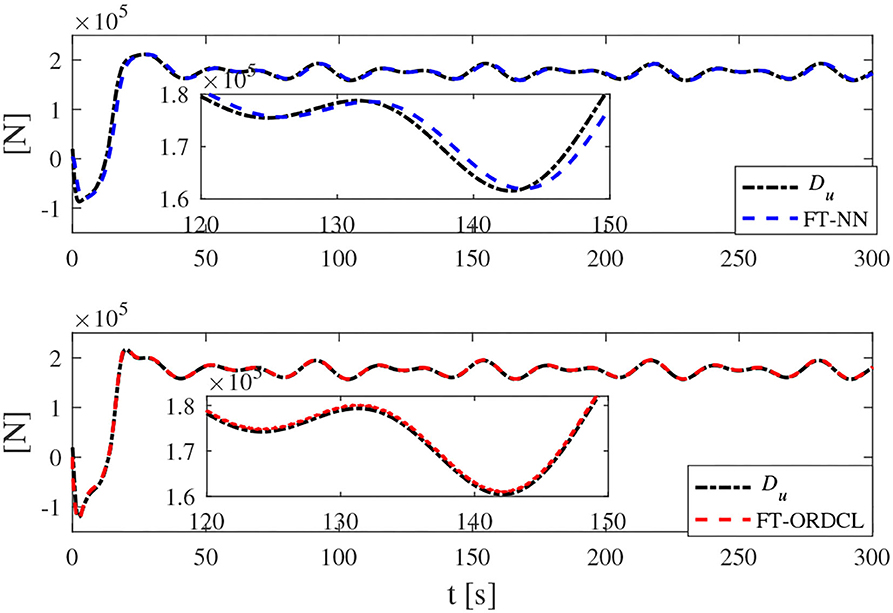
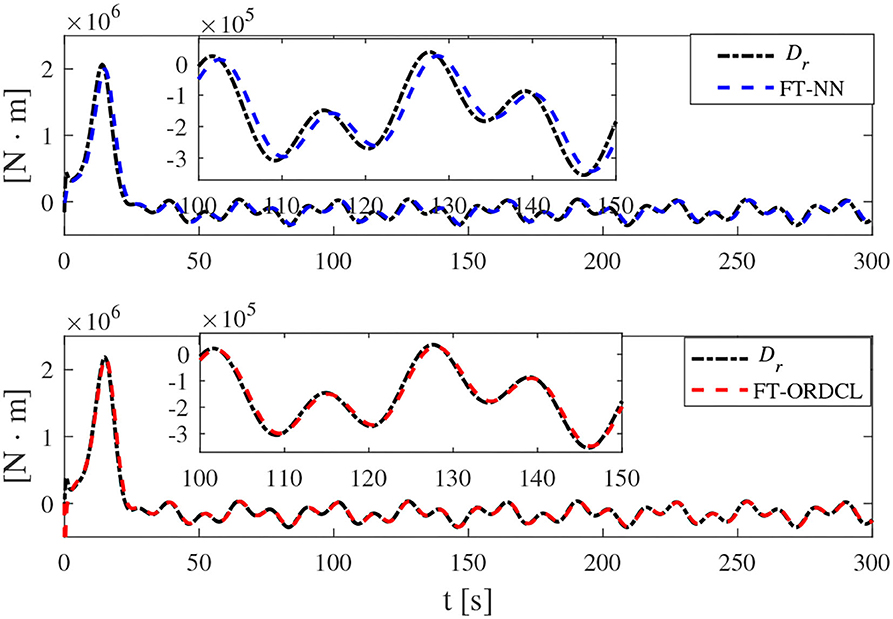
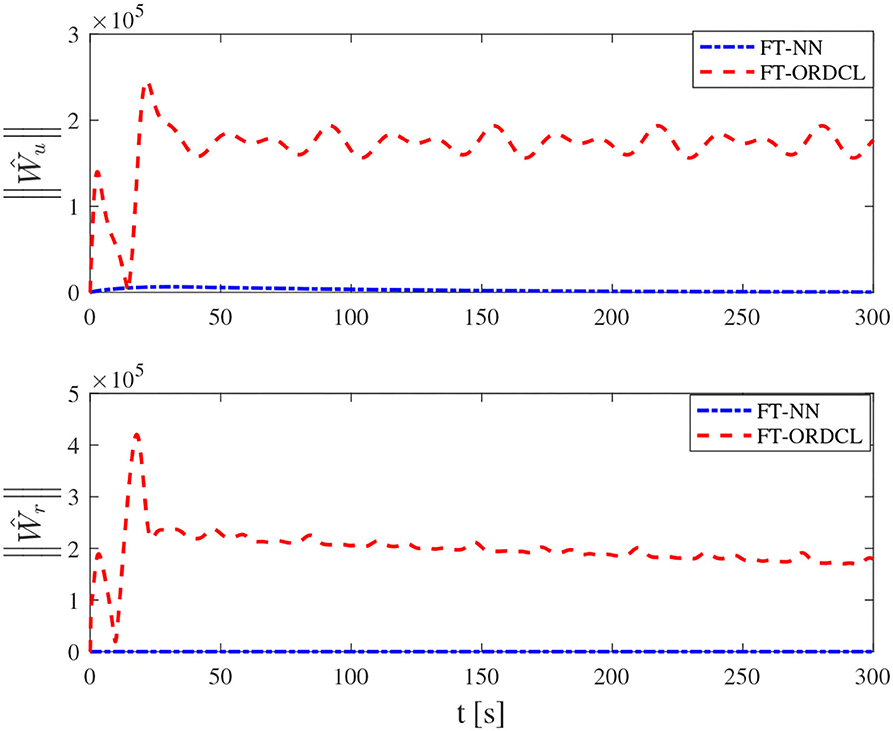
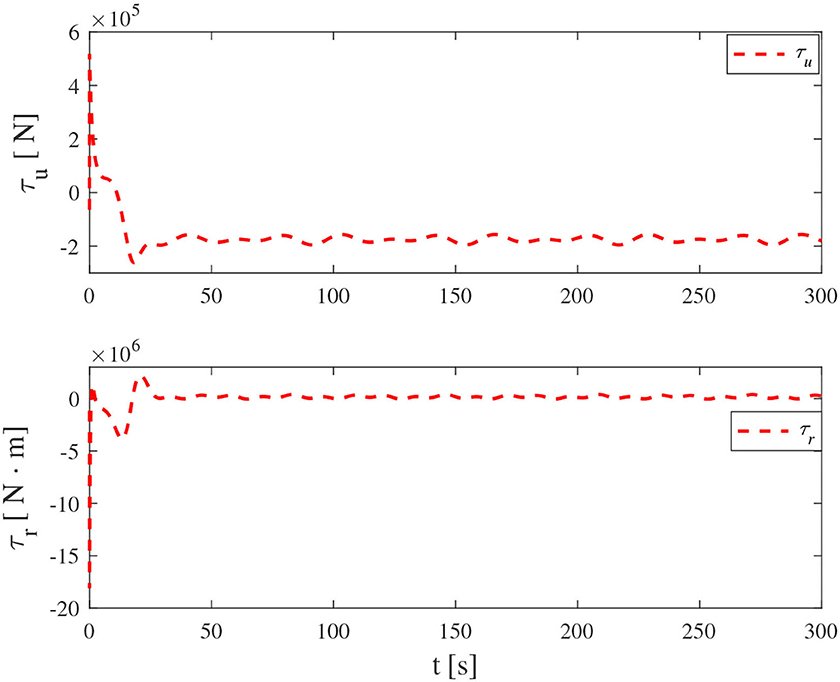
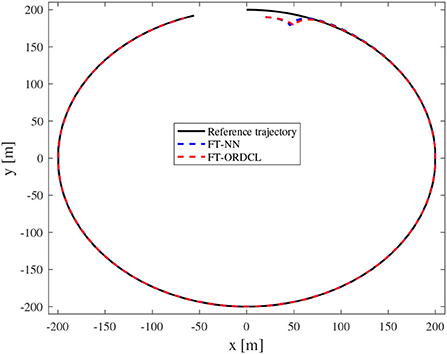
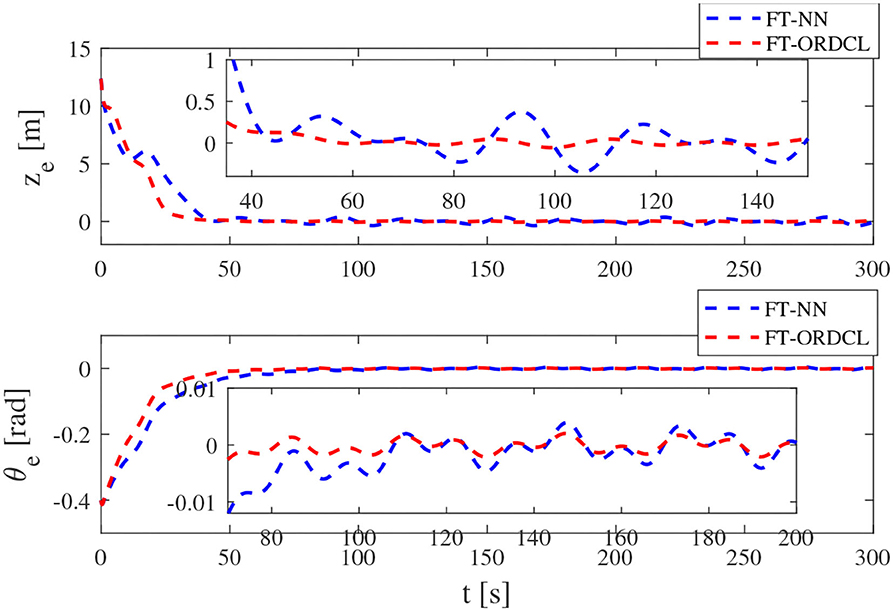
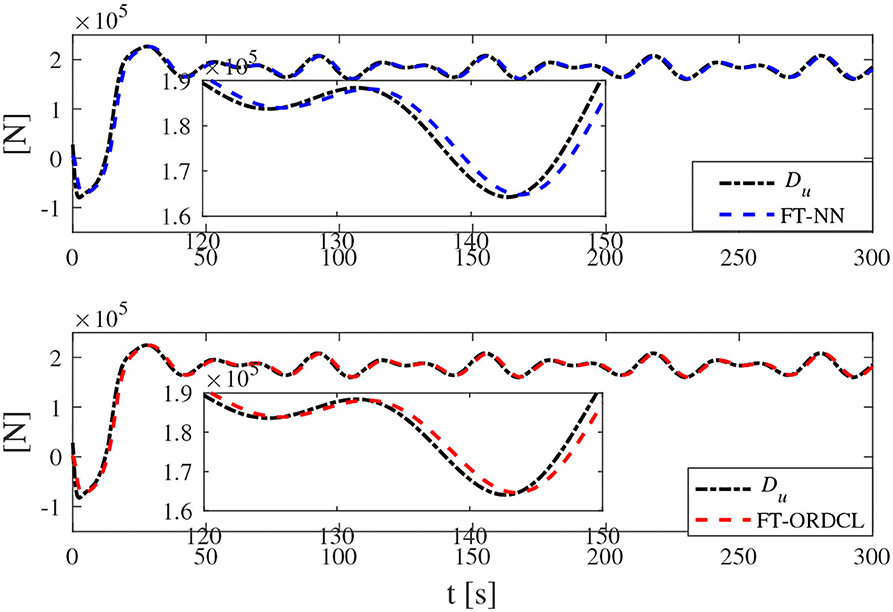
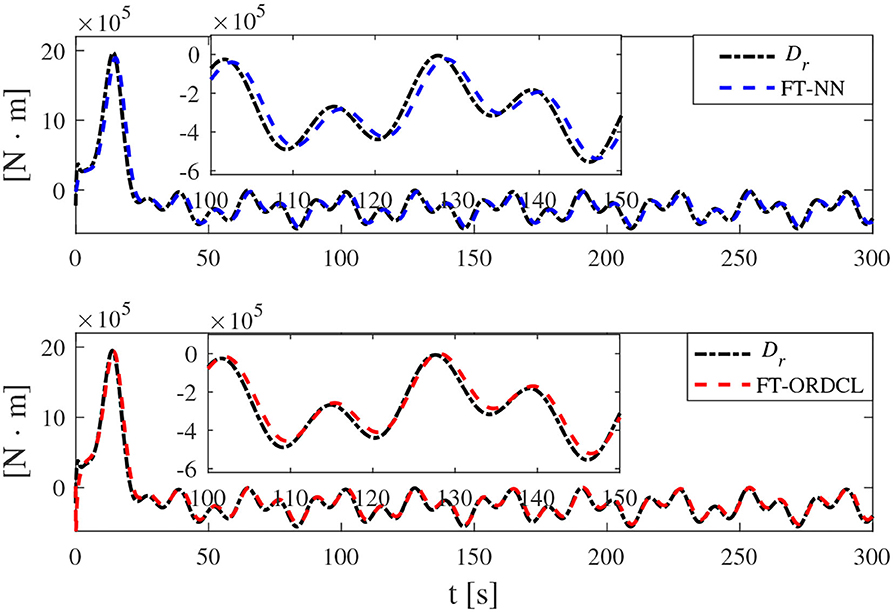
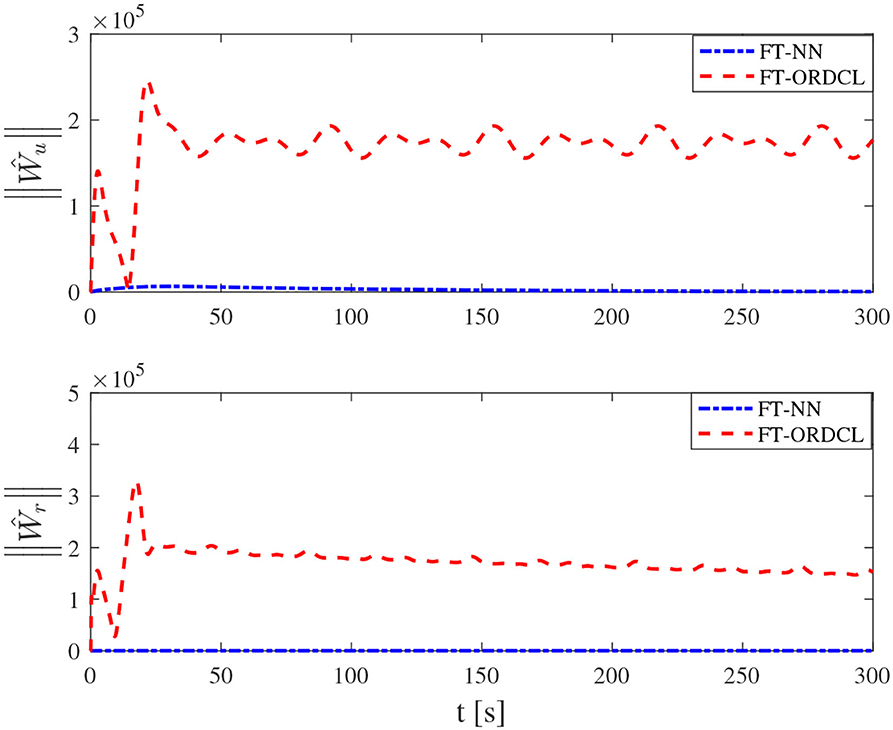
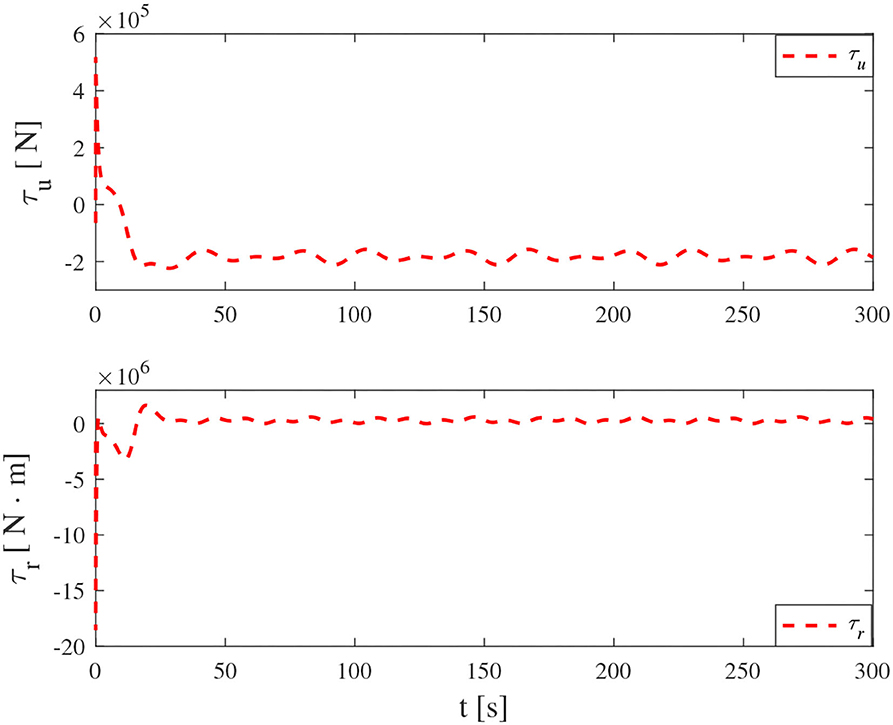
Simulation results under the FT-ORDCL and FT-NN control schemes are illustrated in Figures 1–6. Figure 1 clearly shows that the desired trajectory can be tracked under uncertain dynamics and time-varying disturbances under both control schemes. From Figure 2, the results show that FT-ORDCL can accomplish faster convergence and more accurate tracking of desired trajectories than FT-NN. The approximate results of unknown information are clearly shown in Figures 3, 4, thus further supporting the conclusion in Figure 2. The estimated value of 2-norms of the NN weights are bounded and reasonable as seen in Figure 5. The control force τu and control torque τr are plotted in Figure 6. From a practical point of view, the control force and control torque are bounded and reasonable.
Case 2: The unknown dynamics are increased by +10% and the bigger unknown disturbance is given as [1.2 × 104 sin(0.3t − π/4) + 1.2 × 104 cos(0.2t + π/4) + 2.4 × 104N, 1.2 × 103 sin(0.2t − π/4) + 1.2 × 103 cos(0.3t − π/4) + 3.6 × 103N · m, 1.2 × 105 sin(0.2t + π/6) + 1.2 × 105 cos(0.5t − π/4) − 3.6 × 105N · m]T. The design parameters and the initial conditions are given the same as those in Case 1.
Simulation results under the FT-ORDCL and FT-NN control schemes in Case 2 are provided in Figures 7–12. It is clearly depicted from Figure 7, that MSVs can track the desired trajectory in the presence of uncertain dynamics and time-varying ocean disturbances under both control schemes in Case 2. From Figure 8, the results show that FT-ORDCL can accomplish faster convergence and more accurate tracking of desired trajectories than FT-NN. It can be seen from Figures 9, 10, the same conclusion can be obtained in Case 1. The proposed control scheme has good adaptability and robustness. The estimated value of 2-norms of the NN weights are bounded as seen in Figure 11. The control force τu and control torque τr are plotted in Figure 12. From Figure 12, the corresponding control inputs are bounded and reasonable.
5. Conclusion
In this article, the problem of FT trajectory tracking control for underactuated MSVs, which suffer from uncertain dynamics and unknown external disturbances, has been solved by devising a composite neural control scheme based on online recorded data. The uncertain dynamics and unknown external disturbances were compensated exactly by the composite NNs based on online recorded data and the NDOs, respectively. By virtue of the LOS approach, the underactuation problem of the MSV is addressed. A smooth function is inserted into the design of the proposed control scheme artistically, and the FT trajectory tracking control of MSVs is realized based on online data recording composite NNs. The comparison of simulation results and methods shows the effectiveness and superiority of the developed control scheme.
Furthermore, the developed control scheme in this article can be extended to the trajectory tracking control of multiple-input multiple-output or single-input single-output systems with unknown external disturbances and uncertain dynamics. For extensions to the existing study, the proposed control scheme can be combined with fault-tolerant control and event-triggered schemes to achieve more complex control objectives.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.
Author contributions
CZ: conceptualization and investigation. HY: writing and conceptualization. DG: methodology and formal analysis. All authors contributed to the article and approved the submitted version.
Funding
This study was supported by the National Science Foundation of China under Grant No. 52071201.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Dai, S.-L., Wang, M., and Wang, C. (2015). Neural learning control of marine surface vessels with guaranteed transient tracking performance. IEEE Trans. Ind. Electron. 63, 1717–1727. doi: 10.1109/TIE.2015.2504553
Do, K. D. (2010). Practical control of underactuated ships. Ocean Eng. 37, 1111–1119. doi: 10.1016/j.oceaneng.2010.04.007
Do, K. D. (2016). Global robust adaptive path-tracking control of underactuated ships under stochastic disturbances. Ocean Eng. 111, 267–278. doi: 10.1016/j.oceaneng.2015.10.038
Do, K. D., and Pan, J. (2004). Robust adaptive path following of underactuated ships. Automatica 40, 929–944. doi: 10.1016/j.automatica.2004.01.021
Elhaki, O., and Shojaei, K. (2021). Robust saturated dynamic surface controller design for underactuated fast surface vessels including actuator dynamics. Ocean Eng. 229, 108987. doi: 10.1016/j.oceaneng.2021.108987
Gao, T., Huang, J., Zhou, Y., and Song, Y.-D. (2017). Robust adaptive tracking control of an underactuated ship with guaranteed transient performance. Int. J. Syst. Sci. 48, 272–279. doi: 10.1080/00207721.2016.1179816
Gao, Z., and Guo, G. (2019). Command-filtered fixed-time trajectory tracking control of surface vehicles based on a disturbance observer. Int. J. Robust Nonlinear Control 29, 4348–4365. doi: 10.1002/rnc.4628
Ghommam, J., and Saad, M. (2018). Adaptive leader-follower formation control of underactuated surface vessels under asymmetric range and bearing constraints. IEEE Trans. Veh. Technol. 67, 852–865. doi: 10.1109/TVT.2017.2760367
Gibson, T. E., Annaswamy, A. M., and Lavretsky, E. (2013). On adaptive control with closed-loop reference models: transients, oscillations, and peaking. IEEE Access 1, 703–717. doi: 10.1109/ACCESS.2013.2284005
Guo, G., and Zhang, P. (2020). Asymptotic stabilization of usvs with actuator dead-zones and yaw constraints based on fixed-time disturbance observer. IEEE Trans. Veh. Technol. 69, 302–316. doi: 10.1109/TVT.2019.2955020
He, X., and Geng, Z. (2021). Point stabilization and trajectory tracking of underactuated surface vessels: a geometric control approach. J. Franklin Inst. 358, 7119–7141. doi: 10.1016/j.jfranklin.2021.07.026
Huang, Y., Na, J., Wu, X., Gao, G.-B., and Guo, Y. (2018). Robust adaptive control for vehicle active suspension systems with uncertain dynamics. Trans. Inst. Meas. Control 40, 1237–1249. doi: 10.1177/0142331216678312
Na, J., Huang, Y., Wu, X., Gao, G., Herrmann, G., and Jiang, J. Z. (2017). Active adaptive estimation and control for vehicle suspensions with prescribed performance. IEEE Trans. Control Syst. Technol. 26, 2063–2077. doi: 10.1109/TCST.2017.2746060
Na, J., Mahyuddin, M. N., Herrmann, G., Ren, X., and Barber, P. (2015). Robust adaptive finite-time parameter estimation and control for robotic systems. Int. J. Robust Nonlinear Control 25, 3045–3071. doi: 10.1002/rnc.3247
Ning, W., Xinxiang, P., and Sunfeng, S. (2020). Finite-time fault-tolerant trajectory tracking control of an autonomous surface vehicle. J. Franklin Inst. 357, 11114–11135. doi: 10.1016/j.jfranklin.2019.05.016
Pan, B., Chen, C., Zhu, G., and Su, Y. (2022). Event-triggered composite learning finite-time trajectory tracking control for underactuated msvs subject to uncertainties. IEEE Access 10, 14440–14449. doi: 10.1109/ACCESS.2022.3146315
Park, B. S., and Yoo, S. J. (2016). Robust fault-tolerant tracking with predefined performance for underactuated surface vessels. Ocean Eng. 115, 159–167. doi: 10.1016/j.oceaneng.2016.02.006
Peng, Z., Wang, D., and Wang, J. (2016). Predictor-based neural dynamic surface control for uncertain nonlinear systems in strict-feedback form. IEEE Trans. Neural Netw. Learn. Syst. 28, 2156–2167. doi: 10.1109/TNNLS.2016.2577342
Qi, W., Zong, G., and Karimi, H. R. (2020). Finite-time observer-based sliding mode control for quantized semi-markov switching systems with application. IEEE Trans. Ind. Informat. 16, 1259–1271. doi: 10.1109/TII.2019.2946291
Rout, R., Cui, R., and Han, Z. (2020). Modified line-of-sight guidance law with adaptive neural network control of underactuated marine vehicles with state and input constraints. IEEE Trans. Control Syst. Technol. 28, 1902–1914. doi: 10.1109/TCST.2020.2998798
Seok Park, B. (2014). Neural network-based tracking control of underactuated autonomous underwater vehicles with model uncertainties. J. Dyn. Syst. Meas. Control. 137, 021004. doi: 10.1115/1.4027919
Shojaei, K. (2015). Neural adaptive robust control of underactuated marine surface vehicles with input saturation. Appl. Ocean Res. 53, 267–278. doi: 10.1016/j.apor.2015.09.010
Shojaei, K., and Arefi, M. M. (2015). On the neuro-adaptive feedback linearising control of underactuated autonomous underwater vehicles in three-dimensional space. IET Control Theory Appl. 9, 1264–1273. doi: 10.1049/iet-cta.2014.0472
Van, M. (2019). An enhanced tracking control of marine surface vessels based on adaptive integral sliding mode control and disturbance observer. ISA Trans. 90, 30–40. doi: 10.1016/j.isatra.2018.12.047
Wang, C., and Lin, Y. (2015). Decentralized adaptive tracking control for a class of interconnected nonlinear time-varying systems. Automatica 54, 16–24. doi: 10.1016/j.automatica.2015.01.041
Wang, N., and Deng, Z. (2020). Finite-time fault estimator based fault-tolerance control for a surface vehicle with input saturations. IEEE Trans. Ind. Informat. 16, 1172–1181. doi: 10.1109/TII.2019.2930471
Wang, N., Qian, C., Sun, J.-C., and Liu, Y.-C. (2016). Adaptive robust finite-time trajectory tracking control of fully actuated marine surface vehicles. IEEE Trans. Control Syst. Technol. 24, 1454–1462. doi: 10.1109/TCST.2015.2496585
Wang, N., Qian, C., and Sun, Z.-Y. (2017). Global asymptotic output tracking of nonlinear second-order systems with power integrators. Automatica 80, 156–161. doi: 10.1016/j.automatica.2017.02.026
Wang, N., Sun, J.-C., and Er, M. J. (2018). Tracking-error-based universal adaptive fuzzy control for output tracking of nonlinear systems with completely unknown dynamics. IEEE Trans. Fuzzy Syst. 26, 869–883. doi: 10.1109/TFUZZ.2017.2697399
Wang, Y., Jiang, B., Wu, Z.-G., Xie, S., and Peng, Y. (2020). Adaptive sliding mode fault-tolerant fuzzy tracking control with application to unmanned marine vehicles. IEEE Trans. Syst. Man Cybern. Syst. 51, 6691–6700. doi: 10.1109/TSMC.2020.2964808
Xiao, B., and Yin, S. (2018). Exponential tracking control of robotic manipulators with uncertain dynamics and kinematics. IEEE Trans. Ind. Inform. 15, 689–698. doi: 10.1109/TII.2018.2809514
Xu, B. (2017). Composite learning control of flexible-link manipulator using nn and dob. IEEE Trans. Syst. Man Cybern. Syst. 48, 1979–1985. doi: 10.1109/TSMC.2017.2700433
Xu, B., Shi, Z., Yang, C., and Sun, F. (2014). Composite neural dynamic surface control of a class of uncertain nonlinear systems in strict-feedback form. IEEE Trans. Cybern. 44, 2626–2634. doi: 10.1109/TCYB.2014.2311824
Xu, B., and Shou, Y. (2018). Composite learning control of mimo systems with applications. IEEE Trans. Ind. Electron. 65, 6414–6424. doi: 10.1109/TIE.2018.2793207
Xu, B., Shou, Y., Luo, J., Pu, H., and Shi, Z. (2019). Neural learning control of strict-feedback systems using disturbance observer. IEEE Trans. Neural Netw. Learn. Syst. 30, 1296–1307. doi: 10.1109/TNNLS.2018.2862907
Xu, B., and Sun, F. (2018). Composite intelligent learning control of strict-feedback systems with disturbance. IEEE Trans. Cybern. 48, 730–741. doi: 10.1109/TCYB.2017.2655053
Yang, T., Ma, Y., and Zhang, P. (2022a). Artificial potential field based anti-saturation positioning obstacle avoidance control for wheeled robots. Nonlinear Dyn. 1, 1–11. doi: 10.1007/s11071-022-07778-9
Yang, T., Ma, Y., Zhang, P., and Xu, J. (2021). Prescribed finite time stabilization of linear systems with state constraints. IEEE Access 9, 47677–47686. doi: 10.1109/ACCESS.2021.3068526
Yang, T., Zhang, P., and Chen, H. (2022b). Distributed prescribed-time leader-follower formation control of surface vehicles with unknowns and input saturation. ISA Trans. 1, 1–12. doi: 10.1016/j.isatra.2022.07.033
Yucelen, T., and Haddad, W. M. (2013). Low-frequency learning and fast adaptation in model reference adaptive control. IEEE Trans. Autom. Control 58, 1080–1085. doi: 10.1109/TAC.2012.2218667
Zhang, G., and Zhang, X. (2014). Concise robust adaptive path-following control of underactuated ships using dsc and mlp. IEEE J. Oceanic Eng. 39, 685–694. doi: 10.1109/JOE.2013.2280822
Zhang, P., Yang, T., and Li, D. (2020). Formation control of multiple underactuated surface vehicles based on prescribed-time method. IEEE Access 8, 151371–151382. doi: 10.1109/ACCESS.2020.3016980
Zhu, G., Ma, Y., and Hu, S. (2020). Single-parameter-learning-based finite-time tracking control of underactuated msvs under input saturation. Control Eng. Pract. 105, 104652. doi: 10.1016/j.conengprac.2020.104652
Zhu, G., Ma, Y., Li, Z., Malekian, R., and Sotelo, M. (2021a). Adaptive neural output feedback control for msvs with predefined performance. IEEE Trans. Veh. Technol. 70, 2994–3006. doi: 10.1109/TVT.2021.3063687
Zhu, G., Ma, Y., Li, Z., Malekian, R., and Sotelo, M. (2021b). Event-triggered adaptive neural fault-tolerant control of underactuated msvs with input saturation. IEEE Trans. Intell. Transport. Syst. 99, 1–13. doi: 10.1109/TITS.2021.3066461
Keywords: MSVs, trajectory tracking, online recorded data, finite-time control, composite neural networks
Citation: Zhao C, Yan H and Gao D (2022) Online recorded data-based finite-time composite neural trajectory tracking control for underactuated MSVs. Front. Neurorobot. 16:1029914. doi: 10.3389/fnbot.2022.1029914
Received: 28 August 2022; Accepted: 20 September 2022;
Published: 12 October 2022.
Edited by:
Guibing Zhu, Zhejiang Ocean University, ChinaCopyright © 2022 Zhao, Yan and Gao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huaran Yan, aHVhcmFueWFuMjAyMjAyQDE2My5jb20=
 Chunbo Zhao
Chunbo Zhao Huaran Yan
Huaran Yan