A Fireworks Algorithm Based on Transfer Spark for Evolutionary Multitasking

In recent years, lots of multifactorial optimization evolutionary algorithms have been developed to optimize multiple tasks simultaneously, which improves the overall efficiency using implicit genetic complementarity between different tasks. In this paper, a novel multitask fireworks algorithm is proposed with novel transfer sparks to solve multitask optimization problems. For each task, some transfer sparks would be generated with adaptive length and promising direction vector, which are very helpful to transfer useful genetic information between different tasks. Finally, the proposed algorithm is compared against some chosen state-of-the-art evolutionary multitasking algorithms. The experimental results show that the proposed algorithm provides better performance on several single objectives and multiobjective MTO test suites.

Introduction

Traditional evolutionary algorithms aim to find the optimal solution for a single optimization problem by applying the reproduction and selection operators to generate better individuals iteratively (Coello et al., 2006). With the complexity of the problem increasing, simultaneously solving multiple optimization problems efficiently and quickly becomes an urgent problem (Ong and Gupta, 2016). In this context, inspired by multitasking learning in the machine learning field (Chandra et al., 2017), evolutionary multitasking (EMT) is proposed to solve the multitask optimization (MTO) problem by encoding the solutions from different tasks into a unified search space and utilizing the information of potential complementarity and similarity of different tasks to improve the convergence speed and the quality of the solutions (Gupta et al., 2016b).

The best known and the first instructive work in the EMT area is the multifactorial evolutionary algorithm (MFEA) (Gupta et al., 2016b, 2017). The MFEA algorithm is inspired by the multifactorial inheritance (Rice et al., 1978; Cloninger et al., 1979). Each task corresponds to a cultural bias block, and each cultural bias block will have an impact on the development of the offspring. When individuals with different cultural biases hybridize, they exchange information about each other's cultures and promote optimization by exploiting the potential genetic complementarity between multiple tasks (Gupta and Ong, 2016). Intuitively, an inferior solution of a task may be an exceptional solution for the other task. Similarly, the same solution in a unified space can also be excellent in multiple tasks concurrently. In both cases, the MFEA allows multiple tasks to bundle together to optimize and share genetic information to improve the overall efficiency of the search process (Gupta et al., 2018). To this end, MFEA also proposed the mechanisms of assortative mating and vertical cultural transmission to ensure the efficiency and intensity of information exchange between tasks. These ideas have a profound impact on subsequent algorithms.

Currently, the research on EMT can approximately be summarized into three categories, the practical application of EMT (Sagarna and Ong, 2016; Yuan et al., 2016; Zhou et al., 2016; Cheng et al., 2017; Binh et al., 2018; Thanh et al., 2018; Lian et al., 2019; Wang et al., 2019) and the improved algorithm based on the MFEA framework (Bali et al., 2017; Feng et al., 2017; Wen and Ting, 2017; Joy et al., 2018; Li et al., 2018; Tuan et al., 2018; Zhong et al., 2018; Binh et al., 2019; Liang et al., 2019; Yin et al., 2019; Yu et al., 2019; Zheng et al., 2019; Zhou et al., 2019) and the perfection of EMT theory (Gupta et al., 2016a; Hashimoto et al., 2018; Liu et al., 2018; Zhou et al., 2018; Bali et al., 2019; Chen et al., 2019; Feng et al., 2019; Huang et al., 2019; Shang et al., 2019; Song et al., 2019; Tang et al., 2019). From the above studies, a consensus can be summarized that efficiently utilizing the inter-task related information is the key to improve overall search efficiency in EMT. Therefore, many studies focus on analyzing and optimizing knowledge transfer between tasks. Zhong et al. (2018) proposed a multitask genetic programming algorithm, which adopted a novel scalable chromosome representation to allow cross-domain coding of multiple solutions in a unified representation. The improved evolutionary mechanism takes both the implicit transfer of useful features between tasks and the ability of exploration into account. Liang et al. (2019) introduced genetic transform strategy and hyper-rectangle search strategy to the MFEA to improve the efficiency of knowledge transfer between tasks in the late iteration of the traditional MFEA. Huang et al. (2019) proposed an efficient surrogate-assisted multitask evolutionary framework with adaptive knowledge transfer, which is very superior for solving expensive optimization tasks. The surrogate model is constructed according to the historical search information of each task and reduces the evaluation times. A universal similarity measurement mechanism and an adaptive knowledge transfer mechanism are proposed to help knowledge transfer efficiently. Chen et al. (2019) presented the adaptive selection mechanism to evaluate the correlation between tasks and cumulative return on knowledge transferring to select the appropriate assisted task for a given task to prevent the influence of negative tasks. Feng et al. (2019) proposed an explicit genetic transferring EMT algorithm by autoencoding. This explicit genetic transfer method effectively utilizes multiple preferences embedded in different evolutionary operators to improve search performance. Bali et al. (2019) adopted the online learning mechanism into EMT and initiated a data-driven parameter tuning multitasking approach to mitigate harmful interactions between unrelated tasks to enhance overall optimization efficiency.

It is noted that most of the existing EMT algorithms are affected by the well-known MFEA algorithm. Individuals exchange genetic information through the chromosomal crossover. The hybridization of individuals with the same cultural background contributes to exploit, while individuals from different cultural backgrounds share information about their respective tasks. However, there are two drawbacks. First, the crossover sites and offset directions are randomly generated; therefore, the information transferred from the other task might not necessarily contribute to the optimization of the target task. Second, the intensity of information exchange is artificially set, and the optimization performance lacks effective feedback on it, which makes the search effect of EMT algorithm sensitive to the relationship between the tasks optimized simultaneously.

Swarm intelligence algorithms have the potential to transfer potential genetic information between tasks due to their inherent parallelism (Feng et al., 2019; Song et al., 2019). Inspired by coevolution (Cheng et al., 2017), by mapping multiple tasks into different subpopulations, the same type of subpopulations compete with each other, and subpopulations with different types cooperate, and potentially helpful knowledge blocks can be efficiently transferred between populations and utilized. The fireworks algorithm (FWA) (Tan and Zhu, 2010) is a recently proposed evolutionary algorithm based on swarm intelligence. First, a fixed number of positions in the search space are chosen as fireworks. Then, a set of sparks is generated through the explosion operation from the fireworks. Afterward, the superior solutions from the whole fireworks and sparks are selected as the fireworks for the next generation to continually improve the quality of the solution iteratively. Benefiting from the powerful global search and information utilization capabilities of FWA, it has attracted much research interest (Zheng et al., 2013; Liu et al., 2015; Li et al., 2017; Li and Tan, 2018) and has demonstrated excellent performance in many real-world problems (Yang and Tan, 2014; Bacanin and Tuba, 2015; Bouarara et al., 2015; Ding et al., 2015; Rahmani et al., 2015). In this paper, an innovative transfer vector (TV) is introduced to represent the bias of knowledge transfer between tasks. The TV is constructed by the current fitness information of other tasks and has promising direction and adaptive length. A potential superiority solution with the probability to navigate other tasks called transfer spark (TS) is generated by adding the TV as the bias to the current firework. A novel multitask optimization fireworks algorithm (MTO-FWA) utilizing the TS to exchange implicit information between tasks is proposed.

The rest of this paper is organized as follows. Section Preliminary introduces the basics of MTO and the benchmark EMT algorithm MFEA. Section Method describes the basic FWA algorithm, the proposed MTO-FWA, and the promotion of MTO-FWA on multiobjective optimization problems. Section Experiments demonstrates the experiment results on both single-objective and multiobjective MTO problems to assess the effectiveness of MTO-FWA. Finally, Section Conclusion concludes this paper and elaborates on future work.

Preliminary

The section presents the key concept of MTO and the benchmark EMT algorithm MFEA.

Multitask Optimization

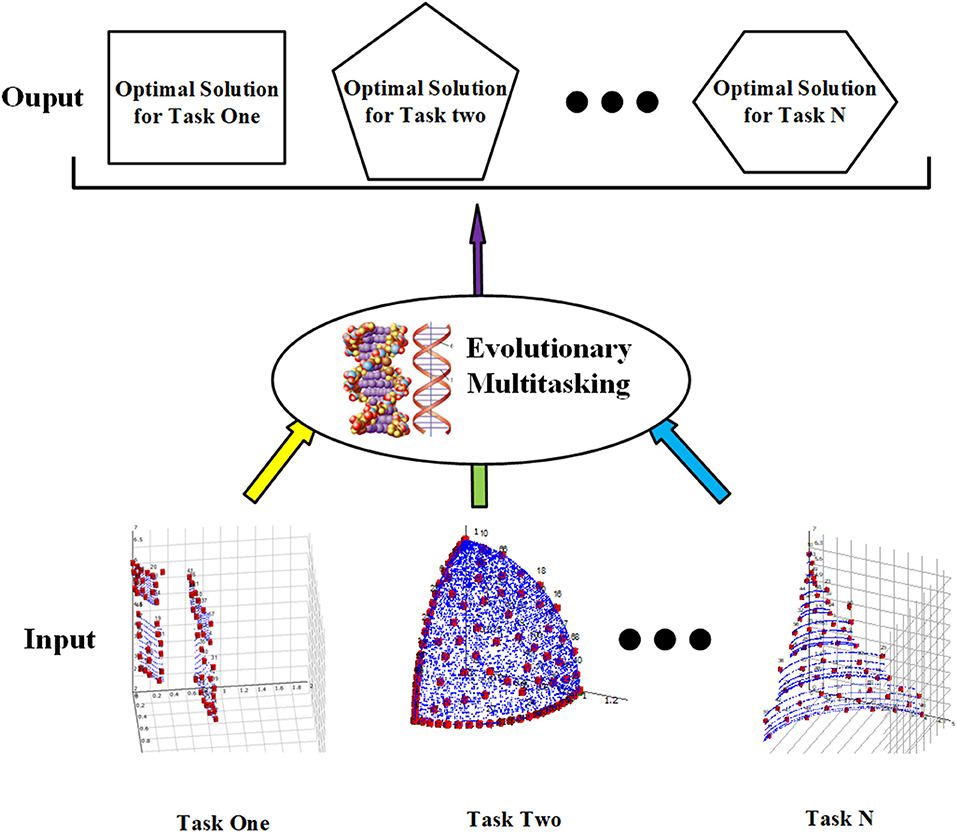
In general, conventional optimization problems can be divided into two categories: single-objective optimization (SOO) problems and multiobjective optimization (MOO) problems (Liang et al., 2019). They are both committed to seeking the optimal solution of an optimization task. The difference is that SOO has only one objective function, while MOO needs to optimize multiple conflicting objective functions. The purpose of the SOO is to search out the solution with the best function value, while the goal of the MOO problem is to obtain a solution set with splendid convergence and diversity. Inspired by the cognitive ability of humans to multitasking, the knowledge acquired from solving the problem can enlighten the optimization of related problems (Gupta et al., 2016b). MTO is devoted to implementing an evolutionary search on multiple optimization tasks simultaneously to improve the convergence by seamlessly transferring knowledge between multiple optimization problems.

Unlike SOO and MOO, MTO is a new paradigm that aims to seek out the optimal solutions for multiple tasks at once. As shown in Figure 1, the input to the MTO consists of multiple optimization tasks, each of which can be a SOO or MOO problem. All the tasks are handled by the MTO paradigms simultaneously, so the output of the MTO contains the optimal solution for each task separately.

$\begin{array}{l}\left\{X_1,X_2,\cdots ,X_K\right\}\\ =\left\{\text{argmin}{T}_1(X_1),\text{argmin}{T}_2(X_2),\cdots ,\text{argmin}{T}_K(X_K)\right\}& (1)\end{array}$

FIGURE 1

Figure 1. Illustration of multitask optimization.

The formal representation of MTO is shown in formula (1), where X_j denotes the optimal solution of the jth task T_j (j = 1,2,…K).

Multifactorial Evolutionary Algorithm

Inspired by the multifactorial inheritance (Rice et al., 1978; Cloninger et al., 1979), a novel EMT paradigm multifactorial optimization is proposed. Each task T_j is considered as a factor affecting individual evolution in the K-factorial environment [4, 5]. MFEA is a popular implementation that integrates genetic operators in genetic algorithm into multifactorial optimization (Gupta et al., 2016b, 2017; Bali et al., 2017; Feng et al., 2017; Wen and Ting, 2017; Binh et al., 2018, 2019; Li et al., 2018; Thanh et al., 2018; Zhong et al., 2018; Zhou et al., 2018, 2019; Liang et al., 2019; Shang et al., 2019; Yin et al., 2019; Yu et al., 2019; Zheng et al., 2019). All the individuals are encoded into a unified search space Y, and each individual can be decoded to optimize different component problems to effectively realize cross-domain knowledge transfer. In general, Y is normalized to [0, 1]^D, where D is the number of dimensions of the unified search space. D = max {D_{j ϵ {1, 2, …K}}}, where D_j indicates the number of dimensions of the jth task. By coding, a single chromosome y ∈ Y can signify a combination of chromosomes corresponding to K different tasks. By decoding, the chromosomes in the unified search space can be differentiated into K chromosomes specific to the task. To evaluate the performance of a solution in the uniform search space on different tasks, MFEA proposes some definitions.

Factorial Cost: The factorial cost of individual p_i is defined as ${\psi }_j^i$ which is applied to measure the performance of individual p_i on a specific task T_j. When the p_i is the feasible solution of task T_j and satisfies the constraint conditions, ${\psi }_j^i$ is the fitness value of T_j. Otherwise, ${\psi }_j^i$ is a very large value and indicates that the individual p_i is not a candidate solution of task T_j.

Factorial Rank: The factorial rank $r_j^i$ indicates the rank of fitness values ${\psi }_j^i$ for an individual p_i on a given task T_j by sorting the ${\psi }_j^i$ in ascending order.

Scalar Fitness: To illustrate the best performance that an individual can achieve in all tasks. The scalar fitness φ_i is defined based on the best factorial rank of individual p_i among all the tasks that can be expressed as φ_i = $\frac{1}{mi{n}_{jϵ\left\{1,2\dots k\right\}}{r}_j^i}$.

Skill Factor: The skill factor τ_i of individual p_i represents the task that p_i shows the best performance, which is defined as ${\tau }_i=argmi{n}_j\left\{r_j^i\right\}$.

Besides the traditional genetic operators, MFEA also applies the assortative mating to control the strength of genetic information transfer between tasks and vertical cultural transmission to enhance the efficiency of implicit knowledge transfer.

Assortative Mating: For two randomly selected individuals, if their skill factor is the same or satisfied the threshold called random mating probability (RMP), they can perform crossover to exchange their respective genetic information or they can only mutate. Intuitively, individuals with the uniform skill factor have a high probability of performing the crossover operator but individuals from different tasks can only exchange their genetic information in a small probability.

Vertical Cultural Transmission: Inspired by the multifactorial inheritance, MFEA believes that offspring will share the same cultural environment with their parents; that is, offspring should inherit their skill factors from their parents. If the offspring is obtained by the crossover operator, it will inherit the skill factor of either parent with equal probability. Otherwise, if the offspring is generated by the mutation operator, its skill factor will be completely inherited from the only parent. Based on the previous definitions, the pseudocode of the basic MFEA algorithm is shown in Algorithm 1.

ALGORITHM 1

Algorithm 1: The Pseudocode of MFEA

Methods

This section introduces the basic FWA, the MTO-FWA based on the TS, and the extended multiobjective MTO-FWA.

The Basic FWA

Illuminated by the phenomenon that fireworks exploding to generate some explosion sparks and illuminate a surrounding area, a novel swarm intelligence algorithm FWA is proposed (Tan and Zhu, 2010). It believes that the fireworks explosion phenomenon is analogical to the process of searching the optimal solution. If there is a promising area around the current search space, fireworks will migrate to that area and generate explosion sparks to perform the local search.

The prime procedure of FWA is as follows: first, randomly initialize a set of fireworks and evaluate each firework according to the objective function Then, each firework performs a local search through an explosion operation. To save computational resources and improve search efficiency, the resource allocation strategy is used to allocate the scope and frequency of each fireworks local search. In general, individuals with better fitness function values are considered more likely to lead to global optimum, and therefore are allocated more search resources. Based on the above ideas, fireworks with better fitness values will generate a mass of sparks and possess smaller explosion amplitudes, and fireworks with worse fitness values can only generate a smaller amount of sparks and have wider explosion amplitudes relatively. After the explosion, the Gaussian mutation operation is applied to produce Gaussian mutation sparks to increase the diversity of the population. Finally, the next generation of fireworks is selected from the candidate set including fireworks, and the sparks produced by explosion and Gaussian mutation based on their performance. The processes repeat iteratively until the maximum number of evaluations is reached.

Explosion Operation

In the basic FWA algorithm (Tan and Zhu, 2010), the number of sparks and explosion amplitude of each firework x_i are shown in formula (2) and (3), respectively:

$\begin{array}{ll}{S}_i=\widehat{S}·\frac{f_{max}-f\left(x_i\right)+ϵ}{{\displaystyle {\sum }_{i=1}^N}\left(f_{max}-f\left(x_i\right)\right)+ϵ}& \left(2\right)\end{array}$

$\begin{array}{ll}{A}_i=\widehat{A}·\frac{f\left(x_i\right)-f_{min}+ϵ}{{\displaystyle {\sum }_{i=1}^N}\left(f\left(x_i\right)-f_{min}\right)+ϵ}& \left(3\right)\end{array}$

where $\widehat{S}$ and $\widehat{A}$ are two artificial parameters to control the total number of fireworks and the total amount of explosion amplitude, respectively, N represents the population size, f_max and f_min denote the maximum and minimum objective values among the total fireworks, and ϵ indicate a tiny real value to prevent zero as the denominator. To avoid this, good fireworks have too many explosion sparks, but bad fireworks have very few explosion sparks. Two other constants parameters a, b ∈ [0,1] are introduced to bound the S_i to a proper range.

$\begin{array}{ll}{S}_i=\{\begin{array}{l}round\left(a·\widehat{S}\right),x<a·\widehat{S}\hfill \\ round\left(b·\widehat{S}\right),x>b·\widehat{S}\hfill \\ round\left(\widehat{S}\right),otherwise\hfill \end{array}& (4)\end{array}$

Conventional FWA does not conduct the explosion operation on each dimension of fireworks, but randomly selects D_explosion dimensions for explosion operation. Each dimension d of explosion spark e_is, which can be indicated as $e_{is}^d$ with s ∈ [1, S_i], d ∈ [1, D_explosion], conducts explosion operation according to formula (5).

$\begin{array}{ll}{e}_{is}^d=x_i^d+A_i·random(-1,1)& (5)\end{array}$

The spark generated by the explosion may exceed the boundary of the search space. FWA proposed the mapping rule to map it back to the search space as expressed in formula (6).

$\begin{array}{ll}{e}_{is}^d=x_{min}^d+e_{is}^{d}mod(x_{max}^d-x_{min}^d)& (6)\end{array}$

The outline of the explosion process is provided in Algorithm 2.

ALGORITHM 2

Algorithm 2: The Pseudocode of explosion

Gaussian Mutation Operator

Some specific sparks are generated by the Gaussian explosion, which adds an offset that satisfies a Gaussian distribution to the spark to increase the diversity of population. The process of the Gaussian explosion is shown in formula (7).

$\begin{array}{ll}{\stackrel{⌣}{e}}_i^d=x_i^d·Gaussian(1,1)& (7)\end{array}$

Similar to the explosion process, the Gaussian mutation also randomly selects D_gaussian dimensions to mutate. ${\stackrel{⌣}{e}}_i^d$ indicates the d dimension of the Gaussian mutation spark with d ∈ [1, D_gaussian].

Selection Mechanism

At each iteration of the algorithm, N individuals should be retained for the next generation. The individual with the best fitness is preferentially kept among all the current sparks and fireworks. Then, the remaining N – 1 individuals are chosen with the probability that is proportional to their distance from other individuals to maintain the diversity of sparks. Manhattan distance (Chiu et al., 2016) is usually used to measure the distance between a solution with other solutions. The choosing probability of the individual x_i represents as Pb(x_i) defined in formula (8), where M denotes the solution set containing all the current individuals of both fireworks and sparks.

$\begin{array}{ll}Pb(x_i)=\frac{Manhattandistance(x_i)}{{\displaystyle {\sum }_{i\in M}}Manhattandistance(x_i)}& (8)\end{array}$

The Structure of the FWA

Algorithm 3 summarizes the FWA framework. After the fireworks explode, the explosion sparks and Gaussian mutation sparks are generated based on Algorithm 2 and formula (7), respectively. The explosion sparks are generated according to the explosion operator, and the number and amplitude of the spark depend on the fitness of the firework. The Gaussian mutation sparks are generated by the Gaussian explosion process, whose number is denoted by Gas. Finally, N individuals remain for the next generation according to the selection mechanism.

ALGORITHM 3

Algorithm 3: The Pseudocode of FWA

Multitask Optimization Firework Algorithm

For MTO problems, the objective function landscape is heterogeneous, and the worst case is that they are not similar or intersecting. The key of EMT is to effectively utilize the implicit genetic information complementation from different tasks to improve the overall efficiency. Therefore, the interaction and transfer of information between different tasks are very important.

Swarm intelligence algorithms frequently possess multiple populations, which can grow the cognition of search space and further the diversity of solutions. This is very promising for exploring the heterogeneous search space of MTO problems. Different tasks can be assigned to different populations, and the cooperation between different populations provides an interpretable theoretical basis for information interaction between tasks. Different from the crossover process of randomly selected individuals in MFEA, information interaction between populations utilizes information from the whole population, which can effectively avoid random noise and negative knowledge transfer.

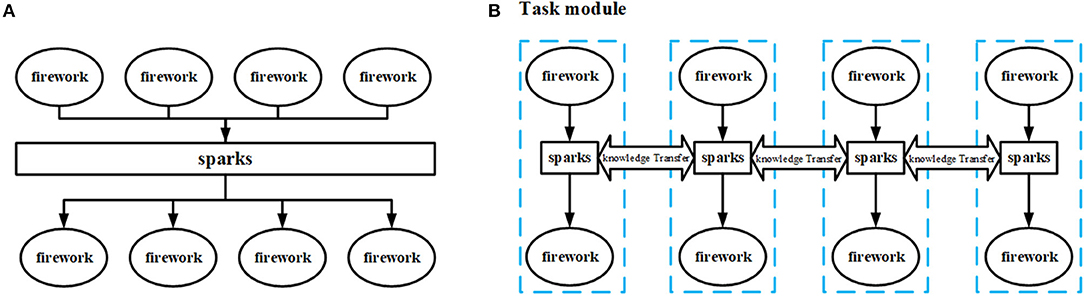
Unlike other swarm intelligence algorithms, FWA naturally possesses multiple populations on account of that every spark is generated near its parent firework and therefore they have similar properties. Just based on such an evolutionary strategy, each firework and its generated sparks are constituted as a task module, and each one is allocated a specific task. Disparate task modules exchange information to facilitate the exchange of implicit genetic information and individuals within a module compete with each other to promote convergence.

Compared with the conventional FWA, the main motivation of MTO-FWA can be summarized as two points.

1) Combine fireworks and their sparks into a task module to solve a specific task. Competition comes from within modules, and communication between tasks is based not on individuals but the module population. The comparison between the task module structure and the conventional FWA structure is shown in Figure 2.

2) A TS is proposed to solve information transfer and knowledge reuse between different tasks.

FIGURE 2

Figure 2. (A) The framework of conventional FWA vs. (B) the framework of MTO-FWA.

Explosion Operation

The traditional method controlling the number of sparks is sensitive to the maximum fitness value in the population, and the resource allocation gap between individuals is uncontrollable. The individuals with the highest adaptive value may get all the resources, while those with the lowest adaptive value may not get any resources. The traditional FWA solves this problem by setting thresholds, but this is crude and inelegant. Therefore, we use the power-law distribution (Li et al., 2017) to allocate spark number, through fitness rank rather than the fitness value to determine the number of spark explosion fireworks, which is shown in formula (9).

$\begin{array}{ll}{S}_r=\widehat{S}·\frac{r^{-\alpha }}{{\displaystyle {\sum }_{r=1}^N}{r}^{-\alpha }}& (9)\end{array}$

N represents the total number of fireworks, r denotes the fitness rank of fireworks, and α indicates the artificial parameter controlling the distribution of resource allocation. The larger the α, more explosion sparks a good firework produces.

For the amplitude, the dynamic control algorithm (Li et al., 2017) is used, and the explosion amplitude of all fireworks is controlled dynamically, as shown in formula (10).

$\begin{array}{ll}f\left(x\right)=\{\begin{array}{ll}{A}_i^1,\hfill & g=1\hfill \\ C_r{A}_i^{g-1},\hfill & f(x_i^g)⩾f(x_i^{g-1})\hfill \\ C_a{A}_i^{g-1},\hfill & f\left(x_i^g\right)<f(x_i^{g-1})\hfill \end{array}& (10)\end{array}$

where $A_i^g$ denotes the explosion amplitude of the ith firework in generation g. In the initialization generation, the explosion amplitude is set to a large real value, usually the diameter of the search space. If the function value of the offspring firework is larger than that of the parent fireworks, the explosion amplitude will be multiplied by a shrink coefficient C_r < 1 to reduce the explosion amplitude so as to exploit a better solution in the local scope. Instead, the amplitude of the explosion is multiplied by an amplification coefficient C_a > 1 to attempt to make the largest progress. In other words, the explosion amplitude is very large at the beginning of the iteration and shrinks to a smaller value in the later stages of the iteration by the dynamic tuning strategy.

It should be emphasized that the proposed MTO-FWA has the same mapping rules as FWA. The difference is that the explosion operator works in each dimension of fireworks instead of the D_explosion dimensions randomly selected, which has been proven to be more effective than the method of randomly selected dimensions (Li and Tan, 2018).

Guiding Spark

Different from the conventional FWA, the proposed MTO-FWA uses the guiding spark (GS) (Li et al., 2017) instead of the Gaussian mutation operator. The GS can guide the fireworks in a good direction by adding a guiding vector that indicates the dominant direction and step size to the fireworks location. The guiding vector is obtained by calculating the average of the differences between the pre-σS_i sparks and the post-σS_i sparks after all the sparks are sorted by their fitness values f (e_is) in the ascending order. By using the deviation between the top population and the bottom population, the random noise can be effectively reduced, the fireworks can be guided in the right direction, and the step length can be adjusted adaptively with the distance from the minimum value of the objective function. The generation of GS for the ith firework is shown in formula (11).

$\begin{array}{l}{\displaystyle {\Delta }_i=\frac{1}{\sigma S_i}({\sum }_{s=1}^{\sigma S_i}{e}_{is}-{\sum }_{s=S_i-\sigma S_i+1}^{S_i}{e}_{is})}\\ G{S}_i=x_i+{\Delta }_i& (11)\end{array}$

where σ is the ratio parameter, e_is represents the sth explosion spark generated by the ith fireworks, Δ_i indicates the guiding vector of the i th fireworks, and GS_i denotes the GS of the i th fireworks. It is worth noting that only one GS is generated for each firework.

Transfer Spark

The TS is proposed to exchange information between different tasks in MTO-FWA. Each firework, explosion spark, and GS will be assigned a skill factor, and the spark inherits the skill factor from their parents. The firework and its sparks constitute a task module with the same skill factor. To avoid excessive evaluations, individuals will only evaluate the fitness values of the tasks they are assigned. In the MTO problem, according to the concept of implicit genetic information complementation, the location information of a task module can greatly help optimize another task. Based on this, assume the ith firework for the optimization task j denoted as $F{W}_j^i$, it generates a unique spark for optimizing the task k according to the information from the task k. This information from task k is denoted as $T{V}_{jk}^i$. This spark is different from other sparks generated by $F{W}_j^i$ as its skill factor is k. Since it can transfer the information from other tasks, this type of spark is named TS. The TS generated by $F{W}_j^i$ under the guiding of $T{V}_{jk}^i$ is represented as $T{S}_{jk}^i$. $T{V}_{jk}^i$ and $T{S}_{jk}^i$ can be obtained by equations (12) and (13), respectively.

$\begin{array}{ll}{\displaystyle T{V}_{jk}^i=\frac{2}{\sigma M_j+\sigma M_k}({\sum }_{i=1}^{\sigma M_k}{x}_k^i-{\sum }_{i=1}^{\sigma M_j}{x}_j^i)\frac{r^{-\alpha }}{{\sum }_{r=1}^{N_j}{r}^{-\alpha }}}& (12)\end{array}$

$\begin{array}{ll}T{S}_{jk}^i=F{W}_j^i+T{V}_{jk}^i& (13)\end{array}$

where M_k and M_j denote the total number of the individuals that the skill factor is k and j, respectively. In general, M_k is equal to M_j. σM_k represents the best σM_k th individuals in ascending order of fitness value of task k, and σM_j indicates the best σM_j th individuals of task j. The average value of the difference of each of the best σMth individuals is taken as a deviation. Then, each firework will be assigned deviation using the power-law distribution according to the fitness rank. The fireworks that perform better on task j are considered to have more genetic advantages and will be given more information from task k. In contrast, individuals who perform poorly on the original task can only be assigned a small amount of exchanged genetic information.

Conventional EMT algorithms randomly select individuals with different skill factors to crossover for genetic information transfer. In FWA, the locations and fitness values of the sparks generated by the explosion contain a lot of information about the objective function. Even the inferior solution that will be eliminated in the selection process still contains the genetic information that can play a great positive role in understanding the fitness landscape of the objective function and transferring the genetic information between tasks. In general, this information is ignored and not effectively utilized. Given this, we use dominant subpopulations rather than a single optimal individual for transferring genetic information in MTO. Second, by using subpopulations for information transfer, the uncorrelated values will be canceled out. Most of the dimensions of the best spark are good, but the rest are not, which means that to learn from the single best individual is to learn its good and bad at the same time. However, learning from a good population is another matter. Only the common characteristics of the population will be transferred, and other information will be regarded as random noise canceling each other, so the transferred knowledge will be more accurate.

Most EMT algorithms use crossover operators to transfer knowledge between tasks, such as SBX crossover operators. The idea is to do a local search around the parents from different tasks, and most of the offspring will fall closer to their parents, and a few will fall in between. TV, which is essentially a similar effect, can be thought of as the average of the σM vectors pointing from task j to task k, and the generated solution TS_jk will fluctuate between the superior subpopulations of x_j and x_k.

Selection Mechanism

All the individuals in the same task module have the same skill factor, and an individual with the best fitness in a task module is kept as candidate firework, instead of selecting from the entire individual pool. Then, all candidate fireworks and TSs are then combined and grouped according to skill factor. Afterward, the selection probability is assigned according to the fitness value of the individual, and each group will select N solutions according to this probability as the next generation of fireworks. For task j, the selection strategy is shown in Algorithm 4.

ALGORITHM 4

Algorithm 4: Selection mechanism

The Structure of the MTO-FWA

Algorithm 5 summarizes the MTO-FWA framework. Assume that K tasks are optimized simultaneously; first, all the fireworks are initialized randomly and each one is evaluated by all the tasks. Then, each firework is assigned a skill factor τ according to their performance. After a firework exploding, S_i sparks with different explosion amplitude A_i are generated according to formulas (9) and (10). After that, a GS is generated by using the knowledge of exploding fireworks according to formula (11), and the skill factors of the explosion sparks and the GS are all set to τ. Afterward, K−1 TS are generated for other K−1 tasks, respectively, to share knowledge according to formulas (12) and (13). Finally, each task applies the selection strategy to pick the appropriate solutions for the next generation according to Algorithm 4.

ALGORITHM 5

Algorithm 5: The overall framework of MTO-FWA

Multitask Optimization Firework Algorithm for MOO

Multiobjective problems have two or more conflicting objectives for simultaneous optimization. Due to the lack of prior knowledge of the objective functions, we always study plentiful obtained solutions and retain the non-dominated solutions, the Pareto solution set, as the approximation of the true Pareto optimal set. Based on the fact that FWA is adept in using a single indicator to conclude the number of explosion sparks and the explosion amplitude, considering that MOO requires both convergence and diversity, the S-metric indicator (Liu et al., 2015) is introduced into FWA instead of the fitness value to select and evaluate the solutions. It should be noted that in the proposed multitask firework algorithm for MOO (MOMTO-FWA), except for the indicator modified to S-metric, the explosion operator, the GS, the TS, and the MTO-FWA are consistent. The following sections highlight the S-metric and the external archive mechanism for preserving non-dominated solutions.

S-Metric

The S-metric indicator can be regarded as the size of the space dominated by the solution or solution set (While et al., 2006). The S-metric for a solution set M = {m₁, m₂, ⋯m_i⋯m_n} is indicated as formula (14) (Emmerich et al., 2005).

$\begin{array}{ll}S(M):=\wedge ({\displaystyle \bigcup _{m\in M}}\left\{x|m\prec x\prec x_{ref}\right\})& (14)\end{array}$

where ∧ denotes the Lebesgue measure, ≺ denotes the dominance relationship, and x_ref indicates the reference point dominated by all the solutions. Homoplastically, the S-metric for a single solution is represented as formula (15).

$\begin{array}{ll}S(m_i)=\Delta S(M,m_i):=S(M)-S(M\backslash \left\{m_i\right\})& (15)\end{array}$

The S-metric of a solution m_i can be considered as the region that is only dominated by m_i but not by other solutions in the population.

External Archive Mechanism

To ensure the quality of the solution, MOMTO-FWA uses an external archive mechanism to save the advantageous solutions for the entire iteration of each task. The number of individuals in the external archive remains at a fixed value E. For a single task k, the E_k solutions are selected from a pool of candidates M_k consisting of all fireworks, explosion sparks, GS, and TS with the same skill factor of τ_k. By selecting the optimal solution with the largest S-metric and updating the S-metric of remaining solutions, the selected E_k solutions gain the maximum S-metric in all the E_k sets. It has been proven that the solution set that has the theoretic maximum of S-metric comes necessarily from the True Pareto Front (Fleischer, 2003). The concrete mechanism of update the external archive of the specific task is shown in Algorithm 6.

ALGORITHM 6

Algorithm 6: Updating strategy for the external archive

Experiments

In this section, the proposed MTO-FWA is compared with other state-of-the-art EMT algorithms. The performance of MTO-FWA is comprehensively evaluated by the single-objective MTO test suite and the performance of MOMTO-FWA is assessed by the multiobjective MTO test suite.

Experiments on MTO for Single-Objective Problems

The performances of EMT algorithms are evaluated by the classical single-objective MTO test suite presented in the evolutionary MTO technical report (Da et al., 2017). The similarity of the fitness landscape and the degree of intersection of the global optima are the two key factors affecting genetic complementarity between different tasks. In other words, if the values of the corresponding dimensions of the global optima of different tasks are closer, the genetic information of the task is more likely to generate complementarity. Homoplastically, the more similar the fitness landscape of the optimization functions of the different tasks, the more helpful the knowledge an individual learns from one task to optimize other tasks indirectly. Therefore, based on the degree of intersection of the global optima, the designed benchmark problems can be divided into complete intersection (CI), partial intersection (PI), and no intersection (NI) categories. According to the similarity in the fitness landscape, the designed benchmark problems can be categorized as High Similarity (HS), Medium Similarity (MS), and Low Similarity (LS) classes. Based on the combination of the above two classification strategies, nine continuous MTO benchmark problems for SOO are proposed, each problem consisting of two classical SOO functions including the Sphere, Rosenbrock, Ackley, Rastrgin, Griewank, Weierstrass, and Schwefel functions.

As a typical swarm intelligence algorithm, the proposed MTO-FWA is compared not only with the classical basic MFEA algorithm but also with MFDE and MFPSO (Feng et al., 2017), the two swarm intelligence EMT algorithms. For a fair comparison, the population number for a single task is set to 100, and the maximum number of fitness evaluation for a single task is set to 100,000, using the average results of 30 independent runs for comparison. The MFEA uses simulated binary crossover operator (SBX) and polynomial mutation methods produce offspring to reproduce offspring, the RMP is set to 0.3, p_c and η_c in SBX are set to 1 and 2, respectively, and the parameters in polynomial mutation p_m and η_m are set to 1 and 5, respectively. In MFPSO, the w decreases linearly from 0.9 to 0.4; c1, c2, and c3 are all set to 0.2; and the RMP is also set to 0.3. In MFDE, the RMP is set to 0.3, and F and CR are set to 0.5 and 0.9. To ensure fairness, in MTO-FWA, the RMP is also set as 0.3; C_r, C_a, σ, and α are set to 0.9, 1.2, 0.2, and 0.

Table 1 shows the average and standard deviation of the objective function values of all algorithms that run 30 times independently on the classical single-objective MTO test suite. The superior average objective value results are highlighted in bold. The Wilcoxon rank sum test is performed at the significance level of 5%, and the proposed MTO-FWA is compared with other EMT algorithms. Significantly better and worse results than the basic MFEA are presented as “+” and “−”.

TABLE 1

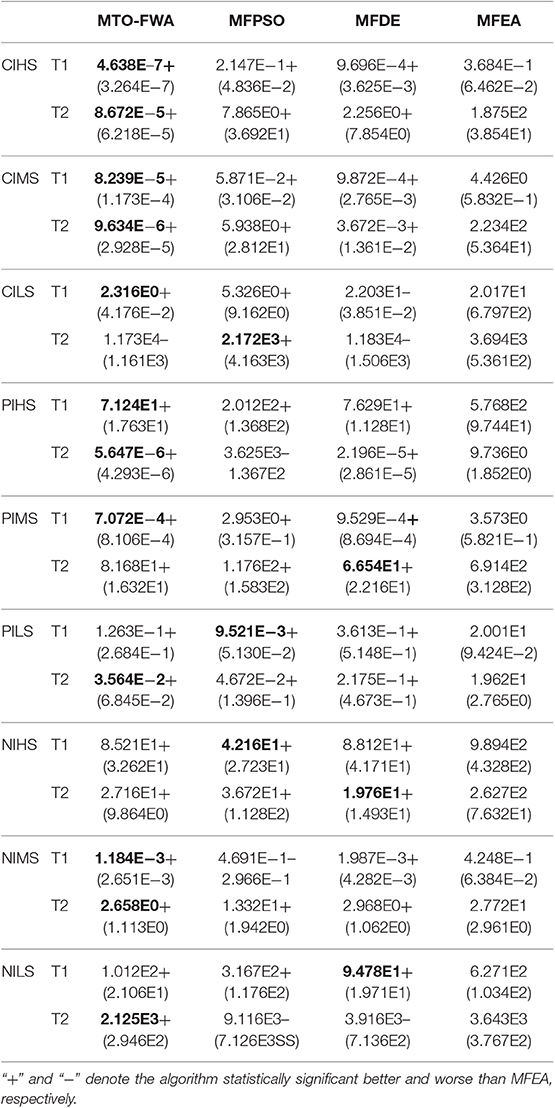
Table 1. Averaged objective value and standard deviation obtained by MTO-FWA, MFPSO, MFDE, and MFEA on the single-objective multitask problem.

As can be seen from Table 1, MTO-FWA shows obvious advantages in the average objective value of all the tasks in the classic MTO test problems compared with the basic MFEA. Compared with MFPSO and MFDE, MTO-FWA also shows better performance on both 15 out of 18 tasks, respectively, in the classical single-objective MTO test suite. The above statistical results verify the competitiveness and potential of the MTO-FWA algorithm in solving single-objective MTO. It is worth emphasizing that MTO-FWA reveals better performance than other EMT algorithms in most low and medium similarity test problems such as CIMS, CILS, PIMS, PILS, NIMS, and NILS. It is mainly due to the fact that the proposed TS can provide useful direction and step size and reduce the probability of negative information transfer by using information about the entire population rather than individual individuals. MFEA cannot mitigate the impact of negative knowledge transfer, which leads to the crossing process randomly happening with a lot of noise. Compared to MFPSO, MTO-FWA achieved better results on NIMS and NILS problems, because TV integrates information about the many sparks around the fireworks; therefore, it can provide better directions than the vector in PSO. Compared with MFDE, the MTO-FWA achieved better results on CIMS, CILS, PILS, and NIMS problems. It can be considered that the information used is the difference between two or more randomly selected individuals in DE, which is unpredictable. The information used in MTO-FWA comes from the difference between the two populations, so it is more specific.

Experiments on MTO for Multiobjective Problems

Similar to the above study for single-objective MTO, this experimental study considers the nine multiobjective multitask problems built in the recent technical report (Yuan et al., 2017). Analogously, the test problems can be classified as high similarity (HS), medium similarity (MS), and low similarity (LS), three categories according to the similarity in the fitness landscape, and each category can be divided into three sub-categories, complete intersection (CI), partial intersection (PI), and no intersection (NI) by the degree of intersection of the value of optima in each dimension. Each MTO problem consists of two MOO problems, each consisting of two or three objective functions commonly studied in the literature. Meanwhile, the proposed MOMTO-FWA is also compared with the well-known NSGA-II (Deb et al., 2002), since it is frequently applied as the underlying basic solver by many multiobjective EMT algorithms. For a fair comparison, the population number for a single task is set to 100, and the maximum number of fitness evaluation for a single task is set to 100,000, using the average results of 30 independent runs for comparison. Both MOMFEA and NSGA-II use SBX, and polynomial variations use the same parameter values. In SBX, p_c and η_c are set to 0.9 and 20, respectively. As for polynomial mutation, p_m and η_m are set to 1/D⁶ and 20, respectively.

Table 2 shows the average and standard deviation of the IGD of all algorithms that run 30 times independently on the classical multiobjective MTO test suite. The superior average IGD values are highlighted in bold. The Wilcoxon rank sum test is performed at the significance level of 5%, and the proposed MOMTO-FWA is compared with other multiobjective EMT algorithms. Significantly better and worse results than the basic MOMFEA are presented as “+” and “−.”

TABLE 2

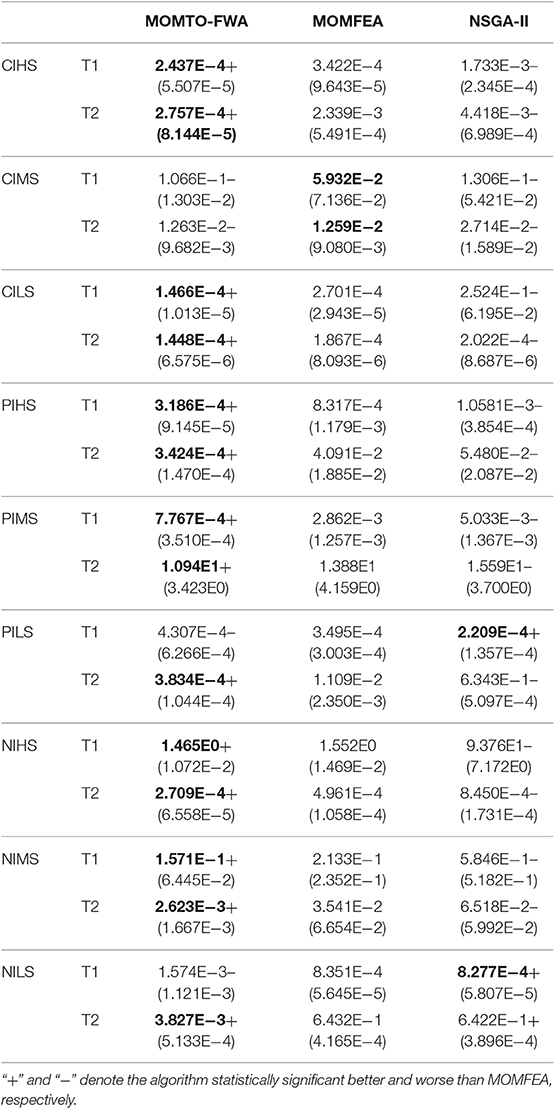
Table 2. Averaged value and standard deviation of the IGD obtained by MOMTO-FWA, MOMFEA, and NSGA-II on the multiobjective multitask problem.

As can be seen from Table 2, MOMTO-FWA shows obvious advantages in the average IGD value on 14 out of 18 tasks in the classic multiobjective MTO test problems compared with the basic MOMFEA. Compared with NSGA-II, MOMTO-FWA also shows better performance on 16 out of 18 tasks in the multiobjective MTO test suite. It is worth emphasizing that MOMTO-FWA reveals better performance than other multiobjective EMT algorithms in most low and medium similarity test problems such as CILS, PIMS, PILS-T2, NIMS, and NILS-T2 problems. Compared to MOMFEA, MOMTO-FWA achieved better results on CIHS, CILS, PIHS, PIMS, PILS-T2, NIHS, NIMS, and NILS-T2 problems, Even if it cannot surpass the performance of MOMFEA on CIMS, PILS-T1, and NILS-T1 problems, the performance of MOMTO-FWA is not much different. This may be because MOMFEA uses non-dominant ranking, while MOMTO-FWA uses S-metric as the evaluation index. In the later stage of the algorithm, the archiving-based mechanism reduces the diversity of solutions. Encouragingly, MOMTO-FWA achieves much better results than MOMFEA and NSGA-II on PIHS-T2, PIMS-T1, PILS-T2, NIMS-T2, and NILS-T2. It can be considered that the knowledge learning from simple tasks provides inspiration for solving difficult tasks and thus improves accuracy.

Figure 3 shows the average IGD values of MOMFEA, NSGA-II, and the proposed MOMTO-FWA after 30 independent runs on the classic multiobjective multitask test set. It should be noted that to indicate the changes in IGD more clearly, the starting point of the evaluation in Figure 3 starts from the 2000th evaluation, not from the 0th evaluation. Therefore, the algorithm has a preeminent starting point on some test problems, which does not mean that the random initialization of the population has undergone artificial intervention, but the population has converged to a state with a better IGD value within 2,000 evaluations. It is obvious from Figure 3 that the proposed MOMTO-FWA has terrific exploration ability and can quickly find out a better solution when the value of the fitness function of the initial population is terrible. In all the test problems, MOMTO-FWA is always on top in terms of IGD value within 20,000 evaluations. Besides, the proposed MOMTO-FWA converges faster than MOMFEA and NSGA-II in most problems.

FIGURE 3

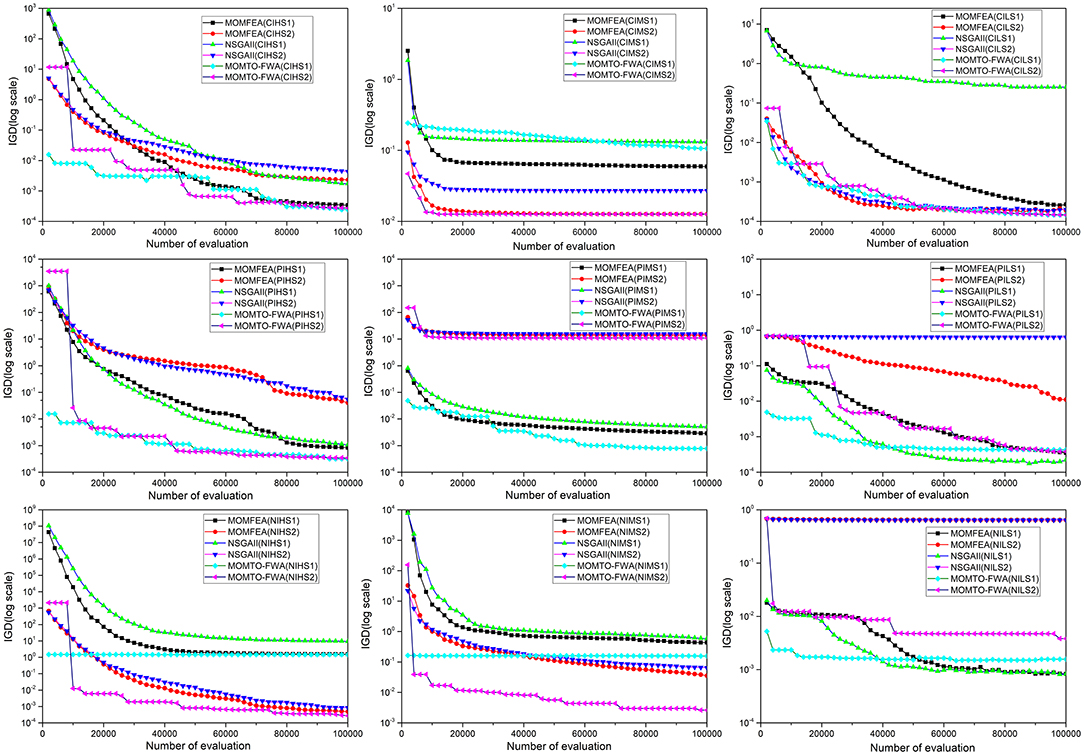
Figure 3. The average IGD with the number of evaluation for MOMFEA, NSGA-II, and MOMTO-FWA on the multiobjective multitask benchmark problem.

Conclusion

In this paper, we propose the strategy named TS to enable the FWA to solve MTO problems. The core idea is to bind a firework and its generated explosion sparks and GS into a task module to solve a specific problem. Through the performance of other task modules, a TS is generated around the firework to transfer the implicit genetic information between tasks. For the single-objective MTO problem, the objective function value corresponding to the task is used as the indicator to measure the performance of the task module to control the number of explosion sparks and the explosion amplitude. For multiobjective multitask problems, S-metric is applied to evaluate individual performance. The evaluation method based on the indicator is simple and effective, which is unified for utilizing the FWA to solve the SOO and MOO in MTO. Experimental results have shown that the proposed MTO-FWA can get promising results compared with the state-of-the-art multitask evolutionary algorithms on both SOO and MOO. There are several future research directions. One direction is to improve the efficiency of information sharing and transfer between fireworks. In addition, our current research focuses on the numerical optimization of two tasks. The many task problems and the simultaneous optimization of discrete and numerical tasks are the focus of the next phase of our research.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

ZX: code implementation and writing the experiment. KZ, JH, and XX: guidance, revision of paper, and discussion.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. U1803262, 61702383, 61602350, and 61472293) and by the Hubei Province Key Laboratory of Intelligent Information Processing and Real-time Industrial System under grant 2016znss11B.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would also like to thank the anonymous reviewers for their valuable remarks and comments.

References

Bacanin, N., and Tuba, M. (2015). “Fireworks algorithm applied to constrained portfolio optimization problem,” in 2015 IEEE Congress on Evolutionary Computation (CEC) (Sendai), 1242–1249. doi: 10.1109/CEC.2015.7257031

CrossRef Full Text | Google Scholar

Bali, K. K., Gupta, A., Feng, L., Ong, Y. S., and Siew, T. P. (2017). “Linearized domain adaptation in evolutionary multitasking,” in 2017 IEEE Congress on Evolutionary Computation (CEC) (San Sebastian), 1295–1302. doi: 10.1109/CEC.2017.7969454

CrossRef Full Text | Google Scholar

Bali, K. K., Ong, Y., Gupta, A., and Tan, P. S. (2019). “Multifactorial evolutionary algorithm with online transfer parameter estimation: MFEA-II,” in IEEE Transactions on Evolutionary Computation, 1. doi: 10.1109/TEVC.2019.2906927

CrossRef Full Text | Google Scholar

Binh, H. T., Thanh, P. D., Trung, T. B., and Thao, L. P. (2018). “Effective multifactorial evolutionary algorithm for solving the cluster shortest path tree problem,” in 2018 IEEE Congress on Evolutionary Computation (CEC) (Rio de Janeiro), 1–8.

Google Scholar

Binh, H. T. T., Tuan, N. Q., and Long, D. C. T. (2019). “A multi-objective multi-factorial evolutionary algorithm with reference-point-based approach,” in 2019 IEEE Congress on Evolutionary Computation (CEC) (Wellington), 2824–2831. doi: 10.1109/CEC.2019.8790034

CrossRef Full Text | Google Scholar

Bouarara, H. A., Hamou, R. M., Amine, A., and Rahmani, A. (2015). A fireworks algorithm for modern web information retrieval with visual results mining. Int. J. Swarm Intell. Res. 6, 1–23. doi: 10.4018/IJSIR.2015070101

CrossRef Full Text | Google Scholar

Chandra, R., Ong, Y.-S., and Goh, C.-K. (2017). Co-evolutionary multi-task learning with predictive recurrence for multi-step chaotic time series prediction. Neurocomputing 243, 21–34. doi: 10.1016/j.neucom.2017.02.065

CrossRef Full Text | Google Scholar

Chen, Y., Zhong, J., Feng, L., and Zhang, J. (2019). An adaptive archive-based evolutionary framework for many-task optimization. IEEE Trans. Emerg. Top. Comput. Intell. 1–16. doi: 10.1109/TETCI.2019.2916051

CrossRef Full Text | Google Scholar

Cheng, M.-Y., Gupta, A., Ong, Y.-S., and Ni, Z.-W. (2017). Coevolutionary multitasking for concurrent global optimization: With case studies in complex engineering design. Eng. Appl. Artif. Intell. 64, 13–24. doi: 10.1016/j.engappai.2017.05.008

CrossRef Full Text | Google Scholar

Chiu, W., Yen, G. G., and Juan, T. (2016). Minimum manhattan distance approach to multiple criteria decision making in multiobjective optimization problems. IEEE Trans. Evol. Comput. 20, 972–985. doi: 10.1109/TEVC.2016.2564158

CrossRef Full Text | Google Scholar

Cloninger, C. R., Rice, J., and Reich, T. (1979). Multifactorial inheritance with cultural transmission and assortative mating. II. a general model of combined polygenic and cultural inheritance. Am. J. Hum. Genet. 31, 176–198.

PubMed Abstract | Google Scholar

Coello, C. A. C., Lamont, G. B., and Veldhuizen, D. A. V. (2006). Evolutionary Algorithms for Solving Multi-Objective Problems (Genetic and Evolutionary Computation). Springer-Verlag. Available online at: http://dl.acm.org/citation.cfm?id=1215640 (accessed September 21, 2019).

Google Scholar

Da, B., Ong, Y.-S., Feng, L., Qin, A. K., Gupta, A., Zhu, Z., et al. (2017). Evolutionary multitasking for single-objective continuous optimization: benchmark problems, performance metric, and baseline results. arXiv:1706.03470.

Google Scholar

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6, 182–197. doi: 10.1109/4235.996017

CrossRef Full Text | Google Scholar

Ding, K., Chen, Y., Wang, Y., and Tan, Y. (2015). “Regional seismic waveform inversion using swarm intelligence algorithms,” in 2015 IEEE Congress on Evolutionary Computation (CEC) (Sendai), 1235–1241. doi: 10.1109/CEC.2015.7257030

CrossRef Full Text | Google Scholar

Emmerich, M., Beume, N., and Naujoks, B. (2005). “An EMO algorithm using the hypervolume measure as selection criterion,” in Evolutionary Multi-Criterion Optimization Lecture Notes in Computer Science, eds C. A. C. Coello, A. Hernández Aguirre, and E. Zitzler (Berlin; Heidelberg: Springer), 62–76. doi: 10.1007/978-3-540-31880-4_5

CrossRef Full Text | Google Scholar

Feng, L., Zhou, L., Zhong, J., Gupta, A., Ong, Y., Tan, K., et al. (2019). Evolutionary multitasking via explicit autoencoding. IEEE Trans. Cybernet. 49, 3457–3470. doi: 10.1109/TCYB.2018.2845361

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, L., Zhou, W., Zhou, L., Jiang, S. W., Zhong, J. H., Da, B. S., et al. (2017). “An empirical study of multifactorial PSO and multifactorial DE,” in 2017 IEEE Congress on Evolutionary Computation (CEC) (San Sebastian), 921–928. doi: 10.1109/CEC.2017.7969407

CrossRef Full Text | Google Scholar

Fleischer, M. (2003). “The measure of pareto optima applications to multi-objective metaheuristics,” in Evolutionary Multi-Criterion Optimization Lecture Notes in Computer Science, eds C. M. Fonseca, P. J. Fleming, E. Zitzler, L. Thiele, and K. Deb (Berlin; Heidelberg: Springer), 519–533. doi: 10.1007/3-540-36970-8_37

CrossRef Full Text | Google Scholar

Gupta, A., and Ong, Y. (2016). “Genetic transfer or population diversification? Deciphering the secret ingredients of evolutionary multitask optimization,” in 2016 IEEE Symposium Series on Computational Intelligence (SSCI) (Athens), 1–7. doi: 10.1109/SSCI.2016.7850038

CrossRef Full Text | Google Scholar

Gupta, A., Ong, Y., and Feng, L. (2016b). Multifactorial evolution: multitasking. IEEE Trans. Evol. Comput. 20, 343–357. doi: 10.1109/TEVC.2015.2458037

CrossRef Full Text | Google Scholar

Gupta, A., Ong, Y., and Feng, L. (2018). Insights on transfer optimization: because experience is the best teacher. IEEE Trans. Emerg. Top. Comput. Intell. 2, 51–64. doi: 10.1109/TETCI.2017.2769104

CrossRef Full Text | Google Scholar

Gupta, A., Ong, Y., Feng, L., and Tan, K. C. (2017). Multiobjective multifactorial optimization in evolutionary multitasking. IEEE Trans. Cybernet. 47, 1652–1665. doi: 10.1109/TCYB.2016.2554622

PubMed Abstract | CrossRef Full Text | Google Scholar

Gupta, A., Ong, Y. S., Da, B., Feng, L., and Handoko, S. D. (2016a). “Landscape synergy in evolutionary multitasking,” in 2016 IEEE Congress on Evolutionary Computation (CEC) (Vancouver, BC), 3076–3083. doi: 10.1109/CEC.2016.7744178

CrossRef Full Text | Google Scholar

Hashimoto, R., Ishibuchi, H., Masuyama, N., and Nojima, Y. (2018). “Analysis of evolutionary multi-tasking as an island model,” in Proceedings of the Genetic and Evolutionary Computation Conference Companion GECCO'18 (New York, NY: ACM), 1894–1897. doi: 10.1145/3205651.3208228

CrossRef Full Text | Google Scholar

Huang, S., Zhong, J., and Yu, W. (2019). Surrogate-assisted evolutionary framework with adaptive knowledge transfer for multi-task optimization. IEEE Trans. Emerg. Topics Comput. 1. doi: 10.1109/TETC.2019.2945775

CrossRef Full Text | Google Scholar

Joy, C. P., Tang, J., Chen, Y., Deng, Z., and Xiang, Y. (2018). “A group-based approach to improve multifactorial evolutionary algorithm,” in Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI-18), 3870–3876. Available online at: https://www.ijcai.org/proceedings/2018/538 (accessed September 22, 2019).

Google Scholar

Li, G., Zhang, Q., and Gao, W. (2018). “Multipopulation evolution framework for multifactorial optimization,” in Proceedings of the Genetic and Evolutionary Computation Conference Companion GECCO'18 (New York, NY: ACM), 215–216. doi: 10.1145/3205651.3205761

CrossRef Full Text | Google Scholar

Li, J., and Tan, Y. (2018). Loser-out tournament-based fireworks algorithm for multimodal function optimization. IEEE Trans. Evol. Comput. 22, 679–691. doi: 10.1109/TEVC.2017.2787042

CrossRef Full Text | Google Scholar

Li, J., Zheng, S., and Tan, Y. (2017). The effect of information utilization: introducing a novel guiding spark in the fireworks algorithm. IEEE Trans. Evol. Comput. 21, 153–166. doi: 10.1109/TEVC.2016.2589821

CrossRef Full Text | Google Scholar

Lian, Y., Huang, Z., Zhou, Y., and Chen, Z. (2019). “Improve theoretical upper bound of jumpk function by evolutionary multitasking,” in Proceedings of the 2019 3rd High Performance Computing and Cluster Technologies Conference HPCCT 2019 (Guangzhou: ACM), 44–50. doi: 10.1145/3341069.3342982

CrossRef Full Text | Google Scholar

Liang, Z., Zhang, J., Feng, L., and Zhu, Z. (2019). A hybrid of genetic transform and hyper-rectangle search strategies for evolutionary multi-tasking. Expert Syst. Appl. 138, 112798. doi: 10.1016/j.eswa.2019.07.015

CrossRef Full Text | Google Scholar

Liu, D., Huang, S., and Zhong, J. (2018). “Surrogate-assisted multi-tasking memetic algorithm,” in 2018 IEEE Congress on Evolutionary Computation (CEC) (Janeiro), 1–8. doi: 10.1109/CEC.2018.8477830

CrossRef Full Text | Google Scholar

Liu, L., Zheng, S., and Tan, Y. (2015). “S-metric based multi-objective fireworks algorithm,” in 2015 IEEE Congress on Evolutionary Computation (CEC) (Sendai), 1257–1264. doi: 10.1109/CEC.2015.7257033

CrossRef Full Text | Google Scholar

Ong, Y.-S., and Gupta, A. (2016). Evolutionary multitasking: a computer science view of cognitive multitasking. Cogn. Comput. 8, 125–142. doi: 10.1007/s12559-016-9395-7

CrossRef Full Text | Google Scholar

Rahmani, A., Amine, A., Hamou, R. M., Rahmasni, M. E., and Bouarara, H. A. (2015). Privacy preserving through fireworks algorithm based model for image perturbation in big data. Int. J. Swarm Intell. Res. 6, 41–58. doi: 10.4018/IJSIR.2015070103

CrossRef Full Text | Google Scholar

Rice, J., Cloninger, C. R., and Reich, T. (1978). Multifactorial inheritance with cultural transmission and assortative mating. I. Description and basic properties of the unitary models. Am. J. Hum. Genet. 30, 618–643.

PubMed Abstract | Google Scholar

Sagarna, R., and Ong, Y. (2016). “Concurrently searching branches in software tests generation through multitask evolution,” in 2016 IEEE Symposium Series on Computational Intelligence (SSCI) (Athens), 1–8. doi: 10.1109/SSCI.2016.7850040

CrossRef Full Text | Google Scholar

Shang, Q., Zhang, L., Feng, L., Hou, Y., Zhong, J., Gupta, A., et al. (2019). “A preliminary study of adaptive task selection in explicit evolutionary many-tasking,” in 2019 IEEE Congress on Evolutionary Computation (CEC) (Wellington), 2153–2159. doi: 10.1109/CEC.2019.8789909

CrossRef Full Text | Google Scholar

Song, H., Qin, A. K., Tsai, P., and Liang, J. J. (2019). “Multitasking multi-swarm optimization,” in 2019 IEEE Congress on Evolutionary Computation (CEC) (Wellington), 1937–1944. doi: 10.1109/CEC.2019.8790009

CrossRef Full Text | Google Scholar

Tan, Y., and Zhu, Y. (2010). “Fireworks algorithm for optimization,” in Advances in Swarm Intelligence Lecture Notes in Computer Science, eds. Y. Tan, Y. Shi, and K. C. Tan (Berlin; Heidelberg: Springer), 355–364. doi: 10.1007/978-3-642-13495-1_44

CrossRef Full Text | Google Scholar

Tang, Z., Gong, M., Jiang, F., Li, H., and Wu, Y. (2019). “Multipopulation optimization for multitask optimization,” in 2019 IEEE Congress on Evolutionary Computation (CEC) (Wellington), 1906–1913. doi: 10.1109/CEC.2019.8790234

CrossRef Full Text | Google Scholar

Thanh, P. D., Dung, D. A., Tien, T. N., and Binh, H. T. T. (2018). “An effective representation scheme in multifactorial evolutionary algorithm for solving cluster shortest-path tree problem,” in 2018 IEEE Congress on Evolutionary Computation (CEC) (Janeiro), 1–8. doi: 10.1109/CEC.2018.8477684

CrossRef Full Text | Google Scholar

Tuan, N. Q., Hoang, T. D., and Binh, H. T. T. (2018). “A guided differential evolutionary multi-tasking with powell search method for solving multi-objective continuous optimization,” in 2018 IEEE Congress on Evolutionary Computation (CEC) (Rio de Janeiro), 1–8. doi: 10.1109/CEC.2018.8477860

CrossRef Full Text | Google Scholar

Wang, C., Ma, H., Chen, G., and Hartmann, S. (2019). “Evolutionary multitasking for semantic web service composition,” in 2019 IEEE Congress on Evolutionary Computation (CEC) (Wellington), 2490–2497. doi: 10.1109/CEC.2019.8790085

CrossRef Full Text | Google Scholar

Wen, Y., and Ting, C. (2017). “Parting ways and reallocating resources in evolutionary multitasking,” in 2017 IEEE Congress on Evolutionary Computation (CEC) (San Sebastian), 2404–2411. doi: 10.1109/CEC.2017.7969596

CrossRef Full Text | Google Scholar

While, L., Hingston, P., Barone, L., and Huband, S. (2006). A faster algorithm for calculating hypervolume. IEEE Trans. Evol. Comput. 10, 29–38. doi: 10.1109/TEVC.2005.851275

CrossRef Full Text | Google Scholar

Yang, X., and Tan, Y. (2014). “Sample index based encoding for clustering using evolutionary computation,” in Advances in Swarm Intelligence Lecture Notes in Computer Science, eds Y. Tan, Y. Shi, and C. A. C. Coello (Springer International Publishing), 489–498. doi: 10.1007/978-3-319-11857-4_55

CrossRef Full Text | Google Scholar

Yin, J., Zhu, A., Zhu, Z., Yu, Y., and Ma, X. (2019). “Multifactorial evolutionary algorithm enhanced with cross-task search direction,” in 2019 IEEE Congress on Evolutionary Computation (CEC) (Wellington), 2244–2251. doi: 10.1109/CEC.2019.8789959

CrossRef Full Text | Google Scholar

Yu, Y., Zhu, A., Zhu, Z., Lin, Q., Yin, J., and Ma, X. (2019). “Multifactorial differential evolution with opposition-based learning for multi-tasking optimization,” in 2019 IEEE Congress on Evolutionary Computation (CEC) (Wellington), 1898–1905. doi: 10.1109/CEC.2019.8790024

CrossRef Full Text | Google Scholar

Yuan, Y., Ong, Y., Gupta, A., Tan, P. S., and Xu, H. (2016). “Evolutionary multitasking in permutation-based combinatorial optimization problems: realization with TSP, QAP, LOP, and JSP,” in 2016 IEEE Region 10 Conference (TENCON) (Singapore), 3157–3164. doi: 10.1109/TENCON.2016.7848632

CrossRef Full Text | Google Scholar

Yuan, Y., Ong, Y.-S., Feng, L., Qin, A. K., Gupta, A., Da, B., et al. (2017). Evolutionary multitasking for multiobjective continuous optimization: benchmark problems, performance metrics and baseline results. arXiv:1706.02766.

Google Scholar

Zheng, X., Lei, Y., Qin, A. K., Zhou, D., Shi, J., and Gong, M. (2019). “Differential evolutionary multi-task optimization,” in 2019 IEEE Congress on Evolutionary Computation (CEC) (Wellington), 1914–1921. doi: 10.1109/CEC.2019.8789933

CrossRef Full Text | Google Scholar

Zheng, Y.-J., Song, Q., and Chen, S.-Y. (2013). Multiobjective fireworks optimization for variable-rate fertilization in oil crop production. Appl. Soft Comput. 13, 4253–4263. doi: 10.1016/j.asoc.2013.07.004

CrossRef Full Text | Google Scholar

Zhong, J., Feng, L., Cai, W., and Ong, Y.-S. (2018). Multifactorial genetic programming for symbolic regression problems. IEEE Trans. Syst. Man Cybern. Syst. 1–14. doi: 10.1109/TSMC.2018.2853719

CrossRef Full Text | Google Scholar

Zhou, L., Feng, L., Liu, K., Chen, C., Deng, S., Xiang, T., et al. (2019). “Towards effective mutation for knowledge transfer in multifactorial differential evolution,” in 2019 IEEE Congress on Evolutionary Computation (CEC) (Wellington), 1541–1547. doi: 10.1109/CEC.2019.8790143

CrossRef Full Text | Google Scholar

Zhou, L., Feng, L., Zhong, J., Ong, Y., Zhu, Z., and Sha, E. (2016). “Evolutionary multitasking in combinatorial search spaces: a case study in capacitated vehicle routing problem,” in 2016 IEEE Symposium Series on Computational Intelligence (SSCI)(Athens: IEEE), 1–8. doi: 10.1109/SSCI.2016.7850039

CrossRef Full Text | Google Scholar

Zhou, L., Feng, L., Zhong, J., Zhu, Z., Da, B., and Wu, Z. (2018). “A study of similarity measure between tasks for multifactorial evolutionary algorithm,” in Proceedings of the Genetic and Evolutionary Computation Conference Companion GECCO'18 (New York, NY: ACM), 229–230. doi: 10.1145/3205651.3205736

CrossRef Full Text | Google Scholar