Passive motion paradigm: an alternative to optimal control

“Nina: I want to be perfect.

Thomas: Perfection is not just about control. It’s also about letting go.”

A conversation between Nina Sayers and Thomas Leroy, the student and the dance teacher in the movie “The Black Swan” directed by Aronofsky (2010).

Putting the Issue into Context

Since the time of Nicholas Bernstein (1967) it has become clear that one of the central issues in neural control of movement is the “Degrees of Freedom (DoFs) Problem,” that is the computational process by which the brain coordinates the action of a high-dimensional set of motor variables for carrying out the tasks of everyday life, typically described, and learnt in a “task-space” of much lower dimensionality. Such dimensionality imbalance is usually expressed by the term “motor redundancy.” This means that the same movement goal can be achieved by an infinite number of combinations of the control variables which are equivalent as far as the task is concerned. But in spite of so much freedom, experimental evidence suggests that the motor system consistently uses a narrow set of solutions. Consider, for example, the task of reaching a point B in space, starting from a point A, in a given time T. In principle, the task could be carried out in an infinite number of ways, with regards to spatial aspects (hand path), timing aspects (speed profile of the hand), and recruitment patterns of the available DoF’s. In contrast, it was found that the spatio-temporal structure of this class of movements is strongly stereotypical, whatever their amplitude, direction, and duration: the path is nearly straight (in the extrinsic, Cartesian space, not the intrinsic, articulatory space) and the speed profile is nearly bell-shaped, with symmetric acceleration and deceleration phases (Morasso, 1981; Abend et al., 1982). That this stereotypicity should be attributed to internal control mechanisms, not to biomechanical effects, is suggested by the observation of reaching movements in different types of neuromotor impaired subjects. For example, in the case of ataxic patients, although they still can reach the target, spatio-temporal invariance is grossly violated: paths are strongly curved, with distortion patterns that change with the direction of movement, and the speed profile is asymmetric (Sanguineti et al., 2003).

Cybernetics of Purposive Actions

A movement, per se, is nothing unless it is associated with a goal and this usually requires recruitment of a number of joints, in the context of an action. Recognizing the crucial importance of multi-joint coordination was really a paradigm shift from the classical Sherringtonian viewpoint (typically focused on single-joint movements), to the Bernsteinian quest for principles of coordination or synergy formation. A coordinated action is a class of movements plus a goal. Redundancy is a side-effect of this connection and thus redundancy is necessarily task-oriented, something to be managed “on-line” and “rapidly” updated as the action unfolds. As descriptive concepts, coordination and synergy are equivalent: both refer to the fact that, in the context of a given set of behaviors, systematic correlations between different effectors can be observed. However, such correlations are just an epiphenomenon, determined by a deeper structure, namely the underlying control mechanisms in the motor system that activates groups of effectors as single units in different moments of an action. Shortly, we suggest calling it the “cybernetics of purposive actions.” Generally speaking, we consider actions as operational modules in which descending motor patterns are produced together with the expectation of the (multimodal) sensory consequences. Mounting evidence accumulated in the last 30 years from different directions and points of view, such as the equilibrium point hypothesis (Asatryan and Feldman, 1965; Feldman, 1966; Bizzi et al., 1976, 1992; Feldman and Levin, 1995), mirror neurons system (Di Pellegrino et al., 1992), motor imagery (Decety, 1996; Crammond, 1997; Grafton, 2009; Kranczioch et al., 2009; Munzert et al., 2009), motor resonance (Borroni et al., 2011), embodied cognition (Wilson, 2002; Gallese and Lakoff, 2005; Gallese and Sinigaglia, 2011; Sevdalis and Keller, 2011), etc., suggest that in order to understand the neural control of movement, the observation, and analysis of overt movements is just the tip of the iceberg because what really matters is the large computational basis shared by action production, action observation, action reasoning, and action learning.

Equilibrium Point Hypothesis – An Extended View

Let us go back to the issue of stereotypicity of reaching movements: where is it coming from? A general concept that was in the background of many studies during the mid-1960s to mid-1980s was the equilibrium point hypothesis (EPH: Asatryan and Feldman, 1965; Feldman, 1966; Bizzi et al., 1976, 1992; Feldman and Levin, 1995). Its power comes from its ability to solve the “DoFs problem” by positing that posture is not directly controlled by the brain in a detailed way but is a “biomechanical consequence” of equilibrium among a large set of muscular and environmental forces. In this view, “movement” is a symmetry-breaking phenomenon, i.e., the transition from an equilibrium state to another. In the quest for motor modules, studies were carried out with intact and spinalized animals (Bizzi et al., 1991; Mussa Ivaldi and Bizzi, 2000; d’Avella and Bizzi, 2005; Roh et al., 2011) showing that motor behaviors may be constructed by muscle synergies, with the associated force fields organized within the brain stem and spinal cord and activated by descending commands from supraspinal areas. Muscle synergies were also shown to be correlated to the control of task-related variables (e.g., end-point kinematics or kinetics, displacement of the center of pressure; (Ivanenko et al., 2003; Torres-Oviedo et al., 2006). Using techniques from control theory, (Berniker et al., 2009) proposed a design of a low-dimensional controller for a frog hind limb model, that balances the advantages of exploiting a system’s natural dynamics with the need to accurately represent the variables relevant for task-specific control. They demonstrated that the low-dimensional controller is capable of producing movements without substantial loss of either efficacy or efficiency, hence providing support for the viability of the muscle synergy hypothesis and the view that the CNS might use such a strategy to produce movement “simply and effectively.”

We emphasize that the additivity of the muscle synergies is ultimately made possible by the additivity of the underlying force fields. In the classical view of EPH, the attractor dynamics that underlies reaching movements is based on the elastic properties of the skeletal neuromuscular system and its ability to store/release mechanical energy. However, this may not be the only possibility. The discovery of motor imagery and the strong similarity of the recorded neural patterns in overt and covert movements, suggests that attractor dynamics and the associated force fields may not be uniquely determined by physical properties of the neuromuscular system but may arise as well from “similar” neural dynamics due to interaction among brain areas that are active in both situations. In this sense, the original EPH viewpoint can be extended by positing that cortico-cortical, cortico-subcortical, and cortico-cerebellar circuits associated with synergy formation may also be characterized by similar attractor mechanisms that cooperate in shaping flexible behaviors of the body schema in the context of ever-changing environmental interactions. The proposed PMP framework goes in this direction.

On the other hand, it is still an open question whether or not the motor system represents equilibrium trajectories (Karniel, 2011). Many motor adaptation studies, starting with the seminal paper by Shadmehr and Mussa-Ivaldi (1994), demonstrate that equilibrium points or equilibrium trajectories per se are not sufficient to account for adaptive motor behavior, but this is not sufficient to rule out the existence of neural mechanisms or internal models capable of generating equilibrium trajectories. Rather, as suggested by Karniel (2011), such findings should induce the research to shift from the lower level analysis of reflex loops and muscle properties to the level of internal representations and the structure of internal models. This is indeed the motivation and the purpose of our proposal: to model the posited internal models in terms of an extension of the EPH.

Optimal Control Theory

The first attempt to formulate in a mathematical manner the process by which the brain singles out a unique spatio-temporal pattern for a reaching task among infinite possible solutions was formulated by Flash and Hogan (1985), in the framework of the classical engineering design technique: optimal control theory (OCT). The general idea is that in order to design the best possible controller of a (robotic/human) system, capable of carrying out a prescribed task, one should define first a “cost function,” i.e., a mathematical combination of the control variables that yields a single number (the “cost”): This function is generally composed of two parts: a part that measures the “distance” of the system from the goal and a part (regularization term) that encodes the required “effort.” The design is then reduced to the computation of the control variables that minimize the cost function, thus finding the best possible trade-off between accuracy and effort. In the case of Flash and Hogan (1985), the regularization term was the “integrated jerk” and they showed that the solution of such minimization task was indeed consistent with the spatio-temporal invariances found by Morasso (1981). Other simulation studies found similar results by choosing different types of cost functions, such as “integrated torque change” (Uno et al., 1989), “minimum end-point variance” (Harris and Wolpert, 1998), “minimum object crackle” (Dingwell et al., 2004), “minimum acceleration criterion” (Ben-Itzhak and Karniel, 2008). In this line of research, optimal control concepts were used for deriving off-line control patterns, to be employed in feed-forward control schemes. A later development (Todorov and Jordan, 2002; Todorov, 2004) suggested using an extension of OCT that incorporates sensory feedback in the computational architecture. In this closed-loop control technique, a block named “Control Policy” generates a stream of motor commands that optimize the pre-defined cost function on the basis of a current estimate of the “state variables”; this estimate integrates in an optimal way (by means of a “Kalman filter”) feedback information (coming from delayed and noise-corrupted sensory signals) with a prediction of the state provided by a “forward model” of the system’s dynamics, driven by an “efference copy” of the motor commands. One of the most attractive features of this formulation, in addition to its elegance and apparent simplicity, is that it blurs the difference between feed-forward and feedback control because the control policy governs both. Recent developments show that OCT has gradually emerged as a powerful theory for interpreting a range of motor behaviors (Scott, 2004; Chhabra and Jacobs, 2006; Li, 2006; Shadmehr et al., 2010), online movement corrections (Saunders and Knill, 2004; Liu and Todorov, 2007), structure of motor variability (Guigon et al., 2008a; Kutch et al., 2008), Fitts’ law and control of precision (Guigon et al., 2008b) among others. At the same time, the framework has also been applied for controlling anthropomorphic robots (Nori et al., 2008; Ivaldi et al., 2010; Mitrovic et al., 2010; Simpkins et al., 2011).

Open challenges in OCT

A basic challenge within this approach is to derive the optimal control signal with non-linear time-varying systems, given a specific cost function and assumptions as to the structure of the noise. It is well known that this process comes with heavy computational costs and requires challenging mathematical contortions to solve even the simplest of the linear control problems (Bryson, 1999; Scott, 2004). Recent reformulations (Todorov, 2009) attempt to specifically address this topic by using concepts from statistical inference and thereby reducing the computation of the optimal “cost to go” function to a linear problem. At the same time, how these formal methods can be implemented through distributed neural networks has been questioned by numerous authors (Scott, 2004; Todorov, 2006; Guigon, 2011). A seemingly unrelated issue that is also worth mentioning here concerns the relationship between posture and movement. OCT based approaches generally speak about “goal directed” movements and speak very little about the integration (and interference) between posture and movement (Ostry and Feldman, 2003; Guigon et al., 2007) in an acting organism. We believe, all these issues are in fact related to the lack of consideration of the characteristics of the underlying neuromuscular system that ultimately generates movement.

Optimal control theory is a sophisticated motor control model directly derived from engineering “servo” theory, extended by integrating internal models and predictors. The “fact” is that such engineering paradigms were designed for high bandwidth, inflexible, consistent systems with precision sensors. The “difficulty” lies in adapting these models to the typical biological situation, characterized by low bandwidth, high transmission delays, variable/flexible behavior, noisy sensors, and actuators. In contrast, evolution naturally aided biological systems to establish “soft” mechanisms that “counteract” these factors and yet produce robust, flexible behaviors. Motor control arises from the interplay between processes both at neural and musculoskeletal levels. Although it is generally believed that the neural level has a dominant role in the control of movements, there is evidence that the mechanics of moving limbs in interaction with the environment can also contribute to control (Chiel and Beer, 1997; Nishikawa et al., 2007). We believe OCT based approaches that begin with the basic assumption that behavior can be understood by minimization of a cost function are too general and do very little to exploit specific properties of the system they intend to control. That such techniques can be applied to a wide range of problems ranging from “animal foraging” to “national policy” making speaks rather about the power of formal mathematical methods. However, when applied to specific problems like coordination of movement in humans or humanoids, it may be possible to simplify the computational machinery by taking into account the properties and constraints of the physical system that is being coordinated (like, stiffness, reflex, local distributed processing/learning etc). This may in turn endow the computational model with greater flexibility, scalability, and robustness.

Optimality entails the choice of a cost function, which indicates a quantity to minimize. The nature of the cost function is a highly debated issue. Part of the confusion arises from the fact that all the proposed cost functions (jerk, energy, torque change, among several others) make similar predictions on basic qualitative characteristics of movement, e.g., trajectories, velocity profiles (Flash and Hogan, 1985; Uno et al., 1989; Harris and Wolpert, 1998; Todorov and Jordan, 2002; Guigon et al., 2007). Yet, a thorough quantitative analysis is in general lacking that could provide more contrasted results. In the standard formulation of OCT, the cost for being in a state and the probability of state transition depending on the action are explicitly given (Doya, 2009). However, in many realistic problems, such costs and transitions are not known a priori. Thus, we have to identify them before applying OCT or learn to act based on past experiences of costs and transitions (using reinforcement learning techniques etc). Similar difficulties also occur in the robotic version of the “DoFs problem” because, for robots interacting with unstructured environments, it is difficult to identify and carefully craft a cost function that may promote the emergence/maturation of purposive, intelligent behavior. This is relevant if we want to go “beyond” reach/grasp movements to more complex manipulation tasks like tool use which in fact “begins” once an object of interest is reached and grasped. It has been recently demonstrated ingeniously that it may be possible to learn the desirability function without explicit knowledge of the costs and transitions using “Z-learning” (Todorov, 2009). It has also been shown to converge considerably faster than the popular “Q learning” (Watkins and Dayan, 1992). But as Doya (2009) suggests, such learning may be trivial for examples like walking on grid-like streets, but may turn out to be very complicated for cases like shifting the body posture by activating several DoFs.

Coming to the topic of redundancy, optimal control can be considered as a solution for such problems by minimizing the norm of the control signal, pseudo-inverse can be used to replace the inverse model block in a non-invertible redundant system. However, a central issue that still remains to be understood is how the brain uses different solutions under different circumstances (Karniel, 2011). Multiple internal models as proposed by different authors (Wolpert and Kawato, 1998; Haruno et al., 2001; Demiris and Khadhouri, 2006) might be the key to represent multiple solutions to the same goal. Nevertheless, the criterion for selecting one of the multiple solutions under various cases is open for future research. This goes to the contentious issue of “Sub–optimality.” The issue of sub-optimality in motor planning and the role of “motor memory” in consolidating the choice of a suboptimal strategy has been recently addressed by Ganesh et al. (2010), by showing the role of motor memory in the local minimization of task-specific variables. Zenzeri et al. (2011) have addressed this issue in relation with bimanual stabilization of an unstable task. The ability of expert users to switch between control strategies with strongly different cost functions was explored recently by Kodl et al. (2011), who showed that in suitable behavioral conditions subjects may randomly select from several available motor plans to perform a task. Generally speaking, the investigation of tasks that attempt to address activities of daily life, rather than artificial lab experiments, shows that the traditional approach to motor control, in the framework of a single plan, characterized by regular patterns related to the minimum of a cost function, can only offer a narrow view of the issue. In contrast, what is needed is a mechanism to hierarchically structure and modulate motion plans “on-line,” in a multi-referential framework, in such a way to allow to mix goals and constraints in a variety of task-related reference systems.

All this is not to say that optimal control concepts are not relevant for addressing motor control and synergy formation in humans and humanoid robots, set aside the successful application of optimization techniques and Bayesian modeling to multisensory and sensorimotor integration (Ernst and Banks, 2002; Kording and Wolpert, 2004; Stevenson et al., 2009). The point is that most studies on application of OCT to motor control were aimed at global optimization, where subjects were supposed to search the unique optimal solution for the given task and the issue of sub-optimality, if considered at all, was limited to address incomplete convergence to the unique optimum (Izawa et al., 2008). In contrast, real life tasks that require skilled control of tools in a variable, partially unknown environment are likely to require the ability to switch from one strategy to another, in the course of an action, accepting suboptimal criteria, in each phase of the action, provided that the overall performance satisfies the task requirements. In this sense, the existence of multiple optima and the ability of the subjects to access them is a key element of skilled behavior. At the same time, taking into account the properties and constraints of the physical (and musculoskeletal) system that is being coordinated can alleviate issues related to “computational cost,” posture–movement integration, local computing principles realized using distributed neural networks, and motor skill learning. The PMP framework, analyzed in the following sections, goes in this direction.

Passive Motion Paradigm: The General Idea

An alternative to OCT (both versions, feed-forward and feedback) as a general theory of synergy formation, is the passive motion paradigm (PMP: Mussa Ivaldi et al., 1988). The focus of attention is shifted from cost functions to force fields. The basic idea can be formulated in qualitative terms by suggesting that the process by which the brain can determine the distribution of work across a redundant set of joints, when the end-effector is assigned the task of reaching a target point in space, can be represented as an “internal simulation process” that calculates how much each joint would move if an externally induced force (i.e., the goal) pulls the end-effector by a small amount toward the target. This internal simulation in turn causes the incremental elastic reconfiguration of the internal body schema involved in generating the action, by disseminating the force field across the kinematic chain (more generally, task-specific kinematic graph) which characterizes the articulated structure of the human or robot. The mechanism is labeled “passive” in line with the EPH because the equilibrium point is not explicitly specified by the brain. Instead, it just contributes to the activation of “task-related” force fields. When motor commands obtained by this process of internal simulation are actively transmitted to the actuators, the robot will reproduce the same motion.

Considering the mounting evidence from neuroscience in support of common neural substrates being activated during both “real and imagined” movements (Jeannerod, 2001; Kranczioch et al., 2009; Munzert et al., 2009; Thirioux et al., 2010), it is not unreasonable to posit that also real, overt actions are the results of an “internal simulation” as in PMP. We further posit that this internal simulation is a result of the interactions between the “internal body model” and the attractor dynamics of force fields induced by the goal and task-specific constraints involved during the performance of an “Action.” If the mental simulation converges (i.e., goal is realized), then the movement can be executed. Otherwise, convergence failure may play the role of a crucial internal event, namely the starting point to break the action plan into a sequence of sub-actions, by recruiting additional DoFs, affordances of tools that may allow the realization of the goal etc. In this sense, PMP can be considered a generalization of EPH from action execution (“overt actions”) to action planning and reasoning about actions (“covert actions”).

Passive motion paradigm: The computational formulation

Let q be the set of all the DoFs that characterize the body of a human or humanoid, possibly extended by including the DoFs of a manipulated object (like a tool). Any given task identifies one or more “end-effectors” and is defined by the motion x(t) of one end-effector with respect to some reference point. The natural reference frame for x(t) is linked to the environmental (extrinsic) space and not the joint (intrinsic) space. Moreover, the dimensionality of q is generally much greater than the dimensionality of x.

The basic idea of the PMP is to express the goal of an action (e.g., “reach a target point P”) by means of an attractive force field, centered in the target position (the target is the “source” of the field) and apply it to the body schema, in particular to the task-related end-effector. The whole body schema will be displaced from the initial equilibrium configuration to a final configuration where the force is null (when the end-effector reaches the target). This relaxation process, from one equilibrium state x_A = f (q_A) to another one x_B = f (q_B)¹, is analogous to the mechanism of coordinating the motion of a wooden marionette by means of strings attached to the terminal parts of the body: the distribution of the motion among the joints is the “passive” consequence of the virtual forces applied to the end-effectors and the “compliance” of different joints.

It is possible to express the dynamics of PMP by means of a graph as in Figure 1 (top panel). In mathematical terms the PMP can be expressed by the following equations:

FIGURE 1

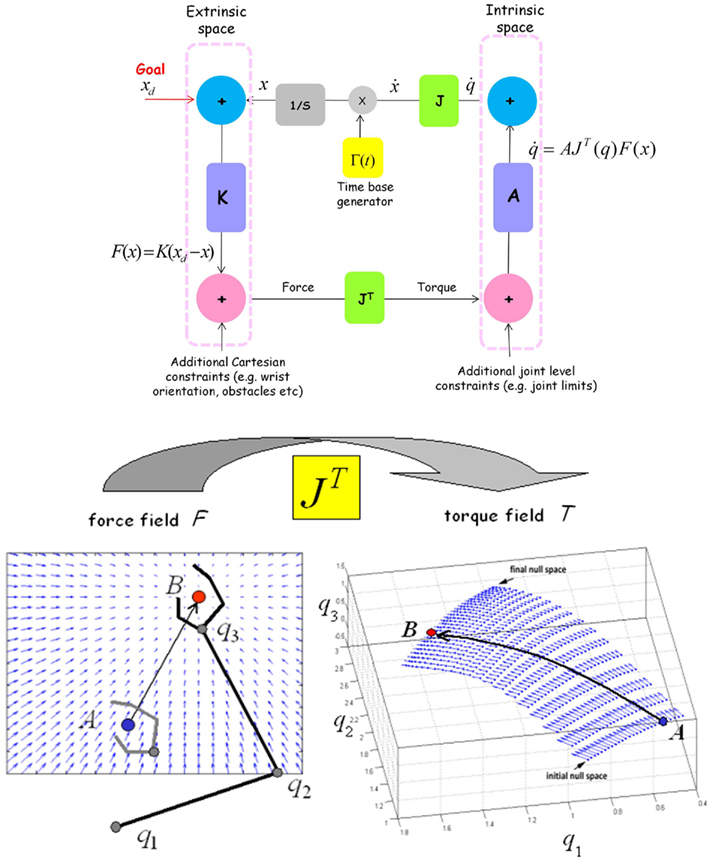
Figure 1. Top panel. Basic kinematic network that implements the passive motion paradigm for a simple kinematic chain (as the arm). In this simple case, the network is grouped into two motor spaces (extrinsic or end effector space and intrinsic or arm joint space). Each motor space consists of a generalized displacement node (blue) and a generalized force node (pink). Vertical connections (purple) denote impedances (K: Stiffness, A: Admittance) in the respective motor spaces and horizontal connections denote the geometric relation between the two motor spaces represented by the Jacobian (Green). The goal induces a force field that causes incremental elastic configurations in the network analogous to the coordination of a marionette with attached strings. The network also includes a time base generator which endows the system with terminal attractor dynamics: this means that equilibrium is not achieved asymptotically but in finite time. External and internal constraints (represented as other task-dependent force/torque fields) bias the path to equilibrium in order to take into account suitable “penalty functions.” This is a multi-referential system of action representation and synergy formation, which integrates a Forward and an Inverse Internal Model. Bottom panel. The figure illustrates the key element of the architecture of Figure 1 for solving the degrees of freedom problem, namely the mapping of the “force field,” defined in the extrinsic space and applied to the end-effector, into the corresponding “torque field,” defined in the intrinsic space and applied to the joints. The mapping is implemented by means of the transpose Jacobian matrix of the kinematic transformation. Dimensionality reduction is obtained implicitly by letting the internal model “slide” in the torque field. Each point of the trajectory in the extrinsic space corresponds to a whole manifold in the intrinsic space (the “null space” of the kinematic transformation). The equilibrium point in the force field corresponds to an equilibrium manifold in the torque field. The selection among the infinite number of possible targets is carried out implicitly by the combination of different force/torque fields.

F is the force field, with intensity and shape determined by the matrix K. In the simplest case, K is proportional to an identity matrix and this corresponds to an isotropic field, converging to the target along straight flow lines. J is the Jacobian matrix of the kinematic mapping from q to x. This matrix is always well defined, whatever the degree of redundancy of the system. For humanoid robots, it can be easily computed analytically. In biological organisms, in which x and q are likely represented in a distributed manner, J can be learnt through “babbling” movements and represented by means of neural networks (Mohan and Morasso, 2007). An important property of kinematic chains is that while the Jacobian matrix maps elementary motions (or speed vectors) from the intrinsic to the extrinsic space, the transpose Jacobian maps forces (or force fields) from the extrinsic to the intrinsic space.

The bottom panel of Figure 1 illustrates the process of mapping the task-oriented “force field” defined in the extrinsic space into a “torque field” in the intrinsic joint space: this is the crucial step in solving the DoF problem because the former field generally has a much smaller dimensionality than the latter and still they are causally related in a flexible way. The dimensionality imbalance implies that each point in the extrinsic space (a given position of the task-selected end-effector) corresponds to a whole manifold in the intrinsic space, what is also known as the “null space” of the kinematic function x = f (q). In the example of Figure 1, this manifold is a curved line that stores all the possible joint configurations compatible with a given position of the end-effector. The shape of the torque field implicitly determines which configuration is chosen. A is a virtual admittance matrix that transforms the torque field to the degree of participation of any individual joint to the collective relaxation process. The fact that trajectories generated according to this mechanism tend to be straight is implicit in the shape of the force field and is not explicitly “programmed.”

Γ(t) is a time-varying gain, or time base generator, that implements “terminal attractor dynamics” (Zak, 1988). A terminal attractor is an equilibrium point which is reached in a specified, finite time, in contrast with the asymptotic behavior of standard attractor systems. Informally stated, the idea behind terminal attractor dynamics is similar to the temporal pressure posed by a deadline in a grant proposal submission. A month before the deadline, the temporal pressure has low intensity and thus the rate of document preparation is scarce. But the pressure builds up as the deadline approaches, in a markedly non-linear way up to a very sharp peak the night before the deadline, and settles down afterward. The technique was originally developed by Zak (1988) for associative memories and later adopted for the PMP both with humans and robots (Morasso et al., 1994, 1997, 2010; Tsuji et al., 2002; Tanaka et al., 2005; Mohan et al., 2009, 2011a). It should be remarked that the mechanism, in spite of its simplicity, is computationally very effective and can be applied to systems with attractor dynamics of any complexity. From the conceptual point of view, Γ(t) has the role of the GO-signal advocated by Bullock and Grossberg (1988) for explaining the dynamics of planned arm movements.

Equation 1 expresses the “Inverse Internal Model” of the computational architecture that generates synergetic activations of all the joints q(t), to be sent to the motor controller. But this is only part of the machinery which is necessary for carrying out mental simulations of virtual and real actions. The missing part is a “Forward Internal Model,” driven by an efference copy of the flow of motor commands. This model generates a prediction of the trajectory of the end-effector which can be compared with the (fixed or moving) target in order to update the driving force field applied to the end-effector:

With this prediction, the loop is closed, defining the PMP as an integrated, multi-referential system of action representation and synergy formation, with a Forward and an Inverse Internal Model.

Task-specific PMP networks: Extracting general principles

Passive motion paradigm is a task-specific model. PMP networks have to be assembled on the fly based on the nature of the motor task and the body segment (and tool) chosen for its execution. We believe that runtime creation/modification of such networks is a fundamental operation in motor planning and action synthesis. In this section, we outline some general principles underlying the creation of task-specific PMP networks, in order to coordinate body/body + tool chains of arbitrary redundancy. At the same time, we also discuss how such a formulation can alleviate some of the open issues with the OCT approach mentioned in “Open Challenges in OCT.” We illustrate the central ideas using two examples: (1) a common day to day bimanual coordination task, namely controlling the steering wheel of a car (Figure 2), which captures both the modularity and computational organization of the framework and (2) Whole upper body coordination in the baby humanoid iCub (Sandini et al., 2004), that captures implementation aspects of such a network (Figure 3) while coordinating a highly redundant body.

FIGURE 2

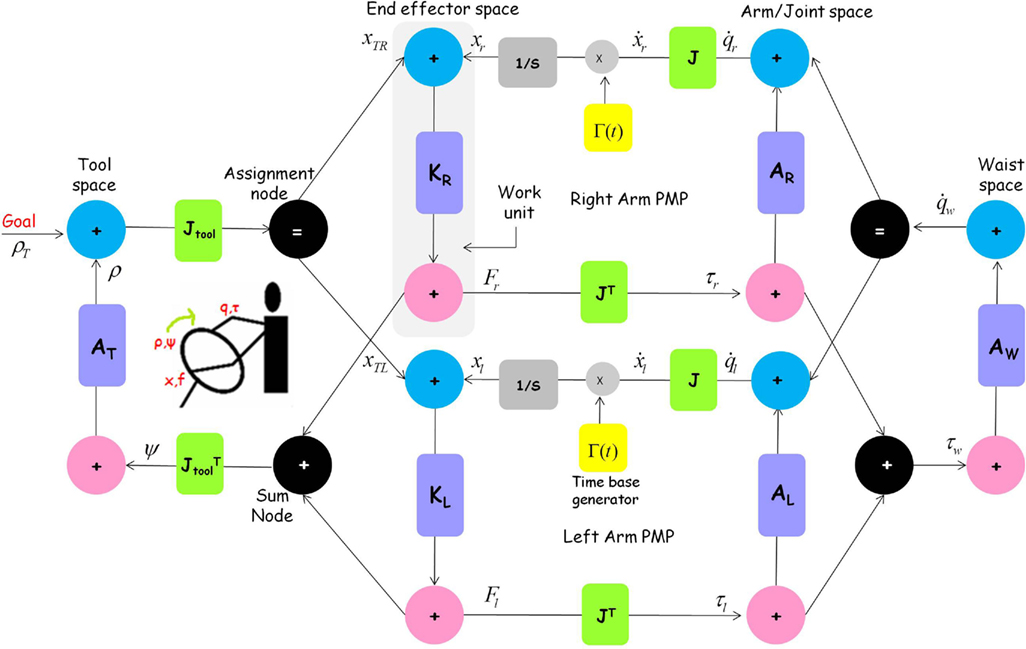
Figure 2. Passive motion paradigm network for a common day to day bimanual task such as controlling the steering wheel of a car. Note that the basic PMP sub network (of Figure 1) is repeated for the right and the left arm. Since the goal is to coordinate bimanually a steering wheel, the network is grouped into the different motor spaces involved in this action, i.e., tool, hand, arm joint, and waist space. Each motor space consists of a displacement (blue) and force node (pink) grouped as a work unit. For example, the blue node in right hand PMP transmits the instantaneous position of the right hand, while the pink node transmits the force exerted by it. Vertical connections (purple) within each work unit denote the impedance, while horizontal connections (green) between two work units denote the geometric transformation between them (Jacobian: J). In this complex PMP network, there are two additional nodes “sum” and “assignment,” that add or assign (forces or displacements) between different motor spaces. Also note that the resulting network is fully connected, connectivity articulated in a fashion that all transformations are “well posed.” Intuitively, as the goal pulls the tool tip, the end-effectors are being simultaneously pulled to respective positions so as to allow the tool to reach the goal. At the same time, the joints (in the two arms and waist) are being pulled to values that allow the two hands to reach positions that allow the tool to reach the goal. This process of incremental updating of every node in the network continues till the time the tool tip reaches the goal (and equivalently the force field in the network is 0). Also note that all computations are local in the sense that every element responds to the pull of the goal based on its own impedance and all these local contributions sum up to create the global synergy achieved by the network.

FIGURE 3

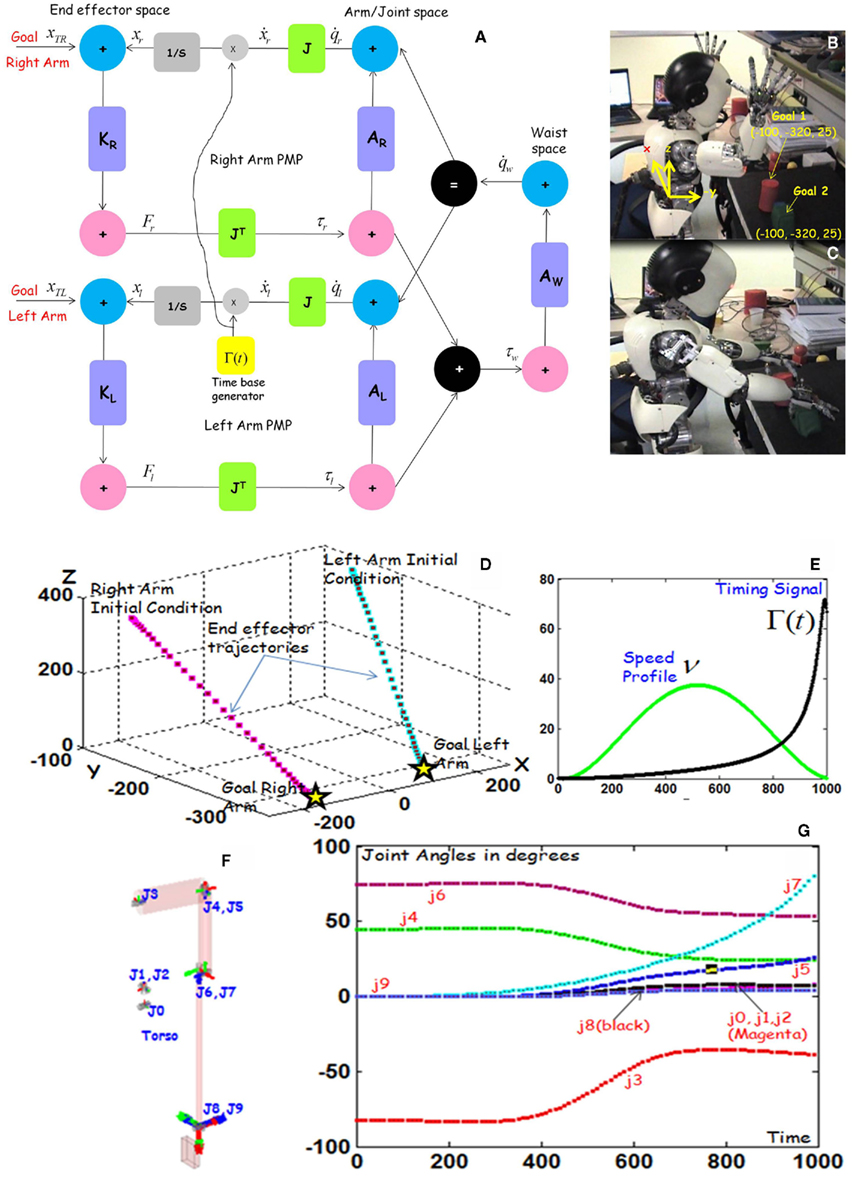
Figure 3. Bimanual coordination task of reaching two objects at the same time. (A) PMP network for the upper body with two target goals and a single time base generator. The network includes three modules: (1) Right arm, (2) Left arm, (3) Waist. The dimensionality of J_R and J_L is 3 × 10 (this includes the seven DoF’s of the arms and the three DoF’s of the waist). The dimensionality of A_j is 7 × 7 and of A_T is 3 × 3. The three sub-networks interact through a pair of nodes (“assignment” and “sum”) that allow the spread of the goal-related activation patterns. (B,C) Show the initial and the final posture of the robot and the two target objects. (D,E) Show the trajectories of the two end-effectors and the corresponding speed profiles (together with the output Γ(t) of the time base generator). (F) Clarifies the intrinsic degrees of freedom in the right arm-torso chain. (G) Shows the time course of the right-arm joint rotation patterns: J0–J2: joint angles of the Waist (yaw, roll, pitch); J3–J9: joint angles of the Right Arm (shoulder pitch/yaw/roll; elbow flexion/extension; wrist prono supination pitch/yaw).

Motor spaces. Consider the common task of bimanually controlling a steering wheel. One of the first things to observe is the diversity of descriptions that are plausible for any motor event. For example, we can describe the same task using a mono-dimensional steering wheel pattern or a 6-dimensional limb space pattern or a 7-dimensional joint rotation pattern or multi-dimensional muscle contraction patterns. Figure 2 gives an explicit PMP network to incrementally derive the 7-D joint rotation patterns for each arm from the 1-D steering wheel plan. Since any motor action can be described simultaneously in multiple motor spaces (tool, end-effector, joint, actuator), PMP networks are “multi-referential.” The type of motor spaces involved in any PMP relaxation depends on the task and body chain responsible for its execution. By default, for action generation using the upper body of a humanoid robot, there are three motor spaces: end effector, arm joints, and waist (see Figure 3A).

Work units. All motor spaces have a pair of generalized force and displacement vectors grouped together as a work unit (in all PMP networks, position nodes are shown in blue, force nodes are shown in pink). For example, x and q denote displacement vectors, i.e., position of the hand and rotation at the arm and waist space respectively; f and τ denote force vectors, i.e., force at the hand space and torques at the joint space, respectively. If a task involves use of a tool, the tool space is also represented similarly with a generalized force and displacement node. Hence, in Figure 2, ρ denotes a generalized displacement (rotation of the steering wheel) and ψ denotes a generalized force (i.e., the steering wheel torque). The scalar work (force × displacement) is the structural invariant across different motor spaces (thus the name work unit: WU). Hence, in PMP the invariance of energy by coordinate transformations (principle of virtual works) is used to relate entities in different motor spaces. The relaxation process achieved by PMP incrementally derives trajectories in all the nodes (force and displacement) of the participating WU’s. For example, in a PMP relaxation for a simple reaching task (like in Figure 3), we get four sets of trajectories (as a function of time): (1) trajectory of joint angles given by the position node in the joint space (arm and waist, see Figure 3G); (2) the resulting consequence, i.e., the trajectory of end-effectors given by the position node in end effector space (Figure 3D); (3) the trajectory of torques at the different joints (arm and waist), given by the force node in the joint space; (4) the resulting consequence, i.e., the trajectory of forces applied by the end effector given by the force node in the end effector space.

Connectivity and circularity. The next thing to observe is that all PMP networks (Figures 2 and 3A) are fully connected in the sense that any node can be reached from any other node. In other words, PMP networks are “circular.” The “goal” can be applied at any node in the network, based on the task. The connectivity allows the force fields induced by a goal to ripple across the whole network. As a simple example, if we deactivate the left arm and the waist space in Figure 3A and enter the network at the right arm end effector dx_r and exit at right arm joint space dq_r, we get the following rule for computing incremental joint angles: dq_r = A_RJ^TK_Rdx_r. The rules become more complex as additional motor spaces participate in the PMP relaxation.

Analogous to electrical circuits, connectivity in any PMP network are of two types: serial and parallel. In a serial connection, position vectors are added. For example, links are serially connected to form a limb. In a parallel connection, force vectors are added. For example, when we push an external object with both arms, the force applied by individual arms is added. In the steering task, the two hands are connected in parallel to the device (wheel), links are connected serially to form the two limbs and muscles are connected in parallel to a link. The task device, tool or effector organ to which the “motor goal” is coupled is always the starting point to build the PMP network. From there we may enter different motor spaces in the body model of the actor, hence branching the PMP network into serial or parallel configurations down to directly controlled elements relevant for a particular task.

Branching nodes (+/=). In complex kinematic structures, where there are several serial and parallel connections, two additional nodes, i.e., Sum (+) and Assignment (=) are used to “add or assign” displacements and forces from one motor space to another. For example, in Figure 3A the assignment node assigns the contribution of the waist (to the overall upper body movement toward a goal), to the right and left arm networks. On the other hand, the net torque seen at the waist is the “sum” of torques coming from the right and left arm PMP sub-networks (because of the individual force fields experienced by the right and left arms respectively). Sum and assignment nodes are dual in nature. If an assignment node appears in the displacement transformation between two WU, then a sum node appears in the force transformation between the same WU’s. This can be understood as a consequence of conservation of energy between two WU’s. Further, sum and assignment nodes can also appear at the interface between the body and a tool, in order to assign/sum forces and displacements from the external object to the end-effectors and vice versa (like in Figure 2).

Geometric causality. This is expressed by the Jacobian matrices that form the horizontal links in the PMP network. They connect two WU’s or motor spaces together. Whether it is a serial or parallel connection, the mapping between one motor space to another is generally “non-linear” and “irreversible.” This mapping can be linearized by considering small displacements (or velocities), whose representations in any two motor spaces are related by the Jacobian matrix: for example, dx_r = J_R(q)dq_r. Further, while the Jacobian determines the mapping of small displacements in one direction, the transpose Jacobian determines the dual relation among forces in the opposite direction (principle of virtual works). For example, in Figure 3A, the space Jacobians J_R and J_L map joint rotation patterns of the two arms and waist into displacements of the two hands, while the corresponding transpose Jacobians project disturbance forces F applied on the hands into corresponding joint torques. The tool Jacobian J_T forms the interface between the body and the tool and represents the geometrical relationship between the tool and the concerned end-effector. While learning to use different tools, it is the tool Jacobians at the interface that are learnt. Based on the tool being coordinated, it is necessary to load the appropriate device Jacobian associated with it.

Elastic causality. This is expressed by the vertical links in the PMP network and is implemented by stiffness and admittance matrices. These links connect generalized force nodes to displacement nodes (or vice versa) in each WU. Hooke’s law of linear elasticity can be generalized to non-linear cases by considering differential variations: dF = K·dX and dX = A·dF, where K is the virtual stiffness and A is the virtual admittance. In the former case, effort is derived from position; whereas in the latter, position is derived from effort. For example, in Figure 3A, the virtual stiffness K_e determines the intensity and shape of the force field applied in the right and left hand networks. In the simplest case, K is proportional to the identity matrix and this corresponds to an isotropic field, converging to the goal target along straight flow lines (see Figure 1, bottom panel, and Figure 3D for the case of bimanual reaching). Curved trajectories (like in hand-written characters of different scripts) can be obtained by actively modulating (or learning) the appropriate values of the virtual stiffness (Mohan et al., 2011b).

Role of admittance in the intrinsic space. In PMP networks, the effect of admittance is “local.” Every intrinsic element (for example, a joint in the arm) responds to the goal induced “force field” based on its own “local” admittance. Hence, it is not the precise values of the admittance of every joint, but the balance between them that affects the final solution achieved. This balance can be altered in a local and “task–specific” fashion. In normal conditions, we consider that all the participating joints are equally compliant. In this case, the admittance is an identity matrix (for a seven DoF arm, it is a 7 × 7 identity matrix). On the other hand, by locally modulating individual values, it is possible to alter the degree of participation of each joint to the coordinated movement while not affecting the solution at the end effector space (see Figure 1 bottom panel). For example, Figure 4A shows the initial condition with the goal being issued to reach the large cylinder (placed far away and asymmetrically with respect to the robot’s body) using both arms. Figure 4B shows the final solution when the admittance of the three DoF of the waist is reduced 10 times as compared to the two arms. Without the contributions of the additional DoF of the torso, it not possible to bimanually reach the target. Figure 4C shows the solution when the waist admittance is made equal to the arms. In this case, note the contributions from all three DoFs of the torso (Figure 4B), hence enabling iCub to bimanually reach the cylinder successfully in this case. An alternative way to interpret this behavior is that, in the former case (Figure 4B) the force field induced by the goal did not propagate through the waist network. In other words, the propagation of goal induced force field across different intrinsic elements of the body can be modified by altering their local admittance. This relates to the issue of “grounding.” Since there are many possible kinematic chains that can be coordinated simultaneously in a complex human/humanoid body, based on the nature of the motor task it is necessary to identify the start and end points in the body schema between which the force fields generated by the goal will propagate, and beyond which the force fields generated by the goal will not propagate. Such grounding can be easily achieved by modulating the local admittance of intrinsic elements in a task-specific fashion. For example, if the waist admittance is very low, this is equivalent to grounding the network at the shoulders. In the steering wheel task the body is grounded at the waist. At the same time, additional DoFs can be “incrementally” recruited in the relaxation process based on the success/failure of the task.

FIGURE 4

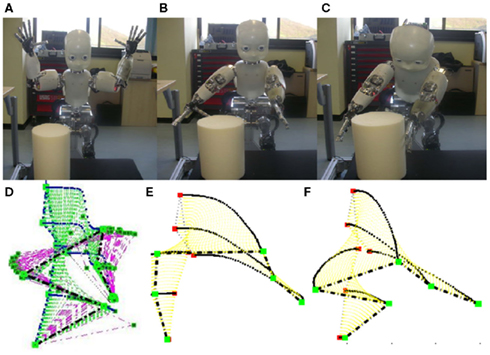
Figure 4. Effects of modulating the admittance in the intrinsic space on the final posture achieved through PMP relaxation. (A) Shows the initial condition with the goal being issued to reach the large cylinder (placed far away and asymmetrically with respect to the robot’s body) using both arms. (B) Shows the final solution when the admittance of the three DoF of the waist is reduced 10 times as compared to the two arms. Without the contributions of the additional DoF of the torso, it is not possible to bimanually reach the target. An alternative way to interpret this behavior is that the force field induced by the goal did not propagate through the waist network because of its lower admittance (in comparison with the arm networks). In other words, the propagation of goal induced force field across different intrinsic elements of the body can be modified by altering their “local” admittance. (C) Shows the solution when the waist admittance is made equal to the arms. In this case, note the contributions from all three degrees of freedom of the torso (B), hence enabling iCub to bimanually reach the cylinder successfully in this case. (D–F) Show a simple scenario where the goal is to reach a target using the whole body but also attain a specific posture as demonstrated by the teacher [(D): Nearby target, (E,F) far way target]. If the admittance of the hip was reduced from 2.5 to 0.1 (rad/s/Nm) in (F) (keeping admittance of other joints constant), and we see two different postures: one that uses the hip more (E) and the other in which the knees compensate for the low admittance of the hip (F). This local and modular nature of motion generation is also evident during injury, when other degrees of freedom compensate for the temporarily “inactive” element, in reaction to the pull of a goal. This is a natural property of the PMP mechanism.

The issue of generating different solutions by actively modulating the admittance of different joints has been demonstrated for whole body reaching (WBR) tasks using the PMP (Morasso et al., 2010). Figures 4D–F show a simple scenario where the goal is to reach a target using the whole body but also attain a specific posture as demonstrated by the teacher (Figure 4D: nearby target, Figures 4E,F far away target). In such cases, it may be “perceptually” possible to determine approximately the contribution of different body parts to the observed movement. Such perceptual information can “locally” modulate the participation of different DoFs, hence influencing the nature of solution obtained. For example, if the admittance of the hip was reduced from 2.5 to 0.1 (rad/s/Nm) in Figure 4F (keeping admittance of other joints constant), and we see two different postures: one that uses the hip more (Figure 4E) and the other in which the knees compensate for the low admittance of the hip (Figure 4F). This local and modular nature of motion generation is also evident during injury (for example, a fracture to elbow), when other DoFs compensate for the temporarily “inactive” element, in reaction to the pull of a goal. This is a natural property of the PMP mechanism (and does not require any additional computation).

Finally, we must note that even though an elastic element is reversible in nature, in articulated elastic systems like in PMP, a coherence of representation dictates the “direction” in which causality is directed.

Directionality. The issue that needs to be understood now is the “direction” in which information should flow in a fully connected network like PMP. This is a critical issue not only while controlling highly redundant bodies, but also when tools with controllable DoFs are coordinated. The short answer to the question is that the direction in which information flows is constrained by the fact that PMP networks always operate through “well posed” computations/transformations. In which direction a transformation is “well posed” depends on the motor spaces involved and the type of connectivity (i.e., serial or parallel) between them.

Serial connections. Consider, for example, a serial kinematic chain like the right arm of iCub, which involves two motor spaces, namely the end effector and the arm joint space (Figures 2 and 3A). In serial connections, vectors of higher dimensionality are transformed into vectors of lower dimensionality (joint angles transform to hand coordinates). Thus the Jacobian matrix has more columns’ than rows (for example, considering that the end effector position is represented in 3D Cartesian space coordinates and the arm has seven joints, the resulting Jacobian matrix has three rows and seven columns). What transformations are well posed in a serial connection? We can observe that given the joint angles of the arm, it is possible to uniquely compute the position of the end effector. So the transformation from position node in joint space to position node in end effector space is well posed. In contrast, the transformation in the opposite direction is not well posed, in the sense that given an end effector position it is not possible to uniquely compute the value of the joint angles. The reason is that there are more unknowns (joint angles) than the equations, thus resulting in infinite solutions. Similarly, coming to transformation between force nodes, note that the transformation from end effector force to joint torques via the transpose Jacobian is well posed (T = J^TF: there are seven equations and seven unknowns if the arm has seven joints). However, the transformation in the opposite direction is ill posed, i.e., given a set of joint torques it is not possible to compute the hand force since there are more constraint equations than unknowns. This is the reason that in the PMP networks of figures 2 and 3A we move from the position node in arm space to the position node in end effector space and force node in end effector space to force node in joint space. Further, this also preserves the circularity in the network.

Parallel connections. The parallel connection is a dual version of the serial connection. A biological example of parallel connection is the relationship between muscle and skeleton. The problem of finding the joint torque given the muscle forces is well posed, but the inverse problem results in infinite solutions (because there are more unknowns than equations). The connection between the two arms and the steering wheel (Figure 2) is also an example of a parallel connection. There can be infinite possible combinations of forces exerted by the two hands “in parallel” to generate a given steering wheel torque, but the transformation in the opposite direction is well posed. Similarly, given a steering wheel rotation it is possible to uniquely compute the position of the two hands. Hence in Figure 2, there is a position to position transformation from the steering wheel space to hand space, and force to force transformation from the hand space to steering wheel space.

In sum, the direction in which causality is directed in a PMP network is constrained by the fact that all computations in the network should be “well posed.” Operating through well posed computations (and avoiding inversion of a generally non-invertible redundant system) significantly reduces the computational overhead. Further, since computations are always “well posed and linearized,” PMP mechanisms do not suffer from the curse of dimensionality and can be easily scaled up to any number of DoFs. This is not the case with OCT where it is well known that non-linearity and high dimensionality can significantly affect the computational overhead and numerical stability of the solution (Bryson, 1999; Scott, 2004).

A more general question can be asked as to “How and Why” computations turn out to be well posed in PMP? The answer is that they are “constrained” by the physical properties of the system they intend to model. For example, natural direction of causality for a muscle is to receive flow and yield force, and the natural direction of causality for the joint is to receive force and yield flow (which is the reason the joint space receives the force field as input and yields joint rotations as output, which in turn uniquely determines end effector displacement). In fact, a detailed analysis of issues related to modularity and causality in physical system modeling goes back to a seminal paper by Hogan (1987), with contributions from Henry Paynter (of the Bond graph approach), that we merely revisit with the PMP model. We think that techniques that start with the assumption that behavior can be understood by minimization of a cost function, even though very general and powerful in explaining observed systematic correlations in wide range of behaviors, often neglect the specific physical properties of the system they intend to model (Guigon, 2011) and that in turn results in unnecessary “costs.”

Local to global, distributed computing. From the perspective of local to global computing, note that, every element in every “work unit” involved in any PMP network always makes a local decision regarding its contribution to the externally induced pull, based on its own impedance. All such local decisions synergistically drive the overall network to a configuration that minimizes its global potential energy. This is analogous to the behavior of well known connectionist models in the field of artificial neural networks like Hopfield networks (Hopfield, 1982). Different implementations of the PMP using back propagation networks (Mohan and Morasso, 2006, 2007) and self organizing maps (Morasso et al., 1997) have already been conceived and implemented on the iCub humanoid. Thus, the local, distributed nature of information processing makes it possible to explain how computations necessary for PMP relaxation can actually be realized using neural networks, whereas this is still an open question for the formal methods employed by OCT (Scott, 2004; Todorov, 2006).

Timing. There are always temporal deadlines associated with any goal. Control over “time and timing” is crucial for successful action synthesis, be it simply reaching a target in a finite time or complex scenarios like synchronization of PMP relaxations with multiple kinematic chains (bimanual coordination), trajectory formation, multi tasking etc. A way to explicitly control time, without using a clock, is to insert in the non-linear dynamics of the PMP, a time-varying gain Γ(t) according to the technique originally proposed by Zak (1988) for speeding up the access to content addressable memories and then applied to a number of problems in neural networks. In this way, the dynamics of the PMP network is characterized by terminal attractor properties (Figure 3E shows the timing signal). This mechanism can be applied to any dynamics where a state vector x is attracted to a target x_T by a potential function, such as V(x) = 1/2(x − x_T)^TK(x − x_T), according to a gradient descent behavior: 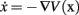, where ▽V(x) is the gradient of the potential function, i.e., the attracting force field. Based on the nature of the task, there can either be single or multiple timing signals, hence allowing action sequencing, synchronization, mixing of force fields generated by multiple spatial goals, generation of a diverse range of spatio-temporal trajectories.

PMP and bond graphs. PMP networks have some similarity with bond graphs (Paynter, 1961). Both are graphical representations of dynamical systems which are port-based, emphasizing the flow of energy rather than the flow of information as it happens in the network diagrams. However, bond graphs represent bi-directional exchange of physical energy among interconnected devices in a given application domain (mechanical, electrical, thermal, hydraulic, etc.), with the purpose of simulating the dynamics of the interconnected system. In contrast, PMP-networks are conceived at a more abstract level, which is concerned with the internal representation of the body schema, not as a static map but as a multi-referential dynamical system. Moreover, PMP-graphs are intrinsically unidirectional, in such a way to restrict the overall dynamics to well-formed transformations between motor spaces of different dimensionality (as described under the “Directionality” subheading).

To sum up, in the example of the steering wheel rotation task, a small wheel rotation incrementally assigns (through the assignment node) motion to the two hands connected in parallel, according to the “weight” J_T (this transformation is well posed). The force disturbance is computed for the imposed displacement in the end effector space “dx” using the stiffness matrix “K.” The resultant force vector determines a torque vector which yields a joint rotation dq via the transpose Jacobian and compliance matrix A, respectively (this transformation is also well posed). Finally, the steering wheel torque is the summed contribution coming from the two arms (through the sum node) and weighted by transpose of the device Jacobian (this transformation is also well posed). The timing signal allows smooth synchronized motion of the two hands, converging to equilibrium in finite time. In sum, the relaxation process of the PMP network allows us to effectively characterize this highly redundant task of bimanual coordination and incrementally derive the multi-dimensional actuator patterns from a mono-dimensional steering wheel rotation plan.

Incorporating Task-Specific “Internal and External” Constraints

Equation 1 can also be seen as the on-line optimization of a cost function, the distance of the end-effector from the target, compatible with the kinematic constraint given by the kinematic structure and represented by the admittance matrix A. However, this is just the simplest situation, which can be expanded easily to include an arbitrary number of constraints or penalty functions, in the form of force fields defined either in the extrinsic space or intrinsic space:

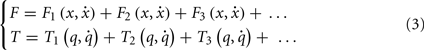
A constraint in the extrinsic space could be an obstacle to avoid, an appropriate hand pose with which to reach an object so as to allow further manipulation actions to be performed (like grasp or push). In the intrinsic space a constraint could take into account the limited range of motion of a joint, the saturation power or torque of an actuator etc. Figure 5A shows a composite PMP network for the right arm kinematic chain, for reaching an object (Goal) with an appropriate wrist orientation/hand pose to support further manipulations (constraint 1) and generating a solution such that the joint angles are well within the permitted range of motion (constraint 2). Hence, in the PMP network of Figure 5A there are three weighted, superimposed force fields that modulate the spatio-temporal behavior of the system: (1) the end-effector field (to reach the target); (2) the wrist field (to achieve the specified hand pose); (3) the force field in joint space for joint limit avoidance. Note that the same timing signal Γ(t) synchronizes all the three relaxation processes. Figure 5B shows results of iCub performing different manipulation tasks driven by such a network.

FIGURE 5

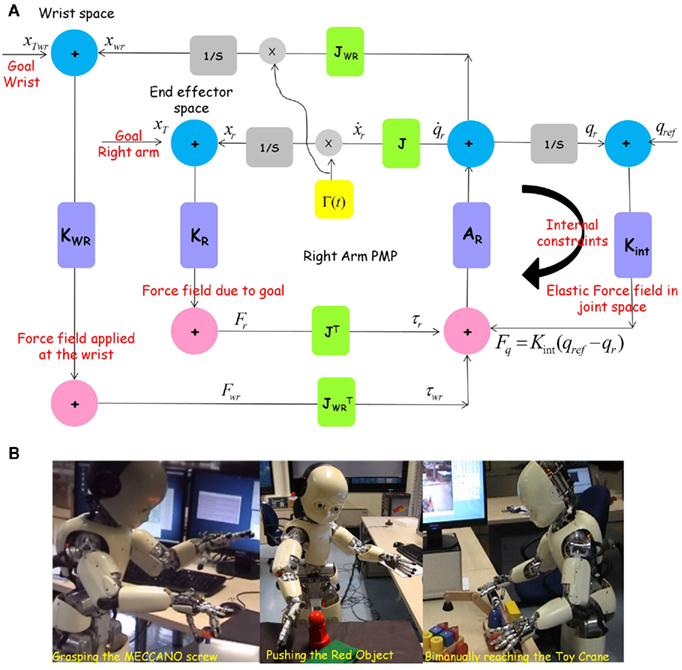
Figure 5. (A) Composite PMP network with three force fields applied to the right arm of iCub: a field F_r that identifies the desired position of the hand/fingertip (Goal); a field F_wr that helps achieving a desired pose of the hand via an attractor applied to the wrist (Constraint 1). Here J_wr is the Jacobian matrix of the subset of the kinematic chain, up to the wrist; an elastic force field F_q in the joint space for generating a solution such that the joint angles are well within the permitted range of motion (constraint 2). Note that the same timing signal synchronizes all three relaxation processes, hence allowing the hand to reach the target with a specific pose and posture. (B) Show three examples of iCub performing manipulation tasks driven by the composite PMP net of (A). In the case of bimanually reaching the crane toy, a similar network also applies to the left arm PMP chain. Note that in all these cases, reaching the goal object with specified hand pose is obligatory for successful realization of the goal.

Recently, this modeling framework was further pursued for explaining the formation of WBR synergies, i.e., coordinated movement of lower and upper limbs, characterized by a focal component (the hand must reach a target) and a postural component (the center of mass or CoM, must remain inside the support base; Morasso et al., 2010). By simulating the network in various conditions it was possible to show that it exhibits several spatio-temporal features found in experimental data of WBR in humans (Stapley et al., 1999; Pozzo et al., 2002; Kaminski, 2007). In particular, it was possible to demonstrate that: (1) during WBR, legs, and trunk play a dual role: not only are they responsible for maintaining postural stability, but they also contribute to transporting the hand to the target. As target distance increases, the reach and postural synergies became coupled resulting in the arms, legs and trunk working together as one functional unit to move the whole body forward (see Figures 4D–F); (2) Analysis of the CoM showed that it is progressively shifted forward, as the reached distance increases, and is synchronized with the finger’s movement. Posture and movement are indeed like Siamese twins: inseparable but, to a certain extent, independent. The article on whole body synergy formation showed how postural and focal synergies can be integrated during goal directed coordination through the PMP framework. Generally, we can see the PMP as a mechanism of multiple constraints satisfaction, which solves implicitly the “DoFs problem” without any fixed hierarchy between the extrinsic and intrinsic spaces. The constraints integrated in the system are task-oriented and can be modified at runtime as a function of performance and success.

Motor Skill Learning and PMP

In the context of PMP, when we learn a motor skill, we basically learn the connecting links in the PMP network associated with the task (i.e., vertical links or impedances, horizontal links or Jacobians, and the timing of the time base generators). We will describe central ideas using a new scenario where iCub learns to bimanually steer a toy crane in order to position its magnetized tip at a goal target (Figure 7A). We choose this example because the task is similar to the bimanual control of the steering wheel, the steering wheel replaced by the two handles of the toy crane. So the structure of the PMP network is the same as shown in Figure 2. In general, while learning to control the toy crane, iCub has to learn: (a) the appropriate stiffness and timing to execute the required “spatio-temporal” trajectories using the body + tool chain (for example, performing synchronized quasi-circular trajectories with both hands while turning the toy crane) and (b) while performing such coordinated movements with the tool, learn the Jacobians that map the relationship between the movements of the body effectors and the corresponding consequence on the tool effector (the magnetized tip). The third issue is of course related to using this learnt knowledge to generate “goal directed” body + tool movements (given a goal to reach/pick up an otherwise “unreachable” environmental object using the toy crane).

Till now we were dealing with point to point reaching actions using the PMP network (for example Figure 3). But using a toy crane is a task that not only requires iCub to reach (and grasp) the tool but also perform coordinated spatio-temporal movements with the tool (both during exploration and performing goal directed movements using the tool). Part of the information as to what kind of movements can be performed with the tool can be acquired by observing a teachers demonstration. The teacher’s demonstration basically constrains the space of explorative actions when iCub practices with the new toy to learn the consequences of its actions. The basic PMP system on the iCub is presently being extended to incorporate these capabilities. With the help of Figure 6, we outline central features of the extended skill learning architecture.

FIGURE 6

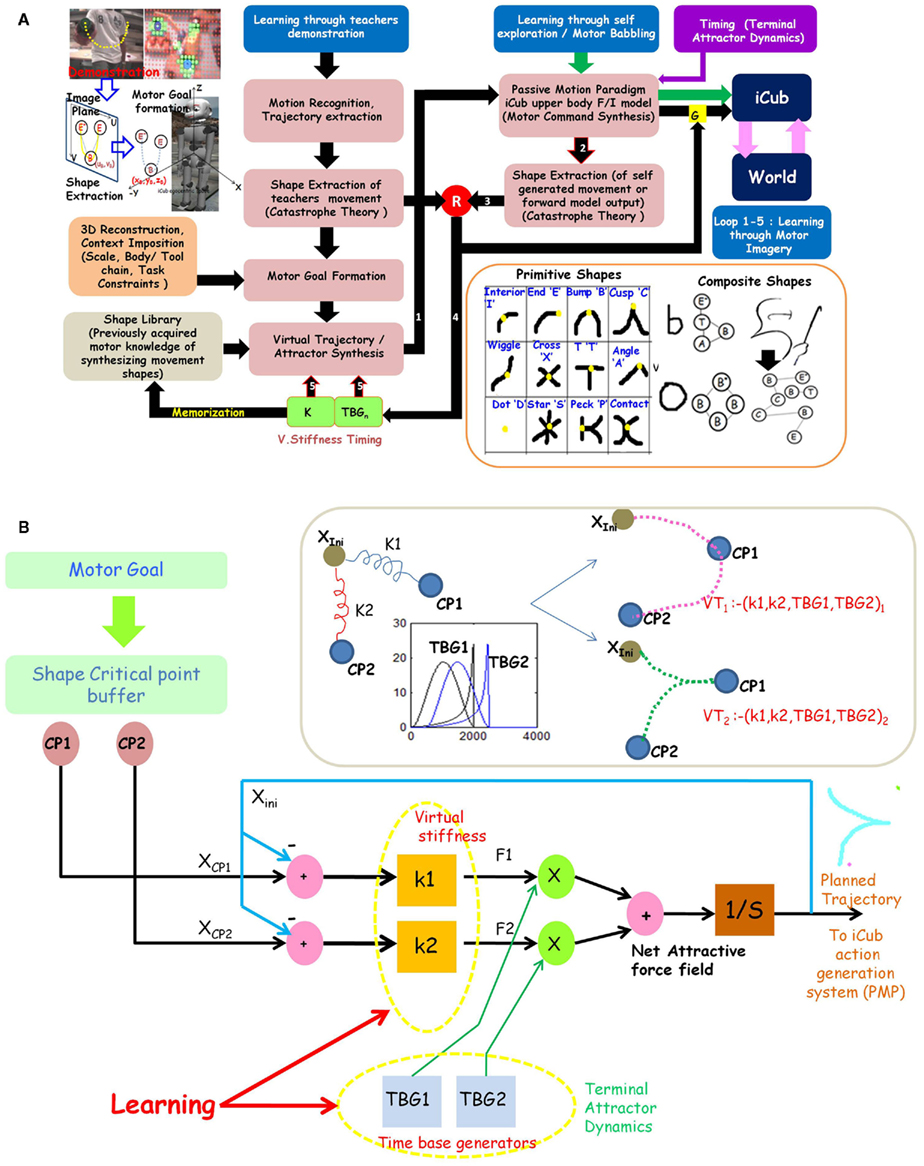
Figure 6. (A) Motor Skill learning and Action generation architecture of iCub: Building blocks and Information flows. (B) Scheme of the virtual trajectory synthesis system (modeled by Eq. (5)), that transforms a discrete set of critical points (shape “type” and its “spatial location”) in the motor goal into a continuous sequence of equilibrium points that act as moving point attractor to the task relevant PMP network. An elastic force field is associated to each spatial location (in the motor goal), with a strength given by the stiffness matrices (K1 and K2). The two force fields are activated in sequence, with a degree of time overlap, as dictated by two time base generators (TBG1 and TBG2). Simulating the dynamics with different values of K and γ, results in different trajectories through the critical points. Inversely, the problem of learning is to acquire the correct values for K and γ (virtual stiffness and temporal overlap) such that the shape of the resulting trajectory correlates with the shape description in the motor goal.

Learning through imitation, exploration, and motor imagery

Three streams of learning, i.e., learning through teacher’s demonstration (information flow in black arrow), learning through physical interaction (blue arrow), and learning through motor imagery (loop 1–5) are integrated into the architecture. The imitation loop initiates with the teachers demonstration and ends with iCub reproducing the observed action. The motor imagery loop is a sub part of the imitation loop, the only difference being that the motor commands synthesized by the PMP are not transmitted to the actuators instead, the forward model output is used to close the learning loop. This loop hence allows iCub to internally simulate a range of motor actions and only execute the ones that have high performance score “R.”

From trajectory to shape, toward “context independent” motor knowledge

Most skilled actions involve synthesis of spatio-temporal trajectories of varying complexity. A central feature in our architecture is the introduction of the notion of “Shape” in the motor domain. The main purpose was to conduct motor learning at an abstract level and thus speed up learning by exploiting the power of “compositionality” and motor knowledge “reuse.” In general, a trajectory may be thought as a sequence of points in space, from a starting position to an ending position. “Shape” is a more abstract description of a trajectory, which captures only the critical events in it. By extracting the “shape” of a trajectory, it is possible to liberate the trajectory from task-specific details like scale, location, coordinate frames and body effectors that underlie its creation and make it “context independent.” Using Catastrophe theory (Thom, 1975; Chakravarthy and Kompella, 2003) have derived a set of 12 primitive shape features (Figure 6, bottom right panel) sufficient to describe the shape of any trajectory in general. As an example, the critical events in a trajectory like “U” is the presence of a minima (or Bump “B” critical point) in between two end points (“E”). Thus, the shape is represented as a graph “E–B–E” (see Figure 6). If the “U” was drawn on a paper or if someone runs a “U” in a playground, the shape representation is “invariant” (there is always a minima in between two end points). More complex shapes can be described as “combinations” of the basic primitives, like a circular trajectory is a composition of four bumps. In short, using the shape extraction system it is possible to move from the visual observation of the end effector trajectory of the teacher to its more abstract “shape” representation.

Imposing “context” while creating the motor goal

The extracted “shape” representation may be thought of as an “abstract” visual goal created by iCub after perceiving the teacher’s demonstration. To facilitate any action generation/learning to begin, this “visual” goal must be transformed into an appropriate “motor” goal in iCub’s egocentric space. To achieve this, we have to transform the location of the shape critical point computed in the image planes of the two cameras (U_left, V_left, U_right, V_right) into corresponding point in the iCub’s egocentric space (x, y, z) through a process of 3D reconstruction (see Figure 6, top left box). Of course the “shape” is conserved by this transformation, i.e., a bump still remains a bump, a cross is still a cross in any coordinate frame. Reconstruction is achieved using Direct Linear Transform (Shapiro, 1978) based stereo camera calibration and 3D reconstruction system already functional in iCub (implementation details of this technique are summarized in the appendix of Mohan et al., 2011b). At this point, other task-related constraints like the scale of the shape, end effector/body chain performing the action can be added to the goal description. So the motor goal for iCub, is an abstract shape representation of the teachers movement (transformed into the egocentric space) and other task-related parameters that needs to be considered while generating the motor action. An example of a motor goal description is like: “use” the left arm-torso chain coupled to the toy crane, generate a trajectory that starts from point 1, ends at point 2, and has a “bump” at point 3 (and observe the consequence through visual and proprioceptive information).

“Virtual trajectories” – motor equivalent action representation

The motor goal basically consists of a discrete set of shape critical points (their spatial location in iCub’s ego centric space and type), that describe in abstract terms the “shape” of the spatio-temporal trajectory that iCub must now generate (with the task relevant body chain). Given a set of points in space an infinite number of trajectories can be shaped through them. How can iCub learn to synthesize a continuous trajectory similar to the teacher’s demonstration using a discrete set of shape descriptors in the Motor goal? The virtual trajectory generation system (VTGS) performs this inverse operation. It transforms the discrete shape representation (in the motor goal) into a continuous set of equilibrium points that act as moving point attractor to the PMP system.

Virtual trajectory generation system preserves the same “force field” based structure as in PMP (Figure 6B). Let X_ini ∈ (x, y, z) be the initial condition, i.e., the point in space from where the creation of shape is expected to commence (usually initial condition will be one of the end points). If there are N shape points in the motor goal, the spatio-temporal evolution of virtual trajectory (x, y, z, t) is equivalent to integrating a differential equation that takes the following form:

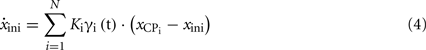
Intuitively, as seen in Figure 6B, we may visualize X_ini as connected to the spatial locations of all shape points by means of virtual springs and hence being attracted by the force fields generated by them F_CP = K_CP(x_CP − x_ini). The strength of these attractive force fields depends on: (1) the virtual stiffness “K_i” of the spring and (2) time-varying modulatory signals Γ_i(t) generated by the respective time base generators that determine the degree of temporal overlap between different force fields. The virtual trajectory is then the set of points created during the evolution X_ini through time, under the influence of the net attractive field generated by different CP’s. Further, by simulating the dynamics of Eq. (4), with different values of K and γ, a wide range of trajectories can be obtained passing through the discrete set of points described in the motor goal. Inversely, learning to “shape” translates into the problem of learning the right set of virtual stiffness and timing such that the “Shape” of the trajectory created by iCub correlates with the shape description in motor goal.

So “how difficult and how long” does it take to learn these parameters given the demonstration of a specific movement by the teacher? It is here we reap the advantage of moving from “trajectory” to “shape,” since compositionality in the domain of shapes can be exploited to speed up learning. In other words, the amount of exploration in the space of “K” and γ is constrained by the fact that once iCub learns to generate the 12 movement shape primitives, any motion trajectory can be expressed as a composition of these primitive features. The main idea is that since more complex trajectories can be “decomposed” into combinations of these primitive shapes, inversely the actions needed to synthesize them can be “composed” using combinations of the corresponding “learnt” primitive actions. Regarding learning the primitives, it has been demonstrated in (Mohan et al., 2011c), that they can be learnt very quickly by just exploring the space of the virtual stiffness “K” in a finite range of 1–10, followed by an evaluation of how closely the shape of the synthesized trajectory (using Eq. (4)) matches the shape described in the goal. Thus effort in terms of motor exploration is required during the initial phases to learn the basics (i.e., primitives). During the synthesis of more complex spatio-temporal trajectories, composition, and recycling of previous knowledge takes the front stage (considering that the correct parameters to generate the primitives already exist in the shape library).

Finally, we note that “virtual trajectories” must not be interpreted as the real trajectories generated by iCub. Instead, the evolving virtual trajectory acts as moving point attractor to the PMP system that in turn generates the motor commands necessary for iCub to actually execute the motion trajectory (it observed). In human experiments also there is evidence of moving equilibrium points as demonstrated by (Shadmehr et al., 1993). In this sense, the VTGS is like a skilled puppeteer who is pulling the task relevant effector (in the PMP network) in a specific fashion. Based on the body/tool PMP network to which the virtual trajectory is coupled, motor commands are generated in that chain. In this sense, virtual trajectories also characterize a “motor equivalent” representation of action.

Using past motor “experience” to generate virtual trajectories on the fly

When iCub learnt to draw trajectories like “U,” “C” etc. (Mohan et al., 2011b), it acquired the correct parameters (K and γ) to synthesize virtual trajectories for shapes that result in “Bump” critical points. When the teacher demonstrates iCub to bimanually steer the toy crane by performing quasi-circular trajectories, the movement “shape” of the teachers “effectors” gives rise to “bump” critical points, which iCub already knows to generate, from its previous drawing experience. Using the previously learnt parameters of K and γ from the shape library, iCub is able to instantaneously generate virtual trajectories (or attractors) that feed the PMP network of the iCub upper body. Here, we reap the benefit of moving from “trajectory” to “shape” and learning actions in a “context independent” fashion thus allowing past experience to be exploited in new contexts.

In general, the straightforward advantage of learning one motor skill in an “abstract” way is that it unlocks the implicit potential to “perceive, mime, and begin to perform” several other skills (that share a similar structure). For example, consider actions like turning a steering wheel, uncorking a bottle, paddling a bicycle, using a screwdriver, among others, all of which result in formation of quasi-circular trajectories in the task-space (or movement shapes of type “E–B–E” which have “bump” as a basic shape point). So does the capability to perceive the underlying structure in these similar actions and “spontaneously imitate” someone performing them with a fair enough “first prototype” becomes possible because the “seeds” already exist in the form of abstract motor knowledge (learnt previously)? Abstraction from “trajectory formation” to “shape formation” could be one possible answer.

At the same time, only being able to synthesize a “virtual trajectory” is not sufficient. What is needed is a system that transforms the “virtual trajectory” into motor commands for the actuators, taking into account task-specific constraints and redundancy of the system (body-tool network) that is generating the action. Further it is necessary to learn the consequences of the generated action in this new “context.” For this we have to rely on the PMP system that comes next in the information flow.

From virtual trajectory to motor commands using PMP: Linking redundancy to task dynamics, timing, and synchronization

The PMP system transforms every point in the virtual trajectory into motor commands in the intrinsic space (upper body chain), hence enabling iCub to mimic the teacher’s action of bimanually steering the toy crane. Of course, this is just the starting point. iCub has to now learn the consequence and utility of the action in this new context (from drawing a “U” shape, to using the toy crane). As the virtual trajectory pulls the relevant end effector in a specific fashion, the rest of the body (arm and waist joints) elastically reconfigure to allow the end effector track the evolving virtual trajectory. When motor commands synthesized by this process are actively fed to the robot, it reproduces the movement, hence enabling iCub to maneuver the toy crane as demonstrated by the teacher. These coordinated movements of iCub (i.e., Figure 7B) with the toy crane now generate sequences of sensorimotor data:

1) The instantaneous position of the two hands Q ∈ (x_R, y_R, z_R, x_L, y_L, z_L) coming from proprioception (and cross-validated by forward model output of PMP, i.e., position node in end effector space).

2) The resulting consequence, i.e., the location of the tool effector X:(x, y, z)_Tool, perceived through vision and reconstructed to Cartesian space (using the same technique to reconstruct teachers movement).

As iCub acquires this sensorimotor data by practicing with the tool, a neural network can be trained to learn the mapping X = f (Q). We used a multilayer feed-forward network with one hidden layer, where Q = {q_i} is the input array (end effector position), X = {x_k} is the output array (tool position), and Z = {z_j} is the output of the hidden units. The mapping can be expressed as shown in Eq. (5), where Ω = {ω_ij} are the connection weights from the input to the hidden layer, W = {w_jk} are the connection weights from the hidden to the output layer, H = {h_j} are the net inputs to the neurons of the hidden layer. The neurons of the hidden layer are characterized by the logistic transfer function; the output layer is composed of linear neurons.

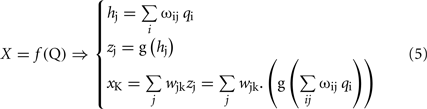
The trick here is that once the neural network is trained on the sequences of sensorimotor data generated by the robot, the tool Jacobian can be extracted from the learnt weight matrix by applying chain rule in the following way:

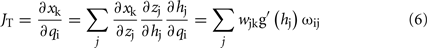
Once the tool Jacobians are learnt by iCub, the PMP network of Figure 2 is complete and fully connected to allow goal directed maneuvering of the toy crane. Note that, the tool admittance “A_T” is a property of the tool itself and can be approximately estimated as the ratio of the total force exerted by iCub with its two hands and the corresponding displacement of the tool. Since the displacement of two handles of the toy crane (connected to iCub) is proportional to the displacement of the iCub’s hands, the tool admittance is approximated as an identity matrix. Of course, there is a possibility that the tool is not compliant, in which case the only way to control it during coordination is to increase the exerted force (for example, one will need to apply more force to “turn” a steering wheel that is jammed). This is a natural property of the PMP network, but is out of scope for discussion in this article. At the same time we note that the admittance of the tool can be controlled during its design (for example, we apply lubricants to mechanical parts to make them more compliant, otherwise we end up spending more energy).

During goal directed movements with the toy crane, the goal now acts on the “tool effector” which is the most distal part of the PMP chain. The pull of the goal acting on the tool tip is incrementally circulated to the proximal spaces (end effector, joints etc.) according to information flow in Figure 2. Figures 7C–G show the trajectories in the tool, end effector, arm joint, and waist spaces, when iCub performs the bimanual action to position the tool tip at the goal. Of course, if the internal simulation of the PMP network does not converge, iCub has a way to know that the toy crane is not useful to realize the goal (or reach the target). This can be the starting point to trigger a new level of reasoning and learning.

FIGURE 7

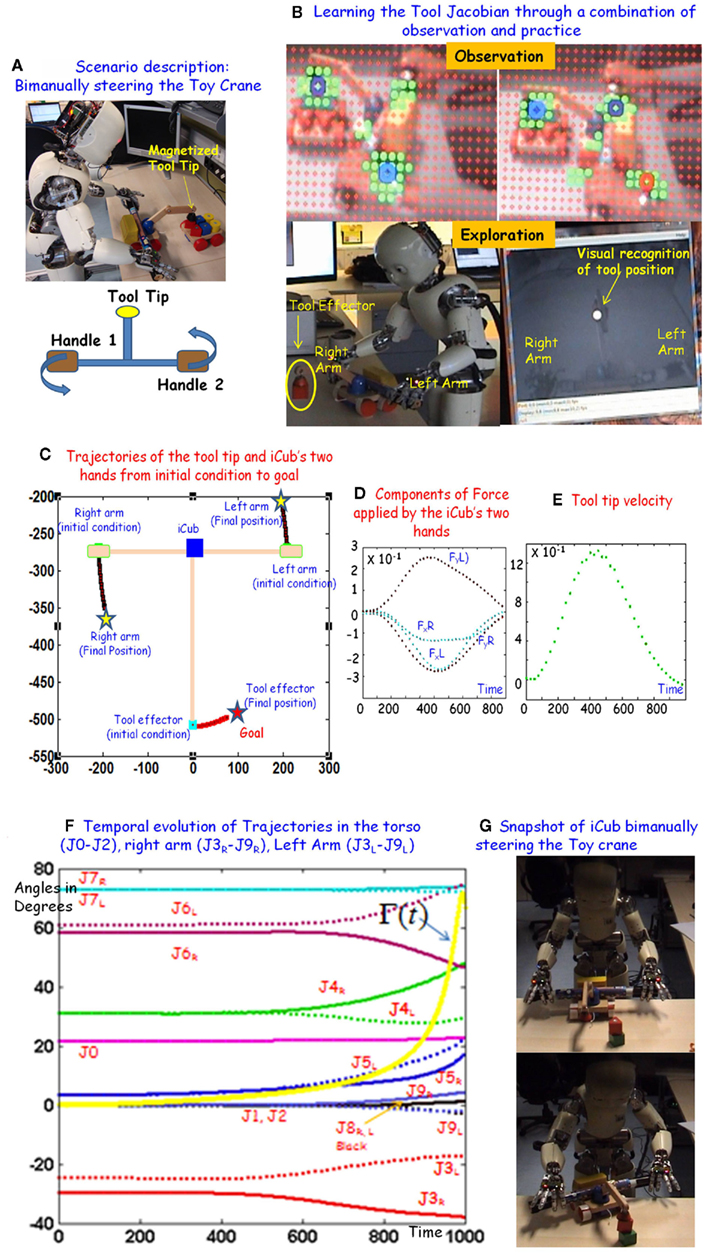
Figure 7. (A) Describes the task. Analogous to controlling a steering wheel, iCub has to bimanually maneuver the toy crane so that the magnetized tool tip reaches the goal. (B) Shows snapshots of the dual processes of observing the teacher to imitate similar spatio-temporal movements with the toy and then interacting directly with the tool in order to learn the tool Jacobian. (C) Shows the trajectories in the tool and end effector space, when iCub steers the crane toy from the initial position to the goal. (D) Shows temporal evolution of the x and y components of force exerted by right and left hand, to steer the toy crane toward the goal. (E) Shows the tool tip velocity. Note that the tool velocity is symmetric and bell-shaped. (F) Shows the temporal evolution of motor commands/joint angles in the 17 joints of the iCub upper body as iCub steers the crane toy from the initial condition [(G): top panel] to the Goal [(G): Bottom panel]. Observe that based on the motion of the two hands (C), the evolution of joint angles in the right and the left arm are approximately mirror symmetric (F).

Summary

In this sub-section, we presented how the basic PMP framework can be extended to support experiments related to motor skill learning, tool use, and imitation in embodied robots. We outlined a scheme through which both observing a “conspecific” as well as previously acquired motor knowledge (stored in an abstract manner) can speed up the acquisition of a new motor skill. To avoid open ended motor exploration in the space of “virtual stiffness,” it is important to “combine and exploit” multiple learning streams mainly imitation, physical interaction, and motor imagery into the skill learning architecture. In the demonstrated example, while the teachers demonstration showed iCub the kind of spatio-temporal trajectories it should perform on the tool, iCub’s past experience of learning to draw (and the compositionality in the domain of shapes) gave iCub the correct parameters to generate the required spatio-temporal trajectories using the “body + tool” network. Of course, in addition iCub had to learn the context specific consequences (Tool Jacobian), to complete the PMP network to perform goal directed actions with the new toy. Note that the learnt tool Jacobian is further represented in a sub-symbolic “distributed” fashion using neural networks. At the same time, through the PMP relaxation there is a way to systematically go down to the directly controlled elements of the body (actuators in the robot) both during exploration and goal directed action. In this sense, our approach is quite different from other attempts of tool use in robotics like those of Stoytchev (2008), that start with a pre-defined set of actions (extend arm 2″, 5″, forward, backward, right, and left), create a look table of the observations and conduct iterations of greedy heuristic search in the look up table, to obtain goal-oriented behavior. Coming back to OCT, how optimal control laws can be learnt through socio-physical interactions, how they can be composed and recycled is still an open question. In this section, we presented a motor skill learning framework using the PMP that incorporates all these features and at the same time validated on a complex humanoid platform.

OCT and PMP as Computational Theories

Is there any connection between OCT and PMP? As observed by Diedrichsen et al. (2009), the idea of distributing motor commands across a set of redundant effectors is shared by OCT and PMP (Mussa Ivaldi et al., 1988). However, the authors wrongly attribute to PMP the absence of a regularization term in the attractor dynamics of the network. In contrast, as illustrated in the previous sections, the possibility of integrating a variety of regularization or penalty terms “at runtime” and in a task-specific manner is the defining feature of PMP. It was only briefly hinted in the 1988 paper, but it was later expanded in great detail (Morasso et al., 1997; Tsuji et al., 2002; Mohan and Morasso, 2007; Mohan et al., 2009, 2011a,b). OCT formulates control problems in terms of scalar cost functions, whereas PMP is based on multi-dimensional force fields. In general, we think that the force field metaphor is closer to the biomechanics and the cybernetics of action than the cost function metaphor if we aim at capturing the variability and adaptability of human behavior in a changing environment in a way that allows compositionality, fast learning, and exploitation of affordances.

In the framework of the Tri-Level Hypothesis² about the levels of analysis in biological information processing systems (Marr and Poggio, 1977; Marr, 1982), both OCT and PMP are computational level theories, i.e., formalizations of what the organism is computing and why. However, PMP also includes an intermediate algorithmic/representational level, which tries to answer the question about how the computational process is actually carried out: the force-field metaphor characterizes the computational level of PMP and the kinematic networks characterize the algorithmic/representation level. We suggest that these two levels of analysis apply equally well to humans and humanoid robots, whereas they differ for the lowest implementation level, which includes sensors, actuators, and early information processing. The importance of integrating these two levels of analysis is also emphasized by the term “embodiment,” which is central in the quest for a human-like cognitive capability in humanoid robotics, by taking into account that adaptive behavior is not a “property of the brain” but emerges from the interactions of the nervous system with body and environment (Varela et al., 1991; Chiel and Beer, 1997). Generally speaking, EPH, as well as the study of force field adaptation (Shadmehr and Mussa-Ivaldi, 1994), suggest that the brain “understands” the “language of force fields,” also providing a theoretical background for an approach to robot-therapy of neuromotor patients based on the use of force fields (Casadio et al., 2009a,b; Vergaro et al., 2010).

Functional Categorization and the Cybernetics of Purposeful Action

In addition to the categorization of “computational levels,” as proposed by Marr (1982), which indeed was primarily conceived for the study of vision, the cybernetics of action also implies a categorization in “functional planning stages,” that complements the previous one. We propose the following categorization which emphasizes the role of generating “goal directed” actions in unstructured environments:

1. Strategic planning stage: given a goal and a general knowledge of the environmental conditions, this stage involves a covert analysis³ of “what is doable and useful, in the context of the goal.” This is an “information foraging” phase where the cognitive agent mentally attends to the Goal, and assembles initial chunks of information “extrinsic (environment state) and intrinsic (task-related memories, current body state),” that might be relevant in realizing the goal. Certainly it includes perception of various Affordances (provided by the environment), retrieval of known Skills (necessary for exploiting the affordances), estimating the Value of each skill (in the context of the goal), using past experiences and memories pertaining to the task;

2. Tactical planning stage: this is a “temporal ordering” or action sequencing phase where the goal is broken down into a sequence of sub-goals/sub-actions (to be carried out by different internal action models), with a prediction of the resulting consequences;

3. Plan execution and monitoring stage: in this stage every specific action/sub-action is translated into a control policy, monitoring the degree of coherence between the predicted and the actual sensory consequences, obtained through sensory feedback, in order to eliminate cognitive dissonance through further learning.

The different stages particularly emphasize the role of mental rehearsal of actions and their consequences, exploiting available affordances, “using and learning to use” environmental objects as tools in the context of the pursued goal (sometimes by imitating a conspecific). Emerging studies in animal cognition reveal that such phases of mental planning, leading to purposeful action synthesis, may not be unique to humans. Research in animal cognition has identified complex goal-oriented behaviors in different animal species, suggesting a cognitive capability well beyond the brute force strategy of trial-and-error. Well known examples are the n-stick paradigm (Visalberghi, 1993; Visalberghi and Limongelli, 1996); Betty’s Hook shaping task (Weir et al., 2002); the Trap tube paradigm (Visalberghi and Tomasello, 1997).

In the two-stick paradigm, the animal has the goal of fetching a chunk of food that cannot be reached with its bare hands. A long stick that could help to solve the problem is unreachable as well. What can be reached is a short stick, which can be used to recover the long stick and ultimately the chunk of food. Chimps can easily solve this problem of combinatorial tool use (Maravita and Iriki, 2004) and since the observation of their behavior rules out the possibility of trial-and-error, the most likely interpretation is as follows: (1) the chimp has an abstract concept of a stick-like object which must have similar computational properties to the body schema in order to be integrated with it, at least temporarily in the course of the task (Iriki et al., 1996); (2) the recognition of crucial “affordances,” such as the fact that the food and the long stick are unreachable and the short stick is reachable and long enough to get the long stick, is carried out by means of covert, “imagined” movements. In a previous work (Mohan and Morasso, 2007, 2011d) we have shown how adding a reasoning system on top of the PMP-based real/mental action generation system can enable a cognitive robot (GNOSYS) to autonomously generate goal directed plans in such scenarios (where use of tools is obligatory for achieving the goal). Figure 8 illustrates the sequences of (real and virtual) actions initiated by iCub using different task-specific PMP networks (illustrated in different examples so far) when it exploits a long green stick as a tool to reach (an otherwise unreachable) red cylinder.

FIGURE 8

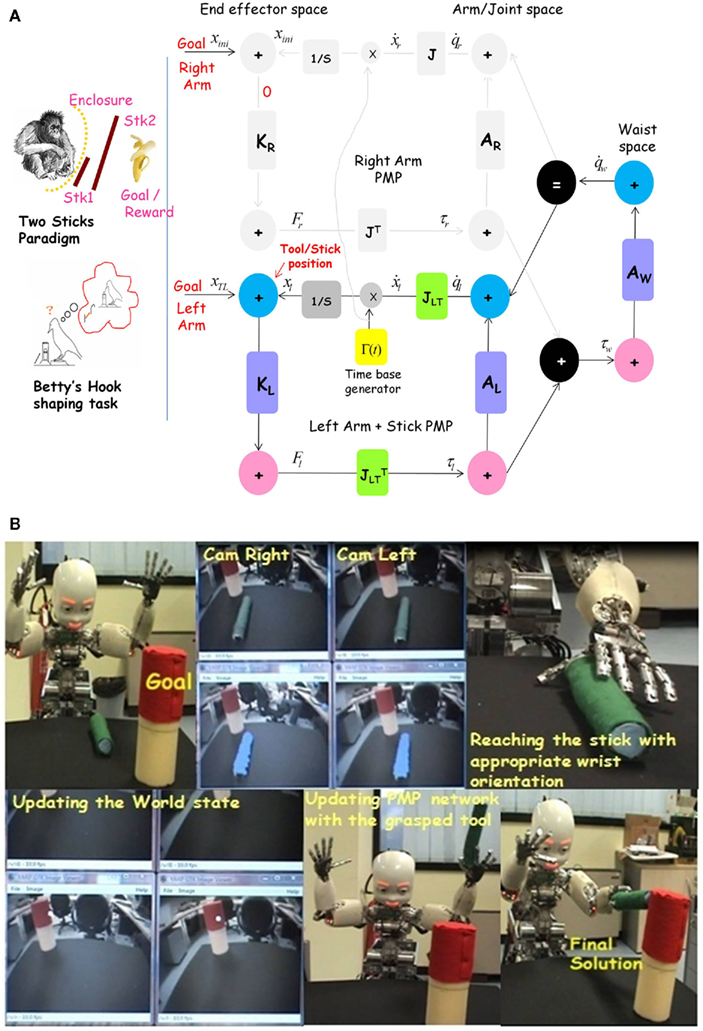
Figure 8. Pictorial illustration of the “Two sticks paradigm” applied to the iCub robot in the simplified case that a single stick is suitable and available. The goal of iCub is the reach the large red cylinder, placed out of reach. As seen, there is a green stick available in the environment. In order to realize its goal in this situation, iCub performs a sequence of overt and covert actions: (1) Mentally estimating weather the goal is directly reachable with either arm using the PMP network for the upper body (Figure 3A); (2) evaluating the size of the required stick-like tool based on the discrepancy between the goal and the final reachable position predicted by the forward model; (3) visually detecting the (green) tool; (4) evaluating whether the long green stick is reachable with an appropriate wrist orientation (using the composite PMP network of Figure 5A); (5) reaching and grasping the stick using the same PMP network; (6) incorporating the stick in the body schema by updating the Jacobian taking into account the length and orientation of the stick coupled to the end effector; (7) using the stick to reach the target cylinder using the PMP network of (A). In (A), since the tool is coupled to the left arm, the right arm network is shown deactivated (goal = initial condition, force field in the right arm network is 0). Since the coordinated tool is the most distal part of the resulting PMP network, goals act on the tool. The field generated by the discrepancy between goal and tool position is mapped into an equivalent torque field by the transpose Jacobian (J_LTT). This torque field is mapped into joint rotation patterns for the left arm by the Admittance matrix. The Jacobian J_LT now transforms this information into next incremental update in the tool position in the end effector space (tool is the end effector now). This process of incremental updating of every node in the PMP network continues till the time the force field in the left arm network is also zero (i.e., the tool tip reaches the target). (B) Shows snapshots of iCub performing the sequence of actions, reasoning and exploiting the available tool (green stick) in order to realize the otherwise unrealizable goal (i.e., reaching the red cylinder).

Summing up, affordances are the seeds of action. Being able to identify and exploit them opportunistically in the “context” of an otherwise unrealizable goal is a sign of cognition. Being able to do this in the mind by performing virtual actions, further allows an agent to evaluate “what additional affordances” it can create in its world, hence enabling it to reason about how the world must “change” such that it becomes a little bit more conducive toward realization of its internal goals. The posited decomposition of a goal into a sequence of sub-goals/sub-actions is a natural side-effect of the mental process of attempting to use tools, exploit environmental affordances to connect the dots from the initial condition to the goal. PMP is an appropriate framework for formulating the two top functional stages of the categorization defined above. The OCT framework, in our opinion, is less appropriate because covert reasoning about actions can hardly be formalized in terms of cost functions and continuous-time control policies. If we agree that internal simulation of action is a key element of purposive behavior (Jeannerod, 2001; Gallese and Lakoff, 2005; Gallese and Sinigaglia, 2011), then it is not clear how to use the “cost function” formalism for treating at the same time overt and covert (imagined) actions.

Finally, we wish to emphasize that proposing PMP as an alternative to OCT as a global framework in the analysis of purposive behavior does not rule out the importance of optimality principles in the field of motor control but, as previously mentioned, suggests that its domain of influence is local rather than global. On the other hand, a recent development on efficient methods of optimal actions (Todorov, 2009; see also the commentary by Doya, 2009) allows to compose optimal control laws by mixing primitives and thus approaches the philosophy underlying the PMP.

Discussion

The PMP has been proposed as a general framework for understanding the organization of task-oriented actions. Extensions of the framework in the direction of motor skill learning, imitation and covert reasoning about actions were presented. How PMP networks of gradually increasing complexity can be created “on the fly” while preserving the inherent “modularity,” “connectivity,” “local,” and “well posed” nature of computations in the basic model was described with a number of examples, implemented on the humanoid iCub (like, control of a single kinematic chain, full upper body coordination, bimanual coordination of a tool, incorporating multiple constraints, performing covert reasoning). In this concluding section, we analyze both positive features and open issues within the framework thereby looking for areas where future research needs to be directed.

PMP and Underexplored Areas for Future Research

In this section, we analyze the PMP framework listing out the under explored areas where novel conceptual developments may be envisaged in the future.

Learning “extended”

Once upon a time, the barter economy prevailed. Goods or services were exchanged for other goods or services. Then someone invented the concept of “currency.” With this, humans started conducting trade and economics at one further level of “Abstraction.” The core idea was to exploit the flexibility resulting from the establishment of an “abstract measure” of value (and ease of storage). Simply, based on ones requirements (i.e., the goal), the right amount of currency can be transformed into any substance or service. What is the brains “currency” for generating skilled goal directed “movement”? Can we arrive at a small set of abstract motor vocabulary that when combined, sequenced, and shaped to “context” (i.e., the goal), allows the emergence of the staggering flexibility, dexterity, and range that human actions possess?

The skill learning architecture based on PMP presented in Section “Motor Skill Learning and PMP” presents some preliminary results in this direction that needs to be further improved and validated through more experiments (both in terms of mathematical advancements and cross validation through behavioral studies). The positive feature of the proposed skill learning architecture is that different aspects of motor knowledge gained while learning a novel task are “distributed” systematically so as to allow task-specific “compositionality” and task independent “knowledge reuse.” At the same time there are areas where improvements need to be made. For example, when we learn a motor skill we learn a number of things listed below:

To perform specific spatio-temporal movements using the “task–specific” effectors/tool. This knowledge is stored in the stiffness and timing parameters that are used by the virtual trajectory synthesis system (i.e., in the shape library of Figure 6). The abstraction from “trajectory” to “shape” allows compositionality in this case. For example consider the crucial human skill of “writing.” It has been shown that 73% of the Latin/English alphabets and 82% of numerals are composed of “simple”⁴ shape features like line, bump, and cusp (Chakravarthy and Kompella, 2003). Inversely, since most letters of the English alphabets and numerals are “synthesized” with these simple shape features, the authors argue that the script is very “stable and robust,” from the “sensory–motor” point of view (i.e., both explaining the diversity in the handwriting of different people and our effortless ability to perceive/read them). Further, even the task-space trajectories of common tool use actions like screwing, uncorking, cycling, use of lever, unwinding, use of a tap, cycling, among many others just require “task–space” trajectories that end up in “bump,” “line,” and “cusp” shape features, that can be very easily “described and generated” in formal terms (Mohan et al., 2011b).

The provocative question is in fact the inverse problem, i.e., not the “use of a tool” but the “design of a tool” itself. Do we prefer design tools that “conform” to these specific movement shapes in the extrinsic space? Is the measure of “user friendliness” of a new tool related to the fact that we can “recycle” our past knowledge of movement and learn to move with new tool applying minimal efforts? Learning the consequence of such movements is another issue (more task-specific) and our system deals with this at a different level (i.e., the Jacobians). But, does the brain “compose” and “recycle” task-space motion by mixing “shape” knowledge? This does seem reasonable from an evolutionary perspective because all basic “sensorimotor” interactions require “shaping” one’s body to the shape of the world with which we are interacting (be it a monkey clinging to a branch of a tree or a couple dancing). Surprisingly, it is not easy to give a precise mathematical or quantitative definition of “shape” or even express it in measurable quantities like length, angles, or topological structures. In general terms, shape is the core information in any object/action that survives the effects of changes in location, scale, orientation, end-effectors/bodies used in its creation, noise, and even minor structural “injury.” We posit that it is this invariance that makes “shape” a crucial piece of information for sensorimotor interaction. Hence, we suggest that an unified treatment of the dual operations of shape perception/synthesis is critical to better understand the perception–action loop, how we recycle past sensorimotor knowledge, and why we design tools the way we do (taking into account how “user friendly” it is). In other words, we posit that “user friendliness” is just a measure of how a “tool designer” can minimize “sensorimotor” exploration required by a “tool user.” Further research needs to be directed in these areas though both experiments with humans and humanoids.

Learning the relationship between the “body effector” and “tool”. This knowledge is specific to the body effector and tool involved in the action and is mapped by the tool Jacobians at the interface. In Section “Motor Skill Learning and PMP,” we have shown how this information can be learnt through an “action–perception” loop and represented in a sub-symbolic manner using standard neural networks.

Learning to attain specific “body postures” that are required by the task. Attaining the right body pose in some tasks may be obligatory but most often simplifies the execution of any motor skill. This can be achieved by learning the right balance of “admittance” in the intrinsic space of the associated PMP network. Similar to the learning of “virtual stiffness and timing” to perform spatio-temporal movements in the end effector space, attaining the right pose with the body may also be learnt through a combination of imitation and practice. In principle it is possible to estimate the approximate contribution of different body parts by observing a teacher or through kinesthetic teaching. Since the effect of admittance is “local” in PMP, such perceptual information can be directly used to “locally” modulate the participation of different DoFs, hence influencing the nature of solution obtained in the intrinsic space. Preliminary results have been obtained in the scenario of whole body synergy formation (Morasso et al., 2010; Zenzeri, 2010) where the task was to learn the right balance of admittance values in the whole body PMP network in order to reproduce the final body pose achieved by the teacher (recorded using a motion capture device). Even though it applies for this specific case, a more comprehensive and general understanding needs to be achieved through experiments in the future. In general, while the link between perception of movement and task-specific regulation of “stiffness” and “timing” in the extrinsic space (VTGS) has been already addressed in detail, further research needs to be conducted to understand the link between perception of movement and swift “task–specific” regulation of admittance in the intrinsic space, in order to also obtain specific body postures while performing these movements.

Integrating all the knowledge in the context of a Goal. The PMP network is the natural site where all the motor knowledge related to stiffness, timing, Jacobians, and admittance comes together. The network structure is organized in a way such that different connecting links play “well defined” roles and can be loaded at “runtime” from memory when a task-specific PMP network is “assembled” to coordinate a motor behavior. What remains is only to “switch on” the task relevant force fields (i.e., the goal and other constraints that apply) and let the network evolve in the resulting attractor dynamics. Part of the motor knowledge related to “movement” per se is context independent and part of the knowledge related to task-specific consequences, other constraints involved are context dependent. These are stored separately in the action learning architecture and integrated in a task-specific fashion by the PMP system to synthesize the motor commands. This modular, distributed, local, and goal directed organization of action is one of the positive features of the framework.

Effects of loading, tighter integration with dynamics

In this section, we are concerned with scenarios such as a firefighter in a self-contained breathing apparatus wearing heavy protective gears and performing a precision task with a tool (for example, a water hose), a soldier often loaded in excess of 40% of his body weight moving both for one’s own survival and performing his/her duties, an infant coping up with a growing body especially during the first few years of life (Adolph and Berger, 2006; Adolph et al., 2008), industrial robots that wield and transport different tools (e.g., assembly lines for car manufacturing etc), or even ourselves performing/learning movements with different physical loads dynamically coupled to our body segments. Often there are functional changes in the mass and moment of inertia of the different body segments that we have to account for dynamically “at runtime.” At the moment, PMP directly does not take into account these effects. It basically solves the DoFs problem, i.e., the how the goal of performing a task-specific movement can be distributed across a large number of contributing elements in a highly redundant motor system (that also includes coupled tools). In this sense, PMP networks should be considered as a “body schema” or an “internal model” that interfaces higher cognitive levels (reasoning and planning) with lower control levels, related to actuators and body dynamics. It does not deal directly with the lower level dynamics at actuator level. In the iCub, whose individual DoFs are separately controlled by means of standard PIDs loops at the actuator level, the output of the PMP network provides the reference trajectory for each PID controller. Still, a tighter “closed–loop” integration of PMP with dynamics at actuator level, taking into account effects of “loading” in various body segments while generating motor actions is necessary. With ongoing hardware developments related to joint level force/torque sensing in iCub (Parmiggiani et al., 2009; Fumagalli et al., 2010), in the next generation PMP networks we plan to integrate and account for dynamics at the lower level in a more refined manner.

An interesting inverse scenario concerns the use of humanoid robots to understand “constraints” that various physically coupled loads place on the movements that needs to be generated under such conditions. New experiments with PMP are being devised to better understand the effects of loading different body segments (trunk, head, hands) of iCub to investigate: (a) postural/focal relations in terms of functional changes in Mass and Moment of Inertia of the different body segments; (b) evaluation of the resulting reduction in available DoF and lack of access to physical and functional workspace due to the loading conditions; (c) compare the results with motion analysis of humans performing similar movements under identical loading conditions. This direction of research can potentially provide greater insights into: (a) the functional capability and survivability of people wearing different kinds of personal protective equipments (PPE) while performing their day to day tasks; (b) use this knowledge to redistribute loading of their bodies in an optimal fashion; (c) create ergonomic designs of PPE’s, safety gears etc worn by people who are expected to perform precision tasks in critical conditions (like soldiers, fire fighters among others).

Towards a Shared Computational Basis for “Execution, Imagination, and Understanding” of Action

Biological plausibility

Mounting evidence accumulated from different directions such as brain imaging studies (Frey and Gerry, 2006; Grafton, 2009; Kranczioch et al., 2009; Munzert et al., 2009), mirror neuron systems (Gallese et al., 1996; Rizzolatti et al., 2001; Rizzolatti and Sinigaglia, 2010) and embodied cognition (Gallese and Lakoff, 2005; Gallese, 2009; Gallese and Sinigaglia, 2011; Sevdalis and Keller, 2011) generally support the idea that action “generation, observation, imagination, and understanding” share similar underlying functional networks in the brain. In general, there is growing evidence for the fact that neural circuits in the predominantly motor areas are also activated in other contexts related to “action” that do not cause any overt movement. Such neural activity occurs not only during imagination of movement (Decety, 1996; Decety and Sommerville, 2007; Caeyenberghs et al., 2008; Holmes and Calmels, 2008, several others) but also during observation and imitation of other’s actions (Grafton et al., 1996; Buccino et al., 2001; Frey and Gerry, 2006; Ulloa and Pineda, 2007; Iacoboni, 2009a) and even comprehension of language, i.e., both action related verbs and nouns (Glenberg, 1997; Barsalou, 1999; Feldman, 2006; Fischer and Zwaan, 2008; Pulvermüller and Fadiga, 2010; Glenberg and Gallese, 2011; Marino et al., 2011). The neural activation patterns include not only premotor and motor areas such as PMC, SMA, and M1 but also subcortical areas of the cerebellum and the basal ganglia. During the observation of movements of others, an entire network of cortical areas called as the “action observation network” that includes the bilateral posterior superior temporal sulcus (STS), inferior parietal lobule (IPL), inferior frontal gyrus (IFG), dorsal premotor cortex, and ventral premotor cortex are activated in a highly reproducible fashion (Grafton, 2009). The central hypothesis that emerges out of these results is that motor imagery and motor execution draw on a shared set of cortical mechanisms underlying motor cognition. In simple terms, it posits that one can reason about an action (reach, grasp etc.) without actually performing the action and yet use the same neural substrate in the sensory motor system. Further, neural substrates that are used in imagination are also used in understanding actions of others, i.e., when observing actions, people recruit motor representations as if they were themselves acting. In other words, understanding is an internal simulation that entails the reuse of our own ability to act with our bodily resources in order to functionally attribute meaning to “others” actions. The extent and reliability of such reuse and functional attribution depends both on the simulator’s bodily resources and their being shared with the target’s bodily resources (Gallese and Sinigaglia, 2011).

A preliminary foundation of such “shared” computational machinery for action generation, action learning through imitation and covert reasoning about action in the humanoid robot iCub has been created through the development of the PMP framework (and illustrated through numerous examples in this paper). In general, PMP networks are activated under a variety of conditions in relation to action, either of oneself or observed from the teacher. Their function is not only to shape the motor output during action execution, but also to provide the self with information on the feasibility, consequence, understanding, and meaning of potential actions. Further, considering that real and imagined actions turn out to be similar indeed, the proposition that even overt actions are a product of an “internal simulation” is a defining feature of PMP architecture. A further hypothesis suggested by the PMP, is that the posited simulation is an attractor dynamics, driven the “task–specific” force fields. This is the crucial difference between EPH and PMP. While in the classical view of EPH, the attractor dynamics that underlies production of movement is attributed to the elastic properties of skeletal neuromuscular system, PMP posits that cortical, subcortical, and cerebellar circuits may also be characterized by similar attractor dynamics. This could explain the similarity of real and imagined movements because, although in the latter case the attractor dynamics associated with the neuromuscular system is not operant, the dynamics due to the interaction among other brain areas are still at play.

The study of the neural basis of imitation is still in its infancy, although the cognitive, social and cultural implications of imitation are well documented (Rizzolatti and Arbib, 1998; Schaal et al., 2003; Argall et al., 2009; Lopes et al., 2010). Experimental evidence from numerous brain imaging studies (Perrett and Emery, 1994; Grafton et al., 1996; Rizzolatti et al., 1996, 2001; Iacoboni et al., 2001; Koski et al., 2002; Iacoboni, 2009b) suggest that the inferior frontal mirror neurons which code the goal of the action to be imitated receive information about the visual description of the observed action from the STS of the cortex and additional somatosensory information regarding the action to be imitated from the posterior parietal mirror neurons. Efferent copies of motor commands providing the predicted sensory consequences of the planned imitative actions are sent back to STS where a matching process between the visual description of the action and the predicted sensory consequences of the planned imitative actions takes place. If there is a good match, the imitative action is initiated; if there is a large error signal, the imitative motor plan is corrected until convergence is reached between the superior temporal description of the action and the description of the sensory consequences of the planned action. It is interesting to note that the imitation learning loop of our skill learning architecture (Figure 6) resonates well with these findings, the visual shape extraction and motor goal formation system coding for the early visual description of the action to be imitated, virtual trajectory coding for a detailed motor representation necessary for action generation, and the forward model output of the PMP (efferent copies) being sent back in the same format of the visual goal description for monitoring purposes. This issue has been dealt with in detail in Mohan et al. (2011b), and emphasizes the point that internal simulations play an important role in allowing the observer to foresee the consequence of an action, predict the intended goal of the actor and learn to replicate the action through imitation.

In this sense, PMP is a young framework that attempts to integrate, in a computational manner, a growing body of neurobiological knowledge on a humanoid robot. Its biological plausibility comes from complementary and converging lines of investigations on the neural basis of purposive behavior: the equilibrium point hypothesis, extended in such a way to take into account the evidence coming from motor imagery, on one side, and the parieto-frontal mirror circuitry, on the other. We understand that this is just the starting point. There exists wide scope for further investigating the neurobiological basis of PMP using a combination of behavioral studies and brain imaging techniques. This requires a comprehensive research program with active participation from the neuroscience, animal cognition and developmental psychology community. This article is just an initiative in this direction.

PMP extended: Ongoing developments

We emphasize that PMP is also a medium through which several findings related to motor cognition coming from the field of neuroscience can be implemented in complex humanoid robots. This opens us the possibility of both conducting a wide range of experiments related to different aspects of “action” on humanoid robots and at the same time endowing them with motor skills necessary to flexibly “assist” us in our needs and in the environments we inhabit and create. In this context, further developments of the architecture are being pursued by the different EU supported projects that use PMP as a computational backbone (ITALK⁵, EFAA, DARWIN, and ROBOCOM).

PMP and Social Interaction

Specifically, EFAA aims to extend the PMP framework in the domain of social interaction, acquisition of motor skills through demonstration, learning to “inter-act,” and cooperate with the teacher in joint goals. Further development of the work on motor knowledge recycling and the “shape” perception/synthesis hypothesis (Mohan et al., 2011b) discussed in Section “Motor Skill Learning and PMP” is also planned. An interesting question in the behavioral side that we are investigating in this context is the possibility of characterizing the shape of “percepts” in general, independent of the modality through which they are sensed (visual, auditory, haptic, all of which is functionally available in iCub). Does multimodal sensory fusion partially result from the resonance between shape critical points computed through different sensory modalities? For example, it is well known that certain forms of music resonate well with certain forms of dance (auditory to motion mapping) or even the existence of numerous metaphors that connect different sensory modalities like “chatter cheese is sharp” (gustatory to tactile mapping). That humans are very good at forming cross modal synesthetic abstractions has been known right from the early experiments of Wolfgang Kohler, the so called “Bouba–Kiki effect” (Ramachandran and Hubbard, 2003). In the same line are recent results from sensory substitution (hearing to seeing for the blind, see Amedi et al., 2007) that show primacy “shape” information in mediating multisensory integration. We hypothesize that a formal framework for perception and synthesis of “shape” backed up with behavioral studies will both shed more light on how cross modal abstractions between senses are made (and at the same time endow iCub with a preliminary capability to perform the same).

PMP, Motor Skill Learning, and Neurorehabilitation

When it comes to motor skill learning a related field of high relevance is neuromotor rehabilitation, considering that functional recovery from motor impairment is similar to learning a new motor skill. In a previous work, we have already investigated the scenario of a master teaching iCub the drawing/writing skill. What about the inverse scenario⁶ of a skilled robot teaching or assisting a neuromotor impaired subject to recover a skill, like writing or drawing? This inverse scenario makes it possible to investigate motor learning as it occurs in human subjects. To investigate this issue, we have ported the PMP framework into the haptic manipulandum BdF (Casadio et al., 2006) and the first set of experiments of teaching subjects to draw “shapes” with their non-dominant hand (coupled to the BDF) is underway (Basteris et al., 2010). An assistance module that “optimally” regulates haptic intervention of the robot based on the performance of the student is being designed. We are also investigating a three way interaction scenario between expert-robot–student (expert and student coupled to the either arms of the manipulandum) during handwriting learning experiments. The goal for the robot here is to acquire an internal model of the training session (case histories) and use this knowledge to intelligently regulate assistance to the trainee when the expert is disconnected in the later stages. This scenario is the subject of the ongoing EU FP7 project HUMOUR.

PMP and the “Blurred” Distinction between “Tool” and the “Body”

An interesting point to observe is that PMP framework does not make any special distinction between the “body” and a “tool.” There are two interesting ramifications.

The tool space is represented exactly in the same manner as any other motor space and during coordination the body and the tool act as one cohesive unit (to realize a goal). The process whereby a tool becomes an extension of the hand to perform a specific task can be related to the flexible view of body schema offered by Head and Holmes (1911). In a seminal paper, Umiltà et al. (2008) have shown that the essence of tool use lies in the capacity to transfer proximal goals to distal goals. Recording from monkeys trained to use pliers to grasp otherwise unreachable food reward, they demonstrated that the end effect of tool use training was the transfer of the temporal discharge pattern that controls “hand grasping” (area F5) to the tool, as if the tool was the hand of the monkey and its tips were the monkey’s fingers. This of course is reminiscent of the results of Iriki and colleagues (Maravita and Iriki, 2004; Iriki and Sakura, 2008), who showed that, with practice, a rake becomes a part of the acting monkey body schema. However, what Umiltà et al demonstrated was that in addition to being incorporated into the body schema, the tool, after learning, is coded in the motor system as if it were an artificial hand able to interact with the external objects, exactly as the natural hand is able to do. In the PMP network for coordinating the toy crane (Figure 2), as the magnetized tip is being pulled toward the goal target, iCub’s end-effectors are simultaneously being pulled toward the required positions so as to allow the tool tip to reach the goal. These positions are the goals for the end effector space. As a consequence, the joints are concurrently pulled so as to allow the end-effectors to reach the position that allows the tool tip to reach the goal. These are the goals for the intrinsic space. If motor commands derived through this incremental internal simulation of action are transmitted to the robot, it will reproduce the motion, hence allowing iCub to perform goal directed movements using the “body + toy crane” network. It is this kind of goal-centered functional organization of cortical motor areas for which Umiltà et al provide evidence through their tool use experiments with monkeys.

An interesting idea proposed in a seminal article by Iriki and Sakura (2008) in this context is that if external objects can be conceived as being parts of the body during coordination, then the converse, i.e., the subject can now “objectify” its own body parts as equivalent to external tools, becomes likewise apparent. In other words, they hypothesize that the ability to literally incorporate external objects into one’s own body schema and the ability to “objectify” the body (other bodies) as another object/tool are just the two sides of the same coin. The consequence is quite remarkable. As soon as one’s own body becomes objectified and separate, one must assume a subject with an independent status that is orchestrating the movements of both the body and its tools. In this way, the “mind” could emerge naturally as a sort of “virtual concept,” a placeholder for the link between the “subject” and the “objects” of manipulation, which includes the body itself (and other bodies). There is already some evidence in this regards. It has been shown that significant intracortical connections between the intraparietal cortex (IPS) and the temporo-parietal junction (TPJ) can be forged by tool use training in adult monkeys (Hihara et al., 2006). In human subjects, activation of the homologous circuitry at the TPJ is detected in self-objectification paradigms (Corradi-Dell’Acqua et al., 2008). In this sense, further research on acquisition of tool use skills in both primates and cognitive robots could open a new window to understand several fundamental issues like the emergence of mind, the sense of self, the continuity of self in time, “other selves” in other bodies and the horizontal spread of skills through culture (through social interactions: human–human, human–humanoid). In this context, work is ongoing to expand the motor skills of iCub using the extended PMP framework and teach it to use common day to day tools like screwdriver, hammer, lever etc., and perform simple assembly operations (using MECCANO 2+ assembly kit) through a combination of social and physical interactions (as in Figure 6). Further, while interacting with these objects we expect it to learn “abstract” sensorimotor knowledge related to contact (using the new touch sensors and skin available in iCub), directionality while pushing/pulling, extension of reach (and its peripersonal space), amplification of force (integration PMP with recently mounted force/torque sensors). The word “abstract” should be taken in the sense that the acquired knowledge can be “recycled” in a number of task-specific contexts. This objective is being pursued through a recently funded EU project DARWIN (www.darwin-project.eu). In general, we look forward towards creating an iCub that learns “Green”!

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The research leading to these results has received funding from the European Community’s Seventh Framework Programme (FP7/2007-2013) projects iTalk (www.italkproject.org, Grant no: FP7-214668), DARWIN (www.darwin-project.eu, Grant No: FP7-270138), EFAA (www.efaa.upf.edu, Grant No: FP7-270490) and ROBOCOM (www.robotcompanions.eu, Grant No: FP7-284951). This research is also supported by IIT (Istituto Italiano di Tecnologia, RBCS dept). We are indebted to the anonymous reviewers for not just their detailed analysis and criticisms to the initial versions of this paper, but also for their attempts to put their own vision into this manuscript, to make it sharp to the context, meaningful and reader friendly.

Supplementary Material

The Movies for this article can be found online at http://www.frontiersin.org/Neurorobotics/10.3389/fnbot.2011.00004/abstract

Footnotes

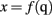1. ^ is the kinematic function that determines the position of any end-effector given the values of the DoFs, i.e., the forward kinematics of the coordinated body chain.
2. ^The three-level hypothesis is articulated in the following levels: (1) computational level (what has to be computed and why, given the task); (2) algorithmic/representational level (how does the system do what it does and. specifically, what representations does it use); (3) implementation level (physical realization of “software” and “hardware”).
3. ^This has similarities with the idea of non-linear model predictive control; a nice review can be found in Camacho and Bordóns (2007). At the same time, we believe that PMP like mechanisms may be quite compatible with recent anthropomimetic robots like ECCEROBOT (http://eccerobot.org/), that not only mimic the human “form” but also its inner structures and mechanisms, i.e., bones, joints, muscles, and tendons and thus have the potential to replicate human-like “action” and “interaction” in the world.
4. ^“Simple” here formally refers to the “codimension” of the resulting shape, i.e., the number of independent parameters necessary to bring back a shape point from its perturbed version to the original state (Chakravarthy and Kompella, 2003). Greater the codimension, the more unstable is the resulting shape.
5. ^EFAA stands for Experimental Functional Android Assistant (http://efaa.upf.edu/). DARWIN stands for Dextrous Assembler Robot Working with embodied INtelligence (http://www.darwin-project.eu/), ITALK stands for Integration and transfer of action and language knowledge in robots (www.italkproject.org), ROBOCOM stands for Robot Companions for Citizens (www.robotcompanions.eu).
6. ^This scenario is the subject of the ongoing EU FP7 project HUMOUR: HUman behavioral Modeling for enhancing learning by Optimizing hUman-Robot interaction.

References

Abend, W., Bizzi, E., and Morasso, P. (1982). Human arm trajectory formation. Brain 105, 331–348.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Adolph, K. E., and Berger, S. A. (2006). “Motor development,” in Handbook of Child Psychology, Vol. 2, Cognition, Perception, and Language, 6th Edn, eds W. Damon, R. Lerner, D. Kuhn, and R. S. Siegler (New York: Wiley), 161–213.

Adolph, K. E., Robinson, S. R., Young, J. W., and Gill-Alvarez, F. (2008). What is the shape of developmental change? Psychol. Rev. 115, 527–543.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Amedi, A., Stern, W., Camprodon, A. J., Bermpohl, F., Merabet, L., Rotman, S., Hemond, C., Meijer, P., and Pascual-Leone, A. (2007). Shape conveyed by visual-to-auditory sensory substitution activates the lateral occipital complex. Nat. Neurosci. 10, 687–689.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Argall, B. D., Chernova, S., Veloso, M., and Browning, B. (2009). A survey of robot learning from demonstration. Rob. Auton. Syst. 57, 469–483.

CrossRef Full Text

Aronofsky, D. (2010). The Black Swan. Movie produced by Ari Handel. Scott Franklin, Mike Medavoy, Arnold Messer, Brian Oliver and starring Natalie Portman, Vincent Cassel, Mila Kunis, Barbara Hershey.

Asatryan, D. G., and Feldman, A. G. (1965). Functional tuning of the nervous system with control of movements or maintenance of a steady posture. Biophysics (Oxf.) 10, 925–935.

Barsalou, L. W. (1999). Perceptual symbol systems. Behav. Brain Sci. 22, 577–609.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Basteris, A., Bracco, L., and Sanguineti, V. (2010). “Intermanual transfer of handwriting skills: role of visual and haptic assistance,” in IMEKO Tc19 International Symposium on Human Function, Prague, Czech Republic.

Ben-Itzhak, K. S., and Karniel, A. (2008). Minimum acceleration criterion with constraints implies bang-bang control as an underlying principle for optimal trajectories of arm reaching movements. Neural. Comput. 20, 779–812.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Berniker, M., Jarc, A., Bizzi, E., and Tresch, M. C. (2009). Simplified and effective motor control based on muscle synergies to exploit musculoskeletal dynamics. Proc. Natl. Acad. Sci. U.S.A. 106, 7601–7606.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bernstein, N. (1967). The Coordination and Regulation of Movements. Oxford: Pergamon Press.

Bizzi, E., Hogan, N., Mussa Ivaldi, F. A., and Giszter, S. (1992). Does the nervous system use equilibrium-point control to guide single and multiple joint movements? Behav. Brain Sci. 15, 603.

Bizzi, E., Mussa Ivaldi, F. A., and Giszter, S. (1991). Computations underlying the execution of movement: a biological perspective. Science 253, 287–291.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bizzi, E., Polit, A., and Morasso, P. (1976). Mechanisms underlying achievement of final position. J. Neurophysiol. 39, 435–444.

Pubmed Abstract | Pubmed Full Text

Borroni, P., Gorini, A., Riva, G., Bouchard, S., and Gabriella Cerri, G. (2011). Mirroring avatars: dissociation of action and intention in human motor resonance. Eur. J. Neurosci. 34, 662–669.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bryson, E. (1999). Dynamic Optimization. Menlo Park, CA: Addison Wesley Longman.

Buccino, G., Binkofski, F., and Fink, G. R. (2001). Action observation activates premotor and parietal areas in a somatotopic manner: an fMRI study. Eur. J. Neurosci. 13, 400–404.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bullock, D., and Grossberg, S. (1988). Neural dynamics of planned arm movements: emergent invariants and speed-accuracy properties. Psychol. Rev. 95, 49–90.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Caeyenberghs, K., van Roon, D., Swinnen, S. P., and Smits-Engelsman, B. C. (2008). Deficits in executed and imagined aiming performance in brain-injured children. Brain Cogn. 69, 154–161.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Camacho, E. F., and Bordóns, C. (2007). Nonlinear Model Predictive Control: An Introductory Review. Assessement and Future Directions of Nonlinear Model Predictive Control. ISBN 3-540-72698-5. (Lecture Notes in Control and Information Science), Vol. 358. New York: Springer, 1–16.

Casadio, M., Morasso, P., Sanguineti, V., and Arrichiello, V. (2006). Braccio di Ferro: a new haptic workstation for neuromotor rehabilitation. Technol. Health Care 14, 123–142.

Pubmed Abstract | Pubmed Full Text

Casadio, M., Morasso, P., Sanguineti, V., and Giannoni, P. (2009a). Minimally assistive robot training for proprioception-enhancement. Exp. Brain Res. 194, 219–231.

CrossRef Full Text

Casadio, M., Giannoni, P., Masia, L., Morasso, P., Sandini, G., Sanguineti, V., Squeri, V., and Vergaro, E. (2009b). Robot therapy of the upper limb in stroke patients: rational guidelines for the principled use of this technology. Funct. Neurol. 24, 195–202.

Chakravarthy, V. S., and Kompella, B. (2003). The shape of handwritten characters. Pattern Recognit. Lett. 24, 1901–1913.

CrossRef Full Text

Chhabra, M., and Jacobs, R. A. (2006). Properties of synergies arising from a theory of optimal motor behavior. Neural. Comput. 18, 2320–2342.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chiel, H. J., and Beer, R. D. (1997). The brain has a body: adaptive behavior emerges from interactions of nervous system, body and environment. Trends Neurosci. 20, 553–557.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Corradi-Dell’Acqua, C., Ueno, K., Ogawa, A., Cheng, K., Rumiati, I., and Iriki, A. (2008). Effects of shifting perspective of the self: an fMRI study. Neuroimage 40, 1902–1911.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Crammond, D. J. (1997). Motor imagery: never in your wildest dream. Trends Neurosci. 20, 54–57.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

d’Avella, A., and Bizzi, E. (2005). Shared and specific muscle synergies in natural motor behaviors. Proc. Natl. Acad. Sci. U.S.A. 102, 3076–3081.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Decety, J. (1996). Do imagined and executed actions share the same neural substrate. Brain Res. Cogn. Brain Res. 3, 87–93.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Decety, J., and Sommerville, J. (2007). “Motor cognition and mental simulation,” in Cognitive Psychology: Mind and Brain, eds S. M. Kosslyn and E. Smith (New York: Prentice Hall), 451–481.

Demiris, Y., and Khadhouri, B. (2006). Hierarchical attentive multiple models for execution and recognition (HAMMER). Rob. Auton. Syst. 54, 361–369.

CrossRef Full Text

Di Pellegrino, G., Fadiga, L., Fogassi, L., Gallese, V., and Rizzolatti, G. (1992). Understanding motor events: a neurophysiological study. Exp. Brain Res. 91, 176–180.

Pubmed Abstract | Pubmed Full Text

Diedrichsen, J., Shadmehr, R., and Ivry, R. B. (2009). The coordination of movement: optimal feedback control and beyond. Trends Cogn. Sci. (Regul. Ed.) 14, 31–39.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dingwell, J. B., Mah, C. D., and Mussa-Ivaldi, F. A. (2004). Experimentally confirmed mathematical model for human control of a non-rigid object. J. Neurophysiol. 91, 1158–1170.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Doya, K. (2009). How can we learn efficiently to act optimally and flexibly? Proc. Natl. Acad. Sci. U.S.A. 106, 11429–11430.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ernst, M. O., and Banks, M. S. (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415, 429–433.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Feldman, A. G. (1966). Functional tuning of the nervous system with control of movement or maintenance of a steady posture, II: controllable parameters of the muscles. Biophysics (Oxf.) 11, 565–578.

Feldman, A. G., and Levin, A. F. (1995). The origin and use of positional frmes of reference in motor control. Behav. Brain Sci. 18, 723.

CrossRef Full Text

Feldman, J. (2006). From Molecule to Metaphor: A Neural Theory of Language. Cambridge, MA: MIT Press.

Fischer, M. H., and Zwaan, R. A. (2008). Embodied language: a review of the role of the motor system in language comprehension. J. Exp. Psychol. 61, 825–850.

CrossRef Full Text

Flash, T., and Hogan, N. (1985). The coordination of arm movements: an experimentally confirmed mathematical model. J. Neurosci. 5, 1688–1703.

Pubmed Abstract | Pubmed Full Text

Frey, S. H., and Gerry, V. E. (2006). Modulation of neural activity during observational learning of actions and their sequential orders. J. Neurosci. 26, 13194–13201.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fumagalli, M., Gijsberts, A., Ivaldi, S., Jamone, L., Metta, G., Natale, L., Nori, F., and Sandini, G. (2010). “Learning to exploit proximal force sensing: a comparison approach,” in From Motor Learning to Interaction Learning in Robots, Vol. 264, eds O. Sigaud and J. Peters (Heidelberg: Springer-Verlag), 159–177.

Gallese, V. (2009). Motor abstraction: a neuroscientific account of how action goals and intentions are mapped and understood. Psychol. Res. 73, 486–498.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gallese, V., Fadiga, L., Fogassi, L., and Rizzolatti, G. (1996). Action recognition in the premotor cortex. Brain 119, 593–609.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gallese, V., and Lakoff, G. (2005). The brain’s concepts: the role of the sensory-motor system in reason and language. Cogn. Neuropsychol. 22, 455–479.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gallese, V., and Sinigaglia, C. (2011). What is so special with embodied simulation. Trends Cogn. Sci. (Regul. Ed.) 15, 512–519.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ganesh, G., Haruno, M., Kawato, M., and Burdet, E. (2010). Motor memory and local minimization of error and effort, not global optimization, determine motor behavior. J. Neurophysiol. 104, 382–390.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Glenberg, A., and Gallese, V. (2011). Action-based language: a theory of language acquisition production and comprehension. Cortex. doi: 10.1016/j.cortex.2011.04.010. [Epub ahead of print].

CrossRef Full Text

Glenberg, A. M. (1997). What memory is for. Behav. Brain Sci. 20, 1–19.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grafton, S. T. (2009). Embodied cognition and the simulation of action to understand others. Ann. N. Y. Acad. Sci. 1156, 97–117.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grafton, S. T., Fagg, A. H., Woods, R. P., and Arbib, M. A. (1996). Functional anatomy of pointing and grasping in humans. Cerebral Cortex 6, 226–237.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Guigon, E. (2011). “Models and architectures for motor control: simple or complex?” in Motor Control, Chap. 20, eds F. Danion and M. L. Latash (Oxford, UK: Oxford University Press), 478–502.

Guigon, E., Baraduc, P., and Desmurget, M. (2007). Computational motor control: redundancy and invariance. J. Neurophysiol. 97, 331–347.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Guigon, E., Baraduc, P., and Desmurget, M. (2008a). Computational motor control: feedback and accuracy. Eur. J. Neurosci. 27, 1003–1016.

CrossRef Full Text

Guigon, E., Baraduc, P., and Desmurget, M. (2008b). Optimality, stochasticity, and variability in motor behavior. J. Comput. Neurosci. 24, 57–68.

CrossRef Full Text

Harris, C. M., and Wolpert, D. M. (1998). Signal-dependent noise determines motor planning. Nature 394, 780–784.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Haruno, M., Wolpert, D. M., and Kawato, M. (2001). MOSAIC model for sensorimotor learning and control. Neural Comput. 13, 2201–2220.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Head, H., and Holmes, G. (1911). Sensory disturbances from cerebral lesions. Brain 34, 102–254.

CrossRef Full Text

Hihara, S., Notoya, T., Tanaka, M., Ichinose, S., Ojima, H., Obayashi, S., Fujii, N., and Iriki, A. (2006). Extension of corticocortical afferents into the anterior bank of the intraparietal sulcus by tool-use training in adult monkeys. Neuropsychologia 44, 2636–2646.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hogan, N. (1987). Modularity and causality in physical system modeling. J. Dyn. Syst. Meas. Control 109, 384–391.

CrossRef Full Text

Holmes, P., and Calmels, C. (2008). A neuroscientific review of imagery and observation use in sport. J. Mot. Behav. 40, 433–445.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U.S.A. 79, 2554–2558.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Iacoboni, M. (2009a). Imitation, empathy, and mirror neurons. Annu. Rev. Psychol. 60, 653–670.

CrossRef Full Text

Iacoboni, M. (2009b). Neurobiology of imitation. Curr. Opin. Neurobiol. 19, 661–665.

CrossRef Full Text

Iacoboni, M., Koski, L. M., Brass, M., Bekkering, H., Woods, R. P., Dubeau, M. C., Mazziotta, J. C., and Rizzolatti, G. (2001). Reafferent copies of imitated actions in the right superior temporal cortex. Proc. Natl. Acad. Sci. U.S.A. 98, 13995–13999.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Iriki, A., and Sakura, O. (2008). Neuroscience of primate intellectual evolution: natural selection and passive and intentional niche construction. Philos. Trans. R. Soc. Lond. B Biol. Sci. 363, 2229–2241.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Iriki, A., Tanaka, M., and Iwamura, Y. (1996). Coding of modified body schema during tool use by macaque postcentral neurones. Neuroreport 7, 2325–2330.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ivaldi, S., Fumagalli, M., Nori, F., Baglietto, M., Metta, G., and Sandini, G. (2010). “Approximate optimal control for reaching and trajectory planning in a humanoid robot,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, 18–22.

Ivanenko, Y. P., Grasso, R., Zago, M., Molinari, M., Scivoletto, G., Castellano, V., Macellari, V., and Lacquaniti, F. (2003). Temporal components of the motor patterns expressed by the human spinal cord reflect foot kinematics. J. Neurophysiol. 90, 3555–3565.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izawa, J., Rane, T., Donchin, O., and Shadmehr, R. (2008). Motor adaptation as a process of reoptimization. J. Neurosci. 28, 2883–2891.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jeannerod, M. (2001). Neural simulation of action: a unifying mechanism for motor cognition. Neuroimage 14, 103–109.

CrossRef Full Text

Kaminski, T. R. (2007). The coupling between upper and lower extremity synergies during whole body reaching. Gait Posture 26, 256–262.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Karniel, A. (2011). Open questions in computational motor control. J. Integr. Neurosci. 10, 385–411.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kodl, J., Ganesh, G., and Burdet, E. (2011). The CNS stochastically selects motor plan utilizing extrinsic and intrinsic representations. PLoS ONE 6, e24229. doi:10.1371/journal.pone.0024229

CrossRef Full Text

Kording, K. P., and Wolpert, D. M. (2004). Bayesian integration in sensorimotor learning. Nature 427, 244–247.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Koski, L., Wohlschlager, A., Bekkering, H., Woods, R. P., Dubeau, M. C., Mazziotta, J. C., and Iacoboni, M. (2002). Modulation of motor and premotor activity during imitation of target-directed actions. Cereb. Cortex 12, 847–855.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kranczioch, C., Mathews, S., Dean, J. A., and Sterr, A. (2009). On the equivalence of executed and imagined movements. Hum. Brain Mapp. 30, 3275–3286.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kutch, J. J., Kuo, A. D., Bloch, A. M., and Rymer, W. Z. (2008). Endpoint force fluctuations reveal flexible rather than synergistic patterns of muscle cooperation. J. Neurophysiol. 100, 2455–2471.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Li, W. (2006). Optimal Control for Biological Movement Systems. Ph. D. thesis, University of California, San Diego.

Liu, D., and Todorov, E. (2007). Evidence for the flexible sensorimotor strategies predicted by optimal feedback control. J. Neurosci. 27, 9354–9368.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lopes, M., Melo, F., Montesano, L., and Santos-Victor, J. (2010). “Abstraction levels for robotic imitation: overview and computational approaches,” in From Motor Learning to Interaction Learning in Robots Series: Studies in Computational Intelligence, eds O. Sigau and J. Peters (Heidelberg: Springer Verlag).

Maravita, A., and Iriki, A. (2004). Tools for the body (schema). Trends Cogn. Sci. 8, 79–86.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Marino, B. F. M., Gough, P. M., Gallese, V., Riggio, L., and Buccino, G. (2011). How the motor system handles nouns: a behavioral study. Psychol. Res. doi: 10.1007/s00426-011-0371-2. [Epub ahead of print].

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Marr, D. (1982). Vision. A computational investigation into the human representation and processing of visual information. San Francisco: W. H. Freeman.

Marr, D., and Poggio, T. (1977). From understanding computation to understanding neural circuitry. Neurosci. Res. Prog. Bull. 15, 470–488.

Mitrovic, D., Klanke, S., and Vijaykumar, S. (2010). “Adaptive optimal feedback control with learned internal dynamics models,” in From Motor Learning to Interaction Learning in Robots SCI, Vol. 264, eds O. Sigaud and J. Peters (Heidelberg: Springer-Verlag), 65–84.

Mohan, V., and Morasso, P. (2006). “A forward/inverse motor controller for cognitive robotics,” in Artificial Neural Networks – ICANN 2006, Lecture Notes in Computer Science, Vol. 4131, eds S. Kollias, A. Stafylopatis, W. Duch, and E. Oja (Berlin: Springer), 602–611.

Mohan, V., and Morasso, P. (2007). Towards reasoning and coordinating action in the mental space. Int. J. Neural Syst. 17, 1–13.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mohan, V., Morasso, P., Metta, G., and Kasderidis, S. (2011a). “Actions and imagined actions in cognitive robots,” in Perception-Reason-Action Cycle: Models, Algorithms and Systems, Vol. 1, Chapter 17, eds V. Cutsuridis, A. Hussain, and J. G. Taylor (Heidelberg: Springer), 539–572.

Mohan, V., Morasso, P., Zenzeri, J., Metta, G., Chakravarthy, V. S., and Sandini, G. (2011b). Teaching a humanoid robot to draw ‘Shapes.’ Auton. Robots 31, 21–53.

CrossRef Full Text

Mohan, V., Morasso, P., and Metta, G. (2011c). What does learning to ‘draw a circle’ have to do with driving, cycling, unwinding and screwing? Front. Comput. Neurosci. Conference Abstract: IEEE ICDL-EPIROB 2011. doi: 10.3389/conf.fncom.2011.52.00028

CrossRef Full Text

Mohan, V., Morasso, P., Metta, G., and Kasderidis, S. (2011d). The distribution of rewards in growing sensory-motor maps. Neurocomputing 74, 3440–3455.

CrossRef Full Text

Mohan, V., Morasso, P., Metta, G., and Sandini, G. (2009). A biomimetic, force-field based computational model for motion planning and bimanual coordination in humanoid robots. Auton. Robots 27, 291–301.

CrossRef Full Text

Morasso, P. (1981). Spatial control of arm movements. Exp. Brain Res. 42, 223–227.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Morasso, P., Casadio, M., Mohan, V., and Zenzeri, J. (2010). A neural mechanism of synergy formation for whole body reaching. Biol. Cybern. 102, 45–55.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Morasso, P., Sanguineti, V., and Spada, G. (1997). A computational theory of targeting movements based on force fields and topology representing networks. Neurocomputing 15, 414–434.

CrossRef Full Text

Morasso, P., Sanguineti, V., and Tsuji, T. (1994). “A model for the generation of virtual targets in trajectory formation,” in Advances in Handwriting and Drawing: A Multidisciplinary Approach, eds C. Faure, P. Keuss, G. Lorette, and A. Vinter (Paris: Europia), 333–348.

Munzert, J., Lorey, B., and Zentgraf, K. (2009). Cognitive motor processes: the role of motor imagery in the study of motor representations. Brain Res. Rev. 60, 306–326.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mussa Ivaldi, F. A., and Bizzi, E. (2000). Motor learning through the combination of primitives. Philos. Trans. R. Soc. Lond. B Biol. Sci. 355, 1755–1769.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mussa Ivaldi, F. A., Morasso, P., and Zaccaria, R. (1988). Kinematic Networks. A distributed model for representing and regularizing motor redundancy. Biol. Cybern. 60, 1–16.

Pubmed Abstract | Pubmed Full Text

Nishikawa, K., Biewener, A. A., Aert, P., Ahn, A. N., Chiel, H. J., Daley, M. A., Daniel, T. L., Full, R. J., Hale, M. E., Hedrick, T. L., Lappin, A. K., Nichols, T. R., Quinn, R. D., Ritzmann, R. E., Satterlie, R. A., and Szymik, B. (2007). Neuromechanics: an integrative approach for understanding motor control. Integr. Comp. Biol. 47, 16–54.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nori, F., Metta, G., and Sandini, G. (2008). “Exploiting motor modules in modular contexts,” in Robust Intelligent Systems, Vol. XII, ed. A. Schuster (London: Springer-Verlag), 81.

Ostry, D. J., and Feldman, A. G. (2003). A critical evaluation of the force control hypothesis in motor control. Exp. Brain Res. 153, 275–288.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Parmiggiani, A., Randazzo, M., Natale, L., Metta, G., and Sandini, G. (2009). “Joint torque sensing for the upper-body of the iCub humanoid robot,” in IEEE-RAS International Conference on Humanoid Robots, Paris, 7–10.

Paynter, H. M. (1961). Analysis and Design of Engineering Systems. Boston: The MIT Press.

Perrett, D. I., and Emery, N. J. (1994). Understanding the intentions of others from visual signals: neurophysiological evidence. Curr. Psychol. Cogn. 13, 683–694.

Pozzo, T., Stapley, P. J., and Papaxanthis, C. (2002). Coordination between equilibrium and hand trajectories during whole body pointing movements. Exp. Brain Res. 144, 343–350.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pulvermüller, F., and Fadiga, L. (2010). Active perception: sensorimotor circuits as a cortical basis for language. Nat. Rev. Neurosci. 11, 351–360.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ramachandran, V. S., and Hubbard, E. M. (2003). Hearing colors, tasting shapes. Sci. Am. 288, 42–49.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rizzolatti, G., and Arbib, M. A. (1998). Language within our grasp. Trends Neurosci. 21, 188–194.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rizzolatti, G., Fadiga, L., Matelli, M., Bettinardi, V., Paulesu, E., Perani, D., and Fazio, F. (1996). Localization of grasp representations in humans by PET: 1.Observation versus execution. Exp. Brain Res. 111, 246–252.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rizzolatti, G., Fogassi, L., and Gallese, V. (2001). Neurophysiological mechanisms underlying action understanding and imitation. Nat. Rev. Neurosci. 2, 661–670.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rizzolatti, G., and Sinigaglia, C. (2010). The functional role of the parieto-frontal mirror circuit: Interpretations and misinterpretations. Nat. Rev. Neurosci. 11, 264–274.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Roh, J., Cheung, V. C. K., and Bizzi, E. (2011). Modules in the brain stem and spinal cord underlying motor behaviors. J. Neurophysiol. 106, 1363–1378.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sandini, G., Metta, G., and Vernon, D. (2004). “RobotCub: an open framework for research in embodied cognition,” in Proceedings of the 4th IEEE/RAS International Conference on Humanoid Robots, Los Angeles, CA, 13–32.

Sanguineti, V., Morasso, P., Baratto, L., Brichetto, G., Mancardi, G. L., and Solaro, C. (2003). Cerebellar ataxia: quantitative assessment and cybernetic interpretations. Hum. Mov. Sci. 22, 189–195.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Saunders, J. A., and Knill, D. C. (2004). Visual feedback control of hand movements. J. Neurosci. 24, 3223–3234.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schaal, S., Ijspeert, A., and Billard, A. (2003). Computational approaches to motor learning by imitation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 358, 537–547.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Scott, S. (2004). Optimal feedback control and the neural basis of volitional motor control. Nat. Rev. Neurosci. 5, 534–546.

CrossRef Full Text

Sevdalis, V., and Keller, P. E. (2011). Captured by motion: dance, action understanding, and social cognition. Brain Cogn. 77, 231–236.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shadmehr, R., and Mussa-Ivaldi, F. A. (1994). Adaptive representation of dynamics during learning of a motor task. J. Neurosci. 14, 3208–3224.

Pubmed Abstract | Pubmed Full Text

Shadmehr, R., Mussa-Ivaldi, F. A., and Bizzi, E. (1993). Postural force fields of the human arm and their role in generating multijoint movements. J. Neurosci. 13, 45–82.

Pubmed Abstract | Pubmed Full Text

Shadmehr, R., Smith, M. A., and Krakauer, J. W. (2010). Error correction, sensory prediction, and adaptation in motor control. Annu. Rev. Neurosci. 33, 89–108.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shapiro, R. (1978). Direct linear transformation method for three-dimensional cinematography. Res. Q. 49, 197–205.

Pubmed Abstract | Pubmed Full Text

Simpkins, A., Kelley, M., and Todorov, E. (2011). “Modular bio-mimetic robots that can interact with the world the way we do,” in International Conference on Robotics and Automation, Shanghai.

Stapley, P. J., Cheron, G., and Grishin, A. (1999). Does the coordination between posture and movement during human whole-body reaching ensure center of mass stabilization. Exp. Brain Res. 129, 134–146.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stevenson, I. H., Fernandes, H. L., Vilares, I., Wei, K., and Kording, K. P. (2009). Bayesian integration and non-linear feedback control in a full-body motor task. PLoS Comput. Biol. 5, e1000629. doi:10.1371/journal.pcbi.1000629

CrossRef Full Text

Stoytchev, A. (2008). “Learning the affordances of tools using a behavior-grounded approach,” in Affordance-Based Robot Control, eds E. Rome, J. Hertzberg, and G. Dorffner (Heidelberg: Springer-Verlag), 140–158.

Tanaka, Y., Tsuji, T., Sanguineti, V., and Morasso, P. G. (2005). Bio-mimetic trajectory generation using a neural time-base generator. J. Robot. Syst. 22, 625–637.

CrossRef Full Text

Thirioux, B., Mercier, M. R., Jorland, G., Berthoz, A., and Blanke, O. (2010). Mental imagery of self-location during spontaneous and active self-other interactions: an electrical neuroimaging study. J. Neurosci. 30, 7202–7214.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thom, R. (1975). Structural Stability and Morphogenesis. Boston, MA: Addison-Wesley.

Todorov, E. (2004). Optimality principles in sensorimotor control. Nat. Neurosci. 7, 907–915

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Todorov, E. (2006). “Optimal control theory,” in Bayesian Brain: Probabilistic Approaches to Neural Coding, Chapter 12, eds K. Doya, S. Ishii, A. Pouget, and R. P.N. Rao (Cambridge, MA: MIT Press), 269–298.

Todorov, E. (2009). Efficient computation of optimal actions. Proc. Natl. Acad. Sci. U.S.A. 106, 11478–11483.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Todorov, E., and Jordan, M. I. (2002). Optimal feedback control as a theory of motor coordination. Nat. Neurosci. 5, 1226–1235.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Torres-Oviedo, G., Macpherson, J. M., and Ting, L. H. (2006). Muscle synergy organization is robust across a variety of postural perturbations. J. Neurophysiol. 96, 1530–1546.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tsuji, T., Tanaka, Y., Morasso, P., Sanguineti, V., and Kaneko, M. (2002). Bio-mimetic trajectory generation of robots via artificial potential field with time base generator. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 88, 426–439.

CrossRef Full Text

Ulloa, E. R., and Pineda, J. A. (2007). Recognition of pointlight biological motion: mu rhythms andmirror neuron activity. Behav. Brain Res. 183, 188–194.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Umiltà, M. A., Escola, L., Intskirveli, I., Grammont, F., Rochat, M., Caruana, F., Jezzini, A., Gallese, V., and Rizzolatti, G. (2008). When pliers become fingers in the monkey motor system. Proc. Natl. Acad. Sci. U.S.A. 105, 2209–2213.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Uno, Y., Kawato, M., and Suzuki, R. (1989). Formation and control of optimal trajectory in human multijoint arm movement. Minimum torque-change model. Biol. Cybern. 61, 89–101.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Varela, F. J., Thomson, E., and Rosch, E. (1991). The Embodied Mind: Cognitive Science and Human Experience. Boston: MIT Press.

Vergaro, E., Casadio, M., Squeri, V., Giannoni, P., Morasso, P., and Sanguineti, V. (2010). Self-adaptive robot-training of stroke patients for continuous tracking movements. J.Neuroeng. Rehabil. 7, 13.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Visalberghi, E. (1993). “Capuchin monkeys: a window into tool use activities by apes and humans,” in Tool, Language and Cognition in Human Evolution, eds K. Gibson and T. Ingold (Cambridge: Cambridge University Press), 138–150.

Visalberghi, E., and Limongelli, L. (1996). Action and understanding: tool use revisited through the mind of capuchin monkeys, in Reaching into thought. The Minds of the Great Apes, eds A. Russon, K. Bard, and S. Parker (Cambridge: Cambridge University Press), 57–79.

Visalberghi, E., and Tomasello, M. (1997). Primate causal understanding in the physical and in the social domains. Behav. Process. 42, 189–203.

CrossRef Full Text

Watkins, C., and Dayan, P. (1992). Q-learning. Mach. Learn. 8, 279–292.

CrossRef Full Text

Weir, A. A. S., Chappell, J., and Kacelnik, A. (2002). Shaping of hooks in New Caledonian Crows. Science 297, 981–983.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilson, M. (2002). Six views of embodied cognition. Psychon. Bull. Rev. 9, 625–636.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wolpert, D. M., and Kawato, M. (1998). Multiple paired forward and inverse models for motor control. Neural. Netw. 11, 1317–1329.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zak, M. (1988). Terminal attractors for addressable memory in neural networks. Phys. Lett. A 133, 218–222.

CrossRef Full Text

Zenzeri, J. (2010). Stabilizzazione posturale durante movimenti globali del corpo, MS thesis, University of Genova, Genova.

Zenzeri, J., Morasso, P., and Saha, D. (2011). “Expert strategy switching in the control of a bimanual manipulandum with an unstable task,” in 33rd Annual International IEEE Engineering in Medicine and Biology Society Conference. Boston.