Sensory feedback plays a significant role in generating walking gait and in gait transition in salamanders: a simulation study

Here, we investigate the role of sensory feedback in gait generation and transition by using a three-dimensional, neuro-musculo-mechanical model of a salamander with realistic physical parameters. Activation of limb and axial muscles were driven by neural output patterns obtained from a central pattern generator (CPG) which is composed of simulated spiking neurons with adaptation. The CPG consists of a body-CPG and four limb-CPGs that are interconnected via synapses both ipsilaterally and contralaterally. We use the model both with and without sensory modulation and four different combinations of ipsilateral and contralateral coupling between the limb-CPGs. We found that the proprioceptive sensory inputs are essential in obtaining a coordinated lateral sequence walking gait (walking). The sensory feedback includes the signals coming from the stretch receptor like intraspinal neurons located in the girdle regions and the limb stretch receptors residing in the hip and scapula regions of the salamander. On the other hand, walking trot gait (trotting) is more under central (CPG) influence compared to that of the peripheral or sensory feedback. We found that the gait transition from walking to trotting can be induced by increased activity of the descending drive coming from the mesencephalic locomotor region and is helped by the sensory inputs at the hip and scapula regions detecting the late stance phase. More neurophysiological experiments are required to identify the precise type of mechanoreceptors in the salamander and the neural mechanisms mediating the sensory modulation.

1. Introduction

Locomotion is an integral part of a whole range of animal behaviors such as searching for food or a place to rest but also for escaping predators or other life threatening situations. For legged locomotion, it is important to use the limbs in a coordinated and efficient manner, adapted to the speed and the environment so that the animal uses energy efficiently and maintains stability (Orlovsky et al., 1999). Rhythmic body or axial movements contribute strongly to the phase shift between movements of the four limbs (i.e., to gait) of a quadruped. Here we use overground stepping of the salamander, an amphibian with a sprawling posture and lateral axial movements (instead of sagittal movements for mammals), since the walking footfall pattern is associated with traveling waves and the trotting one with standing waves (Daan and Belterman, 1968; Harischandra et al., 2010). At low speeds, salamanders adopt the lateral sequence walking gait, where roughly one limb at a time is in swing phase and the first foot to fall after a given hindfoot is the forefoot on the same side of the body and the footfalls of a diagonal limb pair are closely spaced in time. When the speed of locomotion increases they generally switch to the walking trot gait (Hildebrand, 1976). We will refer to these two gaits as walking and trotting respectively. During trotting, opposite limbs are out of phase, while diagonal limbs are in phase. Therefore a symmetry can be seen along the body axis and the body makes S-shaped standing waves coordinated with the movements of the limbs (Hildebrand, 1976; Frolich and Biewener, 1992; Ashley-Ross, 1994a). This coordination is such that it allows the salamander to increase its stride length utilizing its sprawling posture (Roos, 1964; Daan and Belterman, 1968). Even though these gait patterns have been well characterized and observed in intact salamanders, underlying mechanisms behind gait generation and transitions are still not properly understood.

Most of the neurophysiological studies on locomotion in salamanders have focused on generation and transition of locomotor modes (basically swimming and forward trotting) via neural centers in the brain stem and spinal neural circuitry which includes central pattern generators (CPGs; Ashley-Ross, 1994a; Cabelguen et al., 2003; Ashley-Ross et al., 2009). Even though tonic and phasic mechano-sensory inputs play a major role in modulating the activity generated in the spinal locomotor networks, few studies have addressed the sensory modulation concerning locomotion in salamanders (Chevallier et al., 2008). The current hypothesis is that the level of activation of the mesencephalic locomotor region (MLR) controls the initiation, speed, and mode of locomotion via the activation of specific groups of reticulospinal (RS) neurons in the brain stem (Cabelguen et al., 2003; Chevallier et al., 2008). However, we cannot exclude that the sensory feedback is involved in the locomotor mode transition. Moreover, all the previous studies on salamander locomotion have considered only the transition or switching from trotting to swimming (Ashley-Ross and Bechtel, 2004; Ijspeert et al., 2007). For instance, in a modeling and robotic study, Knuesel et al. (2010) proposed that the proprioceptive feedback signals pulsating along the body and acting like closed-loop systems, are useful for entraining the axial oscillators (neural CPG outputs) from a traveling wave pattern (in swimming) to the standing wave pattern that could be seen in trotting. On the other hand, no previous study has addressed the role of sensory feedback in transition from walking to trotting. In the case of mammalian locomotion, several studies have shown that tonic and phasic sensory feedback inputs play a crucial role in patterning the activity of spinal locomotor networks and in gait transition (Ito et al., 1998; Rossignol et al., 2006). For instance, intact, decerebrated, and spinalized cats on a motorized treadmill change the gait pattern depending on the speed of the treadmill. In this study, we use a computer simulation of a salamander model to investigate the contribution from the sensory feedback (peripheral) and the central mechanism (CPGs) in gait generation and in the transition from walking to trotting. In (Harischandra et al., 2010), as a proof of concept, we showed how the walking (lateral sequence) and trotting gaits could be obtained by forcing axial and body (trunk and tail) muscles to follow a set of coordinated prescribed activity patterns. However, the pattern generators did not use a single network of either coupled non-linear oscillators or spiking neurons to generate both gaits and modes of locomotion.

Researchers have found several kinds of cutaneous receptors distributed over the body and the limbs of the salamander (reviewed in Chevallier et al., 2008). Bone et al. (1976) found muscle spindle like receptors in the limb muscles and characterized them as stretch receptors. However, they did not study sensory modulation in locomotion. There is one study concerning the sensory interaction of the ongoing locomotion in salamanders. Cheng et al. (1998), showed that the rhythm of the NMDA-induced stepping movements of the forelimbs in the in vitro mud-puppy preparation is increased following transection of the C2 and C3 dorsal roots. This investigation also provides evidence of a phase-dependent resetting of the ongoing stepping-like rhythm by a low-intensity stimulation of C2 and C3 dorsal roots. Here, we pursue this line of thought and investigate possible neural mechanisms mediating the sensorimotor interactions in the limb and body-CPGs.

Especially when testing a hypothesis that includes isolation of sensory, muscular, or neural mechanisms which is impossible to do in neurophysiological experiments on real animals, computer models, and simulations are very useful tools (Harischandra and Ekeberg, 2008). It has even been argued that proper understanding of the neural and bio-physical mechanisms that modulate locomotion can only be achieved by using physiological experiments together with computer simulations (Pearson et al., 2006). However, the accuracy and reliability of such a method depends on how realistic (inclusion of all relevant features) the model is and to some extent the accuracy of the numerical computations. Not only neural activities in spinal centers that regulate locomotion but also the bio-mechanics of the body (kinematics) and its interactions with the environment play a major role in locomotion. In the recent past, computer simulations have been used to investigate different aspects of locomotion in salamanders, including aquatic and terrestrial gaits, transition from swimming to stepping, spinal central pattern generators, and visual tracking (Ijspeert and Arbib, 2000; Bem et al., 2003; Ijspeert et al., 2005, 2007; Knuesel et al., 2010). For this study, we use a physiologically realistic, three-dimensional (3D) computer model of an animal that incorporates a full neuro-musculo-skeletal-control (NMSC) system for locomotion. This is an extension of the 3D musculo-mechanical model introduced in Harischandra et al. (2010).

The basic rhythmic pattern for locomotion and the synergistic activity of limb and/or body muscles are produced by central pattern generators located in the spinal cord (Brown, 1911; Grillner, 1981) where the sensory motor interactions are taking place (Grillner and Zangger, 1975; Rossignol et al., 2006). The central nervous system of the salamander has many similarities to that of the lamprey (Fetcho, 1987). There is a large number of neurophysiological (Chevallier et al., 2008; Ryczko et al., 2010b) and modeling (Ijspeert et al., 1998, 2007; Bem et al., 2003) studies that shows the generation of motor pattern activity for the axial muscles distributed along the spinal cord as in the lamprey (Williams et al., 1989; Ekeberg and Grillner, 1999; Stefanini et al., 2006). However, the salamander has some additional complexity due to its four limbs which are controlled by interconnected limb-CPGs (Delvolve et al., 1997; Cheng et al., 1998; Ijspeert et al., 2007). The stretch receptors, also referred to as edge cells, are located along the lateral margin of the spinal cord in lampreys (Grillner et al., 1984). Additionally, intraspinal neurons with a morphology similar to that of the lamprey edge cells have been evidenced in the salamander spinal cord (Schroeder and Egar, 1990). For this investigation, we simplified an existing large scale spinal CPG model of a lamprey described in Kozlov et al. (2009) and it is used as the body-CPG for the salamander model.

The central pattern generator network model uses biologically plausible yet simple spiking neurons which include calcium dynamics. The CPG model is equipped with proprioceptive sensory inputs which are believed to exist in the limb and axial muscles of the salamander. Their functional role is explained in detail in the next section. We address the question of the importance of sensory feedback in generating the lateral sequence walking gait and the transition from lateral sequence walking to walking trot. In the last section, the results obtained from the simulation experiments are discussed and compared with known neurophysiological mechanisms related to salamander locomotion.

2. Materials and Methods

All the experiments were carried out with a three-dimensional, forward dynamics, computer simulation model of a salamander which incorporates a neuronal network (CPG), made up of integrate and fire (IF) neurons with adaptation, to drive the trunk, tail, and limb muscles. The neuro-musculo-skeletal (NMS) model was supplemented with proprioceptive sensory feedback via stretch receptor like neurons residing along the body and angle detectors for hip and scapula joints. The 3D mechanical model was developed previously and the skeletal and muscular parameters can be found in Harischandra et al. (2010). The simulator was programmed using the Python language and the neural simulations were done by using the simulation software NEST, available at www.nest-initiative.org (Gewaltig and Diesmann, 2007). Rigid body dynamics were simulated using python wrappers of the open source library open dynamics engine (ODE), available at www.ode.org

2.1. Central Pattern Generators

The activation level of each leg and body (trunk and tail) muscle is controlled by a simulated neuronal network which resembles the biological counterpart, the central pattern generator. The total network is composed of one body-CPG network and four limb-CPG sub-networks mutually coupled via inhibitory and excitatory synaptic connections (see the Sections 1 and 2).

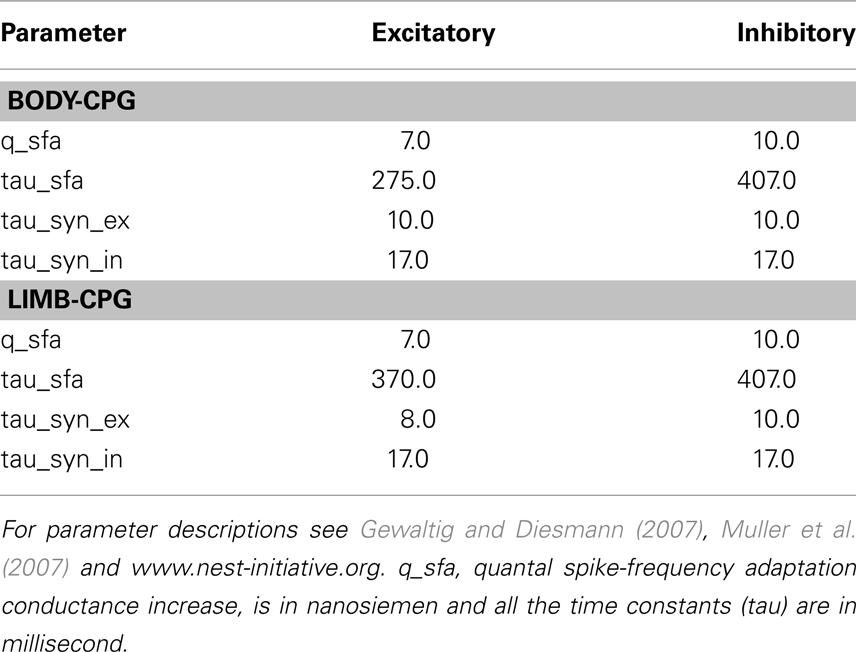
The body-CPG which spans from the head to the tail consists of 800 neurons (total 500E and 300I) in each modeled hemicord and can be considered as 40 segmental oscillatory networks (see Figure 1A) that are locally coupled with short range excitatory (E) and inhibitory (I) synapses. This network is based on the large scale model of the lamprey central pattern generator described in Kozlov et al. (2009) and is a simplified, small scale version which does not include the effects of neuro-modulators and the cellular details of the neurons. Salamanders swim with a lamprey-like undulatory pattern (anguilliform swimming) with the limbs held back to the body (Frolich and Biewener, 1992; Delvolve et al., 1997). Although, there are some significant differences in the cellular mechanism that underlie segmental bursting (Ryczko et al., 2010a), for simplicity, we use the same basic structure of the lamprey spinal locomotor network for generating axial motor patterns for the salamander (Cangiano and Grillner, 2005; Ryczko et al., 2010b). The only difference is that the salamanders have 40 anatomical segments instead of 100 segments of the lamprey. Both E and I neurons project to several segments along the spinal cord in both directions while caudally directed projections dominate. A motor neuron pool (M) on each side of the spinal cord receives projections from the ipsilateral E neurons and the contralateral I neurons which belong to nearby segments (see the Appendix). The M neuron activates one of 14 simulated muscles (ipsilateral) that causes bending around one of the body-joints of the model. Note that, for the sake of simplicity, there are only 14 joints in the model, combining 15 mechanical elements representing the salamander trunk and tail (see Harischandra et al., 2010 for more details of the musculo-mechanical model).

FIGURE 1

Figure 1. (A) Hypothetical segmental oscillatory network residing along the spinal cord of the salamander model. All neuron symbols denote populations rather than single cells. The excitatory interneurons (E) excite all types of spinal neurons, i.e., the motoneurons (M) and the inhibitory interneurons (I) which inhibit all neuron types on the contralateral side and project ipsilaterally. (B) Organization of the synaptic connections in the unit limb oscillatory network. The E neurons in one side (flexion or retraction side) receive tonic excitation whereas the E neurons in the other side (extension or protraction) do not. In both networks (A,B), all the neuron pools receive a descending drive which modulates the total activity level in each pool.

The salamander has four limbs and can control the movement in each leg separately. For instance, during underwater stepping, interlimb coordination patterns can be very flexible (Ashley-Ross et al., 2009; Cabelguen et al., 2010). Independent oscillatory centers for mud-puppy forelimb extensor and flexor motoneuron pools have been identified (Grillner, 1981; Cheng et al., 1998). To date, few data are available concerning the organization of the CPG controlling the leg movements in the salamander (Chevallier et al., 2008). In this study, each limb is regarded as being controlled by an independent limb-CPG. In the model, each limb-CPG consists of three unit CPGs which generate activation patterns for abductor/adductor, protractor/retractor, and knee or shoulder extensor/flexor muscles (for details of the bio-mechanics, see Harischandra et al., 2010) in a coordinated manner with the help of mutual couplings among them (see Figure 2). The different limb-CPGs can be coupled to obtain complex locomotor patterns (see Section 1). Furthermore, the two main phases of the leg movement, stance, and swing, are usually unequal in duration. Similarly flexor and extensor bursts in both limb muscles are also unequal in duration (Orlovsky et al., 1999). In order to replicate the asymmetry in flexion-extension duration in the unit limb-CPGs in the model, E neurons on the flexion side are given tonic excitation (intrinsic) whereas the E neurons on the extension side get excited with the synaptic drive (see Figure 1B). With this asymmetrical connectivity, a unit limb-CPG model is capable of producing motor neuron activity patterns with different duty ratios, especially long lasting activation in retractor or flexor muscles, which matches what is happening during walking. For more details of the network model and the parameters, refer to the Section “Appendix” where some of the network parameters are given and briefly described.

FIGURE 2

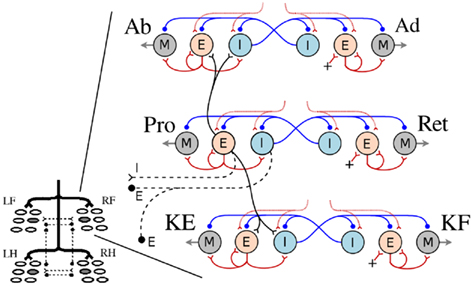
Figure 2. The system of interacting unit CPGs in a limb-CPG network. The four limb-CPGs are turned on by the descending drive from the MLR (Grillner et al., 2008). Within each limb-CPG, there are three paired subdivisions (unit CPGs, see Figure 1B) controlling the muscle synergies at the hip and knee joints; more precisely Abductor (Ab), Adductor (Ad), Protractor (Pro), Retractor (Ret), Knee/shoulder Extensor (KE) and Knee/shoulder Flexor (KF). Only the Protractor neuron pools are involved in intra- (black) and inter (black dash lines) limb-CPG coupling (see the Section 1). RF, LF, RH, and LH represent right front, left front, right hind, and left hind limb-CPGs respectively.

2.1.1. Connectivity within and among limb-CPGs

In the locomotor model, each limb is designed to have three degrees of freedom (DOF), two at the hip/scapula and one at the knee/shoulder. Rotation around each joint is controlled by three pairs of extensor/flexor muscles; Protractor (Pro) and Retractor (Ret), Abductor (Ab) and Adductor (Ad), and Knee/shoulder Extensor (KE) and Knee/shoulder Flexor (KF). Note that the limb musculature is a simplified version as it does not include the muscle action over several joints and the complex pattern, double bursting activity, which is often present in most of the muscles during stepping in salamanders (Ashley-Ross, 1995; Delvolve et al., 1997). The activity of each muscle pair (agonist and antagonist) is controlled by a single unit limb-CPG. As shown in the Figure 2, the E neuron pool of the unit CPG that controls the protractor muscle is coupled to both E and I neuron pools of the other two unit CPGs of the same limb-CPG (only to sub units controlling Ab and KE muscles) via excitatory synaptic connections.

The coordination between the limb-CPGs is important in generating different gaits, for instance, walking and trotting. The two fore limb-CPGs as well as the two hind limb-CPGs are mutually coupled with both excitatory and inhibitory pathways across the mid line (see Figures 2 and 3A). The excitatory projections are such that the E neuron pool of one side excites the I neuron pool of the other side. The fore and hind limb-CPGs are connected ipsilaterally via inhibitory couplings. There are no diagonal connections modeled in this investigation. Moreover, only the neuron pools which belong to unit CPGs that activate protractor muscles are involved in mutual coupling (see Figure 2). By changing the synaptic strength of each connection among the limb-CPGs, it is possible to generate different coordination between the four limbs. Additionally, with proper weight and delay parameters for the excitatory synapses between unit CPGs, the network produces the activity patterns for Ab and Ad slightly leading but proportional to that of Pro and Ret. Hence the limb is lifted before the protraction begins and that makes the swing much easier and smooth. It also helps the limb to settle on the ground before retraction begins (see Appendix for parameters).

FIGURE 3

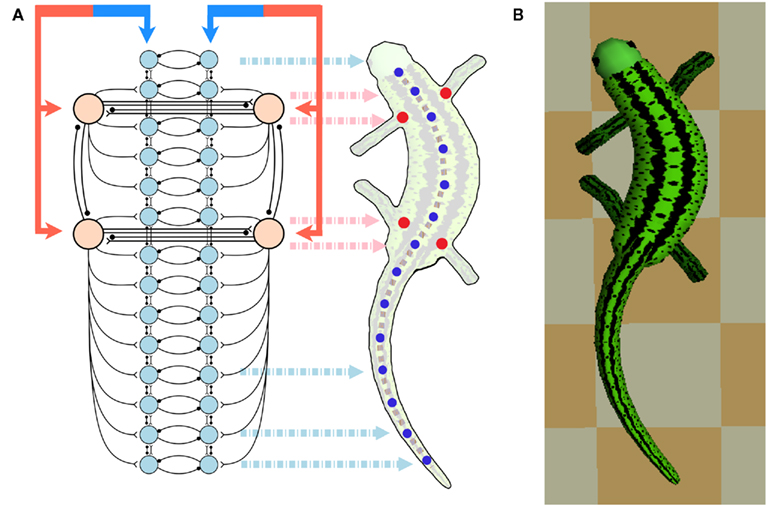
Figure 3. (A) Shows the configuration of the CPG network model. The total network consists of a body-CPG and limb-CPGs interconnected via synapses. The body-CPG is composed of 40 hypothetical segmental unit CPGs connected via excitatory and inhibitory synapses (see Figure 1) and provide the motoneuronal output for 14 paired muscles which generate the torques of the joints along the spine (blue disks). Connections are not only to nearest neighbors but can also be several segments long (see the Appendix). The limb-CPGs are interconnected ipsilaterally and contralaterally (see Figure 2). Front limb-CPGs are coupled bidirectionally to the body-CPG between girdles and the hind limb-CPGs are connected to the body-CPG along the tail. The CPG receives driving signals from the MLR region in the brain stem. (B) Top view of the 3D neuro-musculo-skeletal (NMS) model of the salamander.

2.1.2 Connectivity between body- and limb-CPGs

The salamander uses the curvature of its body (trunk and tail) to increase its stride length but this requires proper coordination between the trunk and the limbs (Daan and Belterman, 1968; Ritter, 1992; Ashley-Ross, 1994a; Ashley-Ross et al., 2009). Therefore the coordination between the body and the limb-CPGs is crucial in generating efficient gaits for terrestrial locomotion. In a previous study based on non-linear oscillator models, different types of possible CPG configurations (connectivity) have been tested (Ijspeert et al., 2005) and for the current investigation we adopted one of the successful configurations with slight modifications which will be described next.

As illustrated in Figure 3A, there are connections from each limb-CPG to the corresponding side (either left or right) of the body-CPG. Note that the forelimb-CPGs are coupled to the segmental oscillator networks residing between the two girdles whereas the hind limb-CPGs are connected with excitatory synapses to the caudal part of the body-CPG, i.e., from the rear girdle to the tail end. In this CPG model, there are local connections from the body-CPG to the limb-CPGs (not shown in the Figure). The excitatory neuron pools belonging to three to four segmental CPGs around both front and rear girdles in one side (left of right), project to the excitatory (E) neuron pools of the unit CPG that (see Figure 1A) controls the protractor muscle of the contralateral limb.

2.2. Descending Drive

In the real salamander, the body- and the limb-CPGs can be selectively activated through tonic input corresponding to descending projections from the brain stem (Cabelguen et al., 2003). For instance, swimming is possible when the body-CPG is activated while the limb-CPG is non-oscillating and tonically active. In the model, four rostral segmental oscillators of the body-CPG are getting extra drive by another descending input which can control the phase lag between the segments (the higher the extra drive the higher the phase lag) and hence the neural traveling wave along the spinal cord. Furthermore, there are two descending paths; left and right (see Figure 3A) and by increasing the activity on one side, the model can bend and turn. In terrestrial locomotion, an increment in the drive signal will increase the speed of locomotion and it, together with the sensory feedback, initiates the transition from walking to trotting. This will be discussed further later in the article.

2.3. Sensory Feedback

In the model, simulated stretch receptors (altogether 28 residing in the spinal cord on both sides of each axial joint), placed along the trunk and tail, have synaptic connections like in the lamprey model (Grillner et al., 2008; Kozlov et al., 2009) and they modulate the activity in the axial muscles. The stretch receptor activation, which is the amount of current injection (i_s) to the receptor neuron (integrate and fire model), is modeled to be proportional to the local curvature of the body. There is no delay involved in signal transduction. The calculations of the i_s current is based on the equation given below.

where k₁ is the proportional constant and Δɸ is the angle of deviation of the model’s body axis from the neutral posture at the corresponding body joint. A lower limit of zero activation is included so that no activity is produced on the contracted side. Fourteen receptor neurons are distributed approximately at equal distance along each side and their axons extend about 1 segment in both directions (rostrally and caudally) and have synaptic connections on E, I, and M neuron pools of those body-CPG segments. These synaptic connections are excitatory (synaptic weight: 1.0 pS and delay: 1.0 ms) on the ipsilateral and inhibitory (synaptic weight: −1.5 pS and delay: 1.5 ms) on the contralateral side as in the lamprey spinal CPG (Kozlov et al., 2009). The synaptic delay is modeled according to the average distance of the synaptic coupling. Furthermore, the two stretch receptors (on one side) local to the each girdle region have excitatory (synaptic weight: 1.0 pS and synaptic delay: 1.0 ms) projections to the E neuron pool of the ipsilateral unit limb-CPG that controls the protractor muscle, helping initiation of forward limb movement (swing).

A second set of sensory inputs included in the model are the limb stretch receptors functioning as hip or scapula angle detectors. These receptor neurons will increase firing rate when a limb is extended more toward the caudal direction (toward the tail in the horizontal plane), i.e., at the later part of the stance phase. The following equation is used to calculate the required current (i_a) to be injected to the receptor neuron (integrate and fire model) via a dc generator in the nest simulation environment (Gewaltig and Diesmann, 2007).

where k₂ is the proportionality constant and Δθ is the hip or scapula angle measured in the horizontal plane from an axis perpendicular to the axis along the body. It is positive and increasing in the direction of the retraction (later stance) and is negative and decreasing while protracting. The receptor neuron will increase its firing when it is more depolarized. These receptor neurons have excitatory (synaptic weight: 10.0 pS and synaptic delay: 1.0 ms) feedback projections to the E neuron pools of the unit CPGs that excite abductor and protractor muscles of the same limb and hence are initiating and facilitating the swing phase.

In a first set of experiments, we used the 3D NMS model (Figure 3B) to investigate its ability to generate walking and trotting gaits without the influence of sensory feedback, that is, only with the CPG. For this, in each experiment, the connectivity strength (level of inhibition) between contralateral and ipsilateral limb-CPGs was changed from NONE or WEAK to STRONG, and the temporal activity patterns that drive the protractor and retractor muscles in the four limbs were observed. Note that at the level of STRONG, one limb-CPG could inhibit another limb-CPG such that the corresponding protractor activities were in 180° phase shift apart, whereas at the level of NONE (synaptic weight of 0.0), they were completely decoupled. The WEAK was set to 50% of the STRONG and the corresponding synaptic weight values are −1.5 and −3.0 respectively (for a comparison with other synapses see the Table A2 in Appendix). We kept the level of excitation between the contralateral limb-CPGs intact as the effect of those connections is to affect the response time, and to a lesser extent on the final phase difference between the contralateral Limb-CPGs (see Section 1). Next, sensory modulation (see above section) was incorporated into the model and the same experiment was carried out with a selected connectivity strength configuration for the limb-CPG coupling.

3. Results

First, the locomotor model was driven only with the CPG without sensory feedback. Different strengths for the inhibitory connections among the four limb-CPGs were systematically analyzed and the resulting activity patterns for the two major limb muscles are shown in the Figure 4. Each sub-figure depicts the motor output pattern from one experiment where the contralateral (↔) and ipsilateral (↕) inhibition was set to one of the following strengths: NONE, WEAK, or STRONG. A coordinated activity pattern for the trotting gait, where diagonal limbs are in simultaneous swing, was obtained with the <↔STRONG↕STRONG> connectivity (see Figure 4C). Note that the protractor and the retractor muscle activities were not symmetrical. This is due to the fact that the intrinsic properties of the unit limb-CPGs are set such that they have asymmetry in the activity of the extensor and the flexor halves (see Section 1 and Figure 1B). Therefore, the trotting gait can be obtained without the sensory feedback with the current configuration of the central pattern generator network (see Figure 3A). On the other hand, none of the combinations was able to produce the muscle activity patterns compatible with the walking gait (see subfigures in Figure 4 and compare those with the walking activity patterns shown in the Figure 5).

FIGURE 4

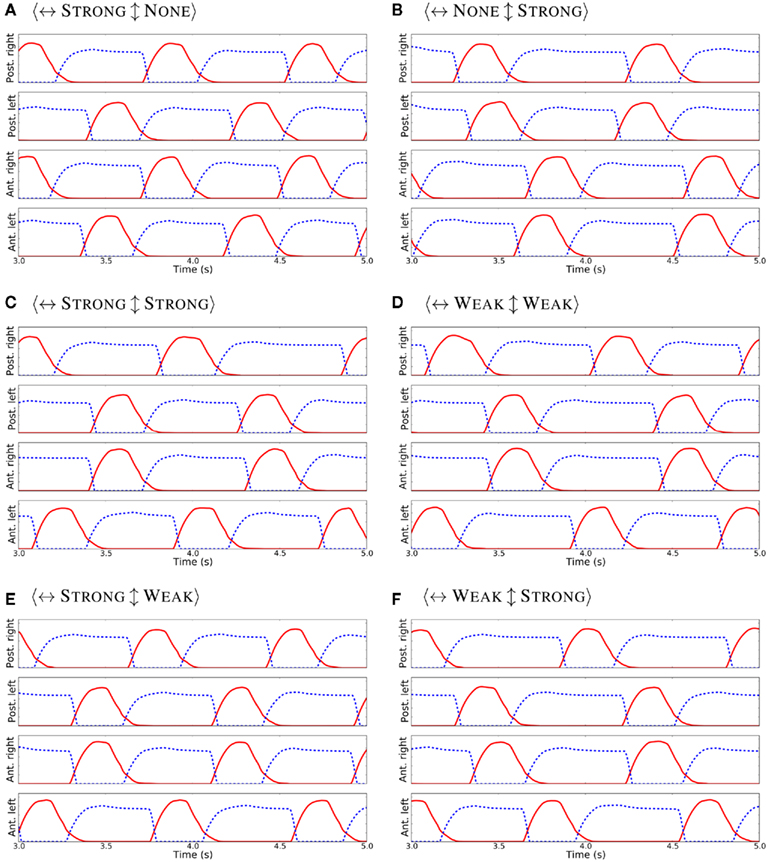
Figure 4. Activity patterns for the protractor (in red) and the retractor (in blue dash) muscles in each limb, when the contralateral (↔) and the ipsilateral (↕) inhibition was set to different strengths (A–F) and with no sensory feedback. Note that, in each case, the excitation from limb to body-CPG and body to limb-CPG was at WEAK level.

FIGURE 5

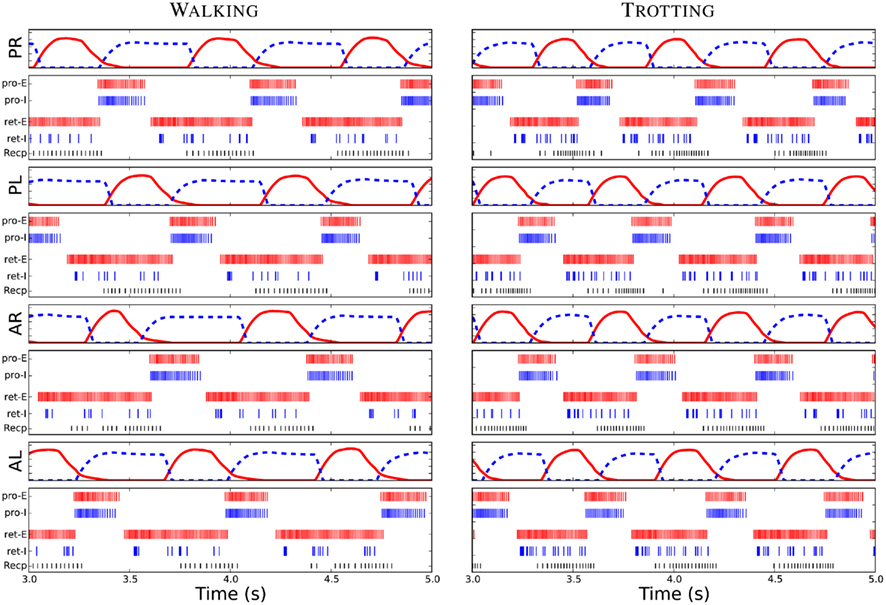
Figure 5. Driving signals for the limb muscles, the protractor (red) and the retractor (blue dash), and the spike plots of neurons within each unit limb-CPG for the walking and trotting gaits. PR, PL, AR, and AL represent posterior right, posterior left, anterior right and anterior left limbs. Furthermore, Pro-E and Pro-I corresponds to an E neuron and an I neuron of the protraction side of the unit limb-CPG respectively. Similarly, ret-E and retextendashI represent an E and an I neuron of the retraction side. Note that the similar firing could be seen in the other neurons of each neuron pool. Recp corresponds to the receptor neuron which detects the hip or scapula angle in each limb. Note the delay between the activity in the inter-neuron pools and the corresponding driving signals or motor output.

After incorporating the sensory feedback to the CPG network, the muscle activity patterns to generate the walking gait was obtained (see Figure 5). Several simulation trials were carried out with different connectivity strengths for contralateral and ipsilateral inhibition among the limb-CPGs as in the above mentioned experiments. We found that the <↔STRONG↕WEAK> connectivity was best for obtaining the walking gait with the sensory modulation. Additionally the excitation of the local projections from the body-CPG near the girdle areas to the limb-CPGs has to be stronger than the connections from the limb-CPGs to the body-CPG (see Section 2 and the Appendix).

With tuned network parameters, the spiking neuronal model of the CPG network, together with the sensory feedback, produce the coordinated activity patterns for the limb musculature (see Figure 5) and for the axial muscles along the trunk and tail. These temporal activation levels were similar to the activity patterns shown in early modeling studies with non-linear coupled oscillator networks (for the trotting gait, see Ijspeert, 2001; Ijspeert et al., 2005) or more abstract time driven, hard wired muscle contraction patterns (for the walking gait, see Harischandra et al., 2010).

When the descending drive (see Figure 3A), which corresponds to the amount of activation in the mesencephalic locomotor region (MLR) in the brain stem, is at a low level, neurons in both body- and limb-CPGs and receptor neurons in the limbs were less active (see “Recp” neuron firing activity in Figure 5) and the salamander adopted the slow walking gait for stepping. An increase in drive causes an increase in the frequency of oscillations in both segmental oscillators along the spine and in unit CPGs controlling the four limbs. Furthermore, the sensitivity (depolarization) of the sensory neurons that detect rotation in hip or scapula joints in the caudal direction also increases (see Recp activity in Figure 5 for trotting). This in turn activates a positive feedback mechanism through the sensory inputs in this area to the protractor and abductor muscles in each limb. This neural mechanism will be discussed in the next section.

In order to test the model’s capability for gait transition, we simulated the transition by changing the descending drive (25%). However, as mentioned above the change in drive will affect the sensitivity (25% change) of the receptor neurons that detect rotation in hip or scapula joints. Additionally, connection strengths among the limb-CPGs have to be changed from <↔STRONG↕WEAK> to <↔STRONG↕STRONG> when switching from walking to trotting or vice versa. This was achieved by changing the synaptic weight parameter of the ipsilateral connections between limb-CPGs at a certain time point while the simulation was running. Even though the changes made were abrupt which could be seen in the activity patterns of the limb muscles (not shown), the gait transition was smooth. This could be due to the mechanical coupling and the sensory motor interactions. In this experiment we could not exclude the sensory modulation as it is necessary to generate the walking gait. Figures 6C,D show the gait diagrams of the transition from walking to trotting and vice versa respectively.

FIGURE 6

Figure 6. Gait diagrams for the terrestrial locomotion of the salamander model. (A,B) Figures cover a time span of 2.1 s whereas the (C,D) cover a time span of 5.4 s. Bars indicate the periods during which the foot is on the ground. (A) This shows the diagram for the walking gait. Most of the time, three legs touch the ground (Ashley-Ross et al., 2009). (B) This shows the quick steps of the trotting gait (Hildebrand, 1976; Ashley-Ross and Bechtel, 2004; Ashley-Ross et al., 2009). (C) This shows the gait pattern during the transition from walking to trotting. (D) Transition from trotting to walking. Vertical dash lines show the onset of parameter change. LH, left hind foot; LF, left front foot; RF, right front foot; and RH, right hind foot.

The locomotor model was able to mimic the two stepping gaits on ground by activating the limbs in proper coordination not only with each other but also with the body, i.e., the trunk and tail. The phase relationship among the four limbs of the neuro-mechanically simulated salamander is shown in Figure 6. Both gaits showed a shorter swing phase and a longer stance phase for all the legs. However, swing duration seems to be less affected when switching from walking to trotting. Hence, during trotting, the speed of locomotion increases by reducing the stance duration. This is clearly seen in the Figures 6A,B as the total number of completed steps over the 2.1 s timespan increases from 3 to approximately 4.5 when the model uses walking or trotting respectively.

4. Discussion

The salamander is an amphibian which is capable of both terrestrial stepping and swimming. On ground, it mainly uses two gaits; walking and trotting depending on the speed of locomotion (Edwards, 1977; Ashley-Ross, 1994a,b) and they differ in their patterns of activation of epaxial and limb muscles. However, the same spinal neuronal network of CPGs together with the limb-CPGs are presumably responsible for generating the patterns of activation in a coordinated manner (Delvolve et al., 1997; Bem et al., 2003; Ijspeert et al., 2007). The limbs are coordinated with the body such that the ipsilateral limb is protracted during contralateral trunk (near the girdle) contractions. In this study, we have explored to what extent the same neuronal network is capable of producing the two gaits with or without the help of sensory feedback (both axial and limb) and with different combinations of interlimb neural connections. Thus we can compare the contribution of central vs. peripheral influences on the generation of two gaits. The same CPG network was able to generate the anguilliform swimming in water by simply reducing the activation of the limb-CPGs and by having a traveling wave of activity along the body-CPGs. We will not discuss swimming capabilities of the model as it is out of the scope of this article.

The foot fall patterns of both gaits showed a clear match to biological data. The gait diagrams in the Figures 6A,B are comparable with the walking and trotting gait patterns of a recent kinematic study on California newts (Ashley-Ross et al., 2009). Furthermore, a qualitative match for the gaits in the simulation could be seen in videos of the real salamander.

Although some studies have suggested that the salamander’s body and the limbs are equipped with mechanoreceptors such as stretch receptors (Bone et al., 1976; Schroeder and Egar, 1990), their role in locomotion or gait transition has not been thoroughly investigated (reviewed in Chevallier et al., 2008). In this investigation, we have hypothesized that the stretch receptors in the limb muscles at the hip or scapula area have a functional role of detecting the extension of the limb in the horizontal plane toward the caudal direction at the later part of the stance phase. This sensory signal was coupled to the neuronal network in a way that helps in initiating the swing phase (see Section 3). At present, there is no concrete neurophysiological evidence for the existence of these types of sensory feedback projections in the salamander. However, a similar effect involving this kind of proprioceptors have been reported in many other locomotor systems, for instance in cats (Rossignol et al., 2006). For instance, Pearson et al. (2006) showed that the unloading signal from the ankle extensor muscle and/or the angle detectors in the hip joint in the hind limb of the cat initiates the transition from stance to swing phase.

During lateral sequence walking (see Figure 6A), approximately one limb is in swing phase at all times (Daan and Belterman, 1968; Frolich and Biewener, 1992; Ashley-Ross et al., 2009). Therefore the rhythmic activation pattern of the retractor muscle (stance phase) in each limb should have approximately a duty ratio of 75% (Harischandra et al., 2010). On the other hand, during trotting, diagonal limbs are simultaneously in swing phase (see Figure 6B) and hence the retractor muscles need to be activated with a motor neuronal output pattern which has approximately a 50% duty ratio (Ijspeert, 2000, 2001). Thus, any transition from walking to trotting needs a neural and/or sensory driven mechanism to change the duty ratio of the activity in the retractor and protractor muscles. In our neural network model, we have set intrinsic parameters of the unit limb-CPG such that it will generate an asymmetric oscillatory motor neuron output, which is required for the walking gait, when the descending drive is at a low level. With the configuration as depicted in the Figure 1B, the activity of the retractor muscle will have a duty ratio of about 75% and be 180° out of phase to that of the protractor muscle (Harischandra et al., 2010). The neural mechanism for this switching can be explained as follows; A slight increase in the descending drive causes faster oscillations in the limb-CPGs. This, in turn increases the stepping frequency which leads to more depolarization of the stretch receptor neurons located in each limb. Thus an increase in firing rate of these neurons (See Figure 5) will give a positive feedback to the E neurons of the unit CPG that controls the protractor muscle (see Sections 1 and 3). Higher excitation in the protractor side will inhibit the E neurons of the retractor side causing them to stop firing. Due to this feedback mechanism, eventually the motor output pattern for both sides (protractor and retractor) will be in symmetry which is suitable for the trotting gait.

When the salamander uses different gaits, proper coordination between the limbs and the body (trunk and tail) is also important for smooth forward locomotion. During walking, the sequence of forward swings in the limbs is as follows; first left front (LF) then right hind (RH) limb and next right front (RF) and finally left hind (LH) limb to complete one step cycle. This phase lag between front and hind limbs has been considered as evidence for the existence of a possible traveling wave between girdles during walking (Harischandra et al., 2010). We have found that the <↔STRONG↕WEAK> coupling is sufficient for maintaining the phase lag between front and hind limb-CPGs. In the isolated body-CPG network (in the model), there is always a neural traveling wave propagated from head to tail. However, depending on the strength of the synaptic connections from the limb-CPGs to the body-CPG, this neural traveling wave in the body-CPG can get altered. In order to obtain the necessary activity patterns for each limb musculature for walking, the strength of the connections from the body-CPG (local to the girdle areas) to the limb-CPGs was set to a higher value than that in the reverse direction (see Section 2). However, this is in contrast with previous investigations (Ijspeert et al., 2005, 2007), where they hypothesize that the connections from limb-CPGs to body segments are stronger than other connections. This stronger connections are indeed useful for imposing slower rhythms in body-CPG and to impose the S-shaped standing waves which could be seen during trotting. It should be noted that, in the current model there are only local projections from the body-CPG to the limb-CPGs while there are global connections in the reverse direction. Therefore, a higher activity in limb-CPGs can still impose the standing wave during trotting. Next we coupled the stretch receptor like neurons residing in the trunk close to the girdle areas to the limb-CPGs in the same way that the body segmental CPGs in the same area connect to the limb-CPGs. With this sensory feedback, the kinematic wave takes part in coordinating the activity patterns for muscles in each limb and the walking gait became possible.

Obtaining the trotting gait with the locomotor model and the neuronal CPG network was reasonably easy and less complex compared to the walking gait. The major difference in the connection strengths within the CPG network compared to that during walking, is the symmetry in ipsilateral and contralateral inhibition (<↔STRONG↕STRONG>) between the limb-CPGs. Furthermore, strong excitation from limb-CPGs (due to the increased activity) to body-CPGs causes the existing intrinsic traveling wave along the body segmental CPGs to diminish and instead a standing neural wave emerges. In fact, this has been verified in previous two dimensional simulation studies where the CPG is modeled using non-linear oscillator networks (Ijspeert et al., 2005, 2007) or leaky integrate and fire neuronal networks (Ijspeert, 2000). It should be mentioned that the trotting gait could even be obtained with the same CPG network with proper connectivity (i.e., if the intrinsic oscillations of the unit limb-CPGs are symmetric) without the sensory modulation introduced in this investigation (not shown). However, the present model was equipped with the sensory feedback in order to obtain the symmetric activity for protraction and retraction. On the other hand the sensory feedback plays a significant role in generating the walking gait and hence the transition from walking to trotting. Therefore, the trotting is more under central influence than the walking gait. For the gait transition, as mentioned previously the most important sensory feedback is coming from the limb receptors that detect hip or scapula retraction. The sensitivity (firing capability) of these neurons has an effect on the duration of the gait transition (see Figures 6C,D). For instance, with reduced sensitivity of those receptor neurons, the transition involves several step cycles (not shown). On the other hand, we cannot exclude the importance of the stretch receptors that couple the body kinematics to the limb-CPGs (see Section 3) for imposing either traveling or standing waves depending on the gait (Knuesel and Ijspeert, 2011). However, we are lacking experimental data from real animals regarding the role of the sensory feedback mechanisms that we modeled in this study. We note that more neurophysiological experiments are required to identify the precise type of mechanoreceptors in the salamander and the neural mechanisms mediating the sensory modulation.

Even in more complex mammalian locomotion, it has been suggested that each limb is being controlled by an independent limb-CPG and that they can be coupled in different ways such that walking, trotting, and galloping is possible (Ito et al., 1998; Grillner, 2006; Grillner et al., 2008). Furthermore, the two main phases of the locomotion can have different durations. That is, the flexor burst remains largely constant, whereas the extensor burst can vary significantly in duration between a slow walk and fast running (Orlovsky et al., 1999). As shown in Figure 6, a similar phenomenon can be seen in the salamander locomotor model when switching from slow walking to fast trotting. Note that here, the intrinsic properties of a unit limb-CPG controlling a protractor muscle were set such that it will generate an activity of almost constant duration. However, the reduction in duration of the activity of the retractor muscle (hence the stance duration) was a result of both the sensory modulation and the increased descending drive. Although the retractor muscle has an activity duration of around 50–55% during trotting (see Figure 5), the actual stance duration was around 60%, as shown in the Figure 6B. Similarly deviations in Pro and Ret activity and the actual swing and stance phase duration could be seen during walking too. One reason for this difference could be delays involved in muscular and skeletal dynamics of the model. Nevertheless, the neuro-musculo-skeletal model of the salamander successfully mimics the two stepping gaits, walking and trotting on level ground.

Recently, Aoi et al. (2011) showed that a simple quadruped locomotor model with an erect posture can produce various gait patterns through dynamic interactions among the body mechanical system, the oscillator network (CPG) and the environment. In their model, the locomotor phase and the rhythm is modulated by phase resetting in response to tactile sensory information coming from the feet. In addition to the stepping speed, they found that the stiffness of the waist joint plays a significant role in gait generation and transition. However, the mechanisms for dynamic changes of the waist joint stiffness is not shown and it could be either peripheral (sensory) or centrally driven. One should be careful when comparing the above findings with the salamander model since it uses a sprawling posture and has a long trunk. An important finding of their study is the hysteresis in the gait transition between the walking and the trotting. A similar phenomenon could be seen in the gait transition of the salamander model. However, we did not quantitatively analyze the hysteresis.

In this study, we found that the proprioceptive sensory inputs are essential in obtaining the lateral sequence walking gait (walking) and that the gait transition from walking to trotting is facilitated by the sensory inputs at the hip and scapula regions detecting the late stance phase. In the future, the same 3D neuro-musculo-skeletal model could be used to investigate the role of sensory modulation especially when stepping on different terrains with different friction coefficients. Moreover, both real and in silico experiments on salamander locomotion on up or down slopes can give more insights into the role of sensory feedback during gait transitions.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the Swedish International Development Cooperation Agency (SIDA), EU FP7 (LAMPETRA) and VINNOVA for the financial support.

Supplementary Material

The Movies S1 and S2 for this article can be found online at http://www.frontiersin.org/Neurorobotics/10.3389/fnbot.2011.00003/abstract

References

Aoi, S., Yamashita, T., and Tsuchiya, K. (2011). Hysteresis in the gait transition of a quadruped investigated using simple body mechanical and oscillator network models. Phys. Rev. E 83, 061909.

CrossRef Full Text

Ashley-Ross, M. (1994a). Hindlimb kinematics during terrestrial locomotion in a salamander (Dicamptodan tenebrosus). J. Exp. Biol. 193, 255–283.

Ashley-Ross, M. (1994b). Metamorphic and speed effects on hindlimb kinematics during terrestrial locomotion in the salamander Dicamptodon tenebrosus. J. Exp. Biol. 193, 285–305.

Ashley-Ross, M. (1995). Patterns of hind limb motor output during walking in the salamander Dicamptodon tenebrosus, with comparisons to other tetrapods. J. Comp. Physiol. A 177, 273–285.

CrossRef Full Text

Ashley-Ross, M., and Bechtel, B. (2004). Kinematics of the transition between aquatic and terrestrial locomotion in the newt Taricha torosa. J. Exp. Biol. 207, 461–474.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ashley-Ross, M., Lundin, R., and Johnson, K. (2009). Kinematics of level terrestrial and underwater walking in the California newt, Taricha torosa. J. Exp. Zool. 311A, 240–257.

CrossRef Full Text

Bem, T., Cabelguen, J., Ekeberg, Ö., and Grillner, S. (2003). From swimming to walking: a single basic network for two different behaviors. Biol. Cybern. 88, 79–90.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bone, Q., Ridge, R., and Ryan, K. (1976). Stretch receptors in urodele limb muscles. J. Cell Tissue Res. 165, 249–266.

Brown, T. (1911). The intrinsic factors in the act of progression in the mammal. Proc. R. Soc. Lond. B 84, 308–319.

CrossRef Full Text

Cabelguen, J., Bourcier-Lucas, C., and Dubuc, R. (2003). Bimodal locomotion elicited by electrical stimulation of the midbrain in the salamander Notophthalmus viridescens. J. Neurosci. 23, 2434–2439.

Pubmed Abstract | Pubmed Full Text

Cabelguen, J., Ijspeert, A., Lamarque, S., and Ryczko, D. (2010). Axial dynamics during locomotion in vertebrates lesson from the salamanderij. Prog. Brain Res. 187, 149–162.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cangiano, L., and Grillner, S. (2005). Mechanisms of rhythm generation in a spinal locomotor network deprived of crossed connections: the lamprey hemicord. J. Neurosci. 25, 923–935.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cheng, J., Stein, R., Jovanovic, K., Yoshida, K., Bennett, D., and Han, Y. (1998). Identification, localization, and modulation of neural networks for walking in the mudpuppy (Necturus maculatus) spinal cord. J. Neurosci. 18, 4295–4304.

Pubmed Abstract | Pubmed Full Text

Chevallier, S., Ijspeert, A., Ryczko, D., Nagy, F., and Cabelguen, J. (2008). Organisation of the spinal central pattern generators for locomotion in the salamander: biology and modelling. Brain Res. Rev. 57, 147–161.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Daan, S., and Belterman, T. (1968). Lateral bending in locomotion of some lower tetrapods, i and ii. Proc. Kon. Ned. Akad. Wetten. C71, 245–266.

Delvolve, I., Bem, T., and Cabelguen, J. (1997). Epaxial and limb muscle activity during swimming and terrestrial stepping in the adult newt, pleurodeles waltl. J. Neurophysiol. 78, 638–650.

Pubmed Abstract | Pubmed Full Text

Edwards, J. (1977). “The evolution of terrestrial locomotion,” in Major Patterns in Vertebrate Evolution, eds M. Hecht, P. Goody, and B. Hecht (New York: Plenum), 553–576.

Ekeberg, Ö., and Grillner, S. (1999). Simulations of neuromuscular control in lamprey swimming. Philos. Trans. R. Soc. Lond. B Biol. Sci. 354, 895–902.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fetcho, J. (1987). A review of the organization and evolution of motoneurons innervating the axial musculature of vertebrates. Brain Res. Rev. 12, 243–280.

CrossRef Full Text

Frolich, L., and Biewener, A. (1992). Kinematic and electromyographic analysis of the functional role of the body axis during terrestrial and aquatic locomotion in the salamander Ambystoma tigrinum. J. Exp. Biol. 162, 107–130.

Gewaltig, M.-O., and Diesmann, M. (2007). Nest: neural simulation tool. Scholarpedia 2, 1430.

CrossRef Full Text

Grillner, S. (1981). “Control of locomotion in bipeds, tetrapods, and fish,” in Handbook of Physiology. The Nervous System II, Motor Control, Vol. 2, ed. V. Bethesda (American Physiological Society), 1179–1236.

Grillner, S. (2006). Biological pattern generation: the cellular and computational logic of networks in motion. Neuron 52, 751–766.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grillner, S., Wallen, P., Saitoh, K., Kozlov, A., and Robertson, B. (2008). Neural bases of goal-directed locomotion in vertebrates an overview. Brain Res. Rev. 57, 2–12.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grillner, S., Williams, T., and Lagerback, P. (1984). The edge cell, a possible intraspinal mechanoreceptor. Science 223, 500–503.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grillner, S., and Zangger, P. (1975). How detailed is the central pattern generation for locomotion? Brain Res. Rev. 88, 367–371.

Harischandra, N., Cabelguen, J., and Ekeberg, Ö. (2010). A 3d musculo-mechanical model of the salamander for the study of different gaits and modes of locomotion. Front. Neurorobot. 4:112. doi:10.3389/fnbot.2010.00112

CrossRef Full Text

Harischandra, N., and Ekeberg, Ö. (2008). System identification of muscle-joint interactions of the cat hind limb during locomotion. Biol. Cybern. 99, 125–138.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hildebrand, M. (1976). “Analysis of tetrapod gaits: general considerations and symmetrical gaits,” in Neural Control of Locomotion eds R. M. Herman, S. Grillner, P. S. G. Stein, and D. G. Stuart (New York: Plenum Press), 203–236.

Ijspeert, A. (2000). “A leaky-integrator neural network for controlling the locomotion of a simulated salamander,” in IEEE-INNS-ENNS International Joint Conference on Neural Networks (IJCNN’00), Vol. 6, Como 6642–6647.

Ijspeert, A. (2001). A connectionist central pattern generator for the aquatic and terrestrial gaits of a simulated salamander. Biol. Cybern. 84, 331–348.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ijspeert, A., and Arbib, M. (2000). “Visual tracking in simulated salamander locomotion,” in Proceedings of the Sixth International Conference of The Society for Adaptive Behavior (SAB2000) (Paris: MIT Press), 88–97.

Ijspeert, A., Crespi, A., and Cabelguen, J. (2005). Simulation and robotics studies of salamander locomotion. Neuroinformatics 3, 171–196.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ijspeert, A., Crespi, A., Ryczko, D., and Cabelguen, J. (2007). From swimming to walking with a salamander robot driven by a spinal cord model. Science 315, 1416–1419.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ijspeert, A., Hallam, J., and Willshaw, D. (1998). “From lampreys to salamanders: evolving neural controllers for swimming and walking,” in From Animals to Animats, Proceedings of the Fifth International Conference of The Society for Adaptive Behavior (SAB98), eds R. Pfeifer, B. Blumberg, J.-M. Meyer, and S. W. Wilson (Zurich: MIT Press), 390–399.

Ito, S., Yuasa, H., Luo, Z., Ito, M., and Yanagihara, D. (1998). A mathematical model of adaptive behavior in quadruped locomotion. Biol. Cybern. 78, 337–347.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Knuesel, J., Cabelguen, J., and Ijspeert, A. (2010). “Decoding the mechanisms of gait generation and gait transition in the salamander using robots and mathematical models,” Motor Control: Theories, Experiments and Applications, eds F. Danion and M. Latash (New York, NY: Oxford University Press), 417–450.

Knuesel, J., and Ijspeert, A. (2011). Effects of muscle dynamics and proprioceptive feedback on the kinematics and cpg activity of salamander stepping. BMC Neurosci. 12(Suppl. 1), P158. doi:10.1186/1471-2202-12-S1-P158

CrossRef Full Text

Kozlov, A., Huss, M., Lansner, A., Kotaleski, J., and Grillner, S. (2009). “Simple cellular and network control principles govern complex patterns of motor behavior,” in Proceedings of the National Academy of Sciences U.S.A., Vol. 106, Washington 20027–20032.

Muller, E., Buessing, L., Schemmel, J., and Meier, K. (2007). Spike-frequency adapting neural ensembles: bmu neural computation yond mean adaptation and renewal theories. Neural Comput. 19, 2958–3010.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Orlovsky, G., Deliagina, T., and Grillner, S. (1999). Neuronal Control of Locomotion: From Mollusc to Man. Oxford: Oxford University Press.

Pearson, K., Ekeberg, Ö., and Buschges, A. (2006). Assessing sensory function in locomotor systems using neuro-mechanical simulations. Trends Neurosci. 29, 625–631.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ritter, D. (1992). Lateral bending during lizard locomotion. J. Exp. Biol. 173, 1–10.

Roos, P. (1964). Lateral bending in newt locomotion. Proc. Kon. Ned. Akad. Wetten. C 67, 223–232.

Rossignol, S., Dubuc, R., and Gossard, J. (2006). Dynamic sensorimotor interactions in locomotion. Physiol. Rev. 86, 89–154.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ryczko, D., Charrier, V., Ijspeert, A., and Cabelguen, J. (2010a). Segmental oscillators in axial motor circuits of the salamander: distribution and bursting mechanisms. J. Neurophysiol. 104, 2677–2692.

CrossRef Full Text

Ryczko, D., Dubuc, R., and Cabelguen, J. (2010b). Rhythmogenesis in axial locomotor networks: an interspecies comparison. Prog. Brain Res. 187, 189–211.

CrossRef Full Text

Schroeder, D., and Egar, M. (1990). Marginal neurons in the urodele spinal cord and the associated denticulate ligaments. J. Comp. Neurol. 301, 93–103.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stefanini, C., Orlandi, G., Menciassi, A., Ravier, Y., La Spina, G., Grillner, S., and Dario, P. (2006). A mechanism for biomimetic actuation in lamprey-like robots. Proc. IEEE RAS EMBS Int. Conf. Biomed. Robot. Biomechatron. 579–584.

CrossRef Full Text

Williams, L., Grillner, S., Smoljaninov, V., Allen, P., Kashin, S., and Rossignol, S. (1989). Locomotion in lamprey and trout: the relative timing of activation and movement. J. Exp. Biol. 143, 559–566.

Appendix

Network Model Parameters

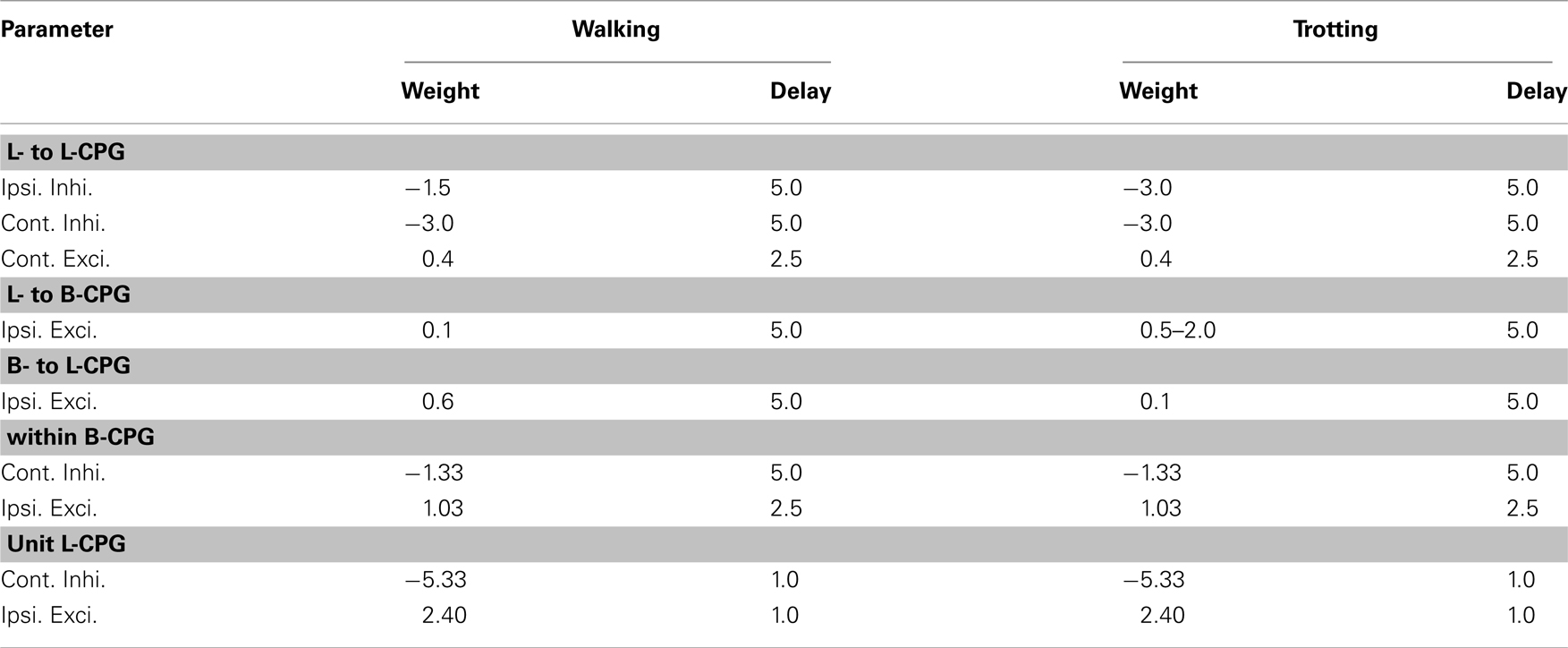
The synaptic connectivity within the body- and limb-CPG is shown in Figure 1. Populations of E an I cells were simulated by using linear leaky IF model with fixed threshold, decaying-exponential post-synaptic conductance, conductance-based spike-frequency adaptation, and a conductance-based relative refractory mechanism (see Muller et al., 2007 for the equations and more details of the model). The parameter values for the both types of neuron pools are given in Table A1 and the rest of the parameters were set to the default values of the corresponding nest neuron model. Model parameters for the simplified neurons in the body-CPG were chosen such that they have the same frequency–current characteristic as in the large scale compartmental model of the lamprey spinal CPG (Kozlov et al., 2009). Axons extended over 1 segment rostrally and 3 segments caudally for the E neurons and 2 segments rostrally and 6 segments caudally for I neurons of each body segment. The synaptic delay for each connection was set proportional to the average distance between the interconnected interneurons. Fourteen motoneurons are distributed approximately in equal distance along each of the hemicord and each motor neuron received the same excitatory and inhibitory input as the E population received in a segment. There is a considerable degree of variability in membrane properties within each pool of interneurons in the spinal cord, and the corresponding variability was introduced in each pool of model neurons. A uniform distribution with ±20% randomness of the parameter values was assigned individually with regard to membrane conductance (g_L) and capacitance (C_m).

Coupling Strengths

All the synaptic weights, except the strength for the ipsilateral inhibition between the front and hind limb-CPGs, were kept constant during each gait. However, we found that the higher synaptic weight for the connectivity from limb-CPGs to body-CPG is advantageous for the trotting gait. The weights for the excitatory and inhibitory connections within a segmental oscillatory network of the body-CPG were chosen to match the total population characteristics of the large scale spinal CPG model for the lamprey (Kozlov et al., 2009). Corresponding default values for the limb-CPGs were chosen such that the motor neuronal output has a duty ratio of about 75%. The parameter values of the coupling strengths and the synaptic delay for both gaits are shown in Table A2.

TABLE A1

Table A1. Parameter values of the E and I modeled neurons.

TABLE A2

Table A2. Default connection strength (pS) and delay (ms) parameters for the synaptic couplings.