Defects go green: using defects in nanomaterials for renewable energy and environmental sustainability

Induction of point defects in nanomaterials can bestow upon them entirely new physics or augment their pre-existing physical properties, thereby expanding their potential use in green energy technology. Predicting structure-property relationships for defects a priori is challenging, and developing methods for precise control of defect type, density, or structural distribution during synthesis is an even more formidable task. Hence, tuning the defect structure to tailor nanomaterials for enhanced device performance remains an underutilized tool in materials design. We review here the state of nanomaterial design through the lens of computational prediction of defect properties for green energy technology, and synthesis methods to control defect formation for optimal performance. We illustrate the efficacy of defect-focused approaches for refining nanomaterial physics by describing several specific applications where these techniques hold potential. Most notably, we focus on quantum dots for reabsorption-free solar windows and net-zero emission buildings, oxide cathodes for high energy density lithium-ion batteries and electric vehicles, and transition metal dichalcogenides for electrocatalytic green hydrogen production and carbon-free fuels.

1 Introduction

The industrial revolution—largely propelled by burning hydrocarbon-containing materials to provide electricity, heating, and power engines (e.g., in motor vehicles)—facilitated over 200 years of sustained human development (Chu and Majumdar, 2012). However, an unfortunate byproduct of burning fossil fuels are large-scale greenhouse gas emissions, which contribute to climate change and ecological deterioration (Chu and Majumdar, 2012; Alstone et al., 2015; Clark et al., 2016; Hallegatte et al., 2016; Schleussner et al., 2016). To ameliorate environmental damage associated with climate change, public policy endeavors must focus on curbing greenhouse gas emissions, while also supporting sustained global development through the expansion of access to inexpensive and reliable energy. Technological innovation will therefore play a pivotal role in achieving a sustainable future. Nanomaterials in particular are poised to contribute to the development of renewable energy production and storage (Chen et al., 2012).

Point defects are single or multiple atom disruptions in the long-range periodicity of crystallographic materials. These atomic impurities often form in nanomaterials, dramatically alter their physical properties (e.g., induce magnetism or metal-insulator transitions) (Lopez-Bezanilla et al., 2015a; Lopez-Bezanilla et al., 2015b; Ganesh et al., 2020; Bennett et al., 2022), and offer a potentially rewarding route for tuning their functionality for enhanced device performance in a broad array of applications. However, predicting the relationship between crystal growth conditions, defect formation, and their corresponding physics is challenging, and has served as a bottleneck to the commercialization of many ubiquitous technologies such as In_xGa_1-xN heterostructure blue light-emitting diodes (LEDs) (Nakamura, 1998). Hence, defect engineering represents an encouraging, but underexplored paradigm to tailor nanostructures for a diverse array of green technology such as solar energy (Giustino and Snaith, 2016) or batteries (Zhao et al., 2020).

Defect engineering efforts will require innovations that link theoretical predictions of defect properties with experimental methods for controlling defect formation in nanomaterials. First principles calculation methods such as density functional theory (DFT) have become a powerful tool in predicting defect physical properties, and guiding experimental efforts to detect and control defect formation during synthesis or post-processing (Freysoldt et al., 2014; Dreyer et al., 2018). Recent advances in scanning transmission electron microscopy (STEM) enable direct measurement and quantification of defects in nanomaterials (Ziatdinov et al., 2017; Madsen et al., 2018; Zhao et al., 2018; Maksov et al., 2019; Ziatdinov et al., 2019; Lee et al., 2020; Guo et al., 2021; Trentino et al., 2021; Yang et al., 2021; Lee et al., 2022; Wu et al., 2022). These ab initio and experimental approaches can be combined with other supplemental experimental techniques such as spectroscopy and scanning tunneling microscopy (STM) to directly resolve nanomaterial defect physics (Ziatdinov et al., 2019). In this context, we review computational and experimental approaches for elucidating defect synthesis-structure-property relationships with the specific aim of unleashing the full potential of defects for green technology. Additionally, we delve into several examples of green technologies where defect engineering has shown promise. These systems of interest include optical defects in quantum dots for Stokes-shift engineered luminescent solar concentrators and net zero-energy buildings, cation-disordered oxides for lithium-ion battery cathodes with improved energy storage capabilities, and defects in transition metal dichalcogenide electrocatalysts for green hydrogen production.

2 Defect formation in nanomaterials: theory and chemistry

2.1 Types of defects

Crystallographic materials exhibit periodicity wherein atoms are arranged in a consistent repeating pattern. The term point defect is generally used to indicate a single or few atom “break” in periodicity such as a missing or misplaced native lattice atom (intrinsic defect), or a foreign atom not normally present in the lattice (extrinsic defect, Figure 1) (Tuller and Bishop, 2011; Freysoldt et al., 2014; Dreyer et al., 2018; Fuhr et al., 2023). Intrinsic defects are generally classified as either vacancies (missing anion or cation), anti-site defects (atomic species in the lattice swap positions such as a cation occupying a lattice site expected to be an anion), or interstitials (cation or anion occupies an interstitial space in the lattice). Extrinsic defects can occupy substitutional or interstitial lattice sites as dopants, or form as adatoms on the surface. The specific lattice site and charge of point defects are commonly described using Kroger-Vink notation (Kröger et al., 1956). Defect atomic identity is indicated by the first letter, and for most defect types (intrinsic or extrinsic), the subscript designates the lattice site where the defect occurs. The exceptions to this rule are vacancies and interstitials for which “V” is used to indicate a vacancy and the subscript “i” is used to indicate interstitial. The superscript indicates the electronic charge at the defect lattice point: “x” signifies no charge, “/” denotes a negative charge, and “•” represents a positive charge. For example, a sulfur anion vacancy with a +2 charge in MoS₂ would be denoted as V_S^•• (a sulfur atom is missing from a sulfur lattice site leaving a +2 charge, Figure 1A), a sulfur interstitial in MoS₂ with a −2 charge would be indicated as S_i^// (Figure 1B) and a O²⁻ dopant on a Te²⁻ site in WTe₂ (net charge of 0) as O_Te^x (Figure 1C) (Kröger et al., 1956).

FIGURE 1

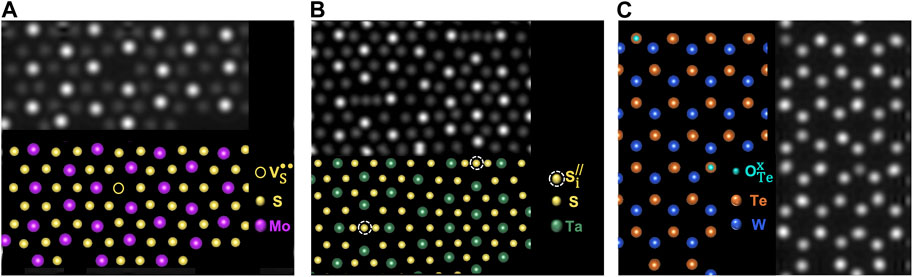
FIGURE 1. (A–C) DFT generated STEM digital twins for defects in monolayer TMDs. Reproduced with permission from Fuhr et al. (2023).

Kroger-Vink theory—in its original conception—describes defect formation under thermodynamic equilibrium by charge-compensated formal reaction pathways. If we consider a simple binary ionic material (MA where M is a 2+ metal cation and A is a chalcogen or oxygen 2− anion), these reaction pathways could include Schottky defects (V_A^•• + V_M^//), Frenkel pairs (V_A^•• + M_i^//, or V_M^•• + M_i^//), antisite defect pairs (M_A^•••• + A_M^////), or non-stoichiometric defects wherein a charged defect is compensated by the oxidation or reduction of another atom (e.g., V_A^•• + 2M_M^/). Regions of lattice disorder, (Cen et al., 2023), distortion (Ding et al., 2018), or non-stoichiometry (Fuhr et al., 2020a) are not always well described by Kroger-Vink reaction pathways, but the notation is still commonly used. Using the notation we described earlier for ionic material MA, metal or anion deficient synthesis conditions could yield M_1-xA or MA_1-x structures with ordered metal vacancies. For this illustrative example the material would not have defects in the traditional sense. Yet, the Kroger-Vink metal vacancy notation is still often used (e.g., as observed with iron sulfides, ceria, or strontium titanate) (Zhuang et al., 2014; Li et al., 2017a; Luo et al., 2021).

2.2 Predicting defect stability

Despite its clarity, consistent bookkeeping of all charge-compensating Kroger-Vink reactions is unrealistic for nanomaterials at-scale (Freysoldt et al., 2014). This problem is even further exacerbated in off-equilibrium processes such as ion implantation. However, the creation of defects alters local chemical bonding (e.g., breaking bonds to form vacancies) in nanomaterials and generally invokes an enthalpic energy penalty. Density functional theory (DFT) or similar electronic structure approaches can therefore be used to calculate formation enthalpies and predict the type and relative concentrations of defects (Freysoldt et al., 2014; Dreyer et al., 2018). This approach assumes a grand canonical material system wherein individual defects interact with an electron reservoir (described by the Fermi level), and their energy can be calculated as a function of the energy of the electron reservoir and relative concentration of each atomic species. The DFT route can shed light onto the likelihood of various defects to form under thermal equilibrium conditions, their relative concentration, local geometry, and corresponding structure-property relationships.

The usual approach for calculating defect formation energy via DFT or related methods is to separately optimize the geometry of a pristine supercell or surface, and compare its energy to the same structure with defect “X” at charge state “q” using Eq. 1:

${\mathrm{E}}_{\mathrm{f}}\left[{\mathrm{X}}^{\mathrm{q}}\right]={\mathrm{E}}_{\text{tot}}\left[{\mathrm{X}}^{\mathrm{q}}\right]-{\mathrm{E}}_{\text{tot}}\left[\text{pristine}\right]-{\displaystyle {\sum }_{\mathrm{i}}}{\mathrm{n}}_{\mathrm{i}}{\mathrm{\mu }}_{\mathrm{i}}+q{\mathrm{E}}_{\mathrm{F}}+{\mathrm{E}}_{\text{corr}}(1)$

where E_tot[X^q] is the total energy of a supercell or surface with the specified defect in charge state q, E_tot[pristine] is the total energy of the defect-free supercell or surface, μ_i represents the chemical potential for atomic species i either added (positive n_i where n notes the number of atoms added by exchange from a chemical reservoir) or subtracted (negative n_i where n notes the number of atoms removed by exchange to a chemical reservoir). The Fermi-level (E_F) describes the energy of the electron reservoir that exchanges electrons with the lattice resulting in a positive or negative charge (q) for electrons removed or gained by the material, respectively. E_F is conventionally described in relation to the valence-band (VB) where E_F = 0 reflects a Fermi-level exactly at the valence band maximum, and the upper bound for E_F is the conduction band (CB) of the material. A correction term E_corr is often added to account for the finite-size of the supercells and k-point meshes on elastic or electrostatic interactions and are described in greater detail elsewhere (Makov and Payne, 1995; Lany and Zunger, 2008; Freysoldt et al., 2009; Komsa et al., 2012; Freysoldt et al., 2014; Dreyer et al., 2018).

The low concentration of defects in materials requires that DFT approaches use large supercells (e.g., 50–200 atoms). Computational expense for DFT based approaches scale with size and the number of electrons in the material, which makes predicting defect stability and structure-property relationships challenging. For example, it is well-known that pure DFT functionals such as the Perdew Burke Ernzerhof (PBE) do not accurately predict semiconductor band gaps (Le Bahers et al., 2014). One route to improve the accuracy of DFT is to include some degree of Hartree Fock direct exchange using a hybrid functional (e.g., HSE06), but this comes at significantly greater computational expense. Hence, predicting optical transitions for defects is much more complicated than for defect-free materials due to the simultaneous requirement of computationally expensive functionals and large supercells. In addition, DFT treatment of surfaces (with or without defects) is often required to predict structure-property relationships at the nanoscale, and similarly scales poorly with hybrid functional or other beyond pure DFT methods. While we do not focus here on specific electronic structure approaches for dealing with large supercells, these are important considerations for predicting defect formation and corresponding physics and are reviewed elsewhere (Makkar and Ghosh, 2021; Broberg et al., 2023).

DFT-calculated formation enthalpy is typically determined at 0 K, and the usually positive value is often interpreted to indicate that entropy and temperature are needed to overcome the enthalpic energy barrier—resulting in a negative Gibbs free energy and enabling defects to spontaneously form. Among the various types of entropy, configurational and vibrational are the most frequently discussed. In the context of understanding defects, configurational entropy pertains to atomic rearrangements resulting from local disruptions of periodicity, while vibrational entropy encompasses modified phonon interactions and changes in chemical bonding. Configurational entropy can be calculated by combining cluster expansion approaches with Monte Carlo, while packages such as Phonopy can be used to determine vibrational entropy using either the Hessian matrix from density functional perturbation theory (DFPT) calculations or the finite displacement method (Freysoldt et al., 2014; Sutton and Levchenko, 2020; Kaczkowski et al., 2021). These additional contributions are typically ignored in most studies due to the high computational cost of performing both enthalpic and entropic calculations. DFT-calculated formation enthalpy is generally considered sufficient to predict structure-property relationships and general trends in the type and relative concentration of defects that will form in nanomaterials under different oxidizing/reductive environments and relative precursor concentration (e.g., metal deficient synthesis vs. chalcogen deficient synthesis). However, interest in high-throughput DFT and beyond 0 K approaches is growing, and are essential to predict more precise relationships between synthesis conditions and defect creation (Balachandran et al., 2017; Choudhary et al., 2023; Mosquera-Lois et al., 2023).

2.3 Synthesis and control of defect formation

The theoretical principles underpinning defect formation predictions have several general implications for nanomaterial synthesis. The type and concentration of defects that form in nanomaterials is strongly influenced by the relative concentration of each atomic species during synthesis or post-processing, as well as whether the experiments are conducted in a more reductive (high E_F) or oxidative (low E_F) environment (Liu et al., 2014a; Du et al., 2021). The set of defects with the lowest formation energies under the specific experimental conditions will prevail. For instance, ignoring kinetic considerations, cation-poor and oxidative growth conditions could favor the creation of negatively charged metal vacancies. Furthermore, the repercussions of local geometric and electrostatic distortions vary by chemical bonding motif. Although the first principles assessment of chemical bonding in the material is not flawless, it remains instructive. For example, closed packed structures less frequently exhibit Frenkel defects due to the additional energy required to squeeze an interstitial ion into the lattice (geometric penalty). On the other hand, materials with metallic or covalent bonds tend to form antisite defects or partial cation disorder due to the lower electrostatic penalty compared to ionically bonded materials (YOO and TULLER, 1987; Tuller and Bishop, 2010; Tuller and Bishop, 2011; Hu et al., 2017).

As discussed earlier, the formation enthalpy of defects is generally positive (unfavorable). Entropic stabilization or external energy is therefore required to overcome the enthalpic penalty to create defects in most materials. These observations are suggestive that growth/post-processing temperature—or the inclusion of external energy sources such as plasmas or light—can be used to control defect formation. Hence, most defect engineering strategies revolve around managing the relative concentrations of each species, establishing an oxidative or reductive environment, and/or controlling external energy factors such as temperature during nanomaterial synthesis or post-processing. For extrinsic defects such as dopants, solubility (maximum concentration attainable by a dopant) and diffusivity (rate at which atomic species spreads across the material at a finite temperature) also need to be taken in consideration (Freysoldt et al., 2014).

The predominant method for managing defect distribution in-situ during nanomaterial synthesis typically entails regulating temperature and atomic species concentration. The synthesis of V_O-rich SnO_2-x nanosheets, achieved through a hot-injection reaction between SnSe nanosheets and organic residue, serves as an illustrative method for creating anion vacancies via temperature control (Zhong et al., 2019). Multinary nanomaterials—such as Cu_xIn_2-xSe_yS_2-y (CISeS) nanocrystals—frequently have their defect distribution tuned by adjusting precursor ratios. In this case, Cu-deficient nanocrystals tend to form V_Cu^/ whereas Cu_In^// are more commonly observed in near-stoichiometric or Cu-rich nanocrystals (Ueng and Hwang, 1989; Ueng and Hwang, 1990; Kim et al., 2012; Jara et al., 2016; Fuhr et al., 2017; Yun et al., 2018; Houck et al., 2019; Fuhr et al., 2020a; Fuhr et al., 2020b; Du et al., 2020; Frick et al., 2020; Liang et al., 2023). Adjusting synthesis temperature and precursor ratios has been shown to enhance the density of vacancies during chemical vapor deposition (CVD) or chemical vapor transport (CVT) synthesis of transition metal dichalcogenides (TMDs, Figure 2) (Enyashin et al., 2013; Lin et al., 2016; Li et al., 2017b; Liang et al., 2021). CVD synthesis occurs at a lower temperature than CVT, and uses more volatile precursors and shorter growth times (Shi et al., 2015). The density of sulfur vacancies can be controlled by the sulfur rate (rate at which sulfur-containing compounds are introduced to the reaction environment) (Gutiérrez et al., 2013; Peimyoo et al., 2013; van der Zande et al., 2013). Both CVD and CVT have also been used to dope nanostructures (Chen et al., 2013; Dumcenco et al., 2013; Zhang et al., 2014a; Feng et al., 2014; Suh et al., 2014; Tongay et al., 2014; Li et al., 2015; Gao et al., 2016; Lin et al., 2016; Deng et al., 2021; Liang et al., 2021). However, the high temperature and long growth times generally leads to greater control of the spatial distribution and density of defects with CVT, which has been demonstrated with Mo_xW_1-xS_y, Mo_xW_1-xS_ySe_2-y, and MoS_xSe_2-x monolayers. Enhanced control of dopant distribution has also been observed in colloidal quantum dots by using hot-injection and diffusion methods to dope Mn in CdSe, ZnSe, and PbSe quantum dots (Mikulec et al., 2000; Norris et al., 2001; Ji et al., 2003; Jian et al., 2003; Vlaskin et al., 2013; Rice et al., 2016; Singh et al., 2019). The high energy of interstitial defects typically precludes their formation in QDs, and dopants are usually assumed to be substitutional unlike nanostructured oxides where both substitutional and interstitial defects are well-known to form (Norris et al., 2001; Robertson et al., 2011; Zhang et al., 2014b).

FIGURE 2

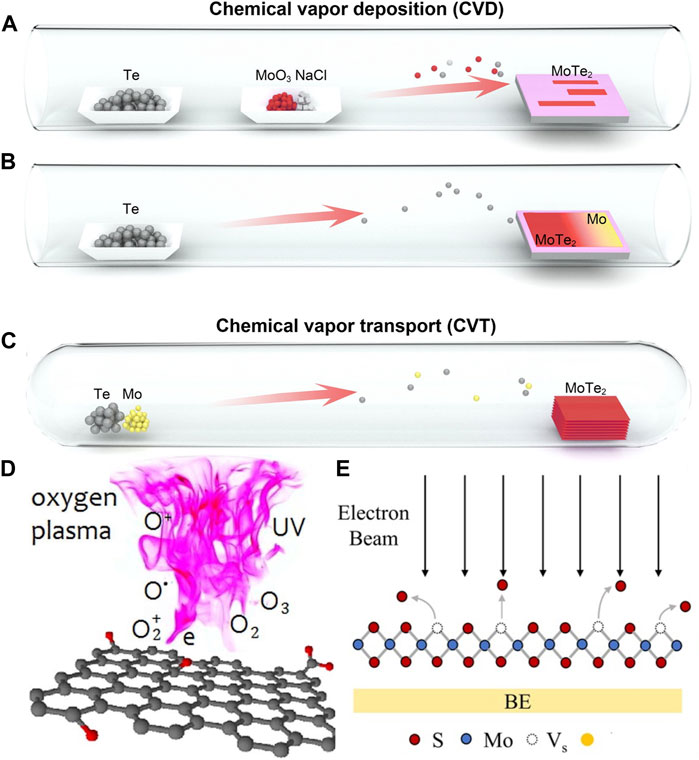
FIGURE 2. Schematic depiction of CVD vs. CVT process for creating defects in TMDs (A–C), light and plasma induced defects in graphene oxide (D), and electron beam induced defects on TMDs (E). Figures reproduced with permission from Deng et al. (2021) for (A–C), Kondratowicz et al. (2018) for (D), and Wu et al. (2022) for (E).

Despite the major advances, controlling the density and distribution of defects in nanomaterials in-situ remains difficult and post-processing methods are often required. Post-synthesis annealing and altering the cooling rate after calcination have been used to create antisite defects and cation site disorder in LiNi_xMn_2-xO₄ and LiNi_0.45Mn_1.45Cr_0.1O₄ phases (Liu et al., 2012; Zheng et al., 2012; Liu et al., 2014b). High-temperature annealing of oxide films in an oxygen deficient environment has been well established to induce oxygen loss and create V_O even in inert environments (Kell et al., 2022). This effect can be further enhanced by inclusion of a reductant such as hydrogen (Merdrignac et al., 1992; Jeong et al., 2003; Chen et al., 2011; Shi et al., 2014; Bonu et al., 2015; Chen et al., 2015; Xiong et al., 2018; Kim et al., 2020; Xiong et al., 2022). Thermal annealing in a pre-determined atmosphere has been extended to non-oxide systems to control the distribution of other anion vacancies such as V_N in C₃N₄ (Niu et al., 2014), or chalcogenide vacancies in MoTe₂, VSe₂, or PdSe₂ (Zhu et al., 2017; Chen et al., 2019; Chua et al., 2020; Zhang et al., 2020). Similar to in-situ methods, control of the heating rate and duration is central to controlling defect density and distribution. This approach can also be extended to nanomaterial doping as exemplified by PdSe₂ wherein the use of an oxidative ozone environment was used to generate oxygen dopants (Liang et al., 2020a). High temperature annealing is not always required to create an oxidative or reductive environment, and solution phase routes can be advantageous for large-scale manufacturing due to their lower energy input requirements, decreased use of harmful chemicals, and overall improved safety. NaBH₄ is a frequently employed solution-phase reducing agent capable of extracting lattice oxygen atoms in materials (e.g., K₄Nb₆O₁₇ ultrathin nanosheets or TiO₂ nanoparticles) to create V_O (Bi et al., 2014; Fang et al., 2014; Mao et al., 2014). Chemical reduction with NaBH₄ can create V_O in ZnO nanorods or SnO₂ nanoparticles at temperatures as low as 30°C–190°C, which is far lower than that required for vacuum annealing (500°C–800°C) (Ansari et al., 2013; Lv et al., 2013; Bonu et al., 2014; Wang et al., 2015a; Wang et al., 2018a; Sahu et al., 2019; Zeng et al., 2020; Xiong et al., 2022). Similar success in controlling the density of V_O has been demonstrated using other solution-phase reductants, including ethylene glycol or glycerol for oxygen vacancy formation in BiOCl or Bi₂WO₆ (Jiang et al., 2013; Ye et al., 2015; Chen et al., 2023).

Temperature and oxidative/reductive environments are not the only post-growth methods capable of generating ample external energy to surmount enthalpic barriers for defect generation. Bi-O bonds in BiOCl nanosheets are long and have a low bond energy, which can be broken with UV photons to create surface oxygen vacancies (Ye et al., 2011; Ye et al., 2012; Jiang et al., 2013; Wu et al., 2018). Photons can also employed to convert chalcogen vacancies to oxygen dopants, as demonstrated in the case of WSe₂ (Lu et al., 2015). Ion-beam bombardment is a common route for substitutional dopant creation—such as Sb-implantation of SnO₂ nanowires (Zhu et al., 2005; Kim et al., 2020). Perhaps counterintuitively, they can also be used to expel lattice atoms and cause atomic rearrangement on the surface without any substitutional doping, as demonstrated with the creation of O_i^// and Sn_i^•••• in SnO₂ nanostructures by high-energy (45–75 MeV) bombardment of Ni⁺ and He²⁺ ions, or vacancy formation in MoSe₂ monolayers via He⁺ ion beam nanoforging (Jeong et al., 2003; Rani et al., 2008; Shi et al., 2014; Iberi et al., 2016; Kwon et al., 2016). Electron beams can create electrons with sufficient kinetic energy to cause knock-on effects. This phenomena can be understood as high-energy electrons from the electron beam transferring enough energy to dislodge atoms from the nanomaterial and create atomic defects (Lingerfelt et al., 2019; Lingerfelt et al., 2020; Lingerfelt et al., 2021). This effect has been demonstrated with nanomaterials such as graphene and TMDs (e.g., MoTe₂, MoS₂, WS₂, and WSE₂) (Algara-Siller et al., 2013; Komsa et al., 2013; Zan et al., 2013; Ziatdinov et al., 2017; Wang et al., 2018b; Elibol et al., 2018; Moody et al., 2018; Nguyen et al., 2018; Maksov et al., 2019; Dyck et al., 2020; Roccapriore et al., 2022). The latter case is particularly well-known due to the high mobility of chalcogen atoms and their relative ease of diffusion out of the structure due to beam-matter interactions. However, these effects are not limited to carbon or chalcogen materials and have been demonstrated in oxides as well (Egdell et al., 1987; Belloni, 2006; Komuro and Matsumoto, 2011). Plasma etching is also a powerful method to create anion vacancies in TMDs, and chalcogen vacancy creation has been demonstrated using Ar plasmas in MoS_2, WSe₂, PdSe₂, and PtSe₂ (Wu et al., 2017; Oyedele et al., 2019; Shawkat et al., 2020; Tsai et al., 2022). Exposure to plasmas can create vacancies in these and other structures, and the defect type and concentration can be controlled by adjusting the plasma gas type (Kondratowicz et al., 2018), irradiation time, or intensity (e.g., generating O-Mo bonds using oxygen plasma) (Islam et al., 2014; Kang et al., 2014; Nan et al., 2014).

3 Energy harvesting: luminescent solar concentrators and net-zero emission buildings

The juxtaposition of global urbanization and the need to lower greenhouse gas emissions require net zero emission buildings wherein annual power consumption is fully counterbalanced by on-site renewable generated energy. Installing conventional photovoltaic (PV) units on a large scale is challenging within dense urban layouts. Energy demands for large buildings frequently exceed those of individual housing units, and PV cells are constrained to rooftop space that is inadequate to meet energy demands (Meinardi et al., 2017). To address these issues, interest has grown in using luminescent solar concentrators (LSCs) as potential building-integrated semi-transparent PV windows (Debije and Verbunt, 2012; Meinardi et al., 2017; Papakonstantinou et al., 2021). LSCs are constructed by doping or coating a glassy or polymeric waveguide with chromophores (Figure 3A) (Debije and Verbunt, 2012; Meinardi et al., 2017). The chromophores absorb broadband solar radiation and re-emit at a specific wavelength, which is guided by internal reflection within the waveguide to the edges or window frame where it is converted into electricity by PV cells (Yablonovitch, 1980; Currie et al., 2008; Sark et al., 2008; Banal et al., 2014). The specific wavelength of re-emission varies by the chromophore material, but near-infrared emission is generally targeted because it is semi-transparent, aesthetically pleasing, and more likely to attain public acceptance (Saifullah et al., 2016).

FIGURE 3

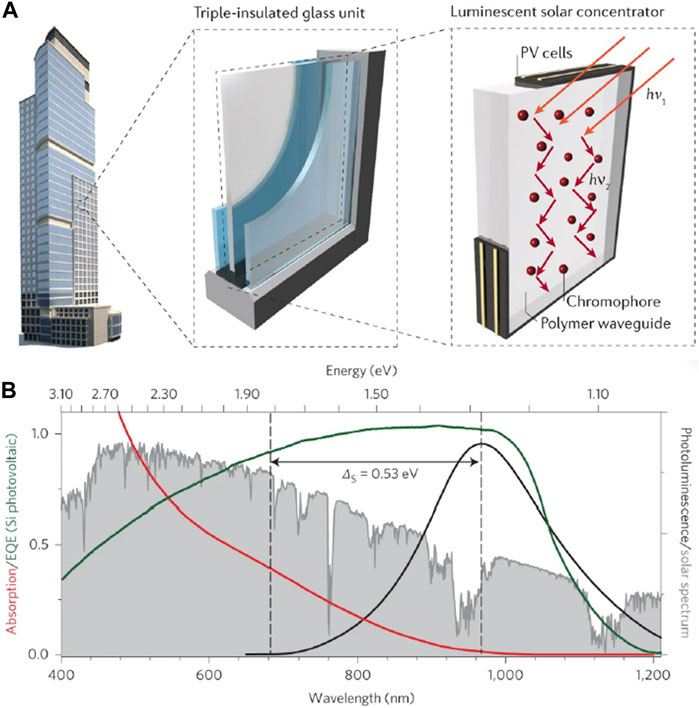
FIGURE 3. (A) Schematic depiction of LSCs, and their potential usage as building-integrated photovoltaic units. Reproduced with permission from Meinardi et al. (2017). (B) CISeS absorption and emission spectra (red and black lines) compared with the solar spectrum (grey shading) and Si solar cell peak EQE (green line). Reproduced with permission from Meinardi et al. (2015).

An ideal LSC chromophore should hold three major optical properties: a large absorption cross-section for capturing sunlight, a high emission efficiency (defined by quantum yield, or $\mathbf{\Phi }=\frac{{\mathbf{N}}_{\mathbf{\text{photons}}\text{emitted}}}{{\mathbf{N}}_{\mathbf{\text{photons}}\text{absorbed}}}$) particularly in the near-infrared region, and a large Stokes shift (Klimov et al., 2016; Gungor et al., 2022). While this review centers on chromophore materials design, other device aspects are important to consider and are discussed elsewhere (Yablonovitch, 1980; Currie et al., 2008; Sark et al., 2008; Banal et al., 2014; Saifullah et al., 2016). Regarding the first two properties, exemplary chromophores should absorb sunlight in both the visible and near-infrared (near-IR) spectral ranges, and re-emit at near 100% quantum yield (QY) allowing for collection by the PV edges. The emitted photons would preferably fall within the near-IR range to achieve both a semi-transparent aesthetic, and also to boost device performance by matching the peak external quantum efficiency (EQE) of the PV device (Figure 3B) (Sark et al., 2008; Meinardi et al., 2015). The chromophore should also have a large Stokes shift, or exhibit peak emission markedly red-shifted from the absorption onset energy. The large Stokes shift is crucial to mitigate reabsorption losses, which are caused by substantial spectral overlap between absorption and emission. Reabsorption losses scale with device dimensions, and chromophores with small Stokes shifts will have poor performance if manufactured at conventional window sizes (Klimov et al., 2016; Gungor et al., 2022).

Several dyes such as 4-dicyanomethyl-6-dimethylaminostiryl-4H-pyran (DCM), CRS040 Yellow, or Lumogen Red have been explored as potential chromophores for LSCs (Batchelder et al., 1979; Sark et al., 2008; Desmet et al., 2012). Though well-studied, molecular dyes struggle to combine all three LSC chromophore optical requirements in the same material: strong broadband optical absorption, high QY, and large Stokes shift with near-IR emission. Quantum dots (QDs) have been proposed as alternative chromophores because of their well-known size-tunable broadband absorption, and the ability to achieve high QY in the near-IR spectral ranges (Pietryga et al., 2016). However, most conventional QDs such as CdSe have a small Stokes shift (tens of meV), which make them unsuitable for LSCs due to prominent reabsorption losses (Pietryga et al., 2016). Several routes have been explored to induce large Stokes shifts in QDs without losing their other potential advantages as LSC chromophores. Most of these approaches involve either doping the QDs with substitutional defects, or designing multinary QD alloys (e.g., ternary or quaternary) that typically form intrinsic defects.

Binary QDs (e.g., CdSe) can be doped directly during crystal growth, or via cation exchange (Mikulec et al., 2000; Norris et al., 2001; Ji et al., 2003; Jian et al., 2003; Meulenberg et al., 2004; Stouwdam and Janssen, 2009; Corrado et al., 2010; Gul et al., 2011; Srivastava et al., 2011; Viswanatha et al., 2011; Vlaskin et al., 2013; Rice et al., 2016; Pinchetti et al., 2018; Singh et al., 2019; Najafi et al., 2021). In the first case, QDs are grown by a conventional strategy such as hot injection wherein precursors are injected into a solvent at high temperature to induce rapid nucleation and growth for size control. During the conventional synthesis route, a dopant is introduced and kinetically competes with host cations during crystal growth. A challenge with this route is that impurity atom binding is unfavorable due to physical attribute mismatching (e.g., differences in charge or ionicity). Cation exchange, on the other hand, involves first synthesizing the QD with conventional methods, and then immersing them in a cation exchange solution with potential dopants. An advantage of such an approach is that the anion sublattice is retained, and crystal composition can be altered without dramatic changes in QD size or shape. This physical process is governed by rapid diffusion driven by the differences in the chemical potential of the QD and impurity solution. While cation exchange often provides for better compositional control than kinetic doping, cation combinations are more limited.

Substitutional transition metal impurities induce red-shifted emission without significantly altering the absorption onset, concurrently increasing the Stokes shift to mitigate reabsorption losses in LSCs. Substitutional Mn²⁺ dopants are the most extensively studied in II-VI QDs—emitting photons via an internal ⁴T₁ → ⁶A₁ d-d transition following excitation by energy transfer from the QD host. The energy of photon emission is fixed at approximately ∼590 nm or 2.1 eV (Figure 4A) (Norris et al., 2001; Erwin et al., 2005; Beaulac et al., 2009), while QD absorption is tunable by nanocrystal size. The absorption onset can therefore be shifted to bluer spectral energies until there is virtually zero overlap between absorption and emission, which results in reabsorption-free LSCs (Erickson et al., 2014). However, the fixed wavelength resulting from the internal emission process for Mn²⁺ dopants yields two key drawbacks. Solar absorption is confined to a narrow spectral region due to the potential of reabsorption when the QD band gap is smaller than 2.2 eV (∼560 nm). Furthermore, the emission exhibits a pronounced yellow-orange hue instead of the preferred semi-transparent shading (Pietryga et al., 2016).

FIGURE 4

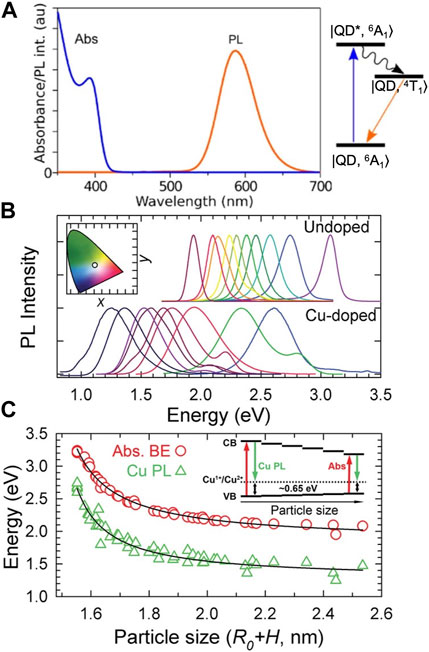
FIGURE 4. Absorption and emission spectra for Mn-doped QDs (A), and a comparison between Cu-doped and undoped QDs in (B,C). Reproduced with permission from Erickson et al. (2014) for (A) and Viswanatha et al. (2011) for (B,C). For Mn-doped QDs the absorption and emission mechanism is depicted schematically in an additional panel to the right of (A), and for Cu-doped QDs it is depicted in the inset of (C).

The emission mechanism for Ag⁺ and Cu²⁺ dopants is markedly different from Mn²⁺ dopants. Radiative recombination occurs via relaxation of a conduction band (CB) electron from the QD host and a hole localized at the dopant energy level (Figures 4B, C) (Lingerfelt et al., 2019, Lingerfelt et al., 2020, Lingerfelt et al., 2021, Wang et al., 2018a, Elibol et al., 2018, Komsa et al., 2013, Algara-Siller et al., 2013, Roccapriore et al., 2022). While the emission transition for both Ag⁺ and Cu⁺ dopants appears to be similar, the hole localization process differs for each structure due to their distinct electron configurations. Cu²⁺ dopants have a 3d⁹ electron configuration, which results in a pre-existing hole in its ground state that can directly recombine with the excited-state CB electron from the host QD (Viswanatha et al., 2011; Knowles et al., 2015; Nelson and Gamelin, 2018; Fuhr et al., 2019; Hughes et al., 2019; Harchol et al., 2022). On the other hand, Ag⁺ has a 3d¹⁰ electron configuration, which must capture a photogenerated hole from the VB (Pinchetti et al., 2018; Najafi et al., 2021). For both cases, the emission wavelength is consequently governed by the energy difference between the hole localized at the Ag⁺ or Cu²⁺ dopant and the CB electron. The Stokes shift is determined by the energy difference between the hole localized at the dopant site and the valence band (VB). The CB electron energy is size-tunable, which allows for larger QDs with redder absorption and near-IR emission to be synthesized without dramatically increasing reabsorption.

The band gap for copper and silver doped QDs is still somewhat large, which limits spectral absorption coverage for LSCs and has driven research interest in Cu_xIn_2-xSe_2-yS_y (CISeS) QDs. CISeS QDs have size tunable absorption all the way to the near-IR range, a large Stokes shift (300–500 meV), a near colorless emission wavelength that well-matches the peak EQE of the LSC PV cells (Figure 3B), and have recently achieved greater than 95% QY (Ueng and Hwang, 1989; Ueng and Hwang, 1990; Kim et al., 2012; Knowles et al., 2015; Jara et al., 2016; Fuhr et al., 2017; Xia et al., 2017; Bergren et al., 2018; Nelson and Gamelin, 2018; Yun et al., 2018; Houck et al., 2019; Hughes et al., 2019; Makarov et al., 2019; Fuhr et al., 2020a; Fuhr et al., 2020b; Du et al., 2020; Frick et al., 2020; Velarde et al., 2020; Hinterding et al., 2021; Xia et al., 2021; Harchol et al., 2022; Liang et al., 2023). The origin of CISeS Stokes shifted emission has commonly been ascribed to defects, but with several other proposed mechanisms depending on the type of defect that forms, and the band-edge transition itself (described later in the review). It has been suggested that near-stoichiometric (and especially Cu-rich) CISeS QDs have antisite (Cu_In^//) defects, and that Cu-deficient QDs have V_Cu^/ charge compensated by oxidation of a lattice Cu⁺ atom to Cu²⁺ (Cu_Cu^•) (Fuhr et al., 2020a; Fuhr et al., 2020b). Considering that Cu_In^// defects are in the +1 oxidation state (3d¹⁰ configuration) and Cu²⁺ defects in the 3d⁹ configuration, hole localization is thought to occur via a similar process as Ag⁺ dopants for Cu_In^// (near-stoichiometric or Cu-rich QDs) and Cu²⁺ dopants for Cu_Cu^• (Cu-deficient QDs).

Both defects involve recombination from a delocalized CB electron, sharing many of the same advantages as Ag⁺ and Cu²⁺-doped structures. However, precise control of synthesis conditions becomes crucial due to variations in emission channels between each defect type. Specifically, the hole localization process for Cu_In^// defects involves intragap absorption, which is absent for Cu_Cu^• defects (Figure 5). A potential conclusion from this observation would be that the sharper absorption edge for Cu-deficient structures arising from the removal of Cu_In^// defects should lead to superior LSC performance via reduced spectral overlap between absorption and emission, and correspondingly improved reabsorption losses. This prediction is partially correct, but misses quantum yield considerations. Moderately Cu-deficient structures exhibit sharper absorption, reduced spectral overlap, and even higher QY due to deactivation of hole trapping pathways (Jara et al., 2016; Fuhr et al., 2020a; Fuhr et al., 2020b). However, if QDs become too Cu-deficient eventually other defects (e.g., In_Cu^••) can form in larger densities and reduce QY via electron trapping (Jara et al., 2016; Fuhr et al., 2020a; Fuhr et al., 2020b). These findings are suggestive that the defect chemistry of CISeS QDs is highly sensitive to synthesis conditions, and that likely the complex distribution of defects and LSC performance will strongly vary with other experimental parameters such as temperature or pH.

FIGURE 5

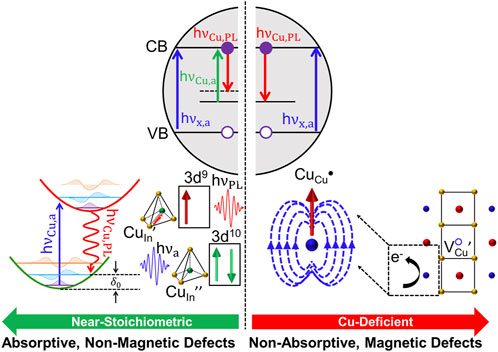
FIGURE 5. Antisite defects in CIS QDs have been predicted to form in near-stoichiometric structures (left panel) and copper vacancies charge compensated by lattice copper oxidation in Cu-deficient structures (right panel). CIS has two absorption pathways if antisite defects are present (h$\mathrm{\upsilon }$_x and h${\mathrm{\upsilon }}_{\mathbf{\text{Cu}},\mathbf{\alpha }}$ for band-edge absorption and Cu¹⁺ absorption, respectively). CIS with V_Cu + Cu_Cu^• only exhibit the h$\mathrm{\upsilon }$_x pathway. Antisite defects undergo excited state reorganization, which further red-shifts emission due to the Cu_In^// → Cu_In^/ Jahn-Teller distorted photoconversion process (similar to the singlet-triplet splitting model). “Near-stoichiometric” CIS therefore has absorption/emission dominated by the antisite defect pathway (similar to Ag⁺-doped QDs), and Cu-deficient CIS by the V_Cu induced Cu_Cu^• pathway (similar to Cu²⁺-doped QDs). Reproduced with permission from Fuhr et al. (2020a).

The precise emission mechanism is still under debate for CISeS QDs, and other models that do not require defects such as the self-trapped exciton or inverted band-edge hole model have been discussed (Knowles et al., 2015; Shabaev et al., 2015; Nagamine et al., 2018; Nelson and Gamelin, 2018; Hughes et al., 2019; Anand et al., 2020; Harchol et al., 2022). For the purposes of this general review on defects in nanomaterials we do not attempt to determine the model that most accurately depicts the exact CISeS emission mechanism. We instead focus on two key points: 1) many of these proposed models are not mutually exclusive, and 2) defects likely affect the emission process, LSC performance, and their formation is sensitive to chemical processing conditions. The predicted Stokes shift for the band-edge hole inversion model is expected to be smaller than the defect-induced emission, and are difficult to resolve experimentally due to partial overlap with strong Cu-defect emission unless defect-free QDs can be synthesized (Batchelder et al., 1979, Desmet et al., 2012, Meinardi et al., 2015). The self-trapped exciton model involves the same hole localization and excited-state reorganization mechanism described for antisite defects and Ag⁺ dopants, but is argued to instead occur via band-edge states to cause the large Stokes shift without the need for defects (Batchelder et al., 1979, Desmet et al., 2012, Meinardi et al., 2015).

These distinctions may prove valuable in future LSC efforts, particularly in resolving routes to reduce spectral linewidths to further diminish reabsorpiton losses. However, it is important to note that regardless of the precise emission mechanism, defects likely strongly impact spectral properties for CISeS QDs and are important to control for LSC performance. There is extensive evidence that the spectral properties of CISeS QDs are highly sensitive to chemical processing in ways that binary QDs are not. Single particle spectroscopy studies have shown radiative lifetimes and photoluminescence (PL) linewidths that can vary by several hundreds of ns or several hundreds of meV, respectively (Zang et al., 2017; Hinterding et al., 2021; Xia et al., 2021). Ensemble absorption and emission spectroscopy has resolved both two channel absorption and two channel emssion (Jara et al., 2016; Fuhr et al., 2020a; Fuhr et al., 2020b; Xia et al., 2021), and the magneto-optical charateristics vary significantly across studies with different QD batches. (Rice et al., 2014; Knowles et al., 2015; Fuhr et al., 2020a; Anand et al., 2020; Fuhr et al., 2020b). These large variations are atypical for QDs, and defect-free structures are atypical for covalently bonded multinary structures—especially those with large variations in stoichiometry (Alvarez-Garcia et al., 2000; Hahn et al., 2001; Paier et al., 2009; Ye et al., 2019; Vijay et al., 2021; Han et al., 2022; Quadir et al., 2022). Given these characteristics and the well-known tendency to form defects in the bulk CISeS phase (Ueng and Hwang, 1989; Ueng and Hwang, 1990; Alvarez-Garcia et al., 2000; Hahn et al., 2001), it is highly likely that defects are impacting the spectral properties in some way, and that regardless of the precise emission mechanism understanding synthesis-defect formation relationships for CISeS QDs could improve LSC performance.

4 Energy storage: batteries and electric vehicles

Fossil fuel powered vehicles are a major contributor to CO₂ emissions and climate change. As such, electric vehicles (EVs) have attracted widespread interest, and their proliferation persists. In this context, lithium-ion batteries (LIBs) power a diverse array of consumer electronics that have become indispensable to modern-society, and their integration into commercial EVs has enabled an alternative to the combustion engine. In conjunction with a greener grid (e.g., utilizing recent innovations in solar and wind technology) EVs powered by LIBs will be critical in lowering CO₂ emissions and reducing the deleterious impacts of climate change (Chu and Majumdar, 2012; Clark et al., 2016). A typical LIB has a solid-state anode and cathode separated by a liquid or gel electrolyte that shuttles ions between the two electrodes during charging and discharging (Manthiram, 2020). For EVs, ideal electrode materials should yield a high energy density, superior rate capability, and long cycle life for consumer acceptability—allowing for extended driving ranges, fast charging, and low maintenance costs.

The achievable energy density of an electrode material is proportional to its capacitance and voltage. Capacitance represents the amount of charge each electrode material can store, and the voltage represents the energy difference between the anode and cathode redox potentials. Hence, an optimal anode would exhibit stable, redox-inactive lower energy levels and a high lying energy band—relative to vacuum or the standard Hydrogen electrode—where redox reactions occur. The opposite is true for the cathode, which should have its highest redox active energy band at the lowest feasible energy (within the limitations of electrolyte stability). Stanley Whittingham demonstrated the first rechargeable LIB at Exxon Corporation using a TiS₂ cathode, which could not be commercialized due to the safety hazards of using Li metal as an anode, and the limited energy density arising from the 2.5 V discharge voltage (Whittingham, 1976). Oxide p-bands lie at lower energies than sulfides (2p vs. 3p electrons), and allow the access of lower lying redox energy states such as the Co^3+/4+ redox couple in LiCoO₂ (Goodenough, 1971; Mizushima et al., 1981). Oxide cathodes, specifically LiCoO₂, extended the voltage range of LIBs to 4V and allowed for the usage of graphite as an anode material by incorporating Li into its as-synthesized lattice structure. These advancements improved the energy density and safety of LIBs, were central to the eventual commercial success of LIBs, and awarded the Nobel prize in chemistry.

The success of LiCoO₂ in commercializing LIBs is laudable, but many challenges persist. LiCoO₂ has a layered cathode structure with a cubic close-packed oxide sublattice and Li⁺ and Co³⁺ ions ordered on alternate (111) planes (Mizushima et al., 1981). The good cation ordering stems from the significant size difference between Li⁺ and Co³⁺ and aids electronic and ionic conduction. Li⁺ ionic conduction occurs via low energy barrier face-sharing tetrahedral voids between octahedra (o-t-o pathway). Shared octahedra along the cobalt plane enable Co-Co interactions for enhanced electronic conductivity. Specifically, Co³⁺ is oxidized to low-spin Co⁴⁺ during LIB charging, leading to the inclusion of holes in the cobalt t₂g^6–x band, and causing Li_1-xCoO₂ to become metallic during charging (Nishizawa and Yamamura, 1998; Chebiam et al., 2001a). However, the overlap between the top of the O²⁻:2p and Co^3+/4+ bands leads to the release of oxygen if charged more than 50% (Chebiam et al., 2001b; Venkatraman et al., 2003). This limits the practical capacity (∼140 mA h g⁻¹), and in conjunction with the high cost of cobalt has driven the search for new rock salt LiMO₂ (where M = a transition metal) alloys.

Cation-ordered LiMO₂ structures crystallize in several common motifs such as the γ-LiFeO₂ (tetragonal structure where Li⁺ and Fe³⁺ ions are well-ordered on octahedral sites, Figure 6A), low-temperature spinel-like LiCoO₂ structure (all Li⁺ ions are ordered on the 16c octahedral sites, Figure 6B), or $\mathit{\alpha }$-NaFeO₂ (Li and M are ordered along alternating (111) planes, Figure 6C). Cation-disordered structures can also form, as exemplified by $\mathit{\alpha }$-LiFeO₂ for which Li and M are randomly distributed (Figure 6D). Li⁺ ions are located on octahedral O_h sites in both ordered and disordered structures, but cation disorder prevents the earlier described o-t-o Li-migration mechanism (Figure 6E) (Sebastian and Gopalakrishnan, 2003; Manthiram, 2020; Wang et al., 2022a) Specifically, the randomness of cation distribution on the octahedral sites means that the intermediate tetrahedral site in the o-t-o diffusion mechanism could now be connected to either Li or M octahedra. The electrostatic interactions between the four cations of the face-sharing octahedra and the size of the tetrahedral diffusion site (T_d) determine the barrier to diffusion. If surrounded only by Li cations (0-TM channel, Figure 6F), Li⁺ ions will have smaller required distances to diffuse through, combined with weaker electrostatic repulsion due to the low valency of lithium. This pathway therefore exhibits facile lithium migration. However, if one or more of the cations are transition metals (1-TM or 2-TM channels, Figures 6G, H) the increase in both migration distances and electrostatic repulsion will lead to a higher energy barrier, which reduces Li⁺ conductivity by disabling the formation of a percolation network for long-distance diffusion (Wang et al., 2022a; Zhang et al., 2023). Inability to efficiently transport Li⁺ through the o-t-o pathway initially led to little interest in cation disordered rock salt structures.

FIGURE 6

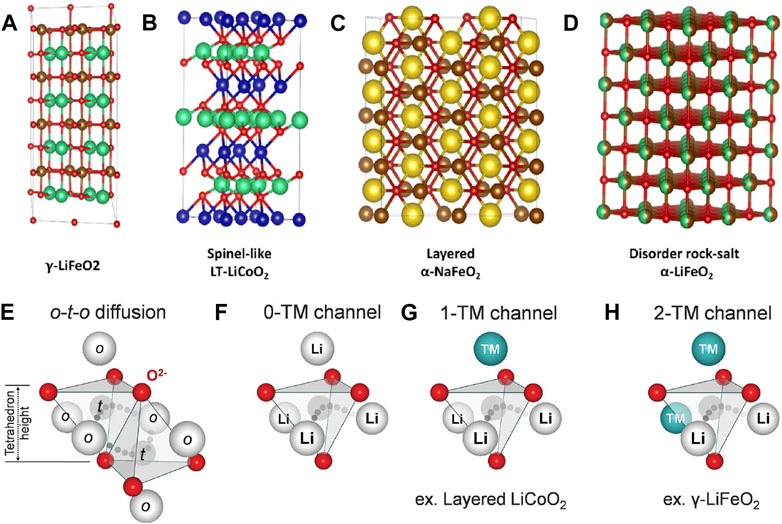
FIGURE 6. (A–D) Types of rock salt cathode structures. The cation ordered structures are shown in (A–C), and an example of cation disorder is shown in (D). Reproduced with permission from Zhang et al. (2023). (E,F) Diffusion models for ordered (E) structures versus disordered structures (F–H). The disordered 0-TM channel (transition metal-free) is shown in (F), while the channels with higher barriers due to transition metals are shown in (G) and (H), for 1 transition metal and 2 transition metals, respectively. Reproduced with permission from Lee et al. (2014).

Monte Carlo simulations have since shown that 0-TM percolation networks can be created if excess lithium (e.g., 10%) in Li_1+xM_1-xO₂ is incorporated into the structure (Lee et al., 2014), giving high conductivity as well as capacity, which has led to renewed interest in these materials (Dixit et al., 2014; Chen et al., 2021a; Szymanski et al., 2022; Patil et al., 2023; Szymanski et al., 2023). Equivalently, when partial Li-occupancies are present, high Li-ion conductivity is expected (Dathar et al., 2017). Lithium-excess cation disordered rock salt structures can be synthesized in any of the structure-types described earlier: γ-LiFeO₂, layered, spinel-like LiCoO₂, and the layered $\mathit{\alpha }$-NaFeO₂ structure-type. Several of these structures have demonstrated capacities beyond currently commercialized LIB cathode materials (Lee et al., 2014; Urban et al., 2014; Wang et al., 2022a; Zhang et al., 2023). Disordered structures that use nickel or manganese for the redox transition metal are the most well-studied. Many nickel alloy (e.g., with Ti, Nb, or Mo) cathodes have been synthesized with high average voltage and tilt slope (Pralong et al., 2012; Lee et al., 2015; Lee et al., 2017a; Källquist et al., 2019; Ouyang et al., 2020). If charged up to 4.6 V, overlap between e_g orbitals in Ni with hybridized Li-O-Li orbitals prevents the complete oxidation/reduction of Ni due to competition with O oxidation (Pralong et al., 2012; Lee et al., 2015; Lee et al., 2017a; Källquist et al., 2019; Ouyang et al., 2020; Zhang et al., 2023). While there are challenges related to the corresponding release of CO₂ and O₂ during the cycling process (surface densification), these materials have exhibited capacities greater than 220 mAh/g (Lee et al., 2015; Yu et al., 2019; Wang et al., 2022a). Manganese structures are also well studied, and Li₄Mn₂O₅ has been shown to exhibit discharge capacities as high as 287 mAh/g (Pralong et al., 2012). Alloying with other metals such as Ti or Nb in Li_1.2Mn_0.4Ti_0.4O₄ or Li_1.3Nb_0.3Mn_0.4³⁺O₂ can further increase the discharge capacity to 300 mAh/g (Yabuuchi et al., 2016a; Lee et al., 2017a). However, irreversible O redox reactions contribute to a large initial discharge capacity, which eventually fades and limits cycle life (Wang et al., 2015b; Lun et al., 2019). Iron and vanadium systems such as Li-Ti-Fe-O and Li-Nb-V-O also show promise. For example, LIBs with discharge capacities equal to or greater than 200 mAh/g have been demonstrated with Li_1.2Ti_0.4Fe_0.4O₂ and Li_1.25Nb_0.25V_0.5O₂ (Yabuuchi et al., 2016b; Nakajima and Yabuuchi, 2017; Wandt et al., 2018; Wang et al., 2019).

Rock salts are not the only class of disordered cathode materials with the potential to improve LIB performance. Spinel LiMn₂O₄ structures have a cubic-closed pack oxygen sublattice where ordered structures consist of Mn³⁺ and Mn⁴⁺ ions occupying octahedral centers (16d) and Li⁺ tetrahedral (8a) sites (Thackeray et al., 1983; Manthiram, 2020). LiMn₂O₄ has a three-dimensional Li⁺ diffusion pathway that enables fast Li conduction; Li⁺ ions migrate between 8a tetrahedral sites via transitioning through low migration barrier empty 16c octahedral sites. Dissimilar to the Li_1-xCoO₂ metallic transition during the charge-discharge process, LiMn₂O₄ remains a small polaron semiconductor. Regardless, Mn-Mn interactions from mixed valence t_2g and e_g states in Mn^3+/4+ facilitates electron hopping and yields good electronic conductivity and high operating voltages (Gul et al., 2011). Jahn-Teller distortions in Mn³⁺:t_2g³e_g¹ contributes to a cubic to tetragonal phase transition, which presents a challenge for LIB performance because of the large volume change induced by the 2Mn³⁺ → Mn²⁺ + Mn⁴⁺ disproportionation reaction (Manthiram, 2020). This leads to dissolution of Mn in the electrolyte and poor cycle life. One route to somewhat circumvent this issue is to alloy LiMn₂O₄ with Ni to form cation disordered LiMn_1.5Ni_0.5O₄ (LMNO). The Ni dopants partially occupy Mn sites, reduce the Mn³⁺ site prevalence, and contribute to a high 4.7 V Ni²⁺/Ni⁴⁺ redox couple (Kan et al., 2017; Liang et al., 2020b; Cen et al., 2023).

LMNO can be synthesized with or without site disorder depending on the temperature (e.g., post synthesis calcination in air above 700°C leads to the formation of the disordered phase and temperatures at or below 700°C the ordered phase, Figure 7) (Kim et al., 2004). Mn atoms are in the +4 oxidation state in the ordered (P4₃32) phase with Ni and Mn located on the 4b and 12d Wyckoff sites, respectively (Kunduraci and Amatucci, 2006; Lee et al., 2017b; Liu et al., 2017). If synthesized at higher temperatures (e.g., greater than 700°C) LMNO forms in the Fd $\overline{\mathbf{3}}$ m space group. The partial reduction of Mn⁴⁺ to Mn³⁺ occurs alongside oxygen vacancy formation, Mn/Ni site disorder, and varied additional impurity phases (e.g., Li_xNi_1-xO) (Chebiam et al., 2001a; Venkatraman et al., 2003; Kunduraci and Amatucci, 2006; Shin et al., 2012; Casas-Cabanas et al., 2016; Aktekin et al., 2019; Haruna et al., 2021; Cen et al., 2023). The partial reduction of Mn⁴⁺ to Mn³⁺ in the cation disordered phase increases the electronic conductivity (>2.5 orders of magnitude) relative to the ordered phase (Kunduraci and Amatucci, 2006). Charging/discharging disordered LMNO as a LIB cathode results in a two-phase reaction when x in Li_xNi_0.5Mn_1.5O₄ is below 0.5 (between Li_0.5Ni_0.5Mn_1.5O₄ and Ni_0.25Mn_0.74O₄), and a solid-solution reaction when x is between 0.5 and 1 due to the Ni^2+/3+ redox couples (Liang et al., 2020b). The solid-solution reaction involves size changes in the parental lattice during charging/discharging, or insertion/extraction of lithium. On the other hand, the two-phase reaction involves interconversion and destruction of the parent cathode structure, which limits lithiation and delithiation kinetics. Notably, the two-phase reaction occurs across the entire x charging range for the ordered LMNO phase (between LiNi_0.5Mn_1.5O₄/Li_0.5Ni_0.5Mn_1.5O₄ and Li_0.5Ni_0.5Mn_1.5O₄/Ni_0.5Mn_1.5O₄), leads to poorer electrochemical stability, reduced rate capability, and lower cycling stability than the disordered structure (Ariyoshi et al., 2004; Liang et al., 2020c).

FIGURE 7

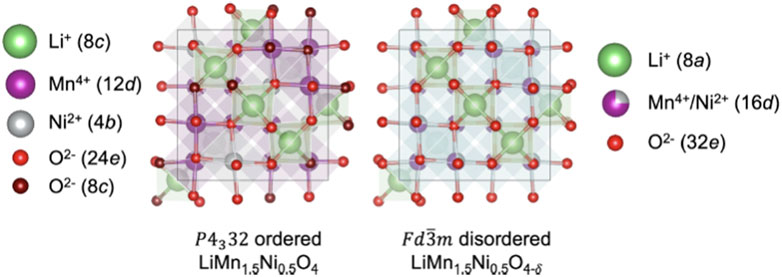
FIGURE 7. Comparing cation ordered and disordered LMNO structures based on their Wyckoff positions. Reproduced with permission from Cen et al. (2023).

Doping LMNO with other metals can further improve the cycling stability and rate capability. Sodium dopants have been shown to enhance cation disorder, decrease particle size, and improve charge transfer by providing extra pathways for electron hopping (Wang et al., 2014). The 5% Na-doped LMNO structure achieved superior rate performance arising from the reduced voltage polarization. Al can be incorporated into LMNO as either substitutional dopants at the Ni/Mn sites via a thermopolymerization method, or in empty surface 16c octahedral sites using atomic layer deposition (ALD), and can prevent transition metal dissolution (Zhong et al., 2011; Piao et al., 2018). This process improves the rate capability and cycling stability by mitigating electrolyte/electrode side-reactions and enabling fast Li⁺ diffusion. The concentration of Mn³⁺ can be increased with iron dopants, which enhances electronic conductivity, reduces voltage polarization, and correspondingly improves cycling performance and rate capability (Liu and Manthiram, 2009). Cr-doped LMNO structures (e.g., LiNi_0.45Cr_0.1Mn_1.45O₄) have also exhibited improved electronic/ionic conductivity with a wide voltage plateau, and cycle-stable structure (Wang et al., 2018c).

5 Energy conversion: electrocatalytic green hydrogen production

Hydrogen has a high energy density (142 MJ/kg), is abundant, and can potentially be used as a clean CO₂ emission-free fuel (Dincer, 2012; Abdin et al., 2020). However, despite these potential advantages over conventional greenhouse gas emitting fuels, H₂ is not readily available in its free form in nature. The predominant industrial routes for hydrogen production rely on thermochemical fossil fuel-related processes such as steam-methane or hydrocarbon reforming, pyrolysis, or coal gasification (Nikolaidis and Poullikkas, 2017; Abdin et al., 2020; Megía et al., 2021). Each of these industrial-scale processes emit greenhouse gases, which has motivated interest in “green hydrogen” production wherein hydrogen is produced via carbon neutral routes. Water electrolysis offers a potentially viable route to produce hydrogen without carbon emissions (Lu et al., 2021; Tan et al., 2023). Catalyst design represents a pertinent challenge for water electrolysis at industrial scales though. To date, the catalysts with the best performance utilize rare metals such as platinum, palladium, iridium, or rhodium (Chen et al., 2021b). These rare earth metals catalysts are known to be commercially expensive and to have negative mining impacts that limit their utility for economically viable and environmentally sustainable hydrogen production at-scale (Glaister and Mudd, 2010; Lu et al., 2021; Tan et al., 2023).

MX₂ phases (where M is a transition metal and X is an oxygen or chalcogenide) are of great interest for many electronic and optical applications (Manzeli et al., 2017). Transition metal dichalcogenides (TMDs) are the most well-studied branch of these materials, and several phases such as MoS₂ and WS₂ are under consideration for replacing platinum group metals catalysts for the hydrogen evolution reaction (HER) (Hinnemann et al., 2005). These two dimensional structures are similar to graphene except that instead of stacked carbon layers separated by weak van der Waals forces (graphite) the bulk structure has stacked metal chalcogen or oxide layers, which similarly can be exfoliated as either a few-layer stacked structure, or as monolayers (Chhowalla et al., 2013). The basal plane of defect-free 2D TMDs is unfortunately catalytically inert, which impedes their electrocatalytic HER performance (Xu et al., 2015). The basal planes can be activated by either inducing defect formation or altering the TMD phase. The latter of these two approaches is often difficult (Kibs et al., 2012; Kong et al., 2013; Voiry et al., 2013; Jiao et al., 2018; Wei et al., 2019; Li et al., 2021; Tan et al., 2023). Using MoS₂ as an example, the 2H phase is a semiconductor and therefore has a lower electron mobility than the metallic 1T phase—yielding reduced HER performance. While converting the 2H phase to 1T could potentially improve charge transfer kinetics, it also involves harsh chemicals and produces only a metastable phase that eventually converts back to the thermodynamically more stable 2H phase (Lukowski et al., 2013). Routes for exposing more catalytically active edge sites on the 2H MoS₂ phase can improve performance, but these do not alter the electronic conductivity significantly.

Alternatively, controlling the density and distribution of defects in TMDs can increase the density of active sites, while simultaneously improving electron mobility by altering the electronic structure. This route is particularly viable with TMDs, which as discussed in the “Synthesis and Control of Defect Formation” section are well-known to form defects in-situ and have many post-processing routes to further control their distribution and density. The Sabatier principle guides HER catalysis design, and states that heterogeneous catalysts that have intermediate binding strengths with reaction intermediates will yield the best performance. Specifically, a catalyst that binds too strongly with the reaction products will not allow for product dissociation, and the active sites of the catalyst will be permanently blocked. On the other hand, a catalyst that binds too weakly to the reactants will not be able to weaken chemical bonds and lower the reaction barrier to improve product yield or selectivity. The most common tool used to illustrate this Goldilocks principle is the volcano plot, which for HER describes $∆$G_H* (binding strength) versus j (exchange current density, Figure 8) (Parsons, 1958).

FIGURE 8

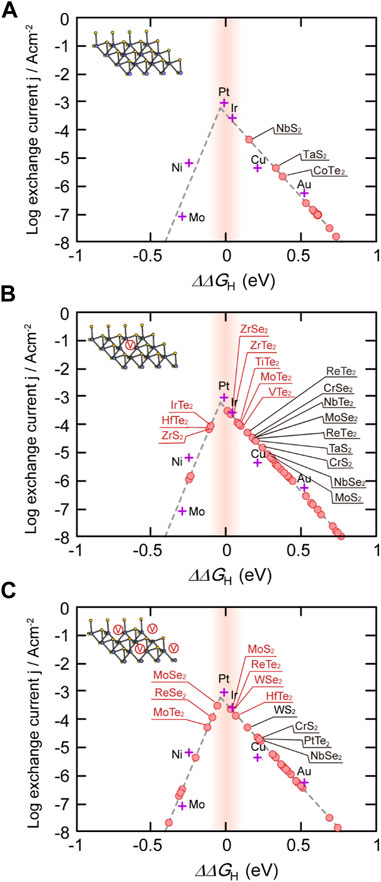
FIGURE 8. (A–C) Volcano plots comparing hydrogen adsorption free energies to Pt for defect-free TMDs (a, depicted by a vacancy-free representative structure in the figure inset), low density anion vacancy concentration (6.25%, b, depicted by a representative structure with a single vacancy), and higher density anion vacancy concentration (25%, c, depicted by a representative structure with four vacancies). Reproduced with permission from Lee et al. (2018).

Among the many defect engineering techniques outlined earlier, the management of vacancy formation in TMDs through a combination of in-situ and ex-situ approaches are the most well-developed, and consequently, the most widely employed for enhancement of $∆$G_H* in TMD-catalyzed HER. First principles calculations have shown that there is an inverse relationship between vacancy formation energy and $∆$G_H* (Lee et al., 2018; Wang et al., 2022b). Localized electronic states resulting from vacancy creation interact with hydrogen electronic states during chemical bonding to reduce the energy cost of bond-breaking from vacancy formation. This process results in stronger hydrogen adsorption for vacancies with larger formation energies. Smaller HOMO-LUMO gaps (highest occupied molecular orbital and lowest unoccupied molecular orbital, respectively), which may encompass localized defect states in addition to band-edges, are also favored. To illustrate the desirability of a small HOMO-LUMO gap, let’s consider group 5 transition metals. As previously described, the hybridization process requires the transfer of two electrons from the HOMO to the bonding state, which necessitates “left-over” electrons occupy the LUMO (Figure 9). This process helps explain the superior performance of ZrSe₂, ZrTe₂, and TiTe₂, which have $∆$G_H* closer to Pt than other TMDs in the volcano plot in Figure 9. An inherent challenge in establishing defect relationships with TMDs lies in the fact that the identical defect types (e.g., vacancies) can elicit distinct effects within the same class of TMDs in different phases. One such example is VS₂ wherein vacancies improve hydrogen adsorption in the 2H phase, but hamper performance in the 1T phase (Zhang et al., 2017). While the general relationships explored so far between vacancy formation and HER performance are informative, each TMD system still requires careful examination.

FIGURE 9

FIGURE 9. Schematic depiction of TMD/hydrogen band diagrams where (A–C) represents defect-free TMDs with group 4, 5, and 6–10 transition metals, and (D–F) represents the same structures with anion vacancies. Reproduced with permission from Lee et al. (2018).

HER performance enhancement via vacancy creation is sensitive to the concentration of defects, and the relationship between vacancy density and performance varies by specific TMD system (Lee et al., 2018). Ab initio computational screening studies have categorized the effects of vacancy density on TMD HER performance into four types. Type-I TMDs exhibit low $∆$G_H* without vacancies. As the vacancy concentration increases the HER performance will improve until it eventually approaches Pt HER performance (e.g., MoS₂, WSe₂, or ReSe₂). Hence, type-I TMDs are initially poor choices for HER catalysts but can be dramatically improved by increasing the vacancy concentration. Type-II TMDs (e.g., MoSe₂ and MoTe₂) have an intermediate $∆$G_H*, or moderately positive $∆∆$G_H* (defined as $∆$G_H* relative to Pt) without vacancies. As the vacancy formation is induced in these structures, there is an initial improvement from their already relatively strong HER performance (eventually matching Pt). However, if the vacancy concentration becomes too large $∆∆$G_H* will become negative and there will be a performance drop. Type-III TMDs (e.g., ZrSe₂ and ZrTe₂) exhibit similar properties as type-II, but with $∆$G_H* already near that of Pt, which indicates that while similar trends hold as described for type-II, the tolerance for including more vacancies is much smaller. The $∆$G_H* for type-I through type-III can therefore be thought of as: TMDs where large vacancy concentrations (type-I), intermediate vacancy concentrations (type-II), and small vacancy concentrations (type-III) are desirable. Type-IV TMDs differ from the other three by exhibiting the opposite $∆$G_H* relationship. For these TMD structures, $∆$G_H* is already larger than Pt, and vacancies will yield a HER performance reduction.

An alternative scheme of modifying TMDs for optimal HER performance is via edge-engineering (Peng et al., 2016; Cui et al., 2017; Hu et al., 2019). As described earlier, the basal plane of non-defective TMDs are catalytically inert. However, stacking 2D TMDs along the edges can increase the exposure of catalytically active edges, and lead to a larger effective surface-area of very active catalytic sites. Recently it was demonstrated using first principles calculations that different types of non-stoichiometric edges in MoSe₂, many of whom have been recently synthesized under a scanning transmission electron microscope (STEM) (Sang et al., 2018), can have near optimal HER activity over conventional stoichiometric edges. They found a strong linear correlation between Bader charges on H and the Gibbs free energy of hydrogen adsorption (ΔG*_H) at these edges, providing a design principle for discovering better HER catalytic edges. HER activity was found to be not only influenced by the formation of H–Se/Mo chemical bonds as previously thought, but also by geometric reconstructions and charge redistribution. The same group subsequently discovered via high-throughput computational screening about nine thermodynamically stable multi-functional edges in MoS₂, many showing optimal HER performance (Hu et al., 2020). STEM was subsequently used as an atomic drill bit for targeted synthesis of specific edge-patterns in 2D TMDs. (Boebinger et al., 2023). Nevertheless, a scalable approach to engineer edges in 2D materials is still lacking, but has significant potential in achieving high HER in TMDs with earth-abundant elements and without involving any critical materials.

These classifications explain many experimental trends, but as observed through other defect systems, a priori prediction of structure-property relationships for defects is complex and difficult. DFT studies on MoS₂ electrocatalysts indicate that high concentrations of sulfur vacancies preferentially agglomerate instead of randomly dispersing throughout the lattice, which partially negates its classification as a type-I defect system (Zhou et al., 2021). However, experimental studies have shown improved performance at high vacancy concentrations because of the unusual interplay between sulfur vacancy formation and exposure of under-coordinated Mo atoms, which become synergistically active as catalytic sites (Li et al., 2019). This is just one of many demonstrations that vacancy formation in TMDs should not only be considered in isolation to other effects in the atomic or electronic structure. Excess vacancy formation can damage the structural integrity of TMDs such as inducing cracks or holes, and the existence of dangling bonds can adsorb other non-hydrogen species (particularly in air) (He et al., 2018; Yang et al., 2019). At low concentrations the co-creation of other defects (e.g., Frenkel pairs) can improve performance by providing additional adsorption sites, or possibly even alternative adsorption mechanisms such as in MoS₂ where the preferred hydrogen adsorption site shifts to a region between the vacancy and interstitial in the Frenkel pair (Xu et al., 2022). This process improved the performance even relative to Pt-doped MoS₂. It is also well-known that defect creation semiconductors leads to localized intragap states, which can contribute to improved electrical conductivity and enhance hydrogen adsorption, but in ways that will wildly vary by which defects form (Li et al., 2016).

6 Challenges and future prospects

Understanding defect formation mechanisms and elucidating their structure-property relationships in nanomaterials is a highly prospective route to commercialize new green energy device architectures, or improve existing ones. A key challenge to address for the future of defect engineering is the development of better integrated theory-experiment workflows wherein the physical properties of a specific defect can be predicted a priori to experiment and the synthesis (or post-synthesis) methods to control the type, concentration, and distribution of defects are known. While partial implementation of such workflows are feasible today, unlocking their full potential requires significant advances in theory and experimental methods. DFT methods for predicting synthesis-structure-property relationships are ever-improving, but the time-scale for calculations is often only marginally faster than running experiments. Avenues for defective material design are continually expanding with the advent of beyond 0 K computational chemistry methods for predicting defect phase stability and advanced electronic structure calculation methods compatible with large supercells for predicting electronic and optical properties of defects. However, each of these routes is computationally expensive and are generally used to explain experimental results posteriori. This problem is further exacerbated if excited-state modeling is considered for gaining mechanistic understanding of QD optical emission processes for optimizing LSCs, or electrochemical-interface modeling is required to improve cation disordered oxides for LIB cathodes or TMDs as catalysts for HER. Hence, further advances in high-throughput calculation methods are required for electronic structure calculations and computational chemistry to be effectively integrated in theory-experiment workflows.

From an experimental perspective, determining synthesis conditions for controlling defect formation in nanomaterials has traditionally relied on an Edisonian trial-and-error methodology. This approach entails selection of initial synthesis conditions, measurement of basic material structure without accounting for defects (e.g., XRD for crystal structure and/or mass spectroscopy for composition), measurement of nanomaterial physical properties (e.g., emission energy), and potentially device performance. The influence of defects on these properties is oftentimes only considered if anomalous characteristics arise. Synthesis methods are then iteratively adjusted to enhance, modify, or eliminate these characteristics. True experimental control of defect chemistry will likely only be achieved if routes for measuring defect structure are regularly integrated in the initial measurement of structure, and the direct impact of synthesis conditions and post-processing on defect distribution are consistently considered. Further advances in in-situ and operando microscopy and spectroscopy techniques, aimed at achieving atomic-level control over defect formation during synthesis (in-situ) or observing their effects on device performance (operando), is equally crucial.

An additional but related challenge is that state-of-the-art techniques for measuring defect structure, such as STEM are also used to create defects. This challenge is particularly pronounced in materials such as TMDs where it is well-known that STEM serves a dual purpose—evaluating the defect distribution in as-synthesized flakes and using the electron beam directly to create defects. Regardless, the prospects for such workflows has been significantly heightened by a recent surge of computational power improving the efficiency of first principles calculations, the synthesis methods outlined here, and advances in material imaging capabilities. The integration of these ever-evolving methods for modeling, synthesis, and imaging into workflows is likely key for defect engineering to reach its full potential. The resulting improvements in nanomaterial design could enable the development of Stokes shift engineered QDs for building integrated photovoltaic units, high-voltage lithium-ion batteries utilizing cation disordered oxides in electric vehicles, and TMD electrocatalysts for green hydrogen production. If the described technologies are then integrated into contemporary cities, a future marked by net-zero emission buildings, fossil fuel-free transportation, and carbon neutral hydrogen production would mark a major step forward in achieving a sustainable future.

Author contributions

AF: Conceptualization, Investigation, Writing–original draft. BS: Conceptualization, Investigation, Writing–review and editing. PG: Conceptualization, Investigation, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Center for Nanophase Materials Science (CNMS) and the Alvin M. Weinberg Fellowship at Oak Ridge National Laboratory.

The authors declare that this study received funding from Oak Ridge National Laboratory. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Acknowledgments

AF acknowledges support from the Alvin M. Weinberg Fellowship at Oak Ridge National Laboratory. This work was carried out at Oak Ridge National Laboratory’s Center for Nanophase Materials Sciences, a US Department of Energy Office of Science User Facility.

Licenses and permissions

This manuscript has been authored by UT-Battelle, LLC, under Contract No. DEAC0500OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for the United States Government purposes.

Conflict of interest

All authors are employees of Oak Ridge National Laboratory, managed by UT-Battelle LLC, an M&O contractor for the U.S. Department of Energy.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdin, Z., Zafaranloo, A., Rafiee, A., Mérida, W., Lipiński, W., and Khalilpour, K. R. (2020). Hydrogen as an energy vector. Renew. Sustain. Energy Rev. 120, 109620. doi:10.1016/j.rser.2019.109620

CrossRef Full Text | Google Scholar

Aktekin, B., Valvo, M., Smith, R. I., Sørby, M. H., Lodi Marzano, F., Zipprich, W., et al. (2019). Cation ordering and oxygen release in LiNi0.5–xMn1.5+xO4–y (LNMO): in situ neutron diffraction and performance in Li ion full cells. ACS Appl. Energy Mater. 2 (5), 3323–3335. doi:10.1021/acsaem.8b02217

CrossRef Full Text | Google Scholar

Algara-Siller, G., Kurasch, S., Sedighi, M., Lehtinen, O., and Kaiser, U. (2013). The pristine atomic structure of MoS2 monolayer protected from electron radiation damage by graphene. Appl. Phys. Lett. 103 (20). doi:10.1063/1.4830036

CrossRef Full Text | Google Scholar

Alstone, P., Gershenson, D., and Kammen, D. M. (2015). Decentralized energy systems for clean electricity access. Nat. Clim. Change 5 (4), 305–314. doi:10.1038/nclimate2512

CrossRef Full Text | Google Scholar

Alvarez-Garcia, J., Marcos-Ruzafa, J., Pérez-Rodriguez, A., Romano-Rodriguez, A., Morante, J. R., and Scheer, R. (2000). MicroRaman scattering from polycrystalline CuInS2 films: structural analysis. Thin Solid Films 361-362, 208–212. doi:10.1016/s0040-6090(99)00847-0

CrossRef Full Text | Google Scholar

Anand, A., Zaffalon, M. L., Gariano, G., Camellini, A., Gandini, M., Brescia, R., et al. (2020). Evidence for the band-edge exciton of CuInS2 nanocrystals enables record efficient large-area luminescent solar concentrators. Adv. Funct. Mater. 30 (4), 1906629. doi:10.1002/adfm.201906629

CrossRef Full Text | Google Scholar

Ansari, S. A., Khan, M. M., Kalathil, S., Nisar, A., Lee, J., and Cho, M. H. (2013). Oxygen vacancy induced band gap narrowing of ZnO nanostructures by an electrochemically active biofilm. Nanoscale 5 (19), 9238–9246. doi:10.1039/c3nr02678g

PubMed Abstract | CrossRef Full Text | Google Scholar

Ariyoshi, K., Iwakoshi, Y., Nakayama, N., and Ohzuku, T. (2004). Topotactic two-phase reactions of Li [ Ni1/2Mn3/2 ] O 4 (P4332) in nonaqueous lithium cells. J. Electrochem. Soc. 151 (2), A296. doi:10.1149/1.1639162

CrossRef Full Text | Google Scholar

Balachandran, J., Lin, L., Anchell, J. S., Bridges, C. A., and Ganesh, P. (2017). Defect genome of cubic perovskites for fuel cell applications. J. Phys. Chem. C 121 (48), 26637–26647. doi:10.1021/acs.jpcc.7b08716

CrossRef Full Text | Google Scholar

Banal, J. L., Ghiggino, K. P., and Wong, W. W. H. (2014). Efficient light harvesting of a luminescent solar concentrator using excitation energy transfer from an aggregation-induced emitter. Phys. Chem. Chem. Phys. 16 (46), 25358–25363. doi:10.1039/c4cp03807j

PubMed Abstract | CrossRef Full Text | Google Scholar

Batchelder, J. S., Zewai, A. H., and Cole, T. (1979). Luminescent solar concentrators. 1: theory of operation and techniques for performance evaluation. Appl. Opt. 18 (18), 3090–3110. doi:10.1364/ao.18.003090

PubMed Abstract | CrossRef Full Text | Google Scholar

Beaulac, R., Schneider, L., Archer, P. I., Bacher, G., and Gamelin, D. R. (2009). Light-induced spontaneous magnetization in doped colloidal quantum dots. Science 325 (5943), 973–976. doi:10.1126/science.1174419

PubMed Abstract | CrossRef Full Text | Google Scholar

Belloni, J. (2006). Nucleation, growth and properties of nanoclusters studied by radiation chemistry: application to catalysis. Catal. Today 113 (3), 141–156. doi:10.1016/j.cattod.2005.11.082

CrossRef Full Text | Google Scholar

Bennett, M. C., Hu, G., Wang, G., Heinonen, O., Kent, P. R. C., Krogel, J. T., et al. (2022). Origin of metal-insulator transitions in correlated perovskite metals. Phys. Rev. Res. 4 (2), L022005. doi:10.1103/physrevresearch.4.l022005

CrossRef Full Text | Google Scholar

Bergren, M. R., Makarov, N. S., Ramasamy, K., Jackson, A., Guglielmetti, R., and McDaniel, H. (2018). High-performance CuInS2 quantum dot laminated glass luminescent solar concentrators for windows. ACS Energy Lett. 3 (3), 520–525. doi:10.1021/acsenergylett.7b01346

CrossRef Full Text | Google Scholar

Bi, W., Ye, C., Xiao, C., Tong, W., Zhang, X., Shao, W., et al. (2014). Spatial location engineering of oxygen vacancies for optimized photocatalytic H2 evolution activity. Small 10 (14), 2820–2825. doi:10.1002/smll.201303548

PubMed Abstract | CrossRef Full Text | Google Scholar

Boebinger, M. G., Brea, C., Ding, L.-P., Misra, S., Olunloyo, O., Yu, Y., et al. (2023). The atomic drill bit: precision controlled atomic fabrication of 2D materials. Adv. Mater. 35 (14), 2210116. doi:10.1002/adma.202210116

CrossRef Full Text | Google Scholar

Bonu, V., Das, A., Amirthapandian, S., Dhara, S., and Tyagi, A. K. (2015). Photoluminescence of oxygen vacancies and hydroxyl group surface functionalized SnO2 nanoparticles. Phys. Chem. Chem. Phys. 17 (15), 9794–9801. doi:10.1039/c5cp00060b

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonu, V., Das, A., Prasad, A. K., Krishna, N. G., Dhara, S., and Tyagi, A. K. (2014). Influence of in-plane and bridging oxygen vacancies of SnO2 nanostructures on CH4 sensing at low operating temperatures. Appl. Phys. Lett. 105 (24). doi:10.1063/1.4904457

CrossRef Full Text | Google Scholar

Broberg, D., Bystrom, K., Srivastava, S., Dahliah, D., Williamson, B. A. D., Weston, L., et al. (2023). High-throughput calculations of charged point defect properties with semi-local density functional theory—performance benchmarks for materials screening applications. npj Comput. Mater. 9 (1), 72. doi:10.1038/s41524-023-01015-6

CrossRef Full Text | Google Scholar

Casas-Cabanas, M., Kim, C., Rodríguez-Carvajal, J., and Cabana, J. (2016). Atomic defects during ordering transitions in LiNi0.5Mn1.5O4 and their relationship with electrochemical properties. J. Mater. Chem. A 4 (21), 8255–8262. doi:10.1039/c6ta00424e

CrossRef Full Text | Google Scholar

Cen, J., Zhu, B., Kavanagh, S. R., Squires, A. G., and Scanlon, D. O. (2023). Cation disorder dominates the defect chemistry of high-voltage LiMn1.5Ni0.5O4 (LMNO) spinel cathodes. J. Mater. Chem. A 11 (25), 13353–13370. doi:10.1039/d3ta00532a

CrossRef Full Text | Google Scholar

Chebiam, R. V., Kannan, A. M., Prado, F., and Manthiram, A. (2001b). Comparison of the chemical stability of the high energy density cathodes of lithium-ion batteries. Electrochem. Commun. 3 (11), 624–627. doi:10.1016/s1388-2481(01)00232-6

CrossRef Full Text | Google Scholar

Chebiam, R. V., Prado, F., and Manthiram, A. (2001a). Soft chemistry synthesis and characterization of layered Li1-xNi1-yCoyO2-δ (0 ≤ x ≤ 1 and 0 ≤ y ≤ 1). Chem. Mater. 13 (9), 2951–2957. doi:10.1021/cm0102537

CrossRef Full Text | Google Scholar

Chen, D., Ahn, J., Self, E., Nanda, J., and Chen, G. (2021a). Understanding cation-disordered rocksalt oxyfluoride cathodes. J. Mater. Chem. A 9 (12), 7826–7837. doi:10.1039/d0ta12179g

CrossRef Full Text | Google Scholar

Chen, J., Ryu, G. H., Sinha, S., and Warner, J. H. (2019). Atomic structure and dynamics of defects and grain boundaries in 2D Pd2Se3 monolayers. ACS Nano 13 (7), 8256–8264. doi:10.1021/acsnano.9b03645

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Xu, B., Jin, M., Chen, L., Yi, G., Xing, B., et al. (2023). Excellent photocatalysis of Bi2WO6 structured with oxygen vacancies in degradation of tetracycline. J. Mol. Struct. 1278, 134911. doi:10.1016/j.molstruc.2023.134911

CrossRef Full Text | Google Scholar

Chen, X., Li, C., Grätzel, M., Kostecki, R., and Mao, S. S. (2012). Nanomaterials for renewable energy production and storage. Chem. Soc. Rev. 41 (23), 7909–7937. doi:10.1039/c2cs35230c

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Liu, L., and Huang, F. (2015). Black titanium dioxide (TiO2) nanomaterials. Chem. Soc. Rev. 44 (7), 1861–1885. doi:10.1039/c4cs00330f

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Liu, L., Yu, P. Y., and Mao, S. S. (2011). Increasing solar absorption for photocatalysis with black hydrogenated titanium dioxide nanocrystals. Science 331 (6018), 746–750. doi:10.1126/science.1200448

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Qiao, Q., Cao, J., Li, H., and Bian, Z. (2021b). Precious metal recovery. Joule 5 (12), 3097–3115. doi:10.1016/j.joule.2021.11.002

CrossRef Full Text | Google Scholar

Chen, Y., Xi, J., Dumcenco, D. O., Liu, Z., Suenaga, K., Wang, D., et al. (2013). Tunable band gap photoluminescence from atomically thin transition-metal dichalcogenide alloys. ACS Nano 7 (5), 4610–4616. doi:10.1021/nn401420h

PubMed Abstract | CrossRef Full Text | Google Scholar

Chhowalla, M., Shin, H. S., Eda, G., Li, L.-J., Loh, K. P., and Zhang, H. (2013). The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5 (4), 263–275. doi:10.1038/nchem.1589

PubMed Abstract | CrossRef Full Text | Google Scholar

Choudhary, K., and Sumpter, B. G. (2023). Can a deep-learning model make fast predictions of vacancy formation in diverse materials? AIP Adv. 13 (9). doi:10.1063/5.0135382

CrossRef Full Text | Google Scholar

Chu, S., and Majumdar, A. (2012). Opportunities and challenges for a sustainable energy future. Nature 488 (7411), 294–303. doi:10.1038/nature11475

PubMed Abstract | CrossRef Full Text | Google Scholar

Chua, R., Yang, J., He, X., Yu, X., Yu, W., Bussolotti, F., et al. (2020). Can reconstructed Se-deficient line defects in monolayer VSe2 induce magnetism? Adv. Mater. 32 (24), 2000693. doi:10.1002/adma.202000693

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, P. U., Shakun, J. D., Marcott, S. A., Mix, A. C., Eby, M., Kulp, S., et al. (2016). Consequences of twenty-first-century policy for multi-millennial climate and sea-level change. Nat. Clim. Change 6 (4), 360–369. doi:10.1038/nclimate2923

CrossRef Full Text | Google Scholar

Corrado, C., Hawker, M., Livingston, G., Medling, S., Bridges, F., and Zhang, J. Z. (2010). Enhanced Cu emission in ZnS: Cu,Cl/ZnS core–shell nanocrystals. Nanoscale 2 (7), 1213–1221. doi:10.1039/c0nr00056f

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, W., Xu, S., Yan, B., Guo, Z., Xu, Q., Sumpter, B. G., et al. (2017). Triphasic 2D materials by vertically stacking laterally heterostructured 2H-/1T′-MoS2 on graphene for enhanced photoresponse. Adv. Electron. Mater. 3 (7), 1700024. doi:10.1002/aelm.201700024

CrossRef Full Text | Google Scholar

Currie, M. J., Mapel, J. K., Heidel, T. D., Goffri, S., and Baldo, M. A. (2008). High-efficiency organic solar concentrators for photovoltaics. Science 321 (5886), 226–228. doi:10.1126/science.1158342

PubMed Abstract | CrossRef Full Text | Google Scholar

Dathar, G. K. P., Balachandran, J., Kent, P. R. C., Rondinone, A. J., and Ganesh, P. (2017). Li-ion site disorder driven superionic conductivity in solid electrolytes: a first-principles investigation of β-Li3PS4. J. Mater. Chem. A 5 (3), 1153–1159. doi:10.1039/c6ta07713g

CrossRef Full Text | Google Scholar

Debije, M. G., and Verbunt, P. P. C. (2012). Thirty years of luminescent solar concentrator research: solar energy for the built environment. Adv. Energy Mater. 2 (1), 12–35. doi:10.1002/aenm.201100554

CrossRef Full Text | Google Scholar

Deng, Y., Zhao, X., Zhu, C., Li, P., Duan, R., Liu, G., et al. (2021). MoTe2: semiconductor or semimetal? ACS Nano 15 (8), 12465–12474. doi:10.1021/acsnano.1c01816

PubMed Abstract | CrossRef Full Text | Google Scholar

Desmet, L., Ras, A. J. M., de Boer, D. K. G., and Debije, M. G. (2012). Monocrystalline silicon photovoltaic luminescent solar concentrator with 4.2% power conversion efficiency. Opt. Lett. 37 (15), 3087–3089. doi:10.1364/ol.37.003087

PubMed Abstract | CrossRef Full Text | Google Scholar

Dincer, I. (2012). Green methods for hydrogen production. Int. J. Hydrogen Energy 37 (2), 1954–1971. doi:10.1016/j.ijhydene.2011.03.173

CrossRef Full Text | Google Scholar

Ding, J., Balachandran, J., Sang, X., Guo, W., Anchell, J. S., Veith, G. M., et al. (2018). The influence of local distortions on proton mobility in acceptor doped perovskites. Chem. Mater. 30 (15), 4919–4925. doi:10.1021/acs.chemmater.8b00502

CrossRef Full Text | Google Scholar

Dixit, H., Zhou, W., Idrobo, J.-C., Nanda, J., and Cooper, V. R. (2014). Facet-Dependent disorder in pristine high-voltage lithium–manganese-rich cathode material. ACS Nano 8 (12), 12710–12716. doi:10.1021/nn505740v

PubMed Abstract | CrossRef Full Text | Google Scholar

Dreyer, C. E., Alkauskas, A., Lyons, J. L., Janotti, A., and Walle, C. G. V. d. (2018). First-principles calculations of point defects for quantum technologies. Annu. Rev. Mater. Res. 48 (1), 1–26. doi:10.1146/annurev-matsci-070317-124453

CrossRef Full Text | Google Scholar

Du, J., Singh, R., Fedin, I., Fuhr, A. S., and Klimov, V. I. (2020). Spectroscopic insights into high defect tolerance of Zn:CuInSe2 quantum-dot-sensitized solar cells. Nat. Energy 5 (5), 409–417. doi:10.1038/s41560-020-0617-6

CrossRef Full Text | Google Scholar

Du, M.-H., Yan, J., Cooper, V. R., and Eisenbach, M. (2021). Tuning Fermi levels in intrinsic antiferromagnetic topological insulators MnBi2Te4 and MnBi4Te7 by defect engineering and chemical doping. Adv. Funct. Mater. 31 (3), 2006516. doi:10.1002/adfm.202006516

CrossRef Full Text | Google Scholar

Dumcenco, D. O., Kobayashi, H., Liu, Z., Huang, Y.-S., and Suenaga, K. (2013). Visualization and quantification of transition metal atomic mixing in Mo1−xWxS2 single layers. Nat. Commun. 4 (1), 1351. doi:10.1038/ncomms2351

PubMed Abstract | CrossRef Full Text | Google Scholar

Dyck, O., Zhang, C., Rack, P. D., Fowlkes, J. D., Sumpter, B., Lupini, A. R., et al. (2020). Electron-beam introduction of heteroatomic Pt–Si structures in graphene. Carbon 161, 750–757. doi:10.1016/j.carbon.2020.01.042

CrossRef Full Text | Google Scholar

Egdell, R. G., Eriksen, S., and Flavell, W. R. (1987). A spectroscopic study of electron and ion beam reduction of SnO2(110). Surf. Sci. 192 (1), 265–274. doi:10.1016/s0039-6028(87)81175-5

CrossRef Full Text | Google Scholar

Elibol, K., Susi, T., Argentero, G., Reza Ahmadpour Monazam, M., Pennycook, T. J., Meyer, J. C., et al. (2018). Atomic structure of intrinsic and electron-irradiation-induced defects in MoTe2. Chem. Mater. 30 (4), 1230–1238. doi:10.1021/acs.chemmater.7b03760

PubMed Abstract | CrossRef Full Text | Google Scholar

Enyashin, A. N., Bar-Sadan, M., Houben, L., and Seifert, G. (2013). Line defects in molybdenum disulfide layers. J. Phys. Chem. C 117 (20), 10842–10848. doi:10.1021/jp403976d

CrossRef Full Text | Google Scholar

Erickson, C. S., Bradshaw, L. R., McDowall, S., Gilbertson, J. D., Gamelin, D. R., and Patrick, D. L. (2014). Zero-reabsorption doped-nanocrystal luminescent solar concentrators. ACS Nano 8 (4), 3461–3467. doi:10.1021/nn406360w

PubMed Abstract | CrossRef Full Text | Google Scholar

Erwin, S. C., Zu, L., Haftel, M. I., Efros, A. L., Kennedy, T. A., and Norris, D. J. (2005). Doping semiconductor nanocrystals. Nature 436 (7047), 91–94. doi:10.1038/nature03832

PubMed Abstract | CrossRef Full Text | Google Scholar

Fang, W., Xing, M., and Zhang, J. (2014). A new approach to prepare Ti3+ self-doped TiO2 via NaBH4 reduction and hydrochloric acid treatment. Appl. Catal. B Environ. 160-161, 240–246. doi:10.1016/j.apcatb.2014.05.031

CrossRef Full Text | Google Scholar

Feng, Q., Zhu, Y., Hong, J., Zhang, M., Duan, W., Mao, N., et al. (2014). Growth of large-area 2D MoS2(1-x)Se2x semiconductor alloys. Adv. Mater. 26 (17), 2648–2653. doi:10.1002/adma.201306095

PubMed Abstract | CrossRef Full Text | Google Scholar

Freysoldt, C., Grabowski, B., Hickel, T., Neugebauer, J., Kresse, G., Janotti, A., et al. (2014). First-principles calculations for point defects in solids. Rev. Mod. Phys. 86 (1), 253–305. doi:10.1103/revmodphys.86.253

CrossRef Full Text | Google Scholar

Freysoldt, C., Neugebauer, J., and Van de Walle, C. G. (2009). Fully ab initio finite-size corrections for charged-defect supercell calculations. Phys. Rev. Lett. 102 (1), 016402. doi:10.1103/physrevlett.102.016402

PubMed Abstract | CrossRef Full Text | Google Scholar

Frick, J. J., Cheng, G., Kushwaha, S., Yao, N., Wagner, S., Bocarsly, A. B., et al. (2020). Observation of [VCu1–ini2+VCu1–] defect triplets in Cu-deficient CuInS2. J. Phys. Chem. C 124 (48), 26415–26427. doi:10.1021/acs.jpcc.0c08872

CrossRef Full Text | Google Scholar

Fuhr, A., Yun, H. J., Crooker, S. A., and Klimov, V. I. (2020b). Spectroscopic and magneto-optical signatures of Cu1+ and Cu2+ defects in copper indium sulfide quantum dots. ACS Nano 14 (2), 2212–2223. doi:10.1021/acsnano.9b09181

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuhr, A. S., Alexandrova, A. N., and Sautet, P. (2020a). Stoichiometry-controllable optical defects in CuxIn2−xSy quantum dots for energy harvesting. J. Mater. Chem. A 8 (25), 12556–12565. doi:10.1039/d0ta03954c

CrossRef Full Text | Google Scholar

Fuhr, A. S., Ganesh, P., Vasudevan, R. K., and Sumpter, B. G. (2023). Bridging theory with experiment: digital twins and deep learning segmentation of defects in monolayer MX2 phases. arXiv:2305.02917. doi:10.48550/arXiv.2305.02917

CrossRef Full Text | Google Scholar

Fuhr, A. S., Sautet, P., and Alexandrova, A. N. (2019). Heterogeneity in local chemical bonding explains spectral broadening in quantum dots with Cu impurities. J. Phys. Chem. C 123 (9), 5705–5713. doi:10.1021/acs.jpcc.8b12023

CrossRef Full Text | Google Scholar

Fuhr, A. S., Yun, H. J., Makarov, N. S., Li, H., McDaniel, H., and Klimov, V. I. (2017). Light emission mechanisms in CuInS2 quantum dots evaluated by spectral electrochemistry. ACS Photonics 4 (10), 2425–2435. doi:10.1021/acsphotonics.7b00560

CrossRef Full Text | Google Scholar

Ganesh, P., Lechermann, F., Kylänpää, I., Krogel, J. T., Kent, P. R. C., and Heinonen, O. (2020). Doping a bad metal: origin of suppression of the metal-insulator transition in nonstoichiometric VO_{2}. Phys. Rev. B 101 (15), 155129. doi:10.1103/physrevb.101.155129

CrossRef Full Text | Google Scholar

Gao, J., Kim, Y. D., Liang, L., Idrobo, J. C., Chow, P., Tan, J., et al. (2016). Transition-metal substitution doping in synthetic atomically thin semiconductors. Adv. Mater. 28 (44), 9735–9743. doi:10.1002/adma.201601104

PubMed Abstract | CrossRef Full Text | Google Scholar

Giustino, F., and Snaith, H. J. (2016). Toward lead-free perovskite solar cells. ACS Energy Lett. 1 (6), 1233–1240. doi:10.1021/acsenergylett.6b00499

CrossRef Full Text | Google Scholar

Glaister, B. J., and Mudd, G. M. (2010). The environmental costs of platinum–PGM mining and sustainability: is the glass half-full or half-empty? Miner. Eng. 23 (5), 438–450. doi:10.1016/j.mineng.2009.12.007

CrossRef Full Text | Google Scholar

Goodenough, J. B. (1971). Metallic oxides. Prog. Solid State Chem. 5, 145–399. doi:10.1016/0079-6786(71)90018-5

CrossRef Full Text | Google Scholar

Gul, S., Cooper, J. K., Corrado, C., Vollbrecht, B., Bridges, F., Guo, J., et al. (2011). Synthesis, optical and structural properties, and charge carrier dynamics of Cu-doped ZnSe nanocrystals. J. Phys. Chem. C 115 (43), 20864–20875. doi:10.1021/jp2047272

CrossRef Full Text | Google Scholar

Gungor, K., Du, J., and Klimov, V. I. (2022). General Trends in the Performance of quantum dot luminescent solar concentrators (LSCs) revealed Using the “effective LSC quality factor”. ACS Energy Lett. 7 (5), 1741–1749. doi:10.1021/acsenergylett.2c00781

CrossRef Full Text | Google Scholar

Guo, Y., Kalinin, S. V., Cai, H., Xiao, K., Krylyuk, S., Davydov, A. V., et al. (2021). Defect detection in atomic-resolution images via unsupervised learning with translational invariance. npj Comput. Mater. 7 (1), 180. doi:10.1038/s41524-021-00642-1

CrossRef Full Text | Google Scholar

Gutiérrez, H. R., Perea-López, N., Elías, A. L., Berkdemir, A., Wang, B., Lv, R., et al. (2013). Extraordinary room-temperature photoluminescence in triangular WS2 monolayers. Nano Lett. 13 (8), 3447–3454. doi:10.1021/nl3026357

PubMed Abstract | CrossRef Full Text | Google Scholar

Hahn, T., Metzner, H., Plikat, B., and Seibt, M. (2001). Order and disorder in epitaxially grown CuInS2. Thin Solid Films 387 (1), 83–85. doi:10.1016/s0040-6090(01)00790-8

CrossRef Full Text | Google Scholar

Hallegatte, S., Rogelj, J., Allen, M., Clarke, L., Edenhofer, O., Field, C. B., et al. (2016). Mapping the climate change challenge. Nat. Clim. Change 6 (7), 663–668. doi:10.1038/nclimate3057

CrossRef Full Text | Google Scholar

Han, D., Rudel, S. S., Schnick, W., and Ebert, H. (2022). Self-doping behavior and cation disorder in MgSnN₂. Phys. Rev. B 105 (12), 125202. doi:10.1103/physrevb.105.125202

CrossRef Full Text | Google Scholar

Harchol, A., Barak, Y., Hughes, K. E., Hartstein, K. H., Jöbsis, H. j., Prins, P. T., et al. (2022). Optically detected magnetic resonance spectroscopy of Cu-doped CdSe/CdS and CuInS2 colloidal quantum dots. ACS Nano 16 (8), 12866–12877. doi:10.1021/acsnano.2c05130

PubMed Abstract | CrossRef Full Text | Google Scholar

Haruna, A. B., Mwonga, P., Barrett, D., Rodella, C. B., Forbes, R. P., Venter, A., et al. (2021). Defect-engineered β-MnO2−δ precursors control the structure–property relationships in high-voltage spinel LiMn1.5Ni0.5O4−δ. ACS Omega 6 (39), 25562–25573. doi:10.1021/acsomega.1c03656

PubMed Abstract | CrossRef Full Text | Google Scholar

He, Z., Zhao, R., Chen, X., Chen, H., Zhu, Y., Su, H., et al. (2018). Defect engineering in single-layer MoS2 using heavy ion irradiation. ACS Appl. Mater. Interfaces 10 (49), 42524–42533. doi:10.1021/acsami.8b17145

PubMed Abstract | CrossRef Full Text | Google Scholar

Hinnemann, B., Moses, P. G., Bonde, J., Jørgensen, K. P., Nielsen, J. H., Horch, S., et al. (2005). Biomimetic hydrogen evolution: MoS2 nanoparticles as catalyst for hydrogen evolution. J. Am. Chem. Soc. 127 (15), 5308–5309. doi:10.1021/ja0504690

PubMed Abstract | CrossRef Full Text | Google Scholar

Hinterding, S. O. M., Mangnus, M. J. J., Prins, P. T., Jöbsis, H. J., Busatto, S., Vanmaekelbergh, D., et al. (2021). Unusual spectral diffusion of single CuInS2 quantum dots sheds light on the mechanism of radiative decay. Nano Lett. 21 (1), 658–665. doi:10.1021/acs.nanolett.0c04239

PubMed Abstract | CrossRef Full Text | Google Scholar

Houck, D. W., Assaf, E. I., Shin, H., Greene, R. M., Pernik, D. R., and Korgel, B. A. (2019). Pervasive cation vacancies and antisite defects in copper indium diselenide (CuInSe2) nanocrystals. J. Phys. Chem. C 123 (14), 9544–9551. doi:10.1021/acs.jpcc.9b00558

CrossRef Full Text | Google Scholar

Hu, C., Zeng, X., Liu, Y., Zhou, M., Zhao, H., Tritt, T. M., et al. (2017). Effects of partial La filling and Sb vacancy defects on CoS b₃ skutterudites. Phys. Rev. B 95 (16), 165204. doi:10.1103/physrevb.95.165204

CrossRef Full Text | Google Scholar

Hu, G., Fung, V., Sang, X., Unocic, R. R., and Ganesh, P. (2019). Superior electrocatalytic hydrogen evolution at engineered non-stoichiometric two-dimensional transition metal dichalcogenide edges. J. Mater. Chem. A 7 (31), 18357–18364. doi:10.1039/c9ta05546k

CrossRef Full Text | Google Scholar

Hu, G., Fung, V., Sang, X., Unocic, R. R., and Ganesh, P. (2020). Predicting synthesizable multi-functional edge reconstructions in two-dimensional transition metal dichalcogenides. npj Comput. Mater. 6 (1), 44. doi:10.1038/s41524-020-0327-4

CrossRef Full Text | Google Scholar

Hughes, K. E., Ostheller, S. R., Nelson, H. D., and Gamelin, D. R. (2019). Copper’s role in the photoluminescence of Ag1–xCuxInS2 nanocrystals, from copper-doped AgInS2 (x ∼ 0) to CuInS2 (x = 1). Nano Lett. 19 (2), 1318–1325. doi:10.1021/acs.nanolett.8b04905

PubMed Abstract | CrossRef Full Text | Google Scholar

Iberi, V., Liang, L., Ievlev, A. V., Stanford, M. G., Lin, M.-W., Li, X., et al. (2016). Nanoforging single layer MoSe2 through defect engineering with focused helium ion beams. Sci. Rep. 6 (1), 30481. doi:10.1038/srep30481

PubMed Abstract | CrossRef Full Text | Google Scholar

Islam, M. R., Kang, N., Bhanu, U., Paudel, H. P., Erementchouk, M., Tetard, L., et al. (2014). Tuning the electrical property via defect engineering of single layer MoS2 by oxygen plasma. Nanoscale 6 (17), 10033–10039. doi:10.1039/c4nr02142h

PubMed Abstract | CrossRef Full Text | Google Scholar

Jara, D. H., Stamplecoskie, K. G., and Kamat, P. V. (2016). Two distinct transitions in CuxInS2 quantum dots. Bandgap versus sub-bandgap excitations in copper-deficient structures. J. Phys. Chem. Lett. 7 (8), 1452–1459. doi:10.1021/acs.jpclett.6b00571

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeong, J., Choi, S.-P., Chang, C. I., Shin, D. C., Park, J. S., Lee, B. T., et al. (2003). Photoluminescence properties of SnO2 thin films grown by thermal CVD. Solid State Commun. 127 (9), 595–597. doi:10.1016/s0038-1098(03)00614-8

CrossRef Full Text | Google Scholar

Ji, T., Jian, W.-B., and Fang, J. (2003). The first synthesis of Pb1-xMnxSe nanocrystals. J. Am. Chem. Soc. 125 (28), 8448–8449. doi:10.1021/ja0351746

PubMed Abstract | CrossRef Full Text | Google Scholar

Jian, W. B., Fang, J., Ji, T., and He, J. (2003). Quantum-size-effect-enhanced dynamic magnetic interactions among doped spins in Cd1−xMnxSe nanocrystals. Appl. Phys. Lett. 83 (16), 3377–3379. doi:10.1063/1.1619564

CrossRef Full Text | Google Scholar

Jiang, J., Zhang, L., Li, H., He, W., and Yin, J. J. (2013). Self-doping and surface plasmon modification induced visible light photocatalysis of BiOCl. Nanoscale 5 (21), 10573–10581. doi:10.1039/c3nr03597b

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiao, Y., Hafez, A. M., Cao, D., Mukhopadhyay, A., Ma, Y., and Zhu, H. (2018). Metallic MoS2 for high performance energy storage and energy conversion. Small 14 (36), 1800640. doi:10.1002/smll.201800640

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaczkowski, J., and Płowaś-Korus, I. (2021). The vibrational and thermodynamic properties of CsPbI3 polymorphs: an improved description based on the SCAN meta-GGA functional. J. Phys. Chem. Lett. 12 (28), 6613–6621. doi:10.1021/acs.jpclett.1c01798

PubMed Abstract | CrossRef Full Text | Google Scholar

Källquist, I., Naylor, A. J., Baur, C., Chable, J., Kullgren, J., Fichtner, M., et al. (2019). Degradation mechanisms in Li2VO2F Li-rich disordered rock-salt cathodes. Chem. Mater. 31 (16), 6084–6096. doi:10.1021/acs.chemmater.9b00829

CrossRef Full Text | Google Scholar

Kan, W. H., Kuppan, S., Cheng, L., Doeff, M., Nanda, J., Huq, A., et al. (2017). Crystal chemistry and electrochemistry of LixMn1.5Ni0.5O4 solid solution cathode materials. Chem. Mater. 29 (16), 6818–6828. doi:10.1021/acs.chemmater.7b01898

CrossRef Full Text | Google Scholar

Kang, N., Paudel, H. P., Leuenberger, M. N., Tetard, L., and Khondaker, S. I. (2014). Photoluminescence quenching in single-layer MoS2 via oxygen plasma treatment. J. Phys. Chem. C 118 (36), 21258–21263. doi:10.1021/jp506964m

CrossRef Full Text | Google Scholar

Kelley, K. P., Morozovska, A. N., Eliseev, E. A., Sharma, V., Yilmaz, D. E., van Duin, A. C. T., et al. (2022). Oxygen vacancy injection as a pathway to enhancing electromechanical response in ferroelectrics. Adv. Mater. 34 (2), 2106426. doi:10.1002/adma.202106426

CrossRef Full Text | Google Scholar

Kibsgaard, J., Chen, Z., Reinecke, B. N., and Jaramillo, T. F. (2012). Engineering the surface structure of MoS2 to preferentially expose active edge sites for electrocatalysis. Nat. Mater. 11 (11), 963–969. doi:10.1038/nmat3439

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, J.-H., Mirzaei, A., Kim, J.-Y., Lee, J.-H., Kim, H. W., Hishita, S., et al. (2020). Enhancement of gas sensing by implantation of Sb-ions in SnO2 nanowires. Sensors Actuators B Chem. 304, 127307. doi:10.1016/j.snb.2019.127307

CrossRef Full Text | Google Scholar

Kim, J. H., Myung, S. T., Yoon, C. S., Kang, S. G., and Sun, Y. K. (2004). Comparative study of LiNi0.5Mn1.5O4-δ and LiNi0.5Mn1.5O4 cathodes having two crystallographic structures: Fd3m and P4332. Chem. Mater. 16 (5), 906–914. doi:10.1021/cm035050s

CrossRef Full Text | Google Scholar

Kim, Y.-K., Ahn, S.-H., Chung, K., Cho, Y.-S., and Choi, C.-J. (2012). The photoluminescence of CuInS2 nanocrystals: effect of non-stoichiometry and surface modification. J. Mater. Chem. 22 (4), 1516–1520. doi:10.1039/c1jm13170b

CrossRef Full Text | Google Scholar

Klimov, V. I., Baker, T. A., Lim, J., Velizhanin, K. A., and McDaniel, H. (2016). Quality factor of luminescent solar concentrators and practical concentration limits attainable with semiconductor quantum dots. ACS Photonics 3 (6), 1138–1148. doi:10.1021/acsphotonics.6b00307

CrossRef Full Text | Google Scholar

Knowles, K. E., Nelson, H. D., Kilburn, T. B., and Gamelin, D. R. (2015). Singlet–triplet splittings in the luminescent excited states of colloidal Cu+:CdSe, Cu+:InP, and CuInS2 nanocrystals: charge-transfer configurations and self-trapped excitons. J. Am. Chem. Soc. 137 (40), 13138–13147. doi:10.1021/jacs.5b08547

PubMed Abstract | CrossRef Full Text | Google Scholar

Komsa, H.-P., Kurasch, S., Lehtinen, O., Kaiser, U., and Krasheninnikov, A. V. (2013). From point to extended defects in two-dimensional MoS₂: evolution of atomic structure under electron irradiation. Phys. Rev. B 88 (3), 035301. doi:10.1103/physrevb.88.035301

CrossRef Full Text | Google Scholar

Komsa, H.-P., Rantala, T. T., and Pasquarello, A. (2012). Finite-size supercell correction schemes for charged defect calculations. Phys. Rev. B 86 (4), 045112. doi:10.1103/physrevb.86.045112

CrossRef Full Text | Google Scholar

Komuro, Y., and Matsumoto, Y. (2011). Electron beam irradiation-induced reduction of SnO2 deposited on TiO2(110) surfaces. J. Phys. Chem. C 115 (14), 6618–6621. doi:10.1021/jp111703p

CrossRef Full Text | Google Scholar

Kondratowicz, I., Nadolska, M., Şahin, S., Łapiński, M., Prześniak-Welenc, M., Sawczak, M., et al. (2018). Tailoring properties of reduced graphene oxide by oxygen plasma treatment. Appl. Surf. Sci. 440, 651–659. doi:10.1016/j.apsusc.2018.01.168

CrossRef Full Text | Google Scholar

Kong, D., Wang, H., Cha, J. J., Pasta, M., Koski, K. J., Yao, J., et al. (2013). Synthesis of MoS2 and MoSe2 Films with Vertically Aligned Layers. Nano Lett. 13 (3), 1341–1347. doi:10.1021/nl400258t

PubMed Abstract | CrossRef Full Text | Google Scholar

Kröger, F. A., and Vink, H. J. (1956). “Relations between the concentrations of imperfections in crystalline solids,” in Solid state physics. Editors F. Seitz, and D. Turnbull (Academic Press), 307–435.

Google Scholar

Kunduraci, M., and Amatucci, G. G. (2006). Synthesis and characterization of nanostructured 4.7 V lix Mn1.5Ni0.5O4 spinels for high-power lithium-ion batteries. J. Electrochem. Soc. 153 (7), A1345. doi:10.1149/1.2198110

CrossRef Full Text | Google Scholar

Kwon, Y. J., Kang, S. Y., Wu, P., Peng, Y., Kim, S. S., and Kim, H. W. (2016). Selective improvement of NO2 gas sensing behavior in SnO2 nanowires by ion-beam irradiation. ACS Appl. Mater. Interfaces 8 (21), 13646–13658. doi:10.1021/acsami.6b01619

PubMed Abstract | CrossRef Full Text | Google Scholar

Lany, S., and Zunger, A. (2008). Assessment of correction methods for the band-gap problem and for finite-size effects in supercell defect calculations: case studies for ZnO and GaAs. Phys. Rev. B 78 (23), 235104. doi:10.1103/physrevb.78.235104

CrossRef Full Text | Google Scholar

Le Bahers, T., Rérat, M., and Sautet, P. (2014). Semiconductors used in photovoltaic and photocatalytic devices: assessing fundamental properties from DFT. J. Phys. Chem. C 118 (12), 5997–6008. doi:10.1021/jp409724c

CrossRef Full Text | Google Scholar

Lee, C.-H., Khan, A., Luo, D., Santos, T. P., Shi, C., Janicek, B. E., et al. (2020). Deep learning enabled strain mapping of single-atom defects in two-dimensional transition metal dichalcogenides with sub-picometer precision. Nano Lett. 20 (5), 3369–3377. doi:10.1021/acs.nanolett.0c00269

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J., Kang, S., Yim, K., Kim, K. Y., Jang, H. W., Kang, Y., et al. (2018). Hydrogen evolution reaction at anion vacancy of two-dimensional transition-metal dichalcogenides: ab initio computational screening. J. Phys. Chem. Lett. 9 (8), 2049–2055. doi:10.1021/acs.jpclett.8b00712

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J., Papp, J. K., Clément, R. J., Sallis, S., Kwon, D.-H., Shi, T., et al. (2017a). Mitigating oxygen loss to improve the cycling performance of high capacity cation-disordered cathode materials. Nat. Commun. 8 (1), 981. doi:10.1038/s41467-017-01115-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J., Seo, D.-H., Balasubramanian, M., Twu, N., Li, X., and Ceder, G. (2015). A new class of high capacity cation-disordered oxides for rechargeable lithium batteries: Li–Ni–Ti–Mo oxides. Energy & Environ. Sci. 8 (11), 3255–3265. doi:10.1039/c5ee02329g

CrossRef Full Text | Google Scholar

Lee, J., Urban, A., Li, X., Su, D., Hautier, G., and Ceder, G. (2014). Unlocking the potential of cation-disordered oxides for rechargeable lithium batteries. Science 343 (6170), 519–522. doi:10.1126/science.1246432

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, K., Park, J., Choi, S., Lee, Y., Lee, S., Jung, J., et al. (2022). STEM image analysis based on deep learning: identification of vacancy defects and polymorphs of MoS2. Nano Lett. 22 (12), 4677–4685. doi:10.1021/acs.nanolett.2c00550

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, K., Yang, G. J., and Kim, Y. (2017b). Improvement of the electrochemical properties of LiNi0.5Mn1.5O4 by controlling the heating atmosphere during synthesis. Ceram. Int. 43 (17), 15510–15518. doi:10.1016/j.ceramint.2017.08.100

CrossRef Full Text | Google Scholar

Li, B., Huang, L., Zhong, M., Huo, N., Li, Y., Yang, S., et al. (2015). Synthesis and transport properties of large-scale alloy Co0.16Mo0.84S2 bilayer nanosheets. ACS Nano 9 (2), 1257–1262. doi:10.1021/nn505048y

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, G., Blake, G. R., and Palstra, T. T. M. (2017a). Vacancies in functional materials for clean energy storage and harvesting: the perfect imperfection. Chem. Soc. Rev. 46 (6), 1693–1706. doi:10.1039/c6cs00571c

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Tsai, C., Koh, A. L., Cai, L., Contryman, A. W., Fragapane, A. H., et al. (2016). Activating and optimizing MoS2 basal planes for hydrogen evolution through the formation of strained sulphur vacancies. Nat. Mater. 15 (1), 48–53. doi:10.1038/nmat4465

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, L., Qin, Z., Ries, L., Hong, S., Michel, T., Yang, J., et al. (2019). Role of sulfur vacancies and undercoordinated Mo regions in MoS2 nanosheets toward the evolution of hydrogen. ACS Nano 13 (6), 6824–6834. doi:10.1021/acsnano.9b01583

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Puretzky, A. A., Sang, X., Kc, S., Tian, M., Ceballos, F., et al. (2017b). Suppression of defects and deep levels using isoelectronic tungsten substitution in monolayer MoSe2. Adv. Funct. Mater. 27 (19), 1603850. doi:10.1002/adfm.201603850

CrossRef Full Text | Google Scholar

Li, Y., Zuo, S., Li, Q.-H., Wu, X., Zhang, J., Zhang, H., et al. (2021). Vertically aligned MoS2 with in-plane selectively cleaved Mo–S bond for hydrogen production. Nano Lett. 21 (4), 1848–1855. doi:10.1021/acs.nanolett.0c04978

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, G., Didier, C., Guo, Z., Pang, W. K., and Peterson, V. K. (2020c). Understanding rechargeable battery function using in operando neutron powder diffraction. Adv. Mater. 32 (18), 1904528. doi:10.1002/adma.201904528

CrossRef Full Text | Google Scholar

Liang, G., Peterson, V. K., See, K. W., Guo, Z., and Pang, W. K. (2020b). Developing high-voltage spinel LiNi0.5Mn1.5O4 cathodes for high-energy-density lithium-ion batteries: current achievements and future prospects. J. Mater. Chem. A 8 (31), 15373–15398. doi:10.1039/d0ta02812f

CrossRef Full Text | Google Scholar

Liang, Q., Zhang, Q., Gou, J., Song, T., Arramel, H., Chen, H., et al. (2020a). Performance improvement by ozone treatment of 2D PdSe2. ACS Nano 14 (5), 5668–5677. doi:10.1021/acsnano.0c00180

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, Q., Zhang, Q., Zhao, X., Liu, M., and Wee, A. T. S. (2021). Defect engineering of two-dimensional transition-metal dichalcogenides: applications, challenges, and opportunities. ACS Nano 15 (2), 2165–2181. doi:10.1021/acsnano.0c09666

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, W., Nie, C., Du, J., Han, Y., Zhao, G., Yang, F., et al. (2023). Near-infrared photon upconversion and solar synthesis using lead-free nanocrystals. Nat. Photonics 17 (4), 346–353. doi:10.1038/s41566-023-01156-6

CrossRef Full Text | Google Scholar

Lin, Z., Carvalho, B. R., Kahn, E., Lv, R., Rao, R., Terrones, H., et al. (2016). Defect engineering of two-dimensional transition metal dichalcogenides. 2D Mater. 3 (2), 022002. doi:10.1088/2053-1583/3/2/022002

CrossRef Full Text | Google Scholar

Lingerfelt, D. B., Ganesh, P., Jakowski, J., and Sumpter, B. G. (2019). Electronically nonadiabatic structural transformations promoted by electron beams. Adv. Funct. Mater. 29 (52), 1901901. doi:10.1002/adfm.201901901

CrossRef Full Text | Google Scholar

Lingerfelt, D. B., Ganesh, P., Jakowski, J., and Sumpter, B. G. (2020). Understanding beam-induced electronic excitations in materials. J. Chem. Theory Comput. 16 (2), 1200–1214. doi:10.1021/acs.jctc.9b00792

PubMed Abstract | CrossRef Full Text | Google Scholar

Lingerfelt, D. B., Yu, T., Yoshimura, A., Ganesh, P., Jakowski, J., and Sumpter, B. G. (2021). Nonadiabatic effects on defect diffusion in silicon-doped nanographenes. Nano Lett. 21 (1), 236–242. doi:10.1021/acs.nanolett.0c03587

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, B., Cooper, V. R., Xu, H., Xiao, H., Zhang, Y., and Weber, W. J. (2014a). Composition dependent intrinsic defect structures in SrTiO3. Phys. Chem. Chem. Phys. 16 (29), 15590–15596. doi:10.1039/c4cp01510j

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, D., Hamel-Paquet, J., Trottier, J., Barray, F., Gariépy, V., Hovington, P., et al. (2012). Synthesis of pure phase disordered LiMn1.45Cr0.1Ni0.45O4 by a post-annealing method. J. Power Sources 217, 400–406. doi:10.1016/j.jpowsour.2012.06.063

CrossRef Full Text | Google Scholar

Liu, D., Zhu, W., Trottier, J., Gagnon, C., Barray, F., Guerfi, A., et al. (2014b). Spinel materials for high-voltage cathodes in Li-ion batteries. RSC Adv. 4 (1), 154–167. doi:10.1039/c3ra45706k

CrossRef Full Text | Google Scholar

Liu, G., Zhang, J., Zhang, X., Du, Y., Zhang, K., Li, G., et al. (2017). Study on oxygen deficiency in spinel LiNi0.5Mn1.5O4 and its Fe and Cr-doped compounds. J. Alloys Compd. 725, 580–586. doi:10.1016/j.jallcom.2017.07.202

CrossRef Full Text | Google Scholar

Liu, J., and Manthiram, A. (2009). Understanding the improved electrochemical performances of Fe-substituted 5 V spinel cathode LiMn1.5Ni0.5O4. J. Phys. Chem. C 113 (33), 15073–15079. doi:10.1021/jp904276t

CrossRef Full Text | Google Scholar

Lopez-Bezanilla, A., Ganesh, P., and Littlewood, P. B. (2015a). Magnetism and metal-insulator transition in oxygen-deficient SrTiO3. Phys. Rev. B 92 (11), 115112. doi:10.1103/physrevb.92.115112

CrossRef Full Text | Google Scholar

Lopez-Bezanilla, A., Ganesh, P., and Littlewood, P. B. (2015b). Research Update: plentiful magnetic moments in oxygen deficient SrTiO3. Apl. Mater. 3 (10). doi:10.1063/1.4932347

CrossRef Full Text | Google Scholar

Lu, J., Carvalho, A., Chan, X. K., Liu, H., Liu, B., Tok, E. S., et al. (2015). Atomic healing of defects in transition metal dichalcogenides. Nano Lett. 15 (5), 3524–3532. doi:10.1021/acs.nanolett.5b00952

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, X. F., Zhang, S. L., Sim, W. L., Gao, S., and Lou, X. W. (2021). Phosphorized CoNi2S4 yolk-shell spheres for highly efficient hydrogen production via water and urea electrolysis. Angew. Chem. Int. Ed. 60 (42), 22885–22891. doi:10.1002/anie.202108563

CrossRef Full Text | Google Scholar

Lukowski, M. A., Daniel, A. S., Meng, F., Forticaux, A., Li, L., and Jin, S. (2013). Enhanced hydrogen evolution catalysis from chemically exfoliated metallic MoS2 nanosheets. J. Am. Chem. Soc. 135 (28), 10274–10277. doi:10.1021/ja404523s

PubMed Abstract | CrossRef Full Text | Google Scholar

Lun, Z., Ouyang, B., Kitchaev, D. A., Clément, R. J., Papp, J. K., Balasubramanian, M., et al. (2019). Improved cycling performance of Li-excess cation-disordered cathode materials upon fluorine substitution. Adv. Energy Mater. 9 (2), 1802959. doi:10.1002/aenm.201802959

CrossRef Full Text | Google Scholar

Luo, S., Li, M., Fung, V., Sumpter, B. G., Liu, J., Wu, Z., et al. (2021). New insights into the bulk and surface defect structures of ceria nanocrystals from neutron scattering study. Chem. Mater. 33 (11), 3959–3970. doi:10.1021/acs.chemmater.1c00156

CrossRef Full Text | Google Scholar

Lv, Y., Pan, C., Ma, X., Zong, R., Bai, X., and Zhu, Y. (2013). Production of visible activity and UV performance enhancement of ZnO photocatalyst via vacuum deoxidation. Appl. Catal. B Environ. 138-139, 26–32. doi:10.1016/j.apcatb.2013.02.011

CrossRef Full Text | Google Scholar

Madsen, J., Liu, P., Kling, J., Wagner, J. B., Hansen, T. W., Winther, O., et al. (2018). A deep learning approach to identify local structures in atomic-resolution transmission electron microscopy images. Adv. Theory Simulations 1 (8), 1800037. doi:10.1002/adts.201800037

CrossRef Full Text | Google Scholar

Makarov, N. S., Ramasamy, K., Jackson, A., Velarde, A., Castaneda, C., Archuleta, N., et al. (2019). Fiber-coupled luminescent concentrators for medical diagnostics, agriculture, and telecommunications. ACS Nano 13 (8), 9112–9121. doi:10.1021/acsnano.9b03335

PubMed Abstract | CrossRef Full Text | Google Scholar

Makkar, P., and Ghosh, N. N. (2021). A review on the use of DFT for the prediction of the properties of nanomaterials. RSC Adv. 11 (45), 27897–27924. doi:10.1039/d1ra04876g

PubMed Abstract | CrossRef Full Text | Google Scholar

Makov, G., and Payne, M. C. (1995). Periodic boundary conditions in ab initio calculations. Phys. Rev. B 51 (7), 4014–4022. doi:10.1103/physrevb.51.4014

PubMed Abstract | CrossRef Full Text | Google Scholar

Maksov, A., Dyck, O., Wang, K., Xiao, K., Geohegan, D. B., Sumpter, B. G., et al. (2019). Deep learning analysis of defect and phase evolution during electron beam-induced transformations in WS2. npj Comput. Mater. 5 (1), 12. doi:10.1038/s41524-019-0152-9

CrossRef Full Text | Google Scholar

Manthiram, A. (2020). A reflection on lithium-ion battery cathode chemistry. Nat. Commun. 11 (1), 1550. doi:10.1038/s41467-020-15355-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Manzeli, S., Ovchinnikov, D., Pasquier, D., Yazyev, O. V., and Kis, A. (2017). 2D transition metal dichalcogenides. Nat. Rev. Mater. 2 (8), 17033. doi:10.1038/natrevmats.2017.33

PubMed Abstract | CrossRef Full Text | Google Scholar

Mao, C., Zuo, F., Hou, Y., Bu, X., and Feng, P. (2014). In situ preparation of a Ti3+ self-doped TiO2 film with enhanced activity as photoanode by N2H4 reduction. Angew. Chem. Int. Ed. 53 (39), 10485–10489. doi:10.1002/anie.201406017

CrossRef Full Text | Google Scholar

Megía, P. J., Vizcaíno, A. J., Calles, J. A., and Carrero, A. (2021). Hydrogen production technologies: from fossil fuels toward renewable sources. A mini review. Energy & Fuels 35 (20), 16403–16415. doi:10.1021/acs.energyfuels.1c02501

CrossRef Full Text | Google Scholar

Meinardi, F., Bruni, F., and Brovelli, S. (2017). Luminescent solar concentrators for building-integrated photovoltaics. Nat. Rev. Mater. 2 (12), 17072. doi:10.1038/natrevmats.2017.72

CrossRef Full Text | Google Scholar

Meinardi, F., McDaniel, H., Carulli, F., Colombo, A., Velizhanin, K. A., Makarov, N. S., et al. (2015). Highly efficient large-area colourless luminescent solar concentrators using heavy-metal-free colloidal quantum dots. Nat. Nanotechnol. 10 (10), 878–885. doi:10.1038/nnano.2015.178

PubMed Abstract | CrossRef Full Text | Google Scholar

Merdrignac, O. M., Moseley, P. T., Peat, R., Sofield, C. J., and Sugden, S. (1992). The modification of gas-sensing properties of semiconducting oxides by treatment with ionizing radiation. Sensors Actuators B Chem. 7 (1), 651–655. doi:10.1016/0925-4005(92)80380-g

CrossRef Full Text | Google Scholar

Meulenberg, R. W., van Buuren, T., Hanif, K. M., Willey, T. M., Strouse, G. F., and Terminello, L. J. (2004). Structure and composition of Cu-doped CdSe nanocrystals using soft X-ray absorption spectroscopy. Nano Lett. 4 (11), 2277–2285. doi:10.1021/nl048738s

CrossRef Full Text | Google Scholar

Mikulec, F. V., Kuno, M., Bennati, M., Hall, D. A., Griffin, R. G., and Bawendi, M. G. (2000). Organometallic synthesis and spectroscopic characterization of manganese-doped CdSe nanocrystals. J. Am. Chem. Soc. 122 (11), 2532–2540. doi:10.1021/ja991249n

CrossRef Full Text | Google Scholar

Mizushima, K., Jones, P. C., Wiseman, P. J., and Goodenough, J. (1981). LixCoO2 (0<x≤1): a new cathode material for batteries of high energy density. Solid State Ionics 3-4, 171–174. doi:10.1016/0167-2738(81)90077-1

CrossRef Full Text | Google Scholar

Moody, G., Tran, K., Lu, X., Autry, T., Fraser, J. M., Mirin, R. P., et al. (2018). Microsecond Valley lifetime of defect-bound excitons in monolayer WSe2. Phys. Rev. Lett. 121 (5), 057403. doi:10.1103/physrevlett.121.057403

PubMed Abstract | CrossRef Full Text | Google Scholar

Mosquera-Lois, I., Kavanagh, S. R., Klarbring, J., Tolborg, K., and Walsh, A. (2023). Imperfections are not 0 K: free energy of point defects in crystals. Chem. Soc. Rev. 52 (17), 5812–5826. doi:10.1039/d3cs00432e

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagamine, G., Nunciaroni, H. B., McDaniel, H., Efros, A. L., de Brito Cruz, C. H., and Padilha, L. A. (2018). Evidence of band-edge hole levels inversion in spherical CuInS2 quantum dots. Nano Lett. 18 (10), 6353–6359. doi:10.1021/acs.nanolett.8b02707

PubMed Abstract | CrossRef Full Text | Google Scholar

Najafi, A., Sharma, M., Delikanli, S., Bhattacharya, A., Murphy, J. R., Pientka, J., et al. (2021). Light-induced paramagnetism in colloidal Ag+-Doped CdSe nanoplatelets. J. Phys. Chem. Lett. 12 (11), 2892–2899. doi:10.1021/acs.jpclett.1c00398

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakajima, M., and Yabuuchi, N. (2017). Lithium-excess cation-disordered rocksalt-type oxide with nanoscale phase segregation: Li1.25Nb0.25V0.5O2. Chem. Mater. 29 (16), 6927–6935. doi:10.1021/acs.chemmater.7b02343

CrossRef Full Text | Google Scholar

Nakamura, S. (1998). The roles of structural imperfections in InGaN-based blue light-emitting diodes and laser diodes. Science 281 (5379), 956–961. doi:10.1126/science.281.5379.956

PubMed Abstract | CrossRef Full Text | Google Scholar

Nan, H., Wang, Z., Wang, W., Liang, Z., Lu, Y., Chen, Q., et al. (2014). Strong photoluminescence enhancement of MoS2 through defect engineering and oxygen bonding. ACS Nano 8 (6), 5738–5745. doi:10.1021/nn500532f

PubMed Abstract | CrossRef Full Text | Google Scholar

Nelson, H. D., and Gamelin, D. R. (2018). Valence-band electronic structures of Cu+-Doped ZnS, alloyed Cu–in–Zn–S, and ternary CuInS2 nanocrystals: a unified description of photoluminescence across compositions. J. Phys. Chem. C 122 (31), 18124–18133. doi:10.1021/acs.jpcc.8b05286

CrossRef Full Text | Google Scholar

Nguyen, G. D., Liang, L., Zou, Q., Fu, M., Oyedele, A. D., Sumpter, B. G., et al. (2018). 3D imaging and manipulation of subsurface selenium vacancies in PdSe2. Phys. Rev. Lett. 121 (8), 086101. doi:10.1103/physrevlett.121.086101

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolaidis, P., and Poullikkas, A. (2017). A comparative overview of hydrogen production processes. Renew. Sustain. Energy Rev. 67, 597–611. doi:10.1016/j.rser.2016.09.044

CrossRef Full Text | Google Scholar

Nishizawa, M., and Yamamura, S. (1998). Irreversible conductivity change of Li1–CoO2 on electrochemical lithium insertion/extraction, desirable for battery applications. Chem. Commun. (16), 1631–1632. doi:10.1039/a802962h

CrossRef Full Text | Google Scholar

Niu, P., Yin, L.-C., Yang, Y.-Q., Liu, G., and Cheng, H.-M. (2014). Increasing the visible light absorption of graphitic carbon nitride (melon) photocatalysts by homogeneous self-modification with nitrogen vacancies. Adv. Mater. 26 (47), 8046–8052. doi:10.1002/adma.201404057

PubMed Abstract | CrossRef Full Text | Google Scholar

Norris, D. J., Yao, N., Charnock, F. T., and Kennedy, T. A. (2001). High-quality manganese-doped ZnSe nanocrystals. Nano Lett. 1 (1), 3–7. doi:10.1021/nl005503h

CrossRef Full Text | Google Scholar

Ouyang, B., Artrith, N., Lun, Z., Jadidi, Z., Kitchaev, D. A., Ji, H., et al. (2020). Effect of fluorination on lithium transport and short-range order in disordered-rocksalt-type lithium-ion battery cathodes. Adv. Energy Mater. 10 (10), 1903240. doi:10.1002/aenm.201903240

CrossRef Full Text | Google Scholar

Oyedele, A. D., Yang, S., Feng, T., Haglund, A. V., Gu, Y., Puretzky, A. A., et al. (2019). Defect-mediated phase transformation in anisotropic two-dimensional PdSe2 crystals for seamless electrical contacts. J. Am. Chem. Soc. 141 (22), 8928–8936. doi:10.1021/jacs.9b02593

PubMed Abstract | CrossRef Full Text | Google Scholar

Paier, J., Asahi, R., Nagoya, A., and Kresse, G. (2009). Cu₂ZnSnS₄ as a potential photovoltaic material: a hybrid Hartree-Fock density functional theory study. Phys. Rev. B 79 (11), 115126. doi:10.1103/physrevb.79.115126

CrossRef Full Text | Google Scholar

Papakonstantinou, I., Portnoi, M., and Debije, M. G. (2021). The hidden potential of luminescent solar concentrators. Adv. Energy Mater. 11 (3), 2002883. doi:10.1002/aenm.202002883

CrossRef Full Text | Google Scholar

Parsons, R. (1958). The rate of electrolytic hydrogen evolution and the heat of adsorption of hydrogen. Trans. Faraday Soc. 54 (0), 1053–1063. doi:10.1039/tf9585401053

CrossRef Full Text | Google Scholar

Patil, S., Darbar, D., Self, E. C., Malkowski, T., Wu, V. C., Giovine, R., et al. (2023). Alternate synthesis method for high-performance manganese rich cation disordered rocksalt cathodes. Adv. Energy Mater. 13 (4), 2203207. doi:10.1002/aenm.202203207

CrossRef Full Text | Google Scholar

Peimyoo, N., Shang, J., Cong, C., Shen, X., Wu, X., Yeow, E. K. L., et al. (2013). Nonblinking, intense two-dimensional light emitter: monolayer WS2 triangles. ACS Nano 7 (12), 10985–10994. doi:10.1021/nn4046002

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, R., Liang, L., Hood, Z. D., Boulesbaa, A., Puretzky, A., Ievlev, A. V., et al. (2016). In-plane heterojunctions enable multiphasic two-dimensional (2D) MoS2 nanosheets as efficient photocatalysts for hydrogen evolution from water reduction. ACS Catal. 6 (10), 6723–6729. doi:10.1021/acscatal.6b02076

CrossRef Full Text | Google Scholar

Piao, J.-Y., Sun, Y.-G., Duan, S.-Y., Cao, A.-M., Wang, X.-L., Xiao, R.-J., et al. (2018). Stabilizing cathode materials of lithium-ion batteries by controlling interstitial sites on the surface. Chem 4 (7), 1685–1695. doi:10.1016/j.chempr.2018.04.020

CrossRef Full Text | Google Scholar

Pietryga, J. M., Park, Y.-S., Lim, J., Fidler, A. F., Bae, W. K., Brovelli, S., et al. (2016). Spectroscopic and device aspects of nanocrystal quantum dots. Chem. Rev. 116 (18), 10513–10622. doi:10.1021/acs.chemrev.6b00169

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinchetti, V., Di, Q., Lorenzon, M., Camellini, A., Fasoli, M., Zavelani-Rossi, M., et al. (2018). Excitonic pathway to photoinduced magnetism in colloidal nanocrystals with nonmagnetic dopants. Nat. Nanotechnol. 13 (2), 145–151. doi:10.1038/s41565-017-0024-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Pralong, V., Gopal, V., Caignaert, V., Duffort, V., and Raveau, B. (2012). Lithium-rich rock-salt-type vanadate as energy storage cathode: Li2–xVO3. Chem. Mater. 24 (1), 12–14. doi:10.1021/cm203281q

CrossRef Full Text | Google Scholar

Quadir, S., Qorbani, M., Sabbah, A., Wu, T.-S., Anbalagan, A. k., Chen, W.-T., et al. (2022). Short- and long-range cation disorder in (AgxCu1–x)2ZnSnSe4 kesterites. Chem. Mater. 34 (15), 7058–7068. doi:10.1021/acs.chemmater.2c01489

CrossRef Full Text | Google Scholar

Rani, S., Bhatnagar, M. C., Roy, S. C., Puri, N. K., and Kanjilal, D. (2008). p-Type gas-sensing behaviour of undoped SnO2 thin films irradiated with a high-energy ion beam. Sensors Actuators B Chem. 135 (1), 35–39. doi:10.1016/j.snb.2008.07.014

CrossRef Full Text | Google Scholar

Rice, W. D., Liu, W., Baker, T. A., Sinitsyn, N. A., Klimov, V. I., and Crooker, S. A. (2016). Revealing giant internal magnetic fields due to spin fluctuations in magnetically doped colloidal nanocrystals. Nat. Nanotechnol. 11 (2), 137–142. doi:10.1038/nnano.2015.258

PubMed Abstract | CrossRef Full Text | Google Scholar

Rice, W. D., McDaniel, H., Klimov, V. I., and Crooker, S. A. (2014). Magneto-optical properties of CuInS2 nanocrystals. J. Phys. Chem. Lett. 5 (23), 4105–4109. doi:10.1021/jz502154m

PubMed Abstract | CrossRef Full Text | Google Scholar

Robertson, J., and Falabretti, B. (2011). “Electronic structure of transparent conducting oxides,” in Handbook of transparent conductors. Editor D. S. Ginley (Boston, MA: Springer US), 27–50.

CrossRef Full Text | Google Scholar

Roccapriore, K. M., Boebinger, M. G., Dyck, O., Ghosh, A., Unocic, R. R., Kalinin, S. V., et al. (2022). Probing electron beam induced transformations on a single-defect level via automated scanning transmission electron microscopy. ACS Nano 16 (10), 17116–17127. doi:10.1021/acsnano.2c07451

PubMed Abstract | CrossRef Full Text | Google Scholar

Sahu, B. K., Das, A., Prasad, A. K., and Mangamma, G. (2019). The role of in-plane oxygen vacancy defects in SnO2 nanoparticles for CH4 sensing. J. Nanosci. Nanotechnol. 19 (12), 7764–7770. doi:10.1166/jnn.2019.16736

PubMed Abstract | CrossRef Full Text | Google Scholar

Saifullah, M., Gwak, J., and Yun, J. H. (2016). Comprehensive review on material requirements, present status, and future prospects for building-integrated semitransparent photovoltaics (BISTPV). J. Mater. Chem. A 4 (22), 8512–8540. doi:10.1039/c6ta01016d

CrossRef Full Text | Google Scholar

Sang, X., Li, X., Zhao, W., Dong, J., Rouleau, C. M., Geohegan, D. B., et al. (2018). In situ edge engineering in two-dimensional transition metal dichalcogenides. Nat. Commun. 9 (1), 2051. doi:10.1038/s41467-018-04435-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Sark, W. G. v., Barnham, K. W. J., Slooff, L. H., Chatten, A. J., Büchtemann, A., Meyer, A., et al. (2008). Luminescent Solar Concentrators - a review of recent results. Opt. Express 16 (26), 21773–21792. doi:10.1364/oe.16.021773

PubMed Abstract | CrossRef Full Text | Google Scholar

Schleussner, C.-F., Rogelj, J., Schaeffer, M., Lissner, T., Licker, R., Fischer, E. M., et al. (2016). Science and policy characteristics of the Paris Agreement temperature goal. Nat. Clim. Change 6 (9), 827–835. doi:10.1038/nclimate3096

CrossRef Full Text | Google Scholar

Sebastian, L., and Gopalakrishnan, J. (2003). Li2MTiO4 (M=Mn, Fe, Co, Ni): new cation-disordered rocksalt oxides exhibiting oxidative deintercalation of lithium. Synthesis of an ordered Li2NiTiO4. J. Solid State Chem. 172 (1), 171–177. doi:10.1016/s0022-4596(03)00010-0

CrossRef Full Text | Google Scholar

Shabaev, A., Mehl, M. J., and Efros, A. L. (2015). Energy band structure of CuInS2 and optical spectra of CuInS2 nanocrystals. Phys. Rev. B 92 (3), 035431. doi:10.1103/physrevb.92.035431

CrossRef Full Text | Google Scholar

Shawkat, M. S., Gil, J., Han, S. S., Ko, T.-J., Wang, M., Dev, D., et al. (2020). Thickness-independent semiconducting-to-metallic conversion in wafer-scale two-dimensional PtSe2 layers by plasma-driven chalcogen defect engineering. ACS Appl. Mater. Interfaces 12 (12), 14341–14351. doi:10.1021/acsami.0c00116

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, S., Gao, D., Xu, Q., Yang, Z., and Xue, D. (2014). Singly-charged oxygen vacancy-induced ferromagnetism in mechanically milled SnO2powders. RSC Adv. 4 (85), 45467–45472. doi:10.1039/c4ra05475j

CrossRef Full Text | Google Scholar

Shi, Y., Li, H., and Li, L.-J. (2015). Recent advances in controlled synthesis of two-dimensional transition metal dichalcogenides via vapour deposition techniques. Chem. Soc. Rev. 44 (9), 2744–2756. doi:10.1039/c4cs00256c

PubMed Abstract | CrossRef Full Text | Google Scholar

Shin, D. W., Bridges, C. A., Huq, A., Paranthaman, M. P., and Manthiram, A. (2012). Role of cation ordering and surface segregation in high-voltage spinel LiMn1.5Ni0.5–xMxO4 (M = Cr, Fe, and Ga) cathodes for lithium-ion batteries. Chem. Mater. 24 (19), 3720–3731. doi:10.1021/cm301844w

CrossRef Full Text | Google Scholar

Singh, R., Liu, W., Lim, J., Robel, I., and Klimov, V. I. (2019). Hot-electron dynamics in quantum dots manipulated by spin-exchange Auger interactions. Nat. Nanotechnol. 14 (11), 1035–1041. doi:10.1038/s41565-019-0548-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Srivastava, B. B., Jana, S., and Pradhan, N. (2011). Doping Cu in semiconductor nanocrystals: some old and some new physical insights. J. Am. Chem. Soc. 133 (4), 1007–1015. doi:10.1021/ja1089809

PubMed Abstract | CrossRef Full Text | Google Scholar

Stouwdam, J. W., and Janssen, R. A. J. (2009). Electroluminescent Cu-doped CdS quantum dots. Adv. Mater. 21 (28), 2916–2920. doi:10.1002/adma.200803223

CrossRef Full Text | Google Scholar

Suh, J., Park, T.-E., Lin, D.-Y., Fu, D., Park, J., Jung, H. J., et al. (2014). Doping against the native propensity of MoS2: degenerate hole doping by cation substitution. Nano Lett. 14 (12), 6976–6982. doi:10.1021/nl503251h

PubMed Abstract | CrossRef Full Text | Google Scholar

Sutton, C., and Levchenko, S. V. (2020). First-principles atomistic thermodynamics and configurational entropy. Front. Chem. 8, 757. doi:10.3389/fchem.2020.00757

PubMed Abstract | CrossRef Full Text | Google Scholar

Szymanski, N. J., Lun, Z., Liu, J., Self, E. C., Bartel, C. J., Nanda, J., et al. (2023). Modeling short-range order in disordered rocksalt cathodes by pair distribution function analysis. Chem. Mater. 35 (13), 4922–4934. doi:10.1021/acs.chemmater.2c03827

CrossRef Full Text | Google Scholar

Szymanski, N. J., Zeng, Y., Bennett, T., Patil, S., Keum, J. K., Self, E. C., et al. (2022). Understanding the fluorination of disordered rocksalt cathodes through rational exploration of synthesis pathways. Chem. Mater. 34 (15), 7015–7028. doi:10.1021/acs.chemmater.2c01474

CrossRef Full Text | Google Scholar

Tan, Z. H., Kong, X. Y., Ng, B.-J., Soo, H. S., Mohamed, A. R., and Chai, S.-P. (2023). Recent advances in defect-engineered transition metal dichalcogenides for enhanced electrocatalytic hydrogen evolution: perfecting imperfections. ACS Omega 8 (2), 1851–1863. doi:10.1021/acsomega.2c06524

PubMed Abstract | CrossRef Full Text | Google Scholar

Thackeray, M. M., David, W. I. F., Bruce, P. G., and Goodenough, J. B. (1983). Lithium insertion into manganese spinels. Mater. Res. Bull. 18 (4), 461–472. doi:10.1016/0025-5408(83)90138-1

CrossRef Full Text | Google Scholar

Tongay, S., Narang, D. S., Kang, J., Fan, W., Ko, C., Luce, A. V., et al. (2014). Two-dimensional semiconductor alloys: monolayer Mo1−xWxSe2. Appl. Phys. Lett. 104 (1). doi:10.1063/1.4834358

CrossRef Full Text | Google Scholar

Trentino, A., Madsen, J., Mittelberger, A., Mangler, C., Susi, T., Mustonen, K., et al. (2021). Atomic-level structural engineering of graphene on a mesoscopic scale. Nano Lett. 21 (12), 5179–5185. doi:10.1021/acs.nanolett.1c01214

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, J.-Y., Pan, J., Lin, H., Bansil, A., and Yan, Q. (2022). Antisite defect qubits in monolayer transition metal dichalcogenides. Nat. Commun. 13 (1), 492. doi:10.1038/s41467-022-28133-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Tuller, H. L., and Bishop, S. R. (2010). Tailoring material properties through defect engineering. Chem. Lett. 39 (12), 1226–1231. doi:10.1246/cl.2010.1226

CrossRef Full Text | Google Scholar

Tuller, H. L., and Bishop, S. R. (2011). Point defects in oxides: tailoring materials through defect engineering. Annu. Rev. Mater. Res. 41 (1), 369–398. doi:10.1146/annurev-matsci-062910-100442

CrossRef Full Text | Google Scholar

Ueng, H. Y., and Hwang, H. L. (1989). The defect structure of CuInS2. part I: intrinsic defects. J. Phys. Chem. Solids 50 (12), 1297–1305. doi:10.1016/0022-3697(89)90403-4

CrossRef Full Text | Google Scholar

Ueng, H. Y., and Hwang, H. L. (1990). The defect structure of CuInS2. part II: thermal annealing defects. J. Phys. Chem. Solids 51 (1), 1–10. doi:10.1016/0022-3697(90)90125-y

CrossRef Full Text | Google Scholar

Urban, A., Lee, J., and Ceder, G. (2014). The configurational space of rocksalt-type oxides for high-capacity lithium battery electrodes. Adv. Energy Mater. 4 (13), 1400478. doi:10.1002/aenm.201400478

CrossRef Full Text | Google Scholar

van der Zande, A. M., Huang, P. Y., Chenet, D. A., Berkelbach, T. C., You, Y., Lee, G.-H., et al. (2013). Grains and grain boundaries in highly crystalline monolayer molybdenum disulphide. Nat. Mater. 12 (6), 554–561. doi:10.1038/nmat3633

PubMed Abstract | CrossRef Full Text | Google Scholar

Velarde, A. R. M., Bartlett, E. R., Makarov, N. S., Castañeda, C., Jackson, A., Ramasamy, K., et al. (2020). Optimizing the aesthetics of high-performance CuInS2/ZnS quantum dot luminescent solar concentrator windows. ACS Appl. Energy Mater. 3 (9), 8159–8163. doi:10.1021/acsaem.0c01288

CrossRef Full Text | Google Scholar

Venkatraman, S., Shin, Y., and Manthiram, A. (2003). Phase relationships and structural and chemical stabilities of charged Li1 − x CoO2 − δ and Li1 − x Ni0.85Co0.15 O 2 − δ cathodes. Electrochem. Solid State Lett. 6, A9. doi:10.1149/1.1525430

CrossRef Full Text | Google Scholar

Vijay, V., Harish, S., Archana, J., and Navaneethan, M. (2021). Cation disorder and bond anharmonicity synergistically boosts the thermoelectric performance of p-type AgSbSe2. CrystEngComm 23 (32), 5522–5530. doi:10.1039/d1ce00599e

CrossRef Full Text | Google Scholar

Viswanatha, R., Brovelli, S., Pandey, A., Crooker, S. A., and Klimov, V. I. (2011). Copper-doped inverted core/shell Nanocrystals with “permanent” optically active holes. Nano Lett. 11 (11), 4753–4758. doi:10.1021/nl202572c

PubMed Abstract | CrossRef Full Text | Google Scholar

Vlaskin, V. A., Barrows, C. J., Erickson, C. S., and Gamelin, D. R. (2013). Nanocrystal diffusion doping. J. Am. Chem. Soc. 135 (38), 14380–14389. doi:10.1021/ja4072207

PubMed Abstract | CrossRef Full Text | Google Scholar

Voiry, D., Salehi, M., Silva, R., Fujita, T., Chen, M., Asefa, T., et al. (2013). Conducting MoS2 nanosheets as catalysts for hydrogen evolution reaction. Nano Lett. 13 (12), 6222–6227. doi:10.1021/nl403661s

PubMed Abstract | CrossRef Full Text | Google Scholar

Wandt, J., Freiberg, A. T. S., Ogrodnik, A., and Gasteiger, H. A. (2018). Singlet oxygen evolution from layered transition metal oxide cathode materials and its implications for lithium-ion batteries. Mater. Today 21 (8), 825–833. doi:10.1016/j.mattod.2018.03.037

CrossRef Full Text | Google Scholar

Wang, C., Wu, D., Wang, P., Ao, Y., Hou, J., and Qian, J. (2015a). Effect of oxygen vacancy on enhanced photocatalytic activity of reduced ZnO nanorod arrays. Appl. Surf. Sci. 325, 112–116. doi:10.1016/j.apsusc.2014.11.003

CrossRef Full Text | Google Scholar

Wang, J., Chen, R., Xiang, L., and Komarneni, S. (2018a). Synthesis, properties and applications of ZnO nanomaterials with oxygen vacancies: a review. Ceram. Int. 44 (7), 7357–7377. doi:10.1016/j.ceramint.2018.02.013

CrossRef Full Text | Google Scholar

Wang, J., Lin, W., Wu, B., and Zhao, J. (2014). Syntheses and electrochemical properties of the Na-doped LiNi0.5Mn1.5O4 cathode materials for lithium-ion batteries. Electrochimica Acta 145, 245–253. doi:10.1016/j.electacta.2014.07.140

CrossRef Full Text | Google Scholar

Wang, J., Nie, P., Xu, G., Jiang, J., Wu, Y., Fu, R., et al. (2018c). High-voltage LiNi0.45Cr0.1Mn1.45O4 cathode with superlong cycle performance for wide temperature lithium-ion batteries. Adv. Funct. Mater. 28 (4), 1704808. doi:10.1002/adfm.201704808

CrossRef Full Text | Google Scholar

Wang, M., Chen, X., Yao, H., Lin, G., Lee, J., Chen, Y., et al. (2022a). Research progress in lithium-excess disordered rock-salt oxides cathode. ENERGY & Environ. Mater. 5 (4), 1139–1154. doi:10.1002/eem2.12413

CrossRef Full Text | Google Scholar

Wang, R., Huang, B., Qu, Z., Gong, Y., He, B., and Wang, H. (2019). Research on the kinetic properties of the cation disordered rock-salt Li-excess Li1.25Nb0.25Mn0.5O2 material. Solid State Ionics 339, 114999. doi:10.1016/j.ssi.2019.06.007

CrossRef Full Text | Google Scholar

Wang, R., Li, X., Liu, L., Lee, J., Seo, D.-H., Bo, S.-H., et al. (2015b). A disordered rock-salt Li-excess cathode material with high capacity and substantial oxygen redox activity: Li1.25Nb0.25Mn0.5O2. Electrochem. Commun. 60, 70–73. doi:10.1016/j.elecom.2015.08.003

CrossRef Full Text | Google Scholar

Wang, S., Robertson, A., and Warner, J. H. (2018b). Atomic structure of defects and dopants in 2D layered transition metal dichalcogenides. Chem. Soc. Rev. 47 (17), 6764–6794. doi:10.1039/c8cs00236c

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Wu, J., Zhang, Y., Sun, Y., Ma, K., Xie, Y., et al. (2022b). Vacancy defects in 2D transition metal dichalcogenide electrocatalysts: from aggregated to atomic configuration. Adv. Mater., 2206576. doi:10.1002/adma.202206576

CrossRef Full Text | Google Scholar

Wei, C., Rao, R. R., Peng, J., Huang, B., Stephens, I. E. L., Risch, M., et al. (2019). Recommended practices and benchmark activity for hydrogen and oxygen electrocatalysis in water splitting and fuel cells. Adv. Mater. 31 (31), 1806296. doi:10.1002/adma.201806296

CrossRef Full Text | Google Scholar

Whittingham, M. S. (1976). Electrical energy storage and intercalation chemistry. Science 192 (4244), 1126–1127. doi:10.1126/science.192.4244.1126

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, S., Sun, W., Sun, J., Hood, Z. D., Yang, S.-Z., Sun, L., et al. (2018). Surface reorganization leads to enhanced photocatalytic activity in defective BiOCl. Chem. Mater. 30 (15), 5128–5136. doi:10.1021/acs.chemmater.8b01629

CrossRef Full Text | Google Scholar

Wu, X., Gu, Y., Ge, R., Serna, M. I., Huang, Y., Lee, J. C., et al. (2022). Electron irradiation-induced defects for reliability improvement in monolayer MoS2-based conductive-point memory devices. npj 2D Mater. Appl. 6 (1), 31. doi:10.1038/s41699-022-00306-8

CrossRef Full Text | Google Scholar

Wu, Z., Zhao, W., Jiang, J., Zheng, T., You, Y., Lu, J., et al. (2017). Defect activated photoluminescence in WSe2 monolayer. J. Phys. Chem. C 121 (22), 12294–12299. doi:10.1021/acs.jpcc.7b03585

CrossRef Full Text | Google Scholar

Xia, C., Meeldijk, J. D., Gerritsen, H. C., and de Mello Donega, C. (2017). Highly luminescent water-dispersible NIR-emitting wurtzite CuInS2/ZnS core/shell colloidal quantum dots. Chem. Mater. 29 (11), 4940–4951. doi:10.1021/acs.chemmater.7b01258

PubMed Abstract | CrossRef Full Text | Google Scholar

Xia, C., Tamarat, P., Hou, L., Busatto, S., Meeldijk, J. D., de Mello Donega, C., et al. (2021). Unraveling the emission pathways in copper indium sulfide quantum dots. ACS Nano 15 (11), 17573–17581. doi:10.1021/acsnano.1c04909

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiong, J., Di, J., Xia, J., Zhu, W., and Li, H. (2018). Surface defect engineering in 2D nanomaterials for photocatalysis. Adv. Funct. Mater. 28 (39), 1801983. doi:10.1002/adfm.201801983

CrossRef Full Text | Google Scholar

Xiong, Y., Lin, Y., Wang, X., Zhao, Y., and Tian, J. (2022). Defect engineering on SnO2 nanomaterials for enhanced gas sensing performances. Adv. Powder Mater. 1 (3), 100033. doi:10.1016/j.apmate.2022.02.001

CrossRef Full Text | Google Scholar

Xu, J., Shao, G., Tang, X., Lv, F., Xiang, H., Jing, C., et al. (2022). Frenkel-defected monolayer MoS2 catalysts for efficient hydrogen evolution. Nat. Commun. 13 (1), 2193. doi:10.1038/s41467-022-29929-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Y., Zheng, C., Wang, S., and Hou, Y. (2015). 3D arrays of molybdenum sulphide nanosheets on Mo meshes: efficient electrocatalysts for hydrogen evolution reaction. Electrochimica Acta 174, 653–659. doi:10.1016/j.electacta.2015.06.040

CrossRef Full Text | Google Scholar

Yablonovitch, E. (1980). Thermodynamics of the fluorescent planar concentrator. J. Opt. Soc. Am. 70 (11), 1362–1363. doi:10.1364/josa.70.001362

CrossRef Full Text | Google Scholar

Yabuuchi, N., Nakayama, M., Takeuchi, M., Komaba, S., Hashimoto, Y., Mukai, T., et al. (2016a). Origin of stabilization and destabilization in solid-state redox reaction of oxide ions for lithium-ion batteries. Nat. Commun. 7 (1), 13814. doi:10.1038/ncomms13814

PubMed Abstract | CrossRef Full Text | Google Scholar

Yabuuchi, N., Takeuchi, M., Komaba, S., Ichikawa, S., Ozaki, T., and Inamasu, T. (2016b). Synthesis and electrochemical properties of Li1.3Nb0.3V0.4O2 as a positive electrode material for rechargeable lithium batteries. Chem. Commun. 52 (10), 2051–2054. doi:10.1039/c5cc08034g

CrossRef Full Text | Google Scholar

Yang, J., Wang, Y., Lagos, M. J., Manichev, V., Fullon, R., Song, X., et al. (2019). Single atomic vacancy catalysis. ACS Nano 13 (9), 9958–9964. doi:10.1021/acsnano.9b05226

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, S.-H., Choi, W., Cho, B. W., Agyapong-Fordjour, F.O.-T., Park, S., Yun, S. J., et al. (2021). Deep learning-assisted quantification of atomic dopants and defects in 2D materials. Adv. Sci. 8 (16), 2101099. doi:10.1002/advs.202101099

CrossRef Full Text | Google Scholar

Ye, K., Siah, S. C., Erslev, P. T., Akey, A., Settens, C., Hoque, M. S. B., et al. (2019). Tuning electrical, optical, and thermal properties through cation disorder in Cu2ZnSnS4. Chem. Mater. 31 (20), 8402–8412. doi:10.1021/acs.chemmater.9b02287

CrossRef Full Text | Google Scholar

Ye, L., Deng, K., Xu, F., Tian, L., Peng, T., and Zan, L. (2012). Increasing visible-light absorption for photocatalysis with black BiOCl. Phys. Chem. Chem. Phys. 14 (1), 82–85. doi:10.1039/c1cp22876e

PubMed Abstract | CrossRef Full Text | Google Scholar

Ye, L., Jin, X., Leng, Y., Su, Y., Xie, H., and Liu, C. (2015). Synthesis of black ultrathin BiOCl nanosheets for efficient photocatalytic H2 production under visible light irradiation. J. Power Sources 293, 409–415. doi:10.1016/j.jpowsour.2015.05.101

CrossRef Full Text | Google Scholar

Ye, L., Zan, L., Tian, L., Peng, T., and Zhang, J. (2011). The {001} facets-dependent high photoactivity of BiOCl nanosheets. Chem. Commun. 47 (24), 6951–6953. doi:10.1039/c1cc11015b

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoo, H.-I., and Tuller, H. L. (1987). Iron-excess manganese ferrite: electrical conductivity and cation distributions. J. Am. Ceram. Soc. 70 (6), 388–392. doi:10.1111/j.1151-2916.1987.tb05656.x

CrossRef Full Text | Google Scholar

Yu, Z., Qu, X., Dou, A., Su, M., Liu, Y., and Wu, F. (2019). Synthesis and redox mechanism of cation-disordered, rock-salt cathode-material Li–Ni–Ti–Nb–O compounds for a Li-ion battery. ACS Appl. Mater. Interfaces 11 (39), 35777–35787. doi:10.1021/acsami.9b12822

PubMed Abstract | CrossRef Full Text | Google Scholar

Yun, H. J., Lim, J., Fuhr, A. S., Makarov, N. S., Keene, S., Law, M., et al. (2018). Charge-transport mechanisms in CuInSexS2–x quantum-dot films. ACS Nano 12 (12), 12587–12596. doi:10.1021/acsnano.8b07179

PubMed Abstract | CrossRef Full Text | Google Scholar

Zan, R., Ramasse, Q. M., Jalil, R., Georgiou, T., Bangert, U., and Novoselov, K. S. (2013). Control of radiation damage in MoS2 by graphene encapsulation. ACS Nano 7 (11), 10167–10174. doi:10.1021/nn4044035

PubMed Abstract | CrossRef Full Text | Google Scholar

Zang, H., Li, H., Makarov, N. S., Velizhanin, K. A., Wu, K., Park, Y.-S., et al. (2017). Thick-Shell CuInS2/ZnS quantum Dots with suppressed “blinking” and narrow single-particle emission line widths. Nano Lett. 17 (3), 1787–1795. doi:10.1021/acs.nanolett.6b05118

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, Q., Cui, Y., Zhu, L., and Yao, Y. (2020). Increasing oxygen vacancies at room temperature in SnO2 for enhancing ethanol gas sensing. Mater. Sci. Semicond. Process. 111, 104962. doi:10.1016/j.mssp.2020.104962

CrossRef Full Text | Google Scholar

Zhang, G., Xie, C., Zhang, S., Zhang, S., and Xiong, Y. (2014b). Defect chemistry of the metal cation defects in the p- and n-doped SnO2 nanocrystalline films. J. Phys. Chem. C 118 (31), 18097–18109. doi:10.1021/jp503059e

CrossRef Full Text | Google Scholar

Zhang, H., Gao, X., Cai, Q., Zhang, X., Tian, Y., Jia, M., et al. (2023). Recent progress and perspectives on cation disordered rock-salt material for advanced Li-ion batteries. J. Mater. Chem. A 11 (16), 8426–8452. doi:10.1039/d3ta00852e

CrossRef Full Text | Google Scholar

Zhang, L., Yang, T., He, X., Zhang, W., Vinai, G., Tang, C. S., et al. (2020). Molecular beam epitaxy of two-dimensional vanadium-molybdenum diselenide alloys. ACS Nano 14 (9), 11140–11149. doi:10.1021/acsnano.0c02124

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, M., Wu, J., Zhu, Y., Dumcenco, D. O., Hong, J., Mao, N., et al. (2014a). Two-dimensional molybdenum tungsten diselenide alloys: photoluminescence, Raman scattering, and electrical transport. ACS Nano 8 (7), 7130–7137. doi:10.1021/nn5020566

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Chen, X., Huang, Y., Zhang, C., Li, F., and Shu, H. (2017). The role of intrinsic defects in electrocatalytic activity of monolayer VS2 basal planes for the hydrogen evolution reaction. J. Phys. Chem. C 121 (3), 1530–1536. doi:10.1021/acs.jpcc.6b11987

CrossRef Full Text | Google Scholar

Zhao, Q., Stalin, S., Zhao, C.-Z., and Archer, L. A. (2020). Designing solid-state electrolytes for safe, energy-dense batteries. Nat. Rev. Mater. 5 (3), 229–252. doi:10.1038/s41578-019-0165-5

CrossRef Full Text | Google Scholar

Zhao, X., Dan, J., Chen, J., Ding, Z., Zhou, W., Loh, K. P., et al. (2018). Atom-by-Atom fabrication of monolayer molybdenum membranes. Adv. Mater. 30 (23), 1707281. doi:10.1002/adma.201707281

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, J., Xiao, J., Yu, X., Kovarik, L., Gu, M., Omenya, F., et al. (2012). Enhanced Li+ ion transport in LiNi0.5Mn1.5O4 through control of site disorder. Phys. Chem. Chem. Phys. 14 (39), 13515–13521. doi:10.1039/c2cp43007j

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhong, G. B., Wang, Y. Y., Zhang, Z. C., and Chen, C. H. (2011). Effects of Al substitution for Ni and Mn on the electrochemical properties of LiNi0.5Mn1.5O4. Electrochimica Acta 56 (18), 6554–6561. doi:10.1016/j.electacta.2011.03.093

CrossRef Full Text | Google Scholar

Zhong, Y., Li, W., Zhao, X., Jiang, X., Lin, S., Zhen, Z., et al. (2019). High-response room-temperature NO2 sensor and ultrafast humidity sensor based on SnO2 with rich oxygen vacancy. ACS Appl. Mater. Interfaces 11 (14), 13441–13449. doi:10.1021/acsami.9b01737

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, W., Dong, L., Tan, L., and Tang, Q. (2021). First-principles study of sulfur vacancy concentration effect on the electronic structures and hydrogen evolution reaction of MoS2. Nanotechnology 32 (14), 145718. doi:10.1088/1361-6528/abd49f

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, B. L., Xie, C. S., Zeng, D. W., Song, W. L., and Wang, A. H. (2005). Investigation of gas sensitivity of Sb-doped ZnO nanoparticles. Mater. Chem. Phys. 89 (1), 148–153. doi:10.1016/j.matchemphys.2004.08.028

CrossRef Full Text | Google Scholar

Zhu, H., Wang, Q., Cheng, L., Addou, R., Kim, J., Kim, M. J., et al. (2017). Defects and surface structural stability of MoTe2 under vacuum annealing. ACS Nano 11 (11), 11005–11014. doi:10.1021/acsnano.7b04984

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhuang, H. L., Ganesh, P., Cooper, V. R., Xu, H., and Kent, P. R. C. (2014). Understanding the interactions between oxygen vacancies at SrTiO₃ (001) surfaces. Phys. Rev. B 90 (6), 064106. doi:10.1103/physrevb.90.064106

CrossRef Full Text | Google Scholar

Ziatdinov, M., Dyck, O., Li, X., Sumpter, B. G., Jesse, S., Vasudevan, R. K., et al. (2019). Building and exploring libraries of atomic defects in graphene: scanning transmission electron and scanning tunneling microscopy study. Sci. Adv. 5 (9), eaaw8989. doi:10.1126/sciadv.aaw8989

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziatdinov, M., Dyck, O., Maksov, A., Li, X., Sang, X., Xiao, K., et al. (2017). Deep learning of atomically resolved scanning transmission electron microscopy images: chemical identification and tracking local transformations. ACS Nano 11 (12), 12742–12752. doi:10.1021/acsnano.7b07504

PubMed Abstract | CrossRef Full Text | Google Scholar