- Centre for Electronics Frontiers, Institute for Integrated Micro and Nano Systems, School of Engineering, The University of Edinburgh, Edinburgh, United Kingdom
The applications of the Artificial Intelligence are currently dominating the technology landscape. Meanwhile, the conventional Von Neumann architectures are struggling with the data-movement bottleneck to meet the ever-increasing performance demands of these data-centric applications. Moreover, The vector-matrix multiplication cost, in the binary domain, is a major computational bottleneck for these applications. This paper introduces a novel digital in-memory stochastic computing architecture that leverages the simplicity of the stochastic computing for in-memory vector-matrix multiplication. The proposed architecture incorporates several new approaches including a new stochastic number generator with ideal binary-to-stochastic mapping, a best seeding approach for accurate-enough low stochastic bit-precisions, a hybrid stochastic-binary accumulation approach for vector-matrix multiplication, and the conversion of conventional memory read operations into on-the-fly stochastic multiplication operations with negligible overhead. Thanks to the combination of these approaches, the accuracy analysis of the vector-matrix multiplication benchmark shows that scaling down the stochastic bit-precision from 16-bit to 4-bit achieves nearly the same average error (less than 3%). The derived analytical model of the proposed in-memory stochastic computing architecture demonstrates that the 4-bit stochastic architecture achieves the highest throughput per sub-array (122 Ops/Cycle), which is better than the 16-bit stochastic precision by 4.36x, while still maintaining a small average error of 2.25%.
1 Introduction
Nowadays we are witnessing the end of Moore’s Law due to the physical limits of the technology scaling. On the other hand, the Artificial Intelligence (AI) revolution has introduced new challenges due to the ever-increasing performance demands of its data-intensive applications such as computer vision, speech recognition, and natural language processing. At the core of these AI applications, the Deep Neural Networks (DNNs) are widely used to mimic the human-brain functionality through layers of neurons that are connected by statistically weighted links. The DNNs may consist of tens of layers to do computations on tens of millions of data weights (Jouppi et al., 2017). The conventional Von Neumann architectures are not originally designed to deal with this gigantic amount of data. Thus, new beyond-Von Neumann architectures became an urgent need to mitigate the data-movement bottleneck of these data-centric applications.
In another direction, the Vector-Matrix Multiplication (VMM), which is the computational core of the DNNs, is the major computational bottleneck due to the binary multiplication complexity. Accelerating the VMM computational core of the DNNs should have a significant contribution to the AI hardware efficiency. This adds more performance demands to the proposed beyond-Von Neumann architectures. The current emerging situation has spotlighted the urgent need to explore not only emerging architectures that are data-centric-oriented but also unconventional computing domains that reduce the computation complexity of the VMM.
To mitigate the data-movement bottleneck, In-Memory Computing (IMC) architectures were proposed to avoid moving data across the chips. The main idea is to process data where it exists in DRAMs (Seshadri et al., 2013; Farmahini-Farahani et al., 2015) or SRAMs (Jeloka et al., 2015; Eckert et al., 2018; Fujiki et al., 2019; Al-Hawaj et al., 2020). In SRAMs, the bitline computing approach is used to compute bitwise AND and NOR operations for two simultaneously activated wordlines. These digital in-memory computing architectures have to add one extra address decoder to activate two wordlines simultaneously which consumes more energy. In addition, compute-logic stacks are added to the SRAM’s peripherals to do more complex operations. These complex operations (like additions and multiplications) require a standalone controller to run micro-algorithms to perform these operations in the digital binary domain. Due to the controller and the micro-algorithms, a multiplication-accumulation operation can consume up to hundreds of cycles (Al-Hawaj et al., 2020). This long latency extremely degrades the benefits of the IMC approach in the binary domain.
Analog in-memory computing architectures were also proposed using emerging technologies like RRAMs (Yao et al., 2020; Kim et al., 2022; Wan et al., 2022). The VMM is done in the analog domain where inputs and weights are converted to analog representations (voltages and resistances) and then analog outputs are converted back to the digital domain. However, these analog architectures suffer from the analog domain’s scalability issues in addition to the high cost of the analog/digital interfacing circuitry (Adam et al., 2018; Liu et al., 2020). Resistivity variations of the RRAMs and manufacturing process variations in Analog-to-Digital Converters (ADCs) are also major obstacles that make the analog computation less accurate and more challenging (Yu et al., 2021). Eventually, the productivity of the analog design is well-known to be much less than the digital one. This makes the analog design’s reusability and time-to-market unpromising for the increasing DNNs’ market demands.
The potential promising approach should inherit the computation simplicity of the analog domain while still utilizing the scalability and robustness of the digital in-memory computing approach. Stochastic Computing (SC) is a promising computing domain which reduces the complexity of the binary multiplication to a simple bitwise AND operation. This unconventional computing domain can fully utilize the digital in-memory computing approach without further logic complexity unlike the binary computing domain. Thus, a digital in-memory stochastic computing architecture is a middle ground that achieves the benefits of both analog and digital in-memory computing approaches while avoiding their drawbacks.
In this paper, we investigate the accuracy of the stochastic computing domain for a VMM benchmark across three different phases: generation, multiplication, and accumulation. Our accuracy analysis targets minimizing the accuracy loss at each phase. It explores two major parameters which are the seeding of the random number generator and the bit-precision of the stochastic bitstream. As part of the accuracy study, we present a new stochastic number generator with an ideal binary-to-stochastic mapping to increase the accuracy of the generation phase. We also introduce a hybrid stochastic-binary accumulation approach to increase the VMM accuracy without dramatically increasing the hardware complexity of the targeted architecture. Additionally, this paper presents a novel digital in-memory stochastic computing architecture for VMM. The proposed architecture converts the conventional memory read operations into on-the-fly stochastic multiplication operations with negligible overhead. An analytical model was built to explore the space of the different architectural design points. This analytical model surveys the different trade-offs among latency, throughput, design complexity, and accuracy for the different stochastic bit-precisions.
2 Stochastic computing
Stochastic computing is a discrete computing system that combines features from both analog and digital domains. The stochastic numbers are represented by random bitstreams of ones and zeros which are interpreted as probabilities. This paper is focusing on the unipolar stochastic numbers where values are calculated as ratios of the number of ones to the total number of bits in the bitstream. This representation makes the stochastic computing more friendly to biological systems where the data is represented by the rate of pulses (Alaghi, 2015).
The stochastic domain inherits the computation simplicity of the analog domain while keeping the same robustness, scalability, and productivity of the digital domain. Figure 1 shows the circuits of stochastic multiplication, addition, and subtraction (Alaghi et al., 2013; Alaghi and Hayes, 2013; Alaghi and Hayes, 2014; Groszewski and Lenz, 2019; Winstead, 2019). The multiplication is done by a bitwise AND operation between X (4/8) and Y (6/8) producing the output Z (3/8). This can be mapped to their equivalent probabilities where X is 0.5 and Y is 0.75 so that the multiplication output should be 0.375 which is equivalent to (3/8). The stochastic computing addition is done by a weighted multiplexer where a stochastic bitstream is forwarded to the select signal. If the select signal (S) has the probability of 0.5, it gives the same weight for the two inputs and the output will be (X+Y)/2 as shown in Figure 1. Regarding the subtraction, it is done by a bitwise XOR operation, however it requires the two stochastic inputs to be correlated to each other. For example, the outputs of the stochastic multiplication and addition in Figure 1 are correlated because they are generated from the same inputs X and Y, so that the XOR gives the absolute value of their subtraction (Alaghi, 2015).
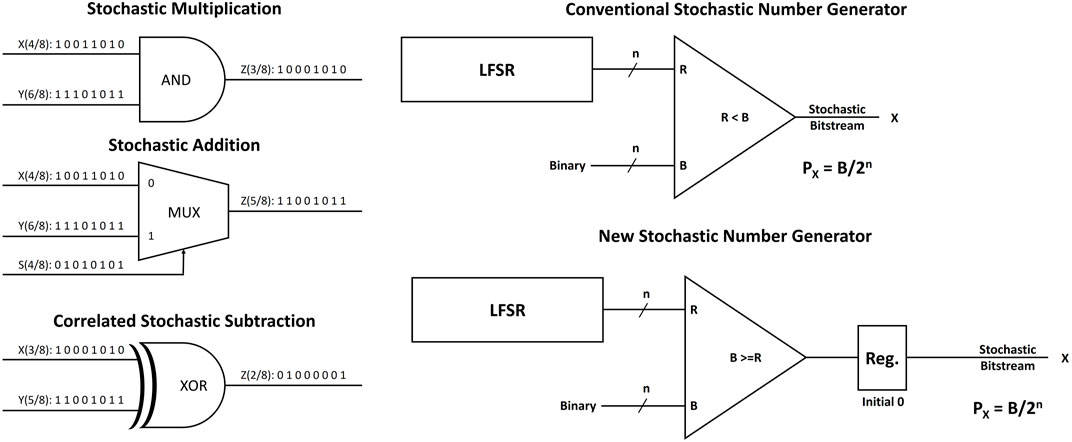
FIGURE 1. The basic circuits of the stochastic computing domain: SC multiplication using AND gate, SC addition using MUX with 50% weighted select signal, SC subtraction for correlated inputs using XOR gate, the conventional stochastic number generator using LFSR with a comparator and a new proposed stochastic number generator where the register has initial state of 0.
Figure 1 also shows the conventional stochastic number generator which is widely used (Alaghi, 2015; Zhang et al., 2019; Salehi, 2020). To convert an n-bit binary number (B) to a 2n stochastic bitstream (X), the binary (B) is compared to a random number (R) with the same bitwidth (n) for 2n cycles and the output bitstream (X) represents the probability Px of B/2n. The Linear Feedback Shift Register (LFSR) generates pseudo random numbers which are still valid for the purpose of stochastic number generation.
The stochastic computing is an approximate computing domain in which the outputs are not exact values in contrast to the binary domain. However, AI applications which mainly depend on DNNs tolerate the approximated results by re-adjusting the weights to be more friendly to the stochastic domain (Lee et al., 2017; Liu et al., 2021). In another direction, the length of the stochastic bitstream creates a trade-off between efficiency and accuracy. By intuition, the longer the bitstream the more accurate results the system can generate. Representing n-bit binary numbers by less than 2n-bit bitstreams reduces the mapping resolution from the binary domain to the stochastic domain which potentially decreases the overall accuracy. In the next section, the accuracy of the stochastic VMM computation is studied through three different phases: generation, multiplication, and accumulation.
3 Stochastic vector-matrix multiplication accuracy
This section investigates the accuracy of the stochastic computing through three different phases: stochastic number generation, stochastic element-by-element multiplication, and stochastic Vector-Matrix Multiplication including the accumulation operations. This accuracy analysis tries to minimize three different sources of errors: 1) the truncation error due to stochastic bit-precision reduction by best seeding at the generation phase, 2) the input correlation error at the multiplication phase by re-exploring the best seeding for less correlation, 3) the approximation error of the accumulation phase by fine-tuning a hybrid stochastic-binary accumulation. The input seed and the stochastic bit-precision are the two major parameters that affect the accuracy of the stochastic computing. Thus, the objective is to find the best seeding while exploring the stochastic bit-precision space of the VMM benchmark. As we keep an eye on the VMM of the DNN applications (like MNIST), a 4-bit binary system was adopted as a case-study where inputs and weights are 4-bit binary values.
3.1 Stochastic generation accuracy
As shown by the conventional stochastic number generator in Figure 1, an LFSR and a comparator are used to generate the stochastic numbers by comparing the binary input against the pseudo random values generated by the LFSR. For full stochastic precision, the 4-bit binary values are mapped to 16-bit stochastic numbers with one-to-one linear mapping from the binary domain to the stochastic/probabilistic domain. However, this conventional stochastic number generator produces non-ideal mapping regardless the input seed as shown by Figure 2. While the ideal linear mapping is shown in blue, it is noticeable that the real mapping (in orange) is being deviated as the value of the seed increases. This deviation is caused by the non-ideal uniform distribution of the pseudo random values generated by the LFSR. The 4-bit LFSR generates values from 1 to 15 but not a 0 value. During the 2n generation cycles, the LFSR starts and ends with the same seed value which means it is able to generate only 2n-1 pseudo random values. Consequently, the (R < B) comparator generates less accurate bitstreams due to ignoring the missing value case, and specially for random seeds with higher values. As the deviation error accumulates in one direction, this can lead to higher error rates during the different stochastic operations (like multiplication).
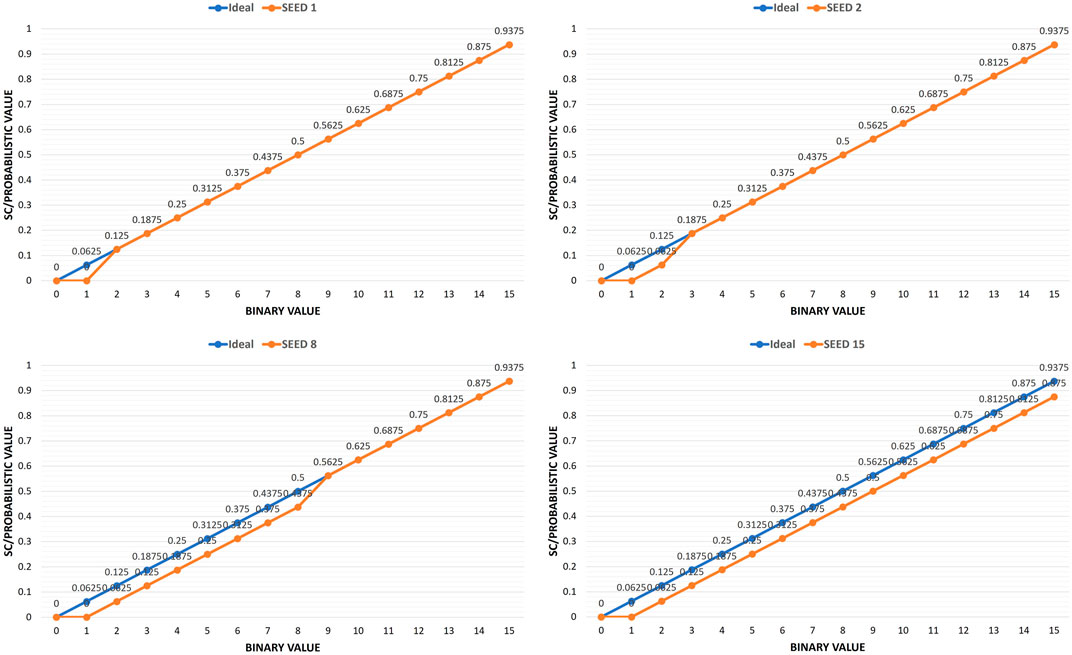
FIGURE 2. Mapping 4-bit binary values to 16-bit full stochastic precision using the conventional stochastic number generator.
To achieve the ideal linear mapping for the 16-bit full stochastic precision, we propose a new stochastic number generator shown in Figure 1. As the expected number of ones per any stochastic bitstream should not exceed 15 for any 4-bit binary input, a zero value is intentionally injected at the beginning of the stochastic bitstream to avoid the repetition of the seed value at the 2n generation cycle. In this case, the LFSR feeds the comparator with 15 pseudo-random values with uniform distribution while the comparison circuit is modified to (B > = R) to overcome the missing 0 case of the pseudo random values. The new proposed circuit generates an ideal mapping from 4-bit binary to 16-bit stochastic for any seed value (from 1 to 15) as shown by the blue line in Figure 3.
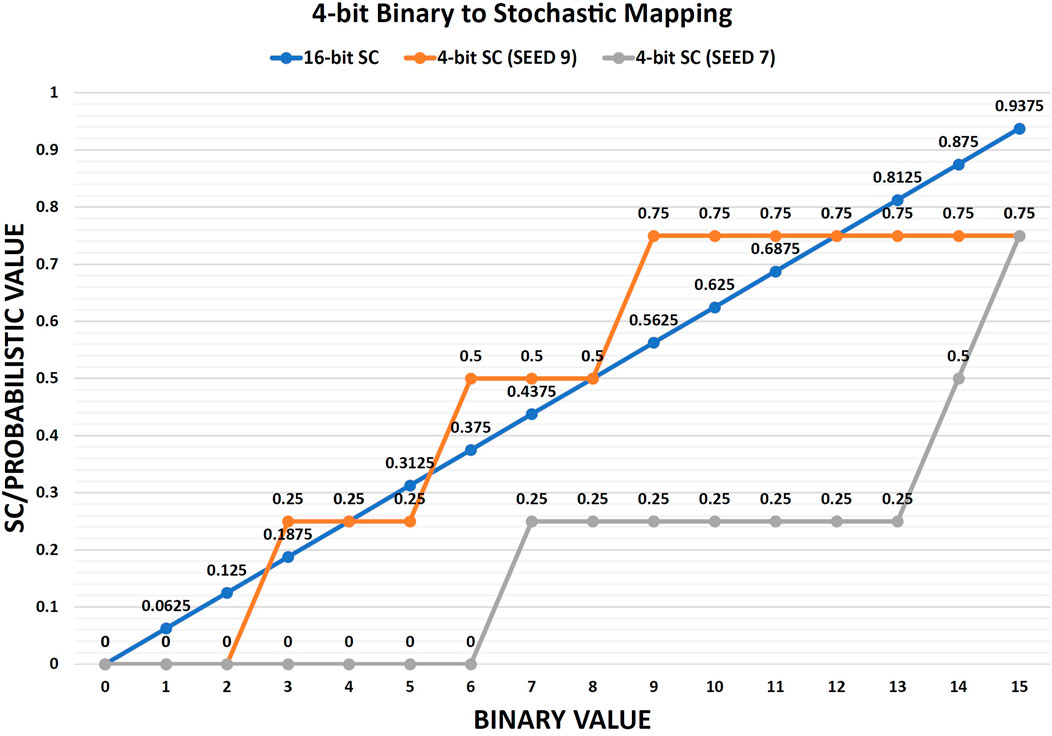
FIGURE 3. Mapping 4-bit binary values to both 16-bit full stochastic precision and 4-bit reduced stochastic precision. The graph shows that SEED 9 gives a more linear mapping (quasi-linear) for the 4-bit stochastic precision which makes it closer to the 16-bit full stochastic precision accuracy. Table 1 shows the accompanied probabilistic values and the absolute errors of the good and bad seedings for the 4-bit stochastic precision versus the 16-bit full stochastic precision (for any seed).
Although the 16-bit stochastic number offers a full accuracy for the data representation, it consumes more resources to save the data (4x) in comparison to the binary domain. The straightforward mitigation approach is to scale down the bit-precision of the stochastic domain to less than 16-bit. However, this may dramatically decrease the accuracy of the generation phase due to a non-linear mapping from binary to stochastic numbers. While the progressive precision approach targets early accurate-enough results from the full stochastic precision (Alaghi and Hayes, 2014; Alaghi, 2015; Chen et al., 2017; Lin et al., 2021; Wu et al., 2021), we propose re-mapping the binary space to a smaller stochastic space with less precision. The target is to accomplish this mapping on-the-fly without going back to the binary domain for quantization. Our approach uses the same proposed new stochastic number generator in addition to the input seed fine-tuning approach to find the best pseudo-random numbers’ distribution. The greater the degree of linear mapping, the higher the generation accuracy we achieve.
The non-linear mapping from 4-bit binary to 4-bit stochastic precision is illustrated by the gray line (bad seeding, SEED 7) in Figure 3. Consequently, the target is to find the best quasi-linear mapping to the binary domain which is close enough to the full stochastic precision mapping as shown by the orange line (good seeding, SEED 9) in Figure 3. As Table 1 shows, the two seeds have two completely different mappings from 4-bit binary to 4-bit stochastic due to the different pseudo-random numbers’ distributions. While the maximum absolute error of SEED 9 is 18.75% (binary 9 and binary 15), the maximum absolute error of SEED 7 is 56.25% (binary 13). It is clear that the 4-bit stochastic number provides 4 probabilities (0.0, 0.25, 0.5, 0.75) for both SEED 9 and SEED 7, but the main advantage of SEED 9 is its ability to map the binary values from 1 to 15 across the 4 probabilities in a quasi-linear way which is close enough to the 16-bit full stochastic precision mapping.
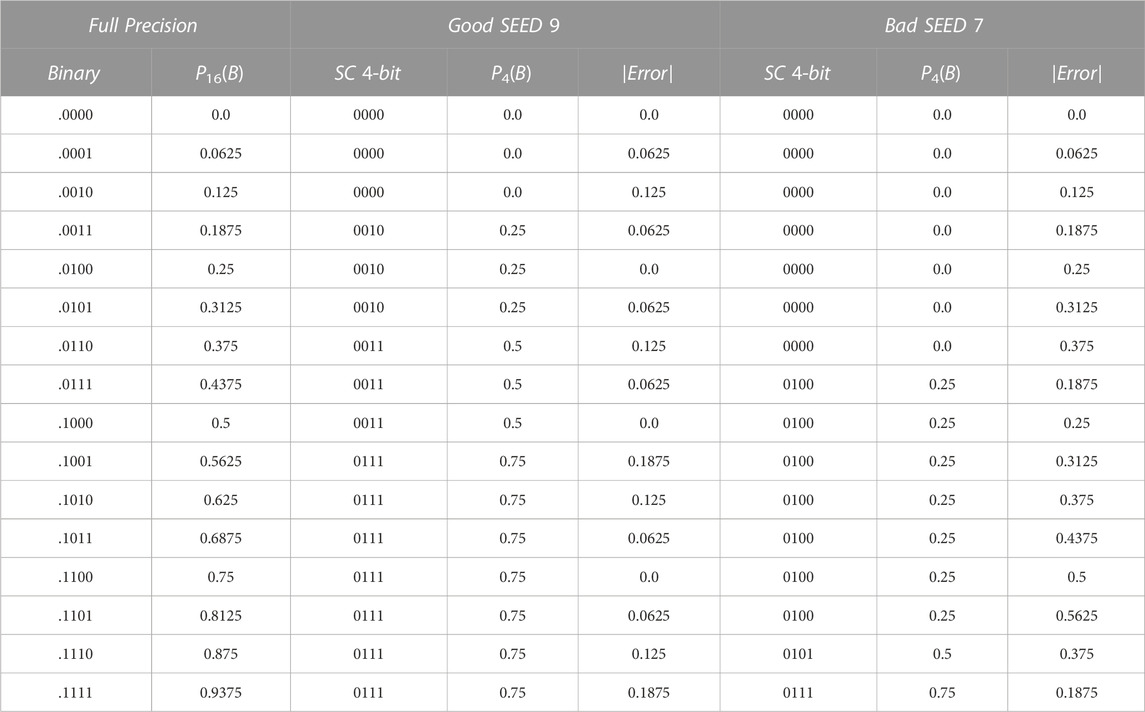
TABLE 1. The absolute errors of mapping the 4-bit binary probabilistic values to 4-bit stochastic precision using good and bad seeding.
Our methodology was to use all possible seeds (from 1 to 15) to convert the 4-bit binary values (from 1 to 15) into stochastic bitstreams with different stochastic precisions (14-bit, 12-bit, 10-bit, 8-bit, 6-bit, and 4-bit). Then we measure the accumulated error for all binary values in comparison to the 16-bit full stochastic precision case. A 4-bit LFSR with reconfigurable seeding was used to forward pseudo random values to the new stochastic number generator. Figure 4 shows the accumulated data-generation errors of the 4-bit binary values per each seed for all targeted stochastic bit-precisions. The average error of the best seed is also shown per each stochastic precision. The results show that choosing a bad seed for any precision increases the average error of the data generation by few times. It is also promising to notice that decreasing the stochastic precision from 16-bit to 4-bit (4x reduction), increases the average error by only 8.33% due to the best seeding. This shows that mapping the binary domain to a less-precision stochastic domain is feasible on-the-fly during the generation phase. The same proposed binary-to-stochastic converter circuit allows us to generate accurate-enough mapping to any stochastic bit-precision not only the 16-bit stochastic precision. This provides the system with a higher level of flexibility for runtime stochastic precision reconfiguration without incurring any additional hardware penalty.
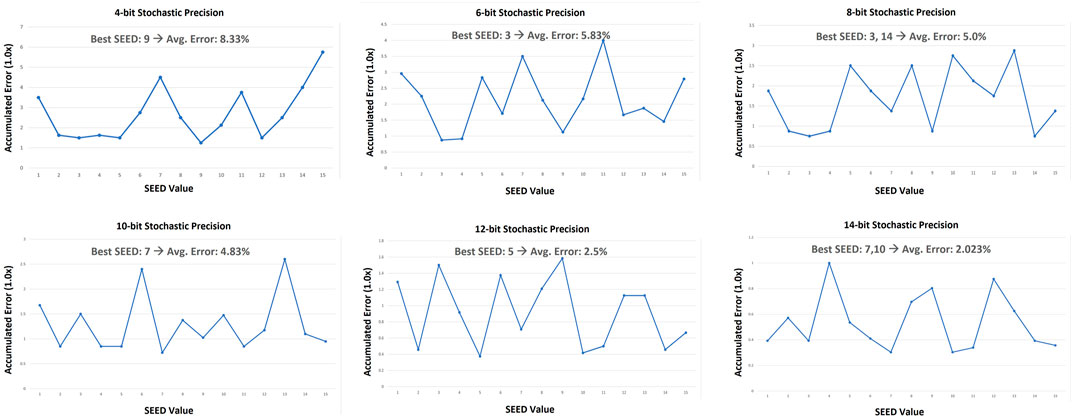
FIGURE 4. The accumulated error (normalized to 1.0x) of representing the 4-bit binary numbers (1–15) using different stochastic bit-precisions while applying all possible seed values for each precision.
3.2 Stochastic multiplication accuracy
Although increasing the accuracy of the generation phase is important, the overall accuracy of the stochastic multiplication has a higher priority. Both seeding and bit-precision affect the accuracy of the generation phase, however the stochastic multiplication has a third important parameter which is the correlation between the input stochastic numbers. To study the stochastic multiplication accuracy, we generated a vector of 1,024 4-bit random binary numbers to act as an input vector V[1 × 1024], and a matrix of 1,024 rows and 10 columns of 4-bit random binary numbers M[1024 × 10]. The benchmark targets element-by-element multiplication of the matrix M by the vector V without accumulating the results to measure the average stochastic multiplication error in isolation from accumulation. The average multiplication error is calculated and updated over the 10,240 stochastic multiplication operations for the different seeding combinations at the 16-bit stochastic precision. After few thousands of operations the average error starts to stabilise around a certain value (as more operations are taken into consideration) which means that the stochastic multiplication is more friendly to AI applications where thousands of multiplications take place. From the stochastic generation accuracy subsection, all seeds have 0.0% average generation error for the 16-bit stochastic precision. However, the different seeding combinations generate different stochastic multiplication accuracy results. The average error is few times higher when the same seed is used to generate both stochastic inputs due to the high input correlation. This means that even for a full stochastic precision, it is necessary to search for the best seeding that generates the most uncorrelated inputs for the best stochastic multiplication results.
Consequently, the benchmark was repeated to execute the element-by-element multiplication of the matrix M by the vector V for the targeted stochastic precisions (16-bit down to 4-bit) for all possible input-seeding combinations. Figure 5 shows the best and worst average stochastic multiplication error per each stochastic precision. As the input correlation starts to contribute to the error, it is reasonable to have some new best seeds that are different from the best seeds of the generation phase. The new best seeds make a balance between the input stochastic generation accuracy and the low input correlation to achieve the optimum overall accuracy. The results show that choosing a better seeding for the stochastic multiplication operation increases the accuracy by few times. For example at 16-bit stochastic precision, choosing SEED 8 for the vector and SEED 10 for the matrix decreases the average error by 3.34x in comparison to using the same seed for both vector and matrix. It is also promising to notice that the best seeding at the lowest precision (SC 4-bit) has a better average error than the worst seeding at the highest precision (SC 16-bit) as shown in Figure 5.
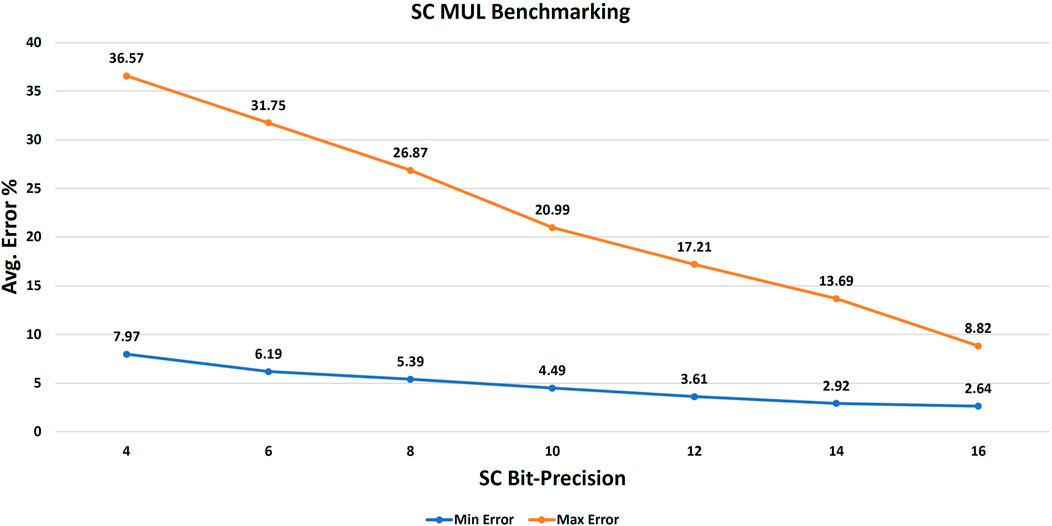
FIGURE 5. The minimum average error (due to best seeding) and the maximum average error (due to worst seeding) of the stochastic multiplication benchmark (10,240 operations) per each targeted stochastic bit-precision.
3.3 Stochastic vector-matrix multiplication accuracy
The accumulation process of the element-by-element stochastic multiplications is crucial to preserve the overall accuracy. Figure 6 shows the errors of the output vector VMM[1 × 10] which is generated by multiplying the matrix M[1024 × 10] by the vector V[1 × 1024]. While the element-by-element multiplication was done in the stochastic domain, the accumulation was done in the binary domain to generate the 10 output values. These output results were compared to the original binary results to calculate the error per each output and then the average error for all targeted stochastic bit-precisions. The results, in Figure 6, show that the average error per each stochastic precision was improved over the only multiplication average error, in Figure 5, due to the accumulation of the negative and positive errors which cancel each others. This in-deterministic behavior makes a lower stochastic precision like 8-bit offers a better accuracy than its higher counterparts like 10-bit and 12-bit. However, the 16-bit stochastic precision still produces the most accurate results as expected. It is also promising to notice that using a fully binary accumulation approach can scale down the stochastic bit-precision from 16-bit to 4-bit while the average error degrades only from 0.35% to 0.85%.
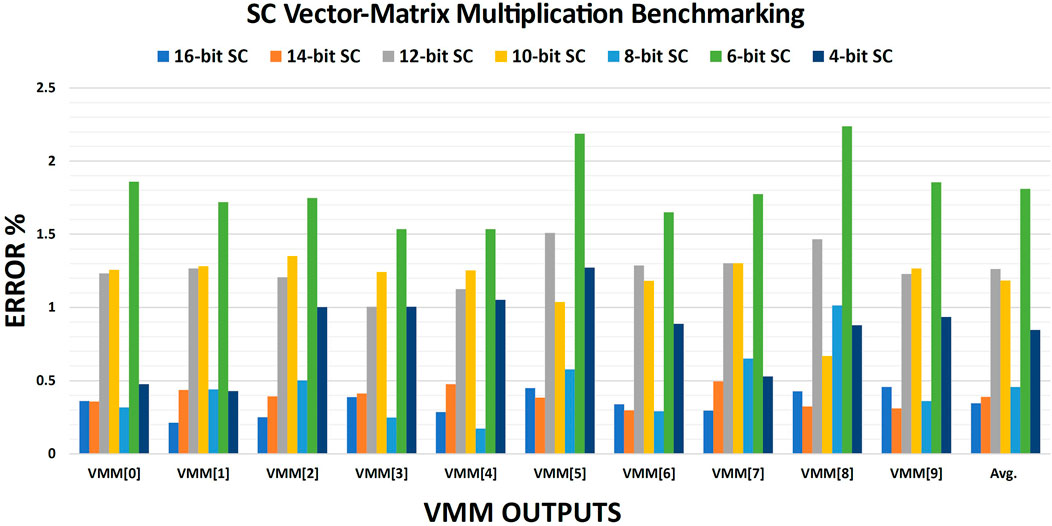
FIGURE 6. The error per each output of the stochastic VMM benchmarking for all targeted precisions. The average error per each stochastic bit-precision is also shown.
This promises a great reduction in the hardware area and energy cost of the stochastic domain, however it increases the design complexity in the binary domain as more bigger counters are required. Although the accumulation can be easily done in the binary domain by integrating it with the stochastic-to-binary converters, it is a hardware-costly solution for large-scale architectures that deal with large DNNs’ datasets. Furthermore, it is not hardware-friendly to the in-memory computing architectures due to the layout pitch-matching constraints of the memory design. Doing the accumulation in the stochastic domain is expected to dramatically degrade the final accuracy of the VMM. To avoid increasing the binary domain design complexity, we propose a hybrid stochastic-binary accumulation approach to trade accuracy for better energy and less design complexity. Our methodology is to repeat the previous VMM benchmark for all stochastic bit-precisions with different numbers of ROWs. The ROW number determines the number of stochastic accumulation operations before the result needs to be converted back to the binary domain for further binary accumulation. Hence, every ROW times of stochastic accumulation operations, one binary accumulation takes place for the stochastic result. The ROW parameter varies from ROW-1 (which means fully binary accumulation approach) to ROW-1024 (which means fully stochastic accumulation approach) including ROW-16, ROW-32, ROW-64, ROW-128, ROW-256 and ROW-512. Figure 7 shows the errors (including the average errors) of the stochastic VMM using the different combinations of the hybrid stochastic-binary accumulation approach for all targeted stochastic bit-precisions. Regarding the 16-bit stochastic precision, the fully stochastic accumulation generates an average error of 18.87% in comparison to 0.35% in case of the fully binary accumulation. However, the ROW-128 hybrid approach generates only 2.94% average error which is 6.4x better than the fully stochastic accumulation approach. On the other side, the fully stochastic accumulation of the 4-bit stochastic precision gives an average error of 7% which is better than expected due to accumulating the positive and negative errors. It also offers an average error of 2.56% at the ROW-64 hybrid approach which is nearly equivalent to the ROW-128 hybrid approach of the 16-bit stochastic precision.
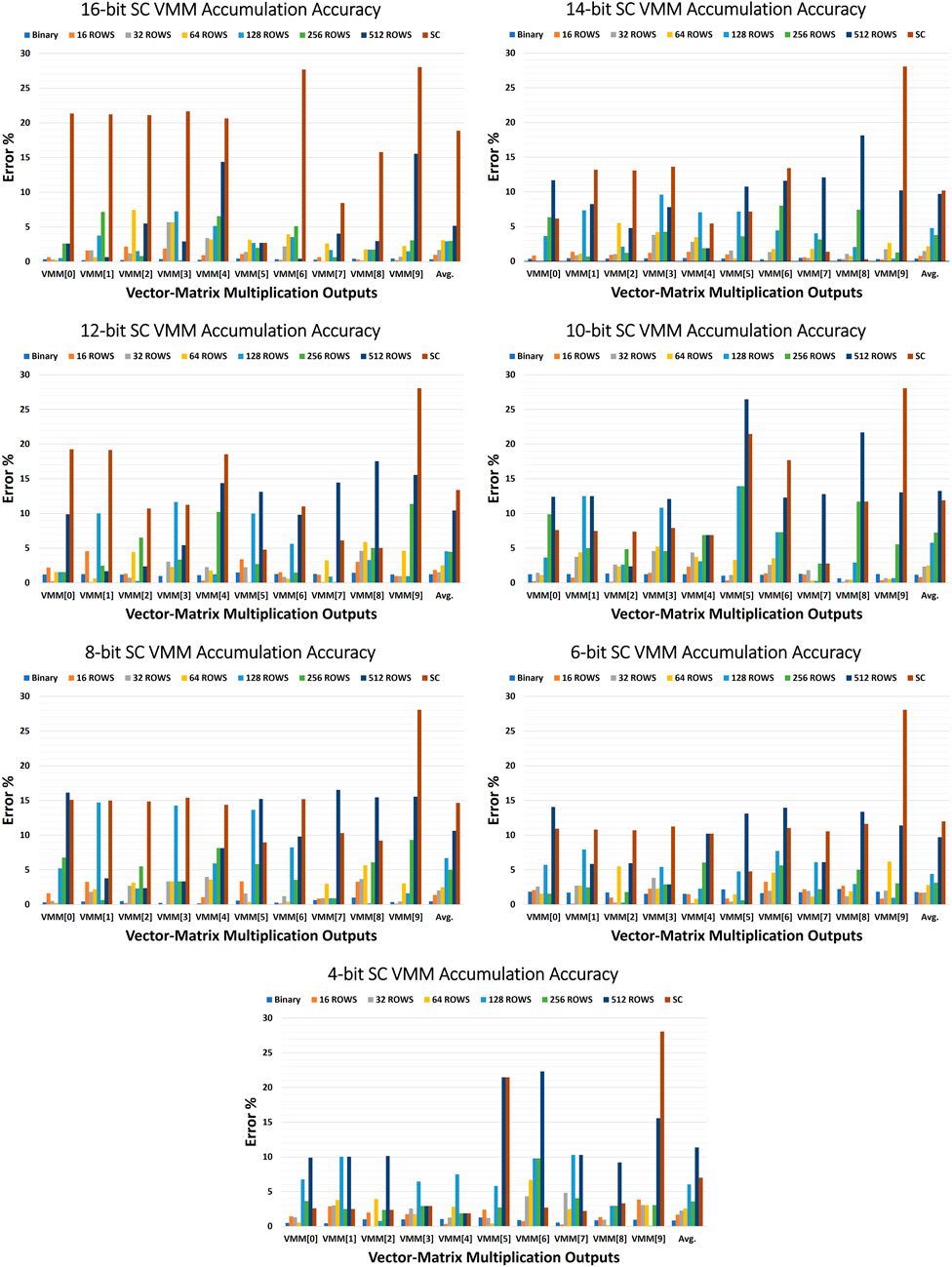
FIGURE 7. The errors including the average error of the stochastic VMM outputs using different hybrid stochastic-binary accumulation combinations for the targeted stochastic bit-precision.
These results show that the stochastic bit-precision can be scaled down for VMMs from 16-bit to only 4-bit without experiencing any significant loss in accuracy. While searching for the best seeding is urgent to increase the element-by-element multiplication accuracy, finding a good ROW value is essential for increasing the VMM accuracy and decreasing the design complexity. Thanks to the hybrid stochastic-binary accumulation approach, the stochastic accumulation reduces the hardware complexity of the design while the periodic binary accumulation mitigates the approximation error of the stochastic accumulation. Therefore, the average errors of all stochastic bit-precisions can be forced to converge below 3% for different good ROW cases. If the AI system tolerates up to 3% average error for a VMM, different hybrid stochastic-binary accumulation setups can be extracted for all stochastic bit-precisions. These different design points have different performance/design-complexity trade-offs, and therefore the accuracy analysis is a vital milestone towards the design space exploration of our novel in-memory stochastic computing architecture.
4 In-memory stochastic computing architecture
The stochastic computing domain is less data-compact due to the bitstream data representation in contrast to the binary domain which represents the same data by a fewer number of bits. This main drawback of the stochastic computing domain adds more insult to injury regarding the data-movement bottleneck. Hence, the conventional Von Neumann architectures are not the best environment for both DNNs and stochastic computing. In-memory computing aims at mitigating the data-movement bottleneck by avoiding, as much as possible, any unnecessary data transmission. High-density on-chip memories are the best candidates to host the relatively long stochastic bitstreams, while performing the in-memory computation avoids transferring these longer bitstreams between the memory and the processing units (potentially through a network-on-chip).
The conventional digital in-memory computing approach using SRAMs depends mainly on the bitline computing technique. During the bitline computing mode, two wordlines are activated simultaneously so the read-data and its complementary (data_bar) represent the bitwise AND and NOR operations between the two wordlines. This requires adding an extra address decoder and modifying the sense-amplifier per each column to a reconfigurable sense-amplifier which nearly doubles the size of the conventional one. Adding one extra address decoder while activating two wordlines simultaneously increases the overall energy footprint of these architectures. To avoid this penalty, we propose a novel in-memory stochastic computing approach which is shown in Figure 8. This new approach converts the conventional memory read operations into on-the-fly bitwise AND operations between the input (IN) and the data saved by the active bitcell. Unlike the conventional bitline computing approach, the proposed architecture has a negligible hardware overhead. While using hardwired AND gates reduces the throughput by 50%, this novel in-memory stochastic computing approach utilizes the full bandwidth of the memory to achieve the full throughput.
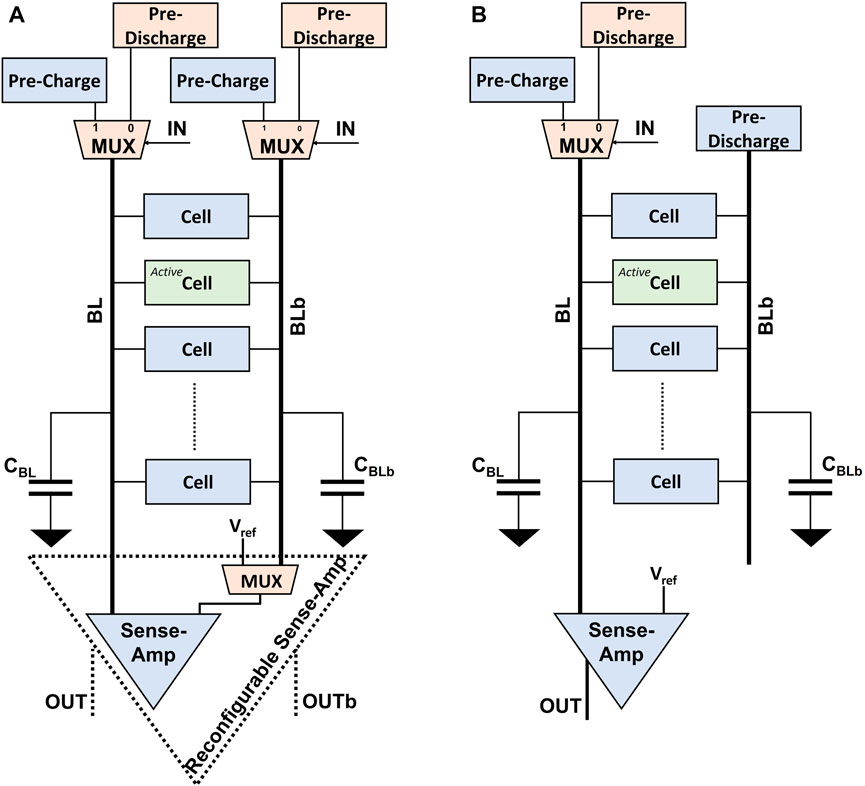
FIGURE 8. The proposed column-wise modifications to convert the conventional read operation into an on-the-fly bitwise AND operation between the input IN and the bitcell data: (A) differential bitcells like 6T CMOS SRAM bitcells, (B) single-ended bitcells like 1T1R RRAM bitcells.
Regarding the conventional 6T CMOS SRAMs shown by Figure 8A, the bitline (BL) is pre-charged to VDD if the input IN is 1 which leads to the conventional read operation functionality. If the active bitcell captures the value of 1 (0), the sense-amplifier reads logic 1 (0) which is the bitwise AND operation. If the input IN is 0, the BL is pre-discharged to GND (or a low voltage) and the sense-amplifier always reads logic 0 regardless the active bitcell’s value, which is the bitwise AND operation. The input should be forwarded in the same way to the bitline_bar (BLb) to avoid any read-disturbance while performing the proposed on-the-fly AND operation.
For the in-memory stochastic computing architecture, we are only interested in the bitwise AND operation which acts as a stochastic multiplication. Thus we are not interested anymore in the complementary of the data and the bitwise NOR operation. The digital 1T1R memory arrays use a single-ended 1T1R bitcell where High Resistance State (HRS) represents logic 1 and Low Resistance State (LRS) represents logic 0 (Agwa et al., 2022). This emerging technology promises a higher on-chip data density and capacity for the in-memory stochastic computing architecture. As shown by Figure 8B, the same approach is proposed to pre-charge BL if IN is 1 and pre-discharge BL if IN is 0, while BLb is pre-discharged regardless the input value. This new approach utilizes the inherent AND behavior of the memory read operations to perform massive parallel stochastic multiplication operations through the in-memory computing architecture.
Data layout, which is how data is physically saved in memory, is an important parameter to explore the design space of this in-memory stochastic computing architecture. Figure 9 shows the logical layout of the input vector and the matrix which should be physically mapped to the memory rows (called wordlines). The in-memory computing architecture has massive parallel computing resources and the target is to maximize the utilization of these resources to do as many stochastic multiplications as possible per cycle. The physical data layout, depicted in Figure 9, shows that the input vector and the matrix columns are divided into multiple batches. Each batch has a certain number of rows and columns with a specific arrangement that makes the accumulation process easier to generate the final VMM outputs. The sizes of these batches depend on the stochastic VMM accuracy analysis done in Section 3. The ROW number of each stochastic bit-precision determines the suitable size of its batch. For example, ROW-128 of 16-bit stochastic precision means that the batch is 128 values of 16-bit stochastic data which can be mapped to 16 rows and 8 columns (16 × 8) in the memory.
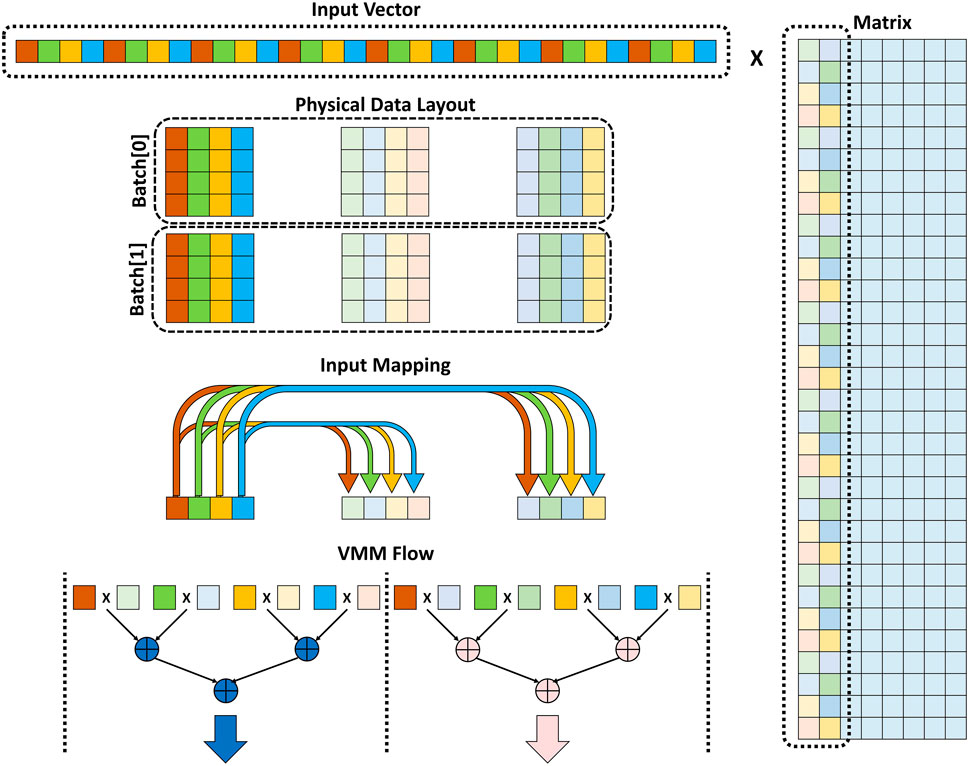
FIGURE 9. Data layout of Vector-Matrix Multiplication including physical data layout saved in the memory sub-array, input vector mapping to different columns of the matrix, and the VMM flow through the accumulation tree.
Figure 10 shows the proposed architecture where the data batches are mapped to virtual clusters. Every cluster consists of a number of virtual ALU lanes and each lane handles one n-bit stochastic multiplication at a time. The outputs of these ALU lanes should be accumulated using a stochastic accumulation tree of multiplexers. The outputs of the stochastic accumulation stage are converted to the binary domain by counters and the latency of these counters is hidden while computing the next batch. Thus, the accumulation is done for one batch in the stochastic domain using a tree of multiplexers and then for the whole dataset in the binary domain using the binary counters to accumulate the batches together. Each cluster is responsible for multiplying one column of the matrix by the input vector to generate one output. Ideally, the cluster should have only one binary counter to accomplish the binary accumulation. However, the cluster may have a few of binary counters and a further accumulation addition tree for smaller batch sizes. The small batch sizing means that more accumulation is done in the binary domain and the architecture has to parallelize the binary accumulation (using more counters) to increase the memory resources’ utilization.
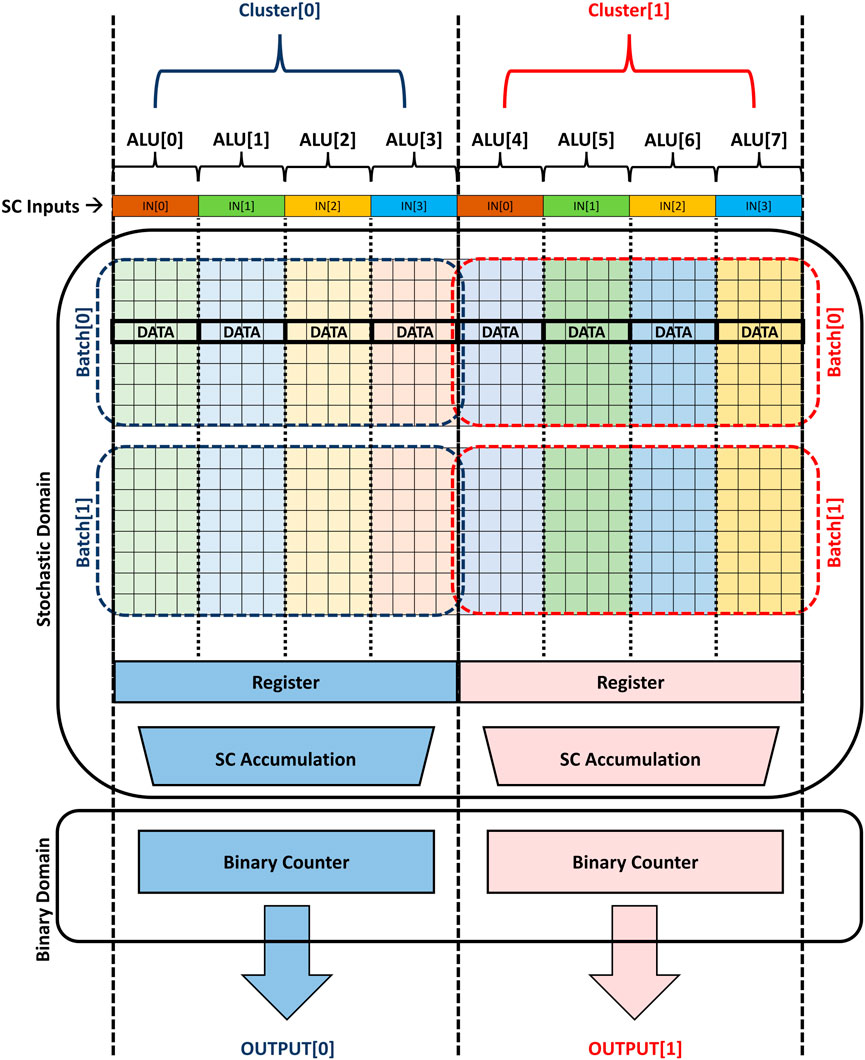
FIGURE 10. An abstract view of the proposed in-memory stochastic computing architecture using hybrid stochastic-binary accumulation for VMM applications.
Our methodology is to fix the memory sub-array size for 128 ROW X 256 COL with 4 KB capacity which is suitable to build on-chip cache memories. Based on the accuracy analysis in Section 3, we consider all design points for all stochastic bit-precisions that have an average error less than 3%. The Verilog-based stochastic VMM benchmarking was utilized to build an analytical model for the proposed architecture. Table 2 shows the definitions of the different parameters of the analytical model while Table 3 shows the extracted equations. We use this model to search for the optimum design point per each stochastic bit-precision depending on different metrics like: throughput, latency, design complexity, memory utilization per sub-array, and accuracy. As each cluster is responsible for generating a standalone output, it has its own counter/counters to complete the hybrid stochastic-binary accumulation independently in parallel with the other running clusters. Increasing the number of counters per sub-array increases the design complexity and the energy footprint of the whole system.
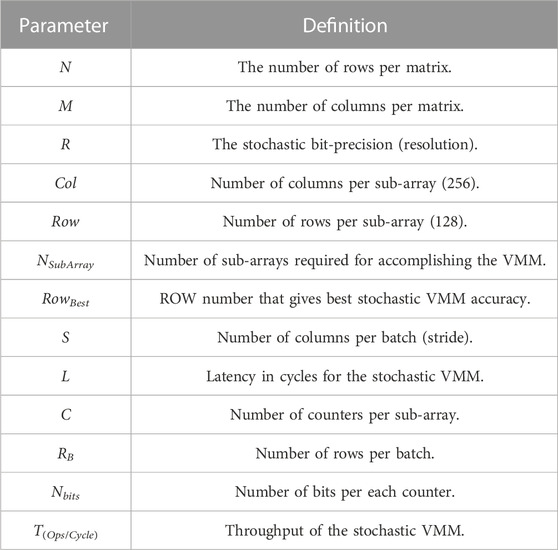
TABLE 2. The analytical Model’s parameters of the in-memory stochastic computing architecture using hybrid stochastic-binary accumulation for VMM.
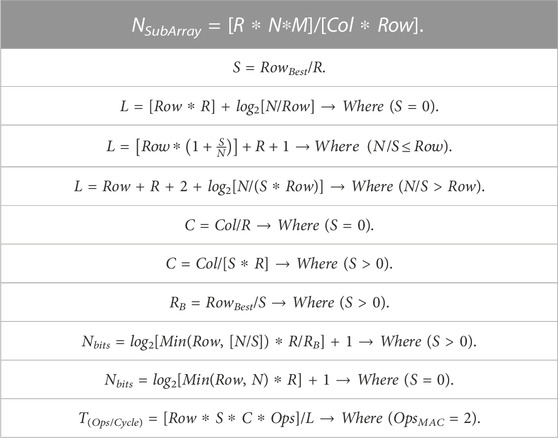
TABLE 3. The analytical Model’s equations of the in-memory stochastic computing architecture using hybrid stochastic-binary accumulation for VMM.
Figure 11 shows the required number of counters per sub-array for each design point of the different stochastic bit-precisions. It is noticeable that decreasing the size of the batch increases the number of counters as expected. The latency and throughput per sub-array for each design point are also shown in Figure 11. The results show how a key factor the stochastic bit-precision is to improve throughput and latency. It determines the number of virtual ALU lanes running in parallel per each sub-array which determines the throughput. The stochastic multiplication operation is done on-the-fly and consumes only one clock cycle regardless its stochastic bit-precision. In contrast, the binary accumulation’s contribution to the overall latency depends on the stochastic bit-precision. The higher the stochastic precision, the more cycles the counter consumes to do the accumulation. However, the binary accumulation has a minor contribution to the overall latency because it is hidden by computing the next batch except the last binary accumulation run.
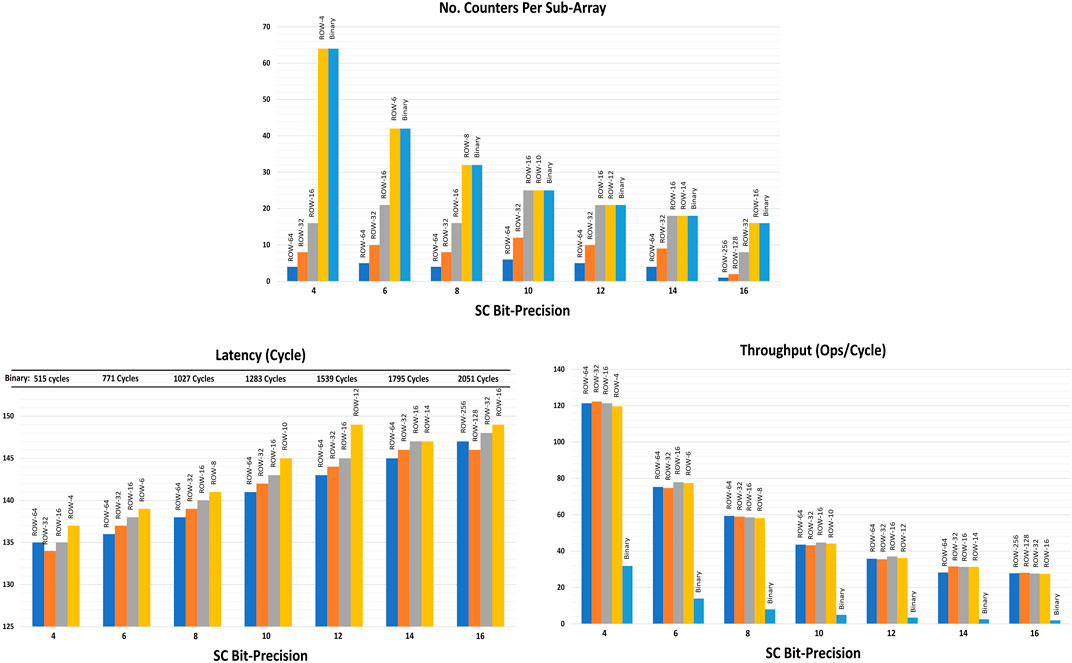
FIGURE 11. The analytical model’s results including number of counters, latency and throughput per sub-array for each architectural design point.
Table 4 shows the most efficient design point per each stochastic bit-precision. The design efficiency was calculated as a ratio of the real throughput versus the ideal throughput, while the ideal one is not considering the cost of the accumulation process and assuming an ideal utilization for the memory sub-array. This design efficiency metric takes into consideration the effects of the latency and the memory utilization on the throughput degradation for each stochastic bit-precision. Thus, it shows how efficient and hardware-friendly the design point is, from the hardware implementation perspective. From Table 4, the stochastic 16-bit architecture with ROW-128 has the maximum batch size and the minimum number of counters (two 8-bit counters) while it shares the maximum memory utilization per sub-array (100%) with stochastic 4-bit (ROW-32) and 8-bit (ROW-64) design points. However, the most efficient design is the stochastic 4-bit with ROW-32 which has the highest throughput (122 Ops/Cycle) and the best latency (134 Cycles) due to its low bit-precision. From accuracy perspective, stochastic 10-bit with ROW-16 has the lowest average error in this table (0.85%) but on the other hand it has the worst design complexity due to the large number of counters per sub-array (25 7-bit counters). These results spotlight the different trade-offs of the architectural design space where each design priority (Accuracy, Energy, Performance, Complexity) has its own matching design point.
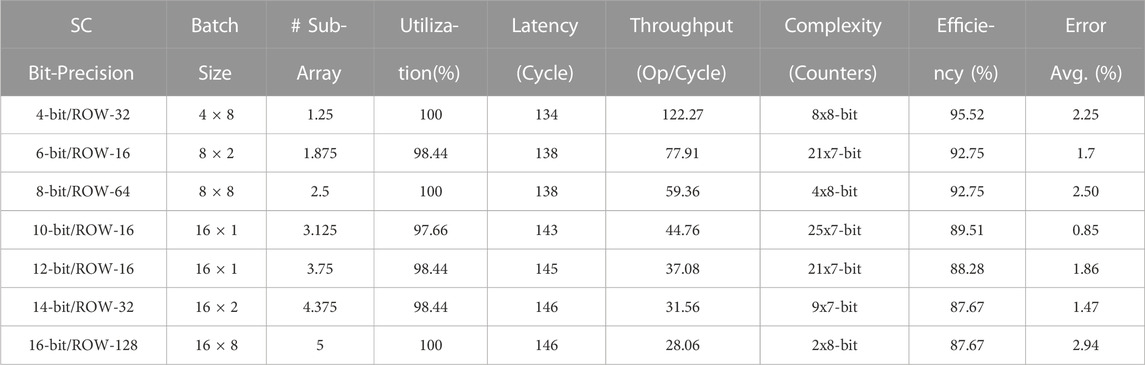
TABLE 4. Comparison among the different stochastic bit-precisions with their best architectural design points.
5 Conclusion
The in-memory computing architectures demonstrate significant potential in mitigating the Von Neumann data-movement bottleneck, while the stochastic computing domain shows promise for combining the computation simplicity of the analog computing with the scalability, productivity and robustness of the digital domain. This paper proposes a novel digital in-memory stochastic computing architecture for Vector-Matrix Multiplications (VMMs). This architecture avoids the scalability and variability challenges associated with analog crossbars, as well as the hardware complexity and long latency of digital in-memory binary computing. The paper introduces a new stochastic number generator that maps the 4-bit binary data ideally to 16-bit stochastic numbers for any seed value. The same circuit is also utilized to map the 4-bit binary domain to lower stochastic bit-precisions with minimal error by fine-tuning the seed value. An accuracy analysis of a stochastic VMM benchmark is presented, incorporating a hybrid stochastic-binary accumulation approach. This accuracy analysis demonstrates the significance of different phases, including generation, multiplication, and accumulation, in achieving optimal accuracy for the VMM benchmark. Therefore, this paper introduces a technology-agnostic accuracy roadmap for stochastic VMM computing, highlighting the importance of all these phases. Thanks to the proposed hybrid stochastic-binary accumulation approach, scaling down the stochastic precision from 16-bit to 4-bit achieves nearly the same average error (less than 3%) across different ROW numbers. Additionally, this work presents a new digital in-memory stochastic computing architecture that turns the conventional memory read operations into on-the-fly stochastic multiplication operations. The proposed architecture’s design space exploration is performed using an analytical model. The extracted analytical model enables the examination of various trade-offs among the different architectural design points, including latency, throughput, design complexity, and accuracy. Thanks to the adopted approaches, the 4-bit stochastic architecture with ROW-32 achieves the highest throughput (122 Ops/Cycle), which is 4.36x better than the 16-bit stochastic precision with a small average error of 2.25%. This technology-agnostic design space exploration study is a key milestone to identify the promising design points for implementation. The transistor-level implementation of the proposed architecture is currently in progress using an in-house RRAM model and a commercial 180 nm technology.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
SA was involved with the conceptualization of the different ideas, conducting the benchmarking tests, extracting the analytical model and writing the manuscript. TP was involved with the conceptualization of the ideas and writing the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work has been funded by the EPSRC FORTE Programme Grant (EP/R024642/2) and the RAEng Chair in Emerging Technologies (CiET1819/2/93).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adam, G. C., Khiat, A., and Prodromakis, T. (2018). Challenges hindering memristive neuromorphic hardware from going mainstream. Nat. Commun. 9, 5267. doi:10.1038/s41467-018-07565-4
Agwa, S., Pan, Y., Abbey, T., Serb, A., and Prodromakis, T. (2022). “High-density digital RRAM-based memory with bit-line compute capability,” in 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, 1199–1200. doi:10.1109/ISCAS48785.2022.9937848
Al-Hawaj, K., Afuye, O., Agwa, S., Apsel, A., and Batten, C. (2020). “Towards a reconfigurable bit-serial/bit-parallel vector accelerator using in-situ processing-in-SRAM,” in 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 1–5. doi:10.1109/ISCAS45731.2020.9181068
Alaghi, A., and Hayes, J. P. (2014). “Fast and accurate computation using stochastic circuits,” in Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 24-28 March 2014.
Alaghi, A., and Hayes, J. P. (2013). Survey of stochastic computing. ACM Trans. Embed. Comput. Syst. 12, 1–19. doi:10.1145/2465787.2465794
Alaghi, A., Li, C., and Hayes, J. P. (2013). “Stochastic circuits for real-time image-processing applications,” in 50th ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, Texas, USA, 29 May - 7 June 2013.
Alaghi, A. (2015). The logic of random pulses: Stochastic computing. Ann Arbor, MI, USA: Ph.D. dissertation, University of Michigan.
Chen, T. H., Ting, P., and Hayes, J. P. (2017). “Achieving progressive precision in stochastic computing,” in IEEE Global Conference on Signal and Information Processing (GlobalSIP), Ottawa, Ontario, Canada, November 11-14 2017, 1320–1324.
Eckert, C., Wang, X., Wang, J., Subramaniyan, A., Iyer, R., Sylvester, D., et al. (2018). “Neural cache: Bit-serial in-cache acceleration of deep neural networks,” in International Symposium on Computer Architecture (ISCA), Los Angeles, CA, USA, June 1 2018 to June 6 2018.
Farmahini-Farahani, A., Ahn, J. H., Morrow, K., and Kim, N. S. (2015). “Nda: Near-dram acceleration architecture leveraging commodity dram devices and standard memory modules,” in International Symposium on High-Performance Computer Architecture (HPCA), Burlingame, CA, USA, Feb 7 2015 to Feb 11 2015.
Fujiki, D., Mahlke, S., and Das, R. (2019). “Duality cache for data parallel acceleration,” in International Symposium on Computer Architecture (ISCA), Phoenix Arizona, June 22 - 26, 2019.
Groszewski, A. J., and Lenz, T. (2019). “Deterministic stochastic computation using parallel datapaths,” in 20th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, March 6-7, 2019, 138–144.
Jeloka, S., Akesh, N. B., Sylvester, D., and Blaauw, D. (2015). “A configurable tcam/bcam/sram using 28nm push-rule 6t bit cell,” in Symposium on Very Large-Scale Integration Circuits (VLSIC), Kyoto, Japan, June 17-19, 2015.
Jouppi, N., Young, C., Patil, N., Patterson, D., Agrawal, G., Bajwa, R., et al. (2017). “In-datacenter performance analysis of a tensor processing unit,” in 44th Annual International Symposium on Computer Architecture (ISCA ’17), Toronto ON Canada, June 24 - 28, 2017.
Kim, D., Yu, C., Xie, S., Chen, Y., Kim, J.-Y., Kim, B., et al. (2022). An overview of processing-in-memory circuits for artificial intelligence and machine learning. IEEE J. Emerg. Sel. Top. Circuits Syst. 12, 338–353. doi:10.1109/JETCAS.2022.3160455
Lee, V. T., Alaghi, A., Hayes, J. P., Sathe, V., and Ceze, L. (2017). “Energy-efficient hybrid stochastic-binary neural networks for near-sensor computing,” in Design, Automation & Test in Europe Conference & Exhibition (DATE), March 27-31 2017, Lausanne, Switzerland. 13–18.
Lin, Z., Xie, G., Wang, S., Han, J., and Zhang, Y. (2021). “A review of deterministic approaches to stochastic computing,” in IEEE/ACM International Symposium on Nanoscale Architectures (NANOARCH), AB, Canada, Nov 8 2021 to Nov 10 2021.
Liu, Q., Gao, B., Yao, P., Wu, D., Chen, J., Pang, Y., et al. (2020). “A fully integrated analog reram based 78.4tops/w compute-in-memory chip with fully parallel mac computing,” in IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, California, USA, 16-20 February 2020, 500–502.
Liu, Y., Liu, S., Wang, Y., Lombardi, F., and Han, J. (2021). A survey of stochastic computing neural networks for machine learning applications. IEEE Trans. Neural Netw. Learn. Syst. 32, 2809–2824. doi:10.1109/TNNLS.2020.3009047
Salehi, S. A. (2020). Low-cost stochastic number generators for stochastic computing. IEEE Trans. Very Large Scale Integration (VLSI) Syst. 28, 992–1001. doi:10.1109/TVLSI.2019.2963678
Seshadri, V., Kim, Y., Fallin, C., Lee, D., Ausavarungnirun, R., Pekhimenko, G., et al. (2013). “Rowclone: Fast and energy-efficient in-dram bulk data copy and initialization,” in International Symposium on Microarchitecture (MICRO), Davis, CA, USA, December 7-11, 2013.
Wan, W., Kubendran, R., Schaefer, C., Eryilmaz, S. B., Zhang, W., Wu, D., et al. (2022). A compute-in-memory chip based on resistive random-access memory. Nature 608, 504–512. doi:10.1038/s41586-022-04992-8
Winstead, C. (2019). “Tutorial on stochastic computing,” in Stochastic computing: Techniques and applications. Editors W. Gross, and V. Gaudet (Berlin, Germany: Springer).
Wu, D., Yin, R., and Miguel, J. S. (2021). “Normalized stability: A cross-level design metric for early termination in stochastic computing,” in 26th Asia and South Pacific Design Automation Conference (ASP-DAC), Tokyo, Japan, January 18-21, 2021, 254–259.
Yao, P., Wu, H., Gao, B., Tang, J., Zhang, Q., Zhang, W., et al. (2020). Fully hardware-implemented memristor convolutional neural network. Nature 577, 641–646. doi:10.1038/s41586-020-1942-4
Yu, S., Jiang, H., Huang, S., Peng, X., and Lu, A. (2021). Compute-in-memory chips for deep learning: Recent trends and prospects. IEEE Circuits Syst. Mag. 21, 31–56. doi:10.1109/MCAS.2021.3092533
Keywords: stochastic computing, in-memory computing, beyond von-neumann architectures, vector-matrix multiplication, RRAM, deep neural network, emerging technologies
Citation: Agwa S and Prodromakis T (2023) Digital in-memory stochastic computing architecture for vector-matrix multiplication. Front. Nanotechnol. 5:1147396. doi: 10.3389/fnano.2023.1147396
Received: 18 January 2023; Accepted: 12 July 2023;
Published: 24 July 2023.
Edited by:
Jeongwon Park, University of Nevada, Reno, United StatesReviewed by:
Jiyong Woo, Kyungpook National University, Republic of KoreaMarc Riedel, University of Minnesota Twin Cities, United States
Copyright © 2023 Agwa and Prodromakis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shady Agwa, c2hhZHkuYWd3YUBlZC5hYy51aw==
 Shady Agwa
Shady Agwa Themis Prodromakis
Themis Prodromakis