Third- and Second-Harmonic Generation in All-Dielectric Nanostructures: A Mini Review

Liu, Tingting; Xiao, Shuyuan; Li, Baoli; Gu, Min; Luan, Haitao; Fang, Xinyuan

doi:10.3389/fnano.2022.891892

MINI REVIEW article

Front. Nanotechnol., 20 May 2022

Sec. Nanophotonics

Volume 4 - 2022 | https://doi.org/10.3389/fnano.2022.891892

Third- and Second-Harmonic Generation in All-Dielectric Nanostructures: A Mini Review

Tingting Liu^1,2

Shuyuan Xiao³

Baoli Li^1,2

Min Gu^1,2

Haitao Luan^1,2*

Xinyuan Fang^1,2*

¹Institute of Photonic Chips, University of Shanghai for Science and Technology, Shanghai, China
²Centre for Artificial-Intelligence Nanophotonics, School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai, China
³Institute for Advanced Study, Nanchang University, Nanchang, China

Frequency conversion such as harmonic generation is a fundamental physical process in nonlinear optics. The conventional nonlinear optical systems suffer from bulky size and cumbersome phase-matching conditions due to the inherently weak nonlinear response of natural materials. Aiming at the manipulation of nonlinear frequency conversion at the nanoscale with favorable conversion efficiencies, recent research has shifted toward the integration of nonlinear functionality into nanophotonics. Compared with plasmonic nanostructures showing high dissipative losses and thermal heating, all-dielectric nanostructures have demonstrated many excellent properties, including low loss, high damage threshold, and controllable resonant electric and magnetic optical nonlinearity. In this review, we cover the recent advances in nonlinear nanophotonics, with special emphasis on third- and second-harmonic generation from all-dielectric nanoantennas and metasurfaces. We discuss the main theoretical concepts, the design principles, and the functionalities of third- and second-harmonic generation processes from dielectric nanostructures and provide an outlook on the future directions and developments of this research field.

1 Introduction

Nonlinear optics is one of the fundamental branches of modern photonic science and technology (Boyd, 2008). It is concerned with the nonlinear light–matter interactions accompanied by the modification of the optical properties in a material system at high light intensities. The discovery of this field is marked by the experimental observation of second-harmonic generation (Franken et al., 1961), shortly after the advent of the laser with intense electromagnetic radiation (Maiman et al., 1960). Ever since, considerable efforts have been devoted to the development of theoretical models and experimental methods of nonlinear phenomena, including high harmonic generation, optical frequency mixing, and self-focusing, leading to its evolution from a laboratory curiosity into a tool that finds applications in a large variety of optical devices. Over these decades, the inherently weak optical nonlinearity of natural materials has been one of the biggest challenges haunting the research community, and thus, a long-standing goal in the field has been the development of materials with large optical nonlinearity.

In the early stage, the bulky structures of nonlinear materials are usually exploited to offer the long interaction lengths for the build-up of nonlinear optical response, while the phase-matching condition involving the extremely precise and cumbersome techniques is required to compensate for the momentum mismatch between the optical pump and generated signals. The typical bulk size and the phase-matching constraint of a conventional nonlinear optical system make it inconvenient to engineer the nonlinear optical responses. In particular, such a system is far from fulfilling the requirements of feasible optical-integrated nonlinear components, hindering the promising applications in telecommunications, all-optical data processing and storage, and quantum information technologies, to name a few.

Fueled by the recent advance in nanofabrication techniques that enable complicated assemblies of nanoscale structures, a renaissance of the nonlinear optics is underway, endowed with the ability to engineer the nonlinear electromagnetic behavior in deep-subwavelength volume. Benefiting from advanced nanotechnology, nonlinear optical components undergo revolutionary transformations as a novel research direction of nanophotonics. The research interest has shifted from the phase-matching optical interactions that occur over the bulk size with many wavelengths scale toward the optical near-field interactions within a few wavelengths or at subwavelength scale (Kravtsov et al., 2016; Mesch et al., 2016; Deka et al., 2017). In this framework, the efficiency of nonlinear processes is determined not by the quality of phase matching between the interacting optical signals but by the degree of confinement and overlap of the optical near-field with the nonlinear nanostructures. For such non-phase-matching nonlinear optical interactions, major research work over the past decade has been focused on the design and fabrication of optimized configurations of nonlinear nanostructures, where not only a good spatial matching between the optical near-field and the optical nanostructure is needed but also the near-field is resonantly enhanced. After years of fruitful developments, nonlinear nanophotonics has become a prominent area of research with potential applications for nonlinear nanoantennas, light sources, nanolasers, and ultrafast miniature devices (Aouani et al., 2012; Schlickriede et al., 2018).

The advances in nonlinear optics are shaped by the evolution of modern nanophotonics. During the past decades, nonlinear nanophotonics has been pioneered in plasmonic nanostructures that are among the first exploited approach to bridge the gap between conventional and modern nonlinear optics. The plasmonic effects of metallic nanostructures arise from the coherent oscillation of free electrons near the surface of noble-metal nanostructures, i.e., the so-called surface plasmons. The resulting strong electromagnetic fields allow the weak nonlinear processes superlinearly dependent on the local field to be significantly enhanced. The combination of the strong near-field intensity in plasmonic system and the intrinsic nonlinearities of metals results in efficient nonlinear optical processes, which have given rise to the new research field of nonlinear plasmonics. The plasmonic nanostructures, including the surface plasmon polariton crystals and waveguides, nanoantennas, and plasmonic metamaterials, can be utilized to control the nonlinear optical response (Shadrivov et al., 2008; Utikal et al., 2011; Husu et al., 2012; Zhang et al., 2016; Collins et al., 2018; Guo et al., 2018). The plasmonic excitation is extremely sensitive to dielectric properties of the metal and the surrounding materials, making it possible to modify the spatial distribution of the optical near-field and the resonance frequency by changing the geometry and optical constants of the nanostructures (Linnenbank et al., 2016; Fischer et al., 2018; Wang and Harutyunyan, 2018). Various nonlinear optical processes have been observed in the plasmonic nanostructures. In this regime, the detailed observation and understanding of the nonlinear optical responses in plasmonic nanostructures are available in review articles (Kauranen and Zayats, 2012; Butet et al., 2015; Ding et al., 2018; Panoiu et al., 2018; Rahimi and Gordon, 2018). Despite the numerous advantages for near-field enhancement, metallic nanostructures suffer from high dissipative losses and inevitable heating effect, leading to irreversible damage under high intensity light. Therefore, the exploration of other materials for nonlinear engineering at the nanoscale has been an active research direction.

Recently, dielectric nanostructures are emerging as promising alternatives for the subwavelength control of light in the nonlinear regime, offering new avenues for a wide range of nonlinear nanophotonic applications (Baranov et al., 2017; Yang et al., 2017; Grinblat, 2021). Compared with their plasmonic counterparts, the dielectric nanostructures show advantages of high refractive index, negligible dissipative loss, and high damage threshold, allowing for the formation of optical resonances with higher quality factors. In particular, in contrast to plasmonics of metallic nanostructures where the electric dipole modes usually dominate the resonance, the multipolar characteristics with the coexistence of electric and magnetic resonant modes known as Mie-type resonances have been demonstrated in different geometries of dielectric resonators (Kivshar, 2018; Xiao et al., 2020a; Wang et al., 2020; Huang L. et al., 2021). The strong localization of electric and magnetic fields arising from Mie-type resonance inside dielectric nanostructures further enhances the nonlinear effects (Volkovskaya et al., 2020). Furthermore, the nonlinear responses can be modified by tuning the electric and magnetic modes (Colom et al., 2019). Therefore, the dielectric nanostructures provide a promising platform for high conversion efficiency and flexible manipulation of nonlinear response, with exclusive prospects for engineering strong optical nonlinearity and ultrafast control at the nanoscale. The research of nonlinear dielectric nanostructures has produced a large body of results and has already been the topic of a few excellent review articles, such as the review of nonlinear metasurfaces, nonlinear silicon photonics, and ultrafast nonlinearity (Zhang et al., 2014; Smirnova and Kivshar, 2016; Rahmani et al., 2018; Reshef et al., 2019; Shcherbakov et al., 2019; Zubyuk et al., 2021). Amongst them, the nonlinear harmonic generation, especially the common third-harmonic generation (THG) and second-harmonic generation (SHG) process, is the fundamental physical processes that lie on the basis of many modern disciplines in nanophotonics, holding great promises in applications of information technology.

In this mini review, we highlight recent progress in the field of nonlinear optical processes with all-dielectric nanostructures, from the nonlinear dielectric materials, and design principles of nonlinear dielectric resonators to the intriguing functionalities of the nonlinear THG and SHG. In Section 2, we present the theoretical concepts and tools to investigate the nonlinear optical properties of the dielectric system and provide a clear insight into the physical mechanisms of the nonlinear harmonic generation. In Sections 3 and 4, we focus on the most recent efforts in engineering optical nonlinear THG and SHG responses from the dielectric nanoantennas and metasurfaces ranging from infrared to ultraviolet regimes. In Section 5, we provide the main conclusions and future perspectives in this field.

2 Enhanced Nonlinear Effects in Dielectric Nanostructures

The response of materials to incident light can be considered as the interference process of the incident optical field with the synchronously oscillating scattered field generated by the collective displacement of electrons. The interference effect between them depends on the incident light intensity. For low and moderate light intensities, the induced scattered field would be linearly proportional to the incident field, which accounts for the linear optical responses and weak light–matter interactions. When the incident light intensity is sufficiently large and the optical field is intense enough to drive the electron beyond the quadratic minimum of the interatomic potential, the response becomes increasingly nonlinear owing to distorted electron orbits. The light intensities needed for nonlinear response can be estimated in the order of 10⁸ V/cm by neglecting saturation effects, which is comparable with the interatomic field (Armstrong et al., 1962). In the electric dipole approximation, the optical response of materials to the electric field of light can be described by a power series of the induced polarization P,

P = ξ_{0} ({\hat{χ}}^{(1)} E + {\hat{χ}}^{(2)} E^{2} + {\hat{χ}}^{(3)} E^{3} + \dots), (1)

where ξ₀ is the vacuum permittivity, ${\hat{χ}}^{(N)}$ is the Nth order nonlinear susceptibility tensor of rank N+1 dependent on the crystal structure of the material, and E is the localized electric field. For the case of low-intensity incident light, only the linear susceptibility ${\hat{χ}}^{(1)}$ is important, and the linear response arising from polarization oscillating at the incident frequency describes the conventional optical effects such as refraction, absorption, and reflection. With increasing field intensity, the nonlinear terms can become apparent due to the electron orbit distortion for most dielectric materials, and the optical response becomes nonlinear at sufficiently strong localized electromagnetic fields, which is usually achievable with powerful coherent light sources. Just as shown in Eq. 1, where the expansion in the field strength mixes the incident fields and produces new fields that oscillate at the sum and differences of the incident frequencies, the nonlinear polarization acts as a source for the new frequency component. Compared to conventional linear optics, nonlinear optics manifests itself as the multiphoton interaction process. Therefore, the nonlinear optical effects provide a rich and diverse set of nontrivial electromagnetic phenomena.

In a perturbative approach, nonlinear optical phenomena can be classified by the number of simultaneously involved photons. The lower-order nonlinear phenomena that arise from second- and third-order interactions with only three or four photons involved are most widely investigated and exploited because of the detectable yields granted by the larger values of the corresponding second- and third-order nonlinear susceptibilities, ${\hat{χ}}^{(2)}$ and ${\hat{χ}}^{(3)}$ . In practical applications, important effects that occur at second- and third-order are the SHG and THG processes related to ${\hat{χ}}^{(2)}$ and ${\hat{χ}}^{(3)}$ , which are routinely used for frequency conversion in the laser system. SHG refers to the interaction process between light and material, where two photons of the same energy are combined to generate a third photon at twice the energy with a frequency two times the original frequency in a coherent fashion. The similar process involved with the three photons generating a three-time frequency photon is known as THG. In addition to them, there are other nonlinear frequency conversion phenomena associated with two or three orders, such as sum and difference frequency generation, spontaneous parametric down-conversion, and four-wave mixing, which are out of the scope of this review, and thorough perspectives on these phenomena can be found in (Bonacina et al., 2020).

Moreover, the basic formalism above reveals the fact that two factors, including the material susceptibility and the localized electric field amplitudes, together play a crucial and critical role in nonlinear optical response. This fundamental principle provides the guideline for the investigation of nonlinear light–matter interaction in the subwavelength regime. In particular, it can be instructive for the nonlinear optical processes in the concerned dielectric nanostructures that can offer a rich selection of materials and be capable of strongly modifying the local-field distribution via the multipolar Mie-type resonances. As shown in Figure 1, we focus on nonlinear THG and SHG processes under the guideline.

FIGURE 1

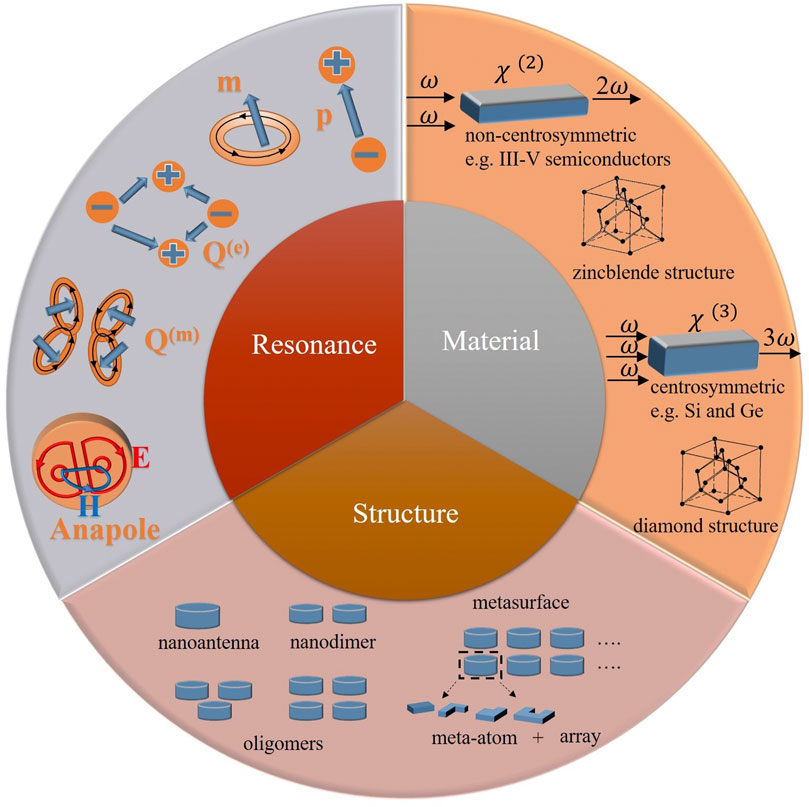
FIGURE 1. Outline of this review with nonlinear THG and SHG processes from dielectric nanostructures.

The first step to describe SHG and THG processes is to determine the properties of the second- and third-order nonlinear susceptibility, ${\hat{χ}}^{(2)}$ and ${\hat{χ}}^{(3)}$ . It is well-established that the symmetry considerations are of particular importance in nonlinear harmonic generations, especially for the SHG process that is inhibited in centrosymmetric materials within the electric approximation of light–matter interaction (Ciracì et al., 2012; Frizyuk et al., 2019). Indeed, if the sign of the applied field is changed as − E for a centrosymmetric structure, the sign of the nonlinear polarization of the SHG process also changes due to the spatial inversion as $- P^{2} = ξ_{0} {\hat{χ}}^{(2)} (- E)$ . After the comparison with Eq. 1, one can deduce − P² = P² = 0, which can only occur if P = 0, implying that ${\hat{χ}}^{2}$ must be zero. This means that the materials with centrosymmetric lattices are forbidden to exhibit the SHG process, regardless of the light intensity. The symmetry constraints explain the unavailability of the second-order nonlinear effects in the bulk of uniform centrosymmetric media such as the metals with face-centered cubic atom lattices and group IV semiconductors. Without the loss of generality, ${\hat{χ}}^{(2)}$ will vanish within the medium that possesses an inversion symmetry which means the invariance of the spatial transformation by inversion of a central point. As a consequence, SHG shows extreme sensitivity to symmetry breaking, and the higher-order susceptibility, i.e., quadrupole and magnetic dipole terms should be taken into account for the evaluation of the SHG efficiency. Similar conclusions can be applied to other even-order nonlinear processes. In contrast, the third-order nonlinear process is not bound by such restrictions, and it can be allowed in the majority of natural materials possessing a center of inversions such as gases, liquids, and centrosymmetric crystalline solids.

With symmetry considerations, the selection of nonlinear optical materials becomes a vital concern in the research community. The use of all-dielectric nanostructures provides a diverse collection of group IV and III–V semiconductors to enrich the nonlinear materials, and these semiconductor materials with advantages of high index, low loss, and large susceptibility have predicted their outstanding capability in the efficient enhancement of the nonlinear optical response. As such, some group IV semiconductors such as silicon (Si) and germanium (Ge) have been considered as excellent material platforms for third-order nonlinear all-dielectric nanostructures. To be exact, Si has a large linear refractive index as n ≈ 3.7 and an intrinsic third-order susceptibility ${\hat{χ}}_{S i}^{(3)} \approx 2.79, \times, 1 0^{- 18}$ m²/V² in the near-infrared band (Yang et al., 2015), and Ge has the refractive index n ≈ 4 and a large third-order susceptibility ${\hat{χ}}_{G e}^{(3)} \approx 5.65 \times 1 0^{- 19}$ m²/V² (Grinblat et al., 2016b). Compared with Si, Ge, and other elemental semiconductors not suitable for SHG, the group of III–V semiconductors that hosts noncentrosymmetric materials benefits from the strong second-order susceptibility. Typically, AlGaAs possess a high dielectric index and relatively large second-order susceptibility ${\hat{χ}}^{(2)} \approx$ 200 pm/V (Carletti et al., 2015), and it has been demonstrated to achieve the strong second-order nonlinearity in the near-infrared spectral ranges.

Following the guideline from Eq. 1, another necessary factor for the nonlinear harmonic generation is the ability to enhance local electric field E. Since the second- and third-order nonlinear light–matter interactions depend correspondingly on the second and third powers of the local electric field E, one can enhance and engineer the local field using various schemes to control the nonlinear response at the harmonic wavelength. In terms of the dielectric nanostructures supporting large displacement currents, the nonlinear interaction with the light field is most often related to resonant excitation due to multipolar modes of Mie-type resonances. Aiming for the higher efficiency of nonlinear harmonic generation, the different types of optical modes, including optically induced magnetic dipole resonances, higher-order multipoles, and composite resonances, have been explored for a high-quality factor in dielectric nanostructures. Some typical and common resonance modes are listed in the following.

The Mie-type resonances introduced as the exact Mie solutions of Maxwell’s equations for light interactions with spherical particles support electric and magnetic resonances of comparable strengths (Kuznetsov et al., 2016). The toroidal resonance is derived from the decomposition of momentum tensors. The produced electromagnetic fields resemble the field produced by an electric current wire wrapped into a coil, with the coil being further arranged into a torus shape, giving rise to an effective magnetic current loop (Kaelberer et al., 2010; Basharin et al., 2015). When the electric field radiation from an electric dipole and a toroidal dipole moment destructively interferes, the resonance excitation of the anapole mode can be realized with the nontrivial radiationless current distribution, as shown in Figure 1 (Xu et al., 2018; Baryshnikova et al., 2019). Furthermore, inspired by the physics of bound states in the continuum (BIC), the quasi-BIC in dielectric nanostructures featuring effective suppression of the radiative loss has been observed. BICs are peculiar states that lie in the radiation continuum but remain perfectly confined without any radiation, which is an exception to the conventional understanding of the confined light in a closed or Hermitian system with no access to radiation channels and the resonant mode with light coupled to the radiation continuum in an open system. In a simple way, BIC can be considered as a resonance with zero leakage and zero line-width or with an infinite quality factor (Hsu et al., 2016; Koshelev et al., 2018; Li et al., 2019). These resonant effects above can intensify electromagnetic fields within nonlinear materials by orders of magnitude, thus dramatically enhancing the efficiency of nonlinear light–matter interactions. Considering the fact that the nonlinear susceptibility ${\hat{χ}}^{(2)}$ and ${\hat{χ}}^{(3)}$ are intrinsic parameters of the constituent materials and can act as a constant, the local field amplitude E that can be engineered via various resonant modes from nanostructures offers a great possibility to control the nonlinear response at the harmonic wavelengths.

3 Third-Harmonic Generation

In contrast with the SHG process only observed in the noncentrosymmetric structures, the THG process is a more general effect because of a relaxed symmetry-induced selection rule. Owing to this major consideration, we start to survey the material choices, structure design, and conversion efficiency enhancement for the nonlinear THG process.

As mentioned in Section 2, silicon and germanium from group IV are centrosymmetric materials and possess large third-order nonlinearity, exhibiting great potential as three-order nonlinear materials in the near-infrared spectral ranges. Benefiting from the compatibility with mature CMOS technology, the silicon and germanium nanostructures can be scaled down to 10 nm at a low cost, allowing for very compact optical devices and large scale integration of functional elements on a single chip (Makarov et al., 2015). Since silicon is widely available as the raw material for the silicon-on-insulator (SOI) platform, it has been the most popular source for all-dielectric nonlinear optics. Unsurprisingly, the first demonstration of the nonlinear response in dielectric nanoparticles was presented in silicon disk nanoparticles (Shcherbakov et al., 2014). By characterizing the magnetoelectric response from silicon nanodisks, the maximum localized enhanced field excited within the disk can be observed at magnetic resonance, leading to the enhanced conversion efficiency of the THG process (conversion efficiency η = P_3ω/P_ω, where P_ω is the pump power and P_3ω is the TH signal power) up to 10^–7 at the pump wavelength of 1.24 μm which has two orders of magnitude enhancement comparing with bulk silicon. The maximum time-averaged yield of the TH radiation is measured to be 4 nW for a pump power of 30 mW (peak intensity ≈5.5 GW/cm²), and the generated 420 nm radiation is bright enough to be observed by the naked eye under the table-lamp illumination conditions, as shown in Figure 2A. This pioneered work demonstrates the experimental possibility for THG response in dielectric nanoparticles and opens an avenue for nonlinear THG driven by the optically induced Mie-type resonances in dielectric nanostructures.

FIGURE 2

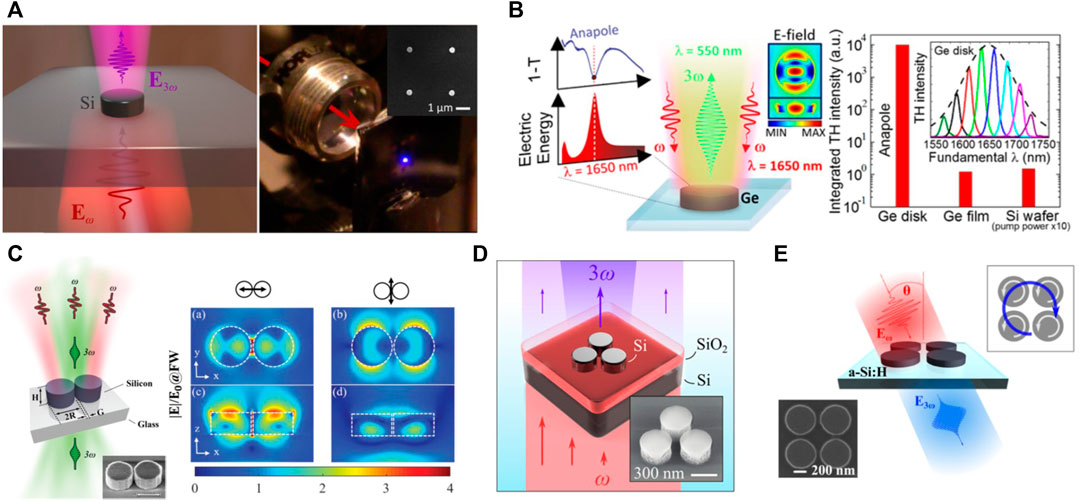
FIGURE 2. Nonlinear THG processes from dielectric nanostructures with different geometries. (A) Illustration of THG from individual Si nanodisks and the photographic image of the sample (Shcherbakov et al., 2014). (B) Illustration of THG for a single Ge nanodisk and the THG performances at anapole resonance compared with unstructured Ge film and the silicon wafer. The insets are the electric field enhancement at anapole resonance and the fundamental wavelength dependence of the TH spectrum (Grinblat et al., 2016a). (C) Illustration of Si nanodimers for THG near electric and magnetic resonances and its electric field distributions at a fundamental wavelength for two polarizations (Wang et al., 2017). (D) Illustration of THG in Si nanodisk trimers and its SEM image (Shcherbakov et al., 2015). (E) Illustration of THG in Si quadrumers. The insets are the SEM image of the sample and the physical origin of magnetic Fano resonance in the quadrumer (Shorokhov et al., 2016).

To understand the essential role of Mie-type resonances in nonlinear THG response, electric and magnetic resonances of nanoparticles have been investigated in nonlinear processes. For subwavelength silicon disk nanoparticles supporting strongly localized Mie-type resonance, the magnetic resonance is able to yield more efficient THG radiation in contrast to the electric resonance, which has been verified by both the nonlinear spectroscopy measurements and the full-wave numerical simulations (Melik-Gaykazyan et al., 2017b). As a further exploration of nonlinear beam engineering via multipolar scattering properties, researchers from the same group selectively excited different multipolar modes of the silicon nanodisks for engineering the strength and polarization of THG radiation where the optically induced electric and magnetic resonances can be enhanced and suppressed by tailoring the vectorial structure of the pumping light (Melik-Gaykazyan et al., 2017a). In addition to the low-order electric and magnetic modes, the anapole mode that can be viewed as a superimposition of electric and toroidal moments of equal amplitude and with a phase difference equal to π exhibits destructive interference in far-field and nontrivial nonradiating current distributions, leading to a zero-scattering condition. In the vicinity of the anapole mode with minimized far-field coupling, the germanium nanodisk with a refractive index greater than 4 and a large third-order susceptibility in the near-infrared region exhibits THG conversion efficiency 10^–6 for pump powers up to 1 μW (5 GW/cm² peak intensity) at a wavelength of 1,650 nm (Grinblat et al., 2016a). As shown in Figure 2B, the THG efficiency is 4 orders of magnitude greater than that of an unstructured germanium reference film and also exceeds by more than an order of magnitude the value reported for a silicon nanodisk at 1,350 nm wavelength (Shcherbakov et al., 2014). The understandings of the low- and high-order Mie-type resonances provide an important pathway to solve the inevitable issue in nonlinear optics of the conversion efficiency enhancement.

The geometry variation is most commonly used in engineering the optical nonlinear effects. For single dielectric nanoparticles such as silicon and germanium disks, they provide two degrees of freedom, i.e., radius and height, to independently tailor the electric and magnetic resonances. When several nanoparticles are placed together with their distance smaller than or on the order of a wavelength, they are termed as oligomers. By adjusting the gap between the nanoparticles, the coupling between individual nanoparticles can be changed, resulting in the controllable nonlinear responses. In a nanodimer consisting of two silicon nanocylinders on a glass substrate in Figure 2C, the nonlinear THG process can be enhanced near electric and magnetic Mie resonances with an engineered radiation directionality (Wang et al., 2017). For the silicon nanodisks arranged in the form of trimer oligomers in Figure 2D, both the electric and magnetic resonances can substantially enhance the intensity of the TH radiation, and a pronounced reshaping of the TH spectra can be observed via the Fano-like interference of nonlinearity generated optical waves (Shcherbakov et al., 2015). Then, the quadrumers of silicon nanodisks of Figure 2E support high-quality collective modes associated with the magnetic Fano resonance, allowing for the extremely enhanced local fields beneficial for the nonlinear THG process (Shorokhov et al., 2016).

When the dielectric nanoparticles are arranged into quasi-infinite arrays with a period of less than a free-space wavelength, the high-quality factor collective mode in the metamaterial or metasurface structures shows the ability to confine optical field inside for further increasing the nonlinear response. The pursuit of a highly confined field using different resonant mechanisms with high-quality mode becomes an important way to enhance the conversion efficiency. The major resonant modes of Mie-type resonances, as shown in Figure 1, including electric dipole, magnetic dipole, electric quadrupole, magnetic quadrupole, and toridorial mode, together with the high-order anapole mode, provide a wide platform for the nonlinear THG process (Chen et al., 2018; Yao et al., 2020). The strong localization of the electric and magnetic fields under the resonant conditions inside the dielectric nanoparticles has demonstrated the ability to give rise to the high-quality factor and thus enhance the nonlinear effects.

In addition to these resonances, Fano resonance arising from the interference of discrete states with broadband states can also be achieved in dielectric nanostructures possessing more complex designs. One of the important concepts for Fano resonance is the near-field interaction between the resonant (bright) and nonresonant (dark) modes, where the near field of the resonant nanoparticle can be remarkably boosted at the Fano frequency (Miroshnichenko et al., 2010). The field enhancement of Fano resonance has been utilized to increase the nonlinear light–matter interaction for conversion efficiency enhancement. As shown in Figure 3A, Yang et al. proposed Fano-resonant Si-based metasurfaces to enhance THG processes consisting of a periodic lattice of the coupled rectangular bar and disk resonators formed from silicon (Yang et al., 2015). The interference between the collective “bright” electric dipole and “dark” magnetic dipoles modes forms a typical three-level Fano-resonant system, resulting in strong near-field enhancement within the volume of the silicon resonator with a THG enhancement factor of 1.5 × 10⁵ with respect to an unpatterned silicon film and accordingly enhanced THG conversion efficiency of 1.2 × 10^–6 with a peak pump intensity of 3.2 GW/cm². In addition to a strong local field enhancement, Fano resonance allows the suppression of the radiative loss of the resonance modes and also accounts for the high-quality factor. By manipulating the trapped modes, Tong et al. proposed a symmetric Fano-resonant silicon metasurface with the THG conversion efficiency enhanced about 300 times with respect to the bulk silicon slab that is sensitive to the polarization direction of the electric field, as shown in Figure 3B (Tong et al., 2016). Other examples of enhanced THG with high conversion efficiency based on Fano resonance can also be found (Strelkov et al., 2014). In addition to the THG process, the Fano-resonant dielectric nanostructures have also been demonstrated for the high-harmonic generation (HHG) process, just as the silicon metasurface that possesses a classical analogue of electromagnetically induced transparency (EIT) show more than two orders of magnitude harmonic emission compared with the unpatterned samples (Liu H. et al., 2018).

FIGURE 3

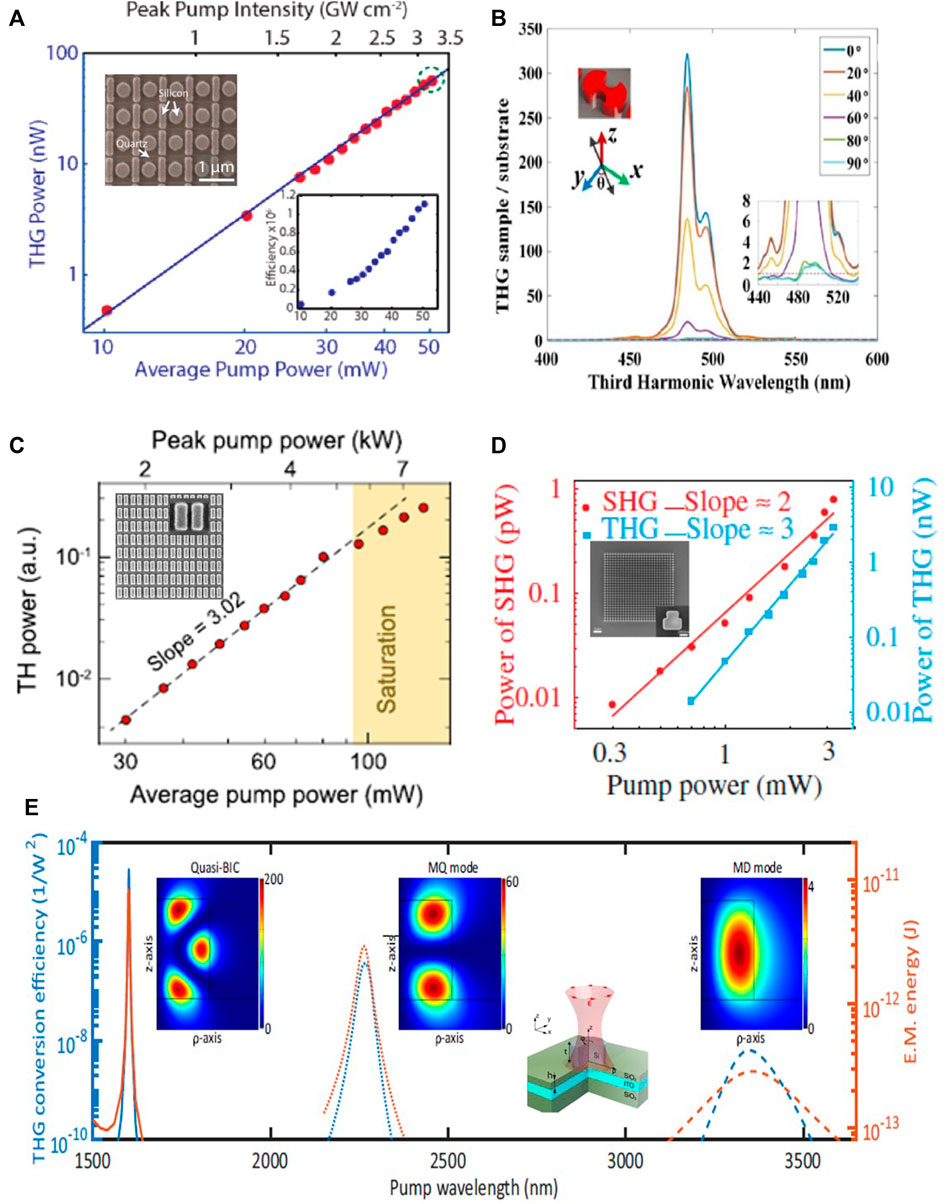
FIGURE 3. Nonlinear THG process enhancement in dielectric nanostructures with different resonance modes. (A) The Fano-resonant Si metasurface with its SEM image and the TH power as a function of the pump power (Yang et al., 2015). (B) The Si metasurface using trapped mode with THG spectra for different polarization angles (Tong et al., 2016). (C) Asymmetric Si metasurfaces associated with quasi-BIC modes and the dependence of the output TH power on the average and peak input power for the sample with α = 0.15 (Koshelev et al., 2019). (D) The high-Q quasi-BICs in Si metasurfaces with power dependences of SHG/THG in a logarithmic scale (Liu et al., 2019). (E)The Si disk resonator and the conversion efficiency for THG as a function of the pump wavelength close to quasi-BIC, MQ mode, and MD mode (Carletti et al., 2019a).

Most recently, BIC has provided a complementary solution to the resonator design and light–matter interactions owing to the high-quality factors. Owing to the finite structures, material absorption, and other perturbations in practice, BIC, which is truly a dark state with infinite radiative lifetime, can be realized in practice as a quasi-BIC with finite quality factor and resonance width. Such BIC-inspired mechanism of light localization has been used to obtain very high-quality resonances in different photonic systems such as optical cavities and photonic crystal slabs, coupled optical waveguides, and even isolated subwavelength dielectric particles (Hsu et al., 2016; Ning et al., 2020; Liu Z. et al., 2021). In a straightforward way, the nonlinear metasurface consisting of the symmetry-broken silicon meta-atoms has been designed as a general example to enhance the THG process, where the sharp BIC resonances control the TH radiation intensity through the degree of asymmetry in Figure 3C (Koshelev et al., 2019). Based on the similar symmetry-breaking quasi-BICs mechanism, an ultrasharp resonance has been achieved in the silicon blocks with a high-quality factor up to 18511 by engineering the symmetry properties and the number of the unit cells in the metasurface of Figure 3D, experimentally exhibiting a normalized THG conversion efficiency of 1.4 × 10^–8/W² which is at least five orders of magnitude higher than the previous silicon metasurfaces (Liu et al., 2019).

Not limited to the periodic array in metasurfaces, optical BICs can also be exploited in a subwavelength particle, and the enhancement ability has been numerically demonstrated. The concept of BIC is combined with an engineered substrate that undergoes a transition from an insulator to a conductor via an epsilon-near-zero (ENZ) regime, and the peak conversion efficiency for the THG process reaches 3 × 10^–5 W⁻² in Figure 3E (Carletti et al., 2019b). Meanwhile, the high-order harmonic generation process can also be enhanced, such as the four-wave mixing process driven by quasi-BIC is about ten times more efficient than that driven by a magnetic quadrupole. Since then, researchers have been exploring to make full use of the advantage of BICs. Lately, the symmetry-broken silicon on silicon dioxide metasurface that is characterized by a high quality factor $> 1 0^{5}$ is demonstrated to enhance THG conversion efficiency up to 10^–2 W⁻² and especially enable the near-unity $> 99.9 %$ nonlinear circular dichroism (CD) (Gandolfi et al., 2021).

The enhanced THG processes in dielectric nanostructures bring new opportunities for the efficient manipulation of phase, amplitude, and polarization in the new frequency regimes, thus making new nonlinear optical functionalities more accessible (Wang et al., 2017; Melik-Gaykazyan et al., 2017a; Wei et al., 2020). Wang et al. suggested a new concept for embedding any functionality into a nonlinear metasurface and demonstrated it in the TH field from silicon-based metasurfaces through producing phase gradients over a full 0–2π phase range based on the generalized Huygens’ principle, as shown in Figure 4A (Wang et al., 2018). In addition, the highly efficient wavefront control of the TH field was achieved in the designed silicon nonlinear metasurface while the nonlinear beams at a designed angle and the nonlinear focusing vortex beams can be generated.

FIGURE 4

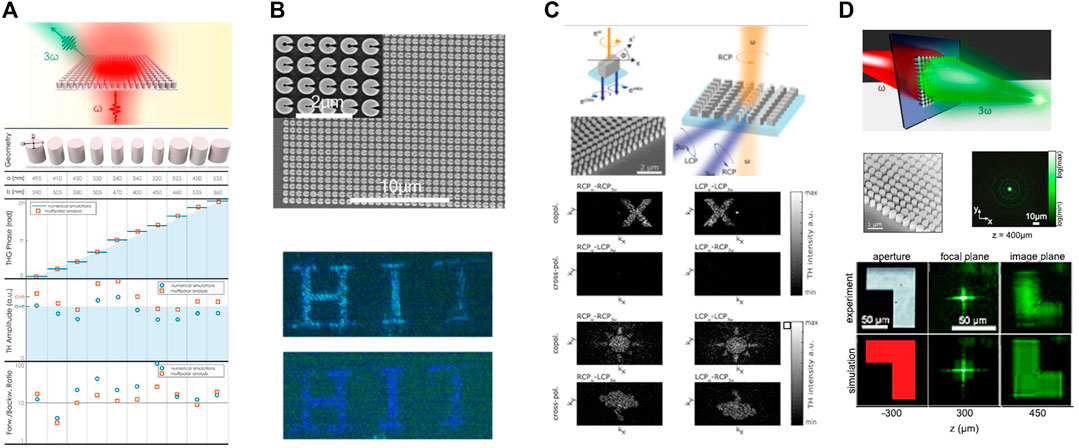
FIGURE 4. Nonlinear THG process for wavefront control with silicon metasurfaces. (A) Nonlinear holography from the silicon nanopillar metasurfaces with the geometries, nonlinear phases, and TH amplitudes of nanopillar meta-atoms (Wang et al., 2018). (B) Nonlinear holography from the C-shaped Si nanoantenna-based metasurface with the SEM image and the experimentally obtained holographic images at 483 (top) and 417 nm (bottom) (Gao et al., 2018). (C) Nonlinear multiplexed holography from geometric-phase silicon metasurface with the working principle and the measured multiplexed holographic image (Reineke et al., 2019). (D) Nonlinear conversion and focusing of the fundamental Gaussian beam from silicon metalens with the SEM image and the measured TH intensity distribution of the focal spot, and the nonlinear TH image formation of the L-shaped aperture at an image distance of 450 um (Schlickriede et al., 2020).

Moreover, all-dielectric metasurface-based nonlinear holograms were proposed and experimentally demonstrated in C-shaped silicon nanoantennas, where the high-efficiency cyan and blue THG holograms were generated by introducing abrupt phase changes from 0–2π by varying the structural parameters of the C elements (Gao et al., 2018), as shown in Figure 4B. In addition, Reineke et al. employed the Pancharatnam–Berry phase concept to encode phase information into the THG of a single silicon nanoresonator by varying the rotation orientation and circularly polarized light and experimentally demonstrated the polarization-dependent wavefront control and the reconstruction of holographic images by THG (Reineke et al., 2019).

In addition to silicon metasurfaces for nonlinear wavefront control for THG, the multiplexed holographic image was also demonstrated for different combinations of the input and output polarizations. Most recently, the ultrathin resonant silicon nanodisk metasurface was designed with an enhanced THG process due to the high-quality factor of quasi-BIC magnetic dipole state, and in particular, the dynamical nonlinear image switching was demonstrated through polarization- and wavelength-tuning methods (Xu et al., 2019a). In addition, the nonlinear dielectric metalens have been demonstrated in silicon nanoparticle metasurface where a generalized form of the Gaussian lens equation for imaging through general nonlinear lenses was suggested in analogy to the thin-lens equation in linear ray optics (Schlickriede et al., 2020), as shown in Figure 4D.

The material choice and the appropriate confined optical mode from nanostructures play the utmost important factors to realize the THG conversion efficiency enhancement. In addition to the most common silicon and germanium used for THG from infrared to visible wavelength, some other dielectric materials are also used for the THG process. For example, titanium dioxide (TiO₂) is well-suited for vacuum ultraviolet (VUV) light generation due to the low absorption in the visible regime, based on which the TiO₂ metasurface was designed to enhance VUV light at 185 nm using the fundamental laser wavelength of 555 nm (Semmlinger et al., 2019). It can be seen that the emerging materials and newly developed mechanisms provide a pathway to further optimization of the THG process in dielectric nanostructures.

4 Second-Harmonic Generation

Different from the THG process, the SHG process exhibits centrosymmetry sensitivity. In the electric dipole approximation, the SH signal vanishes in the far-field if the excited structure possesses a centrosymmetric crystal, and thus the nonzero SHG signal is generally produced in the noncentrosymmetric dielectric materials. With this understanding, dielectric materials such as silicon, germanium, and titanium dioxide are unsuitable for SHG. In contrast, semiconductors from group III–V, such as gallium arsenide (GaAs), gallium phosphide (GaP), aluminum gallium arsenide (AlGaAs), and lithium niobate (LiNbO₃), are noncentrosymmetry materials with large ${\hat{χ}}^{(2)}$ , providing great possibility to intrinsically increase the nonlinear conversion efficiency (Remesh et al., 2019; Sarma et al., 2019; Ma et al., 2021). Meanwhile, the group III–V semiconductors show high refractive indices just like group IV materials and also possess the capability to support strong Mie-type resonances for SH signals enhancement.

The early investigation of SHG from group III–V semiconductor nanostructures was manifested in GaP and LiNbO₃ nanowires, where the strong dependence of SHG intensity was observed on the geometry parameters (Sanatinia et al., 2012; Sergeyev et al., 2015). With the advances in all-dielectric nanophotonics and especially the development of experimental platforms for III–V semiconductor-based metasurfaces, the dielectric nanoresonators for SHG process enhancement were promoted to a new stage. Soon after the enhancement of SHG in dielectric nanostructures was theoretically proposed (Carletti et al., 2015), the SHG process was first experimentally demonstrated in monolithic AlGaAs optical nanoantennas by magnetic Mie-type resonances, revealing a peak conversion efficiency exceeding 10^–5 (Gili et al., 2016), as shown in Figure 5A. In addition, the first resonantly enhanced SHG in GaAs dielectric metasurfaces was experimentally realized at magnetic dipole resonance in Figure 5B, and the absolute nonlinear conversion efficiency of $\sim 2 \times 1 0^{- 5}$ with ∼3.4 GW/cm² pump intensity was measured, as large as 10⁴ relative to unpatterned GaAs (Liu et al., 2016). The GaP nanoantennas have been exploited as an efficient nanophotonic platform for SHG enhancement as well. The single GaP nanodisks were observed to enhance SHG efficiency up to $\sim 2 \times 1 0^{- 6}$ more than three orders of magnitude in comparison with the bulk, and the GaP dimers can enhance up to 3,600 times the fluorescence emission of dyes located in the gap of the nanoantenna, as shown in Figure 5C (Cambiasso et al., 2017). These results open avenues for the optical SHG processes in dielectric nanostructures, and considerable efforts have been made to enhance the nonlinear efficiency based on the early explorations.

FIGURE 5

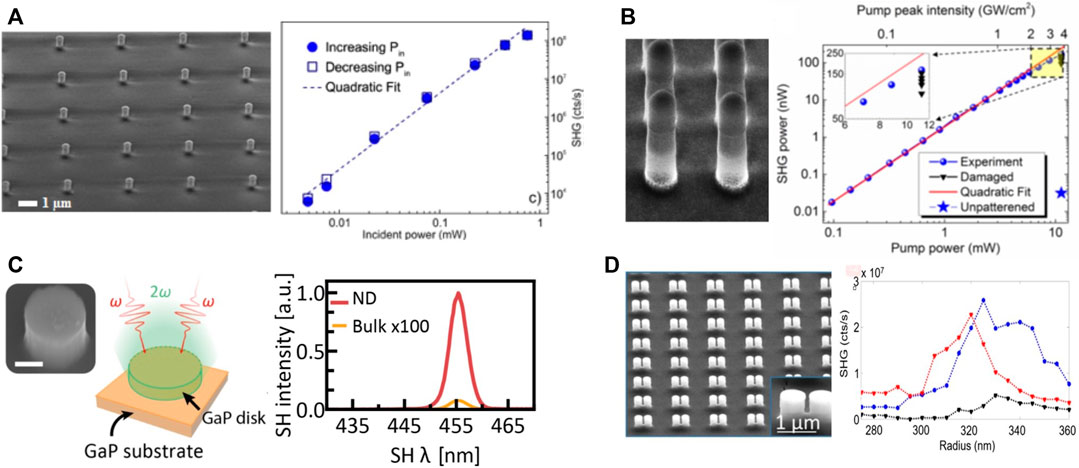
FIGURE 5. Nonlinear SHG process in dielectric nanostructures with different materials and geometries. (A) SEM picture of monolithic AlGaAs-on-AlOx nanoantennas and the SHG efficiency on nanoantennas (Gili et al., 2016). (B) SEM picture of GaAs dielectric metasurface and the quadratic relationship between the average pump and SHG powers at low pump intensities. Inset is the deviation from the quadratic relationship at higher pump intensities due to the damage of GaAs resonators (Liu et al., 2016). (C) SEM picture of GaP nanodisks and the SH spectra of the nanodisks and bulk GaP substrate for an excitation wavelength of 910 nm (Cambiasso et al., 2017). (D) SEM images of AlGaAs-on-AlOx nanodimers and the measured SHG for the dimer structure as a function of radius for two pump polarizations: along the x axis (blue curve) and along the y axis (red curve), and the black line represents the measured SHG for the single-cylinder structure (Rocco et al., 2018).

Similar to THG enhancement, enhanced SHG processes have been widely demonstrated by means of the flexible control of multipolar modes of Mie-type resonances. One of the most common resonances chosen for this is the magnetic dipolar modes, such as the enhanced SHG in GaAs metasurfaces in Figure 5B (Liu et al., 2016). It is also interesting to find that by simultaneously exciting the lowest order magnetic dipole and electric dipole Mie-type resonances of the GaAs nanocylinder in metasurface, an optical frequency mixer was experimentally demonstrated with eleven new frequencies spanning ultraviolet to near-infrared, including the observation of SHG, THG, and fourth-harmonic generation, sum-frequency generation, two-photon absorption-induced photoluminescence, four-wave mixing, and six-wave mixing (Liu S. et al., 2018). These results exhibit the possibility of realizing ultracompact optical mixers with multiple nonlinear processes in the dielectric metasurface platform.

Optical anapole modes with trapped energy and weak radiation can also be generated under the special distributions of polarization currents inside dielectric nanoparticles governed by these low-order multipolar modes, showing great potential for nonlinear SHG enhancement. For example, in Figure 5D, AlGaAs nanodimers was used to demonstrate the electric and magnetic fields enhancement by effective coupling of electric and toroidal modes for anapole modes with minimized optical scattering, while the SHG efficiency was numerically predicted to exceed 4 × 10^–6 using a pump intensity of 1.6 GW/cm² at a wavelength of 1,550 nm (Rocco et al., 2018). Meanwhile, the design of the dimer, with respect to the single AlGaAs nanodisk, adds degrees of freedom to control the polarization and the spatial and frequency properties of photons generated in the SHG process.

The high-quality factor resonances in dielectric nanostructures have also been used to obtain the confined fields for SHG enhancement. Using broken symmetry GaAs metasurface for the interference of radiating modes with the symmetry-protected dark mode in Figure 6A, Fano resonance with high-quality factor ∼600 was achieved with strongly enhanced local fields inside nanoresonators, leading to multifold enhanced SHG process compared with GaAs nanodisc metasurface (Vabishchevich et al., 2018).

FIGURE 6

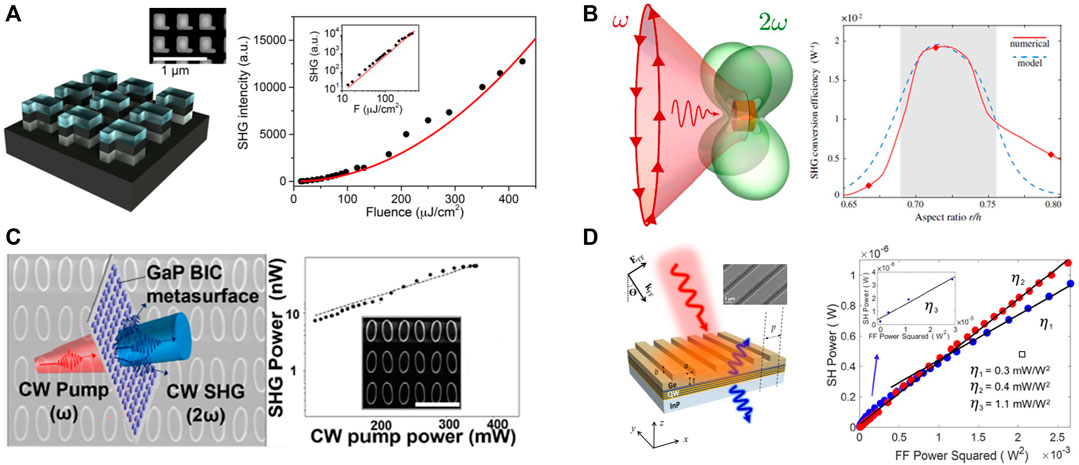
FIGURE 6. Enhancement of nonlinear SHG process from resonant dielectric nanostructures. (A) Symmetry broken GaAs metasurface used to create high-Q Fano resonances and power dependence of the SH intensity plotted against the pump fluence (Vabishchevich et al., 2018). (B) SHG from a subwavelength dielectric nanoparticle pumped by an azimuthally polarized beam at the BIC conditions and the conversion efficiency as a function of the nanoparticle aspect ratio (Carletti et al., 2018a). (C) Illustration of the continuous wave SHG enabled by quasi-BIC on GaP metasurface, and the SHG power as a function of input CW pump power for angles of the dimer 5° (Anthur et al., 2020). (D) Illustration of the dielectric-semiconductor nonlinear device and SH power as a function of the square of incident pump power for the structures with different low incident powers (Sarma et al., 2019).

The concept of BIC has recently attracted interest in the nonlinear SHG community owing to its high-quality factor and confined optical fields (Han et al., 2020; Bernhardt et al., 2020). For example, in Figure 6B, SHG from isolated subwavelength AlGaAs nanoantennas was enhanced via tuning the resonator parameters to the BIC regime and the SHG conversion efficiency could be analytically predicted to increase by at least two orders of magnitude compared to the largest efficiency at magnetic dipole Mie resonances (Carletti et al., 2018a). Then, a comprehensive multipolar theory of SHG from high-quality BIC states in AlGaAs cylindrical nanoresonator was developed (Volkovskaya et al., 2020), and the calculated SHG efficiency of 9.5 × 10^–5 W⁻¹ for 2 ps laser pulses was close to twice higher than the estimate for the case of azimuthally polarized cylindrical vector beam illumination (Koshelev et al., 2020). In another case of linearly polarized plane wave excitation, the BIC-based resonance in a careful design consisting of an array of AlGaAs nanodisk structures with an inner air slot as the defect boosts the SHG signals with a record numerical efficiency of around 0.1 at incident pump intensity of 5 MW/cm², up to six orders of magnitude high than that achieved by magnetic dipole resonances (Han et al., 2020). The continuous wave SHG in GaP metasurfaces combined with BIC can be enhanced with a conversion efficiency of around 5 × 10^–7 W⁻¹ with a wave intensity of 1 kW/cm² at 1,200 nm wavelength (Anthur et al., 2020), as shown in Figure 6C. This efficiency is higher than the values previously reported for dielectric metasurfaces, while the pumping intensity is two orders of magnitude lower. The combination of the BICs concept with the nonlinear dielectric metasurfaces has recently extended to LiNbO₃ with theoretically predicted SHG efficiency exceeding 10^–3 with 30 MW/cm² of the pump intensity (Yang et al., 2020). These investigations using high quality factor resonances have taken SHG in dielectric nanostructures a step closer to practical applications. In Figure 6D, a hybrid approach has also been presented to realize the efficient SHG by combining the advantages of intersubband transitions in multi-quantum-well semiconductor structure and the high-quality factor leaky mode resonances in dielectric metasurfaces. In the hybrid device, the maximum SHG conversion factor reaches 1.1 mW/W² and an efficiency of 2.5 × 10^–5 at modest pump intensities of 10 kW/cm² at pump wavelengths ranging from 8.5 to 11 µm (Sarma et al., 2019).

For most of III–V semiconductors, their zincblende crystal structures define nonlinear tensor ${\hat{χ}}^{(2)}$ with nonzero value ${\hat{χ}}^{(2)} \neq 0$ only for i ≠ j ≠ k. As a consequence, SHG produced by the group III–V based nanostructures exhibits certain polarization and scattering properties. For instance, no SHG signal could be observed under normal incidence when a bulk GaAs wafer with two of its three crystallographic axes is placed within the wafer’s surface (x and y). The only nonlinear polarization will be generated along z, and it will not generate a radiating field along the original z direction. In Ghirardini et al.’s study (2017), an incident plane wave with its electric field linearly polarized along the bisector of two crystalline axes, such as [100] and [010], generates SH radiation that will be linearly polarized along the [001] direction in bulk AlGaAs. Nevertheless, efficient far-field SHG could be observed when an array of Mie-resonant nanoparticles out of such a wafer is made due to the detectable diffraction orders with a larger period than SHG wavelength and the SH radiation at a close-to-normal direction enabled by coupling between local fields along z and far-field, just as shown in Figure 7A. In resonant GaAs metasurfaces, the experimental results reveal that the SH intensity varies with the polarization angle of the fundamental wave as expected from the GaAs nonlinear tensor structure, while the variation characteristics depend on the pump wavelength (Löchner et al., 2018). On the other hand, nanostructures based on III–V semiconductors that are characterized by an intrinsic broken symmetry down to a single elementary cell show certain polarization properties of the SHG radiation (Löchner et al., 2018). A thorough investigation of the emission properties of SHG in AlGaAs monolithic nanoantennas has revealed the control over the polarized emission in these nanoantennas (Ghirardini et al., 2017).

FIGURE 7

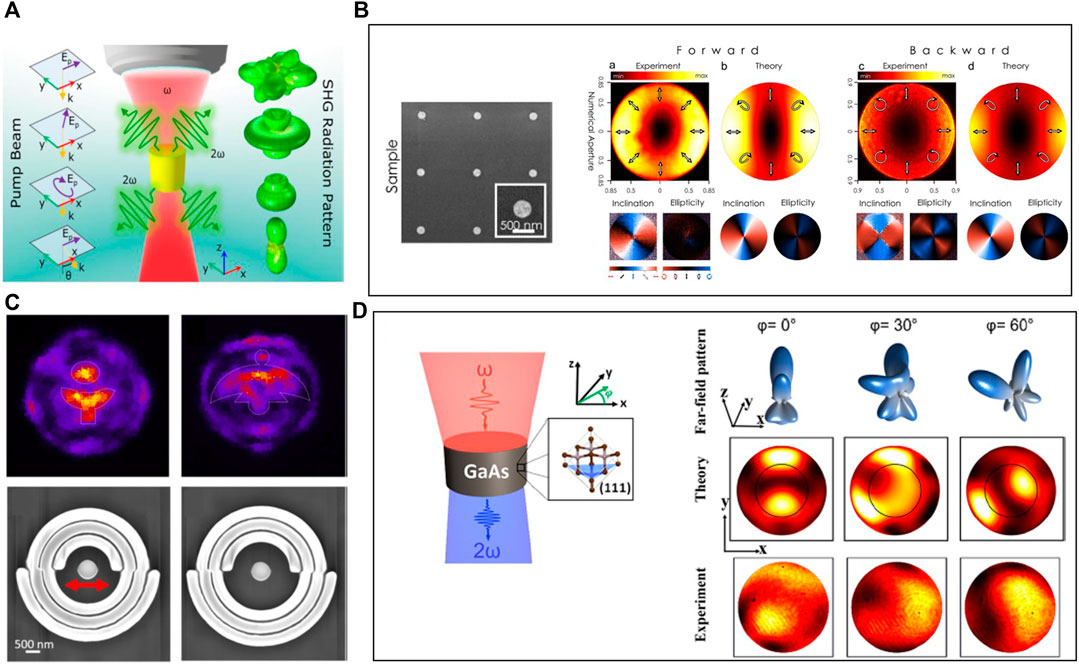
FIGURE 7. Directionality and polarization control of SH signals in dielectric nanostructures. (A) Manipulation of the radiation pattern of THG from AlGaAs all-dielectric nanoantennas by the pump beam polarization, incident angle (Carletti et al., 2016). (B) SH fields control of AlGaAs nanoresonators. The directionality diagrams in forward and backward directions, and the polarization inclination angles and ellipticity for the directionality cases (Camacho-Morales et al., 2016). (C) SHG far-fields resembling a flower and a bird obtained with a single AlGaAs nanodisk antenna using coplanar holographic gratings with d = 450 nm and d = 700 nm (Ghirardini et al., 2018). (D) SHG from a (111)-GaAs nanodisk for different pump polarizations. The simulated radiation patterns and the theoretical and measured back-focal plane (BFP) images in the forward direction (Sautter et al., 2019).

In practice, the specific nonlinear tensor structures of III–V semiconductor-based nanostructures provide great potential for shaping the radiation and polarization patterns of SHG, such as achieving unidirectional emission and nonlinear generation of complex polarization beams. The nanodisk AlGaAs antennas are capable of emitting SH signals in preferential directions, i.e., forward and backward directions and generating complex vector polarization beams, including radial polarization, with SHG efficiency exceeding 10^–4 (Camacho-Morales et al., 2016) in Figure 7B. The same group presented a series of works for shaping the radiation pattern of SHG in AlGaAs dielectric nanoantennas. The interference of different electric and magnetic multipoles in AlGaAs nanodisks has been engineered by manipulating the pump beam polarization, incident angle, and disk geometry, with the aim to shape the radiation pattern and finally increase the SH power (Carletti et al., 2016, 2017, 2018b; Rocco et al., 2020b; Xu et al., 2019b). In a single AlGaAs nanodisk antenna using coplanar holographic gratings in Figure 7C, the SH radiation pattern toward or otherwise forbidden normal direction can be effectively redirected by suitably shifting the phase of the grating pattern in the azimuthal direction, allowing SH power efficiency to increase by two orders of magnitude with respect to an isolated antenna (Ghirardini et al., 2018). At the same time, the control of directionality of SH emission in GaAs antennas has also been manipulated by changing the pump polarization without affecting the linear properties and the total nonlinear conversion efficiency (Sautter et al., 2019), as shown in Figure 7D.

Because of the high sensitivity to symmetry, SHG nanostructures have become a popular technique for achieving optical chirality and circular dichroism, which arise from phase and absorption differences between left and right circularly polarized light passing through the chiral medium. The high-index dielectric nanoparticles that are highly suitable for the nonlinear chiral metasurfaces have recently attracted researchers’ interest (Tang et al., 2019; Kang et al., 2020; Frizyuk et al., 2021). In a dimer structure consisting of two AlGaAs cylinders placed on an engineered substrate, the nonvanishing circular dichroism of the SH signal was first observed due to the interplay of multipolar magnetic and electric Mie resonances when the dimer axes are oriented under an angle to the crystalline lattice of the dielectric material (Frizyuk et al., 2021). Since nonlinear circular dichroism results in different conversion efficiencies for the two circular polarization states of the fundamental wave, the nonlinear circular dichroism can obtain a dramatic enhancement in the vicinity of the Mie-type resonances. The nonlinear dielectric nanostructures with giant nonlinear optical chirality are expected to increase the freedom in the design of innovative chiroptical devices for optoelectronic and biosensing applications.

Moreover, the dielectric nanostructures with the SHG process have found wide applications in wavefront manipulation of electromagnetic waves in the nonlinear regime. By encoding the desired phase pattern at maximum nonlinear conversion efficiency, nonlinear functionalities have been demonstrated. In the (100)-AlGaAs nanochair metasurface, the phase in the 0–2π range at a nearly constant amplitude of the SH signals (with a conversion efficiency of 10^–5) can be obtained through sweeping geometrical parameters. Then, the eight different meta-atoms are devised to construct the unit cell of the beam steering metasurface such that the sawtooth phase profile metasurface is built to direct the SH beam at an angle of 6.2° with respect to the vertical axis (Gigli et al., 2021). The asymmetric structures are also beneficial for light manipulation using the geometric (or Pancharatnam–Berry) phase. For example, the asymmetry of L-shaped a-Si meta-atoms allows us additional degrees of freedom of flipping or reflecting the shape, thus providing great flexibility in controling the diffraction pattern of the SH signal via phase modulation (Bar-David and Levy, 2019).

The group III–V semiconductors have demonstrated their success in achieving high SHG conversion efficiency and the effective manipulation of nonlinear interactions due to their high nonlinear susceptibility values. Meanwhile, an unavoidable issue exists in their relatively small bandgap energy accounting for the higher absorption coefficients in the harmonic generation process, hindering the further enhancement of conversion efficiency in certain spectral ranges. On this aspect, other material platforms have been exploited for efficient SHG at shorter wavelengths, such as the perovskites, silicon carbide, and selenium. Other widegap materials such as ZnO, GaN, and LiNbO₃ could also be an alternative to SHG materials to realize nonlinear dielectric metasurfaces as well (Marino et al., 2018; Li Y. et al., 2020; Yang et al., 2020; Huang Z. et al., 2021; Xu et al., 2021). In addition, in an unconventional way, the SH signal was generated mostly from the surface of the meta-atom in metasurfaces composed of amorphous silicon (a-Si) L-shaped structure fabricated on top of a glass substrate, following the selection rules to support SHG dependent on the meta-atom symmetry. Furthermore, SHG from an a-Si metamaterial fabricated on the tip of an optical fiber achieves conversion efficiency per intensity and square of interaction length 10⁻¹¹W⁻¹, exceeding two orders of magnitude than previous silicon metasurfaces (Xu et al., 2021).

5 Conclusion and Perspectives

The study of nonlinear dielectric nanophotonics has been stimulated by recently rapid progress in nanofabrication techniques such as electron beam lithography and inductively coupled plasma etching and the growing interest in nanophotonics with an optically induced magnetic response. In this review, we have discussed the work that has been done so far in exploiting the dielectric nanoparticles with Mie-type resonances for nonlinear frequency conversion processes, including THG and SHG. The basic concepts are based on the multipolar modes of Mie-type resonances, which provides a unified description of the electromagnetic field and useful insights into the physics underlying the nonlinear process driven by the resonant dielectric nanoparticles. In the new paradigm of nonlinear optics, the intrinsic nonlinearity of dielectric materials and the multipolar resonance modes are associated with the enhancement of the interacting optical near-fields, and the strength of the overlap between optical multipolar modes with subwavelength optical structures is the determinant factor for the nonlinear optical interaction efficiency. On this basis, the focus of this work is on the nonlinear optical frequency conversion processes in dielectric nanostructures from different materials, different nanostructures, and different resonance types. In comparison with the nonlinear plasmonic nanostructures, the huge advantages of dielectric nanosystems, including high index, low dissipative losses, high damage threshold, and coexistence of electric and magnetic resonances, are highly desirable to increase the nonlinear conversion efficiency. It has been demonstrated by the recent advances as we discussed in this review, and meanwhile, the field is quickly growing and many new works appear in literatures almost every week.

Despite the extensive theoretical and experimental studies of nonlinear optical properties of dielectric nanostructures, the study of nonlinear frequency conversion is still a young research field, and more improvements might be needed to fulfill its potential in applications. At this point, some challenges remain to be addressed for the future development of this field. To start with, the quest for giant optical nonlinearity is an indispensable aspect to take the nonlinear process into practice. Here, for nonlinear THG and SHG processes from dielectric nanostructures, the solution might be based on the search for novel materials and the careful combination of materials and electromagnetic resonant engineering from nanostructures. The materials presented in this review are roughly divided due to the symmetry among the harmonic generation background covering the basic theoretical tools and concepts used in nonlinear THG and SHG. Not limited to the presented materials, novel materials with considerably smaller loss and meanwhile showing the efficient ability of the field confinement will be expected. For instance, the transparent oxides such as chalcogenides and 2D materials have been adopted as alternative materials (Rodrigues et al., 2016; Youngblood et al., 2016; Jin et al., 2017; Shan et al., 2018; Cao et al., 2019; Lin et al., 2019; Wang et al., 2019; Yuan et al., 2019; Li C. et al., 2020; Gupta et al., 2021; Nauman et al., 2021; Yue et al., 2021). It is desirable to discover more novel materials with distinguished nonlinearities at the nanoscale in the future. In addition to materials, the novel resonance mechanism with a highly confined field would be necessary to further boost the nonlinear process with the reduced intensity. For the dielectric nanoantennas or metasurfaces, the Mie-type resonance modes allow the flexible control of nonlinear light-matter interactions, including low-order electric and magnetic modes, high-order anapole mode, Fano mode, and the popular BIC mode. Despite the fact that THG and SHG efficiencies have been pushed higher by the confined fields of these modes, it remains unexplored to achieve the efficiency limitations. On this aspect, some strategies have been proposed, such as combining the quantum effects with dielectric nanoresonators, which may provide new channels to achieve the ultimate goal of weak-light nonlinear photonics.

Another notable challenge in the field is the active control of nonlinear behaviors in the subwavelength dielectric structures. The pursuit of tunable nonlinearity is able to bring the nonlinear nanostructures into practical applications such as data manipulation, optical storage, and biosensing technology (Lee et al., 2019; Xiao et al., 2020b). The challenges of tunability and reconfigurability in the nonlinear regime are now attracting considerable interest. As far as the active control in the linear regime is concerned, the strategies have already appeared using different external stimuli for nonlinear manipulation. One of the straightforward ideas is to integrate the nonlinear dielectric nanostructure with active materials (Karl et al., 2020; Liu T. et al., 2021). In a metasurface with AlGaAs nanocylinders embedded into a liquid crystal matrix, it is possible to modulate the SH signal power and the emission pattern by switching the liquid crystal orientation with a realistic voltage bias (Rocco et al., 2020a). The other popular way is all-optical and ultrafast control in a nonlinear regime. As demonstrated by Celebrano et al. (2021), using a control optical beam that is absorbed by the AlGaAs nanoantennas, the refractive index of the radiating antennas can be thermo-optically changed to modulate the SH signal amplitude. For a moderate temperature increase of 40 K, the modulation of SHG efficiency reaches up to 60%. In another example, the AlGaAs nanopillar driven by a control femtosecond ultrashort laser pulse in the visible range can obtain an efficient modulation of SH signal due to the photoinduced permittivity changes within a few tens of picoseconds (Pogna et al., 2021). These strategies of control over nonlinear processes at the nanoscale reported for SHG can be extended to other frequency conversion processes.

Further challenge is the combination with practical engineering applications. Thanks to the design flexibility, tunability, and multifunctionality, dielectric nanostructures, especially metasurfaces, can be widely used in a variety of applications. However, the novel design fields in nonlinear nanostructures remain to be further investigated, such as developing more sophisticated sample designs and functional concepts in the advanced platform offered by nonlinear dielectric nanophotonics. In addition, experimental and engineering applications are still faced with lots of limits in practice. The nonlinear dielectric nanostructures have been explored in unidirectional radiation, holography, and superlense imaging, but these are only a small part of their great potential, and more applications are expected. For example, among the newly emerging research fields, one urgent need for efficient and miniaturized nonlinear devices exists in the all-optical signal process in the diffractive deep neural network, where the nonlinear part serves as the activation function and plays an indispensable role (Yan et al., 2019; Zuo et al., 2019). The combination of the nonlinear dielectric nanostructures with practical applications will become the research focus in the future.

Author Contributions

All the authors conceived the review topic. TL and SX wrote the manuscript. All the authors contributed to the manuscript and approved the submitted version.

Funding

The authors would like to acknowledge the support from the Science and Technology Commission of Shanghai Municipality (Grant no. 21DZ1100500), the Shanghai Municipal Science and Technology Major Project, the Shanghai Frontiers Science Center Program (2021-2025 no. 20), the Zhangjiang National Innovation Demonstration Zone (Grant no. ZJ2019-ZD-005), the Shanghai Rising-Star Program (Grant no. 20QA1404100), the National Natural Science Foundation of China (Grants nos. 11947065, 61901164, 62005164, 62005166, and 12004355), the Natural Science Foundation of Jiangxi Province (Grant no. 20202BAB211007), the Interdisciplinary Innovation Fund of Nanchang University (Grant no. 2019-9166-27060003), and the China Scholarship Council (Grant no. 202008420045).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anthur, A. P., Zhang, H., Paniagua-Dominguez, R., Kalashnikov, D. A., Ha, S. T., Maß, T. W. W., et al. (2020). Continuous Wave Second Harmonic Generation Enabled by Quasi-Bound-States in the Continuum on Gallium Phosphide Metasurfaces. Nano Lett. 20, 8745–8751. doi:10.1021/acs.nanolett.0c03601

PubMed Abstract | CrossRef Full Text | Google Scholar

Aouani, H., Navarro-Cia, M., Rahmani, M., Sidiropoulos, T. P. H., Hong, M., Oulton, R. F., et al. (2012). Multiresonant Broadband Optical Antennas as Efficient Tunable Nanosources of Second Harmonic Light. Nano Lett. 12, 4997–5002. doi:10.1021/nl302665m10.1021/nl302665m

PubMed Abstract | CrossRef Full Text | Google Scholar

Armstrong, J. A., Bloembergen, N., Ducuing, J., and Pershan, P. S. (1962). Interactions between Light Waves in a Nonlinear Dielectric. Phys. Rev. 127, 1918–1939. doi:10.1103/physrev.127.1918