DNA-like Helices as Nanosized Polarizers of Electromagnetic Waves

The possibility of using a conducting double DNA-like helix as the basis of an electromagnetic wave polarizer, which converts an incident linearly polarized wave into a reflected wave with circular polarization, has been shown. A high-frequency resonance is studied, at which the wavelength of the incident radiation is approximately equal to the length of a helical turn. The simulation of a double DNA-like helix has been carried out. The electric currents arising in the helical strands under waves with circular polarization at high-frequency resonance have been analyzed. Fundamentally different behavior of the double DNA-like helix concerning waves with right-hand or left-hand circular polarization has been established, which can be called the effect of polarization selectivity. This effect is manifested in the fact that a double DNA-like helix at high-frequency resonance can create a reflected wave having only one sign of circular polarization. The electric vector of the reflected wave produces a turn in space with the opposite winding direction compared to the double helix. These studies also highlight the electromagnetic forces of interaction between helical strands. The equilibrium of the double DNA-like helix has been studied, including as an element of metamaterials and as an object with a high potential for use in nanotechnology.

1 Introduction

Since the time of the discovery by J. Watson and F. Crick of the DNA molecule structure (Watson and Crick, 1953), the mechanisms of storage and transmission of genetic information by this molecule have become a subject of unfailing interest of researchers (Watson et al., 2013). On the other hand, a DNA molecule is a natural nanoscale object, which creates the possibility of using it in a natural or modified state in nanotechnology. Using a DNA molecule as an element of nanodevices requires careful study and consideration of its physical properties, including electrical conductivity. The presence of conductive properties of the DNA molecule was predicted in (Eley and Spivey, 1962) within the framework of a theoretical approach. Then, the role of charge transfer in the cell’s biochemical processes, such as replication, transcription, and DNA repair, was analyzed in (Demple and Harrison, 1994). The discovery of fast charge transfer between the donor and acceptor in the DNA molecule was reported in (Hall et al., 1996). As a result, a new line of research has emerged, i.e., nanobioelectronics, which represents the development of molecular electronics and uses the DNA conducting properties in new microelectronic devices (Petty et al., 1995; Baker, 2008; Lakhno and Vinnikov, 2018). To analyze the charge transfer problem in biomolecules, including DNA, various models and mutually complementary methods of theoretical analysis are used. Some studies are based on the master equation (Petrov et al., 2002) and the density matrix equation in the Redfield (Segal et al., 2000) and Lindblad (Weiss et al., 2006; Alicki and Lendi, 2007) forms. There are also methods based on numerical solutions of quantum models, considering the effects of many-particle interaction of a charged carrier with molecular vibrations and, possibly, with other degrees of freedom of the environment (Lakhno, 2004; Fialko and Lakhno, 2018; Syurakshin et al., 2021).

DNA has become an advanced material for use in nanotechnology because of its promising properties of structural stability, sequence programmability, and well-defined self-assembly. Therefore, the components of natural biological systems, including DNA, are carefully studied to create innovative nanodevices based on DNA-like elements (Sekhon, 2005). Due to its unique properties, DNA is an excellent intellectual material for the design and manufacture of nanostructures (Seeman, 2010). Single- and double-stranded DNA is used to create one-dimensional, two-dimensional, and three-dimensional structures with complex geometries and high-precision combination of elements. Thus, macroscopic structures with nanoscale details are created (Kallenbach et al., 1983; Aldaye et al., 2008; Shih and Lin, 2010; Pinheiro et al., 2011). DNA nanotechnology is also used to create a variety of programmable devices and sensors. DNA nanotechnology is becoming increasingly important in connection with the required miniaturization of devices and an increase in information processing speed. Materials are created that can be elements of electronic devices, such as nanowires and transistors (Bachtold et al., 2001; DeHon, 2003; Patwardhan et al., 2004; Zahid et al., 2013). The advantage of such devices is related to the property that the DNA density can be significantly increased compared to a typical circuit in a conventional electrical system. In addition, DNA-based nanodevices demonstrate relatively high energy efficiency.

Studies continue in the following areas of nanotechnology as the nanoscale folding of DNA to create arbitrary two- and three-dimensional shapes at the nanoscale (DNA origami) (Wang et al., 2017); synthesizing and characterizing nucleic acid complexes and materials where the assembly has a static, equilibrium endpoint (structural DNA nanotechnology) (Zhang et al., 2014); forming nucleic acid systems with designed dynamic functionalities related to their overall structures, such as computation and mechanical motion (dynamic DNA nanotechnology) (DeLuca et al., 2020).

This research shows that a double DNA-like helix can play a nanoscale polarizer of electromagnetic waves, transforming an incident linearly polarized wave into a reflected wave with circular polarization. A universal theoretical approach, based on Maxwell’s equations and the electromagnetic field potentials, is used. This approach makes it possible to study DNA-like helices in any range of electromagnetic waves, provided that the helix sizes and the resonant wavelength are scaled in a mutually consistent manner. Numerical simulation is carried out for the DNA-like helix in the millimeter range for electromagnetic waves, however, the electrodynamic similarity method allows applying the results to nanoscale DNA-like helices.

The results of the research are universal and reliable in various ranges of electromagnetic waves. This makes it possible (using helical scaling) to obtain metamaterials and metasurfaces resonant for various frequencies, including microwaves, terahertz frequencies and the optical range using available technologies. The use of DNA molecules, during their metallization, would increase the resonant frequency of metamaterials and metasurfaces up to the extreme UV range. Metamaterials and metasurfaces based on DNA-like helices, due to the balance of their dielectric and magnetic properties, can serve as a good tool for controlling the intensity, phase, polarization and direction of wave propagation. A double DNA-like helix is assumed to have electrical conductivity, or this property can be achieved for a modified helix, for example, by metallization. A double DNA-like helix is considered, in which two strands are mutually displaced along a common axis. At this stage, DNA-like helices in a linear state are considered. The applicability of the results for the supercoiled or circular state of DNA molecules requires further study. A high-frequency resonance is investigated, at which the wavelength of the incident radiation is approximately equal to the length of a helical turn. A double DNA-like helix in the field of an incident electromagnetic wave with right or left circular polarization has been considered. Electric currents arising in helical strands under the waves with circular polarization at high-frequency resonance have been analyzed. Suppose the incident wave has a right-hand circular polarization, while the electric vector of the wave produces a right turn in space. In that case, the electric currents arising in two helical strands pass in opposite directions relative to the helix axis. As a result, such oppositely directed currents practically do not emit an electromagnetic field, and the double DNA-like helix does not create a reflected wave. This means that a double DNA-like helix, which, as is known, has a right-hand winding in space, can be regarded as an “orthogonal vibrator” concerning an electromagnetic wave with right-hand circular polarization. If the incident wave has left-hand circular polarization, while the electric vector of the wave produces a left turn in space, then the electric currents induced in two helical strands have the same direction relative to the helix axis. Consequently, such identically directed currents emit an electromagnetic field, and the double DNA-like helix creates a reflected wave with left-hand circular polarization, the same as that of the incident wave. This different behavior of the double DNA-like helix for waves with right-hand or left-hand circular polarization can be called the effect of polarization selectivity.

On the other hand, double DNA-like helices are used to create metamaterials and metasurfaces—artificial structures with pre-designed unique properties not found in natural objects (Lavigne et al., 2018). One of the advantages of such helices over other elements of metamaterials is their strong polarizability in both electric and magnetic fields, which suggests the presence of relatively strong currents in the helical strands. Consequently, the question arises about the interaction of strands in the double helix and its stability. In this regard, all three components of the electric force and magnetic force acting on an arbitrary element of one strand from the side of the whole other strand are calculated in this article. The dependence of all forces on the pitch angle of the double helix is studied. The obtained results can be used when considering the equilibrium of a double-stranded helix, including as an element of metamaterials (Semchenko et al., 2019).

An important advantage of DNA-like helices when creating metamaterials and metasurfaces is the balance or the optimality of such helices in terms of the electromagnetics. This property means that an electric dipole moment and a magnetic moment simultaneously arise under the action of an incident wave in each turn of a DNA-like helix at the resonance under consideration. These induced moments are equally significant, i.e., they make an equal, in absolute magnitude, contribution to the reflected wave. This property of balancing the dielectric and magnetic properties of a single DNA-like helix is promising and can lead, for example, to equality of the dielectric permittivity and magnetic permeability of a metamaterial or a metasurface as a whole.

As for producing metasurfaces based on DNA-like helices, they can be created by nanolithography and three-dimensional nanostructuring. Natural DNA molecules can also be used, which have the ability to self-assemble and arrange in two-dimensional and three-dimensional structures (Kallenbach et al., 1983; Aldaye et al., 2008; Seeman, 2010; Shih and Lin, 2010; Pinheiro et al., 2011).

2 Method for Calculating Electric and Magnetic Fields at High-Frequency Resonance, Taking Into Account the Delay of Electromagnetic Waves

This article considers a DNA-like helix at high-frequency resonance when the wavelength of the electromagnetic field is approximately equal to the period of the helix: ${\lambda }_{res}\approx P$. Under this condition, the electric currents in two helical strands perform a complete oscillation in space within one turn. In other words, the phase of the electric current in each strand changes by $2\pi$ when the coordinate, measured along the helix line, changes by P. A similar change in space occurs for the electric charges induced in two helical strands. Electric currents and charges in two strands are schematically shown in Figure 1. At two points of one strand, the distance between which is equal to half a turn, electric currents have the opposite direction. For two similar points of one helical strand, electric charges have opposite signs.

FIGURE 1

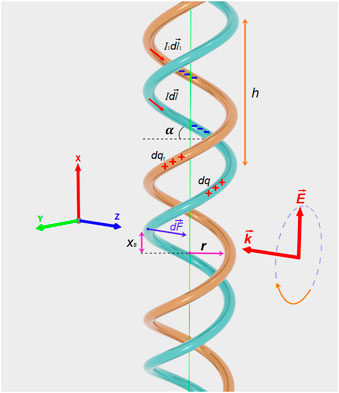
FIGURE 1. Schematic of an asymmetric double-stranded helix (DNA-like type) in the field of an incident electromagnetic wave with left-hand circular polarization. The helix pieces with the maximum concentration of electric currents and charges are indicated for the type of excitation studied. It is assumed that the electric currents in two strands are in the same direction relative to the helix axis. A numerical simulation of a double DNA-like helix as an ideal conductor confirmed this assumption about the direction of the currents at high-frequency resonance, see Section 8.

In Figure 1, the DNA-like helix is schematically represented with its parameters: helix pitch h, helix radius r, axial shift between helices x_s, as well as induced charges $dq$ , $d{q}_1$ and induced currents $I\overrightarrow{dl}$ and $I{\overrightarrow{dl}}_1$. The direction of the currents in two helices depends on the way of exciting the double helix. In our case, the currents pass in same direction relative to the axis of the helix. The charges and the currents are periodically distributed along the helix as they are induced by harmonic standing high-frequency wave with the wavelength ${\lambda }_{res}\approx P$, where P is the period of the helix (the entire length of one turn of the helix). The forces act on a physically small piece of the helix (single-strand) having its maximum current (magnetic force) or maximum charge density (electric force).

Calculations must consider the electromagnetic field delay since electric currents and charges change rapidly within a DNA-like helix. For high-frequency fields, in contrast to the quasi-stationary case, the electric and magnetic vectors $\overrightarrow{E}$ and $\overrightarrow{B}$ can be calculated using the scalar and vector potentials of the electromagnetic field $\phi$ and $\overrightarrow{A }$ (Landau and Lifshits, 1975):

$\overrightarrow{E}=-grad \phi - \frac{\partial \overrightarrow{A}}{\partial t},\overrightarrow{B}=rot\overrightarrow{A}.(1)$

The field potentials $\phi$ and $\overrightarrow{A}$ have the following form

$\phi \left(x,y,z,t\right)=\frac{1}{4\pi {\epsilon }_0}\underset{V_1}{{\displaystyle \int }}\frac{{\rho }_1\left(x_1,y_1,z_1,t_1\right)d{V}_1}{R},(2)$

$\overrightarrow{A}\left(x,y,z,t\right)=\frac{{\mu }_0}{4\pi }\underset{L_1}{{\displaystyle \int }}\frac{I_1\left(x_1,y_1,z_1,t_1\right)\overrightarrow{d{l}_1}}{R}.(3)$

Here $x,y,z$ are the observation point coordinates, $t$ is the current time, ${\epsilon }_0$ and ${\mu }_0$ are the electric and magnetic constants, ${\rho }_1$ is the volumetric electric charge density, $I_1\overrightarrow{d{l}_1}$ is the elementary linear current, which are considered as sources of an electromagnetic field, $x_1,y_1,z_1$ are the coordinates of the point at which electric charges and currents exist, $t_1-\raisebox{1ex}{$R$}\!\left/ \!\raisebox{-1ex}{$c$}\right.$ is the previous moment in time, determined taking into account the delay of waves from the radiating currents and charges to the observation point, R is the distance from elementary charges and currents to the observation point, c is the speed of light in vacuum, $V_1$ and $L_1$ are the integration areas in which there are electric currents and charges, in our case it is the volume of the helical strand and its length, $d{l}_1$ is the helical strand length element, $d{V}_1=S_{0}d{l}_1$ is the helical strand volume element, $S_0$ is the effective cross-sectional area of the strand.

3 The Distribution of Electric Currents and Charges in a Double Helix at High Frequency Resonance

The considered DNA-like helices have a finite length, like the actual DNA molecule. Therefore, a standing wave of electric current is established in each helical strand due to the reflection of waves from the edges of the strands. We assume that the incident wave is quasimonochromatic, and the excitation time is long enough to excite the resonant mode of the helix. When this condition is satisfied, the electric current strength in the first and second helices for the current time can be written as

$I_1\left(l_1,t\right)=I_{1\mathit{max}} \cos \left(k{l}_1\right)\cos \left(\omega t\right), I\left(l,t\right)=I_{\mathit{max}}\cos \left(kl\right)\cos \left(\omega t\right) ,(4)$

where $l_1$ and $l$ are the coordinates calculated along the first and second helical line; $I_{1max}$ and $I_{max}$ are the amplitudes of current standing waves; $k=\frac{\omega }{с}$ is the wavenumber; $\omega$ is the cyclic current frequency.

The distribution of electric charges in the double helix also produces a standing wave, and for the current time can be calculated as follows

${\rho }_1(l_1,t)=\frac{1}{S_{0}c}{I}_{1max}\sin \left(k{l}_1\right)\sin \left(\omega t\right),\rho (l,t)=\frac{1}{S_{0}c}{I}_{max}\sin \left(kl\right)\sin \left(\omega t\right).(5)$

The calculations show that the distribution of currents and charges described by formulae 4, 5 and shown in Figure 1 take place not only with the normal incidence of the wave on a DNA-like helix, but also with an incidence angle less than 45° relative to the axis of the double helix. If the angle between the wave vector and the helical axis exceeds 45°, another eigenmode of electromagnetic oscillations starts to prevail. For this alternative mode, the electric currents in two strands at points lying opposite each other have the opposite direction, and the electric charges at these points have different signs.

This article considers DNA-like helices similar to B-form DNA molecules. Therefore, all structural parameters are provided below for B form of the DNA molecule. It is the electrical conductivity along the helical strands that is essential here, so the effect of the DNA methylation is not considered. The DNA double helix has a significant feature: it is asymmetric, and the second strand is displaced relative to the first one by $x_s$ along their common X-axis (Watson et al., 2013). Further, we will see that such a displacement of the helices leads to the emergence of forces of their interaction directed along the coordinate axes X and Y. These forces can lead to stretching or compression of the turns of the helical strands. The indicated displacement of the helices can cause rotational moments of forces directed along the common X-axis. Under certain conditions, these rotational moments can cause unwinding or winding of the helical strands. Since there is a mutual displacement of the helices by $x_s$, the following relations hold:

$l\sin \alpha =x-x_s,l_1\sin \alpha =x_1,(6)$

where x and $x_1$ are the coordinates of points on the second and first helix, $\alpha$ is the helix pitch angle with respect to the plane, perpendicular to the axis of helix X.

As shown later in this paper, the pitch angle is a universal characteristic of the helix electromagnetic properties, since it is its value that appears in the formulae for electromagnetic forces, and not the radius and pitch of the helix separately. This property of the pitch angle versatility of the helix simplifies the study of helices that exhibit resonance properties in various wavelength ranges, including the nanometer range. In this case, the helices having different radii and periods (pitches), but simultaneously characterized by the same pitch angle, will be similar not only in the geometric, but also in the electromagnetic sense. This makes the study and application of helices easier, including DNA-like ones, in devices operating in various frequency ranges of the electromagnetic field.

The pitch angle satisfies the relations

$\tan \alpha =\frac{h}{2\pi r},\cot \alpha =\pm qr,\sin \alpha =\frac{h}{P}, P=\sqrt{{\left(2\pi r\right)}^2+h^2},(7)$

where $r$ is the helical turn radius; $h=\frac{2\pi }{\left|q\right|}$ is the helix pitch; $q$ is the helix specific winding, which is positive ($q>0$) for a right-handed helix and negative ($q<0$) for a left-handed helix; P is the helical turn length, the plus sign is used in the case of a right-handed helix, and the minus sign is true for a left-handed helix.

The pitch angle of the DNA helix, although not measured directly in the experiment, can be calculated on the basis of experimental data. As the experimental data show (Watson and Crick, 1953), an actual DNA helix has the following parameters:

$r={10}^{-9} \mathrm{m},h=3.4\cdot {10}^{-9} \mathrm{m},q=1.85\cdot {10}^9 \frac{\mathrm{rad}}{\mathrm{m}},{\alpha }_{exp}=28.4 \mathrm{deg},(8)$

According to the geometric properties of the helix, the rotation angle of the radius vector drawn to any point of the helix (polar angle) can be expressed in terms of the x-coordinate of this point: $u=q{x}_{1.}$ According to a book by Watson et al. (Watson et al., 2013), the rotation angle of the second helix for the symmetrical position is $u_s=53\mathrm{deg}=0.93 rad$. Therefore, the following relations are valid, which will be used in further calculations:

$u_s=q{x}_s,x_s=0.5\cdot {10}^{-9} \text{m}=\frac{1}{2}r,u_s=\frac{1}{2}\cot {\alpha }_{exp}.(9)$

The results given below are valid for both electrically conductive and dielectric helices. Conduction currents arise in the helices of the first type, and polarization currents are excited in the helices of the second type, which can lead to the occurrence of magnetic and electric forces of interaction between the strands of the double helix.

4 Calculation of the Magnetic Force of Interaction Between Two Helical Strands

The force acting on the electric current element $Id\overrightarrow{l}$ in the second helix has the following form

${\overrightarrow{dF}}_{\left(mag\right)}=\left[Id\overrightarrow{l}\overrightarrow{B}\right],(10)$

where the magnetic field induction $\overrightarrow{B}$ is determined by expressions (1) and (3) and must be calculated considering the delay of electromagnetic waves propagating from all elements of the first helix to the selected element of the second helix.

Hereinafter, we shall refer to this force as magnetic, as indicated by the corresponding index. This force takes on maximum values in the antinode regions of a standing wave of electric current (4).

Using the integration technique described in (Semchenko et al., 2020), let us calculate all the components of the magnetic force (10) acting on the current element in the second helix from the side of the entire first helix. In this case, integration is performed along the entire first helix to take into account the contribution of all its elements to the generated magnetic field. Infinite limits of integration are used, i.e., the helices are considered as very long, which is typical for an actual DNA molecule. Unlike (Semchenko et al., 2018; Semchenko et al., 2020), where the quasi-stationary case is considered and the Biot–Savart law, and Coulomb law are applied, the delay of electromagnetic waves from various elements of the first helix to the selected element of the second helix is taken into account. The following x-, y-, and z-components of the force are available in the result (10):

$d{F}_{x\left(mag\right)t}=\frac{\Omega }{2}cos\alpha {\left(cot\alpha \right)}^2\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{\left[\left(u_s-u\right)cosu+\mathit{sin}u\right]\cos \left(\frac{Pu}{\lambda }\right)\mathit{cos}\Theta }{w^{3/2}}du(11)$

$d{F}_{y\left(mag\right)t}=-\tan \alpha \cdot d{F}_{x\left(mag\right)t}(12)$

$d{F}_{z\left(mag\right)t}=\frac{\Omega }{2}\mathit{cos}\alpha \cdot \cot \alpha \underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{\left[\left(1-{(\mathit{cot}\alpha )}^2\right)\left(1+\mathit{cos}u\right)-\left(u_s-u\right)\mathit{sin}u\right]\cos \left(\frac{Pu}{\lambda }\right)\mathit{cos}\Theta }{w^{3/2}}du(13)$

Here, the index t means time averaging; the integration variable $u=q{x}_1$, as above, is equal to the polar angle for the first helix; $\lambda =\frac{2\pi с}{\omega }$ is the wavelength of the electromagnetic field in vacuum; $\text{Ω}=I_{\mathit{max}}^2\frac{{\mu }_0}{4\pi r}dl$ is the general normalization constant for the force components; there is also notation to reduce the formulae to a more compact form:

$w={\left(u_s-u\right)}^2+2{(\cot \alpha )}^2\left(1+\mathit{cos}u\right), \text{Θ}=\frac{P}{\lambda }\mathit{sin}\alpha \sqrt{w}.(14)$

To proceed to the quasistationary case $\lambda \gg P$, considered earlier in (Semchenko et al., 2020), it is necessary to perform the passage to the limit $\text{Θ}\to 0$. In this limiting case, formulae 11–formulae 13 take the form obtained in (Semchenko et al., 2020) for quasi-stationary magnetic forces.

5 Calculation of the Electrical Force of Interaction Between Two Helical Strands

In addition to the magnetic force, let us also consider the force acting on the electric charges in the second helix from the side of the entire first helix.

This force takes the maximum value for a physically small element of the helix on which the antinode of the electric charge is located, for example, when $l=\frac{\lambda }{4}$ in formula 5. The force acting on the element of electric charge $dq=\rho dV$ in the second helix has the following form

${\overrightarrow{dF}}_{\left(el\right)}=dq\overrightarrow{E }=\rho \overrightarrow{E}dV(15)$

where $dV=S_{0}dl$ is the volume element of the second helix, $dl$ is the length element of the second helical strand, $\overrightarrow{E}$ is the electric field strength. The vector $\overrightarrow{E}$ is determined by expressions (1), (2) and (3) and must be calculated considering the delay of electromagnetic waves propagating from all elements of the first helix to the selected element of the second helix.

Using the integration technique described in (Semchenko et al., 2020), taking into account the delay of electromagnetic waves, let us calculate all the components of the electric force (15) acting on the charge element in the second helix from the side of the entire first helix. The calculations result in obtaining the x-, y-, and z-components of the force (15), averaged over time:

$d{F}_{x\left(el\right)t}=\frac{\Omega }{2}\mathit{cos}\alpha \left[\frac{1}{{\mathit{sin}}^2\alpha }{I}_1-\frac{P}{\lambda }{I}_2\right](16)$

$d{F}_{y\left(el\right)t}=\frac{\Omega }{2}\mathit{cos}\alpha \cdot \cot \alpha \left[\frac{1}{{\mathit{sin}}^2\alpha }{I}_3+\frac{P}{\lambda }{I}_4\right](17)$

$d{F}_{z\left(el\right)t}=\frac{\Omega }{2}\mathit{cos}\alpha \cdot \cot \alpha \left[-\frac{1}{{\mathit{sin}}^2\alpha }{I}_5+\frac{P}{\lambda }{I}_6\right](18)$

The notation is introduced here

$I_1=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{\left(u_s-u\right)\cos \left(\frac{Pu}{\lambda }\right)\mathit{cos}\text{Θ}}{w^{3/2}}du, I_2=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{\sin \left(\frac{Pu}{\lambda }\right)\mathit{cos}\text{Θ}}{\sqrt{w}}du, I_3=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{\mathit{sin}u\cdot \mathit{cos}\left(\frac{Pu}{\lambda }\right)\mathit{cos}\text{Θ}}{w^{3/2}}du(19)$

$I_4=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{\mathit{cos}u\cdot \sin \left(\frac{Pu}{\lambda }\right)\mathit{cos}\text{Θ}}{\sqrt{w}}du,I_5=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{\left(1+\mathit{cos}u\right)\cos \left(\frac{Pu}{\lambda }\right)\mathit{cos}\text{Θ}}{w^{3/2}}du, I_6=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{\mathit{sin}u\cdot \sin \left(\frac{Pu}{\lambda }\right)\mathit{cos}\text{Θ}}{\sqrt{w}}du(20)$

As in the case of magnetic forces, in order to proceed to the quasi-stationary case $\lambda \gg P$, considered earlier in (Semchenko et al., 2020), it is necessary to perform the passage to the limit $\text{Θ}\to 0$ and neglect the values proportional to ${\left(\frac{P}{\lambda }\right)}^2$. In this limiting case, formulae 16–formulae 18 take the form obtained in (Semchenko et al., 2020) for quasi-stationary electric forces.

6 Graphical Representation of the Interaction Forces Between Helical Strands and a Comparison of Two Types of Resonance

The magnetic and electrical forces of interaction of two helical strands (11–13) and (16–18) at high-frequency resonance, considered in this paper, are presented in the graphical form in Figure 2. Solid lines show the calculated values of the forces. For comparison, in the same figure the dashed lines show the values of the electric and magnetic forces at the main resonance, which can be realized at a lower frequency. This resonance requires an approximate equality of the total length of the helix and half the wavelength of the electromagnetic field. These values of forces, shown by dashed lines, were calculated earlier in (Semchenko et al., 2018; Semchenko et al., 2020).

FIGURE 2

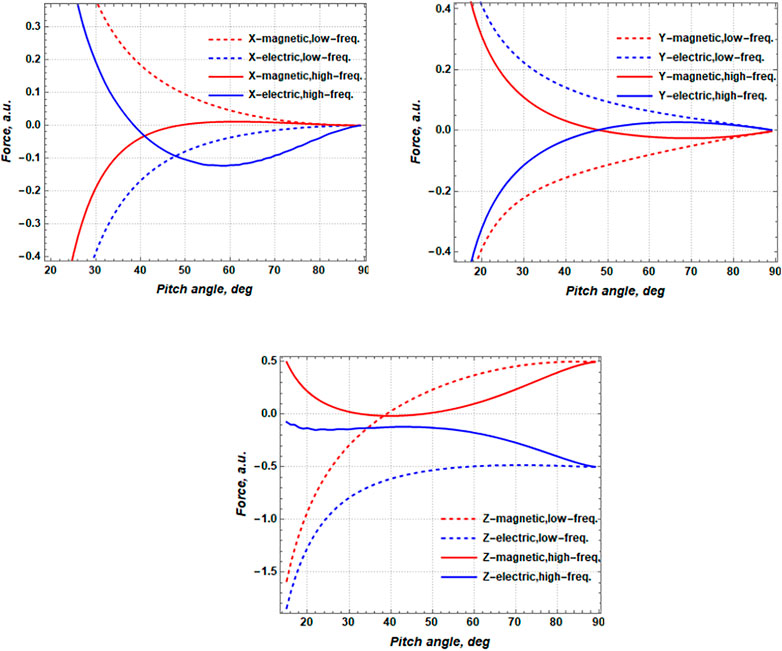
FIGURE 2. X, Y, and Z-components of elementary forces vs. pitch angle calculated both for the low-frequency (dashed lines) and high-frequency (solid lines) cases. All the components of the forces are normalized to a factor $\Omega$.

All three components (X, Y and Z) of the elementary force induced by both electric and magnetic fields are of great interest in the context of their dependence on helix pitch angle (see Figure 2). The first conclusion that can be drawn when comparing the forces for two types of resonance is that low-frequency resonance forces are greater than high-frequency ones almost always (for any pitch angle of the helix).

If the pitch angle of the helix α approaches 90°, the helical strands take on a highly elongated shape and, in the limit, become straight conductors. For such straight parallel conductors, the magnetic and electric forces are well known. Therefore, these forces are convenient to compare with the interaction forces of two helices having an arbitrary pitch angle α.

The X-component of forces may lead to helix compression or stretching. At high-frequency resonance, the X-component of the magnetic interaction force of the strands is close to zero if the pitch angle of the double helix exceeds 48°. On the other hand, the X-component of the electric force is zero only when alpha is equal to 39°, and this force changes sign at this value of the pitch angle. If the pitch angle of the helix satisfies the inequality ${48}^{°}<\alpha <{90}^{°}$, the X-component of the high-frequency electric force exceeds the low-frequency resonance force. There is a maximum (in absolute value) of the X-component of the high-frequency resonant electric force at the pitch angle $\alpha ={55}^{°}.$ If $\alpha \to {90}^{°}$, i.e., for straight parallel conductors, the X-components of all resonant forces go to zero.

The Y-components may lead to the helix winding or unwinding. The Y-components of the electric and magnetic forces behave symmetrically with a change in the pitch angle of the double helix. In this case, the Y-components of the electric and magnetic forces are opposite to each other in sign and approximately equal in magnitude. This means that if the magnetic force unwinds the helix in the antinode of the electric current, then the electric force, on the contrary, winds the helix only in the antinode of the electric charge. At high-frequency resonance, these components are zero when $\alpha \approx {48}^{°}$ and they change their sign at this point. If $\alpha \to {90}^{°}$, i.e., in the limiting case of straight parallel conductors, the Y-components of all resonant forces disappear.

The chosen direction of the coordinate axes is shown in Figure 1 while considering the forces acting on the element of the second helix located on the left. Therefore, the positive Z-component of electric or magnetic force means the radial attraction for the elementary piece of a strand. In contrast, the negative value of the Z-component means the repulsive radial force. If the condition $\alpha \to {90}^{°}$ is satisfied, then the radial electric and magnetic forces become equal with the opposite sign. This equality is consistent with the well-known fact: in straight parallel conductors, currents of the same direction are attracted, and charges are repelled since they have the same sign. In this case, the electric and magnetic forces are equal in magnitude, ensuring the balance of straight parallel conductors. Here, for the double helix, the force of electrical interaction leads to the repulsion of the strands at any pitch angle of the helix. If the pitch angle of the helix satisfies the inequality $\alpha <{50}^{°}$, then the high-frequency radial electric repulsive force of the helical strands is feeble. The high-frequency radial magnetic force is almost equal to zero if the pitch angle of the helix is within a range of ${30}^{°}<\alpha <{50}^{°}$. Consequently, double helices with such a pitch angle are in equilibrium due to the absence of both magnetic and electrical interactions between the strands. As shown by relations (8), an actual DNA molecule is characterized by the helix pitch angle ${\alpha }_{exp}={28.4}^{°}$, which indicates its equilibrium in terms of the electromagnetic interaction of the strands. This equilibrium is a powerful argument in favor of using DNA-like helices in artificial structures and metamaterials, including nanotechnology.

7 Polarization Selectivity of the Effect of Circular Electromagnetic Waves on DNA-like Helices and the Polarization Conversion Upon Reflection of Waves

The DNA double helix is a chiral object, i.e., it differs from its mirror image. As is known in physics since the publication of the classical works of Pasteur, Arago, Biot, Fresnel (Arago, 1811; Biot, 1815; Fresnel, 1822; Pasteur, 1848; Pasteur, 1922), such objects interact differently with circularly polarized electromagnetic waves or show polarization selectivity of optical properties. The indicated polarization selectivity can manifest itself, first of all, in the difference between the refractive indices and absorption coefficients for light waves with right and left circular polarization. For natural objects, for example, quartz crystals, the relative difference between the refractive indices of the right and left circularly polarized waves in the optical range is $\frac{n_{+}-n_{-}}{n_{+}+n_{-}}\sim {10}^{-3}÷ {10}^{-5}$. Consequently, the chiral properties of natural objects in optics are relatively weak.

For artificial structures such as metamaterials based on conducting helices, the chiral properties can be significantly enhanced. Such a stronger manifestation of chiral properties is due to the particular, pre-designed shape of the helical elements. The enhancement of chiral properties can occur in the corresponding frequency range (not only optical but also microwave or terahertz), where the metamaterial interacts with electromagnetic waves in a resonant manner.

It is important to note that there are two different definitions of a circularly polarized wave sign. The first definition is accepted in radiophysics. According to this definition, the wave has right-hand circular polarization if the vector $\overrightarrow{E}$ rotates clockwise over time for an observer looking after the wave. Optics and physical chemistry often use the other definition: a wave has a right-hand circular polarization if the vector $\overrightarrow{E}$ forms a right helix in space. The advantage of the second definition is its independence from the position of the observer. In formula 21 and later in this article, we use the second definition of a circularly polarized wave sign.

It is shown in (Semchenko et al., 2006; Semchenko et al., 2007; Semchenko et al., 2009; Semchenko et al., 2010a; Semchenko et al., 2010b; Semchenko et al., 2010c; Semchenko et al., 2011) that double DNA-like helices have selective properties for the right and left circularly polarized electromagnetic wave if the condition of resonant interaction ${\lambda }_{res}\approx P$ is satisfied. In this case, the double DNA-like helix with the right winding direction strongly interacts with the left circularly polarized wave. It practically does not interact with the wave having the opposite (right) circular polarization. Thus, in relation to the wave with the right circular polarization, the helix can be considered transparent. Consequently, double DNA-like helices at the resonance under consideration can create a reflected wave only with left-hand circular polarization. In connection with this property, a double DNA-like helix can be called an “orthogonal vibrator” for a circularly polarized wave. This term can be introduced by analogy with a straight conductor orthogonal to the vector $\overrightarrow{E}$, if the wave is linearly polarized.

Once again, the key points for the polarization selectivity effect are: 1) double-stranded form of the helix, which leads to a higher symmetry of properties for rotations around the axis of the helix; 2) a certain pitch angle of the helix, close to ${\alpha }_{exp}={28.4}^{°}$, observed for an actual DNA molecule; 3) fulfillment of the condition of resonant interaction ${\lambda }_{res}\approx P$. An important but not fundamental condition for observing the polarization selectivity effect is the electrical conductivity of the helices. Although the effect can occur both for the conduction current and for the polarization current, it is more pronounced in the conduction current. Therefore, DNA-like helices were scaled for microwave and terahertz ranges in (Semchenko et al., 2009; Semchenko et al., 2010c; Semchenko et al., 2011; Semchenko et al., 2012; Semchenko et al., 2017) to observe the effect. The helices were made of metal and periodically arranged in a metamaterial. The DNA-like helices for the microwave range were made by mechanically twisting the wire; then they were placed in a foam plate, which served as a radio-transparent substrate. If such helices were connected into three-dimensional structures, the necessary strength was achieved by using cardboard cylinders on which the helices were wound (Semchenko et al., 2009; Semchenko et al., 2010c; Semchenko et al., 2011; Semchenko et al., 2012). The DNA-like helices having resonant properties in the terahertz range were created within the framework of imprint nanolithography using a unique three-dimensional nanostructuring method developed under the guidance of Academician Viktor Y. Prinz and known as Prinz-technology (Semchenko et al., 2017).

As an example, papers (Gansel et al., 2009; Kaschke et al., 2015), which describe circular polarizers of electromagnetic waves based on metamaterials, should be mentioned as well. Metasurfaces have also generated great research interest due to easy production process, low cost, and powerful functionality for manipulating the electromagnetic waves, including polarization conversion (Li et al., 2020; Li et al., 2021a; Li et al., 2021b; Han et al., 2021).

Unlike (Semchenko et al., 2006; Semchenko et al., 2007; Semchenko et al., 2009; Semchenko et al., 2010a; Semchenko et al., 2010b; Semchenko et al., 2010c; Semchenko et al., 2011), this research deals with not only the reflection of circularly polarized waves by DNA-like helices and the effect of polarization selectivity. We also calculate the currents excited in the helical strands under circularly polarized waves and the interaction forces between these strands. This question is essential in studying the equilibrium in electromagnetic fields of an actual DNA molecule and DNA-like elements of metamaterials and nanodevices.

The electric field strength of the right (+) and left (−) circularly polarized wave propagating in vacuum along the OZ axis is

${\overrightarrow{E}}_{\pm }=E_0\frac{{\overrightarrow{x}}_0\mp i{\overrightarrow{y}}_0}{\surd 2}\mathit{exp}\left(i\left(kz-\omega t\right)\right)(21)$

where $E_0$ is the wave amplitude, ${\overrightarrow{x}}_0$, ${\overrightarrow{y}}_0$, are the unit vectors directed along the OX and OY axes, i is the imaginary unit, the factor $\surd 2$ is introduced to normalize the circular polarization vector, $k=\frac{\omega }{с}$ is the wavenumber; $\omega$ is the cyclic frequency.

The electric vector of a wave incident on the double DNA-like helix with left-hand circular polarization ${\overrightarrow{E}}_{-}$ is presented schematically in Figure 1. This figure shows the direction of the vector ${\overrightarrow{E}}_{-}$ rotation over time for an observer looking after the wave.

8 Simulation of a Conductive DNA-like Double Helix in the Millimeter Wavelength Range of the Electromagnetic Field

Previously in this paper, we noted that the helix pitch angle is a universal characteristic of the electromagnetic properties of a DNA-like double helix. This makes it possible to scale the helix with a pitch angle ${\alpha }_{exp}={28.4}^{°}$ (8), which is characteristic of an actual DNA helix and to simulate its electromagnetic properties in the millimeter wavelength range of the electromagnetic field. In the presence of the helix electrical conductivity and high-frequency resonance, when the wavelength of the electromagnetic field is approximately equal to the period of the helix, the simulated helix will be similar to the DNA double helix not only in the geometric but also in the electromagnetic sense.

This section presents the results of modeling the double DNA-like helix consisting of two and a half turns and having parameters $r={10}^{-3}\text{m}$, $h=3.4\cdot {10}^{-3}m$, $q=1.85\cdot {10}^3 \frac{rad}{m}$, $P=7.14\cdot {10}^{-3}m,$ ${\alpha }_{\exp }=28.4\mathrm{deg}.$ The helical strands are mutually shifted along the helix axis by $x_s=0.5\cdot {10}^{-3}\text{ m}$. The helix under study is in the field of an incident electromagnetic wave, which alternately has right or left circular polarization. The wave vector of the incident wave is directed orthogonal to the double helix axis, i.e., the case of normal incidence is considered. The wavelength of the incident electromagnetic field satisfies the condition of high-frequency resonance ${\lambda }_{res}\approx P$. Therefore, the frequency of the incident wave is close to value ${\nu }_{res}\approx 42\cdot {10}^{9}Hz$. The helix, for which the results are shown in this article section, has 2.5 turns. However, the simulation results do not change significantly for different turns in the range of $0.5\le N_t\le 20.5$. The simulation is carried out using the HFSS software package provided by our scientific partners from Aalto University, Helsinki.

The electric currents in two strands induced by the incident circularly polarized wave are calculated at the first stage. Values are obtained for both the real parts of the electric currents and their imaginary parts.

Figure 3 show that two types of resonance appear simultaneously in the helix under consideration. The first one, which is interesting for us, is associated with the periodicity of the double helix; it occurs near the resonance frequency

${\nu }_{res}=\frac{c}{{\lambda }_{res}} \approx \frac{c}{P} \approx 42\cdot {10}^{9}Hz (22)$

FIGURE 3

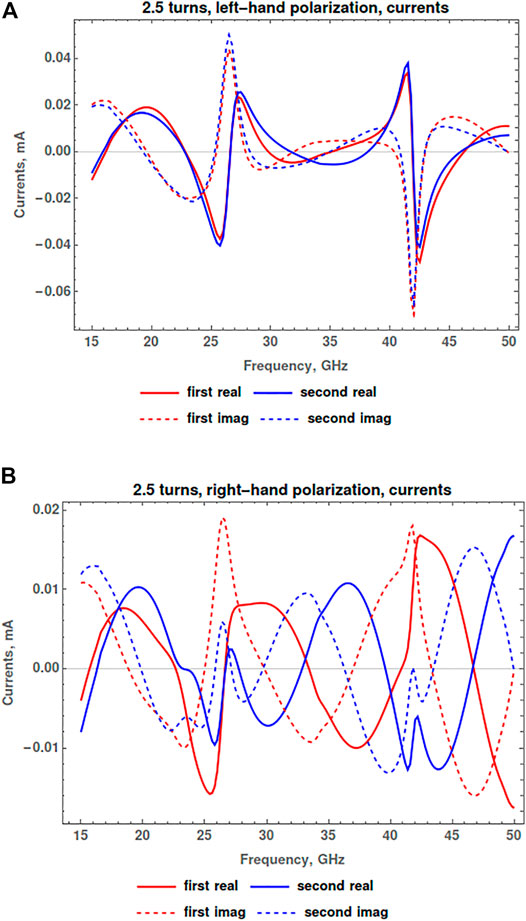
FIGURE 3. (A) Dependence of the real and imaginary parts of the electric currents in two strands of the DNA-like helix in the field of an incident wave with left-hand circular polarization on the wave frequency (the case of strong interaction between the wave and the helix). (B) A similar dependence for currents if the helix is in the wave field with right-hand circular polarization (the case of weak interaction between the wave and the helix).

The second type of resonance is due to the finiteness of the helix; it occurs if the length of the helix in the straightened state L is approximately equal to an integer number of half-waves. Here, the resonant frequencies are as follows

${\nu }_n=n\frac{c}{2L}=n\frac{c}{2N_{t}P}(23)$

At the integer number n = 3, resonance appears at a frequency of ${\nu }_3\approx 25.2\cdot {10}^{9}Hz$, which is noticeable in the considered frequency range.

Figure 3A shows that when a left circularly polarized wave is incident on the helix, electric currents arise in the helical strands that pass in the same direction relative to the helix axis. The real parts of the currents in the two strands have identical signs, and the same is true for the imaginary parts of the currents.

Figure 3B shows that in the other case, if a wave with right-hand circular polarization is incident on the helix, the electric currents excited in the two strands pass in opposite directions relative to the helix axis. The real and the imaginary parts of the currents in the first and second strands have different signs. This rule for the directions of the two currents is violated only near the resonant frequency ${\nu }_3\approx 25.2\cdot {10}^{9}Hz$. In addition, the values of the currents in the second case, for the right-hand circularly polarized incident wave, are approximately two to three times less than the currents in the first case. Consequently, a double DNA-like helix, considered as a whole, as a set of two helical strands, is strongly influenced by a wave with left circular polarization and practically does not interact with a right circularly polarized wave.

9 Simulation of an Intensity and Ellipticity of Wave Reflected by Conductive Double-Stranded and Single-Stranded DNA-like Helices

Significantly different excitation of currents in a double-stranded DNA-like helix under the action of incident waves with left-hand and right-hand circular polarization leads to radically different properties of the wave reflected by the helix. Figure 4 show the intensity and ellipticity of the reflected wave as a function of frequency if the double helix is in the field of incident waves with left-hand circular polarization. In this case, there is a strong interaction between the wave and the helix.

FIGURE 4

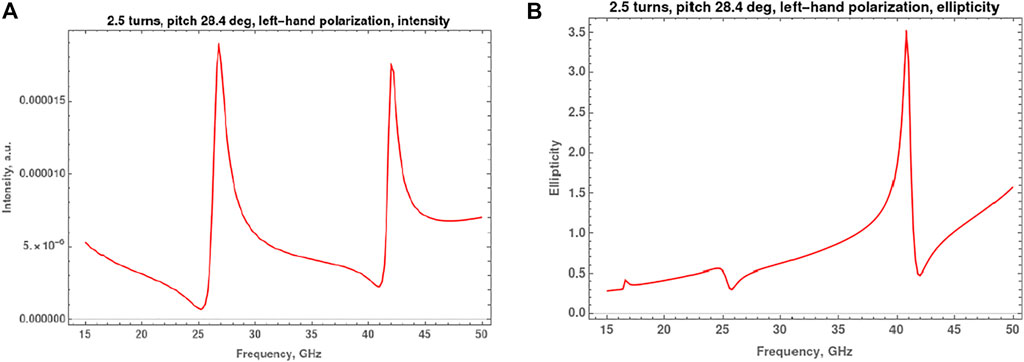
FIGURE 4. (A) Dependence of the intensity of the reflected wave by double-stranded DNA-like helix on the frequency for an incident wave with left-hand circular polarization (the case of strong excitation of currents). (B) Dependence of the ellipticity of the reflected wave under the same conditions.

Figure 4 show that near the resonant frequency ${\nu }_{res}$ (22) the intensity of the reflected wave is high, and at the same time its ellipticity takes values close to unity. This indicates a strong reflected wave with left-hand circular polarization, the same as that of the incident wave.

Figure 5 show, in turn, the dependences of the intensity and ellipticity of the reflected wave on the frequency, if the double helix is in the field of incident waves with right-hand circular polarization. In this case, there is a weak interaction between the wave and the helix. As follows from Figure 5A, the reflected wave intensity is very low in the frequency range from 30 to 45 GHz. These intensity values are approximately 25–80 times less than the intensity in Figure 4A. As for the ellipticity of the reflected wave, its value can also be close to unity near the resonant frequency (22), which confirms the circular polarization of the reflected wave. However, this property is not important due to the very low intensity of the reflected wave.

FIGURE 5

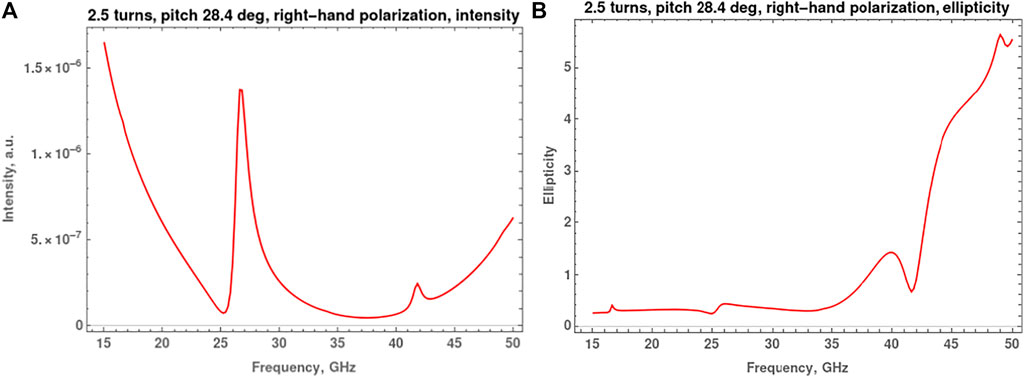
FIGURE 5. (A) Dependence of the intensity of the reflected wave by double-stranded DNA-like helix on the frequency for an incident wave with right-hand circular polarization (the case of weak excitation of currents). (B) Dependence of the ellipticity of the reflected wave under the same conditions.

It is also of interest to compare the reflected waves for a double- and a single-stranded DNA-like helices. Figure 6 show the intensity and ellipticity of the reflected wave as a function of frequency if the single helix is in the field of incident waves with left-hand circular polarization.

FIGURE 6

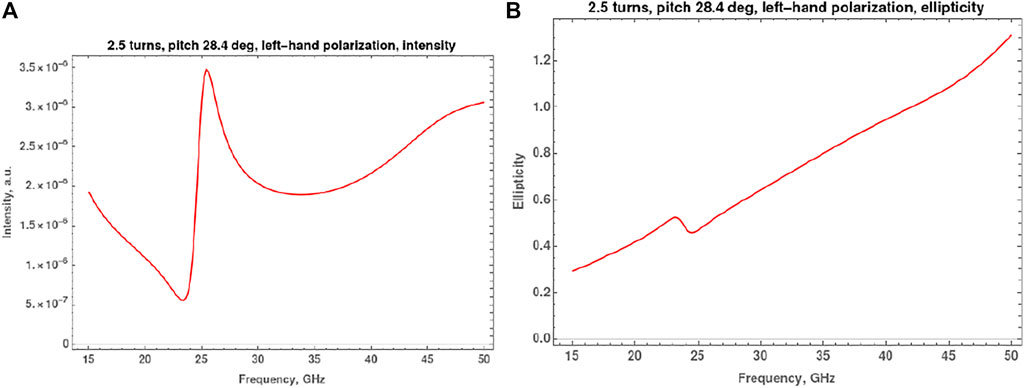
FIGURE 6. (A) Dependence of the intensity of the reflected wave by single-stranded DNA-like helix on the frequency for an incident wave with left-hand circular polarization. (B) Dependence of the ellipticity of the reflected wave under the same conditions.

Figure 6A shows that the reflection of waves by a single helix does not have a resonance character near frequency (22) for an incident wave with left-hand circular polarization. Comparing with Figure 4A, we find that the intensity of the reflected wave for a single helix in the frequency range 30–45 GHz is approximately 3–5 times less than the intensity of the reflected wave for a double helix. As follows from Figure 6B, the reflected wave for a single helix has elliptical polarization.

Figure 7 show, in turn, the dependences of the intensity and ellipticity of the reflected wave on the frequency, if the single helix is in the field of incident waves with right-hand circular polarization. As follows from Figure 7A, the intensity of the reflected wave for a single helix in the field of a wave with right-hand circular polarization in the frequency range 30–45 GHz is approximately the same as for a double helix, that is, very low. According to Figure 7B, the reflected wave for a single helix has elliptical polarization in this frequency range. Near frequency ${\nu }_3$ (23), the reflected wave can be circularly polarized, but its intensity remains very low for this frequency as well.

FIGURE 7

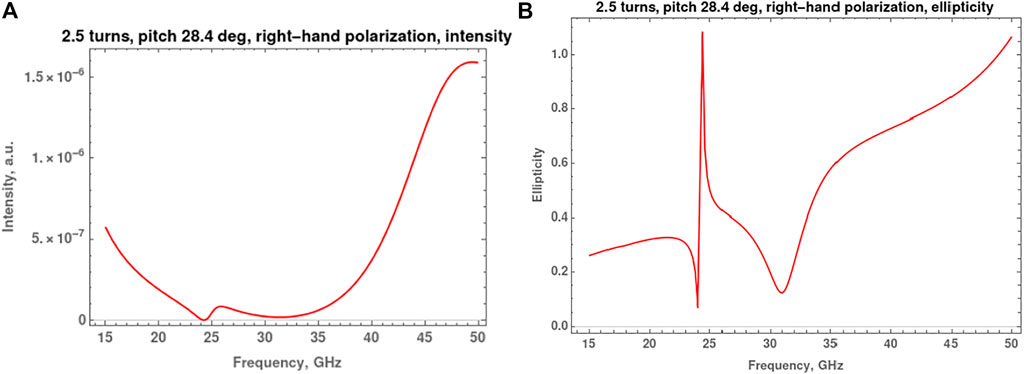
FIGURE 7. (A) Dependence of the intensity of the reflected wave by single-stranded DNA-like helix on the frequency for an incident wave with right-hand circular polarization. (B) Dependence of the ellipticity of the reflected wave under the same conditions.

Thus, the considered effect of polarization selectivity with respect to waves with right-hand and left-hand circular polarization can be fully manifested precisely for a double DNA-like helix. This effect is associated with the transparency of the double DNA-like helix in relation to a wave with circular polarization of a certain sign. Simultaneously, the helix strongly interacts with a wave having a circular polarization of a different sign. Consequently, a double DNA-like helix can be used as a polarization converter from a linear state to a circular one when reflecting a wave, including in the nanometer wavelength range.

10 Conclusion

A double DNA-like helix interacts fundamentally differently with the right and left circularly polarized waves at high-frequency resonance when the wavelength of the electromagnetic field is approximately equal to the period of the helix. This property of the double DNA-like helix can be called the polarization selectivity effect. The essence of this effect is that a double DNA-like helix at high-frequency resonance can create a reflected wave having only one direction of circular polarization. Alternatively, the reflected wave is absent if the helix is in the field of a circularly polarized wave, the electric vector of which produces a turn in space with the same winding direction as the helix itself. The helix is transparent for such an incident wave and may be regarded as an “orthogonal vibrator.” This effect can be achieved in different frequency ranges of the electromagnetic field by scaling the helix. In this case, the helix two-stranded shape, the helix pitch angle, characteristic of the DNA molecule, approximate equality of the wavelength to the length of the helical turn, as well as the electrical conductivity of the helix are required.

In view of the above, DNA-like helices are promising elements of metamaterials for the polarization conversion and absorption of electromagnetic waves, including nanoscale devices. The electrical conductivity of an actual DNA molecule is still currently under study. Modern research shows that the DNA molecule is close in its properties to a nonlinear semiconductor. At the same time, the electrical conductivity of DNA-like helices can be increased by metallization, which expands the possibilities of their use in nanotechnology.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

IS, IM, and SK contributed to conception and design of the study. AS and IM organized the database. IM and AB performed the statistical analysis. IS wrote the first draft of the manuscript. IS, IM, SK, AS, and AB wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aldaye, F. A., Palmer, A. L., and Sleiman, H. F. (2008). Assembling Materials with DNA as the Guide. Science 321 (5897), 1795–1799. doi:10.1126/science.1154533

PubMed Abstract | CrossRef Full Text | Google Scholar

Alicki, R., and Lendi, K. (2007). Quantum Dynamical Semigroups and Applications. Lect. Notes Phys. 717. doi:10.1007/3-540-70861-8

CrossRef Full Text | Google Scholar

Arago, D. F. (1811). Sur Une Modification Remarquable Qu'éprouvent Les Rayons Lumineux Dans Leur Passage a Travers Certains Corps Diaphanes, Et Sur Quelques Autres Nouveaux Phenomnnes D'optique. Mem. Inst. 1, 93.

Google Scholar

Bachtold, A., Hadley, P., Nakanishi, T., and Dekker, C. (2001). Logic Circuits with Carbon Nanotube Transistors. Science 294 (5545), 1317–1320. doi:10.1126/science.1065824

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, R. J. (2008). CMOS: Circuit Design, Layout, and Simulation. New York: Wiley.

Google Scholar

Biot, J. B. (1815). Phénoménes De Polarisation Successive, Observés Dans Des Fluides Homogenes. Bull. Soc. Philomath.,1815 190.

Google Scholar

DeHon, A. (2003). Array-based Architecture for FET-Based, Nanoscale Electronics. IEEE Trans. Nanotechnol. 2 (1), 23–32. doi:10.1109/tnano.2003.808508

CrossRef Full Text | Google Scholar

DeLuca, M., Shi, Z., Castro, C. E., and Arya, G. (2020). Dynamic DNA Nanotechnology: toward Functional Nanoscale Devices. Nanoscale Horiz. 5, 182–201. doi:10.1039/c9nh00529c

CrossRef Full Text | Google Scholar

Demple, B., and Harrison, L. (1994). Repair of Oxidative Damage to DNA: Enzymology and Biology. Annu. Rev. Biochem. 63, 915–948. doi:10.1146/annurev.bi.63.070194.004411

PubMed Abstract | CrossRef Full Text | Google Scholar

Eley, D. D., and Spivey, D. I. (1962). Semiconductivity of Organic Substances. Part 9.-Nucleic Acid in the Dry State. Trans. Faraday Soc. 58, 411–415. doi:10.1039/tf9625800411

CrossRef Full Text | Google Scholar

Fialko, N. S., and Lakhno, V. D. (2018). Charge Transfer in the 1D-Chain "Donor-Bridge-Acceptor. " at T = 300 K. Moscow, Russia: Preprints of the Keldysh Institute of Applied Mathematics [Preprint](in Russian). doi:10.20948/prepr-2018-77

CrossRef Full Text | Google Scholar

Fresnel, A. (1822). Memoire Sur La Double Refraction Que Les Rayons Lumineux Eprouvent En Traversant Les Aiguilles De Cristal De Roche Suivant Des Directions Paralleles A L'axe. Oeuvres 1, 731.

Google Scholar

Gansel, J. K., Thiel, M., Rill, M. S., Decker, M., Bade, K., Saile, V., et al. (2009). Gold Helix Photonic Metamaterial as Broadband Circular Polarizer. Science 325 (5947), 1513–1515. doi:10.1126/science.1177031

PubMed Abstract | CrossRef Full Text | Google Scholar

Hall, D. B., Holmlin, R. E., and Barton, J. K. (1996). Oxidative DNA Damage through Long-Range Electron Transfer. Nature 382, 731–735. doi:10.1038/382731a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, B., Li, S., Li, Z., Huang, G., Tian, J., and Cao, X. (2021). Asymmetric Transmission for Dual-Circularly and Linearly Polarized Waves Based on a Chiral Metasurface. Opt. Express 29 (13), 19643–19654. doi:10.1364/OE.425787

PubMed Abstract | CrossRef Full Text | Google Scholar

Kallenbach, N. R., Ma, R.-I., and Seeman, N. C. (1983). An Immobile Nucleic Acid Junction Constructed from Oligonucleotides. Nature 305 (5937), 829–831. doi:10.1038/305829a0

CrossRef Full Text | Google Scholar

Kaschke, J., Blume, L., Wu, L., Thiel, M., Bade, K., Yang, Z., et al. (2015). A Helical Metamaterial for Broadband Circular Polarization Conversion. Adv. Opt. Mater. 3 (10), 1411–1417. doi:10.1002/adom.201500194

CrossRef Full Text | Google Scholar

Lakhno, V. D., and Vinnikov, A. V. (2018). DNA-based Molecular Devices. Nanobioelectronics Preprints of the Keldysh Institute of Applied Mathematics [Preprint]. (in Russian). doi:10.20948/prepr-2018-137

CrossRef Full Text | Google Scholar

Lakhno, V. D. (2004). Sequence Dependent Hole Evolution in DNA. J. Biol. Phys. 30, 123–138. doi:10.1023/B:JOBP.0000035844.35839.60

PubMed Abstract | CrossRef Full Text | Google Scholar

Landau, L. D., and Lifshits, E. M. (1975). The Classical Theory of Fields: Volume 2 (Course of Theoretical Physics Series). 4th Edition. Butterworth-Heinemann, 402.

Google Scholar

Lavigne, G., Achouri, K., Asadchy, V. S., Tretyakov, S. A., and Caloz, C. (2018). Susceptibility Derivation and Experimental Demonstration of Refracting Metasurfaces without Spurious Diffraction. IEEE Trans. Antennas Propagat. 66, 1321–1330. doi:10.1109/tap.2018.2793958

CrossRef Full Text | Google Scholar

Li, S. J., Li, Y. B., Li, H., Wang, Z. X., Zhang, C., Guo, Z. X., et al. (2020). A Thin Self‐Feeding Janus Metasurface for Manipulating Incident Waves and Emitting Radiation Waves Simultaneously. Ann. Phys. 532 (5), 2000020. doi:10.1002/andp.202000020

CrossRef Full Text | Google Scholar

Li, Z. Y., Li, S. J., Han, B. W., Huang, G. S., Guo, Z. X., and Cao, X. Y. (2021b). Quad‐Band Transmissive Metasurface with Linear to Dual‐Circular Polarization Conversion Simultaneously. Adv. Theory Simul. 4 (9), 2100117. doi:10.1002/adts.202100117

CrossRef Full Text | Google Scholar

Li, S. J, Li, Y. B., Zhang, L., Luo, Z. J., Han, B. W., Li, R. Q., et al. (2021a). Programmable Controls to Scattering Properties of a Radiation Array. Laser & Photonics Rev. 15 (2), 2000449. doi:10.1002/lpor.202000449

CrossRef Full Text | Google Scholar

Pasteur, L. (1848). Recherches Sur Les Relations Qui Peuvent Exister Entre La Forme Crystalline, La Composition Chimique Et Le Sens De La Polarisation Rotatoire. Ann. de chimie de physique 24, 442.

Google Scholar

Pasteur, L. (1922). Recherches Sur La Dissymétrie Moléculaire Des Produits Organiques Naturels. Paris, Masson 1, 314.

Google Scholar

Patwardhan, J. P., Dwyer, C., and Lebeck, A. R. (2004). “Circuit and System Architecture for DNA-Guided Self-Assembly of Nanoelectronics,” in Foundations of Nanoscience: Self-Assembled Architectures and Devices, 344.

Google Scholar

Petrov, E. G., Zelinskyy, Y. R., and May, V. (2002). Bridge Mediated Electron Transfer: A Unified Description of the Thermally Activated and Superexchange Mechanisms. J. Phys. Chem. B 106, 3092–3102. doi:10.1021/jp013427g

CrossRef Full Text | Google Scholar

Petty, M. C., et al. (1995). An Introduction to Molecular Electronics. London: Oxford University Press.

Google Scholar

Pinheiro, A. V., Han, D., Shih, W. M., and Yan, H. (2011). Challenges and Opportunities for Structural DNA Nanotechnology. Nat. Nanotech 6 (12), 763–772. doi:10.1038/nnano.2011.187

PubMed Abstract | CrossRef Full Text | Google Scholar

Seeman, N. C. (2010). Nanomaterials Based on DNA. Annu. Rev. Biochem. 79, 65–87. doi:10.1146/annurev-biochem-060308-102244

PubMed Abstract | CrossRef Full Text | Google Scholar

Segal, D., Nitzan, A., Davis, W. B., Wasielewski, M. R., and Ratner, M. A. (2000). Electron Transfer Rates in Bridged Molecular Systems 2. A Steady-State Analysis of Coherent Tunneling and Thermal Transitions. J. Phys. Chem. B 104, 3817–3829. doi:10.1021/jp993260f

CrossRef Full Text | Google Scholar

Sekhon, B. S. (2005). Nanobiotechnology: an Overview of Drug Discovery, Delivery and Development. Pharmacol. Ther. 69. doi:10.5530/rjps.2012.1.3

CrossRef Full Text | Google Scholar

Semchenko, I. V., Khakhomov, S. A., and Balmakov, A. P. (2006). Polarization Selectivity of Electromagnetic Radiation of DNA. Bianisotropics,2006 45.

Google Scholar

Semchenko, I. V., Khakhomov, S. A., and Balmakov, A. P. (2007). Polarization Selectivity of Electromagnetic Radiation of Deoxyribonucleic Acid. J. Commun. Technol. Electron. 52 (9), 996–1001. doi:10.1134/S1064226907090070

CrossRef Full Text | Google Scholar

Semchenko, I. V., Khakhomov, S. A., and Balmakov, A. P. (2009). “Cube Composed of DNA-like Helices Displays Polarization Selectivity Properties in Microwave.” in 3rd International Congress on Advanced Electromagnetic Materials in Microwaves and Optics Metamaterials, London, United Kingdom, August 30–September 4, 2009, 271.

Google Scholar

Semchenko, I. V., Khakhomov, S. A., and Balmakov, A. P. (2010). Polarization Selectivity of Interaction of DNA Molecules with X-Ray Radiation. Biophysics 55 (2), 194–198. doi:10.1134/s0006350910020053

CrossRef Full Text | Google Scholar

Semchenko, I. V., Khakhomov, S. A., and Balmakov, A. P. (2010). Polarization Selectivity of Artificial Anisotropic Structures Based on DNA-like Helices. Crystallogr. Rep. 55 (6), 921–926. doi:10.1134/S1063774510060040

CrossRef Full Text | Google Scholar

Semchenko, I. V., Khakhomov, S. A., and Balmakov, A. P. (2010). “3D DNA-like Crystals Microwave Analogy for Studying Polarization Selectivity Properties.” in Fourth International Congress on Advanced Electromagnetic Materials in Microwaves and Optics, Karlsruhe, Germany, September 13, 2010, 848.

Google Scholar

Semchenko, I. V., Khakhomov, S. A., and Balmakov, A. P. (2011). Interaction of Artificial DNA-like Structures in the Microwave Range: Polarization Selectivity of Wave Reflection. Telecom Rad. Eng. 70 (20), 1871–1882. doi:10.1615/TelecomRadEng.v70.i20.70

CrossRef Full Text | Google Scholar

Semchenko, I. V., Khakhomov, S. A, and Balmakou, A. P (2012). “Advantages of Metamaterials Based on Double-Stranded DNA-like Helices.” in 6th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics - Metamaterials, Saint Petersburg, Russia, September 7–22, 2012, 309.

Google Scholar

Semchenko, I. V., Khakhomov, S. A., Asadchy, V. S., Golod, S. V., Naumova, E. V., Prinz, V. Y., et al. (2017). Investigation of Electromagnetic Properties of a High Absorptive, Weakly Reflective Metamaterial-Substrate System with Compensated Chirality. J. Appl. Phys. 121, 1015108. doi:10.1063/1.4973679

CrossRef Full Text | Google Scholar

Semchenko, I. V., Khakhomov, S. A, and Balmakou, A. P (2018). Interaction Forces of Electric Currents and Charges in a Double DNA-like Helix and its Equilibrium. 12th International Congress on Artificial Materials for Novel Wave Phenomena. Metamaterials 2018, 281. doi:10.1109/MetaMaterials.2018.8534056

CrossRef Full Text | Google Scholar

Semchenko, I. V., Mikhalka, I. S, Khakhomov, S. A, and Balmakou, A. P (2019). “The Interaction of Strands in a Double DNA-like Helix at High-Frequency Resonance.” in 13th International Congress on Artificial Materials for Novel Wave Phenomena Metamaterials 2019, Rome, Italy, September 16–21, 2019, Italy.

Google Scholar

Semchenko, I. V., Mikhalka, I. S., Faniayeu, I. A., Khakhomov, S. A., Balmakou, A. P., and Tretyakov, S. A. (2020). Optical Forces Acting on a Double DNA-like Helix, its Unwinding and Strands Rupture. Photonics 7, 83. doi:10.3390/photonics7040083

CrossRef Full Text | Google Scholar

Shih, W. M., and Lin, C. (2010). Knitting Complex Weaves with DNA Origami. Curr. Opin. Struct. Biol. 20 (3), 276–282. doi:10.1016/j.sbi.2010.03.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Syurakshin, A. V., Lakhno, V. D., and Yushankhai, V. Y. (2021). Charge Transfer in a DNA Molecule within a Simple Model of an Open Quantum System. Moscow, Russia: Preprints of the Keldysh Institute of Applied Mathematics. [Preprint](in Russian)Available at: https://keldysh.ru/papers/2021/prep2021_23.pdf.

Google Scholar

Wang, P., Meyer, T. A., Pan, V., Dutta, P. K., and Ke, Y. (2017). The Beauty and Utility of DNA Origami. Chem 2, 359–382. doi:10.1016/j.chempr.2017.02.009

CrossRef Full Text | Google Scholar

Watson, J. D., and Crick, F. H. C. (1953). Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature 171, 737–738. doi:10.1038/171737a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, J. D., Baker, T. A., and Bell, S. P. (2013). Molecular Biology of the Gene. London, UK: Pearson.

Google Scholar

Weiss, E. A., Katz, G., Goldsmith, R. H., Wasielewski, M. R., Ratner, M. A., Kosloff, R., et al. (2006). Electron Transfer Mechanism and the Locality of the System-Bath Interaction: A Comparison of Local, Semilocal, and Pure Dephasing Models. J. Chem. Phys. 124, 074501. doi:10.1063/1.2168457

CrossRef Full Text | Google Scholar

Zahid, M., Kim, B., Hussain, R., Amin, R., and Park, S. H. (2013). DNA Nanotechnology: a Future Perspective. Nanoscale Res. Lett. 8, 119. doi:10.1186/1556-276X-8-119

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, F., Nangreave, J., Liu, Y., and Yan, H. (2014). Structural DNA Nanotechnology: State of the Art and Future Perspective. J. Am. Chem. Soc. 136 (32), 11198–11211. doi:10.1021/ja505101a

PubMed Abstract | CrossRef Full Text | Google Scholar