Advances in Memristor-Based Neural Networks

Xu, Weilin; Wang, Jingjuan; Yan, Xiaobing

doi:10.3389/fnano.2021.645995

REVIEW article

Front. Nanotechnol., 24 March 2021

Sec. Nanodevices

Volume 3 - 2021 | https://doi.org/10.3389/fnano.2021.645995

This article is part of the Research Topic Memristive Neuromorphics: Materials, Devices, Circuits, Architectures, Algorithms and their Co-Design View all 13 articles

Advances in Memristor-Based Neural Networks

$\nWeilin Xu,,*&#x;$ Weilin Xu^1,2,3^*^†

Jingjuan Wang¹^†

Xiaobing Yan^1,4^*

¹Key Laboratory of Brain-Like Neuromorphic Devices and Systems of Hebei Province, College of Electron and Information Engineering, Hebei University, Baoding, China
²Guangxi Key Laboratory of Precision Navigation Technology and Application, Guilin University of Electronic Technology, Guilin, China
³Electrical and Computer Engineering Department, Southern Illinois University Carbondale, Carbondale, IL, United States
⁴Department of Materials Science and Engineering, National University of Singapore, Singapore, Singapore

The rapid development of artificial intelligence (AI), big data analytics, cloud computing, and Internet of Things applications expect the emerging memristor devices and their hardware systems to solve massive data calculation with low power consumption and small chip area. This paper provides an overview of memristor device characteristics, models, synapse circuits, and neural network applications, especially for artificial neural networks and spiking neural networks. It also provides research summaries, comparisons, limitations, challenges, and future work opportunities.

Introduction

Resistance, capacitance and inductance are the three basic circuit components in passive circuit theory. In 1971, Professor Leon O. Chua of the University of California at Berkeley first described a basic circuit that relates flux to charge, called the missing fourth memristor element, and was successfully found by a team led by Stanley Williams at HP Labs in 2008 (Chua, 1971; Strukov et al., 2008). As a non-linear two-terminal passive electrical component, studies have shown that the conductance of a memristor is tunable by adjusting the amplitude, direction, or duration of its terminal voltages. Memristors have shown various outstanding properties, such as good compatibility with CMOS technology, small device area for high-density on-chip integration, non-volatility, fast speed, low power dissipation, and high scalability (Lee et al., 2008; Waser et al., 2009; Akinaga and Shima, 2010; Wong et al., 2012; Yang et al., 2013; Choi et al., 2014; Sun et al., 2020; Wang et al., 2020; Zhang et al., 2020). Thus, although memristors took many years to transform from a purely theoretical derivation into a feasible implementation, these devices have been widely used in applications such as machine learning and neuromorphic computing, as well as non-volatile random-access memory (Alibart et al., 2013; Liu et al., 2013; Sarwar et al., 2013; Fackenthal et al., 2014; Prezioso et al., 2015; Midya et al., 2017; Yan et al., 2017, 2019b,d; Ambrogio et al., 2018; Krestinskaya et al., 2018; Li C. et al., 2018, Li et al., 2019; Wang et al., 2018a, 2019a,b; Upadhyay et al., 2020). Furthermore, thanks to its powerful computing and storage capability, a memristor is a promising device for processing tremendous data and increasing the data processing efficiency in neural networks for artificial intelligence (AI) applications (Jeong and Shi, 2018).

This article intends to analyze the memristor theory, models, circuits, and important applications in neural networks. The contents of this paper are organized as follows. Section Memristor Characteristics and Models introduces the memristor theory and models. Section Memristor-Based Neural Networks presents its applications in the second-generation neural networks, namely artificial neural networks (ANNs) and the third-generation neural networks, namely spiking neural networks (SNNs). Section Summary is the conclusions and future research direction.

Memristor Characteristics and Models

The relationship between the physical quantities (namely charge q, voltage v, flux φ, and current i) and basic circuit elements (namely resistor R, capacitor C, inductor L, and memristor M) is shown in Figure 1A (Chua, 1971). Specifically, C defined as a linear relationship between voltage v and electric charge q (C = dq/dv), L is defined as a relationship between magnetic flux φ and current i (L = dφ/di), R is defined as a relationship between voltage v and current i (R = dv/di). The missing link between the electric charge and flux is defined as the memristor M and its differential equation is M = dφ/dq or G = dq/dφ. Figure 1B shows the current-voltage characteristics of the memristor, where the pinched hysteresis loop is its fundamental identifier (Yan et al., 2018c). As a basic element, the memristor I–V curve cannot be obtained using R, C, and L. According to the shape of the pinched curve, it can be roughly classified into a digital type memristor or an analog type memristor. The resistance of a digital memristor exhibits an abrupt change at higher resistance ratios. The high-resistance and low-resistance states in a digital memristor have a long retention period, making it ideal for memory and logic operations. An analog memristor exhibits a gradual change in resistance. Therefore, it is more suitable for analog circuits and hardware-based multi-state neuromorphic system applications.

FIGURE 1

Figure 1. (A) Basic theoretical circuit elements, and (B) pinched hysteresis I–V loop of memristor.

Memristor device technology and modeling research are the cornerstones of system applications. As shown in Figure 2, top-level system applications (brain-machine interface, face or picture recognition, autonomous driving, IoT edge computing, big data analytics, and cloud computing) are built on the device technology and modeling. Memristor-based analog, digital, and memory circuits play a key role in the link between device materials and system applications. The main usage for bi-stable memristors is binary switches, binary memory, and digital logic circuits, while multi-state memristors are used as multi-bit memories, reconfigurable analog circuits, and neuromorphic circuits.

FIGURE 2

Figure 2. Memristor research and applications.

Since the HP labs verified the nanoscale physical implementation, the physical behavior models of memristors have received a lot of attention. Accuracy, convergence, and computational efficiency are the most important factors in memristor models. These behavior models are expected to be simple, intuitive, better understood, and closed form. Up to date, various models have been developed, each with its unique advantages and shortcomings. The models listed in Table 1 are the most popular models, including a linear ion drift memristor model, a non-linear ion drift memristor model, a Simmons tunnel barrier memristor model, a threshold adaptive memristor model (TEAM) (Simmons, 1963; Strukov et al., 2008; Biolek et al., 2009; Pickett et al., 2009; Kvatinsky et al., 2012). In the linear ion drift memristor model, D and u_v represent the full length and device mobility of a memristor film, respectively. ω(t) is a dynamic state variable whose value is limited between 0 and D, taking into account the size of the physical device. The low turn-on resistance R_on is the full doped resistance when dynamic variable ω(t) is equal to D. The high turn-off resistance R_off is a fully undoped resistance when ω(t) is equal to 0. Besides, a window function multiplied by a state variable is needed to nullify the derivative and provide a non-linear transition for the physical boundary simulation. Several window functions have been presented for modeling memristors such as Biolek, Strukov, Joglekar, and Prodromakis window functions (Strukov et al., 2008; Biolek et al., 2009; Joglekar and Wolf, 2009; Strukov and Williams, 2009; Prodromakis et al., 2011). As the first memristor model, the linear ion drift model shows the features of simple, intuitive, and better understood. However, the state variable ω modulation in nano-scale devices is not a linear process, and the memristor experimental results show non-linear I–V characteristics. The non-linear ion drift model provides a better description of non-linear ionic transport and higher accuracy by experimentally fitting the parameters n, β, α, and χ (Biolek et al., 2009). But more physical reaction kinetics still need to be considered. The Simmons tunnel barrier model consists of a resistor in series with an electron tunnel barrier, which provides a more detailed representation of non-linear and asymmetrical features (Simmons, 1963; Pickett et al., 2009). There are nine fitting parameters in this segmentation model, which makes the mathematical model very complicated and computationally inefficient. The TEAM model can be thought of as a simplified version of the Simmons tunnel barrier model (Kvatinsky et al., 2012). However, all of the above models suffer from smoothing problems or mathematical ill-posedness issues, and they cannot provide robust and predictable simulation results in DC, AC, transient analysis, not to mention complicated circuit analysis such as noise analysis and periodic steady-state analysis (Wang and Roychowdhury, 2016). Therefore, in the face of transistor-level circuit design simulation, circuit designers usually have to replace the actual memristor with an emulator (Yang et al., 2019). The emulator is a complex CMOS circuit used to simulate some performance aspect of a special memristor. An emulator is not a true model, and it is very different from the real memristor model (Yang et al., 2014). Thus, it is urgent to establish a complete memristor model. Correct bias definition and right physical characteristics in SPICE or Verilog-a model are important for complex memristor circuit design. Otherwise, non-physical predictions will confuse circuit engineers in physical chip design.

TABLE 1

Table 1. Classic memristor models.

Memristor-Based Neural Networks

Neuron Biological Mechanisms and Memristive Synapse

The human brain can solve complex tasks, such as image recognition and data classification, more efficiently than traditional computers. The reason why a brain excels in complicated functions is the large number of neurons and synapses that process information in parallel. As shown in Figure 3, when an electrical signal is transmitted between two neurons via axon and synapse, the joint strength or weight is adjusted by the synapse. There are approximately 100 billion neurons in an entire human brain, each with about 10,000 synapses. Pre-synaptic and post-synaptic neurons transfer and receive the signal of excitatory and inhibitory post-synaptic potentials by updating synaptic weights. Long-term potentiation (LTP) and long-term depression (LTD) are important mechanisms in a biological nervous system, which indicates a deep-rooted transformation in the connection strengths between neurons. According to the interval between pre-synaptic and post-synaptic action potentials or spikes, the phenomenon of synaptic weight modification is known as spike-timing-dependent plasticity (STDP) (Yan et al., 2018a, 2019c). Due to scalability, low power operation, non-volatile features, and small on-chip area, memristors are good candidates for artificial synaptic devices to mimicking the LTP, LTD, and STDP behaviors (Jo et al., 2010; Ohno et al., 2011; Kim et al., 2015; Wang et al., 2017; Yan et al., 2017).

FIGURE 3

Figure 3. Schematic of two interconnected neurons by synapses.

There are some key requirements for memristive devices in neural network applications. For example, a wide range of resistance is required to enable sufficient resistance states; devices are required to have low resistance fluctuations and low device-to-device variability; a higher absolute resistance is required for low power dissipation; and high durability is required for reprogramming and training (Choi et al., 2018; Yan et al., 2018b, 2019a; Xia and Yang, 2019). A concern with device stability is resistance drift, which occurs over time or with the environment. Resistance drift causes undesirable changes in synapse weight and blurs different resistance states, ultimately affecting the accuracy of neural network computation (Xia and Yang, 2019). To deal with this drift challenge, improvements can be made in three aspects: (1) material device engineering, (2) circuit design, and (3) system design (Alibart et al., 2012; Choi et al., 2018; Jiang et al., 2018; Lastras-Montaño and Cheng, 2018; Yan et al., 2018b, 2019a; Zhao et al., 2020). For example, as for the domain of material engineering, threading dislocations can be used to control programming variation and enhance switching uniformity (Choi et al., 2018). In terms of circuit-level design, a module of two series memristors and a transistor with the smallest size can be used, thus, the resistance ratio of the memristor can be encoded to compensate for the resistance drift (Lastras-Montaño and Cheng, 2018). For the system-design level, device deviation can be reduced by protocols, such as closed loop peripheral circuit with a write-verify function (Alibart et al., 2012). In order to obtain linear and symmetric weight update in LTP and LTD for efficient neural network training, optimized programming pulses can be used to excite memristors with either fixed-amplitude or fixed-width voltage pulses (Jiang et al., 2018; Zhao et al., 2020). Note it is inevitable to increase energy consumption if the memristor resistance value is changed through complex programmable pulses.

The comparison of different memristive synapse circuit structures is shown in Table 2 (Kim et al., 2011a; Wang et al., 2014; Prezioso et al., 2015; Hong et al., 2019; Krestinskaya et al., 2019). Single memristor synapse (1M) crossbar arrays in neural networks have the lowest complexity and low power dissipation. However, it suffers from sneak path problems and complex peripheral switch circuits. Synapses with two memristors (2M) have a more flexible weight range and better symmetric LTP and LTD, but the corresponding chip area will be doubled. A synapse with one memristor and one transistor (1M-1T) has the advantage of solving the sneak path problem, but it also occupies a large area in the large-scale integration of neural networks. A bridge synapse architecture with four memristors (4M) provides a bidirectional programming mechanism with a voltage input voltage output. Due to the significant on-chip area overhead, the 1M-1T and 4M synapses may not be applicable for large-scale neural networks.

TABLE 2

Table 2. Comparison of different structure memristive synapse circuit.

Memristor-Based ANNs

The basic operations of classical hardware ANNs include multiplication, addition, and activation, which are accomplished by CMOS circuits such as GPUs. The weights are typically saved in SRAM or DRAM. Despite the scalability of CMOS circuits, they are still not enough for ANN applications. Furthermore, the SRAM cell size are too big to be integrated at high density. DRAM needs to be refreshed periodically to prevent data decay. Whether it is SRAM or DRAM, it often needs to interact with CMOS cores. No matter SRAM or DRAM, the data needs to be fetched by to the cache and register files of the digital processors before processing and returned through the same databus, leading to significant speed limit and large energy consumption, which is the main challenge for deep learning and big data applications (Xia and Yang, 2019). Nowadays, ANNs feature for large number of computational parameters stored in memory compared to classical computation. For example, a two-layer 784-800-10 fully-connected deep neural network in the MNIST dataset has 635,200 interconnections. A state of the art keep neural network like Visual Geometry Group (VGG) has a few millions of parameters. These factors pose a huge challenge to the implementation of ANN hardware. The memristor's non-volatility, lower power consumption, lower parasitic capacitance, and reconfigureable resistance states, high speed, and adaptability lead to a key role in ANN applications (Xia and Yang, 2019). An ANN is an information processing model which are derived from mathematical optimization. A typical ANN architecture and its memristor crossbar are shown in Figure 4. The system usually consists of three layers: an input layer, a middle layer or a hidden layer, and an output layer. The connected units or nodes are neurons which are usually series by weighted-sum module and activation function module. Neurons also perform tasks of decoding, control, and signal routing. Due to its powerful signal processing capability, CMOS analog and digital logic circuits are the best candidates for neurons hardware implementation. In Figure 4, arrow or connecting lines represent synapses, and their weights represent the connection strengths between two neurons. Assume the weight modulation matrix W_ij in a memristor synapse crossbar is a M × N dimensinal matrix, where i(i = 1, 2, …, N) and j(i = 1, 2, …, M) are the index numbers of the output and input ports of the memristor crossbar. W_ij between pre-neuron input vector X_j and post-neuron output vector Y_i is a matrix-vector multiplication operation, expressed as Equation (1) (Jeong and Shi, 2018).

\begin{array}{l} Y_{i} = Σ W_{i j} \cdot X_{j} & (1) \end{array}

\begin{array}{l} Δ w_{i j} = r [\frac{\partial {(y - y^{^{*}})}^{2}}{\partial w_{i j}}] & (2) \end{array}

The matrix W can be continuously adjusted until the difference between the output value y and the target value y^* is minimized. The Equation (2) shows the synaptic weight tunning process with the gradient of output error (y–y^*)² under a training rate (Huang et al., 2018). Therefore, a memristor crossbar is equal to a CMOS adder plus a CMOS multiplier and an SRAM (Jeong and Shi, 2018), because data are computed, stored, and regenerated on the same local device (i.e., a memristor itself). Besides, a crossbar can be vertically integrated into three dimensions (Seok et al., 2014; Lin et al., 2020; Luo et al., 2020). In this way, it saves much chip area and power consumption. Due to the memristor synapse update and save weight data on itself, the memory wall problem with von Neumann bottleneck is solved.

FIGURE 4

Figure 4. Typical ANN architecture and its memristor crossbar.

Researchers have developed various topologies and learning algorithms for software-based or hardware-based ANNs. Table 3 provides a comparison of typical memristive ANNs, including single-layer perceptron (SLP) or multi-layer perceptron (MLP), CNN, cellular neural network (CeNN), and recurrent neural network (RNN). SLP and MLP are classic neural networks with well-known learning rules such as Hebbian learning, backpropagation. Although a lot of ANN studies have been verified by simulations or small-scale implementation, a single-layer neural network with 128 × 64 1M-1T Ta/HfO₂ memristor array has been experimentally demonstrated with an image recognition accuracy of 89.9% for the MNIST dataset (Hu et al., 2018). CNNs (referred to as space-invariant or shift-invariant ANNs) are regularized versions of MLP. Their hidden layers usually contain multiple complex activation functions, and perform convolution or regional maximum value operations. Researchers have demonstrated an over 70% of accuracy in human behavior video recognition with a memristor-based 3D CNN (Liu et al., 2020). It should be emphasized that this verification is only a software simulation result, while the on-chip hardware demonstration is still very challenging, especially for deep CNNs (Wang et al., 2019a; Luo et al., 2020; Yao et al., 2020). CeNN is a massively parallel computing neural network, whose communication features are limited to between adjacent cell neurons. The cells are dissipative non-linear continuous-time or discrete-time processing units. Due to their dynamic processing capability and flexibility, CeNNs are promising candidates for real-time high frame rate processing or multi-target motion detection. For example, a CeNN with 4M memristive bridge circuit synapse has been proposed for image processing (Duan et al., 2014). Unlike classic feed forward ANNs, RNNs have a feedback connection that enables temporal dynamic behavior. Therefore, it is suitable for speech recognition applications. Long short-term memory (LSTM) is a kind of useful RNN structure for deep learning. Hardware implementation of LSTM networks based on memristors have been reported (Smagulova et al., 2018; Li et al., 2019; Tsai et al., 2019; Wang et al., 2019a).

TABLE 3

Table 3. Typical architectures of Memristive ANNs.

Due to atomic-level random defects and variability in the conductance modulation process, non-ideal memristor characteristics are the main causes of learning accuracy loss in ANNs. This phenomenon is manifested in the following aspects of memristor: asymmetric non-linear weight change between potentiation and depression, limited ON/OFF weight ratio and device variation. Table 4 shows the main strategies for how to deal with these issues. One can mitigate the effects of non-ideal memristor characteristics on ANN accuracy from four levels: device materials, circuits, architectures, and algorithms. At device materials level, switching uniformity and analog on/off ratio can be enhanced by optimizing redox reaction at the metal/oxide interface, adopting threading dislocations technology or heating element (Jeong et al., 2015; Lee et al., 2015; Tanikawa et al., 2018). At circuits level, one can use customized excitation pulse or hybrid CMOS-memristor synapses to mitigate memristor non-ideal effects (Park et al., 2013; Li et al., 2016; Chang et al., 2017; Li S. J. et al., 2018; Woo and Yu, 2018). At architectures level, common techniques are multiple memristors cell for high redundancy, pseudo-crossbar array, and peripheral circuit compensation (Chen et al., 2015). Co-optimization between memristors and ANN algorithms is also reported (Li et al., 2016). However, it should be noted that implementation of these strategies inevitably brings side effects, such as high manufacturing cost, large power consumption, large chip area, complex peripheral circuits, or inefficient algorithm. For example, the non-identical pulse excitation or bipolar-pulse-training methods improve the linearity and symmetry of memristor synapses, but it increases the complexity of peripheral circuits, system power consumption, and chip area. Therefore, trade-offs and co-optimization need to be made at each design level to improve the learning accuracy of ANNs (Gi et al., 2018; Fu et al., 2019). Figure 5 is a collaborative design example from bottom-level memristor devices to top-level training algorithms (Fu et al., 2019). The conductance response (CR) curve of memristors is first measured to obtain its non-linearity factor. Then, the CR curve is divided into piecewise linear segments to obtain their slope, and the pulse width of the excitation pulse is inversely proportional to the slope. These data are stored in memory for comparison and correction by memristor crossbars during the update. Through this method, the ANN recognition accuracy is finally improved.

TABLE 4

Table 4. ANNs learning accuracy improvement by mitigating memristor non-ideal effects.

FIGURE 5

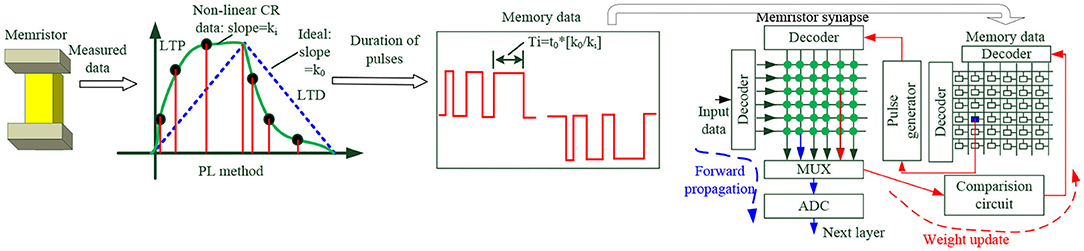
Figure 5. Co-design from memristor non-ideal characteristics to the ANN algorithm (Fu et al., 2019).

The memristor-based ANN applications can be software, hardware or hybrid (Kozhevnikov and Krasilich, 2016). Software networks tend to be more accurate than their hardware counterparts because they do not have the analog element non-uniformity issues. However, hardware networks feature better speed and less power consumption due to non-von Neumann architectures (Kozhevnikov and Krasilich, 2016). In Figure 6, a deep neuromorphic accelerator ANN chip with 2.4 million Al₂O₃/TiO₂-xmemristors was designed and fabricated (Kataeva et al., 2019). This memristor chip consists of a 24 × 43 array with a 48 × 48 memristor crossbar at each intersection, which means its complexity is about 1,000 times higher than previous designs in the literature. This work is a good starting point for the operation of medium-scale memristor ANNs. Similar accelerators have appeared in the last 2 years (Cai et al., 2019; Chen W.-H. et al., 2019; Xue et al., 2020).

FIGURE 6

Figure 6. A deep neuromorphic ANN chip with 2.4 million memristor devices (Kataeva et al., 2019).

Memristive neural networks can be used to understand human emotion and simulate human operational abilities (Bishop, 1995). The well-known PavlTov associative memory experiment has been implemented in memristive ANNs with a novel weighted-input-feedback learning method (Ma et al., 2018). As more input signals, neurons, and memristor synapses, complex emotional processing will be achieved in further AI chips. Due to the material challenge and the lack of effective models, most of the demonstrations are limited to small-scale simulations for simple tasks. The shortcomings of memristors are mainly the non-linearity, asymmetry, and variability, which seriously affect the accuracy of ANNs. Moreover, the peripheral circuits and interface must provide superior energy efficiency and data throughput.

Memristor-Based SNN

Inspired by cognitive and computational methods of animal brains, the third-generation neural network, SNN, makes desirable properties of compact biological neurons mimic and remarkable cognitive performance. The most prominent feature of SNN is that it incorporates the concept of time into operations with discrete values, while the input and output values of the second-generation ANNs are continuous. SNN can better leverage the strength of biological paradigm of information processing, thanks to the hardware emulation of synapses and neurons. ANN is calculated layer by layer, which is relatively simple. However, spike trains in SNN are relatively difficult to understand and efficient coding methods for these spike trains are not easy. These dynamic events driven spikes in SNN enhance the ability to process spatio-temporal or real-world sensory data, with fast adaptation and exponential memorization. The combination of spatio-temporal data allows SNN to process signals naturally and efficiently.

Neuron models, learning rules, and external stimulus coding are key research areas of SNN. The Hodgkin & Huxley (HH) model, leaky Integrate-and-Fire (LIF) model, spike response model (SRM), and Izhikevich model are the most common models of neurons (Hodgkin and Huxley, 1952; Chua, 2013; Ahmed et al., 2014; Pfeiffer and Pfeil, 2018; Wang and Yan, 2019; Zhao et al., 2019; Ojiugwo et al., 2020). The HH model is a continuous-time mathematical model based on conductance. Although this model is based on the study of squid, it is widely used in lower or higher organisms (even humans being). However, since complex non-linear differential equations are set with four variables, this model is difficult to achieve high accuracy. Chua established the memristor model of Hodgkin-Huxley neurons and proved that memristors can be applied to the imitation of complex neurobiology (Chua, 2013). The Izhikevich model integrates the bio-plasticity of HH model with simplicity and higher computational efficiency. The HH and Izhikevich models are calculated by differential equations, while the LIF and SRM models are computed by an integral method. SRM is an extended version of LIF, and the Izhikevich model can be considered as a simplified version of the Hodgkin-Huxley model. These mathematical models are the results of different degrees of customization, trade-offs and biological neural network optimization. Table 5 shows a comparison of several memristor-based SNNs. It can be seen that these SNN studies are based on STDP learning rules and LIF neurons. Most of them are still in simple pattern recognition applications, only a few of which have hardware implementations.

TABLE 5

Table 5. Comparison of several memristor-based SNNs.

The salient features of SNNs are as follows. First, biological neuron models (e.g., HH, LIF) are closer to biological neurons than neurons of ANN. Second, the transmitted information is time or frequency encoded discrete-time spikes, which can contain more information than traditional networks. Third, each neuron can work alone and enter a low power standby mode when there is no input signal. Since SNNs have been proven to be more powerful than ANNs in theory, it is natural to widely use SNNs. Since the spike training cannot be differentiated, the gradient descent method cannot be used to train SNNs without losing accurate temporal information. Another problem is that it takes a lot of computation to simulate SNNs on normal hardware, because it requires analog differential equations (Ojiugwo et al., 2020). Due to the complexity of SNNs, efficient learning rules that meet the characteristics of biological neural networks have not been discovered. This rule is required to model not only synaptic connectivity but also its growth and attenuation. Another challenge is the discontinuous nature of spike sequence, which makes many classic ANN learning rules unsuitable for SNNs, or can only be approximated, because the convergence problem is very serious. Meanwhile, many SNNs studies are limited to theoretical analysis and simulation of simple tasks rather than complex and intelligent tasks (e.g., multiple regression analysis, deductive and inductive reasoning, and their chip implementation) (Wang and Yan, 2019). Although the future of SNNs is still unclear, many researchers believe that SNNs will replace deep ANNs. The reason is that AI is essentially a biological brain mimicking process, and SNNs can provide a perfect mechanism for unsupervised learning.

As shown in Figure 7, a neural network is implemented with CMOS neurons, CMOS control circuits, and memristor synapses (Sun, 2015). The aggregation module, leaky integrate and fire module are equivalent to the role of dendrites and axon hillocks, respectively. Input neurons signals are temporally and spatially summed through a common-drain aggregation amplifier circuit. A memristor synapse gives the action potential signal a weight and its output signal, that is, a post-synaptic potential signal is transmitted to post-neurons. Using the action potential signal and feedback signals from post-neurons, the control circuit and synaptic update phase provide potentiation or depression signals to memristor synapses. According to the STDP learning rules, the transistor-level weight adjustment circuit is composed of a memristor device and CMOS transmission gates. The transmission gates are controlled by potentiation or depression signals. The system is very similar to the main features of biological neurons, which is useful for neuromorphic SNN hardware implementation. A more complete description of SNN circuits and system applications is shown in Figure 8 (Wu and Saxena, 2018). The system consists of event-driven CMOS neurons, a competitive neural coding algorithm [i.e., winner take all (WTA) learning rule], and multi-bit memristor synapse array. A stochastic non-linear STDP learning rule with an exponential shaped window learning function is adopted to update memristor synapse weights in situ. The amplitude and additional temporal delay of the half rectangular half-triangular spike waveform can be adjusted for dendritic-inspired processing. This work demonstrates the feasibility and excellence of emerging memristor devices in neuromorphic applications, with low power consumption and compact on-chip area.

FIGURE 7

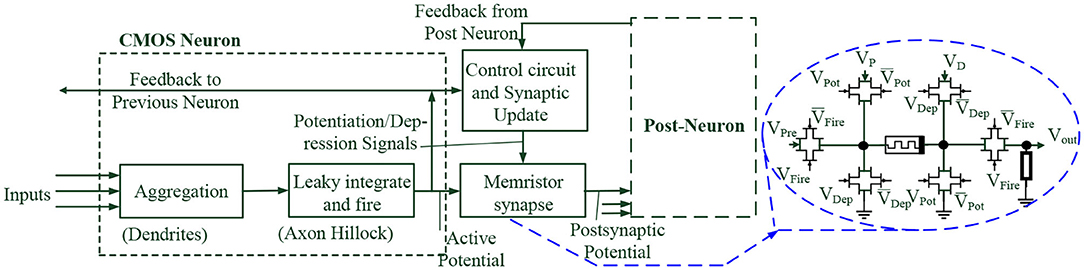
Figure 7. CMOS neuron and memristor synapse weight update circuit (Sun, 2015).

FIGURE 8

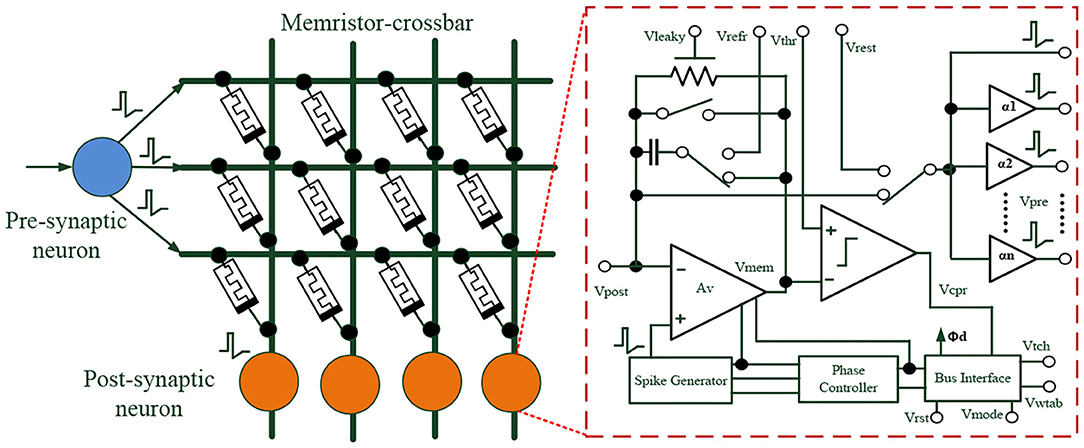
Figure 8. CMOS-Memristor SNN (Wu and Saxena, 2018).

Despite the large on-chip area and power dissipation in CMOS implementation of synaptic circuits (Chicca et al., 2003; Seo et al., 2011), Myonglae Chu adopted Pr_0.7Ca_0.3MnO₃-based memristor synaptic array and CMOS leaky IAF neurons in SNN. As shown in Figure 9, the SNN chip has been successfully developed for visual pattern recognition with modified STDP learning rules. The SNN hardware system includes 30 × 10 neurons and 300 memristor synapses. Although this hardware system only recognizes numbers 0–9, it is a good attempt, as most SNN studies have lingered around the software simulation phase (Kim et al., 2011b; Adhikari et al., 2012; Cantley et al., 2012). One can refer to literatures (Wang et al., 2018b; Ishii et al., 2019; Midya et al., 2019b) for more experimental memristor-SNN demos.

FIGURE 9

Figure 9. A memristor synapse array micrograph for SNN Application (Chu et al., 2014).

Comparison Between ANNs and SNNs

A comparison between ANNs and SNNs is shown in Table 6 (Nenadic and Ghosh, 2001; Chaturvedi and Khurshid, 2011; Zhang et al., 2020). Traditional ANNs require layer-by-layer computation. Therefore, it is computationally intensive and has a relatively large power consumption. An SNN changes from a standby mode to a working mode, when a large nerve spike is coming with its spike threshold exceeding the membrane voltage. As a result, its system power consumption is relatively low.

TABLE 6

Table 6. Comparison between ANNs and SNNs.

SNNs with higher bio-similarity are expected to achieve higher energy efficiency than ANNs. But SNN hardware is harder to implement than ANN hardware. Thus, combining the advantages of ANN and SNN and using ANN-SNN converters to improve SNN performance is a valuable method, which has been experimentally demonstrated (Midya et al., 2019a). The first and second layers of a converter are ordinary ANN structures. The output signals of the second layer are converted to a spike sequence for a 32 × 1 1M-1T drift memristor synapse array at the third layer. This ANN-SNN converter may be a good way for SNN hardware implementation. Despite the enormous potential of SNNs, there is currently no fully satisfactory general learning rules and its computational capability has not been demonstrated. Most of these methods lack comparability and generality. Compared to ANNs, the study of dynamic devices and efficient algorithms in SNNs is very challenging. SNNs only need to compute the activated connections, rather than all connections at every time step in ANNs. However, the encoding and decoding of spikes is one of the challenges in SNN research. In fact, it needs further research in neuroscience. ANN is the recent target of memristors, and SNN is the long-term goal in the future.

For neural networks applications, ANN and SNN memristor grids have some common challenges, such as sneak path problems, IR-drop or ohmic drop, grid latency, and grid power dissipation, as shown as Figure 10 (Zidan et al., 2013; Hu et al., 2014, 2018; Zhang et al., 2017). The large the size of the memristor array, the greater the effect of these parasitic capacitances and resistances. In Figure, the desired weight-update path is the dot-and-dash line, and the sneak path is the dotted line, which is an undesired parallel memristor path due to its relative resistance and non-gated memristor elements. This phenomenon leads to undesired weight changes and a reduction in the accuracy of neural networks. The basic solution for the sneak path is to add a series of connected gate-controlled MOS transistors to memristors as mentioned in Table 2. However, this method will lead to large on-chip synapse array and destroy the advantages of high-density integration of memristors. Grounding an unselected memristor array is another solution without the need to add synaptic area. But this approach leads to more power consumption. There are other techniques such as grounding line, floating line, additional bias, a non-unity aspect ratio of memristor arrays, three-electrode memristor devices. They may be welcome in memristor memory applications, but not necessarily in memristor-based neural network applications (Zidan et al., 2013). In neural network applications, the main concern for memristor arrays is whether the association between input and output signals is correct (Hu et al., 2014). This is one important difference compared to memristor memory applications. IR-drop, memristor grid latency, and power consumption are signal integrity effects caused by grid parasitic resistance Rpar and parasitic capacitance Cpar. These non-ideal factors affect the potential distribution, signal transmission, and ultimately affect the scale of memristor arrays. Similar to CMOS layout and routing techniques, large-scale memristors mesh can be divided into medium-sized modules with high-speed main signal paths for lower parasitic resistance, grid power consumption, and latency. It is worth noting that memristor process variations, gird IR-drop and noise can worsen the sneak path problem.

FIGURE 10

Figure 10. Sneak path, IR-drop, latency, and energy in massive memristor grids of neural networks.

Summary

The advantage of memristors in neural network applications is their fast processing time and energy efficiency in the computational process. At the device level, memristors have very low power dissipation and high on-chip density. At the architecture level, parallel computing is performed at the same location where data is stored, thereby avoiding frequent data movement and memory wall issues. Due to the quantum effect and non-ideal characteristics in the manufacturing of nanometer memristors, the robust performance of memristor neural networks still needs to be improved. Meanwhile, the adaptation range of various memristor models is limited and has not been fully explored in chip design. To date, there are no complete unified memristor models for chip designer. Furthermore, wire resistance, sneak path current, and half-select problems are also challenges for high-density integration of memristor crossbar arrays. Memristor neural network research involves engineering, biology, physics, algorithms, architecture, systems, circuits, equipment, and materials. There is still a long way to go for memristive neural networks, as most research remains in single devices or small-scale prototypes. However, with the marketing promotion of the IoT big data and AI, the breakthrough research of memristor-based ANN will be realized by the joint efforts of academia and industry.

Author Contributions

WX drafted the manuscript, developed the concept, and conceived the experiments. JW revised the manuscript. XY drafted and revised the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was financially supported by the National Natural Science Foundation of China (grant nos. 62064002, 61674050, and 61874158), the Project of Distinguished Young of Hebei Province (grant no. A2018201231), the Hundred Persons Plan of Hebei Province (grant nos. E2018050004 and E2018050003), the Supporting Plan for 100 Excellent Innovative Talents in Colleges and Universities of Hebei Province (grant no. SLRC2019018), Special project of strategic leading science and technology of Chinese Academy of Sciences (grant no. XDB44000000-7), outstanding young scientific research and innovation team of Hebei University, Special support funds for national high level talents (041500120001 and 521000981426), Hebei University graduate innovation funding project in 2021 (grant no. HBU2021bs013), and the Foundation of Guangxi Key Laboratory of Precision Navigation Technology and Application, Guilin University of Electronic Technology (No. DH201908).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Adhikari, S. P., Yang, C., Kim, H., and Chua, L. O. (2012). Memristor bridge synapse-based neural network and its learning. IEEE. Trans. Neur. Netw. Learn. Syst. 23, 1426–1435. doi: 10.1109/TNNLS.2012.2204770