Mathematical Modeling of Blood Flow With the Suspension of Nanoparticles Through a Tapered Artery With a Blood Clot

In this study, some key new developments in nanoscience which highlight the problem of nanoparticles in blood flow through mild stenosis in the presence of a blood clot have been presented. The blood flow behavior through the stenosed artery is considered using the Prandlt fluid model and the flow of blood is considered as suspension of nanoparticles. An appropriate non-linear system of equations governing blood flow is represented in a cylindrical coordinate system and solved exactly under mild stenotic conditions using the geometry of the stenotic artery in the presence of a clot. Heat transfer phenomena have been examined for the physical features of the flow of blood through a stenosed artery, which is tapered in shape and with the presence of a clot. The temperature profile has been discussed with graphs for several different parameters of clot size, stenosis height, heat source, and sink parameter. Tapering phenomena has been analyzed for temperature profile. It is examined that in converging tapering the temperature provides greater values as estimated together with the non-tapered arteries and diverging tapering arteries. In this work, it is also analyzed that with a rise in the clot size (σ) the temperature (θ) increases, whereas the radius of the artery with stenosis h(z) decreases and heat source and sink parameter (D) increases.

Introduction

Heart disease is sometimes called coronary heart disease. It is the leading cause of death among adults all over the world. Learning about the causes and risk factors of this disease may help to avoid heart problems (Akbar and Butt, 2016). According to the WHO's 2016 report, ~17.7 million people died from heart diseases, which makes up 31% of all deaths in that year, with ~7.5 million dying because of Coronary Heart Disease (CHD) and 6.67 million by heart stroke. Coronary heart disease, stroke, and other cardiovascular diseases are the main cause of a lack of oxygen to organs (Ellahi et al., 2013). This occurs when blood is passing through the blood vessels and blood flow passage is reduced, by reducing radius (stenosis), because of the deposition of fatty acids or plaque inside the inner wall of the blood vessels (Young, 1968). Stenosis is an anomalous and an unnatural expansion of cholesterol that grows at several inner layer locations of the cardiovascular system and is responsible for cardiovascular diseases (Fry, 1968). Arterial thrombosis is another form of heart disease, which usually occurs after the erosion or rupture of an atherosclerotic plaque and may hinder blood flow to many of the most important organs. If blood flow in the heart is unexpectedly blocked, then a heart attack occurs in the circulatory system (Dintenfass, 1971). Hemodynamic activities of the blood flow is changed by the existence of arterial stenosis. Many scientists Young and Tsai (1973) and Young (1979) have investigated and created a better interpretation of flow fluid, dynamic of fluid, and rheological blood flow characteristics through arteries in the presence of stenosis, which is essential in the study of cardiovascular diseases. In 2009, Siddiqui et al. (2009) represented the flow of blood by Casson's fluid model in a stenosed artery. Mekheimer and El Kot (2008) studied the axis-symmetric flow of blood in a radially symmetric but axially non-symmetric mild stenosed artery, which is a tapered artery, using blood as a Micropolar fluid model. Mandal (2005) obtained an unsteady flow of blood by remembering that the behavior of blood is like a non-Newtonian fluid, along with an artery that is tapered with mild stenosis. He obtained the numerical solution, expression, and graphical results for the blood flow.

In 2010, Varshney et al. (2010) presented a comprehensive model known as the Power-law fluid model for the flow of blood in blood vessels like arteries and treated blood flow using multiple stenoses. Nadeem et al. (2011) has discussed a model for blood, Power-law fluid, wherein the flow is through a tapered artery with mild stenosis. In 2011, Nadeem and Akbar (2011) again discussed the flow of blood and its analysis in Nadeem et al. (2011) for different fluid models, like Jeffrey fluid model. Mustafa et al. (2011) have investigated and concluded the study for the modified Newtonian fluid blood flow through a pair of arterial mild stenosis which is irregular. Abdullah et al. (2011) have studied the effect of a magnetic field on the flow of blood with an irregular mild stenosis. An annular region has been found in the vessel of blood, between the wall of the stenosis and blood clot. Mekheimer and Elmaboud (2008) studied the Micropolar fluid model in a region which is annular and under a long wavelength. The Reynolds number approximation for peristaltic transport has also been taken into consideration and they assumed the artery as a very small tube with a very small clot and a sinusoidal wave moving down to its wall. Ellahi et al. (2013) calculated mass and heat transfer on blood flow through a mild stenosed artery by using the Homotopy Perturbation method for the Jeffery fluid model with the suspension of nanoparticles. Ajdari et al. (2017) and Akbar and Butt (2016) discussed at which point the stenosis, which starts at a young age with increasing plaque build-up in the major or minor arteries of the human body, such a build-up becomes large enough in the coronary artery. Rahbari et al. (2017) investigated the fluid flow of blood and the effects of the magnetic field and heat transfer with nanoparticles through porous blood vessels.

We have done this work because in several investigations the velocity profile has been discussed but the temperature profile has never been discussed for tapered stenosed artery. So in this work we have aimed to understand the effects of heat transfer phenomenon on the Prandalt fluid model through a tapered stenosed atherosclerotic artery. The non-linear equations governing blood flow are modeled in a cylindrical coordinate system. The convection of heat transfer with a catheterized mild stenotic artery with a clot has been taken into consideration. And the non-linear coupled equations are solved exactly under mild stenotic conditions using the geometry for a mild stenotic artery in the presence of a clot. The heat and mass transfer phenomenon was discussed with distinct values of the temperature profile for some distinct values of flow parameters using graphs. As of now, this model has not been discussed for this kind of blood flow problem.

Mathematical Formulation

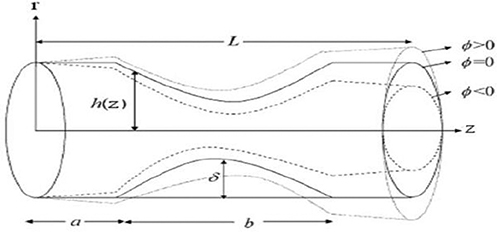
This present study aims to examine an nanoparticles in blood flow with a constant viscosity μ and density ρ in two coaxial tubes with length L; the inner tube contains a clot on its wall and the outer tube contains an axially symmetric mild stenosis. The cylindrical coordinate system (r, θ, and z) is chosen such that u and w are the velocity components in the r and z directions, respectively. Mixed convection is used to calculate the heat transfer by assigning the temperature T0 to the wall of the tube. The consideration of the stenosis in the outer tube and clot in the inner tube is defined by the h (z) and ε (z), respectively, and can be delineated as Rahbari et al. (2017):

$\begin{array}{r}h(z)=\text{d }(\text{z})\left[1-k\left(b^{n-1}(z-a)-{(z-a)}^n\right)\right];a<z\le a+b\\ =d(z);otherwise& (1)\end{array}$

$\begin{array}{r}\epsilon \text{(z)}=\text{d }(\text{z})\left[c+\sigma e^{-{\Pi }^2{(z-z_d-0.5)}^2}\right];a<z\le a+b\\ =cd(z);otherwise& (2)\end{array}$

$\begin{array}{ll}withd(z)=R_0+{\xi }_z& (3)\end{array}$

In the above equations, d(z) is the radius of the tapered arterial segment in the stenotic region, while R₀ is the radius of the artery in the non-stenotic region, ξ is the tapering parameter, b is the length of the stenosis, n ≥ 2 is the parameter determining the shape of the constriction profile and referred to as the shape parameter, a is the stenosis location, and k is given by:

$\begin{array}{ll}\text{k}=\frac{{\delta }^{*}}{{\text{R}}_0{\text{b}}^{\text{n}}}\frac{{\text{n}}^{(\frac{\text{n}}{\text{n}-1})}}{(\text{n}-1)}& (4)\end{array}$

where δ^* is the maximum height of the stenosis located at, $z=a+\frac{b}{n^{\frac{1}{n-1}}}$, σ is the maximum height attained by the clot at z = z_d + 0.5, c d(z) is the radius of the inner tube, and c<<1 and z_d is the axial displacement of the clot as shown in Figure 1.

FIGURE 1

Figure 1. Tapered stenosed artery geometry.

The constitutive equations for the Prandalt fluid model are given by Akbar et al. (2011)

$\begin{array}{ll}\overline{S}=\frac{A{sin}^{-1}\left\{\frac{1}{c_1}{\left[{\left(\frac{\partial u}{\partial z}\right)}^2+{\left(\frac{\partial w}{\partial z}\right)}^2\right]}^{\frac{1}{2}}\right\}}{{\left[{\left(\frac{\partial u}{\partial z}\right)}^2+{\left(\frac{\partial w}{\partial z}\right)}^2\right]}^{\frac{1}{2}}}\frac{\partial w}{\partial r}& (5)\end{array}$

The equations for incompressible nanoparticles in blood flow in the presence of body forces are given by

$\begin{array}{ll}\frac{1}{r}\frac{\partial (ru)}{\partial r}+\frac{\partial w}{\partial z}=0& (6)\end{array}$

$\begin{array}{ll}\rho \left(u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}\right)=-\frac{\partial p}{\partial r}+\frac{1}{r}\frac{\partial }{\partial r}(r{S}_{rr})+\frac{\partial }{\partial z}(S_{rz})-\frac{S_{\theta \theta }}{r}& (7)\end{array}$

$\begin{array}{r}\rho \left(u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\right)=-\frac{\partial p}{\partial z}+\frac{1}{r}\frac{\partial }{\partial r}(r{S}_{rz})+\frac{\partial }{\partial z}(r{S}_{zz})-\rho \\ g\alpha (T-T_0)& (8)\end{array}$

$\begin{array}{ll}u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}=\frac{k}{{(\rho c)}_f}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial z^2}\right)+\frac{Q_0}{{(\rho c)}_f}& (9)\end{array}$

In the presented equations, p is the fluid pressure, μ is the viscosity of the base fluid, g is gravity, and Q₀ is the constant heat absorption or heat generation. To solve the governing equations, we introduce the following dimensionless parameters:-

$\begin{array}{r}{p}^{\prime }=R_0^2\frac{p}{u_{0}b\mu },R_e=\frac{\rho b{u}_0}{\mu },S{\prime }_{rr}=\frac{b{S}_{rr}}{u_0\mu },\theta {= }^{T-T_0}{\text{╱}}_{T_0}\\ \alpha =\frac{A}{\mu c_1},\beta =\frac{A{u}_0^2}{6R_0^2\mu c_1^3},D=\frac{Q_0{R}_0^2}{T_{0}k}& (10)\end{array}$

where u₀ is the average velocity over the section of the channel, A and c₁ are material constants for Prandalt fluid model, D is the dimensionless heat source or sinks parameter with the fluid, and G_r is the Grashof number. Using the above non-dimensional parameters along with the additional conditions:-

$\begin{array}{ll}\frac{\partial p}{\partial z}=\frac{1}{r}\frac{\partial }{\partial r}\left[r\left(\alpha \left(\frac{\partial w}{\partial r}\right)+\beta {\left(\frac{\partial w}{\partial r}\right)}^3\right)\right]+G_r\theta & (11)\end{array}$

$\begin{array}{ll}{\frac{{\partial }^2\theta }{\partial r}}^2+\frac{1}{r}\frac{\partial \theta }{\partial r}+D=0& (12)\end{array}$

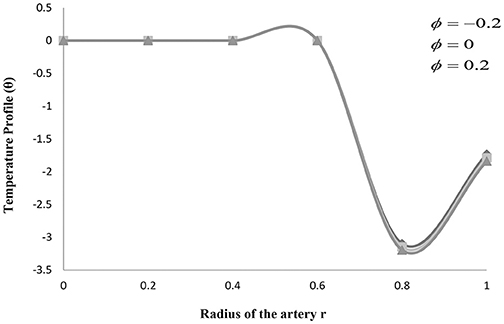
Further, we consider three types of arteries, converging tapering (ϕ < 0), non-tapering (ϕ = 0), and diverging tapering arteries (ϕ > 0). To calculate the heat transfer, the general solution for the temperature profile using the boundary conditions is found exactly, which is given by.

$\begin{array}{ll}\theta =-\frac{D}{4}\left(r^2-h^2\right)+ln(rh-h+\epsilon )\left(1-\frac{D}{4}(h^2-{\epsilon }^2)\right)& (13)\end{array}$

Results and Graphical Discussions

The system of equations has been solved and the expression (Mustafa et al., 2011) has been plotted to study the outcome of the work. The main aim of this mathematical study is to explore the heat transfer phenomena of blood flow through a tapered stenosed artery along with the clot with the flow of blood using the Prandalt fluid model. The effects of Prandalt fluid parameters tapering angle (ϕ), heat source and sink (D), the stenosis shape parameter (n), and a maximum height of the stenosis (δ) are analyzed for (1) converging tapering, (2) diverging tapering, and (3) non-tapered arteries.

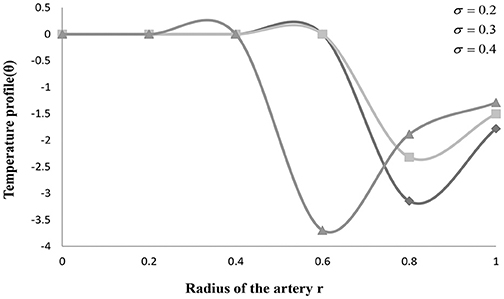
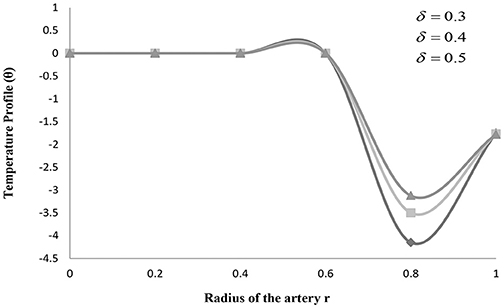
Figures 2–4 explains the heat transfer phenomenon by depicting the changes in temperature profile (θ) for distinct flow parameters graphically. It is obtained here that, due to a rise in the value of the maximum height of the clot (σ), the temperature profile (θ) increases. The temperature profile (θ) shows the identical variation for the maximum height of the stenosis (δ) and the maximum height extended by the clot (σ). The temperature profile (θ) shows quite interesting results for some values of tapering angle (ϕ) and heat source and sink (D).

FIGURE 2

Figure 2. Temperature (θ) for distinct values of clot size (σ) = 0.2, 0.3, 0.4.

The effect of the radius of the artery with a stenosis is understood, and further results are explored in the case of converging tapered artery for distinct values of clot size in the present study. Figure 2 depicts the variation for temperature profile (θ) with the radius of an artery with stenosis h(z) for distinct values of σ, i.e., the maximum height attained by the clot. It is seen in this figure that, due to a rise in the height of the clot, the temperature profile (θ) increases. However, it is also observed in the figure that at σ = 0.4, the temperature attains a minimum value at stenosis size h(z) = 0.6, and then it starts increasing again after attaining certain values of h(z). Figure 3 depicts the variation for temperature profile (θ) with the radius of an artery with stenosis h(z) for distinct values of δ, i.e., the maximum height of the stenosis. It is seen in this figure that, due to an increase in the height of the stenosis, the temperature profile decreases primarily. Whereas, it is also observed in the figure that after attaining minimum value h(z) = 0.8, it is continuously increasing. These figures also show that an increase in the value of the maximum height attained by the clot (σ) and the maximum height attained by the stenosis (δ) will result in an increase in the amount of heat generated. An increase in the amount of heat generated will raise the blood pressure inside the artery. Higher blood pressure has a strong possibility of creating extra pressure that could make the artery burst. Also in a narrow artery, the risk of being blocked is greater.

FIGURE 3

Figure 3. Temperature (θ) for distinct values of stenisis height (δ) = 0.3, 0.4, 0.5.

In both cases, the body part that received its blood from that affected artery will not be able to get the energy and oxygen which is essential for that area of the body and then, because of the lack, the cells in the affected area will die in that body part. If the ruptured blood vessels deliver blood to any part of the heart, then that area of heart muscle, due to lack of blood supply, will die, causing the heart attack.

Figure 4 also depicts how the non-tapered, diverging tapering, and converging tapering arteries affect the temperature profile (θ) with a radius of artery and stenosis h(z) for distinct values of tapering angles (ϕ). It is seen here in the figure that for a decrease in the tapering angle the temperature profile decreases up to h(z) = 0.8, and then increases for the greater values of h(z). However, it is also observed in the figure that the temperature attains a minimum value at stenosis size (r) = 0.8, and then it starts increasing after attaining convinced values of (r). It is shown that, for the case of converging tapering, the temperature gives greater values as compared to the case of diverging tapering. And it is observed that the temperature rises in the case of non-tapered arteries as well.

FIGURE 4

Figure 4. Temperature (θ) for distinct values of tapering angle (ϕ) = (−0.2, 0, 0.2).

Conclusion

This study focus on the heat transfer phenomena of blood flow that happens in the human cardiovascular system and the study aims to contribute to a better understanding of the circulatory system in the presence of minor growth of the stenosis in the artery, where the clot is present inside it. So the objective of the study was to explore the influence of Prandalt fluid parameters like tapering angle (ϕ), heat source and sink (D), the stenosis shape parameter (n), and the maximum height of the stenosis (δ) on temperature profile (θ). In this study, the tapering phenomena have been analyzed for temperature profiles especially. It is found that, for converging tapering, the temperature gives greater results as compared to the case of diverging tapering arteries. It is also observed that the temperature gives superior values in the case of non-tapered arteries as well. It has also been examined that, due to a rise in the clot size (σ), the temperature profile (θ) increases while the radius of the artery with stenosis h(z) decreases and the heat source and sink parameter (D) increases.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

SS: formulation of the problem and mathematical modeling. RK: calculation and the graphical part of the paper. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the School of Computational and Integrative Sciences, Jawaharlal Nehru University, New Delhi-110067 (India), for providing necessary facilities in pursuing this research work.

References

Abdullah, I., Amin, N. S., and Hayat, T. (2011). Magnetohydrodynamic effects on blood flow through irregular stenosis. Int. J. Number. Method Fluids 67, 1624–1636. doi: 10.1002/fld.2436

CrossRef Full Text | Google Scholar

Ajdari, N., Vyas, C., Bogan, S. L., Lwaleed, B. A., and Cousins, B. G. (2017). Gold nanoparticle interactions in human blood: a model evaluation. Nanomed. Nanotechnol. Biol. Med. 13, 1531–1542. doi: 10.1016/j.nano.2017.01.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Akbar, N. S., and Butt, A. W. (2016). Bio-mathematical venture for the metallic nanoparticles due to ciliary motion, Comput. Methods Prog. Biol. 134, 43–51. doi: 10.1016/j.cmpb.2016.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Akbar, N. S., Nadeem, S., and Lee, C. (2011). Peristaltic flow of a Prandtl fluid model in an asymmetric channel. Int. J. Phy. Sci. 7, 687–695. doi: 10.5897/IJPS11.1375

CrossRef Full Text | Google Scholar

Dintenfass, L. (1971). Viscosity factors in hypertensive and cardiovascular diseases. Cardiovasc. Med. 2, 337–349.

Ellahi, R., Rahman, S. U., and Nadeem, S. (2013). Theoretical study of unsteady blood flow of Jeffery fluid through stenosed arteries with permeable walls. Zeitschr Naturforschung A 68, 489–498. doi: 10.5560/zna.2013-0032

CrossRef Full Text | Google Scholar

Fry, D. L. (1968). Acute vascular endothelial changes associated with increased blood velocity gradients. Circ. Res. 22, 165–197. doi: 10.1161/01.RES.22.2.165

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandal, P. K. (2005). An unsteady analysis of non-Newtonian blood flow through tapered arteries with stenosis. Int. J. Non Linear Mech. 40, 151–164. doi: 10.1016/j.ijnonlinmec.2004.07.007

CrossRef Full Text | Google Scholar

Mekheimer, K. H. S., and El Kot, M. A. (2008). The micropolar fluid model for blood flow through a tapered artery with stenosis. Acta Mech. Sin. 24, 637–644. doi: 10.1007/s10409-008-0185-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Mekheimer, K. S., and Elmaboud, Y. A. (2008). The influence of a micropolar fluid on peristaltic transport in an annulus: application of the clot model. Appl. Bionics Biomech. 5:302195. doi: 10.1155/2008/302195

CrossRef Full Text | Google Scholar

Mustafa, N., Mandal, P. K., Abdullah, I., Amin, N. S., and Hayat, T. (2011). Numerical simulation of generalized Newtonian blood flow past a couple of irregular arterial stenosis. Numer. Meth. Partial Diff. Eqs. 27, 960–981. doi: 10.1002/num.20563

CrossRef Full Text | Google Scholar

Nadeem, S., and Akbar, N. S. (2011). Jeffrey fluid model for blood flow through a tapered artery with stenosis. J. Mech. Med. Biol. 11, 529–545 doi: 10.1142/S0219519411003879

CrossRef Full Text | Google Scholar

Nadeem, S., Akbar, N. S., Hayat, T., and Hendi, A. A. (2011). Power-law fluid model for blood flow through a tapered artery with stenosis. Appl. Math. Comput. 217, 7108–7116. doi: 10.1016/j.amc.2011.01.026

CrossRef Full Text | Google Scholar

Rahbari, A., Fakour, M., Hamzehnezhad, A., Vakilabadi, M. A., and Ganji, D. D. (2017). Heat transfer and fluid flow of blood with nanoparticles through porous vessels in a magnetic field: a quasi-one-dimensional analytical approach. Math. Biosci. 283, 38–47. doi: 10.1016/j.mbs.2016.11.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Siddiqui, S. U., Verma, N. K., Mishra, S., and Gupta, R. S. (2009). Mathematical modeling of the pulsatile flow of Casson's fluid in arterial stenosis. Appl. Math. Comput. 210, 1–10. doi: 10.1016/j.amc.2007.05.070

CrossRef Full Text | Google Scholar

Varshney, G., Katiyar, V. K., and Kumar, S. (2010). Effect of magnetic field on the blood flow in an artery having multiple stenoses: a numerical study. Int. J. Eng. Sci. Tech. 2, 67–82. doi: 10.4314/ijest.v2i2.59142

CrossRef Full Text | Google Scholar

Young, D. F. (1968). Effects of a time-dependent stenosis on flow through a tube. J. Eng. Ind. Trans. ASME 90, 248–254. doi: 10.1115/1.3604621

CrossRef Full Text | Google Scholar

Young, D. F. (1979). Fluid mechanics of arterial stenosis. J. Biomech. Eng. Trans. ASME 10, 157–175. doi: 10.1115/1.3426241

CrossRef Full Text | Google Scholar

Young, D. F., and Tsai, F. Y. (1973). Flow characteristic in models of arterial stenosis-I, steady flow. J. Biomech. 6, 395–410. doi: 10.1016/0021-9290(73)90099-7

PubMed Abstract | CrossRef Full Text | Google Scholar