- Department of Biochemistry, All India Institute of Medical Sciences, New Delhi, India
Biochemical networks integrate enzyme-mediated substrate conversions with non-enzymatic complex formation and disassembly to accomplish complex biochemical and physiological functions. The choice of parameters and constraints used in most of these studies is numerically motivated and network-specific. Although sound in theory, the outcomes that result depart significantly from the intracellular milieu and are less likely to retain relevance in a clinical setting. There is a need for a computational tool which is biochemically relevant, mathematically rigorous, and unbiased, and can ascribe functionality to and generate potentially testable hypotheses for a user-defined biochemical network. Here, we present “ReDirection,” an R-package which computes the probable dissociation constant for every reaction of a biochemical network directly from a null space-generated subspace of the stoichiometry number matrix of the modeled network. “ReDirection” delineates this subspace by excluding all trivial and redundant or duplicate occurrences of non-trivial vectors, combinatorially summing the vectors that remain and verifying that the upper or lower bounds of the sequence of terms formed by each row of this subspace belong to the open real-valued intervals
1 Introduction
An undirected biochemical network is converted into a pathway by a combination of physicochemical (temperature, pH, and compartmentalization) and biochemical (small-molecule effectors, shared intermediates, and feedback) factors. Despite the availability and accessibility of advanced data analytical tools, true mechanistic insights into the manner in which a biochemical network accomplishes a complex function are unclear (Ferrara et al., 2008; Keller and Attie, 2010; Biane and Delaplace, 2019; Seyhan and Carini, 2019; Koutrouli et al., 2020). An essential first step in the analysis of a biochemical network is the construction of a suitable model. This is usually data-driven and coarse-grained, where nodes can represent proteins, genes, or cells, and edges indicate lines of supporting evidence (empirical, “omics” datasets, co-expression data, text mining, and knowledge-based databases) (Reinker et al., 2006; Ferrara et al., 2008; Lecca et al., 2009; Keller and Attie, 2010; Haraldsdottir et al., 2012; Shindo et al., 2018; Biane and Delaplace, 2019; Seyhan and Carini, 2019; Koutrouli et al., 2020; Wittenstein et al., 2022). Analyzing such a network results in several network-specific characteristics such as the clustering coefficient and path distance (Reinker et al., 2006; Lecca et al., 2009; Haraldsdottir et al., 2012; Shindo et al., 2018; Wittenstein et al., 2022). This initial characterization can be complemented by a library of equally plausible outcomes, all of which are made to approximate the original architecture (Lecca et al., 2009; Riva et al., 2022). Inverse modeling, for a dataset, generates several possible candidate causal network models, allows hypothesis testing, and may potentially be more informative (Reinker et al., 2006; Lecca et al., 2009; Haraldsdottir et al., 2012; Rottman and Hastie, 2014; Shindo et al., 2018; Riva et al., 2022; Wittenstein et al., 2022).
Causal networks (CNs) are probability-based and can model alternate scenarios for every node of a small network whilst concomitantly ascribing specific states to each node (Rottman and Hastie, 2014). Although CNs have had considerable success in investigating real-world problems, inferring biochemical function from a network of genes/proteins/metabolites remains challenging (Rottman and Hastie, 2014). For example, a causal network is usually modeled as an “acyclic” graph, which is in complete contrast to the plethora of feedback (positive and negative) mechanisms and reverse reactions that exemplify biochemical systems (Rottman and Hastie, 2014). CNs are also inferential, modeled as a homogenous Poisson’s process (discrete event, discrete domain) and inherently Markovian (Lecca et al., 2009; Rottman and Hastie, 2014). Biochemical function, on the other hand, is dependent on thresholds (signal transduction and pattern receptors), characterized by minor perturbations and is memory-driven, all of which are better modeled as continuous events or variables in discrete time. CNs, to be truly informative, also require a significant amount of initial data, which is a major limitation in modeling biochemical networks. These arguments notwithstanding, CNs have contributed to well-defined observables in the presence of ample empirical data, such as phenotype mapping, along with dose- and stimulus-driven response of genes (Goto et al., 2019; Gopalan et al., 2021; Lu et al., 2021; Salvador et al., 2021; Saptarshi et al., 2021). CNs of genes and proteins result in lists which can be utilized for large-scale data mining (parameter selection and candidate genes) and/or analytics, as in precision medicine and biomarker profiling (Biane and Delaplace, 2019; Goto et al., 2019; Seyhan and Carini, 2019; Gopalan et al., 2021; Lu et al., 2021; Salvador et al., 2021; Saptarshi et al., 2021).
Unlike data-driven modeling, optimization- and enumeration-based strategies can be used to investigate and characterize a biochemical network from first principles and at the near-steady state (Segre et al., 2002; Shlomi et al., 2005; Wagner and Urbanczik, 2005; Urbanczik, 2007; Orth et al., 2010; Muller and Regensburger, 2016; Klamt et al., 2017; Klamt et al., 2018; Lee et al., 2020). Algorithms which assess the flux of a reactant (flux balance analysis, flux variability analysis, regulatory on–off minimization, and minimization of metabolic adjustment) will maximize or minimize the biomass of a metabolite of interest and can be used to investigate the effects of deletions and other perturbations on the flux of metabolites through a large network (Segre et al., 2002; Shlomi et al., 2005; Orth et al., 2010; Klamt et al., 2018; Lee et al., 2020). The numerical enumeration of elementary flux modes and vectors, along with extreme pathway analysis, can be used to derive meaningful information about “metabolic” hubs and smaller subsets of cooperating reactions from biochemical networks (Wagner and Urbanczik, 2005; Urbanczik, 2007; Muller and Regensburger, 2016; Klamt et al., 2017). A mathematical model of a biochemical network can also be made to integrate real-time data such as from “omics”-based studies, spectroscopic analysis, and pulse-chase experiments, which allows an investigator to refine and optimize the model (Antoniewicz, 2015; Heuillet et al., 2018; Wang et al., 2020). This approach of combining experimental data with theoretical studies is referred to as metabolic flux analysis (MFA) and is utilized in biotechnological applications to regulate the biomass of a preferred reactant/product (Antoniewicz, 2015; Heuillet et al., 2018; Wang et al., 2020).
The aforementioned limitations to data-driven models and biomass optimization-based strategies advocate the need for a computational tool which can compute biochemically relevant parameters directly from a modeled network. This implies that the parameter should be derivable, measurable and its analysis should be able to generate testable hypotheses. The dissociation constant is an empirically determined parameter, which can be mapped to several biochemically relevant outcomes of a reaction (forward, reverse, equivalent, and tight binding) (Furukawa et al., 2016; Yu and Craciun, 2018; Gerstl et al., 2019; Sparks et al., 2019; Kundu, 2022; Sura and Antalik, 2022). The probable dissociation constant for a reaction is a numerical measure that is computed from a null space-generated subspace of the stoichiometry number matrix for a biochemical network and possesses several desirable properties of the true dissociation constant (Kundu, 2023a). Here, we present “ReDirection,” an R-package which can compute the probable dissociation constant for every reaction of a user-defined biochemical network (Kundu, 2023b). This paper introduces some of the principles and definitions used by “ReDirection” to compute the probable dissociation constant for a user-defined biochemical network. An outline of the functions used by “ReDirection,” their dependencies, rationale, and usage is presented. A stepwise description and brief analysis of the algorithm that “ReDirection” deploys are also described, followed by numerical studies on constrained biochemical networks of human galactose metabolism and heme and cholesterol biosynthesis. The paper concludes with a summary of the salient features, limitations, and future studies which may utilize “ReDirection.”
2 Methods
2.1 Definitions, preliminary concepts, and notations relevant to comprehending the functionality of “ReDirection”
The algorithm deployed by “ReDirection” is mathematically rigorous and biochemically relevant, and has been extensively discussed (Kundu, 2023a; Kundu, 2023b). Briefly, a biochemical network is modeled as the sparse stoichiometry number matrix
“ReDirection” is assessed by the time needed
where
“ReDirection” combinatorially sums the vectors of the null space and, thence, each null space-generated subspace (Kundu, 2023a). This results in several subsets of vectors which contribute to the cardinality of each null space-generated subspace and may be summarized. We describe this comprehensive null space-generated subspace as the set which contains trivial vectors, along with redundant or finite occurrences of non-trivial and identical null space vectors (Kundu, 2023a):
where
Rewriting Def. (4) to include these vectors yields
where
We now enumerate various cases that may arise when we combinatorially sum non-trivial vectors:
We can immediately see from Case 2 that it is possible to have a finite number of subsets of non-trivial identical vectors exist in
We define the exact number of vectors to be reassigned on account of their uniqueness as
For
For
In general, for τ-subsets of identical vectors in
2.2 Generic description, availability, and guidelines for using “ReDirection”
“ReDirection” is freely available and can be updated or installed directly from the graphics user interface (GUI) (R-4.1. x) as “update.packages (‘ReDirection’)” and/or “install.packages (‘ReDirection’)” from any of the CRAN mirrors. “ReDirection” is built in RStudio (1.4.1717) and tested in R-4.1. x. “ReDirection” comprises three functions (calculate_reaction_vector, check_matrix, and reaction_vector). The dependencies for “ReDirection” are the packages “pracma,” “MASS,” “stats,” and the combinations function from the R-package (“gtools”). The downloaded package includes detailed documentation of all the functions, along with ready-to-use examples and tests of functionality. “ReDirection” utilizes these functions sequentially and processes the stoichiometry number matrix of the reactants/products and reactions of a biochemical network that is defined by the user (Figure 1). In addition to implementing “ReDirection” locally, several R-scripts are developed in house, and used to preformat (input and output) and analyze data. The algorithm followed by “ReDirection” can be divided into simpler steps. These include checking the user-defined stoichiometry matrix, searching for a suitable null space-generated subspace, screening and partitioning terms, and computing the probable dissociation constant (Figure 1).
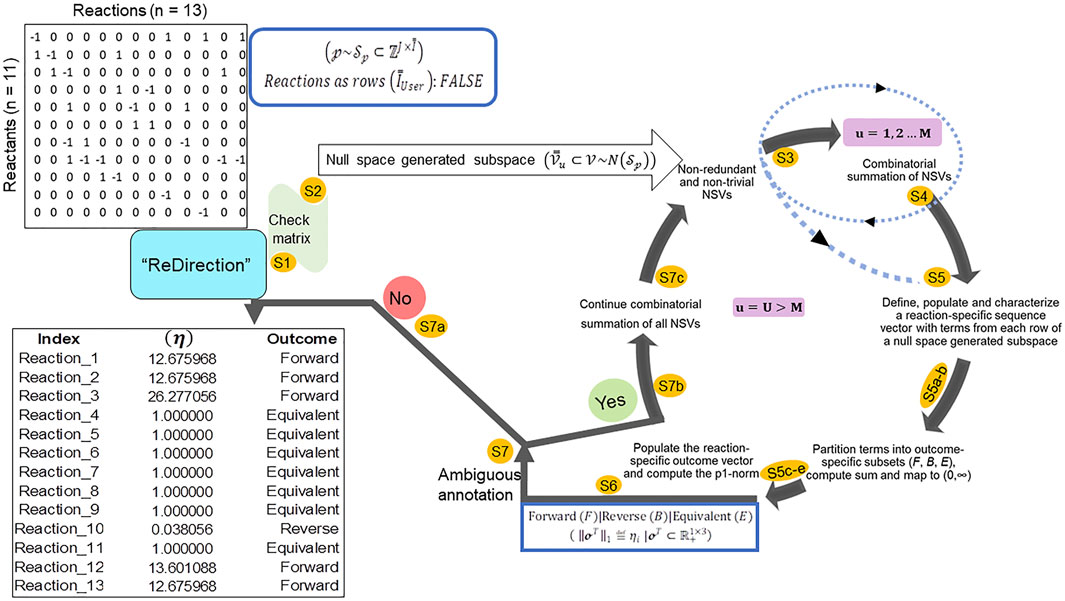
FIGURE 1. Schematic representation of the steps deployed by “ReDirection” to characterize every reaction of a user-defined biochemical network with the probable dissociation constant: “ReDirection” checks the stoichiometry number matrix that is provided by the user for a modeled biochemical network for compliance with pre-defined criteria. If true, then “ReDirection” computes a null space-generated subspace by excluding all redundant and trivial vectors, and combinatorially summing the vectors that remain. “ReDirection” also defines a reaction-specific sequence vector which comprises terms drawn from each row of the resulting subspace. “ReDirection” computes several descriptors (mathematical, statistical) for the numerical values that comprise this vector and partitions these into distinct subsets in accordance with the expected outcomes (forward, reverse, and equivalent) for a reaction. “ReDirection” then maps the sum of the terms of each outcome-specific subset to the strictly positive real number and bins these to a reaction-specific outcome vector. The p1-norm of this vector is the probable dissociation constant for a reaction and is used to annotate the same. “ReDirection” accomplishes this recursively and over several iterations until every reaction of the modeled biochemical network has been assigned an unambiguous outcome. Abbreviations:
2.2.1 Checking the user-defined stoichiometry number matrix for a biochemical network
Although “ReDirection” is simple to operate, there are a few guidelines that the user needs to be aware of whilst using it. “ReDirection” is reaction-centric and requires that the number of reactions and reactants/products of a modeled biochemical network strictly conforms to the lower bounds for each (Kundu, 2023a). Since the user is not expected to validate the stoichiometry number matrix manually, “ReDirection” undertakes this task and carries out this unequivocally prior to commencing the iterations. In addition to the stoichiometry number matrix, the user is expected to provide a logical argument (TRUE, FALSE) that indicates whether the reactions are to be considered rows or columns,
“ReDirection” utilizes these data to assign the appropriate orientation to the stoichiometry number matrix (step 1; Figure 1),
Another checkpoint, albeit internal, is the identification and subsequent exclusion of linear dependent row and column vectors that are contributed by half-reactions (forward, reverse) of the modeled biochemical network (step 1; Figure 1). “ReDirection” accomplishes this by recursively multiplying each reaction vector
It is clear that the final list of reactions that “ReDirection”
The modified stoichiometry number matrix is now
“ReDirection” rechecks the modified stoichiometry number matrix (steps 1–3; Figure 1),
“ReDirection” rechecks the modified stoichiometry number matrix (steps 1–3; Figure 1),
If there are no further deficiencies, “ReDirection” computes the null space (Step 2; Figure 1):
2.2.2 “ReDirection”-mediated search for a suitable null space-generated subspace to compute the probable dissociation constant for every reaction of a biochemical network
“ReDirection” then searches for a suitable null space-generated subspace
where
Rewriting
Clearly, with each iteration, the computational complexity increases with a corresponding increase in the time required by “ReDirection” to completely annotate every reaction of a biochemical network. Therefore, “ReDirection” identifies and excludes these vectors in an attempt to complete the annotations within a reasonable amount of time (steps 3–7; Figure 1). The pseudocode for the case where the nullity of the null space

TABLE 1. Pseudocode to determine cardinality as the function of a finite number of
2.2.3 Row-wise screening and partitioning of terms of the selected null space-generated subspace
Every row of this
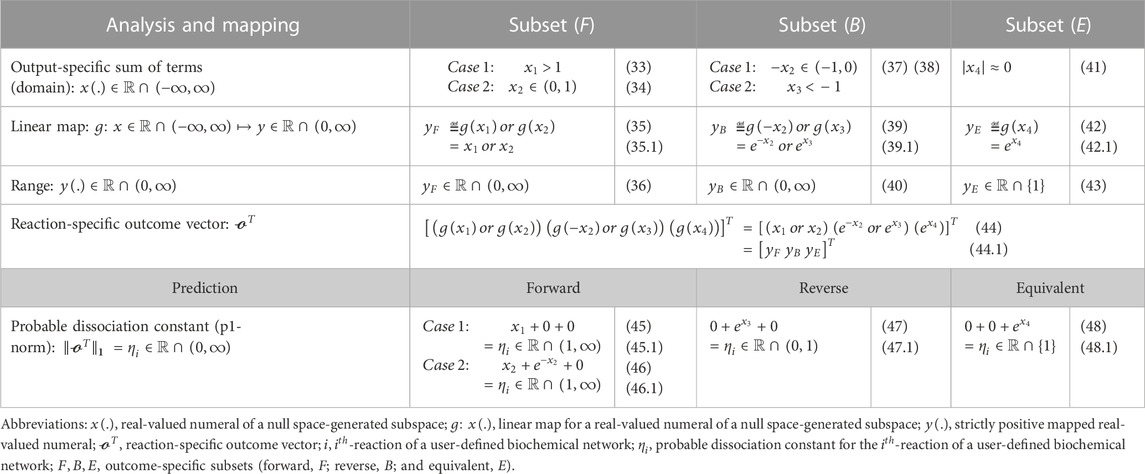
TABLE 2. “ReDirection”-based computation of the probable dissociation constant for the
2.3 “ReDirection”-based numerical studies to ascertain and assess an upper bound for the maximum number of reactions for a user-defined biochemical network
It has already been proven that the algorithm deployed by “ReDirection” is likely to be NP-hard (Kundu, 2023a). This means that for a biochemical network whose output is determined by summing its constituent terms, there is a limit on the maximum number of reaction vectors that can be modeled by a user. Since “ReDirection” utilizes combinatorial summations to identify a suitable null space-generated subspace from where the probable reaction constants for a modeled biochemical network can be computed, the upper bound for the maximum number of reaction vectors is likely to be lower, i.e., there is a narrow permissible limit.
Since “ReDirection” needs to be user-friendly, an indicator of this must be available a priori. We utilize the time metric to ascertain this numerically. In other words, the time
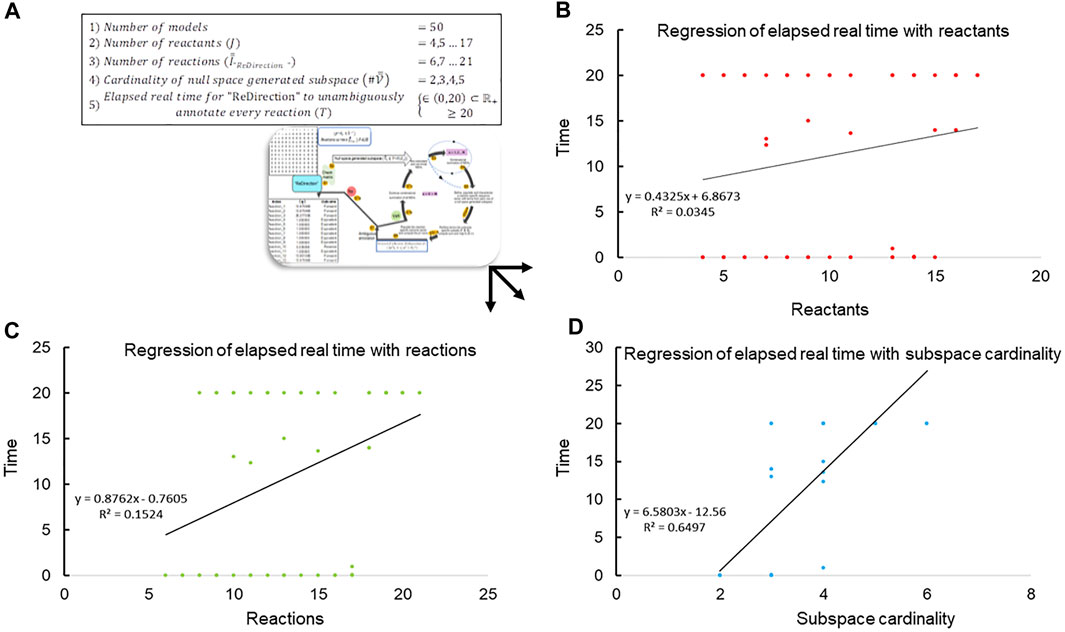
FIGURE 2. Regression of elapsed real time with network-specific parameters. (A) The data, i.e., elapsed run-time (
In order to assess these observations, we compute a truth table with the following assumptions and abbreviations (Defs 26–29):
This yields the following indices to assess our premise:
2.4 “ReDirection”-based studies on physiologically relevant biochemical networks
We conclude this study by examining the relevance of the probable dissociation constants that are computed by “ReDirection” in physiologically relevant biochemical networks for galactose metabolism and heme and cholesterol biosynthesis. The stoichiometry number matrices for these networks are constructed in accordance with the numerical constraints discussed here and in previous work (Figure 3; Figure 4; Figure 5; Supplementary Texts S2–S4) (Kundu, 2023a; Kundu, 2023b).
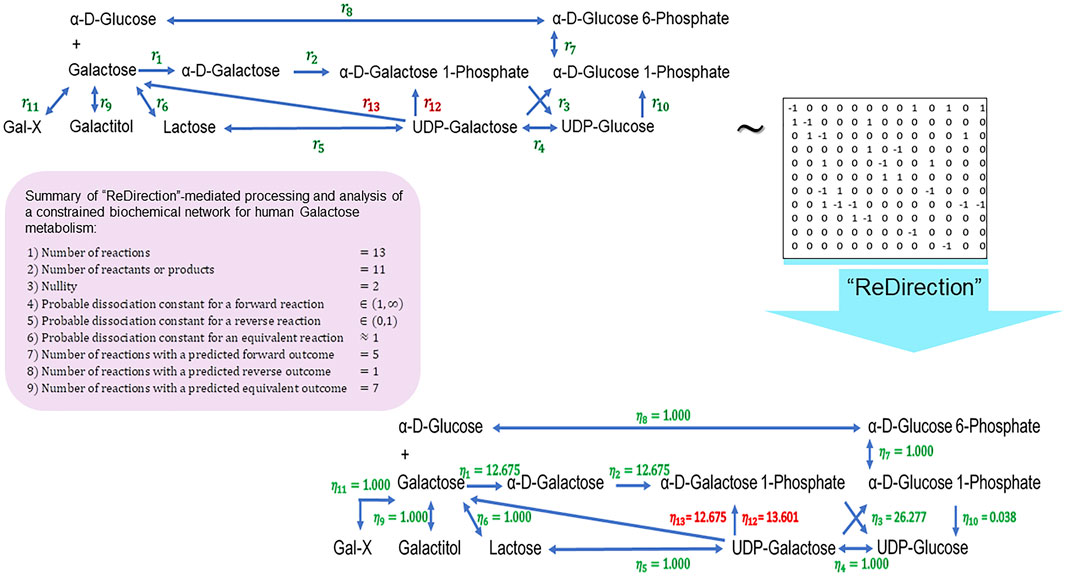
FIGURE 3. Schematic representation of a “ReDirection”-mediated investigation of a constrained biochemical network for human galactose metabolism. The biochemical network for galactose metabolism in Homo sapiens comprises several potentially bidirectional reactions. Here, “ReDirection” investigates the conversion of UDP-galactose to alpha-D-galactose 1-phosphate (
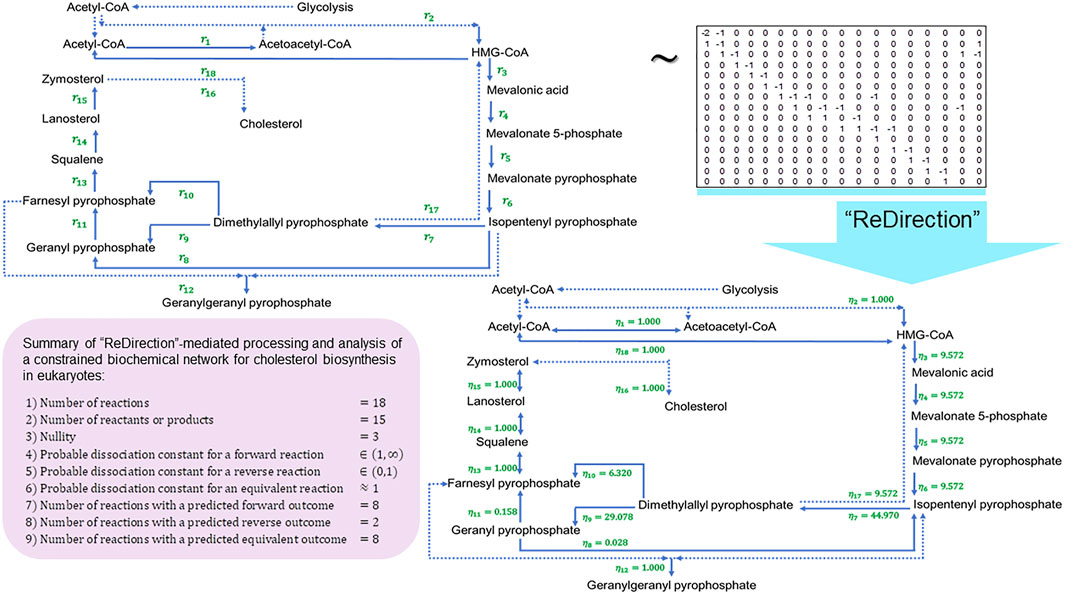
FIGURE 4. Schematic representation of a “ReDirection”-mediated investigation of a constrained biochemical network for eukaryotic cholesterol biosynthesis. The high number of predicted equivalent reactions
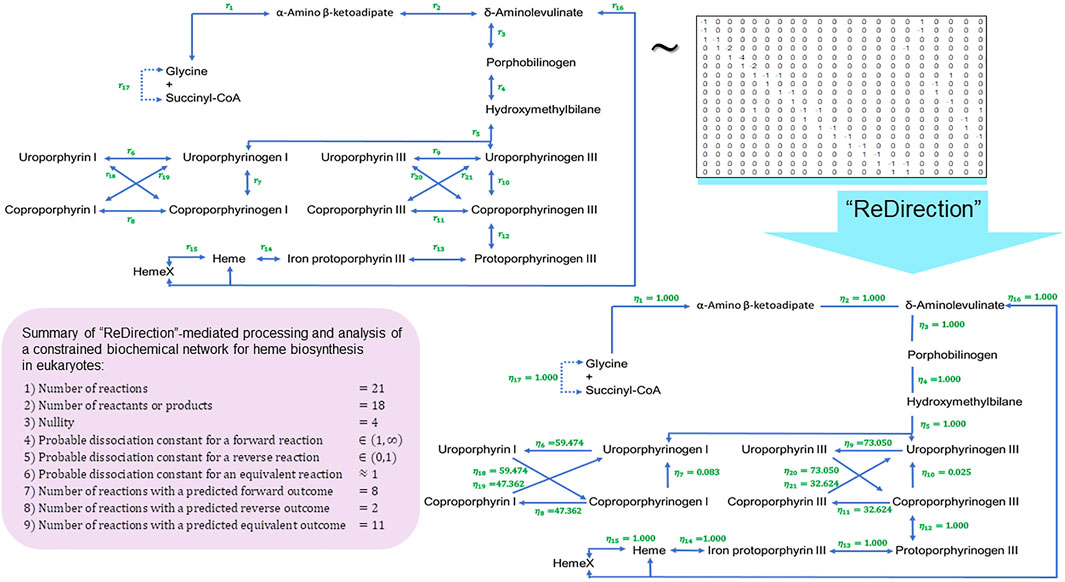
FIGURE 5. Schematic representation of a “ReDirection”-mediated investigation of a constrained biochemical network for heme biosynthesis. Here, we present a biochemical network which examines the effects of the uroporphyrins (I) and (III) and coproporphyrins (I) and (III) on the immediate precursors uroporphyrinogens (I) and (III) or products coproporphyrinogens (I) and (III) on the flux of heme
Galactose–glucose interconversion is readily observed within the cell, catalyzed by the enzyme UDP-galactose 4-epimerase
3 Results and discussion
3.1 Steps deployed by “ReDirection” to compute the probable dissociation constant for every reaction of a user-defined biochemical network
“ReDirection” utilizes the aforementioned functions sequentially and processes the stoichiometric number matrix for the biochemical network that is defined by the user and computes the probable dissociation constant for every reaction (Figure 1). This is conducted sequentially as follows:
Step 1. “ReDirection” checks whether the matrix of stoichiometry numbers that the user inputs is compliant with previously outlined criteria and does not have any linear dependent vectors. If found, “ReDirection” excludes them. The modified input matrix is rechecked.
Step 2. “ReDirection” then computes the null space of the checked/rechecked stoichiometric number matrix of the reactants/products and reactions of the user-defined biochemical network.
Step 3. “ReDirection” processes and screens this null space for redundant and/or trivial vectors and defines a subspace by excluding the same.
Step 4. “ReDirection” combinatorially sums the remaining vectors, i.e., non-redundant and non-trivial, and repeats step 3 for a finite number of
Step 5. For
Step 5a. “ReDirection” tests each term of an
Step 5b. If this term diverges and possesses a numerical value greater than 2 standard deviations from the mean, then this term is binned into the appropriate outcome-specific (forward/reverse/equivalent) subset.
Step 5c. The terms of each outcome-specific subset form a finite series whose sum is computed by “ReDirection.”
Step 5d. “ReDirection” then maps these sums to strictly positive real numbers which are then specific for each outcome-specific subset.
Step 5e. These outcome-specific numerical measures form the
Step 6. “ReDirection” computes the p1-norm of the reaction-specific outcome vector and annotates the reaction.
Step 7. “ReDirection” checks whether the annotations for all the other reactions of the user-defined biochemical network are unambiguous.
Step 7a. If there is no reaction that has been annotated ambiguously, then “ReDirection” outputs the predicted outcomes for every reaction of the user-defined biochemical network.
Step 7b. If there is a reaction that has been annotated ambiguously, then “ReDirection” continues the iterations.
Step 7c. “ReDirection” combinatorially sums all non-redundant and non-trivial null space-generated subspace vectors that remain, defines a new subspace, and repeats steps 5–7.
3.2 “ReDirection”-based delineation of an upper bound for the number of reactions of a biochemical network
The data suggest that the cardinality of the null space-generated subspace that is chosen to compute the probable dissociation constant for a reaction determines not only the time taken to complete the computations but also whether this can be accomplished in real time (Figures 2B–D; Table 3). It was observed that this was achievable, i.e.,
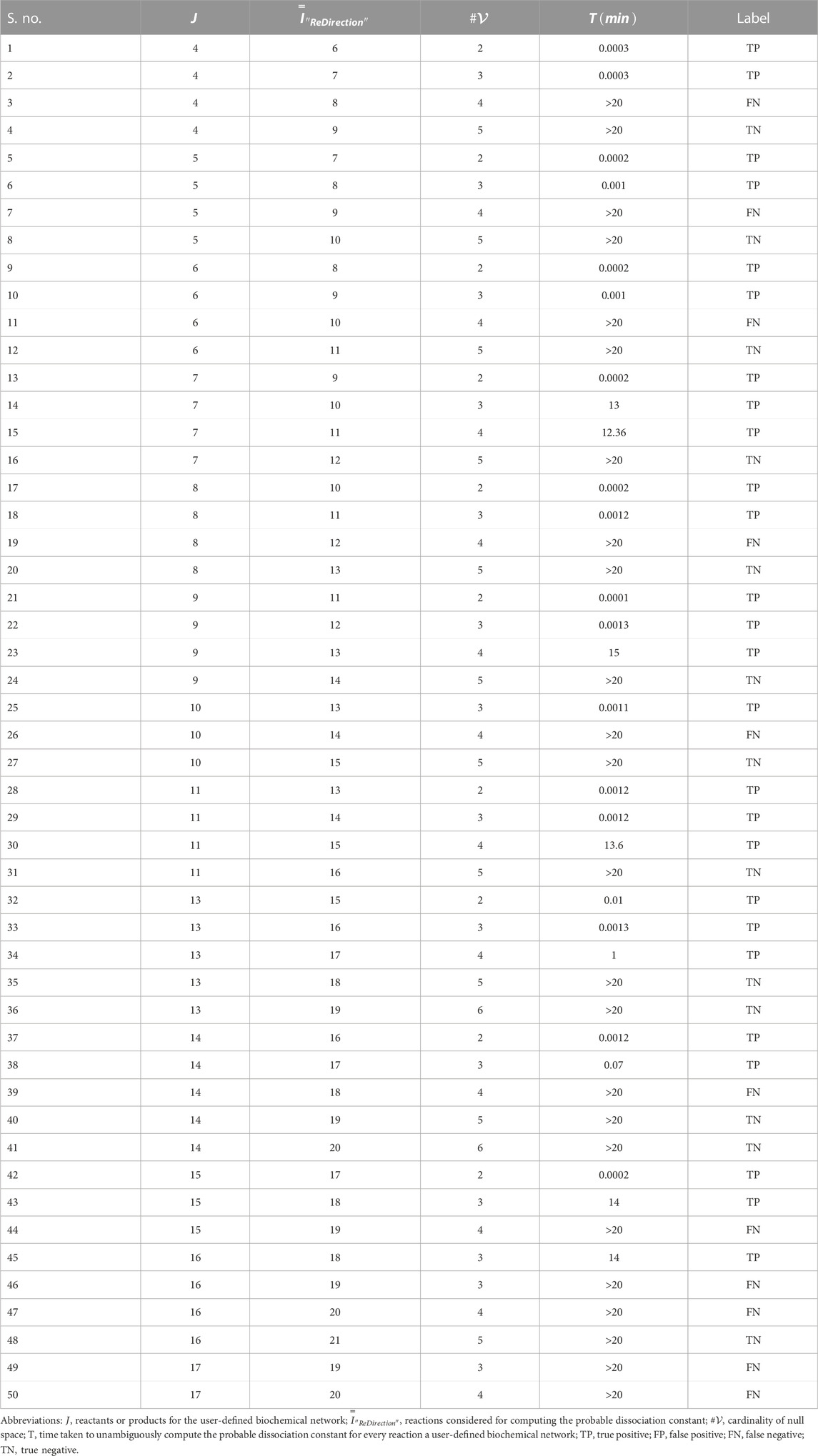
TABLE 3. Run-time characteristics of the “ReDirection”-mediated computation of probable dissociation constants for simulated biochemical networks (
On the basis of the time taken by “ReDirection” to complete the annotations for each simulated biochemical network, we can categorize each outcome in terms of the categorical variables
This yields the following indices to assess our premise:
Clearly, we can achieve significant proportioning of these data on the basis of our estimate of an upper bound for the reactions of these simulated biochemical networks (accuracy, precision, specificity, and recall). We suggest the following bounds for the number of reactions which a user may specify for a modeled biochemical network:
3.3 “ReDirection”-based characterization of physiologically relevant biochemical networks
We now utilize “ReDirection” with these constraints to compute probable dissociation constants and, thence, investigate the biochemical networks of human galactose metabolism and cholesterol biosynthesis.
The presented biochemical network for galactose metabolism comprises a significantly larger fraction
The high number of equivalent reactions
The distribution of equivalent
3.4 The probable dissociation constants for a biochemical network are suitable indices of biochemical function
The probable dissociation constants for a biochemical network provides the user with theoretically sound and biochemically relevant indices by which reactions of a biochemical network can be compared along with the corresponding change in the reactants/products (Reinker et al., 2006; Lecca et al., 2009; Haraldsdottir et al., 2012; Shindo et al., 2018; Wittenstein et al., 2022; Kundu, 2023a). A potentially novel application for these data is to incorporate these into simulation studies with the stochastic simulation algorithms (Gillespie, 2007; Kundu, 2016; Kundu, 2021). However, these studies mandate, by definition, the use of every possible reaction during a simulation run. This precludes the direct usage of data that are generated by “ReDirection” since only half the reactions are considered in computing the probable dissociation constants for the modeled biochemical network. The complete set of reactions for a user-defined biochemical network
We annotate this set of additional half reactions in terms of the probable dissociation constant for the “ReDirection” annotated reaction as (Kundu, 2016; Kundu, 2021; Kundu, 2023a)
This approach has yielded interesting insights into the export of high-affinity peptides to the plasma membrane by the major histocompatibility complex-I (MHC1) (Kundu, 2021). In that study, the authors examined a low-affinity peptide-driven biochemical network that could also be potentially regulatory and, therefore, important in priming circulating CD8+ T-cell lymphocytes into mounting a suitable immune response in the presence of acute and chronic insults (Kundu, 2021). Similarly, a role for reactive oxygen species in facilitating cellular proliferation and transmigration whilst precluding a cell to senescence and apoptosis concomitantly was addressed by creating a biochemical network for an advancing phagocyte toward a noxious stimulus (Kundu, 2016). The transduced signal was modeled to act through lipid raft-interacting actin fibers that could stabilize the actin cytoskeleton of the phagocyte and promote the development of a single dominant lamellipodium in the direction of the noxious stimulus (Kundu, 2016).
4 Conclusion
“ReDirection” is an R-package that computes the probable disassociation constant for every reaction of a biochemical network directly from a null space-generated subspace of a stoichiometry number matrix. Whilst mathematical rigor is ensured at all steps, biological relevance is maintained by utilizing parameters and metrics in accordance with established kinetic paradigms. “ReDirection” computes the probable dissociation constant from first principles and can be used to compare biochemical networks under varying intracellular environments (baseline, perturbed), between cells, and across taxa. Although computationally intense and possibly intractable for larger networks, the predictions are reasonably rapid for fewer reactions and are completed quickly in a desktop environment. Future investigations should strive to improve upon computational time, investigate perturbations, and validate some of the findings by simulation studies. “ReDirection” is not discovery-based and is better suited to addressing known and often empirically intractable biochemical problems in silico with simulations or generating testable hypotheses in a laboratory setting.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
SK: conceptualization, methodology, software, resources, formal analysis, data curation, validation, visualization, investigation, writing—original draft preparation, writing—reviewing and editing, and funding acquisition.
Funding
This study was supported by an extramural grant from the Science and Engineering Research Board (SERB), Department of Science and Technology, Government of India, under the Mathematical Research Impact-Centric Support (MATRICS) scheme to SK (MTR/2021/000290).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmolb.2023.1206502/full#supplementary-material
References
Antoniewicz, M. R. (2015). Methods and advances in metabolic flux analysis: A mini-review. J. Ind. Microbiol. Biotechnol. 42, 317–325. doi:10.1007/s10295-015-1585-x
Biane, C., and Delaplace, F. (2019). Causal reasoning on boolean control networks based on abduction: theory and application to cancer drug discovery. IEEE/ACM Trans. Comput. Biol. Bioinform. 16 (5), 1574–1585. doi:10.1109/TCBB.2018.2889102
Buhaescu, I., and Izzedine, H. (2007). Mevalonate pathway: A review of clinical and therapeutical implications. Clin. Biochem. 40, 575–584. doi:10.1016/j.clinbiochem.2007.03.016
Conte, F., van Buuringen, N., Voermans, N. C., and Lefeber, D. J. (2021). Galactose in human metabolism, glycosylation and congenital metabolic diseases: time for a closer look. Biochim. Biophys. Acta Gen. Subj. 1865 (8), 129898. doi:10.1016/j.bbagen.2021.129898
Edmond, J., and Popjak, G. (1974). Transfer of carbon atoms from mevalonate to n-fatty acids. J. Biol. Chem. 249, 66–71. doi:10.1016/s0021-9258(19)43091-3
Eisenreich, W., Bacher, A., Arigoni, D., and Rohdich, F. (2004). Biosynthesis of isoprenoids via the non-mevalonate pathway. Cell. Mol. Life Sci. 61, 1401–1426. doi:10.1007/s00018-004-3381-z
Ferrara, C. T., Wang, P., Neto, E. C., Stevens, R. D., Bain, J. R., Wenner, B. R., et al. (2008). Genetic networks of liver metabolism revealed by integration of metabolic and transcriptional profiling. PLoS Genet. 4 (3), e1000034. doi:10.1371/journal.pgen.1000034
Furukawa, A., Konuma, T., Yanaka, S., and Sugase, K. (2016). Quantitative analysis of protein-ligand interactions by NMR. Prog. Nucl. Magn. Reson Spectrosc. 96, 47–57. doi:10.1016/j.pnmrs.2016.02.002
Gerstl, M. P., Muller, S., Regensburger, G., and Zanghellini, J. (2019). Flux tope analysis: studying the coordination of reaction directions in metabolic networks. Bioinformatics 35 (2), 266–273. doi:10.1093/bioinformatics/bty550
Gillespie, D. T. (2007). Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 58, 35–55. doi:10.1146/annurev.physchem.58.032806.104637
Gopalan, L., Sebastian, A., Praul, C. A., Albert, I., and Ramachandran, R. (2021). Metformin affects the transcriptomic profile of chicken ovarian cancer cells. Genes. (Basel) 13, 30. doi:10.3390/genes13010030
Goto, T., Fernandes, A. F. A., Tsudzuki, M., and Rosa, G. J. M. (2019). Causal phenotypic networks for egg traits in an F2 chicken population. Mol. Genet. Genomics 294 (6), 1455–1462. doi:10.1007/s00438-019-01588-2
Haraldsdottir, H. S., Thiele, I., and Fleming, R. M. (2012). Quantitative assignment of reaction directionality in a multicompartmental human metabolic reconstruction. Biophys. J. 102, 1703–1711. doi:10.1016/j.bpj.2012.02.032
Heuillet, M., Bellvert, F., Cahoreau, E., Letisse, F., Millard, P., and Portais, J. C. (2018). Methodology for the validation of isotopic analyses by mass spectrometry in stable-isotope labeling experiments. Anal. Chem. 90, 1852–1860. doi:10.1021/acs.analchem.7b03886
Jessen, K. R., Morgan, L., Brammer, M., and Mirsky, R. (1985). Galactocerebroside is expressed by non-myelin-forming Schwann cells in situ. J. Cell. Biol. 101, 1135–1143. doi:10.1083/jcb.101.3.1135
Keller, M. P., and Attie, A. D. (2010). Physiological insights gained from gene expression analysis in obesity and diabetes. Annu. Rev. Nutr. 30, 341–364. doi:10.1146/annurev.nutr.012809.104747
Klamt, S., Regensburger, G., Gerstl, M. P., Jungreuthmayer, C., Schuster, S., Mahadevan, R., et al. (2017). From elementary flux modes to elementary flux vectors: metabolic pathway analysis with arbitrary linear flux constraints. PLoS Comput. Biol. 13 (4), e1005409. doi:10.1371/journal.pcbi.1005409
Klamt, S., Muller, S., Regensburger, G., and Zanghellini, J. (2018). A mathematical framework for yield (vs. rate) optimization in constraint-based modeling and applications in metabolic engineering. Metab. Eng. 47, 153–169. doi:10.1016/j.ymben.2018.02.001
Koutrouli, M., Karatzas, E., Paez-Espino, D., and Pavlopoulos, G. A. (2020). A guide to conquer the biological network era using graph theory. Front. Bioeng. Biotechnol. 8, 34. doi:10.3389/fbioe.2020.00034
Kundu, S. (2016). Stochastic modelling suggests that an elevated superoxide anion - hydrogen peroxide ratio can drive extravascular phagocyte transmigration by lamellipodium formation. J. Theor. Biol. 407, 143–154. doi:10.1016/j.jtbi.2016.07.002
Kundu, S. (2021). Mathematical modeling and stochastic simulations suggest that low-affinity peptides can bisect MHC1-mediated export of high-affinity peptides into "early"- and "late"-phases. Heliyon 7 (7), e07466. doi:10.1016/j.heliyon.2021.e07466
Kundu, S. (2022). Modeling ligand-macromolecular interactions as eigenvalue-based transition-state dissociation constants may offer insights into biochemical function of the resulting complexes. Math. Biosci. Eng. 19, 13252–13275. doi:10.3934/mbe.2022620
Kundu, S. (2023a). A mathematically rigorous algorithm to define, compute and assess relevance of the probable dissociation constant for every reaction of a constrained biochemical network. Res. Square. [Preprint]. doi:10.21203/rs.3.rs-3093545/v1
Kundu, S. (2023b). ReDirection: A numerically robust R-package to characterize every reaction of a user-defined biochemical network with the probable dissociation constant. [Preprint]. [bioRxiv 2023.07.12.548670]. doi:10.1101/2023.07.12.548670
Lecca, P., Palmisano, A., Priami, C., and Sanguinetti, G. (2009). “A new probabilistic generative model of parameter inference in biochemical networks,” in Proceedings of the 2009 ACM symposium on Applied Computing - SAC '09, March 2009, 758–765.
Lee, M. K., Mohamad, M. S., Choon, Y. W., Mohd Daud, K., Nasarudin, N. A., Ismail, M. A., et al. (2020). Comparison of optimization-modelling methods for metabolites production in Escherichia coli. J. Integr. Bioinform 17, 20190073. doi:10.1515/jib-2019-0073
Lu, J., Dumitrascu, B., McDowell, I. C., Jo, B., Barrera, A., Hong, L. K., et al. (2021). Causal network inference from gene transcriptional time-series response to glucocorticoids. PLoS Comput. Biol. 17 (1), e1008223. doi:10.1371/journal.pcbi.1008223
Muller, S., and Regensburger, G. (2016). Elementary vectors and conformal sums in polyhedral geometry and their relevance for metabolic pathway analysis. Front. Genet. 7, 90. doi:10.3389/fgene.2016.00090
Nakanishi, M., Goldstein, J. L., and Brown, M. S. (1988). Multivalent control of 3-hydroxy-3-methylglutaryl coenzyme A reductase. Mevalonate-derived product inhibits translation of mRNA and accelerates degradation of enzyme. J. Biol. Chem. 263, 8929–8937. doi:10.1016/s0021-9258(18)68397-8
Nicoli, E. R., Annunziata, I., d'Azzo, A., Platt, F. M., Tifft, C. J., and Stepien, K. M. (2021). GM1 gangliosidosis-A mini-review. Front. Genet. 12, 734878. doi:10.3389/fgene.2021.734878
Orth, J. D., Thiele, I., and Palsson, B. O. (2010). What is flux balance analysis? Nat. Biotechnol. 28 (3), 245–248. doi:10.1038/nbt.1614
Paoli, M., Marles-Wright, J., and Smith, A. (2002). Structure-function relationships in heme-proteins. DNA Cell. Biol. 21, 271–280. doi:10.1089/104454902753759690
Pappu, A. S., Steiner, R. D., Connor, S. L., Flavell, D. P., Lin, D. S., Hatcher, L., et al. (2002). Feedback inhibition of the cholesterol biosynthetic pathway in patients with Smith-Lemli-Opitz syndrome as demonstrated by urinary mevalonate excretion. J. Lipid Res. 43, 1661–1669. doi:10.1194/jlr.m200163-jlr200
Poulos, T. L. (2014). Heme enzyme structure and function. Chem. Rev. 114, 3919–3962. doi:10.1021/cr400415k
Raff, M. C., Mirsky, R., Fields, K. L., Lisak, R. P., Dorfman, S. H., Silberberg, D. H., et al. (1978). Galactocerebroside is a specific cell-surface antigenic marker for oligodendrocytes in culture. Nature 274, 813–816. doi:10.1038/274813a0
Reinker, S., Altman, R. M., and Timmer, J. (2006). Parameter estimation in stochastic biochemical reactions. Syst. Biol. (Stevenage) 153, 168–178. doi:10.1049/ip-syb:20050105
Riva, S. G., Cazzaniga, P., Nobile, M. S., Spolaor, S., Rundo, L., Besozzi, D., et al. (2022). SMGen: A generator of synthetic models of biochemical reaction networks. Symmetry 14, 119. doi:10.3390/sym14010119
Rottman, B. M., and Hastie, R. (2014). Reasoning about causal relationships: inferences on causal networks. Psychol. Bull. 140 (1), 109–139. doi:10.1037/a0031903
Roullet, J. B., Merkens, L. S., Pappu, A. S., Jacobs, M. D., Winter, R., Connor, W. E., et al. (2012). No evidence for mevalonate shunting in moderately affected children with Smith-Lemli-Opitz syndrome. J. Inherit. Metab. Dis. 35, 859–869. doi:10.1007/s10545-012-9453-6
Salvador, A. C., Arends, D., Barrington, W. T., Elsaadi, A. M., Brockmann, G. A., and Threadgill, D. W. (2021). Sex-specific genetic architecture in response to American and ketogenic diets. Int. J. Obes. (Lond). 45 (6), 1284–1297. doi:10.1038/s41366-021-00785-7
Saptarshi, N., Green, D., Cree, A., Lotery, A., Paraoan, L., and Porter, L. F. (2021). Epigenetic age acceleration is not associated with age-related macular degeneration. Int. J. Mol. Sci. 22 (24), 13457. doi:10.3390/ijms222413457
Segre, D., Vitkup, D., and Church, G. M. (2002). Analysis of optimality in natural and perturbed metabolic networks. Proc. Natl. Acad. Sci. U. S. A. 99, 15112–15117. doi:10.1073/pnas.232349399
Seyhan, A. A., and Carini, C. (2019). Are innovation and new technologies in precision medicine paving a new era in patients centric care? J. Transl. Med. 17 (1), 114. doi:10.1186/s12967-019-1864-9
Shindo, Y., Kondo, Y., and Sako, Y. (2018). Inferring a nonlinear biochemical network model from a heterogeneous single-cell time course data. Sci. Rep. 8, 6790. doi:10.1038/s41598-018-25064-w
Shlomi, T., Berkman, O., and Ruppin, E. (2005). Regulatory on/off minimization of metabolic flux changes after genetic perturbations. Proc. Natl. Acad. Sci. U. S. A. 102, 7695–7700. doi:10.1073/pnas.0406346102
Sparks, R. P., Jenkins, J. L., and Fratti, R. (2019). Use of surface plasmon resonance (SPR) to determine binding affinities and kinetic parameters between components important in fusion machinery. Methods Mol. Biol. 1860, 199–210. doi:10.1007/978-1-4939-8760-3_12
Stein, P. E., Badminton, M. N., and Rees, D. C. (2017). Update review of the acute porphyrias. Br. J. Haematol. 176, 527–538. doi:10.1111/bjh.14459
Sura, R., and Antalik, M. (2022). Determination of proton dissociation constants (pK(a)) of hydroxyl groups of 2,5-dihydroxy-1,4-benzoquinone (DHBQ) by UV-Vis, fluorescence and ATR-FTIR spectroscopy. Spectrochim. Acta A Mol. Biomol. Spectrosc. 271, 120863. doi:10.1016/j.saa.2022.120863
Thom, C. S., Dickson, C. F., Gell, D. A., and Weiss, M. J. (2013). Hemoglobin variants: biochemical properties and clinical correlates. Cold Spring Harb. Perspect. Med. 3, a011858. doi:10.1101/cshperspect.a011858
Urbanczik, R. (2007). Enumerating constrained elementary flux vectors of metabolic networks. IET Syst. Biol. 1 (5), 274–279. doi:10.1049/iet-syb:20060073
Wagner, C., and Urbanczik, R. (2005). The geometry of the flux cone of a metabolic network. Biophys. J. 89 (6), 3837–3845. doi:10.1529/biophysj.104.055129
Wang, Y., Wondisford, F. E., Song, C., Zhang, T., and Su, X. (2020). Metabolic flux analysis-linking isotope labeling and metabolic fluxes. Metabolites 10, 447. doi:10.3390/metabo10110447
Wittenstein, T., Leibovich, N., and Hilfinger, A. (2022). Quantifying biochemical reaction rates from static population variability within incompletely observed complex networks. PLoS Comput. Biol. 18, e1010183. doi:10.1371/journal.pcbi.1010183
Keywords: biochemical network, null space-generated subspaces of combinatorial sums of non-trivial and nonredundant vectors, probable disassociation constant and reaction outcome, “R”-package, reaction-specific sequence and outcome vectors, stoichiometry number matrix
Citation: Kundu S (2023) ReDirection: an R-package to compute the probable dissociation constant for every reaction of a user-defined biochemical network. Front. Mol. Biosci. 10:1206502. doi: 10.3389/fmolb.2023.1206502
Received: 15 April 2023; Accepted: 14 September 2023;
Published: 24 October 2023.
Edited by:
Valentina Tozzini, National Research Council (CNR), ItalyReviewed by:
Onur Serçinoğlu, Gebze Technical University, TürkiyePiero Mazzarisi, University of Siena, Italy
Copyright © 2023 Kundu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Siddhartha Kundu, c2lkZGhhcnRoYV9rdW5kdUB5YWhvby5jby5pbg==, c2lkZGhhcnRoYV9rdW5kdUBhaWltcy5lZHU=
 Siddhartha Kundu
Siddhartha Kundu