High Resolution 31P Field Cycling NMR Reveals Unsuspected Features of Enzyme-Substrate-Cofactor Dynamics

The dynamic interactions of enzymes and substrates underpins catalysis, yet few techniques can interrogate the dynamics of protein-bound ligands. Here we describe the use of field cycling NMR relaxometry to measure the dynamics of enzyme-bound substrates and cofactors in catalytically competent complexes of GMP reductase. These studies reveal new binding modes unanticipated by x-ray crystal structures and reaction-specific dynamic networks. Importantly, this work demonstrates that distal interactions not usually considered part of the reaction coordinate can play an active role in catalysis. The commercialization of shuttling apparatus will make field cycling relaxometry more accessible and expand its use to additional nuclei, promising more intriguing findings to come.

Introduction

The extraordinary power of enzyme catalysis relies on the dynamic alignment of substrates and active site residues. While X-ray crystal structures provide invaluable insights into enzyme-substrate interactions, such structures are typically static views of chemically inert complexes. Tremendous progress has been made using NMR methods to measure protein dynamics, but such studies have largely focused on changes in protein conformation and identification of ligand binding sites, again with typically chemically inert complexes (Akke, 2012; Palmer, 2015; Bax and Clore, 2019; Strotz et al., 2020). These experiments have limited utility for large multimeric proteins. Paramagnetic relaxation can be used to measure ligand binding and infer conformation if the enzyme contains a suitable spin center (Li et al., 2012; Softley et al., 2020). Substrate dynamics can also be addressed computationally, but proper benchmarking is difficult given the few experimental methods available to validate or corroborate such studies (Chakravorty and Merz, 2015). Here we describe the use of high resolution ³¹P field cycling NMR relaxometry to investigate the dynamics of enzyme-bound substrates and cofactors. These experiments provide a unique ligand-centric view of protein-ligand interactions. We describe work in the model system of GMP reductase (GMPR) (Rosenberg et al., 2016; Rosenberg et al., 2018; Rosenberg et al., 2020), where these experiments reveal a novel binding mode unanticipated by crystal structures as well as reaction-specific dynamic networks. Importantly, this work demonstrates that substrate/cofactor phosphates and other interactions not usually considered part of the reaction coordinate can be active participants in catalysis rather than passive bystanders as often assumed.

The Method

The power of subtesla high-resolution field-cycling NMR relaxometry to interrogate the dynamics of enzyme-bound substrates is only beginning to be appreciated (Roberts and Redfield, 2004; Pu et al., 2009; Pu et al., 2010; Redfield, 2012; Gradziel et al., 2014; Wei et al., 2015; Roberts et al., 2021; Wang et al., 2021). Dipolar relaxation results from the interaction of a nucleus of interest, e.g., ³¹P, with nearby dipoles, usually ¹H. An example of potential ³¹P—¹ H dipolar interactions for an enzyme-bound substrate is shown in Figure 1A. Thus dipolar relaxation reflects the structure of the binding site and the mobility of substrate. However, chemical shift anisotropy (CSA) is the mechanism that dominates the spin-lattice/longitudinal rate (R₁) of ³¹P in the high magnetic fields of current spectrometers. Dipolar relaxation can be observed at lower magnetic fields where CSA relaxation is minimal, but differences in the chemical shifts of multiple ³¹P in a sample are lost. In a high resolution field cycling relaxometry experiment, samples are excited at high magnetic field, shuttled up the bore of the magnet to low field for relaxation, then shuttled back to high field to detect the residual magnetization (Figure 1B) (Roberts and Redfield, 2004; Redfield, 2012). This type of field cycling preserves chemical shift information, allowing the magnetic field dependence of R₁ to be measured simultaneously for different ³¹P nuclei. Importantly, the enzyme-bound substrate must be in fast exchange with free substrate, making the observed R₁ the weighted average of the very small R₁ of the free substrate and the much larger R₁ of the enzyme-bound substrate (which is a function of the correlation time of the enzyme•substrate complex) (Pu et al., 2009). Under these conditions, the experiments characterize the ground state Michaelis complex.

FIGURE 1

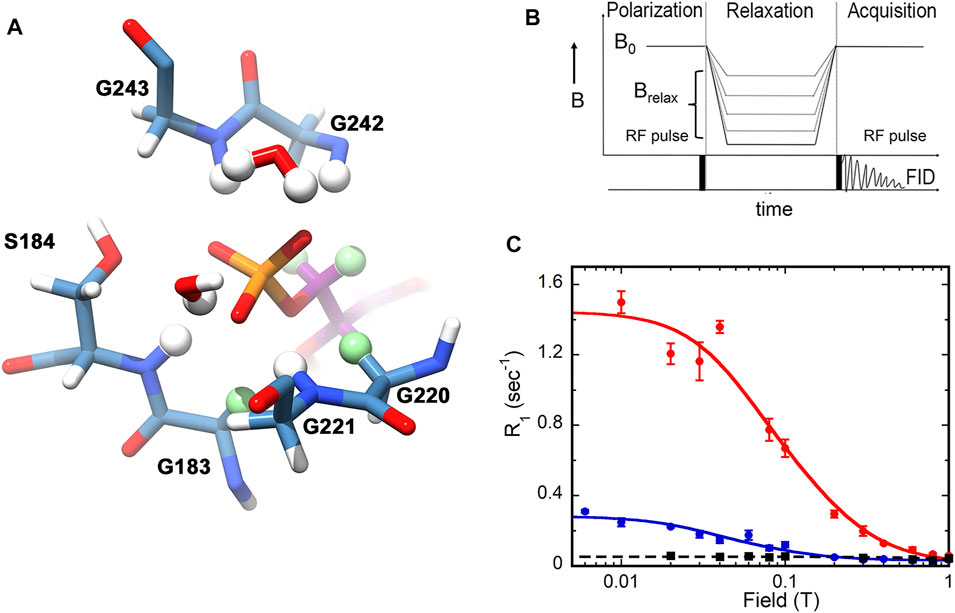
FIGURE 1. ³¹P relaxation as measured by high resolution relaxometry. (A) Structure of the IMP monophosphate binding site in the E•IMP•NADP⁺ complex of GMPR (pdb 2c6q). Residues within 4 Å of the IMP ³¹P are shown. Protein carbon atoms are colored steel blue, IMP carbon atoms are dark magenta, potential ¹H relaxers are shown as balls, nonexchangeable ¹H relaxers are light green. This figure was produced with UCSF Chimera (Pettersen et al., 2004). (B) Design of the field cycling experiment. (C) Examples of field cycling data for substrate monophosphates in ternary complexes with GMPR and cofactor (Rosenberg et al., 2016). The relaxation of IMP is shown in red and GMP in blue. The black trace shows the relaxation of IMP in the absence of enzyme. Note that the CSA component of relaxation is not observed since the field axis is only shown to 1 T and R_CSA is not observed until the magnetic field is greater than 5 T. (B,C) were reprinted with permission from (Rosenberg et al., 2018). Copyright 2020 American Chemical Society.

In a typical high resolution relaxometry experiment (e.g., Figure 1C), R₁ is measured at varying magnetic fields ranging from 0.003 to 11.7 T, yielding two dipolar parameters: 1) R_D(0), the maximum dipolar relaxation rate at zero field; and 2) τ_D, the molecular dipolar correlation time (Roberts and Redfield, 2004; Redfield, 2012). The overall R₁ at any magnetic field is then the sum of dipolar and CSA R₁ values. Importantly, the ratio τ_D/R_D(0) is related to the sixth power of the averaged effective distance (r_eff) between the ³¹P nuclei and the ¹H relaxers. These relationships are described in equations 1-3.

$R_1=\left(\frac{R_D\left(0\right)}{2{\tau }_D}\right)\left\{0.1J\left({\tau }_D,{\omega }_H–{\omega }_P\right)+0.3J\left({\tau }_D,{\omega }_P\right)+0.6J\left({\tau }_D,{\omega }_H+{\omega }_P\right)\right\}+k_D + k_{CSA}{\omega }_P^2 (1)$

${\mathrm{r}}_{\mathrm{e}\mathrm{f}\mathrm{f}}^6=\frac{{\left({\mu }_0/4\mathrm{\pi }\right)}^2{\left(\mathrm{h}/2\mathrm{\pi }\right)}^2{\mathrm{\gamma }}_{\mathrm{P}}^2{\mathrm{\gamma }}_{\mathrm{H}}^2{\mathrm{\tau }}_{\mathrm{D}}}{{\mathrm{R}}_{\mathrm{D}}\left(0\right)}(2)$

where

$\mathrm{J}\left({\tau }_D,\mathrm{\omega }\right)=\frac{2 {\tau }_D}{\left(1+{\mathrm{\omega }}^2{\mathrm{\tau }}_D^2\right)}(3)$

and k_D is the R_D(0) for very fast dipolar relaxation of the ³¹P where τ_D < 0.5 ns (Roberts et al., 2021). The R_CSA term, k_CSA ω_P², assumes that ω²τ_CSA² < 1; the square law increase in R₁ is not detected until the relaxation field, B_relax, is >5 T. In the expression for r_eff, µ₀ is the magnetic permeability in a vacuum, h is Planck’s constant, and the two γ are gyromagnetic ratios for ³¹P and ¹H.

For the purposes of this review, discussion will be limited to τ_D and τ_D/R_D0. If the bound substrate is relatively rigid, then the value of τ_D will be comparable to the overall rotation of the enzyme complex, but if the substrate is mobile, the values of R_D(0) and τ_D can be reduced. As noted above, the sixth root of τ_D/R_D0 is related to the averaged effective distance (r_eff) between the ³¹P nucleus and the ¹H relaxers, so that smaller values of τ_D/R_D0 indicate that the relaxers are closer and/or more relaxers are present. The ¹H relaxers can be intramolecular (e.g., the 5′-¹H nuclei of IMP in Figure 1A), in which case their contribution to relaxation is determined by the conformation of the substrate, or intermolecular (e.g., αC¹H₂ nuclei of Gly183 and Gly220 in Figure 1A), where their contribution is determined by the structure of the binding site. The ¹H relaxers can also be exchangeable protons or even water. Thus, high resolution relaxometry experiments probe critical structural and dynamic features of substrate binding sites.

The System

Given the widespread prevalence of phosphorylated metabolites in critical biochemical pathways, there are surprisingly few studies that utilize ³¹P NMR relaxation, and specifically spin-lattice/longitudinal relaxation, to investigate enzyme-substrate dynamics. GMPR is a particularly attractive system for such studies because the reaction involves four ³¹P nuclei, one on the GMP/IMP substrate and three on the NADP⁺ cofactor. Moreover, the cofactor undergoes a conformational change during the catalytic cycle (Patton et al., 2011), suggesting that relaxation studies will provide new insights into the reaction. As described below, two dead-end yet catalytically competent complexes are available, mimicking each step of the catalytic cycle. GMPR is an (α/β)₈ “TIM” barrel, the most common enzyme fold, with the standard phosphate “gripper” loop conserved throughout the TIM superfamily (Wilmanns et al., 1991; Nagano et al., 2002). Therefore investigation of GMPR is likely to provide insight into many enzyme reactions.

GMPR catalyzes the reduction of GMP to IMP and ammonia with concomitant oxidation of NADPH. The reaction proceeds via two steps (Figure 2A): 1) Deamination of GMP via attack of the catalytic Cys to produce the thioimidate intermediate E-XMP* and ammonia followed by 2) hydride transfer from NADPH to E-XMP* producing IMP. Two catalytically active, yet dead end, complexes provide windows into each step (Figure 2B): 1) The E•GMP•NADP⁺ complex can undergo deamination to form E-XMP*•NH₃•NADP⁺ but cannot proceed to products in the absence of NADPH; 2) hydride transfer can occur in the E•IMP•NADP⁺ complex to form E-XMP*•NADPH, but the reaction cannot proceed to GMP in the absence of ammonia. The cofactor is present throughout the catalytic cycle (Patton et al., 2011), and must adopt different conformations in each step. Two cofactor conformations are found in the x-ray crystal structure of the inactive E•IMP•NADPH complex (Figure 2C) (Patton et al., 2011). The nicotinamide is far from the substrate in the “OUT” conformation, as would be expected during the deamination reaction. In contrast, the nicotinamide is stacked with the substrate as required for hydride transfer in the “IN” conformation. The two ³¹P nuclei of the cofactor diphosphate occupy different sites in the IN and OUT conformations, while the substrate and cofactor monophosphates appear to occupy the same site in both complexes. If the crystal structures accurately reflect catalytically competent structures, then the cofactor diphosphates are expected to be mobile while the substrate and cofactor monophosphates are constrained.

FIGURE 2

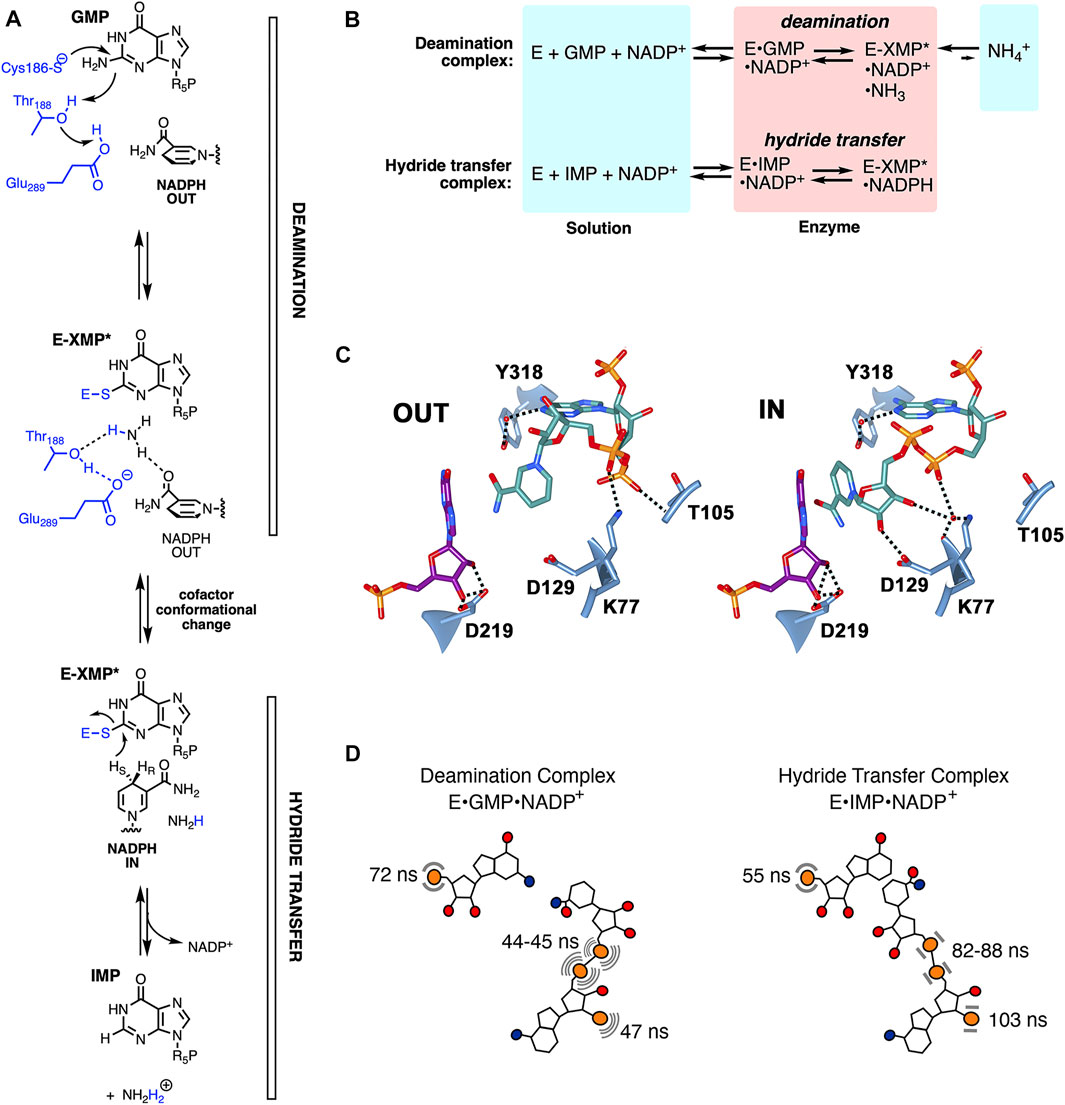
FIGURE 2. The dynamics of enzyme-bound substrate and cofactors in GMPR. (A) The GMPR reaction. (B) Partial reactions catalyzed by GMPR. (C) Cofactor conformations observed in E•IMP•NADP⁺ crystal structure (pdb 2c6q). IMP carbon atoms are shown in dark magenta, NADP⁺ in dark cyan, hydrogen bonds are depicted with dashed lines. This figure was produced with UCSF Chimera (Pettersen et al., 2004). (D) Cartoon showing the values of τ_D in the deamination and hydride transfer complexes. The cofactor is more dynamic than the substrate in the deamination complex while the substrate is more dynamic than the cofactor in the hydride transfer complex. (A,B) were reprinted with permission from (Rosenberg et al., 2020). Copyright 2020 American Chemical Society.

Field Cycling Reveals a Novel Binding Site and Reaction-specific Dynamics

The values of τ_D reveal surprising differences in the mobilities of enzyme bound substrates and cofactors (Rosenberg et al., 2016; 2018). As noted above, if the substrate/cofactor is rigidly bound, then the value of τ_D should approximate the rotational correlation time for the enzyme. GMPR is a homotetramer of 37 kDa subunits. For a spherical protein of this size, the correlation time can be estimated to be ∼70 ns using Stokes law. However, GMPR is disk-like, with multiple rotational axes, each with a distinct correlation time, corresponding to a larger observed τ_D (Ortega and Torre, 2003). The observed values of τ_D for ³¹P nuclei bound to wild-type GMPR complexes are as high as 103 ns (Rosenberg et al., 2016). Mutant enzyme complexes, e.g., K77A and D129A, can display ³¹P τ_D values of 160–195 ns (Rosenberg et al., 2020), which may be the actual correlation time for the protein. The τ_D values were much less than 160 ns in most cases, suggesting that the enzyme-bound substrate and cofactor are mobile. Importantly, if the substrate and cofactor were both rigidly bound to the enzyme, the values of τ_D for all for ³¹P nuclei would be the same. As described in more detail below, the values of τ_D vary for different nuclei in different complexes, such that distinct dynamic signatures are observed for each partial reaction.

The values of τ_D for the ³¹P nuclei of GMP and IMP in their respective binary enzyme complexes were both 43 ns (±4 and ±6 ns, respectively), indicating that the monophosphates are mobile on the enzyme. The values of τ_D/R_D(0) for enzyme bound GMP and IMP are also very similar (1.9–2.0 × 10⁻⁸ s² for τ_D/R_D0), indicating that the binding sites are essentially the same, as found in the crystal structures.

In contrast to the binary substrate complexes, the ternary enzyme-substrate-cofactor complexes display distinct dynamic profiles (Figures 1C, 2D) (Rosenberg et al., 2016; 2018). The dynamic properties of IMP are very similar in the absence and presence of NADP⁺. The cofactor increased the value of τ_D for GMP, suggesting that GMP is more rigidly bound than IMP in the cofactor complex. More importantly, a 10-fold increase is observed in the value of τ_D/R_D(0) for GMP, which indicates that the cofactor induces a new binding mode for GMP where the substrate monophosphate is farther from ¹H relaxers than in the IMP•cofactor complex. This difference in substrate monophosphate binding modes was further substantiated when relaxation was measured in the presence of D₂O, which increases τ_D/R_D(0) for the IMP ³¹P by 2.5-fold but has no effect on the relaxation of GMP ³¹P. Thus exchangeable ¹H relaxers are present near the IMP monophosphate that are absent in the GMP binding site. These observations reveal a novel binding mode for GMP unanticipated by the crystal structures. The reaction-specific interactions induced by the cofactor indicate that the monophosphate does not simply tether the substrate to the active site but instead participates in the catalytic cycle. Since the substrate monophosphate binds in the conserved phosphate gripper motif found throughout the TIM superfamily, similar reaction-specific interactions may well occur in many other enzyme reactions.

The cofactor displays different dynamic properties in the deamination and hydride transfer complexes (Figure 2D). All three cofactor ³¹P nuclei are more mobile than the substrate monophosphate in the deamination complex, with values of τ_D ranging from 44 to 47 ns versus 72 ns for GMP. In contrast, the cofactor is more rigid than the substrate in the hydride transfer complex, with values of τ_D ranging from 82 to 103 ns versus 55 ns for IMP. While the differences in the dynamic behavior of the diphosphate ³¹P nuclei were anticipated from the crystal structures, the cofactor monophosphate was expected to exhibit similar dynamic features in both complexes. Thus, like the substrate monophosphate, the cofactor monophosphate is also intimately coupled to the catalytic cycle.

Although the crystal structure suggested that the cofactor should occupy different sites in the deamination and hydride transfer complexes, the values of τ_D/R_D(0) for the diphosphate ³¹P nuclei were similar, with overlapping errors (e.g., (9.2 ± 2.4) × 10⁻⁸ s² and (6.6 ± 1.2) × 10⁻⁸ s² for the deamination and hydride transfer complex, respectively). Close inspection of the crystal structures revealed similar numbers of ¹H relaxers in the vicinity of the cofactor diphosphate ³¹P nuclei in the OUT and IN conformations (14 and 15, respectively, within 4 Å), which can explain the similar values of τ_D/R_D(0). However, fewer exchangeable ¹H relaxers are observed in the OUT conformation (8) than in the IN conformation (13), suggesting that D₂O should have a larger effect on the dynamic properties of the hydride transfer complex than the deamination complex. Indeed, the presence of D₂O increased the values of τ_D/R_D(0) for the diphosphate ³¹P nuclei by a factor of 2 in the hydride transfer complex versus 1.5 in the GMP complex, as expected if the cofactor has different binding modes as suggested by the crystal structures.

Distinct Enzyme•Substrate•Cofactor Interactions Modulate Reaction-Specific Dynamics

The field cycling experiments indicate that distinct dynamic behavior is associated with each step in the catalytic cycle. Mutagenesis and substrate analogs revealed that this behavior derives from specific enzyme•substrate•cofactor interactions. For example, the substrate 2′-OH forms a hydrogen bond with Asp219 in the crystal structures (Figure 2C). The removal of this interaction by creating an enzyme-cofactor complex with dIMP reduced the rate of hydride transfer by a factor of 6.7 (Rosenberg et al., 2018). The dynamics of this complex were dysregulated, with values of τ_D and τ_D/R_D(0) very similar to those of the native deamination complex. Thus the 2′-OH of IMP differentiates the two dynamic states. Further insight into the nature of the reaction-specific dynamics were revealed by substituting Asp219 with Ala. This mutation reduced the rate of deamination by 50-fold and caused widespread changes in dynamics (Rosenberg et al., 2018). Perhaps counterintuitively, the loss of the Asp219 interaction caused both substrate and cofactor to be constrained relative to the native deamination complex. Moreover, the substrate binding mode was not congruent with deamination but instead resembled that of the native hydride transfer complex. The D219A substitution had little effect on the rate of hydride transfer and dynamics of the E•IMP•cofactor complex. Thus Asp219 is part of a deamination-specific dynamic network.

Further exploration of the roles of active site residues revealed complex networks of dynamic interactions. Asp129 forms a hydrogen bond to the cofactor in the IN conformation in the crystal structure (Figure 2C), suggesting that it holds the cofactor in place for hydride transfer. This interaction is absent in the OUT conformation. Substitution of Asp129 with Ala reduces the rates of both deamination and hydride transfer by factors of 100 (Rosenberg et al., 2020). The dynamic profiles of the deamination and hydride transfer complexes were indistinguishable in the D129A variant, and both substrate and cofactor were constrained when bound to the enzyme, with values of τ_D ranging from 100 to 160 ns for the cofactor ³¹P nuclei. Thus Asp129 is a critical link in the dynamic networks of both reactions.

Lys77 makes hydrogen bonds to the cofactor, either direct or indirect via water, in both the OUT and IN conformations in the crystal structure. Substitution of Lys77 with Ala reduced the rate of deamination and hydride transfer by factors of 100 and 30, respectively (Rosenberg et al., 2020). This substitution had dramatic, yet reaction-specific, effects on the dynamics of both complexes. The dynamics of GMP and cofactor most closely resembled a native hydride transfer complex, and thus are not compatible with deamination, while IMP and cofactor were both constrained when bound to the K77A variant. These observations suggest that Lys77 also participates in the dynamic networks of both reactions. In contrast, Thr105, Tyr318 and Asp219 participate in the deamination-specific network but are not involved in hydride transfer. These findings provide a framework to identify correlated motions required for catalysis in the two steps of the GMPR reaction.

Future Perspectives

While the field cycling experiments described above only begin to map the reaction-specific dynamic networks of GMPR, some themes have already emerged. First, critical dynamic interactions extend far beyond the sites of chemical transformation to seemingly inert moieties like the substrate monophosphate. Second, field cycling can reveal catalytically competent binding modes that elude crystal structures. Lastly, seemingly small structural perturbations of the substrate or enzyme such as the substitution of H for OH, can cause widespread and unpredictable changes in the dynamic behavior of substrates and cofactors. We have only just scratched the surface of the potential of high resolution ³¹P relaxometry given the prevalence of phosphorylated substrates and cofactors.

Until recently, shuttler systems for high resolution solution field cycling have been home-built (Ajoy et al., 2019; Charlier et al., 2013; Chou et al., 2012; Redfield, 2012; Roberts et al., 2004). The method will become more accessible with the availability of commercial add-on shuttling systems compatible with cryo-probes from Field Cycling Technology Ltd., Taiwan (Chou et al., 2012). Such systems will provide enhanced sensitivity and extend the methodology to other ligand nuclei (e.g., ¹H, or specifically enriched ¹³C or ¹⁵N). We believe high resolution field cycling relaxometry is poised to reveal many more unsuspected features of the structure and dynamics of protein-ligand binding.

Author Contributions

The authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Institutes of Health (GM054403 to LH). Molecular graphics images were produced using the UCSF Chimera package from the Computer Graphics Laboratory, University of California, San Francisco (supported by NIGMS P41-GM103311).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ajoy, A., Lv, X., Druga, E., Liu, K., Safvati, B., Morabe, A., et al. (2019). Wide Dynamic Range Magnetic Field Cycler: Harnessing Quantum Control at Low and High fields. Rev. Scientific Instr. 90, 013112. doi:10.1063/1.5064685

PubMed Abstract | CrossRef Full Text | Google Scholar

Akke, M. (2012). Conformational Dynamics and Thermodynamics of Protein-Ligand Binding Studied by NMR Relaxation. Biochem. Soc. Trans. 40, 419–423. doi:10.1042/BST20110750

PubMed Abstract | CrossRef Full Text | Google Scholar

Bax, A., and Clore, G. M. (2019). Protein NMR: Boundless Opportunities. J. Magn. Reson. 306, 187–191. doi:10.1016/j.jmr.2019.07.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakravorty, D. K., and Merz, K. M. (2015). Role of Substrate Dynamics in Protein Prenylation Reactions. Acc. Chem. Res. 48, 439–448. doi:10.1021/ar500321u

PubMed Abstract | CrossRef Full Text | Google Scholar

Charlier, C., Khan, S. N., Marquardsen, T., Pelupessy, P., Reiss, V., Sakellariou, D., et al. (2013). Nanosecond Time Scale Motions in Proteins Revealed by High-Resolution NMR Relaxometry. J. Am. Chem. Soc. 135, 18665–18672. doi:10.1021/ja409820g

PubMed Abstract | CrossRef Full Text | Google Scholar

Chou, C.-Y., Chu, M., Chang, C.-F., and Huang, T.-h. (2012). A Compact High-Speed Mechanical Sample Shuttle for Field-dependent High-Resolution Solution NMR. J. Magn. Reson. 214, 302–308. doi:10.1016/j.jmr.2011.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Gradziel, C. S., Wang, Y., Stec, B., Redfield, A. G., and Roberts, M. F. (2014). Cytotoxic Amphiphiles and Phosphoinositides Bind to Two Discrete Sites on the Akt1 PH Domain. Biochemistry 53, 462–472. doi:10.1021/bi401720v

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Tietz, D. R., Rutaganira, F. U., Kells, P. M., Anzai, Y., Kato, F., et al. (2012). Substrate Recognition by the Multifunctional Cytochrome P450 MycG in Mycinamicin Hydroxylation and Epoxidation Reactions. J. Biol. Chem. 287, 37880–37890. doi:10.1074/jbc.M112.410340

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagano, N., Orengo, C. A., and Thornton, J. M. (2002). One Fold with many Functions: the Evolutionary Relationships between TIM Barrel Families Based on Their Sequences, Structures and Functions. J. Mol. Biol. 321, 741–765. doi:10.1016/s0022-2836(02)00649-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Ortega, A., and Garcı́a de la Torre, J. (2003). Hydrodynamic Properties of Rodlike and Disklike Particles in Dilute Solution. J. Chem. Phys. 119, 9914–9919. doi:10.1063/1.1615967

CrossRef Full Text | Google Scholar

Palmer, A. G. (2015). Enzyme Dynamics from NMR Spectroscopy. Acc. Chem. Res. 48, 457–465. doi:10.1021/ar500340a

PubMed Abstract | CrossRef Full Text | Google Scholar

Patton, G. C., Stenmark, P., Gollapalli, D. R., Sevastik, R., Kursula, P., Flodin, S., et al. (2011). Cofactor Mobility Determines Reaction Outcome in the IMPDH and GMPR (β-Α)8 Barrel Enzymes. Nat. Chem. Biol. 7, 950–958. doi:10.1038/nchembio.693

PubMed Abstract | CrossRef Full Text | Google Scholar

Pettersen, E. F., Goddard, T. D., Huang, C. C., Couch, G. S., Greenblatt, D. M., Meng, E. C., et al. (2004). UCSF Chimera?A Visualization System for Exploratory Research and Analysis. J. Comput. Chem. 25, 1605–1612. doi:10.1002/jcc.20084

PubMed Abstract | CrossRef Full Text | Google Scholar

Pu, M., Feng, J., Redfield, A. G., and Roberts, M. F. (2009). Enzymology with a Spin-Labeled Phospholipase C: Soluble Substrate Binding by 31P NMR from 0.005 to 11.7 T. Biochemistry 48, 8282–8284. doi:10.1021/bi901190j

PubMed Abstract | CrossRef Full Text | Google Scholar

Pu, M., Orr, A., Redfield, A. G., and Roberts, M. F. (2010). Defining Specific Lipid Binding Sites for a Peripheral Membrane Protein In Situ Using Subtesla Field-Cycling NMR. J. Biol. Chem. 285, 26916–26922. doi:10.1074/jbc.M110.123083

PubMed Abstract | CrossRef Full Text | Google Scholar

Redfield, A. G. (2012). High-resolution NMR Field-Cycling Device for Full-Range Relaxation and Structural Studies of Biopolymers on a Shared Commercial Instrument. J. Biomol. NMR 52, 159–177. doi:10.1007/s10858-011-9594-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, M. F., Cai, J., V. Natarajan, S., Khan, H. M., Reuter, N., Gershenson, A., et al. (2021). Phospholipids in Motion: High-Resolution 31P NMR Field Cycling Studies. J. Phys. Chem. B 125, 8827–8838. doi:10.1021/acs.jpcb.1c02105

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, M. F., Cui, Q., Turner, C. J., Case, D. A., and Redfield, A. G. (2004). High-resolution Field-Cycling NMR Studies of a DNA Octamer as a Probe of Phosphodiester Dynamics and Comparison with Computer Simulation. Biochemistry 43, 3637–3650. doi:10.1021/bi035979q

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, M. F., and Redfield, A. G. (2004). High-resolution 31p Field Cycling NMR as a Probe of Phospholipid Dynamics. J. Am. Chem. Soc. 126, 13765–13777. doi:10.1021/ja046658k

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenberg, M. M., Redfield, A. G., Roberts, M. F., and Hedstrom, L. (2018). Dynamic Characteristics of Guanosine-5′-Monophosphate Reductase Complexes Revealed by High-Resolution 31P Field-Cycling NMR Relaxometry. Biochemistry 57, 3146–3154. doi:10.1021/acs.biochem.8b00142

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenberg, M. M., Redfield, A. G., Roberts, M. F., and Hedstrom, L. (2016). Substrate and Cofactor Dynamics on Guanosine Monophosphate Reductase Probed by High Resolution Field Cycling 31P NMR Relaxometry. J. Biol. Chem. 291, 22988–22998. doi:10.1074/jbc.M116.739516

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenberg, M. M., Yao, T., Patton, G. C., Redfield, A. G., Roberts, M. F., and Hedstrom, L. (2020). Enzyme-substrate-cofactor Dynamical Networks Revealed by High-Resolution Field Cycling Relaxometry. Biochemistry 59, 2359–2370. doi:10.1021/acs.biochem.0c00212

PubMed Abstract | CrossRef Full Text | Google Scholar

Softley, C. A., Bostock, M. J., Popowicz, G. M., and Sattler, M. (2020). Paramagnetic NMR in Drug Discovery. J. Biomol. NMR 74, 287–309. doi:10.1007/s10858-020-00322-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Strotz, D., Orts, J., Kadavath, H., Friedmann, M., Ghosh, D., Olsson, S., et al. (2020). Protein Allostery at Atomic Resolution. Angew. Chem. Int. Ed. 59, 22132–22139. doi:10.1002/anie.202008734

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Pisano, S., Ghini, V., Kadeřávek, P., Zachrdla, M., Pelupessy, P., et al. (2021). Detection of Metabolite-Protein Interactions in Complex Biological Samples by High-Resolution Relaxometry: Toward Interactomics by NMR. J. Am. Chem. Soc. 143, 9393–9404. doi:10.1021/jacs.1c01388

CrossRef Full Text | Google Scholar

Wei, Y., Stec, B., Redfield, A. G., Weerapana, E., and Roberts, M. F. (2015). Phospholipid-binding Sites of Phosphatase and Tensin Homolog (PTEN). J. Biol. Chem. 290, 1592–1606. doi:10.1074/jbc.M114.588590

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilmanns, M., Hyde, C. C., Davies, D. R., Kirschner, K., and Jansonius, J. N. (1991). Structural Conservation in Parallel .beta./.alpha.-barrel Enzymes that Catalyze Three Sequential Reactions in the Pathway of Tryptophan Biosynthesis. Biochemistry 30, 9161–9169. doi:10.1021/bi00102a006

PubMed Abstract | CrossRef Full Text | Google Scholar