Recent Developments in Data-Assisted Modeling of Flexible Proteins

Many proteins can fold into well-defined conformations. However, intrinsically-disordered proteins (IDPs) do not possess a defined structure. Moreover, folded multi-domain proteins often digress into alternative conformations. Collectively, the conformational dynamics enables these proteins to fulfill specific functions. Thus, most experimental observables are averaged over the conformations that constitute an ensemble. In this article, we review the recent developments in the concept and methods for the determination of the dynamic structures of flexible peptides and proteins. In particular, we describe ways to extract information from nuclear magnetic resonance small-angle X-ray scattering (SAXS), and chemical cross-linking coupled with mass spectroscopy (XL-MS) measurements. All these techniques can be used to obtain ensemble-averaged restraints or to re-weight the simulated conformational ensembles.

1 Introduction

Proteins exist as dynamic structures. Many proteins undergo often very significant motions while performing their functions (Henzler-Wildman and Kern, 2007; Boehr et al., 2009). The respective conformational states are sometimes stable enough to be captured through X-ray structure determination if appropriate conditions of protein-sample preparation are applied (Bertelsen et al., 2009; Kityk et al., 2012). Nevertheless, in most instances, the structures of multistate proteins, as well as those of intrinsically disordered proteins (IDPs) or proteins with intrinsically-disordered regions (IDRs) can be described only in terms of conformational ensembles. Over 40% of human proteins contain stretches of disorder longer than 30 residues (van der Lee et al., 2014).

Thus, ensemble-averaged quantities are usually obtained from measurements while studying conformational dynamics of multistate proteins, IDPs, or flexible peptides. The composition of an ensemble can be determined only by combining the results of measurements with advanced molecular modeling (Bonomi et al., 2017; Bonomi and Vendruscolo, 2019; Orioli et al., 2020). In this minireview, we summarize the methods for conformational-ensemble determination using molecular modeling, using the data from nuclear magnetic resonance (NMR), small-angle X-ray scattering (SAXS), and chemical cross-linking coupled with mass spectroscopy (XL-MS). In Section 2, we outline the experimental techniques mentioned above and the quantities that they provide, while in Section 3 we describe conformational-sampling methods and two major approaches of implementing the experimental quantities in conformational-ensemble determination: simulations with ensemble-averaged restraints and ensemble reweighting. A scheme summarizing the methodologies discussed is shown in Figure 1.

FIGURE 1

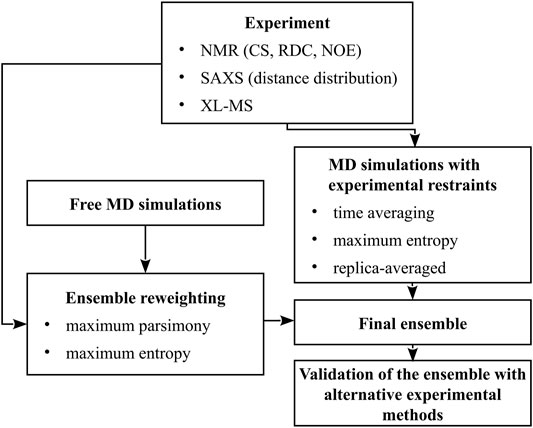
FIGURE 1. A scheme of methods for the determination of conformational ensembles of flexible proteins.

2 Experimental Methods to Study Flexible Proteins

Here we focus on the experimental measurements that can be performed for proteins in solution. We leave out the single-molecule fluorescence resonance energy transfer (FRET), which does not yield ensemble averages and does not have the same issues as those discussed in Section 3 (Tang and Gong, 2020; Lerner et al., 2021).

2.1 Nuclear Magnetic Resonance

The most complete information about the structure and conformational dynamics of proteins and peptides is provided by NMR (Sekhar and Kay, 2019). NMR remains the method of choice to characterize the conformational dynamics of proteins to atomic resolution in near-physiological conditions. NMR observables, including nuclear Overhauser effect (NOE), chemical shift, dipolar coupling constants, and paramagnetic relaxation enhancement (PRE) are ensemble-averaged over a multitude of conformational states (Salmon et al., 2010; Konrat, 2014; Clore, 2015; Huang et al., 2015; Tang and Gong, 2020). Thus, though the flexible regions in a protein can be easily identified by NMR owing to their favorable relaxation properties, it is difficult to obtain a comprehensive description of the ensemble structure of a multi-domain protein or an IDP as a whole and determine the fractions of the constituting conformational states. To this end, many methods have been developed to reconstruct the ensembles based on the NMR data (Bertini et al., 2004; Mittag and Forman-Kay, 2007; Delaforge et al., 2015).

Paramagnetic NMR, in particular, paramagnetic relaxation enhancement (PRE), allows the visualization of protein ensemble structures (Otting, 2010; Liu et al., 2016). The PRE is exquisitely sensitive to the sparsely populated conformations, thanks to the large gyromagnetic ratio of an unpaired electron in the paramagnetic probe and an inverse sixth power dependence on the distances to the observed NMR nuclei (Clore, 2015; Liu et al., 2015). On the other hand, covalent attachment of a paramagnetic probe could perturb the structure, which is more likely for an IDP (Sasmal et al., 2017). As a result, paramagnetic cosolute molecules have been developed (Gu et al., 2014; Gong et al., 2017a), which can also be used to assess the dynamic structures of IDPs (Hartlmüller et al., 2019; Spreitzer et al., 2020). Similar to the PREs, the NOEs also provide ensemble-averaged distances between protein nuclei. However, quantitative interpretation of the NOEs is hampered by the complex relaxation pathways. The exact proton-proton distances and the corresponding conformational states of a protein are best extracted on a perdeuterated background (Vögeli et al., 2009; Vögeli et al., 2016).

2.2 Small-Angle Scattering Methods

Compared to NMR, small-angle X-ray and small-angle neutron scattering (SANS) provide less detailed but more global structural information (Konarev et al., 2003; Forster et al., 2008; Schneidman-Duhovny et al., 2011; Trewhella et al., 2013). For a multi-state protein, the scattering curve is averaged over a multitude of conformational states. The different states and the associated population can, in theory, be obtained from the deconvolution of the scattering curve. To this end, many algorithms have been developed that include ensemble optimization method (EOM) (Bernadó et al., 2007; Tria et al., 2015), minimal ensemble search (MES) (Pelikan et al., 2009), and Bayesian ensemble SAXS (BE-SAXS) (Antonov et al., 2016). Though the scattering intensity at each scattering angle is normally used as a restraint (Forster et al., 2008), pairwise distance distribution could also be employed for the comparison between different sets of structure ensembles (Gorba et al., 2008; Karczyńska et al., 2018). The different approaches fit different numbers of parameters and use different treatments of the displaced solvent, which inevitably leads to somewhat different solutions.

2.3 Chemical Cross-Linking Coupled With Mass Spectroscopy

Cross-linking reactions are initiated either by illumination or chemical reaction followed by enzymatic digestion. The final products are cross-linked peptides, which can be identified by mass spectrometry with high confidence. The cross-linked residues have to be closer in distance than the length of the cross-linker arm. Therefore, each cross-link can be used to derive the restraint imposed on the C^α … , C^α-, C^β … , C^β- or the terminal-atom (e.g., N^ζ … , N^ζ atom pair of lysine side chains) distance of the two cross-linked residues. However, the cross-links may artificially pull two protein regions together, in a so-called zippering effect (Belsom and Rappsilber, 2021), which needs to be carefully controlled and ruled out.

The identified cross-links are often found incompatible with the known protein structure, in which the calculated distance exceeds the maximum length of the cross-linker. Such “over-length” cross-links can be explained by alternative protein conformations, e.g., an open-to-closed transition (Ding et al., 2017), or by the transient oligomerization of the protein. The latter can be ascertained with the mixing of “light” and “heavy” proteins with distinct isotope labeling patterns (Gong et al., 2015). Furthermore, cross-linking mass spectrometry (XL-MS) can be used to elucidate dynamic encounters between two proteins (Gong et al., 2017b).

A crosslink restraint is usually imposed on the straight-line distance between the C^α-atoms of the corresponding residues (Leitner et al., 2014; Merkley et al., 2014; Fajardo et al., 2019). Recently, we developed an approach in which restraints are imposed on side-chain ends and implemented it in all-atom (Gong et al., 2020) and coarse-grained (Kogut et al., 2021) molecular dynamics. This approach is more realistic because such distances are close to those between the solvent-accessible surfaces, which are targeted by the cross-linking reagents in the XL-MS experiments.

3 Modeling Protein Structures With Experimental Restraints

3.1 Conformational Search

Canonical molecular dynamics (MD) (Frenkel and Smit, 2000) and its extensions, namely simulated annealing (SA) (Kirkpatrick et al., 1983), replica-exchange molecular dynamics (REMD) (Hansmann, 1997), and multiplexed replica exchange molecular dynamics (MREMD) (Rhee and Pande, 2003) are usually the methods of choice for sampling the conformational space, owing to their efficiency. All-atom MD is commonly used and a variety of good algorithms and software packages such as e.g., AMBER (Salomon-Ferrer et al., 2013), CHARMM (Brooks et al., 2009), GROMACS (Abraham et al., 2015), LAMMPS (Plimpton, 1995) and DESMOND (Bowers et al., 2006) are available, which also enable the researchers to include experimental information as restraints.

All-atom MD has restricted ability to sample the conformational space extensively (Bottaro and Lindorff-Larsen, 2018). Compared to all-atom approaches, the coarse-grained (CG) approaches, in which several atoms are merged into extended interaction sites, are computationally more efficient and enable us to run simulations at much longer time-scales and for larger systems (Voth, 2008; Kmiecik et al., 2016). The coarse-grained models with which MD for proteins can be run include MARTINI (Marrink and Tieleman, 2013), AWSEM (Davtyan et al., 2012), OPEP (Sterpone et al., 2014), and UNRES (Liwo et al., 2019). CABS (Kolinski, 2004) is another very good CG model of proteins, which was developed to run Monte Carlo dynamics on a high-resolution lattice.

The experimental information can be used as restraints or to filter the conformational ensembles/reweight its conformations to reproduce the experimental observables (Bonomi et al., 2017; Orioli et al., 2020). These two approaches are described in the two subsequent subsections.

3.2 Restrained Simulations of Conformationally Heterogeneous Systems

In restrained simulations, penalty terms are added to the potential energy in MD so that the forces consist of the forces computed from the force field of choice and those due to restraint violation (van Gunsteren et al., 2016). This approach is straightforward if a protein has a well-defined structure and has been implemented in the CYANA (Güntert and Buchner, 2015) and XPLOR-NIH software packages (Schwieters et al., 2018) for structure determination by NMR, as well as is built in the MD packages mentioned in the previous section. For flexible systems, time- and ensemble averaging algorithms to run restrained simulations have been developed.

It should be noted that using restraints from NMR in CG simulations is not straightforward, because the respective quantities depend on all-atom geometry. One method, in which the CG structures are converted into all-atom structures, from which the respective quantities are calculated, was developed (Latek and Koliński, 2011) for use with the CABS model of proteins (Kolinski, 2004). However, this method is not suitable for restrained MD simulations, because it does not provide the forces due to restraints. Recently, we developed ESCASA (Lubecka and Liwo, 2021), an analytical approach to calculating approximate positions of the protons from C^α-trace geometry, thus enabling us to compute the forces due to the penalty function and, consequently, to use the method with coarse-grained MD.

3.2.1 Time-Averaged Restraints

In the time-averaged-restraint method, the quantities obtained from simulations (e.g., interproton distances) are averaged over a time window (Torda et al., 1989; Bonvin et al., 1994). These average quantities are inserted into the penalty terms.

$\bar{f}\left(\mathbf{r}\left(t\right)\right)={\left[\tau \left(1-\exp \left(-t/\tau \right)\right)\right]}^{-1}\underset{0}{\overset{t}{\int }}\exp \left(-t^{\prime }/\tau \right)f\left(\mathbf{r}\left(t-t^{\prime }\right)\right)d{t}^{\prime }(1)$

where f is the quantity being averaged, which depends on the coordinates of the atoms of the system contained in vector r and τ is the length of the time window.

3.2.2 Ensemble Averaged Restraints

The methods that use ensemble-averaged restraints are based on the maximum-entropy and Bayesian principles, according to which a minimally perturbed conformational ensemble compared to that resulting from free simulations is sought and, at the same time, the ensemble-average quantities match their experimental counterparts within the experimental error (Pitera and Chodera, 2012; White et al., 2015; Amirkulova and While, 2019). If the ensemble-averaged restraints are enforced strictly, the potential-energy function is modified to include the experimental quantities with the weight calculated to maximize the entropy (Pitera and Chodera, 2012).

$U_{ME}\left(\mathbf{r};{\alpha }_1,\dots ,{\alpha }_M\right)=U\left(\mathbf{r}\right)+\sum _{i=1}^N{\alpha }_i{f}_i\left(\mathbf{r}\right)(2)$

where f_i(r) is the value of the ith experimental observable calculated for the conformation described by the vector of coordinates r, N is the number of observables, U is the potential-energy function used in MD simulations, U_ME is the extended energy function and the weights α_i are calculated to minimize Γ(α₁, … , α_N).

$\mathrm{\Gamma }\left({\alpha }_1,\dots ,{\alpha }_N\right)=\ln \int \exp \left[-\beta U_{ME}\left(\mathbf{r};{\alpha }_1\dots ,{\alpha }_N\right)\right]d^{3n}\mathbf{r}-\beta \sum _{i=1}^N{\alpha }_i{f}_{i,\mathit{exp}}(3)$

where f_i, exp is the experimental (ensemble-averaged) value of the ith observable, β = 1/RT, R being the universal gas constant and T absolute temperature, and n is the number of atoms in the system. It should be noted that the integral in Equation 3 does not have to be evaluated, because minimization of Γ leads to equations which contain the observables averaged over the conformations, which can readily be calculated from MD simulations (Pitera and Chodera, 2012). With this approach, the distribution of conformations is minimally perturbed with respect to that resulting from the force field used. In other words, the experimental constraints enable us to compensate for the inevitable inaccuracy of the force field and to obtain a distribution of conformations in the ensemble, which is closer to the true (Boltzmann) distribution (Cavalli et al., 2013), provided that the experimental data are sufficient in number and quality. In practical implementation, the replica-averaged method is applied (Camilloni et al., 2013; Hummer and Köfinger, 2015), in which several replicas are run with the extended potential energy, U_ED, containing harmonic restraints on the experimentally measured quantities that are averaged over all replicas.

$U_{ED}\left({\mathbf{r}}_i\right)=U\left({\mathbf{r}}_i\right)+M\sum _j\frac{{\left(\frac{1}{M}\sum _{k=1}^M{f}_j\left({\mathbf{r}}_k\right)-f_{\mathit{exp},j}\right)}^2}{2{\sigma }_j^2}(4)$

where the index i runs over replicas, M is the number of replicas, r_k is the vector of the coordinates of the conformation of the kth replica, and σ_j is the error in the jth observable. It has been demonstrated that this method becomes the maximum-entropy method as the number of replicas increases (Pitera and Chodera, 2012; Cavalli et al., 2013; Roux and Weare, 2013; Hummer and Köfinger, 2015). This approach has been implemented in determining the conformational ensembles from NMR (Camilloni et al., 2013) and SAXS data (Hermann and Hub, 2019). A similar approach termed dynamic ensemble refinement (DER) (Lindorff-Larsen et al., 2005) was developed earlier for the determination of protein dynamical ensembles from NMR data.

3.3 Reweighting the Conformational Ensembles

In the ensemble-reweighting methods, a pool of conformations is generated first in unrestrained simulations and, subsequently, the weights of the conformations are determined to reach the agreement of the conformation-averaged observables with the corresponding experimental quantities (Cavalli et al., 2013; Orioli et al., 2020). An advantage of this approach is that the ensemble can be generated once and used as the results of new experiments are available. However, the state-of-the-art force fields do not produce the true Boltzmann distribution of the conformational states. Consequently, the distribution of conformations obtained in unrestrained simulations could be far from the true distribution; specifically, some regions of conformational space that are, in reality, visited by the system might happen to be under-represented or omitted from the simulated ensemble. It has been demonstrated (Ceriotti et al., 2012) that the more the input distribution diverges from the true distribution the greater the error in reweighting. When the experimental information is included in the simulations as maximum-entropy constraints or replica-averaged restraints, the ensemble is driven towards reproducing the experimental data, i.e., closer to the true (unknown) Boltzmann distribution. An example that the quality of the force field becomes less important with increasing the number of data is the work by Joo et al. (Joo et al., 2015), in which a force field that contained only the van der Waals repulsion, stereochemistry, improper-torsion, and chirality terms, in combination with NOE and dihedral-angle restraints, was used with success to determine protein structures from NMR data.

Because the number of conformations in the ensemble (and, thereby, the number of weights) is usually much greater than the number of observables, the fitting problem is underdetermined. It is solved by using either the maximum-parsimony or the maximum-entropy principle (Bonomi et al., 2017).

In the maximum-parsimony approaches, a minimum set of conformations is determined that can reproduce the experimental observables. This method was originated by Nikiforovich and coworkers (Nikiforovich et al., 1987) and, subsequently evolved into a variety of algorithms, including EOM (Bernadó et al., 2007), ASTEROIDS (Nodet et al., 2009), and SES (Berlin et al., 2013), as well as the algorithms developed in our laboratories to determine the conformational ensembles from the SAXS (Kozak et al., 2010) or SAXS, NMR and XL-MS data (Liu et al., 2018). Usually, the ensemble is clustered first and averages are computed over each cluster, the weights of the clusters being determined by least-square fitting the ensemble-averaged observables to the experimental quantities, subject to the condition that all weights are non-zero and the number of clusters with non-zero weights is minimal.

In the maximum-entropy approach, the weights of conformations are determined so that the ensemble-averaged quantities match the experimental counterparts with minimal perturbation of the input ensembles. Usually, the experimental errors are included in the target function, which results in solving a Bayesian problem, with the prior distribution being equal to that from unrestrained MD simulations.

$\theta \sum _{j=1}^M{w}_j\ln w_j+\sum _{i=1}^N\frac{{\left({\sum }_{j=1}^M{w}_j{f}_{ij}-f_{i,\mathit{exp}}\right)}^2}{2{\sigma }_i^2}=\min (5)$

where the first term is the negative of the Shannon entropy, θ being the weight of this term, and the weights are required to be normalized to unity and non-negative. Many approaches that use this principle, including ENSEMBLE (Marsh and Forman-Kay, 2012; Krzeminski et al., 2013), EROS (Różycki et al., 2011), COPER (Leung et al., 2016), and others (Groth et al., 1999) were developed.

Recently, Pesce and Lindorff-Larsen (Pesce and Lindorff-Larsen, 2021) designed an iterative maximum-entropy reweighting method for the determination of conformational ensembles from SAXS data, in which background intensity and the scaling factor of the computed average SAXS profile are fitted to match the experimental profile. Subsequently, the weights are determined by minimizing the target function of Equation 5. The two steps are iterated until convergence is achieved. The determination of background intensity and scaling factor is a major step forward with respect to the previous approaches, in which only the weights were determined, because these parameters depend on many features of the system studied (e.g., the solvation shell) and on experimental conditions. Also, very recently, an ensemble-reweighting method by using side-chain NMR-relaxation, termed Average Block Selection Using Relaxation Data with Entropy Restraint (ABSURDer), an extension of the ABSURD method of Blackledge and others (Salvi et al., 2016), has been developed by the Lindorff-Larsen group (Kümmerer et al., 2021). This approach takes into account system dynamics, thus enabling us to find the ensemble of trajectories, not just static conformations, consistent with experiment.

4 Conclusion and Outlook

Investigation of the dynamic structures of proteins and other biomolecules in solution is a rapidly growing field, in which the experimental and theoretical methods are complementary to each other (Bonomi et al., 2017; Bonomi and Vendruscolo, 2019; Orioli et al., 2020). Since the experiment provides only average observables (NMR), distance distribution (SAXS, SANS, and WAXS), or just indicates which residues may be close to each other in part of the dynamic structure (XL-MS), dynamic structure determination from the experiment alone is an underdetermined problem. Thus, the development of efficient and reliable conformational-search methods and better force fields is a necessity.

At present, the respective algorithms are based mostly on ensemble reweighting (Bonomi et al., 2017; Bonomi and Vendruscolo, 2019; Orioli et al., 2020), the maximum-entropy variant of which seems to be better, because it does not leave out any part of the ensemble completely, an important feature given the under-determinability of the reweighting problem (Bonomi et al., 2017). Because the conformational ensemble is generated in unrestrained simulations, this approach depends on the quality of a force field used, which is usually still far from being perfect. Therefore, the development of methods based on replica-averaged restraints, which stem from the maximum-entropy principle (Cavalli et al., 2013; Hummer and Köfinger, 2015) seems to be a better approach. Combining this approach with time-averaged restraints (Torda et al., 1989; Bonvin et al., 1994) or posterior ensemble fitting to enrich the averaging is recommended. An efficient conformational search is required regardless of choosing a particular method to include the experimental data, which can be carried out with coarse-grained models (Voth, 2008; Kmiecik et al., 2016). Deep-learning algorithms are also likely to advance the field, especially given their recent tremendous success in predicting the stable structures of proteins at crystallographic accuracy (Baek et al., 2021; Jumper et al., 2021). These methods may be used to generate the initial models for studying the dynamics of multistate proteins.

Another challenge is capturing the full dynamics of the system under study. Time-resolved techniques are an obvious answer here but averages, such as kinetic rate constants, can also be used – an approach has recently been proposed (Brotzakis et al., 2021). This will be particularly important when studying the dynamics of multistate proteins with more than two stable states.

Author Contributions

AL and CT designed the manuscript and wrote part of the text. EL, CC, KX, and ZG participated in writing.

Funding

This work was supported by grants No. 2018YFA0507700 (National Key R&D Program of China), UMO-2017/25/B/ST4/01026, and UMO-2017/26/M/ST4/00044 from the National Science Center of Poland (Narodowe Centrum Nauki).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Computational resources were provided by (a) the Interdisciplinary Center of Mathematical and Computer Modeling (ICM) the University of Warsaw under grant No. GA71-23, (b) the Centre of Informatics - Tricity Academic Supercomputer and Network (CI TASK) in Gdańsk, (c) the Academic Computer Centre Cyfronet AGH in Krakow under grants unres19 and unres2021 and (d) 796-processor Beowulf cluster at the Faculty of Chemistry, University of Gdańsk.

References

Abraham, M. J., Murtola, T., Schulz, R., Páll, S., Smith, J. C., Hess, B., et al. (2015). GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 1-2, 19–25. doi:10.1016/j.softx.2015.06.001

CrossRef Full Text | Google Scholar

Amirkulova, D. B., and White, A. D. (2019). Recent Advances in Maximum Entropy Biasing Techniques for Molecular Dynamics. Mol. Simul. 45, 1285–1294. doi:10.1080/08927022.2019.1608988

CrossRef Full Text | Google Scholar

Antonov, L. D., Olsson, S., Boomsma, W., and Hamelryck, T. (2016). Bayesian Inference of Protein Ensembles from SAXS Data. Phys. Chem. Chem. Phys. 18, 5832–5838. doi:10.1039/c5cp04886a

PubMed Abstract | CrossRef Full Text | Google Scholar

Baek, M., DiMaio, F., Anishchenko, I., Dauparas, J., Ovchinnikov, S., Lee, G. R., et al. (2021). Accurate Prediction of Protein Structures and Interactions Using a Three-Track Neural Network. Science 373, 871–876. doi:10.1126/science.abj8754

PubMed Abstract | CrossRef Full Text | Google Scholar

Belsom, A., and Rappsilber, J. (2021). Anatomy of a Crosslinker. Curr. Opin. Chem. Biol. 60, 39–46. doi:10.1016/j.cbpa.2020.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Berlin, K., Castañeda, C. A., Schneidman-Duhovny, D., Sali, A., Nava-Tudela, A., and Fushman, D. (2013). Recovering a Representative Conformational Ensemble from Underdetermined Macromolecular Structural Data. J. Am. Chem. Soc. 135, 16595–16609. doi:10.1021/ja4083717

CrossRef Full Text | Google Scholar

Bernadó, P., Mylonas, E., Petoukhov, M. V., Blackledge, M., and Svergun, D. I. (2007). Structural Characterization of Flexible Proteins Using Small-Angle X-ray Scattering. J. Am. Chem. Soc. 129, 5656–5664. doi:10.1021/ja069124n

CrossRef Full Text | Google Scholar

Bertelsen, E. B., Chang, L., Gestwicki, J. E., and Zuiderweg, E. R. P. (2009). Solution Conformation of Wild-type E. coli Hsp70 (DnaK) Chaperone Complexed with ADP and Substrate. Proc. Natl. Acad. Sci. 106, 8471–8476. doi:10.1073/pnas.0903503106

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertini, I., Del Bianco, C., Gelis, I., Katsaros, N., Luchinat, C., Parigi, G., et al. (2004). From the Cover: Experimentally Exploring the Conformational Space Sampled by Domain Reorientation in Calmodulin. Proc. Natl. Acad. Sci. 101, 6841–6846. doi:10.1073/pnas.0308641101

PubMed Abstract | CrossRef Full Text | Google Scholar

Boehr, D. D., Nussinov, R., and Wright, P. E. (2009). The Role of Dynamic Conformational Ensembles in Biomolecular Recognition. Nat. Chem. Biol. 5, 789–796. doi:10.1038/nchembio.232

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonomi, M., and Vendruscolo, M. (2019). Determination of Protein Structural Ensembles Using Cryo-Electron Microscopy. Curr. Opin. Struct. Biol. 56, 37–45. doi:10.1016/j.sbi.2018.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonomi, M., Heller, G. T., Camilloni, C., and Vendruscolo, M. (2017). Principles of Protein Structural Ensemble Determination. Curr. Opin. Struct. Biol. 42, 106–116. doi:10.1016/j.sbi.2016.12.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonvin, A. M., Boelens, R., and Kaptein, R. (1994). Time- and Ensemble-Averaged Direct NOE Restraints. J. Biomol. NMR 4, 143–149. doi:10.1007/BF00178343

CrossRef Full Text | Google Scholar

Bottaro, S., and Lindorff-Larsen, K. (2018). Biophysical Experiments and Biomolecular Simulations: A Perfect Match? Science 361, 355–360. doi:10.1126/science.aat4010

PubMed Abstract | CrossRef Full Text | Google Scholar

Bowers, K. J., Chow, E., Xu, H., Dror, R. O., Eastwood, M. P., Gregersen, B. A., et al. (2006). “Scalable Algorithms for Molecular Dynamics Simulations on Commodity Clusters,” in Proceedings of the ACM/IEEE Conference on Supercomputing (SC06), Tampa, FL, November 11–17, 2006 (Tampa, FL), 43. doi:10.1109/sc.2006.54

CrossRef Full Text | Google Scholar

Brooks, B. R., Brooks, C. L., MacKerell, A. D., Nilsson, L., Petrella, R. J., Roux, B., et al. (2009). CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 30, 1545–1614. doi:10.1002/jcc.21287

CrossRef Full Text | Google Scholar

Brotzakis, Z. F., Vendruscolo, M., and Bolhuis, P. G. (2021). A Method of Incorporating Rate Constants as Kinetic Constraints in Molecular Dynamics Simulations. Proc. Natl. Acad. Sci. USA 118, e2012423118. doi:10.1073/pnas.2012423118

PubMed Abstract | CrossRef Full Text | Google Scholar

Camilloni, C., Cavalli, A., and Vendruscolo, M. (2013). Replica-averaged Metadynamics. J. Chem. Theor. Comput. 9, 5610–5617. doi:10.1021/ct4006272

PubMed Abstract | CrossRef Full Text | Google Scholar

Cavalli, A., Camilloni, C., and Vendruscolo, M. (2013). Molecular Dynamics Simulations with Replica-Averaged Structural Restraints Generate Structural Ensembles According to the Maximum Entropy Principle. J. Chem. Phys. 138, 094112. doi:10.1063/1.4793625

CrossRef Full Text | Google Scholar

Ceriotti, M., Brain, G. A. R., Riordan, O., and Manolopoulos, D. E. (2012). The Inefficiency of Re-weighted Sampling and the Curse of System Size in High-Order Path Integration. Proc. R. Soc. A. 468, 2–17. doi:10.1098/rspa.2011.0413

CrossRef Full Text | Google Scholar

Clore, G. M. (2015). Practical Aspects of Paramagnetic Relaxation Enhancement in Biological Macromolecules. Meth. Enzymol. 564, 485–497. doi:10.1016/bs.mie.2015.06.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Davtyan, A., Schafer, N. P., Zheng, W., Clementi, C., Wolynes, P. G., and Papoian, G. A. (2012). AWSEM-MD: Protein Structure Prediction Using Coarse-Grained Physical Potentials and Bioinformatically Based Local Structure Biasing. J. Phys. Chem. B 116, 8494–8503. doi:10.1021/jp212541y

CrossRef Full Text | Google Scholar

Delaforge, E., Milles, S., Bouvignies, G., Bouvier, D., Boivin, S., Salvi, N., et al. (2015). Large-Scale Conformational Dynamics Control H5N1 Influenza Polymerase PB2 Binding to Importin α. J. Am. Chem. Soc. 137, 15122–15134. doi:10.1021/jacs.5b07765

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, Y.-H., Gong, Z., Dong, X., Liu, K., Liu, Z., Liu, C., et al. (2017). Modeling Protein Excited-State Structures from "Over-length" Chemical Cross-Links. J. Biol. Chem. 292, 1187–1196. doi:10.1074/jbc.m116.761841

PubMed Abstract | CrossRef Full Text | Google Scholar

Fajardo, J. E., Shrestha, R., Gil, N., Belsom, A., Crivelli, S. N., Czaplewski, C., et al. (2019). Assessment of Chemical‐crosslink‐assisted Protein Structure Modeling in CASP13. Proteins 87, 1283–1297. doi:10.1002/prot.25816

PubMed Abstract | CrossRef Full Text | Google Scholar

Förster, F., Webb, B., Krukenberg, K. A., Tsuruta, H., Agard, D. A., and Sali, A. (2008). Integration of Small-Angle X-ray Scattering Data into Structural Modeling of Proteins and Their Assemblies. J. Mol. Biol. 382, 1089–1106. doi:10.1016/j.jmb.2008.07.074

CrossRef Full Text | Google Scholar

Frenkel, D., and Smit, B. (2000). Understanding Molecular Simulation: From Algorithms to Applications. New York: Academic Press.

Google Scholar

Gong, Z., Ding, Y.-H., Dong, X., Liu, N., Zhang, E. E., Dong, M.-Q., et al. (2015). Visualizing the Ensemble Structures of Protein Complexes Using Chemical Cross-Linking Coupled with Mass Spectrometry. Biophys. Rep. 1, 127–138. doi:10.1007/s41048-015-0015-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, Z., Gu, X.-H., Guo, D.-C., Wang, J., and Tang, C. (2017a). Protein Structural Ensembles Visualized by Solvent Paramagnetic Relaxation Enhancement. Angew. Chem. Int. Ed. 56, 1002–1006. doi:10.1002/anie.201609830

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, Z., Liu, Z., Dong, X., Ding, Y.-H., Dong, M.-Q., and Tang, C. (2017b). Protocol for Analyzing Protein Ensemble Structures from Chemical Cross-Links Using DynaXL. Biophys. Rep. 3, 100–108. doi:10.1007/s41048-017-0044-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, Z., Ye, S.-X., and Tang, C. (2020). Tightening the Crosslinking Distance Restraints for Better Resolution of Protein Structure and Dynamics. Structure 28, 1160–1167. doi:10.1016/j.str.2020.07.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Gorba, C., Miyashita, O., and Tama, F. (2008). Normal-mode Flexible Fitting of High-Resolution Structure of Biological Molecules toward One-Dimensional Low-Resolution Data. Biophys. J. 94, 1589–1599. doi:10.1529/biophysj.107.122218

PubMed Abstract | CrossRef Full Text | Google Scholar

Groth, M., Malicka, J., Czaplewski, C., Ołdziej, S., Łankiewicz, L., Wiczk, W., et al. (1999). Maximum Entropy Approach to the Determination of Solution Conformation of Flexible Polypeptides by Global Conformational Analysis and NMR Spectroscopy – Application to DNS1-C-[D-A2bu2,Trp4,Leu5]enkephalin and DNS1-C-[D-A2bu2,Trp4,D-Leu5]enkephalin. J. Biomol. NMR 15, 315–330. doi:10.1023/a:1008349424452

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, X.-H., Gong, Z., Guo, D.-C., Zhang, W.-P., and Tang, C. (2014). A Decadentate Gd(III)-coordinating Paramagnetic Cosolvent for Protein Relaxation Enhancement Measurement. J. Biomol. NMR 58, 149–154. doi:10.1007/s10858-014-9817-3

CrossRef Full Text | Google Scholar

Güntert, P., and Buchner, L. (2015). Combined Automated NOE Assignment and Structure Calculation with CYANA. J. Biomol. NMR 62, 453–471. doi:10.1007/s10858-015-9924-9

CrossRef Full Text | Google Scholar

Hansmann, U. H. E. (1997). Parallel Tempering Algorithm for Conformational Studies of Biological Molecules. Chem. Phys. Lett. 281, 140–150. doi:10.1016/s0009-2614(97)01198-6

CrossRef Full Text | Google Scholar

Hartlmüller, C., Spreitzer, E., Göbl, C., Falsone, F., and Madl, T. (2019). NMR Characterization of Solvent Accessibility and Transient Structure in Intrinsically Disordered Proteins. J. Biomol. NMR 73, 305–317. doi:10.1007/s10858-019-00248-2

CrossRef Full Text | Google Scholar

Henzler-Wildman, K., and Kern, D. (2007). Dynamic Personalities of Proteins. Nature 450, 964–972. doi:10.1038/nature06522

PubMed Abstract | CrossRef Full Text | Google Scholar

Hermann, M. R., and Hub, J. S. (2019). SAXS-restrained Ensemble Simulations of Intrinsically Disordered Proteins with Commitment to the Principle of Maximum Entropy. J. Chem. Theor. Comput. 15, 5103–5115. doi:10.1021/acs.jctc.9b00338

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Y. J., Mao, B., Xu, F., and Montelione, G. T. (2015). Guiding Automated NMR Structure Determination Using a Global Optimization Metric, the NMR DP Score. J. Biomol. NMR 62, 439–451. doi:10.1007/s10858-015-9955-2

CrossRef Full Text | Google Scholar

Hummer, G., and Köfinger, J. (2015). Bayesian Ensemble Refinement by Replica Simulations and Reweighting. J. Chem. Phys. 143, 243150. doi:10.1063/1.4937786

CrossRef Full Text | Google Scholar

Joo, K., Joung, I., Lee, J., Lee, J., Lee, W., Brooks, B., et al. (2015). Protein Structure Determination by Conformational Space Annealing Using NMR Geometric Restraints. Proteins 83, 2251–2262. doi:10.1002/prot.24941

PubMed Abstract | CrossRef Full Text | Google Scholar

Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov, M., Ronneberger, O., et al. (2021). Highly Accurate Protein Structure Prediction with Alphafold. Nature 596, 593–589. doi:10.1038/s41586-021-03819-2

CrossRef Full Text | Google Scholar

Karczyńska, A. S., Mozolewska, M. A., Krupa, P., Giełdoń, A., Liwo, A., and Czaplewski, C. (2018). Prediction of Protein Structure with the Coarse-Grained UNRES Force Field Assisted by Small X-ray Scattering Data and Knowledge-Based Information. Proteins 86 (S1), 228–239. doi:10.1002/prot.25421

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirkpatrick, S., Gelatt, C. D. J., and Vecchi, M. P. (1983). Optimization by Simulated Annealing. Science 220, 671–680. doi:10.1126/science.220.4598.671

PubMed Abstract | CrossRef Full Text | Google Scholar

Kityk, R., Kopp, J., Sinning, I., and Mayer, M. P. (2012). Structure and Dynamics of the ATP-Bound Open Conformation of Hsp70 Chaperones. Mol. Cel 48, 863–874. doi:10.1016/j.molcel.2012.09.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Kmiecik, S., Gront, D., Kolinski, M., Wieteska, L., Dawid, A. E., and Kolinski, A. (2016). Coarse-grained Protein Models and Their Applications. Chem. Rev. 116, 7898–7936. doi:10.1021/acs.chemrev.6b00163

PubMed Abstract | CrossRef Full Text | Google Scholar

Kogut, M., Gong, Z., Tang, C., and Liwo, A. (2021). Pseudopotentials for Coarse‐grained Cross‐link‐assisted Modeling of Protein Structures. J. Comput. Chem. 42, 2054–2067. doi:10.1002/jcc.26736

CrossRef Full Text | Google Scholar

Kolinski, A. (2004). Protein Modeling and Structure Prediction with a Reduced Representation. Acta Biochim. Pol. 51, 349–371. doi:10.18388/abp.2004_3575

PubMed Abstract | CrossRef Full Text | Google Scholar

Konarev, P. V., Volkov, V. V., Sokolova, A. V., Koch, M. H. J., and Svergun, D. I. (2003). PRIMUS: a Windows PC-Based System for Small-Angle Scattering Data Analysis. J. Appl. Cryst. 36, 1277–1282. doi:10.1107/s0021889803012779

CrossRef Full Text | Google Scholar

Konrat, R. (2014). NMR Contributions to Structural Dynamics Studies of Intrinsically Disordered Proteins. J. Magn. Reson. 241, 74–85. doi:10.1016/j.jmr.2013.11.011

CrossRef Full Text | Google Scholar

Kozak, M., Lewandowska, A., Ołdziej, S., Rodziewicz-Motowidło, S., and Liwo, A. (2010). Combination of SAXS and NMR Techniques as a Tool for the Determination of Peptide Structure in Solution. J. Phys. Chem. Lett. 1, 3128–3131. doi:10.1021/jz101178t

CrossRef Full Text | Google Scholar

Krzeminski, M., Marsh, J. A., Neale, C., Choy, W.-Y., and Forman-Kay, J. D. (2013). Characterization of Disordered Proteins with Ensemble. Bioinformatics 29, 398–399. doi:10.1093/bioinformatics/bts701

PubMed Abstract | CrossRef Full Text | Google Scholar

Kümmerer, F., Orioli, S., Harding-Larsen, D., Hoffmann, F., Gavrilov, Y., Teilum, K., et al. (2021). Fitting Side-Chain NMR Relaxation Data Using Molecular Simulations. J. Chem. Theor. Comput. 17, 5262–5275. doi:10.1021/acs.jctc.0c01338

CrossRef Full Text | Google Scholar

Latek, D., and Kolinski, A. (2011). CABS-NMR-De Novo Tool for Rapid Global Fold Determination from Chemical Shifts, Residual Dipolar Couplings and Sparse Methyl-Methyl Noes. J. Comput. Chem. 32, 536–544. doi:10.1002/jcc.21640

CrossRef Full Text | Google Scholar

Leitner, A., Joachimiak, L. A., Unverdorben, P., Walzthoeni, T., Frydman, J., Förster, F., et al. (2014). Chemical Cross-Linking/mass Spectrometry Targeting Acidic Residues in Proteins and Protein Complexes. Proc. Natl. Acad. Sci. U.S.A. 111, 9455–9460. doi:10.1073/pnas.1320298111

PubMed Abstract | CrossRef Full Text | Google Scholar

Lerner, E., Barth, A., Hendrix, J., Ambrose, B., Birkedal, V., Blanchard, S. C., et al. (2021). FRET-based Dynamic Structural Biology: Challenges, Perspectives and an Appeal for Open-Science Practices. eLife 10, e60416. doi:10.7554/eLife.60416

PubMed Abstract | CrossRef Full Text | Google Scholar

Leung, H. T. A., Bignucolo, O., Aregger, R., Dames, S. A., Mazur, A., Bernèche, S., et al. (2016). A Rigorous and Efficient Method to Reweight Very Large Conformational Ensembles Using Average Experimental Data and to Determine Their Relative Information Content. J. Chem. Theor. Comput. 12, 383–394. doi:10.1021/acs.jctc.5b00759

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindorff-Larsen, K., Best, R. B., DePristo, M. A., Dobson, C. M., and Vendruscolo, M. (2005). Simultaneous Determination of Protein Structure and Dynamics. Nature 433, 128–132. doi:10.1038/nature03199

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Gong, Z., Jiang, W. X., Yang, J., Zhu, W. K., Guo, D. C., et al. (2015). Lys63-linked Ubiquitin Chain Adopts Multiple Conformational States for Specific Target Recognition. eLife 4, e05767. doi:10.7554/eLife.05767

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Gong, Z., Dong, X., and Tang, C. (2016). Transient Protein-Protein Interactions Visualized by Solution NMR. Biochim. Biophys. Acta Proteins Proteomics 1864, 115–122. doi:10.1016/j.bbapap.2015.04.009

CrossRef Full Text | Google Scholar

Liu, Z., Gong, Z., Cao, Y., Ding, Y.-H., Dong, M.-Q., Lu, Y.-B., et al. (2018). Characterizing Protein Dynamics with Integrative Use of Bulk and Single-Molecule Techniques. Biochemistry 57, 305–313. doi:10.1021/acs.biochem.7b00817

PubMed Abstract | CrossRef Full Text | Google Scholar

Liwo, A., Sieradzan, A. K., Lipska, A. G., Czaplewski, C., Joung, I., Żmudzińska, W., et al. (2019). A General Method for the Derivation of the Functional Forms of the Effective Energy Terms in Coarse-Grained Energy Functions of Polymers. III. Determination of Scale-Consistent Backbone-Local and Correlation Potentials in the UNRES Force Field and Force-Field Calibration and Validation. J. Chem. Phys. 150, 155104. doi:10.1063/1.5093015

CrossRef Full Text | Google Scholar

Lubecka, E. A., and Liwo, A. (2021). ESCASA : Analytical Estimation of Atomic Coordinates from Coarse‐grained Geometry for Nuclear‐magnetic‐resonance ‐assisted Protein Structure Modeling. I. Backbone and H β Protons. J. Comput. Chem. 42, 1579–1589. doi:10.1002/jcc.26695

CrossRef Full Text | Google Scholar

Marrink, S. J., and Tieleman, D. P. (2013). Perspective on the Martini Model. Chem. Soc. Rev. 42, 6801–6822. doi:10.1039/c3cs60093a

PubMed Abstract | CrossRef Full Text | Google Scholar

Marsh, J. A., and Forman-Kay, J. D. (2012). Ensemble Modeling of Protein Disordered States: Experimental Restraint Contributions and Validation. Proteins 80, 556–572. doi:10.1002/prot.23220

PubMed Abstract | CrossRef Full Text | Google Scholar

Merkley, E. D., Rysavy, S., Kahraman, A., Hafen, R. P., Daggett, V., and Adkins, J. N. (2014). Distance Restraints from Crosslinking Mass Spectrometry: Mining a Molecular Dynamics Simulation Database to Evaluate Lysine-Lysine Distances. Protein Sci. 23, 747–759. doi:10.1002/pro.2458

PubMed Abstract | CrossRef Full Text | Google Scholar

Mittag, T., and Forman-Kay, J. D. (2007). Atomic-level Characterization of Disordered Protein Ensembles. Curr. Opin. Struct. Biol. 17, 3–14. doi:10.1016/j.sbi.2007.01.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikiforovich, G. V., Vesterman, B., Betins, J., and Podins, L. (1987). The Space Structure of a Conformationally Labile Oligopeptide in Solution: Angiotensin. J. Biomol. Struct. Dyn. 4, 1119–1135. doi:10.1080/07391102.1987.10507702

CrossRef Full Text | Google Scholar

Nodet, G., Salmon, L., Ozenne, V., Meier, S., Jensen, M. R., and Blackledge, M. (2009). Quantitative Description of Backbone Conformational Sampling of Unfolded Proteins at Amino Acid Resolution from NMR Residual Dipolar Couplings. J. Am. Chem. Soc. 131, 17908–17918. doi:10.1021/ja9069024

CrossRef Full Text | Google Scholar

Orioli, S., Larsen, A. H., Bottaro, S., and Lindorff-Larsen, K. (2020). How to Learn from Inconsistencies: Integrating Molecular Simulations with Experimental Data. Prog. Mol. Biol. Transl. Sci. 170, 123–176. doi:10.1016/bs.pmbts.2019.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Otting, G. (2010). Protein NMR Using Paramagnetic Ions. Annu. Rev. Biophys. 39, 387–405. doi:10.1146/annurev.biophys.093008.131321

PubMed Abstract | CrossRef Full Text | Google Scholar

Pelikan, M., Hura, G., and Hammel, M. (2009). Structure and Flexibility within Proteins as Identified through Small Angle X-ray Scattering. Gen. Physiol. Biophys. 28, 174–189. doi:10.4149/gpb_2009_02_174

PubMed Abstract | CrossRef Full Text | Google Scholar

Pesce, F., and Lindorff-Larsen, K. (2021). Refining Conformational Ensembles of Flexible Proteins against Small-Angle X-ray Scattering Data. Biophys. J. 120, 5124–5135. doi:10.1016/j.bpj.2021.10.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Pitera, J. W., and Chodera, J. D. (2012). On the Use of Experimental Observations to Bias Simulated Ensembles. J. Chem. Theor. Comput. 8, 3445–3451. doi:10.1021/ct300112v

PubMed Abstract | CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Rhee, Y. M., and Pande, V. S. (2003). Multiplexed-replica Exchange Molecular Dynamics Method for Protein Folding Simulation. Biophys. J. 84, 775–786. doi:10.1016/s0006-3495(03)74897-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Roux, B., and Weare, J. (2013). On the Statistical Equivalence of Restrained-Ensemble Simulations with the Maximum Entropy Method. J. Chem. Phys. 138, 084107. doi:10.1063/1.4792208

CrossRef Full Text | Google Scholar

Różycki, B., Kim, Y. C., and Hummer, G. (2011). SAXS Ensemble Refinement of ESCRT-III CHMP3 Conformational Transitions. Structure 19, 109–116. doi:10.1016/j.str.2010.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Salmon, L., Nodet, G., Ozenne, V., Yin, G., Jensen, M. R., Zweckstetter, M., et al. (2010). NMR Characterization of Long-Range Order in Intrinsically Disordered Proteins. J. Am. Chem. Soc. 132, 8407–8418. doi:10.1021/ja101645g

CrossRef Full Text | Google Scholar

Salomon-Ferrer, R., Case, D. A., and Walker, R. C. (2013). An Overview of the Amber Biomolecular Simulation Package. WIREs Comput. Mol. Sci. 3, 198–210. doi:10.1002/wcms.1121

CrossRef Full Text | Google Scholar

Salvi, N., Abyzov, A., and Blackledge, M. (2016). Multi-Timescale Dynamics in Intrinsically Disordered Proteins from NMR Relaxation and Molecular Simulation. J. Phys. Chem. Lett. 7, 2483–2489. doi:10.1021/acs.jpclett.6b00885

PubMed Abstract | CrossRef Full Text | Google Scholar

Sasmal, S., Lincoff, J., and Head-Gordon, T. (2017). Effect of a Paramagnetic Spin Label on the Intrinsically Disordered Peptide Ensemble of Amyloid-β. Biophys. J. 113, 1002–1011. doi:10.1016/j.bpj.2017.06.067

PubMed Abstract | CrossRef Full Text | Google Scholar

Schneidman-Duhovny, D., Hammel, M., and Sali, A. (2011). Macromolecular Docking Restrained by a Small Angle X-ray Scattering Profile. J. Struct. Biol. 173, 461–471. doi:10.1016/j.jsb.2010.09.023

CrossRef Full Text | Google Scholar

Schwieters, C. D., Bermejo, G. A., and Clore, G. M. (2018). Xplor-NIH for Molecular Structure Determination from NMR and Other Data Sources. Protein Sci. 27, 26–40. doi:10.1002/pro.3248

PubMed Abstract | CrossRef Full Text | Google Scholar

Sekhar, A., and Kay, L. E. (2019). An NMR View of Protein Dynamics in Health and Disease. Annu. Rev. Biophys. 48, 297–319. doi:10.1146/annurev-biophys-052118-115647

PubMed Abstract | CrossRef Full Text | Google Scholar

Spreitzer, E., Usluer, S., and Madl, T. (2020). Probing Surfaces in Dynamic Protein Interactions. J. Mol. Biol. 432, 2949–2972. doi:10.1016/j.jmb.2020.02.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Sterpone, F., Melchionna, S., Tuffery, P., Pasquali, S., Mousseau, N., Cragnolini, T., et al. (2014). The OPEP Protein Model: from Single Molecules, Amyloid Formation, Crowding and Hydrodynamics to DNA/RNA Systems. Chem. Soc. Rev. 43, 4871–4893. doi:10.1039/c4cs00048j

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, C., and Gong, Z. (2020). Integrating Non-NMR Distance Restraints to Augment NMR Depiction of Protein Structure and Dynamics. J. Mol. Biol. 432, 2913–2929. doi:10.1016/j.jmb.2020.01.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Torda, A. E., Scheek, R. M., and van Gunsteren, W. F. (1989). Time-dependent Distance Restraints in Molecular Dynamics Simulations. Chem. Phys. Lett. 157, 289–294. doi:10.1016/0009-2614(89)87249-5

CrossRef Full Text | Google Scholar

Trewhella, J., Hendrickson, W. A., Kleywegt, G. J., Sali, A., Sato, M., Schwede, T., et al. (2013). Report of the wwPDB Small-Angle Scattering Task Force: Data Requirements for Biomolecular Modeling and the PDB. Structure 21, 875–881. doi:10.1016/j.str.2013.04.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Tria, G., Mertens, H. D. T., Kachala, M., and Svergun, D. I. (2015). Advanced Ensemble Modelling of Flexible Macromolecules Using X-ray Solution Scattering. Int. Union Crystallogr. J. 2, 207–217. doi:10.1107/s205225251500202x

CrossRef Full Text | Google Scholar

van der Lee, R., Buljan, M., Lang, B., Weatheritt, R. J., Daughdrill, G. W., Dunker, A. K., et al. (2014). Classification of Intrinsically Disordered Regions and Proteins. Chem. Rev. 114, 6589–6631. doi:10.1021/cr400525m

PubMed Abstract | CrossRef Full Text | Google Scholar

van Gunsteren, W. F., Allison, J. R., Daura, X., Dolenc, J., Hansen, N., Mark, A. E., et al. (2016). Deriving Structural Information from Experimentally Measured Data on Biomolecules. Angew. Chem. Int. Ed. Engl. 55, 15990–16010. doi:10.1002/anie.201601828

PubMed Abstract | CrossRef Full Text | Google Scholar

Vögeli, B., Segawa, T. F., Leitz, D., Sobol, A., Choutko, A., Trzesniak, D., et al. (2009). Exact Distances and Internal Dynamics of Perdeuterated Ubiquitin from NOE Buildups. J. Am. Chem. Soc. 131, 17215–17225. doi:10.1021/ja905366h

CrossRef Full Text | Google Scholar

Vögeli, B., Olsson, S., Güntert, P., and Riek, R. (2016). The Exact NOE as an Alternative in Ensemble Structure Determination. Biophys. J. 110, 113–126. doi:10.1016/j.bpj.2015.11.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Voth, G. (2008). Coarse-Graining of Condensed Phase and Biomolecular Systems. 1st edn. Boca Raton: CRC Press, Taylor & Francis Group.

Google Scholar

White, A. D., Dama, J. F., and Voth, G. A. (2015). Designing Free Energy Surfaces that Match Experimental Data with Metadynamics. J. Chem. Theor. Comput. 11, 2451–2460. doi:10.1021/acs.jctc.5b00178

CrossRef Full Text | Google Scholar