- 1Department of Chemical Sciences, University of Naples Federico II, Naples, Italy
- 2Center for Advanced Biomaterials for Healthcare@CRIB, Naples, Italy
The Green Fluorescent Protein (GFP) is a widely studied chemical system both for its large amount of applications and the complexity of the excited state proton transfer responsible of the change in the protonation state of the chromophore. A detailed investigation on the structure of the chromophore environment and the influence of chromophore form (either neutral or anionic) on it is of crucial importance to understand how these factors could potentially influence the protein function. In this study, we perform a detailed computational investigation based on the analysis of ab-initio molecular dynamics simulations, to disentangle the main structural quantities determining the fine balance in the chromophore environment. We found that specific hydrogen bonds interactions directly involving the chromophore (or not), are correlated to quantities, such as the volume of the cavity in which the chromophore is embedded and that it is importantly affected by the chromophore protonation state. The cross-correlation analysis performed on some of these hydrogen bonds and the cavity volume, demonstrates a direct correlation among them and we also identified the ones specifically involved in this correlation. We also found that specific interactions among residues far in the space are correlated, demonstrating the complexity of the chromophore environment and that many structural quantities have to be taken into account to properly describe and understand the main factors tuning the active site of the protein. From an overall evaluation of the results obtained in this work, it is shown that the residues which a priori are perceived to be spectators play instead an important role in both influencing the chromophore environment (cavity volume) and its dynamics (cross-correlations among spatially distant residues).
1. Introduction
The formation and dissociation dynamics of hydrogen-bonding is fundamental to unveil the choreography of several reactions in biology, above all, proton transfer (PT) in condensed phase (Klepeis et al., 2009; Oscar et al., 2014; Wang and Fang, 2019; Fang and Tang, 2020). PT reactions are ubiquitous in nature and are very common in photo-induced processes, such us the ones responsible of the light emission of fluorescent proteins (FPs) (Acharya et al., 2017). FPs are widely used biomarker to visualize in vivo processes in organisms, since their fluorescent states can be easily exploited for bioimaging techniques, as well as genetic markers in cellular biology (Chalfie et al., 1994; Tsien, 1998; Zimmer, 2002; Chen et al., 2019). The well-known green fluorescent protein (GFP) is often employed as a model system for FPs. GFP was first isolated from the jellyfish Aequorea victoria (Shimomura et al., 1962; Shimomura, 2005), even if many similar protein have been found in other organisms. GFP and its mutants are employed in many fields as a marker in cell biology and is responsible for an increasing interest in the whole class of fluorescent proteins that are widely investigated nowadays (Chalfie, 1995). In the wild-type GFP the chromophore 4-(p-hydroxybenzylidene)-imidazolid-5-one (HBDI) is present in the electronic ground state in both its neutral (A) and anionic deprotonated HBDI− (B) form, with a neutral form population six times higher than the anionic one under physiological conditions (Chattoraj et al., 1996). The two forms give absorption bands at ~395 and 480 nm, respectively (Brejc et al., 1997; Creemers et al., 1999). After the excitation of the neutral form, an excited state proton transfer reaction takes place leading to the formation of an anionic form, denoted as I*. Finally the system gives a bright fluorescence near 510 nm, with a quantum yield of ~0.8 and a lifetime of ~3 ns (Striker et al., 1999; Volkmer et al., 2000). Transformations between A and B occur through an intermediate named I, indeed. This form is very similar to the neutral one, differing from A mostly for a protonation change, whereas the change from I to B is considered a slow conformational change (Figure 1) (Grigorenko et al., 2013).
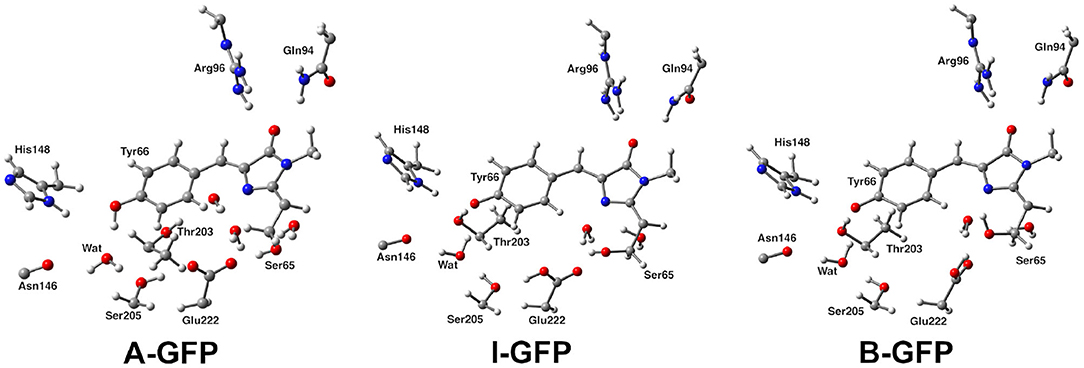
Figure 1. Structural comparison of GFP A, I, and B forms. The distinct protonation states between A and I/B and Glu222 reorientation between I and B can be observed.
Besides characterization of their functions in vivo, a fundamental comprehension of collective atomic motions in correlation with intramolecular and intermolecular interactions on a wide range of timescales, from femtoseconds to seconds, is the grounds for shedding light on the protein photophysics, and more in general, function. Nuclear magnetic resonance and X-ray crystallography have been useful in solving protein structures to provide models for their functions, but a highly desirable visualization of protein motions in real time can be obtained by structural dynamics techniques that are able to provide both high spatial and temporal resolutions. Usually these goals are achieved by time-resolved infrared and Raman Spectroscopies, and we refer the readers to a recent review from Fang et al. on this subject (Fang and Tang, 2020). However, the structure/spectroscopic correlation is not easy to disentangle and in this context the computational approach can be very useful to give the molecular picture behind the different spectroscopic behavior.
Although GFP has been object of several theoretical studies, focusing mostly on either the isolated chromophore (Das et al., 2003 Martin et al., 2004; Wang and Smith, 2006; Vendrell et al., 2008b; Bravaya et al., 2012; Raucci et al., 2020) or the optical properties and related proton transfer mechanism (Lill and Helms, 2002; Toniolo et al., 2004; Zhang et al., 2005; Virshup et al., 2009; Olsen et al., 2010; Bravaya et al., 2011; Conyard et al., 2011; Filippi et al., 2012; Grigorenko et al., 2013; Petrone et al., 2013, 2016a; Armengol et al., 2015; Daday et al., 2015; Nadal-Ferret et al., 2015; Shinobu and Agmon, 2017; Donati et al., 2018b; Chang et al., 2019), the concerted dynamics of the protein and its effect on the chromophore cavity has not been analyzed with the same attention yet. Fewer papers have been focused on the equilibrium properties of ground state forms (Mandal et al., 2004; Patnaik et al., 2004), mostly trying to shown the existence of a volume conserving pathway to isomerization and proving that the friction arising from the packing of the protein about the chromophore is not the only cause responsible for the dramatic effect of the protein matrix preventing the radiationless decay.
Protein hydrogen bond networks are essential to its structure, dynamics, and function. Hydrogen bond dynamics has been indeed extensively studied not only in proteins but also in fluorophores, molecular probes and DNA by a series of powerful experimental techniques, such as optical spectroscopy (Cohen et al., 2002; Pal and Zewail, 2004; Kukura et al., 2006; Frontiera and Mathies, 2007; Groot et al., 2007; Conti Nibal and Havenith, 2014; Fanetti et al., 2014; Patrizi et al., 2014), neutron scattering (Doster and Settles, 2005; Schiro et al., 2015), NMR (Nucci et al., 2011; Lewandowski et al., 2015), and by computational MD simulations (Makarov et al., 2002; Bagchi, 2005; Li et al., 2007; Amadei et a., 2011; D'Alessando et al., 2015; Donati et al., 2018b). In this context, the specific hydrogen bonding interactions and equilibrium dynamics between the GFP protein and the chromophore probably also play a significant role, although an extensive study on this complex interplay in the equilibrium ground state is still missing to the best of our knowledge, indeed. Since the necessity for providing a deeper insight into the equilibrium hydrogen bond dynamics involving HBDI and the protein pocket, in this work we use ab-initio molecular dynamics (AIMD) simulations to mainly investigate about the fluctuations of the hydrogen bond network in the different equilibrium layouts of GFP A, I, B forms. The accurate knowledge of the structural correlation within the GFP pocket dynamics in the ground state and in different forms can be informative also for understanding far from equilibrium relaxation processes in the ultrafast regime and the corresponding spectroscopic behavior. For example, ground state I form can be thought as the fluorescence decay product of the excited I* state. A dynamical picture of H-bond network immediately before absorption and after emission is thus provided by a study of fluctuations around the GFP forms. Moreover, GFP represent a model system to understand how different protonation state affects the hydrogen-bond dynamics in similar systems.
AIMD trajectories are collected according to a hybrid Quantum mechanical (QM)/molecular mechanic (MM) scheme and the energy potential ruling AIMD simulations including QM and MM regions is combined according to the hybrid N-layered integrated molecular orbital and molecular mechanics (ONIOM) extrapolation scheme; more details on the simulations are provided in the Materials and Methods section (Svensson et al., 1996; Morokuma et al., 2006; Vreven et al., 2006). Density functional theory (DFT) is employed for the ab initio treatment of the QM part, since it has an optimal balance between accuracy and computational cost and DFT, in its hybrid version, has been vastly used for the theoretical characterization of both vibrational and dynamical properties of molecules (Wong, 1996; Adamo et al., 2001; Barone et al., 2010; Branduardi et al., 2011; Petrone et al., 2013; Cimino et al., 2016; Lingerfelt et al., 2016; Pepin et al., 2016; Wildman et al., 2019) and the description of the electronic structure of both ground and excited electronic states in macro-molecular systems of material (Hafner et al., 2006; Beaulac et al., 2011; Guido et al., 2013; Lestrange et al., 2015; Aarons et al., 2016; Chong et al., 2016; Petrone et al., 2016b, 2018; Donati et al., 2017, 2018a; Gary et al., 2017; Stein et al., 2017; Crane et al., 2019) or biological interest (Langella et al., 2002; Improta et al., 2005; Lever et al., 2014; Savarese et al., 2014; Battista et al., 2018). An ab-initio treatment of the HBDI chromophore and the surrounding residues is mandatory for an accurate modeling not only of their structure, but also of the non-covalent interactions among them. However, this computationally demanding approach limits the length of the collected trajectories. In particular, we chose to extract and analyze several structural parameters related to the HBDI itself and the dynamic hydrogen bond network involving its neighboring residues. Distributions are provided to show equilibrium main features of the spatial extended hydrogen bond network. Our main goal has been also to retain the temporal information provided by AIMD by performing a cross-correlation analysis to highlight the entangled and complex hydrogen bond dynamics between regions at same, and even opposite, sides with respect to the GFP chromophore, as discussed in the Results and Discussion section. As main goal, we found correlations between the hydrogen bonds dynamics and features, such as the pocket volume where it is known that this one is correlated to spectroscopic parameters involving collective low frequency motions. Conclusions and perspectives are given in the Conclusions section.
2. Materials and Methods
The side chain of residue Thr65 in 1EMA has been modified to Ser65 for modeling both the I and B form according to the wild type GFP. Coordinates were augmented with hydrogen atoms by employing MolProbity (Chen et al., 2010) for both the neutral and anionic forms. Arginine and Lysine residues were considered positively charged while Aspartic and Glutammic acids negatively charged according to a pH condition of about 7. We protonated six histidines in both δ and ϵ positions, while of the remaining three, two were protonated in δ (one of these is His148) and the other one in the ϵ position. As already pointed out in literature (Scharnagl et al., 1999; Oltrogge et al., 2014), His148 δ protonation is required for the interaction with HBDI Tyrosine ring. All the internal crystallographic water molecules were protonated and retained.
The protein environment was modeled recurring to the N-layered integrated molecular orbital and molecular mechanics (ONIOM) scheme, (Svensson et al., 1996; Dapprich et al., 1999; Vreven and Morokuma, 2006; Vreven et al., 2006; Clemente et al., 2010) while implicit solvent effects were taken into account by employing a polarizable continuum model partition scheme (Miertus et al., 1981; Barone and Cossi, 1998; Cossi et al., 2003; Rega et al., 2006). For all the simulations in aqueous solution, solvent was treated more specifically by the so-called ONIOM/CPCM-X (Vreven et al., 2001; Mo et al., 2004) scheme, where a solvent reaction field is computed separately in each ONIOM sub-calculation on the PCM cavity of the real system. In particular, the protein solvent accessible surface was adopted to define the PCM cavity.
Following the ONIOM extrapolative scheme, the GFP has been then portioned into two layers, where a model region was treated at DFT theory level, while the rest of the protein, referred to as real, was represented at molecular mechanics level by employing the AMBER force field (Cornell et al., 1995). Due to the subtractive nature of the ONIOM QM/MM approach: , all the bonded (i.e., bending, stretching, torsions) force field terms are actually not required for the model (QM) part. Moreover, the treatment of the electrostatic interactions between QM and MM atoms was performed at a quantum mechanical level, introducing the charges of the MM layer into the QM model Hamiltonian (the so called “electronic embedding” scheme, as shown in Supplementary Figure 3) (Vreven et al., 2003, 2006). Non-bonding parameters are therefore the only MM parameters required for the HBDI chromophore. Following the approach of Reuter, AMBER Tyr side chain atom types were assigned to the phenol moiety of HBDI and AMBER His side chain atom types to the Imidazol HBDI ring (Reuter et al., 2002). More in details, the wt-GFP chromophore 4-(p-hydroxybenzylidene) imidazolidin-5-one (HBDI), Ser205, Glu222, Ser65, His148, Asn146, Thr203, Arg96, Gln94, and the crystallographic water molecules within a radius of 5 Å of a sphere centered on the methine bridge of the chromophore have been considered as the model region and were treated by using the range-separated version of the hybrid Becke three-parameter Lee-Yang-Parr (B3LYP) density functional (Lee et al., 1988; Becke, 1993; Stephens et al., 1994) with 6-31G(d,p) basis set (as shown in Figure 2). The rest of the protein has been modeled at molecular mechanics level. This partition scheme has been previously shown to be accurate for both ground and excited states properties (Brejc et al., 1997; Scharnagl et al., 1999; Vendrell et al., 2004, 2008a; Virshup et al., 2009; Di Donato et al., 2011; Roy et al., 2011; Wanko et al., 2012; Beerepoot et al., 2013; Petrone et al., 2013; Nadal-Ferret et al., 2015). In order to preserve the chemical nature of peptide bonds for the residues belonging to the DFT/molecular mechanics interface, the cuts have been chosen along single bonds and in general at non-polar or slightly polar bonds, preferably C–C ones. The dangling valence bonds have been capped by link hydrogen atoms.
Figure 2. (Left) Hybrid ONIOM (QM/MM) partition scheme of the neutral GFP structure (PDB code:1GFL). (Right) ONIOM high level model (ball and stick representation) which includes the GFP chromophore, side chains of aminoacids involved in the hydrogen bond network—crystallographic water molecule, Ser205, Glu222, and Ser65—and polar fragments of residues that mimic environmental effects.
This energy potential was used to calculate minimum energy structures in the ground state for the three forms, considered as the reference, and to run AIMD simulations within the Born-Oppenheimer approximation in the ground electronic state. More in detail, a first optimization run was performed in aqueous solution by employing the ONIOM B3LYP/6-31G(d,p)/Amber/CPCM-X level of theory followed by a further optimization run in gas phase. After this optimization procedure, the the root mean square (RMS) of the forces and displacements are within to 0.003 Ha/bohr and 0.03 bohr, respectively. In this work, since we aimed at pointing out the subtle structural differences between the three A/I/B GFP forms, from a dynamical viewpoint, ab-initio molecular dynamics simulations were performed starting from these configurations. The atom-centered density matrix propagation (ADMP) scheme was employed for this aim to allow longer simulations, since this method belonging to the extended Lagrangian approaches can exploit Gaussian basis functions and the direct propagation in time of the density matrix (Iyengar et al., 2001, 2002; Schlegel et al., 2001, 2002; Schlegel, 2003). All ab-initio molecular dynamics trajectories were collected using the previously validated ONIOM B3LYP/6-31G(d,p)/Amber theory level (Rega et al., 2004, 2006). Initial velocities were chosen randomly but enforcing an initial kinetic energy corresponding to the room temperature (T = 298 K) and individual trajectories were collected for 2.5 ps with an integration time step of 0.25 fs. This strategy allows to simultaneously sample the configurational space and dynamical room temperature fluctuations of the system, along with extracting representative correlated motions by employing the following presented analysis.
No back proton transfer event is observed during the simulation for both the I and B forms, while oscillation of the protons between the residues involved in the proton transfer is observed for the A form.
The cavity volume has been computed only for the protein pocket including the chromophore, Ser65, Ser205, and Glu222, and the crystallographic water hydrogen bonded to the phenolic oxygen of the chromophore. For each step of the trajectories for the neutral and anionic forms the cavity was computed as the resulting volume within the surface built using the overlapping spheres created by the PCM machinery on only this region [using the Universal Force Field (Rappe et al., 1992), UFF, atomic radii]. The Oxygen—Oxygen distributions between species directly involved in the proton wire have been computed with a resolution of 0.02 Å, while the cavity volume, the dihedral angles (and bond angle) have a resolution of 1 Å3 and 2.00°, respectively.
All the ab initio calculations were performed with Gaussian (Frisch et al., 2016) electronic structure software package.
Cross-correlations between the hydrogen bond distances and the pocket volume and between different hydrogen bond distances were performed for the three GFP forms. These structural quantities were extracted from the ab-initio molecular dynamics trajectories, and considering x(t) and y(t) as two distinct (average-subtracted) atom distances, their normalized cross-correlation at time-lag τ was evaluated as:
where the average was taken over the length of the trajectory:
The normalization factor (i.e., the inverse square root of the product of the two auto-correlations at τ = 0) allows rxy(τ) to assume values in the [−1, 1] interval. A high positive (negative) correlation rxy(τ) at time-lag τ suggests a high correlation between y(t) and x(t) (−x(t)), shifted by −τ along the time-axis. In order to disclose and analyse the most significant correlations between structural features of GFP pocket, only those with |rxy| > 0.45 were retained.
3. Results and Discussion
3.1. Analysis of Structural Parameter Distributions: A, I, B Forms
We report in Figure 3 the normalized distributions of oxygen—oxygen distances of the residues directly involved in the proton transfer reaction obtained from the ground state ab-initio molecular dynamics trajectories. The labels used in the text are shown in Figure 2. The distribution of the distances between the oxygen atoms of Tyr66 and the surrounding water molecule for the A, I and B forms are presented in Figure 3 (panels A, D, G for the A, I, and B forms, respectively). The distribution of the A form is peaked at 2.76 and 2.93 Å, covering a range of ~1Å. This result reflects small fluctuations around the average value of 2.9 Å (±0.2) calculated from the trajectory. The same distributions for the anionic I and B forms (see Figures 3D,G, respectively) show and cover an increasing range of values, from 2.65 up to 3.68 Å (Figure 3D) and from 2.57 to 4.28 Å (Figure 3G) for the I and B forms, respectively. Additionally, a more defined bimodal trend can be observed where two well-separated maxima can be recognized, a main peak at 2.86 Å (3.00 Å) and a lower one at 3.44 Å (3.46 Å) for the I (or B) form. This result proves the presence of two arrangements explored during the dynamics for both these anionic forms, less pronounced in the neutral one. By a closer inspection of the Tyr66-Wat distance dynamics in the anionic B-form (Supplementary Figure 4), it is clear that the crystallographic water molecule of the proton wire weakens its interaction with the nearby phenoxy ring of Tyr66 with respect to the other two forms. On the other hand, we observe that this water is now more involved in more stable hydrogen bonds with Asn146 and Ser205 residues. On the other side, the underlying Thr203 residue contributes to stabilize the negative charge on the chromophore.
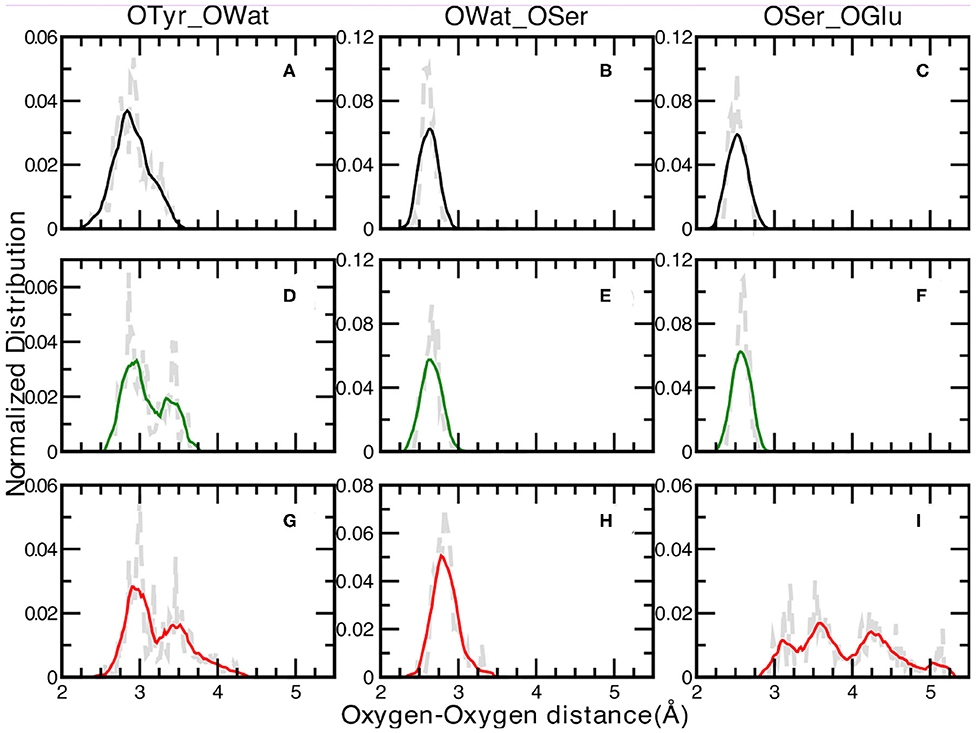
Figure 3. Normalized distributions of Oxygen—Oxygen distances at 0.02 Åresolution of: Tyr66—Wat [(A,D,G) for the A, I, and B forms, respectively], Wat—Ser205 [(B,E,H) for the A, I, and B forms, respectively] and Ser205—Glu222 [(C,F,I) for the A, I, and B forms, respectively]. Average values, shown by colored curves, are calculated every 15 points.
The distribution of the distances between the oxygen atoms of water and Ser205 are analyzed next (Figures 3B,E,H for the A, I, and B forms, respectively). We observe well-defined and unimodal distributions whose maxima are centered at increasing values of 2.61, 2.66, and 2.83 Å for the three forms listed above, respectively. These distributions are also narrower with respect to the previous ones. This observation can be rationalized considering that the Ser205 residue is located on the internal region of one of the eleven β-strands that make up the GFP β-barrel, making this residue less flexible compared to Tyr66. By visually inspecting the interaction maps of the Ser205 residue with the surrounding protein residues side chains, in both neutral and anionic crystallographic forms, it is clear that the distribution around Ser205 is sharper since its environment is more characterized by hydrophobic interactions, making this residue more rigid. On the other hand, by analysing the interaction map of the Tyr66 residue, it is evident that the observed larger mobility is due by three different hydrogen bonded mutual interacting sites (His148, Thr203, and the crystallographic water molecule) which would justify the observed wider and bimodal distributions of Oxygen—Oxygen distances. The interaction maps of both the starting crystallographic structures are reported in the Supplementary Figure 11.
Moreover, the Ser205 closer environment presents no polar or charged residues that could in principle interact with its hydroxyl group, and so competing for its hydrogen bonding interactions. These two factors make Ser205 both conformationally quite rigid and stable in terms of hydrogen bond interactions. This result is also in agreement with experimental data from the crystallographic structures, indeed as in all the three simulated forms the Owat—OSer205 distances show similar values, also in the 1GFL and 1EMA (our references for the neutral and anionic forms) are very close.
A and I forms show sharp and unimodal distributions for the last OSer205—OGlu222 distance (Figures 3C,F, respectively), with two well-defined maxima centered at 2.51 Åfor the A form and at 2.60 Åfor the I form. As concerning the case of the anionic B-form (Figure 3I), this distribution shows a poorly defined shape (almost trimodal) and a wider ranges of values, starting from about 2.30 Å (already a value ~0.6 Å larger than the two previous counterparts) up to 5.18 Å. At least three regions can be recognized, centered around 3.15, 3.50, and 4.25 Å. This result supports the fact that Glu222 residue is in a less favorable orientation to interact through an hydrogen bond with the Ser205 residue in the B-form, while it is in a better arrangement to interact with the crystallographic water molecules behind the molecular plane of the HBDI chromophore (as hydrogen bond acceptor) and with Ser65 (as a donor).
Also this time we provide a closer look at Tyr66-Wat distance dynamics in the anionic B-form collected during ground state sampling as reported in Supplementary Figure 5. We can observe the environment of Tyr66 to be characterized by higher mobility of the water molecule and by the concomitant and competitive hydrogen bond interactions for this form. The negative charged chromophore in this relaxed anionic form can establish, from the Tyr66 phenoxy ring side, both a stable hydrogen bond with the hydroxy group of Thr203 and can partially interact with the NH group of His148, weakening on the contrary the interaction with nearby water molecule.
Summarizing this first analysis, the interaction between Ser205 and water are rather stable for all three forms. The chromophore water interaction shows at least two equilibrium conformations mostly for the anionic forms, while Ser205-Glu222 interactions are more stable for the A- and I-forms only, while this region starts to be more flexible in the B-form, since the Glu222 is spatially distant and more exposed to Ser65 and to two water molecules under the five-membered ring. These results clearly suggest that the chromophore in the three GFP forms is characterized by a structurally different pocket in the equilibrium simulations. The specific interactions have different equilibrium dynamics and stability in the three forms and the observed differences suggest that they have a well-defined and peculiar hydrogen bond network dynamics that will be analyzed in details in the next section.
Given the different observed equilibrium distances of the proton wire described above, the chromophore protein pocket is investigated next. The cavity volume is computed along the trajectories according the procedure explained in the Methods section and the equilibrium distribution for the three forms is reported in Figure 4.
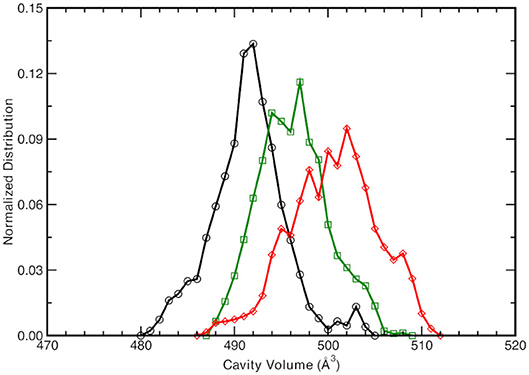
Figure 4. Normalized cavity volume distribution computed for each trajectory step at 1.00 Å3 resolution taking into account the residues participating in the hydrogen bonding network (44 atoms). Black curve refers to the neutral A-form, green and red traces refer to the anionic I- and B-form, respectively.
The neutral A form (black line) shows the sharpest distribution with a peak starting at lowest values with respect to the other two anionic forms. This suggests that the pocket is more compact in the neutral form and this observations is also supported by the previous observed narrower Oxygen—Oxygen distance distributions (see Figures 3A–C). The pocket volume distribution for the I form (dark green) is bimodal and centered at larger volume values, where there are two almost equivalent peaks (shifted of 2 and 5 Å3 with respect the A form). It is interesting to validate the hypothesis that these two larger values are correlated to the different hydrogen bonds arrangements discussed previously. For example, the high mobility of the crystallographic water molecule (previously observed in the OTyr66—OWat distribution of the distances in Figure 3D) can be considered to be the most important structural parameter responsible of these slightly larger pocket. The interactions for hydrogen bond network showed a weaker strength for the anionic B form in the previous analysis of distances distribution (see Figures 3G–I) and we expect a wider distribution of the volume for this last one (red curve). The protein pocket volume computed around this specific partition is wider and less sharp with multiple maxima around the main peak that is located at largest values. These trends prove that the pocket volume is directly correlated to the hydrogen bond network and dynamics, revealing how local variations in the interactions among residues are able to affect a quantity, such as the molecular volume dynamics of the protein pocket. We would also stress that from this molecular analysis based on local specific interactions, insights on larger scale quantities, such as the volume of the active site of the protein, can be obtained. On the other side, changes in volume can be interpreted and disentangled in changes on interactions localized on specific residues that are directly involved in the photo-chemistry of this system (such as the proton transfer in this case). This connection can be very useful in finding the molecular mechanisms hidden behind larger scale effects (volume changes) and can help in improving the efficiency of GFP and in general of biological molecules, when employed in fields, such as technology or drug design (Misteli and Spector, 1997; Errampalli et al., 1999; Ehrhardt, 2003; March et al., 2003; Tromans, 2004; DeLong et al., 2016).
Since the distances distributions analyzed provide a piece-wise description of the hydrogen bond network involved in the PT reactivity, we also decide to report the distribution of the dihedral angle between the planes including either the oxygen atoms of the Tyr66, Wat, and Ser205 or the oxygen atoms of Wat, Ser205 and the accepting oxygen of the Glu222 in Figure 5. A wide distribution of values for the neutral A-form states that the system visits a larger conformational space ranging from −40 to 58° with a main peak at about −9° which indicated that the system oscillates already around a co-planar conformation, although in a very very flexible way. In Figure 5, we also report as example a representative configuration of the atoms in the pocket from the ground state AIMD of the neutral form (top right) in which it is possible to appreciate the relative position of the residue Glu222 with respect to the plane of the chromophore. The anionic I- and B-form dihedral distributions are different with respect to the neutral one. In the I-form, in which we observed previously that the Glu222 side-chain is more prone to a bridge interaction between the two adjacent Serine residues, the distribution is now narrower and covers a more positive range of values. This indicates that the carboxyl group of Glu222 oscillates at equilibrium from a defined co-planar network conformation (about −4°) to a limit one in which lies above the plane defined by the chromophore (28° corresponding to the maximum value of the distribution and can be seen in Figure 5, middle right). On the contrary, for the B form the hydrogen bond network dihedral distributions show mainly negative values and is 10° narrower than the previous ones (from −62 up to 10°). From a detailed analysis of the equilibrium trajectory, it has been observed that the Glu222 moves in the opposite direction from the previously discussed I-form, interacting with the water molecules below the chromophore plane (peaks at −22 and −40°), moving away from Ser205 as also schematically shown in Figure 5 (bottom right).
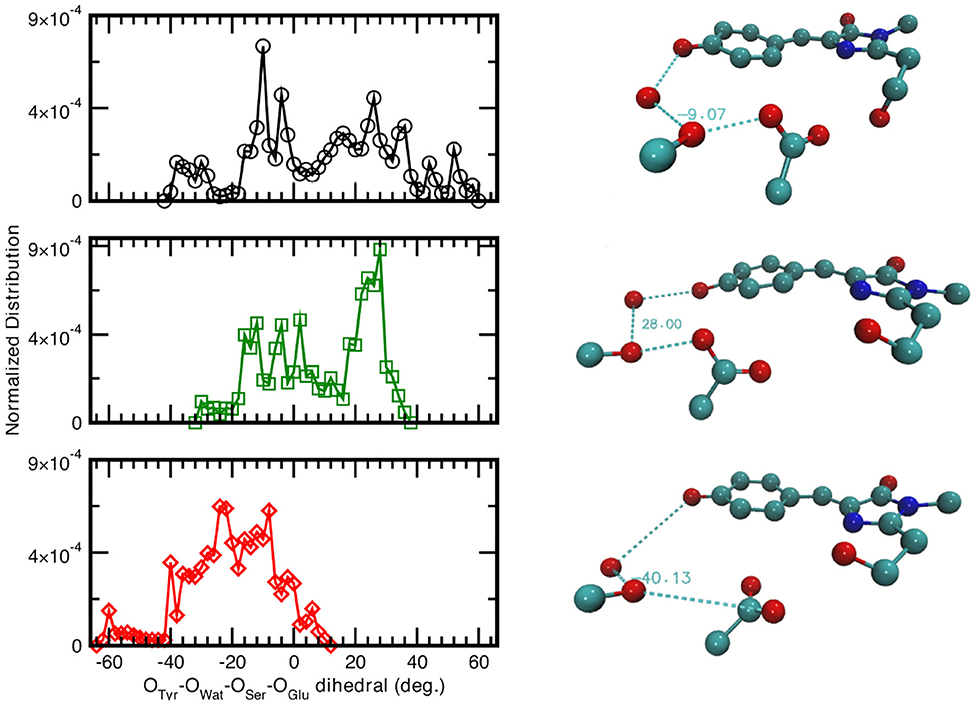
Figure 5. (Left) Normalized distribution computed from equilibrium AIMD trajectories of the dihedral angle identified by oxygens atoms belonging to the species directly involved in the H-bond chain, see X-axis label. Solid black curve and circles refer to the neutral A-form; dark green trace and squares (red trace and diamonds) refer to the anionic I-form (B-). All distributions have a resolution of 2.00°. (Right) Representative configuration of the neutral A-form (−9°), top panel; anionic I- (28°), middle panel and B-form (−40°), bottom panel. Numerical values are reported in degrees.
As also observed in the previous analyses, the distributions of the hydrogen bonds network oxygens reflect the structural rearrangement of the GFP chromophore pocket in the neutral and anionic forms. The A form is characterized by a distribution almost centered at values corresponding to a co-planar conformation, in agreement with the fact that the chromophore environment, also in the ground state, oscillates around a favorable conformation to allow the proton transfer, since this coplanarity has been shown to be important to PT reaction (Petrone et al., 2016a) In the I form case, the peak of the dihedral angles distribution is now shifted at 30°, away from a co-planar arrangement of the residues reflecting the fact that the chromophore is now anionic and the surrounding residues conformation does not need to be planar anymore. This situation is even more enhanced in the B form, where the distribution is substantially centered around non-coplanar values.
Finally, the chromophore flexibility is analyzed by inspecting the distributions of the NCCC(τ) and CCCC(ϕ) dihedral angles affecting the bridging atoms between the tyrosine and imidazolinonic ring of the HBDI chromophore in Supplementary Figure 6. On the contrary with respect to the previous dihedral, we observed here very narrow distributions centered around 0 degrees for both NCCC and CCCC cases. This supports that in the ground state HBDI chromophore is quite rigid and is not the responsible of the main observed distortion of volume of the protein pocket for the three forms. Also, the distribution of the CCC(ω) bond angle, centered at 128° for both the neutral and anionic forms, covers a narrow range of values. The stiffness of the CCC bridge states that, despite the different protonation state in the three forms, there is no mutual scissoring motions of the two chromophoric rings indeed.
To summarize, our results deriving from the study of the distributions of key structural parameters highlight the main differences of the GFP pocket in the three forms. In particular, we observe that the distributions of the distances between oxygen atoms of the proton wire residues are consistent, for all three forms, with the trend of an increasing volume of the pocket cavity. It is clear that, since the chromophore retains co-planarity in both the neutral and anionic form, the increasing trend of volumes is mainly attributable to the relative positions of the residues that participate in the proton hopping reaction.
These results underline that the photoinduced behavior of GFP is a fine balance among the residues of the pocket and of the protein matrix, being this latter the main cause preventing the photoinduced isomerization of the chromophore. Time-resolved infrared and Femtosecond stimulated Raman spectroscopy experiments, supported by theoretical works, revealed the crucial role of chromophore-Glu222 wire for the GFP fluorescence, where a concerted excited state proton transfer is hypothesized during which the protein pocket prevents the non-radiative decay (Stoner-Ma et al., 2005, 2006; Fang et al., 2009; Petrone et al., 2016a). Our finding further supports the importance the hydrogen bond network for the GFP optical properties. Previous computational and experimental works (Ormö et al., 1996; Brejc et al., 1997; Creemers et al., 1999; van Thor et al., 2002; Jung et al., 2005) have underlined the role of amino acids at position 65, 203, 222 and their impact on the optical properties of GFP (both absorption and fluorescence). Point mutations at these positions importantly affect the hydrogen bond network, determining a drastic change in the optical behavior of GFP and the excited state proton transfer reaction. As for our distributions, the role of Ser65 making an hydrogen bond with Glu222 is a crucial prerequisite for the excited state reactivity and fluorescence. Our results highlight not only the differences among the neutral and anionic forms in terms of hydrogen bonds, but also underline the difference in terms of mobility among the different hydrogen bond couples. As a main result, in agreement with experimental data, we found that it is a fine equilibrium, built of specific low energy bonds, such as the hydrogen bond, that is able to rule and change the dynamics of the GFP.
For this reasons we analyze in deep in the next section the dynamic correlation in the residues interacting with the PT hydrogen network and the chromophore.
3.2. Time Cross-Correlation Analysis of GFP Pocket Non-covalent Interactions
The subtle balance among non-covalent interactions in protein structures often gives rise to a complex choreography of delocalized motions (Go et al., 1983; Ichiye and Karplus, 1991; Garcia, 1992; Berendsen and Hayward, 2000; He et al., 2011). As already noticed, a reliable hybrid QM/MM potential is mandatory for an accurate modeling of critical regions of protein systems, such as the GFP HBDI moiety. On the other hand, this imposes practical restraints about the simulation time which, in turn, limits the sampling of the low-frequency modes. In this section, starting from MD simulations of GFP A, I, and B-forms, a cross-correlation-based approach in the time-domain has been employed to give hints about the existence of concerted motions involving distant weak interactions in the GFP HBDI pocket. In particular, the normalized cross-correlation function rxy(τ) was evaluated between each H-bond in the pocket and the cavity volume and between each pair of H-bonds located on opposite sides of the HBDI moiety (one side including His148, Asn146, Thr203, and the other one including Arg96, Gln94, see Figure 2).
As observed in the previous section, the volume of the chromophore cavity is an indirect measure of the packing of the proton-wire around HBDI. To extract potential structural additional determinants affecting the volume and their equilibrium fluctuations and correlations, the most relevant H-bonds/volume cross-correlations were computed and reported in Table 1 and Supplementary Table 1. In this analysis we report significant values of the local maximum (or minimum) and the delay times at which these features appear for several cross-correlation functions between structural determinants. For example, looking first at the proton-wire H-bonds, the correlation between O(Tyr66)—O(Wat) and the volume shows a maximum value of 0.53 at 5 fs as delay time for the I form. This correlation further strengthens presenting a value of 0.62 for the B form and this time the negative −65 fs at which the maximum appears means that the volume lags behind O(Tyr66)—O(Wat) distance. The negative charge acquired by O(Tyr66) in the HBDI deprotonated forms forces the water molecule to oscillate more toward the chromophore, as a consequence of a stronger polar interaction. This reflects into a strong, direct (<100 fs delay) positive correlation for the I and the B-GFP. This result suggests that the volume is very sensitive to the change of the chromophore protonation state and its consequent change in hydrogen bond interaction with water, resulting in an important correlation between them. The short time delay found is also indicative of almost direct correlation between the two quantities. On the other hand, the O(Ser205)—O(Wat) distance appears largely uncorrelated with the volume (Supplementary Table 1). Then, the O(Ser205)—O(Glu222) H-bond shows a lag-free correlation with the pocket volume in the A-form, suggesting a fluctuation of Ser205, which is lost in the I-form. Instead, an intense anti-correlation (negative value) appears in the B-form. The >500 fs delay suggests that this negative correlation is not a direct effect, but it could reflect some delocalized motion involving larger portions of the structure. It is possible that the Glu222 is affected and involved in other motions in the B form (its spatial conformation is actually very different from both the A and I forms, see previous section), and this fact can causes a delay in the correlation of O(Ser205)—O(Glu222) with the volume. However, the intense anti-correlation suggests that the dynamics of the two residues is still involved in influencing the volume changes.

Table 1. Most relevant normalized cross-correlation functions between H-bonding interactions involving residues near the HBDI pocket and the pocket volume for GFP A, I, and B-forms.
Looking instead at the correlations between the pocket volume and the H-bonds external to the proton-wire, the O(Thr203)—O(Wat) interaction is investigated. In this case, significant correlations are found just for the anionic forms. This result supports the hypothesis that the chromophore (and its environment) interacts with Thr203 after the proton transfer reaction (i.e., once the chromophore becomes anionic). More in detail, a high negative correlation is found in the B-form. The negligible delay suggests that the intermittent interaction between the Thr203 OH group and the network water molecule (found only in the B-form) is able to move the water molecule away from the HBDI moiety. Moreover, this result suggests that the interaction with Thr203 (both in terms of degree of correlation and almost absent time-delay) is very important in the B form and that has a direct influence in modifying the volume of the chromophore pocket. On the other side, a large delay and smaller correlation is found for the I form. This fact suggests that this hydrogen bond has an impact on the volume, however it is also influenced by other collective motions and interactions causing the larger observed delay in the correlation. These trends support the hypothesis that the interactions with Thr203 is typical of the anionic forms and it has more impact in the B form that represents the “relaxed” and optimized chromophore pocket after the proton transfer reaction.
N(His148)—O(Wat) always reveals some positive correlation with the volume. Because of the geometry of the pocket, the departure of the water residue from His148 implies also an expansion of GFP main H-bond network. In analogy with the previous case, also in this case a shorter delay is found in the B form with respect to the I one suggesting again that a more direct connection is found when the environment is already rearranged for the anionic chromophore form. Less obvious is the correlation shown by N(His148)—O(Tyr66) in the I and B-forms. The ~±200 fs delays suggest some mechanism also involving residues located outside the pocket. When the correlation involves the chromophore itself, in both the I and B forms similar delays are found. In this case it is not the environment but the chromophore itself involved (anionic in both cases) and affected in the same way by motions involving other residues. The behavior is even more intricate for the O(Asn146)—O(Tyr66)/volume pair, whose correlation starts as positive in the A-form, becoming predominantly negative in the B one. Moreover, the clearly different delays for the positively correlated contribution comparing the A and I with the B-form reveal an abrupt change of the underlying collective motion. H-bonds on the HBDI imidazolinone side show on average weaker correlations with the cavity volume. Notable exceptions [I-form O(Imid)—N(Arg96), A-form O(Imid)—N(Gln94)] are characterized by high (~1 ps) delays and are likely the effect of some low-frequency collective modes. The fact that less significant cross-correlations are found when analyzing parameters from the imidazolinone side support the idea that the perturbation event, i.e., the proton transfer, takes place far in the space from it and so a lower impact on molecular rearrangement affecting the volume on this side is found.
The cross-correlations between non-covalent bond distances on distinct sides of HBDI moiety were then analyzed for regular patterns in Table 2 and Supplementary Table 2. Concerning first the main H-bond network, the O(Tyr66)—O(Wat) distance appears to be strongly related to the O(Imid)—N(Gln94) interaction in the I-form (Figure 7). O(Ser205)—O(Wat) equilibrium dynamics is quite uncorrelated with its counterparts on the opposite side. Just a similarity with O(imid)— N(Arg96) distance is found in the B-form. Interestingly, the only correlations shown by O(Ser205)—O(Glu222) [with O(Imid)—N and N2(Arg96)] are in the B-form, where the H-bond between Ser205 and Glu222 is lost (Supplementary Table 2). Distances involving residues external to the main proton-wire give rise to more evident correlations with the Imid–Arg96 or Gln94 interactions. O(Thr203)—O(Wat) exhibits strong anti-correlations with O(Imid)—N(Arg96) in both I and B-forms and with O(Imid)—N2(Arg96) and O(Imid)—N(Gln94) only in the I-form. These differences between the I and B forms could indicate that structural dynamics in different space regions of the chromophore environment are still correlated. However, this fact is more enhanced in the I form that is the intermediate situation between the stable neutral (A) and anionic (B) forms, indicating that the whole protein region has not completely adapted to new chromophore situation. N(His148)—O(Wat)/O(Imid)—N(Arg96) correlation is stronger in the I and B-forms (Figure 8). The correlation with O(Imid)—N2(Arg96) is in contrast more pronounced in the A-form. Strong correlations are kept with O(imid)—N(Gln94) in the A and I-forms, but they are lost in the B one. Looking at the N(His148)—O(Tyr66) distance, the intense correlations shown in the A (Figure 6) and I-forms with all the three interactions on the HBDI opposite side are not maintained in the anionic B form. The important role of His148 was already observed in Donati et al. (2018b), where this hydrogen bond interactions seems to be highly correlated to proton transfer event starting from the neutral form. It is possible that this interaction is still retained in the I form, but it is weakened in the B form (since it is completely relaxed after the PT), resulting in the observed absence of this correlation.
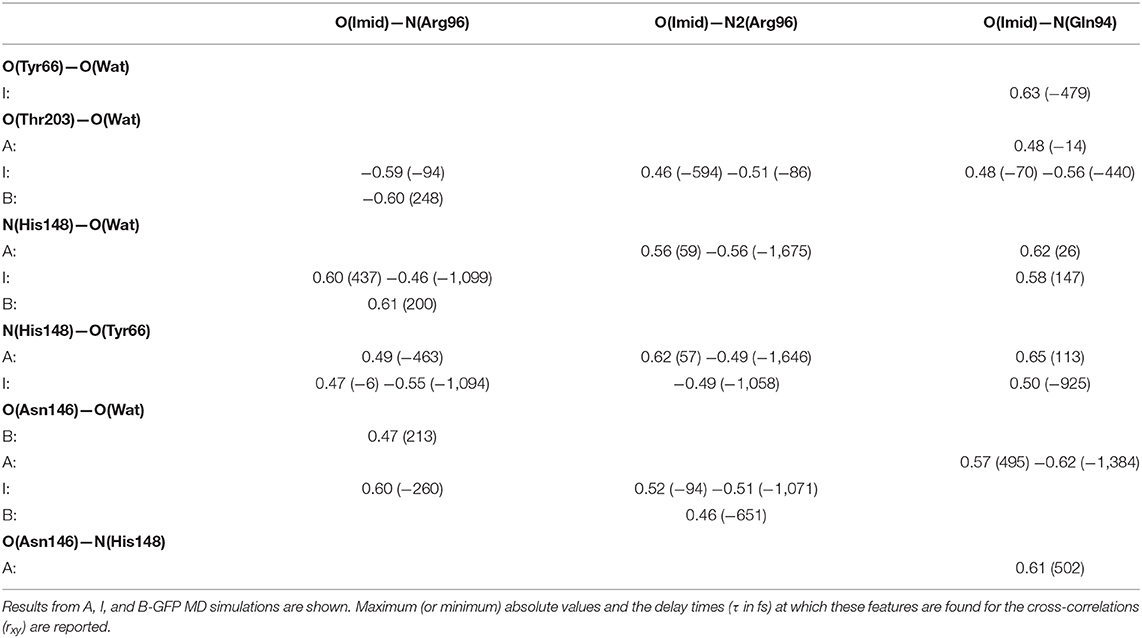
Table 2. Most relevant rxy normalized cross-correlation functions for selected pairs of hydrogen-bonds located on opposite sides of HBDI pocket (one side including His148, Asn146, Thr203, and the other one including Arg96, Gln94, see Figure 2).
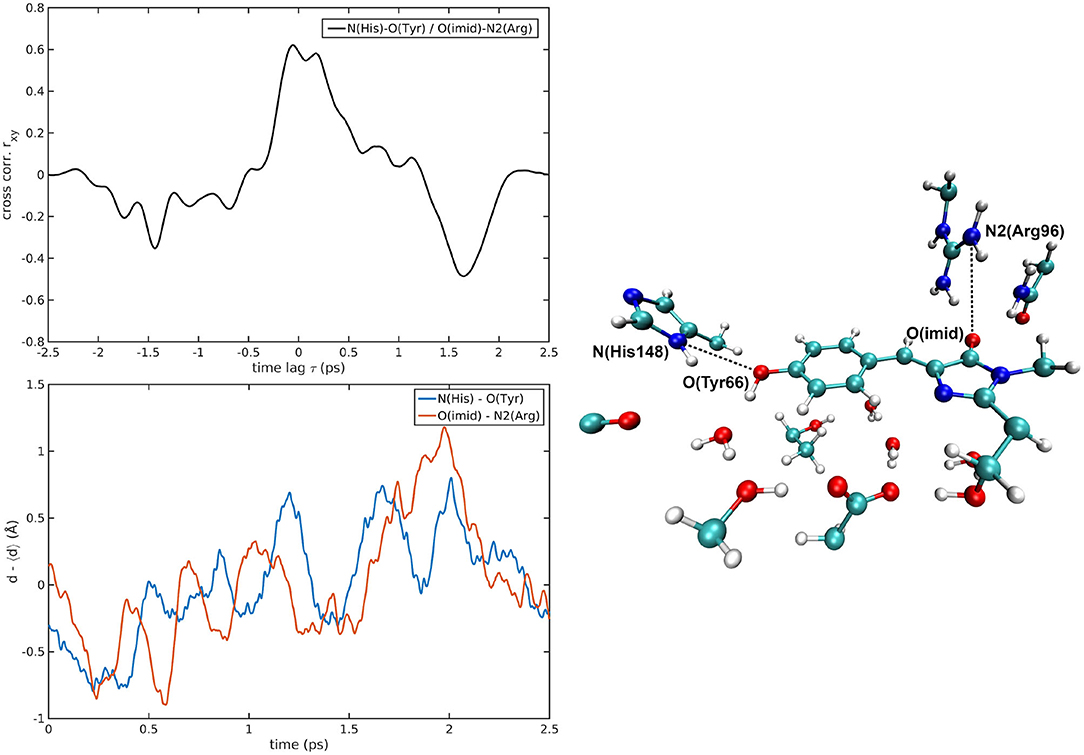
Figure 6. N(His148)—O(Tyr66)/O(Imid)—N2(Arg96) correlated pair in A-GFP MD [rxymax = 0.62 (τ = 57 fs)].
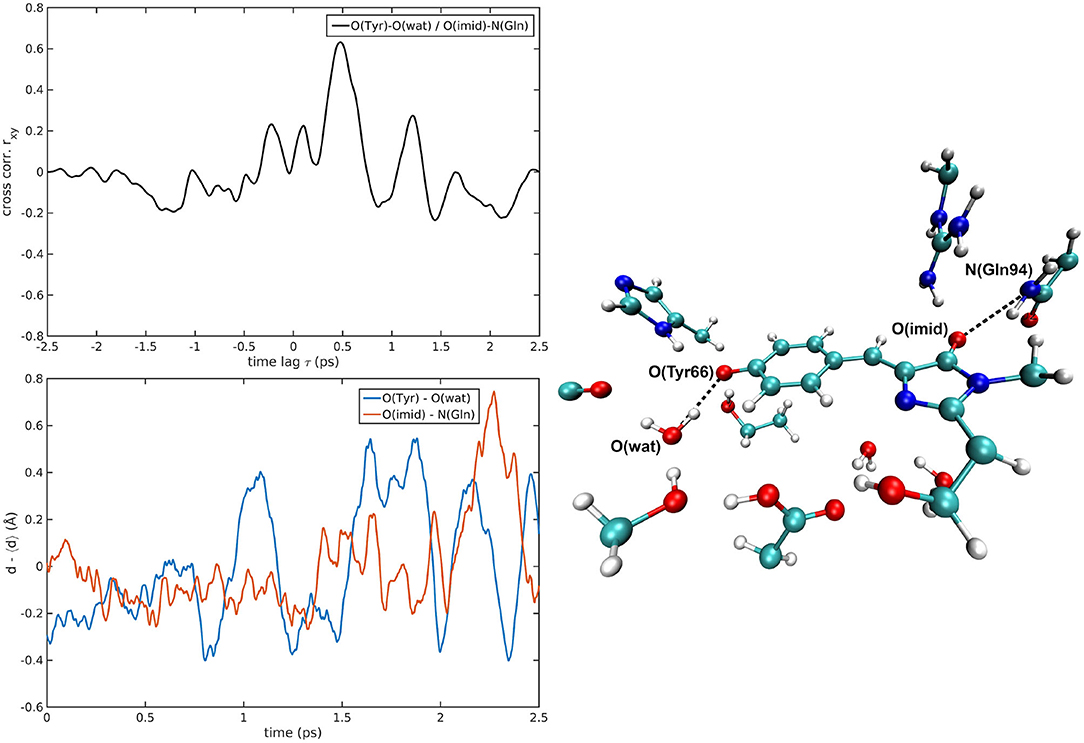
Figure 7. O(Tyr66)—O(wat)/O(Imid)—N(Gln94) correlated pair in I-GFP MD [rxymax = 0.63 (τ = −479 fs)].
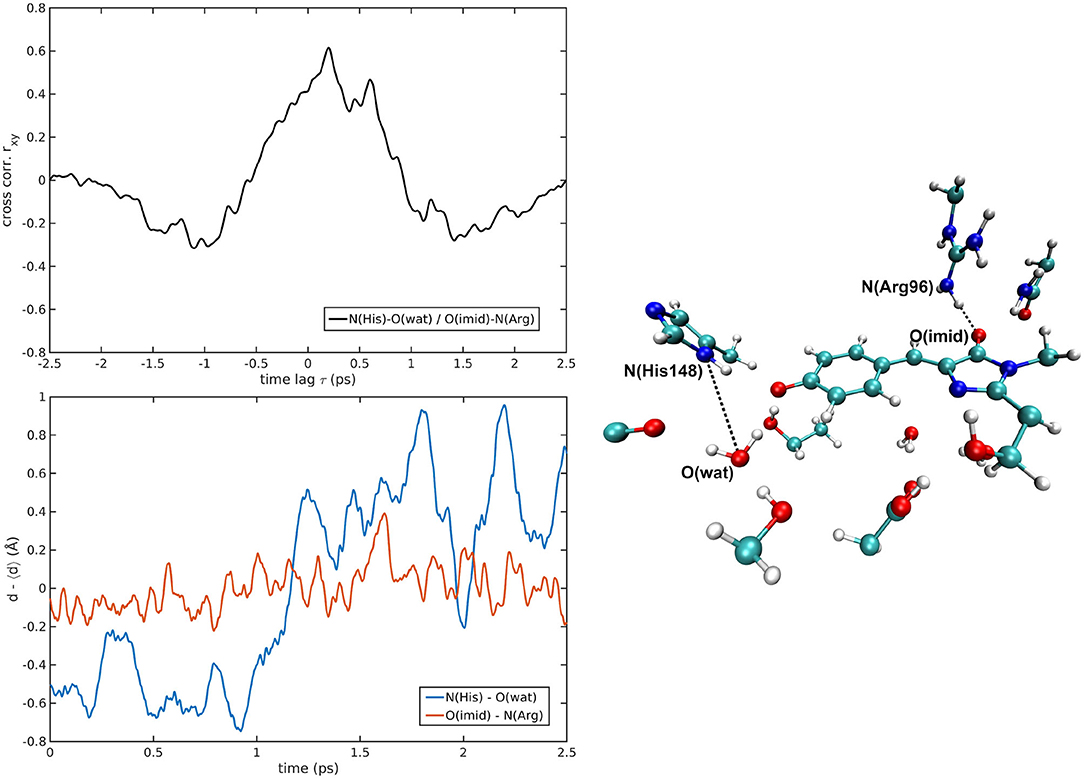
Figure 8. N(His148)—O(wat)/O(Imid)—N(Arg96) correlated pair in B-GFP MD [rxymax = 0.61 (τ = 200 fs)].
O(Asn146)—O(Wat) never shows rxy values above 0.5. Remarkable correlations are found with O(Imid)—N(Arg96) in the B- and with O(Imid)—N(Gln94) in the A-form. Analogously, O(Asn146)—N(His148) distance appears not so well-correlated, particularly for the B and I-forms while a high, delayed, similarity with O(imid)—N(Gln94) is nonetheless found in A-GFP. These results indicate that when dealing with correlations in a wider spatial range not involving the chromophore itself, different pairs of residues are correlated in the anionic form B and the neutral form A. Indeed, while a correlation exists between O(Asn146)—O(wat) and O(Imid)—N(Arg96) for the B form, different couples are correlated in the A form [O(Asn146)—N(His148) with O(Imid)—N(Gln94)].
In a opposite way, when the chromophore is involved all the three forms present correlations. O(Asn146)—O(Tyr66) reveals instead many highly correlated trends. While in the A-GFP the correlation with O(imid)—N(Gln94) is predominant (two equally relevant positive and negative ones with very different delays), in the I-form higher values of rxy are obtained with O(imid)—N(Arg96) and O(Imid)—N2(Arg96) (in the latter case, a positive and negative correlation with distinct delays are found). Distance pairs most strongly correlated (|rxy| > 0.5) in each GFP state are shown in Supplementary Figures 7–10. It is interesting to underline that there is a specificity in the couples involved in the correlation with O(Asn146)—O(Tyr66), indeed while in the A form it takes place with O(imid)—N(Gln94), it switches to O(imid)—N(Arg96) and O(Imid)—N2(Arg96) for the anionic forms. So through this analysis not only correlations among residues far in the space are found, but also the specificity among the different GFP forms is disentangled.
To summarize, our results deriving from the study of the cross-correlation of key structural parameters highlight an entangled dynamics of H-bond network in the pocket and the cavity volume directly involving the chromophore, such as O(Tyr66)—O(Wat), or not, such as O(Thr203)—O(Wat). This is very interesting since it underlines the cooperativity and collective nature of structural events affecting the volume of the cavity. Moreover, the correlations found among some of the H-bonded residues located on opposite sides of the HBDI moiety [O(Tyr66)—O(Wat) with O(Imid)—N(Gln94) or N(His148)—O(Wat)/O(Imid)—N(Arg96)] reveal that the dynamics of apparently uncorrelated residues is instead characterized by an important connection, also in this case, involving or not the chromophore Tyr66 residue. These results importantly underline that disentangling the dynamics of a residue like a chromophore from its environment is tricky since it cannot be confined to it or just few residues apparently actively involved in the reaction event, but it is of crucial importance to take into account a larger portion of the protein surrounding it.
4. Conclusions
This paper presents the complex hydrogen bond equilibrium dynamics involving the GFP chromophore pocket in the A, I, and B forms, relying on accurate hybrid QM/MM approach for simulating the entire protein. The QM/MM ONIOM approach offers the possibility of studying in detail the effect of the protein environment on the chromophore structural and spectroscopic properties as fluorescence. A detailed molecular insight on structural differences in the active site of GFP and correlations among single hydrogen bond interactions and a macroscopic quantity, such as the volume of the chromophore cavity, is given here for the first time. In particular, the intermolecular distances involving the chromophore, such as O(Tyr66)–O(Wat) and O(Asn146)–O(Tyr66) are importantly correlated to the cavity volume in both the anionic forms. Not only the hydrogen bond network involving the chromophore, but also other side residues surrounding it are active parts in tuning the fine balance of the hydrogen bond interactions. Indeed, important differences in non-covalent interactions are found in the A, I and B forms chromophore pocket. Moreover, we found that their dynamics can correlate also residues at opposite sides of the pocket showing either a direct correlation [i.e., N(His148)–O(Tyr66) with O(Imid)–N(Arg96)] or through collective delayed and still (anti)-correlated motions [i.e., O(Thr203)–O(Wat) with O(Imid)–N(Arg96)]. Hydrogen bond pairs not close in the space also show a correlated dynamics, showing the complexity of this system where the synchrony of molecular motions has echoes in the space and that the role of apparently spectator residues is very significant instead. We directly correlate these specific interactions with the cavity volume showing a direct connection among these ones and how the volume reflects changes among the GFP forms. It is also interesting that also between the anionic species, different behaviors are found. Importantly, we were able to disentangle the coupled chromophore/neighboring residues motions over the time, and finely analyze the correlation between the entire protein pocket volume and local atomic displacements, providing a direct link among them.
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material.
Author Contributions
GD, AP, and NR: project. GD: data collections. FC and FP: data analysis. All authors interpretation of data and writing.
Funding
NR, FP, FC, and GD thanked Gaussian Inc., for financial support. AP thanked MIUR (Project AIM1829571-1 CUP E61G19000090002) for financial support. All authors thank MIUR (Project PRIN 2017YJMPZN001) for financial support.
Conflict of Interest
FC, FP, NR, and GD declare that received financial support from Gaussian Inc. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmolb.2020.569990/full#supplementary-material
References
Aarons, J., Sarwar, M., Thompsett, D., and Skylaris, C.-K. (2016). Perspective: methods for large-scale density functional calculations on metallic systems. J. Chem. Phys. 145:220901. doi: 10.1063/1.4972007
Acharya, A., Bogdanov, A. M., Grigorenko, B. L., Bravaya, K. B., Nemukhin, A. V., Lukyanov, K. A., et al. (2017). Photoinduced chemistry in fluorescent proteins: curse or blessing? Chem. Rev. 117, 758–795. doi: 10.1021/acs.chemrev.6b00238
Adamo, C., Cossi, M., Rega, N., and Barone, V. (2001). “Chapter 12 - new computational strategies for the quantum mechanical study of biological systems in condensed phases,” in Theoretical Biochemistry, Vol. 9 of Theoretical and Computational Chemistry. ed L. A. Eriksson (Elsevier), 467–538. doi: 10.1016/S1380-7323(01)80013-3
Amadei, A., Daidone, I., Zanetti-Polzi, L., and Aschi, M. (2011). Modeling quantum vibrational excitations in condensed-phase molecular systems. Theor. Chem. Acc. 129, 31–43. doi: 10.1007/s00214-010-0882-8
Armengol, P., Gelabert, R., Moreno, M., and Lluch, J. M. (2015). Unveiling how an archetypal fluorescent protein operates: theoretical perspective on the ultrafast excited state dynamics of gfp variant s65t/h148d. J. Phys. Chem. B 119, 2274–2291. doi: 10.1021/jp506113g
Bagchi, B. (2005). Water dynamics in the hydration layer around proteins and micelles. Chem. Rev. 105, 3197–3219. doi: 10.1021/cr020661
Barone, V., Bloino, J., and Biczysko, M. (2010). Validation of the dft/n06d computational model on the magnetic, vibrational, and electronic properties of vinyl radical. Phys. Chem. Chem. Phys. 12, 1092–1101. doi: 10.1039/B915246F
Barone, V., and Cossi, M. (1998). Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 102, 1995–2001. doi: 10.1021/jp9716997
Battista, E., Scognamiglio, P. L., Di Luise, N., Raucci, U., Donati, G., Rega, N., et al. (2018). Turn-on fluorescence detection of protein by molecularly imprinted hydrogels based on supramolecular assembly of peptide multi-functional blocks. J. Mater. Chem. B 6, 1207–1215. doi: 10.1039/C7TB03107F
Beaulac, R., Feng, Y., May, J. W., Badaeva, E., Gamelin, D. R., and Li, X. (2011). Orbital pathways for mn2+-carrier sp-d exchange in diluted magnetic semiconductor quantum dots. Phys. Rev. B 84:195324. doi: 10.1103/PhysRevB.84.195324
Becke, A. D. (1993). Becke's three parameter hybrid method using the LYP correlation functional. J. Chem. Phys. 98, 5648–5652. doi: 10.1063/1.464913
Beerepoot, M. T., Steindal, A. H., Kongsted, J., Brandsdal, B. O., Frediani, L., Ruud, K., et al. (2013). A polarizable embedding dft study of one-photon absorption in fluorescent proteins. Phys. Chem. Chem. Phys. 15, 4735–4743. doi: 10.1039/c3cp44659j
Berendsen, H. J., and Hayward, S. (2000). Collective protein dynamics in relation to function. Curr. Opin. Struct. Biol. 10, 165–169. doi: 10.1016/S0959-440X(00)00061-0
Branduardi, D., De Vivo, M., Rega, N., Barone, V., and Cavalli, A. (2011). Methyl phosphate dianion hydrolysis in solution characterized by path collective variables coupled with dft-based enhanced sampling simulations. J. Chem. Theory Comput. 7, 539–543. doi: 10.1021/ct100547a
Bravaya, K. B., Grigorenko, B. L., Nemukhin, A. V., and Krylov, A. I. (2012). Quantum chemistry behind bioimaging: insights from ab initio studies of fluorescent proteins and their chromophores. Acc. Chem. Res. 45, 265–275. doi: 10.1021/ar2001556
Bravaya, K. B., Khrenova, M. G., Grigorenko, B. L., Nemukhin, A. V., and Krylov, A. I. (2011). Effect of protein environment on electronically excited and ionized states of the green fluorescent protein chromophore. J. Phys. Chem. B 115, 8296–8303. doi: 10.1021/jp2020269
Brejc, K., Sixma, T. K., Kitts, P. A., Kain, S. R., Tsien, R. Y., Ormo, M., et al. (1997). Structural basis for dual excitation and photoisomerization of the aequorea victoria green fluorescent protein. Proc. Natl. Acad. Sci. U.S.A. 94, 2306–2311. doi: 10.1073/pnas.94.6.2306
Chalfie, M. (1995). Green fluorescent protein. Photochem. Photobiol. 62, 651–656. doi: 10.1111/j.1751-1097.1995.tb08712.x
Chalfie, M., Tu, Y., Euskirchen, G., Ward, W., and Prasher, D. (1994). Green fluorescent protein as a marker for gene expression. Science 263, 802–805. doi: 10.1126/science.8303295
Chang, J., Romei, M. G., and Boxer, S. G. (2019). Structural evidence of photoisomerization pathways in fluorescent proteins. J. Am. Chem. Soc. 141, 15504–15508. doi: 10.1021/jacs.9b08356
Chattoraj, M., King, B. A., Bublitz, G. U., and Boxer, S. G. (1996). Ultra-fast excited state dynamics in green fluorescent protein: multiple states and proton transfer. Proc. Natl. Acad. Sci. U.S.A. 93, 8362–8367. doi: 10.1073/pnas.93.16.8362
Chen, C., Zhu, L., Baranov, M. S., Tang, L., Baleeva, N. S., Smirnov, A. Y., et al. (2019). Photoinduced proton transfer of gfp-inspired fluorescent superphotoacids: principles and design. J. Phys. Chem. B 123, 3804–3821. doi: 10.1021/acs.jpcb.9b03201
Chen, V. B., Arendall, W. B., Headd, J. J., Keedy, D. A., Immormino, R. M., Kapral, G. J., et al. (2010). Molprobity: all-atom structure validation for macromolecular crystallography. Acta Crystallogr. D 66, 12-21. doi: 10.1107/S0907444909042073
Chong, E. Q., Lingerfelt, D. B., Petrone, A., and Li, X. (2016). Classical or quantum? A computational study of small ion diffusion in II-VI semiconductor quantum dots. J. Phys. Chem. C 120, 19434–19441. doi: 10.1021/acs.jpcc.6b05883
Cimino, P., Raucci, U., Donati, G., Chiariello, M. G., Schiazza, M., Coppola, F., et al. (2016). On the different strength of photoacids. Theor. Chem. Acc. 135:117. doi: 10.1007/s00214-016-1879-8
Clemente, F. R., Vreven, T., and Frisch, M. J. (2010). Getting the most out of ONIOM: guidelines and pitfalls. Quant. Biochem. 61–83. doi: 10.1002/9783527629213.ch2
Cohen, B. E., McAnaney, T. B., Park, E. S., Jan, Y. N., Boxer, S. G., and Jan, L. Y. (2002). Probing protein electrostatics with a synthetic fluorescent amino acid. Science 296, 1700-1703. doi: 10.1126/science.1069346
Conti Nibali, V., and Havenith, M. (2014). New insights into the role of water in biological function: studying solvated biomolecules using terahertz absorption spectroscopy in conjunction with molecular dynamics simulations. J. Am. Chem. Soc. 136, 12800–12807. doi: 10.1021/ja504441h
Conyard, J., Kondo, M., Heisler, I. A., Jones, G., Baldridge, A., Tolbert, L. M., et al. (2011). Chemically modulating the photophysics of the gfp chromophore. J. Phys. Chem. B 115, 1571–1577. doi: 10.1021/jp111593x
Cornell, W. D., Cieplak, P., Bayly, C. I., Gould, I. R., Merz, K. M., Ferguson, D. M., et al. (1995). A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117, 5179–5197. doi: 10.1021/ja00124a002
Cossi, M., Rega, N., Scalmani, G., and Barone, V. (2003). Energies, structures, and electronic properties of molecules in solution with the c-pcm solvation model. J. Comput. Chem. 24, 669–681. doi: 10.1002/jcc.10189
Crane, M. J., Petrone, A., Beck, R. A., Lim, M. B., Zhou, X., Li, X., et al. (2019). High-pressure, high-temperature molecular doping of nanodiamond. Sci. Adv. 5:eaau6073. doi: 10.1126/sciadv.aau6073
Creemers, T., Lock, A., Subramaniam, V., Jovin, T., and Volker, S. (1999). Three photoconvertible forms of green fluorescent protein identified by spectral hole-burning. Nat. Struct. Mol. Biol 6, 557–560. doi: 10.1038/9335
Daday, C., Curutchet, C., Sinicropi, A., Mennucci, B., and Filippi, C. (2015). Chromophore-protein coupling beyond nonpolarizable models: understanding absorption in green fluorescent protein. J. Chem. Theory Comput. 11, 4825–4839. doi: 10.1021/acs.jctc.5b00650
D'Alessando, M., Amadei, A., Stener, M., and Aschi, M. (2015). Essential dynamics for the study of microstructures in liquids. J. Comput. Chem. 36, 399–407. doi: 10.1002/jcc.23814
Dapprich, S., Koma romi, I., Byun, K. S., Morokuma, K., and Frisch, M. J. (1999). A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. J. Mol. Struct. 461, 1–21. doi: 10.1016/S0166-1280(98)00475-8
Das, A. K., Hasegawa, J.-Y., Miyahara, T., Ehara, M., and Nakatsuji, H. (2003). Electronic excitations of the green fluorescent protein chromophore in its protonation states: sac/sac-ci study. J. Comput. Chem. 24, 1421-1431. doi: 10.1002/jcc.10308
DeLong, J. C., Hoffman, R. M., and Bouvet, M. (2016). Current status and future perspectives of fluorescence-guided surgery for cancer. Expert Rev. Anticancer Ther. 16, 71–81. doi: 10.1586/14737140.2016.1121109
Di Donato, M., van Wilderen, L. J., Van Stokkum, I. H., Stuart, T. C., Kennis, J. T., Hellingwerf, K. J., et al. (2011). Proton transfer events in gfp. Phys. Chem. Chem. Phys. 13, 16295–16305. doi: 10.1039/c1cp20387h
Donati, G., Lingerfelt, D. B., Aikens, C. M., and Li, X. (2017). Molecular vibration induced plasmon decay. J. Phys. Chem. C 121, 15368-15374. doi: 10.1021/acs.jpcc.7b04451
Donati, G., Lingerfelt, D. B., Aikens, C. M., and Li, X. (2018a). Anisotropic polarizability-induced plasmon transfer. J. Phys. Chem. C 122, 10621–10626. doi: 10.1021/acs.jpcc.8b02425
Donati, G., Petrone, A., Caruso, P., and Rega, N. (2018b). The mechanism of a green fluorescent protein proton shuttle unveiled in the time-resolved frequency domain by excited state ab initio dynamics. Chem. Sci. 9, 1126-1135. doi: 10.1039/C7SC02803B
Doster, W., and Settles, M. (2005). Protein-water displacement distributions. Biochim. Biophys. Acta 1749, 173-186. doi: 10.1016/j.bbapap.2005.03.010
Ehrhardt, D. (2003). Gfp technology for live cell imaging. Curr. Opin. Plant Biol. 6, 622–628. doi: 10.1016/j.pbi.2003.09.014
Errampalli, D., Leung, K., Cassidy, M., Kostrzynska, M., Blears, M., Lee, H., et al. (1999). Applications of the green fluorescent protein as a molecular marker in environmental microorganisms. J. Microbiol. Methods 35, 187–199. doi: 10.1016/S0167-7012(99)00024-X
Fanetti, S., Lapini, A., Pagliai, M., Citroni, M., Di Donato, M., Scandolo, S., et al. (2014). Structure and dynamics of low-density and high-density liquid water at high pressure. J. Phys. Chem. Lett. 5, 235-240. doi: 10.1021/jz402302z
Fang, C., Frontiera, R. R., Tran, R., and Mathies, R. A. (2009). Mapping GFP structure evolution during proton transfer with femtosecond Raman spectroscopy. Nature 462, 200–204. doi: 10.1038/nature08527
Fang, C., and Tang, L. (2020). Mapping structural dynamics of proteins with femtosecond stimulated raman spectroscopy. Annu. Rev. Phys. Chem. 71, 239–265. doi: 10.1146/annurev-physchem-071119-040154
Filippi, C., Buda, F., Guidoni, L., and Sinicropi, A. (2012). Bathochromic shift in green fluorescent protein: a puzzle for qm/mm approaches. J. Chem. Theory Comput. 8, 112–124. doi: 10.1021/ct200704k
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 09 Developer Version H29P. Wallingford, CT: Gaussian Inc.
Frontiera, R. R., and Mathies, R. A. (2007). Polarization dependence of vibrational coupling signals in femtosecond stimulated raman spectroscopy. J. Chem. Phys. 127:124501. doi: 10.1063/1.2780843
Garcia, A. E. (1992). Large-amplitude nonlinear motions in proteins. Phys. Rev. Lett. 68:2696. doi: 10.1103/PhysRevLett.68.2696
Gary, D. C., Petrone, A., Li, X., and Cossairt, B. M. (2017). Investigating the role of amine in inp nanocrystal syntheses: destabilizing cluster intermediates by z-type ligand displacement. Chem. Commun. 53, 161–164. doi: 10.1039/C6CC07952K
Go, N., Noguti, T., and Nishikawa, T. (1983). Dynamics of a small globular protein in terms of low- frequency vibrational modes. Proc. Natl. Acad. Sci. U.S.A. 80, 3696–3700. doi: 10.1073/pnas.80.12.3696
Grigorenko, B. L., Nemukhin, A. V., Polyakov, I. V., Morozov, D. I., and Krylov, A. I. (2013). First- principles characterization of the energy landscape and optical spectra of green fluorescent protein along the a → i → b proton transfer route. J. Am. Chem. Soc. 135, 11541–11549. doi: 10.1021/ja402472y
Groot, M. L., van Wilderen, L. J. G. W., and Di Donato, M. (2007). Time-resolved methods in biophysics. 5. femtosecond time-resolved and dispersed infrared spectroscopy on proteins. Photochem. Photobiol. Sci. 6, 501–507. doi: 10.1039/b613023b
Guido, C. A., Knecht, S., Kongsted, J., and Mennucci, B. (2013). Benchmarking time-dependent density functional theory for excited state geometries of organic molecules in gas-phase and in solution. J. Chem. Theory Comput. 9, 2209–2220. doi: 10.1021/ct400021c
Hafner, J., Wolverton, C., and Ceder, G. (2006). Toward computational materials design: the impact of density functional theory on materials research. MRS Bull. 31, 659–668. doi: 10.1557/mrs2006.174
He, Y., Chen, J.-Y., Knab, J. R., Zheng, W., and Markelz, A. G. (2011). Evidence of protein collective motions on the picosecond timescale. Biophys. J. 100, 1058–1065. doi: 10.1016/j.bpj.2010.12.3731
Ichiye, T., and Karplus, M. (1991). Collective motions in proteins: a covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulations. Proteins 11, 205–217. doi: 10.1002/prot.340110305
Improta, R., Antonello, S., Formaggio, F., Maran, F., Rega, N., and Barone, V. (2005). Understanding electron transfer across negatively-charged aib oligopeptides. J. Phys. Chem. B 109, 1023–1033. doi: 10.1021/jp045797l
Iyengar, S. S., Schlegel, H. B., Millam, J. M. A, Voth, G., Scuseria, G. E., and Frisch, M. J. (2001). Ab initio molecular dynamics: propagating the density matrix with gaussian orbitals. II. Generalizations based on mass-weighting, idempotency, energy conservation and choice of initial conditions. J. Chem. Phys. 115, 10291–10302. doi: 10.1063/1.1416876
Iyengar, S. S., Schlegel, H. B., Voth, G. A., Millam, J. M., Scuseria, G. E., and Frisch, M. J. (2002). Ab initio molecular dynamics: propagating the density matrix with gaussian orbitals. IV. Formal analysis of the deviations from Born-Oppenheimer dynamics. Israel J. Chem. 42, 191–202. doi: 10.1560/GLW2-8NVQ-4N6T-6C92
Jung, G., Wiehler, J., and Zumbusch, A. (2005). The photophysics of green fluorescent protein: Influence of the key amino acids at positions 65, 203, and 222. Biophys. J. 88, 1932–1947. doi: 10.1529/biophysj.104.044412
Klepeis, J. L., Lindorff-Larsen, K., Dror, R. O., and Shaw, D. E. (2009). Long-timescale molecular dynamics simulations of protein structure and function. Curr. Opin. Struc. Biol. 19, 120–127. doi: 10.1016/j.sbi.2009.03.004
Kukura, P., Frontiera, R. R., and Mathies, R. A. (2006). Direct observation of anharmonic coupling in the time domain with femtosecond stimulated raman scattering. Phys. Rev. Lett. 96:238303. doi: 10.1103/PhysRevLett.96.238303
Langella, E., Rega, N., Improta, R., Crescenzi, O., and Barone, V. (2002). Conformational analysis of the tyrosine dipeptide analogue in the gas phase and in aqueous solution by a density functional/continuum solvent model. J. Comput. Chem. 23, 650–661. doi: 10.1002/jcc.10065
Lee, C., Yang, W., and Parr, R. (1988). Density-functional exchange-energy approximation with correct asymptotic behaviour. Phys. Rev. B 37, 785–789.
Lestrange, P. J., Nguyen, P. D., and Li, X. (2015). Calibration of energy-specific TDDFT for modeling K-edge XAS spectra of light elements. J. Chem. Theory Comput. 11, 2994–2999. doi: 10.1021/acs.jctc.5b00169
Lever, G., Cole, D. J., Lonsdale, R., Ranaghan, K. E., Wales, D. J., Mulholland, A. J., et al. (2014). Large-scale density functional theory transition state searching in enzymes. J. Phys. Chem. Lett. 5, 3614–3619. doi: 10.1021/jz5018703
Lewandowski, J. R., Halse, M. E., Blackledge, M., and Emsley, L. (2015). Direct observation of hierarchical protein dynamics. Science 348, 578–581. doi: 10.1126/science.aaa6111
Li, T., Hassanali, A. A., Kao, Y.-T., Zhong, D., and Singer, S. J. (2007). Hydration dynamics and time scales of coupled water-protein fluctuations. J. Am. Chem. Soc. 129, 3376–3382. doi: 10.1021/ja0685957
Lill, M. A., and Helms, V. (2002). Proton shuttle in green fluorescent protein studied by dynamic simulations. Proc. Natl. Acad. Sci. U.S.A. 99, 2778–2781. doi: 10.1073/pnas.052520799
Lingerfelt, D. B., Williams-Young, D. B., Petrone, A., and Li, X. (2016). Direct ab initio (meta-) surface- hopping dynamics. J. Chem. Theory Comput. 12, 935–945. doi: 10.1021/acs.jctc.5b00697
Makarov, V., Pettitt, B. M., and Feig, M. (2002). Solvation and hydration of proteins and nucleic acids: a theoretical view of simulation and experiment. Acc. Chem. Res. 35, 376–384. doi: 10.1021/ar0100273
Mandal, D., Tahara, T., and Meech, S. R. (2004). Excited-state dynamics in the green fluorescent protein chromophore. J. Phys. Chem. B 108, 1102–1108. doi: 10.1021/jp035816b
March, J., Rao, G., and Bentley, W. (2003). Biotechnological applications of green fluorescent protein. Appl. Microbiol. Biotechnol. 62, 303–315. doi: 10.1007/s00253-003-1339-y
Martin, M. E., Negri, F., and Olivucci, M. (2004). Origin, nature, and fate of the fluorescent state of the green fluorescent protein chromophore at the caspt2//casscf resolution. J. Am. Chem. Soc. 126, 5452–5464. doi: 10.1021/ja037278m
Miertus, S., Scrocco, E., and Tomasi, J. (1981). Electrostatic interaction of a solute with a continuum. A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 55, 117–129. doi: 10.1016/0301-0104(81)85090-2
Misteli, T., and Spector, D. L. (1997). Applications of the green fluorescent protein in cell biology and biotechnology. Nat. Biotechnol. 15, 961–964. doi: 10.1038/nbt1097-961
Mo, S. J., Vreven, T., Mennucci, B., Morokuma, K., and Tomasi, J. (2004). Theoretical study of the SN 2 reaction of Cl-(H O)+CH3Cl using our own N-layered integrated molecular orbital and molecular mechanics polarizable continuum model method (ONIOM, PCM). Theor. Chem. Acc. 111, 154-161. doi: 10.1007/s00214-003-0519-2
Morokuma, K., Wang, Q., and Vreven, T. (2006). Performance evaluation of the three-layer oniom method: case study for a zwitterionic peptide. J. Chem. Theory Comput. 2, 1317–1324. doi: 10.1021/ct600135b
Nadal-Ferret, M., Gelabert, R., Moreno, M., and Lluch, J. M. (2015). Transient low-barrier hydrogen bond in the photoactive state of green fluorescent protein. Phys. Chem. Chem. Phys. 17, 30876–30888. doi: 10.1039/C5CP01067E
Nucci, N. V., Pometun, M. S., and Wand, A. J. (2011). Site-resolved measurement of water-protein interactions by solution nmr. Nat. Struct. Mol. Biol. 18, 245–249. doi: 10.1038/nsmb.1955
Olsen, S., Lamothe, K., and Martínez, T. J. (2010). Protonic gating of excited-state twisting and charge localization in gfp chromophores: a mechanistic hypothesis for reversible photoswitching. J. Am. Chem. Soc. 132, 1192–1193. doi: 10.1021/ja907447k
Oltrogge, L. M., Wang, Q., and Boxer, S. G. (2014). Ground-state proton transfer kinetics in green fluorescent protein. Biochemistry 53, 5947–5957. doi: 10.1021/bi500147n
Ormö, M., Cubitt, A. B., Kallio, K., Gross, L. A., Tsien, R. Y., and Remington, S. J. (1996). Crystal structure of the aequorea victoria green fluorescent protein. Science 273, 1392–1395. doi: 10.1126/science.273.5280.1392
Oscar, B. G., Liu, W., Zhao, Y., Tang, L., Wang, Y., Campbell, R. E., et al. (2014). Excited-state structural dynamics of a dual-emission calmodulin-green fluorescent protein sensor for calcium ion imaging. Proc. Natl. Acad. Sci. U.S.A. 111, 10191-10196. doi: 10.1073/pnas.1403712111
Pal, S. K., and Zewail, A. H. (2004). Dynamics of water in biological recognition. Chem. Rev. 104, 2099-2124. doi: 10.1021/cr020689l
Patnaik, S. S., Trohalaki, S., and Pachter, R. (2004). Molecular modeling of green fluorescent protein: structural effects of chromophore deprotonation. Biopolymers 75, 441–452. doi: 10.1002/bip.20156
Patrizi, B., Lapini, A., Di Donato, M., Marcelli, A., Lima, M., Righini, R., et al. (2014). Role of local structure and dynamics of small ligand migration in proteins: a study of a mutated truncated hemoprotein from thermobifida fusca by time resolved mir spectroscopy. J. Phys. Chem. B 118, 9209–9217. doi: 10.1021/jp504499b
Pepin, R., Petrone, A., Laszlo, K. J., Bush, M. F., Li, X., and Turecek, F. (2016). Does thermal breathing affect collision cross sections of gas-phase peptide ions? An ab initio molecular dynamics study. J. Phys. Chem. Lett. 7, 2765-2771. doi: 10.1021/acs.jpclett.6b01187
Petrone, A., Caruso, P., Tenuta, S., and Rega, N. (2013). On the optical absorption of the anionic GFP chromophore in vacuum, solution, and protein. Phys. Chem. Chem. Phys. 15, 20536–20544. doi: 10.1039/c3cp52820k
Petrone, A., Cimino, P., Donati, G., Hratchian, H. P., Frisch, M. J., and Rega, N. (2016a). On the driving force of the excited-state proton shuttle in the green fluorescent protein: a time-dependent density functional theory (td-dft) study of the intrinsic reaction path. J. Chem. Theory Comput. 12, 4925–4933. doi: 10.1021/acs.jctc.6b00402
Petrone, A., Goings, J. J., and Li, X. (2016b). Quantum confinement effects on optical transitions in nanodiamonds containing nitrogen vacancies. Phys. Rev. B 94:165402. doi: 10.1103/PhysRevB.94.165402
Petrone, A., Williams-Young, D. B., Sun, S., Stetina, T. F., and Li, X. (2018). An efficient implementation of two-component relativistic density functional theory with torque-free auxiliary variables. Euro. Phys. J. B 91:169. doi: 10.1140/epjb/e2018-90170-1
Rappe, A. K., Casewit, C. J., Colwell, K., Goddard, I. I. I. W. A, and Skiff, W. M. (1992). UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 114, 10024-10035. doi: 10.1021/ja00051a040
Raucci, U., Perrella, F., Donati, G., Zoppi, M., Petrone, A., and Rega, N. (2020). Ab-initio molecular dynamics and hybrid explicit-implicit solvation model for aqueous and nonaqueous solvents: Gfp chromophore in water and methanol solution as case study. J. Comput. Chem. 41, 2228–2239. doi: 10.1002/jcc.26384
Rega, N., Brancato, G., and Barone, V. (2006). Non-periodic boundary conditions for ab initio molecular dynamics in condensed phase using localized basis functions. Chem. Phys. Lett. 422, 367–371. doi: 10.1016/j.cplett.2006.02.051
Rega, N., Iyengar, S. S., Voth, G. A., Schlegel, H. B., Vreven, T., and Frisch, M. J. (2004). Hybrid ab-initio/empirical molecular dynamics: combining the ONIOM scheme with the atom-centered density matrix propagation (ADMP) approach. J. Phys. Chem. B 108, 4210–4220. doi: 10.1021/jp0370829
Reuter, N., Lin, H., and Thiel, W. (2002). Green fluorescent proteins: empirical force field for the neutral and deprotonated forms of the chromophore. Molecular dynamics simulations of the wild type and S65T mutant. J. Phys. Chem. B 106, 6310–6321. doi: 10.1021/jp014476w
Roy, A., Field, M. J., Adam, V., and Bourgeois, D. (2011). The nature of transient dark states in a photoactivatable fluorescent protein. J. Am. Chem. Soc. 133, 18586–18589. doi: 10.1021/ja2085355
Savarese, M., Raucci, U., Adamo, C., Netti, P. A., Ciofini, I., and Rega, N. (2014). Non-radiative decay paths in rhodamines: new theoretical insights. Phys. Chem. Chem. Phys. 16, 20681–20688. doi: 10.1039/C4CP02622E
Scharnagl, C., Raupp-Kossmann, R., and Fischer, S. (1999). Molecular basis for ph sensitivity and proton transfer in green fluorescent protein: protonation and conformational substates from electrostatic calculations. Biophys. J. 77, 1839–1857. doi: 10.1016/S0006-3495(99)77028-1
Schiro, G., Fichou, Y., Gallat, F.-X., Wood, K., Gabel, F., Moulin, M., et al. (2015). Translational diffusion of hydration water correlates with functional motions in folded and intrinsically disordered proteins. Nat. Commun. 6:6490. doi: 10.1038/ncomms7490
Schlegel, H. B. (2003). Ab initio molecular dynamics with born-oppenheimer and extended lagrangian methods using atom centered basis functions. Bull. Korean Chem. Soc. 24, 837–842. doi: 10.5012/bkcs.2003.24.6.837
Schlegel, H. B., Iyengar, S. S., Li, X., Millam, J. M., Voth, G. A., Scuseria, G. E., et al. (2002). Ab initio molecular dynamics: propagating the density matrix with gaussian orbitals. III. Comparison with Born-Oppenheimer dynamics. J. Phys. Chem. 117, 8694–8704. doi: 10.1063/1.1514582
Schlegel, H. B., Millam, J. M., Iyengar, S. S., Voth, G. A., Daniels, A. D., Scuseria, G. E., et al. (2001). Ab initio molecular dynamics: propagating the density matrix with gaussian orbitals. J. Chem. Phys. 114, 9758–9763. doi: 10.1063/1.1372182
Shimomura, O. (2005). The discovery of aequorin and green fluorescent protein. J. Microscopy 217, 3-15. doi: 10.1111/j.0022-2720.2005.01441.x
Shimomura, O., Johnson, F. H., and Saiga, Y. (1962). Extraction, purification and properties of aequorin, a bioluminescent protein from the luminous hydromedusan, aequorea. J. Cell. Physiol. 59, 223-239. doi: 10.1002/jcp.1030590302
Shinobu, A., and Agmon, N. (2017). Proton wire dynamics in the green fluorescent protein. J. Chem. Theory Comput. 13, 353–369. doi: 10.1021/acs.jctc.6b00939
Stein, J. L., Steimle, M. I., Terban, M. W., Petrone, A., Billinge, S. J. L., Li, X., et al. (2017). Cation exchange induced transformation of InP magic-sized clusters. Chem. Mater. 29, 7984–7992. doi: 10.1021/acs.chemmater.7b03075
Stephens, P. J., Devlin, F., Chabalowski, C., and Frisch, M. J. (1994). Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 98, 11623–11627. doi: 10.1021/j100096a001
Stoner-Ma, D., Jaye, A. A., Matousek, P., Towrie, M., Meech, S. R., and Tonge, P. J. (2005). Observation of excited-state proton transfer in green fluorescent protein using ultrafast vibrational spectroscopy. J. Am. Chem. Soc. 127, 2864–2865.
Stoner-Ma, D., Melief, E. H., Nappa, J., Ronayne, K. L., Tonge, P. J., and Meech, S. R. (2006). Proton relay reaction in green fluorescent protein (GFP): polarization-resolved ultrafast vibrational spectroscopy of isotopically edited GFP. J. Phys. Chem. B 110, 22009–22018. doi: 10.1021/jp065326u
Striker, G., Subramaniam, V., Seidel, C. A. M., and Volkmer, A. (1999). Photochromicity and fluorescence lifetimes of green fluorescent protein. J. Phys. Chem. B 103, 8612–8617. doi: 10.1021/jp991425e
Svensson, M., Humbel, S., Froese, R. D., Matsubara, T., Sieber, S., and Morokuma, K. (1996). ONIOM: a multilayered integrated MO+MM method for geometry optimizations and single point energy predictions. A test for Diels-Alder reactions and Pt (P(t-Bu)3)2+H2 oxidative addition. J. Phys. Chem. 100, 19357–19363. doi: 10.1021/jp962071j
Toniolo, A., Olsen, S., Manohar, L., and Martinez, T. (2004). Conical intersection dynamics in solution: the chromophore of green fluorescent protein. Faraday Discuss. 127, 149–163. doi: 10.1039/B401167H
Tsien, R. Y. (1998). The green fluorescent protein. Annu. Rev. Biochem 67, 509–544. doi: 10.1146/annurev.biochem.67.1.509
van Thor, J. J., Gensch, T., Hellingwerf, K. J., and Johnson, L. N. (2002). Phototransformation of green fluorescent protein with UV and visible light leads to decarboxylation of glutamate 222. Nat. Struct. Mol. Biol 9, 37–41. doi: 10.1038/nsb739
Vendrell, O., Gelabert, R., Moreno, M., and Lluch, J. M. (2004). Photoinduced proton transfer from the green fluorescent protein chromophore to a water molecule: analysis of the transfer coordinate. Chem. Phys. Lett. 396, 202–207. doi: 10.1016/j.cplett.2004.08.028
Vendrell, O., Gelabert, R., Moreno, M., and Lluch, J. M. (2008a). Operation of the proton wire in green fluorescent protein. A quantum dynamics simulation. J. Phys. Chem. B 112, 5500–5511. doi: 10.1021/jp801169z
Vendrell, O., Gelabert, R., Moreno, M., and Lluch, J. M. (2008b). A potential energy function for heterogeneous proton-wires. Ground and photoactive states of the proton-wire in the green fluorescent protein. J. Chem. Theory Comput. 4, 1138–1150. doi: 10.1021/ct800075w
Virshup, A. M., Punwong, C., Pogorelov, T. V., Lindquist, B. A., Ko, C., and Martinez, T. J. (2009). Photodynamics in complex environments: ab initio multiple spawning quantum mechanical/molecular mechanical dynamics. J. Phys. Chem. B 113, 3280–3291. doi: 10.1021/jp8073464
Volkmer, A., Subramaniam, V., Birch, D. J., and Jovin, T. M. (2000). One- and two-photon excited fluorescence lifetimes and anisotropy decays of green fluorescent proteins. Biophys. J. 78, 1589–1598. doi: 10.1016/S0006-3495(00)76711-7
Vreven, T., Byun, K. S., Komaŕomi, I., Dapprich, S., Montgomery, J. A. Jr, Morokuma, K., et al. (2006). Combining quantum mechanics methods with molecular mechanics methods in ONIOM. J. Chem. Theory Comput. 2, 815–826. doi: 10.1021/ct050289g
Vreven, T., Mennucci, B., da Silva, C. O., Morokuma, K., and Tomasi, J. (2001). The ONIOM-PCM method: combining the hybrid molecular orbital method and the polarizable continuum model for solvation. Application to the geometry and properties of a merocyanine in solution. J. Chem. Phys. 115, 62–72. doi: 10.1063/1.1376127
Vreven, T., and Morokuma, K. (2006). Hybrid methods: ONIOM (QM:MM) and QM/MM. Annu. Rep. Comput. Chem. 2, 35–51. doi: 10.1016/S1574-1400(06)02003-2
Vreven, T., Morokuma, K., Farkas, O., Schlegel, H. B., and Frisch, M. J. (2003). Geometry optimization with QM/MM, ONIOM, and other combined methods. I. Microiterations and constraints. J. Comput. Chem. 24, 760–769. doi: 10.1002/jcc.10156
Wang, S., and Smith, S. C. (2006). Mechanistic aspects of proton chain transfer: a computational study for the green fluorescent protein chromophore. J. Phys. Chem. B 110, 5084–5093. doi: 10.1021/jp056966k
Wang, Y., and Fang, C. (2019). Femtosecond Stimulated Raman Spectroscopy (FSRS) Investigation of Excited-State Hydrogen-Bonding Dynamics and Photoacidity in Solution. Singapore: World Scientific Publishing, 323–367. doi: 10.1142/9781786346087_0013
Wanko, M., García-Risueño, P., and Rubio, A. (2012). Excited states of the green fluorescent protein chromophore: performance of ab initio and semi-empirical methods. Phys. Status Solidi B 249, 392–400. doi: 10.1002/pssb.201100536
Wildman, A., Donati, G., Lipparini, F., Mennucci, B., and Li, X. (2019). Nonequilibrium environment dynamics in a frequency-dependent polarizable embedding model. J. Chem. Theory Comput. 15, 43–51 doi: 10.1021/acs.jctc.8b00836
Wong, M. W. (1996). Vibrational frequency prediction using density functional theory. Chem. Phys. Lett. 256, 391–399. doi: 10.1016/0009-2614(96)00483-6
Zhang, R., Nguyen, M. T., and Ceulemans, A. (2005). A concerted mechanism of proton transfer in green fluorescent protein. A theoretical study. Chem. Phys. Lett. 404, 250–256. doi: 10.1016/j.cplett.2005.01.094
Keywords: hydrogen bond dynamics, fluorescent proteins, ab initio molecular dynamics, structure-function correlation, QM/MM
Citation: Coppola F, Perrella F, Petrone A, Donati G and Rega N (2020) A Not Obvious Correlation Between the Structure of Green Fluorescent Protein Chromophore Pocket and Hydrogen Bond Dynamics: A Choreography From ab initio Molecular Dynamics. Front. Mol. Biosci. 7:569990. doi: 10.3389/fmolb.2020.569990
Received: 05 June 2020; Accepted: 11 September 2020;
Published: 27 October 2020.
Edited by:
Chong Fang, Oregon State University, United StatesReviewed by:
Young Min Rhee, Korea Advanced Institute of Science and Technology, South KoreaErika Anne Taylor, Wesleyan University, United States
Maria Andrea Mroginski, Technical University of Berlin, Germany
Copyright © 2020 Coppola, Perrella, Petrone, Donati and Rega. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alessio Petrone, YWxlc3Npby5wZXRyb25lQHVuaW5hLml0; Greta Donati, Z3JldGEuZG9uYXRpQHVuaW5hLml0; Nadia Rega, bmFkaWEucmVnYUB1bmluYS5pdA==
†These authors have contributed equally to this work
‡Present address: Greta Donati, Department of Chemistry and Biology, University of Salerno, Fisciano, Italy
 Federico Coppola
Federico Coppola Fulvio Perrella
Fulvio Perrella Alessio Petrone
Alessio Petrone Greta Donati
Greta Donati Nadia Rega
Nadia Rega