
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
MINI REVIEW article
Front. Mol. Biosci. , 05 May 2020
Sec. Biological Modeling and Simulation
Volume 7 - 2020 | https://doi.org/10.3389/fmolb.2020.00066
This article is part of the Research Topic Multiscale Modeling from Macromolecules to Cell: Opportunities and Challenges of Biomolecular Simulations View all 27 articles
 Ilda D’Annessa1†
Ilda D’Annessa1† Francesco Saverio Di Leva2†
Francesco Saverio Di Leva2† Anna La Teana3
Anna La Teana3 Ettore Novellino2
Ettore Novellino2 Vittorio Limongelli2,4*
Vittorio Limongelli2,4* Daniele Di Marino3*
Daniele Di Marino3*Peptides and peptidomimetics are strongly re-emerging as amenable candidates in the development of therapeutic strategies against a plethora of pathologies. In particular, these molecules are extremely suitable to treat diseases in which a major role is played by protein–protein interactions (PPIs). Unlike small organic compounds, peptides display both a high degree of specificity avoiding secondary off-targets effects and a relatively low degree of toxicity. Further advantages are provided by the possibility to easily conjugate peptides to functionalized nanoparticles, so improving their delivery and cellular uptake. In many cases, such molecules need to assume a specific three-dimensional conformation that resembles the bioactive one of the endogenous ligand. To this end, chemical modifications are introduced in the polypeptide chain to constrain it in a well-defined conformation, and to improve the drug-like properties. In this context, a successful strategy for peptide/peptidomimetics design and optimization is to combine different computational approaches ranging from structural bioinformatics to atomistic simulations. Here, we review the computational tools for peptide design, highlighting their main features and differences, and discuss selected protocols, among the large number of methods available, used to assess and improve the stability of the functional folding of the peptides. Finally, we introduce the simulation techniques employed to predict the binding affinity of the designed peptides for their targets.
Year by year the use of theoretical approaches to study structural and dynamical features of macromolecules (Di Marino et al., 2014, 2015a; Orozco, 2014; D’Annessa et al., 2018, 2019a) is constantly growing, thanks to the continuous improvement of methodologies and algorithms, as well as of the high performance computing facilities. Theoretical methodologies are achieving an increasing importance in many fields of science and have now gained a primary role in drug design. Indeed, hundreds of examples exist in which the use of computational techniques was crucial to discover new molecules active against different diseases (Sliwoski et al., 2014; D’Annessa et al., 2019b). In the modern era, computer-aided drug design is successfully exploited not only to develop small molecules but also to guide the more challenging design of larger size compounds like peptides or peptide-like molecules (i.e., peptoids or peptidomimetics), which can retain the physicochemical features of bioactive proteins or polypeptide chains. One such feature is the conformational plasticity of peptides that allows them to interact with larger and more shallow surfaces compared to the typically cryptic binding pockets targeted by small molecules (Di Marino et al., 2015b; Vercelli et al., 2015; Di Leva et al., 2018). Therefore, peptides and peptidomimetics represent ideal candidates for targeting protein–protein interactions (PPIs). Indeed, PPIs have emerged as relevant drug targets since they are responsible for numerous cellular processes (Wanner et al., 2011; Otvos and Wade, 2014; Sun, 2016). Nonetheless, most PPIs were until recently considered “undruggable” by small compounds due to the involvement of large binding surfaces where the recognition is ruled by both the physicochemical properties and the shape of the interacting proteins (Bakail and Ochsenbein, 2016). Similar to protein-(small)ligand interactions PPIs are stabilized by non-covalent interactions, but with hydrophobic contacts, usually responsible for recognition and packaging, playing a primary role in stabilizing the complex (Tan et al., 2016). Moreover, upon the formation of macromolecular complexes new pockets can be formed at the interface between two or more proteins, and in some cases their targeting, aimed at stabilizing, instead of disrupting, the complex, can represent a clever therapeutic strategy to treat different diseases. Also in this case, however, small compounds are often not suitable for this purpose, while peptide-like molecules are particularly favored (Henninot et al., 2018; Lee et al., 2019). Furthermore, isolated peptides can compensate for the absence of the whole protein, as in the case of hormones, or can counteract the immune system in autoimmune diseases (Lau and Dunn, 2018). Moreover, peptides have peculiar characteristics that represent advantages in the field of drug development with respect to small molecules. For instance, they show a very low or null toxicity compared to synthetic compounds, being typically degraded in non-toxic metabolites, and are highly selective against a specific target, thus making their use particularly favored (Smith et al., 2019). Finally, many peptides can be easily conjugated either to nanoparticles for targeted delivery (Valcourt et al., 2018; Kalmouni et al., 2019) or to organic molecules working as biomarkers for diagnostic purposes (Wang and Hu, 2019).
In this perspective, much effort was dedicated in the last decades to develop theoretical approaches for the design of therapeutic peptides/peptidomimetics, leading to a new branch of drug development, known as computational peptidology (Zhou et al., 2013). These strategies gave birth to a leading industry producing nearly 20 new peptide-based clinical trials annually. At the time this review was written, more than 400 peptide drugs were under clinical development and over 60 already approved for clinical use in the United States, Europe and Japan (Lee et al., 2019). Several designed peptides have shown great potential for the treatment of different types of cancers (Marqus et al., 2017; Zanella et al., 2019). Although these peptides have an extraordinary effectiveness in cancer cell cultures, they still do not provide encouraging results in vivo (Marqus et al., 2017). This because peptides may suffer from poor metabolic stability and membrane permeability, rapid proteolysis and unstable secondary structure (Zhang et al., 2018). With the aim to overcome such limitations, many strategies have been developed that rely on the application of chemical modifications such as cyclization, N-methylation, stapling or the introduction of amide bond bioisosters and non-natural amino acids. In addition, peptidomimetics can represent a valid alternative to target PPIs. Peptidomimetics are indeed organic molecules featuring physicochemical and structural properties resembling those of classical oligopeptides (Vagner et al., 2008; Zhang et al., 2018) but generally endowed with improved pharmacokinetic profiles.
The possibility to rationally design peptide-based molecules exploiting the structural characteristics of PPIs represents an enormous advantage to achieve the desired effect on the pathological process. The growing number of 3D structures available from X-ray diffraction and NMR has augmented our knowledge on protein–protein recognition and binding process, providing unprecedented insight into the proteins’ structures in the apo form states and in protein–protein and protein–peptide complexes. This information is instrumental in the peptide design process. In this perspective, combining bioinformatics approaches with molecular simulations is a valuable strategy to obtain good drug-candidate peptides. Moreover, the increased accuracy in the calculation of binding free energy allows further characterizing the energetics of the molecular binding interaction, increasing the success rate of the design process (Torrie and Valleau, 1977; Di Marino et al., 2014, 2015b; Kilburg and Gallicchio, 2016). However, the field of peptides design and PPIs prediction/refinement is really extensive and the number of approaches developed for these purposes is constantly growing. Here we provide a concise report of selected computational protocols for peptides/peptidomimetic design, paying particular attention to the most widely employed bioinformatics tools and facilities and docking algorithms available to this end. We also introduce the simulations techniques used to validate protein–peptide complexes obtained by docking procedures and to predict the binding affinity of the designed peptides for their targets.
Since PPIs emerged as druggable targets much effort was dedicated to develop algorithms and tools for peptides/peptidomimetics design. However, this is far from being a fully addressed issue and still poses many hurdles. Indeed, notwithstanding the increasing structural information available, the investigation of protein–peptide recognition is not an easy task to handle and shows several layers of complexity. For a full description of the process: (1) the three-dimensional structure of the investigated protein–protein complex should be available, in order to detect the protein region to use as a template for the design of peptides; (2) in the case the complex is not available, the protein surface that has to be recognized by the PPI disruptor should be detected, or at least predicted, with high accuracy; (3) the structure of the target protein in its apo and holo states should be known, since the binding surface might change undergoing structural rearrangement upon protein or ligand binding; (4) since peptides are highly flexible entities, their conformational flexibility, stability in solution and the ability to achieve and maintain a well-defined active structure should be considered; and (5) finally, a putative structure of the designed peptide in complex with the target protein should be generated, typically by docking, in order to provide a possible mechanism of binding. However, achieving an accurate docking of conformationally flexible peptides to a target protein is a challenging task as discussed in the following sections.
To date numerous bioinformatics tools for peptides design are available. These can be basically classified as ligand-based and target-based (Figure 1), even if in most of the cases the two approaches are combined. Ligand-based approaches can be further distinguished into sequence-based, conformation-based and property-based, with this last possibility still being the least explored.
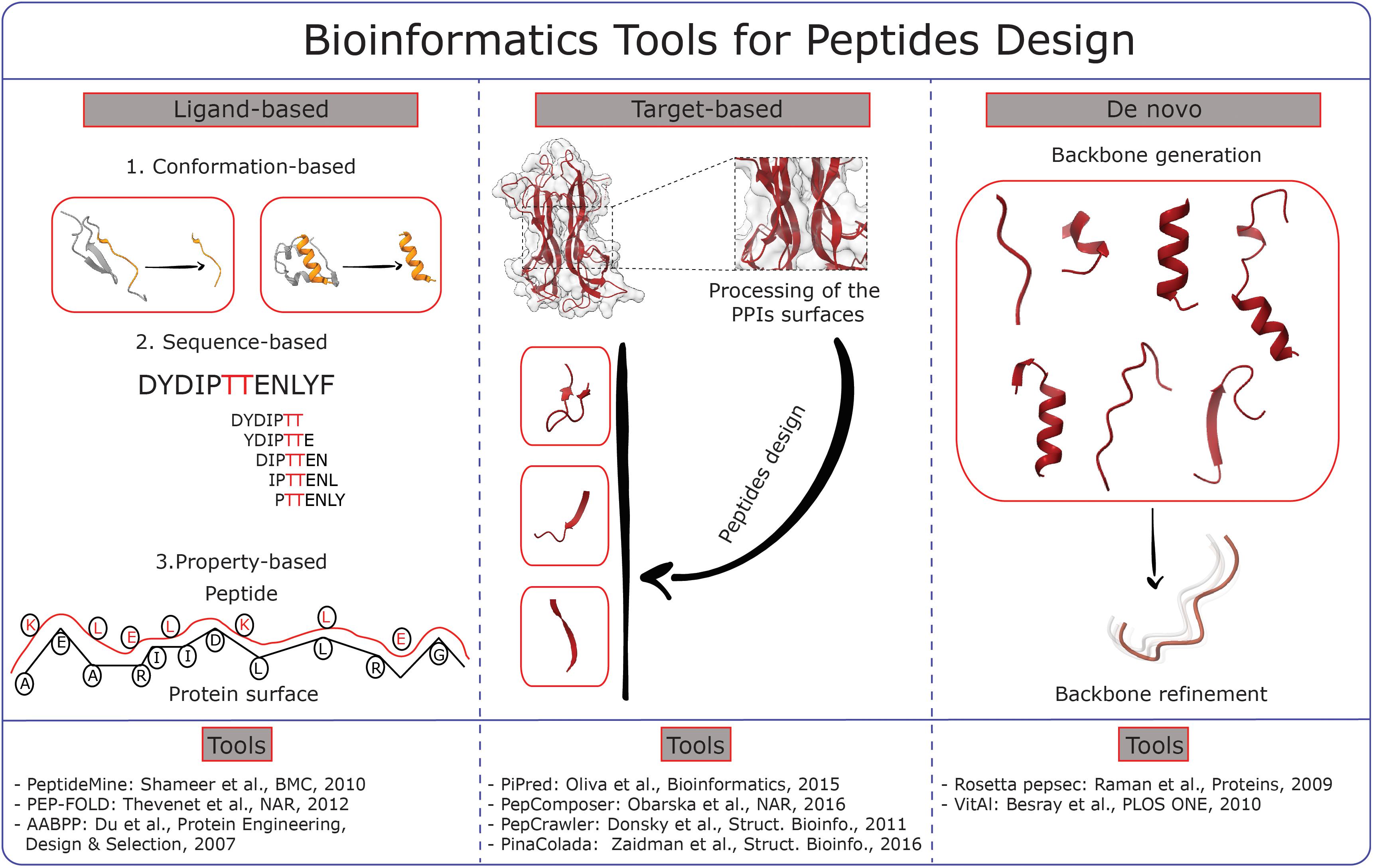
Figure 1. Graphical scheme summarizing different methodologies for peptide design. The core ideas of the main bioinformatics tools available are divided in three major categories: Ligand-based, Target-based and De novo. The references to the tools are reported at the bottom of the picture.
Sequence-based approaches rely on the identification of conserved functional motifs, usually detected through multi-sequences alignment. These sequences are then modified to obtain a ranking of different candidates potentially able to interact with a specific target protein usually blocking an interaction with another protein partner. This is the case of the PeptideMine webserver (Shameer et al., 2010).
Substantially different are the conformation-based approaches that are aimed at building peptides structures and conformational ensembles further refined by investigation of structure-activity relationships. Example is PEP-FOLD that exploits a Hidden Markov Model to derive a structural alphabet to design stretches of “letters” that are assembled into 3D structures then refined by Monte-Carlo calculations (Thévenet et al., 2012).
Target-based strategies include knowledge-based and de novo design approaches. Knowledge-based methods use information from protein complexes, peptides and protein fragments (Vanhee et al., 2011). For instance, PiPred analyses protein complexes to find anchor residues and use them to find the best peptides matching the target surface from databases of fragments (Oliva and Fernandez-Fuentes, 2015). PepComposer explores a pool of protein surfaces and delivers a set of backbone scaffolds that is able to target them. A following Monte Carlo simulation refines the conformation of the newly designed peptides shown in the final peptide-protein complex (Obarska-Kosinska et al., 2016). Similarly, PepCrawler and its cognate PinaColada analyze protein complexes and derive candidate peptides that are subsequently randomly mutated in order to increase their affinity for the target. As final result, the newly designed peptides are ranked according to the predicted binding affinity (Donsky and Wolfson, 2011; Zaidman and Wolfson, 2016).
De novo approaches endeavor to obtain peptides without any a priori structural knowledge. The pepsec tool, included in the Rosetta suite (Raman et al., 2009), provides peptide sequences and structures that are simultaneously optimized. The process is similar to the “anchor and grow” docking algorithms in as much an anchor residue of the peptide is positioned on the protein surface and the chain is assembled starting from that point (King and Bradley, 2010). A significant advance was achieved with the implementation in Rosetta of a rotamers library that allows generating peptoid foldamers for the design of compounds with defined 3D structures thanks to the introduction of non-natural amino acids (Renfrew et al., 2014). Another example of de novo approaches is the VitAl algorithm, which identifies the binding site via a Coarse Grained Gaussian Network model and generates the peptides by sequentially docking pairs of residues and determining the binding energies (Besray Unal et al., 2010).
The described methodologies, especially ligand-based strategies, can be supported by stand-alone protein–peptide docking programs, in order to identify or refine the binding poses of the designed peptides. Notably, these software can be also used to predict the interaction mode of known biologically active peptides with their target, thus guiding the design of novel PPI inhibitors. Nonetheless, protein–peptide docking programs can suffer from some inaccuracies, especially in the solvation and in the conformational sampling of the ligand backbone (Zhou et al., 2013). In the last decade, however, significant progress has been made to address these issues, achieving a satisfactory quality of predictions both by knowledge-based approaches among which HADDOCK and GalaxyPepDock represent some of the most accurate software (Trellet et al., 2013; Lee et al., 2015; Van Zundert et al., 2016), and ab initio programs, including the newest version of the Glide SP algorithm (Glide SP-peptide) and HPEPDOCK, which exploits a hierarchical algorithm to manage peptide flexibility through an ensemble of conformations generated (Antes, 2010; Tubert-Brohman et al., 2013; Li et al., 2014; Ben-Shimon and Niv, 2015; Kurcinski et al., 2015; Schindler et al., 2015; Alam et al., 2017; Zhou et al., 2018). In HADDOCK, experimental information on the targeted PPIs is exploited to drive the docking through the inclusion of interaction restraints during the calculations. The HADDOCK procedure for flexible protein–peptide docking is a multi-step process that combines different solvent models, conformational search and selection, and induced fit algorithms in a highly efficient protocol. The GalaxyPepDock protocol consists of a combination of similarity-based docking and energy-based optimization methods. Given a target protein and a peptide, the server performs a scan of experimentally determined PPIs structures database, in order to identify a proper PPI template. Subsequently, GalaxyPepDock builds a number of protein–peptide complexes that are further refined by energy-based methods to find the best structure interface. Conversely, Glide SP-peptide, pepATTRACT or Rosetta FLexPepDock perform without any a priori experimental information. In particular, Glide SP-peptide relies on a grid-based docking protocol, which takes advantage of advanced sampling algorithms during the search phase. The obtained poses can be further refined by post-processing calculations with physics-based implicit solvent MM-GBSA methods, rescored and ranked by a custom scoring function. PepATTRACT combines a coarse-grained ab initio docking followed by an atomistic refinement protocol. In particular, a fully blind procedure is followed, where the server examines the whole protein surface to find a putative binding site and simultaneously predicts the bound peptide conformation. Finally, FlexPepDock, which is implemented in the Rosetta suite, is able to provide high-resolution protein–peptide complexes starting from a generation of coarse-grained models. These starting coarse-grained models are refined by performing Monte-Carlo Minimization restricting the peptide’s degrees of freedom and allowing the flexibility of the receptor’s binding site side chains.
As reported above, bioinformatics tools show a good degree of accuracy in predicting peptides conformational plasticity, mainly through internal search algorithms that iteratively build different peptide backbone conformations, each one assigned with a specific binding score. However, severe approximations still reside in the docking sampling. For instance, many docking software treat the peptide backbone as rigid during the calculations making the a priori knowledge of its bioactive conformation necessary. In simplest cases, when the ligand assumes a unique, or at least a prevalent conformation in water, this can be straightforwardly computed based on experimental techniques such as proton NMR experiments. This strategy can be, for instance, applied to small cyclic peptides featuring a restricted backbone conformational space. However, in many cases peptides can assume several energetically equivalent states characterized by a rugged conformational free energy landscape. In such cases, it is advisable to support the peptide design with a reliable energy estimation of the different conformations assumed by the new peptide. To this end, atomistic simulations represent a valid tool. In particular, a number of efficient conformational searching methods have been developed or specifically adapted for this purpose. These include simulated annealing (Kirkpatrick et al., 1983; Wilson and Cui, 1990), distance geometry (Donné-Op Den Kelder, 1989), random search Monte Carlo (MC) (Chang et al., 1989; Weinberg and Wolfe, 1994), eigenvector-following (Cerjan and Miller, 1981; Simons et al., 1983), basin-hopping global optimization (Wales and Doye, 1997), discrete path sampling (Wales, 2002, 2004) and molecular dynamics (MD) based algorithms. Extensive reviews are available in literature on the application of simulated annealing (Bernardi et al., 2015) and distance geometry (Mucherino et al., 2013) to study peptides conformational sampling. For this reason, here we will mainly focus on the other approaches.
Among stochastic or random search approaches is the Monte Carlo Multiple Minimum (MCMM) method, commonly known as torsional sampling (Saunders et al., 1990), in which the peptide torsional bonds are randomly rotated through iterative Monte Carlo simulations, each followed by energy minimization, in order to identify local minima in the conformational potential energy surface (PES).
An interesting example of eigenvector-following method is the low mode conformational search (LMCS) (Kolossváry and Guida, 1996), in which local minima in the PES are found through movements along the “low energy eigenvectors” that are identified through a preliminary normal mode analysis, and following energy minimization. The process is then iteratively repeated to find additional minima, eventually leading to the identification of a minimum energy path. In order to improve the performance of LMCS in global searches, a mixed MCMM/LMCS strategy has been also developed (Kolossvàry and Guida, 1999) and successfully applied to the conformational sampling of macrocyclic compounds (Parish et al., 2002).
In basin-hopping global optimization (BHGO), the potential energy landscape is transformed into a series of “basins of attraction” which are explored through a hybrid random search-geometry optimization protocol (Li and Scheraga, 1987; Wales and Doye, 1997). In detail, random structural perturbations such as backbone Cartesian moves or rotations of amino acid side chains are initially applied to the biomolecule. After each perturbation, a geometry optimization cycle is performed to find the nearest local minimum, usually through the quasi-Newton L-BFGS (Limited-memory BFGS) minimization algorithm (Liu and Nocedal, 1989). The transition is finally either accepted or rejected based on a Metropolis criterion. The method allows crossing high barriers that separate the different energy basins, thus leading to the identification of the global minimum. Also, the thermodynamic properties of the system can be computed using the data set of local minima found during the search. Many variants of the technique have been developed to specifically address problems of biological interest including peptides’ conformational sampling. For instance, the efficiency of basin hopping can be improved by including experimental restraints (Carr et al., 2015) or by combining the method with other approaches, such as parallel-tempering (Strodel et al., 2010; Joseph and Wales, 2018). Connected to BHGO, is the discrete path sampling approach. Here, a discrete path is defined as a connected sequence of minima and the intervening transition state(s) between them, which are appropriate for describing dynamical properties but can also be subjected to kinetic analysis (Wales, 2005). Discrete path sampling has been successfully used to explore the conformational energy landscape of both linear and cyclic peptides (Evans and Wales, 2004; Oakley and Johnston, 2013).
Molecular dynamics (MD) based techniques are largely explored for peptides conformational sampling both as stand alone tools or in tandem with experiments. It has been indeed demonstrated that the inclusion of NMR data such as chemical shifts, interatomic distances or residual dipolar couplings (RDCs), as structural restraints in MD simulations can significantly improve the speed and efficiency of sampling algorithms. Ensemble or time-averaged MD represents a first example (Bonvin et al., 1994) followed by more recent advanced methodologies that integrate MD with experimental data. For instance, it was shown that, if geometrical restraints are applied to the system and averaged over simulation replicas, ensembles of conformations compatible with the maximum entropy principle are generated (Cavalli et al., 2013). This approach is known as replica-averaged restrained molecular dynamics and can offer a valid representation of the unknown Boltzmann distribution of a peptide conformational landscape (De Simone et al., 2011). Also, MD simulations can be coupled to Markov State Models (MSM) to predict the folding pathways and kinetics of polypeptides (Chodera and Noé, 2014; Husic and Pande, 2018). An efficient alternative strategy is to employ enhanced sampling methodologies, which allow investigating events that extend beyond the timescale limit of standard simulations. Important examples are umbrella sampling (US) (Torrie and Valleau, 1977) and metadynamics (MetaD) (Laio and Parrinello, 2002), which rely on the application of a bias on a set of user-defined reaction coordinates, specifically designed for the system under investigation, commonly referred to as collective variables (CVs). These methodologies can provide an accurate description of the free energy landscape underlying the process of interest. Particularly, MetaD (Laio and Parrinello, 2002) in its well-tempered variant (Barducci et al., 2008) was largely applied to conformational studies of both linear and cyclic peptides. For instance, Musco and coworkers employed MetaD to predict the bioactive conformation and the pharmacological behavior of cyclic penta- and hexa- peptides designed as RGD-integrin receptors modulators (Spitaleri et al., 2011; Simon et al., 2018). Remarkably, metadynamics can be combined with replica-exchange (RE) methods like parallel-tempering (PT) (Bussi et al., 2006) and bias-exchange (BE) (Piana and Laio, 2007) algorithms in which n exchangeable replicas of the systems are simulated at different temperatures and biasing different set of CVs, respectively. For instance, PT-MetaD was recently applied to predict the turn-helix conformation of a linear peptide reported as a selective ligand of the αvβ6 RGD-integrin, leading to new selective cyclopeptidic ligands with potential clinical applications (Figure 2A; Di Leva et al., 2018). Furthermore, the metadynamics performance can be improved through the inclusion of experimental data either in the user-defined CVs in a BE scheme (Granata et al., 2013) or as replica-averaged structural restraints. The latter approach is known as replica-averaged metadynamics (Camilloni et al., 2013) and is typically performed in the well-tempered ensemble (WTE) where the energy is used as CV (Camilloni et al., 2013). In alternative to CV-based techniques, other enhanced sampling methodologies such as accelerated MD (Hamelberg et al., 2004), replica exchange with solute-tempering (REST) (Liu et al., 2005) and reservoir-REMD (R-REMD) (Okur et al., 2007; Roitberg et al., 2007), have been successfully used for peptides’ conformational sampling. In accelerated MD the sampling is improved through the addition of a boost potential to the potential energy of the system (Hamelberg et al., 2004). This technique demonstrated to provide conformational ensembles for peptidic macrocycles well reproducing the available experimental structures (Kamenik et al., 2018). In replica exchange with solute-tempering, the contribution of solute–solvent and solvent–solvent energies are scaled in order to strengthen solvent interactions at elevated temperatures. As a result, only the solute is simulated at different temperatures as in traditional REMD, while the solvent is kept at original temperature in all replicas. The exchange probabilities exclusively depend on the contribution from solute atoms that generally show broader energy distributions compared to the solvent. Accordingly, a lower number of replicas is needed to cover the desired temperature range compared to standard REMD, thus saving computational time and resources (Liu et al., 2005). Finally, R-REMD is based on a classical PT scheme in which, the highest temperature replica is replaced by a structure reservoir that is pre-generated through standard MD simulations performed at the same temperature (Okur et al., 2007; Roitberg et al., 2007).
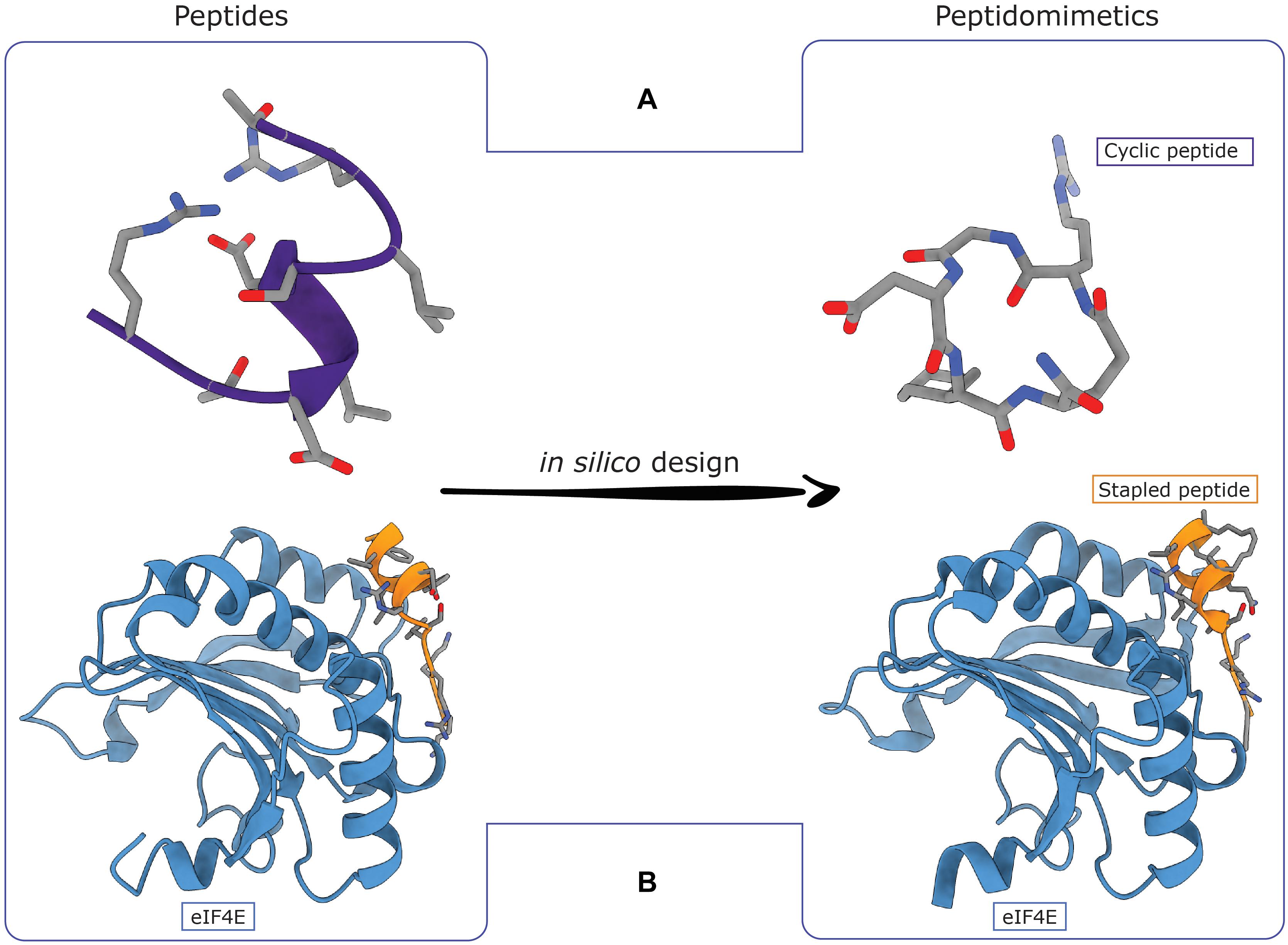
Figure 2. Computational strategies to transform peptides in peptidomimetics. (A) A metadynamics-driven design approach was successfully used to convert a helical peptide able to interact with selective the αvβ6 integrin into a cyclic pentapeptide. (B) A hydrocarbon stapling strategy guided by molecular dynamics (MD) simulations was enabled to successfully convert an eIF4G-derived peptide of two helix turns in a stapled peptide able to inhibit the activity of the eIF4E (PDB IDs: 4AZA and 4BEA).
An accurate estimation of the protein–peptide binding affinity is important to guide key steps in the drug discovery pipeline such as the hit-to-lead and lead optimization processes. This is however, a challenging task to achieve with standard computational methodologies. For instance, docking algorithms can provide rapid qualitative information about the peptide binding modes but generally fail in accurately estimating receptor affinities due to the intrinsic approximations of the method. On the other hand, standard MD would require tens of microseconds of simulations to collect enough statistics to describe the full ligand binding process (Dror et al., 2011; Shan et al., 2011), which are rarely accessible with the current protocols and resources (Salmaso and Moro, 2018). The timescale limitation of classical MD can be overcome by means of free-energy methods, which can be grouped in three main categories: endpoint, alchemical perturbation and physical pathway methods.
Endpoint methods, which include linear interaction energy (LIE) (Aqvist et al., 2002), molecular mechanics Poisson–Boltzmann surface area (MM-PBSA) (Srinivasan et al., 1998), and generalized Born surface area (MM-GBSA) (Kuhn and Kollman, 2000), compute the binding free energy by taking the difference between the absolute free energy of the ligand in unbound and bound states, which are sampled separately. These methods, particularly MM-PBSA and MM-GBSA, offer a good balance between computational efficiency and accuracy, and can be successfully used to predict the binding affinities and identify or rescore the correct binding poses for protein–peptide systems (Weng et al., 2019). Interestingly, a dampened MM-PBSA scoring function was recently introduced in HADDOCK to further improve the predictiveness of the docking protocol and to estimate the protein–peptide binding affinity (Spiliotopoulos et al., 2016). Nevertheless, a large-scale application of endpoint approaches use is partly limited by some approximations to both the sampling and energy calculation which are mainly due to the use of implicit solvent models (Wang et al., 2019).
Alchemical methods are typically more rigorous and accurate, although suffering from the higher demanding computational cost. They include thermodynamic integration (TI) (Kirkwood, 1935), free-energy perturbation (FEP) (Kirkwood, 1935) and Bennett Acceptance Ratio (BAR) (Bennett, 1976; Shirts and Chodera, 2008). In these calculations, ligand and protein are gradually decoupled and the binding free energy computed from a thermodynamic path connecting the bound and unbound states. At each step of the alchemical path, the sampling can be alternatively performed using either MC or MD simulations, with the latter approach being the most widely utilized. Frequently, a translational restrained potential is applied along the path to control the turning off of the molecular interactions between the ligand and the protein binding site. This allows reducing the configurational space to sample between the end-points, thus enhancing the efficiency of the free energy calculation. Alchemical transformations which employ translational restraints are generally referred as to the “double decoupling method” (DDM), while those calculations in which no translational restraint is present are classified as “double annihilation method” (DAM) (Deng and Roux, 2009).
In physical pathway methods, which include steered molecular dynamics (SMD) (Izrailev et al., 1997) and US (Torrie and Valleau, 1977), the ligand and the receptor are physically separated along the binding pathway and finally the potential of mean force (PMF), and in turn the binding free energy, is computed. In SMD, an external force with tuneable spring constant and velocity is applied to pull the ligand out from the binding site. The PMF is then obtained from the average of the irreversible work minus the dissipative work of the process according to the Jarzynski non-equilibrium work theorem (Jarzynski, 1997a, b). Several independent SMD trajectories need to be carried out to provide a statistically significant calculation of the irreversible work, and, accordingly, an accurate estimation of the PMF. Also, the optimization of the pulling force can reduce the dissipative part of the work, which eventually leads to an increased calculations convergence. In US, an external harmonic bias potential is applied on a user-defined CV to physically drive the ligand from the bound state to the unbound state. The pathway is usually divided in n steps, commonly known as windows, in which standard MD calculations are performed in presence of the harmonic potential. The change in free energy between adjacent windows can be computed from the collected MD trajectories using different methods, with the most commonly used being the Weighted Histogram Analysis Method (WHAM) (Souaille and Roux, 2001).
Numerous successful applications of both alchemical and pathway methods are reported in literature. However, also these methodologies can suffer from some limitations such as: (1) a limited use to small-size ligands, for which relatively few conformations must be sampled and (2) the need of a priori knowledge of the ligand binding mode, for alchemical transformation methods; (3) an incomplete sampling of the ligand solvated state (Limongelli et al., 2012); (4) an insufficient sampling of the ligand bound state(s) in case of receptor’s large conformational changes; and (5) the presence of additional degrees of freedom important for the ligand binding/unbinding process which are neglected during the calculation (Limongelli et al., 2012; Limongelli, 2020). In addition, the binding free energy calculation typically converges slowly and might change in dependence of the ligand size and charge, thus hampering the application of such methods in studying peptide/peptidomimetics-protein interaction (Gumbart et al., 2013).
In the attempt to address these problems, many variants of these methodologies were developed over the last decades. In the field of alchemical transformations, for instance, REMD-based approaches were introduced to increase the accuracy and the convergence rate of calculations. Among these is a mixed FEP/REMD strategy that relies on accelerated MD simulations performed in a Hamiltonian replica exchange MD (H-REMD), in which n replicas of the system with a modified Hamiltonian are run in parallel and are exchanged according to specific acceptance criteria (Sugita et al., 2000). The FEP/REMD approach allows the ligand to escape from kinetically trapped conformations, which usually affect the efficiency of standard FEP/MD calculations (Jiang and Roux, 2010). A more recent example is Modeling Employing Limited Data (MELD)-accelerated MD in which experimentally derived constraints are applied in a temperature and H-REMD simulations framework (Morrone et al., 2017). Alternatively, a single decoupling method was proposed, in which a single alchemical calculation is performed in a H-REMD scheme using, however, an implicit solvent model (Kilburg and Gallicchio, 2018). In its original formalism, SDM (Single-Decoupling Binding Free Energy Method) relied on US simulations performed in Hamiltonian replica exchange and combined with the WHAM method for the calculation of the binding free energy. This approach is known as Binding Energy Distribution Analysis Method (BEDAM) and computes the binding constant through a Boltzmann-weighted integral of the probability distribution of the binding energy obtained in the canonical ensemble in which the ligand, while positioned in the binding site, is embedded in the solvent continuum and does not interact with receptor atoms (Gallicchio et al., 2010; Di Marino et al., 2015c).
As mentioned above, physical pathway methods are typically affected by an insufficient sampling of the ligand solvated state. A possible solution to this critical point was provided by the works of Roux and Henchman who introduced a cylindrical restrained potential in US simulations to reduce the sampling space in the unbound state (Woo and Roux, 2005; Doudou et al., 2009). Following this example, geometrically restricted potentials were introduced in other enhanced sampling methodologies such as MetaD. A recent example is Funnel-Metadynamics (FM) in which a funnel-shaped restrained potential is applied to the system along the simulation to reduce the phase space exploration by the ligand in the unbound state. This enhances the sampling of both the target binding site and the ligand solvated state, leading to a thorough characterization of the binding free-energy surface and an accurate calculation of the absolute protein-ligand binding free energy (Limongelli et al., 2013). So far, the method has been employed to study both ligand/protein and ligand/DNA systems (Troussicot et al., 2015; Moraca et al., 2017; Yuan et al., 2018; D’Annessa et al., 2019b), being suitable also in the investigation of peptide-protein binding processes.
Designing peptides able to interact with specific target proteins is only the first step toward the development of compounds that can be considered as drug candidates. Despite their great potential, as largely discussed above, some limitations to the use of peptides in clinical routines still exist, mainly due to their low stability in solution, poor permeability through cellular membranes and physiological barriers, such as the blood–brain barrier (BBB).
The introduction of modifications in the chemical structure that could stabilize a peptide in its bioactive conformation, increasing efficiency, represents the smartest strategy. This can be achieved by introducing non-natural side chains, D-amino acids, non-alpha-amino-acids, peptide bond isosteres, staples and cyclization that change peptides into peptoids or peptidomimetics (Figure 2; Vagner et al., 2008; Zhang et al., 2018). Typically, these modifications are designed by either adding chemical functional groups to a well-characterized active peptide or using small molecules as building blocks that mimic the amino acids backbone with the aim of reproducing the geometry of secondary structure elements (SSE) (i.e., α-helix and β-strand) of bioactive peptides (Vagner et al., 2008; Zhang et al., 2018). Indeed, SSEs play a key role in PPIs, and among them α-helices are the most commonly found at PPI interfaces. Peptidomimetics guarantee enhanced protection against peptidases, improved systemic delivery and cell penetration, high target specificity and poor immune response and they are already in use against different pathologies, such as cancer and diabetes (Vagner et al., 2008; Zhang et al., 2018). In this context, computational approaches such as MetaD (Figure 2A) and classical MD simulations (Figure 2B) demonstrated to be valid tools to drive the conversion of peptides in more active peptoids/peptidomimetics, targeting αvβ6 RGD-integrin in one case (Di Leva et al., 2018) and the eukaryotic translation initiation factor 4E (eIF4E) in the other (Lama et al., 2013, 2019).
As highlighted in this review, peptides and peptidomimetics can play a central role in pharmacological applications, also having a potential strong economic impact on the pharmaceutical industries. Indeed, the use of peptides/peptidomimetics for the treatment of very different pathologies, including some types of cancer, Alzheimer’s disease, metabolic diseases and microbial infections, is now becoming a standard approach (Qvit et al., 2017; Mabonga and Kappo, 2019).
Furthermore, the implementation of “hybrid” approaches that combine theoretical and experimental techniques can sensibly assist drug design, allowing, for instance, to overcome some issues related to the development of peptides, mainly due to their nature and size.
We strongly believe that the improvement of computational peptidology techniques aimed at modifying and increasing the potential of these molecules to obtain multifunctional peptides, cell penetrating peptides and peptide drug conjugates, will help strengthen the efficacy and the applicability of peptides as therapeutics.
In conclusion, peptide design is an appealing but complex process that raises many challenges and for a successful outcome a deep knowledge of the available approaches and how to combine them to overcome some major drawbacks are necessary.
This mini-review article was conceived by DD with contributions from all authors, under the supervision of DD and VL.
VL thanks the support of the Swiss National Science Foundation (Project N. 200021_163281), the Italian MIUR/PRIN 2017 (2017FJZZRC), and the Cost action CA15135 (Multi-target paradigm for innovative ligand identification in the drug discovery process MuTaLig).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Alam, N., Goldstein, O., Xia, B., Porter, K. A., Kozakov, D., and Schueler-Furman, O. (2017). High-resolution global peptide-protein docking using fragments-based PIPER-FlexPepDock. PLoS Comput. Biol. 13:e1005905. doi: 10.1371/journal.pcbi.1005905
Antes, I. (2010). DynaDock: A now molecular dynamics-based algorithm for protein-peptide docking including receptor flexibility. Proteins Struct. Funct. Bioinform. 78, 1084–1104. doi: 10.1002/prot.22629
Aqvist, J., Luzhkov, V. B., and Brandsdal, B. O. (2002). Ligand binding affinities from MD simulations. Acc. Chem. Res. 35, 358–365. doi: 10.1021/ar010014p
Bakail, M., and Ochsenbein, F. (2016). Targeting protein-protein interactions, a wide open field for drug design. Comptes Rendus Chim. 19, 19–27. doi: 10.1016/j.crci.2015.12.004
Barducci, A., Bussi, G., and Parrinello, M. (2008). Well-tempered metadynamics: A smoothly converging and tunable free-energy method. Phys. Rev. Lett. 100:020603. doi: 10.1103/PhysRevLett.100.020603
Bennett, C. H. (1976). Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 22, 245–268. doi: 10.1016/0021-9991(76)90078-4
Ben-Shimon, A., and Niv, M. Y. (2015). AnchorDock: blind and flexible anchor-driven peptide docking. Structure 23, 929–940. doi: 10.1016/j.str.2015.03.010
Bernardi, R. C., Melo, M. C. R., and Schulten, K. (2015). Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta – Gen. Subj. 1850, 872–877. doi: 10.1016/j.bbagen.2014.10.019
Besray Unal, E., Gursoy, A., and Erman, B. (2010). Vital: Viterbi algorithm for de novo peptide design. PLoS ONE 5:e10926. doi: 10.1371/journal.pone.0010926
Bonvin, A. M. J. J., Boelens, R., and Kaptein, R. (1994). Time- and ensemble-averaged direct NOE restraints. J. Biomol. NMR 4, 143–149. doi: 10.1007/BF00178343
Bussi, G., Gervasio, F. L., Laio, A., and Parrinello, M. (2006). Free-energy landscape for β hairpin folding from combined parallel tempering and metadynamics. J. Am. Chem. Soc. 128, 13435–13441. doi: 10.1021/ja062463w
Camilloni, C., Cavalli, A., and Vendruscolo, M. (2013). Replica-averaged metadynamics. J. Chem. Theory Comput. 9, 5610–5617. doi: 10.1021/ct4006272
Carr, J. M., Whittleston, C. S., Wade, D. C., and Wales, D. J. (2015). Energy landscapes of a hairpin peptide including NMR chemical shift restraints. Phys. Chem. Chem. Phys. 17, 20250–20258. doi: 10.1039/c5cp01259g
Cavalli, A., Camilloni, C., and Vendruscolo, M. (2013). Molecular dynamics simulations with replica-averaged structural restraints generate structural ensembles according to the maximum entropy principle. J. Chem. Phys. 138:094112. doi: 10.1063/1.4793625
Cerjan, C. J., and Miller, W. H. (1981). On finding transition states. J. Chem. Phys. 75, 2800–2806. doi: 10.1063/1.442352
Chang, G., Guida, W. C., and Still, W. C. (1989). An internal coordinate monte carlo method for searching conformational space. J. Am. Chem. Soc. 47, 1657–1672. doi: 10.1021/ja00194a035
Chodera, J. D., and Noé, F. (2014). Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 25, 135–144. doi: 10.1016/j.sbi.2014.04.002
D’Annessa, I., Cicconardi, F., and Di Marino, D. (2019a). Handling FMRP and its molecular partners: structural insights into Fragile X Syndrome. Prog. Biophys. Mol. Biol. 141, 3–14. doi: 10.1016/j.pbiomolbio.2018.07.001
D’Annessa, I., Raniolo, S., Limongelli, V., Di Marino, D., and Colombo, G. (2019b). Ligand binding, unbinding, and allosteric effects: deciphering small-molecule modulation of HSP90. J. Chem. Theory Comput. 118:46a. doi: 10.1021/acs.jctc.9b00319
D’Annessa, I., Gandaglia, A., Brivio, E., Stefanelli, G., Frasca, A., Landsberger, N., et al. (2018). Tyr120Asp mutation alters domain flexibility and dynamics of MeCP2 DNA binding domain leading to impaired DNA interaction: atomistic characterization of a Rett syndrome causing mutation. Biochim. Biophys. Acta – Gen. Subj. 1862, 1180–1189. doi: 10.1016/j.bbagen.2018.02.005
De Simone, A., Montalvao, R. W., and Vendruscolo, M. (2011). Determination of conformational equilibria in proteins using residual dipolar couplings. J. Chem. Theory Comput. 137, 14798–14811. doi: 10.1021/ct200361b
Deng, Y., and Roux, B. (2009). Computations of standard binding free energies with molecular dynamics simulations. J. Phys. Chem. B 113, 2234–2246. doi: 10.1021/jp807701h
Di Leva, F. S., Tomassi, S., Di Maro, S., Reichart, F., Notni, J., Dangi, A., et al. (2018). From a helix to a small cycle: metadynamics-inspired αvβ6 integrin selective ligands. Angew. Chemie – Int. Ed. 57, 14645–14649. doi: 10.1002/anie.201803250
Di Marino, D., Achsel, T., Lacoux, C., Falconi, M., and Bagni, C. (2014). Molecular dynamics simulations show how the FMRP Ile304Asn mutation destabilizes the KH2 domain structure and affects its function. J. Biomol. Struct. Dyn. 32, 337–350. doi: 10.1080/07391102.2013.768552
Di Marino, D., Chillemi, G., De Rubeis, S., Tramontano, A., Achsel, T., and Bagni, C. (2015a). MD and docking studies reveal that the functional switch of CYFIP1 is mediated by a butterfly-like motion. J. Chem. Theory Comput. 11, 3401–3410. doi: 10.1021/ct500431h
Di Marino, D., D’Annessa, I., Tancredi, H., Bagni, C., and Gallicchio, E. (2015b). A unique binding mode of the eukaryotic translation initiation factor 4E for guiding the design of novel peptide inhibitors. Protein Sci. 24, 1370–1382. doi: 10.1002/pro.2708
Di Marino, D., D’Annessa, I., Tancredi, H., Bagni, C., and Gallicchio, E. (2015c). A unique binding mode of the eukaryotic translation initiation factor 4E for guiding the design of novel peptide inhibitors. Protein Sci. 24, 1370–1382. doi: 10.1002/pro.2708
Donné-Op Den Kelder, G. M. (1989). Distance geometry and molecular conformation. Trends Pharmacol. Sci. 11, 265–266.
Donsky, E., and Wolfson, H. J. (2011). PepCrawler: a fast RRT-based algorithm for high-resolution refinement and binding affinity estimation of peptide inhibitors. Bioinformatics 27, 2836–2842. doi: 10.1093/bioinformatics/btr498
Doudou, S., Burton, N. A., and Henchman, R. H. (2009). Standard free energy of binding from a one-dimensional potential of mean force. J. Chem. Theory Comput. 5, 909–918. doi: 10.1021/ct8002354
Dror, R. O., Pan, A. C., Arlow, D. H., Borhani, D. W., Maragakis, P., Shan, Y., et al. (2011). Pathway and mechanism of drug binding to G-protein-coupled receptors. Proc. Natl. Acad. Sci. U.S.A. 108, 13118–13123. doi: 10.1073/pnas.1104614108
Evans, D. A., and Wales, D. J. (2004). Folding of the GB1 hairpin peptide from discrete path sampling. J. Chem. Phys. 121, 1080–1090. doi: 10.1063/1.1759317
Gallicchio, E., Lapelosa, M., and Levy, R. M. (2010). Binding energy distribution analysis method (BEDAM) for estimation of protein-ligand binding affinities. J. Chem. Theory Comput. 121, 1080–1090. doi: 10.1021/ct1002913
Granata, D., Camilloni, C., Vendruscolo, M., and Laio, A. (2013). Characterization of the free-energy landscapes of proteins by NMR-guided metadynamics. Proc. Natl. Acad. Sci. U.S.A. 110, 6817–6822. doi: 10.1073/pnas.1218350110
Gumbart, J. C., Roux, B., and Chipot, C. (2013). Standard binding free energies from computer simulations: what is the best strategy? J. Chem. Theory Comput. 9, 794–802. doi: 10.1021/ct3008099
Hamelberg, D., Mongan, J., and McCammon, J. A. (2004). Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules. J. Chem. Phys. 120, 11919–11929. doi: 10.1063/1.1755656
Henninot, A., Collins, J. C., and Nuss, J. M. (2018). The current state of peptide drug discovery: back to the future? J. Med. Chem. 61, 1382–1414. doi: 10.1021/acs.jmedchem.7b00318
Husic, B. E., and Pande, V. S. (2018). Markov state models: from an art to a science. J. Am. Chem. Soc. 140, 2386–2396. doi: 10.1021/jacs.7b12191
Izrailev, S., Stepaniants, S., Balsera, M., Oono, Y., and Schulten, K. (1997). Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 72, 1568–1581. doi: 10.1016/s0006-3495(97)78804-0
Jarzynski, C. (1997a). Equilibrium free-energy differences from nonequilibrium measurements: a master-equation approach. Phys. Rev. E – Stat. Phys. Plasmas Fluids Relat. Interdiscipl. Top. E 56:5018. doi: 10.1103/PhysRevE.56.5018
Jarzynski, C. (1997b). Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 56:5018. doi: 10.1103/PhysRevLett.78.2690
Jiang, W., and Roux, B. (2010). Free energy perturbation Hamiltonian replica-exchange molecular dynamics (FEP/H-REMD) for absolute ligand binding free energy calculations. J. Chem. Theory Comput. 6, 2559–2565. doi: 10.1021/ct1001768
Joseph, J. A., and Wales, D. J. (2018). Intrinsically disordered landscapes for human CD4 receptor peptide. J. Phys. Chem. B. 122, 11906–11921. doi: 10.1021/acs.jpcb.8b08371
Kalmouni, M., Al-Hosani, S., and Magzoub, M. (2019). Cancer targeting peptides. Cell. Mol. Life Sci. 76, 2171–2183.
Kamenik, A. S., Lessel, U., Fuchs, J. E., Fox, T., and Liedl, K. R. (2018). Peptidic macrocycles – Conformational sampling and thermodynamic characterization. J. Chem. Inf. Model. 58, 982–992. doi: 10.1021/acs.jcim.8b00097
Kilburg, D., and Gallicchio, E. (2016). “Recent Advances in Computational Models for the Study of Protein–Peptide Interactions,” in Advances in Protein Chemistry and Structural Biology, ed. R. Donev (Cambridge, MA: Academic Press), doi: 10.1016/bs.apcsb.2016.06.002
Kilburg, D., and Gallicchio, E. (2018). Assessment of a single decoupling alchemical approach for the calculation of the absolute binding free energies of protein-peptide complexes. Front. Mol. Biosci. 5:22. doi: 10.3389/fmolb.2018.00022
King, C. A., and Bradley, P. (2010). Structure-based prediction of protein-peptide specificity in rosetta. Proteins Struct. Funct. Bioinforma. 78, 3437–3449. doi: 10.1002/prot.22851
Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. Science (80-) 220, 671–680. doi: 10.1126/science.220.4598.671
Kirkwood, J. G. (1935). Statistical mechanics of fluid mixtures. J. Chem. Phys. 3:300. doi: 10.1063/1.1749657
Kolossváry, I., and Guida, W. C. (1996). Low mode search. An efficient, automated computational method for conformational analysis: application to cyclic and acyclic alkanes and cyclic peptides. J. Am. Chem. Soc. 118, 5011–5019. doi: 10.1021/ja952478m
Kolossvàry, I., and Guida, W. C. (1999). Low-mode conformational search elucidated: application to C39H80 and flexible docking of 9-deazaguanine inhibitors into PNP. J. Comput. Chem. 20, 1671–1684.
Kuhn, B., and Kollman, P. A. (2000). Binding of a diverse set of ligands to avidin and streptavidin: an accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models. J. Med. Chem. 43, 3786–3791. doi: 10.1021/jm000241h
Kurcinski, M., Jamroz, M., Blaszczyk, M., Kolinski, A., and Kmiecik, S. (2015). CABS-dock web server for the flexible docking of peptides to proteins without prior knowledge of the binding site. Nucleic Acids Res. 43, W419–W424. doi: 10.1093/nar/gkv456
Laio, A., and Parrinello, M. (2002). Escaping free-energy minima. Proc. Natl. Acad. Sci. U.S.A. 99, 12562–12566. doi: 10.1073/pnas.202427399
Lama, D., Liberatore, A. M., Frosi, Y., Nakhle, J., Tsomaia, N., Bashir, T., et al. (2019). Structural insights reveal a recognition feature for tailoring hydrocarbon stapled-peptides against the eukaryotic translation initiation factor 4E protein. Chem. Sci. 10, 2489–2500. doi: 10.1039/C8SC03759K
Lama, D., Quah, S. T., Verma, C. S., Lakshminarayanan, R., Beuerman, R. W., Lane, D. P., et al. (2013). Rational optimization of conformational effects induced by hydrocarbon staples in peptides and their binding interfaces. Sci. Rep. 3:3451. doi: 10.1038/srep03451
Lau, J. L., and Dunn, M. K. (2018). Therapeutic peptides: Historical perspectives, current development trends, and future directions. Bioorganic Med. Chem. 26, 2700–2707. doi: 10.1016/j.bmc.2017.06.052
Lee, A. C. L., Harris, J. L., Khanna, K. K., and Hong, J. H. (2019). A comprehensive review on current advances in peptide drug development and design. Int. J. Mol. Sci. 20, 1–21. doi: 10.3390/ijms20102383
Lee, H., Heo, L., Lee, M. S., and Seok, C. (2015). GalaxyPepDock: a protein-peptide docking tool based on interaction similarity and energy optimization. Nucleic Acids Res. 43, W431–W435. doi: 10.1093/nar/gkv495
Li, H., Lu, L., Chen, R., Quan, L., Xia, X., and Lü, Q. (2014). PaFlexPepDock: parallel ab-initio docking of peptides onto their receptors with full flexibility based on Rosetta. PLoS ONE 9:e94769. doi: 10.1371/journal.pone.0094769
Li, Z., and Scheraga, H. A. (1987). Monte Carlo-minimization approach to the multiple-minima problem in protein folding. Proc. Natl. Acad. Sci. U.S.A. 84, 6611–6615. doi: 10.1073/pnas.84.19.6611
Limongelli, V. (2020). “Ligand binding free energy and kinetics calculation in 2020,” in Wiley Interdisciplinary Reviews: Computational Molecular Science, ed. A. Belkin (Hoboken, NJ: John Wiley & Sons Ltd.), doi: 10.1002/wcms.1455
Limongelli, V., Bonomi, M., and Parrinello, M. (2013). Funnel metadynamics as accurate binding free-energy method. Proc. Natl. Acad. Sci. U.S.A. 110, 6358–6363. doi: 10.1073/pnas.1303186110
Limongelli, V., Marinelli, L., Cosconati, S., La Motta, C., Sartini, S., Mugnaini, L., et al. (2012). Sampling protein motion and solvent effect during ligand binding. Proc. Natl. Acad. Sci. U.S.A. 109, 1467–1472. doi: 10.1073/pnas.1112181108
Liu, D. C., and Nocedal, J. (1989). On the limited memory BFGS method for large scale optimization. Math. Program. 45, 503–528. doi: 10.1007/BF01589116
Liu, P., Kim, B., Friesner, R. A., and Berne, B. J. (2005). Replica exchange with solute tempering: a method for sampling biological systems in explicit water. Proc. Natl. Acad. Sci. U.S.A. 102, 13749–13754. doi: 10.1073/pnas.0506346102
Mabonga, L., and Kappo, A. P. (2019). Peptidomimetics: a synthetic tool for inhibiting Protein–Protein interactions in cancer. Int. J. Pept. Res. Ther. 26, 225–241. doi: 10.1007/s10989-019-09831-5
Marqus, S., Pirogova, E., and Piva, T. J. (2017). Evaluation of the use of therapeutic peptides for cancer treatment. J. Biomed. Sci. 24:21. doi: 10.1186/s12929-017-0328-x
Moraca, F., Amato, J., Ortuso, F., Artese, A., Pagano, B., Novellino, E., et al. (2017). Ligand binding to telomeric G-quadruplex DNA investigated by funnel-metadynamics simulations. Proc. Natl. Acad. Sci. U.S.A. 114, E2136–E2145. doi: 10.1073/pnas.1612627114
Morrone, J. A., Perez, A., MacCallum, J., and Dill, K. A. (2017). Computed binding of peptides to proteins with MELD-accelerated molecular dynamics. J. Chem. Theory Comput. 13, 870-876. doi: 10.1021/acs.jctc.6b00977
Mucherino, A., Lavor, C., Liberti, L., and Maculan, N. (2013). “Distance geometry,” in Theory, Methods, and Applications (Berlin: Springer), 1–420.
Oakley, M. T., and Johnston, R. L. (2013). Exploring the energy landscapes of cyclic tetrapeptides with discrete path sampling. J. Chem. Theory Comput. 9, 650–657. doi: 10.1021/ct3005084
Obarska-Kosinska, A., Iacoangeli, A., Lepore, R., and Tramontano, A. (2016). PepComposer: computational design of peptides binding to a given protein surface. Nucleic Acids Res. 44, W522–W528. doi: 10.1093/nar/gkw366
Okur, A., Roe, D. R., Cui, G., Hornak, V., and Simmerling, C. (2007). Improving convergence of replica-exchange simulations through coupling to a high-temperature structure reservoir. J. Chem. Theory Comput. 3, 557–568. doi: 10.1021/ct600263e
Oliva, B., and Fernandez-Fuentes, N. (2015). Knowledge-based modeling of peptides at protein interfaces: PiPreD. Bioinformatics 31, 1405–1410. doi: 10.1093/bioinformatics/btu838
Orozco, M. (2014). A theoretical view of protein dynamics. Chem. Soc. Rev. 43, 5051–5066. doi: 10.1039/c3cs60474h
Otvos, L., and Wade, J. D. (2014). Current challenges in peptide-based drug discovery. Front. Chem. 2:62. doi: 10.3389/fchem.2014.00062
Parish, C., Lombardi, R., Sinclair, K., Smith, E., Goldberg, A., Rappleye, M., et al. (2002). A comparison of the low mode and monte carlo conformational search methods. J. Mol. Graph. Model. 21, 129–150. doi: 10.1016/s1093-3263(02)00144-4
Piana, S., and Laio, A. (2007). A bias-exchange approach to protein folding. J. Phys. Chem. B 111, 4553–4559. doi: 10.1021/jp0678731
Qvit, N., Rubin, S. J. S., Urban, T. J., Mochly-Rosen, D., and Gross, E. R. (2017). Peptidomimetic therapeutics: scientific approaches and opportunities. Drug Discov. Today 22, 454–462. doi: 10.1016/j.drudis.2016.11.003
Raman, S., Vernon, R., Thompson, J., Tyka, M., Sadreyev, R., Pei, J., et al. (2009). Structure prediction for CASP8 with all-atom refinement using Rosetta. Proteins Struct. Funct. Bioinform. 9 0, 89–99. doi: 10.1002/prot.22540
Renfrew, P. D., Craven, T. W., Butterfoss, G. L., Kirshenbaum, K., and Bonneau, R. (2014). A rotamer library to enable modeling and design of peptoid foldamers. J. Am. Chem. Soc. 136, 8772–8782. doi: 10.1021/ja503776z
Roitberg, A. E., Okur, A., and Simmerling, C. (2007). Coupling of replica exchange simulations to a non-boltzmann structure reservoir. J. Phys. Chem. B 111, 2415–2418. doi: 10.1021/jp068335b
Salmaso, V., and Moro, S. (2018). Bridging molecular docking to molecular dynamics in exploring ligand-protein recognition process: an overview. Front. Pharmacol. 9:923. doi: 10.3389/fphar.2018.00923
Saunders, M., Houk, K. N., Wu, Y. D., Clark Still, W., Lipton, M., Chang, G., et al. (1990). Conformations of cycloheptadecane. A comparison of methods for conformational searching. J. Am. Chem. Soc. 112, 1419–1427. doi: 10.1021/ja00160a020
Schindler, C. E. M., De Vries, S. J., and Zacharias, M. (2015). Fully blind peptide-protein docking with pepATTRACT. Structure 23, 1507–1515. doi: 10.1016/j.str.2015.05.021
Shameer, K., Madan, L. L., Veeranna, S., Gopal, B., and Sowdhamini, R. (2010). PeptideMine – A webserver for the design of peptides for protein-peptide binding studies derived from protein-protein interactomes. BMC Bioinform. 11:473. doi: 10.1186/1471-2105-11-473
Shan, Y., Kim, E. T., Eastwood, M. P., Dror, R. O., Seeliger, M. A., and Shaw, D. E. (2011). How does a drug molecule find its target binding site? J. Am. Chem. Soc. 133, 9181–9183. doi: 10.1021/ja202726y
Shirts, M. R., and Chodera, J. D. (2008). Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 129:124105. doi: 10.1063/1.2978177
Simon, M., Ali, L. M. A., El Cheikh, K., Aguesseau, J., Gary-Bobo, M., Garcia, M., et al. (2018). Can heterocyclic γ-peptides provide polyfunctional platforms for synthetic glycocluster construction? Chem. – A Eur. J. 24, 11426–11432. doi: 10.1002/chem.201802032
Simons, J., Jørgensen, P., Taylor, H., and Ozment, J. (1983). Walking on potential energy surfaces. J. Phys. Chem. 87, 2745–2753. doi: 10.1021/j100238a013
Sliwoski, G., Kothiwale, S., Meiler, J., and Lowe, E. W. (2014). Computational methods in drug discovery. Pharmacol. Rev. 66, 334–395. doi: 10.1124/pr.112.007336
Smith, A., Keane, A., Dumesic, J. A., George, W., and Zavala, V. M. (2019). Antimicrobial peptides as novel therapeutics for nonsmall cell lung cancer. Drug Discov. Today. 25, 238–247. doi: 10.1016/j.apcatb.2019.118257
Souaille, M., and Roux, B. (2001). Extension to the weighted histogram analysis method: combining umbrella sampling with free energy calculations. Comput. Phys. Commun. 135, 40–57. doi: 10.1016/s0010-4655(00)00215-0
Spiliotopoulos, D., Kastritis, P. L., Melquiond, A. S. J., Bonvin, A. M. J. J., Musco, G., Rocchia, W., et al. (2016). dMM-PBSA: a new HADDOCK scoring function for protein-peptide docking. Front. Mol. Biosci. 3:46. doi: 10.3389/fmolb.2016.00046
Spitaleri, A., Ghitti, M., Mari, S., Alberici, L., Traversari, C., Rizzardi, G. P., et al. (2011). Use of metadynamics in the design of isoDGR-based αvβ3 antagonists to fine-tune the conformational ensemble. Angew. Chem. Int. Ed. Engl. 50, 1832–1836. doi: 10.1002/anie.201007091
Srinivasan, J., Cheatham, T. E., Cieplak, P., Kollman, P. A., and Case, D. A. (1998). Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate-DNA helices. J. Am. Chem. Soc. 16, 671–682. doi: 10.1021/ja981844
Strodel, B., Lee, J. W. L., Whittleston, C. S., and Wales, D. J. (2010). Transmembrane structures for Alzheimer’s Aβ1-42 oligomers. J. Am. Chem. Soc. 132, 13300–13312. doi: 10.1021/ja103725c
Sugita, Y., Kitao, A., and Okamoto, Y. (2000). Multidimensional replica-exchange method for free-energy calculations. J. Chem. Phys. 113:6042. doi: 10.1063/1.1308516
Sun, L. (2016). Peptide-based drug development. Mod. Chem. Appl. 1:e103. doi: 10.4172/2329-6798.1000e103
Tan, Y. S., Lane, D. P., and Verma, C. S. (2016). Stapled peptide design: principles and roles of computation. Drug Discov. Today 21, 1642–1653. doi: 10.1016/j.drudis.2016.06.012
Thévenet, P., Shen, Y., Maupetit, J., Guyon, F., Derreumaux, P., and Tufféry, P. (2012). PEP-FOLD: an updated de novo structure prediction server for both linear and disulfide bonded cyclic peptides. Nucleic Acids Res. 40, W288–W293. doi: 10.1093/nar/gks419
Torrie, G. M., and Valleau, J. P. (1977). Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling. J. Comput. Phys. 23, 187–199. doi: 10.1016/0021-9991(77)90121-8
Trellet, M., Melquiond, A. S. J., and Bonvin, A. M. J. J. (2013). A unified conformational selection and induced fit approach to protein-peptide docking. PLoS ONE 8:e58769. doi: 10.1371/journal.pone.0058769
Troussicot, L., Guillière, F., Limongelli, V., Walker, O., and Lancelin, J. M. (2015). Funnel-metadynamics and solution NMR to estimate protein-ligand affinities. J. Am. Chem. Soc. 137, 1273–1281. doi: 10.1021/ja511336z
Tubert-Brohman, I., Sherman, W., Repasky, M., and Beuming, T. (2013). Improved docking of polypeptides with glide. J. Chem. Inform. Model. 53, 1689–1699. doi: 10.1021/ci400128m
Vagner, J., Qu, H., and Hruby, V. J. (2008). Peptidomimetics, a synthetic tool of drug discovery. Curr. Opin. Chem. Biol. 12, 292–296. doi: 10.1016/j.cbpa.2008.03.009
Valcourt, D. M., Harris, J., Riley, R. S., Dang, M., Wang, J., and Day, E. S. (2018). Advances in targeted nanotherapeutics: from bioconjugation to biomimicry. Nano Res. 11, 4999–5016. doi: 10.1007/s12274-018-2083-z
Van Zundert, G. C. P., Rodrigues, J. P. G. L. M., Trellet, M., Schmitz, C., Kastritis, P. L., Karaca, E., et al. (2016). The HADDOCK2.2 web server: user-friendly integrative modeling of biomolecular complexes. J. Mol. Biol. 428, 720–725. doi: 10.1016/j.jmb.2015.09.014
Vanhee, P., van der Sloot, A. M., Verschueren, E., Serrano, L., Rousseau, F., and Schymkowitz, J. (2011). Computational design of peptide ligands. Trends Biotechnol. 29, 231–239. doi: 10.1016/j.tibtech.2011.01.004
Vercelli, A., Biggi, S., Sclip, A., Repetto, I. E., Cimini, S., Falleroni, F., et al. (2015). Exploring the role of MKK7 in excitotoxicity and cerebral ischemia: a novel pharmacological strategy against brain injury. Cell Death Dis. 6, e1854–e1813. doi: 10.1038/cddis.2015.226
Wales, D. J. (2002). Discrete path sampling. Mol. Phys. 100, 3285–3305. doi: 10.1080/00268970210162691
Wales, D. J. (2004). Some further applications of discrete path sampling to cluster isomerization. Mol. Phys. 102, 891–908. doi: 10.1080/00268970410001703363
Wales, D. J. (2005). Energy landscapes and properties of biomolecules. Phys. Biol. 2, S86–S93. doi: 10.1088/1478-3975/2/4/S02
Wales, D. J., and Doye, J. P. K. (1997). Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J. Phys. Chem. A 101, 5111–5116. doi: 10.1021/jp970984n
Wang, E., Sun, H., Wang, J., Wang, Z., Liu, H., Zhang, J. Z. H., et al. (2019). End-point binding free energy calculation with MM/PBSA and MM/GBSA: strategies and applications in drug design. Chem. Rev. 119, 9478–9508. doi: 10.1021/acs.chemrev.9b00055
Wang, W., and Hu, Z. (2019). Targeting peptide-based probes for molecular imaging and diagnosis. Adv. Mater. 31, 1–8. doi: 10.1002/adma.201804827
Wanner, J., Fry, D. C., Peng, Z., and Roberts, J. (2011). Druggability assessment of protein-protein interfaces. Future Med. Chem. 3, 2021–2038. doi: 10.4155/fmc.11.156
Weinberg, N., and Wolfe, S. (1994). A comprehensive approach to the conformational analysis of cyclic compounds. J. Am. Chem. Soc. 116, 9860–9868. doi: 10.1021/ja00101a006
Weng, G., Wang, E., Chen, F., Sun, H., Wang, Z., and Hou, T. (2019). Assessing the performance of MM/PBSA and MM/GBSA methods. 9. Prediction reliability of binding affinities and binding poses for protein-peptide complexes. Phys. Chem. Chem. Phys. 21, 10135–10145. doi: 10.1039/c9cp01674k
Wilson, S. R., and Cui, W. (1990). Applications of simulated annealing to peptides. Biopolymers 29, 225–235. doi: 10.1002/bip.360290127
Woo, H.-J., and Roux, B. (2005). Calculation of absolute protein-ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. U.S.A. 90, 864–877. doi: 10.1073/pnas.0409005102
Yuan, X., Raniolo, S., Limongelli, V., and Xu, Y. (2018). The molecular mechanism underlying ligand binding to the membrane-embedded site of a g-protein-coupled receptor. J. Chem. Theory Comput. 14, 2761–2770. doi: 10.1021/acs.jctc.8b00046
Zaidman, D., and Wolfson, H. J. (2016). PinaColada: peptide-inhibitor ant colony ad-hoc design algorithm. Bioinformatics 32, 2289–2296. doi: 10.1093/bioinformatics/btw133
Zanella, S., Bocchinfuso, G., De Zotti, M., Arosio, D., Marino, F., Raniolo, S., et al. (2019). Rational design of antiangiogenic helical oligopeptides targeting the vascular endothelial growth factor receptors. Front. Chem. 7:170. doi: 10.3389/fchem.2019.00170
Zhang, G., Andersen, J., and Gerona-Navarro, G. (2018). Peptidomimetics targeting protein-protein interactions for therapeutic development. Protein Pept. Lett. 25, 1076–1089. doi: 10.2174/0929866525666181101100842
Zhou, P., Jin, B., Li, H., and Huang, S. Y. (2018). HPEPDOCK: a web server for blind peptide-protein docking based on a hierarchical algorithm. Nucleic Acids Res. 46, W443–W450. doi: 10.1093/nar/gky357
Keywords: peptides design, peptidomimetics, binding free-energy, protein–protein interaction, bioinformatics tools
Citation: D’Annessa I, Di Leva FS, La Teana A, Novellino E, Limongelli V and Di Marino D (2020) Bioinformatics and Biosimulations as Toolbox for Peptides and Peptidomimetics Design: Where Are We? Front. Mol. Biosci. 7:66. doi: 10.3389/fmolb.2020.00066
Received: 10 August 2019; Accepted: 25 March 2020;
Published: 05 May 2020.
Edited by:
Alexandre M. J. J. Bonvin, Utrecht University, NetherlandsReviewed by:
Martin Zacharias, Technical University of Munich, GermanyCopyright © 2020 D’Annessa, Di Leva, La Teana, Novellino, Limongelli and Di Marino. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Vittorio Limongelli, dml0dG9yaW8ubGltb25nZWxsaUBnbWFpbC5jb20=; Daniele Di Marino, ZC5kaW1hcmlub0B1bml2cG0uaXQ=; ZGFuaWVsZS5kaW1hcmlub0BnbWFpbC5jb20=
†These authors have contributed equally to this work
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.